Probing new physics in semileptonic $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ decays

Abstract

Recently, several observed anomalies in semileptonic B meson decays have implied hints of lepton flavor universal violation. Motivated by these inspiring results, we study the baryon decays $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ which are mediated by $b\rightarrow u(c)\tau ^{-}\bar{\nu }_{\tau }$ transitions at quark level in the Standard Model and different New Physics scenarios. In the framework of the extended Standard Model on assuming a general effective theory, we constrain the Wilson coefficients of the NP operators using the experimental measurement results for the $Br(B_{c}^+\rightarrow \tau ^+ \nu _{\tau })$, $R^{l}_{\pi }$, $R_{D^{(*)}}$, $R_{J/\psi }$ and $F_{L}^{D^{*}}$ anomalies and investigate their New Physics effects on several observables relative to the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ decays. We mention the differential branching fraction ${\text {d}}Br/{\text {d}}q^2$, the ratio of branching fractions $R(q^2)$, the lepton-side forward–backward asymmetry $A_{FB}(q^2)$, the longitudinal polarization $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ of the daughter baryons $\Lambda (\Xi _{c})$ and $P_{L}^{\tau }(q^2)$ of the $\tau$ lepton, and the convexity parameter $C_{F}(q^2)$.

1 Introduction

In the Standard Model (SM), the gauge interactions are lepton flavor universal (LFU), but the hints of lepton flavor universal violation (LFUV) have been observed in several anomalies relative to the semileptonic B meson decays. The Belle [1,2,3], BaBar [4, 5] and LHCb [6,7,8] collaborations have reported $R_{D^{(*)}}$ and $R_{J/\psi }$ anomalies in various semileptonic B meson decays mediated by $b\rightarrow c$ charged current interactions. The experimental measurement results for these anomalies show large deviations with their corresponding SM predictions, which may imply the LFUV and the existence of New Physics. The ratios are

$$\begin{aligned} R_{D^{(*)}} =\frac{Br(B\rightarrow D^{(*)} \tau ^{-}\bar{\nu }_{\tau })}{Br(B\rightarrow D^{(*)}l^{-} \bar{\nu }_{l})}, \end{aligned}$$

(1)

with $l= e,\mu$. Very recently, the Belle collaboration announced the latest measurements of $R_{D^{(*)}}$ [9],

$$\begin{aligned} R_{D}^{\mathrm {Bell}}= & {} 0.307\pm 0.037\pm 0.016,\nonumber \\ R^{\mathrm {Bell}}_{D^{*}}= & {} 0.283\pm 0.018 \pm 0.014, \end{aligned}$$

(2)

which agree with their SM predictions within $1.2\sigma$ in combination. Although the tension between the new results and the SM predictions is obviously reduced, it still amounts to $3.08\sigma$ relative to the corresponding SM predictions on combining these measurements in the global average fields, and the new average values reported by the Heavy Flavor Average Group (HFAG) are [10]

$$\begin{aligned} R_{D}^{\mathrm {avg}}= & {} 0.340\pm 0.027 \pm 0.013,\nonumber \\ R^{\mathrm {avg}}_{D^{*}}= & {} 0.295\pm 0.011 \pm 0.008, \end{aligned}$$

(3)

which deviate from their SM predictions at $1.4\sigma$ and $2.5\sigma$ level, respectively. The SM predictions for $R_{D^{(*)}}$ are [10]

$$\begin{aligned} R_{D}^{\mathrm {SM}} = 0.299\pm 0.003, \quad R^{\mathrm {SM}}_{D^{*}}= 0.258\pm 0.005. \end{aligned}$$

(4)

Another anomaly,

$$\begin{aligned} R_{J/\psi }= & {} \frac{Br(B^{+}\rightarrow J/\psi \tau ^{+}\nu _{\tau })}{Br(B^{+} \rightarrow J/\psi \mu ^{+}\mu _{\tau })}=0.71\pm 0.17\pm 0.18,\nonumber \\ \end{aligned}$$

(5)

was reported by [8] and deviated from the central value predicted in the SM 0.25–0.28 within $2\sigma$ range [11, 12].

In addition, there is also discrepancy in the measured ratio [13]

$$\begin{aligned} R_{\pi }^{l} = \frac{\tau _{B^{0}}}{\tau _{B^{-}}}\frac{Br(B^{-}\rightarrow \tau ^{-}\bar{\nu }_{\tau })}{Br(B^{0}\rightarrow \pi ^{+}l^{-} \bar{\nu }_{l})}=0.699\pm 0.156, \end{aligned}$$

(6)

with $l=e,\mu$, which also attracts our attention. The experimental result has about $1\sigma$ tension with its SM prediction, $0.583\pm 0.055$.

Except for the tensions mentioned above, we also investigate the effects of the very recently announced value for $D^{*}$ longitudinal polarization $F_{L}^{D^{*}}$ by the Belle collaboration [14],

$$\begin{aligned} F_{L}^{D^{*}}=\frac{\Gamma _{\lambda _{D^{*}}=0}(B\rightarrow D^{*}\tau ^+\nu _{\tau })}{\Gamma (B\rightarrow D^{*}\tau ^+\nu _{\tau })}=0.60\pm 0.08\pm 0.04, \end{aligned}$$

(7)

which differs from its SM prediction, $0.457\pm 0.010$ [15] $(0.441\pm 0.006$ [16]), by $1.6\sigma (1.8\sigma )$.

It is really interesting and important to investigate the semileptonic baryon decays $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ mediated by the $b\rightarrow u(c)\tau ^{-}\bar{\nu }_{\tau }$ transitions at the quark level. Studying them not only can provide an independent determination of the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements $|V_{ub}|$ and $|V_{cb}|$, but also it may confirm the LFUV again in the ratios of branching fractions $R_{\Lambda (\Xi _{c})}$ having a similar formalism to the $R_{D^{(*)}}$. On the basis of these advantages, many researchers have studied the decays $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ in the SM and NP scenarios [17,18,19,20,21,22,23,24]. In this paper, we set out to explore the NP effects of these B meson decay anomalies in the $\Xi _{b}\rightarrow \Lambda (\Xi _{c}) \tau ^{-}\bar{\nu }_{\tau }$ transitions. Using the Wilson coefficients of the NP operators constrained from the experimental values for $Br(B_{c}^{+}\rightarrow \tau ^{+}\nu _{\tau })$, the $R^{l}_{\pi }$, $R_{D^{(*)}}$, $R_{J/\psi }$ and $F_{L}^{D^{*}}$ anomalies and the form factors for the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})$ transitions calculated by [24], we investigate the NP effects of these anomalies on the differential branching fraction ${\text {d}}Br/{\text {d}}q^2$, the ratio of branching fractions $R(q^2)$, the lepton-side forward–backward asymmetry $A_{FB}(q^2)$, the longitudinal polarization $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ of the daughter baryons $\Lambda (\Xi _{c})$ and $P_{L}^{\tau }(q^2)$ of the $\tau$ lepton, and the convexity parameter $C_{F}^{l}(q^2)$ relative to these baryon decays. It is worthwhile to note that our study is different from [23] whose authors also investigate the decay $\Xi _{b}\rightarrow \Xi _{c}\tau ^{-}\bar{\nu }_{\tau }$ using a model-independent approach. We make the Wilson coefficients complex, though they are real in [23], and also we consider the constraints on the NP Wilson coefficients coming from $R_{J/\psi }$ and $F_{L}^{D^{*}}$ anomalies, which are not mentioned in [23]. In [13], the authors also consider the constraints on the complex NP Wilson coefficients, but they treat the $b\rightarrow u$ and $b\rightarrow c$ transitions separately. Therefore, the constraints on the NP Wilson coefficients are different from ours as is appropriate for both the $b\rightarrow u$ and the $b\rightarrow c$ transitions. In addition, we also consider the interplay of vector and scalar interactions scenarios, which are not mentioned in [13, 23]. In this paper, we consider the $b\rightarrow u$ and $b\rightarrow c$ transitions together in the same framework of effective theory and perform a combined analysis using the constraints on the Wilson coefficients coming from the experimental results for the $Br(B_{c}^{+}\rightarrow \tau ^{+}\nu _{\tau })$, $R^{l}_{\pi }$, $R_{D^{(*)}}$, $R_{J/\psi }$ and $F_{L}^{D^{*}}$ anomalies in the end in determining the NP contributions to the observables aforementioned.

Our paper is organized as follows. In Sect. 2, we introduce the effective theory describing the $b\rightarrow u(c)l^{-}\bar{\nu }_{\tau }$ transitions as well as the form factors, the helicity amplitudes and the observables of the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})l^{-}\bar{\nu }_{\tau }$ decays. In Sect. 3, the Wilson coefficients of the NP operators are constrained from the experimental values for $Br(B_{c}^{+}\rightarrow \tau ^{+}\nu _{\tau })$, $R^{l}_{\pi }$, $R_{D^{(*)}}$, $R_{J/\psi }$ and $F_{L}^{D^{*}}$ anomalies. In Sect. 4, the numerical results for the observables ${\text {d}}Br/{\text {d}}q^2$, $R(q^2)$, $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$ in the SM and different NP scenarios are presented. Finally, we briefly conclude in Sect. 5.

2 Effective Hamiltonian, form factors, helicity amplitude and observables for $\Xi _{b}\rightarrow \Lambda (\Xi _{c})l^{-}\bar{\nu }_{\tau }$ decays

2.1 Effective Hamiltonian

The effective Hamiltonian including both the SM and the NP contributions for the $b\rightarrow q l^{-} \bar{\nu }_{\tau }$, ($q=u,c$) transitions is given by [25, 26],

$$\begin{aligned} \mathcal {H}_{\mathrm {eff}}= & {} -\frac{4G_{F}}{\sqrt{2}}V_{qb}\left\{ (1+V_{L})\bar{l}_{L}\gamma _{\mu }\nu _{L}\bar{q}_{L}\gamma ^{\mu }b_{L}\right. \nonumber \\&+ V_{R}\bar{l}_{L}\gamma _{\mu }\nu _{L}\bar{q}_{R}\gamma ^{\mu }b_{R}+ S_{L}\bar{l}_{R}\nu _{L}\bar{q}_{R}b_{L}\nonumber \\&\left. +S_{R}\bar{l}_{R}\nu _{L}\bar{q}_{L}b_{R}+T_{L}\bar{l}_{R} \sigma _{\mu \nu }\nu _{L}\bar{q}_{R}\sigma ^{\mu \nu }b_{L}\right\} +h.c.,\nonumber \\ \end{aligned}$$

(8)

where $G_{F}$ is the Fermi constant, $V_{qb}$ are the CKM matrix elements and $(q,b,l,\nu )_{L,R}=\frac{1\mp \gamma _{5}}{2}(q,b,l,\nu )$. The vector, scalar and tensor type NP couplings are denoted $V_{L,R}$, $S_{L,R}$ and $T_{L}$, respectively. They are all zero in the SM, and we have assumed that there are only left-handed neutrinos. The right-handed quark current for the tensor operator is omitted because of its zero value. In addition, the NP effects are supposed to appear only in the $\tau$ mode in Eq. (8). This paper we dedicate to a study of the vector and scalar type interactions, excepting the tensor interaction, and we assume that the Wilson coefficients $V_{L,R}$ and $S_{L,R}$ are complex.

Table 1 Form factors for the weak $\Xi _{b}\rightarrow \Lambda$ and $\Xi _{b}\rightarrow \Xi _{c}$ transitions

2.2 Form factors

The hadronic matrix elements of the vector and axial-vector weak currents for the decays $\Xi _{b}\rightarrow \Lambda (\Xi _{c})l^{-}\bar{\nu }_{\tau }$ are parametrized in terms of the six invariant form factors $f_{_{1,2,3}}$ and $g_{_{1,2,3}}$ [24, 27,28,29],

$$\begin{aligned}&\langle \Lambda (\Xi _{c}),\lambda _{2}\vert \bar{u}(\bar{c})\gamma _{\mu }b\vert \Xi _{b},\lambda _{1}\rangle = \bar{u}_{\Lambda ({\Xi }_{c})}(p_{2},\lambda _{2}) \nonumber \\&\times \quad \left[ f_{1}(q^{2})\gamma _{\mu }-i f_{2}(q^{2})\sigma _{\mu \nu } \dfrac{q^{\nu }}{M_{\Xi _{b}}}+f_{3}(q^{2}) \frac{q_{\mu }}{M_{\Xi _{b}}}\right] \nonumber \\&\quad u_{{\Xi }_{b}}(p_{1},\lambda _{1}),\nonumber \\&\times \langle \Lambda (\Xi _{c}),\lambda _{2}\vert \bar{u}(\bar{c})\gamma _{\mu }\gamma _{5}b\vert \Xi _{b},\lambda _{1}\rangle = \bar{u}_{\Lambda ({\Xi }_{c})}(p_{2},\lambda _{2})\nonumber \\&\times \quad \left[ g_{1}(q^{2})\gamma _{\mu }-i g_{2}(q^{2})\sigma _{\mu \nu } \dfrac{q^{\nu }}{M_{\Xi _{b}}}+g_{3}(q^{2}) \frac{q_{\mu }}{M_{\Xi _{b}}}\right] \nonumber \\&\times \quad \gamma _{5}u_{{\Xi }_{b}}(p_{1},\lambda _{1}), \end{aligned}$$

(9)

where $\sigma _{\mu \nu }=\frac{i}{2}(\gamma _{\mu }\gamma _{\nu }-\gamma _{\nu }\gamma _{\mu })$, $q=p_{1}-p_{2}$ is the four-momentum transfer and the $\lambda _{i}=\pm \frac{1}{2}(i=1,2)$ denote the helicities of the parent baryon $\Xi _{b}$ and daughter baryons $\Lambda (\Xi _{c})$, respectively. Using the equations of motion, we can obtain the hadronic matrix elements of the scalar and pseudo-scalar currents between the two baryons. The expressions for them are

$$\begin{aligned}&\langle \Lambda (\Xi _{c}),\lambda _{2}\vert \bar{u}(\bar{c})b\vert \Xi _{b},\lambda _{1}\rangle = \frac{1}{m_{b}-m_{u(c)}}\bar{u}_{\Lambda ({\Xi }_{c})}(p_{2},\lambda _{2})\nonumber \\&\times \quad \left[ f_{1}(q^{2})(M_{\Xi _{b}}-M_{\Lambda (\Xi _{c})})+f_{3}(q^{2}) \frac{q^2}{M_{\Xi _{b}}}\right] u_{{\Xi }_{b}}(p_{1},\lambda _{1}),\nonumber \\&\langle \Lambda (\Xi _{c}),\lambda _{2}\vert \bar{u}(\bar{c})\gamma _{5}b\vert \Xi _{b},\lambda _{1}\rangle = \frac{1}{m_{b}+m_{u(c)}}\bar{u}_{\Lambda ({\Xi }_{c})}(p_{2},\lambda _{2})\nonumber \\&\times \quad \left[ g_{1}(q^{2})(M_{\Xi _{b}}+M_{\Lambda (\Xi _{c})})-g_{3}(q^{2}) \frac{q^2}{M_{\Xi _{b}}}\right] \gamma _{5} u_{{\Xi }_{b}}(p_{1},\lambda _{1}).\nonumber \\ \end{aligned}$$

(10)

The form factors can be approximated with high accuracy by the following analytic expression [24]:

$$\begin{aligned} f(q^2)= & {} g(q^2)=\frac{1}{1-q^2/M^2_{\mathrm {pole}}}\nonumber \\&\times \lbrace a_0+a_1 z(q^2)+a_2[z(q^2)]^2\rbrace , \end{aligned}$$

(11)

where we have the variable

$$\begin{aligned} z(q^2)=\frac{\sqrt{t_+ -q^2}-\sqrt{t_+ -t_0}}{\sqrt{t_+ -q^2}+\sqrt{t_+ -t_0}}, \end{aligned}$$

(12)

with $t_+=(M_{\Xi _{b}}+M_{\Lambda (\Xi _{c})})^2$ and $t_0=(M_{\Xi _{b}}-M_{\Lambda (\Xi _{c})})^2$. The values of $a_{0,1,2}$ and the pole masses are given in Table 1.

2.3 Helicity amplitude and observables

The hadronic helicity amplitudes in the form of the form factors and the NP couplings are [27,28,29]

$$\begin{aligned}&H^{V}_{\frac{1}{2}0}= (1+V_L+V_R)\frac{\sqrt{Q_-}}{\sqrt{q^2}}\nonumber \\&~~~~~~~~~~~~~\times \left[ (M_{\Xi _{b}}+ M_{\Lambda (\Xi _{c})})f_{1}(q^2)+\frac{q^2}{M_{\Xi _{b}}}f_2(q^2)\right] ,\nonumber \\&H^{A}_{\frac{1}{2}0}= (1+V_L-V_R)\frac{\sqrt{Q_+}}{\sqrt{q^2}}\nonumber \\&~~~~~~~~~~~~~\times \left[ (M_{\Xi _{b}}- M_{\Lambda (\Xi _{c})})g_{1}(q^2)-\frac{q^2}{M_{\Xi _{b}}}g_2(q^2)\right] ,\nonumber \\&H^{V}_{\frac{1}{2}1}= (1+V_L+V_R)\sqrt{2Q_-}\nonumber \\&~~~~~~~~~~~~~\times \left[ f_1(q^2)+\frac{(M_{\Xi _{b}}+ M_{\Lambda (\Xi _{c})})}{M_{\Xi _{b}}}f_2(q^2) \right] ,\nonumber \\&H^{A}_{\frac{1}{2}1}= (1+V_L-V_R)\sqrt{2Q_+}\nonumber \\&~~~~~~~~~~~~~\times \left[ g_1(q^2)-\frac{(M_{\Xi _{b}}- M_{\Lambda (\Xi _{c})})}{M_{\Xi _{b}}}g_2(q^2) \right] ,\nonumber \\&H^{V}_{\frac{1}{2}t}= (1+V_L+V_R)\frac{\sqrt{Q_+}}{\sqrt{q^2}}\nonumber \\&~~~~~~~~~~~~~\times \left[ (M_{\Xi _{b}}- M_{\Lambda (\Xi _{c})})f_1(q^2)+\frac{q^2}{M_{\Xi _{b}}}f_3(q^2) \right] ,\nonumber \\&H^{A}_{\frac{1}{2}t}= (1+V_L-V_R)\frac{\sqrt{Q_-}}{\sqrt{q^2}}\nonumber \\&~~~~~~~~~~~~~\times \left[ (M_{\Xi _{b}}+ M_{\Lambda (\Xi _{c})})g_1(q^2)-\frac{q^2}{M_{\Xi _{b}}}g_3(q^2) \right] ,\nonumber \\&H^{S}_{\frac{1}{2}0}= \frac{(S_L+S_R)\sqrt{2Q_+}}{m_b-m_{u(c)}}\nonumber \\&~~~~~~~~~~~~~\times \left[ (M_{\Xi _{b}}- M_{\Lambda (\Xi _{c})})f_1(q^2)+\frac{q^2}{M_{\Xi _{b}}}f_3(q^2) \right] ,\nonumber \\&H^{P}_{\frac{1}{2}0}= \frac{(S_L-S_R)\sqrt{2Q_-}}{m_b+m_{u(c)}}\nonumber \\&~~~~~~~~~~~~~\times \left[ (M_{\Xi _{b}}+ M_{\Lambda (\Xi _{c})})g_1(q^2)-\frac{q^2}{M_{\Xi _{b}}}g_3(q^2) \right] ,\nonumber \\&H_{\lambda _2,\lambda _W}=H_{\lambda _2,\lambda _W}^V-H_{\lambda _2,\lambda _W}^A,\quad \quad H^{SP}_{\lambda _2,0}=H^{S}_{\lambda _2,0}-H^{P}_{\lambda _2,0},\nonumber \\&H_{-\lambda _2,-\lambda _W}^V=H_{\lambda _2,\lambda _W}^V,\quad \quad \quad \quad \quad \quad H^{S}_{-\lambda _2,0}=H^{S}_{\lambda _2,0}, \nonumber \\&H_{-\lambda _2,-\lambda _W}^A=-H_{\lambda _2,\lambda _W}^A,\quad \quad \quad \quad \quad H^{P}_{-\lambda _2,0}=-H^{P}_{\lambda _2,0}, \end{aligned}$$

(13)

where $Q_{\pm }=(M_{\Xi _{b}}\pm M_{\Lambda (\Xi _{c})})^2-q^2$, $\lambda _{2}$ and $\lambda _{W}$ denote the helicities of the daughter baryons $\Lambda (\Xi _{c})$ and the effective (axial-)vector type current, respectively.

Including the NP contributions, the differential decay distributions for the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})l^{-}\bar{\nu }_{\tau }$ decays are written as [27,28,29]

$$\begin{aligned}&\frac{{\text {d}}^2\Gamma }{{\text {d}}q^2\mathrm{d}\cos \theta _{l}}=\frac{G^2_F|V_{u(c)b}|^2q^2\sqrt{\lambda (M^2_{\Xi _{b}},M^2_{\Lambda (\Xi _{c})},q^2)}}{2\times 512\pi ^3 M^3_{\Xi _{b}}}\nonumber \\&\quad \left( 1-\frac{m^2_l}{q^2} \right) ^2\left[ A_1+\frac{m^2_l}{q^2}A_2+2A_3+\frac{4m_l}{\sqrt{q^2}}A_4 \right] \end{aligned}$$

(14)

where

$$\begin{aligned}&A_{1}=2\sin ^{2}\theta _{l}\left( \left| H_{\frac{1}{2},0}\right| ^2+\left| H_{-\frac{1}{2},0}\right| ^2\right) +(1-\cos \theta _{l})^2\nonumber \\&~~~~~~~~\times |H_{\frac{1}{2},1}|^2 +(1+\cos \theta _{l})^2 \left| H_{-\frac{1}{2},-1}\right| ^2,\nonumber \\&A_{2}=2\cos ^{2}\theta _{l}\left( \left| H_{\frac{1}{2},0}|^2+|H_{-\frac{1}{2},0}\right| ^2\right) +\sin ^{2}\theta _{l}\left( \left| H_{\frac{1}{2},1}\right| ^2\right. \nonumber \\&~~~~~~~~\left. +\left| H_{-\frac{1}{2},-1}\right| ^2 \right) +2\left( \left| H_{\frac{1}{2},t}\right| ^2+\left| H_{-\frac{1}{2},t}\right| ^2\right) \nonumber \\&~~~~~~~~~-4\cos \theta _{l}\mathcal {R}e\left[ H_{\frac{1}{2},t}\left( H_{\frac{1}{2},0}\right) ^*+H_{-\frac{1}{2},t}(H_{-\frac{1}{2},0})^*\right] ,\nonumber \\&A_3=|H^{SP}_{\frac{1}{2},0}|^2+|H^{SP}_{-\frac{1}{2},0}|^2,\nonumber \\&A_4=-\cos \theta _l \mathcal {R}e[H_{\frac{1}{2},0}(H^{SP}_{\frac{1}{2},0})^*+H_{-\frac{1}{2},0}(H^{SP}_{-\frac{1}{2},0})^*]\nonumber \\&~~~~~~~~~+\mathcal {R}e[H_{\frac{1}{2},t}(H^{SP}_{\frac{1}{2},0})^*+H_{-\frac{1}{2},t}(H^{SP}_{-\frac{1}{2},0})^*],\nonumber \\&\lambda (a,b,c)=a^2+b^2+c^2-2(ab+bc+ca), \end{aligned}$$

(15)

with $\theta _{l}$ is the angle between the directions of the parent $\Xi _{b}$ baryon and $l^-$ lepton in the dilepton rest frame. One can obtain the $q^2$ dependent differential decay rate by integrating over $\cos \theta _l$. The expressions of the differential branching fraction ${\text {d}}Br/{\text {d}}q^2$, the ratios of the branching fractions $R_{\Lambda (\Xi _{c})}(q^2)$, the lepton-side forward–backward asymmetry $A_{FB}(q^2)$, the longitudinal polarization $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ of the daughter baryons $\Lambda (\Xi _{c})$ and $P_{L}^{\tau }(q^2)$ of the $\tau$ lepton and the convexity parameter $C_{F}^{l}(q^2)$ are written as

$$\begin{aligned}&{\text {d}}\Gamma / {\text {d}}q^2 =\displaystyle \int ^{1}_{-1}\mathrm{d}\cos \theta _l\frac{{\text {d}}^2\Gamma }{{\text {d}}q^2 \mathrm{d}\cos \theta _l},\quad {\text {d}}Br/{\text {d}}q^2= \frac{{\text {d}}\Gamma / {\text {d}}q^2}{\Gamma _{\mathrm {tot}}}, \nonumber \\\end{aligned}$$

(16)

$$\begin{aligned}&R_{\Lambda (\Xi _c)}(q^2)\equiv \dfrac{Br(\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^-\bar{\nu }_{\tau })}{Br(\Xi _{b}\rightarrow \Lambda (\Xi _{c}) l^-\bar{\nu }_{l})}, \end{aligned}$$

(17)

$$\begin{aligned}&A_{FB}(q^2)=\dfrac{ \int ^{1}_{0}\mathrm{d}\cos \theta _l\frac{{\text {d}}^2\Gamma }{{\text {d}}q^2 \mathrm{d}\cos \theta _l}- \int ^{0}_{-1}\mathrm{d}\cos \theta _l\frac{{\text {d}}^2\Gamma }{{\text {d}}q^2 \mathrm{d}\cos \theta _l}}{\int ^{1}_{0} \mathrm{d}\cos \theta _l\frac{{\text {d}}^2\Gamma }{{\text {d}}q^2 \mathrm{d}\cos \theta _l}+ \int ^{0}_{-1}\mathrm{d}\cos \theta _l\frac{{\text {d}}^2\Gamma }{{\text {d}}q^2 \mathrm{d}\cos \theta _l}}, \nonumber \\\end{aligned}$$

(18)

$$\begin{aligned}&P_{L}^{\Lambda (\Xi _{c})}(q^2)=\dfrac{{\text {d}}\Gamma ^{{\lambda }_{2}=1/2}/{\text {d}} q^2-{\text {d}}\Gamma ^{{\lambda }_{2}=-1/2}/{\text {d}} q^2}{{\text {d}}\Gamma ^{{\lambda }_{2}=1/2}/{\text {d}} q^2+{\text {d}}\Gamma ^{{\lambda }_{2}=-1/2}/{\text {d}} q^2}, \end{aligned}$$

(19)

$$\begin{aligned}&P^{\tau }_L (q^2)=\dfrac{{\text {d}}\Gamma ^{{\lambda }_{\tau }=1/2}/{\text {d}} q^2-{\text {d}}\Gamma ^{{\lambda }_{\tau }=-1/2}/{\text {d}} q^2}{{\text {d}}\Gamma ^{{\lambda }_{\tau }=1/2}/{\text {d}} q^2+{\text {d}}\Gamma ^{{\lambda }_{\tau }=-1/2}/{\text {d}} q^2}, \end{aligned}$$

(20)

$$\begin{aligned}&C_{F}(q^2)=\dfrac{1}{\mathcal {H}_{{\text {tot}}}}\dfrac{{\text {d}}^2W(\theta _{l})}{{\text {d}}(\cos \theta _{l})^2},\quad \quad \mathcal {H}_{tot}=\int ^{1}_{-1} W(\theta _{l})\mathrm{d}\cos \theta _{l},\nonumber \\&W(\theta _{l})= \frac{3}{8}\left[ A_1+\frac{m_l^2}{q^2}A_2+2A_3+\frac{4m_l}{\sqrt{q^2}}A_4 \right] ,\nonumber \\&\dfrac{{\text {d}}^2W(\theta _{l})}{{\text {d}}(\cos \theta _{l})^2} = \dfrac{3}{4}\left( 1-\dfrac{m^2_{l}}{q^2}\right) \nonumber \\&\quad \left[ |H_{\frac{1}{2},1}|^2+|H_{-\frac{1}{2},-1}|^2 -2\bigg (|H_{\frac{1}{2},0}|^2+|H_{-\frac{1}{2},0}|^2\bigg )\right] , \end{aligned}$$

(21)

where ${\text {d}}\Gamma ^{\lambda _{2}}=\pm 1/2$ and ${\text {d}}\Gamma ^{\lambda _{\tau }}=\pm 1/2$ are the helicity-dependent differential decay rates, whose expressions are given in [29].

3 Constraints on the NP Wilson coefficients

In this section, we introduce the constraints on the NP Wilson coefficients coming from the experimental results for the $Br(B_{c}^{+}\rightarrow \tau ^{+}\nu _{\tau })$, $R^{l}_{\pi }$, $R_{D^{(*)}}$, $R_{J/\psi }$ and $F_{L}^{D^{*}}$ anomalies. We assume that all the Wilson coefficients of the NP operators are complex and we consider only one new vector (scalar) coefficient or both vector and scalar coefficients existing in Eq. (8) at a time. When using the current world average of the $B_{c}$ lifetime, the upper limit on $Br(B_{c}^{+}\rightarrow \tau ^{+}\nu _{\tau })$ is [30, 31]

$$\begin{aligned} Br(B^+_c\rightarrow \tau ^+ \nu _{\tau })\lesssim 30\%. \end{aligned}$$

(22)

The branching fraction of purely leptonic $B_{c}^+\rightarrow \tau ^+\nu _{\tau }$ decay including NP contributions is written as [31]

$$\begin{aligned}&Br(B_{c}^+\rightarrow \tau ^+\nu _{\tau })\nonumber \\&\quad =\frac{G^2_F|V_{cb}|^2}{8\pi }\tau _{B_{c}}f_{B_{c}}^2 m_{\tau }^2 M_{B_{c}} \left( 1-\frac{m_{\tau }^2}{ M_{B_{c}}^2}\right) ^2\nonumber \\&\qquad \times \left| (1+V_{L}-V_R)-\frac{M_{B_{c}}^2}{m_{\tau }(m_b+m_c)}(S_L-S_R)\right| ^2, \end{aligned}$$

(23)

where $\tau _{B_{c}}$ is the lifetime and $f_{B_{c}}$ is the leptonic decay constant of $B_{c}$ meson.

The differential branching fractions of the decays $B\rightarrow \pi (D)l^{-}\bar{\nu }_{l}$ are expressed as [32, 33]

$$\begin{aligned}&\frac{{\text {d}}Br(B\rightarrow \pi (D)l^{-}\bar{\nu }_{l})}{{\text {d}}q^2}\\&\quad =\tau _{B}\frac{G^2_F|V_{u(c)b}|^2}{192\pi ^3 M^3_{B}}q^2 \sqrt{\lambda _{\pi (D)}(q^2)}\left( 1-\frac{m^2_{l}}{q^2}\right) ^2\\&\quad \times \left\{ |1+V_L+V_R|^2 \left[ \left( 1+\frac{m^2_{l}}{2q^2}\right) H^2_0+\frac{3}{2}\frac{m^2_{l}}{q^2}H^2_t\right] \right. \\&\quad + \frac{3}{2}|S_L+S_R|^2H^2_S+3\mathcal {R}e[(1+V_L+V_R)(S^*_L+S^*_R)]\\&\quad \left. \frac{m^2_{l}}{\sqrt{q^2}}H_SH_t\right\} , \end{aligned}$$

in which $\lambda _{\pi (D)}(q^2)=\lambda (M^2_B, M^2_{\pi (D)}, q^2)$ and the helicity amplitudes can be written in terms of the form factors:

$$\begin{aligned}&H_0=\sqrt{\frac{\lambda _{\pi (D)}(q^2)}{q^2}}F_+(q^2),\quad H_t=\frac{M^2_{B}-M_{\pi (D)}^2}{\sqrt{q^2}}F_0(q^2),\nonumber \\&\quad H_S=\frac{M^2_{B}-M_{\pi (D)}^2}{m_b-m_{u(c)}}F_0(q^2), \end{aligned}$$

(24)

where $F_{+,0}(q^2)$ are the form factors for the $B\rightarrow \pi (D)$ weak transitions and are given in [32, 34].

Fig. 1

The constraints on both real and imaginary parts of the NP Wilson coefficients $V_L$ (a), $V_R$ (b), $S_L$ (c) and $S_R$ (d) coming from $Br(B_{c}^{+}\rightarrow \tau ^{+}\nu _{\tau })$, $R^{l}_{\pi }$, $R_{D^{(*)}}$, $R_{J/\psi }$ and $F_{L}^{D^{*}}$ anomalies within $2\sigma$ range of their corresponding experimental measurement results

The differential branching fractions of the decays $B\rightarrow D^*(J/\psi )l^{-}\bar{\nu }_{l}$ are given by [32, 33, 35]

$$\begin{aligned}&\frac{{\text {d}}Br(B\rightarrow D^*(J/\psi ) l^{-}\bar{\nu }_{l})}{{\text {d}}q^2}\\&\quad =\tau _{B}\frac{G^2_F|V_{cb}|^2}{192\pi ^3 M^3_B}q^2 \sqrt{\lambda _{D^*(J/\psi )}(q^2)}\left( 1-\frac{m^2_{l}}{q^2}\right) ^2\\&\quad \times \left\{ (|1+V_L|^2+|V_R|)^2 \left[ \left( 1+\frac{m^2_{l}}{2q^2}\right) (H^2_{V,0}+H^2_{V,+}\right. \right. \\&\quad \left. +H^2_{V,-})+\frac{3}{2}\frac{m^2_{l}}{q^2}H^2_{V,t}\right] \\&\quad -2\mathcal {R}e[(1+V_{L})V^*_R]\left[ \left( 1+\frac{m^2_{l}}{2q^2} \right) \right. \\&\quad \left. (H^2_{V,0}+2H_{V,+}H_{V,-})+\frac{3}{2}\frac{m^2_{l}}{q^2}H^2_{V,t}\right] \\&\quad + \frac{3}{2}|S_L-S_R|^2H^2_S+3\mathcal {R}e[(1+V_L-V_R)(S^*_L-S^*_R)]\\&\quad \left. \frac{m_{l}}{\sqrt{q^2}}H_SH_{V,t}\right\} , \end{aligned}$$

Fig. 2

The constraints on both real and imaginary parts of the NP Wilson coefficients $V_L$ and $S_L$ (a1–a4), $V_L$ and $S_R$ (b1–b4), $V_R$ and $S_L$ (c1–c4) and $V_R$ and $S_R$ (d1–d4) coming from $Br(B_{c}^{+}\rightarrow \tau ^{+}\nu _{\tau })$, $R^{l}_{\pi }$, $R_{D^{(*)}}$, $R_{J/\psi }$ and $F_{L}^{D^{*}}$ anomalies within $2\sigma$ range of their corresponding experimental results

where

$$\begin{aligned} H_{V,\pm }= & {} (M_{B}+M_{D^*})A_1(q^2)\mp \frac{\sqrt{\lambda _{D^*}(q^2)}}{M_{B}+M_{D^*}}V(q^2),\nonumber \\ H_{V,0}= & {} \frac{M_{B}+M_{D^*}}{2M_{D^*}\sqrt{q^2}}\Bigg [-(M^2_{B}-M^2_{D^*}-q^2)A_1(q^2)\nonumber \\&+\frac{\lambda _{D^*}(q^2)}{(M_B+M_{D^*})^2}A_2(q^2) \Bigg ],\nonumber \\ H_{V,t}= & {} -\sqrt{\frac{\lambda _{D^*}(q^2)}{q^2}}A_0(q^2),\nonumber \\ H_{S}\simeq & {} -\sqrt{\frac{\lambda _{D^*}(q^2)}{m_b+m_c}}A_0(q^2), \end{aligned}$$

(25)

are the hadronic helicity amplitudes for the $B\rightarrow D^*l^{-}\bar{\nu }_{l}$ decays and the form factors $V(q^2), A_0(q^2), A_1(q^2)$ and $A_2(q^2)$ for the $B\rightarrow D^*$ transition can be found in [32].

For the $B_{c}\rightarrow J/\psi l^+\nu _{l}$ transitions, the hadronic helicity amplitudes and the form factors can easily be found in [35, 36].

The $B\rightarrow D^*\tau ^{+}\nu _{\tau }$ differential decay width into the longitudinally-polarized $D^*$ meson ($\lambda _{D^*}=0$) is given by [37]

$$\begin{aligned}&\frac{{\text {d}}\Gamma _{\lambda _{D^*}=0}}{{\text {d}}q^2}\nonumber \\&\quad =\frac{G^2_F|V_{cb}|^2}{192\pi ^3 M^3_B}q^2\sqrt{\lambda _{D^*}(q^2)}\left( 1-\frac{m^2_{\tau }}{q^2}\right) ^2\nonumber \\&\qquad \times \left\{ |1+V_L-V_R|^2\left[ \left( 1+\frac{m^2_{\tau }}{2q^2}\right) ^2H^2_{V,0}+\frac{3}{2}\frac{m^2_{\tau }}{q^2}H^2_{V,t}\right] \right. \nonumber \\&\qquad + \frac{3}{2}|S_L-S_R|^2H^2_S \nonumber \\&\qquad + \left. 3\mathcal {R}e[(1+V_L-V_R)(S^*_L-S^*_R)]\frac{m_{\tau }}{\sqrt{q^2}}H_SH_{V,t}\right\} ;\nonumber \\ \end{aligned}$$

(26)

the helicity amplitudes are in Eq. (25).

Fig. 3

The SM (red) and NP (orange) predictions in the presence of only $V_L$ coupling for the $q^2$ dependent observables ${\text {d}}Br/{\text {d}}q^2$ (a1, b1), $R(q^2)$ (a2, b2), $A_{FB}(q^2)$ (a3, b3), $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ (a4, b4), $P_{L}^{\tau }(q^2)$ (a5, b5) and $C_{F}^{l}(q^2)$ (a6, b6) relative to the decays $\Xi _{b}\rightarrow \Lambda \tau ^{-}\bar{\nu }_{\tau }$ and $\Xi _{b}\rightarrow \Xi _{c} \tau ^{-} \bar{\nu }_{\tau }$, respectively. The bands contain the theoretical uncertainty of the CKM matrix elements $|V_{u(c)b}|$

Fig. 4

The SM (red) and NP (pink) predictions in the presence of only $V_R$ coupling for the $q^2$ dependent observables ${\text {d}}Br/{\text {d}}q^2$ (a1, b1), $R(q^2)$ (a2, b2), $A_{FB}(q^2)$ (a3, b3), $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ (a4, b4), $P_{L}^{\tau }(q^2)$ (a5, b5) and $C_{F}^{l}(q^2)$ (a6, b6) relative to the decays $\Xi _{b}\rightarrow \Lambda \tau ^{-}\bar{\nu }_{\tau }$ and $\Xi _{b}\rightarrow \Xi _{c} \tau ^{-}\bar{\nu }_{\tau }$, correspondingly. The bands contain the theoretical uncertainty of the CKM matrix elements $|V_{u(c)b}|$

Fig. 5

The SM (red) and NP (yellow) predictions in the presence of both the $V_L$ and the $S_L$ couplings for the $q^2$ dependent observables ${\text {d}}Br/{\text {d}}q^2$ (a1, b1), $R(q^2)$ (a2, b2), $A_{FB}(q^2)$ (a3, b3), $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ (a4, b4), $P_{L}^{\tau }(q^2)$ (a5, b5) and $C_{F}^{l}(q^2)$ (a6, b6) relative to the $\Xi _{b}\rightarrow \Lambda \tau ^{-}\bar{\nu }_{\tau }$ and $\Xi _{b}\rightarrow \Xi _{c} \tau ^{-} \bar{\nu }_{\tau }$ decays, respectively. The bands contain the theoretical uncertainty of the CKM matrix elements $|V_{u(c)b}|$

Fig. 6

The SM (red) and NP (purple) predictions in the presence of both $V_L$ and $S_R$ couplings for the $q^2$ dependent observables ${\text {d}}Br/{\text {d}}q^2$ (a1, b1), $R(q^2)$ (a2, b2), $A_{FB}(q^2)$ (a3, b3), $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ (a4, b4), $P_{L}^{\tau }(q^2)$ (a5, b5) and $C_{F}^{l}(q^2)$ (a6, b6) relative to the decays $\Xi _{b}\rightarrow \Lambda \tau ^{-}\bar{\nu }_{\tau }$ and $\Xi _{b}\rightarrow \Xi _{c} \tau ^{-} \bar{\nu }_{\tau }$, respectively. The bands contain the theoretical uncertainty of the CKM matrix elements $|V_{u(c)b}|$

Fig. 7

The SM (red) and NP (cyan) predictions in the presence of both the $V_R$ and the $S_L$ couplings for the $q^2$ dependent observables ${\text {d}}Br/{\text {d}}q^2$ (a1, b1), $R(q^2)$ (a2, b2), $A_{FB}(q^2)$ (a3, b3), $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ (a4, b4), $P_{L}^{\tau }(q^2)$ (a5, b5) and $C_{F}^{l}(q^2)$ (a6, b6) relative to the decays $\Xi _{b}\rightarrow \Lambda \tau ^{-}\bar{\nu }_{\tau }$ and $\Xi _{b}\rightarrow \Xi _{c} \tau ^{-} \bar{\nu }_{\tau }$, respectively. The bands contain the theoretical uncertainty of the CKM matrix elements $|V_{u(c)b}|$

Fig. 8

The SM (red) and NP (brown) predictions in the presence of both $V_R$ and $S_R$ couplings for the $q^2$ dependent observables ${\text {d}}Br/{\text {d}}q^2$ (a1, b1), $R(q^2)$ (a2, b2), $A_{FB}(q^2)$ (a3, b3), $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ (a4, b4), $P_{L}^{\tau }(q^2)$ (a5, b5) and $C_{F}^{l}(q^2)$ (a6, b6) relative to the decays $\Xi _{b}\rightarrow \Lambda \tau ^{-}\bar{\nu }_{\tau }$ and $\Xi _{b}\rightarrow \Xi _{c} \tau ^{-} \bar{\nu }_{\tau }$, correspondingly. The bands contain the theoretical uncertainty of the CKM matrix elements $|V_{u(c)b}|$

Based on these functions, we calculate the predictions of the $Br(B_{c}^{+}\rightarrow \tau ^{+}\nu _{\tau })$, $R^{l}_{\pi }$, $R_{D^{(*)}}$, $R_{J/\psi }$ and $F_{L}^{D^{*}}$ anomalies including only one new vector (scalar) coupling or both the vector and the scalar couplings at a time and compare the results with their corresponding $2\sigma$ range of the observed experimental values, are in Sect. 1. First of all, we display the constrained range of NP Wilson coefficients $V_L$, $V_R$, $S_L$ and $S_R$ with real and imaginary parts in Fig. 1a–d, respectively. One can easily observe the constrained range of $V_L$ and $V_R$ in Fig. 1a, b. We show the constrained range of $S_L$ and $S_R$ more vividly in Fig. 1c, d and one can more easily notice that $S_L$ and $S_R$ are ruled out. The constraints coming from the $F_{L}^{D^{*}}$ anomaly are not shown in Fig. 1c, d since they cannot be parameterized regularly but still have a common range with the other anomalies. This conclusion has been confirmed using the parameter scanning by us. The constraints on $S_L$ coming from $R_{D}$ and $R_{D^{*}}$ as well as the constraints on $S_R$ coming from $R^{l}_{\pi }$ and $R_{D^{(*)}}$ have no area in common on panels c and d, respectively. Secondly, we show the constrained range of $V_L$ and $S_L$, $V_L$ and $S_R$, $V_R$ and $S_L$, and $V_R$ and $S_R$ in Fig. 2a1–a4, b1–b4, c1–c4 and d1–d4, respectively. Taking the constrained range of $V_L$ and $S_L$ as an example, we calculate the predictions of the $Br(B_{c}^{+}\rightarrow \tau ^{+}\nu _{\tau })$, $R^{l}_{\pi }$, $R_{D^{(*)}}$ and $F_{L}^{D^{*}}$ anomalies including the contributions of both the NP couplings $V_L$ and $S_L$, and we then compare the predictions with their corresponding $2\sigma$ range of the experimental measurement values. We show the range (yellow area) of different combinations of two parameters such as $ReV_L$ and $ReS_L$, $ReV_L$ and $ImS_L$, $ImV_L$ and $ReS_L$, and $ImV_L$ and $ImS_L$, contained in the couplings $V_L$ and $S_L$ in Fig. 2a1–a4, respectively. From Fig. 2a1–a4, one can see that the values of $ReS_L$ and $ImS_L$ are in a small range compared with the values of $ReV_L$ and $ImV_L$, since the NP coupling $S_L$ is ruled out when it is considered separately.

4 Numerical results and discussions

In this section, we give the numerical results of the observables ${\text {d}}Br/{\text {d}}q^2$, $R(q^2)$, $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$ relative to the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ transitions including the contributions of only NP vector type couplings and both vector and scalar type couplings except the ones of only scalar type.

Before we present the numerical results, we have to clarify the values of the SM input parameters used for the numerical calculations in Table 2.

Firstly, we suppose that the NP contributions only come from the new coefficient $V_L$ associated with the left-handed vector like quark current. Using the constrained range within $2\sigma$ allowed for real and imaginary parts of $V_L$ in Fig. 1a, we analyze the NP effects of $V_L$ on the $q^2$ dependence of the observables ${\text {d}}Br/{\text {d}}q^2$, $R(q^2)$, $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$, and $C_{F}^{l}(q^2)$ and present the variations of these observables in the reasonable kinematic range in Fig. 3. The red bands represent the SM predictions and the orange bands represent the NP predictions including the contributions of $V_L$. The ${\text {d}}Br/{\text {d}}q^2$ relative to the $\Xi _{b}\rightarrow \Lambda (\Xi _{c}) \tau ^{-}\bar{\nu }_{\tau }$ decays are both largely enhanced in the whole reasonable kinematic region. The red band in Fig. 3a1 is wider than that in Fig. 3b1 because of the larger uncertainty of $|V_{ub}|$ compared with $|V_{cb}|$. Additionally, the ratios $R_{\Lambda }(q^2)$ and $R_{\Xi _{c}}(q^2)$ are also largely enhanced in the whole kinematic region, especially in the large $q^2$ region compared with their corresponding SM predictions. Therefore, measuring the ratios

Table 2 Input parameters in the SM used for our numerical analysis [38]

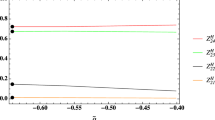
$R_{\Lambda (\Xi _{c})}(q^2)$ in the high kinematic region may be more useful for further confirming the NP effects of the B meson decay anomalies. We only show the SM predictions for $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$ of the two decays in Fig. 3. There is no difference between the NP predictions including contributions of $V_L$ and the SM predictions of the $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$. Because the NP operators have the same Lorentz structure as the SM ones and the SM decay rates of the two transitions are modified by the factor $|1+V_L|^2$. The factor $|1+V_L|^2$ appears both in the numerator and in the denominator of the expressions describing $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$ simultaneously.

Secondly, using the constrained range within $2\sigma$ allowed for real and imaginary parts of the new coefficient $V_R$ in Fig. 1b, the NP predictions including the contributions of $V_R$ and the SM predictions for the ${\text {d}}Br/{\text {d}}q^2$, $R(q^2)$, $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$ relative to the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ decays are displayed in Fig. 4. The red bands represent the SM predictions and the pink bands represent the NP predictions including the contributions of $V_R$. The NP contributions of $V_R$ to ${\text {d}}Br/{\text {d}}q^2$ and $R(q^2)$ in Fig. 4a1, a2, b1, b2 have large deviations from their corresponding SM predictions in the same way as in the $V_L$ scenario. Both ${\text {d}}Br/{\text {d}}q^2$ and $R(q^2)$ are enhanced in the whole reasonable kinematic region. More interesting, the NP contributions of $V_R$ to the observables $A_{FB}(q^2)$ and $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ in Fig. 4a3, a4, b3, b4 similarly have large deviations from their SM predictions, which are really different from the scenario for $V_L$. The $A_{FB}(q^2)$ including NP contributions of $V_R$ are decreased but $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ are enhanced in the whole kinematic region. The extent of the decrement and enhancement vary with the increasing of $q^2$. In the lowest kinematic region, the enhancement of $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ is most prominent. Therefore, it is crucial to measure $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ in the low kinematic region. Additionally, one can see that the $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$ of these two decays including NP contributions of $V_R$ and their SM predictions in Fig. 4a5, a6, b5, b6 are almost the same, which indicates that they are both insensitive to the NP effects of the coupling $V_R$.

Finally, we show the NP contributions of four combinations of vector and scalar type couplings such as $V_L$ and $S_L$, $V_L$ and $S_R$, $V_R$ and $S_L$, and $V_R$ and $S_R$ to ${\text {d}}Br/{\text {d}}q^2$, $R(q^2)$, $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$ relative to the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ decays in Figs. 5, 6, 7 and 8. In these four figures, it is still easily to see that the NP effects of the different combinations of vector or scalar type couplings on ${\text {d}}Br/{\text {d}}q^2$ and $R(q^2)$ relative to the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ decays are all similarly significant. In Fig. 5, different from the scenario only considering the NP couplings $V_L$, the observables $P_{L}^{\tau }(q^2)$ relative to the two decays are also sensitive to $V_L$ and $S_L$. In the highest kinematic region, the deviations between the NP predictions of $P_{L}^{\tau }(q^2)$ including the contributions of $V_L$ and $S_L$ and the SM predictions are largest. Therefore, the observable $P_{L}^{\tau }(q^2)$ is important to distinguish the NP originating from the vector type or from both vector and scalar type couplings. In Fig. 6, except that the ${\text {d}}Br/{\text {d}}q^2$ and $R(q^2)$ observables are sensitive to $V_L$ and $S_R$, the observables $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ are also both enhanced significantly with the NP contributions of $V_L$ and $S_R$; nevertheless they are not sensitive to $V_L$ and $S_L$. Once the observable $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ is measured, they can be used to distinguish the NP contributions provided by $V_L$ and $S_L$ or $V_L$ and $S_R$. The NP predictions of the same observables in Figs. 7 and 8 show a similar variation tendency to the increasing of $q^2$ and have similar deviations to their corresponding SM predictions. The contributions of $V_R$ and $S_L$, and $V_R$ and $S_R$ to the observables ${\text {d}}Br/{\text {d}}q^2$ and $R(q^2)$ are larger than the contributions of only $V_R$ shown in Fig. 4. In addition, the $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ are also more sensitive to $V_R$ and $S_L$, and $V_R$ and $S_R$ than $V_R$, but the contributions of $V_R$ and $S_L$ on $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ are a little higher than those of $V_R$ and $S_R$.

5 Summary and conclusion

Several anomalies $R_{D^{(*)}}$ and $R_{J/\psi }$ observed in the semileptonic B meson decays have indicated the hints of LFUV and attracted many researchers’ attention. Much work has been done as regards the NP effects of these anomalies on the transitions mediated by the $b\rightarrow c$ charged current, such as the baryon decays $\Lambda _{b}\rightarrow \Lambda _{c}l^{-}\bar{\nu }_{l}$. It is important to investigate the semileptonic $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ baryon decays, which are mediated by $b\rightarrow u(c)\tau ^{-}\bar{\nu }_{\tau }$ transitions at quark level. These decays not only can provide an independent determination of the CKM matrix elements $|V_{ub}|$ and $|V_{cb}|$ but also may be further confirmation of the hints of LFUV, which is helpful in exploring NP. Therefore, we investigate the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ decays in the SM and various NP scenarios.

We consider the NP effects of new vector type couplings separately and the combinations of vector and scalar couplings on the observables ${\text {d}}Br/{\text {d}}q^2$, $R(q^2)$, $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$ relative to the $\Xi _{b}\rightarrow \Lambda (\Xi _{c})\tau ^{-}\bar{\nu }_{\tau }$ transitions. The results show that ${\text {d}}Br/{\text {d}}q^2$ and $R(q^2)$ including any kind of NP couplings are all enhanced largely and have significant deviations comparing to their SM predictions. $A_{FB}(q^2)$, $P_{L}^{\Lambda (\Xi _{c})}(q^2)$, $P_{L}^{\tau }(q^2)$ and $C_{F}^{l}(q^2)$ are the same as their corresponding SM predictions in $V_L$ scenario, since the common coefficient $|1+V_L|^2$ appears in the numerator and the denominator of the expressions describing these observables simultaneously. Nevertheless, the contributions of $V_R$ to the $A_{FB}(q^2)$ and $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ are also significant. In the lowest kinematic region, the enhancement of $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ is most prominent. Measuring $R(q^2)$ in the large $q^2$ region and $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ in the low $q^2$ region are more important and useful to further confirm the NP effects of the B meson decay anomalies and can be used to distinguish the new left- and right-handed vector interactions. It is worth noting that the $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ are sensitive to $V_L$ and $S_R$ but not $V_L$ and $S_L$, so detecting $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ is important to confirm the origin of NP effects. For the $V_R$ and $S_L$ and the $V_R$ and $S_R$ scenarios, the characters of the NP effects on $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ are similar and both are more significant than in the scenario with only $V_R$. In addition, the $P_{L}^{\tau }(q^2)$ of these two decays are both sensitive to $V_R$ and $S_L$ and to $V_R$ and $S_R$, but not to only $V_R$. In this case, the observables $P_{L}^{\Lambda (\Xi _{c})}(q^2)$ and $P_{L}^{\tau }(q^2)$ could be an effective target for differentiating the $V_R$ from $V_R$ and $S_L$, and from $V_R$ and $S_R$. We think this investigation will be helpful in exploring and distinguishing different NP scenarios.