1 Introduction

Various astrophysical and cosmological observations provide substantial evidence, firmly establishing the existence of dark matter (DM) in our Universe. However, the nature of DM remains one of the major unsolved problems in fundamental physics. Primordial black holes (PBHs) produced in the radiation-dominated era of the early Universe due to the collapse of large energy density fluctuations, as a promising candidate for dark matter, have attracted much attention [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16].

Two neighboring PBHs can form a binary in the early Universe and coalesce within the age of the Universe. The merge rate of PBH binaries was first estimated through the three-body interaction for the case where all PBHs have the same mass [17, 18]. In the PBH binary formation scenario, the gravitational wave event GW150914 detected by LIGO [19] and the merger rate estimated by the LIGO-Virgo Collaboration can be explained by the coalescence of PBH binaries if PBHs have the mass about \(30 M_{\odot }\) and constitute a tiny fraction of DM [20]. The binary formation was extended to account for an arbitrary PBH mass function based on the three-body approximation [21] or to account for the torque from the surrounding PBHs and the standard large-scale adiabatic perturbations assuming a monochromatic mass function [22]. The mechanism has recently been developed for a general mass function by taking into account the torque from the surrounding PBHs [23,24,25,26].

However, these studies ignore the possibility that a PBH binary merges into a new black hole which together with another PBH forms a new PBH binary. Such a second-merge event can in principle be detected by LIGO-Virgo at the present time. In this paper, we develop an analytic formalism to work out the merger rate density of PBH binaries with a general mass function, by taking into account the merger history of PBHs.

The paper is organized as follows. In the next section, we summarize the basic equation for the primordial input parameters of PBHs and revisit the merger rate for a monochromatic mass function as the first-merger process. In Sect. 3, we develop a formalism to calculate the merger rate density of PBH binaries with a general mass function, by taking into account the merger history of PBHs. In Sect. 4, we consider three specific examples, monochromatic, power-law mass and log-normal functions, to investigate the effects of the merger history on the merger rate density of PBH binaries. The final section is devoted to our conclusions.

In this paper, we use units of \(c = G = 1\). Whenever relevant, we adopt the values of cosmological parameters consistent with the Planck measurements [27]. The scale factor is normalized to unity at the present time.

2 Single-merger events

Let us start with deriving the basic equation of the merger rate of PBH binaries. It could be easily checked that the gravitational attraction between two approximately isolated PBHs dominates their dynamics if their average mass is bigger than the background mass contained in a comoving sphere whose radius equals their conformal distance. Considering the different scaling with time of the two competing effects (their gravitational attraction versus the expansion of the Universe) in the equation of motion for their separation [22]. Following Ref. [20], in this section, we assume that all PBHs have the same mass, M, and PBH binaries decouple from the expansion of the Universe during radiation domination provided that their comoving separation, x, approximately satisfies

$$\begin{aligned} x < x_{\mathrm{max}} \equiv (f_{\mathrm{pbh}}/n_\mathrm{pbh})^{1/3}=\left( M/\rho _{\mathrm{d}m}\right) ^{1/3}, \end{aligned}$$
(1)

where \(f_{\mathrm{pbh}}\) is the fraction of PBHs in DM, \(n_{\mathrm{pbh}}\) denotes the comoving average number density of PBHs and \(\rho _\mathrm{d}m\) denotes the present energy density of DM. The redshift \(z_\mathrm{dec}\) at which the binary decoupling occurs is given by

$$\begin{aligned} 1+z_{\mathrm{dec}}=(1+z_{\mathrm{eq}}) \left( {x_{\mathrm{max}}}/{x}\right) ^3, \end{aligned}$$
(2)

where \(z_{\mathrm{eq}}\simeq 3400\) is the redshift at matter–radiation equality, assuming negligible initial peculiar velocities throughout. Therefore, given PBH mass M and the initial comoving distance of PBHs x, the decoupling time is determined by PBHs. In this work, we assume that accretion and evaporation are negligible before the epoch of binary formation. When two PBHs come closer, the nearest PBH exert torque on the bound system. As a result, the two PBHs avoid a head-on collision and form a highly eccentric binary. The major and minor axes (denoted by a and b, respectively) are given by

$$\begin{aligned} a= & {} A \frac{x}{1+z_{\mathrm{dec}}} = A \frac{\rho _{\mathrm{d}m} x^4}{(1+z_{\mathrm{eq}})M}, \end{aligned}$$
(3)
$$\begin{aligned} b= & {} B \left( \frac{x}{y}\right) ^3 a, \end{aligned}$$
(4)

where y is the comoving distance to the third PBH, A and B are numerical factors of \({{\mathcal {O}}}(1)\). A detailed investigation of the dynamics of the binary formation suggests \(A=0.4\) and \(B=0.8\) [18]. To be exact, in the following calculation, we adopt \(A=0.4\) and \(B=0.8\). The dimensionless angular momentum of PBH binaries is given by

$$\begin{aligned} j \equiv \sqrt{1-e^2} = B \left( \frac{x}{y}\right) ^3, \end{aligned}$$
(5)

where e is the eccentricity of the binary at the formation time. Once two PBHs form a binary, they gradually shrink through the emission of gravitational radiation and eventually merge at the time \(\tau \) after its formation, which can be estimated as [28]

$$\begin{aligned} \tau \simeq \frac{3 { a}^4 j^7}{170 M^3}. \end{aligned}$$
(6)

To calculate the merger rate of PBH binaries, we have to know the spatial distribution of PBHs. Assuming that the spatial distribution of PBHs is random, the probability that the comoving distances, x and y, are in the intervals \((x,x+\mathrm{d}x)\) and \((y,y+\mathrm{d}y)\) is given by

$$\begin{aligned} dP=\frac{4\pi x^2\mathrm{d}x}{n_{\mathrm{pbh}}^{-1}} \frac{4\pi y^2\mathrm{d}y}{n_\mathrm{pbh}^{-1}} \exp \left( -\frac{4\pi y^3}{3n_{\mathrm{pbh}}^{-1}} \right) \Theta (y-x). \end{aligned}$$
(7)

To deal with this probability distribution, we can rewrite Eq. (7) as follows:

$$\begin{aligned} dP=\frac{4\pi x^2\mathrm{d}x}{n_{\mathrm{pbh}}^{-1}} \frac{4\pi y^2\mathrm{d}y}{n_\mathrm{pbh}^{-1}} \Theta (y-x)\Theta (y_{\mathrm{max}}-y), \end{aligned}$$
(8)

where \(y_{\mathrm{max}}={\left( 4\pi n_{\mathrm{pbh}} /3 \right) }^{-1/3}\), which is adopted in [17]. In Fig. 1 we show the merger rate estimated by using the initial distribution (7) and the simplified distribution (8), which indicates that the difference between the two cases is insignificant compared to the uncertainty of the merger rate estimated by the LIGO-Virgo Collaboration.

Fig. 1
figure 1

Event rate of single-mergers of PBH binaries with the mass of \(30 M_{\odot }\) as a function of the PBH abundance. The blue line corresponds to the case of the distribution (7) and the red line corresponds to the case of the distribution (8). The merger rate \(R=12 \)–\( 213\hbox { Gpc}^{-3}\hbox { year}^{-1}\), inferred by the LIGO and Virgo Collaboration, is shown as the shaded region colored orange [29]

Full size image

The fraction of PBHs which have merged before the time t is given by

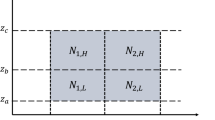
$$\begin{aligned} G(t)=\int \mathrm{d}x\mathrm{d}y \frac{\mathrm{d} P}{\mathrm{d}x\mathrm{d}y} \Theta (t-\tau (x,y))\Theta (x_\mathrm{max}-x). \end{aligned}$$
(9)

In Fig. 2 is a schematic illustration on calculating G(t).

Fig. 2
figure 2

Schematic illustration on calculating G(t)

Full size image

From Eqs. (34), (5) and (6), we can get

$$\begin{aligned} x=\left( \frac{t}{k}\right) ^{1 \over 37} y^{21 \over 37}, \end{aligned}$$
(10)

where

$$\begin{aligned} k=\frac{3}{170} \frac{1}{M^3} \left( \frac{\rho _{\mathrm{dm}}}{(1+z_\mathrm{eq})M}\right) ^{4} A^{4} B^{7}. \end{aligned}$$
(11)

When \(f=f_{c}\), we have

$$\begin{aligned} x_{\mathrm{max}}=\left( \frac{t}{k}\right) ^{1 \over 37} y_{\mathrm{max}}^{21 \over 37}. \end{aligned}$$
(12)

By solving Eq. (12), we get

$$\begin{aligned} f_{c}= & {} \left( \frac{4\pi }{3}\right) ^{-1}\left( \frac{t}{k}\right) ^{1\over 7} \left( M \over \rho _{\mathrm{dm}}\right) ^{-{16 \over 21}} \nonumber \\\approx & {} 1.63 \times 10^{-4} \left( {M \over M_{\odot }}\right) ^{{5 \over 21}} \left( {t\over t_0}\right) ^{{1\over 7}}. \end{aligned}$$
(13)

By solving

$$\begin{aligned} y_1=x, ~~~~x=\left( \frac{t}{k}\right) ^{1 \over 37} y_1^{21 \over 37}, \end{aligned}$$
(14)

we arrive at

$$\begin{aligned} y_1=\left( \frac{t}{k}\right) ^{1 \over 16}. \end{aligned}$$
(15)

By solving

$$\begin{aligned} x_{\mathrm{max}}=\left( \frac{t}{k}\right) ^{1 \over 37} y_{2}^{21 \over 37} \end{aligned}$$
(16)

we arrive at

$$\begin{aligned} y_{2}=\left( \frac{k}{t}\right) ^{1 \over 21} x_{\mathrm{max}}^{37 \over 21}. \end{aligned}$$
(17)

For \(f>f_c\), G(t) is given by

$$\begin{aligned} G(t)= & {} \int _{0}^{y_1} \int _{0}^{y} 4\pi x^2 n_{\mathrm{pbh}} 4\pi y^2 n_{\mathrm{pbh}} \mathrm{d}x\mathrm{d}y \nonumber \\&+\int _{y_1}^{y_{\max }} \int _{0}^{(\frac{t}{k})^{1/37} y^{21/37}} 4\pi x^2 n_{\mathrm{pbh}} 4\pi y^2 n_{\mathrm{pbh}} \mathrm{d}x\mathrm{d}y \nonumber \\= & {} \frac{8 \pi ^2}{261} \left( 37 y_{\max }^{174/37} \left( \frac{t}{k}\right) ^{3/37}-8 \left( \frac{t}{k}\right) ^{3/8}\right) n_{\mathrm{pbh}}^{2} \nonumber \\\approx & {} 2.85\times 10^{-3} \left( { M \over M_{\odot }}\right) ^{{5 \over 37}} \left( {t\over t_0}\right) ^{{3\over 37}} f_{\mathrm{pbh}}^{16 \over 37} \nonumber \\&- 1.86\times 10^{-12}\left( { M \over M_{\odot }}\right) ^{{5 \over 8}} \left( {t\over t_0}\right) ^{{3\over 8}} f_{\mathrm{pbh}}^2 \nonumber \\\approx & {} 2.85\times 10^{-3} \left( { M \over M_{\odot }}\right) ^{{5 \over 37}} \left( {t\over t_0}\right) ^{{3\over 37}} f_{\mathrm{pbh}}^{16 \over 37}. \end{aligned}$$
(18)

For \(f<f_c\), G(t) is given by

$$\begin{aligned} G(t)= & {} \int _{0}^{y_1} \int _{0}^{y} 4\pi x^2 n_{\mathrm{pbh}} 4\pi y^2 n_{\mathrm{pbh}} \mathrm{d}x\mathrm{d}y \nonumber \\&+ \int _{y_1}^{y_2} \int _{0}^{(\frac{t}{k})^{1 \over 37} y_{2}^{21 \over 37}} 4\pi x^2 n_{\mathrm{pbh}} 4\pi y^2 n_{\mathrm{pbh}} \mathrm{d}x\mathrm{d}y \nonumber \\&+ \int _{y_2}^{y_{\mathrm{max}}} \int _{0}^{x_{\mathrm{max}}} 4\pi x^2 n_{\mathrm{pbh}} 4\pi y^2 n_{\mathrm{pbh}} \mathrm{d}x\mathrm{d}y \nonumber \\= & {} -\frac{8 \pi ^2}{261}\left( 8 \left( \frac{t}{k}\right) ^{3\over 8}+(\frac{t}{k})^{3\over 37}y_2^{63\over 37}(-58y_\mathrm{max}^3+21y_2^3)\right) n_{\mathrm{pbh}}^{2} \nonumber \\\approx & {} f_{\mathrm{pbh}}(4.19-1.18\times 10^{-8} \left( { M \over M_{\odot }}\right) ^{{5 \over 8}} \left( {t\over t_0}\right) ^{{3\over 8}} f_{\mathrm{pbh}}\nonumber \\&- 9.32\times 10^{3} \left( { M \over M_{\odot }}\right) ^{-{5 \over 21}} \left( {t\over t_0}\right) ^{-{1\over 7}} f_{\mathrm{pbh}}) \nonumber \\\approx & {} f_{\mathrm{pbh}}(4.19-9.32\times 10^{3} \left( { M \over M_{\odot }}\right) ^{-{5 \over 21}} \left( {t\over t_0}\right) ^{-{1\over 7}} f_{\mathrm{pbh}}) .\nonumber \\ \end{aligned}$$
(19)

Therefore, the merger rate of PBH binaries per unit volume per unit time (at the time t) can be easily obtained by

$$\begin{aligned} R\left( t\right) =\frac{1}{2} n_{\mathrm{pbh}}\lim _{ \mathrm{d}t\rightarrow 0 }{ \frac{G\left( t+\mathrm{d}t\right) -G\left( t\right) }{\mathrm{d}t}}, \end{aligned}$$
(20)

where the factor 1 / 2 accounts for the fact that each merger event involves two PBHs. From Eq. (20), the final result is given by

$$\begin{aligned} \begin{aligned}&R\left( t\right) \approx \\&\quad {\left\{ \begin{array}{ll} 1.61 \times 10^{12} \left( {M \over M_{\odot }}\right) ^{-{26 \over 21}} \left( {t\over t_0}\right) ^{-{8\over 7}} f_{\mathrm{pbh}}^3, ~~~~\mathrm{for}~f_{\mathrm{pbh}}<f_{c},\\ 1.86 \times 10^{6} \left( {M \over M_{\odot }}\right) ^{-{32 \over 37}} \left( {t\over t_0}\right) ^{-{34\over 37}} f_{\mathrm{pbh}}^{53 \over 37},~~~~\mathrm{for}~f_{\mathrm{pbh}}\ge f_{c}, \end{array}\right. } \end{aligned}\nonumber \\ \end{aligned}$$
(21)

which can be interpreted as the merger rate in \(\hbox {Gpc}^{-3}\hbox { year}^{-1}\). We show the single-merger rate of PBH binaries as a function of the PBH abundance in Fig. 3. For \(f_{\mathrm{pbh}}>f_{c}\) it scales as \(f_{\mathrm{pbh}}^{53/37}\) and for \(f_{\mathrm{pbh}}<f_{c}\) it scales as \(f_{\mathrm{pbh}}^3\).

Fig. 3
figure 3

Event rate of single mergers of PBH binaries with the mass \(M=10\) (green), 30 (blue) and 100 (red) in \(M_{\odot }\) at the present time as a function of the PBH abundance. The merger rate of \(R=12 \)–\( 213\hbox { Gpc}^{-3}\hbox { year}^{-1}\), inferred by the LIGO and Virgo Collaboration, is shown as the shaded region colored orange [29]

Full size image

Now we have to see what the difference is between our formalism and the one developed in Ref. [20]. For the single-merger case, the merger rate of PBH binaries is usually calculated by converting the probability distribution function P of x and y into the one of a and e. However, for the multiple-merger case, the probability distribution is a function of more variables than x and y. It becomes hard to convert the probability distribution function of \((x,y,z,\ldots )\) into the one of a and e. Therefore, the known formalism does not work in the multiple-merger case. To get the merger rate of PBH binaries, we directly deal with the probability distribution in the x–y plane to find which PBHs have been merged. It becomes easy to extend our formalism to the second- and third-merger events. In this section, to warm up we consider the merger rate of PBH binaries in the single-merger case. In the next section, we shall extend the formalism to the second- and third-merger cases.

3 Multiple-merger events

So far, several gravitational wave events from black hole binary mergers have been detected by the LIGO-Virgo Collaboration, such as GW150914 (\(36_{-4}^{+5}M_\odot \), \(29_{-4}^{+4}M_\odot \)) [19], GW151226 (\(14.2_{-3.7}^{+8.3}M_\odot \), \(7.5_{-2.3}^{+2.3}M_\odot \)) [30], GW170104 (\(31.2_{-6.0}^{+8.4}M_\odot \), \(19.4_{-5.9}^{+5.3}M_\odot \)) [29], GW170608 (\(12_{-2}^{+7}M_\odot \), \(7_{-2}^{+2}M_\odot \)) [31] and GW170814 (\(30.5_{-3.0}^{+5.7}M_\odot \), \(25.3_{-4.2}^{+2.8}M_\odot \)) [32]. These events detected by LIGO-Virgo suggest that the black holes should have an extended mass function. In this section, we calculate the merger rate distribution for PBH binaries with a general mass function by taking into account the effect of the merger history on the merger rate density of PBH binaries.

First of all, we consider the condition that two neighboring PBHs with the masses \(m_i\) and \(m_j\) decouple from the expansion of the Universe and form a bound system. Their comoving separation, x, approximately satisfies

$$\begin{aligned} x < x_{\mathrm{max}} =\left( \frac{m_b}{2\rho _{\mathrm{dm}}}\right) ^{1/3}, \end{aligned}$$
(22)

where \(m_b=m_i+m_j\) is the total mass of the PBH binary. When two PBHs come closer, the nearest PBH, with the mass \(m_l\), exerts a torque on the bound system. As a result, the two PBHs avoid a head-on collision and form a highly eccentric binary. The major axis a of the binary orbit and the dimensionless angular momentum are given by

$$\begin{aligned}&a \approx A \frac{2\rho _{\mathrm{dm}} x^4}{(1+z_{\mathrm{eq}})m_b}, \end{aligned}$$
(23)
$$\begin{aligned}&j \approx B \frac{2 m_l}{m_b} \left( \frac{x}{y}\right) ^3, \end{aligned}$$
(24)

where y is the comoving distance to the third PBH with the mass \(m_l\). Once two PBHs form a binary, they gradually shrink through the emission of gravitational radiation and eventually merge at the time \(\tau \) after its formation, which can be estimated as [28]

$$\begin{aligned} \tau = \frac{3}{85} \frac{a^4}{m_i m_j m_b} j^7. \end{aligned}$$
(25)

The two neighboring PBHs with the masses \(m_i\) and \(m_j\) merge into a bigger black hole. The mass is given by

$$\begin{aligned} M_2=m_b-E_{\mathrm{GW}} \approx \gamma m_b, \end{aligned}$$
(26)

where \(E_{\mathrm{GW}}\) is the energy of gravitational wave and \(\gamma \) is a factor of \({{\mathcal {O}}}(1)\). In the monochromatic case, \(\gamma =0.95\) is adopted in [33]. For simplicity, in this paper, we take \(\gamma =1\), which means that we assume that the energy of the gravitational wave is zero.

In this paper, the probability distribution function of PBHs, P(m), is normalized to be

$$\begin{aligned} \int \mathrm{d}m P(m) = 1. \end{aligned}$$
(27)

Therefore, the abundance of PBHs in the mass interval \((m, m+\mathrm{d}m)\) can be easily obtained by

$$\begin{aligned} f P(m)\mathrm{d}m, \end{aligned}$$
(28)

where f is a fraction of PBHs in non-relativistic matter including DM and baryons. The fraction of PBHs in DM \(f_{\mathrm{{pbh}}}\) is given by \(f_{\mathrm{{pbh}}}\equiv \Omega _{\mathrm{{pbh}}}/\Omega _{\mathrm{{dm}}} \approx f/0.85\). At the present time, the average number density of PBHs in the mass interval \((m, m+\mathrm{d}m)\) is given by

$$\begin{aligned} n\left( m\right) \mathrm{d}m= \frac{fP(m)\mathrm{d}m \rho _{\mathrm{{m}}}}{m}= \frac{f_{\mathrm{{pbh}}} P(m)\mathrm{d}m \rho _{\mathrm{{dm}}}}{m}, \end{aligned}$$
(29)

where \(\rho _{\mathrm{{m}}}\) is the total energy density of matter and the present total average number density of PBHs, \(n_{T}\), is obtained by

$$\begin{aligned} n_T\equiv f_{\mathrm{{pbh}}}\rho _{\mathrm{{dm}}}\int dm {P(m)\over m}. \end{aligned}$$
(30)

For simplicity, here we define \(m_{\mathrm{pbh}}\) as

$$\begin{aligned} \frac{1}{m_{\mathrm{{pbh}}}}=\int dm {P(m)\over m} . \end{aligned}$$
(31)

We define F(m) as

$$\begin{aligned} F\left( m\right) \equiv \frac{n\left( m\right) }{n_{T}}=P\left( m\right) \frac{m_{\mathrm{{pbh}}}}{m}, \end{aligned}$$
(32)

which is the fraction of the present average number density of PBHs with the mass m in the present total average number density of PBHs.

The result in [22] indicates that in the case of \(f_{\mathrm{pbh}}< f_{c}\), the effects of the linear density perturbations on the merger rate of PBH binaries is significant. Here, we only consider the case of \(f_{\mathrm{pbh}}>f_{c}\), which is shown to be relevant to the LIGO observations [20]. In other words, we ignore the bound (22).

The only essential ingredient that we need is the spatial distribution of PBHs. We firstly consider the spatial distribution of two PBHs. The probability distribution of the comoving separation x between two nearest PBHs with the masses \((m_i, m_i+dm_i)\) and \((m_j, m_j+dm_j)\) and without other PBHs in the comoving volume of \(4\pi x^3/3\) is given by

$$\begin{aligned}&d{\hat{P}} \left( m_i,m_j,x\right) =F\left( m_i\right) dm_i 4\pi x^2 \mathrm{d}x n\left( m_j\right) dm_j \nonumber \\&\qquad \times e^{- {4\pi \over 3}x^3 n(m_j) dm} \prod _{ m\ne m_j }^{ }{ e^{- {4\pi \over 3}x^3 n(m) dm}} \nonumber \\&\quad = F\left( m_i\right) dm_i 4\pi x^2\mathrm{d}x n\left( m_j\right) dm_j e^{- \int dm {4\pi \over 3}x^3 n(m)} \nonumber \\&\quad =F\left( m_i\right) dm_i F\left( m_j\right) dm_j 4\pi x^2 n_{T}\mathrm{d}x e^{- {4\pi \over 3}x^3 n_{T}}. \nonumber \\ \end{aligned}$$
(33)

Clearly, in the non-monochromatic case, to calculate the merger rate in the first-merger process, the differential probability distribution is given by

$$\begin{aligned}&d{P_{1}}\left( m_i,m_j,m_l,x,y\right) \nonumber \\&\quad =F\left( m_i\right) dm_i F\left( m_j\right) dm_j F\left( m_l\right) dm_l \nonumber \\&\qquad \times 4\pi x^2 n_{T}\mathrm{d}x 4\pi y^2 n_{T}\mathrm{d}y e^{- {4\pi \over 3}y^3 n_{T}} \Theta (y-x), \end{aligned}$$
(34)

where x is the comoving separation between two nearest PBHs with the masses \(m_i\) and \(m_j\) and y is the comoving distance to the third PBH with the mass \(m_l\) which provides the angular momentum for the bound system. The fraction of PBHs that have merged before the time t is given by

$$\begin{aligned}&{G_1}(t,m_i,m_j,m_l) \nonumber \\&\quad =\int d\mathrm{d}x\mathrm{d}y \frac{\mathrm{d} P_{1}\left( m_i,m_j,m_l,x,y\right) }{\mathrm{d}x \mathrm{d}y \mathrm{d}m_i \mathrm{d}m_j \mathrm{d}m_l} \Theta (t-\tau (x,y)).\nonumber \\ \end{aligned}$$
(35)

So, we arrive at

$$\begin{aligned}&G_1 (t,m_i,m_j,m_l) =F\left( m_i\right) F\left( m_j\right) F\left( m_l\right) \nonumber \\&\quad \times 1.34\times 10^{-2} \left( { M_{\odot }}\right) ^{-{5 \over 37}} \left( {t\over t_0}\right) ^{{3\over 37}} \left( { m_i m_j}\right) ^{{3 \over 37}} \nonumber \\&\quad \times \left( { m_l}\right) ^{-{21 \over 37}} \left( { m_{\mathrm{pbh}}}\right) ^{-{16 \over 37}} \left( { m_i+m_j}\right) ^{{36 \over 37}} f_{\mathrm{pbh}}^{16 \over 37}.\nonumber \\ \end{aligned}$$
(36)

\({\mathcal {R}}_1(t,m_i,m_j,m_l)\) is given by

$$\begin{aligned}&{\mathcal {R}}_1 (t,m_i,m_j,m_l)=\frac{1}{2} n_{\mathrm{T}} \nonumber \\&\quad \times \lim _{ \mathrm{d}t\rightarrow 0 }{ \frac{G_1\left( t+\mathrm{d}t,m_i,m_j,m_l\right) -G_1\left( t,m_i,m_j,m_l\right) }{\mathrm{d}t}},\nonumber \\ \end{aligned}$$
(37)

where the factor 1 / 2 accounts for the fact that each merger event involves two PBHs. From Eq. (37), one has

$$\begin{aligned}&{\mathcal {R}}_1(t,m_i,m_j,m_l) =F\left( m_i\right) F\left( m_j\right) F\left( m_l\right) \nonumber \\&\quad \times 1.32\times 10^{6} \left( { M_{\odot }}\right) ^{{32 \over 37}} \left( {t\over t_0}\right) ^{-{34\over 37}} \left( { m_i m_j}\right) ^{{3 \over 37}} \nonumber \\&\quad \times \left( { m_l}\right) ^{-{21 \over 37}} \left( { m_{\mathrm{pbh}}}\right) ^{-{53 \over 37}} \left( { m_i+m_j}\right) ^{{36 \over 37}} f_{\mathrm{pbh}}^{53 \over 37}. \end{aligned}$$
(38)

The merger rate density of PBH binaries with the masses \(m_i\) and \(m_j\) in the first-merger process is

$$\begin{aligned} {\mathcal {R}}_1(t,m_i,m_j)=\int dm_l {\mathcal {R}}_1(t,m_i,m_j,m_l) . \end{aligned}$$
(39)

Let us estimate the merger rate density in the second-merger process. In the first-merger process, two neighboring PBHs decouple from the expansion of the Universe and then merge into a new black hole with the mass \(m_i+m_j\). In the second-merger process, the new black hole and the nearest PBH with mass \(m_k\) form a new binary. The merge event of the new binary is detected by LIGO-Virgo at the time t. Statistically, the second coalescence time is larger than the first one, therefore, we can ignore the first coalescence time. The differential probability distribution is given by

$$\begin{aligned}&d{P_{2}}\left( m_i,m_j,m_k,m_l,x,y,z\right) \nonumber \\&\quad =F\left( m_i\right) dm_i F\left( m_j\right) dm_j F\left( m_k\right) dm_k F\left( m_l\right) dm_l \nonumber \\&\qquad 4\pi x^2 n_{T}\mathrm{d}x 4\pi y^2 n_{T}\mathrm{d}y 4\pi z^2 n_{T}\mathrm{d}z e^{- {4\pi \over 3}z^3 n_{T}} \Theta (y-x) \Theta (z-y).\nonumber \\ \end{aligned}$$
(40)

So, the fraction of PBHs that have merged in the second-merger process is given by

$$\begin{aligned}&{G_2}(t,m_i,m_j,m_k,m_l) \nonumber \\&\quad =\int \mathrm{d}x\mathrm{d}y\mathrm{d}z \frac{\mathrm{d} P_{2}\left( m_i,m_j,m_k,m_l,x,y\right) }{\mathrm{d}x \mathrm{d}y \mathrm{d}z \mathrm{d}m_i \mathrm{d}m_j \mathrm{d}m_k \mathrm{d}m_l} \Theta (t-\tau (y,z)).\nonumber \\ \end{aligned}$$
(41)

Then we arrive at

$$\begin{aligned}&G_2(t,m_i,m_j,m_k,m_l) =F\left( m_i\right) F\left( m_j\right) F\left( m_k\right) F\left( m_l\right) \nonumber \\&\quad \times 1.21\times 10^{-4} \left( { M_{\odot }}\right) ^{-{10 \over 37}} \left( {t\over t_0}\right) ^{{6\over 37}} \left( { m_i+ m_j}\right) ^{{6 \over 37}} \left( { m_k}\right) ^{{6 \over 37}} \nonumber \\&\quad \times \left( { m_l}\right) ^{-{42 \over 37}} \left( { m_{\mathrm{pbh}}}\right) ^{-{32 \over 37}} \left( { m_i+m_j+m_k}\right) ^{{72 \over 37}} f_{\mathrm{pbh}}^{32 \over 37}.\nonumber \\ \end{aligned}$$
(42)

\({\mathcal {R}}_2(t,m_i,m_j,m_l)\) is given by

$$\begin{aligned}&{\mathcal {R}}_2(t,m_i,m_k,m_j,m_l)=\frac{1}{3} n_{\mathrm{T}} \nonumber \\&\quad \times \lim _{ \mathrm{d}t\rightarrow 0 }{ \frac{G_2\left( t+\mathrm{d}t,m_i,m_j,m_k,m_l\right) -G_2\left( t,m_i,m_j,m_k,m_l\right) }{\mathrm{d}t}},\nonumber \\ \end{aligned}$$
(43)

where the factor 1 / 3 accounts for the fact that each merger event in second-merger process involves three PBHs. From Eq. (43), the final result is given by

$$\begin{aligned}&{\mathcal {R}}_2(t,m_i,m_j,m_k,m_l) =F\left( m_i\right) F\left( m_j\right) F\left( m_k\right) F\left( m_l\right) \nonumber \\&\quad \times 1.59\times 10^{4} \left( { M_{\odot }}\right) ^{{27 \over 37}} \left( {t\over t_0}\right) ^{-{31\over 37}} \left( { m_i+ m_j}\right) ^{{6 \over 37}} \left( { m_k}\right) ^{{6 \over 37}} \nonumber \\&\quad \times \left( { m_l}\right) ^{-{42 \over 37}} \left( { m_{\mathrm{pbh}}}\right) ^{-{69 \over 37}} \left( { m_i+m_j+m_k}\right) ^{{72 \over 37}} f_{\mathrm{pbh}}^{69 \over 37}. \end{aligned}$$
(44)

The merger rate density of PBH binaries with the masses \(m_i\) and \(m_j\) in the second-merger process is given by

$$\begin{aligned}&{\mathcal {R}}_2(t,m_i,m_j){=}\frac{1}{2}\int dm_ldm_e {\mathcal {R}}_2(t,m_i{-}m_e,m_e,m_j,m_l) \nonumber \\&\quad + \frac{1}{2}\int dm_ldm_e {\mathcal {R}}_2(t,m_j-m_e,m_e,m_i,m_l) . \end{aligned}$$
(45)

Similarly, \(G_3(t,m_i,m_j,m_k,m_f,m_l)\) and \({\mathcal {R}}_3(t,m_i,m_j,m_k,m_f,m_l)\) are given by

$$\begin{aligned}&G_3 (t,m_i,m_j,m_k,m_f,m_l) \nonumber \\&\quad =F\left( m_i\right) F\left( m_j\right) F\left( m_k\right) F\left( m_f\right) F\left( m_l\right) \times 8.88\nonumber \\&\qquad \times 10^{-7} \left( { M_{\odot }}\right) ^{-{15 \over 37}} \left( {t\over t_0}\right) ^{{9\over 37}} \left( { m_i+ m_j+m_k}\right) ^{{9 \over 37}} \left( { m_f}\right) ^{{9 \over 37}} \nonumber \\&\qquad \times \left( { m_l}\right) ^{-{63 \over 37}} \left( { m_{\mathrm{pbh}}}\right) ^{-{48 \over 37}} \left( { m_i+m_j+m_k+m_f}\right) ^{{108 \over 37}} f_{\mathrm{pbh}}^{48 \over 37}, \end{aligned}$$
(46)
$$\begin{aligned}&{\mathcal {R}}_3(t,m_i,m_j,m_k,m_f,m_l) \nonumber \\&\quad =F\left( m_i\right) F\left( m_j\right) F\left( m_k\right) F\left( m_f\right) F\left( m_l\right) \times 1.31\nonumber \\&\qquad \times 10^{2} \left( { M_{\odot }}\right) ^{{22 \over 37}} \left( {t\over t_0}\right) ^{-{28\over 37}} \left( { m_i+ m_j+m_k}\right) ^{{9 \over 37}} \left( { m_f}\right) ^{{9 \over 37}} \nonumber \\&\qquad \times \left( { m_l}\right) ^{-{63 \over 37}} \left( { m_{\mathrm{pbh}}}\right) ^{-{85 \over 37}} \left( { m_i+m_j+m_k+m_f}\right) ^{{108 \over 37}} f_{\mathrm{pbh}}^{85 \over 37}.\nonumber \\ \end{aligned}$$
(47)

The merger rate density of PBH binaries with the masses \(m_i\) and \(m_j\) in the third-merger process is given by

$$\begin{aligned}&{\mathcal {R}}_3 (t,m_i,m_j) \nonumber \\&\quad = \frac{1}{2} \int dm_ldm_edm_f {\mathcal {R}}_3 (t,m_i{-}m_e{-}m_f,m_e,m_f,m_j,m_l) \nonumber \\&\qquad + \frac{1}{2} \int dm_ldm_edm_f {\mathcal {R}}_3 (t,m_j{-}m_e{-}m_f,m_e,m_f,m_i,m_l) .\nonumber \\ \end{aligned}$$
(48)

The total merger rate density of PBH binaries with the masses \(m_i\) and \(m_j\) detected by LIGO-Virgo is given by

$$\begin{aligned} {\mathcal {R}}(t,m_i,m_j) = \sum _{n=1} {\mathcal {R}}_n(t,m_i,m_j) \,. \end{aligned}$$
(49)

In the single-merger case, we have \(\alpha = -(m_i+m_j)^2\partial ^2 \ln {\mathcal {R}}(t,m_i,m_j)/\partial m_i \partial m_j=36/37\), which is independent of the PBH mass function. It is consistent with the result obtained in [23]. However, by taking account into the merger history of PBHs, \(\alpha \) depends on the PBH mass function, which could help us reconstruct the mass function of PBHs.

Fig. 4
figure 4

Event rate of second-merger of PBH binaries with the mass \(M = 10\) (green), 30 (blue) and 100 (red) in \(M_{\odot }\) at the present time as a function of the PBH abundance. The merger rate \(R=12 \)–\( 213\hbox { Gpc}^{-3}\hbox { year}^{-1}\), inferred by the LIGO and Virgo Collaboration, is shown as the shaded region colored orange [29]

Full size image

4 Applications

The total fraction of PBH binaries that have merged before the time t in single-merger events is given by

$$\begin{aligned} G_1 (t) \equiv \int \int G_1(t,m_i,m_j,m_l) dm_idm_j dm_l. \end{aligned}$$
(50)

The merger rate of PBH binaries in single-merger events at the time t is given by

$$\begin{aligned} R_1 (t) \equiv \frac{1}{2} n_{\mathrm{T}} \frac{\mathrm{d}G_1(t)}{\mathrm{d}t} \equiv \int \int {\mathcal {R}}_1(t,m_i,m_j) dm_idm_j. \nonumber \\ \end{aligned}$$
(51)

\(G_N(t)\) is the total fraction of PBH binaries that have merged before the time t in the Nth merger process and \(R_N(t)\) is the merger rate of PBH binaries at time t in the Nth merger process.

Let us consider three typical PBH mass functions: monochromatic, power-law and log-normal functions.

4.1 Monochromatic mass function

In this subsection, we consider the following monochromatic mass function [20, 34, 35]:

$$\begin{aligned} P(m)=\delta (m-M). \end{aligned}$$
(52)

In this case, we can rewrite (31) and (32) as

$$\begin{aligned}&m_{\mathrm{{pbh}}}=M, \end{aligned}$$
(53)
$$\begin{aligned}&F(m)=P(m)=\delta (m-M). \end{aligned}$$
(54)

From Eqs. (36), (38), (2139), (50), (51), (53) and (54), the total fraction of PBH binaries that have merged before the time t and the merger rate of PBH binaries at the time t in the first-merger process are given by

$$\begin{aligned} G_1 \left( t\right)\approx & {} 2.64 \times 10^{-2} \left( {M \over M_{\odot }}\right) ^{{5 \over 37}} \left( {t\over t_0}\right) ^{{3\over 37}} f_{\mathrm{pbh}}^{16 \over 37} \end{aligned}$$
(55)
$$\begin{aligned} R_1\left( t\right)\approx & {} 2.59 \times 10^{6} \left( {M \over M_{\odot }}\right) ^{-{32 \over 37}} \left( {t\over t_0}\right) ^{-{34\over 37}} f_{\mathrm{pbh}}^{53 \over 37}, \end{aligned}$$
(56)

which is consistent with (20). Similarly, the total fraction of PBH binaries that have merged before the time t and the merger rate of PBH binaries at the time t in the second-merger process are given by

$$\begin{aligned} G_2 \left( t\right)\approx & {} 1.15 \times 10^{-3} \left( {M \over M_{\odot }}\right) ^{{10 \over 37}} \left( {t\over t_0}\right) ^{{6\over 37}} f_{\mathrm{pbh}}^{32 \over 37} \end{aligned}$$
(57)
$$\begin{aligned} R_2\left( t\right)\approx & {} 1.51 \times 10^{5} \left( {M \over M_{\odot }}\right) ^{-{27 \over 37}} \left( {t\over t_0}\right) ^{-{31\over 37}} f_{\mathrm{pbh}}^{69 \over 37}. \end{aligned}$$
(58)

In Fig. 4, we show the merger rate of PBH binaries in the second-merger process as a function of \(f_{\mathrm{pbh}}\), which scales as \(f_{\mathrm{pbh}}^{69/37}\). The total fraction of PBH binaries that have merged before the time t and the merger rate of PBH binaries at the time t in the third-merger process are given by

$$\begin{aligned} G_3 \left( t\right)\approx & {} 6.64 \times 10^{-5} \left( {M \over M_{\odot }}\right) ^{{15 \over 37}} \left( {t\over t_0}\right) ^{{9\over 37}} f_{\mathrm{pbh}}^{48 \over 37} \end{aligned}$$
(59)
$$\begin{aligned} R_3 \left( t\right)\approx & {} 9.78 \times 10^{3} \left( {M \over M_{\odot }}\right) ^{-{22 \over 37}} \left( {t\over t_0}\right) ^{-{28\over 37}} f_{\mathrm{pbh}}^{85 \over 37}. \end{aligned}$$
(60)

In Fig. 5, we show the merger rate of PBH binaries in the third-merger process as a function of \(f_{\mathrm{pbh}}\), which scales as \(f_{\mathrm{pbh}}^{69/37}\). In the case of \(M=30M_{\odot }\) and \(f_{\mathrm{pbh}}=0.01\), we can find \(R_1(t_0)=187\hbox { Gpc}^{-3}\hbox { year}^{-1}\), \(R_2(t_0)=2.35\hbox { Gpc}^{-3}\hbox { year}^{-1}\) and \(R_3(t_0)=3.29\times 10^{-2}\hbox { Gpc}^{-3}\hbox { year}^{-1}\), as shown in Fig. 6. It indicates that, in the monochromatic case, although the merger events of both \(30~M_\odot -30~M_\odot \) PBH binaries and \(60~M_\odot -30~M_\odot \) PBH binaries could occur at the same time, the major of merger events detected by LIGO-Vigo is the merger event of \(30~M_\odot -30~M_\odot \) PBH binaries. Therefore, in the monochromatic case, the effect of the merger history on the merger rate of PBH binaries is negligible.

Fig. 5
figure 5

Event rate of third merger of PBH binaries with the mass \(M = 10\) (green), 30 (blue) and 100 (red) in \(M_{\odot }\) at the present time as a function of the PBH abundance. The merger rate \(R=12 \)–\( 213\hbox { Gpc}^{-3}\hbox { year}^{-1}\), inferred by the LIGO and Virgo Collaboration, is shown as the shaded region colored orange [29]

Full size image
Fig. 6
figure 6

Event rate of first merger (green), second merger (blue) and third merger (red) of PBH binaries with the mass \(30M_{\odot }\) at the present time as a function of the PBH abundance. The merger rate \(R=12 \)–\( 213\hbox { Gpc}^{-3}\hbox { year}^{-1}\), inferred by the LIGO and Virgo Collaboration, is shown as the shaded region colored orange [29]

Full size image

4.2 Power-law mass function

In this subsection, we take the PBH mass function in a power-law form [3]:

$$\begin{aligned} P(m)\approx {q-1\over M} \left( {m\over M}\right) ^{-q}, \end{aligned}$$
(61)

with \(500M\ge m\ge M\) and \(q>1.5\). In the power-law case, we can rewrite (31) and (32) as

$$\begin{aligned}&m_{\mathrm{{pbh}}}=M\frac{q}{q-1}\,, \end{aligned}$$
(62)
$$\begin{aligned}&F(m)={q \over m} \left( {m\over M}\right) ^{-q}. \end{aligned}$$
(63)
Fig. 7
figure 7

Contour of the ratio of the total merger rate density to the single-merger one in the PBH mass plane in the case of \(f_{\mathrm{pbh}}=0.01\), \(q=2.3\) and \(M=0.2M_{\odot }\)

Full size image

Choosing \(f_{\mathrm{pbh}}=0.01\), \(q=2.3\), \(M=0.2M_{\odot }\), we can get \(R_1(t_0)=9.66 \times 10^{3}\hbox { Gpc}^{-3}\hbox { year}^{-1}\), \(R_2(t_0)=1.15 \times 10^{2}\hbox { Gpc}^{-3}\hbox { year}^{-1}\), \(R_3(t_0)=5.00\hbox { Gpc}^{-3}\hbox { year}^{-1}\). In the power-law case, the effect of the merger history on the merger rate of PBH binaries is small. However, the effect of the merger history on the merger rate density is significant in some region of the parameter space. For example, \({\mathcal {R}}_1(t_0,30M_{\odot },30M_{\odot })=8.55 \times 10^{-7}\hbox {Gpc}^{-3}\hbox { year}^{-1}M_{\odot }^{-2}\), \({\mathcal {R}}_2(t_0,30M_{\odot },30M_{\odot })=8.90 \times 10^{-7}\hbox {Gpc}^{-3}\hbox { year}^{-1}M_{\odot }^{-2}\), \({\mathcal {R}}_3(t_0,30M_{\odot },30M_{\odot })=4.88 \times 10^{-8}\hbox {Gpc}^{-3}\hbox { year}^{-1}M_{\odot }^{-2}\). In Fig. 7, we show the ratio of the total merger rate density to the single-merger one in the PBH mass plane. There are several gravitational wave events detected by LIGO-Virgo. The masses of the black hole all are in \((5 M_{\odot }, 50 M_{\odot })\). In such a region, in the future, more and more coalescence events of black hole binaries will be detected by LIGO-Virgo [36, 37]. When we use the merger rate distribution to fit the mass function of PBH, the effect of the merger history on the merger rate density of PBH binaries cannot be ignored.

4.3 Log-normal mass function

In this subsection, we take the PBH mass function in a log-normal form [38,39,40]:

$$\begin{aligned} P(m) = \frac{1}{\sqrt{2 \pi } \sigma m} \exp \left( -\frac{\log ^2(m/m_c)}{2 \sigma ^2}\right) . \end{aligned}$$
(64)

In the power-law case, we can rewrite (31) and (32) as

$$\begin{aligned}&m_{\mathrm{{pbh}}}=m_c \exp \left( -\frac{\sigma ^2}{2}\right) . \end{aligned}$$
(65)
$$\begin{aligned}&F(m)=\frac{m_c}{\sqrt{2 \pi } \sigma m^2} \exp \left( -\frac{\sigma ^2}{2}-\frac{\log ^2(m/m_c)}{2 \sigma ^2}\right) . \end{aligned}$$
(66)
Fig. 8
figure 8

Contour of the ratio of the total merger rate density to the single-merger one in the PBH mass plane in the case of \(f_{\mathrm{pbh}}=0.01\), \(m_c=15 M_{\odot }\) and \(\sigma =0.5\)

Full size image
Fig. 9
figure 9

Contour of \(({\mathcal {R}}(t_0,30M_{\odot },30M_{\odot })/{\mathcal {R}}_1(t_0,30M_{\odot },30M_{\odot })-1)\) in the parameter space of PBH mass function

Full size image

Choosing \(f_{\mathrm{pbh}}=0.01\), \(m_c=15 M_{\odot }\), \(\sigma =0.5\), we can get \(R_1(t_0)=423 \hbox { Gpc}^{-3}\hbox { year}^{-1}\), \(R_2(t_0)=6.5 \hbox { Gpc}^{-3}\hbox { year}^{-1}\), \(R_3(t_0)=0.1\hbox { Gpc}^{-3}\hbox { year}^{-1}\). In the log-normal case, the effect of the merger history on the merger rate of PBH binaries is also small. According to \({\mathcal {R}}_1(t_0,30M_{\odot },30M_{\odot })=2.16 \times 10^{-2}\hbox {Gpc}^{-3}\hbox { year}^{-1}M_{\odot }^{-2}\), \({\mathcal {R}}_2(t_0,30M_{\odot },30M_{\odot })=2.14 \times 10^{-3}\hbox {Gpc}^{-3}\hbox { year}^{-1}M_{\odot }^{-2}\), \({\mathcal {R}}_3(t_0,30M_{\odot },30M_{\odot })=2.31 \times 10^{-5}\hbox {Gpc}^{-3}\hbox { year}^{-1}M_{\odot }^{-2}\), the effect of the merger history on the merger rate density of PBH binaries could not be negligible in some region of the parameter space. In Fig. 8, we show the ratio of the total merger rate density to the single-merger one in the PBH mass plane in the case of \(f_{\mathrm{pbh}}=0.01\), \(m_c=15 M_{\odot }\) and \(\sigma =0.5\). In Fig. 9, we also plot the contour of \(({\mathcal {R}}(t_0,30M_{\odot },30M_{\odot })/{\mathcal {R}}_1(t_0,30M_{\odot },30M_{\odot })-1)\) in the parameter space of PBH mass function to show that the effect of the merger history on the merger rate density depend on the mass function.

5 Conclusions

We have developed the formalism to calculate the merger rate density of PBH binaries with a general mass function, by taking into account the merger history of PBHs. In the monochromatic case, we find that \(R_1 \gg R_2 \gg R_3\), which is independent on \(f_{\mathrm{pbh}}\). Therefore, the effect of the merger history on the merger rate of PBH binaries is negligible. However, the multiple-merger events may play an important role in the merger rate density of PBH binaries in the non-monochromatic case. For example, for the power-law and the log-normal mass function, the effect of the merger history on the merger rate density of PBH binaries could not be negligible. In the future, more and more coalescence events of black hole binaries will be detected by LIGO-Virgo. This will provide richer information on the merger rate distribution of black hole binaries to test the PBH scenario.

We calculate the merger rate density of PBH binaries up to three mergers. In principle, one can directly calculate it at more than three mergers by using the formalism developed in the present paper. Since the contribution of the merger history on the merger rate density of PBH binaries depends on the mass function and the mass region, it is hard to judge whether mergers of higher order should be computed for a generic mass function.

The effects of the tidal field from the smooth halo, the encountering with other PBHs, the baryon accretion and present-day halos are carefully investigated in [22]. It is found in [22] that these effects make no significant contributions to the overall merger rate. We therefore neglected these subdominant effects throughout our computation.