Velocity effects on second order contributions to gravitational frequency shift by a moving Kerr–Newman black hole

Abstract

The significance of the radial velocity effects on the leading-order gravitational frequency shift in some special cases was reported recently. This paper investigates the gravitational shift of frequency of light propagating in the equatorial plane of a radially moving Kerr–Newman black hole up to the second post-Minkowskian order, and discusses the radial velocity effects on the second-order contributions to the frequency shift. It is found that a new radial velocity effect appears in the second-order Schwarzschild contribution to the frequency shift, in contrast to no radial velocity effect in the first-order contribution, when both the emission and reception events are far away from the lens. Velocity effects on the gravitational frequency shifts induced respectively by the lens’s electrical charge and spin are also analyzed.

1 Introduction

The translational motion of a gravitational system makes a difference on the propagation of electromagnetic signals, which is the so-called velocity effect [1, 2]. The issue of velocity effects on the gravitational frequency shift of light was discussed in many papers [2,3,4,5,6,7,8,9,10,11]. Birkinshaw and Gull [3] studied the transversal velocity effect of cluster of galaxies and showed that the gravitational frequency shift of light is proportional to the low transverse lens velocity and the deflection angle of light. Since this pioneering work, the conclusion that the transversal velocity effect on the gravitational frequency shift is dominant relative to that of the radial lens motion has been well established in the full relativistic framework [2, 6, 7].

Recently, the radial-velocity effects on the leading-order gravitational frequency shift induced by a constantly moving Schwarzschild black hole were re-examined, and these effects are found to be necessary for the scenarios when the light emitter or the receiver is near to the gravitational lens [12]. As shown in Ref. [12], these velocity effects under these circumstances were, for example, of the order of magnitude of $10^{-9}$, which is larger than the observational precision of current detectors. For example, the precision of the Cassini for measuring gravitational frequency shift is about $\sim 10^{-14}$ [13,14,15]. The Cassini is a sophisticated spacecraft orbiting the ringed planet and its main mission is to explore the Saturnian system, including measuring the plasma density, magnetic field, temperatures and atmospheric composition in Saturn’s atmosphere, as well as studying its largest moon Titan. It bases on the Doppler shift of light signals to and from the spacecraft to determine its speed and the signal timing to measure its distance. When the spacecraft passes behind a massive central body (e.g. the Sun) on its cruise to Saturn, whether the body moves or not, these techniques can be also used to detect frequency shifts caused by gravity with a high accuracy. Highly precise measurements of these velocity effects are thus indeed possible by missions such as the Cassini. Considering the rapid progresses made in the gravitational-frequency-shift measurements (such as the ground-based [16,17,18,19,20,21] and satellite-based [22,23,24] measurements), we expect that the velocity effects on the second-order contributions to the gravitational frequency shift might also be detectable in future. Thus, a full theoretical treatment of the gravitational shift of frequency of light due to a radially moving lens in the second post-Minkowskian (PM) approximation is necessary.

In this work, we extend the method of Ref. [12] to deriving the gravitational frequency shift of light propagating in the equatorial plane of a radially moving Kerr–Newman (KN) black hole, and concentrate on the radial-velocity effects on the second-order Schwarzschild, Kerr, and charge-induced contributions to the frequency shift. We find that for both the emission and reception events far away from the lens, the radial velocity effect makes a significant correction to the second-order Schwarzschild frequency shift, although this effect on the first-order one can be usually neglected.

The structure of this article is as follows. In Sect. 2, we adopt the weak-field metric of the moving KN source to calculate the equatorial frequency shift up to the 2PM order. Section 3 gives the discussions of the velocity effects on the second-order contributions to the frequency shift. Section 4 presents a summary. Our discussions are restricted in the weak-field, small-angle, and thin lens approximation.

Throughout the paper, Latin indices run from 1 to 3, and natural units in which $G = c = 1$ are used.

2 Gravitational frequency shift due to a radially moving KN source

2.1 The weak-field metric for a radially moving Kerr–Newman black hole

Let $\{{\varvec{e}}_1,~{\varvec{e}}_2,~{\varvec{e}}_3\}$ denote the orthonormal basis of a 3D Cartesian coordinate system. The rest frames of the observer and the lens are denoted by (t,  x,  y,  z) and $(X_0,~X_1,~X_2,~X_3)$, respectively. The angular momentum vector ${\varvec{J}}$ of the lens is assumed to be $J{\varvec{e}}_3$. The harmonic metric of a moving KN black hole with a constant radial velocity ${\varvec{v}}=v{\varvec{e_1}}$ up to the 2PM order reads [25]:

$$\begin{aligned} g_{00}= & {} -1+\frac{2\,(1+v^2)\gamma ^2M}{R}-\frac{M^2+\gamma ^2(M^2+Q^2)}{R^2} \nonumber \\&-\frac{4\,v\,\gamma ^2\,a\,M\,X_2}{R^3}+\frac{v^2\,\gamma ^2(M^2-Q^2)\,X_1^2}{R^4} +O(M^3), \end{aligned}$$

(1)

$$\begin{aligned} g_{0i}= & {} \,\gamma \,\zeta _i\,-v\,\gamma ^2\left( \frac{4\,M}{R}-\frac{M^2\,+\,Q^2}{R^2}\right) \delta _{i1} \nonumber \\&-\frac{v\,\gamma \,(M^2-Q^2)\,X_1\left[ \,X_i+(\gamma -1)\,X_1\delta _{i1}\,\right] }{R^4} \nonumber \\&+\frac{2\,(\gamma ^2-\gamma +v^2\gamma ^2)\,a\,M X_2\,\delta _{i1}}{R^3}+O(M^3), \end{aligned}$$

(2)

$$\begin{aligned} g_{ij}= & {} \left( 1+\frac{M}{R}\right) ^2\delta _{ij}+v^2\gamma ^2 \left( \frac{4M}{R}-\frac{M^2+Q^2}{R^2}\right) \delta _{i1}\delta _{j1} \nonumber \\&+\frac{(M^2-Q^2)\left[ X_i + (\gamma -1)X_1\delta _{i1}\right] \left[ X_j + (\gamma -1)X_1\delta _{j1}\right] }{R^4} \nonumber \\&-v\gamma \left[ \zeta _i\,\delta _{j1} + \zeta _j\,\delta _{i1} + \frac{4(\gamma - 1)aM X_2\delta _{i1}\delta _{j1}}{R^3} \right] + O(M^3),\nonumber \\ \end{aligned}$$

(3)

where $\delta _{ij}$ denotes Kronecker delta, $\gamma =(1-v^2)^{-\scriptstyle \frac{1}{2}}$ is the Lorentz factor, and $\frac{X_1^2+X_2^2}{R^2+a^2} + \frac{X_3^2}{R^2} = 1$. M, Q, and $a\equiv J/M$ are the rest mass, the electrical charge, and the angular momentum per mass of the lens, respectively. $\zeta _i=\frac{2aMX_j\epsilon _{ij3}}{R^3}$, with $\epsilon _{ijk}$ being the Levi-Civita symbol. The relation $M^2\ge a^2+Q^2$ is assumed to avoid the naked singularity of the black hole. The coordinates $X_0,~X_1,~X_2$, and $X_3$ are related to t,  x,  y, and z by the Lorentz transformation

$$\begin{aligned}&X_0\equiv T=\gamma (t-vx), \end{aligned}$$

(4)

$$\begin{aligned}&X_1\equiv X=\gamma (x-vt), \end{aligned}$$

(5)

$$\begin{aligned}&X_2\equiv Y=y, \end{aligned}$$

(6)

$$\begin{aligned}&X_3\equiv Z=z. \end{aligned}$$

(7)

2.2 Moving-KN frequency shift up to the 2PM order

Fig. 1

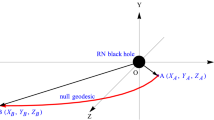
Schematic diagram for the equatorial propagation of light in the gravitational field of the moving KN black hole. We assume that light takes the prograde motion relative to the lens’s spin. The gravitational deflection is greatly exaggerated to distinguish the light path (red line) from the unperturbed path (dashed horizontal line)

For simplicity, we consider the gravitational frequency shift of light which is restricted in the equatorial plane $(z=\frac{\partial }{\partial z}=0)$ of the moving Kerr–Newman black hole, as shown in Fig. 1. b is the impact parameter. The spatial coordinates of the light emitter A and the receiver B are denoted in the observer’s rest frame by $(x_A,~y_A,~0)$ and $(x_B,~y_B,~0)$, respectively, with $y_A<0$, $x_A<0$, and $x_B>0$. The initial velocity of a photon, parallel to the lens’s velocity ${\varvec{v}}$, is assumed to be ${\varvec{w}}|_{x\rightarrow -\infty }~(={\varvec{e}}_1)$. The locations of A and B are denoted in the lens’s rest frame by $(X_A,~Y_A,~0)$ and $(X_B,~Y_B,~0)$, respectively.

The frequency shift of a photon between emission and observation is defined by  [6, 7, 27,28,29]

$$\begin{aligned} \frac{\varDelta \nu }{\nu }\equiv \frac{\nu _B}{\nu _A}-1=\frac{d\tau _A}{dt_A}\frac{dt_A}{dt_B}\frac{dt_B}{d\tau _B}-1. \end{aligned}$$

(8)

Here, $\tau _A$ and $\tau _B$ are the proper times of the light emitter and the receiver, respectively, and $t_A$ and $t_B$ denote respectively their coordinate times. For the case of the light emitter and the receiver being static $({\varvec{v}}_A={\varvec{v}}_B=0)$ in the observer’s rest frame, the explicit forms of $\frac{d\tau _A}{dt_A}$ and $\frac{dt_B}{d\tau _B}$ up to the 2PM order are given as follows:

$$\begin{aligned} \frac{d\tau _A}{dt_A}= & {} \left[ 1-\frac{2(1+v^2)\gamma ^2M}{R_A}+\frac{(1+\gamma ^2)M^2+\gamma ^2Q^2}{R_A^2} \right. \nonumber \\&\left. +\frac{4\,v\,\gamma ^2\,a\,M\,Y_A}{R_A^3}-\frac{v^2\gamma ^2(M^2-Q^2)\,X_A^2}{R_A^4}\right] ^{\frac{1}{2}}, ~~~~~~ \end{aligned}$$

(9)

$$\begin{aligned} \frac{dt_B}{d\tau _B}= & {} \left[ 1-\frac{2(1+v^2)\gamma ^2M}{R_B}+\frac{(1+\gamma ^2)M^2+\gamma ^2Q^2}{R_B^2} \right. \nonumber \\&\left. +\frac{4\,v\,\gamma ^2\,a\,M\,Y_B}{R_B^3} - \frac{v^2\gamma ^2(M^2-Q^2)X_B^2}{R_B^4}\right] ^{-\frac{1}{2}}. ~~~~~~~ \end{aligned}$$

(10)

The analytical form of $\frac{dt_A}{dt_B}$ up to the 2PM order can be obtained from the following gravitational time delay induced by the moving KN black hole [26]

$$\begin{aligned} t_B-t_A=x_B-x_A+\varDelta (t_B,~t_A), ~~ \end{aligned}$$

(11)

with

$$\begin{aligned}&\varDelta (t_B,~t_A)=(1-v)\,\gamma \left[ \,2\,M\,ln\left( \frac{\sqrt{X_B^2+b^2}+X_B}{\sqrt{X_A^2+b^2}+X_A}\right) \right. \nonumber \\&\quad \left. +\,\frac{4M^2 \left( X_B-X_A+\sqrt{X_B^2+b^2}-\sqrt{X_A^2+b^2}\right) }{b^2} \right. \nonumber \\&\quad \left. +\,\frac{15\,M^2-3\,Q^2}{4b}\left( \arctan {\frac{X_B}{b}}-\arctan {\frac{X_A}{b}}\right) \right. \nonumber \\&\quad \left. +\,4\,M^2\left( \frac{1}{\sqrt{X_A^2+b^2}}-\frac{1}{\sqrt{X_B^2+b^2}}\right) \right. \nonumber \\&\quad \left. +\,\frac{M^2-Q^2}{4}\,\left( \frac{X_A}{X_A^2+b^2}\,-\,\frac{X_B}{X_B^2+b^2}\right) \right. \nonumber \\&\quad \left. +\,\frac{2\,aM}{b} \left( \frac{X_A}{\sqrt{X_A^2 + b^2}}-\frac{X_B}{\sqrt{X_B^2 + b^2}} \right) \right] +O(M^3),\nonumber \\ \end{aligned}$$

(12)

where $X_A=\gamma (x_A-vt_A)$ and $X_B=\gamma (x_B-vt_B)$. For the case of ${\varvec{v}}_A={\varvec{v}}_B=0$, Eq. (11) yields [7]

$$\begin{aligned} \frac{dt_A}{dt_B}=\frac{1-\frac{\partial \varDelta (t_B,~t_A)}{\partial t_B}}{1+\frac{\partial \varDelta (t_B,~t_A)}{\partial t_A}}, \end{aligned}$$

(13)

where $\frac{\partial \varDelta (t_B,~t_A)}{\partial t_A}$ and $\frac{\partial \varDelta (t_B,~t_A)}{\partial t_B}$ can be calculated from Eq. (12) as follows:

$$\begin{aligned}&\frac{\partial \varDelta (t_B,~t_A)}{\partial t_A}=\frac{v}{1+v} \left[ \frac{2M}{\sqrt{X_A^2+b^2}} + \frac{4M^2}{b^2} \left( 1 + \frac{X_A}{\sqrt{X_A^2+b^2}} \right) \right. \nonumber \\&\quad \left. +\frac{3(5M^2 - Q^2)}{4\left( X_A^2+b^2\right) } + \frac{4M^2X_A - 2aMb}{\left( X_A^2+b^2\right) ^{\frac{3}{2}}} + \frac{(M^2 - Q^2) \left( X_A^2-b^2\right) }{4\left( X_A^2+b^2\right) ^2} \right] \nonumber \\&\quad +O(M^3), \end{aligned}$$

(14)

$$\begin{aligned}&\frac{\partial \varDelta (t_B,~t_A)}{\partial t_B}=-\frac{v}{1 + v} \left[ \frac{2M}{\sqrt{X_B^2 + b^2}} + \frac{4M^2}{b^2} \left( 1 + \frac{X_B}{\sqrt{X_B^2 + b^2}} \right) \right. \nonumber \\&\quad \left. +\frac{3(5M^2 - Q^2)}{4\left( X_B^2+b^2\right) } + \frac{4M^2X_B - 2aMb}{\left( X_B^2+b^2\right) ^{\frac{3}{2}}} + \frac{(M^2 - Q^2)\left( X_B^2 - b^2\right) }{4\left( X_B^2+b^2\right) ^2} \right] \nonumber \\&\quad +\,O(M^3). \end{aligned}$$

(15)

Moreover, the 1PM form of $X_2$ is given by [26]

$$\begin{aligned} X_2=y=-b \left[ 1 - \frac{2M\left( \sqrt{X_1^2+b^2}+X_1\right) }{b^2}\right] +O(M^2),\nonumber \\ \end{aligned}$$

(16)

which yields

$$\begin{aligned}&R_A=\sqrt{X_A^2 + b^2} \left[ 1 - \frac{2M \left( \sqrt{X_A^2 + b^2}+X_A \right) }{X_A^2+b^2}\right] + O(M^2) , \end{aligned}$$

(17)

$$\begin{aligned}&R_B=\sqrt{X_B^2 + b^2} \left[ 1 - \frac{2M \left( \sqrt{X_B^2 + b^2}+X_B \right) }{X_B^2+b^2}\right] + O(M^2) . \nonumber \\ \end{aligned}$$

(18)

The substitution of Eqs. (9), (10) and (13)–(18) into Eq. (8) yields the explicit form of the gravitational frequency shift up to the 2PM order caused by the moving KN source:

$$\begin{aligned}&\frac{\varDelta \nu }{\nu }=\left( 1 + 2v - v^2\right) \gamma ^2 \left[ \frac{M}{\sqrt{ X_B^2 + b^2}} - \frac{M}{\sqrt{ X_A^2 + b^2}} \right. \nonumber \\&\quad \left. + \frac{2M^2 X_B}{\left( X_B^2 + b^2\right) ^{\frac{3}{2}}} -\frac{2M^2 X_A}{\left( X_A^2 + b^2\right) ^{\frac{3}{2}}} \right] \nonumber \\&\quad + \frac{v\,(M^2 - Q^2)b^2}{4(1+v)} \left[ \frac{1}{\left( X_A^2 + b^2\right) ^2} - \frac{1}{\left( X_B^2 + b^2\right) ^2} \right] \nonumber \\&\quad -\frac{(1 + 2v - v^2)^2\gamma ^4M^2}{\sqrt{X_{ A}^2 + b^2}\sqrt{X_{ B}^2 + b^2}} + \frac{4\,v\,M^2}{(1 + v)\,b^2} \left( \frac{X_B}{\sqrt{ X_B^2 + b^2}} - \frac{X_A}{\sqrt{ X_A^2 + b^2}} \right) \nonumber \\&\quad +\,\frac{(2+3v-5v^2-3v^3+3v^4)\,\gamma ^4\,Q^2}{4} \left( \frac{1}{X_A^2+b^2}-\frac{1}{X_B^2+b^2}\right) \nonumber \\&\quad +\,\frac{v\,(\,M^2\,-\,Q^2\,)}{4\,(1-v)}\left[ \,\frac{X_B^2}{\left( X_B^2\,+\,b^2\right) ^2}\,-\,\frac{X_A^2}{\left( X_A^2\,+\,b^2\right) ^2}\,\right] +\frac{\gamma ^{\,4}\,M^2}{4} \nonumber \\&\quad \times \left( \frac{10 + 23v - 5v^2 - 7v^3 + 3v^4}{X_B^2+b^2} -\frac{6 + 7v - 13v^2 + 9v^3 - v^4}{X_A^2+b^2}\right) \nonumber \\&\quad +\,2\,v^2\gamma ^2a\,M\,b\left[ \frac{1}{\left( X_B^2+b^2\right) ^{\frac{3}{2}}}-\frac{1}{\left( X_A^2+b^2\right) ^{\frac{3}{2}}}\right] . \end{aligned}$$

(19)

Actually, Eq. (19) can also be expressed in terms of the quantities in the observer’s rest frame (t,  x,  y,  z). First, we adopt the following forms of $X_A$ and $X_B$ up to the 1PM order [26]

$$\begin{aligned} X_A= & {} (1-v)\,\gamma \,x_A+O(M^2), \end{aligned}$$

(20)

$$\begin{aligned} X_B= & {} (1 - v)\gamma \,x_B-\frac{2\,vM}{1 + v}\,ln \left[ \frac{S_B + (1 - v)\gamma \,x_B}{S_A + (1 - v)\gamma \,x_A}\right] + O(M^2),\nonumber \\ \end{aligned}$$

(21)

with

$$\begin{aligned} S_A\equiv \sqrt{(1 - v)^2\gamma ^2x_A^2+b^2}, \quad S_B\equiv \sqrt{(1 - v)^2\gamma ^2x_B^2+b^2}. \end{aligned}$$

(22)

Substituting Eqs. (20), (21) into Eq. (19), up to the 2PM order, we obtain

$$\begin{aligned}&\frac{\varDelta \nu }{\nu }=\left( 1 + 2v - v^2\right) \gamma ^2 \left[ \frac{M}{S_B} - \frac{M}{S_A} + 2(1 - v)\gamma \, M^2 \left( \frac{x_B}{S_B^3}-\frac{x_A}{S_A^3}\right) \right] \nonumber \\&\quad +\frac{2v(1 - v)^2(1 + 2v - v^2)\gamma ^5 M^2x_B}{S_B^3}ln \left[ \frac{S_B + (1 - v)\gamma \,x_B}{S_A + (1 - v)\gamma \,x_A} \right] \nonumber \\&\quad + \frac{\gamma ^4 M^2}{4} \nonumber \\&\quad \times \left( \frac{10+23v-5v^2-7v^3+3v^4}{S_B^2} - \frac{6+7v- 13v^2+9v^3- v^4}{S_A^2} \right) \nonumber \\&\quad -\frac{(1+2v-v^2)^2\gamma ^4M^2}{S_AS_B} +\frac{v\,(M^2-Q^2)}{4(1+v)} \left( \frac{x_B^2-b^2}{S_B^4}-\frac{x_A^2-b^2}{S_A^4}\right) \nonumber \\&\quad +\frac{4\,v\,(1-v)^2\,\gamma ^3\,M^2}{b^2}\left( \frac{x_B}{S_B}-\frac{x_A}{S_A}\right) +2\,v^2\gamma ^2\,a\,M\,b\left( \frac{1}{S_B^3}-\frac{1}{S_A^3}\right) \nonumber \\&\quad +\frac{(2+3v-5v^2-3v^3+3v^4)\,\gamma ^4\,Q^2}{4} \left( \frac{1}{S_A^2}-\frac{1}{S_B^2}\right) . \end{aligned}$$

(23)

If all of the second-order contributions are dropped, Eq. (23) reduces to the first-order frequency shift caused by a radially moving Schwarzschild black hole [12]

$$\begin{aligned} \frac{\varDelta \nu }{\nu }=\left( 1+2v-v^2\right) \gamma ^2M \left( \frac{1}{S_B}-\frac{1}{S_A}\right) , \end{aligned}$$

(24)

which is consistent with the result obtained by the method of the Liénard–Wiechert gravitational potential [7], as shown in Appendix A. For the case of no translational motion of the lens ($v=0$), Eq. (23) reduces to the second-order KN frequency shift

$$\begin{aligned} \frac{\varDelta \nu }{\nu }= & {} M \left( \frac{1}{\sqrt{x_B^2 + b^2}} - \frac{1}{\sqrt{x_A^2 + b^2}} \right) + \frac{5M^2 - Q^2}{2(x_B^2 + b^2)}\nonumber \\&-\frac{3M^2 - Q^2}{2(x_A^2 + b^2)} -\frac{M^2}{\sqrt{x_A^2 + b^2}\sqrt{x_B^2 + b^2}}\nonumber \\&+ 2M^2 \left[ \frac{x_B}{(x_B^2 + b^2)^{\frac{3}{2}}} - \frac{x_A}{(x_A^2 + b^2)^{\frac{3}{2}}} \right] . \end{aligned}$$

(25)

In addition, it can be seen from Eq. (23) that the gravitational frequency shift induced by the charge Q can be written as

$$\begin{aligned} \frac{\varDelta \nu }{\nu }= & {} \frac{(1 + 2v - v^2)\gamma ^2Q^2}{2} \left( \frac{1}{S_A^2} - \frac{1}{S_B^2} \right) \nonumber \\&+ \frac{v\gamma ^2Q^2b^2}{2} \left( \frac{1}{S_B^4} - \frac{1}{S_A^4} \right) . \end{aligned}$$

(26)

3 Radial velocity effects on the second-order contributions to the frequency shift

Since the radial velocity effect on the leading-order gravitational frequency shift has been discussed [12], we now focus on the radial velocity effect on the second-order contributions to the frequency shift.

Fig. 2

$\varDelta _{M^2}(v),~\varDelta _{a}(v)$, and $\varDelta _{Q}(v)$ plotted as the functions of the radial velocity v of the lens respectively in linear scale (left column). For the convenience of display of the nonrelativistic cases, we also show $|\varDelta _{M^2}(v)|,~|\varDelta _{a}(v)|$, and $|\varDelta _{Q}(v)|$ vs v respectively in log-log scale (right column), with a sample domain $[\,1.0\times 10^{-8},~0.99\,]$ for v. As an example, we set $\{x_A,~x_B\}=\{-10b,~5b\}$ (red), $\{-1.0\times 10^5b,~10b\}$ (thin blue), $\{-10b,~1.0\times 10^5b\}$ (dotted green), and $\{-1.0\times 10^5b,~2.0\times 10^5b\}$ (dot-dashed purple) for four different scenarios. Here, $b=1.0\times 10^5M$, $a=0.1M$, and $Q=0.01M$ are chosen

3.1 Analytical forms of the radial-velocity effects

The comparison between Eqs. (23) and (25) results in the explicit forms of the radial-velocity effects as follows:

$$\begin{aligned}&\varDelta _{M^2}(v)=\frac{2v(1 - v)^2(1 + 2v - v^2)\gamma ^5 M^2x_B}{S_B^3}ln \left[ \frac{S_B + (1 - v)\gamma \,x_B}{S_A + (1 - v)\gamma \,x_A}\right] \nonumber \\&\quad +\frac{4v(1 - v)^2\gamma ^3 M^2}{b^2} \left( \frac{x_B}{S_B} - \frac{x_A}{S_A} \right) \nonumber \\&\quad + \frac{2(1 + 2v - v^2)\gamma M^2}{1+v} \left( \frac{x_B}{S_B^3} - \frac{x_A}{S_A^3} \right) \nonumber \\&\quad +\frac{\gamma ^4 M^2}{4} \left( \frac{10 + 23v - 5v^2 - 7v^3 + 3v^4}{S_B^2} \right. \nonumber \\&\quad \left. - \frac{6 + 7v - 13v^2 + 9v^3 - v^4}{S_A^2} \right) -\frac{(\,1+2\,v-v^2\,)^2\,\gamma ^4\,M^2}{S_A\,S_B}\nonumber \\&\quad +\frac{v\,M^2}{4\,(\,1+v\,)}\left( \,\frac{x_B^2\,-\,b^2}{S_B^4}-\frac{x_A^2\,-\,b^2}{S_A^4}\,\right) \nonumber \\&\quad -\,2\,\,M^2 \left[ \frac{5}{4\,(x_B^2+b^2)}-\frac{3}{4\,(x_A^2+b^2)}-\frac{1}{2\,\sqrt{x_A^2+b^2}\,\sqrt{x_B^2+b^2}} \right. \nonumber \\&\quad \left. +\,\frac{x_B}{\left( x_B^2+b^2\right) ^{\frac{3}{2}}}-\frac{x_A}{\left( x_A^2+b^2\right) ^{\frac{3}{2}}}\right] , \end{aligned}$$

(27)

$$\begin{aligned}&\varDelta _{a}(v)=2\,v^2\gamma ^2a\,M\,b\left( \frac{1}{S_B^3}-\frac{1}{S_A^3}\right) , \end{aligned}$$

(28)

$$\begin{aligned}&\varDelta _{Q}(v) = \frac{(2 + 3v - 5v^2 - 3v^3 + 3v^4)\gamma ^4Q^2}{4} \left( \frac{1}{S_A^2} - \frac{1}{S_B^2} \right) \nonumber \\&\quad - \frac{v\,Q^2}{4(1 + v)} \nonumber \\&\quad \times \left( \frac{x_B^2 - b^2}{S_B^4} - \frac{x_A^2 - b^2}{S_A^4} \right) - \frac{Q^2}{2} \left( \frac{1}{x_A^2 + b^2} - \frac{1}{x_B^2 + b^2}\right) , \end{aligned}$$

(29)

Fig. 3

$\varDelta _{M}(v)$ and $\varDelta _{M}(v_T)$ plotted as the functions of v and $v_T$ respectively in linear scale (left column). We also show $|\varDelta _{M^2}(v)|,~|\varDelta _{a}(v)|$, and $|\varDelta _{Q}(v)|$ vs v respectively in log-log scale (right column). $\{x_A,~x_B\}=\{-10b,~5b\}$ (red), $\{-1.0\times 10^5b,~10b\}$ (thin blue), $\{-10b,~1.0\times 10^5b\}$ (dotted green), and $\{-1.0\times 10^5b,~2.0\times 10^5b\}$ (dot-dashed purple) for four different scenarios are assumed for comparison. $b=1.0\times 10^5M$ is preset

where $\varDelta _{M^2}(v)$ and $\varDelta _{Q}(v)$ denote the velocity effects on the second-order Schwarzschild and charge-induced contributions to the frequency shift, respectively. $\varDelta _{a}(v)$ denotes the frequency shift induced by the velocity-rotation coupling. Notice that Eq. (25) indicates the second-order Kerr frequency shift is zero. Equations (27)–(29) apply to both non-relativistic and relativistic (such as $v=0.5$) motions of the lens.

3.2 Magnitudes and possible detection of the radial-velocity effects

In this subsection, we discuss the magnitudes of the radial-velocity effects on the second-order contributions to the frequency shift, and analyze the possibilities of their astronomical detection

3.2.1 General cases

We first discuss the magnitudes of the radial-velocity effects for arbitrary radial velocity v of the lens. Figure 2 shows $\varDelta _{M^2}(v)$, $\varDelta _{a}(v)$, and $\varDelta _{Q}(v)$ as the functions of v in four astronomical scenarios. The left column is presented in linear scale ($|v|\le 0.99$) while the right one is in log-log scale ($v\in [\,1.0\times 10^{-8},~0.99\,]$).

It can be seen from Fig. 2b that the magnitudes of $\varDelta _{M^2}(v)$ exceed the precision $\sim 10^{-14}$ of the Cassini [13] for most cases. For example, $\varDelta _{M^2}(v)$ will be about $4.5\times 10^{-13}$ if $x_A=-10b$, $x_B=5b$, and $v=5.0\times 10^{-4}$ (a nonrelativistic radial velocity) are assumed. It indicates that the radial velocity effect on the second-order Schwarzschild contribution to the frequency shift of light may be detected by near future high-accuracy detectors with a relatively large possibility.

According to Fig. 2c or d, we can see that the magnitudes of $\varDelta _{a}(v)$ may be larger than the Cassini’s precision only when the lens has a relativistic radial motion. For instance, $|\varDelta _{a}(v)|$ will exceed $1.0\times 10^{-14}$ when $v>0.38$ for the case of $x_A=-10b$ and $x_B=1.0\times 10^5b$. The possibility of detecting $\varDelta _{a}(v)$ via current projects is thus rather small. In addition, it can also be seen from Fig. 2e or f that there is no possibility of detection of $\varDelta _{Q}(v)$ by current detectors, since its magnitudes are much smaller than the Cassini’s precision. It is only by using the ultrahigh accuracy techniques in future that we may observe these two correctional effects.

However, it should be pointed out that our discussions depend on the choice of the intrinsic parameters of the central body, which implies these velocity effects will be more evident and a easier detection of them if M,  a, and Q become larger.

In addition, we emphasize that the requirements for their realistic detections are more demanding. For instance, the radial velocity of the Sun during the Cassini experiment in 2002 is not larger than 0.0001 in the geocentric frame and $5\times 10^{-8}$ in the barycentric frame of the solar system [15, 30, 31]. The corresponding precision of the measurements for $\varDelta _{M^2}(v)$ should be at least better than $8.0\times 10^{-16}$ in the geocentric frame and $3.2\times 10^{-19}$ in the barycentric frame, for the case of $x_A=-10b,~x_B=1.0\times 10^5b$ and $b=1.0\times 10^6M$ (as an example). Therefore, if we wish to detect conservatively the radial velocity effects on the second-order contributions to the frequency shift in future actual measurements, the central body should move at a higher radial velocity (e.g. $|v|>1.26\times 10^{-3}$, for the case of $x_A=-10b,~x_B=1.0\times 10^5b$ and $b=1.0\times 10^6M$), or a better precision for measurements is required.

In contrast with $\varDelta _{M^2}(v)$, $\varDelta _{a}(v)$, and $\varDelta _{Q}(v)$, Fig. 3 gives the magnitudes of the radial-velocity effect $\varDelta _{M}(v)$ and the transversal-velocity effect $\varDelta _{M}(v_T)$ on the leading-order gravitational frequency shift of light, which have been given analytically in Ref. [12] as follows:

$$\begin{aligned} \varDelta _{M}(v)= & {} \left( 1+2v-v^2\right) \gamma ^2M\left( \frac{1}{S_B}-\frac{1}{S_A}\right) -\frac{M}{\sqrt{x_B^2+b^2}} \nonumber \\&+\frac{M}{\sqrt{x_A^2+b^2}}, \end{aligned}$$

(30)

$$\begin{aligned} \varDelta _{M}(v_T)= & {} \frac{2v_T\gamma _TM \left( v_T+\frac{b+v_Tx_A}{\sqrt{x_A^2+b^2+2\,v_T\,b\,x_A}}\right) }{\sqrt{x_A^2+b^2+2\,v_T\,b\,x_A}+x_A+v_T\,b} \nonumber \\&-\frac{2v_T\gamma _TM \left( v_T+\frac{b+v_Tx_B}{\sqrt{x_B^2+b^2+2\,v_T\,b\,x_B}}\right) }{\sqrt{x_B^2+b^2+2\,v_T\,b\,x_B}+x_B+v_Tb} \nonumber \\&+\frac{(1+v_T^2)\,\gamma _T\,M}{\sqrt{x_B^2+b^2+2\,v_T\,b\,x_B}}-\frac{(1+v_T^2)\,\gamma _T\,M}{\sqrt{x_A^2+b^2+2\,v_T\,b\,x_A}} \nonumber \\&-\frac{M}{\sqrt{x_B^2+b^2}}+\frac{M}{\sqrt{x_A^2+b^2}}, \end{aligned}$$

(31)

where $v_T$ is the magnitude of the transversal velocity ${\varvec{v}}=v_{T}{\varvec{e}}_2$ of a moving Schwarzschild source along y-axis, $\gamma _T=(1-v_T^2)^{-\scriptstyle \frac{1}{2}}$ denotes the Lorentz factor for the transversal motion, and the zeroth-order relations $y_A=-b+O(M)$ and $y_B=-b+O(M)$ have been considered.

3.2.2 The low-velocity limit

We now consider the radial motion effects for four special scenarios in the low-velocity approximation, under which the second- and higher-order terms in velocity are omitted and Eqs. (27)–(29) can be simplified.

(a) The scenario for $x_A\ll -b$ and $x_B\gg b$

For the common astronomical scenario in which both the light emitter A and the receiver B are far away from the moving lens, Eqs. (27)–(29) reduce to

$$\begin{aligned}&\varDelta _{M^2}(v)=\frac{8vM^2}{b^2} , \end{aligned}$$

(32)

$$\begin{aligned}&\varDelta _{a}(v)=0 , \end{aligned}$$

(33)

$$\begin{aligned}&\varDelta _{Q}(v)=0 , \end{aligned}$$

(34)

where the terms with the factor $v/x_A^i$ or $v/x_B^i~(i=1,~2,~4)$ have been dropped since they are much smaller than the term with the factor $v/b^2$.

It can be seen that under this scenario, a radial velocity effect (i.e., $\frac{8M^2v}{b^2}$) on the second-order Schwarzschild frequency shift appears, although the radial velocity effect on the first-order one can be indeed neglected [2, 6, 7]. To some extent, this effect is similar to the famous formula $\frac{Mv_{\bot }}{b}$ for the transversal velocity effect on the first-order frequency shift, with $v_{\bot }$ being the transversal lens velocity. For the case of $M/b=0.0001$ (weak-field), the magnitudes of this effect are $8.0\times 10^{-11}$ and $8.0\times 10^{-13}$ for $v=0.001$ and 0.00001, respectively. Therefore, it is possible to detect this new effect, since its magnitude may still be comparable to the precision $(\sim 10^{-14})$ of the Cassini in the weak-field and low-velocity limit.

(b) The scenario for $x_A\sim -b$ and $x_B\gg b$

If the x position of the light emitter has the same order of magnitude as the impact parameter b while the receiver is far away from the lens, Eqs. (27)–(29) are simplified to

$$\begin{aligned} \varDelta _{M^2}(v)= & {} \frac{4\,v\,M^2}{b^2} \left( 1-\frac{x_A}{\sqrt{x_A^2+b^2}} \right) -\frac{2\,v\,M^2x_A(4\,x_A^2+b^2)}{(x_A^2+b^2)^{\frac{5}{2}}} \nonumber \\&-\frac{vM^2}{4} \left[ \frac{7}{x_A^2+b^2}+\frac{13x_A^2-b^2}{(x_A^2+b^2)^2}\right] , \end{aligned}$$

(35)

$$\begin{aligned} \varDelta _{a}(v)= & {} 0, \end{aligned}$$

(36)

$$\begin{aligned} \varDelta _{Q}(v)= & {} \frac{v\,Q^2}{4}\left[ \frac{3}{x_A^2+b^2}+\frac{5x_A^2-b^2}{(x_A^2+b^2)^2} \right] , \end{aligned}$$

(37)

where the terms with the factor $v/x_B^i~(i=1,~2,~4)$ have been dropped.

(c) The scenario for $x_A\ll -b$ and $x_B\sim b$

Fig. 4

$\varDelta _{M^2}(v)$ and $\varDelta _{Q}(v)$ plotted as the functions of $x_B$ for various $x_A$, respectively. As an example, $b=1.0\times 10^4 M$, $Q=0.01M$, and $v=1.0\times 10^{-4}$ are assumed

When the light emitter is far away from the lens and the observer is relative close to it $(x_B\sim b)$, Eqs. (27)–(29) then reduce to

$$\begin{aligned} \varDelta _{M^2}(v)= & {} \frac{4vM^2}{b^2} \left( 1 + \frac{x_B}{\sqrt{ x_B^2 + b^2}} \right) \nonumber \\&+ \frac{vM^2}{4} \left[ \frac{23}{x_B^2 + b^2} + \frac{21x_B^2 - b^2}{(x_B^2 + b^2)^2} \right] \nonumber \\&+2vM^2 \Biggl \{ \frac{x_B}{(x_B^2 + b^2)^{\frac{3}{2}}} \left[ 1 + ln \left( \frac{\sqrt{x_B^2 + b^2} + x_B}{\sqrt{x_A^2 + b^2} + x_A} \right) \right] \nonumber \\&+ \frac{3\,x_B^3}{(x_B^2 + b^2)^{\frac{5}{2}}} \Biggr \} , \end{aligned}$$

(38)

$$\begin{aligned} \varDelta _{a}(v)= & {} 0 , \end{aligned}$$

(39)

$$\begin{aligned} \varDelta _{Q}(v)= & {} -\frac{v\,Q^2}{4} \left[ \frac{3}{x_B^2+b^2}+\frac{5x_B^2-b^2}{(x_B^2+b^2)^2}\right] , \end{aligned}$$

(40)

where the terms with the factor $v/x_A^i~(i=1,~2,~4)$ have been dropped.

(d) The scenario for $x_A\sim -b$ and $x_B\sim b$

For this case, Eqs. (27)–(29) reduce to

$$\begin{aligned} \varDelta _{M^2}(v)= & {} \frac{4\,v\,M^2}{b^2} \left( \frac{x_B}{\sqrt{x_B^2\,+\,b^2}}-\frac{x_A}{\sqrt{x_A^2\,+\,b^2}} \right) +\frac{2\,v\,M^2x_B}{(x_B^2+b^2)^{\frac{3}{2}}} \nonumber \\&\times \,ln\left( \frac{\sqrt{x_B^2\,+\,b^2}\,+\,x_B}{\sqrt{x_A^2\,+\,b^2}\,+\,x_A}\right) \nonumber \\&-\frac{v\,M^2\left( 4\,+\,\frac{x_B^2}{x_B^2\,\,+\,\,b^2}\,+\,\frac{x_A^2}{x_A^2\,\,+\,\,b^2}\right) }{\sqrt{x_A^2+b^2}\sqrt{x_B^2+b^2}} \nonumber \\&+\frac{vM^2}{4} \left[ \frac{23}{x_B^2 + b^2} - \frac{7}{x_A^2 + b^2}\right. \nonumber \\&\left. + \frac{21x_B^2 - b^2}{(x_B^2 + b^2)^2} - \frac{13x_A^2 - b^2}{(x_A^2 + b^2)^2}\right] + 2vM^2 \nonumber \\&\times \left[ \frac{x_B}{(x_B^2 + b^2)^{\frac{3}{2}}} - \frac{x_A}{(x_A^2 + b^2)^{\frac{3}{2}}}\right. \nonumber \\&\left. +\frac{3x_B^3}{(x_B^2 + b^2)^{\frac{5}{2}}} - \frac{3x_A^3}{(x_A^2 + b^2)^{\frac{5}{2}}} \right] , \end{aligned}$$

(41)

$$\begin{aligned} \varDelta _{a}(v)= & {} 0, \end{aligned}$$

(42)

$$\begin{aligned} \varDelta _{Q}(v)= & {} \frac{v\,Q^2}{4} \left[ \frac{3}{x_A^2 + b^2} - \frac{3}{x_B^2 + b^2}\right. \nonumber \\&\left. + \frac{5x_A^2-b^2}{(x_A^2 + b^2)^2} - \frac{5x_B^2 - b^2}{(x_B^2 + b^2)^2}\right] . \end{aligned}$$

(43)

Figure 4 shows $\varDelta _{M^2}(v)$ and $\varDelta _{Q}(v)$ as the functions of $x_B$ for different $x_A$ in this scenario.

4 Summary

In this paper we have calculated the gravitational frequency shift up to the 2PM order for light propagating in the equatorial plane of a radially moving Kerr–Newman source. It is found that for the astronomical scenario where both the light emitter and observer are far away from the lens, a new radial velocity effect $\frac{8M^2v}{b^2}$ appears in the second-order Schwarzschild contribution to the frequency shift, in contrast to no radial-velocity effect in the first-order frequency shift. The velocity effects on the gravitational frequency shifts induced respectively by the lens’ electrical charge and spin are also analyzed. It might be possible to detect the radial velocity effects on the second-order contributions to the frequency shift by high-accuracy measurements in future.

Appendix A: Comparison between our formulation with that obtained via Liénard–Wiechert representation

In this appendix, we compare Eq. (24) with the analytical form of the first-order gravitational frequency shift obtained from the retarded Liénard–Wiechert gravitational potential [7]. For comparison, we consider a point mass M moving with a constant radial velocity ${\varvec{v}}=v{\varvec{e_1}}$ in the observer’s rest frame (t,  x,  y,  z), and follow the notations used in Ref. [26] for display convenience. According to the results presented in [7], $\frac{d\tau _A}{dt_A}$, $\frac{dt_B}{d\tau _B}$, and $\frac{dt_A}{dt_B}$ in Eq. (8) for the case of the light emitter $A~(t_A,~{\varvec{x}}_A)$ and the receiver $B~(t_B,~{\varvec{x}}_B)$ being non-moving $({\varvec{v}}_A={\varvec{v}}_B=0)$ are written as follows:

$$\begin{aligned}&\frac{d\tau _A}{dt_A}=\sqrt{1-h_{00}^A}=\sqrt{1-\frac{2(1+v^2)\gamma M}{r_A(s_A)-{\varvec{v}}\cdot {\varvec{r}}_A(s_A)}} , \end{aligned}$$

(A.1)

$$\begin{aligned}&\frac{dt_B}{d\tau _B}=\frac{1}{\sqrt{1-h_{00}^B}}=\frac{1}{\sqrt{1-\frac{2(1+v^2)\gamma M}{r_B(s_B)-{\varvec{v}}\cdot {\varvec{r}}_B(s_B)}}} , \end{aligned}$$

(A.2)

$$\begin{aligned}&\frac{dt_A}{dt_B}=\frac{1 - 2M\left( \frac{\partial s_B}{\partial t_B}\frac{\partial \xi }{\partial s_B} +\frac{\partial s_A}{\partial t_B}\frac{\partial \xi }{\partial s_A} +\frac{\partial t^{*}}{\partial t_B}\frac{\partial \xi }{\partial t^{*}} +\frac{\partial k^i}{\partial t_B}\frac{\partial \xi }{\partial k^i}\right) }{1 + 2M\left( \frac{\partial s_B}{\partial t_A}\frac{\partial \xi }{\partial s_B} +\frac{\partial s_A}{\partial t_A}\frac{\partial \xi }{\partial s_A} +\frac{\partial t^{*}}{\partial t_A}\frac{\partial \xi }{\partial t^{*}} +\frac{\partial k^i}{\partial t_A}\frac{\partial \xi }{\partial k^i}\right) } , \nonumber \\ \end{aligned}$$

(A.3)

with

$$\begin{aligned} \frac{\partial s_A}{\partial t_B}= & {} \frac{\partial t^{*}}{\partial t_B}=\frac{\partial k^i}{\partial t_B}=\frac{\partial k^i}{\partial t_A}=0 , \end{aligned}$$

(A.4)

$$\begin{aligned} \frac{\partial s_B}{\partial t_B}= & {} \frac{r_B(s_B)-{\varvec{k}}\cdot {\varvec{r}}_B(s_B)}{r_B(s_B)-{\varvec{v}}\cdot {\varvec{r}}_B(s_B)} , \end{aligned}$$

(A.5)

$$\begin{aligned} \frac{\partial s_B}{\partial t_A}= & {} \frac{{\varvec{k}}\cdot {\varvec{r}}_B(s_B)}{r_B(s_B)-{\varvec{v}}\cdot {\varvec{r}}_B(s_B)} , \end{aligned}$$

(A.6)

$$\begin{aligned} \frac{\partial s_A}{\partial t_A}= & {} \frac{r_A(s_A)}{r_A(s_A)-{\varvec{v}}\cdot {\varvec{r}}_A(s_A)} , \end{aligned}$$

(A.7)

$$\begin{aligned} \frac{\partial t^*}{\partial t_A}= & {} 1 , \end{aligned}$$

(A.8)

$$\begin{aligned} \frac{\partial \xi }{\partial s_B}= & {} \frac{1}{\sqrt{1-v^2}}\frac{\left( 1-{\varvec{k}}\cdot {\varvec{v}}\right) ^2}{r_B(s_B)-{\varvec{k}}\cdot {\varvec{r}}_B(s_B)} , \end{aligned}$$

(A.9)

$$\begin{aligned} \frac{\partial \xi }{\partial s_A}= & {} -\frac{1}{\sqrt{1-v^2}}\frac{\left( 1-{\varvec{k}}\cdot {\varvec{v}}\right) ^2}{r_A(s_A)-{\varvec{k}}\cdot {\varvec{r}}_A(s_A)}, \end{aligned}$$

(A.10)

$$\begin{aligned} \frac{\partial \xi }{\partial t^*}= & {} \frac{1 - {\varvec{k}}\cdot {\varvec{v}}}{\sqrt{1 - v^2}} \left[ \frac{1}{r_A(s_A) - {\varvec{k}}\cdot {\varvec{r}}_A(s_A)} - \frac{1}{r_B(s_B) - {\varvec{k}}\cdot {\varvec{r}}_B(s_B)}\right] , \end{aligned}$$

(A.11)

$$\begin{aligned} \frac{\partial \xi }{\partial k^i}= & {} \frac{1 - {\varvec{k}}\cdot {\varvec{v}}}{\sqrt{1 - v^2}} \left[ \frac{x_M^i(s_A)}{r_A(s_A) - {\varvec{k}}\cdot {\varvec{r}}_A(s_A)} - \frac{x_M^i(s_B)}{r_B(s_B) - {\varvec{k}}\cdot {\varvec{r}}_B(s_B)}\right] \nonumber \\&+\frac{2\,v^i}{\sqrt{1-v^2}}\,ln \left[ \frac{r_B(s_B)-{\varvec{k}}\cdot {\varvec{r}}_B(s_B)}{r_A(s_A)-{\varvec{k}}\cdot {\varvec{r}}_A(s_A)}\right] . \end{aligned}$$

(A.12)

Here, the two retarded times $s_A$ and $s_B$ are related to the emission time $t_A$ and the receiver time $t_B$ by the light-cone equations

$$\begin{aligned}&s_A+|{\varvec{x}}_A(t_A)-{\varvec{x}}_M(s_A)|=t_A, \end{aligned}$$

(A.13)

$$\begin{aligned}&s_B+|{\varvec{x}}_B(t_B)-{\varvec{x}}_M(s_B)|=t_B. \end{aligned}$$

(A.14)

$r_A(s_A)\equiv |{\varvec{r}}_A(s_A)|$ with ${\varvec{r}}_A(s_A)\equiv {\varvec{x}}_A(t_A)-{\varvec{x}}_M(s_A)$ denoting the distance vector from the retarded position ${\varvec{x}}_M(s_A)$ of the moving lens M to the present position ${\varvec{x}}_A(t_A)$ of the emitter. $r_B(s_B)\equiv |{\varvec{r}}_B(s_B)|$ with ${\varvec{r}}_B(s_B)\equiv {\varvec{x}}_B(t_B)-{\varvec{x}}_M(s_B)$ denoting the distance vector from the retarded position ${\varvec{x}}_M(s_B)$ of the moving lens to the present position ${\varvec{x}}_B(t_B)$ of the receiver. ${\varvec{k}}$ denotes the initial velocity of an incoming photon at infinity, which is equal to ${\varvec{e}}_1$ (a unit vector towards the light receiver) in our scenario. $t^*\equiv t_A-{\varvec{k}}\cdot {\varvec{x}}_A(t_A)$. $\xi =\varDelta (t_B,~t_A)/2M$, with $\varDelta (t_B,~t_A)$ being given in Eq. (12). We have used the simplification ${\varvec{v}}(s_A)={\varvec{v}}(s_B)={\varvec{v}}$ and the terms depending on the lens’ acceleration have been dropped, since the velocity of the point mass is constant.

Substituting Eqs. (A.1)–(A.3) into Eq. (8) and considering ${\varvec{k}}\cdot {\varvec{v}}=v$, we can obtain

$$\begin{aligned} \frac{\varDelta \nu }{\nu }=\frac{\sqrt{\frac{1-\frac{2\,(1\,+\,v^2)\,\gamma ^2\,M}{R_A}}{1-\frac{2\,(1\,+\,v^2)\,\gamma ^2\,M}{R_B}}} \left[ 1-\frac{2\,(1-v)^2\,\gamma \, M}{r_B\,(s_B)-{\varvec{v}}\,\cdot \,{\varvec{r}}_B\,(s_B)}\right] }{1+2\,(1-v)\,\gamma \,M\left[ \,(1-v)\,E+F\,\right] }-1 , \end{aligned}$$

(A.15)

with

$$\begin{aligned} E= & {} \frac{{\varvec{k}}\cdot {\varvec{r}}_B(s_B)}{\left[ r_B(s_B)-{\varvec{v}}\cdot {\varvec{r}}_B(s_B)\right] \left[ r_B(s_B)-{\varvec{k}}\cdot {\varvec{r}}_B(s_B)\right] } \nonumber \\&-\frac{r_A(s_A)}{\left[ r_A(s_A)-{\varvec{v}}\cdot {\varvec{r}}_A(s_A)\right] \left[ r_A(s_A)-{\varvec{k}}\cdot {\varvec{r}}_A(s_A)\right] } ,~~~~~~~~~ \end{aligned}$$

(A.16)

$$\begin{aligned} F= & {} \frac{1}{r_A(s_A)-{\varvec{k}}\,\cdot \,{\varvec{r}}_A(s_A)}-\frac{1}{r_B(s_B)-{\varvec{k}}\,\cdot \,{\varvec{r}}_B(s_B)}, \end{aligned}$$

(A.17)

where we have plugged the 1PM form of $h_{00}^A$ and $h_{00}^B$ in terms of the quantities in the lens’s rest frame [2] into Eq. (A.15). Moreover, the retarded quantities in Eq. (A.15) are related to the Lorentz invariant distances $R_A$ and $R_B$ by [32, 33]

$$\begin{aligned}&R_A=\gamma \left[ r_A(s_A)-{\varvec{v}}\cdot {\varvec{r}}_A(s_A)\right] , \end{aligned}$$

(A.18)

$$\begin{aligned}&R_B=\gamma \left[ r_B(s_B)-{\varvec{v}}\cdot {\varvec{r}}_B(s_B)\right] , \end{aligned}$$

(A.19)

$$\begin{aligned}&r_A(s_A)=\gamma \left( R_A+vX_A\right) , \end{aligned}$$

(A.20)

$$\begin{aligned}&r_B(s_B)=\gamma \left( R_B+vX_B\right) , \end{aligned}$$

(A.21)

$$\begin{aligned}&{\varvec{k}}\cdot {\varvec{r}}_A(s_A)=\frac{1}{v}\left[ r_A(s_A)-\frac{R_A}{\gamma }\right] , \end{aligned}$$

(A.22)

$$\begin{aligned}&{\varvec{k}}\cdot {\varvec{r}}_B(s_B)=\frac{1}{v}\left[ r_B(s_B)-\frac{R_B}{\gamma }\right] . \end{aligned}$$

(A.23)

We then substitute Eqs. (A.18)–(A.23) into Eq. (A.15) and get

$$\begin{aligned} \frac{\varDelta \nu }{\nu }= & {} \sqrt{ \frac{1 - \frac{2(1+v^2)\gamma ^2M}{R_A}}{1 - \frac{2(1+v^2)\gamma ^2M}{R_B}}} \left[ 1 - \frac{2(1 - v)^2\gamma ^2M}{R_B}\right] \nonumber \\&\times \Biggl \{ 1 + 2(1 - v)\gamma ^2 M \nonumber \\&\times \left[ \frac{vR_B+X_B}{R_B(R_B - X_B)} - \frac{R_A+vX_A}{R_A(R_A - X_A)}\right. \nonumber \\&\left. + \frac{1+v}{R_A - X_A} - \frac{1+v}{R_B - X_B} \right] \Biggr \}^{ -1} - 1 \nonumber \\= & {} \frac{1-\frac{2(1-v)^2\gamma ^2M}{R_B}}{1 + \frac{2(1-v)\gamma ^2M(vR_B-R_A)}{R_AR_B}} \left[ \frac{1-\frac{2(1+v^2)\gamma ^2M}{R_A}}{1-\frac{2(1+v^2)\gamma ^2M}{R_B}}\right] ^{\frac{1}{2}} - 1. \nonumber \\ \end{aligned}$$

(A.24)

Up to the 1PM order, Eq. (A.24) yields

$$\begin{aligned}&\frac{\varDelta \nu }{\nu }=(1+2v-v^2)\gamma ^2\left( \frac{M}{R_B}-\frac{M}{R_A}\right) \nonumber \\&\quad =(1+2v-v^2)\gamma ^2 \nonumber \\&\qquad \times \left[ \frac{M}{\sqrt{ (1 - v)^2\gamma ^2x_B^2 + b^2}} - \frac{M}{\sqrt{ (1 - v)^2\gamma ^2x_A^2 + b^2}} \right] , \nonumber \\ \end{aligned}$$

(A.25)

which is the same as that given in Eq. (24).