1 Introduction

In the last two decades there has been a growing interest in gravitational solutions with cosmological constant in general relativity (GR) and its extensions. This interest has been generated by seminal observational and theoretical breakthroughs, namely, the discovery of cosmic acceleration [6, 7] and the gauge/gravity dualities [8]. Black hole solutions play a very important role in unraveling several classical and quantum mechanical aspects of the underlying gravitational theory. Therefore, it is viewed as an important tool to study various extensions of GR. Contrary to asymptotically flat black holes, asymptotically de Sitter (dS) and anti-de Sitter (AdS) black hole solutions possess more than one type of horizon topology. They could have spherical, hyperbolic, or flat horizons. dS and AdS black hole solutions have been obtained and studied in GR extensively, as well as teleparallel gravities, please see [1, 2, 9,10,11,12,13,14,15,16,17,18,19], for diverse black hole solutions.

Since the confirmation of the above cosmological observations there have been several proposed extensions of GR which are based on Riemannian as well as other types of geometries. Gravitational theories based on Riemannian geometry have been extended through f(R) gravitational theory which was proposed in [20, 21]. In such a theory, the Ricci scalar R is replaced by an arbitrary function f(R) in Einstein-Hilbert action. Other extensions consider a Lagrangian density on the form of \(f(R,\mathcal{T})\) where \(\mathcal{T}\) the trace of the energy-momentum tensor of the matter component [22], or some f(R, G) where G is Gauss-Bonnet scalar [23,24,25,26,27]. Different approach, however, has been developed within Weitzenböck geometry by introducing the teleparallel torsion scalar, T, as the Lagrangian density instead of the Ricci scalar, that is the teleparallel equivalent of general relativity (TEGR) theory. Motivated by the f(R) gravity extension, TEGR has been generalized to f(T) gravity by replacing T by an arbitrary function f(T) [28]. The f(T) gravity is considered to be one of the simplest extensions of GR, since its field equations are still second order [29,30,31] in spite of having arbitrary torsion scalar terms. Although there is an equivalence between GR and TEGR on the field equations level, their generalizations f(R) and f(T) are not equivalent.

In general, finding an exact nontrivial black hole solution in the above extensions, including f(T) gravity, is not an easy task [3, 32,33,34,35,36,37,38]. In this work, we present a rotating black hole in all dimensions within Maxwell-f(T) theory with a negative cosmological constant, where \(f(T)=T+\alpha T^{2}\). These asymptotically AdS black holes are characterized by cylindrical, toroidal or flat horizons depending on the global identifications of some coordinates. These solutions can be constructed from coordinate transformations which are allowed locally on a manifold but not globally [39]. They are the f(T) analogue of the solutions found in GR by Lemos [1] and their generalizations in higher dimensions that were introduced by one of us in [2]. The charged static configurations obtained in [3] are recovered in the limit of vanishing rotation parameters. These interesting black hole solutions have two different electric multipole terms in the electric potential with related multipole moments. In addition, they have milder singularities at \(r=0\), similar to that of the static solutions obtained in [3], compared to Reissner Nordström solutions in GR. We calculate the energy and the angular momentum of the black hole using the conserved quantities in the framework of teleparallel gravity.

This work is arranged as follow: In Sect. 2, a brief account of f(T) gravitational theories are provided in addition to the previous solutions derived in [3] within the framework of f(T) gravitational theory. In Sect. 3, charged rotating N dimensional exact solutions are derived. These solutions have monopoles and quadrupole moments which are not independent, in addition of being asymptotically AdS. In Sect. 4, we calculate the energy and angular momentum of these solutions. In the final section we comment on some physical aspects of these black hole solutions.

2 Maxwell-f(T) gravity

2.1 Teleparallel geometry

A Vielbein space can be defined as a pair (M, \(e_a\)), where M is an N-dimensional differentiable manifold and the set \(\{e_a\}\) contains N independent vector fields defined globally on M, this set at point p is the basis of its tangent space \(T_{p} M\). Because of the independence of \(e_{a}\), the determinant \(e\equiv \det (e_{a}{^{\mu }})\) is nonzero. The vielbein vector fields satisfy \(e_{a}{^{\mu }}e^{a}{_{\nu }}=\delta ^{\mu }_{\nu }\quad and \quad e_{a}{^{\mu }}e^{b}{_{\mu }}=\delta ^{b}_{a}\), where \(\delta \) is the Kronecker tensor. Thus, we can construct an associated (pseudo-Riemannian) metric and its inverse, respectively, for any set of basis \(g_{\mu \nu } \equiv \eta _{ab}e^{a}{_{\mu }}e^{b}{_{\nu }},\quad g^{\mu \nu } = \eta ^{ab}e_{a}{^{\mu }}e_{b}{^{\nu }}\), where \(\eta _{i j}=(-,+,+,+, \cdots )\) is the metric of N-dimensions Minkowski spacetime. Also, it can be shown that \(e=\sqrt{-g}\), where \(g\equiv \det (g)\). Thus, we go further to define the symmetric Levi-Civita connection. In this sense, the vielbein space is a pseudo-Riemannian as well. However, if we decide not to use curvature as the basic description of gravity, we may begin with the vielbein vector fields as the fundamental field variables. Then, we define the nonsymmetric linear (Weitzenböck) connection [40] \(W^{\alpha }{_{\mu \nu }}\equiv e_{a}{^{\alpha }}\partial _{\nu }e^{a}{_{\mu }}=-e^{a}{_{\mu }}\partial _{\nu }e_{a}{^{\alpha }}\). This connection is characterized by the property that \(\nabla _{\nu }e_{a}{^{\mu }}\equiv \partial _{\nu }{e_a}^\mu +{W^\mu }_{\lambda \nu } {e_a}^\lambda \equiv 0\), where the covariant derivative \(\nabla _{\nu }\) is associated to the Weitzenböck connection. This nonsymmetric connection uniquely determines the teleparallel geometry, since the vielbein vector fields are parallel with respect to it. Indeed, the Weitzenböck connection is curvature free, but it has a non vanishing torsion \({T^\alpha }_{\mu \nu } = {W^\alpha }_{\nu \mu }-{W^\alpha }_{\mu \nu } ={e_i}^\alpha [\partial _\mu {e^i}_\nu -\partial _\nu {e^i}_\mu ]\). Now we can go directly to construct the teleparallel torsion scalar

$$\begin{aligned} T ={T^\alpha }_{\mu \nu } {S_\alpha }^{\mu \nu }, \end{aligned}$$
(1)

where the superpotential tensor is defined as \({S_\alpha }^{\mu \nu } := \frac{1}{2}\left( {K^{\mu \nu }}_\alpha +\delta ^\mu _\alpha {T^{\beta \nu }}_\beta -\delta ^\nu _\alpha {T^{\beta \mu }}_\beta \right) \) and the Contortion tensor is \(K_{\alpha \mu \nu }=\frac{1}{2}\left( T_{\nu \alpha \mu }+T_{\alpha \mu \nu }-T_{\mu \alpha \nu }\right) \).

2.2 The theory

We take the action of the f(T)-Maxwell theory in N-dimensional for asymptotically (Anti)-de-Sitter spacetimes as

$$\begin{aligned} \mathcal {S}_{g}+\mathcal {S}_{em}= & {} \frac{1}{2\kappa }\int d^{N}x~ |e|\left( f(T)-2\Lambda \right) \nonumber \\&-\frac{1}{2\kappa }\int d^{N}x~|e| { F}\wedge ^{\star }{F}, \end{aligned}$$
(2)

where \(\Lambda =-\frac{(N-1)(N-2)}{2l^2}\) is the N-dimensional cosmological constant in N dimensions, l is the length scale of AdS spacetime, \(\kappa \) is a dimensional constant which can be related to the Newton constant \(G_N\) by \(\kappa =2(N-3)\Omega _{N-2} G_N\), where \(\Omega _{N-2} = \frac{2\pi ^{(N-1)/2}}{\Gamma ([N-1]/2)}\) is the volume of \((N-2)\)-dimensional unit sphere and \(\Gamma \) function being the argument that depends on the dimension of the spacetime.Footnote 1\(^{,}\)Footnote 2 Also, in the Maxwell action, \(F = d\mathcal{A}\), with \(\mathcal{A}=\mathcal{A}_{\mu }dx^\mu \) being the gauge potential 1-form [3, 37].

Varying the action (2) with respect to the vielbein and the vector potential \(\mathcal{A}_\mu \), one gets, respectively, the field equations [29]

$$\begin{aligned}&\mathfrak {I{^\nu }{_\mu }}={S_\mu }^{\rho \nu } \partial _{\rho } T f_{TT}\nonumber \\&\quad +\left[ e^{-1}{e^a}_\mu \partial _\rho \left( e{e_a}^\alpha {S_\alpha }^{\rho \nu }\right) -{T^\alpha }_{\lambda \mu }{S_\alpha }^{\nu \lambda }\right] f_T\nonumber \\&\quad -\frac{\delta ^\nu _\mu }{4}\left( f+\frac{(N-1)(N-2)}{l^2}\right) +{\kappa \over 2} {\mathop {\mathfrak {T}}\limits ^{\tiny \mathbf{em }}}{^\nu }{_\mu },\nonumber \\&\quad \partial _\nu \left( \sqrt{-g} F^{\mu \nu } \right) =0, \end{aligned}$$
(3)

where \(f := f(T)\), \(f_{T}:=\frac{\partial f(T)}{\partial T}\), \(f_{TT}:=\frac{\partial ^2 f(T)}{\partial T^2}\) and \({\mathop {\mathfrak {T}}\limits ^{\tiny \mathbf{em }}}{^\nu }{_\mu }\) is the energy momentum tensor of the electromagnetic field which is given by [37]

$$\begin{aligned} {\mathop {\mathfrak {T}}\limits ^{\tiny \mathbf{em }}}{^\nu }{_\mu }=F_{\mu \alpha }F^{\nu \alpha }-\frac{1}{4} \delta _\mu {}^\nu F_{\alpha \beta }F^{\alpha \beta }. \end{aligned}$$

2.3 AdS charged black holes with flat horizons

In a previous work [3] we have introduced the following diagonal vielbein which describes a static configuration in N-dimensions with the coordinates (t, r, \(\phi _1\), \(\phi _2\), \(\ldots \), \(\phi _{n}\), \(z_1\), \(z_2\), \(\ldots \), \(z_k\), \(k=1,2, \ldots \), \(N-n-2\))

$$\begin{aligned} \left( {e^{i}}_{\mu }\right) =\left( \sqrt{A(r)}, \; \frac{1}{\sqrt{B(r)}}, \; r, \; r, \; r\;\cdots \right) , \end{aligned}$$
(4)

where \(0\le r< \infty \), \(-\infty< t < \infty \), \(0\le \phi _{n}< 2\pi \) and \(-\infty< z_k < \infty \). The functions A(r) and B(r) are two unknown functions of the radial coordinate r. Thus, the spacetime which can be generated by (4) is

$$\begin{aligned} ds^2= & {} -A(r)dt^2+\frac{1}{B(r)}dr^2\nonumber \\&+r^2\left( \sum _{i=1}^{n}d\phi ^2_i+\sum _{k=1}^{N-n-2}{dz^2_k \over l^2}\right) . \end{aligned}$$
(5)

Substituting from Eq. (4) into Eq. (1), we evaluate the torsion scalar asFootnote 3

$$\begin{aligned} {\mathrm{T}}=2(N-2)\frac{A'B}{rA}+(N-2)(N-3)\frac{B}{r^2}. \end{aligned}$$
(6)

Using the N-dimensional spacetime of Eq. (4) with Eq. (6) and the vector potential \(\mathcal{A} = \Phi (r) dt\), we obtain the following Eq. (3):

$$\begin{aligned}&{I}^t{}_t= \frac{2(N-2)Bf_{TT} T'}{r}\nonumber \\&\quad + \, \frac{(N-2)f_T[2(N-3)AB+rBA'+rAB']}{r^2A} \nonumber \\&\quad - \, f+2\Lambda +\frac{2\Phi '^2(r)B}{A}=0,\nonumber \\&{I}^r{}_r= 2Tf_T+2\Lambda -f\nonumber \\&\quad + \, \frac{2\Phi '^2(r)B}{A}=0,\nonumber \\&{I}^{\phi _1}{}_{\phi _1}= \mathfrak {I}^{\phi _2}{}_{\phi _2}=\cdots \mathfrak {I}^{\phi _n}{}_{\phi _n}=\mathfrak {I}^{z_1}{}_{z_1}\nonumber \\&\quad =\mathfrak {I}^{z_2}{}_{z_2}\cdots =\mathfrak {I}^{z_k}{}_{z_k}= \frac{f_{TT} [r^2T+(N-2)(N-3)B]T'}{(N-2)r}\nonumber \\&\quad + \, \frac{f_T}{2r^2{A}^2}\Biggl \{2r^2ABA''\nonumber \\&\quad - \, r^ 2BA'^2+4(N-3)^2A^2B\nonumber \\&\quad + \, 2(2N-5)rABA'+r^2AA'B'+2(N-3)rA^2B'\Biggr \}\nonumber \\&\quad - \, f+2\Lambda -\frac{2\Phi '^2(r)B}{A}=0, \end{aligned}$$
(7)

where \(\Phi '=\frac{d\Phi }{dr}\). The general N-dimensional solutions with flat horizons of the Maxwell-f(T) theory, where \(f(T)=T+\alpha T^2\) of the above differential equations takes the form [3]

$$\begin{aligned} A(r)= & {} r^2\Lambda _{eff}-\frac{m}{r^{N-3}}+\frac{3(N-3)q{}^2}{(N-2)r^{2(N-3)}}\nonumber \\&+\frac{2\sqrt{6\left| \alpha \right| }(N-3)^3q{}^3}{(2N-5)(N-2)r^{3N-8}}, \nonumber \\ B(r)= & {} A(r)\left[ 1+\frac{(N-3)q\sqrt{6\left| \alpha \right| }}{r^{N-2}}\right] ^{-2},\nonumber \\ \Phi (r)= & {} \frac{q}{r^{N-3}}+\frac{(N-3)^2q{}^2\sqrt{6\left| \alpha \right| }}{(2N-5)r^{2N-5}}, \end{aligned}$$
(8)

where \(\Lambda _{eff}= \frac{1}{6(N-1)(N-2)\left| \alpha \right| }\), m is the mass parameter, q is the charge parameter and \(\Phi (r)\) is the electric potential which defines the vector potential \(\mathcal{A}=\Phi (r)dt\). As it is clear from Eq. (8), that the potential \(\Phi (r)\) depends on a monopole and quadrupole moments. By setting \(q=0\) both momenta vanish and we get a non-charged solution. It is worth mentioning that the solution (8) has been derived for the quadratic polynomial f(T) theory in the presence of the constraint \(\Lambda =\frac{1}{24\alpha }\). Consequently, one expects the model parameter to be \(\alpha <0\), since the cosmological constant is negative. The reason of the constraint \(\Lambda =\frac{1}{24\alpha }\) is as follows: If one chooses an ansatz for the charged solution in which the functions A(r) and B(r) are equal then one gets constant potential, i.e., a trivial potential for a charged solution! In order to avoid this trivial potential, we choose \(A(r)= C(r) B(r)\). In this case the potential will not be trivial, but A(r) and B(r) are neither unique nor in closed form. For example, for the 5-dimensional uncharged solution, \(\Phi (r)=0\), we have \(C(r)=const.\) and

$$\begin{aligned} A(r)=\frac{[1 \pm \sqrt{1-24 \alpha \Lambda }]r^2}{ 72 \alpha } + \frac{c_1}{r^2} \end{aligned}$$

which shows that A(r) is not unique. An extra complication is obtained when the potential is not constant, in this case, A(r) and B(r) can not be expressed in a closed form. Choosing \(\Lambda =\frac{1}{24\alpha }\) leave the solution unique and in a closed form.

Before closing this section, we note that the black hole solution at hand cannot be considered as a special case of the cubic polynomial f(T) gravity which has been studied in [41]. In the later, the solution has been obtained under a specific constraint whereas the coefficient of cubic term cannot be made to vanish.

3 AdS charged rotating black holes with flat horizons

One way to add an angular momentum for the above solution in four dimensionsFootnote 4

$$\begin{aligned} ds^2= -A(r)dt^2+\frac{1}{B(r)}dr^2+r^2\left( d\phi ^2+{dz^2 \over l^2}\right) . \end{aligned}$$
(9)

We follow the procedure developed in [1, 2], applying the transformations

$$\begin{aligned} \bar{\phi } =-\Xi ~ {\phi }+\frac{ \omega }{l^2}~t,\qquad \qquad \qquad \bar{t}= \Xi ~ t-\omega ~ \phi . \end{aligned}$$
(10)

We note that these transformations are allowed locally but not globally on a manifold as will be clarified below. Thus the spacetime (5) reads

$$\begin{aligned} ds^2= & {} -A(r)\left[ \Xi d\bar{t} - \omega d\bar{\phi } \right] ^2+\frac{dr^2}{B(r)}\nonumber \\&+\frac{r^2}{l^4} \left[ \omega d\bar{t}-\Xi l^2 d\bar{\phi } \right] ^2+ {r^2 \over l^2} dz^2, \end{aligned}$$
(11)

where

$$\begin{aligned} \Xi :=\sqrt{1+\frac{\omega ^2}{l^2}}. \end{aligned}$$

According to Stachel [39] if the first Betti number of the manifold is non-vanishing, which is the case for the equivalent Riemannian manifold of these solutions, there are no global diffeomorphisms that can map one of these metrics to the other, leaving the new manifold with an additional parameter “\(\omega \)”. Since in N dimensions we have more than one rotation parameter, the construction of the rotating tetrad or metric is not as obvious as the one rotation parameter case as was shown in [2]. It requires the addition of other terms which are not obtained by the above coordinate transformations. In the higher dimensional case the proposed form of the tetrad for more than one rotation parameter is given by

$$\begin{aligned} \left( {e^{i}}_{\mu }\right) =\left( \begin{array}{cccccccccccccc} \Xi \sqrt{A(r)} &{} 0 &{} -\omega _1\sqrt{A(r)}&{}-\omega _2\sqrt{A(r)}\cdots &{} -\omega _{n}\sqrt{A(r)}&{}0&{}0&{}\cdots &{}0 \\ 0&{}\frac{1}{\sqrt{B(r)}} &{}0 &{}0\cdots &{}0&{}0&{}0&{}\cdots &{} 0\\ \frac{\omega _1r}{l^2} &{}0 &{}-\Xi r&{}0 \cdots &{}0&{}0&{}0&{}\cdots &{} 0\\ \frac{ \omega _2r}{l^2} &{}0 &{}0 &{}-\Xi r\cdots &{} 0&{}0&{}0&{}\cdots &{} 0\\ \vdots &{} \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{} \cdots &{} \vdots \\ \frac{ \omega _nr}{l^2} &{} 0 &{}0&{}0 \cdots &{} -\Xi r&{}0&{}0&{}\cdots &{} 0 \\ 0 &{} 0 &{}0&{}0 \cdots &{}0&{}r&{}0&{}\cdots &{} 0\\ 0 &{} 0 &{}0&{}0 \cdots &{}0&{}0&{}r&{}\cdots &{} 0\\ 0 &{} 0 &{}0&{}0 \cdots &{}0&{}0&{}0&{}\cdots &{} r\\ \end{array} \right) , \end{aligned}$$
(12)

where \(n= \lfloor (N - 1)/2\rfloor \) is the number of rotation parameters with \(\lfloor y \rfloor \) is the integer part of y, \(\omega _j\) are the rotation parameters and \(\Xi \) is defined as

$$\begin{aligned} \Xi :=\sqrt{1+\sum \limits _{j=1}^{{n}}\frac{ {\omega _j}^2}{l^2}}. \end{aligned}$$

Also, the functions A(r) and B(r) are given by (8). In addition, the gauge potential takes the form

$$\begin{aligned} \bar{\Phi }(r)=-\Phi (r)\left[ \omega _i~ d\bar{\phi }_i-\Xi ~ d\bar{t}\,\right] . \end{aligned}$$
(13)

We note that Eqs. (8) and (13) are also solutions of the stationary configuration (12). Since transformation (10) mixes compact and noncompact coordinates, it leaves the local properties of spacetime the same. However, it does change the spacetime properties globally, c.f. [1]. On other words, the vielbein (4) and (12) can be locally mapped into each other but not globally [1, 2]. One can show that the spacetime which is generated by the vielbein (12) takes the form

$$\begin{aligned} ds^2= & {} -A(r)\left[ \Xi d\bar{t} -\sum \limits _{i=1}^{n} \omega _{i}d\bar{\phi } \right] ^2\nonumber \\&+\frac{dr^2}{B(r)}+\frac{r^2}{l^4}\sum \limits _{i=1 }^{n}\left[ \omega _{i}d\bar{t}-\Xi l^2 d\bar{\phi }_i\right] ^2+ {r^2 \over l^2} d\Sigma ^2\nonumber \\&-\frac{r^2}{l^2}\sum \limits _{i<j }^{n}\left( \omega _{i}d\bar{\phi }_j-\omega _{j}d\bar{\phi }_i\right) ^2, \end{aligned}$$
(14)

where \(0\le r< \infty \), \(-\infty< t < \infty \), \(0 \le \phi _{i}< 2\pi \), \(i=1,2, \ldots , n\) and \(-\infty< z_k < \infty \), \(d\Sigma ^2=dz^kdz^k\) is the Euclidean metric on (\(N-n-2\))-dimensions and \(k = 1,2,\ldots , N-3\). We note that the static configuration (9) can be recovered as a special case when the rotation parameters \(\omega _j\) are chosen to be vanished. These charged rotating solutions do not correspond to any known solutions in GR or TEGR since by sending \(\alpha \rightarrow 0\) we do not get a well defined tetrad or metric. Notice that upon setting the mass parameter \(m=0\) and the charge \(q=0\), the line-element (11) reduces to the N-dimensional AdS metric in an unusual coordinate system. One can easily check that the resulting boundary metric is indeed Minkowski through checking the vanishing of its torsion components. Furthermore, this shows that the whole metric in this limit (i.e., line-element with \(m=0\) and the charge \(q=0\)) is the AdS metric. In the next section, we are going to study the main feature of solution (12).

4 Conserved charges

4.1 Four-momentum

Before we calculate the energy or total mass of these black holes, let us follow [4] deriving the conserved four-momentum for f(T) gravity in few lines. Variation of the action (2) with respect to the vielbein gives the field equations in the form

$$\begin{aligned}&{S_\mu }^{\rho \nu } \partial _{\rho } T f_{TT}\nonumber \\&\quad +\left[ e^{-1}{e^a}_\mu \partial _\rho \left( e{e_a}^\alpha {S_\alpha }^{\rho \nu }\right) -{T^\alpha }_{\lambda \mu }{S_\alpha }^{\nu \lambda }\right] f_T\nonumber \\&\quad -\frac{\delta ^\nu _\mu }{4}\left( f+\frac{(N-1)(N-2)}{l^2}\right) =-{\kappa \over 2}{\mathfrak {T}}{^\nu }{_\mu }, \end{aligned}$$
(15)

where \({\mathfrak {T}}{^\nu }{_\mu }\) is the energy-momentum of the matter. Equation (15) can be rewritten as

$$\begin{aligned} \partial _\rho \left( eS^{a \nu \rho }f_T \right) ={\kappa \over 2} |e| \left( t^{a \nu }+T^{a \nu }\right) , \end{aligned}$$
(16)

where

$$\begin{aligned} t^{a \nu }={2 \over \kappa }\left[ f_TS^{b c \nu } T_{b c}{}^a-\frac{\delta ^\nu _\mu }{4}\left( f+\frac{(N-1)(N-2)}{l^2}\right) \right] .\nonumber \\ \end{aligned}$$
(17)

Taking the derivative of Eq. (16) with respect to \(x^\nu \), we get

$$\begin{aligned}&\partial _\nu \partial _\rho \left( eS^{a \nu \rho }f_T \right) =0 \quad \text {which leads to} \nonumber \\&\quad \partial _\nu \left[ {\kappa \over 2} |e| \left( t^{a \nu }+T^{a \nu }\right) \right] =0. \end{aligned}$$
(18)

Equations (18) give the conserved N-momentum of f(T) gravitational theory in the form

$$\begin{aligned} P^a= \int _{V} d^{N-1}x |e| t^{0 a}. \end{aligned}$$
(19)

Equation (19) which defines the N-momentum of f(T) gravity was derived before in [4]. This has been used, mostly, to calculate energy for asymptotically flat spacetime background. However, the solutions (12) are asymptotically AdS. Here we adopt the point of view of the authors in [42,43,44,45] to calculate conserved quantities of a gravitational solution in reference to a specific background spacetime. These backgrounds are naturally chosen as Minkowski spacetime for asymptotically flat solutions and AdS or dS for asymptotically AdS or dS solutions. Furthermore, infinities due to the asymptotic regions are canceled out in this subtraction prescription leaving the physical quantities finite. For example, the total energy of an AdS black hole, measured by a stationary observer at very large radial distance, is considered to be the difference in energy between the AdS black hole and the AdS space itself. Therefore, in calculating the conserved quantities, it is natural to subtract the contribution due to pure AdS spacetime from that of the solution. Therefore Eqs. (19) and (28) take the form

$$\begin{aligned} P^a=\int _{V} d^{N-1}x \left[ |e|t^{0 a}\right] _{reg}, \end{aligned}$$
(20)

where the subscript “reg” stands for the regularized value of the physical quantity.

Let us now calculate the energy related to the rotating charged black holes given by Eq. (12). Using Eq. (19), it is possible to derive the components that are necessary for the calculations of energy in the formFootnote 5:

$$\begin{aligned} S^{(0)(0)1}= & {} \frac{(N-2){B}}{2r}. \end{aligned}$$
(21)
$$\begin{aligned} P^0= & {} E=\frac{(N-2)[m-\Lambda _{eff}\,r^{(N-1)}]\Xi }{3(N-3)G_N}+\left( \frac{1}{r}\right) +...,\nonumber \\ \end{aligned}$$
(22)

where \(n\ge 1\). expression of Eq. (19) takes the form of a surface integral

$$\begin{aligned} P^a_{reg}:= & {} \frac{2}{\kappa }\int _{\partial V} d^{N-2}x \left[ e{S}^{a 0 \mu }\, n_{\mu } f_T\right] \nonumber \\&-\frac{2}{\kappa }\int _{\partial V} d^{N-2}x \left[ e{S}^{a 0 \mu }\, n_{\mu }\,f_T\right] _{AdS}, \end{aligned}$$
(23)

where \(n_{\mu }\) is the normal vector to the surface \(\partial V\) and AdS means evaluating the second expression of Eq. (19) for pure Anti-de-Sitter space. Using (23) in solution (12), we get

$$\begin{aligned} E_{reg} = \frac{2(N-2)\,\Xi \,M}{3\,(N-3)}, \end{aligned}$$
(24)

where the mass parameter is taken to be \(m=2\,G_N\,M\). As expected, the black hole energy is fully characterized by its mass.

4.2 Angular momentum

Although there is a hamiltonian formulation in teleparallel equivalent of general relativity (i.e., \(f(T)=T\)) which produces some known expressions for the conserved four-momenta and angular momentum [5], there is no known expression for angular momentum in f(T) gravity. But since the angular momentum is independent of the charge q, by sending \(q\rightarrow 0\) we obtain a solution with constant torsion scale T, since the scalar torsion is given by,

$$\begin{aligned} T = {-1 \over 6 \alpha }+{2q\sqrt{6} \over 3 \sqrt{\alpha }\,\, r^3}. \end{aligned}$$
(25)

A solution in f(T) gravity with constant torsion scalars, \(T=T_c\), is equivalent to a solution in TEGR with constant torsion, where \(T'=f(T_c)\). Therefore, one can use Maluf’s expression in [5] to calculate the angular momentum of our solution in this limit. Following [5], the angular momentum tensor can be written in terms of the superpotential \(S^{a b c}\) in the following form

$$\begin{aligned} M^{a \mu c}\equiv & {} |e| e_b{}^\mu \left[ S^{a b c}-S^{c a b}\right] =|e| \left[ S^{a \mu c}-S^{c a \mu }\right] \nonumber \\= & {} -\frac{1}{2}\partial _\nu \{|e| \,[e^{a\nu }e^{c \mu }-e^{a\mu }e^{c \nu }] \, \}. \end{aligned}$$
(26)

From Eq. (26) one can easily show that

$$\begin{aligned} \ \partial _\mu M^{a \mu c}=0. \end{aligned}$$
(27)

Using Eqs. (26) and (27) the conserved angular momentum is given by

$$\begin{aligned}&L^{a b}=\int _{V} d^{N-1} M^{a 0 b}\nonumber \\&\quad =-\frac{1}{\kappa }\int _{V} d^{N-1}x \partial _\nu \{|e| \, [e^{a\nu }e^{b 0}-e^{a0}e^{b \nu }] \, \} \nonumber \\&\quad =-\frac{1}{\kappa }\int _{\partial V} d^{N-2}x\; n_\rho |e| \, [e^{a\rho }e^{b 0}-e^{a0}e^{b \rho }], \end{aligned}$$
(28)

where \(n_\rho \) is the outward unit normal vector.

Now we are going to calculate the angular momentum of solution (12) in the limit \(q\rightarrow 0\). For this aim we are going to list the necessary components needed for these calculations. The non-vanishing components of the torsion tensor, \(T^{a b c}=e^a{}_\mu e^b{}_\nu e^c{}_\rho T^{\mu \nu \rho }\), and the superpotential tensor, \(S^{a b c}=e^a{}_\mu e^b{}_\nu e^c{}_\rho S^{\mu \nu \rho }\), are

$$\begin{aligned}&T_{(0) (1) (0) }=\frac{A'\sqrt{B}}{2A}, \end{aligned}$$
(29)
$$\begin{aligned}&T_{(N-i) (N-j) (1) }=\frac{\Bigg (\Bigg [l^2\Xi ^2-\sum \nolimits _{a=1}^{n}\omega _a{}^2\Bigg ]\delta _{i j}+\omega _i\omega _j\Bigg )\sqrt{B}}{l^2\Xi ^2 r}, \end{aligned}$$
(30)
$$\begin{aligned}&T_{\big (N-n-\sum \nolimits _{k=1}^{(N-n-2)}\;\;k\big ) \big (N-n-\sum \nolimits _{k=1}^{(N-n-2)}\;\;k\big ) (1) }=\frac{\sqrt{B}}{r}, \end{aligned}$$
(31)
$$\begin{aligned}&S_{(0) (0) 1}=\frac{(N-2){B}}{2r}, \end{aligned}$$
(32)
$$\begin{aligned}&S_{(N-i) (1) (N-j) }\nonumber \\&\quad =\frac{\sqrt{B}\Bigg (\Bigg [l^2\Xi ^2-\sum \nolimits _{a=1}^{n}\omega _a{}^2\Bigg ]\delta _{i j}+\omega _i\omega _j\Bigg )\Bigg [2(N-3)A+rA'\Bigg ]}{4Al^2\Xi ^2 r},\nonumber \\ \end{aligned}$$
(33)
$$\begin{aligned}&S_{\big (N-n-\sum \nolimits _{k=1}^{(N-n-2)}\;\;k\big ) (1) \big (N-n-\sum \nolimits _{k=1}^{(N-n-2)}\;\;k\big ) }\nonumber \\&\quad =\frac{\sqrt{B}\Bigg [2(N-3)A+rA'\Bigg ]}{4A r}. \end{aligned}$$
(34)

Similar to the energy calculations, we are going to use the background subtraction prescription to calculate the angular momentum of the black hole relative to the AdS space background.

$$\begin{aligned} L^{i j} =-\frac{1}{\kappa }\int _V d^{N-1}x e^i{}_\mu e^j{}_\nu |e| [(S^{\mu 0\nu }-S^{\nu 0 \mu })]_{reg}. \end{aligned}$$
(35)

Using the above equation one gets

$$\begin{aligned} {J_i|}_{reg}=\frac{ \omega _i M }{2\, (N-3)}, \end{aligned}$$
(36)

where

$$\begin{aligned} {J_i}=\epsilon _{i j k}L^{j k}. \end{aligned}$$
(37)

As clear from the above equations that the angular momentum vanishes when the rotation parameters \(\omega _i\) vanish. In conclusion, under the constraint \(q\rightarrow 0\), Eqs. (24) and (36) show that the black holes are characterized by their masses and angular momenta.

5 Conclusions

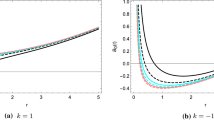
In this work, we present a new class of charged rotating solutions in f(T) theories in N dimensions. These solutions are obtained for \(f(T)=T+\alpha T^2\), where the parameter \(\alpha <0\). It is worth to mention that these solutions cannot be considered as special cases of the solutions of the cubic polynomial f(T) gravity which have been recently studied in [41]. This is because the later are obtained whereas the cubic contribution is parameterized by an extra parameter which cannot be made to vanish. One of the attractive features of the solutions at hand is that their electric potential has related monopole and quadrupole moments. The relation between these moments is a result of demanding an asymptotically AdS solution. It is intriguing to note that all these black holes have a singularity at \(r=0\), which is milder than that of their corresponding solutions in TEGR or GR. The asymptotic behavior of the Kretschmann invariant, the Ricci tensor squared, and the Ricci scalar have the same form of the charged ones presented in [3], i.e. \(K=R_{\mu \nu }R^{\mu \nu } \sim r^{-2(N-2)}\), \(R\sim r^{-(N-2)}\). This is in contrast with their corresponding known solutions in Einstein-Maxwell theory in both GR and TEGR. Also it is important to mention that, in spite that the charged rotating black hole has different components for \(g_{tt}\) and \(g^{rr}\), their Killing and event horizons coincide.

To understand these solutions more, we calculate their total energy and angular momentum. For this aim we have used the mass/energy expression in the framework of f(T) obtained by [4]. For the angular momentum we have used the expression in [5]. We have used the form of the energy-momentum tensor to calculate the total energy of the rotating charged black holes and have shown that the resulting form depends on the mass of the black hole which is consistent with the derived form in [3].

For calculating the angular momentum of the solutions one notices that, although there is a hamiltonian formulation for TEGR, which produces a known expression for the angular momentum, there is no known expression for angular momentum in f(T) gravity. We argue that since the angular momentum in our solution is independent of the charge q, by sending \(q\rightarrow 0\) we obtain a solution with constant torsion scaler T, therefore, one can use the angular momentum expression for TEGR following [5]. As a results we have used the expressions obtained in [4] and [5] to calculate the mass and angular momentum of these solutions together with the subtraction technique used for asymptotically de-Sitter and Anti-de-Sitter solutions. One of the interesting features that we would like to check in future works is that if these milder curvature singularities are weak enough to make these singularities “Tipler weak” according to Tipler’s criteria [46]. If it is weak enough, this might leads to possible extensions of the manifold as was shown in the same theory (i.e., \(f(T)=T+\alpha T^2\)) for some cosmological solutions in [47].