Measurement of the $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\gamma }$ decay form factors in the OKA experiment

Abstract

A precise measurement of the vector and axial-vector form factors difference $F_V-F_A$ in the $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\gamma }$ decay is presented. About 95K events of $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\gamma }$ are selected in the OKA experiment. The result is $F_V-F_A=0.134\pm 0.021(stat)\pm 0.027(syst)$. Both errors are smaller than in the previous $F_V-F_A$ measurements.

Fig. 1

Distribution over the Dalitz-plot ($y,\,x$) for the different terms, contributing to the decay rate as described in Sect. 1: a $f_{IB}(x,y)$, b $f_{INT^-}(x,y)$, c $f_{SD^-}(x,y)$ and $f_{SD^+}(x,y)$, d $f_{INT^+}(x,y)$

Fig. 2

OKA setup. The particle beam goes from left to right

1 Introduction

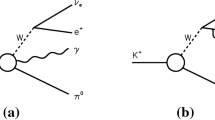
Radiative kaon decays are sensitive to hadronic weak currents in low-energy region and provide a good testing for the chiral perturbation theory (${\chi }PT$). The amplitude of the $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\gamma }$ decay includes two terms: internal bremsstra-hlung (IB) and structure dependent term (SD) [1]. IB contains radiative corrections for $K^+\rightarrow {\mu ^+}{\nu _{\mu }}$ decay. SD is sensitive to the electroweak structure of the kaon.

The differential decay rate can be written in terms of standard kinematic variables $x=2E^{*}_{\gamma }/M_K$ and $y=2E^{*}_{\mu }/M_K$ [2], which are proportional to the photon $E^{*}_{\gamma }$ and muon $E^{*}_{\mu }$ energy in the kaon rest frame ($M_K$ is the kaon mass). It includes IB, SD$^\pm$ terms and their interference INT$^\pm$. The SD$^\pm$ and INT$^\pm$ contributions are determined by two form factors $F_V$ and $F_A$.

The general formula for the decay rate is as follows:

$$\begin{aligned} \frac{d\varGamma }{dxdy}= & {} A_{IB}f_{IB}(x,y)+A_{SD}[(F_V+F_A )^2 f_{SD^+}(x,y)\\&+(F_V-F_A )^2 f_{SD^-}(x,y)]\\&-A_{INT}[(F_V+F_A )f_{INT^+}(x,y)\\&+(F_V-F_A )f_{INT^-}(x,y)], \end{aligned}$$

where

$$\begin{aligned} f_{IB}(x,y)= & {} \left[ \frac{1-y+r}{x^2(x+y-1-r)}\right] \\&\times \left[ x^2+2(1-x)(1-r)-\frac{2xr(1-r)}{x+y-1-r}\right] ,\\ f_{SD^+}(x,y)= & {} [x+y-1-r][(1-x)(1-y)+r], \\ f_{SD^-}(x,y)= & {} [1-y+r][(x+y-1)(1-x)-r], \\ f_{INT^+}(x,y)= & {} \left[ \frac{1-y+r}{x(x+y-1-r)}\right] \\&\times [(1-x)(1-x-y)+r], \\ f_{INT^-}(x,y)= & {} \left[ \frac{1-y+r}{x(x+y-1-r)}\right] \\&\times [x^2-(1-x)(1-x-y)-r], \\ \end{aligned}$$

and $r=[\frac{M_{\mu }}{M_K}]^2$, $A_{IB}=\varGamma _{K_{\mu 2}}\frac{\alpha }{2\pi }\frac{1}{(1-r)^2}$, $A_{SD}=\varGamma _{K_{\mu 2}}\frac{\alpha }{8\pi }\frac{1}{r(1-r)^2}[\frac{M_K}{F_K}]^2$, $A_{INT}=\varGamma _{K_{\mu 2}}\frac{\alpha }{2\pi }\frac{1}{(1-r)^2}[\frac{M_K}{F_K}]$. Here $\alpha$ is the fine structure constant, $F_K$ is $K^+$ decay constant ($F_K = 155.6\pm 0.4\,MeV$ [3]) and $\varGamma _{K_{\mu 2}}$ is the $K_{\mu 2}$ decay width.

Figure 1 shows the kinematic distribution for IB, INT$^-$, INT$^+$, SD$^-$ and SD$^+$. The main goal of the analysis is to measure ${F_V}-{F_A}$ by extracting the INT$^-$ term. Other terms are either suppressed by backgrounds or give negligible contribution to the total decay rate with respect to IB. In the lowest order of ${\chi }PT\,O(p^4)$ $F_V$ and $F_A$ are constant and ${F_V}-{F_A}=0.052$ [2]. The first measurement of ${F_V}-{F_A}$ was made by the ISTRA+ experiment: $F_V-F_A=0.21{\pm }0.04(stat){\pm }0.04(syst)$ [4].

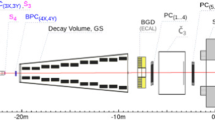
2 OKA detector and separated kaon beam

The OKA setup, Fig. 2, is a double magnetic spectrometer.

The OKA detector includes:

• Beam spectrometer consisting of the magnet M2, 7 beam proportional chambers BPC, 4 beam scintillation counters S and 2 threshold Cherenkov counters $\check{C}_{1,2}$ for the kaon identification;

• 11 m long He filled decay volume DV with the guard system (GS) containing 670 Lead-Scintillator calorimetric modules 20$\times$(5 mm Sc + 1.5 mm Pb) with WLS readout;

• Main magnetic spectrometer on the basis of $200{\times }140$ cm$^2$ wide aperture magnet SP-40A with a field integral 1 Tm, complemented by 13 planes of proportional chambers (PC), straw (ST) and drift tubes (DT);

• 2 gamma detectors: electromagnetic calorimeter GAMS-2000 and large angle detector EGS (EGS is used to supplement GS as a gamma veto at large angles);

• Hadron calorimeter GDA-100 and 4 muon scintillation counters $\mu$C (marked as MC in Fig. 2) used for muon identification;

• Pad (Matrix) Hodoscope MH for the trigger and track reconstruction.

More details can be found in [5].

The data acquisition system of the OKA setup [6] operates at $\sim {25}$ kHz event rate with the mean event size of $\sim {4}$ kByte.

The OKA beam is a separated secondary beam of the U-70 Proton Synchrotron of NRC “Kurchatov Institute”-IHEP, Protvino [7]. RF-separation with the Panofsky scheme [8] is implemented. The beam contains up to $12.5\%$ of kaons with an intensity of about $5\times {10^5}$ kaons per 3 sec U-70 spill. The beam momentum was 17.7 GeV/c during the data taking period used for the analysis (November 2012). The present study uses about half of the statistics collected in 2012, where 504M events were recorded. Another half was taken with a thin copper target inside the decay volume to study the kaon interactions with nucleus. It needs a special consideration, which could be done eventually.

3 Trigger streams and primary selection

The following trigger is used for the analysis: $T_{GAMS}=beam\cdot \overline{\check{C_1}}\cdot \check{C_2}\cdot \overline{S_{bk}}\cdot {E_{GAMS}}$, where $beam={S_1}\cdot {S_2}\cdot {S_3}\cdot {S_4}$ is a coincidence of four beam scintillation counters, $\check{C}_{1,2}$ - threshold Cherenkov counters ($\check{C_1}$ selects pions, $\check{C_2}$ - pions and kaons), $S_{bk}$ (”beam killer”) - two scintillation counters on the beam axis after the magnet aimed to suppress undecayed beam particles. The analog amplitude sum in the GAMS-2000 is required to be higher than $E_{GAMS}$ ($E_{GAMS}$ is chosen to be above the average MIP energy deposit). The 10 times prescaled minimum bias trigger $T_{kaon}=beam\cdot \overline{\check{C_1}}\cdot \check{C_2}\cdot \overline{S_{bk}}$ is used for the trigger efficiency measurement $\epsilon _{trig}={(T_{GAMS}\cap {T_{kaon}})}/{T_{kaon}}$ (Fig. 3).

Fig. 3

Trigger efficiency $\epsilon _{trig}$ as the function of the GAMS total energy deposition. Black points - data, colored curves - fit by the third degree polynomial in four intervals

This trigger efficiency was applied during the Monte Carlo (MC) simulation.

To select the decay channel the following requirements are applied:

• 1 parent $K^+$ track;

• 1 secondary track identified as muon in GAMS-2000, GDA-100 and $\mu$C;

• 1 electromagnetic shower in GAMS-2000 with energy $E_{tot}>1\,GeV$ not associated with charged track;

• GS energy deposition $E_{GS}<10\,MeV$;

• EGS energy deposition $E_{EGS}< 100\,MeV$;

• Decay vertex inside the decay volume DV.

4 Event selection

The main background to the $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\gamma }$ decay comes from 2 decay modes: $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\pi ^0}$ ($K\mu 3$) and $K^+\rightarrow {\pi ^+}{\pi ^0}$ ($K2\pi$) with one $\gamma$ lost from $\pi ^0\rightarrow {\gamma \gamma }$ decay and $\pi$ misidentified as $\mu$. Additional contribution at $y>1$ is given by the decay mode $K^+\rightarrow {\mu ^+}{\nu _{\mu }}$ with an accidental $\gamma$. At low y values there is a small contribution from the $K^+\rightarrow {\pi ^+}{\pi ^-}{\pi ^+}$ ($K3\pi$) decay.

The MC simulation of the OKA setup is done within the GEANT3 framework [9]. Signal and background events are weighted according to corresponding matrix elements. The 22M signal and 624M background MC events are generated.

Fig. 4

Simultaneous fit in the strip 2 (0.15 < x < 0.20): y, $\cos {\theta ^{*}_{\mu \gamma }}$, $m_k$. Black points with errors - data, blue - $K\mu 3$, red - $K2\pi$, yellow - $K\mu 2$, violet - $K3\pi$, green - signal. ${\chi ^2}/NDF=1.7$

The $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\gamma }$ event selection strategy is based on the ISTRA+ approach [4]. Signal extraction procedure starts with dividing all kinematic ($x,\,y$) region into strips in x with $\varDelta {x}=0.05$ width. The following steps are implemented for each x-strip:

• Plot the distribution of the events over y.

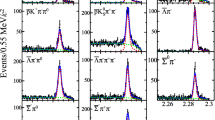
• Select the signal region by a cut $y_{min}<y<y_{max}$ and fill $\cos {\theta ^{*}_{\mu \gamma }}$ plot, where $\theta ^{*}_{\mu \gamma }$ is an angle between $\mu$ and $\gamma$ in the kaon rest frame. $y_{min}$ and $y_{max}$ are selected from the maximization of signal significance defined as $S/\sqrt{S+B}$ where S is the signal and B is the background. For example, the selected cuts for the left plot of Fig. 4 are: $y_{min}=0.85$, $y_{max}=1.0$.

• Apply a cut on $\cos {\theta ^{*}_{\mu \gamma }}$ to futher reject the background. For the middle plot of Fig. 4 the cut is $\cos {\theta ^{*}_{\mu \gamma }}>-0.2$. Plot the distribution of the selected events over $m_k$. $m^{2}_{k}=(P_{\mu }+P_{\nu }+P_{\gamma })^2$, where $P_{\mu }$,$\,P_{\nu }$,$\,P_{\gamma }$ are 4-momenta of decay particles in the laboratory frame, $\mathbf {p}_{\nu }=\mathbf {p}_{K}-\mathbf {p}_{\mu }-\mathbf {p}_{\gamma }$, $E_{\nu }=|\mathbf {p}_{\nu }|$. $m_k$ peaks at the kaon mass for the signal.

• The last step is a simultaneous fit of all 3 histograms ($y, \cos {\theta ^{*}_{\mu \gamma }}, m_k$) with the MINUIT tool [10] where the signal and backgrounds normalization factors are the fit parameters.

For the correct estimation of the statistical error $\sigma _{exp}$, only the $m_k$ histogram is used. The MINOS program [10] is run once with the initial parameter values equal to those obtained in the simultaneous fit. Statistical errors were extracted from the MINOS output.

Figure 5 shows the selected kinematic region for the extraction of the INT$^-$ term. For the further analysis 10 x-strips were selected in the $0.1<x<0.6$ region. The y-width varies from 0.12 to 0.30 inside x-strips.

Fig. 5

INT$^-$ Dalitz-plot density and selected kinematic region (area contoured by the black line)

The result of the simultaneous fit for the strip 2 ($0.15<x<0.2$) is shown in Fig. 4. Both signal and background shapes are taken from the MC simulation. The total normalization of the MC to data is made to the $K\mu 3$ decay at $y<0.6$, where the contribution of other backgrounds is very small. The relative normalization of other backgrounds is done according to their branching ratios. For the $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\gamma }$ decay, only IB term is included in the simultaneous fit. The simultaneous fit gives a reasonable agreement between data and MC with $\chi ^2$ from 1.3 to 1.7 for different x-strips.

5 $F_V-F_A$ calculation

For each x-strip the number of signal events $N_{Data}$ is extracted from the simultaneous fit and the IB event number $N_{IB}$ is obtained from MC. Their ratio is plotted as a function of x (Fig. 6). For the signal containing IB only this ratio would be equal to 1. It is the case for small x, when the IB is dominating and INT$^-$ is negligible. For large x the INT$^-$ term gives significant negative contribution resulting in smaller values of $N_{Data}/N_{IB}$.

Fig. 6

$N_{Data}/N_{IB}$ ratio as a function of x (blue points with errors) and result of the fit with $p_{signal}(x)$ (red line). For the definition of $p_{signal}(x)$, see text

The $N_{Data}/N_{IB}$ distribution is fitted with a function $p_{signal}(x)=p_{0}(1+p_{1}({{\phi }_{INT^-}}(x)/{{\phi }_{IB}}(x)))$, where $p_0$ is normalization factor, $p_1=F_V-F_A$ is the difference of vector and axial-vector form factors, ${{\phi }_{INT^-}}(x)$ is the x-distribution for the reconstructed MC-signal events taken with the weights $({M_K}/{F_K}){f_{INT^-}}(x_{true},y_{true})$, ${{\phi }_{IB}}(x)$ is a similar distribution for the same MC sample, but with the weights ${f_{IB}}(x_{true},y_{true})$. Here $x_{true}$, $y_{true}$ are “true” MC values of x and y.

The result of the fit is $F_V-F_A=0.134{\pm }0.021$. The normalization factor is $p_{0}=1.000{\pm }0.007$. The total number of selected $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\gamma }$ decay events is $95428\pm 309$.

In the next order ${\chi }PT\,O(p^6)$ $F_V$ linearly depends on the momentum transfer $q^2$ [11] with the following parametrization [12]: ${F_V}={F_V(0)}(1+{\lambda }(1-x))$, ${F_A}=const$. The theoretical prediction is tested in three ways:

• The final fit is performed with $F_V$ and $F_A$ fixed from ${\chi }PT\,O(p^6)$ prediction: $F_V(0)=0.082$, $F_A=0.034$, ${\lambda }=0.4$. This fit has bad compliance with ${\chi ^2}/NDF=28.0/9$.

• $F_V(0)$ and $F_A=0.034$ are taken from ${\chi }PT\,O(p^6)$, $\lambda$ is a fit parameter. It gives ${\lambda }=2.28\pm 0.53$ with ${\chi ^2}/NDF=15.8/8$ (Fig. 7).

• $F_V(0)$ is fixed from ${\chi }PT\,O(p^6)$. $F_A$ and $\lambda$ are used as fit parameters. ($F_V,\,\lambda$) correlation is shown in Fig. 8. The theoretical prediction (red star) is slightly out of $3\sigma$-ellipse.

Fig. 7

${\chi }PT\,O(p^6)$ fit, $F_V(0)$ and $F_A$ are taken from theory. The fit gives $\lambda =2.279\pm 0.528$

Fig. 8

($F_V,\,\lambda$) correlation plot. $F_V(0)$ is taken from theory. Red star is theory prediction

6 Systematic errors

The obtained value of $F_V-F_A$ depends on the width of x-strips, y and $\theta ^{*}_{\mu \gamma }$ cuts and the fit procedure. The following sources of the systematic errors were investigated:

• Non ideal description of signal and background by the MC.

  For the estimation of this systematics, the statistical error in each bin of Fig. 6 was scaled by the factor $\sqrt{{\chi ^2}/NDF}$, where ${\chi ^2}/NDF$ is obtained from the simultaneous fit in each x-strip. A new fit of $N_{Data}/N_{IB}$ with the same function $p_{signal}(x)$ gives the best description with ${\chi ^2}/NDF=7.8/8$ compared to ${\chi ^2}/NDF=12.3/8$ of the main fit. The new value of $F_V-F_A=0.138$ is consistent with the main one but the fit error $\sigma _{fit}=0.026$ is larger. Assuming ${\sigma _{fit}}^2={\sigma _{shape}}^2+{\sigma _{stat}}^2$ the systematic error is $\sigma _{shape}=0.015$.

• The fit range in x (number of x-strips in the fit).

  The ratio $N_{Data}/N_{IB}$ was refitted by removing one or two bins on the left (right) edge. For the estimate of systematics the average difference between the new $F_V-F_A$ values and the nominal one is taken. The error is negligible: $\sigma _{x}<0.006$.

• Width of x-strips.

  The $F_V-F_A$ calculation is repeated for 2 different values of x-binning: $\varDelta {x}=0.035$, $\varDelta {x}=0.07$. The deviation of the new $F_V-F_A$ value with respect to the main one gives $\sigma _{\varDelta {x}}=0.011$.

• y limits in x-strips.

  The events inside FWHM of the y-distribution for the signal MC are selected. Such limits are tighter than those used in the main analysis. The difference between the new value and main one gives systematic error $\sigma _{y}=0.008$.

• Possible contribution of INT$^+$.

  The INT$^+$ term is added to the final fit (see Sect. 5). The value $|F_V+F_A|=0.165{\pm }0.013$ measured by the E787 experiment is used [13]. Two fits were repeated for the minimal (−0.178) and maximal (+0.178) possible values of $F_V+F_A$. The fitting function was:

  $p_{signal}(x)=p_{0}(1+({F_V+F_A})({{\phi }_{INT^+}}(x)/{{\phi }_{IB}}(x)) +({F_V-F_A})({{\phi }_{INT^-}}(x)/{{\phi }_{IB}}(x)))$, where ${{\phi }_{INT^+}}(x)$ is the x-distribution similar one as ${{\phi }_{INT^-}}(x)$. The maximal difference between obtained values of $F_V-F_A$ and the main one measured in Sect. 5 is $\sigma _{INT^{+}}=0.018$.

Summing up quadratically all the systematic errors the total error is found to be 0.027.

7 Conclusion

The largest statistics of about 95K events of $K^+\rightarrow {\mu ^+}{\nu _{\mu }}{\gamma }$ is collected by the OKA experiment. The INT$^-$ term is observed and $F_V-F_A$ is measured: $F_V-F_A=0.134{\pm }0.021(stat){\pm }0.027(syst)$. The result is $2.4\sigma$ above ${\chi }PT\,O(p^4)$ prediction.

A recent calculation in the framework of the gauged nonlocal effective chiral action ($E{\chi }A$) gives $F_V-F_A=0.081$ [14]. The OKA result is $1.6\sigma$ above the $E{\chi }A$ prediction.

The obtained value of $F_V-F_A$ is in a reasonable agreement with a similar analysis of the ISTRA+ experiment: $F_V-F_A=0.21{\pm }0.04(stat){\pm }0.04(syst)$ [4].