1 Introduction

As the largest gravitational bound systems in the Universe, galaxy clusters provide a particularly rich source of information about the morphology of our accelerating universe [1]. In particular, X-ray measurements of thermal bremsstrahlung radiation from the hot intracluster medium (ICM) [2,3,4] and the Sunyaev–Zel’dovich (SZ) effect due to inverse Compton scattering of CMB photons by electrons inside the hot ICM [5] became powerful tests. Especially, the latter effect provides us an excellent probe of cosmology [6,7,8] and the dynamical properties of massive galaxy clusters [9,10,11,12]. Much efforts have also been made to explore the sizes of galaxy clusters with the combination of X-ray emission from the ICM and the SZ effect [13, 14]. On the other hand, considering the matter budget, X-ray emitting hot gas constituting the ICM dominates the baryonic mass. The ratio of this gas mass to the total mass (also known as gas mass fraction) in massive clusters of galaxies, is deemed to approximately match the mean universal baryon fraction as \(f_{gas}\propto \gamma (\Omega _b/\Omega _m)\) with a depletion factor \(\gamma \), where \(\Omega _b\) and \(\Omega _m\) are the cosmic baryon density and the total matter density, respectively [15]. It is obvious that such probe provides a robust method to constrain the cosmic matter density \(\Omega _m\), in combination with the constraints on \(\Omega _b\) from cosmic microwave background (CMB) or big bang nucleosynthesis (BBN) data. The idea of using the \(f_{gas}\) measurements in clusters as a cosmological probe was initiated by White et al. [16] and then developed successfully to test modern competing cosmologies [17,18,19], as well as the gas density and temperature profiles of galaxy clusters [20, 21].

However, some problems arise when one uses \(f_{gas}\) observations as a cosmological tool, for instance, the assumption that the gas mass fraction evolves little or does not evolve at all. Therefore, the derived \(f_{gas}\) values should be calibrated with the baryon depletion factor \(\gamma \), the ratio by which the baryon fraction of galaxy clusters is depleted with respect to the universal mean of baryon fraction [17]. This implies that evolutionary behavior of the depletion factor may play a crucial role for the efficiency of \(f_{gas}\) test. In order to quantify the gas content and its possible evolution, parametrized as \(\gamma (z)=\gamma _0(1+\gamma _1z)\), Battaglia et al. [22], Planelles et al. [23] investigated the depletion of X-ray emitting gas relative to the cosmic baryon fraction with hydrodynamic simulations of massive galaxy clusters with \(M_{500}>2\times 10^{14}h^{-1}M_{\odot }\). As usual, \(M_{500}\) denotes the total mass within \(R_{500}\), the radius inside which the mass density is 500 times the critical density of the universe. Their results suggested the depletion factor inside \(R_{500}\) quantified with \(\gamma _{0}=0.85\pm 0.03\) and \(\gamma _1=0.02\pm 0.07\), which indicated that at \(z<1\) the gas mass fraction at intermediate to large cluster radii should have small cluster-to-cluster scatter and should not evolve with redshift. The first attempt of studying the depletion factor with observational data was performed by Holanda et al. [24], who used the luminosity distances from type Ia supernova [25] to calibrate the gas mass fraction inside the \((0.8-1.2)\times r_{2500}\) shell using Chandra X-ray measurements [3]. More recently, with the combination of gas mass fraction obtained from X-ray measurements [26] and angular diameter distances from SZ effect/X-ray measurements, Holanda [27] found a mild redshift evolution of the depletion factor.

Several factors should be taken into account, however, in order to appropriately assess the possible redshift evolution of the gas depletion factor. First of all, either negligible or significant evolution of \(\gamma \) parameter might be just a statistical artefact produced by not particularly rich or deep observational data used in these studies. This suggests that the increased depth and quality of observational data set may result with more firm and robust conclusions [18]. Secondly, accuracy of distance determination may strongly influence the estimated value of the \(\gamma \) parameter. For instance, in the framework of the Planck’s best-fitted \(\Lambda \)CDM cosmology [28], there appears no redshift evolution of the depletion factor for the gas mass fraction from X-ray measurements of several galaxy clusters [27]. In this context, collection of more complete observational data concerning the gas mass fraction does play a crucial role. In our paper we turn to the largest SZ cluster sample derived from observations by the Atacama Cosmology Telescope Polarization experiment (ACTPol) [12], which comprises a catalog of 182 galaxy clusters covering the redshift range of \(0.1<z<1.4\). Our purpose is to probe possible evolution of the gas depletion factor inside \(R_{500}\). Moreover, compared with the previous works using the luminosity distances from type Ia supernova [24, 27], we will use instead, angular diameter distances covering the cluster redshift range derived in a cosmological-model-independent way from cosmic chronometers’ H(z) measurements using Gaussian processes (GP).

The idea of cosmological application of GP technique in general and with respect to H(z) data in particular, was first discussed in Holsclaw et al. [29] and then extensively applied in more recent papers to test the cosmological parameters [30,31,32], the distance-duality relation [33], spatial curvature of the Universe [34,35,36], and the speed of light at higher redshifts [37]. We expect that the newest measurements of \(f_{gas}\) combined with non-parametric distance reconstruction from the most recent H(z) data will shed much more light on the gas content within \(R_{500}\) and its possible evolution. This paper is organized as follows: In Sect. 2, we introduce our methodology, then we briefly describe the galaxy cluster sample from ACTPol and the Hubble parameters from passively evolving galaxies. The results and corresponding discussion are presented in Sect. 3. Finally, the discussion and conclusions are respectively summarized in Sects. 4 and 5.

2 Methodology and data

2.1 Gas mass fraction and depletion factor

The gas mass fraction, \(f_{gas}=M_{gas}/M_{tot}\), is the ratio of the X-ray emitting gas mass \(M_{gas}\) to the cluster total mass \(M_{tot}\). Following Allen et al. [17], the general expression for the gas mass fraction fitted to the reference model can be given by

$$\begin{aligned} f^{ref}_{gas}=K(z)A\gamma (z)\left( \frac{\Omega _b}{\Omega _m}\right) \left[ \frac{D^{ref}_A(z)}{D_A(z)}\right] ^{1.5} \end{aligned}$$
(1)

where K(z) is the calibration constant parameterizing the uncertainty of the instrument calibration and X-ray modeling, which conservatively includes a 10% Gaussian uncertainty \(K=1.0\pm 0.1\) [17]. Throughout this work a flat \(\Lambda \)CDM is assumed as the fiducial cosmological model, with the matter density \(\Omega _m=0.3\), the cosmological constant representing dark energy density \(\Omega _{\Lambda }=0.7\), and the Hubble constant \(H_0=70 \;{\mathrm{km}}^{-1}\,{\mathrm{Mpc}}^{-1}\). The factor A, which quantifies the change in the angle subtended as the cosmology is varied, is always very close to unity. In our analysis, we take the prior of \(\Omega _b=0.0480\pm 0.0002\) and \(\Omega _m=0.3156\pm 0.0091\) from the results of [28]. \(D_A(z)\) is the true angular diameter distance to the cluster, while \(D^{ref}_A(z)\) – its corresponding counterpart calculated in the reference cosmology. Under the assumption of fiducial cosmological model the latter can be calculated as

$$\begin{aligned} D^{ref}_A(z)=\frac{c}{H_0}\frac{1}{1+z}\int ^z_0 \frac{dz'}{\sqrt{\Omega _m(1+z')^3+(1-\Omega _m)}} \end{aligned}$$
(2)

Finally, the gas depletion parameter \(\gamma (z)\), the ratio by which the baryon fraction measured in clusters is depleted with respect to the universal mean, is related to thermodynamic history of X-ray emitting gas in the course of cluster formation. According to Eq. (1), the observed value of \(\gamma (z)\) can be expressed as

$$\begin{aligned} \gamma (z)=\frac{f^{ref}_{gas}}{K} \left( \frac{\Omega _b}{\Omega _m}\right) ^{-1} \left( \frac{D_A(z)}{D^{ref}_A(z)}\right) ^{3/2}. \end{aligned}$$
(3)

It is evident that, with a larger sample of \(f_{gas}\) measurements covering substantial redshift range, the Eq. (3) can provide useful insight into possible redshift evolution of the depletion factor. Moreover, one can see that the uncertainty with respect to the true angular diameter distances may also affect the strength of this test. Contrary to the previous work [24] based on luminosity distances from JLA SNe Ia [25], translated to angular diameter distances by using the distance duality relation \(D_L(z)(1+z)^{-2}/D_A(z)=1\), in this work we derive true angular diameter distances directly from the cosmic chronometers H(z) measurements using publicly available code GaPP (Gaussian Process in Python) [30].

2.2 Galaxy cluster sample

The gas mass fraction data used in this paper comprises 182 clusters [12] covering \(0.1<z<1.4\) with the median redshift \(z=0.49\), observed by the Atacama Cosmology Telescope Polarization experiment (ACTPol). The corresponding cluster redshift was taken from other surveys or measured in their own follow-up observations. In order to obtain the gas mass fraction for these galaxy clusters, we used a semi-empirical relation verified by Vikhlinin et al. [4], in which the gas mass fraction follows a linear relation with the logarithm of the cluster total mass \(M_{500}\) inside the radius \(R_{500}\). It should be noted that different pressure profile models will provide slightly different total mass measurements [12]. In order to estimate this mass for each cluster, the so-called Universal Pressure Profile (UPP) and its associated mass-scaling relation [38] should be considered. After the calibration of the ratio between UPP-based mass and weak-lensing mass [6, 39], the final sample of \(M_{500}\) data is provided in Hilton et al. [12]. Based on these measurements, one can assess the gas mass fraction through the following semi-empirical relation [4]:

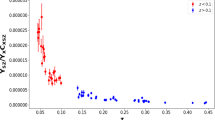
$$\begin{aligned} f_{gas}=0.132+0.039\log {M_{15}} \end{aligned}$$
(4)

where \(M_{15}\) is the cluster total mass in the units of \(10^{15}h^{-1}M_{\odot }\). We remark here that, compared with the statistical uncertainty of \(M_{15}\), uncertainties of two coefficients in the above relation are negligible [12]. Figure 1 displays the derived \(f_{gas}\) measurements and their statistical uncertainties.

Fig. 1
figure 1

The gas mass fraction derived from ACTPol measurements [12]. Blue circles with red bars represent central values and corresponding \(1\sigma \) uncertainties calculated from cluster total mass based on the semi-empirical relation

Full size image

2.3 Cosmic chronometer sample

Observational values of the Hubble parameter H(z) at different redshifts can be obtained through two distinct methods: cosmic chronometers, i.e., the differential ages of passively evolving galaxies and the BAO peak position in the radial direction. However, as extensively discussed in the literature [40], systematic differences between these two approaches should be better understood before one can use them jointly to get unbiased results. Considering the fact that the only assumption for the cosmic chronometer method is the stellar population model, which is independent of the cosmological model, we prefer cosmic chronometers in this paper. (See [41,42,43] for the cosmological applications of the Hubble parameter measurements). In particular, following Zheng et al. [40, 44], Qi et al. [45] we used the recent compilation of 30 H(z) measurements from the differential age technique, covering the redshift range \(0.07<z<1.965\) corresponding to the redshifts of clusters for which the gas mass fraction was measured. Using the aforementioned Gaussian processes we were able to reconstruct the profile of H(z) function up to the redshifts \(z=2\), which can subsequently be used to reconstruct the distance. The results are shown in Fig. 2, where the reconstructed H(z) function with corresponding \(1\sigma \) and \(2\sigma \) uncertainty strips are displayed.

3 Analysis and results

In the first step, we reconstructed the gas depletion factor as a function of redshift. The procedure was carried out in the following way: (1) we firstly used the GPs to reconstruct \(f_{gas}(z)\) function based on the derived discrete gas mass fraction from Eq. (4). The choice of covariance functions from the Mantérn family has negligible influence on the final result [24]. (2) Then the \(D_A(z)\) function was reconstructed form H(z) data (assuming flat universe). (3) Based on the reconstructed functions of \(f_{gas}(z)\) and \(D_A(z)\), combined with the priors of other relevant parameters as discussed in Sect. 2.1, the \(\gamma (z)\) function was reconstructed. Results are shown in Fig. 3.

Fig. 2
figure 2

Hubble parameter measurements from cosmic chronometers (red points) and the reconstruction of H(z) function (green envelope). Blue line corresponds to the fiducial cosmological model

Full size image
Fig. 3
figure 3

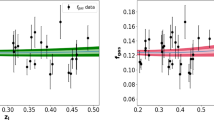
Reconstructed gas depletion factor \(\gamma (z)\) for the full (green solid line) and reduced (magenta dashed line) ACTPol cluster sample, with the shadow regions showing the 1\(\sigma \) region calculated with the error propagation. The gray dashed region corresponds to the hydrodynamical simulation results

Full size image

Contrary to the previous works, the negative time evolution of the gas depletion factor \(\gamma _{500}\) can be clearly seen from the full ACTPol cluster sample. This result is different from the previous analysis with a smaller sample focusing on the inner region of galaxy clusters (\(r<r_{2500}\)), combined with angular diameter distances derived from the SN Ia observations. For instance, with 40 \(f_{gas}\) measurements in the redshift range of \(z\in [0.063,1.063]\) [17] and 42 \(f_{gas}\) measurements in the redshift range of \(z\in [0.078,1.063]\) [3], no significant evolution of \(\gamma (z)\) was found within \(R_{2500}\) [24]. In order to compare our reconstruction with the results of hydrodynamical simulations Battaglia et al. [22] and Planelles et al. [23] the gray strip \(\gamma =0.85\pm 0.03\) is also plotted in Fig. 3. One can see that central values of our reconstructed \(\gamma (z)\) are consistent with hydrodynamical simulations up to the redshift \(z=0.4\), afterwards the reconstructed \(\gamma (z)\) continues decreasing. Not only central values but also associated \(1\sigma \) strips of the reconstructed \(\gamma (z)\) display decreasing trend. If the sample of clusters was deeper than \(z=1.4\) and trend did not reverse, the strips would disconnect. Because the simulations of Battaglia et al. [22] and Planelles et al. [23] comprised cluster redshifts \(z<1\), one might worry whether a larger redshift coverage of the ACTPol data could be responsible for the difference in trends seen in Fig. 3. Therefore we repeated calculations on the reduced ACTPol sample (ACTPol-re hereafter) where 10 higher redshift (i.e. \(z>1\)) clusters were excluded. One can see in Fig. 3 that the difference between the full and reduced ACTPol samples is negligible. This means that the evolutionary trend \(\partial \gamma /\partial z<0\) of the depletion factor cannot be simply attributed to the leverage of galaxy clusters located at \(z>1\). Therefore, the trend of \(\gamma (z)\) decreasing with redshift revealed in our study could reflect real evolutionary processes of intracluster medium within \(R_{500}\). Let us remark here that the gas mass fraction obtained under hydrostatic equilibrium assumption could be overestimated, or the true mass is underestimated especially at large radii, which is strongly supported by recent numerical simulations and comparisons between X-ray and lensing masses [2, 46]. This effect could manifest itself as lower gas depletion factor, which still needs to be investigated with more available data.

In the second step, we investigated the issue of \(\gamma (z)\) evolution using a parametric approach first used (with different notations) in [17]

$$\begin{aligned} \gamma (z)=\gamma _0(1+\gamma _{1}z) \end{aligned}$$
(5)

where \(\gamma _0\) denotes the depletion factor normalization and \(\gamma _1\) quantifies its possible evolution with redshift. Using the Python package emcee [57], which includes Markov chain Monte Carlo (MCMC) sampler, we calculated the posterior likelihood \(\mathcal {L}\sim exp(-\chi ^2/2)\), where

$$\begin{aligned} \chi ^2=\sum ^n_{i=1}\frac{(\gamma _{th}(z_i)-\gamma _{obs}(z_i))^2}{\sigma ^2_{i,obs}}. \end{aligned}$$
(6)
Fig. 4
figure 4

Confidence contours for the \(\gamma (z)\) parameters in \(\gamma (z)=\gamma _0(1+\gamma _{1}z)\). Green solid lines and magenta dashed lines correspond to the fits obtained on the the full and reduced ACTPol cluster sample

Full size image
Fig. 5
figure 5

Gas mass fraction derived from ACT compilation [11] (left panel) and the corresponding reconstruction of the gas depletion factor \(\gamma (z)\)

Full size image

Theoretical expression for the depletion factor \(\gamma _{th}\) and the corresponding observational counterpart \(\gamma _{obs}\) are respectively calculated from Eqs. (5) and (3), \(\sigma ^2_{i,obs}\) denotes the uncertainty of \(\gamma _{obs}\) calculated according to the standard law of uncertainty propagation using uncertainties of K, \(\Omega _b\), \(\Omega _m\), \(D_A\). Performing fits on the full and restricted ACTPol sample, we obtained the results displayed in Fig. 4. The best-fitted \(\gamma \) parameters are \(\gamma _0=0.840^{+0.025}_{-0.025}(1\sigma )^{+0.048}_{-0.048}(2\sigma )\), \(\gamma _1=-0.072^{+0.044}_{-0.049}(1\sigma )^{+0.095}_{-0.086}(2\sigma )\) for the full ACTPol sample and \(\gamma _0= 0.835^{+0.028}_{-0.028}(1\sigma )^{+0.056}_{-0.056}(2\sigma )\), \(\gamma _1=-0.060^{+0.056}_{-0.063}(1\sigma )^{+0.120}_{-0.110}(2\sigma )\) for the ACTPol-re sample, respectively. One can see that the fit on \(\gamma _0\) is essentially consistent with previous hydrodynamical simulations [22, 23] and observational tests with smaller cluster sample [24, 27]. However, we also find that \(\gamma _1=0\) is excluded at \(1\sigma \) confidence level for both (i.e. full and reduced) cluster samples. This is in agreement with the reconstruction of the \(\gamma _{500}(z)\) function and indicates a mild evolutionary trend of the gas depletion factor, which is independently supported by the angular diameter distance measurements obtained from the SZ/X-ray technique [27].

Table 1 Summary of the best-fitted gas depletion factor parameters and the corresponding \(1\sigma \) uncertainty in this analysis and in the literature [23, 24, 27], obtained at different cluster radius (\(R_{500}\) and \(R_{2500}\)) from non-radiative(NR) simulations [23] and different \(f_{gas}\) samples [12, 26]. In the previous works, the luminosity distances/angular diameter distances are derived from recent SN Ia observations, SZ effect/X-ray measurements of Cluster I [13] and Cluster II [14], or in the framework of Planck’s best-fitted \(\Lambda \)CDM cosmology [28]
Full size table

Some sources of systematic effects that might influence our results should be discussed. First of all, it is evident from Eq. (3) that \(\gamma (z)\) functional dependence on redshift is determined by the angular diameter distance ratio \(\frac{D_A(z)}{D^{ref}_A(z)}\) and possible redshift dependence of the \(f_{gas}\). However, one can see in Fig. 2, that H(z) function reconstructed non-parametrically from cosmic chronometers agrees very well with the reference cosmological model. Indeed, noticeable divergence between them can be seen at redshifts \(z>1.5\) which are larger than the depth of the cluster sample. In order to check the influence of the cosmological model on the results quantitatively, we also repeated the calculations assuming that the fiducial cosmological model is the true one, i.e. \(D_A(z)=D^{ref}_A(z)\). We found this influence negligible. This means that evolutionary trend of \(\gamma (z)\) discussed above could be attributed to possible evolution of \(f_{gas}\). One might raise an objection that our result was obtained on a particular sample of clusters and therefore could not be representative. In order to address this issue we studied in the same way the sample of 91 SZ detected clusters (ACT compilation) reported in Hasselfield et al. [11] and a consistent result is given in Fig. 5. Using it we made an extrapolation to \(z=1.4\) and the question arises if it was justified. The validity or recalibration of \(M_{tot}\)–\(f_{gas}\) relation at higher redshifts remains open and should be addressed in a separate study. It should be stressed, that the gas mass fraction has been derived from semi-empirical relation commonly used in cosmology. Such approach was used for example, to test the validity of distance duality relation (DDR) [47], the evolution of dark energy equation of state [48] and the evolution of the fine-structure constant [49]. Finally, the well-known distance duality relation could potentially be the third important source of systematic error on the final results. As it was extensively discussed in the literature [50], the equivalence of the gas mass fraction obtained from the two major techniques, SZ effect and X-ray surface brightness observations, might be slightly affected by the possible deviation from the distance duality relation. Based on the \(f_{gas}\) observations derived from ACT compilation, Gonca̧lves et al. [47, 51] addressed the question of DDR on SZ gas mass fraction measurements and concluded that the major source of uncertainty comes from the gas mass fraction derived from SZ effect. A more detailed study of such possibilities will be the subject of a separate paper.

4 Discussion

Now one important issue is the comparison of our results with those of earlier studies done using other, alternative methodologies. The numerical results are summarized in Table 1. Using a set of hydrodynamical simulations of galaxy clusters characterized by different physical processes, Planelles et al. [23] explored how the fraction and spatial distribution of baryons (contributed both by the stellar component and the hot X-ray emitting gas), are affected by the feedback from supernova (SN) and active galactic nuclei (AGN) within \(R_{500}\) and \(R_{2500}\). More specifically, the depletion factor \(\gamma (z)\), as well as its dependence on redshift, baryonic physics, and cluster radius were thoroughly discussed. Their results showed that the depletion in baryon content within \(R_{500}\) is more pronounced, with a stronger mass dependence for the simulations including AGN feedback. However, in the framework of the functional form of \(\gamma (z)=\gamma _0+\gamma _1z\), the baryon depletion factor does not evolve significantly with redshift (\(z<1\)), regardless of the considered radius or physics. At last, the simulation results gave the best-fit parameter: \(\gamma _0=0.85\pm 0.03\), \(\gamma _1=0.02\pm 0.05\) at \(R_{500}\) and \(\gamma _0=0.79\pm 0.07\), \(\gamma _1=0.07\pm 0.12\) at \(R_{2500}\) [23]. On the other hand, the attempt to determine the baryon depletion factor with currently available observations was presented in Holanda et al. [24], which investigated the viability of using 40 X-ray emitting gas mass fraction measurements [26] and luminosity distance measurements from SNe Ia [25] (based on the validity of distance duality relation [52]) to place additional constraints on the behavior of \(\gamma (z)\). It was found that \(\gamma _0=0.85\pm 0.08\) and \(\gamma _1=0.00\pm 0.05\) within \(R_{2500}\), from which one may observe the well consistency between fits obtained from current observations and hydrodynamical simulations. Further papers have also studied the possible time evolution for \(\gamma (z)\), in light of exclusively galaxy cluster data. More recently, Ref. [27] proposed a new method to investigate the depletion factor, in light of X-ray gas mass fraction and angular diameter distance measurements from Sunyaev–Zel’dovich effect plus X-ray observations [13, 14]. Note that in their analysis, the electron density and temperature profiles of galaxy clusters, which provide the measurements of angular diameter distances, are described by the non-isothermal double \(\beta \)-model or under the assumptions of spherical symmetry and hydrostatic equilibrium [13, 14]. Different from the findings of the simulations, the analysis has revealed a non-negligible time evolution for the depletion factor: \(\gamma _1=-0.42^{+0.42}_{-0.40}\) and \(\gamma _1=0.16\pm 0.36\). Such conclusion, however, disagrees with the constraints on depletion factor (\(\gamma _0=0.84\pm 0.07\), \(\gamma _1=-0.02\pm 0.14\)) by using the same \(f_{gas}\) sample and angular diameter distances obtained from the flat \(\Lambda \)CDM model (Planck results) [27]. Therefore, the importance of non-parametric reconstruction of angular diameter distance using Hubble parameters from cosmic chronometers are indeed revealed in this analysis.

We also provide a graphical representation of the comparison results in Fig. 6, which directly shows the depletion factor parameters obtained in this analysis and the previous works (see Table 1 for details). The red circle and square denote the best-fitted gas depletion factor within the cluster radius of \(R_{500}\), concerning the whole ACTPol and reduced ACTPol sample, respectively. The grey dashed and white netted region show the hydrodynamical simulation results (\(1\sigma \) uncertainties) at different cluster radius (\(R_{500}\) and \(R_{2500}\)), while the triangles with different directions represent the best-fitted gas depletion factor parameters within \(R_{2500}\), concerning the LaRoque et al. [26] \(f_{gas}\) sample and different distance indicators (SN Ia observations, SZ effect/X-ray measurements of galaxy clusters, and Planck’s best-fitted \(\Lambda \)CDM cosmology). On the one hand, we find that the \(\gamma _0\) value is in full agreement with the simulated results derived within \(R_{500}\). On the other hand, although the \(\gamma _1\) value in our analysis is compatible with \(\gamma _1=0\) within 2\(\sigma \), a non-negligible time evolution for the depletion factor is still supported by the current observations. Such tendency is clearly in tension with the results of cosmological hydrodynamical simulations [23], but well consistent with the self-consistent observational constraints by using exclusively galaxy cluster data [27].

Fig. 6
figure 6

Comparison of the best-fitted gas depletion factor parameters (\(\gamma _0, \gamma _1\)). The red circle and square denote the best-fitted gas depletion factor within the cluster radius of \(R_{500}\), concerning the whole ACTPol and reduced ACTPol sample, respectively. The grey dashed and white netted region show the hydrodynamical simulation results (\(1\sigma \) uncertainties) at different cluster radius (\(R_{500}\) and \(R_{2500}\)), while the triangles represent the best-fitted gas depletion factor parameters within \(R_{2500}\), given the same \(f_{gas}\) sample and different distance indicators

Full size image

5 Conclusions

We studied the evolution of the gas depletion factor \(\gamma (z)\) inside the radius \(R_{500}\), using the largest SZ cluster sample obtained by the Atacama Cosmology Telescope Polarization experiment (ACTPol) [12]. The sample comprised 182 galaxy clusters covering the redshift range of \(0.1<z<1.4\). Using two methods: non-parametric reconstruction of \(\gamma (z)\) and fitting \(\gamma _0, \gamma _1\) parameters in the evolutionary model \(\gamma (z)=\gamma _0(1+\gamma _{1}z)\) we revealed an unambiguous trend of \(\gamma (z)\) decreasing with redshift. This is contrary to recent claims of Holanda et al. [24] who found no evidence for such evolution. However, their analysis was focused on \(\gamma (z)\) inside the inner region of galaxy clusters (\(r<r_{2500}\)) and performed on a smaller sample. It should be noted that the best-fitted value our reconstructed \(\gamma (z)\) is well consistent with the hydrodynamical simulations at \(z<0.4\) [22, 23]. However, when the 1\(\sigma \) uncertainty is taken into account, the \(\gamma (z)\) reconstructed from the full ACTPol sample and hydrodynamical simulations overlap with each other. On the other hand, the reconstructed uncertainty strip displays an unambiguous trend while the simulation results stay constant. They would eventually detach once we had access to cluster data at higher redshifts. Moreover, parametric fits excluded no evolution case of \(\gamma _1=0\) at \(1\sigma \) confidence level. These results have been confirmed on the reduced ACTPol measurements, the redshift coverage of which is consistent with that of hydrodynamical simulations (\(z<1\)) and on the alternative sample of 91 SZ clusters reported earlier in ACT compilation. Discussion of possible systematic effects leaves one open question about validity of the empirical relation \(M_{tot}\)–\(f_{gas}\) obtained on very close clusters.

Summarizing, the results presented in this paper could pave the way to explore the hot gas fraction within large radii of galaxy clusters as well as its possible evolution with redshift, which should be studied further on larger galaxy cluster samples available in the upcoming X-ray/SZ cluster surveys. With the dawn of the era of GW astronomy, which was opened by the first direct detection of gravitational waves (GWs) by the LIGO/Virgo collaboration [53], one could expect the possibility of testing \(\gamma (z)\) at much higher precision in the future, along with the observational search for more GW events with smaller statistical and systematic uncertainties [54,55,56].