Quasi-two-body decays $B \rightarrow D K^*(892) \rightarrow D K \pi$ in the perturbative QCD approach

Abstract

We study the quasi-two-body decays $B\rightarrow D K^*(892) \rightarrow D K\pi$ by employing the perturbative QCD approach. The two-meson distribution amplitudes $\Phi _{K\pi }^{P\text {-wave}}$ are adopted to describe the final state interactions of the kaon–pion pair in the resonance region. The resonance line shape for the P-wave $K\pi$ component $K^*(892)$ in the time-like form factor $F_{K\pi }(s)$ is parameterized by the relativistic Breit-Wigner function. For most considered decay modes, the theoretical predictions for their branching ratios are consistent with currently available experimental measurements within errors. We also disscuss some ratios of the branching fractions of the concerned decay processes. More precise data from LHCb and Belle-II are expected to test our predictions.

1 Introduction

Many three-body hadronic B meson decays including $B \rightarrow DK\pi$ have been studied experimentally in recent years [1, 2]. The $B \rightarrow DK\pi$ decays have demonstrated the potential to determine the CKM angles precisely. Suggestions for the determination of the unitarity triangle angle $\gamma$ through Dalitz plot [3] analyses of the decays $B^\pm \rightarrow D K^\pm \pi ^0$ and $B^0 \rightarrow DK^+\pi ^-$ were proposed in [4,5,6], respectively. And the measurement has been performed by LHCb [7]. The ${ BABAR}$ Collaboration has presented a measurement of the weak phase $2\beta +\gamma$ from the time-dependent Dalitz plot analysis of the $B^0 \rightarrow D^{\mp } K^0 \pi ^{\pm }$ decays [8]. In addition, the decay modes $B\rightarrow DK\pi$ have provided rich opportunities to investigate the spectroscopy of excited charm mesons and the significant components originated from $K\pi$ system, corresponding results have been acquired from Dalitz plot analyses of $B^0 \rightarrow D^{(*)\pm }K^0\pi ^{\mp }$ [9], $B_s^0 \rightarrow \bar{D}^0K^-\pi ^+$ [10, 11], $B^- \rightarrow D^+K^-\pi ^-$ [12] and $B^+ \rightarrow D^+K^+\pi ^-$ [13] decays. In the amplitude analyses of $B \rightarrow D K \pi$ decays, contributions from the P-wave $K\pi$ resonant state $K^*(892)$¹ were found to be the largest proportion in most cases, and the $B \rightarrow DK^*$ decays have been substantially studied in experiment by quasi-two-body approach [14,15,16,17,18,19,20,21,22,23].

On the theoretical side, the charmed hadronic B meson decays $B\rightarrow DK^*$ have been studied by using rather different methods in Refs. [24,25,26,27,28,29,30,31,32]. The $K^*$ was treated as a stable particle in the framework of two-body decays while as a resonance with the cascade decay $K^*\rightarrow K\pi$ in the three-body decays. Several approaches have been adopted to describe those three-body B decays involving $K\pi$ systems. For instance, within the QCD factorization [33,34,35], the authors studied the CP violation and the contribution of the strong kaon–pion interactions in the three-body $B\rightarrow K\pi \pi$ decays [36, 37] where the $K^*(892)$ and $K_0^*(1430)$ resonance effects were mainly taken into account. In Ref. [38], the calculation of the localized CP violation in $B^-\rightarrow K^-\pi ^+\pi ^-$ decays has been done with the $K\pi$ channels including $K^*(892)$, $K_0^*(1430)$, $K^*(1410)$, $K^*(1680)$ and $K_2^*(1430)$. Using a simple model on the basis of the factorization approach, the branching ratios and direct CP violation for the charmless three-body hadronic decays $B_{(s)} \rightarrow KK\pi$ and $B_{(s)} \rightarrow K\pi \pi$ have been calculated in Refs. [39,40,41,42]. In the recent works, the $K\pi$ contributions to the decay channels $B\rightarrow \psi K\pi$ [43] and $B\rightarrow P K\pi$ [44], with $\psi =(J/\psi ,\psi (2S))$ and $P=(K,\pi )$, were analyzed by employing the perturbative QCD (PQCD) factorization approach [45,46,47,48]. In addition, phenomenological studies of the processes $\bar{B}^0 \rightarrow D^0\pi ^+\pi ^-$ and $\bar{B}_s^0 \rightarrow D^0 K^+\pi ^-$ based on results of the chiral unitary approach has been performed in Ref. [49]. Motivated by the abundant experimental data and theoretical studies, we shall analyse the contributions of the resonance $K^*$ in the $B \rightarrow DK\pi$ decays in this work.

In the framework of the PQCD factorization approach, the two-body charmed hadronic decays $B \rightarrow D M$ have been studied for many years [26, 28, 30, 50,51,52,53,54,55,56,57,58,59,60,61,62]. In Refs. [50, 51], the authors examined the PQCD formalism to B to D transitions and discussed some related two-body nonleptonic decays. Assuming the hierachy $m_B\gg m_D\gg \bar{\Lambda }$ with $\bar{\Lambda }=m_B-m_b$, the $B \rightarrow D^{(*)}$ form factors in the heavy-quark and large-recoil limits were calculated in Ref. [52]. The next-to-leading-power corrections were found to be less than $20\%$ of the leading contribution, indicating that the power expansion made sense, and the results of the $B\rightarrow D \pi$ branching ratios were consistent with the experimental results. It is worth to mention that the contribution from nonfactorizable and annihilation-type diagrams is also important in the $B \rightarrow DM$ decays [53]. As a feature of PQCD, all topologies of decay amplitudes are calculable which makes it advantageous to study those charmed B decays including the pure annihilation type decays and the color suppressed decays in the PQCD approach. Some separate calculations for the two-body charmed decays of B meson were carried out in Refs. [26, 54,55,56,57]. In Ref. [55], specifically, the authors studied the annihilation type decay $B \rightarrow D_s K$ and gave the PQCD prediction for a sizable branching ratio $\mathcal{B}(B^0 \rightarrow D^-_s K^+)\sim 10^{-5}$, which has already been confirmed by experiments [1, 2]. In the past decade, the two-body charmed decays $B\rightarrow DS, DP, DV, DA, DT$, where S, P, V, A, T denote the scalar, pseudoscalar, vector, axial-vector and tensor mesons, have been studied systematically in [28, 30, 58,59,60,61,62] by employing the PQCD approach and most of the predictions are in good agreement with the available experimental data. Therefore, it is interesting and meaningful to analyse the relevant three-body charmed hadronic B meson decays within the same method.

Theoretically, the three-body hadronic B meson decays are much more complicated than the two-body cases because of their non-trivial kinematics and the different phase space distributions. While these three-body decay processes are known to be dominated by the low energy scalar, vector and tensor resonant states, which could be handled in the quasi-two-body framework by neglecting the three-body and rescattering effects [63,64,65,66,67]. In the quasi-two-body region of the phase space, the three final states are quasi-aligned in the rest frame of the B meson and two of them almost collimate to each other, the related processes can be denoted as $B\rightarrow h_1R\rightarrow h_1h_2h_3$ where $h_1$ represents the bachelor particle and the $h_2h_3$ pair proceeds by the intermediate state R. In our previous works, the S-, P- and D-wave $\pi \pi$ and $K\pi$ resonance contributions to a series of charmed or charmless three-body $B_{(s)}$ meson decays have been studied in [43, 44, 66, 68,69,70,71,72,73,74,75,76,77] within the PQCD approach by introducing two-meson distribution amplitudes [78,79,80,81,82,83,84]. The consistency of the theoretical studies and experimental results indicates the PQCD factorization approach are applicable to the three-body and quasi-two-body hadronic B meson decays. More recently, several quasi-two-body decays involving $D^*_0(2400)$ [85], $D^*(2007)^0$ and $D^*(2010)^\pm$ [67] as the intermediate states have been studied. And the isovector scalar resonances $a_0(980)$ and $a_0(1450)$ in the $B\rightarrow \psi (K\bar{K},\pi \eta )$ decays were presented in [86]. In this work, we will extend the previous studies to the quasi-two-body decays $B\rightarrow DK^*\rightarrow DK\pi$.

This paper is organized as follows. In Sec. II, we give a brief introduction for the theoretical framework and perturbative calculations for the considered decays. Then, the numerical values and phenomenological analyses are given in Sec. III. Finally, the last section contains a short summary.

2 The theoretical framework

In the framework of the PQCD approach for the quasi-two-body decays, the nonperturbative dynamics associated with the pair of the mesons are absorbed into two-meson distribution amplitudes, then the relevant decay amplitude $\mathcal A$ for the quasi-two-body decays $B \rightarrow D K^* \rightarrow D K \pi$ can be written as the convolution [78, 79]

$$\begin{aligned} \mathcal{A}=\Phi _B\otimes H\otimes \Phi _{D}\otimes \Phi _{K\pi }^{P\text {-wave}}, \end{aligned}$$

(1)

where the symbol $\otimes$ means the convolution integrations over the parton momenta and the hard kernel H includes the leading-order contributions. The B meson (D meson, P-wave $K\pi$ pair) distribution amplitude $\Phi _B$ ($\Phi _{D}$,$\Phi _{K\pi }^{P\text {-wave}}$) absorbs the nonperturbative dynamics in the decay processes.

2.1 Coordinates and wave functions

In the rest frame of the B meson, we define the B meson momentum $p_{B}$, the kaon momentum $p_1$, the pion momentum $p_2$, the $K^*$ meson momentum $p=p_1+p_2$ and the D meson momentum $p_3$ in the light-cone coordinates as

$$\begin{aligned} p_{B}= & {} \frac{m_{B}}{\sqrt{2}}(1,1,\mathbf 0 _\mathrm{T}), ~\quad p=\frac{m_{B}}{\sqrt{2}}(1-r^2,\eta ,\mathbf 0 _\mathrm{T}),\nonumber \\ p_3= & {} \frac{m_{B}}{\sqrt{2}}(r^2,1-\eta ,\mathbf 0 _\mathrm{T}), \nonumber \\ p_1= & {} \left( \frac{m_{B}}{\sqrt{2}}\zeta (1-r^2), \frac{m_{B}}{\sqrt{2}}(1-\zeta )\eta , \mathbf p _{1\mathrm T}\right) , \nonumber \\ p_2= & {} \left( \frac{m_{B}}{\sqrt{2}}(1-\zeta )(1-r^2),\frac{m_{B}}{\sqrt{2}} \zeta \eta , \mathbf p _{2\mathrm T}\right) , \end{aligned}$$

(2)

with the mass ratio $r = m_{D}/m_{B}$, $m_{B(D)}$ is the mass of the B(D) meson. The variable $\eta$ is defined as $\eta =\omega ^2/[(1-r^2)m^2_{B}]$ with the invariant mass squared $\omega ^2=p^2=m^2(K\pi )$ of the kaon–pion pair and $\zeta$ is the momentum fraction for the kaon meson. The momenta of the light quarks in the B meson, the $K^*$ meson and the D meson are chosen as $k_B$, k and $k_3$ respectively

$$\begin{aligned}&k_B=(0,x_Bp_B^-,\mathbf k _{B \mathrm T}),~\quad k=(zp^+,0,\mathbf k _\mathrm{T}),\nonumber \\&k_3=(0,x_3p_3^-,\mathbf k _{3\mathrm T}), \end{aligned}$$

(3)

where the corresponding momentum fractions $x_{B}$, z and $x_3$ run between zero and unity.

The P-wave kaon–pion distribution amplitudes are defined in the same way as in Refs. [78, 79],

(4)

with the functions [44]

$$\begin{aligned} \phi _0= & {} \frac{3F_{K\pi }(s)}{\sqrt{2N_c}} z (1-z)\left[ 1+a_{1K^*}^{||}3(2z-1)\right. \nonumber \\&\left. +\, a_{2K^*}^{||}\frac{3}{2}(5(2z-1)^2-1)\right] P_1(2\zeta -1)\;, \end{aligned}$$

(5)

$$\begin{aligned} \phi _s= & {} \frac{3F_s(s)}{2\sqrt{2N_c}}(1-2z)P_1(2\zeta -1) \;, \end{aligned}$$

(6)

$$\begin{aligned} \phi _t= & {} \frac{3F_t(s)}{2\sqrt{2N_c}}(2z-1)^2P_1(2\zeta -1) \;, \end{aligned}$$

(7)

where the Legendre polynomial $P_1(2\zeta -1)=2\zeta -1$ and the variable $s=\omega ^2=m^2(K\pi )$. For the Gegenbauer moments, we adopt $a_{1K^*}^{||}=0.05\pm 0.02$ and $a_{2K^*}^{||}=0.15\pm 0.05$ determined in Ref. [44]. The relativistic Breit-Wigner (RBW) function is an appropriate model for narrow resonances which are well separated from any other resonant or nonresonant contributions with the same spin, and it is widely used in the experimental data analyses. Here, the time-like form factor $F_{K\pi }(s)$ is parameterized with the RBW line shape and can be expressed as the following form [7, 11, 12]

$$\begin{aligned} F_{K\pi }(s)= & {} \frac{m_{K^*}^2}{(m^2_{K^*} -s)-im_{K^*}\Gamma (s)}, \end{aligned}$$

(8)

with the mass-dependent decay width $\Gamma (s)$

$$\begin{aligned} \Gamma (s)= & {} \Gamma _{K^*}\frac{m_{K^*}}{\sqrt{s}}\left( \frac{|\overrightarrow{p_1}|}{|\overrightarrow{p_0}|}\right) ^3 \frac{1+(|\overrightarrow{p_0}|r_{BW})^2}{1+(|\overrightarrow{p_1}|r_{BW})^2}. \end{aligned}$$

(9)

The $|\overrightarrow{p_1}|$ is the momentum of one of the resonance daughters evaluated in the $K\pi$ rest frame and $|\overrightarrow{p_0}|$ is the value of $|\overrightarrow{p_1}|$ when $\sqrt{s}=m_{K^*}$. The pole mass $m_{K^*}$ and width $\Gamma _{K^*}$ of the resonance state $K^*$ are chosen as $m_{K^{*0}}=895.55\pm 0.20~(m_{K^{*\pm }}=891.76\pm 0.25)$ MeV and $\Gamma _{K^{*0}}=47.3\pm 0.5~(\Gamma _{K^{*\pm }} =50.3\pm 0.8)$ MeV, respectively [1]. The parameter $r_{BW}$ is the barrier radius which is set to 4.0 GeV $^{-1}$ as in Refs. [7, 11, 12]. Following Ref. [66], we also assume that $F_s(s) = F_t(s) \approx (f_{K^*}^T/f_{K^*}) F_{K\pi }(s)$ with $f_{K^*}=0.217 \pm 0.005$ GeV and $f^T_{K^*}=0.185 \pm 0.010$ GeV [87].

In this work, we use the same distribution amplitudes for the B and D meson as in Refs. [72, 75] where one can easily find their expressions and the relevant parameters.

2.2 Analytic formulae

For the quasi-two-body decays $B \rightarrow D K^* \rightarrow D K \pi$, the effective Hamiltonian is defined as [88]

$$\begin{aligned} \mathcal{H}_{eff}= & {} \left\{ \begin{array}{ll} \frac{G_F}{\sqrt{2}}V^*_{cb}V_{ud(s)}\left[ C_1(\mu )O_1(\mu )+C_2(\mu )O_2(\mu )\right] , &{} \ \ \mathrm{for} \ \ B_{(s)} \rightarrow \bar{D}_{(s)} K^* \rightarrow \bar{D}_{(s)} K \pi \ \ \mathrm{decays},\\ \frac{G_F}{\sqrt{2}} V^*_{ub}V_{cd(s)}\left[ C_1(\mu )O'_1(\mu )+C_2(\mu )O'_2(\mu )\right] , &{} \ \ \mathrm{for} \ \ B_{(s)} \rightarrow D_{(s)} K^* \rightarrow D_{(s)} K \pi \ \ \mathrm{decays},\\ \end{array} \right. \end{aligned}$$

(10)

where the Fermi coupling constant $G_F=1.16638\times 10^{-5}$ GeV$^{-2}$, $V_{ij}$ are the CKM matrix elements and $C_{1,2}(\mu )$ denote the Wilson coefficients at the renormalization scale $\mu$. The $O^{(\prime )}_{1,2}$ represent the effective four quark operators and can be expressed as

$$\begin{aligned}&O_1=(\bar{b}_\alpha c_\beta )_{V-A} (\bar{u}_\beta d(s)_\alpha )_{V-A},\nonumber \\&O_2=(\bar{b}_\alpha c_\alpha )_{V-A} (\bar{u}_\beta d(s)_\beta )_{V-A},\end{aligned}$$

(11)

$$\begin{aligned}&O'_1=(\bar{b}_\alpha u_\beta )_{V-A} (\bar{c}_\beta d(s)_\alpha )_{V-A},\nonumber \\&O'_2=(\bar{b}_\alpha u_\alpha )_{V-A} (\bar{c}_\beta d(s)_\beta )_{V-A}, \end{aligned}$$

(12)

with the color indices $\alpha$ and $\beta$. Here $V-A$ refers to the Lorentz structure $\gamma _\mu (1-\gamma _5)$ and $(\bar{q}_1q_2)_{V-A}=\bar{q}_1 \gamma _\mu (1-\gamma _5)q_2$.

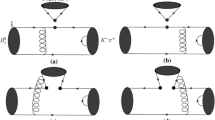
The typical Feynman diagrams at the leading order for the quasi-two-body decays $B_{(s)} \rightarrow \bar{D}_{(s)} K^* \rightarrow \bar{D}_{(s)} K \pi$ (through $\bar{b} \rightarrow \bar{c}$ transition) and $B_{(s)} \rightarrow D_{(s)} K^* \rightarrow D_{(s)} K \pi$ (through $\bar{b} \rightarrow \bar{u}$ transition) are shown in Figs. 1 and 2, respectively. By making analytical evaluations for those Feynman diagrams in Figs. 1 and 2, we can obtain the total decay amplitudes of these concerned decays.

Fig. 1

The leading-order Feynman diagrams for the quasi-two-body decays $B_{(s)} \rightarrow \bar{D}_{(s)} K^* \rightarrow \bar{D}_{(s)} K\pi$ where $B_{(s)}$ = ($B^0$, $B^+$, $B^0_s$) and $\bar{D}_{(s)}$ =( $\bar{D}^0$, $D^-$, $D_s^-$). The $h_1h_2$ denotes the $K\pi$ pair and the blue ellipse represents the intermediate state $K^*$. The “$\otimes \otimes$” in the diagrams represents the insertion of the 4-fermion operator $O_i$ in the effective theory [88]. When considering the color structure of the diagrams for the single-gluon exchange between two color-singlet weak-currents, the operators $O_1$ and $O_2$, with the same flavor form but different color structure, have to be introduced. The expressions for the relevant operators $O_{1,2}$ and $O^{\prime }_{1,2}$ (for Fig. 2) can be found in Eqs. (11) and (12)

Fig. 2

The leading-order Feynman diagrams for the quasi-two-body decays $B_{(s)} \rightarrow D_{(s)} K^* \rightarrow D_{(s)} K \pi$ where $B_{(s)}$ =($B^0$, $B^+$, $B^0_s$) and $D_{(s)}$=($D^0$, $D^+$, $D_s^+$). The $h_1h_2$ denotes the $K\pi$ pair and the blue ellipse represents the intermediate state $K^*$

For the $B_{(s)} \rightarrow \bar{D}_{(s)} K^* \rightarrow \bar{D}_{(s)} K\pi$ decays, their total decay amplitudes can be written explicitly in the following form

$$\begin{aligned}&\mathcal{A}(B^+ \rightarrow \bar{D}^0K^{*+} \rightarrow \bar{D}^0K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{cb}^*V_{us}\left[ \left( C_1+\frac{C_2}{3}\right) F^{LL}_{eK^{*}}\right. \nonumber \\&\qquad \left. +\,C_2M^{LL}_{eK^{*}}+\left( \frac{C_1}{3}+C_2\right) F^{LL}_{eD}+C_1M^{LL}_{eD}\right] , \end{aligned}$$

(13)

$$\begin{aligned}&\mathcal{A}(B^0 \rightarrow \bar{D}^0K^{*0} \rightarrow \bar{D}^0K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{cb}^*V_{us}\left[ \left( C_1+\frac{C_2}{3}\right) F^{LL}_{eK^{*}}+C_2M^{LL}_{eK^{*}}\right] , \end{aligned}$$

(14)

$$\begin{aligned}&\mathcal{A}(B^0 \rightarrow D^- K^{*+} \rightarrow D^-K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{cb}^*V_{us}\left[ \left( \frac{C_1}{3}+C_2\right) F^{LL}_{eD}+C_1M^{LL}_{eD}\right] , \end{aligned}$$

(15)

$$\begin{aligned}&\mathcal{A}(B^0 \rightarrow D_s^- K^{*+} \rightarrow D_s^- K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{cb}^*V_{ud}\left[ \left( C_1+\frac{C_2}{3}\right) F^{LL}_{aK^{*}}+C_2M^{LL}_{aK^{*}}\right] , \end{aligned}$$

(16)

$$\begin{aligned}&\mathcal{A}(B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0} \rightarrow \bar{D}^0K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{cb}^*V_{ud}\left[ \left( C_1+\frac{C_2}{3}\right) F^{LL}_{eK^{*}}+C_2M^{LL}_{eK^{*}}\right] , \end{aligned}$$

(17)

$$\begin{aligned}&\mathcal{A}(B_s^0 \rightarrow D_s^- K^{*+} \rightarrow D_s^- K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{cb}^*V_{us}\left[ \left( \frac{C_1}{3}+C_2\right) F^{LL}_{eD}\right. \nonumber \\&\qquad \left. +C_1M^{LL}_{eD}+\left( C_1+\frac{C_2}{3}\right) F^{LL}_{aK^{*}}+C_2M^{LL}_{aK^{*}}\right] , \end{aligned}$$

(18)

while the total decay amplitudes for $B_{(s)} \rightarrow D_{(s)} K^* \rightarrow D_{(s)} K\pi$ decays can be written as

$$\begin{aligned}&\mathcal{A}(B^+ \rightarrow D^0 K^{*+} \rightarrow D^0K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{ub}^*V_{cs}\left[ \left( C_1+\frac{C_2}{3}\right) F^{LL}_{eK^{*}}\right. \nonumber \\&\qquad \left. +\,C_2M^{LL}_{eK^{*}}+\left( \frac{C_1}{3}+C_2\right) F^{LL}_{aD}+C_1M^{LL}_{aD}\right] , \end{aligned}$$

(19)

$$\begin{aligned}&\mathcal{A}(B^+ \rightarrow D^+ K^{*0} \rightarrow D^+ K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{ub}^*V_{cs}\left[ \left( \frac{C_1}{3}+C_2\right) F^{LL}_{aD}+C_1M^{LL}_{aD}\right] , \end{aligned}$$

(20)

$$\begin{aligned}&\mathcal{A}(B^+ \rightarrow D_s^+ \bar{K}^{*0} \rightarrow D_s^+K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{ub}^*V_{cd}\left[ \left( \frac{C_1}{3}+C_2\right) F^{LL}_{aD}+C_1M^{LL}_{aD}\right] , \end{aligned}$$

(21)

$$\begin{aligned}&\mathcal{A}(B^0 \rightarrow D^0 K^{*0} \rightarrow D^0K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{ub}^*V_{cs}\left[ \left( C_1+\frac{C_2}{3}\right) F^{LL}_{eK^{*}}+C_2M^{LL}_{eK^{*}}\right] , \end{aligned}$$

(22)

$$\begin{aligned}&\mathcal{A}(B^0 \rightarrow D_s^+ K^{*-} \rightarrow D_s^+K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{ub}^*V_{cd}\left[ \left( C_1+\frac{C_2}{3}\right) F^{LL}_{aD}+C_2M^{LL}_{aD}\right] , \end{aligned}$$

(23)

$$\begin{aligned}&\mathcal{A}(B_s^0 \rightarrow D^0 \bar{K}^{*0} \rightarrow D^0 K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{ub}^*V_{cd}\left[ \left( C_1+\frac{C_2}{3}\right) F^{LL}_{eK^{*}}+C_2M^{LL}_{eK^{*}}\right] , \end{aligned}$$

(24)

$$\begin{aligned}&\mathcal{A}(B_s^0 \rightarrow D^+ K^{*-} \rightarrow D^+K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{ub}^*V_{cd}\left[ \left( \frac{C_1}{3}+C_2\right) F^{LL}_{eK^{*}}+C_1M^{LL}_{eK^{*}}\right] , \end{aligned}$$

(25)

$$\begin{aligned}&\mathcal{A}(B_s^0 \rightarrow D_s^+ K^{*-} \rightarrow D_s^+K \pi ) \nonumber \\&\quad = \frac{G_F}{\sqrt{2}} V_{ub}^*V_{cs}\left[ \left( \frac{C_1}{3}+C_2\right) F^{LL}_{eK^{*}}\right. \nonumber \\&\qquad \left. +\,C_1M^{LL}_{eK^{*}}+\left( C_1+\frac{C_2}{3}\right) F^{LL}_{aD}+C_2M^{LL}_{aD}\right] , \end{aligned}$$

(26)

where the individual amplitude $F_{eK^{*}}^{LL},$ $M_{eK^{*}}^{LL},$ $F_{eD}^{LL},$ $M_{eD}^{LL}, F_{aK^{*}}^{LL}$ and $M_{aK^{*}}^{LL}$ are the amplitudes from different sub-diagrams in Figs. 1 and 2. Since the P-wave kaon–pion distribution amplitudes in Eq. (4) have the same Lorentz structure as that of two-pion ones in Refs. [66, 72], the concerned expressions of those individual amplitudes in Ref. [72] can be employed in this work directly by replacing the distribution amplitudes ($\phi _0$, $\phi _s$, $\phi _t$) of the $\pi \pi$ system with the corresponding twists of the $K\pi$ ones in Eqs. (5)–(7). The parameter c in the Eq. (33) of [72] is adopted to be 0.4 in this work according to the Refs. [89, 90].

For the $B \rightarrow D K^* \rightarrow D K \pi$ decays, the differential decay rate can be described as

$$\begin{aligned} \frac{d\mathcal{B}}{d\omega ^2}=\tau _{B}\frac{|\vec {p}_1| |\vec {p}_3 | }{64\pi ^3m^3_{B}}|\mathcal{A}|^2, \end{aligned}$$

(27)

where $\tau _{B}$ is the mean lifetime of B meson, the kinematic variables $|\vec {p}_1|$ and $|\vec {p}_3|$ denote the magnitudes of the K and D momenta in the center-of-mass frame of the kaon–pion pair,

$$\begin{aligned} |\vec {p}_1|= & {} \frac{1}{2} \sqrt{[(m^2_{K}-m^2_\pi )^2-2(m^2_{K}+m^2_\pi )w^2+w^4]/w^2}, \nonumber \\ |\vec {p}_3|= & {} \frac{1}{2} \sqrt{[(m^2_{B}-m^2_D)^2-2(m^2_{B}+m^2_D)w^2+w^4]/w^2}.\nonumber \\ \end{aligned}$$

(28)

3 Numerical results and discussions

The adopted input parameters in our numerical calculations are summarized as following (the masses, decay constants and QCD scale are in units of GeV) [1]:

$$\begin{aligned} \Lambda ^{(f=4)}_{ \overline{MS} }= & {} 0.25,\quad m_{B^+}=5.279,\quad m_{B^0}=5.280,\nonumber \\&m_{B_s}=5.367,\quad m_{D^\pm }=1.870,\nonumber \\ \quad m_{D^0/\bar{D}^0}= & {} 1.865,\quad m_{D_s^\pm }=1.968,\nonumber \\&m_{b}=4.8,\quad m_{c}=1.275,\quad m_{\pi ^\pm }=0.140,\nonumber \\ \quad m_{\pi ^0}= & {} 0.135,\quad m_{K^\pm }=0.494,\quad m_{K^0/\bar{K}^0}=0.498,\nonumber \\&f_{B}=0.19,\quad f_{B_s}=0.236,\nonumber \\ \quad f_{D}= & {} 0.2119, \quad f_{D_s}=0.249, \quad \tau _{B^+}= 1.638\; \mathrm{ps},\nonumber \\&\tau _{B^0}= 1.520\; \mathrm{ps},\quad \tau _{B_s^0}= 1.509\; \mathrm{ps}. \end{aligned}$$

(29)

For the Wolfenstein parameters $(A, \lambda ,\bar{\rho },\bar{\eta })$ of the CKM mixing matrix, we use $A=0.836\pm 0.015,~\lambda =0.22453\pm 0.00044$, $\bar{\rho } = 0.122^{+0.018}_{-0.017},~\bar{\eta }= 0.355^{+0.012}_{-0.011}$ [1].

Table 1 The PQCD predictions for the branching ratios of the $B_{(s)} \rightarrow \bar{D}_{(s)} K^* \rightarrow \bar{D}_{(s)} K \pi$ decays in the quasi-two-body framework together with experimental data

Table 2 The PQCD predictions for the branching ratios of the CKM suppressed $B_{(s)} \rightarrow D_{(s)} K^* \rightarrow D_{(s)} K \pi$ decays in the quasi-two-body framework together with experimental data

By using the decay amplitudes as given in Eqs. (13–26) and the differential branching ratio in Eq. (27), integrating over the full $K\pi$ invariant mass region $(m_K+m_{\pi })\le \omega \le (m_B-m_D)$ for the resonant components, we obtain the branching ratios for the quasi-two-body decays $B_{(s)} \rightarrow \bar{D}_{(s)} K^* \rightarrow \bar{D}_{(s)} K \pi$ and $B_{(s)} \rightarrow D_{(s)} K^* \rightarrow D_{(s)} K \pi$, and list the numerical results in Tables 1 and 2. The first error of these PQCD predictions comes from the $B(B_{s})$ meson shape parameter uncertainty $\omega _B = 0.40 \pm 0.04$ ($\omega _{B_s}=0.50 \pm 0.05$) GeV, the following two errors are from the Gegenbauer coefficients in the kaon–pion distribution amplitudes: $a_{1K^*}^{||}=0.05\pm 0.02$, $a_{2K^*}^{||}=0.15\pm 0.05$ and the last one is induced by $C_D=0.5 \pm 0.1$ ($C_{D_s}= 0.4\pm 0.1$) for $D(D_s)$ meson wave function. One can see that the dominant theoretical error comes from the uncertainty of $\omega _{B_{(s)}}$: about 10% for the decays $B^+ \rightarrow D^+ K^{*0} \rightarrow D^+K \pi$ and $B^+ \rightarrow D_s^+ \bar{K}^{*0} \rightarrow D_s^+K \pi$, and about 20% to 40% for other remaining decays. It can be roughly understood from the analytic formulas of Eqs. (20) and (21). Since $C_2$ is much more than $C_1$, the main contribution for those two pure annihilation type decays $B^+ \rightarrow D^+ K^{*0} \rightarrow D^+K \pi$ and $B^+ \rightarrow D_s^+ \bar{K}^{*0} \rightarrow D_s^+K \pi$ comes from the term which is proportional to $F^{LL}_{aD}$, the amplitude of the factorizable annihilation diagram. While the amplitude $F^{LL}_{aD}$ does not contain any term about $\omega _{B_{(s)}}$, the corresponding theoretical error due to $\omega _{B_{(s)}}$ is reduced for those two decays naturally. One can also see that the error stemming from $a_{1K^*}^{||}, a_{2K^*}^{||}$ and $C_{D_{(s)}}$ is less than 15% respectively. The errors come from the uncertainties of the parameters, for instance, the Wolfenstein parameters, the pole mass $m_{K^*}$ and width $\Gamma _{K^*}$, are very small and have been neglected. Although the three-body B meson decay offers an ideal ground to study the distribution of CP asymmetry, there are no direct CP violations for these decays in this work because only the tree diagrams contribute to the considered decay processes.

In this work, the Gegenbauer moments for $K^*$ at the scale of 1 GeV are chosen, similar to the definitions for the ordinary distribution amplitudes used in the PQCD approach. In principle, the Gegenbauer moments should depend on the factorization scale. As a test of the effect of the scale evolution for the Gegenbauer moments in the kaon–pion distribution amplitudes, we calculate the branching ratios of the decays $B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K \pi$ and $B^0 \rightarrow D^- K^{*+} \rightarrow D^-K \pi$ by considering the $a_{1K^*}^{||}, a_{2K^*}^{||}$ with the evolution from 1 GeV to the hard scale $\sqrt{\Lambda m_B}$. The new results for $B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K \pi$ and $B^0 \rightarrow D^- K^{*+} \rightarrow D^-K \pi$ are $5.28 \times 10^{-4}$ and $3.51 \times 10^{-4}$, respectively, and the variations are found to be less than 4% for the corresponding values in Table 1. Which mean that we can neglect the scale evolution for the kaon–pion system Gegenbauer moments when considering that the current data for the three-body B decays still have larger uncertainties.

From the calculations and the numerical results as listed in Tables 1 and 2, one can find the following points:

• (1) By assuming the $\mathcal{B}(K^*\rightarrow K\pi ) \approx 100$ % [1] and accepting a simple relation between the branching ratio of the same kind of decay evaluated in the quasi-two-body and the two-body framework, it is easy to have

  $$\begin{aligned}&\mathcal{B}(B \rightarrow D K^* \rightarrow D K \pi )\nonumber \\&\quad = \mathcal{B}(B \rightarrow D K^*) \cdot \mathcal{B}(K^* \rightarrow K \pi ) \approx \mathcal{B}(B \rightarrow D K^*).\nonumber \\ \end{aligned}$$

  (30)

  • This relation can be examined roughly from the predictions in this work and the results calculated in the PQCD framework for two-body decays [28, 30]. For examples, $\mathcal{B}(B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K \pi )=5.38\times 10^{-4}$ and $\mathcal{B}(B_s^0 \rightarrow D_s^- K^{*+} \rightarrow D_s^-K \pi )=2.06\times 10^{-4}$ in Table 1 consistent with the $\mathcal{B}(B^+ \rightarrow \bar{D}^0 K^{*+})=6.37\times 10^{-4}$ and $\mathcal{B}(B_s^0 \rightarrow D_s^- K^{*+} )=2.81\times 10^{-4}$ in the Ref. [28]. While because of the updated parameters, there are also relatively large differences between the results for some decays, especially for those channels with the branching ratios less than $10^{-5}$. The same situation exists in the relevant decays with the resonance $\rho$ since $\mathcal{B}(\rho \rightarrow \pi \pi ) \approx 100$%. With the same input parameters, the PQCD predictions for the branching ratios of all considered decays obtained in both the quasi-two-body and the two-body decay frameworks were found to agree very well with each other [72].

  • One can extract the PQCD predictions for the decay rates of the related quasi-two-body decays from the results in Tables 1 and 2. Take the quasi-two-body decay $B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K^+ \pi ^0$ for example, the relation between $\mathcal{B}(B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K^+ \pi ^0)$ and $\mathcal{B}(B^+ \rightarrow \bar{D}^0 K^{*+})$ can be described as

    $$\begin{aligned}&\mathcal{B}(B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K^+ \pi ^0)\nonumber \\&\quad = \mathcal{B}(B^+ \rightarrow \bar{D}^0 K^{*+}) \cdot \mathcal{B}(K^{*+} \rightarrow K^+ \pi ^0), \end{aligned}$$

    (31)

    where the isospin relation $\mathcal{B}(K^{*+} \rightarrow K^+ \pi ^0)=\frac{1}{3}$. Combining with the central value of $\mathcal{B}(B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K \pi )=5.38\times 10^{-4}$ in Table 1, one can obtain the PQCD prediction for $\mathcal{B}(B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K^+\pi ^0)=1.79\times 10^{-4}$ easily.

• (2) Compare our numerical results with the experimental data in Table 1, one can see that:

  • The PQCD prediction for the branching ratio of the decay $B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K \pi$ agrees well with the value $(5.29 \pm 0.30 \pm 0.34) \times 10^{-4}$ [15] measured by the ${ BABAR}$ detector at the PEP-II B Factory. In Ref. [9], the branching ratio of $B^0 \rightarrow D^- K^{*+}$ decay was measured to be $(4.6 \pm 0.6 \pm 0.5)\times 10^{-4}$ and the $K^*$ resonant fraction $\frac{\mathcal{B}(B^0 \rightarrow D^-K^{*+})\mathcal{B}(K^{*+} \rightarrow K^0 \pi ^{+})}{\mathcal{B}(B^0 \rightarrow D^- K^0 \pi ^{+})}=0.63 \pm 0.08\pm 0.04$ has been also obtained. $\mathcal{B}(B^0 \rightarrow D^-K^{*+}\rightarrow D^-K\pi )=(3.63^{+1.61+0.04+0.02+0.35}_{-0.91-0.05-0.11-0.36})\times 10^{-4}$ predicted in this work agrees with the result within the measurement uncertainties. We also have the PQCD prediction $\frac{\mathcal{B}(B^0 \rightarrow D^-K^{*+})\mathcal{B}(K^{*+} \rightarrow K^0 \pi ^{+})}{\mathcal{B}(B^0 \rightarrow D^- K^0 \pi ^{+})}\approx 0.5$ by taking $\mathcal{B}(B^0 \rightarrow D^- K^0 \pi ^{+})=(4.9 \pm 0.7 \pm 0.5) \times 10^{-4}$ from Ref. [9].

  • For the decay $B^0 \rightarrow \bar{D}^0 K^{*0} \rightarrow \bar{D}^0K \pi$, the central value of the branching fraction predicted by PQCD is less than 50% of the available experimental measurements but agrees with the PQCD prediction in the ordinary two-body framework in [28] within errors. The prediction $\mathcal{B}(B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0} \rightarrow \bar{D}^0K \pi )=(2.33^{+0.94+0.31+0.60+0.25}_{-0.66-0.13-0.11-0.07})\times 10^{-4}$ in this work is more close to $(3.3\pm 0.3\pm 0.1\pm 0.3\pm 0.5)\times 10^{-4}$ in Ref. [21] than other two results from LHCb [11, 20]. Furthermore, in Ref. [20], the measurement of the ratio of branching fractions for the decays $B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0}$ and $B^0 \rightarrow \bar{D}^0 \rho ^0$ was found to be

    $$\begin{aligned} \frac{\mathcal{B}(B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0})}{\mathcal{B}(B^0 \rightarrow \bar{D}^0 \rho ^0)}=1.48\pm 0.34\pm 0.15\pm 0.12,\nonumber \\ \end{aligned}$$

    (32)

    while a similar ratio between $\mathcal{B}(B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0})$ and $\mathcal{B}(B^0 \rightarrow \bar{D}^0 K^{*0})$ was measured in Ref. [21]

    $$\begin{aligned} \frac{\mathcal{B}(B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0})}{\mathcal{B}(B^0 \rightarrow \bar{D}^0 K^{*0})}=7.8\pm 0.7\pm 0.3\pm 0.6. \end{aligned}$$

    (33)

    Utilize the PQCD predictions in Table 1 and $\mathcal{B}(B^0 \rightarrow \bar{D}^0 \rho ^0)=1.39\times 10^{-4}$ taken from our previous work in Ref. [72], we estimate the ratio of branching fractions $\frac{\mathcal{B}(B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0})}{\mathcal{B}(B^0 \rightarrow \bar{D}^0 \rho ^0)}=1.68$, in agreement with the data, while our prediction $\frac{\mathcal{B}(B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0})}{\mathcal{B}(B^0 \rightarrow \bar{D}^0 K^{*0})}=12.07$ is a bit larger than the value announced by LHCb [21] after taking errors into consideration. If we accept $\mathcal{B}(B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0})=4.29 \times 10^{-4}$ [11] ($4.72 \times 10^{-4}$ [20]) and $\mathcal{B}(B^0 \rightarrow \bar{D}^0 K^{*0})= 4.0 \times 10^{-5}$ in Ref. [18], our result for the ratio $\frac{\mathcal{B}(B_s^0 \rightarrow \bar{D}^0 \bar{K}^{*0})}{\mathcal{B}(B^0 \rightarrow \bar{D}^0 K^{*0})}$ is still consistent with the data.

  • The branching fraction for the pure annihilation decay $B^0 \rightarrow D_s^- K^{*+}$: $\mathcal{B}=(0.35^{+0.10}_{-0.09}\pm 0.04)\times 10^{-4}$ selected from ${ BABAR}$ [19] is smaller than the values $1.05\times 10^{-4}$ obtained from this work and $1.82\times 10^{-4}$ acquired from the PQCD framework for two-body decays [28]. More theoretical studies and experimental measurements are needed to improve the estimation for the pure annihilation decays.

• (3) For the branching ratios of eight CKM suppressed $B_{(s)} \rightarrow D_{(s)} K^* \rightarrow D_{(s)} K \pi$ decays as listed in Table 2, the PQCD predictions are in the order of $10^{-8}$ to $10^{-5}$ and we have some comments as follows:

  • Since no enough significant signals have been observed, there were hardly any specific data for the branching fractions of those decays but the upper limits. As shown in Table 2, the experimental collaborations have determined the upper limits for three of the considered decays at 90(95)% confidence level and it is easy to see that all the PQCD predictions for the branching ratios are consistent with the corresponding experimental ones.

  • In Ref. [13], the ratio of branching fractions was measured to be

    $$\begin{aligned}&\frac{\mathcal{B}(B^+ \rightarrow D^+ K^{*0} \rightarrow D^+ K^+ \pi ^-)}{\mathcal{B}(B^+ \rightarrow D^- K^+ \pi ^+)}\nonumber \\&\quad < 0.0044(0.0055), \end{aligned}$$

    (34)

    at 90(95)% confidence level. By adopting the measured value $\mathcal{B}(B^+ \rightarrow D^- K^+ \pi ^+)=(7.31\pm 0.19\pm 0.22\pm 0.39)\times 10^{-5}$ [12], the isospin relation $\mathcal{B}(K^{*0} \rightarrow K^+ \pi ^-)=\frac{2}{3}$, and our result $\mathcal{B}(B^+ \rightarrow D^+ K^{*0} \rightarrow DK \pi )=(6.27^{+0.58+0.14+0.04+0.39}_{-0.79-0.10-0.04-0.35})\times 10^{-7}$, we estimate the ratio $\frac{\mathcal{B}(B^+ \rightarrow D^+ K^{*0} \rightarrow D^+ K^+ \pi ^-)}{\mathcal{B}(B^+ \rightarrow D^- K^+ \pi ^+)}\approx 0.0057$. It is to be tested further since the upper limit for the branching fraction of $B^+ \rightarrow D^+ K^{*0} \rightarrow DK \pi$ given by Ref. [13] is much less than that in the Refs. [22, 23].

  • We suggest more studies for those CKM suppressed $B_{(s)} \rightarrow D_{(s)} K^* \rightarrow D_{(s)} K \pi$ decays in which the decay mode $B_s^0 \rightarrow D_s^+ K^{*-} \rightarrow D_s^+K \pi$ has a large branching ratio, and could be measured in the LHCb and Belle-II experiments.

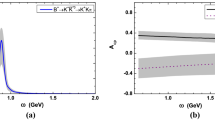
• (4) Different from the fixed kinematics of the two-body B meson decays, the decay amplitudes of the quasi-two-body B meson decays show a strong dependence on the $K\pi$ invariant mass $\omega$. In Fig. 3, we plot the differential decay branching ratio of the decay mode $B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K \pi$ versus the invariant mass $\omega$ in the range of $[m_K+m_{\pi }, 2 \mathrm{GeV}]$. The main portion of the branching ratio lies obviously in the region around the pole mass of the resonant state which presented as a narrow peak in the plot, the contributions from the energy region $\omega >1.2$ GeV can be omitted safely.

Fig. 3

The PQCD prediction for the $\omega$-dependence of the differential branching ratio for the decay mode $B^+ \rightarrow \bar{D}^0 K^{*+} \rightarrow \bar{D}^0 K \pi$

4 Summary

Motivated by the abundant experimental data, we studied the contributions of the P-wave resonant states $K^*$ to the decays $B_{(s)} \rightarrow \bar{D}_{(s)} K \pi$ and the CKM suppressed decays $B_{(s)} \rightarrow D_{(s)}K \pi$ by employing the PQCD factorization approach. The final-state interactions between the $K\pi$ pair are factorized into the two-meson distribution amplitudes in which the resonant line shape for the resonance $K^*$ in the time-like form factor $F_{K\pi }$ is described by the RBW function.

By the numerical evaluations and the phenomenological analyses, we found the following points:

• (1) By adopting the $\mathcal{B}(K^*\rightarrow K\pi ) \approx 100$ %, one can obtain $\mathcal{B}(B \rightarrow D K^* \rightarrow D K \pi ) \approx \mathcal{B}(B \rightarrow D K^*)$ easily, and it provides us a new way to study those two-body B meson decays in the framework for the quasi-two-body cases.

• (2) The PQCD predictions for the branching fractions of the decay processes $B_{(s)} \rightarrow \bar{D}_{(s)} K^* \rightarrow \bar{D}_{(s)}K \pi$ do agree with the experimental data, except for the cases of the color-suppressed decay $B^0 \rightarrow \bar{D}^0 K^{*0} \rightarrow \bar{D}^0K \pi$ and the pure annihilation decay $B^0 \rightarrow D_s^- K^{*+} \rightarrow D_s^- K\pi$. More precise data from the LHCb and the Belle-II experiments can help us to test our predictions and to improve the theoretical framework itself.

• (3) For the CKM suppressed $B_{(s)} \rightarrow D_{(s)} K^* \rightarrow D_{(s)} K \pi$ decays, all the PQCD predictions for the branching ratios are consistent with currently available experimental measurements. Experimentally, the upper limit for the branching fraction of $B^+ \rightarrow D^+ K^{*0} \rightarrow DK \pi$ given by Ref. [13] is much less than that in the Refs. [22, 23], and it is to be verified further.

• (4) Unlike the fixed kinematics of the two-body B meson decays, the decay amplitudes of the quasi-two-body B meson decays have a strong dependence on the $K\pi$ invariant mass $\omega$ and the main portion lies in the region around the pole mass of the resonant state.