1 Introduction

The theoretical study of the nature and properties of the strange quark stars is an attractive topic of research, not only due to a distinct branch of compact stars but also the strange matter EOS is worthy of explaining a few astrophysical compact objects. The possibility of strange quark matter (SQM) [1,2,3,4,5,6], made up of equal unconfined up, down and strange quarks may be counted as the basic state of the strong interaction, proposed by Bodmer [7] and later on by Witten [8]. Theoretical presence of strange quark star was proposed by Itoh [9].

To provide the chemical equilibrate of the strange stars, a small number of electrons should be included in SQM. This small number of electrons (not bounded by any strong interaction) plays a significant role in the constitution of an electric dipole layer at the surface. Therefore, a non-negligible electrical energy density comparable to radial pressure has developed a local non-neutral strong electric field within the star, i.e. between the electron layer and positively charged core. Strange quark stars in the presence of the strong electric field can be modelled using the Maxwell-Einstein field equations. Strong impacts of this electric filed on the gravitationally bounded system is already shown by the authors [10,11,12]. The electric field on the surface region is in the order of \( 10^{19} \sim 10^{20}\) V/m. This surface electric field would be more extreme if the strange matter is made up of color superconducting strange matter [13]. The strange star demands more charge to be in stable equilibrium in a strong gravitational field. A significant amount of charge can induce an acute electric field. Non-zero charge modulate the structure of the strange star in a different manner: (1) curvature of space-time, i.e. the metric, (2) energy density affiliated to the electric field enriches the total mass of the system, (3) coulombian interaction has a finite contribution to the hydrostatic equilibrium of the system, (4) charge also contributes to the anisotropic stress. It reduces the amount of anisotropic stress of the system. The charge and mass density contribute finitely to form an equilibrium configuration of the charged fluid.

Within last two decades, various charge distribution has been frequently applied to describe the effects of charge on the interior of strange stars [14,15,16]. Polytropic stars with charge density related to the energy density have been studied in [17, 18]. In their pioneer work, Negreiros et al. [14] investigated the strange star with the Gaussian charge distribution. They found that the charge gradient (dQ/dr) is not dependent on the width of charge distribution. This is true for any relativistic stellar object, provided that the distribution is narrowly spread over the system. Several authors worked with the charge distribution in the form of power law \(q(r)=Q(r/R)^n\), where Q and R are total charge and radius of the system respectively. Felice et al. [19, 20], in his works studied the system for n\( \ge \) 3 to make sure that the charge density does not diverge at the origin. Arbañil and Malheiro, in their work [16] studied for \(n=3\) for perfect fluid system and later on, Deb et al. [21] studied the strange star for the same. Anninos and Rothman [22] studied the stellar system with a complex type of charge distribution.

Considering the homogeneous distribution of matter and constant surface charge, the stability of the charged star investigated in [23] and found that the incompressible star with no charge is less stable than a star with small surface charge and constant energy density. Glazer developed Chandrasekhar’s pulsation equation for the charged fluid system [24]. Stability of an incompressible fluid star can be increased by introducing charge [25]. The hydrostatic equilibrium and collapse of a charged fluid system studied in [26]. An extensive study of the equilibrium dependency and stability on the charge distribution is provided in [16]. They found that the stability of the strange star inversely varies with the total charge due to a certain range of the central energy density, whereas for a range of total mass stability increases with the increment of charge. Also, studied the hydrostatic equilibrium and stability with the radial perturbation for the varying central density, charge and charge-radius ratio. The behaviour of the anisotropic fluids in the static spherically symmetric system has been extensively studied in Refs. [27,28,29] in different coordinate systems. Over the range of charge and anisotropic parameters, the variation has been studied.

In this article, we have studied the generalized structure of strange stars in the presence of electric charge, in the framework of Finsler geometry, and study the stability of the system. The reasons for choosing Finsler geometry are as follows: Firstly, its length elements are not bounded by any quadratic restriction and the geometry depends on dynamics along with the position of the system [30]. The measurement of time required between two events that pass to an observer is equivalent to the distance measured along the observer’s world-line, connecting the events. Secondly, the measurement is based on the tangent bundle of a homogeneous function. Here the arc is not the only function of length but also the function of velocity. Thirdly, the current Finsler space \(\bar{F^2}\) is quadratic in (\(y^\theta \) and \(y^\phi \)) which can be resolved from a Riemannian manifold \((M, g_{\mu \nu }(x))\) as we consider \(F(x,y) =\sqrt{g_{\mu \nu }(x)y^\mu y^\nu }.\) It is actually a semi-definite Finsler space and for that one can use the covariant derivative of the Riemannian space. The Bianchi identities, in this case, are similar to those of the Riemannian space and the current Finsler space reduces to the Riemannian space and as a result, the gravitational field equations can be found.

Extensions of Einstein gravity in Fineslerain geometry is studied in the literatures [31,32,33]. Nowadays several authors are using Finsler geometry to describe the violation of Lorentzian invariance and anisotropy of the Universe [34,35,36,37,38,39,40,41]. The modified form of Singularity theorem, as well as the Raychaudhuri equation for the Finsler geometry has been studied in [42]. In Finsler–Rander spacetime the generalized form of Raychaudhuri equation and scalar-tensor theory has been introduced by Stavrinos and Alexious [43]. On the other hand, For Finslerian set up, Penrose’s singularity theorem is discussed in [44]. The study of non charged compact stars is considered in the literature [45]. Pfeifer and Wohlfarth [46] studied the casual structure and the generalized theory of electrodynamics in Finslerian space-time. However, the solutions to the field equations are not discussed. Li [47] has obtained a Finslerian Reissner-Nordström solution for vacuum space and also found the eigenfunction of the Finslerian Laplacian operator. The generalized form of the Maxwell–Einstein Field equation in the following geometry is obtained from the geodesic equation of motion in the geometry. We have considered the simplified MIT bag model EOS and the charge distribution in the form as assumed in [16] (power law). For simplicity, we constrained ourselves in constant flag curvature. Akbar-Zahed [48] already discussed the helpfulness of considering constant flag curvature and generality remain same.

We obtained the exact solution of the Maxwell-Einstein Field equation. As a consequence, obtained maximum enclosed charge and field on the surface. The generalized variation of mass-radius relation for the strange stars due to a definite value of bag has been enumerated. We found a range of total mass, radius and charge respective of central density along with the theoretical bounds. The explicit study of the system are shown graphically and in tabular format for \({\overline{Ric}} =1.2\) and bag value \(83~Mev/fm^3 \), which is within the well accepted range.

Our paper is structured as follows: Definition and formation of the field equation of Finsler geometry are outlined in Sect. 2. Ad hoc relations are stated in Sect. 3. We provided the formalism of basic stellar equations in Sect. 4, we have presented the solution of the Maxwell-Einstein field equations. Physical acceptability and stability of the stellar system are verified in Sect. 5 by studying mass-radius relation, energy conditions verification, the stability of the stellar model and compactification. Finally, the conclusion of our study with a discussion is provided in Sect. 6.

2 Basic stellar equations

We briefly present fundamental geometrical concepts from the theory of Finsler spaces and generates the respective field equations, as well as discuss about the EOS of the stellar system.

2.1 Basic formalism

We consider on a manifold , the Finsler metric is F. In standard coordinate notation, \(F = F( x, y)\) is the function of \((x^\mu , y^\mu )\) in .

The equation of Geodesic of the Finsler metric (F) can be written as follows:

$$\begin{aligned} \frac{d^2x^\mu }{d \tau ^2}+2G^\mu (x, y) =0 , \end{aligned}$$
(1)

where the geodesic spray is given by

$$\begin{aligned} G^\mu = \frac{1}{4} g^{\mu \nu } \left( \frac{\partial ^2F^2}{\partial x^\lambda \partial y^\nu } y^\lambda -\frac{\partial F^2}{\partial x^\nu } \right) . \end{aligned}$$
(2)

The metric structure coefficient is given by

$$\begin{aligned} g_{\mu \nu } = \frac{\partial }{\partial y^\mu } \frac{\partial }{ \partial y^\nu } \left( \frac{1}{2} F^2 \right) , \end{aligned}$$
(3)

with \((g ^{\mu \nu } )\) = \( (g_{\mu \nu })^{-1} \).

Let, the Finsler structure be

$$\begin{aligned} F^2= -e^{\lambda (r)} y^t y^t + e^{\nu (r)} y^r y^r +r^2 {\overline{F}}^2(\theta , \phi , y^\theta , y^\phi ). \end{aligned}$$
(4)

Smoothness of the line element is discussed elaborately for the standard static spacetime in [49, 50].

Using Eq. (1), the Finsler metric potential can be defined as

$$\begin{aligned}&g_{\mu \nu } = diag(-e^{\lambda (r)}, e^{\nu (r)}, r^2{\overline{g}}_{ij}). \end{aligned}$$
(5)

where, the term \({\overline{g}}_{ij}\) is the metric potential derived from the Finsler structure \( {\overline{F}}^2 \).

The respective geodesics sprays of the system are as follows:

$$\begin{aligned}&G^t = \frac{1}{2}\lambda ' y^t y^r, \end{aligned}$$
(6)
$$\begin{aligned}&G^r = \frac{1}{4} \left( \nu ' y^r y^r +\lambda ' e^{\lambda -\nu } y^t y^t -2re^{-\nu }{\overline{F}}^2 \right) , \end{aligned}$$
(7)
$$\begin{aligned}&G^\theta = \frac{1}{r} y^\theta y^r +{\overline{G}}^\theta , \end{aligned}$$
(8)
$$\begin{aligned}&G^\phi = \frac{1}{r} y^\theta y^r +{\overline{G}}^\phi . \end{aligned}$$
(9)

the term \( {\overline{G}}^{\mu } \) corresponds to geodesic spray of Finsler structure \( {\overline{F}}^2 \).

In Finsler geometry, Ricci tensor is introduced by Akbar-Zadeh [48], given by

$$\begin{aligned} Ric_{\mu \nu }= \frac{\partial ^2}{\partial y^\mu \partial y^\nu }\left( \frac{1}{2}F^2 Ric \right) . \end{aligned}$$
(10)

Ricci scalar in the Finsler geometry is,

$$\begin{aligned}&Ric =R^\mu _\mu \nonumber \\&\quad =\frac{1}{F^2} \left[ 2 \frac{\partial G^\mu }{\partial x^\mu }- y^\lambda \frac{\partial ^2 G^\mu }{\partial x^\lambda \partial y^\mu } +2 G^\lambda \frac{\partial ^2 G^\mu }{\partial y^\lambda \partial y^\mu } \right. \nonumber \\&\left. \qquad - \frac{\partial G^\mu }{\partial y^\lambda }\frac{\partial G^\lambda }{\partial y^\mu } \right] , \end{aligned}$$
(11)

where, \(R^\mu _\mu \) is insensitive to connections, it only depends on Finsler structure.

With the help of Eqs. (2), (4) and (11), we obtain

$$\begin{aligned}&F^2 Ric= \left[ \frac{\lambda ''}{2}+\frac{\lambda '^2}{4}-\frac{\lambda ' \nu '}{4} +\frac{\lambda '}{r} \right] e^{(\lambda -\nu )} y^t y^t \nonumber \\&\quad + \left[ - \frac{\lambda ''}{2}-\frac{\lambda '^2}{4} +\frac{\lambda ' \nu '}{4} +\frac{\nu '}{r} \right] y^r y^r \nonumber \\&\quad +\left( {\overline{Ric}}-e^{-\nu } +\frac{r \nu ' e^{-\nu }}{2}-\frac{r \lambda ' e^{-\nu }}{2}\right) . \end{aligned}$$
(12)

Ricci scalar, \({\overline{Ric}}\) derived from the Finsler structure \({\overline{F}}^2\).

The scalar curvature can define as \(S = g^{\mu \nu } Ric_{\mu \nu }\).

Therefore, in Finsler geometry, the modified form of Einstein tensor reads,

$$\begin{aligned} G^{\mu }_{\nu } = g^{\mu \nu }Ric_{\mu \nu }-\frac{1}{2} S. \end{aligned}$$
(13)

The explicit form of S for the Finsler structure Eq. 4 as follows:

$$\begin{aligned}&S = e^{-\nu }\left[ \lambda ''+\frac{\lambda '^2}{2}- \frac{\lambda ' \nu '}{2} +\frac{\lambda '-\nu '}{r} \right] \nonumber \\&\qquad -\frac{2}{r^2} \left[ {\overline{Ric}}-e^{-\nu } +\frac{r e^{-\nu }}{2} (\nu '- \lambda ')\right] . \end{aligned}$$
(14)

The energy momentum tensor for the anisotropic fluid distribution and electromagnetic field within the system has the following forms respectively,

$$\begin{aligned}&T^{i}_{j}= (\rho +p_t)u^{i}u_{j} - p_t \delta ^{i}_{j} - (p_t-p_r)v^{i}v_{j}, \end{aligned}$$
(15)
$$\begin{aligned}&E^{i}_{j}= \frac{1}{4 \pi }(-{\mathcal {F}}^{im}{\mathcal {F}}_{jm} + \delta ^i_j{\mathcal {F}}^{mn}{\mathcal {F}}_{mn}), \end{aligned}$$
(16)

where \(\rho \), \(p_r\) and \(p_t\) represent the energy density, radial and tangential pressures, respectively. Here, \( u_{i} \) and \( v_{i} \) represents four-velocity and radial four-vector, respectively. \({\mathcal {F}}^i_j\) is the anti-symmetric electromagnetic field tensor.

Hence, in the Finsler geometry the Einstein-Maxwell field equations is

$$\begin{aligned} G^\mu _\nu = 8 \pi _F(T^{i}_{j} +E^{i}_{j}) =8 \pi _F T^\mu _\nu , \end{aligned}$$
(17)

where, we consider the geometrized unit, i.e., \(G=1=c\).

The covariant divergence of the stress-energy tensor is

$$\begin{aligned} T^\mu _{~\nu ;\mu } = 0. \end{aligned}$$
(18)

The effective energy-momentum tensor for the locally anisotropic charged fluid distribution can be written as

$$\begin{aligned} T^\mu _\nu = \left( \begin{array}{cccc} -\rho +\frac{q^2}{8\pi r^4} &{} 0 &{} 0 &{} 0 \\ 0 &{} (p_r-\frac{q^2}{8\pi r^4}) &{} 0 &{} 0 \\ 0 &{} 0 &{} (p_t+\frac{q^2}{8\pi r^4}) &{} 0\\ 0 &{} 0 &{} 0 &{} (p_t+\frac{q^2}{8\pi r^4}) \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$
(19)

where the electric charge (\({\mathbf {q}}\)) and the corresponding field (\({\mathbf {E}}\)) is related as \( \frac{E^2}{8 \, \pi } = \frac{q^2}{8 \, \pi \,r^4} \).

Hence, the components of the Einstein-Maxwell field equations are given by

$$\begin{aligned} \frac{\nu ' e^{-\nu }}{r} - \frac{ e^{-\nu }}{r^2} +\frac{{\overline{Ric}}}{r^2}&= 8 \pi _F \rho +E^2, \end{aligned}$$
(20)
$$\begin{aligned} \frac{\lambda ' e^{-\nu }}{r} + \frac{ e^{-\nu }}{r^2} - \frac{{\overline{Ric}}}{r^2}&= 8 \pi _F p_r -E^2, \end{aligned}$$
(21)
$$\begin{aligned} e^{-\nu }\left[ \frac{\lambda ''}{2}+\frac{\lambda '^2}{4}-\frac{\lambda ' \nu '}{4} +\frac{\lambda '-\nu '}{2r} \right]&= 8 \pi _F p_t +E^2. \end{aligned}$$
(22)

The effective gravitational mass equation due to the spherically symmetric charged compact stellar object is defined by

$$\begin{aligned} \frac{dm}{dr}=4\, \pi \,r^2 \rho + \frac{q}{r}\frac{dq}{dr}. \end{aligned}$$

2.2 Junction condition

The stellar structure extended from the centre towards the surface of the system within the following constrains

$$\begin{aligned} m(0) = 0, ~~q(0)=0,~~ \rho (0) = \rho _{c}~~and~~p_r(0)=p_c. \end{aligned}$$

The interior spacetime of the stellar system should be matched smoothly at the boundary with the exterior spacetime. The Finslerian Ressiner-Nordström metric to represent the exterior spacetime of the following form [47],

$$\begin{aligned} F^2= -f_{RN} y^t y^t + g^{-1}_{RN} y^r y^r +r^2 {\overline{F}}^2(\theta , \phi , y^\theta , y^\phi ), \end{aligned}$$
(23)

where \(f_{RN}=1-\frac{2GM}{CR}+\frac{GQ^2}{R^2}\) and \(g_{RN}=C-\frac{2GM}{R}+\frac{GQ^2}{R^2}\) with M and Q being the total mass and charge of the system, respectively, and C is a constant.

3 Charge distribution, density profile and equation of state

To study the effects of charge on the anisotropic strange stars, the charge distribution definitely should have a form. Considered the charge distribution is in the form of power law following Felice et al. [19] as \( q(r)= Q (r/R)^n \). For the simplicity, we assume that \(n=3\) as follows

$$\begin{aligned} q(r)=Q\left( \frac{r}{R}\right) ^3 = \alpha r^3, \end{aligned}$$
(24)

where, Q is the total charge and R is the radius of the system, respectively. \( \alpha \left( =\frac{Q}{R^3}\right) \) is a constant (charge constant).

We consider that the energy density of the fluid inside the strange stars maintaining the form [51]

$$\begin{aligned} \rho (r)=\rho _c\left[ 1-\left( 1-\frac{\rho _0}{\rho _c}\right) \frac{r^{2}}{R^{2}}\right] , \end{aligned}$$
(25)

where \(\rho _c\) and \(\rho _0\) are the central and surface density, respectively.

The SQM within the system is described by the phenomenal MIT bag model. We assumed that the quarks are massless and non-interacting [here we considered up (u), down (d) and strange (s) quarks]. The corrected form of pressure can be defined after introduction of ad hoc bag function (B) as follows

$$\begin{aligned} p_r = \sum _{f=u,d,s} p^f-B, \end{aligned}$$
(26)

where \(p^f\) is the pressure of each type of quarks, i.e. u, d and s. The corresponding corrected energy density is as follows

$$\begin{aligned} \rho = \sum _{f=u,d,s} \rho ^f+B. \end{aligned}$$
(27)

On substituting the relation between the pressure and energy density due to each quark flavor, given by \(p^f=\frac{1}{3}\rho ^f\) and Eq. 27 in Eq. 26, the final form obtained of the MIT bag EOS as follows

$$\begin{aligned} p_r=\frac{1}{3}(\rho -4B). \end{aligned}$$
(28)

The radial pressure (\( p_r \)) vanishes on the surface. Therefore, we can consider the surface density (\( \rho _0 \)) as 4B. Following that the Eqs. (28) can be rewritten as

$$\begin{aligned} p_r=\frac{1}{3}(\rho -\mathbf {\rho _0}). \end{aligned}$$

4 Solution of the Einstein–Maxwell field equation

We obtained the following expression for the gravitational potentials (\(\nu \) and \(\lambda \)), density, radial and tangential pressures, respectively, by solving the Eqs. 20–22 with the help of Eqs. 24, 25 and 28, as

$$\begin{aligned}&\nu \left( r \right) =-\ln \left( {\frac{ \nu _1 {r}^{4}+ \nu _2 {r}^{2}+A{R}^{5}}{{R}^{5}}} \right) , \end{aligned}$$
(29)
$$\begin{aligned} \lambda (r)= & {} -\frac{32}{\lambda _{{1}}\nu _{1}} \Bigg [\lambda _{1}\,\mathrm{arctanh} \left( {\frac{{R}^{5}{\alpha }^{2}+16\,B\pi \,{R}^{3}-M}{\lambda _{{2}}}}\right) \nonumber \\&+\lambda _{1}\,\mathrm{arctanh} \left( {\frac{2 \nu _{1}r^2+2\,\nu _{2}}{\lambda _{{2}}{R}^{2}}}\right) + \lambda _{{2}} \left( \lambda _{3}-\lambda _{4} \right) \ln \lambda _{5} \nonumber \\&+\left\{ \phantom {\left( {\frac{3\,{R}^{5}{\alpha }^{2}}{40}}\right) }\lambda _{4}\,\ln \left( \left( \nu _{1}r^2+\nu _{2} \right) {r}^{2}+\overline{{ Ric}} {R}^{5} \right) -\lambda _{3}\,\ln \overline{{ Ric}} \right. \nonumber \\&\left. +\frac{5}{2}\left( {\frac{3\,{R}^{5}{\alpha }^{2}}{40}}+B\pi \,{R}^{3}-\frac{3}{16}\,M \right) \,\ln R \right\} \lambda _{{2}} \Bigg ], \end{aligned}$$
(30)
$$\begin{aligned} \rho= & {} {\frac{9\,{R}^{5}{\alpha }^{2}{r}^{2}+80\,B\pi \,{R}^{3}{r}^{2} -15\,M{r}^{2}-3\,\nu _2}{8 \pi {R}^{5}}},\end{aligned}$$
(31)
$$\begin{aligned} p_{{r}}= & {} -\frac{1}{24}\,{\frac{ \left( 9\,{R}^{5}{\alpha }^{2}+80\,B\pi \,{R}^{3}-15\,M \right) \left( R+r \right) \left( R-r \right) }{\pi {R}^{5}}},\nonumber \\ \end{aligned}$$
(32)
Fig. 1
figure 1

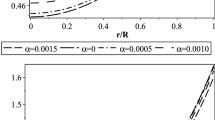
Variation of \(e^{-\lambda (r)}\) and \(e^{\nu (r)}\) as a function of the fractional radial coordinate r / R for \(LMC ~X-4\). Here and in what follows the bag constant \(B_g = 83 MeV/fm^3\). In this figure blue, orange, green and red colour stands for \(\alpha =0.0015\),\(\alpha =0.0010\),\(\alpha =0.0005\) and \(\alpha =0.0000\), respectively. Dot and dashdot line style represent \(e^{-\lambda (r)}\) with \({\overline{Ric}} =1.2\) and 1, respectively. Dash and longdash line style represent \(e^{\nu (r)}\) with \({\overline{Ric}} =1.2\) and 1, respectively

Full size image
Fig. 2
figure 2

Variation of \(\rho \) as a function of the fractional radial coordinate r / R for the \(LMC ~X-4\)

Full size image
$$\begin{aligned} p_{{t}}= & {} -\frac{1}{72\,\pi \,(\left( \nu _1 r^2 +\nu _2 \right) r^2 +{\overline{Ric}} R^5) {R}^{5}}\Bigg [ -81\,{R}^{14}{\alpha }^{4}{r}^{2} \nonumber \\&-54\,{R}^{10}{\alpha }^{4}{r}^{6}-1008\,B\pi \,{R}^{12}{\alpha }^{2}{r}^{2}\nonumber \\&+1632\,B\pi \,{R}^{10}{\alpha }^{2}{r}^{4}-720\,B\pi \,{R}^{8}{\alpha }^{2} {r}^{6} \nonumber \\&-3328\,{B}^{2}{\pi }^{2}{R}^{10}{r}^{2} +5888\,{B}^{2}{\pi }^{2}{R}^{8}{r}^{4}\nonumber \\&-2560\,{B}^{2}{\pi }^{2}{R}^{6}{r}^{6}+1680\,BM\pi \,{R}^{7}{r}^{2}\nonumber \\&-2304\,BM\pi \,{R}^{5}{r}^{4}\nonumber \\&+270\,M{R}^{9}{\alpha }^{2}{r}^{2} -360\,M{R}^{7}{\alpha }^{2}{r}^{4}+240\,\overline{{ Ric}}B\pi \, {R}^{10}\nonumber \\&-480\,\overline{{ Ric}}B\pi \,{R}^{8}{r}^{2} +135\,M{R}^{5}{\alpha }^{2}{r}^{6}+27\,\overline{{ Ric}}{R}^{12}{\alpha }^{2}\nonumber \\&-27\,\overline{{ Ric}}{R}^{10}{\alpha }^{2}{r}^{2}+960\,BM\pi \,{R}^{3}{r}^{6}-45\,\overline{{ Ric}}M{R}^{7}\nonumber \\&+90\,\overline{{ Ric}}M{R}^{5}{r}^{2}-225\,{M}^{2}{R}^{4}{r}^{2}+225\,{M}^{2}{R}^{2}{r}^{4}\nonumber \\&-90\,{M}^{2}{r}^{6}+135\,{R}^{12}{\alpha }^{4}{r}^{4}\Bigg ] , \end{aligned}$$
(33)

where \(\nu _1, \nu _2,\lambda _{1},\lambda _{2},\lambda _{3},\lambda _{4}\) and \(\lambda _{5}\) are constants and their expressions are provided at the Appendix A.

Fig. 3
figure 3

Variation of (i) \(p_r\) (upper panel) and (ii) \(p_r\) (lower panel) as a function of the fractional radial coordinate r/R for the \(LMC ~X-4\). Here and in what follows \({\overline{Ric}} =1.2\)

Full size image

The variation of the gravitational potentials, viz. \(\text {e}^\nu \) and \(\text {e}^{-\lambda }\) as a function of the fractional radial coordinates (r/R) at the interior of the stellar system are exhibited in the upper and lower panel of Fig. 1, respectively. The variations of the physical quantities like \(\rho \), \(p_r\) and \(p_t\) are shown in Fig. 2 and in the upper and lower panel of Fig. 3, respectively.

The anisotropic stress (\( \varDelta \)) of a stellar system can be expressed as additional tangential pressure over radial direction, i.e. \(p_t-p_r\), is given by

$$\begin{aligned} \varDelta (r)= & {} \frac{10}{3\pi \,(\left( \nu _1 r^2 +\nu _2 \right) r^2 +{\overline{Ric}} R^5) {R}^{5}} {r}^{2} \Bigg [ {\frac{27}{40}}\,{R}^{14}{\alpha }^{4}\nonumber \\&-\frac{9}{4}\,M{R}^{9}{\alpha }^{2}+\Big ( {\frac{9\,{r}^{4}{\alpha }^{4}}{20}}-{\frac{77\,B{r}^{2}\pi \,{\alpha }^{2}}{5}} +{\frac{448\,{B}^{2}{\pi }^{2}}{15}} \Big ) {R}^{10} \nonumber \\&+{\frac{15}{8}}\,{M}^{2}{R}^{4} -15\,M\left( B\pi -{\frac{89\,{r}^{2}{\alpha }^{2}}{400}} \right) {R}^{7}+ \big (9\,B\pi \,{\alpha }^{2} \nonumber \\&-{\frac{9}{8}}\,{r}^{2}{\alpha }^{4} \big ) {R}^{12} +B\pi \, \left( {\frac{34\,{\alpha }^{2}{r}^{4}}{5}}-{\frac{848\,B\pi \,{r}^{2}}{15}}+{\overline{Ric}} \right) {R}^{8}\nonumber \\&-10\,BM\pi \,{R}^{3}{r}^{4}+{\frac{80\,{B}^{2}{\pi }^{2}{R}^{6}{r}^{4}}{3}} -\frac{3}{16}\,M \Big ( {\frac{34\,{\alpha }^{2}{r}^{4}}{5}}\nonumber \\&-{\frac{1888\,B\pi \,{r}^{2}}{15}}+{\overline{Ric}}\Big ) {R}^{5} -{\frac{39\,{M}^{2}{R}^{2}{r}^{2}}{16}}+{\frac{15\,{M}^{2}{r}^{4}}{16}} \Bigg ].~\nonumber \\ \end{aligned}$$
(34)

The variation of the anisotropic stress of the stellar system as a function of fractional radial coordinates (r / R) is shown in Fig. 4.

Fig. 4
figure 4

Variation of anisotropic stress \((\varDelta )\) as a function of the fractional radial coordinate r / R for the \(LMC ~X-4\)

Full size image

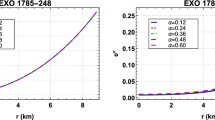
The variation of the electrical charge distribution (q(r)) and respective electrical energy density (\( E^2/8\,\pi \)) are exhibited in Fig. 5 in the upper and lower panel respectively as a function of fractional radial coordinate. It is clear from the plots that there are no charge density and corresponding field at the centre of the stellar distribution.

Fig. 5
figure 5

Variation of (i) q(r) (upper panel) and (ii) \( E^2/8\,\pi \) (lower panel) as a function of the fractional radial coordinate r / R for the \(LMC ~X-4\)

Full size image

5 Physical features of the stellar system

In this section, we are going to verify whether our model is in the stable equilibrium and physically valid.

5.1 Physically acceptable behaviour

5.1.1 Energy conditions

Energy conditions depict the observer’s measurement of the matter distribution in the space-time. The conditions are always positive, which define that the flow of matter should be along null or time-like world line. Stavrinos and Alexiou [62] provided the required energy conditions for the Finslerian system. A stellar system is said to be a physically valid system if the following inequalities are simultaneously satisfied:

$$\begin{aligned} \begin{array}{ll} &{}NEC:\rho +p_r\ge 0,~\rho +p_t+\frac{E^2}{4 \pi }\ge 0, \\ &{}WEC: \rho +p_r\ge 0,~\rho +\frac{E^2}{8 \pi }\ge 0,~\rho +p_t+\frac{E^2}{4 \pi }\ge 0, \\ &{}SEC: \rho +p_r\ge 0,~\rho +p_r+2p_t +\frac{E^2}{4 \pi }\ge 0, \\ &{}DEC:\rho +\frac{E^2}{8 \pi }\ge 0,~ {{\rho }-{p_r}}+\frac{E^2}{4 \pi }\ge 0, ~{{\rho }-{p_t}}\ge 0. \end{array} \end{aligned}$$

Here, NEC, WEC, SEC and DEC denote the null energy condition, weak energy condition, strong energy condition and dominant energy condition, respectively. The variation of the different energy conditions with the fractional radial coordinate due to different values of \(\alpha \) is shown in Fig. 6.

Fig. 6
figure 6

Variation of the different energy conditions as a function of the fractional radial coordinate r / R for the \(LMC ~X-4\). Here, blue, red, green, black, burgundy and purple colour linestyle stand for \(\rho +p_{r}+2\,p_{t}+{\frac{{E}^{2}}{4 \pi }}\), \( \rho +p_t+{\frac{{E}^{2}}{4 \pi }}\), \(\rho +p_r\), \(\rho +{\frac{{E}^{2}}{ 8 \pi }}\), \(\rho -p_{r}+{\frac{{E}^{2}}{4 \pi }}\) and \( \rho -p_t\), respectively. Solid line for \( \alpha \) = 0.0015; long dash line for \( \alpha \) = 0.0010; dash line for \( \alpha \) = 0.0005; dot line for \( \alpha \) = 0.000

Full size image

5.1.2 Mass-radius relation

According to [65], the mass-radius ratio for a stable stellar system should maintain \(2m(r)/r \le 1\) throughout the region. Andréasson [66] generalized the maximum mass-radius ratio for a charged stellar system in the following form

$$\begin{aligned} \frac{2M}{R}\le \frac{2}{9R^2}\left[ 3Q^2 + 2R^2+ 2R \sqrt{3Q^2 + R^2}\right] . \end{aligned}$$

For the present stellar system the mass variation can be written as

$$\begin{aligned} m \left( r \right)= & {} \frac{{r}^{3}}{2{R}^{5}}\, \big [ -3{R}^{7}{\alpha }^{2 }+3{R}^{5}{\alpha }^{2}{r}^{2}-16B\pi {R}^{5} \nonumber \\&+16B\pi {R}^{3}{r}^{2}+5M{R}^{2}-3M{r}^{2} \big ]. \end{aligned}$$
(35)

The variation of total mass respect to total radius is exhibited in Fig. 7. The variation is drawn for different charge constant. As a result from variation, we obtain that the mass increases with the charge constant. Stellar mass is normalized in solar mass (\(M_\odot \)).

Fig. 7
figure 7

The variation of M (normalized in solar mass \(M_{\odot }\)) of a strange star as a function of radius shown in the upper panel, whereas in the lower panel we show enlarged version of \(M/M_\odot \) vs R curve. Solid circles are representing the maximum mass and radius of the respective curves

Full size image

5.1.3 Compactification factor and red shift

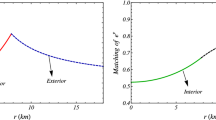
The compactification factor of a stellar system can express as,

$$\begin{aligned} u(r)= \frac{m(r)}{r}= & {} \frac{{r}^{2}}{2{R}^{5}}\, \Big ( -3\,{R}^{7}{\alpha }^{2}+3\,{R}^{5}{\alpha }^{2}{r}^{2}-16\,B\pi \,{R}^{5}\nonumber \\&+16\,B\pi \,{R}^{3}{r}^{2} +5\,M{R}^{2}-3\,M{r}^{2} \Big ). \end{aligned}$$
(36)

The redshift function (\(Z_s\)) of a stellar system is defined as,

$$\begin{aligned} Z_s= & {} \text {e}^{-\lambda /2}-1\nonumber \\= & {} \exp -\frac{32}{\lambda _{{1}}\nu _{1}} \Bigg [\lambda _{1}\,\mathrm{arctanh} \left( {\frac{{R}^{5}{\alpha }^{2}+16\,B\pi \,{R}^{3}-M}{\lambda _{{2}}}}\right) \nonumber \\&+\lambda _{1}\,\mathrm{arctanh} \left( {\frac{2 \nu _{1}r^2+2\,\nu _{2}}{\lambda _{{2}}{R}^{2}}}\right) + \lambda _{{2}} \left( \lambda _{3}-\lambda _{4} \right) \ln \lambda _{5} \nonumber \\&+\Big \{\lambda _{4}\,\ln \left( \left( \nu _{1}r^2+\nu _{2} \right) {r}^{2}+\overline{{ Ric}} {R}^{5} \right) -\lambda _{3}\,\ln \overline{{ Ric}} \nonumber \\&+\frac{5}{2}\left( {\frac{3\,{R}^{5}{\alpha }^{2}}{40}}+B\pi \,{R}^{3}-\frac{3}{16}\,M \right) \,\ln R \Big \} \lambda _{{2}} \Bigg ]-1. \nonumber \\ \end{aligned}$$
(37)

The variation of \(Z_s\) is shown in the Fig. 8 as function of radial coordinate.

Fig. 8
figure 8

The variation of the redshift function with respect to the fractional radial coordinate for \(LMC~X-4\)

Full size image

5.2 Verification of the stability

To justify the stability of the present stellar configuration, we considered (i) TOV equation, (ii) Herrera cracking condition and (iii) Adiabatic Index.

5.2.1 (i) TOV equation

A stellar system is said to be in equilibrium if the resultant of forces on a system is nil. Imbalance in force drives the system to an unstable configuration. For the stellar system these counterbalancing forces are given by Tolman [67] and Oppenheimer-Volkoff [68].

According to TOV equation

$$\begin{aligned} -p_r'-\frac{\lambda '}{2}(\rho +p_r)+ \sigma \frac{q}{r^2} e^{\nu /2}+\frac{2}{r}(p_t-p_r) = 0. \end{aligned}$$
(38)

Here, the terms are defined as hydrostatic force (\( F_{h} \)), gravitational force (\( F_{g} \)), electrostatic force (\( F_{e} \)) and the last term defines the anisotropic force (\( F_{a} \)) respectively of the Eq. 38. To maintain the equilibrium, the outward forces \( F_{e} \), \( F_{a} \) and \( F_{h} \) must be balance by the attractive pull \( F_{g} \).

Fig. 9
figure 9

Variation of different forces as a function of the fractional radial coordinate r / R for the \(LMC ~X-4\)

Full size image

The variation of the forces for different charge distributions are exhibit in Fig. 9.

5.2.2 (ii) Herrera cracking condition

The physical stability of a stellar system can be verified with respect to the causality condition also. According to the condition, the square of the radial (\( v_{sr}^2 =\frac{dp_r}{d\rho } \)) and the tangential (\( v_{st}^2 =\frac{dp_t}{d\rho }\)) sound speed lies between 0 \(\rightarrow \) 1, i.e. 0 \(\le v_{si}^2 \le 1 \) (where, \(i=r, t\)). The region is called potentially stable if the radial sound speed is greater than the tangential sound speed.

According to the following works [69, 70] the difference of the squares of tangential and radial sound speeds must hold the sign inside the stellar system. Hence, according to Herrera’s condition \( \mid v_{st}^2 -v_{sr}^2 \mid \le \) 1.

In Fig. 10 the variation of the radial and tangential sound speeds and their differences are shown in the upper panel and lower panel, respectively.

Fig. 10
figure 10

Variation of (i) \(v_{sr}^2\) and \(v_{st}^2\) (upper panel) and (ii) \( \mid v_{st}^2 -v_{sr}^2 \mid \) (lower panel) as a function of the fractional radial coordinate r / R for the \(LMC ~X-4\)

Full size image

5.2.3 (iii) Adiabatic index

The study of the adiabatic index plays an important role in the case of a spherically symmetric system by exploring the characterization of the stiffness of the equation of state (EOS) [53, 54]. Clearly, the adiabatic index develops a clear bridge between the spherically symmetric relativistic stellar system and the EOS which describes interior matter distribution by including all the required fundamental characteristics of EOS into the instability criterion. It is worth mentioning that the adiabatic index is a function of baryon density and exhibits a radial dependency on the instability equation. The pioneering work by Chandrasekhar [55, 56] presents an efficient technique via the adiabatic index in examining the criteria of stability of a relativistic stellar object against an infinitesimal radial adiabatic perturbation. For an infinitesimal radial perturbation, the dynamical stability has been studied by several authors [57,58,59,60]. Later on, Heintzmann and Hillebrandt [61] in their work had shown that for a dynamically stable stellar system the value of adiabatic index should lie above 4 / 3 in all the interior points of the stellar system. In relativistic stars, with anisotropic fluid distribution, the consideration is more perplex. The gamma is higher than the normal considered critical limit [63, 64]. As a consequence, with increment of the charge, it is observed that the adiabatic index is also increases and hence the EOS of the stars becomes stiffer. The adiabatic index (\(\mathrm {\Gamma } \)) for our system is defined as follows:

$$\begin{aligned} \mathrm {\Gamma } = \left( \frac{p_r + \rho }{p_r}\right) \frac{dp_r}{d \rho } = \frac{p_r + \rho }{p_r} v_{sr}^2. \end{aligned}$$
(39)

The variation of the adiabatic index as a function of the fractional radial coordinate is shown in Fig. 11.

Fig. 11
figure 11

Variation of the adiabatic index as a function of the fractional radial coordinate r / R for the \(LMC ~X-4\)

Full size image
Table 1 The physical parameters are predicted from the proposed model where \(1~{{M}_{\odot }}=1.475\) km for \(G=c=1\). The set is valid for \(\hbox {B} _g = 83 \hbox {Mev/fm}{^3}\), \( {\overline{Ric}} = 1.2\) and \(\alpha = 0.0010~\hbox {km}^{-2}\)
Full size table

6 Discussion and conclusion

In the paper at hand, we have performed a detail investigation of the physical impacts of the charge distribution on the structure and behaviour of the strange stars. We have generalized the description of the charged strange stars in Finslerian background by studying the modified form of the Maxwell-Einstein field equation. We derived the gravitational potentials from the family of field equations and smoothly matched them with exterior Finslerian Ressiner-Nordström solution. Fig. 1 indicates the variation of the metric potentials viz., \( e^{\nu (r)} \) and \( e^{\lambda (r)} \), which are monotonically increasing and geometrically non-singular by nature. The variation of \(\hbox {e}^{\nu }\) and \(\hbox {e}^{-\lambda }\) meet at the surface, i.e., \(r=R\) for \({\overline{Ric}}=1\) only. Note that for other numerically considered values of \({\overline{Ric}}\), \(\hbox {e}^{\nu }\) and \(\hbox {e}^{-\lambda }\) must not meet at the surface, due to the presence of \({\overline{Ric}}\) in numerator and denominator, respectively. This aspect is also clear from Eq. (23). The interior quarks and electrons distribution profile of the system is related to the radial pressure of the system by the MIT bag equation. The density profile of the system decreases from the central density \(\rho _c\) (A.8) holding the same sign of the slope. The radius of the stellar body is predicted when, there is no overlying matter against the gravitational attractive force, which endorses zero radial pressure. Due to the reason, the surface density is constant, this is one of the limitations of the approach. The radial and tangential pressure also decreases monotonically with the radial variation. The expression and variation of density, radial and tangential pressure are provided in Eqs. 31–33, in Fig. 2 and in Fig. 3 respectively. As a consequence of using anisotropic fluid, our model shows that the anisotropic stress is maximum at surface area and there is no anisotropy at the centre of the system, as predicted by Deb et al. [71] in Riemannian frame. Due to the introduction of charge, the anisotropy reduces with the increment of the charge constant, i.e., charge can remove the anisotropy of a system. The expression is provided in Eq. (33) and the Fig. 4. The variation of charge distribution and the corresponding field is portrayed in Fig. 5.

Fig. 12
figure 12

The variation of M (normalized in \(M_{\odot }\)) with respect to the central density \(({\rho }_c)\) is shown in the upper panel, whereas in the lower panel we show the enlarged version of \(M/M_\odot \) vs \({\rho }_c\) curve. Solid circles are representing the maximum mass for the system

Full size image

With the considered assumption, the charge and the following electric field reaches its maximum at the surface. The acceptability of the system is examined on the basis of the energy conditions, Herrera cracking condition, TOV equation and mass-radius relation.

Table 2 Numerical values of physical parameters for different charge constant \(\alpha \) for the strange star \(LMC~X-4\) of mass \(1.29M_\odot \) (\(1~{{M}_{\odot }}=1.475~\hbox {km}\)) with \(B _g = 83\hbox { Mev/fm}{^3}\)
Full size table
Fig. 13
figure 13

The variation of R with respect to \({\rho }_c\) is shown in the upper panel, whereas in the lower panel we show the enlarged version of R vs \({\rho }_c\) curve. Solid circles are representing the maximum radius for the system

Full size image
Fig. 14
figure 14

The variation of the total charge (Q) with respect to \({\rho }_c\) is shown in the figure. Solid circles are representing the maximum charge for the system

Full size image

The anisotropic flow along with the pressure gradient and coulomb repulsion is supported by the gravitational pull of the matter (mass), inwards to it. It defines the overlying matter density reduces radially. The variation of the forces endorses that our stellar structure is non-varying in terms of the equilibrium of forces.

Cracking concept describes the nature of the deviation of the system from equilibrium. The notion depends on the theory of gravitation, not on the geometry. We found that our stellar structure is consistent with both conditions (i) the causality relation and (ii) the Herrera cracking concept.

The redshift is monotonically decreasing with radial variation toward the surface. Variation of the redshift as a function of fractional radial coordinate (r / R) for the strange star \(LMC~X-4\) is portrait in Fig. 8, where the compactification factor defines the mass boundness of the structure.

In GR, the Schwarzschild type metric keeps the spherical symmetry. The spherical symmetry of Riemannian space is defined by “Finslerian sphere” in Finslerian geometry, that maintains maximal symmetry [72]. In mathematics, which is topologically equivalent to a sphere. In Finsler geometry, the flag curvature is equivalent of sectional curvature of Riemannian geometry. Constant Ricci scalar is also equivalent to the constant flag curvature, which imposes the spherical symmetric system.

We have predicted the radii of few candidates of strange stars by using their observed masses. In addition, we studied different physical parameters related to the structure for the predicted radius. All studies are provided in the tabular form, Ref. Table 1.

Table 3 Numerical values of physical parameters for different \({\overline{Ric}}\) for the strange star \(LMC~X-4\) of mass \(1.29M_\odot (1~{{M}_{\odot }}=1.475~\hbox {km})\) with \(\hbox {B} _g = 83\hbox { Mev/fm}{^3}\) and \(\alpha = 0.0010~\hbox {km}^{-2}\)
Full size table
Table 4 Numerical values of physical parameters for different Bag values for the strange star \(LMC~X-4\) of mass \(1.29M_\odot (1~{{M}_{\odot }}=1.475~\hbox {km}\)) with \( {\overline{Ric}} = 1.2\) and a = 0.0010 km\(^{-2}\)
Full size table

The maximum limiting mass and correlated radius gradually increase with the increasing values of \( \alpha \) ref. Fig. 7 (the solid circles in the variation of the total mass M of the stellar structure corresponds to the maximum mass limit of the model for a given value of \( {\overline{Ric}} =1.2 \) and \( B_g=83 \) MeV\(/{\text {fm}}{^3}\) ). We found that the maximum mass (\(M_{max} \)) for \( \alpha = 0.0015 ~km^{-2}\) is higher than \(M _{max} \) for zero charge by \(4.77 \%\) and the respective radius \(R _{max} \) is increased by 0.98%. A stellar configuration is in stable or unstable equilibrium, can be categorized from the relation \(\frac{dM}{d \rho _c} \). The positive slope indicates a stable configuration. Maximum mass point for \( \alpha = 0.0015\) km\(^{-2}\) is increased by \(7.6\%\) than the maximum mass point for zero charge respective of \(\rho _c\) variation. The variations of M (normalized in \(M_\odot \)) and R with respect to \(\rho _c\) are shown in the Figs. 12 and 13, respectively. In addition, the variation of total charge (Q) with respect to central density is shown in Fig. 14, which features that with the increasing values of Q the central density of the strange stars decreases gradually. Again, for the charge constant \(\alpha = 0.0015\) km\(^{-2}\) the maximum total charge is obtained at \(\rho _c=963\)  MeV\(/{\text {fm}}{^3}\), whereas the maximum mass \(M_{max}=5.03 M_\odot \) is obtained for \(\rho _c=965\)  MeV\(/{\text {fm}}{^3}\). From the above numerical study, it is interesting to mention that, in the presence of charge, the amount of total mass increases more intensely than the radius, which indicates that the more compact systems can be justified in the framework.

In the recent discovery of extremely luminous supernovas, e.g. SN 2003fg, SN 2006gz, SN 2007if and SN 2009dc [82, 83] as a part of SNLS, reveals a huge Ni-mass system and endorse the super-massive Chandrasekhar white dwarfs of over mass range 2.1-2.8 \(\hbox {M}_\odot \) [84,85,86,87]. Recent discovery of massive pulsar of \(2.27^{+0.17}_{-0.15}\) \(\hbox {M}_\odot \), in observation of binary \(PSR~J2215+5135\), [88] supports the existence of massive compact stars. In the framework of Finslerian geometry, the expansion of the universe and the corresponding anisotropic behaviour has been studied [39,40,41]. Our study enunciates that in the Finslerian frame, the limiting mass of an compact stellar system can be higher than the standard mass limit in Riemannian frame for a chosen parametric value of the flag curvature and can explain the observed massive stellar system.

To have a better understanding of the present model in Tables 2 and 3 we present a comparative study of the different physical parameters, viz., radius, central density, central pressure, surface redshift, total charge of the structure and the corresponding field, etc., due to the chosen parametric values of \(\alpha \) and \( {\overline{Ric}}\), respectively. Further, we have predicted values of the above mentioned physical parameters due to the chosen values of bag constant, viz. \(B=70, 80\) and \(90~MeV/fm^3\) in Table 4. Interestingly, the numerical analysis reveals that with the increasing values of \( {\overline{Ric}} \) it is possible to pack more mass in the stellar system and the total charge of the system also increases gradually.

There are also few limitations in our approach, due to which simulation is not completely analogues with the real life system, formally applicable to define a static stellar structure. Within all constraints, it is worthy of noting that in Finslerian geometry the ultra-high dense strange stars can be successfully represented, which leaves a very interesting area for future research.