Anisotropic compact objects in f(T) gravity with Finch–Skea geometry

Abstract

We study relativistic solutions of anisotropic compact stars with Finch–Skea (FS) metric in f(T) gravity framework. The modified FS geometry is considered to obtain the equation of state (EoS) for different known stellar objects with given mass and radius. The modified Chaplygin gas (MCG) EoS is also considered to obtain stellar objects as the EoS inside the star is not yet known. The results obtained here is important in the two cases to understand properties of known stars, which are however not known observationally. The physical features of known stars are analyzed here and found that compact star formation may be possible with repulsive core. In the case of MCG in f(T) gravity compact stars may be obtained with anisotropic fluid ($p_t>p_r$), with maximum anisotropy at the center of the star, which however is not found when MCG is absent.

1 Introduction

It is known that General theory of Relativity (GR) is a geometric theory of gravitation based on the assumption that gravity manifests itself as the curvature of spacetime. In GR the spacetime structure may be determined using Lorentzian metric (g) and a linear Levi-Civita connection ($\Gamma$). Although GR is a fairly successful theory it presents some serious issues at ultraviolet and infrared limits. Recent observational evidences of Galactic, extra Galactic and cosmic dynamics can not be understood by GR unless one considers some exotic forms of matter energy viz. dark matter and dark energy [1, 2]. Alternatively, one can modify the gravitational sector to fit the missing matter-energy of the observed universe. In recent times there is a huge effort to modify gravity [3,4,5,6] to describe the evolution of the observed universe as well as to solve the issues of non-renormalizability [7, 8] in GR.

The spacetime connections considered by Einstein are torsionless. However apart from simplicity there is no reason to consider that spacetime is torsionless. Torsion in the theory may arise from the consideration of spin or from a gradient of scalar field. The issues to modify GR with torsion [9,10,11] arises whether the spacetime connection is a symmetric or not. Essentially GR is a classical theory which does not accounted quantum effects, a situation which deals with gravity at a fundamental level. The paradigm is that the mass-energy is the source of curvature and in general, spin is the source of torsion.

The consideration of a spacetime with torsion is an alternate approach equivalent to GR, was first introduced by Einstein himself known as Teleparallel Equivalent of General Relativity (TEGR) [12,13,14]. The most significant difference between GR and TEGR is that in the later case tetrad fields are present [15, 16]. In this case the tetrad fields are used to define a linear anti-symmetric Weitzenböck connection related to torsion without curvature [17, 18]. Although both GR and TEGR provides similar results there are some fundamental differences between the two theories. According to GR, curvature represents the geometrical picture of spacetime which describes gravity. In contrast TEGR represents the same gravitational interactions in terms of torsion which acts as a force. This implies that in TEGR the geodesic equations are analogous to the Lorentz force equations of electrodynamics [19].

The need of constructing a modified gravitational theory arose from the observational evidences that our universe is passing through an accelerating phase of expansion [20]. Most of the works in the literature addressed curvature-based formulation, and modify the Einstein–Hilbert action with f(R) paradigm in which the Lagrangian is considered to be a non-linear function of the curvature scalar. However, one can reasonably think to start from TEGR, and use it as a basis to build a gravitational modification. The simplest class of these torsion-based modifications is the paradigm of f(T) gravity [21,22,23,24], in which the Lagrangian is taken to be a non-linear function of the TEGR Lagrangian T. TEGR coincides completely with general relativity at the level of equations, f(T) gravity may be simple compared to f(R) gravity as they give rise to second order differential equations whereas it is fourth order in case of f(R) theories.

In recent times, TEGR formalism and f(T) gravity are found successful to study cosmological and astrophysical phenomena. Ferraro and Fiorini [21] solved the particle horizon problem in a spatially flat FRW universe considering a modified version of TEGR in Born–Infeld approach. The solution of the equations of motion for the extended BTZ black hole with a cosmological constant has been studied in this model [22]. Li et al. [25] showed that in f(T) gravity the action and the field equations are not invariant under local Lorentz transformations, however, the usual teleparallel Lagrangian (TEGR) is an exception. The first law of black-hole thermodynamics is violated in f(T) framework which is a result of the lack of local Lorentz invariance [26]. Recently Wang et al. [27] studied spherically symmetric static solution in f(T) models with Maxwell terms in a particular frame based on the conformally Cartesian coordinates. It is found that only a limited class of f(T) models can be solved in this frame. Momeni et al. [28] obtained a new exact solution of anisotropic star in f(T) gravity considering Krori and Barua metric. Deliduman et al. [29] investigated neutron stars under modified f(T) gravity framework and found that, the relativistic neutron star solution in f(T) gravity models is possible only if f(T) is a linear function of the torsion scalar T, that is in the case of TEGR.

The motivation of the present paper is to obtain relativistic solution for an anisotropic compact object whose interior spacetime is described by the modified Finch–Skea (FS) geometry, for linear form of f(T) gravity. The metric proposed by Dourah and Ray [30] was modified by Finch and Skea [31] for investigating compact objects under various situations. Recently, FS geometry was modified to accommodate isotropic charged star [32] and it was also modified further incorporating anisotropic stars [33]. A number of research work in relativistic astrophysics using FS metric in 4- dimensions [34,35,36,37,38,39,40] and higher dimensions [41, 42] also came up.

In order to study the physical properties of a stellar system, it is important to predict a proper equation of state (EoS), i.e., $p=p(\rho )$. In the absence of a reliable information about the EoS at very high densities, assumption of the metric potentials, based on the geometry has been found to be a reasonable approach to construct a stellar model. In our paper, we obtain EoS of a compact object with FS geometry in a linear f(T) gravity which corresponds to TEGR.

With the introduction of the existence of dark energy, Lobo [43] and coworkers considered stellar models which are called dark stars where the equation of state was taken in the linear form given by $p=\omega \rho$ with $-1<\omega <1/3$. Chaplygin gas was considered to obtain acceleration of the universe and structure formation. Later a modification to the Chaplygin EoS with a more generalized form of equation of state [44, 45]. Dark energy provides sufficient repulsive force to counteract the continued gravitational collapse of the dark stars. The process reaches a stable configuration which is free from horizons and singularities. Recently Saha et al. [46] studied anisotropic stellar models with interior space-time geometry described by Krori-Barua metric with modified Chaplygin gas in f(T) gravity. Motivated by the above works, we also analyzed anisotropic compact stellar models with Finch–Skea geometry in f(T) framework with modified Chaplygin gas (MCG).

The paper is organized as follows: In Sect. 2, fundamentals of f(T) gravity is presented. The general form of the field equation is obtained by varying the action with respect to the tetrad field. In Sect. 3, the field equations are presented for a spherically symmetric static spacetime in terms of the torsion scalar, T and it’s derivative, and we have discussed that for a neutron star model only the linear form of f(T) (TEGR) is permitted. In Sect. 4, the exterior region of the stellar model is described by Schwarzschild metric and the junction conditions joining the interior modified FS metric and exterior region have been obtained. In Sect. 5, the field equations are solved and determine the unknown parameters from matching conditions and studied the various physical features of compact object e.g. energy-density, pressure, anisotropy etc. We analyzed the stability condition also and obtained a mass–radius relation. The probable EoS for the matter are determined. In Sect. 6, we compare the results obtained from the f(T) model to the results obtained previously in GR. In Sect. 7, for a compact object the EoS described by the modified Chaplygin gas in a f(T) gravity is considered to describe the physical features. Finally in Sect. 8, we summarize the results obtained.

2 Field equations of f(T) gravity for anisotropic sources

The line element of a manifold is,

$$\begin{aligned} ds^2= & {} g_{\mu \nu } {dx^\mu } {dx^\nu } = \eta _{ij} {\theta ^{i}}_\mu {\theta ^{j}}_\nu {dx^\mu } {dx^\nu }, \end{aligned}$$

(1)

$$\begin{aligned} dx^\mu= & {} {e^{\mu }}_i {\theta ^{i}}, {\theta ^{i}}={e^{i}}_\mu {dx^{\mu }}, \end{aligned}$$

(2)

where $\eta _{ij}=diag[1,-1,-1,-1]$, $e^\mu _i e^\nu _i=\delta ^\mu _\nu$ or $e^\mu _i e^\nu _j=\delta ^j_i$, the indices i, j are related to the tetrad field $\theta ^i_\mu$ and the greek letters $\mu ,\nu$ corresponds to the space time coordinates. The root of the metric determinant is $\sqrt{-g}=det[e^i_\mu ]=e$. The Weitzenböck’s anti-symmetric connections for the vanishing Riemann tensor with non vanishing torsion is defined as

$$\begin{aligned} \Gamma ^\alpha _{\mu \nu }=e^\alpha _i \partial _\nu e^i_\mu =-e^\mu _i \partial _\nu e^\alpha _i. \end{aligned}$$

(3)

The torsion and con-torsion tensors are:

$$\begin{aligned} T^\alpha _{\mu \nu }=\Gamma ^\alpha _{\nu \mu }-\Gamma ^\alpha _{\mu \nu }=e^\alpha _i \left( \partial _\mu e^i_\nu - \partial _\nu e^i_\mu \right) . \end{aligned}$$

(4)

$$\begin{aligned} K^{\mu \nu }_\alpha =-\frac{1}{2} \left( T^{\mu \nu }_\alpha -T^{\nu \mu }_\alpha -T^{\mu \nu }_\alpha \right) . \end{aligned}$$

(5)

The above two tensors given by Eqs. (3) and (4) are used to construct a new tensor given by,

$$\begin{aligned} S^{\mu \nu }_\alpha =\frac{1}{2}\left( K^{\mu \nu }_\alpha +\delta ^\mu _\alpha T^{\beta \nu }_\beta -\delta ^\nu _\alpha T^{\beta \mu }_\beta \right) . \end{aligned}$$

(6)

The torsion scalar now can be expressed as:

$$\begin{aligned} T=T^\alpha _{\mu \nu } S^{\mu \nu }_\alpha . \end{aligned}$$

(7)

Analogous to modified gravitational action in f(R) theory one can obtain another modified gravity f(T) replacing R by T, as,

$$\begin{aligned} S=\int d^4x \left[ \frac{1}{16\pi } f(T)+ {L_{ {matter}}}\right] e \end{aligned}$$

(8)

where, $G=c=1$ and $L_{ {matter}}$ is the matter Lagrangian. Variation of Eq. (8) with respect to tetrad field yield the following set of equations of motion:

$$\begin{aligned}&e_{i}^{\alpha } S^{\mu \nu }_{\alpha } \partial _{\mu } T f_{TT}+e^{-1} \partial _{\mu }(e e^{\alpha }_{i} S^{\mu \nu }_{\alpha }) f_{T}+e_{i}^{\mu } T_{\mu k}^{\lambda } S^{\nu k}_{\lambda } f_{T} \nonumber \\&\quad -\frac{1}{4} e^{\nu }_{i} f=-4\pi e^{\lambda }_{i}T^{\nu }_{\lambda }, \end{aligned}$$

(9)

where $T_{\mu \nu }$ is the energy–momentum tensor of a particular matter, whereas $f_{T}$ and $f_{TT}$ represent first and second derivatives of f(T) with respect to the torsion scalar T respectively. For an anisotropic fluid the energy–momentum tensor is described by,

$$\begin{aligned} T^\nu _\mu =( \rho + p_t ) u_\mu u^\nu - p_t\delta ^\nu _\mu + (p_r-p_t) v_\mu v^\nu \end{aligned}$$

(10)

where $u^\mu$ and $v^\mu$ are the four velocity and radial four vectors, $p_r$ and $p_t$ represents pressures in radial and transverse directions.

In covariant derivative formalism, f(T) field equations can be recasted as,

$$\begin{aligned} \Upsilon _{\mu \nu }f_{TT} +\frac{T}{2}\Big ( \frac{f}{T}-f_{T}\Big ) g_{\mu \nu }+G_{\mu \nu } f_{T}=\frac{1}{16 \pi } T_{\mu \nu }^{(m)} \end{aligned}$$

(11)

where, $\Upsilon _{\mu \nu }=S^{\alpha }_{\nu \mu } \nabla _{\alpha } T$, while $G_{\mu \nu }$ is the Einstein tensor. In the stream of GR as well as f(R) field equations, Eq. (9) can be rewritten as,

$$\begin{aligned} G_{\mu \nu }=\frac{1}{16\pi f_{T}} \left( T_{\mu \nu }^{(T)}+T_{\mu \nu }^{(m)}\right) , \end{aligned}$$

(12)

where,

$$\begin{aligned} T_{\mu \nu }^{(T)}=\frac{1}{16\pi }\Bigg (-\Upsilon _{\mu \nu } f_{TT}-\frac{1}{4}(T-\Upsilon f_{TT}+Rf_{T})g_{\mu \nu } \Big )\nonumber \\ \end{aligned}$$

(13)

is a tensor incorporating corrections coming from torsion scalar. It is evident that for a linear f(T) i.e., $f(T)=T$, Eq. (11) leads to GR equations.

3 Model of anisotropic compact stars in f(T) gravity with Finch–Skea geometry

We consider a spherically symmetric static space-time metric given by,

$$\begin{aligned} ds^2=- e^{2\nu (r)} dt^{2} + e^{2\lambda (r)} dr^{2} + r^{2}d\Omega _2^{2} \end{aligned}$$

(14)

where, $\nu (r)$ and $\lambda (r)$ are the two unknown metric potentials, and $d\Omega _2^{2} = d\theta ^{2} + sin^2 \theta d\phi ^{2}$ represents the metric on the 2-sphere in polar co-ordinates. We consider the energy momentum tensor for an anisotropic compact object in 4-dimensions as,

$$\begin{aligned} T_{ab}=diag(-\rho ,p_r,p_t,p_t) \end{aligned}$$

(15)

where, $\rho$ is the energy density, $p_r$ is the radial pressure and $p_t$ is the tangential pressure.The pressure anisotropy is defined by $\varDelta =p_t-p_r$. The value of the anisotropy depends on the metric potentials $\lambda (r)$ and $\nu (r)$. The tetrad matrix for the metric in Eq. (10) is given by,

$$\begin{aligned}{}[e^i_{\mu }]=diag[e^\nu (r),e^\lambda (r),r,rsin(\theta )]. \end{aligned}$$

(16)

The determinant of the tetrad matrix is given by $e=det[e^i_{\mu }]=e^{\nu +\lambda }r^2 sin(\theta )$, the torsion scalar and its derivative in terms of r is given by,

$$\begin{aligned} T(r)= & {} \frac{2e^{-2\lambda }}{r} \Big (2\nu ' + \frac{1}{r}\Big ) \end{aligned}$$

(17)

$$\begin{aligned} T'(r)= & {} \frac{2e^{-2\lambda }}{r}\bigg [ 2\nu '' - \frac{1}{r^2} - \Big (2\nu ' + \frac{1}{r} \Big )\Big ( 2\lambda ' + \frac{1}{r}\Big )\bigg ] \end{aligned}$$

(18)

where the prime ()$'$ denotes the derivative with respect to the radial coordinates.

Now substituting the above tetrad field (16) and inserting the values of torsion scalar and its derivative in Eq. (9), one can find out the Einstein field equations explicitly in f(T) gravity for an anisotropic fluid as,

$$\begin{aligned} 4\pi \rho= & {} \frac{f}{4}-\frac{f_T}{2}\bigg [T-\frac{1}{r^2}-2\frac{e^{-2\lambda }}{r}\Big (\nu '+\lambda '\Big )\bigg ], \end{aligned}$$

(19)

$$\begin{aligned} 4\pi p_r= & {} \frac{f_T}{2}\bigg (T-\frac{1}{r^2}\bigg )-\frac{f}{4}, \end{aligned}$$

(20)

$$\begin{aligned} 4\pi p_t&{=}&\bigg [ \frac{T}{2}{+}e^{-2\lambda }\Big (\nu ''{+}(\frac{\nu '}{2}{+}\frac{1}{2r})(2\nu '-2\lambda ')\Big )\bigg ] \frac{f_T}{2}-\frac{f}{4},\nonumber \\ \end{aligned}$$

(21)

It is evident from Eqs. (19)–(21) that the above field equations lead to the corresponding field equations in GR for $f(T)=T$. In f(T) gravity one gets an extra non-diagonal Eq. (22) which is different from the case of GR.

$$\begin{aligned} \frac{cot\theta }{2r^2} T' f_{TT} = 0. \end{aligned}$$

(22)

One obtains the following cases corresponding to Eq. (22), (i) $T'=0\;\;$and (ii) $f_{TT}=0$ in the second case one obtains a linear form of f(T) function as,

$$\begin{aligned} f(T)=\beta T+\beta _1 \end{aligned}$$

(23)

where, $\beta$ and $\beta _1$ are integration constants. Equation (22) puts a strict constraint on the possible f(T) functions. Since f(T) may be a linear function only in the case of teleparallel equivalent of general relativity (TEGR) the corresponding solutions permits a relativistic neutron star. If one sets $T'=0$ it may not require to set $f_{TT}=0$, in which case it corresponds to a general f(T) gravity theory with constant torsion scaler ($T_{0}$) everywhere. However in the later case ($T'=0$), it make no sense as relativistic star solution which is evident from Eq. (20) [29]. For a constant torsion the rhs of Eq. (20) blows up as r goes to zero. This is not acceptable as interior pressure in this case also blows up. Thus this solution can not be considered to accommodate a neutron star. Therefore, if the torsion scaler is set to a constant value it leads to some ill consequences. Therefore, plausible choice is to set $f_{TT}= 0$, in which case no f(T) gravity theory other than the TEGR would be possible. However, the claim made above is concerned solely with the neutron star case in f(T) gravity where it is expected that both the energy-density and pressure have non-zero finite values only up to the surface of the neutron star. It may be possible in the framework of f(T) gravity accommodating a solution where either pressure or energy-density have everywhere non-zero values or one or both take infinite values at some points, but such solutions are not permitted in the context of TOV equation.

We consider the interior space-time of the star described by the modified Finch–Skea metric which is given by,

$$\begin{aligned} e^{2\lambda (r)}= & {} (1+Cr^2), \end{aligned}$$

(24)

$$\begin{aligned} e^{2\nu (r)}= & {} D^2\left[ (B{-}A\sqrt{(1{-}\alpha )(1{+}Cr^2)})Cos\sqrt{(1{-}\alpha )(1{+}Cr^2)}\right. \nonumber \\&\left. +\,(A{+}B\sqrt{(1{-}\alpha )(1{+}Cr^2)})Sin\sqrt{(1{-}\alpha )(1{+}Cr^2)}\right] ^2\nonumber \\ \end{aligned}$$

(25)

where A, B, C, D and $\alpha$ are arbitrary constants. The metric parameters are to be determined from the boundary conditions for a physical viable stellar model. In the above the parameter $\alpha$ is taken to satisfy ($0<\alpha <1$) for a modified Finch–Skea space-time, as for $\alpha =0$ the metric becomes the original Finch–Skea metric [31].

4 Conditions for physically realistic stellar model

To begin with we consider following conditions:

• (i) At the boundary of a star (i.e. at $r=b$), the interior space-time solution should be matched with the exterior Schwarzschild solution. For the continuity of the metric functions at the surface. One obtains,

  $$\begin{aligned}&D^2\left[ (B{-}A\sqrt{(1{-}\alpha )(1{+}Cb^2)})Cos\sqrt{(1{-}\alpha )(1{+}Cb^2)}\right. \nonumber \\&\qquad \left. {+}(A{+}B\sqrt{(1{-}\alpha )(1{+}Cb^2)})Sin\sqrt{(1{-}\alpha )(1{+}Cb^2)}\right] ^2 \nonumber \\&\quad =\left( 1-\frac{2M}{b}\right) \end{aligned}$$

  (26)
  $$\begin{aligned}&(1+Cb^2)=\left( 1-\frac{2M}{b}\right) ^{-1} \end{aligned}$$

  (27)

• (ii) The radial pressure drops from its maximum value ( at center ) to zero at the boundary, i.e.

  $$\begin{aligned} p_{r}|_{ (r=b)} =0 \end{aligned}$$

  (28)

• (iii) The density and pressure are positive inside a star, and at the center $\rho (0)=\rho _0$, $p_r(0)=p_{0}$, these are finite. For density this coincides with the null energy condition (NEC).

• (iv) The model must satisfy the dominant energy condition (DEC) at the center, i.e. $\rho _0> \mid p_0 \mid$.

• (v) Inside the star the square of the sound velocity $v^2 = \frac{dp}{d\rho } \leqslant 1$, to satisfy causality.

• (vi) The gradient of the pressure and energy-density should be negative inside the stellar configuration, i.e., $\frac{dp_r}{dr} < 0$, $\frac{d\rho }{dr} < 0$ and $\frac{dp_t}{dr} < 0$.

In our model there are seven unknowns $A,B,C,D, \alpha ,\beta$ and $\beta _{1}$ for a given mass (M) and radius (b) of a star which are to be determined from four equations viz. Eqs. (22), (26), (27) and (28). Thus to solve the relativistic equations we consider possible values of $\alpha$, $\beta$ and $\beta _{1}$ to obtain stellar models.

5 Physical analysis

5.1 Density and pressure of a compact object in f(T) gravity

We now solve Eq. (19) using the expressions of T(r), $\mu (r)$, $\nu (r)$ and f(T) as described in the previous section to obtain the energy-density as (taking $c=1$ and $G=1$),

$$\begin{aligned} \rho = \frac{\beta _1+2 C\;(3 \beta +r^{2} \beta _1)+C^{2}(2 \;r^{2}\beta +r^{4}\beta _1)}{16 \pi (1+C\;r^{2})^{2}} \end{aligned}$$

(29)

which is a function of r, determined by $\beta$, $\beta _1$ and C. Similarly, Eqs. (20) and (21) can be solved for finding the expression of $p_r$ and $p_{t}$. The radial pressure ($p_{r}$) can be given by,

$$\begin{aligned} p_r=\frac{(AK_{1}Z- B Y_1) Cos K_1 - (BK_1 Z+ A Y_1) Sin K_1}{16\pi K^2 X _1}\nonumber \\ \end{aligned}$$

(30)

where $Y_1= \beta _1+C (-2 \beta +4\alpha \beta + r^2 \beta _1)$, $K=\sqrt{1+C r^2}$, $Z= 2C\beta + \beta _1 + Cr^2 \beta _1$ and $X_1=(B-AK_1) Cos K_1 + (A+BK_1) Sin K_1$, $K_1=K\sqrt{(1-\alpha )}$.

The expression for $p_{t}$ is given by,

$$\begin{aligned} p_{t}=\frac{(AK_{1}Z^{'}- B Y_1^{'}) Cos K_1 - (BK_1 Z^{'}+ A Y_1^{'}) Sin K_1}{16\pi K^4 X _1}\nonumber \\ \end{aligned}$$

(31)

where, $Z^{'}=Z+Cr^{2}[\beta _{1}(1+Cr^2)+2\beta C(1-\alpha )]$ and $Y_{1}^{'}=Y_{1}+Cr^{2}[\beta _{1}(1+Cr^2)-2\beta C(1-\alpha )]$. It is noted that both the radial- pressure and transverse pressure depend on $\alpha$, though density is independent of $\alpha$.

Now, in the absence of anisotropy (i.e. $\alpha =0$), then the expression for radial pressure becomes,

$$\begin{aligned} p_r=\frac{(BY+AKZ) Cos K + (AY-BKZ) Sin K}{16\pi K^2 X} \end{aligned}$$

(32)

where $Y=2C\beta -\beta _1-C r^{2} \beta _1$ and $X=(B-AK) Cos K + (A+BK) Sin K$.

In our model we choose $\beta _1=0$. In Fig. 1, we plot the variation of energy-density with different $\beta$ values taking $\beta _1=0$, for a known compact object. Here, we have seen that for different $\beta$, at the center the density of compact object in f(T) gravity is maximum and it decreases radially outward. Therefore, in this case $\beta$ plays role of a scale factor which is evident from Fig. 1. So we can say that for a star of particular radius higher $\beta$ values allows the star to accommodate more mass. It is evident from Eq. (28) that $\rho$ is independent of the anisotropy parameter $\alpha$. Thus the modified Finch–Skea geometry doesn’t change with the density of stellar matter.

Fig. 1

Radial variation of energy-density of PSR J0348+0432 for $\beta = 1$ (red), $\beta = 2$ (black) and $\beta = 3$ (blue)

Fig. 2

Variation of radial pressure with r of PSR J0348+0432 for $\beta = 1$ (red), $\beta = 2$ (black) and $\beta = 3$ (blue) (considering $\alpha = 0.4$)

Fig. 3

Variation of radial pressure with r of PSR J0348+0432 for $\alpha = 0$ (dot dashed) and $\alpha \ne 0$ (red)

The radial pressure is plotted in Fig. 2, it is observed that the radial pressure is a monotonically decreasing function of r with its maximum value at the center of the star. The radial pressure increases when $\beta$ increases for same r. We plot $p_{r}$ with r for a particular $\beta$ and found that for $\alpha = 0$ pressure is greater than that for $\alpha \ne 0$ in Fig. 3. For both $\alpha = 0$ and $\alpha \ne 0$ , we found that the radial pressure reaches a maximum value at the center of the star. The plot of transverse pressure is shown in Fig. 4, and it is evident that transverse pressure also follows the same profile as the radial pressure with increasing $\beta$. In Fig. 5 the radial variation of $p_{r}$ and $p_{t}$ are plotted for a particular $\beta$ value. From the plot it is clear that both $p_r$ and $p_t$ are equal at the center of the star, however at the boundary of the compact object $p_t \ne p_r$ which implies the presence of anisotropic stress and it becomes more prominent near the boundary of the star.

Fig. 4

Variation of transverse pressure with r of PSR J0348+0432 for $\beta = 1$ (red), $\beta = 2$ (black) and $\beta = 3$ (blue) (considering $\alpha = 0.4$)

Fig. 5

Variation of $p_r$ (solid line) and $p_t$ (dot dashed) with r of PSR J0348+0432 for $\beta = 1$ (considering $\alpha = 0.4$)

The radial variation of the gradients of energy-density and radial pressure for $\alpha \ne 0$ is shown in Figs. 6 and 7 for different $\beta$ values, which are negative.

Fig. 6

Radial variation of the energy-density gradient of PSR J0348+0432 for $\beta = 1$ (red), $\beta = 2$ (black) and $\beta = 3$ (blue) (considering $\alpha = 0.4$)

Fig. 7

Variation of the radial pressure gradient of PSR J0348+0432 for $\beta = 1$ (red), $\beta = 2$ (black) and $\beta = 3$ (blue) (considering $\alpha = 0.4$)

5.2 Anisotropic behaviour

The anisotropic pressure behaviour is studied by several authors for a spherically symmetric stellar model. Ruderman [47] showed that a high density ($>10^{15}\,\text {g/cm}^3$) nuclear matter object can be treated relativistically and exhibits anisotropy as an intrinsic property. The reason for incorporating anisotropy is due to the fact that in the high-density regime of compact stars the radial pressure ($p_r$) and the transverse pressure ($p_t$) need not be equal which was invented by Canuto [48]. Anisotropy might occur in astrophysical objects for various reasons namely, viscosity, phase transition, pion condensation, the presence of strong electromagnetic field [49], the existence of a solid core or type 3A super fluid [50], the slow rotation of fluids [51] etc. We define the anisotropic stress parameter as,

$$\begin{aligned} \varDelta =p_t-p_r \end{aligned}$$

(33)

In modified Finch–Skea geometry the measure of anisotropy in f(T) gravity is obtained using Eqs. (20) and (21), which is given by,

$$\begin{aligned} \varDelta =\frac{\alpha C^{2} r^{2} \beta }{8\pi (1+Cr^{2})^{2}} \end{aligned}$$

(34)

It is evident that $\alpha =0$ and $\beta = 0$ leads to $\varDelta =0$. Thus $\alpha =0$ may be considered for a star with isotropic pressure in 4-dimension and $\alpha \ne 0$ corresponds to anisotropic pressure situation which also can be obtained in Finch–Skea geometry in higher dimension [42]. In Fig. 8 we plot the radial variation of $\varDelta$ for different $\beta$ values and it is found that for $\beta >0$, $\varDelta$ is positive i.e, $p_t>p_r$ which in turn implies that the anisotropic stress is directed outwards, hence there exists a repulsive gravitational force that allows the formation of super massive stars. However for negative $\beta$ values the energy-density turns out to be negative inside the star and also the causality condition is violated which is not physically acceptable.

Fig. 8

Variation of the anisotropic parameter of PSR J0348+0432 considering $\alpha = 0.4$

5.3 Stability

The stability of a stellar model is studied by plotting the radial speed of sound ($v_{sr}^{2}$) and the transverse speed of sound ( $v_{st}^{2}$ ) with r which lie between 0 and 1. The radial variation of the radial and transverse speed of sound are plotted in Figs. 9 and 10 respectively. It is also noted that the value of $|v_{st}^{2}-v_{sr}^{2}|$ must be less than 1 [52, 53] for a stable model of an anisotropic compact object found to exist in our model and plotted in Fig. 11.

Fig. 9

Variation of $v_{sr}^{2}$ with r of PSR J0348+0432

Fig. 10

Variation of $v_{st}^{2}$ with r of PSR J0348+0432

Fig. 11

Variation of $|v_{st}^{2}-v_{sr}^{2}|$ with r of PSR J0348+0432

5.4 Mass–radius relation

The compactification factor (u) for a spherically symmetric object is defined as the ratio between its mass and radius and it plays a significant role to understand the physical properties of a compact object. According to Buchdahl, the maximum allowable ratio of mass to radius for a compact object can be than $\frac{4}{9}$ ($\frac{2m}{b}<\frac{8}{9}$) [54]. In our model the gravitational mass in terms of $\rho$ is given by,

$$\begin{aligned} m=4\pi \int _{0}^{r} \rho (r') r'^2 dr'=\frac{r^3(6C\beta + \beta _1 + Cr^2 \beta _1)}{12(1+Cr^2)} \end{aligned}$$

(35)

From the above equation it is observed that the mass function is regular inside the star and it vanishes at the center. The variation of the mass function with radius is shown in Fig. 12. The observed mass of PSR J0348+0432 is also plotted in the mass radius curve.

Fig. 12

Variation of the mass function at the interior of a stellar object with r for PSR J0348+0432 with $\beta =1$ and $\beta _1=0$

In our model the compactification factor is given by,

$$\begin{aligned} u=\frac{m(r)}{r}=\frac{r^2(6C\beta + \beta _1 + Cr^2 \beta _1)}{12(1+Cr^2)} \end{aligned}$$

(36)

Fig. 13

Variation of $p_r$ with $\rho$ for PSR J0348+0432 with $\beta =1$ (the solid line (red) denotes quadratic fit and the dashed line (blue) denotes linear fit)

Table 1 Parameter values for different known compact objects with $\alpha =0.4$ and $\beta =1$

Table 2 Values of different physical parameters considering different values of the model parameter $\beta$ for PSR J0348+0432

For different stellar objects it is evident that u will depends on the model parameters C, $\beta$ and $\beta _1$. In Table 2, we have obtained the values of radius for a fixed mass object considering different $\beta$ values with $\beta _1=0$. We have also determined the central density ($\rho _0$), radial pressure at the center ($p_{r0}$) and density at the boundary ($\rho _b$) of the star. From the table it is evident that the radius obtained from our model agrees well with the observational value when we consider $\beta =1, \beta _1=0$ case. We note that for a given mass object the value of $\beta$ lies between 0 and 3 ($0<\beta <3$), as $\beta$ can not be negative for physically realizable models and also $\beta \ge 3$ leads to $\frac{2M}{b} >\frac{8}{9}$, which is not acceptable.

5.5 Equation of state

The variation of the energy-density and radial pressure are plotted in Figs. 1 and 2 from which one can predict possible EoS. Because of the complex form of the expressions of $\rho$ and $p_r$ it is not possible to obtain a known analytic relation between them. However a numerical analysis can be performed to predict the EoS. Here we obtain the best fitted relation between $\rho$ and $p_r$, the expressions so obtained for different compact objects have been listed in Table 1. In Fig. 13 both the linear and quadratic variation of $p_r$ with $\rho$ have been found to satisfy for PSR J0348+0432. It is predicted that the model permits both linear and quadratic fitting however the goodness of fit for the quadratic fit is better than the linear one as is evident from the figure also. Also it is noted that MIT bag model is not permitted here.

6 Comparative study of Finch–Skea star under f(T) and GR framework

In this section the results obtained in our model using f(T) gravity are compared with that obtained in GR model. In Sect. 5.2 we have studied the anisotropic behaviour of compact star with FS geometry in f(T) gravity. In GR, anisotropic stellar models with a modified FS geometry is studied [33] and an expression for $\varDelta$ is obtained. In f(T) gravity model, it is noted that for non-zero value of a parameter $\alpha$ the anisotropy is found as a function of parameter $\beta$, a coupling parameter in linear f(T) gravity. The anisotropy parameter in f(T) gravity is found more compared to GR model as $\beta >0$. It is noted that in f(T) gravity, $\varDelta >0$ corresponds to a repulsive gravity which is found to be more than the GR model. It is evident from Table 2, that the radius for a given star estimated from our model satisfies the observed Neutron star radius, which is in good agreement with the GR model for $\beta = 1$ and $\beta _{1}=0$. For a given mass of a compact object, as $\beta$ increases the radius is found to decrease, leading to a more compact object for higher $\beta$ values, which is displayed in Table 2.

Table 3 Parameter values for different known compact objects for matter distribution following Chaplygin EoS for $\alpha \ne 0$ ($\beta =1$, $\beta _{1}=0$ and $\gamma = 1$)

Table 4 Parameter values for different known compact objects for matter distribution following Chaplygin EoS for $\alpha = 0$ ($\beta =1$, $\beta _{1}=0$ and $\gamma = 1$)

7 Anisotropic Finch–Skea stars with modified Chaplygin gas in f(T) gravity

In this section, stellar models are obtained when the EoS is known. We consider modified Chaplygin gas ($MCG$) to determine the physical properties of compact objects in f(T) gravity. The equation of state for the modified Chaplygin gas is,

$$\begin{aligned} p_{rc}=\xi \rho _{c} - \frac{\zeta }{\rho _{c}^{\gamma }} \end{aligned}$$

(37)

where, $\xi$, $\gamma$ and $\zeta$ are free parameters and subscript c stands for Chaplygin gas. The energy-density for modified Chaplygin gas ($\rho _{c}$), is determined using Eqs. (17)–(25) which depends on $\nu$ and $\lambda$ as a function of r and is given by,

$$\begin{aligned} 8\pi (1+\xi )\rho _{c}^{\gamma +1} - 8\pi \zeta - \frac{2(\beta \rho _{c}^{\gamma })}{r(1+Cr^2)}(\nu '+\lambda ')=0 \end{aligned}$$

(38)

For simplicity we choose $\gamma =1$, $\beta =1$ and $\beta _{1}=0$, and it leads to a quadratic equation in $\rho _{c}$. Solving the equation the energy-density is given by,

$$\begin{aligned} \rho _{c}=\chi \left[ -\frac{CrP_1}{K^{4}X_1} \pm \sqrt{r^{2}(64\pi ^{2}\zeta (1+\xi ) + \frac{C^{2}P_{1}^{2}}{K^{8}X_1^{2}}}\right] \end{aligned}$$

(39)

where, $P=-AK_1-B(1+K_1^{2})$, $Q=-BK_1-A(1+K_1^{2})$ and $P_1=PCosK_1+QSinK_1$ and $\chi =\frac{1}{8\pi r(1+\xi )}$. The negative sign is not considered here as it leads to negative energy-density which is a unphysical result.

The radial pressure in this case will be of the form,

$$\begin{aligned} p_{rc}= & {} \xi \chi \left[ -\frac{CrP_1}{K^{4}X_1} + \sqrt{r^{2}(64\pi ^{2}\zeta (1+\xi ) + \frac{C^{2}P_{1}^{2}}{K^{8}X_1^{2}}}\right] \nonumber \\&-\frac{\zeta }{\chi \left[ -\frac{CrP_1}{K^{4}X_1} + \sqrt{r^{2}(64\pi ^{2}\zeta (1+\xi ) + \frac{C^{2}P_{1}^{2}}{K^{8}X_1^{2}}}\right] } \end{aligned}$$

(40)

The transverse pressure ($p_{tc}$) in this case is found to be same as Eq. (21). In case of $\alpha =0$, the modified Finch–Skea geometry leads to the original Finch–Skea geometry. We have studied both cases ($\alpha = 0$ and $\alpha \ne 0$) in the following sections.

7.1 Physical analysis of stellar model with Chaplygin gas

To study the physical behaviour of the energy density, pressure, anisotropy etc. inside the star the values of the model parameters A, B, C and $\xi$ are obtained using the matching condition at the boundary together with the condition that the radial pressure vanishes as $r=b$ for both $\alpha \ne 0$ and $\alpha = 0$ cases. The value of the parameter $\zeta$ is then obtained for different stars of known mass–radius values for a physically viable stellar model which are tabulated in Tables 3 and Table 4 respectively.

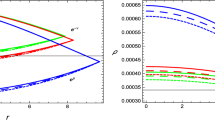
We plot the radial variation of $\rho _c$, $p_{rc}$, $v_{rc}^{2}$ and $v_{tc}^{2}$ for PSR-J0348+0432 in Figs. 14, 15, 16, 17 choosing $\xi =0.3$ and $\zeta =7.44 \times 10^{-8}$ for both $\alpha \ne 0$ and $\alpha = 0$. From the plots, it is evident that the values of energy density and radial pressure both at the center of the star will be less in case of modified Finch–Skea geometry than the original Finch–Skea geometry. All the physical conditions as mentioned in Sect. 4, are tested and found working satisfactorily for a stellar model. From Figs. 16, 17, 18, we have observed that $v_{rc}^{2}$ , $v_{tc}^{2}$ and $|v_{tc}^{2} - v_{rc}^{2}|$ always lies between 0 and 1. Finally, we have ensured that our model is potentially stable.

Fig. 14

Variation of energy-density ($\rho _{c}$) with r for PSR J0348+0432 considering $\beta =1$ and matter distribution following Chaplygin EoS [($\alpha = 0$ (blue) and $\alpha \ne 0$ (red)]

Fig. 15

Variation of radial pressure ($p_{rc}$) with r for PSR J0348+0432 considering $\beta =1$ and matter distribution following Chaplygin EoS [($\alpha = 0$ (blue) and $\alpha \ne 0$ (red)]

Fig. 16

Variation of $v_{rc}^{2}$ with r for PSR J0348+0432 considering $\beta =1$ and matter distribution following Chaplygin EoS [$\alpha = 0$ (blue) and $\alpha \ne 0$ (red)]

Fig. 17

Variation of $v_{tc}^{2}$ with r for PSR J0348+0432 considering $\beta =1$ and matter distribution following Chaplygin EoS [$\alpha = 0$ (blue) and $\alpha \ne 0$ (red)]

Fig. 18

Variation of $|v_{tc}^{2}-v_{rc}^{2}|$ with r for PSR J0348+0432 considering $\beta =1$ and matter distribution following Chaplygin EoS [$\alpha = 0$ (blue) and $\alpha \ne 0$ (red)]

7.2 Pressure anisotropy

The anisotropic stress parameter is defined as, $\varDelta = p_{tc} - p_{rc}$. In Sect. 5.2, it is observed that for the stellar systems with interior space-time described by modified Finch–Skea geometry, the anisotropy depends on the parameter $\alpha$. However when $\alpha =0$ it leads to an isotropic star as can be seen from Eq. (34). In this section we obtain the anisotropic stress for modified Chaplygin gas for $\alpha = 0$ and $\alpha \ne 0$ and it is also found that the anisotropy does not vanish even when $\alpha =0$, this is a new result and it may be due to the introduction of modified Chaplygin gas in the stellar system under f(T) framework. The radial variation of anisotropic parameter, $\varDelta$ is plotted in Fig. 19 for $\alpha = 0$ (blue) and $\alpha \ne 0$ (red) considering the modified Chaplygin gas. It is evident from Figs. 8 and 19 that the behaviour of anisotropic stress factor with modified Chaplygin gas is different from that without MCG i.e., $\varDelta$ is maximum at the center and decreases outward. It is interesting to note that there exists a critical value of radius ($r= 8.02 \;km$ for PSR J0348+0432) at which the value of $\varDelta$ for $\alpha = 0$ and $\alpha \ne 0$ coincide.

Fig. 19

Variation of the anisotropic parameter of PSR J0348+0432 with matter distribution following Chaplygin EoS [$\alpha = 0$ (blue) and $\alpha \ne 0$ (red)]

8 Discussion

In this paper we consider a modified gravity described by $f(T)=\beta T + \beta _1$, which is recently considered in describing issues in cosmology and astrophysics. Two different cases are considered, (1) considering only f(T) gravity with modified Finch–Skea geometry we predict the possible EoS of compact objects and (2) considering EoS described by the modified Chaplygin gas we determine the physical properties of compact objects. In the first case we found compact objects with quadratic EoS determined by fitting the model values of pressure and density numerically.

We note the following observations,

(i):

In Fig. 1, we plot the variation of energy-density with different $\beta$ values for a known compact object. It is found that for different $\beta$, at the center the density of compact object in f(T) gravity is maximum and it monotonically decreases radially outward. In this case $\beta$ plays the role of a scale and for a star of particular radius higher $\beta$ values allows a star with more mass. It is also evident that $\rho$ is independent of $\alpha$, the modified Finch–Skea parameter.

(ii):

In Fig. 2, we plot the variation of radial pressure for a known star. It is seen that the radial pressure is a monotonically decreasing function of r with its maximum value at the center of the stellar system. The value of the pressure increases with increasing $\beta$ at a particular distance from the center of the star. The radial pressures for the isotropic ($\alpha = 0$) and anisotropic cases ($\alpha \ne 0$ ) with a fixed value of the parameter $\beta$ has been shown in Fig. 3 and it is seen that for the isotropic case the radial pressure for any value of r is greater than that of the anisotropic case except at the boundary, reaching a maximum value at the center of the star. In Fig. 4 we have plotted the radial variation of transverse pressure $p_t$ and it is evident from the figure that the transverse pressure follows the same profile as the radial pressure. Figure 5 shows a variation of $p_r$ and $p_t$ for a particular value of $\beta$. From the figure we see that both the pressures are equal at the center of the star and the difference between them increases with increasing r, reaching maximum at the surface of the star. This in turn implies a presence of anisotropy.

(iii):

From Figs. 6 and 7, it is evident that energy-density and pressure gradient are negative for different $\beta$ values.

(iv):

From Eq. (33) we found that for non-zero values of $\alpha$ the anisotropy depends on the parameter $\beta$ which is a multiplicative constant in the torsional term of f(T) gravity. In Fig. 8 we have shown the radial variation of $\varDelta$ for $\beta >0$. It is evident that for $\beta >0$, $\varDelta$ is positive i.e, $p_t>p_r$ which implies that the anisotropic stress is directed outwards, hence there exists a repulsive gravitational force that allows the formation of super massive stars. However for $\beta <0$, the energy-density inside the star turns out to be negative also the causality of the speed of sound is violated which is not physically acceptable. If $\alpha =0$, i.e for the Finch–Skea metric, the anisotropy vanishes in 4 dimensions, which corresponds to the isotropic case, although $\alpha \ne 0$ leads to anisotropic compact star.

(v):

We have shown the variation of the radial and transverse speed of sound in Figs. 9 and 10 respectively. It is also noted that the value of $|v_{st}^{2}-v_{sr}^{2}|$ is less than 1 complying the condition for a stable model of an anisotropic compact object, which is shown in Fig. 11. Thus the stability condition in the model described is satisfied.

(vi):

From Fig. 12 it can be seen that the variation of mass function is regular inside the star and vanishes at the center. The compactification factor is also obtained in Eq. (35), which depends on C and f(T) model parameters for different stellar objects.

(vii):

For a physically acceptable stellar model we have obtained the range of $\beta$ value considering $\beta _1=0$ for a given mass object. The range of allowed values is found to be $0<\beta <3$ as can be seen from Table 2. If $\beta \ge 3$ then the value of $\frac{2M}{b}$ exceeds $\frac{8}{9}$ which is not acceptable.

(viii):

In Sect. 5.5, it is found that the EoS satisfies a non-linear relation between $p_r$ and $\rho$. In Fig. 11 we plot the variation of $p_r$ with $\rho$ which is fitted with linear as well as quadratic equations. It is evident from the Fig. 13 that the quadratic fitting gives better acceptability for the model.

(ix):

In Table 1, we tabulated the values of A, B, C and probable EoS for different known stellar objects considering their mass and radius from observations.

(x):

In Sect. 7, we have considered the modified Finch–Skea metric and solved the field equations considering Chaplygin gas as matter distribution. The radial variations of $\rho _{c}$, $p_{rc}$, $v_{tc}^{2}$ and $v_{rc}^{2}$ are shown in Figs. 14, 15, 16, 17. It is evident from the curves that they are all well behaved inside the star.

(xi):

In Sect. 5.2, it is seen that, stellar systems whose interior space-time is described by the modified Finch–Skea geometry, the anisotropy depends on the modification parameter, $\alpha$. If $\alpha =0$ then anisotropy vanishes which is evident from Eq. (34). For Chaplygin gas model, the anisotropy is non-zero even in the case of generalized Finch–Skea metric (i.e. $\alpha =0$). The variation of anisotropic parameter, $\varDelta$ inside the star is shown in Fig. 19 considering $\beta >0$. It is evident that for positive $\beta$ values anisotropy is positive and has a maximum value at the center of the star, which is opposite to that noted without Chaplygin gas which is an interesting result. It may be due to the introduction of modified Chaplygin gas in the stellar system under f(T) framework.

(xii):

In Tables 3 and 4, the values of A, B, C are tabulated along with the parameters $\xi$ and $\zeta$ for different stellar objects considering modified Chaplygin Gas for both $\alpha \ne 0$ and $\alpha = 0$ respectively . It is noted that the modified Chaplygin gas plays an important role to understand the physical behaviour of a compact stellar object. We see that Finch- Skea geometry with modified Chaplygin gas (MCG) permits an anisotropic star which is not possible in $4-$dimensions without MCG.