$k_T$-factorization approach to the Higgs boson production in $ZZ^*\rightarrow 4\ell$ channel at the LHC

Abstract

We calculated a differential cross section of the Higgs boson production in the $h\rightarrow ZZ^*\rightarrow 4\ell$ decay channel within the framework of $k_T$-factorization. Results are obtained using an off-shell matrix element for the $g^*g^*\rightarrow h\rightarrow ZZ^*\rightarrow 4\ell$ process together with Ciafaloni–Catani–Fiorani–Marchesini (CCFM) evolution equations for an unintegrated gluon distribution function. We have presented a comparison of our results with the latest experimental measurements at $\sqrt{S} = 8\hbox { TeV}$ and $\sqrt{S} = 13\ \hbox {TeV}$ from the ATLAS and CMS collaborations at the LHC. In addition to this, we have compared our results with the results from the collinear factorization formalism calculated up to next-to-next-to-leading order plus next-to-next-to-leading logarithm (NNLO + NNLL) accuracy obtained using the HRes code for the Higgs boson production in the gluon-gluon fusion process. Our estimates are consistently close to NNLO + NNLL results obtained using a collinear factorization formalism and are also in agreement with experimental measurements.

1 Introduction

The Higgs boson discovery at the LHC, by ATLAS and CMS collaborations [1, 2], has enabled experimental measurements to be taken to investigate its properties. The ATLAS and CMS collaborations have performed an improved measurement of the Higgs boson mass, considering an invariant mass spectra of the $h\rightarrow \gamma \gamma$ and $h\rightarrow ZZ^*\rightarrow 4\ell$ decay channels [3, 4]. Further studies of spin and the parity quantum number of the Higgs boson have established that it is a neutral scalar boson, with a mass equal to 125.09 GeV, rather than a pseudoscalar boson [5,6,7]. Its coupling strength to vector bosons and to fermions is studied by analyzing various decay modes of the Higgs boson [4, 8,9,10]. Establishing various aspects of the Higgs boson’s properties and coupling strength allows us to study other aspects of it.

A dominant channel for the inclusive Higgs boson production at the LHC is gluon–gluon fusion [11,12,13]. Hence, the Higgs boson production at the LHC can be effectively used to understand the gluon dynamics inside a proton. The gluon density $xf_g(x,\mu ^2_F)$ in a proton is a function of the Bjorken variable x and the hard scale $\mu ^2_F$. The scale evolution of parton densities, in general, is described using the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) evolution equation [14, 16, 18, 19], where large logarithmic terms proportional to $\ln \mu ^2_F$ are resummed up to all orders.

The factorization theorem in perturbative quantum chromodynamics (pQCD) allows us to write a convolution of the matrix element of the short distance process and the universal parton distribution functions to obtain an inclusive cross section for a given scattering process [21]. The QCD collinear factorization theorem is based on the collinear approach where the parton distribution function depends on the longitudinal momentum fraction x and the hard scale $\mu ^2_F$. The Higgs boson production cross section at leading order and higher order QCD corrections to it, up to next-to-next-to-next-to-leading order ($\hbox {N}^3\hbox {LO}$), have been computed within the collinear factorization framework [22,23,24,25,26,27]. However, it should be noted that the NNLO and $\hbox {N}^3\hbox {LO}$ results that were obtained so far are using an effective theory and in the heavy top quark mass limit. Study of the Higgs boson’s transverse momentum spectrum resummed at NNLL accuracy is shown in Refs. [28,29,30]. Recently, the state-of-the-art predictions for the Higgs boson’s transverse momentum at the LHC, at next-to-next-to-next-to-leading-logarithmic accuracy ($\hbox {N}^3\hbox {LL}$) matched, at NNLO is presented in Ref. [31].

For the inclusive Higgs boson production at the LHC, the longitudinal momentum fraction of the incident gluons is small ($x_1 x_2\sim$ 0.0089–0.0175). This domain of small longitudinal momentum fraction (x) is still in the perturbative regime where is it expected that collinear factorization should break down because the large logarithmic term proportional to 1 / x becomes dominant [32,33,34]. The contribution from the terms proportional to 1 / x is taken into account in the Balitsky–Fadin–Kuraev–Lipatov (BFKL) evolution equation [35, 37, 39]. An unintegrated parton densities (uPDFs) obeying BFKL evolution, convoluted with an off-shell matrix element within a generalized factorization is called $k_T$-factorization [41, 42, 44,45,46]. The evolution equation is valid for both small x and large x is given by the Ciafaloni–Catani–Fiorani–Marchesini (CCFM) evolution equation [47,48,49,50]. CCFM evolution is equivalent to BFKL evolution in the limit of very small x and is equivalent to the DGLAP evolution for a large x region.

In this work, we have not implemented the reggeized parton approach [51,52,53,54,55] based on the Lipatov effective action formalism, which ensures a gauge invariance of the off-shell amplitude [56, 57]. However, our investigation is based on the assumption that the off-shell partonic amplitudes being gauge-invariant in a small-x limit. The approach, which is based on Lipatov effective action formalism that has been employed recently in the calculation using $k_T$-factorization approach for the inclusive prompt photon production at LHC [58].

In this paper, the inclusive Higgs boson production within the $k_T$-factorization approach, together with CCFM evolution equations have been studied and demonstrated importance of higher order corrections included within the $k_T$-factorization [59]. The authors of Ref. [60] have shown that $k_T$-factorization gives a description of an experimental data from ATLAS experiment for the differential cross section of the Higgs boson production in the diphoton decay channel. They have calculated a leading order (LO) matrix element for the partonic subprocess $gg\rightarrow h\rightarrow \gamma \gamma$ considering gluons to be off-shell. Inclusive Higgs boson production analysis based on off-shell gluon-gluon fusion, and considering $H\rightarrow \gamma \gamma$, $H\rightarrow ZZ^*\rightarrow 4\ell$ (where $\ell = e,\mu$) and $H\rightarrow W^+W^- \rightarrow e^{\pm }\mu ^{\mp }\nu \bar{\nu }$ decay channel is given in Ref. [61].

The ATLAS and CMS collaboration at the LHC presented a measurement of a fiducial differential cross section of the Higgs boson decay into four-leptons at $\sqrt{S} =8\hbox { TeV}$ [62, 63] and $\sqrt{S} = 13\hbox { TeV}$ [64]. We compare the results obtained using the $k_T$-factorization approach with the recent ATLAS and CMS data. We have evaluated the off-shell matrix element for the partonic subprocess $g^*g^*\rightarrow h\rightarrow ZZ^*\rightarrow 4\ell , \ell =e,\mu$. Convolution of the off-shell matrix element of partonic subprocess with CCFM uPDFs [65] is used to obtain a differential cross section.

This article is organized as follows: We discuss in detail the formalism behind our study and the necessary expressions for further numerical analysis in Sect. 2. In Sect. 3, we give the results of our numerical simulation. Here we also discuss the details of the analyses that have gone into the study. Finally, we conclude and draw inferences from the analysis in Sect. 4.

2 Formalism

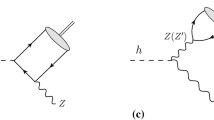
In the present section, we briefly discuss the formalism we have used in our study. The details are in the Appendix A and B. In Sect. 1, we have mentioned that to explore the effects of $k_T$-factorization, we need to take the initial state partons to be off-shell. In calculating the off-shell matrix element for the process $g^*\!g^*\!\rightarrow \!h\!\rightarrow \!ZZ^*\!\rightarrow \!4\ell$ (see Fig. 1), we have used the effective field theory approach. The effective Lagrangian in the large top quark mass limit, $m_t \rightarrow \infty$, for the Higgs boson coupling to gluon is [66, 67]:

Fig. 1

Momentum assignment for the process $g^*\!g^*\!\rightarrow \!h\!\rightarrow \!ZZ^*\!\rightarrow \!4\ell$

$$\begin{aligned} \mathcal{L}_{ggh} = \frac{\alpha _s}{12 \pi } (\surd {2} G_F)^{1/2} G^a_{\mu \nu } G^{a\mu \nu } h, \end{aligned}$$

(1)

where $\alpha _s$ and $G_F$ are the strong and Fermi coupling constants, respectively. $G^a_{\mu \nu }$ is the gluon field strength tensor and h is the Higgs scalar field. The effective ggh triangle vertex (see Eq. (11)) thus becomes

$$\begin{aligned} T^{\mu \nu , ab}_{ggh} (k_1, k_2) = \delta ^{ab} \frac{\alpha _S}{3 \pi } (\surd {2} G_F)^{1/2} [k_2^\mu k_1^\nu - (k_1 \cdot k_2) g^{\mu \nu }]. \nonumber \\ \end{aligned}$$

(2)

The non-zero transverse momentum for an initial gluon leads to the corresponding polarization sum [41, 42]:

$$\begin{aligned} \overline{\sum } \epsilon ^{*k}_\mu \epsilon ^{k}_\nu \simeq \frac{k_{\perp \mu } k_{\perp \nu }}{k^2_{\perp }}. \end{aligned}$$

(3)

Using Eqs. (2) and (3), we derived the off-shell matrix element for the hard scattering process. The matrix element thus obtained is given by Eq. (23) as:

$$\begin{aligned} \overline{|\mathcal{M}|^2}=&\frac{2}{9} \frac{\alpha ^2_S}{\pi ^2} \frac{m^4_Z}{v^4} \frac{\left[ \hat{s} + \left( \sum _{i=1}^2 \mathbf{k}_{i\perp }\right) ^2\right] ^2}{\left[ (\hat{s} - m^2_h)^2 - m^2_h \varGamma ^2_h\right] } \cos ^2\varphi \nonumber \\&\times \frac{[g^4_L + g^4_R] (p_1 \cdot p_3) (p_2 \cdot p_4) + 2 g^2_L g^2_R (p_1 \cdot p_4) (p_2 \cdot p_3)}{[(2 p_1 \cdot p_2 - m^2_Z)^2 + m^2_Z \varGamma ^2_Z] \ [(2 p_3 \cdot p_4 - m^2_Z)^2 + m^2_Z \varGamma ^2_Z]}, \nonumber \\ \end{aligned}$$

(4)

where

$$\begin{aligned} g_L =&\frac{g_W}{\cos \theta _W} \Big ( - \frac{1}{2} + \sin ^2\theta _W \Big ),\\ g_R =&\frac{g_W}{\cos \theta _W} \sin ^2\theta _W, \quad \text {and} \quad v=(\surd {2}G_F)^{-1/2}. \end{aligned}$$

Here $\varGamma _h$ and $\varGamma _Z$ are the total decay widths of the Higgs boson and Z boson, respectively. $\mathbf{k}_{i\perp }$ are the intrinsic transverse momenta of the initial gluons. $\varphi$ is the azimuthal angle between $\mathbf{k}_{1\perp }$ and $\mathbf{k}_{2\perp }$. $m_h$ and $m_Z$ are the Higgs boson and Z boson masses, respectively. The partonic center of mass energy is denoted by $\hat{s}$. $\theta _W$ and $g_W$ are the weak mixing angle and the coupling of weak interaction, respectively.

Finally, we arrived at the hadronic cross section for the off-shell hard scattering amplitude of Eq. (4) within the framework of $k_T$-factorization as¹ (see Eq. (36))

$$\begin{aligned} \sigma =\int \prod _{i=1}^2 \frac{f_g(x_i,\mathbf{k}^2_{i\perp },\mu ^2_F)}{x^2_i S^2} d\mathbf{k}^2_{i\perp } \frac{d\varphi _i}{2 \pi } \prod _{f=1}^3 d^2\mathbf{p}_{f\perp } dy_f dy_4 \frac{\overline{|\mathcal{M}|^2}}{2^{12}\ \pi ^5}, \end{aligned}$$

(5)

with the longitudinal momentum fractions $x_1$ and $x_2$ of initial gluons to be

$$\begin{aligned} x_1 = \sum _{f=1}^4\frac{|\mathbf{p}_{f\perp }|}{\sqrt{S}} e^{y_f}, \qquad x_2 = \sum _{f=1}^4\frac{|\mathbf{p}_{f\perp }|}{\sqrt{S}} e^{-y_f}, \end{aligned}$$

(6)

and the transverse momenta:

$$\begin{aligned} \sum _{i=1}^2 \mathbf{k}_{i\perp } = \sum _{f=1}^4 \mathbf{p}_{f\perp }. \end{aligned}$$

(7)

In Eq. (5), $\varphi _{1,2}$ are the azimuthal angle of $\mathbf{k}_{1\perp ,2\perp }$. y and $\mathbf{p}_{\perp }$ are rapidities and transverse momenta of the final state leptons, respectively. The hadronic center of mass energy is denoted by S.

3 Results and discussion

With all the calculational tools at our disposal, we proceed to perform a numerical calculation using Eq. (5) together with the off-shell hard scattering amplitude given in Eq. (4). We estimate the cross section of the Higgs boson production as a function of transverse momentum ($p_T$) and rapidity (y) of the Higgs boson in the four-lepton decay channel. Results are obtained using CCFM A0 the set of uPDFs [65] which is commonly used for such phenomenological studies. Recently a fit to a high precision data from deeply inelastic scattering at the HERA is performed using a $k_T$-factorization and CCFM evolution [69]. A transverse momentum dependent gluon density function including experimental and theoretical uncertainties were obtained. The application of these unintegrated gluon densities to vector boson + jet production processes at LHC is given in Ref. [70]. Unintegrated gluon densities including experimental and theoretical uncertainties are given in the CCFM JH2013-set in TMDlib library [71, 72]. We have used the TMDlib library to calculate our results using CCFM JH2013-set. For our phenomenological study, we have used the CCFM JH2013-set2 which is determined from the fit to both stucture functions $F^{(charm)}_2$ and $F_2$ data whereas CCFM JH2013-set1 is determined from the fit to inclusive $F_2$ data only.

Total decay width and mass of the Higgs boson is set to be equal to 4.0 MeV and 125.09 GeV, respectively [7]. We have implemented kinematical cuts on the rapidity and transverse momentum of leptons used by ATLAS and CMS experiments in their measurements. For the ATLAS experiment, the absolute value of rapidity is $|\eta |< 2.5$ and the leading transverse momentum of the lepton is $p_T < 20$ GeV. The transverse momenta of sub-leading leptons are $p_T < 15, 10, 7$ GeV. Similarly for the CMS experiment, the absolute value of rapidity is $|\eta |< 2.5$ and the ordered transverse momenta of the leptons are $p_T < 20, 10, 7, 7$ GeV. The cross section in Eq. (5) depends on the renormalization and factorization scales $\mu _R$ and $\mu _F$, respectively. The scale uncertainty in the cross section is estimated by varying the scale between $\mu _R = \mu _F = m_h/2$ and $\mu _R = \mu _F = 2 m_h$.

We have also calculated a total inclusive cross section for the Higgs boson production with $k_T \rightarrow 0$ and averaged over an azimuthal angle of the Higgs boson. This result of the inclusive cross section is equivalent to the cross section obtained using the collinear factorization approach at LO while using collinear parton densities. We have used the Martin–Stirling–Thorne–Watt (MSTW) set [73] for collinear parton densities. We have also obtained results of the total inclusive cross section for the Higgs production with $k_T$-factorization formalism using the CCFM JH2013-set2 of uPDFs.

Table 1 Total inclusive cross section ($\sigma ^{tot}$) for the Higgs boson production in gluon-gluon fusion channel

In Table 1, we have given our results for the total inclusive cross section for the Higgs production, using both collinear and $k_T$-factorization framework. Our results, for total inclusive cross section, obtained using collinear approach, are consistent with the results obtained in Ref. [74] at $\sqrt{S} = 8\hbox { TeV}$. The results obtained with $k_T$-factorization is close to next-to-leading order (NNLO) results given in Ref. [74] at $\sqrt{S} = 8\hbox { TeV}$. The cross section estimates given here are for a gluon–gluon fusion process only. The inclusive cross section for the Higgs boson production can be obtained using a hadron level Monte Carlo event generator called CASCADE [75]. CASCADE uses the CCFM evolution equation in the initial state with the off-shell parton level matrix element.

Fig. 2

Differential cross section of the Higgs boson production as a function of transverse momentum ($p_T$) and rapidity (y) of the Higgs boson in four-lepton decay channel at $\sqrt{S} = 8\hbox { TeV}$. Solid (red) line and dashed (purple) line is a result obtained using $k_T$-factorization approach with CCFM JH2013-set2 and CCFM A0 unintegrated gluon densities respectively. Filled triangle and filled square points corresponds to estimates obtained using HRes tool [28, 76] up to NNLO + NNLL accuracy and shaded region corresponds to scale uncertainty in renormalization and factorization scale. Experimental data points are from ATLAS [62]. The error bars on the data points shows total (statistical $\oplus$ systematic) uncertainty

Fig. 3

Differential cross section of the Higgs boson production as a function of transverse momentum ($p_T$) and rapidity (y) of the Higgs boson in four-lepton decay channel at $\sqrt{S} = 8\hbox { TeV}$. Notations of all the histograms are the same as in fig. 2. Higher order pQCD predictions up to NNLO + NNLL accuracy are obtained using HRes tool [28, 76]. Experimental data points are from CMS [63]

Fig. 4

Differential cross section of the Higgs boson production as a function of transverse momentum ($p_T$) and rapidity (y) of the Higgs boson in four-lepton decay channel at $\sqrt{S} = 13\hbox { TeV}$. Notations of all the histograms are the same as in Fig. 2. Higher order pQCD predictions up to NNLO + NNLL accuracy are obtained using HRes tool [28, 76]

We have presented our results in Figs. 2, 3 and 4. Figures 2, 4 shows the result of the differential cross section for the Higgs boson production in the four-lepton decay channel at $\sqrt{S} = 8\hbox { TeV}$ and $\sqrt{S} = 13\hbox { TeV}$, respectively. We have compared our results of the differential cross section obtained using the $k_T$-factorization approach with experimental measurements from the ATLAS at $\sqrt{S} = 8\hbox { TeV}$, 13 TeV and CMS collaboration at $\sqrt{S} = 8\hbox { TeV}$ [62, 63]. The solid (red) and dashed (purple) histogram corresponds to our results obtained using the CCFM JH2013-set2 set of uPDFs and CCFM A0 set of uPDFs respectively. We also see that the results obtained using CCFM JH2013-set2 has a better agreement with experimetal measurements than A0 set.

Our results are plotted against state-of-the-art results for the cross section calculated up to next-to-leading order plus next-to-leading logarithm (NLO + NLL) and next-to-next-to-leading order plus next-to-next-leading logarithm (NNLO + NNLL) obtained using the HRes tool [28, 76] within the collinear factorization framework. Our results of both the differential cross section in $p_T$ and y using the $k_T$-factorization framework with CCFM unintegrated PDFs are consistently close to NNLO + NNLL results at $\sqrt{S} = 8\hbox { TeV}$ and $\sqrt{S} = 13\hbox { TeV}$. This can be explained considering the fact that the main part of higher order corrections are included in the $k_T$-factorization approach [59, 77, 78]. For the $p_T$ distribution, we are using the convention that NLO + NLL and NNLO + NNLL results are labelled as LO + NLL and NLO + NNLL, respectively considering that the $p_T$ distribution is non-zero at NLO.

4 Conclusions

In this paper, we present a phenomenological study of the Higgs boson production in the four-lepton decay channel within the $k_T$-factorization framework. Here CCFM unintegrated parton densities were convoluted with the hard matrix element, considering initial gluons to be off-shell. We present a comparison of our results with experimental measurements. Our results are evaluated using same experimental conditions (i.e., the same $p_T$ and y cuts were used for our estimates as given by the experimental results) for both the ATLAS and CMS at $\sqrt{S} = 8\hbox { TeV}$ and at $\sqrt{S} = 13\hbox { TeV}$, respectively.

Further comparison of our estimates with the state-of-the-art results of a differential cross section within collinear factorization up to NLO + NLL and NNLO + NNLL obtained using HRes code is presented. We have also estimated a total inclusive cross section for the Higgs boson production within both collinear factorization and $k_T$-factorization framework. Within $k_T$ factorization approach, we have compared the results obtained using CCFM JH2013-set2 and CCFM A0 uPDF set. Our results for the differential cross section with CCFM JH2012-set2 are close to the NNLO + NNLL results obtained using the HRes tool.

Our results show that the observed $p_T$ distribution of the final state can be generated at leading order subprocesses, using unintegrated gluon distributions. Moreover, gluons in the initial state have finite transverse momenta, which results in the transverse momenta of the final state. The total inclusive cross section estimated using $k_T$-factorization is close to the NNLO results obtained using collinear factorization. The main reason for this behavior is that the main part of higher order correction in collinear pQCD is already included in the $k_T$-factorization [79] framework.

The higher order corrections within $k_T$-factorization at the parton level would be an interesting study, to see any additional effect. The cross section for the Higgs boson production has been calculated using a mixture of LO and NLO partonic diagrams and unintegrated PDFs from the $k_T$-factorization. Considering the effect of the transverse momentum of the initial gluon on the transverse momentum distribution of the final state, our study, as well as further studies in this direction could impose constraints on uPDFs of gluons.

Appendices

Appendices

A Amplitude of $g^*\!g^*\!\rightarrow \!h\!\rightarrow \!ZZ^*\!\rightarrow \!4\ell$

In this appendix, we give details of our calculations that went into our analysis. Figure 1 shows the assignment of the momenta. In the limit of large top quark mass $m_t \rightarrow \infty$, the effective Lagrangian for the Higgs boson coupling to gluons given in Eq. (1) can be written as

$$\begin{aligned} \mathcal{L}_{ggh} = \frac{\alpha _s}{12 \pi v} G^a_{\mu \nu } G^{a\mu \nu } h,&\quad [ \text {Using } v = (\surd {2} G_F)^{-1/2} ] \end{aligned}$$

(8)

where v is the vacuum expectation value of the scalar field. The amplitude of the process $g^*\!g^*\!\rightarrow \!h\!\rightarrow \!ZZ^*\!\rightarrow \!\ell \bar{\ell }\ell ^\prime \bar{\ell }^\prime$ is

$$\begin{aligned}&\mathrm{i}\mathcal{M} =\epsilon ^{*k_1}_{\mu } \epsilon ^{*k_2}_{\nu }\nonumber \\&\quad \times \,\frac{\left[ \mathrm{i}T^{\mu \nu , ab}_{ggh} (k_1, k_2)\right] \mathrm{i}\left[ \mathrm{i}T_{h \rightarrow ZZ^* \rightarrow 4\ell } (p_1, p_2, p_3, p_4)\right] }{(\hat{s} - m^2_h) + i m_h \varGamma _h}, \end{aligned}$$

(9)

where

$$\begin{aligned}&T^{\mu \nu , ab}_{ggh} (k_1, k_2) = \delta ^{ab} \frac{\alpha _s}{3 \pi v} \left[ k_2^\mu k_1^\nu - (k_1 \cdot k_2) g^{\mu \nu }\right] ,\end{aligned}$$

(10)

$$\begin{aligned}&T_{h \rightarrow ZZ^* \rightarrow 4\ell } (p_1, p_2, p_3, p_4) \nonumber \\&\quad = - 2 \frac{m^2_Z}{v} \ \frac{\bar{u}(p_1) \gamma ^\rho [g^{(1)}_L P_L + g^{(1)}_R P_R] v(p_2)}{[(p_1 + p_2)^2 - m^2_Z + i m_Z \varGamma _Z]} \nonumber \\&\quad \quad \times \frac{\bar{u}(p_3) \gamma _\rho [g^{(2)}_L P_L + g^{(2)}_R P_R] v(p_4)}{[(p_3 + p_4)^2 - m^2_Z + i m_Z \varGamma _Z]}, \end{aligned}$$

(11)

where

$$\begin{aligned} g^{(i)}_L = \frac{g_W}{\mathrm{c}_W} \Big ( - \frac{1}{2} + \mathrm{s}^2_W \Big ), \quad g^{(i)}_R = \frac{g_W}{\mathrm{c}_W} \mathrm{s}^2_W, \quad i = 1,2. \end{aligned}$$

(12)

Hence we shall denote them only by $g_L$ and $g_R$ hereafter.

Now using the above expressions into Eq. (9) we can get $\overline{|\mathcal{M}|^2}$ for the process as

$$\begin{aligned} \overline{|\mathcal{M}|^2} =&|T^{\mu \nu , ab}_{ggh} (k_1, k_2)|^2 \frac{|T_{h \rightarrow ZZ^* \rightarrow 4\ell } (p_1, p_2, p_3, p_4)|^2}{(\hat{s} - m^2_h)^2 + m^2_h \varGamma ^2_h}, \end{aligned}$$

(13)

where

$$\begin{aligned}&|T_{h \rightarrow ZZ^* \rightarrow 4\ell } (p_1, p_2, p_3, p_4)|^2 = 64 \frac{m^4_Z}{v^2}\nonumber \\&\quad \times \frac{[g^4_L + g^4_R] (p_1 \cdot p_3) (p_2 \cdot p_4) + 2 g^2_L g^2_R (p_1 \cdot p_4) (p_2 \cdot p_3)}{\left[ (2 p_1 \cdot p_2 - m^2_Z)^2 + m^2_Z \varGamma ^2_Z\right] \ \left[ (2 p_3 \cdot p_4 - m^2_Z)^2 + m^2_Z \varGamma ^2_Z\right] },\nonumber \\ \end{aligned}$$

(14)

whereas

$$\begin{aligned}&|T_{ggh}^{\mu \nu ,ab}(k_1,k_2)|^2= \overline{\delta ^{ab}\delta ^{ab}} \frac{1}{9} \frac{\alpha ^2_s}{\pi ^2} \frac{1}{v^2} \nonumber \\&\quad \times \overline{\sum } \epsilon ^{*k_1}_{\mu }\epsilon ^{k_1}_{\mu ^\prime } \ \overline{\sum } \epsilon ^{*k_2}_{\nu }\epsilon ^{k_2}_{\nu ^\prime } \left[ k_2^\mu k_1^\nu - (k_1 \cdot k_2) g^{\mu \nu }\right] \nonumber \\&\quad \times \ \left[ k_2^{\mu ^\prime } k_1^{\nu ^\prime } - (k_1 \cdot k_2) g^{\mu ^\prime \nu ^\prime }\right] . \end{aligned}$$

(15)

To calculate the gluon part of the above amplitude we use the Sudakov decomposition of momenta as followed in Ref. [45, 46]. Accordingly, we can write the gluon momenta $k_{1,2}$ as

$$\begin{aligned} \begin{aligned} k_1 =\,&z_1 P_1 + {\bar{z}}_1 P_2 + k_{1\perp }, \\ k_2 =\,&z_2 P_1 + {\bar{z}}_2 P_2 + k_{2\perp }, \end{aligned} \quad \text {where} \begin{aligned} k_{1\perp } = (0, \mathbf{k}_{1\perp }, 0), \\ k_{2\perp } = (0, \mathbf{k}_{2\perp }, 0). \end{aligned} \end{aligned}$$

(16)

In the above equation, $k_{1\perp ,2\perp }$ are vectors transverse to the momenta $P_{1,2}$ of the incoming hadrons. It is convenient to take both $P_{1,2}$ to be light-like (i.e. $P^2_{1,2} = 0$). Because of this, $P_{1,2}$ are slightly different from the actual momenta of the incoming hadrons. Let us take $P_{1,2}$ to be as follows

$$\begin{aligned} P_{1,2} = \frac{\sqrt{S}}{2} (1, \mathbf{0}, \pm 1), \end{aligned}$$

(17)

where $\sqrt{S}$ is the center of mass energy of the hadrons. In the high energy limit, the introduction of strong ordering in longitudinal momenta gives

$$\begin{aligned} \begin{aligned} k_1 =\,&z_1 P_1 + k_{1\perp }, \\ k_2 =\,&{\bar{z}}_2 P_2 + k_{2\perp }. \end{aligned} \end{aligned}$$

(18)

Therefore using Eqs. (17) and (18) we get

$$\begin{aligned}&k_1 \cdot k_2 = z_1 {\bar{z}}_2 P_1 \cdot P_2 + k_{1\perp } \cdot k_{2\perp }, \end{aligned}$$

(19)

$$\begin{aligned}&\hat{s} = (k_1 + k_2)^2 = 2 z_1 {\bar{z}}_2 P_1 \cdot P_2 - (\mathbf{k}_{1\perp } + \mathbf{k}_{2\perp })^2. \end{aligned}$$

(20)

In the last step, we have used the definition of $k_{1\perp ,2\perp }$ introduced in Eq. (16).

With the help of the above expressions, we are now ready to calculate the gluon part of Eq. (15). Using the polarization sum for the off-shell gluons given by

$$\begin{aligned} \overline{\sum } \epsilon ^{*k}_\mu \epsilon ^{k}_\nu \simeq \frac{k_{\perp \mu } k_{\perp \nu }}{k^2_{\perp }}, \end{aligned}$$

(21)

we can calculate

$$\begin{aligned} \overline{\sum } \epsilon ^{*k_1}_{\mu }\epsilon ^{k_1}_{\mu ^\prime }&\overline{\sum } \epsilon ^{*k_2}_{\nu }\epsilon ^{k_2}_{\nu ^\prime } \left[ k_2^\mu k_1^\nu - (k_1 \cdot k_2) g^{\mu \nu }\right] \nonumber \\ \times&\ \left[ k_2^{\mu ^\prime } k_1^{\nu ^\prime } - (k_1 \cdot k_2) g^{\mu ^\prime \nu ^\prime }\right] \nonumber \\ =&\frac{1}{4} \left[ \hat{s} + (\mathbf{k}_{1\perp } + \mathbf{k}_{2\perp })^2\right] ^2 \cos ^2\varphi . \nonumber \\&[\text {Using Eq.}\,~(19)\text { and then Eq.}\,(20)] \end{aligned}$$

(22)

Therefore putting the expression of Eq. (22) into Eq. (15) we get the total spin averaged squared amplitude of the process $g^*\!g^*\!\rightarrow \!h\!\rightarrow \!ZZ^*\!\rightarrow \!\ell \bar{\ell }\ell ^\prime \bar{\ell }^\prime$ as

$$\begin{aligned}&\overline{|\mathcal{M}|^2} = \frac{2}{9} \frac{\alpha ^2_S}{\pi ^2} \frac{m^4_Z}{v^4} \frac{[\hat{s} + (\mathbf{k}_{1\perp } + \mathbf{k}_{2\perp })^2]^2}{(\hat{s} - m^2_h)^2 + m^2_h \varGamma ^2_h} \cos ^2\varphi \nonumber \\&\quad \times \frac{[g^4_L + g^4_R] (p_1 \cdot p_3) (p_2 \cdot p_4) + 2 g^2_L g^2_R (p_1 \cdot p_4) (p_2 \cdot p_3)}{[(2 p_1 \cdot p_2 - m^2_Z)^2 + m^2_Z \varGamma ^2_Z] \ [(2 p_3 \cdot p_4 - m^2_Z)^2 + m^2_Z \varGamma ^2_Z]}. \nonumber \\ \end{aligned}$$

(23)

Phase space calculation

In this appendix, we give details of the phase space calculations related to our analysis. Let us express the 4-momentum p in a 3-component vector in terms of the transverse momentum $\mathbf{p}_T$ and the rapidity y as follows

$$\begin{aligned} p = \left( E_T \cosh y, \mathbf{p}_T, E_T \sinh y\right) {,} \end{aligned}$$

(24)

where the transverse energy $E_T = \sqrt{\mathbf{p}^2_T + m^2}$ and m is the mass. We can write the measure of the phase space integration as

$$\begin{aligned} \frac{d^3\mathbf{p}}{p_{_0}} = d^2\mathbf{p}_T dy. \end{aligned}$$

(25)

Let us further express the 4-momentum p in a 4-component vector in terms of $p_T (\equiv |\mathbf{p}_T|)$, y and the azimuthal angle $\varphi$ as

$$\begin{aligned} p = (E_T \cosh y, p_T \cos \varphi , p_T \sin \varphi , E_T \sinh y). \end{aligned}$$

(26)

Now the measure of integration over the phase space becomes

$$\begin{aligned} \frac{d^3\mathbf{p}}{p_{_0}} = p_T dp_T d\varphi dy. \end{aligned}$$

(27)

The above can be easily understood if we express the 2-component vector $\mathbf{p}_T$ in polar coordinates $(p_T \cos \varphi , p_T \sin \varphi )$. Then we can write $d^2\mathbf{p}_T = p_T dp_T d\varphi$.

Now let us turn our attention to the phase space integration of a 4-body final state process in a hadron collider. The hadronic cross section in the $k_T$-factorization approach for the off-shell hard scattering amplitude of appendix A is (see Eq. 2.1 of Ref. [80])

$$\begin{aligned} \sigma= & {} \int \frac{1}{x_1 x_2 S} \prod _{i=1}^2 \frac{dx_i}{x_i} f_g(x_i,\mathbf{k}^2_{i\perp },\mu ^2_F) \frac{d^2\mathbf{k}_{i\perp }}{\pi } \nonumber \\&\times \prod _{f=1}^4 \frac{d^3\mathbf{p}_f}{(2\pi )^3 2p_{f0}} \overline{|\mathcal{M}|^2} \times (2\pi )^4 \delta ^{(4)} \bigg (\sum _{i=1}^2 k_i - \sum _{f=1}^4 p_i\bigg ). \nonumber \\ \end{aligned}$$

(28)

Introducing the azimuthal angles $\varphi _{1,2}$ of the off-shell gluons into Eq. (28) we can write the gluon phase space as

$$\begin{aligned} \int \frac{d^2\mathbf{k}_{i\perp }}{\pi } = \int \frac{k_{i\perp } dk_{i\perp } d\varphi _i}{\pi } = \int d\mathbf{k}^2_{i\perp } \frac{d\varphi _i}{2 \pi }. \end{aligned}$$

(29)

Let us write the 4-momenta of the partons, using Eq. (18), as

$$\begin{aligned} \begin{aligned} k_1 = \,&\bigg ( x_1 \frac{\sqrt{S}}{2}, \mathbf{k}_{1\perp }, x_1 \frac{\sqrt{S}}{2} \bigg ), \\ k_2 = \,&\bigg ( x_2 \frac{\sqrt{S}}{2}, \mathbf{k}_{2\perp }, - x_2 \frac{\sqrt{S}}{2} \bigg ). \end{aligned} \end{aligned}$$

(30)

Here $z_1 \rightarrow x_1$ and ${\bar{z}}_2 \rightarrow x_2$. Also the 4-momenta of the leptons are

$$\begin{aligned} p_f = (|\mathbf{p}_{f\perp }| \cosh y_f, \mathbf{p}_{f\perp }, |\mathbf{p}_{f\perp }| \sinh y_f). \end{aligned}$$

(31)

Using the above designation of the gluon and lepton momenta we can simplify the delta function of Eq. (28) as

$$\begin{aligned}&\delta ^{(4)} \bigg (\sum _{i=1}^2 k_i - \sum _{f=1}^4 p_i\bigg ) = \frac{1}{S} \delta ^{(2)} \bigg ( \sum _{i=1}^2 \mathbf{k}_{i\perp } - \sum _{f=1}^4 \mathbf{p}_{f\perp } \bigg ) \nonumber \\&\quad \times \delta \bigg ( x_1 - \sum _{f=1}^4\frac{|\mathbf{p}_{f\perp }|}{\sqrt{S}} e^{y_f} \bigg ) \ \delta \bigg ( x_2 - \sum _{f=1}^4\frac{|\mathbf{p}_{f\perp }|}{\sqrt{S}} e^{-y_f} \bigg ). \end{aligned}$$

(32)

Putting the results from Eqs. (29) and (32) into Eq. (28) and integrating over $x_1$ and $x_2$ we get

$$\begin{aligned} \sigma =&\int \prod _{i=1}^2 \frac{f_g(x_i,\mathbf{k}^2_{i\perp },\mu ^2_F)}{x^2_i S^2} d\mathbf{k}^2_{i\perp } \frac{d\varphi _i}{2 \pi } \nonumber \\&\times \prod _{f=1}^4 d^2\mathbf{p}_{f\perp } dy_f \frac{\overline{|\mathcal{M}|^2}}{2^{12}\ \pi ^8} \ \delta ^{(2)} \bigg ( \sum _{i=1}^2 \mathbf{k}_{i\perp } - \sum _{f=1}^4 \mathbf{p}_{f\perp } \bigg ). \end{aligned}$$

(33)

where

$$\begin{aligned}&x_1 = \sum _{f=1}^4\frac{|\mathbf{p}_{f\perp }|}{\sqrt{S}} e^{y_f}, \qquad x_2 = \sum _{f=1}^4\frac{|\mathbf{p}_{f\perp }|}{\sqrt{S}} e^{-y_f}, \end{aligned}$$

(34)

$$\begin{aligned}&\sum _{i=1}^2 \mathbf{k}_{i\perp } = \sum _{f=1}^4 \mathbf{p}_{f\perp }. \end{aligned}$$

(35)

Now integration over $\mathbf{p}_{4\perp }$ in Eq. (33) gives us

$$\begin{aligned} \sigma = \int \prod _{i=1}^2 \frac{f_g(x_i,\mathbf{k}^2_{i\perp }, \mu ^2_F)}{x^2_i S^2} d\mathbf{k}^2_{i\perp } \frac{d\varphi _i}{2 \pi } \prod _{f=1}^3 d^2\mathbf{p}_{f\perp } dy_f dy_4 \frac{\overline{|\mathcal{M}|^2}}{2^{12}\ \pi ^5}. \nonumber \\ \end{aligned}$$

(36)

In the last step above we have used $d^2\mathbf{p}_{f\perp } = 2\pi p_{f\perp } dp_{f\perp } = \pi d\mathbf{p}^2_{f\perp }, (f=1,2,3)$.