1 Introduction

In the past decades, the B meson three-body decays have attracted a lot of attention both as regards experiments and theoretical studies. On the experimental side, many data for the three-body B meson decays have been measured by different collaborations, such as Belle [1,2,3,4,5] and BaBar [6,7,8,9], which provide valuable information about complicated strong dynamics. Especially large regional CP violation in \(KKK,K\pi \pi ,KK\pi ,\pi \pi \pi \) final states [10,11,12] are revealed. All of these have raised great interest and are a severe challenge to the theorists. On the theoretical side, substantial progress on three-body B meson decays has been made through the symmetry principles and factorization theorems. The former includes isospin, U-spin, flavor SU(3) symmetries and CPT invariance [13,14,15,16,17,18]. The latter includes the naive factorization [19,20,21], QCD factorization (QCDF) [22,23,24,25,26,27, 29, 30] and the perturbative QCD approach [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46]. It is noticed that the rigorous justification of these approaches for the three-body decays is not yet available, so these approaches worked in the phenomenological factorization. Compared with two-body decays, the three-body decays are much more complicated because of receiving both nonresonant and resonant contributions. It is difficult to separated them clearly [47]. Furthermore, the final-state interactions (FSIs) may be more significant in the three-body decays than those in the two-body decays. This is so because there exist two distinct FSIs mechanisms. One is the interactions between the meson pair in the resonant region associated with various intermediate states. The other is the rescattering between the third particle (usually referred to as “bachelor”) and the pair of mesons. Most difficult for the three-body decays is the evaluation of the matrix elements for the B meson transition into two hadrons. An enormous number of diagrams will need to be calculated if one evaluates directly the hard kernels for the three-body decays, which contain two virtual gluons at lowest order. Fortunately, the region with the two gluons being hard simultaneously is power suppressed and not important, which corresponds to the central region of a Dalitz plot [30]. The dominant contributions come from the kinematic region corresponding to the edges of the Dalitz plots, where the two light mesons move almost in parallel. It is possible to catch the dominant contributions in a simple way through introducing a new nonperturbative inputs, two-meson distribution amplitudes (DAs) [48,49,50,51]. This just is one crucial step for the perturbative QCD approach (pQCD) in dealing with the three-body B meson decays, which are simplified into the two-body decays. The two-meson DAs (distribution amplitudes) describe the hadronization of two collinear quarks, together with two other quarks popped out of the vacuum, into two collimated mesons. For the PP system, the two-meson DAs from not only S wave [31,32,33,34,35,36,37] but also P wave [38,39,40,41,42,43,44] have been studied and used widely in B meson decays. For the VP system, the two-meson DAs with more complicated structures have been studied in a few works [45, 46].

In view of the status of B meson three-body decays, we would like to study the three-body radiative decay \(B_s\rightarrow \phi {\bar{K}}^0 \gamma \) in pQCD approach. In this decay, we can avoid the aforementioned difficulties such as the entangled nonresonant and resonant contributions, significant final-state interactions. At the same time, it provides a clean platform to study the two-meson distribution amplitudes for the \(\phi K\) pair. The similar decay \(B\rightarrow \phi K \gamma \) has been researched by experiments [1, 5, 6] and theoretical studies [45, 46]. These studies show that no clear evidence is found for the existence of a kaonic resonance decaying to \(\phi K\). In the pQCD approach [46], the decay \(B\rightarrow \phi K \gamma \) was studied by introducing the two-meson DAs for the \(\phi K\) pair, where some parameters are extracted from the data [52]. So it is meaningful to check if the \(\phi K\) pair DAs can be used in the decay \(B_s\rightarrow \phi K \gamma \) to predict its branching ratio and direct CP violation.

The layout of this paper is as follows: we analyze the decay \(B_s\rightarrow \phi {\bar{K}}^0 \gamma \) using the perturbative QCD approach in Sect. 2. The numerical results and discussions are given in Sect. 3, where the theoretical uncertainties are also considered. The conclusions are presented in the final part.

2 The perturbative calculations

The effective Hamiltonian which includes a flavor changing \(b\rightarrow d\gamma \) transition is given by [53]

$$\begin{aligned} H_{eff}= & {} \frac{G_F}{\sqrt{2}}\Bigg [\sum _{q=u,c}V_{qb}V^*_{qd} \left( C_1(\mu )O^q_1(\mu )+ C_2(\mu )O_2^q(\mu )\right) \nonumber \\&\quad -V_{tb}V^*_{td}\sum _{i=3\sim 8g}C_i(\mu )O_i(\mu )\Bigg ]+h.c. \end{aligned}$$
(1)

Under the light-cone coordinates, the momenta of the B meson and the \(\phi K\) pair can be written as

$$\begin{aligned} P_{B_s}=\frac{M_{B_s}}{\sqrt{2}}(1,1,0_T),\;\; P=\frac{M_{B_s}}{\sqrt{2}}(1,\eta ,0_T), \end{aligned}$$
(2)

where the parameter \(\eta =\omega ^2/M^2_{B_s}\) with \(\omega \) being the invariant mass of the \(\phi K\) pair. If we define \(P_1\) and \(P_2\) as the momenta of the \(\phi \) and K mesons, respectively, we have \(P=P_1+P_2\), with

$$\begin{aligned} P^+_1= & {} \zeta P^+, P^-_1=[(1-\zeta )\eta +r^2_\phi ]P^+,\nonumber \\ P_{1T}= & {} \sqrt{(\zeta \omega ^2-m^2_\phi )(1-\zeta )},\ \end{aligned}$$
(3)
$$\begin{aligned} P^+_2= & {} (1-\zeta )P^+, P^-_2=(\zeta \eta -r^2_\phi )P^+,\nonumber \\ P_{2T}= & {} -P_{1T}=-\sqrt{(\zeta \omega ^2-m^2_\phi )(1-\zeta )}, \end{aligned}$$
(4)

where \(\zeta \) is the \(\phi \) meson momentum fraction and the mass ratio \(r_\phi =m_\phi /m_{B_s}\). The on-shell condition \(P^2_1=m^2_\phi , P^2_2=0\) is used to obtain \(P_{1T(2T)}\). The momenta of the spectator quarks in \(B_s\) and K mesons can be defined as

$$\begin{aligned} k_1=\left( 0,\frac{M_{B_s}}{\sqrt{2}}x_1,\mathbf{k }_{1T}\right) ,\;\; k_2=\left( \frac{M_{B_s}}{\sqrt{2}}z,0,\mathbf{k }_{2T}\right) . \end{aligned}$$
(5)

The momentum of the photon \(\gamma \) in the final state is written as \(P_3=(M_{B_s}/\sqrt{2})(0,1-\eta ,0_T)\). The transverse polarization vectors of \(\gamma \) and \(\phi K\) pair are given as

$$\begin{aligned} \epsilon ^*_\gamma (\pm )= & {} \left( 0,0,\frac{1}{\sqrt{2}}(\mp 1,-i)\right) , \end{aligned}$$
(6)
$$\begin{aligned} \epsilon ^*_{\phi K}(\pm )= & {} \left( 0,0,\frac{1}{\sqrt{2}}(\pm 1,-i)\right) . \end{aligned}$$
(7)

The \(\phi K\) pair distribution amplitudes can be related to the \(\phi \) and kaon distribution amplitudes [54,55,56] through calculating perturbatively the matrix elements \(\langle \phi (P_1,\epsilon _\phi )K^+(P_2)|\bar{u}(y^-)\Gamma s(0)|0\rangle \), where \(\Gamma =\gamma _\mu \gamma _5, \sigma _{\mu \nu }\gamma _5, \gamma _5, \gamma _\mu , I\) represent the different Lorentz structures. The matrix elements can be written as the products of the kinematic factors with the corresponding form factors [45]:

$$\begin{aligned}&\langle \phi {\bar{K}}^0| {\bar{s}}(y^-)\gamma _{\mu }\gamma _5 d(0)|0\rangle \nonumber \\&\quad =P_\mu \int ^1_0 \mathrm{d}z e^{izP\cdot y} \phi _\parallel (z,\zeta ,\omega )\nonumber \\&\qquad +\omega \epsilon ^*_{T{\mu }}\int ^1_0\mathrm{d}z e^{izP\cdot y}\varPhi _a(z,\zeta ,\omega ), \end{aligned}$$
(8)
$$\begin{aligned}&\langle \phi {\bar{K}}^0|\bar{s}(y^-)\sigma _{\mu \nu }\gamma _5 d(0)|0\rangle =-i\Bigg \{(\epsilon _{T\mu } P_{1\nu }-\epsilon _{T\nu } P_{1\mu })\nonumber \\&\times \quad \left. \int ^1_0\mathrm{d}ze^{izP\cdot y} \phi _T(z,\zeta ,\omega )\nonumber \right. \\&\quad +\frac{2}{\omega }(P_{1\mu }P_{2\nu }-P_{1\nu }P_{2\mu })\int ^1_0\mathrm{d}z e^{izP\cdot y}\varPhi _3(z,\zeta ,\omega ) \Bigg \} \end{aligned}$$
(9)
$$\begin{aligned}&\quad \langle \phi {\bar{K}}^0 |{\bar{s}}(y^-)\gamma _5 d(0)|0\rangle \nonumber \\&\quad =\omega \int ^1_0\mathrm{d}z e^{izP\cdot y}\varPhi _p(z,\zeta ,\omega ), \end{aligned}$$
(10)
$$\begin{aligned}&\quad \langle \phi {\bar{K}}^0|{\bar{s}}(y^-)\gamma _\mu d(0)|0\rangle \nonumber \\&\quad =i\frac{\omega }{P\cdot n_-}\epsilon _{\mu \nu \rho \sigma }\epsilon ^\nu _T P^\rho n^\sigma _-\int ^1_0\mathrm{d}z e^{izP\cdot y\varPhi _v(z,\zeta ,\omega )}, \end{aligned}$$
(11)
$$\begin{aligned}&\quad \langle \phi {\bar{K}}^0 |{\bar{s}}(y^-)I d(0)|0\rangle =0. \end{aligned}$$
(12)

Some explanations are in order. The perturbative calculation is only in order to obtain the \(\zeta \) dependence of the \(\phi K\) pair distribution amplitudes, which arises from the Lorentz structure of the associated hadronic matrix element, irrespective of whether the form factor is nonperturbative. To obtain the upper expansions, the following approximations to the kinematic factors have been used:

$$\begin{aligned}&(P_1-P_2)_\mu \approx (2\zeta -1)P_\mu , \end{aligned}$$
(13)
$$\begin{aligned}&\epsilon _{T\mu }(\phi ) P_{1\nu }-\epsilon _{T\nu }(\phi ) P_{1\mu }\approx \zeta (\epsilon _{T\mu } P_{\nu }-\epsilon _{T\nu } P_{\mu }), \end{aligned}$$
(14)
$$\begin{aligned}&\frac{2}{\omega }(P_{1\mu }P_{2\nu }-P_{1\nu }P_{2\mu })\approx (2\zeta -1)(\epsilon _{L\mu } P_{\nu }-\epsilon _{L\nu } P_{\mu }),\nonumber \\ \end{aligned}$$
(15)
$$\begin{aligned}&\frac{2}{\omega }\epsilon _{\mu \nu \rho \sigma }\epsilon _T^\nu (\phi ) P^\rho _1P^\sigma _2 \approx \frac{\omega }{P\cdot n_{-}}(2\zeta -1)\sigma _{\mu \nu \rho \sigma }\epsilon ^\nu _T P^\rho n^\sigma _-.\nonumber \\ \end{aligned}$$
(16)

Then the \(\phi K\) pair distribution amplitudes up to twist-3 can be given as [45]:

$$\begin{aligned}&\langle \phi K(P, \epsilon _L)|\bar{u}(y^-)_js(0)_l|0\rangle =\frac{1}{\sqrt{2N_c}}\int ^1_0\mathrm{d}ze^{izP\cdot y}\nonumber \\&\quad \left\{ (\gamma _5 P / )_{lj}\phi _\parallel (z,\zeta ,\omega ) +(\gamma _5)_{lj}\omega \phi _p(z,\zeta ,\omega )\nonumber \right. \\&\quad \left. +(\gamma _5 \epsilon / _L P / )_{lj}\phi _3(z,\zeta ,\omega )\right\} , \end{aligned}$$
(17)
$$\begin{aligned}&\quad \langle \phi K(P, \epsilon _T)|\bar{u}(y^-)_js(0)_l|0\rangle =\frac{1}{\sqrt{2N_c}}\int ^1_0\mathrm{d}ze^{izP\cdot y}\nonumber \\&\times \quad \left\{ \phantom {\left. \times \phi _a(z,\zeta ,\omega )+i\frac{\omega }{P\cdot n_-}\epsilon _{\mu \nu \rho \sigma }(\gamma ^\mu )_{lj}\epsilon ^\nu _TP^\rho n^\sigma _-\varPhi _v(z,\zeta ,\omega )\right\} }(\gamma _5 \epsilon / _T P / )_{lj}\phi _t(z,\zeta ,\omega ) +(\gamma _5 \epsilon / _{T\mu })_{lj}\omega \right. \nonumber \\&\left. \times \phi _a(z,\zeta ,\omega )+i\frac{\omega }{P\cdot n_-}\epsilon _{\mu \nu \rho \sigma }(\gamma ^\mu )_{lj}\epsilon ^\nu _TP^\rho n^\sigma _-\varPhi _v(z,\zeta ,\omega )\right\} ,\nonumber \\ \end{aligned}$$
(18)

where the transversely polarized distribution amplitudes can be expressed as the products of the time-like form factors \(F(\omega )\) and the \(z,\zeta \)-dependent functions:

$$\begin{aligned} \phi _t(z,\zeta ,\omega )= & {} \frac{3F_T(\omega )}{\sqrt{2N_c}}z(1-z)\zeta , \end{aligned}$$
(19)
$$\begin{aligned} \phi _a(z,\zeta ,\omega )= & {} \frac{3F_a(\omega )}{\sqrt{2N_c}}z(1-z) \left[ 1+a_1C^{3/2}_1(2z-1)\right] ,\nonumber \\ \end{aligned}$$
(20)
$$\begin{aligned} \phi _v(z,\zeta ,\omega )= & {} \frac{3F_v(\omega )}{\sqrt{2N_c}}z(1-z)(2\zeta -1). \end{aligned}$$
(21)

Here the z dependence of each DA except \(\phi _a\) is assumed to be in the asymptotic form \(z(1-z)\). In order to make the \(\phi K\) pair DA \(\phi _a\) a bit asymmetric, the first Gegenbauer moment is included. For our considered decays, only the transverse components are used. It is similar for the longitudinal polarized distribution amplitudes,

$$\begin{aligned} \phi _\parallel (z,\zeta ,\omega )= & {} \frac{3F_\parallel (\omega )}{\sqrt{2N_c}}z(1-z)(2\zeta -1),\end{aligned}$$
(22)
$$\begin{aligned} \phi _p(z,\zeta ,\omega )= & {} \frac{3F_p(\omega )}{\sqrt{2N_c}}z(1-z),\end{aligned}$$
(23)
$$\begin{aligned} \phi _3(z,\zeta ,\omega )= & {} \frac{3F_3(\omega )}{\sqrt{2N_c}}z(1-z)(2\zeta -1). \end{aligned}$$
(24)

Here the time-like form factors \(F_{T,2,v}(\omega )\) are used to define the normalization of different twist distribution amplitudes,

$$\begin{aligned} F_{T,\parallel }(\omega )= & {} \frac{m^2_{T\parallel }}{(\omega -m_l)^2+m^2_{T\parallel }},\end{aligned}$$
(25)
$$\begin{aligned} F_{a,v,p,3}(\omega )= & {} \frac{m_0m^2_{T\parallel }}{(\omega -m_l)^3+m_0m^2_{T\parallel }}, \end{aligned}$$
(26)

where \(m_0\approx 1.7 GeV\) is the chiral scale and the threshold invariant mass \(m_l=m_\phi +m_K\). The parameters \(m_\parallel \) and \(m_T\) are associated with the longitudinally and transversely polarized \(\phi \) meson. Both of them are expected to be few GeV [31] and can be determined by fitting the measured branching ratios of \(\tau \rightarrow \phi K \nu \) and \(B \rightarrow \phi K \gamma \) [52]. In the latter calculations, we set \(m_T=m_\parallel =m_{T\parallel }=3\) GeV. To construct these form factors, these two points must be considered: first, respecting the kinematic threshold of the decay spectra, \(F_{i}(m_l)=1, i=T,\parallel ,a,v,p,3\); second, the power behaviors of the form factors in the asymptotic region with large \(\omega \) satisfy \(F_{T,\parallel }(\omega )\approx 1/\omega ^2, F_{a,v,p,3}(\omega )\approx m_0/\omega ^3\) [57,58,59,60].

For the wave function of the heavy B meson, we take

$$\begin{aligned} \varPhi _{{B_s}}(x,b)= \frac{1}{\sqrt{2N_c}} ( P / _{{B_s}} +m_{{B_s}}) \gamma _5 \phi _{{B_s}} (x,b). \end{aligned}$$
(27)

Here only the contribution of Lorentz structure \(\phi _{{B_s}} (x,b)\) is taken into account, since the contribution of the second Lorentz structure \({\bar{\phi }}_{{B_s}}\) is numerically small and has been neglected. For the distribution amplitude \(\phi _{{B_s}}(x,b)\) in Eq. (27), we adopt the following model:

$$\begin{aligned} \phi _{{B_s}}(x,b)=N_{{B_s}}x^2(1-x)^2\exp \left[ -\frac{M^2_{{B_s}} x^2}{2\omega ^2_b}-\frac{1}{2}(\omega _bb)^2\right] ,\nonumber \\ \end{aligned}$$
(28)

where \(\omega _b\) is a free parameter, and we take \(\omega _b=0.5\pm 0.05\) GeV in the numerical calculations; \(N_{B_s}=63.7\) is the normalization factor for \(\omega _b=0.5\).

The decay spectrum is written as

$$\begin{aligned} \frac{d\Gamma }{d\omega }=\tau _{B_s}\frac{G^2_F\omega |\vec {P}|| \vec {P}_3|}{64\pi ^3M^3_{B_s}}|{\mathcal {M}}|^2 =\tau _{B_s}\frac{G^2_F\sqrt{\eta }(1-\eta )|{\mathcal {M}}|^2}{256\pi ^3},\nonumber \\ \end{aligned}$$
(29)

where the conditions \(|\vec {P}||\vec {P_3}|=\frac{M^2_{B_s}}{4}(1-\eta ), \omega =\sqrt{\eta }M_{B_s}\) are used. For simplicity, we define the common factor F in each amplitude as

$$\begin{aligned} F_i=\frac{G_FeM^5_{B_s}C_F}{\sqrt{2} \pi }V_i, \end{aligned}$$
(30)

where \(C_F\) is the color factor, and \(V_i\) is for \(V^*_{ib}V_{is}\). If both \(\phi K\) pair and \(\gamma \) are left-handed, the explicit factorization formula from the \(O_{7\gamma }\) operator can be written as

$$\begin{aligned} {\mathcal {M}}^R_{7\gamma }= & {} 4F_i(1-\eta )\int _0^1 \mathrm{d}x_1 \mathrm{d}x_2\nonumber \\&\quad \times \int _{0}^{\infty }b_1 d b_1 b_2 db_2\phi _{B_s}(x_1,b_1)\left\{ E_e(t_a)S_t(z)\right. \nonumber \\&\times \left. \left[ \sqrt{\eta }(2z-1)(\phi _a+\phi _v)-(z+1)\phi _t\right] h_e(x_1 z,z,b_1,b_2)\right. \nonumber \\&\left. -\sqrt{\eta }(\phi _a+\phi _v)E_e(t_b)S_t(x_1)h_e(x_1 z,x_1-\eta ,b_2,b_1)\right\} ,\nonumber \\ \end{aligned}$$
(31)
Fig. 1
figure 1

Feynman diagrams of electromagnetic penguin operator \(O_{7\gamma }\). A photon is emitted through the \(O_{7\gamma }\) operator, and one hard gluon is exchanged between an energy quark and the spectator quark

Full size image

where the hard scales are given as

$$\begin{aligned} t_a= & {} \max (\sqrt{z}M_B,\sqrt{\beta _{ab}}M_B,1/b_1,1/b_2),\nonumber \\ t_b= & {} \max (\sqrt{|\eta -x_1|}M_B,\sqrt{\beta _{ab}}M_B,1/b_1,1/b_2),\;\;\;\;\;\; \end{aligned}$$
(32)

and the hard function \(h_e\) in the amplitude is from the propagators of virtual quark and gluon:

$$\begin{aligned}&h_e(\alpha ,\beta ,b_1,b_2)=\left[ \theta (\beta )K_0(\sqrt{\beta } M_{B_s}b_1)\nonumber \right. \\&\quad \left. +\theta (-\beta )i\frac{\pi }{2} H_0(\sqrt{-\beta }M_{B_s}b_1)\right] ,\nonumber \\&\quad \times \left\{ \theta (b_1-b_2)\left[ \theta (\alpha )K_0(\sqrt{\alpha } M_{B_s}b_1)I_0(\sqrt{\alpha }M_{B_s}b_2)\right. \right. \nonumber \\&\quad \left. \left. +\theta (-\alpha )\frac{i\pi }{2}H^{(1)}_0\nonumber \right. \right. \\&\quad \left. \left. (\sqrt{-\alpha }M_{B_s}b_1)J_0(\sqrt{-\alpha }M_{B_s}b_2)\right] +(b_1\leftrightarrow b_2)\right\} . \end{aligned}$$
(33)

The Sudakov factor \(S_t(x)\) from the threshold resummation is parameterized as

$$\begin{aligned} S_t(x)=\frac{2^{1+2c}\Gamma (3/2+c)}{\sqrt{\pi }\Gamma (1+c)}[x(1-x)]^c, \end{aligned}$$
(34)

with \(c=0.4\). The evolution factor is given as

$$\begin{aligned} E_e(t)=\alpha _s(t)\exp [-S_{B_s}(t)-S_{\phi K}(t)] \end{aligned}$$
(35)

with the Sudakov exponents \(S_{B_s}(t), S_{\phi K}(t)\) being given in Ref. [46]. To be compared with the right-helicity amplitude, the left-helicity amplitude is proportional to the ratio \(r_s=m_s/m_b\), which is obviously highly suppressed, \({\mathcal {M}}^L_{7\gamma }=0\), by neglecting the mass of s quark.

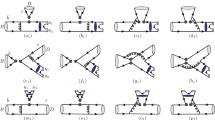
If the hard gluon which is required to kick the soft spectator quark is generated from the \({\mathcal {O}}_{8g}\) operator, one can obtain the four diagrams from the \(O_{8g}\) operator given in Fig. 3. The amplitudes for the first two diagrams are listed now:

$$\begin{aligned}&{\mathcal {M}}^{R,ab}_{8g}=2F_t\int _0^1 \mathrm{d}x_1 \mathrm{d}x_2\int _{0}^{\infty }b_1 d b_1 b_2 db_2\phi _{B_s}(x_1,b_1)\nonumber \\&\quad \times \left\{ Q_bE_e(t_a^\prime )S_t(x_1)(\eta -x_1-1)\right. \nonumber \\&\quad \left. \left. \times [x_1\phi _t+\sqrt{\eta }z(\phi _a+\phi _v)\right] \right. \nonumber \\&\times \qquad \left. h_e(\alpha _a,\beta _{ab},b_2,b_1) +Q_sE_e(t_b^\prime )S_t(z)\right. \nonumber \\&\quad \left. \times \left[ (x_1-2z)\phi _t+3z\sqrt{\eta }(\phi _a+\phi _v)\right] \right. \nonumber \\&\times \qquad \left. h_e(\alpha _b,\beta _{ab},b_1,b_2)\right\} , \end{aligned}$$
(36)
$$\begin{aligned}&{\mathcal {M}}^{R,cd}_{8g}=2F_tQ_u(1-\eta )\int _0^1 \mathrm{d}x_1 \mathrm{d}x_2\nonumber \\&\quad \times \int _{0}^{\infty }b_1 d b_1 b_2 db_2\phi _{B_s}(x_1,b_1)\left\{ E_e(t_c)S_t(x_1)\right. \nonumber \\&\quad \times \left. \left[ (\phi _a+\phi _v)\sqrt{\eta }(x_1-z)+x_1\phi _t\right] h_e(\alpha _c,\beta _{cd},b_2,b_1) \right. \nonumber \\&\quad \left. -E_e(t_d)S_t(z)\left[ 3z\sqrt{\eta }\times (\phi _a+\phi _v) right\right. \right. \nonumber \\&\quad \left. \left. -(x_1+2\eta -2-z)\phi _t\right] \right. \nonumber \\&\quad \left. \times h_e(\alpha _d,\beta _{cd},b_1,b_2)\right\} , \end{aligned}$$
(37)
$$\begin{aligned}&{\mathcal {M}}^{L,ab}_{8g}=2F_tQ_s\int _0^1 \mathrm{d}x_1 \mathrm{d}x_2 \int _{0}^{\infty }b_1 d b_1 b_2 db_2\phi _{B_s}(x_1,b_1)\nonumber \\&\quad \times \left\{ E_e(t_b^\prime )S_t(x_1)(1-z)\right. \nonumber \\&\quad \left. \times \left[ \eta (2x_1-z)\phi _t-3x_1\sqrt{\eta } (\phi _a-\phi _v)\right] \right. \nonumber \\&\times \qquad \left. h_e(\alpha _b,\beta _{ab},b_1,b_2)\right\} , \end{aligned}$$
(38)
$$\begin{aligned}&{\mathcal {M}}^{L,cd}_{8g}=2F_tQ_u\int _0^1 \mathrm{d}x_1 \mathrm{d}x_2\nonumber \\&\quad \times \int _{0}^{\infty }b_1 d b_1 b_2 db_2\phi _{B_s}(x_1,b_1)\left\{ E_e(t_c)S_t(x_1)\right. \nonumber \\&\quad \left. \times (1-\eta )\left[ \eta (x_1-z)\phi _t\nonumber \right. \right. \\&\quad \left. \left. +x_1\sqrt{\eta } (\phi _a-\phi _v)\right] h_e(\alpha _c,\beta _{cd},b_2,b_1) \right. \nonumber \\&\quad \left. +E_e(t_d)S_t(z)\left[ \eta z(2 x_1+\eta -2z-1)\nonumber \right. \right. \\&\quad \times \left. \left. \phi _t-3\sqrt{\eta }(1-\eta ) (z-x_1)(\phi _a-\phi _v)\right] \right. \nonumber \\&\quad \left. \times h_e(\alpha _c,\beta _{cd},b_1,b_2)\right\} , \end{aligned}$$
(39)

where

$$\begin{aligned} \alpha _a= & {} 1-\eta +x_1, \alpha _b=z-1,\beta _{ab}=x_1z, \end{aligned}$$
(40)
$$\begin{aligned} \alpha _c= & {} (1-\eta )x_1, \alpha _d=-z(1-\eta ), \beta _{cd}=(x_1-z)(1-\eta ), \nonumber \\ \end{aligned}$$
(41)
$$\begin{aligned} t^\prime _a= & {} \max (\sqrt{\alpha _a}M_{B_s},\sqrt{\beta _{ab}}M_{B_s},1/b_1,1/b_2), \end{aligned}$$
(42)
$$\begin{aligned} t^\prime _b= & {} \max (\sqrt{-\alpha _b}M_{B_s},\sqrt{\beta _{ab}}M_{B_s},1/b_1,1/b_2),\end{aligned}$$
(43)
$$\begin{aligned} t_c= & {} \max (\sqrt{\alpha _c}M_{B_s},\sqrt{|\beta _{cd}|}M_{B_s},1/b_1,1/b_2),\end{aligned}$$
(44)
$$\begin{aligned} t_d= & {} \max (\sqrt{-\alpha _d}M_{B_s},\sqrt{|\beta _{cd}|}M_{B_s},1/b_1,1/b_2). \end{aligned}$$
(45)
Fig. 2
figure 2

Feynman diagrams of chromomagnetic penguin operator \(O_{8g}\). A hard gluon is emitted through the \(O_{8g}\) operator, and a photon is emitted by bremsstrahlung of external quark lines

Full size image
Fig. 3
figure 3

Feynman diagrams of quark line photon emission. The charm or up loop to the gluon is attached to the spectator quark line. A photon is emitted through the external quark lines

Full size image

There are two kinds of charm/up quark-loop contributions specified as the type of photon emission: Quark line photon emission and loop line photon emission. The former means that a photon is emitted through the external quark lines (shown in Fig. 3), the gauge invariant c / u quark-loop function combined with the \( b\rightarrow dg\) vertex is written as \({\bar{d}} \gamma ^\mu (1-\gamma ^5)I_{\mu \nu }b\) where the explicit formula \(I_{\mu \nu }\) is as follows [61]:

$$\begin{aligned} I^a_{\mu \nu }= & {} \frac{gT^a}{2\pi ^2}(k^2g_{\mu \nu }-k_{\mu } k_{\nu })\int _0^1\mathrm{d}x (1-x)\nonumber \\&\quad \left[ 1+\log \frac{m^2_i-x(1-x)k^2}{t^2}\right] \nonumber \\= & {} -\frac{gT^2}{8\pi ^2}(k^2g_{\mu \nu }-k_\mu k_\nu )\left[ G(m^2_i,k^2,t)-\frac{2}{3}\right] , \end{aligned}$$
(46)

where k is the gluon momentum and \(m_i\) is the loop internal quark mass. The loop function G is given as [62]

$$\begin{aligned} G(m^2_i,k^2,t)= & {} \theta (-k^2)\frac{2}{3}\left[ \frac{5}{3} +\frac{4m^2_i}{k^2}-\ln \frac{m^2_i}{t^2}+\left( 1+\frac{2m^2_i}{k^2}\right) \right. \nonumber \\&\left. \times \quad \sqrt{1-\frac{4m^2_i}{k^2}}\ln \frac{\sqrt{1-4m^2_i/k^2}-1}{\sqrt{1-4m^2_i/k^2}+1}\right] \nonumber \\&\quad +\theta (k^2)\theta (4m^2_i-k^2)\frac{2}{3}\nonumber \\&\times \left[ \frac{5}{3}+\frac{4m^2_i}{k^2}-\ln \frac{m^2_i}{t^2} -2\left( 1+\frac{2m^2_i}{k^2}\right) \right. \nonumber \\&\left. \times \sqrt{\frac{4m^2_i}{k^2}-1}\arctan \left( \frac{1}{\sqrt{4m^2_i/k^2-1}}\right) \right] \nonumber \\&\quad +\theta (k^2-4m^2_i)\frac{2}{3}\left[ \frac{5}{3} +\frac{4m^2_i}{k^2}-\ln \frac{m^2_i}{t^2}\right. \nonumber \\&\quad \left. \left. +(1+\frac{2m^2_i}{k^2})\sqrt{1-\frac{4m^2_i}{k^2}}\nonumber \right. \right. \\&\times \left. \left[ \ln \frac{1-\sqrt{1-4m^2_i/k^2}}{1+\sqrt{1-4m^2_i/k^2}}+i\pi \right] \right] . \end{aligned}$$
(47)

It is noticed that there is no singularity when we take the limit of \(k\rightarrow 0\), so we can neglect the \(k_T\) components of \(k^2\) in the loop function G. This kind of contribution can be expressed as follows:

$$\begin{aligned}&{\mathcal {M}}^{R,ab}_{1i}=F_iQ_s\int _0^1 \mathrm{d}x_1 \mathrm{d}x_2\int _{0}^{\infty }b_1 d b_1 b_2 db_2\phi _{B_s}(x_1,b_1)\nonumber \\&\quad \times \left[ G(m^2_i, -\beta _{ab}M^2_{B_s},t^\prime _b)-\frac{2}{3}\right] \nonumber \\&E_e(t_b^\prime )S_t(z)z\nonumber \\&\quad \times \left[ \sqrt{\eta }(2x_1-z) (\phi _a+\phi _v)-3x_1\phi _t\right] \nonumber \\&\times \qquad h_e(\alpha _b,\beta _{ab},b_1,b_2), \end{aligned}$$
(48)
$$\begin{aligned}&{\mathcal {M}}^{L,ab}_{1i}=F_i\int _0^1 \mathrm{d}x_1 \mathrm{d}x_2\int _{0}^{\infty }b_1 d b_1 b_2 db_2\phi _{B_s}(x_1,b_1)\sqrt{\eta }\nonumber \\&\quad \times \left\{ Q_b\left[ G(m^2_i,-\beta _{ab}M^2_{B_s}, t^\prime _a)-\frac{2}{3}\right] \right. \nonumber \\&\quad \left. \times E_e(t^\prime _a)S_t(x_1)z(1+x_1-\eta )\nonumber \right. \\&\quad \times \left. \left[ x_1(\phi _a-\phi _v)+\sqrt{\eta }z\phi _t\right] h_e(\alpha _a,\beta _{ab},b_2,b_1) \right. \nonumber \\&\quad \left. +\left[ G(m^2_i,-\beta _{ab}M^2_{B_s}, t_b^\prime )-\frac{2}{3}\right] x_1(z-1)\nonumber \right. \\&\quad \times \left. \left[ (x_1-2z)(\phi _a-\phi _v)+3\sqrt{\eta }z\phi _t\right] \right. \nonumber \\&\quad \left. \times Q_sE_e(t_b^\prime )S_t(z)h_e(\alpha _b,\beta _{ab},b_1,b_2)\right\} , {\mathcal {M}}^{R,cd}_{1i} \end{aligned}$$
(49)
$$\begin{aligned}&{\mathcal {M}}^{R,cd}_{1i}=F_iQ_u\int _0^1 \mathrm{d}x_1 \mathrm{d}x_2\nonumber \\&\quad \times \int _{0}^{\infty }b_1 d b_1 b_2 db_2\phi _{B_s}(x_1,b_1)(\eta -1)\nonumber \\&\quad \times \left\{ \left[ G(m^2_i,-\beta _{cd}M^2_{B_s},t_c) -\frac{2}{3}\right] \right. \nonumber \\&\quad \left. \times E_e(t_c)S_t(x_1)(\eta -1)\nonumber \right. \\&\quad \times \left. \left[ \sqrt{\eta }(z-x_1)(\phi _a+\phi _v) -x_1\phi _t\right] h_e(\alpha _c,\beta _{cd},b_1,b_2)\right. \nonumber \\&\quad \left. + G(m^2_i,-\beta _{cd}M^2_{B_s},t_d)E_e(t_d)S_t(z)\nonumber \right. \\&\quad \times \left. \left[ 3(\eta -1)(z-x_1)\phi _t+(\phi _a+\phi _v)\right. \right. \nonumber \\&\quad \left. \left. \times z\sqrt{\eta }(\eta +2x_1-1-2z)\right] h_e(\alpha _d,\beta _{cd},b_1,b_2) \right\} , \end{aligned}$$
(50)
$$\begin{aligned}&{\mathcal {M}}^{L,cd}_{1i}=F_iQ_u\int _0^1 \mathrm{d}x_1 \mathrm{d}x_2\nonumber \\&\quad \times \int _{0}^{\infty }b_1 d b_1 b_2 db_2\phi _{B_s}(x_1,b_1)(\eta -1)(x_1-z)\nonumber \\&\quad \times \sqrt{\eta } \left\{ E_e(t_c)S_t(x_1) G(m^2_i,-\beta _{cd}M^2_{B_s},t_c)\nonumber \right. \\&\quad \times \left. \left[ \sqrt{\eta }(z-x_1) \phi _t-x_1(\phi _a-\phi _v)\right] h_e(\alpha _c,\beta _{cd},b_1,b_2)\right. \nonumber \\&\quad \left. + G(m^2_i,-\beta _{cd}M^2_{B_s},t_d)E_e(t_d)S_t(z) \right. \nonumber \\&\times \quad \left. \left[ 3\sqrt{\eta }z\phi _t+(\phi _a-\phi _v)\right. \right. \nonumber \\&\quad \left. \left. \times (2+z-2\eta -x_1)\right] h_e(\alpha _d,-\beta _{cd},b_1,b_2)\right\} , \end{aligned}$$
(51)

where the hard function and the hard scales have been defined in Eq. (33) and Eqs. (40–45), respectively. When the photon is emitted from the c / u quark-loop line (shown in Fig. 4), the \( b\rightarrow d g \gamma \) amplitude is expressed as [63,64,65,66]

$$\begin{aligned} A( b\rightarrow d g\gamma )={\bar{d}} \gamma ^\rho \frac{(1-\gamma _5)}{2} T^abI_{\mu \nu \rho }\epsilon ^\mu _\gamma \epsilon ^\nu _{g}, \end{aligned}$$
(52)

where the vertex function \(I_{\mu \nu \rho }\) is defined as follows:

$$\begin{aligned} I_{\mu \nu \rho }= & {} A_4\left[ (k\cdot q)\epsilon _{\mu \nu \rho \sigma }(q^\sigma -k^\sigma )\nonumber \right. \\&\left. +\epsilon _{\nu \rho \sigma \tau }q^\sigma k^\tau k_\mu -\epsilon _{\mu \rho \sigma \tau }q^\sigma k^\tau q_\nu \right] \nonumber \\&+A_5\left[ \epsilon _{\mu \rho \sigma \tau }q^\sigma k^\tau k_\nu -k^2\epsilon _{\mu \nu \rho \sigma }q^\sigma \right] , \end{aligned}$$
(53)
$$\begin{aligned} A_4= & {} \frac{4i}{3\pi ^2}eg\int _0^1 \mathrm{d}x\int _0^{1-x}\mathrm{d}y\nonumber \\&\times \frac{xy}{x(1-x)k^2+2xyq\cdot k-m^2_i}, \end{aligned}$$
(54)
$$\begin{aligned} A_5= & {} \frac{4i}{3\pi ^2}eg\int _0^1 \mathrm{d}x\int _0^{1-x} \mathrm{d}y\nonumber \\&\times \frac{x(1-x)}{x(1-x)k^2+2xyq\cdot k-m^2_i}, \end{aligned}$$
(55)

where k is the gluon momentum and q is the momentum of the photon. The amplitudes can be expressed as follows:

$$\begin{aligned}&{\mathcal {M}}^R_{2i}=\frac{8F_{i}}{3}\int _0^1 \mathrm{d}x\int _0^{1-x} \mathrm{d}y\int _0^1 \mathrm{d}x_1\mathrm{d}x_2\nonumber \\&\quad \times \int _0^\infty b_1d b_1\phi _{B_s}(x_1,b_1)E_e(t_2)h^\prime _{e}(A,B,b_1)\nonumber \\&\quad \times \frac{(\eta -1)z}{xyz(1-\eta )M^2_{B_s}-m^2_i}\nonumber \\&\quad \times \left\{ xy\left[ \sqrt{\eta }(\eta +z-x_1-1)(\phi _a+\phi _v) \right. \right. \nonumber \\&\quad \left. \left. +(1+2x_1-\eta )\phi _t \right] \right. \nonumber \\&\quad \left. -x(1-x)\left[ 3x_1\phi _t+\sqrt{\eta }(z-2x_1) (\phi _a+\phi _v)\right] \right\} , \end{aligned}$$
(56)
$$\begin{aligned}&{\mathcal {M}}^L_{2i}=\frac{8F_{i}}{3}\int _0^1 \mathrm{d}x\int _0^{1-x} \mathrm{d}y\int _0^1 \mathrm{d}x_1\mathrm{d}x_2\nonumber \\&\quad \times \int _0^\infty b_1d b_1\phi _{B_s}(x_1,b_1)E_e(t_2)h^\prime _{e}(A,B,b_1)\nonumber \\&\quad \times \frac{(\eta -1)z}{xyz(1-\eta )M^2_{B_s}-m^2_i}\nonumber \\&\quad \times \left\{ xy\left[ \sqrt{\eta }(z-x_1)(\phi _a-\phi _v)-2\eta z\phi _t \right] \right. \nonumber \\&\quad \left. +x(1-x)\left[ \eta z\phi _t+\sqrt{\eta }x_1(\phi _a-\phi _v)\right] \right\} , \end{aligned}$$
(57)
Fig. 4
figure 4

Feynman diagrams of loop line photon emission. The charm or up loop to the gluon is attached to the spectator quark line. A photon is emitted through the quark-loop line

Full size image
Fig. 5
figure 5

Annihilation diagrams by tree and penguin operators. There are no hard gluons for these cases because they belong to the four Fermi interactions and do not include the spectator quarks

Full size image

where

$$\begin{aligned}&A=x_1 z, B=x_1z-\frac{y}{1-x}z(1-\eta )+\frac{r^2_i}{x(1-x)}, \end{aligned}$$
(58)
$$\begin{aligned}&t_2=\max (\sqrt{A}M_{B_s},\sqrt{|B|}M_{B_s},1/b_1),\end{aligned}$$
(59)
$$\begin{aligned}&h^\prime _e(A,B,b_1)=K_0(\sqrt{A}M_{B_s}b_1)\nonumber \\&\qquad -\Bigg [\theta (B)K_0(\sqrt{B}M_{B_s}b_1) +\theta (-B)\frac{i\pi }{2} \nonumber \\&\qquad H_0(\sqrt{-B}M_{B_s}b_1)\Bigg ], \end{aligned}$$
(60)

where we have the ratio \(r^2_i=m^2_i/M^2_{B_s}\) with \(m_i\) being the c / u quark mass.

For the annihilation diagrams, three kinds of operators are used: Both \({\bar{b}}\otimes {\bar{s}}\) and \({\bar{d}}\otimes s\) are left-handed currents, denoted as LL; \({\bar{b}} \otimes {\bar{s}}\) is a left-handed current and \({\bar{d}} \otimes s\) is a right-handed current, denoted as LR; the third kind of current SP is from the Fierz transformation of the LR current. So the factorization formulas for these annihilation diagrams are written as

$$\begin{aligned}&M^{R,LL}_{ann1}=4\sqrt{6\eta }eM^3_{B_s}Q_s(1-\eta )F_v\zeta \int _0^1 \mathrm{d}x_1\nonumber \\&\quad \times \int _{0}^{\infty }b_1 d b_1\phi _{B_s}(x_1,b_1)E_{a1}(t'_c)\nonumber \\&\quad \times S_t(x_1)K_0(\sqrt{\alpha _c}M_{B_s} b_1), \end{aligned}$$
(61)
$$\begin{aligned}&M^{L,LL}_{ann1}=4\sqrt{6\eta }eM^3_{B_s}F_v(1-\zeta )\int _0^1 \mathrm{d}x_1\nonumber \\&\quad \times \int _{0}^{\infty }b_1 d b_1\phi _{B_s}(x_1,b_1)S_t(x_1) \left\{ Q_b\right. \nonumber \\&\quad \left. \times (\eta -x_1-1)E_{a1}(t_a{''})K_0(\sqrt{\alpha _a}M_{B_s}b_1)\nonumber \right. \\&\qquad \left. -Q_s x_1 E_{a1}(t'_c)K_0(\sqrt{\alpha _c}M_{B_s} b_1)\right\} , \end{aligned}$$
(62)
$$\begin{aligned}&M^{R,LR}_{ann1}=4\sqrt{6\eta }eM^3_{B_s}Q_s(1-\eta )F_v(\zeta -1)\int _0^1 \mathrm{d}x_1\nonumber \\&\quad \times \int _{0}^{\infty }b_1 d b_1\phi _{B_s}(x_1,b_1)E_{a1}(t'_c)\nonumber \\&\quad \times S_t(x_1)K_0(\sqrt{\alpha _c}M_{B_s} b_1), \end{aligned}$$
(63)
$$\begin{aligned}&M^{L,LL}_{ann1}=-4\sqrt{6\eta }eM^3_{B_s}F_v\zeta \int _0^1 \mathrm{d}x_1\nonumber \\&\quad \times \int _{0}^{\infty }b_1 d b_1\phi _{B_s}(x_1,b_1)S_t(x_1) \left\{ Q_b\right. \nonumber \\&\quad \left. \times (\eta -x_1-1)E_{a1}(t_a{''})K_0(\sqrt{\alpha _a}M_{B_s}b_1)\nonumber \right. \\&\qquad \left. -Q_s x_1 E_{a1}(t'_c)K_0(\sqrt{\alpha _c}M_{B_s} b_1)\right\} , \end{aligned}$$
(64)
$$\begin{aligned}&M^{R,LL}_{ann2}=-M^{L,LR}_{ann2}=-2\sqrt{6\eta }ef_{B_s}M^3_{B_s}\int _0^1 d z\nonumber \\&\quad \times \int _{0}^{\infty }b_2 d b_2 (\phi _a+\phi _v) S_t(z)\left\{ Q_dE_{a2}(t_b'')\right. \nonumber \\&\quad \left. \times \frac{i\pi }{2}H^{(1)}_0(\sqrt{-\alpha _b}M_{B_s}b_2)\nonumber \right. \\&\qquad \left. -Q_s z\frac{i\pi }{2}E_{a2}(t_d')H^{(1)}_0(\sqrt{-\alpha _d}M_{B_s}b_2)\right\} , \end{aligned}$$
(65)
$$\begin{aligned}&M^{L,LL}_{ann2}=-M^{R,LR}_{ann2}=2\sqrt{6\eta }ef_{B_s}M^3_{B_s}\int _0^1 d z\nonumber \\&\quad \times \int _{0}^{\infty }b_2 d b_2 (\phi _a-\phi _v) \left\{ \frac{i\pi }{2}H^{(1)}_0(\sqrt{-\alpha _b}M_{B_s}b_2)\right. \nonumber \\&\quad \left. \times (z-1)Q_dE_{a2}(t_b'')-Q_s (\eta -1)\nonumber \right. \\&\quad \times \left. \frac{i\pi }{2}E_{a2}(t_d')H^{(1)}_0(\sqrt{-\alpha _d}M_{B_s}b_2)\right\} S_t(z), \end{aligned}$$
(66)
$$\begin{aligned}&M^{R,SP}_{ann2}=4\sqrt{6}ef_{B_s}M^3_{B_s}\int _0^1 d z\int _{0}^{\infty }b_2 d b_2 \phi _t \nonumber \\&\quad \times \left\{ Q_dE_{a2}(t_b{''}) \frac{i\pi }{2}H^{(1)}_0(\sqrt{-\alpha _b}M_{B_s}b_2)\right. \nonumber \\&\qquad \left. -Q_s (\eta -1)E_{a2}(t_d')\frac{i\pi }{2}H^{(1)}_0 (\sqrt{-\alpha _d}M_{B_s}b_2)\right\} S_t(z), \nonumber \\ \end{aligned}$$
(67)
$$\begin{aligned}&M^{L,SP}_{ann2}=4\sqrt{6}ef_{B_s}M^3_{B_s}\int _0^1 d z\int _{0}^{\infty }b_2 d b_2 \phi _t\nonumber \\&\quad \times \left\{ (1-z)\eta Q_dE_{a2}(t_b{''}) \frac{i\pi }{2}H^{(1)}_0(\sqrt{-\alpha _b}M_{B_s}b_2)\right. \nonumber \\&\qquad \left. +Q_s \eta z E_{a2}(t_d')\frac{i\pi }{2}H^{(1)}_0(\sqrt{-\alpha _d}M_{B_s}b_2)\right\} S_t(z), \end{aligned}$$
(68)

where the time-like form factor \(F_v\) is given in Eq. (26), the hard scales \(t_a'', t_b'', t_c', t_d'\) and the evolution factors \(E_{ann1}, E_{ann2}\) are defined as

$$\begin{aligned}&t_a''=\max (\sqrt{\alpha _a}M_{B_s},1/b_1),t_b''=\max (\sqrt{-\alpha _b}M_{B_s},1/b_2),\nonumber \\ \end{aligned}$$
(69)
$$\begin{aligned}&t_c'=\max (\sqrt{\alpha _c}M_{B_s},1/b_1),t_d'=\max (\sqrt{-\alpha _d}M_{B_s},1/b_2),\nonumber \\ \end{aligned}$$
(70)
$$\begin{aligned}&E_{ann1}(t)=\alpha _s(t)\exp [-S_{B_s}(t)],E_{ann2}(t)\nonumber \\&\quad =\alpha _s(t)\exp [-S_{\phi K}(t)].\nonumber \\ \end{aligned}$$
(71)

By combining these amplitudes from the different Feynman diagrams, one can get the total decay amplitude for the decay \(B_s\rightarrow \phi {\bar{K}}^0\gamma \):

$$\begin{aligned}&M^i(B_s\rightarrow \phi {\bar{K}}^0\gamma )=V^*_{ub}V_{us}C_2\left( {\mathcal {M}} ^{j,ab}_{1u}+{\mathcal {M}}^{j,cd}_{1u}+{\mathcal {M}}^{j}_{2u}\right) \nonumber \\&+V^*_{cb}V_{cs}C_2\left( {\mathcal {M}}^{j,ab}_{1c} +{\mathcal {M}}^{j,cd}_{1c}+{\mathcal {M}}^{j}_{2c}\right) \nonumber \\&-V^*_{tb}V_{ts}\left[ C_{7\gamma }{\mathcal {M}}^j_{7\gamma } +C_{8g}({\mathcal {M}}^{j,ab}_{8g}+{\mathcal {M}}^{j,cd}_{8g})\right. \nonumber \\&\left. +(a_4-\frac{1}{2}a_{10})\left( {\mathcal {M}}^{j,LL}_{ann1} +{\mathcal {M}}^{j,LL}_{ann2}\right) +(a_6-\frac{a_8}{2}) {\mathcal {M}}^{j,SP}_{ann2}\right] ,\nonumber \\ \end{aligned}$$
(72)

where the combinations of the Wilson coefficients are defined as

$$\begin{aligned} a_4= & {} C_4+C_3/3, a_6=C_6+C_5/3, \end{aligned}$$
(73)
$$\begin{aligned} a_8= & {} C_8+C_7/3,a_{10}=C_{10}+C_9/3. \end{aligned}$$
(74)

3 The numerical results and discussions

The input parameters in the numerical calculations [52, 67] are listed as follows:

$$\begin{aligned}&f_{B_s} = 230 \ \mathrm{MeV}, \tau _{B_s} = 1.510\times 10^{-12} s, M_{B_s}=5.3667 \ \mathrm{GeV}\nonumber \\ \end{aligned}$$
(75)
$$\begin{aligned}&\lambda = 0.22506\pm 0.00050, A=0.811\pm 0.026, \end{aligned}$$
(76)
$$\begin{aligned}&{\bar{\rho }}=0.124^{+0.019}_{-0.018}, \quad {\bar{\eta }}=0.356\pm 0.011. \end{aligned}$$
(77)

Using the input parameters and the wave functions as specified in this section and Sect. 1, it is easy to get the branching ratios for the decays \(B_s\rightarrow \phi {\bar{K}}^0 \gamma \)

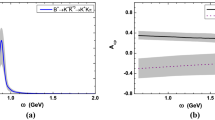
$$\begin{aligned} Br(B_s\rightarrow \phi {\bar{K}}^0\gamma )= & {} (9.26^{+1.79+3.12+0.64} _{-1.61-3.86-0.49})\times 10^{-8}, \end{aligned}$$
(78)

where the first error is from the \(B_s\) meson wave function shape parameter \(\omega _b=(0.5\pm 0.05)\) GeV, the second one is from the hard scale t from 0.5t to 2t (without changing \(1/b_i\)), and the third one is from the Wolfenstein parameter \(A=0.811\pm 0.026\). It is noticed that the result for the region with the \(\phi K\) invariant mass as large as 4 GeV is not reliable, and the main contribution to the branching ratio is from the peak near the threshold value for the \(\phi K\) invariant mass as shown in Fig. 6. So the cut with \(M_{\phi K}<2.5\) GeV is given to the \(\phi K\) invariant mass. From the result, one can find that the main errors are from the scale-dependent uncertainty, which can be reduced only if the next-to-leading order contributions are included. In the future, even if the high order corrections are considered, the corresponding error is still large, it just reflects considerable nonperturbative effects. Certainly, we chose a wider range for the hard scale from 0.5t to 2t. It is noticed that the hard scale usually varies from 0.75t to 1.25t in previous work.

Fig. 6
figure 6

\(B_s\rightarrow \phi {\bar{K}}^0\gamma \) decay spectrum in the \(\phi K\) invariant mass

Full size image

We also predicted the \(B_s\rightarrow \phi {\bar{K}}^0\gamma \) decay spectrum shown in Fig. 6, which exhibits a maximum at the \(\phi K\) invariant mass around 1.95 GeV.

The direct CP asymmetry of the \(B_s\rightarrow \phi {\bar{K}}^0 \gamma \) is defined by

$$\begin{aligned}&A^{dir}_{CP}(B_s\rightarrow \phi K \gamma )\nonumber \\&\quad =\frac{Br({\bar{B}}^0_s\rightarrow \phi K^0 \gamma )-Br(B^0_s\rightarrow \phi {\bar{K}}^0 \gamma )}{Br({\bar{B}}^0_s\rightarrow \phi K^0 \gamma )+Br(B^0_s\rightarrow \phi {\bar{K}}^0 \gamma )}. \end{aligned}$$
(79)

We predict the direct CP asymmetry as

$$\begin{aligned} A^{dir}_{CP}(B_s\rightarrow \phi {\bar{K}}^0 \gamma )=(-4.1^{+0.4+1.7+0.2}_{-0.6-1.2-0.1})\%, \end{aligned}$$
(80)

where the errors are the same as those in Eq. (78). The main error is still from the hard scale t varying from 0.5t to 2t. The errors are induced by the hadronic uncertainties, such as the decay constants, the Gegenbauer moments and the shape parameter \(\omega _b\); they can be dropped out partly in the ratio. Similar conditions also occur in the direct CP asymmetries of the \(B_s\) two-body decays [69]. Some comments are in order:

  • The branching ratio for the decay \(B_s\rightarrow \phi {\bar{K}}^0\gamma \) is of order near \(10^{-7}\), which can be tested by the present running LHCb experiments. The ratio of the branching ratios for the decays \(B\rightarrow \phi K\) and \(B\rightarrow \phi K\gamma \) is given as [52]

    $$\begin{aligned} \frac{Br(B^+\rightarrow \phi K^+)}{Br(B^+\rightarrow \phi K^+\gamma )}= & {} \frac{(8.8^{+0.7}_{-0.6})\times 10^{-6}}{(2.7\pm 0.4)\times 10^{-6}}\sim 3.3, \end{aligned}$$
    (81)
    $$\begin{aligned} \frac{Br(B^0\rightarrow \phi K^0)}{Br(B^0\rightarrow \phi K^0\gamma )}= & {} \frac{(7.3\pm 0.7) \times 10^{-6}}{(2.7\pm 0.7)\times 10^{-6}}\sim 2.7. \end{aligned}$$
    (82)

    For the decay \(B_s\rightarrow \phi {\bar{K}}^0\), it has not been measured by experiment, while it was studied by the QCDF approach [68] and the pQCD approach [69] and predicted to be \((2.7^{+7.4}_{-2.5})\times 10^{-7}\) and \((1.6^{+1.0}_{-0.5})\times 10^{-7}\), respectively. Combined with our prediction we find the ratio

    $$\begin{aligned} \frac{Br(B_s\rightarrow \phi {\bar{K}}^0)}{Br(B_s\rightarrow \phi {\bar{K}}^0\gamma )}\sim 2.9 \;\text {or} \;1.7, \end{aligned}$$
    (83)

    that is to say, the branching ratios of decays \(B_{u,d,s}\rightarrow \phi K\) are larger by about \(1\sim 2\) times than that of the corresponding one photon radiation decays.

  • For the \(B_s\rightarrow \phi {\bar{K}}^0\gamma \) decay, the nonresonant contributions are dominant, and the resonant contributions from \(K_1(1650), K_2(1770)\) and K(1830) mesons through the \(\phi K\) channel are expected to be negligible. This is so because the branching ratios of these resonant mesons decaying into a \(\phi K\) pair are not yet available. So this decay \(B_s\rightarrow \phi {\bar{K}}^0\gamma \) provides a clean test for the application of two-meson distribution amplitudes to the B meson three-body decays. It is similar to the decay \(B\rightarrow \phi K\gamma \).

  • For the decay \(B_s\rightarrow \phi {\bar{K}}^0\gamma \), the prominent feature of the decay spectra is the enhancement near the threshold, which reaches the maximum at around \(m_{\phi K}\sim 1.95 GeV\). To be compared with the decay spectra of the \(B^0\rightarrow \phi K^0\gamma \) channel, the peak position moves toward the larger \(m_{\phi K}\) region because \(B_s\) is heavier than B meson. Indeed, the decay \(B^0\rightarrow \phi K^0\gamma \) spectrum exhibits a maximum at the \(\phi K\) invariant mass around 1.8 GeV [46]. However, the shapes of the differential decay rates for the two decay channels should be very similar.

  • In the \(b\rightarrow d\gamma \) process, although the dominant contribution to the decay amplitudes comes from the chiral-odd dipole operator \(O_{7\gamma }\), we also considered contributions from the \(O_{8g}\) operator, the annihilation type amplitudes, especially \(O_2\) operator from the quark-loop corrections, which is necessary to induce the direct CP violation. The CKM matrix element for the \(O_{7\gamma }\) is \(V^*_{tb}V_{td}\sim \lambda ^3\), while the tree operator \(O_2\) is either proportional to \(V^*_{ub}V_{ud}\sim \lambda ^3\) or \(V^*_{cb}V_{cd}\sim \lambda ^3\). Then the tree contribution is not suppressed and can give bigger direct CP asymmetries than that of the decay \(B^0\rightarrow \phi K^0\gamma \). For the \(B^0\rightarrow \phi K^0\gamma \) decay, the CKM matrix for the \(O_{7\gamma }\) and tree operators are proportional to \(V^*_{tb}V_{ts}\sim \lambda ^2\) and \(V^*_{ub}V_{ud}\sim \lambda ^4\), respectively. The difference between these two interfering amplitudes is large, so the corresponding direct CP asymmetry is small [46].

  • U-spin can connect \(b\rightarrow s\gamma \) and \(b\rightarrow d\gamma \), two different kinds of weak decays, by exchange of \(d\leftrightarrow s\) [70,71,72]. Using the U-spin symmetry and the CKM unitarity relation

    $$\begin{aligned} Im(V^*_{ub}V_{us}V_{cd}V^*_{cs})=-Im(V^*_{ub}V_{ud}V_{cd}V^*_{cd}), \end{aligned}$$
    (84)

    one can obtain

    $$\begin{aligned}&|{\mathcal {A}}({\bar{B}}^0\rightarrow \phi {\bar{K}}^0\gamma )|^2-|{\mathcal {A}}( B^0\rightarrow \phi K^0\gamma )|^2\nonumber \\&\quad =|{\mathcal {A}}( B_s\rightarrow \phi {\bar{K}}^0\gamma )|^2-|{\mathcal {A}}( {\bar{B}}_s\rightarrow \phi K^0\gamma )|^2.\;\;\; \end{aligned}$$
    (85)

    Certainly, U-spin symmetry breaking is introduced through the form factors \(F_{B\rightarrow \phi K}\) and \(F_{B_s\rightarrow \phi K}\). So we can expect that

    $$\begin{aligned}&A^{dir}_{CP}(B_s\rightarrow \phi {\bar{K}}^0\gamma )\nonumber \\&\quad \approx A^{dir}_{CP}(B^0\rightarrow \phi K^0\gamma )\frac{Br(B^0\rightarrow \phi K^0\gamma )}{Br(B_s\rightarrow \phi {\bar{K}}^0\gamma )}. \end{aligned}$$
    (86)

    Combining the predictions for the decay \(B^0\rightarrow \phi K^0\gamma \) given in Ref. [46], one finds that this relation is well supported.

4 Conclusion

In this paper, we calculate the branching ratio and the direct CP asymmetry for the decay \(B_s\rightarrow \phi {\bar{K}}^0\gamma \), which induced by \(b\rightarrow d \gamma \) transition. In addition to the dominant electromagnetic penguin operator, the subleading contributions including the chromomagnetic penguin operator, quark-loop corrections and annihilation amplitudes are also calculated. Compared with the decay \(B^0\rightarrow \phi K^0\gamma \), the branching ratio for the decay \(B_s\rightarrow \phi {\bar{K}}^0\gamma \) is very small and less than \(10^{-7}\) because of the smaller CKM element matrix being proportional to \(\lambda ^3\). Although the subleading contribution from the quark-loop corrections is small, it is necessary for the direct CP asymmetry, which is predicted as \((-4.1^{+0.4+1.7+0.2}_{-0.6-1.2-0.1})\%\). These predictions can be well explained by using the U-spin asymmetry approach when combining the results for the decay \(B^0\rightarrow \phi K^0\gamma \). We also give the shape of the differential decay rate, which is similar to that for the decay \(B^0\rightarrow \phi K^0\gamma \) but with a different peak position for the \(m_{\phi K}\). In the upper calculations, the two-meson \(\phi K\) DAs are introduced to absorb the infrared dynamics in the \(\phi K\) pair, so the three-body decay amplitude can be factorized, just similar to the two-body case, into the convolution of the wave functions and hard kernels.