1 Introduction

Despite its amazing success in explaining gravitational and cosmological dynamics on scales ranging from the Solar System to the Hubble radius, general relativity was confronted from its early stages of existence with a plethora of alternative gravity theories. An interesting but less investigated way of explaining gravity was related to field theoretical models of gravity, in which the gravitational interaction, similarly to the other interactions of nature, is mediated by a spin two particle, called the graviton. The early field theoretical approaches to gravity were formulated in a flat geometry, and the first such model was proposed by Fierz and Pauli [1] in 1939. This linear approach to gravity succeeded to give to the graviton a mass, introduced five degrees of freedom in the model, and avoided the propagation of the sixth’s one. A theory of gravitation using a massless tensor field was proposed by Thirring in [2]. In this model the field equations require a conserved source and admit a gauge-group, while the equations of motion of particles are gauge invariant only if the gauge transformation of the field is supplemented by a linear coordinate transformation.

An important moment in the development of the massive gravity theory was represented by the paper [3], where it was found that there exists a discrete difference between the zero-mass theories and the very small, but non-zero mass theories (the vDVZ discontinuity). In this context it is important to mention that massive gravity is a classical field theory that does not need to be formulated in terms of the graviton, a particle mediating the gravitational interaction in a way similar to the electromagnetic or nuclear interactions. Based on its transformation properties, a classical gravitational field has spin two, and it can have a mass that follows from its dispersion relation. These properties are general, and they are valid without the need of introducing a particle representation of the gravitational interaction. In the following we will use, for simplicity, the term “graviton” as defined above, and which does not imply an explicit particle interaction picture. In the case of gravitation, a comparison of massive and massless theories with experiment, in particular the perihelion movement of Mercury, did show that the massive gravity theory must be excluded, and therefore the graviton mass must be rigorously zero.

A possible way to get around the physical consequences of the vDVZ discontinuity was proposed in [4], and was based on the idea that the linearized approximation of the gravitational field breaks down near massive objects like, for example, the Sun. Therefore an improved expansion must be used, which, also including the previously ignored nonlinear effects, leads to a continuous zero mass limit. Static, spherically symmetric, and asymptotically flat numerical solutions of massive gravity with a source were obtained in [5], and they led to a recovery of the Schwarzschild solution of standard general relativity via the Vainshtein mechanism. The massive gravity theory seemed to face insurmountable problems after the publication of the paper [6], where it was claimed that no acceptable tensor gravitational theory with arbitrarily long but finite range could exist. The main points to support this result are the facts that in the massive version of the full Einstein theory, there are necessarily six rather than the five tensor degrees of freedom, the energy has no lower bound, the infinite-range limit does not exist at all, and lowest-order forces are the same as in the massive linearized theory, respectively. The Boulware–Deser (BD) ghost instability raised serious questions about the viability of any massive gravity theory.

However, de Rham, Gabadadze and Tolley (dRGT) [7, 8] succeeded in 2010 to construct the first (and probably unique) nonlinear fulfillment of the Fierz–Pauli theory that is free of the Boulware–Deser ghost instability. To achieve this goal the Lagrangian of gravity was covariantly amended by mass and polynomial interaction terms with arbitrary coefficients. The consistency of the theory was investigated in the decoupling limit, up to the fifth order in the nonlinearities. The ghost-like pathologies in these interactions cancel for special choices of the polynomial interactions, and it was suggested that this result remains true to all orders in the decoupling limit. It was also pointed out that the mixing between the helicity-0 and 2 modes can be at most quartic in the decoupling limit. The problem of the ghosts in the non-linear massive gravity was analyzed within the ADM formalism in [9,10,11], and it was shown that, in the entire two-parameter family of actions, the Hamiltonian constraint is maintained at the complete non-linear level. This result implies the absence of the pathological Boulware–Deser ghost to all orders. In [12] it was shown that there can be no new Lorentz invariant kinetic interactions free from the Boulware-Deser ghost in four dimensions in the metric formulation of gravity, beyond the standard Einstein–Hilbert, up to total derivatives. By performing a general perturbative analysis in four dimensions, it follows that the only term with two derivatives that does not introduce a ghost is the Einstein–Hilbert term. Moreover, this result extends to all orders in perturbations. For reviews on the theoretical aspects of massive gravity see [13, 14], and [15], respectively.

The establishment of a firm theoretical foundation of the massive gravity theory has opened the possibility of the investigation of its cosmological and astrophysical applications. The effect of helicity-0 mode which remains elusive after analysis of cosmological perturbation around an open Friedmann–Lemaitre–Robertson–Walker universe was investigated in [16] . The non-linear form of the effective energy-momentum tensor stemming from the mass term was also derived for the spherically symmetric case. By solving the spherically symmetric gravitational equations of motion in vacuum to the linear order, a solution which has an arbitrary time-dependent parameter was obtained. In general relativity, this parameter corresponds to the mass of a star. Hence Birkhoff’s theorem may no longer hold in the non-linear massive gravity, and the energy can probably be emitted superluminously (with infinite speed) on the self-accelerating background by the helicity-0 mode.

Homogeneous and isotropic cosmological solutions have been presented in [17], which suffer from either Higuchi ghost or a non-linear ghost instability. By relaxing the symmetry of the background by e.g. breaking isotropy in the hidden sector, it is possible to accommodate a stable cosmological solution. Alternatively, extending the theory to allow for new dynamical degrees of freedom can also remove the conditions that lead to the instability. The stability of the linear perturbations in the bimetric theory was examined in [18]. Instabilities were presented for several classes of models, and simple criteria for the cosmological stability of massive bigravity were derived. A particular self-accelerating bigravity model, infinite-branch bigravity, which exhibits both viable background evolution and stable linear perturbations was also found. In [19] it was shown that by taking the Planck mass for the second metric to be small, the instabilities of the bimetric theory describing gravitational interactions in the presence of an extra spin-2 field can be moved back to unobservably early times, when the theory approaches general relativity with an effective cosmological constant determined by the spin-2 interaction scale. The late-time expansion history of the theory becomes extremely close to the standard \(\Lambda \)CDM model, with a natural value for the cosmological constant. In order for the cosmological perturbations to be stable by Big-Bang nucleosynthesis the Planck mass for the second metric \(M_f\) must be smaller than the electroweak scale.

The scalar gravitational radiation from a binary pulsar system in the simplest model that exhibits the Vainshtein mechanism was computed in [20]. The gravitational radiation is less suppressed relative to its general relativity predictions than static fifth forces effects within the pulsar system. Spherically symmetric solutions of the field equations in the dRGT massive gravity model have also been extensively investigated. In [21] it was shown that the Schwarzschild–de Sitter and Reissner–Nordström–de Sitter black hole metrics appear as exact solutions in the dRGT model, where the mass term sets the curvature scale. They occur within a two-parameter family of dGRT mass terms. In the limit of vanishing graviton mass they go smoothly to the Schwarzschild and Reissner–Nordström metrics. Static charged black hole solutions in nonlinear massive gravity were found in [22], in the parameter space of two gravitational potential parameters \((\alpha ,\beta )\). In the simplest case with \(\alpha =\beta =0\), the solution exhibits the vDVZ discontinuity but ordinary General Relativity is recovered deep inside the horizon due to the existence of electric charge. Spherically symmetric solutions in the bigravity formulation of massive gravity were obtained in [23]. The solutions admit both a Lorentz invariant and a Lorentz breaking asymptotically flat behaviour and also fall in two branches. In the first branch, all solutions can be found analytically, and are Schwarzschild-like. In the second branch, Yukawa-like modifications of the static potential were found. Spherically-symmetric solutions in massive gravity generated by matter sources with polytropic equation of state were studied in [24], in the non-perturbative regime where the mass term non-linearities are important. A detailed study of the spherically symmetric solutions in Lorentz breaking massive gravity was presented in [25]. The stability of the gravitational field by the analysis of the Komar integral was also discussed. Static spherically symmetric black hole solutions of dRGT massive gravity theory in the presence of cosmological constant were obtained in [26]. The unitary and non-unitary gauges are used to find the solutions in three, four and five dimensions. Two general classes of solutions were found, and in the first one the effect of massive potential appears as the effective cosmological constant. The quasi-stationary profile of massive charged scalar field in a class of charged black hole in dRGT massive gravity was investigated in [27]. For asymptotically dRGT anti de Sitter (AdS) black holes, unstable modes have been found, with their frequency satisfying the condition of superradiance. The properties of the black holes in massive gravity theory have been investigated in [28,29,30,31,32,33,34].

Relativistic stars in the simplest model of the de Rham–Gabadadze–Tolley massive gravity, which describes the massive graviton without ghost propagating mode were studied in [35]. The modified Tolman–Oppenheimer–Volkoff equation and the constraint equation coming from the potential terms in the gravitational action were derived, and analytical and numerical results for quark and neutron stars were obtained. The deviations were compared with the corresponding results in standard General Relativity and f(R) gravity theory, respectively. The dRGT gravity theory leads to small deviations from the General Relativity in terms of density profiles and mass-radius relation. The structure of neutron stars in the context of massive gravity was studied in [36]. The modifications of hydrostatic equilibrium equation in the presence of massive gravity have been explored in four and higher dimensions. The consideration of the effects of the Massive Gravity gives specific contributions into the structure of neutron stars. A relation between the mass and radius of neutron stars versus the Planck mass was also obtained.

The study of the stability of compact objects in the general relativistic framework is of central importance for understanding the behavior of astrophysical systems such as black holes or neutron stars. A simple but very powerful stability criterion was obtained by Buchdahl [37, 38], and it gives the condition for the stability of a compact object with mass M and radius R as,

$$\begin{aligned} \frac{2GM}{c^2R}\le \frac{8}{9}. \end{aligned}$$
(1)

The condition given in Eq. (1) is a stability condition in static spherical symmetry against the collapse of massive objects in General Relativity. If the condition is not satisfied, the gravitating object collapses, thus leading to the formation of a black hole. The equality sign (also called the Buchdahl limit) corresponds to the case of constant density stars, and gives the maximum mass-radius ratio for stable massive compact objects. The Buchdahl upper bound was generalized in [39] to take into account the effect of the cosmological constant \(\Lambda \). Sharp bounds on the mass-radius ratio were obtained in [40,41,42]. For example, in [42] it was shown that if the energy condition \(p+2p_{\perp } \le \rho \) is satisfied, where \(p\ge 0\) is the radial pressure, and \(p_{\perp }\) is the tangential pressure, then the condition,

$$\begin{aligned} \frac{GM}{c^2R}\le \frac{2}{9}-\frac{\Lambda R^2}{3}+\frac{2}{9} \sqrt{1+3\Lambda R^2 }, \end{aligned}$$
(2)

must hold. Buchdahl type upper limits for the mass radius ratio have been obtained for charged particles [43,44,45], and for anisotropic stars [46]. In [45] it was shown that for an object with charge q, if the condition \(0\le q^2/r^2+\Lambda r^2\le 1\) is satisfied, then the inequality,

$$\begin{aligned} \frac{Gm}{c^2r}\le \frac{2}{9}+\frac{q^2}{3r^2}\frac{\Lambda r^2}{3}+\frac{2}{9}\sqrt{1+\frac{3q^2}{r^2}+3\Lambda r^2}, \end{aligned}$$
(3)

must hold. Mass-radius ratio bounds were derived for arbitrary dimensional spheres in [47], and for Gauss-Bonnet gravity in [48].

A lower bound of the mass-radius ratio in the presence of a cosmological constant, as well as a cosmological constant related minimum density was found in [49], and further explored in [50, 51]. These lower bounds can be formulated as,

$$\begin{aligned} \frac{2GM}{c^{2}R}\ge \frac{1}{6}\Lambda R^2, \rho =\frac{3M}{4\pi R^3}\ge \rho _{\Lambda }\equiv \frac{\Lambda c^2}{16 \pi G}. \end{aligned}$$
(4)

In the case of a charged particle with total charge Q the lower bound for the mass-radius ratio is given by [51],

$$\begin{aligned} M\ge \frac{3}{4} \frac{Q^2}{Rc^2}+\frac{\Lambda R^3c^2}{12G}. \end{aligned}$$
(5)

By using the minimum mass-cosmological constant relation, as well as dimensional analysis [52], one can obtain a representation of the cosmological constant in terms of the fundamental physical constants as [50, 53, 54],

$$\begin{aligned} \Lambda \approx \frac{\hbar ^2G^2m_e^6c^6}{e^{12}}, \end{aligned}$$
(6)

where \(m_e\) is the electron mass. For a review of the relation between fundamental physics and the cosmological constant see [55].

The mass-radius relations, as well as the possible existence of a minimum mass have been in different theoretical contexts, and for different physical models, in [56,57,58,59,60,61]. The generalized Buchdahl inequalities in arbitrary space-time dimensions in the presence of a non-zero cosmological constant were obtained in [56], by considering both the de Sitter and anti-de Sitter cases. The dependence on the number of space-time dimensions of the minimum and maximum masses for stable spherical objects was explicitly obtained. Bounds for the minimum and maximum mass/radius ratio of a stable, charged, spherically symmetric compact object in a D-dimensional space-times were obtained, in the presence of dark energy, in [57]. By combining the lower mass bound, in four space-time dimensions, with minimum length uncertainty relations (MLUR) motivated by quantum gravity, an alternative bound for the maximum charge/mass ratio of a stable, gravitating, charged quantum mechanical object, expressed in terms of fundamental constants, was obtained. This limit leads to the correct order of magnitude value for the charge/mass ratio of the electron, as required by the stability conditions. The physical interpretation of the mass scale \(\left( \hbar ^2\sqrt{\Lambda }/G\right) ^{1/3} \) was discussed in [58]. Based on the Generalized Uncertainty Relation, it was shown that a black hole with age comparable to the age of the Universe would stop radiating when the mass reaches a new mass scale \( M^{\prime }_T=c\left( \hbar /G^2\sqrt{\Lambda }\right) ^{1/3}\). Upper and lower bounds on the mass-radius ratio of stable compact objects in extended gravity theories, in which modifications of the gravitational dynamics are described by an effective contribution to the matter energy-momentum tensor, were obtained in [59]. The possibility of a variable coupling between the matter sector and the gravitational field was considered, and the obtained results are valid for a large class of generalized gravity models. As an applications of the obtained formalism compact bosonic objects, described by scalar-tensor gravitational theories with self-interacting scalar field potentials, and charged compact objects, respectively, were considered. By assuming a static, spherically symmetric geometry, the strong gravity equilibrium properties of compact hadronic objects were investigated in [60]. The generalized Buchdahl inequalities for a strong gravity ‘particles’ were derived, and the upper and lower bounds of the mass/radius ratio of stable, compact, strongly interacting objects were obtained. The existence of the lower mass bound is induced by the presence of the effective cosmological constant, which produces a mass gap, while the upper bound corresponds to a deconfinement phase transition. Upper and lower limits for the mass-radius ratio of spin-fluid spheres in Einstein–Cartan theory in the presence of a cosmological constant were considered in [61], under the assumption that matter satisfies a linear barotropic equation of state. In the case of the spin-generalized strong gravity model for baryons/mesons, show the existence of quantum spin imposes a lower mass bound for spinning particles, which almost exactly reproduces the electron mass. The mass-radius relations for neutron stars in f(R) and other modified theories of gravity were investigated in [62,63,64,65].

Massive gravity theories are formulated with the help of a fixed fiducial metric \(f_{\mu \nu }\), and the general properties of the theory depend very much on the choice of the metric \(f_{\mu \nu }\). Therefore, each f-metric gives rise to a different massive gravity theory. It is the goal of this work to consider the mass-radius ratio bounds in the framework of the dRGT massive gravity theory with Lorentz-violating fiducial metric. This represents a generalization of the previous works on the mass-radius upper and lower bounds to this interesting approach to the gravitational force. After writing down the gravitational field equations of dRGT massive gravity, we specialize our analysis to the case of the spherically symmetric static gravitational field. For this particular geometry the hydrostatic equilibrium equations are obtained, which represent the generalizations of the standard Tolman–Oppenheimer–Volkoff equation of general relativity, and of the mass continuity equation, respectively. We investigate through numerical analysis the solutions of these equations for the simple but theoretically important case of the constant density stars. The upper and lower bounds for the mass-radius ratios are obtained, and discussed systematically for the three possible cases determined by the sign and numerical value of the parameter \(\gamma \) of the model, which is proportional to the mass square of the graviton. As possible physical applications of our results we discuss the corrections to the minimum mass of particles due to the non-zero graviton mass, as well as the modifications of the surface redshift of the compact gravitational objects.

The present paper is organized as follows. The field equations of the dRGT massive gravity model are introduced in Sect. 2, where the hydrostatic equilibrium equations of compact objects in static spherical symmetry are derived. The case of the constant density stars is also investigated. The mass-radius bounds for dense stars are derived in Sect.  3 for arbitrary values of the model parameter \(\gamma \). We discuss and conclude our results in Sect. 4. The rescaling of the metric function is explained in “Appendix”.

2 Field equations, geometry, hydrostatic equilibrium, and constant density stars in dRGT massive gravity

2.1 The field equations of dRGT massive gravity with the Lorentz-violating fiducial metric

We start with the well-known Einstein-Hilbert gravitational action plus consistent nonlinear interaction terms interpreted as a graviton mass which is given by [8],

$$\begin{aligned} S = \int d^4x \sqrt{-\mathrm {g}}\frac{1}{2\kappa } \bigg [ R+ 2\kappa {\mathcal {L}}_{m} + m^2_{\mathrm {g}}\ {\mathcal {U}}(\mathrm {g},\phi ^a)\bigg ] , \end{aligned}$$
(7)

where \(\kappa = 8\pi G/c^4\), R is the scalar curvature, \({\mathcal {L}}_{m}\) is the matter Lagrangian, and \({\mathcal {U}}\) is a graviton potential with the parameter \(m_{\mathrm {g}}\) interpreted as graviton mass. The nonlinear interaction potential, which is constructed to the fourth order in the four-dimensional spacetime, is given by,

$$\begin{aligned} {\mathcal {U}}(\mathrm {g},\phi ^a) = {\mathcal {U}}_{2} + \alpha _{3}{\mathcal {U}}_{3} + \alpha _{4}{\mathcal {U}}_{4}, \end{aligned}$$
(8)

where the coefficients \(\alpha _{3}\) and \(\alpha _{4}\) are dimensionless free parameters. The potentials on the second, the third, and the fourth terms are defined as,

$$\begin{aligned} {\mathcal {U}}_{2}\equiv & {} [{\mathcal {K}}]^2 - [{\mathcal {K}}^2], \end{aligned}$$
(9)
$$\begin{aligned} {\mathcal {U}}_{3}\equiv & {} [{\mathcal {K}}]^3 - 3[{\mathcal {K}}][{\mathcal {K}}^2] + 2[{\mathcal {K}}^3], \end{aligned}$$
(10)
$$\begin{aligned} {\mathcal {U}}_{4}\equiv & {} [{\mathcal {K}}]^4 - 6[{\mathcal {K}}]^2[{\mathcal {K}}^2] + 8[{\mathcal {K}}][{\mathcal {K}}^3] + 3[{\mathcal {K}}^2]^2 - 6[{\mathcal {K}}^4],\nonumber \\ \end{aligned}$$
(11)

respectively. The building block tensor is defined as,

$$\begin{aligned} {\mathcal {K}}^\mu _\nu = \delta ^\mu _\nu - \sqrt{\mathrm {g}^{\mu \sigma }f_{ab} \partial _\sigma \phi ^a \partial _\nu \phi ^b}, \end{aligned}$$
(12)

where,

$$\begin{aligned}{}[{\mathcal {K}}] = {\mathcal {K}}^\mu _\mu , [{\mathcal {K}}^n] = ({\mathcal {K}} ^n)^\mu _\mu . \end{aligned}$$
(13)

This choice of interaction eliminates the BD ghost order by order. We follow the previous works by choosing a simple form of the fiducial metric to be the Lorentz-violating  [66, 67],

$$\begin{aligned} f_{\mu \nu } = \mathrm {diag}(0, 0, \lambda ^2, \lambda ^2\sin ^2\theta ), \end{aligned}$$
(14)

where \(\lambda \) is a constant, and we choose the unitary gauge \(\phi ^a = x^\mu \delta ^a_\mu \) for the Stückelberg scalars. In fact, the analysis of [8] was initially performed for a flat Minkowski f-metric, and the expression of the potential as introduced in [8], is valid for such an f metric. On the other hand in [10] it was shown that the dRGT theory with a generic f-metric is also ghost free, and this result is valid for the case of the singular metric (14). It should be emphasized that this choice of fiducial metric is Lorentz-violating and the resulting massive gravity model is the Lorentz-violating variation of the dRGT model. The “1-K” formulation [68] is more convenient to obtain nonlinear solutions, and it leads more easily to the field equations, as well as to the parameters of the final solution.

In order to simplify the form of the metric, we will reparametrize the parameters \(\alpha _3\) and \(\alpha _4\) to two parameters \(\alpha \) and \(\beta \), defined by,

$$\begin{aligned} \alpha _3 = \frac{\alpha -1}{3}, \quad \alpha _4 = \frac{\beta }{4} + \frac{ 1-\alpha }{12}. \end{aligned}$$
(15)

After varying the total action \(S=S_g+S_m\), where \(S_m\) is the matter action, the modified Einstein field equations in the presence of the graviton potential are

$$\begin{aligned} G_{\mu \nu }-\kappa T_{\mu \nu }+m^2_{\mathrm {g}}X_{\mu \nu }=0, \end{aligned}$$
(16)

where \(T_{\mu \nu }\) is the energy-momentum tensor of the matter.

The effective energy-momentum tensor of massive graviton, obtained by varying the graviton potential term in the action, takes the following form  [66, 67],

$$\begin{aligned} X_{\mu \nu }= & {} {\mathcal {K}}_{\mu \nu } - {\mathcal {K}}\mathrm {g}_{\mu \nu } \nonumber \\&-\alpha \ \Bigg \{{\mathcal {K}}^2_{\mu \nu } - {\mathcal {K}}{\mathcal {K}}_{\mu \nu } + \frac{[{\mathcal {K}}]^2 - [{\mathcal {K}}^2]}{2}\mathrm {g}_{\mu \nu }\Bigg \} \nonumber \\&+3\beta \ \Bigg \{{\mathcal {K}}^3_{\mu \nu } - {\mathcal {K}}{\mathcal {K}}^2_{\mu \nu } + \frac{1}{2}{\mathcal {K}}_{\mu \nu }\ \Big \{[{\mathcal {K}}]^2 - [\mathcal {K }^2]\Big \} \nonumber \\&-\frac{1}{6}\mathrm {g}_{\mu \nu }\ \Big \{[{\mathcal {K}}]^3 - 3[\mathcal { K}][{\mathcal {K}}^2] + 2[{\mathcal {K}}^3]\Big \}\Bigg \}. \end{aligned}$$
(17)

We will assume that the constraint from Bianchi identities gives separately the covariant derivatives of \(T_{\mu \nu }\) and \(X_{\mu \nu }\) equal to zero, according to the equations,

$$\begin{aligned} \nabla ^\mu X_{\mu \nu } = 0,\quad \nabla ^\mu T_{\mu \nu } = 0. \end{aligned}$$
(18)

2.2 The spherically symmetric case

In four space-time dimensions, we consider a static and spherically symmetric metric of the following form,

$$\begin{aligned} ds^2 = -n(r)d(ct)^2 + \frac{dr^2}{f(r)} + r^2d\Omega ^2, \end{aligned}$$
(19)

where \(d\Omega ^2 = d\theta ^2+\sin ^2\theta d\phi ^2\).

We will assume that the energy-momentum tensor of the matter is given by,

$$\begin{aligned} T^{\mu }_{\nu } = (\rho c^2+P)u^{\mu }u_{\nu } + P\mathrm {\delta ^{\mu }_{\nu },} \end{aligned}$$
(20)

i.e., by a perfect fluid, characterized by only two thermodynamic parameters, the matter density \(\rho \), and the thermodynamic pressure P, respectively, as well as by its four-velocity \(u^{\mu }\), satisfying the normalization condition \(u^{\mu }u_{\mu }=-1\). In the following we adopt the comoving reference frame, in which the components of the four velocity are given by \(u^{\mu }=\left( -n(r)^{-1/2},0,0,0\right) \).

For the metric given by Eq. (19), the components of Einstein tensor become

$$\begin{aligned} G^t_t= & {} \frac{f^{\prime }}{r}+\frac{f}{r^2}-\frac{1}{r^2}, \end{aligned}$$
(21)
$$\begin{aligned} G^r_r= & {} \frac{f(rn^{\prime }+n)}{nr^2}-\frac{1}{r^2}, \end{aligned}$$
(22)
$$\begin{aligned} G^\theta _\theta= & {} G^\phi _\phi \nonumber \\= & {} f^{\prime }\left( \frac{n^{\prime }}{4n}+\frac{1}{2r}\right) + f\left( \frac{ n^{\prime \prime }}{2n} + \frac{n^{\prime }}{2nr}-\frac{n^{\prime 2}}{4n^2} \right) , \end{aligned}$$
(23)

where a prime denotes the derivative with respect to r. The components of the effective energy-momentum tensor of the massive graviton are given by,

$$\begin{aligned} X^t_t= & {} -\bigg [\frac{\alpha (3r-\lambda )(r-\lambda )}{r^2}+\frac{ 3\beta (r-\lambda )^2}{r^2}+\frac{3r - 2\lambda }{r}\bigg ], \end{aligned}$$
(24)
$$\begin{aligned} X^r_r= & {} -\bigg [\frac{\alpha (3r-\lambda )(r-\lambda )}{r^2}+\frac{ 3\beta (r-\lambda )^2}{r^2}+\frac{3r - 2\lambda }{r}\bigg ], \end{aligned}$$
(25)
$$\begin{aligned} X^\theta _\theta= & {} X^\phi _\phi = \frac{\alpha (2\lambda -3r)}{r}+\frac{ 3\beta (\lambda -r)}{r}+\frac{\lambda -3r}{r}. \end{aligned}$$
(26)

Substitute all components in Eq. (16), the modified Einstein field equations become

$$\begin{aligned} \frac{f^{\prime }}{r}+\frac{f}{r^2}-\frac{1}{r^2}= & {} m^2_{\mathrm {g}}\bigg [ \frac{\alpha (3r-\lambda )(r-\lambda )}{r^2}+\frac{3\beta (r-\lambda )^2}{r^2} \nonumber \\&+\frac{3r - 2\lambda }{r}\bigg ] - \frac{8\pi G}{c^2}\rho , \end{aligned}$$
(27)
$$\begin{aligned} \frac{f(rn^{\prime }+n)}{nr^2}-\frac{1}{r^2}= & {} m^2_{\mathrm {g}}\bigg [\frac{ \alpha (3r-\lambda )(r-\lambda )}{r^2}+\frac{3\beta (r-\lambda )^2}{r^2} \nonumber \\&+\frac{3r - 2\lambda }{r}\bigg ] + \frac{8\pi G}{c^4}P, \end{aligned}$$
(28)
$$\begin{aligned}&f^{\prime }\Big (\frac{n^{\prime }}{4n}+\frac{1}{2r}\Big ) + f\Big [\frac{ n^{\prime \prime }}{2n} + \frac{n^{\prime }}{2nr}-\frac{n^{\prime 2}}{4n^2} \Big ] \nonumber \\&\quad = -m^2_{\mathrm {g}}\bigg [\frac{\alpha (2\lambda -3r)}{r}+\frac{3\beta (\lambda -r)}{r } \nonumber \\&\qquad +\frac{\lambda -3r}{r}\bigg ] + \frac{8\pi G}{c^4}P. \end{aligned}$$
(29)

2.3 The hydrostatic equilibrium equations

The functional form of f is obtained from Eq. (27), and can be expressed as,

$$\begin{aligned} f(r) = 1 - \frac{2G}{c^2}\frac{M(r)}{r} - \frac{\Lambda }{3}r^2 + \gamma r + \xi , \end{aligned}$$
(30)

where,

$$\begin{aligned} \Lambda= & {} -3m^2_{\mathrm {g}}(1+\alpha +\beta ), \end{aligned}$$
(31)
$$\begin{aligned} \gamma= & {} -\lambda m^2_{\mathrm {g}}(1+2\alpha +3\beta ), \end{aligned}$$
(32)
$$\begin{aligned} \xi= & {} \lambda ^2 m^2_{\mathrm {g}}(\alpha +3\beta ), \end{aligned}$$
(33)

and,

$$\begin{aligned} M(r) = 4\pi \int \limits _{0}^{r} \rho (r^{\prime })r^{\prime 2}dr^{\prime }, \end{aligned}$$
(34)

respectively, with M(r) representing the total mass inside the radius r of a spherically symmetric object. The graviton mass \(m_{\mathrm {g}}\) is included in the cosmological constant term, namely \(\Lambda \), and the extra terms, \(\gamma \) and \(\xi \), respectively. The coordinate r can be rescaled without any loss of generality by setting \(\xi =0\) (for details see “Appendix”). Hence, the expression of f can be written as,

$$\begin{aligned} f(r) = 1 - \frac{2G}{c^2}\frac{M(r)}{r} - \frac{\Lambda }{3}r^2 + \gamma r. \end{aligned}$$
(35)

From the continuity equation,\(\nabla ^\mu T_{\mu \nu } = 0\), it follows that,

$$\begin{aligned} \frac{n^{\prime }}{n} = -\frac{2P^{\prime }}{\rho c^2+P}. \end{aligned}$$
(36)

By substituting Eqs. (35) and (36) in Eq. (28), the TOV equation in the presence of a massive graviton in the dRGT massive gravity theory can be obtained as,

$$\begin{aligned} \frac{dP}{dr} = -\frac{(\rho c^2+P)\Big [\Big (\frac{8\pi G}{c^4}P-\frac{2}{3} \Lambda \Big )r^3 + \gamma r^2 +\frac{2G}{c^2}M(r)\Big ]}{2r^2\Big [1 - \frac{2G }{c^2}\frac{M}{r} - \frac{\Lambda }{3}r^2 + \gamma r\Big ]}. \end{aligned}$$
(37)

In order to obtain the structure of stars the hydrostatic equilibrium equation (37) must be integrated together with the mass continuity equation,

$$\begin{aligned} \frac{dM(r)}{dr}=4\pi \rho r^2, \end{aligned}$$
(38)

after the equation of state of the matter, \(P=P(\rho )\), was specified. The boundary conditions that must be imposed at the center and on the surface of the star are \(\rho (0)=\rho _c\), and \(P(R)=0\), where \(\rho _c\) is the central density, and R is the radius of the compact object.

The hydrostatic equilibrium and the mass continuity equations can be written in a dimensionless form with the help of the set of the dimensionless quantities \(\left( \eta , \theta , \Pi \right) \), defined as,

$$\begin{aligned} r=a\eta , M=M^{*}\mu ,\rho =\rho _c\theta , P=\rho _cc^2\Pi , \end{aligned}$$
(39)

where,

$$\begin{aligned} a=\frac{c}{\sqrt{4\pi G\rho _c}}, M^{*}=4\pi \rho _ca^3=\frac{c^3}{\sqrt{ 4\pi G^3\rho _c}}. \end{aligned}$$
(40)

In the new variables the mass continuity and the hydrostatic equilibrium equations take the form,

$$\begin{aligned} \frac{d\mu }{d\eta }= & {} \theta \eta ^2, \end{aligned}$$
(41)
$$\begin{aligned} \frac{d\Pi }{d\eta }= & {} -\frac{\left( \theta +\Pi \right) \left[ \left( \Pi -\psi \right) \eta ^3+\frac{\sigma \eta ^2}{2}+\mu \right] }{\eta ^2\left( 1-\frac{2\mu }{\eta }-\psi \eta ^2+\sigma \eta \right) }, \end{aligned}$$
(42)

where we have denoted,

$$\begin{aligned} \psi =\frac{\Lambda }{3}a^2=\frac{\Lambda c^2}{12\pi G\rho _c}, \sigma =\gamma a=\frac{\gamma c}{\sqrt{4\pi G\rho _c}}. \end{aligned}$$
(43)

In order to close the system of Eqs. (41) and (42) one must specify the equation of state of the matter \(\Pi =\Pi (\theta )\). The boundary conditions for the integration of the system are \(\theta (0)=1\) and \(\Pi \left( \eta _S\right) =0\), where \(\eta _S\) defines the vacuum boundary of the compact object.

2.4 Constant density stars in Lorentz-violating dRGT massive gravity

Constant density stars can give in some astrophysical circumstances an acceptable physical description of realistic astrophysical objects. Moreover, they are important from theoretical point of view since they allow some insights into the general properties of the relativistic compact objects. In the following we will investigate the properties of the constant density stars in dRGT massive gravity.

The requirement of the constant density \(\rho =\rho _c=\mathrm {constant}, \forall r\in [0,R]\) fixes the dimensionless density \(\theta \) as \(\theta =1\) inside the star. Then Eq. (41) can be immediately integrated to give the dimensionless mass density distribution as,

$$\begin{aligned} \mu (\eta )=\frac{\eta ^3}{3}. \end{aligned}$$
(44)

Substituting this expression of the mass into the hydrostatic equilibrium equation (42) it follows that the pressure \(\Pi \) obeys the first order differential equation given by,

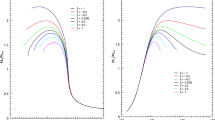
$$\begin{aligned} \frac{d\Pi }{d\eta }=-\frac{\eta \left( 1+\Pi \right) \left( \Pi -\psi +\frac{1}{3} +\frac{\sigma }{2\eta }\right) }{1-\left( \frac{2}{3}+\psi \right) \eta ^2+\sigma \eta }. \end{aligned}$$
(45)

Equation (45) must be integrated with the boundary conditions \(\Pi (0)=\Pi _c\), and \(\Pi \left( \eta _S\right) =0\). The variations of the dimensionless pressure profile inside the constant density star in massive gravity theory are presented for positive and negative numerical values of \(\sigma \) in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Variation of the dimensionless pressure \(\Pi \) as a function of the dimensionless radial coordinate \(\eta \) for a constant density star in dRGT massive gravity theory for \(\psi =0.06\), and different values of \( \sigma \): \(\sigma =0.25\) (dotted curve), \(\sigma =0.50 \) (dashed-dotted curve), \(\sigma =0.75\) (short dashed curve), \( \sigma =1\) (dashed curve), and \(\sigma =1.25\) (long dashed curve). For the sake of comparison we have also presented the standard general relativistic case, corresponding to \(\psi =\sigma =0\) (solid curve). The boundary condition used to integrate the TOV equation are \(\Pi (0)=1\), and \(\Pi \left( \eta _s\right) =0\), respectively

Full size image
Fig. 2
figure 2

Variation of the dimensionless pressure \(\Pi \) as a function of the dimensionless radial coordinate \(\eta \) for a constant density star in dRGT massive gravity theory for \(\psi =0.06\), and different values of \( \sigma \): \(\sigma =-0.05\) (dotted curve), \(\sigma =-0.25\) (dashed-dotted curve), \(\sigma =-0.50\) (short dashed curve), \(\sigma =-0.75\) (dashed curve), \(\sigma =-1\) (long dashed curve), and \(\sigma =-1.25\) (long dashed-double dotted curve). The standard general relativistic case also corresponds to \(\psi = \sigma =0\) (solid curve)

Full size image

As one can see from Fig. 1, the vanishing of the pressure at the vacuum boundary of the star is dependent on the adopted values of the positive dimensionless parameter \(\sigma \). In the general relativistic case, corresponding to \(\psi =\sigma =0\), the (dimensionless) radius of the star is given by \(\eta _S=1.06\), while \(\eta _S=1.10, 1.12, 1.11, 1.09,\) and 1.06 for \(\sigma =0.25, 0.50, 0.75, 1.00,\) and 1.25, respectively. This implies an increase at first, and then a decrease in the radius of the star with increasing \(\sigma \) and for the fixed value \(\psi =0.06\).

On the other hand, Fig. 2 shows the pressure profile inside the sphere for negative \(\sigma \). A remarkable feature is the increase of pressure near the central region of the sphere. It can be shown that this is generic for any negative value of \(\sigma \). For sufficiently small \(\eta \), the term \(-\sigma /2\eta \) in Eq. (45) becomes dominant and,

$$\begin{aligned} \frac{d\Pi }{d\eta }\simeq -\left( 1+\Pi \right) \left( \frac{\sigma }{2}\right) . \end{aligned}$$
(46)

Consequently, for sufficiently small \(\eta \) and negative (positive) \(\sigma \) , \(\Pi (\eta )\) is always an increasing (decreasing) function.

At first sight, the increase of the pressure with radius for small \(\eta \) seems to imply the existence of an instability of this spherical configuration around the center. The reason is we normally need pressure force (\(\propto -\vec {\nabla } P\)) to exert outward to balance inward gravitational attractive force. However, for sufficiently small \(\eta \), the force of gravity in the massive gravity model with negative \(\sigma ~(\text {or} ~\gamma )\) actually is always repulsive, i.e. antigravity. We can prove this statement by the following. Generically, the gravity force (per mass) from the massive gravity metric is given by,

$$\begin{aligned} -f^{\prime }(r)=\frac{8\pi G r}{c^{2}}(\rho (r)-\frac{{\bar{\rho }}(r)}{3})+\frac{2\Lambda r}{3}-\gamma . \end{aligned}$$
(47)

For sufficiently small r, the dominant term is the constant force from massive gravity contribution \(\gamma \). If \(\gamma <0\), this force is repulsive, i.e. exerting outwardly from the center of the sphere. Note also that for sufficiently large r, another repulsive “cosmological constant” term becomes dominant.

From Eq. (47) when \(\gamma <0\), the critical radius \(r_{c}\) where gravity changes from repulsive in \(r<r_{c}\) region to attractive in \(r>r_{c}\) region is given by \(f^{\prime }(r_{c})=0\) (for constant density profile, there is no \(r_{c}\), gravity is always repulsive throughout the object). On the other hand, Eq. (37) tells us that the pressure is an increasing function of radius until,

$$\begin{aligned} \frac{8\pi G}{c^{4}}Pr= & {} \frac{2\Lambda r}{3}-\gamma -\frac{2GM}{c^{2} r^{2}}, \nonumber \\= & {} -\frac{8\pi G}{c^{2}}\rho r-f^{\prime }(r), \end{aligned}$$
(48)

then it will start to decrease with respect to r. Therefore, the region of increasing pressure will always be accompanied by antigravity with positive \(-f'(r)\) force until \(-f'(r)=8\pi G(P+\rho c^{2}) r/c^{4}\) where the pressure starts to decrease with r while gravity is still repulsive. Beyond this radius, the pressure force becomes repulsive while gravity is still repulsive thus we have instability of the spherical shell. Interestingly, the static sphere in the negative \(\gamma \) scenario is stable with repulsive gravity balancing inward pressure gradient force! The radius of the stable compact object in this case is then given by Eq. (48). Having high pressure boundary and vacuum outside requires high surface tension for such object to be truly stable under dissipation.

Another interesting possibility of static configuration in negative \(\gamma \) scenario is the halo or spherical shell. This can only occur when \(\rho \) is not constant as we can see from Eq. (47). For \(r>r_{c}\) in generic profile, Eq. (37) guarantees that the pressure gradient force is outward balancing the attractive gravity. A static halo with inner radius larger than \(r_{c}\) is thus stable.

In physical units the radius of the constant density compact objects in dRGT massive gravity Theory (for \(\sigma \ge 0\)) is given by,

$$\begin{aligned} R=10.362\times \left( \frac{\rho _c}{10^{15}\;\mathrm {g/cm^3 }} \right) ^{-1/2}\times \eta _S\;\mathrm {km}. \end{aligned}$$
(49)

Hence the mass effects associated to the possible existence of the graviton may change the mass of a neutron star with a central density of the order of \(\rho _c=10^{15}\;\mathrm {g/cm^3}\) from \(R\approx 11.0\) km, a value corresponding to the standard general relativistic case, to \(R\approx 11.6\) km, for \(\psi =0.06\) and \(\sigma =0.50\).

The interior mass profiles of these models are presented in Fig. 3.

Fig. 3
figure 3

Variation of the dimensionless mass \(\mu \) as a function of the dimensionless radial coordinate \(\eta \) for a constant density star in dRGT massive gravity theory

Full size image

For constant density stars all the interior mass profiles follow the same law, \(\mu =\eta ^3/3\). The physical maximum mass \(M_S\) of the constant density star can be obtained as,

$$\begin{aligned} M_S=M^*\mu \left( \eta _S\right) =2.33\times \left( \frac{\rho _c}{10^{15}\; \mathrm {g/cm^3 }}\right) ^{-1/2}\times \eta _S^3\;M_{\odot }. \end{aligned}$$
(50)

Hence the mass of a constant density star can vary from \(M_S=2.78M_{\odot }\) for \(\psi =\sigma =0\), corresponding to the general relativistic case, to \( M_S=3.27M_{\odot }\), corresponding to \(\psi =0.06\) and \(\sigma =0.50\).

3 The Buchdahl limits in the Lorentz-violating dRGT massive gravity

We introduce now the generalized Buchdahl variables (\(x, \omega , \zeta , y\)), defined as follows,

$$\begin{aligned} x= & {} r^2,\quad \omega (r)=\frac{G}{c^2}\frac{M(r)}{r^3},\quad \zeta =n^{1/2}, \end{aligned}$$
(51)
$$\begin{aligned} y^2= & {} f(r)=1-2\omega (r)r^2-\frac{\Lambda }{3}r^2+\gamma r. \end{aligned}$$
(52)

Then Eqs. (36) and (37) can be rewritten as,

$$\begin{aligned} \frac{1}{\zeta }\frac{d\zeta }{dx}=-\frac{1}{\rho c^2+P}\frac{dP}{dx} \leftrightarrow \frac{d}{dx}(\zeta P)=-\rho c^2\frac{d\zeta }{dx}, \end{aligned}$$
(53)

and,

$$\begin{aligned} \frac{dP}{dx}=-\frac{(\rho c^2+P)}{y^2}\bigg [\frac{2\pi G}{c^4}P-\frac{ \Lambda }{6}+\frac{\gamma }{4}x^{-1/2}+\frac{\omega }{2}\bigg ], \end{aligned}$$
(54)

respectively. By using the above equations, in terms of new variables, we obtain,

$$\begin{aligned} \frac{d}{dx}\bigg (y\frac{d\zeta }{dx}\bigg )-\frac{1}{2}\frac{\zeta }{y}\frac{ d\omega }{dx}+\frac{\gamma }{8}\frac{\zeta }{y}x^{-3/2}=0. \end{aligned}$$
(55)

We will introduce a new independent variable \(\ell \), obtained by changing the derivative \(2y(d/dx)\rightarrow d/d\ell \), and defined as,

$$\begin{aligned} \ell (r) = \int _{0}^{r} r^{\prime }\bigg [1-\frac{2G}{c^2}\frac{M(r^{\prime })}{r^{\prime }}-\frac{\Lambda }{3}r^{\prime 2}+\gamma r^{\prime }\bigg ]^{- \frac{1}{2}}dr^{\prime }, \end{aligned}$$
(56)

with \(\ell (0)=0\). We define the mean density of the star as,

$$\begin{aligned} {\bar{\rho }}=\frac{M(r)}{\frac{4}{3}\pi r^3}. \end{aligned}$$
(57)

Both the local density \(\rho \) and the mean density \({\bar{\rho }}\) are required to be decreasing functions of r inside the spherically symmetric object. The requirement that the matter density is a decreasing function throughout the star implies that,

$$\begin{aligned} \frac{d}{dr}\bigg (\frac{M(r)}{r^3}\bigg )< 0, \end{aligned}$$
(58)

leading to \(d\omega /dx< 0\).

3.1 Mass-radius bounds in dRGT massive gravity for compact objects for \(\gamma >0\)

As a first case in the analysis of the mass-radius bounds in dRGT massive gravity we assume the condition that \(\gamma >0\). Then for the function \(\zeta \) we obtain immediately the following constraint,

$$\begin{aligned} \frac{d^2 \zeta }{d\ell ^2}<0. \end{aligned}$$
(59)

This condition must hold for all points inside the vacuum boundary of the compact spherically symmetric object. By using the mean value theorem, we obtain the inequality,

$$\begin{aligned} \frac{d\zeta }{d\ell }\le \frac{\zeta (\ell )-\zeta (0)}{\ell -0}\le \frac{ \zeta (\ell )}{\ell }. \end{aligned}$$
(60)

Since \(\zeta (0)>0\), it follows that,

$$\begin{aligned} \frac{1}{\zeta }\frac{d\zeta }{d\ell }\le \frac{1}{\ell }. \end{aligned}$$
(61)

We introduce now the new function \(\alpha \)(r), defined as,

$$\begin{aligned} \alpha (r)=1-\frac{c^2 r}{2GM}\left( -\frac{\Lambda }{3}r^2+\gamma r\right) . \end{aligned}$$
(62)

This leads to,

$$\begin{aligned} y^2=1-\frac{2G}{c^2}\frac{M(r)}{r}\alpha (r). \end{aligned}$$
(63)

By using the condition  (58), for all \(r^{\prime }<r\) we obtain the inequality,

$$\begin{aligned} \frac{M(r^{\prime })}{r^{\prime 3}}\ge \frac{M(r)}{r^3}, r^{\prime }<r. \end{aligned}$$
(64)

Furthermore, we will assume that inside the star the following condition,

$$\begin{aligned} \alpha (r^{\prime })\frac{M(r^{\prime })}{r^{\prime }}\ge \alpha (r)\frac{M(r) }{r}\left( \frac{r^{\prime }}{r}\right) ^2, \end{aligned}$$
(65)

also holds. The above inequality follows directly from the requirement,

$$\begin{aligned} \frac{d}{dr}\Big (\alpha (r)\frac{M(r)}{r^3}\Big )<0, \end{aligned}$$
(66)

leading to,

$$\begin{aligned} \gamma< \frac{8\pi G}{c^2}({\bar{\rho }}-\rho )r, r<R, \end{aligned}$$
(67)

which is valid for all \(r<R\) where R is the radius of the compact spherically symmetric object. From Eq. (65), it follows that,

$$\begin{aligned} \left[ 1-\frac{2G}{c^2}\frac{M(r^{\prime })\alpha (r^{\prime })}{r^{\prime }} \right] ^{-\frac{1}{2}}\ge \left[ 1-\frac{2G}{c^2}\frac{M(r)\alpha (r)}{r^3} r^{\prime 2}\right] ^{-\frac{1}{2}}. \end{aligned}$$
(68)

Therefore, the right-hand side of inequality (61) is bounded by,

$$\begin{aligned}&\left\{ \int _{0}^{r} r'\left[ 1-\frac{2G}{c^2}\frac{M(r')\alpha (r')}{r'}\right] ^{-\frac{1}{2}}dr'\right\} ^{-1}\nonumber \\&\quad \le \frac{2G}{c^2}\frac{M(r)\alpha (r)}{r^3}\left[ 1-\sqrt{1-\frac{2G}{c^2}\frac{M(r)\alpha (r)}{r}}\right] ^{-1}. \end{aligned}$$
(69)

The left-hand side of inequality (61) can be rewritten with the use of Eqs. (53) and (54), and thus we eventually obtain the generalized Buchdahl inequality for dRGT massive gravity, in the form,

$$\begin{aligned} \bigg (\frac{4\pi G}{c^4}P-\frac{\Lambda }{3}\bigg )r^2+\frac{G}{c^2}\frac{M(r) }{r}+\frac{\gamma }{2}r\le y(1+y). \end{aligned}$$
(70)

This relation is valid for \(r\in [0,R]\). The upper bound of the mass-radius ratio follows by estimating the generalized Buchdahl inequality at the vacuum boundary of the compact object, where \(r=R\), \(P(R)=0\), and \(M(R)=M\), respectively. Then it follows that,

$$\begin{aligned} \frac{\frac{GM}{c^{2}R}+\frac{\gamma R}{2}-\frac{\Lambda R^{2}}{3}}{\sqrt{1-\frac{2GM}{c^{2}R}-\frac{\Lambda R^{2}}{3}+\gamma R}} \le \frac{\frac{2GM}{c^{2}R}+\frac{\Lambda R^{2}}{3}-\gamma R}{1-\sqrt{1-\frac{2GM}{c^{2}R}-\frac{\Lambda R^{2}}{3}+\gamma R}}, \nonumber \\ \end{aligned}$$
(71)

or in an alternative form,

$$\begin{aligned} \frac{3G}{c^2}\frac{M}{R}\le \sqrt{1-\frac{2G}{c^2}\frac{M}{R}-\frac{\Lambda }{3}R^2+\gamma R}+1+\frac{\gamma }{2}R. \end{aligned}$$
(72)

For convenience, the physical variables in the above inequality are redefined by introducing the dimensionless quantities,

$$\begin{aligned} u:=\frac{G}{c^2}\frac{M}{R},\quad a:=\frac{\Lambda }{3}R^2,\quad b:=\gamma R. \end{aligned}$$
(73)

Consequently, the inequality (72) becomes,

$$\begin{aligned} 3u-1-\frac{b}{2}\le \sqrt{1-2u-a+b}. \end{aligned}$$
(74)

In order to find the lower and upper bounds on the mass/radius ratio, we would square the inequality to get rid of the square root. However, this can be done only when the Left Hand Side of (74) is bounded from below, i.e. \( |3u-1-b/2|\le \sqrt{1-2u-a+b}\). Since the Left Hand Side is always negative for sufficiently small u (for large u, the Left Hand Side is positive and squaring is justified naturally), the inequality is trivially satisfied and there is no lower bound on u.

However, there is an additional physical condition to be imposed here. For the matter sphere to exist physically, we need the matter pressure to compensate for the pressure from the cosmological constant or the pressure generated by the massive gravity in this case, i.e.,

$$\begin{aligned} P_{\mathrm {total}}=P+P_{\Lambda }\ge 0, \end{aligned}$$
(75)

is required inside the sphere. For negative \(P_{\Lambda }\), this condition implies positive matter pressure P. The equation of state of matter thus demands the matter density \(\rho \ge -P_{\Lambda }/wc^{2}>0\) and consequently,

$$\begin{aligned} {\bar{\rho }}=3M/4\pi R^{3}\gtrsim \Lambda c^{2}/8\pi G, \end{aligned}$$
(76)

inside the sphere. Since \(u=4\pi G {\bar{\rho }}R^{2}/3c^{2}\), the condition \( |3u-1-b/2|\le \sqrt{1-2u-a+b}\) is valid when

$$\begin{aligned} {\bar{\rho }}\ge \frac{1}{2}\frac{\Lambda c^{2}}{8\pi G}, \end{aligned}$$
(77)

and for small u, a, and b, respectively. This is always true for the condition (76) above, therefore squaring the inequality is justified.

By reorganizing the above relation, we obtain,

$$\begin{aligned} 9u^2-(4+3b)u+\left( \frac{b^2}{4}+a\right) \le 0, \end{aligned}$$
(78)

or, equivalently,

$$\begin{aligned} (u-u_1)(u-u_2)\le 0, \end{aligned}$$
(79)

where,

$$\begin{aligned} u_1= & {} \frac{4+3\gamma R}{18}\left[ 1-\sqrt{1-\frac{3\left( 3\gamma ^2+4\Lambda \right) R^2}{\left( 4+3\gamma R\right) ^2}}\right] , \end{aligned}$$
(80)
$$\begin{aligned} u_2= & {} \frac{4+3\gamma R}{18}\left[ 1+\sqrt{1-\frac{3\left( 3\gamma ^2+4\Lambda \right) R^2}{\left( 4+3\gamma R\right) ^2}}\right] . \end{aligned}$$
(81)

Hence, under the condition \(\gamma >0\), in the presence of massive graviton, the mass-radius ratio of compact objects is bounded by,

$$\begin{aligned}&\frac{4+3\gamma R}{9}\left[ 1-\sqrt{1-\frac{3\left( 3\gamma ^2+4\Lambda \right) R^2}{\left( 4+3\gamma R\right) ^2}}\right] \nonumber \\&\quad \le \frac{2GM}{c^2R}\le \frac{4+3\gamma R}{9}\left[ 1+\sqrt{1-\frac{3\left( 3\gamma ^2+4\Lambda \right) R^2}{\left( 4+3\gamma R\right) ^2}}\right] .\nonumber \\ \end{aligned}$$
(82)

The validity of this inequality demands that the value in the square root be greater than zero, a requirement which leads to the constraint,

$$\begin{aligned} \Lambda <\frac{4+6\gamma R}{3R^2}. \end{aligned}$$
(83)

Nontrivial (positive) lower bounds do exist only when the fraction in the square root is greater than zero, which gives another constraint for the negative \(\Lambda \) case,

$$\begin{aligned} \gamma >\sqrt{-\frac{4\Lambda }{3}}, \Lambda <0, \end{aligned}$$
(84)

whilst it is trivially satisfied for \(\Lambda >0\) as long as (83) is valid.

3.2 Mass-radius ratios in the presence of a cosmological constant only: the case \(\gamma =0\)

For the case \(\gamma =0\), Eq. (82) leads to the condition for the existence of a lower and an upper mass-radius bound, which is given by,

$$\begin{aligned} \frac{4}{9}\left[ 1-\sqrt{1-\frac{3}{4}\Lambda R^2}\right] \le \frac{2GM}{c^2R} \le \frac{4}{9}\left[ 1+\sqrt{1-\frac{3}{4}\Lambda R^2}\right] . \end{aligned}$$
(85)

This relation implies the existence of a minimum mass/radius ratio for a matter particle, which is induced by the presence of a cosmological constant, as shown first in [49]. The existence of \(\Lambda \) also determines modifications of the Buchdahl upper limit of general relativity [39]. The generalized Buchdahl inequality (85) gives a nontrivial solution only when the condition,

$$\begin{aligned} 0<\Lambda <\left( \frac{4}{3}\right) R^{-2}, \end{aligned}$$
(86)

corresponding to a Schwarzschild-de Sitter type geometry, is satisfied.

3.3 Mass-radius bounds in dRGT massive gravity for dense stars for \(\gamma <0\)

For the case \(\gamma < 0\), we can write the generalized Buchdahl equation for spherically symmetric objects in the following form,

$$\begin{aligned} y(y\zeta ^{\prime })^{\prime }=\frac{1}{2}\omega ^{\prime }\zeta +\frac{|\gamma | }{8}\frac{\zeta }{x^{3/2}}. \end{aligned}$$
(87)

Subsequently, we introduce four new variables \(\Gamma , \psi , \eta \) and z, defined as,

$$\begin{aligned} \Gamma (r)\equiv & {} \frac{|\gamma |}{8}\frac{\zeta }{r^2}, \end{aligned}$$
(88)
$$\begin{aligned} \psi= & {} \zeta -\eta , \end{aligned}$$
(89)

where,

$$\begin{aligned} \eta =4\int _{0}^{r} \Bigg (\int _{0}^{r_{1}} \frac{\Gamma (r_{2})}{\sqrt{1-\frac{ \Theta (r_{2})}{r_{2}}}}dr_{2}\Bigg )\frac{r_{1}}{\sqrt{1-\frac{\Theta (r_{1})}{ r_{1}}}} dr_{1}, \end{aligned}$$
(90)

while the last variable z is given by,

$$\begin{aligned} dz=\frac{1}{y(x)}dx \rightarrow z(r)=\int _{0}^{r} \frac{2r^{\prime }}{\sqrt{ 1-\frac{\Theta (r^{\prime })}{r^{\prime }}}}dr^{\prime }. \end{aligned}$$
(91)

The function \(\Theta (r)\) is obviously defined by,

$$\begin{aligned} y^2=1-\frac{\Theta (r)}{r}, \end{aligned}$$
(92)

where,

$$\begin{aligned} \Theta (r)=\frac{2GM(r)}{c^2}+\frac{\Lambda }{3}r^3+|\gamma |r^2. \end{aligned}$$
(93)

In terms of the new variables defined above, the Buchdahl equation Eq. (87) can be written as,

$$\begin{aligned} \frac{d^2 \psi (z)}{dz^2}=\frac{1}{2}\omega ^{\prime }(x)\zeta (x). \end{aligned}$$
(94)

We assume first the condition that, for \(r^{\prime }<r\),

$$\begin{aligned} \frac{\Theta (r^{\prime })}{r^{\prime }}\ge \frac{\Theta (r)}{r}\bigg (\frac{ r^{\prime }}{r}\bigg )^2,r^{\prime }<r, \end{aligned}$$
(95)

and use the assumption that the density inside the object does not increase with r in the above relation. Finally, the above assumptions lead to the condition,

$$\begin{aligned} |\gamma | > -\frac{8\pi G}{c^2}({\bar{\rho }}-\rho )r, \end{aligned}$$
(96)

which is valid for all \(r\le R\) as long as the matter density is a decreasing function of the radial coordinate r. Next, as a second condition we assume that for \(r^{\prime }<r\),

$$\begin{aligned} \Gamma (r^{\prime })\ge \Gamma (r), \end{aligned}$$
(97)

that is, \(\Gamma (r)\) is a decreasing function of r. This condition leads to a constraint on \(|\gamma |\) given by,

$$\begin{aligned} |\gamma | < \frac{4}{3r}- \frac{40\pi G}{9c^2}{\bar{\rho }}r+\frac{2}{9}\Lambda r-\frac{8\pi G}{3c^{4}}Pr. \end{aligned}$$
(98)

This relation is trivially valid for \(r\rightarrow 0\), and at the surface \(r=R\) it gives a constraint,

$$\begin{aligned} |\gamma | < \frac{4}{3R}- \frac{10G}{3c^2}\frac{M}{R^{2}}+\frac{2}{9}\Lambda R. \end{aligned}$$
(99)

Alternatively, it can be written with the help of the dimensionless parameters already defined in Eq. (43) as,

$$\begin{aligned} \sigma >-\frac{4}{3\eta }+\frac{10}{9}\eta -\frac{2}{3}\psi \eta . \end{aligned}$$
(100)

For example, when \(\psi \) is equal to 0.06, all cases with \(\sigma = -0.05, -0.25, -0.50, -0.75, -1\), and \(-1.25\) satisfy this condition at the surface.

From the condition \(\omega ^{\prime }(x)<0\), we obtain the inequality,

$$\begin{aligned} \frac{d^2}{dz^2}\psi (z)<0, \end{aligned}$$
(101)

which holds for all r in the range \(0\le r\le R\). Again, by using the mean value theorem, we find,

$$\begin{aligned} \frac{d\psi }{dz}\le \frac{\psi (z)-\psi (0)}{z}\le \frac{\psi (z)}{z}. \end{aligned}$$
(102)

Since \(\psi (0)=\zeta (0)-\eta (0)=\zeta (0)>0\), it follows that,

$$\begin{aligned} \frac{d\psi }{dz}\le \frac{\psi (z)}{z}\rightarrow \frac{d\zeta }{dz}-\frac{d\eta }{dz}\le \frac{\zeta -\eta }{z}. \end{aligned}$$
(103)

After substituting the new variables (90) and (91) in the above relation, we obtain,

$$\begin{aligned}&\frac{1}{2r}\sqrt{1-\frac{\Theta (r)}{r}}\frac{d\zeta }{dr}-2\int _{0}^{r}\frac{\Gamma (r')}{\sqrt{1-\frac{\Theta (r')}{r'}}}dr'\nonumber \\&\quad \le \frac{1}{2\int _{0}^{r}\frac{r'}{\sqrt{1-\frac{\Theta (r')}{r'}}}dr'}\left[ \zeta -4\int _{0}^{r}\frac{r_{1}}{\sqrt{1-\frac{\Theta (r_{1})}{r_{1}}}}\right. \nonumber \\&\qquad \left. \times \left( \int _{0}^{r_{1}}\frac{\Gamma (r_{2})}{\sqrt{1-\frac{\Theta (r_{2})}{r_{2}}}}dr_{2}\right) dr_{1}\right] . \end{aligned}$$
(104)

The denominator of the right-hand side of Eq. (104) is bounded from above as a result of using the condition,  (95). Hence we have,

$$\begin{aligned} \left( \int _{0}^{r} \frac{r^{\prime }}{\sqrt{1-\frac{\Theta (r^{\prime })}{ r^{\prime }}}}dr^{\prime }\right) ^{-1} \le \frac{\Theta (r)}{r^3}\left( 1- \sqrt{1-\frac{\Theta (r)}{r}}\right) ^{-1}. \end{aligned}$$
(105)

As for the term related to \(\Gamma \), it is also bounded as a consequence of the conditions  (95) and  (97), such that,

$$\begin{aligned} \int _{0}^{r} \frac{\Gamma (r^{\prime })}{\sqrt{1-\frac{\Theta (r^{\prime })}{ r^{\prime }}}}dr^{\prime }\ge & {} \Gamma (r)\int _{0}^{r} \Bigg (1-\frac{ \Theta (r)}{r}\bigg (\frac{r^{\prime }}{r}\bigg )^2\Bigg )^{-\frac{1}{2} }dr^{\prime } \nonumber \\= & {} \Gamma (r)\bigg (\frac{\Theta (r)}{r^3}\bigg )^{-\frac{1}{2}}\arcsin \Bigg ( \sqrt{\frac{\Theta (r)}{r}}\Bigg ).\nonumber \\ \end{aligned}$$
(106)

Hence the term in the numerator on the right-handed side of Eq. (104) has a lower bound, which can be obtained as,

$$\begin{aligned}&\int _{0}^{r} \frac{r_{1}}{\sqrt{1-\frac{\Theta (r_{1})}{r_{1}}}}\Bigg (\int _{0}^{r_{1}}\frac{\Gamma (r_{2})}{\sqrt{1-\frac{\Theta (r_{2})}{r_{2}}}}dr_{2}\Bigg )dr_{1}\nonumber \\&\quad \ge \int _{0}^{r} r_{1}\bigg (1-\frac{\Theta (r_{1})}{r_{1}}\bigg )^{-\frac{1}{2}}\left( \frac{\Gamma (r)}{\Big (\frac{\Theta (r)}{r^3}\Big )^{\frac{1}{2}}}\arcsin \left( \sqrt{\frac{\Theta (r)}{r}}\right) \right) dr_{1} \nonumber \\&\quad \ge \int _{0}^{r} r_{1}\bigg (1-\frac{\Theta (r)}{r^3}r_{1}^2\bigg )^{-\frac{1}{2}}\left( \frac{\Gamma (r)}{\Big (\frac{\Theta (r)}{r^3}\Big )^{\frac{1}{2}}}\arcsin \left( \sqrt{\frac{\Theta (r)}{r}}\right) \right) dr_{1} \nonumber \\&\quad = \left( \frac{1-\sqrt{1-\frac{\Theta (r)}{r}}}{\frac{\Theta (r)}{r^3}}\right) \frac{\Gamma (r)}{\Big (\frac{\Theta (r)}{r^3}\Big )^{\frac{1}{2}}}\arcsin \left( \sqrt{\frac{\Theta (r)}{r}}\right) \nonumber \\&\quad =\frac{\Gamma (r)}{\Big (\frac{\Theta (r)}{r^3}\Big )^{\frac{3}{2}}}\left[ \arcsin \left( \sqrt{\frac{\Theta (r)}{r}}\right) -\sqrt{1-\frac{\Theta (r)}{r}}\arcsin \left( \sqrt{\frac{\Theta (r)}{r}}\right) \right] \nonumber \\&\quad \ge \frac{\Gamma (r)}{\Big (\frac{\Theta (r)}{r^3}\Big )^{\frac{3}{2}}}\left[ \sqrt{\frac{\Theta (r)}{r}}-\sqrt{1-\frac{\Theta (r)}{r}}\arcsin \left( \sqrt{\frac{\Theta (r)}{r}}\right) \right] , \end{aligned}$$
(107)

where we have used the identity \(\arcsin x \ge x\). Subsequently, we insert the inequalities  (105),  (106) and  (107) into Eq. (104) and use the relation \(y^2=1-\Theta (r)/r\). Afterwards, we obtain,

$$\begin{aligned} \frac{y}{r}\frac{d\zeta }{dr}\le & {} \frac{1+y}{r^2}\left[ \zeta (r)-4\Gamma (r)r^3\left( \frac{1}{1-y^2}-\frac{y\arcsin \left( \sqrt{1-y^2}\right) }{(1-y^2)^{3/2}}\right) \right] \nonumber \\&+4\Gamma (r)\frac{r}{\sqrt{1-y^2}}\arcsin \left( \sqrt{1-y^2}\right) . \end{aligned}$$
(108)

Since for ordinary matter the energy condition \(\rho c^2+P\ge 0\) always holds, it allows us to replace \(1/\zeta \) with 1 / y, such that,

$$\begin{aligned}&\left( \frac{4\pi G}{c^4}P-\frac{\Lambda }{3}\right) r^2+\frac{G}{c^2}\frac{M(r)}{r}-\frac{|\gamma |}{2}r\nonumber \\&\quad \le y(1+y)+\frac{4\Gamma (r)r^3}{1-y}\left( \frac{y\arcsin \left( \sqrt{1-y^2}\right) }{\sqrt{1-y^2}}-1\right) \nonumber \\&\qquad +4\Gamma (r)r^3\frac{\arcsin \left( \sqrt{1-y^2}\right) }{\sqrt{1-y^2}} \le y(1+y)+4r^3\frac{\Gamma (r)}{y},\nonumber \\ \end{aligned}$$
(109)

where we have also used the relation,

$$\begin{aligned} \arcsin \left( \sqrt{1-y^2}\right) \le \frac{\sqrt{1-y^2}}{y}. \end{aligned}$$
(110)

Hence we have obtained the Buchdahl inequality for the mass-radius ratio of a compact object in dRGT massive gravity theory for the case \(\gamma <0\). This inequality is valid for all values of the radial coordinate inside the star, \(r\in [0,R]\). The upper and lower bounds on the mass-radius ratio are determined by considering the Buchdahl inequality at the surface of the object, where \(r=R\), \(P(R)=0\) and \(M(R)=M\), respectively. Then it follows that,

$$\begin{aligned} \frac{3G}{c^2}\frac{M}{R}\le \sqrt{1-\frac{2G}{c^2}\frac{M}{R}-\frac{\Lambda }{3}R^2 - |\gamma | R}+1. \end{aligned}$$
(111)

For convenience, the variables in the above inequality are redefined as follows,

$$\begin{aligned} u=\frac{G}{c^2}\frac{M}{R}, \quad a=\frac{\Lambda }{3}R^2,\quad b=|\gamma | R. \end{aligned}$$
(112)

Consequently, the inequality (111) becomes,

$$\begin{aligned} 3u\le \sqrt{1-2u-a-b}+1. \end{aligned}$$
(113)

After squaring and simplifying the above relation, we obtain,

$$\begin{aligned} u^2-\frac{4u}{9}+\frac{(a+b)}{9}\le 0, \end{aligned}$$
(114)

or, equivalently,

$$\begin{aligned} (u-u_{-})(u-u_{+})\le 0, \end{aligned}$$
(115)

where,

$$\begin{aligned} u_{\pm }=\frac{2}{9}\left[ 1\pm \sqrt{1-\frac{3\left( \Lambda R+3|\gamma |\right) R }{4}}\right] . \end{aligned}$$
(116)

Hence we have obtained the following lower and upper bounds for the mass-radius ratio of compact objects in dRGT massive gravity,

$$\begin{aligned} \frac{4}{9}\left[ 1-\sqrt{1-\frac{3\left( \Lambda R+3|\gamma |\right) R}{4}} \right]\le & {} \frac{2GM}{c^2R} \nonumber \\\le & {} \frac{4}{9}\left[ 1+\sqrt{1-\frac{3\left( \Lambda R+3|\gamma |\right) R}{4}} \right] .\nonumber \\ \end{aligned}$$
(117)

The inequality demands the value in the square root greater than zero which leads to a constraint,

$$\begin{aligned} |\gamma | < \frac{4}{9R}-\frac{\Lambda }{3}R. \end{aligned}$$
(118)

A nontrivial (positive) lower bound in this case exists only when the fraction in the square root is greater than zero giving another constraint,

$$\begin{aligned} |\gamma | > -\frac{\Lambda }{3}R. \end{aligned}$$
(119)

4 Discussions and final remarks

Massive gravity is an interesting theory of gravitation, inspired by the quantum field theoretical approach to gravity, and which assumes a non-zero mass of the quanta intermediating the gravitational interaction, the graviton. Despite the initial many complicated theoretical problems raised by this approach, a consistent formulation proposed in [7, 8] seems to offer the possibility of an alternative to standard general relativity, which allows us to go beyond the theoretical limits imposed by Einstein’s theory. The dRGT model of massive gravity is ghost-free, and, at least at the classical level, it has strictly five (or seven in the bimetric case) gravitational degrees of freedom [9,10,11]. However, when applied to cosmology, it turns out that the theory with Minkowski fiducial metric does not have flat and closed Friedmann-Lemaitre-Robertson-Walker solutions [69]. In the context of the very early Universe cosmology, that is, during inflation, the propagation of the gravitational waves would also be affected by the non-trivial mass of the graviton [70,71,72,73].

In the present paper we have investigated in the framework of Lorentz-violating dRGT massive gravity theory an important property of compact general relativistic objects, namely, their mass-radius ratio bounds, which are important indicators of their stability properties. These bounds can be obtained from the generalized Buchdahl inequality, from which the existence of a minimum value of this ratio, as well as an upper stability limit do follow. In order to obtain the mass-radius ratio bounds we have adopted a specific form for the \(g_{11}\) component of the metric tensor, in which the corrections to the standard Schwarzschild-de Sitter geometry are represented by a correction term of the form \(\gamma r\), where the coefficient \(\gamma \), proportional to the graviton mass square, gives the new contribution coming from the ghost-free massive gravity. After adopting the functional form of the metric, we have obtained the basic equations describing the hydrostatic equilibrium properties of high density stars. As compared to the standard general relativistic case, a new term of the form \( \gamma r^2\), depending on the mass of the graviton, does appear in the TOV equation. We have first investigated the role this term may play in the description of stellar properties for the case of constant density stars. In some astrophysical situations the assumption of constant density may give a good description of the global parameters of high density objects. As opposed to the standard general relativistic case, in dRGT massive gravity theory there is no exact solution of the gravitational field equations, and hence a numerical investigation is required. The pressure distribution inside the star, and consequently its radius, shows a significant theoretical dependence on the numerical values of the dimensionless parameter \(\sigma \), constructed from \(\gamma \), the density of the star, and the fundamental constants of physics.

We also explored the stability of a static sphere in dRGT massive gravity model. Interestingly, the linear term \(\gamma r\) in the metric has a crucial role in the stability condition. When \(\gamma \) is negative, the massive-gravity TOV equation demonstrates the universal gravitational stability of a static sphere between repulsive gravity and inward pressure gradient force in contrast to the conventional gravitational stability of compact object. Such object, however, requires high surface tension to maintain the high pressure boundary condition. Interestingly enough, stable static hollow spheres or halo configurations are also possible for the \( \gamma <0\) case as long as the inner radius is larger than the turnover radius \(r_{c}\) of gravity.

We have obtained, and investigated in detail the Buchdahl inequality for both a positive and negative \(\gamma \) (the case \(\gamma =0\) reduces the model to the standard general relativistic case). In the case \(\gamma >0\), the Buchdahl inequality implies the existence of an absolute minimum particle mass, which is given by,

$$\begin{aligned} \frac{2GM}{c^2R}\ge \frac{\gamma ^2}{8}\frac{\left( 1+4\Lambda /3 \gamma ^2\right) R^2}{\left( 1+3\gamma R/4\right) }, \quad \gamma >0. \end{aligned}$$
(120)

Alternatively, this relation can be formulated in terms of an absolute minimum density \(\rho _{min}\), so that the density \(\rho =3M/4\pi R^3\) of any matter configuration must satisfy the constraint,

$$\begin{aligned} \rho \ge \rho _{min}\equiv \frac{3c^{2}\gamma ^2}{64\pi G}\frac{ \left( 1+4\Lambda /3 \gamma ^2\right) }{\left( 1+3\gamma R/4\right) },\quad \gamma >0. \end{aligned}$$
(121)

However, the minimum density is radius-dependent, and the above inequality can also be interpreted as a matter density-radius relation. It is important to mention that a lower limit for the mass does exist in massive gravity even in the absence of the cosmological constant, when \(\Lambda =0\). In this case we have,

$$\begin{aligned} \frac{2GM}{c^2R}\ge \frac{\gamma ^2}{8}\frac{R^2}{\left( 1+3\gamma R/4\right) },\quad \gamma >0, \end{aligned}$$
(122)

and,

$$\begin{aligned} \rho \ge \rho _{min}\equiv \frac{3c^{2}\gamma ^2}{64\pi G}\frac{1}{ \left( 1+3\gamma R/4\right) },\quad \gamma >0, \end{aligned}$$
(123)

respectively. Therefore there is a straightforward relation between the minimum mass an elementary particle can have, and the mass of the graviton. If a quantum of gravity does exist, its existence would impose a strong limit on the minimum mass a particle can have. From a physical point of view one can assume that it is the graviton mass that determines the gravitational mass of the elementary particles, and mediates their gravitational interactions.

A very different minimum mass expression is obtained in the case \(\gamma <0\) . From Eq. (117) we immediately obtain,

$$\begin{aligned} \frac{2GM}{c^2R}\ge \frac{|\gamma |\left( 1+\Lambda R/3|\gamma |\right) R}{2},\quad \gamma <0. \end{aligned}$$
(124)

As for the particle mass density, it satisfies a lower bound given by,

$$\begin{aligned} \rho \ge \rho _{min}\equiv \frac{3c^{2}|\gamma | }{16\pi G}\frac{ \left( 1+\Lambda R/3|\gamma | \right) }{R},\quad \gamma <0. \end{aligned}$$
(125)

Similarly to the \(\gamma >0\) case, a minimum mass does exist even in the absence of the cosmological constant, \(\Lambda =0\), and it is given by,

$$\begin{aligned} \frac{2GM}{c^2R}\ge \frac{|\gamma |R}{2},\quad \gamma <0. \end{aligned}$$
(126)

A similar relation is obtained if the condition \(\Lambda R/3|\gamma |<<1\) is satisfied for all R. As for the minimum matter density, it is given by a relation of the form,

$$\begin{aligned} \rho _{min}\equiv \frac{3c^{2}|\gamma | }{16\pi G R},\quad \gamma <0. \end{aligned}$$
(127)

As for the upper bounds of the mass-radius ratios of the compact stars in massive gravity, they are given by,

$$\begin{aligned} \frac{2GM}{c^2R}\le & {} \frac{4}{9}\left( 1+\frac{3\gamma R}{4}\right) \nonumber \\&\times \left[ 2- \frac{9\gamma ^2\left( 1+4\Lambda /3\gamma ^2\right) R^2}{32\left( 1+3\gamma R/4\right) ^2}\right] ,\quad \gamma >0, \end{aligned}$$
(128)

and

$$\begin{aligned} \frac{2GM}{c^2R}\le \frac{4}{9}\left[ 2-\frac{3\left( \Lambda R+3|\gamma |\right) R}{8}\right] ,\quad \gamma <0. \end{aligned}$$
(129)

In both cases in the limit \(\gamma =0\), \(\Lambda =0\), the corresponding expressions reduce to the standard Buchdahl limit \(2GM/c^2R\le 8/9\).

The existence of upper/lower bounds of the mass-radius ratio for compact objects also leads to the existence of some limiting values for other physical and geometrical quantities of observational interest. One such important quantity is the surface red shift z of the high density star, which can be defined in the massive gravity effects corrected Schwarzschild-de Sitter geometry as

$$\begin{aligned} z\equiv \frac{1}{\sqrt{f(r)}}-1=\frac{1}{\sqrt{ 1 - 2GM(r)/c^2r - \Lambda r^2/3 + \gamma r}}-1. \end{aligned}$$
(130)

We consider first the case \(\gamma >0\). Then, from Eq. (71), written as

$$\begin{aligned}&\frac{1}{y}\left[ -\frac{\Lambda }{3}R^2+\frac{GM}{c^2R}+\frac{\gamma R}{2} \right] \nonumber \\&\quad \le \frac{1}{1-y}\left[ \frac{2GM}{c^2R} + \frac{\Lambda }{3}R^2 - \gamma R\right] , \end{aligned}$$
(131)

we obtain

$$\begin{aligned} z\le \frac{2GM/c^2R-\gamma R+\Lambda R^2/3}{GM/c^2R+\gamma R/2-\Lambda R^2/3 }. \end{aligned}$$
(132)

In the case \(\gamma \equiv 0\) and \(\Lambda \equiv 0\), we reobtain the standard general relativistic gravitational redshift restriction \(z\le 2\). Alternatively, the redshift bound can be reformulated as

$$\begin{aligned} z\le \frac{2\left[ 1-\left( c^{2}/8\pi G{\bar{\rho }}\right) \left( 3\gamma /R-\Lambda \right) \right] }{1+\left( c^{2}/8\pi G{\bar{\rho }}\right) \left( 3\gamma /R-2\Lambda \right) }. \end{aligned}$$
(133)

Hence, at least in principle, observations of the gravitational redshift from compact high density astrophysical objects may offer the possibility of discriminating between massive gravity and other modified theories of gravity.

To conclude, in the present paper we have investigated some of the implications of the dRGT massive gravity theory with Lorentz-violating fiducial metric, which are relevant at both microscopic and macroscopic scale. The results obtained in the present analysis may provide some insights for the possible experimental/observational testing of this particular class of massive gravity theory at both elementary particle and astrophysical levels, as well as on its theoretical foundations.