1 Introduction

Stars are considered as the most fundamental building blocks of galaxy and known as widely recognized astronomical objects. The study of their age, structure and evolution has gained much attention in cosmology as well as astrophysics. The age of a star depends upon its size such as larger stars have shorter lives. In the core of stars, a fusion process occurs that produces heat and pressure to counter balance the gravitational effects generated by a star’s mass. During the development of stars, a phase arises when the nuclear fuel is completely burnt out and outward directed radiation pressure no longer counter balances the inward directed strong gravitational pull resulting the stellar death. Consequently, new remnants are formed known as compact stars that are entirely determined by original mass of the star. Similar to other ordinary stars, compact stars are also very common and are categorized into white dwarfs, neutron stars and black holes. As compared to normal stars, compact stars possess larger masses and smaller radii.

In astrophysics, the study of nature and exact constitution of compact objects motivates researchers to explore their internal features and different phases of their evolution. In compact stars, neutron stars have gained much attention due to their interesting features and structures. Neutron stars are the most strange as well as curious objects in which the attractive effects of gravity are balanced by the degeneracy pressure of neutrons. The presence of neutron stars was predicted soon after the discovery of neutrons [1] and later, this notion received a strong observational support from the evidences of pulsars [2]. Pulsars are considered as the rotating neutron stars and some examples of their candidates are Her X-1, 4U 1820-30, RXJ 1856-37 and SAX J 1808.4-3658. These pulsars captivated the attraction of many researchers due to their distinct pulse periods and much work has been done to examine various features of these star candidates.

In order to understand the interior geometry and evolutionary stages of stellar objects, the anisotropic fluid distribution plays a fundamental role. As the compact stars have dense cores and their density exceed the nuclear density, therefore, pressure must be anisotropic inside the stellar object [3]. In anisotropic matter distribution, it is observed that pressure is partitioned into transverse and radial components. In this context, many researchers investigated characteristics of dense compact stars with anisotropic fluid configuration. Hossein et al. [4] analyzed the features of anisotropic relativistic objects with cosmological constant and found stable structure of stellar objects. Kalam et al. [5] examined the relativistic modeling of anisotropic neutron stars and checked the validity of energy conditions, anisotropy measurement and stability with quintessence dark energy. For anisotropic distribution, Paul and Deb [6] formulated new relativistic exact solutions of compact stars which maintain the hydrostatic equilibrium.

In compact stars, the densest neutron stars can further be collapsed to form a black hole whereas for lesser dense neutron stars, there is a possibility to turn into a quark star. It is predicted that the interior matter distribution of quark stars is computed through MIT bag model equation of state (EoS) [7, 8]. During the last few years, the study of quark stars has motivated many researchers to analyze its features as well as interior composition. In this regard, Rahaman et al. [9] proposed a new mass interpolation function for strange star candidates using MIT bag model and investigated the physical behavior of stars from 6km to the boundary surface. Bhar [10] examined characteristics of SAX J 1808.4-3658, PSR J1614-2230 and 4U1820-30 stars with MIT bag model EoS and obtained stable configuration of these stars.

Murad [11] investigated the effect of charge on candidates of anisotropic strange stars using MIT bag model EoS. Arbañil and Malheiro [12] analyzed the influence of anisotropy in the equilibrium as well as stability of strange stars through numerical solution of the hydrostatic equilibrium equation, radial oscillation equation and MIT bag model. In the same context, Deb et al. [13] found singularity free solutions of Einstein field equations for strange quark stars by employing MIT bag model EoS and observed that anisotropy of compact stars increases with the radial coordinate. It attains its maximum value at the surface which seems an inherent property for the singularity free anisotropic compact stellar objects. They also represented the graphical analysis of pressure as well as energy density for LMC X-4 strange star candidate.

In 1915, Einstein proposed general theory of relativity which resolved many hidden mysteries of the universe. However, some observational facts reveal that general relativity (GR) is not sufficient enough to explore some of the physical phenomena. Recent astrophysical observations about the problem of dark matter (DM) and accelerating cosmic expansion have stimulated many relativistic astrophysicists to modify GR. It is claimed that this cosmic expansion is carried out by a mysterious source of energy with unknown features named as dark energy (DE). Alternative theories to GR have played a dynamical role to unveil hidden mysteries of DE and DM. Qadir et al. [14] discussed various characteristics of modified relativistic dynamics and obtained that GR may need to modify as possible resolutions for some cosmological issues, like quantum gravity and DM problem. In this context, different theoretical approaches have been considered as a way to handle these issues.

In the field of astrophysics, modified theories of gravity at large scales have been suggested to observe DE as well as DM in the dynamical and kinematical properties of stars. Though the DE and DM models are able to resolve the issues successfully but still they suffer from some limitations that motivate the researchers to consider alternative theories of gravity. The potential effects of such theories are more difficult to examine but one can derive the precise set of equations that governs the internal stable structure of fluids and then consider the specific models of interest such as relativistic stars or compact objects which unavoidably requires the use of numerical methods. Despite all these difficulties, the study of the effects of modified theories on the structure, formation and evolution of compact objects has attracted much attention in the context of modified theories of gravity of different types. It is claimed that the study of stellar structures as well as their features in the extensions of GR could provide new perceptions to test the strong field regime of gravitation and set limits to potential corrections to Einstein’s equations.

Some modifications in gravitational portion of the GR action have been provided with the passage of time in which the most smooth modification of GR is f(R) gravity [15] formulated by taking an arbitrary function f(R) in place of scalar curvature (R) in the Einstein–Hilbert action. Modified gravity theories have attained much attention due to combined motivation coming from high-energy physics, cosmology, and astrophysics. Among numerous alternatives to Einstein’s theory of gravity, theories that include higher-order curvature invariants such as f(R) and \(f(\mathcal {G})\) (\(\mathcal {G}\) denotes the Gauss–Bonnet invariant) have provided a number of interesting results [16,17,18,19,20,21]. An interesting characteristic of modified theories is the coupling of matter and curvature components. Such coupling yields a source term which may produce stimulating results and helps to examine mysteries behind the expansion of the cosmos. Motivated by this argument, various modified theories that involve strong matter-curvature coupling are developed such as f(R, T) gravity, where T symbolizes the trace of energy-momentum tensor (EMT) [22], \(f(R,T, R_{\alpha \beta }T^{\alpha \beta })\) gravity [23, 24] and \(f(\mathcal {G},T)\) gravity in which \(\mathcal {G}\) denotes the Gauss–Bonnet invariant [25].

The f(R, T) gravity as a generalization of f(R) gravity has inspired many researchers and is used to discuss various cosmological applications [26,27,28,29,30,31,32,33,34,35]. The study of physical features of compact stars using MIT bag model EoS has gained much importance and developed interesting results in this gravity. Moraes et al. [36] discussed the equilibrium configuration of quark stars with MIT bag model and numerically solved the field equations to obtain the behavior of matter variables. Deb et al. [37] analyzed the isotropic as well as anisotropic spherically symmetric compact stars and represented the graphical behavior of LMC X-4 star model. They also found the validity of energy conditions, hydrostatic equilibrium and stability corresponding to a fixed value of the bag constant. Sharif and Siddiqa [38] investigated the effect of higher curvature terms present in f(R, T) model on the evolution of compact stars using polytropic as well as MIT bag model EoS and obtained stable structures for particular values of the model parameters. Deb et al. [39] evaluated the solutions of f(R, T) field equations with anisotropic matter distribution for strange quark stars using MIT bag model EoS and studied the physical features of LMC X-4 as the representative of strange stars.

Recently, Biswas et al. [40] explored the features of three quark stars (Cen X-3, Vela X-1 and PSR J 1614-2230) by employing MIT bag model EoS for \(R+2\gamma T\) model. In this paper, we analyze the impact of MIT bag constant on anisotropic configuration of Her X-1, SAX J 1808.4-3658, RXJ 1856-37 and 4U1820-30 compact star candidates to observe the stable structure of stellar objects corresponding to \(R+\sigma R^{2}+\gamma T\) gravity model. The paper is arranged in the following format. In Sect. 2, we construct the field equations using Krori–Barua solutions corresponding to anisotropic fluid configuration and discuss a viable model of f(R, T) gravity. In Sect. 3, we figure out the values of unknown constants by employing a strong relation between interior and exterior spacetimes for chosen values of the model parameters. Section  4 represents the graphical representation of physical behavior of considered quark stars. In the last section, we compile our results.

2 Matter distribution and field equations

The f(R, T) theory in the presence of matter Lagrangian (\(\mathcal {L}_{m}\)) is presented by the action [22]

$$\begin{aligned} A=\int d^{4}x\sqrt{-g}\left[ \frac{f(R, T)}{2\kappa }+{\mathcal {L}}_{m}\right] , \end{aligned}$$
(1)

where \(\kappa =1\) represents the coupling constant and g acts as a determinant of the metric tensor (\(g_{\xi \eta }\)). The field equations corresponding to action (1) are

$$\begin{aligned}&f_{R}(R,T)R_{\xi \eta }-\frac{1}{2}g_{\xi \eta }f(R,T) -(\nabla _{\xi }\nabla _{\eta }-g_{\xi \eta }\Box )f_{R}(R,T) \nonumber \\&\quad =T_{\xi \eta } -(T_{\xi \eta }+\Theta _{\xi \eta })f_{T}(R,T), \end{aligned}$$
(2)

where \(f_{R}=\frac{\partial f}{\partial R},~f_{T}=\frac{\partial f}{\partial T}\), \(\Box =g^{\xi \eta }\nabla _{\xi }\nabla _{\eta }\), \(\nabla _{\xi }\) corresponds to covariant derivative, \(\Theta _{\xi \eta }\) is evaluated by

$$\begin{aligned} \Theta _{\xi \eta }=g^{\mu \upsilon }\frac{\delta T_{\mu \upsilon }}{\delta g^{\xi \eta }}= -2T_{\xi \eta }+g_{\xi \eta }\mathcal {L}_{m}- 2g^{\mu \upsilon }\frac{\partial ^{2}\mathcal {L}_{m}}{\partial g^{\xi \eta }\partial g^{\mu \upsilon }}. \end{aligned}$$
(3)

In order to interpret the interior geometry of stellar objects, we consider a static spherically symmetric line element given by

$$\begin{aligned} ds^{2}_{-}=e^{\mu (r)}dt^{2}-e^{\lambda (r)}dr^{2} -r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(4)

where \(\mu \) and \(\lambda \) are the metric potentials and depend only on radial coordinate. In gravitational physics, the matter distribution is illustrated through EMT \((T_{\xi \eta })\) in which every non-zero entity indicates dynamical variables with some physical effects. In relativistic compact objects, pressure anisotropy is an essential matter constituent which affects their evolution. It is well-known that stellar models are mostly rotating and anisotropic in nature. The anisotropic factor has convincing influences in various dynamical aspects of stellar evolution. The impact of anisotropy arises when the radial pressure component makes difference from the transverse component. Here, we study physical characteristics of compact star models with the effect of pressure anisotropy. For this purpose, we consider that the interior geometry of the stellar models is filled with anisotropic fluid whose EMT is

$$\begin{aligned} T_{\xi \eta }=(\rho +p_{t})U_{\xi }U_{\eta } -p_{t}g_{\xi \eta }+(p_{r}-p_{t})V_{\xi }V_{\eta }, \end{aligned}$$
(5)

where \(\rho \) represents energy density, \(p_{t}\) and \(p_{r}\) denote transverse and radial pressure ingredients, respectively, \(U_{\xi }\) stands for four velocity and \(V_{\xi }\) indicates four-vector in radial direction.

In comoving coordinates, the four velocity and four-vector execute the following relations

$$\begin{aligned} U_{\xi }U^{\xi }=1,\quad V_{\xi }V^{\xi }=-1. \end{aligned}$$

There are different choices of matter Lagrangian corresponding to fluid distributions. In this work, we consider \(\mathcal {L}_{m}=\rho \), where \(\rho \) does not depend upon the corresponding metric tensor which yields \(\frac{\partial ^{2}\mathcal {L}_{m}}{\partial g^{\xi \eta }\partial g^{\mu \upsilon }}=0\) [22]. Consequently, the expression for \(\Theta _{\xi \eta }\) becomes

$$\begin{aligned} \Theta _{\xi \eta }=-2T_{\xi \eta }+\rho g_{\xi \eta }. \end{aligned}$$

Inserting the expression of \(\Theta _{\xi \eta }\) in Eq. (2), it follows that

$$\begin{aligned} G_{\xi \eta }= & {} \frac{1}{f_{R}}\left[ T_{\xi \eta } (1+f_{T}) +\frac{1}{2}\left( f-Rf_{R}\right) \right. g_{\xi \eta }-\left. \rho g_{\xi \eta }f_{T}\right. \nonumber \\&-\,\left. \left( g_{\xi \eta }\Box - \nabla _{\xi }\nabla _{\eta }\right) f_{R}\phantom {\frac{1}{2}}\right] . \end{aligned}$$
(6)

The field equations of f(R, T) gravity (6) corresponding to anisotropic spherically symmetric line element are

$$\begin{aligned} \rho= & {} e^{-\lambda }\left[ \left\{ \frac{\mu '^{2}}{4}+\frac{\mu ''}{2} +\frac{\mu '}{r}-\frac{\mu '\lambda '}{4}\right\} f_{R}\right. \nonumber \\&\left. +\,\left( \frac{\lambda '}{2}-\frac{2}{r}\right) f_{R}' -f_{R}''\right] -\frac{f}{2}, \end{aligned}$$
(7)
$$\begin{aligned} p_{r}= & {} \frac{e^{-\lambda }}{1+f_{T}}\left[ \left\{ \frac{\lambda '}{r} -\frac{\mu '^{2}}{4}-\frac{\mu ''}{2}+\frac{\mu '\lambda '}{4}\right\} f_{R}\right. \nonumber \\&\left. +\,\left( \frac{\mu '}{2}+\frac{2}{r}\right) f_{R}'\right] -\rho f_{T}+\frac{f}{2}, \end{aligned}$$
(8)
$$\begin{aligned} p_{t}= & {} \frac{e^{-\lambda }}{1+f_{T}}\left[ \left\{ \frac{\lambda '}{2r} -\frac{\mu '}{2r}-\frac{1}{r^{2}}+\frac{e^{\lambda }}{r^{2}}\right\} f_{R}\right. \nonumber \\&\left. +\,\left( \frac{\mu '-\lambda '}{2}+\frac{1}{r}\right) f_{R}' +f_{R}''\right] -\rho f_{T}+\frac{f}{2}, \end{aligned}$$
(9)

where prime shows derivative with respect to radial coordinate.

In the current phase of cosmos, it is revealed that several stellar systems presently exist in non-linear regime. In order to obtain entire description of their structure transformation, we need to analyze their linear behavior. In order to discuss the coupling effects of matter and curvature components in f(R, T) gravity on the relativistic structures, we consider a separable functional form presented by

$$\begin{aligned} f(R,T)=f_{1}(R)+\mathrm {g}(T). \end{aligned}$$
(10)

This class of separable models can provide an appropriate linear extension of f(R) gravity. The various viable models of f(R, T) gravity can be formulated from this model by choosing different forms of \(f_{1}(R)\) along with linear combination of \(\mathrm {g}(T)\). Here, we take \(\mathrm {g}(T)=\gamma T\), where \(\gamma \) ia a small positive constant and \(T=\rho -p_{r}-2p_{t}\). In this regard, the field equations (7)–(9) become

$$\begin{aligned}&\left( 1+\frac{\gamma }{2}\right) \rho -\frac{\gamma }{2}p_{r}-\gamma p_{t}\nonumber \\&\quad = e^{-\lambda }\left[ \left\{ \frac{\mu '^{2}}{4}+\frac{\mu ''}{2} +\frac{\mu '}{r}-\frac{\mu '\lambda '}{4}\right\} f_{1R} +\left( \frac{\lambda '}{2}-\frac{2}{r}\right) \right. \nonumber \\&\qquad \times \, \left. f_{1R}' -f_{1R}''-\frac{e^{\lambda }f_{1}}{2}\right] , \end{aligned}$$
(11)
$$\begin{aligned}&\frac{\gamma }{2}\rho +\left( 1+\frac{3\gamma }{2}\right) p_{r}+\gamma p_{t}\nonumber \\&\quad =e^{-\lambda }\left[ \left\{ \frac{\lambda '}{r} -\frac{\mu '^{2}}{4}-\frac{\mu ''}{2}+\frac{\mu '\lambda '}{4}\right\} f_{1R}+\left( \frac{\mu '}{2}+\frac{2}{r}\right) \right. \nonumber \\&\qquad \times \, \left. f_{1R}' +\frac{e^{\lambda }f_{1}}{2}\right] , \end{aligned}$$
(12)
$$\begin{aligned}&\frac{\gamma }{2}\rho +\frac{\gamma }{2}p_{r}+(1+2\gamma )p_{t}\nonumber \\&\quad = e^{-\lambda }\left[ \left\{ \frac{\lambda '}{2r} -\frac{\mu '}{2r} -\frac{1}{r^{2}}+\frac{e^{\lambda }}{r^{2}}\right\} f_{1R}+\left( \frac{\mu '-\lambda '}{2}+\frac{1}{r}\right) \right. \nonumber \\&\qquad \times \, \left. f_{1R}' +f_{1R}''+\frac{e^{\lambda }f_{1}}{2}\right] . \end{aligned}$$
(13)

In order to discuss the anisotropic stellar system, we consider a relationship between matter variables of the fluid configuration which expresses the state of matter under some physical influences known as EoS. In compact objects, masses of white dwarfs are nearly equal to the solar mass and their radii are hundred times less than that of the Sun whereas the neutron stars can have masses upto \(3M_{\odot }\) or twice as that of the Sun [41]. In white dwarfs, the attractive gravitational force is balanced by the degeneracy pressure of electrons while in neutron stars, neutrons play their role to balance the degeneracy pressure. Neutron stars are the most exotic objects and if they are dense enough then they can be further collapsed to form a black hole whereas lesser dense neutron stars turn into quark stars. The conversion of neutron stars into quark stars has been studied in literature [42,43,44]. The hypothetical forms of neutron stars possessed by up, down and strange quark flavors are termed as quark stars. These stars are extremely dense as well as small and possess a very high gravitational field.

In the relativistic modeling of quark stars, we assume that the fluid distribution in the interior of these stars is influenced by MIT bag model EoS [7, 8]. The quark pressure is defined as follows

$$\begin{aligned} p_{r}=\sum _{\begin{array}{c} i=u,d,s \end{array}}p^{i}-\mathfrak {B}. \end{aligned}$$
(14)

Here, \(p^{i}\) represents the respective pressure of up (u), down (d) and strange (s) quark flavors whereas \(\mathfrak {B}\) is a constant known as bag constant. The individual quark pressure is related with the energy density of respective quark flavor as \(p^{i}=\frac{1}{3}\rho ^{i}\). Thus, the energy density is presented by

$$\begin{aligned} \rho =\sum _{\begin{array}{c} i=u,d,s \end{array}}\rho ^{i}+\mathfrak {B}. \end{aligned}$$
(15)

From Eqs. (14) and (15), the MIT bag model EoS for quark matter is constructed as

$$\begin{aligned} p_{r}=\frac{1}{3}(\rho -4\mathfrak {B}). \end{aligned}$$
(16)

It is observed that in the framework of GR as well as in modified theories, several researchers have successfully used the simplified form of this EoS to analyze the features of quark star candidates. In order to investigate the physical properties of compact relativistic objects, Krori–Barua solutions have gained much attention during the last few years due to singularity free solutions. These solutions provide a convincing as well as realistic method in the study of stellar evolution defined as [45]

$$\begin{aligned} \mu (r)=\mathcal {B}r^{2}+\mathcal {C}, \quad \lambda (r)=\mathcal {A}r^{2}, \end{aligned}$$

where \(\mathcal {A}\), \(\mathcal {B}\) and \(\mathcal {C}\) are unknown constants that can be evaluated by means of some observational values of quark star candidates. In the framework of these solutions, Eqs. (11)–(13) along with (16) turn out to be

$$\begin{aligned} \rho= & {} \frac{3e^{-\mathcal {A}r^{2}}}{4(1+\gamma )} \left[ \phantom {r(\mathcal {A} +\mathcal {B})f_{1R}'-f_{1R}''}2(\mathcal {A}+\mathcal {B})f_{1R}\right. \nonumber \\&\left. +\,r(\mathcal {A} +\mathcal {B})f_{1R}'-f_{1R}''\right] +\mathfrak {B}, \end{aligned}$$
(17)
$$\begin{aligned} p_{r}= & {} \frac{e^{-\mathcal {A}r^{2}}}{4(1+\gamma )} \left[ \phantom {r(\mathcal {A} +\mathcal {B})f_{1R}'-f_{1R}''}2(\mathcal {A}+\mathcal {B})f_{1R}\right. \nonumber \\&\left. +\,r(\mathcal {A} +\mathcal {B})f_{1R}'-f_{1R}''\right] -\mathfrak {B}, \end{aligned}$$
(18)
$$\begin{aligned} p_{t}= & {} \frac{e^{-\mathcal {A}r^{2}}}{2(1+\gamma )(1+2\gamma )} \left[ \left\{ 2(\mathcal {A}-\mathcal {B})\right. \right. \nonumber \\&\left. \left. -\,2(1+\gamma ) \left( \frac{1-e^{\mathcal {A}r^{2}}}{r^{2}}\right) \right. \right. \nonumber \\&+\,\left. \left. \gamma (\mathcal {A} -3\mathcal {B})\right\} f_{1R} +\left\{ 2r(\mathcal {B} -\mathcal {A})\right. \right. \nonumber \\&\left. \left. +\,\frac{2(1+\gamma )}{r}+\gamma r(\mathcal {B} -3\mathcal {A})\right\} \right. \nonumber \\&\times \,\left. f_{1R}' +(2+3\gamma )f_{1R}''+(1+\gamma )e^{\mathcal {A}r^{2}}f_{1}\right] . \end{aligned}$$
(19)

Now, we analyze the influence of a viable f(R, T) model on the structure evolution and stability of relativistic compact objects in the context of some physical observations. Different models of f(R, T) gravity can be served as mathematical tools to investigate various hidden characteristics of gravitational dynamics at large scales. The dynamics present in this gravity contain extension of T that describe more extended form of GR as compared to f(R) gravity. In general, a viable and compatible model depicts the selection of model parameters whose values will be according to the observational data. The choice of such astrophysical functional forms depends upon their cosmological consistency that must be fulfilled to satisfy solar system tests. Depending upon the choice of \(f_{1}(R)\) given in Eq. (10), one can formulate different f(R, T) models.

In this work, we consider the extension of quadratic R which was initially suggested by Starobinsky [46]. Using this modification, the f(R, T) model (10) becomes

$$\begin{aligned} f(R,T)=R+\sigma R^{2}+\gamma T, \end{aligned}$$
(20)

where \(\sigma \) is an arbitrary constant. This model successfully interprets the current exponential increase of the expanding cosmos and can be analyzed as an alternative candidate for DE. Inserting \(\sigma =0=\gamma \) in this model, the field equations of GR can be retrieved. This model has widely been found in literature to discuss the stellar evolution as well as gravitational collapse. Moraes et al. [47] formulated this model and found that this functional form efficiently illustrates the cosmological scenario of a radiation-dominated universe. Sharif and Siddiqa [38] discussed spherically symmetric stellar structure using polytropic as well as MIT bag model EoS for this functional form.

In the following section, we explain some physical conditions which have significant importance in analyzing the interior region of stellar models.

3 Physical conditions

In order to observe the nature as well as exact composition of charged compact stars, there must be a direct relation between the interior and exterior geometries of stars. For this purpose, we have taken the Schwarzschild metric which well describes the exterior region of compact stars given as

$$\begin{aligned} ds^{2}_{+}= & {} \left( 1-\frac{2M}{r}\right) dt^{2} -\frac{1}{\left( 1-\frac{2M}{r}\right) }dr^{2}\nonumber \\&-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(21)

where M represents total mass within the boundary \((r=\mathcal {R})\) of compact star. At the boundary surface between the interior and exterior metrics of compact stars, the continuity of spacetime variables \(g_{tt}\), \(g_{rr}\) and \(g_{tt,r}\) yields the following constraints

$$\begin{aligned} g_{tt}= & {} e^{\mathcal {B}\mathcal {R}^{2}+\mathcal {C}}=1 -\frac{2M}{\mathcal {R}} , \end{aligned}$$
(22)
$$\begin{aligned} g_{rr}= & {} e^{\mathcal {-A}\mathcal {R}^{2}}= 1-\frac{2M}{\mathcal {R}}, \end{aligned}$$
(23)
$$\begin{aligned} \frac{\partial g_{tt}}{\partial r}= & {} \mathcal {B}\mathcal {R} e^{\mathcal {B}\mathcal {R}^{2} +\mathcal {C}}=\frac{M}{\mathcal {R}^{2}}. \end{aligned}$$
(24)

The expressions of unknown triplet \((\mathcal {A,B,C})\) in the combination of total mass and radius can be evaluated by solving Eqs. (22)–(24) which yield

$$\begin{aligned} \mathcal {A}= & {} \frac{-1}{\mathcal {R}^{2}}\ln \left( 1 -\frac{2M}{\mathcal {R}}\right) , \end{aligned}$$
(25)
$$\begin{aligned} \mathcal {B}= & {} \frac{1}{\mathcal {R}^{2}} \left( \frac{M}{\mathcal {R}} \right) \left( 1 -\frac{2M}{\mathcal {R}}\right) ^{-1}, \end{aligned}$$
(26)
$$\begin{aligned} \mathcal {C}= & {} \ln \left( 1-\frac{2M}{\mathcal {R}} \right) -\left( \frac{M}{\mathcal {R}} \right) \left( 1-\frac{2M}{\mathcal {R}}\right) ^{-1}. \end{aligned}$$
(27)
Table 1 Approximate values of unknown parameters \(\mathcal {A}\), \(\mathcal {B}\) and \(\mathfrak {B}\) for compact star candidates Her X-1, RXJ 1856-37, SAX J 1808.4-3658 and 4U 1820-30
Full size table

In stellar structure at the boundary surface \((r=\mathcal {R})\), the radial pressure vanishes leading to the following expression

$$\begin{aligned} p_{r}(r=\mathcal {R})= & {} \frac{e^{-2\mathcal {A}\mathcal {R}^{2}}}{2(1 +\gamma )} \left[ \phantom {\frac{4\mathcal {A}}{\mathcal {R}^{2}}}e^{\mathcal {A}\mathcal {R}^{2}} (\mathcal {A}+\mathcal {B}) \right. \nonumber \\&\left. +\,\sigma \left\{ \phantom {\frac{4\mathcal {A}}{\mathcal {R}^{2}}}8\mathcal {B}^{2} +12\mathcal {A}^{3}\mathcal {R}^{2}(2+\mathcal {B}\mathcal {R}^{2}) \right. \right. \\&+\,\left. \left. 8\mathcal {B}^{3} \mathcal {R}^{2}-4\mathcal {A}^{2}(7+14\mathcal {B}\mathcal {R}^{2}+\,2\mathcal {B}^{2}\mathcal {R}^{4}) \right. \right. \nonumber \\&\left. \left. -\, 12\left( \frac{1 -e^{\mathcal {A}\mathcal {R}^{2}}}{\mathcal {R}^{4}}\right) -\frac{4\mathcal {A}}{\mathcal {R}^{2}} \right. \right. \\&\times \,\left. \left. \left( 3 -4\mathcal {B}\mathcal {R}^{2} -2\mathcal {B}^{2}\mathcal {R}^{4} +\mathcal {B}^{3} \mathcal {R}^{6}\right) \phantom {{\frac{4\mathcal {A}}{\mathcal {R}^{2}}}}\right\} \right] -\mathfrak {B}=0. \end{aligned}$$

Using the values of \(\mathcal {A}\) and \(\mathcal {B}\) from Eqs. (25) and (26), the expression for bag constant is evaluated as

$$\begin{aligned} \mathfrak {B}= & {} \frac{M-(\mathcal {R}-2M)\ln (1-\frac{2M}{\mathcal {R}})}{2\mathcal {R}^{3}(1+\gamma )}\nonumber \\&-\, \frac{2\sigma }{\mathcal {R}^{6}(1+\gamma ) (2M-\mathcal {R})}\left[ \phantom {\left( 1 -\frac{2M}{\mathcal {R}}\right) }22M^{3} +6M\mathcal {R}^{2}\right. \nonumber \\&-\, \left. 22M^{2}\mathcal {R} +\ln \left( 1-\frac{2M}{\mathcal {R}}\right) \left\{ \phantom {\left( 1 -\frac{2M}{\mathcal {R}}\right) }35M^{3} -3\mathcal {R}^{3}\right. \right. \nonumber \\&\left. \left. -\, 50M^{2}\mathcal {R}+22M\mathcal {R}^{2}+(4M^{3} \right. \right. \nonumber \\&+\, \left. \left. 28M\mathcal {R}^{2} -30M^{2}\mathcal {R}-7\mathcal {R}^{3})\ln \left( 1 -\frac{2M}{\mathcal {R}}\right) \right. \right. \nonumber \\&\left. \left. +\, 3(3M-2\mathcal {R})(\mathcal {R} -2M)^{2} \times \ln \left( 1 -\frac{2M}{\mathcal {R}}\right) ^{2}\right\} \right] .\nonumber \\ \end{aligned}$$
(28)

For \(\sigma =0\), this expression reduces to the bag constant for the simplest \(R+2\gamma T\) gravity model [40]. Here, the values of \(\mathcal {A}\), \(\mathcal {B}\) and \(\mathfrak {B}\) can be evaluated using the values of masses and radii of strange star candidates given in [48,49,50]. These stellar objects are consistent with the bound suggested by Buchdahl, i.e., the values of \(\frac{2M}{\mathcal {R}}\) are less than \(\frac{8}{9}\) [51]. In order to evaluate the values of bag constant for our proposed stellar models, we take \(\sigma =15\) and \(\gamma =8\). The evolution of stellar structures has been analyzed successfully using these values of model parameters. In Table 1, we have demonstrated the values of \(\mathcal {A}\), \(\mathcal {B}\) and \(\mathfrak {B}\) with respect to the radii and masses of considered stellar models.

It would be interesting to mention here that the values of bag constant obtained by considering the values of radii and masses strange quark stars candidates are 180.44, 144.5, 192.3 and 209 Mev/fm\(^{3}\), respectively. These values are greater than the observed range of bag constant for stable quark stars. However, experimental results from CERN-SPS and RHIC show that a wide range of values of the bag constant is possible for a density dependent bag model [52].

4 Physical attributes of compact stars

This section studies various physical features of considered anisotropic dense stellar candidates. Substituting the observed data shown in Table 1 along with the proposed model (20), we obtain the values of matter variables. We explore the graphical behavior of energy density, radial as well as transverse pressures, energy conditions, anisotropic factor, compactness, redshift parameter and stability for chosen values of the model parameters. This graphical analysis may provide some mysterious realities in the context of both theoretical and astrophysical regimes.

4.1 Evolution of matter variables

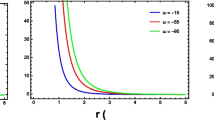
The densest nature of compact relativistic objects implies that the impact of energy density as well as pressure components inside the stellar system should be maximum. The variation of energy density, transverse and radial pressures in the interior of considered compact stars with respect to radial coordinate for our proposed model are presented in Fig. 1. These plots clearly indicate that at the center (\(r=0\)) of anisotropic compact objects, the energy density and pressure components show maximum values which lead to the presence of highly compact cores. It is also found that at the boundary surface, the radial ingredient of pressure vanishes, the density as well as pressure components are monotonically decreasing functions of radial coordinate and possess positive values inside the stars corresponding to the calculated values of bag constant. The consequences of these physical behavior provide a highly compact profile of considered stars that ensure the existence of anisotropic configuration of dense stars in f(R, T) gravity.

In all plots, blue color represents Her X-1, red color indicates RXJ 1856-37, magenta color expresses SAX J 1808.4-3658 star whereas the compact star model 4U 1820-30 is shown by green color.

Fig. 1
figure 1

Plots of energy density, radial pressure and transverse pressure versus r for different compact star candidates

Full size image

4.2 Energy conditions

In order to examine the presence of realistic matter distribution, there are physical properties known as energy conditions. These conditions play a crucial role to observe normal or exotic nature of matter inside the stellar model. These energy conditions are partitioned into null, dominant, strong and weak energy conditions. For curvature-matter coupled gravity, these conditions in the presence of anisotropic fluid are expressed as [53]

  • NEC: \(\rho + p_{r}-E\ge 0,\quad \rho + p_{t}-E\ge 0\),

  • DEC: \(\rho -p_{r}-E\ge 0,\quad \rho - p_{t}-E\ge 0\),

  • SEC: \(\rho + p_{r}-E\ge 0,\quad \rho + p_{t}-E\ge 0,\) \(\rho + p_{r}+ 2p_{t}-E\ge 0\),

  • WEC: \(\rho -E\ge 0,\quad \rho + p_{r}-E\ge 0, \quad \rho + p_{t}-E\ge 0\),

where \(E=\nabla _{\mu }(U^{\nu }\nabla _{\nu }U^{\mu })\) appears due to non-geodesic motion of massive particles and is given as

$$\begin{aligned} E=e^{-\lambda }\left( \frac{\mu ''}{2}+\frac{\mu '}{r} +\frac{\mu '^{2}}{4}-\frac{\mu '\lambda '}{4}\right) . \end{aligned}$$

Using Krori–Barua solutions in the expression of E, the energy conditions are plotted in Fig. 2. It is observed that all energy conditions are satisfied for considered compact stars which confirm the presence of normal matter in the interior region of quark star candidates. Hence the anisotropy as well as bag constant characterize the realistic origin of gravitational effects of stellar objects.

Fig. 2
figure 2

Plots of energy conditions for different compact star models

Full size image

4.3 Effect of anisotropy

To investigate the behavior of anisotropic pressure on the evolution of stellar structures, the anisotropic factor \((\Delta )\) using Eqs. (18) and (19) is calculated as

$$\begin{aligned} \Delta= & {} \frac{e^{-\mathcal {A}r^{2}}}{2(1+\gamma )(1+2\gamma )} \left[ \left\{ \phantom {\left( \frac{1 -e^{\mathcal {A}r^{2}}}{r^{2}}\right) }\mathcal {A}-3\mathcal {B} -\gamma (\mathcal {A} +5\mathcal {B})\right. \right. \nonumber \\&\left. -\, 2(1+\gamma )\left( \frac{1 -e^{\mathcal {A}r^{2}}}{r^{2}}\right) \right\} \times f_{1R} \nonumber \\&+\, \left\{ \frac{r}{2}(3\mathcal {B}-5\mathcal {A})-4\gamma r \mathcal {A}+\frac{2(1+\gamma )}{r}\right\} \nonumber \\&\left. \times \, f_{1R}' +\left( \frac{5}{2}+4\gamma \right) f_{1R}'' +(1+\gamma )e^{\mathcal {A}r^{2}}f_{1}\right] +\mathfrak {B}.\nonumber \\ \end{aligned}$$
(29)

Here, f is the generic function and on substituting its form from Eq. (20), we obtain the anisotropic factor in terms of \(\mathcal {A}\), \(\mathcal {B}\) and \(\mathfrak {B}\). We analyze the behavior of anisotropy graphically with the help of observational data of considered anisotropic compact stars presented in Table  1. If \(p_{t}> p_{r}\), then it leads to \(\Delta > 0\) which describes the outward directed anisotropic pressure whereas \(p_{t} < p_{r}\) yields \(\Delta < 0\) specifying that the anisotropic pressure is directed inward. The behavior of anisotropic measurement for compact star candidates corresponding to viable functional form of f(R, T) gravity is shown in Fig. 3. It is found that the variation of \(\Delta \) remains positive which depicts the presence of a repelling force that allows the evolution of more massive distribution in the interior geometry of stellar models.

4.4 Effective mass, compactness and surface redshift

Fig. 3
figure 3

Behavior of \(\Delta \) and \(M_{eff}\) for considered compact stars

Full size image

Here, we analyze the graphical behavior of effective mass, compactness factor and gravitational surface redshift. For static spherically symmetric stellar models governed by anisotropic fluid, Buchdahl [51] found a limit for the mass to radius ratio, i.e., \(\frac{2M}{\mathcal {R}}<\frac{8}{9}\). In the context of our proposed model, the effective mass is of the form

$$\begin{aligned} M_{eff}=\int _{0}^{\mathcal {R}}4\pi r^{2}\rho dr, \end{aligned}$$
(30)

where \(\rho \) is given in Eq. (17). Inserting the expression of \(\rho \) along with the proposed model in the above equation, the behavior of effective mass is presented in Fig. 3. From the graphical analysis of effective mass, it is observed that the maximum mass point \(2.5 M_{\odot }\) corresponding to MIT bag model EoS is obtained which is in well agreement with the predicted mass of compact stars. The mass to radius ratio, also known as compactness factor, is defined as

$$\begin{aligned} u_{eff}=\frac{M_{eff}}{\mathcal {R}}. \end{aligned}$$

The surface redshift plays a dynamic role to understand strong physical interaction between particles inside the star and its EoS. In the context of effective compactness factor, the surface redshift (\(z_{eff}\)) is of the form

$$\begin{aligned} z_{eff}=\frac{1}{\sqrt{1-2u_{eff}}}-1. \end{aligned}$$

The variation of compactness factor and surface redshift with respect to radial coordinate is expressed in Fig. 4 which vanishes at the center and increases towards the boundary surface of compact stars. It is also observed that in our proposed model, all stars satisfy the Buchdahl condition (\(\frac{2M}{\mathcal {R}}<\frac{8}{9}\)) and the maximum value of surface redshift is \(z_{eff}\le 5.211\) [54].

Fig. 4
figure 4

Behavior of \(u_{eff}\) and \(z_{eff}\) for different compact star candidates

Full size image
Fig. 5
figure 5

Variation of speed of sound versus r corresponding to MIT bag model EoS for different compact star candidates

Full size image

4.5 Analysis of stable structure

The stability of stellar structure has a vital role in analyzing physically consistent models. Such stellar objects are more fascinating to observe that represent stable behavior against external fluctuations. Thus the phenomenon of stability has gained much attention to study the evolution of stellar structures. Here, we examine the stability of our considered stars through the techniques of speed of sound \(v^{2}_{s}\) based on Herrera’s cracking concept [3] and adiabatic index. According to causality condition, the speed of sound defined by \(v^{2}_{s} = dp/d\rho \) should lie in the range [0, 1], i.e., \(0 \le v^{2}_{s} \le 1\) everywhere in the interior of stars for a physically stable stellar object. For anisotropic fluid, we have \(0\le v^{2}_{sr}\le 1\) and \(0\le v^{2}_{st}\le 1\), where \(v_{sr}\) and \(v_{st}\) indicate radial as well as transverse components of sound speed, respectively.

Herrera [3] presented the notion of cracking using a different approach to explore potentially stable/unstable structures of compact objects. The potentially stable/unstable regions are computed through the difference of sound speed in radial and transverse directions. If the difference between radial and transverse components of speed of sound is positive, then it leads to potentially stable regions whereas for unstable regions, their difference does not satisfy the inequality \(0 \le \mid v^{2}_{st}- v^{2}_{sr}\mid \le 1\). The stability analysis of our proposed stars corresponding to specific values of bag constant is shown in Fig. 5. It is found that \(0\le v^{2}_{sr}\le 1\), \(0\le v^{2}_{st}\le 1\) and \(0\le \mid v^{2}_{st}- v^{2}_{sr}\mid \le 1\).

The stiffness of the EoS for given energy density is characterized by adiabatic index which has significant importance to discuss the stability of relativistic as well as non-relativistic compact objects. Chandrasekhar (as a pioneer) [55] and many researchers [56,57,58] studied the dynamical stability against infinitesimal radial adiabatic perturbation of the stellar system. It is evaluated that the value of adiabatic index should be greater than \(\frac{4}{3}\) in the interior of a dynamically stable stellar object [56,57,58]. For anisotropic fluid, the expressions for adiabatic index is given by

$$\begin{aligned} \Gamma =\frac{\rho +p_{r}}{p_{r}}\left( dp_{r}/d\rho \right) . \end{aligned}$$

The graphical representation of adiabatic index is shown in Fig. 6 for MIT bag model EoS. This indicates that our considered compact star models show dynamical stable structure for the chosen values of coupling parameters \(\sigma \) and \(\gamma \) as the value of \(\Gamma \) \(>\frac{4}{3}\). This demonstrates that our considered anisotropic stellar models are within the stability range even in the existence of higher curvature terms present in f(R, T) functional form.

5 Concluding remarks

The coupling between matter and geometry components in alternative theories plays a crucial role to narrate the attractive issue of current cosmic accelerated expansion. In this context, the f(R, T) gravity provides a captivating perspective without including any mysterious energy component. The coupling effects of geometry and matter components in this theory yields the non-zero covariant derivative of EMT which is a dominant property to discuss the attributes of gravity at quantum level and examines the influence of non-geodesic motion of test particles.

This paper explores the impacts of anisotropy as well as MIT bag constant on physical attributes of four particular compact stars Her X-1, 4U 1820-30, RXJ 1856-37 and SAX J 1808.4-3658 in the framework of f(R, T) gravity. To analyze the influence of matter-curvature coupling present in a viable model on the evolution of anisotropic quark star candidates, we have considered that the fluid distribution inside the stellar structure is computed through MIT bag model EoS. For the realistic modeling of compact stars, we have applied the Krori–Barua solutions in which the unknown constants \(\mathcal {A}\), \(\mathcal {B}\) and \(\mathcal {C}\) are evaluated through a smooth connection of interior and exterior geometries of anisotropic stellar models. Using the values of radii and masses of proposed compact star models, the values of \(\mathcal {A}\), \(\mathcal {B}\) and \(\mathfrak {B}\) are calculated for \(\sigma =15\) and \(\gamma =8\) (Table 1).

We have observed graphically the evolution of energy density, transverse and radial pressure components corresponding to particular value of the bag constant. It is observed that these physical quantities show finite as well as regular behavior in the interior of quark star candidates and the values of these quantities decrease towards the boundary of compact objects. It is also found that the radial pressure vanishes at \(r=0\). These graphical analysis confirm the presence of most dense stellar interiors.

Fig. 6
figure 6

Variation of adiabatic index versus r corresponding to MIT bag model EoS for different compact star candidates

Full size image

We have examined that all energy conditions are satisfied for different quark star candidates which ensure the existence of normal matter in the interior region of neutron stars. The effect of anisotropic factor is also analyzed, i.e., \(\Delta >0\), which leads to the presence of a repelling anisotropic force that permits the formulation of more massive configuration. We have obtained that the maximum value of effective mass is \(2.5 M_{\odot }\) which is in well agreement with the observed masses of quark star models. Similarly, the values of compactness factor and redshift parameter also lie within the required limits.

It is shown that the stability conditions are fulfilled and the inequality \(0 \le \mid v^{2}_{st}- v^{2}_{sr}\mid \le 1\) holds for all proposed compact stars which indicates that the potentially stable structure of compact stars exists. We have also examined the stability criteria through adiabatic index and found that the value of \(\Gamma \) is greater than \(\frac{4}{3}\) for all star models which depict the stability against an infinitesimal radial adiabatic perturbation. It is worth mentioning here that in the context of MIT bag model EoS, stellar objects show smooth and stable structures even in the presence of higher-curvature terms in f(R, T) gravity that indicates the viability of our proposed f(R, T) functional form (20).