Collapse of the wavefunction, the information paradox and backreaction

Abstract

We consider the black hole information problem within the context of collapse theories in a scheme that allows the incorporation of the backreaction to the Hawking radiation. We explore the issue in a setting of the two dimensional version of black hole evaporation known as the Russo-Susskind-Thorlacius model. We summarize the general ideas based on the semiclassical version of Einstein’s equations and then discuss specific modifications that are required in the context of collapse theories when applied to this model.

1 Introduction

The black hole information question has been with us for more than four decades, ever since Hawking’s discovery that black holes emit thermal radiation and therefore evaporate, leading either to their complete disappearance or to a small Planck mass scale remnant [1]. The basic issue can be best illustrated by considering an initial setting where an essentially flat space-time in which a single quantum field is in a pure quantum state of relative high excitation corresponding to a spatial concentration of energy, that, when left on its own will, collapses gravitationally leading to the formation of a black hole. As the black hole evaporates, the energy that was initially localized in a small spatial region, ends up in the form of Hawking radiation that, for much of this evolution must be almost exactly thermal [2]. The point, of course, is that if this process ends with the complete evaporation of the black hole (or even if a small remnant is left) the overwhelming majority of the initial energy content would correspond to a state of the quantum field possessing almost no information (except that encoded in the radiation’s temperature) and it is very difficult to reconcile this with the general expectation that in any quantum process the initial and final states should be related by a unitary transformation, and thus all information encoded in the initial state must be somehow present in the final one. The issue, of course, is far more subtle and the above should be taken as only a approximate account of the problem.

There have been many attempts to deal with this conundrum, with none of them resulting in a truly satisfactory resolution of the problem [3, 4]. In fact there is even a debate as to the extent to which this is indeed a problem or as some people like to call it a “paradox” [5, 6].

In previous works [7,8,9] we helped to clarify the basis of the dispute, and proposed a scheme where the resolution of the issue is tied to a proposal to address another lingering problem of theoretical physics: the so called measurement problem [10] in quantum theory.

The first task was dealt with [7,8,9] by noting that the true problem arises only when one takes the point of view that a satisfactory theory of quantum gravity must resolve the singularity, and that, as a result of such resolution, there will be no need to introduce a new boundary of space-time in the region where the classical black hole singularity stood. Otherwise the problem can be fully understood by noting that the region in the black hole exterior, at late times corresponding to those where most of the energy takes the form of thermal Hawking radiation, contains no Cauchy hypersurfaces and thus any attempt to provide a full description of the quantum state in terms of the quantum field modes in the black hole exterior is simply wrongheaded. In order to provide a complete description of such late quantum state one needs to include the modes that register on the part of the Cauchy hypersurface that goes deep into the black hole interior, in particular one that treads close to the singularity, as described in detail in [5].

The second task was carried out by considering the application of one particular dynamical collapse theory designed to address the measurement problem in quantum theory, to a simple two dimensional black hole model known as the Callan-Giddings-Harvey-Strominger (CGHS) model [11]. The proposal was then to associate to the intrinsic breakdown of unitary evolution, which is typical of these dynamical collapse theories [12,13,14,15,16,17,18], (which were developed to deal with the measurement problem in standard quantum mechanics) all the information loss that takes place during the formation and subsequent Hawking evaporation of the black hole. The first concrete treatments along this line are [19, 20].

In those works we noted that the treatment at that point left various issues to be worked out, and that substantial progress in those would be required before the proposal could be considered to be fully satisfactory. Among these issues that two most pressing ones are the replacement of the treatment presented, by one that is fully consistent with relativistic covariance, and to show how the important question of back reaction due to Hawking radiation on the spacetime and vice-versa can be incorporated in such a scheme (i.e., in presence of the collapse of wavefunction type setting). A first step in this direction was accomplished in [21] where the simple two dimensional problem is considered using a relativistic version of collapse theories.

The objective of the present work is to continue the research path initiated in [19,20,21,22] and explore an example where the remaining issue of backreaction in the setting of collapse theories. For this we will again consider a two dimensional black hole model known due to Russo-Susskind-Thorlacius (RST) [23, 24] which presents a solution of the semiclassical (Einstein) equation in 2D.

The paper is organized as follows: We start by reviewing the semi-classical CGHS model in Sect. 2 and then move to the RST model in Sect. 3 and discuss the quantization of matter fields on RST in Sect. 4. It is important to emphasize that all those sections contain nothing novel and represent just a review, which is however needed in order to make sense of what follows. Section 5 contains necessary ingredients for the adaptation of collapse of the wave-function in a general setting as well as for the specific case of 2D RST model. In Sect. 6 we discuss the Hawking radiation and the information paradox. There are two appendices (A and B) discussing important issues related with the renormalization of the energy-momentum tensor and a specific example of the treatment of back reaction of the space-time metric (and dilaton field) to a discrete collapse of the wave-function.

2 Semiclassical CGHS model with backreaction

A natural way to incorporate backreaction effects of a quantum field on the background geometry is to modify the Einstein equations where the expectation value of the stress tensor is included on the right hand side of the equations of motion (E.O.M), so that,

$$\begin{aligned} G_{ab} = T_{ab}^{Class} + \langle {\Psi }| T_{ab} |{\Psi } \rangle , \end{aligned}$$

(1)

where $G_{ab}$ is the Einstein tensor of the classical metric, $T_{ab}^{Class}$ represents the energy-momentum tensor of whatever matter is being described at the classical level, and $\langle {\Psi }| T_{ab} |{\Psi } \rangle$ is the renormalized expectation value of the energy-momentum tensor of the matter fields that are treated quantum mechanically, evaluated in the corresponding quantum state $|\Psi \rangle$ of such fields.

In the two dimensional CGHS model with a single freely propagating massless scalar field, characterized by the action [11]:

$$\begin{aligned} S_{CGHS}= & {} \frac{1}{2\pi } \int {d^2x \sqrt{-g}[e^{-2\phi } (R + 4(\nabla \phi )^2 + 4\Lambda ^2) - (\nabla f)^2]}, \nonumber \\ \end{aligned}$$

(2)

where $\Lambda$ is a constant. The dilaton field $\phi$ is usually treated classically, and the scalar field f is treated quantum mechanically.

Working in the conformal gauge with null coordinates the metric is described by:

$$\begin{aligned} ds^2 = -e^{2\rho } dx^+ dx^-. \end{aligned}$$

(3)

The semiclassical E.O.M involve now the energy-momentum contribution from the classical dilaton field and the cosmological constant as well as the part coming from the expectation value of the quantum field f. Those take now the following form (with respect to the appropriate variation mentioned on the left)

$$\begin{aligned} \rho&: e^{-2\phi } \left( 2\partial _{x^+}\partial _{x^-}\phi - 4\partial _{x^+}\phi \partial _{x^-}\phi - \Lambda ^2e^{2\rho }\right) \nonumber \\&- \langle {\Psi }| T_{x^+ x^-} |{\Psi } \rangle = 0 , \end{aligned}$$

(4)

$$\begin{aligned} g^{\pm \pm }&: e^{-2\phi } \left( -2\partial _{x^\pm }^2\phi + 4\partial _{x^\pm }\rho \partial _{x^\pm }\phi \right) \nonumber \\&+ \langle {\Psi }| T_{x^\pm x^\pm } |{\Psi } \rangle = 0 , \end{aligned}$$

(5)

$$\begin{aligned} \phi&: 2e^{-2\phi }\partial _{x^+}\partial _{x^-}(\rho -\phi ) + \partial _{x^+}\partial _{x^-}e^{-2\phi } \nonumber \\&+ \Lambda ^2e^{2(\rho -\phi )} = 0 . \end{aligned}$$

(6)

Note that even though the unperturbed metric has $g^{\pm \pm } =0$ the general variations do not share this property in these coordinates, and their consideration results in Eq. (5).

In order to solve the above differential equations, it is necessary to calculate the expectation value of various components of the renormalized energy-momentum tensor in a particular state of the quantum field denoted by $|{\Psi }\rangle$. The state is usually taken to be the “in vacuum state”. We review this calculation, from a slightly different perspective that the usual one, in Appendix A.

One interesting feature of the Eqs. (4)–(6), is that one can write down a formal action, given by

$$\begin{aligned} S = S_{CGHS} + S_P, \end{aligned}$$

(7)

where $S_P$ is the Polyakov effective action [25]

$$\begin{aligned} S_{P} = -\frac{\hbar }{96\pi } \int d^2x \sqrt{-g} R \frac{1}{\Box } R, \end{aligned}$$

(8)

and whose variation leads to the same set of Eqs. (4)–(6). This is because, in the effective action formalism, the expectation value of the renormalized energy-momentum tensor corresponding to the quantum field ${\hat{f}}$, is given by the derivative of the Polyakov term

$$\begin{aligned}&-\frac{2}{\sqrt{-g}} \frac{\delta S_P}{\delta g^{ab}} = \langle \psi |T_{ab}|\psi \rangle \nonumber \\&\quad = -\frac{\hbar }{48\pi }\left[ \nabla _a\xi \nabla _b\xi - 2\nabla _a\nabla _b\xi + g_{ab}\left( 2R - \frac{1}{2}\nabla _c\xi \nabla ^c\xi \right) \right] , \nonumber \\ \end{aligned}$$

(9)

where $\xi$ is an auxiliary scalar field constrained to obey the equation $\Box \xi =R$ and $|\psi \rangle$ is the state of the quantum (scalar) field. We note that the freedom in the choice of the quantum state, correspond, in the effective action treatment, to the freedom of choice of boundary conditions for the solution $\xi$. We refer the interested reader to [26] for more discussions on the effective action formalism.

This is a very delicate issue that can generate serious confusion in our approach, and care must be taken to ensure one goes back and forth from the two formalism in a consistent manner. We will have to do so in particular if we want to consider the changes in the quantum states of the ${\hat{f}}$ field (for which the treatment without the effective action is more convenient) and at the same time consider explicitly solving for the spacetime metric and dilaton field (for which the reliance on the effective action is most suitable). We will explore this issue in detail in section V.A. and appendix B. In the meanwhile we return to the review of the original RST model.

It has been found difficult to solve the set of differential Eqs. (4)–(6) without a numerical handle. The advantage of using “effective action formalism” is that it allows one to play with the E.O.M without going into a rigorous quantum field theory calculation, and indeed that approach was subsequently exploited in Russo-Susskind-Thorlacius (RST) [23], where a local term was added in (7), allowing one to solve the new semiclassical equations analytically. We review this model in the next section.

3 Review of the RST Model

In the RST model a local term is added to the CGHS and Polyakov actions such that the complete action, with a scalar field f, which are however, treated via an effective term , is given by [23, 26]

$$\begin{aligned} S = S_{CGHS} + S_{P} + S_{RST}, \end{aligned}$$

(10)

where $S_{CGHS}$ is given by (2), $S_P$ is (8) and the local term is

$$\begin{aligned} S_{RST} = -\frac{\hbar }{48\pi } \int {d^2x\sqrt{-g}~\phi R}, \end{aligned}$$

(11)

which adds a direct coupling between the dilaton and the Ricci scalar. Again, the above scheme should be seen as effectively characterizing a model where the Polyakov term replaces quantum effects of the massless scalar field.

3.1 Equations of motion

Next we present the equations of motion that result from the model’s action (10).

Varying (10) with respect to $g^{ab}$ we obtain

$$\begin{aligned}&e^{-2\phi } \left[ - 2\nabla _a \nabla _b \phi + \frac{1}{2} g_{ab} (- 4 (\nabla \phi )^2 + 4\nabla ^2\phi + 4\Lambda ^2)\right] \end{aligned}$$

(12)

$$\begin{aligned}&\quad = \frac{ \hbar }{48\pi }\left( \nabla _a\xi \nabla _b\xi - \frac{1}{2} g_{ab} (\nabla \xi )^2\right) \nonumber \\&\quad -\frac{N \hbar }{24\pi } (\nabla _a\nabla _b\xi - g_{ab}\Box \xi ) -\frac{ \hbar }{24\pi } (\nabla _a\nabla _b\phi - g_{ab}\Box \phi ),\nonumber \\ \end{aligned}$$

(13)

On the other hand the E. O. M. for $\phi$ is:

$$\begin{aligned} e^{-2\phi } \left[ -2R - 8\Lambda ^2 + 8 (\nabla \phi )^2 - 8\nabla ^2\phi \right] -\frac{\hbar }{24\pi }R = 0.\nonumber \\ \end{aligned}$$

(14)

In 2D conformal gauge¹ the above equations take the following form (with respect to the appropriate variations indicated below):

$$\begin{aligned} \rho&: e^{-2\phi } \left( 2\partial _{x^+}\partial _{x^-}\phi - 4\partial _{x^+}\phi \partial _{x^-}\phi - \Lambda ^2e^{2\rho }\right) \nonumber \\&+\frac{\hbar }{12\pi }\partial _{x^+}\partial _{x^-}\rho + \frac{\hbar }{24\pi } \partial _{x^+}\partial _{x^-}\phi = 0, \end{aligned}$$

(15)

$$\begin{aligned} g^{\pm \pm }&: \left( e^{-2\phi }- \frac{\hbar }{48\pi }\right) \left( -2\partial _{x^{\pm }}^2\phi + 4\partial _{x^{\pm }}\rho \partial _{x^{\pm }}\phi \right) \nonumber \\&+ \langle {\Psi }| T_{x^{\pm \pm }} |{\Psi } \rangle = 0 , \end{aligned}$$

(16)

$$\begin{aligned} \phi&: 2e^{-2\phi }\partial _{x^+}\partial _{x^-}(\rho -\phi ) + \partial _{x^+}\partial _{x^-}e^{-2\phi } \nonumber \\&+ \Lambda ^2e^{2(\rho -\phi )} + \frac{\hbar }{24\pi }\partial _{x^+}\partial _{x^-}\rho = 0, \end{aligned}$$

(17)

where the expectation values of the energy-momentum tensor are those found in (97) and (98). The only choice yet to implement is the selection of a particular state $|\Psi \rangle$ to solve the above set of equations. An important feature of these equations is that if one uses (15) and (17) one still finds the “free field equation”:

$$\begin{aligned} \partial _{x^+}\partial _{x^-}(\rho -\phi )=0, \end{aligned}$$

(18)

which is typical of the CGHS model without backreaction. This feature is what in this model facilitates the finding of a specific solution for the spacetime geometry in presence of backreaction.

3.2 Solving semiclassical equations

It is convenient to introduce the new variables [23]

$$\begin{aligned} \Omega\equiv & {} \frac{\sqrt{\kappa }}{2}\phi +\frac{e^{-2\phi }}{\sqrt{\kappa }}, \end{aligned}$$

(19)

$$\begin{aligned} \chi\equiv & {} \sqrt{\kappa }\rho -\frac{\sqrt{\kappa }}{2}\phi +\frac{e^{-2\phi }}{\sqrt{\kappa }}, \end{aligned}$$

(20)

where $\kappa =\frac{\hbar }{12\pi }$.

In these variables (15)–(17) take the following form

$$\begin{aligned}&\partial _{x^+}\partial _{x^-}\Omega =-\frac{\Lambda ^2}{\sqrt{\kappa }}e^{\frac{2}{\sqrt{\kappa }}(\chi -\Omega )}, \end{aligned}$$

(21)

$$\begin{aligned}&\partial _{x^+}\partial _{x^-}\chi =-\frac{\Lambda ^2}{\sqrt{\kappa }}e^{\frac{2}{\sqrt{\kappa }}(\chi -\Omega )}, \end{aligned}$$

(22)

$$\begin{aligned}&-\partial _{x^\pm }\chi \partial _{x^\pm }\chi +\sqrt{\kappa }\partial ^{2}_{x^\pm }\chi +\partial _{x^\pm }\Omega \partial _{x^\pm }\Omega \nonumber \\&\quad - \frac{\kappa }{4x^{\pm ^2}}+\langle \Psi |:T_{x^\pm x^\pm }:_{in}|\Psi \rangle =0, \end{aligned}$$

(23)

whereas the free field Eq. (18) becomes

$$\begin{aligned} \partial _{x^+}\partial _{x^-}(\chi -\Omega )=0. \end{aligned}$$

(24)

The above equation allows us to write

$$\begin{aligned} \chi -\Omega =\frac{\sqrt{\kappa }}{2}\left( W_{+}(x^+)+W_{-}(x^-)\right) , \end{aligned}$$

(25)

where $W_{+}$ and $W_{-}$ are arbitrary functions of $x^{+}$ and $x^{-}$ respectively. Then (21) and (22) become

$$\begin{aligned} \partial _{x^+}\partial _{x^-}\chi =-\frac{\Lambda ^2}{\sqrt{\kappa }}e^{W_{+}+W_{-}} \end{aligned}$$

(26)

and

$$\begin{aligned} \partial _{x^+}\partial _{x^-}\Omega =-\frac{\Lambda ^2}{\sqrt{\kappa }}e^{W_{+}+W_{-}}. \end{aligned}$$

(27)

In the RST model one restricts oneself to the choice $\Omega = \chi$, i.e., $W_{+} = 0 = W_{-}$ and then the solution is found to be

$$\begin{aligned} \Omega = \chi = D-\frac{\Lambda ^2 x^+ x^-}{\sqrt{\kappa }}-\frac{F(x^+)+G(x^-)}{\sqrt{\kappa }}, \end{aligned}$$

(28)

where D is an arbitrary constant and the functions $F(x^+)$, $G(x^-)$ can be found by substituting (28) in (23) and integrating

$$\begin{aligned} F(x^+)= & {} \int ^{x^+}dx'^+\int ^{x'^+}dx''^+ \nonumber \\&\times \left( -\frac{1}{4x^{+2}} + \langle \Psi |:T_{x^{+} x^{+}} (x''^{+}):_{in}|\Psi \rangle \right) , \end{aligned}$$

(29)

$$\begin{aligned} G(x^-)= & {} \int ^{x^-}dx'^-\int ^{x'^-}dx''^{-} \nonumber \\&\times \left( - \frac{1}{4x^{-2}} + \langle \Psi |:T_{x^{-}x^{-}} (x''^{-}) :_{in}|\Psi \rangle \right) . \end{aligned}$$

(30)

Now using these expressions one can find particular solutions depending on the choice for the state of the quantum field ($|\Psi \rangle$). Specifically, we will focus on those ones which correspond to solutions representing the formation and evolution of black holes.

For future convenience let us note that in new variables the Ricci scalar, $R=8e^{-2\rho }\partial _{+}\partial _{-}\rho$ turns out to be

$$\begin{aligned} R=\frac{8e^{-2\rho }}{\Omega '}\left( \partial _{+}\partial _{-}\chi -\frac{\Omega ''}{\Omega '^2}\partial _{+}\Omega \partial _{-}\Omega \right) , \end{aligned}$$

(31)

where

$$\begin{aligned} \Omega '\equiv \frac{d\Omega }{d\phi }=\frac{\sqrt{\kappa }}{2}-\frac{2}{\sqrt{\kappa }}e^{-2\phi }. \end{aligned}$$

(32)

3.3 Dynamical case of black hole formation and evaporation

Now we will consider the case where a sharp pulse of matter forms a black hole. This pulse can be well approximated by choosing $|\Psi \rangle$ to be a coherent state build on top of the in vacuum, corresponding to a wave packet peaked around a particular classical value. In particular, we only need a left moving pulse to create a black hole, therefore, we can chose $|\Psi \rangle = |Pulse\rangle ^{L}\otimes |0_{in}\rangle ^R$ where $|Pulse\rangle ^{L} = \hat{\mathcal{O}} |0_{in}\rangle ^{L}$ with $\hat{\mathcal{O}}$ a suitable creation operator for the sharply peaked wave packet. In this case the state dependent functions turns out to be

$$\begin{aligned}&\langle \Psi |:T_{x^+ x^+}:_{in}|\Psi \rangle =\frac{m}{\Lambda x_{0}^+}\delta \left( x^+ -x_{0}^+\right) , \end{aligned}$$

(33)

$$\begin{aligned}&\quad \langle \Psi |:T_{x^- x^-}:_{in}|\Psi \rangle = 0. \end{aligned}$$

(34)

This choice when used in (28) leads to the following solution

$$\begin{aligned} \chi= & {} \Omega =-\frac{\Lambda ^2x^+x^-}{\sqrt{\kappa }}-\frac{\sqrt{\kappa }}{4}\ln \left( -\Lambda ^2x^+x^-\right) \nonumber \\&-\frac{m}{\Lambda \sqrt{\kappa }x_{0}^+}\left( x^+-x_{0}^+\right) \theta \left( x^+-x_{0}^+\right) . \end{aligned}$$

(35)

This solution contains a singularity. To see this we refer to Eqs. (31) and (32). The singularity occurs when $\Omega ' = 0$ and (32) gives $e^{-2\phi _{s}} = \frac{\kappa }{4}$. As we have restricted ourselves to the case $\rho =\phi$, one can use the relation (20), to find the value of $\Omega _s = \frac{\sqrt{\kappa }}{4}(1-\ln \frac{\kappa }{4})$ associated with the singularity. Therefore the location of the singularity turns out to be:

$$\begin{aligned}- & {} \frac{\Lambda ^2x^+}{\sqrt{\kappa }}\left( x^- +\frac{m}{\Lambda ^3x_{0}^+}\right) -\frac{\sqrt{\kappa }}{4}\ln \left( -\Lambda ^2x^+x^-\right) + \frac{m}{\Lambda \sqrt{\kappa }}\nonumber \\&\quad =\frac{\sqrt{\kappa }}{4}\left( 1-\ln \frac{\kappa }{4}\right) . \end{aligned}$$

(36)

This singularity is hidden by the apparent horizon located at $\partial _{+}\phi =0$ which is given by

$$\begin{aligned} -\Lambda ^2x^+\left( x^- +\frac{m}{\Lambda ^3x_{0}^+}\right) =\frac{\kappa }{4}. \end{aligned}$$

(37)

The apparent horizon and the singularity meet at

$$\begin{aligned} x_{s}^+= & {} \frac{\kappa \Lambda x_{0}^+}{4m}(e^{\frac{4m}{\kappa \Lambda }}-1), \end{aligned}$$

(38)

$$\begin{aligned} x_{s}^-= & {} -\frac{m}{\Lambda ^3x_{0}^+}\frac{1}{\left( 1-e^{-\frac{4m}{\kappa \Lambda }}\right) }. \end{aligned}$$

(39)

The physical meaning of this point is that it could be interpreted as the end point of the black hole evaporation [23]. This is confirmed by the fact that at $x^-=x_{s}^-$ the solution (35) with $x^+ > x_0^+$ takes the form

$$\begin{aligned} \chi= & {} \Omega = -\frac{\Lambda ^2x^+}{\sqrt{\kappa }}\left( x_{s}^- +\frac{m}{\Lambda ^3x_{0}^+}\right) \nonumber \\&-\frac{\sqrt{\kappa }}{4}\ln \left( -\Lambda ^2x^+\left( x_{s}^- +\frac{m}{\Lambda ^3x_{0}^+}\right) \right) , \end{aligned}$$

(40)

which is nothing but the vacuum configuration, commonly known as the linear dilaton vacuum (L. D. V.).

Thus the spacetime for $x^+ > x_{s}^+$ is given by

$$\begin{aligned} \chi= & {} \Omega =-\frac{\Lambda ^2x^+}{\sqrt{\kappa }}\left( x^- +\frac{m}{\Lambda ^3x_{0}^+}\right) \nonumber \\&+\left[ -\frac{\sqrt{\kappa }}{4}\ln \left( -\Lambda ^2x^+x^-\right) +\frac{m}{\Lambda \sqrt{\kappa }}\right] \theta \left( x_{s}^- -x^-\right) \nonumber \\&- \frac{\sqrt{\kappa }}{4}\ln \left( -\Lambda ^2x^+\left( x^- +\frac{m}{\Lambda ^3x_{0}^+}\right) \right) \theta \left( x^- -x_{s}^-\right) . \nonumber \\ \end{aligned}$$

(41)

Fig. 1

RST spacetime in Kruskal coordinates where a black hole is created due to the matter collapse and evaporated due to the Hawking effect

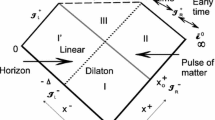
Now we can construct the complete spacetime metric so that for $x^+ < x_s^+$ one has (35) and for $x^+ \ge x_s^+$ the appropriate expression of the metric is given by (41). We show the overall spacetime in Kruskal coordinates in Fig. 1. Note that there are two different linear dilaton vacuums—(1) for $x^+ <x_0^+$ and (2) for $x^+ \ge x_{s}^{+},~ x^- \ge x_s^-$. These L. D. V. s are glued together with the black hole regions (Reg. I and II) by the pulse of matter (for L. D. V.-I) and radiation (for L. D. V.-II). The pulse of the matter at $x^+ =x_0^+$ carries positive energy and forms the black hole, whereas, the pulse of the radiation at $x^- = x_s^- , ~ x^+ \ge x_s^+$ carries negative energy associated with the singularity and usually called thunderpop. The space-time metric, although, is continuous at those gluing points but clearly it is not differentiable.

The Penrose diagram of the RST spacetime can be constructed following Ref. [27]. The asymptotic past and future regions are specified with respect to the Minkowskian coordinates. First, in the asymptotic past, where the metric corresponds to a linear dilaton vacuum, so that, $ds^2 = \frac{1}{\Lambda ^2 x^+ x^-}$, one can use the coordinates,

$$\begin{aligned} y^+= & {} \frac{1}{\Lambda } \ln (\Lambda x^+) - y_0^+, \end{aligned}$$

(42)

$$\begin{aligned} y^-= & {} -\frac{1}{\Lambda } \ln (-\Lambda x^-) \end{aligned}$$

(43)

to write $ds^2 = -dy^+ dy^-$, where $y_0^+$ is introduced to set the origin of the coordinates $y^+$.

Fig. 2

Penrose diagram for RST spacetime where a black hole is created due to the matter collapse and evaporated due to the Hawking effect

There is also a subtle issue regarding the extensions of the linear dilaton vacuum regions. The expression for the for the Ricci scalar (31) implies that at $\Omega '=0$ it diverges. Since even in the linear dilaton vacuum regions this value can be reached one has to put some boundary conditions so that such an artifact does not show up in the solution [23]. In the literature this issue is bypassed by putting reflecting boundary conditions there. The conformal/Penrose diagram for the RST model is given by Fig. 2. For a discussion about the boundary conditions to make finite curvature in $\Omega _{crit}$ see [24].

Let us now consider the asymptotic structure of the spacetime. Particularly we want to check the asymptotic behavior and viability of defining $\mathcal{J}^+$. Let us focus on the metric in Reg. I and Reg. II (inside and outside the black hole apparent horizon), given by

$$\begin{aligned} \chi= & {} \Omega = -\frac{\Lambda ^2 x^+}{\sqrt{\kappa }} \left( x^- + \frac{m}{\Lambda ^3 x_0^+}\right) \nonumber \\&- \frac{\sqrt{\kappa }}{4}\ln (-\Lambda ^2 x^+ x^-) + \frac{m}{\Lambda \sqrt{\kappa }}. \end{aligned}$$

(44)

If we want to find out the physical metric coefficient in the conformal gauge (3) we need to use the relations (20) and (20). By using those we obtain the following equation

$$\begin{aligned} \frac{\sqrt{\kappa }}{2}\rho +\frac{e^{-2\rho }}{\sqrt{\kappa }} - \Omega = 0, \end{aligned}$$

(45)

whose solution determines $\rho$. However, practically this equation is not invertible and therefore we cannot find an exact solution for $\rho$ from the known expression of $\Omega$. But we can perform certain analysis to unfold the asymptotic behavior. First, we check the staticity of the metric by expressing (44) in the standard Schwarzschild like coordinates (t,  r). These are related with Kruskal ($x^{\pm }$) coordinates in the following way

$$\begin{aligned} x^+= & {} \frac{1}{\Lambda } e^{\Lambda \left( t + \frac{1}{2\Lambda }\ln \left( e^{2\Lambda r} - \frac{m}{\Lambda }\right) \right) }, \end{aligned}$$

(46)

$$\begin{aligned} x^-= & {} -\frac{m}{\Lambda ^3 x_0^+} - \frac{1}{\Lambda } e^{-\Lambda \left( t- \frac{1}{2\Lambda }\ln \left( e^{2\Lambda r} - \frac{m}{\Lambda }\right) \right) }. \end{aligned}$$

(47)

Using these relations the metric function takes the following form

$$\begin{aligned} \chi= & {} \Omega = \frac{1}{\sqrt{\kappa }} e^{2\Lambda \sigma } \nonumber \\&- \frac{\sqrt{\kappa }}{2} \Lambda \sigma - \frac{\sqrt{k}}{4} \ln \left( 1 + \frac{m}{\Lambda ^2 x_0^+} e^{\Lambda (t - \sigma )}\right) , \end{aligned}$$

(48)

$$\begin{aligned} \sigma= & {} \frac{1}{2\Lambda } \ln \left( e^{2\Lambda r - \frac{m}{\Lambda }}\right) . \end{aligned}$$

(49)

Now note that for $t= const.$ and $r \rightarrow \infty$ (i.e., at spatial infinity $i_0$) the last term which is time dependent vanishes altogether. This makes $\Omega$ time independent and therefore any solution for $\rho$ in (45) will be time independent. This guaranties the staticity of the metric at $i_0$. Furthermore, as one moves up in $\mathcal{J}_R^+$ where $t \rightarrow \infty , ~ \sigma \rightarrow \infty$ keeping $t-\sigma = \text {finite}$, the time-dependent term becomes least dominant and one can approximately define an asymptotic time-like Killing vector field near $\mathcal{J}_R^+$. We shall use this asymptotic Killing time to be associated with the physical observers as usually done in the RST model. To talk about the asymptotic flatness let us focus on (4849). Near $\mathcal{J}_R^+$ as $\sigma ,~t,~x^+$ all tends to infinity, from (44) and (45) and, by comparing the dominating coefficients of $\kappa$, we have $\lim _{x^+\rightarrow \infty } e^{2\rho } = \frac{1}{-\Lambda ^2 x^+ (x^- + \frac{m}{\Lambda ^3 x_0^+})}$, which is the asymptotic form of the LDV-II. Thus in entire $\mathcal{J}^+_R$ one has a flat metric. This is essential for discussions related with Hawking radiation and information paradox.

Up to this point we have presented the standard RST model which incorporates the backreaction of the spacetime to the Hawking evaporation, corresponding to the usual quantum evolution of the matter field, and which indicates that information is either lost at the singularity or somehow conveyed to the exterior in some unknown fashion encoded in the very late outward flux of energy known as the thunderpop.

However, in the context of our proposal, the state of the quantum field will be affected by the modified quantum evolution prescribed by the modified dynamics involving spontaneous collapse of the wavefunction. The specific model that we shall consider is given by the Continuous-Spontaneous-Collapse (CSL) theory, a brief introduction of which will be provided in section V. In light of this modification the backreaction of the quantum matter on the spacetime metric will be modified as well. We will discuss this in the reminder of this work.

4 Quantization on RST

In order to discuss in some detail the modifications, brought in by the CSL version of quantum theory, it is convenient to describe the two relevant constructions of the quantum theory of the scalar field f on RST spacetime.

We note, however that the power of this model resides in the fact that one is able to obtain the whole space-time, including the back reaction of the space-time metric to the quantum energy momentum stress tensor, before one actually discusses the construction of the quantum field theory for the matter field ${\hat{f}}$. This, in turn, allows for that construction to be carried out in the appropriate spacetime which already includes backreaction.

Thus one might think that one can safely ignore this part of the treatment and just go ahead with the usage of the effective action and never actually carry out the explicit construction of the quantum field. This would be correct except that in our approach we will need to further consider the changes in the state of the quantum field brought about by the dynamical collapse theory. Doing that requires the quantum field theory for ${\hat{f}}$ and we proceed with this now.

We can express the scalar field both in the in region and the out region. The out region consists of the modes having support in the inside and outside of the event horizon. Since in the discussion related with Hawking radiation one only considers the modes in the “right moving” sector we shall only use them in various expressions here. In the in region one can write

$$\begin{aligned} f=\sum _{\omega }\left( a_{\omega }u_{\omega }+a_{\omega }^{\dagger }u_{\omega }^{*}\right) , \end{aligned}$$

(50)

where the in vacuum is defined by $a_{\omega }|0\rangle _{in}=0$. In the out region one has

$$\begin{aligned} f=\sum _{\omega '}\left( b_{\omega '}v_{\omega '}+b_{\omega '}^{\dagger }v_{\omega '}^{*}\right) +\sum _{\tilde{\omega }'}\left( c_{\tilde{\omega }'}\tilde{v}_{\tilde{\omega }'}+c_{\tilde{\omega }'}^{\dagger }\tilde{v}_{\tilde{\omega }'}^{*}\right) , \end{aligned}$$

(51)

where the modes with and without tildes respectively have supports inside and outside the horizon. Vacuum within the Fock spaces interior and exterior to black hole are respectively $c_{\tilde{\omega }'}|0\rangle _{int} = 0$ and $b_{\omega '}|0\rangle _{ext} = 0$. Using Bogolyubov coefficients one can express the creation or annihilation operators of the in region in terms of a linear combination of creation and annihilation operators (defined in either Fock spaces) of the out region. Specifically, there are two sets of Bogolyubov coefficients connecting the in region to black hole interior and exterior regions (only for the right moving sector of the scalar field modes).

The field modes appearing in above expressions of f are respectively given by

$$\begin{aligned} u_{\omega }= & {} \frac{1}{\sqrt{2\omega }}e^{-i\omega y^{+}}, \end{aligned}$$

(52)

$$\begin{aligned} v_{\omega '}= & {} \frac{1}{\sqrt{2\omega '}}e^{-i\omega '\sigma ^{-}}, \end{aligned}$$

(53)

where $y^{+}$ is defined in (42) and $\sigma ^{-}=-\frac{1}{\Lambda }\ln \left( \frac{\Lambda x^{-}+\pi M/\Lambda \kappa }{\Lambda x_{s}^{-}+\pi M/\Lambda \kappa }\right)$ [27]. Whereas the mode in the interior of the black hole can be defined from the expression of $v_{\omega }$, in the following way

$$\begin{aligned} \widetilde{v}_{\tilde{\omega }'}(y^-)=v_{-\omega '}^{*}(-y^-), \end{aligned}$$

(54)

with $y^-$ given by (43). One should also note that in the continuous basis (using $\omega , \omega '$) modes are in fact not ortho-normalized and to talk about particle creation in a particular quantum number one has to introduce a discrete basis to make sense of the particle definition. Moreover, the discrete basis allows for a relatively simple characterization of localization of the modes which in the continuous basis would require the use of wave packets. We will rely on the discrete basis in our work. It is easily obtained from the continuous counterpart by defining the modes,

$$\begin{aligned} v_{jn}=\frac{1}{\sqrt{\epsilon }}\int _{j\epsilon }^{(j+1)\epsilon }d\omega e^{2\pi \omega n/\epsilon }v_{\omega }^{out} \end{aligned}$$

(55)

with n and $j\ge 0$ are integer numbers. These wave packets are peaked about $u_{out} = 2\pi n/\epsilon$ with width $2\pi /\epsilon$. The Bogolyubov coefficients between the $u_{\omega }$ modes and $v_{\omega '}$ (and its complex conjugate) modes turns out to satisfy the following relationship in the late time limit [27]

$$\begin{aligned} \alpha _{\omega \omega '}\approx e^{-\pi \omega /\Lambda }\beta _{\omega \omega '}. \end{aligned}$$

(56)

It is also possible to express the Bogolyubov coefficients in the discrete basis just by using the transformation (55).

A standard calculation from the above expression immediately leads us to the Hawking radiation. Also, as it is well known, with this relation one can express the in vacuum (defined in the Fock space at $\mathcal{J}^-_R$) as a superposition of the particle states in the joint basis in the out region defined inside and outside the event horizon (i.e., interior to black hole and at $\mathcal{J}^+_R$) [28, 29]. Later, we need to consider the initial state of the quantum field which will be evolved using the CSL evolution, with the CSL term taken as an interaction hamiltonian. We will take this state, to be the in vacuum for right moving sector and a pulse for the left moving sector, as discussed in subsection 3.3. Using Bogolyubov transformation we can express

$$\begin{aligned} |\Psi _{i}\rangle= & {} |0_{in}\rangle ^R\otimes |Pulse\rangle ^{L}, \nonumber \\= & {} N\sum _{{F}}C_{F}|F\rangle ^{int}\otimes |F\rangle ^{ext}\otimes |Pulse\rangle ^{L}, \end{aligned}$$

(57)

where the in vacuum for right moving sector is expressed as a linear combination of $|F\rangle$ states interior and exterior to the black hole. Each of these states is characterized by a set of excitation numbers corresponding to various modes. Entanglement between the interior and exterior modes, in the above state, implies that corresponding to a $|F\rangle ^{ext}$ there is a single $|F\rangle ^{int}$ with the same particle excitation number but with negative energy/wave-vector. It is this initial quantum state (57) that had led to the formation of the black hole. We should also state that using the late time characterization, the usual thermal nature of the radiation can be seen in the fact that $C_F = e^{-\pi E_F/\Lambda }$ , where $E_F = \sum _F{\omega _{nj}F_{nj}}$ is the total late time energy of the $|F\rangle$ state.

Now that we have characterized the initial quantum state we move to the next section to incorporate the CSL evolution on this state.

5 Incorporating collapse mechanism in the RST model

We will be addressing the question of the fate of information in the evaporation of the black hole by considering a modified version of quantum theory proposed to address the “measurement problem” of the standard quantum theory. The specific version that we will be using is the CSL theory proposed in [16]. This theory is a continuous version of the so called Ghirardi-Rimini-Weber (GRW) theory [14, 15] where the unitary evolution is accompanied by occasional discrete collapse of the wavefunction that happens for a very small amount of time. As these theories were developed in the context of many particle non-relativistic quantum mechanics we will need to adapt it to the present context involving quantum field theory in curved spacetime².

5.1 Collapse of the quantum state and Einstein’s semiclassical equations

One of the main difficulties that must be dealt with when considering a semi-classical treatment of gravitation in the context of modified quantum theories involving a collapse of the quantum state is the fact that Einstein’s equations simply will not hold when the energy-momentum tensor is replaced by its quantum expectation value and the quantum state of the matter fields undergoes a stochastic collapse. In fact this is connected to the intrinsic problem of treating gravitation in a classical language, and it is expected to be fully solved only in the context of a complete theory of quantum gravity. This is illustrated in [35] where it is argued that semi-classical gravity is either inconsistent when we assume the state of quantum matter undergoes some sort of collapse, or, it is simply at odds with experiments when we do not make such an assumption. Unfortunately, we do not have at this point a fully workable quantum gravity theory to explore these issues. Furthermore, even when, and if we eventually get our hands on such a theory, in which as expected the classical spacetime metric is replaced by some more fundamental set of quantum variables, the recovery the standard notions of classical spacetime, a task that seems unavoidable if we want to be able to describe such things a formation and evaporation of black holes, can be expected to be a rather complex process, that, moreover, might only work in some approximate sense.

These considerations lead us to adopt the following approach: We will consider semi-classical gravity as an approximate and effective description, valid in limited circumstances, of a more fundamental theory of quantum gravity including matter fields. This seems to be, in fact, the position that would be adopted in this regard by a good segment of our community working on these questions, but we describe our posture explicitly in order to avoid misunderstandings. The analogy to keep in mind is the hydrodynamic description of fluids, which as we know, works rather well in a large class of circumstances, but does not represent the behavior of the truly fundamental degrees of freedom involved. We know, that at a deeper level fluids are made of molecules that interact in a complex manner, and that, there are only certain aspects of their collective behavior describable in the hydrodynamic language. The semi-classical Einstein equations therefore cannot be trusted to hold precisely at the fundamental microscopic level, just like the Navier-Stokes equations, which cannot be thought to represent the true behavior of the fluid molecules, but must be taken as holding only in an approximate sense. Moreover, just as the hydrodynamic characterization of a fluid is known to break down rather dramatically in certain circumstances, such as when a ocean wave breaks at the beach, we can also expect that Einstein’s semiclassical equations should become invalid under some situations. We thus must take the situations associated with the collapse of the quantum state of matter fields to be one of such circumstance.

Now we must consider a way out to formally implement such ideas in order to be able to further explore them and their consequences, and in particular to apply them to the problem at hand.

Below, we discuss the issue, first in the realistic setting of a 3+1 dimensional spacetime and second in the particularly simple situation concerning the RST model in 1+1 dimensions.

Here we will describe an approach initially proposed in [36] in the context of inflationary cosmology and the problem of emergence of the primordial inhomogeneities [37]. The staring point is the notion of Semi classical Self- consistent Configurations (SSC), defined for the case of a single matter field (for simplicity), as follows:

Definition The set $\lbrace g_{ab}(x),\hat{\varphi }(x), \hat{\pi }(x), \mathcal{H}, \vert \xi \rangle \in \mathcal{H}\rbrace$ represents a SSC if and only if $\hat{\varphi }(x)$, $\hat{\pi }(x)$ and $\mathcal{H}$ correspond a to quantum field theory constructed over a space-time with metric $g_{ab}(x)$ and the state $\vert \xi \rangle$ in $\mathcal{H}$ is such that

$$\begin{aligned} G_{ab}[g(x)]=8\pi G\langle \xi \vert \hat{T}_{ab}[g(x),\hat{\varphi }(x)]\vert \xi \rangle , \end{aligned}$$

(58)

where $\langle \xi | \hat{T}_{\mu \nu }[g(x),\hat{\varphi }(x)]|\xi \rangle$ stands for the renormalized energy momentum tensor of the quantum matter field $\hat{\varphi }(x)$ (in the state $\vert \xi \rangle$) constructed with the space-time metric $g_{ab}$. This corresponds, in a sense, to the general relativistic version of Schrödinger–Newton equation [38,39,40,41,42,43]. The point of this setting is to ensure a consistency between the description of the quantum matter and that of gravitation by considering their influences on each other³.

To this setting we want to add an extra element: the collapse of the wave function. That is, besides the unitary evolution describing the change in time of the state of a quantum field, we consider situations such as those envisaged in discrete collapse theories such as GRW, where there will be, sometimes, spontaneous jumps in the quantum state. We will consider the situation when we are given a dynamical collapse theory that, given an SSC (dubbed as SSC1 and considered to describe the situation before the collapse), specifies, a space-like hypersurface $\Sigma _{Collapse}$ (perhaps through some stochastic recipe that we can overlook at this point) on which the collapse of the quantum state takes place, and also the final quantum state (generally, again in a similar stochastic manner). The remaining task is now twofold – (i) to describe the construction of the new SSC, (to be called SSC2) that will be taken to describe the situation after the collapse and, (ii) to join the two SSC’s in a manner to generate something to call, in its closest sense, a “global space-time”.

In order to have a picture in our mind we can think of the above scheme as something akin to an effective description of a fluid involving a situation where “instantaneously”, the Navier-Stokes equations do not hold. Let us think, for instance, once more, about an ocean wave breaking at the beach. The situation just before the wave breaks should be describable to a very good approximation by the Navier-Stokes equations, and should the situation, well after the wave breaks and the water surface becomes rather smooth again. The particular regime where the breakdown of the wave is taking place, and its immediate aftermath, will, of course, not be the one where fluid description and the Navier Stokes equations can be expected to provide an accurate picture. This is because such regime involves large amounts of energy and information flowing between the macroscopic degrees of freedom that are well characterized in the fluid language, and the underlying molecular degrees of freedom, (accompanied by other complex process including such things as incorporation of air molecules into the water, the mechanism by which ocean water is oxigenated). All these represent aspects would that have been “averaged out” in passing from the molecular to the fluid description. If we now take the limit in which this complex non-fluid characterization is essential to be instantaneous, then we will be in possession of two regimes that are susceptible to a fluid description using Navier-Stokes equations, joined through an instantaneous collapse of the wavefunction (to be identified with the space-like hypersurface $\Sigma _{Collapse}$) where the said equations cannot hold.

The specific proposal for the effective characterization of these situations, that we will have in mind is based on the $3+ 1$ decomposition of the space-time associated with the hypersurface $\Sigma _{Collapse}$ and inspired by the application of these ideas in the specific case treated in [36].

The spacetime metric of the SSC1 defined on $\Sigma _{Collapse}$ has the induced spatial metric $h_{ab}^{(1)}$, the unit normal $n^{a (1)}$ and the extrinsic curvature ${K^{ab}}^{(1)}$. The fact that the SSC1 corresponds to a semi-classical solution of Einstein’s equations then ensures that the Hamiltonian and momentum constrains are satisfied on $\Sigma _{Collapse}$ viewed as a hypersurface embedded in the space-time of the SSC1.

The task at hand now, would be to specify the quantum state and initial conditions for the construction of the SSC to the future of the collapse hypersurface, assuming that we are given the expectation of the energy-momentum tensor for the SSC2, i.e., assuming that the collapse theory allows us to determine ${\langle \xi \vert \hat{T}_{bc}[g(x),\hat{\varphi }(x)]\vert \xi }\rangle ^{(2)}$. That is, as we are considering the treatment for the case where the collapse is taken to be instantaneous, we will assume that the collapse theory, in our case CSL, determines (by some scheme involving stochastic components) the quantum state at the hypersurface lying “just to the future of the collapse hypesurface” (assuming that the initial, pre-collapse, state was given) on $\Sigma _{Collpase}$, and given that, one would need is to construct the complete, corresponding SSC2. The first thing would be to obtain suitable initial data for the space-time metric of SSC2. That is we need to find $h_{ab}^{(2)}$ and the extrinsic curvature ${K^{ab}}^{(2)}$ satisfying the Hamiltonian and momentum constrains, involving the expectation value of the energy-momentum tensor corresponding to the SSC2.

We have previously used the ansatz of taking $h_{ab}^{(2)} = h_{ab}^{(1)}$ on $\Sigma _{Collapse}$ and finding a suitable expression $K_{ab}^{(2)}$, on $\Sigma _{Collapse}$ determined so as to ensure the Hamiltonian and momentum constraints for the SSC2 are satisfied.

This determination of the initial data for the SSC2 metric will be referred as Step 2. Next one would have to carry out the completion of the SSC2, namely to specify the construction of the quantum field theory, identify the quantum state and show how the full space-time metric can be determined.

The completion of the process would then involve finding the state of the new Hilbert space such that its expectation value of the (renormalized) energy-momentum tensor corresponds to the values given in Step 1 above. One must then ensure that with the integration of the space-time metric and the mode functions given those initial data can be done effectively. An explicit example showing the completion of this process in the inflationary cosmological context representing a single mode perturbation with specific co-moving wave vector was presented in [36]. There one can see that in general the tasks involved are rather non-trivial.

The point is that this scheme will allow the construction of a space-time made of two four dimensional regions characterized by the SSC constructions and joined along a collapse hypersurface where Einstein’s equations do not hold.

In the case of the RST model, in 1 + 1 dimensions, the situation is substantially simplified by the fact that the space-time is two dimensional and thus the Einstein tensor vanishes identically. The violation of the equations of motion during a collapse of the quantum state are thus a bit more subtle and, at the same time easier to deal with.

Again, one can make use of the fact that the most general spacetime (smooth) metric can be written as:

$$\begin{aligned} ds^2 = -e^{2\rho } dx^+ dx^-, \end{aligned}$$

(59)

where $\rho$ is a smooth function. Thus both the space-time metric for SSC1 and SSC2 can be put in this form. The issue is now joining these two space-times along $\Sigma _{Collapse}$. Thus we can regard, as a complete generalized space-time, the result obtained by this gluing procedure where the price we have paid by doing so is that now the function $\rho$ will not necessarily be a smooth function. Note that something similar happens when the linear dilaton vacuum region is glued with the black hole space-time in CGHS or RST model.

Also the remaining SSC 2 construction, i.e., the specification of the corresponding Hilbert space and identification of the quantum state needs to be dealt with. The specification of the mode functions that determine the Fock space, can be taken to be done at the level of initial data on $\Sigma _{Collapse}$, and this can be achieved by making use of the fact that the general solution of the Klein-Gordon equation for a massless scalar field f on any space-time metric of the form (59) is of the form

$$\begin{aligned} f = f_{+} ( x_+) + f_{-} ( x_-). \end{aligned}$$

(60)

As we mentioned before, the idea is then to take take the modes used in the SSC1 Fock space as providing initial data for the SSC2 Hilbert space construction. However it is easy to see that using such procedure on $\Sigma _{Collapse}$ with functions satisfying (60) both in the regions to the past and future of $\Sigma _{Collapse}$ corresponds, simply, to functions satisfying (60) in all our generalized space-time ( i.e. after incorporating the discontinuity in the derivative of $\rho$). All this will work fine as long as the spatial-metric is continuous along $\Sigma _{Collapse}$ and the space-time metric is continuous as one crosses it.

The point is that we can take the modes of the SSC2 and the corresponding Fock space to be the same as those of the SSC1. This represents a very nice simplification provided by the two dimensional nature of the situation of interest.

The last step would be the identification of the state in the Hilbert space of SSC 2 with the appropriate expectation values of the renormalized energy-momentum tensor, but again as the Hilbert space of two SSC’s are the same we can take this as being provided by the collapse theory in Step 1.

This shows that the program described at the start of this section, regarding a single instantaneous collapse of the state of the quantum matter field, can be easily implemented in the present situation. The details of the general application of that scheme for situations in higher dimensions is an open problem.

The final issue that needs to be considered before applying collapse theories to the problem at hand, has to do with generalizing the above procedure, from the case of a single instantaneous collapse to a continuous collapse theory. That is, if instead of considering a single collapse taking place on the space-like hypersurface $\Sigma _{Collapse}$ we want to consider a foliation of space-time by space-like “collapse” hypersurfaces $\Sigma _{Collapse} (\tau )$ parametrized by a real valued time function $\tau$ on the space-time manifold, and a theory like CSL to be described in the next section, describing the change in the quantum state, as one “passes form one hypersurface to the other”.

We can deal with this, first for the case of a finite interval $[\tau _{start}, \tau _{end}]$ in the time function by considering a partition of the corresponding interval $\tau _0=\tau _{start}, \tau _1......\tau _i... \tau _N= \tau _{end}$, performing the procedure describing the individual discrete collapse at each step i in the partition, and eventually taking the limit $N\rightarrow \infty$.

With these considerations in hand we now turn to the description of the specific type of collapse theory will be using in this work.

5.2 CSL theory

We first consider the theory in the non-relativistic quantum mechanical setting in which it was first postulated. The CSL theory is generically described in terms of two equations. The first is a modified version of Schrödinger equation, whose general solution, in the case of a single non-relativistic particle is:

$$\begin{aligned} |\psi ,t\rangle ^{CSL}_{w}=\mathcal{T}e^{-\int _{0}^{t}dt'\big [i{\hat{H}}+\frac{1}{4\lambda }[w(t')-2\lambda {\hat{A}}]^{2}\big ]}|\psi ,0\rangle , \end{aligned}$$

(61)

where $\mathcal{T}$ is the time-ordering operator. ${\hat{A}}$ is a smeared position operator for the particle. w(t) is a random classical function of time, of white noise type, whose probability is given by the second equation, the Probability Rule:

$$\begin{aligned} PDw(t)\equiv \langle \psi ,t|\psi ,t\rangle \prod _{t_{i}=0}^{t}\frac{dw(t_{i})}{\sqrt{ 2\pi \lambda /dt}}. \end{aligned}$$

(62)

The state vector norm evolves dynamically (not equal 1), so Eq. (62) says that the state vectors with largest norm are most probable. It is straightforward to see that the total probability is 1, that is

$$\begin{aligned} \int PDw(t) =\langle \psi ,0|\psi ,0\rangle =1. \end{aligned}$$

(63)

The way we will incorporate the CSL modifications in our situation is by relying on the formalism of interaction picture version of quantum evolution, where the free part of the evolution corresponding to the standard quantum evolution will be absorbed in the construction of the quantum field operators, while the interaction corresponding to the CSL modifications will be used to evolve the quantum states. One more thing that needs to be modified is related to the fact that the quantum field is a system with infinite number of degrees of freedom (DOF), and thus instead of a single operator ${\hat{A}}$ and a single stochastic function w(t) we will have an infinite set of those labeled by the index $\alpha$. Thus in our case we will have:

$$\begin{aligned} |\Psi ,t\rangle ^{CSL}_{ \lbrace w_{\alpha } \rbrace }=\mathcal{T}e^{-\int _{0}^{t}dt'\big [\frac{1}{4\lambda } \sum _{\alpha } [w_{\alpha }{} (t')-2\lambda {\hat{A}}_{\alpha }]^{2}\big ]}|\Psi ,0\rangle , \end{aligned}$$

(64)

with a corresponding probability rule for the joint realization of the functions $\lbrace w_{\alpha } (t)\rbrace$.

It is not our aim to review various physical and technical features of CSL theory here for which we refer the reader to our previous papers [19, 20] as well as well established papers and review articles in the literature [10]. However, we would like to add an important point that is worthy to highlight here. Since CSL theory adds a non-linear, stochastic term to the otherwise deterministic Schrödinger equation, there is an inevitable loss of information associated with it. Given an initial quantum state we cannot predict the final state after CSL evolution with 100% accuracy even in Minkowski space-time. Given the tiny numerical value of the collapse parameter $\lambda \sim 10^{-16}sec^{-1}$ this departure is so small that no observable effect can be found in practical situations while dealing within laboratory systems and hence making the theory phenomenologically viable. Nevertheless, it is an important insight that stochasticity that was brought in by CSL theory allows information destruction in quantum evolution. The major challenge that we overcame in our earlier proposals [19, 20] was making this tiny effect substantially larger inside a black hole in a sensible manner. We review this important feature in the next subsection.

5.3 Gravitationally induced collapse rate

The basic hypothesis we want to consider in the specific models we are studying is that all the information that is encoded in the quantum state of the fields, that might be considered as entering the black hole region, will eventually be erased by a CSL type mechanism before the singularity (or more precisely the region that requires a full quantum gravity description) is reached. As in our previous works, we find that this can be achieved by postulating that usually small rate of information loss of information controlled by a fixed $\lambda$ is intensified as the singularity is approached. This is achieved through the hypothesis that $\lambda$ is a function of local curvature of the space-time. Mathematically we expressed [19, 20]

$$\begin{aligned} \lambda (R) = \lambda _0\left( 1 + \left( \frac{R}{\mu }\right) ^\gamma \right) , \end{aligned}$$

(65)

where $\mu$ is an appropriate scale and $\gamma \ge 1$. In flat spacetime this reduces to standard CSL theory.

Further motivation for such idea comes from arguments of Penrose [41] and Díosi [38] suggesting that spontaneous the collapse itself has gravitational origins. Furthermore, there are strong indications that, at the phenomenological level, a theory in which $\lambda$ depends on the mass of the particle species is preferred over theories where it is taken to be constant [44], and such a mass dependence is very suggestive of a possible connection to local curvature. In any event, the above assumption tunes the rate of collapse in a manner that naturally leads to the scenario we want to explore.

The large value of $\lambda$ in highly curved regions of space-time in fact leads to the dominance of the stochastic term over that of the usual term in (61). The non-unitary term breaks the linear superposition (in terms of the vector basis adapted to the collapse operators) and stochasticity brings a high degree of indeterminism in the quantum evolution. These two effects together cause the destruction of information as the black hole singularity is approached. Of course at present, we cannot directly test the hypothesis behind (65), but future technological developments might one day provide evidence in favour or against our proposal. We consider this as a clear advantage over other approaches existing in the literature. It is however important to note here that our proposal does not depend on the particular function that we have chosen in (65) as long as it satisfies, the following conditions—(1) $\lambda$ is a (sufficiently rapidly) increasing function of local curvature (so that the collapse rate diverges as the singularity is approached), (2) it is not in contradiction with the flat space-time constraints and various constraints that comes from astrophysical and cosmological observations and, (3) is a manifestly Lorentz invariant quantity. In previous works we have argued that $\lambda$ could naturally be taken to a function of the Weyl curvature scalar ($W_{abcd}W^{abcd}$) simply because in realistic scenarios (in 4 dimensions) the singularity in the black hole interiors can be approached through paths where R vanished, but, all paths in the black hole interior that approach the singularity involve a divergence of Weyl curvature scalar. However in two dimensions the Weyl tensor vanishes, and so in our model we substitute it by what seems as the simplest alternative, the scalar curvature R (65).

Now we need to mathematically implement the above ideas in RST model and the first step towards this is to foliate the spacetime with Cauchy slices.

5.4 Spacetime foliation

In order to describe the evolution of quantum states we will need to foliate the space-time with Cauchy slices and introduce a suitable global time parameter labeling the foliation. We perform an analysis similar to that used in works [19, 20] for CGHS model, with some needed modifications. The relevant patch of the black hole space-time is referred as Region I and Region II in Fig. 1. Region I is further divided into two regions Region I(a) and I(b) which are within the event horizon and apparent horizon respectively. A Cauchy slice has the following characteristics– $R= const.$ curve in Regions I(a) and I(b), joined with a $t=const.$, curve in Region II. Note that this time t, defined with respect to an asymptotic observer, is well defined in regions II and I(b), i.e., outside the event horizon. The family of slices are determined once we specify the intersecting points between the $R=const.$ and $t=const.$ curves. For that we have to find out a curve which stays within Region I(b). This is needed to ensure that the Cauchy slices are spacelike and forward driven with respect to the asymptotic Killing time t. There might be many such curves and any of them should be as good as others to do the job. We choose the curve

$$\begin{aligned}&-\Lambda ^2 x^+ \left( x^- + \frac{m}{\Lambda ^3 x_0^+}\right) \nonumber \\&\quad - \frac{\kappa }{4}\left( 1+ a_0 \left( x^- - x_s^-\right) \left( x^+ - x_0^+\right) \right) = 0, \end{aligned}$$

(66)

where $a_0$ is a constant and we shall use a fixed value for this in our analysis.

Let us now comment on the quantitative aspect of making these slices. The targeted regions are I and II as shown in Fig. 1. We start by calculating R in (31) by using (44) which gives

$$\begin{aligned} R= & {} -\frac{16}{\Lambda x^- x^+ x_0^+ \left( \kappa e^{2 \rho }-4\right) ^3} \nonumber \\&\times \left( e^{2 \rho } \left( \Lambda \kappa ^2 x_{0}^{+} + 4 \kappa m x^+ + 16 \Lambda ^2 x^- x^{+2} \left( m+\Lambda ^3 x^- x_0^+ \right) \right) \right. \nonumber \\&\times \left. + \kappa ^2 \Lambda ^3 e^{4 \rho } x^- x^+ x_0^+ + 16 \Lambda ^3 x^- x^+ x_0^+\right) . \end{aligned}$$

(67)

In principle it is straightforward to find the $R = const. = R_0$ slices in the following way. First we can solve (67) for $e^{2\rho }$ as a function of coordinates $x^\pm$ and other parameters ($\kappa , m, \Lambda , x_0^+$) since the equation $R-R_0 = 0$ is a cubic equation in $e^{2\rho }$. Among the three solutions for $e^{2\rho }$ one has to take the real solution and put it in (20) to find $\Omega _c$ which now corresponds to $R=R_0$. The next step is to equate (44) with $\Omega _c$ and this in turn allows one to write $x^+ = f_{R_c}(x^-)$ where $f_{R_c}(x^-)$ is a function of $x^-$ on the collapse hypersurface with curvature $R = R_c$. The resulting analytic expression for the $R=R_c$ curve is too cumbersome to put in a paper and therefore not included here.

Fig. 3

Spacetime foliation plots for RST model. The family of Cauchy slices are given by $R=const.$ curves inside the apparent horizon joined with $t=const.$ lines outside. We have set $k=1, m=2, \Lambda =1, x_0^+ = 0.1$ for all plots. Values of curvature $R = 50, 30, 25$ for blue curves from top to bottom. As required for this slicing to be Cauchy, hypersurfaces with larger R (more closer to the singularity) are joined together with larger values of asymptotic Killing time t

However, it is possible to plot the $R= const.$ curve numerically along with other relevant curves, namely, the singularity (36), the apparent horizon (37), the intersection curve (66) and $t=const.$ lines to complete the foliation. This family of Cauchy slices is plotted in Fig. 3. It is clear that slices with increasingly higher curvature are those that are closer to the singularity. Making the collapse parameter a function of the spacetime curvature intensify the collapse of the wave function near singularity. This, in effect, erase almost all the information about the matter that had once created the black hole.

5.5 CSL evolution and the modified back reaction

Now we are in a position to use the construction made so far and evolve the initial quantum state as given in (57). We have assumed the curvature dependent collapse rate in (65) and prepared our Cauchy slices in the preceding subsection. The only thing that is missing is to define the set of collapse operators appearing in (64). As we have indicated before that it is convenient to use the discrete basis in order to have at our disposal simple notions of localized excitations or “particles”. Therefore it is convenient to characterize the collapse operators also in terms of this discrete basis. Following our earlier works, and for simplicity we chose

$$\begin{aligned} A_{\alpha } := N_{nj}=N^{int}_{nj}\otimes \mathbb {I}^{ext}. \end{aligned}$$

(68)

Here $N^{int}_{n,j}$ is the number operator in the discrete basis (which was used to discretize the mode function in (55)) interior of the black hole and $\mathbb {I}^{ext}$ is the identity in the exterior of the black hole basis. The number operator acts on the particle states as follows

$$\begin{aligned} N_{nj}|F\rangle ^{int}\otimes |F\rangle ^{ext}=F_{nj}|F\rangle ^{int}\otimes |F\rangle ^{ext}, \end{aligned}$$

(69)

where $F_{nj}$ is the particle excitation in a state corresponding to quantum numbers n, j.

At this point we must consider the fact that when we introduce the CSL modification of the evolution of the quantum state of the field, we also have a modification of the expectation value of the renormalized energy-momentum tensor (REMT), and this will in turn modify the back reaction of the quantum field on the background spacetime.

One issue that needs to be mentioned here is that such simple collapse operator might not be physically appropriate (or acceptable) as it might fail to take Hadamard states into Hadamard states. The issue of what are the kind of operators that when used as collapse generating operators would ensure this essential property has been studied with some generality in [34], however the results suggest that there are suitable choices of acceptable operators that are very close to the one described above.

In order to consider the modification of the back reaction we should in principle study the expression for the REMT in the quantum state $|\psi _{CSL}\rangle$ which according to (89) can be written in the following form:

$$\begin{aligned}&\langle \psi _{CSL} | T_{\mu \nu }(x)| \psi _{CSL} \rangle _R \nonumber \\&\quad = \langle \psi _{CSL} |: T_{\mu \nu }(x) :_{in}| \psi _{CSL} \rangle + \text {Geometric terms}, \end{aligned}$$

(70)

where the first term on the r.h.s is normal ordered with respect to the “in” quantization. Here we shall be considering the right moving sector of field modes and concentrate how the REMT evolves due to CSL evolution (for a brief account on the issue see Appendix A).

In fact what we would need to do is to compute the quantities $\langle \psi _{CSL} |: T_{\pm \pm }(x) :_{in}| \psi _{CSL} \rangle$ that should be used in (97) or more specifically within the full RST model in (29) and (30).

The in normal ordered energy-momentum tensor can be easily expressed in terms of the objects used to construct the “in” quantization region and takes the following form

$$\begin{aligned} : T_{\pm \pm } (x) :_{in}= & {} \lim _{x\rightarrow x'} : \frac{1}{2}(\partial _\pm {\hat{f}} (x)) (\partial _\pm {\hat{f}} (x')) :_{in}\nonumber \\= & {} \frac{1}{2} \int {d\omega _1} {d\omega _2} \left\{ \lim _{x\rightarrow x'}\left( {\hat{a}}_{\omega _1} {\hat{a}}_{\omega _2} u_{\omega _1, \pm } (x) u_{\omega _2, \pm }(x') \right. \right. \nonumber \\&+ 2{\hat{a}}_{\omega _1}^\dagger {\hat{a}}_{\omega _2} u_{\omega _1, \pm } (x)^* u_{\omega _2, \pm }(x') \nonumber \\&\left. + {\hat{a}}_{\omega _1}^\dagger {\hat{a}}_{\omega _2}^\dagger u_{\omega _1, \pm } (x)^* u_{\omega _2, \pm }(x')^* \right\} , \end{aligned}$$

(71)

where $_{,\pm }$ represents ordinary derivative with respect to $x^{\pm }$. Note that the normal ordering procedure has been explicitly performed in the above expression. Also it should be cleared that although the modes appearing in the above expression are naturally associated with the early flat dilaton vacuum region they are defined everywhere, so the expression is valid for evaluations of the expectation value anywhere in the space-time.

As we mentioned before we shall focus only on the right moving modes for CSL effect. The changes in the state due to the CSL modified evolution are expected to be relevant only at late times, due to the fact that this is where the parameter $\lambda$ becomes large due to the large values of the curvature as the singularity is approached. Thus in principle we only need to consider the CSL modifications of the state after the pulse.

The state in fact can be written as

$$\begin{aligned} | \psi _{CSL} \rangle= & {} \mathcal{T}e^{-\int _{0}^{t}dt'\big [\frac{1}{4\lambda } \sum _{nj} [w_{nj}{} (t')-2\lambda {\hat{N}}_{nj}]^{2}\big ]} N \nonumber \\&\times \sum _{F}C_{F}|F\rangle ^{int}\otimes |F\rangle ^{ext} \nonumber \\= & {} N \sum _{F}C_{F} e^{-\int _{0}^{t}dt'\big [\frac{1}{4\lambda } \sum _{nj} [w_{nj}{} (t')-2\lambda F_{nj}]^{2}\big ]} \nonumber \\&\times |F\rangle ^{int}\otimes |F\rangle ^{ext} \end{aligned}$$

(72)

with $C_F = e^{-\frac{\pi E_F}{\Lambda }}$ in the late time limit. One of the complications in evaluating the quantity of interest is that while in the above expression all the operators refer to the out quantization, the expression (71) uses the in quantization. In principle one could rewrite all the operators appearing in (71) using the Bogolyubov relations and end up with an expression for $\langle \psi _{CSL} |: T_{\pm \pm }(x) :_{in}| \psi _{CSL} \rangle$ where everything is expressed in terms of the out quantization. Furthermore once one considers a specific realization of the stochastic functions $\lbrace w_{nj}\rbrace$, one would have a well defined expression, which could, in turn, be used to compute the modifications of the spacetime metric given by the functions $F \& G$ in (29) and (30). That is in (71) we can express the creation and annihilation operators defined in the “in” region, by using Bogolyubov transformations, by operators associated with the black hole interior and the exterior region:

$$\begin{aligned} \hat{a}_{\omega } = \sum _{j,n} \left[ \alpha _{jn,\omega } \hat{b}_{jn} + \beta ^*_{jn,\omega } {\hat{b} }^\dagger _{jn}\right] + \sum _{\tilde{j},\tilde{n}} \left[ \zeta _{\tilde{j}\tilde{n},\omega } \hat{c}_{\tilde{j}\tilde{n}} + \theta ^*_{\tilde{j}\tilde{n},\omega } {\hat{c} }^\dagger _{\tilde{j}\tilde{n}}\right] ,\nonumber \\ \end{aligned}$$

(73)

where we have only discretized the modes in the out region which is sufficient for our purpose and expressions with and without tildes are again belong to the interior and exterior of the black hole event horizon. Using this and the corresponding expression for ${{\hat{a}}_{\omega }}^\dagger$ we could write $: T_{\pm \pm } (x) :_{in}$ as a sum of quadratic terms in the operators $\lbrace {\hat{b}}_{jn} , {\hat{b}}^\dagger _{jn}, {\hat{c}}_{jn}, {\hat{c} }^\dagger _{jn}\rbrace$ which act in a simple form on the states $|F\rangle ^{int}\otimes |F\rangle ^{ext}$.

Unfortunately such calculation turns out to be extremely difficult, even when one takes some simple form for the functions $\lbrace w_{nj}\rbrace$ (we had considered the case where those functions are just constants).

As evident, so far, with the above analysis we can write down a formal general expression of the backreacted metric in presence of wavefunction collapse. As we have mentioned, the normal ordering contributes to $\Omega$ in (28) via (29) and (30). Of course, if we consider (72), the CSL evolved state of the in vacuum for the right movers, we can no longer neglect the normal ordered part and an appropriate expression for them should be

$$\begin{aligned} \langle \psi _{CSL} |: T_{\pm \pm }(x) :_{in}| \psi _{CSL} \rangle= & {} t_{\pm \pm }(x) \end{aligned}$$

(74)

and we shall end up with a backreacted spacetime, given by

$$\begin{aligned} \chi= & {} \Omega =-\frac{\Lambda ^2x^+x^-}{\sqrt{\kappa }}-\frac{\sqrt{\kappa }}{4}\ln \left( -\Lambda ^2x^+x^-\right) \nonumber \\&-\frac{m}{\Lambda \sqrt{\kappa }x_{0}^+}\left( x^+-x_{0}^+\right) \theta \left( x^+-x_{0}^+\right) \nonumber \\&+ \frac{1}{\sqrt{\kappa }}\left( \int ^{x^+} dx^{'+} \int ^{x^{'+}} dx^{''+} t_{++} \right. \nonumber \\&\left. + \int ^{x^-} dx^{'-} \int ^{x^{'-}} dx^{''-} t_{--} \right) \end{aligned}$$

(75)

where new undetermined functions $t_{\pm \pm }$ appear due to the CSL excitation of the vacuum state. One shortcoming of not having the explicit expression of the normal order expectation value in general CSL state (72) is that we cannot compute an exact backreacted spacetime which needs to be a continuous change over the standard RST space-time. However, for completeness, in Appendix B, we explicitly compute the backreacted and modified RST space-time for a single, GRW type of collapse event. Even in this situation the metric can be glued continuously on the collapse hypersurface. The case of continuous collapse would need to generalize this situation for multiple collapse events and gluing the spacetime for each of those events over the family of such collapse hypersurfaces. This task, however, is beyond the scope of this paper.

The point is that we know from construction of the CSL type of evolution, together with our assumption that $\lambda$ depends on curvature (65) and diverges as one approaches the singularity and that as one considers a hypersurface very close to the singularity, the state there would have collapsed to a state with definite occupation number, giving

$$\begin{aligned} | \psi _{CSL} \rangle = N C_{F_0}|F_0\rangle ^{int}\otimes |F_0\rangle ^{ext} \end{aligned}$$

(76)

where $F_0$ stands collectively for a complete set of the occupation numbers in each mode i.e. $\lbrace F_0^{nj} \rbrace$. This state is associated with a flux of positive energy towards future null infinity given by $E_0 \approx \sum _{nj} F_0^{nj} \omega '_{nj}$ where $\omega '_{nj}$ is the mean frequency of the mode n, j. The state is also associated with a corresponding (equal) negative energy flux into the black hole. Therefore, associated with the black hole at late times we would have a total energy corresponding the mass associated with the pulse that led to the formation of the black hole $M-E_0$ while the Hawking radiation would have carried to $\mathcal {I}^+$ the energy $E_0$. If quantum gravity cures the singularity without leading to large violations of energy-momentum, and if we ignore the actual violation of energy-momentum associated with CSL⁴ then the thunderpop which we know in this model, associated with the final and complete evaporation of the black hole, would have to carry the extra energy in the amount $E^{thunderpop} =M-E_0$.

Thus taking into account the assumption that quantum gravity resolves the singularity, and the above characterization of the thunderpop can describe the full evolution of the initial state from asymptotic past to the null future infinity as starting with the initial state

$$\begin{aligned}&|0\rangle _{in}^{R}\otimes |Pulse \rangle ^{L} \nonumber \\&\quad =\sum _{F}C_{F}|F\rangle ^{int, R}\otimes |F\rangle ^{ext,R}\otimes |Pulse \rangle ^{L}, \end{aligned}$$

(77)

transforming as a result of the CSL collapse into

$$\begin{aligned} |F\rangle ^{int, R}\otimes |F\rangle ^{ext,R}\otimes |Pulse \rangle ^{L}, \end{aligned}$$

(78)

on an hypersurface extending to null infinity but staying behind and very close to the singularity ( or QG region) and eventually leading to the state at $\mathcal{I}^+$ given by

$$\begin{aligned} |F\rangle ^{ext}\otimes |thunderpop, M-E_0 \rangle . \end{aligned}$$

(79)

The point however is that this state is undetermined because we can not predict which realization of the stochastic functions $w_{nj} (t)$ will occur in a specific situation.

6 Recovering the thermal Hawking radiation

In order to deal with the indeterminacy, brought in by the stochasticity of the CSL evolution, it is convenient to consider an ensemble of systems, all prepared in the same initial state and, described by the pure density matrix

$$\begin{aligned} \rho _{0}=|\Psi _i\rangle \langle \Psi _i|, \end{aligned}$$

(80)

which can, by using (57), be written as

$$\begin{aligned} \rho _{0}=\rho (\tau _{0})\otimes |Pulse^L\rangle \langle Pulse^L |, \end{aligned}$$

(81)

where

$$\begin{aligned} \rho (\tau _{0})=\sum _{F,G}C_{F, G}|F\rangle ^{int}\otimes |F\rangle ^{ext}\langle G|^{ext}\otimes \langle G|^{int}, \end{aligned}$$

(82)

and $C_{F, G}$ are determined by the Bogolyubov coefficients between various mode functions. Now time evolution according to the CSL dynamics suggests [19]

$$\begin{aligned} \rho (\tau )=\mathcal {T}e^{-\int _{\tau _{0}}^{\tau }d\tau '\frac{\lambda (\tau ')}{2}\sum _{n,j}\left[ N_{n,j}^L-N_{n,j}^R\right] ^2} \rho (\tau _{0}). \end{aligned}$$

(83)

In the late time limit we have

$$\begin{aligned} \rho (\tau )= & {} \sum _{F, G}e^{-\frac{\pi }{\Lambda }(E_{F}+E_{G})}e^{-\sum _{n,j}(F_{n,j}-G_{n,j})^2 \int _{\tau _{0}}^{\tau }d\tau '\frac{\lambda (\tau ')}{2}} \nonumber \\&\times |F\rangle ^{int}\otimes |F\rangle ^{out}\langle G|^{out}\otimes \langle G|^{int}. \end{aligned}$$

(84)

Taking into account the dependence of $\lambda$ on R and the fact that inside the black hole and the foliation makes R a function of $\tau$, we conclude that for the evolution under consideration, $\lambda$ becomes effectively that function of $\tau$. Noting the manner in which $\lambda (\tau )$ in (65) depends on R we conclude that the integral diverges near the singularity. Therefore the only surviving terms are the diagonal ones and thus very close to the singularity we will have,

$$\begin{aligned}&\lim _{\tau \rightarrow \tau _{s}}\rho (\tau ) =\sum _{F}e^{-\frac{2\pi }{\Lambda }E_{F}}|F\rangle ^{int}\otimes |F\rangle ^{out}\langle F|^{out}\otimes \langle F|^{int}.\nonumber \\ \end{aligned}$$

(85)

Next we explicitly include the left moving pulse, so that the complete density matrix very close to the singularity is given by

$$\begin{aligned} \lim _{\tau \rightarrow \tau _{s}}\rho '(\tau )= & {} \sum _{F}e^{-\frac{2\pi }{\Lambda }E_{F}} \nonumber \\&\times |F\rangle ^{int}\otimes |F\rangle ^{out}\langle F|^{out}\otimes \langle F|^{int}\otimes |Pulse\rangle \langle Pulse|.\nonumber \\ \end{aligned}$$

(86)

Note that $E_{F}$ represents the energy of state $|F\rangle ^{ext}$ as measured by late time observers. The operator given by eq. (86) represents the ensemble when the evolution has almost reached the singularity.

Next by taking into account the effects of the quantum gravity region,⁵ on each one of the components of the ensemble characterized by the above density matrix, we can write the corresponding density matrix for the ensemble at $\mathcal{I}^+$ namely:

$$\begin{aligned} \rho '( \mathcal{I}^+)= & {} \sum _{F} e^{-\frac{2\pi }{\Lambda }E_{F}} |F\rangle ^{out} \langle F|^{out}\otimes |T, M-E_0(F) \rangle \nonumber \\&\times \langle T, M-E_0(F)|, \end{aligned}$$

(87)

where T stands for the thunderpop and the state has energy $M-E_0(F)$.

As far as the information is concerned we do not believe that the correlations between the thunderpop energy and that in the early parts of the Hawking radiation can be of any help in restituting a unitary relation between the initial and final states. This is because the same considerations concerning the possibility that a remnant might help in this regard, apply to the thunderpop. That is, the amount of energy available to the thunderpop is expected to be rather small and to a large extent independent of the initial mass of the matter that collapsed to form a black hole, and thus for large enough initial masses, the overwhelming part of the initial energy would be emitted in the form of Hawking radiation. The small, and essentially fixed, amount of energy available to the thunderpop is not expected to be sufficient for the excitation of the arbitrarily large number of degrees of freedom necessary to restore unitarity to en entangle the Hawking radiation and thunderpop state. Thus the resulting picture emerging from the present work is consistent with a full loss of information during the evaporation of a black hole that was present in our previous treatments.

7 Discussion

The black hole information problem continuous to be a topic attracting wide spread interest. A proposal to deal with the issue in a scheme which unified it with the general measurement problem in quantum mechanics, has been advocated in [7, 8] and initially studied in detail in [19, 20]. Those initial proposals left out two important aspects: relativistic covariance of the proposal and the issue of back reaction. The former was explored in [21] while the later is the object of the present work.

We have studied the incorporation of spontaneous collapse dynamics into the back reaction of an evaporating black hole using the RST model. We have shown in detail how a single collapse leads to the modification of the space-time and discussed in general how the full continuous collapse dynamics might be used in this case and might be expanded to deal with more realistic Black hole models.

Appendices

Appendix A: The renormalized energy-momentum tensor

Here we review, and to a certain degree clarify, the method to calculate $\langle {\Psi }| T_{ab} |{\Psi } \rangle$ using the properties of CGHS model and a result for the renormalized energy-momentum tensor as found by Wald [45].

Let us start with the expression for the renormalized energy-momentum tensor obtained in [45]. The result is described using Penrose’s abstract index notation for clarity. It applies to a two dimensional spacetime where the metric is conformally related to the flat metric so that $g_{ab} = \Omega ^2 \eta _{ab }$ and where, in the past the metric (is or approaches asymptotically) the flat Minkowski metric, so that there $\Omega ^2 = 1$. It offers an expression of the renormalized expectation value of the energy-momentum tensor, in terms of the derivative operator $\nabla ^{(\eta )}_a$ associated with the flat metric $\eta _{ab}$. The expression is:

$$\begin{aligned} \langle \Psi | T_{ab} | \Psi \rangle= & {} \langle \Psi |:T_{ab}:_{in}| \Psi \rangle + \frac{1}{12\pi } \left( \nabla ^{(\eta )}_{a}\nabla ^{(\eta )}_{b} C \right. \nonumber \\&- \eta _{ab} \eta ^{cd} \nabla ^{(\eta )}_{c} \nabla ^{(\eta )}_{d} C -\nabla ^{(\eta )}_a C \nabla ^{(\eta )}_b C \nonumber \\&\left. + \frac{\eta _{ab}}{2} \eta ^{cd}\nabla ^{(\eta )}_{c} C \nabla ^{(\eta )}_{d} C\right) , \end{aligned}$$

(88)

where the first expression on the right hand side is the normal ordering with respect to the construction of the quantum field theory that leads to the in vacuum, $\eta _{ab}$ is the flat metric, and $C = \ln \Omega$. In [45], the derivation of this expression is obtained using an axiomatic approach to renormalize the stress tensor. We emphasize that the above expression is fully covariant when all the objects are properly understood, (in particular $\nabla ^{(\eta )}_a$ is derivative operator associated with the flat metric $\eta _{ab}$), and it is valid in all regions of space-time and not only in the flat region in the past (where the expression would simply be $\langle \Psi |:T_{ab}:_{in}| \Psi \rangle$ as there $C =$ constant).

Note that as (88) is expressed in terms of the derivative operator associated with the flat metric $\eta _{ab}$, thus it can be simply written in terms of the ordinary derivative operator $\partial ^{(y)}$ associated with Minkowski coordinates $y^\mu$ in which one can write the flat metric components as $\eta _{\mu \nu }$ ( i.e. $\eta _{ab} =\eta _{\mu \nu } dy^\mu _a {dy^\nu }_b = -dy^0_a dy^0_b + dy^1_a {dy^1}_b$ (because this operator coincides with the covariant derivative operator associated with the flat metric). That is, we can write the expression in terms of the explicit components in these coordinates as:

$$\begin{aligned} \langle \Psi | T_{\mu \nu } | \Psi \rangle= & {} \langle \Psi |:T_{\mu \nu }:_{in}| \Psi \rangle + \frac{1}{12\pi } \left( \partial ^{(y)}_{\mu }\partial ^{(y)}_{\nu } C \right. \nonumber \\&- \eta _{\mu \nu } \eta ^{\alpha \beta } \partial ^{(y)}_{\alpha } \partial ^{(y)}_{\beta } C -\partial ^{(y)}_\mu C \partial ^{(y)}_\nu C \nonumber \\&\left. + \frac{\eta _{\mu \nu }}{2} \eta ^{\alpha \beta }\partial ^{(y)}_{\alpha } C \partial ^{(y)}_{\beta } C\right) , \end{aligned}$$

(89)

where the derivative operators are just partial derivatives with respect to the coordinates $y^{\mu }$ above. In order to use this expression at an arbitrary point, where the space-time is expressed in other generic coordinates one needs to rely on in appropriate covariant form (88).

When evaluating the expectation value in any state we must ensure that we use the normal ordering with respect to the in quantization, so that the first term on the r.h.s will be zero if we chose $|\Psi \rangle$ to be the in vacuum.

In our calculations, we will be using the relationship between the derivative operators corresponding to the flat metric and that corresponding to the general metric. Recall that relationship between two derivative operators is represented by is a tensor of type (1,2) denoted $C_{ab}^c$ which specifies how it acts on a dual vector field $A_b$ [46]

$$\begin{aligned} \nabla _{a} A_{b} = \nabla '_{a}A_{b} - C_{ab}^{c} A_{c}. \end{aligned}$$

(90)

Such expression is of course valid in all coordinate systems.

In order to use (88) for computing (89) we have to write the ordinary derivative operator associated with the asymptotic past “in” coordinates which as we noted is the same as the covariant derivative operator $\nabla ^{(\eta )}_a$ associated with the flat metric $\eta _{ab}$ in terms of the derivative operators associated with the coordinates that cover the whole space-time (that is the coordinates $x^{\pm }$). We denote these latter derivative operators as $\partial _a^{(x)}$.

Next we compute the $C_{ab}^{c}$ which becomes the Christoffel symbol relating the covariant derivative operator $\nabla ^{(\eta )}_a$ with the ordinary derivative operator $\partial _a^{(x)}$. In the x coordinate basis it is

$$\begin{aligned} \Gamma _{\mu \nu }^{\rho } = \frac{1}{2}g^{\rho \sigma } (\partial _{\mu }g_{\sigma \nu } + \partial _{\nu }g_{\mu \sigma } -\partial _{\sigma }g_{\mu \nu }) . \end{aligned}$$

(91)

Note that here the Christoffel symbol is a tensor field associated with the derivative operator $\nabla _a^{(\eta )}$ and the coordinate chart $x^{\mu }$ associated with the ordinary derivative operators $\partial ^{(x)}_a$.

The in flat metric can be expressed in the global coordinates $x^+, x^-$ as $ds^2_{\eta _{\mu \nu }} = \frac{dx^+ dx^-}{ (-\Lambda ^2 x^+ x^-)}$ and can also be expressed in the in coordinates as $\eta _{\mu \nu } dy^\mu {dy^\nu }$. The relation between the coordinates $x^{\pm }$ and the coordinates $y^{\pm }$ is given by $dy ^{\pm }=d x^{\pm }/ \Lambda x^{\pm }$ while $dy^+ = dy^0 + dy^1$ and $dy^- = dy^0 - dy^1$. Thus we have the metric components $g_{x^+ x^+} =g_{x^- x^-} =0$ and $g_{x^+ x^-} = g_{x^- x^+} = -(2 \Lambda ^2 x^+ x^-)^{-1}$.

Next we find the appropriate expression for the conformal factor relating the flat and curved metrics. For that let us recall the spacetime metric in the conformal gauge is

$$\begin{aligned} ds^2= & {} -e^{2\rho } dx^+ dx^-, \nonumber \\= & {} e^{2\rho } \left( -\Lambda ^2 x^+ x^-\right) ds^2_{\eta _{\mu \nu }}, \end{aligned}$$

(92)

where is the flat linear-dilaton spacetime and the conformal factor or subsequently C is found to be

$$\begin{aligned} \Omega ^2= & {} e^{2\rho } (-\Lambda ^2 x^+ x^-), \nonumber \\ \implies C= & {} \ln \Omega = \rho + \frac{1}{2}\ln (-\Lambda ^2x^+ x^-). \end{aligned}$$

(93)

Using (90), (91), (92) and (93), a simple calculation yields

$$\begin{aligned} \langle {\Psi }| T_{x^\pm x^\pm } |{\Psi } \rangle= & {} -\frac{\hbar }{12\pi } \left( (\partial _{x^\pm }\rho )^2 - \partial _{x^\pm }^2\rho - \frac{1}{4{x^\pm }^2}\right) \nonumber \\&+ \langle {\Psi }|: T_{x^\pm x^\pm }:_{in} |{\Psi } \rangle , \end{aligned}$$

(94)

$$\begin{aligned} \langle {\Psi }| T_{x^+ x^-} |{\Psi } \rangle= & {} -\frac{\hbar }{12\pi }\partial _{x^+}\partial _{x^-}\rho \nonumber \\&+ \langle {\Psi }|: T_{x^+x^-}:_{in}|{\Psi } \rangle . \end{aligned}$$

(95)

As it is well known [47, 48], the covariant behavior of the renormalized stress tensor (which is a direct consequence of semi-classical Einstein equations) requires a specific nonzero trace of the expectation value of the energy-momentum tensor that should be in fact state independent. That is :

$$\begin{aligned} g^{\mu \nu } \langle \Psi | T_{\mu \nu } | \Psi \rangle = \frac{\hbar R}{24\pi }. \end{aligned}$$

(96)

In the conformal gauge where the only non-vanishing metric components are $g^{x^+ x^-}$ one can easily find the off-diagonal components of renormalized energy-momentum tensor $\langle \Psi | T_{x^{\pm }{x^\mp }} | \Psi \rangle$ which matches with (95) given the fact that $\langle {\Psi }|: T_{x^+x^-}:_{in}|{\Psi } \rangle$ must vanish (this vanishing is a consequence of the conservation law $\nabla ^\mu \langle {\Psi }|T_{\mu \nu }|{\Psi } \rangle =0$). This is a direct consequence of the fact that trace of the energy-momentum tensor which appears in (96) is independent of the state of the quantum field.

Thus we now have the explicit expressions for various components of the renormalized energy-momentum tensor that appear in semi-classical Einstein Eqs. (4) and (5), given by

$$\begin{aligned} \langle {\Psi }| T_{x^\pm x^\pm } |{\Psi } \rangle= & {} \frac{\hbar }{12\pi } \left( \partial _{x^\pm }^2\rho -(\partial _{x^\pm }\rho )^2 - \frac{1}{4{x^\pm }^2}\right) \nonumber \\&+ \langle {\Psi }|: T_{x^\pm x^\pm }:_{in} |{\Psi } \rangle , \end{aligned}$$

(97)

$$\begin{aligned} \langle {\Psi }| T_{x^+ x^-} |{\Psi } \rangle= & {} -\frac{\hbar }{12\pi }\partial _{x^+}\partial _{x^-}\rho . \end{aligned}$$

(98)

As a check on the above expressions we consider them for the in vacuum state in the linear dilaton vacuum region, where components of the renormalized energy-momentum tensor should vanish. The conformal factor in linear dilaton vacuum $e^{2\rho (x^\pm )} = -\frac{1}{\Lambda ^2 x^+ x^-}$ which implies that the first term in (97) vanishes and the normal ordered part is trivially zero since we have chosen $|\Psi \rangle$ to be the vacuum state. Similarly it is easy to see that (98) vanishes as well. This provides one consistency check for the expressions of the renormalized energy-momentum tensor.

Fig. 4

Modified RST spacetime due to the collapse of wavefunction in Kruskal frame. The energy-momentum tensor due to the collapse of the “in” vacuum state has support in the region $c\le x^+ \le c+b$ which modifies the spacetime after the collapse hypersurface. The modification to RST spacetime is the intersection of the future light cone of the point $(x^+=c, x^-=x^-_1)$ and the causal future of all the points on the collapse hypersurface

Appendix B: The backreacted spacetime with GRW type collapse

Here we want to explicitly calculate the backreacted spacetime assuming a single collapse event of GRW type [15] on one of the collapse hypersurfaces chosen stochastically. Also, we would only consider a situation where the right-moving modes are subjected to collapse. In this situation the backreacted metric due to collapse has the following form

$$\begin{aligned} \chi= & {} \Omega =-\frac{\Lambda ^2x^+x^-}{\sqrt{\kappa }} \nonumber \\&-\frac{\sqrt{\kappa }}{4}\ln (-\Lambda ^2x^+x^-) \nonumber \\&-\frac{m}{\Lambda \sqrt{\kappa }x_{0}^+} \left( x^+-x_{0}^+\right) \theta \left( x^+-x_{0}^+\right) \nonumber \\&+ \frac{1}{\sqrt{\kappa }} \int _0^{x^+} dx^{'+} \int _0^{x^{'+}} dx^{''+} t_{++} \end{aligned}$$

(99)

where $t_{++}$ is a state dependent function, defined in (74), and it vanishes if and only if we chose the quantum state to be the “in” vacuum. In that case we have the RST spacetime. However, if the state is different than vacuum, such as when the wavefunction is modified by a the collapse dynamics, we must find out the new spacetime.

We will consider here a single collapse event, associated with a certain space-like hypersurface, which we take here as given by one of the hypersurfaces of the folliation introduced in section V.D. That is the hypersurface that corresponds to say to a specific value of R say $R= R_c$ (which in the distant exterior region is matched to something else as shown in Fig. 3). In order to further simplify matters we will chose chose $t_{++}$ to be proportional to a (localized) function of compact support along $x^+$. This is further motivated by the form of the collapse operators which are associated to the modes n, j which as we know are highly localized. However as we noted, the meaningful use of the semi-classical setting, requires that the precise form of the collapse operators should be such as to ensure the Hadamard nature of the states that result from the collapse dynamics.

We represent the fact that $t_{++}$ is nonzero only to the future of the collapse hypersurface characterized by the equation $x^+ = f_{R_c}(x^{-})$, by including a theta function. Keeping these considerations in mind we have

$$\begin{aligned} t_{++} (x^+, x^-) = \epsilon h(x^+) \Theta \left[ x^+ - f_{R_c}(x^-)\right] , \end{aligned}$$

(100)

where $\epsilon$ is small number, $x^+ - f_{R_c}(x^-) =0$ specifies the collapse hypersurface and the theta function makes sure that the energy-momentum tensor vanishes to all the points past to the collapse hypersurface⁶. The resulting backreacted spacetime is then found by putting (100) in (99) and integrating.

As an example, where the calculation can be made explicitly we considered the function

$$\begin{aligned} h(x^+) = \left\{ \begin{array}{ll} 0 &{} \quad x^+\le c \\ \alpha (x^+ - c) &{} \quad c\le x^+ \le c+b/2 \\ \alpha b -\alpha (x^+ - c) &{} \quad c+b/2\le x^+ \le c+b \\ 0 &{} \quad b+c<x^+ \end{array} \right. \nonumber \\ \end{aligned}$$

(101)

and checked that the resulting space-time metric is smooth, everywhere except on the collapse hypersurface where it is only continuous. The spacetime is modified only to the future of the support of $t_{++}$.

The analysis proves that as we move along the $x^-$ axis (with fixed $x^+$) the metric changes nontrivially as one crosses the hypersurface, but, the change is always continuous.

As one moves along a line of fixed $x^-$ by changing $x^+$, the modification appears only to the future of the collapse hypersurface and change is continuous The pictorial description of these results is depicted in Fig. 4.

By observing Figs. 4 and 3 we note that the collapse can result in modifications of the metric and quantum state at asymptotic infinity, in the black hole region and on the thunderpop.

The actual changes will of course depend on the specific realization of the stochastic parameters/functions that control the collapse evolution, as these will determine the actual state of the quantum field that results from the collapse. The treatment presented here is limited to a single instantaneous collapse event and the treatment involving the continuous and multi-mode CSL dynamics, presented in section V. B., is more complicated but can be generalized as a continuous version of what we showed here.