1 Introduction

Decays of B mesons to two-body final states including a charmonium meson, proceed via a \(b\rightarrow s c\bar{c}\) or \(b\rightarrow d c\bar{c}\) quark transition, provide us with a playground for understanding the features of CP violation in the B meson system. For the Cabibbo-favored \(b\rightarrow s c\bar{c}\) modes, such as \(B\rightarrow J/\psi K\), the tree and penguin contributions have the same weak phase to order \(\lambda ^2\) and thus no direct CP violation is expected. In the Cabibbo-suppressed \(b\rightarrow d c\bar{c}\) transitions, however, the tree and penguin contributions have different phases and the CP asymmetries may appear at the percent level, e.g. \(B\rightarrow J/\psi \pi \). Any asymmetry larger than this magnitude would be the harbingers of new physics and of significant interest. The current experimental measurements of the direct CP violations for exclusive decays of B mesons to charmonium and kaon or pion final states, which have been averaged by the Particle Data Group (PDG) [1], are summarized below:

$$\begin{aligned} A_{J/\psi K^+}= & {} 0.003\pm 0.006, \nonumber \\ A_{\psi (2S) K^+}= & {} 0.012\pm 0.020, \nonumber \\ A_{\chi _{c1} K^+}= & {} -0.009\pm 0.033, \nonumber \\ A_{J/\psi \pi ^+}= & {} 0.001\pm 0.028, \nonumber \\ A_{\psi (2S) \pi ^+}= & {} 0.03\pm 0.06, \nonumber \\ A_{\chi _{c1} \pi ^+}= & {} 0.07\pm 0.18, \end{aligned}$$
(1)

where statistical and systematic uncertainties have been added in quadrature. The neutral B decays to CP eigenstates containing a charmonium and \(K_S^0\) are regarded as the golden mode for extracting the mixing-induced CP asymmetry parameter \(S_f=-\eta \sin {2\beta }\), \(\beta \) being the weak phase of the CKM matrix element \(V_{td}\) and \(\eta \) is the CP eigenvalue of the final state f. The latest average of Heavy Flavor Averaging Group (HFAVG) [2] gave \(S_{J/\psi K^0_S}=0.665 \pm 0.024 \), \(S_{\psi (2S) K^0_S}=0.807\pm 0.067\), and \(S_{\chi _{c1} K^0_S}=0.632\pm 0.099\) corresponding to the \(\eta =-1\) modes \(J/\psi K^0_S\), \(\psi (2S) K^0_S\), and \(\chi _{c1} K^0_S\), respectively. The small spread in the CP asymmetry parameters between different charmonia may indicate the penguin contributions in these decays are split according to different \(c\bar{c}\) systems.

On the other hand, the dominant mechanism for charmonium production in the B meson decay is color-suppressed, so precise measurements of rates to the exclusive modes can provide valuable insight into the dynamics of strong interactions in heavy meson systems. In particular, any mode involving various excitations of the \(c\bar{c}\) assignments such as P-wave charmonium productions could be an alternative to that for S-wave counterparts, and they could give additional and complementary information about the exclusive charmonium decays of the B meson. Under the factorization hypothesis, those decays are allowed when the charm-anticharm pair hadronizes to \(\chi _{c1}\), but suppressed when the quark pair hadronizes to \(\chi _{c0,c2}\) and \(h_c\) due to the spin-parity and vector current conservation [3]. Of course it is possible if there is an exchange of an additional gluon, which is the so-called non-factorizable contributions. Therefore, these modes are particularly illuminating as they provide valuable information for understanding of the non-factorizable mechanism. In fact, both the BABAR [4, 5] and Belle [6, 7] have found a surprisingly large branching ratios of \(B\rightarrow \chi _{c0,c2}K^{(*)}\) decays, which are even comparable to that of the factorization-allowed decay, such as \(B\rightarrow \chi _{c1}K\). Besides, some other P-wave charmonium productions in B meson decay have been observed by several experimental collaborations, such as \(B\rightarrow \chi _{c1} \pi \) [8, 9], \(B\rightarrow \chi _{c1} K^{(*)}\) [10,11,12], \(B\rightarrow h_{c} K^{(*)}\) [13, 14], and so on. Most recently, the Belle collaboration present the measurement of the absolute branching fractions of \(B^+\rightarrow X_{cc} K^+\), where \(X_{cc}\) denotes nine charmonium states: \(\eta _c\), \(J/\psi \), \(\chi _{c0}\), \(\chi _{c1}\), \(\eta _c(2S)\), \(\psi (2S)\), X(3870), X(3872), and X(3915) [15]. As for hadronic \(B_s\) decays, the first observation of the decay \(B_{s}\rightarrow \chi _{c1}\phi \) [16] are reported by the LHCb experiment, meanwhile, some relative ratios of the branching ratios for B meson decays into \(\chi _{c1}\) and \(J/\psi \) mesons are also measured, which would discriminate the mass dependence from the quantum number dependence [17].

Phenomenologically the B meson decays into various P-wave charmonium have been studied in different approaches. In Ref. [18], the authors analyze the soft nonfactorizable contributions to \(B\rightarrow (\eta _c,J/\psi ,\chi _{c0,c1})K\) decays by using the light-cone sum rules (LCSR) approach, and they found the nonfactorizable contributions are sizable for \(B\rightarrow (\chi _{c1},J/\psi ) K\), while for the B decays into a (pseudo) scalar charmonia, the nonfactorizable contributions are too small to accommodate the data. In Ref. [19], the same decay modes are studied by using a hybrid PQCD approach, in which the factorizable contributions are treated in naive factorization (FA). The nonfactorizable diagrams are evaluated utilizing the conventional PQCD formalism, which is free from the endpoint singularities. Within the framework of QCD factorization (QCDF) [20,21,22], the exclusive B decays to P-wave charmonium states were discussed earlier [23,24,25,26,27,28,29], and they found the soft contributions may be large since there exist infrared divergences in the vertex corrections and end-point singularities in the leading twist spectator corrections. Subsequently, the explicit calculations in Refs. [28, 29] show that the infrared divergences arising from vertex corrections cancel in the \(B\rightarrow \chi _{c1} K\) decay as in the case of \(B\rightarrow J/\psi K\).

Based on the \(k_T\) factorization theorem, after including the parton transverse momentum \(k_T\) and threshold resummations, both factorizable and nonfactorizable decay amplitudes are calculable without endpoint singularity. For detailed discussions of this approach, one can consult Refs. [30, 31]. In general, the PQCD approach is suitable for describing various charmonium decays of B meson [32,33,34,35,36,37,38] and has a good predictive power. In our previous work [39], the PQCD approach had been applied to study the \(B\rightarrow J/\psi V, \psi (2S) V\) decays with V encompasses \(\rho , \omega , K^{*}, \phi \) and gave satisfactory results. The main focus of this work lies on the \(B\rightarrow \chi _{c1} K(\pi )\) decays, while other factorization forbidden decays are beyond the scope of the present analysis because of the appearance of nonvanishing infrared divergences arising from nonfactorizable vertex corrections. As mentioned above, the \(B\rightarrow \chi _{c1}K\) decay had been analyzed in a hybrid PQCD approach [19], where the factorizable contributions were parameterized in FA with the \(B\rightarrow K\) form factors taken from the light-front QCD [40]. Here both the factorizable and nonfactorizable contributions are evaluated utilizing the conventional PQCD formalism. This is the main difference between [19] and our calculations. Besides, we update the \(\chi _{c1}\) distribution amplitudes (DAs) according to our recent work [41], where the new universal nonperturbative objects are successful in describing various P-wave charmonium productions in the case of \(B_c\) meson decays. Thus it is motivated to check for validity of the same scenario in the B meson decays. For the vertex corrections, we employ the most recent updated results from the QCDF [28, 29]. Finally, we also investigate the CP asymmetry parameters including the Cabibbo-suppressed \(B\rightarrow \chi _{c1} \pi \) and \(B_s\rightarrow \chi _{c1} \bar{K}\) decays, which may be tested by the LHCb and Belle-II with continuously increasing high precision measurements.

The presentation of the paper is as follows. After this introduction, we formulate the decay amplitudes of \(B\rightarrow \chi _{c1}K(\pi )\) in the PQCD approach. In Sect. 3, we give the numerical results and discussions. Finally, we conclude in Sect. 4 with a summary.

2 Theoretical details

The effective Hamiltonian relevant for \(B\rightarrow \chi _{c1} K(\pi )\) has the following form [42]:

$$\begin{aligned} \mathcal {H}_{eff}= & {} \frac{G_F}{\sqrt{2}}\Bigg \{\xi _c\big [C_1(\mu )(\bar{q}_ic_j)_{V-A}(\bar{c}_jb_i)_{V-A}\nonumber \\&+C_2(\mu )(\bar{q}_ic_i)_{V-A}(\bar{c}_jb_j)_{V-A}\big ]\nonumber \\&-\xi _t\big [C_3(\mu )(\bar{q}_ib_i)_{V-A}(\bar{q}'_jq'_j)_{V-A}\nonumber \\&+C_4(\mu )(\bar{q}_ib_j)_{V-A}(\bar{q}'_jq'_i)_{V-A}\nonumber \\&+C_5(\mu )(\bar{q}_ib_i)_{V-A}(\bar{q}'_jq'_j)_{V+A}\nonumber \\&+C_6(\mu )(\bar{q}_ib_j)_{V-A}(\bar{q}'_jq'_i)_{V+A}\nonumber \\&+C_7(\mu )\frac{3}{2}(\bar{q}_ib_i)_{V-A} \sum _{q'}e_{q'}(\bar{q}'_jq'_j)_{V+A}\nonumber \\&+C_8(\mu )\frac{3}{2}(\bar{q}_ib_j)_{V-A} \sum _{q'}e_{q'}(\bar{q}'_jq'_i)_{V+A}\nonumber \\&+C_9(\mu )\frac{3}{2}(\bar{q}_ib_i)_{V-A} \sum _{q'}e_{q'}(\bar{q}'_jq'_j)_{V-A}\nonumber \\&+C_{10}(\mu )\frac{3}{2}(\bar{q}_ib_j)_{V-A} \sum _{q'}e_{q'}(\bar{q}'_jq'_i)_{V-A}\big ]\Bigg \}, \end{aligned}$$
(2)

where \(V\pm A\equiv \gamma _{\mu }(1\pm \gamma _5)\), i, j are colour indices, \(e_{q'}\) are the electric charges of the quarks in units of |e|, and a summation over \(q'=u,d,s,c,b\) is implied. \(G_F\) is the Fermi constant and \(\xi _{c(t)}=V^*_{c(t)b}V_{c(t)q}\) with \(q=d,s\) are the products of CKM matrix element. \(C_i(\mu )\) are the QCD corrected Wilson coefficients at the renormalization scale \(\mu \).

In the PQCD framework, the decay amplitude is factorized into the convolution of the meson wave functions, the hard scattering kernels and the Wilson coefficients, which stand for the dynamics below, around, and above the b quark mass, respectively. The formalism can be written as

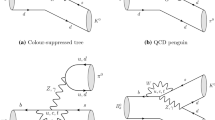
$$\begin{aligned}&\mathcal {A}(B\rightarrow \chi _{c1} K(\pi )) \nonumber \\&\quad = \int d^4k_1d^4k_2d^4k_3Tr\nonumber \\&\qquad \times \left[ C(t)\Phi _B(k_1)\Phi _{\chi _{c1}}(k_2)\Psi _{K(\pi )}(k_3) H(k_1,k_2,k_3,t)\right] ,\nonumber \\ \end{aligned}$$
(3)

where \(k_i\) are the quark momentum in each meson, and “Tr” denotes the trace over all Dirac structures and color indices. C(t) is the standard perturbative QCD coefficient, which evolve from the W boson mass down to the renormalization scale t. The meson wave functions \(\Phi \) absorb the nonperturbative dynamics in the hadronization processes. The explicit expression of \(\Phi _{\chi _{c1}}\) refer to our previous work [41], while for \(\Phi _{B}\) and \(\Phi _{K(\pi )}\) including some relevant parameters are the same as those used in [43]. The remaining finite contribution is assigned to a hard amplitude H, which contains the four quark operator and a hard gluon connecting the spectator quark. This renders the perturbative calculations in an effective six quark interaction form. The relevant Feynman diagrams are shown in Fig. 1. Below we present the calculation of the hard amplitude in the PQCD approach.

Fig. 1
figure 1

The typical leading-order Feynman diagrams for the decays \(B_c \rightarrow \chi _{c1} K(\pi )\). a, b The factorizable diagrams, and c, d the nonfactorizable diagrams

Full size image

The calculation is carried out in the rest frame of B meson. The B meson momentum \(P_1\), the \(\chi _{c1}\) meson momentum \(P_2\), the light meson momentum \(P_3\), and the quark momenta \(k_1\), \(k_2\), and \(k_3\) corresponding to B, \(\chi _{c1}\), and light mesons, respectively, whose notation are displayed in Fig. 1a, are chosen as

$$\begin{aligned} P_1= & {} \frac{M}{\sqrt{2}}\left( 1,1,\mathbf 0 _\mathrm{T}\right) ,\nonumber \\ P_2= & {} \frac{M}{\sqrt{2}}\left( 1,r^2,\mathbf 0 _\mathrm{T}\right) ,\nonumber \\ P_3= & {} \frac{M}{\sqrt{2}}\left( 0,1-r^2,\mathbf 0 _\mathrm{T}\right) ,\nonumber \\ k_1= & {} \left( \frac{M}{\sqrt{2}}x_1,0,\mathbf k _\mathrm{1T}\right) ,\nonumber \\ k_2= & {} \left( \frac{M}{\sqrt{2}}x_2,\frac{M}{\sqrt{2}}x_2r^2,\mathbf k _{2\mathrm T}\right) ,\nonumber \\ k_3= & {} \left( 0,\frac{M}{\sqrt{2}}x_3(1-r^2),\mathbf k _\mathrm{3T}\right) , \end{aligned}$$
(4)

with the mass ratio \(r=m_{\chi _{c1}}/M\) and \(m_{\chi _{c1}},M\) are the masses of the charmonium and B meson, respectively. The \(k_{iT}\), \(x_i\) represent the transverse momentum and longitudinal momentum fraction of the quark inside the meson. Like vector mesons, axial-vector charmonium \(\chi _{c1}\) also carry spin degrees of freedom. For the decays under study, only longitudinally polarized \(\chi _{c1}\) produced with the polarization vector \(\epsilon _{2L}=\frac{1}{\sqrt{2}r}(1,-r^2,\mathbf 0 _\mathrm{T})\), which satisfy the normalization \((\epsilon _{2L})^2 =-1\) and the orthogonality \(\epsilon _{2L} \cdot P_2=0\). According to Eq. (3), the full decay amplitudes for the considered decays is written as

$$\begin{aligned} \mathcal {A}= & {} \xi _c \Big [a_2\mathcal {F}^{LL} +C_2\mathcal {M}^{LL} \Big ] \nonumber \\&-\xi _t\Big [(a_3+a_9)\mathcal {F}^{LL}+ (a_5+a_7)\mathcal {F}^{LR}\nonumber \\&+(C_4+C_{10})\mathcal {M}^{LL}+(C_6+C_8)\mathcal {M}^{SP}\Big ]. \end{aligned}$$
(5)

The QCD factors \(a_i\) appear in decay amplitudes, which encode dynamics of the decay, are related to \(C_i\) as follows:

$$\begin{aligned} a_2=C_1+\frac{1}{3}C_2, \quad a_{i}=C_i+\frac{1}{3}C_{i+1} \quad \text {for} \quad i=3,5,7,9.\nonumber \\ \end{aligned}$$
(6)

The superscript LL, LR, and SP refers to the contributions from \((V-A)\otimes (V-A)\), \((V-A)\otimes (V+A)\) and \((S-P)\otimes (S+P)\) operators, respectively. \(\mathcal {F}(\mathcal {M})\) describes the contributions from the factorizable (nonfactorizable) diagrams in Fig. 1, which can be expressed as

$$\begin{aligned} \mathcal {F}^{LL}= & {} 8\pi C_f f_{\chi _{c1}} M^4\int _0^1dx_1dx_3\nonumber \\&\times \int _0^{\infty }b_1b_3db_1db_3 \phi _B(x_1,b_1)\nonumber \\&\times \Bigg \{ \Big [(r^2-1)\phi ^A(x_3)((r^2-1)x_3-1)\nonumber \\&+(r^2-1)\phi ^P(x_3)r_p(2x_3-1)\nonumber \\&-\phi ^T(x_3)r_p(2x_3-1-r^2(1+2x_3))\Big ]\nonumber \\&\times \alpha _s(t_a)S_{ab}(t_a)h(\alpha _e,\beta _a,b_1,b_3)S_t(x_1)\nonumber \\&-2r_{p}(1-r^2)\phi ^P(x_3)\alpha _s(t_b)S_{ab}(t_b)\nonumber \\&\times h(\alpha _e,\beta _b,b_1,b_3)S_t(x_3)\Bigg \}, \end{aligned}$$
(7)
$$\begin{aligned} \mathcal {M}^{LL}= & {} -16\sqrt{\frac{2}{3}}\pi C_f M^4\int _0^1dx_1dx_2dx_3\nonumber \\&\times \int _0^{\infty }b_1b_2db_1db_2 \phi _B(x_1,b_1)\nonumber \\&\times \left[ (r^2-1)\phi ^A(x_3)+2r_p\phi ^T(x_3)\right] \nonumber \\&\times \left[ \psi ^L(x_2)(r^2(x_1+x_3-2x_2)-x_3) +2rr_c\psi ^t(x_2)\right] \nonumber \\&\times \alpha _s(t_d)S_{cd}(t_d)h(\alpha _e,\beta _d,b_1,b_2), \end{aligned}$$
(8)
$$\begin{aligned} \mathcal {F}^{LR}= & {} -\mathcal {F}^{LL},\nonumber \\ \mathcal {M}^{SP}= & {} \mathcal {M}^{LL}, \end{aligned}$$
(9)

with \(r_c=m_c/M\) and \(m_c\) is the charm quark mass; \(C_f=4/3\) is a color factor; \(f_{\chi _{c1}}\) is the vector decay constant of the \(\chi _{c1}\) meson. The hard scales t, functions h, Sudakov factors S(t), and the threshold resummation factor \(S_t(x)\) refer to Appendix A of Ref. [39] for details. Note that the coefficient \(-\frac{1}{\sqrt{2}}\) appears for \(B\rightarrow \chi _{c1}\pi ^0\) mode due to the \(\pi ^0\) meson generated from a pure \(d\bar{d}\) source.

In addition, we also consider the vertex corrections to the factorizable diagrams in Fig. 1. As stated in Refs. [28, 29], the infrared divergences cancel when one sums over all the vertex corrections for the \(B\rightarrow \chi _{c1}K\) decay, just like the decays to S-wave charmonia, where the same hard vertex corrections are infrared finite.

Therefore, it is not necessary to introduce the quark transverse momentum \(k_T\) at the end-point region [44]. The calculations are then performed in the collinear factorization theorem instead of the \(k_T\) factorization theorem. As a consequence, we can simply quote the QCDF expressions for the vertex corrections. According to the power counting of QCDF [20,21,22], the hard spectator (nonfactorizable) interaction is of the same order in \(\alpha _s\) as the vertex corrections in the heavy-quark limit. So the corrections to the nonfactorizable diagrams Fig. 1c, d are further power suppressed. In fact, the full next-to-leading-order (NLO) corrections to the charmonium B decays under the PQCD framework are still unavailable, but the significant vertex corrections should be included in this work when comparing with the predictions of the QCDF. As usual, the vertex corrections effects can be combined into the coefficients \(a_i\) in Eq. (5) as [20,21,22]

$$\begin{aligned}&a_2\rightarrow a_2 +\frac{\alpha _s}{4\pi }\frac{C_f}{N_c}C_2 \left[ -18-12\text {ln}(\frac{t}{m_b})+f_I\right] ,\nonumber \\&a_3+a_9 \rightarrow a_3+a_9 +\frac{\alpha _s}{4\pi }\frac{C_f}{N_c}(C_4+C_{10}) \nonumber \\&\quad \times \left[ -18 -12\text {ln}\left( \frac{t}{m_b}\right) +f_I\right] ,\nonumber \\&a_5+a_7 \rightarrow a_5+a_7-\frac{\alpha _s}{4\pi }\frac{C_f}{N_c}(C_6+C_{8}) \nonumber \\&\quad \times \left[ -6-12\text {ln}\left( \frac{t}{m_b}\right) +f_I\right] , \end{aligned}$$
(10)

where \(N_c\) is the color factor. The quantity \(f_I\) account for vertex corrections, whose detail calculations can be found in Refs. [28, 29].

3 Numerical results and discussions

To proceed the numerical analysis, it is useful to summarize all of the input quantities entering the PQCD approach below:

  • For the masses (in GeV) [1]: \(M_B=5.28\),    \(M_{B_s}=5.37\),    \(m_{\chi _{c1}}=3.511\),   \(m_b(\text {pole})=4.8\),    \(\bar{m_c} (\bar{m_c})=1.275\).

  • For the lifetimes (in ps) [1]: \(\tau _{B_s}=1.51, \quad \tau _{B_0}=1.52,\quad \tau _{B^+}=1.638\).

  • For the Wolfenstein parameters [1]: \(\lambda = 0.22506\),   \(A=0.811\),    \(\bar{\rho }=0.124\),   \(\bar{\eta }=0.356\).

  • For the Gegenbauer moments at the scale of \(\mu =1\) GeV [43]: \(a_1^K=0.17\),    \(a_2^K=0.2\),    \(a_1^{\pi }=0\),    \(a_2^{\pi }=0.44\).

  • For the decay constants (in GeV): \(f_B=0.19\) [1],    \(f_{B_s}=0.227\) [1],    \(f_{\chi _{c1}}=0.335\) [19],    \(f_{\pi }=0.131\) [43],    \(f_{K}=0.16\) [43].

The chiral factor \(m_0\) relates the pseudoscalar meson mass to the quark mass is set as \(1.6\pm 0.2\) GeV [45].

For the concerned decays, the branching ratios can be written as

$$\begin{aligned} \mathcal {B}(B\rightarrow \chi _{c1} K(\pi ))=\frac{G_F^2\tau _{B}}{32\pi M}(1-r^2) |\mathcal {A}|^2. \end{aligned}$$
(11)

Using the above formulas and inputs, we derive the CP-averaged branching ratios for the concerned decays,

$$\begin{aligned} \mathcal {B}(B^+\rightarrow \chi _{c1}K^+)= & {} \left( 4.4^{+1.4+0.9+0.7+0.2+0.5}_{-1.1-0.8-0.7-0.4-0.4}\right) \times 10^{-4}\nonumber \\= & {} (4.4^{+1.9}_{-1.6})\times 10^{-4},\nonumber \\ \mathcal {B}(B^0\rightarrow \chi _{c1}K^0)= & {} \left( 4.1^{+1.3+0.9+0.6+0.2+0.5}_{-1.1-0.8-0.7-0.4-0.4}\right) \times 10^{-4}\nonumber \\= & {} (4.1^{+1.8}_{-1.6})\times 10^{-4},\nonumber \\ \mathcal {B}(B^+\rightarrow \chi _{c1}\pi ^+)= & {} \left( 1.7^{+0.4+0.4+0.2+0.2+0.1}_{-0.4-0.3-0.2-0.2-0.2}\right) \times 10^{-5}\nonumber \\= & {} (1.7\pm 0.6)\times 10^{-5},\nonumber \\ \mathcal {B}(B^0\rightarrow \chi _{c1}\pi ^0)= & {} \left( 0.8^{+0.2+0.2+0.1+0.1+0.1}_{-0.2-0.2-0.1-0.1-0.1}\right) \times 10^{-5}\nonumber \\= & {} (0.8\pm 0.3)\times 10^{-5},\nonumber \\ \mathcal {B}(B_s\rightarrow \chi _{c1}\bar{K}^{0})= & {} \left( 1.4^{+0.5+0.3+0.2+0.0+0.2}_{-0.4-0.3-0.2-0.1-0.2}\right) \times 10^{-5}\nonumber \\= & {} (1.4\pm 0.6)\times 10^{-5}, \end{aligned}$$
(12)

where the second equal-sign in each row denote the central value with all uncertainties added in quadrature. There are some theoretical uncertainties in our calculations. The first one comes from the nonperturbative parameters \(\omega _{b_{(s)}}\) in \(B_{(s)}\) meson wave functions. For B decays, we adopt the value \(\omega _b=0.40\pm 0.04\) GeV, which is supported by intensive PQCD studies [46,47,48,49]. For \(B_s\) meson, we will follow the authors in Ref. [43] and adopt the value \(\omega _{b_s}=0.50 \pm 0.05\) GeV. The second error comes from the decay constant of \(\chi _{c1}\) meson, which varies \(10\%\) for error estimates. The third error is induced by the chiral scale parameter \(m_0=1.6\pm 0.2\) GeV [45] associated with kaon or pion, which reflect the uncertainty in the current quark masses. The fourth one is from the uncertainty of the heavy quark masses. In the evaluation, we also vary the values of \(m_{b,c}\) within a \(10\%\) range. The last one is caused by the variation of the hard scale from 0.75t to 1.25t, which characterizes the size of higher-order corrections to the hard amplitudes. It is found that the first three errors are comparable and contribute the main uncertainties in our approach. While the last scale-dependent uncertainty is less than \(15\%\) due to the inclusion of the vertex corrections.

As noted previously, many other work have performed a systematic study on the Cabibbo-favored decays. For comparison, we also collect their results in Table 1, as well as the current world average values from the PDG [1]. The branching ratios of \(\mathcal {B}(B^+\rightarrow \chi _{c1}K^+)\) evaluated within LCSR method [18] is \((5.1\pm 0.5)\times 10^{-4}\), which match well with our results. Two earlier papers [23, 29] also discuss the concerned decays in the QCDF. In Ref. [29], the authors treat \(\chi _{c1}\) as nonrelativistic bound states and gave \(\mathcal {B}(B^0\rightarrow \chi _{c1}K^0)=1.79\times 10^{-4}\), while in Ref. [23], where the light-cone wave function is used to describe the \(\chi _{c1}\) meson, the corresponding value is in the range \((0.87\sim 0.97)\times 10^{-4}\). Both of the two predictions yield much smaller values. However, in another paper [28], the authors revisited the exclusive B decays to P-wave charmonia in the same framework, where the colour-octet contributions are included and the charmonium is described as a Coulomb bound state. Their theoretical calculations, with reasonable parameter choices, can be in qualitative agreement with ours as well as the experimental data. It also can be seen that, for the K decay modes, our calculations in the conventional PQCD scheme are somewhat larger than the previous hybrid PQCD ones [19] due to the different scheme about the factorizable contributions, the \(\chi _{c1}\) DAs, and the vertex corrections as mentioned in the Sect. 1.

Comparing with the data, our predicted branching ratios of the Cabibbo-favored modes in Eq. (12) comply with the world average \(\mathcal {B}(B^+\rightarrow \chi _{c1}K^+)=(4.79\pm 0.23)\times 10^{-4}\) [1] from the measurements [5, 7, 50, 51]

$$\begin{aligned}&\mathcal {B}(B^+\rightarrow \chi _{c1}K^+)\\&\quad =\left\{ \begin{array}{ll} (4.94 \pm 0.11(\text {stat})\pm 0.33(\text {syst}))\times 10^{-4} &{}\quad \text {Belle (2011)}, \\ (4.5 \pm 0.1(\text {stat})\pm 0.3(\text {syst}))\times 10^{-4} &{} \quad \textit{BABAR}~ (2009), \\ (8.1 \pm 1.4(\text {stat})\pm 0.7(\text {syst}))\times 10^{-4} &{}\quad \textit{BABAR}~ (2006), \\ (15.5 \pm 5.4(\text {stat})\pm 2.0(\text {syst}))\times 10^{-4} &{}\quad \text {CDF (2002)}, \\ \end{array}\right. \end{aligned}$$

and \(\mathcal {B}(B^0\rightarrow \chi _{c1}K^0)=(3.93\pm 0.27)\times 10^{-4}\) from [5, 7, 52]

$$\begin{aligned}&\mathcal {B}(B^0\rightarrow \chi _{c1}K^0)\\&\quad =\left\{ \begin{array}{ll} (3.78 ^{ +0.17}_{ -0.16}(\text {stat})\pm 0.33(\text {syst}))\times 10^{-4} &{}\quad \text {Belle (2011)}, \\ (4.2 \pm 0.3(\text {stat})\pm 0.3(\text {syst}))\times 10^{-4} &{}\quad \textit{BABAR}~ (2009), \\ (3.1 ^{ +1.6}_{ -1.1}(\text {stat})\pm 0.1(\text {syst}))\times 10^{-4} &{}\quad \text {CLEO (2000)}. \\ \end{array}\right. \end{aligned}$$
Table 1 The branching ratios (in units of \(10^{-4}\)) of the Cabibbo-favored decays from different theoretical work [18, 19, 23, 28, 29]. The data are taken from the PDG 2016 [1]. The original experimental results can be found in [5, 7, 50,51,52]
Full size table

Now, we turn our attention to the Cabibbo-suppressed decays. From Eq. (12), the value of \(\mathcal {B}(B_s \rightarrow \chi _{c1} \bar{K}^{0} )\) have a tendency to be smaller than 2\(\mathcal {B}(B^0 \rightarrow \chi _{c1} \pi ^{0} )\). Although the \(B_s\) and K meson decay constants are larger than those of the \(B^0\) and \(\pi ^0\) meson, the SU(3) breaking effects in the twist-2 distribution amplitudes of the K meson, parametrized by the first Gegenbauer moment \(a_{1}^K\), gives a negative contribution to the \(B_s \rightarrow \chi _{c1} \bar{K}^{0}\) decay, which induces the smaller branching ratio. This is similar to the case of \(B_s \rightarrow \psi (2S) \bar{K}^{*0}\) and \(B^0 \rightarrow \psi (2S) \rho ^{0}\) decays [39]. Experimentally, only the Belle collaboration reported the results \(\mathcal {B}(B^+\rightarrow \chi _{c1}\pi ^+)=(2.4 \pm 0.4(\text {stat})\pm 0.3(\text {syst}))\times 10^{-5}\) [8] and \(\mathcal {B}(B^+\rightarrow \chi _{c1}\pi ^0)=(1.12 \pm 0.25(\text {stat})\pm 0.12(\text {syst}))\times 10^{-5}\) [9], which are a little larger than our predictions. None the less, taking the errors into consideration, the theoretical predictions and experimental data can still agree with each other. Since these Cabibbo-suppressed decays are still received less attention in other approaches, and we wait for future comparison.

As a cross-check, the ratio of the decay rates for the \(B\rightarrow \chi _{c1}\pi \) and \(B\rightarrow \chi _{c1}K\) decays, called \(\mathcal {R}_{\pi /K}\) below, can be calculated from Eq. (12), and are estimated as

$$\begin{aligned} \mathcal {R}_{\pi ^+/K^+}= & {} \frac{\mathcal {B}(B\rightarrow \chi _{c1}\pi ^+)}{\mathcal {B}(B\rightarrow \chi _{c1}K^+)}=\left( 3.9^{+0.2}_{-0.3}\right) \%,\nonumber \\ \mathcal {R}_{\pi ^0/K^0}= & {} \frac{\mathcal {B}(B\rightarrow \chi _{c1}\pi ^0)}{\mathcal {B}(B\rightarrow \chi _{c1}K^0)}=\left( 2.0^{+0.1}_{-0.2}\right) \%, \end{aligned}$$
(13)

where all uncertainties are added in quadrature. Because most theoretical uncertainties are cancelled by the flavor symmetries in the relative branching ratios, the total error of \(\mathcal {R}\) are only a few percent, much smaller than those for the absolute branching ratios. As can be seen that the first ratio is comparable with the Belle measurement [8],

$$\begin{aligned} \mathcal {R}_{\pi ^+/K^+}=(4.3\pm 0.8\pm 0.3)\%. \end{aligned}$$
(14)

Next, we consider the CP asymmetries in these decays. The direct CP violation for the charged modes, which arise from the interference between the tree contributions and the penguin contributions, can be written as

$$\begin{aligned} A^{\text {dir}}=\frac{|\mathcal {\bar{A}}|^2-|\mathcal {A}|^2}{|\mathcal {\bar{A}}|^2+|\mathcal {A}|^2}, \end{aligned}$$
(15)

where \(\mathcal {\bar{A}}\) is the CP-conjugate amplitude of \(\mathcal {A}\). In decays of neutral B mesons to a final state accessible to both B and \(\bar{B}\), the interference between the direct decay and the decay via oscillation leads to time-dependent CP asymmetry, which takes the form,

$$\begin{aligned} A(t)=-C_f \text {cos}(\Delta m t)+S_f \text {sin}(\Delta m t), \end{aligned}$$
(16)

where \(\Delta m>0\) is the mass difference of the two neutral B meson mass eigenstates. \(S_f\) is referred to as mixing-induced CP asymmetry and \(A_f=-C_f\) is the direct CP asymmetry, which can be expressed as

$$\begin{aligned} C_f=\frac{1-|\lambda _f|^2}{1+|\lambda _f|^2},\quad S_{f}=\frac{2\text {Im}(\lambda _f)}{1+|\lambda _f|^2}, \end{aligned}$$
(17)

with \(\lambda _f=\eta e^{-2i\beta _{(s)}}\frac{\mathcal {\bar{A}}}{\mathcal {A}}\). \(\eta \) is the CP eigenvalue of the final state f. \(\beta _{(s)}\) is the CKM angle defined as usual [1]. The numerical results for the direct CP asymmetries yield

$$\begin{aligned} A_{\chi _{c1}K}= & {} -\left( 1.5^{+0.0+0.0+0.0+0.1+0.4}_{-0.1-0.0-0.1-0.1-0.4}\right) \times 10^{-3}\nonumber \\= & {} -(1.5\pm 0.4)\times 10^{-3},\nonumber \\ A_{\chi _{c1}\pi }= & {} \left( 1.1^{+0.0+0.0+0.0+0.2+0.5}_{-0.0-0.0-0.1-0.3-0.5}\right) \times 10^{-2}\nonumber \\= & {} (1.1^{+0.5}_{-0.6})\times 10^{-2}, \nonumber \\ A_{\chi _{c1}\bar{K}}= & {} \left( 2.5^{+0.1+0.0+0.0+0.2+0.9}_{-0.1-0.0-0.1-0.3-0.9}\right) \times 10^{-2} \nonumber \\= & {} (2.5\pm 0.9)\times 10^{-2}, \end{aligned}$$
(18)

where the errors induced by the same sources as in Eq. (12). Unlike the branching ratios, the direct CP asymmetry is not sensitive to the nonperturbative parameters related to the initial and final states wave functions, but suffer from large uncertainties due to the hard scale t. Since the charged and neutral decay modes differ only in the lifetimes and isospin factor in our formalism, they have the same direct CP violations. It is found that the direct CP violations are rather small (only \(10^{-3}\sim 10^{-2}\)) due to the penguin contributions are loop suppressed with respect to the tree contributions. On the experimental side, some direct CP violations were measured by the Belle collaboration [8]:

$$\begin{aligned} A^{\text {dir}}_{CP}(B^+\rightarrow \chi _{c1}\pi ^+)= & {} 0.07\pm 0.18\pm 0.02,\nonumber \\ A^{\text {dir}}_{CP}(B^+\rightarrow \chi _{c1}K^+)= & {} -0.01\pm 0.03\pm 0.02, \end{aligned}$$
(19)

and BABAR collaboration [12]:

$$\begin{aligned} A^{\text {dir}}_{CP}(B^+\rightarrow \chi _{c1}K^+)=0.003\pm 0.076\pm 0.017. \end{aligned}$$
(20)

Their weighted average, in fact, enter the numbers given in Eq. (1) are in accordance with our calculations.

Since the neutral final state \(\chi _{c1}K^0\) and its CP conjugate are flavor-specific, here, we replace it with the CP-odd eigenstate \(f=\chi _{c1}K_S\) to analyze the mixing-induced CP asymmetries. The obtained results are listed as:

$$\begin{aligned} S(B^0\rightarrow \chi _{c1}K_S)= & {} 0.70^{+0.00+0.00+0.00+0.00+0.00}_{-0.00-0.00-0.00-0.00-0.01}\nonumber \\= & {} 0.70^{+0.0}_{-0.1},\nonumber \\ S(B^0\rightarrow \chi _{c1}\pi ^0)= & {} -0.62^{+0.01+0.00+0.00+0.01+0.02}_{-0.00-0.00-0.00-0.01-0.01}\nonumber \\= & {} -0.62^{+0.02}_{-0.01}, \nonumber \\ S(B_s\rightarrow \chi _{c1}K_S)= & {} -0.06^{+0.00+0.00+0.00+0.00+0.01}_{-0.00-0.00-0.00-0.00-0.01}\nonumber \\= & {} -0.06\pm 0.01, \end{aligned}$$
(21)

which are less sensitive to the those parameters within their uncertainties. Experimentally only the first value was direct measured. The HFAVG [2] quotes \(S(B^0\rightarrow \chi _{c1}K_S)=0.632\pm 0.099\) [2] as the average of the Belle [53] and BABAR [54] data, which is also compatible within \(1.0\sigma \) with our result in Eq. (21). In the limit of negligible higher-order contributions, S can be identified as \(\sin {2\beta }\). As can be seen, both theory and experiment are close to the current world average value \(\sin {2\beta }=0.677\pm 0.020\) [1], which suggests that this mode can serve as an alternative place to extract CKM phase \(\beta \). The \(B_s\rightarrow \chi _{c1}\bar{K}_S\) decay has not been observed so far. For a similar \(B_s\rightarrow J/\psi \bar{K}_S\) mode, the time-dependent CP-violation parameters have been measured by the LHCb [55] collaboration,

$$\begin{aligned} S(B_s \rightarrow J/\psi K_S)=-0.08\pm 0.40\pm 0.08. \end{aligned}$$
(22)

The small discrepancy is understandable with respect to the different charmonium states. It is hope that the future experiment will provide a direct measurement to the \(B_s\rightarrow \chi _{c1} K_S\) mode. Our predictions can be used to further explore the properties of the \(B_s\) system.

4 Conclusion

In the wake of recent measurements of the P-wave charmonium productions in the hadronic B decays, we performed the calculations of the \(B_{(s)}\rightarrow \chi _{c1}K(\pi )\) decays by employing the PQCD factorization approach. The predicted branching ratios for the \(B\rightarrow \chi _{c1}K\) modes are consistent with the data and those from LCSR method, while the expectations from the earlier QCDF and PQCD are somewhat smaller than the measured values. Our results for \(\mathcal {B}(B^0\rightarrow \chi _{c1}\pi )\) are smaller than those of the Belle measurement but the discrepancies do not exceed two standard deviations if one take into account the experimental uncertainty. For the \(B_s\) modes, the branching ratios amounts to the order of \(10^{-5}\), letting the corresponding measurement appear feasible. We further investigate the measurable CP asymmetries. The present predictions indicate that the direct CP asymmetries in these channels are very small due to the suppressed penguin contributions as we mentioned before. The mixing-induced CP asymmetry \(S(B^0\rightarrow \chi _{c1}K_S)\) is not far away from \(\sin {2\beta }\), and this mode can play an important role in the extraction of the CKM angle \(\beta \). These numbers will be further tested by the LHCb and Belle-II experiments in the near future.