Exclusive diffractive resonance production in proton–proton collisions at high energies

Abstract

A model for exclusive diffractive resonance production in proton–proton collisions at high energies is presented. This model is able to predict double differential distributions with respect to the mass and the transverse momentum of the produced resonance in the mass region $\sqrt{M^2}\lesssim$ 5 GeV. The model is based on convoluting the Pomeron distribution in the proton with the Pomeron–Pomeron–meson total cross section. The Pomeron–Pomeron–meson cross section is saturated by direct-channel contributions from the Pomeron as well as from two different f trajectories, accompanied by the isolated f$_0(500)$ resonance dominating the $\sqrt{M^{2}}\lesssim 1$ GeV region. A slowly varying background is taken into account.

1 Introduction

Central production in proton–proton collisions has been analysed from the low energy range $\sqrt{s} = 12.7-63$ GeV of the ISR at CERN up to the presently highest energy available of $\sqrt{s} = 13$ TeV achieved in Run II at the LHC. The CDF Collaboration has analysed central exclusive pion pair production in proton–antiproton collisions at the TEVATRON energies of $\sqrt{s} = 0.9$ and 1.96 TeV [1]. A physics programme of central exclusive production in proton–proton collisions is being pursued by the STAR Collaboration at RHIC [2]. Results from analyses of centrally produced exclusive two track events from Run I and II at the LHC are available from the ALICE [3], ATLAS [4], CMS [5] and LHCb [6] experiments. A comprehensive survey of central exclusive production has been published in a review article [7].

The analysis of centrally produced states necessitates the simulation of such events to study the acceptance and efficiency of the complex large detector systems. Such events can either be recognized by identifying rapidity gaps, or by measuring the very forward scattered protons with Roman Pots. In order to be able to compare the efficiency of these two approaches, the information of the complete kinematics of the final state is needed, including the central state and the two outgoing protons. With the ongoing detector upgrade programmes at RHIC and at the LHC, much larger data samples of central production events are expected in the next few years. These larger data samples will allow much improved data analyses of differential distributions, such as for example the investigation of resonance parameters by a partial wave analysis (PWA). The aim of the study presented here is the formulation of a model for simulating such differential distributions.

This article is organized as follows. In the introduction in Sect. 1, the development of a model for central exclusive production in proton–proton collisions is motivated. In Sect. 2, the experimental situation regarding exclusive resonance production at RHIC, the TEVATRON and the LHC is reviewed. In Sect. 3, the basics of the Regge pole model used for extracting the Pomeron–Pomeron–meson cross section are summarized. The total meson production cross section at hadron level is defined in Sect. 4. The meson cross section double differential with respect to meson mass and transverse momentum is derived in Sect. 5. A summary and an outlook for future studies of the topic presented here is given in Sect. 6. The parameterisation of the proton–Pomeron kinematics is explained in Appendix A. In Appendix B, the parameterisation of the Pomeron–Pomeron–meson kinematics is derived. The parameterisation of the three-body final state phase space is defined in Appendix C.

2 Central exclusive production at the TEVATRON, at RHIC and at the LHC

Central production in proton–proton collisions is characterized by the hadronic state produced at or close to mid-rapidity, and by the two forward scattered protons, or remnants thereof. No particles are produced between the mid-rapidity system and the two beam rapidities on either side of the central system. Experimentally, these event topologies can be identified by the presence of the two rapidity gaps, by detecting the forward protons or its remnants, or by a combination of these two approaches. Forward scattered neutral fragments can, for example, be measured in Zero Degree Calorimeters.

Fig. 1

(Figure taken from Ref. [1])

Invariant mass distribution of pion pairs measured by the CDF Collaboration

The mass distribution of two oppositely charged tracks within pseudorapidity $|\eta |<$ 1.3, assumed to be pions, has been measured by the CDF Collaboration at the TEVATRON energy of $\sqrt{s} = 1.96$ TeV. This mass distribution, shown in Fig. 1, has been measured in events where otherwise no particles have been registered in the range $|\eta |<$ 5.9. A clear signal is seen in the region of the f$_{2}$(1270) resonance. The acceptance of pairs at low masses $M{<}1$ GeV and low transverse momenta $p_{T}$ is severely reduced, as shown for example on page 11 of Ref. [8]. A low pair transverse momentum threshold is hence applied in the data shown in Fig. 1. For pair masses $M{<}1$ GeV, only the high-end tail of the transverse momentum distribution is visible, and conclusions on possible resonance structures at masses below 1 GeV are therefore difficult to infer in Fig. 1.

Fig. 2

(Figure taken from Ref. [2])

Invariant mass distributions of pion pairs measured by the STAR Collaboration

The invariant mass distribution of exclusively produced pion pairs measured by the STAR Collaboration at RHIC at $\sqrt{s} = 200$ GeV is shown in Fig. 2. The exclusivity of the event is provided by measuring the pion pair in the STAR central barrel, and the forward scattered protons in Roman Pots installed around 16 m away from the interaction point. The opposite-sign pair distribution is displayed in black, whereas the like-sign pair distribution reflecting the background is shown in red. Clearly visible is a strong signal in the mass regions of the f$_{0}$(980) and the f$_{2}$(1270) resonance.

Fig. 3

(Figure taken from Ref. [3])

Invariant mass distributions of pion pairs measured by the ALICE Collaboration

The invariant mass distributions of pion pairs shown in Fig. 3 were taken by the ALICE Collaboration at mid-rapidity in Run I of the LHC [3]. This distribution is shown in red for double gap events, and in black for minimum bias events. The two distributions are normalized to unity for better comparison of the shape. Clearly visible is an enhancement of the f$_{0}$(980) and f$_{2}$(1270) resonances in the red distribution, thereby validating the double gap technique at LHC energies.

Fig. 4

(Figure taken from Ref. [4])

The differential cross section measured by the ATLAS Collaboration as function of the dipion invariant mass

In Fig. 4, the central exclusive differential cross section $pp \rightarrow p + \pi \pi + p$ analysed by the ATLAS Collaboration is displayed as function of the dipion mass [4]. Here, the pions are identified in the ATLAS central barrel, and the final state protons are measured in the ALFA detector. Shown in Fig. 4 are bare Breit–Wigner fits without interference for the individual resonances (f$_{0}$(980) in yellow, f$_{2}$(1270) in blue), and the sum of all resonances, continua and interferences (in red).

Fig. 5

(Figure taken from Ref. [5])

Differential cross section measured by the CMS Collaboration as function of the pion pair invariant mass

In Fig. 5, the differential cross section $pp \rightarrow p(p^{*}) + (\pi ^{+}\pi ^{-}) + p (p^{*})$ measured by the CMS Collaboration is shown as function of the pion pair invariant mass [5]. For comparison, the model predictions from DIME for the continuum (solid and dashed curves) [9] and from $\rho$ photoproduction from STARlight (long dashed curve) are shown [10]. The results are also compared to the predictions by PYTHIA and MBR (open squares).

In Fig. 6, the invariant mass distribution of pion pairs in the pseudorapidity range 2.0 $< \eta<$ 5.0 taken by the LHCb Collaboration in proton-lead collisions at $\sqrt{s_{NN}}$ = 8.16 TeV is displayed [6]. This pair distribution is derived from events where there are exactly two oppositely charged pions in the event and significant energy in the forward shower counter HeRSCel, suggesting proton dissociation. This histogram is dominated by the photoproduction of the $\rho$-resonance, with a visible signal of the f$_{2}$(1270) resonance, and an indication of a signal of the f$_{0}$(980).

Fig. 6

(Figure taken from Ref. [6])

Invariant mass distribution of pion pairs measured by the LHCb Collaboration

The comparison of the pion pair spectra by the CDF Collaboration, and the preliminary data from the STAR, ALICE, ATLAS, CMS and LHCb experiments shown in Figs. 1, 2, 3, 4, 5 and 6 clearly demonstrates the existence of the f$_{0}$(980) and the f$_{2}$(1270) resonance in central exclusive production. The in-depth analysis of these two resonances will play a pivotal role in future studies of central exclusive production at high energies. Such analyses provide the opportunity to compare the results from high statistics data of the different experiments.

3 Dual resonance model of Pomeron–Pomeron scattering

We summarize here the main ideas of the dual resonance model of Pomeron–Pomeron scattering. A detailed discussion of this model is presented in Ref. [11]

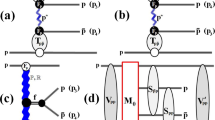
The triple Reggeon formalism is used in most studies on single and double diffraction dissociation, and in central diffraction. This approach is valid in the smooth Regge region, beyond the resonance region, but is not useful at low masses which is dominated by resonances. We solve this problem by using a dual model.

Fig. 7

Connection, through unitarity (generalized optical theorem) and Veneziano-duality, between the Pomeron–Pomeron cross section and the sum of direct-channel resonances

A sequence of resonances contributes at low masses, where the one-by-one account of single resonances is possible, but not economic for the calculation of cross sections. These resonances overlap and gradually disappear in the higher mass continuum. Based on the idea of duality with a limited number of resonances lying on non-linear Regge trajectories, an approach to account for many resonances was suggested in Ref. [12]. This approach was used in Ref. [13] to calculate low mass single- and double-diffractive dissociation at the LHC.

The main idea behind this approach is illustrated in Fig. 7, realized by dual amplitudes with Mandelstam analyticity (DAMA) [14]. For $s\rightarrow \infty$ and fixed t it is Regge-behaved. Contrary to the Veneziano model, DAMA not only allows for, but rather requires the use of non-linear complex trajectories providing the resonance widths via the imaginary part of the trajectory. In the case of limited real part, a finite number of resonances is produced. More specifically, the asymptotic rise of the trajectories in DAMA is limited by the condition, in accordance with an important upper bound,

$$\begin{aligned} \big |{\alpha (s)\over {\sqrt{s}\ln s}}\big |\le const, \ \ s\rightarrow \infty . \end{aligned}$$

(1)

In our study of central production, the direct-channel pole decomposition of the dual amplitude $A(M_{X}^{2},t)$ is relevant. Different trajectories $\alpha _{i}(M_X^2)$ contribute to the amplitude, with $\alpha _{i}(M_X^2)$ a non-linear, complex Regge trajectory in the Pomeron-Pomeron (PP) system,

$$\begin{aligned} A(M_X^2,t)=a\sum _{i=f,P}\sum _{J}\frac{[f_{i}(t)]^{J+2}}{J-\alpha _i(M_X^2)}. \end{aligned}$$

(2)

In Eq. (2), the pole decomposition of the dual amplitude $A(M_{X}^{2},t)$ is shown with t the squared momentum transfer in the $PP\rightarrow PP$ reaction. The index i sums over the trajectories which contribute to this amplitude. Within each trajectory, the second sum extends over the bound states of spin J. The prefactor a in Eq. (2) is of numerical value a = 1 GeV$^{-2} = 0.389$ mb.

The pole residue f(t) appearing in the $PP\rightarrow PP$ system is fixed by the dual model, in particular by the compatibility of its Regge asymptotics with Bjorken scaling and reads

$$\begin{aligned} f(t) = (1-t/t_0)^{-2}, \end{aligned}$$

(3)

where $t_0$ is a parameter to be fitted to data. However, due to the absence of data so far, we set $t_0=0.71$ GeV$^2$ for the moment as in the proton elastic form factor. Note that the residue enters with a power ($J{+}2$) in Eq. (2), thereby strongly damping higher spin resonance contributions. The imaginary part of amplitude $A(M_X^2,t)$ given in Eq. (2) is defined by

$$\begin{aligned}&\mathfrak {I}m\, A(M_{X}^2,t)\nonumber \\&\quad =a\sum _{i=f,P}\sum _{J}\frac{[f_{i}(t)]^{J+2} \mathfrak {I}m\,\alpha _{i}(M_{X}^2)}{(J-Re\,\alpha _{i}(M_{X}^2))^2+ (\mathfrak {I}m\,\alpha _{i}(M_{X}^2))^2}.\nonumber \\ \end{aligned}$$

(4)

For the PP total cross section we use the norm

$$\begin{aligned} \sigma _{t}^{PP} (M_{X}^2)= {\mathfrak {I}m\; A}(M_{X}^2, t=0), \end{aligned}$$

(5)

and recall that the amplitude A and the cross section $\sigma _{t}$ carry dimensions of mb due to the parameter a discussed above. The Pomeron–Pomeron channel, $PP\rightarrow M_X^2$, couples to the Pomeron and f channels dictated by conservation of quantum numbers. For calculating the PP cross section, we hence consider the trajectories associated to the f$_0$(980) and f$_2$(1270) resonance which are seen as strong signals in the experiment data as shown in Sect. 2, and the Pomeron trajectory [11].

The experimental data on central exclusive pion pair production measured at the ISR, RHIC, TEVATRON and the LHC all show a broad continuum for pair masses $m_{\pi ^+\pi ^-}<$ 1 GeV. This mass region is experimentally difficult to access due to the missing acceptance for pairs of low mass and low transverse momentum $p_{T}$ [8]. The population of this mass region is attributed to the f$_{0}$(500), a resonance which has been controversial for many decades. The non-ordinary nature of the f$_{0}$(500) state is corroborated by the fact that it does not fit into the Regge description of classifying $q\bar{q}$-states into trajectories [15]. In spite of the complexity of the f$_{0}$(500) resonance, and the controversy on its interpretation and description, we take the practical but simple-minded approach of a Breit–Wigner resonance [16]

$$\begin{aligned} A(M^{2}) = a\; \frac{-M_0\Gamma }{M^{2}-M_{0}^{2}+iM_{0}\Gamma }. \end{aligned}$$

(6)

In Eq. (6), the parameterisation of the relativistic Breit–Wigner amplitude is shown with $M_{0}$ and $\Gamma$ the mass and width, respectively. The Breit–Wigner amplitude of Eq. (6) is used below for calculating the contribution of the f$_{0}$(500) resonance to the PP cross section.

The PP cross section is calculated from the imaginary part of the amplitude by use of the optical theorem

$$\begin{aligned} \sigma _{t}^{PP} (M^2)= & {} {\mathfrak {I}m\; A}(M^2, t=0) \;\; \nonumber \\= & {} a\sum _{i=f,P}\sum _{J}\frac{[f_{i}(0)]^{J+2} \mathfrak {I}m \alpha _{i}(M^{2})}{(J{-}\mathfrak {R}e\alpha _{i}(M^{2}))^{2}{+}(\mathfrak {I}m \alpha _{i}(M^{2}))^{2}}.\nonumber \\ \end{aligned}$$

(7)

In Eq. (7), the index i sums over the trajectories which contribute to the cross section, in our case the $f_{1}$, $f_{2}$ and the Pomeron trajectory. For a discussion of the $f_{1},f_{2}$ trajectories, and a listing of the resonances defining these trajectories, see Ref. [11]. Within each trajectory, the summation extends over the poles of spin J as expressed by the second summation sign. The value $f_{i}(0) =f_{i}(t)\big |_{\text{ t }=0}$ is not known a priori, but can be extracted from the experimental data by analysing relative strengths of resonances within a trajectory.

The Breit–Wigner parameterisation of the isolated f$_{0}$(500) resonance contributes to the cross section with

$$\begin{aligned} \sigma _{\text {f}_{0}(500)}^{PP}(M^{2}) = a \sqrt{1.-\frac{4\,m_{\pi }^{2}}{M^{2}}} \frac{{M}_{0}^{2}\Gamma ^{2}}{({M}^{2}-{M}_{0}^{2})^{2}+{M}_{0}^{2}\Gamma ^{2}}, \end{aligned}$$

(8)

with the resonance mass of $M_{0} = (0.40-0.55)$ GeV and a width $\Gamma = (0.40-0.70)$ GeV [16]. The quantity $\sqrt{1.-4\,m_{\pi }^{2}/M^{2}}$ in Eq. (8) is the threshold phase space factor for the two-pion decay, and the prefactor a the same as used in Eq. (2).

In the treatment of the background we follow the approach put forward in Ref. [12], by which the background is dual to Pomeron exchange (two-component duality, introduced by Freund and Harari many years ago [17, 18]). In dual amplitude with Mandelstam analyticity Regge trajectories are non-linear complex functions, their real part being limited to highest resonances spins [12]. Contrary to ordinary meson and baryon trajectories, the real part of the direct channel exotic trajectory, dual to Pomeron exchange (Freund–Harari), by construction does not reach spin J in Eq. (7), thus the relevant background amplitude is smooth, structureless. Any smooth (logarithmic) background would be acceptable from the phenomenological point of view, however conceptually a background in terms of a dual, direct-channel exotic trajectory is preferable. The specific realization of the background term used below in Eq. (9), the values of its parameters, such as the constant c, to some extent are model-dependent.

A background term of form

$$\begin{aligned} \sigma _{backgr.}^{PP}(M^{2}) = c\cdot (0.1+ \text {log}(M^{2}))\text {\;mb} \end{aligned}$$

(9)

is added, with the numerical value of the parameter c fitted to data [19].

Fig. 8

Contributions of the f$_{0}$(500) resonance, the $f_{1}$, $f_{2}$ and the Pomeron trajectory, and of the background to the PP total cross section

The different contributions to the PP total cross section are shown in Fig. 8. The contribution of the f$_{0}$(500) resonance according to Eq. (8) is displayed by the dashed cyan line, with a central value for the mass $M_{0}$ as well as for the width $\Gamma$, $M_{0} = 0.475\,$GeV and $\Gamma = 0.55\,$GeV, respectively. The contribution of the $f_{1}$ and $f_{2}$ trajectory are shown by the solid green and by the dashed blue line, respectively. The contribution from the Pomeron trajectory is displayed by the dashed magenta line. The Pomeron–Pomeron total cross section is calculated by summing over the contributions discussed above, and is shown by the solid black line.

4 Total meson cross section at hadron level

In order to derive the meson production cross section at hadron level, we start from the definition of an infinitesimal cross section element

$$\begin{aligned} d\sigma = \frac{|\mathcal {M}|^{2}}{\text {flux}} dQ, \end{aligned}$$

(10)

with $\mathcal {M}$ the invariant amplitude, dQ the Lorentz-invariant phase space and flux the flux factor. Above Eq. (10) can be written at hadron and Pomeron level, and hence yields an equation

$$\begin{aligned} |\mathcal {M}|^{2} dQ = \text {flux}_{\text {prot}}\; d\sigma _{\text {prot}} = \text {flux}_{\text {Pom}} F^{\text {Pom}}_{\text {prot}}\; d\sigma _{\text {Pom}}. \end{aligned}$$

(11)

In Eq. (11), the parameter $F^{\text {Pom}}_{\text {prot}}$ characterizes the distribution of Pomerons in the proton. Equation (11) can be rearranged, and the infinitesimal cross section element at hadron level can be expressed as function of the corresponding element at Pomeron level,

$$\begin{aligned} d\sigma _{\text {prot}} = \frac{\text {flux}_{\text {Pom}}}{\text {flux}_{\text {prot}}} F^{\text {Pom}}_{\text {prot}} d\sigma _{\text {Pom}}. \end{aligned}$$

(12)

The flux factor for two-body collisions of A and B is defined in manifestly invariant form [20],

$$\begin{aligned} \text {flux} = 4.*\big ( (p_{A}\cdot p_{B})^{2}-m_{A}^{2} m_{B}^{2}\big )^{1/2}. \end{aligned}$$

(13)

The distribution $F^{\text {Pom}}_{\text {prot}}$ of Pomerons in the proton has been examined in the study of the structure of the Pomeron, and has been parameterised as function of the two kinematical variables $(t,\xi )$ [21],

$$\begin{aligned} F^{\text {Pom}}_{\text {prot}}(t,\xi ) = \frac{9 \beta _{0}^{2}}{4\pi ^{2}}\;\big [F_{1}(t)\big ]^{2}\xi ^{1-2\alpha (t)}. \end{aligned}$$

(14)

The distribution $F^{\text {Pom}}_{\text {prot}}$ in Eq. (14) is integrated over the azimuthal angle of the final state proton. The variable t represents the squared four-momentum transfer of the proton (Mandelstam t), $\xi$ denotes the proton fractional longitudinal momentum loss, and $\beta _{0}$=1.8 GeV$^{-1}$. The Regge factor $\xi ^{1-2\alpha (t)}$ enters instead of propagators for the Pomerons, with $\alpha (t)$ the Pomeron trajectory

$$\begin{aligned} \alpha (t)=1.+\varepsilon +\alpha ^{'}t, \quad \varepsilon \sim 0.085, \quad \alpha ^{'}=0.25\, \text {GeV}^{-2}.\nonumber \\ \end{aligned}$$

(15)

The factor $F_{1}(t)$ in Eq. (14) represents the elastic form factor, and is taken as

$$\begin{aligned} F_{1}(t) = \frac{4 m^{2} - 2.8 t}{4 m^{2} - t}\left( \frac{1}{1-t/0.7\;\mathrm{{GeV}}^{2}}\right) ^{2}. \end{aligned}$$

(16)

Note that the form factor as given by Eq. (16) resembles the pole residue in the dual amplitude as depicted in Eq. (3), except for the prefactor which depends on the mass of the proton.

The meson production cross section at hadron level can be expressed as an integral over the 6 kinematical variables ($t_{A},\xi _{A},\phi _{A},t_{B},\xi _{B},\phi _{B}$) which parameterise the Pomeron distribution in the two protons,

$$\begin{aligned} \sigma _{pp}= & {} \int \frac{\text {flux}_{\text {Pom}}}{\text {flux}_{\text {prot}}} \cdot F^{\text {Pom}}_{\text {prot}_{A}}(t_{A},\xi _{A},\phi _{A}) F^{\text {Pom}}_{\text {prot}_{B}}(t_{B},\xi _{B},\phi _{B})\nonumber \\&\times \, \sigma ^{PP}(M_{x},t_{A,B})\,dt_{A}d\xi _{A}d \phi _{A}dt_{B}d\xi _{B}d\phi _{B}. \end{aligned}$$

(17)

5 Double differential meson cross section

From the expression given in Eq. (17), the cross section can be derived double differentially with respect to the mass M and transverse momentum $p_{T}$ of the produced meson. Such a derivation can be achieved by a transformation of the total cross section to the parameters M and $p_{T}$ as integration variables. The Pomeron distribution in the proton as expressed in Eq. (14) is integrated over the azimuthal angle, and the Pomeron distributions entering Eq. (17) therefore have no explicit azimuthal dependence. One of the azimuthal angles of the two protons can hence be integrated out, and one azimuthal angle $\phi = \phi _{A} - \phi _{B}$ representing the azimuthal opening angle between the two protons remains.

We hence look for a change of variables

$$\begin{aligned} (t_{A},\xi _{A},t_{B},\xi _{B},cos(\phi )) \longmapsto (u_{+},u_{-},v_{-}, M, p_{T}). \end{aligned}$$

(18)

Such a transformation is accompanied by a transformation of the differentials according to the Jacobian determinant J

$$\begin{aligned} dt_{A}\,d\xi _{A}\,dt_{B}\,d\xi _{B}\,dcos(\phi ) = J\; du_{+}du_{-}dv_{-}dMdp_{T}. \end{aligned}$$

(19)

This transformation is derived in Appendices A, B and C, with the Jacobian J defined by

$$\begin{aligned} J = \frac{4}{\beta ^{2}} \frac{2 M p_{T}}{G \gamma ^{2} \frac{\partial H}{\partial v_{+}}}. \end{aligned}$$

(20)

Here, G and H are functions of the transformed kinematic variables $(u_{+},u_{-},v_{-}, M, p_{T})$ and are defined in Appendix B. In these transformed variables, the meson production cross section is written as

$$\begin{aligned} \sigma _{pp}= & {} \int \frac{\text {flux}_{\text {Pom}}}{\text {flux}_{\text {prot}}} \cdot \tilde{F}^{\text {Pom}}_{\text {prot}_{A}} \tilde{F}^{\text {Pom}}_{\text {prot}_{B}} \sigma ^{PP}(M,u_{+},u_{-})\nonumber \\&\times \;J\,du_{+}du_{-}dv_{-}dMdp_{T}. \end{aligned}$$

(21)

Here, the quantity $\tilde{F}^{\text {Pom}}_{\text {prot}}$ denotes the Pomeron distribution $F^{\text {Pom}}_{\text {prot}}$ written in the transformed variables $(u_{+},\!u_{-},\!v_{-},\! M,\! p_{T})$. The double differential meson cross section can be extracted from Eq. (21) as

$$\begin{aligned} \frac{d\sigma _{pp}}{dMdp_{T}}= & {} \int \frac{\text {flux}_{\text {Pom}}}{\text {flux}_{\text {prot}}} \cdot \tilde{F}^{\text {Pom}}_{\text {prot}_{A}} \tilde{F}^{\text {Pom}}_{\text {prot}_{B}} \sigma ^{PP}(M,u_{+},u_{-})\nonumber \\&\times \;J\,du_{+}du_{-}dv_{-}. \end{aligned}$$

(22)

The numerical evaluation of the double differential cross section $d\sigma _{pp}/dMdp_{T}$ involves an integration over the three parameters ($u_{+},u_{-},v_{-}$). In this integration, the value of $f_{i}(0) =f_{i}(t)\big |_{\text{ t }=0}$ of Eq. (7) is taken as $f_{i}(0)$ = 0.6. The integration limits in this parameter space can be determined according to the kinematically allowed range as shown in Fig. 13 of Appendix A.

The double differential meson production cross section $d\sigma _{pp}/dMdp_{T}$ at hadron level is shown in Fig. 9 for the contribution of the $f_{1}$ trajectory.

Fig. 9

Double differential meson cross section for contribution of $f_{1}$ trajectory

The double differential meson production cross section $d\sigma _{pp}/dMdp_{T}$ at hadron level is shown in Fig. 10 for the contribution of the $f_{2}$ trajectory.

Fig. 10

Double differential meson cross section for contribution of $f_{2}$ trajectory

The model presented here does not make any prediction on the absolute value of these two contributions to the total meson production cross section. The strength of these contributions needs to be extracted from experimental data.

Fig. 11

Contributions of the f$_{0}$(500) resonance, the $f_{1}$, $f_{2}$ and the Pomeron trajectory, and of the background to the meson differential cross section d$\sigma$/dM at hadron level

The contributions to the differential meson cross section $d\sigma _{pp}/dM$ at hadron level are shown in Fig. 11. The contributions of the $f_{1},f_{2}$ trajectory are derived by integrating the differential cross section $d\sigma _{pp}/dMdp_{T}$ over the transverse momentum $p_{T}$, and are shown by the dashed green and dashed blue line, respectively. The contribution of the f$_{0}$(500) resonance results from the Breit–Wigner parameterisation of Eq. (8), taken with the resonance mass $M_{0}$ = 0.475 GeV and the width $\Gamma$ = 0.55 GeV, and is shown by the dashed cyan line. Even though this state is the lowest mass resonance contributing to the spectrum shown in Fig. 11, the f$_{0}$(500) with the chosen central values for the mass $M_{0}$ and the width $\Gamma$ dominates the distribution in the high mass region. The numerical ranges given by the Particle Data Group for the mass $M_{0}$ and the width $\Gamma$ put, however, considerable uncertainty to this contribution in the high mass range. The contribution of the Pomeron trajectory is shown by the dashed magenta line, whereas the background is represented by the dashed black line. The contributions of the f$_{0}$(500), the $f_{1},f_{2}$ and the Pomeron trajectory, and background, are normalized such that they correspond to cross sections of 1 mb, 50 $\mu$b, 120 $\mu$b, 2 $\mu$b and 0.1 $\mu$b per unit of rapidity at mid-rapidity, respectively.

6 Summary and outlook

A model is presented for calculating double differential distributions in mass and transverse momentum for exclusive diffractive meson production at high energies. This model is based on convoluting the Pomeron distribution in the proton with the Pomeron–Pomeron–meson cross section. Such double differential distributions are presented for the f$_{0}$(980) and f$_{2}$(1270) resonances. The absolute contribution of these resonances to the total meson cross section cannot be derived within this approach, and must hence be deduced from experimental data. Fitting the parameter of this model to future published data from the LHC experiments will allow to extract the relative strengths of the different contributions shown in Fig. 11. Moreover, the analysis of published LHC data will also allow the extraction of the presently unknown value of $f_{i}(0) =f_{i}(t)\big |_{\text{ t }=0}$ in Eq. (7). This model can be expanded to include photon–Pomeron interactions, and hence distributions of diffractive photoproduction of low mass vector mesons $\rho ,\omega ,\phi$ can be calculated. With such a model, a multitude of resonances with different spin-parity assignments can be generated in order to validate the fitting procedures of a Partial Wave Analysis framework. The model presented here can be extended to lower beam energies where not only Pomeron–Pomeron, but also Pomeron–Reggeon and Reggeon–Reggeon diagrams need to be considered. To make realistic predictions for exclusive resonance production at the LHC, diffractive excitations of protons must be included. The results discussed here are necessary and essential for such calculations.

Appendices

Appendix A

Kinematics Proton–Pomeron vertex

The kinematics at the proton–Pomeron vertex is parameterised as function of three variables, the squared four-momentum transfer t to the proton (Mandelstam t), the fractional longitudinal momentum loss $\xi$ of the proton $(\xi > 0)$, and the scattered proton azimuthal angle $\phi$ ($0 \le \phi < 2 \pi$).

Fig. 12

Proton–Pomeron vertex

The elementary proton–Pomeron vertex is shown in Fig. 12. Here, the four-momentum of the proton before and after scattering is denoted by $p_{A}$ and $p_{A'}$, respectively, with $Q_{A}$ the four-momentum of the exchange,

$$\begin{aligned} Q_{A} = P_{A} - P_{A'}. \end{aligned}$$

(23)

The squared four-momentum transfer t to the proton is negative ($t < 0$), and is defined by

$$\begin{aligned} t = Q_{A}^{2} = (P_{A} - P_{A'})^{2}. \end{aligned}$$

(24)

The components of the four-momentum $P_{A}$ are defined by $(E_{A},p_{A,x},p_{A,y},p_{A,z})$, with an analogous definition for $P_{A'}$. We introduce a temporary variable $\zeta$ for the fractional energy loss of the proton $(\zeta > 0)$,

$$\begin{aligned} \zeta = \frac{E_{A}-E_{A'}}{E_{A}}, \end{aligned}$$

(25)

which can be rewritten for $E_{A'}$ as

$$\begin{aligned} E_{A'} = E_{A}(1 - \zeta ). \end{aligned}$$

(26)

With $\gamma$ the Lorentz-factor of the beam, the four-momenta $P_{A}$, $P_{A'}$ and $Q_{A}$ are written as

$$\begin{aligned} P_{A}= & {} (\gamma m, \,0, \,0, \,\gamma \beta m), \end{aligned}$$

(27)

$$\begin{aligned} P_{A'}= & {} (\gamma m (1-\zeta ), \,p_{T}\,cos \phi , \,p_{T}\,sin\phi , \,\gamma \beta m (1-\xi )),\nonumber \\ \end{aligned}$$

(28)

$$\begin{aligned} Q_{A}= & {} (\gamma m \zeta , \,-p_{T}\,cos\phi , \,-p_{T}\,sin\phi , \,\gamma \beta m \xi ), \end{aligned}$$

(29)

with m the proton mass, and $p_{T}$ the transverse momentum of the final state proton. From Eqs. (24), (27) and (28), the fractional energy loss $\zeta$ and transverse momentum $p_{T}$ of the scattered proton are deduced as

$$\begin{aligned} \zeta= & {} \frac{t}{2\gamma ^{2}m^{2}} + \beta ^{2}\xi , \end{aligned}$$

(30)

$$\begin{aligned} p_{T}^{2}= & {} f(t,\xi ) = \frac{t^{2}}{4 \gamma ^{2} m^{2}} - t + t \xi \beta ^{2} - m^{2} \beta ^{2} \xi ^{2}. \end{aligned}$$

(31)

The function $f(t,\xi )$ in Eq. (31) can be transformed into a bilinear form by quadratic completion. This procedure defines a transformation to a set of variables on the principal axes of the bilinear form. These principal axes coordinates (u, v) are determined as

$$\begin{aligned} u= & {} \frac{-t}{2 m} +m, \end{aligned}$$

(32)

$$\begin{aligned} v= & {} m \beta \xi - \frac{t \beta }{2 m}. \end{aligned}$$

(33)

The transformation to the variables (u, v) is associated with a Jacobian determinant

$$\begin{aligned} dudv = \Bigl | \frac{\partial (u,v)}{\partial (t,\xi )} \Bigr |\; dtd\xi = \frac{\beta }{2}\; dtd\xi . \end{aligned}$$

(34)

The transformation defined by Eqs. (32), (33) is non-singular due to the constant finite value of the Jacobian J = $\beta$/2, and can hence be inverted to express the variables $(t,\xi )$ as function of the new coordinates (u, v)

$$\begin{aligned} t= & {} -2m (u-m), \end{aligned}$$

(35)

$$\begin{aligned} \xi= & {} \frac{v}{m \beta } - \frac{u}{m} +1. \end{aligned}$$

(36)

Our region of interest ($\xi >0, t<0$) is transformed by Eqs. (32), (33) into a section of the (u, v)-plane defined by ($u> 0, v > 0$). The fractional energy loss $\zeta$ and the transverse momentum $p_{T}$ are expressed in the new coordinates (u, v) as

$$\begin{aligned} \zeta= & {} \frac{v \beta }{m} - \frac{u}{m} +1, \end{aligned}$$

(37)

$$\begin{aligned} p_{T}^{2}= & {} u^{2} - v^{2} - m^{2}. \end{aligned}$$

(38)

The loci of constant transverse momentum $p_{T}$ lie on the branch ($u>0, v>0$) of the hyperbola defined in canonical form by

$$\begin{aligned} \frac{u^{2}}{p_{T}^{2}+m^{2}} - \frac{v^{2}}{p_{T}^{2}+m^{2}} = 1. \end{aligned}$$

(39)

Fig. 13

Proton–Pomeron kinematics in (u,v)-plane

The hyperbolae of transverse momenta $p_{T} = 0$, 1 and 4 GeV/c are shown in Fig. 13 by solid blue lines. The solid and dashed red lines represent the constant fractional energy loss of $\zeta = 0$ and $\zeta = 0.1$, respectively. The kinematically allowed (u,v)-values are indicated by the grey shaded area. The requirement of positive fractional momentum loss $(\xi >0)$ is not shown in Fig. 13 since the condition of positive fractional energy loss $(\zeta > 0)$ is more restrictive. A fixed value of $t=t_{0}$ corresponds to a value of $u_{0} = m-t_{0}/2m$. The allowed v-values are hence in the range defined by the line of energy loss $\zeta =0$ and the hyperbola $p_{T} = 0$ GeV/c,

$$\begin{aligned} \frac{u_{0}-m}{\beta }< v < \sqrt{u_{0}^{2}-m^{2}}. \end{aligned}$$

(40)

Appendix B

Kinematics Pomeron–Pomeron–meson vertex

Fig. 14

Pomeron–Pomeron–meson vertex

The kinematics of the Pomeron–Pomeron–meson vertex is derived from two uncorrelated proton–Pomeron vertices. The exchanges $Q_{A}$ and $Q_{B}$ shown in Fig. 14 combine to generate the meson of four-momentum X,

$$\begin{aligned} X= & {} Q_{A} + Q_{B}\nonumber \\= & {} (\gamma m (\zeta _{A}+\zeta _{B}), \,-p_{T,A}\,cos\phi _{A}-p_{T,B}\,cos\phi _{B},\nonumber \\&-p_{T,A}\,sin\phi _{A}-p_{T,B}\,sin\phi _{B}, \,\gamma \beta m (\xi _{A}-\xi _{B})). \end{aligned}$$

(41)

From the four-momentum X shown in Eq. (41), the invariant mass M of the meson can be derived as

$$\begin{aligned} M^{2}= & {} \gamma ^{2}m^{2}(\zeta _{A}+\zeta _{B})^{2}- \gamma ^{2}\beta ^{2}m^{2}(\xi _{A}-\xi _{B})^{2}\nonumber \\&-p_{T,A}^{2}-p_{T,B}^{2}-2\, p_{T,A}\, p_{T,B} \,cos(\phi ). \end{aligned}$$

(42)

The quantity $\phi$ in Eq. (42) denotes the difference in azimuthal angle of the two protons in the final state, $\phi = \phi _{A}-\phi _{B}$. The transverse momentum $p_{T}$ of the meson is given by

$$\begin{aligned} p_{T}^{2} = p_{T,A}^{2} + p_{T,B}^{2} + 2\, p_{T,A}\, p_{T,B} \,cos(\phi ). \end{aligned}$$

(43)

In the new coordinates (u, v) defined in Appendix A, the mass M is expressed as

$$\begin{aligned} M^{2}= & {} \gamma ^{2} \bigl [\beta (v_{A} + v_{B}) - (u_{A} + u_{B}) + 2m\bigr ]^{2}\nonumber \\&-\gamma ^{2}\bigl [(v_{A}-v_{B})-\beta (u_{A}-u_{B})\bigr ]^{2} - p_{T}^{2}. \end{aligned}$$

(44)

It is convenient to introduce new variables $(u_{+},u_{-})$ and $(v_{+},v_{-})$ with a Jacobian determinant equal to unity,

$$\begin{aligned} u_{+}= & {} \frac{u_{A}+u_{B}}{\sqrt{2}}, \quad u_{-} = \frac{u_{A}-u_{B}}{\sqrt{2}},\nonumber \\ v_{+}= & {} \frac{v_{A}+v_{B}}{\sqrt{2}}, \quad v_{-} = \frac{v_{A}-v_{B}}{\sqrt{2}}. \end{aligned}$$

(45)

The transverse momentum $p_{T}$ is expressed in the variables $(u_{+},u_{-},v_{+},v_{-},cos(\phi ))$ as

$$\begin{aligned} p_{T}^{2}=F(u_{+},u_{-},v_{+},v_{-})+G(u_{+},u_{-},v_{+},v_{-})\,cos(\phi ), \end{aligned}$$

(46)

with $F(u_{+},u_{-},v_{+},v_{-})$ and $G(u_{+},u_{-},v_{+},v_{-})$ defined as

$$\begin{aligned} F(u_{+},u_{-},v_{+},v_{-})= & {} u_{+}^{2} + u_{-}^{2} - v_{+}^{2} - v_{-}^{2} - 2 m^{2}, \end{aligned}$$

(47)

$$\begin{aligned} G(u_{+},u_{-},v_{+},v_{-})= & {} \sqrt{(u_{+}+u_{-})^{2}-(v_{+}+v_{-})^{2}- 2m^{2}}\nonumber \\&\times \sqrt{(u_{+}-u_{-})^{2}-(v_{+}-v_{-})^{2}-2m^{2}}.\nonumber \\ \end{aligned}$$

(48)

The mass M is expressed as

$$\begin{aligned} M^{2} = 2\gamma ^{2} H(u_{+},u_{-},v_{+},v_{-}) - p_{T}^{2}, \end{aligned}$$

(49)

with $H(u_{+},u_{-},v_{+},v_{-})$ defined by

$$\begin{aligned} H(u_{+},u_{-},v_{+},v_{-})=(\beta v_{+}- u_{+}+\sqrt{2}m)^{2} -(\beta u_{-}-v_{-})^{2}. \end{aligned}$$

(50)

Appendix C

Phase space parameterisation

The parameterisation of the final state consisting of two protons and a meson necessitates ten variables (not considering polarisation). These ten parameters consist of the two three-momentum vectors of the protons, in addition to the four-momentum of the central meson system. Imposing conservation of energy-momentum of the initial state reduces the ten parameters to six. These six variables can be taken as the squared four-momentum transfer t, the fractional longitudinal momentum loss $\xi$ and the azimuthal angle $\phi$ of each of the two protons. The distribution of Pomerons in the proton used in this study does not have an azimuthal dependence, and the azimuthal angle of one of the protons can hence be integrated out. This integration leaves the difference in azimuthal angle of the two final state protons as a phase space parameter. In the present study, this azimuthal opening angle is uniformly distributed. Our approach permits to assign a weight function to this opening angle, thereby allowing the study of azimuthal angle correlations between the two final state protons. The set of five variables ($u_{+},u_{-},v_{+},v_{-},cos(\phi )$) derived in Appendix B defines the phase space of the final state unambiguously.

Differential cross sections can be derived by a kinematical transformation onto the corresponding parameters. In particular, we would like to derive the meson cross section differential with respect to meson mass M and meson transverse momentum $p_{T}$, hence we are looking for a change of variables

$$\begin{aligned} (u_{+},u_{-},v_{+},v_{-},cos(\phi )) \longmapsto (u_{+},u_{-},v_{-},M,p_{T}),\nonumber \\ \end{aligned}$$

(51)

with an associated Jacobian determinant

$$\begin{aligned}&du_{+}du_{-}dv_{+}dv_{-}dcos(\phi )\nonumber \\&\quad = \biggl |\frac{\partial (u_{+},u_{-},v_{+},v_{-},cos(\phi ))}{\partial (u_{+},u_{-},v_{-},M,p_{T})}\biggr |\,du_{+}du_{-}dv_{-}dMdp_{T} \nonumber \\&\quad =\biggl |\frac{\partial (v_{+},cos(\phi ))}{\partial (M,p_{T})}\biggr |\,du_{+}du_{-}dv_{-}dMdp_{T}. \end{aligned}$$

(52)

The Jacobian determinant J of Eq. 52 can be evaluated with the use of Eqs. (46), (49),

$$\begin{aligned}&J=\biggl |\frac{\partial (v_{+},cos(\phi ))}{\partial (M,p_{T})}\biggr |= 4 M p_{T} \biggl |\frac{\partial (M^{2},p_{T}^{2})}{\partial (v_{+},cos(\phi ))}\biggr |^{-1}\nonumber \\&\quad =\frac{2 M p_{T}}{G \gamma ^{2} \frac{\partial H}{\partial v_{+}}}. \end{aligned}$$

(53)

Here, G and H are the functions $G(u_{+},u_{-},v_{+},v_{-})$ and $H(u_{+},u_{-},v_{+},v_{-})$ defined in Eqs. (48), (50).