1 Introduction

Over the last two decades models with extra spatial dimensions [1,2,3,4,5,6,7,8,9,10,11,12,13] have been increasingly playing a central role in physics beyond the standard model of particle [14] and cosmological [15] physics. Apart from the phenomenological approach, higher dimensional scenarios occur naturally in string theory. Depending on different possible compactification schemes for the extra dimensions, a large number of models have been constructed, and their predictions are yet to be observed in the current experiments. In all these models, our visible universe is identified as one of the three branes embedded within a higher dimensional spacetime. The low energy effective description [16,17,18] of the dynamical three brane turned out to be a very powerful tool in studying the dynamics ranging from particle to cosmology. In our present work we will take this ansatz to understand cosmological bouncing phenomena in the early universe cosmology considering the Randall–Sundrum two brane model.

Among various extra dimensional models proposed over the last several years, the Randall–Sundrum (RS) warped extra dimensional model [6] earned special attention since it can resolve the gauge hierarchy problem without introducing any intermediate scale (between Planck and TeV) in the theory. The RS model is a five dimensional AdS space with \(S^1/Z_2\) orbifolding along the extra dimension while two three branes are placed at the orbifold fixed points. The bulk negative cosmological constant along with appropriate boundary conditions generate exponentially warped geometry along the extra dimension. Due to this exponential warping, the Planck scale on one brane gets suppressed along the extra dimension and emerges as TeV scale [6] on the visible brane. In the RS model the interbrane separation (known as modulus or radion) is \(\sim \) Planck length and generates the required hierarchy between the branes. Subsequently, Goldberger and Wise (GW) proposed a modulus stabilzation mechanism [19] by introducing a massive scalar field in the bulk with appropriate boundary conditions. Different variants of the RS model and its modulus stabilization are extensively studied in [21,22,23,24,25,26,27,28]. In this paper we will consider a specific variant of RS scenario and study the cosmological dynamics from the perspective of low energy effective field theory induced on the visible brane.

It is well known that standard Big Bang scenario is quite successful in explaining many aspects of cosmological evolution of our universe. However, the big-bang model is plagued with a singularity (known as “cosmological singularity”) in the finite past. Resolving this time like cosmological singularity is an important issue which is a subject of great research in theoretical cosmology for the last several decades. It is widely believed that quantum theory of gravity, if any, should play very important role in resolving this singularity. One of the important aspects of all the known non-singular cosmological models is the existence of pre Big-Bang universe [29]. In terms of effective theory, different models of non-singular cosmologies, such as ekpyrotic universe [30, 31], loop quantum cosmology [32, 33], Galileon genesis [34,35,36], or the classical bouncing model, can be described by gravity coupled to a scalar field which generically violates the null energy condition at the background level. Therefore, the scale factor of the universe undergoes a non-singular bounce from a pre-existing universe to the present universe. This fact resulted in a reasonable amount of work on classical bouncing cosmology [37,38,39,40,41,42,43], with/without the presence of matter components (see also [44,45,46,47]).

In the present work, we will study the dynamics of the induced low energy theory which contains modes originating from bulk physics. The dynamics of such a mode in the context of usual cosmology [48,49,50,51,52,53] has been studied extensively. However, here we ask the following question:

  • Can the effect of extra dimension trigger a non-singular bounce on the brane scale factor and allow one to remove the “big-bang singularity” ?

In the context of a two brane scenario, the ekpyrotic model [30, 31] and its various other variants are known to have cosmological bouncing solutions. An important point to emphasize is that in those scenarios the bounce occurs at the time when two branes collapse. However, in this paper we will be studying the possibility of bouncing phenomena strictly in the Randall–Sundrum framework, where the gauge hierarchy will impose a further restriction on the moduli (radion) dynamics. In this regard, we have employed the radion stabilization mechanism in the time dependent RS background so that it does not spoil the bouncing phenomena. Our classical effective field theory computation shows that the required gauge hierarchy can be obtained in the asymptotic limit after the bounce.

The aim of this paper is to address the aforementioned question in the backdrop of a generalized scenario of the RS model proposed in [16]. The effective on-brane action we used in this paper has been formulated by Kanno and Soda in [16] by the method of a “low energy expansion scheme”.

Our paper is organized as follows: in Sect. 2, we briefly describe the generalized RS model and its effective action on the visible brane. In Sect. 3, we present the cosmological solutions of the effective Friedmann equations. The stabilization mechanism of the radion field is discussed in Sect. 4 and finally we end the paper with some conclusive remarks.

2 Low energy effective action on the visible brane

In the RS model, the Einstein equations are derived for a fixed interbrane separation as well as for flat three branes. However, the scenario changes if the distance between the branes becomes a function of spacetime coordinates and the brane geometry is curved. These generalizations are incorporated while deriving the effective action on the TeV brane via the “low energy expansion scheme” proposed in [16].

The model we considered in the present paper is described by a five dimensional anti-de Sitter (AdS) spacetime with two three branes embedded within the spacetime. The spacetime geometry has \(S^1/Z_2\) orbifolding along the extra dimension. Taking \(\varphi \) as the extra dimensional angular coordinate, the branes are situated at orbifolded fixed points i.e. at \(\varphi =0\) (Planck brane) and \(\varphi =\pi \) (TeV brane), respectively, while our visible universe is identified with the TeV scale brane. The proper distance between the branes is considered as a function of spacetime coordinates. The action of this model [16] is the following:

$$\begin{aligned} S= & {} \frac{1}{2\kappa ^2} \int \mathrm{d}^4x d\varphi \sqrt{-G} \bigg [R^{(5)}+ (12/l^2)\bigg ] \nonumber \\&- \int \mathrm{d}^4x \bigg [\sqrt{-g_{\mathrm{hid}}} V_{\mathrm{hid}} + \sqrt{-g_{\mathrm{vis}}} V_{\mathrm{vis}}\bigg ] \end{aligned}$$
(1)

with \(x^\mu =(x^0,x^1,x^2,x^3)\) the brane coordinates. \(\frac{1}{2\kappa ^2} = M^3\), M is the five dimensional Planck mass. \(R^{(5)}\) and l (\(\sim \) Planck length) are the Ricci scalar and curvature radius of the five dimensional spacetime, respectively. Critical brane tensions of hidden and visible brane are, respectively, given by \(V_{\mathrm{hid}}\) and \(V_{\mathrm{vis}}\).

We use the following metric ansatz [16]:

$$\begin{aligned} \mathrm{d}s^2 = b^2(x)\mathrm{d}\varphi ^2 + e^{-2A(\varphi ,x)}h_{\mu \nu }(x)\mathrm{d}x^\mu \mathrm{d}x^\nu , \end{aligned}$$
(2)

where \(A(\varphi ,x)\) is the spacetime dependent warp factor along the extra dimension, and b(x) is the radius of the compactified extra dimension.

Equation (2) leads to the separation between hidden and visible brane along the path of constant \(x^\mu \) as follows:

$$\begin{aligned} \mathrm{d}(x) = \int _{0}^{\pi }\mathrm{d}\varphi b(x) = \pi b(x). \end{aligned}$$
(3)

Equation (3) clearly indicates that the proper distance between the branes depends on the brane coordinates and that is why d(x) can be treated as a field. From the perspective of four dimensional effective theory, this field is termed the ’radion field’ (or modulus field).

For the metric ansatz in Eq. (2), the five dimensional Einstein equations are given by

$$\begin{aligned}&\frac{e^{-2\xi }}{b}(K^\mu _\nu )_{,\varphi } {-} e^{-2\xi }KK^\mu _\nu {+} R^{(4)^\mu }_\nu (h) {-} \nabla ^\mu \nabla _\nu \xi - \nabla ^\mu \xi \nabla _\nu \xi \nonumber \\&\quad =-\frac{4}{l^2}\delta ^\mu _\nu + \kappa ^2\bigg (\frac{1}{3}\delta ^\mu _\nu V_{\mathrm{hid}}\bigg ) \frac{e^{-\xi }}{b}\delta (\varphi ) \nonumber \\&\qquad +\, \kappa ^2\bigg (\frac{1}{3}\delta ^\mu _\nu V_{\mathrm{vis}}\bigg )\frac{e^{-\xi }}{b}\delta (\varphi -\pi ), \end{aligned}$$
(4)
$$\begin{aligned}&\frac{e^{-2\xi }}{b}K_{,\varphi } - e^{-2\xi }K^{\mu \nu } K_{\mu \nu } - \nabla ^\mu \nabla _\mu \xi - \nabla ^\mu \xi \nabla _\mu \xi \nonumber \\&\quad =-\frac{4}{l^2} + \frac{4\kappa ^2e^{-\xi }}{3b}V_{\mathrm{hid}} \delta (\varphi ) - \frac{4\kappa ^2e^{-\xi }}{3b}V_{\mathrm{vis}} \delta (\varphi -\pi ),\nonumber \\ \end{aligned}$$
(5)
$$\begin{aligned}&\nabla _\nu (e^{-\xi }K^\nu _\mu ) - \nabla _\mu (e^{-\xi }K) = 0, \end{aligned}$$
(6)

where \(R^{(4)^\mu }_\nu (h)\) is the Ricci curvature, formed by the metric \(h_{\mu \nu }\). \(K_{\mu \nu }=\frac{1}{b(x)}A'(\varphi )e^{-2A}h_{\mu \nu }\) denotes the extrinsic curvature of the \(\varphi =\) constant hypersurface and \(\nabla _{\mu }\) is the covariant derivative with respect to \(h_{\mu \nu }\). Moreover, we introduce \(e^{\xi }= \frac{b(x)}{l}\pi \).

In order to solve the five dimensional Einstein equations, it is assumed that the brane curvature radius L is much larger than the bulk curvature l i.e. \(\epsilon = (\frac{l}{L})^2 \ll 1\). Then the bulk Einstein equations can be solved perturbatively where \(\epsilon \) is taken as the perturbation parameter. This method is known as “low energy expansion scheme” [16] in which the metric is expanded with increasing power of \(\epsilon \). The zeroth order perturbation solution replicates the RS situation where the interbrane separation is constant. The effective on-brane action can be obtained up to first order perturbation, and it incorporates the fluctuation of modulus as well as non-zero value of the brane matter. Taking these generalizations into account, the \(\varphi \) dependence of the warp factor can be obtained as follows (due to Kanno and Soda; see [16]):

$$\begin{aligned} A(\varphi ,x) = \frac{b(x)}{l}\varphi . \end{aligned}$$
(7)

However, Eqs. (4), (5) and (6) lead to the junction conditions:

$$\begin{aligned} \bigg (K^{\mu }_{\nu } - \delta ^{\mu }_{\nu }K\bigg )_{\varphi =0}= & {} -\frac{\kappa ^2}{2}V_{\mathrm{hid}}\delta ^{\mu }_{\nu }, \end{aligned}$$
(8)
$$\begin{aligned} \bigg (K^{\mu }_{\nu } - \delta ^{\mu }_{\nu }K\bigg )_{\varphi =\pi }= & {} \frac{\kappa ^2}{2}V_{\mathrm{vis}}\delta ^{\mu }_{\nu }, \end{aligned}$$
(9)

where we use the property that the spacetime is \(S^1/Z_2\) orbifolded along the extra dimension. Using the solution of the warp factor \(A(\varphi ,x) = \frac{b(x)}{l}\varphi \) (see Eq. (7)), we obtain the extrinsic curvature as follows:

$$\begin{aligned} K_{\mu \nu } = \frac{1}{l}\exp {\big (-2b\varphi /l\big )} h_{\mu \nu }, \end{aligned}$$

and we have

$$\begin{aligned} K = K_{\mu \nu } \exp {\big (2b\varphi /l\big )} h^{\mu \nu } = \frac{4}{l}. \end{aligned}$$

Plugging the above expression of \(K_{\mu \nu }\) and K into the junction equations yields the brane tensions:

$$\begin{aligned} V_{\mathrm{hid}} = -V_{\mathrm{vis}} = \frac{6}{\kappa ^2l}. \end{aligned}$$
(10)

Furthermore, using the five dimensional line element (shown in Eq. 2) along with the solution of warp factor (see Eq. (7)), one determines the five dimensional Ricci scalar \(R^{(5)}\), which contains a constant part \(= - \frac{20}{l^2}\). As a result:

  • The effective four dimensional action from the constant part of \(R^{(5)}\) is

    $$\begin{aligned} S_{1}= & {} \frac{1}{2\kappa ^2} \int \mathrm{d}^4x\nonumber \\&\times \int ^{\pi }_{-\pi } \mathrm{d}\varphi \sqrt{-G} \bigg [\frac{16}{bl}\big [\delta (\varphi )-\delta (\varphi -\pi )\big ] - \frac{20}{l^2}\bigg ]\nonumber \\= & {} \frac{3}{\kappa ^2l} \int \mathrm{d}^4x \sqrt{-h} \bigg [1 - e^{-4\frac{b}{l}\pi }\bigg ] \end{aligned}$$
    (11)

    where we use the expression of \(A(\varphi ,x)\) (see Eq. (6) below) and the fact that the spacetime has \(S^1/Z_2\) orbifolding along \(\varphi \).

  • The effective action from the bulk cosmological constant is

    $$\begin{aligned} S_{2}= & {} \frac{1}{2\kappa ^2} \int \mathrm{d}^4x \int ^{\pi }_{-\pi } \mathrm{d}\varphi \sqrt{-G} \frac{12}{l^2}\nonumber \\= & {} \frac{3}{\kappa ^2l} \int \mathrm{d}^4x \sqrt{-h} \bigg [1 - e^{-4\frac{b}{l}\pi }\bigg ]. \end{aligned}$$
    (12)

  • The effective action from the brane tensions is

    $$\begin{aligned} S_{3}= & {} - \int \mathrm{d}^4x \sqrt{-h} \bigg [V_{\mathrm{hid}} + e^{-4\frac{b}{l}\pi }V_{\mathrm{vis}}\bigg ]\nonumber \\= & {} -\frac{6}{\kappa ^2l} \int \mathrm{d}^4x \sqrt{-h} \bigg [1 - e^{-4\frac{b}{l}\pi }\bigg ] \end{aligned}$$
    (13)

    where we use the expressions of the brane tensions obtained in Eq. (10).

From the above three equations, it is clear that \(S_{1}\), \(S_{2}\) and \(S_{3}\) cancel among each other. This indicates that, while deriving the effective four dimensional action from Eq. (1), the contribution comes only from the \(R^{(5)}\) term. As a consequence the original five dimensional action (in Eq. (1)) yields the effective four dimensional action for the visible brane (see [16]),

$$\begin{aligned} S_{\mathrm{eff}}= & {} \frac{l}{2\kappa ^2} \int \mathrm{d}^4x \sqrt{-f} \bigg [\Phi (x)R^{(4)}(f) \nonumber \\&-\frac{3}{2(1+\Phi )}h^{\mu \nu }\partial _\mu \Phi \partial _\nu \Phi \bigg ] \end{aligned}$$
(14)

where \(\Phi (x) = [\exp {(2\pi \frac{b(x)}{l}})-1]\) and \(R^{(4)}(f)\) is the Ricci scalar formed by the induced metric of the visible brane i.e. \(f_{\mu \nu }\) (\(= e^{-A(\pi ,x)}h_{\mu \nu }\)). It may be noticed from Eq. (14) that upon projecting the bulk gravity on the brane, the extra degrees of freedom of \(R^{(5)}\) (with respect to \(R^{(4)}(f)\)) appear as a scalar field \(\Phi (x)\) which directly couples with the four dimensional Ricci scalar. Hence the effective on-brane action is a Brans–Dicke like theory. For such an effective four dimensional theory, we now explore the cosmological evolution of the universe.

3 Cosmological solution for effective on-brane theory

Considering the effective four dimensional action presented in Eq. (14), one obtains the equations of motion for gravitational and scalar field as follows:

$$\begin{aligned} E_{\mu \nu }= & {} \frac{1}{\Phi } \bigg [-f_{\mu \nu }[\Box \Phi + \frac{3}{4(1+\Phi )} \nabla _{\alpha }\Phi \nabla ^{\alpha }\Phi ]\nonumber \\&+\nabla _{\mu }\nabla _{\nu }\Phi + \frac{3}{2(1+\Phi )}\nabla _{\mu }\Phi \nabla _{\nu } \Phi \bigg ] \end{aligned}$$
(15)

where \(E_{\mu \nu }\) is the Einstein tensor and the covariant derivatives are formed by the visible brane metric \(f_{\mu \nu }\). It is clear from the above equation that the radion field \(\Phi \) acts as an energy-momentum tensor on the brane. Furthermore, the scalar radion field equation of motion is given by

$$\begin{aligned} \frac{3}{(1+\Phi )}\Box \Phi - \frac{3}{2(1+\Phi )^2}\nabla _{\mu }\Phi \nabla ^{\mu }\Phi = 0. \end{aligned}$$
(16)

Consider the on-brane metric ansatz as the FRW metric with negative curvature parameter,

$$\begin{aligned} \mathrm{d}s_{(4)}^2= & {} f_{\mu \nu }\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }\nonumber \\= & {} -\mathrm{d}t^2 + a^2(t)\left[ \frac{\mathrm{d}r^2}{(1+r^2)} + r^2\mathrm{d}\Omega ^2\right] \end{aligned}$$
(17)

where a(t) is the scale factor and \(x^{\mu }=(t,r,\Omega )\) are the spherical polar coordinates. Using this metric ansatz, the field equations (Eqs. (15) and (16)) take the following form:

$$\begin{aligned} H^2 = \frac{1}{a^2} - H\frac{\dot{\Phi }}{\Phi } - \frac{(\dot{\Phi })^2}{4\Phi (1+\Phi )} \end{aligned}$$
(18)

and

$$\begin{aligned} \ddot{\Phi } = -3H\dot{\Phi } + \frac{(\dot{\Phi })^2}{2(1+\Phi )}. \end{aligned}$$
(19)

An overdot denotes \(\frac{\mathrm{d}}{\mathrm{d}t}\), \(H=\dot{a}/a\) is known as the Hubble parameter and we assume that the radion field \(\Phi \) is homogeneous in space.

In order to solve the above coupled equations (Eqs. (18) and (19)), we adopt the procedure formulated in [54]. Introducing the conformal time through

$$\begin{aligned} a \mathrm{d}\eta = \mathrm{d}t \end{aligned}$$
(20)

and denoting \(\frac{\mathrm{d}}{\mathrm{d}\eta }\) by a prime, Eq. (19) becomes

$$\begin{aligned} \Phi '' + 2\frac{a'}{a}\Phi ' = \frac{(\Phi ')^2}{2(1+\Phi )}. \end{aligned}$$
(21)

Integrating Eq. (21), we have the following solution:

$$\begin{aligned} \Phi ' a^2 = B\sqrt{1+\Phi } \end{aligned}$$
(22)

where B is a constant. Defining a new variable,

$$\begin{aligned} y = \Phi a^2 \end{aligned}$$
(23)

Eq. (18) becomes

$$\begin{aligned} (y')^2 = 4y^2 + \frac{(\Phi ')^2 a^4}{1+\Phi }, \end{aligned}$$

which, along with Eq. (22) yields

$$\begin{aligned} (y')^2 = 4y^2 + B^2. \end{aligned}$$
(24)

Once the Friedmann equations are expressed in terms of the variable y, the solutions of the scale factor (a(t)) and radion field (\(\Phi (t)\)) can be obtained by performing the following steps:

3.1 Step 1: solution for \(y=y(\eta )\)

Integrating Eq. (24), we obtain the solution for \(y=y(\eta )\):

$$\begin{aligned} y(\eta ) = \frac{1}{2}B \sinh [2(\eta +\eta _0)] \end{aligned}$$
(25)

where \(\eta _0\) is an integration constant.

3.2 Step 2: solution for \(\Phi =\Phi (\eta )\)

Dividing both sides of Eq. (22) by y, we get the integral of \(\Phi (\eta )\):

$$\begin{aligned} \int \frac{\mathrm{d}\Phi }{\Phi \sqrt{1+\Phi }} = B \int \frac{\mathrm{d}\eta }{y(\eta )} \end{aligned}$$

where we use the definition \(y=\Phi a^2\). By putting the solution of \(y(\eta )\) into the above equation, one ends up with the following form of \(\Phi =\Phi (\eta )\):

$$\begin{aligned} \Phi (\eta ) = \frac{4D \tanh (\eta +\eta _0)}{[1-D \tanh (\eta +\eta _0)]^2} \end{aligned}$$
(26)

with D an integration constant.

Fig. 1
figure 1

b(t) vs. t for \(B=1\) and \(D=0.5\)

Full size image

3.3 Step 3: solution for \(a=a(\eta )\)

Plugging the solutions of \(y(\eta )\) and \(\Phi (\eta )\) into the expression \(y=\Phi a^2\), the solution of the scale factor with respect to the conformal time is found to be

$$\begin{aligned} a^2(\eta ) = \frac{B}{4D} \bigg [\cosh (\eta +\eta _0) - D \sinh (\eta +\eta _0)\bigg ]^2. \end{aligned}$$
(27)

3.4 Step 4: solution for \(a=a(t)\) and \(\Phi =\Phi (t)\)

From the above solutions of \(a(\eta )\), \(\Phi (\eta )\) and using Eq. (20), we obtain the scale factor and radion field with respect to cosmic time (t):

$$\begin{aligned} a(t)= & {} \bigg [t^2 + \frac{B}{4D}(1-D^2)\bigg ]^{1/2}, \end{aligned}$$
(28)
$$\begin{aligned} \Phi (t)= & {} \frac{D}{(1-D^2)^2}\nonumber \\&\times \bigg [\frac{32\frac{D^2}{B}t^2 - 8\sqrt{\frac{D}{B}}(1+D^2)t\sqrt{4t^2\frac{D}{B}{+}(1-D^2)}}{4t^2 \frac{D}{B}+(1-D^2)}\bigg ].\nonumber \\ \end{aligned}$$
(29)

It is evident from Eq. (28) that a(t) has a non-zero minimum at \(t=0\) for \(0<D<1\), where the minimum value is given by

$$\begin{aligned} a(0) = \bigg [\frac{B}{4D}(1-D^2)\bigg ]^{1/2}. \end{aligned}$$

Thus the presence of a warped extra dimension allows for a non-singular bounce of the scale factor (at \(t=0\)) in our four dimensional universe, as long as the parameter D is constrained to be less than unity.

However, it can be checked from Eq. (29) that \(\Phi (t)\) has a positive asymptotic value as \(t\rightarrow -\infty \) and goes to zero at \(t=\frac{\sqrt{BD}}{2}\). Using Eq. (29) and the relation \(\Phi (t)=[\exp {\big (2\pi \frac{b(t)}{l}\big )} -1]\), we obtain Fig. 1, demonstrating the variation of the interbrane separation (b(t)) with time.

Figure 1 clearly reveals that the branes collapse into each other within a finite time \(t=\frac{\sqrt{BD}}{2}\), which indicates the instability of the entire set-up. Thus we need a suitable mechanism to stabilize the modulus. Following the procedure adopted in [19, 20], the stabilization method for the present set-up is discussed in the next section.

4 Radion stabilization

In order to address the stabilization of the time dependent radion field, one needs to consider a dynamical stabilization mechanism, which can be achieved by a time dependent generalization of the Goldberger–Wise (GW) mechanism [19]. Earlier, a similar approach was adopted in [20]. Introducing a time dependent scalar field (with quartic brane interactions) in the bulk [19, 20], we address the dynamics of modulus stabilization without sacrificing the conditions necessary to resolve the gauge hierarchy problem.

The action for the time dependent bulk scalar field is given by

$$\begin{aligned} S_5=\frac{1}{2}\int \mathrm{d}^4x\mathrm{d}\varphi \sqrt{-G}\bigg [G^{MN}\partial _M\Psi \partial _N\Psi + m^2\Psi ^2\bigg ] \end{aligned}$$
(30)

where M and N symbolize \((\mu ,\varphi )\). The hidden and visible brane interaction terms with the bulk stabilizing scalar field can be written as

$$\begin{aligned} S_4=\int \mathrm{d}^4x \int _{-\pi }^{+\pi }\mathrm{d}\varphi \sqrt{-g_h}\lambda _v\bigg [\Psi ^2-\tilde{v}_{h}^{2}\bigg ]^2 \delta (\varphi -0) \end{aligned}$$
(31)

and

$$\begin{aligned} S_4=\int \mathrm{d}^4x \int _{-\pi }^{+\pi }\mathrm{d}\varphi \sqrt{-g_v}\lambda _h\bigg [\Psi ^{2} -\tilde{v}_{v}^{2}\bigg ]^2 \delta (\varphi -\pi ) \end{aligned}$$
(32)

where \(g_h, g_v\) are the determinants of the metrics induced on the hidden and visible brane, respectively. The scalar field action (in Eq. (30)) leads to the field equation for \(\Psi =\Psi (\varphi ,t)\) as follows:

$$\begin{aligned}&\frac{\partial }{\partial t}\bigg [e^{-2A}a^3(t)b(t)\frac{\partial \Psi }{\partial t}\bigg ] -\frac{\partial }{\partial \varphi }\bigg [e^{-4A}\frac{a^3(t)}{b(t)} \frac{\partial \Psi }{\partial \varphi }\bigg ]\nonumber \\&\quad +\,m^2 e^{-4A}a^3(t)b(t)\Psi + 4e^{-4A}a^3(t)\lambda _h \psi \bigg (\Psi ^2- \tilde{v}_{h}^{2}\bigg )\delta (\varphi )\nonumber \\&\quad +\,4e^{-4A}a^3(t)\lambda _v \psi \bigg (\Psi ^2- \tilde{v}_{v}^{2}\bigg ) \delta (\varphi -\pi )=0. \end{aligned}$$
(33)

In the limit of large \(\lambda _h\) and \(\lambda _v\), the boundary conditions for \(\Psi (\varphi ,t)\) turns out to be

$$\begin{aligned} \Psi (0,t)=\tilde{v}_h(t)=F(t)v_h\quad \Psi (\pi ,t)=\tilde{v}_v(t)=F(t)v_v \end{aligned}$$
(34)

where F(t) carries the time dependence of \(\tilde{v}_{h}(t)\) and \(\tilde{v}_v(t)\). We choose a generalized solution for the stabilizing scalar field as

$$\begin{aligned} \Psi (\varphi ,t)=F(t)\bigg [P(t)e^{(2+\nu )A} + Q(t)e^{(2-\nu )A}\bigg ] \end{aligned}$$
(35)

where \(\nu = \sqrt{4+\frac{m^2}{k^2}}\), \(k=\frac{1}{l}\) and recall that \(A(\varphi ,t) = kb(t)\varphi \). Using the boundary conditions we obtain

$$\begin{aligned} P(t)=v_ve^{-(2+\nu )k\pi b(t)} - v_h e^{-2\nu k\pi b(t)} \end{aligned}$$
(36)

and

$$\begin{aligned} Q(t)=v_h(1+e^{-2\nu k\pi b(t)}) - v_ve^{-(2+\nu )k \pi b(t)}. \end{aligned}$$
(37)

Moreover, using the scalar field solution presented in Eq. (35), the time dependent part of the differential Eq. (33) takes the following form:

$$\begin{aligned}&a^3(t)b(t)\bigg [e^{\nu A}\bigg \{F(t)P_t + P(t)\bigg (F_t+(\nu +2) F(t)A_t\bigg )\bigg \}\nonumber \\&\qquad +\,e^{-\nu A}\bigg \{F(t)Q_t+Q(t)\bigg (F_t + (2-\nu )F(t)A_t\bigg ) \bigg \}\bigg ] \nonumber \\&\quad = C(\varphi ) \end{aligned}$$
(38)

where \(F_t, P_t, Q_t, A_t\) are the derivatives of F, P, Q, A with respect to t and \(C(\varphi )\) is a \(\varphi \) dependent integration constant.

Plugging back the solutions of P(t) and Q(t) (obtained in Eqs. (36) and (37)) into Eq. (38), one obtains a differential equation for F(t) as follows:

$$\begin{aligned} \frac{\partial F}{\partial t}\propto k\frac{e^{2k \pi b(t)}}{a^3(t)} \end{aligned}$$
(39)

where we assume that the scalar field mass (m) is less than the bulk curvature (k). Finally,

$$\begin{aligned} \frac{\partial F}{\partial t}= f_0 k\frac{e^{2k \pi b(t)}}{a^3(t)} \end{aligned}$$
(40)

with \(f_0\) a dimensionless constant. Using the solutions of a(t) and b(t) obtained in Eqs. (28) and (29), the function F(t) can be determined (from Eq. (40)) as follows:

$$\begin{aligned} F(t)= & {} \bigg [f_0k \bigg (\frac{8D\sqrt{\frac{D}{B}}\sqrt{\frac{D}{B}-DB+4t^2}}{3(1-D^{2})^3\big [4D t^2+B(1-D^{2})\big ]^2}\bigg )\nonumber \\&\times \bigg (4D(3+10D^{2}+3D^{4})\nonumber \\&+\,\sqrt{\frac{D}{B}}t^3-3(D^{4}-1)B\bigg \{(1+D^{2})\sqrt{\frac{D}{B}}t\nonumber \\&+\,D\sqrt{1-D^{2}+4\frac{D}{B}t^2}\bigg \}\bigg ) + E_0\bigg ] \end{aligned}$$
(41)

where \(E_0\) is an integration constant. After obtaining the explicit form of F(t), the GW stabilization mechanism can be implemented in this framework, where \(\Psi (\varphi ,t)\) acts as a stabilizing field. Plugging the solution of \(\Psi (\varphi ,t)\) (see Eq. (35)) in the five dimensional scalar field action (Eq. (30)) and integrating over \(\varphi \) yield the effective radion potential (\(V_{eff}\)) as follows:

$$\begin{aligned} V_{\mathrm{eff}}= & {} \bigg (v_ve^{-(2+\nu )k\pi \frac{b(t)}{F(t)}} - v_h e^{-2\nu k\pi \frac{b(t)}{F(t)}}\bigg )^2\nonumber \\&\times \, k(2+\nu )\exp {\bigg (2\nu k\pi \frac{b(t)}{F(t)}\bigg )}\nonumber \\&+\,\bigg (v_h(1+e^{-2\nu k\pi \frac{b(t)}{F(t)}}) \!-\! v_ve^{-(2+\nu )k \pi \frac{b(t)}{F(t)}}\bigg )^2k(\nu \!-\!2).\nonumber \\ \end{aligned}$$
(42)

Minimizing this radion potential, we obtain the value of \(b_{\mathrm{min}}(t)\):

$$\begin{aligned} k\pi b_{\mathrm{min}}(t)=4\frac{k^2}{m^2}\mathrm{ln}\bigg (\frac{v_h}{v_v}\bigg )\times F(t) \end{aligned}$$
(43)

where \(b_{\mathrm{min}}(t)\) is the stabilized value of the modulus and F(t) is given in Eq. (41). It can be checked that \(b_{\mathrm{min}}(t)\) is positive for all t and has asymptotic values at \(t\rightarrow \pm \infty \). Thus the branes are never going to be collapsed in the presence of the bulk massive scalar field (\(\Psi (\varphi ,t)\)) and the stabilized interbrane separation (i.e. \(b_{\mathrm{min}}(t)\)) acquires a saturated value at large time.

4.1 Determination of the constants: \(f_0\) and \(E_0\)

The solution of F(t) (in Eq. (41)) immediately leads the asymptotic values of \(b_{\mathrm{min}}(t)\) as follows:

$$\begin{aligned}&k\pi b_{\mathrm{min}}(t\rightarrow -\infty )=4\frac{k^2}{m^2}\mathrm{ln}\bigg (\frac{v_h}{v_v} \bigg )\nonumber \\&\quad \times \,\bigg [-f_0k\bigg (\frac{4D}{3B}\bigg ) \frac{(1+3D^{2})(3+D^{2})}{(1-D^{2})^3} + E_0\bigg ] \end{aligned}$$
(44)

and

$$\begin{aligned}&k\pi b_{\mathrm{min}}(t\rightarrow \infty )=4\frac{k^2}{m^2}\mathrm{ln}\bigg (\frac{v_h}{v_v} \bigg )\nonumber \\&\quad \times \,\bigg [f_0k\bigg (\frac{4D}{3B}\bigg ) \frac{(1+3D^{2})(3+D^{2})}{(1-D^{2})^3} + E_0\bigg ]. \end{aligned}$$
(45)
Fig. 2
figure 2

\(b_{\mathrm{min}}(t)\) vs. t for \(B=1\) and \(D=0.5\)

Full size image

Now, the constants (\(f_0\) and \(E_0\)) can be determined by equating these asymptotic values (as shown in Eqs. (44) and (45)) with that obtained in Eq. (29) (for \(t\rightarrow -\infty \)) and with the GW result (for \(t\rightarrow +\infty \)), as follows:

  • \(k\pi b_{\mathrm{min}}(t\rightarrow -\infty ) = \ln {\bigg (\frac{1+D}{1-D}\bigg )}\), obtained from Eq. (29).

  • \(k\pi b_{\mathrm{min}}(t\rightarrow +\infty ) = 4\frac{k^2}{m^2}\mathrm{ln}\bigg (\frac{v_h}{v_v}\bigg )\) (in consonance with the GW result [19]).

With the help of the above two conditions, one finds the constants \(f_0\) and \(E_0\) (in terms of B, D) as follows:

$$\begin{aligned} E_0 = \bigg [\frac{1}{2} + \frac{m^2/8k^2}{\ln (v_h/v_v)}\ln \bigg (\frac{1+D}{1-D}\bigg )\bigg ] \end{aligned}$$
(46)

and

$$\begin{aligned}&f_0 = \bigg (\frac{1}{k}\bigg )\frac{(1-D^{2})^3}{(3+D^{2})(1+3D^{2})}\nonumber \\&\quad \times \bigg [1-\frac{m^2/8k^2}{\ln (v_h/v_v)}\mathrm{ln}\bigg [\frac{1+D}{1-D}\bigg ]\bigg ]. \end{aligned}$$
(47)

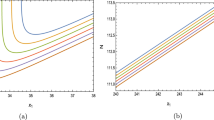
Using the above expressions of \(f_0\), \(E_0\) and Eq. (43), we obtain Fig. 2 showing the stabilized modulus (\(\frac{b_{\mathrm{min}}(t)}{b_{\mathrm{GW}}}\)) versus t (where \(k\pi b_{\mathrm{GW}}=4\frac{k^2}{m^2}\ln (v_h/v_v)\)).

Figure 2 clearly depicts \(b_{\mathrm{min}}(t)\), showing it to be non-vanishing for the entire range of t (\(-\infty<t< \infty \)) and saturating at the Goldberger–Wise value (\(b_{\mathrm{GW}}\)) at large time. Thus the time dependent modulus can be stabilized by imposing a time dependent massive scalar field in the bulk. Moreover, we fix the integration constants (\(f_0\), \(E_0\)) in such a way that the solution of the gauge hierarchy problem is ensured.

However, the question may arise whether the introduction of stabilizing scalar field can affect the bouncing phenomena or not. To examine this, we substitute the solution of the stabilized modulus (i.e. \(b_{\mathrm{min}}(t)\)) into the effective Friedmann equation and find

$$\begin{aligned} \bigg (\frac{\dot{a}}{a}\bigg )^2= & {} \frac{1}{a^2} - 8\frac{k^2}{m^2}\mathrm{ln}\bigg (\frac{v_h}{v_v}\bigg )\dot{F}(t) \frac{\dot{a}}{a}\bigg [\frac{\big (\frac{v_h}{v_v}\big )^{8\frac{k^2}{m^2}F(t)}}{\big (\frac{v_h}{v_v}\big )^{8\frac{k^2}{m^2}F(t)}-1}\bigg ]\nonumber \\&+\bigg (8\frac{k^2}{m^2}\mathrm{ln}\bigg (\frac{v_h}{v_v}\bigg )\dot{F}(t)\bigg )^2 \bigg [\frac{\big (\frac{v_h}{v_v}\big )^{8\frac{k^2}{m^2}F(t)}}{\big (\frac{v_h}{v_v}\big )^{8\frac{k^2}{m^2}F(t)}-1}\bigg ]. \end{aligned}$$
(48)

Using the form of F(t) given in Eq. (41), we solve the Hubble parameter (\(=\dot{a}/a\)) numerically and compare this numerical solution with the Hubble parameter obtained earlier (in the absence of \(\Psi (\varphi ,t)\); see Eq. (28)). This comparison is shown in Fig. 3.

Fig. 3
figure 3

H(t) vs. t, with/without the stabilizing field for \(B=1\), \(D=0.5\), \(\frac{v_h}{v_v}=1.5\) and \(\frac{m}{k}=0.2\)

Full size image

Figure 3 clearly demonstrates that the feature of the bouncing phenomena remains unaffected due to the effect of the stabilizing scalar field.

Before concluding we want to mention that the free kinetic energy density of the radion field remains always positive while the interaction energy between radion and gravitational field becomes negative for a certain time regime, which causes the bounce at \(t=0\). Equation (18) immediately leads to the effective energy density (\(\rho _{\mathrm{eff}}\)) as follows:

$$\begin{aligned} \rho _{\mathrm{eff}} = \frac{3}{4} \bigg (\bigg [-\frac{\dot{\Phi }}{\Phi } - \bigg (\frac{\dot{\Phi }^2}{\Phi ^2(1+\Phi )} + \frac{4}{a^2}\bigg )^{\frac{1}{2}}\bigg ]\bigg )^2 . \end{aligned}$$
(49)

Now the curvature energy density is given by \(\rho _{\mathrm{cur}}=\frac{3}{a^2}\) and the expression of the effective action \(S_{\mathrm{eff}}\) (see Eq. (14)) leads to the free kinetic energy density of the radion field, \(\rho _{\mathrm{rad}}=\frac{3}{4}\dot{\Phi }^2\), which is always positive definite. Therefore \(\rho _{\mathrm{eff}}\) can be written as

$$\begin{aligned} \rho _{\mathrm{eff}} = \rho _{\mathrm{cur}} + \rho _{\mathrm{rad}} + \rho _{\mathrm{coup}} \end{aligned}$$

where \(\rho _{\mathrm{coup}}\) denotes the interaction energy density between gravitational field and radion field. Using the solution of the stabilized radion field (see Eq. (43)) and the scale factor (obtained numerically from Eq. (48)), we obtain Fig. 4, which gives the variation of energy densities (\(\rho _{\mathrm{cur}}\), \(\rho _{\mathrm{rad}}\), \(\rho _{\mathrm{coup}}\)) with time (t).

Fig. 4
figure 4

\(\rho _{\mathrm{eff}}\), \(\rho _{\mathrm{cur}}\), \(\rho _{\mathrm{rad}}\) and \(\rho _{\mathrm{coup}}\) vs. t for \(B=1\), \(D=0.5\)

Full size image

Figure 4 clearly demonstrates that the free kinetic energy density of the radion field remains always positive while the interaction energy density (between radion and gravitational field) becomes negative for a certain regime of time. The negativity of \(\rho _{\mathrm{coup}}\) along with the positive value of \(\rho _{\mathrm{cur}}\) and \(\rho _{\mathrm{rad}}\) cancel each other to generate a zero effective energy density at \(t=0\), which causes the bounce.

5 Conclusion

We consider a five dimensional AdS compactified warped geometric model with two three branes residing at the orbifold fixed points. Our universe is identified with the visible brane. Instead of considering the five dimensional dynamics of the brane under gravity, we studied the low energy effective theory induced on our brane following Ref. [16]. In the high bulk curvature limit, the induced four dimensional effective theory appeared to be a Brans–Dicke type theory where the scalar field is playing the role of the distance modulus between the two branes. In this paper, we investigate the possibility of having a classical bouncing solution in the visible three brane (i.e. our universe). Out of three possible spatial curvatures of the Friedmann–Robertson–Walker brane, the bouncing solution exists only for hyperbolic spatial curvature \((\kappa = -1)\). Following the procedure as mentioned in Sect. III, it can be shown easily that, for \(\kappa = 0\) and for \(\kappa = +1\), one cannot have any bouncing solution. While finding the solution for \(\kappa =-1\), we also introduce the stabilization mechanism to make sure that the two branes do not collapse, and maintain the hierarchy of scale in the asymptotic limit. In addition, we also need to satisfy the specific constraint \(0<D< 1\) to ensure the real valued bouncing solution for the scale factor.

As the solution of the radion field presented in Eq. (29) clearly implies, in the epoch after the bouncing, (depicted in Fig. 1), the two branes would collapse, leading to instability. Therefore, in order to stabilize this, a time dependent massive scalar field is introduced in the bulk. Thus we have a dynamical stabilization of the RS model, where in the asymptotic past the hierarchy of scales was larger than that of the present Goldberger–Wise value, which is achieved in the asymptotic future. This is clearly demonstrated in Fig. 2. We have determined the stabilization condition in Eq. (39), and finally taking this into account, we numerically solve the Hubble parameter as shown in Fig. 3. This clearly reveals that the “bouncing” phenomenon is not affected by the stabilizing scalar field.