1 Introduction

The late time cosmic acceleration is revealed by various observations [1,2,3,4,5,6]. Substantial efforts were made by a number of authors to explore the cause of cosmic acceleration, by introducing a new player with negative pressure termed dark energy (DE) [7,8,9,10]. Apart from dark energy, there are other theoretical models, such as void and back-reaction models, which all provide late time cosmic acceleration [11,12,13,14,15,16,17,18,19].

The simplest candidate of DE is the cosmological constant \(\Lambda \) with the equation of state \(w=-1\). However, it suffers two severe problems, the cosmological constant (fine tuning) and coincidence problems [20,21,22,23]. Though the \(\Lambda \)CDM model is supported by the present observations, yet it has no satisfactory argument for the fine tuning and coincidence problems; why is the vacuum energy so small? Why are the densities of DE and dark matter (DM) nearly equal at present, while their time evolution is very different? Therefore, one can explore the dynamical DE models that can fit into the observations. Such models have been studied in the past few decades [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55].

The simplest models of dynamical DE are scalar fields, dubbed “quintessence”. If the quintessence is coupled with the DM, then one can get similar energy densities in the dark sector at present. A conclusive way is if the DE models have \(\Omega _\mathrm{DE}/ \Omega _\mathrm{DM}\) of the order 1 and an accelerated scaling attractor solution, then the coincidence problem can be alleviated. Therefore, to sort out the coincidence problem, the interaction of DE with DM is one novel approach.

It has been found that the form of dark energy that dominates the present Universe could be a phantom energy, quintessence or cosmological constant. The available cosmological data do not fix a microscopic theory of dark energy. But the overall uncertainty is reflected by the existence of various phenomenological models. To reduce the number of models one way is to consider only the ones that do not violate any of the fundamental theories. The number can be further reduced by testing the models against the cosmological data. The phantom field can be a source of dark energy and may arise from higher order theories of gravity; for example, the Brans–Dicke and non-minimally coupled scalar field theories [56,57,58,59,60]. Recently, the dynamics of a coupled phantom field with dark matter has been discussed [61,62,63,64,65,66,67,68]. To solve the long standing coincidence problem, we consider scalar fields (specifically phantom and tachyon) as a dynamical dark energy interacting with dark matter by transferring energy between the two dark components. For an exponential potential, the quantity \(\lambda =- V'/\kappa V\), which corresponds to the relative slope of the potential, is constant. Therefore, it is easy to study the stability of the stationary points in the phase space [69, 70].

In the literature, it has been proposed that rolling tachyon condensates, in a class of string theories, may have important cosmological outcomes. Ashoke Sen [71, 72] has shown that the decay of D-branes generates a pressure-less gas having definite energy density that looks like classical dust. The equation of state of a rolling tachyon lies between 0 and −1 [73]. The tachyon is an unstable field, which is vital in string theory and which is used in Dirac–Born–Infeld (DBI) action. It also acts as a source of dark energy for a particular class of potentials [74,75,76,77,78,79]. In this case, we consider an inverse square potential for which \(\lambda \) is constant, an analog of exponential potential for the standard scalar field. Coupling with matter might lead to late time acceleration. The tachyon field also has implications for inflation, namely, the tensor to scalar ratio is very low in this case.

A dynamical system plays a central role in the understanding of the asymptotic behavior of the cosmological models and belongs to the class of autonomous systems [69, 70]. For an autonomous system, the dimensionless set of variables are chosen due to a number of reasons.

  1. (a)

    These variables give rise to a bounded dynamical system.

  2. (b)

    They are well behaved and regularly have a direct physical interpretation.

  3. (c)

    Due to a symmetry in the equations, the number of equations can be reduced and then resulting simplified system is investigated. A brief analysis of the dynamical system is given in the appendix.

In this letter, we investigate the stationary points and their stability for coupled phantom and tachyon fields. We apply dynamical system analysis to study the asymptotic behavior of the cosmological models mentioned above. We consider the forms of coupling that are proportional to the time derivative of their energy densities. The different forms of coupling have been studied in [80,81,82,83,84,85,86]. There also exist studies of the models without such particular forms of coupling [87]. The rest of the paper is organized as follows: In Sect. 2 we discuss the coupled phantom dynamics and construct the autonomous system which is useful for phase space analysis. In Sect. 3 we study phase space trajectories, and we obtain stationary points and their stabilities for different forms of coupling. The stationary points and their stabilities of a tachyon field with the coupling \(Q=\beta \dot{\rho _{\phi }}\) is discussed in Sect. 4. We summarize our results in Sect. 5.

2 Coupled phantom dynamics

In a spatially flat Universe, we consider two components, namely phantom field and matter (baryonic+DM). The energy density of each component may not be conserved, although the total energy density of the Universe is. Therefore, the conservation laws of energy can be written as

$$\begin{aligned}&\dot{\rho }_{m}+3H(\rho _{m}+p_m)=Q, \nonumber \\&\dot{\rho }_{\phi }+3H(\rho _{\phi }+p_{\phi })=-Q, \\&\dot{\rho }_\mathrm{tot}+3H(\rho _\mathrm{tot}+p_\mathrm{tot})=0, \nonumber \end{aligned}$$
(1)

where \(\rho _\mathrm{tot}=\rho _{\phi }+\rho _{m}\) and \(p_\mathrm{tot}=p_{\phi }+p_{m}\), and \(\rho _m, \rho _{\phi }, p_m\) and \(p_{\phi }\) are the energy densities and pressures of matter (dust) and phantom field, respectively. The coupling is through the function Q, and H denotes the Hubble parameter.

The flow of energy between two components depends on the sign of Q. If \(Q > 0\), the transfer of energy takes place from phantom to matter, whereas for \(Q< 0\) it occurs from matter to phantom. At present, several forms of Q have been investigated [88,89,90,91,92,93,94,95,96,97,98,99,100,101]. Following Eq. (1), it is clear that Q should be a function of \(H, \rho _m\) and \(\rho _{\phi }\),

$$\begin{aligned} Q= Q(H, \rho _m, \rho _{\phi }). \end{aligned}$$
(2)

We consider three particular forms of Q: \(\alpha \dot{\rho }_{{m}}, \beta \dot{\rho _{\phi }}\) and \(\sigma (\dot{\rho }_{{m}}+\dot{\rho _{\phi }})\). In these forms, H is not directly involved, as it has the dimension of the inverse of time, and the latter is already present in \({\dot{\rho }}_i\).

In a spatially flat Friedmann–Lemaitre–Robertson–Walker (FLRW) Universe, the evolution equations are given by

$$\begin{aligned} \begin{aligned} H^{2}&=\frac{\kappa ^2}{3} (\rho _{m}+\rho _{\phi })\\ 2\dot{H}+3H^2&=-\kappa ^2 p_{\phi } \end{aligned} \end{aligned}$$
(3)

where \(\kappa ^2= 8\pi G, \rho _{\phi }=-\frac{1}{2}\dot{\phi ^2}+ V(\phi )\) and \(p_{\phi }=-\frac{1}{2}\dot{\phi ^2}- V(\phi )\). To cast the evolution equations in the form of an autonomous system, we introduce the following dimensionless quantities:

$$\begin{aligned} x=\frac{\kappa \dot{\phi }}{\sqrt{6}H}; \quad y=\frac{\kappa \sqrt{V}}{\sqrt{3}H}; \quad \lambda =-\frac{V'}{\kappa V}. \end{aligned}$$
(4)

Hence, we find

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm{d}x}{\mathrm{d}N}&= x \left( \frac{\ddot{\phi }}{H \dot{\phi }}-\frac{\dot{H}}{H^2}\right) ,\\ \dfrac{\mathrm{d}y}{\mathrm{d}N}&=-y\left( \sqrt{\frac{3}{2}}\lambda x +\frac{\dot{H}}{H^{2}}\right) , \end{aligned} \end{aligned}$$
(5)

where \(N=\ln a\). For an exponential potential, we find that \(\lambda \) is constant, and

$$\begin{aligned} \frac{\dot{H}}{H^2}= & {} \frac{3(x^2+y^2-1)}{2}\end{aligned}$$
(6)
$$\begin{aligned} \frac{\ddot{\phi }}{H \dot{\phi }}= & {} -3-\sqrt{3/2}~\frac{\lambda y^2}{x}+\frac{Q}{H\dot{\phi ^2}} . \end{aligned}$$
(7)

Then the effective equation of state, the field density parameter and the equation of state for a phantom field are given, respectively, by

$$\begin{aligned} w_\mathrm{eff}= & {} -1 - \frac{2\dot{H}}{3H^2}, \nonumber \\ \Omega _{\phi }= & {} \frac{\kappa ^2 \rho _{\phi }}{3H^2}=-x^2+y^2 \\ w_{\phi }= & {} \frac{w_\mathrm{eff}}{\Omega _{\phi }}.\nonumber \end{aligned}$$
(8)

For an accelerating Universe, we have \(w_\mathrm{eff} < -\frac{1}{3}\).

3 Stationary points and their stabilities

To study stationary points and their stabilities, let us consider the autonomous system (5), from which we can find the stationary points by setting the left-hand side of these equations to zero. Then the signs of the eigenvalues will tell us the stability of the points. In the following sub-sections, we consider different forms of the coupling.

3.1 Coupling \(Q=\alpha \dot{\rho }_{m}\)

For this coupling, Eq. (7) takes the form

$$\begin{aligned} \frac{\ddot{\phi }}{H \dot{\phi }}= & {} -3-\sqrt{3/2}~\frac{\lambda y^2}{x}-\frac{3\alpha \Omega _m}{2(1-\alpha )x^2} \end{aligned}$$
(9)

where \(\Omega _m=1-\Omega _{\phi }\). Then the autonomous system can be written as

$$\begin{aligned} \dfrac{\mathrm{d}x}{\mathrm{d}N}= & {} x \left( -3-\sqrt{3/2}~\frac{\lambda y^2}{x}-\frac{3\alpha \Omega _m}{2(1-\alpha )x^2}-\frac{3(x^2+y^2-1)}{2}\right) , \nonumber \\ \dfrac{\mathrm{d}y}{\mathrm{d}N}= & {} -y\left( \sqrt{\frac{3}{2}}\lambda x +\frac{3(x^2+y^2-1)}{2}\right) . \end{aligned}$$
(10)

The critical points can be obtained by putting \(\frac{\mathrm{d}x}{\mathrm{d}N}=0\) and \(\frac{\mathrm{d}y}{\mathrm{d}N}=0\), simultaneously. Therefore, we have the following stationary points:

  1. 1.

    \(x= -\sqrt{\frac{\alpha }{\alpha -1}},~ y= 0\). In this case, the corresponding eigenvalues are

    $$\begin{aligned} \mu _1= & {} -6 - \frac{3}{\alpha -1}< 0,\quad { \text{ for }}\quad \alpha \> 1, \nonumber \\ \mu _2= & {} \frac{-3 + \sqrt{6 \alpha (\alpha -1)}~ \lambda }{2(\alpha -1)} < 0, \;\;\; { \text{ for }} \;\;\; \alpha \ > 1,\\&\sqrt{6 \alpha (\alpha -1)}~ \lambda \le 0. \end{aligned}$$

    The point has negative eigenvalues for \(\alpha > 1\) and \(\sqrt{6 \alpha (\alpha -1)}~ \lambda \le 0 \). Thus, it is a stable point.

  2. 2.

    \(x= \sqrt{\frac{\alpha }{\alpha -1}},~ y= 0\). Then we have the following eigenvalues:

    $$\begin{aligned} \mu _1= & {} -6 - \frac{3}{\alpha -1}< 0,\quad { \text{ for }}\quad \alpha \> 1, \nonumber \\ \mu _2= & {} \frac{-3 - \sqrt{6 \alpha (\alpha -1)}~ \lambda }{2(\alpha -1)} < 0, { \text{ for }}\;\;\; \alpha \ > 1, \\&\sqrt{6 \alpha (\alpha -1)}~ \lambda \ge 0 . \end{aligned}$$

    The eigenvalues of this point show they are negative for \(\alpha \ > 1\) and \(\sqrt{6 \alpha (\alpha -1)}~ \lambda \ge 0 \). Therefore, it is a stable point.

  3. 3.

    \(x= -\frac{\lambda }{\sqrt{6}},~ y= -\sqrt{1+\frac{\lambda ^{2}}{6}}\). In this case, the eigenvalues are given by

    $$\begin{aligned} \mu _1= & {} -3 - \lambda ^2/2< 0, \quad { \text{ for }}\quad \lambda \> 0,\nonumber \\ \mu _2= & {} 3/(\alpha -1) - \lambda ^2 < 0, \quad { \text{ for }}\quad \alpha \> 1,\quad \lambda \ > \sqrt{3/( \alpha -1)} . \nonumber \end{aligned}$$

    The point is stable under the conditions given above.

  4. 4.

    \(x= -\frac{\lambda }{\sqrt{6}},~ y= \sqrt{1+\frac{\lambda ^{2}}{6}}\). In this case, we get the same eigenvalues as (3).

  5. 5.

    \(x= \frac{\sqrt{\frac{3}{2}}}{\lambda (1-\alpha )},~ y= -\frac{\sqrt{(\alpha -1)\alpha \lambda ^2-\frac{3}{2}}}{\lambda (\alpha -1)}\). In this case, the corresponding eigenvalues are

    $$\begin{aligned} \mu _1= & {} -\frac{1}{4}\left( 12+\frac{9}{\alpha -1}-2\alpha \lambda ^2+\delta _1\right)< 0, \\&{ \text{ for }}\quad 12+\frac{9}{\alpha -1}-2\alpha \lambda ^2+\delta _1>0,\\ \mu _2= & {} -\frac{1}{4}\left( 12+\frac{9}{\alpha -1}-2\alpha \lambda ^2-\delta _1\right) < 0, \\&{ \text{ for }}\quad 12+\frac{9}{\alpha -1}-2\alpha \lambda ^2-\delta _1>0, \end{aligned}$$

    where \(\delta _1=\) \(\frac{\sqrt{(\alpha -1)\lambda ^2(216+(\alpha -1)\lambda ^2(-63+4\alpha (-54+36\alpha -3(\alpha -1)(4\alpha -5)\lambda ^2+(\alpha -1)^2\alpha \lambda ^4)))}}{\lambda ^{2}(\alpha -1)^{2}}\). The point now is a saddle point.

Fig. 1
figure 1

The figure shows the phase space trajectories for point (3) of the coupling \(Q=\alpha \dot{\rho }_{m}\). The stable fixed point is an attractive node and corresponds to \(\alpha =5\) and \(\lambda =1\). The black dot represents the stable attractor point

Full size image
Fig. 2
figure 2

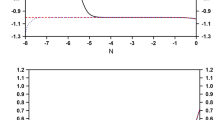
This figure represents the phase portrait, evolution of \(w_{\phi }\) and \(\Omega _{\phi }\) of point (5) for \(Q=\alpha \dot{\rho }_{m}\). This is an unstable point and acts as a saddle point that is shown in the left panel for \(\alpha =-0.3\) and \(\lambda =1.9\). The middle and right panels are plotted for different values of \(\alpha \). The solid, dashed, dot-dashed and dotted lines correspond to \(\alpha =-1, -2, -3\) and \(-5\), respectively. The values of \(\lambda \) below the horizontal line are not allowed

Full size image
Table 1 We display stationary points for the coupling \(Q=\alpha \dot{\rho _m}\). We also show the expressions of \(\Omega _{\phi }, w_\mathrm{eff}, w_{\phi }\) and the conditions to have an accelerating phase
Full size table

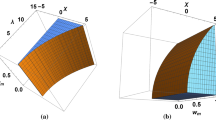
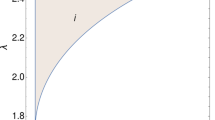
In this coupling, we are interested in Cases (3) and (5), as Case (3) is stable and has an accelerating period, whereas Case (5) is a saddle point and also has an accelerating period. For Case (3), we solve the autonomous system (10) numerically for \(\alpha =5\) and \(\lambda =1\), and the result is displayed in Fig. 1. The stable point of Case (3) acts as an attractive node under the chosen parameters, which is confirmed by Fig. 1. Additionally, in this case we obtain \(\Omega _{\phi }=1\), which corresponds to the case where dark energy totally dominates. However, we find that Case (3) is a stable fixed point with a late accelerating Universe (\(w_\mathrm{eff} < -1/3\)), but it cannot solve the coincidence problem as it has \(\Omega _\mathrm{DE}=1\) rather than \(\Omega _\mathrm{DE}/\Omega _\mathrm{DM} \simeq \mathcal{{O}}(1)\). In Case (5), we evolve the system (10) numerically for \(\alpha =-0.3\) and \(\lambda =1.9\), and find that this point is a saddle point, which is shown at the left panel of Fig. 2. We also find the cosmological observables \(\Omega _{\phi }, w_\mathrm{eff}\) and \(w_{\phi }\). The middle and right panels of Fig. 2 show the evolution of \(w_{\phi }\) and \(\Omega _{\phi }\) versus \(\lambda \). They also show in which range of \(\lambda \) (having different values of \(\alpha \)) both physical observables are allowed. The general properties of this coupling are summarized in Table 1.

3.2 Coupling \(Q=\beta \dot{\rho _{\phi }}\)

For the coupling \(Q=\beta \dot{\rho _{\phi }}\), Eq. (7) becomes

$$\begin{aligned} \frac{\ddot{\phi }}{H \dot{\phi }}=-3-\sqrt{3/2}~\frac{\lambda y^2}{x}+\frac{3\beta }{1+\beta } . \end{aligned}$$
(11)

Therefore, Eq. (5) takes the form

$$\begin{aligned} \dfrac{\mathrm{d}x}{\mathrm{d}N}= & {} x \left( -3-\sqrt{3/2}~\frac{\lambda y^2}{x}+\frac{3\beta }{1+\beta }-\frac{3(x^2+y^2-1)}{2}\right) , \nonumber \\ \dfrac{\mathrm{d}y}{\mathrm{d}N}= & {} -y\left( \sqrt{\frac{3}{2}}\lambda x +\frac{3(x^2+y^2-1)}{2}\right) . \end{aligned}$$
(12)

For this coupling, we have the following stationary points:

  1. 1.

    \(x= 0,~ y= 0\). In this case, the corresponding eigenvalues are

    $$\begin{aligned}&\mu _1 = \frac{3}{2}-\frac{3}{1+\beta }< 0, \quad { \text{ for }}\quad 0< \beta < 1, \nonumber \\&\mu _2 = \frac{3}{2} .\nonumber \end{aligned}$$

    As one of the eigenvalues is positive, the stationary point is unstable for any value of \(\beta \).

  2. 2.

    \(x= -\sqrt{\frac{\beta -1}{\beta +1}},~ y= 0\). In this case, the eigenvalues are given by

    $$\begin{aligned} \mu _1= & {} -3+\frac{6}{1+\beta }< 0, \quad { \text{ for }}\quad \beta< -1, \nonumber \\ \mu _2= & {} \frac{3}{1+\beta }+\sqrt{\frac{3}{2}-\frac{3}{1+\beta }}\lambda< 0, \\&{ \text{ for }}\quad -2 \le \beta< -1 \quad \text {and} \quad 0<\lambda \le 1. \nonumber \end{aligned}$$

    The eigenvalues of this point show the negativity for \(-2 \le \beta < -1\) and \(0<\lambda \le 1\). Therefore, it is a stable point.

  3. 3.

    \(x= \sqrt{\frac{\beta -1}{\beta +1}},~ y= 0\). In this case, the corresponding eigenvalues are

    $$\begin{aligned} \mu _1= & {} -3+\frac{6}{1+\beta }< 0,\quad { \text{ for }}\quad \beta< -1, \nonumber \\ \mu _2= & {} \frac{3}{1+\beta }-\sqrt{\frac{3}{2}-\frac{3}{1+\beta }}\lambda< 0,\\&{ \text{ for }}\quad \beta < -1 \quad \text {and} \quad \lambda > \ 0. \end{aligned}$$

    It is a stable point for the above given conditions.

  4. 4.

    \(x= \frac{9-(1+\beta )^2\lambda ^4+\delta _2}{2\sqrt{6}\lambda (1+\beta )(3+(1+\beta )\lambda ^2)},~ y= -\frac{\sqrt{6(1+\beta )^2\lambda ^2-9+\lambda ^4(1+\beta )^2-\delta _2}}{2\sqrt{3}(1+\beta )\lambda }\). In this case, we have the following eigenvalues:

$$\begin{aligned} \mu _1= & {} -\frac{2\delta _{2}^2-6(1+\beta )\delta _2 \epsilon \lambda ^2+2\epsilon ^2(-9+(1+\beta )\lambda ^2(9+2(1+\beta )\lambda ^2))+\nu }{16(1+\beta )^2\epsilon ^2\lambda ^2}< 0, \nonumber \\&{ \text{ for }}\;\;\; 2\delta _{2}^2+2\epsilon ^2(-9+(1+\beta )\lambda ^2(9+2(1+\beta )\lambda ^2))+\nu< 0, \nonumber \\ \nonumber \\ \nonumber \\ \mu _2= & {} -\frac{2\delta _{2}^2-6(1+\beta )\delta _2 \epsilon \lambda ^2+2\epsilon ^2(-9+(1+\beta )\lambda ^2(9+2(1+\beta )\lambda ^2))-\nu }{16(1+\beta )^2\epsilon ^2\lambda ^2}< 0,\nonumber \\&{ \text{ for }}\quad 2\delta _{2}^2+2\epsilon ^2(-9+(1+\beta )\lambda ^2(9+2(1+\beta )\lambda ^2))-\nu < 0, \nonumber \end{aligned}$$

where

$$\begin{aligned} \delta _2= & {} \sqrt{(3+(1+\beta )\lambda ^2)^2(9+(1+\beta )\lambda ^2(6+\lambda ^2+ \beta (12+\lambda ^2)))}\nonumber \\ \epsilon= & {} 3+(1+\beta )\lambda ^2 \nonumber \\ \nu= & {} \surd \left( \delta _{2}^4-12(1+\beta )\lambda ^2\delta _{2}^3\epsilon -6\delta _{2}^2 \epsilon ^2(3-4(\beta -6)(1+\beta )\lambda ^2\right. \\&\left. +3(1+\beta )^2\lambda ^4)+\epsilon ^4(-9+12(1+\beta )(2+\beta )\lambda ^2 \right. \\&\left. +5(1+\beta )^2\lambda ^4)^2+4(1+\beta )\lambda ^2\delta _2\epsilon ^3(-117+(1+\beta )\right. \\&\left. \times \lambda ^2(24+\lambda ^2+\beta (60+\lambda ^2))))\right) . \end{aligned}$$

The eigenvalues of this point show the negativity under the above conditions. Hence, it is a stable point. \(\Omega _{\phi }, w_\mathrm{eff}\) and \(w_{\phi }\) are given by

$$\begin{aligned} \Omega _{\phi }= & {} -\frac{9-(1+\beta )^2 \lambda ^4+\sqrt{\delta _2}}{2(1+\beta )^2 \lambda ^2 \epsilon } ,\end{aligned}$$
(13)
$$\begin{aligned} w_\mathrm{eff}= & {} -\frac{9+18\beta +6(1+\beta )^2 \lambda ^2+(1+\beta )^2 \lambda ^4-\sqrt{\delta _2}}{6(1+\beta ) \epsilon } , \end{aligned}$$
(14)
$$\begin{aligned} w_{\phi }= & {} \frac{-9-(1+\beta ) \lambda ^2(6+(1+\beta ) \lambda ^2)+\sqrt{\gamma }}{6 \epsilon } , \end{aligned}$$
(15)

where

$$\begin{aligned} \gamma= & {} 81+(1+\beta )^2 \lambda ^2 \Big (108+18(3+4\beta )\lambda ^2\nonumber \\&+12(1+\beta )^2 \lambda ^4+(1+\beta )^2 \lambda ^6 \Big ). \end{aligned}$$
(16)

For this coupling, we pay particular attention to Cases (2) and (4). In Case (2), we evolve the autonomous system (12) numerically for the values \(\beta =-2\) and \(\lambda =1\), and we get \(\Omega _{\phi }, w_\mathrm{eff}\) and \(w_{\phi }\). With the chosen parameters, the point is stable and behaves as an attractive node (see Fig. 3), but there does not exist an accelerating phase of the Universe, as the equation of state \(w_{\phi }\) for the phantom field is always positive. Therefore, it does not solve the coincidence problem. In Case (4), we elaborate the system for \(\beta =-2.5\) and \(\lambda =1\), and we find that it is stable and acts as an attractive node. The phase portrait of this stable point is shown in the left panel of Fig. 4, the middle and right panels of Fig. 4 show the evolution of \(w_{\phi }\) and \(\Omega _{\phi }\). For this point, we consider two cases: (a) \(\beta =-2.5\) and \(1 \le \lambda < 1.5\), in which Case (4) behaves as a stable point but does not give rise to an accelerating Universe as \(w_{\phi }\) is always positive. (b) \(\beta =-2.5\) and \(\lambda > 1.5\), in which Case (4) acts as a saddle point and has an accelerating phase as \(w_{\phi }<-1\) (see Table 2). Hence, it does not alleviate the coincidence problem. The results of the coupling are summarized in Table 2.

Fig. 3
figure 3

The figure displays the phase space trajectories of Case (2) for \(Q=\beta \dot{\rho _{\phi }}\). It is plotted for \(\beta =-2\) and \(\lambda =1\). The point is stable and behaves as an attractive node

Full size image
Fig. 4
figure 4

The left panel shows the phase portrait of Case (4) for \(Q=\beta \dot{\rho _{\phi }}\) and corresponds to \(\beta =-2.5\) and \(\lambda =1\). The middle and right panels show the evolution of \(w_{\phi }\) and \(\Omega _{\phi }\) versus \(\lambda \) for various values of \(\beta \). The solid, dashed, dot-dashed and dotted lines correspond to \(\beta =-0.5, -2, -3\) and \(-5\), respectively. The values of \(\lambda \) below the horizontal line are not accepted. This is a stable point and acts as an attractive node

Full size image

3.3 Coupling \(Q=\sigma (\dot{\rho }_{m}+ \dot{\rho _{\phi }})\)

In this case, the coupling Q is a linear combination of \(\dot{\rho }_{m}\) and \(\dot{\rho _{\phi }}\). For this coupling, Eq. (7) can be written as

$$\begin{aligned} \frac{\ddot{\phi }}{H \dot{\phi }}= & {} -3-\sqrt{3/2}~\frac{\lambda y^2}{x}-\frac{3\sigma \Omega _m }{2(1-\sigma )x^2}+\frac{3\sigma }{1+\sigma }. \end{aligned}$$
(17)

Thus, the autonomous system (5) becomes

$$\begin{aligned} \dfrac{\mathrm{d}x}{\mathrm{d}N}= & {} x \left( -3-\sqrt{3/2}~\frac{\lambda y^2}{x} -\frac{3\sigma \Omega _m }{2(1-\sigma )x^2}\right. \nonumber \\&\left. +\frac{3\sigma }{1+\sigma }-\frac{3(x^2+y^2-1)}{2}\right) ,\nonumber \\ \dfrac{\mathrm{d}y}{\mathrm{d}N}= & {} -y\left( \sqrt{\frac{3}{2}}\lambda x +\frac{3(x^2+y^2-1)}{2}\right) . \end{aligned}$$
(18)

For this coupling, we have the following stationary points:

  1. 1.

    \(x= -\frac{\sqrt{1-\sigma +2\sigma ^2-\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}}}{\sqrt{2(\sigma ^2-1)}},~ y= 0\). In this case, the corresponding eigenvalues are

    $$\begin{aligned} \mu _1= & {} \frac{3\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}}{\sigma ^2-1}<0, ~~ \text {for} \ \sigma ^2 < 1, \nonumber \\ \mu _2= & {} \frac{1}{8}\left( \frac{6(\sigma -3+\sqrt{1+\sigma (\sigma +8\sigma ^3-6)})}{\sigma ^2-1}\right. \\&\left. +\,4\sqrt{3}\lambda \sqrt{\frac{1-\sigma +2\sigma ^2-\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}}{\sigma ^2-1}}\right) >0,\\&\text {for all}\ \sigma . \nonumber \end{aligned}$$
    Table 2 We present stationary points and their stability for the coupling \(Q=\beta \dot{\rho _{\phi }}\)
    Full size table

    As one of the eigenvalues is positive, the stationary point is a saddle point for any value of \(\sigma \).

  2. 2.

    \(x= \frac{\sqrt{1-\sigma +2\sigma ^2-\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}}}{\sqrt{2(\sigma ^2-1)}},~ y= 0\). In this case, the eigenvalues are given by

    $$\begin{aligned} \mu _1= & {} \frac{3\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}}{\sigma ^2-1}<0,~~ \text {for}\ \sigma ^2 < 1, \nonumber \\ \mu _2= & {} \frac{1}{8}\left( \frac{6(\sigma -3+\sqrt{1+\sigma (\sigma +8\sigma ^3-6)})}{\sigma ^2-1}\right. \\&\left. -\,4\sqrt{3}\lambda \sqrt{\frac{1-\sigma +2\sigma ^2-\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}}{\sigma ^2-1}}\right) >0,\\&\text {for all} \ \sigma .\nonumber \end{aligned}$$

    This is a saddle point.

  3. 3.

    \(x= \sqrt{\frac{1+\sigma (2\sigma -1)+\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}}{2(\sigma ^2-1)}},~ y= 0\). In this case, the eigenvalues take the form

    $$\begin{aligned} \mu _1= & {} -\frac{3\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}}{\sigma ^2-1}<0,~~ \text {for} \ \sigma ^2 \> 1, \nonumber \\ \mu _2= & {} \frac{1}{8}\left( -\frac{6(3-\sigma +\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}) }{\sigma ^2-1}\right. \\&\left. -4\sqrt{3}\lambda \sqrt{\frac{1+\sigma (2\sigma -1)+\sqrt{1+\sigma (\sigma +8\sigma ^3-6)}}{\sigma ^2-1}}\right) <0,\nonumber \\&\text {for}\ \sigma ^2> 1 \quad \text {and}\quad \lambda \ >0.\nonumber \end{aligned}$$

    The eigenvalues of the point show the negativity for \(\sigma ^2 > 1\) and \(\lambda >0\). Therefore, it is a stable point.

For this coupling, the stationary point in Case (3) is stable for \(\sigma ^2>1\) and \(\lambda >0\). We numerically evolve the autonomous system (18) for the choices \(\sigma =2\) and \(\lambda =1\). The phase space trajectories of the stable point is displayed in Fig. 5, and the point behaves as an attractive node. For this point we do not find any accelerating solution as it has a positive equation of state. Hence, it cannot solve the coincidence problem. The main results of this coupling are summarized in Table 3.

In Ref. [80], we studied the coupled quintessence with scaling potential for different forms of the coupling and discussed phase space analysis. For all the models, we obtained a late time accelerated scaling attractor having \(\Omega _\mathrm{DE}/\Omega _\mathrm{DM}= O(1)\). Therefore all the models considered in the said reference are viable to solving the coincidence problem. In the present paper, we perform the same analysis with the coupled phantom field and inspect whether the coincidence problem can be alleviated or not. In the case of the coupling term \(Q=\alpha \dot{\rho }_m\), the point (3) is a stable fixed point with an accelerating phase, but it cannot solve the coincidence problem as \(\Omega _\mathrm{DE}=1\) (see Table 1). In the case of \(Q=\beta \dot{\rho }_{\phi }\), we focus on points (2) and (4), and notice that both are unable to solve the coincidence problem (see Table 2). In the case of \(Q=\sigma (\dot{\rho }_m + \dot{\rho }_{\phi })\), the point (3) is stable with a non-accelerating phase as the equation of state is positive (see Table 3). Therefore, in the interacting phantom field models, the coincidence problem cannot be solved. Similar results were discussed in Ref. [102].

Table 3 We show stationary points for the coupling \(Q=\sigma (\dot{\rho }_{m}+ \dot{\rho _{\phi }})\)
Full size table
Fig. 5
figure 5

The figure represents the evolution of the phase space trajectories of Case (3) for \(Q=\sigma (\dot{\rho }_{m}+ \dot{\rho _{\phi }})\), and it is plotted for \(\sigma =2\) and \( \lambda =1\). The stable point acts as an attractive node, and the black dot designates a stable attractor point

Full size image

4 Coupled tachyon dynamics

The tachyon acts as a source of dark energy, depending on the shape of the potentials [74,75,76,77,78,79]. We consider that dark energy and dark matter are interacting with each other, but the total energy density is conserved. The conservation equations for both components are written as

$$\begin{aligned} \dot{\rho }_{{m}}+3H(\rho _{m}+p_m)= & {} Q, \nonumber \\ \dot{\rho }_{{\phi }}+3H(\rho _{\phi }+p_{\phi })= & {} -Q, \end{aligned}$$
(19)

where

$$\begin{aligned} \rho _{\phi }= & {} \frac{V(\phi )}{\sqrt{1-\dot{\phi }^{2}}},\nonumber \\ p_{\phi }= & {} -V(\phi )\sqrt{1-\dot{\phi }^{2}}. \end{aligned}$$
(20)

Then the evolution equations take the form

$$\begin{aligned}&H^{2}=\frac{\kappa ^{2}}{3}\left[ \frac{V(\phi )}{\sqrt{1-\dot{\phi }^{2}}} + \rho _{m} \right] , \end{aligned}$$
(21)
$$\begin{aligned}&\frac{\ddot{\phi }}{1-\dot{\phi }^2}+3H\dot{\phi }+\frac{V'(\phi )}{V(\phi )}=-\frac{Q\sqrt{1-\dot{\phi }^2}}{\dot{\phi }V(\phi )}, \end{aligned}$$
(22)

where a prime and a dot denote derivatives with respect to field and cosmic time, respectively.

Let us define the following dimensionless parameters:

$$\begin{aligned} x=\dot{\phi }, \quad y=\frac{\kappa \sqrt{V}}{\sqrt{3}H}, \quad \Omega _m=\frac{\kappa ^2 \rho _{m}}{3H^2}, \quad \lambda =-\frac{V'}{\kappa V\sqrt{V}}. \end{aligned}$$
(23)

Then we obtain the autonomous system

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}N}= & {} \frac{\ddot{\phi }}{H\dot{\phi }}~x ,\nonumber \\ \frac{\mathrm{d}y}{\mathrm{d}N}= & {} -\frac{\sqrt{3}}{2}y^2\lambda x -y\left( \frac{\dot{H}}{H^2}\right) . \end{aligned}$$
(24)

Here we take inverse square potential for which \(\lambda \) is constant. Also, we consider the coupling \(Q=\beta \dot{\rho _{\phi }}\) only. For this coupling we have the following equations:

$$\begin{aligned} \frac{\dot{H}}{H^2}&=\frac{3\left( y^2\sqrt{1-x^2}-1\right) }{2},\end{aligned}$$
(25)
$$\begin{aligned} \frac{\ddot{\phi }}{H\dot{\phi }}&=-3\left( 1-x^2 \right) +\sqrt{3}\lambda y\frac{\left( 1-x^2\right) }{x}+\frac{3 \beta \left( 1-x^2\right) }{1+\beta }. \end{aligned}$$
(26)

The equation of state for the tachyon field is given by

$$\begin{aligned} w_\mathrm{eff}&= -1 -\frac{2\dot{H}}{3H^2},\end{aligned}$$
(27)
$$\begin{aligned} w_{\phi }&= \frac{w_\mathrm{eff}-w_m \Omega _m}{1-\Omega _m}, \end{aligned}$$
(28)

where \(w_m = 0\) for standard dust matter. Setting the left-hand sides of the autonomous system (24) to zero, we obtain the following stationary points:

  1. (1)

    \(x= 0,~ y= 0\). In this case, the corresponding eigenvalues are

    $$\begin{aligned} \mu _1= & {} -\frac{3}{1+\beta }<0,~~ \text {for} \ 0< \ \beta < 1, \\ \mu _2= & {} \frac{3}{2}, \end{aligned}$$

    As one of the eigenvalues is positive, the stationary point is a saddle point.

  2. (2)

    \(x= \pm 1,~ y= \pm \frac{\sqrt{3}}{\lambda }\). In this case, the metric is indeterminate.

  3. (3)
    $$\begin{aligned} x= & {} -\dfrac{1}{3\sqrt{6}} (1 + \beta ) \lambda \surd \left( ((-81(2\times 2^{1/3} \delta ^{2/3}_{3} + 18(18+ \delta _{5}))\right. \\&\left. +\,2^{2/3}\delta _{3}^{1/3}(18+\delta _{5}))+ 9(1+\beta )^{2} (243\beta ^{2}(18+2^{2/3}\delta ^{1/3}_{4})\right. \\&\left. +\, 12\beta (486+27\times 2^{2/3}\delta _{4}^{1/3}-2^{1/3}\delta _{4}^{2/3}) \right. \\&\left. +\, 135\times 2^{2/3}\delta _{4}^{1/3} -8\times 2^{1/3}\delta _{4}^{2/3} +18(153+\delta _{5}))\lambda ^{4} \right. \\&\left. -\, 2(1+\beta )^{4}(243+2187\beta ^{2}-81\beta (-18+2^{2/3}\delta _{4}^{1/3})\right. \\&\left. -\,54 \times 2^{2/3}\delta _{4}^{1/3}+2^{1/3}\delta _{4}^{2/3})\lambda ^{8} +2(1+\beta )^{6} \right. \\&\left. \times \, (-90-162\beta +2^{2/3}\delta _{4}^{1/3})\lambda ^{12}-4(1+\beta )^{8}\lambda ^{16} \right. \\&\left. / ((1+\beta )^{2}\lambda ^{2}(-81(18+\delta _{5}) +243(1+\beta )^{2}\right. \\&\left. \times \, (5+3\beta (4+3\beta ))\lambda ^{4}+54(1+\beta )^{4}(2+3\beta )\lambda ^{8}\right. \\&\left. +\,2(1+\beta )^{6}\lambda ^{12}))) \right) , \\ y= & {} -\dfrac{1}{3\sqrt{2}} \surd \left( ((-81(324+18\times 2^{2/3}\delta _{3}^{1/3} +2\times 2^{1/3}\delta _{3}^{2/3} \right. \\&\left. +\,18\delta _{5} +2^{2/3}\delta _{3}^{1/3}\delta _{5}) + 9(1+\beta )^{2}(2754+243\beta ^{2} \right. \\&\left. \times \, (18+2^{2/3}\delta _{4}^{1/3})+12\beta (486 +27\times 2^{2/3}\delta _{4}^{1/3}\right. \\&\left. -\,2^{1/3}\delta _{4}^{2/3})+135\times 2^{2/3}\delta _{4}^{1/3}\right. \\&\left. -\, 8\times 2^{1/3}\delta _{4}^{2/3} +18\delta _{5})\lambda ^{4}-2(1+\beta )^{4} \right. \\&\left. \times \, (243+2187\beta ^{2}-81\beta (-18+2^{2/3}\delta _{4}^{1/3})\right. \\&\left. -\,54\times 2^{2/3}\delta _{4}^{1/3} +2^{1/3}\delta _{4}^{2/3})\lambda ^{8} \right. \\&\left. +\,2(1+\beta )^{6}(-90-162\beta +2^{2/3}\delta _{4}^{1/3}) \lambda ^{12}\right. \\&\left. \times \,-4(1+\beta )^{8}\lambda ^{16})/ ((1+\beta )^{2}\lambda ^{2}(-81(18+\delta _{5})\right. \\&\left. +\,243(1+\beta )^{2}\times (5+3 \beta (4+3\beta ))\lambda ^{4}+54(1+\beta )^{4}(2+3\beta )\right. \\&\left. \lambda ^{8}+2(1+\beta )^{6}\lambda ^{12}))) \right) . \end{aligned}$$

For this point, we get the following eigenvalues:

$$\begin{aligned}&\mu _1 = \dfrac{-\dfrac{\eta _{2}}{2}+3\beta \left( \dfrac{-\eta _{2}}{6}+\sqrt{\eta _{6}}\right) +\dfrac{\eta _{4} \left( \dfrac{\eta _{3}}{18}+2\sqrt{\eta 6}\right) }{6\eta 5} -3\sqrt{\eta _{6}}-\eta _{8}-\dfrac{1}{3}(1+\beta )^{2} \sqrt{\eta _{2}}\sqrt{\eta _{6}}\sqrt{\eta _{7}}\lambda ^{2}}{4(1+\beta )\sqrt{\eta _{6}}}<0\\&\text {for } \beta \ne -1 \text { and } 3\beta \left( \dfrac{-\eta _{2}}{6}+\sqrt{\eta _{6}}\right) +\dfrac{\eta _{4} \left( \dfrac{\eta _{3}}{18}+2\sqrt{\eta 6}\right) }{6\eta 5}<0 ,\\&\mu _{2}=\dfrac{\dfrac{\eta _{10}}{2}+3\beta \left( \dfrac{\eta _{10}}{6}+\sqrt{\eta _{6}}\right) +\dfrac{\eta _{4} \left( \dfrac{\eta _{3}}{18}+2\sqrt{\eta 6}\right) }{6\eta _{5}} -3\sqrt{\eta _{6}}+\eta _{8}- \dfrac{(1+\beta )^{2}\sqrt{\eta 2} \sqrt{3- \dfrac{\eta _{4}}{18\eta _{5}}}\sqrt{\eta _{7}}\lambda ^{2}}{3\sqrt{3}} }{4(1+\beta )\sqrt{\eta _{6}}}<0\\&\text {for } \beta \ne -1 \text { and } \dfrac{\eta _{10}}{2}+3\beta \left( \dfrac{\eta _{10}}{6}+\sqrt{\eta _{6}}\right) +\dfrac{\eta _{4} \left( \dfrac{\eta _{3}}{18}+2\sqrt{\eta 6}\right) }{6\eta 5} +\eta _8<0 , \end{aligned}$$

where

$$\begin{aligned} \delta _3= & {} -243 (1+\beta )^2 \left( 5+3 \beta (4+3 \beta )\right) \lambda ^4\\&-54 (1+\beta )^4 (2+3 \beta ) \lambda ^8-2 (1+\beta )^6 \lambda ^{12}+81 (18+\delta _5),\\ \delta _4= & {} 1458-243 (1+\beta )^2 (5+3 \beta (4+3 \beta )) \lambda ^4\\&-54 (1+\beta )^4 (2+3 \beta ) \lambda ^8-2 (1+\beta )^6 \lambda ^{12}+81 \delta _5, \end{aligned}$$
$$\begin{aligned} \delta _5= & {} \sqrt{3 (1+\beta )^4 \lambda ^4 \left( -324+9 (1+\beta )^2 (-1+9 \beta (2+3 \beta )) \lambda ^4+4 \beta (1+\beta )^4 \lambda ^8 \right) }, \end{aligned}$$
$$\begin{aligned} \eta _{1}= & {} (-81(324 +18 \times 2^{2/3}\delta _{3}^{1/3} + 2\times 2^{1/3} \delta _{3}^{2/3} +18\delta _{5} +2^{2/3}\delta _{3}^{1/3} \delta _{5})\\&+ 9(1+\beta )^{2}(2754+243\beta ^{2}(18+2^{2/3}\delta _{4}^{1/3}) \\&+12\beta (486+27\times 2^{2/3}\delta _{4}^{1/3}-2^{1/3}\delta _{4}^{2/3})\\&+ 135\times 2^{2/3}\delta _{4}^{1/3}- 8\times 2^{1/3}\delta _{4}^{2/3}+18\delta _{5})\lambda ^{4}-2(1+\beta )^{4} \\&\times (243+2187\beta ^{2}-81\beta (-18+2^{2/3}\delta _{4}^{1/3})\\&-54\times 2^{2/3}\delta _{4}^{1/3}+2^{1/3}\delta _{4}^{2/3})\lambda ^{8}\\&+ 2(1+\beta )^{6}(-90-162\beta +2^{2/3}\delta _{4}^{1/3})\lambda ^{12}-4(1+\beta )^{8}\lambda ^{16}, \end{aligned}$$
$$\begin{aligned} \eta _{2}= & {} \dfrac{\eta _{1}}{(1+\beta )^{2}\lambda ^{2}(-81(18+\delta _{5})+243(1+\beta )^{2}(5+3\beta (4+3\beta ))\lambda ^{4} +54(1+\beta )^{4}(2+3\beta )\lambda ^{8}+2(1+\beta )^{6}\lambda ^{12}) }, \\ \eta _{3}= & {} \dfrac{\eta _{1}}{(1+\beta )\lambda ^{2}(-81(18+\delta _{5})+243(1+\beta )^{2}(5+3\beta (4+3\beta ))\lambda ^{4} +54(1+\beta )^{4}(2+3\beta )\lambda ^{8}+2(1+\beta )^{6}\lambda ^{12}) }, \end{aligned}$$
$$\begin{aligned} \eta _{4}= & {} (-81(2\times 2^{1/3}\delta _{3}^{2/3}+18(18+\delta _{5})\\&+2^{2/3}\delta _{3}^{1/3}(18+\delta _{5})) + 9(1+\beta )^{2}(243\beta ^{2}(18+2^{2/3}\delta _{4}^{1/3})\\&+12\beta (486 +27\times 2^{2/3}\delta _{4}^{1/3}-2^{1/3}\delta _{4}^{2/3})+135\times 2^{2/3}\delta _{4}^{1/3}\\&-8\times 2^{1/3}\delta _{4}^{2/3}+18(153+\delta _{5}))\lambda ^{4}-2(1+\beta )^{4}\\&\times (243+2187\beta ^{2}-81\beta (-18+2^{2/3}\delta _{4}^{1/3})\\&-54\times 2^{2/3}\delta _{4}^{1/3}+2^{1/3}\delta _{4}^{2/3}\lambda ^{8}\\&+2(1+\beta )^{6}(-90-162\beta +2^{2/3}\delta _{4}^{1/3})\lambda ^{12} \\&-4(1+\beta )^{8}\lambda ^{16}), \\ \eta _{5}= & {} -81(18+\delta _{5})+243(1+\beta )^{2} (5+3\beta (4+3\beta ))\lambda ^{4}\\&+54(1+\beta )^{4}(2+3\beta )\lambda ^{8} +2(1+\beta )^{6}\lambda ^{12}, \\ \eta _{6}= & {} 1-\dfrac{\eta _{4}}{54\eta _{5}}, \\ \eta _{7}= & {} \dfrac{\eta _{4}}{(1+\beta )^{2}\eta _{5}\lambda ^{2}}, \end{aligned}$$
$$\begin{aligned} \eta _{8}= & {} \sqrt{3}\surd \left( \phantom {\left. +\dfrac{\eta _{4}(-12(3+\beta )+ \dfrac{1}{18} \eta _{3}(36\sqrt{\eta _{6}}-\dfrac{\eta _{1}}{2(1+\beta )\eta _{5}\lambda ^{2}}+4(1+\beta )\lambda ^{2})) }{18\eta _{5}} \Big ) \right) }\eta _{6} \Big (3(3+\beta )^{2}+ \dfrac{\eta ^{2}_{3}}{12}\right. \\&\left. + \dfrac{\eta ^{2}_{4}}{27\eta ^{2}_{5}} -\dfrac{2}{9}(1+\beta )^{2}\sqrt{\eta _{2}}\left( -3-\beta +\dfrac{\eta _{3}\sqrt{\eta _{6}}}{18}\right) \right. \\&\left. \sqrt{\eta _{7}}\lambda ^{2}-\dfrac{2}{81}(1+\beta )^{4} \sqrt{\eta _{2}}\eta ^{3/2}_{7}\lambda ^{4} \right. \\&\left. -\dfrac{1}{9} \eta _{3}\left( \phantom {\left. +\dfrac{\eta _{4}\left( -12(3+\beta )+ \dfrac{1}{18} \eta _{3}\left( 36\sqrt{\eta _{6}}-\dfrac{\eta _{1}}{2(1+\beta )\eta _{5}\lambda ^{2}}+4(1+\beta )\lambda ^{2}\right) \right) }{18\eta _{5}}\right) }27\sqrt{\eta _{6}}+9\beta \sqrt{\eta _{6}}+4(1+\beta ) \lambda ^{2}\right. \right. \\&\left. \left. +\dfrac{\eta _{4}\left( -12(3+\beta )+ \dfrac{1}{18} \eta _{3}\left( 36\sqrt{\eta _{6}}-\dfrac{\eta _{1}}{2(1+\beta )\eta _{5}\lambda ^{2}}+4(1+\beta )\lambda ^{2}\right) \right) }{18\eta _{5}}\right) \right) ,\ \end{aligned}$$
$$\begin{aligned} \eta _{9}= & {} 81(324+18\times 2^{2/3}\delta ^{1/3}_{3}+2\times 2^{1/3}\delta ^{2/3}_{3}\\&+18\delta _{5}+2^{2/3}\delta ^{1/3}_{3}\delta _{5})-9(1+\beta )^{2} (2754+243\beta ^{2}(18+2^{2/3}\delta ^{1/3}_{4})\\&+ 12\beta (486+27\times 2^{2/3}\delta ^{1/3}_{4}-2^{1/3}\delta ^{2/3}_{4})+135\times 2^{2/3}\delta ^{1/3}_{4}\\&-8\times 2^{1/3}\delta ^{2/3}_{4}+18\delta _{5})\lambda ^{4}+2(1+\beta )^{4}(243+2187\beta ^{2}\\&- 81\beta (-18+2^{2/3}\delta ^{1/3}_{4})-54\times 2^{2/3}\delta ^{1/3}_{4}\\&+2^{1/3}\delta ^{2/3}_{4}) \lambda ^{8}-2(1+\beta )^{6}(-90-162\beta +2^{2/3} \delta ^{1/3}_{4})\lambda ^{12}\\&+4(1+\beta )^{8}\lambda ^{16},\\ \eta _{10}= & {} \dfrac{\eta _{9}}{(1+\beta )^{2}\eta _{5}\lambda ^{2}}. \end{aligned}$$
Fig. 6
figure 6

The figure shows the phase space trajectories for the coupled tachyon field. The stable fixed point is an attractive node and corresponds to \(\beta =0.9\) and \(\lambda =1\). The black dot represents the stable attractor point

Full size image

In the case of a tachyon field, we consider only the coupling \(Q=\beta \dot{\rho _{\phi }}\). The point (3) shows the negativity of the eigenvalues under the given conditions. Hence, it is a stable point. The phase portrait is shown in Fig. 6.

5 Conclusions

We investigated the interaction of a phantom field with a dark matter component in a spatially flat FLRW Universe. The choices of the coupling Q in the conservation equations were phenomenological and heuristic as there is no fundamental theory of the coupling strength in the dark sector that was involved. We examined three different couplings and studied the corresponding dynamical behavior and phase space. We paid attention to the stable point, which could give rise to an accelerating phase. For all the three different couplings, we found \(\Omega _{\phi }, w_\mathrm{eff}\) and \(w_{\phi }\). Our primary goal was to see if there exists a late time scaling attractor with an accelerating phase and having the property \(\Omega _\mathrm{DE}/\Omega _\mathrm{DM} \simeq \mathcal{{O}}(1)\). For the coupling \(Q=\alpha \dot{\rho _m}\), we focused on Cases (3) and (5). In both cases the stationary points have an accelerating phase, but one of the stationary point is stable and the other is a saddle point. In Case (3) the point is stable for \(\alpha >1\) and \(\lambda > \sqrt{3/ (\alpha -1)}\), and behaves as an attractive node. In this case, we obtained a stable fixed point with an accelerating Universe (\(w_\mathrm{eff}<-1/3\)), however, it corresponds to the case where dark energy completely dominates, as now we have \(\Omega _{\phi }=1\). Therefore, it does not solve the coincidence problem. The results are shown in Figs. 1 and 2. In the case of the coupling \(Q=\beta \dot{\rho _{\phi }}\), we concentrated on Cases (2) and (4), and in both cases the points are stable but possessing non-accelerating phases as now \(w_{\phi }\) is always positive (see Table 2). In Case (4), we considered two sets of the parameters as \(\beta =-2.5, 1 \le \lambda < 1.5\) and \(\beta =-2.5, \lambda > 1.5\). In the first set, the point in Case (4) behaves as a stable point and give rise to a non-accelerating Universe (\(w_{\phi }\) always positive). In the second set, it acts as a saddle point and has an accelerating Universe (\(w_{\phi }<-1\)). Thus, it cannot solve coincidence problem either. The phase portrait and the evolution of \(w_{\phi }\) and \(\Omega _{\phi }\) are displayed in Figs. 3 and 4. For the linear combination of the coupling \(Q=\sigma (\dot{\rho }_{m}+\dot{\rho _{\phi }})\), we noticed that the stationary point in Case (3) is stable for \(\sigma ^2>1\) and \(\lambda >0\), but could not give rise to an accelerating Universe as the equation of state is always positive. The phase portrait for this case is shown in Fig. 5, and it acts as an attractive node.

For all the couplings considered here, our analysis showed that the coincidence problem cannot be alleviated in the coupled phantom field models. Similar results were also shown in [102] for different couplings.

We also studied the dynamical behavior and stabilities for the coupled tachyon field with the coupling \(Q=\beta \dot{\rho _{\phi }}\). In this case, the eigenvalues of the stationary point in Case (3) are negative. Therefore, it is a stable point.