1 Introduction

In 2002, Amelino-Camelia constructed a famous theory with two observer-independent constants (including the speed of light “c” and the Planck length “\(L_p\)”) of relativity, which was known as Double Special Relativity (DSR) [1]. In the DSR, the modified dispersion relation naturally leads to the Planck-scale departure from the Lorentz symmetry, which is referred to as the Lorentz-invariance violation of dispersion relations (LIV-DRs) [1]. In the past few decades, since the spontaneous violation of Lorentz symmetries in the framework of the string theory was proposed in [2], the study of the LIV has attracted great research enthusiasm, which appeared to bear much fruit [3,4,5,6,7,8,9]. For instance, Coleman and Glashow have suggested a self-consistent framework for discussing the possible LIV [4]. In the standard model extension (SEM), the Lorentz-invariance violation has been described by the effective field theory [5, 6]. More importantly, Lorentz invariance violation has also been intensively investigated in the framework of quantum-gravity theories. In string theory, the spontaneous breakdown of Lorentz symmetry can be found when some tensor fields acquired the nonzero vacuum expectation value [7]. In loop gravity and Hořava–Lifshitz gravity, one finds that also Lorentz-invariance violation is incorporated [8, 9]. At present, it is generally believed that the LIV might act as a relic probe for quantum gravity. Furthermore, there are a lot of remarkable experimental phenomena that have been studied, in which constraints on the LIV have attracted a lot of attention [10,11,12,13,14,15,16,17,18,19,20,21]. Succinctly stated, one can see that the Lorentz-invariance violation typically at the Planck scale has received more and more interests both theoretically and experimentally in recent years.

For simplicity, we here consider the preferred frames in which the dispersion relation breaks the boost invariance but preserves rotation invariance. In this case, by considering the phenomenological levels, the LIV-DR that may be induced by quantum gravity can be expected to take the following form for the massive particles [10,11,12,13,14]:

$$\begin{aligned} {E^2} = {p^2} + {m^2} - {\eta _ \pm }{p^2}{\left( {\frac{E}{{{\xi _n}{M_{\text {QG}}}}}} \right) ^n}, \end{aligned}$$
(1)

where this relation occurs at high energy scales. Also, it is only convenient for us to choose the form (1) to work in the current context. In the SME, other different forms of LIV-DR can and do arise [6, 22,23,24,25]. The quantities E, m and p denote the energy, the mass and the 3-component momentum of particles, respectively. \({\eta _ \pm }\) is the “sign of the LIV” [10], and the sign \(\eta _+=1\) represents a subluminal correction and the sign \(\eta _-=-1\) denotes a superluminal one [14]. However, it is worth noting that one should employ the sign \( \eta _+ = 1 \) to coincide with the experimental astrophysical phenomena, which is emphasized by Jacob and Amelino-Camelia [10, 14]. The energy scale of quantum gravity \({E_{\text {QG}}}\) can be expected to be in the neighborhood of the Planck energy scale \(({E_p} \approx {10^{28}}\text {eV})\) [26, 27]. The coefficient \({\xi _n}\) is a dimensionless parameter, and lower bounds from gamma-ray bursts (GRBs) have been obtained for the case \(n = 1\), \({\xi _1} \ge 0.01\), and \({\xi _2} \ge {10^{ - 9}}\) from flaring active galactic nuclei (AGNs) for the case \(n = 2\) [14, 15]. Here, n is also a dimensionless parameter, usually appearing as an integer. In our consideration, values at \(n \le 0\) should be excluded on a high energy scale, because huge deviations at low energies would occur at these levels and lead to a strong limit [28]. In the case of \(n \ge 3\), the quantum-gravity corrections would be too small to be observed [10, 21]. As a result, more and more researchers have come to have confidence in the values of \(n = 1\) for linear suppression and \(n = 2\) for higher-price quadratic suppression by the Planck mass (\(1/M_p\) or \(L_p\)) [3, 10, 14, 21]. For \(n=1\), Jacobson has shown that the observation of 100-\(M\text {eV}\) synchrotron radiation from the Crab Nebula provides a new constraint \(\eta > -7 \times 10^{-8}\) on the electron parameter \(\eta \) in the context of the effective field theory [3].Footnote 1 Clearly, this condition is so strong that Jacobson concludes that quantum-gravity scenarios implying this sort of the Lorentz violation are not viable, and the fact that \(n=1\) was ruled out might consequently be a result of the CPT symmetry,Footnote 2 rather than the Lorentz symmetry. Later, by reviewing Jacobson’s paper [3], Ellis has reported that the synchrotron constraint provided by the Crab Nebula on the electron’s dispersion relation implies that the situation \(n \le 1.74\) for the electron should be removed [29]. In brief, we have good reason to believe that if one expects Eq. (1) to act as a candidate of quantum gravity, we should choose the case \(n=2\) with a form of constraining the Lorentz violation suppressed by the second power, \({E^2}/({\xi _2^2 M_p^2})\). However, one may argue that it would be impossible to test this quadratically suppressed LIV effects in experiments. To answer this question, Amelino-Camelia has observed that the photon and neutrino observatories do have the required capability for providing the first elements of an experimental program [10]. For \(n=2\), in the spirit of the time-of-arrival analysis of gamma-ray bursts, especially when we compared the time of arrival of these neutrinos emitted by gamma-ray bursts with the corresponding time of arrival of low-energy photons, one finds that the expected time-of-arrival difference can reach \(\varDelta t \sim 10^{-6}~\text {s}\). These remarkable LIV effects in the case \(n=2\) are within the realm of possibilities of future observatories, as described by Amelino-Camelia [10]. Based on the above viewpoints, the most popular LIV-DR should always be fixed to the case of \(n=2\), which is usually expressed as

$$\begin{aligned} {E^2} = {p^2} + {m^2} - {p^2}E^2 l_p^2, \end{aligned}$$
(2)

where \(l_p={L_p}/{\xi _2}\) and \( {L_p} = {1}/{M_p}\) is the Planck length.

A black hole, as a special object with the strong gravitational field, has many interesting thermodynamic properties such as a negative heat capacity and so on. So, when the particle is gradually emitted from the black hole horizon, the black hole temperature becomes higher and higher till the final stage of the black hole evaporation. Thus, the energy of the emitted particle is getting higher and higher during black hole emission. As a result, the quantum effect of gravity becomes more and more important in the study of black hole radiation. The introduction of gravity into quantum theory brings about an observer-independent minimum length scale. A minimal length also occurs in string theory [7], loop quantum gravity [8], Hořava–Lifshitz gravity [9], noncommutative geometry [31], etc. Moreover, some Gedanken experiments in the spirit of black hole physics have also supported the idea of the existence of a minimal measurable length [7,8,9, 31,32,33,34]. Therefore, the existence of a minimal observable length is a common feature of all promising quantum-gravity candidates. In the quantum-gravity candidate of doubly special relativity (DSR), a minimal and observer-independent length is preserved at the expense of the Planck-scale violation from the Lorentz invariance for the dispersion relation [1], which we name the LIV-DR. In another quantum-gravity candidate, the generalized uncertainty principle (GUP), a minimal observable length is preserved by modifying the uncertainty principle in quantum physics, where the dispersion relation is not modified and the minimal length is described as an observer-dependent parameter due to the Lorentz symmetry [35,36,37,38,39,40,41,42]. Obviously, in the LIV-DR and GUP candidates, quantum gravity is phenomenologically analyzed from different perspectives, so it is interesting to compare with their results. On the other hand, when the quantum-gravity effects are present, many physical phenomena that are absent at low energies appear at high energies, which maybe provide an effective window to solve some physical paradoxes that always occur in the semiclassical theory. Motivated by these facts, our primary aim in this paper is to apply the LIV-DR with the dimensionless parameter \(n=2\) and the “sign of LIV” \(\eta _\pm = 1\) to phenomenologically study the effect of quantum gravity in a strong gravitational field. Specifically, we have studied the effect of the LIV-DR induced quantum gravity on the Schwarzschild black hole thermodynamics and compared our results with the earlier findings by the GUP.

The outlines of this paper are as follows. In Sect. 2, we rewrite the Dirac equation with the inclusion of the LIV-DR in the curved spacetime, and we study the LIV-DR effect on the emission rate of the Schwarzschild black hole in the tunneling framework.Footnote 3 In Sect. 3, in the presence of the LIV-DR induced quantum gravity, we further analyze the thermodynamic properties at the final stage of the black hole evaporation, and we reconsider the well-known singularity problem and the critical problem that often occur in a semiclassical theory. Also, we compare our results with the GUP findings by Nozari [38] and Chen [41, 42]. Section 4 ends up with conclusions and discussions.

2 Quantum gravity and fermions’ tunneling

In this section, we attempt to study the effect of the LIV-DR induced quantum gravity on fermions’ tunneling radiation. Before that, we should first rewrite the Dirac equation with the inclusion of the LIV-DR. In the presence of the LIV-DR (2), it is easy to write the modified Dirac equation for spin-1/2 particles asFootnote 4 [64]

$$\begin{aligned} \begin{aligned} \left[ {{{\overline{\gamma }}^\mu }{\partial _\mu } + \overline{m} - i l_p \left( {{{\overline{\gamma }}^t}{\partial _t}} \right) \left( {{{\overline{\gamma }}^j}{\partial _j}} \right) } \right] \times \varPsi = 0. \end{aligned} \end{aligned}$$
(3)

Here \(\mu \) is for the spacetime coordinates, j is for the space coordinates, and \({\overline{\gamma }^\mu }\) is the ordinary gamma matrix. This modified Dirac equation has been proved to be compatible with the quadratically suppressed dispersion relation (2) when one adopts the wave function as the plane-wave solution \(\varPsi \left( x \right) = \varPsi \left( p \right) \exp \left[ {i}\left( {\overrightarrow{p} \cdot \overrightarrow{x} - {p_0}\cdot {x_0}} \right) \right] \) to Eq. (3) [64]. Here, if we want to study the fermions’ tunneling radiation in curved spacetime, we should first replace the gamma matrix and the partial derivative in (3) with , where \({\gamma ^\mu }\) satisfies the relation \(\left\{ {{\gamma ^\mu },{\gamma ^\nu }} \right\} = {\gamma ^\mu }{\gamma ^\nu } + {\gamma ^\nu }{\gamma ^\mu } = 2{g^{\mu \nu }}I\), \(e{A_\mu }\) is the charge term of the Dirac equation, and \({\varOmega _\mu }\) is the spin connection. So, in curved spacetime, the deformed Dirac equation with the inclusion of the LIV-DR can be written as

(4)

Following the standard ansatz, it is necessary for us to rewrite the wave function of the Dirac equation as

(5)

where S is the action of the tunneling fermions. Substituting this wave function into the deformed Dirac equation (4) and carrying out the separation of variables,

$$\begin{aligned} \begin{aligned} S = - \omega t + W( r ) + \varTheta ( {\theta ,\varphi } ) \end{aligned} \end{aligned}$$
(6)

for the spherically symmetric spacetime, we finally obtain the following motion for the action S:

$$\begin{aligned}&\left[ i \gamma ^{\mu }(\partial _{\mu }S + e A_{\mu })+ m - i l_p \gamma ^t (\omega - e A_t) \gamma ^j (\partial _{j}S + e A_j)\right] \nonumber \\&\quad \times \,\xi (t,r,\theta ,\varphi )=0, \end{aligned}$$
(7)

where \({\partial _t}S =-\omega \), and \(\omega \) is the energy of the emitted Dirac particles. The terms of have been neglected at high energies. In this paper, we take the Schwarzschild black hole as an example to study the effect of LIV-DR induced quantum gravity on the fermions’ tunneling radiation. For the Schwarzschild black hole, the line element is \(\text {d}{s^2} = - f( r )\text {d}{t^2} + {{g( r )}^{-1}}\text {d}{r^2} + {r^2}\left( {\text {d}{\theta ^2} + {{\sin }^2}\theta \text {d}{\varphi ^2}} \right) \), where \(f\left( r \right) = g\left( r \right) = 1 - {{2M}}/{r}\), and \({r_h} = 2M\) is the event horizon of the black hole. For the Dirac particles with spin 1 / 2, there are two spin states, i.e. a spin-up state (\(\uparrow \)) and a spin-down state (\(\downarrow \)). In our case, we choose the spin-up state without loss of generality. So, we have

$$\begin{aligned} \begin{aligned} \xi _{\uparrow } ( {t,r,\theta ,\varphi } ) = \left( {\begin{array}{c} {A( {t,r,\theta ,\varphi } )\zeta _{\uparrow }}\\ {B( {t,r,\theta ,\varphi } )\zeta _{\uparrow }}\\ \end{array}} \right) , \end{aligned} \end{aligned}$$
(8)

where \(\zeta _{\uparrow }=\Big ( {\begin{array}{c} {1}\\ {0}\\ \end{array}} \Big )\) for the spin-up state. Now, we choose the suitable gamma matrices to further simplify the Dirac equation (7). For the Schwarzschild spacetime, we choose

$$\begin{aligned} \begin{array}{l} {\gamma ^t} = \sqrt{ f^{-1}} \Big ( {\begin{array}{cc} 0&{}I\\ { - I}&{}0 \end{array}} \Big ),{\gamma ^r} = \sqrt{g} \Big ( {\begin{array}{cc} 0&{}{{\sigma ^3}}\\ {{\sigma ^3}}&{}0 \end{array}} \Big ),\\ {\gamma ^\theta } = \sqrt{{g^{\theta \theta }}} \Big ( {\begin{array}{cc} 0&{}{{\sigma ^1}}\\ {{\sigma ^1}}&{}0 \end{array}} \Big ),{\gamma ^\varphi } = \sqrt{{g^{\varphi \varphi }}} \Big ( {\begin{array}{cc} 0&{}{{\sigma ^2}}\\ {{\sigma ^2}}&{}0 \end{array}} \Big ), \end{array} \end{aligned}$$
(9)

where \({\sigma ^i}\left( {i = 1,2,3} \right) \) represent the Pauli matrices. Substituting \(\xi _{\uparrow } ( {t,r,\theta ,\varphi } )\) and Eq. (9) into Eq. (7), we finally obtain four simplified equations related to the functions A and B. Two of them are

$$\begin{aligned} B\Big ( { - {{i\omega }}/{{\sqrt{f} }} + i\sqrt{g} {\partial _r}W} \Big ) + A\Big ( {m - i l_p \omega {\partial _r}W} \Big ) = 0, \end{aligned}$$
(10)
$$\begin{aligned} A\Big ( {{{i\omega }}/{{\sqrt{f} }} + i\sqrt{g} {\partial _r}W} \Big ) + B\Big ( {m + i l_p \omega {\partial _r}W} \Big ) = 0. \end{aligned}$$
(11)

In Eqs. (10) and (11), if the functions A and B are required to have non-trivial solutions, the determinant of the coefficient matrices must be zero. That requires

$$\begin{aligned} \begin{aligned} {\partial _r}W( r ) = \pm \sqrt{\Big ( {\frac{{{\omega ^2}}}{{{f^2}}} - \frac{{{m^2}}}{f}} \Big )} \times \Big ( 1-\frac{l_p^2 \omega ^2}{2 f}\Big ), \end{aligned} \end{aligned}$$
(12)

where we have carried out the Taylor expansion with respect to \(l_p\), and the high-order terms, i.e. \(O (l_p^4)\), have already been neglected. Basing on the value of \({\partial _r}W( r )\), by using the residue principle near the event horizon of the Schwarzschild black hole [65, 66], we have

$$\begin{aligned} W_{ \pm } = \pm 2i\pi \omega M\Big ( {1 + l_p^2 \big ( {{{{m^2}}}/{4} - {\omega ^2}} \big )} \Big ), \end{aligned}$$
(13)

where the sign ± corresponds to the outgoing/ingoing Dirac particle across the event horizon of the black hole. Based on the WKB approximation, the relationship between the imaginary part of the action and the tunneling probability is given by . Then, during the Dirac particle’s tunneling across the black hole horizon, the total emission rate is

$$\begin{aligned} \begin{aligned} \varGamma&= \frac{{{P_{\text {out}}}}}{{{P_{\text {in}}}}} = \frac{{\exp ( { - 2{\mathrm{Im}} {W_ + }} )}}{{\exp ( { - 2{\mathrm{Im}} {W_ - }} )}} \\&= \exp \left[ { - 8\pi M\omega \left( {1 - {l_p^2}\left( {{\omega ^2} - \frac{{{m^2}}}{4}} \right) } \right) } \right] . \end{aligned} \end{aligned}$$
(14)

Clearly, a small correction to the tunneling rate has been exhibited by the effect of the LIV-DR induced quantum gravity. At first sight, this correction speeds up the black hole evaporation, which is consistent with the findings by Nozari [38,39,40] and Banerjee [67], but it is in contradiction with those by Chen [41, 42]. In [38,39,40, 67], the effect of quantum gravity was present by demanding the generalized uncertainty principle (GUP) with the incorporation of both a minimal observable length and a maximal momentum. Instead, the simplest GUP relation which implies only the appearance of a nonzero minimal length was incorporated in [41, 42]. Magueijo and Smolin have shown that in the context of the DSR, a test particle’s momentum cannot be arbitrarily imprecise and therefore there is an upper bound for momentum fluctuations [68, 69]. Then, it has been shown that this may lead to a maximal measurable momentum for a test particle [70]. That means that, in the GUP model, the appearance of the maximal momentum could provide a better description of the effect of quantum gravity. Combined with these facts, it also is confirmed by (14) that, as a candidate for describing quantum gravity, the LIV-DR with the dimensionless parameter \(n=2\) and the “sign of LIV” \(\eta _\pm = 1\) can always do as well as the GUP with a minimal observable length and a maximal momentum. On the other hand, this correction (14) due to the presence of LIV-DR induced quantum gravity becomes drastic at the Planck scale, and the final stage of the black hole evaporation would exhibit some interesting properties, which will be detailed in Sect. 3. In addition, the quantum-gravity correction of the tunneling rate (14) is related not only to the mass of black hole, but also to the Planck length and the emitted fermions’ mass and energy. So, we see that in the presence of the quantum-gravity effect, the emission spectrum cannot be strictly thermal. This happens to coincide with Parikh–Wilczek’s observation [47], where a leading correction to the tunneling rate has been present by the incorporation of the emitted particle’s self-gravitational interaction. However, because of the lack of correlation between different emitted modes in the black hole emission spectrum, the form of the Parikh–Wilczek correction is not adequate by itself to recover information [93]. This semiclassical correction with the incorporation of a minimal measurable length and possible resolution of the information loss problem in this framework has been studied in [39]. Later, in the tunneling framework, further research with the GUP including all natural cutoffs showed that information emerges continuously during the evaporation process at the quantum-gravity level [38]. This property has the potential to answer some questions about the black hole information loss problem and provides a more realistic background for treating the black hole evaporation in its final stage. In fact, these observations only provide evidence of correlations between the two tunneling particles in the presence of quantum gravity, but they are not adequate by themselves to recover information. Section 4 ends up with some discussion of the information loss.

3 Remnant values of temperature, mass and entropy

At the quantum-gravity level, an interesting attempt is to observe the Planck-scale physics. At the final stage of the black hole evaporation, some exciting findings due to the presence of the quantum-gravity effect would be exhibited. In this section, with the inclusion of the LIV-DR induced quantum-gravity effect, we attempt to obtain the Planck-scale thermodynamic quantities at the final stage of the black hole evaporation. Before that, we should first find the quantum-gravity induced thermodynamic relations. As defined by [41, 42, 71,72,73,74,75,76,77], using the principle of “detailed balance” for the emission rate (14), it is easy for us to obtain the effective temperature of the Schwarzschild black hole, that is, \(T = {T_h}\left( {1 + {l_p^2}\Big ( {{\omega ^2} - {{{m^2}}}/{4}} \Big )} \right) \), where \(l_p={L_p}/{\xi _2}\) and \( {L_p} = {1}/{M_p}\) is the Planck length, \(T_h = {M_p^2}/({8 \pi M k_\text {B}})\) is the standard semiclassical temperature of the black hole and other terms are the corrections due to the quantum-gravity effect, and we use the relations and . To further facilitate our calculations, deforming the effective temperature at the final stage of black hole evaporation, we have

$$\begin{aligned} {M} = \frac{{M_p^2}}{{8\pi T k_\text {B}}}\left( {1 + {\frac{k_\text {B}^2{T^2} L_p^2}{\xi _2^2}}} \right) , \end{aligned}$$
(15)

where we have approximately replaced \(\omega \) in the effective temperature with the characteristic energy of the emitted particle [37, 67]. For the particle with temperature T, its characteristic energy is given by \( k_\text {B}T \) [67]. Normally, a black hole has a negative heat capacity, so its temperature would increase when the black hole loses mass and energy by the emission process. In Fig. 1, we show the LIV-DR induced black hole heat capacity versus its mass for different values for \(\xi _2\). Obviously, the heat capacity of the black hole under the quantum-gravity corrections is bigger than that of the semiclassical case. With the increase of the parameter \(\xi _2\), the corrected heat capacity is much closer to the semiclassical one.

Fig. 1
figure 1

The LIV-DR induced black hole heat capacity versus its mass, where \(L_p = k_\text {B} = 1\)

Full size image

When considering the quantum-gravity effect into the emission process, the negative heat capacity increases monotonically as the energy gradually reaches the Planck energy. There is a point at which the heat capacity vanishes. The corresponding temperature is considered to be the maximum temperature attainable by black hole evaporation. So, at the final stage of the black hole evaporation, there is no further change of the black hole mass with its temperature. This means that the heat capacity of the black hole defined by \({C} = \frac{{\text {d}M}}{{\text {d}T}}\) becomes zero, at which the emission process ends with a finite remnant mass and temperature. According to Eq. (15), the final stage of the black hole evaporation leaves the remnant temperature

$$\begin{aligned} {{{T}}_{\text {rem}}} = \frac{{\xi _2 {M_p}}}{{{k_\text {B}}}}, \end{aligned}$$
(16)

and the corresponding remnant mass given by

$$\begin{aligned} {{{M}}_{\text {rem}}} = \frac{{{M_p}}}{{4\pi \xi _2}}. \end{aligned}$$
(17)

Alternatively, the remnant mass can also be obtained by minimizing the black hole entropy, that is, \(\frac{{\text {d}S}}{{\text {d}M}}=0\), and for the second derivative \(\frac{\text {d}^2S}{\text {d}M^2}>0\). In Fig. 2, we show the LIV-DR induced black hole temperature versus its mass for different values for \(\xi _2\). Obviously, in the presence of the LIV-DR effect, the quantum-gravity corrected temperature is higher than the semiclassical case. With the increase of the parameter \(\xi _2\), the corrected temperature is much closer to the semiclassical temperature, meanwhile the final stage of the black hole evaporation leaves a higher remnant temperature and a smaller remnant mass.

Fig. 2
figure 2

The LIV-DR induced black hole temperature versus its mass

Full size image

Next, we attempt to obtain the modified black hole entropy in the presence of the LIV-DR effect. According to the first law of black hole thermodynamics, the black hole entropy is given by

$$\begin{aligned} {S}= \int \frac{\text {d}M}{T} = \int \frac{C\text {d}T}{T} = \frac{k_\text {B}}{16\pi }\Big [\Big (\frac{M_p}{k_\text {B}T}\Big )^2 +\frac{1}{\xi _2^{2}} ln\Big (\frac{k_\text {B}T}{M_p}\Big )^2\Big ]. \end{aligned}$$
(18)

So, at the final stage of the black hole evaporation, we are left with the remnant entropy,

$$\begin{aligned} {{{S}}_\text {rem}} = \frac{k_\text {B}}{16\pi \xi _2^2}\Big (1- ln \frac{1}{\xi _2^2} \Big ). \end{aligned}$$
(19)

In (18), the corrected black hole entropy is expressed in terms of the corrected temperature, so it is inconvenient to observe the quantum-gravity corrections to the semiclassical Bekenstein–Hawking entropy. To specifically exhibit the quantum-gravity induced black hole entropy in terms of the semiclassical Bekenstein–Hawking entropy, we should first find an expression for \(T^2\) in terms of M. We can do this by squaring (15), that is,

$$\begin{aligned} \Big (\frac{k_\text {B} T}{M_p}\Big )^2 = \frac{\Big [\Big (\frac{8\pi M}{M_p}\Big )^2-\frac{2}{\xi _2^{2}}\Big ]\pm \sqrt{\Big [\Big (\frac{8\pi M}{M_p}\Big )^2-\frac{2}{\xi _2^{2}}\Big ]^2-\frac{4}{\xi _2^{4}}}}{2\xi _2^{-4}}.\nonumber \\ \end{aligned}$$
(20)

Here, only the part with the (−) sign is acceptable, since the (\(+\)) part cannot produce the semiclassical mass–temperature result in the absence of the quantum-gravity effect (i.e. \(\xi _2^{-2}=0\)). Now, rearranging (20) with the binomial expansion, we have

$$\begin{aligned} \Big (\frac{k_\text {B}T}{M_p}\Big )^2 = \frac{1}{\Big [\Big (\frac{8\pi M}{M_p}\Big )^2-\frac{2}{\xi _2^{2}}\Big ]}\left[ 1+\frac{\xi _2^{-4}}{\Big [\Big (\frac{8\pi M}{M_p}\Big )^2-\frac{2}{\xi _2^{2}}\Big ]^2}+\cdot \cdot \cdot \right] . \nonumber \\ \end{aligned}$$
(21)

Substituting (21) into (18), we can obtain the modified black hole entropy

$$\begin{aligned} \frac{S}{k_{\text {B}}}= & {} \Big (\frac{S_{\text {BH}}}{k_{\text {B}}}-\frac{2}{16\pi \xi _2^{2}}\Big )-\frac{1}{16\pi \xi _2^{2}}ln \Big (\frac{S_{\text {BH}}}{k_{\text {B}}}-\frac{2}{16\pi \xi _2^{2}}\Big )\nonumber \\&+\sum _{j=0}^\infty c_j(\xi _2^{-2})\Big (\frac{S_{\text {BH}}}{k_{\text {B}}}-\frac{2}{16\pi \xi _2^{2}}\Big )^{-j}-\frac{1}{16\pi \xi _2^{2}} ln 16\pi , \nonumber \\ \end{aligned}$$
(22)

where the semiclassical Bekenstein–Hawking entropy is given by \(S_{\text {BH}}=k_{\text {B}}\frac{4\pi M^2}{M_p^2}\), and the coefficients \(c_j\) are functions of \(\xi _2^{-2}\). This is the modified black hole entropy in the presence of the LIV-DR induced quantum-gravity effect, and the semiclassical Bekenstein–Hawking entropy would be reproduced when the quantum-gravity effect is absent (i.e. \(\xi _2^{-2}=0\)). We subsequently attempt to obtain the area theorem from the expression of the modified black hole entropy (22). Before that, we introduce a new variable \(\widetilde{\mathbf{A }}\) defined by \(\widetilde{\mathbf{A }}=16\pi G^2 M^2-\frac{2}{4\pi \xi _2^{2} }G^2M_p^2=\mathbf A -\frac{2}{4\pi \xi _2^{2} } L_p^2\), which is named the reduced area, and \(\mathbf A =16\pi G^2 M^2\) is the usual area of the black hole horizon. In terms of the reduced area, the modified black hole entropy can be written in a familiar form,

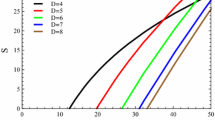
$$\begin{aligned} \begin{aligned} \frac{S}{k_B} =&\frac{\widetilde{\mathbf{A }}}{4L_p^2}-\frac{1}{16\pi \xi _2^{2}}ln \Big (\frac{\widetilde{\mathbf{A }}}{4L_p^2}\Big )\\&+ \sum _{j=0}^\infty c_j(\xi _2^{-2})\Big (\frac{\widetilde{\mathbf{A }}}{4L_p^2}\Big )^{-j}-\frac{1}{16\pi \xi _2^{2}} ln 16\pi . \end{aligned} \end{aligned}$$
(23)

This is the area theorem in the presence of the LIV-DR induced quantum-gravity effect. The usual Bekenstein–Hawking semiclassical area law is reproduced for \(\xi _2^{-2}=0\). This quantum-gravity induced area theorem looks like the standard modified area theorem [71,72,73, 78,79,80,81,82,83,84,85,86,87,88,89,90,91], with the role of the usual area \(\mathbf A \) being played by the reduced area \(\widetilde{\mathbf{A }}\). We also note that as usual the leading order correction term to the black hole entropy has a logarithmic nature, which is consistent with the earlier findings by the loop quantum gravity considerations [71,72,73, 79, 91], the field theory calculations [84, 85], the quantum geometry method [78, 90], and the statistical method [87, 88]. The higher order corrections involve inverse powers of the reduced area \(\widetilde{\mathbf{A }}\). In Fig. 3, we have shown the LIV-DR induced black hole entropy versus its mass in the different values for \(\xi _2\). Obviously, the quantum-gravity corrected entropy is lower than the semiclassical case. With the increase of the parameter \(\xi _2\), the corrected entropy is much closer to the semiclassical entropy.

Fig. 3
figure 3

The LIV-DR induced black hole entropy versus its mass

Full size image

Also, in Fig. 4, we have shown the LIV-DR induced remnant entropy versus \(\xi _2\). Obviously, when \(0.6065\le \xi _2 \le 1 \), the remnant entropy increases with the increasing parameter \(\xi _2\). When \(\xi _2>1\), the remnant entropy decreases with the increasing parameter \(\xi _2\). At the point \(\xi _2=1\), the remnant entropy reaches a maximum.

Fig. 4
figure 4

The LIV-DR induced remnant entropy versus \(\xi _2\)

Full size image

When the reduced area is zero (i.e. \(\widetilde{\mathbf{A }}=0\)), there is a singularity for the modified black hole entropy (23), which corresponds to the singular mass given by

$$\begin{aligned} M_{sin}=\frac{\sqrt{2}{{M_p}}}{{8\pi \xi _2}}. \end{aligned}$$
(24)

On the other hand, the critical mass below which the temperature (20) becomes a complex quantity is given by

$$\begin{aligned} M_{\text {cri}}=\frac{{{M_p}}}{{4\pi \xi _2}}. \end{aligned}$$
(25)

In short, the quantum-gravity induced LIV-DR speeds up the black hole evaporation, and its corresponding black hole entropy undergoes a leading logarithmic correction to the “reduced Bekenstein–Hawking entropy”. At the final stage of the black hole evaporation when the heat capacity reaches zero, the quantum-gravity effect stops the further collapse of the black hole with the remnant mass \(M_{\text {rem}}\), the remnant temperature \(T_{\text {rem}}\) and the remnant entropy \(S_{\text {rem}}\). We also note that the remnant mass \(M_{\text {rem}}\) is greater than the singular mass \(M_{\text {sin}}\) but equal to the critical mass \(M_{\text {cri}}\). So, during the black hole evaporation, we can easily find that the singularity problem is naturally avoided, and the reduced area is always positive. Meanwhile, we manage to avoid the critical problem of dealing with the complex values for the thermodynamic entities. Consequently, ill-defined situations are naturally bypassed in the presence of LIV-DR induced quantum-gravity effects. In addition, we have shown in Figs. 1, 2 and 3 that the quantum-gravity effect lowers the black hole entropy, but it elevates the black hole heat capacity and temperature. In Fig. 4, we have shown that the remnant entropy increases with the increasing parameter \(0.6065\le \xi _2 \le 1\), and it decreases with the increasing parameter \(\xi _2>1\). At the point \(\xi _2=1\), the remnant entropy reaches a maximum.

To put our results in a proper perspective, let us compare with the earlier findings by another quantum-gravity candidates, i.e. the generalized uncertainty principle (GUP) [35,36,37,38,39,40,41,42, 92], where the dispersion relation is not modified and the minimal length is instead described as an observer-dependent parameter due to the Lorentz symmetry. In Figs. 5, 6 and 7 Footnote 5, when employing the GUP parameters \(\beta _0=\alpha =1\) and the LIV parameter \(\xi _2 =1\), we have specifically compared the LIV-DR induced results with the GUP induced findings by Nozari [38,39,40] and Chen [41, 42] without loss of generality. In Fig. 5, we show that the LIV-DR induced heat capacity is higher than the semiclassical one, but is lower than the GUP induced one. In Fig. 6, we show that the LIV-DR induced black hole temperature is higher than the semiclassical one, but lower than that of the GUP case. Meanwhile, at the final stage of the black hole evaporation, the LIV-DR induced quantum-gravity effect leaves a smaller remnant mass, and a higher remnant temperature than in the case of GUP induced quantum gravity. In Fig. 7, we note that the LIV-DR induced black hole entropy is lower than the semiclassical one, but higher than that of the GUP case. And, at the final stage of the black hole evaporation, the remnant entropy induced by the LIV-DR quantum gravity is smaller than that induced by GUP quantum gravity.

Fig. 5
figure 5

The black hole’s modified heat capacity versus its mass when employing the GUP parameters \(\beta _0=\alpha =1\) and the LIV parameter \(\xi _2 =1\)

Full size image
Fig. 6
figure 6

The black hole’s modified temperature versus its mass when employing the GUP parameters \(\beta _0=\alpha =1\) and the LIV parameter \(\xi _2 =1\)

Full size image
Fig. 7
figure 7

The black hole’s modified entropy versus its mass when employing the GUP parameters \(\beta _0=\alpha =1\) and the LIV parameter \(\xi _2 =1\)

Full size image

4 Conclusions and discussions

In this paper, we have applied the Lorentz-invariance-violation (LIV) class of dispersion relations (DR) with the dimensionless parameter \(n=2\) and the “sign of LIV” \(\eta _\pm = 1\), to a phenomenological study of the effect of quantum gravity in a strong gravitational field. Specifically, we have studied the effect of LIV-DR induced quantum gravity on the Schwarzschild black hole thermodynamics. First, we have written out the modified Dirac equation in accordance with the deformed dispersion relation with the Lorentz-invariance violation. Then, in the tunneling framework, we have applied the deformed Dirac equation to study the effect of quantum gravity on the black hole emission. Finally, we have shown some peculiar properties of LIV-DR induced quantum gravity at the final stage of the black hole evaporation and compared them with the GUP induced observations. The result shows that, the effect of the LIV-DR induced quantum gravity speeds up the black hole evaporation, and its corresponding black hole entropy undergoes a leading logarithmic correction to the “reduced Bekenstein–Hawking entropy”, and the ill-defined situations (i.e. the singularity problem and the critical problem) are naturally bypassed in the presence of this quantum-gravity effect. Our work once again provides a piece of evidence for the dimensionless parameter \(n=2\) in the LIV-DR. Also, the result shows that, for the same quantum-gravity-dependent parameters, the LIV-DR induced black hole heat capacity and temperature are lower than the GUP induced ones, but the LIV-DR induced black hole entropy is higher than the GUP induced one; meanwhile, at the final stage of the black hole evaporation, the LIV-DR effect leaves a smaller remnant mass, a higher remnant temperature, and a smaller remnant entropy than the case of the GUP.

In the standard view of black hole thermodynamics, a black hole should emit blackbody radiation, thereby becoming lighter and hotter, and so on, leading to an explosive end when the mass approaches zero. However, when including of the effect of quantum gravity during the emission process, a black hole stops further collapse at a remnant mass, temperature and entropy, and it becomes an inert remnant, possessing only gravitational interactions. Obviously, the black hole’s remnants contain information of quantum gravity, and need not have a classical black hole horizon structure. In this paper, we have shown that, when the quantum-gravity-dependent parameters \(\xi _2^{-1}=\beta _0=\alpha \), the LIV-DR induced remnant entropy is smaller than the GUP induced one, which suggests that the final structure of the black hole is unstable in the GUP induced remnant entropy, and it can further evolve till its final entropy at least reaches the LIV-DR induced remnant entropy. This also suggests that in the information theory, if the remnant entropy (information) is used to describe the basic structure of quantum gravity (in fact, this is well done in accordance with the following discussion on the information loss), the LIV-DR induced remnants contain more information of quantum gravity than the GUP induced one. So, by analyzing the influence of the two quantum-gravity candidates on the final stage of black hole evaporation, we find that, the LIV-DR acts as a more suitable candidate for describing quantum gravity in comparison with the GUP. However, it is noteworthy that, the above discussions are only valid when the LIV-DR parameter is exactly equal to the GUP parameter. Normally, when \(\xi _2^{-1}> \beta _0, \alpha \), we can always adjust the model-dependent parameters to make the LIV-DR and GUP induced remnant entropy equal. We also note that, when the GUP includes all natural cutoffs and higher order corrections [67], its induced remnant entropy is exactly equal to the LIV-DR induced one (19) when \(\xi _2^{-1}=a_1'\). This shows that at the final stage of black hole evaporation, the GUP with all natural cutoffs and higher order corrections contains the same amount of information of quantum gravity as the LIV-DR. On the other hand, the third law of thermodynamics requires that the remnant entropy at the final stage of black hole evaporation should be greater than zero (i.e. \(S_{\text {rem}}\ge 0\)), which, in our case, determines the LIV-DR parameter \(\xi _2\ge 0.6065\). Obviously, this parameter range is within a range of parameters from flaring active galactic nucleus(AGNs) for the case \(n = 2\), \({\xi _2} \ge {10^{ - 9}}\), and gamma-ray bursts(GRBs) for the case \(n = 1\), \({\xi _1} \ge 0.01\).

The information loss paradox occurring during the Hawking radiation is an outstanding issue for black hole physics. As a heuristic method to proceed, the semiclassical method that treats the Hawking radiation as tunneling has been proposed by Parikh and Wilczek to recover the unitarity for the black hole emission [47]. However, further research also by Parikh has shown that there is a lack of correlations between the tunneling radiation of two particles [93]. This means that, although the tunneling picture might recover the unitarity for the black hole emission, it is not sufficient by itself to relay information. Later on, with the inclusion of quantum gravity, some attempts have been proposed to recover information in the tunneling picture [38, 39]. In fact, these observations only provide evidence of correlations between the two tunneling particles in the presence of quantum gravity, but they are not adequate by themselves to recover information. Recently, an interesting observation has shown that the Hawking radiation as tunneling is an entropy conservation process, which leads naturally to the conclusion that the process of Hawking radiation is unitary, and no information loss occurs [94]. When the effect of quantum gravity is included, more information would be present in the black hole radiation, but we assert that the Hawking radiation as tunneling is still an entropy conservation process, which will be reported by us in the near future. So, at the final stage of black hole evaporation, the inert remnant contains information of quantum gravity, possessing only gravitational interactions.