Decoherence and disentanglement of qubits detecting scalar fields in an expanded spacetime

Abstract

We consider Unruh–Wald qubit detector model adopted for the far future region of an exactly solvable $1+1$ dimensional scalar field theory in a toy model of Robertson–Walker expanding spacetime. It is shown that the expansion of the spacetime in its history enhances the decoherence of the qubit coupled with a scalar field. Moreover, we consider two entangled qubits, each locally coupled with a scalar field. The expansion of the spacetime in its history degrades the entanglement between the qubits, and it can lead to entanglement’s sudden death if the initial entanglement is small enough. The details depend on the parameters characterizing the expansion of the spacetime. This work, on a toy model, suggests that the history of the spacetime might be probed through the coherent and entanglement behavior of the future detectors of quantum fields. In the present toy model, the two cosmological parameters can be determined from the quantum informational quantities of the detectors.

1 Introduction

Recently, the concepts developed in quantum foundations and quantum information theory have been exploited to understand quantum effects of spacetime, including the quantum effects of the expansion of the metric [1]. Concepts such as quantum entanglement can shed new light on the topic of the particle creation in an expanding spacetime [2, 3]. Investigations have been made on the entanglement generated between different field modes by the expansion of a model spacetime, and scalar, Dirac and some other fields have been studied [5,6,7,8,9]. It was also shown that the entanglement in the field can be swapped to detectors [10]. The response of a detector switched on since the early universe was also studied [11]. Basic issues concerning the entanglement created in a time-dependent spacetime were carefully examined and clarified [12].

In this paper, we investigate the cosmological effect on the coherence and entanglement of detectors, rather than field modes. Specifically, we consider an exactly solvable model of scalar field in a toy model of expanded spacetime [4], which is a common model in the present subject. To study entanglement effect on the detectors is more practically useful than that on the field modes. While the latter is interesting in theoretical analyses, the cosmological effect on entanglement between detectors may provide a new way of probing cosmological parameters. The field theory model and the qubit detector model are introduced in Sects. 2 and 3, with the single mode approximation justified. The decoherence of a single qubit is discussed in Sect. 4, by studying the dependence of its purity on the two parameters characterizing the expansion of this model spacetime. Then in Sect. 5, we move on to two initially entangled qubits, studying the mutual information, which is a quantifying measure of the total correlation including both classical correlation and quantum entanglement, and the concurrence, which is a quantifying measure of entanglement. Afterwards, in Sect. 6, we consider quantum teleportation in the presence of the coupling with the fields in the expanded spacetime, and calculate its fidelity. In Sect. 7, we explain the common features in the dependence of different quantities on the two cosmic parameters. Finally, we give a summary and a discussion in Sect. 8.

2 Scalar field in a model of expanding spacetime

Consider a $1+1$ dimensional Robertson–Walker metric, the line element being $\mathrm{d}s^{2}=\mathrm{d}t^{2}-a^{2}(t)\mathrm{d}x^{2}$, where a(t) is the scale factor. By using the conformal time $\eta$ defined as $\mathrm{d}\eta =\frac{\mathrm{d}t}{a(t)}$, the line element is rewritten as

$$\begin{aligned} \mathrm{d}s^{2}=R^{2}(\eta )(\mathrm{d}\eta ^{2}-\mathrm{d}x^{2}). \end{aligned}$$

(1)

Suppose the conformal scale factor is [4, 5]

$$\begin{aligned} R^{2}(\eta )=1+\varepsilon [1+\tanh (\sigma \eta )], \end{aligned}$$

(2)

with the parameters $\varepsilon$ and $\sigma$ characterizing the volume and the rapidity of the expansion of the spacetime, respectively. It can be seen that the spacetime is flat in the distant past and in the far future, that is, $\mathrm{d}s^{2}= \mathrm{d}\eta ^{2}-\mathrm{d}x^{2}$ as $\eta \rightarrow -\infty$, while $\mathrm{d}s^{2}= (1+2\varepsilon )(\mathrm{d}\eta ^{2}-\mathrm{d}x^{2})$ as $\eta \rightarrow +\infty$. Consequently, the timelike Killing vector and thus the particle content of the field are well defined in these two limits.

In this metric, consider a real scalar field $\Phi (x,\eta )$, which satisfies the Klein–Gordon equation,

$$\begin{aligned} (\Box +m^{2})\Phi =0, \end{aligned}$$

(3)

with $\Box \Phi \equiv \partial _\mu \big (\sqrt{-g}g^{\mu \nu }\partial _\nu \Phi \big )/\sqrt{-g}$. Following the literature, it is assumed that the scale factor is given, ignoring the backaction of the matter field on it. Corresponding to the limits of $\eta \rightarrow \pm \infty$, there exists a set of basis solutions $u^{{\mathrm {in}}}_\mathbf {k}$ in the distant past or “in” region, and a set of basis solutions $u^{{\mathrm {out}}}_\mathbf {k}$ in the far future or “out” region, and they are related as [4, 13]

$$\begin{aligned} u^{{\mathrm {in}}}_\mathbf {k}(x,\eta ) =\alpha _\mathbf {k}u^{{\mathrm {out}}}_\mathbf {k}(x,\eta )+ \beta _\mathbf {k}u^{{\mathrm {out}}*}_{-\mathbf {k}}(x,\eta ), \end{aligned}$$

(4)

where

$$\begin{aligned}&\alpha _\mathbf {k}\equiv \left( \dfrac{\omega _{{\mathrm {out}}}}{\omega _{{\mathrm {in}}}}\right) ^{1/2}\dfrac{\Gamma \left( 1-\dfrac{i\omega _{{\mathrm {in}}}}{\sigma }\right) \Gamma \left( -\dfrac{i\omega _{{\mathrm {out}}}}{\sigma }\right) }{\Gamma \left( -\dfrac{i\omega _{+}}{\sigma }\right) \Gamma \left( 1-\dfrac{i\omega _{+}}{\sigma }\right) }, \end{aligned}$$

(5)

$$\begin{aligned}&\beta _\mathbf {k}\equiv \left( \dfrac{\omega _{{\mathrm {out}}}}{\omega _{{\mathrm {in}}}}\right) ^{1/2}\dfrac{\Gamma \left( 1-\dfrac{i\omega _{{\mathrm {in}}}}{\sigma }\right) \Gamma \left( \dfrac{i\omega _{{\mathrm {out}}}}{\sigma }\right) }{\Gamma \left( \dfrac{i\omega _{-}}{\sigma }\right) \Gamma \left( 1+\dfrac{i\omega _{-}}{\sigma }\right) }, \end{aligned}$$

(6)

with $\omega _{{\mathrm {in}}}=[k^{2}+m^{2}]^{1/2},$ $\omega _{{\mathrm {out}}}=[k^{2}+m^{2}(1+2\varepsilon )]^{1/2}$, $\omega _{\pm } \equiv \frac{1}{2}(\omega _{{\mathrm {out}}}\pm \omega _{{\mathrm {in}}})$, $\Gamma$ being the gamma function, $k\equiv |\mathbf {k}|$. It can be seen that $|\alpha _\mathbf {k}|^{2}= \frac{\sinh ^{2}(\pi \omega _{+}/\sigma )}{\sinh (\pi \omega _{{\mathrm {in}}}/ \sigma ) \sinh (\pi \omega _{{\mathrm {out}}}/\sigma )}$, $|\beta _\mathbf {k}|^{2}= \frac{\sinh ^{2}(\pi \omega _{-}/\sigma )}{\sinh (\pi \omega _{{\mathrm {in}}}/\sigma ) \sinh (\pi \omega _{{\mathrm {out}}}/\sigma )}$, satisfying $|\alpha _\mathbf {k}|^{2}-|\beta _\mathbf {k}|^{2}=1$. For convenience, we define

$$\begin{aligned} \gamma _k = { \left| {\frac{{{\beta _{\mathbf {k}}}}}{{{\alpha _{\mathbf {k}}}}}} \right| ^2} = \frac{{{{\sinh }^2}\left( {\pi {{{\omega _ - }} / \sigma }} \right) }}{{{{\sinh }^2} \left( {\pi {{{\omega _ + }} /\sigma }} \right) }}, \end{aligned}$$

(7)

which measures the degree of mixing between the “in” modes $\mathbf {k}$ and $-\mathbf {k}$. It also measures the average number of particles created at “out” mode $\mathbf {k}$, which equals $|\beta _\mathbf {k}|^2$ [3],

$$\begin{aligned} |\beta _\mathbf {k}|^2 = \frac{1}{\gamma _k^{-1}-1}. \end{aligned}$$

(8)

Hence $\gamma _k \rightarrow 0$ means that the average number of the particles created at the “out” mode $\mathbf {k}$ is vanishing, $\gamma _k \rightarrow 1$ means that the average number of the particles created at the “out” mode $\mathbf {k}$ approaches infinity. It can be seen that when $m=0$, $\omega _{{\mathrm {in}}}=\omega _{{\mathrm {out}}}$, the effect of expansion of the scale factor disappears, and there is no particle created by the expansion. This feature is shared by all Friedmann spacetimes, including the realistic one, as particle creation takes place only if the conformal symmetry is broken by a mass, which then represents a length scale. Thus it is instructive to consider this exactly solvable toy model, even though the time dependence of the scale factor is prescribed thus rather than from gravitational dynamics.

The annihilation and creation operators satisfy

$$\begin{aligned}&\hat{a}^{{\mathrm {in}}}_\mathbf {k}= \alpha ^{*}_\mathbf {k}\hat{a}^{{\mathrm {out}}}_\mathbf {k}- \beta ^{*}_\mathbf {k}\hat{a}^{{\mathrm {out}}\dagger }_{-\mathbf {k}}, \end{aligned}$$

(9)

$$\begin{aligned}&\hat{a}^{{\mathrm {in}}\dagger }_\mathbf {k}= \alpha _\mathbf {k}\hat{a}^{{\mathrm {out}}\dagger }_\mathbf {k} - \beta _\mathbf {k}\hat{a}^{{\mathrm {out}}}_{-\mathbf {k}}. \end{aligned}$$

(10)

As the Bogoliubov transformation only mixes the “out” modes $\mathbf {k}$ and $-\mathbf {k}$ in the “in” mode $\mathbf {k}$, the “in” vacuum in the sector for the (unordered) pair $\mathbf {k}$ and $-\mathbf {k}$ is thus

$$\begin{aligned} |0\rangle _\mathbf {k}^{\mathrm {in}}|0\rangle _{-\mathbf {k}}^{\mathrm {in}} = \sum _n A_{n,\mathbf {k}} |n\rangle _\mathbf {k}^\mathrm{{out}} |n\rangle _{- \mathbf {k}}^\mathrm{{out}}, \end{aligned}$$

(11)

where n denotes the particle number, $A_{n,\mathbf {k}} = { \left( {\frac{{\beta _{\mathbf {k}}^*}}{{\alpha _{\mathbf {k}}^*}}} \right) ^n}\sqrt{1 - \gamma _k}$. After creation, each pair of modes with opposite momenta are separated on cosmological scale [3]. A local detector at the far future accesses only one of each pair of modes, say $\mathbf {k}$, hence feels a mixed state, with the other mode $-\mathbf {k}$ traced out. In (11), the reduced density matrix of mode $\mathbf {k}$ is

$$\begin{aligned} \rho _\mathbf {k}^\mathrm{{out}}= & {} \mathrm {Tr}_{ -\mathbf {k} } [| 0 \rangle _{\mathbf {k}}^{\mathrm {in}} | 0 \rangle _{-\mathbf {k}}^{\mathrm {in}} {_{-\mathbf {k}}^\mathrm {in}} \langle 0 | {_{\mathbf {k}}^\mathrm {in}} \langle 0 | ]\nonumber \\= & {} ( 1 - \gamma _k) \sum \limits _n \gamma _k^n |n \rangle _{\mathbf {k}} \langle n |, \end{aligned}$$

(12)

where $|n \rangle _{\mathbf {k}}\langle n |$ on the rightmost is a shorthand for $|n \rangle _{\mathbf {k}}^{\mathrm {out}} {_{\mathbf {k}}^{\mathrm {out}}} \langle n |$. From now on, the superscript “out” is dropped without causing confusion. The density matrix of all the modes accessible to the local detector is $\mathop \prod \nolimits _{\mathbf {k}} {\rho _{\mathbf {k}}^\mathrm{{out}}}$, where the direct product is only over those accessible modes.

3 Coupling between the detector qubit and the scalar field

Suppose in the far future of the expanded spacetime described by (2), a detector couples locally with a scalar field. For simplicity, we adopt for the present purpose the Unruh–Wald qubit detector model, which is originally a detector model for Unruh effect [14]. The Hamiltonian is $H_{\Phi }+H_q+H_{I}$, where $H_{\Phi }$ is the Klein–Gordon Hamiltonian for the scalar field. $H_q$ is the Hamiltonian of the qubit detector, given by

$$\begin{aligned} H_q=\Omega Q^\dagger Q, \end{aligned}$$

(13)

where $Q^\dagger$ and Q are creation and annihilation operators acting on two basis states $|0\rangle$ and $|1\rangle$ of the qubit as $Q | 0 \rangle = Q^\dagger | 1 \rangle = 0,$ $Q^\dagger | 0 \rangle = | 1 \rangle$, $Q | 1 \rangle = | 0\rangle$. $\Omega$ is the energy level difference between $|1\rangle$ and $|0\rangle$. The interaction $H_{I}$ is

$$\begin{aligned} H_{I}(t) = \epsilon ( t ) \int _{\Sigma } {\Phi ( \mathbf {x},t ) [ {\psi ( \mathbf { x} )Q + {\psi ^*} ( \mathbf {x} ){Q^\dag }} ]\sqrt{ - g} \mathrm{d}x}, \end{aligned}$$

(14)

where $\mathbf {x}$ and t are proper coordinates of the qubit, the integral is over the spacelike Cauchy surface $\Sigma$ at given time t, $\epsilon ( t )$ is the coupling constant with a finite duration of qubit–field interaction, $\psi (\mathbf { x} )$ is a smooth function nonvanishing within a small volume around the qubit. In the interaction picture, the unitary transformation induced by the Hamiltonian can be written as [14]

$$\begin{aligned} U\approx & {} 1-i \int \Phi (\mathbf {x},t')\epsilon (t') [Q e^{-i\Omega t'} \psi (\mathbf {x})\nonumber \\&+\, Q^\dagger e^{i\Omega t'} \psi ^*(\mathbf {x})]\sqrt{-g'} \mathrm{d}x \mathrm{d}t', \end{aligned}$$

(15)

which, because of resonant effect, can be simplified as

$$\begin{aligned} U \approx 1+iQ a^\dagger (\Gamma ^*) - i Q^\dagger a(\Gamma ^*), \end{aligned}$$

(16)

where $a(\Gamma ^*)$ and $a^\dagger (\Gamma ^*)$ are the annihilation and the creation operators of the mode $\Gamma _q^*$, with

$$\begin{aligned} \Gamma (x)\equiv & {} -2i \int [G_R(x;x')-G_A(x;x')]\nonumber \\&\times \,\epsilon (t')e^{i\Omega t'}\psi ^*(\mathbf {x}')\sqrt{-g'} \mathrm{d}^2x', \end{aligned}$$

(17)

$G_{R}$ and $G_{A}$ being the retarded and advanced Green functions of the field $\Phi$, respectively. We stay in the interaction picture, in which the results we shall be interested in are the same as those in the Schrödinger picture.

For each mode $\chi _\mathbf {k}$, the action of $a(\Gamma ^*)$ and $a^\dagger (\Gamma ^*)$ is

$$\begin{aligned} a(\Gamma ^*)|n\rangle _\mathbf {k}= & {} \sqrt{n} \mu _\mathbf {k} |n-1\rangle _\mathbf {k}, \end{aligned}$$

(18)

$$\begin{aligned} a^\dagger (\Gamma ^*)|n\rangle _\mathbf {k}= & {} \sqrt{n+1} \mu _\mathbf {k}^* |n+1\rangle _\mathbf {k}, \end{aligned}$$

(19)

where $\mu _\mathbf {k}\equiv \langle \Gamma _q^*,\chi _\mathbf {k}\rangle = \int \epsilon _q(t) e^{i\Omega _q t}\psi _q^*(\mathbf {x}) \chi (t,\mathbf {x})\sqrt{-g} \mathrm{d}^2 x$ is the inner product [14].

As a single mode approximation, we may ignore the coupling between the detector qubit and all the field modes except the mode $\mathbf {k}_0$ with energy equal to $\Omega$. $-\mathbf {k}_0$ is out of access because of the separation on a cosmological scale.

Therefore, the effect of the interaction between the detector qubit and the field mode $\mathbf {k}_0$ can be simplified as

$$\begin{aligned}&| n \rangle \otimes | 0 \rangle \rightarrow | n \rangle \otimes | 0 \rangle - i\sqrt{n} \mu | {n - 1} \rangle \otimes | 1 \rangle , \nonumber \\&| n \rangle \otimes | 1 \rangle \rightarrow | n \rangle \otimes | 1 \rangle + i\sqrt{n + 1} {\mu ^*} | {n + 1} \rangle \otimes | 0 \rangle , \end{aligned}$$

(20)

where we omit the mode index $\mathbf {k}_0$ of the Fock state $|n\rangle$ and the inner product

$$\begin{aligned} \mu \equiv \langle \Gamma _q^*,\chi _{\mathbf {k}_0}\rangle . \end{aligned}$$

(21)

For a particle created by the expansion of the spacetime, the lower bound of the energy is $m\sqrt{1 + 2\varepsilon }$, as ${\omega _\mathrm {out}} = \sqrt{{k^2} + {m^2}( {1 + 2\varepsilon } )} \ge m\sqrt{1 + 2\varepsilon }$. In order that the qubit is affected by the field modes, there must be

$$\begin{aligned} \Omega \ge m\sqrt{1 + 2\varepsilon }, \end{aligned}$$

(22)

that is,

$$\begin{aligned} \varepsilon \le \varepsilon _\mathrm{max} = \frac{1}{2}\left( \frac{\Omega ^2}{m^2}-1\right) . \end{aligned}$$

(23)

For example, for $\Omega /m=200$, in order for the field to be coupled with the qubit, the maximal volume of the expansion of the spacetime is ${\varepsilon _{\max }} = 19{,}999.5$.

4 Decoherence of a single qubit

We now consider a single-qubit detector. Its initial state is

$$\begin{aligned} | \psi \rangle = \alpha | 0 \rangle + \beta | 1 \rangle , \end{aligned}$$

(24)

with ${ | \alpha |^2} + { | \beta |^2} = 1$.

In the case that there has not been expansion of the spacetime, the state of the field remains as the vacuum $|0\rangle$ when its interaction with the qubit switched on. In order to be coupled with the field, the qubit must satisfy $\Omega \ge m$. Then as a special case of (20), we have

$$\begin{aligned}&| 0 \rangle \otimes | 0 \rangle \rightarrow | 0 \rangle \otimes | 0 \rangle , \nonumber \\&| 0 \rangle \otimes | 1 \rangle \rightarrow | 0 \rangle \otimes | 1 \rangle + i {\mu ^*} | 1 \rangle \otimes | 0 \rangle . \end{aligned}$$

(25)

Therefore the state of the field mode $\mathbf {k}_0$ and the qubit evolves as

$$\begin{aligned} | 0 \rangle \otimes (\alpha | 0 \rangle + \beta | 1 \rangle ) \rightarrow | 0 \rangle \otimes (\alpha | 0 \rangle + \beta | 1 \rangle ) + i\beta {\mu ^*} | 1 \rangle \otimes | 0 \rangle . \end{aligned}$$

(26)

If $\beta \ne 0$, the qubit becomes entangled with the field. The reduced density matrix of the qubit is

$$\begin{aligned} \rho = \frac{1}{1+|\beta |^2|\mu |^2} \left( \begin{array}{cc} |\alpha |^2+|\beta |^2|\mu |^2 &{} \alpha \beta ^* \\ \alpha ^* \beta &{} |\beta |^2 \end{array} \right) . \end{aligned}$$

(27)

Its mixedness can be characterized by its purity

$$\begin{aligned} \mathrm {Tr}(\rho ^2)= \frac{(|\alpha |^2+|\beta |^2|\mu |^2 )^2+2|\alpha |^2|\beta |^2+|\beta |^4}{(1+|\beta |^2|\mu |^2)^2}, \end{aligned}$$

(28)

which reduces to unity when $\beta =0$, then the state of the field and the qubit remains as the initial state $| 0 \rangle \otimes | 0 \rangle$.

We now turn to the case that there has been expansion of the spacetime. The particles generated by the expansion of the spacetime become the environment of the detector, and causes the decoherence of the detector. After the expansion, the qubit starts with the initial state (24). Hence the state of the qubit and the field mode $\mathbf {k}_0$ start as the separable mixed state

$$\begin{aligned} {\rho _{\mathbf {k}_0}} \otimes | \psi \rangle \langle \psi |= & {} ( {1 - \gamma } )\sum \limits _n^{} {\gamma ^n} [ { | n \rangle ( {\alpha | 0 \rangle + \beta | 1 \rangle } )} ] \nonumber \\&\times \, [ { \langle n | ( {{\alpha ^*} \langle 0 | + {\beta ^*} \langle 1 |} )} ]. \end{aligned}$$

(29)

According to (20), after the interaction between the qubit and scalar field,

$$\begin{aligned}&| n \rangle ( \alpha | 0 \rangle + \beta | 1 \rangle ) \rightarrow |\phi _n\rangle \equiv \frac{1}{{\sqrt{{Q_n}} }} [ | n \rangle ( \alpha | 0 \rangle + \beta | 1 \rangle ) \nonumber \\&\quad -\, i\alpha \sqrt{n} \mu | {n - 1} \rangle | 1 \rangle + i\beta \sqrt{n + 1} {\mu ^*} | {n + 1} \rangle | 0 \rangle ], \end{aligned}$$

(30)

where ${Q_n} = 1 + { | \alpha |^2}n{ | \mu |^2} + { | \beta |^2} ( {n + 1} ){ | \mu |^2}$ is the normalization factor. Hence the state of the field mode $\mathbf {k}_0$ and the qubit becomes

$$\begin{aligned} (1 - \gamma ) \sum _n \gamma ^n |\phi _n\rangle \langle \phi _n|. \end{aligned}$$

(31)

By tracing out the field mode, one obtains the density matrix of the final state of the qubit,

$$\begin{aligned} \rho= & {} ( 1 - \gamma ) \sum _n \frac{\gamma ^n}{Q_n} [ (\alpha | 0 \rangle + \beta | 1 \rangle ) ( \alpha ^*\langle 0 | + \beta ^*\langle 1 | ) \nonumber \\&+\, | \beta |^2 ( {n + 1} )| \mu |^2 | 0 \rangle \langle 0 | + | \alpha |^2 n | \mu |^2 | 1 \rangle \langle 1 | ], \end{aligned}$$

(32)

which, in the basis $\{|0\rangle , |1\rangle \}$, can be written as

$$\begin{aligned} \rho = \left( {\begin{array}{*{20}{c}} {{{| \alpha |}^2}{M_0} + {{| \beta |}^2}{M_{2}}}&{}{\alpha {\beta ^*}{M_0}}\\ {{\alpha ^*}\beta {M_0}}&{}{{{| \beta |}^2}{M_0} + {{| \alpha |}^2}{M_{1}}} \end{array}} \right) , \end{aligned}$$

(33)

where ${M_0} \equiv ( {1 - \gamma } )\sum \nolimits _n^{} {\frac{{{\gamma ^n}}}{{{Q_n}}}},$ ${M_{1}} \equiv ( {1 - \gamma } ){| \mu |^2}\sum \nolimits _n^{} {\frac{{n{\gamma ^n}}}{{{Q_n}}}},$ ${M_{2}} \equiv ( {1 - \gamma } ){| \mu |^2}\sum \nolimits _n^{} {\frac{{( {n + 1} ){\gamma ^n}}}{{{Q_n}}}},$ satisfying $M_0+|\alpha |^2 M_1+|\beta |^2 M_2=1$.

The case without cosmic expansion corresponds to $\varepsilon =0$ and thus $\gamma =0$, then (33) indeed reduces to (27).

For $\varepsilon \ne 0$, even if $\beta =0$, the final state $\rho$ of the qubit is a mixed state, in contrast with the case without cosmic expansion.

We calculate the purity $\mathrm {Tr}( {\rho ^2} )$ of the qubit. Its dependence on the parameters $\varepsilon$ and $\sigma$ is as shown in Figs. 1 and 2.

Fig. 1

The purity $\mathrm {Tr}( {\rho ^2} )$ of the final state of the qubit as a function of the volume $\varepsilon$ of the cosmic expansion. The expansion rapidity is $\sigma =5$. The qubit energy level difference is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$, the mass of the scalar field particle is $m=0.01$. The initial state of the qubit is $\alpha |0\rangle +\beta |1\rangle$

Fig. 2

The purity $\mathrm {Tr}( {\rho ^2} )$ of the final state of the qubit as a function of the expansion rapidity $\sigma$ of the cosmic expansion. The qubit energy level difference is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$, the mass of the scalar field particle is $m=0.01$. The volume of the cosmic expansion is chosen to be $\varepsilon = {\varepsilon _{\max }} = 19{,}999.5$. The initial state of the qubit is $\alpha |0\rangle +\beta |1\rangle$

Fig. 3

The purity $\mathrm {Tr}( {\rho ^2} )$ of the final state of the qubit as a function of the volume $\varepsilon$ and the rapidity $\sigma$ of the cosmic expansion. The qubit energy level difference is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$, the mass of the scalar field particle is $m=0.01$. The initial state of the qubit is $\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle )$

As shown in Fig. 1, the purity slowly decreases with the increase of $\varepsilon$. When $\varepsilon$ is close to $\varepsilon _{\max }$, the purity decreases rapidly to the minimum.

For $\varepsilon > {\varepsilon _{\max }}$, $\omega _\mathrm{{out}} > \Omega$ even if $k=0$, hence all the field modes are decoupled with the qubit, and the purity of the qubit remains as the initial. In other words, in order to be decohered by the scalar field, the qubit must satisfy Eq. (22). If there has not been expansion of the spacetime, the qubit must satisfy $\Omega \ge m$ in order to be coupled and thus decohered by the field.

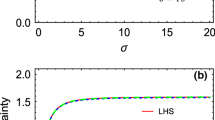
The dependence of the purity on the expansion rapidity $\sigma$ is shown in Fig. 2. When $\sigma$ is very small, the purity decreases rapidly with the increase of $\sigma$. Then it slowly approaches an asymptotic value, which is dependent on $\varepsilon$ and the initial state.

With given values of $\varepsilon$ and $\sigma$, for $|\alpha | \le 1/\sqrt{2}$, the smaller $|\alpha |$, the smaller the purity.

For $\alpha =1/\sqrt{2}$, the 2D plot of the purity as a function of the two parameters is shown in Fig. 3. The larger $\sigma$, the larger the rate of decrease of the purity with respect to $\varepsilon$. When $\sigma$ is small enough, the dependence of the purity on $\varepsilon$ is saturated.

5 Two entangled qubits

Now we study the effect of the expansion of the spacetime on two entangled qubits. Suppose each qubit $q = A, B$ interacts locally with a scalar field $\Phi _q$, and does not interact with the scalar field around the other qubit, as the qubits are so far away from each other that there is no causal contact between one qubit on one hand, and the other qubit and its ambient field on the other.

For each qubit q and its ambient field $\Phi _q$, the discussion in Sect. 4 applies. For qubit q, the energy difference between the two basis states $|1\rangle _q$ and $|0\rangle _q$ in the Schrödinger picture is $\Omega _q$. As noted above, for qubit q, only the coupling with the field mode $\mathbf {k}_{q0}$ with energy $\Omega _q$ needs to be considered.

Suppose the initial two-qubit entangled state is

$$\begin{aligned} | \Psi \rangle = \alpha |0 \rangle _A |1 \rangle _B + \beta |1\rangle _A |0 \rangle _B, \end{aligned}$$

(34)

with ${| \alpha |^2} + {| \beta |^2} = 1$. The entanglement in $|\Psi \rangle$ is quantified as the entanglement entropy $-|\alpha |^2 \log _2 |\alpha |^2 - (1-|\alpha |^2 ) \log _2 (1-|\alpha |^2)$, hence is symmetric between $|\alpha |^2$ and $1-|\alpha |^2$, and is maximal when $|\alpha |=1/\sqrt{2}$. Without loss of generality, we will only consider examples with $|\alpha | \le 1/\sqrt{2}$.

There having been expansion of the spacetime, the initial state of the field modes $\mathbf {k}_{A0}$, $\mathbf {k}_{B0}$ and the two-qubit case is

$$\begin{aligned} \rho _{\mathbf {k}_{A0}} \otimes \rho _{\mathbf {k}_{B0}} \otimes | \Psi \rangle \langle \Psi | \end{aligned}$$

(35)

where

$$\begin{aligned} \rho _{\mathbf {k}_{q0}} = ( 1 - \gamma _q)\sum _n \gamma _{q}^n |n\rangle _{q0}\langle n| \end{aligned}$$

(36)

is the density matrix of the field mode $\mathbf {k}_{q0}$, n is the particle number in this mode. After the interaction between each qubit and its ambient field, the density matrix of the qubits and the field modes evolves to

$$\begin{aligned} ( 1 - \gamma _A )( 1 - \gamma _B) \sum _{n,m} \gamma _{A}^n\gamma _{B}^m |\phi _{nm}\rangle \langle \phi _{nm} |, \end{aligned}$$

(37)

where

$$\begin{aligned} |\phi _{nm}\rangle\equiv & {} \frac{1}{\sqrt{Q_{nm}} } \big \{ \alpha \big (|n\rangle _{A0}|0\rangle _A - i\sqrt{n} {\mu _A} |n - 1\rangle _{A0}|1\rangle _A \big ) \nonumber \\&\times \, \big (|m\rangle _{B0}|1\rangle _B+ i\sqrt{m + 1} \mu _B^*|m + 1\rangle _{B0}|0\rangle _B\big ) \nonumber \\&+\,\beta \big (|n\rangle _{A0}|1 \rangle _A+ i\sqrt{n + 1} \mu _A^* | n + 1 \rangle _{A0}|0\rangle _A \big ) \nonumber \\&\times \,\big (|m\rangle _{B0}|0\rangle _B - i\sqrt{m } \mu _B|m - 1\rangle _{B0}|1\rangle _B\big ) \big \},\nonumber \\ \end{aligned}$$

(38)

with

$$\begin{aligned} Q_{nm}= & {} |\alpha |^2\big (1 + n|\mu _{A}|^2 + ( m + 1 ) |\mu _{B}|^2\nonumber \\&+\, n( m + 1 )| \mu _{A}|^2|\mu _{B}|^2\big ) \nonumber \\&+\, |\beta |^2 \big (1 + m |\mu _{B}|^2 + ( n + 1 ) |\mu _{A}|^2 \nonumber \\&+\, m(n + 1) |\mu _{A}|^2 |\mu _{B}|^2\big ). \end{aligned}$$

(39)

Tracing out the field modes yields the final reduced density matrix of the qubits,

$$\begin{aligned} \rho ^{AB}= & {} ( 1 - \gamma _A )(1 - \gamma _B ) \displaystyle \sum _{n,m} \frac{\gamma _{A}^n\gamma _{B}^m}{ Q_{nm}} \nonumber \\&\times \, \big [ ( | \alpha |^2 + |\beta |^2 m( n + 1 ) |\mu _{A}|^2|\mu _{B}|^2) |01\rangle \langle 01| \nonumber \\&+\, \alpha \beta ^*|01\rangle \langle 10| + \alpha ^* \beta | 10 \rangle \langle 01| \nonumber \\&+\, \big ( | \alpha |^2( {m + 1} ) | \mu _{B} |^2+ |\beta |^2( {n + 1} )|\mu _{A}| ^2\big )|00\rangle \langle 00 | \nonumber \\&+\, \big ( | \alpha |^2 n | \mu _{A} | ^2 + | \beta | ^2 m | \mu _{B} | ^2 \big )| 11 \rangle \langle {11} | \nonumber \\&+\, \big ( | \alpha | ^2 n( {m + 1} ) | \mu _{A} | ^2 | \mu _{B} | ^2 + | \beta | ^2 \big ) | 10 \rangle \langle 10 | \big ],\nonumber \\ \end{aligned}$$

(40)

where $|ij\rangle \equiv | i \rangle _A| j \rangle _{B}$. Using $| {00} \rangle$, $| {01} \rangle$, $| {10} \rangle$, $| {11} \rangle$ as the basis states, the density matrix can be written as

$$\begin{aligned} {\rho ^{AB} } = \left( {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {{{| \alpha |}^2}{S_4} + {{| \beta |}^2}{S_3}} &{}0&{}0&{}0\\ 0&{}{{{| \alpha |}^2}{S_0} + {{| \beta |}^2}{S_5}}&{}{\alpha {\beta ^*}{S_0}}&{}0\\ 0&{}{{\alpha ^*}\beta {S_0}}&{}{{{| \alpha |}^2}{S_6} + {{| \beta |}^2}{S_\mathrm{{0}}}}&{}0\\ 0&{}0&{}0&{}{{{| \alpha |}^2}{S_1} + {{| \beta |}^2}{S_2}} \end{array}} \right) , \end{aligned}$$

(41)

where

$$\begin{aligned}&{S_0} \equiv ( {1 - {\gamma _{A}}} )( {1 - {\gamma _{B}}} )\sum \limits _{n,m}^{} {\frac{{\gamma _{A}^n\gamma _{B}^m}}{{{Q_{nm}}}}}, \end{aligned}$$

(42)

$$\begin{aligned}&{S_1} \equiv ( {1 - {\gamma _{A}}} )( {1 - {\gamma _{B}}} ){| {{\mu _{A}}} |^2}\sum \limits _{n,m}^{} {\frac{{n\gamma _{A}^n\gamma _{B}^m}}{{{Q_{nm}}}}}, \end{aligned}$$

(43)

$$\begin{aligned}&{S_2} \equiv ( {1 - {\gamma _{A}}} )( {1 - {\gamma _{B}}} ){| {{\mu _{B}}} |^2}\sum \limits _{n,m}^{} {\frac{{m\gamma _{A}^n\gamma _{B}^m}}{{{Q_{nm}}}}}, \end{aligned}$$

(44)

$$\begin{aligned}&{S_3} \equiv ( {1 - {\gamma _{A}}} )( {1 - {\gamma _{B}}} ){| {{\mu _{A}}} |^2}\sum \limits _{n,m}^{} {\frac{{( {n + 1} )\gamma _{A}^n\gamma _{B}^m}}{{{Q_{nm}}}}}, \end{aligned}$$

(45)

$$\begin{aligned}&S_4 \equiv ( 1 - \gamma _{A} )(1 - \gamma _{B} ) |\mu _{B} |^2 \sum \limits _{n,m} \frac{( m + 1 )\gamma _{A}^n\gamma _{B}^m}{Q_{nm}}, \end{aligned}$$

(46)

$$\begin{aligned}&{S_5} \equiv ( {1 - {\gamma _{A}}} )( {1 - {\gamma _{B}}} ){| {{\mu _{A}}} |^2}{| {{\mu _{B}}} |^2}\sum \limits _{n,m}^{} {\frac{{m( {n + 1} )\gamma _{A}^n\gamma _{B}^m}}{{{Q_{nm}}}}}, \nonumber \\\end{aligned}$$

(47)

$$\begin{aligned}&{S_6} = ( {1 - {\gamma _{A}}} )( {1 - {\gamma _{B}}} ){| {{\mu _{A}}} |^2}{| {{\mu _{B}}} |^2}\sum \limits _{n,m}^{} {\frac{{n( {m + 1} )\gamma _{A}^n\gamma _{B}^m}}{{{Q_{nm}}}}},\nonumber \\ \end{aligned}$$

(48)

satisfying $S_0+|\alpha |^2(S_1+S_4+S_6)+|\beta |^2(S_2+S_3+S_5)=1$.

The eigenvalues of $\rho ^{AB}$ are

$$\begin{aligned}&{\lambda ^{AB} _1} = {| \alpha |^2}{S_4} + {| \beta |^2}{S_3}, \end{aligned}$$

(49)

$$\begin{aligned}&{\lambda ^{AB} _2} = {| \alpha |^2}{S_1} + {| \beta |^2}{S_2}, \end{aligned}$$

(50)

$$\begin{aligned}&\begin{array}{rl} \lambda ^{AB}_{3,4} &{}= \frac{1}{2} \Big [ S_0 + |\alpha |^2 S_6 + |\beta |^2 S_5 \\ &{}\quad \pm \, \sqrt{S_0^2 + ( | \alpha |^2 S_6 - |\beta |^2 S_5 )^2 + 2(|\alpha |^2 - |\beta |^2 ) S_0 (|\beta |^2 S_5 - |\alpha |^2 S_6 ) } \Big ]. \end{array}\nonumber \\ \end{aligned}$$

(51)

The reduced density matrix of A is

$$\begin{aligned} \rho ^{A} = \left( {\begin{array}{*{20}{c}} {{{| \alpha |}^2}( {{S_0} + {S_4}} ) + {{| \beta |}^2}( {{S_3} + {S_5}} )}&{}0\\ 0&{}{{{| \alpha |}^2}( {{S_1} + {S_6}} ) + {{| \beta |}^2}( {{S_0} + {S_2}} )} \end{array}} \right) ,\nonumber \\ \end{aligned}$$

(52)

with eigenvalues

$$\begin{aligned}&\lambda _1^{A} = {| \alpha |^2}( {{S_0} + {S_4}} ) + {| \beta |^2}( {{S_3} + {S_5}} ), \end{aligned}$$

(53)

$$\begin{aligned}&\lambda _2^{A} = {| \alpha |^2}( {{S_1} + {S_6}} ) + {| \beta |^2}( {{S_0} + {S_2}} ). \end{aligned}$$

(54)

The reduced density matrix of B is

$$\begin{aligned}&\rho ^{B} = \left( {\begin{array}{*{20}{c}} {{{| \alpha |}^2}( {{S_4} + {S_6}} ) + {{| \beta |}^2}( {{S_0} + {S_3}} )}&{}0\\ 0&{}{{{| \alpha |}^2}( {{S_0} + {S_1}} ) + {{| \beta |}^2}( {{S_2} + {S_5}} )} \end{array}} \right) ,\nonumber \\ \end{aligned}$$

(55)

with eigenvalues

$$\begin{aligned} \lambda _1^{B}= & {} {| \alpha |^2}( {{S_4} + {S_6}} ) + {| \beta |^2}( {{S_0} + {S_3}} ), \end{aligned}$$

(56)

$$\begin{aligned} \lambda _2^{B}= & {} {| \alpha |^2}( {{S_0} + {S_1}} ) + {| \beta |^2}( {{S_2} + {S_5}} ). \end{aligned}$$

(57)

We now study the mutual information

$$\begin{aligned} I = S( {\rho ^{A}} ) + S( {\rho ^{B}} ) - S( {{\rho ^{AB} }} ), \end{aligned}$$

(58)

which is a quantifying measure of the total correlation, contributed by both quantum entanglement and classical correlation. One obtains

$$\begin{aligned} I= & {} - \lambda _1^{A}{\log _2}\lambda _1^{A} - \lambda _2^{A}{\log _2}\lambda _2^{A} - \lambda _1^{B}{\log _2}\lambda _1^{B} - \lambda _2^{B}{\log _2}\lambda _2^{B}\nonumber \\&+\, {\lambda ^{AB} _1}{\log _2}{\lambda ^{AB} _1} + {\lambda ^{AB} _2}{\log _2}{\lambda ^{AB} _2}\nonumber \\&+\, {\lambda ^{AB} _3}{\log _2}{\lambda ^{AB} _3} + {\lambda ^{AB} _4}{\log _2}{\lambda ^{AB} _4}. \end{aligned}$$

(59)

Fig. 4

The mutual information I of the final state of two entangled qubits as a function of the volume $\varepsilon$ of the cosmic expansion. The expansion rapidity is $\sigma =5$. The parameters of the two qubits are the same. The qubit energy level difference is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$, the mass of the scalar field particle is $m=0.01$. The initial state of the qubits is $\alpha |01\rangle +\beta |10\rangle$

Fig. 5

The mutual information I of the final state of two entangled qubits as a function of the rapidity $\sigma$ of the expansion of the spacetime. The parameters of the two qubits are the same. The qubit energy level difference is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$, the mass of the scalar field particle is $m=0.01$. The volume of the expansion is chosen to be ${\varepsilon =\varepsilon _{\max }} = 19{,}999.5$. The initial state of the qubits is $\alpha |01\rangle +\beta |10\rangle$

The dependence of the mutual information I on the parameters $\varepsilon$ and $\sigma$ is shown in Figs. 4 and 5, respectively. $\varepsilon =0$ corresponds to the case that there has not been expansion of the spacetime. It can be seen that, for a given value of $\sigma$, as far as $0 < \varepsilon \le {\varepsilon _{\max }}$, the mutual information I monotonically decreases with the increase of $\varepsilon$, and decreases more rapidly when $\varepsilon$ is closer to ${\varepsilon _{\max }}$. For a given value of $0< \varepsilon \le {\varepsilon _{\max }}$, the mutual information also monotonically decreases with the increase of $\sigma$. The larger $\sigma$, the smaller the rate of the decrease, and the mutual information approaches an asymptotic value as $\sigma$ increases. Moreover, for $|\alpha | \le 1/\sqrt{2}$, the smaller $|\alpha |$, i.e. the smaller the initial entanglement, the smaller the mutual information at given values of $\varepsilon$ and $\sigma$.

For $\alpha =1/\sqrt{2}$, the 2D plot of the mutual information as a function of the two parameters $\varepsilon$ and $\sigma$ is shown in Fig. 6. The larger $\sigma$, the larger the rate of decrease of the mutual information with respect to $\varepsilon$. When $\sigma$ is small enough, the dependence on $\varepsilon$ is saturated.

Now we study how the entanglement between the two qubits is degraded in an expanded spacetime. The entanglement between qubits A and B in a mixed state is quantified by the concurrence [15]

$$\begin{aligned} C( \rho ^{AB} ) = \max \left\{ {0,\sqrt{{\lambda _1}} - \sqrt{{\lambda _2}} - \sqrt{{\lambda _3}} - \sqrt{{\lambda _4}} } \right\} , \end{aligned}$$

(60)

where ${\lambda _i}$’s are the eigenvalues of

$$\begin{aligned} X\equiv {\rho ^{{AB}}}( {{\sigma _y} \otimes {\sigma _y}} ) (\rho ^{AB})^* ( {{\sigma _y} \otimes {\sigma _y}} ), \end{aligned}$$

(61)

satisfying ${\lambda _1} \ge {\lambda _2} \ge {\lambda _3} \ge {\lambda _4}$, $(\rho ^{AB})^*$ is the complex conjugate of ${\rho ^{{AB}}}$, ${\sigma _y} = \left( {\begin{array}{*{20}{c}} 0&{}{ - i}\\ i&{}0 \end{array}} \right)$.

We obtain

$$\begin{aligned} X = \left( {\begin{array}{cccc} W&{}0&{}0&{}0 \\ 0&{}V&{}Y&{}0\\ 0&{}Z&{}V&{}0\\ 0&{}0&{}0&{}W \end{array}} \right) , \end{aligned}$$

(62)

where

$$\begin{aligned}&V \equiv {| \alpha |^4}{S_0}{S_6} + {| \beta |^4}{S_0}{S_5} + {| \alpha |^2}{| \beta |^2}\big ( {2S_0^2 + {S_5}{S_6}} \big ), \end{aligned}$$

(63)

$$\begin{aligned}&W \equiv {| \alpha |^4}{S_1}{S_4} + {| \beta |^4}{S_2}{S_3} + {| \alpha |^2}{| \beta |^2}\big ( {{S_2}{S_4} + {S_1}{S_3}} \big ), \end{aligned}$$

(64)

$$\begin{aligned}&Y \equiv 2\alpha {\beta ^*}\big ( {{{| \alpha |}^2}{S_0} + {{| \beta |}^2}{S_5}} \big ){S_0}, \end{aligned}$$

(65)

$$\begin{aligned}&Z\equiv 2{\alpha ^*}\beta \big ( {{{| \alpha |}^2}{S_6} + {{| \beta |}^2}{S_0}} \big ){S_0}. \end{aligned}$$

(66)

The eigenvalues of X can be obtained:

$$\begin{aligned}&\lambda _{1,2} = {| \alpha |^4}{S_1}{S_4} + {| \beta |^4}{S_2}{S_3} + {| \alpha |^2}{| \beta |^2}( {{S_2}{S_4} + {S_1}{S_3}} ), \end{aligned}$$

(67)

$$\begin{aligned}&\lambda _{3,4} = \left[ {| \alpha || \beta |{S_0} \pm \sqrt{\big ( {{{| \alpha |}^2}{S_0} + {{| \beta |}^2}{S_5}} \big )\big ( {{{| \alpha |}^2}{S_6} + {{| \beta |}^2}{S_0}} \big )} } \right] ^2,\nonumber \\ \end{aligned}$$

(68)

using which the concurrence is calculated, as a function of $\varepsilon$ and $\sigma$, respectively.

Fig. 6

The mutual information I of the final state of two entangled qubits as a function of the volume $\varepsilon$ and the rapidity $\sigma$ of the cosmic expansion. The parameters of the two qubits are the same. The qubit energy level difference is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$, the mass of the scalar field particle is $m=0.01$. The initial state of the qubits is $\frac{1}{\sqrt{2}}(|01\rangle + |10\rangle )$

As shown in Fig. 7, the concurrence monotonically decreases with the increase of $\varepsilon$, reaching the minimum at ${\varepsilon _{\max }}$. As shown in Fig. 8, the concurrence also decreases with the increase of $\sigma$. The larger $\sigma$, the smaller the rate of the decrease, and the concurrence approaches an asymptotic value as $\sigma$ increases.

Moreover, with given values of $\varepsilon$ and $\sigma$, for $|\alpha | \le 1/\sqrt{2}$ and larger than a certain value, the smaller $\alpha$, i.e. the smaller the initial entanglement, the smaller the final concurrence. A significant feature is that when $|\alpha |$ is smaller than a certain value, i.e. when the initial entanglement is not too large, there exists entanglement’s sudden death [16] at a finite value of $\sigma$, that is, for $\sigma$ larger than this critical value, the entanglement remains vanishing.

Fig. 7

The concurrence of the final state of two entangled qubits as a function of the volume $\varepsilon$ of the cosmic expansion. The expansion rapidity is $\sigma =5$. The parameters of the two qubits are the same. The qubit energy level difference is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$, the mass of the scalar field particle is $m=0.01$. The initial state of the qubits is $\alpha |01\rangle +\beta |10\rangle$

Fig. 8

The concurrence of the final state of two entangled qubits as a function of the rapidity $\sigma$ of the expansion of the spacetime. The parameters of the two qubits are the same. The qubit energy level difference is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$, the mass of the scalar field particle is $m=0.01$. The volume of the expansion is chosen to be ${\varepsilon =\varepsilon _{\max }} = 19{,}999.5$. The initial state of the qubits is $\alpha |01\rangle +\beta |10\rangle$

Fig. 9

The concurrence of the final state of two entangled qubits as a function of the volume $\varepsilon$ and the rapidity $\sigma$ of the cosmic expansion. The parameters of the two qubits are the same. The qubit energy level difference is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$, the mass of the scalar field particle is $m=0.01$. The initial state of the two qubits is $\frac{1}{\sqrt{2}}(|01\rangle + |10\rangle )$

For $\alpha =1/\sqrt{2}$, the 2D plot of the concurrence as a function of the two parameters is shown in Fig. 9. The larger $\sigma$, the larger the rate of decrease of the concurrence with respect to $\varepsilon$. When $\sigma$ is small enough, the dependence of the concurrence on $\varepsilon$ is saturated.

If there has not been an expansion of the spacetime, the initial states of the field modes are vacua, hence the evolution of the state of the field modes and the qubits is

$$\begin{aligned}&| 0 \rangle _{\mathbf {k}_{A0} } \otimes | 0 \rangle _{\mathbf {k}_{B0} } \otimes |\Psi \rangle \rightarrow |0\rangle _{\mathbf {k}_{A0} } |0\rangle _{\mathbf {k}_{B0} }|\Psi \rangle \nonumber \\&\quad +\, i\big (\alpha \mu _B^* |0\rangle _{\mathbf {k}_{A0} } |1\rangle _{\mathbf {k}_{B0} } +\beta \mu _A^* |1\rangle _{\mathbf {k}_{A0} } |0\rangle _{\mathbf {k}_{B0} }\big ) |00\rangle . \end{aligned}$$

(69)

Hence the reduced density matrix of the qubits is

$$\begin{aligned} \rho ^{AB}= & {} \frac{1}{1+|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2}\nonumber \\&\times \,\big [ |\Psi \rangle \langle \Psi | + (|\alpha |^2|\mu _B|^2 +|\beta |^2|\mu _A|^2)|00\rangle \langle 00|\big ] \end{aligned}$$

(70)

$$\begin{aligned}= & {} \frac{1}{1+|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2}\nonumber \\&\times \, \left( {\begin{array}{cccc} |\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2 &{}0&{}0&{}0\\ 0&{} | \alpha |^2 &{} \alpha {\beta ^*} &{}0\\ 0&{} \alpha ^* \beta &{} | \beta |^2 &{}0\\ 0&{}0&{}0&{}0 \end{array}} \right) , \end{aligned}$$

(71)

which is a mixed state even if $\alpha =0$ or $\beta =0$.

It can be seen that, in this case, the mutual information is

$$\begin{aligned} I= & {} \log _2(1+|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2)\nonumber \\&-\,\frac{1}{1+|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2}\nonumber \\&\times \,[|\alpha |^2\log _2 |\alpha |^2+|\beta |^2\log _2 |\beta |^2\nonumber \\&+\,(|\alpha |^2+|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2) \nonumber \\&\times \, \log _2 (|\alpha |^2+|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2) \nonumber \\&+\, (|\beta |^2+|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2) \nonumber \\&\times \, \log _2 (|\beta |^2+|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2)\nonumber \\&-\, (|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2) \nonumber \\&\times \, \log _2 (|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2) ], \end{aligned}$$

(72)

which vanishes when $\alpha =0$ or $\beta =0$, and is nonzero if $\alpha \ne 0$ and $\beta \ne 0$. Moreover, without the coupling with the fields, $\mu _A = \mu _B=0$, the mutual information reduces to $I=-2|\alpha |^2 \log _2 |\alpha |^2 - 2 |\beta |^2 \log _2 |\beta |^2$, which is that of the original state $| \Psi \rangle = \alpha |0 \rangle _A |1 \rangle _B + \beta |1\rangle _A |0 \rangle _B$.

In this case, the concurrence is

$$\begin{aligned} C(\rho ^{AB}) = \frac{2|\alpha ||\beta |}{1+|\alpha |^2|\mu _B|^2+|\beta |^2|\mu _A|^2}, \end{aligned}$$

(73)

implying that in the case that there has not expansion of the spacetime, if and only if the initial state is an entangled state, i.e. $\alpha \ne 0$ and $\beta \ne 0$, the final state is entangled. Moreover, without the coupling with the fields, $\mu _A = \mu _B=0$, the concurrence reduces to $2|\alpha ||\beta |$, which is that of the original state $| \Psi \rangle = \alpha |0 \rangle _A |1 \rangle _B + \beta |1\rangle _A |0 \rangle _B$.

6 Quantum teleportation

Another way of characterizing the entanglement degradation of a maximally entangled state is in terms of the fidelity of quantum teleportation. Quantum teleportation is a quantum information protocol based on a maximally entangled state [17]. In the ideal case, without environmental disturbance, two qubits initially entangled remain entangled no matter how far they are separated. The coupling with a scalar field causes the qubits entangled with the field modes, hence the entanglement between the two qubits degrades. Consequently the teleportation based on the two-qubit entanglement is disturbed. The fidelity of the teleportation measures how well the teleportation is completed in the presence of the coupling with a field. As we have seen in the last section, the entanglement degradation is greatly enhanced by the expansion of the spacetime. Hence the teleportation fidelity provides a witness of the cosmic expansion.

Consider in the far future a two-qubit state, which was initially a maximally entangled state but has been degraded by the scalar field. We study how the teleportation fidelity depends on the parameters of the cosmic expansion.

Suppose the two qubits A and B are prepared to be one of the four Bell states

$$\begin{aligned} | {{\Phi ^\pm }} \rangle = \frac{1}{{\sqrt{2} }}({| 0 \rangle | 0 \rangle \pm | 1 \rangle | 1 \rangle }),\nonumber \\ | {{\Psi ^ \pm }} \rangle = \frac{1}{{\sqrt{2} }}( {| 0 \rangle | 1 \rangle \pm | 1 \rangle | 0 \rangle }), \end{aligned}$$

(74)

say, $|\Psi ^+\rangle$.

A and B are separated at two locations far away from each other. Each of the two qubits interacts locally with the scalar field around it. Hence the state of the two qubits together with the two relevant field modes is given by Eq. (37), with $\alpha =\beta =1/\sqrt{2}$.

As in the usual protocol of teleportation, A and B are, respectively, controlled by Alice and Bob. Alice also controls another qubit C, which is in the state

$$\begin{aligned} |\psi \rangle _C = u |0\rangle _C+ v |1\rangle _C. \end{aligned}$$

(75)

Our interest lies in the teleportation fidelity decrease due to the effect of scalar field on the resource, namely the entangled state $|\Psi ^+\rangle$, which is shared by two qubits far away from each other. The teleportation can start immediately after $|\psi \rangle _C$ is prepared, which is thus not considered to be affected by the scalar field.

The composite state of the three qubits and the two field modes is

$$\begin{aligned} \rho ^\mathrm{{all}}= ( 1 - \gamma _A )( 1 - \gamma _B) \sum _{n,m} \gamma _{A}^n\gamma _{B}^m |\Phi _{nm},\psi \rangle \langle \Phi _{nm},\psi |,\nonumber \\ \end{aligned}$$

(76)

where

$$\begin{aligned}&|\Phi _{nm},\psi \rangle \nonumber \\&\quad \equiv \frac{1}{ 2\sqrt{Q_{nm}}} \big \{ \big [\big (u | n \rangle _{A0}- iv \sqrt{n} \mu _{A}|n-1 \rangle _{A0}\big )\nonumber \\&\qquad \times \,\big ( | m\rangle _{B0} |1\rangle _B + i\sqrt{m + 1} \mu _{B}^*| m+1\rangle _{B0} |0\rangle _B\big )\nonumber \\&\qquad +\,\big (v | n \rangle _{A0}+ iu \sqrt{n+1} \mu _{A}^*|n + 1 \rangle _{A0}\big ) \nonumber \\&\qquad \times \,\big ( | m\rangle _{B0} |0\rangle _B - i\sqrt{m} \mu _{B}| m-1\rangle _{B0} |1\rangle _B\big )\big ]| \Phi ^+ \rangle _{AC}\nonumber \\&\qquad +\, \big [\big (u | n \rangle _{A0} + iv \sqrt{n} \mu _{A}|n-1 \rangle _{A0}\big ) \nonumber \\&\qquad \times \,\big ( | m\rangle _{B0} |1\rangle _B + i\sqrt{m + 1} \mu _{B}^*| m+1\rangle _{B0} |0\rangle _B\big )\nonumber \\&\qquad +\,\big ({-}v | n \rangle _{A0}+ iu \sqrt{n+1} \mu _{A}^*|n + 1 \rangle _{A0}\big ) \nonumber \\&\qquad \times \,\big ( | m\rangle _{B0} |0\rangle _B - i\sqrt{m} \mu _{B}| m-1\rangle _{B0} |1\rangle _B\big )\big ]| \Phi ^- \rangle _{AC}\nonumber \\&\qquad +\, \big [\big (v | n \rangle _{A0}- iu \sqrt{n} \mu _{A}|n-1 \rangle _{A0}\big ) \nonumber \\&\qquad \times \, \big ( | m \rangle _{B0} |1\rangle _B+ i\sqrt{m + 1} \mu _{B}^*| m + 1\rangle _{B0} |0\rangle _B \big )\nonumber \\&\qquad +\,\big (u | n \rangle _{A0}+ iv \sqrt{n+1} \mu _{A}^*|n + 1 \rangle _{A0}\big ) \nonumber \\&\qquad \times \, \big ( | m\rangle _{B0} |0\rangle _B- i\sqrt{m} \mu _{B}| m-1\rangle _{B0} |1\rangle _B\big )\big ]| \Psi ^+ \rangle _{AC}\nonumber \\&\qquad +\, \big [\big (v | n \rangle _{A0}+ i u \sqrt{n} \mu _{A}|n-1 \rangle _{A0}\big ) \nonumber \\&\qquad \times \,\big ( | m\rangle _{B0} |1\rangle _B+ i\sqrt{m + 1} \mu _{B}^*| m + 1\rangle _{B0}|0\rangle _B \big )\nonumber \\&\qquad +\, \big ({-} u | n \rangle _{A0}+ iv \sqrt{n+1} \mu _{A}^*|n + 1 \rangle _{A0}\big ) \nonumber \\&\qquad \times \,\big ( | m\rangle _{B0} |0\rangle _B - i\sqrt{m} \mu _{B}| m-1\rangle _{B0} |1\rangle _B\big )\big ]| \Psi ^- \rangle _{AC} \},\nonumber \\ \end{aligned}$$

(77)

where $Q_{nm}$ is given by (39) with $\alpha = \beta =1/\sqrt{2}$. For convenience, one can write

$$\begin{aligned} |\Phi _{nm},\psi \rangle \equiv \frac{1}{ 2\sqrt{Q_{nm}}} \sum _{i=1}^4 |\Phi ^i_{nm}\rangle |\mathrm{{Bell}}^i\rangle _{AC}, \end{aligned}$$

(78)

where the terms $i=1,2,3,4$ referrs to the four terms consecutively, $|\mathrm{{Bell}}^1\rangle =| \Phi ^+ \rangle$, $|\mathrm{{Bell}}^2\rangle =| \Phi ^- \rangle$, $|\mathrm{{Bell}}^3\rangle =| \Psi ^+ \rangle$, $|\mathrm{{Bell}}^4\rangle =| \Psi ^-\rangle$, $|\Phi ^i_{nm}\rangle$ is not normalized, and one can find

$$\begin{aligned} \langle \Phi ^1_{nm}|\Phi ^1_{nm}\rangle= & {} \langle \Phi ^2_{nm} |\Phi ^2_{nm}\rangle = Q_{nm}^{v u } \nonumber \\\equiv & {} 1+ [ {{{| v |}^2}n + {{| u |}^2}( {n + 1} )} ]{| {{\mu _{A}}} |^2} \nonumber \\&+\, [ {{{|v |}^2}m + {{| u |}^2}( {m + 1} )} ]{| {{\mu _{B}}} |^2}\nonumber \\&+\, [ {{|v |}^2}n( {m + 1} )\nonumber \\&+\, {{| u |}^2}( {n + 1} )m ]{| {{\mu _{A}}} |^2}{| {{\mu _{B}}} |^2},\end{aligned}$$

(79)

$$\begin{aligned} \langle \Phi ^3_{nm}|\Phi ^3_{nm}\rangle= & {} \langle \Phi ^4_{nm}|\Phi ^4_{nm}\rangle = Q_{nm}^{u v } \nonumber \\\equiv & {} 1 + [ {{| u |}^2}n+ {{| v |}^2}( {n + 1} ) ]{| {{\mu _{A}}} |^2} \nonumber \\&+\, [ {{{| u |}^2}m + {{| v |}^2}( {m + 1} )} ]{| {{\mu _{B}}} |^2} \nonumber \\&+\, [ {{| u |}^2}n( {m + 1} )\nonumber \\&+ {{| v |}^2}( {n + 1} )m ]{| {{\mu _{A}}} |^2}{| {{\mu _{B}}} |^2}, \end{aligned}$$

(80)

satisfying $Q_{nm}^{v u }+Q_{nm}^{u v }=2Q_{nm}$. By setting $\mu _A=\mu _B=0$, $\gamma =0$, and keeping only $n=m=0$ term, (76) reduces to the ideal case of a pure state.

On qubits A and C, Alice makes a Bell measurement, i.e. a measurement in the basis of Bell states. In the ideal quantum teleportation, the state of qubit B is a pure state. After Alice informs Bob of her measurement result through classical communication, Bob can transform the state of qubit B to $|\psi \rangle$, which was the original state of C, by using a one-qubit unitary transformation, with a one-to-one correspondence with the four Bell states of qubits A and C. If the result of the Bell measurement is $|\Phi ^+\rangle$, then the state of qubit B is $u |1\rangle + v |0\rangle$, which can be transformed to $|\psi \rangle$ by $\sigma _x$. If the result of the Bell measurement is $|\Phi ^-\rangle$, then the state of qubit B is $u |1\rangle - v |0\rangle$, which can be transformed to $|\psi \rangle$ by $i\sigma _y$. If the result of Bell measurement is $|\Psi ^+\rangle$, then the state of qubit B is $u |0\rangle + v |1\rangle$, which is just $|\psi \rangle$. If the result of the Bell measurement is $|\Psi ^-\rangle$, then the state of qubit B is $u |0\rangle - v |1\rangle$, which can be transformed to $|\psi \rangle$ by $\sigma _z$.

In the presence of the coupling with the field modes, the procedure of the teleportation remains the same. Although usually the $|\Phi ^i_{nm}\rangle$ are not orthogonal to each other, Bell states are orthogonal to each other, therefore after Bell measurement of qubits A and C, each $|\Phi _{nm},\psi \rangle$ does collapse into one of the four terms in (77), i.e. $|\Phi ^i_{nm}\rangle |\mathrm{{Bell}}^i\rangle$, with the Bell state of qubits A and C disentangled with the state of qubit B and the field modes. Hence if qubits A and C are measured to be in $|\mathrm{{Bell}}^i\rangle$, the density matrix of qubit B and the field modes becomes

$$\begin{aligned} \rho _{i}= ( 1 - \gamma _A )( 1 - \gamma _B) \sum _{n,m} \gamma _{A}^n\gamma _{B}^m \frac{|\Phi ^i_{nm}\rangle \langle \Phi ^i_{nm}|}{\langle \Phi ^i_{nm}|\Phi ^i_{nm}\rangle }. \end{aligned}$$

(81)

The probability for the result of the Bell measurement to be $|\mathrm{{Bell}}^i\rangle$ and thus $\rho ^\mathrm{all}$ collapses to $\rho _i\otimes |\mathrm{{Bell}}^i\rangle \langle \mathrm{{Bell}}^i|$ is

$$\begin{aligned} p_i= ( 1 - \gamma _A )( 1 - \gamma _B) \sum _{n,m} \gamma _{A}^n\gamma _{B}^m \frac{\langle \Phi ^i_{nm}|\Phi ^i_{nm}\rangle }{4Q_{nm}}. \end{aligned}$$

(82)

Thus

$$\begin{aligned} p_1=p_2= & {} ( 1 - \gamma _A )( 1 - \gamma _B)\displaystyle \sum _{n,m} \gamma _{A}^n\gamma _{B}^m \frac{Q_{nm}^{vu}}{4Q_{nm}},\end{aligned}$$

(83)

$$\begin{aligned} p_3=p_4= & {} ( 1 - \gamma _A )( 1 - \gamma _B)\displaystyle \sum _{n,m} \gamma _{A}^n\gamma _{B}^m \frac{Q_{nm}^{uv}}{4Q_{nm}}, \end{aligned}$$

(84)

the sum of which is unity.

From each $\rho _i$, one obtains the mixed state of qubit B, $\mathrm {Tr}_{A0,B0}(\rho _i)$, by tracing out the field modes. This mixed state is nothing but a modification of the pure state in the ideal case. After learning the measurement result of Alice on A and C, Bob transforms the mixed state of qubit B to the corresponding destined mixed state by using a one-qubit unitary transformation, which is the same as in the ideal case. Denote the one-qubit unitary transformation corresponding to $|\mathrm {Bell}^i\rangle$, which has been described above, by $U_i$. Then the destined density matrix is

$$\begin{aligned} \rho ^B_i = U_i \mathrm {Tr}_{A0,B0}(\rho _i) U_i^\dagger , \end{aligned}$$

(85)

It can be seen that

$$\begin{aligned} \rho ^B_3= & {} \rho ^B_4= ( {1 - {\gamma _{A}}} )( {1 - {\gamma _{B}}} )\nonumber \\&\times \,\mathop \sum \limits _{n,m} \frac{{\gamma _{A}^n\gamma _{B}^m}}{{Q_{nm}^{u v }}} \big \{ {[ {{{| u |}^2} + {{| v |}^2}( {n + 1} ){{| {{\mu _{A}}} |}^2} } } \nonumber \\&+\, {| v |^2}( {m + 1} ){| {{\mu _{B}}} |^2} + {{{| u |}^2}n( {m + 1} ){{| {{\mu _{A}}} |}^2}{{| {{\mu _{B}}} |}^2}} ]{| 0 \rangle _{B}}\langle 0 | \nonumber \\&+\, u {v ^*}{| 0 \rangle _{B}} \langle 1 | + {u ^*}v {| 1 \rangle _{B}}\langle 0 | + [ {{{| v |}^2} + {{| u |}^2}n{{| {{\mu _{A}}} |}^2} } \nonumber \\&+\, { {{{| u |}^2}m{{| {{\mu _{B}}} |}^2} + {{| v |}^2}( {n + 1} )m{{| {{\mu _{A}}} |}^2}{{| {{\mu _{B}}} |}^2}} ]{{| 1 \rangle }_{B}}\langle 1 |} \big \}.\nonumber \\ \end{aligned}$$

(86)

$\rho ^B_1=\rho ^B_2$ is given by this expression with u and v exchanged.

The fidelity $F_i$ is the overlap between the destined mixed state of qubit B and $|\psi \rangle$, the teleported state originally carried by qubit C, that is,

$$\begin{aligned} F_i=\langle \psi |\rho ^B_i|\psi \rangle . \end{aligned}$$

(87)

It is seen that

$$\begin{aligned} F_3=F_4= & {} ( {1 - {\gamma _{A}}} )( {1 - {\gamma _{B}}} ) \nonumber \\&\times \,\mathop \sum \limits _{n,m} \frac{{\gamma _{A}^n\gamma _{B}^m}}{{Q_{nm}^{u v }}}\big \{ {1 + {{| u |}^2}{{| v |}^2}( {2n + 1} ){{| {{\mu _{A}}} |}^2} } \nonumber \\&+\, {{| u |}^2}{{| v |}^2}( {2m + 1} ){{| {{\mu _{B}}} |}^2}+ [ {{| u |}^4}n( {m + 1} )\nonumber \\&+\, {{| v |}^4}( {n + 1} )m ]{{| {{\mu _{A}}} |}^2}{{| {{\mu _{B}}} |}^2} \big \}. \end{aligned}$$

(88)

$F_1=F_2$ is given by this expression with u and v exchanged.

Fig. 10

The fidelity of quantum teleportation, $F_3$ as defined in (88), as a function of the volume $\varepsilon$ of the expansion of the spacetime. The rapidity of the cosmic expansion is $\sigma =5$. The parameters of the two originally entangled qubits A and B are the same. The energy gap of each of them is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$. The mass of the scalar field particle is $m=0.01$. The state teleported from qubit C to B is $u|0\rangle +v|1\rangle$

Fig. 11

The fidelity of quantum teleportation, $F_3$ as defined in (88), as a function of the rapidity $\sigma$ of the expansion of the spacetime. The parameters of the two originally entangled qubits A and B are the same. The energy gap of each of them is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$. The mass of the scalar field particle is $m=0.01$. The volume of the expansion is chosen to be ${\varepsilon =\varepsilon _{\max }} = 19{,}999.5$. The state teleported from qubit C to B is $u|0\rangle +v|1\rangle$

Fig. 12

The fidelity of the quantum teleportation, $F_3$ as defined in (88), as a function of the volume $\varepsilon$ and the rapidity $\sigma$ of the cosmic expansion. The parameters of the two originally entangled qubits A and B are the same. The energy gap of each of them is $\Omega =2$, the inner product of the mode functions, defined in Eq. (21), is $\mu = 0.1$. The mass of the scalar field particle is $m=0.01$. The state teleported from qubit C to B is $\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle )$

Only one of these four fidelities needs to be numerically calculated. It is $F_3$, for which the one-qubit unitary transformation is just unity, that is shown in Figs. 10, 11 and 12. $F_4=F_3$. For the plots of $F_1$ and $F_2$, one only needs to replace u as v in these figures.

The dependence of the teleportation fidelity $F_3$ on the cosmic parameter $\varepsilon$ is shown in Fig. 10. For a given value of $\sigma$, the fidelity monotonically decreases with the increase of $\varepsilon$, till $\varepsilon _\mathrm{max}$.

The dependence of the teleportation fidelity $F_3$ on the cosmic parameter $\sigma$ is shown in Fig. 11. The fidelity monotonically decreases with the increase of $\sigma$ towards an asymptotic value. The larger $\sigma$, the smaller the rate of decrease of the fidelity.

Fig. 13

$\gamma$ as a function of the volume $\varepsilon$ and the rapidity $\sigma$ of the cosmic expansion, for $m=0.0001, 0.001, 0.01, 0.1, 1$, respectively. The parameters of the two originally entangled qubits A and B are the same. The energy gap of the qubit is $\Omega =2$, which is supposed to be equal to the energy of the field mode $\mathbf {k}_0$ coupled with the qubit

For $|u| \le 1/\sqrt{2}$ and given values of $\varepsilon$ and $\sigma$, the smaller |u|, the smaller $F_3$ and the larger $F_1$.

For $u = 1/\sqrt{2}$, the 2D plot of the teleportation fidelity $F_3$ as a function of the two cosmic parameters $\varepsilon$ and $\sigma$ is shown in Fig. 12. In this case all the four fidelities are equal. The larger $\sigma$, the larger the rate of decrease of the teleportation fidelity with respect to $\varepsilon$. When $\sigma$ is small enough, the dependence of the teleportation fidelity on $\varepsilon$ is saturated.

In the case that there has not been an expansion of the spacetime, the fidelity can be obtained:

$$\begin{aligned} F_3=F_4 = \frac{1+ |uv|^2 ( | \mu _{A}|^2 + |\mu _B|^2) }{ 1+|v|^2( | \mu _{A}|^2 + |\mu _B|^2)}, \end{aligned}$$

(89)

which reduces to unity when $\mu _A=\mu _B=0$. $F_1=F_2$ is given by this expression with u and v exchanged.

7 Common features of different quantities

One may note from the above figures that all the quantities share some similarities in their dependence on the two cosmic parameters $\varepsilon$ and $\sigma$. In most of the range of $\varepsilon$, except near $\varepsilon _\mathrm{max}$, the deviation from the static case ($\varepsilon =0$) is limited. Certainly there are also special features. Most notable is that only concurrence can have sudden death.

The reason for the similarity is that each quantity depends on these two parameters only through $\gamma$, which is a measure of the mixture of the pair of “in” modes $\mathbf {k}_0$ and $-\mathbf {k}_0$, and is a measure of the average number of particles created at the “out” mode $\mathbf {k}_0$. Moreover, the following nature of the dependence of $\gamma$ on the two parameters leads to the common features in all the quantities studied above.

In Fig. 13, we show $\gamma$ as a function of $\varepsilon$ and $\sigma$, for $m=0.0001, 0.001, 0.01, 0.1, 1$, representing five orders of magnitudes, under the constraint $\Omega \ge m$. $m=0.01$ is the value used in the above calculations. It can be seen that, for each value of m, $\gamma$ remains close to 0 in a large parameter regime. The smaller m, the larger this regime. Only when m is of the same order of magnitude as $\Omega$, represented by $m=1$, there is a significantly large regime in which $\gamma$ is significantly larger than 0. As depicted in Fig. 13, for the other four values of m, i.e. when the order of magnitude of m is smaller than that of $\Omega$, $\gamma$ is significantly larger than 0 only when $\varepsilon$ is close to $\varepsilon _\mathrm{max}$. For even smaller value of m, the regime in which $\gamma$ is significantly larger than 0 is even smaller.

Consequently, all the quantities calculated above significantly deviate from the static case in a limited parameter regime.

8 Summary and discussions

In this paper, we have studied the behavior of one- or two-qubit detectors of scalar fields in a $1+1$ dimensional conformally flat spacetime. We have compared the case that the scale factor is static with the case that the scale factor describes an expanding spacetime. In this model of expanding spacetime, the particle content is well defined in the distant past and in the far future. Note that it is in the far future that the detectors are considered to be coupled with the fields for a period of time.

In the static case, i.e. if there has not been expansion of the spacetime, the initial state of the field is assumed to be the vacuum. Unless its initial state is the ground state $|0\rangle$, the coupling of a single qubit with the field causes it to be decohered to a mixed state. For two initially entangled qubits A and B, their coupling with two ambient scalar fields degrades their total correlation, quantified by the mutual information, as well as quantum entanglement, quantified by the concurrence and the teleportation fidelity. For each of these quantity, there is a perturbative correction due to the qubit–field interaction, parameterized by $\mu _A$ and $\mu _B$, as defined in Eq. (21).

In the case that there has been expansion of the spacetime, the vacuum sector of each pair of momenta $\pm \mathbf {k}$ in the distant past becomes in the far future a squeezed superposition of all possible Fock states of equal occupation numbers in the pair of modes. The particles with opposite momenta are separated on cosmological scale. A detector at the far future sees only particles with one sign, hence a mixed state of the accessible field modes. After the interaction between the detector and the field, the state of detector becomes entangled with the field as the environment, hence the state of the detector becomes mixed. For two entangled detectors, the interaction with the scalar fields in the expanded spacetime causes the degradation of the mutual information and entanglement, and even entanglement’s sudden death if the initial entanglement is small enough. Consequently, the fidelity of quantum teleportation based on this entanglement becomes less than unity. Our analysis of teleportation in the presence of coupling with field modes may be useful also in other areas.

We have calculated how the purity, the mutual information, the concurrence and the teleportation fidelity depend on the two parameters characterizing the expansion of the spacetime, namely the total volume $\varepsilon$ and the rapidity $\sigma$ of the expansion. It turns out that each quantity monotonically decreases, and the rate of change increases, with the increase of $\varepsilon$, until the maximal value $\varepsilon _\mathrm{max}$, above which the field mode becomes off-resonant with the qubit. Each quantity also monotonically decreases, and the rate of change decreases, with the increase of $\sigma$. The reason for the common feature is that the dependence on $\varepsilon$ and $\sigma$ is only through $\gamma$, characterizing the mixing of the “in” modes or the number of particles created by the cosmic expansion. $\gamma$ is significantly larger than 0 in limited parameter regimes.

In general, one can measure these quantum information quantities and even other physical quantities not calculated here of the detectors, and compare the results with the theoretical results calculated by taking into account the cosmic expansion as presented here. Consequently the cosmological parameters can be determined or some constraints can be obtained. In our present toy model, in which there are only two cosmological parameters $\varepsilon$ and $\sigma$, this comparison and determination is simple in principle.

Moreover, one can tune the transition frequency $\Omega$, such that the transition starts to occur, which is at the value $m\sqrt{1+\epsilon }$, as given in Eq. (22). Thus $\epsilon$ can be determined. Then the other parameter $\sigma$ can also be determined from those quantum informational quantities for a given initial state. In the present work, as a model study, the state in the distant past is assumed to be the vacuum for simplicity. One could assume other initial state according to different the cosmological theories.

A possible direction into which more realistic extension could be made is inflationary cosmology, in which the exponentially expanding metric leads to the quantum fluctuation of a scalar field as the primordial inhomogeneity that has acted as the seeds for the formation of large scale structures and imprinted the cosmic microwave background. The role of the detectors in this paper could possibly be played by some particles in post-inflation era. Nevertheless, much work is still needed to address the realistic cosmology.

In the present work, we presume the scale factor a(t) or $R(\eta )$ to be given, as in Eq. (2). In a satisfactory approach, the scale factor depends on the matter content, through its equation of motion derived from the Einstein field equation. Unfortunately, it cannot be done for this toy model, as it is one-dimensional, for which general relativity does not apply. In three dimensions, Einstein equation applied to Robertson–Walker metric leads to the Friedmann equation $\mathrm{d}^2 a/\mathrm{d}t^2 =-(4\pi /3)G(\rho + 3 p)a$, where the energy density $\rho$ and the pressure p can be determined from the Lagrangian of the scalar field. This equation is then solved consistently, together with the Klein–Gordon equation (3) for the scalar field.

Information is physical. Studying quantum informational quantities in cosmological setting might shed new light on quantum information. With the input of quantum field theory, particle physics and gravitational physics, our understanding of quantum information will be deepened.

Physics is informational. Wheeler said: “It from bit”. Using ideas from quantum information in cosmology can also bring about new tools for the latter. For example, these quantum informational quantities encode information as regards cosmological parameters, thus one might learn about the parameters of the whole spacetime in its history through the properties of one or a few qubits in a finite time. Whether the idea can be extended to three dimensions remains to be investigated. The idea could be captured fittingly by William Blake’s lines:

To see a World in a Grain of Sand

And a Heaven in a Wild Flower,

Hold Infinity in the palm of your hand

And Eternity in an hour.