Possible $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ molecular states in the extended constituent quark models

Abstract

The possible neutral $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ molecular states are studied in the framework of the constituent quark models, which is extended by including the s-channel one-gluon exchange. Using different types of quark–quark potentials, we solve the four-body Schrödinger equation by means of the Gaussian expansion method. The bound states of $D^{(*)}\bar{D}^{(*)}$ with $J^{PC}=1^{++},2^{++}$ and $B^{(*)}\bar{B}^{(*)}$ with $J^{PC}=0^{++},1^{+-},1^{++},2^{++}$ are obtained. The molecular states $D^{*}\bar{D}$ with $J^{PC}=1^{++}$ and $B^{*}\bar{B}$ with $J^{PC}=1^{+-}$ are good candidates for X(3872) and $Z^0_b(10610)$, respectively. The dependence of the results on the model parameters is also discussed.

1 Introduction

Since 2003, more than 20 new meson states (called XYZ particles) [1,2,3] have been observed by Belle, BaBar, BES, LHCb and other collaborations in hadronic final states that contain either a $c\bar{c}$ or a $b\bar{b}$ quark pair. In general, the properties of these states do not match to the expectations for any of the currently unassigned $c\bar{c}$ charmonium or $b\bar{b}$ bottomonium states. A well-established one among these XYZ states is X(3872), which was first discovered in 2003 by Belle Collaboration [4] in the $\pi ^+\pi ^-J/\psi$ invariant mass spectrum in $B\rightarrow K\pi ^+\pi ^-J/\psi$, and later confirmed by six other experiments [5,6,7,8,9,10]. Its quantum numbers have been studied by Belle, BaBar, CDF and LHCb, and were determined to be $I^GJ^{PC}=0^{+}1^{++}$ [11]. The most striking feature of X(3872) is the narrow total width about 1.2 MeV and the average mass $3871.69 \pm 0.17$ MeV, which is extremely close to the $D^0\bar{D}^{0*}$ mass threshold [12].

It is unlikely for most XYZ states that they can be interpreted as a conventional $c\bar{c}$ or $b\bar{b}$ meson because of their unusual properties. During the past decades, various pictures like the molecular state, the compact tetraquark state, the hybrid state, and so on, have been proposed to explain their nature. For explaining the structure of X(3872), the most popular explanation is the molecular state. Swanson [14] proposed the interpretation of X(3872) as a $D^0\bar{D}^{0*}$ molecular state with $J^{PC}=1^{++}$ which is bound by both pion and quark exchange. However, no $D^0\bar{D}^{0*}$ molecular state was obtained in Ref. [14] if only taking into account of one-pion exchange between $D^0$ and $\bar{D}^{0*}$. Wong [13] applied a quark-based model, which is similar to adding a short-range quark–gluon force, to study the molecular states composed of two heavy mesons. They found an S-wave $\bar{D}^{0}\bar{D}^{0*}$ molecular state with a binding energy of about 7.5 MeV. Suzuki [15] believes that the one-pion-exchange potential cannot bind $\bar{D}^0$ and $D^{0*}$ to a molecular state. Thomas and Close [16] found that the $D^{0}\bar{D}^{0*}$ can be a bound state, when the one-pion exchange between charm and bottom mesons is considered. However, their results are very sensitive to a poorly constrained parameter. In Ref. [17], the authors also obtained a $D^{0}\bar{D}^{0*}$ bound state when they systematically studied possible $D\bar{D}$, $D\bar{D}^{*}$ and $D^*\bar{D}^{*}$ molecular states by considering vector, pseudoscalar and scalar meson exchanges. In the framework of a potential model generated by the exchange of scalar, pseudoscalar and vector mesons, based on the effective Lagrangian of heavy hadron chiral perturbation theory, a $D^*\bar{D}^{*}$ bound state was got by Lee et al. [18] as well. In Ref. [19], the authors believe that X(3872) should be understood as a molecular state of $D\bar{D}^{*}$–cc, and they extrapolate this information to make predictions of $B\bar{B}^{*}$–cc molecules [20]. Oset et al. [21] obtained a $D\bar{D}$ bound state both by a model using a chiral Lagrangian already used to study flavor symmetry breaking in Skyrme models, and another model by taking into account a SU(4) symmetric Lagrangian with heavy meson exchanges. They also analyzed the $e^{+}e^{-}\rightarrow J/\psi D\bar{D}, J/\psi D\bar{D}^{*}$ reactions of Belle, and they found a hidden charm scalar meson with mass around 3700 MeV [22], which is compatible with the $D\bar{D}$ bound state. In Ref. [23], Molina and Oset interpret Y(3940) and Z(3940) as molecular states of $D^*\bar{D}^{*}$ with quantum number $J^{PC}=0^{++},~2^{++}$ and X(4160) as a $D_s^*\bar{D}_s^{*}$ molecular state with $J^{PC}=~2^{++}$, respectively.

In the constituent quark model, Vijande et al. [24] studied the four-quark system $c\bar{c}n\bar{n}$ by means of the hyperspherical harmonic formalism. However, no bound states have been found whether taking into account the exchange of scalar and pseudoscalar mesons or not. Yang and Ping [26] systematically studied $D\bar{D}$, $D\bar{D}^{*}$ and $D^*\bar{D}^{*}$ by means of the Gaussian expansion method (GEM). No neutral bound state of $D^{(*)}\bar{D}^{(*)}$ was found as well. Liu and Zhang [25] obtained a $D^{0}\bar{D}^{0*}$ bound state in a chiral quark model on including $\pi , \sigma$, $\omega$ and $\rho$ meson exchanges into it.

In nature only the colorless hadron is allowed, so there is no one-gluon annihilation interaction between quark and antiquark with the same flavor in a conventional colorless $q\bar{q}$ meson. However, the s-channel one-gluon-exchange interaction can exist in the neutral $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ system and maybe plays an important role in binding them, since the color structure of a four-quark state is much richer than that of a $q\bar{q}$ conventional meson. Based on the Bhaduri, Cohler and Nogami model (BCN), Wang et al. [27] believe that the s-channel one-gluon-exchange interaction is important for binding a $D^*\bar{D}^{*}$ molecular state, which is a good candidate for X(3872).

In this work, we would like to study the possible neutral molecular states $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ by two constituent quark models, which are extended by including the one-gluon annihilation interaction between $u\bar{u}$ or $d\bar{d}$ light quark pairs. We solve the four-body Schrödinger equation by means of GEM, which is a high accuracy method for few-body systems developed by Kamimura, Hiyama et al. [28] and extensively performed in studying the mass spectrum of a multi-quark system [29,30,31,32,33,34].

This paper is organized as follows. After the introduction, we present the extended constituent quark models in Sect. 2. The wave functions of $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ are constructed by considering the isospin, total angular momentum, color and the Gaussian expansion method and listed in Sect. 3. We summarize our numerical results and perform some analysis in Sect. 4 and draw some conclusions in Sect. 5.

2 The constituent quark model with s-channel one-gluon exchange

2.1 Bhaduri, Cohler and Nogami model

This quark model was proposed by Bhaduri et al. [35, 36]. The Hamiltonian takes the form

$$\begin{aligned} H=\sum _{i=1}^4\left( m_i+\frac{\mathbf {p}_i^2}{2m_i}\right) -T_{c.m.}+\sum _{j>i=1}^4 (V_{ij}^C+V_{ij}^G) \end{aligned}$$

(1)

with

$$\begin{aligned} V_{ij}^G= & {} \alpha _s\frac{\varvec{\lambda }_i^c\cdot \varvec{\lambda }^c_j}{4} \left( \frac{1}{r_{ij}}-\frac{1}{m_im_j}\frac{e^{-r_{ij}/r_0}}{r_0^2r_{ij}} \varvec{\sigma }_i\cdot \varvec{\sigma }_j\right) ,\end{aligned}$$

(2)

$$\begin{aligned} V_{ij}^{C}= & {} \varvec{\lambda }^c_{i}\cdot \varvec{\lambda }^c_{j}~(-a_{c}r_{ij} - \Delta ), \end{aligned}$$

(3)

where $r_{ij}=|\mathbf {r}_i-\mathbf {r}_j|$ and $T_{c.m.}$ is the kinetic energy of the center-of-mass motion. $\varvec{\sigma }$, $\varvec{\lambda }$ are the SU(2) Pauli matrices and the SU(3) Gell-Mann matrices, respectively. $\varvec{\lambda }$ should be replaced by $-\varvec{\lambda }^{*}$ for the antiquark.

2.2 The chiral constituent quark model (ChQM)

The chiral constituent quark model(ChQM) [37] includes the Goldstone-boson-exchange potential in addition to a color confinement potential and a t-channel one-gluon-exchange (OGE) potential between quarks (antiquarks). The chiral partner, the $\sigma$-meson-exchange potential, is also introduced here, although its effect is still controversial [38,39,40,41]. The Hamiltonian of the ChQM used here is given as follows:

$$\begin{aligned} H= & {} \sum _{i=1}^4 \left( m_i+\frac{\mathbf {p}_i^2}{2m_i} \right) -T_{c.m.} \nonumber \\&+\sum _{j>i=1}^4 (V_{ij}^G+V_{ij}^C+V_{ij}^\chi +V_{ij}^\sigma ), ~~\chi =\pi ,K,\eta . \end{aligned}$$

(4)

The OGE potential reads

$$\begin{aligned} V_{ij}^G = \alpha _{s} \frac{\varvec{\lambda }^{c}_{i}\cdot \varvec{\lambda }^{c}_{j}}{4} \left[ {\frac{1}{r_{ij}}}-{\frac{2\pi }{3m_im_j}}~(\varvec{\sigma }_{i} \cdot \varvec{\sigma }_{j})~\delta (\mathbf {r}_{ij}) \right] , \end{aligned}$$

(5)

where $T_{c.m.}$, $\varvec{\sigma }$, $\varvec{\lambda }$ have the same meaning as the above. In the non-relativistic quark model, the function $\delta (\mathbf {r}_{ij})$ should be regularized [42,43,44,45]. It reads

$$\begin{aligned} \delta (\mathbf {r}_{ij})=\frac{1}{4\pi r_{ij}~r_0^2(\mu )}~ e^{-r_{ij}/r_0(\mu )}, \end{aligned}$$

(6)

where $r_0(\mu )=\hat{r}_0/\mu$ and $\mu$ is the reduced mass of the interacting quark/antiquark–quark/antiquark pair, $\hat{r}_0$ is a parameter to be determined from the experimental data. In the non-relativistic quark model, the wide energy covered from light to heavy quark requires an effective scale-dependent strong coupling constant $\alpha _s$ in Eq. (5) that cannot be obtained from the usual one-loop expression of the running coupling constant because it diverges when $Q\rightarrow \Lambda _{QCD}$. So one uses an effective scale-dependent strong coupling constant given by

$$\begin{aligned} \alpha _s(\mu )=\frac{\alpha _0}{\ln \left[ (\mu ^{2}+\mu _0^2)/\Lambda _0^2\right] }~, \end{aligned}$$

(7)

where $\mu _0$ and $\Lambda _0$ are the parameters to be obtained by fitting the conventional meson spectra.

A screened potential simulating the results of unquenched lattice calculations is given by

$$\begin{aligned} V_{ij}^{C} =\varvec{\lambda }^c_{i}\cdot \varvec{\lambda }^c_{j} ~\{-a_{c}(1-e^{-\mu _c r_{ij}})+ \Delta \}, \end{aligned}$$

(8)

where $\Delta$ is a global constant to be fixed by experimental data.

Due to the spontaneous breaking of original $SU(3)_L\otimes SU(3)_R$ chiral symmetry at some momentum scale, the Goldstone-meson-exchange occurs between quarks (antiquarks). The potential takes the form

$$\begin{aligned}&V_{ij}^{\pi } =C(g_{ch},\Lambda _{\pi },m_{\pi }){\frac{m_{\pi }^{2}}{{12m_{i}m_{j}}}} H_1(m_{\pi },\Lambda _{\pi },r_{ij}) \nonumber \\&~~~~~~~~~~~ \times (\varvec{\sigma }_{i}\cdot \varvec{\sigma }_{j})~\sum _{a=1}^3\lambda _{i}^{a} \lambda _{j}^{a}, \end{aligned}$$

(9)

$$\begin{aligned}&V_{ij}^{\eta } =C(g_{ch},\Lambda _{\eta },m_{\eta }){\frac{m_{\eta }^{2}}{{12m_{i}m_{j}}}} H_1(m_{\eta },\Lambda _{\eta },r_{ij}) \nonumber \\&~~~~~~~~~~~ \times (\varvec{\sigma }_{i}\cdot \varvec{\sigma }_{j})~\left[ \cos \theta _P(\lambda _{i}^{8} \lambda _{j}^{8})-\sin \theta _P(\lambda _{i}^{0} \lambda _{j}^{0})\right] , \end{aligned}$$

(10)

$$\begin{aligned}&V_{ij}^{\sigma } = -C(g_{ch},\Lambda _{\sigma },m_{\sigma })~H_2(m_{\sigma },\Lambda _{\sigma },r_{ij}), \end{aligned}$$

(11)

$$\begin{aligned}&H_1(m,\Lambda ,r)=\left[ Y(mr)-{\frac{\Lambda ^{3}}{m^{3}}} Y(\Lambda r)\right] , \end{aligned}$$

(12)

$$\begin{aligned}&H_2(m,\Lambda ,r)=\left[ Y(mr)-{\frac{\Lambda }{m}} Y(\Lambda r)\right] , \end{aligned}$$

(13)

$$\begin{aligned}&C(g_{ch},\Lambda ,m)={\frac{g_{ch}^{2}}{{4\pi }}}{\frac{\Lambda ^{2}}{{\Lambda ^{2}-m^{2}}}} m, \end{aligned}$$

(14)

where Y(x) is the standard Yukawa function defined by $Y(x)=e^{-x}/x$ and rest symbols have their usual meaning. The chiral coupling constant $g_{ch}$ is determined from the $\pi NN$ coupling constant through

$$\begin{aligned} \frac{g_{ch}^{2}}{4\pi }=\left( \frac{3}{5}\right) ^{2}{\frac{g_{\pi NN}^{2} }{{4\pi }}}{\frac{m_{u,d}^{2}}{m_{N}^{2}}}, \end{aligned}$$

(15)

and flavor SU(3) symmetry is assumed.

2.3 s-Channel one-gluon-exchange interaction

In the case of heavy-light meson and antimeson system, the contribution of s-channel annihilation interaction should be taken into account. The one-gluon annihilation of quark and antiquark is shown in Fig. 1.

Fig. 1

The one-gluon annihilation diagrams for quark and antiquark

According to the Feynman rules, we can write down the T-matrix of the process

$$\begin{aligned} T_{fi}= & {} \frac{g^2_s}{s} \bar{u} (p^{\prime }_i,s^{\prime }_i) \chi ^{\dag }_{c^{\prime }_i} \chi ^{\dag }_{f^{\prime }_i} \frac{\lambda ^a}{2} \gamma ^{\mu } v(p^{\prime }_j,s^{\prime }_j) \chi _{c^{\prime }_j}\chi _{f^{\prime }_j} \nonumber \\&\times \bar{v}(p_j,s_j)\chi ^{\dag }_{c_j} \chi ^{\dag }_{f_j} \frac{\lambda ^{a}}{2}\gamma _{\mu }u(p_i,s_i)\chi _{c_i}\chi _{f_i}, \end{aligned}$$

(16)

where $s=(p_i+p_j)^2$ and p is a four-vector momentum; $u(p_i,s_i),~v(p_j,s_j)$ are the free Dirac spinors of ith quark and jth antiquark; $\chi _{c},~\chi _{f}$ represent color and flavor wave functions, respectively. After a Fierz transformation [46] of the SU(n) group and taking the lowest order in the non-relativistic limit, the contributions from one-gluon annihilation to the potential between quark and antiquark in the momentum representation can be written as

$$\begin{aligned} V_{ij}^{\mathrm{Anni}-G}(s)= & {} \frac{4 \pi \alpha _s}{s}\frac{1}{4}\left( \frac{16}{9}-\frac{1}{3}\mathbf {\lambda }^{c}_{i}\cdot \mathbf {\lambda }^{*c}_{j}\right) \nonumber \\&\times \left( \frac{1}{3}+\frac{1}{2}\mathbf {f}^a_{i}\cdot \mathbf {f}^{*a}_{j}\right) \left( \frac{3}{2}+\frac{\mathbf {\sigma }_{i}\cdot \mathbf {\sigma }_{j}}{2}\right) . \end{aligned}$$

(17)

In coordinate space, and under the static approximation, $s=(m_i+m_j)^2=4m_q^2$, the potential reads

$$\begin{aligned} V_{ij}^{\mathrm{Anni}-G}(r_{ij})= & {} \frac{\pi \alpha _s}{4m_q^2}\left( \frac{16}{9}-\frac{1}{3}\mathbf {\lambda }^{c}_{i}\cdot \mathbf {\lambda }^{*c}_{j}\right) \nonumber \\&\times \left( \frac{1}{3}+\frac{1}{2}\mathbf {f}^a_{i}\cdot \mathbf {f}^{*a}_{j}\right) \left( \frac{3}{2}+\frac{\mathbf {\sigma }_{i}\cdot \mathbf {\sigma }_{j}}{2}\right) \delta (\mathbf {r}_{ij}).\nonumber \\ \end{aligned}$$

(18)

As the annihilation interaction is inversely proportional to the masses of the interacting quarks, the one-gluon-annihilation process must be very weak for heavy quarks. Thus we only consider here $u\bar{u}$ and $d\bar{d}$, and $\mathbf {f}^a$ are the SU(3) matrices in flavor space. The factor of the first bracket represents that this interaction never occurs inside a color singlet. Obviously, the last two factors in the brackets mean that this interaction only occurs when the $\bar{q}q$ pair is in the same flavor with spin $S = 1$. This interaction is always repulsive in molecular states of the four-quark system, since the color matrix elements are zero and $-\frac{14}{3}$ in $1\otimes 1$ and $8\otimes 8$, respectively.

However, the earliest lattice simulations of the gluon propagator in the Landau gauge, by Gupta et al. [47], were interpreted in terms of a massive particle propagator. In order to study the $I=0~\pi \pi$ and $I=\frac{1}{2}~K\pi$ S-wave phase shift, Barnes and Swanson [48] modified the gluon propagator by including an effective gluon mass. To analyze the mixing of the scalar glueball with scalar–isoscalar quarkonia states above 1 GeV [49], and investigate mesonic content of the nucleon and Roper resonance [50], the massive gluon propagator is also employed. So here we choose the gluon propagator [49, 51, 52]

$$\begin{aligned} D(s)=\frac{1}{s-m_g^2}, \end{aligned}$$

(19)

where $m_g$ is effective gluon mass, which should be larger than the half of the bare glueball mass deduced from lattice simulations. Typical values for the effective gluon mass are in the range 0.6–1.2 GeV [49].

After taking into account the massive gluon propagator, Eq. (19) turns out to become

$$\begin{aligned} V_{ij}^{Anni-G}(r_{ij})= & {} \frac{\pi \alpha _s}{4m_q^2-m_g^2}\left( \frac{16}{9}-\frac{1}{3}\mathbf {\lambda }^{c}_{i}\cdot \mathbf {\lambda }^{*c}_{j}\right) \nonumber \\&\times \left( \frac{1}{3}+\frac{1}{2}\mathbf {f}^a_{i}\cdot \mathbf {f}^{*a}_{j}\right) \left( \frac{3}{2}+\frac{\mathbf {\sigma }_{i}\cdot \mathbf {\sigma }_{j}}{2}\right) \delta (\mathbf {r}_{ij}).\nonumber \\ \end{aligned}$$

(20)

Obviously, this interaction is attractive if $m_g>2m_q$.

3 Wave function

The total wave function of the four-quark system can be written as

$$\begin{aligned} \Psi ^{I,I_z}_{J,J_z}=\left| \xi \right\rangle \left| \eta \right\rangle _{II_z}\Phi _{JJ_z}, \end{aligned}$$

(21)

with

$$\begin{aligned} \Phi _{JJ_z}=\left[ \left| \chi \right\rangle _{S}\otimes \left| \Phi \right\rangle _{L_T}\right] _{JJ_z} \end{aligned}$$

where $\left| \xi \right\rangle$, $\left| \eta \right\rangle _{II_z}$, $\left| \chi \right\rangle _{SM_S}$, $\left| \Phi \right\rangle _{L_{T}M_L}$ represent color, flavor, spin and spatial wave functions with the quantum numbers color singlet, isospin I, spin S and orbital angular momentum $L_T$, respectively.

The molecular states of the $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ systems can be conveniently classified in terms of total angular momentum, J, parity, P and charge conjugation, C. In this work we only consider the low-lying states, the orbital angular momentum $L_T$ is set to 0. In this case we have the following states for the $D^{(*)}\bar{D}^{(*)}$ system:

• (i) Two states with $J^{PC}=0^{++}$: $[D\bar{D}]_{0}$, $[D^*\bar{D}^*]_{0}$, where the subscript is the total angular momentum J.

• (ii) One state with $J^{PC}=1^{++}$:

  $$\begin{aligned} \frac{1}{\sqrt{2}}\left( [D\bar{D}^*]_{1}+[D^*\bar{D}]_1\right) , \end{aligned}$$

  and two states with $J^{PC}=1^{+-}$:

  $$\begin{aligned} \frac{1}{\sqrt{2}}\left( [D\bar{D}^*]_{1}-[D^*\bar{D}]_1\right) \text{ and } [D^*\bar{D}^*]_{1}. \end{aligned}$$

• (iii) One state with $J^{PC}=2^{++}$: $[D^*\bar{D}^*]_{2}$.

For the $B^{(*)}\bar{B}^{(*)}$ system, we replace the D mesons in the above with the B mesons.

The total spin function $\left| \chi \right\rangle _{SM_S}$ and the flavor function $\left| \eta \right\rangle _{II_z}$ can easily be constructed from the above expressions. For example, for $[D^*\bar{D}^*]_{1}$,

$$\begin{aligned} |\chi \rangle _{11}= & {} \sqrt{\frac{1}{2}}(|11\rangle |10\rangle -|10\rangle |11\rangle ) \\= & {} \frac{1}{2}(\alpha \alpha \alpha \beta +\alpha \alpha \beta \alpha -\alpha \beta \alpha \alpha -\beta \alpha \alpha \alpha ) \nonumber \\ |\eta \rangle _{00}= & {} \sqrt{\frac{1}{2}}(D^0\bar{D}^0+D^-D^+) =\sqrt{\frac{1}{2}}(u\bar{c}c\bar{u}+d\bar{c}c\bar{d}). \end{aligned}$$

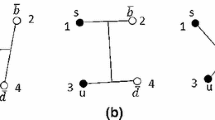
The spatial structure of molecular states are pictured in Fig. 2. We define the relative coordinate as follows:

$$\begin{aligned}&\mathbf {r}=\mathbf {r}_1-\mathbf {r}_2,\ ~~~~ \mathbf {R}=\mathbf {r}_3-\mathbf {r}_4,\end{aligned}$$

(22)

$$\begin{aligned}&\varvec{\rho }=\frac{m_1\mathbf {r}_1+m_2\mathbf {r}_2}{m_1+m_2} -\frac{m_3\mathbf {r}_3+m_4\mathbf {r}_4}{m_3+m_4}, \end{aligned}$$

(23)

and the center-of-mass coordinate is

$$\begin{aligned} \mathbf {R}_{cm}=\sum _{i=1}^4 m_i \mathbf {r}_i/\sum _{i=1}^4 m_i, \end{aligned}$$

(24)

where $m_i$ is the mass of the ith quark (or antiqark).

Fig. 2

The relative coordinates for the molecular state. Dark and open circles represent quarks and antiquarks, respectively

Table 1 Parameters of two quark models. ChQM: the masses of $\pi ,\eta$ take the experimental values, $m_\pi =0.7$ fm$^{-1}$, $m_{\eta }=2.77$ fm$^{-1}$; $m_{\sigma },\Lambda _{\pi }$, $\Lambda _{\eta }$, $\theta _p$ are taken from Ref. [37], namely $m_{\sigma }=3.42$ fm$^{-1}$, $\Lambda _{\pi }=\Lambda _{\sigma }=4.2$ fm$^{-1}$, $\Lambda _{\eta }=5.2$ fm$^{-1}$, $\theta _p=-15^o$, $g^2_{ch}/4\pi$=0.54. BCN: the parameters take from Refs. [35, 36]

Then the outer products of space and spin are

$$\begin{aligned} \Phi _{JJ_z}= & {} \left[ \left[ \left[ \phi ^G_{lm}(\mathbf {r})\chi _{s_1m_{s_1}}\right] _{J_1M_1} \right. \right. \nonumber \\&\times \left. \left. \left[ \psi ^G_{LM}(\mathbf {R})\chi _{s_2m_{s_2}} \right] _{J_2M_2} \right] _{J_{12}M_{12}} \varphi ^G_{\beta \gamma }(\varvec{\rho })\right] _{JJ_z}. \end{aligned}$$

(25)

Here $\chi _{sm_{s}}$ is a spin wave function of a conventional meson, which is composed of a quark–antiquark. The spatial wave functions $\phi ^G_{lm}(\mathbf {r}), \psi ^G_{LM}(\mathbf {R})$ and $\varphi ^G_{\beta \gamma }(\varvec{\rho })$ are written as

$$\begin{aligned} \phi ^G_{lm}(\mathbf {r})=\sum _{n=1}^{n_\mathrm{max}}c_nN_{nl}r^le^{-\nu _nr^2}Y_{lm}(\hat{\mathbf {r}}), \end{aligned}$$

(26)

$$\begin{aligned} \psi ^G_{LM}(\mathbf {R})=\sum _{N=1}^{N_\mathrm{max}}c_NN_{NL}R^Le^{-\zeta _NR^2}Y_{LM}(\hat{\mathbf {R}}), \end{aligned}$$

(27)

$$\begin{aligned} \varphi ^G_{\beta \gamma }(\varvec{\rho })=\sum _{\alpha =1}^{\alpha _\mathrm{max}}c_{\alpha } N_{\alpha \beta }\rho ^{\beta }e^{-\omega _\alpha \rho ^2}Y_{\beta \gamma }(\hat{\varvec{\rho }}). \end{aligned}$$

(28)

The Gaussian size parameters are taken as a geometric progression

$$\begin{aligned} \nu _{n}=\frac{1}{s^2_n},&s_n=s_1 a^{n-1},&a=\left( \frac{s_{n_\mathrm{max}}}{s_1}\right) ^{\frac{1}{n_\mathrm{max}-1}}. \end{aligned}$$

(29)

The expressions of $\zeta _N,\omega _\alpha$ in Eqs. (27)–(28) are similar to Eq. (29).

The color wave function of possible molecular states reads

$$\begin{aligned} \left| \xi \right\rangle =&\frac{1}{3}\left( \left| r\bar{r}r\bar{r}\right\rangle + \left| g\bar{g}g\bar{g}\right\rangle +\left| b\bar{b}b\bar{b}\right\rangle +\left| r\bar{r}g\bar{g}\right\rangle +\left| r\bar{r}b\bar{b}\right\rangle \right. \nonumber \\&+\left. \left| g\bar{g}r\bar{r}\right\rangle +\left| g\bar{g}b\bar{b}\right\rangle + \left| b\bar{b}r\bar{r}\right\rangle +\left| b\bar{b}g\bar{g}\right\rangle \right) . \end{aligned}$$

(30)

4 Numerical results and discussion

The energy of a meson composed of quark–antiquark, and four-quark systems $D^{(*)}\bar{D}^{(*)}$, $B^{(*)}\bar{B}^{(*)}$ can be obtained by solving the Schrödinger equation,

$$\begin{aligned} \left( H-E\right) \Psi ^{I,I_z}_{J,J_z}=0, \end{aligned}$$

(31)

with Rayleigh–Ritz variational principle.

To study the spectrum of a four-quark state, one believes that whether or not the state is bound is judged by the threshold of two conventional mesons, and the same parameters should be used in the calculation of conventional mesons and four-quark states [36, 43,44,45, 53,54,55,56].

For the calculating spectra of the conventional meson, there is only one relative motion between quark and antiquark, so Eq. (26) is employed. The model parameters of the ChQM and the BCN used in this work are shown in Table 1, which are from Refs. [35,36,37], respectively. To study the $D^{(*)}\bar{D}^{(*)}$, $B^{(*)}\bar{B}^{(*)}$ systems, fitting masses of the $D, D^{*}, B, B^{*}$ mesons to the experimental data exactly is more reasonable, so we introduce a set of new parameters which are denoted ‘BCN$_\mathrm{new}$’ and ‘ChQM$_\mathrm{new}$’ in Table 1. The calculated results of the conventional meson spectra listed in Table 2 converge with $n_\mathrm{max}=7$, $s_1=0.1$ fm and $s_{n_\mathrm{max}}=2$ fm, as discussed in detail in Ref. [29]. Obviously, the meson spectra in Table 2 calculated by GEM agree well with the experimental data [12] and Refs. [35,36,37].

Table 2 Numerical results of conventional meson spectra (in MeV) for the ChQM and BCN models. The column of BCN1 and ChQM1 are taken from Refs. [35, 36] and [37] respectively. The BCN2 and ChQM2 are calculated by GEM. The last column takes from the latest Particle Data Group [12]

Table 3 Threshold energies (in MeV) of S-wave $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ configurations

Generally, the binding energy of the four-quark system is defined by

$$\begin{aligned} \Delta E=E_T-E_{th}, \end{aligned}$$

(32)

with

$$\begin{aligned} E_{th}=E_{M_1}+E_{M_2} \end{aligned}$$

where $E_{M}$ and $E_T$ represent the energy of $Q\bar{q}~(Q=c,b$ and $q=u,d)$ and $Q\bar{q}q\bar{Q}$ systems, respectively. If $\Delta E < 0$, then the system is stable against the strong interaction. According to Table 2, the thresholds of the S-wave $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ of the ChQM and BCN models are listed in Table 3. Obviously, the threshold calculated by new parameters, which are denoted ‘BCN$_\mathrm{new}$’ and ‘ChQM$_\mathrm{new}$’, respectively, match the experimental data well.

To calculate the spectra of the four-quark states $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$, the Schrödinger equation, Eq. (31), is solved by using the four-quark wave function in Eq. (21). The converging results are obtained by taking the parameters of GEM $\alpha =12, ~n=7,~N=7$, and the ranges of $s_n$ for $\varvec{\rho }$ are from 0.1 to 6 fm, and 0.1 to 2 fm for $\mathbf {R}$ and $\mathbf {r}$, respectively. Entem and Fern$\grave{a}$ndez believe the effective gluon mass $m_g$ ranges from 0.6 to 1.2 GeV [49], so we calculated the spectra of $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ with $m_g$=0, 0.9, 1 GeV and without annihilation interaction. The results are listed in Tables 4, 5, 6 and 7, which are calculated by different model parameters for BCN and ChQM, respectively.

Table 4 Energies (in MeV) of S-wave $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ with different effective gluon mass for the BCN model. ‘No-anni’ means without annihilation interaction

Table 5 Energies (in MeV) of S-wave $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ for the ChQM. ‘No-anni’ means without annihilation interaction

Table 6 Same as Table 4 for the BCN model with new parameters

Table 7 Same as Table 5 for the ChQM with new parameters

From Tables 4 and 5, obtained by the conventional parameters of BCN and ChQM, we can find several interesting features. (1) If we do not take into account the annihilation interaction, no bound states of $D^{(*)}\bar{D}^{(*)}$ are found both in BCN and ChQM. However, there are three states of $B^{(*)}\bar{B}^{(*)}$ with $J^{PC}=0^{++},1^{++},2^{++}$ having energies lower than the corresponding thresholds in ChQM, due to the larger mass of the b quark than that of the c quark, which induces the fact that the kinetic energy of the former is lower than of the latter. No state appears in BCN means that the meson-exchange interaction between u(d, s) and $\bar{u}(\bar{d}, \bar{s})$ plays an important role. (2) If we do not take into account the effective mass of the gluon in annihilation interaction, namely $m_g=0$ in Eq. (20), no bound states of $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ are found both in BCN and ChQM since the annihilation interaction is repulsive in this case. (3) With a finite effective mass of the gluon, almost all states under investigation can form molecules, having energies lower than the corresponding thresholds, and the binding energies decrease with the increasing effective mass of gluon. These results can be understood with the expression of Eq. (20), where the magnitude of the denominator $4m_q^2-m_g^2$ increases with the increasing $m_g$ when $m_g> 2m_q \approx 626{-}674$ MeV. So the results are sensitive to the effective mass of gluon. We choose 0.9–1.0 GeV for the effective gluon mass, which is in accord with the effective constituent gluon mass found in the study of gluon dynamics in Ref. [57] and the glueball–quarkonia content of the scalar–isoscalar mesons in Ref. [49]. For the $D^{*}\bar{D}$ system, $D^{*}\bar{D}$ with $J^{PC}=1^{++}$ has about 2.5 and 16.2 MeV binding energy for ChQM and BCN, respectively. The reason for the difference between the two models is that different masses of the u, d quarks in BCN and ChQM are used, and the annihilation interaction of Eq. (20) is sensitive to the quark mass. If we take 1 GeV for effective gluon mass in BCN, which was chosen in Ref. [27], the same binding energy as that of ChQM, 2.6 MeV is obtained. It is well known that X(3872) was first found by the Belle Collaboration in the $J/\psi \pi ^+\pi ^-$ invariant mass spectrum in the decays of $B^\pm \longrightarrow K\pm J/\psi \pi ^+\pi ^-$. D0, BaBar, CDF, CMS, BESIII, and LHCb have later confirmed X(3872) by decays of the $B^{\pm ,0}$ mesons and pp collisions, and one affirmed the quantum numbers $I^G(J^{PC})=0^+(1^{++})$. The average mass of X(3872) listed in PDG is $3871.69\pm 0.17$ MeV, which is lower by about 1 MeV than the threshold of $D^{*}\bar{D}$. Obviously, our results listed in Tables 4 and 5 agree well with the experimental data when we choose the reasonable parameters which are suggested by Giacosa, Gutsche, and Faessler in Ref. [49]. The weakly bound states of $D^{*}\bar{D}^{*}$ with $J^{PC}=2^{++}$ are also obtained in our calculation. (4) For the $B^{(*)}\bar{B}^{(*)}$ system, four bound states are obtained when we take into account the annihilation interaction. The bound state of $B^{*}\bar{B}$ with $J^{PC}=1^{+-}$ is a good candidate for $Z_b^0(10610)$, which was firstly found in the $\Upsilon (2,3S)\pi ^0$ invariant mass spectrum in the $\Upsilon (10860)\rightarrow \Upsilon (1,2,3S)\pi ^0\pi ^0$ by the Belle Collaboration [58].

With the new parameters of BCN and ChQM shown in Table 1, we obtain the spectra of the S-wave $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ listed in Tables 6 and 7. Almost the same bound states as those listed in Tables 4 and 5 are obtained with the same effective mass of gluon, respectively. Obviously, the energy spectra of two molecular states $D^{*}\bar{D}$ with $I^G(J^{PC})=0^+(1^{++})$ and $B^{*}\bar{B}$ with $J^{PC}=1^{+-}$ agree well with the experimental data $3871.69\pm 0.17$ MeV for X(3872) and $10{,}609\pm 4\pm 4$ MeV for $Z_b^0(10{,}610)$, respectively. Two sets of model parameters give almost the same results, which is reasonable, because the difference between the energy of the four-quark system and the sum of the theoretical masses of the involved two mesons is taken as the binding energy. The error in calculating the masses of the mesons and the error in calculating the energy of the four-quark state are expected to cancel each other. Of course, the cancelation cannot be exact. $D\bar{D}$ with $m_g=0.9$ GeV in Table 7 is a bound state ($\Delta E=-0.7$ MeV), whereas the corresponding state in Table 5 is unbound. The reason is that the larger mass of c-quark is used in the new parameters; the kinetic energy for the relative motion is smaller. To see more clearly which terms in the Hamiltonian are responsible for the binding behavior of the system, for example, $D\bar{D}^*$, we list the individual contributions of ChQM model with the parameters ‘ChQM$_\mathrm{new}$’ and $m_g = 1$ GeV in Table 8. From the table, we can see that the contribution of kinetic energy and mass terms are positive, which almost cancel with that from OGE + OBE + confinement. Finally, the contribution from the annihilation between $u\bar{u}$ makes the system bound. In Table 8, the contribution from annihilation between $c\bar{c}$ is also listed, which is very small, $-0.2$ MeV, compared with that from the annihilation between $u\bar{u}$, which is $-5.8$ MeV.

Table 8 The contribution from the terms of ChQM with the parameter set ‘ChQM$_\mathrm{new}$’ and $m_g = 1$ GeV (unit: MeV)

5 Summary

The constituent quark models are extended by introducing the s-channel one-gluon-exchange interaction, which does not appear in the conventional mesons of $q\bar{q}$. We dynamically calculate the spectra of the S-wave $D^{(*)}\bar{D}^{(*)}$ and $B^{(*)}\bar{B}^{(*)}$ systems in the extended quark models. The annihilation interaction is repulsive if the effective gluon mass is not taken into account. However, if we take a massive gluon propagator and a reasonable effective gluon mass in the s-channel one-gluon-exchange interaction, two molecular states $D^{*}\bar{D}$ with $I^G(J^{PC})=0^+(1^{++})$ and $B^{*}\bar{B}$ with $J^{PC}=1^{+-}$ are obtained, which are good candidates for X(3872) and $Z^0_b(10610)$, respectively. $D^{*}\bar{D}^{*}$, $B^{*}\bar{B}^{*}$ with $J^{PC}=2^{++}$, $B^{*}\bar{B}$ with $J^{PC}=1^{++}$ and $B\bar{B}$ with $J^{PC}=0^{++}$ are also predicted in these extended constituent quark models. Further experimental searches by LHCb, BaBar, Belle and other collaborations are needed to clarify whether these states exist or not.

In the present calculation, the one-gluon-annihilation interaction with effective gluon mass plays an important role. The interaction does show up in the ordinary mesons even with the same flavor because of the color structure. The effective mass of the gluon is a model parameter, which is not much constrained by the experimental data. Because the calculated results are sensitive to the effective mass of the gluon, a better way to fix this parameter is expected to be found.