Non-minimal flavored ${S}_{3}\otimes {Z}_{2}$ left–right symmetric model

Abstract

We propose a non-minimal left–right symmetric model with parity symmetry where the fermion mixings arise as a result of imposing an $\mathbf{S}_{3}\otimes \mathbf{Z}_{2}$ flavor symmetry, and an extra $\mathbf{Z}^{e}_{2}$ symmetry is considered in the lepton sector. Then the neutrino mass matrix possesses approximately the $\mu$–$\tau$ symmetry. The breaking of the $\mu$–$\tau$ symmetry induces sizable non-zero $\theta _{13}$, and the deviation of $\theta _{23}$ from $45^{\circ }$ is strongly controlled by an $\epsilon$ free parameter and the neutrino masses. So, an analytic study of the CP parities in the neutrino masses is carried out to constrain the $\epsilon$ parameter and the lightest neutrino mass that accommodate the mixing angles. The results are: (a) the normal hierarchy is ruled out for any values of the Majorana phases; (b) for the inverted hierarchy the values of the reactor and atmospheric angles are compatible up to $2, 3~\sigma$ C.L.; (c) the degenerate ordering is the most favorable such that the reactor and atmospheric angle are compatible with the experimental data for a large set of values of the free parameters. The model predicts defined regions for the effective neutrino mass, the neutrino mass scale and the sum of the neutrino masses for the favored cases. Therefore, this model may be testable by the future experiments.

1 Introduction

Currently, we know that neutrinos oscillate and have a tiny mass. In the theoretical framework of three active neutrinos, the difference of the squared neutrino masses for a normal (inverted) hierarchy are given by  $\Delta m^{2}_{21} \left( 10^{-5} \, \text {eV}^{2} \right) = 7.60_{-0.18}^{+0.19},$ and $\left| \Delta m^{2}_{31} \right| \left( 10^{-3} \, \text {eV}^{2} \right) = 2.48_{-0.07}^{+0.05}~ (2.38_{-0.06}^{+0.05})$. Additionally, we have the values of the mixing angles $\sin ^{2} \theta _{12} / 10^{-1} = 3.23 \pm 0.16,$ $\sin ^{2} \theta _{23} / 10^{-1} = 5.67_{-1.24}^{+0.32}~(5.73_{-0.39}^{+0.25})$ and $\sin ^{2} \theta _{13} / 10^{-2}= 2.26 \pm 0.12~(2.29 \pm 0.12)$ [1]. At present, there is not yet solid evidence on the Dirac CP-violating phase and the ordering that respects the neutrino masses. The NO $\nu$ A [2] and KamLAND-Zen [3] collaborations can shed light on the hierarchy in the coming years.

In spite of the fact that the Standard Model (SM) works almost perfectly, the neutrino experimental data cannot be explained within this framework. If the neutrino sector opens the window to the new physics, then what is the new model and the extra ingredients that are needed to accommodate the masses and mixings? Along this line of thought, a simplest route to include small neutrino masses and mixings to the SM is to add the missing right-handed neutrinos (RHNs) states to the matter content, and then invoking the see-saw mechanism [4,5,6,7,8,9,10]. However, we should point out that the RHN mass scale is introduced by hand with no relation whatsoever to the Higgs mechanism, which gives mass to all other fields. Nonetheless, this problem may be alleviated if the minimal extension of the SM is replaced by the left–right symmetric model (LRSM) [7, 11,12,13,14] where the RHNs are already included in the matter content. Additionally, the see-saw mechanism comes in rather naturally in the context of left–right symmetric scenarios; aside from other nice features, as for instance the recovery of parity symmetry, and the appearance of right-handed currents at high energy, which also makes such extensions very appealing. Recently, the left–right scenarios have been revised [15,16,17,18,19,20,21,22,23,24,25] in order to make contact with the latest experimental data of LHC. Moreover, the dark matter problem [26,27,28] and the diphoton excess anomaly [29,30,31,32,33] have been explored in this kind of scenarios.

Explaining the peculiar neutrino mixing pattern (besides the CKM mixing matrix) has been a hard task. Along this line, the mass textures have played an important role in trying to solve this puzzle [34]. In fact, discrete symmetries may be the missing ingredient to understand the mixings so that several groups have been proposed [35,36,37] to get in an elegant way the mass textures. Along this line of thought, the $\mathbf{S}_{3}$ flavor symmetry, in particular, is a good candidate to handle the Yukawa couplings for leptons and quarks; and this has been studied exhaustively in different frameworks [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. In most of this work, the meaning of the flavor has been extended to the scalar sector such that three Higgs doublets are required to accommodate the PMNS and CKM mixing matrices. One motivation to use the $\mathbf{S}_{3}$ flavor symmetry in the lepton sector is to generate the $\mu$–$\tau$ symmetry [60,61,62,63,64,65] which could be the origin of the tribimaximal mixing matrix [66, 67]. In the quark sector, on the other hand, the $\mathbf{S}_{3}$ symmetry may be responsible to get the generalized Fritzsch mass textures which fit quite well the CKM mixing matrix [34, 48, 68].

Although there are too many flavored models in the literature, the LRSM has received few attention in the context of the flavored puzzle [69,70,71]. It is not an easy task to study the mixings in the LRSM since the structure of the gauge group increases the Yukawa sector parameters compared to the SM. However, as was shown in the early work, parity symmetry might reduce substantially the gauge and Yukawa couplings; this last issue gives the opportunity to calculate the right-handed CKM matrix [21, 22], which is crucial to study in great detail the $W_{R}$ gauge boson that comes out being a prediction of the LRMS. Then it is fundamental to face the flavor puzzle in this kind of theoretical frameworks.

Therefore, we propose a non-minimal LRSM with parity symmetry where the fermion mixings arise as a result of imposing an $\mathbf{S}_{3}\otimes \mathbf{Z}_{2}$ flavor symmetry, and an extra $\mathbf{Z}^{e}_{2}$ symmetry is considered to get both diagonal charged lepton and Dirac neutrino mass matrices. Additionally, taking into account the remarkable hierarchy in the quark sector (in contrast to the leptons) a non-conventional assignment is done for the fermion families under the $\mathbf{S}_{3}$ symmetry. As a consequence, the quark mass matrices have implicitly the generalized Fritzsch textures but this sector will be discussed exhaustively in a future work, however, on some preliminary results will be commented. On the other hand, in the lepton sector, the effective neutrino mass matrix possesses approximately the $\mu$–$\tau$ symmetry; for recent work see [72,73,74,75,76,77,78,79]. The breaking of the $\mu$–$\tau$ symmetry induces sizable non-zero $\theta _{13}$, and the deviation of $\theta _{23}$ from $45^{\circ }$ is strongly controlled by an $\epsilon$ free parameter and the complex neutrino masses. Then an analytic study of the CP parity phases is done since these turn out to be relevant to enhance or suppress the reactor and atmospheric angle. Thus, we can constrain the parameter space for the parameter $\epsilon$ and the lightest neutrino mass that accommodate the mixing angles. The highlighted results are: (a) the normal hierarchy is ruled out since the reactor angle comes out being tiny, for any values of the Majorana phases; (b) for the inverted hierarchy there is one combination in the CP parities where the values of the reactor and atmospheric angles are compatible up to $2, 3~\sigma$ C.L., but the parameter space is tight; (c) the model favors the degenerate ordering for one combination in the CP parities. In this case, the reactor and atmospheric angle are compatible with the experimental data for a large set of values of the free parameters. As model predictions, for the favored cases, we obtain the allowed region for the effective neutrino mass, the neutrino mass scale and the sum of the neutrino masses.

The paper is organized as follows: we introduce briefly, in Sect. 2, the minimal LRSM and the $\mathbf{S}_{3}$ discrete symmetry. In addition, we comment the matter content of the model and its non-conventional assignment under the $\mathbf{S}_{3}$ symmetry. At the same time, we argue about the need to include the $\mathbf{Z}^{e}_{2}$ symmetry in the lepton sector. In Sect. 3, the fermion mass matrices are obtained with special attention on the lepton sector for getting the mixing matrices. We present, in Sect. 4, the PMNS matrix that the model predicts and the respective mixing angles. Finally, we present an analytic study of the mixing angles, the results and the predictions in Sect. 5, and we close our discussion with a summary of conclusions.

2 Flavored left–right symmetric model

The minimal LRSM is based on the usual, $SU(3)_{c}\otimes SU(2)_{L}\otimes SU(2)_{R}\otimes U(1)_{B-L}$, gauge symmetry where parity symmetry, $\mathcal {P}$, is assumed to be a symmetry a high energy but it is broken at electroweak scale since there are no right-handed currents. The matter fields and their respective quantum numbers (in parentheses) under the gauge symmetry are given by

$$\begin{aligned}&Q_{(L, R)}=\left( \begin{array}{c} u \\ d \\ \end{array} \right) _{(L, R)}\sim {\left( 3, (2,1), (1,2), 1/3\right) },\nonumber \\&(L, R)=\left( \begin{array}{c} \nu \\ \ell \\ \end{array} \right) _{(L, R)}\sim { (1, (2,1), (1,2), -1)},\nonumber \\&\Phi =\left( \begin{array}{c@{\quad }c} \phi ^{0} &{} \phi ^{'+} \\ \phi ^{-} &{} \phi ^{'0} \\ \end{array} \right) \sim \left( 1, 2, 2, 0 \right) ;\nonumber \\&\Delta _{(L, R)}=\left( \begin{array}{c@{\quad }c} \frac{\delta ^{+}}{2} &{} \delta ^{++} \\ \delta ^{0} &{} -\frac{\delta ^{+}}{2} \\ \end{array} \right) _{(L, R)}\sim \left( 1, (3,1), (1,3), 2 \right) . \end{aligned}$$

(1)

The gauge invariant Yukawa mass term is given by

$$\begin{aligned} -\mathcal {L}_{Y}= & {} \bar{Q}_{L}\big [y^{q}\Phi + \tilde{y}^{q}\tilde{\Phi } \big ]Q_{R}+ \bar{L}\big [y^{\ell }\Phi + \tilde{y}^{\ell }\tilde{\Phi } \big ]\nonumber \\&\times \, R+ y^{L}\bar{L}\Delta _{L}L^{c}+y^{R}\bar{R}^{c}\Delta _{R}R+h.c. \end{aligned}$$

(2)

where the family indices have been suppressed and $\tilde{\Phi }_{i}=-i\sigma _{2}\Phi ^{*}_{i}i\sigma _{2}$. Here, parity symmetry will be assumed in the above Lagrangian, then this requires that $\Psi _{i L}\leftrightarrow \Psi _{i R}$, $\Phi _{i} \leftrightarrow \Phi ^{\dagger }_{i}$ and $\Delta _{i L}\leftrightarrow \Delta ^{\dagger }_{i R}$ for fermions and scalar fields, respectively. Thereby, the Yukawa couplings may reduce substantially and the gauge couplings too. In particular, for the former issue we have $y=y^{\dagger }$, $\tilde{y}=\tilde{y}^{\dagger }$ and $y^{R}=y^{L}$. On the other hand, due to our purpose the scalar potential will be left aside. But in the minimal LRMS the spontaneous symmetry breaking is as follows: parity symmetry is broken at the same scale where the $\Delta _{R}$ right-handed scale acquires its vacuum expectation value (VEV). At the first stage, the RHNs are massive particles, then the rest of the particles turn out massive since the Higgs scalars get their VEVs. Explicitly,

$$\begin{aligned} \langle \Delta _{L, R}\rangle&= \left( \begin{array}{c@{\quad }c} 0 &{} 0 \\ v_{L,R} &{} 0 \\ \end{array} \right) ,\quad \langle \Phi \rangle = \left( \begin{array}{c@{\quad }c} k &{} 0 \\ 0 &{} k^{\prime } \\ \end{array} \right) , \nonumber \\ \langle \tilde{\Phi }\rangle&= \left( \begin{array}{c@{\quad }c} k^{\prime *} &{} 0 \\ 0 &{} k^{*} \\ \end{array} \right) . \end{aligned}$$

(3)

As a result, the Yukawa mass term is given by

$$\begin{aligned} -\mathcal {L}_{Y}&=\bar{q}_{i L} \left( \mathbf{M}_{q} \right) _{ij}q_{j R}+\bar{\ell }_{i L} \left( \mathbf{M}_{\ell }\right) _{ij}\ell _{j R} +\dfrac{1}{2}\bar{\nu }_{i L}\left( \mathbf{M}_{\nu }\right) _{ij}\nu ^{c}_{j L}\nonumber \\&\quad +\dfrac{1}{2}\bar{\nu }^{c}_{i R}\left( \mathbf{M}_{R}\right) _{ij}\nu _{j R}+h.c. \end{aligned}$$

(4)

where the type I see-saw mechanism has been realized, $\mathbf{M}_{\nu }=-\mathbf{M}_{D} \mathbf{M}^{-1}_{R} \mathbf{M}^{T}_{D}$; so that the $\mathbf{M}_{L}$ were neglected for simplicity.

In the present model, the Yukawa mass term will be controlled by the $\mathbf{S}_{3}$ flavor symmetry. The non-Abelian group $\mathbf{S}_{3}$ is the permutation group of three objects and this has three irreducible representations: two 1-dimensional, $\mathbf{1}_{S}$ and $\mathbf{1}_{A}$, and one 2-dimensional representation, $\mathbf{2}$ (for a detailed study see [35]). So, the 3-dimensional real representation can be decomposed as $\mathbf{3}_{S}=\mathbf{2}\oplus \mathbf{1}_{S}$ or $\mathbf{3}_{A}=\mathbf{2}\oplus \mathbf{1}_{A}$. The multiplication rules among the irreducible representations are

(5)

Having introduced briefly the gauge and the non-Abelian group, let us build the gauge and flavored Yukawa mass term. To do this, we will consider three Higgs bidoublets as well as three left–right triplets with the purpose of getting the mixing in the lepton sector. Here, we want to emphasize a clear difference between this model and the previous ones with the $\mathbf{S}_{3}$ symmetry. As is well known, the quark masses exhibit a notable hierarchy among families which means that the physical masses satisfy $m_{u}\ll m_{c}\ll m_{t}$ and $m_{d}\ll m_{s}\ll m_{b}$, this mass spectrum may explain the almost diagonal CKM mixing matrix as was suggested in [34]. Contrarily, at least in the neutrino sector, this hierarchy is not remarkable as regards leptons. Because of this, in our model, the quark and lepton families have been assigned in a different way under the irreducible representations of $\mathbf{S}_{3}$. Explicitly, for the former and the Higgs sector respectively, the first and second family have been put together in a flavor doublet $\mathbf{2}$, and the third family is a singlet $\mathbf{1}_{S}$ ($\mathbf{2}\,\oplus \, \mathbf{1}_{S}$); this choice predicts hierarchical quark mass matrices which may be put into two mass textures (generalized Fritzsch mass textures) fashion that fit the CKM matrix very well as can be found in [34, 48, 68]. On the contrary, for the leptonic sector, the first family is a singlet $\mathbf{1}_{S}$ and the second and third families are put in a doublet $\mathbf{2}$ ($\mathbf{1}_{S}\oplus \mathbf{2}$); this assignation is a natural way to get the $\mu$–$\tau$ symmetry [63, 80,81,82,83]. Remarkably, the NO $\nu$ A collaboration is testing the $\mu$–$\tau$ symmetry and some results have been released [2].

The main aim of this non-conventional assignation for the fermion families is to try of understanding the contrast between the CKM and PMNS mixing matrices. However, this idea might go against the spirit of a unification theory.

The matter content of the model transforms in a non-trivial way under the $\mathbf{S}_{3}$ symmetry and this is displayed in Table 1. Here, the $\mathbf{Z_{2}}$ symmetry has been added in order to prohibit some Yukawa couplings in the lepton sector. Thus, the most general Yukawa mass term that respects the $\mathbf{S}_{3}\otimes \mathbf{Z}_{2}$ flavor symmetry and the gauge group is given as

$$\begin{aligned}&-\mathcal {L}_{Y}=y^{q}_{1}\left[ \bar{Q}_{1 L}\left( \Phi _{1} Q_{2 R}+\Phi _{2} Q_{1 R}\right) +\bar{Q}_{2 L}\left( \Phi _{1} Q_{1 R}-\Phi _{2}Q_{2 R}\right) \right] \nonumber \\&\quad +y^{q}_{2}\left[ \bar{Q}_{1 L}\Phi _{3}Q_{1 R}+\bar{Q}_{2 L}\Phi _{3} Q_{2 R}\right] +y^{q}_{3}\left[ \bar{Q}_{1 L}\Phi _{1}+\bar{Q}_{2 L}\Phi _{2}\right] Q_{3 R}\nonumber \\&\quad +y^{q}_{4}\bar{Q}_{3 L}\left[ \Phi _{1}Q_{1 R}+\Phi _{2}Q_{2 R}\right] +y^{q}_{5}\bar{Q}_{3 L}\Phi _{3}Q_{3 R}\nonumber \\&\quad +\tilde{y}^{q}_{1}\left[ \bar{Q}_{1 L}\left( \tilde{\Phi }_{1} Q_{2 R}+\tilde{\Phi }_{2}Q_{1 R}\right) +\bar{Q}_{2 L}\left( \tilde{\Phi }_{1} Q_{1 R}-\tilde{\Phi }_{2}Q_{2 R}\right) \right] \nonumber \\&\quad +\tilde{y}^{q}_{2}\left[ \bar{Q}_{1 L}\tilde{\Phi }_{3}Q_{1 R}+\bar{Q}_{2 L}\tilde{\Phi }_{3} Q_{2 R}\right] +\tilde{y}^{q}_{3}\left[ \bar{Q}_{1 L}\tilde{\Phi }_{1}+\bar{Q}_{2 L}\tilde{\Phi }_{2}\right] Q_{3 R}\nonumber \\&\quad +\tilde{y}^{q}_{4}\bar{Q}_{3 L}\left[ \tilde{\Phi }_{1}Q_{1 R}+\tilde{\Phi }_{2}Q_{2 R}\right] +\tilde{y}^{q}_{5}\bar{Q}_{3 L}\tilde{\Phi }_{3}Q_{3 R} +y^{\ell }_{1}\bar{L}_{1}\Phi _{3}R_{1}\nonumber \\&\quad +y^{\ell }_{2}\left[ (\bar{L}_{2}\Phi _{2}+\bar{L}_{3}\Phi _{1})R_{2}+(\bar{L}_{2}\Phi _{1}-\bar{L}_{3}\Phi _{2})R_{3} \right] \nonumber \\&\quad +y^{\ell }_{3}\left[ \bar{L}_{2}\Phi _{3}R_{2}+\bar{L}_{3}\Phi _{3}R_{3}\right] + \tilde{y}^{\ell }_{1}\bar{L}_{1}\tilde{\Phi }_{3}R_{1}\nonumber \\&\quad +\tilde{y}^{\ell }_{2}\left[ (\bar{L}_{2}\tilde{\Phi }_{2}+\bar{L}_{3}\tilde{\Phi }_{1})R_{2}+(\bar{L}_{2}\tilde{\Phi }_{1}-\bar{L}_{3}\tilde{\Phi }_{2})R_{3} \right] \nonumber \\&\quad +\tilde{y}^{\ell }_{3}\left[ \bar{L}_{2}\tilde{\Phi }_{3}R_{2}+\bar{L}_{3}\tilde{\Phi }_{3}R_{3}\right] \nonumber \\&\quad +y^{L}_{1}\bar{L}_{1}\Delta _{3L}L^{c}_{1}+y^{L}_{2}\bar{L}_{1}\left[ \Delta _{1 L}L^{c}_{2}+\Delta _{2 L}L^{c}_{3}\right] \nonumber \\&\quad +y^{L}_{3} \left[ \bar{L}_{2}\Delta _{1 L}+\bar{L}_{3}\Delta _{2 L}\right] L^{c}_{1}+y^{L}_{4}\left[ \bar{L}_{2}\Delta _{3 L}L^{c}_{2}+\bar{L}_{3}\Delta _{3 L}L^{c}_{3}\right] \nonumber \\&\quad +y^{R}_{1}\bar{R}^{c}_{1}\Delta _{3 R}R_{1}+ y^{R}_{2}\bar{R}^{c}_{1}\left[ \Delta _{1 R}R_{2}+\Delta _{2 R}R_{3}\right] \nonumber \\&\quad +y^{R}_{3}\left[ \bar{R}^{c}_{2}\Delta _{1 R}+\bar{R}^{c}\Delta _{2 R}\right] R_{1}\nonumber \\&\quad + y^{R}_{4}\left[ \bar{R}^{c}_{2}\Delta _{3 R}R_{2}+\bar{R}^{c}_{3}\Delta _{3 R}R_{3}\right] +h.c. \end{aligned}$$

(6)

Table 1 Non-minimal left–right model. Here, $I=1,2$ and $J=2,3$

In this flavored model, we have to keep in mind that parity symmetry will be assumed in the above Lagrangian in such a way that the number of Yukawa couplings is reduced. Moreover, we do stress that an extra symmetry $\mathbf{Z}^{e}_{2}$ is used to get a diagonal charged lepton and Dirac neutrino mass matrix whereas the Majorana mass matrices retain their forms. Explicitly, in the above Lagrangian, we require that

$$\begin{aligned}&L_{3}\leftrightarrow -L_{3},\quad R_{3}\leftrightarrow -R_{3},\quad \Delta _{2 L}\leftrightarrow -\Delta _{2 L},\nonumber \\&\quad \Delta _{2 R}\leftrightarrow -\Delta _{2 R}, \end{aligned}$$

(7)

so that the terms $\bar{L}_{2}R_{3}$ and $\bar{L}_{3}R_{2}$ are absent in the lepton sector. As was already commented on, because of our interest in studying masses and mixings for fermions, the scalar potential will not be analyzed for the moment. We ought to comment that this study is not trivial since the scalar sector has been augmented, so that the potential is rather complicated, but this study has to be done eventually since is crucial for theoretical and phenomenological purpose.

From Eqs. (3) and (6), the mass matrices have the following structure:

$$\begin{aligned}&\mathbf{M}_{q}= \begin{pmatrix} a_{q}+b^{\prime }_{q} &{}\quad b_{q} &{}\quad c_{q} \\ b_{q} &{}\quad a_{q}-b^{\prime }_{q} &{}\quad c^{\prime }_{q} \\ f_{q} &{}\quad f^{\prime }_{q} &{}\quad g_{q} \end{pmatrix},\nonumber \\&\mathbf{M}_{\ell }= \begin{pmatrix} a_{\ell } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad b_{\ell }+c_{\ell } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad b_{\ell }-c_{\ell } \end{pmatrix} ,\nonumber \\&\mathbf{M}_{(L, R)}= \begin{pmatrix} a_{(L, R)} &{}\quad b_{(L, R)} &{}\quad b^{\prime }_{(L, R)} \\ b_{(L, R)} &{}\quad c_{(L, R)} &{}\quad 0 \\ b^{\prime }_{(L, R)} &{}\quad 0 &{}\quad c_{(L, R)} \end{pmatrix}, \end{aligned}$$

(8)

where the $q= u, d$ and $\ell =e, \nu _{D}$. Explicitly, the matrix elements for quarks and leptons are given as

$$\begin{aligned}&a_{u}=y^{q}_{2}k_{3}+\tilde{y}^{q}_{2}k^{\prime *}_{3},\quad b^{\prime }_{u}=y^{q}_{1}k_{2}+\tilde{y}^{q}_{1}k^{\prime *}_{2},\nonumber \\&b_{u}=y^{q}_{1}k_{1}+\tilde{y}^{q}_{1}k^{\prime *}_{1},\quad c_{u}=y^{q}_{3}k_{1}+\tilde{y}^{q}_{3}k^{\prime *}_{1},\,\nonumber \\&c^{\prime }_{u}=y^{q}_{3}k_{2}+\tilde{y}^{q}_{3}k^{\prime *}_{2},\quad f_{u}= y^{\dagger q}_{3}k_{1}+\tilde{y}^{\dagger q}_{3}k^{\prime *}_{1},\nonumber \\&f^{\prime }_{u}= y^{\dagger q}_{3}k_{2}+\tilde{y}^{\dagger q}_{3}k^{\prime *}_{2} ,\quad g_{u}=y^{q}_{5}k_{3}+\tilde{y}^{q}_{5}k^{\prime *}_{3},\nonumber \\&a_{d}=y^{q}_{2}k^{\prime }_{3}+\tilde{y}^{q}_{2}k^{*}_{3},\quad b^{\prime }_{d}=y^{q}_{1}k^{\prime }_{2}+\tilde{y}^{q}_{1}k^{*}_{2},\nonumber \\&b_{d}=y^{q}_{1}k^{\prime }_{1}+\tilde{y}^{q}_{1}k^{*}_{1},\quad c_{d}=y^{q}_{3}k^{\prime }_{1}+\tilde{y}^{q}_{3}k^{*}_{1};\nonumber \\&c^{\prime }_{d}=y^{q}_{3}k^{\prime }_{2}+\tilde{y}^{q}_{3}k^{*}_{2},\quad f_{d}= y^{\dagger q}_{3}k^{\prime }_{1}+\tilde{y}^{\dagger q}_{3}k^{*}_{1},\nonumber \\&f^{\prime }_{d}= y^{\dagger q}_{3}k^{\prime }_{2}+\tilde{y}^{\dagger q}_{3}k^{*}_{2} ,\quad g_{d}=y^{q}_{5}k^{\prime }_{3}+\tilde{y}^{q}_{5}k^{*}_{3},\nonumber \\&a_{D}=y^{\ell }_{1}k_{3}+\tilde{y}^{\ell }_{1}k^{\prime *}_{3},\quad b_{D}=y^{\ell }_{3}k_{3}+\tilde{y}_{3}k^{\prime *}_{3},\nonumber \\&c_{D}=y^{\ell }_{2}k_{2}+\tilde{y}_{2}k^{\prime *}_{2},\quad a_{e}=y^{\ell }_{1}k^{\prime }_{3}+\tilde{y}^{\ell }_{1}k^{*}_{3},\nonumber \\&b_{e}=y^{\ell }_{3}k^{\prime }_{3}+\tilde{y}_{3}k^{*}_{3},\quad c_{e}=y^{\ell }_{2}k^{\prime }_{2}+\tilde{y}_{2}k^{*}_{2},\nonumber \\&a_{(L, R)}=y^{R}_{1}v_{1(L, R)},\quad b_{(L, R)}=y^{R}_{2}v_{2(L, R)},\nonumber \\&b^{\prime }_{(L, R)}=y^{R}_{2}v_{3(L, R)},\quad c_{(L, R)}=y^{R}_{4}v_{1(L, R)}, \end{aligned}$$

(9)

where parity symmetry has been considered. Remarkably, we will end up having a complex symmetric (diagonal) quark (lepton) mass matrix if the VEVs are complex; in the literature this scenario is known as the pseudomanifest left–right symmetry [84, 85]. If the VEVs are real, the quark (lepton) mass matrix is hermitian (real) and the number of CP phases are reduced, this framework is known as the manifest left–right symmetry [84, 86]. In this work, we will discuss only the first framework and the second one will be studied in an extended version of the model and its consequences on the quark sector.

3 Masses and mixings

In principle, in the mass matrices, we can reduce a further the number of free parameters considering certain alignment in the VEVs; see Eq. (9). Thus, for the moment, we will assume that the VEVs of $\Phi _{1}$ and $\Phi _{2}$ are degenerate. Explicitly, we demand that $k_{1}=k_{2}\equiv k$ and $k^{\prime }_{1}=k^{\prime }_{2}\equiv k^{\prime }$. Additionally, $v_{1 R}=v_{2 R}=v_{R}$. Therefore, we have the following.

Pseudomanisfest left–right theory

$$\begin{aligned}&\mathbf{M}_{q}= \begin{pmatrix} a_{q}+b_{q} &{}\quad b_{q} &{}\quad c_{q} \\ b_{q} &{}\quad a_{q}-b_{q} &{}\quad c_{q} \\ c_{q} &{}\quad c_{q} &{}\quad g_{q} \end{pmatrix},\nonumber \\&\mathbf{M}_{\ell }= \begin{pmatrix} a_{\ell } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad b_{\ell }+c_{\ell } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad b_{\ell }-c_{\ell } \end{pmatrix} ,\nonumber \\&\mathbf{M}_{(L, R)}= \begin{pmatrix} a_{(L, R)} &{}\quad b_{(L, R)} &{}\quad b_{(L, R)} \\ b_{(L, R)} &{}\quad c_{(L, R)} &{}\quad 0 \\ b_{(L, R)} &{}\quad 0 &{}\quad c_{(L, R)} \end{pmatrix}. \end{aligned}$$

(10)

Manifest left–right theory

$$\begin{aligned}&\mathbf{M}_{q}= \begin{pmatrix} a_{q}+b_{q} &{}\quad b_{q} &{}\quad c_{q} \\ b_{q} &{}\quad a_{q}-b_{q} &{}\quad c_{q} \\ c^{*}_{q} &{}\quad c^{*}_{q} &{}\quad g_{q} \end{pmatrix},\nonumber \\&\mathbf{M}_{\ell }= \begin{pmatrix} a_{\ell } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad b_{\ell }+c_{\ell } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad b_{\ell }-c_{\ell } \end{pmatrix} ,\nonumber \\&\mathbf{M}_{(L, R)}= \begin{pmatrix} a_{(L, R)} &{}\quad b_{(L, R)} &{}\quad b_{(L, R)} \\ b_{(L, R)} &{}\quad c_{(L, R)} &{}\quad 0 \\ b_{(L, R)} &{}\quad 0 &{}\quad c_{(L, R)} \end{pmatrix}. \end{aligned}$$

(11)

As was already commented on at the beginning, the full analysis of the quark masses and mixings will be left aside for this moment. However, we just make a brief comment on the results that one expects. In the pseudomanifest framework, the $\mathbf{M}_{q}$ mass matrix may be put into two mass textures fashion that fit the CKM matrix very well. To be more specific, $\mathbf{M}_{q}$ is diagonalized by $\mathbf{U}_{q (L, R)}=\mathbf{U}_{\pi /4}\tilde{\mathbf{u}}_{q (L,R)}$ where $\hat{\mathbf{M}}_{q}=\text {diag.}(m_{q_{1}},m_{q_{2}},m_{q_{3}})=\mathbf{U}^{\dagger }_{q L}{} \mathbf{M}_{q}{} \mathbf{U}_{q R}=\tilde{\mathbf{u}}^{\dagger }_{q L}{} \mathbf{m}_{q}\tilde{\mathbf{u}}_{q R}$ with

$$\begin{aligned}&\mathbf{m}_{q}=\mathbf{U}^{T}_{\pi /4}{} \mathbf{M}_{q}{} \mathbf{U}_{\pi /4}= \begin{pmatrix} B_{q}&{}\quad b_{q} &{}\quad 0 \\ b_{q} &{}\quad A_{q} &{}\quad \sqrt{2}c_{q} \\ 0 &{}\quad \sqrt{2} c_{q} &{}\quad g_{q} \end{pmatrix},\nonumber \\&\mathbf{u}_{\pi /4}= \begin{pmatrix} \dfrac{1}{\sqrt{2}} &{}\quad \dfrac{1}{\sqrt{2}} &{}\quad 0 \\ -\dfrac{1}{\sqrt{2}} &{}\quad \dfrac{1}{\sqrt{2}} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{pmatrix}, \end{aligned}$$

(12)

where $A_{q}\equiv a_{q}+b_{q}$ and $B_{q}\equiv a_{q}-b_{q}$. Factorizing the CP phases of $\mathbf{m}_{q}$ as $\mathbf{m}_{q}=\mathbf{P}_{q} \bar{\mathbf{m}}_{q} \mathbf{P}_{q}$, we choose appropriately, $\tilde{\mathbf{u}}_{q L}= \mathbf{P}_{q}{} \mathbf{O}_{q}$ and $\tilde{\mathbf{u}}_{q R}= \mathbf{P}^{\dagger }_{q} \mathbf{O}_{q}$. In this way, $\mathbf{P}_{q}=\text {diag.}(\exp {i\eta _{q_{1}}}, \exp {i\eta _{q_{2}}}, \exp {i\eta _{q_{3}}})$ where the phases should satisfy

$$\begin{aligned}&\eta _{q_{1}}=arg[B_{q}]/2,\quad \eta _{q_{2}}=arg[A_{q}]/2,\quad \eta _{q_{3}}=arg[d_{q}]/2,\nonumber \\&\quad \eta _{q_{1}}+\eta _{q_{2}}=2 arg[b_{q}],\quad \eta _{q_{2}}+\eta _{q_{3}}=2 arg[c_{q}]. \end{aligned}$$

(13)

Thus, we obtain $\mathbf{O}^{T}_{q}\bar{\mathbf{m}}_{q} \mathbf{O}_{q}=\hat{\mathbf{M}}_{q}$. Actually, $\bar{\mathbf{m}}_{q}$ can be rewritten as

$$\begin{aligned} \bar{\mathbf{m}}_{q}=\vert B_{q}\vert \mathbf{1}_{3\times 3}+ \begin{pmatrix} 0 &{}\quad \vert b_{q} \vert &{}\quad 0 \\ \vert b_{q} \vert &{}\quad \vert A_{q}\vert -\vert B_{q}\vert &{}\quad \sqrt{2}\vert c_{q} \vert \\ 0 &{}\quad \sqrt{2}\vert c_{q} \vert &{}\quad \vert g_{q} \vert -\vert B_{q}\vert \end{pmatrix} \end{aligned}$$

(14)

where the second matrix, in the right side, possesses two zero textures but displacement by the $\vert B_{q}\vert \mathbf{1}_{3\times 3}$ matrix. This kind of matrices accommodated the CKM matrix as was showed in [34, 48, 68]. In a similar way, the manifest framework may be tackled. In this case, the quark mass matrix has fewer free parameters than the above framework since this is hermitian; the study, and its predictions on the mixing angles on the former and latter scenario is a work in progress.

3.1 Charged leptons

The $\mathbf{M}_{e}$ mass matrix is complex and diagonal then one could identify straight the physical masses, however, we will make a similarity transformation in order to prohibit a fine tuning in the free parameters. What we mean is the following: the $\mathbf{M}_{e}$ mass matrix is diagonalized by $\mathbf{U}_{e L}=\mathbf{S}_{23}\mathbf{P}_{e}$ and $\mathbf{U}_{e R}=\mathbf{S}_{23}{} \mathbf{P}^{\dagger }_{e}$, this is, ${\hat{\mathbf{M}}_{e}}=\text {diag.}(\vert m_{e}\vert , \vert m_{\mu }\vert ,\vert m_{\tau }\vert )=\mathbf{U}^{\dagger }_{e L}{} \mathbf{M}_{e}{} \mathbf{U}_{e R} =\mathbf{P}^{\dagger }{} \mathbf{m}_{e}{} \mathbf{P}^{\dagger }_{e}$ with $\mathbf{m}_{e}=\mathbf{S}^{T}_{23}{} \mathbf{M}_{e}{} \mathbf{S}_{23}$. After factorizing the phases, we have $\mathbf{m}_{e}=\mathbf{P}_{e}{\bar{\mathbf{m}}_\mathbf{e}}{} \mathbf{P}_{e}$ where

$$\begin{aligned}&\mathbf{m}_{e}=\text {diag.}(m_{e}, m_{\mu }, m_{\tau }),\quad \mathbf{S}_{23}= \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 1 &{}\quad 0 \end{pmatrix},\nonumber \\&\quad \mathbf{P}_{e}=\text {diag.}(e^{i\eta _{e}}, e^{i\eta _{\mu }}, e^{i\eta _{\tau }}) \end{aligned}$$

(15)

As result, one obtains that $\vert m_{e}\vert =\vert a_{e}\vert$, $\vert m_{\mu }\vert =\vert b_{e}-c_{e}\vert$ and $\vert m_{\tau }\vert =\vert b_{e}+c_{e}\vert$.

3.2 Neutrinos

On the other hand, the $\mathbf{M}_{\nu }$ effective neutrino mass matrix is given as

$$\begin{aligned}&\mathbf{M}_{\nu }= \begin{pmatrix} \mathcal {X}a^{2}_{D}&{}\quad -a_{D}\mathcal {Y}(b_{D}+c_{D}) &{}\quad -a_{D}\mathcal {Y}(b_{D}-c_{D}) \\ -a_{D}\mathcal {Y}(b_{D}+c_{D})&{}\quad \mathcal {W}(b_{D}+c_{D})^{2} &{}\quad \mathcal {Z}(b^{2}_{D}-c^{2}_{D}) \\ -a_{D}\mathcal {Y}(b_{D}-c_{D})&{}\quad \mathcal {Z}(b^{2}_{D}-c^{2}_{D}) &{}\quad \mathcal {W}(b_{D}-c_{D})^{2} \end{pmatrix}\nonumber \\&\text {where}\quad \mathbf{M}^{-1}_{R}\equiv \begin{pmatrix} \mathcal {X}&{} -\mathcal {Y} &{} -\mathcal {Y} \\ -\mathcal {Y} &{} \mathcal {W} &{} \mathcal {Z} \\ -\mathcal {Y} &{} \mathcal {Z} &{} \mathcal {W} \end{pmatrix}. \end{aligned}$$

(16)

Now as a hypothesis, we will assume that $b_{D}$ is larger than $c_{D}$, in this way the effective mass matrix can be written as

$$\begin{aligned} \mathbf{M}_{\nu }\equiv \begin{pmatrix} A_{\nu }&{}\quad -B_{\nu }(1+\epsilon ) &{}\quad -B_{\nu }(1-\epsilon ) \\ -B_{\nu }(1+\epsilon )&{}\quad C_{\nu }(1+\epsilon )^{2} &{}\quad D_{\nu }(1-\epsilon ^{2}) \\ -B_{\nu }(1-\epsilon )&{}\quad D_{\nu }(1-\epsilon ^{2}) &{}\quad C_{\nu }(1-\epsilon )^{2} \end{pmatrix} \end{aligned}$$

(17)

where $A_{\nu }\equiv \mathcal {X}a^{2}_{D}$, $B_{\nu } \equiv \mathcal {Y}a_{D}b_{D}$, $C_{\nu }\equiv \mathcal {W}b^{2}_{D}$ and $D_{\nu }\equiv \mathcal {Z}b^{2}_{D}$ are complex. Besides, $\epsilon \equiv c_{D}/b_{D}$ is complex too. Here, we want to stress that the last parameter will be considered as a perturbation to the effective mass matrix such that $\vert \epsilon \vert \lll 1$. To be more specific, $\vert \epsilon \vert \le 0.3$ in order to break softly the $\mu$–$\tau$ symmetry. Thus, hereafter, we will neglect the $\epsilon ^{2}$ quadratic terms in the above matrix. Having done this, we go back to the effective neutrino mass matrix. In order to cancel the $\mathbf{S}_{23}$ contribution that comes from the charged lepton sector, we deal as follows with $\mathbf{M}_{\nu }$. We know that $\hat{\mathbf{M}}_{\nu }=\text {diag.}(m_{\nu _{1}}, m_{\nu _{2}}, m_{\nu _{3}})=\mathbf{U}^{\dagger }_{\nu }{} \mathbf{M}_{\nu }{} \mathbf{U}^{*}_{\nu }$, then $\mathbf{U}_{\nu }=\mathbf{S}_{23}{} \mathbf{\mathcal {U}_{\nu }}$ where the latter mixing matrix will be obtained below. Then $\hat{\mathbf{M}}_{\nu }=\mathbf{\mathcal {U}^{\dagger }_{\nu }}{} \mathbf{\mathcal {M}_{\nu }}{} \mathbf{\mathcal {U}^{*}_{\nu }}$ with

$$\begin{aligned} \mathbf{\mathcal {M}_{\nu }}&= \mathbf{S}^{T}_{23}{} \mathbf{M}_{\nu }{} \mathbf{S}_{23}\nonumber \\ {}&\approx \begin{pmatrix} A_{\nu }&{}\quad -B_{\nu }(1-\epsilon ) &{}\quad -B_{\nu }(1+\epsilon ) \\ -B_{\nu }(1-\epsilon )&{}\quad C_{\nu }(1-2\epsilon ) &{}\quad D_{\nu } \\ -B_{\nu }(1+\epsilon )&{}\quad D_{\nu } &{}\quad C_{\nu }(1+2\epsilon ) \end{pmatrix}. \end{aligned}$$

(18)

When the $\epsilon$ parameter is switched off the effective mass matrix, which is denoted by $\mathbf{\mathcal {M}^{0}_{\nu }}$, possesses the $\mu$–$\tau$ symmetry and this is diagonalized by

$$\begin{aligned} \mathbf{\mathcal {U}}^{0}_{\nu }= \begin{pmatrix} \cos {\theta }_{\nu }~e^{i(\eta _{\nu }+\pi )} &{}\quad \sin {\theta }_{\nu }~e^{i(\eta _{\nu }+\pi )} &{}\quad 0 \\ -\frac{\sin {\theta }_{\nu }}{\sqrt{2}}&{}\quad \frac{\cos {\theta }_{\nu }}{\sqrt{2}} &{}\quad -\frac{1}{\sqrt{2}} \\ -\frac{\sin {\theta }_{\nu }}{\sqrt{2}}&{}\quad \frac{\cos {\theta }_{\nu }}{\sqrt{2}} &{}\quad \frac{1}{\sqrt{2}} \end{pmatrix} \end{aligned}$$

(19)

where the $\mathbf{\mathcal {M}^{0}_{\nu }}$ matrix elements are fixed in terms of the complex neutrinos physical masses, the $\theta _{\nu }$ free parameter and the $\eta _{\nu }$ Dirac CP phase. To be more explicit,

$$\begin{aligned}&A_{\nu }=(m^{0}_{\nu _{1}}\cos ^{2}{\theta }_{\nu }+m^{0}_{\nu _{2}}\sin ^{2}{\theta }_{\nu })e^{2i(\eta _{\nu }+\pi )},\nonumber \\&-B_{\nu }=\frac{\sin {2\theta _{\nu }}}{\sqrt{8}}(m^{0}_{\nu _{2}}-m^{0}_{\nu _{1}})e^{i(\eta _{\nu }+\pi )};\nonumber \\&C_{\nu }=\frac{1}{2}(m^{0}_{\nu _{1}}\sin ^{2}{\theta }_{\nu }+m^{0}_{\nu _{2}}\cos ^{2}{\theta }_{\nu }+m^{0}_{\nu _{3}}),\nonumber \\&D_{\nu }=\frac{1}{2}(m^{0}_{\nu _{1}}\sin ^{2}{\theta }_{\nu }+m^{0}_{\nu _{2}}\cos ^{2}{\theta }_{\nu }-m^{0}_{\nu _{3}}). \end{aligned}$$

(20)

Including the $\epsilon$ parameter we can write the effective mass matrix as $\mathbf{\mathcal {M}}_{\nu }=\mathbf{\mathcal {M}^{0}_{\nu }}+\mathbf{\mathcal {M}^{\epsilon }_{\nu }}$ where the second matrix contains the perturbation, then, when we apply $\mathbf{\mathcal {U}^{0}_{\nu }}$, we get $\mathbf{\mathcal {M}}_{\nu }=\mathbf{\mathcal {U}^{0\dagger }_{\nu }}(\mathbf{\mathcal {M}^{0}_{\nu }}+\mathbf{\mathcal {M}^{\epsilon }_{\nu }})\mathbf{\mathcal {U}^{0 *}_{\nu }}$. Explicitly

$$\begin{aligned}&\mathbf{\mathcal {M}}_{\nu }=\text {Diag.}(m^{0}_{\nu _{1}}, m^{0}_{\nu _{2}}, m^{0}_{\nu _{3}})+\begin{pmatrix} 0 &{}\quad &{}\quad -\sin {\theta _{\nu }}(m^{0}_{\nu _{3}}+m^{0}_{\nu _{1}})\epsilon \\ 0 &{}\quad 0 &{}\quad \cos {\theta _{\nu }}(m^{0}_{\nu _{3}}+m^{0}_{\nu _{2}})\epsilon \\ -\sin {\theta _{\nu }}(m^{0}_{\nu _{3}}+m^{0}_{\nu _{1}})\epsilon &{}\quad \cos {\theta _{\nu }}(m^{0}_{\nu _{3}}+m^{0}_{\nu _{2}})\epsilon &{}\quad 0 \end{pmatrix}. \end{aligned}$$

(21)

The contribution of second matrix to the mixing one is given by

$$\begin{aligned} \mathbf{\mathcal {U}}^{\epsilon }_{\nu }\approx \begin{pmatrix} N_{1}&{} 0 &{} -N_{3}\sin {\theta _{\nu }}r_{1}\epsilon \\ 0 &{} N_{2} &{} N_{3}\cos {\theta _{\nu }}r_{2}\epsilon \\ N_{1}\sin {\theta _{\nu }}r_{1}\epsilon &{} -N_{2}\cos {\theta _{\nu }}r_{2}\epsilon &{} N_{3} \end{pmatrix} \end{aligned}$$

(22)

where we have defined the complex mass ratios $r_{(1, 2)}\equiv (m^{0}_{\nu _{3}}+m^{0}_{\nu _{(1, 2)}})/(m^{0}_{\nu _{3}}-m^{0}_{\nu _{(1, 2)}})$. Here, $N_{1}$, $N_{2}$ and $N_{3}$ are the normalization factors which are given as

$$\begin{aligned}&N_{1}{=}\left( 1{+}\sin ^{2}{\theta _{\nu }}\vert r_{1}\epsilon \vert ^{2}\right) ^{-1/2},\,N_{2}{=}\left( 1{+}\cos ^{2}{\theta _{\nu }}\vert r_{2}\epsilon \vert ^{2}\right) ^{-1/2},\nonumber \\&N_{3}=\left( 1+\sin ^{2}{\theta _{\nu }}\vert r_{1}\epsilon \vert ^{2}+\cos ^{2}{\theta _{\nu }}\vert r_{2}\epsilon \vert ^{2}\right) ^{-1/2}. \end{aligned}$$

(23)

Finally, the effective mass matrix given in Eq.(17) is diagonalized approximately by $\mathbf{U}_{\nu }\approx \mathbf{S}_{23}\mathbf{\mathcal {U}^{0}_{\nu }{} \mathbf{\mathcal {U}^{\epsilon }_{\nu }}}$. Therefore, the theoretical PMNS mixing matrix is written as $V_{PMNS}=\mathbf{U}^{\dagger }_{e L}{} \mathbf{U}_{\nu }\approx \mathbf{P}^{\dagger }_{e}\mathbf{\mathcal {U}^{0}_{\nu }{} \mathbf{\mathcal {U}^{\epsilon }_{\nu }}}$.

4 PMNS mixing matrix

The PMNS mixing matrix is given explicitly as

$$\begin{aligned}&{} \mathbf{V}_\mathrm{PMNS}\approx \mathbf{P}^{\dagger }_{e}\begin{pmatrix} \cos {\theta _{\nu }}N_{1}e^{i(\eta _{\nu }+\pi )}&{}\quad \sin {\theta _{\nu }}N_{2}e^{i(\eta _{\nu }+\pi )} &{}\quad \sin {2\theta _{\nu }}\frac{N_{3}}{2}(r_{2}-r_{1})\epsilon e^{i(\eta _{\nu }+\pi )} \\ -\frac{\sin {\theta _{\nu }}}{\sqrt{2}}N_{1}(1+r_{1}\epsilon )&{}\quad \frac{\cos {\theta _{\nu }}}{\sqrt{2}}N_{2}(1+r_{2}\epsilon ) &{}\quad -\frac{N_{3}}{\sqrt{2}}\left[ 1-\epsilon ~r_{3}\right] \\ -\frac{\sin {\theta _{\nu }}}{\sqrt{2}}N_{1}(1-r_{1}\epsilon )&{}\quad \frac{\cos {\theta _{\nu }}}{\sqrt{2}}N_{2}(1-r_{2}\epsilon ) &{}\quad \frac{N_{3}}{\sqrt{2}}\left[ 1+\epsilon ~ r_{3}\right] \end{pmatrix} \end{aligned}$$

(24)

where $r_{3}\equiv r_{2}\cos ^{2}{\theta _{\nu }}+r_{1}\sin ^{2}{\theta _{\nu }}$. On the other hand, comparing the magnitude of entries $\mathbf{V}_\mathrm{PMNS}$ with the mixing matrix in the standard parametrization of the PMNS, we obtain the following expressions for the lepton mixing angles:

$$\begin{aligned}&\sin ^{2}{\theta }_{13}=\vert \mathbf{V}_{13}\vert ^{2} =\frac{\sin ^{2}{2\theta _{\nu }}}{4}N^{2}_{3}\vert \epsilon \vert ^{2}~\vert r_{2}-r_{1} \vert ^{2},\nonumber \\&\sin ^{2}{\theta }_{23}=\dfrac{\vert \mathbf{V}_{23}\vert ^{2}}{1-\vert \mathbf{V}_{13}\vert ^{2}}=\dfrac{N^{2}_{3}}{2}\frac{\vert 1-\epsilon ~r_{3} \vert ^{2}}{1- \sin ^{2}{\theta _{13}}},\nonumber \\&\sin ^{2}{\theta _{12}}=\dfrac{\vert \mathbf{V}_{12}\vert ^{2}}{1-\vert \mathbf{V}_{13}\vert ^{2}}= \dfrac{N^{2}_{2}\sin ^{2}{\theta _{\nu }}}{1-\sin ^{2}{\theta }_{13}}. \end{aligned}$$

(25)

As can be noticed, if $\epsilon$ vanishes, one would recover the exact $\mu$–$\tau$ symmetry where $\theta _{13}=0^{\circ }$ and $\theta _{23}=45^{\circ }$. Additionally, we have to point out that the reactor and atmospheric angles depend strongly on the neutrino masses ratios so that these angles are sensitive to the Majorana phases. At the same time, the reactor angle does not depend on the phase of the parameter $\epsilon$, but on the other hand, the atmospheric one has a clear dependency on this phase.

5 Analytic study and results

In order to make an analytic study of the above formulas, let us emphasize that we are working in a perturbative regime, which means that $\vert \epsilon \vert \le 0.3$. Then $N_{i}$ normalization factors should be the order of 1, so that, as is usual in models where the $\mu$–$\tau$ symmetry is broken softly, the solar angle is directly related to the free parameter $\theta _{\nu }$, as can be seen in Eq. (25). Therefore, at the leading order we have

$$\begin{aligned} \sin ^{2}{\theta _{12}}=\sin ^{2}{\theta _{\nu }},\qquad \text {then},\qquad \theta _{12}=\theta _{\nu }. \end{aligned}$$

(26)

Therefore, throughout the analytic study we will consider $\sin {\theta _{\nu }}\approx 1/\sqrt{3}$ [66, 87,88,89,90], which is a good approximation to the solar angle. Additionally, we will analyze the CP parities for the complex neutrino masses, $m^{0}_{\nu _{j}}=\vert m^{0}_{\nu _{j}} \vert e^{i \beta _{j}}$ for $j=1, 2, 3$, for each hierarchy, which means that these can be either 0 or $\pi$. Explicitly, $m^{0}_{\nu _{j}}=\pm \vert m^{0}_{\nu _{j}}\vert$ where $\vert m^{0}_{\nu _{j}}\vert$ is the absolute mass. As we will see, these CP parities can be relevant to enhancing or suppressing the reactor and atmospheric angles. We want to remark that no Majorana phase was factorized as in the standard parametrization so that our results may be equivalent to this up to one phase which is irrelevant for the observables. In the following, the lightest neutrino mass and the $\vert \epsilon \vert$ parameter will be constrained.

5.1 Mixing angles

Normal hierarchy From experimental data, the absolute neutrino masses are $\vert m^{0}_{\nu _{3}}\vert = \sqrt{\Delta m^{2}_{31}+\vert m^{0 }_{\nu _{1}}\vert ^{2}}$ and $\vert m^{0}_{\nu _{2}}\vert =\sqrt{\Delta m^{2}_{21}+\vert m^{0}_{\nu _{1}}\vert ^{2} }$. Now, the mass ratios $r_{1}$, $r_{2}$ and $r_{3}$ can be approximated as follows:

$$\begin{aligned}&r_{1}\approx 1+2\frac{m^{0}_{\nu _{1}}}{m^{0}_{\nu _{3}}}\approx 1,\qquad r_{2}\approx 1+2\frac{m^{0}_{\nu _{2}}}{m^{0}_{\nu _{3}}},\nonumber \\&r_{3}\approx 1+2\frac{m^{0}_{\nu _{2}}}{m^{0}_{\nu _{3}}}\cos ^{2}{\theta _{\nu }} \end{aligned}$$

(27)

and, as a results of this, we obtain

$$\begin{aligned}&\sin ^{2}{\theta }_{13}\approx \sin ^{2}{2\theta _{\nu }}\vert \epsilon \vert ^{2} \left| \frac{m^{0}_{\nu _{2}}}{m^{0}_{\nu _{3}}}\right| ^{2},\nonumber \\&\sin ^{2}{\theta }_{23}\approx \dfrac{1}{2}\dfrac{ \left| 1-\epsilon \left( 1+2\frac{m^{0}_{\nu _{2}}}{m^{0}_{\nu _{3}}}\cos ^{2}{\theta _{\nu }} \right) \right| ^{2} }{1-\sin ^{2}{\theta }_{13}}. \end{aligned}$$

(28)

As can be noticed, if the strict normal hierarchy is assumed then the reactor angle turns out to be very small since $\vert m^{0}_{\nu _{2}}/m^{0}_{\nu _{3}}\vert ^{2}\approx \Delta m^{2}_{21}/\Delta m^{2}_{31}$, and $\vert \epsilon \vert \le 0.3$. This holds for any CP parities in the neutrino masses and this result does not change substantially if the $m^{0}_{\nu _{1}}$ is non-zero. Therefore, the normal spectrum is ruled out for $\vert \epsilon \vert \le 0.3$.

Inverted hierarchy In this case, we have $\vert m^{0}_{\nu _{2}}\vert =\sqrt{\Delta m^{2}_{13}+\Delta m^{2}_{21}+\vert m^{0 }_{\nu _{3}}\vert ^{2}}$ and $\vert m^{0}_{\nu _{1}}\vert =\sqrt{\Delta m^{2}_{13}+\vert m^{0}_{\nu _{3}}\vert ^{2}}$. The mass ratios $r_{1}$, $r_{2}$ and $r_{3}$ are written approximately as

$$\begin{aligned}&r_{(1, 2)}\approx -\left( 1+2\frac{m^{0}_{\nu _{3}}}{m^{0}_{\nu _{(1,2)}}}\right) ,\quad r_{2}-r_{1}\approx 2m^{0}_{\nu _{3}}\left[ \frac{m^{0}_{\nu _{2}}-m^{0}_{\nu _{1}}}{m^{0}_{\nu _{2}}m^{0}_{\nu _{1}}}\right] ,\nonumber \\&r_{3}\approx -\left[ 1+2\frac{m^{0}_{\nu _{3}}\left( m^{0}_{\nu _{1}}\cos ^{2}{\theta _{\nu }}+m^{0}_{\nu _{2}}\sin ^{2}{\theta _{\nu }}\right) }{m^{0}_{\nu _{2}}m^{0}_{\nu _{1}}}\right] . \end{aligned}$$

(29)

Due to the mass difference $m^{0}_{\nu _{2}}-m^{0}_{\nu _{1}}$ in the factor $r_{2}-r_{1}$, the reactor angle can be small or large since the relative signs in these two masses may conspire to achieve it. Then there are four independent cases where the signs in the masses can affect substantially the mixing angles:

• Case A If $m_{\nu _{i}}> 0$.

  $$\begin{aligned}&r_{2}-r_{1}\approx 2\vert m^{0}_{\nu _{3}}\vert \left[ \frac{\vert m^{0}_{\nu _{2}}\vert -\vert m^{0}_{\nu _{1}}\vert }{\vert m^{0}_{\nu _{2}}\vert \vert m^{0}_{\nu _{1}}\vert }\right] ,\nonumber \\&r_{3}\approx -\left[ 1+2\frac{\vert m^{0}_{\nu _{3}}\vert \left( \vert m^{0}_{\nu _{2}}\vert \sin ^{2}{\theta _{\nu }}+\vert m^{0}_{\nu _{1}}\vert \cos ^{2}{\theta _{\nu }}\right) }{\vert m^{0}_{\nu _{2}}\vert \vert m^{0}_{\nu _{1}}\vert } \right] . \end{aligned}$$

  (30)

• Case B If $m^{0}_{\nu _{(2, 1)}}> 0$ and $m^{0}_{\nu _{3}}<0$.

  $$\begin{aligned}&r_{2}-r_{1}\approx -2\vert m^{0}_{\nu _{3}}\vert \left[ \frac{\vert m^{0}_{\nu _{2}}\vert -\vert m^{0}_{\nu _{1}}\vert }{\vert m^{0}_{\nu _{2}}\vert \vert m^{0}_{\nu _{1}}\vert }\right] ,\nonumber \\&r_{3}\approx -\left[ 1-2\frac{\vert m^{0}_{\nu _{3}}\vert \left( \vert m^{0}_{\nu _{2}}\vert \sin ^{2}{\theta _{\nu }}+\vert m^{0}_{\nu _{1}}\vert \cos ^{2}{\theta _{\nu }}\right) }{\vert m^{0}_{\nu _{2}}\vert \vert m^{0}_{\nu _{1}}\vert } \right] . \end{aligned}$$

  (31)

• Case C If $m^{0}_{\nu _{(3, 2)}}> 0$ and $m^{0}_{\nu _{1}}<0$.

  $$\begin{aligned}&r_{2}-r_{1}\approx -2\vert m^{0}_{\nu _{3}}\vert \left[ \frac{\vert m^{0}_{\nu _{2}}\vert +\vert m^{0}_{\nu _{1}}\vert }{\vert m^{0}_{\nu _{2}}\vert \vert m^{0}_{\nu _{1}}\vert }\right] ,\nonumber \\&r_{3}\approx -\left[ 1-2\frac{\vert m^{0}_{\nu _{3}}\vert \left( \vert m^{0}_{\nu _{2}}\vert \sin ^{2}{\theta _{\nu }}-\vert m^{0}_{\nu _{1}}\vert \cos ^{2}{\theta _{\nu }}\right) }{\vert m^{0}_{\nu _{2}}\vert \vert m^{0}_{\nu _{1}}\vert } \right] . \end{aligned}$$

  (32)

• Case D If $m^{0}_{\nu _{2}}>0$ and $m^{0}_{\nu _{(3, 1)}}< 0$.

  $$\begin{aligned}&r_{2}-r_{1}\approx 2\vert m^{0}_{\nu _{3}}\vert \left[ \frac{\vert m^{0}_{\nu _{2}}\vert +\vert m^{0}_{\nu _{1}}\vert }{\vert m^{0}_{\nu _{2}}\vert \vert m^{0}_{\nu _{1}}\vert }\right] ,\nonumber \\&r_{3}\approx -\left[ 1+2\frac{\vert m^{0}_{\nu _{3}}\vert \left( \vert m^{0}_{\nu _{2}}\vert \sin ^{2}{\theta _{\nu }}-\vert m^{0}_{\nu _{1}}\vert \cos ^{2}{\theta _{\nu }}\right) }{\vert m^{0}_{\nu _{2}}\vert \vert m^{0}_{\nu _{1}}\vert } \right] . \end{aligned}$$

  (33)

Notice, if the strict inverted hierarchy were realized, $r_{2}-r_{1}=0$ and $r_{3}=-1$, we would have $\sin ^{2}{\theta _{13}}=0$ and $\sin ^{2}{\theta _{23}}=N^{2}_{3}\vert 1+\epsilon \vert ^{2}/2$, which is not compatible with the observations. Nonetheless, this strict ordering allows us to infer that the $\vert \epsilon \vert e^{i\alpha _{\epsilon }}$ parameter magnitude has to be small in order to make the atmospheric angle deviate sufficiently from $45^{\circ }$ and, the same time, this has to be large enough to enhance the reactor one. The $\alpha _{\epsilon }$ associated phase determines if we are above or below of $45^{\circ }$. Along this line, the NO $\nu$ A experiment has discarded the lower octant [2]. On the contrary, if the constraint, on the lightest neutrino mass, is relaxed, the reactor angle turns out to be non-zero and the atmospheric one has an extra contribution, $r_{3}$, which can enlarge or reduce the $\vert \epsilon \vert$ magnitude, since this may be greater or smaller than 1. Thus, the factor $\vert \epsilon ~r_{3}\vert$ might drastically make the atmospheric angle deviate beyond $45^{\circ }$.

Notice that, roughly speaking, the reactor angle turns out to be equal for Cases A and B, and also, for C and D. The key difference among them comes from the atmospheric angle as can be seen in Eqs. (30)–(33). Now, from the absolute value of the neutrino masses we have $\vert m^{0}_{\nu _{2}}\vert \approx \vert m^{0}_{\nu _{1}}\vert (1+2R_{1})$, then

$$\begin{aligned}&\vert m^{0}_{\nu _{2}}\vert -\vert m^{0}_{\nu _{1}}\vert \approx 2\vert m^{0}_{\nu _{1}}\vert R_{1} ,\nonumber \\&\quad \vert m^{0}_{\nu _{2}}\vert +\vert m^{0}_{\nu _{1}}\vert \approx 2 \vert m^{0}_{\nu _{1}}\vert \left[ 1+R_{1}\right] ,\nonumber \\&\quad \vert m^{0}_{\nu _{1}}\vert \vert m^{0}_{\nu _{2}}\vert \approx \vert m^{0}_{\nu _{1}}\vert ^{2}\left[ 1+2 R_{1} \right] , \end{aligned}$$

(34)

where $R_{1}\equiv \Delta m^{2}_{21}/4 \vert m^{0}_{\nu _{1}}\vert ^{2}\approx \mathcal {O}(10^{-3})$, if the $\vert m^{0}_{\nu _{3}}\vert$ lightest neutrino mass is tiny. Therefore, for Cases A and B, we have

$$\begin{aligned}&\sin ^{2}{\theta _{13}}\approx \frac{32}{9} | \epsilon |^{2} R^{2}_{1} \left| \frac{m^{0}_{\nu _{3}}}{m^{0}_{\nu _{1}}} \right| ^{2},\nonumber \\&\sin ^{2}{\theta _{23}}\approx \frac{1}{2}\frac{\left| 1+\epsilon \left( 1\pm 2 \left| \frac{m^{0}_{\nu _{3}}}{m^{0}_{\nu _{1}}}\right| \right) \right| ^{2}}{1-\sin ^{2}{\theta _{13}}} , \end{aligned}$$

(35)

where the upper (lower) sign, in the atmospheric angle, stands for Case A (Case B). Here, we have to keep in mind that $\vert m^{0}_{\nu _{3}}\vert /\vert m^{0}_{\nu _{1}}\vert < 1$ so that we can conclude that the first two scenarios are ruled out since the reactor angle is proportional to the small quantity $(\vert m^{0}_{\nu _{3}}\vert /\vert m^{0}_{\nu _{1}}\vert )R_{1}\vert \epsilon \vert$, where $\vert \epsilon \vert \le 0.3$.

For Case C ( Case D) the corresponding sign is the upper (lower) one; then the mixing angles are given as

$$\begin{aligned}&\sin ^{2}{\theta }_{13}\approx \frac{32}{9}\vert \epsilon \vert ^{2} \left| \frac{ m^{0}_{\nu _{3}} }{ m^{0}_{\nu _{1}}}\right| ^{2}(1-R_{1})^{2},\nonumber \\&\sin ^{2}{\theta }_{23}\approx \frac{1}{2}\frac{\left| 1+\epsilon \left( 1\pm \frac{2}{3} \left| \frac{m^{0}_{\nu _{3}}}{m^{0}_{\nu _{1}}}\right| \right) \right| ^{2}}{1-\sin ^{2}{\theta _{13}}}. \end{aligned}$$

(36)

From these formulas, in general, a large value of $\vert \epsilon \vert$ will be needed to compensate the $\vert m^{0}_{\nu _{3}}\vert$ lightest neutrino mass to get the allowed region for the reactor angle. But the atmospheric angle prefers small values for $\vert \epsilon \vert$. In addition, since $r_{3}<0$, the complex parameter phase is taken to be $\alpha _{\epsilon }=0$ to increase the atmospheric angle value. In order to be definite, we obtain for Case C: (a) if $\vert \epsilon \vert \approx 0.3$, it is required that $\vert m^{0}_{\nu _{3}}\vert /\vert m^{0}_{\nu _{1}}\vert \approx 0.26$, to obtain $\sin ^{2}{\theta _{13}}\approx 0.0229$. As a consequence, we get $\sin ^{2}{\theta _{23}}\approx 0.94$, which is too large; (b) if $\vert \epsilon \vert \approx 0.1$, then we need $\vert m^{0}_{\nu _{3}}\vert /\vert m^{0}_{\nu _{1}}\vert \approx 0.8$ to get $\sin ^{2}{\theta _{13}}\approx 0.0229$, and therefore, $\sin ^{2}{\theta _{23}}\approx 0.68$, which is still large in comparison to the central value.

Fig. 1

$\sin ^{2}{\theta _{23}}$ versus $\sin ^{2}{\theta _{13}}$. The left and right panels stand for Case C and Case D, respectively. The dot-dashed, dashed and thick lines stand for $1~\sigma$, $2~\sigma$ and $3~\sigma$ C.L., respectively for each case

For Case D, the reactor angle has approximately the same values for $\vert \epsilon \vert \approx 0.3$, $\vert \epsilon \vert \approx 0.1$ and their respective $\vert m^{0}_{\nu _{3}}\vert /\vert m^{0}_{\nu _{1}}\vert$ mass ratios as the above case. Then, with these values of $\vert \epsilon \vert$, we obtain $\sin ^{2}{\theta _{23}}\approx 0.79$ and $\sin ^{2}{\theta _{23}}\approx 0.56$, respectively. Notice that both values are approaching the allowed region for this mixing angle, then this case is more favorable than Case C. This happens since a large contribution of $\vert \epsilon \vert$, in the atmospheric angle, is suppressed by $r_{3}$, which is smaller than 1 and the reactor angle prefers large values of $\vert \epsilon \vert$.

Let us remark the following: if $\vert \epsilon \vert$ is tiny, we require that $\vert m^{0}_{\nu _{3}}\vert /\vert m^{0}_{\nu _{1}}\vert$ neutrino mass ratio should be larger than 1 to enhance the reactor angle but this mass ratio violates the inverted ordering. This statement is valid for Cases C and D. At the same time, if $\alpha _{\epsilon }=\pi$ is chosen in the atmospheric angle, this would be tiny for the same values of $\vert \epsilon \vert$ and the $\vert m^{0}_{\nu _{3}}\vert /\vert m^{0}_{\nu _{1}}$, as can be verified straightforwardly from Eq. (36).

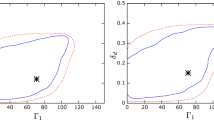
In order to get a complete view of the parameter space, let us show some plots for the reactor and atmospheric angles. We have considered the exact formulas given in Eq. (25), for the observables as the $\theta _{12}$ solar angle, $\Delta m^{2}_{21}$ and $\Delta m^{2}_{13}$, their values were taken up to $3~\sigma$ C.L. Then Fig. 1 shows the atmospheric angle versus the reactor one for Case C and D. These scattering plots clearly support our analytic result in Case C, that is, the two mixing angles cannot be accommodate simultaneously. In Case D, the reactor angle is consistent with the experimental data but the atmospheric one is large but consistent up to 2–3 $\sigma$ C.L. in its allowed region. In addition, for Case D, the parameter space is shown in Fig. 2. As can be seen, the atmospheric angle prefers small values for $\vert \epsilon \vert$ whereas the reactor one needs a large value, as was already pointed out. Moreover, the set of values for $\vert \epsilon \vert$ and $\vert m^{0}_{\nu _{3}}\vert$ is tight.

Fig. 2

Case D: Allowed region for $\sin ^{2}{\theta _{23}}$. The dot-dashed, dashed and thick lines stand for $1~\sigma$, $2~\sigma$ and $3~\sigma$ of C. L

Degenerate hierarchy In this case, $\vert m^{0}_{\nu _{3}}\vert \approxeq \vert m^{0}_{\nu _{2}}\vert \approxeq \vert m^{0}_{\nu _{1}}\vert \approxeq m_{0}$, with $m_{0}\gtrsim 0.1~eV$. Then the absolute neutrino masses can be written as $\vert m^{0}_{\nu _{3}} \vert = \sqrt{\Delta m^{2}_{31}+m^{2}_{0}}\approx m_{0}(1+\Delta m^{2}_{31}/2m^{2}_{0})$ and $\vert m^{0}_{\nu _{2}} \vert =\sqrt{\Delta m^{2}_{21}+m^{2}_{0}}\approx m_{0}(1+\Delta m^{2}_{21}/2m^{2}_{0})$. As in the inverted case, there are four independent cases for the signs, which are shown below.

• Case A If $m^{0}_{\nu _{i}}>0$,

  $$\begin{aligned}&r^{A}_{1}=\frac{\vert m^{0}_{\nu _{3}}\vert +m_{0}}{\vert m^{0}_{\nu _{3}}\vert -m_{0}},\qquad r^{A}_{2}=\frac{\vert m^{0}_{\nu _{3}}\vert +\vert m^{0}_{\nu _{2}}\vert }{\vert m^{0}_{\nu _{3}}\vert -\vert m^{0}_{\nu _{2}}\vert },\nonumber \\&r^{A}_{3}=r^{A}_{2}\cos ^{2}{\theta _{\nu }}+r^{A}_{1}\sin ^{2}{\theta _{\nu }}. \end{aligned}$$

  (37)

• Case B If $m^{0}_{\nu _{(2, 1)}}>0$ and $m^{0}_{\nu _{3}}<0$,

  $$\begin{aligned}&r^{B}_{1}=\frac{\vert m^{0}_{\nu _{3}}\vert -m_{0}}{\vert m^{0}_{\nu _{3}}\vert +m_{0}}=\frac{1}{r^{A}_{1}},\qquad r^{B}_{2}=\frac{\vert m^{0}_{\nu _{3}}\vert -\vert m^{0}_{\nu _{2}}\vert }{\vert m^{0}_{\nu _{3}}\vert +\vert m^{0}_{\nu _{2}}\vert }=\frac{1}{r^{A}_{2}},\nonumber \\&r^{B}_{3}=r^{B}_{2}\cos ^{2}{\theta _{\nu }}+r^{B}_{1}\sin ^{2}{\theta _{\nu }}. \end{aligned}$$

  (38)

• Case C If $m^{0}_{\nu _{(3, 2)}}>0$ and $m^{0}_{\nu _{1}}=-m_{0}$,

  $$\begin{aligned}&r^{C}_{1}=\frac{\vert m^{0}_{\nu _{3}}\vert -m_{0}}{\vert m^{0}_{\nu _{3}}\vert +m_{0}}=\frac{1}{r^{A}_{1}},\qquad r^{C}_{2}=\frac{\vert m^{0}_{\nu _{3}}\vert +\vert m^{0}_{\nu _{2}}\vert }{\vert m^{0}_{\nu _{3}}\vert -\vert m^{0}_{\nu _{2}}\vert }=r^{A}_{2},\nonumber \\&r^{C}_{3}=r^{C}_{2}\cos ^{2}{\theta _{\nu }}+r^{C}_{1}\sin ^{2}{\theta _{\nu }}. \end{aligned}$$

  (39)

• Case D If $m^{0}_{\nu _{2}}>0$ and $m^{0}_{\nu _{(3, 1)}}<0$,

  $$\begin{aligned}&r^{D}_{1}=\frac{\vert m^{0}_{\nu _{3}}\vert +m_{0}}{\vert m^{0}_{\nu _{3}}\vert -m_{0}}=r^{A}_{1},\qquad r^{D}_{2}=\frac{\vert m^{0}_{\nu _{3}}\vert -\vert m^{0}_{\nu _{2}}\vert }{\vert m^{0}_{\nu _{3}}\vert +\vert m^{0}_{\nu _{2}}\vert }=\frac{1}{r^{A}_{2}}, \nonumber \\&r^{D}_{3}=r^{D}_{2}\cos ^{2}{\theta _{\nu }}+r^{D}_{1}\sin ^{2}{\theta _{\nu }}. \end{aligned}$$

  (40)

Notice that

$$\begin{aligned}&\vert m^{0}_{\nu _{3}}\vert - m_{0}\approx 2 m_{0}R_{2},\quad \vert m^{0}_{\nu _{3}}\vert + m_{0}\approx 2m_{0}\left( 1+R_{2}\right) ,\nonumber \\&\quad \vert m^{0}_{\nu _{3}}\vert - \vert m^{0}_{\nu _{2}}\vert \approx 2m_{0}R_{2}\left( 1-R_{3}\right) ,\nonumber \\&\quad \vert m^{0}_{\nu _{3}}\vert + \vert m^{0}_{\nu _{2}}\vert \approx 2 m_{0}\left[ 1+R_{2}+R_{4}\right] , \end{aligned}$$

(41)

with $R_{2}\equiv \Delta m^{2}_{31}/4m^{2}_{0}$, $R_{3}=\Delta m^{2}_{21}/\Delta m^{2}_{31}$ and $R_{4}=\Delta m^{2}_{21}/4m^{2}_{0}$, where $R_{4}< R_{3}\lesssim R_{2}$. Thus, $r^{A}_{1}\approx (1+R_{2})/R_{2}$ and $r^{A}_{2}\approx r^{A}_{1}(1+R_{3})$. To be definite on the order of magnitude of each defined quantity, we use the data for the inverted hierarchy and their respective central values. Thus, $R_{2}\sim 6\times 10^{-2}$, $R_{3}\sim 3\times 10^{-2}$, $R_{4}\sim 2\times 10^{-3}$ and $r^{A}_{1}\sim 17$ with $m_{0}=0.1~eV$. Indeed, $R_{2}$ and $R_{4}$ might be fairly small, and therefore $r^{A}_{1}$ so large since $m_{0}\gtrsim 0.1~eV$.

Therefore, in Cases A, $r^{A}_{2}-r^{A}_{1}\approx r^{A}_{1}R_{3}$ and $r^{A}_{3}\approx r^{A}_{1}$; then

$$\begin{aligned} \sin ^{2}{\theta _{13}}&\approx \frac{2}{9}\left| \epsilon \right| ^{2}\left[ r^{A}_{1} R_{3}\right] ^{2},\qquad \sin ^{2}{\theta _{23}}\approx \frac{1}{2}\frac{\left| 1-\epsilon r^{A}_{1}\right| ^{2}}{1-\sin ^{2}{\theta _{13}}}. \end{aligned}$$

(42)

In Case B, $r^{B}_{2}-r^{B}_{1}\approx -r^{A}_{1}/R_{3}$ and $r^{B}_{3}\approx 1/r^{A}_{1}$ so that

$$\begin{aligned}&\sin ^{2}{\theta _{13}}\approx \frac{2}{9}\left| \epsilon \right| ^{2}\left[ \frac{R_{3}}{r^{A}_{1}}\right] ^{2},\nonumber \\&\sin ^{2}{\theta _{23}}\approx \frac{1}{2}\frac{\left| 1-\frac{\epsilon }{ r^{A}_{1}}\right| ^{2}}{1-\sin ^{2}{\theta _{13}}}. \end{aligned}$$

(43)

Thus, in the former case if the reactor angle is fixed to its central value ($\sin ^{2}{\theta _{13}}\approx 0.0229$), with the above values for $r^{A}_{1}$ and $R_{3}$, we obtain $\vert \epsilon \vert \approx 0.5$, which means a strong breaking of the $\mu$–$\tau$ symmetry. As result, the atmospheric angle turns out to be too large. Analogously, for the second case one gets that $\vert \epsilon \vert \approx 10^{2}$ if the reactor angle is fixed to its central value. As consequence, the atmospheric angle is also quite large. Therefore, these two cases are excluded, the only feasible cases are the last ones.

For Case C, from Eq. (39), we have $r^{C}_{2}-r^{C}_{1}\approx r^{A}_{1}(1+R_{3})$ and $r^{C}_{3}\approx r^{A}_{1}\cos ^{2}{\theta _{\nu }}$, so that

$$\begin{aligned}&\sin ^{2}{\theta }_{13}\approx \frac{2}{9}\vert \epsilon \vert ^{2}\big [r^{A}_{1}(1+R_{3})\big ]^{2},\nonumber \\&\sin ^{2}{\theta _{23}}\approx \frac{1}{2}\frac{\left| 1-\frac{2}{3}r^{A}_{1}\epsilon \right| ^{2} }{1-\sin ^{2}{\theta _{13}}}. \end{aligned}$$

(44)

For Case D, from Eq. (40), we obtain $r^{D}_{2}-r^{D}_{1}\approx -r^{A}_{1}$ and $r^{D}_{3}\approx r^{A}_{1}\sin ^{2}{\theta _{\nu }}$. Then

$$\begin{aligned}&\sin ^{2}{\theta }_{13}\approx \frac{2}{9}\vert \epsilon \vert ^{2} \big [r^{A}_{1} \big ]^{2},\nonumber \\&\sin ^{2}{\theta _{23}}\approx \frac{1}{2}\frac{\left| 1-\frac{1}{3}r^{A}_{1}\epsilon \right| ^{2}}{1-\sin ^{2}{\theta _{13}}}. \end{aligned}$$

(45)

Fig. 3

$\sin ^{2}{\theta _{23}}$ versus $\sin ^{2}{\theta _{13}}$. The left and right panels stand for the Case C and Case D, respectively. The dot-dashed, dashed and thick lines stand for $1~\sigma$, $2~\sigma$ and $3~\sigma$ of C. L., respectively for each case

Roughly speaking, as in the inverted case, the reactor angle has approximately the same behavior for both cases but the atmospheric angle comes out being different. In here, on the other hand, notice that $r_{3}>0$ for both cases then if $\alpha _{\epsilon }=0$, the atmospheric angle would be smaller than $45^{\circ }$, which is far away from the experimental data, as can be verified from Eqs. (44) and (45). In order to increase this value, we need $\alpha _{\epsilon }=\pi$. Additionally, because of $r^{A}_{1}\ggg 1$, the value of $\vert \epsilon \vert$ should be of the order of $10^{-2}$ in order to not enhance too much the atmospheric angle; of course, we must be careful not to spoil the reactor angle or vice versa.

Now, in Case C and D, if the reactor angle is fixed to its central value ($\sin ^{2}{\theta _{13}}\approx 0.0229$) then it is required that $\vert \epsilon \vert \sim 2\times 10^{-2}$, so that one obtains $\sin ^{2}{\theta _{23}}\approx 0.74$ and $\sin ^{2}{\theta _{23}}\approx 0.63$, respectively. As can be seen, the favored case is the latter due to the $\epsilon r^{D}_{3}$ contribution, in the atmospheric angle, being less than $\epsilon r^{C}_{3}$ such that the atmospheric angle is softly being deviated from $45^{\circ }$. Now, an interesting fact is the following: if $m_{0}$ is increased to the allowed value, then $r^{A}_{1}$ becomes quite large and therefore, a tiny $\vert \epsilon \vert$ value is needed to not deviate so much from $45^{\circ }$ the atmospheric angle and at the same time, to get an allowed region for the reactor angle. In this hierarchy, the $\mu$–$\tau$ symmetry is being broken softly.

We will now show the complete parameter space for both cases. The exact formulas for the mixing angles have been used, apart from the allowed values for $\Delta m^{2}_{21}$, $\Delta m^{2}_{13}$ and $\theta _{\nu }$ the solar angle for the inverted ordering as a good approximation. Therefore, in Fig. 3, the atmospheric versus the reactor angle is show up to $3~\sigma$ C.L. These panels allow us compare the two cases and these support our analytic result, in Case D, both angles of interest are accommodated very well. In Fig. 4, as can be seen, the parameter space is large where the atmospheric angle, and therefore the reactor one, is accommodated in good agreement with the experimental data. At the end of the day, the degenerate ordering is favored instead of the inverted case.

Fig. 4

Case D: Allowed region for $\sin ^{2}{\theta _{23}}$. The dot-dashed, dashed and thick lines stand for $1~\sigma$, $2~\sigma$ and $3~\sigma$ of C. L

5.2 The effective neutrinoless mass decay

Having obtained the PMNS mixing matrix, an immediate result is the effective neutrino mass, $\vert m_{ee}\vert$, which comes from neutrinoless double beta decay in the presence of light Majorana neutrinos [91,92,93]. As is well known, this is given by

$$\begin{aligned} \vert m_{ee} \vert = \vert m_{1}V^{2}_{e 1}+m_{2}V^{2}_{e 2}+ m_{3}V^{2}_{e 3}\vert . \end{aligned}$$

(46)

The lowest upper bound on $\vert m_{ee}\vert$ is provided by GERDA phase-I data [94], and this is 0.22 eV. At the same time, we have the neutrino mass scale [95, 96]

$$\begin{aligned} m_{e}= \sqrt{ m^{2}_{1}\vert V_{e 1}\vert ^{2}+m^{2}_{2}\vert V_{e 2}\vert ^{2}+ m^{2}_{3}\vert V_{e 3}\vert ^{2}}, \end{aligned}$$

(47)

which has been measured to be $m_{e}=0.2~\mathrm{eV}$ [97]. Additionally, the sum of neutrino masses has been measured by the Planck collaboration and the upper bound is $\Sigma _{i}\vert m_{\nu _{i}}\vert =0.23~\mathrm{eV}$ [98].

For the inverted and degenerate hierarchy in Case D, which turns out to be the most favorable to accommodate the reactor and atmospheric angles as was shown, the above observables will be calculated. To this aim, we have to keep in mind that the parameter that breaks the $\mu$–$\tau$ symmetry is small in both cases so that the normalization factors are $N_{i}\approx \mathcal {O}(1)$. In addition, $\vert m_{ee}\vert$ becomes a real quantity since CP parities have been considered in the neutrino masses. Along with this, for the effective neutrino mass, we have to point out that there will be a cancellation among the involved terms due to the CP parities in the neutrino masses; as a consequence, we expect small values in comparison to the GERDA phase-I data.

Inverted hierarchy

From Eqs. (24) and (46), we get the following:

$$\begin{aligned} \vert m_{ee}\vert \approx \frac{2}{3} \vert m^{0}_{\nu _{1}}\vert \left| R_{1}-\frac{16}{3} \left| \frac{m^{0}_{\nu _{3}}}{ m^{0}_{\nu _{1}}}\right| ^{3} \vert \epsilon \vert ^{2} (1-2R_{1})\right| , \end{aligned}$$

(48)

where Eq. (36) was used and $\vert m^{0}_{\nu _{2}}\vert \approx \vert m^{0}_{\nu _{1}}\vert (1+2R_{1})$ with $R_{1}=\Delta m^{2}_{21}/4\vert m^{0}_{\nu _{1}}\vert ^{2}$. The associated phase value, $\alpha _{\epsilon }=0$, has been taken into account and $\sin {\theta _{\nu }}\approx 1/\sqrt{3}$. In the strict inverted hierarchy, $\vert m^{0}_{\nu _{3}}\vert =0$, we obtain $\vert m_{ee}\vert \approx 10^{-4}~\mathrm{eV}$, but the lightest neutrino mass is non-zero from the previous analytical study; then one expects $\vert m_{ee}\vert > 10^{-4}~\mathrm{eV}$.

Fig. 5

$\vert m_{ee}\vert$ versus $\vert m^{0}_{\nu _{3}} \vert$ and $\vert \epsilon \vert$, respectively

Fig. 6

Neutrino mass scale and the sum of the neutrino masses versus $\vert m^{0}_{\nu _{3}} \vert$, respectively

Fig. 7

$\vert m_{ee}\vert$ versus $\vert m_{0} \vert$ and $\vert \epsilon \vert$, respectively

In order to get the allowed values of the effective neutrino mass as a function of the lightest neutrino mass and the $\epsilon$ free parameter, we consider the exact formula for $\vert m_{ee}\vert$ and the entries of the PMNS mixing matrix; the observables as $\theta _{12}$, $\Delta m^{2}_{21}$ and $\Delta m^{2}_{13}$ have been considered up to $3~\sigma$ C.L. The plots given in Fig. 5 are the predictions of the model on this quantity. Let us remind the reader that the parameter space for $\vert m^{0}_{\nu _{3}} \vert$ and $\vert \epsilon \vert$ has been constrained in the previous analysis. Actually, this is shown in Fig. 2 where we have approximately $0.02~\mathrm{eV}\le \vert m^{0}_{\nu _{3}} \vert \le 0.06~\mathrm{eV}$ and $0.02\le \vert \epsilon \vert \le 0.19$. So, the allowed values of $\vert m_{ee}\vert$ are below the GERDA phase-I data. However, GERDA phase-II data [99] can reach the predicted region by our model.

For the neutrino mass scale and the sum of neutrino masses, we have, respectively,

$$\begin{aligned}&m_{e}\approx \sqrt{\Delta m^{2}_{13}}\left[ 1+\frac{\vert m^{0}_{\nu _{3}}\vert ^{2}}{\Delta m^{2}_{13}}(1+\sin ^{2}{\theta _{13}})+\frac{1}{3}\frac{\Delta m^{2}_{21}}{\Delta m^{2}_{13}}\right] ^{1/2},\nonumber \\&\quad \Sigma _{i}\vert m_{\nu _{i}}\vert \approx 2\vert m^{0}_{\nu _{1}}\vert \left[ 1+R_{1}+\frac{1}{2} \frac{\vert m^{0}_{\nu _{3}}\vert }{\vert m^{0}_{\nu _{1}}\vert }\right] \end{aligned}$$

(49)

where $m_{e}\approx 0.049~\mathrm{eV}$ and $\Sigma _{i}\vert m_{\nu _{i}}\vert \approx 0.098~\mathrm{eV}$ with $\vert m^{0}_{\nu _{3}} \vert =0$. As was already pointed out the lightest neutrino mass is non-zero so the those observables will be increased when $\vert m^{0}_{\nu _{3}} \vert$ is increased. The predicted regions on these quantities are shown in Fig. 6. Notice that the upper bound on the sum of the neutrino masses that Planck provides can be reached if the lightest neutrino mass is allowed to be large.

Fig. 8

Neutrino mass and the sum of the neutrino masses versus $m_{0}$, respectively

Degenerate hierarchy

In similar way to the above case

$$\begin{aligned} \vert m_{ee} \vert \approx \frac{m_{0}}{3} \big [1+ 3\sin ^{2}{\theta _{13}} \big ], \end{aligned}$$

(50)

where $\vert m^{0}_{\nu _{3}}\vert \approx m_{0}(1+2 R_{2})$, $\vert m^{0}_{\nu _{2}}\vert \approx m_{0}(1+2 R_{4})$ and $\sin {\theta }_{\nu }\approx 1/\sqrt{3}$. Let us remind the reader that $R_{2}=\Delta m^{2}_{13}/4m^{2}_{0}$ and $R_{4}=\Delta m^{2}_{21}/4m^{2}_{0}$; besides that, Eq. (45) was considered. In this case, we obtain $\vert m_{ee}\vert \approx 0.035$ with $m_{0}=0.1~\mathrm{eV}$ and central values for the observables so that $\vert m_{ee}\vert > 0.035$ when the $m_{0}$ is increasing. The predicted region of $\vert m_{ee} \vert$, as a function of the $m_{0}$ common neutrino mass and the $\vert \epsilon \vert$ parameter, is shown in Fig. 7. In this case the parameter space for $m_{0}$ and $\epsilon$ is shown in Fig. 4, from this panel we have approximately that $0.1~\mathrm{eV}\le m_{0}\le 0.25~\mathrm{eV}$ and $0.005\le \vert \epsilon \vert \le 0.023$. As we can observe, the allowed values are smaller than GERDA phase-I data but this region will be explored by GERDA phase-II data. Finally, we obtain

$$\begin{aligned}&m_{e}\approx m_{0}\left[ 1+\frac{1}{2}\sin ^{2}{\theta _{13}}\right] ,\nonumber \\&\Sigma _{i}\vert m_{\nu _{i}}\vert \approx 3 m_{0}\left[ 1+\frac{2}{3}\left( R_{2}+R_{4}\right) \right] . \end{aligned}$$

(51)

Then we expect that $m_{e}>0.1~\mathrm{eV}$ and $\Sigma _{i}\vert m_{\nu _{i}}\vert >0.3~\mathrm{eV}$, since the reactor angle is tiny but not negligible. For the neutrino mass and the sum of the neutrino masses, the allowed region is shown in Fig. 8. Let us point out that the neutrino mass scale is below the experimental limit 0.2 eV [97], but this upper bound can be reached if $m_{0}$ is large. In this degenerate ordering, the sum of the neutrino mass is predicted to be large in comparison to the cosmological data [98].

6 Conclusions

We have extended the scalar sector of the LRSM in order to get masses and mixings for fermions. In the lepton sector, neutrino masses and mixings have been studied in the limit of a slightly broken $\mu$–$\tau$ symmetry where the reactor and atmospheric angles depend strongly on the $\epsilon$ free parameter, which characterizes the $\mu$–$\tau$ symmetry breaking, and the neutrino masses. Due to this last fact, the mixing angles are sensitive to the CP parities in the neutrino masses which may increase or decrease their respective values. Therefore, we have made an analytic study of the role that these signs in masses might play in each hierarchy and their impact to constrain the $\epsilon$ free parameter and the lightest neutrino mass.

The main results are the following: (a) The model predicts a tiny value for the reactor angle in the normal hierarchy and this result holds for whatever CP parities in the neutrino masses. Then the normal ordering is completely ruled out for $\vert \epsilon \vert \le 0.3$. (b) In the inverted hierarchy there is one combination in the neutrino masses signs where the reactor and atmospheric angles are compatible up to 2–3 $\sigma$ C.L., within the allowed region for the latter angle. This scenario is fairly constrained since the parameter space is so tight. (c) The degenerate ordering is the most viable scenario to accommodate simultaneously the reactor and atmospheric angles. In this case, there is one combination in the CP parities where both angles are consistent with the current limits imposed by the experimental data for $\sin ^{2}\theta _{23}$ and $\sin ^{2}\theta _{13}$. In this ordering, a set of values for $\epsilon$ and the lightest neutrino mass was found such that the $\mu$–$\tau$ symmetry is broken softly. Remarkably, the viable cases predict that $\theta _{23}>45^{\circ }$.

As model predictions the effective neutrino mass, the neutrino mass scale and the sum of the neutrino masses were obtained in the favored cases for the inverted and degenerate hierarchies. In the former ordering, for the above observables the allowed regions of values are below the experimental limit. In particular, the allowed values for the effective neutrino mass can be reached by GERDA phase-II data. Similar results were obtained in the degenerate ordering for the effective neutrino mass and the neutrino mass scale. However, the sum of the neutrino mass is beyond the experimental result that the Planck collaboration provides.

For the moment, the quark sector has been left aside for future work but we have pointed out that the mass matrices possess textures that might fit the CKM matrix. Although the model is quite elaborate, it is fairly predictive and testable by the future results that the experiments will provide.