CP violation induced by the double resonance for pure annihilation decay process in perturbative QCD

Abstract

In a perturbative QCD approach we study the direct CP violation in the pure annihilation decay process of $\bar{B}^0_{s}\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$ induced by the $\rho$ and $\omega$ double resonance effect. Generally, the CP violation is small in the pure annihilation type decay process. However, we find that the CP violation can be enhanced by double $\rho$–$\omega$ interference when the invariant masses of the $\pi ^+\pi ^-$ pairs are in the vicinity of the $\omega$ resonance. For the decay process of $\bar{B}^0_{s}\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$, the CP violation can reach $A_{CP}(\bar{B}^0_{s}\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-)=27.20^{+0.05+0.28+7.13}_{-0.15-0.31-6.11}\%$.

1 Introduction

CP violation is an important area in searching new physics signals beyond the standard model (SM). It is generally believed that the B meson system provides rich information as regards CP violation. Theoretical work has been done in this direction in the past few years. CP violation arises from the weak phase in the Cabibbo–Kobayasgi–Maskawa (CKM) matrix [1, 2] in SM. Meanwhile, it is remarkable that CP violation can still be produced by the interference effects between the tree and penguin amplitudes. Since the kinematic suppression, the strong phase associated with long distance rescattering is generally neglected during the past decades. The appearance of the $\rho$ and $\omega$ resonance is associated with complex strong phase which is responsible for the CP violation except for the weak phase. The CP violation can be enhanced in the decay process of $B^{\pm }\rightarrow \pi ^{\pm }\pi ^{+}\pi ^{-}$ via a $\rho$–$\omega$ mixing mechanism [3]. Recently, the LHCb Collaboration found the large CP violation in the three-body decay channels of $B^{\pm }\rightarrow \pi ^{\pm }\pi ^{+}\pi ^{-}$ and $B^{\pm }\rightarrow K^{\pm }\pi ^{+}\pi ^{-}$ [4,5,6]. Hence, the nonleptonic B meson decay from the three-body and four-body decay channels has been become an important area in searching for CP violation via the $\rho$ and $\omega$ resonance.

A mixing between the u and d flavor leads to the breaking of isospin symmetry for the $\rho$–$\omega$ system. The chiral dynamics has been shown to restore the isospin symmetry [7]. The $\rho$–$\omega$ mixing matrix element ${\Pi }_{\rho \omega }$ gives rise to isospin violation which refers to the contribution of the mixing of $\omega \rightarrow \rho \rightarrow 2\pi$. The magnitude has been extracted by the pion form factor through the cross section of $e^{+}e^{-}\rightarrow \pi ^{+}\pi ^{-}$ from relatively broad $\rho$ resonance region [8,9,10,11,12,13]. The appearance of the $\rho$ and $\omega$ resonance is associated with a complex strong phase. Especially, there is perhaps larger strong phase from double $\rho$ and $\omega$ interference. The CP violation origins from the weak phase difference and the strong phase difference. Hence, the decay process of $\bar{B}^0_{s}\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$ is a great candidate for studying the origin of the CP violation.

Meanwhile, it is well known that the CP violation is extremely tiny from the pure annihilation decay process in experiment. There is relatively large error in dealing with the decay amplitudes from the QCD factorization approach [14, 15]. The perturbative QCD (PQCD) factorization approach [16,17,18,19,20,21,22,23,24] is based on $k_{T}$ factorization. The amplitude can be divided into the convolution of the Wilson coefficients, the light-cone wave function, and hard kernels by the low energy effective Hamiltonian. The endpoint singularity can be eliminated by introducing the transverse momentum. However, the transverse momentum integration leads to the double logarithm term, which is resummed into the Sudakov form factor. The nonperturbative dynamics is included in the meson wave function which can be extracted from experiment. The perturbative contribution can be calculated by perturbation theory.

The remainder of this paper is organized as follows. In Sect. 2 we present the form of the effective Hamiltonian. In Sect. 3 we give the calculation formalism and details of CP violation from $\rho$–$\omega$ mixing in the $\bar{B}^0_{s}\rightarrow \rho ^0(\omega )\rho ^0(\omega )\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$ decay. In Sect. 4 we show the input parameters. We present the numerical results in Sect. 5. A summary and discussion are included in Sect. 6. The related functions defined in the text are given in the appendix.

2 The effective hamiltonian

With the operator product expansion, the effective weak Hamiltonian can be written as [25]

$$\begin{aligned} \mathcal{H}_{eff}= & {} \frac{G_{F}}{\sqrt{2}} \Bigg \{ V_{ub} V_{uq}^{*} \Big [ C_{1}({\mu }) Q^{u}_{1}({\mu }) + C_{2}({\mu }) Q^{u}_{2}({\mu })\Big ]\nonumber \\&-\,V_{tb} V_{tq}^{*} \Big [{\sum \limits _{i=3}^{10}} C_{i}({\mu }) Q_{i}({\mu }) \Big ] \Bigg \} + \text{ H.c. } , \end{aligned}$$

(1)

where $q=(d, s)$, $G_F$ represents Fermi constant, $C_i$ ($i=1,\ldots ,10$) are the Wilson coefficients, $V_{q_1q_2}$ ($q_1$ and $q_2$ represent quarks) is the CKM matrix element, and $O_i$ is the four quark operator. The operators $O_i$ have the following forms:

$$\begin{aligned} \begin{aligned}&O^{u}_1= \bar{d}_\alpha \gamma _\mu (1-\gamma _5)u_\beta \bar{u}_\beta \gamma ^\mu (1-\gamma _5)b_\alpha ,\\&O^{u}_2= \bar{d} \gamma _\mu (1-\gamma _5)u\bar{u}\gamma ^\mu (1-\gamma _5)b,\\&O_3= \bar{d} \gamma _\mu (1-\gamma _5)b \sum _{q'} \bar{q}' \gamma ^\mu (1-\gamma _5) q',\\&O_4 = \bar{d}_\alpha \gamma _\mu (1-\gamma _5)b_\beta \sum _{q'} \bar{q}'_\beta \gamma ^\mu (1-\gamma _5) q'_\alpha ,\\&O_5=\bar{d} \gamma _\mu (1-\gamma _5)b \sum _{q'} \bar{q}' \gamma ^\mu (1+\gamma _5)q',\\&O_6 = \bar{d}_\alpha \gamma _\mu (1-\gamma _5)b_\beta \sum _{q'} \bar{q}'_\beta \gamma ^\mu (1+\gamma _5) q'_\alpha ,\\&O_7= \frac{3}{2}\bar{d} \gamma _\mu (1-\gamma _5)b \sum _{q'} e_{q'}\bar{q}' \gamma ^\mu (1+\gamma _5) q',\\&O_8 =\frac{3}{2} \bar{d}_\alpha \gamma _\mu (1-\gamma _5)b_\beta \sum _{q'} e_{q'}\bar{q}'_\beta \gamma ^\mu (1+\gamma _5) q'_\alpha ,\\&O_9=\frac{3}{2}\bar{d} \gamma _\mu (1-\gamma _5)b \sum _{q'} e_{q'}\bar{q}' \gamma ^\mu (1-\gamma _5)q',\\&O_{10} = \frac{3}{2}\bar{d}_\alpha \gamma _\mu (1-\gamma _5)b_\beta \sum _{q'} e_{q'}\bar{q}'_\beta \gamma ^\mu (1-\gamma _5) q'_\alpha , \end{aligned} \end{aligned}$$

(2)

where $\alpha$ and $\beta$ are color indices, and $q^\prime =u, d, s, c$ or b quarks. In Eq. (2) $O_1^u$ and $O_2^u$ are tree operators, $O_3$–$O_6$ are QCD penguin operators and $O_7$–$O_{10}$ are the operators associated with electroweak penguin diagrams. $C_i(m_b)$ can be written [24],

$$\begin{aligned}&C_1 =-0.2703, \quad C_2=1.1188,\nonumber \\&C_3 = 0.0126,\quad C_4 = -0.0270,\nonumber \\&C_5 = 0.0085,\quad C_6 = -0.0326,\nonumber \\&C_7 = 0.0011,\quad C_8 = 0.0004,\nonumber \\&C_9= -0.0090,\quad C_{10} = 0.0022. \end{aligned}$$

(3)

So, we can obtain numerical values of $a_i$. The combinations $a_i$ of Wilson coefficients are defined as usual [19,20,21]:

$$\begin{aligned} \begin{aligned}&a_1=C_2+C_1/3,\;\; \;a_2=C_1+C_2/3,\\&a_3=C_3+C_4/3,\;\; \;a_4=C_4+C_3/3,\\&a_5=C_5+C_6/3,\;\; \;a_6=C_6+C_5/3,\\&a_7=C_7+C_8/3,\;\; \;a_8=C_8+C_7/3,\\&a_9=C_9+C_{10}/3,\;\; \;a_{10}= C_{10}+C_{9}/3. \end{aligned} \end{aligned}$$

(4)

3 CP violation in $\bar{B}_{s}^{0}\rightarrow \rho ^0(\omega )\rho ^0(\omega )\rightarrow \pi ^+\pi ^{-}\pi ^+\pi ^{-}$

3.1 Formalism

The amplitudes $A^{\sigma }$ of the process $\bar{B}_s(p) \rightarrow V_1(p_1,\epsilon _{1}) + V_2(p_2,\epsilon _{2})$ can be written [26]

$$\begin{aligned} A^{\sigma }=\epsilon _{1\mu }^{*}({\sigma })\epsilon _{2\nu }^{*}({\sigma }) \left( ag^{\mu \nu }+\frac{b}{m_{1}m_{2}}p^{\mu }p^{\nu }+\frac{ic}{m_{1}m_{2}} \epsilon ^{\mu \nu \alpha \beta }p_{1\alpha }p_{2\beta }\right) \end{aligned}$$

(5)

where $\sigma$ is the helicity of the vector meson. $\epsilon _1$($p_1$) and $\epsilon _2$($p_2$) are the polarization vectors (momenta) of $V_{1}$ and $V_{2}$, respectively. $m_{1}$ and $m_{2}$ refer to the masses of the vector mesons $V_{1}$ and $V_{2}$. The invariant amplitudes a, b, c are associated with the amplitude $A_{i}$ (i refers to the three kind of polarizations, longitudinal (L), normal (N) and transverse (T)). Then we have

$$\begin{aligned} A^{\sigma }= & {} M^2_{B_{s}}A_{L}+M^2_{B_{s}}A_{N}\epsilon _{1\mu }^{*} (\sigma =T)\cdot \epsilon _{2\mu }^{*}(\sigma =T)\nonumber \\&+\,iA_{T} \epsilon ^{\alpha \beta \gamma \rho }\epsilon _{1\alpha }^{*}(\sigma ) \epsilon _{2\alpha }^{*}(\sigma )p_{1\gamma }p_{2\rho }. \end{aligned}$$

(6)

The longitudinal $H_{0}$, transverse $H_{\pm }$ of helicity amplitudes can be expressed $H_{0}=M^2_{B_{s}}A_{L}$, $H_{\pm }=M^2_{B_{s}}A_{N}\mp m_{1}m_{2} \sqrt{r^2-1}A_{T}$. The decay width is written

$$\begin{aligned} \Gamma =\frac{P_c}{8\pi M^{2}_{B_s} } A^{(\sigma )+}A^{(\sigma )}=\frac{P_c}{8\pi M^{2}_{B_s} }|H_{0}|^{2}+|H_{+}|^{2}+|H_{-}|^{2}. \end{aligned}$$

(7)

The interaction of the photon and the hadronic matter can be described by the vector meson dominance model (VMD) [27]. The photon can couple to the hadronic field through a $\rho$ meson. The mixing matrix element ${\Pi }_{\rho \omega }(m_{\rho }^2)$ is precisely extracted by fitting to recent data from the cross section for $e^{+}e^{-}\rightarrow \pi ^{+}\pi ^{-}$, which does not include the non-resonant contribution of direct $\omega \rightarrow \pi ^+\pi ^-$ [12, 13]. We can express $\Pi _{\rho \omega }(m_{\rho }^2)=\mathfrak {Re}\Pi _{\rho \omega }(m_{\rho }^2)+{\mathfrak {Im}}\Pi _{\rho \omega }(m_{\rho }^2)$ for the real part of $\mathfrak {Re}\Pi _{\rho \omega }(m_{\rho }^2)$ and the imaginary part of ${\mathfrak {Im}}\Pi _{\rho \omega }(m_{\rho }^2)$ at the $\rho$ mass.

The $\rho$–$\omega$ mixing parameters were recently determined precisely by Wolfe and Maltman [12, 13]:

$$\begin{aligned} \begin{aligned} \mathfrak {Re}\Pi _{\rho \omega }(m_{\rho }^2)&=-4600\pm {220}_{\mathrm{model}}\pm {170}_{\mathrm{data}} \ \mathrm{MeV}^2,\\ {\mathfrak {Im}}\Pi _{\rho \omega }(m_{\rho }^2)&=-6100\pm {1800}_{\mathrm{model}}\pm {1110}_{\mathrm{data}}\ \text {MeV}^2. \end{aligned} \end{aligned}$$

(8)

One can find the mixing parameters is the momentum dependence absorbing the non-resonant contribution of direct decay $\omega \rightarrow \pi ^{+}\pi ^{-}$. We introduce the momentum dependence of the $\rho$–$\omega$ mixing parameters $\widetilde{\Pi }_{\rho \omega }(s)$ where $\sqrt{s}$ is the invariant mass of $\pi ^{+}\pi ^{-}$. It is sensible to devote one’s energies to search the mixing process at the $\omega$ mass where the two pions can be produced. We write $\widetilde{\Pi }_{\rho \omega }(s)=\mathfrak {Re}\widetilde{\Pi }_{\rho \omega } (m_{\omega }^2)+\mathfrak {Im}\widetilde{\Pi }_{\rho \omega }(m_{\omega }^2)$ as follows:

$$\begin{aligned} \begin{aligned} \mathfrak {Re}\widetilde{\Pi }_{\rho \omega }(m_{\omega }^2)&=-4900\pm {400}\ \mathrm{MeV}^2,\\ {\mathfrak {Im}}\widetilde{\Pi }_{\rho \omega }(m_{\omega }^2)&=-6500\pm {3100}\ \text {MeV}^2. \end{aligned} \end{aligned}$$

(9)

The formalism of the CP violation is presented for the $\bar{B}_{s}^{0}$ meson decay process in the following. The amplitude A ($\bar{A}$) for the decay process $\bar{B}_{s}^{0}\rightarrow \pi ^+\pi ^{-}\pi ^+\pi ^{-}$ (${B}_{s}^{0}\rightarrow \pi ^+\pi ^{-}\pi ^+\pi ^{-}$) can be written as

$$\begin{aligned} A=\langle \pi ^+\pi ^{-}\pi ^+\pi ^{-}|H^T|\bar{B}_{s}^{0} \rangle + \langle \pi ^+\pi ^{-}\pi ^+\pi ^{-} |H^P|\bar{B}_{s}^{0} \rangle ,\nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned} \bar{A}= \langle \pi ^+\pi ^{-}\pi ^+\pi ^{-}|H^T|{B}_{s}^{0} \rangle +\langle \pi ^+\pi ^-\pi ^+\pi ^{-}|H^P|{B}_{s}^{0}\rangle ,\nonumber \\ \end{aligned}$$

(11)

where $H^T$ and $H^P$ refer to the tree and penguin operators in the Hamiltonian, respectively. We define the relative magnitudes and phases between the tree and penguin operator contributions as follows:

$$\begin{aligned} A= & {} \left\langle \pi ^+\pi ^{-}\pi ^+\pi ^{-}|H^T| \bar{B}_{s}^{0} \right\rangle [1+re^{i(\delta +\phi )}],\end{aligned}$$

(12)

$$\begin{aligned} \bar{A}= & {} \left\langle \pi ^+\pi ^-\pi ^+\pi ^{-} |H^T|{B}_{s}^{0} \right\rangle [1+re^{i(\delta -\phi )}], \end{aligned}$$

(13)

where $\delta$ and $\phi$ are strong and weak phases, respectively. The weak phase difference $\phi$ can be expressed as a combination of the CKM matrix elements: $\phi =\arg [(V_{tb}V_{ts}^{*})/(V_{ub}V_{us}^{*})]$. The parameter r is the absolute value of the ratio of tree and penguin amplitudes:

$$\begin{aligned} r\equiv \Bigg |\frac{\left\langle \pi ^+\pi ^{-}\pi ^+\pi ^{-}|H^P|\bar{B}_{s}^{0}\right\rangle }{\left\langle \pi ^+\pi ^{-}\pi ^+\pi ^{-}|H^T|\bar{B}_{s}^{0}\right\rangle }\Bigg |. \end{aligned}$$

(14)

The parameter of CP violating asymmetry, $A_{cp}$, can be written as

$$\begin{aligned} A_{CP}= & {} \frac{|A|^{2}-|\bar{A}|^{2}}{|A|^{2}+|\bar{A}|^{2}}\nonumber \\= & {} \frac{-2(T_{0}^2r_{0}\sin \delta _0+T_{+}^2r_{+}\sin \delta _{+} \,{+}\,T_{-}^2r_{-}\sin \delta _-)\sin \phi }{\sum _{i=0+-}T_{i}^2(1\,{+}\,r_{i}^2+2r_{i}\cos \delta _i\cos \phi )},\nonumber \\ \end{aligned}$$

(15)

where

$$\begin{aligned} |A|^{2}=\sum _{\sigma }A^{(\sigma )+}A^{(\sigma )}=|H_{0}|^{2} +|H_{+}|^{2}+|H_{-}|^{2} \end{aligned}$$

(16)

and the $T_{i}(i=0,+,-)$ are the tree-level helicity amplitudes. The $r_{j}(j=0,+,-)$ refer to the absolute value of the ratio of tree and penguin amplitude for the three kinds of polarizations, respectively. The $\sin \delta _{k}(k=0,+,-)$ represent the relative strong phases between the tree and penguin operator contributions from three kinds of helicity amplitudes. We can see explicitly from Eq. (15) that both weak and strong phase differences are responsible for CP violation. $\rho$–$\omega$ mixing introduces the strong phase difference and is well known for the three-body decay processes of the bottom hadron [28,29,30,31,32,33,34]. Due to $\rho$–$\omega$ interference from u and d quark mixing, we can write the formalism in an approximate form in terms of the first order isospin violation:

$$\begin{aligned} \left\langle \pi ^+\pi ^-\pi ^+\pi ^-|H^T|\bar{B}^0_{s} \right\rangle =\frac{2g_{\rho }^2}{s_{\rho }^{2}s_{\omega }}\widetilde{\Pi }_{\rho \omega }t_{\rho \omega } +\frac{g_{\rho }^2}{s_{\rho }^2}t_{\rho \rho }, \end{aligned}$$

(17)

$$\begin{aligned} \left\langle \pi ^+\pi ^-\pi ^+\pi ^-|H^P|\bar{B}^0_{s} \right\rangle =\frac{2g_{\rho }^2}{s_{\rho }^{2}s_{\omega }}\widetilde{\Pi }_{\rho \omega }p_{\rho \omega } +\frac{g_{\rho }^2}{s_{\rho }^2}p_{\rho \rho }, \end{aligned}$$

(18)

where $t_{\rho \rho }(p_{\rho \rho })$ and $t_{\rho \omega }(p_{\rho \omega })$ are the tree (penguin) amplitudes for $\bar{B}_{s}\rightarrow \rho ^0\rho ^0$ and $\bar{B}_{s}\rightarrow \rho ^0\omega$, respectively. $g_{\rho }$ is the coupling for $\rho ^0\rightarrow \pi ^+\pi ^-$. $\widetilde{\Pi }_{\rho \omega }$ refers to the effective $\rho$–$\omega$ mixing amplitude which also effectively includes the direct coupling $\omega \rightarrow \pi ^+\pi ^-$. $s_{V}$, $m_{V}$ and $\Gamma _V$(V=$\rho$ or $\omega$) is the inverse propagator, mass and decay rate of the vector meson V, respectively.

$$\begin{aligned} s_V=s-m_V^2+\mathrm{{i}}m_V\Gamma _V, \end{aligned}$$

(19)

with $\sqrt{s}$ being the invariant masses of the $\pi ^+\pi ^-$ pairs. There are double $\rho$–$\omega$ interference in the decay process of $\bar{B}^0_{s}\rightarrow \rho ^0(\omega )\rho ^0(\omega )\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$. Hence, a factor of 2 appears in Eqs. (17) and (18) compared with the case of single $\rho$–$\omega$ interference [28,29,30,31,32,33,34,35,36]. From Eqs. (10), (11), (17) and (18) one has

$$\begin{aligned} re^{i\delta }e^{i\phi }=\frac{2\widetilde{\Pi }_{\rho \omega }p_{\rho \omega } +s_{\omega }p_{\rho \rho }}{2\widetilde{\Pi }_{\rho \omega }t_{\rho \omega }+s_{\omega }t_{\rho \rho }}. \end{aligned}$$

(20)

Defining

$$\begin{aligned} \frac{p_{\rho \omega }}{t_{\rho \rho }}\equiv r^\prime e^{i(\delta _q+\phi )},\quad \frac{t_{\rho \omega }}{t_{\rho \rho }}\equiv \alpha e^{i\delta _\alpha },\quad \frac{p_{\rho \rho }}{p_{\rho \omega }}\equiv \beta e^{i\delta _\beta }, \end{aligned}$$

(21)

where $\delta _\alpha$, $\delta _\beta$ and $\delta _q$ are strong phases, one finds the following expression from Eqs. (20) and (21):

$$\begin{aligned} re^{i\delta }=r^\prime e^{i\delta _q}\frac{2\widetilde{\Pi }_{\rho \omega }+\beta e^{i\delta _\beta }s_{\omega }}{2\widetilde{\Pi }_{\rho \omega }\alpha e^{i\delta _\alpha }+s_{\omega }}. \end{aligned}$$

(22)

In order to obtain the CP violating asymmetry in Eq. (15), $\sin \phi$ and $\cos \phi$ are needed, where $\phi$ is determined by the CKM matrix elements. In the Wolfenstein parametrization [37, 38], one has

$$\begin{aligned} \begin{aligned} \mathrm{sin}\phi&=-\frac{\eta }{\sqrt{\rho ^2+\eta ^2}}, \\ \mathrm{cos}\phi&=-\frac{\rho }{\sqrt{\rho ^2+\eta ^2}}. \end{aligned} \end{aligned}$$

(23)

3.2 Calculation details

We can decompose the decay amplitude for the decay process $\bar{B}_{s}^0\rightarrow \rho ^{0}(\omega )\rho ^{0}(\omega )$ in terms of tree-level and penguin-level contributions depending on the CKM matrix elements of $V_{ub}V^{*}_{us}$ and $V_{tb}V^{*}_{ts}$. Due to Eqs. (15), (20) and (21), we can calculate the amplitudes $t_{\rho \rho }$, $t_{\rho \omega }$, $p_{\rho \rho }$ and $p_{\rho \omega }$ in a perturbative QCD approach. The F and M function associated with the decay amplitudes can be found in the appendix from the perturbative QCD approach.

There are four types of Feynman diagrams contributing to $\bar{B}_{s} \rightarrow M_{2}M_{3}$($M_{2}$, $M_{3}=\rho$ or $\omega$) annihilation decay mode at leading order. The pure annihilation type process can be classified into factorizable diagrams and non-factorizable diagrams [39, 40]. Through calculating these diagrams, we can get the amplitudes $A^{(i)}$, where $i=L, N, T$ stand for the longitudinal and two transverse polarizations. Because these diagrams are the same as those of $B\rightarrow K^*\phi$ and $B\rightarrow K^*\rho$ decays [39, 40], the formulas of $\bar{B}_{s} \rightarrow \rho \rho$ or $\bar{B}_{s} \rightarrow \rho \omega$ are similar to those of $B\rightarrow K^*\phi$ and $B\rightarrow K^*\rho$. We just need to replace some corresponding wave functions, Wilson coefficients and corresponding parameters.

With the Hamiltonian (1), depending on CKM matrix elements of $V_{ub}V^{*}_{us}$ and $V_{tb}V^{*}_{ts}$, the decay amplitudes $A^{(i)}(i=L, N, T)$ for $\bar{B}_{s}^0\rightarrow \rho ^{0}\rho ^{0}$ in PQCD can be written as

$$\begin{aligned} \sqrt{2}A^{(i)}(\bar{B}_{s}^0\rightarrow \rho ^{0}\rho ^{0})=V_{ub}V_{us}^{*}t_{\rho \rho }^{i}-V_{tb} V_{ts}^{*}p_{\rho \rho }^{i}. \end{aligned}$$

(24)

The tree-level amplitude $t_{\rho \rho }$ can written as

$$\begin{aligned} t_{\rho \rho }^{i}= & {} \frac{G_F}{\sqrt{2}} \Big \{ f_{B_s} F_{\mathrm{ann}}^{LL,i}\left[ a_{2}\right] + M_{\mathrm{ann}}^{LL,i}[C_2]\Big \}, \end{aligned}$$

(25)

where $f_{B_s}$ refers to the decay constant of $\bar{B}_{s}$ meson.

The penguin-level amplitude are expressed as follows:

$$\begin{aligned} p_{\rho \rho }^{i}= & {} \frac{G_F}{\sqrt{2}} \bigg \{ f_{B_s} F_{\mathrm{ann}}^{LL,i}\left[ 2a_{3} +\frac{1}{2}a_{9} \right] +f_{B_s} F_{\mathrm{ann}}^{LR,i}\left[ 2a_{5} +\frac{1}{2}a_{7} \right] \nonumber \\&+\,M_{\mathrm{ann}}^{LL,i}\left[ 2C_{4}+\frac{1}{2}C_{10}\right] +M_{\mathrm{ann}}^{SP,i}\left[ 2C_{6}+\frac{1}{2}C_{8}\right] \bigg \}.\nonumber \\ \end{aligned}$$

(26)

The decay amplitude for $\bar{B}_{s}^0\rightarrow \rho ^{0}\omega$ can be written as

$$\begin{aligned} 2A^{(i)}(\bar{B}_{s}^0\rightarrow \rho ^{0}\omega )= & {} V_{ub}V_{us}^{*} t_{\rho \omega }^{i} - V_{tb}V_{ts}^{*} p_{\rho \omega }^{i}. \end{aligned}$$

(27)

We can give the tree-level contribution as follows:

$$\begin{aligned} t_{\rho \omega }^{i}= & {} \frac{G_F}{\sqrt{2}}\Big \{ f_{B_s}F_{\mathrm{ann}}^{LL,i}\left[ a_{2}\right] + M_{\mathrm{ann}}^{LL,i}[C_{2}] \Big \}, \end{aligned}$$

(28)

and the penguin-level contributions are given as follows:

Table 1 Input parameters used in this paper

$$\begin{aligned} p_{\rho \omega }^{i}= & {} \frac{G_F}{\sqrt{2}} V_{tb}V_{ts}^{*}\left\{ f_{B_s} F_{\mathrm{ann}}^{LL,i}\left[ \frac{3}{2}a_9 \right] + f_{B_s}F_{\mathrm{ann}}^{LR,i}\left[ \frac{3}{2}a_7 \right] \right. \nonumber \\&\left. +\,M_{\mathrm{ann}}^{LL,i}\left[ \frac{3}{2}C_{10}\right] +M_{\mathrm{ann}}^{SP,i}\left[ \frac{3}{2}C_8\right] \right\} +\left[ \rho ^0 \leftrightarrow \omega \right] . \nonumber \\ \end{aligned}$$

(29)

Based on the definition of (21), we can get

$$\begin{aligned} \alpha e^{i\delta _\alpha }= & {} \frac{t_{\rho \omega }}{t_{\rho \rho }}, \end{aligned}$$

(30)

$$\begin{aligned} \beta e^{i\delta _\beta }= & {} \frac{p_{\rho \rho }}{p_{\rho \omega }}, \end{aligned}$$

(31)

$$\begin{aligned} r^\prime e^{i\delta _q}= & {} \frac{p_{\rho \omega }}{t_{\rho \rho }} \times \bigg |\frac{V_{tb}V_{ts}^*}{V_{ub}V_{us}^*}\bigg |, \end{aligned}$$

(32)

where

$$\begin{aligned} \left| \frac{V_{tb}V^{*}_{ts}}{V_{ub}V^{*}_{us}}\right| =\frac{\sqrt{\rho ^2+\eta ^2}}{\lambda ^2(\rho ^2+\eta ^2)}. \end{aligned}$$

(33)

4 Input parameters

The CKM matrix, which elements are determined from experiments, can be expressed in terms of the Wolfenstein parameters A, $\rho$, $\lambda$ and $\eta$ [37, 38, 41]:

$$\begin{aligned} \left( \begin{array}{ccc} 1-\tfrac{1}{2}\lambda ^2 &{}\quad \lambda &{}\quad A\lambda ^3(\rho -\mathrm {i}\eta ) \\ -\lambda &{}\quad 1-\tfrac{1}{2}\lambda ^2 &{}\quad A\lambda ^2 \\ A\lambda ^3(1-\rho -\mathrm {i}\eta ) &{}\quad -A\lambda ^2 &{}\quad 1\\ \end{array} \right) , \end{aligned}$$

(34)

where $\mathcal {O} (\lambda ^{4})$ corrections are neglected. The latest values for the parameters in the CKM matrix are [42]:

$$\begin{aligned}&\lambda =0.22506\pm 0.00050,\quad A=0.811\pm 0.026,\nonumber \\&\bar{\rho }=0.124_{-0.018}^{+0.019},\quad \bar{\eta }=0.356\pm {0.011}, \end{aligned}$$

(35)

where

$$\begin{aligned} \bar{\rho }=\rho \left( 1-\frac{\lambda ^2}{2}\right) ,\quad \bar{\eta }=\eta \left( 1-\frac{\lambda ^2}{2}\right) . \end{aligned}$$

(36)

From Eqs. (35) and (36) we have

$$\begin{aligned} 0.109<\rho<0.147,\quad 0.354<\eta <0.377. \end{aligned}$$

(37)

The other parameters and the corresponding references are listed in Table 1.

5 The numerical results of CP violation in $\bar{B}^0_{s}\rightarrow \rho ^0(\omega )\rho ^0(\omega )\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$

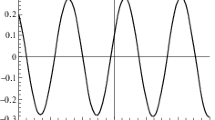
In the numerical results, we find that the CP violation can be enhanced via double $\rho$–$\omega$ mixing for the pure annihilation type decay channel $\bar{B}^0_{s}\rightarrow \rho ^0(\omega )\rho ^0(\omega )\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$ when the invariant mass of $\pi ^{+}\pi ^{-}$ is in the vicinity of the $\omega$ resonance within perturbative QCD scheme. The CP violation depends on the weak phase difference from CKM matrix elements and the strong phase difference. The CKM matrix elements, which relate to $\rho$, $\eta$, $\lambda$ and A, are given in Eq. (35). The uncertainties due to the CKM matrix elements come from $\rho$, $\eta$, $\lambda$ and A. In our numerical calculations, we let $\rho$, $\eta$, $\lambda$ and A vary among the limiting values. The numerical results are shown from Figs. 1, 2 and 3 with the different parameter values of the CKM matrix elements. The dash line, dot line and solid line corresponds to the maximum, middle, and minimum CKM matrix element for the decay channel of $\bar{B}^0_{s}\rightarrow \rho ^0(\omega )\rho ^0(\omega )\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$, respectively. We find the results are not sensitive to the values of $\rho$, $\eta$, $\lambda$ and A. In Fig. 1, we give the plot of the CP violating asymmetry as a function of $\sqrt{s}$. From Fig. 1, one can see that the CP violation parameter is dependent on $\sqrt{s}$ and changes rapidly due to $\rho$–$\omega$ mixing when the invariant mass of $\pi ^{+}\pi ^{-}$ is in the vicinity of the $\omega$ resonance [see Eq. (15)]. From the numerical results, it is found that the maximum CP violating parameter reaches $27.25\%$ in the case of ($\rho _{\mathrm{mini}}$, $\eta _{\mathrm{mini}}$).

Fig. 1

The CP violating asymmetry, $A_{cp}$, as a function of $\sqrt{s}$ for different CKM matrix elements. The dash line, dot line and solid line corresponds to the maximum, middle, and minimum CKM matrix element for the decay channel of $\bar{B}^0_{s}\rightarrow \rho ^0(\omega )\rho ^0(\omega )\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$, respectively

Fig. 2

$\sin \delta$ as a function of $\sqrt{s}$ corresponding to central parameter values of the CKM matrix elements for $\bar{B}^0_{s}\rightarrow \rho ^0(\omega )\rho ^0(\omega )\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$. The dash line, dot line and solid line corresponds to $\sin {\delta _{0}}$, $\sin {\delta _{+}}$ and $\sin {\delta _{-}}$, respectively

From Eqs. (15) and (22), one can see that the CP violating parameter depends on both $\sin \delta$ and r. The plots of $\sin \delta$ and r as a function of $\sqrt{s}$ are shown in Figs. 2, and 3, respectively. It can be seen that $\sin \delta _{0}$ ($\sin \delta _{-}$ and $\sin \delta _{+}$) vary sharply in the range of the resonance in Fig. 2. One can see that r changes largely in the vicinity of the $\omega$ resonance.

Fig. 3

Plot of r as a function of $\sqrt{s}$ corresponding to central parameter values of the CKM matrix elements for $\bar{B}^0_{s}\rightarrow \rho ^0(\omega )\rho ^0(\omega )\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$. The dash line, dot line and solid line corresponds to $r_{0}$, $r_{+}$ and $r_{-}$, respectively

6 Summary and conclusion

In this paper, we study the CP violation for the pure annihilation type decay process of $\bar{B}^0_{s}\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$ in perturbative QCD. It has been found that the CP violation can be enhanced greatly in the neighborhood of the $\rho$–$\omega$ resonance. There is the double resonance effect via $\rho$–$\omega$ mixing which can produce large strong phase in this decay process. The maximum CP violation value can reach $27.25\%$ due to double $\rho$ and $\omega$ resonance in Fig. 1. Hence, this decay process may be a good channel to test the $\rho$–$\omega$ mixing mechanism. The LHC experiment may search the large CP violation by reconstructing the $\pi ^{+}\pi ^{-}$ pairs at the region of the $\rho$ and $\omega$ mass. It is impossible to produce the decay process of $B_{s}\rightarrow \rho (\omega )\rightarrow \pi ^{+}\pi ^{-}$. So we could not obtain large CP violation by this decay process via $\rho$–$\omega$ mixing.

The theoretical errors are large, which follows from the uncertainties of the results. Generally, power corrections beyond the heavy quark limit give the major theoretical uncertainties. This implies the necessity of introducing $1/m_b$ power corrections. Unfortunately, there are many possible $1/m_b$ power suppressed effects and they are generally nonperturbative in nature and hence not calculable by the perturbative method. There are more uncertainties in this scheme. The first error refers to the variation of the CKM parameters, which are given in Eq. (35). The second error comes from the hadronic parameters: the shape parameters, form factors, decay constants, and the wave function of the $B_s$ meson. The third error corresponds to the choice of the hard scales, which vary from 0.75 to 1.25t, characterizing the size of next-to-leading order QCD contributions. Therefore, the results for CP violating asymmetry of the decay process $\bar{B}^0_{s}\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-$ is given as follows:

$$\begin{aligned} A_{CP}(\bar{B}^0_{s}\rightarrow \pi ^+\pi ^-\pi ^+\pi ^-)=27.20^{+0.05+0.28+7.13}_{-0.15-0.31-6.11}\%. \end{aligned}$$

(38)

When $\sqrt{s}=0.76$ GeV, the CP violating asymmetry varies from around $20.63\%$ to around $34.64\%$. Here the first uncertainty corresponds to the CKM parameters, the second comes from the hadronic parameters, and the third is associated with the hard scales.

Appendix: Related functions defined in the text

In this appendix we present explicit expressions of the factorizable and non-factorizable amplitudes with perturbative QCD in Eqs. (24) and (27) [22,23,24, 45, 46]. The factorizable amplitudes $F_{\mathrm{ann}}^{LL,i}(a_i)$, and $F_{\mathrm{ann}}^{SP,i}(a_i)$ ($i=L,N,T$) are written as

$$\begin{aligned}&f_{B_s}F_{\mathrm{ann}}^{LL,N}(a_i)= f_{B_s}F_{\mathrm{ann}}^{LR,N}(a_i), \end{aligned}$$

(39)

$$\begin{aligned}&f_{B_s}F_{\mathrm{ann}}^{LL,N}(a_i) = -8\pi C_FM_{B_s}^4f_{B_s}r_2 r_3\int ^1_0\mathrm{d}x_2\mathrm{d}x_3\nonumber \\&\quad \times \int ^\infty _0b_2\mathrm{d}b_2b_3\mathrm{d}b_3 \Big \{E_a(t_c)a_i(t_c)h_a(x_2,1-x_3,b_2,b_3) )\nonumber \\&\quad \times \left[ (2-x_3)\left( \phi _2^v(x_2)\phi _3^v(x_3) +\phi _2^a(x_2)\phi _3^a(x_3)\right) \right. \nonumber \\&\quad \left. +\,x_3(\phi _2^v(x_2)\phi _3^a(x_3)+\phi _2^a(x_2)\phi _3^v(x_3))\right] \nonumber \\&\quad -\,h_a(1-x_3,x_2,b_3,b_2)[(1+x_2) (\phi _2^v(x_2)\phi _3^v(x_3)\nonumber \\&\quad +\,\phi _2^a(x_2)\phi _3^a(x_3)) -(1-x_2)(\phi _2^v(x_2)\phi _3^a(x_3)\nonumber \\&\quad +\,\phi _2^a(x_2)\phi _3^v(x_3))] E_a(t_c')a_i(t_c')\Big \}, \end{aligned}$$

(40)

$$\begin{aligned} f_{B_s}F_{\mathrm{ann}}^{LL,T}(a_i)= & {} -f_{B_s}F_{\mathrm{ann}}^{LR,T}(a_i), \end{aligned}$$

(41)

$$\begin{aligned}&f_{B_s}F_{\mathrm{ann}}^{LL,T}(a_i) = -16\pi C_FM_{B_s}^4f_{B_s}r_2 r_3\int ^1_0\mathrm{d}x_2\mathrm{d}x_3\nonumber \\&\quad \times \int ^\infty _0b_2\mathrm{d}b_2b_3\mathrm{d}b_3\nonumber \\&\quad \Big \{ [x_3(\phi _2^v(x_2)\phi _3^v(x_3)+\phi _2^a(x_2)\phi _3^a(x_3))\nonumber \\&\quad +\,(2-x_3)(\phi _2^v(x_2)\phi _3^a(x_3)+\phi _2^a(x_2)\phi _3^v(x_3))]\nonumber \\&\quad \times E_a(t_c)a_i(t_c)h_a(x_2,1-x_3,b_2,b_3)\nonumber \\&\quad +\,h_a(1-x_3,x_2,b_3,b_2)[(1-x_2) (\phi _2^v(x_2)\phi _3^v(x_3)\nonumber \\&\quad +\,\phi _2^a(x_2)\phi _3^a(x_3)) \nonumber \\&\quad -\,(1+x_2)(\phi _2^v(x_2)\phi _3^a(x_3)\nonumber \\&\quad +\,\phi _2^a(x_2)\phi _3^v(x_3))] E_a(t_c')a_i(t_c')\Big \}, \end{aligned}$$

(42)

$$\begin{aligned}&f_{B_s} F_{\mathrm{ann}}^{LL,L}( a_i)=8\pi C_FM_{B_s}^4f_{B_s}\int ^1_0\mathrm{d}x_2\mathrm{d}x_3\int ^\infty _0b_2\mathrm{d}b_2b_3\mathrm{d}b_3\nonumber \\&\quad \times \Big \{a_i(t_c) E_a(t_c) \nonumber \\&\quad \times \Big [(x_3-1)\phi _2(x_2)\phi _3(x_3)-4r_2r_3\phi _2^s(x_2) \phi _3^s(x_3)\nonumber \\&\quad +2r_2r_3x_3\phi _2^s(x_2)(\phi _3^s(x_3)-\phi _3^t(x_3))\Big ] h_a(x_2,1-x_3,b_2,b_3)\nonumber \\&\quad +\,\Big [x_2\phi _2(x_2) \phi _3(x_3)+2r_2r_3(\phi _2^s(x_2)-\phi _2^t(x_2)) \phi _3^s(x_3)\nonumber \\&\quad +\, 2r_2r_3x_2(\phi _2^s(x_2)+\phi _2^t(x_2))\phi _3^s(x_3)\Big ]\nonumber \\&\quad \times a_i(t_c^\prime ) E_a(t_c^\prime )h_a(1-x_3,x_2,b_3,b_2)\Big \}, \end{aligned}$$

(43)

$$\begin{aligned} F_{\mathrm{ann}}^{LR,L}( a_i)=F_{\mathrm{ann}}^{LL,L}(a_i), \end{aligned}$$

(44)

with the color factor ${C_F} = 3/4$ and $f_{B_s}$ refer to the decay constant of the $\bar{B}_{s}$ meson and $a_i$ represents the corresponding Wilson coefficients for annihilation decay channels. In the above functions, $r_{2} (r_{3}) = m_{V} /m_{B_s}$ and $\phi _{2} (\phi _{3}) = \phi _{V}$ $(V=\rho$ or $\omega )$, where $m_{V}$ is the chiral scale parameter.

The non-factorizable amplitudes $M_{\mathrm{ann}}^{LL,i}(a_i)$, and $M_{\mathrm{ann}}^{SP,i}(a_i)$ ($i=L,N,T$) are written as

$$\begin{aligned} M_{\mathrm{ann}}^{LL,N}(a_i)= & {} M_{\mathrm{ann}}^{SP,N}(a_i), \end{aligned}$$

(45)

$$\begin{aligned} M_{\mathrm{ann}}^{LL,N}(a_i)= & {} -64\pi C_FM_{B_s}^4r_2 r_3/\sqrt{6}\int ^1_0\mathrm{d}x_1\mathrm{d}x_2\mathrm{d}x_3\nonumber \\&\times \int ^\infty _0b_1\mathrm{d}b_2b_2\mathrm{d}b_2\phi _{B_s}(x_1,b_1) [\phi _2^v(x_2)\phi _3^v(x_3)\nonumber \\&+\,\phi _2^a(x_2)\phi _3^a(x_3)] E_a'(t_d)a_i(t_d)h_{na}(x_1,x_2,x_3,b_1,b_2),\nonumber \\ \end{aligned}$$

(46)

$$\begin{aligned} M_{\mathrm{ann}}^{LL,T}(a_i)= & {} -M_{\mathrm{ann}}^{SP,T}(a_i), \end{aligned}$$

(47)

$$\begin{aligned}&M_{\mathrm{ann}}^{LL,T}(a_i) =-128 \pi C_FM_{B_s}^4r_2 r_3/\sqrt{6}\int ^1_0\mathrm{d}x_1\mathrm{d}x_2\mathrm{d}x_3\nonumber \\&\quad \times \int ^\infty _0b_1\mathrm{d}b_2b_2\mathrm{d}b_2\phi _{B_s}(x_1,b_1) [\phi _2^v(x_2)\phi _3^a(x_3)\nonumber \\&\quad +\,\phi _2^a(x_2)\phi _3^v(x_3)] E_a'(t_d)a_i(t_d)h_{na}(x_1,x_2,x_3,b_1,b_2), \end{aligned}$$

(48)

$$\begin{aligned}&M_{\mathrm{ann}}^{LL,L}( a_i)=32\pi C_FM_{B_s}^4/\sqrt{6}\int ^1_0\mathrm{d}x_1\mathrm{d}x_2\mathrm{d}x_3\nonumber \\&\quad \times \int ^\infty _0b_1\mathrm{d}b_2b_2\mathrm{d}b_2 \phi _{B_s}(x_1,b_1)\nonumber \\&\quad \times \Big \{h_{na}(x_1,x_2,x_3,b_1,b_2)\Big [-x_2\phi _2(x_2) \phi _3(x_3)\nonumber \\&\quad -\,4r_2r_3 \phi _2^s(x_2)\phi _3^s(x_3)\nonumber \\&\quad +\,r_2r_3(1-x_2)(\phi _2^s(x_2)+\phi _2^t(x_2)) (\phi _3^s(x_3)-\phi _3^t(x_3)) \nonumber \\&\quad +\,r_2r_3x_3(\phi _2^s(x_2)-\phi _2^t(x_2))(\phi _3^s(x_3)\nonumber \\&\quad +\,\phi _3^t(x_3))\Big ]a_i(t_d) E_a^\prime (t_d)\nonumber \\&\quad +\,h_{na}^\prime (x_1,x_2,x_3,b_1,b_2)\Big [(1-x_3) \phi _2(x_2)\phi _3(x_3) \nonumber \\&\quad +\,(1-x_3)r_2r_3(\phi _2^s(x_2)+\phi _2^t(x_2)) (\phi _3^s(x_3)-\phi _3^t(x_3)) \nonumber \\&\quad +\,x_2r_2r_3(\phi _2^s(x_2)-\phi _2^t(x_2)) (\phi _3^s(x_3)+\phi _3^t(x_3))\Big ] a_i(t_d^\prime ) E_a^\prime (t_d^\prime )\Big \},\nonumber \\ \end{aligned}$$

(49)

$$\begin{aligned}&M_{\mathrm{ann}}^{SP,L}( a_i)=32\pi C_F M_{B_s}^4/\sqrt{6}\int ^1_0\mathrm{d}x_1\mathrm{d}x_2\mathrm{d}x_3\nonumber \\&\quad \times \int ^\infty _0b_1\mathrm{d}b_1b_2\mathrm{d}b_2 \phi _{B_s}(x_1,b_1)\nonumber \\&\quad \times \Big \{a_i(t_d)E_a^\prime (t_d)h_{na}(x_1,x_2,x_3,b_1,b_2)\nonumber \\&\quad \times \Big [(x_3-1) \phi _2(x_2)\phi _3(x_3)\nonumber \\&\quad -\,4r_2r_3\phi _2^s(x_2)\phi _3^s(x_3)+r_2r_3x_3(\phi _2^s(x_2)\nonumber \\&\quad +\,\phi _2^t(x_2)) (\phi ^s_3(x_3)-\phi _3^t(x_3))\nonumber \\&\quad +\,r_2r_3(1-x_2)(\phi _2^s(x_2)-\phi _2^t(x_2))(\phi ^s_3(x_3) +\phi _3^t(x_3))\Big ] \nonumber \\&\quad +\,a_i(t_d^\prime ) E_a^\prime (t_d^\prime )h_{na}^\prime (x_1,x_2,x_3,b_1,b_2) \Big [x_2\phi _2(x_2)\phi _3(x_3)\nonumber \\&\quad +\,x_2r_2r_3(\phi _2^s(x_2)+\phi _2^t(x_2)) (\phi _3^s(x_3)-\phi _3^t(x_3)))\nonumber \\&\quad +\,r_2r_3(1-x_3)(\phi _2^s(x_2)-\phi _2^t(x_2))(\phi _3^s(x_3) +\phi _3^t(x_3))\Big ]\Big \}.\nonumber \\ \end{aligned}$$

(50)

The hard scale t is chosen as the maximum of the virtuality of the internal momentum transition in the hard amplitudes, including $1/b_i$:

$$\begin{aligned}&t_a=\text{ max }\{{\sqrt{x_3}M_{B_s},1/b_1,1/b_3}\},\end{aligned}$$

(51)

$$\begin{aligned}&t_a^\prime =\text{ max }\{{\sqrt{x_1}M_{B_s},1/b_1,1/b_3}\},\end{aligned}$$

(52)

$$\begin{aligned}&t_b=\text{ max }\{\sqrt{x_1x_3}M_{B_s},\sqrt{|1-x_1-x_2|x_3}M_{B_s},1/b_1,1/b_2\},\end{aligned}$$

(53)

$$\begin{aligned}&t_b^\prime =\text{ max }\{\sqrt{x_1x_3}M_{B_s},\sqrt{|x_1-x_2|x_3}M_{B_s},1/b_1,1/b_2\},\end{aligned}$$

(54)

$$\begin{aligned}&t_c=\text{ max }\{\sqrt{1-x_3}M_{B_s},1/b_2,1/b_3\},\end{aligned}$$

(55)

$$\begin{aligned}&t_c^\prime =\text{ max }\{\sqrt{x_2}M_{B_s},1/b_2,1/b_3\},\end{aligned}$$

(56)

$$\begin{aligned}&t_d=\text{ max }\{\sqrt{x_2(1-x_3)}M_{B_s}, \sqrt{1-(1-x_1-x_2)x_3}M_{B_s},1/b_1,1/b_2\},\nonumber \\\end{aligned}$$

(57)

$$\begin{aligned}&t_d^\prime =\text{ max }\{\sqrt{x_2(1-x_3)}M_{B_s},\sqrt{|x_1-x_2|(1-x_3)} M_{B_s},1/b_1,1/b_2\}.\nonumber \\ \end{aligned}$$

(58)

The hard functions h are written as [47]

$$\begin{aligned}&h_e(x_1,x_3,b_1,b_3)=\left[ \theta (b_1-b_3)I_0(\sqrt{x}_3M_{B_s}b_3)\right. \nonumber \\&\quad K_0(\sqrt{x}_3 M_{B_s}b_1) +\theta (b_3-b_1)I_0(\sqrt{x}_3M_{B_s}b_1)\nonumber \\&\quad \times \left. K_0(\sqrt{x}_3M_{B_s}b_3)\right] K_0(\sqrt{x_1x_3}M_{B_s}b_1)S_t(x_3),\nonumber \\&h_n(x_1,x_2,x_3,b_1,b_2)\nonumber \\&\quad =\left[ \theta (b_2-b_1)K_0(\sqrt{x_1x_3}M_{B_s}b_2) I_0(\sqrt{x_1x_3}M_{B_s}b_1)\right. \nonumber \\&\quad \left. +\,\theta (b_1-b_2)K_0(\sqrt{x_1x_3}M_{B_s}b_1)I_0(\sqrt{x_1x_3}M_{B_s}b_2)\right] \nonumber \\&\quad \times \left\{ \begin{array}{ll} \frac{i\pi }{2}H_0^{(1)}(\sqrt{(x_2-x_1)x_3} M_{B_s}b_2),&{} x_1-x_2<0\\ K_0(\sqrt{(x_1-x_2)x_3}M_{B_s}b_2),&{} x_1-x_2>0 \end{array} \right. , \end{aligned}$$

(59)

$$\begin{aligned}&h_a(x_2,x_3,b_2,b_3)=\left( \frac{i\pi }{2}\right) ^2 S_t(x_3)\Big [\theta (b_2-b_3)H_0^{(1)}\nonumber \\&\quad \times (\sqrt{x_3}M_{B_s}b_2)J_0(\sqrt{x_3}M_{B_s}b_3)\nonumber \\&\quad +\,\theta (b_3-b_2)H_0^{(1)}(\sqrt{x_3}M_{B_s}b_3)\nonumber \\&\quad \times J_0(\sqrt{x_3}M_{B_s}b_2)\Big ]H_0^{(1)}(\sqrt{x_2x_3}M_{B_s}b_2),\nonumber \\&h_{na}(x_1,x_2,x_3,b_1,b_2)=\frac{i\pi }{2}\left[ \theta (b_1-b_2)H^{(1)}_0\right. \nonumber \\&\quad \left. \times (\sqrt{x_2(1-x_3)}M_{B_s}b_1)J_0(\sqrt{x_2(1-x_3)}M_{B_s}b_2)\right. \nonumber \\&\quad \left. +\,\theta (b_2-b_1)H^{(1)}_0(\sqrt{x_2(1-x_3)}M_{B_s}b_2)\right. \nonumber \\&\quad \left. \times J_0(\sqrt{x_2(1-x_3)}M_{B_s}b_1)\right] \nonumber \\&\quad \times K_0(\sqrt{1-(1-x_1-x_2)x_3}M_{B_s}b_1),\nonumber \\&h_{na}^\prime (x_1,x_2,x_3,b_1,b_2)=\frac{i\pi }{2}\left[ \theta (b_1-b_2) H^{(1)}_0\right. \nonumber \\&\quad \left. \times (\sqrt{x_2(1-x_3)}M_{B_s}b_1)J_0(\sqrt{x_2(1-x_3)}M_{B_s}b_2)\right. \nonumber \\&\quad \left. +\,\theta (b_2-b_1)H^{(1)}_0(\sqrt{x_2(1-x_3)}M_{B_s}b_2)\right. \nonumber \\&\quad \times \left. J_0(\sqrt{x_2(1-x_3)}M_{B_s}b_1)\right] \nonumber \\&\quad \times \left\{ \begin{array}{ll} \frac{i\pi }{2}H^{(1)}_0(\sqrt{(x_2-x_1)(1-x_3)}M_{B_s}b_1),&{} x_1-x_2<0,\\ K_0(\sqrt{(x_1-x_2)(1-x_3)}M_{B_s}b_1),&{} x_1-x_2>0, \end{array}\right. \nonumber \\ \end{aligned}$$

(60)

where $J_0$ and ${Y}_0$ are Bessel functions with $H_0^{(1)}(z) = \mathrm {J}_0(z) + i\, \mathrm {Y}_0(z)$.

The threshold re-sums factor $S_t$ follows the parameterized [48]

$$\begin{aligned} S_t(x)=\frac{2^{1+2c}\Gamma (3/2+c)}{\sqrt{\pi }\Gamma (1+c)}[x(1-x)]^c, \end{aligned}$$

(61)

where the parameter $c=0.4$. In the non-factorizable contributions, $S_t(x)$ has a very small numerical effect on the amplitude [49]. Therefore, we drop $S_t(x)$ in $h_n$ and $h_{na}$.

The evolution factors $E^{(\prime )}_e$ and $E^{(\prime )}_a$ entering in the expressions for the matrix elements are given by

$$\begin{aligned} E_e(t)= & {} \alpha _s(t) \exp [-S_B(t)-S_3(t)],\nonumber \\ E'_e(t)= & {} \alpha _s(t) \exp [-S_B(t)-S_2(t)-S_3(t)]|_{b_1=b_3},\end{aligned}$$

(62)

$$\begin{aligned} E_a(t)= & {} \alpha _s(t) \exp [-S_2(t)-S_3(t)],\nonumber \\ E'_a(t)= & {} \alpha _s(t) \exp [-S_B(t)-S_2(t)-S_3(t)]|_{b_2=b_3}, \end{aligned}$$

(63)

in which the Sudakov exponents are defined as

$$\begin{aligned} S_B(t)= & {} s\left( x_1\frac{M_{B_s}}{\sqrt{2}},b_1\right) +\frac{5}{3}\int ^t_{1/b_1}\frac{d\bar{\mu }}{\bar{\mu }}\gamma _q(\alpha _s(\bar{\mu })),\end{aligned}$$

(64)

$$\begin{aligned} S_2(t)= & {} s\left( x_2\frac{M_{B_s}}{\sqrt{2}},b_2\right) +s\left( (1-x_2)\frac{M_{B_s}}{\sqrt{2}},b_2\right) \nonumber \\&+\,2\int ^t_{1/b_2}\frac{d\bar{\mu }}{\bar{\mu }}\gamma _q(\alpha _s(\bar{\mu })), \end{aligned}$$

(65)

where $\gamma _q=-\alpha _s/\pi$ is the anomalous dimension of the quark. The explicit form for the function s(Q, b) is

$$\begin{aligned} s(Q,b)= & {} \frac{A^{(1)}}{2\beta _{1}}\hat{q}\ln \left( \frac{\hat{q}}{\hat{b}}\right) -\frac{A^{(1)}}{2\beta _{1}}\left( \hat{q}-\hat{b}\right) + \frac{A^{(2)}}{4\beta _{1}^{2}}\left( \frac{\hat{q}}{\hat{b}}-1\right) \nonumber \\&-\left[ \frac{A^{(2)}}{4\beta _{1}^{2}}-\frac{A^{(1)}}{4\beta _{1}} \ln \left( \frac{e^{2\gamma _E-1}}{2}\right) \right] \ln \left( \frac{\hat{q}}{\hat{b}}\right) \nonumber \\&+\frac{A^{(1)}\beta _{2}}{4\beta _{1}^{3}}\hat{q}\left[ \frac{\ln (2\hat{q})+1}{\hat{q}}-\frac{\ln (2\hat{b})+1}{\hat{b}}\right] \nonumber \\&+\frac{A^{(1)}\beta _{2}}{8\beta _{1}^{3}}\left[ \ln ^{2}(2\hat{q})-\ln ^{2}(2\hat{b})\right] , \end{aligned}$$

(66)

where the variables are defined by

$$\begin{aligned} {\hat{q}}\equiv \text{ ln }[Q/(\sqrt{2}\Lambda )],~~~ \hat{b}\equiv \text{ ln }[1/(b\Lambda )], \end{aligned}$$

(67)

and the coefficients $A^{(i)}$ and $\beta _i$ are

$$\begin{aligned}&\beta _1=\frac{33-2n_f}{12},~~\beta _2=\frac{153-19n_f}{24},\nonumber \\&A^{(1)}=\frac{4}{3},~~A^{(2)}=\frac{67}{9} -\frac{\pi ^2}{3}-\frac{10}{27}n_f+\frac{8}{3}\beta _1\text{ ln } (\frac{1}{2}e^{\gamma _E}),\nonumber \\ \end{aligned}$$

(68)

with $n_f$ is the number of the quark flavors and $\gamma _E$ the Euler constant. We will use the one-loop expression of the running coupling constant.

In this study, we use the model function

$$\begin{aligned} \phi _{B_s}(x,b) = N_{B_s} x^2(1-x)^2 \exp \left[ -\frac{M_{B_s}^2\ x^2}{2 \omega _b^2} -\frac{1}{2} (\omega _b b)^2 \right] , \end{aligned}$$

(69)

where the share parameter $\omega _b=0.5\pm 0.05$ GeV, and the normalization constant $N_{B_s}=63.5688$ GeV is related to the $B_s$ decay constant ${f_{{B_s}}} = 0.23 \pm 0.03$ GeV.

For $\rho$ and $\omega$ vector mesons, we use ${\rho ^0} = \frac{1}{{\sqrt{2} }}\left( {u\overline{u} - d\overline{d} } \right)$ and $\omega = \frac{1}{{\sqrt{2} }}\left( {u\overline{u} + d\overline{d} } \right)$. The distribution amplitudes of a vector meson (v=$\rho$ or $\omega$), $\phi _{\rho }$, $\phi _{\omega }$, $\phi ^t_{V}$, $\phi ^s_{V}$, $\phi ^v_{V}$, and $\phi ^a_{V}$, are calculated using the light-cone QCD sum rule [50, 51]:

$$\begin{aligned} \phi _\rho (x)= & {} \frac{3f_\rho }{\sqrt{6}} x (1-x)\left[ 1+0.15C_2^{3/2} (t) \right] ,\end{aligned}$$

(70)

$$\begin{aligned} \phi _\omega (x)= & {} \frac{3f_\omega }{\sqrt{6}} x (1-x)\left[ 1+0.15C_2^{3/2} (t)\right] ,\end{aligned}$$

(71)

$$\begin{aligned} \phi ^t_V(x)= & {} \frac{3f^T_V}{2\sqrt{6}}t^2,\end{aligned}$$

(72)

$$\begin{aligned} \phi ^s_V(x)= & {} \frac{3f_V^T}{2\sqrt{6}} (-t),\end{aligned}$$

(73)

$$\begin{aligned} \phi _V^v(x)= & {} \frac{3f_V}{8\sqrt{6}}(1+t^2),\end{aligned}$$

(74)

$$\begin{aligned} \phi _V^a(x)= & {} \frac{3f_V}{4\sqrt{6}}(-t), \end{aligned}$$

(75)

where $t=2x-1$. Here $f_{V}$ is the decay constant of the vector meson with longitudinal polarization, whose values are shown in Table 1.

The Gegenbauer polynomials $C^{\nu }_{n}(t)$ read

$$\begin{aligned} \begin{array}{ll} C_2^{1/2} (t) = \frac{1}{2} (3t^2-1),&{}\quad C_4^{1/2} (t) = \frac{1}{8}(35t^4-30t^2+3),\\ C_2^{3/2} (t) = \frac{3}{2} (5t^2-1),&{}\quad C_4^{3/2} (t) = \frac{15}{8}(1-14t^2+21t^4),\\ C_1^{3/2}(t)= 3t. \end{array} \end{aligned}$$

(76)