1 Introduction

Over the past 100 years General Relativity (GR) has matured into what is now arguably one of the most successful theories of modern physics. It has allowed us to explain gravitational phenomena from solar system scales [1,2,3,4,5] all the way to some of the largest scales in the observable universe. With the first two direct detections of gravitational waves from coalescing black holes by LIGO [6, 7], the past year has been a particularly triumphant period for GR.

Despite these successes, most well-established tests of GR still only involve weak gravitational fields and motions with speeds much less that the speed of light. While the recent LIGO events represented the first real strong-field tests of the theory and were consistent with GR, many more such observations will be needed to probe the dynamical features of the strong-field regime, before we can be certain that all extensions of Einstein gravity can be ruled out. Some of the most natural and promising extensions to GR are those which appear as the low energy limit of fundamental theories such as string or M-theory (e.g., [8, 9]). Examples of such modifications of GR can be found in a particularly popular and now very extensively studied class of fourth order theories of gravity, the so called f(R) theories of gravity. In these theories, the modification to the gravitational action is described by the addition of a general function of the Ricci scalar R, which leads to field equations which are of fourth order in the metric tensor \(g_{ab}\) (in GR the field equations are second order in \(g_{ab}\)).This implies that the gravitational interaction is generated by the usual spin-2 graviton degrees of freedom together with a scalar degree of freedom. These deviations from GR derive from the work on scalar-tensor theory by Brans and Dicke, Jordan and Fierz [10,11,12].

On cosmological scales, we require that f(R) theories reproduce cosmological dynamics consistent with type Ia supernovae, BAO, Large Scale Structure and CMB measurements. They should be free from tachyonic instabilities, sudden singularities and ghosts and they should have valid Newtonian and post-Newtonian limits [13]. We should also expect that well-defined solutions found in GR, such as the Schwarzschild solution, are stable against generic perturbations in this more general context. Failure to satisfy the aforementioned criteria disfavours the theory as a viable alternative to GR.

In GR, linear perturbations of Schwarzschild black holes were first studied in detail by Chandrasekhar using the metric approach together with the Newman–Penrose formalism [14]. More recently, the standard results of Black Hole perturbation theory were reproduced using the \(1+1+2\) covariant approach [15]. In the metric approach, perturbations are described by two wave equations, i.e., the Regge–Wheeler equation for odd parity modes and the Zerilli equation in the even parity case. These wave equations are described by functions (and their derivatives) in the perturbed metric which are not gauge-invariant, as general coordinate transformations do not preserve the form of the wave equation. However, using the \(1+1+2\) covariant approach, Clarkson and Barrett [15] demonstrated that both the odd and the even parity perturbations may be unified in a single covariant wave equation, which is equivalent to the Regge–Wheeler equation. This wave equation is governed by a single covariant, gauge and frame-independent, transverse-traceless tensor. These results were extended to include couplings (at second order) to a homogeneous magnetic field leading to an accompanying electromagnetic signal alongside the standard tensor (gravitational wave modes) [16] and to electromagnetic perturbations on general locally rotationally symmetric spacetimes [17].

The \(1+1+2\) covariant approach was later applied to f(R) gravity in [18, 19] where all calculations were performed in the Jordan frame. The dynamics of the extra gravitational degree of freedom inherent in these fourth order theories was determined by the trace of the effective Einstein equations, leading to a linearised scalar wave equation for the Ricci scalar. One of the key results that came out of this analysis was: at the linearised level, the Regge Wheeler equation in general f(R) gravity (which admits the Schwarzschild solution), for gravitational perturbation around a black hole is exactly same as in GR. Therefore, any measurement of gravitational waves emitted from a black hole will not have any signatures of the modification of gravity. This brings us to the following important question.

At the observational level, what are the properties of the extra degree of freedom that manifests itself in the Ricci scalar of the spacetime, due to the higher order modifications in the theory of gravity? The answer to this question may then provide us with observational templates that can be used to verify GR at strong gravity regimes near the black hole horizon.

In this paper we address the above question in the following way:

  1. 1.

    We consider a small perturbation in the Ricci scalar from its zero value for a Schwarzschild spacetime in f(R)-gravity. We note that this is unique to higher order gravity and not possible in GR, where the Ricci scalar must be zero in vacuum. We then study the scattering of this disturbance of Ricci scalar by the black hole. Since all the calculations are done in the Jordan frame, the results can be directly linked to observables.

  2. 2.

    We would like to emphasise the following important point here: We know that at the action level and in the Einstein frame, f(R) gravity is equivalent to a scalar-tensor theory (GR with a massive scalar field) [25]. Hence studying the propagation of the scalar perturbations on a Schwarzschild background should be equivalent to studying the Klein–Gordon equation for a massive scalar field on that background (see for example [26] and the references therein). However, this equivalence may miss certain important features in the observational level, as in this case there is no real scalar field, but the geometry of space time behaving like a scalar field. Therefore, it will be unwise to assume beforehand that this geometrical effect will obey all physically realistic conditions (e.g. energy conditions) like a real massive scalar field would. Hence in this paper we perform all our calculations in Jordan frame (the physical frame), to find what fraction of the in-falling Ricci scalar perturbation would be reflected by the black hole potential barrier.

  3. 3.

    To study the problem of reflection and transmission of the perturbations of Ricci scalar, we use the method of Jost functions. This is a powerful mathematical tool that enables us to model the problem in terms of a Volterra integral equation of second kind. It is interesting to note that in the context of the Ricci scalar perturbations, the convergence of the numerical solution to this equation is guaranteed.

  4. 4.

    We explicitly calculate the reflection coefficient for the Ricci scalar perturbations for wavelengths much smaller than the ratio of the second order coefficient to the first order coefficient of the Taylor expansion of the function f around \(R=0\), and compare them to that of the gravity waves. Our analysis brings out certain interesting features which may provide a novel observational signature for modified gravity.

Unless otherwise specified, geometric units (\(8\pi G=c=1\)) will be used throughout this paper.

2 Higher order gravity

In general relativity the Einstein–Hilbert action is given as

$$\begin{aligned} \mathcal{S} =\frac{1}{2} \int \mathrm{d}V \left[ \sqrt{-g} \left( R-2\Lambda \right) +2\, \mathcal{L}_{M}(g_{ab}, \psi )\right] , \end{aligned}$$
(1)

where \( \mathcal{L}_{M} \) is the Lagrangian density of the matter fields \(\psi \), R is the Ricci scalar and \( \Lambda \) is the cosmological constant. The invariant 4-volume element is given by the expression \(\sqrt{-g}\,dV\) and the gravitational Lagrangian density as \( \mathcal{L}_{g} = \sqrt{-g} \left( R-2\Lambda \right) \), where g is the determinant of the metric tensor \(g_{ab}\). A generalisation of this action is done by replacing R in (1) with a \(C^2\) function of the quadratic contractions of the Riemann curvature tensor \(R^{2}\), \(R_{ab}R^{ab}\), \(R_{abcd}R^{abcd}\) and \(\varepsilon ^{klmn} R_{klst}R^{st}{}_{mn}\) where \(\varepsilon ^{klmn}\) is the antisymmetric 4-volume element. In fact, in the quantum field picture, the effects of renormalisation are expected to add such terms to the Lagrangian giving a first approximation to some quantised theory of gravity [27, 28]. The Lagrangian density that can be constructed from the generalisation is of the form

$$\begin{aligned} \mathcal{L}_{g}=\ \sqrt{-g} ~f(R, R_{ab}\,R^{ab}, R_{abcd}\,R^{abcd}). \end{aligned}$$
(2)

It is a well-known result that [29,30,31]

$$\begin{aligned} (\delta /\delta g_{ab})\int&\mathrm{d}V \left( R_{abcd}\,R^{abcd}-4R_{ab}\,R^{ab}+R^2\right) =0,\end{aligned}$$
(3)
$$\begin{aligned} (\delta /\delta g_{ab})\int&\mathrm{d}V \,\varepsilon ^{klmn} R_{klst}\,R^{st}{}_{mn}= 0, \end{aligned}$$
(4)

that is, the functional derivative of the Gauss–Bonnet invariant and \(\epsilon ^{iklm}R_{ikst}\,R^{st}{}_{lm}\) vanish with respect to \(g_{ab}\). If we consider the function f to be linear in the square of Riemann tensor, we can use this symmetry to rewrite it in terms of the other two invariants and as a result the action for FOG can be written as:

$$\begin{aligned} \mathcal{S}= & {} \frac{1}{2} \int \mathrm{d}V \left\{ \sqrt{-g} \left( c_{0}\,R+ c_{1}\,R^{2} + c_{2}\,R_{ab}\,R^{ab}\right) \right. \nonumber \\&\left. +\,2\,\mathcal{L}_{M}(g_{ab}, \psi ) \right\} . \end{aligned}$$
(5)

where the coefficients \(c_{0}\), \(c_{1}\) and \(c_{2}\) have the appropriate dimensions. Now it is well known that the theory of gravity obeying the above Lagrangian suffers from several instabilities (see for example [32] and the references therein). One of the major problems arises in the weak field limit, where these theories represent two massive modes with two different mass scales. For a certain parameter set of these mass scales the usual PPN constraints are violated. Apart from that there exist open sets for these mass parameters for which gravity is repulsive at small scales and attractive at larger scales. Also being a higher order curvature theory, this action suffers from the usual Ostrogradski instabilities [33], which cannot be avoided. To avoid such pathologies in the theory we set the constant \(c_2=0\) and therefore we can write the action as

$$\begin{aligned} \mathcal{S}= \frac{1}{2} \int \mathrm{d}V \left[ \sqrt{-g}\,f(R)+ 2\,\mathcal{L}_{M}(g_{ab}, \psi )\right] . \end{aligned}$$
(6)

The action (6) represents the simplest generalisation of the Einstein–Hilbert density. Demanding that the action be invariant under some symmetry ensures that the resulting field equations also respect that symmetry. That being the case, since the Lagrangian is a function R only, and R is a generally covariant and locally Lorentz invariant scalar quantity, then the field equations derived from the action (6) are generally covariant and Lorentz invariant. Also it is quite interesting that we can avoid the Ostrogradski instabilities in f(R)-theories. This corresponds to removing the ghost degrees of freedom from both the fourth order and the third order derivative terms from the equations of motion [34, 35].

There are different variational principles that can be applied to the action \(\mathcal S\) in order to obtain the field equations. One approach is the standard metric formalism where variation of the action is with respect to the metric \(g_{ab}\) and the connection \(\Gamma ^a_{~~bc}\) in this case is the Levi-Civita one, that is, the metric connection,

$$\begin{aligned} \Gamma ^a{}_{bc}=\frac{1}{2}\,g^{ad} \left( g_{bd,c}+g_{dc,b}-g_{bc,d}\right) . \end{aligned}$$
(7)

3 Field equations in metric formalism

Varying the action (6) with respect to the metric \(g_{ab}\) over a 4-volume yields

$$\begin{aligned} \delta \mathcal{S}= & {} -\frac{1}{2} \int \mathrm{d}V \, \sqrt{-g} \left\{ \frac{1}{2} f \, g_{ab} \, \delta g^{ab}\right. \nonumber \\&\left. -f^{\prime }\,\delta R +T^{M}_{ab} \, \delta g^{ab}\right\} , \end{aligned}$$
(8)

where \( ' \) denotes differentiation with respect to R, and \( T^{M}_{ab} \) is the matter energy momentum tensor (EMT) defined as

$$\begin{aligned} T^{M}_{ab}=- \frac{2}{\sqrt{-g}} \, \frac{\delta \mathcal{L}_{M}}{\delta g^{ab} }. \end{aligned}$$
(9)

Writing the Ricci scalar as \(R= g^{ab}\,R_{ab}\) and assuming the connection is the Levi-Civita one, we can write

$$\begin{aligned} f^{\prime }\,\delta R \simeq \delta g^{ab}\left( f^{\prime }\, R_{ab} + g_{ab} \, \Box f^{\prime }- \nabla _{a}\nabla _{b} f^{\prime }\right) , \end{aligned}$$
(10)

where the \(\simeq \) sign denotes equality up to surface terms and \(\Box \equiv \nabla _{c}\nabla ^{c}\). By requiring that \(\delta \mathcal{S} =0\) with respect to variations in the metric, ergo a stationary action, one has finally

$$\begin{aligned} f^{\prime }\left( R_{ab}-\frac{1}{2} g_{ab} \, R\right)= & {} \frac{1}{2} g_{ab}\,(f-R \, f^{\prime }) +\nabla _{a}\nabla _{b}f^{\prime }\nonumber \\&-\, g_{ab} \,\Box f^{\prime }+ T^{M}_{ab}. \end{aligned}$$
(11)

The special case \(f = R\) gives the standard Einstein field equations.

It is convenient to write (11) in the form of effective Einstein equations as

$$\begin{aligned} G_{ab} = \left( R_{ab}-\frac{1}{2} g_{ab} \, R\right) = \tilde{T}^{M}_{ab} + T^{R}_{ab} = T_{ab}, \end{aligned}$$
(12)

where we define \(T_{ab}\) as the total EMT with

$$\begin{aligned} \tilde{T}^{M}_{ab} = \frac{T^{M}_{ab}}{ f^{\prime }} \end{aligned}$$
(13)

and

$$\begin{aligned} T^{R}_{ab} = \frac{1}{ f^{\prime }} \left[ \frac{1}{2}g_{ab} \,(f-R\, f^{\prime }) +\nabla _{a}\nabla _{b} f^{\prime }- g_{ab}\,\Box f^{\prime }\right] .\quad \end{aligned}$$
(14)

The field equation (12) contain fourth order derivatives of the metric functions, which can be seen from the existence of the \(\nabla _{a}\nabla _{b} f^{\prime }\) term in (14). This result also follows from a corollary of Lovelock’s theorem [36, 37], which states that in a four-dimensional Riemannian manifold, the construction of a metric theory of modified gravity must admit higher than second order derivatives in the field equations.

4 Schwarzschild solution and its stability

We know that in general relativity, the rigidity of spherically symmetric vacuum solutions of Einstein’s field equations continues even in the perturbed case. Particularly, almost spherical symmetry and/or almost vacuum implies almost static or almost spatially homogeneous [20,21,22]. This result emphasises the stability of Schwarzschild solution in general relativity.

In f(R)-gravity, the extension of this result is not so obvious due to the presence of an extra scalar degree of freedom. However, it has been shown recently that a Birkhoff-like theorem does exist in these theories [23], which states the following: For f(R) gravity, where the function f is of class \(C^3\) at \(R=0\), with \(f(0) = 0\) and \(f'_{0} \ne 0\), the only spherically symmetric solution with vanishing Ricci scalar in empty space in an open set \(\mathcal {S}\), is one that is locally equivalent to part of maximally extended Schwarzschild solution in \(\mathcal {S}\). The stability of this local theorem in the perturbed case has been formulated as: For f(R) gravity, where the function f is of class \(C^3\) at \(R=0\), with \(f(0) = 0\) and \(f'_{0} \ne 0\), any almost spherically symmetric solution with almost vanishing Ricci scalar in empty space in an open set \(\mathcal {S}\), is locally almost equivalent to part of maximally extended Schwarzschild solution in \(\mathcal {S}\). The important point to note here is that the size of the open set \({\mathcal S}\) depends on the parameters of the theory (namely the quantity \(f^{\prime \prime }(0)\)) and the Schwarzschild mass) and they can be always tuned such that the perturbations continue to remain small for a time period which is greater than the age of the universe. This clearly indicates that the local spacetime around almost spherical stars will be stable in the regime of linear perturbations in these modified gravity theories. A more direct perturbative analysis of Schwarzschild black holes in f(R) gravity [24] does establish the stability in a more rigorous way.

4.1 Linear perturbation of Schwarzschild black hole in f(R) gravity

In general relativity, the two fundamental second order wave equations govern the gravitational perturbations of the Schwarzschild black holes are the Regge–Wheeler equation [40] and the Zerilli equation [41]. The former equation describes the odd perturbations and the latter equation describes the even perturbations. Both equations satisfy a Schrödinger-like equation and the effective potential of these equations is shown to have the same spectra [42]. These waves are tensorial, and they are sourced by a small deviation from the spherical symmetry of the Schwarzschild black hole in vacuum.

For f(R) gravity, we can easily see from the almost Birkhoff like theorem stated in the previous section that there can be two types of perturbations. The first is the tensor perturbation driven by small departure from the spherical symmetry (like GR), whereas the second one is the scalar perturbation that is sourced by perturbations in the Ricci scalar, which vanishes in the unperturbed background. This is an extra mode, which is generated by the extra scalar degree of freedom in these theories and is absent in GR. The detection of these modes are of a crucial importance in asserting the validity or otherwise of GR as the theory of gravity. We will now briefly discuss the wave-equations governing these two different kind of perturbations in f(R)-gravity.

4.1.1 Tensor perturbations

In [18], it has been explained in detail that in f(R) gravity, one can construct a transverse traceless gauge independent 2-tensor, whose coefficients of harmonic decomposition \(M_T\) obey the same Regge–Wheeler equation as in GR. In terms of the ‘tortoise’ coordinate \(r_*\), which is related to the usual radial coordinate r by

$$\begin{aligned} r_*=r+2m\,\ln \left( \frac{r}{2m}-1\right) , \end{aligned}$$
(15)

this equation can be written in the form

$$\begin{aligned} \left( \frac{\mathrm{d}^2}{\mathrm{d}r_*^2}+\kappa ^2-V_T\right) M_T= 0, \end{aligned}$$
(16)

with the effective potential \(V_T\)

$$\begin{aligned} V_T=\left( 1-\frac{2m}{r}\right) \left[ \frac{\ell \left( \ell +1\right) }{r^2} -\frac{6m}{r^3}\right] , \end{aligned}$$
(17)

and we have factored out the harmonic time dependence part of \(M_T\), which is \(\exp (i\kappa t)\). \(V_T\) is the Regge–Wheeler potential for gravitational perturbations. This clearly indicates that the tensorial modes of the gravitational perturbations in f(R)-gravity have the same spectrum as in GR and hence observationally it is impossible to differentiate between the two through these modes.

4.1.2 Perturbation of Ricci scalar

Taking the trace of Eq. (12) in vacuum we get

$$\begin{aligned} 3\Box f^{\prime }+Rf^{\prime }-2f=0, \end{aligned}$$
(18)

which is a wave equation in terms of the Ricci scalar R associated with scalar modes. These modes are not present in GR as can be seen by substituting \(f(R)=R\) in the above equation, which gives \(R=0\). Hence in vacuum spacetimes in GR there cannot be any perturbations in Ricci scalar. However, this is possible in f(R) gravity and we can Taylor expand the function f around \(R=0\) (using \(f(0)=0\) for the existence of Schwarzschild solution) to get

$$\begin{aligned} f(R) = f'_0R + \frac{f''_0}{2}R^2 + \cdots \;. \end{aligned}$$
(19)

Using the tortoise coordinates, rescaling \(R=r^{-1}\mathcal {R}\), and factoring out the time dependence part \(\exp (i\kappa t)\) from \(\mathcal {R}\) we get

$$\begin{aligned} \left( \frac{\mathrm{d}^2}{\mathrm{d}r^{2}_{*}}+\kappa ^{2}-V_{S}\right) \mathcal {R}=0, \end{aligned}$$
(20)

where

$$\begin{aligned} V_{S}=\left( 1-\frac{2m}{r}\right) \left[ \frac{l(l+1)}{r^2}+\frac{2m}{r^3}+{U}^2\right] \end{aligned}$$
(21)

is the Regge–Wheeler potential for the scalar perturbations and

$$\begin{aligned} {U}^{2}=\frac{f'_{0}}{3f''_{0}}. \end{aligned}$$
(22)

The form of the wave equation (20) is similar to a one dimensional Schrödinger equation and hence the potential corresponds to a single potential barrier. This equation can be made dimensionless by multiplying through with the square of the black hole mass m. In this way the potential (21) becomes

$$\begin{aligned} V_S= & {} \left( 1-\frac{2}{r}\right) \left[ \frac{\ell \left( \ell +1\right) }{r^2} +\frac{2}{r^3}+u^2\right] , \end{aligned}$$
(23)

where we have defined (and dropped the tildes),

$$\begin{aligned} \tilde{r} = \frac{r}{m}, \quad \tilde{u} = m\,{U}, \quad \tilde{\kappa }=m\kappa . \end{aligned}$$
(24)

For scalar perturbations with \(u = 0\), the potential has two extrema, one in the unphysical region \(r<0\) and the other in \(r>0\). In the case of the scalar perturbations with \(u \ne 0\), for a certain range of u, the potential has three extrema: one in the unphysical region \(r<0\), a local maximum at \(r_\mathrm{max}\) and local minimum at \(r_\mathrm{min}\) such that \(2<r_\mathrm{max}<r_\mathrm{min}\).

5 Infra-red cut-off for incoming waves of disturbance of Ricci scalar

Let us now look at the equation governing the Ricci scalar perturbations (20) and the form of the potential (23), to study the limiting behaviour of the waves generated by these perturbations. This will help us specify the physically realistic boundary conditions. At \(r_{*}\rightarrow -\infty \), (which implies the horizon at \(r=2\)), we have \(V_{S}=0\), and Eq. (20) becomes

$$\begin{aligned} \left( \frac{\mathrm{d}^2}{\mathrm{d}r^{2}_{*}}+\kappa ^{2}\right) \mathcal {R}=0, \end{aligned}$$
(25)

which is an usual harmonic equation with two linearly independent solutions,

$$\begin{aligned} \mathcal {R}\sim C_1 \exp {(i\kappa r_{*})} + C_2 \exp {(-i\kappa r_{*})}. \end{aligned}$$
(26)

Since we do not have any outgoing mode at the horizon, this implies \(C_2=0\). On the other hand, at \(r_{*} = +\infty \), Eq. (20) becomes

$$\begin{aligned} \left( \frac{\mathrm{d}^2}{\mathrm{d}r^{2}_{*}}+\kappa ^{2}-u^2\right) \mathcal {R}=0, \end{aligned}$$
(27)

with

$$\begin{aligned} \mathcal {R}\sim C_3\exp {(i\sqrt{\kappa ^2-u^2}r_*)} +C_4\exp {(-i\sqrt{\kappa ^2-u^2}r_*)}. \end{aligned}$$
(28)

At this point, we come to a very important proposition, which we state as follows.

Proposition 1

The parameters of the theory in f(R) gravity provide a cut-off for long wavelength spherical incoming Ricci scalar waves from infinity.

Proof

When \(u^2 > \kappa ^2\), we can immediately see for the incoming modes,

$$\begin{aligned} \lim _{r_* \rightarrow \infty } \mathcal {R}_{in} = C_3\exp {(-\sqrt{-\kappa ^2+u^2}r_*)}\rightarrow 0. \end{aligned}$$
(29)

Hence, there are no incoming scalar waves at \(r_* \rightarrow \infty \) for \(\kappa <u.\)

As we are interested in the scattering of incoming Ricci scalar waves from infinity by the black hole potential barrier, in the following sections we choose the parameters of the theory, such that \(u^2<< \kappa ^2\). Hence for all practical purposes we have \({\kappa '}\equiv \sqrt{\kappa ^2 - u^2}=\kappa \).

6 Study of potential scattering using Jost functions

In this section we investigate in detail, how the Ricci scalar waves from infinity get scattered by the black holes in f(R) gravity. This scattering (which shows the reflexion and transmission) is due to the one dimensional potential barrier of the Schrödinger-like equation governing the perturbations. We set our boundary conditions in a way that there is no outgoing wave from the event horizon. Considering an influx of incoming waves from infinity, we would like to know that what fraction of these waves gets reflected by the potential barrier and what fraction gets transmitted to the black hole. Our analysis here is quite similar to the analysis presented in [14]. We use the method of the Jost function, which is the Wronskian of the regular solution and the (irregular) Jost solution to the differential equation.

Equation (20) is an ODE integrable over \((-\infty , \infty )\). Moreover, \(V_{S}(-\infty ) = 0\) and \(V_{S}(\infty ) = u^2\). If we let \(r_{*}\rightarrow \pm \infty \) in Eq. (20), we obtain two particular solutions with the asymptotic behaviours

$$\begin{aligned} \mathcal {R}_{1}(r_{*}, \kappa )\sim e^{-i\kappa ' r_{*}}\sim e^{-i\kappa r_{*}}, \quad (r_{*} \rightarrow +\infty ) \end{aligned}$$

and

$$\begin{aligned} \mathcal {R}_{2}(r_{*}, \kappa ) \sim e^{i\kappa r_{*}}, \quad (r_{*} \rightarrow -\infty ), \end{aligned}$$

which are independent since their Wronskian

$$\begin{aligned} \left[ \mathcal {R}_{1}(r_{*}, \kappa ), \mathcal {R}_{2}(r_{*}, \kappa )\right]&= +2i\kappa \ne 0. \end{aligned}$$
(30)

For real \(\kappa \), the solution represents ingoing and outgoing waves at \(\pm \infty \). This problem becomes one of reflection and transmission of incident waves by the potential barrier, \(V_{S}\). We seek solutions satisfying the wave Eq. (20) and the boundary conditions,

$$\begin{aligned} \mathcal {R}_{2}(r_{*}, \kappa ) = \frac{R_{1}(\kappa )}{T_1(\kappa )} \mathcal {R}_1(r_{*}, \kappa ) + \frac{1}{T_1(\kappa )} \mathcal {R}_{1}(r_{*}, -\kappa ) \end{aligned}$$
(31)

and

$$\begin{aligned} \mathcal {R}_{1}(r_{*}, \kappa ) = \frac{R_2(\kappa )}{T_2(\kappa )} \mathcal {R}_2(r_{*}, \kappa ) + \frac{1}{T_2(\kappa )} \mathcal {R}_{2}(r_{*}, -\kappa ), \end{aligned}$$
(32)

where \(R_1(\kappa )\), \(R_2(\kappa )\), \(T_1(\kappa )\), \(T_2(\kappa )\) are distinct functions that exist if \(\kappa \ne 0\). Here we can easily see that \(T_1(\kappa )\mathcal {R}_{2}(r_{*}, \kappa ) \) corresponds to an incident wave of unit amplitude from \(+\infty \) giving rise to a reflected wave of amplitude \({R}_1(\kappa )\) and a transmitted wave of amplitude \(T_1(\kappa )\). In the theory of potential scattering, the Jost functions are defined by

$$\begin{aligned} m_{1}(r_{*}, \kappa ) = e^{+ i \kappa r_{*}} \mathcal {R}_{1}(r_{*}, \kappa ) \end{aligned}$$
(33)

and

$$\begin{aligned} m_{2}(r_{*}, \kappa ) = e^{- i \kappa r_{*}} \mathcal {R}_{2}(r_{*}, \kappa ), \end{aligned}$$
(34)

which satisfy the boundary conditions

$$\begin{aligned} m_{1}(r_{*}, \kappa )&\rightarrow 1 \quad \text {as} \quad r_{*} \rightarrow +\infty \nonumber \\ \text {and} \quad m_{2}(r_{*}, \kappa )&\rightarrow 1 \quad \text {as} \quad r_{*} \rightarrow -\infty . \end{aligned}$$
(35)

Equations (31) and (32) can, respectively, be written in terms of the Jost functions as

$$\begin{aligned} T(\kappa ) m_{2}(r_{*}, \kappa )&= R_{1}(\kappa ) e^{-2 i \kappa r_{*}} m_{1}(r_{*}, \kappa ) + m_{1}(r_{*}, -\kappa ), \end{aligned}$$
(36)

and

$$\begin{aligned} T(\kappa ) m_{1}(r_{*}, \kappa ) = R_{2}(\kappa ) e^{+2 i \kappa r_{*}} m_{2}(r_{*}, \kappa ) + m_{2}(r_{*}, -\kappa ), \end{aligned}$$
(37)

where \(T_1(\kappa ) = T_2(\kappa )= T(\kappa )\). From the conditions imposed in (35), it follows that

$$\begin{aligned} m_{1}(r_{*}, \kappa ) = \frac{R_{2}(\kappa )}{T(\kappa )} e^{+2 i \kappa r_{*}} + \frac{1}{T(\kappa )} + o(1) \quad (r_{*} \rightarrow -\infty ) \end{aligned}$$
(38)

and

$$\begin{aligned} m_{2}(r_{*}, \kappa ) = \frac{R_{1}(\kappa )}{T(\kappa )} e^{-2 i \kappa r_{*}} + \frac{1}{T(\kappa )} + o(1) \quad (r_{*} \rightarrow +\infty ) . \end{aligned}$$
(39)

Let us now write

$$\begin{aligned} \mathcal {R}_{2}(r_{*}, \kappa ) = e^{i \kappa r_{*}} + \psi (r_{*}, \kappa ). \end{aligned}$$
(40)

We note that \(\psi \rightarrow 0\) as \(r_{*} \rightarrow -\infty \), and \(\psi \) satisfies the differential equation

$$\begin{aligned} \left( \frac{\mathrm{d}^{2}}{\mathrm{d} r_{*}^{2}} + \kappa ^{2}\right) \psi = \left( e^{i \kappa r_{*}} + \psi \right) V_{s}. \end{aligned}$$
(41)
Fig. 1
figure 1

Potential profile \(V_S\) for \(l=2, 3, 4\)

Full size image

Now we know that, given any linear ODE of the form \(L \psi (x) = -f(x)\), where L is the linear harmonic differential operator, the solution is given by Green’s function

$$\begin{aligned} \psi (x) = \int G(x, x')f(x') \mathrm{d}x', \end{aligned}$$
(42)

where

$$\begin{aligned} G(x, x') = \frac{1}{\kappa } \left[ \frac{1}{2 i} \left( e^{i \kappa (x-x')} - e^{-i \kappa (x-x')}\right) \right] . \end{aligned}$$
(43)

Therefore we can write the solution \(\psi (x)\) in the form

$$\begin{aligned} \psi (r _{*}, \kappa ) =&\, \frac{1}{2 i \kappa } \int _{-\infty }^{r_{*}}\left[ e^{i \kappa (r_{*}' - r_{*})} - e^{-i \kappa (r_{*}' - r_{*})} \right] V_{S}(r_{*}') \nonumber \\&\times \left[ e^{i \kappa r_{*}} + \psi (r_{*}, \kappa ) \right] \mathrm{d}r_{*}'. \end{aligned}$$
(44)

Using the above equations we now get an integral equation for the Jost function as

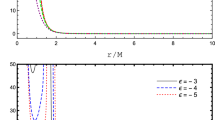
$$\begin{aligned} m_{2}(r _{*}, \kappa ) =\,&1 - \frac{1}{2 i \kappa } \int _{-\infty }^{r _{*}} \left( e^{2 i \kappa (r_{*}' - r_{*})} - 1 \right) \nonumber \\&\times V_{s}(r_{*}') m_{2}(r_{*}', \kappa ) \mathrm{d}r_{*}', \end{aligned}$$
(45)

which is a Volterra integral equation of the second kind. In the next section we give a numerical scheme to solve this equation, which will then provide us the required expressions for reflected and transmitted waves. In Fig. 1, we have plotted the form of the Jost function \(m_2(r_{*}', \kappa )\).

7 Numerical solution

Given a Volterra integral equation of the second kind (45), which is of the form

$$\begin{aligned} u (x) = f(x) + \lambda \int _a^x K(x,y)u(t)\mathrm{d}t, \end{aligned}$$
(46)

we divide the interval of integration (a, x) into n equal subintervals, \(\Delta t = \frac{x_n - a}{n}\), where \(n \ge 1\) and \(x_n = n.\) Also let \(y_0 = a\), \(x_0 = t_0\), \(x_n = t_n = x\), \(t_j = a + j\Delta t = t_0 + j\Delta t\), \(x_0 + i\Delta t = a + i\Delta t = t_i.\) Using the trapezoid rule, the integral can now be written as

$$\begin{aligned} \int _{a}^x K(x,t) u(t) \mathrm{d}t\approx & {} \Delta t \left[ \frac{1}{2}K(x,t_0) u(t_0) + K(x,t_1) u(t_1) \right. \nonumber \\&+\, \cdots + K(x,t_{n-1}) u(t_{(n-1)})\nonumber \\&\left. +\, \frac{1}{2} K(x,t_n) u(t_n) \right] , \end{aligned}$$
(47)

where \(\Delta t = \frac{t_j - a}{j} = \frac{x-a}{n}, \) \(t_j \le x, \) \(j \ge 1, \) \(x = x_n = t_n.\)

Using the above, Eq. (46) can be discretised as

$$\begin{aligned} u(x)= & {} f(x) + \lambda \Delta t \left[ \frac{1}{2}K(x,t_0) u(t_0) + K(x,t_1) u(t_1) \right. \nonumber \\&\left. + \cdots + K(x,t_{n-1}) u(t_{(n-1)}) + \frac{1}{2} K(x,t_n) u(t_n) \right] .\nonumber \\ \end{aligned}$$
(48)

Since \(K(x,t) \equiv 0\) when \(t > x\) (the upper limit of the integration ends at \(t = x\)), then \(K(x_i, t_j) = 0\) for \(t_j > x_i\). Numerically, Eq. (48) becomes

$$\begin{aligned} u(x_i) =&\, f(x_i) + \lambda \Delta t \left[ \frac{1}{2}K(x_i,t_0) u(t_0) + K(x_i, t_1) u(t_1) \right. \nonumber \\&+ \cdots + \left. K(x_i,t_{j-1}) u(t_{(j-1)}) + \frac{1}{2} K(x_i,t_j) u(t_j) \right] , \end{aligned}$$
(49)

where \(i = 1, 2, \ldots ,n \quad t_j \le x_i\) and \(u(x_0) = f(x_0).\) Denoting \(u_i = u(x_i)\), \(f_i = f(x_i)\) and \(K_{ij} = K(x_i, t_j)\), we can write the numeric equation in a simpler form as

$$\begin{aligned} u_0= & {} f_0 \nonumber \\ u_i= & {} f_i + \lambda \Delta t \left[ \frac{1}{2}K_{i0} u_0 + K_{i1} u_1 + \cdots + K_{i(j-1)} u_{j-1}\right. \nonumber \\&\qquad \qquad \qquad \left. +\, \frac{1}{2} K_{ij} u_j \right] , \end{aligned}$$
(50)

with \(i = 1, 2, \ldots ,n\) and \(j \le i\). Therefore there are \(n+1\) linear equations

$$\begin{aligned} u_0&= f_0 ,\nonumber \\ u_1&= f_1 + \lambda \Delta t \left[ \frac{1}{2}K_{10} u_0 + K_{11} u_1\right] ,\nonumber \\ u_2&= f_2 + \lambda \Delta t \left[ \frac{1}{2}K_{20} u_0 + K_{21} u_1 + \frac{1}{2} K_{22}u_2\right] ,\nonumber \\ \vdots&\qquad \vdots \nonumber \\ u_n&= f_n + \lambda \Delta t \left[ \frac{1}{2}K_{n0} u_0 + K_{n1} u_1 + \cdots \right. \nonumber \\&\quad \left. +\,K_{n(n-1)} u_{n-1} + \frac{1}{2} K_{nn}u_n\right] \;. \end{aligned}$$
(51)

Hence a general equation can be written in compact form as

$$\begin{aligned} u_i = \frac{f_i + \lambda \Delta t \left[ \frac{1}{2}K_{i0} u_0 + K_{i1} u_1 + \cdots + K_{i(i-1)} u_{i-1} \right] }{1 - \frac{\lambda \Delta t}{2} K_{ii}} \end{aligned}$$
(52)

and can be evaluated by substituting \(u_0, u_1, \ldots , u_{i-1}\) recursively from previous calculations. A MATLAB code was written to evaluate this system of linear equations for (45) and the results were used to evaluate the reflexion and transmission coefficients by coding the numerical solution for \(m_{2}(x, \kappa )\) with the potential (23) for different values of u (Fig. 2).

Fig. 2
figure 2

Jost function for \(l=2; u=0.001\)

Full size image

8 Reflection of Ricci scalar perturbations: results and discussions

It is well known [14] that the solution to the Volterra integral Eq. (45) is analytic in the lower half of the complex \(\kappa \) plane and is continuous for \(\mathfrak {I}(\kappa )\le 0\). In this case, the solution obtained by repeated iterations always converges and \(m_{2}(r _{*}, \kappa )\) can be expanded as a power series in \(1/\kappa \). These facts indicate the following:

$$\begin{aligned} m_{2}(x, \kappa )= & {} 1 -e^{-2 i \kappa r_{*}} \frac{1}{2 i \kappa } \int _{-\infty }^{+\infty } e^{2 i \kappa r_{*}'} V_{S}m_{2} \mathrm{d}r_*' \nonumber \\&+\, \frac{1}{2 i \kappa } \int _{-\infty }^{+\infty }V_{S}m_{2} \mathrm{d}r_{*}' + o(1). \end{aligned}$$
(53)

Comparing the above result with Eq. (39) immediately gives the relation between reflexion and transmission coefficients and the Jost function as

$$\begin{aligned} \frac{R_{1}(\kappa )}{T(\kappa )} =\, - \frac{1}{2 i \kappa } \int _{-\infty }^{+\infty } e^{2 i \kappa r_{*}'} V_{S} m_{2} \mathrm{d}r_{*}', \end{aligned}$$
(54)
$$\begin{aligned} \frac{1}{T(\kappa )} = 1 + \frac{1}{2 i \kappa } \int _{-\infty }^{+\infty } V_{s} m_{2} \mathrm{d}r_{*}'. \end{aligned}$$
(55)

From the above expression, the following conservation condition can be verified easily:

$$\begin{aligned} \varvec{R}+\varvec{T}\equiv |R_1|^2+|T|^2=1, \end{aligned}$$
(56)

The reflection wave amplitude \(\varvec{R}\) for various frequencies and for different values of l and u, are summarised in Tables 2, 3 and 4. From this analysis we attain a few interesting insights, which are as follows:

  1. 1.

    First of all, the Ricci waves have \(l=0,1\) modes, which are absent for the gravitational waves. It is interesting to note that for the monopole term (\(l=0\) mode) the reflection coefficients are much less than those with higher values of l for all wavelengths and for all values of the parameter u. This shows that a large fraction of monopole modes gets transmitted through the black hole potential barrier.

  2. 2.

    This analysis also provides a nice observational template to constrain the parameters of the higher order gravity theory. Assuming in the near future we will have an interferometer to detect scalar waves that are backscattered from an astrophysical black hole, we can in principle constrain the parameter u through the observation of the amplitude of these waves. We recall that the parameter u is linked to the parameters of the theory as \( u^2=m\sqrt{{\textstyle {f'_{0}\over 3f''_{0}}}}\), where m is the black hole mass.

  3. 3.

    If we compare the reflection coefficients of the tensor waves for \(l=2\) in GR from [14] (tabulated in Table 1), which will be the same in f(R) gravity, then we see that, for all wavelengths, a larger fraction of the scalar waves get reflected (in comparison to tensor waves) from the black hole potential barrier. This may provide a novel observational signature for modified gravity or otherwise.

  4. 4.

    Furthermore from Tables 2, 3 and 4 we can immediately see that, for all values of l, as u increases, the tendency of reflection increases for long wavelength scalar waves. This trait continues till the infra-red cut-off happens for a given frequency.

  5. 5.

    Also these calculations indicate that, for \(l=2\), as u increases, reflection wave amplitude attains a plateau near \(\varvec{R}=1\) for long wavelengths that suddenly drop off for higher frequencies, which is not the case for tensor waves tabulated in Table 1.

Table 1 The reflection amplitude (\(\varvec{R}\)) of gravitational waves for \(l=2\), for various frequencies (\(\kappa \)) as calculated in [14]
Full size table
Table 2 The reflection amplitude (\(\varvec{R}\)), where \(l=0\), for various frequencies (\(\kappa \)) and for different values of u
Full size table
Table 3 The reflection amplitude (\(\varvec{R}\)), where \(l=1\), for various frequencies (\(\kappa \)) and for different values of u.
Full size table
Table 4 The reflection amplitude (\(\varvec{R}\)), where \(l=2\), for various frequencies (\(\kappa \)) and for different values of u.
Full size table

We would like to emphasise here that these results are only applicable in the scenario where the frequency of the scalar waves are much larger than u (which is given by the parameters of the theory of gravity considered). An interesting limiting case occurs when \(\kappa \rightarrow u\). We can immediately see from the Ricci wave equation that the inner boundary condition at the black hole horizon remains unchanged, whereas for the outer boundary condition both ingoing and outgoing modes reaches a non-oscillating constant value at spatial infinity, which can be rescaled to zero without any loss of generality. A detailed analysis of this limiting case was performed in [43] for rotating Kerr black holes. A similar Jost function analysis as presented in this paper with the modified outer boundary condition would replicate the results of this paper for the special case of vanishing rotation. For \(\kappa>>u\) there will be a completely different scenario in terms of localisation of the scalar waves, which will be reported elsewhere.