The S-wave resonance contributions in the $B^{0}_{s}$ decays into $\psi (2S,3S)$ plus pion pair

Abstract

The three-body decays $B^0_s \rightarrow \psi (2S,3S) \pi ^+ \pi ^-$ are studied based on the perturbative QCD approach. With the help of the nonperturbative two-pion distribution amplitudes, the analysis is simplified into the quasi-two-body processes. Besides the traditional factorizable and nonfactorizable diagrams at the leading order, the next-to-leading order vertex corrections are also included to cancel the scale dependence. The $f_0(980)$, $f_0(1500)$ resonance contributions as well as the nonresonant contributions are taken into account using the presently known $\pi \pi$ time-like scalar form factor for the $s\bar{s}$ component. It is found that the predicted $B^0_s \rightarrow \psi (2S) \pi ^+ \pi ^-$ decay spectra in the pion pair invariant mass shows a similar behavior as the experiment. The calculated S-wave contributions to the branching ratio of $B^0_s \rightarrow \psi (2S) \pi ^+ \pi ^-$ is $6.0\times 10^{-5}$, which is in agreement with the LHCb data $\mathcal {B}(B^0_s \rightarrow \psi (2S) \pi ^+ \pi ^-)=(7.2\pm 1.2)\times 10^{-5}$ within errors. The estimate of $\mathcal {B}(B^0_s \rightarrow \psi (3S) \pi ^+ \pi ^-)$ can reach the order of $10^{-5}$, pending the corresponding measurements.

1 Introduction

The decays of the neutral B mesons to the charmonium state plus light meson pair have attracted lots of attentions recently. These decay processes could be used to study the spectroscopy in various meson pair systems, and they also have significant roles in understanding of the substructure of different resonant states. Up to now, several experimental collaborations, like LHCb and BaBar, have measured the decays $B_s^0\rightarrow J/\psi \pi ^+\pi ^-$ [1, 2], $B_s^0\rightarrow J/\psi K^+ K^-$ [3, 4], $B^0\rightarrow J/\psi \pi ^+\pi ^-$[5,6,7,8], $B^0\rightarrow J/\psi K^+ K^-$ [9], $B^0_s\rightarrow J/\psi \phi \phi$ [10], $B^0_s\rightarrow \psi (2S) K^+\pi ^-$ [11].

Fig. 1

The leading-order Feynman diagrams for the quasi-two-body decays $B^0_s\rightarrow \psi (2S,3S)f_0\rightarrow \psi (2S,3S)\pi ^+\pi ^-$, where $f_0$ stands for the S-wave intermediate state

On the theoretical side, the studies of B mesons decay into three hadronic final states have been performed using different approaches [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] in recent years. The perturbative QCD approach (PQCD) [37, 38] has some unique features that are particularly suitable for dealing with the three-body B meson decays. First, by introducing two-meson distribution amplitudes [39,40,41,42,43,44,45], the analysis of three-body hadronic B meson decays is simplified into the one for two-body decays. As pointed out in [46, 47], it is not practical to make a direct calculation for the three-body processes due to the enormous number of diagrams which contain two gluon exchange at lowest order. Besides, its contribution is not important because the region with the two gluons being hard simultaneously is power suppressed. The dominant contributions come from the kinematic region where the two light mesons move almost parallelly for producing a resonance with an invariant mass below $O(\bar{\Lambda }M_B)$ ($\bar{\Lambda }$ being the heavy-meson and heavy-quark mass difference), which can be catched by this new nonperturbative inputs. Second, the three-body decays of B meson receive both resonant and nonresonant contributions, it is difficult to separate the two parts clearly [27]. After absorbing the nonperturbative dynamics associated with the meson pair into the complex time-like form factors in the two-meson distribution amplitudes, both resonant and nonresonant contributions [46, 47] are included in the PQCD approach. Third, in the above dominant contribution region, the end-point singularities are smeared by the two-meson invariant mass, which suggest that the PQCD approach has a good predictive power without any arbitrary cutoffs. Finally, different from the two-body cases, some possible final state interactions (FSIs) may be significant in the three-body decays [31, 48]. According to [48], there are two distinct FSIs mechanisms. One is the interactions between the meson pair in the resonant region associated with various intermediate states. The other is the rescattering between the third particle and the pair of mesons. In our opinion, the former can be factorized into two-meson distribution amplitudes while the latter is ignored in the quasi-two-body approximation. Over past few years, the braching ratios and direct CP asymmetries of the three-body decays such as $B^{\pm }\rightarrow \pi ^{\pm }(K^{\pm })\pi ^+\pi ^-$ [49], $B^0_{(s)}\rightarrow J/\psi \pi ^+ \pi ^-$ [50], $B^0_{(s)}\rightarrow \eta _c \pi ^+\pi ^-$ [51], $B^+_c\rightarrow D^+_{(s)}\pi ^+\pi ^-$ [52], $B_{(s)}\rightarrow (D_{(s)}, \bar{D}_{(s)})\pi ^+\pi ^-$ [53], $B_{(s)}\rightarrow P\pi ^+\pi ^-$ [54] and $B^0_{(s)}\rightarrow \eta _c (2S)\pi ^+\pi ^-$ [55] have been studied systematically in the PQCD approach. In a recent work, the P-wave resonance contributions have been calculated in the $B\rightarrow K \pi \pi$ decays [56].

The three-body hadronic B meson decays with the radially excited charmonium mesons in the final state have not received much attentions in the literature. As the LHC gathering more and more data, the processes of the B mesons decays including excited charmonium states must have much possibilities to be found. Recently, the LHCb Collaboration have measured the three-body decay channels of $B^0_{(s)}\rightarrow \psi (2S) \pi ^+ \pi ^-$ with pp collision data collected at $\sqrt{s}=7$ TeV recently [57]. In the quark model, $\psi (2S)$ ($\psi (3S)$) is the first (second) radially excited vector charmonium with the radial quantum number $n=2(3)$ and the orbital angular momentum $l=0$. Both $\psi (2S)$ and $\psi (3S)$ were observed by the processes of the $e^+e^-$ annihilation into hadronic [58, 59]. The properties for the two high excited charmonium were updated in PDG 2016 [60]; they are listed in Table 1.

Table 1 The properties of $\psi (2S)$ and $\psi (3S)$ mesons

We have previously studied the semileptonic and two-body nonleptonic decays of the $B_c$ meson to radially excited charmonium mesons in the PQCD approach by using the harmonicosillator wave functions for the charmonium states [61, 62]. In the present work, we will extend our analysis to the three-body decays $B^0_s\rightarrow \psi (2S,3S)\pi ^+\pi ^-$ to provide an order of magnitude estimation. By introducing the two-pion distribution amplitudes, the S-wave contributions, which are the main contributions in the three-body decays $B^0_s\rightarrow \psi (2S,3S)\pi ^+\pi ^-$ [57], could be described by the quasi-two-body processes $B^0_s\rightarrow \psi (2S,3S)f_0\rightarrow \psi (2S,3S)\pi ^+\pi ^-$ containing the S-wave resonant states $f_0$, $f_0(980)$ and $f_0(1500)$ as two examples. Following the steps in Ref. [50], the decay amplitude $\mathcal {A}(B^0_s\rightarrow \psi (2S,3S)\pi ^+\pi ^-)$ can be written as the convolution

$$\begin{aligned} \mathcal {A}(B^0_s\rightarrow \psi (2S,3S)\pi ^+\pi ^-)=H \otimes \phi _B\otimes \phi _{\psi } \otimes \phi ^S_{\pi \pi }, \end{aligned}$$

(1)

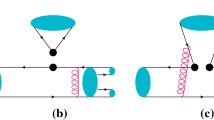
where the hard function H could be treated by PQCD including both factorizable and nonfactorizable contributions in the expansion at the leading order in $\alpha _s$ (single gluon exchange as depicted in Fig. 1). The hadron wave functions $\phi _B, \phi _{\psi }$ and $\phi ^S_{\pi \pi }$ absorb the nonperturbative dynamics, and they can be extracted from experimental data or other nonperturbative methods.

Following the introduction, in Sect. 2, we shall define kinematics and describe the wave functions of the initial and final states, then we will briefly review the related theoretical formulas. In Sect. 3, we will calculate the $B^0_s\rightarrow \psi (2S,3S)\pi ^+\pi ^-$ decays in the PQCD approach with discussions. Finally we will close this paper with a conclusion.

2 Framework

It is convenient to work in the rest frame of the $B_s^0$ meson. Its momentum $p_B$, along with the charmonium meson momentum $p_3$, the pion pair momentum p and other quark momenta $k_i$ in each meson, is chosen as [50]

$$\begin{aligned} p_B= & {} \frac{M_B}{\sqrt{2}}(1,1,\mathbf 0 _\mathrm{T}),\quad p_3=\frac{M_B}{\sqrt{2}}(r^2,1-\eta ,\mathbf 0 _\mathrm{T}),\nonumber \\ p= & {} \frac{M_B}{\sqrt{2}}(1-r^2,\eta ,\mathbf 0 _\mathrm{T}),\nonumber \\ k_B= & {} \left( 0,\frac{M_B}{\sqrt{2}}x_B,\mathbf k _\mathrm{BT}\right) ,\quad \nonumber \\ k_3= & {} \left( \frac{M_B}{\sqrt{2}}r^2x_3,\frac{M}{\sqrt{2}}(1-\eta )x_3,\mathbf k _{3\mathrm T}\right) ,\nonumber \\ k= & {} \left( \frac{M_B}{\sqrt{2}}z(1-r^2),0,\mathbf k _\mathrm{T}\right) , \end{aligned}$$

(2)

with the ratio $r=m/M_B$ and $m (M_B)$ is the mass of the charmonium ($B^0_s$) meson. The factor $\eta =\omega ^2/(M_B^2-m^2)$ with the invariant mass squared $\omega ^2=p^2$ for the pion pair. The $k_{iT}$, $x_i$ represent the transverse momentum and longitudinal momentum fraction of the quark inside the meson, respectively. If we choose the $\zeta =p_1^+/p^+$ as the $\pi ^+$ meson momentum fraction, the two pion momenta $p_{1,2}$ can be written as

$$\begin{aligned}&p_1=\frac{M_B}{\sqrt{2}}((1-r^2)\zeta , \eta (1-\zeta ),\mathbf p _{1\mathrm T}),\nonumber \\&p_2=\frac{M_B}{\sqrt{2}}((1-r^2)(1-\zeta ), \eta \zeta ,\mathbf p _{2\mathrm T}). \end{aligned}$$

(3)

Similar to the situation of the B meson [63], $B^0_s$ meson could also be treated as a heavy–light system, its wave function in the b space can be expressed by [64,65,66,67]

(4)

where b is the conjugate space coordinate of the transverse momentum $k_\mathrm{BT}$, and $N_c$ is the color factor. Here, we only consider one of the dominant Lorentz structures in our calculation. The distribution amplitude $\phi _{B_s}$ is adopt the same form as it in Refs. [68, 69]

$$\begin{aligned} \phi _{B_s}(x,b)=N x^2(1-x)^2\exp \left[ -\frac{x^2M_B^2}{2\omega ^2_b}-\frac{\omega ^2_bb^2}{2}\right] , \end{aligned}$$

(5)

with shape parameter $\omega _b=0.50\pm 0.05$ GeV and the normalization constant N being related to the decay constant $f_{B_s}$ through

$$\begin{aligned} \int _0^1\phi _{B_s}(x,b=0)\mathrm{{d}} x=\frac{f_{B_s}}{2\sqrt{2N_c}}. \end{aligned}$$

(6)

For the considered decays, the vector charmonium meson is longitudinally polarized. The longitudinal polarized component of the wave function is defined as [61, 62]

(7)

with the longitudinal polarization vector $\epsilon _L=\frac{M}{\sqrt{2}m}(-r^2,1-\eta , \mathbf 0 _{T})$. For the twist-2 (twist-3) distribution amplitudes $\phi ^L (\phi ^t)$ of 2S and 3S states, the same form and parameters are adopted as in Refs. [61, 62].

According to [50], the S-wave two-pion distribution amplitudes are organized into

(8)

where $n=(1,0,\mathbf 0 _{T})$ and $v=(0,1,\mathbf 0 _{T})$ are two dimensionless vectors. The asymptotic models for the twist-2 distribution amplitude $\Phi _{v \nu =-}$ and the twist-3 distribution amplitude $\Phi _{s},\Phi _{t \nu =+}$ and relevant time-like scalar form factor can be found in [50].

Now, we write down the differential branching ratio for $B^0_s\rightarrow \psi (2S,3S) \pi ^+\pi ^-$ decays,

$$\begin{aligned} \frac{\mathrm{d} \mathcal {B}}{\mathrm{d} \omega }=\frac{\tau \omega |\overrightarrow{p_1}||\overrightarrow{p_3}|}{32\pi ^3M_B^3}|\mathcal {A}|^2, \end{aligned}$$

(9)

where $\tau =1.512\times 10^{-12}s$ is the lifetime of $B^0_s$ meson. The three-momenta of the pion in the pion pair center-of-mass system $\overrightarrow{p_1}$ and that of the charmonium $\overrightarrow{p_3}$ are given by

$$\begin{aligned}&|\overrightarrow{p_1}|=\frac{1}{2}\sqrt{\omega ^2-4 m^2_{\pi }},\nonumber \\&|\overrightarrow{p_3}|=\frac{1}{2\omega }\sqrt{[M_B^2-(\omega +m)^2][M_B^2-(\omega -m)^2]}, \end{aligned}$$

(10)

with $m_{\pi }$ the pion mass.

Fig. 2

a The $\omega$ dependence of the differential decay rates $\mathrm{d}\mathcal {B}/\mathrm{d}\omega$ in a $B^0_s\rightarrow \psi (2S)\pi ^+\pi ^-$ and b $B^0_s\rightarrow \psi (3S)\pi ^+\pi ^-$ decays

The decay amplitude $\mathcal {A}$ is written as

$$\begin{aligned} \mathcal {A}= & {} V^*_{cb} V_{cs}(F^{LL}+M^{LL})\nonumber \\&-V^*_{tb} V_{ts}(F'^{LL}+F^{LR}+M'^{LL}+M^{SP}), \end{aligned}$$

(11)

with $V_{ij}$ the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements. The detailed expressions of F (the factorizable emission contributions) and M (the nonfacorizable contributions) are the same as the $B^0_s\rightarrow J/\psi \pi ^+\pi ^-$ process in the appendix of Ref. [50], except for the replacement $J/\psi \rightarrow \psi (2S,3S)$. In this work, we also consider the vertex corrections to the factorizable amplitudes F at the current known next-to-leading order (NLO) level. Their effects can be combined in the Wilson coefficients as usual [63, 70, 71]. In the NDR scheme we have

$$\begin{aligned} a_1= & {} C_1+\frac{C_2}{3}+\frac{\alpha _s}{9\pi }C_2\nonumber \\&\times \left[ -18-12\text {ln}\left( \frac{\mu }{m_b}\right) +f_I+g_I(1-r^2)\right] ,\nonumber \\ a_2= & {} C_3+\frac{C_4}{3}+C_9+\frac{C_{10}}{3}+\frac{\alpha _s}{9\pi }\times (C_4+C_{10})\nonumber \\&\times \left[ -18-12\text {ln}\left( \frac{\mu }{m_b}\right) +f_I+g_I(1-r^2)\right] ,\nonumber \\ a_3= & {} C_5+\frac{C_6}{3}+C_7+\frac{C_{8}}{3}+\frac{\alpha _s}{9\pi }\nonumber \\&\times (C_6+C_{8})\left[ 6+12\text {ln}\left( \frac{\mu }{m_b}\right) -f_I^h-g_I(1-r^2)\right] .\nonumber \\ \end{aligned}$$

(12)

The functions $f_I$ and $g_I$ arise from the vertex corrections; they can be found in [72].

3 Results

The mesons and quark masses (in units of GeV) and the Wolfenstein parameters are taken from the Particle Data Group [60],

$$\begin{aligned} M_B= & {} 5.367,\quad m_{\psi (2S)}=3.686,\quad m_{\psi (3S)}=4.040,\nonumber \\ m_{\pi }= & {} 0.14,\quad m_b=4.2, \quad m_c=1.27,\nonumber \\ \lambda= & {} 0.22506\pm 0.00050, \quad A=0.811\pm 0.026, \nonumber \\ \bar{\rho }= & {} 0.124^{+0.019}_{-0.018}, \quad \bar{\eta }=0.356\pm 0.011. \end{aligned}$$

(13)

The decay constants needed (in units of MeV) are [61, 73]

$$\begin{aligned} f_{B_s}=259\pm 32 ,\quad f_{\psi (2S)}=296^{+3}_{-2} ,\quad f_{\psi (3S)}=187\pm 8.\nonumber \\ \end{aligned}$$

(14)

Fig. 3

$\pi ^+\pi ^-$ invariant mass distributions for the $B^0_s\rightarrow \psi (2S)\pi ^+\pi ^-$ decay. a The S-wave contributions in this work, and b from the LHCb Collaboration [57]

Table 2 Contributions to the branching ratios (in unit of $10^{-5}$) of $B^0_s\rightarrow \psi (2S,3S)\pi ^+\pi ^-$ decays from the factorizable amplitudes F, from the nonfactorizable amplitudes M, and from the interference between F and M

By using Eq. (9), we have the predictions of the branching ratios as

$$\begin{aligned}&\mathcal {B}(B^0_s\rightarrow \psi (2S) f_0(980)\rightarrow \psi (2S)\pi ^+\pi ^- )\nonumber \\&\quad =[5.1^{+1.6}_{-1.2}(\omega _b)^{+1.4}_{-1.2}(f_{B_s}) ^{+1.0}_{-0.7}(a_2^{I=0})^{+0.6}_{-0.4}(t)]\times 10^{-5}, \nonumber \\&\mathcal {B}(B^0_s\rightarrow \psi (2S) f_0(1500)\rightarrow \psi (2S)\pi ^+\pi ^- )\nonumber \\&\quad =[2.3^{+1.3}_{-0.5}(\omega _b)^{+0.7}_{-0.5}(f_{B_s}) ^{+0.2}_{-0.1}(a_2^{I=0})^{+0.4}_{-0.1}(t)]\times 10^{-6},\nonumber \\ \end{aligned}$$

(15)

where the errors are induced by the shape parameter $\omega _b=0.50\pm 0.05$ GeV, the decay constant $f_{B_s}=0.259\pm 0.032$, the Gegenbauer coefficient $a_2^{I=0}=0.2\pm 0.2$ for the two-pion system, and the hard scale t, which varies from 0.75t to 1.25t, respectively. The errors from the uncertainty of the CKM matrix elements and the decay constants of charmonia are very small, and have been neglected. It is found that the main uncertainties in our approach come from the $B_s$ meson wave function (the first two errors), which can reach 30–50%. The uncertainties caused by the Gegenbauer coefficient are less than 20% which is similar to that of $B^0_s \rightarrow J/\psi \pi ^+ \pi ^-$ [50]. The scale-dependent uncertainty is largely reduced due to the inclusion of the next-to-leading order vertex corrections. Summing the two resonances $f_0(980)$ and $f_0(1500)$ in the strange scalar form factors, we have the total S-wave contribution for $B^0_s \rightarrow \psi (2S) \pi ^+ \pi ^-$ decay as

$$\begin{aligned}&\mathcal {B}(B^0_s\rightarrow \psi (2S)(\pi ^+\pi ^- )_{\mathrm{{S}}{\text {-}}\mathrm{{wave}}})\nonumber \\&\quad =\left[ 6.0^{+1.7}_{-1.4}(\omega _b)^{+1.6}_{-1.4}(f_{B_s}) ^{+0.9}_{-0.9}(a_2^{I=0})^{+0.6}_{-0.5}(t)\right] \times 10^{-5},\nonumber \\ \end{aligned}$$

(16)

which is compatible with the LHCb data $(7.2\pm 1.2)\times 10^{-5}$ [60] when considering its uncertainty.

The measured ratio between the branching ratios of $B^0_s \rightarrow \psi (2S) \pi ^+ \pi ^-$ and $B^0_s \rightarrow J/\psi \pi ^+ \pi ^-$ is [57]

$$\begin{aligned}&\frac{\mathcal {B}(B^0_s\rightarrow \psi (2S) \pi ^+ \pi ^-)}{\mathcal {B}(B^0_s\rightarrow J/\psi \pi ^+ \pi ^-)}\nonumber \\&\quad =0.34\pm 0.04 ({\text {stat}})\pm 0.03 ({\text {syst}})\pm 0.01(\mathcal {B}), \end{aligned}$$

(17)

which is consistent with the PQCD prediction $0.37^{+0.25}_{-0.18}$ (uncertainties added in quadrature), where the $\mathcal {B}(B^0_s\rightarrow J/\psi \pi ^+ \pi ^-)$ is read from [50]. Because the mass of the $f_0(1500)$ resonance is beyond the $\pi ^+\pi ^-$ invariant mass spectra ($2m_{\pi }<\omega <M-m$) in $B^0_s \rightarrow \psi (3S) \pi ^+ \pi ^-$ decay, there is only one resonant state $f_0(980)$ contributing to this decay. We have the branching ratio:

$$\begin{aligned}&\mathcal {B}(B^0_s\rightarrow \psi (3S) f_0(980)\rightarrow \psi (3S)\pi ^+\pi ^-)\nonumber \\&\quad =\left[ 1.7^{+0.5}_{-0.3}(\omega _b)^{+0.5}_{-0.4}(f_{B_s}) ^{+0.3}_{-0.1}(a_2^{I=0})^{+0.2}_{-0.0}(t)\right] \times 10^{-5}.\nonumber \\ \end{aligned}$$

(18)

In Fig. 2, we plot the differential branching ratio for $B^0_s\rightarrow \psi (2S,3S)\pi ^+\pi ^-$ as a function of the $\pi ^+\pi ^-$ invariant mass $\omega$. The red dashed and blue dotted curves represent the contributions from the resonances $f_0(980)$ and $f_0(1500)$, respectively. As expected, the $f_0(980)$ production is clearly dominant. From the branching ratios in Eqs. (15) and (16) one could find that the $f_0(980)$ resonance accounts for $85.0\%$ of the total branching ratio, the $f_0(1500)$ resonance $3.8\%$, and positive interference between the two terms is for $11.2\%$.

For a more direct comparison with the available experimental data [57], we also present the S-wave $\pi ^+\pi ^-$ invariant mass distributions for the $B^0_s\rightarrow \psi (2S)\pi ^+\pi ^-$ decay in this work as well as the Fig. 4b in Ref. [57]. One observes an appreciable peak arising form the $f_0(980)$ resonance and a less strong, but clearly visible peak for the $f_0(1500)$ in Fig. 3a. Comparing with the data, our distribution below 1.4 GeV for the resonances agrees quite well, showing a similar behavior in this region.

Different from the fixed kinematics of the two-body decays, the decay amplitudes of the quasi-two-body decays are dependent on the $\pi ^+\pi ^-$ invariant mass. Therefore, it is more convenient to compare these contributions to the branching ratios, whose results are displayed separately in Table 2, where the labels FF, MM, FM correspond to the contribution of the factorizable, nonfactorizable cases, and the interferences between them, respectively, while the label “Total” denotes the total contribution. It can be found that the dominant contributions to the branching ratios coming from the factorizable topology due to the vertex corrections, which are enhanced by the Wilson coefficient $C_2$ (see Eq. (12)). The interference contributions are of the same order as the factorizable ones with an opposite sign, which reflects the importance of nonfactorizable effects in the color-suppressed processes. This is similar to the case of the two-body B meson decays into charmonia [74,75,76].

4 Conclusion

In this work, the quasi-two-body decays $B^0_s\rightarrow \psi (2S,3S)\pi ^+\pi ^-$ have been analyzed in the PQCD approach, assuming dominance of the S-wave resonance states $f_0(980)$ and $f_0(1500)$ in the invariant $\pi ^+\pi ^-$ mass distributions. Both the factorizable (including the vertex corrections) and nonfactorizable contributions are taken into account. We discussed theoretical uncertainties arising from the nonperturbative shape parameters, the decay constant, the Gegenbauer coefficient, and the scale dependence. It is found that the main uncertainties of the concerned processes come from the shape parameters and the decay constant of the $B_s$ meson. The predicted branching ratio and the invariant mass distributions for $B^0_s\rightarrow \psi (2S)\pi ^+\pi ^-$ decay are in agreement with the results from LHCb Collaboration. The decay mode $B^0_s\rightarrow \psi (3S) \pi ^+\pi ^-$ has not been measured yet, while the large value of the prediction $\mathcal {B}=1.7^{+0.8}_{-0.5}\times 10^{-5}$ for it in this work waits future measurements.