Impact of resonance decays on critical point signals in net-proton fluctuations

Abstract

The non-monotonic beam energy dependence of the higher cumulants of net-proton fluctuations is a widely studied signature of the conjectured presence of a critical point in the QCD phase diagram. In this work we study the effect of resonance decays on critical fluctuations. We show that resonance effects reduce the signatures of critical fluctuations, but that for reasonable parameter choices critical effects in the net-proton cumulants survive. The relative role of resonance decays has a weak dependence on the order of the cumulants studied with a slightly stronger suppression of critical effects for higher-order cumulants.

1 Introduction

Hot and dense strongly interacting matter is studied experimentally in heavy-ion collisions at different beam energies $\sqrt{s}$. One of the major scientific goals of these experiments is to explore the phases of QCD matter as a function of temperature T and baryon chemical potential $\mu _\mathrm{B}$. At vanishing $\mu _\mathrm{B}$ the transition between the high-T partonic and low-T hadronic phases is an analytic crossover [1], but many models predict that the transition is first order at large $\mu _\mathrm{B}$ [2,3,4]. Experimental searches for the first-order phase transition and the associated critical endpoint are based on the observation that the baryon chemical potential at chemical freeze-out increases with decreasing $\sqrt{s}$ in the regime probed at the Relativistic Heavy Ion Collider (RHIC) and the SPS fixed target program at CERN. Promising observable signatures for the presence of a critical point include event-by-event fluctuations [5,6,7], in particular fluctuations of conserved quantum numbers such as baryon number or electric charge [8, 9]. The influence of a phase transition, or a change of its order, should be reflected in a non-monotonic $\sqrt{s}$-dependence of these observables [10,11,12,13,14,15]. Moreover, non-uniform structures in e.g. the net-baryon number distributions due to domain formation in the spinodal region of the phase diagram may be expected [16, 17].

Motivated by these ideas a substantial experimental effort has been made in studying event-by-event multiplicity fluctuations of identified particle species [18,19,20]. Considered as a proxy for net-baryon number fluctuations, net-proton number fluctuations are particularly interesting. For these, intriguing non-monotonic patterns were observed within phase I of the RHIC beam energy scan (BES) program as $\sqrt{s}$ was decreased [21,22,23]. To deduce from the observed behavior unambiguously the presence of a first-order phase transition or a critical point is, nonetheless, a non-trivial task which requires additional work. On the experimental side the main issue is to reduce systematic and statistical uncertainties, which is one of the central goals of the upcoming phase II of the BES. Moreover, the strong sensitivity of the current data on reconstruction efficiency, kinematic acceptance or collision-centrality needs to be better understood. On the theoretical side a list of challenges has to be resolved before the data can be interpreted meaningfully. For example, net-proton number fluctuations serve, at best, as a proxy for net-baryon number fluctuations. In particular at lower $\sqrt{s}$, aspects of exact charge conservation [24, 25], repulsive interactions [26] or late stage hadronic phase processes such as resonance regeneration [27, 28] or decay have to be considered carefully. Further details and more fluctuation sources were discussed in the recent review [29].

The present work addresses one of the theoretical challenges to data interpretation, namely the role of resonance decays. Resonance decays contribute significantly to the final state particle multiplicities and, consequently, to event-by-event multiplicity distributions. Their impact on net-proton number fluctuations, ignoring the possible presence of a critical point, was previously studied in [30, 31]. It was found that the decay processes do not significantly modify the primordial (without resonance decays) ratios of net-proton number cumulants if the probabilistic decay contributions are properly taken into account [31]. This is because a thermal distribution of particles is being folded with a binomial decay distribution yielding again a nearly thermal distribution. However, critical fluctuations lead to sizable deviations from the thermal baseline. In [28] it was argued that the isospin randomization through resonance regeneration processes suppresses strongly the critical fluctuation signals in the net-proton number distribution, in particular, in the higher-order cumulants. It is natural to ask if resonance decays similarly obscure critical point signals in fluctuation observables.

Critical fluctuations can be described in terms of an order parameter field $\sigma$. In the thermodynamic limit the equilibrium correlation length $\xi$ of the order parameter diverges at the critical point. Under the assumption that QCD belongs to the same universality class as the three-dimensional Ising model [3, 4] one finds that the cumulants of the order parameter fluctuations scale as $\langle (\delta \sigma )^2 \rangle \propto \xi ^2$, $\langle (\delta \sigma )^3 \rangle \propto \xi ^{9/2}$ and $\langle (\delta \sigma )^4 \rangle _c \propto \xi ^7$, where small anomalous dimension corrections are neglected in these scaling relations [10]. Thus, higher-order cumulants depend more sensitively on the value of the equilibrium correlation length.

This is important for heavy-ion collisions, because the actual value of $\xi$ is limited due to finite size and time effects. Most significantly, the temporal growth of the correlation length is controlled by the relaxation time $\tau _\xi$, which increases as a power of the equilibrium correlation length. Near the critical point $\tau _\xi \sim \xi ^z$ with $z\approx 3$ [32], and critical slowing down places significant limits on the actual growth of the correlation length. In [33], the non-equilibrium evolution of the correlation length was studied and a maximal value of about 2–3 fm was found. Thus, critical fluctuation signals in observables will be weaker than expected based on equilibrium considerations. Within the model of non-equilibrium chiral fluid dynamics [34, 35] fluctuations of the order parameter are explicitly propagated in a fluid dynamical evolution of heavy-ion collisions. The effect of such a dynamics on the time evolution of net-proton fluctuations has been investigated recently [36]. It was found that critical fluctuations are affected by the dynamics, and that the location on the hydrodynamic trajectory where fluctuations freeze out determines the magnitude and shape of the fluctuation signals. However, it was also found that a critical point signal remains visible on top of thermal and initial state fluctuations. An analytic model for the time evolution of order parameter fluctuations was recently studied in [37]. The authors found that relaxation time effects introduce a significant lag in the cumulants relative to equilibrium expectations, and that non-equilibrium effects modify the simple scaling relations discussed in [10].

In this work we assume that there is a critical point in the QCD phase diagram, that this point causes critical fluctuations in the primordial net-proton number at chemical freeze-out, and that these fluctuations are determined by the growth of the correlation length. We study quantitatively the impact of resonance decays on the higher-order net-proton number cumulant ratios. We do not take into account dynamical effects such as the role of the relaxation time and critical slowing down. We assume that (a) the fluctuations reflect thermal equilibrium at chemical freeze-out, and that (b) freeze-out takes place in proximity to the QCD phase transition. These assumptions are motivated by the success of fluid dynamics, based on the assumption of rapid local thermalization, in describing bulk observables [38, 39], and by the successful extraction of freeze-out parameters from fluctuation observables [40]. Certainly, results obtained in the limit of rapid local thermalization provide an important benchmark for more sophisticated studies based on non-equilibrium thermodynamics.

2 Net-proton fluctuations and the impact of a critical point

In this section, we discuss in detail the framework used in our work. We start by describing the thermal, i.e. non-critical, baseline which we assume to be given by a grand-canonical hadron resonance gas model. It was shown that such a model is quite successful in quantitatively describing both lattice QCD results of the thermodynamics in the hadronic phase [41, 42] and measured particle yields [43]. Critical fluctuations are then included by making use of universality class arguments and coupling (anti-)particles with the order parameter field, the critical mode, via a phenomenological approach. We discuss how the critical fluctuations can be quantified at the chemical freeze-out and, furthermore, propose different phenomenological ansätze to study, in addition, the impact resonance decays have on the net-proton number fluctuations in the presence of a critical point.

2.1 Non-critical baseline model

As a baseline theory that exhibits no critical behavior we consider a hadron resonance gas model containing baryons and mesons up to masses of approximately 2 GeV in line with [44]. Starting point for our study is the particle density of species i given by the momentum-integral

$$\begin{aligned} n_i(T,\mu _i)=d_i \int \frac{\mathrm{d}^3k}{(2\pi )^3}\, f_i^0(T,\mu _i) \end{aligned}$$

(1)

with degeneracy factor $d_i$ and distribution function

$$\begin{aligned} f_i^0(T,\mu _i)=\frac{1}{(-1)^{B_i+1}+e^{(E_i-\mu _i)/T}}. \end{aligned}$$

(2)

In Eq. (2), $E_i=\sqrt{k^2+m_i^2}$ is the energy of particles of species i with mass $m_i$, and $\mu _i=B_i\mu _\mathrm{B}+S_i\mu _\mathrm{S}+Q_i\mu _\mathrm{Q}$ is their chemical potential, where $\mu _X$ are conjugate to the conserved charges $N_X$ and $B_i,\, S_i,\, Q_i$ represent the corresponding quantum numbers of baryon number, strangeness and electric charge, respectively.

For the grand-canonical ensemble of a non-interacting hadron resonance gas, one defines the mean particle number $\langle N_i\rangle$ of species i in a fixed volume V as $\langle N_i\rangle =Vn_i$. The cumulants with $n>1$, measuring thermal ensemble fluctuations in the particle number, can be related to derivatives of $n_i/T^3$ with respect to $\mu _i/T$ for fixed T,

$$\begin{aligned} C_n^i = VT^3 \left. \frac{\partial ^{n-1}(n_i/T^3)}{\partial (\mu _i/T)^{n-1}}\right| _T\,. \end{aligned}$$

(3)

In this work, we are interested in the first four cumulants $C_n$ of the net-proton number $N_{p-\bar{p}}=N_p-N_{\bar{p}}$, which read (note that cumulant and central moment are the same for order $n\le 3$)

$$\begin{aligned} C_1&= \langle N_{p-\bar{p}}\rangle = \langle N_p\rangle - \langle N_{\bar{p}}\rangle ,\end{aligned}$$

(4)

$$\begin{aligned} C_2&= \langle (\Delta N_{p-\bar{p}})^2\rangle = C_2^p+C_2^{\bar{p}}, \end{aligned}$$

(5)

$$\begin{aligned} C_3&= \langle (\Delta N_{p-\bar{p}})^3\rangle = C_3^p-C_3^{\bar{p}},\end{aligned}$$

(6)

$$\begin{aligned} C_4&= \langle (\Delta N_{p-\bar{p}})^4\rangle _c = C_4^p+C_4^{\bar{p}} \end{aligned}$$

(7)

with $\langle (\Delta N_{p-\bar{p}})^4\rangle _c = \langle (\Delta N_{p-\bar{p}})^4\rangle - 3\!\left. \langle (\Delta N_{p-\bar{p}})^2\rangle \right. ^{\!\!2}$ and $\Delta N_{p-\bar{p}}=N_{p-\bar{p}}-\langle N_{p-\bar{p}}\rangle$. The second equalities in Eqs. (5)–(7) are specific for our baseline model, for which correlations among different particle species vanish.

It is useful to consider particular ratios of these cumulants. Assuming that the fluctuations originate from a source with fixed thermal conditions, we may define

$$\begin{aligned} \frac{C_2}{C_1} = \frac{\sigma ^2}{M}, \quad \frac{C_3}{C_2} = S\sigma , \quad \frac{C_4}{C_2} = \kappa \sigma ^2 \end{aligned}$$

(8)

and compare model calculations for the cumulant ratios with combinations of mean $M=C_1$, variance $\sigma ^2=C_2$, skewness $S=C_3/C_2^{3/2}$ and kurtosis $\kappa =C_4/C_2^2$ of measured event-by-event multiplicity distributions. An advantage of considering ratios is that to first approximation volume fluctuations, which are inherent in the individual cumulants $C_n$, cancel out.

2.2 Critical mode fluctuations and coupling to physical observables

In the scaling region near a critical point different physical systems, which belong to the same universality class, exhibit a universal critical behavior [45]. Assuming that QCD belongs to the same universality class as the three-dimensional Ising model allows us to relate the order parameter $\sigma$ of the chiral phase transition in QCD with the order parameter of the spin model, the magnetization M. In the Ising model, the magnetization is a function of reduced temperature $r=(T-T_\mathrm{c})/T_\mathrm{c}$ and reduced external magnetic field $h=H/H_0$, where $T_\mathrm{c}$ is the critical temperature in the spin model and $H_0$ is a normalization constant. In these variables, the critical point is located at $r=h=0$. For $r<0$ and $h=0$ the transition is of first order, while $r>0$ marks the crossover regime.

The equilibrium cumulants of the critical mode are then obtained via

$$\begin{aligned} \langle (\delta \sigma )^n\rangle _c = \left( \frac{T}{VH_0}\right) ^{n-1}\left. \frac{\partial ^{n-1}M}{\partial h^{n-1}}\right| _r \end{aligned}$$

(9)

from appropriate derivatives of M with respect to the classical field keeping r fixed [14, 15, 37]. A parametric representation of M based on [46] can be found in Appendix A. This gives rise to parametric expressions for the cumulants of the critical mode, which are also given in Appendix A. These expressions are, strictly speaking, only valid for the scaling region close to the critical point. Nevertheless, we employ them for all considered $\sqrt{s}$ because (a) the size of the scaling region is not known, and (b) the influence of critical fluctuations on observables is suppressed further away from the critical point as we discuss in Sect. 3.

Fluctuations of the critical mode are not directly measurable. Instead, we focus on observables that couple to the critical mode, such as the number of pions or protons [6, 7]. In general, the coupling of these observables to the critical mode has to be modeled. In the following we will take the order parameter to be the chiral field $\sigma$, and model the coupling of (anti-)particles to the critical mode in a way that is suggested by models in which the chiral field has a linear relation to the dynamically generated mass, $\delta m_i=g_i\delta \sigma$ [6, 12, 14]. As a consequence, fluctuations

$$\begin{aligned} \delta f_i = - \delta \sigma \frac{g_i}{T} \frac{v_i^2}{\gamma _i} \end{aligned}$$

(10)

associated with the variations in the particle masses arise in addition to the thermal ensemble fluctuations discussed in Sect. 2.1. In Eq. (10), $\gamma _i=E_i/m_i$, $v_i^2=f_i^0\left( (-1)^{B_i}f_i^0+1\right)$ and $\langle \delta \sigma \rangle =0$ such that $\langle \delta m_i\rangle =0$ on average.

The coupling of protons and anti-protons to the critical mode with coupling strength $g_p$ influences the net-proton number fluctuations near the critical point. According to Eq. (10), critical fluctuations do not affect the mean value $C_1$ but modify the variance $C_2=\langle (\Delta N_p)^2 \rangle + \langle (\Delta N_{\bar{p}})^2 \rangle - 2 \langle \Delta N_p\Delta N_{\bar{p}} \rangle$ via

$$\begin{aligned}&\langle (\Delta N_i)^2 \rangle = C_2^i + \langle (V\delta \sigma )^2\rangle I_i^2 \,, \end{aligned}$$

(11)

$$\begin{aligned}&\langle \Delta N_i\Delta N_j \rangle = \langle (V\delta \sigma )^2\rangle I_i I_j \end{aligned}$$

(12)

with

$$\begin{aligned} I_i = \frac{g_id_i}{T} \int \frac{d^3k}{(2\pi )^3} \frac{v_i^2}{\gamma _i} \,. \end{aligned}$$

(13)

In these expressions we assumed that non-critical and critical fluctuations are uncorrelated. The coupling to the critical mode induces correlations between protons and anti-protons in $C_2$, which reduce the variance compared to that in the case of an independent production. Simultaneously, critical fluctuations enhance the individual proton and anti-proton variances according to Eq. (11). With the help of Eq. (13) we can write $C_2$ in compact form as

$$\begin{aligned} C_2 = C_2^p + C_2^{\bar{p}} + \langle (V\delta \sigma )^2 \rangle \left( I_p-I_{\bar{p}}\right) ^2 \end{aligned}$$

(14)

and find as net-effect an enhancement of the net-proton variance due to critical fluctuations.

Similarly, $C_3$ and $C_4$ are modified. For $C_3 = \langle (\Delta N_p)^3 \rangle - \langle (\Delta N_{\bar{p}})^3 \rangle - 3 \langle (\Delta N_p)^2\Delta N_{\bar{p}} \rangle + 3 \langle \Delta N_p(\Delta N_{\bar{p}})^2 \rangle$ we find

$$\begin{aligned}&\langle (\Delta N_i)^3 \rangle = C_3^i - \langle (V\delta \sigma )^3\rangle I_i^3 \,, \end{aligned}$$

(15)

$$\begin{aligned}&\langle (\Delta N_i)^2\Delta N_j \rangle = - \langle (V\delta \sigma )^3\rangle I_i^2 I_j \,, \end{aligned}$$

(16)

where we neglected subdominant critical fluctuation contributions of order lower than $\mathcal{O}(\xi ^{9/2})$. Accordingly, we can write

$$\begin{aligned} C_3 = C_3^p - C_3^{\bar{p}} - \langle (V\delta \sigma )^3 \rangle \left( I_p-I_{\bar{p}}\right) ^3 \,. \end{aligned}$$

(17)

For $C_4 = \langle (\Delta N_p)^4 \rangle _c + \langle (\Delta N_{\bar{p}})^4 \rangle _c - 4 \langle (\Delta N_p)^3\Delta N_{\bar{p}} \rangle _c + 6 \langle (\Delta N_p)^2(\Delta N_{\bar{p}})^2 \rangle _c - 4 \langle \Delta N_p(\Delta N_{\bar{p}})^3 \rangle _c$ one has

$$\begin{aligned}&\langle (\Delta N_i)^4 \rangle _c = C_4^i + \langle (V\delta \sigma )^4\rangle _c \,I_i^4 \,, \end{aligned}$$

(18)

$$\begin{aligned}&\langle (\Delta N_i)^m(\Delta N_j)^n \rangle _c = \langle (V\delta \sigma )^4\rangle _c \,I_i^m I_j^n \end{aligned}$$

(19)

for $m+n=4$, where we also neglected subdominant critical fluctuation contributions, here of order lower than $\mathcal{O}(\xi ^7)$. In compact form one may write

$$\begin{aligned} C_4 = C_4^p + C_4^{\bar{p}} + \langle (V\delta \sigma )^4 \rangle _c \left( I_p-I_{\bar{p}}\right) ^4 \,. \end{aligned}$$

(20)

We note that if non-critical and critical fluctuations are independent, then Eqs. (17) and (20) will represent the full results for $C_3$ and $C_4$, respectively, in line with the model assumption Eq. (10).

2.3 Mapping to QCD thermodynamics

In order to quantify the effect of the critical point on net-proton number fluctuations, we have to specify the cumulants of the critical mode $\langle (\delta \sigma )^n\rangle _c$ at chemical freeze-out. In this work we use the chemical freeze-out conditions reported in [40], which are shown in Fig. 1 (squares). These were determined by analyzing the STAR data [18, 19] on net-proton number and net-electric charge fluctuations. A discussion and practical parametrization of the results (exhibited by the solid curve in Fig. 1) is relegated to Appendix B.

Fig. 1

Sketch of the set-up in the QCD phase diagram considered in this work. The filled band between the two dashed curves comprises available information from lattice QCD on the crossover region as known for small $\mu _\mathrm{B}$, which we extrapolate to larger $\mu _\mathrm{B}$. The dashed curves are obtained by solving Eq. (21) to leading order with $\kappa _\mathrm{c}=0.007$ (upper curve, $T_{\mathrm{c},0}=0.163$ GeV) and $\kappa _\mathrm{c}=0.02$ (lower curve, $T_{\mathrm{c},0}=0.145$ GeV). The location of the critical point and of the adjacent first-order phase transition is not known. The placement in this figure corresponds to the choice of parameters specified in Sect. 3.2. The spin model coordinate system (r, h) has its origin in the critical point. Details of the mapping are described in the text. We also show the chemical freeze-out conditions determined in [40] (squares) and a practical parametrization of these results (solid curve), which is discussed in Appendix B

For any set of values of Ising model variables r and h, we can determine the cumulants $\langle (\delta \sigma )^n\rangle _c$ from the parametric representation discussed in detail in Appendix A by using the transformations in Eqs. (A.2) and (A.3). Therefore, we only have to map the thermal variables in QCD, T and $\mu _\mathrm{B}$, to the variables of the spin model. This mapping is non-universal: The relation between r and h on the one hand, and T and $\mu _\mathrm{B}$ on the other, depends sensitively on model assumptions. The easiest approach, used frequently in the literature [37, 47], is a linear map $r(T,\mu _\mathrm{B})$ and $h(T,\mu _\mathrm{B})$ subject to two conditions: (a) the conjectured QCD critical point $(\mu _\mathrm{B}^{\text {cp}},T^{\text {cp}})$ is located in Ising coordinates at $r=h=0$, and (b) the r-axis must lie tangentially to the first-order phase transition line in the QCD critical point and be oriented such that positive r-values correspond to the crossover regime in QCD (see the sketch in Fig. 1).

The exact location of the critical point and the slope of the adjacent first-order phase transition line are not known. In this work we use lattice information on the location of the pseudo-critical line in the $(\mu _\mathrm{B},T)$-plane, indicated by the filled band between the two dashed curves in Fig. 1. The lattice data can be parameterized as

$$\begin{aligned} T_\mathrm{c}(\mu _\mathrm{B})=T_{\mathrm{c},0}\left[ 1-\kappa _\mathrm{c}\left( \frac{\mu _\mathrm{B}}{T_\mathrm{c}(\mu _\mathrm{B})}\right) ^2+\cdots \right] , \end{aligned}$$

(21)

where $T_{\mathrm{c},0}=(0.145\cdots 0.163)$ GeV is the pseudo-critical temperature at vanishing $\mu _\mathrm{B}$ [48, 49] and $\kappa _\mathrm{c}\simeq 0.007\cdots 0.059$ is the chiral crossover curvature [50,51,52,53,54].

The mapping to h is not well constrained. A typical choice made in the literature is to define the h-axis perpendicular to the r-axis [37, 47]. However, since the first-order phase transition line is expected to have some curvature in the $(\mu _\mathrm{B},T)$-plane it is clear that, in general, the map must be more complicated. In this work, we follow [37] and define

$$\begin{aligned} h = \frac{(T-T^{\text {cp}})}{\Delta T^{\text {cp}}} \end{aligned}$$

(22)

such that the h-axis is simply parallel to the T-axis (see Fig. 1). We also define the auxiliary variable

$$\begin{aligned} \tilde{r} = \frac{(\mu _\mathrm{B}-\mu _\mathrm{B}^{\text {cp}})}{\Delta \mu _\mathrm{B}^{\text {cp}}}. \end{aligned}$$

(23)

The parameters $\Delta T^{\text {cp}}$ and $\Delta \mu _\mathrm{B}^{\text {cp}}$ determine the size of the critical region. The Ising variable r is then obtained by rotating $\tilde{r}$, where the slope of the r-axis is determined by using the slope of $T_\mathrm{c}(\mu _\mathrm{B})$ at $\mu _\mathrm{B}^{\text {cp}}$.

2.4 Resonance decays

The cumulants of a multiplicity distribution influenced by resonance decays were derived in [26, 55]. These results take the probabilistic nature of the decay process into account. As critical fluctuations do not alter mean values, cf. Eq. (10), the mean of the final net-proton number reads

$$\begin{aligned} \hat{C}_1 = \langle N_p\rangle - \langle N_{\bar{p}}\rangle + \sum _R \langle N_R\rangle \left( \langle n_p\rangle _R - \langle n_{\bar{p}}\rangle _R\right) , \end{aligned}$$

(24)

where the notation $\hat{C}_n$ refers to a cumulant that includes resonance decays. We also define $\langle n_i\rangle _R=\sum _r b_r^R n_{i,r}^R$ as the decay-average number of particles of species i created from resonance R, where $n_{i,r}^R$ are created in decay branch r with branching ratio $b_r^R$. Note that the sum in Eq. (24) includes all resonances and anti-resonances of the baseline hadron resonance gas model. Analogous formulas for the higher cumulants, which contain critical fluctuation contributions, are given in Appendix C.

To study the impact of resonance decays on the higher-order cumulants of the net-proton number in the presence of a critical point we must quantify the coupling strengths $g_R$ between the critical mode and the (anti-)resonances. In line with the chiral model study [56] we may assume that $g_R$ is proportional to $g_p$ for non-strange baryonic resonances like $\Delta ^{++}$ with a proportionality factor that reflects the mass difference between the resonance and the proton. For strangeness carrying resonances like $\Lambda (1520)$ we must, in addition, account for the fact that their mass generation is less dominated by the coupling to the chiral field [56]. To accommodate these features we advocate as a phenomenological ansatz

$$\begin{aligned} g_{R}=\frac{g_{p}}{3}\frac{m_{R}}{m_{p}}(3-|S_{R}|) \end{aligned}$$

(25)

for the $\sigma$-(anti-)resonance couplings. To analyze the impact of other possible scenarios, we also consider the two cases that either all resonances couple like protons, $g_{R}=g_{p}$, or that resonances do not couple to the critical mode at all, $g_{R}=0$. This allows us to study how sensitively the final results depend on the choice for the couplings $g_{R}$.

3 Numerical results

In this section we present numerical results of our study. We start by discussing how to implement kinematic cuts in order to take into account the experimental acceptance. Then, we quantify the effect of resonance decays on critical point signatures in net-proton number fluctuations. We compare our results to preliminary STAR data [23]. We should note that there are sizable uncertainties in both the data and the theoretical analysis. Our goal in this work is not to establish or constrain the existence of a critical point, but to quantify the role of resonance decays.

3.1 Kinematic cuts

In the analyses [18, 21,22,23] of net-proton number fluctuations the detector acceptance was limited. Coverage in kinematic rapidity was restricted to the mid-rapidity region $|y|\le 0.5$, with a full coverage in azimuthal angle $\phi$, and in transverse momentum cuts of $0.4~\mathrm{GeV}\le k_T\le k_T^\mathrm{max}$ with $k_T^\mathrm{max}=0.8$ GeV [18] or $k_T^\mathrm{max}=2$ GeV [21,22,23] were applied. For a smaller experimentally analyzed phase space, one expects critical fluctuation signals in observables to be diminished because the momentum-space correlations, which are caused by the potentially large spatial correlations through thermal smearing, may exceed the considered kinematic acceptance window [57, 58]. Indeed, the pronounced structures seen in the preliminary data of the higher-order net-proton number cumulant ratios [21,22,23] disappear to a large extent in the published data [18] for smaller $k_T^\mathrm{max}$.

In this work, we include the kinematic cuts on the level of the momentum-integrals, cf. Eqs. (1) and (13). For this purpose, we rewrite following [30]

$$\begin{aligned} \int \mathrm{d}^3k \,\rightarrow \, \int k_\mathrm{T}\sqrt{k_\mathrm{T}^2+m_i^2}\cosh (y) \,\mathrm{d}k_T \,\mathrm{d}y \,\mathrm{d}\phi , \end{aligned}$$

(26)

limit the integrations to $-0.5\le y\le 0.5$, $0\le \phi \le 2\pi$ and $0.4~\mathrm{GeV}\le k_\mathrm{T}\le k_\mathrm{T}^\mathrm{max}$ and replace $E_i$ by $\cosh (y)\sqrt{k_\mathrm{T}^2+m_i^2}$. This implies that we apply the kinematic cuts to evaluate quantities at the chemical freeze-out and neglect the subsequent modifications of particle multiplicity distributions in a given acceptance window due to elastic scatterings until kinetic freeze-out.

3.2 Cumulant ratios

Before we can show our results we have to fix the parameters that enter into our calculation. These include the pseudo-critical line parameters $T_{\mathrm{c},0}$ and $\kappa _c$, the coordinates of the critical point $(\mu _\mathrm{B}^{\text {cp}},T^{\text {cp}})$, the width of the critical regime $(\Delta \mu _\mathrm{B}^{\text {cp}}, \Delta T^{\text {cp}})$, the normalizations of the critical equation of state $M_0$ and $H_0$, and the coupling strength $g_{p}$.

We assume $T_{\mathrm{c},0}=0.156$ GeV and $\kappa _\mathrm{c}=0.007$ based on the lattice data cited in Sect. 2.3. The STAR data show tentative hints of critical behavior in the kurtosis in the regime $\sqrt{s}=(14.5-19.6)$ GeV. We choose $\mu _\mathrm{B}^{\text {cp}}=0.39$ GeV to illustrate the effects of possible critical behavior in this regime. The pseudo-critical line then predicts $T^{\text {cp}}\simeq 0.149$ GeV. We use $\Delta T^{\text {cp}}=0.02$ GeV and $\Delta \mu _\mathrm{B}^{\text {cp}}=0.42$ GeV, and set the spin model normalization constants to $M_0/$GeV$=5.52\times 10^{-2}$ and $H_0/$GeV$^3=3.44\times 10^{-4}$. The resulting behavior of the correlation length along the chemical freeze-out curve is shown in Fig. 5 (see Appendix A). We observe that the maximum of the correlation length is about 2 fm, comparable to estimates based on dynamical models.

Fig. 2

Cumulant ratios $S\sigma$ and $\kappa \sigma ^2$ for net-protons as functions of $\sqrt{s}$ without including resonance decays. The results shown are based on Eqs. (5)–(7) as baseline (thin dashed curves) without critical fluctuations, and based on Eqs. (14), (17) and (20) including critical fluctuations for the exemplary $\sigma$-(anti-)proton couplings $g=g_{p}=3,\,5,\,7$. These results are obtained along the chemical freeze-out curve shown in Fig. 1 and include the kinematic cuts applied in [23]. For guidance, the preliminary data [23] are also shown. See text for more details

To quantify the influence of critical fluctuations on the net-proton number cumulant ratios, we also need to specify the value of the coupling strength $g_{p}$ between the (anti-)protons and the critical mode, which enters the cumulants via the factors $I_{p}$ and $I_{\bar{{p}}}$, cf. Eq. (13). In the context of the linear sigma model the coupling constant $g_{p}$ in the ground state can be related to the pion decay constant [7, 10], $g_{p}\simeq m_{p}/f_\pi \simeq 10$. In chiral models, parameters are typically fixed to reproduce the vacuum masses of baryons and mesons as well as other known properties of nuclear matter at saturation density. In the non-linear chiral model considered in [59] to describe QCD matter in neutron stars, for example, $|g_{p}|\lesssim 10$ was used. Quark model calculations [60] of nucleon–meson couplings find $g_{p}$ in the range of 3–7, instead. To illustrate the importance of the actual value of $g_{p}$, we use three different values $g_{p}=3,\,5$ and 7 in the following.

In Fig. 2, we show the net-proton number cumulant ratios $S\sigma$ and $\kappa \sigma ^2$ defined in Eq. (8) without including the contributions from resonance decays. The non-critical baseline (thin dashed curves) is determined using Eqs. (5)–(7). The relevant expressions, cf. Eq. (3), are evaluated along a chemical freeze-out curve, where we employ the $\sqrt{s}$-parametrizations of the thermal variables $T^{\text {fo}}$ and $\mu _X^{\text {fo}}$ summarized in Appendix B. Kinematic cuts are applied as described in Sect. 3.1, where we use $k_T^\mathrm{max}=2$ GeV in line with [23]. To include critical fluctuation contributions we use Eqs. (14), (17) and (20). The relevant cumulants of the critical mode $\langle (\delta \sigma )^n\rangle _c$ are obtained via Eqs. (A.4)–(A.6) by mapping T and $\mu _\mathrm{B}$ at chemical freeze-out to the Ising variables r and h as explained in Sect. 2.3.

Fig. 3

Similar to Fig. 2, but including resonance decays both in the baseline results (thin dashed curves), cf. [31] for more details, and for the case $g=g_{p}=5$. Resonance decays are found to reduce the influence of critical fluctuations on the net-proton number cumulant ratios visibly. The filled bands contain the results of the three different ansätze for $g_{R}$ discussed in this work: the strongest reduction of baseline deviations is seen for $g_{R}=0$ when resonances do not couple to the critical mode, while critical fluctuations are least suppressed by resonance decays for $g_{R}$ following the phenomenological ansatz Eq. (25). The case $g_{R}=g_{p}$ lies in between, but closer to the phenomenological ansatz

As expected, critical fluctuations cause a non-monotonic behavior of the net-proton number cumulant ratios. The qualitative features are driven by the sign changes in $\langle (\delta \sigma )^3\rangle$ and $\langle (\delta \sigma )^4\rangle _c$ as discussed in Appendix A. The effects are found to be stronger for larger $g_{p}$ and in the region of beam energies, where the correlation length $\xi$ at chemical freeze-out is largest, cf. Fig. 5 in Appendix A. Further away from this region, at small and large $\sqrt{s}$, the contributions from critical fluctuations are suppressed and the net-proton number cumulant ratios fall back to the baseline results. At small $\sqrt{s}$, this is a consequence of the smallness of $\xi$ further away from the critical point. But more importantly, in particular for large $\sqrt{s}$, this is caused by the thermal factor $(I_{p}-I_{\bar{{p}}})/g_{p}$, which is positive definite and a monotonically decreasing function with increasing $\sqrt{s}$ along the chemical freeze-out curve.

In Fig. 3 we show the impact of resonance decays, focusing on the case $g_{p}=5$. We determine the final net-proton number cumulants including critical fluctuations via the expressions summarized in Appendix C and consider the three different scenarios for the couplings $g_{R}$ between the critical mode and (anti-)resonances discussed in Sect. 2.4. We find that resonance decays influence the net-proton number cumulant ratios visibly, reducing the non-monotonicity induced by the critical fluctuations. Critical fluctuation signals are suppressed in $S\sigma$ by about 40% and in $\kappa \sigma ^2$ by about 50%, i.e. the reduction effect is slightly stronger for higher-order cumulants. This behavior is qualitatively in agreement with the predicted impact of isospin randomization processes on critical fluctuation signals [28].

The results shown in Fig. 3 indicate that resonance decays have significant effects on the cumulant ratios, but that for a sufficiently strong coupling $g_{p}$ between critical mode and (anti-)protons critical fluctuations survive final state processes such as resonance decays. Details in the couplings $g_{R}$ play a rather minor role as evident from Fig. 3. The strongest suppression of critical fluctuation signals is found for $g_{R}=0$, while the least is observed for $g_{R}$ in line with the phenomenological ansatz Eq. (25).

3.3 Discussion

The results discussed in Sect. 3.2 are obtained for fixed values of $g_{p}$. In general, it is reasonable to assume that the coupling strengths between the critical mode and (anti-)particles depend on $\sqrt{s}$. For example, in [6] it was argued that at the critical point the $\sigma$-pion coupling could be significantly smaller than in vacuum. Moreover, quark–meson model [61] and Nambu–Jona-Lasinio (NJL) model [62] studies find that meson–nucleon couplings decrease both with increasing T and/or $\mu _\mathrm{B}$. Thus, by phenomenologically adjusting $g_{p}(\sqrt{s})$, as done in [63], a quantitative model-to-data comparison would certainly be feasible, which is, however, beyond the scope of the present work.

Fig. 4

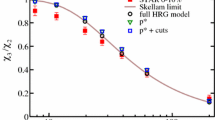
Cumulant ratio $\sigma ^2/M$ as a function of $\sqrt{s}$ including resonance decays and critical fluctuation contributions for $g_{p}=5$ (both filled bands). As in Fig. 3, for $g_{R}=0$ the results are closest to the non-critical baseline (thin dashed curve). For guidance, we also show the preliminary data [23]. Reducing the kinematic acceptance, for example by decreasing the value for $k_T^{\text {max}}$ from 2 GeV (upper band) to 0.8 GeV (lower band), reduces the non-monotonic behavior caused by critical fluctuations slightly

The specific behavior of the skewness, which shows a reduction of $S\sigma$ compared to the baseline result, depends on our choices for the direction of the h-axis relative to the T-axis, the relative sign of $\delta \sigma$ and h, and the sign of $g_{p}$. For simplicity we have taken all these signs to be positive. It is important to note that the sign of the critical contribution changes, leading to an enhancement of $S\sigma$ relative to the non-critical baseline, if either of these signs is changed. Indeed, in the case of the liquid–gas phase transition in ordinary liquids, the order parameter is $\delta n = n-n_{\text {cr}}$, which is mapped to the positive h-direction in the Ising model. This supports the idea of aligning h with the positive T-axis in the QCD phase diagram, but it also suggests, based on Eq. (10) and $g>0$, that $\delta \sigma$ is aligned with the negative h-axis. The assumption $g>0$ is consistent with the simple sigma model picture that g controls the dynamically generated mass, $m\sim g\sigma$. An NJL model study [64] of the $\sigma$-mode finds that in the critical region positive fluctuations in $\sigma$ are associated with positive fluctuations in the net-baryon density. In our simple phenomenological approach this corresponds to $g<0$, cf. Eq. (10). A different NJL model study [65] shows that the baryon skewness is negative on the high $(\mu _\mathrm{B},T)$ side of the transition line. Again, this result corresponds to changing one of the signs in our model.

It is also important to quantify the influence of a critical point on the lowest-order cumulant ratio $\sigma ^2/M$. According to Eq. (14), $\sigma ^2/M$ is, compared to the non-critical baseline, increased through the critical fluctuation contributions in $C_2$. In contrast, neither the published [18] nor the preliminary STAR data [23] show within errors any sign of non-monotonic behavior in $\sigma ^2/M$. This puts significant constraints on the values of $g_{p}$, $\Delta \mu _\mathrm{B}^{\text {cp}}$, $\Delta T^{\text {cp}}$, $M_0$ and $H_0$, and the location of the critical point relative to the chemical freeze-out in the QCD phase diagram.

In Fig. 4, we show $\sigma ^2/M$ including the contributions from resonance decays for the case $g_{p}=5$ along the parametrized freeze-out curve. The filled bands comprise again the results of the three different ansätze for $g_{R}$, cf. Fig. 3. For comparison also the preliminary STAR data [23] and the non-critical baseline (thin dashed curve) are shown. The non-monotonic structures seen in Fig. 4 are caused by the critical fluctuations. By decreasing $k_T^{\text {max}}$ from 2 GeV (upper band) to 0.8 GeV (lower band), the non-monotonic behavior is only slightly reduced. The observed reduction is a consequence of the fact that the thermal factors $I_i$ in the cumulants correlate (anti-)particles of different momenta in the distribution with each other. By decreasing the considered kinematic acceptance, these correlations are reduced, as is also discussed e.g. in [57, 58]. The effect is found to be stronger for higher-order cumulant ratios. Moreover, increasing the considered rapidity range from $|y|\le 0.5$ to $|y|\le 0.75$ instead of changing $k_T^{\text {max}}$ from 0.8 to 2 GeV has a quantitatively comparable influence, cf. also [57].

4 Conclusions

In this work, we have quantified the impact of resonance decays on higher-order net-proton number cumulant ratios for the case that the primordial net-proton number distribution contains critical fluctuations induced by the presence of a QCD critical point. The critical fluctuations were included on top of a non-critical background described by a thermal hadron resonance gas model. The coupling of particle and anti-particle resonances to the critical mode was modeled using a sigma model coupling. Fluctuations of the critical mode were determined, applying universality class arguments, from derivatives of the order parameter in the three-dimensional Ising model. We employed a linear map to relate QCD chemical freeze-out parameters $(\mu _\mathrm{B}^{\text {fo}},T^{\text {fo}})$ to the Ising variables (r, h).

We find that resonance decays reduce, but do not completely obscure, the non-monotonic beam energy dependence of cumulant ratios induced by a critical point. The suppression is found to be slightly stronger for higher-order cumulants, in qualitative agreement with the influence of isospin randomization processes in the hadronic phase [28]. This is fairly independent of the strength of the coupling between (anti-)resonances and the critical mode. Shrinking the kinematic acceptance reduces the critical point signals as expected. The coupling to the critical mode results in correlations between protons and anti-protons both from the direct coupling and from the indirect coupling via resonances. The correlations turn out to be fairly small, modifying the cumulant ratios by a few percent at most.

Clearly, there are many issues that need to be addressed in order to make more quantitative model-to-data comparisons. This includes, in particular, the role of dynamical effects, both in the evolution of the order parameter and in the coupling to resonances.

Appendices

Appendix A: Critical mode fluctuations based on universality class arguments

A suitable parametric representation of the magnetization M(r, h) in the three-dimensional Ising model, which is valid in the scaling region around the critical point, is given in terms of the auxiliary variables R and $\theta$ as [46]

$$\begin{aligned} M&= M_0 R^\beta \theta \,,\end{aligned}$$

(A.1)

$$\begin{aligned} r&= R (1-\theta ^2) \,,\end{aligned}$$

(A.2)

$$\begin{aligned} h&\equiv H/H_0 = R^{\beta \delta } \tilde{h}(\theta ) \end{aligned}$$

(A.3)

with $\tilde{h}(\theta )=c\theta \left( 1+a\theta ^2+b\theta ^4\right)$ being an odd function of $\theta$ which is regular near $\theta =0$ and $\theta =\pm 1$. The parametric representation [46] uses the universal critical exponents $\beta =0.3250$ and $\delta =4.8169$, while the coefficients in $\tilde{h}(\theta )$ read $a=-0.76145$, $b=0.00773$ and $c=1$ such that the relevant non-trivial roots of $\tilde{h}(\theta )$ are located at $\theta _0=\pm \sqrt{1.33128}$. Furthermore, the representation Eqs. (A.1)–(A.3) is uniquely defined for $R\ge 0$ and $-|\theta _0|\le \theta \le |\theta _0|$. For $R>0$ and $\theta =0$, we have $h=0$ and positive r, which corresponds to the crossover transition, while $\theta =\theta _0$ corresponds to the first-order phase transition line. The normalization constants $M_0$ and $H_0$ [66, 67] are of mass dimension one and three, respectively, and the magnetization M is positive for $(r<0,h\rightarrow 0^+)$ and for $(r\rightarrow 0,h>0)$.

We obtain the equilibrium cumulants of the critical mode within this parametrization from Eq. (9). They read as functions of R and $\theta$

$$\begin{aligned}&\langle (\delta \sigma )^2\rangle = \frac{T}{V} \frac{M_0}{cH_0} R^{\beta -\beta \delta }\times \frac{\left( 1+(2\beta -1)\theta ^2\right) }{\left( 1 + (3a+2\beta \delta -1)\theta ^2 + (a(2\beta \delta -3)+5b)\theta ^4 + b(2\beta \delta -5)\theta ^6\right) }, \end{aligned}$$

(A.4)

$$\begin{aligned}&\langle (\delta \sigma )^3\rangle = - 2 \frac{T^2}{V^2} \frac{M_0}{(cH_0)^2} R^{\beta -2\beta \delta }\times \frac{\theta \left( A_0+A_1\theta ^2+A_2\theta ^4+A_3\theta ^6+A_4\theta ^8\right) }{\left( 1 + (3a+2\beta \delta -1)\theta ^2 + (a(2\beta \delta -3)+5b)\theta ^4 + b(2\beta \delta -5)\theta ^6\right) ^3}, \end{aligned}$$

(A.5)

$$\begin{aligned}&\langle (\delta \sigma )^4\rangle _c = 2 \frac{T^3}{V^3} \frac{M_0}{(cH_0)^3} R^{\beta -3\beta \delta }\times \frac{\left( B_0 + B_1\theta ^2 + B_2\theta ^4 + B_3\theta ^6 + B_4\theta ^8 + B_5\theta ^{10} + B_6\theta ^{12} + B_7\theta ^{14} + B_8\theta ^{16}\right) }{\left( 1 + (3a+2\beta \delta -1)\theta ^2 + (a(2\beta \delta -3)+5b)\theta ^4 + b(2\beta \delta -5)\theta ^6\right) ^5}. \end{aligned}$$

(A.6)

The variance $\langle (\delta \sigma )^2\rangle$ is, by definition, a positive function. The coefficients in $\langle (\delta \sigma )^3\rangle$ are

$$\begin{aligned} A_0 =&\,\,3a+3\beta (\delta -1),\end{aligned}$$

(A.7)

$$\begin{aligned} A_1 =&\,\,a\left[ \beta (7\delta -3)-9\right] +2\beta (\delta -1)(\beta \delta +\beta -2)+10b,\end{aligned}$$

(A.8)

$$\begin{aligned} A_2 =&\,\,a\left[ 2\beta (\beta (\delta (\delta +4)-3)-6\delta )+9\right] \nonumber \\&+\beta (2\beta -1)(\delta -1)(2\beta \delta -1)+b\left[ 11\beta \delta +5\beta -30\right] ,\end{aligned}$$

(A.9)

$$\begin{aligned} A_3 =&\,\,a\left[ (2\beta -1)(\beta (\delta -1)-1)(2\beta \delta -3)\right] \nonumber \\&+2b\left[ \beta ^2(\delta (\delta +8)-5)-10\beta (\delta +1)+15\right] ,\end{aligned}$$

(A.10)

$$\begin{aligned} A_4 =&\,\,b\left[ (2\beta -1)(\beta (\delta -1)-2)(2\beta \delta -5)\right] , \end{aligned}$$

(A.11)

and in $\langle (\delta \sigma )^4\rangle _c$ they read

$$\begin{aligned} B_0 =&\,\,-A_0 \,,\end{aligned}$$

(A.12)

$$\begin{aligned} B_1 =&\,\,45a^2+3a\left[ 2\beta (11\delta -7)+5\right] \nonumber \\&+\,12\beta ^2(\delta -1)(3\delta -1)-30b \,, \end{aligned}$$

(A.13)

$$\begin{aligned} B_2 =&\,\,15a^2\left[ 11\beta \delta -3(\beta +5)\right] \nonumber \\&+6a\left[ 2\beta \left( 17\beta \delta ^2-3(6\beta +7) \delta + 3\beta +17\right) -5\right] +255ab \nonumber \\&+2\beta (\delta -1)(2\beta (\beta (\delta (11\delta -4)-1)-18\delta +6)+5)\nonumber \\&+30b\left[ 7\beta (\delta -1)+5\right] , \end{aligned}$$

(A.14)

$$\begin{aligned} B_3= & {} \,\,30a^2(2\beta \delta -3)\left[ \beta (4\delta -2)-5\right] \nonumber \\&+\,a\left[ 4\beta \bigg (82\delta +\beta \bigg (38\beta \delta ^3-3\delta ^2(6\beta +41)\right. \nonumber \\&\left. +6\delta (19-3\beta ) +6\beta -9\bigg )-78\bigg )+30\right] \nonumber \\&+\,15ab\left[ 54\delta \beta -14\beta -85\right] +4\beta (\delta -1)(2\beta \delta -1)\nonumber \\&\times (\beta (2\beta (\delta (\delta +2)-1)-7\delta +3)+2) \nonumber \\&+12b\left[ 2\beta (\delta (2\beta (8\delta -7)-29)+35)-25\right] + 450b^2,\nonumber \\ \end{aligned}$$

(A.15)

$$\begin{aligned} B_4&= \,\,6a^2\left[ \beta (161\delta +2\beta (\delta (6-53\delta )\right. \nonumber \\&\quad \left. +\,\beta (\delta (\delta (9\delta +11)-15)+3) +9)-33)-75\right] \nonumber \\&\quad +\,a\left[ 4\beta \left( \beta \left( 4\delta \beta ^2(\delta (2\delta (\delta +5)-15)+4)\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -\,4\beta \left( 16\delta ^3 -15\delta +3\right) +\delta (97\delta -74)-9\right) \right. \right. \nonumber \\&\left. \left. \quad -\,41\delta +45\right) -15\right] \nonumber \\&\quad +\,6ab\left[ 2\beta (\beta (\delta (67\delta +2)-15)-263\delta +55)+425\right] \nonumber \\&\quad +\,\beta (2\beta -1)(\delta -1)(1-2\beta \delta )^2(\beta (4\delta -2)-1) \nonumber \\&\quad +\,4b\left[ 2\beta ^3\left( 3\delta \left( 9\delta ^2+3\delta -11\right) +5\right) \right. \nonumber \\&\quad \left. +\,6\beta ^2(\delta (34-41\delta ) +5)\right. \nonumber \\&\quad \left. +\,5\beta (39\delta -59)+75\right] \nonumber \\&\quad +\,15b^2\left[ \beta (59\delta +5)-150\right] , \end{aligned}$$

(A.16)

$$\begin{aligned} B_5&= a^2(2\beta \delta -3)\left[ 2\beta \left( 4\beta ^2(\delta (\delta (\delta +9)-12)+3)\right. \right. \nonumber \\&\quad \left. \left. -\,6\beta (\delta (7\delta +6)-6)+77\delta -6\right) -75\right] \nonumber \\&\quad +\,a\left[ (2\beta -1)(2\beta \delta -3)(2\beta \delta -1)\right. \nonumber \\&\quad \left. \times \left( 2\beta \left( \beta \left( 4\delta ^2-6\delta +2\right) -5\delta +4\right) -1\right) \right] \nonumber \\&\quad +\,2ab\left[ 2\beta \left( 2\beta ^2(\delta (\delta (35\delta +87)-93)+15)\right. \right. \nonumber \\&\quad \left. \left. -\,9\beta (\delta (61\delta +26)-25) +8(142\delta -15)\right) -1275\right] \nonumber \\&\quad +\,2b\big [4\beta \big (85+2\beta \big (2\beta ^2\delta ^4+6\beta \delta ^3(3\beta -4)\nonumber \\&\quad +\,\delta ^2(52-3\beta (8\beta +7)) \nonumber \\&\quad +\,6\delta (\beta (\beta +7)-7)-5(\beta +3)\big )-39\delta \big )-75\big ] \nonumber \\&\quad +\,12b^2\big [\beta \left( 53\beta \delta ^2+10\delta (4\beta -29)-25(\beta +2)\right) +375\big ], \end{aligned}$$

(A.17)

$$\begin{aligned} B_6&= a^2\left[ (2\beta -1)(\beta (\delta -1)-1)(\beta (4\delta -2)-5)(3-2\beta \delta )^2\right] \nonumber \\&\quad +\,ab\left[ 4\beta \left( \beta \left( 4\delta \beta ^2(\delta (2\delta (\delta +13)-33)+8)\right. \right. \right. \nonumber \\&\quad -\,4\beta (\delta (2\delta (16\delta +51)-105)+15) \nonumber \\&\quad \left. \left. \left. +\delta (499\delta +434)-315\right) -5(143\delta +9)\right) +1275\right] \nonumber \\&\quad +\,2b\left[ (2\beta -1)(2\beta \delta -5)(2\beta \delta -1)\right. \nonumber \\&\quad \times \left. \left( \beta \left( \beta \left( 4\delta ^2- 6\delta +\,2\right) -9\delta +7\right) -3\right) \right] \nonumber \\&\quad +\,2b^2\left[ \beta \left( \beta ^2(2\delta (\delta (43\delta +177)-165)+50)\right. \right. \nonumber \\&\quad \left. \left. - \,24\beta (\delta (37\delta +45)-25)+2545\delta +775\right) -2250\right] , \end{aligned}$$

(A.18)

$$\begin{aligned} B_7 =&\,\,ab(2\beta \delta -5)\left[ (2\beta -1)(2\beta \delta -3)\right. \nonumber \\&\times \left. \left( 2\beta \left( \beta \left( 4\delta ^2- 6\delta +2\right) -13\delta +10\right) +17\right) \right] \nonumber \\&+b^2(2\beta \delta -5)\left[ 4\beta \left( 2\beta ^2(\delta (\delta (\delta +17)-21)+5)\right. \right. \nonumber \\&\left. \left. -5\beta (\delta (7\delta +22)-15)+119\delta +80\right) -450\right] , \end{aligned}$$

(A.19)

$$\begin{aligned} B_8 =&\,\,b^2\left[ (2\beta -1)(\beta (\delta -1)-2)(5-2\beta \delta )^2(\beta (4\delta -2)-9)\right] \,. \end{aligned}$$

(A.20)

In the limit of the so called linear parametric representation with critical exponents $\beta =1/3$ and $\delta =5$ and coefficients $a=-2/3$, $b=0$ and $c=3$ these expressions simplify to the cumulants reported in [14, 37].

One can study the dependence of the cumulants of the critical mode on the spin model variables by analyzing, for example, the dimensionless skewness $\tilde{S}=\langle (\delta \sigma )^3\rangle /\langle (\delta \sigma )^2\rangle ^{3/2}$ and kurtosis $\tilde{\kappa }=\langle (\delta \sigma )^4\rangle _c/\langle (\delta \sigma )^2\rangle ^2$, which both diverge at the critical point. For this purpose, we use Eqs. (A.2) and (A.3) to convert given values for r and h into R and $\theta$. The skewness is an odd function of h, cf. also [15, 37], which is positive for $h<0$ and changes sign continuously (discontinuously) for positive (negative) r when h becomes positive. The kurtosis, instead, is an even function of h, which for a given $r>0$ is negative within an interval $|h|<h^*(r)$ which depends on r. For $r<0$, one finds positive $\tilde{\kappa }$ as function of h with a cusp at $h=0$. As a function of r, $\tilde{S}$ exhibits a maximum (minimum) for negative (positive) h at an $r>0$ which itself depends on h, while $\tilde{\kappa }$ exhibits with decreasing positive r first a minimum followed by a maximum whose locations depend on the non-zero value of |h|.

Let us compare the parametric expressions for the cumulants of the critical mode in Eqs. (A.4)–(A.6) with those obtained from the corresponding Ginzburg–Landau effective potential. Including cubic and quartic interactions one finds [10, 37]

$$\begin{aligned} \langle (\delta \sigma )^2 \rangle&= \frac{T}{V}\xi ^2 ,\end{aligned}$$

(A.21)

$$\begin{aligned} \langle (\delta \sigma )^3 \rangle&= -2\tilde{\lambda }_3\frac{T^{3/2}}{V^2}\xi ^{9/2},\end{aligned}$$

(A.22)

$$\begin{aligned} \langle (\delta \sigma )^4 \rangle _c&= 6\left( 2\tilde{\lambda }_3^2-\tilde{\lambda }_4\right) \frac{T^2}{V^3} \xi ^7, \end{aligned}$$

(A.23)

where the correlation length dependence of the cubic and quartic coupling strengths as known in the scaling region has already been taken into account, such that $\tilde{\lambda }_3$ and $\tilde{\lambda }_4$ are dimensionless parameters.

Fig. 5

Beam energy dependence of $\xi$ along the considered chemical freeze-out curve (see Fig. 1). The correlation length falls off slower in the crossover regime, i.e. at larger $\sqrt{s}$, as is expected from the underlying universality class. The depicted result will be described qualitatively with the phenomenological ansatz for $\xi$ introduced in [12], if a comparable size of the critical region is considered

Comparing $\langle (\delta \sigma )^2\rangle$ in Eq. (A.4) with Eq. (A.21) allows us to determine the $\sqrt{s}$-dependence of $\xi$ along the chemical freeze-out curve considered in this work. This is shown in Fig. 5. One finds that the correlation length falls off slower in the crossover regime of the QCD phase diagram in line with the underlying universality class. Details of this behavior depend very sensitively on the chosen values for the normalization constants $M_0$ and $H_0$, but also on the details of the mapping such as the size of the critical region and the proximity of the chemical freeze-out to the QCD phase transition. For the parameter choices specified in Sect. 3.2 we find that $\xi$ becomes as large as 2.3 fm for $\sqrt{s}\simeq 19.2$ GeV, which corresponds to a freeze-out baryon chemical potential $\mu _\mathrm{B}^{\text {fo}}$ significantly smaller than $\mu _\mathrm{B}^{\text {cp}}$. A similar comparison of the higher-order cumulants can be made to determine the behavior of the dimensionless parameters $\tilde{\lambda }_3$ and $\tilde{\lambda }_4$. These are found to be independent of R and, thus, remain finite in the domain $-|\theta _0|\le \theta \le |\theta _0|$ of the parametric representation. In particular, $\tilde{\lambda }_3$ turns out to be negative for $h<0$. This implies that the sign of the skewness $\tilde{S}$ depends sensitively on the probed values of h.

Appendix B: Parametrization of the chemical freeze-out curve

The chemical freeze-out conditions reported in [40] were determined by analyzing the published STAR data [18, 19] of $\sigma ^2/M$ for event-by-event net-proton number and net-electric charge distributions. The qualitative behavior of these observables is dominated by charged pions and (anti-)protons. The published results for net-proton number fluctuations [18] were obtained by considering a significantly smaller kinematic acceptance in transverse momentum $k_T$ compared to [21,22,23]. Within errors, no pronounced deviation from non-critical baseline expectations was found in the data [18, 19] for the lowest-order cumulant ratios. This justified the application of the non-critical baseline model in the analysis [40].

In particular for larger $\sqrt{s}$, the chemical freeze-out temperatures found in [40] are significantly lower than those obtained in traditional approaches in which yields or yield ratios are analyzed, cf. e.g. [68]. Moreover, for small $\mu _\mathrm{B}$ a positive slope of the chemical freeze-out curve is found, cf. Fig. 1. This is opposite to the curvature of the crossover line obtained in lattice QCD, as can be seen from Eq. (21) and the cited values for $\kappa _\mathrm{c}$. Nonetheless, both small values for the chemical freeze-out temperature [69, 70] and a positive slope of the freeze-out curve for small $\mu _\mathrm{B}$ [70] have also been obtained in lattice QCD analyses of the same fluctuation observables [18, 19].

A practical parametrization of the freeze-out conditions [40] can be given in form of functions of the beam energy $\sqrt{s}$. We define analytic functions for the chemical potentials at chemical freeze-out $\mu _X^{\text {fo}}$ similar to [68] reading

$$\begin{aligned} \mu _X^{\text {fo}}(\sqrt{s}) = \frac{d_X}{\left( e_X\sqrt{s}+f_X\right) ^{g_X}}, \end{aligned}$$

(B.1)

which yield $\mu _X^{\text {fo}}$ in GeV given $\sqrt{s}$ in GeV for the parameter values listed in Table 1. The chemical freeze-out temperature $T^{\text {fo}}$ is best parametrized as a function of $\mu _\mathrm{B}^{\text {fo}}$ via

$$\begin{aligned} T^{\text {fo}}(\mu _\mathrm{B}^{\text {fo}}) = t_0 + t_1\mu _\mathrm{B}^{\text {fo}} + t_2\left( \mu _\mathrm{B}^{\text {fo}}\right) ^2 + t_4\left( \mu _\mathrm{B}^{\text {fo}}\right) ^4 + t_6\left( \mu _\mathrm{B}^{\text {fo}}\right) ^6 \end{aligned}$$

(B.2)

with parameter values $t_0=0.146$ GeV, $t_1=0.079$, $t_2=-0.366$ GeV$^{-1}$, $t_4=0.251$ GeV$^{-3}$ and $t_6=-0.107$ GeV$^{-5}$ yielding $T^{\text {fo}}$ in GeV for $\mu _\mathrm{B}^{\text {fo}}$ in GeV. The fit is shown in Fig. 1 by the solid curve. These parametrizations give reasonable descriptions of the freeze-out conditions [40] and hold for beam energies $\sqrt{s}\ge 7$ GeV. The non-vanishing values for $\mu _Q$ and $\mu _S$ for a given $\sqrt{s}$ are a consequence of physical side conditions for first cumulants, namely overall strangeness neutrality and an initial proton to baryon ratio of about 0.4 as realized in Au $+$ Au or Pb $+$ Pb heavy-ion collisions. Due to the smallness of $\mu _\mathrm{B}^{\text {fo}}$ at high beam energies, the latter condition is still quantitatively appropriate at high $\sqrt{s}$ even though the created system is almost isospin symmetric at mid-rapidity.

Table 1 Parameter values for the parametrizations of $\mu _X^{\text {fo}}$ as functions of $\sqrt{s}$ in Eq. (B.1)

Appendix C: Resonance decay contributions to net-proton cumulants including critical fluctuations

The variance of the final net-proton number is given by $\hat{C}_2=\langle (\Delta \hat{N}_p)^2 \rangle + \langle (\Delta \hat{N}_{\bar{p}})^2 \rangle - 2 \langle \Delta \hat{N}_p\Delta \hat{N}_{\bar{p}} \rangle$, where the two-particle correlators including resonance decays read [26, 55]

$$\begin{aligned} \langle (\Delta \hat{N}_i)^2\rangle =&\,\, \langle (\Delta N_i)^2\rangle + \sum _R \langle (\Delta N_R)^2\rangle \langle n_i\rangle _R^2 \nonumber \\&+ \sum _R \langle N_R \rangle \langle (\Delta n_i)^2 \rangle _R \,,\end{aligned}$$

(C.1)

$$\begin{aligned} \langle \Delta \hat{N}_i\Delta \hat{N}_j\rangle =&\,\, \langle \Delta N_i\Delta N_j\rangle + \sum _R \langle \Delta N_R\Delta N_{\bar{R}}\rangle \langle n_i\rangle _R \langle n_j\rangle _{\bar{R}} \end{aligned}$$

(C.2)

with $\langle (\Delta n_i)^2\rangle _R=\sum _r b_r^R (n_{i,r}^R)^2 - \langle n_i\rangle _R^2$. Note again that the sums over R include all resonances and anti-resonances of the non-critical baseline model such that if R denotes an anti-resonance like $\bar{\Lambda }(1520)$, the corresponding $\bar{R}$ is the resonance $\Lambda (1520)$.

According to Eq. (C.2), resonance decays can induce correlations between different particle species. Nonetheless, without critical fluctuations protons and anti-protons would remain uncorrelated in our grand-canonical hadron resonance gas model approach because of baryon charge conservation in each decay. The individual contributions $\langle (\Delta N_R)^2\rangle$ and $\langle \Delta N_R\Delta N_{\bar{R}}\rangle$ in Eqs. (C.1) and (C.2), which include critical fluctuations, follow from Eqs. (11) and (12) analogous to $\langle (\Delta N_i)^2\rangle$ and $\langle \Delta N_i\Delta N_j\rangle$ for (anti-)protons. Critical point induced correlations between a resonance and its anti-resonance are, therefore, inherited by their decay products. This induces additional correlations between protons and anti-protons on top of the primordial correlations discussed in Sect. 2.2.

From Eqs. (C.1) and (C.2) we find that $\hat{C}_2$ contains non-critical fluctuation contributions, which are independent of the correlation length, and critical fluctuation contributions of order $\mathcal{O}(\xi ^2)$. This implies that the critical contribution to the resonance terms scales with the same power of $\xi$ as in the primordial result Eq. (14). The situation is more complicated in the case of the cumulants of third and fourth order, see [26]. Consider the third-order cumulant. The critical contribution to the primordial term, Eq. (15), scales as $\xi ^{9/2}$. The resonance terms contain a contribution, induced by fluctuations $\langle (\Delta N_R)^3\rangle$, that scales with the same power of $\xi$, but they also contain contributions, induced by the probabilistic nature of branching, that scale with lower powers of $\xi$. Since we do not keep subdominant terms, we drop these contributions in the resonance terms. The same statement applies to the fourth-order cumulant.

For $\hat{C}_3 = \langle (\Delta \hat{N}_p)^3\rangle - \langle (\Delta \hat{N}_{\bar{p}})^3\rangle - 3 \langle (\Delta \hat{N}_p)^2\Delta \hat{N}_{\bar{p}}\rangle + 3 \langle \Delta \hat{N}_p(\Delta \hat{N}_{\bar{p}})^2\rangle$ the three-particle correlators including resonance decays were derived in [26]. Taking only non-critical fluctuation contributions and critical fluctuation contributions of order $\mathcal{O}(\xi ^{9/2})$ into account, we find for these correlators

$$\begin{aligned} \langle (\Delta \hat{N}_i)^3 \rangle&= \langle (\Delta N_i)^3 \rangle + \sum _R \langle (\Delta N_R)^3\rangle \langle n_i\rangle _R^3 \nonumber \\&\quad + 3 \sum _R C_2^R \langle (\Delta n_i)^2\rangle _R \langle n_i\rangle _R \nonumber \\&\quad + \sum _R \langle N_R\rangle \langle (\Delta n_i)^3\rangle _R \,,\end{aligned}$$

(C.3)

$$\begin{aligned} \langle (\Delta \hat{N}_i)^2 \Delta \hat{N}_j \rangle&= \langle (\Delta N_i)^2 \Delta N_j \rangle \nonumber \\&\quad + \sum _R \langle (\Delta N_R)^2 \Delta N_{\bar{R}} \rangle \langle n_i\rangle _R^2 \langle n_j\rangle _{\bar{R}} \,, \end{aligned}$$

(C.4)

where $\langle (\Delta n_i)^3\rangle _R = \sum _r b_r^R (n_{i,r}^R)^3 - 3 \langle n_i\rangle _R \sum _r b_r^R (n_{i,r}^R)^2 + 2 \langle n_i\rangle _R^3$. The individual contributions in Eq. (C.3) follow from Eqs. (3) and (15) and in Eq. (C.4) from Eq. (16).

For $\hat{C}_4 = \langle (\Delta \hat{N}_p)^4 \rangle _c + \langle (\Delta \hat{N}_{\bar{p}})^4 \rangle _c - 4 \langle (\Delta \hat{N}_p)^3\Delta \hat{N}_{\bar{p}} \rangle _c + 6 \langle (\Delta \hat{N}_p)^2(\Delta \hat{N}_{\bar{p}})^2 \rangle _c - 4 \langle \Delta \hat{N}_p(\Delta \hat{N}_{\bar{p}})^3 \rangle _c$ the individual fourth-order cumulants follow from the four-particle correlators including resonance decays, cf. [26]. Taking for $\hat{C}_4$ only non-critical fluctuation contributions and critical fluctuation contributions of order $\mathcal{O}(\xi ^7)$ into account, we find

$$\begin{aligned} \langle (\Delta \hat{N}_i)^4 \rangle _c =&\,\, \langle (\Delta N_i)^4 \rangle _c + \sum _R \langle (\Delta N_R)^4\rangle _c \langle n_i\rangle _R^4 \nonumber \\&+ 6 \sum _R C_3^R \langle (\Delta n_i)^2\rangle _R \langle n_i\rangle _R^2 \nonumber \\&\,\, + \sum _R C_2^R \left[ 3 \langle (\Delta n_i)^2\rangle _R^2 + 4 \langle (\Delta n_i)^3\rangle _R \langle n_i\rangle _R \right] \nonumber \\&+ \sum _R \langle N_R\rangle \langle (\Delta n_i)^4\rangle _{R,c},\end{aligned}$$

(C.5)

$$\begin{aligned} \langle (\Delta \hat{N}_i)^m(\Delta \hat{N}_j)^n \rangle _c =&\,\, \langle (\Delta N_i)^m(\Delta N_j)^n \rangle _c \nonumber \\&+ \sum _R \langle (\Delta N_R)^m(\Delta N_{\bar{R}})^n \rangle _c \langle n_i\rangle _R^m \langle n_j\rangle _{\bar{R}}^n \end{aligned}$$

(C.6)

for $m+n=4$, where $\langle (\Delta n_i)^4\rangle _{R,c} = \langle (\Delta n_i)^4\rangle _R - 3 \langle (\Delta n_i)^2\rangle _R^2$ with $\langle (\Delta n_i)^4\rangle _R=\sum _r b_r^R (n_{i,r}^R)^4 - 4 \langle n_i\rangle _R \sum _r b_r^R (n_{i,r}^R)^3 + 6 \langle n_i\rangle _R^2 \sum _r b_r^R (n_{i,r}^R)^2 - 3 \langle n_i\rangle _R^4$. The individual contributions in Eq. (C.5) follow from Eqs. (3) and (18) and in Eq. (C.6) from Eq. (19).