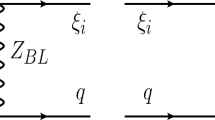Neutrino masses and superheavy dark matter in the 3-3-1-1 model

Abstract

In this work, we interpret the 3-3-1-1 model when the $B-L$ and 3-3-1 breaking scales behave simultaneously as the inflation scale. This setup not only realizes the previously achieved consequences of inflation and leptogenesis, but also provides new insights in superheavy dark matter and neutrino masses. We argue that the 3-3-1-1 model can incorporate a scalar sextet, which induces both small masses for the neutrinos via a combined type I and II seesaw and large masses for the new neutral fermions. Additionally, all the new particles have large masses in the inflation scale. The lightest particle among the W-particles that have abnormal (i.e., wrong) $B-L$ number in comparison to those of the standard model particles may be superheavy dark matter as it is stabilized by W-parity. The dark matter candidate may be a Majorana fermion, a neutral scalar, or a neutral gauge boson, which was properly created in the early universe due to gravitational effects on the vacuum or thermal production after cosmic inflation.

1 Introduction

The $SU(3)_\mathrm{C}\,\otimes \, SU(2)_\mathrm{L}\,\otimes \, U(1)_\mathrm{Y}$ standard model of strong and electroweak interactions with three quark and lepton families and a scalar doublet is an excellent description of the physics of our world down to $10^{-18}$ m order. However, it also leaves many crucial questions of nature unanswered [1]. Indeed, the standard model predicts only normal matter that occupies roundly 5% mass–energy density of the universe. What remains beyond the standard model is about 25% dark matter and 70% dark energy. The standard model provides null masses for the neutrinos, but the experiments have proved that the neutrinos have nonzero, small masses and flavor mixing. Besides, the standard model cannot solve the issues concerning the early universe such as the baryon-number asymmetry and the inflationary expansion. On the theoretical side, the standard model cannot explain how the Higgs mass is stabilized against radiative corrections, why there are only three families of fermions, and what makes the electric charges quantized.

Alternative to the popular proposals of grand unification, extra dimensions, and supersymmetry [1], a simple extension of the gauge symmetry to $SU(3)_\mathrm{C}\otimes SU(3)_\mathrm{L}\otimes U(1)_\mathrm{X}\otimes U(1)_\mathrm{N}$ (3-3-1-1) might address numerous questions [2,3,4,5,6]. Here, $SU(3)_\mathrm{L}$ is an enlargement of the weak-isospin symmetry, while the last two factors determine the electric charge (Q) and baryon-minus-lepton number ($B-L$), respectively. The 3-3-1-1 model overhauls the mathematical and phenomenological aspects of the known 3-3-1 models [7,8,9,10,11,12]. Indeed, $U(1)_\mathrm{N}$ is necessarily included since $B-L$ does not commute and is non-closed algebraically with $SU(3)_\mathrm{L}$. Consequently, $B-L$ and thus N charge must be gauged, and the electroweak and $B-L$ interactions are unified similar to the Glashow–Weinberg–Salam theory. The small neutrino masses can be achieved via seesaw mechanisms [13,14,15,16,17,18,19,20] as a result of the 3-3-1-1 symmetry breaking. The dark matter candidates naturally appear as W-particles that possess abnormal (i.e., wrong) $B-L$ number, which transform nontrivially and are thus stabilized under W-parity (like R-parity)—a remnant of the gauge symmetry unbroken by the vacuum. If the $U(1)_\mathrm{N}$ breaking scale is large, the corresponding $U(1)_\mathrm{N}$ breaking field could act as an inflaton, explaining the cosmological inflation. The CP-asymmetry decays of the right-handed neutrinos into normal matter or dark matter can generate the matter–antimatter asymmetry appropriately. The 3-3-1-1 model provides plausible solutions to the electric charge quantization and flavor problems. Particularly, the large flavor-changing neutral currents and potential CPT violation due to the unwanted vacuums and interactions in the 3-3-1 model with right-handed neutrinos are excellently prevented.

In the 3-3-1-1 model [2], the new neutral fermions $N_\mathrm{R}$ have vanishing masses at tree level. However, their masses can be generated by the effective operators that couple lepton triplets $\psi _\mathrm{L}$ to scalar triplet $\chi$. Such effective operators which are invariant under the gauge symmetry and W-parity can be radiatively induced by the model itself. Alternatively, the neutral fermion masses can be given at tree level by introducing their left-handed counterparts, $N_\mathrm{L}$, which transform as gauge symmetry singlets, so-called the truly sterile particles [3]. In all cases discussed, the new particles of the corresponding 3-3-1 model including $N_\mathrm{R}$ have masses in the 3-3-1 breaking scale. On the other hand, the observed neutrino masses in this model are generated by a type I seesaw mechanism. It is natural to impose the seesaw scale of $B-L$ breaking as the inflation scale, which is close to a hypothetical grand unification scale of $10^{16}$ GeV order [21,22,23,24] (however, see Appendix B), which is required for the successful inflation and leptogenesis scenarios [4]. Hence, the remaining particles such as the inflaton, right-handed neutrinos, and $B-L$ gauge boson all pick up a mass in the inflation regime.

Let us ask which size the 3-3-1 breaking scale has? A possibility for it is at TeV scale as investigated in the literatures [4, 7,8,9,10,11,12]. The new observation of this work is that it can be as large as the $B-L$ breaking scale associated with the seesaw and inflation ones. Such a large size for the 3-3-1 breaking scale is made available by the implement of a scalar sextet. This new scalar sextet will couple to $\psi _\mathrm{L} \psi _\mathrm{L}$, which consequently provides small masses for the neutrinos via a type II seesaw mechanism, in addition to the type I one. In contradiction to the previous proposals, the new neutral fermion masses are naturally large as given at tree level via the vacuum value of the scalar sextet, without necessarily acquiring either their sterile counterparts $N_\mathrm{L}$ or the effective operators. The implication of the scalar sextet for lepton-flavor-changing and leptogenesis processes is further hinted at. Despite a previous study [4], the scalar sextet may decay into two light leptons, possibly involving heavy lepton modes, which may dominate over generated lepton number. It is noteworthy that since the unitarity of the 3-3-1 model is cured as well as the proton stability is ensured [5], a large energy scale with regard to the 3-3-1 breaking is possible.

Interestingly enough, the dark matter candidates, which are the lightest particles among W-particles carrying abnormal $B-L$ numbers, are superheavy in the inflation regime, and this is called superheavy dark matter [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. They are stabilized by W-parity as a residual gauge symmetry. It is to be noted that the often-studied global symmetries could not keep the candidates stable since they are subsequently broken by the non-perturbative effects due to the gravitational anomalies. See, for instance [44]. The superheavy dark matter candidates are suitable to be non-thermally generated, because by contrast the thermal relics should overclose the universe due to the unitarity constraint [45].

Let us recall that in the previous work [2,3,4,5], the $SU(3)_\mathrm{L}$ symmetry breaking is at the TeV scale, which provides the dark matter candidates as thermal relics, limited below some hundreds of TeV. Hence, the above proposal is an alternative solution to the dark matter question. With the perspective of TeV dark matter, we hope that the search for thermal dark matter may be connected to the discovery of new physics at TeV scale. In fact, there are the extensive experimental programs that set up to detect the thermal dark matter such as direct and indirect detections as well as accelerator searches. However, none of these efforts have discovered a clear thermal dark matter and no evidence for new physics related to dark matter has been observed at the large hadron collider. The lack of evidence of thermal dark matter candidates may provide an additional source of dark matter in form of non-thermal candidates. The non-thermal dark matter candidates can provide the dominant source of dark matter and their self-annihilation rates can be larger than that of thermal dark matter. Therefore we do not only expect for experimental search but also other probes of the microscopic nature of dark matter [46]. Specially if dark matter and scalar perturbations can grow during the non-thermal phase, an additional enhancement of dark matter sub-structure on the small scale and important implication for indirect detection signals as well as the process of structure formation are expected to obtain [47,48,49,50,51]. On the other hand, if the existence of dark matter derives from the inflaton dynamics [52], it can be tested via measurements of inflationary parameter and/or the CMB isocurvature perturbations.

The rest of this work is organized as follows. In Sect. 2, we briefly review the 3-3-1-1 model, introducing the scalar sextet and concentrating on its effects for the mass spectrum of neutrinos and new fermions. Section 3 is devoted to the scalar potential when including the contribution of the scalar sextet. We show that the type II seesaw scale appearing naturally small in the considering model. We also identify the dark matter candidates, gauge bosons, and their masses. The inflation and reheating are discussed in Sect. 4. Section 5 considers the lightest W-particle as superheavy dark matter, and it estimates their contribution to the present critical density, where the scenarios for superheavy dark matter production are briefly studied. Finally, we conclude this work and make outlooks in Sect. 6.

2 The 3-3-3-1 model with scalar sextet

Let $SU(2)_\mathrm{L}$ extend to $SU(3)_\mathrm{L}$. The $[SU(3)_\mathrm{L}]^3$ anomaly does not vanish for each complex representation unlike $SU(2)_\mathrm{L}$. The fundamental representations (triplets/antitriplets) of $SU(3)_\mathrm{L}$ decompose as $3=2\oplus 1$ and $3^*=2^*\oplus 1$ under $SU(2)_\mathrm{L}$. Thus, all the left-handed fermion doublets will be embedded into 3 or $3^*$, where for the second case $(f_2,-f_1)$ is an antidoublet, provided that $(f_1,f_2)$ is a doublet. Suppose that all the right-handed fermion singlets transform as $SU(3)_\mathrm{L}$ singlets (note that they cannot be put in the above 3 or $3^*$ except for leptons because $SU(3)_\mathrm{C}$, $SU(3)_\mathrm{L}$, and spacetime symmetry commute). Since the $[SU(3)_\mathrm{L}]^3$ anomaly for 3 and $3^*$ are opposite, this anomaly is canceled out if the number of 3 is equal that of $3^*$, which determines the number of families to match that of colors. Hence, the fermion representations under $SU(3)_\mathrm{L}$ are arranged as given below, there $N_\mathrm{R}$, U, D, and $\nu _\mathrm{R}$ are new particles added to complete the representations as well as canceling other anomalies. In principle, the new leptons $N_\mathrm{R}$ may have arbitrary Q and $B-L$ charges [5], but in this work we consider the simplest, nontrivial case, $Q(N_\mathrm{R})=[B-L](N_\mathrm{R})=0$ (their partners $N_\mathrm{L}$ are thus gauge singlets, which are truly sterile and not imposed). The lepton triplets obey $Q=\mathrm {diag}(0,-1,0)$ and $B-L=\mathrm {diag}(-1,-1,0)$, which indicate that Q and $B-L$ neither commute nor close algebraically with $SU(3)_\mathrm{L}$. Hence, two new Abelian gauge groups arise as a result to close those symmetries by $SU(3)_\mathrm{C}\otimes SU(3)_\mathrm{L}\otimes U(1)_\mathrm{X}\otimes U(1)_\mathrm{N}$ (called 3-3-1-1), where the color group is also included for completeness, and X, N, respectively, define $Q,B-L$ by the forms as obtained below when acting on a lepton triplet. The Q and $B-L$ charges for new quarks are thus seen when acting such operators on quark triplets/antitriplets. Note that the left-handed and right-handed fermions have the same Q and $B-L$. The X and N charges are determined as $X=\mathrm {Tr}(Q)/D$ and $N=\mathrm {Tr}(B-L)/D$, where D is the dimension of corresponding $SU(3)_\mathrm{L}$ representation.

The fermion content in the 3-3-1-1 model under consideration is given by

$$\begin{aligned}&\psi _{a\mathrm{L}} = \left( \begin{array}{c} \nu _{a\mathrm{L}}\\ e_{a\mathrm{L}}\\ (N_{a\mathrm{R}})^c \end{array}\right) \sim (1,3, -1/3,-2/3),\end{aligned}$$

(1)

$$\begin{aligned}&\nu _{a\mathrm{R}}\sim (1,1,0,-1),\quad e_{a\mathrm{R}} \sim (1,1, -1,-1),\end{aligned}$$

(2)

$$\begin{aligned}&Q_{\alpha \mathrm{L}}=\left( \begin{array}{c} d_{\alpha \mathrm{L}}\\ -u_{\alpha \mathrm{L}}\\ D_{\alpha \mathrm{L}} \end{array}\right) \sim (3,3^*,0,0),\\&Q_\mathrm{3L}=\left( \begin{array}{c} u_\mathrm{3L}\\ d_\mathrm{3L}\\ U_\mathrm{L} \end{array}\right) \sim \left( 3,3,1/3,2/3\right) ,\nonumber \end{aligned}$$

(3)

$$\begin{aligned}&u_{a \mathrm{R}}\sim \left( 3,1,2/3,1/3\right) ,\quad d_{a \mathrm{R}} \sim \left( 3,1,-1/3,1/3\right) ,\end{aligned}$$

(4)

$$\begin{aligned}&U_\mathrm{R}\sim \left( 3,1,2/3,4/3\right) ,\quad D_{\alpha \mathrm{R}} \sim \left( 3,1,-1/3,-2/3\right) , \end{aligned}$$

(5)

where $a=1,2,3$ and $\alpha =1,2$ are family indices [2]. The quantum numbers in the parentheses are provided upon the 3-3-1-1 subgroups, respectively. The electric charge, baryon-minus-lepton charge, and W-parity (P) are embedded in the 3-3-1-1 symmetry as

$$\begin{aligned} Q= & {} T_3-\frac{1}{\sqrt{3}}T_8 + X,\quad B-L=-\frac{2}{\sqrt{3}}T_8+N,\nonumber \\ P= & {} (-1)^{3(B-L)+2s}=(-1)^{-2\sqrt{3}T_8+3 N+2 s}, \end{aligned}$$

(6)

where $T_i$ $(i=1,2,3,\ldots ,8)$, X, and N are $SU(3)_\mathrm{L}$, $U(1)_\mathrm{X}$, and $U(1)_\mathrm{N}$ charges, respectively, and s is spin. Additionally, we will denote the $SU(3)_\mathrm{C}$ charges as $t_i$. The new observation is that $B-L$ is a noncommutative gauge charge like Q, which is nontrivially unified with the weak forces, which is unlike the standard model $B-L$ symmetry. W-parity is nontrivial for the new particles that carry abnormal (wrong) $B-L$ charges unlike those defined for the standard model particles, called W-particles. The residual gauge operators Q and P are actually conserved by the vacuum. The new fermions $N_\mathrm{R}$, U, and D possess $(Q,B-L)$ as (0, 0), (2 / 3, 4 / 3), and $(-1/3,-2/3)$, respectively. Here, we see that they have $B-L$ unlike the ordinary leptons/quarks and are W-odd, while all the ordinary fermions are W-even.

The fermion content as provided is also free from all the other anomalies. Indeed, the $[SU(3)_\mathrm{C}]^3$ anomaly always vanishes since all the quarks are vector-like. Additionally, we have $X=Q-T_3+T_8/\sqrt{3}$ and $N=B-L+2 T_8/\sqrt{3}$, in which the anomalies as coupled to Q, $B-L$, and $T_{3,8}$ obviously vanish. Hence, the anomalies associated with X, N are canceled too. To see this explicitly, the nontrivial anomalies which make troublesome can be calculated as presented in Appendix A. Here, note that $\nu _\mathrm{R}$ as supposed are in order to cancel the gravity anomaly $[\mathrm {gravity}]^2U(1)_\mathrm{N}$ and the self-anomaly $[U(1)_\mathrm{N}]^3$. Although the B and L charges are anomalous, regarding $B-L$ as a fundamental charge makes the model free from all the B and L anomalies. Further, it is easy to show that the anomalies are always canceled, independent of the Q and $B-L$ embedding coefficients in the gauge group, i.e. those charges of the new particles (cf. [5]).

The scalar content actually contains

$$\begin{aligned} \rho= & {} \left( \begin{array}{c} \rho ^+_1\\ \rho ^0_2\\ \rho ^+_3\end{array}\right) \sim (1,3,2/3,1/3),\\ \eta= & {} \left( \begin{array}{c} \eta ^0_1\\ \eta ^-_2\\ \eta ^0_3\end{array}\right) \sim (1,3,-1/3,1/3),\nonumber \end{aligned}$$

(7)

$$\begin{aligned} \chi= & {} \left( \begin{array}{c} \chi ^0_1\\ \chi ^-_2\\ \chi ^0_3\end{array}\right) \sim (1,3,-1/3,-2/3), \quad \phi \sim (1,1,0,2). \end{aligned}$$

(8)

Here, the scalars $\eta _3$, $\rho _3$, and $\chi _{1,2}$ carry $B-L$ charge with one unit and are W-odd, whereas the remaining scalars possess $[B-L](\eta _{1,2}, \rho _{1,2}, \chi _3)=0$ and $[B-L](\phi )=2$ and are W-even. The vacuum expectation values (VEVs) that conserve Q and P are obtained:

$$\begin{aligned} \langle \rho \rangle= & {} \frac{1}{\sqrt{2}}(0,v,0)^\mathrm{T}, \quad \langle \eta \rangle =\frac{1}{\sqrt{2}}(u,0,0)^\mathrm{T},\\ \langle \chi \rangle= & {} \frac{1}{\sqrt{2}}(0,0,w)^\mathrm{T}, \quad \langle \phi \rangle =\frac{1}{\sqrt{2}}\Lambda .\nonumber \end{aligned}$$

(9)

The 3-3-1-1 symmetry is broken down to $SU(3)_\mathrm{C}\otimes U(1)_{Q}\otimes U(1)_{{B}-{L}}$ due to w, u, v, while $U(1)_{{B}-{L}}$ is broken down to P due to $\Lambda$. Under the standard model symmetry we have three scalar doublets $(\rho _1,\rho _2)$, $(\eta _1,\eta _2)$, and $(\chi _1,\chi _2)$, where the third one is W-odd and integrated out. The first two are W-even, behaving in the weak scale, and the standard model like Higgs boson is a combination of $\rho _2$ and $\eta _1$.

Observe that $N_{a\mathrm{R}}$ are still massless at the renormalizable level. To generate the appropriate masses for $N_{a\mathrm{R}}$, we additionally introduce a scalar sextet,

$$\begin{aligned} S= \left( \begin{array}{ccc} S_{11}^0 &{} \frac{S_{12}^-}{\sqrt{2}}&{} \frac{S_{13}^0}{\sqrt{2}} \\ \frac{S_{12}^-}{\sqrt{2}} &{} S_{22}^{--} &{} \frac{S_{23}^{-}}{\sqrt{2}}\\ \frac{S_{13}^0}{\sqrt{2}}&{} \frac{S_{23}^{-}}{\sqrt{2}}&{} S^0_{33} \\ \end{array} \right) \sim (1,6,-2/3,-4/3), \end{aligned}$$

(10)

which couples to two $\psi _\mathrm{L}$’s. The VEV of S that conserves W-parity takes the form

$$\begin{aligned} \left\langle S \right\rangle = \frac{1}{\sqrt{2}}\left( \begin{array}{ccc} \kappa &{} 0 &{} 0\\ 0 &{} 0&{} 0 \\ 0 &{} 0&{} \Delta \\ \end{array} \right) . \end{aligned}$$

(11)

Note that $S_{13}$ and $S_{23}$ have $B-L=-1$ and are W-odd, while the other components possess $[B-L](S_{11},S_{12},S_{22})=-2$, $[B-L](S_{33})=0$, and they are W-even.

The Lagrangian of the considering model includes the ones in [3] (some parameters will be renamed for easy reading) plus the kinetic mixing term in [6] and new contributions relevant to the scalar sextet. Up to the gauge fixing and ghost terms, it is given by

$$\begin{aligned} \mathcal {L}= & {} \sum _{\mathrm {fermion\ multiplets}}\bar{\Psi }i\gamma ^\mu D_\mu \Psi \nonumber \\&+\, \sum _{\mathrm {scalar\ multiplets}}(D^\mu \Phi )^\dagger (D_\mu \Phi )\nonumber \\&-\frac{1}{4}G_{i\mu \nu }G_i^{\mu \nu } -\frac{1}{4} A_{i\mu \nu }A_i^{\mu \nu }-\frac{1}{4} B_{\mu \nu } B^{\mu \nu }-\frac{1}{4}C_{\mu \nu } C^{\mu \nu }\nonumber \\&-\frac{\delta }{2} B_{\mu \nu }C^{\mu \nu }-V(\rho ,\eta ,\chi ,\phi ,S) + \mathcal {L}_{\mathrm {Yukawa}}, \end{aligned}$$

(12)

where $D_\mu =\partial _\mu +ig_s G_{i\mu }t_i+ig A_{i\mu }T_i+ig_\mathrm{X} B_\mu X+ig_\mathrm{N} C_\mu N$ is covariant derivative. The field strength tensors, $G_{i\mu \nu }$, $A_{i\mu \nu }$, $B_{\mu \nu }$, and $C_{\mu \nu }$, are given as coupled to the gauge fields, $G_{i\mu }$, $A_{i\mu }$, $B_\mu$, and $C_\mu$, as well as the coupling constants, $g_\mathrm{s}$, g, $g_\mathrm{X}$, and $g_\mathrm{N}$, of the 3-3-1-1 subgroups, respectively. The Yukawa Lagrangian is

$$\begin{aligned} \mathcal {L}_{\mathrm {Yukawa}}= & {} h^e_{ab}\bar{\psi }_{a\mathrm{L}}\rho e_{b\mathrm{R}} +h^\nu _{ab}\bar{\psi }_{a\mathrm{L}}\eta \nu _{b\mathrm{R}}\nonumber \\&+\,h'^\nu _{ab}\bar{\nu }^c_{a\mathrm{R}}\nu _{b\mathrm{R}}\phi +f_{ab} \bar{\psi }_{a\mathrm{L}}^c S^\dagger \psi _{b\mathrm{L}} \nonumber \\&+\,h^U\bar{Q}_\mathrm{3L}\chi U_\mathrm{R} + h^D_{\alpha \beta }\bar{Q}_{\alpha \mathrm{L}} \chi ^* D_{\beta R}\nonumber \\&+\, h^u_a \bar{Q}_\mathrm{3L}\eta u_{a\mathrm{R}}+h^d_a\bar{Q}_\mathrm{3L}\rho d_{a\mathrm{R}} \nonumber \\&+\, h^d_{\alpha a} \bar{Q}_{\alpha \mathrm{L}}\eta ^* d_{a\mathrm{R}} +h^u_{\alpha a } \bar{Q}_{\alpha \mathrm{L}}\rho ^* u_{a\mathrm{R}} + \mathrm{H.c.} \end{aligned}$$

(13)

The scalar potential is separated into two parts, $V(\rho ,\eta ,\chi , \phi ,S)=V(\rho ,\eta ,\chi ,\phi )+V(S)$, where

$$\begin{aligned} V(\rho ,\eta ,\chi ,\phi )= & {} \mu ^2_\phi \phi ^\dagger \phi + \mu ^2_\rho \rho ^\dagger \rho + \mu ^2_\chi \chi ^\dagger \chi + \mu ^2_\eta \eta ^\dagger \eta \nonumber \\&+ \,\lambda (\phi ^\dagger \phi )^2 + \lambda _1 (\rho ^\dagger \rho )^2 + \lambda _2 (\chi ^\dagger \chi )^2 \nonumber \\&+ \lambda _3 (\eta ^\dagger \eta )^2+ \,\lambda _4 (\rho ^\dagger \rho )(\chi ^\dagger \chi )\nonumber \\&+\lambda _5 (\rho ^\dagger \rho )(\eta ^\dagger \eta ) +\lambda _6 (\chi ^\dagger \chi )(\eta ^\dagger \eta ) \nonumber \\&+\,\lambda _7 (\rho ^\dagger \chi )(\chi ^\dagger \rho ) +\lambda _8 (\rho ^\dagger \eta )(\eta ^\dagger \rho )\nonumber \\&+\lambda _9 (\chi ^\dagger \eta )(\eta ^\dagger \chi )+\lambda _{10} (\phi ^\dagger \phi )(\rho ^\dagger \rho ) \nonumber \\&+\lambda _{11}(\phi ^\dagger \phi )(\chi ^\dagger \chi )+\lambda _{12}(\phi ^\dagger \phi )(\eta ^\dagger \eta ) \nonumber \\&+\, (f_1 \epsilon ^{mnp}\eta _m\rho _n\chi _p+\mathrm{H.c.}), \end{aligned}$$

(14)

$$\begin{aligned} V(S)= & {} \mu _\mathrm{S}^2 \mathrm {Tr}(SS^\dagger )+\zeta _{1}\mathrm {Tr}^2(SS^\dagger )+\zeta _{2} \mathrm {Tr}(SS^\dagger )^2 \nonumber \\&+\, (\zeta _{3} \eta ^\dagger \eta +\zeta _{4} \rho ^\dagger \rho +\zeta _{5} \chi ^\dagger \chi +\zeta _{6} \phi ^\dagger \phi )\mathrm {Tr}(SS^\dagger ) \nonumber \\&+ \,\zeta _{7} (\eta ^\dagger S)(S^\dagger \eta )+\zeta _8 (\chi ^\dagger S)(S^\dagger \chi )+\zeta _9(\rho ^\dagger S)(S^\dagger \rho ) \nonumber \\&+ \,(\zeta _{10} \eta ^\mathrm{T} S^\dagger \eta \phi ^*+f_2 \chi ^\mathrm{T} S^\dagger \chi +\mathrm{H.c.}). \end{aligned}$$

(15)

To ensure that the scalar potential $V = V(\rho ,\eta ,\chi ,\phi ,S)$ is bounded from below (i.e., vacuum stability), the necessary conditions are

$$\begin{aligned} \lambda>0,\quad \lambda _1>0,\quad \lambda _2>0,\quad \lambda _3>0,\quad \zeta _1+\zeta _2>0, \end{aligned}$$

(16)

which could be obtained for $V>0$ when $\phi$, $\rho$, $\chi$, $\eta$, and S separately tend to infinity, respectively. Additional conditions are $V>0$ for any two of the $\phi$, $\rho$, $\chi$, $\eta$, and S fields simultaneously tending to infinity, which yield

$$\begin{aligned}&\lambda _4+\lambda _7\theta (-\lambda _7)>-2\sqrt{\lambda _1\lambda _2}, \nonumber \\&\lambda _5+\lambda _8\theta (-\lambda _8)>-2\sqrt{\lambda _1\lambda _3}, \nonumber \\&\lambda _6+\lambda _9\theta (-\lambda _9)>-2\sqrt{\lambda _2\lambda _3},\nonumber \\&\lambda _{10}>-2\sqrt{\lambda \lambda _1},\lambda _{11}>-2\sqrt{\lambda \lambda _2}, \lambda _{12}>-2\sqrt{\lambda \lambda _3},\\&\zeta _6>-2\sqrt{\lambda (\zeta _1+\zeta _2)},\nonumber \\&\zeta _3+\zeta _7\theta (-\zeta _7)>-2\sqrt{\lambda _3(\zeta _1+\zeta _2)},\nonumber \\&\zeta _4+\zeta _9\theta (-\zeta _9)>-2\sqrt{\lambda _1(\zeta _1+\zeta _2)},\nonumber \\&\zeta _5+\zeta _8\theta (-\zeta _8)>-2\sqrt{\lambda _2(\zeta _1+\zeta _2)},\nonumber \end{aligned}$$

(17)

where $\theta (x)$ is the Heaviside step function. Furthermore, $V>0$ for any three, any four, and the five of the $\phi$, $\rho$, $\chi$, $\eta$, and S fields, respectively, simultaneously tending to infinity also provide extra conditions for vacuum stability. We might also have the constraints (but most of them should be equivalent to the above conditions) for physical scalar masses as squared to be positive. On the other hand, to have a desirable vacuum structure, i.e. the VEVs, the necessary conditions are $\mu ^2_{\phi }<0$, $\mu ^2_{\rho }<0$, $\mu ^2_{\chi }<0$, $\mu ^2_{\eta }<0$, and $\mu ^2_\mathrm{S}<0$.

We see that the appearance of the scalar sextet does not affect the mass spectrum of the charged leptons and quarks, which were presented in [2]. Because W-parity is conserved, i.e. $\langle S_{13}\rangle =\langle \eta _3\rangle =0$, the left-handed and right-handed neutrinos do not mix with the neutral fermions, $N_{a\mathrm{R}}$. The neutral fermions by themselves couple to $S_{33}$, which yields their masses in $\Delta$ scale of the form, $-\frac{1}{2} \bar{N}_\mathrm{R} m_\mathrm{N} N^c_\mathrm{R} + \mathrm{H.c.}$, where

$$\begin{aligned} \, [m_\mathrm{N}]_{ab} =- \sqrt{2} f_{ab}\Delta , \end{aligned}$$

(18)

which is different from the criteria in [2]. On the other hand, the left-handed neutrinos gain Majorana masses since they couple to $S_{11}$, $[m_\mathrm{L}]_{ab}=-\sqrt{2}\kappa f_{ab}$. The right-handed neutrinos obtain Majorana masses because they interact with $\phi$, $[m_\mathrm{R}]_{ab}=-\sqrt{2} \Lambda h'^\nu _{ab}$. Whereas the left-handed and right-handed neutrinos couple to $\eta _1$, their Dirac masses are obtained as $[m^*_\mathrm{D}]_{ab}=-uh^\nu _{ab}/\sqrt{2}$ [2]. Hence, the total mass Lagrangian for the neutrinos is

$$\begin{aligned} \mathcal {L}^\nu _{\mathrm {mass}}=-\frac{1}{2}\left( \begin{array}{cc} \bar{\nu }_\mathrm{L}^c &{} \bar{\nu }_\mathrm{R} \\ \end{array} \right) m_\nu \left( \begin{array}{c} \nu _\mathrm{L} \\ \nu _\mathrm{R}^c \\ \end{array} \right) +\mathrm{H.c.}, \end{aligned}$$

(19)

where $m_\nu$ has the form

$$\begin{aligned} m_\nu =\left( \begin{array}{cc} m_\mathrm{L}&{} m_\mathrm{D} \\ m^\mathrm{T}_\mathrm{D} &{} m_\mathrm{R} \\ \end{array} \right) . \end{aligned}$$

(20)

First note that $w, \Delta , \Lambda$ break $SU(3)_\mathrm{L}\otimes U(1)_\mathrm{X}\otimes U(1)_\mathrm{N}$ down to $SU(2)_\mathrm{L}\otimes U(1)_\mathrm{Y}$ and provide the masses for the new particles, whereas $u,v, \kappa$ break $SU(2)_\mathrm{L}\otimes U(1)_\mathrm{Y}$ down to $U(1)_{Q}$ and give the masses for the standard model particles. To be consistent with the present data, we assume $u,v, \kappa \ll w, \Lambda , \Delta$. In this limit, the scalar sextet shifts the $\rho$-parameter by $\Delta \rho \equiv \rho -1 \simeq - \frac{2 \kappa ^2}{v^2+u^2} + \mathcal {O}[\kappa ^4/(v^4,u^4),(u^2,v^2)/(w^2, \Lambda ^2, \Delta ^2)]$, which is negative. The positive contributions that come from the mass splittings of the fermion, scalar and vector doublets could make it overall positive and comparable to the global fit [1]. We thus expect $2\kappa ^2/(u^2+v^2)\sim 0.0004$, which implies $\kappa \sim 3.5\ \mathrm {GeV}$. Note that the W mass can be approximated by $m^2_{W}\simeq \frac{g^2}{4}(v^2+u^2)$, which yields $u^2+v^2 \simeq (246\ \mathrm {GeV})^2$, as used. Now that, due to the constraints, $\kappa \ll u,v \ll w,\Lambda ,\Delta$, $m_\mathrm{L}\ll m_\mathrm{D}\ll m_\mathrm{R}$, the observed, light neutrinos $\sim \nu _\mathrm{L}$ receive masses via a combinational mechanism of type I and II seesaw, by

$$\begin{aligned} m_{\mathrm {light}}\simeq & {} m_\mathrm{L}-m_\mathrm{D} m^{-1}_\mathrm{R} m^\mathrm{T}_\mathrm{D}\nonumber \\= & {} -\sqrt{2} \left[ \kappa f - \frac{u^2}{4\Lambda } (h^{\nu })^* (h^{\prime \nu })^{-1}(h^{\nu })^\dagger \right] , \end{aligned}$$

(21)

which are naturally small since $\kappa$ and $u^2/\Lambda$ can be in the eV scale, as shown below. The heavy neutrinos $\sim \nu _\mathrm{R}$ have the masses, $m_{\mathrm {heavy}}\simeq -\sqrt{2} h^{\prime \nu } \Lambda$, as retained, which are proportional to the $U(1)_\mathrm{N}$ breaking scale, $\Lambda$.

We would like to emphasize that the VEVs u, v (including $\kappa$) break the electroweak symmetry. Whereas the VEVs $w, \Delta$ break the $SU(3)_\mathrm{L}\otimes U(1)_\mathrm{X}\otimes U(1)_\mathrm{N}$ symmetry, they do not break the $U(1)_{B-L}$ symmetry, and we have the well-known 3-3-1 scales. The VEV $\Lambda$ (including $\kappa$) breaks $B-L$, thus $U(1)_\mathrm{N}$ totally. It is natural to suppose $w\sim \Delta$ and $u\sim v$, because they mainly break $SU(3)_\mathrm{L}$ and $SU(2)_\mathrm{L}$, respectively. The phenomenological aspects of the 3-3-1-1 model can be divided into the corresponding regimes, such that

• 1. $w\sim \Lambda \sim \mathrm {TeV}$, as explicitly studied in [3].

• 2. $w \sim \mathrm {TeV} \ll \Lambda \sim m_{\mathrm {inflaton}}$, as explicitly investigated in [2, 4].

• 3. $w\sim \Lambda \sim m_{\mathrm {inflaton}}$, which is the new case under consideration.

Below, we will show that both the 3-3-1 and the $B-L$ breaking scales, w and $\Lambda$, can be kept at a very high energy scale as the inflation scale, which is close to a hypothetical grand unification scale (however, see Appendix B for extra discussion). By this regime, it is best understood why the seesaw contributions, $\kappa$ and $u^2/\Lambda$, are naturally small. The introduction of S, thus $\Delta$, provides (i) $N_{a\mathrm{R}}$ are realized in the inflation energy regime, (ii) the neutrino masses of the type II seesaw fit the observed range in eV, and (iii) rich phenomenology in inflation, leptogenesis, and dark matter candidates. Of course, the leading conclusions of this work would remain if one omitted the scalar sextet.

3 Scalar sector

First of all, we recall that the considering model provides the type II seesaw neutrino masses, given that $S_{11}$ has a tiny VEV, $\kappa$. Because the lepton number is a gauge charge, the Goldstone boson, well known as a Majoron, that is associated with this broken charge can be eliminated by the corresponding gauge field. There is no invisible decay mode of the Z boson into the Majoron and its Higgs partner (however, see [53]). The Majoron problem is solved, which is unlike [54]. We will also show that $\kappa$ is naturally small, as suppressed and protected by the $B-L$ dynamics, due to the interaction, $-\zeta _{10} \eta ^\mathrm{T} S^\dagger \eta \phi ^*$. Here, when $\phi$ gets a VEV, $\Lambda$, it becomes $-\frac{1}{\sqrt{2}}\zeta _{10}\Lambda \eta ^\mathrm{T} S^\dagger \eta$, which works as that in the theory of explicit lepton-number violation [53]. The violation strength is set by $\Lambda$.

Expanding the neutral scalars around their VEVs, we have

$$\begin{aligned} \rho= & {} \left( \begin{array}{cc} \rho ^+_1\\ \frac{1}{\sqrt{2}}(v+S_2+iA_2)\\ \rho ^+_3\end{array}\right) ,\quad \eta = \left( \begin{array}{cc} \frac{1}{\sqrt{2}}(u+S_1+iA_1)\\ \eta ^-_2\\ \frac{1}{\sqrt{2}}(S_3^\prime +iA_3^\prime )\end{array}\right) ,\nonumber \\ \chi= & {} \left( \begin{array}{c} \frac{1}{\sqrt{2}}(S_1^\prime +i A_1^\prime )\\ \chi ^-_2\\ \frac{1}{\sqrt{2}}(\omega +S_3+iA_3) \end{array}\right) ,\nonumber \\ \phi= & {} \frac{1}{\sqrt{2}}(\Lambda +S_4+i A_4), \end{aligned}$$

(22)

and for the sextet

$$\begin{aligned} S= \left( \begin{array}{ccc} \frac{1}{\sqrt{2}}(\kappa +S_5+iA_5) &{} \frac{S^-_{12}}{\sqrt{2}}&{} \frac{1}{2}(S_2^\prime +iA_2^\prime ) \\ \frac{S^-_{12}}{\sqrt{2}} &{} S^{--}_{22} &{} \frac{S^-_{23}}{\sqrt{2}} \\ \frac{1}{2}(S_2^\prime +iA_2^\prime ) &{} \frac{S^-_{23}}{\sqrt{2}} &{} \frac{1}{\sqrt{2}}(\Delta + S_6+iA_6) \\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(23)

Here, all the fields superscripted by a prime, $S^\prime$ and $A^\prime$, are W-odd, while the others, S and A, are W-even. There is no mixing between the two kinds of fields, due to W-parity conservation. Also, the W-odd and W-even charged scalars do not mix.

The potential minimization conditions are derived as

$$\begin{aligned}&\sqrt{2}f_1 vw+u(\zeta _7 \kappa ^2+2\zeta _{10} \kappa \Lambda +\lambda _{12} \Lambda ^2+\zeta _{3}(\kappa ^2+\Delta ^2)\\&\quad +2\lambda _3 u^2+\lambda _5 v^2+\lambda _6w^2+2\mu _\eta ^2) =0, \\&\sqrt{2}f_1 uw+v(2\lambda _1 v^2+\lambda _{10} \Lambda ^2\\&\quad +\zeta _{4}(\kappa ^2+\Delta ^2)+\lambda _4 w^2+ \lambda _5 u^2+ 2\mu _\rho ^2)=0, \\&\sqrt{2}f_1 uv+w(2\sqrt{2}f_2 \Delta + \lambda _{11}\Lambda ^2+ \zeta _{5} \kappa ^2+\Delta ^2(\zeta _8+\zeta _{5})\\&\quad +2\lambda _2 w^2+\lambda _4 v^2+\lambda _6 u^2+2\mu _\chi ^2) =0, \\&\zeta _{10} u^2 \kappa +\Lambda (2\lambda \Lambda ^2+\lambda _{10} v^2\\&\quad +\lambda _{11}w^2+\lambda _{12}u^2+\zeta _{6}(\kappa ^2+\Delta ^2)+2 \mu ^2_\phi )= 0, \\&u^2(\zeta _{10} \Lambda +\kappa (\zeta _7+\zeta _{3}))+\kappa (2\zeta _{1}\Delta ^2 +2(\zeta _{1}+\zeta _{2})\kappa ^2\\&\quad +\zeta _{4}v^2+\zeta _{5}w^2+\zeta _{6}\Lambda ^2 +2\mu _\mathrm{S}^2 )=0, \\&\sqrt{2}f_2w^2+\Delta (2\zeta _{1}\kappa ^2+2(\zeta _{1} +\zeta _{2})\Delta ^2+\zeta _{3}u^2\\&\quad +\zeta _{4}v^2 +(\zeta _{5}+\zeta _8)w^2+\zeta _{6} \Lambda ^2+2 \mu _\mathrm{S}^2)=0. \end{aligned}$$

To have the desirable vacuum, we set $\mu _\chi$, $\mu _\phi$, and $\mu _\mathrm{S}$ in the inflation scale as mentioned. Correspondingly, the VEVs $w,\Lambda ,\Delta$ that reduce the 3-3-1-1 symmetry down to the standard model one are large in such a regime. Indeed, for $\kappa ,u,v=0$, we obtain

$$\begin{aligned}&2 \mu ^2_\phi + \lambda _{11}w^2+ 2\lambda \Lambda ^2+\zeta _6\Delta ^2 = 0, \nonumber \\&2\mu ^2_\chi +2\lambda _2 w^2+\lambda _{11}\Lambda ^2+ (\zeta _8+\zeta _5) \Delta ^2+ 2\sqrt{2}f_2 \Delta =0, \\&2\mu _\mathrm{S}^2+ (\zeta _8+\zeta _5)w^2+\zeta _6 \Lambda ^2\nonumber \\&\quad +2(\zeta _1 +\zeta _2)\Delta ^2 +\sqrt{2}f_2w^2/\Delta = 0, \nonumber \end{aligned}$$

(24)

which provide the $(w,\Lambda ,\Delta )$ solution proportionally to $(\mu _\chi ,\mu _\phi ,\mu _\mathrm{S})$, with an appropriate choice of the signs of the parameters. These three equations can also be deduced from the above six conditions if one uses $\mu _\eta ,\mu _\rho ,u,v,\kappa \ll \mu _\chi ,\mu _\phi ,\mu _S,w,\Lambda , \Delta$.

At the low energy regime as of the standard model, all the heavy particles are integrated out. We work with the effective potential,

$$\begin{aligned} V_{\mathrm {eff}}= & {} \mu ^2_\rho \rho ^\dagger \rho + \mu ^2_\eta \eta ^\dagger \eta +\lambda _1 (\rho ^\dagger \rho )^2+\lambda _3(\eta ^\dagger \eta )^2\nonumber \\&+\,(\lambda _5+f_1^2/\mu ^2_\chi )(\rho ^\dagger \rho )(\eta ^\dagger \eta )\nonumber \\&+\,(\lambda _8-f_1^2/\mu ^2_\chi )(\rho ^\dagger \eta )(\eta ^\dagger \rho ), \end{aligned}$$

(25)

where the last two terms received a contribution due to the $-f_1\eta \rho \chi$ interaction and its Hermitian conjugate; the other contributions are smaller and neglected. Note also that the fields $\eta$, $\rho$ denote only their doublet components, while their third components were integrated away. This potential yields the minimization conditions,

$$\begin{aligned}&\mu ^2_\eta +\lambda _3 u^2+\frac{1}{2} (\lambda _5+f^2_1/\mu ^2_\chi )v^2=0,\\&\mu ^2_\rho +\lambda _1 v^2+\frac{1}{2} (\lambda _5+f^2_1/\mu ^2_\chi )u^2=0,\nonumber \end{aligned}$$

(26)

which define the weak scales (u, v), as usual.

Also in this regime, since the left-handed neutrinos couple to the sextet by $f_{ab}\bar{\psi }^c_{a\mathrm{L}}\psi _{b\mathrm{L}} S^*$ and then the sextet couples to the standard model Higgs bosons by $-\zeta _{10}\eta \eta S^* \phi ^*$, we obtain the effective interaction,

$$\begin{aligned} -\frac{\Lambda }{\sqrt{2}}\frac{1}{m^2_\mathrm{S}}\zeta _{10}f_{ab} (\bar{\psi }^c_{a\mathrm{L}}\eta ^*)(\psi _{b\mathrm{L}}\eta ^*), \end{aligned}$$

(27)

after integrating S out as well as breaking the $B-L$ charge by $\langle \phi \rangle$ simultaneously. Here, $m_\mathrm{S}$ denotes the mass of the scalar triplet located in the sextet, satisfying $m^2_\mathrm{S}=\mu ^2_\mathrm{S}+\frac{1}{2} \zeta _5 w^2 +\frac{1}{2} \zeta _6 \Lambda ^2+\zeta _1 \Delta ^2$. This interaction is responsible for the type II seesaw neutrino masses,

$$\begin{aligned} \, [m_\mathrm{L}]_{ab}=\frac{\Lambda }{\sqrt{2}}\frac{u^2}{m^2_\mathrm{S}}\zeta _{10}f_{ab}, \end{aligned}$$

(28)

which must agree with the result in the previous section. Indeed, the fifth minimization condition above implies a solution for $\kappa$,

$$\begin{aligned} \kappa =-\frac{\zeta _{10}u^2\Lambda }{2m^2_\mathrm{S}}, \end{aligned}$$

(29)

which matches the two results. It also implies $\kappa \sim u^2/\Lambda$, which fits eV scale naturally.

In the pseudo-scalar sector, all the W-even fields, $A_1, A_2, A_3, A_4, A_5, A_6$, mix by themselves via the mass matrix in such order as

$$\begin{aligned} \frac{1}{2} M_\mathrm{A}^2=\left( \begin{array}{cccccc} -\frac{\sqrt{2}f_1 vw+4\zeta _{10} u\kappa \Lambda }{4u} &{} -\frac{f_1 w}{2\sqrt{2}} &{} -\frac{f_1 v}{2\sqrt{2}} &{} \frac{\zeta _{10} u \kappa }{2} &{} \frac{\zeta _{10} u \Lambda }{2} &{} 0 \\ -\frac{f_1 w}{2\sqrt{2}} &{} -\frac{f_1 uw}{2\sqrt{2}v} &{} -\frac{f_1 u}{2\sqrt{2}} &{} 0 &{} 0 &{} 0\\ -\frac{f_1 v}{2\sqrt{2}} &{} -\frac{f_1 u}{2\sqrt{2}} &{} -\frac{f_1 uv+4f_2 \Delta w}{2\sqrt{2} w} &{} 0 &{} 0 &{} \frac{f_2 w}{\sqrt{2}} \\ \frac{\zeta _{10} u \kappa }{2} &{} 0 &{} 0 &{} -\frac{ \zeta _{10} u^2 \kappa }{4 \Lambda } &{} \frac{- \zeta _{10} u^2}{4} &{} 0 \\ \frac{\zeta _{10} u \Lambda }{2} &{} 0 &{} 0 &{} -\frac{\zeta _{10} u^2}{4} &{} -\frac{\zeta _{10} u^2 \Lambda }{4\kappa } &{} 0 \\ 0 &{} 0 &{} \frac{f_2 w}{\sqrt{2}} &{} 0 &{} 0 &{} -\frac{f_2 w^2}{2\sqrt{2}\Delta } \\ \end{array} \right) . \end{aligned}$$

(30)

Also, in the scalar sector, all the W-even fields, $S_1, S_2, S_3, S_4,S_5,S_6$, mix by themselves through a mass matrix, $\frac{1}{2} M^2_S$, given in such order as

$$\begin{aligned} \left( \begin{array}{cccccc} -\frac{f_1 vw}{2\sqrt{2}u} +\lambda _3 u^2&{} \frac{\sqrt{2}}{4}(f_1 w+\sqrt{2}\lambda _5uv) &{} \frac{\sqrt{2}}{4}(f_1 v+\sqrt{2}\lambda _6uw) &{} \frac{u}{2}(\zeta _{10} \kappa +\lambda _{12} \Lambda ) &{} m^2_{{15}}&{} \frac{\zeta _{3}u \Delta }{2} \\ \frac{\sqrt{2}}{4}(f_1 w+\sqrt{2}\lambda _5 uv) &{} -\frac{f_1 uw}{2\sqrt{2}v}+\lambda _1v^2 &{} \frac{\sqrt{2}}{4}(f_1 u+\sqrt{2}\lambda _4 vw) &{} \frac{\lambda _{10}v \Delta }{2} &{} \frac{\zeta _{4}v \kappa }{2}&{} \frac{\zeta _{4}v \Delta }{2} \\ \frac{\sqrt{2}}{4}(f_1 v+\sqrt{2}\lambda _{6}uw) &{} \frac{\sqrt{2}}{4}(f_1 u+\sqrt{2} \lambda _4vw) &{} -\frac{f_1 uv}{2\sqrt{2}w}+\lambda _2 w^2 &{} \frac{\lambda _{11}w \Lambda }{2} &{} \frac{\zeta _{5}\kappa w}{2} &{} \frac{f_2 w}{\sqrt{2}}\\ \frac{u}{2}(\zeta _{10} \kappa +\lambda _{12}\Lambda ) &{}\frac{\lambda _{10}v\Lambda }{2} &{} \frac{\lambda _{11}w\Lambda }{2} &{} -\frac{\zeta _{10} \kappa u^2}{4 \Lambda } +\lambda \Lambda ^2 &{} m^2_{{45}} &{}\frac{\zeta _{6}\Delta \Lambda }{2} \\ m^2_{{15}} &{} \frac{\zeta _{4}\kappa v}{2} &{} \frac{\zeta _{5} \kappa w}{2} &{} m^2_{{45}} &{}m^2_{{55}}&{}\zeta _{1} \kappa \Delta \\ \frac{\zeta _{3}u \Delta }{2} &{} \frac{\zeta _{4}v \Delta }{2} &{} \frac{f_2 w}{\sqrt{2}} &{} \frac{\zeta _{6}\Delta \Lambda }{2} &{} \zeta _{1}\kappa \Delta &{}m^2_{{66}} \\ \end{array} \right) , \end{aligned}$$

where we have defined

$$\begin{aligned} m^2_{{15}}= & {} \frac{u}{2}(\zeta _{10} \Lambda +\kappa (\zeta _7+\zeta _{3})), \\ m^2_{{55}}= & {} -\frac{\zeta _{10} u^2 \Lambda }{4 \kappa } +(\zeta _{1}+\zeta _{2})\kappa ^2 ,\nonumber \end{aligned}$$

(31)

$$\begin{aligned} m^2_{{45}}= & {} \frac{1}{4}(\zeta _{10} u^2+2 \zeta _{6}\kappa \Lambda ),\\ m^2_{{66}}= & {} -\frac{f_2 w^2}{2\sqrt{2} \Delta } +(\zeta _{1}+\zeta _{2})\Delta ^2.\nonumber \end{aligned}$$

(32)

Above, we have investigated that the S, $\eta$, and $\phi$ interaction, i.e. $-\zeta _{10} \eta \eta S^*\phi ^*$, is crucial to produce the observed neutrino masses as well as to make the model viable. Let us show this explicitly. First, we turn, by contrast, this interaction off, i.e. $\zeta _{10}=0$. The condition for the potential minimization in the $S_{11}$ direction becomes

$$\begin{aligned} \kappa ^2=-\frac{2 \mu ^2_\mathrm{S}+\zeta _{6}\Lambda ^2+\zeta _{5}w^2+2\zeta _{1}\Delta ^2+(\zeta _7 +\zeta _{3})u^2+\zeta _{4}v^2}{2(\zeta _{1}+\zeta _{2})}.\nonumber \\ \end{aligned}$$

(33)

Because $\mu _\mathrm{S},\Lambda ,w, \Delta$ are proportional to the inflation scale, while u, v are proportional to the weak scale, it is impossible to impose a small value in eV for $\kappa$, unless unnatural fine-tunings among the two kinds of large scales are taken place. Thus, the $\kappa$ scale lies in the inflation energy regime, which ruins the standard model. Even if the fine-tuning is allowed, in this case, the pseudo-scalar mass matrix implies four massless fields. Three of them are the Goldstone bosons of the $Z,Z^\prime ,C$ gauge bosons, such that $G_{Z}\simeq \frac{1}{\sqrt{u^2+v^2}}(-u A_1+v A_2), G_{Z^\prime } \simeq \frac{1}{\sqrt{w^2+ 4 \Delta ^2}}(wA_3+2 \Delta A_6), G_\mathrm{C}\simeq A_4$. The remaining massless field is $A_5$, which is a physical particle, acting similarly as a Majoron. On the other hand, the scalar mass matrix, $M^2_\mathrm{S}$, also provides a physical partner of the Majoron, $S_5$, with mass $m^2_{S_5} \simeq (\zeta _{1}+\zeta _{2}) \kappa ^2$, given at the leading order. Of course, this mass is as small as the neutrino mass. Therefore, the Z boson would decay invisibly into $S_5 A_5$, having a rate equal to that of the Z decay into two light neutrinos, which has experimentally been ruled out [1]. By this view, the $\zeta _{10}$ coupling must be turned on, matching the fact that it conserves any symmetry of the theory and is renormalizable. Indeed, there is no reason why it is not present in this model.

Above, the presence of the $\zeta _{10}$ interaction may help us understanding why the type II seesaw neutrino masses are very tiny, $\kappa \propto \frac{u^2}{\Lambda }$. This is because $\phi$ may play a role of inflaton field during the cosmological inflation time, i.e. its VEV, $\Lambda$, is very large, in $10^{13}$–$10^{14}$ GeV order [4], whereas u, v are the electroweak scales, by which it obtains such a small mass $\kappa \sim \mathrm {eV}$. Note that the type I seesaw mechanism works analogously, where the mediators are right-handed neutrinos instead of the sextet, while $B-L$ is also broken by $\phi$ that directly couples to those right-handed neutrinos. See [5] for details of the neutrino mass generation diagrams. Consequently, the natural small masses of the neutrinos might be originally correlated to the inflationary expansion of the early universe as all derived by the $\phi$ inflaton field. Furthermore, when $\zeta _{10} \ne 0$, the pseudo-scalar mass matrix (30) shows that besides the three massless Goldstone bosons for $Z,Z^\prime ,C$, the Majoron becomes massive. At the leading order, the Majoron mass is given by

$$\begin{aligned} m^2_{A_5} \simeq -\frac{\zeta _{10} u^2 \Lambda }{2 \kappa }. \end{aligned}$$

(34)

The mass of its partner, $S_5$, is now

$$\begin{aligned} m^2_{S_5}\simeq -\frac{\zeta _{10} u^2 \Lambda }{2\kappa }. \end{aligned}$$

(35)

All these particles have mass in the inflation energy scale as expected.

Consider the W-odd scalars. The pseudo-scalar sector yields a massless state:

$$\begin{aligned} A_{1p}\simeq \frac{1}{\sqrt{w^2+2\Delta ^2}}(w A_1^\prime +\sqrt{2}\Delta A_2^\prime ), \end{aligned}$$

(36)

and two massive states with respective masses,

$$\begin{aligned} A_{2p}\simeq & {} \frac{1}{\sqrt{w^2+2\Delta ^2}}( -\sqrt{2}\Delta A_{1}^\prime +w A_{2}^\prime ),\\ m^2_{A_{2p}}\simeq & {} -\frac{2\Delta ^2+w^2}{4\Delta } (2\sqrt{2}f_2 +\zeta _{8}\Delta ),\nonumber \end{aligned}$$

(37)

$$\begin{aligned} A_{3p}\simeq & {} A_3^\prime ,\quad m^2_{A_{3p}} \nonumber \\\simeq & {} \frac{1}{2}[(\zeta _3+\zeta _7)\Delta ^2-2\zeta _{10}\Delta \Lambda +\lambda _{12}\Lambda ^2+(\lambda _6+\lambda _9)w^2].\nonumber \\ \end{aligned}$$

(38)

Similarly, the scalar sector contains a massless state, called $S_{1p}$, and two massive states, named $S_{2p}$ and $S_{3p}$, determined as

$$\begin{aligned} S_{1p}\simeq & {} \frac{1}{\sqrt{w^2+2\Delta ^2}}(wS_1^\prime +\sqrt{2}\Delta S_2^\prime ), \end{aligned}$$

(39)

$$\begin{aligned} S_{2p}\simeq & {} \frac{1}{\sqrt{w^2+2\Delta ^2}}(-\sqrt{2}\Delta S_1^\prime +w S_2^\prime ), \end{aligned}$$

(40)

$$\begin{aligned} S_{3p}\simeq & {} S_3^\prime , \end{aligned}$$

(41)

with respective masses

$$\begin{aligned} m_{S_{1p}}= & {} 0,\quad m^2_{S_{2p}} \simeq -\frac{2\Delta ^2+w^2}{4\Delta } (2\sqrt{2}f_2 + \zeta _{8}\Delta ),\end{aligned}$$

(42)

$$\begin{aligned} m^2_{S_{3p}}\simeq & {} \frac{1}{2}[(\zeta _3+\zeta _7)\Delta ^2+2\zeta _{10} \Delta \Lambda +\lambda _{12}\Lambda ^2+(\lambda _6+\lambda _9) w^2].\nonumber \\ \end{aligned}$$

(43)

Observe that the fields, $S_{1p}$ and $A_{1p}$, are the Goldstone bosons of the real and imaginary parts of the neutral, non-Hermitian X gauge boson, respectively. Hence their combination, $G_{X}=\frac{1}{\sqrt{2}}(S_{1p}+iA_{1p})$, forms the Goldstone boson of X. Furthermore, $S_{2p}$ and $A_{2p}$ have the same mass. They can be identified as a physical neutral complex field, $H^\prime = \frac{1}{\sqrt{2}} \left( S_{2p}+iA_{2p}\right)$, which is orthogonal to $G_\mathrm{X}$.

Consider the W-odd, charged scalars. There are two massless Goldstone bosons, $G^\pm _\mathrm{Y}$, as associated with the $Y^{\pm }$ gauge bosons, and four massive charged Higgs bosons, $H^\pm _{p1,p2}$. In the limit $\Lambda , \Delta , w \gg u,v,\kappa$, their eigenstates and masses can be approximated by

$$\begin{aligned}&G_\mathrm{Y}^\pm = \frac{1}{\sqrt{2\Delta ^2+w^2}}( w \chi _2^\pm +\sqrt{2}\Delta S^{\pm }_{23} ), \quad m_{G_\mathrm{Y}}=0,\end{aligned}$$

(44)

$$\begin{aligned}&H^\pm _{p1} = \frac{1}{\sqrt{2\Delta ^2+w^2}}( -\sqrt{2} \Delta \chi _2^\pm +w S^{\pm }_{23}),\nonumber \\&m_{H_{p1}}^2= -\frac{(2\Delta ^2+w^2)(2\sqrt{2}f_2+\zeta _8 \Delta )}{4\Delta }, \end{aligned}$$

(45)

$$\begin{aligned}&H^\pm _{p2} = \rho _3^\pm , \;\; m_{H_{p2}}^2 =\frac{1}{2}[(\lambda _4+\lambda _7) w^2+(\zeta _4+\zeta _9) \Delta ^2 +\zeta _{10}\Lambda ^2].\nonumber \\ \end{aligned}$$

(46)

The doubly charged scalars, $S^{\pm \pm }_{22}$, are physical fields by themselves and have large masses,

$$\begin{aligned} m^2_{S_{22}}=-\frac{\sqrt{2}f_2w^2+2\zeta _2 \Delta ^3+\zeta _8 \Delta w^2}{2\Delta }. \end{aligned}$$

(47)

Let us note that the sextet affects negligibly the mass spectrum of the non-Hermitian W, X, Y gauge bosons, as identified in [3]. Their states are

$$\begin{aligned} W^\pm= & {} \frac{1}{\sqrt{2}}(A_1\mp i A_2),\quad X^{0,0*}=\frac{1}{\sqrt{2}}(A_4\mp i A_5),\nonumber \\ Y^\mp= & {} \frac{1}{\sqrt{2}}(A_6\mp i A_7), \end{aligned}$$

(48)

with respective masses

$$\begin{aligned} m^2_{W}\simeq \frac{g^2}{4}(u^2+v^2),\quad m_\mathrm{X}\simeq m_\mathrm{Y}\simeq \frac{gw}{2}. \end{aligned}$$

(49)

The neutral gauge bosons, $A_{3},\ A_{8},\ B,\ C$, mix, as given in [6]. This mass spectrum would be changed due to the contribution of the sextet. However, because of the limit, $u,v,\kappa \ll w, \Delta , \Lambda$, the Z boson decouples (i.e. mixes infinitesimally) from the heavy $Z^\prime , C$ bosons, with mass $m^2_Z\simeq m^2_W/c^2_W$, whereas the $Z^\prime , C$ bosons may largely mix due to the contributions of $w,\Lambda ,\Delta$ and the kinetic mixing parameter. Lastly, the $\rho$-parameter can be derived due to the contribution of $\kappa$, as mentioned before.

Further, from the potential minimization in $S_{11}$ and $S_{33}$ directions, we obtain a condition,

$$\begin{aligned} \frac{f_2 w^2}{\sqrt{2} \Delta } -\frac{\zeta _7 u^2}{2} +\frac{\zeta _8 w^2}{2} -\frac{\zeta _{10} \Lambda u^2}{2 \kappa } +\zeta _{2}(\Delta ^2-\kappa ^2)=0.\nonumber \\ \end{aligned}$$

(50)

Combining (50) and (29), we find that at least one of the two 3-3-1 breaking scales, w or $\Delta$, must have the same magnitude as the $B-L$ breaking scale, $\Lambda$. It may also be derived from the three equations for the large scales in (24). Therefore, relaxing the condition, $w\sim \Delta$, as above proposed, leads to three hypotheses as follows:

• 1. $w \sim O(1)\ \mathrm {TeV} \ll \Delta \sim \Lambda$. In this case, the mass spectrum of the new particles is separated into two parts: The new gauge bosons $X^0, Y^\pm$, the exotic quarks, and some new Higgs (but not $H'$, $A'_3$, and $S'_3$) live in the TeV scale. Some other new Higgs including $H'$, $A'_3$, and $S'_3$, neutral fermions $N_\mathrm{R}$, and new gauge bosons, $Z^\prime , C$, are heavy, with masses close to the inflation scale. This scenario does not provide any dark matter candidate, since the $X^0$ abundance completely vanishes, i.e. it annihilates totally before freeze-out [2]. See also [55,56,57] for other proposals.

• 2. $\Delta \sim O(1)\ \mathrm {TeV} \ll w \sim \Lambda$. All the new gauge bosons, exotic quarks, and most new Higgs bosons, including the W-odd scalars, receive masses in the inflation scale. Exclusively, the neutral fermions $N_\mathrm{R}$ have mass in TeV scale. The lightest $N_\mathrm{R}$ can be a thermal dark matter candidate [2].

• 3. $w\sim \Delta \sim \Lambda$ being in the inflation scale. The considering model induces non-thermal superheavy dark matter (see, for other proposals, [38,39,40,41,42,43]), because there are two necessary conditions: (i) the candidate is the lightest W-odd particle, LWP, which is stabilized by W-parity, (ii) the candidate was not in thermal equilibrium with the cosmic plasma, since by contrast, it could overclose the universe due to the unitarity condition [45]. Hence, such a candidate would be produced by various mechanisms for non-thermal relics [25,26,27,28,29,30,31,32,33,34,35,36,37]. We will show that if its mass is as large as the inflation scale, it can be created by the gravitational mechanism, which is common in most models. If it has a smaller mass, just above the reheating temperature, it is naturally produced by the inflaton decay or thermal fusion. This observation is an interesting alternative connecting the 3-3-1-1 model to the physics at the early stage of the universe. Depending on the parameter space, the superheavy dark matter or LWP may be a neutral fermion (a combination of $N_{a\mathrm{R}}$), a scalar (among $H'$, $S'_3$, and $A'_3$), or possibly a $X^0$ gauge boson. It is noteworthy that a non-thermal relic for the last one is viable, which is unlike its previous variant [2].

Before examining the superheavy dark matter, it is necessary to obtain the consistent inflation scenarios in order to fix the inflation scale, inflaton mass, and reheating temperature. Let us stress again that the inflation presenting in the current model is substantially different from the previous study [4].

4 Inflation and reheating

We would like to note that the scalar fields, singlet $\phi$, triplet $\chi$, and sextet S can have large VEVs, $\Lambda , w, \Delta$, respectively, proportional to the inflation scale of the early universe. At this energy scale, all the mentioned scalar fields can play the role as inflaton field(s) deriving the cosmic inflation (see, for an example [4]). Indeed, we can have a single-field inflation scenario as governed by one combination of the scalars or multi-field inflation scenarios as cooperated by a number of the combinations of the scalars, in the field space. Recall that $\chi _3$ and $S_{33}$ break $SU(3)_\mathrm{L}\otimes U(1)_\mathrm{X}\otimes U(1)_\mathrm{N}$ down to $SU(2)_\mathrm{L}\otimes U(1)_\mathrm{Y}\otimes U(1)_{B-L}$, whereas $\phi$ breaks both $U(1)_\mathrm{N}$ and $U(1)_{B-L}$ down to W-parity since $N(\phi )=[B-L](\phi ) = 2\ne 0$, where note that these breakings as indicated is effectively translated to $S_{11}$, which along with $\eta _1$ and $\rho _2$ break both the electroweak symmetry and $B-L$. That said, inflation may be related to the first kind symmetry breaking (i.e., 3-3-1 breaking) due to $\chi _3$, $S_{33}$ and/or the second kind symmetry breaking (i.e., $B-L$ breaking) due to $\phi$.

Let us first consider a single-field inflation scenario linked to the $U(1)_{B-L}$ symmetry breaking as driven by the singlet $\phi$. The inflaton sector which is impacted from the model’s potential in (14) and (15) is thus extracted as

$$\begin{aligned} V_{\mathrm {tot}}= & {} \mu ^2_\phi \phi ^\dag \phi +\lambda (\phi ^\dag \phi )^2+\lambda _{11}(\phi ^\dag \phi )(\chi ^\dag \chi )\nonumber \\&+\,\zeta _6(\phi ^\dagger \phi )\mathrm {Tr}(S^\dagger S)+ \mu ^2_\chi \chi ^\dagger \chi +\lambda _2 (\chi ^\dagger \chi )^2\nonumber \\&+ \mu ^2_\mathrm{S}\mathrm {Tr}(S^\dagger S) +\,\zeta _1[\mathrm {Tr}(S^\dagger S)]^2+\zeta _2 \mathrm {Tr}[(S^\dagger S)^2] \nonumber \\&+ \,\zeta _5 (\chi ^\dag \chi ) \mathrm {Tr}(S S^\dag ) +\,\zeta _8(\chi ^\dagger S)(S^\dagger \chi )\nonumber \\&+ (f_2 \chi ^\mathrm{T} S^\dag \chi +\mathrm{H.c.}), \end{aligned}$$

(51)

where $\phi$ is the inflaton field involving during inflation, while $\chi , S$ may be the water-fall fields. One might also include $\eta ,\rho$ as water-fall fields, but they are radically light, subdominant, and thus omitted. During inflation, the inflaton potential reads $V_{\mathrm {inflation}} = \mu ^2_\phi \phi ^\dag \phi +\lambda (\phi ^\dag \phi )^2$, while the interactions of $\phi$ with $\chi , S$ as well as the self-terms of $\chi , S$ might terminate the inflation, where the inflation ends due to an instability triggered by $\phi$ when it reaches a critical value determined by the largest scalar mass between $\chi$ and S [58]. As associated with the $B-L$ breaking, the inflaton slowly rolls down to the potential minimum from above $\phi >\Lambda /\sqrt{2}$, and the inflation ends corresponding to a 3-3-1 symmetry breaking.¹

As specified in [4], all the scalar couplings would be constrained to be radically small under the present data. Therefore, we further consider the inflaton potential to be radiatively induced as an effective potential, due to the interactions of $\phi$ with the $U(1)_\mathrm{N}$ gauge boson (C), the scalar fields ($\phi ,\chi ,S$), and the right-handed neutrinos ($\nu _\mathrm{R}$). To be concrete, we denote the inflaton as $\Phi =\sqrt{2}\mathfrak {R}(\phi )$, while $\mathfrak {I}(\phi )$ is a Goldstone boson which could be gauged away. We parametrize the effective potential in the leading-log approximation as [59]

$$\begin{aligned} V(\Phi )\simeq \frac{\lambda }{4}(\Phi ^2-\Lambda ^2)^2+ \frac{a}{64\pi ^2}\Phi ^4 \ln \frac{\Phi ^2}{\Lambda ^2} +V_0, \end{aligned}$$

(52)

where

$$\begin{aligned} a= & {} -8 \sum _{i=1}^3 (h^{ \prime \nu }_{ii})^4 + 48 g_\mathrm{N}^4+\frac{1}{4} (\lambda _{11}^2+\zeta _6^2)+36\lambda ^2\nonumber \\\simeq & {} 8\left[ 6g^4_\mathrm{N}-\sum _{i=1}^3 (h^{ \prime \nu }_{ii})^4\right] , \end{aligned}$$

(53)

with $h'^\nu$ assumed to be flavor-diagonal, and the renormalization scale is fixed at $\Lambda ^2=-\mu ^2_\phi /\lambda$, which is compatible to $w^2$ and $\Delta ^2$, but which should be significantly larger than $\mu ^2_{\chi ,\mathrm{S}}$. The effective potential reveals a consistent local minimum if $a/\lambda >-63.165$. Provided that $\Lambda$ is bounded below the Planck scale, the effective potential is governed by the quartic and log terms. Otherwise, when one put $\Lambda$ beyond the Planck scale, the Coleman–Weinberg corrections would be negligible, and the tree-level potential dominates.

We note that the inflation occurs as the inflaton slowly rolls down to the potential minimum at $\Phi \sim \Lambda$. The slow roll parameters read

$$\begin{aligned} \epsilon (\Phi )= & {} \frac{1}{2}m_P^2 \left( \frac{V^\prime }{V}\right) ^2, \quad \eta (\Phi )=m_P^2 \left( \frac{V^{\prime \prime }}{V}\right) ,\\ \xi ^2 (\Phi )= & {} m_P^4 \frac{V^\prime V^{\prime \prime \prime }}{V^2},\nonumber \end{aligned}$$

(54)

which satisfy $\epsilon (\Phi ) \ll 1,\ \eta (\Phi ) \ll 1,\ \xi (\Phi ) \ll 1$, where $m_P=(8\pi G_\mathrm{N})^{-1/2}\simeq 2.4 \times 10^{18}$ GeV is the reduced Planck mass. The spectral index $n_\mathrm{s}$, the tensor-to-scalar ratio r, and the running index $\alpha$ can be approximated by

$$\begin{aligned} n_\mathrm{s}\simeq 1-6\epsilon +2\eta , \quad r\simeq 16\epsilon , \quad \alpha \simeq 16\epsilon \eta -24\epsilon ^2-2\xi ^2. \end{aligned}$$

(55)

The experimental bounds for these quantities were summarized in [1] as $n_\mathrm{s}=0.968\pm 0.006$, $\alpha =-0.003\pm 0.007$, and $r<0.07$. The curvature perturbation is determined by

$$\begin{aligned} \triangle ^2_\mathcal {R}= \frac{V}{24\pi ^2m_P^4\epsilon (\Phi )}, \end{aligned}$$

(56)

which satisfies $\triangle ^2_\mathcal {R}=2.215 \times 10^{-9}$ at the pivot scale $k_0=0.05\ \mathrm {Mpc}^{-1}$ to fit the CMB measurements [1]. The number of e-folds is

$$\begin{aligned} N=\frac{1}{\sqrt{2}m_P} \int ^{\Phi _0}_{\Phi _e}\frac{\mathrm{d} \Phi }{\sqrt{\epsilon (\Phi )}}, \end{aligned}$$

(57)

where $\Phi _e$ is given at the end of inflation specified by $\epsilon (\Phi _e)\simeq 1$, and $\Phi _0$ is given at the horizon exit corresponding to $k_0$, and $N=60$ is taken regarding a large inflation scale.

The $\lambda$ coupling is determined from the $\triangle ^2_{\mathcal {R}}$ constraint, which yields $\lambda \sim 10^{-12}$–$10^{-11}$ in the actual parameter regime. We are left with $r,n_\mathrm{s},\alpha$ correlatively related as functions of $\Phi$ involving from $\Phi _0$ to $\Phi _e$ for fixed values of the parameters, $a'=a/\lambda >-63.165$ and $\Lambda$ selected in the range $(10^{13}\ \mathrm {GeV},m_P)$. As numerically evaluated, the values of $n_\mathrm{s}$ and r in agreement with the experimental constraints make the effective coupling reasonably large, $-60<a^\prime < -20$, and the $B-L$ breaking scale typically recovered in $\Lambda \sim 10^{14}$–$10^{18}$ GeV. Since $a'$ is a function of the various couplings, the present inflation scenario does not constrain solely the gauge coupling $g_\mathrm{N}$. However, the strength is set as $g_\mathrm{N}\sim h'^\nu \sim (\lambda |a'|)^{1/4}\sim 10^{-2.5}$, which is quite smaller than the electroweak couplings. Therefore, it is seemingly impossible to choose the values of the Yukawa couplings so that $g_\mathrm{N}$ is compatible with a unified gauge coupling, to a small extent responsible for a hypothetical, higher gauge symmetry if one proposes to search for (for further details, see Appendix B).

The effective potential provides a VEV, $\langle \Phi \rangle \sim \Lambda$, from the minimization condition $V'=0$. The inflaton mass is given at this VEV as

$$\begin{aligned} m_\Phi= & {} \sqrt{V''}\nonumber \\ {}= & {} \sqrt{2\lambda \Lambda ^2+\frac{a}{8\pi ^2}\langle \Phi \rangle ^2}\sim \sqrt{\lambda }\Lambda \sim 10^{8}-10^{12}\ \mathrm {GeV}, \end{aligned}$$

(58)

which should be smaller than the $U(1)_\mathrm{N}$ gauge boson mass, $m_\mathrm{C}=2g_\mathrm{N}\langle \Phi \rangle$, due to $\sqrt{\lambda }\ll g_\mathrm{N}$. If one supposes hierarchical Yukawa couplings, $h'^\nu _{11}\ll h'^\nu _{22,33}\sim g_\mathrm{N}$, for the leptogenesis mechanism to work [4], it follows that

$$\begin{aligned} m_{\nu _{2,3\mathrm{R}}}= & {} -\sqrt{2}h'^\nu _{22,33}\langle \Phi \rangle \sim m_\mathrm{C} > m_\Phi \sim m_{\nu _{1\mathrm{R}}}\nonumber \\ {}= & {} -\sqrt{2}h'^\nu _{11}\langle \Phi \rangle . \end{aligned}$$

(59)

The inflaton cannot decay into the gauge boson C as well as the heavy right-handed neutrinos $\nu _{2,3\mathrm{R}}$ although they have interactions $\mathcal {L}_{\mathrm {int}}\supset 4g^2_\mathrm{N}\langle \Phi \rangle \Phi C_\mu C^\mu +(\frac{1}{\sqrt{2}}h'^\nu _{ii}\Phi \bar{\nu }^c_{i\mathrm{R}}\nu _{i\mathrm{R}}+\mathrm{H.c.})$ for $i=2,3$. However, after the inflation, the inflaton might decay into a pair of scalars ($\chi ,S$, and even $\rho ,\eta$ if the previous modes are suppressed) or a pair of the light right-handed neutrinos ($\nu _{1\mathrm{R}}$) with subsequent thermalization with the standard model particles. The interaction Lagrangian is given by

$$\begin{aligned}&\mathcal {L}_{\mathrm {int}}\supset \langle \Phi \rangle \Phi [\lambda _{11}\chi ^\dagger \chi +\zeta _6 \mathrm {Tr}(S^\dagger S)]\nonumber \\&\quad +\left( \frac{1}{\sqrt{2}} h'^\nu _{11} \Phi \bar{\nu }^c_{1\mathrm{R}}\nu _{1\mathrm{R}}+\mathrm{H.c.}\right) . \end{aligned}$$

(60)

If the inflaton mass is much larger than the products, $m^2_\Phi \gg m^2_{\chi ,S,\nu _{1\mathrm{R}}}$, the decay rates are

$$\begin{aligned} \Gamma _\chi = \frac{\lambda ^2_{11}\langle \Phi \rangle ^2}{16\pi m_\Phi },\quad \Gamma _\mathrm{S}= \frac{\zeta ^2_{6}\langle \Phi \rangle ^2}{16\pi m_\Phi },\quad \Gamma _{\nu _{1\mathrm{R}}}= \frac{(h'^\nu _{11})^2 m_\Phi }{8\pi }.\nonumber \\ \end{aligned}$$

(61)

If $\lambda ^2_{11}/\lambda ,\zeta ^2_6/\lambda \gg (h'^\nu _{11})^2$, the inflaton mainly decays into $\chi ,S$ with the total width $\Gamma =\Gamma _\chi +\Gamma _\mathrm{S}$. The reheating temperature is given by

$$\begin{aligned} T_\mathrm{R}= & {} \left( \frac{90}{\pi ^2g_*}\right) ^{1/4}(m_P \Gamma )^{1/2}\nonumber \\\simeq & {} 10^{9}\left( \frac{\Lambda }{10^{14}\ \mathrm {GeV}}\right) ^{1/2}\left( \frac{10^{-12}}{\lambda }\right) ^{1/4}\frac{(\lambda ^2_{11}+\zeta ^2_6)^{1/2}}{10^{-9}}\ \mathrm {GeV},\nonumber \\ \end{aligned}$$

(62)

where $g_*=106.75$ is the effective number of degrees of freedom given at the temperature of the asymmetric production. With the parameters as obtained, taking $(\lambda ^2_{11}+\zeta ^2_6)^{1/2}\sim 10^{-9}$ yields $T_\mathrm{R}\sim 10^9$ GeV, which is in agreement with the upper bound for the reheating temperature to prevent the gravitino problem [60, 61]. In this case, the right-handed neutrinos may be thermally produced, recognizing a thermal leptogenesis scenario [4].

By contrast, when $\lambda ^2_{11}/\lambda ,\zeta ^2_6/\lambda \ll (h'^\nu _{11})^2$, the inflaton substantially decays into $\nu _{1R}$. The reheating temperature is bounded by

$$\begin{aligned} T_\mathrm{R}= & {} \left( \frac{90}{\pi ^2g_*}\right) ^{1/4}(m_P \Gamma _{\nu _{1\mathrm{R}}})^{1/2}\nonumber \\\simeq & {} 1.6 \times 10^{12}\left( \frac{\Lambda }{10^{14}\ \mathrm {GeV}}\right) ^{1/2}\left( \frac{\lambda }{10^{-12}}\right) ^{1/4}h'^\nu _{11}\ \mathrm {GeV}.\nonumber \\ \end{aligned}$$

(63)

Taking the condition $h'^\nu _{11} \le \sqrt{\lambda }\sim 10^{-6}$ and with the other parameters as given, the reheating temperature is limited by $T_\mathrm{R}\lesssim 10^6$ GeV, which is significantly smaller than the right-handed neutrino masses. This case realizes a non-thermal leptogenesis scenario since the light right-handed neutrinos are produced by inflaton decay.

Note that both cases considered always satisfy the total width to be less than $m_\Phi$ for perturbative decay. On the other hand, the model predicts the value of the reheating temperature to be compatible with thermal productions (see below) after the cosmic inflation [27]. Similarly, we can consider the other single-field inflation scenarios, where the scalar triplet $\chi$ or sextet S plays a role of inflaton.

The above single-field inflation scenarios predict a good approximation to the Gaussian spectrum of primordial fluctuations. The size of non-Gaussian contribution $f_{\mathrm {NL}}$ is suppressed by the slow-roll parameters. However, a combined analysis of the Planck temperature and polarization data shows that $f^{\mathrm {local}}_{\mathrm {NL}}=0.8 \pm 5.0$ [1]. There are popular multi-field inflation models which may generate the observably large non-Gaussianity [62]. It is natural to consider the multi-field inflation in our model due to the presence of a large number of scalar fields behaving in this regime. Let us consider the model where inflation is driven by the multiple scalar consisting of $S_{33}, \chi _3, \phi$ fields. For simplicity, we ignore the soft interaction, $\chi ^\mathrm{T} S^\dag \chi$, which can be suppressed by some global symmetry. We conveniently define $\phi _1 = \phi ^2-\Lambda ^2/2$, $\phi _2= S_{33}^2-\Delta ^2/2$, $\phi _3 = \chi _3^2 -w^2/2$, and using the potential minimization conditions as obtained in (24). The inflation potential (51) can be rewritten as follows:

$$\begin{aligned} V_{\mathrm {tot}}= & {} \lambda \phi _1^2+(\zeta _1+\zeta _2) \phi _2^2+\lambda _2 \phi _3^2\nonumber \\&+\,\zeta _6 \phi _1 \phi _2+\lambda _{11}\phi _1 \phi _3+(\zeta _5+\zeta _8)\phi _2 \phi _3. \end{aligned}$$

(64)

The potential given in (64) contains cross coupling terms between the scalar fields as $\phi _1\phi _2$, $\phi _2\phi _3$, and $\phi _3\phi _1$. In order to make the cross coupling terms disappeared, we can change to the canonical basis system by diagonalizing the corresponding $3\times 3$ matrix. Without loss of generality, we define the new fields as follows:

$$\begin{aligned}&\phi _1^\prime =\frac{-a_{23}\phi _1+\phi _2 +a_{12}a_{23}\phi _3}{1+a_{12}a_{23}a_{31}},\end{aligned}$$

(65)

$$\begin{aligned}&\phi _2^\prime = \frac{a_{23}a_{31}\phi _1-a_{31}\phi _2+\phi _3}{1+a_{12}a_{23}a_{31}},\end{aligned}$$

(66)

$$\begin{aligned}&\phi _3^\prime = \frac{\phi _1+a_{12}a_{31}\phi _2-a_{12}\phi _3}{1+a_{12}a_{23}a_{31}}, \end{aligned}$$

(67)

where

$$\begin{aligned} a_{12}= & {} -\frac{ \lambda (\zeta _5+\zeta _8)^2-\lambda _{11}^2(\zeta _1+\zeta _2)+\lambda _2(\zeta _6^2-4\lambda \zeta _1-4\lambda \zeta _2)+\sqrt{A}}{2\zeta _6(\zeta _5+\zeta _8)\lambda -4(\zeta _1+\zeta _2)\lambda \lambda _{11}}, \end{aligned}$$

(68)

$$\begin{aligned} a_{23}= & {} -\frac{ \lambda (\zeta _5+\zeta _8)^2+\lambda _{11}^2(\zeta _1+\zeta _2)-\lambda _2(\zeta _6^2+4\lambda \zeta _1+4\lambda \zeta _2)+\sqrt{A}}{2(\zeta _1+\zeta _2)[(\zeta _5+\zeta _8)\lambda _{11}-2\zeta _6 \lambda _2]}, \end{aligned}$$

(69)

$$\begin{aligned} a_{31}= & {} \frac{ -\lambda (\zeta _5+\zeta _8)^2+\lambda _{11}^2(\zeta _1+\zeta _2)+\lambda _2(\zeta _6^2-4\zeta _1 \lambda -4\zeta _2 \lambda )+\sqrt{A}}{2\lambda _2(2\lambda \zeta _5+2\lambda \zeta _8-\lambda _{11}\zeta _6)},\nonumber \\ \end{aligned}$$

(70)

$$\begin{aligned} A= & {} -4(\zeta _1+\zeta _2)\lambda [(\zeta _5+\zeta _8)\lambda _{11}-2\lambda _2 \zeta _6]^2 + \{(\zeta _1+\zeta _2)\lambda _{11}^2-\lambda _2\zeta _6^2\nonumber \\&+\,\lambda [(\zeta _5+\zeta _8)^2-4(\zeta _1+\zeta _2)\lambda _2]\}^2. \end{aligned}$$

(71)

On the basis of the new fields $\phi _1^\prime , \phi _2^\prime , \phi _2^\prime$, the inflation potential in (64) can be written as

$$\begin{aligned} V_{\mathrm {tot}}= & {} [\zeta _1+\zeta _2+a_{31}(\zeta _5+\zeta _8)-a_{31}\lambda _2]\phi _1^{ \prime 2} +(a_{12}^2 \lambda +a_{12}\lambda _{11}+\lambda _2) \phi _2^{\prime 2}\nonumber \\&+\, [a_{23}^2(\zeta _1+\zeta _2)+a_{23}\zeta _6 +\lambda ]\phi _3^{\prime 2}. \end{aligned}$$

(72)

If $\phi _1^\prime , \phi _2^\prime , \phi _3^\prime$ play a role of inflation, we have a model of multi-field inflation with a separable potential. This inflationary scenario was appropriately considered in [63]. The general expression for the nonlinear parameter characterizing non-Gaussianities $f_\mathrm{NL}$ is suppressed by the number of e-folding for model with a narrow mass spectrum, and this suppression is enhanced for model with a broad spectrum of masses. We would like to emphasize that in the case, the fields $\phi _1, \phi _2, \phi _3$ play a role of inflation and are non-canonical. In the physical basis, the cross coupling terms between various fundamental scalar fields should be considered, and this might present another source making a large non-Gaussianity.

5 Superheavy dark matter

The recent developments in understanding how matter was created in the early universe suggests that dark matter might be supermassive. The idea is currently favored since the well-established, thermal weakly interacting massive particles have been searched for, but they were not found. Its mass can be much greater than the weak scale, say the inflation scale, which was created very early, at the end of inflation, in a non-thermal state. It never reached chemical equilibrium with plasma, avoiding the unitarity constraint [45]. A small ratio of thermal energy transferred at the beginning, smaller than $10^{-18}$, suffices to explain the present dark matter abundance, via cosmological mechanisms such as gravitational production [33,34,35,36,37], thermal production at reheating [25,26,27,28], non-perturbative parametric resonance effects at preheating [29,30,31], and topological defects [25, 32]. The last one is irrelevant to this model, while the non-perturbative parametric resonance mechanism is inaccessible since the inflaton couplings to superheavy dark matter always contribute to the Coleman–Weinberg potential which are required to be perturbative as well as retaining the flatness of potential. The remaining mechanisms are viable as discussed below.

All the dark matter candidates in this model, say $X^0$, $N_{a\mathrm{R}}$, $H'$, $S'_3$, and $A'_3$, have mass proportional to the large scales $\Lambda ,w,\Delta$ as the inflation scale. The lightest particle of which (as called LWP) is stabilized by W-parity conservation, responsible for the mentioned superheavy dark matter. When they are created by some source after the end of inflation, they are never to thermalize. The condition for the candidate to lie out of thermal equilibrium and its comoving number density to be constant is that its self-annihilation rate is less than the Hubble parameter, i.e. $n\langle \sigma v \rangle \lesssim H$. Here, the self-annihilation cross-section times the Møller velocity takes the form $\langle \sigma v \rangle \simeq \alpha ^2_{\mathrm {LWP}}/m^2_{\mathrm {LWP}}$, and $H=\frac{1}{m_P}\sqrt{\frac{V}{3}}\sim \frac{1}{m_P}\sqrt{\lambda }\Lambda ^2$. The condition leads to a bound on the dark matter mass [33]

$$\begin{aligned} \frac{m_{\mathrm {LWP}}}{m_P}\gtrsim 10^{-9}\left( \frac{\alpha _{\mathrm {LWP}}}{\alpha }\right) ^{2/3}\left( \frac{\sqrt{\lambda }}{10^{-6}}\right) ^{1/3}\left( \frac{\Lambda }{m_P}\right) ^{2/3}\left( \frac{10^9\ \mathrm {GeV}}{T_\mathrm{R}}\right) ^{1/3}.\nonumber \\ \end{aligned}$$

(73)

Thus, the superheavy dark matter is not to thermalize if its mass satisfies, for instance, $m_{\mathrm {LWP}}\gtrsim 10^{9}$ GeV, which is compatible to the inflaton mass as well as those given in the above references. This typical bound tends to change, depending on the self-annihilation coupling $\alpha _{\mathrm {LWP}}$ and the inflation scenarios to be used. The correct abundance of the candidates is explicitly studied below when we investigate their sources.

The gravitational mechanism is common and model-independent. That being said, due to the interaction of gravitational field with vacuum quantum fluctuations of the dark matter field, our candidate can be generated with an appropriate density, provided that it has a mass proportional to the inflaton mass, $m_{\mathrm {LWP}}\sim m_{\mathrm {inflaton}}\sim 10^{13}$ GeV [33,34,35,36,37]. In this case, any lightest particle among $X^0$, $N_{a\mathrm{R}}$, $H'$, $S'_3$, or $A'_3$ which is identified as LWP is viable. Indeed, considering the single-field inflation scenario with the $B-L$ breaking inflaton field, the present-day density of dark matter is approximated by [64]

$$\begin{aligned} \Omega _{\mathrm {LWP}}h^2\sim 10^{3}\left( \frac{T_\mathrm{R}}{10^{9}\ \mathrm {GeV}}\right) \left( \frac{m_{\mathrm {LWP}}}{10^{13}\ \mathrm {GeV}}\right) ^2\left( \frac{m_{\mathrm {LWP}}}{H}\right) ^{1/2}e^{-2m_{\mathrm {LWP}}/H},\nonumber \\ \end{aligned}$$

(74)

where H is given at the end of inflation as obtained, $H\sim \frac{\Lambda }{m_P}m_\Phi$. The dark matter mass is proportional to the $B-L$ breaking scale, $m_{\mathrm {LWP}}\simeq g_{\mathrm {LWP}}\Lambda \sim m_\Phi$, thus $m_{\mathrm {LWP}}/H\sim m_P/\Lambda$. The data $\Omega _{\mathrm {LWP}}h^2\sim 0.1$ implies $m_P/\Lambda \gtrsim 6$ for $m_{\mathrm {LWP}}\simeq 3\times 10^{13}$ GeV and $T_\mathrm{R}\simeq 10^9$ GeV. Hence, to have the appropriate dark matter density by the gravitational production, the $B-L$ breaking scale $\Lambda$ should be close to the Planck scale.

This gravitational production mechanism might also affect the observable quantities such as r and $n_\mathrm{s}$ as well as giving rise to considerable isocurvature perturbations. However, the contribution size to the former should be small in comparison to the obtained ones, while the latter would be of interest under the light of the recent experiments, which possibly favors having a further look, to be published elsewhere. For the former, as referred to the single-field inflation scenario with the $B-L$ breaking inflaton field, $\phi$ is a 3-3-1 singlet. It does not interact with the $X^0$ gauge boson nor with the neutral fermions $N_\mathrm{R}$. However, it can interact with the scalar candidates such as $H'$, $S'_3$, and $A'_3$ via the cross coupling constants between scalars in the potential as $\lambda _{11}$, $\lambda _{12}$, and $\zeta _6$. As obtained, the interaction strengths $\lambda _{11},\zeta _6$ are very weak, $\lambda _{11},\zeta _6\lesssim 10^{-9}$, and $\lambda _{12}\sim (\lambda _{11},\zeta _6)$ should be imposed in order to maintain the flatness of the inflaton effective potential since it gets a contribution from the $\lambda _{12}$ coupling between $\phi ,\eta$. Therefore, the effective coupling a is only governed by $g_\mathrm{N}$ and $h'^\nu$ as achieved, due to $g^2_\mathrm{N},(h'^\nu )^2\gg \lambda _{11},\lambda _{12},\zeta _6$. The contributions of the scalar candidates do not affect $r,n_\mathrm{s}$ as the effective potential remains unchanged. Additionally, with an appropriate choice of the parameters, the inflaton might decay into the scalar dark matter. But the contribution to the reheating temperature is at most only comparable to the one in (62), which is again in agreement with the existing bounds. Further, the radiation density at the reheating time is given by $\rho _\mathrm{R}=(\pi ^2/30)g_*T^4_\mathrm{R}$, which is not affected too. Correspondingly, the contribution of this density to the number of e-folds, thus to $r,n_\mathrm{s}$, is also negligible.

An alternative interesting origin for LWP results from thermal production during reheating. In this scenario, the radiation is produced as the inflaton decays, but it is only dominated over the universe when the temperature is below the reheating temperature. In fact, the direct decay products of inflaton can rapidly thermalize, forming a plasma with the temperature much beyond the convenient reheating temperature. With this high-temperature background $\sim 10^3 T_\mathrm{R}$, the LWP can be created by scattering of light states. Another possibility is that they can be produced directly from the inflaton decay or from the thermalization of the water-fall fields and right-handed neutrinos.

On the theoretical side, the upper bound for $T_\mathrm{R}$ is model-dependent. As referred to Appendix B, our theory proved is as an alternative to the grand unified theories. In addition, the proton is always stabilized due to W-parity as a residual symmetry of the 3-3-1-1 gauge symmetry. There is no reason for the existence of supersymmetry, and thus the gravitino. Neglecting this obstacle, the reheating temperature may be raised much higher. For this case, the LWP can be produced by thermal fusions, e.g. from radiations too.

To find the LWP relic density, it is necessary to solve the system of Boltzmann equations describing the redshift and interchange in the energy densities for components, including the inflaton density, the radiation density, and the LWP density. Generalizing the result in [27], the present LWP density is given as

$$\begin{aligned} \Omega _{\mathrm {LWP}} h^2 = m_{\mathrm {LWP}}^2 \langle \sigma v\rangle \left( \frac{g_*}{200} \right) ^{\frac{-3}{2}}\left( \frac{2000 T_{\mathrm{R}}}{m_{\mathrm {LWP}}} \right) ^7, \end{aligned}$$

(75)

where $g_*$ is the effective number of degrees of freedom in the radiation, and $\langle \sigma v\rangle$ is the thermal averaged LWP annihilation cross-section times the Møller velocity. We would like to stress again that all the LWPs are heavy with masses proportional to $\Lambda , \Delta , w$ as the inflation scale, and that these candidates are electrically neutral and colorless as expected. Thus, this ensures that the LWP is stable and is a suitable candidate for superheavy dark matter, thermally produced in the $10^3T_\mathrm{R}$ scale.

Depending on the parameter space, we have the following possibilities:

• 1. The LWP is the W-odd gauge boson, $X^0$. The appearance of the scalar sextet does not contribute to the mass of the neutral, complex gauge boson as well as its couplings to the standard model particles. Hence, the annihilation of $X^0$ into the standard model particles is analogous to those in [2], where the dominant contribution is the channel, $X^0X^{0*}\rightarrow W^+ W^-$. The thermal average of the annihilation cross-section times the velocity was evaluated as [2]

  $$\begin{aligned} \langle \sigma v\rangle _\mathrm{X} \simeq \frac{5\alpha ^2 m_\mathrm{X}^2}{8 s_W^4 m_W^4}. \end{aligned}$$

  (76)

  Hereafter, we take $\frac{\alpha ^2}{(150^2\ \mathrm {GeV}^2)} \simeq 1$ pb and $s_W^2 \simeq 0.23$. Additionally, the reheating temperature as calculated in the previous section is $T_\mathrm{R} \lesssim 10^9$ GeV, so we choose $T_\mathrm{R}=10^9$ GeV. Hence, the present density of X gauge bosons is

  $$\begin{aligned} \Omega _\mathrm{X} h^2 \simeq 6.0340 g_*^{-\frac{3}{2}} \left( \frac{10^{27}\ \mathrm {GeV}}{m_\mathrm{X}} \right) ^3. \end{aligned}$$

  (77)

  It is evident that $g_* \sim 100$–200 and $m_\mathrm{X}$ is limited below the Planck scale. Hence, X cannot be a candidate for dark matter since it overpopulates, $\Omega _\mathrm{X} h^2\gg 1$.

• 2. The LWP is the lightest neutral fermion among $N_{a\mathrm{R}}$, denoted $N_\mathrm{R}$. The fermions $N_\mathrm{R}$ annihilate into the standard model particles due to the contribution of the new neutral gauge bosons $Z'$ and $Z''$ via s-channels as well as the new complex gauge bosons X, Y via t-channels. Here, the annihilation modes into $Z,H,t,\tau ,\nu _\tau$ where the leptons have t-channels are dominated. Using the limit $m_{N_\mathrm{R}}\gg m_\mathrm{t}, m_{Z}, m_\mathrm{H}\gg m_\mathrm{lep}$, the thermal average of the annihilation cross-section times the velocity is approximated by [2]

  $$\begin{aligned} \langle \sigma v\rangle _{\mathrm{N}_\mathrm{R}} \simeq \frac{\alpha ^2}{(150\ \mathrm {GeV})^2} \frac{(2557.5\ \mathrm {GeV})^2m^2_{\mathrm{N}_\mathrm{R}}}{m^4_{Z^\prime }}, \end{aligned}$$

  (78)

  with the assumption that $m_\mathrm{X}\sim m_\mathrm{Y}\sim \frac{\sqrt{3-t^2_W}}{2}m_{Z'}\sim \frac{\sqrt{3-t^2_W}}{2}m_{Z''}$. In this case, the relic density of the fermion dark matter can be written as

  $$\begin{aligned} \Omega _{\mathrm{N}_\mathrm{R}} h^2 \simeq \frac{6.08121}{g_*^{3/2}z^4} \left( \frac{10^{13}\ \mathrm {GeV}}{m_{\mathrm{N}_\mathrm{R}}} \right) ^7, \end{aligned}$$

  (79)

  where $z\equiv \frac{m_{Z^\prime }}{m_{\mathrm{N}_\mathrm{R}}}\sim 1$, since these masses are both proportional to the large scale, $\Lambda ,\Delta , w$. The correct density as observed demands $m_{\mathrm{N}_\mathrm{R}}\sim 10^{13}$ GeV.

• 3. The LWP is a scalar among the $H',S'_3,A'_3$ states, by which we choose $H'$ for investigation. The annihilation cross-section of $H'$ into the standard model particles was obtained in [3] by the Higgs portal as follows:

  $$\begin{aligned} \langle \sigma v \rangle _{H'} \simeq \frac{\alpha ^2}{(150\ \mathrm {GeV})^2} \lambda ^\prime \left( \frac{1.328\ \mathrm {GeV}}{m_{H^\prime }} \right) ^2, \end{aligned}$$

  (80)

  where $\lambda ^\prime$ is the effective coupling between two $H^\prime$ scalars with two standard model Higgs bosons. The $H^\prime$ relic density is

  $$\begin{aligned} \Omega _{H^\prime } h^2 \simeq 1.63967 \lambda ^\prime g_*^{-\frac{3}{2}} \left( \frac{10^{12}\ \mathrm {GeV}}{m_{H^\prime }} \right) ^7. \end{aligned}$$

  (81)

  Given that the scalar coupling is proportional to one, $\lambda '\sim 1$, the observed abundance of dark matter is recovered if $m_{H'}\sim 10^{12}$ GeV.

6 Conclusions

We have shown that the 3-3-1-1 model can work under the three distinct regimes of the energy scale, characterized by the VEVs as $\kappa \sim m_\nu$, $(u,v)\sim m_{W,Z}$, and $(w,\Delta ,\Lambda )\sim m_{\mathrm {inflaton}}$. The $B-L$ breaking scale, $\Lambda$, is responsible for the type I seesaw mechanism and inflation scenario, so it naturally picked up a value in the large energy regime. The introduction of the scalar sextet implies that the 3-3-1 breaking scales, $\Delta$ and w, are also large, proportional to $\Lambda$, recognizing the fact that the $B-L$ and 3-3-1 symmetries are nontrivially unified. Therefore, the new physics regime of the 3-3-1-1 model is actually realized in the inflation scale as governed by $(w,\Delta ,\Lambda )$. The consistent smallness of $\kappa$ and neutrino masses are ensured by the type I and II seesaw mechanisms as a result of the 3-3-1-1 gauge symmetry breaking, and that they are naturally suppressed by the large scales. In other words, the conventional seesaw mechanisms can be manifestly explained by a noncommutative $B-L$ dynamics associated with the 3-3-1 gauge symmetry. The resulting 3-3-1-1 model provides not only the neutrino masses and leptogenesis but also other consequences such as inflation scenarios and superheavy dark matter.

The 3-3-1-1 breaking fields can behave as inflatons driving the inflationary expansion of the early universe. The several single-field inflation scenarios have been interpreted, in which the case associated with the $B-L$ breaking was explicitly shown, taking the contribution of the superheavy particles to the inflaton effective potential. The inflaton can have a mass in the $10^{8}$–$10^{12}$ GeV order, corresponding to $\Lambda =10^{14}$–$10^{18}$ GeV. The reheating temperature is naturally bounded by $10^{9}$ GeV if the inflaton decays into the scalars or by a lower value if it decays into the right-handed neutrinos. The multi-field inflation scenarios can be explicitly implemented in this model as corroborated by the superheavy Higgs fields, but their contribution to the isocurvature and non-Gaussian perturbations should be small due to the slow-role approximation. When turning on the coupling terms between inflatons, these effects may be enhanced, which was not evaluated by this work.

The breakdown of the 3-3-1-1 gauge symmetry induces W-parity, i.e. R-parity, as a residual gauge symmetry, making the W-particles that carry abnormal $B-L$ number odd. The W-particles include a non-Hermitian gauge boson $X^0$, scalars $H'$, $S'_3$, $A'_3$, and fermions $N_{a\mathrm{R}}$ besides the other electrically charged states, which all have a mass proportional to the large scales ($\Lambda , w,\Delta$). The lightest W-particle or the LWP is stabilized, responsible for superheavy dark matter. $X^0$ as LWP can only be gravitationally produced, with a mass $m_\mathrm{X}\sim 10^{13}$ GeV. Alternatively, the LWP as a lightest neutral fermion among $N_{1,2,3\mathrm{R}}$ or a neutral scalar among $H'$, $S'_3$, and $A'_3$ can be created in the early universe by either gravitational or thermal production, which depends on their mass in the $10^{13}$–$10^{12}$ GeV range or possibly lower according to the thermal mechanism. The contribution of superheavy dark matter to the slow-roll parameters $r,n_\mathrm{s}$ and the reheating temperature is negligible. However, their effects for the isocurvature and non-Gaussian perturbations may be considerable compared to the mentioned multi-field inflation scenarios.

Conclusively, the 3-3-1-1 model at the large energy regime recognizes an actual unification of the $B-L$ and 3-3-1 symmetries, yielding the potential solution to the important issues of particle physics and cosmology, such as neutrino masses, baryon asymmetry, dark matter, and inflation. Although it is presented as an alternative to the grand unified theories, at an extremely high energy regime, a possible unification of the gauge couplings along with a more fundamental gauge symmetry might emerge, to be addressed in further studies [65].

Appendices

Appendix A: Anomaly checking

With the X, N charges as given in the text, we have

$$\begin{aligned}&[SU(3)_\mathrm{C}]^2U(1)_\mathrm{X} \sim \sum _{\mathrm {quarks}} (X_{q_\mathrm{L}}-X_{q_\mathrm{R}}) \nonumber \\&\quad = 3X_{Q_3}+2\times 3 X_{{Q}_\alpha }-3X_{u_a}-3X_{d_a}-X_\mathrm{U}-2X_{\mathrm{D}_\alpha }\nonumber \\&\quad =3\left( 1/3\right) +6\left( 0\right) -3\left( 2/3\right) -3\left( -1/3\right) -\left( 2/3\right) \nonumber \\&\qquad -2\left( -1/3\right) =0, \end{aligned}$$

(A1)

$$\begin{aligned}&[SU(3)_\mathrm{C}]^2U(1)_\mathrm{N} \sim \sum _{\mathrm {quarks}} (N_{q_\mathrm{L}}-N_{q_\mathrm{R}}) \nonumber \\&\quad = 3N_{Q_3}+2\times 3 N_{Q_\alpha }-3N_{u_a}-3N_{d_a}-N_\mathrm{U}-2N_{D_\alpha }\nonumber \\&\quad = 3\left( 2/3\right) +6\left( 0\right) -3\left( 1/3\right) -3\left( 1/3\right) \nonumber \\&\qquad -\left( 4/3\right) -2\left( -2/3\right) =0, \end{aligned}$$

(A2)

$$\begin{aligned}&[SU(3)_\mathrm{L}]^2 U(1)_\mathrm{X} \sim \sum _{\mathrm {(anti)triplets}} X_{F_\mathrm{L}}\nonumber \\&\quad = 3X_{\psi _a}+3X_{Q_3}+2\times 3 X_{Q_\alpha }\nonumber \\&\quad = 3\left( -1/3\right) +3\left( 1/3\right) +6\left( 0\right) =0, \end{aligned}$$

(A3)

$$\begin{aligned}&[SU(3)_\mathrm{L}]^2 U(1)_\mathrm{N} \sim \sum _{\mathrm {(anti)triplets}} N_{F_\mathrm{L}}\nonumber \\&\quad = 3N_{\psi _a}+3N_{Q_3}+2\times 3 N_{Q_\alpha } \nonumber \\&\quad = 3\left( -2/3\right) +3\left( 2/3\right) +6\left( 0\right) =0. \end{aligned}$$

(A4)

The last two anomalies have taken the color number, i.e. 3’s in the second and last terms, into account, and below the presence of this number should be understood. Note also that, for antitriplets, we have $\mathrm {Tr}[(-T^*_i)(-T^*_j)X]=\mathrm {Tr}[T_i T_j X]$ and similarly for the N charge. We have

$$\begin{aligned}&[\mathrm {gravity}]^2U(1)_\mathrm{X}\sim \sum _{\mathrm {fermions}}(X_{f_\mathrm{L}}-X_{f_\mathrm{R}})\nonumber \\&\quad =3\times 3 X_{\psi _a}+3\times 3 X_{Q_3}+2\times 3 \times 3 X_{Q_\alpha }-3\times 3 X_{u_a}\nonumber \\&\qquad -3\times 3 X_{d_a}-3X_\mathrm{U}-2\times 3 X_{D_\alpha }-3X_{e_a}-3X_{\nu _a}\nonumber \\&\quad =3\times 3 (-1/3)+3\times 3 (1/3)+2\times 3\times 3 (0)\nonumber \\&\qquad -3\times 3 (2/3)-3\times 3 (-1/3) -3(2/3)\nonumber \\&\qquad -2\times 3 (-1/3)-3(-1)-3(0)=0, \end{aligned}$$

(A5)

$$\begin{aligned}&[\mathrm {gravity}]^2U(1)_\mathrm{N}\sim \sum _{\mathrm {fermions}}(N_{f_\mathrm{L}}-N_{f_\mathrm{R}})\nonumber \\&\quad =3\times 3 N_{\psi _a}+3\times 3 N_{Q_3}+2\times 3 \times 3 N_{Q_\alpha }\nonumber \\&\qquad -3\times 3 N_{u_a}-3\times 3 N_{d_a}-3N_\mathrm{U}-2\nonumber \\&\qquad \times 3 N_{D_\alpha }-3N_{e_a}-3N_{\nu _a}\nonumber \\&\quad =3\times 3 (-2/3)+3\times 3 (2/3)+2\times 3\times 3 (0)\nonumber \\&\qquad -3\times 3 (1/3)-3\times 3 (1/3) -3(4/3)\nonumber \\&\qquad -2\times 3 (-2/3)-3(-1)-3(-1)=0, \end{aligned}$$

(A6)

$$\begin{aligned}{}[U(1)_\mathrm{X}]^2U(1)_\mathrm{N}= & {} \sum _{\mathrm {fermions}}(X^2_{f_\mathrm{L}}N_{f_\mathrm{L}}-X^2_{f_\mathrm{R}}N_{f_\mathrm{R}})\nonumber \\= & {} 3\times 3 X^2_{\psi _a}N_{\psi _a}+3\times 3 X^2_{Q_3} N_{Q_3}\nonumber \\&+\,2\times 3\times 3 X^2_{Q_{\alpha }}N_{Q_{\alpha }}-3\times 3 X^2_{u_a}N_{u_a}\nonumber \\&-3\times 3 X^2_{d_a}N_{d_a}-3X^2_\mathrm{U} N_\mathrm{U}\nonumber \\&-2\times 3 X^2_{D_\alpha }N_{D_\alpha }-3X^2_{e_a} N_{e_a}-3X^2_{\nu _a}N_{\nu _a}\nonumber \\= & {} 3\times 3 (-1/3)^2(-2/3)\nonumber \\&+\,3\times 3 (1/3)^2(2/3)\nonumber \\&+\,2\times 3\times 3 (0)^2(0)-3\times 3(2/3)^2(1/3)\nonumber \\&-3\times 3(-1/3)^2(1/3)-3(2/3)^2(4/3)\nonumber \\&-2\times 3(-1/3)^2(-2/3)\nonumber \\&-3(-1)^2(-1)-3(0)^2(-1)=0, \end{aligned}$$

(A7)

$$\begin{aligned} U(1)_\mathrm{X}[U(1)_\mathrm{N}]^2= & {} \sum _{\mathrm {fermions}}(X_{f_\mathrm{L}}N^2_{f_\mathrm{L}}-X_{f_\mathrm{R}}N^2_{f_\mathrm{R}})\nonumber \\= & {} 3\times 3 X_{\psi _a}N^2_{\psi _a}+3\times 3 X_{Q_3} N^2_{Q_3}\nonumber \\&+\,2\times 3\times 3 X_{Q_{\alpha }}N^2_{Q_{\alpha }}-3\times 3 X_{u_a}N^2_{u_a}\nonumber \\&-3\times 3 X_{d_a}N^2_{d_a}-3X_\mathrm{U} N^2_\mathrm{U}\nonumber \\&-2\times 3 X_{D_\alpha }N^2_{D_\alpha }-3X_{e_a} N^2_{e_a}-3X_{\nu _a}N^2_{\nu _a}\nonumber \\= & {} 3\times 3 (-1/3)(-2/3)^2+3\times 3 (1/3)(2/3)^2\nonumber \\&+\,2\times 3\times 3 (0)(0)^2-3\times 3(2/3)(1/3)^2\nonumber \\&-3\times 3(-1/3)(1/3)^2-3(2/3)(4/3)^2\nonumber \\&-2\times 3(-1/3)(-2/3)^2-3(-1)(-1)^2\nonumber \\&-3(0)(-1)^2=0, \end{aligned}$$

(A8)

$$\begin{aligned}{}[U(1)_\mathrm{X}]^3= & {} \sum _{\mathrm {fermions}}(X^3_{f_\mathrm{L}}-X^3_{f_\mathrm{R}})=3\times 3 X^3_{\psi _a}\nonumber \\&+\,3\times 3 X^3_{Q_3}+2\times 3\times 3 X^3_{Q_\alpha }\nonumber \\&-3\times 3 X^3_{u_a}-3\times 3 X^3_{d_a}-3X^3_\mathrm{U}\nonumber \\&-2\times 3 X^3_{D_\alpha }-3X^3_{e_a}-3X^3_{\nu _a}\nonumber \\= & {} 3\times 3 (-1/3)^3+3\times 3 (1/3)^3\nonumber \\&+\,2\times 3\times 3 (0)^3-3\times 3(2/3)^3\nonumber \\&-3\times 3(-1/3)^3-3(2/3)^3\nonumber \\&-2\times 3(-1/3)^3-3(-1)^3-3(0)^3=0, \end{aligned}$$

(A9)

$$\begin{aligned}{}[U(1)_\mathrm{N}]^3= & {} \sum _{\mathrm {fermions}}(N^3_{f_\mathrm{L}}-N^3_{f_\mathrm{R}})=3\times 3 N^3_{\psi _a}\nonumber \\&+\,3\times 3 N^3_{Q_3}+2\times 3\times 3 N^3_{Q_\alpha }\nonumber \\&-3\times 3 N^3_{u_a}-3\times 3 N^3_{d_a}-3N^3_\mathrm{U}\nonumber \\&-2\times 3 N^3_{D_\alpha }-3N^3_{e_a}-3N^3_{\nu _a}\nonumber \\= & {} 3\times 3 (-2/3)^3+3\times 3 (2/3)^3\nonumber \\&+\,2\times 3\times 3 (0)^3-3\times 3(1/3)^3\nonumber \\&-3\times 3(1/3)^3-3(4/3)^3\nonumber \\&-2\times 3(-2/3)^3-3(-1)^3-3(-1)^3=0. \end{aligned}$$

(A10)

Appendix B: GUT embedding

Let us study the possibility of embedding the 3-3-1-1 model into a grand unified theory. We assume that the 3-3-1-1 model can be unified by a simple group such as SU(n) or SO(n). Of course the gauge group $SU(3)_\mathrm{C} \otimes SU(3)_\mathrm{L} \otimes U(1)_\mathrm{X} \otimes U(1)_\mathrm{N}$ should be a subgroup of the grand unified group, and thus the fermion content in our model is included in the matter representations of the grand unified group. Since the 3-3-1-1 group is embedded into the simple group, the X and N charges are determined as a combination of the Cartan generators of the grand unified group. Therefore, the X and N generators are traceless. It means that the total X and N charges in every matter representation of the grand unified group must add up to zero. Furthermore, if we look at the representation of each fermion multiplet given in Eqs. (1)–(5), we see that the X and N charges have different values, by which we cannot arrange the fermion multiplets in the 3-3-1-1 model into the matter representations of the unified group so that the total X and N charges simultaneously add up to zero.

To embed our fermion content into the representations of the unified group, we have to rearrange the fermion representations of the original model as in [66,67,68,69,70,71], or otherwise we introduce new fermion multiplets. Let us illustrate this by selecting a grand unified group $SU(7) \supset$ 3-3-1-1 group. The anomaly-free combination of SU(7) representations is $7^* + 21+ 35^*$. Each irreducible representation of SU(7) can decompose into irreducible representations of 3-3-1-1 group, which depends on the choice of the intermediate subgroup. Let us consider two cases. The first case is that $SU(7)\rightarrow SU(6) \otimes U(1)_a \rightarrow SU(3)\otimes SU(3) \otimes U(1)_b \otimes U(1)_a$. The representations, $7^*+21+35^*$, decompose into the 3-3-1-1 representations,

$$\begin{aligned} 7^*+21+35^*= & {} \left[ (1,1,0,6a) \oplus (1,3^*, 3b, -a)\right. \nonumber \\&\left. \oplus \, (3^*,1, -3b, -a) \right] \nonumber \\&+\, \left[ (3^*,1,6b,2a) \oplus (3,3,0,2a)\right. \nonumber \\&\oplus \, (1,3^*, -6b, 2a)\oplus \, (3,1,3c,-5a) \nonumber \\&\left. \oplus (1,3,-3c,-5a) \right] + \left[ (1,3,6b,4a) \right. \nonumber \\&\oplus \, (3^*, 3^*, 0, 4a)\oplus \, (3,1,-6b,4a)\nonumber \\&\oplus \,(1,1,9c,-3a) \oplus \, (1,1,-9c,-3a)\nonumber \\&\left. \oplus (3^*,3,3d,-3a) \oplus (3,3^*,-3d,-3a)\right] .\nonumber \\ \end{aligned}$$

(B1)

The second case is if $SU(7)\rightarrow SU(4) \otimes SU(3) \otimes U(1)_a \rightarrow SU(3)\otimes SU(3) \otimes U(1)_b \times U(1)_a$, the representations, $7^*+21+35^*$, decompose into 3-3-1-1 subgroups as follows:

$$\begin{aligned} 7^*+21+35^*= & {} \left[ (1,3^*,0,4a) \oplus (1,1,3c,-3a)\right. \nonumber \\&\left. \oplus \, (3^*,1,-c,-3a)\right] + \left[ (3^*,1,2b,6a) \right. \nonumber \\&\oplus \, (3,1,-2b,6a) \oplus (3,3,c,-a) \nonumber \\&\left. \oplus \,(1,3,-3c,-a) \oplus (1,3^*,0,-8a) \right] \nonumber \\&+ \,\left[ (1,1,0,12a) \oplus (1,3,3c,5a) \right. \nonumber \\&\oplus \,(3^*,3,-c,5a) \oplus (3,3^*,2d,-2a) \nonumber \\&\oplus \, (3,3^*,-2d,-2a) \oplus (3,1,e,-9a)\nonumber \\&\left. \oplus \,(1,1,-3e,-9a) \right] . \end{aligned}$$

(B2)

Due to the separation of SU(7) representations given in (B1) or (B2), it is easy to see that there is no choice the value of (a, b, c, d, e) so that each SU(7) representation contains at least two different fermion multiplets of the 3-3-1-1 model. Therefore, if embedding the 3-3-1-1 model into SU(7), the number of irreducible representations of SU(7) must equal that of the present fermion multiplets containing in the 3-3-1-1 model. It means that, for each fermion family, we have to introduce three sets of $7^*+21+35^*$ representations of the SU(7) group. So the fermion content in the SU(7) grand unified model will appear much more new fermions beyond the 3-3-1-1 model. This is not a favorite choice, and other issues may arise because the QCD asymptotic freedom is not ensured due to a largely numerical contribution of new quark fields.

To avoid the appearance of much more new fermions in the SU(7) unified theory, we have to change the quantum numbers X and N for each fermion multiplets or in other words we have to modify the fermion content in the 3-3-1-1 model as similarly done in the 3-3-1 models [66,67,68,69,70,71]. There may be another option: that the interactions and their gauge symmetries need not necessarily be unified at a grand unified scale. The 3-3-1-1 symmetry as it stands is enough to describe the physics at such a large scale.