The strong decays of X(3940) and X(4160)

Abstract

The new mesons X(3940) and X(4160) have been found by Belle Collaboration in the processes $e^+e^-\rightarrow J/\psi D^{(*)}{\bar{D}}^{(*)}$. Considering X(3940) and X(4160) as $\eta _c(3S)$ and $\eta _c(4S)$ states, the two-body open charm OZI-allowed strong decay of $\eta _c(3S)$ and $\eta _c(4S)$ are studied by the improved Bethe–Salpeter method combined with the $^3P_0$ model. The strong decay width of $\eta _c(3S)$ is $\Gamma _{\eta _c(3S)}=(33.5^{+18.4}_{-15.3})$ MeV, which is close to the result of X(3940); therefore, $\eta _c(3S)$ is a good candidate of X(3940). The strong decay width of $\eta _c(4S)$ is $\Gamma _{\eta _c(4S)}=(69.9^{+22.4}_{-21.1})$ MeV, considering the errors of the results, it is close to the lower limit of X(4160). But the ratio of the decay width $\frac{\Gamma (D{\bar{D}}^*)}{\Gamma (D^*{\bar{D}}^*)}$ of $\eta _c(4S)$ is larger than the experimental data of X(4160). According to the above analysis, $\eta _c(4S)$ is not the candidate of X(4160), and more investigations of X(4160) is needed.

1 Introduction

In the past few years, many more new charmonium-like states, so-called XYZ states, have been observed by the Belle, BABAR and BESIII Collaborations [1]. The discovery of these states not only enriched the spectroscopy of charmonium-like states but also provided us with an opportunity to research the properties of charmonium-like states. For example, the X(3940) state was observed from the inclusive process $e^+e^-\rightarrow J/\psi X(3940)$ and had the decay mode $X(3940)\rightarrow D^*{\bar{D}}$ by the Belle Collaboration at a mass of $(3943\pm 6\pm 6)$ MeV. The decay width of these state was less than 52 MeV at the $90\%$ C.L. which has taken into the systematics [2]. Later the Belle Collaboration confirmed the observation of X(3940) with a significance of $5.7\sigma$, they got the mass and width of X(3940), which were $M=(3942^{+7}_{-6}\pm 6)$ MeV, $\Gamma =(37^{+26}_{-15}\pm 8)$ MeV. At the same time, they also observed a new charmonium-like state X(4160) in the process $e^+e^-\rightarrow J/\psi D^*{\bar{D}}^*$, the mass and width of X(4160) were $M=(4156^{+25}_{-20}\pm 15)$ MeV, $\Gamma =(139^{+111}_{-61}\pm 21)$ MeV [3].

The observations of these XYZ states much inspired addressing their physical natures. There are already many theoretical approaches which have been used to study the properties of these XYZ states [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. In this paper, we mainly discuss the properties and decays of two X states: X(3940) and X(4160). References [4, 5] have assigned to the C parity of X(3940) and X(4160) values that should be even, $C=+$. Assuming X(3940) as $3^1S_0$ or one of $2^3P_J$ charmonium-like states, Ref. [6] studied the $e^+e^-\rightarrow J/\psi X(3940)$ process by the light-cone formalism, and they considered the X(3940) to be $3^1S_0$($\eta _c(3S)$). Reference [7, 8] investigated the properties of X(3940) and X(4160), which were $\eta _c(3S)$ and $\chi _{c0}(3P)$, respectively. Reference [13] calculated the strong decays of $\eta _c(nS)$; one found that the explanation of X(3940) as $\eta _c(3S)$ is possible and the assignment of X(4160) as $\eta _c(4S)$ cannot be excluded. In Ref. [14], the authors studied the vector–vector interaction of X(4160), which was basically a $D_\mathrm{s}^*{\bar{D}}_\mathrm{s}^*$ molecular state with $J^\mathrm{PC}=2^{++}$. References [16] had studied the inclusive production of X(3940) in the decay of the ground bottomonium state $\eta _b$ by the NRQCD factorization formula, and one also considered X(3940) as the excited $\eta _c(3S)$ state. Reference [17] calculated the strong decay of X(4160), which was assumed as $\chi _{c0}(3P)$, $\chi _{c1}(3P)$, $\eta _{c2}(2D)$ or $\eta _c(4S)$ by the $^3P_0$ model. In Ref. [18], one also explored the properties of X(3940) and X(4160) as the $\eta _c(3S)$ and $\eta _c(4S)$, respectively. But the results suggested X(3940) as $\eta _c(3S)$ and the explanation of X(4160) taken to be $\eta _c(4S)$ is fully excluded. Using the NRQCD factorization approach, Ref. [19] calculated the branching fractions of $\Upsilon (nS)\rightarrow J/\psi +X$ with $X=X(3940)$ or $X=X(4160)$; one thought that the X(3940) and X(4160) can be explained as $3^1S_0$ and $4^1S_0$ charmonium-like states, respectively. Up to now, it is very difficult to confirm the constructions of X(3940) and X(4160), because of the lack of enough experimental data. Many more theoretical predictions and experimental data are needed for X(3940) and X(4160).

The mesons can be described by the Bethe–Salpeter (BS) equation. Reference [21] took the BS equation to describe the light mesons $\pi$ and K, then one calculated the mass and decay constant of $\pi$ by the BS amplitudes [22, 23], and one also studied the weak decays [24,25,26] and the strong decays [27, 28] combined with the Dyson–Schwinger equation.

We will use the BS equation to study the properties of heavy mesons. In Ref. [29], we had calculated the spectrum of heavy quarkonia by the improved BS method, for the charmonium state with the quantum numbers $J^\mathrm{PC} =0^{-+}$, the mass of $3^1S_0$ ($\eta _c(3S)$) is $M=3948.8$ MeV, which is close to the mass of X(3940) with error, the mass of $4^1S_0$ ($\eta _c(4S)$) was $M=4224.6$ MeV, which was larger than the center mass of X(4160) about 70 MeV. In this paper, to check if the X(4160) is the charmonium $\eta _c(4S)$; we calculate the strong decay of $\eta _c(4S)$, but we assign the mass of $\eta _c(4S)$ to 4156 MeV by varying the parameter $V_0$ in the interaction potential, where in the potential model the parameter $V_0$ is added to move the theoretical mass spectra parallel to match the experimental data.

Using the improved BS method, we calculated the weak decay of $B_c$ to $\eta _c(1S)$ and $\eta _c(2S)$ [30], and the weak decay of $B_c$ to $\eta _c(3S)$ and $\eta _c(4S)$ [31]. Nobody has calculated $B_c$ to $\eta _c(4S)$, but the results of $B_c$ to $\eta _c(1S)$, $\eta _c(2S)$, $\eta _c(3S)$ were close to the other theoretical results. We also studied the properties of some XYZ states, such as radiative E1 decay of X(3872) [9, 10], two-body strong decay of Z(3930), which was a $\chi _{c2}(2P)$ state combined with the $^3P_0$ model [11], the strong decay of X(3915) as $\chi _{c0}(2P)$ state [32], and the strong decay of $\Upsilon$ [33]. All the theoretical results are consistent with the experimental data or other theoretical results. Because the higher excited states have a larger relativistic correction than the corresponding ground state, a relativistic model is needed in a careful study. The improved BS method is a relativistic model that describes bound states with definite quantum numbers, and the corresponding relativistic form of wave functions are solutions of the full Salpeter equations. So the improved BS method is a good method to describe the properties and decays of the radially highly excited states, In this paper, we focus on the strong decays of X(3940) and X(4160) as radially highly excited states $\eta _c(3S)$ and $\eta _c(4S)$ by the improved BS method.

In our method, we study the natures of the heavy mesons by the coupling of $L+S$ for the quark and anti-quark in mesons. According to the $L+S$ coupling, we show the wave functions of the heavy mesons in terms of the quantum number $J^P$ (or $J^\mathrm{PC}$) which are very good in describing the equal mass systems in heavy mesons. The quantum numbers $J^\mathrm{PC}$ of $\eta _c(3S)$ and $\eta _c(4S)$ both are $0^{-+}$, and the C parities are even, which agrees with the results of Refs. [4, 5]. The corresponding Okubo–Zweig–Iizuka (OZI) [34,35,36] rule-allowed two-body open charm strong decay modes are $0^-\rightarrow 0^-1^-$ and $0^-\rightarrow 1^-1^-$, while the other strong decays in the final state are ruled out by the kinematic possible mass region. In order to calculate the two-body open charm strong decay, we adopt the $^3P_0$ model, which assumes that a quark–antiquark pair is created with vacuum quantum numbers, $J^\mathrm{PC}=0^{++}$ [37,38,39]. The $^3P_0$ model was proposed in Ref. [37]; then Refs. [38, 39] applied the $^3P_0$ model to a study of the open-flavor strong decays of the light mesons. Now, one has extended this model to a study of the natures of the heavy-light mesons [40, 41] and heavy quarkonia [33, 42, 43]. In Refs. [11, 33], we have calculated the OZI-allowed two-body strong decays of charmonium and bottomonium in the $^3P_0$ model with the relativistic BS wave functions. The results were well according with the experimental data and the other theoretical results. Furthermore, the strong decay widths are related to the parameter $\gamma$, but the ratio of the decay width $\frac{\Gamma (\eta _c(4S)\rightarrow D\bar{D}^*}{\Gamma (\eta _c(4S)\rightarrow D^*\bar{D}^*}$ and $\frac{\Gamma (\eta _c(4S)\rightarrow D\bar{D}}{\Gamma (\eta _c(4S)\rightarrow D^*\bar{D}^*}$ was independent of the parameter $\gamma$, so the results of the ratios are more reliable than the decay widths. In this paper, we take the same method as Refs. [11, 33] to study strong decays of $\eta _c(3S)$ and $\eta _c(4S)$ states.

The paper is organized as follows. In Sect. 2, we introduce the instantaneous BS equation; we show the relativistic wave functions of the initial mesons and final mesons in Sect. 3; In Sect. 4, we give the formulation of two-body open charm strong decays; the corresponding results and conclusions are presented in Sect. 5.

2 Instantaneous Bethe–Salpeter equation

In this section, we briefly review the Bethe–Salpeter equation and its instantaneous one, the Salpeter equation.

The BS equation reads [44]

$$\begin{aligned} (\not \!{p_{1}}-m_{1})\chi (q)(\not \!{p_{2}}+m_{2})= i\int \frac{\mathrm{d}^{4}k}{(2\pi )^{4}}V(P,k,q)\chi (k),\nonumber \\ \end{aligned}$$

(1)

where $\chi (q)$ is the BS wave function, P is the total momentum of the meson, q is relative quantum between quark and anti-quark, V(P, k, q) is the interaction kernel between the quark and anti-quark, $p_{1}, p_{2}$ and $m_1$, $m_2$ are the momentum and mass of the quark 1 and anti-quark 2, respectively.

We divide the relative momentum q into two parts, $q_{\parallel }$ and $q_{\perp }$,

$$\begin{aligned} q^{\mu }&=q^{\mu }_{\parallel }+q^{\mu }_{\perp },\\ q^{\mu }_{\parallel }&\equiv (P\cdot q/M^{2})P^{\mu },\quad q^{\mu }_{\perp }\equiv q^{\mu }-q^{\mu }_{\parallel }. \end{aligned}$$

Correspondingly, we have two Lorentz invariants:

$$\begin{aligned} q_{p}=\frac{(P\cdot q)}{M}, \quad q_{_T}=\sqrt{q^{2}_{p}-q^{2}}=\sqrt{-q^{2}_{\perp }}. \end{aligned}$$

When $\mathop {P}\limits ^{\rightarrow }=0$, $q_p=q_{0}$ and $q_T=|{\vec {q}}|$, respectively.

In instantaneous approach, the kernel V(P, k, q) takes the simple form [45]

$$\begin{aligned} V(P,k,q) \Rightarrow V(|{\vec {k}}-{\vec {q}}|). \end{aligned}$$

Let us introduce the notations $\varphi _{p}(q^{\mu }_{\perp })$ and $\eta (q^{\mu }_{\perp })$ for the three dimensional wave function as follows:

$$\begin{aligned}&\varphi _{p}(q^{\mu }_{\perp })\equiv i\int \frac{\mathrm{d}q_{p}}{2\pi }\chi (q^{\mu }_{\parallel },q^{\mu }_{\perp }),\nonumber \\&\eta (q^{\mu }_{\perp })\equiv \int \frac{\mathrm{d}k_{\perp }}{(2\pi )^{3}} V(k_{\perp },q_{\perp })\varphi _{p}(k^{\mu }_{\perp }). \end{aligned}$$

(2)

Then the BS equation can be rewritten as

$$\begin{aligned} \chi (q_{\parallel },q_{\perp })=S_{1}(p_{1})\eta (q_{\perp })S_{2}(p_{2}). \end{aligned}$$

(3)

The propagators of the two constituents can be decomposed as

$$\begin{aligned} S_{i}(p_{i})= & {} \frac{\Lambda ^{+}_{ip}(q_{\perp })}{J(i)q_{p} +\alpha _{i}M-\omega _{i}+i\epsilon }\nonumber \\&+ \frac{\Lambda ^{-}_{ip}(q_{\perp })}{J(i)q_{p}+\alpha _{i}M+\omega _{i}-i\epsilon }, \end{aligned}$$

(4)

with

$$\begin{aligned} \omega _{i}= & {} \sqrt{m_{i}^{2}+q^{2}_{_T}},\quad \Lambda ^{\pm }_{ip}(q_{\perp })\nonumber \\= & {} \frac{1}{2\omega _{ip}}\left[ \frac{\not \!{P}}{M}\omega _{i}\pm J(i)(m_{i}+{\not \!q}_{\perp })\right] , \end{aligned}$$

(5)

where $i=1, 2$ for quark and anti-quark, respectively, and $J(i)=(-1)^{i+1}$.

Introducing the notations $\varphi ^{\pm \pm }_{p}(q_{\perp })$ as

$$\begin{aligned} \varphi ^{\pm \pm }_{p}(q_{\perp })\equiv \Lambda ^{\pm }_{1p}(q_{\perp }) \frac{\not \!{P}}{M}\varphi _{p}(q_{\perp }) \frac{\not \!{P}}{M} \Lambda ^{{\pm }}_{2p}(q_{\perp }). \end{aligned}$$

(6)

With contour integration over $q_{p}$ on both sides of Eq. (3), we obtain

$$\begin{aligned} \varphi _{p}(q_{\perp })= & {} \frac{ \Lambda ^{+}_{1p}(q_{\perp })\eta _{p}(q_{\perp })\Lambda ^{+}_{2p}(q_{\perp })}{(M-\omega _{1}-\omega _{2})}\\&- \frac{ \Lambda ^{-}_{1p}(q_{\perp })\eta _{p}(q_{\perp })\Lambda ^{-}_{2p}(q_{\perp })}{(M+\omega _{1}+\omega _{2})}, \end{aligned}$$

and the full Salpeter equation:

$$\begin{aligned} (M-\omega _{1}-\omega _{2})\varphi ^{++}_{p}(q_{\perp })= & {} \Lambda ^{+}_{1p}(q_{\perp })\eta _{p}(q_{\perp })\Lambda ^{+}_{2p}(q_{\perp }),\nonumber \\ (M+\omega _{1}+\omega _{2})\varphi ^{--}_{p}(q_{\perp })= & {} - \Lambda ^{-}_{1p}(q_{\perp })\eta _{p}(q_{\perp })\Lambda ^{-}_{2p}(q_{\perp }),\nonumber \\ \varphi ^{+-}_{p}(q_{\perp })= & {} \varphi ^{-+}_{p}(q_{\perp })=0. \end{aligned}$$

(7)

For the different $J^\mathrm{PC}$ (or $J^{P}$) states, we give the general form of wave functions. Reducing the wave functions by the last equation of Eq. (7), then solving the first and second equations in Eq. (7) to get the wave functions and mass spectrum. We have discussed the solution of the Salpeter equation in detail in Refs. [29, 46].

The normalization condition for the BS wave function is

$$\begin{aligned} \int \frac{q_{_T}^2\mathrm{d}q_{_T}}{2{\pi }^2}Tr\left[ \overline{\varphi }^{++} \frac{{/}\!\!\! {P}}{M}\varphi ^{++}\frac{{/}\!\!\!{P}}{M}-\overline{\varphi }^{--} \frac{{/}\!\!\! {P}}{M}\varphi ^{--}\frac{{/}\!\!\! {P}}{M}\right] =2P_{0}.\nonumber \\ \end{aligned}$$

(8)

In our model, the instantaneous interaction kernel V is the Cornell potential, which is the sum of a linear scalar interaction and a vector interaction:

$$\begin{aligned} V(r)= & {} V_\mathrm{s}(r)+V_0+\gamma _{_0}\otimes \gamma ^0 V_\mathrm{v}(r)\nonumber \\= & {} \lambda r+V_0-\gamma _{_0}\otimes \gamma ^0\frac{4}{3}\frac{\alpha _\mathrm{s}}{r}, \end{aligned}$$

(9)

where $\lambda$ is the string constant and $\alpha _\mathrm{s}({\vec {q}})$ is the running coupling constant. In order to fit the data of heavy quarkonia, a constant $V_0$ is often added to confine the potential. To avoid the infrared divergence $V_\mathrm{v}({{\vec {q}}})$ at $q=0$ in the momentum space, we introduce a factor $e^{-\alpha r}$ to avoid the divergence:

$$\begin{aligned} V_\mathrm{s}(r)=\frac{\lambda }{\alpha }(1-e^{-\alpha r}), \quad V_\mathrm{v}(r)=-\frac{4}{3}\frac{\alpha _\mathrm{s}}{r}e^{-\alpha r}. \end{aligned}$$

(10)

It is easy to see that when $\alpha r\ll 1$, the potential becomes to Eq. (9). In the momentum space and the C.M.S. of the bound state, the potential reads

$$\begin{aligned}&V({\vec {q}})=V_\mathrm{s}({\vec {q}}) +\gamma _{_0}\otimes \gamma ^0 V_\mathrm{v}({\vec {q}}),\nonumber \\&V_\mathrm{s}({\vec {q}})=-\left( \frac{\lambda }{\alpha }+V_0\right) \delta ^3({\vec {q}})+\frac{\lambda }{\pi ^2} \frac{1}{{({\vec {q}}}^2+{\alpha }^2)^2},\nonumber \\&V_\mathrm{v}({\vec {q}})=-\frac{2}{3{\pi }^2}\frac{\alpha _\mathrm{s}( {\vec {q}})}{{({\vec {q}}}^2+{\alpha }^2)}, \end{aligned}$$

(11)

where the running coupling constant $\alpha _\mathrm{s}({\vec {q}})$ is:

$$\begin{aligned} \alpha _\mathrm{s}({\vec {q}})=\frac{12\pi }{33-2N_{f}}\frac{1}{\log \left( a+\frac{{{\vec {q}}}^2}{\Lambda ^{2}_\mathrm{QCD}}\right) }. \end{aligned}$$

We introduce a small parameter a to avoid the divergence in the denominator. The constants $\lambda$, $\alpha$, $V_0$ and $\Lambda _\mathrm{QCD}$ are the parameters that characterize the potential. $N_{f}=3$ for ${\bar{bq}}$ (and ${\bar{cq}}$) system.

3 The Relativistic Wave Functions

In this paper, we focus on the two-body open charm strong decay of X(3940) and X(4160), which are considered as $\eta _c(3S)$ $\eta _c(4S)$ states. $\eta _c(3S)$ $\eta _c(4S)$ states have two decay modes: $0^-\rightarrow 0^-1^-$ and $0^-\rightarrow 1^-1^-$. So we only discuss the relativistic wave functions of $J^{P}$ equal to $0^{-}(^1S_0)$ and $1^-(^3S_1)$ states.

3.1 For pseudoscalar meson with quantum numbers $J^{P}=0^{-}$

The general form for the relativistic wave function of the pseudoscalar meson can be written as [46]

$$\begin{aligned} \varphi _{0^-}({\vec {q}})= & {} \left[ f_1({\vec {q}}){\not \!P}+f_2({\vec {q}})M+ f_3({\vec {q}})\not \!{q_\bot }+f_4({\vec {q}})\frac{{\not \!P}\not \!{q_\bot }}{M}\right] \gamma _5,\nonumber \\ \end{aligned}$$

(12)

where M is the mass of the pseudoscalar meson, and $f_i({\vec {q}})$ are functions of $|{\vec {q}}|^2$. Due to the last two equations of Eq. (7): $\varphi _{0^-}^{+-}=\varphi _{0^-}^{-+}=0$, we have

$$\begin{aligned} f_3({\vec {q}})= & {} \frac{f_2({\vec {q}}) M(-\omega _1+\omega _2)}{m_2\omega _1+m_1\omega _2},\quad \nonumber \\ f_4({\vec {q}})= & {} -\frac{f_1({\vec {q}}) M(\omega _1+\omega _2)}{m_2\omega _1+m_1\omega _2}, \end{aligned}$$

(13)

where $m_1, m_2$ and $\omega _1=\sqrt{m_1^{2}+\vec {q}^2},\omega _2=\sqrt{m_2^{2}+\vec {q}^2}$ are the masses and the energies of quark and anti-quark in the mesons, $q_{\bot }^2=-|{\vec {q}}|^2$.

The numerical values of the radial wave functions $f_1$, $f_2$ and eigenvalue M can be obtained by solving the first two Salpeter equations in Eq. (7). In Ref. [31], we have plotted the wave functions of X(3940) and X(4160), which are considered as $\eta _c(3S)$ and $\eta _c(4S)$, respectively.

According to Eq. (6) the relativistic positive wave function of the pseudoscalar meson in C.M.S. can be written as [46]

$$\begin{aligned} {\varphi }^{++}_{0^-}(\vec {q})=b_1 \left[ b_2+\frac{\not \!{P}}{M}+b_3\not \!{q_{\bot }} +b_4\frac{\not \!{q_{\bot }}\not \!{P}}{M}\right] {\gamma }_5, \end{aligned}$$

(14)

where the $b_i$s ($i=1,~2,~3,~4$) are related to the original radial wave functions $f_1$, $f_2$, quark masses $m_1$, $m_2$, quark energy $w_1$, $w_2$, and meson mass M:

$$\begin{aligned} b_1= & {} \frac{M}{2}\left( {f}_{1}(\vec {q}) +{f}_{2}(\vec {q})\frac{m_1+m_2}{\omega _1+\omega _2}\right) ,\quad b_2=\frac{\omega _1+\omega _2}{m_1+m_2},\nonumber \\ b_3= & {} -\frac{(m_1-m_2)}{m_1\omega _2+m_2\omega _1},\quad b_4=\frac{(\omega _1+\omega _2)}{(m_1\omega _2+m_2\omega _1)}. \end{aligned}$$

3.2 For vector meson with quantum numbers $J^{P}=1^{-}$

The general form for the relativistic wave functions of vector state $J^P=1^-$(or $J^\mathrm{PC}=1^{--}$ for quarkonium) can be written as eight terms, which are constructed by $P_{f1}$, $q_{f1\perp }$, $\epsilon _1$ and the gamma matrices [47],

$$\begin{aligned} \varphi _{1^{-}}({\vec {q}}_{f1})= & {} q_{f1\perp }\cdot {\epsilon }_1 \Bigg [f'_1+\frac{\not \!P_{f1}}{M_{f1}}f'_2+ \frac{{\not \!q}_{f1\perp }}{M_{f1}}f'_3\nonumber \\&+\frac{{\not \!P_{f1}} {\not \!q}_{f1\perp }}{M_{f1}^2} f'_4\Bigg ]+M_{f1}{\not \!\epsilon _1}f'_5\nonumber \\&+ {\not \!\epsilon _1}{\not \!P_{f1}}f'_6+ ({\not \!q}_{f1\perp }{\not \!\epsilon _1}- q_{f1\perp }\cdot {\epsilon _1}) f'_7\nonumber \\&+\frac{1}{M_{f1}}({\not \!P_{f1}}{\not \!\epsilon _1} {\not \!q}_{f1\perp }-{\not \!P_{f1}}q_{f1\perp }\cdot {\epsilon _1}) f'_8,\nonumber \\ \end{aligned}$$

(15)

where ${\epsilon }_1$ is the polarization vector of the vector meson in the final state.

Due to the last two equations of Eq. (7): $\varphi _{0^-}^{+-}=\varphi _{0^-}^{-+}=0$, we have [48]

$$\begin{aligned}&f'_1=\frac{\left[ q_{f1\perp }^2 f'_3+M_{f1}^2f'_5 \right] (m'_1m'_2-w'_1w'_2+q_{f1\perp }^2)}{M_{f1}(m'_1+m'_2)q_{f1\perp }^2},\quad \\&f'_7=\frac{f'_5M_{f1}(-w'_1+w'_2)}{(m'_1w'_2+m'_2w'_1)},\\&f'_2=\frac{\left[ -q_{f1\perp }^2 f'_4+M_{f1}^2f'_6\right] (m'_1w'_2-m'_2w'_1)}{M_{f1}(w'_1+w'_2)q_{f1\perp }^2},\quad \\&f'_8=\frac{f'_6M_{f1}(w'_1w'_2-m'_1m'_2-q_{f1\perp }^2)}{(m'_1+m'_2)q_{f1\perp }^2}. \end{aligned}$$

The relativistic positive wave functions of $^3S_1$ state can be written as [49]

$$\begin{aligned} {\varphi }_{1^{-}}^{++}(\vec {q}_{f1})= & {} b_1\not \!{\epsilon }_1+b_2\not \!{\epsilon }_1\not \!{P_{f1}} +b_3(\not \!{q_{f1\bot }}\not \!{\epsilon }_1-q_{f1\bot }\cdot {\epsilon }_1)\nonumber \\&+\,b_4(\not \!{P_{f1}}\not \!{\epsilon }_1\not \!{q_{f1\bot }}-\not \!{P_{f1}}q_{f1\bot }\cdot {\epsilon }_1) +q_{f1\bot }\nonumber \\&\cdot \,{\epsilon }_1(b_5+b_6\not \!{P_{f1}}+b_7\not \!{q_{f1\bot }}+b_8\not \!{q_{f1\bot }}\not \!{P_{f1}}),\nonumber \\ \end{aligned}$$

(16)

where we first define the parameters $n_i$, which are functions of the $f'_i$ ($^3S_1$ wave functions):

$$\begin{aligned} n_1= & {} f'_5 -f'_6\frac{(w'_1+w'_2)}{(m'_1+m'_2)},\quad n_2=f'_5 -f'_6\frac{(m'_1+m'_2)}{(w'_1+w'_2)},\\ n_3= & {} f'_3 +f'_4\frac{(m'_1+m'_2)}{(w'_1+w'_2)}, \end{aligned}$$

then we define the parameters $b_i$, which are functions of $f'_i$ and $n_i$:

$$\begin{aligned}&b_1=\frac{M_{f1}}{2}n_1,\quad b_2=-\frac{(m'_1+m'_2)}{2(w'_1+w'_2)}n_1,\\&b_3=\frac{M_{f1}(w'_2-w'_1)}{2(m'_1w'_2+m'_2w'_1)}n_1,\\&b_4=\frac{(w'_1+w'_2)}{2(w'_1w'_2+m'_1m'_2-{q_{f1\bot }^{2}})}n_1,\\&b_5=\frac{1}{2M_{f1}}\frac{(m'_1+m'_2)(M_{f1}^2n_2+{q_{f1\bot }^{2}}n_3)}{(w'_1w'_2+m'_1m'_2+{q_{f1\bot }^{2}})},\\&b_6=\frac{1}{2M_{f1}^2}\frac{(w'_1-w'_2)(M_{f1}^2n_2+{q_{f1\bot }^{2}}n_3)}{(w'_1w'_2+m'_1m'_2+{q_{f1\bot }^{2}})},\\&b_7=\frac{n_3}{2M_{f1}}-\frac{f'_6M_{f1}}{(m'_1w'_2+m'_2w'_1)},\\&b_8=\frac{1}{2M_{f1}^2}\frac{w'_1+w'_2}{m'_1+m'_2}n_3\\&\quad \qquad -f'_5\frac{w'_1+w'_2}{(m'_1+m'_2)(w'_1w'_2+m'_1m'_2-{q_{f1\bot }^{2}})}. \end{aligned}$$

4 The formulation of two-body open charm strong decays

For the two-body OZI-allowed open charm strong decays, such as $\eta _c(3S)\rightarrow D{\bar{D}}^*$, we adopt the $^3P_0$ model to calculate the strong decay amplitude. The non-relativistic $^3P_0$ model describe the decay matrix elements by the $q{\bar{q}}$ pair-production Hamiltonian: $H=g\int \mathrm{d}^3x{\bar{\psi }}\psi$ [42]. According to the improved BS method which is a relativistic model, we can extend the non-relativistic $^3P_0$ model to the relativistic form: $H=-ig\int \mathrm{d}^4x{\bar{\psi }}\psi$ [11, 33]. Here $\psi$ is the Dirac quark field, $g=2m_q\gamma$, $m_q$ is the quark mass of the light quark pairs, $\gamma$ is a dimensionless constant which describes the pair-production strength and can be obtained by fitting the experimental data. In this paper, we choose $\gamma =0.483$ [43] which gives a reasonable calculation of $\eta _c(3S)$, then we use the same value for $\eta _c(4S)$.

Fig. 1

The Feynman diagram of two-body open charm strong decay

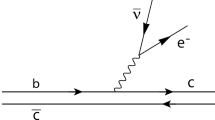
Using the $q{\bar{q}}$ pair-production Hamiltonian, the amplitude of two-body OZI-allowed open charm strong decays $A\rightarrow B+C$ in Fig. 1, can be written as [11, 33]

$$\begin{aligned} \langle BC|H|A\rangle= & {} -ig\int \frac{\mathrm{d}^4q}{(2\pi )^4} \mathrm{Tr}[\chi _P(q)S_2^{-1}(p_2) {\bar{\chi }}_{P_{f2}}(q_{f2})\nonumber \\&\times {\bar{\chi }}_{P_{f1}}(q_{f1})S_1^{-1}(p_1)]\nonumber \\= & {} g\int \frac{\mathrm{d}^3{\vec {q}}}{(2\pi )^3}\mathrm{Tr}\left[ \frac{\not \!{P}}{M}\varphi ^{++}_P({\vec {q}}) \frac{\not \!{P}}{M}{\bar{\varphi }}^{++}_{P_{f2}}({\vec {q}}_{f2})\right. \nonumber \\&\times \left. {\bar{\varphi }}^{++}_{P_{f1}}({\vec {q}}_{f1})\right] \left( 1-\frac{M-w_1-w_2}{2w_{12}}\right) , \end{aligned}$$

(17)

where $\varphi ^{++}_P({\vec {q}})$, $\varphi ^{++}_{P_{f1}}({\vec {q}}_{f1})$ and $\varphi ^{++}_{P_{f2}}({\vec {q}}_{f2})$ are the relativistic positive wave functions of the initial meson A, the final mesons B and C, respectively. ${\bar{\varphi }}=\gamma ^0\varphi ^\dagger \gamma ^0$. We have given the detailed form of wave functions in Sect. 3. P, $P_{f1}$, $P_{f2}$ and ${\vec {q}}$, ${\vec {q}}_{f1}$, ${\vec {q}}_{f2}$ are the momentum and the three-dimensional relative momentum between quark and anti-quark of the initial meson A, the final mesons B and C, respectively. We have $\vec {q}_{f1}={\vec {q}}-\frac{m_c}{m_c+m_{u,d,s}}\vec {P}_{f1}$, $\vec {q}_{f2}={\vec {q}}+\frac{m_c}{m_c+m_{u,d,s}}\vec {P}_{f2}$. $\vec {P}_{f1}$ and $\vec {P}_{f2}$ are the three momenta of the final mesons B and C. $w_{12}=\sqrt{m_{u,d,s}^2+{\vec {q}}^2_{f1}}$.

Using the BS wave functions in Sect. 3 and the formula for the amplitude, Eq. (17), the two-body open charm strong decay amplitude can be defined as

$$\begin{aligned}&\mathcal M(A\rightarrow D{\bar{D}}^*)=\epsilon _{1\mu }P^\mu t_1,\nonumber \\&\mathcal M(A\rightarrow D^*{\bar{D}}^*)=\varepsilon _{\mu \nu \alpha \beta }P^\mu P^\nu _{f1}\epsilon ^{\alpha }_1\epsilon ^{\beta }_2 t_2, \end{aligned}$$

(18)

where A denotes $\eta _c(3S)$ or $\eta _c(4S)$, $\epsilon _{1}$ and $\epsilon _{2}$ are the polarization vector of the final mesons B and C. $t_1$ and $t_2$ are the strong decay coupling constants, which are related to the BS wave functions.

Finally, using Eq. (18) the two-body open charm strong decay width can be written as

$$\begin{aligned} \Gamma =\frac{|{\vec {P}}_{f1}|}{8\pi M^2}\sum _{\lambda }|\mathcal M|^2, \end{aligned}$$

(19)

where $|{\vec {P}}_{f1}|=\sqrt{[M^2-(M_{f1}-M_{f2})^2][M^2-(M_{f1}+M_{f2})^2]}/(2M)$, which is the three momentum of the final mesons.

Table 1 The exclusive strong decay widths of $\eta _c(3S)$ and $\eta _c(4S)$ (unit in MeV)

5 Number results and discussions

In order to fix the Cornell potential in Eq. (11) and the masses of the quarks, we take these parameters: $a=e=2.7183, \lambda =0.210$ GeV$^2$, ${\Lambda }_\mathrm{QCD}=0.270$ GeV, $\alpha =0.060$ GeV, $m_u=0.305$ GeV, $m_d=0.311$ GeV, $m_\mathrm{s}=0.500$ GeV, $m_b=4.96$ GeV, $m_c=1.62$ GeV, etc. [29], which are best to fit the mass spectra of the ground states B, D mesons and the other heavy mesons. We get the masses $M_{D^\pm }=1.869$ GeV, $M_{D^0}=1.865$ GeV, $M_{D_\mathrm{s}^\pm }=1.968$ GeV, $M_{D^{*0}}=2.007$ GeV, $M_{D^{*\pm }}=2.010$ GeV, $M_{D_\mathrm{s}^{*\pm }}=2.112$ GeV, $M_{\eta _c(3S)}=3.942$ GeV, $M_{\eta _c(4S)}=4.156$ GeV.

Considering X(3940) as the $\eta _c(3S)$ state, there is only one decay mode: $0^-\rightarrow 1^-0^-$, According to the kinematic ranges, the corresponding final states are $D^{0}{\bar{D}}^{*0}$, ${\bar{D}}^{0} D^{*0}$, $D^{+}D^{*-}$ and $D^{*+}D^{-}$. Considering the X(4160) as $\eta _c(4S)$ state, there are two decay modes: $0^-\rightarrow 1^-0^-$ and $0^-\rightarrow 1^-1^-$, within the kinematic ranges, the corresponding decay channels include $D^{0}{\bar{D}}^{*0}$, ${\bar{D}}^{0} D^{*0}$, $D^{+}D^{*-}$, $D^{*+}D^{-}$, $D^+_\mathrm{s}D^{*-}_\mathrm{s}$, $D^-_\mathrm{s}D^{*+}_\mathrm{s}$, $D^{*0}{\bar{D}}^{*0}$ and $D^{*-} D^{*+}$. We have shown the exclusive two-body open charm strong decay widths of $\eta _c(3S)$ and $\eta _c(4S)$ in Table 1, where $D{\bar{D}}^*$ means $D^0{\bar{D}}^{*0}$+$D^+D^{*-}$ and $D^*{\bar{D}}^*$ means $D^{*0}{\bar{D}}^{*0}$+$D^{*-} D^{*+}$. For $D^0{\bar{D}}^{*0}$, $D^+D^{*-}$ and $D^-_\mathrm{s}D^{*+}_\mathrm{s}$, we have considered theisospin conservation of the final mesons. In Table 2, we have presented the total widths with different theoretical models and the experimental data for convenience. We also consider the uncertainties by varying all the input parameters simultaneously within ±5$\%$ of the central values in Tables 1 and 2.

Table 2 The total strong decay widths of $\eta _c(3S)$ and $\eta _c(4S)$ (unit in MeV). ‘Ex.’ means the experimental data of X(3940) and X(4160) from PDG [1]

Fig. 2

The relation of decay width to the mass of $\eta _c(3S)$

Fig. 3

The relation of different decay width with the mass of $\eta _c(4S)$

In Table 1, we find that the dominant strong decay channel of $\eta _c(3S)$ is $D{\bar{D}}^*$, and we have agreement with the experimental observation by Belle Collaboration [2, 3]. The total two-body open charm strong decay width of $\eta _c(3S)$ is $\Gamma _{\eta _c(3S)}=(33.5^{+18.4}_{-15.3})$ MeV, which is smaller than the result of Ref. [20], but it is in accordance with experimental results. So $\eta _c(3S)$ could be a good candidate of the X(3940). Because of the mass of X(3940) having errors, we plot the relations of the decay widths of $\eta _c(3S)$ with the masses of $\eta _c(3S)$ in Fig. 2, the relations of the decay widths with the masses of $\eta _c(3S)$ are linear. The decay widths increase with the increase of the masses of $\eta _c(3S)$.

For the $\eta _c(4S)$ state, the main strong decay channels are $D{\bar{D}}^*$ and $D^*{\bar{D}}^*$, $\eta _c(4S)\rightarrow D^-_\mathrm{s}D^{*+}_\mathrm{s}$ is very small with the small phase space, and the decay $\eta _c(4S)\rightarrow D{\bar{D}}$ is forbidden. In Table 2, the total two-body open charm strong decay width of $\eta _c(4S)$ is $\Gamma _{\eta _c(4S)}=(69.9^{+22.4}_{-21.1})$ MeV. Our result is larger than the result of Ref. [17], but considering the uncertainties of the results, our result is close to the lower limit of X(4160) for the experimental data [3]. In our calculation, the ratio of the decay width $\frac{\Gamma (\eta _c(4S)\rightarrow D{\bar{D}})}{\Gamma (\eta _c(4S)\rightarrow D^*{\bar{D}}^*)}=0$, which is consistent with the experimental data $\frac{\Gamma (X(4160)\rightarrow D{\bar{D}})}{\Gamma (X(4160)\rightarrow D^*{\bar{D}}^*)}<0.09$ [3]. There is another ratio of the decay width: $\frac{\Gamma (\eta _c(4S)\rightarrow D{\bar{D}}^*)}{\Gamma (\eta _c(4S)\rightarrow D^*{\bar{D}}^*)}=3.67$, which is much larger than the upper limit of the experimental data $\frac{\Gamma (X(4160)\rightarrow D{\bar{D}}^*)}{\Gamma (X(4160)\rightarrow D^*{\bar{D}}^*)}<0.22$ which is reported by Belle [3]. In order to find the relation of the decay width to the mass of $\eta _c(4S)$, we plot the relation of the different decay width and decay ratio to the mass of $\eta _c(4S)$ in Figs. 3 and 4. Especially in Fig. 4, the decay ratio is decreased with the increased mass of $\eta _c(4S)$, but the decay ratio is larger than the experimental data at large mass, so $\eta _c(4S)$ is not a candidate of X(4160), and more investigations of X(4160) are needed in the future.

Fig. 4

The relation of $\Gamma _{\eta _c(4S)\rightarrow D{\bar{D}}^*}/\Gamma _{\eta _c(4S)\rightarrow D^*{\bar{D}}^*}$ with the mass of $\eta _c(4S)$

In summary, considering X(3940) and X(4160) as $\eta _c(3S)$ and $\eta _c(4S)$ states, we study the two-body open charm OZI-allowed strong decay of $\eta _c(3S)$ and $\eta _c(4S)$ by the improved BS method combined with the $^3P_0$ model. For the strong decay of $\eta _c(3S)$, the dominant strong decay is $\eta _c(3S)\rightarrow D{\bar{D}}^*$, the corresponding strong decay width is $\Gamma _{\eta _c(3S)}=(33.5^{+18.4}_{-15.3})$ MeV, which is close to the experimental data; therefore, $\eta _c(3S)$ is a good candidate of X(3940). For the $\eta _c(4S)$ state, the main strong decay channels are $D{\bar{D}}^*$ and $D^*{\bar{D}}^*$, $\eta _c(4S)$ cannot decay to $D{\bar{D}}$, which has not been observed for X(4160) in experiment. $\Gamma (D^*{\bar{D}}^*)$ is smaller than $\Gamma (D{\bar{D}}^*)$, the ratio of the decay widths $\frac{\Gamma (D{\bar{D}}^*)}{\Gamma (D^*{\bar{D}}^*)}$ is larger than the experimental data by Belle. We also find that the ratio of the decay widths $\frac{\Gamma (D{\bar{D}}^*)}{\Gamma (D^*{\bar{D}}^*)}$ is dependent on the mass of $\eta _c(4S)$. Finally, we calculate the strong decay width of $\eta _c(4S)$: $\Gamma _{\eta _c(4S)}=(69.9^{+22.4}_{-21.1})$ MeV; considering the errors of the results, it is close to the lower limit of X(4160). With large errors of the full decay width, it is hard to confirm that $\eta _c(4S)$ is a candidate of X(4160). But the ratio of the decay widths $\frac{\Gamma (D{\bar{D}}^*)}{\Gamma (D^*{\bar{D}}^*)}$ is not consistent with the experimental data, so taking the $\eta _c(4S)$ as an assignment of X(4160) can be excluded and more investigations are needed in the future.