LHC di-photon excess and gauge coupling unification in extra $Z^\prime$ heterotic-string derived models

Abstract

A di-photon excess at the LHC can be explained as a Standard Model singlet that is produced and decays by heavy vector-like colour triplets and electroweak doublets in one-loop diagrams. The characteristics of the required spectrum are well motivated in heterotic-string constructions that allow for a light $Z^\prime$. Anomaly cancellation of the $U(1)_{Z^\prime }$ symmetry requires the existence of the Standard Model singlet and vector-like states in the vicinity of the $U(1)_{Z^\prime }$ breaking scale. In this paper we show that the agreement with the gauge coupling data at one-loop is identical to the case of the Minimal Supersymmetric Standard Model, owing to cancellations between the additional states. We further show that effects arising from heavy thresholds may push the supersymmetric spectrum beyond the reach of the LHC, while maintaining the agreement with the gauge coupling data. We show that the string-inspired model can indeed produce an observable signal and discuss the feasibility of obtaining viable scalar mass spectrum.

1 Introduction

The Standard Model of particle physics provides viable parameterisation for all subatomic data to date. The most striking feature of the Standard Model, augmented by right-handed neutrinos that are required by the neutrino data, is the embedding of its chiral spectrum in three chiral 16 representations of SO(10). Heterotic-string models give rise to spinorial 16 representations in the perturbative spectrum and therefore preserve the SO(10) embedding of the Standard Model states [1, 2].

Recently, a possible signal has been reported by the ATLAS [3] and CMS [4] collaborations that would indicate a clear deviation from the Standard Model. Both experiments reported early indications for enhancement of di-photon events with a resonance at 750 GeV, and generated substantial interest [5–78]. A plausible explanation for this enhancement is obtained if the resonant state is assumed to be a Standard Model singlet state, and the production and decay are mediated by heavy vector-like quark and lepton states [5–95]. These characteristics arise naturally in heterotic-string models that allow for a light extra $Z^\prime$ [96].

We note that the construction of heterotic-string models that allow for a light $Z^\prime$ is highly non-trivial [97–105]. The reason is that the extra family universal U(1) symmetries that are typically discussed in the string-inspired literature tend to be anomalous and are therefore broken near the string scale [106–108]. The relevant symmetries tend to be anomalous due to the symmetry breaking pattern $E_6\rightarrow SO(10)\times U(1)_\zeta$, induced at the string level by the Gliozzi–Scherk–Olive (GSO) projection [109]. In Ref. [105] we used the spinor–vector duality property of $Z_2\times Z_2$ orbifolds [110–114] to construct a string derived model with anomaly free $U(1)_\zeta$, thus enabling it to remain unbroken down to low scales.

An additional constraint imposed by the heterotic-string is that the gauge, as well as the gravitational, couplings are unified at the string scale [115, 116]. Since the early 1990s, much of the research on the phenomenology of supersymmetric grand unified theories has been motivated by the observation that the unification of the gauge couplings in SUSY GUTs is compatible with the measured gauge coupling data at the electroweak scale, provided that we assume that the spectrum between the two scales consists of that of the Minimal Supersymmetric Standard Model (MSSM) [117–122]. Following Witten we may assume that the string and GUT scales may coincide in the framework of M-theory [123].

A vital question therefore is to examine what is the corresponding situation in the heterotic-string derived $Z^\prime$ models. We find that, quite remarkably, in the $Z^\prime$ models the compatibility of gauge coupling unification with the data at the electroweak scale is identical to the case of the MSSM. We further show that effects arising from heavy thresholds may push the supersymmetric spectrum beyond the reach of the LHC, while maintaining the agreement with the gauge coupling data. We show that the string-inspired model can indeed account for the observed signal and discuss the feasibility of obtaining viable scalar mass spectrum.

While further data from the LHC did not substantiate the observation of the di-photon excess [124, 125], a di-photon excess is a general signature of this class of $Z^\prime$ models. The results presented in this paper are therofore relevant for continuing $Z^\prime$ searches at the LHC.

2 The string model and extra $Z^\prime$

The difficulty in constructing heterotic-string models with light $Z^\prime$ symmetries arises due to the breaking of the observable $E_6$ symmetry in the string constructions by discrete Wilson lines to $SO(10)\times U(1)_\zeta$. Application of the symmetry breaking at the string level results in the projection of some states from the physical spectrum. The consequence is that $U(1)_\zeta$ is in general anomalous in the string vacua, and cannot remain unbroken to low scales. The extra U(1) symmetry which is embedded in SO(10), and is orthogonal to the Standard Model weak hypercharge, is typically broken at the high scale to generate sufficiently light neutrino masses. Flavour non-universal U(1) symmetries must be broken above the deca-TeV scale to avoid conflict with Flavour Changing Neutral Current (FCNC) constraints [126].

The string derived model of Ref. [105] was constructed in the free fermionic formulation [127–129] of the heterotic-string. The details of the construction, the massless spectrum of the model and its superpotential are given in Ref. [105] and will not be repeated here. We review here the properties of the model that are relevant for the anomaly free extra $Z^\prime$ symmetry.

The model utilises the spinor–vector duality symmetry that was observed in the space of fermionic $Z_2\times Z_2$ orbifold compactifications [110–114]. The spinor–vector duality operates under exchange of the total number of spinorial $({16}\oplus \overline{16})$ representations of SO(10) with the total number of vectorial 10 representations. For every string vacuum with a $\#_1$ of $({16}\oplus \overline{16})$ representations and $\#_2$ of 10 representations there is a dual vacuum in which $\#_1\leftrightarrow \#_2$. The understanding of this duality is facilitated by considering the vacua in which the $SO(10)\times U(1)_\zeta$ symmetry is enhanced to $E_6$. The chiral representations of $E_6$ are the 27 and $\overline{27}$ and their decomposition under $SU(10)\times U(1)_\zeta$ is

$$\begin{aligned} 27= & {} 16_{+{1/2}} + 10_{-1} + 1_{+2},\\ \overline{27}= & {} \overline{16}_{-{1/2}} + 10_{+1} + 1_{-2}, \end{aligned}$$

where the subscript denotes the $U(1)_\zeta$ charge. Thus, the string vacua with $E_6$ symmetry are self-dual with respect to the spinor–vector duality, i.e. in these vacua $\#_1(16\oplus \overline{16})=\#_2(10)$. In this case $U(1)_\zeta$ is anomaly free by virtue of its embedding in $E_6$. There exist a discrete Wilson line that reduce $E_6$ symmetry to $SO(10)\times U(1)_\zeta$ with $\#_1(16\oplus \overline{16})~ \& ~\#_2(10)$, and a corresponding discrete Wilson line with $\#_2(16\oplus \overline{16})~ \& ~ \#_1(10)$ [113, 114].

The string vacua with enhanced $E_6$ symmetry correspond to heterotic-string vacua with (2, 2) worldsheet supersymmetry. We can realise the $E_6$ symmetry by breaking the ten dimensional untwisted gauge symmetry to $SO(8)^4$ [110–112]. One of the SO(8) factors is reduced further to $SO(2)^4$ and the $E_6$ symmetry is generated from additional sectors in the string vacua. In parallel to the spectral flow operator on the supersymmetric side of the heterotic-string that maps between different spacetime spin representations, there exists a spectral flow operator on the bosonic side. In the vacua with enhanced $E_6$ symmetry the spectral flow operator exchanges between the spinorial and vectorial components in the $E_6$ representations. The spectral flow operator is the U(1) generator of the $N=2$ worldsheet supersymmetry on the bosonic side of the heterotic-string. In the vacua with broken $E_6$ symmetry, the $N=2$ worldsheet supersymmetry on the bosonic side is broken and the spectral flow operator induces the map between the spinor–vector dual vacua. The picture was extended to other internal CFTs in Ref. [130].

Table 1 Observable sector field notation and associated states in [105]

The class of $Z_2\times Z_2$ vacua affords another possibility. It is possible to construct self-dual vacua with $\#_1(16\oplus \overline{16})=\#_2(10)$, without enhancing the gauge symmetry to $E_6$. This is the case if the different components of the $E_6$ representations are obtained from different fixed points of the $Z_2\times Z_2$ orbifold. The spectrum then forms complete $E_6$ representations, but the gauge symmetry is not enhanced to $E_6$ and remains $SO(10)\times U(1)_\zeta$, with $U(1)_\zeta$ being anomaly free due to the fact that the chiral spectrum still forms complete $E_6$ multiplets. It is important to note that this is possible only because the spinorial and vectorial SO(10) representations are obtained from different fixed points. Obtaining the 16 and $(10+1)$ components at the same fixed point necessarily implies that the gauge symmetry is enhanced to $E_6$.

The construction of Ref. [105] utilises the classification methods developed in Ref. [131] for type IIB string and in Refs. [132, 133] for heterotic-string vacua with unbroken SO(10) gauge group. The heterotic-string classification was extended to vacua with the Pati–Salam and flipped SU(5) subgroups of O(10) in Refs. [134–136], respectively. In this method a space of the order of $10^{12}$ is spanned and models with specific phenomenological characteristics can be extracted. The string vacuum with anomaly free $U(1)_{Z^\prime }$ is obtained by first trawling a self-dual SO(10) model with six chiral families and subsequently breaking the SO(10) symmetry to the Pati–Salam subgroup [105]. The chiral spectrum of the models forms complete $E_6$ representations, whereas the additional vector-like multiplets may reside in incomplete multiplets. This is in fact an additional important property of the string, which affects compatibility with the gauge coupling data. The complete massless spectrum of the model was presented in Ref. [105]. Spacetime vector bosons are obtained solely from the untwisted sector and generate the observable and hidden gauge symmetries, given by

$$\begin{aligned} \mathrm{observable}&: \; SO(6)\times SO(4) \times U(1)_1 \times U(1)_2\times U(1)_3 \\ \mathrm{hidden}&:\;SO(4)^2\times SO(8). \end{aligned}$$

The $E_6$ combination,

$$\begin{aligned} U(1)_\zeta = U(1)_1+U(1)_2+U(1)_3, \end{aligned}$$

(2.1)

is anomaly free whereas the orthogonal combinations of $U(1)_{1,2,3}$ are anomalous. The complete massless spectrum of the string model and the charges under the gauge symmetries are given in Ref. [105]. Tables 1 and 2 show a glossary of the states in the model and their charges under the $SU(4)\times SO(4)\times U(1)_\zeta$ group factors, where we adopt the notation of Ref. [96]. The sextet states are in vector-like representations with respect to the Standard Model, but are chiral under $U(1)_\zeta$. Thus, if $U(1)_\zeta$ is part of an unbroken $U(1)_{Z^\prime }$ combination down to low scales, it protects the sextets, and the corresponding bi-doublets, from acquiring a mass above the $U(1)_{Z^\prime }$ breaking scale. The model also contains vector-like states that transform under the hidden $SU(2)^4\times SO(8)$ group factors, with charges $Q_\zeta =\pm 1$ or $Q_\zeta =0$.

Table 2 Hidden sector field notation and associated states in [105]

As noted from Table 1 the string model contains the Higgs representations required to break the non-Abelian Pati–Salam gauge symmetry [137]. These are $\mathcal{H}=F_R$ and $\bar{\mathcal{H}}$, being a linear combination of the four $\bar{F}_R$ fields. The decomposition of these fields under the Standard Model group is given by

$$\begin{aligned}&{\bar{\mathcal H}}(\bar{\mathbf{4}},\mathbf{1,2}) \rightarrow u^{c}_{H}\left( \bar{\mathbf{3}},\mathbf{1},\frac{2}{3}\right) +d^{c}_H\left( {\bar{\mathbf{3}}},\mathbf{1},-\frac{1}{3}\right) \\&\quad +\,{\bar{\mathcal N}}\left( \mathbf{1,1},0\right) + e^{c}_H\left( \mathbf{1,1},-1\right) \\&{\mathcal H}\left( \mathbf{4,1,2}\right) \rightarrow u_{H}\left( \mathbf{3,1},-\frac{2}{3}\right) + d_{H}\left( \mathbf{3,1},\frac{1}{3}\right) \\&\quad +\, {\mathcal N}\left( \mathbf{1,1},0\right) + e_{H}\left( \mathbf{1,1},1\right) \end{aligned}$$

Table 3 Spectrum and $SU(3)_C\times SU(2)_L\times U(1)_{Y}\times U(1)_{{Z}^\prime }$ quantum numbers, with $i=1,2,3$ for the three light generations

The suppression of the left-handed neutrino masses favours the breaking of the Pati–Salam (PS) gauge symmetry at the high scale [138–143]. The possibility of breaking the PS symmetry at a low scale was considered in Refs. [144–148]. Here we will take the PS breaking scale to be in the vicinity of the string scale or slightly below. The VEVs of the heavy Higgs fields that break the PS gauge group leave an unbroken $U(1)_{Z^\prime }$ symmetry given by

$$\begin{aligned} U(1)_{{Z}^\prime } = {1\over {2}} U(1)_{B-L} -{2\over 3} U(1)_{T_{3_R}} - {5\over 3}U(1)_\zeta ~\notin ~ SO(10),\nonumber \\ \end{aligned}$$

(2.2)

which may remain unbroken down to low scales provided that $U(1)_\zeta$ is anomaly free. Cancellation of the anomalies requires that the additional vector-like quarks and leptons, which arise from the 10 representation of SO(10), as well as the SO(10) singlet in the 27 of $E_6$, remain in the light spectrum. The three right-handed neutrino states are neutral under the low scale gauge symmetry and receive a mass of the order of Pati–Salam breaking scale. The spectrum below the PS breaking scale is displayed schematically in Table 3. The spectrum is taken to be supersymmetric down to the TeV scale. As in the MSSM, compatibility of gauge coupling unification with the experimental data requires the existence of one vector-like pair of Higgs doublets, beyond the number of vector-like triplets. This is possible in the free fermionic heterotic-string models due to the stringy doublet–triplet splitting mechanism [149, 150]. We allow also for the possibility of light states that are neutral under the low scale gauge group. In Ref. [96] we showed that the string model contains all the ingredients to account for the LHC di-photon excess, provided that the vector-like pairs of colour triplets and electroweak doublets receive a mass of the order of the TeV scale. This explanation is particularly appealing if the $U(1)_{Z^\prime }$ remains unbroken down to low scales. In this case the mass of the vector-like states can only be generated by the VEV of the SO(10) singlets $S_i$ and/or ${\phi _{1,2}}$ that breaks the $U(1)_{Z^\prime }$ gauge symmetry. In this scenario the scale of the di-photon excess fixes the scale of the $U(1)_{Z^\prime }$ breaking to be of the order of the TeV scale. It is therefore of interest to examine the compatibility of this picture with the gauge coupling data.

Table 4 Beta-function coefficients of the light thresholds in the string-inspired $Z^\prime$ model

3 Gauge coupling analysis

In this section we analyse the compatibility of gauge coupling unification in the string-inspired model with the low-energy gauge coupling data, where we may assume that the unification scale is either at the GUT or string scales [123]. We examine the case in which the PS symmetry is broken at the string scale as well as the case in which is broken at an intermediate scale. We take the following values for the input parameters at the Z-mass scale [151]:

$$\begin{aligned} \begin{array}{ll} M_Z = 91.1876\pm 0.0021 \text{ GeV }\\ \quad \left. \sin ^2\theta _W\left( M_Z\right) \right| _{\overline{\text{ MS }}} =0.23116\pm 0.00012\\ \alpha ^{-1}\equiv \alpha _{\text{ e.m. }}^{-1}\left( M_Z\right) =127.944\pm 0.014\\ \quad \alpha _3\left( M_Z\right) =0.1184\pm 0.0007. \end{array} \end{aligned}$$

(3.1)

We also include the top-quark mass of $M_t\sim 173.5$ GeV [151] and the Higgs boson mass of $M_H\sim 125$ GeV [152, 153] in our analysis. String unification implies that the Standard Model gauge couplings are unified at the heterotic-string scale. The one-loop renormalisation group equations (RGEs) for the gauge couplings are given by

$$\begin{aligned} \frac{1}{\alpha \left( M_X\right) } = \frac{1}{k_i\alpha _i\left( \mu \right) } -\frac{b_i}{2\pi } \log \frac{M_X}{\mu ^2} + \Delta _i^{\left( \text{ total }\right) }, \end{aligned}$$

(3.2)

where $b_i$ are the one-loop beta-function coefficients, $\Delta _i^{\left( \text{ total }\right) }$ represents corrections two-loop and mixing effects, and $k_i=\{1,1,5/3\}$ for $i=3,2,1$. The analysis is most revealing at the one-loop level. Therefore, for the most part we limit our exposition to the one-loop investigation and give an estimate of the higher order corrections, which do not affect the overall picture. We obtain algebraic expressions for $\sin ^2\theta _W\left( M_Z\right)$ and $\alpha _3\left( M_Z\right)$ by solving the one-loop RGEs. In our analysis, we initially assume the full spectrum of the $Z^\prime$ model between the unification scale, $M_X$, and the Z-boson scale, $M_Z$, and treat all perturbations as effective threshold terms. At the unification scale we have

$$\begin{aligned} \alpha _S\equiv \alpha _3(M_X)=\alpha _2(M_X)=k_1\alpha _Y(M_X), \end{aligned}$$

(3.3)

where $k_1={5}/{3}$ is the canonical SO(10) normalisation. We initially study the case in which the PS symmetry is broken at the string scale. In this case the expression for $\left. \sin ^2\theta _W\left( M_Z\right) \right| _{\overline{MS}}$ takes the general form

$$\begin{aligned} \left. \sin ^2\theta _W\left( M_Z\right) \right| _{\overline{MS}} = \Delta _{{Z^\prime }}^{\sin ^2\theta _W}+ \Delta _{\text{ L.T. }}^{\sin ^2\theta _W}+ \Delta _{ \text{ T.C. }}^{\sin ^2\theta _W} \end{aligned}$$

(3.4)

with $\left. \alpha _3\left( M_Z\right) \right| _{\tiny {\overline{MS}}}$ having a similar form with corresponding $\Delta ^{\alpha _3}$ corrections. Here $\Delta _{Z^\prime }$ is the one-loop contribution from the states of the $Z^\prime$ model between the unification scale and the Z-boson mass scale. $\Delta _{\text{ L.T. }}$ are corrections from the light thresholds, which consist of the light supersymmetric thresholds; the Higgs and the top mass thresholds; and the mass thresholds of the heavy vector-like matter states in the $Z^\prime$ model. The last term,

$$\begin{aligned} \Delta _{\text{ T.C. }}^{\sin ^2\theta _W} = \Delta _{ \text{ Yuk. }}^{\sin ^2\theta _W}+ \Delta _{ \text{2-loop }}^{\sin ^2\theta _W}+ \Delta _{ \text{ Conv. }}^{\sin ^2\theta _W}, \end{aligned}$$

(3.5)

includes the two-loop; kinetic mixing; Yukawa couplings and scheme conversion corrections. These corrections are found to be small and do not affect the overall picture. These effects can be absorbed into modifications of the light thresholds, which in any case are not fixed and can be varied. For $\sin ^2\theta _W\left( M_Z\right)$ we obtain

$$\begin{aligned} \Delta _{{Z^\prime }}^{\sin ^2\theta _W}&= \frac{3}{8} +\frac{5\alpha }{16\pi } \left( b_2^{{Z^\prime }} - b_1^{{Z^\prime }} \right) \log \frac{M_X}{M_Z}; \nonumber \\ \Delta _{\text{ L.T. }}^{\sin ^2\theta _W}&= \frac{5\alpha }{16\pi } \sum _i \left( b^{\text{ L.T. }}_{1_i}- b^{\text{ L.T. }}_{2_i} \phantom {\frac{1}{1}} \right) \log \frac{M_i}{M_Z}, \end{aligned}$$

(3.6)

where $M_i$ are the light mass thresholds and $\alpha =\alpha _{\text{ e.m. }}\left( M_Z\right)$. Similarly for $\alpha _3\left( M_Z\right)$, we have

$$\begin{aligned} \Delta _{{Z^\prime }}^{\alpha _3}= & {} \frac{3}{8\alpha }+ \frac{1}{2\pi } \left( \phantom {\frac{1}{1}} b_3^{{Z^\prime }} - \frac{3}{8} b_2^{{Z^\prime }} - \frac{5}{8} b_1^{{Z^\prime }} \right) \log \frac{M_S}{M_Z}; \nonumber \\ \Delta _{\text{ L.T. }}^{\alpha _3}= & {} \frac{1}{2\pi } \sum _i \left( \frac{5}{8} b^{\text{ L.T. }}_{1_i} + \frac{3}{8} b^{\text{ L.T. }}_{2_i} - b^{\text{ L.T. }}_{3_i} \phantom {\frac{1}{1}} \right) \log \frac{M_i}{M_Z}.\nonumber \\ \end{aligned}$$

(3.7)

The predictions for gauge coupling observables at the Z-scale can therefore be seen to correspond to 0th order predictions consisting of the first lines of Eqs. (3.6) and (3.7) plus the threshold corrections due to the decoupling of the different particles at their mass thresholds. The values of the beta-function coefficients of these light thresholds are shown in Table 4. The 0th order coefficients are given by

$$\begin{aligned} b_3^{{Z^\prime }}~~=&0&= ~~b_3^{\text{ MSSM }}+ ~3, \\ b_2^{{Z^\prime }}~~=&4&= ~~b_2^{\text{ MSSM }}+ ~3, \\ b_1^{{Z^\prime }}~~=&\frac{48}{5}&= ~~b_1^{\text{ MSSM }} + ~3. \end{aligned}$$

Hence, the $b_i^{{Z^\prime }}$ are identical to the $b_i^{\text{ MSSM }}$ up to a common shift by 3, arising from the vector-like colour triplets and electroweak doublets. As the 0th order predictions for $\sin \theta (M_Z)$ and $\alpha _3(M_Z)$ only depend on the differences of the beta-function coefficients, the zeroes order predictions are identical to those that are obtained in the MSSM.

Fig. 1

Gauge coupling data at the electroweak scale in the presence of a light $Z^\prime$ and assuming unification at the heterotic-string scale

The corrections due to the light thresholds are given by

$$\begin{aligned} \delta \sin ^2\big (\theta _W\big )_\mathrm{light}= & {} \frac{5\alpha }{16\pi }\bigg ( -{4\over 3} \log {M_{\tilde{w}} \over M_{Z}} -{1\over 5}\log {M_{{\tilde{\ell }}_\ell }\over M_{Z}} \nonumber \\&+{3\over 5}\log {M_{{\tilde{\ell }}_r}\over M_{Z}} +{1\over 5}\log {M_{{\tilde{d}}_r}\over M_{Z}} \nonumber \\&-{7\over 5}\log {M_{{\tilde{Q}}_r}\over M_{Z}} +{4\over 5}\log {M_{{\tilde{u}}_r}\over M_{Z}} \nonumber \\&-{4\over 15}\log {M_{\tilde{h}}\over M_{Z}} -{2\over 15}\log {M_{h}\over M_{Z}}\nonumber \\&+{1\over 15}\log {M_{t}\over M_{Z}} +{6\over 5}\log {M_{D}\over M_{Z}} -{6\over 5}\log {M_{H}\over M_{Z}}\bigg ), \nonumber \\ \end{aligned}$$

(3.8)

$$\begin{aligned} \delta \big (\alpha _3^{-1}\big )_\mathrm{light}= & {} \frac{1}{2\pi }\bigg ( -2 \log {M_{\tilde{g}}\over M_{Z}} + {1\over 2}\log {M_{\tilde{w}}\over M_{Z}} \nonumber \\&-{3\over 8}\log {M_{{\tilde{\ell }}_\ell }\over M_{Z}} +{3\over 8}\log {M_{{\tilde{\ell }}_r}\over M_{Z}} \nonumber \\&-{3\over 8}\log {M_{{\tilde{d}}_r}\over M_{Z}} -{3\over 8}\log {M_{{\tilde{Q}}_r}\over M_{Z}} \nonumber \\&+{1\over 2}\log {M_{\tilde{h}}\over M_{Z}} +{1\over 4}\log {M_{h}\over M_{Z}}\nonumber \\&-{1\over 8}\log {M_{t}\over M_{Z}} -{9\over 4}\log {M_{D}\over M_{Z}} +{9\over 4}\log {M_{H}\over M_{Z}}\bigg ) .\nonumber \\ \end{aligned}$$

(3.9)

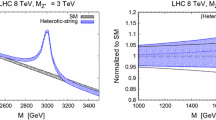
It is noted from Eqs. (3.8) and (3.9) that if the vector-like colour triplets are degenerate in mass with the vector-like electroweak doublets, then their threshold corrections exactly cancel. In that case the predictions for $\sin ^2\theta _W(M_Z)$ and $\alpha _3(M_Z)$ coincide exactly with those of the MSSM. The exact masses of these states depend of course on the details of their couplings to the $Z^\prime$ breaking VEV. Allowing for mass splitting of the order of a few TeV may be compensated by contributions from the supersymmetric states. Imposing the experimental limits on the supersymmetric particles and allowing for such mass differences Fig. 1 shows a scatter plot of $\sin ^2\theta _W(M_Z)$ and $\alpha _3(M_Z)$, where the masses of the supersymmetric particles are varied independently.

Fig. 2

The effect of intermediate Pati–Salam symmetry breaking scale in the $Z^\prime$ model pushes the supersymmetric thresholds beyond the LHC reach. The figure on the left displays the predictions for the gauge coupling parameters. The one on the right displays the PS scale versus a common SUSY scale on a logarithmic scale $\log ({M_\mathrm{PS}/M_Z})$ vs. $\log ({M_\mathrm{SUSY}/M_Z})$

Fig. 3

The effect of additional heavy thresholds and an intermediate symmetry breaking pushes the unification scale toward the perturbative heterotic-string scale, while producing viable low scale predictions. The figure on the right displays the PS scale versus a common SUSY scale on a logarithmic scale $\log \left( {M_\mathrm{PS}/M_Z}\right)$ vs. $\log \left( {M_\mathrm{SUSY}/M_Z}\right)$

Next we study the predictions for the gauge coupling parameters with Pati–Salam breaking at an intermediate energy scale $M_{PS}$. The gauge symmetry is $SU(4)_C\times SU(2)_L\times SU(2)_R\times U(1)_\zeta$, and $SU(3)_C\times SU(2)_L\times U(1)_Y\times U(1)_{Z^\prime }$, above and below the intermediate Pati–Salam breaking scale, respectively. The weak hypercharge is given by¹

$$\begin{aligned} U(1)_Y~=~\frac{1}{3} U(1)_C + T_{3_R} \end{aligned}$$

(3.10)

with $k_C= 6$. When solving the RGEs for the low scale predictions we have to distinguish the running above and below the intermediate breaking scale. The RGEs and beta-function coefficients below the symmetry breaking scale coincide with those of the $Z^\prime$ model discussed above. Above the symmetry breaking scale the spectrum differs from the standard Pati–Salam model due to the anomaly cancellation requirement of $U(1)_\zeta$. To ensure that $U(1)_\zeta$ is anomaly free, all the additional states above the intermediate breaking scale have to be vector-like with respect to $U(1)_\zeta$. The Pati–Salam model contains an additional sextet field required for the missing-partner-like mechanism that gives heavy mass to the heavy Higgs states [154]. Hence, anomaly cancellation with respect to $U(1)_\zeta$ demands another sextet in the spectrum with opposite $U(1)_\zeta$ charge. Similarly, the spectrum above the intermediate symmetry breaking scale contains two bi-doublet states with opposite $U(1)_{\zeta }$ charges, whereas only one pair of Higgs doublets remain below the intermediate scale. The beta-function coefficients above the intermediate breaking scale are therefore

$$\begin{aligned} b_4^{\text{ PS }}=1,\quad b_2^{\text{ PS }}=5,\quad b_{\text{ R }}^{\text{ PS }}=9, \end{aligned}$$

(3.11)

which also takes into account the contribution of the heavy Higgs states, and $b_2^{\text{ PS }}, ~b_{\text{ R }}^{\text{ PS }}$ are the beta-function coefficients of $SU(2)_L~,SU(2)_R$, respectively. The effect of the intermediate symmetry breaking scale is to add correction terms to Eqs. (3.6) and (3.7), given by

$$\begin{aligned}&\Delta _{\text{ I.S. }}^{\sin ^2\theta _W}=\frac{5\alpha }{16\pi } \left( b^{{Z^\prime }}_{1}- \frac{3}{5}b^{\text{ PS }}_{\text{ R }}- \frac{2}{5}b^{\text{ PS }}_{4}- b^{{Z^\prime }}_{2}+ b^{\text{ PS }}_{2} \phantom {\frac{1}{1}} \right) \log \frac{M_X}{M_{PS}}, \end{aligned}$$

(3.12)

$$\begin{aligned}&\Delta _{\text{ I.S. }}^{\alpha _3}=\frac{1}{2\pi } \left( \frac{3}{4} b^{\text{ PS }}_{4}- b^{{Z^\prime }}_{3}- \frac{3}{8} b^{\text{ PS }}_{\text{ R }}+ \frac{5}{8} b^{{Z^\prime }}_{1}+ \frac{3}{8} b^{{Z^\prime }}_{2}- \frac{3}{8} b^{\text{ PS }}_{2} \phantom {\frac{1}{1}} \right) \log \frac{M_X}{M_{PS}}.\nonumber \\ \end{aligned}$$

(3.13)

Restricting to experimentally viable predictions for $\sin ^2\theta _W(M_Z)$ and $\alpha _3(M_Z)$, and varying $M_{PS}$ and a common SUSY breaking scale $M_{SUSY}$, while keeping $M_X=1.1\times 10^{16}\mathrm{GeV}$ we obtain a relation between $M_{PS}$ and $M_{SUSY}$, which is displayed in Fig. 2. From the figure we note that reducing the intermediate Pati–Salam symmetry breaking scale pushes the supersymmetric thresholds beyond the LHC reach. Nevertheless, the $Z^\prime$ breaking scale remains at the TeV scale as the contribution of the extra vector-like colour triplets is cancelled by that of the extra vector-like doublets.

The effects of the extra vector-like states above the Pati–Salam breaking scale may also mitigate the unification of the gauge coupling closer to the perturbative heterotic-string scale. Assuming an additional pair of sextet fields, fixing $M_{SUSY}\sim 2\mathrm{TeV}$ and $M_X\sim 1\times 10^{17}\mathrm{GeV}$, we note that by varying the PS breaking scale we obtain viable predictions for $\sin ^2\theta _W(M_Z)$ and $\alpha _3(M_Z)$. These results are displayed in Fig. 3.

Split bi-doublet and sextet multiplets naturally appear in string models due to the stringy doublet–triplet stringy mechanism, which depends on the assignment of boundary conditions in the basis vectors that break the SO(10) symmetry to the Pati–Salam subgroup [149]. The model of [105] contains three such pairs of untwisted sextets, and one additional pair from the twisted sectors, whereas there is no excess of vector-like bi-doublets. This is the case because the model of [105] utilises symmetric boundary conditions with respect to the internal manifold, whereas a model with asymmetric assignment would generate corresponding extra bi-doublets. The string models therefore contain all the ingredients to naturally produce agreement with a di-photon excess as well as agreement with the gauge coupling data at the electroweak scale.

Fig. 4

The effect of intermediate left–right symmetry breaking scale in the $Z^\prime$ model pushes the supersymmetric thresholds beyond the LHC reach. The figure on the left displays the predictions for the gauge coupling parameters. The one on the right displays the LRS scale versus a common SUSY scale, on a logarithmic scale $\log ({M_\mathrm{R}/M_Z})$ vs. $\log ({M_\mathrm{SUSY}/M_Z})$

We may also consider the case of the left–right symmetric model in which the SO(10) symmetry is broken to $SU(3)\times U(1)_C\times SU(2)_L\times SU(2)_R$. We assume that $U(1)_\zeta$ charges admit the $E_6$ embedding. In this case the heavy Higgs states consists of the pair $\mathcal{N}\left( \mathbf{1},\mathbf{\frac{3}{2}},\mathbf{1},\mathbf{2},\mathbf{\frac{1}{2}}\right) ,~ {\bar{\mathcal{N}}}\left( \mathbf{1},-\mathbf{\frac{3}{2}},\mathbf{1},\mathbf{2}, -\mathbf{\frac{1}{2}}\right) .$ The VEV along the electrically neutral component leaves unbroken the Standard Model gauge group and the $U(1)_{Z^\prime }$ combination in Eq. (2.2). We remark, however, that in the free fermionic LRS models [155, 156] the $U(1)_\zeta$ charges do not admit the $E_6$ embedding and we will argue in [157] that in a large class of string models such construction is not possible. Here, we consider such models as purely field theory models and study the effect on the low scale gauge coupling parameters. Above the symmetry breaking scale the spectrum coincides with that of Table 3 with the right-handed fields arranged into doublet representations of $SU(2)_R$. Additionally, the spectrum contains the heavy Higgs states and a pair of Higgs bi-doublets with opposite $U(1)_\zeta$ charges. Crucially, here, the intermediate symmetry breaking does not require the existence of coloured states in the interval between $M_R$ and $M_X$, which may be incorporated in non-minimal extensions. Consequently, the beta-function coefficients above the intermediate symmetry breaking scale $M_R$ are

$$\begin{aligned} b_3^{\text{ R }}= 0,\quad b_2^{\text{ R }}= 5,\quad b_{\text{ R }}^{\text{ R }}= 6,\quad b^{\text{ R }}_{{\hat{C}}}= 9, \end{aligned}$$

(3.14)

whereas the $b^{Z^{\prime }}_i$ below the intermediate breaking scale coincide with those given above. Here, $b_2^\mathrm{R}$ is the beta-function coefficient of $SU(2)_L$; $b_\mathrm{R}^\mathrm{R}$ is that of $SU(2)_R$; and $b^\mathrm{R}_{\hat{C}}$ is that of the normalised $U(1)_C$ generator. The effect of the intermediate scale symmetry breaking is to add correction terms for $\sin ^2\theta _W(M_Z)$ and $\alpha _3(M_Z)$ given by

$$\begin{aligned}&\Delta _{\text{ I.S. }}^{\sin ^2\theta _W}\nonumber \\&\quad = \frac{5\alpha }{16\pi } \left( b^{{Z^\prime }}_{1}- \frac{3}{5}b^{\text{ R }}_{\text{ R }}- \frac{2}{5}b^{\text{ R }}_{{\hat{C}}}- b^{{Z^\prime }}_{2}+ b^{\text{ R }}_{2} \phantom {\frac{1}{1}} \right) \log \frac{M_X}{M_{R}},\nonumber \\ \end{aligned}$$

(3.15)

$$\begin{aligned}&\Delta _{\text{ I.S. }}^{\alpha _3}\nonumber \\&\quad = \frac{1}{2\pi } \left( \frac{3}{8} \left( b^{{Z^\prime }}_{2}- b^{\text{ R }}_{2}- b^{\text{ R }}_{\text{ R }}- \frac{2}{3} b^{\text{ R }}_{{\hat{C}}} \right) + \frac{5}{8} b^{{Z^\prime }}_{1} \phantom {\frac{1}{1}} \right) \log \frac{M_X}{M_{R}}.\nonumber \\ \end{aligned}$$

(3.16)

As seen in Fig. 4 similar to the PS case the effect of the intermediate scale corrections to $\sin ^2\theta _W(M_Z)$ and $\alpha _3(M_Z)$ is to shift the common SUSY threshold beyond the reach of the LHC. The figures should be viewed as illustrative, indicating the substantial impact that a low scale $Z^\prime$ may have on the anticipated signatures at accessible energy scales. This should be contrasted with the corresponding intermediate scale models [158], in which the impact of the intermediate scale corrections is milder.

4 The di-photon events

In the low-energy regime the superpotential [105] provides different interaction terms of the singlet fields $S_i$ and $\zeta _i$, which can be extracted from Table  3, among them we have

$$\begin{aligned}&\lambda ^{ijk}_D S_i D_j \bar{D}_k + \lambda ^{ijk}_H S_i H_j \bar{H}_k + \lambda ^{ij}_h S_i H_j \bar{h}\nonumber \\&\quad +\, \eta ^i_{ \mathcal D} \zeta _i {\mathcal D} \bar{ \mathcal D} + \eta ^i_{ h} \zeta _i h \bar{h} . \end{aligned}$$

(4.1)

All these terms may comply with the di-photon excess reported by both the ATLAS and the CMS experiments with a resonance around 750 GeV described by either the singlets $S_i$ or $\zeta _i$. Indeed, the presence of vector-like quarks, which is natural in heterotic-string models, facilitates the production of these states at the LHC. In the following discussion we will consider the most simple and economic scenario in order to highlight the effects of the vector-like coloured states $D, \bar{D}$ and their role in the explanation of the di-photon excess. For this reason we assume that the resonance is reproduced by exchange of one of the singlet $S_i$ and we ignore the contribution of the $\zeta _i$ fields and of the coupling $S H \bar{H}$. The real scalar component of one of the $S_i$ superfields acquires a VEV $v_S$ and breaks the extra $U(1)_{Z'}$ symmetry thus providing the mass of the $Z'$ gauge boson and of the $D, \bar{D}$ field through the coupling $\lambda _D$ in the superpotential (4.1). Provided $v_S$ around the TeV scale, the mass of the singlet $S_i$, of the vector-like states $D, \bar{D}$ and of the $Z'$ lay in the TeV ballpark, thus establishing a intimate relationship between the 750 GeV di-photon resonance and the presence of an additional spontaneously broken $U(1)_{Z'}$ gauge symmetry. Interestingly this can also be probed at the LHC in the lepto-production channel [148, 160]. Moreover, as we have already stated, in order to reproduce the di-photon excess it is enough to consider the impact of the vector-like coloured superfields $D, \bar{D}$ only. Therefore we assume $\lambda \equiv \lambda ^{3ii}_D$ and we neglect all the other couplings. The fermionic components of $D_i$ and $\bar{D}_i$ can be rearranged into three Dirac spinors $\psi _{D_i}$, while the scalar components will provide six complex scalars $\tilde{D}_j$. The corresponding interaction Lagrangian can be parameterised as

$$\begin{aligned} {\mathcal L} = - Y_D \, S \bar{\psi }_{D_i} \psi _{D_i} - \mu \, S |\tilde{D}_j|^2 , \end{aligned}$$

(4.2)

where S is the real scalar component of one of the $S_i$ singlet whose mass $M_S$ is identified with the 750 GeV resonance, $Y_D = \lambda /\sqrt{2}$ and $\mu$ is the corresponding soft-breaking term.

Fig. 5

$\sigma (pp \rightarrow S) \times \mathrm {BR}(S \rightarrow \gamma \gamma )$ at 13 TeV LHC in a the $(M_D, \mu )$ plane for two values of the Yukawa coupling $Y_D$ and b in the $(M_D, Y_D)$ plane for two values of the scalar coupling $\mu$. The coloured regions correspond to a $2\sigma$ region of the measured cross section $4.5\pm 1.9$ fb

The LHC cross section of the di-photon production through the exchange of a scalar resonance in the s-channel is, in the narrow width approximation,

$$\begin{aligned} \sigma (pp \rightarrow S \rightarrow \gamma \gamma ) = \frac{1}{M_S \, s} C_{gg} \Gamma (S \rightarrow g g) \mathrm {Br}(S \rightarrow \gamma \gamma )\nonumber \\ \end{aligned}$$

(4.3)

where $M_S$ is the resonance mass, $C_{gg}$ the luminosity factor in the gluon–gluon channel and $\sqrt{s}$ the centre-of-mass energy. We assume that the main production mechanism occurs via gluon fusion with the corresponding luminosity factor at 13 TeV given by

$$\begin{aligned} C_{gg} = \frac{\pi ^8}{8} \int _{M_S^2/s}^1 \frac{\mathrm{d}x}{x} g(x) g \left( \frac{M_S^2}{sx} \right) \simeq 2137 , \end{aligned}$$

(4.4)

where g(x) is the gluon distribution function and the value has been computed for $\sqrt{s} = 13$ TeV and for $M_S = 750$ GeV using MSTW2008NLO [159].

The partial decay widths of S into gluons and photons are

$$\begin{aligned}&\Gamma (S \rightarrow gg)\nonumber \\&\quad = \frac{\alpha _S^2}{128 \pi ^3} M_S^3 \bigg | \sum _f \frac{y_f}{m_f} A_{1/2}(\tau _f) + \sum _s \frac{\mu _s}{2 m_s^2} A_0(\tau _s) \bigg |^2 ,\nonumber \\ \end{aligned}$$

(4.5)

$$\begin{aligned} \Gamma (S \rightarrow \gamma \gamma )= & {} \frac{\alpha ^2}{256 \pi ^3} M_S^3 \bigg | \sum _f N_c^f q_f^2 \frac{y_f}{m_f} A_{1/2}(\tau _f) \nonumber \\&+\sum _s N_c^s q_s^2 \frac{\mu _s}{2 m_s^2} A_0(\tau _s) \bigg |^2, \end{aligned}$$

(4.6)

where $m_f$ and $m_s$ are the masses of a generic fermion and scalar running in the loops, $y_f$ and $\mu _s$ the corresponding couplings to S and $N_c$ the colour factor. As $D, ~\bar{D}$ are singlets of $SU(2)_L$, their electric charge q coincides with the hypercharge Y. The fermionic and scalar loop functions are given by

$$\begin{aligned} A_{1/2}(\tau )= & {} 2 [\tau + (\tau -1) f(\tau )]/\tau ^2, \nonumber \\ A_{0}(\tau )= & {} - [\tau - f(\tau )]/\tau ^2 \end{aligned}$$

(4.7)

with $\tau _i = M_S^2/(4 m_i^2)$ and

$$\begin{aligned} f(\tau ) = {\left\{ \begin{array}{ll} \arcsin ^2 \sqrt{\tau }, &{} \text{ if } \tau \le 1 ,\\ -\frac{1}{4} \left[ \log \frac{1 + \sqrt{1 - \tau ^{-1}}}{1 - \sqrt{1- \tau ^{-1}}} - i \, \pi \right] ^2 , &{} \text{ if } \tau > 1. \end{array}\right. } \end{aligned}$$

(4.8)

Assuming $\Gamma _\mathrm{tot} = \Gamma (S \rightarrow gg) + \Gamma (S \rightarrow \gamma \gamma )$, we show in Fig. 5 the portion of the parameters space in which the di-photon excess can be reproduced in a $2\sigma$ region around the measured value $\sigma = 4.5\pm 1.9$ fb reported by the ATLAS and CMS collaborations at 13 TeV. For simplicity we assume $M_{\psi _{D_i}} \simeq M_{\tilde{D}_i} \simeq M_D$ and we present our results in the $(M_D, \mu )$ and $(M_D, Y_D)$ planes. The cross section is dominated by the complex scalar loops while the fermionic components of the supermultiplets $D, ~\bar{D}$ only provide a small contribution. Therefore, a huge Yukawa coupling is not strictly necessary as usually required in the literature, as its effect is compensated by a large soft-breaking term and relatively light squark-like states. Nevertheless, the di-photon cross section is also reproduced in regions of the parameter space characterised by big values of $Y_D$. Therefore, it is natural to ask if the running of the Yukawa coupling up to the unification scale does not induce a loss of pertubativity at high energies. For this purpose we have computed the corresponding $\beta$ function

$$\begin{aligned}&\beta _{Y_D}= Y_D \left( - \frac{4}{15} g_1^2 - \frac{19}{10} g_1'^2 - \frac{16}{3} g_3^2+ 22 Y_D^2 + 2 \lambda _h^2 + 2 \lambda _H^2\right) \nonumber \\ \end{aligned}$$

(4.9)

where, for the sake of simplicity, we have neglected the kinetic mixing and the tensor structure of the couplings. The contributions from the gauge sector, and in particular of the strong gauge group, provide a decreasing evolution for $Y_D$, which could be prevented mainly by the $Y_D^3$ term. This behaviour, due to the SU(3) charge of the supermultiplets D and $\bar{D}$, is similar to that of the top quark in the SM in which the QCD corrections are responsible for a monotonically decreasing $Y_t$ along all the RG running. We have explicitly verified that $Y_D \sim 0.6$ still preserves its perturbativiy up to $10^{16}$ GeV. The inclusion of the kinetic mixing would improve the perturbativity limit, even if only slightly.

For smaller values of the Yukawa coupling $Y_D$, the $D, ~\bar{D}$ scalar components running in the loops, which interact with the singlet S through the soft-breaking term $\mu$, represent the dominant contribution to the cross section. However, a large trilinear term may spoil the stability of the potential or induce a coloured and electric charged vacuum (see for instance [161, 162] for studies related to the 750 GeV excess). Preventing this situation will introduce an upper bound on the $\mu$ term whose exact value obviously depends on the details of the soft-breaking Lagrangian. This would clearly require a dedicated study of the parameter space, here we give some comments. The relevant part of the scalar potential can be parameterised in the following form:

$$\begin{aligned} V(S, D, \bar{D})= & {} m_{D_i}^2 |D_i |^2 + m_{\bar{D}_i}^2 |\bar{D}_i |^2 \nonumber \\&+\, \frac{1}{2} M_S^2 S^2 + \frac{\mu _S}{3} S^3 + \frac{\lambda _1}{4} S^4 + \mu \, S (|D_i |^2\nonumber \\&+\, |\bar{D}_i |^2 )+ \frac{ \lambda _2}{2} S^2 |D_i |^2 \nonumber \\&+\, \frac{\lambda '_2}{2} S^2 |\bar{D}_i |^2 + \lambda _3 ( D_i \bar{D}_i ) ( D_i^\dag \bar{D}_i^\dag ) \nonumber \\&+\, \lambda _4 \left( ( D_i^\dag D_j ) ( D_j^\dag D_i ) + ( \bar{D}_i^\dag \bar{D}_j ) ( \bar{D}_j^\dag \bar{D}_i ) \right. \nonumber \\&\left. +\, 2 ( D_i \bar{D}_j ) ( D_j^\dag \bar{D}_i^\dag ) \right) \nonumber \\&+\, \lambda _5 |D_i |^2 |D_j |^2 + \lambda '_5 |\bar{D}_i |^2 |\bar{D}_j |^2\nonumber \\&+\, \lambda _6 |D_i |^2 |\bar{D}_j |^2 , \end{aligned}$$

(4.10)

where S is the physical real scalar component, $i,j = 1,2,3$, and the quartic couplings have been extracted from the F and D terms,

$$\begin{aligned}&\lambda _1 = \frac{1}{8} g_1'^2 Q^{' 2}_S, \quad \lambda _2 = \lambda _D^2 + g_1'^2 Q^{' }_S Q^{' }_{D}, \quad \nonumber \\&\lambda '_2 = \lambda _D^2 + g_1'^2 Q^{' }_S Q^{' }_{\bar{D}} ,\end{aligned}$$

(4.11)

$$\begin{aligned}&\lambda _3 = \lambda _D^2, \quad \lambda _4 = \frac{1}{4} g_3^2 ,\quad \nonumber \\&\lambda _5 = - \frac{1}{12} g_3^2 + \frac{1}{18} g_1^2 + \frac{1}{2} g_1'^2 Q^{' 2}_{D} ,\end{aligned}$$

(4.12)

$$\begin{aligned}&\lambda '_5 = - \frac{1}{12} g_3^2 + \frac{1}{18} g_1^2 + \frac{1}{2} g_1'^2 Q^{' 2}_{\bar{D}} , \quad \nonumber \\&\lambda _6 = - \frac{1}{6} g_3^2 - \frac{1}{9} g_1^2 + g_1'^2 Q^{' }_{D} Q^{'}_{\bar{D}} , \end{aligned}$$

(4.13)

with $Q'$ being the charge under the $U(1)_{Z'}$ gauge group. We require $\langle S \rangle = 0$ (notice that in the parameterisation of the scalar potential given above, the scalar singlet has already undergone spontaneous symmetry breaking) and $\langle D_i \rangle = \langle \bar{D}_i \rangle = 0$, thus identifying the region of the parameter space in which the occurrence of a coloured vacuum is avoided. To simplify the discussion we study the scenario of a flavour independent vacuum, namely $v_D \equiv \langle D_i \rangle = \langle \bar{D}_i^\dag \rangle$. In this case the minimisation conditions read

$$\begin{aligned}&6 \mu |v_D|^2 + ( M_S^2 + 6 \alpha |v_D|^2 ) v_S + \mu _S v_S^2 + \lambda _1 v_S^3 = 0, \nonumber \\&|v_D| (2 M_D^2 + 6 \beta |v_D|^2 + \alpha \, v_S^2 + 2 \mu \, v_S) = 0 , \end{aligned}$$

(4.14)

with $\alpha = \lambda _2/2 + \lambda '_2/2$ and $\beta = \lambda _3 + 4\lambda _4 + \lambda _5 + \lambda '_5 + \lambda _6$. In general, the destabilising effect of a large $\mu$ term can be counterweighted by large quartic couplings. In this scenario the latter are mainly controlled by $Y_D = \lambda _D/\sqrt{2}$ and the strong coupling constant $g_3$. We show in Fig. 6 the $2\sigma$ band around the central value of the di-photon cross section for $Y_D = 0.6$ and the corresponding excluded region in the $(M_D, \mu )$ plane. The bound is quite restrictive allowing, in this simplified setup, for a parameter space with $\mu \lesssim 2$ TeV and $M_D \lesssim 500$ GeV. We stress again that this analysis is far from being exhaustive, while its only purpose is to show how the di-photon excess can be naturally accommodated in heterotic-string scenarios where the $U(1)_{Z'}$ gauge symmetry is broken around the TeV scale. We have neglected, for instance, the impact of the $S H \bar{H}$ interaction which would increase, in general, the partial decay width into photons and thus broaden the preferred parameter space. As a side effect this would relax the necessity of either a large Yukawa coupling or soft-breaking term and it will also provide more involved decay patterns through the mixing with the H and $\bar{H}$ fields.

Fig. 6

$\sigma (pp \rightarrow S) \times \mathrm {BR}(S \rightarrow \gamma \gamma )$ at 13 TeV LHC in the $(M_D, \mu )$ plane for $Y_D = 0.6$. The coloured region corresponds to a $2\sigma$ interval around the measured cross section $4.5\pm 1.9$ fb, while the hatched region is excluded by the requirement of colourless and electric neutral vacuum

5 The impact of the D-terms

The presence of an extra abelian factor together with the dynamical generation of a $\mu$-term supply our model with the minimal set of tools to relieve the tree-level MSSM hierarchy between the Z and Higgs masses. To explore the low-energy scalar spectrum that can be naturally covered by the parameter space, we focus on the simple scenario involving only the fields interacting through the coupling $\lambda ^{ijk}_H$ in (4.1). The neutral scalar components will then include 9 supermultiplets; 6 from $H, \bar{H}$ plus other 3 from the SM singlet S. Among different possible settings a viable one is achievable from

$$\begin{aligned} \langle H_{1,2} \rangle \, =\, \langle \bar{H}_{1,2} \rangle \,= \,\langle S_{1,2} \rangle \,=\, 0, \end{aligned}$$

(5.1)

with non-zero VEVs concerning only the third generation

$$\begin{aligned} \langle H_3\rangle = \frac{1}{\sqrt{2}} \left( \begin{array}{c} v_d \\ 0 \end{array}\right) , \quad \langle \bar{H}_3\rangle = \frac{1}{\sqrt{2}} \left( \begin{array}{c} 0 \\ v_u \end{array}\right) , \quad \langle S_3\rangle = \frac{v_S}{\sqrt{2}} ,\nonumber \\ \end{aligned}$$

(5.2)

where $v_u = v \sin \beta$ and $v_d = v \cos \beta$. The setting in (5.1–5.2) is not the only one capable to minimise the scalar potential and break the symmetry down to $SU(3)\times U(1)_{em}$. It is nevertheless the one with the simplest and more MSSM-like structure. Given the illustrative purpose of this section, we take $\lambda ^{ijk}_H$ and the soft-SUSY masses to be flavour-diagonal and real parameters. The part of the potential relevant to the spontaneous breaking analysis contains only the (scalar component of the) fields $H_3, \bar{H}_3,$ and $S_3$

$$\begin{aligned} V_\mathrm{Higgs}= & {} \tilde{m}^2_H |H|^2 + \tilde{m}^2_{\bar{H}} |\bar{H}|^2 + \tilde{m}^2_S |S|^2 \nonumber \\&-\, \left( \lambda _H \,A_{\lambda } H\,\bar{H}\,S + \text {h.c.} \right) \nonumber \\&+\, \lambda _H^2 \left( |H \bar{H}|^2 + |H|^2|S|^2 + |\bar{H}|^2|S|^2 \right) \nonumber \\&+\, \frac{1}{2}\,g_2^2 \left( H^{\dagger }\frac{\sigma ^{\mu }}{2}H + \bar{H}^{\dagger }\frac{\sigma ^{\mu }}{2}\bar{H}\right) ^2 \nonumber \\&+\,\frac{1}{2} g_1^2 \left( \frac{1}{2}|\bar{H}|^2 - \frac{1}{2}|H|^2 \right) ^2 \nonumber \\&+\, \frac{1}{2} {g'_1}^2 \left( Q'_{\bar{H}}|\bar{H}|^2 + Q'_{H}|H|^2 + Q'_{S}|S|^2 \right) ^2 ,\nonumber \\ \end{aligned}$$

(5.3)

with the generator of the extra Abelian group given in the form which includes the mixing $g'_1\,Q'_{f} = g'_1 Y_{f}' + \tilde{g} Y_{f}$, where $Y_{f}'$ and $Y_{f}$ are, respectively, the charges under $U(1)_{Z'}$ and $U(1)_Y$. As customary, the trilinear (dimensionful) coefficient has been written in the form $\lambda _H\,A_{\lambda }$. The three soft masses $\tilde{m}_{H\, 3,3}^2, \tilde{m}_{\bar{H}\,3,3}^2, \tilde{m}_{S\,3,3}^2$ non-trivially solve the tadpole-conditions to accommodate for the VEVs structure of (5.1–5.2). Putting such values in the neutral-boson mass matrices and considering the large $v_S$ limit we obtain

$$\begin{aligned} m^2_{Z} = \frac{v^2}{4} \left( g_1^2 + g_2^2\right) , \quad m^2_{Z'} = \left( Q'_{S}\, g'_1\, v_S\right) ^2 = \left( Y'_{S}\,g'_1\,v_S\right) ^2 .\nonumber \\ \end{aligned}$$

(5.4)

By requiring

$$\begin{aligned} \tilde{m}_{H\,1,1}^2 = \tilde{m}_{H\,2,2}^2, \quad \tilde{m}_{\bar{H}\,1,1}^2 = \tilde{m}_{\bar{H}\,2,2}^2, \quad \tilde{m}_{S\,1,1}^2 = \tilde{m}_{S\, 2,2}^2,\nonumber \\ \end{aligned}$$

(5.5)

the $9\times 9$ CP-odd mass matrix can be analytically diagonalised. In the Landau gauge the two massless Goldstone bosons are promptly found and the remaining 7 masses are a degenerate ensemble of the independent set:

$$\begin{aligned} \left( m^2_{1}, m^2_{2}, m^2_{3},m^2_{A_{\lambda }} \right) . \end{aligned}$$

(5.6)

The eigenvalues $m^2_{1-3}$ are uniquely linked to the three independent soft masses of (5.5) and consequently are all double degenerate. The eigenvalue dubbed $m^2_{A_{\lambda }}$ is connected to the trilinear soft term. In the limit of large $v_S$ we find

$$\begin{aligned} m^2_{A_{\lambda }} = \sqrt{2}\, v_S\, \lambda _H \frac{A_{\lambda }}{\sin (2\beta )} , \end{aligned}$$

(5.7)

where $\tan \beta$ $= v_u / v_d$. The correspondence with the MSSM is clear once we identify the effective $\mu$-term $\mu _{eff} = v_S\,\lambda _H\,/\sqrt{2}$. All the soft masses in (5.3) can thus be traded for the CP-odd eigenvalues and, via tadpole conditions, for the non-zero VEVs. The mass matrix for the charged Higgs scalars² can similarly be analytically diagonalised. The eigenvalues are simply linked to the W mass and the CP-odd masses. In the Landau gauge we find one massless Goldstone while the remaining independent masses are given by (for $v_S \gg v$)

$$\begin{aligned} \left( m^2_{1} + M_W^2\,\cos (2\beta ), \,m^2_{2} - M_W^2\,\cos (2\beta ), m^2_{A_{\lambda }} + M_W^2 - \frac{\lambda ^2 v^2}{2} \right) ,\nonumber \\ \end{aligned}$$

(5.8)

with degeneracy inherited from the CP-odd structure. The CP-even mass matrix is mostly diagonal with mixing involving only the third generations of $H, \bar{H}$, and S. The 6 eigenvalues in the diagonal are degenerate to the corresponding CP-odd partners $m^2_{i= 1,2,3}$. The remaining $3\times 3$ block to be diagonalised includes the matrix elements

$$\begin{aligned} m^2_{1,1}= & {} M_Z^2\, \cos ^2 \beta + 4\,M_Z^2\,\left( \frac{g'_1\,Q'_{H}}{\bar{g}}\right) ^2\,\cos ^2 \beta + \Delta \,\,\sin ^2 \beta , \nonumber \\ m^2_{2,2}= & {} M_Z^2\, \sin ^2 \beta + 4\,M_Z^2\,\left( \frac{g'_1\,Q'_{\bar{H}}}{\bar{g}}\right) ^2\,\sin ^2 \beta + \Delta \,\,\cos ^2 \beta , \nonumber \\ m^2_{3,3}= & {} {M'_Z}^2 + \Delta \left( \frac{M_Z\,\sin (2\beta )}{\bar{g}\,v_S}\right) ^2 , \nonumber \\ m^2_{1,2}= & {} \, \cos \beta \,\sin \beta \, \left( - M^2_Z - \Delta + \frac{4\,M_Z^2}{\bar{g}^2}\,\left( \lambda ^2 + {g'_1}^2\,Q'_{H}\,Q'_{\bar{H}} \right) \right) , \nonumber \\ m^2_{1,3}= & {} \,\cos \beta \left( 2\,\frac{M_Z\,v_S}{\bar{g}}\right) \,\left( - \frac{\Delta }{v_S^2}\,\sin ^2 \beta + \lambda ^2 + {g'_1}^2\,Q'_{H}\,Q'_{S} \right) ,\nonumber \\ m^2_{2,3}= & {} \,\sin \beta \left( 2\,\frac{M_Z\,v_S}{\bar{g}}\right) \,\left( - \frac{\Delta }{v_S^2}\,\cos ^2 \beta + \lambda ^2 + {g'_1}^2\,Q'_{S}\,Q'_{\bar{H}} \right) \nonumber \\ \end{aligned}$$

(5.9)

where

$$\begin{aligned} \bar{g}^2= & {} g_1^2 + g_2^2,\quad \Delta = \frac{\bar{g}^2\, M^2_{A_{\lambda }}\,v^2_S}{M_Z^2\, \sin ^2 (2 \beta )+ \bar{g}^2\,v_S^2}. \end{aligned}$$

(5.10)

The numerical diagonalisation of the previous mass matrices easily reveals large branches of the parameter space with tree-level eigenvalues that elude the MSSM hierarchy between the lightest scalar (LS) and $M_Z$ (Fig. 7). To obtain an analytical estimation of the impact of the D-terms we minimise the expectation value of the CP-even mass matrix with the vector $(\cos \beta , \sin \beta ,0)$ [163]. The result represents an upper limit for its smallest eigenvalue,

$$\begin{aligned} M^2_{h}\le & {} M^2_Z\,\cos ^2(2\,\beta ) + \frac{v^2}{2}\,\lambda ^2\,\sin ^2(2\,\beta ) \nonumber \\&+\,{g'_1}^2\,v^2\,\left( Q'_{H}\,\cos ^2 \beta + Q'_{\bar{H}}\,\sin ^2 \beta \right) ^2 . \end{aligned}$$

(5.11)

Fig. 7

Contour plot of lightest scalar eigenvalue of matrix (5.9). $v_S = 2.5$ TeV $M_{A_{\lambda }} = 500$ GeV

Fig. 8

Contour plot of upper bounds for LS mass

Fig. 9

Production and di-photon decay of the Standard Model singlet scalar state

In the formal limit $g'_1,\tilde{g} \rightarrow 0$ we recover the upper bound of the NMSSM [163, 164] and a further limit, $\lambda _H \rightarrow 0$, we obtain the MSSM one. As known, the singlet extension of the MSSM is a first step to increase the tree-level value of the LS. The positive contribution of the $U(1)_{Z'}$-related D-terms in (5.11) allows even larger upper bounds (Fig. 8).

6 Conclusions

The Standard Model of particle physics continues to reign supreme in providing viable parameterisation for subatomic observational data. Incorporating gravitational phenomena mandates the extension of the Standard Model, with string theory providing:

• minimal departure from the point particle hypothesis underlying the Standard Model;

• a mathematically self-consistent framework for perturbative quantum gravity;

• a mathematically self-consistent framework to develop a phenomenological approach to explore the synthesis of the gauge and gravitational interactions.

Phenomenological string models constructed in the so called fermionic formulation [138–140, 155, 156, 165–171] correspond to $Z_2\times Z_2$ orbifolds at enhanced symmetry points in the toroidal moduli space [172–176]. These models reproduce the main characteristic of the Standard Model spectrum, i.e. the existence of three chiral generations and their embedding in spinorial 16 representations of SO(10).

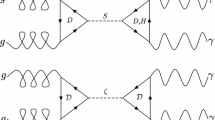
Indications for di-photon excess at the LHC will provide a vital clue in seeking the fundamental origins of the Standard Model. Such excess, and absence of any other observed signatures, is well explained as a resonance of a Standard Model singlet scalar field, which is produced and decays via triangular loops incorporating heavy vector-like states as depicted schematically in Fig. 9. All the ingredients for producing the diagram depicted in Fig. 9 arise naturally in the string derived $Z^\prime$ model [96, 105]. The chirality of the Standard Model singlet and the vector-like states under $U(1)_{Z^\prime }$ symmetry mandates that their masses are generated by the VEV that breaks the $U(1)_{Z^\prime }$ gauge symmetry. In this paper we showed that the observed low scale gauge coupling parameters are also in good agreement with the $Z^\prime$ model. The situation is in fact identical to that of the MSSM at one-loop level, whereas two-loop effects are small and can be absorbed into the unknown mass thresholds. Kinetic mixing effects are also small and can be neglected in the analysis. Above the intermediate breaking scale the weak hypercharge is embedded in a non-Abelian group and kinetic mixing cannot arise. Below the intermediate breaking scale kinetic mixing arises due to the extra pair of electroweak doublets, but it is found to be small and does not affect the results. We further showed that the $Z^\prime$ model can indeed account for the observed signal, while providing for a rich scalar sector that includes the Standard Model Higgs and the scalar resonance, as well as numerous other states that should be generated in the vicinity of this resonance. If such a resonance is observed in forthcoming data, future higher energy colliders will be required to decipher the underlying physics.

7 Note added

While this paper was under review the ATLAS and CMS collaborations reported that accumulation of further data did not substantiate the observation of the di-photon excess [124, 125], indicating that the initial observation was a statistical fluctuation. In our view, rather than being a negative outcome of the initial signal, it reflects the robustness and expediency of collider based experiments, and we eagerly look forward for future such ventures. We further remark that while a di-photon excess at 750 GeV was not substantiated by additional data, a di-photon excess at energy scales accessible at the LHC provides a general signature of the string derived $Z^\prime$ model of Ref. [105]. We are indebted to our colleagues in ATLAS and CMS, as well as those in Refs. [5–78] for drawing our attention to this possibility. Similarly, the gauge coupling analysis and the pertaining analysis that we presented in this paper is valid for $Z^\prime$ and di-photon excess in the multi-TeV energy scale.