Abstract
We review lattice results related to pion, kaon, D-meson, B-meson, and nucleon physics with the aim of making them easily accessible to the nuclear and particle physics communities. More specifically, we report on the determination of the light-quark masses, the form factor \(f_+(0)\) arising in the semileptonic \(K \rightarrow \pi \) transition at zero momentum transfer, as well as the decay constant ratio \(f_K/f_\pi \) and its consequences for the CKM matrix elements \(V_{us}\) and \(V_{ud}\). Furthermore, we describe the results obtained on the lattice for some of the low-energy constants of \(SU(2)_L\times SU(2)_R\) and \(SU(3)_L\times SU(3)_R\) Chiral Perturbation Theory. We review the determination of the \(B_K\) parameter of neutral kaon mixing as well as the additional four B parameters that arise in theories of physics beyond the Standard Model. For the heavy-quark sector, we provide results for \(m_c\) and \(m_b\) as well as those for D- and B-meson decay constants, form factors, and mixing parameters. These are the heavy-quark quantities most relevant for the determination of CKM matrix elements and the global CKM unitarity-triangle fit. We review the status of lattice determinations of the strong coupling constant \(\alpha _s\). Finally, in this review we have added a new section reviewing results for nucleon matrix elements of the axial, scalar and tensor bilinears, both isovector and flavor diagonal.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flavour physics provides an important opportunity for exploring the limits of the Standard Model of particle physics and for constraining possible extensions that go beyond it. As the LHC explores a new energy frontier and as experiments continue to extend the precision frontier, the importance of flavour physics will grow, both in terms of searches for signatures of new physics through precision measurements and in terms of attempts to construct the theoretical framework behind direct discoveries of new particles. Crucial to such searches for new physics is the ability to quantify strong-interaction effects. Large-scale numerical simulations of lattice QCD allow for the computation of these effects from first principles. The scope of the Flavour Lattice Averaging Group (FLAG) is to review the current status of lattice results for a variety of physical quantities that are important for flavour physics. Set up in November 2007, it comprises experts in Lattice Field Theory, Chiral Perturbation Theory and Standard Model phenomenology. Our aim is to provide an answer to the frequently posed question “What is currently the best lattice value for a particular quantity?” in a way that is readily accessible to those who are not expert in lattice methods. This is generally not an easy question to answer; different collaborations use different lattice actions (discretizations of QCD) with a variety of lattice spacings and volumes, and with a range of masses for the u- and d-quarks. Not only are the systematic errors different, but also the methodology used to estimate these uncertainties varies between collaborations. In the present work, we summarize the main features of each of the calculations and provide a framework for judging and combining the different results. Sometimes it is a single result that provides the “best” value; more often it is a combination of results from different collaborations. Indeed, the consistency of values obtained using different formulations adds significantly to our confidence in the results.
The first three editions of the FLAG review were made public in 2010 [1], 2013 [2], and 2016 [3] (and will be referred to as FLAG 10, FLAG 13 and FLAG 16, respectively). The third edition reviewed results related to both light (u-, d- and s-), and heavy (c- and b-) flavours. The quantities related to pion and kaon physics were light-quark masses, the form factor \(f_+(0)\) arising in semileptonic \(K \rightarrow \pi \) transitions (evaluated at zero momentum transfer), the decay constants \(f_K\) and \(f_\pi \), the \(B_K\) parameter from neutral kaon mixing, and the kaon mixing matrix elements of new operators that arise in theories of physics beyond the Standard Model. Their implications for the CKM matrix elements \(V_{us}\) and \(V_{ud}\) were also discussed. Furthermore, results were reported for some of the low-energy constants of \(SU(2)_L \times SU(2)_R\) and \(SU(3)_L \times SU(3)_R\) Chiral Perturbation Theory. The quantities related to D- and B-meson physics that were reviewed were the masses of the charm and bottom quarks together with the decay constants, form factors, and mixing parameters of B- and D-mesons. These are the heavy–light quantities most relevant to the determination of CKM matrix elements and the global CKM unitarity-triangle fit. Last but not least, the current status of lattice results on the QCD coupling \(\alpha _s\) was reviewed.
In the present paper we provide updated results for all the above-mentioned quantities, but also extend the scope of the review by adding a section on nucleon matrix elements. This presents results for matrix elements of flavor nonsinglet and singlet bilinear operators, including the nucleon axial charge \(g_A\) and the nucleon sigma terms. These results are relevant for constraining \(V_{ud}\), for searches for new physics in neutron decays and other processes, and for dark matter searches. In addition, the section on up and down quark masses has been largely rewritten, replacing previous estimates for \(m_u\), \(m_d\), and the mass ratios R and Q that were largely phenomenological with those from lattice QED+QCD calculations. We have also updated the discussion of the phenomenology of isospin-breaking effects in the light meson sector, and their relation to quark masses, with a lattice-centric discussion. A short review of QED in lattice-QCD simulations is also provided, including a discussion of ambiguities arising when attempting to define “physical” quantities in pure QCD.
Our main results are collected in Tables 1, 2 and 3. As is clear from the tables, for most quantities there are results from ensembles with different values for \(N_f\). In most cases, there is reasonable agreement among results with \(N_f=2\), \(2\,+\,1\), and \(2\,+\,1\,+\,1\). As precision increases, we may some day be able to distinguish among the different values of \(N_f\), in which case, presumably \(2\,+\,1\,+\,1\) would be the most realistic. (If isospin violation is critical, then \(1\,+\,1+1\) or \(1\,+\,1+1\,+\,1\) might be desired.) At present, for some quantities the errors in the \(N_f=2\,+\,1\) results are smaller than those with \(N_f=2\,+\,1\,+\,1\) (e.g., for \(m_c\)), while for others the relative size of the errors is reversed. Our suggestion to those using the averages is to take whichever of the \(N_f=2\,+\,1\) or \(N_f=2\,+\,1\,+\,1\) results has the smaller error. We do not recommend using the \(N_f=2\) results, except for studies of the \(N_f\)-dependence of condensates and \(\alpha _s\), as these have an uncontrolled systematic error coming from quenching the strange quark.
Our plan is to continue providing FLAG updates, in the form of a peer reviewed paper, roughly on a triennial basis. This effort is supplemented by our more frequently updated website http://flag.unibe.ch [4], where figures as well as pdf-files for the individual sections can be downloaded. The papers reviewed in the present edition have appeared before the closing date 30 September 2018.Footnote 1
This review is organized as follows. In the remainder of Sect. 1 we summarize the composition and rules of FLAG and discuss general issues that arise in modern lattice calculations. In Sect. 2, we explain our general methodology for evaluating the robustness of lattice results. We also describe the procedures followed for combining results from different collaborations in a single average or estimate (see Sect. 2.2 for our definition of these terms). The rest of the paper consists of sections, each dedicated to a set of closely connected physical quantities. Each of these sections is accompanied by an Appendix with explicatory notes.Footnote 2 Finally, in Appendix A we provide a glossary in which we introduce some standard lattice terminology (e.g., concerning the gauge, light-quark and heavy-quark actions), and in addition we summarize and describe the most commonly used lattice techniques and methodologies (e.g., related to renormalization, chiral extrapolations, scale setting).
1.1 FLAG composition, guidelines and rules
FLAG strives to be representative of the lattice community, both in terms of the geographical location of its members and the lattice collaborations to which they belong. We aspire to provide the nuclear- and particle-physics communities with a single source of reliable information on lattice results.
In order to work reliably and efficiently, we have adopted a formal structure and a set of rules by which all FLAG members abide. The collaboration presently consists of an Advisory Board (AB), an Editorial Board (EB), and eight Working Groups (WG). The rôle of the Advisory Board is to provide oversight of the content, procedures, schedule and membership of FLAG, to help resolve disputes, to serve as a source of advice to the EB and to FLAG as a whole, and to provide a critical assessment of drafts. They also give their approval of the final version of the preprint before it is rendered public. The Editorial Board coordinates the activities of FLAG, sets priorities and intermediate deadlines, organizes votes on FLAG procedures, writes the introductory sections, and takes care of the editorial work needed to amalgamate the sections written by the individual working groups into a uniform and coherent review. The working groups concentrate on writing the review of the physical quantities for which they are responsible, which is subsequently circulated to the whole collaboration for critical evaluation.
The current list of FLAG members and their Working Group assignments is:
Advisory Board (AB): S. Aoki, M. Golterman, R. Van De Water, and A. Vladikas
Editorial Board (EB): G. Colangelo, A. Jüttner, S. Hashimoto, S.R. Sharpe, and U. Wenger
Working Groups (coordinator listed first):
Quark masses: T. Blum, A. Portelli, and A. Ramos;
\(V_{us},V_{ud}\): S. Simula, T. Kaneko, and J. N. Simone;
LEC: S. Dürr, H. Fukaya, and U.M. Heller;
\(B_K\): P. Dimopoulos, G. Herdoiza, and R. Mawhinney;
\(f_{B_{(s)}}\), \(f_{D_{(s)}}\), \(B_B\): D. Lin, Y. Aoki, and M. Della Morte;
\(B_{(s)}\), D semileptonic and radiative decays: E. Lunghi, D. Becirevic, S. Gottlieb, and C. Pena;
\(\alpha _s\): R. Sommer, R. Horsley, and T. Onogi;
NME: R. Gupta, S. Collins, A. Nicholson, and H. Wittig;
The most important FLAG guidelines and rules are the following:
the composition of the AB reflects the main geographical areas in which lattice collaborations are active, with members from America, Asia/Oceania, and Europe;
the mandate of regular members is not limited in time, but we expect that a certain turnover will occur naturally;
whenever a replacement becomes necessary this has to keep, and possibly improve, the balance in FLAG, so that different collaborations, from different geographical areas are represented;
in all working groups the three members must belong to three different lattice collaborations;Footnote 3\(^{,}\)Footnote 4
a paper is in general not reviewed (nor colour-coded, as described in the next section) by any of its authors;
lattice collaborations will be consulted on the colour coding of their calculation;
there are also internal rules regulating our work, such as voting procedures.
For this edition of the FLAG review, we sought the advice of external reviewers once a complete draft of the review was available. For each review section, we have asked one lattice expert (who could be a FLAG alumnus/alumna) and one nonlattice phenomenologist for a critical assessment. This is similar to the procedure followed by the Particle Data Group in the creation of the Review of Particle Physics. The reviewers provide comments and feedback on scientific and stylistic matters. They are not anonymous, and enter into a discussion with the authors of the WG. Our aim with this additional step is to make sure that a wider array of viewpoints enter into the discussions, so as to make this review more useful for its intended audience.
1.2 Citation policy
We draw attention to this particularly important point. As stated above, our aim is to make lattice-QCD results easily accessible to those without lattice expertise, and we are well aware that it is likely that some readers will only consult the present paper and not the original lattice literature. It is very important that this paper not be the only one cited when our results are quoted. We strongly suggest that readers also cite the original sources. In order to facilitate this, in Tables 1, 2, and 3, besides summarizing the main results of the present review, we also cite the original references from which they have been obtained. In addition, for each figure we make a bibtex file available on our webpage [4] which contains the bibtex entries of all the calculations contributing to the FLAG average or estimate. The bibliography at the end of this paper should also make it easy to cite additional papers. Indeed, we hope that the bibliography will be one of the most widely used elements of the whole paper.
1.3 General issues
Several general issues concerning the present review are thoroughly discussed in Sect. 1.1 of our initial 2010 paper [1], and we encourage the reader to consult the relevant pages. In the remainder of the present section, we focus on a few important points. Though the discussion has been duly updated, it is similar to that of Sect. 1.2 in the previous two reviews [2, 3], with the addition of comments on the contributions from excited states that are particularly relevant for the new section on NMEs.
The present review aims to achieve two distinct goals: first, to provide a description of the relevant work done on the lattice; and, second, to draw conclusions on the basis of that work, summarizing the results obtained for the various quantities of physical interest.
The core of the information about the work done on the lattice is presented in the form of tables, which not only list the various results, but also describe the quality of the data that underlie them. We consider it important that this part of the review represents a generally accepted description of the work done. For this reason, we explicitly specify the quality requirements used and provide sufficient details in appendices so that the reader can verify the information given in the tables.Footnote 5
On the other hand, the conclusions drawn on the basis of the available lattice results are the responsibility of FLAG alone. Preferring to err on the side of caution, in several cases we draw conclusions that are more conservative than those resulting from a plain weighted average of the available lattice results. This cautious approach is usually adopted when the average is dominated by a single lattice result, or when only one lattice result is available for a given quantity. In such cases, one does not have the same degree of confidence in results and errors as when there is agreement among several different calculations using different approaches. The reader should keep in mind that the degree of confidence cannot be quantified, and it is not reflected in the quoted errors.
Each discretization has its merits, but also its shortcomings. For most topics covered in this review we have an increasingly broad database, and for most quantities lattice calculations based on totally different discretizations are now available. This is illustrated by the dense population of the tables and figures in most parts of this review. Those calculations that do satisfy our quality criteria indeed lead, in almost all cases, to consistent results, confirming universality within the accuracy reached. In our opinion, the consistency between independent lattice results, obtained with different discretizations, methods, and simulation parameters, is an important test of lattice QCD, and observing such consistency also provides further evidence that systematic errors are fully under control.
In the sections dealing with heavy quarks and with \(\alpha _s\), the situation is not the same. Since the b-quark mass can barely be resolved with current lattice spacings, most lattice methods for treating b quarks use effective field theory at some level. This introduces additional complications not present in the light-quark sector. An overview of the issues specific to heavy-quark quantities is given in the introduction of Sect. 8. For B- and D-meson leptonic decay constants, there already exists a good number of different independent calculations that use different heavy-quark methods, but there are only one or two independent calculations of semileptonic B and D meson form factors and B meson mixing parameters. For \(\alpha _s\), most lattice methods involve a range of scales that need to be resolved and controlling the systematic error over a large range of scales is more demanding. The issues specific to determinations of the strong coupling are summarized in Sect. 9.
Number of sea quarks in lattice simulations
Lattice-QCD simulations currently involve two, three or four flavours of dynamical quarks. Most simulations set the masses of the two lightest quarks to be equal, while the strange and charm quarks, if present, are heavier (and tuned to lie close to their respective physical values). Our notation for these simulations indicates which quarks are nondegenerate, e.g., \(N_{ f}=2\,+\,1\) if \(m_u=m_d < m_s\) and \(N_{ f}=2\,+\,1\,+\,1\) if \(m_u=m_d< m_s < m_c\). Calculations with \(N_{ f}=2\), i.e., two degenerate dynamical flavours, often include strange valence quarks interacting with gluons, so that bound states with the quantum numbers of the kaons can be studied, albeit neglecting strange sea-quark fluctuations. The quenched approximation (\(N_f=0\)), in which all sea-quark contributions are omitted, has uncontrolled systematic errors and is no longer used in modern lattice simulations with relevance to phenomenology. Accordingly, we will review results obtained with \(N_f=2\), \(N_f=2\,+\,1\), and \(N_f = 2\,+\,1\,+\,1\), but omit earlier results with \(N_f=0\). The only exception concerns the QCD coupling constant \(\alpha _s\). Since this observable does not require valence light quarks, it is theoretically well defined also in the \(N_f=0\) theory, which is simply pure gluodynamics. The \(N_f\)-dependence of \(\alpha _s\), or more precisely of the related quantity \(r_0 \Lambda _{\overline{\mathrm {MS}}}\), is a theoretical issue of considerable interest; here \(r_0\) is a quantity with the dimension of length that sets the physical scale, as discussed in Appendix A.2. We stress, however, that only results with \(N_f \ge 3\) are used to determine the physical value of \(\alpha _s\) at a high scale.
Lattice actions, simulation parameters, and scale setting
The remarkable progress in the precision of lattice calculations is due to improved algorithms, better computing resources, and, last but not least, conceptual developments. Examples of the latter are improved actions that reduce lattice artifacts and actions that preserve chiral symmetry to very good approximation. A concise characterization of the various discretizations that underlie the results reported in the present review is given in Appendix A.1.
Physical quantities are computed in lattice simulations in units of the lattice spacing so that they are dimensionless. For example, the pion decay constant that is obtained from a simulation is \(f_\pi a\), where a is the spacing between two neighboring lattice sites. (All simulations with results quoted in this review use hypercubic lattices, i.e., with the same spacing in all four Euclidean directions.) To convert these results to physical units requires knowledge of the lattice spacing a at the fixed values of the bare QCD parameters (quark masses and gauge coupling) used in the simulation. This is achieved by requiring agreement between the lattice calculation and experimental measurement of a known quantity, which thus “sets the scale” of a given simulation. A few details on this procedure are provided in Appendix A.2.
Renormalization and scheme dependence
Several of the results covered by this review, such as quark masses, the gauge coupling, and B-parameters, are for quantities defined in a given renormalization scheme and at a specific renormalization scale. The schemes employed (e.g., regularization-independent MOM schemes) are often chosen because of their specific merits when combined with the lattice regularization. For a brief discussion of their properties, see Appendix A.3. The conversion of the results obtained in these so-called intermediate schemes to more familiar regularization schemes, such as the \({\overline{\mathrm {MS}}}\)-scheme, is done with the aid of perturbation theory. It must be stressed that the renormalization scales accessible in simulations are limited, because of the presence of an ultraviolet (UV) cutoff of \(\sim \pi /a\). To safely match to \({\overline{\mathrm {MS}}}\), a scheme defined in perturbation theory, Renormalization Group (RG) running to higher scales is performed, either perturbatively or nonperturbatively (the latter using finite-size scaling techniques).
Extrapolations
Because of limited computing resources, lattice simulations are often performed at unphysically heavy pion masses, although results at the physical point have become increasingly common. Further, numerical simulations must be done at nonzero lattice spacing, and in a finite (four-dimensional) volume. In order to obtain physical results, lattice data are obtained at a sequence of pion masses and a sequence of lattice spacings, and then extrapolated to the physical pion mass and to the continuum limit. In principle, an extrapolation to infinite volume is also required. However, for most quantities discussed in this review, finite-volume effects are exponentially small in the linear extent of the lattice in units of the pion mass, and, in practice, one often verifies volume independence by comparing results obtained on a few different physical volumes, holding other parameters fixed. To control the associated systematic uncertainties, these extrapolations are guided by effective theories. For light-quark actions, the lattice-spacing dependence is described by Symanzik’s effective theory [93, 94]; for heavy quarks, this can be extended and/or supplemented by other effective theories such as Heavy-Quark Effective Theory (HQET). The pion-mass dependence can be parameterized with Chiral Perturbation Theory (\(\chi \)PT), which takes into account the Nambu-Goldstone nature of the lowest excitations that occur in the presence of light quarks. Similarly, one can use Heavy–Light Meson Chiral Perturbation Theory (HM\(\chi \)PT) to extrapolate quantities involving mesons composed of one heavy (b or c) and one light quark. One can combine Symanzik’s effective theory with \(\chi \)PT to simultaneously extrapolate to the physical pion mass and the continuum; in this case, the form of the effective theory depends on the discretization. See Appendix A.4 for a brief description of the different variants in use and some useful references. Finally, \(\chi \)PT can also be used to estimate the size of finite-volume effects measured in units of the inverse pion mass, thus providing information on the systematic error due to finite-volume effects in addition to that obtained by comparing simulations at different volumes.
Excited-state contamination
In all the hadronic matrix elements discussed in this review, the hadron in question is the lightest state with the chosen quantum numbers. This implies that it dominates the required correlation functions as their extent in Euclidean time is increased. Excited-state contributions are suppressed by \(e^{-\Delta E \Delta \tau }\), where \(\Delta E\) is the gap between the ground and excited states, and \(\Delta \tau \) the relevant separation in Euclidean time. The size of \(\Delta E\) depends on the hadron in question, and in general is a multiple of the pion mass. In practice, as discussed at length in Sect. 10, the contamination of signals due to excited-state contributions is a much more challenging problem for baryons than for the other particles discussed here. This is in part due to the fact that the signal-to-noise ratio drops exponentially for baryons, which reduces the values of \(\Delta \tau \) that can be used.
Critical slowing down
The lattice spacings reached in recent simulations go down to 0.05 fm or even smaller. In this regime, long autocorrelation times slow down the sampling of the configurations [95,96,97,98,99,100,101,102,103,104]. Many groups check for autocorrelations in a number of observables, including the topological charge, for which a rapid growth of the autocorrelation time is observed with decreasing lattice spacing. This is often referred to as topological freezing. A solution to the problem consists in using open boundary conditions in time [105], instead of the more common antiperiodic ones. More recently two other approaches have been proposed, one based on a multiscale thermalization algorithm [106, 107] and another based on defining QCD on a nonorientable manifold [108]. The problem is also touched upon in Sect. 9.2.1, where it is stressed that attention must be paid to this issue. While large scale simulations with open boundary conditions are already far advanced [109], only one result reviewed here has been obtained with any of the above methods (results for \(\alpha _s\) from Ref. [79] which use open boundary conditions). It is usually assumed that the continuum limit can be reached by extrapolation from the existing simulations, and that potential systematic errors due to the long autocorrelation times have been adequately controlled. Partially or completely frozen topology would produce a mixture of different \(\theta \) vacua, and the difference from the desired \(\theta =0\) result may be estimated in some cases using chiral perturbation theory, which gives predictions for the \(\theta \)-dependence of the physical quantity of interest [110, 111]. These ideas have been systematically and successfully tested in various models in [112, 113], and a numerical test on MILC ensembles indicates that the topology dependence for some of the physical quantities reviewed here is small, consistent with theoretical expectations [114].
Simulation algorithms and numerical errors
Most of the modern lattice-QCD simulations use exact algorithms such as those of Refs. [115, 116], which do not produce any systematic errors when exact arithmetic is available. In reality, one uses numerical calculations at double (or in some cases even single) precision, and some errors are unavoidable. More importantly, the inversion of the Dirac operator is carried out iteratively and it is truncated once some accuracy is reached, which is another source of potential systematic error. In most cases, these errors have been confirmed to be much less than the statistical errors. In the following we assume that this source of error is negligible. Some of the most recent simulations use an inexact algorithm in order to speed up the computation, though it may produce systematic effects. Currently available tests indicate that errors from the use of inexact algorithms are under control [117].
2 Quality criteria, averaging and error estimation
The essential characteristics of our approach to the problem of rating and averaging lattice quantities have been outlined in our first publication [1]. Our aim is to help the reader assess the reliability of a particular lattice result without necessarily studying the original article in depth. This is a delicate issue, since the ratings may make things appear simpler than they are. Nevertheless, it safeguards against the common practice of using lattice results, and drawing physics conclusions from them, without a critical assessment of the quality of the various calculations. We believe that, despite the risks, it is important to provide some compact information about the quality of a calculation. We stress, however, the importance of the accompanying detailed discussion of the results presented in the various sections of the present review.
2.1 Systematic errors and colour code
The major sources of systematic error are common to most lattice calculations. These include, as discussed in detail below, the chiral, continuum, and infinite-volume extrapolations. To each such source of error for which systematic improvement is possible we assign one of three coloured symbols: green star, unfilled green circle (which replaced in Ref. [2] the amber disk used in the original FLAG review [1]) or red square. These correspond to the following ratings:
 the parameter values and ranges used to generate the data sets allow for a satisfactory control of the systematic uncertainties;
the parameter values and ranges used to generate the data sets allow for a satisfactory control of the systematic uncertainties; the parameter values and ranges used to generate the data sets allow for a reasonable attempt at estimating systematic uncertainties, which however could be improved;
the parameter values and ranges used to generate the data sets allow for a reasonable attempt at estimating systematic uncertainties, which however could be improved; the parameter values and ranges used to generate the data sets are unlikely to allow for a reasonable control of systematic uncertainties.
the parameter values and ranges used to generate the data sets are unlikely to allow for a reasonable control of systematic uncertainties.
The appearance of a red tag, even in a single source of systematic error of a given lattice result, disqualifies it from inclusion in the global average.
Note that in the first two editions [1, 2], FLAG used the three symbols in order to rate the reliability of the systematic errors attributed to a given result by the paper’s authors. Starting with the previous edition [3] the meaning of the symbols has changed slightly – they now rate the quality of a particular simulation, based on the values and range of the chosen parameters, and its aptness to obtain well-controlled systematic uncertainties. They do not rate the quality of the analysis performed by the authors of the publication. The latter question is deferred to the relevant sections of the present review, which contain detailed discussions of the results contributing (or not) to each FLAG average or estimate.
For most quantities the colour-coding system refers to the following sources of systematic errors: (i) chiral extrapolation; (ii) continuum extrapolation; (iii) finite volume. As we will see below, renormalization is another source of systematic uncertainties in several quantities. This we also classify using the three coloured symbols listed above, but now with a different rationale: they express how reliably these quantities are renormalized, from a field-theoretic point of view (namely, nonperturbatively, or with 2-loop or 1-loop perturbation theory).
Given the sophisticated status that the field has attained, several aspects, besides those rated by the coloured symbols, need to be evaluated before one can conclude whether a particular analysis leads to results that should be included in an average or estimate. Some of these aspects are not so easily expressible in terms of an adjustable parameter such as the lattice spacing, the pion mass or the volume. As a result of such considerations, it sometimes occurs, albeit rarely, that a given result does not contribute to the FLAG average or estimate, despite not carrying any red tags. This happens, for instance, whenever aspects of the analysis appear to be incomplete (e.g., an incomplete error budget), so that the presence of inadequately controlled systematic effects cannot be excluded. This mostly refers to results with a statistical error only, or results in which the quoted error budget obviously fails to account for an important contribution.
Of course, any colour coding has to be treated with caution; we emphasize that the criteria are subjective and evolving. Sometimes, a single source of systematic error dominates the systematic uncertainty and it is more important to reduce this uncertainty than to aim for green stars for other sources of error. In spite of these caveats, we hope that our attempt to introduce quality measures for lattice simulations will prove to be a useful guide. In addition, we would like to stress that the agreement of lattice results obtained using different actions and procedures provides further validation.
2.1.1 Systematic effects and rating criteria
The precise criteria used in determining the colour coding are unavoidably time-dependent; as lattice calculations become more accurate, the standards against which they are measured become tighter. For this reason FLAG reassesses criteria with each edition and as a result some of the quality criteria (the one on chiral extrapolation for instance) have been tightened up over time [1,2,3].
In the following, we present the rating criteria used in the current report. While these criteria apply to most quantities without modification there are cases where they need to be amended or additional criteria need to be defined. For instance, when discussing results obtained in the \(\epsilon \)-regime of chiral perturbation theory in Sect. 5 the finite volume criterion listed below for the p-regime is no longer appropriate.Footnote 6 Similarly, the discussion of the strong coupling constant in Sect. 9 requires tailored criteria for renormalization, perturbative behaviour, and continuum extrapolation. In such cases, the modified criteria are discussed in the respective sections. Apart from only a few exceptions the following colour code applies in the tables:
Chiral extrapolation:
 \(M_{\pi ,\mathrm {min}}< 200\) MeV, with three or more pion masses used in the extrapolation
\(M_{\pi ,\mathrm {min}}< 200\) MeV, with three or more pion masses used in the extrapolationor two values of \(M_\pi \) with one lying within 10 MeV of 135MeV (the physical neutral pion mass) and the other one below 200 MeV
 200 MeV \(\le M_{\pi ,{\mathrm {min}}} \le \) 400 MeV, with three or more pion masses used in the extrapolation
200 MeV \(\le M_{\pi ,{\mathrm {min}}} \le \) 400 MeV, with three or more pion masses used in the extrapolationor two values of \(M_\pi \) with \(M_{\pi ,{\mathrm {min}}}<\) 200 MeV
or a single value of \(M_\pi \), lying within 10 MeV of 135 MeV (the physical neutral pion mass)
 otherwise
otherwise
This criterion has changed with respect to the previous edition [3].
Continuum extrapolation:
 at least three lattice spacings and at least two points below 0.1 fm and a range of lattice spacings satisfying \([a_{\mathrm {max}}/a_{\mathrm {min}}]^2 \ge 2\)
at least three lattice spacings and at least two points below 0.1 fm and a range of lattice spacings satisfying \([a_{\mathrm {max}}/a_{\mathrm {min}}]^2 \ge 2\) at least two lattice spacings and at least one point below 0.1 fm and a range of lattice spacings satisfying \([a_{\mathrm {max}}/a_{\mathrm {min}}]^2 \ge 1.4\)
at least two lattice spacings and at least one point below 0.1 fm and a range of lattice spacings satisfying \([a_{\mathrm {max}}/a_{\mathrm {min}}]^2 \ge 1.4\) otherwise
otherwise
It is assumed that the lattice action is \({\mathcal {O}}(a)\)-improved (i.e., the discretization errors vanish quadratically with the lattice spacing); otherwise this will be explicitly mentioned. For unimproved actions an additional lattice spacing is required. This condition is unchanged from Ref. [3].
Finite-volume effects:
The finite-volume colour code used for a result is chosen to be the worse of the QCD and the QED codes, as described below. If only QCD is used the QED colour code is ignored.
– For QCD:
 \([M_{\pi ,\mathrm {min}} / M_{\pi ,\mathrm {fid}}]^2 \exp \{4-M_{\pi ,\mathrm {min}}[L(M_{\pi ,\mathrm {min}})]_{\mathrm {max}}\} < 1\), or at least three volumes
\([M_{\pi ,\mathrm {min}} / M_{\pi ,\mathrm {fid}}]^2 \exp \{4-M_{\pi ,\mathrm {min}}[L(M_{\pi ,\mathrm {min}})]_{\mathrm {max}}\} < 1\), or at least three volumes \([M_{\pi ,\mathrm {min}} / M_{\pi ,\mathrm {fid}}]^2 \exp \{3-M_{\pi ,\mathrm {min}}[L(M_{\pi ,\mathrm {min}})]_{\mathrm {max}}\} < 1\), or at least two volumes
\([M_{\pi ,\mathrm {min}} / M_{\pi ,\mathrm {fid}}]^2 \exp \{3-M_{\pi ,\mathrm {min}}[L(M_{\pi ,\mathrm {min}})]_{\mathrm {max}}\} < 1\), or at least two volumes otherwise
otherwise
where we have introduced \([L(M_{\pi ,\mathrm {min}})]_{\mathrm {max}}\), which is the maximum box size used in the simulations performed at the smallest pion mass \(M_{\pi ,\mathrm{min}}\), as well as a fiducial pion mass \(M_{\pi ,\mathrm{fid}}\), which we set to 200 MeV (the cutoff value for a green star in the chiral extrapolation). It is assumed here that calculations are in the p-regime of chiral perturbation theory, and that all volumes used exceed 2 fm. This condition has been improved between the second [2] and the third [3] edition of the FLAG review but remains unchanged since. The rationale for this condition is as follows. Finite volume effects contain the universal factor \(\exp \{- L~M_\pi \}\), and if this were the only contribution a criterion based on the values of \(M_{\pi ,\text {min}} L\) would be appropriate. This is what we used in Ref. [2] (with \(M_{\pi ,\text {min}} L>4\) for
 and \(M_{\pi ,\text {min}} L>3\) for
and \(M_{\pi ,\text {min}} L>3\) for  ). However, as pion masses decrease, one must also account for the weakening of the pion couplings. In particular, 1-loop chiral perturbation theory [118] reveals a behaviour proportional to \(M_\pi ^2 \exp \{- L~M_\pi \}\). Our new condition includes this weakening of the coupling, and ensures, for example, that simulations with \(M_{\pi ,\mathrm {min}} = 135~\mathrm{MeV}\) and \(L~M_{\pi ,\mathrm {min}} = 3.2\) are rated equivalently to those with \(M_{\pi ,\mathrm {min}} = 200~\mathrm{MeV}\) and \(L~M_{\pi ,\mathrm {min}} = 4\).
). However, as pion masses decrease, one must also account for the weakening of the pion couplings. In particular, 1-loop chiral perturbation theory [118] reveals a behaviour proportional to \(M_\pi ^2 \exp \{- L~M_\pi \}\). Our new condition includes this weakening of the coupling, and ensures, for example, that simulations with \(M_{\pi ,\mathrm {min}} = 135~\mathrm{MeV}\) and \(L~M_{\pi ,\mathrm {min}} = 3.2\) are rated equivalently to those with \(M_{\pi ,\mathrm {min}} = 200~\mathrm{MeV}\) and \(L~M_{\pi ,\mathrm {min}} = 4\).– For QED (where applicable):
 \(1/([M_{\pi ,\mathrm {min}}L(M_{\pi ,\mathrm {min}})]_{\mathrm {max}})^{n_{\mathrm {min}}}<0.02\), or at least four volumes
\(1/([M_{\pi ,\mathrm {min}}L(M_{\pi ,\mathrm {min}})]_{\mathrm {max}})^{n_{\mathrm {min}}}<0.02\), or at least four volumes \(1/([M_{\pi ,\mathrm {min}}L(M_{\pi ,\mathrm {min}})]_{\mathrm {max}})^{n_{\mathrm {min}}}<0.04\), or at least three volumes
\(1/([M_{\pi ,\mathrm {min}}L(M_{\pi ,\mathrm {min}})]_{\mathrm {max}})^{n_{\mathrm {min}}}<0.04\), or at least three volumes otherwise
otherwise
Because of the infrared-singular structure of QED, electromagnetic finite-volume effects decay only like a power of the inverse spatial extent. In several cases like mass splittings [119, 120] or leptonic decays [121], the leading corrections are known to be universal, i.e., independent of the structure of the involved hadrons. In such cases, the leading universal effects can be directly subtracted exactly from the lattice data. We denote \(n_{\mathrm {min}}\) the smallest power of \(\frac{1}{L}\) at which such a subtraction cannot be done. In the widely used finite-volume formulation \(\mathrm {QED}_L\), one always has \(n_{\mathrm {min}}\le 3\) due to the nonlocality of the theory [122]. While the QCD criteria have not changed with respect to Ref. [3] the QED criteria are new. They are used here only in Sect. 3.
Isospin breaking effects (where applicable):
 all leading isospin breaking effects are included in the lattice calculation
all leading isospin breaking effects are included in the lattice calculation isospin breaking effects are included using the electro-quenched approximation
isospin breaking effects are included using the electro-quenched approximation otherwise
otherwise
This criterion is used for quantities which are breaking isospin symmetry or which can be determined at the sub-percent accuracy where isospin breaking effects, if not included, are expected to be the dominant source of uncertainty. In the current edition, this criterion is only used for the up and down quark masses, and related quantities (\(\epsilon \), \(Q^2\) and \(R^2\)). The criteria for isospin breaking effects feature for the first time in the FLAG review.
Renormalization (where applicable):
 nonperturbative
nonperturbative 1-loop perturbation theory or higher with a reasonable estimate of truncation errors
1-loop perturbation theory or higher with a reasonable estimate of truncation errors otherwise
otherwise
In Ref. [1], we assigned a red square to all results which were renormalized at 1-loop in perturbation theory. In Ref. [2], we decided that this was too restrictive, since the error arising from renormalization constants, calculated in perturbation theory at 1-loop, is often estimated conservatively and reliably. We did not change these criteria since.
Renormalization Group (RG) running (where applicable):
For scale-dependent quantities, such as quark masses or \(B_K\), it is essential that contact with continuum perturbation theory can be established. Various different methods are used for this purpose (cf. Appendix A.3): Regularization-independent Momentum Subtraction (RI/MOM), the Schrödinger functional, and direct comparison with (resummed) perturbation theory. Irrespective of the particular method used, the uncertainty associated with the choice of intermediate renormalization scales in the construction of physical observables must be brought under control. This is best achieved by performing comparisons between nonperturbative and perturbative running over a reasonably broad range of scales. These comparisons were initially only made in the Schrödinger functional approach, but are now also being performed in RI/MOM schemes. We mark the data for which information about nonperturbative running checks is available and give some details, but do not attempt to translate this into a colour code.
The pion mass plays an important role in the criteria relevant for chiral extrapolation and finite volume. For some of the regularizations used, however, it is not a trivial matter to identify this mass. In the case of twisted-mass fermions, discretization effects give rise to a mass difference between charged and neutral pions even when the up- and down-quark masses are equal: the charged pion is found to be the heavier of the two for twisted-mass Wilson fermions (cf. Ref. [123]). In early works, typically referring to \(N_f=2\) simulations (e.g., Refs. [123] and [48]), chiral extrapolations are based on chiral perturbation theory formulae which do not take these regularization effects into account. After the importance of accounting for isospin breaking when doing chiral fits was shown in Ref. [124], later works, typically referring to \(N_f=2\,+\,1\,+\,1\) simulations, have taken these effects into account [9]. We use \(M_{\pi ^\pm }\) for \(M_{\pi ,\mathrm {min}}\) in the chiral-extrapolation rating criterion. On the other hand, we identify \(M_{\pi ,\mathrm {min}}\) with the root mean square (RMS) of \(M_{\pi ^+}\), \(M_{\pi ^-}\) and \(M_{\pi ^0}\) in the finite-volume rating criterion.Footnote 7
In the case of staggered fermions, discretization effects give rise to several light states with the quantum numbers of the pion.Footnote 8 The mass splitting among these “taste” partners represents a discretization effect of \({\mathcal {O}}(a^2)\), which can be significant at large lattice spacings but shrinks as the spacing is reduced. In the discussion of the results obtained with staggered quarks given in the following sections, we assume that these artifacts are under control. We conservatively identify \(M_{\pi ,\mathrm {min}}\) with the root mean square (RMS) average of the masses of all the taste partners, both for chiral-extrapolation and finite-volume criteria.Footnote 9
The strong coupling \(\alpha _s\) is computed in lattice QCD with methods differing substantially from those used in the calculations of the other quantities discussed in this review. Therefore, we have established separate criteria for \(\alpha _s\) results, which will be discussed in Sect. 9.2.1.
In the new section on nuclear matrix elements, Sect. 10, an additional criterion has been introduced. This concerns the level of control over contamination from excited states, which is a more challenging issue for nucleons than for mesons. In addition, the chiral-extrapolation criterion in this section is somewhat stricter than that given above.
2.1.2 Heavy-quark actions
For the b quark, the discretization of the heavy-quark action follows a very different approach from that used for light flavours. There are several different methods for treating heavy quarks on the lattice, each with its own issues and considerations. Most of these methods use Effective Field Theory (EFT) at some point in the computation, either via direct simulation of the EFT, or by using EFT as a tool to estimate the size of cutoff errors, or by using EFT to extrapolate from the simulated lattice quark masses up to the physical b-quark mass. Because of the use of an EFT, truncation errors must be considered together with discretization errors.
The charm quark lies at an intermediate point between the heavy and light quarks. In our earlier reviews, the calculations involving charm quarks often treated it using one of the approaches adopted for the b quark. Since the last report [3], however, we found more recent calculations to simulate the charm quark using light-quark actions. This has become possible thanks to the increasing availability of dynamical gauge field ensembles with fine lattice spacings. But clearly, when charm quarks are treated relativistically, discretization errors are more severe than those of the corresponding light-quark quantities.
In order to address these complications, we add a new heavy-quark treatment category to the rating system. The purpose of this criterion is to provide a guideline for the level of action and operator improvement needed in each approach to make reliable calculations possible, in principle.
A description of the different approaches to treating heavy quarks on the lattice is given in Appendix A.1.3, including a discussion of the associated discretization, truncation, and matching errors. For truncation errors we use HQET power counting throughout, since this review is focused on heavy-quark quantities involving B and D mesons rather than bottomonium or charmonium quantities. Here we describe the criteria for how each approach must be implemented in order to receive an acceptable ( ) rating for both the heavy-quark actions and the weak operators. Heavy-quark implementations without the level of improvement described below are rated not acceptable (
) rating for both the heavy-quark actions and the weak operators. Heavy-quark implementations without the level of improvement described below are rated not acceptable ( ). The matching is evaluated together with renormalization, using the renormalization criteria described in Sect. 2.1.1. We emphasize that the heavy-quark implementations rated as acceptable and described below have been validated in a variety of ways, such as via phenomenological agreement with experimental measurements, consistency between independent lattice calculations, and numerical studies of truncation errors. These tests are summarized in Sect. 8.
). The matching is evaluated together with renormalization, using the renormalization criteria described in Sect. 2.1.1. We emphasize that the heavy-quark implementations rated as acceptable and described below have been validated in a variety of ways, such as via phenomenological agreement with experimental measurements, consistency between independent lattice calculations, and numerical studies of truncation errors. These tests are summarized in Sect. 8.
Relativistic heavy-quark actions
 at least tree-level \({\mathcal {O}}(a)\) improved action and weak operators
at least tree-level \({\mathcal {O}}(a)\) improved action and weak operators
This is similar to the requirements for light-quark actions. All current implementations of relativistic heavy-quark actions satisfy this criterion.
NRQCD
 tree-level matched through \({\mathcal {O}}(1/m_h)\) and improved through \({\mathcal {O}}(a^2)\)
tree-level matched through \({\mathcal {O}}(1/m_h)\) and improved through \({\mathcal {O}}(a^2)\)
The current implementations of NRQCD satisfy this criterion, and also include tree-level corrections of \({\mathcal {O}}(1/m_h^2)\) in the action.
HQET
 tree-level matched through \({\mathcal {O}}(1/m_h)\) with discretization errors starting at \({\mathcal {O}}(a^2)\)
tree-level matched through \({\mathcal {O}}(1/m_h)\) with discretization errors starting at \({\mathcal {O}}(a^2)\)
The current implementation of HQET by the ALPHA collaboration satisfies this criterion, since both action and weak operators are matched nonperturbatively through \({\mathcal {O}}(1/m_h)\). Calculations that exclusively use a static-limit action do not satisfy this criterion, since the static-limit action, by definition, does not include \(1/m_h\) terms. We therefore include static computations in our final estimates only if truncation errors (in \(1/m_h\)) are discussed and included in the systematic uncertainties.
Light-quark actions for heavy quarks
 discretization errors starting at \({\mathcal {O}}(a^2)\) or higher
discretization errors starting at \({\mathcal {O}}(a^2)\) or higher
This applies to calculations that use the tmWilson action, a nonperturbatively improved Wilson action, domain wall fermions or the HISQ action for charm-quark quantities. It also applies to calculations that use these light quark actions in the charm region and above together with either the static limit or with an HQET-inspired extrapolation to obtain results at the physical b-quark mass. In these cases, the continuum-extrapolation criteria described earlier must be applied to the entire range of heavy-quark masses used in the calculation.
2.1.3 Conventions for the figures
For a coherent assessment of the present situation, the quality of the data plays a key role, but the colour coding cannot be carried over to the figures. On the other hand, simply showing all data on equal footing might give the misleading impression that the overall consistency of the information available on the lattice is questionable. Therefore, in the figures we indicate the quality of the data in a rudimentary way, using the following symbols:
 corresponds to results included in the average or estimate (i.e., results that contribute to the black square below);
corresponds to results included in the average or estimate (i.e., results that contribute to the black square below); corresponds to results that are not included in the average but pass all quality criteria;
corresponds to results that are not included in the average but pass all quality criteria; corresponds to all other results;
corresponds to all other results; corresponds to FLAG averages or estimates; they are also highlighted by a gray vertical band.
corresponds to FLAG averages or estimates; they are also highlighted by a gray vertical band.
The reason for not including a given result in the average is not always the same: the result may fail one of the quality criteria; the paper may be unpublished; it may be superseded by newer results; or it may not offer a complete error budget.
Symbols other than squares are used to distinguish results with specific properties and are always explained in the caption.Footnote 10
Often, nonlattice data are also shown in the figures for comparison. For these we use the following symbols:
 corresponds to nonlattice results;
corresponds to nonlattice results; corresponds to Particle Data Group (PDG) results.
corresponds to Particle Data Group (PDG) results.
2.2 Averages and estimates
FLAG results of a given quantity are denoted either as averages or as estimates. Here we clarify this distinction. To start with, both averages and estimates are based on results without any red tags in their colour coding. For many observables there are enough independent lattice calculations of good quality, with all sources of error (not merely those related to the colour-coded criteria), as analyzed in the original papers, appearing to be under control. In such cases, it makes sense to average these results and propose such an average as the best current lattice number. The averaging procedure applied to this data and the way the error is obtained is explained in detail in Sect. 2.3. In those cases where only a sole result passes our rating criteria (colour coding), we refer to it as our FLAG average, provided it also displays adequate control of all other sources of systematic uncertainty.
On the other hand, there are some cases in which this procedure leads to a result that, in our opinion, does not cover all uncertainties. Systematic errors are by their nature often subjective and difficult to estimate, and may thus end up being underestimated in one or more results that receive green symbols for all explicitly tabulated criteria. Adopting a conservative policy, in these cases we opt for an estimate (or a range), which we consider as a fair assessment of the knowledge acquired on the lattice at present. This estimate is not obtained with a prescribed mathematical procedure, but reflects what we consider the best possible analysis of the available information. The hope is that this will encourage more detailed investigations by the lattice community.
There are two other important criteria that also play a role in this respect, but that cannot be colour coded, because a systematic improvement is not possible. These are: i) the publication status, and ii) the number of sea-quark flavours \(N_{ f}\). As far as the former criterion is concerned, we adopt the following policy: we average only results that have been published in peer-reviewed journals, i.e., they have been endorsed by referee(s). The only exception to this rule consists in straightforward updates of previously published results, typically presented in conference proceedings. Such updates, which supersede the corresponding results in the published papers, are included in the averages. Note that updates of earlier results rely, at least partially, on the same gauge-field-configuration ensembles. For this reason, we do not average updates with earlier results. Nevertheless, all results are listed in the tables,Footnote 11 and their publication status is identified by the following symbols:
Publication status:
A published or plain update of published results
P preprint
C conference contribution
In the present edition, the publication status on the 30th of September 2018 is relevant. If the paper appeared in print after that date, this is accounted for in the bibliography, but does not affect the averages.Footnote 12
As noted above, in this review we present results from simulations with \(N_f=2\), \(N_f=2\,+\,1\) and \(N_f=2\,+\,1\,+\,1\) (except for \( r_0 \Lambda _{\overline{\mathrm {MS}}}\) where we also give the \(N_f=0\) result). We are not aware of an a priori way to quantitatively estimate the difference between results produced in simulations with a different number of dynamical quarks. We therefore average results at fixed \(N_{ f}\) separately; averages of calculations with different \(N_{ f}\) are not provided.
To date, no significant differences between results with different values of \(N_f\) have been observed in the quantities listed in Tables 1, 2, and 3. In the future, as the accuracy and the control over systematic effects in lattice calculations increases, it will hopefully be possible to see a difference between results from simulations with \(N_{ f}= 2\) and \(N_{ f}= 2 + 1\), and thus determine the size of the Zweig-rule violations related to strange-quark loops. This is a very interesting issue per se, and one which can be quantitatively addressed only with lattice calculations.
The question of differences between results with \(N_{ f}=2\,+\,1\) and \(N_{ f}=2\,+\,1\,+\,1\) is more subtle. The dominant effect of including the charm sea quark is to shift the lattice scale, an effect that is accounted for by fixing this scale nonperturbatively using physical quantities. For most of the quantities discussed in this review, it is expected that residual effects are small in the continuum limit, suppressed by \(\alpha _s(m_c)\) and powers of \(\Lambda ^2/m_c^2\). Here \(\Lambda \) is a hadronic scale that can only be roughly estimated and depends on the process under consideration. Note that the \(\Lambda ^2/m_c^2\) effects have been addressed in Refs. [130, 131]. Assuming that such effects are small, it might be reasonable to average the results from \(N_{ f}=2\,+\,1\) and \(N_{ f}=2\,+\,1\,+\,1\) simulations.
2.3 Averaging procedure and error analysis
In the present report, we repeatedly average results obtained by different collaborations, and estimate the error on the resulting averages. Here we provide details on how averages are obtained.
2.3.1 Averaging: generic case
We follow the procedure of the previous two editions [2, 3], which we describe here in full detail.
One of the problems arising when forming averages is that not all of the data sets are independent. In particular, the same gauge-field configurations, produced with a given fermion discretization, are often used by different research teams with different valence-quark lattice actions, obtaining results that are not really independent. Our averaging procedure takes such correlations into account.
Consider a given measurable quantity Q, measured by M distinct, not necessarily uncorrelated, numerical experiments (simulations). The result of each of these measurement is expressed as
where \(x_i\) is the value obtained by the \(i{\mathrm{th}}\) experiment (\(i = 1, \ldots , M\)) and \(\sigma ^{(k)}_i\) (for \(k = 1, \ldots , E\)) are the various errors. Typically \(\sigma ^{(1)}_i\) stands for the statistical error and \(\sigma ^{(\alpha )}_i\) (\(\alpha \ge 2\)) are the different systematic errors from various sources. For each individual result, we estimate the total error \(\sigma _i \) by adding statistical and systematic errors in quadrature:
With the weight factor of each total error estimated in standard fashion,
the central value of the average over all simulations is given by
The above central value corresponds to a \(\chi _{\mathrm{min}}^2\) weighted average, evaluated by adding statistical and systematic errors in quadrature. If the fit is not of good quality (\(\chi _\mathrm{min}^2/\mathrm{dof} > 1\)), the statistical and systematic error bars are stretched by a factor \(S = \sqrt{\chi ^2/\mathrm{dof}}\).
Next, we examine error budgets for individual calculations and look for potentially correlated uncertainties. Specific problems encountered in connection with correlations between different data sets are described in the text that accompanies the averaging. If there is reason to believe that a source of error is correlated between two calculations, a \(100\%\) correlation is assumed. The correlation matrix \(C_{ij}\) for the set of correlated lattice results is estimated by a prescription due to Schmelling [132]. This consists in defining
with \(\sum _{\alpha }^\prime \) running only over those errors of \(x_i\) that are correlated with the corresponding errors of the measurement \(x_j\). This expresses the part of the uncertainty in \(x_i\) that is correlated with the uncertainty in \(x_j\). If no such correlations are known to exist, then we take \(\sigma _{i;j} =0\). The diagonal and off-diagonal elements of the correlation matrix are then taken to be
Finally, the error of the average is estimated by
and the FLAG average is
2.3.2 Nested averaging
We have encountered one case where the correlations between results are more involved, and a nested averaging scheme is required. This concerns the B-meson bag parameters discussed in Sect. 8.2. In the following, we describe the details of the nested averaging scheme. This is an updated version of the section added in the web update of the FLAG 16 report.
The issue arises for a quantity Q that is given by a ratio, \(Q=Y/Z\). In most simulations, both Y and Z are calculated, and the error in Q can be obtained in each simulation in the standard way. However, in other simulations only Y is calculated, with Z taken from a global average of some type. The issue to be addressed is that this average value \({\overline{Z}}\) has errors that are correlated with those in Q.
In the example that arises in Sect. 8.2, \(Q=B_B\), \(Y=B_B f_B^2\) and \(Z=f_B^2\). In one of the simulations that contribute to the average, Z is replaced by \({\overline{Z}}\), the PDG average for \(f_B^2\) [133] (obtained with an averaging procedure similar to that used by FLAG). This simulation is labeled with \(i=1\), so that
The other simulations have results labeled \(Q_j\), with \(j\ge 2\). In this set up, the issue is that \({\overline{Z}}\) is correlated with the \(Q_j\), \(j\ge 2\).Footnote 13
We begin by decomposing the error in \(Q_1\) in the same schematic form as above,
Here the last term represents the error propagating from that in \({\overline{Z}}\), while the others arise from errors in \(Y_1\). For the remaining \(Q_j\) (\(j\ge 2\)) the decomposition is as in Eq. (1). The total error of \(Q_1\) then reads
while that for the \(Q_j\) (\(j\ge 2\)) is
Correlations between \(Q_j\) and \(Q_k\) (\(j,k\ge 2\)) are taken care of by Schmelling’s prescription, as explained above. What is new here is how the correlations between \(Q_1\) and \(Q_j\) (\(j\ge 2\)) are taken into account.
To proceed, we recall from Eq. (7) that \(\sigma _{{\overline{Z}}}\) is given by
Here the indices \(i'\) and \(j'\) run over the \(M'\) simulations that contribute to \({\overline{Z}}\), which, in general, are different from those contributing to the results for Q. The weights \(\omega [Z]\) and correlation matrix C[Z] are given an explicit argument Z to emphasize that they refer to the calculation of this quantity and not to that of Q. C[Z] is calculated using the Schmelling prescription [Eqs. (5)–(7)] in terms of the errors, \(\sigma [Z]_{i'}^{(\alpha )}\), taking into account the correlations between the different calculations of Z.
We now generalize Schmelling’s prescription for \(\sigma _{i;j}\), Eq. (5), to that for \(\sigma _{1;k}\) (\(k\ge 2\)), i.e., the part of the error in \(Q_1\) that is correlated with \(Q_k\). We take
The first term under the square root sums those sources of error in \(Y_1\) that are correlated with \(Q_k\). Here we are using a more explicit notation from that in Eq. (5), with \((\alpha ) \leftrightarrow k\) indicating that the sum is restricted to the values of \(\alpha \) for which the error \(\sigma _{Y_1}^{(\alpha )}\) is correlated with \(Q_k\). The second term accounts for the correlations within \({\overline{Z}}\) with \(Q_k\), and is the nested part of the present scheme. The new matrix \(C[Z]_{i'j'\leftrightarrow k}\) is a restriction of the full correlation matrix C[Z], and is defined as follows. Its diagonal elements are given by
where the summation \(\sum ^\prime _{(\alpha )\leftrightarrow k}\) over \((\alpha )\) is restricted to those \(\sigma [Z]_{i'}^{(\alpha )}\) that are correlated with \(Q_k\). The off-diagonal elements are
where the summation \(\sum ^\prime _{(\alpha )\leftrightarrow j'k}\) over \((\alpha )\) is restricted to \(\sigma [Z]_{i'}^{(\alpha )}\) that are correlated with both \(Z_{j'}\) and \(Q_k\).
The last quantity that we need to define is \(\sigma _{k;1}\).
where the summation \(\sum ^\prime _{(\alpha )\leftrightarrow 1}\) is restricted to those \(\sigma _k^{(\alpha )}\) that are correlated with one of the terms in Eq. (11).
In summary, we construct the correlation matrix \(C_{ij}\) using Eq. (6), as in the generic case, except the expressions for \(\sigma _{1;k}\) and \(\sigma _{k;1}\) are now given by Eqs. (14) and (19), respectively. All other \(\sigma _{i;j}\) are given by the original Schmelling prescription, Eq. (5). In this way we extend the philosophy of Schmelling’s approach while accounting for the more involved correlations.
3 Quark masses
Authors: T. Blum, A. Portelli, A. Ramos
Quark masses are fundamental parameters of the Standard Model. An accurate determination of these parameters is important for both phenomenological and theoretical applications. The bottom- and charm-quark masses, for instance, are important sources of parametric uncertainties in several Higgs decay modes. The up-, down- and strange-quark masses govern the amount of explicit chiral symmetry breaking in QCD. From a theoretical point of view, the values of quark masses provide information about the flavour structure of physics beyond the Standard Model. The Review of Particle Physics of the Particle Data Group contains a review of quark masses [134], which covers light as well as heavy flavours. Here we also consider light- and heavy-quark masses, but focus on lattice results and discuss them in more detail. We do not discuss the top quark, however, because it decays weakly before it can hadronize, and the nonperturbative QCD dynamics described by present day lattice simulations is not relevant. The lattice determination of light- (up, down, strange), charm- and bottom-quark masses is considered below in Sects. 3.1, 3.2, and 3.3, respectively.
Quark masses cannot be measured directly in experiment because quarks cannot be isolated, as they are confined inside hadrons. From a theoretical point of view, in QCD with \(N_f\) flavours, a precise definition of quark masses requires one to choose a particular renormalization scheme. This renormalization procedure introduces a renormalization scale \(\mu \), and quark masses depend on this renormalization scale according to the Renormalization Group (RG) equations. In mass-independent renormalization schemes the RG equations reads
where the function \(\tau ({{\bar{g}}})\) is the anomalous dimension, which depends only on the value of the strong coupling \(\alpha _s=\bar{g}^2/(4\pi )\). Note that in QCD \(\tau ({{\bar{g}}})\) is the same for all quark flavours. The anomalous dimension is scheme dependent, but its perturbative expansion

has a leading coefficient \(d_0 = 8/(4\pi )^2\), which is scheme independent.Footnote 14 Equation (20), being a first order differential equation, can be solved exactly by using Eq. (21) as boundary condition. The formal solution of the RG equation reads
where \(b_0 = (11-2N_f/3) / (4\pi )^2\) is the universal leading perturbative coefficient in the expansion of the \(\beta \)-function \(\beta ({{\bar{g}}})\). The renormalization group invariant (RGI) quark masses \(M_i\) are formally integration constants of the RG Eq. (20). They are scale independent, and due to the universality of the coefficient \(d_0\), they are also scheme independent. Moreover, they are nonperturbatively defined by Eq. (22). They only depend on the number of flavours \(N_f\), making them a natural candidate to quote quark masses and compare determinations from different lattice collaborations. Nevertheless, it is customary in the phenomenology community to use the \(\overline{\mathrm{MS}}\) scheme at a scale \(\mu = 2\) GeV to compare different results for light-quark masses, and use a scale equal to its own mass for the charm and bottom quarks. In this review, we will quote the final averages of both quantities.
Results for quark masses are always quoted in the four-flavour theory. \(N_{\mathrm{f}}=2\,+\,1\) results have to be converted to the four flavour theory. Fortunately, the charm quark is heavy \((\Lambda _\mathrm{QCD}/m_c)^2<1\), and this conversion can be performed in perturbation theory with negligible (\(\sim 0.2\%\)) perturbative uncertainties. Nonperturbative corrections in this matching are more difficult to estimate. Since these effects are suppressed by a factor of \(1/N_{\mathrm{c}}\), and a factor of the strong coupling at the scale of the charm mass, naive power counting arguments would suggest that the effects are \(\sim 1\%\). In practice, numerical nonperturbative studies [130, 131] have found this power counting argument to be an overestimate by one order of magnitude in the determination of simple hadronic quantities or the \(\Lambda \)-parameter. Moreover, lattice determinations do not show any significant deviation between the \(N_{\mathrm{f}}=2\,+\,1\) and \(N_\mathrm{f}=2\,+\,1\,+\,1\) simulations. For example, the difference in the final averages for the mass of the strange quark \(m_s\) between \(N_f=2\,+\,1\) and \(N_f=2\,+\,1\,+\,1\) determinations is about a 0.8%, and negligible from a statistical point of view.
We quote all final averages at 2 GeV in the \(\overline{\mathrm{MS}}\) scheme and also the RGI values (in the four flavour theory). We use the exact RG Eq. (22). Note that to use this equation we need the value of the strong coupling in the \(\overline{\mathrm{MS}}\) scheme at a scale \(\mu = 2\) GeV. All our results are obtained from the RG equation in the \(\overline{\mathrm{MS}}\) scheme and the 5-loop beta function together with the value of the \(\Lambda \)-parameter in the four-flavour theory \(\Lambda ^{(4)}_{\overline{\mathrm{MS}}} = 294(12)\, \mathrm{MeV}\) obtained in this review (see Sect. 9). In the uncertainties of the RGI massses we separate the contributions from the determination of the quark masses and the propagation of the uncertainty of \(\Lambda ^{(4)}_{\overline{\mathrm{MS}}}\). These are identified with the subscripts m and \(\Lambda \), respectively.
Conceptually, all lattice determinations of quark masses contain three basic ingredients:
- 1.
Tuning the lattice bare-quark masses to match the experimental values of some quantities. Pseudo-scalar meson masses provide the most common choice, since they have a strong dependence on the values of quark masses. In pure QCD with \(N_f\) quark flavours these values are not known, since the electromagnetic interactions affect the experimental values of meson masses. Therefore, pure QCD determinations use model/lattice information to determine the location of the physical point. This is discussed at length in Sect. 3.1.1.
- 2.
Renormalization of the bare-quark masses. Bare-quark masses determined with the above-mentioned criteria have to be renormalized. Many of the latest determinations use some nonperturbatively defined scheme. One can also use perturbation theory to connect directly the values of the bare-quark masses to the values in the \(\overline{\mathrm{MS}}\) scheme at 2 GeV. Experience shows that 1-loop calculations are unreliable for the renormalization of quark masses: usually at least two loops are required to have trustworthy results.
- 3.
If quark masses have been nonperturbatively renormalized, for example, to some MOM/SF scheme, the values in this scheme must be converted to the phenomenologically useful values in the \(\overline{\mathrm{MS}}\) scheme (or to the scheme/scale independent RGI masses). Either option requires the use of perturbation theory. The larger the energy scale of this matching with perturbation theory, the better, and many recent computations in MOM schemes do a nonperturbative running up to \(3{-}4\) GeV. Computations in the SF scheme allow us to perform this running nonperturbatively over large energy scales and match with perturbation theory directly at the electro-weak scale \(\sim 100\) GeV.
Note that quark masses are different from other quantities determined on the lattice since perturbation theory is unavoidable when matching to schemes in the continuum.
We mention that lattice-QCD calculations of the b-quark mass have an additional complication which is not present in the case of the charm and light quarks. At the lattice spacings currently used in numerical simulations the direct treatment of the b quark with the fermionic actions commonly used for light quarks is very challenging. Only one determination of the b-quark mass uses this approach, reaching the physical b-quark mass region at two lattice spacings with \(am\sim 0.9\) and 0.64, respectively (see Sect. 3.3). There are a few widely used approaches to treat the b quark on the lattice, which have been already discussed in the FLAG 13 review (see Sect. 8 of Ref. [2]). Those relevant for the determination of the b-quark mass will be briefly described in Sect. 3.3.
3.1 Masses of the light quarks
Light-quark masses are particularly difficult to determine because they are very small (for the up and down quarks) or small (for the strange quark) compared to typical hadronic scales. Thus, their impact on typical hadronic observables is minute, and it is difficult to isolate their contribution accurately.
Fortunately, the spontaneous breaking of \(SU(3)_L\times SU(3)_R\) chiral symmetry provides observables which are particularly sensitive to the light-quark masses: the masses of the resulting Nambu-Goldstone bosons (NGB), i.e., pions, kaons, and eta. Indeed, the Gell-Mann-Oakes-Renner relation [136] predicts that the squared mass of a NGB is directly proportional to the sum of the masses of the quark and antiquark which compose it, up to higher-order mass corrections. Moreover, because these NGBs are light, and are composed of only two valence particles, their masses have a particularly clean statistical signal in lattice-QCD calculations. In addition, the experimental uncertainties on these meson masses are negligible. Thus, in lattice calculations, light-quark masses are typically obtained by renormalizing the input quark mass and tuning them to reproduce NGB masses, as described above.
3.1.1 The physical point and isospin symmetry
As mentioned in Sect. 2.1, the present review relies on the hypothesis that, at low energies, the Lagrangian \(\mathcal{L}_{ \text{ QCD }}+{{{\mathcal {L}}}}_{ \text{ QED }}\) describes nature to a high degree of precision. However, most of the results presented below are obtained in pure QCD calculations, which do not include QED. Quite generally, when comparing QCD calculations with experiment, radiative corrections need to be applied. In pure QCD simulations, where the parameters are fixed in terms of the masses of some of the hadrons, the electromagnetic contributions to these masses must be discussed. How the matching is done is generally ambiguous because it relies on the unphysical separation of QCD and QED contributions. In this section, and in the following, we discuss this issue in detail. Of course, once QED is included in lattice calculations, the subtraction of electromagnetic contributions is no longer necessary.
Let us start from the unambiguous case of QCD+QED. As explained in the introduction of this section, the physical quark masses are the parameters of the Lagrangian such that a given set of experimentally measured, dimensionful hadronic quantities are reproduced by the theory. Many choices are possible for these quantities, but in practice many lattice groups use pseudoscalar meson masses, as they are easily and precisely obtained both by experiment, and through lattice simulations. For example, in the four-flavour case, one can solve the system
where we assumed that
all the equations are in the continuum and infinite-volume limits;
the overall scale has been set to its physical value, generally through some lattice-scale setting procedure involving a fifth dimensionful input;
the quark masses \(m_q\) are assumed to be renormalized from the bare, lattice ones in some given continuum renormalization scheme;
\(\alpha =\frac{e^2}{4\pi }\) is the fine-structure constant expressed as function of the positron charge e, generally set to the Thomson limit \(\alpha =0.007297352\dots \) [137];
the mass \(M_{h}(m_u,m_d,m_s,m_c,\alpha )\) of the meson h is a function of the quark masses and \(\alpha \). The functional dependence is generally obtained by choosing an appropriate parameterization and performing a global fit to the lattice data;
the superscript exp. indicates that the mass is an experimental input, lattice groups use in general the values in the Particle Data Group review [137].
However, ambiguities arise with simulations of QCD only. In that case, there is no experimentally measurable quantity that emerges from the strong interaction only. The missing QED contribution is tightly related to isospin-symmetry breaking effects. Isospin symmetry is explicitly broken by the differences between the up- and down-quark masses \(\delta m=m_u-m_d\), and electric charges \(\delta Q=Q_u-Q_d\). Both these effects are, respectively, of order \({\mathcal {O}}(\delta m/\Lambda _{\mathrm {QCD}})\) and \({\mathcal {O}}(\alpha )\), and are expected to be \({\mathcal {O}}(1\%)\) of a typical isospin-symmetric hadronic quantity. Strong and electromagnetic isospin-breaking effects are of the same order and therefore cannot, in principle, be evaluated separately without introducing strong ambiguities. Because these effects are small, they can be treated as a perturbation:
for a given hadronic quantity X, where \(m_{ud}=\frac{1}{2}(m_u+m_d)\) is the average light-quark mass. There are several things to notice here. Firstly, the neglected higher-order \({\mathcal {O}}(\delta m^2,\alpha \delta m,\alpha ^2)\) corrections are expected to be \({\mathcal {O}}(10^{-4})\) relatively to X, which at the moment is way beyond the relative statistical accuracy that can be delivered by a lattice calculation. Secondly, this is not strictly speaking an expansion around the isospin-symmetric point, the electromagnetic interaction has also symmetric contributions. From this last expression the previous statements about ambiguities become clearer. Indeed, the only unambiguous prediction one can perform is to solve Eqs. (23)–(26) and use the resulting parameters to obtain a prediction for X, which is represented by the left-hand side of Eq. (27). This prediction will be the sum of the QCD isospin-symmetric part \({\bar{X}}\), the strong isospin-breaking effects \( X^{SU(2)}=\delta mA_X\), and the electromagnetic effects \(X^{\gamma }=\alpha B_X\). Obtaining any of these terms individually requires extra, unphysical conditions to perform the separation. To be consistent with previous editions of FLAG, we also define \({\hat{X}}={\bar{X}}+X^{SU(2)}\) to be the \(\alpha \rightarrow 0\) limit of X.
With pure QCD simulations, one typically solves Eqs. (23)–(26) by equating the QCD, isospin-symmetric part of a hadron mass \({\bar{M}}_h\), result of the simulations, with its experimental value \(M_h^{\mathrm {exp.}}\). This will result in an \({\mathcal {O}}(\delta m,\alpha )\) mis-tuning of the theory parameters which will propagate as an error on predicted quantities. Because of this, in principle, one cannot predict hadronic quantities with a relative accuracy higher than \({\mathcal {O}}(1\%)\) from pure QCD simulations, independently on how the target X is sensitive to isospin breaking effects. If one performs a complete lattice prediction of the physical value of X, it can be of phenomenological interest to define in some way \({\bar{X}}\), \(X^{SU(2)}\), and \(X^{\gamma }\). If we keep \(m_{ud}\), \(m_s\) and \(m_c\) at their physical values in physical units, for a given renormalization scheme and scale, then these three quantities can be extracted by setting successively and simultaneously \(\alpha \) and \(\delta m\) to 0. This is where the ambiguity lies: in general the \(\delta m=0\) point will depend on the renormalization scheme used for the quark masses. In the next section, we give more details on that particular aspect and discuss the order of scheme ambiguities.
3.1.2 Ambiguities in the separation of isospin-breaking contributions
In this section, we discuss the ambiguities that arise in the individual determination of the QED contribution \(X^{\gamma }\) and the strong-isospin correction \(X^{SU(2)}\) defined in the previous section. Throughout this section, we assume that the isospin-symmetric quark masses \(m_{ud}\), \(m_s\) and \(m_c\) are always kept fixed in physical units to the values they take at the QCD+QED physical point in some given renormalization scheme. Let us assume that both up and down masses have been renormalized in an identical mass-independent scheme which depends on some energy scale \(\mu \). We also assume that the renormalization procedure respects chiral symmetry so that quark masses renormalize multiplicatively. The renormalization constants of the quark masses are identical for \(\alpha =0\) and therefore the renormalized mass of a quark has the general form
up to \({\mathcal {O}}(\alpha ^2)\) corrections, where \(m_{q,0}\) is the bare quark mass, and where \(Q_{\mathrm {tot.}}\) and \(Q_{\mathrm {tot.}}^2\) are the sum of all quark charges and squared charges, respectively. Throughout this section, a subscript ud generally denotes the average between up and down quantities and \(\delta \) the difference between the up and the down quantities. The source of the ambiguities described in the previous section is the mixing of the isospin-symmetric mass \(m_{ud}\) and the difference \(\delta m\) through renormalization. Using Eq. (28) one can make this mixing explicit at leading order in \(\alpha \):
with the mixing matrices
Now let us assume that for the purpose of determining the different components in Eq. (27), one starts by tuning the bare masses to obtain equal up and down masses, for some small coupling \(\alpha _0\) at some scale \(\mu _0\), i.e., \(\delta m(\mu _0)=0\). At this specific point, one can extract the pure QCD, and the QED corrections to a given quantity X by studying the slope of \(\alpha \) in Eq. (27). From these quantities the strong isospin contribution can then readily be extracted using a nonzero value of \(\delta m(\mu _0)\). However, if now the procedure is repeated at another coupling \(\alpha \) and scale \(\mu \) with the same bare masses, it appears from Eq. (29) that \(\delta m(\mu )\ne 0\). More explicitly,
with
up to higher-order corrections in \(\alpha \) and \(\alpha _0\). In other words, the definitions of \({\bar{X}}\), \(X^{SU(2)}\), and \(X^{\gamma }\) depend on the renormalization scale at which the separation was made. This dependence, of course, has to cancel in the physical sum X. One can notice that at no point did we mention the renormalization of \(\alpha \) itself, which, in principle, introduces similar ambiguities. However, the corrections coming from the running of \(\alpha \) are \({\mathcal {O}}(\alpha ^2)\) relatively to X, which, as justified above, can be safely neglected. Finally, important information is provided by Eq. (31): the scale ambiguities are \({\mathcal {O}}(\alpha m_{ud})\). For physical quark masses, one generally has \(m_{ud}\simeq \delta m\). So by using this approximation in the first-order expansion Eq. (27), it is actually possible to define unambiguously the components of X up to second-order isospin-breaking corrections. Therefore, in the rest of this review, we will not keep track of the ambiguities in determining pure QCD or QED quantities. However, in the context of lattice simulations, it is crucial to notice that \(m_{ud}\simeq \delta m\) is only accurate at the physical point. In simulations at larger-than-physical pion masses, scheme ambiguities in the separation of QCD and QED contributions are generally large. Once more, the argument made here assumes that the isospin-symmetric quark masses \(m_{ud}\), \(m_s\), and \(m_c\) are kept fixed to their physical value in a given scheme while varying \(\alpha \). Outside of this assumption there is an additional isospin-symmetric \(O(\alpha m_q)\) ambiguity between \({\bar{X}}\) and \(X^{\gamma }\).
Such separation on lattice-QCD+QED simulation results appeared for the first time in RBC 07 [138] and Blum 10 [139], where the scheme was implicitly defined around the \(\chi \)PT expansion. In that setup, the \(\delta m(\mu _0)=0\) point is defined in pure QCD, i.e., \(\alpha _0=0\) in the previous discussion. The QCD part of the kaon-mass splitting from the first FLAG review [1] is used as an input in RM123 11 [140], which focuses on QCD isospin corrections only. It therefore inherits from the convention that was chosen there, which is also to set \(\delta m(\mu _0)=0\) at zero QED coupling. The same convention was used in the follow-up works RM123 13 [141] and RM123 17 [19]. The BMW collaboration was the first to introduce a purely hadronic scheme in its electro-quenched study of the baryon octet mass splittings [142]. In this work, the quark mass difference \(\delta m(\mu )\) is swapped with the mass splitting \(\Delta M^2\) between the connected \({\bar{u}}u\) and \({\bar{d}}d\) pseudoscalar masses. Although unphysical, this quantity is proportional [143] to \(\delta m(\mu )\) up to \({\mathcal {O}}(\alpha m_{ud})\) chiral corrections. In this scheme, the quark masses are assumed to be equal at \(\Delta M^2=0\), and the \({\mathcal {O}}(\alpha m_{ud})\) corrections to this statement are analogous to the scale ambiguities mentioned previously. The same scheme was used with the same data set for the determination of light-quark masses BMW 16 [20]. The BMW collaboration used a different hadronic scheme for its determination of the nucleon-mass splitting BMW 14 [119] using full QCD+QED simulations. In this work, the \(\delta m=0\) point was fixed by imposing the baryon splitting \(M_{\Sigma ^+}-M_{\Sigma ^-}\) to cancel. This scheme is quite different from the other ones presented here, in the sense that its intrinsic ambiguity is not \({\mathcal {O}}(\alpha m_{ud})\). What motivates this choice here is that \(M_{\Sigma ^+}-M_{\Sigma ^-}=0\) in the limit where these baryons are point particles, so the scheme ambiguity is suppressed by the compositeness of the \(\Sigma \) baryons. This may sounds like a more difficult ambiguity to quantify, but this scheme has the advantage of being defined purely by measurable quantities. Moreover, it has been demonstrated numerically in BMW 14 [119] that, within the uncertainties of this study, the \(M_{\Sigma ^+}-M_{\Sigma ^-}=0\) scheme is equivalent to the \(\Delta M^2=0\) one, explicitly \(M_{\Sigma ^+}-M_{\Sigma ^-}=-0.18(12)(6)\,\mathrm {MeV}\) at \(\Delta M^2=0\). The calculation QCDSF/UKQCD 15 [144] uses a “Dashen scheme,” where quark masses are tuned such that flavour-diagonal mesons have equal masses in QCD and QCD+QED. Although not explicitly mentioned by the authors of the paper, this scheme is simply a reformulation of the \(\Delta M^2=0\) scheme mentioned previously. Finally, the recent preprint MILC 18 [145] also used the \(\Delta M^2=0\) scheme and noticed its connection to the “Dashen scheme” from QCDSF/UKQCD 15.
In the previous edition of this review, the contributions \({\bar{X}}\), \(X^{SU(2)}\), and \(X^{\gamma }\) were given for pion and kaon masses based on phenomenological information. Considerable progress has been achieved by the lattice community to include isospin-breaking effects in calculations, and it is now possible to determine these quantities precisely directly from a lattice calculation. However, these quantities generally appear as intermediate products of a lattice analysis, and are rarely directly communicated in publications. These quantities, although unphysical, have a phenomenological interest, and we encourage the authors of future calculations to quote them explicitly.
3.1.3 Inclusion of electromagnetic effects in lattice-QCD simulations
Electromagnetism on a lattice can be formulated using a naive discretization of the Maxwell action \(S[A_{\mu }]=\frac{1}{4}\int d^4 x\,\sum _{\mu ,\nu }[\partial _{\mu }A_{\nu }(x)-\partial _{\nu }A_{\mu }(x)]^2\). Even in its noncompact form, the action remains gauge-invariant. This is not the case for non-Abelian theories for which one uses the traditional compact Wilson gauge action (or an improved version of it). Compact actions for QED feature spurious photon-photon interactions which vanish only in the continuum limit. This is one of the main reason why the noncompact action is the most popular so far. It was used in all the calculations presented in this review. Gauge-fixing is necessary for noncompact actions. It was shown [146, 147] that gauge fixing is not necessary with compact actions, including in the construction of interpolating operators for charged states.
Although discretization is straightforward, simulating QED in a finite volume is more challenging. Indeed, the long range nature of the interaction suggests that important finite-size effects have to be expected. In the case of periodic boundary conditions, the situation is even more critical: a naive implementation of the theory features an isolated zero-mode singularity in the photon propagator. It was first proposed in [148] to fix the global zero-mode of the photon field \(A_{\mu }(x)\) in order to remove it from the dynamics. This modified theory is generally named \(\mathrm {QED}_{\mathrm {TL}}\). Although this procedure regularizes the theory and has the right classical infinite-volume limit, it is nonlocal because of the zero-mode fixing. As first discussed in [119], the nonlocality in time of \(\mathrm {QED}_{\mathrm {TL}}\) prevents the existence of a transfer matrix, and therefore a quantum-mechanical interpretation of the theory. Another prescription named \(\mathrm {QED}_{\mathrm {L}}\), proposed in [149], is to remove the zero-mode of \(A_{\mu }(x)\) independently for each time slice. This theory, although still nonlocal in space, is local in time and has a well-defined transfer matrix. Wether these nonlocalities constitute an issue to extract infinite-volume physics from lattice-QCD+\(\mathrm {QED}_{\mathrm {L}}\) simulations is, at the time of this review, still an open question. However, it is known through analytical calculations of electromagnetic finite-size effects at \(O(\alpha )\) in hadron masses [119, 120, 122, 141, 149,150,151], meson leptonic decays [151], and the hadronic vacuum polarization [152] that \(\mathrm {QED}_{\mathrm {L}}\) does not suffer from a problematic (e.g., UV divergent) coupling of short and long-distance physics due to its nonlocality. Another strategy, first prosposed in [153] and used by the QCDSF collaboration, is to bound the zero-mode fluctuations to a finite range. Although more minimal, it is still a nonlocal modification of the theory and so far finite-size effects for this scheme have not been investigated. More recently, two proposals for local formulations of finite-volume QED emerged. The first one described in [154] proposes to use massive photons to regulate zero-mode singularities, at the price of (softly) breaking gauge invariance. The second one presented in [147] avoids the zero-mode issue by using anti-periodic boundary conditions for \(A_{\mu }(x)\). In this approach, gauge invariance requires the fermion field to undergo a charge conjugation transformation over a period, breaking electric charge conservation. These local approaches have the potential to constitute cleaner approaches to finite-volume QED. All the calculations presented in this review used \(\mathrm {QED}_{\mathrm {L}}\) or \(\mathrm {QED}_{\mathrm {TL}}\), with the exception of QCDSF.
Once a finite-volume theory for QED is specified, there are various ways to compute QED effects themselves on a given hadronic quantity. The most direct approach, first used in [148], is to include QED directly in the lattice simulations and assemble correlation functions from charged quark propagators. Another approach proposed in [141], is to exploit the perturbative nature of QED, and compute the leading-order corrections directly in pure QCD as matrix elements of the electromagnetic current. Both approaches have their advantages and disadvantages and as shown in [19], are not mutually exclusive. A critical comparative study can be found in [155].
Finally, most of the calculations presented here made the choice of computing electromagnetic corrections in the electro-quenched approximation. In this limit, one assumes that only valence quarks are charged, which is equivalent to neglecting QED corrections to the fermionic determinant. This approximation reduces dramatically the cost of lattice-QCD + QED calculations since it allows the reuse of previously generated QCD configurations. It also avoids computing disconnected contributions coming from the electromagnetic current in the vacuum, which are generally challenging to determine precisely. The electromagnetic contributions from sea quarks are known to be flavour-SU(3) and large-\(N_c\) suppressed, thus electro-quenched simulations are expected to have an \(O(10\%)\) accuracy for the leading electromagnetic effects. This suppression is in principle rather weak and results obtained from electro-quenched simulations might feature uncontrolled systematic errors. For this reason, the use of the electro-quenched approximation constitutes the difference between  and
and  in the FLAG criterion for the inclusion of isospin breaking effects.
in the FLAG criterion for the inclusion of isospin breaking effects.
3.1.4 Lattice determination of \(m_s\) and \(m_{ud}\)
We now turn to a review of the lattice calculations of the light-quark masses and begin with \(m_s\), the isospin-averaged up- and down-quark mass \(m_{ud}\), and their ratio. Most groups quote only \(m_{ud}\), not the individual up- and down-quark masses. We then discuss the ratio \(m_u/m_d\) and the individual determinations of \(m_u\) and \(m_d\).
Quark masses have been calculated on the lattice since the mid-nineties. However, early calculations were performed in the quenched approximation, leading to unquantifiable systematics. Thus, in the following, we only review modern, unquenched calculations, which include the effects of light sea quarks.
Tables 4 and 5 list the results of \(N_{ f}=2\,+\,1\) and \(N_{ f}=2\,+\,1\,+\,1\) lattice calculations of \(m_s\) and \(m_{ud}\). These results are given in the \({\overline{\mathrm {MS}}}\) scheme at \(2\,\mathrm {GeV}\), which is standard nowadays, though some groups are starting to quote results at higher scales (e.g., Ref. [156]). The tables also show the colour coding of the calculations leading to these results. As indicated earlier in this review, we treat calculations with different numbers, \(N_f\), of dynamical quarks separately.
\(N_{ f}=2\,+\,1\) lattice calculations
We turn now to \(N_{ f}=2\,+\,1\) calculations. These and the corresponding results for \(m_{ud}\) and \(m_s\) are summarized in Table 4. Given the very high precision of a number of the results, with total errors on the order of 1%, it is important to consider the effects neglected in these calculations. Isospin-breaking and electromagnetic effects are small on \(m_{ud}\) and \(m_s\), and have been approximately accounted for in the calculations that will be retained for our averages. We have already commented that the effect of the omission of the charm quark in the sea is expected to be small, below our current precision. In contrast with previous editions of the FLAG report, we do not add any additional uncertainty due to these effects in the final averages.
The only new calculation since FLAG 16 is the \(m_s\) determination of Maezawa 16 [157]. This new result agrees well with other determinations; however because it is computed with a single pion mass of about 160 MeV, it does not meet our criteria for entering the average. RBC/UKQCD 14 [10] significantly improves on their RBC/UKQCD 12 [156] work by adding three new domain wall fermion simulations to three used previously. Two of the new simulations are performed at essentially physical pion masses (\(M_\pi \simeq 139\,\mathrm {MeV}\)) on lattices of about \(5.4\,\mathrm{fm}\) in size and with lattice spacings of \(0.114\,\mathrm{fm}\) and \(0.084\,\mathrm{fm}\). It is complemented by a third simulation with \(M_\pi \simeq 371\,\mathrm {MeV}\), \(a\simeq 0.063\) and a rather small \(L\simeq 2.0\,\mathrm{fm}\). Altogether, this gives them six simulations with six unitary (\(m_{\mathrm{sea}}=m_{\mathrm{val}}\)) \(M_\pi \)’s in the range of 139 to \(371\,\mathrm {MeV}\), and effectively three lattice spacings from 0.063 to \(0.114\,\mathrm{fm}\). They perform a combined global continuum and chiral fit to all of their results for the \(\pi \) and K masses and decay constants, the \(\Omega \) baryon mass and two Wilson-flow parameters. Quark masses in these fits are renormalized and run nonperturbatively in the RI-SMOM scheme. This is done by computing the relevant renormalization constant for a reference ensemble, and determining those for other simulations relative to it by adding appropriate parameters in the global fit. This new calculation passes all of our selection criteria. Its results will replace the older RBC/UKQCD 12 results in our averages.
\(N_{ f}=2\,+\,1\) MILC results for light-quark masses go back to 2004 [166, 167]. They use rooted staggered fermions. By 2009 their simulations covered an impressive range of parameter space, with lattice spacings going down to 0.045 fm, and valence-pion masses down to approximately 180 MeV [17]. The most recent MILC \(N_{ f}=2\,+\,1\) results, i.e., MILC 10A [14] and MILC 09A [17], feature large statistics and 2-loop renormalization. Since these data sets subsume those of their previous calculations, these latest results are the only ones that must be kept in any world average.
The PACS-CS 12 [158] calculation represents an important extension of the collaboration’s earlier 2010 computation [159], which already probed pion masses down to \(M_\pi \simeq 135\,\mathrm {MeV}\), i.e., down to the physical-mass point. This was achieved by reweighting the simulations performed in PACS-CS 08 [162] at \(M_\pi \simeq 160\,\mathrm {MeV}\). If adequately controlled, this procedure eliminates the need to extrapolate to the physical-mass point and, hence, the corresponding systematic error. The new calculation now applies similar reweighting techniques to include electromagnetic and \(m_u\ne m_d\) isospin-breaking effects directly at the physical pion mass. Further, as in PACS-CS 10 [159], renormalization of quark masses is implemented nonperturbatively, through the Schrödinger functional method [172]. As it stands, the main drawback of the calculation, which makes the inclusion of its results in a world average of lattice results inappropriate at this stage, is that for the lightest quark mass the volume is very small, corresponding to \(LM_\pi \simeq 2.0\), a value for which finite-volume effects will be difficult to control. Another problem is that the calculation was performed at a single lattice spacing, forbidding a continuum extrapolation. Further, it is unclear at this point what might be the systematic errors associated with the reweighting procedure.
The BMW 10A, 10B [11, 12] calculation still satisfies our stricter selection criteria. They reach the physical up- and down-quark mass by interpolation instead of by extrapolation. Moreover, their calculation was performed at five lattice spacings ranging from 0.054 to 0.116 fm, with full nonperturbative renormalization and running and in volumes of up to (6 fm)\(^3\), guaranteeing that the continuum limit, renormalization, and infinite-volume extrapolation are controlled. It does neglect, however, isospin-breaking effects, which are small on the scale of their error bars.
Finally, we come to another calculation which satisfies our selection criteria, HPQCD 10 [13]. It updates the staggered-fermions calculation of HPQCD 09A [24]. In these papers, the renormalized mass of the strange quark is obtained by combining the result of a precise calculation of the renormalized charm-quark mass, \(m_c\), with the result of a calculation of the quark-mass ratio, \(m_c/m_s\). As described in Ref. [171] and in Sect. 3.2, HPQCD determines \(m_c\) by fitting Euclidean-time moments of the \({{\bar{c}}}c\) pseudoscalar density two-point functions, obtained numerically in lattice-QCD, to fourth-order, continuum perturbative expressions. These moments are normalized and chosen so as to require no renormalization with staggered fermions. Since \(m_c/m_s\) requires no renormalization either, HPQCD’s approach displaces the problem of lattice renormalization in the computation of \(m_s\) to one of computing continuum perturbative expressions for the moments. To calculate \(m_{ud}\) HPQCD 10 [13] use the MILC 09 determination of the quark-mass ratio \(m_s/m_{ud}\) [129].
HPQCD 09A [24] obtains \(m_c/m_s=11.85(16)\) [24] fully nonperturbatively, with a precision slightly larger than 1%. HPQCD 10’s determination of the charm-quark mass, \(m_c(m_c)=1.268(6)\),Footnote 15 is even more precise, achieving an accuracy better than 0.5%.
This discussion leaves us with five results for our final average for \(m_s\): MILC 09A [17], BMW 10A, 10B [11, 12], HPQCD 10 [13] and RBC/UKQCD 14 [10]. Assuming that the result from HPQCD 10 is 100% correlated with that of MILC 09A, as it is based on a subset of the MILC 09A configurations, we find \(m_s=92.03(88)\,\mathrm {MeV}\) with a \(\chi ^2/\)dof = 1.2.
For the light-quark mass \(m_{ud}\), the results satisfying our criteria are RBC/UKQCD 14B, BMW 10A, 10B, HPQCD 10, and MILC 10A. For the error, we include the same 100% correlation between statistical errors for the latter two as for the strange case, resulting in \(m_{ud}=3.364(41)\) at 2 GeV in the \(\overline{\mathrm{MS}}\) scheme (\(\chi ^2/\)d.of.=1.1). Our final estimates for the light-quark masses are

And the RGI values

\(N_{ f}=2\,+\,1\,+\,1\) lattice calculations
Since the previous FLAG review, two new results for the strange-quark mass have appeared, HPQCD 18 [15] and FNAL/MILC/TUMQCD 18 [8]. In the former quark masses are renormalized nonperturbatively in the RI-SMOM scheme. The mass of the (fictitious) \({{\bar{s}}} s\) meson is used to tune the bare strange mass. The “physical” \({{\bar{s}}} s\) mass is given in QCD from the pion and kaon masses. In addition, they use the same HISQ ensembles and valence quarks as those in HPQCD 14A, where the quark masses were computed from time moments of vector-vector correlation functions. The new results are consistent with the old, with roughly the same size error, but of course with different systematics. In particular the new results avoid the use of high-order perturbation theory in the matching between lattice and continuum schemes. It is reassuring that the two methods, applied to the same ensembles, agree well.
The \(N_{ f}=2\,+\,1\,+\,1\) results are summarized in Table 5. Note that the results of Ref. [16] are reported as \(m_s(2\,\mathrm {GeV};N_f=3)\) and those of Ref. [9] as \(m_{ud(s)}(2\,\mathrm {GeV};N_f=4)\). We convert the former to \(N_f=4\) and obtain \(m_s(2\,\mathrm {GeV}; N_f=4)=93.12(69)\mathrm {MeV}\). The average of FNAL/MILC/TUMQCD 18, HPQCD 18, ETM 14 and HPQCD 14A is 93.44(68)\(\mathrm {MeV}\) with \(\chi ^2/\text{ dof }=1.7\). For the light-quark average we use ETM 14A and FNAL/MILC/TUMQCD 18 with an average 3.410(43) and a \(\chi ^2/\text{ dof }=3\). We note these \(\chi ^2\) values are large. For the case of the light-quark masses this is mostly due to ETM 14(A) masses lying significantly above the rest, but in the case of \(m_s\) there is also some tension between the recent and very precise results of HPQCD 18 and FNAL/MILC/TUMQCD 18. Also note that the 2 + 1-flavour values are consistent with the four-flavour ones, so in all cases we have decided to simply quote averages according to FLAG rules, including stretching factors for the errors based on \(\chi ^2\) values of our fits.

and the RGI values

In Figs. 1 and 2 the lattice results listed in Tables 4 and 5 and the FLAG averages obtained at each value of \(N_f\) are presented and compared with various phenomenological results.
\({\overline{\mathrm {MS}}}\) mass of the strange quark (at 2 GeV scale) in MeV. The upper two panels show the lattice results listed in Tables 4 and 5, while the bottom panel collects sum rule results [173,174,175,176,177]. Diamonds and squares represent results based on perturbative and nonperturbative renormalization, respectively. The black squares and the grey bands represent our estimates (33) and (35). The significance of the colours is explained in Sect. 2
3.1.5 Lattice determinations of \(m_s/m_{ud}\)
The lattice results for \(m_s/m_{ud}\) are summarized in Table 6. In the ratio \(m_s/m_{ud}\), one of the sources of systematic error – the uncertainties in the renormalization factors – drops out.
\(N_{ f}=2\,+\,1\) lattice calculations
For \(N_f = 2\,+\,1\) our average has not changed since the last version of the review and is based on the result RBC/UKQCD 14B, which replaces RBC/UKQCD 12 (see Sect. 3.1.4), and on the results MILC 09A and BMW 10A, 10B. The value quoted by HPQCD 10 does not represent independent information as it relies on the result for \(m_s/m_{ud}\) obtained by the MILC collaboration. Averaging these results according to the prescriptions of Sect. 2.3 gives \(m_s / m_{ud} = 27.42(12)\) with \(\chi ^2/\text{ dof } \simeq 0.2\). Since the errors associated with renormalization drop out in the ratio, the uncertainties are even smaller than in the case of the quark masses themselves: the above number for \(m_s/m_{ud}\) amounts to an accuracy of 0.5%.
At this level of precision, the uncertainties in the electromagnetic and strong isospin-breaking corrections might not be completely negligible. Nevertheless, we decide not to add any uncertainty associated with this effect. The main reason is that most recent determinations try to estimate this uncertainty themselves and found an effect smaller than naive power counting estimates (see \(N_{ f}=2\,+\,1\,+\,1\) section).
\(N_{ f}=2\,+\,1\,+\,1\) lattice calculations
For \(N_f = 2\,+\,1\,+\,1\) there are three results, MILC 17 [5], ETM 14 [9] and FNAL/MILC 14A [18], all of which satisfy our selection criteria.
MILC 17 uses 24 HISQ staggered-fermion ensembles at six values of the lattice spacing in the range \(0.15\, \mathrm{fm}\)–\(0.03\, \mathrm{fm}\).
ETM 14 uses 15 twisted mass gauge ensembles at three lattice spacings ranging from 0.062 to 0.089 fm (using \(f_\pi \) as input), in boxes of size ranging from 2.0 to 3.0 fm, and pion masses from 210 to 440 MeV (explaining the tag  in the chiral extrapolation and the tag
in the chiral extrapolation and the tag  for the continuum extrapolation). The value of \(M_\pi L\) at their smallest pion mass is 3.2 with more than two volumes (explaining the tag
for the continuum extrapolation). The value of \(M_\pi L\) at their smallest pion mass is 3.2 with more than two volumes (explaining the tag  in the finite-volume effects). They fix the strange mass with the kaon mass.
in the finite-volume effects). They fix the strange mass with the kaon mass.
FNAL/MILC 14A employs HISQ staggered fermions. Their result is based on 21 ensembles at four values of the coupling \(\beta \) corresponding to lattice spacings in the range from 0.057 to 0.153 fm, in boxes of sizes up to 5.8 fm, and with taste-Goldstone pion masses down to 130 MeV, and RMS pion masses down to 143 MeV. They fix the strange mass with \(M_{{{\bar{s}}}s}\), corrected for electromagnetic effects with \(\epsilon = 0.84(20)\) [179]. All of our selection criteria are satisfied with the tag  . Thus our average is given by \(m_s / m_{ud} = 27.23 ~ (10)\), where the error includes a large stretching factor equal to \(\sqrt{\chi ^2/\text{ dof }} \simeq 1.6\), coming from our rules for the averages discussed in Sect. 2.2. As mentioned already this is mainly due to ETM 14(A) values lying significantly above the averages for the individual masses.
. Thus our average is given by \(m_s / m_{ud} = 27.23 ~ (10)\), where the error includes a large stretching factor equal to \(\sqrt{\chi ^2/\text{ dof }} \simeq 1.6\), coming from our rules for the averages discussed in Sect. 2.2. As mentioned already this is mainly due to ETM 14(A) values lying significantly above the averages for the individual masses.
which corresponds to an overall uncertainty equal to 0.4%. It is worth noting that [5] estimates the EM effects in this quantity to be \(\sim 0.18\%\).
All the lattice results listed in Table 6 as well as the FLAG averages for each value of \(N_f\) are reported in Fig. 3 and compared with \(\chi \)PT and sum rules.
3.1.6 Lattice determination of \(m_u\) and \(m_d\)
In addition to reviewing computations of individual \(m_u\) and \(m_d\) quark masses, we will also determine FLAG averages for the parameter \(\epsilon \) related to the violations of Dashen’s theorem
where \(\Delta M_{\pi }^{2}=M_{\pi ^+}^{2}-M_{\pi ^0}^{2}\) and \(\Delta M_{K}^{2}=M_{K^+}^{2}-M_{K^0}^{2}\) are the pion and kaon squared mass splittings, respectively. The superscript \(\gamma \), here and in the following, denotes corrections that arise from electromagnetic effects only. This parameter is often a crucial intermediate quantity in the extraction of the individual light-quark masses. Indeed, it can be shown using the G-parity symmetry of the pion triplet that \(\Delta M_{\pi }^{2}\) does not receive \(O(\delta m)\) isospin-breaking corrections. In other words
at leading-order in the isospin-breaking expansion. The difference \((\Delta M_{\pi }^{2})^{SU(2)}\) was estimated in previous editions of FLAG through the \(\epsilon _m\) parameter. However, consistent with our leading-order truncation of the isospin-breaking expansion, it is simpler to ignore this term. Once known, \(\epsilon \) allows one to consistently subtract the electromagnetic part of the kaon splitting to obtain the QCD splitting \((\Delta M_{K}^{2})^{SU(2)}\). In contrast with the pion, the kaon QCD splitting is sensitive to \(\delta m\), and, in particular, proportional to it at leading order in \(\chi \)PT. Therefore, the knowledge of \(\epsilon \) allows for the determination of \(\delta m\) from a chiral fit to lattice-QCD data. Originally introduced in another form in [184], \(\epsilon \) vanishes in the SU(3) chiral limit, a result known as Dashen’s theorem. However, in the 1990’s numerous phenomenological papers pointed out that \(\epsilon \) might be an O(1) number, indicating a significant failure of SU(3) \(\chi \)PT in the description of electromagnetic effects on light meson masses. However, the phenomenological determinations of \(\epsilon \) feature some level of controversy, leading to the rather imprecise estimate \(\epsilon =0.7(5)\) given in the first edition of FLAG. In this edition of the review, we quote below more precise averages for \(\epsilon \), directly obtained from lattice-QCD+QED simulations. We refer the reader to the previous editions of FLAG, and to the review [185] for discusions of the phenomenological determinations of \(\epsilon \).
Regarding finite-volume effects for calculations including QED, this edition of FLAG uses a new quality criterion presented in Sect. 2.1.1. Indeed, due to the long-distance nature of the electromagnetic interaction, these effects are dominated by a power law in the lattice spatial size. The coefficients of this expansion depend on the chosen finite-volume formulation of QED. For \(\mathrm {QED}_{\mathrm {L}}\), these effects on the squared mass \(M^2\) of a charged meson are given by [119, 120, 122]
with \(c_1\simeq -2.83730\). It has been shown in [119] that the two first orders in this expansion are exactly known for hadrons, and are equal to the pointlike case. However, the \({\mathcal {O}}[1/(ML)^{3}]\) term and higher orders depend on the structure of the hadron. The universal corrections for \(\mathrm {QED}_{\mathrm {TL}}\) can also be found in [119]. In all this part, for all computations using such universal formulae, the QED finite-volume quality criterion has been applied with \(n_{\mathrm {min}}=3\), otherwise \(n_{\mathrm {min}}=1\) was used.
Since FLAG 16, six new results have been reported for nondegenerate light-quark masses. In the \(N_f=2\,+\,1\,+\,1\) sector, MILC 18 [145] computed \(\epsilon \) using \(N_f=2\,+\,1\) asqtad electro-quenched QCD+\(\mathrm {QED}_{\mathrm {TL}}\) simulations and extracted the ratio \(m_u/m_d\) from a new set of \(N_f=2\,+\,1\,+\,1\) HISQ QCD simulations. Although \(\epsilon \) comes from \(N_f=2\,+\,1\) simulations, \((\Delta M_{K}^{2})^{SU(2)}\), which is about three times larger than \((\Delta M_{K}^{2})^{\gamma }\), has been determined in the \(N_f=2\,+\,1\,+\,1\) theory. We therefore chose to classify this result as a four-flavour one. This result is explicitly described by the authors as an update of MILC 17 [5]. In MILC 17 [5], \(m_u/m_d\) is determined as a side-product of a global analysis of heavy-meson decay constants, using a preliminary version of \(\epsilon \) from MILC 18 [145]. In FNAL/MILC/TUMQCD 18 [8] the ratio \(m_u/m_d\) from MILC 17 [5] is used to determine the individual masses \(m_u\) and \(m_d\) from a new calculation of \(m_{ud}\). The work RM123 17 [19] is the continuation the \(N_f=2\) result named RM123 13 [141] in the previous edition of FLAG. This group now uses \(N_f=2\,+\,1\,+\,1\) ensembles from ETM 10 [186], however still with a rather large minimum pion mass of \(270~\mathrm {MeV}\), leading to the  rating for chiral extrapolations. In the \(N_f=2\,+\,1\) sector, BMW 16 [20] reuses the data set produced from their determination of the light baryon octet mass splittings [142] using electro-quenched QCD+\(\mathrm {QED}_{\mathrm {TL}}\) smeared clover fermion simulations. Finally, MILC 16 [187], which is a preliminary result for the value of \(\epsilon \) published in MILC 18 [145], also provides a \(N_f=2\,+\,1\) computation of the ratio \(m_u/m_d\).
rating for chiral extrapolations. In the \(N_f=2\,+\,1\) sector, BMW 16 [20] reuses the data set produced from their determination of the light baryon octet mass splittings [142] using electro-quenched QCD+\(\mathrm {QED}_{\mathrm {TL}}\) smeared clover fermion simulations. Finally, MILC 16 [187], which is a preliminary result for the value of \(\epsilon \) published in MILC 18 [145], also provides a \(N_f=2\,+\,1\) computation of the ratio \(m_u/m_d\).
MILC 09A [17] uses the mass difference between \(K^0\) and \(K^+\), from which they subtract electromagnetic effects using Dashen’s theorem with corrections, as discussed in the introduction of this section. The up and down sea quarks remain degenerate in their calculation, fixed to the value of \(m_{ud}\) obtained from \(M_{\pi ^0}\). To determine \(m_u/m_d\), BMW 10A, 10B [11, 12] follow a slightly different strategy. They obtain this ratio from their result for \(m_s/m_{ud}\) combined with a phenomenological determination of the isospin-breaking quark-mass ratio \(Q=22.3(8)\), from \(\eta \rightarrow 3\pi \) decays [188] (the decay \(\eta \rightarrow 3\pi \) is very sensitive to QCD isospin breaking but fairly insensitive to QED isospin breaking). Instead of subtracting electromagnetic effects using phenomenology, RBC 07 [138] and Blum 10 [139] actually include a quenched electromagnetic field in their calculation. This means that their results include corrections to Dashen’s theorem, albeit only in the presence of quenched electromagnetism. Since the up and down quarks in the sea are treated as degenerate, very small isospin corrections are neglected, as in MILC’s calculation. PACS-CS 12 [158] takes the inclusion of isospin-breaking effects one step further. Using reweighting techniques, it also includes electromagnetic and \(m_u-m_d\) effects in the sea. However, they do not correct for the large finite-volume effects coming from electromagnetism in their \(M_{\pi }L\sim 2\) simulations, but provide rough estimates for their size, based on Ref. [149]. QCDSF/UKQCD 15 [189] uses QCD+QED dynamical simulations performed at the SU(3)-flavour-symmetric point, but at a single lattice spacing, so they do not enter our average. The smallest partially quenched (\(m_{\mathrm{sea}}\ne m_{\mathrm{val}}\)) pion mass is greater than 200 MeV, so our chiral-extrapolation criteria require a  rating. Concerning finite-volume effects, this work uses three spatial extents L of \(1.6~\mathrm {fm}\), \(2.2~\mathrm {fm}\), and \(3.3~\mathrm {fm}\). QCDSF/UKQCD 15 claims that the volume dependence is not visible on the two largest volumes, leading them to assume that finite-size effects are under control. As a consequence of that, the final result for quark masses does not feature a finite-volume extrapolation or an estimation of the finite-volume uncertainty. However, in their work on the QED corrections to the hadron spectrum [189] based on the same ensembles, a volume study shows some level of compatibility with the \(\mathrm {QED}_{\mathrm {L}}\) finite-volume effects derived in [120]. We see two issues here. Firstly, the analytical result quoted from [120] predicts large, \(O(10\%)\) finite-size effects from QED on the meson masses at the values of \(M_{\pi }L\) considered in QCDSF/UKQCD 15, which is inconsistent with the statement made in the paper. Secondly, it is not known that the zero-mode regularization scheme used here has the same volume scaling as \(\mathrm {QED}_{\mathrm {L}}\). We therefore chose to assign the
rating. Concerning finite-volume effects, this work uses three spatial extents L of \(1.6~\mathrm {fm}\), \(2.2~\mathrm {fm}\), and \(3.3~\mathrm {fm}\). QCDSF/UKQCD 15 claims that the volume dependence is not visible on the two largest volumes, leading them to assume that finite-size effects are under control. As a consequence of that, the final result for quark masses does not feature a finite-volume extrapolation or an estimation of the finite-volume uncertainty. However, in their work on the QED corrections to the hadron spectrum [189] based on the same ensembles, a volume study shows some level of compatibility with the \(\mathrm {QED}_{\mathrm {L}}\) finite-volume effects derived in [120]. We see two issues here. Firstly, the analytical result quoted from [120] predicts large, \(O(10\%)\) finite-size effects from QED on the meson masses at the values of \(M_{\pi }L\) considered in QCDSF/UKQCD 15, which is inconsistent with the statement made in the paper. Secondly, it is not known that the zero-mode regularization scheme used here has the same volume scaling as \(\mathrm {QED}_{\mathrm {L}}\). We therefore chose to assign the  rating for finite volume to QCDSF/UKQCD 15. Finally, for \(N_f=2\,+\,1\,+\,1\), ETM 14 [9] uses simulations in pure QCD, but determines \(m_u-m_d\) from the slope \(\partial M_K^2/\partial m_{ud}\) and the physical value for the QCD kaon-mass splitting taken from the phenomenological estimate in FLAG 13 (Fig. 4).
rating for finite volume to QCDSF/UKQCD 15. Finally, for \(N_f=2\,+\,1\,+\,1\), ETM 14 [9] uses simulations in pure QCD, but determines \(m_u-m_d\) from the slope \(\partial M_K^2/\partial m_{ud}\) and the physical value for the QCD kaon-mass splitting taken from the phenomenological estimate in FLAG 13 (Fig. 4).
Lattice results for \(m_u\), \(m_d\) and \(m_u/m_d\) are summarized in Table 7. It is important to notice two major changes in the grading of these results: the introduction of an “isospin breaking” criterion and the modification of the “finite volume” criterion in the presence of QED. The colour coding is specified in detail in Sect. 2.1. Considering the important progress in the last years on including isospin-breaking effects in lattice simulations, we are now in a position where averages for \(m_u\) and \(m_d\) can be made without the need of phenomenological inputs. Therefore, lattice calculations of the individual quark masses using phenomenological inputs for isospin-breaking effects will be coded  .
.
We start by recalling the \(N_f=2\) FLAG estimate for the light-quark masses, entirely coming from RM123 13 [141],
with errors of roughly 10%, 5% and 8%, respectively. In these results, the errors are obtained by combining the lattice statistical and systematic errors in quadrature. For \(N_{ f}=2\,+\,1\), the only result, which qualifies for entering the FLAG average for quark masses, is BMW 16 [20],
with errors of roughly 4%, 2% and 4%, respectively. This estimate is slightly more precise than in the previous edition of FLAG. More importantly, it now comes entirely from a lattice-QCD+QED calculation, whereas phenomenological input was used in previous editions. These numbers result in the following RGI averages
Finally, for \(N_{ f}=2\,+\,1\,+\,1\), only RM123 17 [19] enters the average, giving
with errors of roughly 7%, 4% and 6%, respectively. In the previous edition of FLAG, ETM 14 [9] was used for the average. The RM123 17 result used here is slightly more precise and is free of phenomenological input. The value of \(m_u/m_d\) in MILC 17 [5] depends critically on the value of \(\epsilon \) given in MILC 18 [145], which was unpublished at the time of the review deadline. As a consequence we did not include the result MILC 17 [5] in the average. The value will appear in the average of the online version of the review. It is, however important to point out that both MILC 17 and MILC 18 results show a marginal discrepancy with RM123 17 [19] of 1.7 standard deviations. The RGI averages are
Every result for \(m_u\) and \(m_d\) used here to produce the FLAG averages relies on electro-quenched calculations, so there is some interest to comment on the size of quenching effects. Considering phenomenology and the lattice results presented here, it is reasonable for a rough estimate to use the value \((\Delta M_{K}^{2})^{\gamma }\sim 2000~\mathrm {MeV}^2\) for the QED part of the kaon splitting. Using the arguments presented in Sect. 3.1.3, one can assume that the QED sea contribution represents \(O(10\%)\) of \((\Delta M_{K}^{2})^{\gamma }\). Using SU(3) PQ\(\chi \)PT+QED [143, 191] gives a \(\sim 5\%\) effect. Keeping the more conservative \(10\%\) estimate and using the experimental value of the kaon splitting, one finds that the QCD kaon splitting \((\Delta M_{K}^{2})^{SU(2)}\) suffers from a reduced \(3\%\) quenching uncertainty. Considering that this splitting is proportional to \(m_u-m_d\) at leading order in SU(3) \(\chi \)PT, we can estimate that a similar error will propagate to the quark masses. So the individual up and down masses look mildly affected by QED quenching. However, one notices that \(\sim 3\%\) is the level of error in the new FLAG averages, and increasing significantly this accuracy will require using fully unquenched calculations.
In view of the fact that a massless up-quark would solve the strong CP-problem, many authors have considered this an attractive possibility, but the results presented above exclude this possibility: the value of \(m_u\) in Eq. (43) differs from zero by 25 standard deviations. We conclude that nature solves the strong CP-problem differently.
Finally, we conclude this section by giving the FLAG averages for \(\epsilon \) defined in Eq. (39). For \(N_{ f}=2\,+\,1\,+\,1\), we average the RM123 17 [19] result with the value of \((\Delta M_{K}^{2})^{\gamma }\) from BMW 14 [119] combined with Eq. (40), giving
Although BMW 14 [119] focuses on hadron masses and did not extract the light-quark masses, they are the only fully unquenched QCD+QED calculation to date that qualifies to enter a FLAG average. With the exception of renormalization which is not discussed in the paper, this work has a  rating for every FLAG criterion considered for the \(m_u\) and \(m_d\) quark masses. For \(N_{ f}=2\,+\,1\) we use the results from BMW 16 [20]
rating for every FLAG criterion considered for the \(m_u\) and \(m_d\) quark masses. For \(N_{ f}=2\,+\,1\) we use the results from BMW 16 [20]
These results are entirely determined from lattice-QCD+QED and represent an improvement of the error by a factor of two to three on the FLAG 16 phenomenological estimate.
It is important to notice that the \(\epsilon \) uncertainties from BMW 16 and RM123 17 are dominated by estimates of the QED quenching effects. Indeed, in contrast with the quark masses, \(\epsilon \) is expected to be rather sensitive to the sea quark-QED constributions. Using the arguments presented in Sect. 3.1.3, if one conservatively assumes that the QED sea contributions represent \(O(10\%)\) of \((\Delta M_{K}^{2})^{\gamma }\), then Eq. (40) implies that \(\epsilon \) will have a quenching error of \(\sim 0.15\) for \((\Delta M_{K}^{2})^{\gamma }\sim 2000~\mathrm {MeV}^2\), representing a large \(\sim 20\%\) relative error. It is interesting to observe that such a discrepancy does not appear between BMW 15 and RM123 17, although the \(\sim 10\%\) accuracy of both results might not be sufficient to resolve these effects. To conclude, although the controversy around the value of \(\epsilon \) has been significantly reduced by lattice-QCD+QED determinations, computing this quantity precisely requires fully unquenched simulations.
3.1.7 Estimates for R and Q
The quark-mass ratios
compare SU(3) breaking with isospin breaking. Both numbers only depend on the ratios \(m_s/m_{ud}\) and \(m_u/m_d\),
The quantity Q is of particular interest because of a low-energy theorem [192], which relates it to a ratio of meson masses,
Chiral symmetry implies that the expansion of \(Q_M^2\) in powers of the quark masses (i) starts with \(Q^2\) and (ii) does not receive any contributions at NLO:

We recall here the \(N_f=2\) estimates for Q and R from FLAG 16,
where the second error comes from the phenomenological inputs that were used. For \(N_{ f}=2\,+\,1\), we use Eqs. (37) and (43) and obtain
where now only lattice results have been used. For \(N_{ f}=2\,+\,1\,+\,1\) we obtain
which are quite compatible with two- and three-flavour results. It is interesting to notice that the most recent phenomenological determination of R and Q from \(\eta \rightarrow 3\pi \) decay [193] gives the values \(R=34.4(2.1)\) and \(Q=22.1(7)\), which are marginally discrepant with the averages presented here. For \(N_{ f}=2\,+\,1\), the discrepancy is 1.4 standard deviations for both R and Q. For \(N_{ f}=2\,+\,1\,+\,1\) it is 1.8 standard deviations. The authors of [193] point out that this discrepancy is due to surprisingly large corrections to the approximation (52) used in the phenomenological analysis.
Our final results for the masses \(m_u\), \(m_d\), \(m_{ud}\), \(m_s\) and the mass ratios \(m_u/m_d\), \(m_s/m_{ud}\), R, Q are collected in Tables 8 and 9. We separate \(m_u\), \(m_d\), \(m_u/m_d\), R and Q from \(m_{ud}\), \(m_s\) and \(m_s/m_{ud}\), because the latter are completely dominated by lattice results while the former still include some phenomenological input.
3.2 Charm quark mass
In the following, we collect and discuss the lattice determinations of the \(\overline{\mathrm{MS}}\) charm-quark mass \({\overline{m}}_c\). Most of the results have been obtained by analyzing the lattice-QCD simulations of two-point heavy–light- or heavy–heavy-meson correlation functions, using as input the experimental values of the D, \(D_s\), and charmonium mesons. Other groups use the moments method. The latter is based on the lattice calculation of the Euclidean time moments of pseudoscalar-pseudoscalar correlators for heavy-quark currents followed by an OPE expansion dominated by perturbative QCD effects, which provides the determination of both the heavy-quark mass and the strong-coupling constant \(\alpha _s\).
The heavy-quark actions adopted by various lattice collaborations have been discussed in previous FLAG reviews [2, 3], and their descriptions can be found in Sect. A.1.3. While the charm mass determined with the moments method does not need any lattice evaluation of the mass-renormalization constant \(Z_m\), the extraction of \({\overline{m}}_c\) from two-point heavy-meson correlators does require the nonperturbative calculation of \(Z_m\). The lattice scale at which \(Z_m\) is obtained, is usually at least of the order 2–3 GeV, and therefore it is natural in this review to provide the values of \({\overline{m}}_c(\mu )\) at the renormalization scale \(\mu = 3~\mathrm {GeV}\). Since the choice of a renormalization scale equal to \({\overline{m}}_c\) is still commonly adopted (as by PDG [170]), we have collected in Table 10 the lattice results for both \({\overline{m}}_c({\overline{m}}_c)\) and \({\overline{m}}_c(\text{3 } \text{ GeV })\), obtained for \(N_f =2\,+\,1\) and \(2\,+\,1\,+\,1\). This year’s review does not contain results for \(N_f=2\), and interested readers are referred to previous reviews [2, 3].
When not directly available in the published work, we apply a conversion factor equal either to 0.900 between the scales \(\mu = 2\) GeV and \(\mu = 3\) GeV or to 0.766 between the scales \(\mu = {\overline{m}}_c\) and \(\mu = 3\) GeV, obtained using perturbative QCD evolution at four loops assuming \(\Lambda _{QCD} = 300\) MeV for \(N_f = 4\).
In the next sections, we review separately the results of \({\overline{m}}_c({\overline{m}}_c)\) for the various values of \(N_f\).
3.2.1 \(N_f = 2\,+\,1\) results
The HPQCD 10 [13] result is computed from moments, using a subset of \(N_f = 2\,+\,1\) Asqtad-staggered-fermion ensembles from MILC [129] and HISQ valence fermions. The charm mass is fixed from the \(\eta _c\) meson, \(M_{\eta _c} = 2.9852 (34) ~ \mathrm {GeV}\), corrected for \({{\bar{c}}}c\) annihilation and electromagnetic effects. HPQCD 10 supersedes the HPQCD 08B [171] result using valence-Asqtad-staggered fermions.
\(\chi \)QCD 14 [22] uses a mixed-action approach based on overlap fermions for the valence quarks and domain-wall fermions for the sea quarks. They adopt six of the gauge ensembles generated by the RBC/UKQCD collaboration [160] at two values of the lattice spacing (0.087 and 0.11 fm) with unitary pion masses in the range from 290 to 420 MeV. For the valence quarks no light-quark masses are simulated. At the lightest pion mass \(M_\pi \simeq \) 290 MeV, \(M_\pi L=4.1\), which satisfies the tag  for finite-volume effects. The strange- and charm-quark masses are fixed together with the lattice scale by using the experimental values of the \(D_s\), \(D_s^*\) and \(J/\psi \) meson masses.
for finite-volume effects. The strange- and charm-quark masses are fixed together with the lattice scale by using the experimental values of the \(D_s\), \(D_s^*\) and \(J/\psi \) meson masses.
JLQCD 15B [194] determines the charm mass by using the moments method and Möbius domain-wall fermions at three values of the lattice spacing, ranging from 0.044 to 0.083 fm. They employ 15 ensembles in all, including several different pion masses and volumes. The lightest pion mass is \(\simeq 230\) MeV with \(M_\pi L\) is \(\simeq 4.4\). The linear size of their lattices is in the range 2.6–3.8 fm.
Since FLAG 16 there have been two new results, JLQCD 16 [23] and Maezawa 16 [157]. The former supersedes JLQCD 15B as it is a published update of their previous preliminary result. The latter employs the moments method using pseudoscalar correlation functions computed with HISQ fermions on a set of 11 ensembles with lattices spacing in the range 0.04 to 0.14 fm. Only a single pion mass of 160 MeV is studied. The linear size of the lattices take on values between 2.5 and 5.2 fm.
Thus, according to our rules on the publication status, the FLAG average for the charm-quark mass at \(N_f = 2\,+\,1\) is obtained by combining the results HPQCD 10, \(\chi \)QCD 14, and JLQCD 16,
where the error on \( {\overline{m}}_c(\text{3 } \text{ GeV })\) includes a stretching factor \(\sqrt{\chi ^2/\text{ dof }} \simeq 1.18\) as discussed in Sect. 2.2. This result corresponds to the following RGI average
3.2.2 \(N_f = 2\,+\,1\,+\,1\) results
In FLAG 16 three results employing four dynamical quarks in the sea were discussed. ETM 14 [9] uses 15 twisted-mass gauge ensembles at three lattice spacings ranging from 0.062 to 0.089 fm, in boxes of size ranging from 2.0 to 3.0 fm and pion masses from 210 to 440 MeV (explaining the tag  in the chiral extrapolation and the tag
in the chiral extrapolation and the tag  for the continuum extrapolation). The value of \(M_\pi L\) at their smallest pion mass is 3.2 with more than two volumes (explaining the tag
for the continuum extrapolation). The value of \(M_\pi L\) at their smallest pion mass is 3.2 with more than two volumes (explaining the tag  in the finite-volume effects). They fix the strange mass with the kaon mass and the charm one with that of the \(D_s\) and D mesons.
in the finite-volume effects). They fix the strange mass with the kaon mass and the charm one with that of the \(D_s\) and D mesons.
ETM 14A [21] uses 10 out of the 15 gauge ensembles adopted in ETM 14 spanning the same range of values for the pion mass and the lattice spacing, but the latter is fixed using the nucleon mass. Two lattice volumes with size larger than 2.0 fm are employed. The physical strange and the charm mass are obtained using the masses of the \(\Omega ^-\) and \(\Lambda _c^+\) baryons, respectively.
HPQCD 14A [16] employs the moments method with HISQ fermions. Their results are based on 9 out of the 21 ensembles produced by the MILC collaboration [18]. Lattice spacings range from 0.057 to 0.153 fm, with box sizes up to 5.8 fm and taste-Goldstone-pion masses down to 130 MeV. The RMS-pion masses go down to 173 MeV. The strange- and charm-quark masses are fixed using \(M_{{{\bar{s}}}s} = 688.5 (2.2)~\mathrm {MeV}\), calculated without including \({{\bar{s}}}s\) annihilation effects, and \(M_{\eta _c} = 2.9863(27)~\mathrm {GeV}\), obtained from the experimental \(\eta _c\) mass after correcting for \({{\bar{c}}}c\) annihilation and electromagnetic effects. All of the selection criteria of Sect. 2.1.1 are satisfied with the tag  .Footnote 16
.Footnote 16
Since FLAG 16 two groups, FNAL/MILC/TUMQCD and HPQCD have produced new values for the charm-quark mass [8, 15]. The latter use nonperturbative renormalization in the RI-SMOM scheme as described in the strange quark section and the same HISQ ensembles and valence quarks as those described in HPQCD 14A [16].
The FNAL/MILC/TUMQCD groups use a new minimal-renormalon-subtraction scheme (MRS) [195] and a sophisticated, but complex, fit strategy incorporating three effective field theories: heavy quark effective theory (HQET), heavy-meson rooted all-staggered chiral perturbation theory (HMrAS\(\chi \)PT), and Symanzik effective theory for cutoff effects. heavy–light meson masses are computed from fits to lattice-QCD correlation functions. They employ HISQ quarks on 20 MILC \(2\,+\,1\,+\,1\) flavour ensembles with six lattice spacings between 0.03 and 0.15 fm (the largest is used only in the estimation of the systematic error in the continuum-limit extrapolation). The pion mass is physical on several ensembles except the finest, and \(M_\pi L=3.7\)–3.9 on the physical mass ensembles. The light-quark masses are fixed from meson masses in pure QCD, which have been shifted from their physical values using \(O(\alpha )\) electromagnetic effects recently computed by the MILC collaboration [145], see Sect. 3.1.6 for details. The heavy–light mesons are shifted using a phenomenological formula. Using chiral perturbation theory at NLO and NNLO, the results are corrected for exponentially small finite-volume effects. They find that nonexponential finite-volume effects due to nonequilibration of topological charge are negligible compared to other quoted errors. These allow for a combined continuum, chiral, and infinite-volume limit from a global fit including 77 free parameters to 324 data points which satisfies all of the FLAG criteria.
All four results enter the FLAG average for \(N_f = 2\,+\,1\,+\,1\) quark flavours. We note however that while the determinations of \({\overline{m}}_c\) by ETM 14 and 14A agree well with each other, they are incompatible with HPQCD 14A, HPQCD 18, and FNAL/MILC/TUMQCD 18 by several standard deviations. While the latter use the same configurations, the analyses are quite different and independent. As mentioned earlier, \(m_{ud}\) and \(m_s\) are also systematically high compared to their respective averages. In addition, the other four-flavour values are consistent with the three-flavour average. Combining all four results yields


where the errors include large stretching factors \(\sqrt{\chi ^2/\text{ dof }}\approx 2.0\) and 1.7, respectively. We have assumed 100% correlation for statistical errors between ETM results. For HPQCD 14A, HPQCD 18, and FNAL/MILC/TUMQCD 18 we use the correlations given in Ref. [15]. Our fits have \(\chi ^2/\text{ dof }=3.9\) and 2.8, respectively. The RGI average reads as follows
Figure 5 presents the results given in Table 10 along with the FLAG averages obtained for \(2\,+\,1\) and \(2\,+\,1\,+\,1\) flavours.
3.2.3 Lattice determinations of the ratio \(m_c/m_s\)
Because some of the results for the light-quark masses given in this review are obtained via the quark-mass ratio \(m_c/m_s\), we review these lattice calculations, which are listed in Table 11.
The \(N_f = 2\,+\,1\) results from \(\chi \)QCD 14 and HPQCD 09A [24] are the same as described for the charm-quark mass, and in addition the latter fixes the strange mass using \(M_{{{\bar{s}}}s} = 685.8(4.0)\,\mathrm {MeV}\). Since FLAG 16 another result has appeared, Maezawa 16 which does not pass our chiral-limit test (as described in the previous section), though we note that it is quite consistent with the other values. Combining \(\chi \)QCD 14 and HPQCD 09A, we obtain the same result reported in FLAG 16,
with a \(\chi ^2/\text{ dof } \simeq 0.85\).
Lattice results for the ratio \(m_c / m_s\) listed in Table 11 and the FLAG averages corresponding to \(2\,+\,1\) and \(2\,+\,1\,+\,1\) quark flavours. The latter average includes a large stretching factor on the error due a poor \(\chi ^2\) from our fit
Turning to \(N_f = 2\,+\,1\,+\,1\), in addition to the HPQCD 14A and ETM 14 calculations, already described in Sect. 3.2.2, we consider the recent FNAL/MILC/TUMQCD 18 value [8] (which updates and replaces [18]), where HISQ fermions are employed as described in the previous section. As for the HPQCD 14A result, all of our selection criteria are satisfied with the tag  . However, some tension exists between the HPQCD and FNAL/MILC/TUMQCD results. Combining all three yields
. However, some tension exists between the HPQCD and FNAL/MILC/TUMQCD results. Combining all three yields
where the error includes the stretching factor \(\sqrt{\chi ^2/\text{ dof }} \simeq 1.5\), and \(\chi ^2/dof=2.28\). We have assumed a 100% correlation of statistical errors for FNAL/MILC/TUMQCD 18 and HPQCD 14A.
Results for \(m_c/m_s\) are shown in Fig. 6 together with the FLAG averages for \(2\,+\,1\) and \(2\,+\,1\,+\,1\) flavours.
3.3 Bottom quark mass
Now we review the lattice results for the \(\overline{\mathrm{MS}}\)-bottom-quark mass \({\overline{m}}_b\). Related heavy-quark actions and observables have been discussed in the FLAG 13 and 17 reviews [2, 3], and descriptions can be found in Sect. A.1.3. In Table 12 we collect results for \({\overline{m}}_b({\overline{m}}_b)\) obtained with \(N_f =2\,+\,1\) and \(2\,+\,1\,+\,1\) quark flavours in the sea. Available results for the quark-mass ratio \(m_b / m_c\) are also reported. After discussing the various results we evaluate the corresponding FLAG averages.
3.3.1 \(N_f=2\,+\,1\)
HPQCD 13B [197] extracts \({\overline{m}}_b\) from a lattice determination of the \(\Upsilon \) energy in NRQCD and the experimental value of the meson mass. The latter quantities yield the pole mass which is related to the \(\overline{\mathrm{MS}}\) mass in 3-loop perturbation theory. The MILC coarse (0.12 fm) and fine (0.09 fm) Asqtad-2 + 1-flavour ensembles are employed in the calculation. The bare light-(sea)-quark masses correspond to a single, relatively heavy, pion mass of about 300 MeV. No estimate of the finite-volume error is given. This result is not used in our average.
The value of \({\overline{m}}_b({\overline{m}}_b)\) reported in HPQCD 10 [13] is computed in a very similar fashion to the one in HPQCD 14A described in the following section on \(2\,+\,1\,+\,1\) flavour results, except that MILC \(2\,+\,1\)-flavour-Asqtad ensembles are used under HISQ valence quarks. The lattice spacings of the ensembles range from 0.18 to 0.045 fm and pion masses down to about 165 MeV. In all, 22 ensembles were fit simultaneously. An estimate of the finite-volume error based on leading-order perturbation theory for the moment ratio is also provided. Details of perturbation theory and renormalization systematics are given in Sect. 9.7.
Maezawa 16 reports a new result for the b-quark mass since the last FLAG review. However as discussed in the charm-quark section, this calculation does not satisfy the criteria to be used in the FLAG average. As in the previous review, we take the HPQCD 10 result as our average,
Since HPQCD quotes \({\overline{m}}_b({\overline{m}}_b)\) using \(N_f = 5\) running, we used that value in the average. The corresponding 4-flavour RGI average is
3.3.2 \(N_f=2\,+\,1\,+\,1\)
Results have been published by HPQCD using NRQCD and HISQ-quark actions (HPQCD 14B [25] and HPQCD 14A [16], respectively). In both works the b-quark mass is computed with the moments method, that is, from Euclidean-time moments of two-point, heavy–heavy-meson correlation functions (see also Sect. 9.7 for a description of the method).
In HPQCD 14B the b-quark mass is computed from ratios of the moments \(R_n\) of heavy current-current correlation functions, namely,
where \(r_n\) are the perturbative moments calculated at \(\hbox {N}^3\)LO, \({\bar{M}}_{\mathrm{kin}}\) is the spin-averaged kinetic mass of the heavy–heavy vector and pseudoscalar mesons and \({\bar{M}}_{\Upsilon ,\eta _b}\) is the experimental spin average of the \(\Upsilon \) and \(\eta _b\) masses. The average kinetic mass \({\bar{M}}_{\mathrm{kin}}\) is chosen since in the lattice calculation the splitting of the \(\Upsilon \) and \(\eta _b\) states is inverted. In Eq. (66), the bare mass \(m_b\) appearing on the left-hand side is tuned so that the spin-averaged mass agrees with experiment, while the mass \({\overline{m}}_b\) at the fixed scale \(\mu = 4.18\) GeV is extrapolated to the continuum limit using three HISQ (MILC) ensembles with \(a \approx \) 0.15, 0.12 and 0.09 fm and two pion masses, one of which is the physical one. Their final result is \({\overline{m}}_b(\mu = 4.18\, \mathrm {GeV}) = 4.207(26)\) GeV, where the error is from adding systematic uncertainties in quadrature only (statistical errors are smaller than \(0.1 \%\) and ignored). The errors arise from renormalization, perturbation theory, lattice spacing, and NRQCD systematics. The finite-volume uncertainty is not estimated, but at the lowest pion mass they have \( m_\pi L \simeq 4\), which leads to the tag  .
.
In HPQCD 14A the quark mass is computed using a similar strategy as above but with HISQ heavy quarks instead of NRQCD. The gauge field ensembles are the same as in HPQCD 14B above plus the one with \(a = 0.06\) fm (four lattice spacings in all). Since the physical b-quark mass in units of the lattice spacing is always greater than one in these calculations, fits to correlation functions are restricted to \(am_h \le 0.8\), and a high-degree polynomial in \(a m_{\eta _{h}}\), the corresponding pseudoscalar mass, is used in the fits to remove the lattice-spacing errors. Finally, to obtain the physical b-quark mass, the moments are extrapolated to \(m_{\eta _b}\). Bare heavy-quark masses are tuned to their physical values using the \(\eta _h\) mesons, and ratios of ratios yield \(m_h/m_c\). The \(\overline{\mathrm{MS}}\)-charm-quark mass determined as described in Sect. 3.2 then gives \(m_b\). The moment ratios are expanded using the OPE, and the quark masses and \(\alpha _S\) are determined from fits of the lattice ratios to this expansion. The fits are complicated: HPQCD uses cubic splines for valence- and sea-mass dependence, with several knots, and many priors for 21 ratios to fit 29 data points. Taking this fit at face value results in a  rating for the continuum limit since they use four lattice spacings down to 0.06 fm. See however the detailed discussion of the continuum limit given in Sect. 9.7 on \(\alpha _S\).
rating for the continuum limit since they use four lattice spacings down to 0.06 fm. See however the detailed discussion of the continuum limit given in Sect. 9.7 on \(\alpha _S\).
The third four-flavour result [26] is from the ETM collaboration and updates their preliminary result appearing in a conference proceedings [196]. The calculation is performed on a set of configurations generated with twisted-Wilson fermions with three lattice spacings in the range 0.06–0.09 fm and with pion masses in the range 210–440 MeV. The b-quark mass is determined from a ratio of heavy–light pseudoscalar meson masses designed to yield the quark pole mass in the static limit. The pole mass is related to the \(\overline{\mathrm{MS}}\) mass through perturbation theory at \(\hbox {N}^3\)LO. The key idea is that by taking ratios of ratios, the b-quark mass is accessible through fits to heavy–light(strange)-meson correlation functions computed on the lattice in the range \(\sim 1\)–\(2\times m_c\) and the static limit, the latter being exactly 1. By simulating below \({\overline{m}}_b\), taking the continuum limit is easier. They find \({\overline{m}}_b({\overline{m}}_b) = 4.26(3)(10)\) GeV, where the first error is statistical and the second systematic. The dominant errors come from setting the lattice scale and fit systematics.
The next new result since FLAG 16 is from Gambino, et al. [27]. The authors use twisted-mass-fermion ensembles from the ETM collaboration and the ETM ratio method as in ETM 16. Three values of the lattice spacing are used, ranging from 0.062 to 0.089 fm. Several volumes are also used. The light-quark masses produce pions with masses from 210 to 450 MeV. The main difference with ETM 16 is that the authors use the kinetic mass defined in the heavy-quark expansion (HQE) to extract the b-quark mass instead of the pole mass.
The final b-quark mass result is FNAL/MILC/TUM 18 [8]. The mass is extracted from the same fit and analysis that is described in the charm quark mass section. Note that relativistic HISQ quarks are used (almost) all the way up to the b-quark mass (0.9 \(am_b\)) on the finest two lattices, \(a=0.03\) and 0.042 fm. The authors investigated the effect of leaving out the heaviest points from the fit, and the result did not noticeably change.
All of the above results enter our average. We note that here the updated ETM result is consistent with the average and a stretching factor on the error is not used. The average and error is dominated by the very precise FNAL/MILC/TUM 18 value.
Since HPQCD quotes \({\overline{m}}_b({\overline{m}}_b)\) using \(N_f= 5\) running, we used that value in the average. We have included a 100% correlation on the statistical errors of ETM 16 and Gambino 17 since the same ensembles are used in both. This translates to the following RGI average
All the results for \({\overline{m}}_b({\overline{m}}_b)\) discussed above are shown in Fig. 7 together with the FLAG averages corresponding to \(N_f=2\,+\,1\) and \(2\,+\,1\,+\,1\) quark flavours.
The b-quark mass, \(N_f =2\,+\,1\) and \(2\,+\,1\,+\,1\). The updated PDG value from Ref. [137] is reported for comparison
4 Leptonic and semileptonic kaon and pion decay and \(|V_{ud}|\) and \(|V_{us}|\)
Authors: T. Kaneko, J. N. Simone, S. Simula
This section summarizes state-of-the-art lattice calculations of the leptonic kaon and pion decay constants and the kaon semileptonic-decay form factor and provides an analysis in view of the Standard Model. With respect to the previous edition of the FLAG review [3] the data in this section has been updated. As in Ref. [3], when combining lattice data with experimental results, we take into account the strong SU(2) isospin correction, either obtained in lattice calculations or estimated by using chiral perturbation theory (\(\chi \)PT), both for the kaon leptonic decay constant \(f_{K^\pm }\) and for the ratio \(f_{K^\pm } / f_{\pi ^\pm }\).
4.1 Experimental information concerning \(|V_{ud}|\), \(|V_{us}|\), \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\)
The following review relies on the fact that precision experimental data on kaon decays very accurately determine the product \(|V_{us}|f_+(0)\) [200] and the ratio \(|V_{us}/V_{ud}|f_{K^\pm }/f_{\pi ^\pm }\) [200, 201]:
Here and in the following, \(f_{K^\pm }\) and \(f_{\pi ^\pm }\) are the isospin-broken decay constants, respectively, in QCD. We will refer to the decay constants in the SU(2) isospin-symmetric limit as \(f_K\) and \(f_\pi \) (the latter at leading order in the mass difference (\(m_u - m_d\)) coincides with \(f_{\pi ^\pm }\)). The parameters \(|V_{ud}|\) and \(|V_{us}|\) are elements of the Cabibbo-Kobayashi-Maskawa matrix and \(f_+(q^2)\) represents one of the form factors relevant for the semileptonic decay \(K^0\rightarrow \pi ^-\ell \,\nu \), which depends on the momentum transfer q between the two mesons. What matters here is the value at \(q^2 = 0\):  . The pion and kaon decay constants are defined byFootnote 17
. The pion and kaon decay constants are defined byFootnote 17

In this normalization, \(f_{\pi ^\pm } \simeq 130\) MeV, \(f_{K^\pm }\simeq 155\) MeV.
In Eq. (69), the electromagnetic effects have already been subtracted in the experimental analysis using \(\chi \)PT. Recently, a new method [206] has been proposed for calculating the leptonic decay rates of hadrons including both QCD and QED on the lattice, and successfully applied to the case of the ratio of the leptonic decay rates of kaons and pions [207]. The correction to the tree-level \(K_{\mu 2} / \pi _{\mu 2}\) decay rate, including both electromagnetic and strong isospin-breaking effects, is found to be equal to \(-1.22 (16) \%\) to be compared to the estimate \(-1.12 (21) \%\) based on \(\chi \)PT [133, 208]. Using the experimental values of the \(K_{\mu 2} \) and \(\pi _{\mu 2}\) decay rates the result of Ref. [207] implies
where the last error in brackets is the sum in quadrature of the experimental and theoretical uncertainties, and the ratio of the decay constants is the one corresponding to isosymmetric QCD. The single calculation of Ref. [207] is clearly not ready for averaging, but it demonstrates that the determination of \(V_{us} / V_{ud}\) using only lattice-QCD+QED and the ratio of the experimental values of the \(K_{\mu 2} \) and \(\pi _{\mu 2}\) decay rates is feasible with good accuracy.
The measurement of \(|V_{ud}|\) based on superallowed nuclear \(\beta \) transitions has now become remarkably precise. The result of the update of Hardy and Towner [209], which is based on 20 different superallowed transitions, readsFootnote 18
The matrix element \(|V_{us}|\) can be determined from semi-inclusive \(\tau \) decays [217,218,219,220]. By separating the inclusive decay \(\tau \rightarrow \text{ hadrons }+\nu \) into nonstrange and strange final states, e.g., HFLAV 16 [221] obtains \(|V_{us}|=0.2186(21)\) and both Maltman et al. [219, 222, 223] and Gamiz et al. [224, 225] arrive at very similar values. Inclusive hadronic \(\tau \) decay offers an interesting way to measure \(|V_{us}|\), but the above value of \(|V_{us}|\) differs from the result one obtains from assuming three-flavour SM-unitarity by more than three standard deviations [221]. This apparent tension has been recently solved in Ref. [226] thanks to the use of a different experimental input and to a new treatment of higher orders in the operator product expansion and of violations of quark-hadron duality. A much larger value of \(|V_{us}|\) is obtained, namely,
which is in much better agreement with CKM unitarity. Recently, in Ref. [227], a new method, which includes also the lattice calculation of the hadronic vacuum polarization function, has been proposed for the determination of \(|V_{us}|\) from inclusive strange \(\tau \) decays.
The experimental results in Eq. (69) are for the semileptonic decay of a neutral kaon into a negatively charged pion and the charged pion and kaon leptonic decays, respectively, in QCD. In the case of the semileptonic decays the corrections for strong and electromagnetic isospin breaking in chiral perturbation theory at NLO have allowed for averaging the different experimentally measured isospin channels [228]. This is quite a convenient procedure as long as lattice-QCD simulations do not include strong or QED isospin-breaking effects. Several lattice results for \(f_K/f_\pi \) are quoted for QCD with (squared) pion and kaon masses of \(M_\pi ^2=M_{\pi ^0}^2\) and \(M_K^2=\frac{1}{2} \left( M_{K^\pm }^2\,+\,M_{K^0}^2-M_{\pi ^\pm }^2\,+\,M_{\pi ^0}^2\right) \) for which the leading strong and electromagnetic isospin violations cancel. While the modern trend is to include strong and electromagnetic isospin breaking in the lattice simulations (e.g., Refs. [140, 141, 162, 185, 206, 207, 229,230,231]), in this section contact with experimental results is made by correcting leading SU(2) isospin breaking guided either by chiral perturbation theory or by lattice calculations.
4.2 Lattice results for \(f_+(0)\) and \(f_{K^\pm }/f_{\pi ^\pm }\)
The traditional way of determining \(|V_{us}|\) relies on using estimates for the value of \(f_+(0)\), invoking the Ademollo-Gatto theorem [241]. Since this theorem only holds to leading order of the expansion in powers of \(m_u\), \(m_d\), and \(m_s\), theoretical models are used to estimate the corrections. Lattice methods have now reached the stage where quantities like \(f_+(0)\) or \(f_K/f_\pi \) can be determined to good accuracy. As a consequence, the uncertainties inherent in the theoretical estimates for the higher order effects in the value of \(f_+(0)\) do not represent a limiting factor any more and we shall therefore not invoke those estimates. Also, we will use the experimental results based on nuclear \(\beta \) decay and \(\tau \) decay exclusively for comparison – the main aim of the present review is to assess the information gathered with lattice methods and to use it for testing the consistency of the SM and its potential to provide constraints for its extensions.
The database underlying the present review of the semileptonic form factor and the ratio of decay constants is listed in Tables 13 and 14. The properties of the lattice data play a crucial role for the conclusions to be drawn from these results: range of \(M_\pi \), size of \(L M_\pi \), continuum extrapolation, extrapolation in the quark masses, finite-size effects, etc. The key features of the various data sets are characterized by means of the colour code specified in Sect. 2.1. Note that with respect to the previous edition [3] we have dropped old results with two red tags. More detailed information on individual computations are compiled in Appendix B.2, which in this edition is limited to new results and to those entering the FLAG averages. For other calculations the reader should refer to the Appendix B.2 of Ref. [3].
The quantity \(f_+(0)\) represents a matrix element of a strangeness-changing null-plane charge, \(f_+(0)\,{=}\,\langle K|Q^{{\bar{u}}s}|\pi \rangle \) (see Ref. [242]). The vector charges obey the commutation relations of the Lie algebra of SU(3), in particular \([Q^{{\bar{u}}s},Q^{{\bar{s}}u}]=Q^{{\bar{u}}u-{\bar{s}}s}\). This relation implies the sum rule \(\sum _n |\langle K|Q^{{\bar{u}}s}|n \rangle |^2-\sum _n |\langle K|Q^{{\bar{s}}u}|n \rangle |^2=1\). Since the contribution from the one-pion intermediate state to the first sum is given by \(f_+(0)^2\), the relation amounts to an exact representation for this quantity [243]:
While the first sum on the right extends over nonstrange intermediate states, the second runs over exotic states with strangeness \(\pm 2\) and is expected to be small compared to the first.
The expansion of \(f_+(0)\) in SU(3) chiral perturbation theory in powers of \(m_u\), \(m_d\), and \(m_s\) starts with \(f_+(0)=1+f_2\,+\,f_4+\ldots \,\) [244]. Since all of the low-energy constants occurring in \(f_2\) can be expressed in terms of \(M_\pi \), \(M_K\), \(M_\eta \) and \(f_\pi \) [242], the NLO correction is known. In the language of the sum rule (73), \(f_2\) stems from nonstrange intermediate states with three mesons. Like all other nonexotic intermediate states, it lowers the value of \(f_+(0)\): \(f_2=-0.023\) when using the experimental value of \(f_\pi \) as input. The corresponding expressions have also been derived in quenched or partially quenched (staggered) chiral perturbation theory [30, 245]. At the same order in the SU(2) expansion [246], \(f_+(0)\) is parameterized in terms of \(M_\pi \) and two a priori unknown parameters. The latter can be determined from the dependence of the lattice results on the masses of the quarks. Note that any calculation that relies on the \(\chi \)PT formula for \(f_2\) is subject to the uncertainties inherent in NLO results: instead of using the physical value of the pion decay constant \(f_\pi \), one may, for instance, work with the constant \(f_0\) that occurs in the effective Lagrangian and represents the value of \(f_\pi \) in the chiral limit. Although trading \(f_\pi \) for \(f_0\) in the expression for the NLO term affects the result only at NNLO, it may make a significant numerical difference in calculations where the latter are not explicitly accounted for. (Lattice results concerning the value of the ratio \(f_\pi /f_0\) are reviewed in Sect. 5.3.)
Comparison of lattice results (squares) for \(f_+(0)\) and \(f_{K^\pm }/ f_{\pi ^\pm }\) with various model estimates based on \(\chi \)PT (blue circles). The ratio \(f_{K^\pm }/f_{\pi ^\pm }\) is obtained in pure QCD including the SU(2) isospin-breaking correction (see Sect. 4.3). The black squares and grey bands indicate our estimates. The significance of the colours is explained in Sect. 2
The lattice results shown in the left panel of Fig. 8 indicate that the higher order contributions \(\Delta f\equiv f_+(0)-1-f_2\) are negative and thus amplify the effect generated by \(f_2\). This confirms the expectation that the exotic contributions are small. The entries in the lower part of the left panel represent various model estimates for \(f_4\). In Ref. [251], the symmetry-breaking effects are estimated in the framework of the quark model. The more recent calculations are more sophisticated, as they make use of the known explicit expression for the \(K_{\ell 3}\) form factors to NNLO in \(\chi \)PT [250, 252]. The corresponding formula for \(f_4\) accounts for the chiral logarithms occurring at NNLO and is not subject to the ambiguity mentioned above.Footnote 19 The numerical result, however, depends on the model used to estimate the low-energy constants occurring in \(f_4\) [247,248,249,250]. The figure indicates that the most recent numbers obtained in this way correspond to a positive or an almost vanishing rather than a negative value for \(\Delta f\). We note that FNAL/MILC 12I [30] and Ref. [253] have made an attempt at determining a combination of some of the low-energy constants appearing in \(f_4\) from lattice data.
4.3 Direct determination of \(f_+(0)\) and \(f_{K^\pm }/f_{\pi ^\pm }\)
Many lattice results for the form factor \(f_+(0)\) and for the ratio of decay constants, which we summarize here in Tables 13 and 14, respectively, have been computed in isospin-symmetric QCD. The reason for this unphysical parameter choice is that there are only a few simulations of isospin-breaking effects in lattice QCD, which is ultimately the cleanest way for predicting these effects [139,140,141, 148, 185, 206, 207, 231, 254, 255]. In the meantime, one relies either on chiral perturbation theory [166, 244] to estimate the correction to the isospin limit or one calculates the breaking at leading order in \((m_u-m_d)\) in the valence quark sector by extrapolating the lattice data for the charged kaons to the physical value of the up(down)-quark mass (the result for the pion decay constant is always extrapolated to the value of the average light-quark mass \({{\hat{m}}}\)). This defines the prediction for \(f_{K^\pm }/f_{\pi ^\pm }\).
Since the majority of results that qualify for inclusion into the FLAG average include the strong SU(2) isospin-breaking correction, we confirm the choice made in the previous edition of the FLAG review [3] and we provide in Fig. 8 the overview of the world data of \(f_{K^\pm }/f_{\pi ^\pm }\). For all the results of Table 14 provided only in the isospin-symmetric limit we apply individually an isospin correction that will be described later on (see Eqs. (78)–(79)).
The plots in Fig. 8 illustrate our compilation of data for \(f_+(0)\) and \(f_{K^\pm }/f_{\pi ^\pm }\). The lattice data for the latter quantity is largely consistent even when comparing simulations with different \(N_f\), while in the case of \(f_+(0)\) a slight tendency to get higher values for increasing \(N_f\) seems to be visible, even if it does not exceed one standard deviation. We now proceed to form the corresponding averages, separately for the data with \(N_{ f}=2\,+\,1\,+\,1\), \(N_{ f}=2\,+\,1\), and \(N_{ f}=2\) dynamical flavours, and in the following we will refer to these averages as the “direct” determinations.
4.3.1 Results for \(f_+(0)\)
For \(f_+(0)\) there are currently two computational strategies: FNAL/MILC uses the Ward identity to relate the \(K\rightarrow \pi \) form factor at zero momentum transfer to the matrix element \(\langle \pi |S|K\rangle \) of the flavour-changing scalar current \(S = {\bar{s}} u\). Peculiarities of the staggered fermion discretization used by FNAL/MILC (see Ref. [30]) makes this the favoured choice. The other collaborations are instead computing the vector current matrix element \(\langle \pi | {\bar{s}} \gamma _\mu u |K\rangle \). Apart from FNAL/MILC 13C, FNAL/MILC 13E and RBC/UKQCD 15A all simulations in Table 13 involve unphysically heavy quarks and, therefore, the lattice data needs to be extrapolated to the physical pion and kaon masses corresponding to the \(K^0\rightarrow \pi ^-\) channel. We note also that the recent computations of \(f_+(0)\) obtained by the FNAL/MILC and RBC/UKQCD collaborations make use of the partially-twisted boundary conditions to determine the form-factor results directly at the relevant kinematical point \(q^2=0\) [266, 267], avoiding in this way any uncertainty due to the momentum dependence of the vector and/or scalar form factors. The ETM collaboration uses partially-twisted boundary conditions to compare the momentum dependence of the scalar and vector form factors with the one of the experimental data [29, 240], while keeping at the same time the advantage of the high-precision determination of the scalar form factor at the kinematical end-point \(q_{max}^2 = (M_K - M_\pi )^2\) [32, 268] for the interpolation at \(q^2 = 0\).
According to the colour codes reported in Table 13 and to the FLAG rules of Sect. 2.2, only the result ETM 09A with \(N_{ f}=2\), the results FNAL/MILC 12I and RBC/UKQCD 15A with \(N_{ f}=2\,+\,1\) and the results FNAL/MILC 13E and ETM 16 with \(N_{ f}=2\,+\,1\,+\,1\) dynamical flavours of fermions, respectively, can enter the FLAG averages.
At \(N_{ f}=2\,+\,1\,+\,1\) the result from the FNAL/MILC collaboration, \(f_+(0) = 0.9704 (24) (22)\) (FNAL/MILC 13E), is based on the use of the Highly Improved Staggered Quark (HISQ) action (for both valence and sea quarks), which has been tailored to reduce staggered taste-breaking effects, and includes simulations with three lattice spacings and physical light-quark masses. These features allow to keep the uncertainties due to the chiral extrapolation and to the discretization artifacts well below the statistical error. The remaining largest systematic uncertainty comes from finite-size effects, which have been investigated in Ref. [269] using 1-loop \(\chi \)PT (with and without taste-violating effects). Recently [232] the FNAL/MILC collaboration presented a more precise determination of \(f_+(0)\), \(f_+(0) = 0.9696 (15) (11)\) (see the entry FNAL/MILC 18 in Table 13), in which the improvement of the precision with respect to FNAL/MILC 13E is obtained mainly by using an estimate of finite-size effects based on ChPT only. We do not consider FNAL/MILC 18 as a plain update of FNAL/MILC 13E.
The new result from the ETM collaboration, \(f_+(0) = 0.9709 (45) (9)\) (ETM 16), makes use of the twisted-mass discretization adopting three values of the lattice spacing in the range \(0.06{-}0.09\) fm and pion masses simulated in the range \(210{-}450\) MeV. The chiral and continuum extrapolations are performed in a combined fit together with the momentum dependence, using both a SU(2)-\(\chi \)PT inspired ansatz (following Ref. [240]) and a modified z-expansion fit. The uncertainties coming from the chiral extrapolation, the continuum extrapolation and the finite-volume effects turn out to be well below the dominant statistical error, which includes also the error due to the fitting procedure. A set of synthetic data points, representing both the vector and the scalar semileptonic form factors at the physical point for several selected values of \(q^2\), is provided together with the corresponding correlation matrix.
At \(N_{ f}=2\,+\,1\) there is a new result from the JLQCD collaboration [234], which however does not satisfy all FLAG criteria for entering the average. The two results eligible to enter the FLAG average at \(N_{ f}=2\,+\,1\) are the one from RBC/UKQCD 15A, \(f_+(0) = 0.9685 (34) (14)\) [31], and the one from FNAL/MILC 12I, \(f_+(0)=0.9667(23)(33)\) [30]. These results, based on different fermion discretizations (staggered fermions in the case of FNAL/MILC and domain wall fermions in the case of RBC/UKQCD) are in nice agreement. Moreover, in the case of FNAL/MILC the form factor has been determined from the scalar current matrix element, while in the case of RBC/UKQCD it has been determined including also the matrix element of the vector current. To a certain extent both simulations are expected to be affected by different systematic effects.
RBC/UKQCD 15A has analyzed results on ensembles with pion masses down to 140 MeV, mapping out the complete range from the SU(3)-symmetric limit to the physical point. No significant cut-off effects (results for two lattice spacings) were observed in the simulation results. Ensembles with unphysical light-quark masses are weighted to work as a guide for small corrections toward the physical point, reducing in this way the model dependence in the fitting ansatz. The systematic uncertainty turns out to be dominated by finite-volume effects, for which an estimate based on effective theory arguments is provided.
The result FNAL/MILC 12I is from simulations reaching down to a lightest RMS pion mass of about 380 MeV (the lightest valence pion mass for one of their ensembles is about 260 MeV). Their combined chiral and continuum extrapolation (results for two lattice spacings) is based on NLO staggered chiral perturbation theory supplemented by the continuum NNLO expression [250] and a phenomenological parameterization of the breaking of the Ademollo-Gatto theorem at finite lattice spacing inherent in their approach. The \(p^4\) low-energy constants entering the NNLO expression have been fixed in terms of external input [270].
The ETM collaboration uses the twisted-mass discretization and provides at \(N_{ f}=2\) a comprehensive study of the systematics [32, 240], by presenting results for four lattice spacings and by simulating at light pion masses (down to \(M_\pi = 260\) MeV). This makes it possible to constrain the chiral extrapolation, using both SU(3) [242] and SU(2) [246] chiral perturbation theory. Moreover, a rough estimate for the size of the effects due to quenching the strange quark is given, based on the comparison of the result for \(N_{ f}=2\) dynamical quark flavours [40] with the one in the quenched approximation, obtained earlier by the SPQcdR collaboration [268].
We now compute the \(N_f = 2\,+\,1\,+\,1\) FLAG-average for \(f_+(0)\) using the FNAL/MILC 13E and ETM 16 (uncorrelated) results, the \(N_f =2\,+\,1\) FLAG-average based on FNAL/MILC 12I and RBC/UKQCD 15A, which we consider uncorrelated, while for \(N_f = 2\) we consider directly the ETM 09A result, respectively:
where the brackets in the third line indicate the statistical and systematic errors, respectively. We stress that the results (74) and (75), corresponding to \(N_f = 2\,+\,1\,+\,1\) and \(N_f = 2\,+\,1\), respectively, include already simulations with physical light-quark masses.
4.3.2 Results for \(f_{K^\pm }/f_{\pi ^\pm }\)
In the case of the ratio of decay constants the data sets that meet the criteria formulated in the introduction are HPQCD 13A [33], ETM 14E [34] and FNAL/MILC 17 [5] (which updates FNAL/MILC 14A [18]) with \(N_f=2\,+\,1\,+\,1\), HPQCD/UKQCD 07 [35], MILC 10 [36], BMW 10 [37], RBC/UKQCD 14B [10], Dürr 16 [38, 260] and QCDSF/UKQCD 16 [39] with \(N_{ f}=2\,+\,1\) and ETM 09 [40] with \(N_{ f}=2\) dynamical flavours.
ETM 14E uses the twisted-mass discretization and provides a comprehensive study of the systematics by presenting results for three lattice spacings in the range \(0.06 - 0.09\) fm and for pion masses in the range \(210 - 450\) MeV. This makes it possible to constrain the chiral extrapolation, using both SU(2) [246] chiral perturbation theory and polynomial fits. The ETM collaboration always includes the spread in the central values obtained from different ansätze into the systematic errors. The final result of their analysis is \({f_{K^\pm }}/{f_{\pi ^\pm }}= 1.184(12)_{\mathrm{stat+fit}}(3)_{\mathrm{Chiral}}(9)_{\mathrm{a}^2}(1)_{Z_P}(3)_{FV}(3)_{IB}\) where the errors are (statistical + the error due to the fitting procedure), due to the chiral extrapolation, the continuum extrapolation, the mass-renormalization constant, the finite-volume and (strong) isospin-breaking effects.
FNAL/MILC 17 [5] has determined the ratio of the decay constants from a comprehensive set of HISQ ensembles with \(N_f = 2\,+\,1\,+\,1\) dynamical flavours. They have generated 24 ensembles for six values of the lattice spacing (\(0.03 - 0.15\) fm, scale set with \(f_{\pi ^+}\)) and with both physical and unphysical values of the light sea-quark masses, controlling in this way the systematic uncertainties due to chiral and continuum extrapolations. With respect to FNAL/MILC 14A they have increased the statistics and added three ensembles at very fine lattice spacings, \(a \simeq 0.03\) and 0.042 fm, including for the latter case also a simulation at the physical value of the light-quark mass. The final result of their analysis is \({f_{K^\pm }}/{f_{\pi ^\pm }}=1.1950(14)_{\mathrm{stat}}(_{-17}^{+0})_{\mathrm{a}^2} (2)_{FV} (3)_{f_\pi , PDG} (3)_{EM} (2)_{Q^2}\), where the errors are statistical, due to the continuum extrapolation, finite-volume, pion decay constant from PDG, electromagnetic effects and sampling of the topological charge distribution.
HPQCD 13A has analyzed ensembles generated by MILC and therefore its study of \({f_{K^\pm }}/{f_{\pi ^\pm }}\) is based on the same set of ensembles bar the ones at the finest lattice spacings (namely, only \(a = 0.09 - 0.15\) fm, scale set with \(f_{\pi ^+}\) and relative scale set with the Wilson flow [271, 272]) supplemented by some simulation points with heavier quark masses. HPQCD employs a global fit based on continuum NLO SU(3) chiral perturbation theory for the decay constants supplemented by a model for higher-order terms including discretization and finite-volume effects (61 parameters for 39 data points supplemented by Bayesian priors). Their final result is \(f_{K^\pm }/f_{\pi ^\pm }=1.1916(15)_{\mathrm{stat}}(12)_{\mathrm{a}^2}(1)_{FV}(10)\), where the errors are statistical, due to the continuum extrapolation, due to finite-volume effects and the last error contains the combined uncertainties from the chiral extrapolation, the scale-setting uncertainty, the experimental input in terms of \(f_{\pi ^+}\) and from the uncertainty in \(m_u/m_d\).
In the two previous editions of the FLAG review [2, 3] the error budget of HPQCD 13A was compared with the ones of MILC 13A and FNAL/MILC 14A and discussed in detail. It was pointed out that, despite the overlap in primary lattice data, both collaborations arrive at surprisingly different error budgets, particularly in the cases of the cutoff dependence and of the finite volume effects. The error budget of the latest update FNAL/MILC 17, which has a richer lattice setup with respect to HPQCD 13A, is consistent with the one of HPQCD 13A.
Adding in quadrature all the uncertainties one gets: \(f_{K^\pm }/f_{\pi ^\pm } = 1.1916(22)\) (HPQCD 13A) and \({f_{K^\pm }}/{f_{\pi ^\pm }}=1.1944(18)\)Footnote 20 (FNAL/MILC 17). It can be seen that the total errors are very similar and the central values are consistent within approximately one standard deviation. Thus, the HPQCD 13A and FNAL/MILC 17 are averaged, assuming a \(100 \%\) statistical and systematic correlations between them, together with the (uncorrelated) ETM 14E result, obtaining
For \(N_f=2\,+\,1\) the result Dürr 16 [38, 260] is now eligible to enter the FLAG average as well as the new result [39] from the QCDSF collaboration. Dürr 16 [38, 260] has analyzed the decay constants evaluated for 47 gauge ensembles generated using tree-level clover-improved fermions with two HEX-smearings and the tree-level Symanzik-improved gauge action. The ensembles correspond to five values of the lattice spacing (\(0.05{-}0.12\) fm, scale set by \(\Omega \) mass), to pion masses in the range \(130{-}680\) MeV and to values of the lattice size from 1.7 to 5.6 fm, obtaining a good control over the interpolation to the physical mass point and the extrapolation to the continuum and infinite volume limits.
QCDSF/UKQCD 16 [39] has used the nonperturbatively \(\mathcal{{O}}(a)\)-improved clover action for the fermions (mildly stout-smeared) and the tree-level Symanzik action for the gluons. Four values of the lattice spacing (\(0.06{-}0.08\) fm) have been simulated with pion masses down to \(\sim 220\) MeV and values of the lattice size in the range \(2.0{-}2.8\) fm. The decay constants are evaluated using an expansion around the symmetric SU(3) point \(m_u = m_d = m_s = (m_u + m_d + m_s)^{phys}/3\).
Note that for \(N_f=2\,+\,1\) MILC 10 and HPQCD/UKQCD 07 are based on staggered fermions, BMW 10, Dürr 16 and QCDSF/UKQCD 16 have used improved Wilson fermions and RBC/UKQCD 14B’s result is based on the domain-wall formulation. In contrast to RBC/UKQCD 14B and Dürr 16 the other simulations are for unphysical values of the light-quark masses (corresponding to smallest pion masses in the range \(220 - 260\) MeV in the case of MILC 10, HPQCD/UKQCD 07 and QCDSF/UKQCD 16) and therefore slightly more sophisticated extrapolations needed to be controlled. Various ansätze for the mass and cutoff dependence comprising SU(2) and SU(3) chiral perturbation theory or simply polynomials were used and compared in order to estimate the model dependence. While BMW 10, RBC/UKQCD 14B and QCDSF/UKQCD 16 are entirely independent computations, subsets of the MILC gauge ensembles used by MILC 10 and HPQCD/UKQCD 07 are the same. MILC 10 is certainly based on a larger and more advanced set of gauge configurations than HPQCD/UKQCD 07. This allows them for a more reliable estimation of systematic effects. In this situation we consider both statistical and systematic uncertainties to be correlated.
For \(N_f=2\) no new result enters the corresponding FLAG average with respect to the previous edition of the FLAG review [3], which therefore remains the ETM 09 result, which has simulated twisted-mass fermions down to (charged) pion masses equal to 260 MeV.
We note that the overall uncertainties quoted by ETM 14E at \(N_{ f}=2\,+\,1\,+\,1\) and by Dürr 16 and QCDSF/UKQCD 16 at \(N_{ f}=2\,+\,1\) are much larger than the overall uncertainties obtained with staggered (HPQCD 13A, FNAL/MILC 17 at \(N_{ f}=2\,+\,1\,+\,1\) and MILC 10, HPQCD/UKQCD 07 at \(N_{ f}=2\,+\,1\)) and domain-wall fermions (RBC/UKQCD 14B at \(N_{ f}=2\,+\,1\)).
Before determining the average for \(f_{K^\pm }/f_{\pi ^\pm }\), which should be used for applications to Standard Model phenomenology, we apply the strong isospin correction individually to all those results that have been published only in the isospin-symmetric limit, i.e., BMW 10, HPQCD/UKQCD 07 and RBC/UKQCD 14B at \(N_f = 2\,+\,1\) and ETM 09 at \(N_f = 2\). To this end, as in the previous edition of the FLAG reviews [2, 3], we make use of NLO SU(3) chiral perturbation theory [208, 244], which predicts
where [208]

We use as input \(\epsilon _{SU(2)} = \sqrt{3} / (4 R)\) with the FLAG result for R of Eq. (54), \(F_0 = f_0 / \sqrt{2} = 80\,(20)\) MeV, \(M_\pi = 135\) MeV and \(M_K = 495\) MeV (we decided to choose a conservative uncertainty on \(f_0\) in order to reflect the magnitude of potential higher-order corrections). The results are reported in Table 15, where in the last column the last error is due to the isospin correction (the remaining errors are quoted in the same order as in the original data).
The plot compares the information for \(|V_{ud}|\), \(|V_{us}|\) obtained on the lattice for \(N_f = 2\,+\,1\) and \(N_f = 2\,+\,1\,+\,1\) with the experimental result extracted from nuclear \(\beta \) transitions. The dotted line indicates the correlation between \(|V_{ud}|\) and \(|V_{us}|\) that follows if the CKM-matrix is unitary. For the \(N_f = 2\) results see the previous FLAG edition [3]
For \(N_f=2\) and \(N_f=2\,+\,1\,+\,1\) dedicated studies of the strong-isospin correction in lattice QCD do exist. The updated \(N_f=2\) result of the RM123 collaboration [141] amounts to \(\delta _{SU(2)}=-0.0080(4)\) and we use this result for the isospin correction of the ETM 09 result. Note that the above RM123 value for the strong-isospin correction is incompatible with the results based on SU(3) chiral perturbation theory, \(\delta _{SU(2)}=-0.004(1)\) (see Table 15). Moreover, for \(N_f=2\,+\,1\,+\,1\) HPQCD [33], FNAL/MILC [5] and ETM [273] estimate a value for \(\delta _{SU(2)}\) equal to \(-0.0054(14)\), \(-0.0052(9)\) and \(-0.0073(6)\), respectively. Note that the RM123 and ETM results are obtained using the insertion of the isovector scalar current according to the expansion method of Ref. [140], while the HPQCD and FNAL/MILC results correspond to the difference between the values of the decay constant ratio extrapolated to the physical u-quark mass \(m_u\) and to the average \((m_u + m_d) / 2\) light-quark mass.
One would not expect the strange and heavier sea-quark contributions to be responsible for such a large effect. Whether higher-order effects in chiral perturbation theory or other sources are responsible still needs to be understood. More lattice-QCD simulations of SU(2) isospin-breaking effects are therefore required. To remain on the conservative side we add a \(100 \%\) error to the correction based on SU(3) chiral perturbation theory. For further analyses we add (in quadrature) such an uncertainty to the systematic error.
Using the results of Table 15 for \(N_f = 2\,+\,1\) we obtain
for QCD with broken isospin.
The averages obtained for \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\) at \(N_{ f}=2\,+\,1\) and \(N_{ f}=2\,+\,1\,+\,1\) [see Eqs. (74-75) and (80-81)] exhibit a precision better than \(\sim 0.3 \%\). At such a level of precision QED effects cannot be ignored and a consistent lattice treatment of both QED and QCD effects in leptonic and semileptonic decays becomes mandatory.
4.3.3 Extraction of \(|V_{ud}|\) and \(|V_{us}|\)
It is instructive to convert the averages for \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\) into a corresponding range for the CKM matrix elements \(|V_{ud}|\) and \(|V_{us}|\), using the relations (69). Consider first the results for \(N_{ f}=2\,+\,1\,+\,1\). The range for \(f_+(0)\) in Eq. (74) is mapped into the interval \(|V_{us}|=0.2231(7)\), depicted as a horizontal red band in Fig. 9, while the one for \({f_{K^\pm }}/{f_{\pi ^\pm }}\) in Eq. (80) is converted into \(|V_{us}|/|V_{ud}|= 0.2313(5)\), shown as a tilted red band. The red ellipse is the intersection of these two bands and represents the 68% likelihood contour,Footnote 21 obtained by treating the above two results as independent measurements. Repeating the exercise for \(N_{ f}=2\,+\,1\) leads to the green ellipse. The plot indicates a slight tension of both the \(N_f=2\,+\,1\,+\,1\) and \(N_f=2\,+\,1\) results with the one from nuclear \(\beta \) decay.
4.4 Tests of the Standard Model
In the Standard Model, the CKM matrix is unitary. In particular, the elements of the first row obey
The tiny contribution from \(|V_{ub}|\) is known much better than needed in the present context: \(|V_{ub}|= 3.94 (36) \cdot 10^{-3}\) [201]. In the following, we first discuss the evidence for the validity of the relation (83) and only then use it to analyse the lattice data within the Standard Model.
Results for \(|V_{us}|\) and \(|V_{ud}|\) that follow from the lattice data for \(f_+(0)\) (triangles) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\) (squares), on the basis of the assumption that the CKM matrix is unitary. The black squares and the grey bands represent our estimates, obtained by combining these two different ways of measuring \(|V_{us}|\) and \(|V_{ud}|\) on a lattice. For comparison, the figure also indicates the results obtained if the data on nuclear \(\beta \) decay and \(\tau \) decay is analysed within the standard model
In Fig. 9, the correlation between \(|V_{ud}|\) and \(|V_{us}|\) imposed by the unitarity of the CKM matrix is indicated by a dotted line (more precisely, in view of the uncertainty in \(|V_{ub}|\), the correlation corresponds to a band of finite width, but the effect is too small to be seen here). The plot shows that there is a slight tension with unitarity in the data for \(N_f = 2 + 1 + 1\): Numerically, the outcome for the sum of the squares of the first row of the CKM matrix reads \(|V_u|^2 = 0.9797(74)\), which deviates from unity at the level of \(\simeq 2.7\) standard deviations. Still, it is fair to say that at this level the Standard Model passes a nontrivial test that exclusively involves lattice data and well-established kaon decay branching ratios. Combining the lattice results for \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\) in Eqs. (74) and (80) with the \(\beta \) decay value of \(|V_{ud}|\) quoted in Eq. (71), the test sharpens considerably: the lattice result for \(f_+(0)\) leads to \(|V_u|^2 = 0.99884(53)\), which highlights again a \(\simeq 2.2\sigma \)-tension with unitarity, while the one for \({f_{K^\pm }}/{f_{\pi ^\pm }}\) implies \(|V_u|^2 = 0.99986(46)\), confirming the first-row CKM unitarity below the permille level.Footnote 22 Note that the largest contribution to the uncertainty on \(|V_u|^2\) comes from the error on \(|V_{ud}|\) given in Eq. (71).
The situation is similar for \(N_{ f}=2\,+\,1\): with the lattice data alone one has \(|V_u|^2 = 0.9832(89)\), which deviates from unity at the level of \(\simeq 1.9\) standard deviations. Combining the lattice results for \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\) in Eqs. (75) and (81) with the \(\beta \) decay value of \(|V_{ud}|\), the test sharpens again considerably: the lattice result for \(f_+(0)\) leads to \(|V_u|^2 = 0.99914(53)\), implying only a \(\simeq 1.6\sigma \)-tension with unitarity, while the one for \({f_{K^\pm }}/{f_{\pi ^\pm }}\) implies \(|V_u|^2 = 0.99999(54)\), thus confirming again CKM unitarity below the permille level.
For the analysis corresponding to \(N_f = 2\) the reader should refer to the previous FLAG edition [3].
Note that the above tests also offer a check of the basic hypothesis that underlies our analysis: we are assuming that the weak interaction between the quarks and the leptons is governed by the same Fermi constant as the one that determines the strength of the weak interaction among the leptons and the lifetime of the muon. In certain modifications of the Standard Model, this is not the case and it need not be true that the rates of the decays \(\pi \rightarrow \ell \nu \), \(K\rightarrow \ell \nu \) and \(K\rightarrow \pi \ell \nu \) can be used to determine the matrix elements \(|V_{ud}f_\pi |\), \(|V_{us}f_K|\) and \(|V_{us}f_+(0)|\), respectively, and that \(|V_{ud}|\) can be measured in nuclear \(\beta \) decay. The fact that the lattice data is consistent with unitarity and with the value of \(|V_{ud}|\) found in nuclear \(\beta \) decay indirectly also checks the equality of the Fermi constants.
4.5 Analysis within the Standard Model
The Standard Model implies that the CKM matrix is unitary. The precise experimental constraints quoted in (69) and the unitarity condition (83) then reduce the four quantities \(|V_{ud}|,|V_{us}|,f_+(0),{f_{K^\pm }}/{f_{\pi ^\pm }}\) to a single unknown: any one of these determines the other three within narrow uncertainties.
As Fig. 10 shows, the results obtained for \(|V_{us}|\) and \(|V_{ud}|\) from the data on \({f_{K^\pm }}/{f_{\pi ^\pm }}\) (squares) are quite consistent with the determinations via \(f_+(0)\) (triangles). In order to calculate the corresponding average values, we restrict ourselves to those determinations that we have considered best in Sect. 4.3. The corresponding results for \(|V_{us}|\) are listed in Table 16 (the error in the experimental numbers used to convert the values of \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\) into values for \(|V_{us}|\) is included in the statistical error).
For \(N_{ f}=2\,+\,1\,+\,1\) we consider the data both for \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\), treating ETM 16 and ETM 14E on the one hand and FNAL/MILC 13E, FNAL/MILC 17 and HPQCD 13A on the other hand, as statistically correlated according to the prescription of Sect. 2.3. We obtain \(|V_{us}|=0.2249(7)\), where the error includes the inflation factor due to the value of \(\chi ^2/\mathrm{dof} \simeq 2.5\). This result is indicated on the left hand side of Fig. 10 by the narrow vertical band. In the case \(N_f = 2\,+\,1\) we consider MILC 10, FNAL/MILC 12I and HPQCD/UKQCD 07 on the one hand and RBC/UKQCD 14B and RBC/UKQCD 15A on the other hand, as mutually statistically correlated, since the analysis in the two cases starts from partly the same set of gauge ensembles. In this way we arrive at \(|V_{us}| = 0.2249(5)\) with \(\chi ^2/\mathrm{dof} \simeq 0.8\). For \(N_{ f}=2\) we consider ETM 09A and ETM 09 as statistically correlated, obtaining \(|V_{us}|=0.2256(19)\) with \(\chi ^2/\mathrm{dof} \simeq 0.7\). The figure shows that the results obtained for the data with \(N_{ f}=2\), \(N_{ f}=2\,+\,1\) and \(N_{ f}=2\,+\,1\,+\,1\) are consistent with each other.
Alternatively, we can solve the relations for \(|V_{ud}|\) instead of \(|V_{us}|\). Again, the result \(|V_{ud}|=0.97437(16)\), which follows from the lattice data with \(N_{ f}=2\,+\,1\,+\,1\), is perfectly consistent with the values \(|V_{ud}|=0.97438(12)\) and \(|V_{ud}|=0.97423(44)\) obtained from the data with \(N_{ f}=2\,+\,1\) and \(N_{ f}=2\), respectively. The reduction of the uncertainties in the result for \(|V_{ud}|\) due to CKM unitarity is to be expected from Fig. 9: the unitarity condition reduces the region allowed by the lattice results to a nearly vertical interval.
Next, we determine the values of \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\) that follow from our determinations of \(|V_{us}|\) and \(|V_{ud}|\) obtained from the lattice data within the Standard Model. We find \(f_+(0) = 0.9627(35)\) for \(N_{ f}=2\,+\,1\,+\,1\), \(f_+(0) = 0.9627(28)\) for \(N_{ f}=2\,+\,1\), \(f_+(0) = 0.9597(83)\) for \(N_{ f}=2\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}= 1.196(3)\) for \(N_{ f}=2\,+\,1\,+\,1\), \({f_{K^\pm }}/{f_{\pi ^\pm }}= 1.196(3)\) for \(N_{ f}=2\,+\,1\), \({f_{K^\pm }}/{f_{\pi ^\pm }}= 1.192(9) \) for \(N_{ f}=2\), respectively. These results are collected in the upper half of Table 17. In the lower half of the table, we list the analogous results found by working out the consequences of the CKM unitarity using the values of \(|V_{ud}|\) and \(|V_{us}|\) obtained from nuclear \(\beta \) decay and \(\tau \) decay, respectively. The comparison shows that the lattice result for \(|V_{ud}|\) not only agrees very well with the totally independent determination based on nuclear \(\beta \) transitions, but is also remarkably precise. On the other hand, the values of \(|V_{ud}|\), \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\) that follow from the \(\tau \)-decay data if the Standard Model is assumed to be valid were initially not all in agreement with the lattice results for these quantities. The disagreement is reduced considerably if the analysis of the \(\tau \) data is supplemented with experimental results on electroproduction [223]: the discrepancy then amounts to little more than one standard deviation. The disagreement disappears when recent implementations of the relevant sum rules and a different experimental input are considered [226].
4.6 Direct determination of \(f_{K^\pm }\) and \(f_{\pi ^\pm }\)
It is useful for flavour physics studies to provide not only the lattice average of \(f_{K^\pm } / f_{\pi ^\pm }\), but also the average of the decay constant \(f_{K^\pm }\). The case of the decay constant \(f_{\pi ^\pm }\) is different, since the the PDG value [201] of this quantity, based on the use of the value of \(|V_{ud}|\) obtained from superallowed nuclear \(\beta \) decays [209], is often used for setting the scale in lattice QCD (see Appendix A.2). However, the physical scale can be set in different ways, namely, by using as input the mass of the \(\Omega \)-baryon (\(m_\Omega \)) or the \(\Upsilon \)-meson spectrum (\(\Delta M_\Upsilon \)), which are less sensitive to the uncertainties of the chiral extrapolation in the light-quark mass with respect to \(f_{\pi ^\pm }\). In such cases the value of the decay constant \(f_{\pi ^\pm }\) becomes a direct prediction of the lattice-QCD simulations. It is therefore interesting to provide also the average of the decay constant \(f_{\pi ^\pm }\), obtained when the physical scale is set through another hadron observable, in order to check the consistency of different scale setting procedures.
Our compilation of the values of \(f_{\pi ^\pm }\) and \(f_{K^\pm }\) with the corresponding colour code is presented in Table 18 and it is unchanged from the corresponding one in the previous FLAG review [3].
In comparison to the case of \(f_{K^\pm } / f_{\pi ^\pm }\) we have added two columns indicating which quantity is used to set the physical scale and the possible use of a renormalization constant for the axial current. For several lattice formulations the use of the nonsinglet axial-vector Ward identity allows to avoid the use of any renormalization constant.
One can see that the determinations of \(f_{\pi ^\pm }\) and \(f_{K^\pm }\) suffer from larger uncertainties with respect to the ones of the ratio \(f_{K^\pm } / f_{\pi ^\pm }\), which is less sensitive to various systematic effects (including the uncertainty of a possible renormalization constant) and, moreover, is not exposed to the uncertainties of the procedure used to set the physical scale.
According to the FLAG rules, for \(N_f = 2 + 1 + 1\) three data sets can form the average of \(f_{K^\pm }\) only: ETM 14E [34], FNAL/MILC 14A [18] and HPQCD 13A [33]. Following the same procedure already adopted in Sect. 4.3 in the case of the ratio of the decay constant we treat FNAL/MILC 14A and HPQCD 13A as statistically correlated. For \(N_f = 2 + 1\) three data sets can form the average of \(f_{\pi ^\pm }\) and \(f_{K^\pm }\) : RBC/UKQCD 14B [10] (update of RBC/UKQCD 12), HPQCD/UKQCD 07 [35] and MILC 10 [36], which is the latest update of the MILC program. We consider HPQCD/UKQCD 07 and MILC 10 as statistically correlated and use the prescription of Sect. 2.3 to form an average. For \(N_f = 2\) the average cannot be formed for \(f_{\pi ^\pm }\), and only one data set (ETM 09) satisfies the FLAG rules in the case of \(f_{K^\pm }\).
Thus, our estimates read
The lattice results of Table 18 and our estimates (84)–(85) are reported in Fig. 11. Note that the FLAG estimates of \(f_{K^\pm }\) for \(N_f = 2\) and \(N_f = 2 + 1 + 1\) are based on calculations in which \(f_{\pi ^\pm }\) is used to set the lattice scale, while the \(N_f = 2 + 1\) estimate does not rely on that.
5 Low-energy constants
Authors: S. Dürr, H. Fukaya, U. M. Heller
In the study of the quark-mass dependence of QCD observables calculated on the lattice, it is common practice to invoke chiral perturbation theory (\(\chi \)PT). For a given quantity this framework predicts the nonanalytic quark-mass dependence and it provides symmetry relations among different observables. These relations are best expressed with the help of a set of linearly independent and universal (i.e., process-independent) low-energy constants (LECs), which first appear as coefficients of the polynomial terms (in \(m_q\) or \(M_{\pi }^2\)) in different observables. When numerical simulations are done at heavier than physical (light) quark masses, \(\chi \)PT is usually invoked in the extrapolation to physical quark masses.
5.1 Chiral perturbation theory
\(\chi \)PT is an effective field theory approach to the low-energy properties of QCD based on the spontaneous breaking of chiral symmetry, \(SU(N_{ f})_L \times SU(N_{ f})_R \rightarrow SU(N_{ f})_{L+R}\), and its soft explicit breaking by quark-mass terms. In its original implementation, in infinite volume, it is an expansion in \(m_q\) and \(p^2\) with power counting \(M_{\pi }^2 \sim m_q \sim p^2\).
If one expands around the SU(2) chiral limit, there appear two LECs at order \(p^2\) in the chiral effective Lagrangian,

and seven at order \(p^4\), indicated by \({{\bar{\ell }}}_i\) with \(i=1,\ldots ,7\). In the analysis of the SU(3) chiral limit there are also just two LECs at order \(p^2\),

but ten at order \(p^4\), indicated by the capital letter \(L_i(\mu )\) with \(i=1,\ldots ,10\). These constants are independent of the quark masses,Footnote 23 but they become scale dependent after renormalization (sometimes a superscript r is added). The SU(2) constants \({\bar{\ell }}_i\) are scale independent, since they are defined at scale \(\mu =M_{\pi ,\mathrm {phys}}\) (as indicated by the bar). For the precise definition of these constants and their scale dependence we refer the reader to Refs. [244, 277].
5.1.1 Patterns of chiral symmetry breaking
If the box size is finite but large compared to the Compton wavelength of the pion, \(L\gg 1/M_{\pi }\), the power counting generalizes to \(m_q \sim p^2 \sim 1/L^2\), as one would assume based on the fact that \(p_\mathrm {min}=2\pi /L\) is the minimum momentum in a finite box with periodic boundary conditions in the spatial directions. This is the so-called p-regime of \(\chi \)PT. It coincides with the setting that is used for standard phenomenologically oriented lattice-QCD computations, and we shall consider the p-regime the default in the following. However, if the pion mass is so small that the box-length L is no longer large compared to the Compton wavelength that the pion would have, at the given \(m_q\), in infinite volume, then the chiral series must be reordered. Such finite-volume versions of \(\chi \)PT with correspondingly adjusted power counting schemes, referred to as \(\epsilon \)- and \(\delta \)-regime, are described in Sects. 5.1.6 and 5.1.7, respectively.
Lattice calculations can be used to test if chiral symmetry is indeed spontaneously broken along the path \(SU(N_{ f})_L \times SU(N_{ f})_R \rightarrow SU(N_{ f})_{L+R}\) by measuring nonzero chiral condensates and by verifying the validity of the GMOR relation \(M_{\pi }^2\propto m_q\) close to the chiral limit. If the chiral extrapolation of quantities calculated on the lattice is made with the help of fits to their \(\chi \)PT forms, apart from determining the observable at the physical value of the quark masses, one also obtains the relevant LECs. This is an important by-product for two reasons:
- 1.
All LECs up to order \(p^4\) (with the exception of B and \(B_0\), since only the product of these times the quark masses can be estimated from phenomenology) have either been determined by comparison to experiment or estimated theoretically, e.g., in large-\(N_c\) QCD. A lattice determination of the better known LECs thus provides a test of the \(\chi \)PT approach.
- 2.
The less well-known LECs are those which describe the quark-mass dependence of observables – these cannot be determined from experiment, and therefore the lattice, where quark masses can be varied, provides unique quantitative information. This information is essential for improving phenomenological \(\chi \)PT predictions in which these LECs play a role.
We stress that this program is based on the nonobvious assumption that \(\chi \)PT is valid in the region of masses and momenta used in the lattice simulations under consideration, something that can and should be checked. With the ability to create data at multiple values of the light-quark masses, lattice QCD offers the possibility to check the convergence of \(\chi \)PT. Lattice data may be used to verify that higher order contributions, for small enough quark masses, become increasingly unimportant. In the end one wants to compare lattice and phenomenological determinations of LECs, much in the spirit of Ref. [278]. An overview of many of the conceptual issues involved in matching lattice data to an effective field theory framework like \(\chi \)PT is given in Refs. [279,280,281].
The fact that, at large volume, the finite-size effects, which occur if a system undergoes spontaneous symmetry breakdown, are controlled by the Nambu-Goldstone modes, was first noted in solid state physics, in connection with magnetic systems [282, 283]. As pointed out in Ref. [284] in the context of QCD, the thermal properties of such systems can be studied in a systematic and model-independent manner by means of the corresponding effective field theory, provided the temperature is low enough. While finite volumes are not of physical interest in particle physics, lattice simulations are necessarily carried out in a finite box. As shown in Refs. [285,286,287], the ensuing finite-size effects can be studied on the basis of the effective theory – \(\chi \)PT in the case of QCD – provided the simulation is close enough to the continuum limit, the volume is sufficiently large and the explicit breaking of chiral symmetry generated by the quark masses is sufficiently small. Indeed, \(\chi \)PT represents a useful tool for the analysis of the finite-size effects in lattice simulations.
In the remainder of this section we collect the relevant \(\chi \)PT formulae that will be used in the two following sections to extract SU(2) and SU(3) LECs from lattice data.
5.1.2 Quark-mass dependence of pseudoscalar masses and decay constants
A. SU(2) formulae
The expansionsFootnote 24 of \(M_{\pi }^2\) and \(F_\pi \) in powers of the quark mass are known to next-to-next-to-leading order (NNLO) in the SU(2) chiral effective theory. In the isospin limit, \(m_u=m_d=m\), the explicit expressions may be written in the form [288]
Here the expansion parameter is given by
but there is another option as discussed below. The scales \(\Lambda _3,\Lambda _4\) are related to the effective coupling constants \({\bar{\ell }}_3,{\bar{\ell }}_4\) of the chiral Lagrangian at scale \(\mu =M_{\pi ,\mathrm {phys}}\) by
Note that in Eq. (88) the logarithms are evaluated at \(M^2\), not at \(M_{\pi }^2\). The coupling constants \(k_M,k_F\) in Eq. (88) are mass-independent. The scales of the squared logarithms can be expressed in terms of the \({\mathcal {O}}(p^4)\) coupling constants as
Hence by analysing the quark-mass dependence of \(M_{\pi }^2\) and \(F_\pi \) with Eq. (88), possibly truncated at NLO, one can determineFootnote 25 the \({\mathcal {O}}(p^2)\) LECs B and F, as well as the \({\mathcal {O}}(p^4)\) LECs \({{\bar{\ell }}}_3\) and \({{\bar{\ell }}}_4\). The quark condensate in the chiral limit is given by \(\Sigma =F^2B\). With precise enough data at several small enough pion masses, one could in principle also determine \(\Lambda _M\), \(\Lambda _F\) and \(k_M\), \(k_F\). To date this is not yet possible. The results for the LO and NLO constants will be presented in Sect. 5.2.
Alternatively, one can invert Eq. (88) and express \(M^2\) and F as an expansion in
and the corresponding expressions then take the form
The scales of the quadratic logarithms are determined by \(\Lambda _1,\ldots ,\Lambda _4\) through
In practice, many results are expressed in terms of the LO constants F and \(\Sigma \) and the NLO constants \({{\bar{\ell }}}_i\). The LO constants relate to the LO constants used above through \(B=\Sigma /F^2\). At the NLO the relation is a bit more involved, since the \({{\bar{\ell }}}_i\) bear the notion of the physical pion mass, see (90). For instance, Eqs. (93) may be rewritten as
and this implies that fitting some lattice data (say at a single lattice spacing a) with Eq. (95) requires some a-priori knowledge of the lattice spacing. On the other hand, doing the same job with Eq. (93) yields the scales \(a\Lambda _3, a\Lambda _4\) in lattice units (which may be converted to \({{\bar{\ell }}}_3,{{\bar{\ell }}}_4\) at a later stage of the analysis when the scale is known more precisely).
B. SU(3) formulae
While the formulae for the pseudoscalar masses and decay constants are known to NNLO for SU(3) as well [289], they are rather complicated and we restrict ourselves here to next-to-leading order (NLO). In the isospin limit, the relevant SU(3) formulae take the form [244]

where \(m_{ud}\) is the joint up/down quark mass in the simulation [which may be taken different from the average light-quark mass \(\frac{1}{2}(m_u^\mathrm {phys}+m_d^\mathrm {phys})\) in the real world]. And \(B_0=\Sigma _0/F_0^2\), \(F_0\) denote the condensate parameter and the pseudoscalar decay constant in the SU(3) chiral limit, respectively. In addition, we use the notation
At the order of the chiral expansion used in these formulae, the quantities \(\mu _\pi \), \(\mu _K\), \(\mu _\eta \) can equally well be evaluated with the leading-order expressions for the masses,

Throughout, \(L_i\) denotes the renormalized low-energy constant/coupling (LEC) at scale \(\mu \), and we adopt the convention that is standard in phenomenology, \(\mu =M_\rho =770\,\mathrm {MeV}\). The normalization used for the decay constants is specified in footnote 24.
5.1.3 Pion form factors and charge radii
The scalar and vector form factors of the pion are defined by the matrix elements
where the operators contain only the lightest two quark flavours, i.e., \(\tau ^1\), \(\tau ^2\), \(\tau ^3\) are the Pauli matrices, and \(t\equiv (p_1-p_2)^2\) denotes the momentum transfer.
The vector form factor has been measured by several experiments for time-like as well as for space-like values of t. The scalar form factor is not directly measurable, but it can be evaluated theoretically from data on the \(\pi \pi \) and \(\pi K\) phase shifts [290] by means of analyticity and unitarity, i.e., in a model-independent way. Lattice calculations can be compared with data or model-independent theoretical evaluations at any given value of t. At present, however, most lattice studies concentrate on the region close to \(t=0\) and on the evaluation of the slope and curvature, which are defined as
The slopes are related to the mean-square vector and scalar radii, which are the quantities on which most experiments and lattice calculations concentrate.
In \(\chi \)PT, the form factors are known at NNLO for SU(2) [291]. The corresponding formulae are available in fully analytical form and are compact enough that they can be used for the chiral extrapolation of the data (as done, for example, in Refs. [53, 292]). The expressions for the scalar and vector radii and for the \(c_{S,V}\) coefficients at 2-loop level in SU(2) terminology read
where
and \(k_{r_S},k_{r_V}\) and \(k_{c_S},k_{c_V}\) are independent of the quark masses. Their expression in terms of the \(\ell _i\) and of the \({\mathcal {O}}(p^6)\) constants \(c_M,c_F\) is known but will not be reproduced here.
The SU(3) formula for the slope of the pion vector form factor reads, to NLO [242],

while the expression \(\langle r^2\rangle _S^\mathrm {oct}\) for the octet part of the scalar radius does not contain any NLO low-energy constant at 1-loop order [242] – contrary to the situation in SU(2), see Eq. (101).
The difference between the quark-line connected and the full (i.e., containing the connected and the disconnected pieces) scalar pion form factor has been investigated by means of \(\chi \)PT in Ref. [293]. It is expected that the technique used can be applied to a large class of observables relevant in QCD phenomenology.
As a point of practical interest let us remark that there are no finite-volume correction formulae for the mean-square radii \(\langle r^2\rangle _{V,S}\) and the curvatures \(c_{V,S}\). The lattice data for \(F_{V,S}(t)\) need to be corrected, point by point in t, for finite-volume effects. In fact, if a given \(\sqrt{t}\) is realized through several inequivalent \(p_1\!-\!p_2\) combinations, the level of agreement after the correction has been applied is indicative of how well higher-order and finite-volume effects are under control.
5.1.4 Goldstone boson scattering in a finite volume
The scattering of pseudoscalar octet mesons off each other (mostly \(\pi \)–\(\pi \) and \(\pi \)–K scattering) is a useful approach to determine \(\chi \)PT low-energy constants [288, 294,295,296,297]. This statement holds true both in experiment and on the lattice. We would like to point out that the main difference between these approaches is not so much the discretization of space-time, but rather the Minkowskian versus Euclidean setup.
In infinite-volume Minkowski space-time, 4-point Green’s functions can be evaluated (e.g., in experiment) for a continuous range of (on-shell) momenta, as captured, for instance, by the Mandelstam variable s. For a given isospin channel \(I=0\) or \(I=2\) the \(\pi \)–\(\pi \) scattering phase shift \(\delta ^{I}(s)\) can be determined for a variety of s values, and by matching to \(\chi \)PT some low-energy constants can be determined (see below). In infinite-volume Euclidean space-time, such 4-point Green’s functions can only be evaluated at kinematic thresholds; this is the content of the so-called Maiani-Testa theorem [298]. However, in the Euclidean case, the finite volume comes to our rescue, as first pointed out by Lüscher [299,300,301,302]. By comparing the energy of the (interacting) two-pion system in a box with finite spatial extent L to twice the energy of a pion (with identical bare parameters) in infinite volume information on the scattering length can be obtained. In particular in the (somewhat idealized) situation where one can “scan” through a narrowly spaced set of box-sizes L such information can be reconstructed in an efficient way.
We begin with a brief summary of the relevant formulae from \(\chi \)PT in SU(2) terminology. In the x-expansion the formulae for \(a_\ell ^I\) with \(\ell =0\) and \(I=0,2\) are found in Ref. [277]
where we deviate from the \(\chi \)PT habit of absorbing a factor \(-M_{\pi }\) into the scattering length (relative to the convention used in quantum mechanics), since we include just a minus sign but not the factor \(M_{\pi }\). Hence, our \(a_\ell ^I\) have the dimension of a length so that all quark- or pion-mass dependence is explicit (as is most convenient for the lattice community). But the sign convention is the one of the chiral community (where \(a_\ell ^IM_{\pi }>0\) means attraction and \(a_\ell ^IM_{\pi }<0\) means repulsion).
An important difference between the two scattering lengths is evident already at tree-level. The isospin-0 S-wave scattering length (104) is large and positive, while the isospin-2 counterpart (105) is by a factor \(\sim 3.5\) smaller (in absolute magnitude) and negative. Hence, in the channel with \(I=0\) the interaction is attractive, while in the channel with \(I=2\) the interaction is repulsive and significantly weaker. In this convention experimental results, evaluated with the unitarity constraint genuine to any local quantum field theory, read \(a_0^0M_{\pi }=0.2198(46)_\mathrm {stat}(16)_\mathrm {syst}(64)_\mathrm {theo}\) and \(a_0^2M_{\pi }=-0.0445(11)_\mathrm {stat}(4)_\mathrm {syst}(8)_\mathrm {theo}\) [288, 303,304,305]. The ratio between the two (absolute) central values is larger than 3.5, and this suggests that NLO contributions to \(a_0^0\) might be more relevant than NLO contributions to \(a_0^2\).
By means of \(M^2/(4\pi F)^2=M_{\pi }^2/(4\pi F_\pi )^2\{1+\frac{1}{2}\xi \ln (\Lambda _3^2/M_{\pi }^2)+2\xi \ln (\Lambda _4^2/M_{\pi }^2)+{\mathcal {O}}(\xi ^2)\}\) or equivalently through \(M^2/(4\pi F)^2=M_{\pi }^2/(4\pi F_\pi )^2\{1+\frac{1}{2}\xi {{\bar{\ell }}}_3+2\xi {{\bar{\ell }}}_4+{\mathcal {O}}(\xi ^2)\}\) Eqs. (104, 105) may be brought into the form
Finally, this expression can be summarized as
with the abbreviations
where \(\lambda _\ell ^I\) with \(\ell =0\) and \(I=0,2\) are scales like the \(\Lambda _i\) in \({{\bar{\ell }}}_i=\ln (\Lambda _i^2/M_{\pi ,\mathrm {phys}}^2)\) for \(i\in \{1,2,3,4\}\) (albeit they are not independent from the latter). Here we made use of the fact that \(M_{\pi }^2/M_{\pi ,\mathrm {phys}}^2=1+{\mathcal {O}}(\xi )\) and thus \(\xi \ln (M_{\pi }^2/M_{\pi ,\mathrm {phys}}^2)={\mathcal {O}}(\xi ^2)\). In the absence of any knowledge on the \({{\bar{\ell }}}_i\) one would assume \(\lambda _0^0\simeq \lambda _0^2\), and with this input Eqs. (108, 109) suggest that the NLO contribution to \(|a_0^0|\) is by a factor \(\sim 9\) larger than the NLO contribution to \(|a_0^2|\). The experimental numbers quoted before clearly support this view.
Given that all of this sounds like a complete success story for the determination of the scattering lengths \(a_0^0\) and \(a_0^2\), one may wonder whether lattice QCD is helpful at all. It is, because the “experimental” evaluation of these scattering lengths builds on a constraint between these two quantities that, in turn, is based on a (rather nontrivial) dispersive evaluation of scattering phase shifts [288, 303,304,305]. Hence, to overcome this possible loophole, an independent lattice determination of \(a_0^0\) and/or \(a_0^2\) is highly welcome.
On the lattice \(a_0^2\) is much easier to determine than \(a_0^0\), since the former quantity does not involve quark-line disconnected contributions. The main upshot of such activities (to be reviewed below) is that the lattice determination of \(a_0^2M_{\pi }\) at the physical mass point is in perfect agreement with the experimental numbers quoted before, thus supporting the view that the scalar condensate is – at least in the SU(2) case – the dominant order parameter, and the original estimate \({{\bar{\ell }}}_3=2.9\pm 2.4\) is correct (see below). Still, from a lattice perspective it is natural to see a determination of \(a_0^0M_{\pi }\) and/or \(a_0^2M_{\pi }\) as a means to access the specific linear combinations of \({{\bar{\ell }}}_i\) with \(i\in \{1,2,3,4\}\) defined in Eqs. (110, 111).
In passing we note that an alternative version of Eqs. (108, 109) is used in the literature, too. For instance Refs. [306,307,308,309,310] give their results in the form
where the quantities (used to quote the results of the lattice calculation)
amount to linear combinations of the \(\ell _i^\mathrm {ren}(\mu ^\mathrm {ren})\) that, due to the explicit logarithms in Eqs. (114, 115), are effectively renormalized at the scale \(\mu _\mathrm {ren}=f_{\pi ,\mathrm {phys}}=\sqrt{2}F_{\pi ,\mathrm {phys}}\). Note that in these equations the dependence on the physical pion mass in the logarithms cancels the one that comes from the \({{\bar{\ell }}}_i\), so that the left-hand-sides bear no knowledge of \(M_{\pi ,\mathrm {phys}}\). This alternative form is slightly different from Eqs. (108, 109). Exact equality would be reached upon substituting \(F_\pi ^2 \rightarrow F_{\pi ,\mathrm {phys}}^2\) in the logarithms of Eqs. (112, 113). Upon expanding \(F_\pi ^2/F_{\pi ,\mathrm {phys}}^2\) and subsequently the logarithm, one realizes that this difference amounts to a term \(O(\xi )\) within the square bracket. It thus makes up for a difference at the NNLO, which is beyond the scope of these formulae.
We close by mentioning a few works that elaborate on specific issues in \(\pi \)–\(\pi \) scattering relevant to the lattice. Ref. [311] does mixed action \(\chi \)PT for 2 and 2 + 1 flavors of staggered sea quarks and Ginsparg-Wilson valence quarks, Refs. [312, 313] work out scattering formulae in Wilson fermion \(\chi \)PT, and Ref. [314] lists connected and disconnected contractions in \(\pi \)–\(\pi \) scattering.
5.1.5 Partially quenched and mixed action formulations
The term “partially quenched QCD” is used in two ways. For heavy quarks (c, b and sometimes s) it usually means that these flavours are included in the valence sector, but not into the functional determinant, i.e., the sea sector. For the light quarks (u, d and sometimes s) it means that they are present in both the valence and the sea sector of the theory, but with different masses (e.g., a series of valence quark masses is evaluated on an ensemble with fixed sea-quark masses).
The program of extending the standard (unitary) SU(3) theory to the (second version of) “partially quenched QCD” has been completed at the 2-loop (NNLO) level for masses and decay constants [315]. These formulae tend to be complicated, with the consequence that a state-of-the-art analysis with \({\mathcal {O}}(2000)\) bootstrap samples on \({\mathcal {O}}(20)\) ensembles with \({\mathcal {O}}(5)\) masses each [and hence \({\mathcal {O}}(200\,000)\) different fits] will require significant computational resources. For a summary of recent developments in \(\chi \)PT relevant to lattice QCD we refer to Ref. [316]. The SU(2) partially quenched formulae can be obtained from the SU(3) ones by “integrating out the strange quark”; this involves a matching of the two theories. At NLO, they can be found in Ref. [317] by setting the lattice artifact terms from the staggered \(\chi \)PT form to zero.
The theoretical underpinning of how “partial quenching” is to be understood in the (properly extended) chiral framework is given in Ref. [318]. Specifically, for partially quenched QCD with staggered quarks it is shown that a transfer matrix can be constructed that is not Hermitian but bounded, and can thus be used to construct correlation functions in the usual way. The program of calculating all observables in the p-regime in finite-volume to two loops, first completed in the unitary theory [319, 320], has been carried out for the partially quenched case, too [321].
A further extension of the \(\chi \)PT framework concerns the lattice effects that arise in partially quenched simulations where sea and valence quarks are implemented with different lattice fermion actions [245, 322,323,324,325,326,327,328]. This extension is usually referred to as “mixed-action \(\chi \)PT” or “mixed-action partially-quenched \(\chi \)PT”.
5.1.6 Correlation functions in the \(\epsilon \)-regime
The finite-size effects encountered in lattice calculations can be used to determine some of the LECs of QCD. In order to illustrate this point, we focus on the two lightest quarks, take the isospin limit \(m_u=m_d=m\) and consider a box of size \(L_s\) in the three space directions and size \(L_t\) in the time direction. If m is sent to zero at fixed box size, chiral symmetry is restored, and the zero-momentum mode of the pion field becomes nonperturbative. An intuitive way to understand the regime with \(ML<1\) ( ) starts from considering the pion propagator \(G(p)=1/(p^2\,+\,M^2)\) in finite volume. For
) starts from considering the pion propagator \(G(p)=1/(p^2\,+\,M^2)\) in finite volume. For  and \(p\sim 1/L\), \(G(p)\sim L^2\) for small momenta, including \(p=0\). But when M becomes of order \(1/L^2\), \(G(0)\propto L^4\gg G(p\ne 0)\sim L^2\). The \(p=0\) mode of the pion field becomes nonperturbative, and the integration over this mode restores chiral symmetry in the limit \(m\rightarrow 0\).
and \(p\sim 1/L\), \(G(p)\sim L^2\) for small momenta, including \(p=0\). But when M becomes of order \(1/L^2\), \(G(0)\propto L^4\gg G(p\ne 0)\sim L^2\). The \(p=0\) mode of the pion field becomes nonperturbative, and the integration over this mode restores chiral symmetry in the limit \(m\rightarrow 0\).
The pion effective action for the zero-momentum field depends only on the combination \(\mu =m\Sigma V\), the symmetry-restoration parameter, where \(V=L_s^3 L_t\) [329]. In the \(\epsilon \)-regime, where \(ML\ll 1\) with \(L\equiv V^{1/4}\) and hence \(m \ll 1/(2BL^2)\), all other terms in the effective action are sub-dominant in powers of \(\epsilon \sim 1/L\). This amounts to a reordering of the chiral expansion, based on \(m\sim \epsilon ^4\) in the \(\epsilon \)-regime [329]. In the p-regime, with \(m\sim \epsilon ^2\) or equivalently  , finite-volume corrections are of order \(\int d^4p\,e^{ipx}\,G(p)|_{x\sim L}\sim e^{-ML}\). In the \(\epsilon \)-regime the chiral expansion is an expansion in powers of \(1/(\Lambda _\mathrm {QCD}L)\sim 1/(FL)\).
, finite-volume corrections are of order \(\int d^4p\,e^{ipx}\,G(p)|_{x\sim L}\sim e^{-ML}\). In the \(\epsilon \)-regime the chiral expansion is an expansion in powers of \(1/(\Lambda _\mathrm {QCD}L)\sim 1/(FL)\).
As an example, we consider the correlator of the axial charge carried by the two lightest quarks, \(q(x)=\{u(x),d(x)\}\). The axial current and the pseudoscalar density are given by
where \(\tau ^1, \tau ^2,\tau ^3\) are the Pauli matrices in flavour space. In Euclidean space, the correlators (at zero spatial momentum) of the axial charge and the pseudoscalar density are given by
\(\chi \)PT yields explicit finite-size scaling formulae for these quantities [287, 330, 331]. In the \(\epsilon \)-regime, the expansion starts with
where the coefficients \(a_A\), \(b_A\), \(a_P\), \(b_P\) stand for quantities of \({\mathcal {O}}(\epsilon ^0)\). They can be expressed in terms of the variables \(L_s\), \(L_t\) and m and involve only the two leading low-energy constants F and \(\Sigma \). In fact, at leading order only the combination \(\mu =m\,\Sigma \,L_s^3 L_t\) matters, the correlators are t-independent and the dependence on \(\mu \) is fully determined by the structure of the groups involved in the pattern of spontaneous symmetry breaking. In the case of \(SU(2)\times SU(2)\) \(\rightarrow \) SU(2), relevant for QCD in the symmetry restoration region with two light quarks, the coefficients can be expressed in terms of Bessel functions. The t-dependence of the correlators starts showing up at \({\mathcal {O}}(\epsilon ^2)\), in the form of a parabola, viz., \(h_1(\tau )=\frac{1}{2}\left[ \left( \tau -\frac{1}{2} \right) ^2-\frac{1}{12}\right] \). Explicit expressions for \(a_A\), \(b_A\), \(a_P\), \(b_P\) can be found in Refs. [287, 330, 331], where some of the correlation functions are worked out to NNLO. By matching the finite-size scaling of correlators computed on the lattice with these predictions one can extract F and \(\Sigma \). A way to deal with the numerical challenges germane to the \(\epsilon \)-regime has been described [332].
The fact that the representation of the correlators to NLO is not “contaminated” by higher-order unknown LECs, makes the \(\epsilon \)-regime potentially convenient for a clean extraction of the LO couplings. The determination of these LECs is then affected by different systematic uncertainties with respect to the standard case; simulations in this regime yield complementary information that can serve as a valuable cross-check to get a comprehensive picture of the low-energy properties of QCD.
The effective theory can also be used to study the distribution of the topological charge in QCD [329] and the various quantities of interest may be defined for a fixed value of this charge. The expectation values and correlation functions then not only depend on the symmetry restoration parameter \(\mu \), but also on the topological charge \(\nu \). The dependence on these two variables can explicitly be calculated. It turns out that the two-point correlation functions considered above retain the form (118), but the coefficients \(a_A\), \(b_A\), \(a_P\), \(b_P\) now depend on the topological charge as well as on the symmetry restoration parameter (see Refs. [333,334,335] for explicit expressions).
A specific issue with \(\epsilon \)-regime calculations is the scale setting. Ideally one would perform a p-regime study with the same bare parameters to measure a hadronic scale (e.g., the proton mass). In the literature, sometimes a gluonic scale, like the static force scale \(r_0\) [336] or the gradient flow scales \(t_0\) [271] or \(w_0\) [272], is used to avoid such expenses. However, it seems not entirely obvious to us that it is legitimate to identify such a gluonic scale with the length determined in the p-regime (e.g., by using \(r_0\simeq 0.48\,\mathrm{fm}\)).
It is important to stress that in the \(\epsilon \)-expansion higher-order finite-volume corrections might be significant, and the physical box size (in fm) should still be large in order to keep these distortions under control. The criteria for the chiral extrapolation and finite-volume effects are obviously different with respect to the p-regime. For these reasons we have to adjust the colour coding defined in Sect. 2.1 (see Sect. 5.2 for more details).
Recently, the effective theory has been extended to the “mixed regime” where some quarks are in the p-regime and some in the \(\epsilon \)-regime [337, 338]. In Ref. [339] a technique is proposed to smoothly connect the p- and \(\epsilon \)-regimes. In Ref. [340] the issue is reconsidered with a counting rule that is essentially the same as in the p-regime. In this new scheme, one can treat the IR fluctuations of the zero-mode nonperturbatively, while keeping the logarithmic quark-mass dependence of the p-regime.
Also first steps towards calculating higher n-point functions in the \(\epsilon \)-regime have been taken. For instance the electromagnetic pion form factor in QCD has been calculated to NLO in the \(\epsilon \)-expansion, and a way to get rid of the pion zero-momentum part has been proposed [341].
5.1.7 Energy levels of the QCD Hamiltonian in a box and \(\delta \)-regime
At low temperature, the properties of the partition function are governed by the lowest eigenvalues of the Hamiltonian. In the case of QCD, the lowest levels are due to the Nambu-Goldstone bosons and can be worked out with \(\chi \)PT [342]. In the chiral limit the level pattern follows the one of a quantum-mechanical rotator, i.e., \(E_\ell =\ell (\ell +1)/(2\,\Theta )\) with \(\ell =0,1,2,\ldots \). For a cubic spatial box and to leading order in the expansion in inverse powers of the box size \(L_s\), the moment of inertia is fixed by the value of the pion decay constant in the chiral limit, i.e., \(\Theta =F^2L_s^3\).
In order to analyse the dependence of the levels on the quark masses and on the parameters that specify the size of the box, a reordering of the chiral series is required, the so-called \(\delta \)-expansion. Regarding the spatial box-size, this regime is similar to the \(\epsilon \)-regime, i.e., \(ML_s\ll 1\), where \(M=\sqrt{2Bm}\) is the mass the pion would have in infinite volume. But the temporal box size is effectively infinite, since \(1\ll ML_t\) (and \(ML_t\ll 4\pi FL_t\) to enable the chiral approach at all), whereupon \(L_s\ll L_t\). The region where the properties of the system are controlled by this expansion is referred to as the \(\delta \)-regime [342]. Evaluating the chiral series in this regime, one finds that the expansion of the partition function goes in even inverse powers of \(FL_s\), that the rotator formula for the energy levels holds up to NNLO and the expression for the moment of inertia is now also known up to and including terms of order \((FL_s)^{-4}\) [343,344,345]. Since the level spectrum is governed by the value of the pion decay constant in the chiral limit, an evaluation of this spectrum on the lattice can be used to measure F. More generally, the evaluation of various observables in the \(\delta \)-regime offers an alternative method for a determination of some of the low-energy constants occurring in the effective Lagrangian. At present, however, the numerical results obtained in this way [346, 347] are not yet competitive with those found in the p- or \(\epsilon \)-regime. For recent theoretical investigations concerning the \(\delta \)-regime and how it matches onto the \(\epsilon \)-regime see Refs. [348, 349].
5.1.8 Other methods for the extraction of the low-energy constants
An observable that can be used to extract LECs is the topological susceptibility
where \(\omega (x)\) is the topological charge density,
At infinite volume, the expansion of \(\chi _t\) in powers of the quark masses starts with [350]
The condensate \(\Sigma \) can thus be extracted from the properties of the topological susceptibility close to the chiral limit. The behaviour at finite volume, in particular in the region where the symmetry is restored, is discussed in Ref. [331]. The dependence on the vacuum angle \(\theta \) and the projection on sectors of fixed \(\nu \) have been studied in Ref. [329]. For a discussion of the finite-size effects at NLO, including the dependence on \(\theta \), we refer to Refs. [335, 351].
The role that the topological susceptibility plays in attempts to determine whether there is a large paramagnetic suppression when going from the \(N_{ f}=2\) to the \(N_{ f}=2\,+\,1\) theory has been highlighted in Ref. [352]. And the potential usefulness of higher moments of the topological charge distribution to determine LECs has been investigated in Ref. [353].
Another method for computing the quark condensate has been proposed in Ref. [354], where it is shown that starting from the Banks–Casher relation [355] one may extract the condensate from suitable (renormalizable) spectral observables, for instance the number of Dirac operator modes in a given interval. For those spectral observables higher-order corrections can be systematically computed in terms of the chiral effective theory. For recent implementations of this strategy, see Refs. [41, 50, 356]. As an aside let us remark that corrections to the Banks–Casher relation that come from a finite quark mass, a finite four-dimensional volume and (with Wilson-type fermions) a finite lattice spacing can be parameterized in a properly extended version of the chiral framework [357, 358].
An alternative strategy is based on the fact that at LO in the \(\epsilon \)-expansion the partition function in a given topological sector \(\nu \) is equivalent to the one of a chiral Random Matrix Theory (RMT) [359,360,361,362]. In RMT it is possible to extract the probability distributions of individual eigenvalues [363,364,365] in terms of two dimensionless variables \(\zeta =\lambda \Sigma V\) and \(\mu =m\Sigma V\), where \(\lambda \) represents the eigenvalue of the massless Dirac operator and m is the sea quark mass. More recently this approach has been extended to the Hermitian (Wilson) Dirac operator [366], which is easier to study in numerical simulations. Hence, if it is possible to match the QCD low-lying spectrum of the Dirac operator to the RMT predictions, then one may extractFootnote 26 the chiral condensate \(\Sigma \). One issue with this method is that for the distributions of individual eigenvalues higher-order corrections are still not known in the effective theory, and this may introduce systematic effects that are hardFootnote 27 to control. Another open question is that, while it is clear how the spectral density is renormalized [370], this is not the case for the individual eigenvalues, and one relies on assumptions. There have been many lattice studies [371,372,373,374,375] that investigate the matching of the low-lying Dirac spectrum with RMT. In this review the results of the LECs obtained in this wayFootnote 28 are not included.
5.2 Extraction of SU(2) low-energy constants
In this and the following sections we summarize the lattice results for the SU(2) and SU(3) LECs, respectively. In either case we first discuss the \({\mathcal {O}}(p^2)\) constants and then proceed to their \({\mathcal {O}}(p^4)\) counterparts. The \({\mathcal {O}}(p^2)\) LECs are determined from the chiral extrapolation of masses and decay constants or, alternatively, from a finite-size study of correlators in the \(\epsilon \)-regime. At order \(p^4\) some LECs affect two-point functions while others appear only in three- or four-point functions; the latter need to be determined from form factors or scattering amplitudes. The \(\chi \)PT analysis of the (nonlattice) phenomenological quantities is nowadaysFootnote 29 based on \({\mathcal {O}}(p^6)\) formulae. At this level the number of LECs explodes and we will not discuss any of these. We will, however, discuss how comparing different orders and different expansions (in particular the x versus \(\xi \)-expansion) can help to assess the theoretical uncertainties of the LECs determined on the lattice.
5.2.1 General remarks on the extraction of low-energy constants
The lattice results for the SU(2) LECs are summarized in Tables 19, 20, 21, 22 and Figs. 12, 13 and 14. The tables present our usual colour coding, which summarizes the main aspects related to the treatment of the systematic errors of the various calculations.
 in \(\,\mathrm {MeV}\) units, in the \(\overline{\mathrm{MS}}\)-scheme, at the renormalization scale \(\mu =2\,\mathrm {GeV}\). All ETM values that were available only in \(r_0\) units were converted on the basis of \(r_0=0.48(2)\,\mathrm{fm}\) [386, 400, 401], with this error being added in quadrature to any existing systematic error
in \(\,\mathrm {MeV}\) units, in the \(\overline{\mathrm{MS}}\)-scheme, at the renormalization scale \(\mu =2\,\mathrm {GeV}\). All ETM values that were available only in \(r_0\) units were converted on the basis of \(r_0=0.48(2)\,\mathrm{fm}\) [386, 400, 401], with this error being added in quadrature to any existing systematic errorA delicate issue in the lattice determination of chiral LECs (in particular at NLO), which cannot be reflected by our colour coding, is a reliable assessment of the theoretical error that comes from the chiral expansion. We add a few remarks on this point:
- 1.
Using both the x and the \(\xi \) expansion is a good way to test how the ambiguity of the chiral expansion (at a given order) affects the numerical values of the LECs that are determined from a particular set of data [44, 376]. For instance, to determine \({{\bar{\ell }}}_4\) (or \(\Lambda _4\)) from lattice data for \(F_\pi \) as a function of the quark mass, one may compare the fits based on the parameterization \(F_\pi =F\{1+x\ln (\Lambda _4^2/M^2)\}\) [see Eq. (88)] with those obtained from \(F_\pi =F/\{1-\xi \ln (\Lambda _4^2/M_{\pi }^2)\}\) [see Eq. (93)]. The difference between the two results provides an estimate of the uncertainty due to the truncation of the chiral series. Which central value one chooses is in principle arbitrary, but we find it advisable to use the one obtained with the \(\xi \) expansion,Footnote 30 in particular because it makes the comparison with phenomenological determinations (where it is standard practice to use the \(\xi \) expansion) more meaningful.
- 2.
Alternatively one could try to estimate the influence of higher chiral orders by reshuffling irrelevant higher-order terms. For instance, in the example mentioned above one might use \(F_\pi =F/\{1-x\ln (\Lambda _4^2/M^2)\}\) as a different functional form at NLO. Another way to establish such an estimate is through introducing by hand “analytical” higher-order terms (e.g., “analytical NNLO” as done, in the past, by MILC [129]). In principle it would be preferable to include all NNLO terms or none, such that the structure of the chiral expansion is preserved at any order (this is what ETM [48] and JLQCD/TWQCD [376] have done for SU(2) \(\chi \)PT and MILC for both SU(2) and SU(3) \(\chi \)PT [14, 17, 36]). There are different opinions in the field as to whether it is advisable to include terms to which the data is not sensitive. In case one is willing to include external (typically: nonlattice) information, the use of priors is a theoretically well founded option (e.g., priors for NNLO LECs if one is interested exclusively in LECs at LO/NLO).
- 3.
Another issue concerns the s-quark mass dependence of the LECs \({{\bar{\ell }}}_i\) or \(\Lambda _i\) of the SU(2) framework. As far as variations of \(m_s\) around \(m_s^\mathrm {phys}\) are concerned (say for \(0<m_s<1.5m_s^\mathrm {phys}\) at best) the issue can be studied in SU(3) \(\chi \)PT, and this has been done in a series of papers [244, 377, 378]. However, the effect of sending \(m_s\) to infinity, as is the case in \(N_{ f}=2\) lattice studies of SU(2) LECs, cannot be addressed in this way. A way to analyse this difference is to compare the numerical values of LECs determined in \(N_{ f}=2\) lattice simulations to those determined in \(N_{ f}=2\,+\,1\) lattice simulations (see, e.g., Ref. [379] for a discussion).
- 4.
Last but not least let us recall that the determination of the LECs is affected by discretization effects, and it is important that these are removed by means of a continuum extrapolation. In this step invoking an extended version of the chiral Lagrangian [323, 380,381,382,383,384] may be usefulFootnote 31 in case one aims for a global fit of lattice data involving several \(M_{\pi }\) and a values and several chiral observables.
In the tables and figures we summarize the results of various lattice collaborations for the SU(2) LECs at LO (F or \(F_\pi /F\), B or \(\Sigma \)) and at NLO (\({\bar{\ell }}_1-{\bar{\ell }}_2\), \({\bar{\ell }}_3\), \({\bar{\ell }}_4\), \({\bar{\ell }}_6\)). Throughout we group the results into those which stem from \(N_{ f}=2\,+\,1\,+\,1\) calculations, those which come from \(N_{ f}=2\,+\,1\) calculations and those which stem from \(N_{ f}=2\) calculations (since, as mentioned above, the LECs are logically distinct even if the current precision of the data is not sufficient to resolve the differences). Furthermore, we make a distinction whether the results are obtained from simulations in the p-regime or whether alternative methods (\(\epsilon \)-regime, spectral densities, topological susceptibility, etc.) have been used (this should not affect the result). For comparison we add, in each case, a few representative phenomenological determinations.
Cubic root of the SU(2) quark condensate  in the \(\overline{\mathrm{MS}}\)-scheme, at the renormalization scale \(\mu =2\,\mathrm {GeV}\). Green and red squares indicate determinations from correlators in the p-regime. Up triangles refer to extractions from the topological susceptibility, diamonds to determinations from the pion form factor, and star symbols refer to the spectral density method
in the \(\overline{\mathrm{MS}}\)-scheme, at the renormalization scale \(\mu =2\,\mathrm {GeV}\). Green and red squares indicate determinations from correlators in the p-regime. Up triangles refer to extractions from the topological susceptibility, diamonds to determinations from the pion form factor, and star symbols refer to the spectral density method
Comparison of the results for the ratio of the physical pion decay constant \(F_\pi \) and the leading-order SU(2) low-energy constant F. The meaning of the symbols is the same as in Fig. 12
A generic comment applies to the issue of the scale setting. In the past none of the lattice studies with \(N_{ f}\ge 2\) involved simulations in the p-regime at the physical value of \(m_{ud}\). Accordingly, the setting of the scale \(a^{-1}\) via an experimentally measurable quantity did necessarily involve a chiral extrapolation, and as a result of this dimensionful quantities used to be particularly sensitive to this extrapolation uncertainty, while in dimensionless ratios such as \(F_\pi /F\), \(F/F_0\), \(B/B_0\), \(\Sigma /\Sigma _0\) this particular problem is much reduced (and often finite lattice-to-continuum renormalization factors drop out). Now, there is a new generation of lattice studies with \(N_{ f}=2\) [386], \(N_{ f}=2\,+\,1\) [10,11,12, 30, 43,44,45, 117, 156, 161], and \(N_{ f}=2\,+\,1\,+\,1\) [33, 387], which does involve simulations at physical pion masses. In such studies the uncertainty that the scale setting has on dimensionful quantities is much mitigated.
It is worth repeating here that the standard colour-coding scheme of our tables is necessarily schematic and cannot do justice to every calculation. In particular there is some difficulty in coming up with a fair adjustment of the rating criteria to finite-volume regimes of QCD. For instance, in the \(\epsilon \)-regimeFootnote 32 we re-express the “chiral extrapolation” criterion in terms of \(\sqrt{2m_\mathrm {min}\Sigma }/F\), with the same threshold values (in MeV) between the three categories as in the p-regime. Also the “infinite volume” assessment is adapted to the \(\epsilon \)-regime, since the \(M_{\pi }L\) criterion does not make sense here; we assign a green star if at least 2 volumes with \(L>2.5\,\mathrm{fm}\) are included, an open symbol if at least 1 volume with \(L>2\,\mathrm{fm}\) is invoked and a red square if all boxes are smaller than \(2\,\mathrm{fm}\). Similarly, in the calculation of form factors and charge radii the tables do not reflect whether an interpolation to the desired \(q^2\) has been performed or whether the relevant \(q^2\) has been engineered by means of “twisted boundary conditions” [390]. In spite of these limitations we feel that these tables give an adequate overview of the qualities of the various calculations.
5.2.2 Results for the LO SU(2) LECs
We begin with a discussion of the lattice results for the SU(2) LEC \(\Sigma \). We present the results in Table 19 and Fig. 12. We remind the reader that results which include only a statistical error are listed in the table but omitted from the plot. Regarding the \(N_{ f}=2\) computations there are six entries without a red tag. We form the average based on ETM 09C, ETM 13 (here we deviate from our “superseded” rule, since the two works use different methods), Brandt 13, and Engel 14. Here and in the following we take into account that ETM 09C, ETM 13 share configurations, and the same statement holds true for Brandt 13 and Engel 14. Regarding the \(N_{ f}=2\,+\,1\) computations there are six published or updated papers (MILC 10A, Borsanyi 12, BMW 13, RBC/UKQCD 15E, JLQCD 16B and JLQCD 17A) that qualify for the \(N_{ f}=2\,+\,1\) average. Here we deviate again from the “superseded” rule, since JLQCD 17A [47] uses a completely different methodology than JLQCD 16B [46]. Unfortunately, the new error-bar (from an indirect determination, via the topological susceptibility) is about an order of magnitude larger than the old one, hence it barely affects our average. Finally, the single complete \(N_{ f}=2\,+\,1\,+\,1\) calculation available so far, ETM 13 [41], was recently complemented by ETM 17E [42]. Again we deviate from the “supersede” rule, since both authors and methodologies differ.
In slight deviation from the general recipe outlined in Sect. 2.2 we use these values as a basis for our estimates (as opposed to averages) of the \(N_{ f}=2\), \(N_{ f}=2\,+\,1\), and \(N_{ f}=2\,+\,1\,+\,1\) condensates. In each case the central value is obtained from our standard averaging procedure, but the (symmetrical) error is just the median of the overall uncertainties of all contributing results (see the comment below for details). This leads to the values
in the \({\overline{\mathrm {MS}}}\) scheme at the renormalization scale \(2\,\mathrm {GeV}\), where the errors include both statistical and systematic uncertainties. In accordance with our guidelines we ask the reader to cite the appropriate set of references as indicated in Eq. (122) when using these numbers.
As a rationale for using estimates (as opposed to averages) for \(N_{ f}=2\), \(N_{ f}=2\,+\,1\), and \(N_{ f}=2\,+\,1\,+\,1\), we add that for \(\Sigma ^{1/3}|_{N_{ f}=2}\), \(\Sigma ^{1/3}|_{N_{ f}=2\,+\,1}\), and \(\Sigma ^{1/3}|_{N_{ f}=2\,+\,1\,+\,1}\) the standard averaging method would yield central values as quoted in Eq. (122), but with (overall) uncertainties of \(4\,\mathrm {MeV}\), \(1\,\mathrm {MeV}\), and \(16\,\mathrm {MeV}\), respectively. It is not entirely clear to us that the scale is sufficiently well known in all contributing works to warrant a precision of up to 0.37% on our \(\Sigma ^{1/3}\), and a similar statement can be made about the level of control over the convergence of the chiral expansion. The aforementioned uncertainties would tend to suggest an \(N_{ f}\)-dependence of the SU(2) chiral condensate, which (especially in view of similar issues with other LECs, see below) seems premature to us. Therefore we choose to form the central value of our estimate with the standard averaging procedure, but its uncertainty is taken as the median of the uncertainties of the participating results. We hope that future high-quality determinations (with any of \(N_f=2\), \(N_f=2\,+\,1\), or \(N_f=2\,+\,1\,+\,1\)) will help determine whether there is a noticeable \(N_f\)-dependence of the SU(2) chiral condensate or not.
The next quantity considered is F, i.e., the pion decay constant in the SU(2) chiral limit (\(m_{ud}\rightarrow 0\), at fixed physical \(m_s\) for \(N_f > 2\) simulations). As argued on previous occasions we tend to give preference to \(F_\pi /F\) (here the numerator is meant to refer to the physical-pion-mass point) wherever it is available, since often some of the systematic uncertainties are mitigated. We collect the results in Table 20 and Fig. 13. In those cases where the collaboration provides only F, the ratio is computed on the basis of the phenomenological value of \(F_\pi \), and the respective entries in Table 20 are in slanted fonts. We encourage authors to provide both F and \(F_\pi /F\) from their analysis, since the ratio is less dependent on the scale setting, and errors tend to partially cancel. Among the \(N_{ f}=2\) determinations five (ETM 08, ETM 09C, QCDSF 13, Brandt 13 and Engel 14) are without red tags. Since the third one is without systematic error, only four of them enter the average. Among the \(N_{ f}=2\,+\,1\) determinations five values (MILC 10 as an update of MILC 09, NPLQCD 11, Borsanyi 12, BMW 13, and RBC/UKQCD 15E) contribute to the average. Here and in the following we take into account that MILC 10 and NPLQCD 11 share configurations. Finally, there is a single \(N_{ f}=2\,+\,1\,+\,1\) determination (ETM 11) which forms the current best estimate in this category.
In analogy to the condensates discussed above, we use these values as a basis for our estimates (as opposed to averages) of the decay constant ratios
where the errors include both statistical and systematic uncertainties. We ask the reader to cite the appropriate set of references as indicated in Eq. (123) when using these numbers. For \(N_{ f}=2\) and \(N_{ f}=2\,+\,1\) these estimates are obtained through the well-defined procedure described next to Eq. (122). For \(N_{ f}=2\,+\,1\,+\,1\) the result of ETM 11 (as an update to ETM 10) is the only oneFootnote 33 available.
For \(N_{ f}=2\) and \(N_{ f}=2\,+\,1\) the standard averaging method would yield the central values as quoted in Eq. (123), but with (overall) uncertainties of 6 and 1, respectively, on the last digit quoted. In this particular case the single \(N_{ f}=2\,+\,1\,+\,1\) determination lies significantly higher than the \(N_{ f}=2\,+\,1\) average (with the small error-bar), basically on par with the \(N_{ f}=2\) average (ditto), and this makes such a standard average look even more suspicious to us. At the very least, one should wait for one more qualifying \(N_f=2\,+\,1\,+\,1\) determination before attempting any conclusions about the \(N_f\)-dependence of \(F_\pi /F\). While we are not aware of any theorem that excludes a nonmonotonic behavior in \(N_f\) of a LEC, standard physics reasoning would suggest that quark-loop effects become smaller with increasing quark mass, hence a dynamical charm quark will influence LECs less significantly than a dynamical strange quark, and even the latter one seems to bring rather small shifts. As a result, we feel that a nonmonotonic behavior of \(F_\pi /F\) with \(N_{ f}\), once established, would represent a noteworthy finding. We hope this reasoning explains why we prefer to stay in Eq. (123) with estimates that obviously are on the conservative side.
5.2.3 Results for the NLO SU(2) LECs
We move on to a discussion of the lattice results for the NLO LECs \({\bar{\ell }}_3\) and \({\bar{\ell }}_4\). We remind the reader that on the lattice the former LEC is obtained as a result of the tiny deviation from linearity seen in \(M_{\pi }^2\) versus \(Bm_{ud}\), whereas the latter LEC is extracted from the curvature in \(F_\pi \) versus \(Bm_{ud}\). The available determinations are presented in Table 21 and Fig. 14. Among the \(N_{ f}=2\) determinations ETM 08, ETM 09C, Brandt 13, and Gülpers 15 come with a systematic uncertainty and without red tags. Given that the former two use different approaches, all four determinations enter our average. The colour coding of the \(N_{ f}=2\,+\,1\) results looks very promising; there is a significant number of lattice determinations without any red tag. Applying our superseding rule, MILC 10 (as an updateFootnote 34 to MILC 09), NPLQCD 11, Borsanyi 12, BMW 13, and RBC/UKQCD 15E contribute to the average. For \(N_{ f}=2\,+\,1\,+\,1\) there is only the single work ETM 11 (as an update to ETM 10).
In analogy to our processing of the LECs at LO, we use these determinations as the basis of our estimate (as opposed to average) of the NLO quantities
where the errors include both statistical and systematic uncertainties. Again we ask the reader to cite the appropriate set of references as indicated in Eq. (124) or Eq. (125) when using these numbers. For \(N_{ f}=2\) and \(N_{ f}=2\,+\,1\) these estimates are obtained through the well-defined procedure described next to Eq. (122). For \(N_{ f}=2\,+\,1\,+\,1\) once again ETM 11 (as an update to ETM 10) is the single reference available.
We remark that our preprocessing procedureFootnote 35 symmetrizes the asymmetric error of ETM 09C with a slight adjustment of the central value. Regarding the difference between the estimates as given in Eqs. (124, 125) and the result of the standard averaging procedure we add that the latter would yield the overall uncertainties 25 and 12 for \({{\bar{\ell }}}_3\), and the overall uncertainties 17 and 5 for \({{\bar{\ell }}}_4\). In all cases the central value would be unchanged. Especially for \({{\bar{\ell }}}_4\) such numbers would suggest a clear difference between the value with \(N_{ f}=2\) dynamical flavours and the one at \(N_{ f}=2\,+\,1\). Similarly to what happened with \(F_\pi /F\), the single determination with \(N_{ f}=2\,+\,1\,+\,1\) is more on the \(N_{ f}=2\) side, which, if confirmed, would suggest a nonmonotonicity of a \(\chi \)PT LEC with \(N_{ f}\). Again we think that currently such a conclusion would be premature, and this is why we give preference to the estimates quoted in Eqs. (124, 125).
From a more phenomenological point of view there is a notable difference between \({\bar{\ell }}_3\) and \({\bar{\ell }}_4\) in Fig. 14. For \({\bar{\ell }}_4\) the precision of the phenomenological determination achieved in Colangelo 01 [288] represents a significant improvement compared to Gasser 84 [277]. Picking any \(N_{ f}\), the lattice estimate of \({\bar{\ell }}_4\) is consistent with both of the phenomenological values and comes with an error-bar that is roughly comparable to or somewhat larger than the one in Colangelo 01 [288]. By contrast, for \({\bar{\ell }}_3\) the error of an individual lattice computation is usually much smaller than the error of the estimate given in Gasser 84 [277], and even our conservative estimates (124) have uncertainties that represent a significant improvement on the error-bar of Gasser 84 [277]. Evidently, our hope is that future determinations of \({{\bar{\ell }}}_3,{{\bar{\ell }}}_4\), with \(N_{ f}=2\), \(N_{ f}=2\,+\,1\) and \(N_{ f}=2\,+\,1\,+\,1\), will allow us to further shrink our error-bars in a future edition of FLAG.
Let us add that Ref. [414] determines \(\ell _1,\ell _2,\ell _3,\ell _4\) (or equivalently \({{\bar{\ell }}}_1,{{\bar{\ell }}}_2,{{\bar{\ell }}}_3,{{\bar{\ell }}}_4\)) individually, with some assumptions and various fits from lattice data at a single lattice spacing and two (heavier than physical) pion masses.
We continue with a discussion of the lattice results for \({\bar{\ell }}_6\) and \({\bar{\ell }}_1-{\bar{\ell }}_2\). The LEC \({\bar{\ell }}_6\) determines the leading contribution in the chiral expansion of the pion vector charge radius, see Eq. (101). Hence from a lattice study of the vector form factor of the pion with several \(M_{\pi }\) one may extract the radius \(\langle r^2\rangle _V^\pi \), the curvature \(c_V\) (both at the physical pion-mass point) and the LEC \({\bar{\ell }}_6\) in one go. Similarly, the leading contribution in the chiral expansion of the scalar radius of the pion determines \({\bar{\ell }}_4\), see Eq. (101). This LEC is also present in the pion-mass dependence of \(F_\pi \), as we have seen. The difference \({\bar{\ell }}_1-{\bar{\ell }}_2\), finally, may be obtained from the momentum dependence of the vector and scalar pion form factors, based on the 2-loop formulae of Ref. [291]. The top part of Table 22 collects the results obtained from the vector form factor of the pion (charge radius, curvature and \({\bar{\ell }}_6\)). Regarding this low-energy constant two \(N_{ f}=2\) calculations are published works without a red tag; we thus arrive at the average (actually the first one in the LEC section)
which is represented as a grey band in the last panel of Fig. 14. Here we ask the reader to cite Refs. [49, 53] when using this number.
The experimental information concerning the charge radius is excellent and the curvature is also known very accurately, based on \(e^+e^-\) data and dispersion theory. The vector form factor calculations thus present an excellent testing ground for the lattice methodology. The first data column of Table 22 shows that most of the available lattice results pass the test. There is, however, one worrisome point. For \({\bar{\ell }}_6\) the agreement seems less convincing than for the charge radius, even though the two quantities are closely related. In particular the \({\bar{\ell }}_6\) value of JLQCD 14 [408] seems inconsistent with the phenomenological determinations of Refs. [277, 291], even though its value for \(\langle r^2\rangle _V^\pi \) is consistent. So far we have no explanation (other than observing that lattice computations which disagree with the phenomenological determination of \({\bar{\ell }}_6\) tend to have red tags), but we urge the groups to pay special attention to this point. Similarly, the bottom part of Table 22 collects the results obtained for the scalar form factor of the pion and the combination \({\bar{\ell }}_1-{\bar{\ell }}_2\) that is extracted from it. A new feature is that Ref. [387] gives both the (flavour) octet and singlet part in SU(3), finding \(\langle r^2\rangle _{S,\mathrm {octet}}^\pi =0.431(38)(46)\) and \(\langle r^2\rangle _{S,\mathrm {singlet}}^\pi =0.506(38)(53)\). For reasons of backward compatibility they also give \(\langle r^2\rangle _{S,ud}^\pi \) defined with a \({\bar{u}}u+{\bar{d}}d\) density, and this number is shown in Table 22. Another notable feature is that they find the ordering \(\langle r^2\rangle _{S,\mathrm {conn}}^\pi< \langle r^2\rangle _{S,\mathrm {octet}}^\pi< \langle r^2\rangle _{S,ud}^\pi < \langle r^2\rangle _{S,\mathrm {singlet}}^\pi \) [387].
Those data of Table 22 that come with a systematic error are shown in Fig. 15. The overall impression is that the majority of lattice results come with a fair assessment of the respective systematic uncertainties. Yet it is clear that it is a nontrivial endeavor to match the precision obtained in experiment and subsequent phenomenological analysis.
The last set of observables we wish to discuss includes the \(\pi \)–\(\pi \) scattering lengths \(a_0^0\) and \(a_0^2\) in the isopin channels \(I=0\) and \(I=2\), respectively. As can be seen from Eqs. (108, 110), the \(I=0\) scattering length carries information about \(\frac{20}{21}{{\bar{\ell }}}_1+\frac{40}{21}{{\bar{\ell }}}_2-\frac{5}{14}{{\bar{\ell }}}_3+2{{\bar{\ell }}}_4\). And from Eqs. (109, 111) it follows that the \(I=2\) counterpart carries information about the linear combination \(\frac{4}{3}{{\bar{\ell }}}_1+\frac{8}{3}{{\bar{\ell }}}_2-\frac{1}{2}{{\bar{\ell }}}_3-2{{\bar{\ell }}}_4\). We prefer quoting the dimensionless products \(a_0^{I}M_{\pi }\) (at the physical mass point) over the aforementioned linear combinations to ease comparison with phenomenology. In Table 23 we summarize the lattice information on \(a_0^{I=0}M_{\pi }\) and \(a_0^{I=2}M_{\pi }\) at the physical mass point. We are aware of at least one additional work, Ref. [422], which has a technical focus and determines a scattering length away from the physical point, and which, for this reason, is not included in Table 23. We remind the reader that a lattice computation of \(a_0^{I=0}M_{\pi }\) involves quark-loop disconnected contributions, which tend to be very noisy and hence require lots of statistics. To date there are three pioneering calculations, but none of them is free of red tags. The situation is slightly better for \(a_0^{I=2}M_{\pi }\); there is one computation at \(N_{ f}=2\) and one at \(N_{ f}=2\,+\,1\,+\,1\) that would qualify for a FLAG average. Still, since in the much better populated category of \(N_{ f}=2\,+\,1\) studies there is currently no computation without a red tag, we feel it is appropriate to postpone any form of averaging to the next edition of FLAG, when hopefully qualifying computations (at least for \(a_0^{I=2}M_{\pi }\)) are available at each \(N_{ f}\) considered.
5.2.4 Epilogue
In this section there are several quantities for which only one qualifying (“all-green”) determination is available for a given SU(2) LEC. Obviously the phenomenologically oriented reader is encouraged to use such a value (as provided in our tables) and to cite the original work. We hope that the lattice community will come up with further computations, in particular for \(N_{ f}=2\,+\,1\,+\,1\), such that a fair comparison of different works is possible at any \(N_{ f}\), and eventually a statement can be made about the presence or absence of an \(N_{ f}\)-dependence of SU(2) LECs.
What can be learned about the convergence pattern of SU(2) \(\chi \)PT from varying the fit ranges (in \(m_{ud}\)) of the pion mass and decay constant (i.e., the quantities from which \({\bar{\ell }}_3,{\bar{\ell }}_4\) are derived) is discussed in Ref. [423], where also the usefulness of comparing results from the x and the \(\xi \) expansion (with material taken from Ref. [44]) is emphasized.
Perhaps the most important physics result of this section is that the lattice simulations confirm the approximate validity of the Gell–Mann–Oakes–Renner formula and show that the square of the pion mass indeed grows in proportion to \(m_{ud}\). The formula represents the leading term of the chiral series and necessarily receives corrections from higher orders. At first nonleading order, the correction is determined by the effective coupling constant \({\bar{\ell }}_3\). The results collected in Table 21 and in the top panel of Fig. 14 show that \({\bar{\ell }}_3\) is now known quite well. They corroborate the conclusion drawn already in Ref. [424]: the lattice confirms the estimate of \({\bar{\ell }}_3\) derived in Ref. [277]. In the graph of \(M_{\pi }^2\) versus \(m_{ud}\), the values found on the lattice for \({\bar{\ell }}_3\) correspond to remarkably little curvature. In other words, the Gell-Mann-Oakes-Renner formula represents a reasonable first approximation out to values of \(m_{ud}\) that exceed the physical value by an order of magnitude.
As emphasized by Stern and collaborators [425,426,427], the analysis in the framework of \(\chi \)PT is coherent only if (i) the leading term in the chiral expansion of \(M_{\pi }^2\) dominates over the remainder and (ii) the ratio \(m_s/m_{ud}\) is close to the value 25.6 that follows from Weinberg’s leading-order formulae. In order to investigate the possibility that one or both of these conditions might fail, the authors proposed a more general framework, referred to as “generalized \(\chi \)PT”, which includes (standard) \(\chi \)PT as a special case. The results found on the lattice demonstrate that QCD does satisfy both of the above conditions. Hence, in the context of QCD, the proposed generalization of the effective theory does not appear to be needed. There is a modified version, however, referred to as “re-summed \(\chi \)PT” [428], which is motivated by the possibility that the Zweig-rule violating couplings \(L_4\) and \(L_6\) might be larger than expected. The available lattice data does not support this possibility, but they do not rule it out either (see Sect. 5.3 for details).
5.3 Extraction of SU(3) low-energy constants
To date, there are three comprehensive SU(3) papers with results based on lattice QCD with \(N_{ f}\!=\!2\,+\,1\) dynamical flavours [129, 162, 163], and one more with results based on \(N_{ f}\!=\!2\,+\,1\,+\,1\) dynamical flavours [33]. It is an open issue whether the data collected at \(m_s \simeq m_s^\mathrm {phys}\) allows for an unambiguous determination of SU(3) low-energy constants (cf. the discussion in Ref. [163]). To make definite statements one needs data at considerably smaller \(m_s\), and so far only MILC has some [129]. We are aware of a few papers with a result on one SU(3) low-energy constant each, which we list for completeness. Some particulars of the computations are listed in Table 24.
5.3.1 Results for the LO and NLO SU(3) LECs
Results for the SU(3) low-energy constants of leading order are found in Table 24 and analogous results for some of the effective coupling constants that enter the chiral SU(3) Lagrangian at NLO are collected in Tables 25 and 26. From PACS-CS [162] only those results are quoted that have been corrected for finite-size effects (misleadingly labelled “w/FSE” in their tables). For staggered data our colour-coding rule states that \(M_{\pi }\) is to be understood as \(M_{\pi }^\mathrm {RMS}\). The rating of Refs. [36, 129] is based on the information regarding the RMS masses given in Ref. [17]. Finally, Boyle 14 [431] and Boito 15 [430] are “hybrids” in the sense that they combine lattice data and experimental information.Footnote 36
A graphical summary of the lattice results for the coupling constants \(L_4\), \(L_5\), \(L_6\) and \(L_8\), which determine the masses and the decay constants of the pions and kaons at NLO of the chiral SU(3) expansion, is displayed in Fig. 17, along with the two phenomenological determinations quoted in the above tables. The overall consistency seems fairly convincing. In spite of this apparent consistency, there is a point that needs to be clarified as soon as possible. Some collaborations (RBC/UKQCD and PACS-CS) find that they are having difficulties in fitting their partially quenched data to the respective formulae for pion masses above \(\simeq \) 400 MeV. Evidently, this indicates that the data is stretching the regime of validity of these formulae. To date it is, however, not clear which subset of the data causes the troubles, whether it is the unitary part extending to too large values of the quark masses or whether it is due to \(m^\mathrm {val}/m^\mathrm {sea}\) differing too much from one. In fact, little is known, in the framework of partially quenched \(\chi \)PT, about the shape of the region of applicability in the \(m^\mathrm {val}\) versus \(m^\mathrm {sea}\) plane for fixed \(N_{ f}\). This point has also been emphasized in Ref. [379].
To date only the computations MILC 10 [36] (as an update of MILC 09 and MILC 09A) and HPQCD 13A [33] are free of red tags. Since they use different \(N_{ f}\) (in the former case \(N_{ f}=2\,+\,1\), in the latter case \(N_{ f}=2\,+\,1\,+\,1\)) we stay away from averaging them. Hence the situation remains unsatisfactory in the sense that for each \(N_{ f}\) only a single determination of high standing is available. Accordingly, for the phenomenologically oriented reader there is no alternative to using the results of MILC 10 [36] for \(N_{ f}=2\,+\,1\) and HPQCD 13A [33] for \(N_{ f}=2\,+\,1\,+\,1\), as given in Table 25.
5.3.2 Epilogue
In this subsection we find ourselves again in the unpleasant situation that only one qualifying (“all-green”) determination is available (at a given \(N_{ f}\)) for several LECs in the SU(3) framework, both at LO and at NLO. Obviously the phenomenologically oriented reader is encouraged to use such a value (as provided in our tables) and to cite the original work. Again our hope is that further computations would become available in forthcoming years, such that a fair comparison of different works will become possible both at \(N_{ f}=2\,+\,1\) and \(N_{ f}=2\,+\,1\,+\,1\).
In the large-\(N_c\) limit, the Zweig rule becomes exact, but the quarks have \(N_c=3\). The work done on the lattice is ideally suited to confirm or disprove the approximate validity of this rule for QCD. Two of the coupling constants entering the effective SU(3) Lagrangian at NLO disappear when \(N_c\) is sent to infinity: \(L_4\) and \(L_6\). The upper part of Table 25 and the left panels of Fig. 17 show that the lattice results for these quantities are in good agreement. At the scale \(\mu =M_\rho \), \(L_4\) and \(L_6\) are consistent with zero, indicating that these constants do approximately obey the Zweig rule. As mentioned above, the ratios \(F/F_0\), \(B/B_0\) and \(\Sigma /\Sigma _0\) also test the validity of this rule. Their expansion in powers of \(m_s\) starts with unity and the contributions of first order in \(m_s\) are determined by the constants \(L_4\) and \(L_6\), but they also contain terms of higher order. Apart from measuring the Zweig-rule violations, an accurate determination of these ratios will thus also allow us to determine the range of \(m_s\) where the first few terms of the expansion represent an adequate approximation. Unfortunately, at present, the uncertainties in the lattice data on these ratios are too large to draw conclusions, both concerning the relative size of the subsequent terms in the chiral series and concerning the magnitude of the Zweig-rule violations. The data seems to confirm the paramagnetic inequalities [427], which require \(F/F_0>1\), \(\Sigma /\Sigma _0>1\), and it appears that the ratio \(B/B_0\) is also larger than unity, but the numerical results need to be improved before further conclusions can be drawn.
The matching formulae in Ref. [244] can be used to calculate the SU(2) couplings \({{\bar{\ell }}}_i\) from the SU(3) couplings \(L_j\). Results obtained in this way are included in Table 21, namely, the entries explicitly labelled “SU(3)-fit” as well as MILC 10. Within the still rather large errors, the converted LECs from the SU(3) fits agree with those directly determined within SU(2) \(\chi \)PT. We plead with every collaboration performing \(N_{ f}=2\,+\,1\) simulations to also directly analyse their data in the SU(2) framework. In practice, lattice simulations are performed at values of \(m_s\) close to the physical value and the results are then corrected for the difference of \(m_s\) from its physical value. If simulations with more than one value of \(m_s\) have been performed, this can be done by interpolation. Alternatively one can use the technique of re-weighting (for a review see, e.g., Ref. [436]) to shift \(m_s\) to its physical value. From a conceptual view, the most pressing issue is the question about the convergence of the SU(3) framework for \(m_s\simeq m_s^\mathrm {phys}\). In line with what has been said in the very first paragraph of this section, we plead with every collaboration involved in \(N_{ f}=2\,+\,1\) (or \(2\,+\,1\,+\,1\)) simulations, to add ensembles with \(m_s \ll m_s^\mathrm {phys}\) to their database, as this allows them to address the issue properly.
5.3.3 Outlook
A relatively new development is that several lattice groups started extracting low-energy constants from \(\pi \)–\(\pi \) scattering data. In the isospin \(I=0\) and \(I=2\) channels the results of these studies are typically expressed in SU(2) terminology [i.e., through the linear combinations of \({{\bar{\ell }}}_i\) that appear in Eqs. (110, 111)], even if the studies are performed with \(N_{ f}=2\,+\,1\) or \(N_{ f}=2\,+\,1\,+\,1\) lattices. This is why the respective compilation, in the form of Table 23, is found in Sect. 5.2. Still, we remind the reader that the most generic way of presenting the results is through the scattering lengths \(a_0^0,a_0^2\), as featured in Fig. 16.
In the isospin \(I=1\) channel the situation is different. The most obvious difference is that this channel is dominated by a low-lying (and fairly broad) resonance, the well-known \(\rho (770)\). Lattice data would naturally include contributions where this resonance features in internal propagators. In the chiral SU(2) and SU(3) frameworks, on the other hand, there is no degree of freedom with the quantum numbers of a vector meson [244, 277]. Its contributions are subsumed in the low-energy constants, and an important insight is that the theory is built in such a way that it would correctly describe the low-energy tail of such contributions [437, 438]. Of course, one may extend the theory as to include vector mesons as explicit degrees of freedom, but this raises the issue of how to avoid double counting. Another way of phrasing this is to say that the low-energy constants in such an extended theory are logically different from those of \(\chi \)PT, since they should not include the vector meson contributions. Moreover, such extensions of \(\chi \)PT seem to lack a clear-cut power-counting scheme. In any case, since the literature on this topic is mostly in terms of the SU(3) chiral Lagrangian (and its extensions), it is natural to expect that lattice results concerning the \(I=1\) channel will be expressed in terms of SU(3) LECs.
In this spirit we like to mention that there are considerable efforts, on the lattice, to get a better handle on the \(I=1\) channel of \(\pi \)–\(\pi \) scattering; we are aware of Refs. [422, 439,440,441,442,443,444,445,446,447,448,449,450,451,452]. Some of these try to extract the NLO LEC combinations \(2L_4+L_5\) and \(2L_1-L_2\,+\,L_3\), sometimes with a single lattice spacing and with little or limited variation in the pion mass. We feel confident that these calculations will mature quickly, and eventually yield results on LECs (or linear combinations thereof) that might appear here, in the SU(3) section of a future edition.
We should add that there are claims that low-order calculations in extended chiral frameworks might allow for a simpler description of lattice data with an extended range of light (\(m_{ud}\)) and strange (\(m_s\)) quark masses than high-order calculations in the standard (vector-meson free) SU(3) \(\chi \)PT framework, see, e.g., Ref. [453]. While it is too early to jump to conclusions, we see nothing wrong in testing such frameworks as an effective (or model) description of lattice data on masses and decay constants of pseudoscalar mesons. But we caution that whenever LECs are extracted, it is worth scrutinizing the details of how this is done, for reasons that are intricately linked to the “double counting” issue mentioned above.
Last but not least we should mention that also baryon \(\chi \)PT results can be used to learn something about the chiral LECs in the meson sector. For instance Refs. [454, 455] give values for \(2L_6-L_4\), \(2L_8-L_5\), and \(L_8+3L_7\) from three different fits to lattice-QCD baryon masses by other groups. The quoted LECs enter via the pion- and kaon-mass dependence on quark masses. In our view checking whether the indirect determination of SU(3) meson LECs, via baryonic properties, agrees with the direct determination in the meson sector is a promising direction for forthcoming years.
6 Kaon mixing
Authors: P. Dimopoulos, G. Herdoíza, R. Mawhinney
The mixing of neutral pseudoscalar mesons plays an important role in the understanding of the physics of CP violation. In this section we discuss \(K^0 - {{\bar{K}}}^0\) oscillations, which probe the physics of indirect CP violation. Extensive reviews on the subject can be found in Refs. [456,457,458,459,460]. For the most part, we shall focus on kaon mixing in the SM. The case of Beyond-the-Standard-Model (BSM) contributions is discussed in Sect. 6.3.
6.1 Indirect CP violation and \(\epsilon _{K}\) in the SM
Indirect CP violation arises in \(K_L \rightarrow \pi \pi \) transitions through the decay of the \(\mathrm CP=+1\) component of \(K_L\) into two pions (which are also in a \(\mathrm CP=+1\) state). Its measure is defined as
with the final state having total isospin zero. The parameter \(\epsilon _{K}\) may also be expressed in terms of \(K^0 - {{\bar{K}}}^0\) oscillations. In the Standard Model, \(\epsilon _{K}\) receives contributions from: (i) short-distance (SD) physics given by \(\Delta S = 2\) “box diagrams” involving \(W^\pm \) bosons and u, c and t quarks; (ii) the long-distance (LD) physics from light hadrons contributing to the imaginary part of the dispersive amplitude \(M_{12}\) used in the two component description of \(K^0-{\bar{K}}^0\) mixing; (iii) the imaginary part of the absorptive amplitude \(\Gamma _{12}\) from \(K^0-{\bar{K}}^0\) mixing; and (iv) \(\text {Im}(A_0)/\text {Re}(A_0)\), where \(A_0\) is the \(K \rightarrow (\pi \pi )_{I=0}\) decay amplitude. The various factors in this decomposition can vary with phase conventions. In terms of the \(\Delta S = 2\) effective Hamiltonian, \({{{\mathcal {H}}}}_\text {eff}^{\Delta S = 2}\), it is common to represent contribution (i) by
and contribution (ii) by \(\text {Im}\,M_{12}^\text {LD}\). Contribution (iii) can be related to \(\text {Im}(A_0)/\text {Re}(A_0)\) since \((\pi \pi )_{I=0}\) states provide the dominant contribution to absorptive part of the integral in \(\Gamma _{12}\). Collecting the various pieces yields the following expression for the \(\epsilon _{K}\) factor [459, 461,462,463,464]
where the phase of \(\epsilon _{K}\) is given by
The quantities \(\Delta M_K\) and \(\Delta \Gamma _K\) are the mass and decay width differences between long- and short-lived neutral kaons. The experimentally known values of the above quantities read [137]:
where the latter three measurements have been obtained by imposing CPT symmetry.
We will start by discussing the short-distance effects (i) since they provide the dominant contribution to \(\epsilon _K\). To lowest order in the electroweak theory, the contribution to the \(K^0 - \bar{K}^0\) oscillations arises from so-called box diagrams, in which two W bosons and two “up-type” quarks (i.e., up, charm, top) are exchanged between the constituent down and strange quarks of the K mesons. The loop integration of the box diagrams can be performed exactly. In the limit of vanishing external momenta and external quark masses, the result can be identified with an effective four-fermion interaction, expressed in terms of the effective Hamiltonian
In this expression, \(G_F\) is the Fermi coupling, \(M_{\mathrm{W}}\) the W-boson mass, and
is a dimension-six, four-fermion operator. The function \({{{\mathcal {F}}}}^0\) is given by
where \(\lambda _a = V^*_{as} V_{ad}\), and \(a=c\,,t\) denotes a flavour index. The quantities \(S_0(x_c),\,S_0(x_t)\) and \(S_0(x_c,x_t)\) with \(x_c=m_c^2/M_{\mathrm{W}}^2\), \(x_t=m_t^2/M_{\mathrm{W}}^2\) are the Inami-Lim functions [465], which express the basic electroweak loop contributions without QCD corrections. The contribution of the up quark, which is taken to be massless in this approach, has been taken into account by imposing the unitarity constraint \(\lambda _u + \lambda _c + \lambda _t = 0\).
When strong interactions are included, \(\Delta {S}=2\) transitions can no longer be discussed at the quark level. Instead, the effective Hamiltonian must be considered between mesonic initial and final states. Since the strong coupling is large at typical hadronic scales, the resulting weak matrix element cannot be calculated in perturbation theory. The operator product expansion (OPE) does, however, factorize long- and short- distance effects. For energy scales below the charm threshold, the \(K^0-{{\bar{K}}}^0\) transition amplitude of the effective Hamiltonian can be expressed as
where \({\bar{g}}(\mu )\) and \(Q^{\Delta S=2}_{\mathrm{R}}(\mu )\) are the renormalized gauge coupling and four-fermion operator in some renormalization scheme. The factors \(\eta _1, \eta _2\) and \(\eta _3\) depend on the renormalized coupling \({\bar{g}}\), evaluated at the various flavour thresholds \(m_t, m_b, m_c\) and \( M_{\mathrm{W}}\), as required by the OPE and RG-running procedure that separate high- and low-energy contributions. Explicit expressions can be found in Refs. [458] and references therein, except that \(\eta _1\) and \(\eta _3\) have been calculated to NNLO in Refs. [466, 467], respectively. We follow the same conventions for the RG equations as in Ref. [458]. Thus the Callan-Symanzik function and the anomalous dimension \(\gamma ({\bar{g}})\) of \(Q^{\Delta S=2}\) are defined by
with perturbative expansions
We stress that \(\beta _0, \beta _1\) and \(\gamma _0\) are universal, i.e., scheme independent. As for \(K^0-{{\bar{K}}}^0\) mixing, this is usually considered in the naive dimensional regularization (NDR) scheme of \({\overline{\mathrm {MS}}}\), and below we specify the perturbative coefficient \(\gamma _1\) in that scheme:
Note that for QCD the above expressions must be evaluated for \(N=3\) colours, while \(N_{ f}\) denotes the number of active quark flavours. As already stated, Eq. (138) is valid at scales below the charm threshold, after all heavier flavours have been integrated out, i.e., \(N_{ f}= 3\).
In Eq. (138), the terms proportional to \(\eta _1,\,\eta _2\) and \(\eta _3\), multiplied by the contributions containing \({\bar{g}}(\mu )^2\), correspond to the Wilson coefficient of the OPE, computed in perturbation theory. Its dependence on the renormalization scheme and scale \(\mu \) is canceled by that of the weak matrix element \(\langle {{\bar{K}}}^0 \vert Q^{\Delta S=2}_{\mathrm{R}} (\mu ) \vert K^0 \rangle \). The latter corresponds to the long-distance effects of the effective Hamiltonian and must be computed nonperturbatively. For historical, as well as technical reasons, it is convenient to express it in terms of the B-parameter \(B_{K}\), defined as
The four-quark operator \(Q^{\Delta S=2}(\mu )\) is renormalized at scale \(\mu \) in some regularization scheme, for instance, NDR-\({\overline{\mathrm {MS}}}\). Assuming that \(B_{K}(\mu )\) and the anomalous dimension \(\gamma (g)\) are both known in that scheme, the renormalization group independent (RGI) B-parameter \({\hat{B}}_{K}\) is related to \(B_{K}(\mu )\) by the exact formula
At NLO in perturbation theory the above reduces to
To this order, this is the scale-independent product of all \(\mu \)-dependent quantities in Eq. (138).
Lattice-QCD calculations provide results for \(B_K(\mu )\). These results are, however, usually obtained in intermediate schemes other than the continuum \({\overline{\mathrm {MS}}}\) scheme used to calculate the Wilson coefficients appearing in Eq. (138). Examples of intermediate schemes are the RI/MOM scheme [468] (also dubbed the “Rome-Southampton method”) and the Schrödinger functional (SF) scheme [172]. These schemes are used as they allow a nonperturbative renormalization of the four-fermion operator, using an auxiliary lattice simulation. This allows \(B_K(\mu )\) to be calculated with percent-level accuracy, as described below.
In order to make contact with phenomenology, however, and in particular to use the results presented above, one must convert from the intermediate scheme to the \({\overline{\mathrm {MS}}}\) scheme or to the RGI quantity \({\hat{B}}_{K}\). This conversion relies on one or 2-loop perturbative matching calculations, the truncation errors in which are, for many recent calculations, the dominant source of error in \({\hat{B}}_{K}\) (see, for instance, Refs. [10, 57, 58, 156, 469]). While this scheme-conversion error is not, strictly speaking, an error of the lattice calculation itself, it must be included in results for the quantities of phenomenological interest, namely, \(B_K({\overline{\mathrm {MS}}},2\,\mathrm{GeV})\) and \({\hat{B}}_{K}\). Incidentally, we remark that this truncation error is estimated in different ways and that its relative contribution to the total error can considerably differ among the various lattice calculations. We note that this error can be minimized by matching between the intermediate scheme and \({\overline{\mathrm {MS}}}\) at as large a scale \(\mu \) as possible (so that the coupling which determines the rate of convergence is minimized). Recent calculations have pushed the matching \(\mu \) up to the range \(3-3.5\,\)GeV. This is possible because of the use of nonperturbative RG running determined on the lattice [10, 56, 156]. The Schrödinger functional offers the possibility to run nonperturbatively to scales \(\mu \sim M_{\mathrm{W}}\) where the truncation error can be safely neglected. However, so far this has been applied only for two flavours for \(B_K\) in Ref. [470] and for the case of the BSM bag parameters in Ref. [471], see more details in Sect. 6.3.
Perturbative truncation errors in Eq. (138) also affect the Wilson coefficients \(\eta _1\), \(\eta _2\) and \(\eta _3\). It turns out that the largest uncertainty arises from the charm quark contribution \(\eta _1=1.87(76)\) [466]. Although it is now calculated at NNLO, the series shows poor convergence. The net effect from the uncertainty on \(\eta _1\) on the amplitude in Eq. (138) is larger than that of present lattice calculations of \(B_K\).
We will now proceed to discuss the remaining contributions to \(\epsilon _K\) in Eq. (129). An analytical estimate of the leading contribution from \(\mathrm{Im} M_{12}^\text {LD}\) based on \(\chi \)PT, shows that it is approximately proportional to \(\xi \equiv \mathrm{{Im}}(A_0)/\mathrm{{Re}}(A_0)\) so that Eq. (129) can be written as follows [463, 464]
where the deviation of \(\rho \) from one parameterizes the long-distance effects in \(\mathrm{Im} M_{12}\).
An estimate of \(\xi \) has been obtained from a direct evaluation of the ratio of amplitudes \(\mathrm{Im}(A_0)/\mathrm{{Re}}(A_0)\) where \(\mathrm{{Re}}(A_0)\) is determined from a lattice-QCD computation [472] at one value of the lattice spacing, while \(\mathrm{Re}(A_0) \simeq |A_0|\) and the value \(|A_0| = 3.320(2) \times 10^{-7}\) GeV are used based on the relevant experimental input [137] from the decay to two pions. This leads to a result for \(\xi \) with a rather large relative error,
A more precise estimate can be been obtained through a lattice-QCD computation of the ratio of amplitudes \(\mathrm{Im}(A_2)/\mathrm{Re}(A_2)\) [473] where the continuum limit result is based on data at two values of the lattice spacing; \(A_2\) denotes the \(\Delta {I}=3/2\) \(K\rightarrow \pi \pi \) decay amplitude. For the computation of \(\xi \), the experimental values of \(\mathrm{Re}(\epsilon ^{\prime }/\epsilon )\), \(|\epsilon _K|\) and \(\omega = \mathrm{Re}(A_2)/\mathrm{Re}(A_0)\) have been used. The result for \(\xi \) reads
A phenomenological estimate can also be obtained from the relationship of \(\xi \) to \(\mathrm{Re} (\epsilon ^\prime /\epsilon )\), using the experimental value of the latter and further assumptions concerning the estimate of hadronic contributions. The corresponding value of \(\xi \) reads [463, 464]
We note that the use of the experimental value for \(\mathrm{Re}(\epsilon ^\prime /\epsilon )\) is based on the assumption that it is free from New Physics contributions. The value of \(\xi \) can then be combined with a \({\chi }\mathrm PT\)-based estimate for the long-range contribution, \(\rho =0.6(3)\) [464]. Overall, the combination \(\rho \xi \) appearing in Eq. (145) leads to a suppression of the SM prediction of \(|\epsilon _K|\) by about \(3(2)\%\) relative to the experimental measurement of \(|\epsilon _K|\) given in Eq. (131), regardless of whether the phenomenological estimate of \(\xi \) [see Eq. (148)] or the most precise lattice result [see Eq. (147)] are used. The uncertainty in the suppression factor is dominated by the error on \(\rho \). Although this is a small correction, we note that its contribution to the error of \(\epsilon _K\) is larger than that arising from the value of \(B_{K}\) reported below.
Efforts are under way to compute the long-distance contributions to \(\epsilon _{K}\) [474] and to the \(K_L-K_S\) mass difference in lattice QCD [475,476,477,478]. However, the results are not yet precise enough to improve the accuracy in the determination of the parameter \(\rho \).
The lattice-QCD study of \(K \rightarrow \pi \pi \) decays provides crucial input to the SM prediction of \(\epsilon _{K}\). Besides the RBC-UKQCD collaboration programme [472, 473] using domain-wall fermions, an approach based on improved Wilson fermions [479, 480] has presented a determination of the \(K \rightarrow \pi \pi \) decay amplitudes, \(A_0\) and \(A_2\), at unphysical quark masses. A first proposal aiming at the inclusion of electromagnetism in lattice-QCD calculations of these decays was reported in Ref. [481]. For an ongoing analysis of the scaling with the number of colours of \(K \rightarrow \pi \pi \) decay amplitudes using lattice-QCD computations, we refer to Refs. [482, 483].
Finally, we notice that \(\epsilon _{K}\) receives a contribution from \(|V_{cb}|\) through the \(\lambda _t\) parameter in Eq. (137). The present uncertainty on \(|V_{cb}|\) has a significant impact on the error of \(\epsilon _{K}\) (see, e.g., Ref. [484] and a recent update [485]).
6.2 Lattice computation of \(B_{K}\)
Lattice calculations of \(B_{K}\) are affected by the same systematic effects discussed in previous sections. However, the issue of renormalization merits special attention. The reason is that the multiplicative renormalizability of the relevant operator \(Q^{\Delta S=2}\) is lost once the regularized QCD action ceases to be invariant under chiral transformations. For Wilson fermions, \(Q^{\Delta S=2}\) mixes with four additional dimension-six operators, which belong to different representations of the chiral group, with mixing coefficients that are finite functions of the gauge coupling. This complicated renormalization pattern was identified as the main source of systematic error in earlier, mostly quenched calculations of \(B_{K}\) with Wilson quarks. It can be bypassed via the implementation of specifically designed methods, which are either based on Ward identities [486] or on a modification of the Wilson quark action, known as twisted mass QCD [487,488,489].
An advantage of staggered fermions is the presence of a remnant U(1) chiral symmetry. However, at nonvanishing lattice spacing, the symmetry among the extra unphysical degrees of freedom (tastes) is broken. As a result, mixing with other dimension-six operators cannot be avoided in the staggered formulation, which complicates the determination of the B-parameter. In general, taste conserving mixings are implemented directly in the lattice computation of the matrix element. The effects of the broken taste symmetry are usually treated through an effective field theory, staggered Chiral Perturbation Theory (S\(\chi \)PT) [327, 490], parameterizing the quark-mass and lattice-spacing dependences.
Fermionic lattice actions based on the Ginsparg-Wilson relation [491] are invariant under the chiral group, and hence four-quark operators such as \(Q^{\Delta S=2}\) renormalize multiplicatively. However, depending on the particular formulation of Ginsparg-Wilson fermions, residual chiral symmetry breaking effects may be present in actual calculations. For instance, in the case of domain-wall fermions, the finiteness of the extra 5th dimension implies that the decoupling of modes with different chirality is not exact, which produces a residual nonzero quark mass in the chiral limit. Furthermore, whether a significant mixing with dimension-six operators of different chirality is induced must be investigated on a case-by-case basis.
The only existing lattice-QCD calculation of \(B_K\) with \(N_{ f}=2\,+\,1\,+\,1\) dynamical quarks [55] was reviewed in the FLAG 16 report. Considering that no direct evaluation of the size of the excess of charm quark effects included in \(N_{ f}=2\,+\,1\,+\,1\) computations of \(B_K\) has appeared since then, we wish to reiterate a discussion about a few related conceptual issues.
As described in Sect. 6.1, kaon mixing is expressed in terms of an effective four-quark interaction \(Q^{{\Delta }S=2}\), considered below the charm threshold. When the matrix element of \(Q^{{\Delta }S=2}\) is evaluated in a theory that contains a dynamical charm quark, the resulting estimate for \(B_K\) must then be matched to the three-flavour theory that underlies the effective four-quark interaction.Footnote 37 In general, the matching of \(2\,+\,1\)-flavour QCD with the theory containing \(2\,+\,1\,+\,1\) flavours of sea quarks below the charm threshold can be accomplished by adjusting the coupling and quark masses of the \(N_{ f}=2\,+\,1\) theory so that the two theories match at energies \(E<m_c\). The corrections associated with this matching are of order \((E/m_c)^2\), since the subleading operators have dimension eight [492].
When the kaon mixing amplitude is considered, the matching also involves the relation between the relevant box graphs and the effective four-quark operator. In this case, corrections of order \((E/m_c)^2\) arise not only from the charm quarks in the sea, but also from the valence sector, since the charm quark propagates in the box diagrams. We note that the original derivation of the effective four-quark interaction is valid up to corrections of order \((E/m_c)^2\). The kaon mixing amplitudes evaluated in the \(N_{ f}=2\,+\,1\) and \(2\,+\,1\,+\,1\) theories are thus subject to corrections of the same order in \(E/m_c\) as the derivation of the conventional four-quark interaction.
Regarding perturbative QCD corrections at the scale of the charm quark mass on the amplitude in Eq. (138), the uncertainty on \(\eta _1\) and \(\eta _3\) factors is of \({\mathcal {O}}(\alpha _s(m_c)^3)\) [466, 467], while that on \(\eta _2\) is of \({\mathcal {O}}(\alpha _s(m_c)^2)\) [493]. On the other hand, a naive power counting argument suggests that the corrections of order \((E/m_c)^2\) due to dynamical charm-quark effects in the matching of the amplitudes are suppressed by powers of \(\alpha _s(m_c)\) and by a factor of \(1/N_c\). It is therefore essential that any forthcoming calculation of \(B_K\) with \(N_{ f}=2\,+\,1\,+\,1\) flavours addresses properly the size of these residual dynamical charm effects in a quantitative way.
Another issue in this context is how the lattice scale and the physical values of the quark masses are determined in the \(2\,+\,1\) and \(2\,+\,1\,+\,1\) flavour theories. Here it is important to consider in which way the quantities used to fix the bare parameters are affected by a dynamical charm quark. Apart from a brief discussion in Ref. [55], these issues have not yet been directly addressed in the literature.Footnote 38 Given the hierarchy of scales between the charm quark mass and that of \(B_K\), we expect these errors to be modest, but a more quantitative understanding is needed as statistical errors on \(B_K\) are reduced. Within this review we will not discuss this issue further. However, we wish to point out that the present discussion also applies to \(N_{ f}=2\,+\,1\,+\,1\) computations of the kaon BSM B-parameters discussed in Sect. 6.3.
A compilation of results with \(N_{ f}=2, 2\,+\,1\) and \(2\,+\,1\,+\,1\) flavours of dynamical quarks is shown in Tables 27 and 28, as well as Fig. 18. An overview of the quality of systematic error studies is represented by the colour coded entries in Tables 27 and 28. In Appendix B.4 we gather the simulation details and results that have appeared since the previous FLAG review [3]. The values of the most relevant lattice parameters, and comparative tables on the various estimates of systematic errors are also collected.
Some of the groups whose results are listed in Tables 27 and 28 do not quote results for both \(B_{K}(\overline{\mathrm{MS}},2\,\mathrm{GeV})\) – which we denote by the shorthand \(B_{K}\) from now on – and \({\hat{B}}_{K}\). This concerns Refs. [59, 494] for \(N_{ f}=2\), Refs. [10, 57, 58, 156] for \(2\,+\,1\) and Ref. [55] for \(2\,+\,1\,+\,1\) flavours. In these cases we perform the conversion ourselves by evaluating the proportionality factor in Eq. (144) using perturbation theory at NLO at a renormalization scale \(\mu =2\,\mathrm {GeV}\). For \(N_{ f}=2\,+\,1\), by using the world average value \(\Lambda _{{\overline{\mathrm {MS}}}}^{(3)}=332\) MeV from PDG [137] and the 4-loop \(\beta \)-function we obtain, \({\hat{B}}_{K}/B_{K}=1.369\) in the three-flavour theory. Had we used the 5-loop \(\beta \)-function we would get \({\hat{B}}_{K}/B_{K}=1.373\). If we use instead the average lattice results from Sect. 9 of the present FLAG report, \(\Lambda _{{\overline{\mathrm {MS}}}}^{(3)}=343\) MeV, together with the four and 5-loop \(\beta \)-function, we obtain \({\hat{B}}_{K}/B_{K}=1.365\) and \({\hat{B}}_{K}/B_{K}=1.369\), respectively. In FLAG 16, we used \({\hat{B}}_{K}/B_{K}=1.369\) based on the 2014 edition of the PDG [170]. The relative deviations among these various estimates is below the 3 permille level and amounts to a tiny fraction of the uncertainty on the average value of the B-parameter. We have therefore used in this edition the value, \({\hat{B}}_{K}/B_{K}=1.369\), which was also used in FLAG 16. The same value for the conversion factor has also been applied to the result computed in QCD with \(N_{ f}=2\,+\,1\,+\,1\) flavours of dynamical quarks [55].
In two-flavour QCD one can insert into the NLO expressions for \(\alpha _s\) the estimate \(\Lambda _{{\overline{\mathrm {MS}}}}^{(2)}=330\) MeV, which is the average value for \(N_{ f}=2\) obtained in Sect. 9, and get \({\hat{B}}_K/B_K = 1.365\) and \({\hat{B}}_K/B_K = 1.368\) for running with four and 5-loop \(\beta \)-function, respectively. We again note that the difference between the conversion factors for \(N_{ f}=2\) and \(N_{ f}=2\,+\,1\) will produce a negligible ambiguity, which, in any case, is well below the overall uncertainties in Refs. [59, 494]. We have therefore chosen to apply the conversion factor of 1.369 not only to results obtained for \(N_{ f}=2\,+\,1\) flavours but also to the two-flavour theory (in cases where only one of \({\hat{B}}_K\) and \(B_K\) are quoted). We have indicated explicitly in Table 28 in which way the conversion factor 1.369 has been applied to the results of Refs. [59, 494]. We wish to encourage authors to provide both \({\hat{B}}_{K}\) and \(B_{K}\) together with the values of the parameters appearing in the perturbative running.
We discuss here one recent result for the kaon B-parameter reported by the RBC/UKQCD collaboration, RBC/UKQCD 16 [60], where \(N_f=2\,+\,1\) dynamical quarks have been employed. For a detailed description of previous calculations – and in particular those considered in the computation of the average values – we refer the reader to the FLAG 16 [3] and FLAG 13 [2] reports.
In Ref. [60], RBC/UKQCD presented a determination of \(B_K\) obtained as part of their study of kaon mixing in extensions of the SM. In this calculation two values of the lattice spacing, \(a \simeq 0.11\) and 0.08 fm, are used, employing ensembles generated using the Iwasaki gauge action and the Shamir domain-wall fermionic action. The lattice volumes are \(24^3 \times 64 \times 16\) for the coarse and \(32^3 \times 64 \times 16\) for the fine lattice spacing. The lowest simulated values for the pseudoscalar mass are about 340 MeV and 300 MeV, respectively. The renormalization of four-quark operators was performed nonperturbatively in two RI-SMOM schemes, namely, \(({/}\!\!\!{q},{/}\!\!\!{q})\) and \((\gamma _{\mu }, \gamma _{\mu })\), where the latter was used for the final estimate of \(B_K\). While the procedure to determine \(B_K\) is very similar to RBC/UKQCD 14B, the calculation in RBC/UKQCD 16 [60] is based only on a subset of the ensembles studied in Ref. [10]. Therefore, the result for \(B_K\) reported in Ref. [60] can neither be considered an update of RBC/UKQCD 14B, nor an independent new result.
We now describe our procedure for obtaining global averages. The rules of Sect. 2.1 stipulate that results free of red tags and published in a refereed journal may enter an average. Papers that at the time of writing are still unpublished but are obvious updates of earlier published results can also be taken into account.
There is only one result for \(N_f=2\,+\,1\,+\,1\), computed by the ETM collaboration [55]. Since it is free of red tags, it qualifies as the currently best global estimate, i.e.,
The bulk of results for the kaon B-parameter has been obtained for \(N_{ f}=2\,+\,1\). As in the previous editions of the FLAG review [2, 3] we include the results from SWME [58, 469, 495], despite the fact that nonperturbative information on the renormalization factors is not available. Instead, the matching factor has been determined in perturbation theory at one loop, but with a sufficiently conservative error of 4.4%. As described above, the result in RBC/UKQCD 16 [60] cannot be considered an update of the earlier estimate in RBC/UKQCD 14B, and hence it is not included in the FLAG average.
Thus, for \(N_{ f}=2\,+\,1\) our global average is based on the results of BMW 11 [56], Laiho 11 [57], RBC/UKQCD 14B [10] and SWME 15A [58]. The last three are the latest updates from a series of calculations by the same collaborations. Our procedure is as follows: in a first step statistical and systematic errors of each individual result for the RGI B-parameter, \({\hat{B}}_{K}\), are combined in quadrature. Next, a weighted average is computed from the set of results. For the final error estimate we take correlations between different collaborations into account. To this end we note that we consider the statistical and finite-volume errors of SWME 15A and Laiho 11 to be correlated, since both groups use the Asqtad ensembles generated by the MILC collaboration. Laiho 11 and RBC/UKQCD 14B both use domain-wall quarks in the valence sector and also employ similar procedures for the nonperturbative determination of matching factors. Hence, we treat the quoted renormalization and matching uncertainties by the two groups as correlated. After constructing the global covariance matrix according to Schmelling [132], we arrive at
with \(\chi ^2/\mathrm{dof}=0.675\). After applying the NLO conversion factor \({\hat{B}}_{K}/B_{K}^{\overline{\mathrm {MS}}}(2\,\mathrm{GeV})=1.369\), this translates into
Note that the statistical errors of each calculation entering the global average are small enough to make their results statistically incompatible. It is only because of the relatively large systematic errors that the weighted average produces a value of \({\mathcal {O}}(1)\) for the reduced \(\chi ^2\).
Passing over to describing the results computed for \(N_{ f}=2\) flavours, we note that there is only the set of results published in ETM 12D [59] and ETM 10A [494] that allow for an extensive investigation of systematic uncertainties. We identify the result from ETM 12D [59], which is an update of ETM 10A, with the currently best global estimate for two-flavour QCD, i.e.,
The result in the \({\overline{\mathrm {MS}}}\) scheme has been obtained by applying the same conversion factor of 1.369 as in the three-flavour theory.
6.3 Kaon BSM B-parameters
We now report on lattice results concerning the matrix elements of operators that encode the effects of physics beyond the Standard Model (BSM) to the mixing of neutral kaons. In this theoretical framework both the SM and BSM contributions add up to reproduce the experimentally observed value of \(\epsilon _K\). Since BSM contributions involve heavy but unobserved particles they are short-distance dominated. The effective Hamiltonian for generic \({\Delta }S=2\) processes including BSM contributions reads
where \(Q_1\) is the four-quark operator of Eq. (136) that gives rise to the SM contribution to \(\epsilon _K\). In the so-called SUSY basis introduced by Gabbiani et al. [501] the operators \(Q_2,\ldots ,Q_5\) read Footnote 39
where a and b denote colour indices. In analogy to the case of \(B_{K}\) one then defines the B-parameters of \(Q_2,\ldots ,Q_5\) according to
The factors \(\{N_2,\ldots ,N_5\}\) are given by \(\{-5/3, 1/3, 2, 2/3\}\), and it is understood that \(B_i(\mu )\) is specified in some renormalization scheme, such as \({\overline{\mathrm {MS}}}\) or a variant of the regularization-independent momentum subtraction (RI-MOM) scheme.
The SUSY basis has been adopted in Refs. [55, 59, 60, 502]. Alternatively, one can employ the chiral basis of Buras, Misiak and Urban [503]. The SWME collaboration prefers the latter since the anomalous dimension that enters the RG running has been calculated to two loops in perturbation theory [503]. Results obtained in the chiral basis can be easily converted to the SUSY basis via
The remaining B-parameters are the same in both bases. In the following we adopt the SUSY basis and drop the superscript.
Older quenched results for the BSM B-parameters can be found in Refs. [504,505,506]. For a nonlattice approach to get estimates for the BSM B-parameters see Ref. [507].
Estimates for \(B_2,\ldots ,B_5\) have been reported for QCD with \(N_{ f}=2\) (ETM 12D [59]), \(N_{ f}=2+1\) (RBC/UKQCD 12E [502], SWME 13A [495], SWME 14C [508], SWME 15A [58], RBC/UKQCD 16 [60, 509]) and \(N_{ f}=2\,+\,1\,+\,1\) (ETM 15 [55]) flavours of dynamical quarks. They are listed and compared in Table 29 and Fig. 19. In general one finds that the BSM B-parameters computed by different collaborations do not show the same level of consistency as the SM kaon mixing parameter \(B_K\) discussed previously. Control over systematic uncertainties (chiral and continuum extrapolations, finite-volume effects) in \(B_2,\ldots ,B_5\) is expected to be at the same level as for \(B_{K}\), as far as the results by ETM 12D, ETM 15 and SWME 15A are concerned. The calculation by RBC/UKQCD 12E has been performed at a single value of the lattice spacing and a minimum pion mass of 290 MeV. Thus, the results do not benefit from the same improvements regarding control over the chiral and continuum extrapolations as in the case of \(B_{K}\) [10].
Lattice results for the BSM B-parameters defined in the \({\overline{\mathrm {MS}}}\) scheme at a reference scale of 3 GeV, see Table 29
The RBC/UKQCD collaboration has recently extended its calculation of BSM B-parameters [60, 509] for \(N_f=2\,+\,1\), by considering two values of the lattice spacing, \(a \simeq 0.11\) and 0.08 fm, employing ensembles generated using the Iwasaki gauge action and the Shamir domain-wall fermionic action. The lattice volumes in the RBC/UKQCD 16 calculation are \(24^3 \times 64 \times 16\) for the coarse and \(32^3 \times 64 \times 16\) for the fine lattice spacing, while the lowest simulated values for the pseudoscalar mass are about 340 MeV and 300 MeV, respectively. As in the related calculation of \(B_K\) (RBC/UKQCD 14B [10]) the renormalization of four-quark operators was performed nonperturbatively in two RI-SMOM schemes, namely, \(({/}\!\!\!{q},{/}\!\!\!{q})\) and \((\gamma _{\mu }, \gamma _{\mu })\), where the latter was used for the final estimates of \(B_2,\ldots ,B_5\) quoted in Ref. [60]. By comparing the results obtained in the conventional RI-MOM and the two RI-SMOM schemes, RBC/UKQCD 16 report significant discrepancies for \(B_4\) and \(B_5\) in the \({\overline{\mathrm{MS}}}\) scheme at the scale of 3 GeV, which amount up to 2.8\(\sigma \) in the case of \(B_5\). By contrast, the agreement for \(B_2\) and \(B_3\) determined for different intermediate scheme is much better. Based on these findings they claim that these discrepancies are due to uncontrolled systematics coming from the Goldstone boson pole subtraction procedure that is needed in the RI-MOM scheme, while pole subtraction effects are much suppressed in RI-SMOM thanks to the fact that the latter is based on nonexceptional momenta. The RBC/UKQCD collaboration has presented an ongoing study [510] in which simulations with two values of the lattice spacing at the physical point and with a third finer lattice spacing at \(M_\pi = 234\) MeV are employed in order to obtain the BSM matrix elements in the continuum limit. Results are still preliminary.
The findings by RBC/UKQCD 16 [60, 509] provide evidence that the nonperturbative determination of the matching factors depends strongly on the details of the implementation of the Rome-Southampton method. The use of nonexceptional momentum configurations in the calculation of the vertex functions produces a significant modification of the renormalization factors, which affects the matching between \({\overline{\mathrm{MS}}}\) and the intermediate momentum subtraction scheme. This effect is most pronounced in \(B_4\) and \(B_5\). Furthermore, it can be noticed that the estimates for \(B_4\) and \(B_5\) from RBC/UKQCD 16 are much closer to those of SWME 15A. At the same time, the results for \(B_2\) and \(B_3\) obtained by ETM 15, SWME 15A and RBC/UKQCD 16 are in good agreement within errors.
A nonperturbative computation of the running of the four-fermion operators contributing to the \(B_2\), ..., \(B_5\) parameters has been carried out with two dynamical flavours using the Schrödinger functional renormalization scheme [471]. Renormalization matrices of the operator basis are used to build step-scaling functions governing the continuum-limit running between hadronic and electroweak scales. A comparison to perturbative results using NLO (2-loops) for the four-fermion operator anomalous dimensions indicates that, at scales of about 3 GeV, nonperturbative effects can induce a sizeable contribution to the running.
A detailed look at the most recent calculations reported in ETM 15 [55], SWME 15A [58] and RBC/UKQCD 16 [60] reveals that cutoff effects appear to be larger for the BSM B-parameters compared to \(B_K\). Depending on the details of the renormalization procedure and/or the fit ansatz for the combined chiral and continuum extrapolation, the results obtained at the coarsest lattice spacing differ by 15–30%. At the same time the available range of lattice spacings is typically much reduced compared to the corresponding calculations of \(B_K\), as can be seen by comparing the quality criteria in Tables 27 and 29. Hence, the impact of the renormalization procedure and the continuum limit on the BSM B-parameters certainly requires further investigation.
Finally we present our estimates for the BSM B-parameters, quoted in the \({\overline{\mathrm {MS}}}\)-scheme at scale 3 GeV. For \(N_f=2\,+\,1\) our estimate is given by the average between the results from SWME 15A and RBC/UKQCD 16, i.e.,
For \(N_f=2\,+\,1\,+\,1\) and \(N_f=2\), our estimates coincide with the ones by ETM 15 and ETM 12D, respectively, since there is only one computation for each case. Thus we quote
Based on the above discussion on the effects of employing different intermediate momentum subtraction schemes in the nonperturbative renormalization of the operators, the discrepancy for \(B_4\) and \(B_5\) results between \(N_f=2, 2\,+\,1\,+\,1\) and \(N_f=2\,+\,1\) computations should not be considered an effect associated with the number of dynamical flavours. As a closing remark, we encourage authors to provide the correlation matrix of the \(B_i\) parameters.
7 D-meson decay constants and form factors
Authors: Y. Aoki, D. Bečirević, M. Della Morte, S. Gottlieb, D. Lin, E. Lunghi, C. Pena
Leptonic and semileptonic decays of charmed D and \(D_s\) mesons occur via charged W-boson exchange, and are sensitive probes of \(c \rightarrow d\) and \(c \rightarrow s\) quark flavour-changing transitions. Given experimental measurements of the branching fractions combined with sufficiently precise theoretical calculations of the hadronic matrix elements, they enable the determination of the CKM matrix elements \(|V_{cd}|\) and \(|V_{cs}|\) (within the Standard Model) and a precise test of the unitarity of the second row of the CKM matrix. Here we summarize the status of lattice-QCD calculations of the charmed leptonic decay constants. Significant progress has been made in charm physics on the lattice in recent years, largely due to the availability of gauge configurations produced using highly-improved lattice-fermion actions that enable treating the c quark with the same action as for the u, d, and s quarks.
This section updates the corresponding one in the last FLAG review [3] for results that appeared after November 30, 2015. As already done in Ref. [3], we limit our review to results based on modern simulations with reasonably light pion masses (below approximately 500 MeV). This excludes results obtained from the earliest unquenched simulations, which typically had two flavours in the sea, and which were limited to heavier pion masses because of the constraints imposed by the computational resources and methods available at that time.
Following our review of lattice-QCD calculations of \(D_{(s)}\)-meson leptonic decay constants and semileptonic form factors, we then interpret our results within the context of the Standard Model. We combine our best-determined values of the hadronic matrix elements with the most recent experimentally-measured branching fractions to obtain \(|V_{cd(s)}|\) and test the unitarity of the second row of the CKM matrix.
7.1 Leptonic decay constants \(f_D\) and \(f_{D_s}\)
In the Standard Model, and up to electromagnetic corrections, the decay constant \(f_{D_{(s)}}\) of a pseudoscalar D or \(D_s\) meson is related to the branching ratio for leptonic decays mediated by a W boson through the formula
where q is d or s and \(V_{cd}\) (\(V_{cs}\)) is the appropriate CKM matrix element for a D (\(D_s\)) meson. The branching fractions have been experimentally measured by CLEO, Belle, Babar and BES with a precision around 4–5\(\%\) for both the D and the \(D_s\)-meson decay modes [133]. When combined with lattice results for the decay constants, they allow for determinations of \(|V_{cs}|\) and \(|V_{cd}|\).
In lattice-QCD calculations the decay constants \(f_{D_{(s)}}\) are extracted from Euclidean matrix elements of the axial current
with \(q=d,s\) and \( A^{\mu }_{cq} ={\bar{c}}\gamma _\mu \gamma _5 q\). Results for \(N_f=2,\; 2\,+\,1\) and \(2\,+\,1\,+\,1\) dynamical flavours are summarized in Table 30 and Fig. 20. Since the publication of the last FLAG review, a handful of results for \(f_D\) and \(f_{D_s}\) have appeared, as described below. We consider isospin-averaged quantities, although in a few cases results for \(f_{D^+}\) are quoted (see, for example, the FNAL/MILC 11,14A and 17 computations, where the difference between \(f_D\) and \(f_{D^+}\) has been estimated to be around 0.5 MeV).
One new result has appeared for \(N_f=2\). Blossier 18 [66] employs a subset of the gauge field configuration ensembles entering the earlier study presented in ALPHA 13B [511] by the ALPHA collaboration, however, it is independent of it; in particular, in [66] a different strategy is used to analyse the raw data, based on matrices of correlation functions and by solving a Generalized Eigenvalue Problem. It describes a determination of the \(D_s\) and \(D_s^*\) decay constants computed on six \(N_f=2\) ensembles of nonperturbatively O(a) improved Wilson fermions at lattice spacings of 0.065 and 0.048 fm. Pion masses range between 440 and 194 MeV and the condition \(Lm_\pi \ge 4\) is always met. Chiral/continuum extrapolations are performed adopting a fit ansatz linear in \(m_\pi ^2\) and \(a^2\). The systematic errors are dominated by the uncertainty on the absolute lattice scale, which is fixed through \(f_K\). Cutoff effects on \(f_{D_s}\) instead appear to be small and are at the 1% level at the coarsest lattice spacing.
Decay constants of the D and \(D_s\) mesons [values in Table 30 and Eqs. (162–170)]. As usual, full green squares are used in the averaging procedure, pale green squares have been superseded by later determinations, while pale red squares do not satisfy the criteria. The black squares and grey bands indicate our averages
The \(N_f=2\) averages for \(f_D\) and \({{f_{D_s}}/{f_D}}\) coincide with those in the previous FLAG review and are given by the values in ETM 13B [64], while the estimate for \(f_{D_s}\) is the result of the weighted average of the numbers in ETM 13B [64] and Blossier 18 [66]. They read
where the error on the average of \(f_{D_s}\) has been rescaled by the factor \(\sqrt{\chi ^2/\text{ dof }}=1.34\) (see Sect. 2).
The RBC/UKQCD collaboration presented in RBC/UKQCD 17 [63] the final results for the computation of the D- and \(D_s\)-mesons decay constants based on the \(N_f=2\,+\,1\) dynamical ensembles generated using Domain Wall Fermions (DWF). Three lattice spacings have been considered with pion masses ranging between the physical value (reached at the two coarsest lattice spacings) and 430 MeV. Two different Domain Wall discretizations (Möbius and Shamir) have been used for both (light) valence and sea quarks. They correspond to two different choices for the DWF kernel. The Möbius DWF are loosely equivalent to Shamir DWF at twice the extension in the fifth dimension [10]. For the actual implementation by the RBC/UKQCD collaboration O\((a^2)\) cutoff effects in the two formulations are expected to agree and results are therefore extrapolated jointly to the continuum limit. For the quenched charm quark Möbius DWF are always used, with a domain-wall height slightly different from the one adopted for light valence quarks. The choice helps to keep cutoff effects under control, according to the study in Ref. [517]. The continuum/physical-mass extrapolations are performed by using a Taylor expansion in \(a^2\) and \(m_\pi ^2-m_\pi ^{2 \, phys}\) and the associated systematic error is estimated by essentially applying cuts in the pion mass. This error dominates the uncertainties on the final results.
The updated FLAG estimates then read



where the error on the \(N_{ f}=2\,+\,1\) average of \(f_{D_s}\) has been rescaled by the factor \(\sqrt{\chi ^2/\text{ dof }}=1.1\). Those come from the results in HPQCD 12A [61], FNAL/MILC 11 [62] as well as RBC/UKQCD 17 [63] concerning \(f_D\) while for \(f_{D_s}\) also the \(\chi \)QCD 14 [22] result contributes, and instead of the value in HPQCD 12A [61] the one in HPQCD 10A [65] is used. In addition, the statistical errors between the results of FNAL/MILC and HPQCD have been everywhere treated as 100% correlated since the two collaborations use overlapping sets of configurations. The same procedure had been used in the past reviews.
For \(N_f=2\,+\,1\,+\,1\) one new determination (FNAL/MILC 17) appeared in [5], which is actually an extension of FNAL/MILC 14A [18] (described in detail in the previous FLAG review). While in FNAL/MILC 14A the finest lattice spacing considered was 0.06 fm, in FNAL/MILC 17 three new ensembles have been employed; two with resolution 0.042 fm and light-quark masses equal to either one fifth of the strange-quark mass (\(m_s/5\)) or to the physical up-down average mass, and one at \(a\approx \) 0.03 fm with light-quark masses equal to \(m_s/5\). In addition, the statistics on the \(a\approx \) 0.06 fm ensemble have been increased. As in FNAL/MILC 14A, the HISQ fermionic regularization and the 1-loop tadpole improved Symanzik gauge action have been used for the generation of configurations, produced by a combination of the RHMC and the RHMD algorithms. The analysis, absolute and relative scale setting, and the chiral/continuum extrapolations are performed in essentially the same way as in FNAL/MILC 14A and the latter rely on the use of heavy-meson rooted all-staggered chiral perturbation theory (HMrAS\(\chi \)PT) [518] at NNLO with the inclusion of \(\hbox {N}^3\)LO mass-dependent analytic terms. A novel aspect is represented by the inclusion of corrections due to the nonequilibration of the topological charge. Such freezing of the topology is particularly severe at the two new fine lattice spacings. Following [114] such corrections are computed in the context of heavy-meson \(\chi \)PT, through an expansion in \(1/\chi _TV\), with \(\chi _T\) being the topological susceptibility in a fully-sampled, large-volume ensemble. The resulting systematic error turns out to be of the same size as other systematic uncertainties such as the scale setting. The final total errors (below 0.5%) however are dominated by statistics and the systematic due to chiral/continuum extrapolations. As in FNAL/MILC 14A the results for the decay constants are used in combination with the experimental decay rates for \(D_{(s)}^+ \rightarrow \ell \nu _\ell \) in order to perform a unitarity test of the second row of the CKM matrix. After correcting the experimental decay rates from PDG by the known long- and short-distance electroweak contributions and including a 0.6% uncertainty to account for unknown electromagnetic corrections (as done in FNAL/MILC 14A and discussed in the previous FLAG review), the FNAL/MILC collaboration obtains \(1- |V_{cd}|^2 - |V_{cs}|^2 - |V_{cb}|^2 =-0.049(32)\), which is compatible with CKM unitarity within 1.5 standard deviations.
The results in FNAL/MILC 17 [5] replace those from FNAL/MILC 14A [18] in our \(N_f=2\,+\,1\,+\,1\) final estimates, which are therefore obtained by performing a weighted average with ETM 14E [34] and read
where the error on the average of \(f_{D}\) has been rescaled by the factor \(\sqrt{\chi ^2/\text{ dof }}=1.22\).
7.2 Form factors for \(D\rightarrow \pi \ell \nu \) and \(D\rightarrow K \ell \nu \) semileptonic decays
The SM prediction for the differential decay rate of the semileptonic processes \(D\rightarrow \pi \ell \nu \) and \(D\rightarrow K \ell \nu \) can be written as
where \(x = d, s\) is the daughter light quark, \(P= \pi , K\) is the daughter light-pseudoscalar meson, \(q = (p_D - p_P)\) is the momentum of the outgoing lepton pair, and \(E_P\) is the light-pseudoscalar meson energy in the rest frame of the decaying D. The vector and scalar form factors \(f_+(q^2)\) and \(f_0(q^2)\) parameterize the hadronic matrix element of the heavy-to-light quark flavour-changing vector current \(V_\mu = {\overline{x}} \gamma _\mu c\),
and satisfy the kinematic constraint \(f_+(0) = f_0(0)\). Because the contribution to the decay width from the scalar form factor is proportional to \(m_\ell ^2\), within current precision standards it can be neglected for \(\ell = e, \mu \), and Eq. (171) simplifies to
In models of new physics, decay rates may also receive contributions from matrix elements of other parity-even currents. In the case of the scalar density, partial vector current conservation allows one to write matrix elements of the latter in terms of \(f_+\) and \(f_0\), while for tensor currents \(T_{\mu \nu }={{\bar{x}}}\sigma _{\mu \nu }c\) a new form factor has to be introduced, viz.,
Recall that, unlike the Noether current \(V_\mu \), the operator \(T_{\mu \nu }\) requires a scale-dependent renormalization.
Lattice-QCD computations of \(f_{+,0}\) allow for comparisons to experiment to ascertain whether the SM provides the correct prediction for the \(q^2\)-dependence of \(d\Gamma (D\rightarrow P\ell \nu )/dq^2\); and, subsequently, to determine the CKM matrix elements \(|V_{cd}|\) and \(|V_{cs}|\) from Eq. (171). The inclusion of \(f_T\) allows for analyses to constrain new physics. Currently, state-of-the-art experimental results by CLEO-c [519] and BESIII [520, 521] provide data for the differential rates in the whole \(q^2\) range available, with a precision of order 2–3% for the total branching fractions in both the electron and muon final channels.
Calculations of the \(D\rightarrow \pi \ell \nu \) and \(D\rightarrow K \ell \nu \) form factors typically use the same light-quark and charm-quark actions as those of the leptonic decay constants \(f_D\) and \(f_{D_s}\). Therefore many of the same issues arise; in particular, considerations about cutoff effects coming from the large charm-quark mass, or the normalization of weak currents, apply. Additional complications arise, however, due to the necessity of covering a sizeable range of values in \(q^2\):
Lattice kinematics imposes restrictions on the values of the hadron momenta. Because lattice calculations are performed in a finite spatial volume, the pion or kaon three-momentum can only take discrete values in units of \(2\pi /L\) when periodic boundary conditions are used. For typical box sizes in recent lattice D- and B-meson form-factor calculations, \(L \sim 2.5\)–3 fm; thus the smallest nonzero momentum in most of these analyses lies in the range \(|\vec {p}_P| \sim 400\)–500 MeV. The largest momentum in lattice heavy–light form-factor calculations is typically restricted to \( |\vec {p}_P| \le 4\pi /L\). For \(D \rightarrow \pi \ell \nu \) and \(D \rightarrow K \ell \nu \), \(q^2=0\) corresponds to \(|\vec {p}_\pi | \sim 940\) MeV and \(|\vec {p}_K| \sim 1\) GeV, respectively, and the full recoil-momentum region is within the range of accessible lattice momenta. This has implications for both the accuracy of the study of the \(q^2\)-dependence, and the precision of the computation, since statistical errors and cutoff effects tend to increase at larger meson momenta. As a consequence, many recent studies have incorporated the use of nonperiodic (“twisted”) boundary conditions [522, 523] as a means to circumvent these difficulties and study other values of momentum including, perhaps, that for which \(q^2=0\) [67, 524,525,526,527,528].
Final-state pions and kaons can have energies \(\gtrsim 1~\mathrm{GeV}\), given the available kinematical range \(0 \lesssim q^2 \le q_{\mathrm{max}}^2=(m_D-m_P)^2\). This makes the use of (heavy-meson) chiral perturbation theory to extrapolate to physical light-quark masses potentially problematic.
Accurate comparisons to experiment, including the determination of CKM parameters, requires good control of systematic uncertainties in the parameterization of the \(q^2\)-dependence of form factors. While this issue is far more important for semileptonic B decays, where existing lattice computations cover just a fraction of the kinematic range, the increase in experimental precision requires accurate work in the charm sector as well. The parameterization of semileptonic form factors is discussed in detail in Appendix A.5.
The most advanced \(N_f = 2\) lattice-QCD calculation of the \(D \rightarrow \pi \ell \nu \) and \(D \rightarrow K \ell \nu \) form factors is by the ETM collaboration [524]. This work, for which published results are still at the preliminary stage, uses the twisted-mass Wilson action for both the light and charm quarks, with three lattice spacings down to \(a \approx 0.068\) fm and (charged) pion masses down to \(m_\pi \approx 270\) MeV. The calculation employs the method of Ref. [529] to avoid the need to renormalize the vector current, by introducing double-ratios of lattice three-point correlation functions in which the vector current renormalization cancels. Discretization errors in the double ratio are of \({{\mathcal {O}}}((am_c)^2)\), due to the automatic \({{\mathcal {O}}}(a)\) improvement at maximal twist. The vector and scalar form factors \(f_+(q^2)\) and \(f_0(q^2)\) are obtained by taking suitable linear combinations of these double ratios. Extrapolation to physical light-quark masses is performed using SU(2) heavy–light meson \(\chi \)PT. The ETM collaboration simulates with twisted boundary conditions for the valence quarks to access arbitrary momentum values over the full physical \(q^2\) range, and interpolate to \(q^2=0\) using the Bečirević–Kaidalov ansatz [530]. The statistical errors in \(f_+^{D\pi }(0)\) and \(f_+^{DK}(0)\) are 9% and 7%, respectively, and lead to rather large systematic uncertainties in the fits to the light-quark mass and energy dependence (7% and 5%, respectively). Another significant source of uncertainty is from discretization errors (5% and 3%, respectively). On the finest lattice spacing used in this analysis \(am_c \sim 0.17\), so \({\mathcal {O}}((am_c)^2)\) cutoff errors are expected to be about 5%. This can be reduced by including the existing \(N_f = 2\) twisted-mass ensembles with \(a \approx 0.051\) fm discussed in Ref. [48].
The first published \(N_f = 2\,+\,1\) lattice-QCD calculation of the \(D \rightarrow \pi \ell \nu \) and \(D \rightarrow K \ell \nu \) form factors came from the Fermilab Lattice, MILC, and HPQCD collaborations [531].Footnote 40 This work uses asqtad-improved staggered sea quarks and light (u, d, s) valence quarks and the Fermilab action for the charm quarks, with a single lattice spacing of \(a \approx 0.12\) fm, and for a minimum RMS pion mass is \(\approx 510\) MeV, dictated by the presence of fairly large staggered taste splittings. The vector current is normalized using a mostly nonperturbative approach, such that the perturbative truncation error is expected to be negligible compared to other systematics. Results for the form factors are provided over the full kinematic range, rather than focusing just at \(q^2=0\) as was customary in previous work, and fitted to a Bečirević-Kaidalov ansatz. In fact, the publication of this result predated the precise measurements of the \(D\rightarrow K \ell \nu \) decay width by the FOCUS [532] and Belle experiments [533], and showed good agreement with the experimental determination of the shape of \(f_+^{DK}(q^2)\). Progress on extending this work was reported in [534]; efforts are aimed at reducing both the statistical and systematic errors in \(f_+^{D\pi }(q^2)\) and \(f_+^{DK}(q^2)\) by increasing the number of configurations analyzed, simulating with lighter pions, and adding lattice spacings as fine as \(a \approx 0.045\) fm.
The most precise published calculations of the \(D \rightarrow \pi \ell \nu \) [68] and \(D \rightarrow K \ell \nu \) [69] form factors in \(N_f=2\,+\,1\) QCD are by the HPQCD collaboration. They are also based on \(N_f = 2\,+\,1\) asqtad-improved staggered MILC configurations, but use two lattice spacings \(a \approx 0.09\) and 0.12 fm, and a HISQ action for the valence u, d, s, and c quarks. In these mixed-action calculations, the HISQ valence light-quark masses are tuned so that the ratio \(m_l/m_s\) is approximately the same as for the sea quarks; the minimum RMS sea-pion mass \(\approx 390\) MeV. Form factors are determined only at \(q^2=0\), by using a Ward identity to relate matrix elements of vector currents to matrix elements of the absolutely normalized quantity \((m_{c} - m_{x} ) \langle P | {\bar{x}}c | D \rangle \), and exploiting the kinematic identity \(f_+(0) = f_0(0)\) to yield \(f_+(q^2=0) = (m_{c} - m_{x} ) \langle P | {\bar{x}}c | D \rangle / (m^2_D - m^2_P)\). A modified z-expansion (cf. Appendix A.5) is employed to simultaneously extrapolate to the physical light-quark masses and continuum and interpolate to \(q^2 = 0\), and allow the coefficients of the series expansion to vary with the light- and charm-quark masses. The form of the light-quark dependence is inspired by \(\chi \)PT, and includes logarithms of the form \(m_\pi ^2 \mathrm{log} (m_\pi ^2)\) as well as polynomials in the valence-, sea-, and charm-quark masses. Polynomials in \(E_{\pi (K)}\) are also included to parameterize momentum-dependent discretization errors. The number of terms is increased until the result for \(f_+(0)\) stabilizes, such that the quoted fit error for \(f_+(0)\) not only contains statistical uncertainties, but also reflects relevant systematics. The largest quoted uncertainties in these calculations are from statistics and charm-quark discretization errors. Progress towards extending the computation to the full \(q^2\) range have been reported in [525, 526]; however, the information contained in these conference proceedings is not enough to establish an updated value of \(f_+(0)\) with respect to the previous journal publications.
The most recent \(N_f=2\,+\,1\) computation of D semileptonic form factors has been carried out by the JLQCD collaboration, and so far published in conference proceedings only; the most recent update is Ref. [535]. They use their own Möbius domain-wall configurations at three values of the lattice spacing \(a=0.080, 0.055, 0.044~\mathrm{fm}\), with several pion masses ranging from 226 to 501 MeV (though there is so far only one ensemble, with \(m_\pi =284~\mathrm{MeV}\), at the finest lattice spacing). The vector and scalar form factors are computed at four values of the momentum transfer for each ensemble. The computed form factors are observed to depend mildly on both the lattice spacing and the pion mass. The momentum dependence of the form factors is fitted to a BCL z-parameterization with a Blaschke factor that contains the measured value of the \(D_{(s)}^*\) mass in the vector channel, and a trivial Blaschke factor in the scalar channel. The systematics of this latter fit is assessed by a BCL fit with the experimental value of the scalar resonance mass in the Blaschke factor. Continuum and chiral extrapolations are carried out through a linear fit in the squared lattice spacing and the square pion and \(\eta _c\) masses. A global fit that uses hard-pion HM\(\chi \)PT to model the mass dependence is furthermore used for a comparison of the form factor shapes with experimental data.Footnote 41 Since the computation is only published in proceedings so far, it will not enter our \(N_f=2\,+\,1\) average.Footnote 42
The first full computation of both the vector and scalar form factors in \(N_f=2\,+\,1\,+\,1\) QCD has been achieved by the ETM collaboration [67]. They have furthermore provided a separate determination of the tensor form factor, relevant for new physics analyses [528]. Both works use the available \(N_f = 2\,+\,1\,+\,1\) twisted-mass Wilson lattices [186], totaling three lattice spacings down to \(a\approx 0.06\) fm, and a minimal pion mass of 220 MeV. Matrix elements are extracted from suitable double ratios of correlation functions that avoid the need of nontrivial current normalizations. The use of twisted boundary conditions allows both for imposing several kinematical conditions, and considering arbitrary frames that include moving initial mesons. After interpolation to the physical strange- and charm-quark masses, the results for form factors are fitted to a modified z-expansion that takes into account both the light-quark mass dependence through hard-pion SU(2) \(\chi \)PT [537], and the lattice-spacing dependence. In the case of the latter, a detailed study of Lorentz-breaking effects due to the breaking of rotational invariance down to the hypercubic subgroup is performed, leading to a nontrivial momentum-dependent parameterization of cutoff effects. The z-parameterization itself includes a single-pole Blaschke factor (save for the scalar channel in \(D\rightarrow K\), where the Blaschke factor is trivial), with pole masses treated as free parameters. The final quoted uncertainty on the form factors is about 5–6% for \(D\rightarrow \pi \), and 4% for \(D\rightarrow K\). The dominant source of uncertainty is quoted as statistical+fitting procedure+input parameters – the latter referring to the values of quark masses, the lattice spacing (i.e., scale setting), and the LO SU(2) LECs.
The FNAL/MILC collaboration has also reported ongoing work on extending their computation to \(N_f=2\,+\,1\,+\,1\), using MILC HISQ ensembles at four values of the lattice spacing down to \(a=0.042~\mathrm{fm}\) and pion masses down to the physical point. The latest updates on this computation, focusing on the form factors at \(q^2=0\), but without explicit values of the latter yet, can be found in Refs. [538, 539]. A similar update of the HPQCD collaboration is ongoing, for which results for the \(D \rightarrow K\) vector and scalar form factors are being determined for the full \(q^2\) range based on MILC \(N_f=2\,+\,1\,+\,1\) ensembles [540]. This supersedes previously reported progress by HPQCD in extending their \(N_f=2\,+\,1\) computation to nonvanishing \(q^2\), see Refs. [525, 526].
Table 31 contains our summary of the existing calculations of the \(D \rightarrow \pi \ell \nu \) and \(D \rightarrow K \ell \nu \) semileptonic form factors. Additional tables in Appendix B.5.1 provide further details on the simulation parameters and comparisons of the error estimates. Recall that only calculations without red tags that are published in a refereed journal are included in the FLAG average. We will quote no FLAG estimate for \(N_f=2\), since the results by ETM have only appeared in conference proceedings. For \(N_f=2\,+\,1\), only HPQCD 10B,11 qualify, which provides our estimate for \(f_+(q^2=0)=f_0(q^2=0)\). For \(N_f=2\,+\,1\,+\,1\), we quote as FLAG estimate the only available result by ETM 17D:


In Fig. 21 we display the existing \(N_f =2\), \(N_f = 2\,+\,1\), and \(N_f=2\,+\,1\,+\,1\) results for \(f_+^{D\pi }(0)\) and \(f_+^{DK}(0)\); the grey bands show our estimates of these quantities. Sect. 7.4 discusses the implications of these results for determinations of the CKM matrix elements \(|V_{cd}|\) and \(|V_{cs}|\) and tests of unitarity of the second row of the CKM matrix.
\(D\rightarrow \pi \ell \nu \) and \(D\rightarrow K\ell \nu \) semileptonic form factors at \(q^2=0\). The HPQCD result for \(f_+^{D\pi }(0)\) is from HPQCD 11, the one for \(f_+^{DK}(0)\) represents HPQCD 10B (see Table 31)
7.3 Form factors for \(\Lambda _c\rightarrow \Lambda \ell \nu \) semileptonic decays
In recent years, Meinel and collaborators have pioneered the computation of form factors for semileptonic heavy-baryon decays (see also Sect. 8.6). In particular, Ref. [541] deals with \(\Lambda _c\rightarrow \Lambda \ell \nu \) transitions. The motivation for this study is twofold: apart from allowing for a new determination of \(|V_{cs}|\) in combination with the recent pioneering experimental measurement of the decay rates in Refs. [542, 543], it allows one to test the techniques previously employed for b baryons in the better-controlled (from the point of view of systematics) charm environment.
The amplitudes of the decays \(\Lambda _c\rightarrow \Lambda \ell \nu \) receive contributions from both the vector and the axial components of the current in the matrix element \(\langle \Lambda |\bar{s}\gamma ^\mu ({\mathbf {1}}-\gamma _5)c|\Lambda _c\rangle \), and can be parameterized in terms of six different form factors – see, e.g., Ref. [544] for a complete description. They split into three form factors \(f_+\), \(f_0\), \(f_\perp \) in the parity-even sector, mediated by the vector component of the current, and another three form factors \(g_+,g_0,g_\perp \) in the parity-odd sector, mediated by the axial component. All of them provide contributions that are parametrically comparable.
The computation in Meinel 16 [541] uses RBC/UKQCD \(N_f=2\,+\,1\) DWF ensembles, and treats the c quarks within the Columbia RHQ approach. Two values of the lattice spacing (\(a\sim 0.11,~0.085~\mathrm{fm}\)) are considered, with the absolute scale set from the \(\Upsilon (2S)\)–\(\Upsilon (1S)\) splitting. In one ensemble the pion mass \(m_\pi =139~\mathrm{MeV}\) is at the physical point, while for other ensembles they range roughly in the 300–350 MeV interval. Results for the form factors are obtained from suitable three-point functions, and fitted to a modified z-expansion ansatz that combines the \(q^2\)-dependence with the chiral and continuum extrapolations. The paper goes on to quote the predictions for the total rates in the e and \(\mu \) channels (where errors are statistical and systematic, respectively)
The combination with the recent experimental determination of the total branching fractions by BESIII in Refs. [542, 543] to extract \(|V_{cs}|\) is discussed in Sect. 7.4 below.
7.4 Determinations of \(|V_{cd}|\) and \(|V_{cs}|\) and test of second-row CKM unitarity
We now interpret the lattice-QCD results for the \(D_{(s)}\) meson decays as determinations of the CKM matrix elements \(|V_{cd}|\) and \(|V_{cs}|\) in the Standard Model.
For the leptonic decays, we use the latest experimental averages from Rosner, Stone and Van de Water for the Particle Data Group [137]
By combining these with the average values of \(f_D\) and \(f_{D_s}\) from the individual \(N_f = 2\), \(N_f = 2\,+\,1\) and \(N_f=2\,+\,1\,+\,1\) lattice-QCD calculations that satisfy the FLAG criteria, we obtain the results for the CKM matrix elements \(|V_{cd}|\) and \(|V_{cs}|\) in Table 32. For our preferred values we use the averaged \(N_f=2\) and \(N_f = 2\,+\,1\) results for \(f_D\) and \(f_{D_s}\) in Eqs. (162–170). We obtain
where the errors shown are from the lattice calculation and experiment (plus nonlattice theory), respectively. For the \(N_f = 2\,+\,1\) and the \(N_f=2\,+\,1\,+\,1\) determinations, the uncertainties from the lattice-QCD calculations of the decay constants are smaller than the experimental uncertainties in the branching fractions. Although the results for \(|V_{cs}|\) are slightly larger than one, they are consistent with unity within at most 1.5 standard deviations.
The leptonic determinations of these CKM matrix elements have uncertainties that are reaching the few-percent level. However, higher-order electroweak and hadronic-structure dependent corrections to the rate have not been computed for the case of \(D_{(s)}\) mesons, whereas they have been estimated to be around 1–2% for pion and kaon decays [545]. It is therefore important that such theoretical calculations are tackled soon, perhaps directly on the lattice, as proposed in Ref. [206].
For D meson semileptonic decays, there is no update on the lattice side from the previous version of our review for \(N_f=2\,+\,1\), where the only works entering the FLAG averages are HPQCD 10B/11 [68, 69], that provide values for \(f_+^{DK}(0)\) and \(f_+^{D\pi }(0)\), respectively, cf. Eq. (175). The latter can be combined with the latest experimental averages from the HFLAV collaboration [221]:
where we have combined the experimental statistical and systematic errors in quadrature, to determine the CKM parameters.
The new \(N_f=2\,+\,1\,+\,1\) result for form factors in ETM 17D [67] has a broader scope, in that a companion paper [546] provides a determination of \(|V_{cd}|\) and \(|V_{cs}|\) from a joint fit to lattice and experimental data. This procedure is a priori preferable to the matching at \(q^2=0\), and we will therefore use the values in Ref. [546] for our CKM averages. It has to be stressed that this entails a measure of bias in the comparison with the above \(N_f=2\,+\,1\) result; to quantify the effect, we also show in Fig. 22 the values of \(|V_{cd}|\) and \(|V_{cs}|\) obtained by using the values for \(f_+(0)\) quoted in [67], cf. Eq. (176), together with Eq. (182).
Finally, Meinel 16 has determined the form factors for \(\Lambda _c\rightarrow \Lambda \ell \nu \) decays for \(N_f=2\,+\,1\), which results in a determination of \(|V_{cs}|\) in combination with the experimental measurement of the branching fractions for the \(e^+\) and \(\mu ^+\) channels in Refs. [542, 543]. In Ref. [541] the value \(|V_{cs}|=0.949(24)(14)(49)\) is quoted, where the first error comes from the lattice computation, the second from the \(\Lambda _c\) lifetime, and the third from the branching fraction of the decay. While the lattice uncertainty is competitive with meson channels, the experimental uncertainty is far larger.
Comparison of determinations of \(|V_{cd}|\) and \(|V_{cs}|\) obtained from lattice methods with nonlattice determinations and the standard model prediction based on CKM unitarity. When two references are listed on a single row, the first corresponds to the lattice input for \(|V_{cd}|\) and the second to that for \(|V_{cs}|\). The results denoted by squares are from leptonic decays, while those denoted by triangles are from semileptonic decays. The points indicated as ETM 17D (\(q^2=0\)) do not contribute to the average, and are shown for comparison purposes (see text)
We thus proceed to quote our estimates from semileptonic decay as
where the errors for \(N_f=2\,+\,1\) are lattice and experimental (plus nonlattice theory), respectively. It has to be stressed that all errors are largely theory-dominated. The above values are compared with individual leptonic determinations in Table 32.
In Table 33 we summarize the results for \(|V_{cd}|\) and \(|V_{cs}|\) from leptonic and semileptonic decays, and compare them to determinations from neutrino scattering (for \(|V_{cd}|\) only) and CKM unitarity. These results are also plotted in Fig. 22. For both \(|V_{cd}|\) and \(|V_{cs}|\), the errors in the direct determinations from leptonic and semileptonic decays are approximately one order of magnitude larger than the indirect determination from CKM unitarity. The direct and indirect determinations are still always compatible within at most \(1.2\sigma \), save for the leptonic determinations of \(|V_{cs}|\) – that show a \(\sim 2\sigma \) deviation for all values of \(N_f\) – and \(|V_{cd}|\) using the \(N_f=2\,+\,1\,+\,1\) lattice result, where the difference is \(1.8\sigma \).
In order to provide final estimates, we average all the available results separately for each value of \(N_f\). In all cases, we assume that results that share a significant fraction of the underlying gauge ensembles have statistical errors that are 100% correlated; the same applies to the heavy-quark discretization and scale setting errors in HPQCD calculations of leptonic and semileptonic decays. Finally, we include a 100% correlation in the fraction of the error of \(|V_{cd(s)}|\) leptonic determinations that comes from the experimental input, to avoid an artificial reduction of the experimental uncertainty in the averages. We finally quote
where the errors include both theoretical and experimental uncertainties. These averages also appear in Fig. 22. The mutual consistency between the various lattice results is always good, save for the case of \(|V_{cd}|\) with \(N_f=2\,+\,1\,+\,1\), where a \(\sim 2\sigma \) tension between the leptonic and semileptonic determinations shows up. Currently, the leptonic and semileptonic determinations of \(V_{cd}\) are controlled by experimental and lattice uncertainties, respectively. The leptonic error will be reduced by Belle II and BES III. It would be valuable to have other lattice calculations of the semileptonic form factors.
Using the lattice determinations of \(|V_{cd}|\) and \(|V_{cs}|\) in Table 33, we can test the unitarity of the second row of the CKM matrix. We obtain
Again, tensions at the 2\(\sigma \) level with CKM unitarity are visible, as also reported in the PDG review [133], where the value 0.063(34) is quoted for the quantity in the equations above. Given the current level of precision, this result does not depend on \(|V_{cb}|\), which is of \({\mathcal {O}}(10^{-2})\).
8 B-meson decay constants, mixing parameters and form factors
Authors: Y. Aoki, D. Bečirević, M. Della Morte, S. Gottlieb, D. Lin, E. Lunghi, C. Pena
The (semi)leptonic decay and mixing processes of \(B_{(s)}\) mesons have been playing a crucial role in flavour physics. In particular, they contain important information for the investigation of the \(b{-}d\) unitarity triangle in the Cabibbo-Kobayashi-Maskawa (CKM) matrix, and can be ideal probes of physics beyond the Standard Model. The charged-current decay channels \(B^{+} \rightarrow l^{+} \nu _{l}\) and \(B^{0} \rightarrow \pi ^{-} l^{+} \nu _{l}\), where \(l^{+}\) is a charged lepton with \(\nu _{l}\) being the corresponding neutrino, are essential in extracting the CKM matrix element \(|V_{ub}|\). Similarly, the B to \(D^{(*)}\) semileptonic transitions can be used to determine \(|V_{cb}|\). The flavour-changing neutral current (FCNC) processes, such as \(B\rightarrow K^{(*)} \ell ^+ \ell ^-\) and \(B_{d(s)} \rightarrow \ell ^+ \ell ^-\), occur only beyond the tree level in weak interactions and are suppressed in the Standard Model. Therefore, these processes can be sensitive to new physics, since heavy particles can contribute to the loop diagrams. They are also suitable channels for the extraction of the CKM matrix elements involving the top quark which can appear in the loop. The decays \(B\rightarrow D^{(*)}\ell \nu \) and \(B\rightarrow K^{(*)} \ell \ell \) can also be used to test lepton flavour universality by comparing results for \(\ell = e\), \(\mu \) and \(\tau \). In particular, anomalies have been seen in the ratios \(R(D^{(*)}) = {{{\mathcal {B}}}} (B\rightarrow D^{(*)}\tau \nu ) /{{{\mathcal {B}}}} (B\rightarrow D^{(*)}\ell \nu )_{\ell =e,\mu }\) and \({{{{R}}}}(K^{(*)}) = {{{\mathcal {B}}}} (B\rightarrow K^{(*)}\mu \mu ) /{{{\mathcal {B}}}} (B\rightarrow K^{(*)}ee)\). In addition, the neutral \(B_{d(s)}\)-meson mixings are FCNC processes and are dominated by the 1-loop “box” diagrams containing the top quark and the W bosons. Thus, using the experimentally measured neutral \(B^0_{d(s)}\)-meson oscillation frequencies, \(\Delta M_{d(s)}\), and the theoretical calculations for the relevant hadronic mixing matrix elements, one can obtain \(|V_{td}|\) and \(|V_{ts}|\) in the Standard Model.Footnote 43
Accommodating the light quarks and the b quark simultaneously in lattice-QCD computations is a challenging endeavour. To incorporate the pion and the b hadrons with their physical masses, the simulations have to be performed using the lattice size \({\hat{L}} = L/a \sim {\mathcal {O}}(10^{2})\), where a is the lattice spacing and L is the physical (dimensionful) box size. The most ambitious calculations are now using such volumes; however, many ensembles are smaller. Therefore, in addition to employing Chiral Perturbation Theory for the extrapolations in the light-quark mass, current lattice calculations for quantities involving b hadrons often make use of effective theories that allow one to expand in inverse powers of \(m_{b}\). In this regard, two general approaches are widely adopted. On the one hand, effective field theories such as Heavy-Quark Effective Theory (HQET) and Nonrelativistic QCD (NRQCD) can be directly implemented in numerical computations. On the other hand, a relativistic quark action can be improved à la Symanzik to suppress cutoff errors, and then re-interpreted in a manner that is suitable for heavy-quark physics calculations. This latter strategy is often referred to as the method of the Relativistic Heavy-Quark Action (RHQA). The utilization of such effective theories inevitably introduces systematic uncertainties that are not present in light-quark calculations. These uncertainties can arise from the truncation of the expansion in constructing the effective theories (as in HQET and NRQCD), or from more intricate cutoff effects (as in NRQCD and RQHA). They can also be introduced through more complicated renormalization procedures which often lead to significant systematic effects in matching the lattice operators to their continuum counterparts. For instance, due to the use of different actions for the heavy and the light quarks, it is more difficult to construct absolutely normalized bottom-light currents.
Complementary to the above “effective theory approaches”, another popular method is to simulate the heavy and the light quarks using the same (normally improved) lattice action at several values of the heavy-quark mass \(m_{h}\) with \(a m_{h} < 1\) and \(m_{h} < m_{b}\). This enables one to employ HQET-inspired relations to extrapolate the computed quantities to the physical b mass. When combined with results obtained in the static heavy-quark limit, this approach can be rendered into an interpolation, instead of extrapolation, in \(m_{h}\). The discretization errors are the main source of the systematic effects in this method, and very small lattice spacings are needed to keep such errors under control.
In recent years, it has also been possible to perform lattice simulations at very fine lattice spacings and treat heavy quarks as fully relativistic fermions without resorting to effective field theories. Such simulations are of course very demanding in computing resources.
Because of the challenge described above, the efforts that have been made to obtain reliable, accurate lattice-QCD results for physics of the b quark have been enormous. These efforts include significant theoretical progress in formulating QCD with heavy quarks on the lattice. This aspect is briefly reviewed in Appendix A.1.3.
In this section, we summarize the results of the B-meson leptonic decay constants, the neutral B-mixing parameters, and the semileptonic form factors, from lattice QCD. To be focused on the calculations that have strong phenomenological impact, we limit the review to results based on modern simulations containing dynamical fermions with reasonably light pion masses (below approximately 500 MeV). There has been significant progress for b-quark physics since the previous review. There are also a number of calculations that are still in a preliminary stage. We have made note of some of these in anticipation of later publications, whose results will contribute to future averages.
Following our review of \(B_{(s)}\)-meson leptonic decay constants, the neutral B-meson mixing parameters, and semileptonic form factors, we then interpret our results within the context of the Standard Model. We combine our best-determined values of the hadronic matrix elements with the most recent experimentally-measured branching fractions to obtain \(|V_{ub}|\) and \(|V_{cb}|\), and compare these results to those obtained from inclusive semileptonic B decays.
Recent lattice-QCD averages for \(B^+\)- and \(B_s\)-meson decay constants were also presented by the Particle Data Group (PDG) in Ref. [133]. The PDG three- and four-flavour averages for these quantities differ from those quoted here because the PDG provides the charged-meson decay constant \(f_{B^+}\), while we present the isospin-averaged meson-decay constant \(f_B\).
8.1 Leptonic decay constants \(f_B\) and \(f_{B_s}\)
The B- and \(B_s\)-meson decay constants are crucial inputs for extracting information from leptonic B decays. Charged B mesons can decay to the lepton-neutrino final state through the charged-current weak interaction. On the other hand, neutral \(B_{d(s)}\) mesons can decay to a charged-lepton pair via a flavour-changing neutral current (FCNC) process.
In the Standard Model the decay rate for \(B^+ \rightarrow \ell ^+ \nu _{\ell }\) is described by a formula identical to Eq. (160), with \(D_{(s)}\) replaced by B, and the relevant CKM matrix element \(V_{cq}\) replaced by \(V_{ub}\),
The only charged-current B-meson decay that has been observed so far is \(B^{+} \rightarrow \tau ^{+} \nu _{\tau }\), which has been measured by the Belle and Babar collaborations [549, 550]. Both collaborations have reported results with errors around \(20\%\). These measurements can be used to determine \(|V_{ub}|\) when combined with lattice-QCD predictions of the corresponding decay constant.
Neutral \(B_{d(s)}\)-meson decays to a charged-lepton pair \(B_{d(s)} \rightarrow l^{+} l^{-}\) is a FCNC process, and can only occur at one loop in the Standard Model. Hence these processes are expected to be rare, and are sensitive to physics beyond the Standard Model. The corresponding expression for the branching fraction has the form
where the light quark \(q=s\) or d, and the function Y includes NLO QCD and electro-weak corrections [465, 551]. Evidence for both \(B_s \rightarrow \mu ^+ \mu ^-\) and \(B_s \rightarrow \mu ^+ \mu ^-\) decays was first observed by the CMS and the LHCb collaborations, and a combined analysis was presented in 2014 in Ref. [547]. In 2017, the LHCb collaboration reported their latest measurements as [548]
which are compatible with the Standard Model predictions [552].
The decay constants \(f_{B_q}\) (with \(q=u,d,s\)) parameterize the matrix elements of the corresponding axial-vector currents \(A^{\mu }_{bq} = {\bar{b}}\gamma ^{\mu }\gamma ^5q\) analogously to the definition of \(f_{D_q}\) in Sect. 7.1:
For heavy–light mesons, it is convenient to define and analyse the quantity
which approaches a constant (up to logarithmic corrections) in the \(m_B \rightarrow \infty \) limit because of the heavy-quark symmetry. In the following discussion we denote lattice data for \(\Phi \)(f) obtained at a heavy-quark mass \(m_h\) and light valence-quark mass \(m_{\ell }\) as \(\Phi _{h\ell }\)(\(f_{hl}\)), to differentiate them from the corresponding quantities at the physical b- and light-quark masses.
The SU(3)-breaking ratio \(f_{B_s}/f_B\) is of phenomenological interest. This is because in lattice-QCD calculations for this quantity, many systematic effects can be partially reduced. These include discretization errors, heavy-quark mass tuning effects, and renormalization/ matching errors, amongst others. On the other hand, this SU(3)-breaking ratio is still sensitive to the chiral extrapolation. Given that the chiral extrapolation is under control, one can then adopt \(f_{B_s}/f_B\) as input in extracting phenomenologically-interesting quantities. In addition, it often happens to be easier to obtain lattice results for \(f_{B_{s}}\) with smaller errors. Therefore, one can combine the \(B_{s}\)-meson decay constant with the SU(3)-breaking ratio to calculate \(f_{B}\). Such a strategy can lead to better precision in the computation of the B-meson decay constant, and has been adopted by the ETM [26, 64] and the HPQCD collaborations [73].
It is clear that the decay constants for charged and neutral B mesons play different roles in flavour-physics phenomenology. As already mentioned above, the knowledge of the \(B^{+}\)-meson decay constant \(f_{B^{+}}\) is essential for extracting \(|V_{ub}|\) from leptonic \(B^{+}\) decays. The neutral B-meson decay constants \(f_{B^{0}}\) and \(f_{B_{s}}\) are inputs for the search of new physics in rare leptonic \(B^{0}\) decays. In view of this, it is desirable to include isospin-breaking effects in lattice computations for these quantities, and have results for \(f_{B^{+}}\) and \(f_{B^{0}}\). With the increasing precision of recent lattice calculations, isospin splittings for B-meson decay constants are significant, and will play an important role in the foreseeable future. A few collaborations reported \(f_{B^{+}}\) and \(f_{B^{0}}\) separately by taking into account strong isospin effects in the valence sector, and estimated the corrections from electromagnetism. To properly use these results for extracting phenomenologically relevant information, one would have to take into account QED effects in the B-meson leptonic decay rates.Footnote 44 Currently, errors on the experimental measurements on these decay rates are still very large. In this review, we will then concentrate on the isospin-averaged result \(f_{B}\) and the \(B_{s}\)-meson decay constant, as well as the SU(3)-breaking ratio \(f_{B_{s}}/f_{B}\). For the world average for lattice determination of \(f_{B^{+}}\) and \(f_{B_{s}}/f_{B^{+}}\), we refer the reader to the latest work from the Particle Data Group (PDG) [133]. Notice that the \(N_{f} = 2\,+\,1\) lattice results used in Ref. [133] and the current review are identical. We will discuss this in further detail at the end of this section.
The status of lattice-QCD computations for B-meson decay constants and the SU(3)-breaking ratio, using gauge-field ensembles with light dynamical fermions, is summarized in Tables 34 and 35, while Figs. 23 and 24 contain the graphical presentation of the collected results and our averages. Many results in these tables and plots were already reviewed in detail in the previous FLAG report. Below we will describe the new results that appeared after January 2016.
Decay constants of the B and \(B_s\) mesons. The values are taken from Table 34 (the \(f_B\) entry for FNAL/MILC 11 represents \(f_{B^+}\)). The significance of the colours is explained in Sect. 2. The black squares and grey bands indicate our averages in Eqs. (196), (199), (202), (197), (200) and (203)
Ratio of the decay constants of the B and \(B_s\) mesons. The values are taken from Table 35. Results labelled as FNAL/MILC 17 1 and FNAL/MILC 17 2 correspond to those for \(f_{B_{s}}/f_{B^{0}}\) and \(f_{B_{s}}/f_{B^{+}}\) reported in FNAL/MILC 17. The significance of the colours is explained in Sect. 2. The black squares and grey bands indicate our averages in Eqs. (198), (201) and (204)
No new \(N_{f}=2\) and \(N_{f}=2\,+\,1\) project for computing \(f_{B}\), \(f_{B_{s}}\) and \(f_{B_{s}}/f_{B}\) were completed after the publication of the previous FLAG review [3]. Therefore, our averages for these cases stay the same as those in Ref. [3],
There have been results for \(f_{B_{(s)}}\) and \(f_{B_{s}}/f_{B}\) from three collaborations, ETMC, HPQCD and FNAL/MILC since the last FLAG report. In Tables 34 and 35, these results are labelled ETM 16B [26], HPQCD 17A [71] and FNAL/MILC 17 [5].
In ETM 16B [26], simulations at three values of lattice spacing, \(a=0.0885\), 0.0815 and 0.0619 fm are performed with twisted-mass Wilson fermions and the Iwasaki gauge action. The three lattice spacings correspond to the bare couplings \(\beta =1.90\), 1.95 and 2.10. The pion masses in this work range from 210 to 450 MeV, and the lattice sizes are between 1.97 and 2.98 fm. An essential feature in ETM 16B [26] is the use of the ratio method [560]. In the application of this approach to the B-decay constants, one first computes the quantity \({{\mathcal {F}}}_{hq} \equiv f_{hq}/M_{hq}\), where \(f_{hq}\) and \(M_{hq}\) are decay constant and mass of the pseudoscalar meson composed of valence (relativistic) heavy quark h and light (or strange) quark q. The matching between the lattice and the continuum heavy–light currents for extracting the above \(f_{hq}\) is straightforward because the valence heavy quark is also described by twisted-mass fermions. In the second step, the ratio \(z_{q} ({\bar{\mu }}^{(h)}, \lambda ) \equiv [{{\mathcal {F}}}_{hq}C_{A}^{{\mathrm {stat}}}({\bar{\mu }}^{(h^{\prime })})(\mu _{{\mathrm {pole}}}^{(h)})^{3/2}]/[{{\mathcal {F}}}_{h^{\prime }q}C_{A}^{{\mathrm {stat}}}({\bar{\mu }}^{(h)})(\mu _{{\mathrm {pole}}}^{(h^{\prime })})^{3/2}]\) is calculated, where \(\mu _{{\mathrm {pole}}}^{(h)}\) is the pole mass of the heavy quark h with \({\bar{\mu }}^{(h)}\) being the corresponding renormalized mass in a scheme (chosen to be the \({\overline{\mathrm{MS}}}\) scheme in ETM 16B [26]), \(C_{A}^{{\mathrm {stat}}}({\bar{\mu }}^{(h)})\) is the matching coefficient for the (hq)-meson decay constant in QCD and its counterpart in HQET, and \({\bar{\mu }}^{(h)} = \lambda {\bar{\mu }}^{(h^{\prime })}\) with \(\lambda \) being larger than, but close to, one. The authors of ETM 16B [26] use the NNLO perturbative result of \(C_{A}^{{\mathrm {stat}}}({\bar{\mu }}^{(h)})\) in their work. Notice that in practice one never has to determine the heavy-quark pole mass in this strategy, since it can be matched to the \({\overline{\mathrm{MS}}}\) mass, and the matching coefficient is known to NNNLO [169, 563, 564]. By starting from a “triggering” point with the heavy-quark mass around that of the charm, one can proceed with the calculations in steps, such that \({\bar{\mu }}^{(h)}\) is increased by a factor of \(\lambda \) at each step. In ETM 16B [26], the authors went up to heavy-quark mass around 3.3 GeV, and observed that all systematics were under control. In this approach, it is also crucial to employ the information that \(z_{q} ({\bar{\mu }}^{(h)}, \lambda ) \rightarrow 1\) in the limit \({\bar{\mu }}^{(h)} \rightarrow \infty \). Designing the computations in such a way that in the last step, \({\bar{\mu }}^{(h)}\) is equal to the pre-determined bottom-quark mass in the same renormalization scheme, one obtains \(f_{B_{(s)}}/M_{B_{(s)}}\). Employing experimental results for \(M_{B_{(s)}}\), the decay constants can be extracted. In ETM 16B [26], this strategy was implemented to compute \(f_{B_{s}}\). It was also performed for a double ratio to determine \((f_{B_{s}}/f_{B})/(f_{K}/f_{\pi })\), hence \(f_{B_{s}}/f_{B}\), using information of \(f_{K}/f_{\pi }\) from Ref. [34]. This double ratio leads to the advantage that it contains small coefficients for chiral logarithms. The B-meson decay constant is then computed with \(f_{B} = f_{B_{s}}/(f_{B_{s}}/f_{B})\). The authors estimated various kinds of systematic errors in their work. These include discretization errors, the effects of perturbative matching between QCD and HQET, those of chiral extrapolation, and errors associate with the value of \(f_{K}/f_{\pi }\).
The authors of HPQCD 17A [71] reanalysed the data in Ref. [70] (HPQCD 13 in Tables 34 and 35) employing a different method for computing B-decay constants with NRQCD heavy quarks and HISQ light quarks on the lattice. The NRQCD action used in this work is improved to \(O(\alpha _{s} v_{b}^{4})\), where \(v_{b}\) is the velocity of the b quark. In Ref. [70], the determination of the decay constants is carried out through studying matrix elements of axial currents. On the other hand, the same decay constants can be obtained by investigating \((m_{b} + m_{l}) \langle 0 | P | B \rangle \), where \(m_{b}\) (\(m_{l}\)) is the b- (light-)quark mass and P stands for the pseudoscalar current. The matching of this pseudoscalar current between QCD and NRQCD is performed at the precision of \({{\mathcal {O}}}(\alpha _{s})\), \({{\mathcal {O}}}(\alpha _{s}\Lambda _{{\mathrm {QCD}}}/m_{b})\) and \({{\mathcal {O}}}(\alpha _{s} a \Lambda _{{\mathrm {QCD}}})\), using lattice perturbation theory. This requires the inclusion of three operators in the NRQCD-HISQ theory. The gauge configurations used in this computation were part of those generated by the MILC collaboration, with details given in Ref. [117]. They are the ensembles obtained at three values of bare gauge coupling (\(\beta = 6.3, 6.0\) and 5.8), corresponding to lattice spacings, determined using the \(\Upsilon (2S-1A)\) splitting, between 0.09 and 0.15 fm. Pion masses are between 128 and 315 MeV. For each lattice spacing, the MILC collaboration performed simulations at several lattice volumes, such that \(M_{\pi } L \) lies between 3.3 and 4.5 for all the data points. This ensures that the finite-size effects are under control [565]. On each ensemble, the bare NRQCD quark mass is tuned to the b-quark mass using the spin-average for the masses \(\Upsilon \) and \(\eta _{b}\). In this work, a combined chiral-continuum extrapolation is performed, with the strategy of using Bayesian priors as explained in Ref. [566]. Systematic effects estimated in HPQCD 17A [71] include those from lattice-spacing dependence, the chiral fits, the \(B{-}B^{*}{-}\pi \) axial coupling, the operator matching, and the relativistic corrections to the NRQCD formalism. Although these errors are estimated in the same fashion as in Ref. [70] (HPQCD 13), most of them involve the handling of fits to the actual data. This means that most of the systematics effects from HPQCD 13 [70] and HPQCD 17A [71] are not correlated, although the two calculations are performed on exactly the same gauge field ensembles. The only exception is the error in the relativistic corrections. For this, the authors simply take \((\Lambda _{{\mathrm {QCD}}}/m_{b})^{2} \approx 1\%\) as the estimation in both computations. Therefore, we will correlate this part of the systematic effects in our average.Footnote 45
The third new calculation for the B-meson decay constants since the last FLAG report was performed by the FNAL/MILC collaboration (FNAL/MILC 17 [5] in Tables 34 and 35). In this work, Ref. [5], the simulations are performed for six lattice spacings, ranging from 0.03 to 0.15 fm. For the two finest lattices (\(a = 0.042\) and 0.03 fm), it is found that the topological charge is not well equilibrated. The effects of this nonequilibration are estimated using results of chiral perturbation theory in Ref. [114]. Another feature of the simulations is that both RHMC and RHMD algorithms are used. The authors investigated the effects of omitting the Metropolis test in the RHMD simulations by examining changes of the plaquette values, and found that they do not result in any variation with statistical significance. The light-quark masses used in this computation correspond to pion masses between 130 to 314 MeV. The values of the valence heavy-quark mass \(m_{h}\) are in the range of about 0.9 and 5 times the charm-quark mass. Notice that on the two coarsest lattices, the authors only implement calculations at \(m_{h} \sim m_{c}\) in order to avoid uncontrolled discretization errors, while only on the two finest lattices, is \(m_{h}\) chosen to be as high as \(\sim 5 m_{c}\). For setting the scale and the quark masses, the approach described in Ref. [18] is employed, with the special feature of using the decay constant of the “fictitious” meson that is composed of degenerate quarks with mass \(m_{p4s} = 0.4 m_{s}\). The overall scale is determined by comparing \(f_{\pi }\) to its PDG average as reported in Ref. [133]. In the analysis procedure of extrapolating/interpolating to the physical quark masses and the continuum limit, the key point is the use of heavy-meson rooted all-staggered chiral perturbation theory (HMrA\(\chi \)PT) [518]. In order to account for lattice artifacts and the effects of the heavy-quark mass in this chiral expansion, appropriate polynomial terms in a and \(1/m_{h}\) are included in the fit formulae. The full NLO terms in the chiral effective theory are incorporated in the analysis, while only the analytic contributions from the NNLO are considered. Furthermore, data obtained at the coarsest lattice spacing, \(a \approx 0.15\) fm, are discarded for the central-value fits, and are subsequently used only for the estimation of systematic errors. In this analysis strategy, there are 60 free parameters to be determined by about 500 data points. Systematic errors estimated in FNAL/MILC 17 include excited-state contamination, choices of fit models with different sizes of the priors, scale setting, quark-mass tuning, finite-size correction, electromagnetic (EM) contribution, and topological nonequilibration. The dominant effects are from the first two in this list. For the EM effects, the authors also include an error associated with choosing a specific scheme to estimate their contributions.
In our current work, the averages for \(f_{B_{s}}\), \(f_{B^{0}}\) and \(f_{B_{s}}/f_{B^{0}}\) with \(N_{f}=2\,+\,1\,+\,1\) lattice simulations are updated, because of the three published papers (FNAL/MILC 17 [5], HPQCD 17A [71] and ETM 16B [26] in Tables 34 and 35) that appeared after the release of the last FLAG review [3]. In the updated FLAG averages, we include results from these three new computations, as well as those in HPQCD 13 [70]. Since the decay constants presented in HPQCD 13 [70], HPQCD 17A [71] and FNAL/MILC 17 have been extracted with a significant overlap of gauge-field configurations, we correlate statistical errors from these works. Furthermore, as explained above, the systematic effects arising from relativistic corrections in HPQCD 13 [70] and HPQCD 17A [71] are correlated. Notice that the authors of FNAL/MILC 17 [5] computed \(f_{B_{s}}/f_{B^{+}}\) and \(f_{B_{s}}/f_{B^{0}}\) without performing an isospin average to obtain \(f_{B_{s}}/f_{B}\). This is the reason why in Fig. 24 we show two results, FNAL/MILC 17 1 (\(f_{B_{s}}/f_{B^{0}}\)) and FNAL/MILC 17 2 (\(f_{B_{s}}/f_{B^{+}}\)), from this reference. To determine the global average for \(f_{B_{s}}/f_{B}\), we first perform the average of \(f_{B_{s}}/f_{B^{+}}\) and \(f_{B_{s}}/f_{B^{0}}\) in FNAL/MILC 17 [5] by following the procedure in Sect. 2, with all errors correlated. This gives us the estimate of \(f_{B_{s}}/f_{B}\) from this work by the FNAL/MILC collaboration.
Following the above strategy, and the procedure explained in Sect. 2, we compute the average of \(N_f = 2\,+\,1\,+\,1\) results for \(f_{B_{(s)}}\) and \(f_{B_{s}}/f_{B}\),
The PDG presented their averages for the \(N_{f}=2\,+\,1\) and \(N_{f}=2\,+\,1\,+\,1\) lattice-QCD determinations of \(f_{B^{+}}\), \(f_{B_{s}}\) and \(f_{B_{s}}/f_{B^{+}}\) in 2015 [133]. The \(N_{f}=2\,+\,1\) lattice-computation results used in Ref. [133] are identical to those included in our current work. Regarding our isospin-averaged \(f_{B}\) as the representative for \(f_{B^{+}}\), then the current FLAG and PDG estimations for these quantities are compatible, although the errors of \(N_{f}=2\,+\,1\,+\,1\) results in this report are significantly smaller. In the PDG work, they “corrected” the isospin-averaged \(f_{B}\), as reported by various lattice collaborations, using the \(N_{f}=2\,+\,1\,+\,1\) strong isospin-breaking effect computed in HPQCD 13 [70] (see Table 34 in this section). However, since only unitary points (with equal sea- and valence-quark masses) were considered in HPQCD 13 [70], this procedure only correctly accounts for the effect from the valence-quark masses, while introducing a spurious sea-quark contribution. We notice that \(f_{B^{+}}\) and \(f_{B^{0}}\) are also separately reported in FNAL/MILC 17 [5] by taking into account the strong-isospin effect, and it is found that these two decay constants are well compatible. Notice that the new FNAL/MILC results were obtained by properly keeping the averaged light sea-quark mass fixed when varying the quark masses in their analysis procedure. Their finding indicates that the strong isospin-breaking effects could be smaller than what was suggested by previous computations.
8.2 Neutral B-meson mixing matrix elements
Neutral B-meson mixing is induced in the Standard Model through 1-loop box diagrams to lowest order in the electroweak theory, similar to those for short-distance effects in neutral kaon mixing. The effective Hamiltonian is given by
with
where \(q=d\) or s. The short-distance function \({{{\mathcal {F}}}}^0_q\) in Eq. (205) is much simpler compared to the kaon mixing case due to the hierarchy in the CKM matrix elements. Here, only one term is relevant,
where
and where \(S_0(x_t)\) is an Inami-Lim function with \(x_t=m_t^2/M_W^2\), which describes the basic electroweak loop contributions without QCD [465]. The transition amplitude for \(B_q^0\) with \(q=d\) or s can be written as
where \(Q^q_{\mathrm{R}} (\mu )\) is the renormalized four-fermion operator (usually in the NDR scheme of \({\overline{\mathrm {MS}}}\)). The running coupling \({\bar{g}}\), the \(\beta \)-function \(\beta (g)\), and the anomalous dimension of the four-quark operator \(\gamma (g)\) are defined in Eqs. (139) and (140). The product of \(\mu \)-dependent terms on the second line of Eq. (209) is, of course, \(\mu \)-independent (up to truncation errors arising from the use of perturbation theory). The explicit expression for the short-distance QCD correction factor \(\eta _{2B}\) (calculated to NLO) can be found in Ref. [458].
For historical reasons the B-meson mixing matrix elements are often parameterized in terms of bag parameters defined as
The RGI B parameter \({\hat{B}}\) is defined as in the case of the kaon, and expressed to 2-loop order as
with \(\beta _0\), \(\beta _1\), \(\gamma _0\), and \(\gamma _1\) defined in Eq. (141). Note, as Eq. (209) is evaluated above the bottom threshold (\(m_b<\mu <m_t\)), the active number of flavours here is \(N_f=5\).
Nonzero transition amplitudes result in a mass difference between the CP eigenstates of the neutral B-meson system. Writing the mass difference for a \(B_q^0\) meson as \(\Delta m_q\), its Standard Model prediction is
Experimentally the mass difference is measured as oscillation frequency of the CP eigenstates. The frequencies are measured precisely with an error of less than a percent. Many different experiments have measured \(\Delta m_d\), but the current average [170] is based on measurements from the B-factory experiments Belle and Babar, and from the LHC experiment LHCb. For \(\Delta m_s\) the experimental average is dominated by results from LHCb [170]. With these experimental results and lattice-QCD calculations of \(f_{B_q}^2{\hat{B}}_{B_q}\) at hand, \(\lambda _{tq}\) can be determined. In lattice-QCD calculations the flavour SU(3)-breaking ratio
can be obtained more precisely than the individual \(B_q\)-mixing matrix elements because statistical and systematic errors cancel in part. With this the ratio \(|V_{td}/V_{ts}|\) can be determined, which can be used to constrain the apex of the CKM triangle.
Neutral B-meson mixing, being loop-induced in the Standard Model, is also a sensitive probe of new physics. The most general \(\Delta B=2\) effective Hamiltonian that describes contributions to B-meson mixing in the Standard Model and beyond is given in terms of five local four-fermion operators:
where \({{{\mathcal {Q}}}}_1\) is defined in Eq. (206) and where
with the superscripts \(\alpha ,\beta \) denoting colour indices, which are shown only when they are contracted across the two bilinears. There are three other basis operators in the \(\Delta B=2\) effective Hamiltonian. When evaluated in QCD, however, they give identical matrix elements to the ones already listed due to parity invariance in QCD. The short-distance Wilson coefficients \({{{\mathcal {C}}}}_i\) depend on the underlying theory and can be calculated perturbatively. In the Standard Model only matrix elements of \({{{\mathcal {Q}}}}^q_1\) contribute to \(\Delta m_q\), while all operators do, for example, for general SUSY extensions of the Standard Model [501]. The matrix elements or bag parameters for the non-SM operators are also useful to estimate the width difference in the Standard Model, where combinations of matrix elements of \({{{\mathcal {Q}}}}^q_1\), \({{{\mathcal {Q}}}}^q_2\), and \({{{\mathcal {Q}}}}^q_3\) contribute to \(\Delta \Gamma _q\) at \({\mathcal {O}}(1/m_b)\) [567, 568].
In this section, we report on results from lattice-QCD calculations for the neutral B-meson mixing parameters \({\hat{B}}_{B_d}\), \({\hat{B}}_{B_s}\), \(f_{B_d}\sqrt{{\hat{B}}_{B_d}}\), \(f_{B_s}\sqrt{{\hat{B}}_{B_s}}\) and the SU(3)-breaking ratios \(B_{B_s}/B_{B_d}\) and \(\xi \) defined in Eqs. (210), (211), and (213). The results are summarized in Tables 36 and 37 and in Figs. 25 and 26. Additional details about the underlying simulations and systematic error estimates are given in Appendix B.6.2. Some collaborations do not provide the RGI quantities \({\hat{B}}_{B_q}\), but quote instead \(B_B(\mu )^{{\overline{MS}},NDR}\). In such cases we convert the results to the RGI quantities quoted in Table 36 using Eq. (211). More details on the conversion factors are provided below in the descriptions of the individual results. We do not provide the B-meson matrix elements of the other operators \({{{\mathcal {Q}}}}_{2-5}\) in this report. They have been calculated in Ref. [64] for the \(N_f=2\) case and in Refs. [78, 569] for \(N_f=2\,+\,1\).
There are no new results for \(N_f=2\) reported after the previous FLAG review. In this category one work (ETM 13B) [64] passes the quality criteria. A description of this work can be found in the FLAG 13 review [2] where it did not enter the average as it had not appeared in a journal. Because this is the only result available for \(N_f=2\), we quote their values as our averages in this version:
For the \(N_f=2\,+\,1\) case the FNAL/MILC collaboration reported their new results on the neutral B-meson mixing parameters in 2016. As the paper [78] appeared after the closing date of FLAG 16 [3], the results had not been taken into our average then. However, the subsequent web update of FLAG took the results into the average, and was made public in November 2017.
Their estimate of the \(B^0{-}\overline{B^0}\) mixing matrix elements are far improved compared to their older ones as well as all the prior \(N_f=2\,+\,1\) results. Hence, including the new FNAL/MILC results makes our averages much more precise. The study uses the asqtad action for light quarks and the Fermilab action for the b quark. They use MILC asqtad ensembles spanning four lattice spacings in the range \(a\approx 0.045{-}0.12\) fm and RMS pion mass of 257 MeV as the lightest. The lightest Goldstone pion of 177 MeV, at which the RMS mass is 280 MeV, helps constraining the combined chiral and continuum limit analysis with the HMrS\(\chi \)PT (heavy-meson rooted-staggered chiral perturbation theory) to NLO with NNLO analytic terms using a Bayesian prior. The extension to the finer lattice spacing and closer to physical pion masses together with the quadrupled statistics of the ensembles compared with those used in the earlier studies, as well as the inclusion of the wrong spin contribution [573], which is a staggered fermion artifact, make it possible to achieve the large improvement of the overall precision. Although for each parameter only one lattice volume is available, the finite-volume effects are well controlled by using a large enough lattice ( ) for all the ensembles. The operator renormalization is done by 1-loop lattice perturbation theory with the help of the mostly nonperturbative renormalization method where a perturbative computation of the ratio of the four-quark operator and square of the vector-current renormalization factors is combined with the nonperturbative estimate of the latter. Let us note that in the report [78] not only the SM \(B^0{-}\overline{B^0}\) mixing matrix element, but also those with all possible four-quark operators are included. The correlation among the different matrix elements are given, which helps to properly assess the error propagation to phenomenological analyses where combinations of the different matrix elements enter. The authors estimate the effect of omitting the charm-quark dynamics, which we have not propagated to our \(N_f=2\,+\,1\) averages. It should also be noted that their main new results are for the \(B^0-\overline{B^0}\) mixing matrix elements, that are \(f_{B_d}\sqrt{B_{B_d}}\), \(f_{B_s}\sqrt{B_{B_s}}\) and the ratio \(\xi \). They reported also on \(B_{B_d}\), \(B_{B_s}\) and \(B_{B_s}/B_{B_d}\). However, the B-meson decay constants needed in order to isolate the bag parameters from the four-fermion matrix elements are taken from the PDG [133] averages, which are obtained using a procedure similar to that used by FLAG. They plan to compute the decay constants on the same gauge field ensembles and then complete the bag parameter calculation on their own in the future. As of now, for the bag parameters we need to use the nested averaging scheme, described in Sect. 2.3.2, to take into account the possible correlations with this new result to the other ones through the averaged decay constants. The detailed procedure to apply the scheme for this particular case is provided in Sect. 8.2.1.
) for all the ensembles. The operator renormalization is done by 1-loop lattice perturbation theory with the help of the mostly nonperturbative renormalization method where a perturbative computation of the ratio of the four-quark operator and square of the vector-current renormalization factors is combined with the nonperturbative estimate of the latter. Let us note that in the report [78] not only the SM \(B^0{-}\overline{B^0}\) mixing matrix element, but also those with all possible four-quark operators are included. The correlation among the different matrix elements are given, which helps to properly assess the error propagation to phenomenological analyses where combinations of the different matrix elements enter. The authors estimate the effect of omitting the charm-quark dynamics, which we have not propagated to our \(N_f=2\,+\,1\) averages. It should also be noted that their main new results are for the \(B^0-\overline{B^0}\) mixing matrix elements, that are \(f_{B_d}\sqrt{B_{B_d}}\), \(f_{B_s}\sqrt{B_{B_s}}\) and the ratio \(\xi \). They reported also on \(B_{B_d}\), \(B_{B_s}\) and \(B_{B_s}/B_{B_d}\). However, the B-meson decay constants needed in order to isolate the bag parameters from the four-fermion matrix elements are taken from the PDG [133] averages, which are obtained using a procedure similar to that used by FLAG. They plan to compute the decay constants on the same gauge field ensembles and then complete the bag parameter calculation on their own in the future. As of now, for the bag parameters we need to use the nested averaging scheme, described in Sect. 2.3.2, to take into account the possible correlations with this new result to the other ones through the averaged decay constants. The detailed procedure to apply the scheme for this particular case is provided in Sect. 8.2.1.
The other results for \(N_f=2\,+\,1\) are RBC/UKQCD 14A [74], which had been included in the averages at FLAG 16 [3], and HPQCD 09 [77] to which a description is available in FLAG 13 [2]. Now our averages for \(N_f=2\,+\,1\) are:
Here all the above equations have been updated from the paper version of FLAG 16. The new results from FNAL/MILC 16 [78] entered the average for Eqs. (219), (220), and replaced the earlier FNAL/MILC 12 [572] for Eq. (221).
As discussed in detail in the FLAG 13 review [2] HPQCD 09 does not include wrong-spin contributions [573], which are staggered fermion artifacts, to the chiral extrapolation analysis. It is possible that the effect is significant for \(\xi \) and \(B_{B_s}/B_{B_d}\), since the chiral extrapolation error is a dominant one for these flavour SU(3)-breaking ratios. Indeed, a test done by FNAL/MILC 12 [572] indicates that the omission of the wrong spin contribution in the chiral analysis may be a significant source of error. We therefore took the conservative choice to exclude \(\xi \) and \(B_{B_s}/B_{B_d}\) by HPQCD 09 from our average and we follow the same strategy in this report as well.
We note that the above results within same \(N_f\) are all correlated with each other, due to the use of the same gauge field ensembles for different quantities. The results are also correlated with the averages obtained in Sect. 8.1 and shown in Eqs. (196)–(198) for \(N_f=2\) and Eqs. (199)–(201) for \(N_f=2\,+\,1\), because the calculations of B-meson decay constants and mixing quantities are performed on the same (or on similar) sets of ensembles, and results obtained by a given collaboration use the same actions and setups. These correlations must be considered when using our averages as inputs to unitarity triangle (UT) fits. For this reason, if one were for example to estimate \(f_{B_s}\sqrt{{\hat{B}}_s}\) from the separate averages of \(f_{B_s}\) and \({\hat{B}}_s\), one would obtain a value about one standard deviation below the one quoted above. While these two estimates lead to compatible results, giving us confidence that all uncertainties have been properly addressed, we do not recommend combining averages this way, as many correlations would have to be taken into account to properly assess the errors. We recommend instead using the numbers quoted above. In the future, as more independent calculations enter the averages, correlations between the lattice-QCD inputs to UT fits will become less significant.
8.2.1 Error treatment for B-meson bag parameters
The latest FNAL/MILC computation (FNAL/MILC 16) uses B-meson decay constants averaged for PDG [133] to isolate the bag parameter from the mixing matrix elements. The bag parameters so obtained have correlation to those from the other computations in two ways: through the mixing matrix elements of FNAL/MILC 16 and through the PDG average. Since the PDG average is obtained similarly as the FLAG average, estimating the bag parameter average with FNAL/MILC 16 requires a nested scheme. The nested scheme discussed in Sect. 2.3.2 is applied as follows.
Three computations contribute to the \(N_f=2\,+\,1\) average of the \(B_d\) meson bag parameter \(B_{B_d}\), FNAL/MILC 16 [78], RBC/UKQCD 14A [74], HPQCD 09 [77]. FNAL/MILC 16 uses \(f_{B^0}\) of PDG [133], which is an average of RBC/UKQCD 14, RBC/UKQCD 14A, HPQCD 12/11A, FNAL/MILC 11 in Table 34.Footnote 46 \(B_{B_d}\) (RBC/UKQCD 14A) has correlation with that of FNAL/MILC 16, through \(f_B\) (RBC/UKQCD 14A). Also some correlation exists through \(f_B\) (RBC/UKQCD 14), which uses the same set of gauge field configurations as \(B_{B_d}\) (RBC/UKQCD 14A).
In Eq. (9) for this particular case, \(Q_1\) is \(B_{B_d}\) (FNAL/MILC 16), \(Y_1\) is \(f_{B^0}^2 B_{B_d}\) (FNAL/MILC 16), and \({\overline{Z}}\) is the PDG average of \(f_{B^0}^2\). The most nontrivial part of the nested averaging is to construct the restricted errors \(\sigma [f_B^2]_{i'\leftrightarrow k}\) [Eq. (16)] and \(\sigma [f_B^2]_{i';j'\leftrightarrow k}\) [Eq. (18)], which goes into the final correlation matrix \(C_{ij}\) of \(B_{B_d}\) through \(\sigma _{1;k}\) [Eq. (14)]. The restricted summation over \((\alpha )\) labeling the origin of errors in this analysis turns out to be either the whole error or the statistical error only.
For the correlation of \(f_B\) and \(B_{B_d}\) both with RBC/UKQCD 14A, not knowing the information of the correlation, we take total errors 100 % correlated. For example, the heavy-quark error, which is \(O(1/m_b)\) and most dominant, is common for both. For the correlation of \(f_B\) (RBC/UKQCD 14) and \(B_{B_d}\) (RBC/UKQCD 14A), which uses different heavy-quark formulations but based on the same set of gauge field configurations, only the statistical error is taken as correlated. In a similar way, correlation among the other computations is determined. In principle, we take the whole error as correlated between \(f_B\) and \(B_{B_d}\) if both results are based on the exact same lattice action for light and heavy quarks and are sharing (at least a part of) the gauge field ensemble. Otherwise, only the statistical error is taken as correlated if two computations share the gauge field ensemble, or no correlation for the rest, which is summarized in Table 38. Also in a similar way, correlations of \(f_{B_s}\) and \(B_{B_s}\), \(f_{B_s}/f_{B}\) and \(B_{B_s}/B_{B_d}\) are determined, which are also summarized in Table 38.
The necessary information for constructing the second term in the square root of Eq. (14) has already been provided. For completeness, let us also summarize the correlation pattern needed to construct the other part of \(\sigma _{i;j}\) for the bag parameters, which is shown in Table 39.
8.3 Semileptonic form factors for B decays to light flavours
The Standard Model differential rate for the decay \(B_{(s)}\rightarrow P\ell \nu \) involving a quark-level \(b\rightarrow u\) transition is given, at leading order in the weak interaction, by a formula analogous to the one for D decays in Eq. (171), but with \(D \rightarrow B_{(s)}\) and the relevant CKM matrix element \(|V_{cq}| \rightarrow |V_{ub}|\):
Again, for \(\ell =e,\mu \) the contribution from the scalar form factor \(f_0\) can be neglected, and one has a similar expression to Eq. (173), which, in principle, allows for a direct extraction of \(|V_{ub}|\) by matching theoretical predictions to experimental data. However, while for D (or K) decays the entire physical range \(0 \le q^2 \le q^2_{\mathrm{max}}\) can be covered with moderate momenta accessible to lattice simulations, in \(B \rightarrow \pi \ell \nu \) decays one has \(q^2_{\mathrm{max}} \sim 26~\mathrm{GeV}^2\) and only part of the full kinematic range is reachable. As a consequence, obtaining \(|V_{ub}|\) from \(B\rightarrow \pi \ell \nu \) is more complicated than obtaining \(|V_{cd(s)}|\) from semileptonic D-meson decays.
In practice, lattice computations are restricted to large values of the momentum transfer \(q^2\) (see Sect. 7.2) where statistical and momentum-dependent discretization errors can be controlled,Footnote 47 which in existing calculations roughly cover the upper third of the kinematically allowed \(q^2\) range. Since, on the other hand, the decay rate is suppressed by phase space at large \(q^2\), most of the semileptonic \(B\rightarrow \pi \) events are selected in experiment at lower values of \(q^2\), leading to more accurate experimental results for the binned differential rate in that region.Footnote 48 It is therefore a challenge to find a window of intermediate values of \(q^2\) at which both the experimental and lattice results can be reliably evaluated.
In current practice, the extraction of CKM matrix elements requires that both experimental and lattice data for the \(q^2\)-dependence be parameterized by fitting data to a specific ansatz. Before the generalization of the sophisticated ansätze that will be discussed below, the most common procedure to overcome this difficulty involved matching the theoretical prediction and the experimental result for the integrated decay rate over some finite interval in \(q^2\),
In the most recent literature, it has become customary to perform a joint fit to lattice and experimental results, keeping the relative normalization \(|V_{ub}|^2\) as a free parameter. In either case, good control of the systematic uncertainty induced by the choice of parameterization is crucial to obtain a precise determination of \(|V_{ub}|\). A detailed discussion of the parameterization of form factors as a function of \(q^2\) can be found in Appendix A.5.
8.3.1 Form factors for \(B\rightarrow \pi \ell \nu \)
The semileptonic decay processes \(B\rightarrow \pi \ell \nu \) enable determinations of the CKM matrix element \(|V_{ub}|\) within the Standard Model via Eq. (222). Early results for \(B\rightarrow \pi \ell \nu \) form factors came from the HPQCD [575] and FNAL/MILC [576] collaborations. Only HPQCD provided results for the scalar form factor \(f_0\). Our previous review featured a significantly extended calculation of \(B\rightarrow \pi \ell \nu \) from FNAL/MILC [577] and a new computation from RBC/UKQCD [578]. All the above computations employ \(N_f=2\,+\,1\) dynamical configurations, and provide values for both form factors \(f_+\) and \(f_0\). In addition, HPQCD using MILC ensembles had published the first \(N_f=2\,+\,1\,+\,1\) results for the \(B\rightarrow \pi \ell \nu \) scalar form factor, working at zero recoil and pion masses down to the physical value [579]; this adds to previous reports on ongoing work to upgrade their 2006 computation [580, 581]. Since this latter result has no immediate impact on current \(|V_{ub}|\) determinations, which come from the vector-form-factor-dominated decay channels into light leptons, we will from now on concentrate on the \(N_f=2\,+\,1\) determinations of the \(q^2\)-dependence of \(B\rightarrow \pi \) form factors.
Results presented at Lattice 2017 are preliminary or blinded, so not yet ready for inclusion in this review. However, the reader will be interested to know that the JLQCD collaboration is using Möbius Domain Wall fermions with \(a\approx 0.08\), 0.055, and 0.044 fm and pion masses down to 300 MeV to study this process [582]. FNAL/MILC is using \(N_f=2\,+\,1\,+\,1\) HISQ ensembles with \(a\approx 0.15\), 0.12, and 0.088 fm, with Goldstone pion mass down to its physical value [583]. Both groups updated their results for Lattice 2018, but do not have final values for the form factors.
Returning to the works that contribute to our averages, both the HPQCD and the FNAL/MILC computations of \(B\rightarrow \pi \ell \nu \) amplitudes use ensembles of gauge configurations with \(N_f=2\,+\,1\) flavours of rooted staggered quarks produced by the MILC collaboration; however, the latest FNAL/MILC work makes a much more extensive use of the currently available ensembles, both in terms of lattice spacings and light-quark masses. HPQCD have results at two values of the lattice spacing (\(a\sim 0.12,~0.09~\mathrm{fm}\)), while FNAL/MILC employs four values (\(a\sim 0.12,~0.09,~0.06,~0.045~\mathrm{fm}\)). Lattice-discretization effects are estimated within HMrS\(\chi \)PT in the FNAL/MILC computation, while HPQCD quotes the results at \(a\sim 0.12~\mathrm{fm}\) as central values and uses the \(a\sim 0.09~\mathrm{fm}\) results to quote an uncertainty. The relative scale is fixed in both cases through \(r_1/a\). HPQCD set the absolute scale through the \(\Upsilon \) 2S–1S splitting, while FNAL/MILC uses a combination of \(f_\pi \) and the same \(\Upsilon \) splitting, as described in Ref. [62]. The spatial extent of the lattices employed by HPQCD is \(L\simeq 2.4~\mathrm{fm}\), save for the lightest mass point (at \(a\sim 0.09~\mathrm{fm}\)) for which \(L\simeq 2.9~\mathrm{fm}\). FNAL/MILC, on the other hand, uses extents up to \(L \simeq 5.8~\mathrm{fm}\), in order to allow for light-pion masses while keeping finite-volume effects under control. Indeed, while in the 2006 HPQCD work the lightest RMS pion mass is \(400~\mathrm{MeV}\), the latest FNAL/MILC work includes pions as light as \(165~\mathrm{MeV}\) – in both cases the bound \(m_\pi L \gtrsim 3.8\) is kept. Other than the qualitatively different range of MILC ensembles used in the two computations, the main difference between HPQCD and FNAL/MILC lies in the treatment of heavy quarks. HPQCD uses the NRQCD formalism, with a 1-loop matching of the relevant currents to the ones in the relativistic theory. FNAL/MILC employs the clover action with the Fermilab interpretation, with a mostly nonperturbative renormalization of the relevant currents, within which light-light and heavy–heavy currents are renormalized nonperturbatively and 1-loop perturbation theory is used for the relative normalization. (See Table 40; full details about the computations are provided in tables in Appendix B.6.3.)
The RBC/UKQCD computation is based on \(N_f=2\,+\,1\) DWF ensembles at two values of the lattice spacing (\(a\sim 0.12,~0.09~\mathrm{fm}\)), and pion masses in a narrow interval ranging from slightly above \(400~\mathrm{MeV}\) to slightly below \(300~\mathrm{MeV}\), keeping \(m_\pi L \gtrsim 4\). The scale is set using the \(\Omega ^-\) baryon mass. Discretization effects coming from the light sector are estimated in the \(1\%\) ballpark using HM\(\chi \)PT supplemented with effective higher-order interactions to describe cutoff effects. The b quark is treated using the Columbia RHQ action, with a mostly nonperturbative renormalization of the relevant currents. Discretization effects coming from the heavy sector are estimated with power-counting arguments to be below \(2\%\).
Given the large kinematical range available in the \(B\rightarrow \pi \) transition, chiral extrapolations are an important source of systematic uncertainty: apart from the eventual need to reach physical pion masses in the extrapolation, the applicability of \(\chi \)PT is not guaranteed for large values of the pion energy \(E_\pi \). Indeed, in all computations \(E_\pi \) reaches values in the \(1~\mathrm{GeV}\) ballpark, and chiral extrapolation systematics is the dominant source of errors. FNAL/MILC uses SU(2) NLO HMrS\(\chi \)PT for the continuum-chiral extrapolation, supplemented by NNLO analytic terms and hard-pion \(\chi \)PT terms [537];Footnote 49 systematic uncertainties are estimated through an extensive study of the effects of varying the specific fit ansatz and/or data range. RBC/UKQCD uses SU(2) hard-pion HM\(\chi \)PT to perform its combined continuum-chiral extrapolation, and obtains sizeable estimates for systematic uncertainties by varying the ansätze and ranges used in fits. HPQCD performs chiral extrapolations using HMrS\(\chi \)PT formulae, and estimates systematic uncertainties by comparing the result with the ones from fits to a linear behaviour in the light-quark mass, continuum HM\(\chi \)PT, and partially quenched HMrS\(\chi \)PT formulae (including also data with different sea and valence light-quark masses).
FNAL/MILC and RBC/UKQCD describe the \(q^2\)-dependence of \(f_+\) and \(f_0\) by applying a BCL parameterization to the form factors extrapolated to the continuum limit, within the range of values of \(q^2\) covered by data. RBC/UKQCD generate synthetic data for the form factors at some values of \(q^2\) (evenly spaced in z) from the continuous function of \(q^2\) obtained from the joint chiral-continuum extrapolation, which are then used as input for the fits. After having checked that the kinematical constraint \(f_+(0)=f_0(0)\) is satisfied within errors by the extrapolation to \(q^2=0\) of the results of separate fits, this constraint is imposed to improve fit quality. In the case of FNAL/MILC, rather than producing synthetic data a functional method is used to extract the z-parameterization directly from the fit functions employed in the continuum-chiral extrapolation. In the case of HPQCD, the parameterization of the \(q^2\)-dependence of form factors is somewhat intertwined with chiral extrapolations: a set of fiducial values \(\{E_\pi ^{(n)}\}\) is fixed for each value of the light-quark mass, and \(f_{+,0}\) are interpolated to each of the \(E_\pi ^{(n)}\); chiral extrapolations are then performed at fixed \(E_\pi \) (i.e., \(m_\pi \) and \(q^2\) are varied subject to \(E_\pi \)=constant). The interpolation is performed using a BZ ansatz. The \(q^2\)-dependence of the resulting form factors in the chiral limit is then described by means of a BZ ansatz, which is cross-checked against BK, RH, and BGL parameterizations. Unfortunately, the correlation matrix for the values of the form factors at different \(q^2\) is not provided, which severely limits the possibilities of combining them with other computations into a global z-parameterization.
Based on the parameterized form factors, HPQCD and RBC/UKQCD provide values for integrated decay rates \(\Delta \zeta ^{B\pi }\), as defined in Eq. (223); they are quoted in Table 40. The latest FNAL/MILC work, on the other hand, does not quote a value for the integrated ratio. Furthermore, as mentioned above, the field has recently moved forward to determine CKM matrix elements from direct joint fits of experimental results and theoretical form factors, rather than a matching through \(\Delta \zeta ^{B\pi }\). Thus, we will not provide here a FLAG average for the integrated rate, and focus on averaging lattice results for the form factors themselves.
The different ways in which the current results are presented do not allow a straightforward averaging procedure. RBC/UKQCD only provides synthetic values of \(f_+\) and \(f_0\) at a few values of \(q^2\) as an illustration of their results, and FNAL/MILC does not quote synthetic values at all. In both cases, full results for BCL z-parameterizations defined by Eq. (448) are quoted. In the case of HPQCD 06, unfortunately, a fit to a BCL z-parameterization is not possible, as discussed above.
In order to combine these form factor calculations we start from sets of synthetic data for several \(q^2\) values. HPQCD and RBC/UKQCD provide directly this information; FNAL/MILC presents only fits to a BCL z-parameterization from which we can easily generate an equivalent set of form factor values. It is important to note that in both the RBC/UKQCD synthetic data and the FNAL/MILC z-parameterization fits the kinematic constraint at \(q^2=0\) is automatically included (in the FNAL/MILC case the constraint is manifest in an exact degeneracy of the \((a_n^+ ,a_n^0)\) covariance matrix). Due to these considerations, in our opinion the most accurate procedure is to perform a simultaneous fit to all synthetic data for the vector and scalar form factors. Unfortunately, the absence of information on the correlation in the HPQCD result between the vector and scalar form factors even at a single \(q^2\) point makes it impossible to include consistently this calculation in the overall fit. In fact, the HPQCD and FNAL/MILC statistical uncertainties are highly correlated (because they are based on overlapping subsets of MILC \(N_f=2\,+\,1\) ensembles) and, without knowledge of the \(f_+ - f_0\) correlation we are unable to construct the HPQCD-FNAL/MILC off-diagonal entries of the overall covariance matrix.
In conclusion, we will present as our best result a combined vector and scalar form factor fit to the FNAL/MILC and RBC/UKQCD results that we treat as completely uncorrelated. For sake of completeness we will also show the results of a vector form factor fit alone in which we include one HPQCD datum at \(q^2=17.34~\,\mathrm {GeV}^2\) assuming conservatively a 100% correlation between the statistical error of this point and of all FNAL/MILC synthetic data. In spite of contributing just one point, the HPQCD datum has a significant weight in the fit due to its small overall uncertainty. We stress again that this procedure is slightly inconsistent because FNAL/MILC and RBC/UKQCD include information on the kinematic constraint at \(q^2=0\) in their \(f_+\) results.
The resulting data set is then fitted to the BCL parameterization in Eqs. (448) and (449). We assess the systematic uncertainty due to truncating the series expansion by considering fits to different orders in z. In Fig. 27, we show the FNAL/MILC, RBC/UKQCD, and HPQCD data points for \((1-q^2/m_{B^*}^2) f_+(q^2)\) and \(f_0 (q^2)\) versus z. The data is highly linear and we get a good \(\chi ^2/\mathrm{dof}\) with \(N^+ = N^0 = 3\). Note that this implies three independent parameters for \(f_+\) corresponding to a polynomial through \({\mathcal {O}}(z^3)\) and two independent parameters for \(f_0\) corresponding to a polynomial through \({\mathcal {O}}(z^2)\) (the coefficient \(a_2^0\) is fixed using the \(q^2=0\) kinematic constraint). We cannot constrain the coefficients of the z-expansion beyond this order; for instance, including a fourth parameter in \(f_+\) results in 100% uncertainties on \(a_2^+\) and \(a_3^+\). The outcome of the five-parameter \(N^+ =N^0=3\) BCL fit to the FNAL/MILC and RBC/UKQCD calculations is shown in Table 41. The uncertainties on \(a_0^{+,0}\), \(a_1^{+,0}\) and \(a_2^+\) encompass the central values obtained from \(N^+=2,4\) and \(N^0=2,4,5\) fits and thus adequately reflect the systematic uncertainty on those series coefficients. This can be used as the averaged FLAG result for the lattice-computed form factor \(f_+(q^2)\). The coefficient \(a_3^+\) can be obtained from the values for \(a_0^+\)–\(a_2^+\) using Eq. (447). The coefficient \(a_2^0\) can be obtained from all other coefficients imposing the \(f_+(q^2=0) = f_0(q^2=0)\) constraint. The fit is illustrated in Fig. 27. It is worth stressing that, with respect to our average in the 2015 edition of the FLAG report, the relative error on \(a_0^+\), which dominates the theory contribution to the determination of \(|V_{ub}|\), has decreased from \(7.3\%\) to \(3.2\%\). The dominant factor in this remarkable improvement is the new FNAL/MILC determination of \(f_+\). We emphasize that future lattice-QCD calculations of semileptonic form factors should publish their full statistical and systematic correlation matrices to enable others to use the data. It is also preferable to present a set of synthetic form factors data equivalent to the z-fit results, since this allows for an independent analysis that avoids further assumptions about the compatibility of the procedures to arrive at a given z-parameterization.Footnote 50 It is also preferable to present covariance/correlation matrices with enough significant digits to calculate correctly all their eigenvalues.
For the sake of completeness, we present also a standalone z-fit to the vector form factor. In this fit we are able to include the single \(f_+\) point at \(q^2 = 17.34\; \mathrm{GeV}^2\) that we mentioned above. This fit uses the FNAL/MILC and RBC/UKQCD results that do make use of the kinematic constraint at \(q^2=0\), but is otherwise unbiased. The results of the three-parameter BCL fit to the HPQCD, FNAL/MILC and RBC/UKQCD calculations of the vector form factor are:
Note that the \(a_0^+\) coefficient, that is the most relevant for input to the extraction of \(V_{ub}\) from semileptonic \(B\rightarrow \pi \ell \nu _\ell (\ell =e,\mu )\) decays, shifts by about a standard deviation.
8.3.2 Form factors for \(B_s\rightarrow K\ell \nu \)
Similar to \(B\rightarrow \pi \ell \nu \), measurements of \(B_s\rightarrow K\ell \nu \) enable determinations of the CKM matrix element \(|V_{ub}|\) within the Standard Model via Eq. (222). From the lattice point of view the two channels are very similar – as a matter of fact, \(B_s\rightarrow K\ell \nu \) is actually somewhat simpler, in that the fact that the kaon mass region is easily accessed by all simulations makes the systematic uncertainties related to chiral extrapolation smaller. On the other hand, \(B_s\rightarrow K\ell \nu \) channels have not been measured experimentally yet, and therefore lattice results provide SM predictions for the relevant rates.
At the time of our previous review, results for \(B_s\rightarrow K\ell \nu \) form factors were provided by HPQCD [584] and RBC/UKQCD [577] for both form factors \(f_+\) and \(f_0\), in both cases using \(N_f=2\,+\,1\) dynamical configurations. The ALPHA collaboration determination of \(B_s\rightarrow K\ell \nu \) form factors with \(N_f=2\) was also well underway [585]; however, we have not seen final results. HPQCD has recently emphasized the value of form factor ratios for the processes \(B_s\rightarrow K\ell \nu \) and \(B_s\rightarrow D_s\ell \nu \) for determination of \(|V_{ub}/V_{cb}|\) [586]. Preliminary results from FNAL/MILC have been reported for \(N_f=2\,+\,1\) [587] and \(N_f=2\,+\,1\,+\,1\) [583]. Archival papers are expected soon.
The RBC/UKQCD computation has been published together with the \(B\rightarrow \pi \ell \nu \) computation discussed in Sect. 8.3.1, all technical details being practically identical. The main difference is that errors are significantly smaller, mostly due to the reduction of systematic uncertainties due to the chiral extrapolation; detailed information is provided in tables in Appendix B.6.3. The HPQCD computation uses ensembles of gauge configurations with \(N_f=2\,+\,1\) flavours of asqtad rooted staggered quarks produced by the MILC collaboration at two values of the lattice spacing (\(a\sim 0.12,~0.09~\mathrm{fm}\)), for three and two different sea-pion masses, respectively, down to a value of \(260~\mathrm{MeV}\). The b quark is treated within the NRQCD formalism, with a 1-loop matching of the relevant currents to the ones in the relativistic theory, omitting terms of \({\mathcal {O}}(\alpha _s\Lambda _{\mathrm{QCD}}/m_b)\). The HISQ action is used for the valence s quark. The continuum-chiral extrapolation is combined with the description of the \(q^2\)-dependence of the form factors into a modified z-expansion (cf. Appendix A.5) that formally coincides in the continuum with the BCL ansatz. The dependence of form factors on the pion energy and quark masses is fitted to a 1-loop ansatz inspired by hard-pion \(\chi \)PT [537], that factorizes out the chiral logarithms describing soft physics. See Table 42 and the tables in Appendix B.6.3 for full details.
Both RBC/UKQCD and HPQCD quote values for integrated differential decay rates over the full kinematically available region. However, since the absence of experiment makes the relevant integration interval subject to change, we will not discuss them here, and focus on averages of form factors. In order to combine the results from the two collaborations, we will follow a similar approach to the one adopted above for \(B\rightarrow \pi \ell \nu \): we will take as direct input the synthetic values of the form factors provided by RBC/UKQCD, use the preferred HPQCD parameterization to produce synthetic values, and perform a joint fit to the two data sets.
Note that the kinematic constraint at \(q^2=0\) is included explicitly in the results presented by HPQCD (the coefficient \(b_0^0\) is expressed analytically in terms of all others) and implicitly in the synthetic data provided by RBC/UKQCD. Therefore, following the procedure we adopted for the \(B\rightarrow \pi \) case, we present a joint fit to the vector and scalar form factors and implement explicitly the \(q^2=0\) constraint by expressing the coefficient \(b^0_{N^0-1}\) in terms of all others.
For the fits we employ a BCL ansatz with \(t_+=(M_{B_s}+M_{K^\pm })^2 \simeq 34.35~\,\mathrm {GeV}^2\) and \(t_0=(M_{B_s}+M_{K^\pm })(\sqrt{M_{B_s}}-\sqrt{M_{K^\pm }})^2 \simeq 15.27~\,\mathrm {GeV}^2\). Our pole factors will contain a single pole in both the vector and scalar channels, for which we take the mass values \(M_{B^*}=5.325~\,\mathrm {GeV}\) and \(M_{B^*(0^+)}=5.65~\,\mathrm {GeV}\).Footnote 51
The outcome of the five-parameter \(N^+ = N^0 = 3\) BCL fit, which we quote as our preferred result, is shown in Table 43. The uncertainties on \(a_0\) and \(a_1\) encompass the central values obtained from \({\mathcal {O}}(z^2)\) fits, and thus adequately reflect the systematic uncertainty on those series coefficients.Footnote 52 These can be used as the averaged FLAG results for the lattice-computed form factors \(f_+(q^2)\) and \(f_0(q^2)\). The coefficient \(a_3^+\) can be obtained from the values for \(a_0^+\)–\(a_2^+\) using Eq. (447). The fit is illustrated in Fig. 28.
The form factors \((1 - q^2/m_{B^*}^2) f_+(q^2)\) and \((1 - q^2/m_{B^*(0+)}^2) f_0(q^2)\) for \(B_s \rightarrow K\ell \nu \) plotted versus z. (See text for a discussion of the data sets.) The grey and salmon bands display our preferred \(N^+=N^0=3\) BCL fit (five parameters) to the plotted data with errors
8.3.3 Form factors for rare and radiative B-semileptonic decays to light flavours
Lattice-QCD input is also available for some exclusive semileptonic decay channels involving neutral-current \(b\rightarrow q\) transitions at the quark level, where \(q=d,s\). Being forbidden at tree level in the SM, these processes allow for stringent tests of potential new physics; simple examples are \(B\rightarrow K^*\gamma \), \(B\rightarrow K^{(*)}\ell ^+\ell ^-\), or \(B\rightarrow \pi \ell ^+\ell ^-\) where the B meson (and therefore the light meson in the final state) can be either neutral or charged.
The corresponding SM effective weak Hamiltonian is considerably more complicated than the one for the tree-level processes discussed above: after integrating out the top and the W boson, as many as ten dimension-six operators formed by the product of two hadronic currents or one hadronic and one leptonic current appear.Footnote 53 Three of the latter, coming from penguin and box diagrams, dominate at short distances and have matrix elements that, up to small QED corrections, are given entirely in terms of \(B\rightarrow (\pi ,K,K^*)\) form factors. The matrix elements of the remaining seven operators can be expressed, up to power corrections whose size is still unclear, in terms of form factors, decay constants and light-cone distribution amplitudes (for the \(\pi \), K, \(K^*\) and B mesons) by employing OPE arguments (at large di-lepton invariant mass) and results from Soft Collinear Effective Theory (at small di-lepton invariant mass). In conclusion, the most important contributions to all of these decays are expected to come from matrix elements of current operators (vector, tensor, and axial-vector) between one-hadron states, which in turn can be parameterized in terms of a number of form factors (see Ref. [589] for a complete description).
In channels with pseudoscalar mesons in the final state, the level of sophistication of lattice calculations is similar to the \(B\rightarrow \pi \) case and there are results for the vector, scalar, and tensor form factors for \(B\rightarrow K\ell ^+\ell ^-\) decays by HPQCD [590], and more recent results for both \(B\rightarrow \pi \ell ^+\ell ^-\) [592] and \(B\rightarrow K\ell ^+\ell ^-\) [591] from FNAL/MILC. Full details about these two calculations are provided in Table 44 and in the tables in Appendix B.6.4. Both computations employ MILC \(N_f=2\,+\,1\) asqtad ensembles. HPQCD [593] and FNAL/MILC [594] have also companion papers in which they calculate the Standard Model predictions for the differential branching fractions and other observables and compare to experiment. The HPQCD computation employs NRQCD b quarks and HISQ valence light quarks, and parameterizes the form factors over the full kinematic range using a model-independent z-expansion as in Appendix A.5, including the covariance matrix of the fit coefficients. In the case of the (separate) FNAL/MILC computations, both of them use Fermilab b quarks and asqtad light quarks, and a BCL z-parameterization of the form factors.
Reference [592] includes results for the tensor form factor for \(B\rightarrow \pi \ell ^+\ell ^-\) not included in previous publications on the vector and scalar form factors [577]. Nineteen ensembles from four lattice spacings are used to control continuum and chiral extrapolations. The results for \(N_z=4\) z-expansion of the tensor form factor and its correlations with the expansions for the vector and scalar form factors, which we consider the FLAG estimate, are shown in Table 45. Partial decay widths for decay into light leptons or \(\tau ^+\tau ^-\) are presented as a function of \(q^2\). The former is compared with results from LHCb [595], while the latter is a prediction.
The averaging of the HPQCD and FNAL/MILC results for the \(B\rightarrow K\) form factors is similar to our treatment of the \(B\rightarrow \pi \) and \(B_s\rightarrow K\) form factors. In this case, even though the statistical uncertainties are partially correlated because of some overlap between the adopted sets of MILC ensembles, we choose to treat the two calculations as independent. The reason is that, in \(B\rightarrow K\), statistical uncertainties are subdominant and cannot be easily extracted from the results presented by HPQCD and FNAL/MILC. Both collaborations provide only the outcome of a simultaneous z-fit to the vector, scalar and tensor form factors, that we use to generate appropriate synthetic data. We then impose the kinematic constraint \(f_+(q^2=0) = f_0(q^2=0)\) and fit to \((N^+ = N^0 = N^T = 3)\) BCL parameterization. The functional forms of the form factors that we use are identical to those adopted in Ref. [594].Footnote 54 The results of the fit are presented in Table 46. The fit is illustrated in Fig. 29. Note that the average for the \(f_T\) form factor appears to prefer the FNAL/MILC synthetic data. This happens because we perform a correlated fit of the three form factors simultaneously (both FNAL/MILC and HPQCD present covariance matrices that include correlations between all form factors). We checked that the average for the \(f_T\) form factor, obtained neglecting correlations with \(f_0\) and \(f_+\), is a little lower and lies in between the two data sets. There is still a noticeable tension between the FNAL/MILC and HPQCD data for the tensor form factor; indeed, a standalone fit to these data results in \(\chi ^2_{\mathrm{red}}=7.2/3\), while a similar standalone joint fit to \(f_+\) and \(f_0\) has \(\chi ^2_{\mathrm{red}}=7.3/7\). Finally, the global fit that is shown in the figure has \(\chi ^2_{\mathrm{red}}=16.4/10\).
The \(B\rightarrow K\) form factors \((1 - q^2/m_{B^*}^2) f_+(q^2)\), \((1 - q^2/m_{B^*(0+)}^2) f_0(q^2)\) and \((1 - q^2/m_{B^*}^2) f_T(q^2)\) plotted versus z. (See text for a discussion of the data sets.) The grey, salmon and blue bands display our preferred \(N^+=N^0=N^T=3\) BCL fit (eight parameters) to the plotted data with errors
Lattice computations of form factors in channels with a vector meson in the final state face extra challenges with respect to the case of a pseudoscalar meson: the state is unstable, and the extraction of the relevant matrix element from correlation functions is significantly more complicated; \(\chi \)PT cannot be used as a guide to extrapolate results at unphysically heavy pion masses to the chiral limit. While field-theory procedures to take resonance effects into account are available [300,301,302, 597,598,599,600,601,602], they have not yet been implemented in the existing preliminary computations, which therefore suffer from uncontrolled systematic errors in calculations of weak decay form factors into unstable vector meson final states, such as the \(K^*\) or \(\rho \) mesons.Footnote 55
As a consequence of the complexity of the problem, the level of maturity of these computations is significantly below the one present for pseudoscalar form factors. Therefore, we will only provide below a short guide to the existing results.
Concerning channels with vector mesons in the final state, Horgan et al. have obtained the seven form factors governing \(B \rightarrow K^* \ell ^+ \ell ^-\) (as well as those for \(B_s \rightarrow \phi \, \ell ^+ \ell ^-\)) in Ref. [603] using NRQCD b quarks and asqtad staggered light quarks. In this work, they use a modified z-expansion to simultaneously extrapolate to the physical light-quark masses and continuum and extrapolate in \(q^2\) to the full kinematic range. As discussed in Sect. 7.2, the modified z-expansion is not based on an underlying effective theory, and the associated uncertainties have yet to be fully studied. Horgan et al. use their form-factor results to calculate the differential branching fractions and angular distributions and discuss the implications for phenomenology in a companion paper [604]. Finally, preliminary results on \(B\rightarrow K^*\ell ^+\ell ^-\) and \(B_s\rightarrow \phi \ell ^+\ell ^-\) by RBC/UKQCD, have been reported in Refs. [605,606,607].
8.4 Semileptonic form factors for \(B_{(s)} \rightarrow D_{(s)} \ell \nu \) and \(B \rightarrow D^* \ell \nu \)
The semileptonic processes \( B_{(s)} \rightarrow D_{(s)} \ell \nu \) and \(B \rightarrow D^* \ell \nu \) have been studied extensively by experimentalists and theorists over the years. They allow for the determination of the CKM matrix element \(|V_{cb}|\), an extremely important parameter of the Standard Model. The matrix elememt \(V_{cb}\) appears in many quantities that serve as inputs to CKM unitarity triangle analyses and reducing its uncertainties is of paramount importance. For example, when \(\epsilon _K\), the measure of indirect CP violation in the neutral kaon system, is written in terms of the parameters \(\rho \) and \(\eta \) that specify the apex of the unitarity triangle, a factor of \(|V_{cb}|^4\) multiplies the dominant term. As a result, the errors coming from \(|V_{cb}|\) (and not those from \(B_K\)) are now the dominant uncertainty in the Standard Model (SM) prediction for this quantity.
The decay rate for \(B \rightarrow D\ell \nu \) can be parameterized in terms of vector and scalar form factors in the same way as, e.g., \(B\rightarrow \pi \ell \nu \), see Sect. 8.3. The decay rate for \(B \rightarrow D^*\ell \nu \) is different because the final-state hadron is spin-1. There are four form factors used to describe the vector and axial-vector current matrix elements that are needed to calculate this decay. We define the 4-velocity of the meson P as \(v_P= p_P/m_P\) and the polarization vector of the \(D^*\) as \(\epsilon \). When the light lepton \(\ell =e\), or \(\mu \), it is traditional to use \( w=v_B\cdot v_{D^{(*)}}\) rather than \(q^2\) as the variable upon which the form factors depend. Then, the form factors \(h_V\), and \(h_{A_i}\), with \(i=1\), 2 or 3 are defined by
The differential decay rates can then be written as
where \(w = v_B \cdot v_{D^{(*)}}\) (depending on whether the final-state meson is D or \(D^*\)) and \(\eta _\mathrm {EW}=1.0066\) is the 1-loop electroweak correction [608]. The function \(\chi (w)\) in Eq. (228) depends on the recoil w and the meson masses, and reduces to unity at zero recoil [588]. These formulas do not include terms that are proportional to the lepton mass squared, which can be neglected for \(\ell = e, \mu \). Further details of the definitions of \({{{\mathcal {F}}}}\) and \({{{\mathcal {G}}}}\) may be found, e.g., in Ref. [588]. Until recently, most unquenched lattice calculations for \(B \rightarrow D^* \ell \nu \) and \(B \rightarrow D \ell \nu \) decays focused on the form factors at zero recoil \({{{\mathcal {F}}}}^{B \rightarrow D^*}(1)\) and \({{{\mathcal {G}}}}^{B \rightarrow D}(1)\); these can then be combined with experimental input to extract \(|V_{cb}|\). The main reasons for concentrating on the zero recoil point are that (i) the decay rate then depends on a single form factor, and (ii) for \(B \rightarrow D^*\ell \nu \), there are no \({\mathcal {O}}(\Lambda _{QCD}/m_Q)\) contributions due to Luke’s theorem [609]. Further, the zero recoil form factor can be computed via a double ratio in which most of the current renormalization cancels and heavy-quark discretization errors are suppressed by an additional power of \(\Lambda _{QCD}/m_Q\). Recent work on \(B \rightarrow D^{(*)}\ell \nu \) transitions has started to explore the dependence of the relevant form factors on the momentum transfer, using a similar methodology to the one employed in \(B\rightarrow \pi \ell \nu \) transitions; we refer the reader to Sect. 8.3 for a detailed discussion.
Early computations of the form factors for \(B \rightarrow D\ell \nu \) decays include \(N_f=2\,+\,1\) results by FNAL/MILC [610, 611] for \({{{\mathcal {G}}}}^{B \rightarrow D}(1)\) and the \(N_f=2\) study by Atoui et al. [612], that in addition to providing \(\mathcal{G}^{B \rightarrow D}(1)\) explored the \(w>1\) region. This latter work also provided the first results for \(B_s \rightarrow D_s\ell \nu \) amplitudes, again including information about the momentum-transfer dependence; this will allow for an independent determination of \(|V_{cb}|\) as soon as experimental data is available for these transitions. The first published unquenched results for \({{{\mathcal {F}}}}^{B \rightarrow D^*}(1)\), obtained by FNAL/MILC, date from 2008 [613]. In 2014 and 2015, significant progress was achieved in \(N_f=2\,+\,1\) computations: the FNAL/MILC value for \({{{\mathcal {F}}}}^{B \rightarrow D^*}(1)\) was updated in Ref. [614], and full results for \(B \rightarrow D\ell \nu \) at \(w \ge 1\) were published by FNAL/MILC [615] and HPQCD [616]. These works also provided full results for the scalar form factor, allowing analysis of the decay with a final-state \(\tau \). Since the previous version of this review, there are new results for \(B_s \rightarrow D_s\ell \nu \) form factors over the full kinematic range for \(N_f=2\,+\,1\) from HPQCD [617, 618], and for \({{B}_{(s)}\rightarrow D_{(s)}^{*}\ell {\nu }}\) form factors at zero recoil with \(N_f=2\,+\,1\,+\,1\) also from HPQCD [619, 620]. There has also been significant progress on heavy-baryon decay. Reference [621] calculates the tensor form factors for decay \({\Lambda }_b\rightarrow {\Lambda }_c\tau {{\overline{\nu }}}_{\tau }\) and considers the phenomenological implications.
In the discussion below, we mainly concentrate on the latest generation of results, which supersedes previous \(N_f=2\,+\,1\) determinations and allows for an extraction of \(|V_{cb}|\) that incorporates information about the \(q^2\)-dependence of the decay rate (cf. Sect. 8.8).
8.4.1 \(B_{(s)} \rightarrow D_{(s)}\) decays
We will first discuss the \(N_f=2\,+\,1\) computations of \(B \rightarrow D \ell \nu \) by FNAL/MILC and HPQCD mentioned above, both based on MILC asqtad ensembles. Full details about all the computations are provided in Table 48 and in the tables in Appendix B.6.5.
The FNAL/MILC study [615] employs ensembles at four values of the lattice spacing ranging between approximately 0.045 and \(0.12~\mathrm{fm}\), and several values of the light-quark mass corresponding to pions with RMS masses ranging between 260 and \(670~\mathrm{MeV}\) (with just one ensemble with \(M_\pi ^{\mathrm{RMS}} \simeq 330~\mathrm{MeV}\) at the finest lattice spacing). The b and c quarks are treated using the Fermilab approach. The quantities directly studied are the form factors \(h_\pm \) defined by
which are related to the standard vector and scalar form factors by
with \(r=m_D/m_B\). (Recall that \(q^2=(p_B-p_D)^2=m_B^2\,+\,m_D^2-2 w m_B m_D\).) The hadronic form factor relevant for experiment, \({\mathcal {G}}(w)\), is then obtained from the relation \({\mathcal {G}}(w)=4rf_+(q^2)/(1+r)\). The form factors are obtained from double ratios of three-point functions in which the flavour-conserving current renormalization factors cancel. The remaining matching factor \(\rho _{V^\mu _{cb}}\) is estimated with 1-loop lattice perturbation theory. In order to obtain \(h_\pm (w)\), a joint continuum-chiral fit is performed to an ansatz that contains the light-quark mass and lattice-spacing dependence predicted by next-to-leading order HMrS\(\chi \)PT, and the leading dependence on \(m_c\) predicted by the heavy-quark expansion (\(1/m_c^2\) for \(h_+\) and \(1/m_c\) for \(h_-\)). The w-dependence, which allows for an interpolation in w, is given by analytic terms up to \((1-w)^2\), as well as a contribution from the logarithm proportional to \(g^2_{D^*D\pi }\). The total resulting systematic error is \(1.2\%\) for \(f_+\) and \(1.1\%\) for \(f_0\). This dominates the final error budget for the form factors. After \(f_+\) and \(f_0\) have been determined as functions of w within the interval of values of \(q^2\) covered by the computation, synthetic data points are generated to be subsequently fitted to a z-expansion of the BGL form, cf. Sect. 8.3, with pole factors set to unity. This in turn enables one to determine \(|V_{cb}|\) from a joint fit of this z-expansion and experimental data. The value of the zero-recoil form factor resulting from the z-expansion is
The HPQCD computations [616, 618] use ensembles at two values of the lattice spacing, \(a=0.09,~0.12~\mathrm{fm}\), and two and three values of light-quark masses, respectively. The b quark is treated using NRQCD, while for the c quark the HISQ action is used. The form factors studied, extracted from suitable three-point functions, are
where \(V_\mu \) is the relevant vector current and the \(B_{(s)}\) rest frame is assumed. The standard vector and scalar form factors are retrieved as
The currents in the effective theory are matched at 1-loop to their continuum counterparts. Results for the form factors are then fitted to a modified BCL z-expansion ansatz, that takes into account simultaneously the lattice spacing, light-quark masses, and \(q^2\)-dependence. For the mass dependence NLO chiral logarithms are included, in the form obtained in hard-pion \(\chi \)PT. As in the case of the FNAL/MILC computation, once \(f_+\) and \(f_0\) have been determined as functions of \(q^2\), \(|V_{cb}|\) can be determined from a joint fit of this z-expansion and experimental data. The works quote for the zero-recoil vector form factor the result
The HPQCD and FNAL/MILC results for \(B\rightarrow D\) differ by less than half a standard deviation (assuming they are uncorrelated, which they are not as some of the ensembles are common) primarily because of lower precision of the former result. The HPQCD central value is smaller by 1.8 of the FNAL/MILC standard deviations than the FNAL/MILC value. The dominant source of errors in the \(|V_{cb}|\) determination by HPQCD are discretization effects and the systematic uncertainty associated with the perturbative matching.
In order to combine the form factors determinations of HPQCD and FNAL/MILC into a lattice average, we proceed in a similar way as with \(B\rightarrow \pi \ell \nu \) and \(B_s\rightarrow K\ell \nu \) above. FNAL/MILC quotes synthetic values for the form factors at three values of w (or, alternatively, \(q^2\)) with a full correlation matrix, which we take directly as input. In the case of HPQCD, we use their preferred modified z-expansion parameterization to produce synthetic values of the form factors at two different values of \(q^2\). This leaves us with a total of five data points in the kinematical range \(w\in [1.00,1.11]\). As in the case of \(B\rightarrow \pi \ell \nu \), we conservatively assume a 100% correlation of statistical uncertainties between HPQCD and FNAL/MILC. We then fit this data set to a BCL ansatz, using \(t_+=(M_{B^0}+M_{D^\pm })^2 \simeq 51.12~\,\mathrm {GeV}^2\) and \(t_0=(M_{B^0}+M_{D^\pm })(\sqrt{M_{B^0}}-\sqrt{M_{D^\pm }})^2 \simeq 6.19~\,\mathrm {GeV}^2\). In our fits, pole factors have been set to unity – i.e., we do not take into account the effect of sub-threshold poles, which is then implicitly absorbed into the series coefficients. The reason for this is our imperfect knowledge of the relevant resonance spectrum in this channel, which does not allow us to decide the precise number of poles needed.Footnote 56 This in turn implies that unitarity bounds do not rigorously apply, which has to be taken into account when interpreting the results (cf. Appendix A.5).
With a procedure similar to what we adopted for the \(B\rightarrow \pi \) and \(B_s\rightarrow K\) cases, we impose the kinematic constraint at \(q^2=0\) by expressing the \(a^0_{N^0-1}\) coefficient in the z-expansion of \(f_0\) in terms of all other coefficients. As mentioned above, FNAL/MILC provides synthetic data for \(f_+\) and \(f_0\) including correlations; HPQCD presents the result of simultaneous z-fits to the two form factors including all correlations, thus enabling us to generate a complete set of synthetic data for \(f_+\) and \(f_0\). Since both calculations are based on MILC ensembles, we then reconstruct the off-diagonal HPQCD-FNAL/MILC entries of the covariance matrix by conservatively assuming that statistical uncertainties are 100% correlated. The Fermilab/MILC (HPQCD) statistical error is 58% (31%) of the total error for every \(f_+\) value, and 64% (49%) for every \(f_0\) one. Using this information we can easily build the off-diagonal block of the overall covariance matrix (e.g., the covariance between \([f_+(q_1^2)]_{\mathrm{FNAL}}\) and \([f_0(q_2^2)]_\mathrm{HPQCD}\) is \((\delta [f_+(q_1^2)]_{\mathrm{FNAL}} \times 0.58)\; (\delta [f_0(q_2^2)]_{\mathrm{HPQCD}} \times 0.49)\), where \(\delta f\) is the total error).
For our central value, we choose an \(N^+ =N^0=3\) BCL fit, shown in Table 47. The coefficient \(a_3^+\) can be obtained from the values for \(a_0^+\)–\(a_2^+\) using Eq. (447). The fit is illustrated in Fig. 30.
Reference [612] is the only existing \(N_f=2\) work on \(B \rightarrow D\ell \nu \) transitions, that furthermore provided the first available results for \(B_s \rightarrow D_s\ell \nu \). This computation uses the publicly available ETM configurations obtained with the twisted-mass QCD action at maximal twist. Four values of the lattice spacing, ranging between 0.054 and \(0.098~\mathrm{fm}\), are considered, with physical box lengths ranging between 1.7 and \(2.7~\mathrm{fm}\). At two values of the lattice spacing two different physical volumes are available. Charged-pion masses range between \(\approx 270\) and \(\approx 490~\mathrm{MeV}\), with two or three masses available per lattice spacing and volume, save for the \(a \approx 0.054~\mathrm{fm}\) point at which only one light mass is available for each of the two volumes. The strange- and heavy-valence quarks are also treated with maximally twisted-mass QCD.
The quantities of interest are again the form factors \(h_\pm \) defined above. In order to control discretization effects from the heavy quarks, a strategy similar to the one employed by the ETM collaboration in their studies of B-meson decay constants (cf. Sect. 8.1) is employed: the value of \({{{\mathcal {G}}}}(w)\) is computed at a fixed value of \(m_c\) and several values of a heavier quark mass \(m_h^{(k)}=\lambda ^k m_c\), where \(\lambda \) is a fixed scaling parameter, and step-scaling functions are built as
Each ratio is extrapolated to the continuum limit, \(\sigma _k(w)=\lim _{a \rightarrow 0}\Sigma _k(w)\). One then exploits the fact that the \(m_h \rightarrow \infty \) limit of the step-scaling is fixed – in particular, it is easy to find from the heavy-quark expansion that \(\lim _{m_h\rightarrow \infty }\sigma (1)=1\). In this way, the physical result at the b-quark mass can be reached by interpolating \(\sigma (w)\) between the charm region (where the computation can be carried out with controlled systematics) and the known static limit value.
In practice, the values of \(m_c\) and \(m_s\) are fixed at each value of the lattice spacing such that the experimental kaon and \(D_s\) masses are reached at the physical point, as determined in Ref. [622]. For the scaling parameter, \(\lambda =1.176\) is chosen, and eight scaling steps are performed, reaching \(m_h/m_c=1.176^9\simeq 4.30\), approximately corresponding to the ratio of the physical b- and c-masses in the \(\overline{\mathrm{MS}}\) scheme at \(2~\mathrm{GeV}\). All observables are obtained from ratios that do not require (re)normalization. The ansatz for the continuum and chiral extrapolation of \(\Sigma _k\) contains a constant and linear terms in \(m_{\mathrm{sea}}\) and \(a^2\). Twisted boundary conditions in space are used for valence-quark fields for better momentum resolution. Applying this strategy the form factors are finally obtained at four reference values of w between 1.004 and 1.062, and, after a slight extrapolation to \(w=1\), the result is quoted
The authors also provide values for the form factor relevant for the meson states with light-valence quarks, obtained from a similar analysis to the one described above for the \(B_s\rightarrow D_s\) case. Values are quoted from fits with and without a linear \(m_\mathrm{sea}/m_s\) term in the chiral extrapolation. The result in the former case, which safely covers systematic uncertainties, is
Given the identical strategy, and the small sensitivity of the ratios used in their method to the light valence- and sea-quark masses, we assign this result the same ratings in Table 48 as those for their calculation of \({{{\mathcal {G}}}}^{B_s \rightarrow D_s}(1)\). Currently the precision of this calculation is not competitive with that of \(N_f=2\,+\,1\) works, but this is due largely to the small number of configurations analysed by Atoui et al. The viability of their method has been clearly demonstrated, however, which leaves significant room for improvement on the errors of both the \(B \rightarrow D\) and \(B_s \rightarrow D_s\) form factors with this approach by including either additional two-flavour data or analysing more recent ensembles with \(N_f>2\).
Finally, Atoui et al. also study the scalar and tensor form factors, as well as the momentum-transfer dependence of \(f_{+,0}\). The value of the ratio \(f_0(q^2)/f_+(q^2)\) is provided at a reference value of \(q^2\) as a proxy for the slope of \({{{\mathcal {G}}}}(w)\) around the zero-recoil limit.
8.4.2 Ratios of \(B\rightarrow D\ell \nu \) form factors
The availability of results for the scalar form factor \(f_0\) for \(B\rightarrow D\ell \nu \) amplitudes allows us to study interesting observables that involve the decay in the \(\tau \) channel. One such quantity is the ratio
which is sensitive to \(f_0\), and can be accurately determined by experiment.Footnote 57 Indeed, the recent availability of experimental results for R(D) has made this quantity particularly relevant in the search for possible physics beyond the Standard Model. Both FNAL/MILC and HPQCD provide values for R(D) from their recent form factor computations, discussed above. The quoted values by FNAL/MILC and HPQCD are
These results are in excellent agreement, and can be averaged (using the same considerations for the correlation between the two computations as we did in the averaging of form factors) into
This result is about \(2.3\sigma \) lower than the current experimental average for this quantity. It has to be stressed that achieving this level of precision critically depends on the reliability with which the low-\(q^2\) region is controlled by the parameterizations of the form factors. It is also worth mentioning that if experimental data for \(B \rightarrow D\ell \nu \) are used to further constrain R(D) as part of a global fit, it is possible to decrease the error substantially, cf. the value \(R(D)=0.299(3)\) quoted in [623].
HPQCD also computes a new value for \(R(D_s)\), the analog of R(D), with both heavy–light mesons containing a strange quark [618]:
Another area of immediate interest in searches for physics beyond the Standard Model is the measurement of \(B_s \rightarrow \mu ^+ \mu ^-\) decays, recently studied at the LHC.Footnote 58 In addition to the \(B_s\) decay constant (see Sect. 8.1), one of the hadronic inputs required by the LHCb analysis is the ratio of \(B_q\) meson (\(q = d,s\)) fragmentation fractions \(f_s / f_d\). A dedicated \(N_f=2\,+\,1\) study by FNAL/MILCFootnote 59 [624] addresses the ratios of scalar form factors \(f_0^{(q)}(q^2)\), and quotes:
where the first error is statistical and the second systematic. The more recent results from HPQCD [618] are:
Results from both groups lead to fragmentation fraction ratios \(f_s/f_d\) that are consistent with LHCb’s measurements via other methods [625].
8.4.3 \(B \rightarrow D^*\) decays
The most precise computation of the zero-recoil form factors needed for the determination of \(|V_{cb}|\) from exclusive B semileptonic decays comes from the \(B \rightarrow D^* \ell \nu \) form factor at zero recoil \({{{\mathcal {F}}}}^{B \rightarrow D^*}(1)\), calculated by the FNAL/MILC collaboration. The original computation, published in Ref. [613], has now been updated [614] by employing a much more extensive set of gauge ensembles and increasing the statistics of the ensembles originally considered, while preserving the analysis strategy. There is currently no unquenched computation of the relevant form factors at nonzero recoil.
This work uses the MILC \(N_f = 2 + 1\) ensembles. The bottom and charm quarks are simulated using the clover action with the Fermilab interpretation and light quarks are treated via the asqtad staggered fermion action. Recalling the definition of the form factors in Eq. (226), at zero recoil \({{{\mathcal {F}}}}^{B \rightarrow D^*}(1)\) reduces to a single form factor \(h_{A_1}(1)\) coming from the axial-vector current
where \(\epsilon ^\prime \) is the polarization of the \(D^*\). The form factor is accessed through a ratio of three-point correlators, viz.,
Simulation data is obtained on MILC ensembles with five lattice spacings, ranging from \(a \approx 0.15~\mathrm{fm}\) to \(a \approx 0.045~\mathrm{fm}\), and as many as five values of the light-quark masses per ensemble (though just one at the finest lattice spacing). Results are then extrapolated to the physical, continuum/chiral, limit employing staggered \(\chi \)PT.
The \(D^*\) meson is not a stable particle in QCD and decays predominantly into a D plus a pion. Nevertheless, heavy–light meson \(\chi \)PT can be applied to extrapolate lattice simulation results for the \(B\rightarrow D^*\ell \nu \) form factor to the physical light-quark mass. The \(D^*\) width is quite narrow, 0.096 MeV for the \(D^{*\pm }(2010)\) and less than 2.1 MeV for the \(D^{*0}(2007)\), making this system much more stable and long lived than the \(\rho \) or the \(K^*\) systems. The fact that the \(D^* - D\) mass difference is close to the pion mass leads to the well-known “cusp” in \(\mathcal{R}_{A_1}\) just above the physical pion mass [626,627,628]. This cusp makes the chiral extrapolation sensitive to values used in the \(\chi \)PT formulas for the \(D^*D \pi \) coupling \(g_{D^*D\pi }\). The error budget in Ref. [614] includes a separate error of 0.3% coming from the uncertainty in \(g_{D^*D \pi }\) in addition to general chiral extrapolation errors in order to take this sensitivity into account.
The final updated value presented in Ref. [614] is
where the first error is statistical, and the second the sum of systematic errors added in quadrature, making up a total error of 1.4% (down from the original 2.6% of Ref. [613]). The largest systematic uncertainty comes from discretization errors followed by effects of higher-order corrections in the chiral perturbation theory ansatz.
Since the previous version of this review, the HPQCD collaboration has published the first study of \({{B}_{(s)}\rightarrow D_{(s)}^{*}\ell {\nu }}\) form factors at zero recoil for \(N_f=2\,+\,1\,+\,1\) using eight MILC ensembles with lattice spacing \(a\approx 0.15\), 0.12, and 0.09 [618]. There are three ensembles with varying light-quark masses for the two coarser lattice spacings and two choices of light-quark mass for the finest lattice spacing. In each case, there is one ensemble for which the light-quark mass is very close to the physical value. The b quark is treated using NRQCD and the light quarks are treated using the HISQ action. The resulting zero-recoil form factors are:
At Lattice 2018, two groups presented preliminary results for the \(B\rightarrow D^* \ell \nu \) semileptonic decay. From JLQCD, there was a poster describing their calculations for zero and nonzero recoil using \(N_f=2\,+\,1\) Möbius domain-wall ensembles. Two lattice spacings of roughly 0.079 and 0.055 fm were used with bottom-quark mass limited to 2.4 times the charm-quark mass to control the heavy-quark discretization effects. In addition, JLQCD is studying \(B\rightarrow D\ell \nu \). From FNAL/MILC there was a presentation of preliminary results using 15 \(N_f=2\,+\,1\) asqtad sea-quark ensembles with lattice spacing between approximately 0.15 and 0.045 fm. The heavy quarks are treated using the clover action with the Fermilab interpretation. In addition, HPQCD presented preliminary results for \(B_s \rightarrow D_s^{(*)}\ell \nu \) using HISQ quarks for all valence and sea quarks. The calculation uses three of MILC’s \(N_f=2\,+\,1\,+\,1\) HISQ ensembles with \(a\approx 0.09\), 0.06 and 0.045 fm. An advantage of the all-HISQ approach is that there is no need for perturbative renormalization of the axial-vector- or vector-current.
8.5 Semileptonic form factors for \(B_c\rightarrow \eta _c\ell \nu \) and \(B_c\rightarrow J/\psi \ell \nu \)
In 2016, preliminary results for the decays \(B_c\rightarrow \eta _c\ell \nu \) and \(B_c\rightarrow J/\psi \ell \nu \) were presented at two conferences by the HPQCD collaboration [629, 630]. The calculations use both NRQCD and HISQ actions for the valence b quark, and the HISQ action for the c quark (both valence and sea). The calculations were done using five ensembles from the MILC collaboration with \(N_f=2\,+\,1\,+\,1\) and lattice spacings between approximately 0.15 and 0.045 fm. Only ensembles with \(m_l/m_s=0.2\) are used although ones with a physical light-quark mass are available. For the HISQ formalism, a range of heavy-quark masses obeying \(am_h<0.8\) is used and an extrapolation \(m_h\rightarrow m_b\) is made. Comparison of results using NRQCD and HISQ allows an improved normalization for the NRQCD currents as the HISQ currents do not require renormalization.
8.6 Semileptonic form factors for \(\Lambda _b\rightarrow p\ell \nu \) and \(\Lambda _b\rightarrow \Lambda _c\ell \nu \)
Lattice-QCD computations for heavy-quark physics has been extended to the study of semileptonic decays of the \(\Lambda _b\) baryon, with first unquenched results away from the static limit provided in a work by Detmold, Lehner, and Meinel [631].Footnote 60 The importance of this result is that, together with a recent analysis by LHCb of the ratio of decay rates \(\Gamma (\Lambda _b\rightarrow p\ell \nu )/\Gamma (\Lambda _b\rightarrow \Lambda _c\ell \nu )\) [634], it allows for an exclusive determination of the ratio \(|V_{ub}|/|V_{cb}|\) largely independent from the outcome of different exclusive channels, thus contributing a very interesting piece of information to the existing tensions in the determination of third-column CKM matrix elements (cf. Sects. 8.7, and 8.8).
The amplitudes of the decays \(\Lambda _b\rightarrow p\ell \nu \) and \(\Lambda _b\rightarrow \Lambda _c\ell \nu \) receive contributions from both the vector and the axial components of the current in the matrix elements \(\langle p|\bar{q}\gamma ^\mu ({\mathbf {1}}-\gamma _5)b|\Lambda _b\rangle \) and \(\langle \Lambda _c|{{\bar{q}}}\gamma ^\mu ({\mathbf {1}}-\gamma _5)b|\Lambda _b\rangle \), and can be parameterized in terms of six different form factors – see, e.g., Ref. [544] for a complete description. They split into three form factors \(f_+\), \(f_0\), \(f_\perp \) in the parity-even sector, mediated by the vector component of the current, and another three form factors \(g_+,g_0,g_\perp \) in the parity-odd sector, mediated by the axial component. All of them provide contributions that are parametrically comparable.
The computation of Detmold et al. uses RBC/UKQCD \(N_f=2\,+\,1\) DWF ensembles, and treats the b and c quarks within the Columbia RHQ approach. Two values of the lattice spacing (\(a\sim 0.112,~0.085~\mathrm{fm}\)) are considered, with the absolute scale set from the \(\Upsilon (2S)\)–\(\Upsilon (1S)\) splitting. Sea pion masses lie in a narrow interval ranging from slightly above \(400~\mathrm{MeV}\) to slightly below \(300~\mathrm{MeV}\), keeping \(m_\pi L \gtrsim 4\); however, lighter pion masses are considered in the valence DWF action for the u, d quarks, leading to partial quenching effects in the chiral extrapolation. More importantly, this also leads to values of \(M_{\pi ,\mathrm{min}}L\) close to 3.0 (cf. Appendix B.6.3 for details); compounded with the fact that there is only one lattice volume in the computation, an application of the FLAG criteria would lead to a  rating for finite-volume effects. It has to be stressed, however, that our criteria have been developed in the context of meson physics, and their application to the baryon sector is not straightforward; as a consequence, we will refrain from providing a conclusive rating of this computation for the time being.
rating for finite-volume effects. It has to be stressed, however, that our criteria have been developed in the context of meson physics, and their application to the baryon sector is not straightforward; as a consequence, we will refrain from providing a conclusive rating of this computation for the time being.
Results for the form factors are obtained from suitable three-point functions, and fitted to a modified z-expansion ansatz that combines the \(q^2\)-dependence with the chiral and continuum extrapolations. The main results of the paper are the predictions (errors are statistical and systematic, respectively)
which are the input for the LHCb analysis. Predictions for the total rates in all possible lepton channels, as well as for ratios similar to R(D) (cf. Sect. 8.4) between the \(\tau \) and light-lepton channels are also available.
Since the previous version of this review, there have been three papers [621, 635, 636] extending study of the \(\Lambda _b\) and two [541, 637] studying the \(\Lambda _c\). Reference [635] studies the rare decay \(\Lambda _b \rightarrow \Lambda \ell ^+ \ell ^-\). The lattice setup is identical, and similar considerations as above thus apply. Furthermore, the renormalization of the tensor current is carried out adopting a mostly nonperturbative renormalization strategy, without however computing the residual renormalization factor \(\rho _{T^{\mu \nu }}\), which is set to its tree-level value. While the matching systematic uncertainty is augmented to take this fact into account, the procedure implies that the current retains an uncanceled logarithmic divergence at \({\mathcal {O}}(\alpha _s)\).
Reference [636] is an exploratory study of the decay \(\Lambda _b \rightarrow \Lambda (1520) \ell ^+ \ell ^-\) using a single gauge ensemble presented at Lattice 2016. Reference [621] includes new results for \({\Lambda }_b\rightarrow {\Lambda }_c\) for the tensor form factors. The main focus of this paper is the phenomenology of the \( {\Lambda }_b\rightarrow {\Lambda }_c\tau {{\overline{\nu }}}_{\tau } \) decay and how it can be used to limit contributions from beyond the standard model physics.
8.7 Determination of \(|V_{ub}|\)
We now use the lattice-determined Standard Model transition amplitudes for leptonic (Sect. 8.1) and semileptonic (Sect. 8.3) B-meson decays to obtain exclusive determinations of the CKM matrix element \(|V_{ub}|\). In this section, we describe the aspect of our work that involves experimental input for the relevant charged-current exclusive decay processes. The relevant formulae are Eqs. (191) and (222). Among leptonic channels the only input comes from \(B\rightarrow \tau \nu _\tau \), since the rates for decays to e and \(\mu \) have not yet been measured. In the semileptonic case we only consider \(B\rightarrow \pi \ell \nu \) transitions (experimentally measured for \(\ell =e,\mu \)). As discussed in Sects. 8.3 and 8.6, there are now lattice predictions for the rates of the decays \(B_s\rightarrow K\ell \nu \) and \(\Lambda _b\rightarrow p\ell \nu \); however, in the former case the process has not been experimentally measured yet, while in the latter case the only existing lattice computation does not meet FLAG requirements for controlled systematics.
We first investigate the determination of \(|V_{ub}|\) through the \(B\rightarrow \tau \nu _\tau \) transition. This is the only experimentally measured leptonic decay channel of the charged B meson. The experimental measurements of the branching fraction of this channel, \(B(B^{-} \rightarrow \tau ^{-} {\bar{\nu }})\), have not been updated since the publication of the previous FLAG report [3]. In Table 49 we summarize the current status of experimental results for this branching fraction.
It is obvious that all the measurements listed in Table 49 have significance smaller than \(5\sigma \), and the large uncertainties are dominated by statistical errors. These measurements lead to the averages of experimental measurements for \(B(B^{-}\rightarrow \tau {\bar{\nu }})\) [549, 550],
where, following our standard procedure we perform a weighted average and rescale the uncertainty by the square root of the reduced chi-squared. Note that the Particle Data Group [133] did not inflate the uncertainty in the calculation of the averaged branching ratio.
Combining the results in Eqs. (253–255) with the experimental measurements of the mass of the \(\tau \)-lepton and the B-meson lifetime and mass we get
which can be used to extract \(|V_{ub}|\), viz.,
where the first error comes from the uncertainty in \(f_B\) and the second comes from experiment.
Let us now turn our attention to semileptonic decays. The experimental value of \(|V_{ub}|f_+(q^2)\) can be extracted from the measured branching fractions for \(B^0\rightarrow \pi ^\pm \ell \nu \) and/or \(B^\pm \rightarrow \pi ^0\ell \nu \) applying Eq. (222);Footnote 61 \(|V_{ub}|\) can then be determined by performing fits to the constrained BCL z-parameterization of the form factor \(f_+(q^2)\) given in Eq. (448). This can be done in two ways: one option is to perform separate fits to lattice and experimental results, and extract the value of \(|V_{ub}|\) from the ratio of the respective \(a_0\) coefficients; a second option is to perform a simultaneous fit to lattice and experimental data, leaving their relative normalization \(|V_{ub}|\) as a free parameter. We adopt the second strategy, because it combines the lattice and experimental input in a more efficient way, leading to a smaller uncertainty on \(|V_{ub}|\).
The available state-of-the-art experimental input consists of five data sets: three untagged measurements by BaBar (6-bin [640] and 12-bin [641]) and Belle [642], all of which assume isospin symmetry and provide combined \(B^0\rightarrow \pi ^-\) and \(B^+\rightarrow \pi ^0\) data; and the two tagged Belle measurements of \({{\bar{B}}}^0\rightarrow \pi ^+\) (13-bin) and \(B^-\rightarrow \pi ^0\) (7-bin) [643]. Including all of them, along with the available information about cross-correlations, will allow us to obtain a meaningful final error estimate.Footnote 62 The lattice input data set will be the same discussed in Sect. 8.3.
We perform a constrained BCL fit of the vector and scalar form factors (this is necessary in order to take into account the \(f_+(q^2=0) = f_0 (q^2=0)\) constraint) together with the combined experimental data sets. We find that the error on \(|V_{ub}|\) stabilizes for \((N^+ = N^0 = 3)\). The result of the combined fit is presented in Table 50.
In Fig. 31 we show both the lattice and experimental data for \((1-q^2/m_{B^*}^2)f_+(q^2)\) as a function of \(z(q^2)\), together with our preferred fit; experimental data has been rescaled by the resulting value for \(|V_{ub}|^2\). It is worth noting the good consistency between the form factor shapes from lattice and experimental data. This can be quantified, e.g., by computing the ratio of the two leading coefficients in the constrained BCL parameterization: the fit to lattice form factors yields \(a_1^+/a_0^+=-1.67(35)\) (cf. the results presented in Sect. 8.3.1), while the above lattice+experiment fit yields \(a_1^+/a_0^+=-1.19(13)\).
Lattice and experimental data for \((1-q^2/m_{B^*}^2)f_+^{B\rightarrow \pi }(q^2)\) and \(f_0^{B\rightarrow \pi } (q^2)\) versus z. Green symbols denote lattice-QCD points included in the fit, while blue and indigo points show experimental data divided by the value of \(|V_{ub}|\) obtained from the fit. The grey and orange bands display the preferred \(N^+ = N^0 = 3\) BCL fit (six parameters) to the lattice-QCD and experimental data with errors
We plot the values of \(|V_{ub}|\) we have obtained in Fig. 33, where the (GGOU) determination through inclusive decays by the Heavy Flavour Averaging Group (HFLAV) [221], yielding \(|V_{ub}| = 4.52(15)({}^{+11}_{-14}) \times 10^{-3}\), is also shown for comparison. In this plot the tension between the BaBar and the Belle measurements of \(B(B^{-} \rightarrow \tau ^{-} {\bar{\nu }})\) is manifest. As discussed above, it is for this reason that we do not extract \(|V_{ub}|\) through the average of results for this branching fraction from these two collaborations. In fact this means that a reliable determination of \(|V_{ub}|\) using information from leptonic B-meson decays is still absent; the situation will only clearly improve with the more precise experimental data expected from Belle II [644, 645]. The value for \(|V_{ub}|\) obtained from semileptonic B decays for \(N_f=2\,+\,1\), on the other hand, is significantly more precise than both the leptonic and the inclusive determinations, and exhibits the well-known \(\sim 3\sigma \) tension with the latter.
8.8 Determination of \(|V_{cb}|\)
We will now use the lattice-QCD results for the \(B \rightarrow D^{(*)}\ell \nu \) form factors in order to obtain determinations of the CKM matrix element \(|V_{cb}|\) in the Standard Model. The relevant formulae are given in Eq. (228).
Let us summarize the lattice input that satisfies FLAG requirements for the control of systematic uncertainties, discussed in Sect. 8.4. In the (experimentally more precise) \(B\rightarrow D^*\ell \nu \) channel, there is only one \(N_f=2\,+\,1\) lattice computation of the relevant form factor \({\mathcal {F}}^{B\rightarrow D^*}\) at zero recoil. Concerning the \(B \rightarrow D\ell \nu \) channel, for \(N_f=2\) there is one determination of the relevant form factor \({\mathcal {G}}^{B\rightarrow D}\) at zero recoil;Footnote 63 while for \(N_f=2\,+\,1\) there are two determinations of the \(B \rightarrow D\) form factor as a function of the recoil parameter in roughly the lowest third of the kinematically allowed region. In this latter case, it is possible to replicate the analysis carried out for \(|V_{ub}|\) in Sect. 8.7, and perform a joint fit to lattice and experimental data; in the former, the value of \(|V_{cb}|\) has to be extracted by matching to the experimental value for \({\mathcal {F}}^{B\rightarrow D^*}(1)\eta _{\mathrm{EW}}|V_{cb}|\) and \({\mathcal {G}}^{B\rightarrow D}(1)\eta _{\mathrm{EW}}|V_{cb}|\).
The latest experimental average by HFLAV [221] for the \(B\rightarrow D^*\) form factor at zero recoil makes use of the CLN [646] parameterization of the \(B\rightarrow D^*\) form factor and is
Recently the Belle collaboration presented an updated measurement of the \(B\rightarrow D^* \ell \nu \) branching ratio [647] in which, as suggested in Refs. [648,649,650], the impact of the form factor parameterization has been studied by comparing the CLN [646] and BGL [651, 652] ansätze. The fit results using the two parameterizations are perfectly compatible. In light of the fact that the BGL parameterization imposes much less stringent constraints on the shape of the form factor than the CLN one we choose to focus on the BGL fit:
where the first error is statistical and the second is systematic. In the following we present determinations of \(|V_{cb}|\) obtained from Eqs. (268) and (269). By using \(\eta _{\mathrm{EW}}=1.00662\) Footnote 64 and the \(N_f = 2 +1\) lattice value for \({\mathcal {F}}^{B\rightarrow D^*}(1)\) in Eq. (248),Footnote 65 we thus extract the averages
where the first uncertainty comes from the lattice computation and the second from the experimental input.
For the zero-recoil \(B \rightarrow D\) form factor, HFLAV [221] quotes
yielding the following average for \(N_f=2\):
where the first uncertainty comes from the lattice computation and the second from the experimental input.
Finally, for \(N_f=2\,+\,1\) we perform, as discussed above, a joint fit to the available lattice data, discussed in Sect. 8.4, and state-of-the-art experimental determinations. In this case, we will combine the aforementioned recent Belle measurement [653], which provides partial integrated decay rates in 10 bins in the recoil parameter w, with the 2010 BaBar data set in Ref. [654], which quotes the value of \({\mathcal {G}}^{B\rightarrow D}(w)\eta _{\mathrm{EW}}|V_{cb}|\) for ten values of w.Footnote 66 The fit is dominated by the more precise Belle data; given this, and the fact that only partial correlations among systematic uncertainties are to be expected, we will treat both data sets as uncorrelated.Footnote 67
A constrained \((N^+ = N^0 = 3)\) BCL fit using the same ansatz as for lattice-only data in Sect. 8.4, yields our average, which we present in Table 51. The fit is illustrated in Fig. 32. In passing, we note that, if correlations between the FNAL/MILC and HPQCD calculations are neglected, the \(|V_{cb}|\) central value rises to \(40.3 \times 10^{-3}\) in nice agreement with the results presented in Ref. [623].
Lattice and experimental data for \(f_+^{B\rightarrow D}(q^2)\) and \(f_0^{B\rightarrow D}(q^2)\) versus z. Green symbols denote lattice-QCD points included in the fit, while blue and indigo points show experimental data divided by the value of \(|V_{cb}|\) obtained from the fit. The grey and orange bands display the preferred \(N^+=N^0=3\) BCL fit (six parameters) to the lattice-QCD and experimental data with errors
In order to combine the determinations of \(|V_{cb}|\) from exclusive \(B\rightarrow D\) and \(B\rightarrow D^*\) semileptonic decays, we need to estimate the correlation between the lattice uncertainties in the two modes. We assume conservatively that the statistical component of the lattice error in both determinations are 100% correlated because they are based on the same MILC configurations (albeit on different subsets). Considering separately the BGL and CLN determination of \(|V_{cb}|\) from \(B\rightarrow D^*\) semileptonic decays, we obtain:
where we applied a rescaling factor 1.35 to the BGL case.
Our results are summarized in Table 52, which also shows the HFLAV inclusive determination of \(|V_{cb}|=42.00(65) \times 10^{-3}\) [655] for comparison, and illustrated in Fig. 33.
Left: Summary of \(|V_{ub}|\) determined using: i) the B-meson leptonic decay branching fraction, \(B(B^{-} \rightarrow \tau ^{-} {\bar{\nu }})\), measured at the Belle and BaBar experiments, and our averages for \(f_{B}\) from lattice QCD; and ii) the various measurements of the \(B\rightarrow \pi \ell \nu \) decay rates by Belle and BaBar, and our averages for lattice determinations of the relevant vector form factor \(f_+(q^2)\). Right: Same for determinations of \(|V_{cb}|\) using semileptonic decays. The HFLAV inclusive results are from Refs. [221, 655]
In Fig. 34 we present a summary of determinations of \(|V_{ub}|\) and \(|V_{cb}|\) from \(B\rightarrow (\pi ,D^{(*)})\ell \nu \) and \(B\rightarrow \tau \nu \). For comparison purposes, we also add the determination of \(|V_{ub}/V_{cb}|\) obtained from \(\Lambda _b\rightarrow (p,\Lambda _c)\ell \nu \) decays in Refs. [631, 634] – which, as discussed in the text, does not meet the FLAG criteria to enter our averages – as well as the results from inclusive \(B\rightarrow X_{u,c} \ell \nu \) decays. Currently, the determinations of \(V_{cb}\) from \(B\rightarrow D^*\) and \(B\rightarrow D\) decays are quite compatible; however, a sizeable tension involving the extraction of \(V_{cb}\) from inclusive dedecays remains. In the determination of the \(1\sigma \) and \(2\sigma \) contours for our average we have included an estimate of the correlation between \(|V_{ub}|\) and \(|V_{cb}|\) from semileptonic B decays: the lattice inputs to these quantities are dominated by results from the Fermilab/MILC and HPQCD collaborations which are both based on MILC \(N_f=2\,+\,1\) ensembles, leading to our conservatively introducing a 100% correlation between the lattice statistical uncertainties of the three computations involved. The results of the fit are
for the BGL and CLN \(B\rightarrow D^*\) parameterizations, respectively.
Summary of \(|V_{ub}|\) and \(|V_{cb}|\) determinations. Left and right panels correspond to using the BGL and CLN parameterization for the \(B\rightarrow D^*\) form factor, respectively. The solid and dashed lines correspond to 68% and 95% C.L. contours. As discussed in the text, baryonic modes are not included in our averages. The results of the fit in the two cases are \((|V_{cb}^{}|,|V_{ub}^{}|) \times 10^3 = (39.09\pm 0.68, 3.73 \pm 0.14)\) with a p-value of 0.32 and \((|V_{cb}^{}|,|V_{ub}^{}|) \times 10^3 = (39.41\pm 0.61, 3.74 \pm 0.14)\) with a p-value of 0.55, for the BGL and CLN \(B\rightarrow D^*\) parameterizations, respectively
References [623, 648, 650] published in 2016 and 2017 presented evidence that there can be a considerable difference in the CKM matrix elements when choosing between the CLN and BGL parameterizations of form factors. In mid-2018, it appeared that switching to BGL might resolve the difference between the inclusive and exclusive determinations of \(|V_{cb}|\); however, it did not seem to shed light on \(|V_{ub}|\). In September, 2018, a new analysis of Belle [647] appeared to find a 10% difference between CNL and BGL parametrizations for \({\mathcal {F}}^{B\rightarrow D^*}(1)\eta _\mathrm{EW}|V_{cb}|\), supporting previous findings. However, in April, 2019, a new version of that preprint found the two parametrizations completely compatible. Further, in March, 2019, a BaBar preprint [656] presented an angular analysis of the full dataset from that experiment. This unbinned fit using the BGL parametrization of the form factors and the FNAL/MILC result for \({\mathcal {F}}^{B\rightarrow D^*}(1)\) finds \(|V_{cb}| = (38.36\pm 0.90)\times 10^{-3},\) quite compatible with previous exclusive determinations and not indicating a resolution of the difference from the inclusive value. A recent paper by Gambino et al. [657] reviews the history, presents numerous fits of the Belle tagged and untagged data, and finds about a \(2 \sigma \) difference between exclusive and inclusive values for \(|V_{cb}|\).
It will be interesting to see what happens when both experimental and theoretical precisions are improved. At least four groups are working to improve the form factor calculations: FNAL/MILC, HPQCD, JLQCD, and LANL/SWME. It would also be good to have additional results on the \(\Lambda _b\) form factors. We can expect new measurements from Belle II and LHCb.
9 The strong coupling \(\alpha _{\mathrm{s}}\)
Authors: R. Horsley, T. Onogi, R. Sommer
9.1 Introduction
The strong coupling \({\bar{g}}_s(\mu )\) defined at scale \(\mu \), plays a key role in the understanding of QCD and in its application to collider physics. For example, the parametric uncertainty from \(\alpha _s\) is one of the dominant sources of uncertainty in the Standard Model prediction for the \(H \rightarrow b{\bar{b}}\) partial width, and the largest source of uncertainty for \(H \rightarrow gg\). Thus higher precision determinations of \(\alpha _s\) are needed to maximize the potential of experimental measurements at the LHC, and for high-precision Higgs studies at future colliders and the study of the stability of the vacuum [658,659,660,661,662,663,664,665]. The value of \(\alpha _s\) also yields one of the essential boundary conditions for completions of the standard model at high energies.
In order to determine the running coupling at scale \(\mu \)
we should first “measure” a short-distance quantity \({{\mathcal {Q}}}\) at scale \(\mu \) either experimentally or by lattice calculations, and then match it to a perturbative expansion in terms of a running coupling, conventionally taken as \(\alpha _{\overline{\mathrm{MS}}}(\mu )\),
The essential difference between continuum determinations of \(\alpha _s\) and lattice determinations is the origin of the values of \({\mathcal {Q}}\) in Eq. (278).
The basis of continuum determinations are experimentally measurable cross sections or decay widths from which \({\mathcal {Q}}\) is defined. These cross sections have to be sufficiently inclusive and at sufficiently high scales such that perturbation theory can be applied. Often hadronization corrections have to be used to connect the observed hadronic cross sections to the perturbative ones. Experimental data at high \(\mu \), where perturbation theory is progressively more precise, usually have increasing experimental errors, and it is not easy to find processes that allow one to follow the \(\mu \)-dependence of a single \({\mathcal {Q}}(\mu )\) over a range where \(\alpha _s(\mu )\) changes significantly and precision is maintained.
In contrast, in lattice gauge theory, one can design \({\mathcal {Q}}(\mu )\) as Euclidean short-distance quantities that are not directly related to experimental observables. This allows us to follow the \(\mu \)-dependence until the perturbative regime is reached and nonperturbative “corrections” are negligible. The only experimental input for lattice computations of \(\alpha _s\) is the hadron spectrum which fixes the overall energy scale of the theory and the quark masses. Therefore experimental errors are completely negligible and issues such as hadronization do not occur. We can construct many short-distance quantities that are easy to calculate nonperturbatively in lattice simulations with small statistical uncertainties. We can also simulate at parameter values that do not exist in nature (for example, with unphysical quark masses between bottom and charm) to help control systematic uncertainties. These features mean that precise results for \(\alpha _s\) can be achieved with lattice gauge theory computations. Further, as in the continuum, the different methods available to determine \(\alpha _s\) in lattice calculations with different associated systematic uncertainties enable valuable cross-checks. Practical limitations are discussed in the next section, but a simple one is worth mentioning here. Experimental results (and therefore the continuum determinations) of course have all quarks present, while in lattice gauge theories in practice only the lighter ones are included and one is then forced to use the matching at thresholds, as discussed in the following section.
It is important to keep in mind that the dominant source of uncertainty in most present day lattice-QCD calculations of \(\alpha _s\) are from the truncation of continuum/lattice perturbation theory and from discretization errors. Perturbative truncation errors are of particular concern because they often cannot easily be estimated from studying the data itself. Further, the size of higher-order coefficients in the perturbative series can sometimes turn out to be larger than naive expectations based on power counting from the behaviour of lower-order terms. We note that perturbative truncation errors are also the dominant source of uncertainty in several of the phenomenological determinations of \(\alpha _s\).
The various phenomenological approaches to determining the running coupling, \(\alpha ^{(5)}_{\overline{\mathrm{MS}}}(M_Z)\) are summarized by the Particle Data Group [137]. The PDG review lists five categories of phenomenological results used to obtain the running coupling: using hadronic \(\tau \) decays, hadronic final states of \(e^+e^-\) annihilation, deep inelastic lepton–nucleon scattering, electroweak precision data, and high energy hadron collider data. Excluding lattice results, the PDG quotes the weighted average as
compared to \( \alpha ^{(5)}_{\overline{\mathrm{MS}}}(M_Z) = 0.1183(12) \) of the older review [170]. For a general overview of the various phenomenological and lattice approaches see, e.g., Ref. [666]. The extraction of \(\alpha _s\) from \(\tau \) data, which is the most precise and has the largest impact on the nonlattice average in Eq. (279) is especially sensitive to the treatment of higher-order perturbative terms as well as the treatment of nonperturbative effects. This is important to keep in mind when comparing our chosen range for \(\alpha ^{(5)}_{\overline{\mathrm{MS}}}(M_Z)\) from lattice determinations in Eq. (344) with the nonlattice average from the PDG.
9.1.1 Scheme and scale dependence of \(\alpha _s\) and \(\Lambda _{\mathrm{QCD}}\)
Despite the fact that the notion of the QCD coupling is initially a perturbative concept, the associated \(\Lambda \) parameter is nonperturbatively defined
where \(\beta \) is the full renormalization group function in the scheme which defines \({\bar{g}}_s\), and \(b_0\) and \(b_1\) are the first two scheme-independent coefficients of the perturbative expansion
with
Thus the \(\Lambda \) parameter is renormalization-scheme-dependent but in an exactly computable way, and lattice gauge theory is an ideal method to relate it to the low-energy properties of QCD. In the \(\overline{\mathrm{MS}}\) scheme presently \(b_{n_l}\) with \(n_l = 4\) is known.
The change in the coupling from one scheme S to another (taken here to be the \(\overline{\mathrm{MS}}\) scheme) is perturbative,
where \(c^{(i)}_g, \, i\ge 1\) are finite renormalization coefficients. The scale \(\mu \) must be taken high enough for the error in keeping only the first few terms in the expansion to be small. On the other hand, the conversion to the \(\Lambda \) parameter in the \(\overline{\mathrm{MS}}\) scheme is given exactly by
The fact that \(\Lambda _{\overline{\mathrm {MS}}}\) can be obtained exactly from \(\Lambda _S\) in any scheme S where \(c^{(1)}_g\) is known together with the high order knowledge (5-loop by now) of \(\beta _{\overline{\mathrm {MS}}}\) means that the errors in \(\alpha _{\overline{\mathrm {MS}}}(m_\mathrm {Z})\) are dominantly due to the errors of \(\Lambda _S\). We will therefore mostly discuss them in that way. Starting from Eq. (280), we have to consider (i) the error of \({\bar{g}}_S^2(\mu )\) (denoted as \(\left( \frac{\Delta \Lambda }{\Lambda }\right) _{\Delta \alpha _S}\) ) and (ii) the truncation error in \(\beta _S\) (denoted as \(\left( \frac{\Delta \Lambda }{\Lambda }\right) _{\mathrm{trunc}}\)). Concerning (ii), note that knowledge of \(c_g^{(n_l)}\) for the scheme S means that \(\beta _S\) is known to \(n_l+1\) loop order; \(b_{n_l}\) is known. We thus see that in the region where perturbation theory can be applied, the following errors of \(\Lambda _S\) (or consequently \(\Lambda _{\overline{\mathrm{MS}}}\)) have to be considered
where k is proportional to \(b_{n_\mathrm {l}+1}\) and in typical good schemes such as \({\overline{\mathrm {MS}}}\) it is numerically of order one. Statistical and systematic errors such as discretization effects contribute to \(\Delta \alpha _{S}(\mu )\). In the above we dropped a scheme subscript for the \(\Lambda \)-parameters because of Eq. (284).
By convention \(\alpha _{\overline{\mathrm {MS}}}\) is usually quoted at a scale \(\mu =M_Z\) where the appropriate effective coupling is the one in the 5-flavour theory: \(\alpha ^{(5)}_{\overline{\mathrm{MS}}}(M_Z)\). In order to obtain it from a result with fewer flavours, one connects effective theories with different number of flavours as discussed by Bernreuther and Wetzel [667]. For example, one considers the \({\overline{\mathrm {MS}}}\) scheme, matches the 3-flavour theory to the 4-flavour theory at a scale given by the charm-quark mass [668,669,670], runs with the 5-loop \(\beta \)-function [168, 671,672,673,674] of the 4-flavour theory to a scale given by the b-quark mass, and there matches to the 5-flavour theory, after which one runs up to \(\mu =M_Z\) with the 5-loop \(\beta \) function. For the matching relation at a given quark threshold we use the mass \(m_\star \) which satisfies \(m_\star = {\overline{m}}_{\overline{\mathrm {MS}}}(m_\star )\), where \({\overline{m}}\) is the running mass (analogous to the running coupling). Then
(where \(\zeta _3\) is the Riemann zeta-function) provides the matching at the thresholds in the \({\overline{\mathrm {MS}}}\) scheme. Often the package RunDec is used for quark-threshold matching and running in the \({\overline{\mathrm {MS}}}\)-scheme [676, 677].
While \(t_2,\,t_3,\,t_4\) are numerically small coefficients, the charm threshold scale is also relatively low and so there are nonperturbative uncertainties in the matching procedure, which are difficult to estimate but which we assume here to be negligible. Obviously there is no perturbative matching formula across the strange “threshold”; here matching is entirely nonperturbative. Model dependent extrapolations of \({\bar{g}}^2_{N_f}\) from \(N_f=0,2\) to \(N_f=3\) were done in the early days of lattice gauge theory. We will include these in our listings of results but not in our estimates, since such extrapolations are based on untestable assumptions.
9.1.2 Overview of the review of \(\alpha _s\)
We begin by explaining lattice-specific difficulties in Sect. 9.2.1 and the FLAG criteria designed to assess whether the associated systematic uncertainties can be controlled and estimated in a reasonable manner. We then discuss, in Sects. 9.3–9.8, the various lattice approaches. For completeness, we present results from calculations with \(N_f = 0, 2, 3\), and 4 flavours. Finally, in Sect. 9.10, we present averages together with our best estimates for \(\alpha _{\overline{\mathrm{MS}}}^{(5)}\). These are determined from 3- and 4-flavour QCD simulations. The earlier \(N_f = 0, 2\) works obtained results for \(N_f = 3\) by extrapolation in \(N_f\). Because this is not a theoretically controlled procedure, we do not include these results in our averages. For the \(\Lambda \) parameter, we also give results for other number of flavours, including \(N_f=0\). Even though the latter numbers should not be used for phenomenology, they represent valuable nonperturbative information concerning field theories with variable numbers of quarks.
9.1.3 Additions with respect to the FLAG 13 report
Computations added in FLAG 16 were
Karbstein 14 [678] and Bazavov 14 [80] based on the static-quark potential (Sect. 9.4),
FlowQCD 15 [679] based on a tadpole-improved bare coupling (Sect. 9.6),
HPQCD 14A [16] based on heavy-quark current two-point functions (Sect. 9.7).
They influenced the final ranges marginally.
9.1.4 Additions with respect to the FLAG 16 report
For the benefit of the readers who are familiar with our previous report, we list here where changes and additions can be found which go beyond slight improvements of the presentation.
Our criteria are slightly updated, keeping up-to-date with the cited precisions of computations. In particular, in the criterion for perturbative behaviour we specify that the requirement may be less stringent if a larger uncertainty is quoted.
The FLAG 19 additions are
ALPHA 17 [79] and Ishikawa 17 [680] from step-scaling methods (Sect. 9.3).
Husung 17 [681], Karbstein 18 [682] and Takaura 18 [683, 684] from the static-quark potential (Sect. 9.4).
Hudspith 18 [685] based on the vacuum polarization (Sect. 9.5).
Kitazawa 16 [686] based on a tadpole-improved bare coupling (Sect. 9.6).
JLQCD 16 [23] and Maezawa 16 [157] based on heavy-quark current two-point functions (Sect. 9.7).
Nakayama 18 [687] from the eigenvalue spectrum of the Dirac operator (Sect. 9.9).
9.2 General issues
9.2.1 Discussion of criteria for computations entering the averages
As in the PDG review, we only use calculations of \(\alpha _s\) published in peer-reviewed journals, and that use NNLO or higher-order perturbative expansions, to obtain our final range in Sect. 9.10. We also, however, introduce further criteria designed to assess the ability to control important systematics, which we describe here. Some of these criteria, e.g., that for the continuum extrapolation, are associated with lattice-specific systematics and have no continuum analogue. Other criteria, e.g., that for the renormalization scale, could in principle be applied to nonlattice determinations. Expecting that lattice calculations will continue to improve significantly in the near future, our goal in reviewing the state of the art here is to be conservative and avoid prematurely choosing an overly small range.
In lattice calculations, we generally take \({{\mathcal {Q}}}\) to be some combination of physical amplitudes or Euclidean correlation functions which are free from UV and IR divergences and have a well-defined continuum limit. Examples include the force between static quarks and two-point functions of quark bilinear currents.
In comparison to values of observables \({{\mathcal {Q}}}\) determined experimentally, those from lattice calculations require two more steps. The first step concerns setting the scale \(\mu \) in GeV, where one needs to use some experimentally measurable low-energy scale as input. Ideally one employs a hadron mass. Alternatively convenient intermediate scales such as \(\sqrt{t_0}\), \(w_0\), \(r_0\), \(r_1\), [271, 272, 336, 688] can be used if their relation to an experimental dimensionful observable is established. The low-energy scale needs to be computed at the same bare parameters where \({{\mathcal {Q}}}\) is determined, at least as long as one does not use the step-scaling method (see below). This induces a practical difficulty given present computing resources. In the determination of the low-energy reference scale the volume needs to be large enough to avoid finite-size effects. On the other hand, in order for the perturbative expansion of Eq. (278) to be reliable, one has to reach sufficiently high values of \(\mu \), i.e., short enough distances. To avoid uncontrollable discretization effects the lattice spacing a has to be accordingly small. This means
(where L is the box size) and therefore
The currently available computer power, however, limits L/a, typically to \(L/a = 32-96\). Unless one accepts compromises in controlling discretization errors or finite-size effects, this means one needs to set the scale \(\mu \) according to
(Here \(\lll \) or \(\ggg \) means at least one order of magnitude smaller or larger.) Therefore, \(\mu \) can be \(1-3\, \text{ GeV }\) at most. This raises the concern whether the asymptotic perturbative expansion truncated at 1-loop, 2-loop, or 3-loop in Eq. (278) is sufficiently accurate. There is a finite-size scaling method, usually called step-scaling method, which solves this problem by identifying \(\mu =1/L\) in the definition of \({{\mathcal {Q}}}(\mu )\), see Sect. 9.3.
For the second step after setting the scale \(\mu \) in physical units (\(\text{ GeV }\)), one should compute \({{\mathcal {Q}}}\) on the lattice, \({{\mathcal {Q}}}_{\mathrm{lat}}(a,\mu )\) for several lattice spacings and take the continuum limit to obtain the left hand side of Eq. (278) as
This is necessary to remove the discretization error.
Here it is assumed that the quantity \({{\mathcal {Q}}}\) has a continuum limit, which is regularization-independent. The method discussed in Sect. 9.6, which is based on the perturbative expansion of a lattice-regulated, divergent short-distance quantity \(W_\mathrm{lat}(a)\) differs in this respect and must be treated separately.
In summary, a controlled determination of \(\alpha _s\) needs to satisfy the following:
- 1.
The determination of \(\alpha _s\) is based on a comparison of a short-distance quantity \({{\mathcal {Q}}}\) at scale \(\mu \) with a well-defined continuum limit without UV and IR divergences to a perturbative expansion formula in Eq. (278).
- 2.
The scale \(\mu \) is large enough so that the perturbative expansion in Eq. (278) is precise to the order at which it is truncated, i.e., it has good asymptotic convergence.
- 3.
If \({{\mathcal {Q}}}\) is defined by physical quantities in infinite volume, one needs to satisfy Eq. (292).
Nonuniversal quantities need a separate discussion, see Sect. 9.6.
Conditions (2) and (3) give approximate lower and upper bounds for \(\mu \) respectively. It is important to see whether there is a window to satisfy (2) and (3) at the same time. If it exists, it remains to examine whether a particular lattice calculation is done inside the window or not.
Obviously, an important issue for the reliability of a calculation is whether the scale \(\mu \) that can be reached lies in a regime where perturbation theory can be applied with confidence. However, the value of \(\mu \) does not provide an unambiguous criterion. For instance, the Schrödinger Functional, or SF-coupling (Sect. 9.3) is conventionally taken at the scale \(\mu =1/L\), but one could also choose \(\mu =2/L\). Instead of \(\mu \) we therefore define an effective \(\alpha _{\mathrm{eff}}\). For schemes such as SF (see Sect. 9.3) or qq (see Sect. 9.4) this is directly the coupling of the scheme. For other schemes such as the vacuum polarization we use the perturbative expansion Eq. (278) for the observable \({{\mathcal {Q}}}\) to define
If there is an \(\alpha _s\)-independent term it should first be subtracted. Note that this is nothing but defining an effective, regularization-independent coupling, a physical renormalization scheme.
Let us now comment further on the use of the perturbative series. Since it is only an asymptotic expansion, the remainder \(R_n({{\mathcal {Q}}})={{\mathcal {Q}}}-\sum _{i\le n}c_i \alpha _s^i\) of a truncated perturbative expression \({{\mathcal {Q}}}\sim \sum _{i\le n}c_i \alpha _s^i\) cannot just be estimated as a perturbative error \(k\,\alpha _s^{n+1}\). The error is nonperturbative. Often one speaks of “nonperturbative contributions”, but nonperturbative and perturbative cannot be strictly separated due to the asymptotic nature of the series (see, e.g., Ref. [689]).
Still, we do have some general ideas concerning the size of nonperturbative effects. The known ones such as instantons or renormalons decay for large \(\mu \) like inverse powers of \(\mu \) and are thus roughly of the form
with some positive constant \(\gamma \). Thus we have, loosely speaking,
For small \(\alpha _s\), the \(\exp (-\gamma /\alpha _s)\) is negligible. Similarly the perturbative estimate for the magnitude of relative errors in Eq. (297) is small; as an illustration for \(n=3\) and \(\alpha _s = 0.2\) the relative error is \(\sim 0.8\%\) (assuming coefficients \(|c_{n+1} /c_1 | \sim 1\)).
For larger values of \(\alpha _s\) nonperturbative effects can become significant in Eq. (297). An instructive example comes from the values obtained from \(\tau \) decays, for which \(\alpha _s\approx 0.3\). Here, different applications of perturbation theory (fixed order and contour improved) each look reasonably asymptotically convergent but the difference does not seem to decrease much with the order (see, e.g., the contribution of Pich in Ref. [690]). In addition nonperturbative terms in the spectral function may be nonnegligible even after the integration up to \(m_\tau \) (see, e.g., Refs. [691, 692]). All of this is because \(\alpha _s\) is not really small.
Since the size of the nonperturbative effects is very hard to estimate one should try to avoid such regions of the coupling. In a fully controlled computation one would like to verify the perturbative behaviour by changing \(\alpha _s\) over a significant range instead of estimating the errors as \(\sim \alpha _s^{n+1}\) . Some computations try to take nonperturbative power ‘corrections’ to the perturbative series into account by including such terms in a fit to the \(\mu \)-dependence. We note that this is a delicate procedure, both because the separation of nonperturbative and perturbative is theoretically not well defined and because in practice a term like, e.g., \(\alpha _s(\mu )^3\) is hard to distinguish from a \(1/\mu ^2\) term when the \(\mu \)-range is restricted and statistical and systematic errors are present. We consider it safer to restrict the fit range to the region where the power corrections are negligible compared to the estimated perturbative error.
The above considerations lead us to the following special criteria for the determination of \(\alpha _s\):
Renormalization scale
 all points relevant in the analysis have \(\alpha _\mathrm {eff} < 0.2\)
all points relevant in the analysis have \(\alpha _\mathrm {eff} < 0.2\) all points have \(\alpha _\mathrm {eff} < 0.4\) and at least one \(\alpha _\mathrm {eff} \le 0.25\)
all points have \(\alpha _\mathrm {eff} < 0.4\) and at least one \(\alpha _\mathrm {eff} \le 0.25\) otherwise
otherwise
Perturbative behaviour
 verified over a range of a factor 4 change in \(\alpha _\mathrm {eff}^{n_\mathrm {l}}\) without power corrections or alternatively \(\alpha _\mathrm {eff}^{n_\mathrm {l}} \le \frac{1}{2} \Delta \alpha _\mathrm {eff} / (8\pi b_0 \alpha _\mathrm {eff}^2) \) is reached
verified over a range of a factor 4 change in \(\alpha _\mathrm {eff}^{n_\mathrm {l}}\) without power corrections or alternatively \(\alpha _\mathrm {eff}^{n_\mathrm {l}} \le \frac{1}{2} \Delta \alpha _\mathrm {eff} / (8\pi b_0 \alpha _\mathrm {eff}^2) \) is reached agreement with perturbation theory over a range of a factor \((3/2)^2\) in \(\alpha _\mathrm {eff}^{n_\mathrm {l}}\) possibly fitting with power corrections or alternatively \(\alpha _\mathrm {eff}^{n_\mathrm {l}} \le \Delta \alpha _\mathrm {eff} / (8\pi b_0 \alpha _\mathrm {eff}^2)\) is reached
agreement with perturbation theory over a range of a factor \((3/2)^2\) in \(\alpha _\mathrm {eff}^{n_\mathrm {l}}\) possibly fitting with power corrections or alternatively \(\alpha _\mathrm {eff}^{n_\mathrm {l}} \le \Delta \alpha _\mathrm {eff} / (8\pi b_0 \alpha _\mathrm {eff}^2)\) is reached otherwise
otherwise
Here \(\Delta \alpha _\mathrm {eff}\) is the accuracy cited for the determination of \(\alpha _\mathrm {eff}\) and \(n_\mathrm {l}\) is the loop order to which the connection of \(\alpha _\mathrm {eff}\) to the \({\overline{\mathrm {MS}}}\) scheme is known. Recall the discussion around Eqs. (285, 286) The \(\beta \)-function of \(\alpha _\mathrm {eff}\) is then known to \(n_\mathrm {l}+1\) loop order.Footnote 68
Continuum extrapolation
At a reference point of \(\alpha _{\mathrm{eff}} = 0.3\) (or less) we require
 three lattice spacings with \(\mu a < 1/2\) and full \({\mathcal {O}}(a)\) improvement,
three lattice spacings with \(\mu a < 1/2\) and full \({\mathcal {O}}(a)\) improvement,or three lattice spacings with \(\mu a \le 1/4\) and 2-loop \({\mathcal {O}}(a)\) improvement,
or \(\mu a \le 1/8\) and 1-loop \({\mathcal {O}}(a)\) improvement
 three lattice spacings with \(\mu a < 3/2\) reaching down to \(\mu a =1\) and full \({\mathcal {O}}(a)\) improvement,
three lattice spacings with \(\mu a < 3/2\) reaching down to \(\mu a =1\) and full \({\mathcal {O}}(a)\) improvement,or three lattice spacings with \(\mu a \le 1/4\) and 1-loop \({\mathcal {O}}(a)\) improvement
 otherwise
otherwise
We also need to specify what is meant by \(\mu \). Here are our choices:
where q is the magnitude of the momentum, \({\bar{m}}_\mathrm {c}\) the heavy-quark mass, usually taken around the charm quark mass and \(\lambda _{\overline{\mathrm {MS}}}\) is the eigenvalue of the Dirac operator, see Sect. 9.9. We note again that the above criteria cannot be applied when regularization dependent quantities \(W_\mathrm {lat}(a)\) are used instead of \({{\mathcal {O}}}(\mu )\). These cases are specifically discussed in Sect. 9.6.
In principle one should also account for electro-weak radiative corrections. However, both in the determination of \(\alpha _{s}\) at intermediate scales \(\mu \) and in the running to high scales, we expect electro-weak effects to be much smaller than the presently reached precision. Such effects are therefore not further discussed.
The attentive reader will have noticed that bounds such as \(\mu a < 3/2\) or at least one value of \(\alpha _\mathrm {eff}\le 0.25\) which we require for a  are not very stringent. There is a considerable difference between
are not very stringent. There is a considerable difference between  and
and  . We have chosen the above bounds, unchanged as compared to FLAG 16, since not too many computations would satisfy more stringent ones at present. Nevertheless, we believe that the
. We have chosen the above bounds, unchanged as compared to FLAG 16, since not too many computations would satisfy more stringent ones at present. Nevertheless, we believe that the  criteria already give reasonable bases for estimates of systematic errors. In the future, we expect that we will be able to tighten our criteria for inclusion in the average, and that many more computations will reach the present
criteria already give reasonable bases for estimates of systematic errors. In the future, we expect that we will be able to tighten our criteria for inclusion in the average, and that many more computations will reach the present  rating in one or more categories.
rating in one or more categories.
In addition to our explicit criteria, the following effects may influence the precision of results:
Topology sampling In principle a good way to improve the quality of determinations of \(\alpha _s\) is to push to very small lattice spacings thus enabling large \(\mu \). It is known that the sampling of field space becomes very difficult for the HMC algorithm when the lattice spacing is small and one has the standard periodic boundary conditions. In practice, for all known discretizations the topological charge slows down dramatically for \(a\approx 0.05\,\mathrm{fm}\) and smaller [97, 100,101,102,103,104, 401]. Open boundary conditions solve the problem [105] but are not frequently used. Since the effect of the freezing on short distance observables is not known, we also do need to pay attention to this issue. Remarks are added in the text when appropriate.
Quark-mass effects We assume that effects of the finite masses of the light quarks (including strange) are negligible in the effective coupling itself where large, perturbative, \(\mu \) is considered.
Scale determination The scale does not need to be very precise, since using the lowest-order \(\beta \)-function shows that a 3% error in the scale determination corresponds to a \(\sim 0.5\%\) error in \(\alpha _s(M_Z)\). So as long as systematic errors from chiral extrapolation and finite-volume effects are well below 3% we do not need to be concerned about those at the present level of precision in \(\alpha _s(M_Z)\). This may change in the future.
9.2.2 Physical scale
A popular scale choice has been the intermediate \(r_0\) scale. One should bear in mind that its determination from physical observables also has to be taken into account. The phenomenological value of \(r_0\) was originally determined as \(r_0 \approx 0.49\,\text{ fm }\) through potential models describing quarkonia [336]. Of course the quantity is precisely defined, independent of such model considerations. But a lattice computation with the correct sea-quark content is needed to determine a completely sharp value. When the quark content is not quite realistic, the value of \(r_0\) may depend to some extent on which experimental input is used to determine (actually define) it.
The latest determinations from two-flavour QCD are \(r_0\) = 0.420(14)–0.450(14) fm by the ETM collaboration [40, 48], using as input \(f_\pi \) and \(f_K\) and carrying out various continuum extrapolations. On the other hand, the ALPHA collaboration [693] determined \(r_0\) = 0.503(10) fm with input from \(f_K\), and the QCDSF collaboration [90] cites 0.501(10)(11) fm from the mass of the nucleon (no continuum limit). Recent determinations from three-flavour QCD are consistent with \(r_1\) = 0.313(3) fm and \(r_0\) = 0.472(5) fm [36, 276, 694]. Due to the uncertainty in these estimates, and as many results are based directly on \(r_0\) to set the scale, we shall often give both the dimensionless number \(r_0 \Lambda _{\overline{\mathrm{MS}}}\), as well as \(\Lambda _{\overline{\mathrm{MS}}}\). In the cases where no physical \(r_0\) scale is given in the original papers or we convert to the \(r_0\) scale, we use the value \(r_0\) = 0.472 fm. In case \(r_1 \Lambda _{\overline{\mathrm{MS}}}\) is given in the publications, we use \(r_0 /r_1 = 1.508\) [694], to convert, which remains well consistent with the update [401] neglecting the error on this ratio. In some, mostly early, computations the string tension, \(\sqrt{\sigma }\) was used. We convert to \(r_0\) using \(r_0^2\sigma = 1.65-\pi /12\), which has been shown to be an excellent approximation in the relevant pure gauge theory [695, 696].
The new scales \(t_0,w_0\) based on the gradient flow are very attractive alternatives to \(r_0\) but their discretization errors are still under discussion [697,698,699,700] and their values at the physical point are not yet determined with great precision. We remain with \(r_0\) as our main reference scale for now. A general discussion of the various scales is given in [701].
9.2.3 Studies of truncation errors of perturbation theory
As discussed previously, we have to determine \(\alpha _s\) in a region where the perturbative expansion for the \(\beta \)-function, Eq. (281) in the integral Eq. (280), is reliable. In principle this must be checked, however this is difficult to achieve as we need to reach up to a sufficiently high scale. A frequently used recipe to estimate the size of truncation errors of the perturbative series is to vary the renormalization-scale dependence around the chosen ‘optimal’ scale \(\mu _*\), of an observable evaluated at a fixed order in the coupling from \(\mu =\mu _*/2\) to \(2\mu _*\). For an example see Fig. 35. Alternatively, or in addition, the renormalization scheme chosen can be varied, which investigates the perturbative conversion of the chosen scheme to the perturbatively defined \(\overline{\mathrm{MS}}\) scheme and in particular ‘fastest apparent convergence’ when the ‘optimal’ scale is chosen so that the \(O(\alpha _s^2)\) coefficient vanishes.
The ALPHA collaboration in Ref. [702] and ALPHA 17 [703], within the SF approach defined a set of \(\nu \) schemes where the third scheme-dependent coefficient of the \(\beta \)-function for \(N_f = 2\,+\,1\) flavours was computed to be \(b_2^\nu = -(0.064(27)+1.259(1)\nu )/(4\pi )^3\). The standard SF scheme has \(\nu = 0\). For comparison, \(b_2^{\overline{\mathrm {MS}}}= 0.324/(4\pi )^3\). A range of scales from about \(4\,\text{ GeV }\) to \(128\,\text{ GeV }\) was investigated. It was found that while the procedure of varying the scale by a factor 2 up and down gave a correct estimate of the residual perturbative error for \(\nu \approx 0 \ldots 0.3\), for negative values, e.g., \(\nu = -0.5\), the estimated perturbative error is much too small to account for the mismatch in the \(\Lambda \)-parameter of \(\approx 8\%\) at \(\alpha _s=0.15\). This mismatch, however, did, as expected, still scale with \(\alpha _s^{n_l}\) with \(n_l=2\). In the schemes with negative \(\nu \), the coupling \(\alpha _s\) has to be quite small for scale-variations of a factor 2 to correctly signal the perturbative errors.
A similar \(\approx 8\%\) deviation in the \(\Lambda \)-parameter extracted from the qq-scheme (c.f. Sect. 9.4) is found by Husung 17 [681], but at \(\alpha _s\approx 0.2\) and with \(n_l=3\).
9.3 \(\alpha _s\) from Step-Scaling Methods
9.3.1 General considerations
The method of step-scaling functions avoids the scale problem, Eq. (291). It is in principle independent of the particular boundary conditions used and was first developed with periodic boundary conditions in a two-dimensional model [704].
The essential idea of the step-scaling strategy is to split the determination of the running coupling at large \(\mu \) and of a hadronic scale into two lattice calculations and connect them by ‘step-scaling’. In the former part, we determine the running coupling constant in a finite-volume scheme in which the renormalization scale is set by the inverse lattice size \(\mu = 1/L\). In this calculation, one takes a high renormalization scale while keeping the lattice spacing sufficiently small as
In the latter part, one chooses a certain \({\bar{g}}^2_\mathrm {max}={\bar{g}}^2(1/L_\mathrm {max})\), typically such that \(L_\mathrm {max}\) is around 0.5–1 fm. With a common discretization, one then determines \(L_\mathrm {max}/a\) and (in a large volume \(L \ge \) 2–3 fm) a hadronic scale such as a hadron mass, \(\sqrt{t_0}/a\) or \(r_0/a\) at the same bare parameters. In this way one gets numbers for, e.g., \(L_\mathrm {max}/r_0\) and by changing the lattice spacing a carries out a continuum limit extrapolation of that ratio.
In order to connect \({\bar{g}}^2(1/L_\mathrm {max})\) to \({\bar{g}}^2(\mu )\) at high \(\mu \), one determines the change of the coupling in the continuum limit when the scale changes from L to L/s, starting from \(L=L_{\mathrm{max}}\) and arriving at \(\mu = s^k /L_{\mathrm{max}}\). This part of the strategy is called step-scaling. Combining these results yields \({\bar{g}}^2(\mu )\) at \(\mu = s^k \,(r_0 / L_\mathrm {max})\, r_0^{-1}\), where \(r_0\) stands for the particular chosen hadronic scale. Most applications use a scale factor \(s=2\).
At present most applications in QCD use Schrödinger functional boundary conditions [172, 705] and we discuss this below in a little more detail. (However, other boundary conditions are also possible, such as twisted boundary conditions and the discussion also applies to them.) An important reason is that these boundary conditions avoid zero modes for the quark fields and quartic modes [706] in the perturbative expansion in the gauge fields. Furthermore the corresponding renormalization scheme is well studied in perturbation theory [707,708,709] with the 3-loop \(\beta \)-function and 2-loop cutoff effects (for the standard Wilson regularization) known.
In order to have a perturbatively well-defined scheme, the SF scheme uses Dirichlet boundary conditions at time \(t = 0\) and \(t = T\). These break translation invariance and permit \({{\mathcal {O}}}(a)\) counter terms at the boundary through quantum corrections. Therefore, the leading discretization error is \({{\mathcal {O}}}(a)\). Improving the lattice action is achieved by adding counter terms at the boundaries whose coefficients are denoted as \(c_t,{{\tilde{c}}}_t\). In practice, these coefficients are computed with 1-loop or 2-loop perturbative accuracy. A better precision in this step yields a better control over discretization errors, which is important, as can be seen, e.g., in Refs. [695, 710].
Also computations with Dirichlet boundary conditions do in principle suffer from the insufficient change of topology in the HMC algorithm at small lattice spacing. However, in a small volume the weight of nonzero charge sectors in the path integral is exponentially suppressed [711]Footnote 69 and in a Monte Carlo run of typical length very few configurations with nontrivial topology should appear. Considering the issue quantitatively Ref. [712] finds a strong suppression below \(L\approx 0.8\,\mathrm{fm}\). Therefore the lack of topology change of the HMC is not a serious issue. Still Ref. [713] includes a projection to zero topology into the definition of the coupling. We note also that a mix of Dirichlet and open boundary conditions is expected to remove the topology issue entirely [714] and may be considered in the future.
Apart from the boundary conditions, the very definition of the coupling needs to be chosen. We briefly discuss in turn, the two schemes used at present, namely, the ‘Schrödinger Functional’ (SF) and ‘Gradient Flow’ (GF) schemes.
The SF scheme is the first one, which was used in step-scaling studies in gauge theories [172]. Inhomogeneous Dirichlet boundary conditions are imposed in time,
for \(k=1,2,3\). Periodic boundary conditions (up to a phase for the fermion fields) with period L are imposed in space. The matrices
just depend on the dimensionless parameter \(\eta \). The coupling \({\bar{g}}_\mathrm {SF}\) is obtained from the \(\eta \)-derivative of the effective action,
For this scheme, the finite \(c^{(i)}_g\), Eq. (283), are known for \(i=1,2\) [708, 709].
More recently, gradient flow couplings have been used frequently because of their small statistical errors at large couplings (in contrast to \({\bar{g}}_\mathrm {SF}\), which has small statistical errors at small couplings). The gradient flow is introduced as follows [271, 715]. Consider the flow gauge field \(B_\mu (t,x)\) with the flow time t, which is a one parameter deformation of the bare gauge field \(A_\mu (x)\), where \(B_\mu (t,x)\) is the solution to the gradient flow equation
with initial condition \(B_\mu (0,x) = A_\mu (x)\). The renormalized coupling is defined by [271]
with \({{{\mathcal {N}}}} = 16\pi ^2/3 + O((a/L)^2)\) and where E(t, x) is the action density given by
In a finite volume, one needs to specify additional conditions. In order not to introduce two independent scales one sets
for some fixed number c [716]. Schrödinger functional boundary conditions [717] or twisted boundary conditions [680, 718] have been employed. Matching of the GF coupling to the \(\overline{\mathrm{MS}}\) scheme coupling is known to 1-loop for twisted boundary conditions with zero quark flavours and SU(3) group [680] and to 2-loop with SF boundary conditions with zero quark flavours [719]. The former is based on a MC evaluation at small couplings and the latter on numerical stochastic perturbation theory.
9.3.2 Discussion of computations
In Table 53 we give results from various determinations of the \(\Lambda \) parameter. For a clear assessment of the \(N_f\)-dependence, the last column also shows results that refer to a common hadronic scale, \(r_0\). As discussed above, the renormalization scale can be chosen large enough such that \(\alpha _s < 0.2\) and the perturbative behaviour can be verified. Consequently only  is present for these criteria except for early work where the \(n_l=2\) loop connection to \({\overline{\mathrm {MS}}}\) was not yet known and we assigned a
is present for these criteria except for early work where the \(n_l=2\) loop connection to \({\overline{\mathrm {MS}}}\) was not yet known and we assigned a  concerning the renormalization scale. With dynamical fermions, results for the step-scaling functions are always available for at least \(a/L = \mu a =1/4,1/6, 1/8\). All calculations have a nonperturbatively \({\mathcal {O}}(a)\) improved action in the bulk. For the discussed boundary \({\mathcal {O}}(a)\) terms this is not so. In most recent calculations 2-loop \({\mathcal {O}}(a)\) improvement is employed together with at least three lattice spacings.Footnote 70 This means a
concerning the renormalization scale. With dynamical fermions, results for the step-scaling functions are always available for at least \(a/L = \mu a =1/4,1/6, 1/8\). All calculations have a nonperturbatively \({\mathcal {O}}(a)\) improved action in the bulk. For the discussed boundary \({\mathcal {O}}(a)\) terms this is not so. In most recent calculations 2-loop \({\mathcal {O}}(a)\) improvement is employed together with at least three lattice spacings.Footnote 70 This means a  for the continuum extrapolation. In other computations only 1-loop \(c_t\) was available and we arrive at
for the continuum extrapolation. In other computations only 1-loop \(c_t\) was available and we arrive at  . We note that the discretization errors in the step-scaling functions of the SF coupling are usually found to be very small, at the percent level or below. However, the overall desired precision is very high as well, and the results in CP-PACS 04 [710] show that discretization errors at the below percent level cannot be taken for granted. In particular with staggered fermions (unimproved except for boundary terms) few percent effects are seen in Perez 10 [721].
. We note that the discretization errors in the step-scaling functions of the SF coupling are usually found to be very small, at the percent level or below. However, the overall desired precision is very high as well, and the results in CP-PACS 04 [710] show that discretization errors at the below percent level cannot be taken for granted. In particular with staggered fermions (unimproved except for boundary terms) few percent effects are seen in Perez 10 [721].
In the work by PACS-CS 09A [81], the continuum extrapolation in the scale setting is performed using a constant function in a and with a linear function. Potentially the former leaves a considerable residual discretization error. We here use, as discussed with the collaboration, the continuum extrapolation linear in a, as given in the second line of PACS-CS 09A [81] results in Table 53. After perturbative conversion from a three-flavour result to five flavours (see Sect. 9.2.1), they obtain
In Ref. [79], the ALPHA collaboration determined \(\Lambda ^{(3)}_{{\overline{\mathrm {MS}}}}\) combining step-scaling in \({\bar{g}}^2_\mathrm{GF}\) in the lower scale region \(\mu _{\mathrm{had}} \le \mu \le \mu _0\), and step-scaling in \({\bar{g}}^2_{\mathrm{SF}}\) for higher scales \(\mu _0 \le \mu \le \mu _{\mathrm{PT}}\). Both schemes are defined with SF boundary conditions. For \({\bar{g}}^2_{\mathrm{GF}}\) a projection to the sector of zero topological charge is included, Eq. (304) is restricted to the magnetic components, and \(c=0.3\). The scales \(\mu _{\mathrm{had}}\), \(\mu _0\), and \(\mu _{\mathrm{PT}}\) are defined by \({\bar{g}}^2_{\mathrm{GF}} (\mu _{\mathrm{had}})= 11.3\), \({\bar{g}}^2_{\mathrm{SF}}(\mu _0) = 2.012\), and \(\mu _{\mathrm{PT}} = 16 \mu _0\) which are roughly estimated as
Step-scaling is carried out with an O(a)-improved Wilson quark action [725] and Lüscher-Weisz gauge action [726] in the low-scale region and an O(a)-improved Wilson quark action [727] and Wilson gauge action in the high-energy part. For the step-scaling using steps of \(L/a \,\rightarrow \,2L/a\), three lattice sizes \(L/a=8,12,16\) were simulated for \({\bar{g}}^2_{\mathrm{GF}}\) and four lattice sizes \(L/a=(4,)\, 6, 8, 12\) for \({\bar{g}}^2_{\mathrm{SF}}\). The final results do not use the small lattices given in parenthesis. The parameter \(\Lambda ^{(3)}_{{\overline{\mathrm {MS}}}}\) is then obtained via
where the hadronic scale \(f_{\pi K}\) is \(f_{\pi K}= \frac{1}{3}(2 f_K + f_\pi ) = 147.6 (5) \text{ MeV }\). The first term on the right hand side of Eq. (308) is obtained from \(\alpha _\mathrm{SF}(\mu _{\mathrm{PT}})\) which is the output from SF step-scaling using Eq. (280) with \(\alpha _{\mathrm{SF}}(\mu _{\mathrm{PT}})\approx 0.1\) and the 3-loop \(\beta \)-function and the exact conversion to the \({\overline{\mathrm {MS}}}\)-scheme. The second term is essentially obtained from step-scaling in the GF scheme and the measurement of \({\bar{g}}^2_\mathrm{SF}(\mu _0)\) except for the trivial scaling factor of 16 in the SF running. The third term is obtained from a measurement of the hadronic quantity at large volume.
A large volume simulation is done for three lattice spacings with sufficiently large volume and reasonable control over the chiral extrapolation so that the scale determination is precise enough. The step-scaling results in both schemes satisfy renormalization criteria, perturbation theory criteria, and continuum limit criteria just as previous studies using step-scaling. So we assign green stars for these criteria.
The dependence of \(\Lambda \), Eq. (280) with 3-loop \(\beta \)-function, on \(\alpha _s\) and on the chosen scheme is discussed in [702]. This investigation provides a warning on estimating the truncation error of perturbative series. Details are explained in Sect. 9.2.3.
The result for the \(\Lambda \) parameter is \(\Lambda ^{(3)}_{\overline{\mathrm{MS}}} = 341(12)~\text{ MeV }\), where the dominant error comes from the error of \(\alpha _{\mathrm{SF}}(\mu _\mathrm{PT})\) after step-scaling in SF scheme. Using 4-loop matching at the charm and bottom thresholds and 5-loop running one finally obtains
Several other results do not have a sufficient number of quark flavours or do not yet contain the conversion of the scale to physical units (ALPHA 10A [720], Perez 10 [721]). Thus no value for \(\alpha _{\overline{\mathrm {MS}}}^{(5)}(M_Z)\) is quoted.
The computation of Ishikawa et al. [680] is based on the gradient flow coupling with twisted boundary conditions [718] (TGF coupling) in the pure gauge theory. Again they use \(c=0.3\). Step-scaling with a scale factor \(s=3/2\) is employed, covering a large range of couplings from \(\alpha _s\approx 0.5\) to \(\alpha _s\approx 0.1\) and taking the continuum limit through global fits to the step-scaling function on \(L/a=12,16,18\) lattices with between 6 and 8 parameters. Systematic errors due to variations of the fit functions are estimated. Two physical scales are considered: \(r_0/a\) is taken from [695] and \(\sigma a^2\) from [163] and [728]. As the ratio \(\Lambda _\mathrm {TGF}/\Lambda _{{\overline{\mathrm {MS}}}}\) has not yet been computed analytically, Ref. [680] determines the 1-loop relation between \({\bar{g}}_\mathrm {SF}\) and \({\bar{g}}_\mathrm {TGF}\) from MC simulations performed in the weak coupling region and then uses the known \(\Lambda _\mathrm {SF}/\Lambda _{{\overline{\mathrm {MS}}}}\). Systematic errors due to variations of the fit functions dominate the overall uncertainty.
9.4 \(\alpha _s\) from the potential at short distances
9.4.1 General considerations
The basic method was introduced in Ref. [729] and developed in Ref. [730]. The force or potential between an infinitely massive quark and antiquark pair defines an effective coupling constant via
The coupling can be evaluated nonperturbatively from the potential through a numerical differentiation, see below. In perturbation theory one also defines couplings in different schemes \(\alpha _{{\bar{V}}}\), \(\alpha _V\) via
where one fixes the unphysical constant in the potential by \(\lim _{r\rightarrow \infty }V(r)=0\) and \({\tilde{V}}(Q)\) is the Fourier transform of V(r). Nonperturbatively, the subtraction of a constant in the potential introduces an additional renormalization constant, the value of \(V(r_\mathrm {ref})\) at some distance \(r_\mathrm {ref}\). Perturbatively, it is believed to entail a renormalon ambiguity. In perturbation theory, the different definitions are all simply related to each other, and their perturbative expansions are known including the \(\alpha _s^4,\,\alpha _s^4 \log \alpha _s\) and \(\alpha _s^5 \log \alpha _s ,\,\alpha _s^5 (\log \alpha _s)^2\) terms [731,732,733,734,735,736,737,738].
The potential V(r) is determined from ratios of Wilson loops, W(r, t), which behave as
where t is taken as the temporal extension of the loop, r is the spatial one and \(V_n\) are excited-state potentials. To improve the overlap with the ground state, and to suppress the effects of excited states, t is taken large. Also various additional techniques are used, such as a variational basis of operators (spatial paths) to help in projecting out the ground state. Furthermore some lattice-discretization effects can be reduced by averaging over Wilson loops related by rotational symmetry in the continuum.
In order to reduce discretization errors it is of advantage to define the numerical derivative giving the force as
where \(r_\mathrm {I}\) is chosen so that at tree level the force is the continuum force. \(F(r_\mathrm {I})\) is then a ‘tree-level improved’ quantity and similarly the tree-level improved potential can be defined [739].
Lattice potential results are in position space, while perturbation theory is naturally computed in momentum space at large momentum. Usually, the Fourier transform of the perturbative expansion is then matched to lattice data.
Finally, as was noted in Sect. 9.2.1, a determination of the force can also be used to determine the scales \(r_0,\,r_1\), by defining them from the static force by
9.4.2 Discussion of computations
In Table 54, we list results of determinations of \(r_0\Lambda _{{\overline{\mathrm {MS}}}}\) (together with \(\Lambda _{{\overline{\mathrm {MS}}}}\) using the scale determination of the authors). Since the last review, FLAG 16, there have been three new computations, Husung 17 [681], Karbstein 18 [682] and Takaura 18 [683, 684].
The first determinations in the three-colour Yang Mills theory are by UKQCD 92 [730] and Bali 92 [743] who used \(\alpha _\mathrm {qq}\) as explained above, but not in the tree-level improved form. Rather a phenomenologically determined lattice artifact correction was subtracted from the lattice potentials. The comparison with perturbation theory was on a more qualitative level on the basis of a 2-loop \(\beta \)-function (\(n_l=1\)) and a continuum extrapolation could not be performed as yet. A much more precise computation of \(\alpha _\mathrm {qq}\) with continuum extrapolation was performed in Refs. [695, 739]. Satisfactory agreement with perturbation theory was found [739] but the stability of the perturbative prediction was not considered sufficient to be able to extract a \(\Lambda \) parameter.
In Brambilla 10 [742] the same quenched lattice results of Ref. [739] were used and a fit was performed to the continuum potential, instead of the force. Perturbation theory to \(n_l=3\) loop was used including a resummation of terms \(\alpha _s^3 (\alpha _s \ln \alpha _s)^n \) and \(\alpha _s^4 (\alpha _s \ln \alpha _s)^n \). Close agreement with perturbation theory was found when a renormalon subtraction was performed. Note that the renormalon subtraction introduces a second scale into the perturbative formula which is absent when the force is considered.
Bazavov 14 [80] updates Bazavov 12 [740] and modifies this procedure somewhat. They consider the perturbative expansion for the force. They set \(\mu = 1/r\) to eliminate logarithms and then integrate the force to obtain an expression for the potential. The resulting integration constant is fixed by requiring the perturbative potential to be equal to the nonperturbative one exactly at a reference distance \(r_{\mathrm{ref}}\) and the two are then compared at other values of r. As a further check, the force is also used directly.
For the quenched calculation Brambilla 10 [742] very small lattice spacings, \(a \sim 0.025\,\text{ fm }\), were available from Ref. [739]. For ETM 11C [741], Bazavov 12 [740], Karbstein 14 [678] and Bazavov 14 [80] using dynamical fermions such small lattice spacings are not yet realized (Bazavov 14 reaches down to \(a \sim 0.041\,\text{ fm }\)). They all use the tree-level improved potential as described above. We note that the value of \(\Lambda _{\overline{\mathrm {MS}}}\) in physical units by ETM 11C [741] is based on a value of \(r_0=0.42\) fm. This is at least 10% smaller than the large majority of other values of \(r_0\). Also the values of \(r_0/a\) on the finest lattices in ETM 11C [741] and \(r_1/a\) for Bazavov 14 [80] come from rather small lattices with \(m_\pi L \approx 2.4\), 2.2 respectively.
Instead of the procedure discussed previously, Karbstein 14 [678] reanalyzes the data of ETM 11C [741] by first estimating the Fourier transform \({{\tilde{V}}}(p)\) of V(r) and then fitting the perturbative expansion of \({{\tilde{V}}}(p)\) in terms of \(\alpha _{\overline{\mathrm {MS}}}(p)\). Of course, the Fourier transform requires some modelling of the r-dependence of V(r) at short and at large distances. The authors fit a linearly rising potential at large distances together with string-like corrections of order \(r^{-n}\) and define the potential at large distances by this fit.Footnote 71 Recall that for observables in momentum space we take the renormalization scale entering our criteria as \(\mu =q\), Eq. (298). The analysis (as in ETM 11C [741]) is dominated by the data at the smallest lattice spacing, where a controlled determination of the overall scale is difficult due to possible finite-size effects. Karbstein 18 [682] is a reanalysis of Karbstein 14 and supersedes it. Some data with a different discretization of the static quark is added (on the same configurations) and the discrete lattice results for the static potential in position space are first parameterized by a continuous function, which then allows for an analytical Fourier transformation to momentum space.
Similarly also for Takaura 18 [683, 684] the momentum space potential \({\tilde{V}}(Q)\) is the central object. Namely, they assume that renormalon / power law effects are absent in \({\tilde{V}}(Q)\) and only come in through the Fourier transformation. They provide evidence that renormalon effects (both \(u=1/2\) and \(u=3/2\)) can be subtracted and arrive at a nonperturbative term \(k\,\Lambda _{\overline{\mathrm {MS}}}^3 r^2\). Two different analysis are carried out with the final result taken from “Analysis II”. Our numbers including the evaluation of the criteria refer to it. Together with the perturbative 3-loop (including the \( \alpha _s^4\log \alpha _s\) term) expression, this term is fitted to the nonperturbative results for the potential in the region \(0.04\,\mathrm{fm}\, \le \, r \,\le 0.35\,\mathrm{fm}\), where \(0.04\,\mathrm{fm}\) is \(r=a\) on the finest lattice. The NP potential data originate from JLQCD ensembles (Symanzik improved gauge action and Möbius domain-wall quarks) at three lattice spacings with a pion mass around \(300\,\,\mathrm {MeV}\). Since at the maximal distance in the analysis we find \(\alpha _{\overline{\mathrm {MS}}}(2/r) = 0.43\), the renormalization scale criterion yields a  . The perturbative behavior is
. The perturbative behavior is  because of the high order in PT known. The continuum limit criterion yields a
because of the high order in PT known. The continuum limit criterion yields a  .
.
One of the main issues for all these computations is whether the perturbative running of the coupling constant has been reached. While for \(N_f=0\) fermions Brambilla 10 [742] reports agreement with perturbative behavior at the smallest distances, Husung 17 [681] (which goes to shorter distances) finds relatively large corrections beyond the 3-loop \(\alpha _\mathrm {qq}\). For dynamical fermions, Bazavov 12 [740] and Bazavov 14 [80] report good agreement with perturbation theory after the renormalon is subtracted or eliminated.
A second issue is the coverage of configuration space in some of the simulations, which use very small lattice spacings with periodic boundary conditions. Affected are the smallest two lattice spacings of Bazavov 14 [80] where very few tunnelings of the topological charge occur [401]. With present knowledge, it also seems possible that the older data by Refs. [695, 739] used by Brambilla 10 [742] are partially obtained with (close to) frozen topology.
The recent computation Husung 17 [681], for \(N_f = 0\) flavours first determines the coupling \({\bar{g}}_{\mathrm{qq}}^2(r,a)\) from the force and then performs a continuum extrapolation on lattices down to \(a \approx 0.015\,\text{ fm }\), using a step-scaling method at short distances,  . Using the 4-loop \(\beta ^{\mathrm{qq}}\) function this allows \(r_0\Lambda _{\mathrm{qq}}\) to be estimated, which is then converted to the \(\overline{\mathrm{MS}}\) scheme. \(\alpha _{\mathrm{eff}} = \alpha _{\mathrm{qq}}\) ranges from \(\sim 0.17\) to large values; we give
. Using the 4-loop \(\beta ^{\mathrm{qq}}\) function this allows \(r_0\Lambda _{\mathrm{qq}}\) to be estimated, which is then converted to the \(\overline{\mathrm{MS}}\) scheme. \(\alpha _{\mathrm{eff}} = \alpha _{\mathrm{qq}}\) ranges from \(\sim 0.17\) to large values; we give  for renormalization scale and
for renormalization scale and  for perturbative behaviour. The range \(a\mu = 2a/r \approx 0.37\) - 0.14 leads to a
for perturbative behaviour. The range \(a\mu = 2a/r \approx 0.37\) - 0.14 leads to a  in the continuum extrapolation.
in the continuum extrapolation.
We note that the \(N_{ f}=3\) determinations of \(r_0 \Lambda _{\overline{\mathrm{MS}}}\) agree within their errors of 4-6%.
9.5 \(\alpha _s\) from the vacuum polarization at short distances
9.5.1 General considerations
The vacuum polarization function for the flavour nonsinglet currents \(J^a_\mu \) (\(a=1,2,3\)) in the momentum representation is parameterized as
where \(Q_\mu \) is a space-like momentum and \(J_\mu \equiv V_\mu \) for a vector current and \(J_\mu \equiv A_\mu \) for an axial-vector current. Defining \(\Pi _J(Q)\equiv \Pi _J^{(0)}(Q)+\Pi _J^{(1)}(Q)\), the operator product expansion (OPE) of the vacuum polarization function \(\Pi _{V+A}(Q)=\Pi _V(Q)+\Pi _A(Q)\) is given by
for large \(Q^2\). The perturbative coefficient functions \(C_X^{V+A}(Q^2)\) for the operators X (\(X=1\), \({\bar{q}}q\), GG) are given as \(C_X^{V+A}(Q^2)=\sum _{i\ge 0}\left( C_X^{V+A}\right) ^{(i)}\alpha _s^i(Q^2)\) and \({{\bar{m}}}\) is the running mass of the mass-degenerate up and down quarks. \(C_1\) is known including \(\alpha _s^4\) in a continuum renormalization scheme such as the \(\overline{\mathrm{MS}}\) scheme [744,745,746,747]. Nonperturbatively, there are terms in \(C_X\) that do not have a series expansion in \(\alpha _s\). For an example for the unit operator see Ref. [748]. The term c is Q-independent and divergent in the limit of infinite ultraviolet cutoff. However the Adler function defined as
is a scheme-independent finite quantity. Therefore one can determine the running coupling constant in the \(\overline{\mathrm{MS}}\) scheme from the vacuum polarization function computed by a lattice-QCD simulation. In more detail, the lattice data of the vacuum polarization is fitted with the perturbative formula Eq. (316) with fit parameter \(\Lambda _{\overline{\mathrm{MS}}}\) parameterizing the running coupling \(\alpha _{\overline{\mathrm{MS}}}(Q^2)\).
While there is no problem in discussing the OPE at the nonperturbative level, the ‘condensates’ such as \({\langle \alpha _s GG\rangle }\) are ambiguous, since they mix with lower-dimensional operators including the unity operator. Therefore one should work in the high-\(Q^2\) regime where power corrections are negligible within the given accuracy. Thus setting the renormalization scale as \(\mu \equiv \sqrt{Q^2}\), one should seek, as always, the window \(\Lambda _{\mathrm{QCD}} \ll \mu \ll a^{-1}\).
9.5.2 Discussion of computations
Results using this method are, to date, only available using overlap fermions or domain wall fermions. Since the last review, FLAG 16, there has been one new computation, Hudspith 18 [685]. These are collected in Table 55 for \(N_f=2\), JLQCD/TWQCD 08C [751] and for \(N_f = 2\,+\,1\), JLQCD 10 [750] and Hudspith 18 [685].
We first discuss the results of JLQCD/TWQCD 08C [751] and JLQCD 10 [750]. The fit to Eq. (316) is done with the 4-loop relation between the running coupling and \(\Lambda _{{\overline{\mathrm {MS}}}}\). It is found that without introducing condensate contributions, the momentum scale where the perturbative formula gives good agreement with the lattice results is very narrow, \(aQ \simeq 0.8{-}1.0\). When a condensate contribution is included the perturbative formula gives good agreement with the lattice results for the extended range \(aQ \simeq 0.6-1.0\). Since there is only a single lattice spacing \(a \approx 0.11\,\text{ fm }\) there is a  for the continuum limit. The renormalization scale \(\mu \) is in the range of \(Q=1.6-2\,\text{ GeV }\). Approximating \(\alpha _{\mathrm{eff}}\approx \alpha _{\overline{\mathrm{MS}}}(Q)\), we estimate that \(\alpha _{\mathrm{eff}}=0.25-0.30\) for \(N_f=2\) and \(\alpha _\mathrm{eff}=0.29-0.33\) for \(N_f=2\,+\,1\). Thus we give a
for the continuum limit. The renormalization scale \(\mu \) is in the range of \(Q=1.6-2\,\text{ GeV }\). Approximating \(\alpha _{\mathrm{eff}}\approx \alpha _{\overline{\mathrm{MS}}}(Q)\), we estimate that \(\alpha _{\mathrm{eff}}=0.25-0.30\) for \(N_f=2\) and \(\alpha _\mathrm{eff}=0.29-0.33\) for \(N_f=2\,+\,1\). Thus we give a  and
and  for \(N_{ f}=2\) and \(N_{ f}=2\,+\,1\), respectively, for the renormalization scale and a
for \(N_{ f}=2\) and \(N_{ f}=2\,+\,1\), respectively, for the renormalization scale and a  for the perturbative behaviour.
for the perturbative behaviour.
A further investigation of this method was initiated in Hudspith 15 [749] and completed by Hudspith 18 [685] (see also [752]) based on domain wall fermion configurations at three lattice spacings, \(a^{-1} = 1.78,\, 2.38,\, 3.15 \,\,\mathrm {GeV}\), with three different light quark masses on the two coarser lattices and one on the fine lattice. An extensive discussion of condensates, using continuum finite energy sum rules was employed to estimate where their contributions might be negligible. It was found that even up to terms of \(O((1/Q^2)^8)\) (a higher order than depicted in Eq. (316) but with constant coefficients) no single condensate dominates and apparent convergence was poor for low \(Q^2\) due to cancellations between contributions of similar size with alternating signs. (See, e.g., the list given by Hudspith 15 [749].) Choosing \(Q^2\) to be at least \(\sim 3.8\,\text{ GeV }^2\) mitigated the problem, but then the coarest lattice had to be discarded, due to large lattice artifacts. So this gives a  for continuum extrapolation. With the higher \(Q^2\) the quark-mass dependence of the results was negligible, so ensembles with different quark masses were averaged over. A range of \(Q^2\) from 3.8 – \(16\,\text{ GeV }^2\) gives \(\alpha _{\mathrm{eff}} = 0.31\) – 0.22, so there is a
for continuum extrapolation. With the higher \(Q^2\) the quark-mass dependence of the results was negligible, so ensembles with different quark masses were averaged over. A range of \(Q^2\) from 3.8 – \(16\,\text{ GeV }^2\) gives \(\alpha _{\mathrm{eff}} = 0.31\) – 0.22, so there is a  for the renormalization scale. The value of \(\alpha _{\mathrm{eff}}^3\) reaches \(\Delta \alpha _\mathrm{eff}/(8\pi b_0 \alpha _{\mathrm{eff}})\) and thus gives a
for the renormalization scale. The value of \(\alpha _{\mathrm{eff}}^3\) reaches \(\Delta \alpha _\mathrm{eff}/(8\pi b_0 \alpha _{\mathrm{eff}})\) and thus gives a  for perturbative behaviour. In Hudspith 15 [749] (superseded by Hudspith 18 [685]) about a 20% difference in \(\Pi (Q^2)\) was seen between the two lattice lattice spacings and a result is quoted only for the smaller a.
for perturbative behaviour. In Hudspith 15 [749] (superseded by Hudspith 18 [685]) about a 20% difference in \(\Pi (Q^2)\) was seen between the two lattice lattice spacings and a result is quoted only for the smaller a.
9.6 \(\alpha _s\) from observables at the lattice spacing scale
9.6.1 General considerations
The general method is to evaluate a short-distance quantity \({{\mathcal {Q}}}\) at the scale of the lattice spacing \(\sim 1/a\) and then determine its relationship to \(\alpha _{\overline{\mathrm{MS}}}\) via a perturbative expansion.
This is epitomized by the strategy of the HPQCD collaboration [753, 754], discussed here for illustration, which computes and then fits to a variety of short-distance quantities, Y,
The quantity Y is taken as the logarithm of small Wilson loops (including some nonplanar ones), Creutz ratios, ‘tadpole-improved’ Wilson loops and the tadpole-improved or ‘boosted’ bare coupling (\({\mathcal {O}}(20)\) quantities in total). The perturbative coefficients \(c_n\) (each depending on the choice of Y) are known to \(n = 3\) with additional coefficients up to \(n_{\mathrm{max}}\) being fitted numerically. The running coupling \(\alpha _{\mathrm {V'}}\) is related to \(\alpha _{\mathrm {V}}\) from the static-quark potential (see Sect. 9.4).Footnote 72
The coupling constant is fixed at a scale \(q^* = d/a\). The latter is chosen as the mean value of \(\ln q\) with the one gluon loop as measure [755, 756]. (Thus a different result for d is found for every short-distance quantity.) A rough estimate yields \(d \approx \pi \), and in general the renormalization scale is always found to lie in this region.
For example, for the Wilson loop \(W_{mn} \equiv \langle W(ma,na) \rangle \) we have
for the tadpole-improved version, where \(c_1\), \(c_2\,, \ldots \) are the appropriate perturbative coefficients and \(u_0 = W_{11}^{1/4}\). Substituting the nonperturbative simulation value in the left hand side, we can determine \(\alpha _{\mathrm {V'}}(q^*)\), at the scale \(q^*\). Note that one finds empirically that perturbation theory for these tadpole-improved quantities have smaller \(c_n\) coefficients and so the series has a faster apparent convergence compared to the case without tadpole improvement.
Using the \(\beta \)-function in the \(\mathrm V'\) scheme, results can be run to a reference value, chosen as \(\alpha _0 \equiv \alpha _{\mathrm {V'}}(q_0)\), \(q_0 = 7.5\,\text{ GeV }\). This is then converted perturbatively to the continuum \({\overline{\mathrm {MS}}}\) scheme
where \(d_1, d_2\) are known 1- and 2-loop coefficients.
Other collaborations have focused more on the bare ‘boosted’ coupling constant and directly determined its relationship to \(\alpha _{\overline{\mathrm{MS}}}\). Specifically, the boosted coupling is defined by
again determined at a scale \(\sim 1/a\). As discussed previously, since the plaquette expectation value in the boosted coupling contains the tadpole diagram contributions to all orders, which are dominant contributions in perturbation theory, there is an expectation that the perturbation theory using the boosted coupling has smaller perturbative coefficients [755], and hence smaller perturbative errors.
9.6.2 Continuum limit
Lattice results always come along with discretization errors, which one needs to remove by a continuum extrapolation. As mentioned previously, in this respect the present method differs in principle from those in which \(\alpha _s\) is determined from physical observables. In the general case, the numerical results of the lattice simulations at a value of \(\mu \) fixed in physical units can be extrapolated to the continuum limit, and the result can be analyzed as to whether it shows perturbative running as a function of \(\mu \) in the continuum. For observables at the cutoff-scale (\(q^*=d/a\)), discretization effects cannot easily be separated out from perturbation theory, as the scale for the coupling comes from the lattice spacing. Therefore the restriction \(a\mu \ll 1\) (the ‘continuum extrapolation’ criterion) is not applicable here. Discretization errors of order \(a^2\) are, however, present. Since \(a\sim \exp (-1/(2b_0 g_0^2)) \sim \exp (-1/(8\pi b_0 \alpha (q^*))\), these errors now appear as power corrections to the perturbative running, and have to be taken into account in the study of the perturbative behaviour, which is to be verified by changing a. One thus usually fits with power corrections in this method.
In order to keep a symmetry with the ‘continuum extrapolation’ criterion for physical observables and to remember that discretization errors are, of course, relevant, we replace it here by one for the lattice spacings used:
Lattice spacings
 3 or more lattice spacings, at least 2 points below \(a = 0.1\,\text{ fm }\)
3 or more lattice spacings, at least 2 points below \(a = 0.1\,\text{ fm }\) 2 lattice spacings, at least 1 point below \(a = 0.1\,\text{ fm }\)
2 lattice spacings, at least 1 point below \(a = 0.1\,\text{ fm }\) otherwise
otherwise
9.6.3 Discussion of computations
Note that due to \(\mu \sim 1/a\) being relatively large the results easily have a  or
or  in the rating on renormalization scale.
in the rating on renormalization scale.
The work of El-Khadra 92 [762] employs a 1-loop formula to relate \(\alpha ^{(0)}_{\overline{\mathrm{MS}}}(\pi /a)\) to the boosted coupling for three lattice spacings \(a^{-1} = 1.15\), 1.78, \(2.43\,\text{ GeV }\). (The lattice spacing is determined from the charmonium 1S-1P splitting.) They obtain \(\Lambda ^{(0)}_{\overline{\mathrm{MS}}}=234\,\text{ MeV }\), corresponding to \(\alpha _{\mathrm{eff}} = \alpha ^{(0)}_{\overline{\mathrm{MS}}}(\pi /a) \approx \) 0.15–0.2. The work of Aoki 94 [761] calculates \(\alpha ^{(2)}_V\) and \(\alpha ^{(2)}_{\overline{\mathrm{MS}}}\) for a single lattice spacing \(a^{-1}\sim 2\,\text{ GeV }\), again determined from charmonium 1S-1P splitting in two-flavour QCD. Using 1-loop perturbation theory with boosted coupling, they obtain \(\alpha ^{(2)}_V=0.169\) and \(\alpha ^{(2)}_{\overline{\mathrm{MS}}}=0.142\). Davies 94 [760] gives a determination of \(\alpha _{\mathrm {V}}\) from the expansion
neglecting higher-order terms. They compute the \(\Upsilon \) spectrum in \(N_f=0\), 2 QCD for single lattice spacings at \(a^{-1} = 2.57\), \(2.47\,\text{ GeV }\) and obtain \(\alpha _{\mathrm {V}}(3.41/a)\simeq \) 0.15, 0.18, respectively. Extrapolating the inverse coupling linearly in \(N_f\), a value of \(\alpha _{\mathrm {V}}^{(3)}(8.3\,\text{ GeV }) = 0.196(3)\) is obtained. SESAM 99 [758] follows a similar strategy, again for a single lattice spacing. They linearly extrapolated results for \(1/\alpha _{\mathrm {V}}^{(0)}\), \(1/\alpha _{\mathrm {V}}^{(2)}\) at a fixed scale of \(9\,\text{ GeV }\) to give \(\alpha _{\mathrm {V}}^{(3)}\), which is then perturbatively converted to \(\alpha _{\overline{\mathrm{MS}}}^{(3)}\). This finally gave \(\alpha _{\overline{\mathrm{MS}}}^{(5)}(M_Z) = 0.1118(17)\). Wingate 95 [759] also follows this method. With the scale determined from the charmonium 1S-1P splitting for single lattice spacings in \(N_f = 0\), 2 giving \(a^{-1}\simeq 1.80\,\text{ GeV }\) for \(N_f=0\) and \(a^{-1}\simeq 1.66\,\text{ GeV }\) for \(N_f=2\), they obtain \(\alpha _{\mathrm {V}}^{(0)}(3.41/a)\simeq 0.15\) and \(\alpha _{\mathrm {V}}^{(2)}\simeq 0.18\), respectively. Extrapolating the coupling linearly in \(N_f\), they obtain \(\alpha _{\mathrm {V}}^{(3)}(6.48\,\text{ GeV })=0.194(17)\).
The QCDSF/UKQCD collaboration, QCDSF/UKQCD 05 [757, 763,764,765], use the 2-loop relation (re-written here in terms of \(\alpha \))
where \(t_1^{\mathrm{P}}\) and \(t_2^{\mathrm{P}}\) are known. (A 2-loop relation corresponds to a 3-loop lattice \(\beta \)-function.) This was used to directly compute \(\alpha _{{\overline{\mathrm{MS}}}}\), and the scale was chosen so that the \({\mathcal {O}}(\alpha _{\mathrm {P}}^0)\) term vanishes, i.e.,
The method is to first compute \(\alpha _{\mathrm {P}}(1/a)\) and from this, using Eq. (323) to find \(\alpha _{\overline{\mathrm{MS}}}(\mu ^*)\). The RG equation, Eq. (280), then determines \(\mu ^*/\Lambda _{\overline{\mathrm{MS}}}\) and hence using Eq. (324) leads to the result for \(r_0\Lambda _{\overline{\mathrm{MS}}}\). This avoids giving the scale in \(\text{ MeV }\) until the end. In the \(N_{ f}=0\) case seven lattice spacings were used [695], giving a range \(\mu ^*/\Lambda _{\overline{\mathrm{MS}}} \approx \) 24–72 (or \(a^{-1} \approx \) 2–7 GeV) and \(\alpha _{\mathrm{eff}} = \alpha _{\overline{\mathrm{MS}}}(\mu ^*) \approx \) 0.15–0.10. Neglecting higher-order perturbative terms (see discussion after Eq. (325) below) in Eq. (323) this is sufficient to allow a continuum extrapolation of \(r_0\Lambda _{\overline{\mathrm{MS}}}\). A similar computation for \(N_f = 2\) by QCDSF/UKQCD 05 [757] gave \(\mu ^*/\Lambda _{\overline{\mathrm{MS}}} \approx \) 12–17 (or roughly \(a^{-1} \approx \) 2–3 GeV) and \(\alpha _{\mathrm{eff}} = \alpha _{\overline{\mathrm{MS}}}(\mu ^*) \approx \) 0.20–0.18. The \(N_f=2\) results of QCDSF/UKQCD 05 [757] are affected by an uncertainty which was not known at the time of publication: It has been realized that the values of \(r_0/a\) of Ref. [757] were significantly too low [693]. As this effect is expected to depend on a, it influences the perturbative behaviour leading us to assign a  for that criterion.
for that criterion.
Since FLAG 13, there has been one new result for \(N_f = 0\) by FlowQCD 15 [679], later updated and published in Kitazawa 16 [686]. They also use the techniques as described in Eqs. (323), (324), but together with the gradient flow scale \(w_0\) (rather than the \(r_0\) scale) leading to a determination of \(w_0\Lambda _{\overline{\mathrm{MS}}}\). The continuum limit is estimated by extrapolating the data at 6 lattice spacings linearly in \(a^2\). The data range used is \(\mu ^*/\Lambda _{\overline{\mathrm{MS}}} \approx \) 50–120 (or \(a^{-1} \approx \) 5–11 GeV) and \(\alpha _{\overline{\mathrm{MS}}}(\mu ^*) \approx \) 0.12–0.095. Since a very small value of \(\alpha _{\overline{\mathrm {MS}}}\) is reached, there is a  in the perturbative behaviour. Note that our conversion to the common \(r_0\) scale unfortunately leads to a significant increase of the error of the \(\Lambda \) parameter compared to using \(w_0\) directly [701]. Again we note that the results of QCDSF/UKQCD 05 [757] (\(N_f = 0\)) and Kitazawa 16 [686] may be affected by frozen topology as they have lattice spacings significantly below \(a = 0.05\,\text{ fm }\). Kitazawa 16 [686] investigate this by evaluating \(w_0/a\) in a fixed topology and estimate any effect at about \(\sim 1\%\).
in the perturbative behaviour. Note that our conversion to the common \(r_0\) scale unfortunately leads to a significant increase of the error of the \(\Lambda \) parameter compared to using \(w_0\) directly [701]. Again we note that the results of QCDSF/UKQCD 05 [757] (\(N_f = 0\)) and Kitazawa 16 [686] may be affected by frozen topology as they have lattice spacings significantly below \(a = 0.05\,\text{ fm }\). Kitazawa 16 [686] investigate this by evaluating \(w_0/a\) in a fixed topology and estimate any effect at about \(\sim 1\%\).
The work of HPQCD 05A [753] (which supersedes the original work [766]) uses three lattice spacings \(a^{-1} \approx 1.2\), 1.6, \(2.3\,\text{ GeV }\) for \(2\,+\,1\) flavour QCD. Typically the renormalization scale \(q \approx \pi /a \approx \) 3.50–7.10 GeV, corresponding to \(\alpha _\mathrm {V'} \approx \) 0.22–0.28.
In the later update HPQCD 08A [754] twelve data sets (with six lattice spacings) are now used reaching up to \(a^{-1} \approx 4.4\,\text{ GeV }\), corresponding to \(\alpha _\mathrm {V'}\approx 0.18\). The values used for the scale \(r_1\) were further updated in HPQCD 10 [13]. Maltman 08 [82] uses most of the same lattice ensembles as HPQCD 08A [754], but not the one at the smallest lattice spacing, \(a\approx 0.045\) fm. Maltman 08 [82] also considers a much smaller set of quantities (three versus 22) that are less sensitive to condensates. They also use different strategies for evaluating the condensates and for the perturbative expansion, and a slightly different value for the scale \(r_1\). The central values of the final results from Maltman 08 [82] and HPQCD 08A [754] differ by 0.0009 (which would be decreased to 0.0007 taking into account a reduction of 0.0002 in the value of the \(r_1\) scale used by Maltman 08 [82]).
As mentioned before, the perturbative coefficients are computed through 3-loop order [767], while the higher-order perturbative coefficients \(c_n\) with \( n_{\mathrm{max}} \ge n > 3\) (with \(n_{\mathrm{max}} = 10\)) are numerically fitted using the lattice-simulation data for the lattice spacings with the help of Bayesian methods. It turns out that corrections in Eq. (319) are of order \(|c_i/c_1|\alpha ^i=\) 5–15% and 3–10% for i = 2, 3, respectively. The inclusion of a fourth-order term is necessary to obtain a good fit to the data, and leads to a shift of the result by 1 – 2 sigma. For all but one of the 22 quantities, central values of \(|c_4/c_1|\approx \) 2–4 were found, with errors from the fits of \(\approx 2\).
An important source of uncertainty is the truncation of perturbation theory. In HPQCD 08A [754], 10 [13] it is estimated to be about 0.4% of \(\alpha _{\overline{\mathrm {MS}}}(M_Z)\). In FLAG 13 we included a rather detailed discussion of the issue with the result that we prefer for the time being a more conservative error based on the above estimate \(|c_4/c_1| = 2\). From Eq. (318) this gives an estimate of the uncertainty in \(\alpha _{\mathrm{eff}}\) of
at the scale \(\mu _1\) where \(\alpha _{\mathrm{eff}}\) is computed from the Wilson loops. This can be used with a variation in \(\Lambda \) at lowest order of perturbation theory and also applied to \(\alpha _s\) evolved to a different scale \(\mu _2\),Footnote 73
With \(\mu _2 = M_Z\) and \(\alpha _s(\mu _1)=0.2\) (a typical value extracted from Wilson loops in HPQCD 10 [13], HPQCD 08A [754] at \(\mu = 5\,\text{ GeV }\)) we have
which we shall later use as the typical perturbative uncertainty of the method with \(2\,+\,1\) fermions.
Table 56 summarizes the results. Within the errors of 3–5% \(N_f=3\) determinations of \(r_0 \Lambda \) nicely agree.
9.7 \(\alpha _s\) from heavy-quark current two-point functions
9.7.1 General considerations
The method has been introduced in HPQCD 08, Ref. [171], and updated in HPQCD 10, Ref. [13], see also Ref. [768]. In addition there is a 2 + 1 + 1 flavour result, HPQCD 14A [16]. Since FLAG 16 two new results have appeared: JLQCD 16 [23] and Maezawa 16 [157].
The basic observable is constructed from a current
of two mass-degenerate heavy-valence quarks, c, \(c^\prime \), usually taken to be at or around the charm quark mass. The pre-factor \(m_c\) denotes the bare mass of the quark. When the lattice discretization respects chiral symmetry, J(x) is a renormalization group invariant local field, i.e., it requires no renormalization. Staggered fermions and twisted mass fermions have such a residual chiral symmetry. The (Euclidean) time-slice correlation function
(\(J^\dagger (x) = im_c{{\overline{\psi }}}_{c'}(x)\gamma _5\psi _c(x)\)) has a \(\sim x_0^{-3}\) singularity at short distances and moments
are nonvanishing for even n and furthermore finite for \(n \ge 4\). Here T is the time extent of the lattice. The moments are dominated by contributions at t of order \(1/m_c\). For large mass \(m_c\) these are short distances and the moments become increasingly perturbative for decreasing n. Denoting the lowest-order perturbation theory moments by \(G_n^{(0)}\), one defines the normalized moments
of even order n. Note that Eq. (328) contains the variable (bare) heavy-quark mass \(m_c\). The normalization \(G_n^{(0)}\) is introduced to help in reducing lattice artifacts. In addition, one can also define moments with different normalizations,
While \({{\tilde{R}}}_n\) also remains renormalization group invariant, it now also has a scale which might introduce an additional ambiguity [23].
The normalized moments can then be parameterized in terms of functions
with \({\bar{m}}_c(\mu )\) being the renormalized charm-quark mass. The reduced moments \(r_n\) have a perturbative expansion
where the written terms \(r_{n,i}(\mu /{\bar{m}}_c(\mu ))\), \(i \le 3\) are known for low n from Refs. [769,770,771,772,773]. In practice, the expansion is performed in the \(\overline{\mathrm{MS}}\) scheme. Matching nonperturbative lattice results for the moments to the perturbative expansion, one determines an approximation to \(\alpha _{\overline{\mathrm{MS}}}(\mu )\) as well as \({{\bar{m}}}_c(\mu )\). With the lattice spacing (scale) determined from some extra physical input, this calibrates \(\mu \). As usual suitable pseudoscalar masses determine the bare quark masses, here in particular the charm mass, and then through Eq. (333) the renormalized charm-quark mass.
A difficulty with this approach is that large masses are needed to enter the perturbative domain. Lattice artifacts can then be sizeable and have a complicated form. The ratios in Eq. (331) use the tree-level lattice results in the usual way for normalization. This results in unity as the leading term in Eq. (334), suppressing some of the kinematical lattice artifacts. We note that in contrast to, e.g., the definition of \(\alpha _\mathrm {qq}\), here the cutoff effects are of order \(a^k\alpha _s\), while there the tree-level term defines \(\alpha _s\) and therefore the cutoff effects after tree-level improvement are of order \(a^k\alpha _s^2\).
Finite-size effects (FSE) due to the omission of \(|t| > T /2\) in Eq. (330) grow with n as \((m_{\eta _c}T/2)^n\, \exp {(-m_{\eta _c} T/2)}\). In practice, however, since the (lower) moments are short-distance dominated, the FSE are expected to be irrelevant at the present level of precision.
Moments of correlation functions of the quark’s electromagnetic current can also be obtained from experimental data for \(e^+e^-\) annihilation [774, 775]. This enables a nonlattice determination of \(\alpha _s\) using a similar analysis method. In particular, the same continuum perturbation theory computation enters both the lattice and the phenomenological determinations.
9.7.2 Discussion of computations
The method has originally been applied in HPQCD 08B [171] and in HPQCD 10 [13], based on the MILC ensembles with \(2 + 1\) flavours of Asqtad staggered quarks and HISQ valence quarks. Both use \(R_n\) while the latter also used a range of quark masses \(m_c\) in addition to the physical charm mass.
The scale was set using \(r_1 = 0.321(5)\,\text{ fm }\) in HPQCD 08B [171] and the updated value \(r_1 = 0.3133(23)\,\text{ fm }\) in HPQCD 10 [13]. The effective range of couplings used is here given for \(n = 4\), which is the moment most dominated by short (perturbative) distances and important in the determination of \(\alpha _s\). The range is similar for other ratios. With \(r_{4,1} = 0.7427\) and \(R_4 = 1.28\) determined in the continuum limit at the charm mass in Ref. [171], we have \(\alpha _{\mathrm{eff}} = 0.38\) at the charm-quark mass, which is the mass value where HPQCD 08B [171] carries out the analysis. In HPQCD 10 [13] a set of masses is used, with \({\tilde{R}}_4 \in [1.09, 1.29]\), which corresponds to \(\alpha _{\mathrm{eff}} \in [0.12, 0.40]\). The available data of HPQCD 10 [13] is reviewed in FLAG 13. For the continuum limit criterion, we choose the scale \(\mu = 2{{\bar{m}}}_c \approx m_{\eta _c}/1.1\), where we have taken \({{\bar{m}}}_c\) in the \({\overline{\mathrm {MS}}}\) scheme at scale \({{\bar{m}}}_c\) and the numerical value 1.1 was determined in HPQCD 10B [69]. With these choices for \(\mu \), the continuum limit criterion is satisfied for three lattice spacings when \(\alpha _\mathrm {eff} \le 0.3\) and \(n=4\).
Larger-n moments are more influenced by nonperturbative effects. For the n values considered, adding a gluon condensate term only changed error bars slightly in HPQCD’s analysis. We note that HPQCD in their papers perform a global fit to all data using a joint expansion in powers of \(\alpha _s^n\), \((\Lambda /(m_{\eta _c}/2))^j\) to parameterize the heavy-quark mass dependence, and \(( am_{\eta _c}/2)^{2i}\) to parameterize the lattice-spacing dependence. To obtain a good fit, they must exclude data with \(am_{\eta _c} > 1.95\) and include lattice-spacing terms \(a^{2i}\) with i greater than 10. Because these fits include many more fit parameters than data points, HPQCD uses their expectations for the sizes of coefficients as Bayesian priors. The fits include data with masses as large as \(am_{\eta _c}/2 \sim 0.86\), so there is only minimal suppression of the many high-order contributions for the heavier masses. It is not clear, however, how sensitive the final results are to the larger \(am_{\eta _c}/2\) values in the data. The continuum limit of the fit is in agreement with a perturbative scale dependence (a 5-loop running \(\alpha _{\overline{\mathrm{MS}}}\) with a fitted 5-loop coefficient in the \(\beta \)-function is used). Indeed, Fig. 2 of Ref. [13] suggests that HPQCD’s fit describes the data well.
A more recent computation, HPQCD 14A [16] uses \({\tilde{R}}_n\) and is based on MILC’s 2 + 1 + 1 HISQ staggered ensembles. Compared to HPQCD 10 [13] valence- and sea-quarks now use the same discretization and the scale is set through the gradient flow scale \(w_0\), determined to \(w_0=0.1715(9)\,\mathrm{fm}\) in Ref. [566]. A number of data points satisfy our continuum limit criterion \(a\mu < 1.5\), at two different lattice spacings. This does not by itself lead to a  but the next-larger lattice spacing does not miss the criterion by much We therefore assign a
but the next-larger lattice spacing does not miss the criterion by much We therefore assign a  in that criterion.
in that criterion.
Two new computations have appeared since the last FLAG report. Maezawa and Petreczky, [157] computed the two-point functions of the \(c{\bar{c}}\) pseudoscalar operator and obtained \(R_4\), \(R_6/R_8\) and \(R_8/R_{10}\) based on the HotQCD collaboration HISQ staggered ensembles, [401]. The scale is set by measuring \(r_1=0.3106(18)\) fm. Continuum limits are taken fitting the lattice spacing dependence with \(a^2\,+\,a^4\) form as the best fit. For \(R_4\), they also employ other forms for fit functions such as \(a^2\), \(\alpha _s^{\mathrm{boosted}} a^2\,+\,a^4\), etc., the results agreeing within errors. Matching \(R_4\) with the 3-loop formula Eq. (334) through order \(\alpha _{\overline{\mathrm {MS}}}^3\) [769], where \(\mu \) is fixed to \(m_c\), they obtain \(\alpha ^{(3)}_{\overline{\mathrm{MS}}}(\mu =m_c) = 0.3697(54)(64)(15)\). The first error is statistical, the second is the uncertainty in the continuum extrapolation, and the third is the truncation error in the perturbative approximation of \(r_4\). This last error is estimated by the “typical size” of the missing 4-loop contribution, which they assume to be \(\alpha ^4_{\overline{\mathrm{MS}}}(\mu )\) multiplied by 2 times the 3-loop coefficient \(2 \times r_{4,3} \times \alpha ^4_{{\overline{\mathrm {MS}}}}(\mu ) = 0.2364 \times \alpha ^4_{{\overline{\mathrm {MS}}}}(\mu )\). The result is converted to
Since \(\alpha _{\mathrm{eff}}(2m_c)\) reaches 0.25, we assign  for the criterion of the renormalization scale. As \(\Delta \Lambda / \Lambda \sim \alpha _{\mathrm{eff}}^2\), we assign
for the criterion of the renormalization scale. As \(\Delta \Lambda / \Lambda \sim \alpha _{\mathrm{eff}}^2\), we assign  for the criterion of perturbative behaviour. The lattice cutoff ranges as \(a^{-1} \) = 1.42–4.89 GeV with \(\mu =2m_c\sim 2.6\) GeV so that we assign
for the criterion of perturbative behaviour. The lattice cutoff ranges as \(a^{-1} \) = 1.42–4.89 GeV with \(\mu =2m_c\sim 2.6\) GeV so that we assign  for continuum extrapolation.
for continuum extrapolation.
JLQCD 16 [23] also computed the two-point functions of the \(c{\bar{c}}\) pseudoscalar operator and obtained \(R_6\), \(R_8\), \(R_{10}\) and their ratios based on 2 + 1 flavour QCD with Möbius domain-wall quark for three lattice cutoff \(a^{-1}\) = 2.5, 3.6, 4.5 GeV. The scale is set by \(\sqrt{t_0}=0.1465(21)(13)\,\text{ fm }\). The continuum limit is taken assuming linear dependence on \(a^2\). They find a sizeable lattice-spacing dependence of \(R_4\), which is therefore not used in their analysis, but for \(R_6,R_8, R_{10}\) the dependence is mild giving reasonable control over the continuum limit. They use the perturbative formulae for the vacuum polarization in the pseudoscalar channel \(\Pi _{PS}\) through order \(\alpha _{\overline{\mathrm {MS}}}^3\) in the \(\overline{\mathrm{MS}}\) scheme [771, 772] to obtain \(\alpha ^{(4)}_{\overline{\mathrm{MS}}}\). Combining the matching of lattice results with continuum perturbation theory for \(R_6\), \(R_6/R_8\) and \(R_{10}\), they obtain \(\alpha ^{(4)}_{\overline{\mathrm{MS}}}(\mu =3\,\,\mathrm {GeV})=0.2528(127)\), where the error is dominated by the perturbative truncation error. To estimate the truncation error they study the dependence of the final result on the choice of the renormalization scales \(\mu _\alpha , \;\mu _\mathrm {m}\) which are used as renormalization scales for \(\alpha \) and the quark mass. Independently [776] the two scales are varied in the range of 2 GeV to 4 GeV. The above result is converted to \(\alpha ^{(5)}_{\overline{\mathrm {MS}}}(M_Z)\) as
Since \(\alpha _{\mathrm{eff}}\) roughly reaches 0.25, they have  for the renormalization scale criterion. Since \(\Delta \Lambda / \Lambda > \alpha _{\mathrm{eff}}^2\), we also assign
for the renormalization scale criterion. Since \(\Delta \Lambda / \Lambda > \alpha _{\mathrm{eff}}^2\), we also assign  for the criterion of perturbative behaviour. The lattice cutoff ranges over \(a^{-1}\) = 2.5–4.5 GeV with \(\mu =3\) GeV so we also give them a
for the criterion of perturbative behaviour. The lattice cutoff ranges over \(a^{-1}\) = 2.5–4.5 GeV with \(\mu =3\) GeV so we also give them a  for continuum extrapolation.
for continuum extrapolation.
There is a significant difference in the perturbative error estimate of JLQCD 16 [23] and Maezawa 16 [157], both of which use the moments at the charm mass. JLQCD 16 uses the scale dependence (see also Sect. 9.2.3) but Maezawa 16 looks at the perturbative coefficients at \(\mu =m_*\), with \({{{\bar{m}}}_c}(m_*)=m_*\). While the Maezawa 16 result derives from \(R_4\), JLQCD 16 did not use that moment and therefore did not show its renormalization-scale dependence. We provide it here and show \(\alpha (m_*)\) extracted from \(R_4\) expanded in \(\alpha (\mu )\) for \(\mu =s\,m_*\) (and evolved to \(\mu =m_*\)) in Fig. 35. Note that the perturbative error estimated by Maezawa 16 is a small contribution to the total error, while the scale dependence in Fig. 35 is significant between, e.g., \(s=1\) and \(s=4\). This is a confirmation of our  in the perturbative error criterion which is linked to the cited overall error as spelled out in Sect. 9.2.1.
in the perturbative error criterion which is linked to the cited overall error as spelled out in Sect. 9.2.1.
Aside from the final results for \(\alpha _s(m_Z)\) obtained by matching with perturbation theory, it is interesting to make a comparison of the short distance quantities in the continuum limit \(R_n\) which are available from HPQCD 08 [171], JLQCD 16 [23] and Maezawa 16 [157] (all using \(2\,+\,1\) flavours). In Fig. 36 we plot the various results based on the numbers collated in Table 58. These results are in quite good agreement with each other. For future studies it is of course interesting to check agreement of these numbers before turning to the more involved determination of \(\alpha _s\).
Ratios from Table 58. Note that constants have been subtracted from \(R_4\), \(R_6\) and \(R_{10}\), to be able to plot all results in a similar range
In Table 57 we summarize the results for the latter.
9.8 \(\alpha _s\) from QCD vertices
9.8.1 General considerations
The most intuitive and in principle direct way to determine the coupling constant in QCD is to compute the appropriate three- or four-point gluon vertices or alternatively the quark-quark-gluon vertex or ghost-ghost-gluon vertex (i.e., \( q{\overline{q}}A\) or \(c{\overline{c}}A\) vertex, respectively). A suitable combination of renormalization constants then leads to the relation between the bare (lattice) and renormalized coupling constant. This procedure requires the implementation of a nonperturbative renormalization condition and the fixing of the gauge. For the study of nonperturbative gauge fixing and the associated Gribov ambiguity, we refer to Refs. [777,778,779] and references therein. In practice the Landau gauge is used and the renormalization constants are defined by requiring that the vertex is equal to the tree level value at a certain momentum configuration. The resulting renormalization schemes are called ‘MOM’ scheme (symmetric momentum configuration) or ‘\(\mathrm {\widetilde{MOM}}\)’ (one momentum vanishes), which are then converted perturbatively to the \(\overline{\mathrm{MS}}\) scheme.
A pioneering work to determine the three-gluon vertex in the \(N_f = 0\) theory is Alles 96 [780] (which was followed by Ref. [781] for two flavour QCD); a more recent \(N_f = 0\) computation was Ref. [782] in which the three-gluon vertex as well as the ghost-ghost-gluon vertex was considered. (This requires a computation of the propagator of the Faddeev–Popov ghost on the lattice.) The latter paper concluded that the resulting \(\Lambda _{\overline{\mathrm{MS}}}\) depended strongly on the scheme used, the order of perturbation theory used in the matching and also on nonperturbative corrections [783].
Subsequently in Refs. [784, 785] a specific \(\widetilde{\mathrm{MOM}}\) scheme with zero ghost momentum for the ghost-ghost-gluon vertex was used. In this scheme, dubbed the ‘MM’ (Minimal MOM) or ‘Taylor’ (T) scheme, the vertex is not renormalized, and so the renormalized coupling reduces to
where \(D^{\mathrm{ghost}}_{\mathrm{lat}}\) and \(D^{\mathrm{gluon}}_{\mathrm{lat}}\) are the (bare lattice) dressed ghost and gluon ‘form factors’ of these propagator functions in the Landau gauge,
and we have written the formula in the continuum with \(D^\mathrm{ghost/gluon}(p)=D^{\mathrm{ghost/gluon}}_{\mathrm{lat}}(p, 0)\). Thus there is now no need to compute the ghost-ghost-gluon vertex, just the ghost and gluon propagators.
9.8.2 Discussion of computations
For the calculations considered here, to match to perturbative scaling, it was first necessary to reduce lattice artifacts by an H(4) extrapolation procedure (addressing O(4) rotational invariance), e.g., ETM 10F [791] or by lattice perturbation theory, e.g., Sternbeck 12 [789]. To match to perturbation theory, collaborations vary in their approach. In ETM 10F [791], it was necessary to include the operator \(A^2\) in the OPE of the ghost and gluon propagators, while in Sternbeck 12 [789] very large momenta are used and \(a^2p^2\) and \(a^4p^4\) terms are included in their fit to the momentum dependence. A further later refinement was the introduction of higher nonperturbative OPE power corrections in ETM 11D [788] and ETM 12C [787]. Although the expected leading power correction, \(1/p^4\), was tried, ETM finds good agreement with their data only when they fit with the next-to-leading-order term, \(1/p^6\). The update ETM 13D [786] investigates this point in more detail, using better data with reduced statistical errors. They find that after again including the \(1/p^6\) term they can describe their data over a large momentum range from about 1.75 GeV to 7 GeV.
In all calculations except for Sternbeck 10 [790], Sternbeck 12 [789] , the matching with the perturbative formula is performed including power corrections in the form of condensates, in particular \(\langle A^2 \rangle \). Three lattice spacings are present in almost all calculations with \(N_f=0\), 2, but the scales ap are rather large. This mostly results in a  on the continuum extrapolation (Sternbeck 10 [790], Boucaud 01B [781] for \(N_f=2\). Ilgenfritz 10 [792], Boucaud 08 [785], Boucaud 05 [782], Becirevic 99B [797], Becirevic 99A [798], Boucaud 98B [799], Boucaud 98A [800], Alles 96 [780] for \(N_f=0\)). A
on the continuum extrapolation (Sternbeck 10 [790], Boucaud 01B [781] for \(N_f=2\). Ilgenfritz 10 [792], Boucaud 08 [785], Boucaud 05 [782], Becirevic 99B [797], Becirevic 99A [798], Boucaud 98B [799], Boucaud 98A [800], Alles 96 [780] for \(N_f=0\)). A  is reached in the \(N_{ f}=0\) computations Boucaud 00A [796], 00B [795], 01A [794], Soto 01 [793] due to a rather small lattice spacing, but this is done on a lattice of a small physical size. The \(N_f=2\,+\,1\,+\,1\) calculation, fitting with condensates, is carried out for two lattice spacings and with \(ap>1.5\), giving
is reached in the \(N_{ f}=0\) computations Boucaud 00A [796], 00B [795], 01A [794], Soto 01 [793] due to a rather small lattice spacing, but this is done on a lattice of a small physical size. The \(N_f=2\,+\,1\,+\,1\) calculation, fitting with condensates, is carried out for two lattice spacings and with \(ap>1.5\), giving  for the continuum extrapolation as well. In ETM 10F [791] we have \(0.25< \alpha _{\mathrm{eff}} < 0.4\), while in ETM 11D [788], ETM 12C [787] (and ETM 13 [41]) we find \(0.24< \alpha _{\mathrm{eff}} < 0.38\), which gives a green circle in these cases for the renormalization scale. In ETM 10F [791] the values of ap violate our criterion for a continuum limit only slightly, and we give a
for the continuum extrapolation as well. In ETM 10F [791] we have \(0.25< \alpha _{\mathrm{eff}} < 0.4\), while in ETM 11D [788], ETM 12C [787] (and ETM 13 [41]) we find \(0.24< \alpha _{\mathrm{eff}} < 0.38\), which gives a green circle in these cases for the renormalization scale. In ETM 10F [791] the values of ap violate our criterion for a continuum limit only slightly, and we give a  .
.
In Sternbeck 10 [790], the coupling ranges over \(0.07 \le \alpha _{\mathrm{eff}} \le 0.32\) for \(N_f=0\) and \(0.19 \le \alpha _{\mathrm{eff}} \le 0.38\) for \(N_f=2\) giving  and
and  for the renormalization scale, respectively. The fit with the perturbative formula is carried out without condensates, giving a satisfactory description of the data. In Boucaud 01A [794], depending on a, a large range of \(\alpha _{\mathrm{eff}}\) is used which goes down to 0.2 giving a
for the renormalization scale, respectively. The fit with the perturbative formula is carried out without condensates, giving a satisfactory description of the data. In Boucaud 01A [794], depending on a, a large range of \(\alpha _{\mathrm{eff}}\) is used which goes down to 0.2 giving a  for the renormalization scale and perturbative behaviour, and several lattice spacings are used leading to
for the renormalization scale and perturbative behaviour, and several lattice spacings are used leading to  in the continuum extrapolation. The \(N_{ f}=2\) computation Boucaud 01B [794], fails the continuum limit criterion because both \(a\mu \) is too large and an unimproved Wilson fermion action is used. Finally in the conference proceedings Sternbeck 12 [789], the \(N_f\) = 0, 2, 3 coupling \(\alpha _\mathrm {T}\) is studied. Subtracting 1-loop lattice artifacts and subsequently fitting with \(a^2p^2\) and \(a^4p^4\) additional lattice artifacts, agreement with the perturbative running is found for large momenta (\(r_0^2p^2 > 600\)) without the need for power corrections. In these comparisons, the values of \(r_0\Lambda _{\overline{\mathrm {MS}}}\) from other collaborations are used. As no numbers are given, we have not introduced ratings for this study.
in the continuum extrapolation. The \(N_{ f}=2\) computation Boucaud 01B [794], fails the continuum limit criterion because both \(a\mu \) is too large and an unimproved Wilson fermion action is used. Finally in the conference proceedings Sternbeck 12 [789], the \(N_f\) = 0, 2, 3 coupling \(\alpha _\mathrm {T}\) is studied. Subtracting 1-loop lattice artifacts and subsequently fitting with \(a^2p^2\) and \(a^4p^4\) additional lattice artifacts, agreement with the perturbative running is found for large momenta (\(r_0^2p^2 > 600\)) without the need for power corrections. In these comparisons, the values of \(r_0\Lambda _{\overline{\mathrm {MS}}}\) from other collaborations are used. As no numbers are given, we have not introduced ratings for this study.
In Table 59 we summarize the results. Presently there are no \(N_f \ge 3\) calculations of \(\alpha _s\) from QCD vertices that satisfy the FLAG criteria to be included in the range.
9.9 \(\alpha _s\) from the eigenvalue spectrum of the Dirac operator
9.9.1 General considerations
Consider the spectral density of the continuum Dirac operator
where V is the volume and \(\lambda _k\) are the eigenvalues of the Dirac operator in a gauge background.
Its perturbative expansion
is known including \(\rho _3\) in the \(\overline{\mathrm {MS}}\) scheme [801, 802]. In renormalization group improved form one sets the renormalization scale \(\mu \) to \(\mu =s\lambda \) with \(s=\mathrm{O}(1)\) and the \(\rho _i\) are pure numbers. Nakayama 18 [687] initiated a study of \(\rho (\lambda )\) in the perturbative regime. They prefer to consider \(\mu \) independent from \(\lambda \). Then \(\rho _i\) are polynomials in \(\log (\lambda /\mu )\) of degree i. One may consider
where the four coefficients \(F_i\), again polynomials of degree i in \(\log (\lambda /\mu )\), are known. Choosing instead the renormalization group improved form with \(\mu =s\lambda \) in Eq. (340) would have led to
with pure numbers \({{\bar{F}}}_i\) and \({{\bar{F}}}_1=0\). Determinations of \(\alpha _s\) can be carried out by a computation and continuum extrapolation of \(\rho (\lambda )\) and/or \(F(\lambda )\) at large \(\lambda \). Such computations are made possible by the techniques of [46, 354, 687].
We note that according to our general discussions in terms of an effective coupling, we have \(n_\mathrm {l}=2\); the 3-loop \(\beta \) function of a coupling defined from Eq. (340) or Eq. (342) is known.Footnote 74
9.9.2 Discussion of computations
There is one pioneering result to date using this method by Nakayama 18 [687]. They computed the eigenmode distributions of the Hermitian operator \(a^2 D^{\dagger }_\mathrm{ov}(m_f=0,am_{\mathrm{PV}}) D_{\mathrm{ov}}(m_f=0,am_{\mathrm{PV}})\) where \(D_\mathrm{ov}\) is the overlap operator and \(m_{\mathrm{PV}}\) is the Pauli–Villars regulator on ensembles with 2 + 1 flavours using Möbius domain-wall quarks for three lattice cutoff \(a^{-1}= 2.5, 3.6, 4.5 \) GeV, where \(am_{\mathrm{PV}} = 3\) or \(\infty \). The bare eigenvalues are converted to the \({\overline{\mathrm {MS}}}\) scheme at \(\mu = 2\,\text{ GeV }\) by multiplying with the renormalization constant \(Z_m(2\,\text{ GeV })\), which is then transformed to those renormalized at \(\mu =6\,\text{ GeV }\) using the renormalization group equation. The scale is set by \(\sqrt{t_0}=0.1465(21)(13)\,\text{ fm }\). The continuum limit is taken assuming a linear dependence in \(a^2\), while the volume size is kept about constant: 2.6–2.8 fm.
Choosing the renormalization scale \(\mu = 6\,\text{ GeV }\), Nakayama 18 [687], extracted \(\alpha _{\overline{\mathrm{MS}}}^{(3)}(6\,\text{ GeV })=0.204(10)\). The result is converted to
The lattice cutoff ranges over \(a^{-1} = 2.5-4.5\,\text{ GeV }\) with \(\mu =\lambda =0.8-1.25\,\text{ GeV }\) yielding quite small values \(a\mu \). However, our continuum limit criterion does not apply as it requires us to consider \(\alpha _s=0.3\). We thus deviate from the general rule and give a  which would result at the smallest value \(\alpha _{\overline{\mathrm {MS}}}(\mu )=0.4\) considered by Nakayama 18 [687]. The values of \(\alpha _{\overline{\mathrm {MS}}}\) lead to a
which would result at the smallest value \(\alpha _{\overline{\mathrm {MS}}}(\mu )=0.4\) considered by Nakayama 18 [687]. The values of \(\alpha _{\overline{\mathrm {MS}}}\) lead to a  for the renormalization scale, while perturbative behavior is rated
for the renormalization scale, while perturbative behavior is rated  .
.
In Table 60 we list this result.
9.10 Summary
After reviewing the individual computations, we are now in a position to discuss the overall result. We first present the current status and for that briefly consider \(r_0\Lambda \) with its flavour dependence from \(N_f = 0\) to 4 flavours. Then we discuss the central \(\alpha _{\overline{\mathrm{MS}}}(M_Z)\) results, which just use \(N_f \ge 3\), give ranges for each sub-group discussed previously, and give final FLAG average as well as an overall average together with the current PDG nonlattice numbers. Finally we return to \(r_0\Lambda \), presenting our estimates for the various \(N_f\).
 . A weighted average of the pre-ranges gives 0.11824(58), using the smallest pre-range uncertainty gives 0.11824(81) while the average uncertainty of the ranges used as an error gives 0.11824(131). We note that Bazavov 12 is superseded by Bazavov 14
. A weighted average of the pre-ranges gives 0.11824(58), using the smallest pre-range uncertainty gives 0.11824(81) while the average uncertainty of the ranges used as an error gives 0.11824(131). We note that Bazavov 12 is superseded by Bazavov 149.10.1 The present situation
We first summarize the status of lattice-QCD calculations of the QCD scale \(\Lambda _{\overline{\mathrm {MS}}}\). Figure 37 shows all the results for \(r_0\Lambda _{\overline{\mathrm{MS}}}\) discussed in the previous sections.
\(r_0\Lambda _{\overline{\mathrm{MS}}}\) estimates for \(N_f = 0\), 2, 3, 4 flavours. Full green squares are used in our final ranges, pale green squares also indicate that there are no red squares in the colour coding but the computations were superseded by later more complete ones or not published, while red open squares mean that there is at least one red square in the colour coding
Many of the numbers are the ones given directly in the papers. However, when only \(\Lambda _{\overline{\mathrm{MS}}}\) in physical units (\(\text{ MeV }\)) is available, we have converted them by multiplying with the value of \(r_0\) in physical units. The notation used is full green squares for results used in our final average, while a lightly shaded green square indicates that there are no red squares in the previous colour coding but the computation does not enter the ranges because either it has been superseded by an update or it is not published. Red open squares mean that there is at least one red square in the colour coding.
For \(N_f=0\) there is relatively little spread in the more recent numbers.
When two flavours of quarks are included, the numbers extracted by the various groups show a considerable spread, as in particular older computations did not yet control the systematics sufficiently. This illustrates the difficulty of the problem and emphasizes the need for strict criteria. The agreement among the more modern calculations with three or more flavours, however, is quite good.
We now turn to the status of the essential result for phenomenology, \(\alpha _{\overline{\mathrm{MS}}}^{(5)}(M_Z)\). In Table 61 and the upper plot in Fig. 38 we show all the results for \(\alpha _{\overline{\mathrm{MS}}}^{(5)}(M_Z)\) (i.e., \(\alpha _{\overline{\mathrm{MS}}}\) at the Z mass) obtained from \(N_f=2\,+\,1\) and \(N_f = 2\,+\,1\,+\,1\) simulations. The conversion from \(N_{ f}= 3\) or \(N_{ f}= 4\) to \(N_{ f}= 5\) is made by matching the coupling constant at the charm and bottom quark thresholds and using the scale as determined or used by the authors.
\(\alpha _{\overline{\mathrm{MS}}}^{(5)}(M_Z)\), the coupling constant in the \(\overline{\mathrm{MS}}\) scheme at the Z mass. Left: Lattice results, pre-ranges from different calculation methods, and final average. Right: Comparison of the lattice pre-ranges and average with the nonlattice ranges and average. The first PDG 18 entry gives the outcome of their analysis excluding lattice results (see Sect. 9.10.4)
As can be seen from the tables and figures, at present there are several computations satisfying the criteria to be included in the FLAG average. Since FLAG 16 two new computations of \(\alpha _{\overline{\mathrm{MS}}}^{(5)}(M_Z)\) pass all our criteria with at least a  and one computation with all
and one computation with all  . The results agree quite well within the stated uncertainties. The uncertainties vary significantly.
. The results agree quite well within the stated uncertainties. The uncertainties vary significantly.
9.10.2 Our range for \(\alpha _{\overline{\mathrm{MS}}}^{(5)}\)
We now explain the determination of our range. We only include those results without a red tag and that are published in a refereed journal. We also do not include any numbers that were obtained by extrapolating from theories with less than three flavours. They are not controlled and can be looked up in the previous FLAG reviews.
A general issue with most determinations of \(\alpha _{\overline{\mathrm {MS}}}\), both lattice and nonlattice, is that they are dominated by perturbative truncation errors, which are difficult to estimate. Further, all results discussed here except for those of Sects. 9.3, 9.6 are based on extractions of \(\alpha _{\overline{\mathrm {MS}}}\) that are largely influenced by data with \(\alpha _\mathrm {eff}\ge 0.3\). At smaller \(\alpha _s\) the momentum scale \(\mu \) quickly is at or above \(a^{-1}\). We have included computations using \(a\mu \) up to 1.5 and \(\alpha _\mathrm {eff}\) up to 0.4, but one would ideally like to be significantly below that. Accordingly we choose to not simply perform weighted averages with the individual errors estimated by each group. Rather, we use our own more conservative estimates of the perturbative truncation errors in the weighted average.
In the following we repeat aspects of the methods and calculations that inform our estimates of the perturbative truncation errors. We also provide separate estimates for \(\alpha _s\) obtained from step-scaling, the heavy-quark potential, Wilson loops, and heavy-quark current two-point functions to enable a comparison of the different lattice approaches; these are summarized in Table 61.
Step-scaling
The step-scaling computations of PACS-CS 09A [81] and ALPHA 17 [79] reach energies around the Z-mass where perturbative uncertainties in the three-flavour theory are negligible. Perturbative errors do enter in the conversion of the \(\Lambda \)-parameters from three to five flavours, but successive order contributions decrease rapidly and can be neglected. We form a weighted average of the two results and obtain \(\alpha _{{\overline{\mathrm {MS}}}}=0.11848(81)\).
Potential computations
Brambilla 10 [742], ETM 11C [741] and Bazavov 12 [740] give evidence that they have reached distances where perturbation theory can be used. However, in addition to \(\Lambda \), a scale is introduced into the perturbative prediction by the process of subtracting the renormalon contribution. This subtraction is avoided in Bazavov 14 [80] by using the force and again agreement with perturbative running is reported. Husung 17 [681] (unpublished) studies the reliability of perturbation theory in the pure gauge theory with lattice spacings down to \(0.015\,\mathrm{fm}\) and finds that at weak coupling there is a downwards trend in the \(\Lambda \)-parameter with a slope \(\Delta \Lambda / \Lambda \approx 9 \alpha _s^3\). While it is not very satisfactory to use just Husung 17 to estimate the perturbative error, we do not have additional information at present. Further studies are needed to better understand the errors of \(\alpha _s\) determinations from the potential.
Only Bazavov 14 [80] satisfies all of the criteria to enter the FLAG average for \(\alpha _s\). Given the findings of [681] we estimate a perturbative error of \(\Delta \Lambda / \Lambda = 9(\alpha _s^{\mathrm{min}})^3 \) with \(\alpha _s^{\mathrm{min}} \approx 0.19\) the smallest value reached in [80]. This translates into \(\Delta \alpha _{\overline{\mathrm {MS}}}(M_Z)=0.0014\). A different way to estimate the effect is to take the actual difference of the \(\Lambda \)-parameters estimated in \(N_{ f}=0\) by Brambilla 10 [742] and Husung 17 [681]: \(\Delta \Lambda / \Lambda \approx (0.637-0.590)/0.637 = 0.074\) or \(\Delta \alpha _{\overline{\mathrm {MS}}}(M_Z)=0.0018\). We use the mean of these two error estimates together with the central value of Bazavov 14 and obtain \(\alpha _{{\overline{\mathrm {MS}}}}= 0.1166(16)\).
Small Wilson loops
Here the situation is unchanged as compared to FLAG 16. In the determination of \(\alpha _s\) from observables at the lattice spacing scale, there is an interplay of higher-order perturbative terms and lattice artifacts. In HPQCD 05A [753], HPQCD 08A [754] and Maltman 08 [82] both lattice artifacts (which are power corrections in this approach) and higher-order perturbative terms are fitted. We note that Maltman 08 [82] and HPQCD 08A [754] analyze largely the same data set but use different versions of the perturbative expansion and treatments of nonperturbative terms. After adjusting for the slightly different lattice scales used, the values of \(\alpha _{\overline{\mathrm {MS}}}(M_Z)\) differ by 0.0004 to 0.0008 for the three quantities considered. In fact the largest of these differences (0.0008) comes from a tadpole-improved loop, which is expected to be best behaved perturbatively. We therefore replace the perturbative-truncation errors from [13, 82] with our estimate of the perturbative uncertainty Eq. (327). Taking the perturbative errors to be 100% correlated between the results, we obtain for the weighted average \(\alpha _{{\overline{\mathrm {MS}}}}=0.11871(128)\).
Heavy quark current two-point functions
Other computations with small errors are HPQCD 10 [13] and HPQCD 14A [16], where correlation functions of heavy valence quarks are used to construct short-distance quantities. Due to the large quark masses needed to reach the region of small coupling, considerable discretization errors are present, see Fig. 30 of FLAG 16. These are treated by fits to the perturbative running (a 5-loop running \(\alpha _{\overline{\mathrm{MS}}}\) with a fitted 5-loop coefficient in the \(\beta \)-function is used) with high-order terms in a double expansion in \(a^2\Lambda ^2\) and \(a^2 m_\mathrm {c}^2\) supplemented by priors which limit the size of the coefficients. The priors play an especially important role in these fits given the much larger number of fit parameters than data points. We note, however, that the size of the coefficients does not prevent high-order terms from contributing significantly, since the data includes values of \(am_{\text {c}}\) that are rather close to 1.
More recent calculations use the same method but just at the charm quark mass, where discretization errors are considerably smaller. Here the dominating uncertainty is the perturbative error. JLQCD 16 [23] estimates it at \(\Delta \alpha _s= 0.0011\) from independent changes of the renormalization scales of coupling and mass, \(\mu _\alpha ,\mu _\mathrm {m}\). Figure 35 for the residual scale dependence of \(\alpha _s\) from \(R_4\) yields 0.0017 from scale change \(1\le s\le 3\) and 0.0025 for \(2\le s\le 4\). For the figure we set \(\mu _\alpha = \mu _\mathrm {m}\). Independent changes of \(\mu _\alpha ,\,\mu _\mathrm {m}\) would yield a larger estimate of the uncertainty [776]. We note also that there are small differences in the continuum-extrapolated results in the moments themselves, cf. Table 58. The relative difference in \(R_6/R_8 -1 \sim k \alpha _s\) between Maezawa 16 [157], and JLQCD 16 [23], is about 4.5(2.5)%, which translates into a difference of 0.0023(13) in \(\alpha _s\) at the Z-mass, close to the total cited uncertainty of JLQCD 16 [23]. A further estimate of the uncertainty is the difference of the JLQCD 16 [23] and Maezawa 16 [157] final numbers,Footnote 75 which is \(\Delta \alpha _{\overline{\mathrm {MS}}}(M_Z)= 0.0015\)
We settle for an intermediate value of \(\Delta \alpha _s=0.0015\). Replacing the perturbative truncation errors from HPQCD 10 [13], HPQCD 14A [16], and JLQCD 16 [23] with this value, and including a 100% correlation between the perturbative errors, we obtain for the weighted average \(\alpha _{{\overline{\mathrm {MS}}}}= 0.11818(156)\).
Other methods
Computations using other methods do not qualify for an average yet, predominantly due to a lacking
 in the continuum extrapolation.
in the continuum extrapolation.
We obtain the central value for our range of \(\alpha _s\) from the weighted average of the four pre-ranges listed in Table 61. The error of this weighted average is 0.0006, which is quite a bit smaller than the most precise entry. Because, however, the errors on almost all of the \(\alpha _s\) calculations that enter the average are dominated by perturbative truncation errors, which are especially difficult to estimate, we choose instead to take a larger range for \(\alpha _s\) of 0.0008. This is the error on the pre-range for \(\alpha _s\) from step-scaling, because perturbative-truncation errors are sub-dominant in this method. Our final range is then given by
Almost all of the eight calculations that are included are within 1\(\sigma \) of this range. Further, the range for \(\alpha _{\overline{\mathrm{MS}}}^{(5)}(M_Z)\) presented here is based on results with rather different systematics (apart from the matching across the charm threshold). We therefore believe that the true value is very likely to lie within this range.
All computations which enter this range, with the exception of HPQCD 14A [16], rely on a perturbative inclusion of the charm and bottom quarks. Perturbation theory for the matching of \({\bar{g}}^2_{N_f}\) and \({\bar{g}}^2_{N_f-1}\) looks very well behaved even at the mass of the charm. Worries that still there may be purely nonperturbative effects at this rather low scale have been removed by nonperturbative studies of the accuracy of perturbation theory. While the original study in Ref. [130] was not precise enough, the extended one in Ref. [131] estimates effects in the \(\Lambda \)-parameter to be significantly below 1% and thus negligible for the present and near future accuracy.
9.10.3 Ranges for \([r_0 \Lambda ]^{(N_{ f})}\) and \(\Lambda _{{\overline{\mathrm {MS}}}}\)
In the present situation, we give ranges for \([r_0 \Lambda ]^{(N_{ f})}\) and \(\Lambda _{{\overline{\mathrm {MS}}}}\), discussing their determination case by case. We include results with \(N_{ f}<3\) because it is interesting to see the \(N_{ f}\)-dependence of the connection of low- and high-energy QCD. This aids our understanding of the field theory and helps in finding possible ways to tackle it beyond the lattice approach. It is also of interest in providing an impression on the size of the vacuum polarization effects of quarks, in particular with an eye on the still difficult-to-treat heavier charm and bottom quarks. Even if this information is rather qualitative, it may be valuable, given that it is of a completely nonperturbative nature. We emphasize that results for \([r_0 \Lambda ]^{(0)}\) and \([r_0 \Lambda ]^{(2)}\) are not meant to be used in phenomenology.
For \(N_{ f}=2\,+\,1\,+\,1\), we presently do not quote a range as there is a single result: HPQCD 14A [16] found \([r_0 \Lambda ]^{(4)} = 0.70(3)\).
For \(N_{ f}=2\,+\,1\), we take as a central value the weighted average of ALPHA 17 [79], JLQCD 16 [23], Bazavov 14 [80], HPQCD 10 [13] (Wilson loops and current two-point correlators), PACS-CS 09A [81] and Maltman 08 [82]. Since the uncertainty in \(r_0\) is small compared to that of \(\Lambda \), we can directly propagate the error from the analog of Eq. (344) with the 2 + 1 + 1 number removed and arrive at
(The error of the straight weighted average is 0.012.) It is in good agreement with all 2 + 1 results without red tags. In physical units, using \(r_0=0.472\) fm and neglecting its error, this means
where the error of the straight weighted average is \(5\,\mathrm {MeV}\).
For \(N_f=2\), at present there is one computation with a  rating for all criteria, ALPHA 12 [693]. We adopt it as our central value and enlarge the error to cover the central values of the other three results with filled green boxes. This results in an asymmetric error. Our range is unchanged as compared to FLAG 13,
rating for all criteria, ALPHA 12 [693]. We adopt it as our central value and enlarge the error to cover the central values of the other three results with filled green boxes. This results in an asymmetric error. Our range is unchanged as compared to FLAG 13,
and in physical units, using \(r_0=0.472\)fm,
A weighted average of the four eligible numbers would yield \([r_0 \Lambda _{{\overline{\mathrm {MS}}}}]^{(2)} = 0.689(23)\), not covering the best result and in particular leading to a smaller error than we feel is justified, given the issues discussed previously in Sect. 9.4.2 (Karbstein 18 [682], ETM 11C [741]) and Sect. 9.8.2 (ETM 10F [791]). Thus we believe that our estimate is a conservative choice; the low values of ETM 11C [741] and Karbstein 18 [682] lead to a large downward error. We note that this can largely be explained by different values of \(r_0\) between ETM 11C [741] and ALPHA 12 [693]. We still hope that future work will improve the situation.
For \(N_f=0\) we take into account ALPHA 98 [724], QCDSF/UKQCD 05 [757], Brambilla 10 [742], Kitazawa 16 [686] and Ishikawa 17 [680] for forming a range.Footnote 76 Taking a weighted average of the five numbers, we obtain \([r_0 \Lambda _{{\overline{\mathrm {MS}}}}]^{(0)} = 0.615(5)\), dominated by the QCDSF/UKQCD 05 [757] result.
Since the errors are dominantly systematic, due to missing higher orders of PT, we prefer to presently take a range which encompasses all five central values and whose uncertainty comes close to our estimate of the perturbative error in QCDSF/UKQCD 05 [757]: based on \(|c_4/c_1| \approx 2\) as before, we find \(\Delta [r_0 \Lambda _{{\overline{\mathrm {MS}}}}]^{(0)} = 0.018\). We then have
Converting to physical units, again using \(r_0=0.472\,\text{ fm }\) yields
While the conversion of the \(\Lambda \) parameter to physical units is quite unambiguous for \(N_{ f}=2\,+\,1\), our choice of \(r_0=0.472\) fm also for smaller numbers of flavour amounts to a convention, in particular for \(N_{ f}=0\). Indeed, in the Tables 53, 54, 55, 56, 57, 58 and 59 somewhat different numbers in MeV are found.
How sure are we about our ranges for \([r_0 \Lambda _{{\overline{\mathrm {MS}}}}]^{(N_f)}\)? In one case we have a result, Eq. (347) that easily passes our criteria; in another one [Eq. (349)] we have four compatible results that are close to that quality and agree. For \(N_{ f}=2\,+\,1\) the range [Eq. (345)] takes account of results with rather different systematics. We therefore find it difficult to imagine that the ranges could be violated by much.
9.10.4 Conclusions
With the present results our range for the strong coupling is (repeating Eq. (344))
and the associated \(\Lambda \) parameters
Compared with FLAG 16, the errors have been reduced by about 30% due to new computations. As can be seen from Fig. 38, when surveying the green data points, the individual lattice results agree within their quoted errors. Furthermore those points are based on different methods for determining \(\alpha _s\), each with its own difficulties and limitations. Thus the overall consistency of the lattice \(\alpha _s\) results and the large number of  in Table 38, engenders confidence in our range.
in Table 38, engenders confidence in our range.
It is interesting to compare with the Particle Data Group average of nonlattice determinations of recent years,
(there was no update in [137]). There is good agreement with Eq. (344). Due to recent new determinations the lattice average is by now a factor two more precise than the nonlattice world average and an average of the two [Eq. (344) and Eq. (279)] yields
In the lower plot in Fig. 38 we show as blue circles the various PDG pre-averages which lead to the PDG 2018/2016 nonlattice average. They are on a similar level as our pre-ranges (green squares) : each one corresponds to an estimate (by the PDG) of \(\alpha _s\) determined from one set of input quantities. Within each pre-average multiple groups did the analysis and published their results as displayed in Ref. [137]. The PDG performed an average within each group;Footnote 77 we only display the latter in Fig. 38.
The fact that our range for the lattice determination of \(\alpha _{\overline{\mathrm{MS}}}(M_Z)\) in Eq. (344) is in excellent agreement with the PDG nonlattice average Eq. (279) is an excellent check for the subtle interplay of theory, phenomenology and experiments in the nonlattice determinations. The work done on the lattice provides an entirely independent determination, with negligible experimental uncertainty, which reaches a better precision even with our quite conservative estimate of its uncertainty.
Given that the PDG has not updated their number, Eq. (357) is presently the up-to-date world average.
We finish by commenting on perspectives for the future. The step-scaling methods have been shown to yield a very precise result and to satisfy all criteria easily. A downside is that dedicated simulations have to be done and the method is thus hardly used. It would be desirable to have at least one more such computation by an independent collaboration, as also requested in the review [666]. For now, we have seen a decrease of the error by 30% compared to FLAG 16. There is potential for a further reduction. Likely there will be more lattice calculations of \(\alpha _s\) from different quantities and by different collaborations. This will enable increasingly precise determinations, coupled with stringent cross-checks.
The two- and three-point correlation functions (illustrated by Feynman diagrams) that need to be calculated to extract the ground state nucleon matrix elements. (Left) the nucleon two-point function. (Middle) the connected three-point function with source-sink separation \(\tau \) and operator insertion time slice t. (Right) the disconnected three-point function with operator insertion at time t
10 Nucleon matrix elements
Authors: S. Collins, R. Gupta, A. Nicholson, H. Wittig
A large number of experiments testing the Standard Model (SM) and searching for physics Beyond the Standard Model (BSM) involve either free nucleons (proton and neutron beams) or the scattering of electrons, protons, neutrinos and dark matter off nuclear targets. Necessary ingredients in the analysis of the experimental results are the matrix elements of various probes (fundamental currents or operators in a low energy effective theory) between nucleon or nuclear states. The goal of lattice-QCD calculations in this context is to provide high precision predictions of these matrix elements, the simplest of which give the nucleon charges and form factors. Determinations of the charges are the most mature and in this review we summarize the results for six quantities, the isovector and flavour diagonal axial vector, scalar and tensor charges. Other quantities that are not being reviewed but for which significant progress has been made in the last five years are the nucleon axial vector and electromagnetic form factors [804,805,806,807,808,809,810,811,812] and parton distribution functions [813]. The more challenging calculations of nuclear matrix elements, that are needed, for example, to calculate the cross-sections of neutrinos or dark matter scattering off nuclear targets, are proceeding along three paths. First is direct evaluation of matrix elements calculated with initial and final states consisting of multiple nucleons [814, 815]. Second, convoluting nucleon matrix elements with nuclear effects [816], and third, determining two and higher body terms in the nuclear potential via the direct or the HAL QCD methods [817, 818]. We expect future FLAG reviews to include results on these quantities once a sufficient level of control over all the systematics is reached.
10.1 Isovector and flavour diagonal charges of the nucleon
The simplest nucleon matrix elements are composed of local quark bilinear operators, \(\overline{q_i} \Gamma _\alpha q_j\), where \(\Gamma _\alpha \) can be any of the sixteen Dirac matrices. In this report, we consider two types of flavour structures: (a) when \(i = u\) and \(j = d\). These \({\overline{u}} \Gamma _\alpha d\) operators arise in \(W^\pm \) mediated weak interactions such as in neutron or pion decay. We restrict the discussion to the matrix elements of the axial vector (A), scalar (S) and tensor (T) currents, which give the isovector charges, \(g_{A,S,T}^{u-d}\).Footnote 78 (b) When \(i = j \) for \(j \in \{u, d, s, c\}\), there is no change of flavour, e.g., in processes mediated via the electromagnetic or weak neutral interaction or dark matter. These \(\gamma \) or \(Z^0\) or dark matter mediated processes couple to all flavours with their corresponding charges. Since these probes interact with nucleons within nuclear targets, one has to include the effects of QCD (to go from the couplings defined at the quark and gluon level to those for nucleons) and nuclear forces in order to make contact with experiments. The isovector and flavour diagonal charges, given by the matrix elements of the corresponding operators calculated between nucleon states, are these nucleon level couplings. Here we review results for the light and strange flavours, \(g_{A,S,T}^{u}\), \(g_{A,S,T}^{d}\), and \(g_{A,S,T}^{s}\).
The isovector and flavour diagonal operators also arise in BSM theories due to the exchange of novel force carriers or as effective interactions due to loop effects. The associated couplings are defined at the energy scale \(\Lambda _{\mathrm{BSM}}\), while lattice-QCD calculations of matrix elements are carried out at a hadronic scale, \(\mu \), of a few GeV. The tool for connecting the couplings at the two scales is the renormalization group. Since the operators of interest are composed of quark fields (and more generally also of gluon fields), the predominant change in the corresponding couplings under a scale transformation is due to QCD. To define the operators and their couplings at the hadronic scale \(\mu \), one constructs renormalized operators, whose matrix elements are finite in the continuum limit. This requires calculating both multiplicative renormalization factors, including the anomalous dimensions and finite terms, and the mixing with other operators. We discuss the details of the renormalization factors needed for each of the six operators reviewed in this report in Sect. 10.1.3.
Once renormalized operators are defined, the matrix elements of interest are extracted using expectation values of two-point and three-point correlation functions illustrated in Fig. 39, where the latter can have both quark line connected and disconnected contributions. In order to isolate the ground state matrix element, these correlation functions are analyzed using their spectral decomposition. The current practice is to fit the n-point correlation functions (or ratios involving three- and two-point functions) including contributions from one or two excited states.
The ideal situation occurs if the time separation \(\tau \) between the nucleon source and sink positions, and the distance of the operator insertion time from the source and the sink, t and \(\tau - t\), respectively, are large enough such that the contribution of all excited states is negligible. In the limit of large \(\tau \), the ratio of noise to signal in the nucleon two and three-point correlation functions grows exponentially as \(e^{(M_N - \frac{3}{2}M_\pi )\tau }\) [819, 820], where \(M_N\) and \(M_\pi \) are the masses of the nucleon and the pion, respectively. Therefore, in particular at small pion masses, maintaining reasonable errors for large \(\tau \) is challenging, with current calculations limited to \(\tau \lesssim 1.5\) fm. In addition, the mass gap between the ground and excited (including multi-particle) states is smaller than in the meson sector and at these separations, excited-state effects can be significant. The approach commonly taken is to first obtain results with high statistics at multiple values of \(\tau \), using the methods described in Sect. 10.1.1. Then, as mentioned above, excited-state contamination is removed by fitting the data using a fit form involving one or two excited states. The different strategies that have been employed to minimize excited-state contamination are discussed in Sect. 10.1.2.
Usually, the quark-connected part of the three-point function (corresponding to the plot in the centre of Fig. 39) is computed via the so-called “sequential propagator method”, which uses the product of two quark propagators between the positions of the initial and the final nucleons as a source term for another inversion of the lattice Dirac operator. This implies that the position of the sink timeslice is fixed at some chosen value. Varying the value of the source-sink separation \(\tau \) then requires the calculation of another sequential propagator.
The evaluation of quark-disconnected contributions is computationally more challenging as the disconnected loop (which contains the operator insertion, as illustrated in Fig. 39 right) is needed at all points on a particular timeslice or, in general, over the whole lattice. The quark loop is computed stochastically and then correlated with the nucleon two-point function before averaging this three-point function over the ensemble of gauge configurations. The associated statistical error, therefore, is a combination of that due to the stochastic evaluation (on each configuration) and that from the gauge average. The number of stochastic sources employed on each configuration is, typically, optimized to reduce the overall error for a given computational cost. The statistical errors of the connected contributions, in contrast, usually come only from the ensemble average since they are often evaluated exactly on each configuration, for a small number of source positions. If these positions are well-separated in space and time, then each measurement is statistically independent. The methodology applied for these calculations and the variance reduction techniques are summarized in Sect. 10.1.1. By construction, arbitrary values of \(\tau \) across the entire temporal extent of the lattice can be realized when computing the quark-disconnected contribution, since the source-sink separation is determined by the part of the diagram that corresponds to the two-point nucleon correlator. However, in practice statistical fluctuations of both the connected and disconnected contributions increase sharply, so that the signal is lost in the statistical noise for \(\tau \gtrsim 1.5\) fm.
The lattice calculation is performed for a given number of quark flavours and at a number of values of the lattice spacing a, the pion mass \(M_\pi \), and the lattice size represented by \(M_\pi L\). The results need to be extrapolated to the physical point defined by \(a=0\), \(M_\pi = 135\) MeV and \(M_\pi L \rightarrow \infty \). This is done by fitting the data simultaneously in these three variables using a theoretically motivated ansatz. The ansätze used and the fitting strategy are described in Sect. 10.1.4.
The procedure for rating the various calculations and the criteria specific to this chapter are discussed in Sect. 10.2, which also includes a brief description of how the final averages are constructed. The physics motivation for computing the isovector charges, \(g_{A,S,T}^{u-d}\), and the review of the lattice results are presented in Sect. 10.3. This is followed by a discussion of the relevance of the flavour diagonal charges, \(g_{A,S,T}^{u,d,s}\), and a presentation of the lattice results in Sect. 10.4.
10.1.1 Technical aspects of the calculations of nucleon matrix elements
The calculation of n-point functions needed to extract nucleon matrix elements requires making four essential choices. The first involves choosing between the suite of background gauge field ensembles one has access to. The range of lattice parameters should be large enough to facilitate the extrapolation to the continuum and infinite volume limits, and the evaluation at the physical pion mass taken to be \(M_\pi =135\) MeV. Such ensembles have been generated with a variety of discretization schemes for the gauge and fermion actions that have different levels of improvement and preservation of continuum symmetries. The actions employed at present include (i) Wilson gauge with nonperturbatively improved Sheikholeslami–Wohlert fermions (nonperturbatively improved clover fermions) [85, 90, 402, 821,822,823,824], (ii) Iwasaki gauge with nonperturbatively improved clover fermions [812, 825], (iii) Iwasaki gauge with twisted mass fermions with a clover term [826,827,828,829,830], (iv) tadpole Symanzik improved gauge with highly improved staggered quarks (HISQ) [7, 83, 84, 86, 831,832,833,834,835], (v) Iwasaki gauge with domain wall fermions (DW) [6, 89, 836,837,838,839,840] and (vi) Iwasaki gauge with overlap fermions [841,842,843]. For details of the lattice actions, see Glossary A.1.
The second choice is of the valence quark action. Here there are two choices, to maintain a unitary formulation by choosing exactly the same action as is used in the generation of gauge configurations or to choose a different action and tune the quark masses to match the pseudoscalar meson spectrum in the two theories. Such mixed action formulations are nonunitary but are expected to have the same continuum limit as QCD. The reason for choosing a mixed action approach is expediency. For example, the generation of 2 + 1 + 1 flavour HISQ and 2 + 1 flavour DW ensembles with physical quark masses has been possible even at the coarse lattice spacing of \(a=0.15\) fm and there are indications that cut-off effects are reasonably small. These ensembles have been analyzed using clover-improved Wilson fermions, DW and overlap fermions since the construction of baryon correlation functions with definite spin and parity is much simpler compared to staggered fermions.
The third choice is the combination of the algorithm for inverting the Dirac matrix and variance reduction techniques. Efficient inversion and variance reduction techniques are needed for the calculation of nucleon correlation functions with high precision because the signal to noise degrades exponentially as \(e^{({\frac{3}{2}M_\pi -M_N}) \tau }\) with the source-sink separation \(\tau \). Thus, the number of measurements needed for high precision is much larger than in the meson sector. Commonly used inversion algorithms include the multigrid [844] and the deflation-accelerated Krylov solvers [845], which can handle linear systems with large condition numbers very efficiently, thereby enabling calculations of correlation functions at the physical pion mass.
The sampling of the path integral is limited by the number \(N_\mathrm{conf}\) of gauge configurations generated. One requires sufficiently large \(N_{\mathrm{conf}}\) such that the phase space (for example, different topological sectors) has been adequately sampled and all the correlation functions satisfy the expected lattice symmetries such as C, P, T, momentum and translation invariance. Thus, one needs gauge field generation algorithms that give decorrelated large volume configurations cost-effectively. On such large lattices, to reduce errors one can exploit the fact that the volume is large enough to allow multiple measurements of nucleon correlation functions that are essentially statistically independent. Two other common variance reduction techniques that reduce the cost of multiple measurements on each configuration are: the truncated solver with bias correction method [846] and deflation of the Dirac matrix for the low lying modes followed by sloppy solution with bias correction for the residual matrix consisting predominately of the high frequency modes [846, 847].
A number of other variation reduction methods are also being used and developed. These include deflation with hierarchical probing for disconnected diagrams [848, 849], the coherent source sequential propagator method [850, 851], low mode averaging [332, 852], the hopping parameter expansion [853, 854] and partitioning [855] (also known as dilution [856]).
The final choice is of the interpolating operator used to create and annihilate the nucleon state, and of the operator used to calculate the matrix element. Along with the choice of the interpolating operator (or operators if a variational method is used) one also chooses a “smearing” of the source used to construct the quark propagator. By tuning the width of the smearing, one can optimize the spatial extent of the nucleon interpolating operator to reduce the overlap with the excited states. Two common smearing algorithms are Gaussian (Wuppertal) [857] and Jacobi [858] smearing.
Having made all the above choices, for which a reasonable recipe exists, one calculates a statistical sample of correlation functions from which the desired ground state nucleon matrix element is extracted. Excited states, unfortunately, contribute significantly to nucleon correlation functions in present studies. To remove their contributions, calculations are performed with multiple source-sink separations \(\tau \) and fits are made to the correlation functions using their spectral decomposition as discussed in the next section.
10.1.2 Controlling excited-state contamination
Nucleon matrix elements are determined from a combination of two- and three-point correlation functions. To be more specific, let \(B^\alpha (\vec {x},t)\) denote an interpolating operator for the nucleon. Placing the initial state at timeslice \(t=0\), the two-point correlation function of a nucleon with momentum \(\vec {p}\) reads
where the projector \({\mathbb {P}}\) selects the polarization, and \(\alpha , \beta \) denote Dirac indices. The three-point function of two nucleons and a quark bilinear operator \(O_\Gamma \) is defined as
where \(\vec {p},\ \vec {p\,}^\prime \) denote the momenta of the nucleons at the source and sink, respectively, and \(\vec {q}\equiv \vec {p\,}^\prime -\vec {p}\) is the momentum transfer. The bilinear operator is inserted at timeslice t, and \(\tau \) denotes the source-sink separation. Both \(C_2\) and \(C_3^\Gamma \) are constructed using the nonperturbative quark propagators, \(D^{-1}(y,x)\), where D is the lattice Dirac operator.
The framework for the analysis of excited-state contamination is based on spectral decomposition. After inserting complete sets of eigenstates of the transfer matrix, the expressions for the correlators \(C_2\) and \(C_3^\Gamma \) read
where \(|\Omega \rangle \) denotes the vacuum state, and \(E_n\) represents the energy of the \(n^{\mathrm{th}}\) eigenstate \(|n\rangle \) in the nucleon channel. Here we restrict the discussion to vanishing momentum transfer, \(\vec {q}=0\) and label the ground state by \(n=0\). The matrix element of interest, \(g_\Gamma \equiv \langle 0|O_\Gamma |0\rangle \) can, for instance, be obtained from the asymptotic behaviour of the ratio
where \(\Delta \equiv E_1-E_0\) denotes the energy gap between the ground state and the first excitation. Here we assume that the bilinear operator \(O_\Gamma \) is appropriately renormalized (see Sect. 10.1.3).
Excited states with the same quantum numbers as the nucleon include resonances such as a Roper-like state with a mass of about 1.5 GeV, or multi-particle states consisting of a nucleon and one or more pions [859, 860]. The latter are expected to be responsible for the most relevant sub-leading contributions to two- and three-point correlators in Eqs. (358) and (359) or their ratios (362) as the pion mass approaches its physical value. Ignoring the interactions between the individual hadrons, one can easily identify the lowest-lying multi-particle states: they include the \(N\pi \pi \) state with all three particles at rest at \(\sim 1.2\) GeV, as well as \(N\pi \) states with both hadrons having nonzero and opposite momentum. Depending on the spatial box size L in physical units (with the smallest nonzero momentum equal to \(2\pi /L\)), there may be a dense spectrum of \(N\pi \) states before the first nucleon resonance is encountered. Corrections to nucleon correlation functions due to the pion continuum have been studied using chiral effective theory [859,860,861,862] and Lüscher’s finite-volume quantization condition [863].
The well-known noise problem of baryonic correlation functions implies that the long-distance regime, \(t, (\tau -t)\rightarrow \infty \), where the correlators are dominated by the ground state, is difficult to reach. Current lattice calculations of baryonic three-point functions are typically confined to source-sink separations of \(\tau \lesssim 1.5\) fm, despite the availability of efficient noise reduction methods. In view of the dense excitation spectrum encountered in the nucleon channel, one has to demonstrate that the contributions from excited states are sufficiently suppressed to guarantee an unbiased determination of nucleon matrix elements. There are several strategies to address this problem:
Multi-state fits to correlator ratios or individual two- and three-point functions;
Three-point correlation functions summed over the operator insertion time t;
Increasing the projection of the interpolator \(B^\alpha \) onto the ground state.
The first of the above methods includes excited state contributions explicitly when fitting to the spectral decomposition of the correlation functions, Eqs. (360, 361) or, alternatively, their ratio (see Eq. (362)). In its simplest form, the resulting expression for \(R_\Gamma \) includes the contributions from the first excited state, i.e.,
where \(c_{01}, c_{10}, c_{11}\) and \(\Delta \) are treated as additional parameters when fitting \(R_\Gamma (t,\tau )\) simultaneously over intervals in the source-sink separation \(\tau \) and the operator insertion timeslice t. Multi-exponential fits become more difficult to stabilize for a growing number of excited states, since an increasing number of free parameters must be sufficiently constrained by the data. Therefore, a high level of statistical precision at several source-sink separations is required. One common way to address this issue is to introduce Bayesian constraints, as described in [864]. Alternatively, one may try to reduce the number of free parameters by fixing the energy gap \(\Delta \) (see, for instance, Ref. [805]), by assuming that the lowest-lying excitations are described by noninteracting multi-particle states consisting of the nucleon and at least one pion.
Ignoring the explicit contributions from excited states and fitting \(R_\Gamma (t,\tau )\) to a constant in t for fixed \(\tau \) amounts to applying what is called the “plateau method”. The name derives from the ideal situation that sufficiently large source-sink separations \(\tau \) can be realized, which would cause \(R_\Gamma (t,\tau )\) to exhibit a plateau in t independent of \(\tau \). The ability to control excited-state contamination is rather limited in this approach, since the only option is to check for consistency in the estimate of the plateau as \(\tau \) is varied. In view of the exponential degradation of the statistical signal for increasing \(\tau \), such stability checks are difficult to perform reliably.
Summed operator insertions, originally proposed in Ref. [865], have also emerged as a widely used method to address the problem of excited state contamination. One way to implement this method [866, 867] proceeds by summing \(R_\Gamma (t,\tau )\) over the insertion time t, resulting in the correlator ratio \(S_\Gamma (\tau )\),
The asymptotic behaviour of \(S_\Gamma (\tau )\), including sub-leading terms, for large source-sink separations \(\tau \) can be easily derived from the spectral decomposition of the correlators and is given by [868]
where \(K_\Gamma \) is a constant, and the coefficients \(d_\Gamma \) and \(f_\Gamma \) contain linear combinations of transition matrix elements involving the ground and first excited states. Thus, the matrix element of interest, \(g_\Gamma \), is obtained from the linear slope of \(S_\Gamma (\tau )\) with respect to the source-sink separation \(\tau \). While the leading corrections from excited states are parametrically smaller than those of the original ratio \(R_\Gamma (t,\tau )\) (see Eq. (362)), extracting the slope from a linear fit to \(S_\Gamma (\tau )\) typically results in relatively large statistical errors. In principle, one could include the contributions from excited states explicitly in the expression for \(S_\Gamma (\tau )\). However, in practice it is often difficult to constrain an enlarged set of parameters reliably, in particular if one cannot afford to determine \(S_\Gamma (\tau )\) except for a handful of source-sink separations.
The original summed operator insertion technique described in Refs. [857, 865, 869, 870] avoids the explicit summation over the operator insertion time t at every fixed value of \(\tau \). Instead, one replaces one of the quark propagators that appear in the representation of the two-point correlation function \(C_2(t)\) by a “sequential” propagator, according to
In this expression, the position \(z\equiv (\vec {z},t)\) of the insertion of the quark bilinear operator is implicitly summed over, by inverting the lattice Dirac operator D on the source field \(\Gamma D^{-1}(z,x)\). While this gives access to all source-sink separations \(0\le \tau \le T\), where T is the temporal extent of the lattice, the resulting correlator also contains contact terms, as well as contributions from \(\tau<t<T\) that must be controlled. This methodFootnote 79 has been adopted recently by the CalLat collaboration in their calculation of the isovector axial charge [84, 835].
As in the case of explicitly summing over the operator insertion time, the matrix element of interest is determined from the slope of the summed correlator. For instance, in Ref. [84], the axial charge was determined from the summed three-point correlation function, by fitting to its asymptotic behaviour [871] including sub-leading terms.
In practice, one often uses several methods simultaneously [e.g., multi-state fits and the summation method based on Eq. (365)], in order to check whether the results converge towards a common value. All of the approaches for controlling excited-state contributions proceed by fitting data obtained in a finite interval in \(\tau \) to a function that describes the approach to the asymptotic behaviour derived from the spectral decomposition. Obviously, the accessible values of \(\tau \) must be large enough so that the model function provides a good representation of the data that enter such a fit. It is then reasonable to impose a lower threshold on \(\tau \) above which the fit model is deemed reliable. We will return to this issue when explaining our quality criteria in Sect. 10.2.
The third method for controlling excited-state contamination aims at optimizing the projection onto the ground state in the two-point and three-point correlation functions [823, 851, 874]. The RQCD collaboration has chosen to optimize the parameters in the Gaussian smearing procedure, so that the overlap of the nucleon interpolating operator onto the ground state is maximized [823]. In this way it may be possible to use shorter source-sink separations without incurring a bias due to excited states.
The variational method, originally designed to provide detailed information on energy levels of the ground and excited states in a given channel [875,876,877,878], has also been adapted to the determination of hadron-to-hadron transition elements [868]. In the case of nucleon matrix elements, the authors of Ref. [874] have employed a basis of operators to construct interpolators that couple to individual eigenstates in the nucleon channel. The method has produced promising results when applied to calculations of the axial and other forward matrix elements at a fixed value of the pion mass [851, 874, 879]. However, a more comprehensive study aimed at providing an estimate at the physical point has, until now, not been performed.
10.1.3 Renormalization and Symanzik improvement of local currents
In this section we discuss the matching of the normalization of lattice operators to a continuum reference scheme such as \({\overline{\mathrm {MS}}}\), and the application of Symanzik improvement to remove O(a) contributions. The relevant operators for this review are the axial (\(A_\mu \)), tensor (\(T_{\mu \nu }\)) and scalar (S) local operators of the form \({{{\mathcal {O}}}}_\Gamma ={\overline{q}}\Gamma q\), with \(\Gamma =\gamma _\mu \gamma _5\), \(i\sigma _{\mu \nu }\) and \({\mathbf {1}}\), respectively, whose matrix elements are evaluated in the forward limit. The general form for renormalized operators in the isovector flavour combination, at a scale \(\mu \), reads
where \(Z_{{{\mathcal {O}}}}^{{\overline{\mathrm {MS}}},\mathrm{Latt}}(\mu a,g^2)\) denotes the multiplicative renormalization factor determined in the chiral limit and the second and third terms represent all possible mass dependent and mass independent Symanzik improvement terms, respectively.Footnote 80 The chiral properties of overlap, domain-wall fermions (with improvement up to \(O(m_{\mathrm{res}}^n)\) where \(m_{\mathrm{res}}\) is the residual mass) and twisted mass fermions (at maximal twist [884, 885]) mean that the O(a) improvement terms are absent, while for nonperturbatively improved Sheikholeslami–Wohlert–Wilson (nonperturbatively-improved clover) fermions all terms appear in principle. For the operators of interest here there are several mass dependent terms but at most one (higher dimensional) \({{{\mathcal {O}}}}_\Gamma ^{\mathrm{imp}}\), see, e.g., Refs. [886, 887]. However, the latter involve external derivatives whose corresponding matrix elements vanish in the forward limit. Note that no mention is made of staggered fermions as they are not, currently, widely employed as valence quarks in nucleon matrix element calculations.
In order to illustrate the above remarks we consider the renormalization and improvement of the isovector axial current. This current has no anomalous dimension and hence the renormalization factor, \(Z_A=Z_A^{{\overline{\mathrm {MS}}},\mathrm{Latt}}(g^2)\), is independent of the scale. The factor is usually computed nonperturbatively via the axial Ward identity [888] or the Rome-Southampton method [468] (see Sect. A.3 for details). In some studies, the ratio with the corresponding vector renormalization factor, \(Z_A/Z_V\), is determined for which some of the systematics cancel. In this case, one constructs the combination \(Z_A g_A/(Z_V g_V)\), where \(Z_V g_V=1\) and \(g_A\) and \(g_V\) are the lattice forward matrix elements, to arrive at the renormalized axial charge [834]. For domain wall fermions the ratio is employed in order to remove \(O(am_{\mathrm{res}})\) terms and achieve leading discretisation effects starting at \(O(a^2)\) [10]. Thus, as mentioned above, O(a) improvement terms are only present for nonperturbatively-improved clover fermions. For the axial current, Eq. (367) takes the explicit form,
where \(m_{\mathrm{val}}\) and \(m_{\mathrm{sea}}\) are the average valence- and sea-quark masses derived from the vector Ward identity [881, 887, 888], and P is the pseudoscalar operator \({\overline{q}}\gamma _5 q\). The matrix element of the derivative term is equivalent to \(q_\mu \langle N(p^\prime )|P|N(p)\rangle \) and hence vanishes in the forward limit when the momentum transfer \(q_\mu =0\). The improvement coefficients \(b_A\) and \({\tilde{b}}_A\) are known perturbatively for a variety of gauge actions [886, 889, 890] and nonperturbatively for the tree-level Symanzik-improved gauge action for \(N_{ f}=2\,+\,1\) [891].
Turning to operators for individual quark flavours, these can mix under renormalization and the singlet and nonsinglet renormalization factors can differ. For the axial current, such mixing occurs for all fermion formulations just like in the continuum, where the singlet combination acquires an anomalous dimension due to the \(\hbox {U}_A\)(1) anomaly. The ratio of singlet to nonsinglet renormalization factors, \(r_{{{\mathcal {O}}}}=Z^{\mathrm{s.}}_{{{\mathcal {O}}}}/Z^{\mathrm{n.s.}}_{{{\mathcal {O}}}}\) for \({{{\mathcal {O}}}}=A\) differs from 1 at \(O(\alpha _s^2)\) in perturbation theory (due to quark loops), suggesting that the mixing is a small effect. The nonperturbative determinations performed so far find \(r_A\approx 1\) [808, 828], supporting this. For the tensor current the disconnected diagram vanishes in the continuum due to chirality and consequently on the lattice \(r_T=1\) holds for overlap and DW fermions (assuming \(m_{\mathrm{res}}=0\) for the latter). For twisted-mass and clover fermions the mixing is expected to be small with \(r_T=1+O(\alpha _s^3)\) [892] and this is confirmed by the nonperturbative studies of Refs. [830, 893].
The scalar operators for the individual quark flavours, \({\overline{q}}q\), are relevant not only for the corresponding scalar charges, but also for the sigma terms, \(\sigma _q=m_q\langle N|{\overline{q}}q|N\rangle \), when combined with the quark masses (\(m_q\)). For overlap and DW fermions \(r_S=1\), like in the continuum and all \({\overline{q}}q\) renormalize multiplicatively with the isovector \(Z_S\). The latter is equal to the inverse of the mass renormaliation and hence \(m_q{\overline{q}}q\) is renormalization group (RG) invariant. For twisted mass fermions, through the use of Osterwalder–Seiler valence fermions, the operators \(m_{ud}({\overline{u}}u+{\overline{d}}d)\) and \(m_s{\overline{s}}s\) are also invariant [894].Footnote 81 In contrast, the lack of good chiral properties leads to significant mixing between quark flavours for clover fermions. Nonperturbative determinations via the axial Ward identity [693, 824] have found the ratio \(r_S\) to be much larger than the perturbative expectation \(1+O(\alpha _s^2)\) [892] may suggest. While the sum over the quark flavours which appear in the action, \(\sum ^{N_{ f}}_q m_q {\overline{q}}q\), is RG invariant, large cancellations between the contributions from individual flavours can occur when evaluating, e.g., the strange sigma term. Note that for twisted mass and clover fermions there is also an additive contribution \(\propto a^{-3}{\mathbf {1}}\) (or \(\propto \mu a^{-2}{\mathbf {1}}\)) to the scalar operator. This contribution is removed from the nucleon scalar matrix elements by working with the subtracted current, \({\overline{q}}q - \langle {\overline{q}}q\rangle \), where \(\langle {\overline{q}}q\rangle \) is the vacuum expectation value of the current [887].
Symanzik improvement for the singlet currents follows the same pattern as in the isovector case with O(a) terms only appearing for nonperturbatively-improved clover fermions. For the axial and tensor operators only mass dependent terms are relevant in the forward limit while for the scalar there is an additional gluonic operator \({{{\mathcal {O}}}}_S^{\mathrm{imp}}=\text {Tr}(F_{\mu \nu }F_{\mu \nu })\) with a coefficient of \(O(\alpha _s)\) in perturbation theory. When constructing the sigma terms from the quark masses and the scalar operator, the improvement terms remain and they must be included to remove all O(a) effects for nonperturbatively-improved clover fermions, see Ref. [887] for a discussion.
10.1.4 Extrapolations in a, \(M_\pi \) and \(M_\pi L\)
To obtain physical results which can be used to compare to or make predictions for experiment, all quantities must be extrapolated to the continuum and infinite volume limits. In general, either a chiral extrapolation or interpolation must also be made to the physical pion mass. These extrapolations need to be performed simultaneously since discretization and finite volume effects are themselves dependent upon the pion mass. Furthermore, in practice it is not possible to hold the pion mass fixed while the lattice spacing is varied, as some variation in a occurs when tuning the quark masses at fixed gauge coupling. Thus, one performs a simultaneous extrapolation in all three variables using a theoretically motivated formula of the form,
where \(g_{\mathrm {phys}}\) is the desired extrapolated result, and \(\delta _{M_{\pi }}\), \(\delta _a\), \(\delta _L\) are the deviations due to the pion mass, the lattice spacing, and the volume, respectively. Below we outline the forms for each of these terms.
All observables discussed in this section are dimensionless, therefore the extrapolation formulae may be parameterized by a set of dimensionless variables:
Here, \(\Lambda _{\chi } \sim 1\) GeV is a chiral symmetry breaking scale, which, for example, can be set to \(\Lambda _{\chi } = 4 \pi F_{\pi }\), where \(F_{\pi } = 92.2\) MeV is the pion decay constant, and \(\Lambda _a\) is a discretization scale, e.g., \(\Lambda _a = \frac{1}{4\pi w_0}\), where \(w_0\) is a gradient-flow scale [272].
Effective field theory methods may be used to determine the form of each of these extrapolations. For the single nucleon charges, Heavy-Baryon \(\chi \)PT (HB\(\chi \)PT) is a common choice [895], however, other formulations, such as unitarized \(\chi \)PT [896], are also employed. Various formulations of HB\(\chi \)PT exist, including those for two- and three-flavours, as well as with and without explicit \(\Delta \) degrees of freedom. Two-flavour HB\(\chi \)PT is typically used due to issues with convergence of the three-flavour theory [825, 897,898,899,900]. The convergence properties of all known formulations for baryon \(\chi \)PT, even at the physical pion mass, have not been well-established, and are generally believed to be poor compared to purely mesonic \(\chi \)PT.
To \({\mathcal {O}}\left( \epsilon _{\pi }^2\right) \), the two-flavour chiral expansion for the nucleon charges is known to be of the form [901],
where \(g_1=0\) for all charges g except \(g_S^{u,d}\). The dimensionless coefficients \(g_{0,1,2}, {\tilde{g}}_2\) are assumed to be different for each of the different charges. The coefficients in front of the logarithms, \({\tilde{g}}_2\), are known functions of the lower order coefficients (LECs), and do not represent new, independent LECs. Mixed action calculations will have further dependence upon the mixed valence-sea pion mass, \(m_{vs}\).
Given the potential difficulties with convergence of the chiral expansion, known values of the \({\tilde{g}}_2\) in terms of LECs are not typically used, but are left as free fit parameters. Furthermore, many quantities have been found to display mild pion mass dependence, such that Taylor expansions, i.e., neglecting logarithms in the above expressions, are also often employed. The lack of a rigorously established theoretical basis for the extrapolation in the pion mass thus requires data close to the physical pion mass for obtaining high precision extrapolated/interpolated results.
Discretization effects depend upon the lattice action used in a particular calculation, and their form may be determined using the standard Symanzik power counting. In general, for an unimproved action, the corrections due to discretization effects, \(\delta _a\), include terms of the form,
where \(c_{1,2}\) are dimensionless coefficients. Additional terms of the form \({\tilde{c}}_n \left( \epsilon _{\pi } \epsilon _a\right) ^n\), where n is an integer whose lowest value depends on the combined discretization and chiral properties, will also appear. Improved actions systematically remove correction terms, e.g., an \({\mathcal {O}}\left( a\right) \) improved action, combined with an similarly improved operator, will contain terms in the extrapolation ansatz beginning at \(\epsilon _a^2\) (see Sect. 10.1.3).
Finite volume corrections, \(\delta _L\), may be determined in the usual way from effective field theory, by replacing loop integrals over continuous momenta with discrete sums. Finite volume effects therefore introduce no new undetermined parameters to the extrapolation. For example, at next-to-leading order, and neglecting contributions from intermediate delta baryons, the finite volume corrections for the axial charge in two-flavour HB\(\chi \)PT take the form [902],
where
and \(K_{\nu }(z)\) are the modified Bessel functions of the second kind. Some extrapolations are performed using the form for asymptotically large \(M_{\pi } L\),
and neglecting contributions due to \(K_1\). Care must, however, be taken to establish that these corrections are negligible for all included values of \(M_{\pi } L\). The numerical coefficients, for example, 8/3 in Eq. (373), are often taken to be additional free fit parameters, due to the question of convergence of the theory discussed above.
Given the lack of knowledge about the convergence of the expansions and the resulting plethora of possibilities for extrapolation models at differing orders, it is important to include statistical tests of model selection for a given set of data. Bayesian model averaging [903] or use of the Akaike Information Criterion [904] are common choices which penalize over-parameterized models.
10.2 Quality criteria for nucleon matrix elements and averaging procedure
There are two specific issues which call for a modification and extension of the FLAG quality criteria listed in Sect. 2. The first concerns the rating of the chiral extrapolation: The FLAG criteria reflect the ability of \(\chi \)PT to provide accurate descriptions of the pion mass dependence of observables. Clearly, this ability is linked to the convergence properties of \(\chi \)PT in a particular mass range. Quantities extracted from nucleon matrix elements are extrapolated to the physical pion mass using some variant of baryonic \(\chi \)PT, whose convergence is not as well established compared to the mesonic sector. Therefore, we have opted for stricter quality criteria concerning the chiral extrapolation of nucleon matrix elements, i.e.,
 \(M_{\pi ,\mathrm {min}}< 200\) MeV with three or more pion masses used in the extrapolation or two values of \(M_\pi \) with one lying within 10 MeV of 135 MeV (the physical neutral pion mass) and the other one below 200 MeV
\(M_{\pi ,\mathrm {min}}< 200\) MeV with three or more pion masses used in the extrapolation or two values of \(M_\pi \) with one lying within 10 MeV of 135 MeV (the physical neutral pion mass) and the other one below 200 MeV 200 MeV \(\le M_{\pi ,\mathrm {min}} \le 300\) MeV with three or more pion masses used in the extrapolation; or two values of \(M_\pi \) with \(M_{\pi ,\mathrm {min}}< 200\) MeV; or a single value of \(M_\pi \) lying within 10 MeV of 135 MeV (the physical neutral pion mass)
200 MeV \(\le M_{\pi ,\mathrm {min}} \le 300\) MeV with three or more pion masses used in the extrapolation; or two values of \(M_\pi \) with \(M_{\pi ,\mathrm {min}}< 200\) MeV; or a single value of \(M_\pi \) lying within 10 MeV of 135 MeV (the physical neutral pion mass) Otherwise
Otherwise
In Sect. 10.1.2 we have discussed that insufficient control over excited state contributions, arising from the noise problem in baryonic correlation functions, may lead to a systematic bias in the determination of nucleon matrix elements. We therefore introduce an additional criterion that rates the efforts to suppress excited state contamination in the final result. As described in Sect. 10.1.2, the source-sink separation \(\tau \), i.e., the Euclidean distance between the initial and final nucleons, is the crucial variable. The rating scale concerning control over excited state contributions is thus
 Three or more source-sink separations \(\tau \), at least two of which must be above 1.0 fm.
Three or more source-sink separations \(\tau \), at least two of which must be above 1.0 fm. Two or more source-sink separations, \(\tau \), with at least one value above 1.0 fm.
Two or more source-sink separations, \(\tau \), with at least one value above 1.0 fm. Otherwise
Otherwise
Despite the enormous progress achieved in reducing excited state contamination, we emphasize that more stringent quality criteria may have to be adopted in future editions of the FLAG report to control this important systematic effect at the stated level of precision.
As explained in Sect. 2, FLAG averages are distinguished by the sea-quark content. Hence, for a given configuration of the quark sea (i.e., for \(N_f=2\), \(2\,+\,1\) or \(2\,+\,1\,+\,1\)), we first identify those calculations that pass the FLAG and the additional quality criteria defined in this section, i.e., excluding any calculation that has a red tag in one or more of the categories. We then add statistical and systematic errors in quadrature and perform a weighted average. If the fit is of bad quality (i.e., if \(\chi ^2_{\mathrm{min}}/\mathrm{dof}>1\)), the errors of the input quantities are scaled by \(\sqrt{\chi ^2/\mathrm{dof}}\). In the following step, correlations among different calculations are taken into account in the error estimate by applying Schmelling’s procedure [132].
10.3 Isovector charges
The axial, scalar and tensor isovector charges are needed to interpret the results of many experiments and phenomena mediated by weak interactions, including probes of new physics. The most natural process from which isovector charges can be measured is neutron beta decay (\(n \rightarrow p^{+} e^{-} {\overline{\nu }}_e\)). At the quark level, this process occurs when a down quark in a neutron transforms into an up quark due to weak interactions, in particular due to the axial current interaction. While scalar and tensor currents have not been observed in nature, effective scalar and tensor interactions arise in the SM due to loop effects. At the TeV and higher scales, contributions to these three currents could arise due to new interactions and/or loop effects in BSM theories. These super-weak corrections to standard weak decays can be probed through high precision measurements of the neutron decay distribution by examining deviations from SM predictions as described in Ref. [905]. The lattice-QCD methodology for the calculation of isovector charges is well-established, and the control over statistical and systematic uncertainties is becoming robust.
The axial charge \(g_A^{u-d}\) is an important parameter that encapsulates the strength of weak interactions of nucleons. It enters in many analyses of nucleon structure and of SM and BSM physics. For example, it enters in (i) the extraction of \(V_{ud}\) and tests of the unitarity of the Cabibbo–Kobayashi–Maskawa (CKM) matrix; (ii) the analysis of neutrinoless double-beta decay, (iii) neutrino-nucleus quasi-elastic scattering cross-section; (iv) the rate of proton–proton fusion, the first step in the thermonuclear reaction chains that power low-mass hydrogen-burning stars like the Sun; (v) solar and reactor neutrino fluxes; (vi) muon capture rates, etc.. The current best determination of the ratio of the axial to the vector charge, \(g_A/g_V\), comes from measurement of neutron beta decay using polarized ultracold neutrons by the UCNA collaboration, 1.2772(20) [906, 907], and by PERKEO II, \(1.2761{}^{+14}_{-17}\) [908]. Note that, in the SM, \(g_V=1\) up to second order corrections in isospin breaking [909, 910] as a result of the conservation of the vector current. Given the accuracy with which \(g_A^{u-d}\) has been measured in experiments, the goal of lattice-QCD calculations is to calculate it directly with \(O(1\%)\) accuracy.
Isovector scalar or tensor interactions contribute to the helicity-flip parameters, called b and B, in the neutron decay distribution. By combining the calculation of the scalar and tensor charges with the measurements of b and B, one can put constraints on novel scalar and tensor interactions at the TeV scale as described in Ref. [905]. To optimally bound such scalar and tensor interactions using measurements of b and B parameters in planned experiments targeting \(10^{-3}\) precision [911,912,913], we need to determine \(g_S^{u-d}\) and \(g_T^{u-d}\) at the \(10\%\) level as explained in Refs. [834, 905]. Future higher-precision measurements of b and B would require correspondingly higher-precision calculations of the matrix elements to place even more stringent bounds on these couplings at the TeV-scale.
One can estimate \(g_S^{u-d}\) using the conserved vector current (CVC) relation, \(g_S/g_V = (M_N-M_P)^{\mathrm{QCD}}/ (m_d-m_u)^\mathrm{QCD}\), as done by Gonzalez-Alonso et al. [914]. In their analysis, they took estimates of the two mass differences on the right-hand side from the global lattice-QCD data [2] and obtained \(g_S^{u-d}=1.02(8)(7)\).
The tensor charge \(g_T^{u-d}\) can be extracted experimentally from semi-inclusive deep-inelastic scattering (SIDIS) data [915,916,917,918]. A sample of these phenomenological estimates is shown in Fig. 42, and the noteworthy feature is that the current uncertainty in these estimates is large.
10.3.1 Results for \(g_A^{u-d}\)
Calculations of the isovector axial charge have a long history, as can be seen from the compilation given in Table 62 and plotted in Fig. 40. There are results in two-flavour QCD, as well as for QCD with \(N_f=2\,+\,1\) and \(2\,+\,1\,+\,1\) dynamical flavours. All calculations discussed below use renormalization factors that were determined nonperturbatively, either via Ward identities or the Rome-Southampton method.
The issue of excited state contamination received little if any attention before 2010. As a consequence, the range of source-sink separations employed in many of the early calculations prior to that year was rather limited, offering little control over this important systematic effect. This concerns the calculations by LHPC 05 [921], LHPC 10 [850], RBC 08 [922], RBC/UKQCD 08 [836], RBC/UKQCD 09B [837] and QCDSF 06 [821].
The Mainz group has performed calculations in two-flavour QCD, based on the ensembles generated by the Coordinated Lattice Simulations (CLS) effort, using nonperturbatively improved Wilson fermions and the Wilson gauge action. In their first calculation (Mainz 12 [822]) they computed three-point correlators over several source-sink separations up to \(\tau \approx 1.3\) fm. By comparing the technique of summed operator insertions (the “summation method”) to the more traditional plateau method, they found that the former gave consistently larger estimates for \(g_A^{u-d}\), which were in better agreement with the experimental value. In a follow-up paper (Mainz 17 [85]) they added more statistics, extended the range of pion masses towards lower values and used two-state fits in addition to the summation method.
Two flavours of O(a) improved Wilson quarks were also used in the calculations performed by QCDSF 06 [821], QCDSF 13 [402] and RQCD 14 [823]. QCDSF 13 [402] is an extension of the earlier study QCDSF 06 [821], including ensembles at smaller lattice spacing. Control over excited-state effects is still limited, since a range of several source-sink separations was studied only on one ensemble, and the main result was derived from the plateau method at a single source-sink separation of about 1 fm. The calculation by the Regensburg group (RQCD 14 [823]) was performed on a large part of the same ensembles used by QCDSF 13, supplemented by a larger volume at the smallest pion mass of 150 MeV and by an additional ensemble at coarser lattice spacing with \(M_\pi =290\) MeV. The strategy employed in RQCD 14 to control excited-state contamination was focused on optimizing the overlap of the nucleon interpolator onto the ground state, by choosing appropriate parameters in the smearing procedure. The efficacy of this approach was studied on a subset of ensembles for \(\tau \sim 0.5{-}1.2\) fm. In both QCDSF 13 and RQCD 14, the axial charge was determined from the ratio \(g_A/f_\pi \) in which finite-volume effects and other systematic errors are expected to cancel approximately.
The ETM collaboration has published results for the axial charge [826, 828], obtained using \(N_f=2\) flavours of twisted-mass Wilson fermions. In ETM 15D [826], three different source-sink separations were studied, and the range of pion masses was extended down to the physical values. The quoted result for \(g_A^{u-d}\) originates from a single lattice spacing and was obtained using the plateau method at the largest value of the source-sink separation \(\tau \) where agreement with the summation method was found. A further extension of the analysis (ETM 17B [828]) was performed at a single (but almost physical) pion mass value and single lattice spacing. ETMC quote the result at the smallest source-sink separation \(\tau \) for which the plateau value agrees with the two-state fit as their main estimate. Agreement with the summation method is also observed, albeit within the larger statistical errors of the latter.
Estimates for the axial charge with \(N_f=2\,+\,1\) have been published by the LHPC [850, 920, 921] and RBC/UKQCD collaborations [836, 837] and, more recently, by JLQCD 18 [843], \(\chi \)QCD 18 [6], PACS 18 [812], and Mainz 18 [919].
The calculations in LHPC 05 [921] and LHPC 10 [850] were performed employing a mixed-action setup, combining domain wall fermions in the valence sector with staggered (Asqtad) gauge ensembles generated by MILC. Although the dependence of the results on the source-sink separation was studied to some extent in LHPC 10, excited state effects are not sufficiently controlled according to our quality criteria described in Sect. 10.2. A different discretization of the quark action was used in their later study (LHPC 12A [920]), based on tree-level improved Wilson fermions with smeared gauge links, both in the sea and valence sectors. While this setup does not realize full O(a) improvement, it was found that smeared gauge links reduce the leading discretization effects of O(a) substantially. Three source-sink separations were studied in LHPC 12A on each ensemble down to nearly the physical quark mass at a single value of the lattice spacing. The quoted estimate for the axial charge is uncharacteristically low. While other quantities determined in the same study agreed well with experiment or other groups, the reasons for such a low value of \(g_A^{u-d}\) could not be established.
The RBC/UKQCD collaboration has employed \(N_f=2\,+\,1\) flavours of domain wall fermions in their calculations. The results quoted in RBC/UKQCD 08B [836] and RBC/UKQCD 09B [837] were obtained at relatively heavy pion masses at a single value of the lattice spacing, with only limited control over excited state effects. A systematic investigation of different source-sink separations has only been performed more recently [923], however, without quoting an estimate for \(g_A^{u-d}\).
The JLQCD collaboration (JLQCD 18 [843]) have performed a calculation using \(N_f=2\,+\,1\) flavours of overlap fermions and the Iwasaki gauge action. Owing to the large numerical cost of overlap fermions, which preserve exact chiral symmetry at nonzero lattice spacing, they have only simulated four light quark masses with \(290< M_\pi < 540\) MeV and at a single lattice spacing so far. Their simultaneous fit to the data for the correlator ratio \(R_A(t,\tau )\) computed at six values of \(\tau \) to a constant, gives a low value for \(g_A^{u-d}\) at the physical point. Overlap valence quarks were also used by the \(\chi \)QCD collaboration in their study of various nucleon matrix elements (\(\chi \)QCD 18 [6]), utilizing the gauge ensembles generated by RBC/UKQCD with domain wall fermions. The quoted estimate for the axial charge was obtained from a combination of two-state fits and the summation method, applied over a range of source-sink separations.
Two recent calculations with \(N_f=2\,+\,1\) have used O(a) improved Wilson fermions. The focus of the study by the PACS collaboration (PACS 18 [812]) was on the use of very large volumes at the physical pion mass. The calculation comprises only one lattice spacing and a single source-sink separation. Therefore, at the current stage, the study does not offer sufficient control over several systematic effects. The Mainz group (Mainz 18 [919]) has presented preliminary results for the axial charge, obtained by performing two-state fits to six different nucleon matrix elements (including the scalar and tensor charges), assuming that the mass gap to the excited state can be more reliably constrained in this way. Up to six source-sink separations per ensemble have been studied.
Two groups, PNDME and CalLat, have published results for \(N_f=2\,+\,1\,+\,1\), i.e., PNDME 16 [834], PNDME 18 [83], CalLat 17 [835] CalLat 18 [84]. While both groups share the staggered (HISQ) gauge ensembles generated by the MILC collaboration, they employ different discretizations in the valence quark sector: PNDME use O(a) improved Wilson fermions with the improvement coefficient \(c_{\mathrm{sw}}\) set to its tadpole-improved tree-level value. By contrast, CalLat use the Möbius variant of domain wall fermions, which are fully O(a) improved. The CalLat set of ensembles includes three values of the lattice spacing, i.e., \(a=0.09\), 0.12, and 0.15 fm, while PNDME added another set of ensembles at the finer lattice spacing of 0.06 fm to this collection. Both groups have included physical pion mass ensembles in their calculations. The operator matrix elements are renormalized nonperturbatively, using the Rome–Southampton method.
In order to control excited state contamination, PNDME perform multi-state fits, including up to four (three) energy levels in the two-point (three-point) correlation functions. By contrast, CalLat have employed the Feynman-Hellmann-inspired implementation of summed operator insertions described in Sect. 10.1.2. Plotting the summed correlator \(S_A(\tau )\) as a function of the source-sink separation, they find that excited-state effects cannot be detected for \(\tau \gtrsim 1.0\) fm at their level of statistics. After subtracting the leading contributions from excited states determined from two-state fits, they argue that the data for \(S_A(\tau )\) can be described consistently down to \(\tau \simeq 0.3\) fm.
We now proceed to discuss global averages for the axial charge, in accordance with the procedures in Sect. 10.2. For QCD with \(N_f=2\,+\,1\,+\,1\), the calculations of PNDME and CalLat pass all our quality criteria, and hence the latest results, i.e., PNDME 18 [83] and CalLat 18 [84] qualify for being included in a global average. Since both PNDME and CalLat use the gauge ensembles produced by MILC, we assume that the quoted statistical errors are 100% correlated, even though the range of pion masses and lattice spacings explored in Refs. [83] and [84] is not exactly identical. Since the two calculations differ by the valence quark action, and since systematic errors have been estimated independently, we restrict the correlations between PNDME 18 and CalLat 18 to the statistical error only. Performing a weighted average yields \(g_A^{u-d} = 1.266(18)\) with \(\chi ^2/\mathrm{dof}=1.68\), where the error has been scaled by about 30% because of the large \(\chi ^2/\mathrm{dof}\). Given that the calculations of PNDME 18 and CalLat 18 are correlated, the large value of \(\chi ^2/\mathrm{dof}\) indicates a tension between the two results. In this situation it is appropriate to adopt a more conservative approach: We estimate the axial charge to be represented by the interval \(1.218\le g_A^{u-d}\le 1.284\), where the lower bound is identified with the result of PNDME 18, while the upper bound is the weighted average plus the scaled 1\(\sigma \) uncertainty. Hence, for \(N_f=2\,+\,1\,+\,1\) we quote \(g_A^{u-d}=1.251(33)\) as the FLAG estimate, where the central value marks the mid-point of the interval, and half the width is taken to be the error.
For QCD with \(N_f=2\,+\,1\) dynamical quarks, the calculations of \(\chi \)QCD 18 [6] and Mainz 18 [919] are free of red tags. However, since the result from the latter is preliminary and published only as a proceedings article, it does not qualify for being included in a global average. Hence, for \(N_f=2\,+\,1\) we identify the FLAG average with the result quoted in \(\chi \)QCD 18 [6], i.e., \(g_A^{u-d}=1.254(16)(30)\).
In the two-flavour case, the results by the Mainz group [85, 822] qualify for an average, since other recent calculations employed only a single source-sink separation on most ensembles (RQCD 14 [823], QCDSF 13 [402]) or because only a single lattice spacing was used (ETM 15D [826], ETM 17B [828]). For \(N_f=2\) we quote the latest estimate \(g_A^{u-d}\) from Mainz 17 [85], adding statistical and systematic errors in quadrature and symmetrizing the error. To summarize, the FLAG averages for the axial charge read
Within errors, these averages are all compatible with the result of \(g_A^{u-d}=1.2724(23)\) quoted by the PDG. While the most recent lattice calculations reproduce the axial charge at the level of a few percent or even better, the experimental result is more precise by an order of magnitude.
10.3.2 Results for \(g_S^{u-d}\)
Calculations of the isovector scalar charge have, in general, larger errors than the isovector axial charge as can be seen from the compilation given in Table 63 and plotted in Fig. 41. For comparison, Fig. 41 also shows a phenomenological result produced using the conserved vector current (CVC) relation [914].
Lattice results and FLAG averages for the isovector scalar charge \(g^{u-d}_S\) for \(N_{ f}= 2\), \(2\,+\,1\), and \(2\,+\,1\,+\,1\) flavour calculations. Also shown is a phenomenological result obtained using the conserved vector current (CVC) relation [914] (circle)
Only a single calculation, PNDME 18 [83], which supersedes PNDME 16 [834] and PNDME 13 [831], meets all the criteria for inclusion in the average.
This \(2\,+\,1\,+\,1\) flavour mixed-action calculation was performed using the MILC HISQ ensembles, with a clover valence action. The 11 ensembles used include three pion mass values, \(M_{\pi } \sim \) 135, 225, 320 MeV, and four lattice spacings, \(a \sim \) 0.06, 0.09, 0.12, 0.15 fm. Note that four lattice spacings are required to meet the green star criteria, as this calculation is not fully O(a) improved. Lattice size ranges between \(3.3 \lesssim M_{\pi } L \lesssim 5.5\), and the set of ensembles includes three different volumes at a fixed pion mass \(M_{\pi } \sim 225\) MeV and lattice spacing \(a\sim 0.12\) fm. Physical point extrapolations were performed simultaneously, keeping only the leading order terms in the various expansion parameters. For the chiral extrapolation, these are the terms proportional to \(M_{\pi }^2\), while the continuum extrapolation is performed using the term proportional to a, because the action and operators are not fully O(a) improved. For the finite volume extrapolation, the asymptotic limit of the \(\chi \)PT prediction, Eq. (375), is used. The Akaike Information Criterion is used to conclude that including more fit parameters is not justified based on the data.
Excited state contamination is controlled using two-state fits to between three and five source-sink time separations. Time separations range between \(0.72 \lesssim \tau \lesssim 1.68\) fm, with all ensembles having at least two time separations greater than 1 fm. Renormalization was performed nonperturbatively using the RI-SMOM scheme and converted to \({\overline{\mathrm {MS}}}\) at 2 GeV using 2-loop perturbation theory.
Regarding \(2\,+\,1\)-flavour calculations, the Mainz 18 calculation meets all criteria for averaging, however as it is only a preliminary result published in proceedings it is not considered. The calculation was performed on the Wilson CLS ensembles, using four lattice spacings down to 0.05 fm and several pion masses down to \(\sim 200\) GeV. Excited states were controlled using multi-state fits to several source-sink separations. The JLQCD 18 calculation, performed using overlap fermions on the Iwasaki gauge action, covered four pion masses down to 290 MeV. The lattice size was adjusted to keep \(M_\pi L \ge 4\) in all four cases. However, the single lattice spacing of \(a=0.11\) fm does not meet the criteria for continuum extrapolation. The calculations presented in LHPC 12A used three different lattice actions, Wilson-clover, domain wall, and mixed action. Pion masses ranged down to near the physical pion mass. Data at two lattice spacings were produced with the domain wall and Wilson actions, however, the final result utilized only the single lattice spacing of \(a=0.116\) fm from the Wilson action. Because the action is not fully O(a) improved, two lattice spacings are not sufficient for meeting the quality criteria for the continuum extrapolation.
The two-flavour calculations in Table 63 include ETM 17, which employed twisted mass fermions on the Iwasaki gauge action.Footnote 82 This work utilized a single physical pion mass ensemble with lattice spacing \(a\sim 0.09\) fm, and therefore does not meet the criteria for continuum extrapolation. The RQCD 14 calculation included three lattice spacings down to 0.06 fm and several pion masses down to near the physical point. While a study of excited state contamination was performed on some ensembles using multiple source-sink separations, many ensembles included only a single time separation, so it does not meet the criteria for excited states.
The final FLAG average for \(g_S^{u-d}\) is
10.3.3 Results for \(g_T^{u-d}\)
Estimates of the isovector tensor charge are currently the most precise of the isovector charges with values that are stable over time, as can be seen from the compilation given in Table 64 and plotted in Fig. 42. This is a consequence of the smaller statistical fluctuations in the raw data and the very mild dependence on a, \(M_\pi \), and the lattice size \(M_\pi L\). As a result, the uncertainty due to the various extrapolations is small. Also shown for comparison in Fig. 42 are phenomenological results using measures of transversity [925,926,927,928,929].
Only the PNDME 18 [83] calculation, which supersedes PNDME 16 [834], PNDME 15 [832, 833] and PNDME 13 [831], meets all the criteria for inclusion in the average. The details for this calculation are the same as those for \(g_S^{u-d}\) described in the previous section (Sect. 10.3.2), except that three-state fits were used to remove excited-state effects.
For \(2\,+\,1\)-flavour calculations, details for the Mainz 18, JLQCD 18, and LHPC 12A, calculations are identical to those presented previously in Sect. 10.3.2. The earlier RBC/UKQCD 10 calculation was performed using domain wall fermions on the Iwasaki gauge action, with two volumes and several pion masses. The lowest pion mass used was \(M_{\pi }\sim 330\) MeV and does not meet the criteria for chiral extrapolation. In addition, the single lattice spacing and single source-sink separation do not meet the criteria for continuum extrapolation and excited states.
Two-flavour calculations include RQCD 14, with details identical to those described in Sect. 10.3.2. There are two calculations, ETM 15D and ETM 17, which employed twisted mass fermions on the Iwasaki gauge action. The earlier work utilized three ensembles, with three volumes and two pion masses down to the physical point. The more recent work used only the physical pion mass ensemble. Both works used only a single lattice spacing \(a\sim 0.09\) fm, and therefore do not meet the criteria for continuum extrapolation. The early work by RBC 08 with domain wall fermions used three heavy values for the pion mass, and a single value for the lattice spacing, volume, and source-sink separation, and therefore do not meet many of the criteria.
The final FLAG average for \(g_T^{u-d}\) is
10.4 Flavour diagonal charges
Three examples of interactions for which matrix elements of flavour-diagonal operators (\(q \Gamma q\) where \(\Gamma \) defines the Lorentz structure of the bilinear quark operator) are needed are the neutral current interactions of neutrinos, elastic scattering of electrons off nuclei, and the scattering of dark matter off nuclei. In addition, these matrix elements also probe intrinsic properties of nucleons (the spin, the strangeness contribution and the electric dipole moment of the quarks) as explained below. For brevity, all operators are assumed to be appropriately renormalized as discussed in Sect. 10.1.3.
The matrix elements of the scalar operator, \({\overline{q}} q\) with flavour q, give the rate of change in the nucleon mass due to nonzero values of the corresponding quark mass. This relationship is given by the Feynman–Hellmann theorem. The quantities of interest are the nucleon \(\sigma \)-term, \(\sigma _{\pi N}\), and the strange and charm content of the nucleon, \(\sigma _{s}\) and \(\sigma _{c}\),
Here \(m_{ud}\) is the average of the up and down quark masses and \(m_s\) (\(m_c\)) is the strange (charm) quark mass. The \(\sigma _{\pi N, s, c}\) give the shift in \(M_N\) due to nonzero light-, strange- and charm-quark masses. The same matrix elements are also needed to quantify the spin independent interaction of dark matter with nucleons. Note that, while \(\sigma _b\) and \(\sigma _t\) are also phenomenologically interesting, they are unlikely to be calculated on the lattice. In principle, the heavy sigma terms can be estimated using \(\sigma _{u,d,s}\) by exploiting the heavy-quark limit [930,931,932].
The matrix elements of the axial operator, \({\overline{q}} \gamma _\mu \gamma _5 q\), give the contribution, \(\Delta q\), of quarks of flavour q to the spin of the nucleon:
The charge \(g_A^q\) is thus the contribution of the spin of a quark of flavour q to the spin of the nucleon. It is also related to the first Mellin moment of the polarized parton distribution function (PDF), \(\Delta q\), as shown in the second line in Eq. (384). Measurements by the European Muon collaboration in 1987 of the spin asymmetry in polarized deep inelastic scattering showed that the sum of the spins of the quarks contributes less than half of the total spin of the proton [933]. To understand this unexpected result, called the “proton spin crisis”, it is common to start with Ji’s sum rule [934] that provides a gauge invariant decomposition of the nucleon’s total spin as
where \(\Delta q /2 \equiv g_A^q /2 \) is the contribution of the intrinsic spin of a quark with flavour q; \(L_q\) is the orbital angular momentum of that quark; and \(J_g\) is the total angular momentum of the gluons. Thus, to obtain the spin of the proton starting from QCD, requires calculating the contributions of the three terms: the spin and orbital angular momentum of the quarks, and the angular momentum of the gluons. Lattice-QCD calculations of the various matrix elements needed to extract the three contributions are underway. An alternate decomposition of the spin of the proton has been provided by Jaffe and Manohar [935]. The two formulations differ in the decomposition of the contributions of the quark orbital angular momentum and of the gluons. The contribution of the quark spin, which is the subject of this review and given in Eq. (384), is the same in both formulations.
The tensor charges are defined as the matrix elements of the tensor operator, \({\overline{q}} \sigma ^{\mu \nu } q\) with \(\sigma ^{\mu \nu } = \{\gamma _\mu ,\gamma _\nu \}/2\):
These flavour-diagonal tensor charges \(g_T^{u,d,s,c}\) quantify the contributions of the u, d, s, c quark electric dipole moments (EDM) to the neutron electric dipole moment (nEDM) [832, 936]. Since particles can have an EDM only due to P and T (or CP assuming CPT is a good symmetry) violating interactions, the nEDM is a very sensitive probe of new sources of CP violation that arise in most extensions of the SM designed to explain nature at the TeV scale. The current experimental bound on the nEDM is \(d_n < 2.9 \times 10^{-26}\ e\) cm [937], while the known CP violation in the SM implies \(d_n < 10^{-31}\ e\) cm [938]. A nonzero result over the intervening five orders of magnitude would signal new physics. Planned experiments aim to reduce the bound to around \( 10^{-28}\ e\) cm. A discovery or reduction in the bound from these experiments will put stringent constraints on many BSM theories, provided the matrix elements of novel CP-violating interactions, of which the quark EDM is one, are calculated with the required precision.
One can also extract these tensor charges from the zeroth moment of the transversity distributions that are measured in many experiments including Drell–Yan and semi-inclusive deep inelastic scattering (SIDIS). Of particular importance is the active program at Jefferson Lab (JLab) to measure them [915, 916]. Transversity distributions describe the net transverse polarization of quarks in a transversely polarized nucleon. Their extraction from the data taken over a limited range of \(Q^2\) and Bjorken x is, however, not straightforward and requires additional phenomenological modeling. At present, lattice-QCD estimates of \(g_T^{u,d,s}\) are the most accurate [832, 917, 918] as can be deduced from Fig. 42. Future experiments will significantly improve the extraction of the transversity distributions. Thus, accurate calculations of the tensor charges using lattice QCD will continue to help elucidate the structure of the nucleon in terms of quarks and gluons and provide a benchmark against which phenomenological estimates utilizing measurements at JLab and other experimental facilities worldwide can be compared.
The methodology for the calculation of flavour-diagonal charges is also well-established. The major challenges are the much larger statistical errors in the disconnected contributions for the same computational cost and the need for the additional calculations of the isosinglet renormalization factors.
10.4.1 Results for \(g_A^{u,d,s}\)
A compilation of recent results for the flavour-diagonal axial charges for the proton is given in Table 65 and plotted in Fig. 43. Results for the neutron can be obtained by interchanging the u and d flavor indices. Only two calculations qualify for global averages, the PNDME 18A for 2 + 1 + 1 flavours [86] and the \(\chi \)QCD 18 for 2 + 1 flavours [6]. The global averages given below are, therefore, the same as the corresponding results given in Table 65.
The 2 + 1 + 1 flavour FLAG results for the axial charges \(g_A^{u,d,s}\) of the proton are
These PNDME 18A [86] results were obtained using the \(2\,+\,1\,+\,1\) flavour clover-on-HISQ formulation. The connected contributions were obtained on 11 HISQ ensembles generated by the MILC collaboration with \(a \approx 0.057\), 0.87, 0.12 and 0.15 fm, \( M_\pi \approx 135\), 220 and 320 MeV, and \(3.3< M_\pi L < 5.5\). The light disconnected contributions were obtained on six of these ensembles with the lowest pion mass \(M_\pi \approx 220\) MeV, while the strange disconnected contributions were obtained on seven ensembles, i.e., including an additional one at \(a \approx 0.087\) fm and \(M_\pi \approx 135\) MeV. The excited state and the chiral-continuum fits were done separately for the connected and disconnected contributions, which introduces a systematic that is hypothesied to be small as explained in Ref. [86]. The analysis of the excited-state contamination, discussed in Sect. 10.1.2, was done using three-state fits for the connected contribution and two-state fits for the disconnected contributions. The chiral-continuum extrapolation was done keeping the leading correction terms proportional to \(M_\pi ^2\) and a in both cases, and the leading finite volume correction in \(M_\pi L\) was included in the analysis of the connected contributions. The isovector renormalization factor, used for all three flavour diagonal operators, was calculated on the lattice in the RI-SMOM scheme and converted to \({\overline{\mathrm {MS}}}\). The difference due to flavor mixing for the singlet case is small as discussed in Sect. 10.1.3.
The \(2\,+\,1\) flavour FLAG results from \(\chi \)QCD 18 were obtained using the overlap-on-domain-wall formalism [6]. Three domain-wall ensembles with lattice spacings 0.143, 0.11 and 0.083 fm and sea-quark pion masses \(M_\pi = 171\), 337 and 302 MeV, respectively, were analyzed. In addition to the three approximately unitary points, the paper presents data for an additional 4–5 valence quark masses on each ensemble, i.e., partially quenched data. Separate excited-state fits were done for the connected and disconnected contributions. The continuum, chiral and volume extrapolation to the combined unitary and nonunitary data is made including terms proportional to both \(M_{\pi ,\mathrm{valence}}^2\) and \(M_{\pi ,\mathrm{sea}}^2\), and two \(O(a^2)\) discretization terms for the two different domain wall actions. With just three unitary points, not all the coefficients are well constrained. The \(M_{\pi ,sea}\) dependence is omitted and considered as a systematic, and a prior is used for the coefficients of the \(a^2\) terms to stabilize the fit. These \(\chi \)QCD 18 2 + 1 flavour results for the proton, which supersede the \(\chi \)QCD 15 [840] analysis, are
The JLQCD 18 [843], ETM 17C [829] and Engelhardt 12 [939] calculations were not considered for the averages as they did not satisfy the criteria for the continuum extrapolation. All three calculations were done at a single lattice spacing. The JLQCD 18 calculation used overlap fermions and the Iwasaki gauge action. They perform a chiral fit using data at four pion masses in the range 290–540 MeV. Finite volume corrections are assumed to be negligible since each of the two pairs of points on different lattice volumes satisfy \(M_\pi L \ge 4\). The ETM 17C calculation is based on a single twisted mass ensemble with \(M_\pi =130\) MeV, \(a=0.094\) and a relatively small \(M_\pi L = 2.98\). Engelhardt 12 calculation was done on three asqtad ensembles with \(M_\pi = 293\), 356 and 495 MeV, but all at a single lattice spacing \(a=0.124\) fm.
Results for \(g_A^s\) were also presented recently by LHPC in Ref. [808]. However, this calculation is not reviewed as it has been performed on a single ensemble with \(a=0.114\) and a heavy pion mass value of \(M_\pi \approx 317\) MeV.
10.4.2 Results for \(g_S^{u,d,s}\) from direct and hybrid calculations of the matrix elements
The sigma terms \(\sigma _q=m_q\langle N|{\bar{q}}q|N\rangle =m_q g_S^q\) or the quark mass fractions \(f_{T_q}=\sigma _q/M_N\) are normally computed rather than \(g_S^q\). These combinations have the advantage of being renormalization group invariant in the continuum, and this holds on the lattice for actions with good chiral properties, see Sect. 10.1.3 for a discussion. In order to aid comparison with phenomenological estimates, e.g., from \(\pi \)–N scattering [940,941,942], the light quark sigma terms are usually added to give the \(\pi N\) sigma term, \(\sigma _{\pi N}=\sigma _u+\sigma _d\). The direct evaluation of the sigma terms involves the calculation of the corresponding three-point correlation functions for different source-sink separations \(\tau \). For \(\sigma _{\pi N}\) there are both connected and disconnected contributions, while for most lattice fermion formulations only disconnected contributions are needed for \(\sigma _s\). The techniques typically employed lead to the availability of a wider range of \(\tau \) for the disconnected contributions compared to the connected ones (both, however, suffer from signal to noise problems for large \(\tau \), as discussed in Sect. 10.1) and we only comment on the range of \(\tau \) computed for the latter in the following.
Recent results for \(\sigma _{\pi N}\) and for \(\sigma _s\) from the direct approach are compiled in Table 66. For both quantities, only the results from \(\chi \)QCD 15A [89] qualify for global averaging. In this mixed action study, three RBC/UKQCD \(N_{ f}=2\,+\,1\) domain wall ensembles are analysed comprising two lattice spacings, \(a=0.08\) fm with \(M_{\pi ,\mathrm sea}=300\) MeV and \(a=0.11\) fm with \(M_{\pi ,\mathrm sea}=330\) MeV and 139 MeV. Overlap fermions are employed with a number of nonunitary valence quark masses. The connected three-point functions are measured with three values of \(\tau \) in the range 0.9–1.4 fm. A combined chiral, continuum and volume extrapolation is performed for all data with \(M_\pi <350\) MeV. The leading order expressions are taken for the lattice-spacing and volume dependence while partially quenched SU(2) HB\(\chi \)PT up to \(M_\pi ^3\) terms models the chiral behaviour for \(\sigma _{\pi N}\). The strange quark sigma term has a milder dependence on the pion mass and only the leading order quadratic terms are included in this case.
The lack of other qualifying studies is an indication of the difficulty and computational expense of performing these calculations. Nonetheless, this situation is likely to improve in the future. We note that although the recent analyses, ETM 16A [827] and JLQCD 18 [843], are both performed at a single lattice spacing (\(a=0.09\) fm and 0.11 fm, respectively), they satisfy the criteria for chiral extrapolation, finite volume and excited states. ETM 16A is a single ensemble study with \(N_{ f}=2\) twisted mass fermions with a pion mass close to the physical point and \(M_\pi L=3.0\). Excited states are investigated utilizing \(\tau =0.9\) fm up to \(\tau =1.7\) fm for the connected three-point functions. JLQCD utilize \(N_{ f}=2\,+\,1\) overlap fermion ensembles with pion masses reaching down to 293 MeV (\(M_\pi L=4.0\)) and apply techniques which give a wide range of \(\tau \) for the connected contribution, with the final results extracted from \(\tau \ge 1.2\) fm.
RQCD in RQCD 16 [824] investigate the continuum, physical quark mass and infinite volume limits, where the lattice spacing spans the range 0.06–0.08 fm, the minimum \(M_\pi \) is 150 MeV and \(M_\pi L\) is varied between 3.4 and 6.7 at \(M_\pi =290\) MeV. This \(N_{ f}=2\) study has a red tag for the excited state criterion as multiple source-sink separations for the connected three-point functions are only computed on a subset of the ensembles. Clover fermions are employed and the lack of good chiral properties for this action means that there is mixing between quark flavours under renormalization when determining \(\sigma _s\) and a gluonic term needs to be considered for full O(a) improvement (which has not been included, see Sect. 10.1.3 for a discussion).
Earlier work focuses only on \(\sigma _s\). The analysis of JLQCD 12A [842], is performed on the same set of ensembles as the JLQCD 18 study discussed above and in addition includes smaller volumes for the lightest two pion masses.Footnote 83 No significant finite volume effects are observed. Engelhardt 12 [939] and \(\chi \)QCD 13A [839] have less control over the systematics. The former is a single lattice spacing analysis restricted to small spatial volumes while the latter is a partially quenched study on a single ensemble with unitary \(M_\pi >300\) MeV.
MILC have also computed \(\sigma _s\) using a hybrid method [943] which makes use of the Feynman–Hellmann (FH) theorem and involves evaluating the matrix element \(\langle N|\int \! d^4\!x\, {\bar{s}}s|N\rangle \).Footnote 84 This method is applied in MILC 09D [943] to the \(N_{ f}=2\,+\,1\) Asqtad ensembles with lattice spacings \(a=0.06,0.09,0.12\) fm and values of \(M_\pi \) ranging down to 224 MeV. A continuum and chiral extrapolation is performed including terms linear in the light-quark mass and quadratic in a. As the coefficient of the discretisation term is poorly determined, a Bayesian prior is used, with a width corresponding to a 10% discretisation effect between the continuum limit and the coarsest lattice spacing.Footnote 85 A similar updated analysis is presented in MILC 12C [91], with an improved evaluation of \(\langle N|\int \! d^4\!x\, {\bar{s}}s|N\rangle \) on a subset of the \(N_{ f}=2\,+\,1\) Asqtad ensembles. The study is also extended to HISQ \(N_{ f}=2\,+\,1\,+\,1\) ensembles comprising four lattice spacings with \(a=0.06-0.15\) fm and a minimum pion mass of 131 MeV. Results are presented for \(g_S^s=\langle N|{\bar{s}}s|N\rangle \) (in the \({\overline{\mathrm {MS}}}\) scheme at 2 GeV) rather than for \(\sigma _s\). The scalar matrix element is renormalized for both three and four flavours using the 2-loop factor for the Asqtad action [165]. The error incurred by applying the same factor to the HISQ results is expected to be small.Footnote 86
Both MILC 09D and MILC 12C achieve green tags for all the criteria, see Table 66. As the same set of Asqtad ensembles is utilized in both studies we take MILC 12C as superseding MILC 09D for the three flavour case. The global averaging is discussed in Sect. 10.4.4.
10.4.3 Results for \(g_S^{u,d,s}\) using the Feynman–Hellmann theorem
An alternative approach for accessing the sigma terms is to determine the slope of the nucleon mass as a function of the quark masses, or equivalently, the squared pseudoscalar meson masses. The Feynman–Hellman (FH) theorem gives
where the fictitious \({\bar{s}}s\) meson has a mass squared \(M^2_{{\bar{s}}s}=2M_K^2-M_\pi ^2\). In principle this is a straightforward method as the nucleon mass can be extracted from fits to two-point correlation functions, and a further fit to \(M_N\) as a function of \(M_\pi \) (and also \(M_K\) for \(\sigma _s\)) provides the slope. Nonetheless, this approach presents its own challenges: a functional form for the chiral behaviour of the nucleon mass is needed, and while baryonic \(\chi \)PT (B\(\chi \)PT) is the natural choice, the convergence properties of the different formulations are not well established. Results are sensitive to the formulation chosen and the order of the expansion employed. If there is an insufficient number of data points when implementing higher order terms, the coefficients are sometimes fixed using additional input, e.g., from analyses of experimental data. This may influence the slope extracted. Simulations with pion masses close to or bracketing the physical point can alleviate these difficulties. In some studies the nucleon mass is used to set the lattice spacing. This naturally forces the fit to reproduce the physical nucleon mass at the physical point and may affect the extracted slope.
An overview of recent determinations of \(\sigma _{\pi N}\) and \(\sigma _s\) is given in Table 67. Note that the renormalization and excited state criteria are not applied.Footnote 87 We do not impose the latter since a wide range of source-sink separations are available for nucleon two-point functions and ground state dominance is normally achieved.
There are several results for \(\sigma _{\pi N}\) that can be included in a global average. For \(N_{ f}=2\), one study meets the selection criteria.Footnote 88 The analysis of QCDSF 12 [90] employs nonperturbatively improved clover fermions over three lattice spacings (\(a=0.06-0.08\) fm) with pion masses reaching down to around 160 MeV. Finite volume corrected nucleon masses are extrapolated via \(O(p^4)\) covariant B\(\chi \)PT with three free parameters. The other coefficients are taken from experiment, phenomenology or FLAG, with the corresponding uncertainties accounted for in the fit for those coefficients that are not well known. The nucleon mass is used to set the scale. A novel feature of this study is that a direct determination of \(\sigma _{\pi N}\) at around \(M_\pi =290\) MeV was used as an additional constraint on the slope.
Turning to \(N_{ f}=2\,+\,1\), two studies performed by the BMW collaboration are relevant. In BMW 11A [87], stout smeared tree-level clover fermions are employed on 15 ensembles with simulation parameters encompassing a = 0.06–0.12 fm, \(M_\pi \sim \) 190–550 MeV and  . Taylor, Padé and covariant SU(3) B\(\chi \)PT fit forms are considered. Due to the use of smeared gauge links, discretisation effects are found to be mild even though the fermion action is not fully O(a) improved. Fits are performed including an O(a) or \(O(a^2)\) term and also without a lattice-spacing dependent term. Finite volume effects were assessed to be small in an earlier work [952]. The final results are computed considering all combinations of the fit ansatz weighted by the quality of the fit. In BMW 15 [88], a more extensive analysis on 47 ensembles is presented for HEX-smeared clover fermions involving five lattice spacings and pion masses reaching down to 120 MeV. Bracketing the physical point reduces the reliance on a chiral extrapolation. Joint continuum, chiral and infinite volume extrapolations are carried out for a number of fit parameterisations with the final results determined via the Akaike information criterion procedure [904]. Although only \(\sigma _{\pi N}\) is accessible in the FH approach in the isospin limit, the individual quark fractions \(f_{T_q}=\sigma _q/M_N\) for \(q=u,d\) for the proton and the neutron are also quoted in BMW 15, using isospin relations.Footnote 89
. Taylor, Padé and covariant SU(3) B\(\chi \)PT fit forms are considered. Due to the use of smeared gauge links, discretisation effects are found to be mild even though the fermion action is not fully O(a) improved. Fits are performed including an O(a) or \(O(a^2)\) term and also without a lattice-spacing dependent term. Finite volume effects were assessed to be small in an earlier work [952]. The final results are computed considering all combinations of the fit ansatz weighted by the quality of the fit. In BMW 15 [88], a more extensive analysis on 47 ensembles is presented for HEX-smeared clover fermions involving five lattice spacings and pion masses reaching down to 120 MeV. Bracketing the physical point reduces the reliance on a chiral extrapolation. Joint continuum, chiral and infinite volume extrapolations are carried out for a number of fit parameterisations with the final results determined via the Akaike information criterion procedure [904]. Although only \(\sigma _{\pi N}\) is accessible in the FH approach in the isospin limit, the individual quark fractions \(f_{T_q}=\sigma _q/M_N\) for \(q=u,d\) for the proton and the neutron are also quoted in BMW 15, using isospin relations.Footnote 89
Regarding \(N_{ f}=2\,+\,1\,+\,1\), there is only one recent study. In ETM 14A [21], fits are performed to the nucleon mass utilizing SU(2) \(\chi \)PT for data with \(M_\pi \ge 213\) MeV as part of an analysis to set the lattice spacing. The expansion is considered to \(O(p^3)\) and \(O(p^4)\), with two and three of the coefficients as free parameters, respectively. The difference between the two fits is taken as the systematic error. No discernable discretisation or finite volume effects are observed where the lattice spacing is varied over the range a = 0.06–0.09 fm and the spatial volumes cover \(M_\pi L=3.4\) up to \(M_\pi L>5\). The results are unchanged when a near physical point \(N_{ f}=2\) ensemble is added to the analysis in Ref. [949].
Lattice results and FLAG averages for the nucleon sigma term, \(\sigma _{\pi N}\), for the \(N_{ f}= 2\), \(2\,+\,1\), and \(2\,+\,1\,+\,1\) flavour calculations. Determinations via the direct approach are indicated by squares and the Feynman–Hellmann method by triangles. Results from calculations which analyse more than one lattice data set within the Feynman–Hellmann approach [454, 455, 949, 954,955,956,957,958,959,960] are shown for comparison (pentagons) along with those from recent analyses of \(\pi \)-N scattering [940,941,942, 961] (circles)
Other determinations of \(\sigma _{\pi N}\) in Table 67 receive one or more red tags. JLQCD 08B [841], PACS-CS 09 [825] and QCDSF 11 [947] are single lattice spacing studies. In addition, the volume for the minimum pion mass is rather small for JLQCD 08B and PACS-CS 09, while QCDSF 11 is restricted to heavier pion masses.
We also consider publications that are based on results for baryon masses found in the literature. As different lattice setups (in terms of \(N_{ f}\), lattice actions, etc.) will lead to different systematics, we only include works in Table 67 which utilize a single setup. These correspond to Shanahan 12 [946] and Martin Camalich 10 [948], which fit PACS-CS data [162] (the PACS-CS 09 study is also based on these results). Note that Shanahan 12 avoids a red tag for the volume criterion as the lightest pion mass ensemble is omitted. Recent studies which combine data from different setups/collaborations are displayed for comparison in Figs. 44 and 45 in the next section.
Several of the above studies have also determined the strange quark sigma term. This quantity is difficult to access via the Feynman-Hellmann method since in most simulations the physical point is approached by varying the light-quark mass, keeping \(m_s\) approximately constant. While additional ensembles can be generated, it is hard to resolve a small slope with respect to \(m_s\). Such problems are illustrated by the large uncertainties in the results from BMW 11A and BMW 15. Alternative approaches have been pursued in QCDSF 11, where the physical point is approached along a trajectory keeping the average of the light- and strange-quark masses fixed, and JLQCD 12A [842], where quark mass reweighting is applied. The latter is a single lattice spacing study. One can also fit to the whole baryon octet and apply SU(3) flavour symmetry constraints as investigated in, e.g., Martin Camalich 10, Shanahan 12, QCDSF 11 and BMW 11A.
Lattice results and FLAG averages for \(\sigma _s\) for the \(N_{ f}= 2\), \(2\,+\,1\), and \(2\,+\,1\,+\,1\) flavour calculations. Determinations via the direct approach are indicated by squares, the Feynman–Hellmann method by triangles and the hybrid approach by circles. Results from calculations which analyse more than one lattice data set within the Feynman–Hellmann approach [454, 455, 955, 956, 958] are shown for comparison (pentagons)
The determinations of \(\sigma _s\) in BMW 11A and BMW 15 qualify for averaging. The mixed action study of Junnarkar 13 [92] with domain wall valence fermions on MILC \(N_{ f}=2\,+\,1\) Asqtad ensembles also passes the FLAG criteria. The derivative \(\partial M_N/\partial m_s\) is determined from simulations above and below the physical strange quark mass for \(M_\pi \) around 240–675 MeV. The resulting values of \(\sigma _s\) are extrapolated quadratically in \(M_\pi \). The quark fraction \(f_{T_s}=\sigma _s/M_N\) exhibits a milder pion-mass dependence and extrapolations of this quantity were also performed using ansätze linear and quadratic in \(M_\pi \). A weighted average of all three fits was used to form the final result. Two lattice spacings were analysed, with a around 0.09 fm and 0.12 fm, however, discretisation effects could not be resolved. The global averaging of all calculations that qualify is discussed in the next section.
10.4.4 Summary of results for \(g_S^{u,d,s}\)
We consider computing global averages of results determined via the direct, hybrid and Feynman-Hellmann (FH) methods. Beginning with \(\sigma _{\pi N}\), Tables 66 and 67 show that for \(N_{ f}=2\,+\,1\,+\,1\) only ETM 14A (FH) satisfies the selection criteria. We take this result as our average for the four flavour case.
For \(N_{ f}=2\,+\,1\) we form an average from the BMW 11A (FH), BMW 15 (FH) and \(\chi \)QCD 15A (direct) results, yielding
Note that both BMW results are included as they were obtained on independent sets of ensembles (employing different fermion actions). The average is dominated by the BMW 15 calculation, which has much smaller overall errors compared to the other two studies.
Turning to the results for \(N_{ f}=2\), only QCDSF 12 (FH) qualifies. This result forms our average
Considering \(\sigma _s\) and the calculations detailed in Table 66, there is again only a single 2 + 1 + 1 flavour study, MILC 12C (hybrid), which satisfies the quality criteria. In order to convert the result for \(\langle N|{\bar{s}}s|N\rangle \) given in this work to a value for \(\sigma _s\), we multiply by the appropriate FLAG average for \(m_s\) given in Eq. (35). This gives our average for four flavours.
For \(N_{ f}=2\,+\,1\) we perform a weighted average of BMW 11A (FH), MILC 12C (hybrid), Junnarkar 13 (FH), BMW 15 (FH) and \(\chi \)QCD 15A (direct). MILC 09D [943] also passes the FLAG selection rules, however, this calculation is superseded by MILC 12C. As for Eq. (397), the strangeness scalar matrix element determined in the latter study is multiplied by the three flavour FLAG average for \(m_s\) given in Eq. (33). There are correlations between the MILC 12C and Junnarkar 13 results as there is some overlap between the sets of Asqtad ensembles used in both cases. To be conservative we take the statistical errors for these two studies to be 100% correlated. The global average is
Given that all of the \(N_{ f}=2\) studies have at least one red tag we are not able to give an average in this case.
All the results for \(\sigma _{\pi N}\) and \(\sigma _s\) are displayed in Figs. 44 and 45 along with the averages given above. Note that where \(f_{T_s}\) is quoted in Tables 66 and 67, we multiply by the experimental proton mass in order to include the results in the figures. Those results which pass the FLAG criteria, shown in green, are consistent within one standard deviation with the averages for each \(N_{ f}\), and considering the size of the uncertainties in the averages no significant \(N_{ f}\)-dependence is observed. However, there is some fluctuation in the central values, in particular, when taking the lattice results as a whole into account, and we caution the reader that the averages may change as new results become available.
Also shown for comparison in the figures are determinations from the FH method which utilize more than one lattice data set [454, 455, 949, 954,955,956,957,958,959,960] as well as results for \(\sigma _{\pi N}\) obtained from recent analyses of \(\pi \)-N scattering [940,941,942, 961]. There is some tension, at the level of three to four standard deviations, between the lattice average for \(N_{ f}=2\,+\,1\) and Hoferichter et al. [942], who quote a precision similar to that of the average.
Finally we remark that, by exploiting the heavy-quark limit, the light- and strange-quark sigma terms can be used to estimate \(\sigma _q\) for the charm, bottom and top quarks [930,931,932]. The resulting estimate for the charm quark, see, e.g., the RQCD 16 \(N_{ f}=2\) analysis of Ref. [824] that reports \(f_{T_c}=0.075(4)\) or \(\sigma _c=70(4)\) MeV, is consistent with the direct determinations of ETM 16A [827] for \(N_{ f}=2\) of \(\sigma _c=79(21)(^{12}_{8})\) MeV and \(\chi \)QCD 13A [839] for \(N_{ f}=2\,+\,1\) of \(\sigma _c=94(31)\) MeV. MILC in MILC 12C [91] find \(\langle N|{\bar{c}}c|N\rangle =0.056(27)\) in the \({\overline{\mathrm {MS}}}\) scheme at a scale of 2 GeV for \(N_{ f}=2\,+\,1\,+\,1\) via the hybrid method. Considering the large uncertainty, this is consistent with the other results once multiplied by the charm quark mass.
10.4.5 Results for \(g_T^{u,d,s}\)
A compilation of recent results for the flavour-diagonal tensor charges \(g_T^{u,d,s}\) for the proton in the \({\overline{\mathrm {MS}}}\) scheme at 2 GeV is given in Table 68 and plotted in Fig. 46. Results for the neutron can be obtained by interchanging the u and d flavor indices. Only the PNDME 2 + 1 + 1 flavour calculations qualify for the global average.
The FLAG averages are the same as the PNDME 18B [7] results, which supersede the PNDME 16 [834] and the PNDME 15A [832] values:
The ensembles and the analysis strategy used in PNDME 18B is the same as described in Sect. 10.4.1 for \(g_A^{u,d,s}\). The only difference for the tensor charges was that a one-state (constant) fit was used for the disconnected contributions as the data did not show significant excited-state contamination. The isovector renormalization constant, used for all three flavour diagonal tensor operators, was calculated on the lattice in the RI-SMOM scheme and converted to \({\overline{\mathrm {MS}}}\) at 2 GeV using 2-loop perturbation theory. As discussed in Sect. 10.1.3, the difference between the singlet and isovector factors is expected to be small.
The JLQCD 18 [843] and ETM 17 calculations [830] were not considered for the final averages because they did not satisfy the criteria for the continuum extrapolation as already discussed in Sect. 10.4.1.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a review article for which no new simulations were performed. Fits done to results in the literature are contained within the article.]
Notes
Working groups were given the option of including papers submitted to arxiv.org before the closing date but published after this date. This flexibility allows this review to be up-to-date at the time of submission. Three papers of this type were included: Ref. [5] in Sects. 7 and 8, and Refs. [6, 7] in Sect. 10.
The WG on semileptonic D and B decays currently has four members, but only three of them belong to lattice collaborations.
The NME WG, new in this addition of the FLAG review, has been formed with four members (all members of lattice collaborations) rather than three. This reflects the large amount of work needed to create a section for which some of the systematic errors are substantially different from those described in other sections, and to provide a better representation of relevant collaborations.
We also use terms like “quality criteria”, “rating”, “colour coding”, etc., when referring to the classification of results, as described in Sect. 2.
This is a change from FLAG 13, where we used the charged pion mass when evaluating both chiral-extrapolation and finite-volume effects.
In FLAG 13, the RMS value was used in the chiral-extrapolation criteria throughout the paper. For the finite-volume rating, however, \(M_{\pi ,\mathrm {min}}\) was identified with the RMS value only in Sects. 4 and 6, while in Sects. 3, 5, 7 and 8 it was identified with the mass of the lightest pseudoscalar state.
For example, for quark-mass results we distinguish between perturbative and nonperturbative renormalization, for low-energy constants we distinguish between the p- and \(\epsilon \)-regimes, and for heavy-flavour results we distinguish between those from leptonic and semi-leptonic decays.
Whenever figures turn out to be overcrowded, older, superseded results are omitted. However, all the most recent results from each collaboration are displayed.
As noted above in footnote 1, three exceptions to this deadline were made.
There is also a small correlation between \(Y_1\) and \({\overline{Z}}\), but we follow the original Ref. [78] and do not take this into account. Thus, the error in \(Q_1\) is obtained by simple error propagation from those in \(Y_1\) and \({\overline{Z}}\). Ignoring this correlation is conservative, because, as in the calculation of \(B_K\), the correlations between \(B_B f_B^2\) and \(f_B^2\) tend to lead to a cancelation of errors. By ignoring this effect we are making a small overestimate of the error in \(Q_1\).
We follow the conventions of Gasser and Leutwyler [135].
To obtain this number, we have used the conversion from \(\mu =3\,\) GeV to \(m_c\) given in Ref. [171].
Note that in Sect. 9.7.2 different quality criteria are adopted and the HPQCD 14A paper is tagged differently for the continuum extrapolation.
The pion decay constant represents a QCD matrix element – in the full Standard Model, the one-pion state is not a meaningful notion: the correlation function of the charged axial current does not have a pole at \(p^2=M_{\pi ^+}^2\), but a branch cut extending from \(M_{\pi ^+}^2\) to \(\infty \). The analytic properties of the correlation function and the problems encountered in the determination of \(f_\pi \) are thoroughly discussed in Ref. [202]. The “experimental” value of \(f_\pi \) depends on the convention used when splitting the sum \({{{\mathcal {L}}}}_{ \text{ QCD }}+\mathcal{L}_{ \text{ QED }}\) into two parts. The lattice determinations of \(f_{\pi }\) do not yet reach the accuracy where this is of significance, but at the precision claimed by the Particle Data Group [170, 201], the numerical value does depend on the convention used [202,203,204,205].
Fortran programs for the numerical evaluation of the form factor representation in Ref. [250] are available on request from Johan Bijnens.
Here we have symmetrized the asymmetric systematic error and shifted the central value by half the difference as will be done throughout this section.
In a recent paper [274] the size of the radiative corrections entering the extraction of \(|V_{ud}|\) from superallowed nuclear \(\beta \) decays has been reanalyzed obtaining \(|V_{ud}| = 0.97366~(15)\). This value differs by \(\simeq 1.5 \sigma \) from Eq. (71) and leads to \(|V_u|^2 = 0.99778~(44)\) and \(|V_u|^2 = 0.99875~(37)\) using the lattice results for \(f_+(0)\) and \({f_{K^\pm }}/{f_{\pi ^\pm }}\), respectively. This would correspond to a \(\simeq 5 \sigma \) (\(\simeq 3.4 \sigma \)) violation of the unitarity of the first-row of the CKM matrix.
More precisely, they are independent of the 2 or 3 light-quark masses that are explicitly considered in the respective framework. However, all low-energy constants depend on the masses of the remaining quarks s, c, b, t or c, b, t in the SU(2) and SU(3) framework, respectively, although the dependence on the masses of the c, b, t quarks is expected to be small.
Here and in the following, we stick to the notation used in the papers where the \(\chi \)PT formulae were established, i.e., we work with \(F_\pi \equiv f_\pi /\sqrt{2}=92.2(1)\,\mathrm {MeV}\) and \(F_K\equiv f_K/\sqrt{2}\). The occurrence of different normalization conventions is not convenient, but avoiding it by reformulating the formulae in terms of \(f_\pi \), \(f_K\) is not a good way out. Since we are using different symbols, confusion cannot arise.
Notice that one could analyse the quark-mass dependence entirely in terms of the parameter \(M^2\) defined in Eq. (89) and determine equally well all other LECs. Using the determination of the quark masses described in Sect. 3 one can then extract B or \(\Sigma \). No matter the strategy of extraction, determination of B or \(\Sigma \) requires knowledge of the scale and scheme dependent quark mass renormalization factor \(Z_m(\mu )\).
By introducing an imaginary isospin chemical potential, the framework can be extended such that the low-lying spectrum of the Dirac operator is also sensitive to the pseudoscalar decay constant F at LO [367].
Some of the \({\mathcal {O}}(p^6)\) formulae presented below have been derived in an unpublished note by two of us (GC and SD), Jürg Gasser and Heiri Leutwyler. We thank them for allowing us to publish them here.
There are theoretical arguments suggesting that the \(\xi \) expansion is preferable to the x expansion, based on the observation that the coefficients in front of the squared logs in Eq. (88) are somewhat larger than in Eq. (93). This can be traced to the fact that a part of every formula in the x expansion is concerned with locating the position of the pion pole (at the previous order) while in the \(\xi \) expansion the knowledge of this position is built in exactly. Numerical evidence supporting this view is presented in Ref. [376].
This means that for any given lattice formulation one needs to determine additional lattice-artifact low-energy constants. For certain formulations, e.g., the twisted-mass approach, first steps in this direction have already been taken [385], while with staggered fermions MILC routinely does so, see, e.g., Refs. [129, 166].
Note that in previous editions of this report the result of ETM 10 was mistakenly used, since the fact that \((a_\mathrm {max}/a_\mathrm {min})^2<1.4\) in that work, leading to the red square in Tables 20 and 21, escaped our attention. Here we consider the proceedings contribution ETM 11 a straightforward update of the published work ETM 10, and this is why it qualifies for the FLAG average.
The fits in MILC 10 are straightforward updates to those in MILC 09, and the SU(2) NLO LECs are obtained directly from the SU(3) ones, a conversion just not performed in MILC 09. This is why MILC 10 can be an update to a refereed publication that does not show up in Table 21.
There are two naive procedures to symmetrize an asymmetric systematic error: (i) keep the central value untouched and enlarge the smaller error, (ii) shift the central value by half of the difference between the two original errors and enlarge/shrink both errors by the same amount. Our procedure (iii) is to average the results of (i) and (ii). In other words a result \(c(s)\left( {\begin{array}{c}+u\\ -\ell \end{array}}\right) \) with \(\ell >u\) is changed into \(c+(u-\ell )/4\) with statistical error s and a symmetric systematic error \((u+3\ell )/4\). The case \(\ell <u\) is handled accordingly.
It is worth emphasizing that our rating cannot do justice to “hybrid” papers, since it is exclusively based on the lattice information that makes it into the analysis. This is a consequence of us being unable to rate the quality of the experimental information involved.
We thank Martin Lüscher for an interesting discussion on this issue.
Thanks to QCD parity invariance lattice computations for three more dimension-six operators, whose parity conserving parts coincide with the corresponding parity conserving contributions of the operators \(Q_1, Q_2\) and \(Q_3\), can be ignored.
Because only two of the authors of this work are members of HPQCD, and to distinguish it from other more recent works on the same topic by HPQCD, we hereafter refer to this work as “FNAL/MILC.”
It is important to stress the finding in [536] that the factorization of chiral logs in hard-pion \(\chi \)PT breaks down, implying that it does not fulfill the expected requisites for a proper effective field theory. Its use to model the mass dependence of form factors can thus be questioned.
The ensemble parameters quoted in Ref. [535] appear to show that the volumes employed at the lightest pion masses are insufficient to meet our criteria for finite-volume effects. There is however a typo in the table which result in a wrong assignment of lattice sizes, whereupon the criteria are indeed met. We thank T. Kaneko for correspondence on this issue.
The neutral B-meson leptonic decays, \(B_{d,s} \rightarrow \mu ^{+} \mu ^{-}\), were initially observed at the LHC experiments, and the corresponding branching fractions were obtained by combining the data from the CMS and the LHCb collaborations [547], resulting in some tension with the SM prediction. More recently, the LHCb collaboration [548] has improved the measurement of \(B^0_s\rightarrow \mu ^+\mu ^-\) and provided a bound on \(B^0\rightarrow \mu ^+\mu ^-\) that eliminate the tension with the SM. Nevertheless, the errors of these experimental results are currently too large to enable a precise determination of \(|V_{td}|\) and \(|V_{ts}|\).
See Ref. [206] for a strategy that has been proposed to account for QED effects.
Following the guideline in Sect. 2.3, these systematic errors are assumed to be \(100\%\) correlated. It should be noted that this correlation cannot be taken at face value.
In Ref. [133] an “isospin correction” is applied to \(f_{B^+}\) to obtain \(f_{B^0}\) for RBC/UKQCD 14A, HPQCD 12/11A, FNAL/MILC 11 before averaging.
The variance of hadron correlation functions at nonzero three-momentum is dominated at large Euclidean times by zero-momentum multiparticle states [574]; therefore the noise-to-signal grows more rapidly than for the vanishing three-momentum case.
Upcoming data from Belle II are expected to significantly improve the precision of experimental results, in particular, for larger values of \(q^2\).
It is important to stress the finding in [536] that the factorization of chiral logs in hard-pion \(\chi \)PT breaks down, implying that it does not fulfill the expected requisites for a proper effective field theory. Its use to model the mass dependence of form factors can thus be questioned.
Note that generating synthetic data is a trivial task, but less so is choosing the number of required points and the \(q^2\) values that lead to an optimal description of the form factors.
The values of the scalar resonance mass in \(B\pi \) scattering taken by HPQCD and RBC/UKQCD are \(M_{B^*(0+)}=5.6794(10)~\,\mathrm {GeV}\) and \(M_{B^*(0+)}=5.63~\,\mathrm {GeV}\), respectively. We use an average of the two values, and have checked that changing it by \(\sim 1\%\) has a negligible impact on the fit results.
In this case, \({\mathcal {O}}(z^4)\) fits with just two degrees of freedom, are significantly less stable. Still, the results for \(a_0^+\) and \(a_1^+\) are always compatible with the ones at \({\mathcal {O}}(z^2)\) and \({\mathcal {O}}(z^3)\) within one standard deviation.
See, e.g., Ref. [588] and references therein.
Note in particular that not much is known about the sub-threshold poles for the scalar form factor. FNAL/MILC includes one pole at the \(B_{s0}^*\) mass as taken from the calculation in Ref. [596].
In cases such as \(B\rightarrow D^*\) transitions, that will be discussed below, this is much less of a practical problem due to the very narrow nature of the resonance.
As noted above, this is the same approach adopted by FNAL/MILC in their fits to a BGL ansatz. HPQCD, meanwhile, uses one single pole in the pole factors that enter their modified z-expansion, using their spectral studies to fix the value of the relevant resonance masses.
A similar ratio \(R(D^*)\) can be considered for \(B \rightarrow D^*\) transitions – as a matter of fact, the experimental value of \(R(D^*)\) is significantly more accurate than the one of R(D). However, the absence of lattice results for the \(B\rightarrow D^*\) scalar form factor, and indeed of results at nonzero recoil (see below), takes \(R(D^*)\) out of our current scope.
This work also provided a value for R(D), now superseded by Ref. [615].
Since \(\ell =e,\mu \) the contribution from the scalar form factor in Eq. (222) is negligible.
See, e.g., Sect. V.D of [577] for a detailed discussion.
The same work provides \({\mathcal {G}}^{B_s\rightarrow D_s}\), for which there are, however, no experimental data.
Note that this determination does not include the electromagnetic Coulomb correction roughly estimated in Ref. [614]. Currently the numerical impact of this correction is negligible.
In light of our policy not to average \(N_f=2\,+\,1\) and \(N_f = 2\,+\,1\,+\,1\) calculations and of the controversy over the use of the CLN vs. BGL parameterizations, we prefer to simply use only the more precise \(N_f=2\,+\,1\) determination of \({\mathcal {F}}^{B\rightarrow D^*}(1)\) in Eq. (248) for the extraction of \(V_{cb}\).
We thank Marcello Rotondo for providing the ten bins result of the BaBar analysis.
We have checked that results using just one experimental data set are compatible within \(1\sigma \). In the case of BaBar, we have taken into account the introduction of some EW corrections in the data.
Once one is in the perturbative region with \(\alpha _\mathrm{eff}\), the error in extracting the \(\Lambda \) parameter due to the truncation of perturbation theory scales like \(\alpha _\mathrm{eff}^{n_\mathrm {l}}\), as discussed around Eq. (286). In order to detect/control such corrections properly, one needs to change the correction term significantly; we require a factor of four for a
 and a factor \((3/2)^2\) for a
and a factor \((3/2)^2\) for a  . An exception to the above is the situation where the correction terms are small anyway, i.e., \(\alpha _{\mathrm{eff}}^{n_\mathrm {l}} = \Delta \Lambda /\Lambda \approx \Delta \alpha _{\mathrm{eff}} / (8\pi b_0 \alpha _{\mathrm{eff}}^2)\) is reached.
. An exception to the above is the situation where the correction terms are small anyway, i.e., \(\alpha _{\mathrm{eff}}^{n_\mathrm {l}} = \Delta \Lambda /\Lambda \approx \Delta \alpha _{\mathrm{eff}} / (8\pi b_0 \alpha _{\mathrm{eff}}^2)\) is reached.We simplify here and assume that the classical solution associated with the used boundary conditions has charge zero. In practice this is the case.
With 2-loop \({\mathcal {O}}(a)\) improvement we here mean \(c_\mathrm {t}\) including the \(g_0^4\) term and \({{\tilde{c}}}_\mathrm {t}\) with the \(g_0^2\) term. For gluonic observables such as the running coupling this is sufficient for cutoff effects being suppressed to \({\mathcal {O}}(g^6 a)\).
Note that at large distances, where string breaking is known to occur, this is not any more the ground state potential defined by Eq. (312).
\(\alpha _{\mathrm {V'}}\) is defined by \(\Lambda _\mathrm {V'}=\Lambda _\mathrm {V}\) and \(b_i^\mathrm {V'}=b_i^\mathrm {V}\) for \(i=0,1,2\) but \(b_i^\mathrm {V'}=0\) for \(i\ge 3\).
From Eq. (287) we see that at low order in PT the coupling \(\alpha _s\) is continuous and differentiable across the mass thresholds (at the same scale). Therefore to leading order \(\alpha _s\) and \(\Delta \alpha _s\) are independent of \(N_f\).
In the present situation, the effective coupling would be defined by \({\bar{g}}^2_\lambda (\mu ) = \bar{F}_2^{-1/2}\,(3 - F(\lambda ))^{1/2}\) with \(\mu =\lambda \), preferably taken as the renormalization group invariant eigenvalue.
One may wonder why we consider Maezawa 16 which has a
 in the perturbative behaviour. This rating is, however, due to the overall estimated uncertainty, not to the rest of the data and analysis, which we use here.
in the perturbative behaviour. This rating is, however, due to the overall estimated uncertainty, not to the rest of the data and analysis, which we use here.Note that these are not straight weighted averages since often individual results within one group are not in good agreement.
In the isospin symmetric limit \(\langle p|{\bar{u}}\Gamma d|n\rangle =\langle p|{\bar{u}}\Gamma u-{\bar{d}}\Gamma d|p\rangle =\langle n|{\bar{d}}\Gamma d-{\bar{u}}\Gamma u|n\rangle \) for nucleon and proton states \(|p\rangle \) and \(|n\rangle \), respectively. The latter two (equivalent) isovector matrix elements are computed on the lattice.
Here \(a(g^2)\) refers to the lattice spacing in the chiral limit, however, lattice simulations are usually carried out by fixing the value of \(g^2\) while varying the quark masses. This means \(a=a({\tilde{g}}^2)\) where \({\tilde{g}}^2=g^2(1+b_g am_q)\) [880, 881] is the improved coupling that varies with the average sea-quark mass \(m_q\). The difference between the Z factors calculated with respect to \(g^2\) and \({\tilde{g}}^2\) can effectively be absorbed into the \(b_{{\mathcal {O}}}\) coefficients [882, 883].
Note that for twisted mass fermions the pseudoscalar renormalization factor is the relevant factor for the scalar operator. The isovector (isosinglet) scalar current in the physical basis becomes the isosinglet (isovector) pseudoscalar current in the twisted basis. Perturbatively \(r_P=1+O(\alpha _s^3)\) and nonperturbative determinations have found \(r_P\approx 1\) [830].
The earlier work, ETM 15D [826], did not give a final value for \(g_S^{u-d}\) and is therefore not included in the tables.
JLQCD also determine \(f_{T_s}\) in Ref. [944] in a single lattice spacing study on small volumes with heavy pion masses.
Note that in the direct method the matrix element \(\langle N|\int \! d^3\!x\, {\bar{s}}s|N\rangle \), involving the spatial volume sum, is evaluated for a fixed timeslice.
This is consistent with discretisation effects observed in other quantities at \(a=0.12\) fm.
At least at 1-loop the Z factors for HISQ and Asqtad are very similar, cf. Ref. [945].
Renormalization is normally not required in the Feynman-Hellmann approach when computing the sigma terms. However, when employing clover fermions one must take care of the mixing between quark flavours when renormalizing the quark masses that appear in Eq. (393).
ETMC also determine \(\sigma _{\pi N}\) in Ref. [951] as part of an \(N_{ f}=2\) analysis to determine the lattice spacing from the nucleon mass. However, no final result is given.
These isospin relations were also derived in Ref. [953].
A more complicated analytic structure may arise in other cases, such as channels with vector mesons in the final state. We will however not discuss form-factor parameterizations for any such process.
We are grateful to G. Herdoíza, R.J. Hill, A. Kronfeld and A. Szczepaniak for illuminating discussions on this issue.
References
[FLAG 10] G. Colangelo, S. Dürr, A. Jüttner, L. Lellouch, H. Leutwyler et al., Review of lattice results concerning low energy particle physics. Eur. Phys. J. C 71, 1695 (2011). https://doi.org/10.1140/epjc/s10052-011-1695-1. arXiv:1011.4408
[FLAG 13] S. Aoki, Y. Aoki, C. Bernard, T. Blum, G. Colangelo et al., Review of lattice results concerning low-energy particle physics. Eur. Phys. J. C 74, 2890 (2014). https://doi.org/10.1140/epjc/s10052-014-2890-7. arXiv:1310.8555
[FLAG 16] S. Aoki et al., Review of lattice results concerning low-energy particle physics. Eur. Phys. J. C 77, 112 (2017). https://doi.org/10.1140/epjc/s10052-016-4509-7. arXiv:1607.00299
Flavour Lattice Averaging Group (FLAG), Review of lattice results concerning low energy particle physics. http://flag.unibe.ch/
[FNAL/MILC 17] A. Bazavov et al., \(B\)- and \(D\)-meson leptonic decay constants from four-flavor lattice QCD. Phys. Rev. D 98, 074512 (2018). https://doi.org/10.1103/PhysRevD.98.074512. arXiv:1712.09262
[\(\chi \)QCD 18] J. Liang, Y.-B. Yang, T. Draper, M. Gong, K.-F. Liu, Quark spins and anomalous ward identity. Phys. Rev. D 98, 074505 (2018). https://doi.org/10.1103/PhysRevD.98.074505. arXiv:1806.08366
[PNDME 18B] R. Gupta, B. Yoon, T. Bhattacharya, V. Cirigliano, Y.-C. Jang, H.-W. Lin, Flavor diagonal tensor charges of the nucleon from (2+1+1)-flavor lattice QCD. Phys. Rev. D 98, 91501 (2018). https://doi.org/10.1103/PhysRevD.98.091501. arXiv:1808.07597
[FNAL/MILC/TUMQCD 18] A. Bazavov et al., Up-, down-, strange-, charm-, and bottom-quark masses from four-flavor lattice QCD. Phys. Rev. D 98, 054517 (2018). https://doi.org/10.1103/PhysRevD.98.054517. arXiv:1802.04248
[ETM 14] N. Carrasco et al., Up, down, strange and charm quark masses with N\(_f\) = 2+1+1 twisted mass lattice QCD. Nucl. Phys. B 887, 19–68 (2014). https://doi.org/10.1016/j.nuclphysb.2014.07.025. arXiv:1403.4504
[RBC/UKQCD 14B] T. Blum et al., Domain wall QCD with physical quark masses. Phys. Rev. D 93 074505 (2016). https://doi.org/10.1103/PhysRevD.93.074505. arXiv:1411.7017
[BMW 10A] S. Dürr, Z. Fodor, C. Hoelbling, S. Katz, S. Krieg et al., Lattice QCD at the physical point: light quark masses. Phys. Lett. B 701, 265–268 (2011). https://doi.org/10.1016/j.physletb.2011.05.053. arXiv:1011.2403
[BMW 10B] S. Dürr, Z. Fodor, C. Hoelbling, S. Katz, S. Krieg et al., Lattice QCD at the physical point: simulation and analysis details. JHEP 1108, 148 (2011). https://doi.org/10.1007/JHEP08(2011)148. arXiv:1011.2711
[HPQCD 10] C. McNeile, C.T.H. Davies, E. Follana, K. Hornbostel, G.P. Lepage, High-precision c and b masses and QCD coupling from current-current correlators in lattice and continuum QCD. Phys. Rev. D 82, 034512 (2010). https://doi.org/10.1103/PhysRevD.82.034512. arXiv:1004.4285
[MILC 10A] A. Bazavov et al., Staggered chiral perturbation theory in the two-flavor case and SU(2) analysis of the MILC data. PoS LAT2010, 083 (2010). arXiv:1011.1792
[HPQCD 18] A.T. Lytle, C.T.H. Davies, D. Hatton, G.P. Lepage, C. Sturm, Determination of quark masses from \(\bf n\it _{{\rm f}}={\bf 4}\) lattice QCD and the RI-SMOM intermediate scheme. Phys. Rev. D 98, 014513. https://doi.org/10.1103/PhysRevD.98.014513. arXiv:1805.06225
[HPQCD 14A] B. Chakraborty, C.T.H. Davies, G.C. Donald, R.J. Dowdall, B. Galloway, P. Knecht et al., High-precision quark masses and QCD coupling from \(n_f=4\) lattice QCD. Phys. Rev. D 91, 054508 (2015). https://doi.org/10.1103/PhysRevD.91.054508. arXiv:1408.4169
[MILC 09A] A. Bazavov et al., MILC results for light pseudoscalars. PoS CD09, 007 (2009). arXiv:0910.2966
[FNAL/MILC 14A] A. Bazavov et al., Charmed and light pseudoscalar meson decay constants from four-flavor lattice QCD with physical light quarks. Phys. Rev. D 90, 074509 (2014). https://doi.org/10.1103/PhysRevD.90.074509. arXiv:1407.3772
[RM123 17] D. Giusti, V. Lubicz, C. Tarantino, G. Martinelli, S. Sanfilippo, S. Simula et al., Leading isospin-breaking corrections to pion, kaon and charmed-meson masses with Twisted-Mass fermions. Phys. Rev. D 95, 114504 (2017). https://doi.org/10.1103/PhysRevD.95.114504. arXiv:1704.06561
[BMW 16] Z. Fodor, C. Hoelbling, S. Krieg, L. Lellouch, T. Lippert, A. Portelli et al., Up and down quark masses and corrections to Dashen’s theorem from lattice QCD and quenched QED. Phys. Rev. Lett. 117, 082001 (2016). https://doi.org/10.1103/PhysRevLett.117.082001. arXiv:1604.07112
[ETM 14A] C. Alexandrou, V. Drach, K. Jansen, C. Kallidonis, G. Koutsou, Baryon spectrum with \(N_f=2+1+1\) twisted mass fermions. Phys. Rev. D 90, 074501 (2014). https://doi.org/10.1103/PhysRevD.90.074501. arXiv:1406.4310
[\(\chi \)QCD 14] Y. Yi-Bo et al., Charm and strange quark masses and \(f\_{D\_s}\) from overlap fermions. Phys. Rev. D 92, 034517 (2015). https://doi.org/10.1103/PhysRevD.92.034517. arXiv:1410.3343
[JLQCD 16] K. Nakayama, B. Fahy, S. Hashimoto, Short-distance charmonium correlator on the lattice with Möbius domain-wall fermion and a determination of charm quark mass. Phys. Rev. D 94, 054507 (2016). https://doi.org/10.1103/PhysRevD.94.054507. arXiv:1606.01002
[HPQCD 09A] C. T. H. Davies et al., Precise charm to strange mass ratio and light quark masses from full lattice QCD. Phys. Rev. Lett. 104, 132003 (2010). https://doi.org/10.1103/PhysRevLett.104.132003. arXiv:0910.3102
[HPQCD 14B] B. Colquhoun, R.J. Dowdall, C.T.H. Davies, K. Hornbostel, G.P. Lepage, \(\Upsilon \) and \(\Upsilon ^{\prime }\) Leptonic widths, \(a_{\mu }^b\) and \(m_b\) from full lattice QCD. Phys. Rev. D 91, 074514 (2015). https://doi.org/10.1103/PhysRevD.91.074514. arXiv:1408.5768
[ETM 16B] A. Bussone et al., Mass of the b quark and B -meson decay constants from N\(_f\)=2+1+1 twisted-mass lattice QCD. Phys. Rev. D 93, 114505. https://doi.org/10.1103/PhysRevD.93.114505. arXiv:1603.04306
P. Gambino, A. Melis S. Simula, Extraction of heavy-quark-expansion parameters from unquenched lattice data on pseudoscalar and vector heavy-light meson masses. Phys. Rev. D 96, 014511 (2017). https://doi.org/10.1103/PhysRevD.96.014511. arXiv:1704.06105
[FNAL/MILC 13E] A. Bazavov et al., Determination of \(|V_{us}|\) from a lattice-QCD calculation of the \(K\rightarrow \pi \ell \nu \) semileptonic form factor with physical quark masses. Phys. Rev. Lett. 112, 112001 (2014). https://doi.org/10.1103/PhysRevLett.112.112001. arXiv:1312.1228
[ETM 16] N. Carrasco, P. Lami, V. Lubicz, L. Riggio, S. Simula, C. Tarantino, \(K \rightarrow \pi \) semileptonic form factors with \(N_f=2+1+1\) twisted mass fermions. Phys. Rev. D 93, 114512 (2016). https://doi.org/10.1103/PhysRevD.93.114512. arXiv:1602.04113
[FNAL/MILC 12I] A. Bazavov, C. Bernard, C. Bouchard, C. DeTar, D. Du et al., Kaon semileptonic vector form factor and determination of \(|V_{us}|\) using staggered fermions. Phys. Rev. D 87, 073012 (2013). https://doi.org/10.1103/PhysRevD.87.073012. arXiv:1212.4993
[RBC/UKQCD 15A] P.A. Boyle et al., The kaon semileptonic form factor in N\(_{f}\) = 2 + 1 domain wall lattice QCD with physical light quark masses. JHEP 1506, 164 (2015). https://doi.org/10.1007/JHEP06(2015)164. arXiv:1504.01692
[ETM 09A] V. Lubicz, F. Mescia, S. Simula, C. Tarantino, \(K \rightarrow \pi \,\ell \,\nu \) semileptonic form factors from two-flavor lattice QCD. Phys. Rev. D 80, 111502 (2009). https://doi.org/10.1103/PhysRevD.80.111502. arXiv:0906.4728
[HPQCD 13A] R. Dowdall, C. Davies, G. Lepage, C. McNeile, \(V_{us}\) from \(\pi \) and \(K\) decay constants in full lattice QCD with physical \(u\), \(d\), \(s\) and \(c\) quarks. Phys. Rev. D 88, 074504 (2013). https://doi.org/10.1103/PhysRevD.88.074504. arXiv:1303.1670
[ETM 14E] N. Carrasco, P. Dimopoulos, R. Frezzotti, P. Lami, V. Lubicz et al., Leptonic decay constants \(f_K\), \(f_D\) and \(f_{D_s}\) with \(N_f = 2+1+1\) twisted-mass lattice QCD. Phys. Rev. D 91, 054507 (2015). https://doi.org/10.1103/PhysRevD.91.054507. arXiv:1411.7908
[HPQCD/UKQCD 07] E. Follana, C.T.H. Davies, G.P. Lepage, J. Shigemitsu, High precision determination of the \(\pi \), \(K\), \(D\) and \(D_s\) decay constants from lattice QCD. Phys. Rev. Lett. 100, 062002 (2008). https://doi.org/10.1103/PhysRevLett.100.062002. arXiv:0706.1726
[MILC 10] A. Bazavov et al., Results for light pseudoscalar mesons. PoS LAT2010, 074 (2010). arXiv:1012.0868
[BMW 10] S. Dürr, Z. Fodor, C. Hoelbling, S. Katz, S. Krieg et al., The ratio \(F_K/F_\pi \) in QCD. Phys. Rev. D 81, 054507 (2010). https://doi.org/10.1103/PhysRevD.81.054507. arXiv:1001.4692
S. Dürr et al., Leptonic decay-constant ratio \(f_K/f_\pi \) from lattice QCD using 2+1 clover-improved fermion flavors with 2-HEX smearing. Phys. Rev. D 95, 054513 (2017). https://doi.org/10.1103/PhysRevD.95.054513. arXiv:1601.05998
[QCDSF/UKQCD 16] V.G. Bornyakov, R. Horsley, Y. Nakamura, H. Perlt, D. Pleiter, P.E.L. Rakow et al., Flavour breaking effects in the pseudoscalar meson decay constants. Phys. Lett. B 767, 366–373 (2017). https://doi.org/10.1016/j.physletb.2017.02.018. arXiv:1612.04798
[ETM 09] B. Blossier et al., Pseudoscalar decay constants of kaon and D-mesons from \(N_f=2\) twisted mass lattice QCD. JHEP 0907, 043 (2009). https://doi.org/10.1088/1126-6708/2009/07/043. arXiv:0904.0954
[ETM 13] K. Cichy, E. Garcia-Ramos, K. Jansen, Chiral condensate from the twisted mass Dirac operator spectrum. JHEP 1310, 175 (2013). https://doi.org/10.1007/JHEP10(2013)175. arXiv:1303.1954
[ETMC 17E] C. Alexandrou, A. Athenodorou, K. Cichy, M. Constantinou, D.P. Horkel, K. Jansen et al., Topological susceptibility from twisted mass fermions using spectral projectors and the gradient flow. Phys. Rev. D 97 074503 (2018). https://doi.org/10.1103/PhysRevD.97.074503. arXiv:1709.06596
S. Borsanyi, S. Dürr, Z. Fodor, S. Krieg, A. Schäfer et al., SU(2) chiral perturbation theory low-energy constants from 2+1 flavor staggered lattice simulations. Phys. Rev. D 88, 014513 (2013). https://doi.org/10.1103/PhysRevD.88.014513. arXiv:1205.0788
[BMW 13] S. Dürr, Z. Fodor, C. Hoelbling, S. Krieg, T. Kurth et al., Lattice QCD at the physical point meets SU(2) chiral perturbation theory. Phys. Rev. D 90, 114504 (2014). https://doi.org/10.1103/PhysRevD.90.114504. arXiv:1310.3626
[RBC/UKQCD 15E] P.A. Boyle et al., Low energy constants of SU(2) partially quenched chiral perturbation theory from N\(_f\)=2+1 domain wall QCD. Phys. Rev. D 93, 054502 (2016). https://doi.org/10.1103/PhysRevD.93.054502. arXiv:1511.01950
[JLQCD 16B] G. Cossu, H. Fukaya, S. Hashimoto, T. Kaneko, J.-I. Noaki, Stochastic calculation of the Dirac spectrum on the lattice and a determination of chiral condensate in 2+1-flavor QCD. PTEP 2016, 093B06 (2016). https://doi.org/10.1093/ptep/ptw129. arXiv:1607.01099
[JLQCD 17A] S. Aoki, G. Cossu, H. Fukaya, S. Hashimoto, T. Kaneko, Topological susceptibility of QCD with dynamical Möbius domain wall fermions. PTEP 2018, 043B07 (2018). https://doi.org/10.1093/ptep/pty041. arXiv:1705.10906
[ETM 09C] R. Baron et al., Light meson physics from maximally twisted mass lattice QCD. JHEP 08, 097 (2010). https://doi.org/10.1007/JHEP08(2010)097. arXiv:0911.5061
B.B. Brandt, A. Jüttner, H. Wittig, The pion vector form factor from lattice QCD and NNLO chiral perturbation theory. JHEP 1311, 034 (2013). https://doi.org/10.1007/JHEP11(2013)034. arXiv:1306.2916
G.P. Engel, L. Giusti, S. Lottini, R. Sommer, Spectral density of the Dirac operator in two-flavor QCD. Phys. Rev. D 91, 054505 (2015). https://doi.org/10.1103/PhysRevD.91.054505. arXiv:1411.6386
[ETM 11] R. Baron et al., Light hadrons from \(N_f=2+1+1\) dynamical twisted mass fermions. PoS LAT2010, 123 (2010). arXiv:1101.0518
[NPLQCD 11] S.R. Beane, W. Detmold, P. Junnarkar, T. Luu, K. Orginos et al., SU(2) low-energy constants from mixed-action lattice QCD. Phys. Rev. D 86, 094509 (2012). https://doi.org/10.1103/PhysRevD.86.094509. arXiv:1108.1380
[ETM 08] R. Frezzotti, V. Lubicz, S. Simula, Electromagnetic form factor of the pion from twisted-mass lattice QCD at \(N_f=2\). Phys. Rev. D 79, 074506 (2009). https://doi.org/10.1103/PhysRevD.79.074506. arXiv:0812.4042
V. Gülpers, G. von Hippel, H. Wittig, The scalar radius of the pion from lattice QCD in the continuum limit. Eur. Phys. J. A 51, 158 (2015). https://doi.org/10.1140/epja/i2015-15158-0. arXiv:1507.01749
[ETM 15] N. Carrasco, P. Dimopoulos, R. Frezzotti, V. Lubicz, G.C. Rossi, S. Simula et al., \(\Delta S=2\) and \(\Delta C=2\) bag parameters in the standard model and beyond from \(N_f=2+1+1\) twisted-mass lattice QCD. Phys. Rev. D 92, 034516 (2015). https://doi.org/10.1103/PhysRevD.92.034516. arXiv:1505.06639
[BMW 11] S. Dürr, Z. Fodor, C. Hoelbling, S. Katz, S. Krieg et al., Precision computation of the kaon bag parameter. Phys. Lett. B 705, 477–481 (2011). https://doi.org/10.1016/j.physletb.2011.10.043. arXiv:1106.3230
J. Laiho, R.S. Van de Water, Pseudoscalar decay constants, light-quark masses and \(B_K\) from mixed-action lattice QCD. PoS LATTICE2011, 293 (2011). arXiv:1112.4861
[SWME 15A] Y.-C. Jang et al., Kaon BSM B-parameters using improved staggered fermions from \(N_f=2+1\) unquenched QCD. Phys. Rev. D 93, 014511 (2016). https://doi.org/10.1103/PhysRevD.93.014511. arXiv:1509.00592
[ETM 12D] V. Bertone et al., Kaon mixing beyond the SM from N\(_{f}\)=2 tmQCD and model independent constraints from the UTA. JHEP 03, 089 (2013). https://doi.org/10.1007/JHEP07(2013)143, https://doi.org/10.1007/JHEP03(2013)089. arXiv:1207.1287
[RBC/UKQCD 16] N. Garron, R.J. Hudspith, A.T. Lytle, Neutral Kaon mixing beyond the standard model with \(n_f=2+1\) chiral fermions part 1: Bare matrix elements and physical results. JHEP 11, 001 (2016). https://doi.org/10.1007/JHEP11(2016)001. arXiv:1609.03334
[HPQCD 12A] H. Na, C.T. Davies, E. Follana, G.P. Lepage, J. Shigemitsu, \(|V_{cd}|\) from D meson leptonic decays. Phys. Rev. D 86, 054510 (2012). https://doi.org/10.1103/PhysRevD.86.054510. arXiv:1206.4936
[FNAL/MILC 11] A. Bazavov et al., \(B\)- and \(D\)-meson decay constants from three-flavor lattice QCD. Phys. Rev. D 85, 114506 (2012). https://doi.org/10.1103/PhysRevD.85.114506. arXiv:1112.3051
[RBC/UKQCD 17] P.A. Boyle, L. Del Debbio, A. Jüttner, A. Khamseh, F. Sanfilippo, J.T. Tsang, The decay constants \({\bf f}_{{\bf D}}\) and \({\bf f}_{{\bf D}_{{\bf s}}}\) in the continuum limit of \({\bf N}_{\bf f} = {\bf 2}+{\bf 1}\) domain wall lattice QCD. JHEP 12, 008 (2017). https://doi.org/10.1007/JHEP12(2017)008. arXiv:1701.02644
[ETM 13B] N. Carrasco et al., B-physics from \(N_f\) = 2 tmQCD: the Standard Model and beyond. JHEP 1403, 016 (2014). https://doi.org/10.1007/JHEP03(2014)016. arXiv:1308.1851
[HPQCD 10A] C.T.H. Davies, C. McNeile, E. Follana, G. Lepage, H. Na et al., Update: precision \(D_s\) decay constant from full lattice QCD using very fine lattices. Phys. Rev. D 82, 114504 (2010). https://doi.org/10.1103/PhysRevD.82.114504. arXiv:1008.4018
B. Blossier, J. Heitger, M. Post, Leptonic D\(_s\) decays in two-flavour lattice QCD. Phys. Rev. D 98, 054506 (2018). https://doi.org/10.1103/PhysRevD.98.054506. arXiv:1803.03065
[ETM 17D] V. Lubicz, L. Riggio, G. Salerno, S. Simula, C. Tarantino, Scalar and vector form factors of \(D \rightarrow \pi (K) \ell \nu \) decays with \(N_f=2+1+1\) twisted fermions. Phys. Rev. D 96, 054514 (2017). https://doi.org/10.1103/PhysRevD.96.054514. arXiv:1706.03017
[HPQCD 11] H. Na et al., \(D \rightarrow \pi \ell \nu \) semileptonic decays, \(|V_{cd}|\) and 2\(^{nd}\) row unitarity from lattice QCD. Phys. Rev. D 84, 114505 (2011). https://doi.org/10.1103/PhysRevD.84.114505. arXiv:1109.1501
[HPQCD 10B] H. Na, C.T.H. Davies, E. Follana, G.P. Lepage, J. Shigemitsu, The \(D \rightarrow K\ell \nu \) semileptonic decay scalar form factor and \(|V_{cs}|\) from lattice QCD. Phys. Rev. D 82, 114506 (2010). https://doi.org/10.1103/PhysRevD.82.114506. arXiv:1008.4562
[HPQCD 13] R.J. Dowdall, C. Davies, R. Horgan, C. Monahan, J. Shigemitsu, B-meson decay constants from improved lattice NRQCD and physical u, d, s and c sea quarks. Phys. Rev. Lett. 110, 222003 (2013). https://doi.org/10.1103/PhysRevLett.110.222003. arXiv:1302.2644
[HPQCD 17A] C. Hughes, C.T.H. Davies, C.J. Monahan, New methods for B meson decay constants and form factors from lattice NRQCD, Phys. Rev. D 97, 054509 (2018). https://doi.org/10.1103/PhysRevD.97.054509. arXiv:1711.09981
[HPQCD 11A] C. McNeile, C.T.H. Davies, E. Follana, K. Hornbostel, G.P. Lepage, High-precision \(f_{B_s}\) and HQET from relativistic lattice QCD. Phys. Rev. D 85, 031503 (2012). https://doi.org/10.1103/PhysRevD.85.031503. arXiv:1110.4510
[HPQCD 12] H. Na, C.J. Monahan, C.T. Davies, R. Horgan, G.P. Lepage et al., The \(B\) and \(B_s\) meson decay constants from lattice QCD. Phys. Rev. D 86, 034506 (2012). https://doi.org/10.1103/PhysRevD.86.034506. arXiv:1202.4914
[RBC/UKQCD 14A] Y. Aoki, T. Ishikawa, T. Izubuchi, C. Lehner, A. Soni, Neutral \(B\) meson mixings and \(B\) meson decay constants with static heavy and domain-wall light quarks. Phys. Rev. D 91, 114505 (2015). https://doi.org/10.1103/PhysRevD.91.114505. arXiv:1406.6192
[RBC/UKQCD 14] N.H. Christ, J.M. Flynn, T. Izubuchi, T. Kawanai, C. Lehner et al., B-meson decay constants from 2+1-flavor lattice QCD with domain-wall light quarks and relativistic heavy quarks. Phys. Rev. D 91, 054502 (2015). https://doi.org/10.1103/PhysRevD.91.054502. arXiv:1404.4670
[ALPHA 14] F. Bernardoni et al., Decay constants of B-mesons from non-perturbative HQET with two light dynamical quarks. Phys. Lett. B 735, 349–356 (2014). https://doi.org/10.1016/j.physletb.2014.06.051. arXiv:1404.3590
[HPQCD 09] E. Gamiz, C.T. Davies, G.P. Lepage, J. Shigemitsu, M. Wingate, Neutral \(B\) meson mixing in unquenched lattice QCD. Phys. Rev. D 80, 014503 (2009). https://doi.org/10.1103/PhysRevD.80.014503. arXiv:0902.1815
[FNAL/MILC 16] A. Bazavov et al., \(B^0_{(s)}\)-mixing matrix elements from lattice QCD for the Standard Model and beyond. Phys. Rev. D 93, 113016 (2016). https://doi.org/10.1103/PhysRevD.93.113016. arXiv:1602.03560
[ALPHA 17] M. Bruno, M. Dalla Brida, P. Fritzsch, T. Korzec, A. Ramos, S. Schaefer et al., QCD coupling from a nonperturbative determination of the three-flavor \(\Lambda \) Parameter. Phys. Rev. Lett. 119, 102001 (2017). https://doi.org/10.1103/PhysRevLett.119.102001. arXiv:1706.03821
A. Bazavov, N. Brambilla, X. Garcia i Tormo, P. Petreczky, S. Joan, A. Vairo, Determination of \(\alpha _s\) from the QCD static energy: An update. Phys. Rev. D 90, 074038 (2014). https://doi.org/10.1103/PhysRevD.90.074038. arXiv:1407.8437
[PACS-CS 09A] S. Aoki et al., Precise determination of the strong coupling constant in \(N_f = 2+1\) lattice QCD with the Schrödinger functional scheme. JHEP 0910, 053 (2009). https://doi.org/10.1088/1126-6708/2009/10/053. arXiv:0906.3906
K. Maltman, D. Leinweber, P. Moran, A. Sternbeck, The realistic lattice determination of \(\alpha _s(M_Z)\) revisited. Phys. Rev. D 78, 114504 (2008). arXiv:0807.2020
[PNDME 18] R. Gupta, Y.-C. Jang, B. Yoon, H.-W. Lin, V. Cirigliano, T. Bhattacharya, Isovector charges of the nucleon from 2+1+1-flavor lattice QCD. Phys. Rev. D 98, 034503 (2018). https://doi.org/10.1103/PhysRevD.98.034503. arXiv:1806.09006
[CalLat 18] C.C. Chang et al., A per-cent-level determination of the nucleon axial coupling from quantum chromodynamics. Nature (2018). https://doi.org/10.1038/s41586-018-0161-8. arXiv:1805.12130
[Mainz 17] S. Capitani, M. Della Morte, D. Djukanovic, G.M. von Hippel, J. Hua, B. Jäger et al., Iso-vector axial form factors of the nucleon in two-flavor lattice QCD. Int. J. Mod. Phys. A 34, 1950009 (2019). https://doi.org/10.1142/S0217751X1950009X. arXiv:1705.06186
[PNDME 18A] H.W. Lin, R. Gupta, B. Yoon, Y.-C. Jang, T. Bhattacharya, Quark contribution to the proton spin from 2+1+1-flavor lattice QCD. Phys. Rev. D 98, 094512 (2018). https://doi.org/10.1103/PhysRevD.98.094512. arXiv:1806.10604
[BMW 11A] S. Dürr et al., Sigma term and strangeness content of octet baryons. Phys. Rev. D 85, 014509 (2012). https://doi.org/10.1103/PhysRevD.85.014509, https://doi.org/10.1103/PhysRevD.93.039905. arXiv:1109.4265
[BMW 15] S. Dürr et al., Lattice computation of the nucleon scalar quark contents at the physical point. Phys. Rev. Lett. 116, 172001 (2016). https://doi.org/10.1103/PhysRevLett.116.172001. arXiv:1510.08013
[\(\chi \)QCD 15A] Y.-B. Yang, A. Alexandru, T. Draper, J. Liang, K.-F. Liu, \(\pi \)N and strangeness sigma terms at the physical point with chiral fermions. Phys. Rev. D 94, 054503 (2016). https://doi.org/10.1103/PhysRevD.94.054503. arXiv:1511.09089
[QCDSF 12] G. Bali, P. Bruns, S. Collins, M. Deka, B. Glasle et al., Nucleon mass and sigma term from lattice QCD with two light fermion flavors. Nucl. Phys. B 866, 1–25 (2013). https://doi.org/10.1016/j.nuclphysb.2012.08.009. arXiv:1206.7034
[MILC 12C] W. Freeman, D. Toussaint, Intrinsic strangeness and charm of the nucleon using improved staggered fermions. Phys. Rev. D 88, 054503 (2013). https://doi.org/10.1103/PhysRevD.88.054503. arXiv:1204.3866
P. Junnarkar, A. Walker-Loud, Scalar strange content of the nucleon from lattice QCD. Phys. Rev. D 87, 114510 (2013). https://doi.org/10.1103/PhysRevD.87.114510. arXiv:1301.1114
K. Symanzik, Continuum limit and improved action in lattice theories. 1. Principles and \(\phi ^4\) theory. Nucl. Phys. B 226, 187 (1983). https://doi.org/10.1016/0550-3213(83)90468-6
K. Symanzik, Continuum limit and improved action in lattice theories. 2. O(N) nonlinear sigma model in perturbation theory. Nucl. Phys. B 226, 205 (1983). https://doi.org/10.1016/0550-3213(83)90469-8
[RBC 07A] D. J. Antonio et al., Localization and chiral symmetry in 3 flavor domain wall QCD. Phys. Rev. D 77, 014509 (2008). https://doi.org/10.1103/PhysRevD.77.014509. arXiv:0705.2340
[MILC 10] A. Bazavov et al., Topological susceptibility with the asqtad action. Phys. Rev. D 81, 114501 (2010). https://doi.org/10.1103/PhysRevD.81.114501. arXiv:1003.5695
[ALPHA 10C] S. Schaefer, R. Sommer, F. Virotta, Critical slowing down and error analysis in lattice QCD simulations. Nucl. Phys. B 845, 93–119 (2011). https://doi.org/10.1016/j.nuclphysb.2010.11.020. arXiv:1009.5228
M. Lüscher, Topology, the Wilson flow and the HMC algorithm. PoS LATTICE2010, 015 (2010). arXiv:1009.5877
S. Schaefer, Algorithms for lattice QCD: progress and challenges. AIP Conf. Proc. 1343, 93–98 (2011). https://doi.org/10.1063/1.3574948. arXiv:1011.5641
A. Chowdhury, A. Harindranath, J. Maiti, P. Majumdar, Topological susceptibility in lattice Yang-Mills theory with open boundary condition. JHEP 02, 045 (2014). https://doi.org/10.1007/JHEP02(2014)045. arXiv:1311.6599
[LSD 14] R.C. Brower et al., Maximum-likelihood approach to topological charge fluctuations in lattice gauge theory. Phys. Rev. D 90, 014503 (2014). https://doi.org/10.1103/PhysRevD.90.014503. arXiv:1403.2761
[JLQCD 15] H. Fukaya, S. Aoki, G. Cossu, S. Hashimoto, T. Kaneko, J. Noaki, \(\eta ^\prime \) meson mass from topological charge density correlator in QCD. Phys. Rev. D 92, 111501 (2015). https://doi.org/10.1103/PhysRevD.92.111501. arXiv:1509.00944
L. Del Debbio, H. Panagopoulos, E. Vicari, Theta dependence of SU(N) gauge theories. JHEP 08, 044 (2002). https://doi.org/10.1088/1126-6708/2002/08/044. arXiv:hep-th/0204125
C. Bernard et al., Topological susceptibility with the improved Asqtad action. Phys. Rev. D 68, 114501 (2003). https://doi.org/10.1103/PhysRevD.68.114501. arXiv:hep-lat/0308019
M. Lüscher, S. Schaefer, Lattice QCD without topology barriers. JHEP 1107, 036 (2011). https://doi.org/10.1007/JHEP07(2011)036. arXiv:1105.4749
M.G. Endres, R.C. Brower, W. Detmold, K. Orginos, A.V. Pochinsky, Multiscale Monte Carlo equilibration: Pure Yang-Mills theory. Phys. Rev. D 92, 114516 (2015). https://doi.org/10.1103/PhysRevD.92.114516. arXiv:1510.04675
W. Detmold, M.G. Endres, Scaling properties of multiscale equilibration. Phys. Rev. D 97, 074507 (2018). https://doi.org/10.1103/PhysRevD.97.074507. arXiv:1801.06132
S. Mages, B.C. Toth, S. Borsanyi, Z. Fodor, S. Katz, K.K. Szabo, Lattice QCD on Non-Orientable Manifolds. Phys. Rev. D 95, 094512 (2017). https://doi.org/10.1103/PhysRevD.95.094512. arXiv:1512.06804
M. Bruno et al., Simulation of QCD with N\(_{f} =\) 2 \(+\) 1 flavors of non-perturbatively improved Wilson fermions. JHEP 02, 043 (2015). https://doi.org/10.1007/JHEP02(2015)043. arXiv:1411.3982
R. Brower, S. Chandrasekharan, J.W. Negele, U. Wiese, QCD at fixed topology. Phys. Lett. B 560, 64–74 (2003). https://doi.org/10.1016/S0370-2693(03)00369-1. arXiv:hep-lat/0302005
S. Aoki, H. Fukaya, S. Hashimoto, T. Onogi, Finite volume QCD at fixed topological charge. Phys. Rev. D 76, 054508 (2007). https://doi.org/10.1103/PhysRevD.76.054508. arXiv:0707.0396
I. Bautista, W. Bietenholz, A. Dromard, U. Gerber, L. Gonglach, C.P. Hofmann et al., Measuring the topological susceptibility in a fixed sector. Phys. Rev. D 92, 114510 (2015). https://doi.org/10.1103/PhysRevD.92.114510. arXiv:1503.06853
W. Bietenholz, C. Czaban, A. Dromard, U. Gerber, C.P. Hofmann, H. Mejía-Díaz et al., Interpreting numerical measurements in fixed topological sectors. Phys. Rev. D 93, 114516 (2016). https://doi.org/10.1103/PhysRevD.93.114516. arXiv:1603.05630
C. Bernard, D. Toussaint, Effects of nonequilibrated topological charge distributions on pseudoscalar meson masses and decay constants. Phys. Rev. D 97, 074502 (2018). https://doi.org/10.1103/PhysRevD.97.074502. arXiv:1707.05430
S. Duane, A.D. Kennedy, B.J. Pendleton, D. Roweth, Hybrid Monte Carlo. Phys. Lett. B 195, 216–222 (1987). https://doi.org/10.1016/0370-2693(87)91197-X
M.A. Clark, A.D. Kennedy, Accelerating staggered fermion dynamics with the rational hybrid Monte Carlo (RHMC) algorithm. Phys. Rev. D 75, 011502 (2007). https://doi.org/10.1103/PhysRevD.75.011502. arXiv:hep-lat/0610047
[MILC 12B] A. Bazavov et al., Lattice QCD ensembles with four flavors of highly improved staggered quarks. Phys. Rev. D 87, 054505 (2013). https://doi.org/10.1103/PhysRevD.87.054505. arXiv:1212.4768
G. Colangelo, S. Dürr, C. Haefeli, Finite volume effects for meson masses and decay constants. Nucl. Phys. B 721, 136–174 (2005). https://doi.org/10.1016/j.nuclphysb.2005.05.015. arXiv:hep-lat/0503014
[BMW 14] Sz. Borsanyi et al., Ab initio calculation of the neutron-proton mass difference. Science 347, 1452–1455 (2015). https://doi.org/10.1126/science.1257050. arXiv:1406.4088
Z. Davoudi, M.J. Savage, Finite-volume electromagnetic corrections to the masses of mesons, baryons and nuclei. Phys. Rev. D 90, 054503 (2014). https://doi.org/10.1103/PhysRevD.90.054503. arXiv:1402.6741
V. Lubicz, G. Martinelli, C.T. Sachrajda, F. Sanfilippo, S. Simula, N. Tantalo, Finite-volume QED corrections to decay amplitudes in lattice QCD. Phys. Rev. D 95, 034504 (2017). https://doi.org/10.1103/PhysRevD.95.034504. arXiv:1611.08497
Z. Davoudi, J. Harrison, A. Jüttner, A. Portelli, M.J. Savage, Theoretical aspects of quantum electrodynamics in a finite volume with periodic boundary conditions. Phys. Rev. D 99, 034510 (2019). https://doi.org/10.1103/PhysRevD.99.034510. arXiv:1810.05923
[ETM 07A] Ph. Boucaud et al., Dynamical twisted mass fermions with light quarks. Phys. Lett. B 650, 304–311 (2007). https://doi.org/10.1016/j.physletb.2007.04.054. arXiv:hep-lat/0701012
O. Bär, Chiral logs in twisted mass lattice QCD with large isospin breaking. Phys. Rev. D 82, 094505 (2010). https://doi.org/10.1103/PhysRevD.82.094505. arXiv:1008.0784
S. Dürr, Theoretical issues with staggered fermion simulations. PoS LAT2005, 021 (2006). arXiv:hep-lat/0509026
S.R. Sharpe, Rooted staggered fermions: good, bad or ugly?. PoS LAT2006, 022 (2006). arXiv:hep-lat/0610094
A.S. Kronfeld, Lattice gauge theory with staggered fermions: how, where, and why (not). PoS LAT2007, 016 (2007). arXiv:0711.0699
M. Golterman, QCD with rooted staggered fermions. PoS CONFINEMENT8, 014 (2008). arXiv:0812.3110
[MILC 09] A. Bazavov et al., Full nonperturbative QCD simulations with 2+1 flavors of improved staggered quarks. Rev. Mod. Phys. 82, 1349–1417 (2010). arXiv:0903.3598
[ALPHA 14A] M. Bruno, J. Finkenrath, F. Knechtli, B. Leder, R. Sommer, Effects of Heavy Sea Quarks at Low Energies. Phys. Rev. Lett. 114, 102001 (2015). https://doi.org/10.1103/PhysRevLett.114.102001. arXiv:1410.8374
A. Athenodorou, J. Finkenrath, F. Knechtli, T. Korzec, B. Leder, M.K. Marinkovic et al., How perturbative are heavy sea quarks? Nucl. Phys. B 943, 114612 (2019). https://doi.org/10.1016/j.nuclphysb.2019.114612. arXiv:1809.03383
M. Schmelling, Averaging correlated data. Phys. Scripta 51, 676–679 (1995). https://doi.org/10.1088/0031-8949/51/6/002
J. L. Rosner, S. Stone, R.S. Van de Water, Leptonic decays of charged pseudoscalar mesons, in review of particle physics [170] 2015 update. arXiv:1509.02220
A. Manohar, C.T. Sachrajda, Quark masses, in review of particle physics., Chin. Phys. C 38, 090001 (2014). https://doi.org/10.1088/1674-1137/38/9/090001
J. Gasser, H. Leutwyler, Quark masses. Phys. Rept. 87, 77–169 (1982). https://doi.org/10.1016/0370-1573(82)90035-7
M. Gell-Mann, R.J. Oakes, B. Renner, Behavior of current divergences under SU(3)\(\times \)SU(3). Phys. Rev. 175, 2195–2199 (1968). https://doi.org/10.1103/PhysRev.175.2195
Particle Data Group collaboration, M. Tanabashi et al., Review of particle physics. Phys. Rev. D 98, 030001 (2018). https://doi.org/10.1103/PhysRevD.98.030001
[RBC 07] T. Blum, T. Doi, M. Hayakawa, T. Izubuchi, N. Yamada, Determination of light quark masses from the electromagnetic splitting of pseudoscalar meson masses computed with two flavors of domain wall fermions. Phys. Rev. D 76, 114508 (2007). https://doi.org/10.1103/PhysRevD.76.114508. arXiv:0708.0484
T. Blum et al., Electromagnetic mass splittings of the low lying hadrons and quark masses from 2+1 flavor lattice QCD+QED. Phys. Rev. D 82, 094508 (2010). https://doi.org/10.1103/PhysRevD.82.094508. arXiv:1006.1311
[RM123 11] G.M. de Divitiis, P. Dimopoulos, R. Frezzotti, V. Lubicz, G. Martinelli et al., Isospin breaking effects due to the up-down mass difference in lattice QCD. JHEP 1204, 124 (2012). https://doi.org/10.1007/JHEP04(2012)124. arXiv:1110.6294
[RM123 13] G.M. de Divitiis, R. Frezzotti, V. Lubicz, G. Martinelli, R. Petronzio et al., Leading isospin breaking effects on the lattice. Phys.Rev. D 87, 114505 (2013). https://doi.org/10.1103/PhysRevD.87.114505. arXiv:1303.4896
[BMW 13A] Sz. Borsanyi et al., Isospin splittings in the light baryon octet from lattice QCD and QED. Phys. Rev. Lett. 111, 252001 (2013). https://doi.org/10.1103/PhysRevLett.111.252001. arXiv:1306.2287
J. Bijnens, N. Danielsson, Electromagnetic corrections in partially quenched chiral perturbation theory. Phys. Rev. D 75, 014505 (2007). https://doi.org/10.1103/PhysRevD.75.014505. arXiv:hep-lat/0610127
[QCDSF/UKQCD 15A] R. Horsley et al., QED effects in the pseudoscalar meson sector. JHEP 04, 093 (2016). https://doi.org/10.1007/JHEP04(2016)093. arXiv:1509.00799
[MILC 18] Basak, S. et al., Lattice computation of the electromagnetic contributions to kaon and pion masses. Phys. Rev. D 99, 034503 (2019). https://doi.org/10.1103/PhysRevD.99.034503. arXiv:1807.05556
M. Hansen, B. Lucini, A. Patella, N. Tantalo, Gauge invariant determination of charged hadron masses. JHEP 05, 146 (2018). https://doi.org/10.1007/JHEP05(2018)146. arXiv:1802.05474
B. Lucini, A. Patella, A. Ramos, N. Tantalo, Charged hadrons in local finite-volume QED+QCD with C\(^{*}\) boundary conditions. JHEP 02, 076 (2016). https://doi.org/10.1007/JHEP02(2016)076. arXiv:1509.01636
A. Duncan, E. Eichten, H. Thacker, Electromagnetic splittings and light quark masses in lattice QCD. Phys. Rev. Lett. 76, 3894–3897 (1996). https://doi.org/10.1103/PhysRevLett.76.3894. arXiv:hep-lat/9602005
M. Hayakawa, S. Uno, QED in finite volume and finite size scaling effect on electromagnetic properties of hadrons. Prog. Theor. Phys. 120, 413–441 (2008). https://doi.org/10.1143/PTP.120.413. arXiv:0804.2044
Z. Fodor, C. Hoelbling, S.D. Katz, L. Lellouch, A. Portelli, K.K. Szabo et al., Quantum electrodynamics in finite volume and nonrelativistic effective field theories. Phys. Lett. B 755, 245–248 (2016). https://doi.org/10.1016/j.physletb.2016.01.047. arXiv:1502.06921
N. Tantalo, V. Lubicz, G. Martinelli, C.T. Sachrajda, F. Sanfilippo, S. Simula, Electromagnetic corrections to leptonic decay rates of charged pseudoscalar mesons: finite-volume effects. arXiv:1612.00199
J. Bijnens, J. Harrison, N. Hermansson-Truedsson, T. Janowski, A. Jüttner, A. Portelli, Finite-size effects on the leading electromagnetic corrections to the hadronic vacuum polarisation. Phys. Rev. D 100, 014508 (2019). https://doi.org/10.1103/PhysRevD.100.014508
M. Göckeler, R. Horsley, E. Laermann, P.E.L. Rakow, G. Schierholz, R. Sommer et al., QED: A Lattice Investigation of the chiral phase transition and the nature of the continuum limit. Nucl. Phys. B 334, 527–558 (1990). https://doi.org/10.1016/0550-3213(90)90490-5
M.G. Endres, A. Shindler, B.C. Tiburzi, A. Walker-Loud, Massive photons: an infrared regularization scheme for lattice QCD+QED. Phys. Rev. Lett. 117, 072002 (2016). https://doi.org/10.1103/PhysRevLett.117.072002. arXiv:1507.08916
P. Boyle, V. Gülpers, J. Harrison, A. Jüttner, C. Lehner, A. Portelli et al., Isospin breaking corrections to meson masses and the hadronic vacuum polarization: a comparative study. JHEP 09, 153 (2017). https://doi.org/10.1007/JHEP09(2017)153. arXiv:1706.05293
[RBC/UKQCD 12] R. Arthur et al., Domain wall QCD with near-physical pions. Phys. Rev. D 87 (2013) 094514. https://doi.org/10.1103/PhysRevD.87.094514. arXiv:1208.4412
Y. Maezawa, P. Petreczky, Quark masses and strong coupling constant in 2+1 flavor QCD. Phys. Rev. D 94, 034507 (2016). https://doi.org/10.1103/PhysRevD.94.034507. arXiv:1606.08798
[PACS-CS 12] S. Aoki, K.-I. Ishikawa, N. Ishizuka, K. Kanaya, Y. Kuramashi et al., 1+1+1 flavor QCD + QED simulation at the physical point. Phys. Rev. D 86, 034507 (2012). https://doi.org/10.1103/PhysRevD.86.034507. arXiv:1205.2961
[PACS-CS 10] S. Aoki et al., Non-perturbative renormalization of quark mass in \(N_f = 2+1\) QCD with the Schrödinger functional scheme. JHEP 1008, 101 (2010). https://doi.org/10.1007/JHEP08(2010)101. arXiv:1006.1164
[RBC/UKQCD 10A] Y. Aoki et al., Continuum limit physics from 2+1 flavor domain wall QCD. Phys. Rev. D 83, 074508 (2011). https://doi.org/10.1103/PhysRevD.83.074508. arXiv:1011.0892
[PACS-CS 09] S. Aoki et al., Physical point simulation in 2+1 flavor lattice QCD. Phys. Rev. D 81, 074503 (2010). https://doi.org/10.1103/PhysRevD.81.074503. arXiv:0911.2561
[PACS-CS 08] S. Aoki et al., 2+1 flavor lattice QCD toward the physical point. Phys. Rev. D 79, 034503 (2009). https://doi.org/10.1103/PhysRevD.79.034503. arXiv:0807.1661
[RBC/UKQCD 08] C. Allton et al., Physical results from 2+1 flavor domain wall QCD and SU(2) chiral perturbation theory, Phys. Rev. D 78, 114509 (2008). https://doi.org/10.1103/PhysRevD.78.114509. arXiv:0804.0473
[CP-PACS/JLQCD 07] T. Ishikawa et al., Light quark masses from unquenched lattice QCD. Phys. Rev. D 78, 011502 (2008). https://doi.org/10.1103/PhysRevD.78.011502. arXiv:0704.1937
[HPQCD 05] Q. Mason, H.D. Trottier, R. Horgan, C.T.H. Davies, G.P. Lepage, High-precision determination of the light-quark masses from realistic lattice QCD. Phys. Rev. D 73, 114501 (2006). https://doi.org/10.1103/PhysRevD.73.114501. arXiv:hep-ph/0511160
[MILC 04] C. Aubin et al., Light pseudoscalar decay constants, quark masses and low energy constants from three-flavor lattice QCD. Phys. Rev. D 70, 114501 (2004). https://doi.org/10.1103/PhysRevD.70.114501. arXiv:hep-lat/0407028
[HPQCD/MILC/UKQCD 04] C. Aubin et al., First determination of the strange and light quark masses from full lattice QCD. Phys. Rev. D 70 (2004) 031504. https://doi.org/10.1103/PhysRevD.70.031504. arXiv:hep-lat/0405022
T. van Ritbergen, J.A.M. Vermaseren, S.A. Larin, The four-loop \(\beta \)-function in Quantum Chromodynamics. Phys. Lett. B 400, 379–384 (1997). https://doi.org/10.1016/S0370-2693(97)00370-5. arXiv:hep-ph/9701390
K.G. Chetyrkin, A. Retey, Renormalization and running of quark mass and field in the regularization invariant and \({\overline{{\rm MS}}}\) schemes at three and four loops. Nucl. Phys. B 583, 3–34 (2000). https://doi.org/10.1016/S0550-3213(00)00331-X. arXiv:hep-ph/9910332
Particle Data Group collaboration, K.A. Olive et al., Review of particle physics. Chin. Phys. C 38, 090001 (2014). https://doi.org/10.1088/1674-1137/38/9/090001(2015 update)
[HPQCD 08B] I. Allison et al., High-precision charm-quark mass from current-current correlators in lattice and continuum QCD. Phys. Rev. D 78, 054513 (2008). https://doi.org/10.1103/PhysRevD.78.054513. arXiv:0805.2999
M. Lüscher, R. Narayanan, P. Weisz, U. Wolff, The Schrödinger functional: a renormalizable probe for non-abelian gauge theories. Nucl. Phys. B 384, 168–228 (1992). https://doi.org/10.1016/0550-3213(92)90466-O. arXiv:hep-lat/9207009
C.A. Dominguez, N.F. Nasrallah, R. Röntsch, K. Schilcher, Light quark masses from QCD sum rules with minimal hadronic bias. Nucl. Phys. Proc. Suppl. 186, 133–136 (2009). https://doi.org/10.1016/j.nuclphysbps.2008.12.031. arXiv:0808.3909
K.G. Chetyrkin, A. Khodjamirian, Strange quark mass from pseudoscalar sum rule with \(O(\alpha _s^4)\) accuracy. Eur. Phys. J. C 46, 721–728 (2006). https://doi.org/10.1140/epjc/s2006-02508-8. arXiv:hep-ph/0512295
M. Jamin, J.A. Oller, A. Pich, Scalar \(K\pi \) form factor and light quark masses. Phys. Rev. D 74, 074009 (2006). https://doi.org/10.1103/PhysRevD.74.074009. arXiv:hep-ph/0605095
S. Narison, Strange quark mass from \(e^+e^-\) revisited and present status of light quark masses. Phys. Rev. D 74, 034013 (2006). https://doi.org/10.1103/PhysRevD.74.034013. arXiv:hep-ph/0510108
A.I. Vainshtein et al., Sum rules for light quarks in quantum chromodynamics. Sov. J. Nucl. Phys. 27, 274 (1978)
K. Maltman, J. Kambor, \(m_u+m_d\) from isovector pseudoscalar sum rules. Phys. Lett. B 517, 332–338 (2001). https://doi.org/10.1016/S0370-2693(01)00987-X. arXiv:hep-ph/0107060
[MILC 14] S. Basak et al., Finite-volume effects and the electromagnetic contributions to kaon and pion masses. PoS LATTICE2014, 116 (2014). arXiv:1409.7139
J.A. Oller, L. Roca, Non-perturbative study of the light pseudoscalar masses in chiral dynamics. Eur. Phys. J. A 34, 371–386 (2007). https://doi.org/10.1140/epja/i2006-10516-7. arXiv:hep-ph/0608290
R. Kaiser, The \(\eta \)and the \(\eta ^{\prime }\)at large \(N_c\), diploma work (University of Bern, Bern, 1997) [H. Leutwyler, On the 1/N-expansion in chiral perturbation theory. Nucl. Phys. Proc. Suppl. 64, 223–231 (1998). https://doi.org/10.1016/S0920-5632(97)01065-7. arXiv:hep-ph/9709408]
H. Leutwyler, The ratios of the light quark masses. Phys. Lett. B 378, 313–318 (1996). https://doi.org/10.1016/0370-2693(96)00386-3. arXiv:hep-ph/9602366
S. Weinberg, The problem of mass. Trans. N. Y. Acad. Sci. 38, 185–201 (1977)
R.F. Dashen, Chiral SU(3)\(\times \)SU(3) as a symmetry of the strong interactions. Phys. Rev. 183, 1245–1260 (1969). https://doi.org/10.1103/PhysRev.183.1245
A. Portelli, Inclusion of isospin breaking effects in lattice simulations. PoS LATTICE2014, 013 (2015)
[ETM 10] R. Baron et al., Light hadrons from lattice QCD with light (u, d), strange and charm dynamical quarks. JHEP 1006, 111 (2010). https://doi.org/10.1007/JHEP06(2010)111. arXiv:1004.5284
[MILC 16] S. Basak et al., Electromagnetic effects on the light pseudoscalar mesons and determination of \(m_u/m_d\). PoS LATTICE2015, 259 (2016). arXiv:1606.01228
H. Leutwyler, Light quark masses. PoS CD09, 005 (2009). arXiv:0911.1416
[QCDSF/UKQCD 15] R. Horsley et al., Isospin splittings of meson and baryon masses from three-flavor lattice QCD + QED. J. Phys. G 43, 10LT02 (2016). https://doi.org/10.1088/0954-3899/43/10/10LT02. arXiv:1508.06401
[ALPHA 05] M. Della Morte et al., Non-perturbative quark mass renormalization in two-flavor QCD. Nucl. Phys. B 729, 117–134 (2005). https://doi.org/10.1016/j.nuclphysb.2005.09.028. arXiv:hep-lat/0507035
[BMW 12] A. Portelli, S. Dürr, Z. Fodor, J. Frison, C. Hoelbling et al., Systematic errors in partially-quenched QCD plus QED lattice simulations. PoS LAT2011, 136 (2011). arXiv:1201.2787
J. Gasser, H. Leutwyler, \(\eta \rightarrow 3 \pi \) to one loop. Nucl. Phys. B 250, 539 (1985). https://doi.org/10.1016/0550-3213(85)90494-8
G. Colangelo, S. Lanz, H. Leutwyler, E. Passemar, Dispersive analysis of \(\eta \rightarrow 3 \pi \). Eur. Phys. J. C 78, 947 (2018). https://doi.org/10.1140/epjc/s10052-018-6377-9. arXiv:1807.11937
[JLQCD 15B] K. Nakayama, B. Fahy, S. Hashimoto, Charmonium current-current correlators with Möbius domain-wall fermion. In Proceedings, 33rd International Symposium on Lattice Field Theory (Lattice 2015), vol. LATTICE2015 (2016), p. 267. arXiv:1511.09163
[TUMQCD 17] N. Brambilla, J. Komijani, A.S. Kronfeld, A. Vairo, Relations between Heavy-light Meson and Quark Masses. Phys. Rev. D 97, 034503 (2018). https://doi.org/10.1103/PhysRevD.97.034503. arXiv:1712.04983
[ETM 14B] A. Bussone et al., Heavy flavour precision physics from \(N_f = 2 + 1 + 1\) lattice simulations. In International Conference on High Energy Physics 2014 (ICHEP 2014), vol. 273–275 (Valencia, 2016), pp. 273–275. https://doi.org/10.1016/j.nuclphysbps.2015.09.265. arXiv:1411.0484
[HPQCD 13B] A.J. Lee et al., Mass of the b quark from lattice NRQCD and lattice perturbation theory. Phys. Rev. D 87, 074018 (2013). https://doi.org/10.1103/PhysRevD.87.074018. arXiv:1302.3739
[ALPHA 13C] F. Bernardoni et al., The b-quark mass from non-perturbative \(N_f=2\) Heavy Quark Effective Theory at \(O(1/m_h)\). Phys. Lett. B 730, 171–177 (2014). https://doi.org/10.1016/j.physletb.2014.01.046. arXiv:1311.5498
[ETM 11A] P. Dimopoulos et al., Lattice QCD determination of \(m_b\), \(f_B\) and \(f_{B_s}\) with twisted mass Wilson fermions. JHEP 1201, 046 (2012). https://doi.org/10.1007/JHEP01(2012)046. arXiv:1107.1441
M. Moulson, Experimental determination of \(V_{us}\) from kaon decays. PoS CKM2016, 033 (2017). arXiv:1704.04104
Particle Data Group collaboration, C. Patrignani et al., Review of particle physics. Chin. Phys. C 40, 100001 (2016). https://doi.org/10.1088/1674-1137/40/10/100001
J. Gasser, G.R.S. Zarnauskas, On the pion decay constant. Phys. Lett. B 693, 122–128 (2010). https://doi.org/10.1016/j.physletb.2010.08.021. arXiv:1008.3479
J. Gasser, A. Rusetsky, I. Scimemi, Electromagnetic corrections in hadronic processes. Eur. Phys. J. C 32, 97–114 (2003). https://doi.org/10.1140/epjc/s2003-01383-1. arXiv:hep-ph/0305260
A. Rusetsky, Isospin symmetry breaking. PoS CD09, 071 (2009). arXiv:0910.5151
J. Gasser, Theoretical progress on cusp effect and \(K_{\ell 4}\) decays. PoS KAON07, 033 (2008). arXiv:0710.3048
N. Carrasco, V. Lubicz, G. Martinelli, C.T. Sachrajda, N. Tantalo, C. Tarantino et al., QED corrections to hadronic processes in lattice QCD. Phys. Rev. D 91, 074506 (2015). https://doi.org/10.1103/PhysRevD.91.074506. arXiv:1502.00257
D. Giusti, V. Lubicz, G. Martinelli, C.T. Sachrajda, F. Sanfilippo, S. Simula et al., First lattice calculation of the QED corrections to leptonic decay rates. Phys. Rev. Lett. 120, 072001 (2018). https://doi.org/10.1103/PhysRevLett.120.072001. arXiv:1711.06537
V. Cirigliano, H. Neufeld, A note on isospin violation in \(P_{\ell 2}(\gamma )\) decays. Phys. Lett. B 700, 7–10 (2011). https://doi.org/10.1016/j.physletb.2011.04.038. arXiv:1102.0563
J. Hardy, I.S. Towner, \(|V_{ud}|\) from nuclear \(\beta \) decays. PoS CKM2016, 028 (2016)
I.S. Towner, J.C. Hardy, An improved calculation of the isospin-symmetry- breaking corrections to superallowed Fermi \(\beta \) decay. Phys. Rev. C 77, 025501 (2008). https://doi.org/10.1103/PhysRevC.77.025501. arXiv:0710.3181
G.A. Miller, A. Schwenk, Isospin-symmetry-breaking corrections to superallowed Fermi \(\beta \) decay: formalism and schematic models. Phys. Rev. C 78, 035501 (2008). https://doi.org/10.1103/PhysRevC.78.035501. arXiv:0805.0603
N. Auerbach, Coulomb corrections to superallowed \(\beta \) decay in nuclei. Phys. Rev. C 79, 035502 (2009). https://doi.org/10.1103/PhysRevC.79.035502. arXiv:0811.4742
H. Liang, N. Van Giai, J. Meng, Isospin corrections for superallowed Fermi \(\beta \) decay in self-consistent relativistic random-phase approximation approaches. Phys. Rev. C 79, 064316 (2009). https://doi.org/10.1103/PhysRevC.79.064316. arXiv:0904.3673
G.A. Miller, A. Schwenk, Isospin-symmetry-breaking corrections to superallowed Fermi \(\beta \) decay: radial excitations. Phys. Rev. C 80, 064319 (2009). https://doi.org/10.1103/PhysRevC.80.064319. arXiv:0910.2790
I. Towner, J. Hardy, Comparative tests of isospin-symmetry-breaking corrections to superallowed \(0^+\rightarrow 0^+\) nuclear \(\beta \) decay. Phys. Rev. C 82, 065501 (2010). https://doi.org/10.1103/PhysRevC.82.065501. arXiv:1007.5343
J.C. Hardy, I.S. Towner, Superallowed \(0^+\rightarrow 0^+\) nuclear \(\beta \) decays: 2014 critical survey, with precise results for \(V_{ud}\) and CKM unitarity. Phys. Rev. C C91, 025501 (2015). https://doi.org/10.1103/PhysRevC.91.025501. arXiv:1411.5987
E. Gamiz, M. Jamin, A. Pich, J. Prades, F. Schwab, Determination of \(m_s\) and \(|V_{us}|\) from hadronic \(\tau \) decays. JHEP 01, 060 (2003). arXiv:hep-ph/0212230
E. Gamiz, M. Jamin, A. Pich, J. Prades, F. Schwab, \(V_{us}\) and \(m_s\) from hadronic \(\tau \) decays. Phys. Rev. Lett. 94, 011803 (2005). https://doi.org/10.1103/PhysRevLett.94.011803. arXiv:hep-ph/0408044
K. Maltman, A mixed \(\tau \)-electroproduction sum rule for \(V_{us}\). Phys. Lett. B 672, 257–263 (2009). https://doi.org/10.1016/j.physletb.2009.01.036. arXiv:0811.1590
A. Pich, R. Kass, talks given at CKM 2008. http://ckm2008.roma1.infn.it
[HFLAV 16] Y. Amhis et al., Averages of \(b\)-hadron, \(c\)-hadron, and \(\tau \)-lepton properties as of summer 2016. Eur. Phys. J. C 77, 895 (2017). https://doi.org/10.1140/epjc/s10052-017-5058-4. arXiv:1612.07233
K. Maltman, C.E. Wolfe, S. Banerjee, J.M. Roney, I. Nugent, Status of the hadronic \(\tau \) determination of \(V_{us}\). Int. J. Mod. Phys. A 23, 3191–3195 (2008). https://doi.org/10.1142/S0217751X08041803. arXiv:0807.3195
K. Maltman, C.E. Wolfe, S. Banerjee, I.M. Nugent, J.M. Roney, Status of the hadronic \(\tau \) decay determination of \(|V_{us}|\). Nucl. Phys. Proc. Suppl. 189, 175–180 (2009). https://doi.org/10.1016/j.nuclphysbps.2009.03.031. arXiv:0906.1386
E. Gamiz, M. Jamin, A. Pich, J. Prades, F. Schwab, Theoretical progress on the \(V_{us}\) determination from \(\tau \) decays. PoS KAON07, 008 (2008). arXiv:0709.0282
E. Gamiz, \(|V_{us}|\) from hadronic \(\tau \) decays, CKM (2012). arXiv:1301.2206
R.J. Hudspith, R. Lewis, K. Maltman, J. Zanotti, A resolution of the inclusive flavor-breaking \(\tau \) \(|V_{us}|\) puzzle. Phys. Lett. B 781, 206–212 (2018). https://doi.org/10.1016/j.physletb.2018.03.074. arXiv:1702.01767
[RBC/UKQCD 18] P. Boyle, R.J. Hudspith, T. Izubuchi, A. Jüttner, C. Lehner, R. Lewis et al., \(|Vus|\) determination from inclusive strange tau decay and lattice HVP. EPJ Web Conf. 175 13011 (2018). https://doi.org/10.1051/epjconf/201817513011. arXiv:1803.07228
M. Antonelli et al., An evaluation of \(|V_{us}|\) and precise tests of the Standard Model from world data on leptonic and semileptonic kaon decays. Eur. Phys. J. C 69, 399–424 (2010). https://doi.org/10.1140/epjc/s10052-010-1406-3. arXiv:1005.2323
T. Ishikawa, T. Blum, M. Hayakawa, T. Izubuchi, C. Jung et al., Full QED+QCD low-energy constants through reweighting. Phys. Rev. Lett. 109, 072002 (2012). https://doi.org/10.1103/PhysRevLett.109.072002. arXiv:1202.6018
T. Izubuchi, Lattice QCD + QED - from Isospin breaking to g-2 light-by-light, talk given at Lattice 2012, Cairns, Australia. http://www.physics.adelaide.edu.au/cssm/lattice2012
N. Tantalo, Isospin breaking effects on the lattice. PoS LATTICE2013, 007 (2014). arXiv:1311.2797
[FNAL/MILC 18] A. Bazavov et al., \(|V_{us}|\) from \(K_{\ell 3}\) decay and four-flavor lattice QCD. Phys. Rev. D 99 114509 (2019). https://doi.org/10.1103/PhysRevD.99.114509. arXiv:1809.02827
[FNAL/MILC 13C] E. Gamiz, A. Bazavov, C. Bernard, C. Bouchard, C. DeTar et al., K semileptonic form factor with HISQ fermions at the physical point. PoS LATTICE2013, 395 (2013). arXiv:1311.7264
[JLQCD 17] S. Aoki, G. Cossu, X. Feng, H. Fukaya, S. Hashimoto, T. Kaneko et al., Chiral behavior of \(K \rightarrow \pi l \nu \) decay form factors in lattice QCD with exact chiral symmetry. Phys. Rev. D 96, 034501 (2017). https://doi.org/10.1103/PhysRevD.96.034501. arXiv:1705.00884
[RBC/UKQCD 13] P.A. Boyle, J.M. Flynn, N. Garron, A. Jüttner, C.T. Sachrajda et al., The kaon semileptonic form factor with near physical domain wall quarks. JHEP 1308, 132 (2013). https://doi.org/10.1007/JHEP08(2013)132. arXiv:1305.7217
[JLQCD 12] T. Kaneko et al., Chiral behavior of kaon semileptonic form factors in lattice QCD with exact chiral symmetry. PoS LAT2012, 111 (2012). arXiv:1211.6180
[JLQCD 11] T. Kaneko et al., Kaon semileptonic form factors in QCD with exact chiral symmetry. PoS LAT2011, 284 (2011). arXiv:1112.5259
[RBC/UKQCD 10] P.A. Boyle et al., \(K\rightarrow \pi \) form factors with reduced model dependence. Eur. Phys. J. C 69, 159–167 (2010). https://doi.org/10.1140/epjc/s10052-010-1405-4. arXiv:1004.0886
[RBC/UKQCD 07] P.A. Boyle, A. Jüttner, R. Kenway, C. Sachrajda, S. Sasaki et al., \(K_{l3}\) semileptonic form-factor from 2+1 flavour lattice QCD. Phys.Rev.Lett. 100, 141601 (2008). https://doi.org/10.1103/PhysRevLett.100.141601. arXiv:0710.5136
[ETM 10D] V. Lubicz, F. Mescia, L. Orifici, S. Simula, C. Tarantino, Improved analysis of the scalar and vector form factors of kaon semileptonic decays with \(N_f = 2\) twisted-mass fermions. PoS LAT2010, 316 (2010). arXiv:1012.3573
M. Ademollo, R. Gatto, Nonrenormalization theorem for the strangeness violating vector currents. Phys. Rev. Lett. 13, 264–265 (1964). https://doi.org/10.1103/PhysRevLett.13.264
J. Gasser, H. Leutwyler, Low-energy expansion of meson form factors. Nucl. Phys. B 250, 517–538 (1985). https://doi.org/10.1016/0550-3213(85)90493-6
G. Furlan, F. Lannoy, C. Rossetti, G. Segré, Symmetry-breaking corrections to weak vector currents. Nuovo Cim. 38, 1747 (1965)
J. Gasser, H. Leutwyler, Chiral perturbation theory: expansions in the mass of the strange quark. Nucl. Phys. B 250, 465 (1985). https://doi.org/10.1016/0550-3213(85)90492-4
C. Bernard, J. Bijnens, E. Gamiz, Semileptonic kaon decay in staggered chiral perturbation theory. Phys. Rev. D 89, 054510 (2014). https://doi.org/10.1103/PhysRevD.89.054510. arXiv:1311.7511
[RBC 08A] J.M. Flynn, C.T. Sachrajda, SU(2) chiral perturbation theory for \(K_{\ell 3}\) decay amplitudes. Nucl. Phys. B 812, 64–80 (2009). https://doi.org/10.1016/j.nuclphysb.2008.12.001. arXiv:0809.1229
A. Kastner, H. Neufeld, The \(K_{l3}\) scalar form factors in the Standard Model. Eur. Phys. J. C 57, 541–556 (2008). https://doi.org/10.1140/epjc/s10052-008-0703-6. arXiv:0805.2222
V. Cirigliano et al., The Green function and SU(3) breaking in \(K_{l3}\) decays. JHEP 04, 006 (2005). arXiv:hep-ph/0503108
M. Jamin, J.A. Oller, A. Pich, Order \(p^{6}\) chiral couplings from the scalar \(K \pi \) form factor. JHEP 02, 047 (2004). arXiv:hep-ph/0401080
J. Bijnens, P. Talavera, \(K_{l3}\) decays in chiral perturbation theory. Nucl. Phys. B 669, 341–362 (2003). https://doi.org/10.1016/S0550-3213(03)00581-9. arXiv:hep-ph/0303103
H. Leutwyler, M. Roos, Determination of the elements \(V_{us}\) and \(V_{ud}\) of the Kobayashi-Maskawa matrix. Z. Phys. C 25, 91 (1984). https://doi.org/10.1007/BF01571961
P. Post, K. Schilcher, \(K_{l3}\) form factors at order \(p^6\) in chiral perturbation theory. Eur. Phys. J. C 25, 427–443 (2002). https://doi.org/10.1007/s10052-002-0967-1. arXiv:hep-ph/0112352
V. Bernard, E. Passemar, Matching chiral perturbation theory and the dispersive representation of the scalar K pi form-factor. Phys. Lett. B 661, 95–102 (2008). https://doi.org/10.1016/j.physletb.2008.02.004. arXiv:0711.3450
[MILC 08] S. Basak et al., Electromagnetic splittings of hadrons from improved staggered quarks in full QCD. PoS LAT2008, 127 (2008). arXiv:0812.4486
[BMW 10C] A. Portelli et al., Electromagnetic corrections to light hadron masses. PoS LAT2010, 121 (2010). arXiv:1011.4189
[ETM 13F] P. Dimopoulos, R. Frezzotti, P. Lami, V. Lubicz, E. Picca et al., Pseudoscalar decay constants \(f_K/f_\pi \), \(f_D\) and \(f_{D_s}\) with \(N_f = 2 + 1 + 1\) ETMC configurations. PoS LATTICE2013, 314 (2014). arXiv:1311.3080
[MILC 13A] A. Bazavov, C. Bernard, C. DeTar, J. Foley, W. Freeman et al., Leptonic decay-constant ratio \(f_{K^+}/f_{\pi ^+}\) from lattice QCD with physical light quarks. Phys. Rev. Lett. 110, 172003 (2013). https://doi.org/10.1103/PhysRevLett.110.172003. arXiv:1301.5855
[MILC 11] A. Bazavov et al., Properties of light pseudoscalars from lattice QCD with HISQ ensembles. PoS LAT2011, 107 (2011). arXiv:1111.4314
[ETM 10E] F. Farchioni, G. Herdoiza, K. Jansen, M. Petschlies, C. Urbach et al., Pseudoscalar decay constants from \(N_f=2+1+1\) twisted mass lattice QCD. PoS LAT2010, 128 (2010). arXiv:1012.0200
E.E. Scholz, S. Dürr, Leptonic decay-constant ratio \(f_K/f_\pi \) from clover-improved \(N_f=2+1\) QCD. PoS LATTICE2016, 283 (2016). arXiv:1610.00932
[JLQCD/TWQCD 10] J. Noaki et al., Chiral properties of light mesons in \(N_f = 2+1\) overlap QCD. PoS LAT2010, 117 (2010)
C. Aubin, J. Laiho, R.S. Van de Water, Light pseudoscalar meson masses and decay constants from mixed action lattice QCD. PoS LAT2008, 105 (2008). arXiv:0810.4328
[ETM 14D] A. Abdel-Rehim, C. Alexandrou, P. Dimopoulos, R. Frezzotti, K. Jansen et al., Progress in simulations with twisted mass fermions at the physical point. PoS LATTICE2014, 119 (2014). arXiv:1411.6842
[ALPHA 13A] S. Lottini, Chiral behaviour of the pion decay constant in \(N_f=2\) QCD. PoS LATTICE2013, 315 (2013). arXiv:1311.3081
[QCDSF/UKQCD 07] G. Schierholz et al., Probing the chiral limit with clover fermions I: the meson sector, talk given at Lattice, Regensburg, Germany. PoS LAT2007, 133 (2007)
D. Guadagnoli, F. Mescia, S. Simula, Lattice study of semileptonic form-factors with twisted boundary conditions. Phys. Rev. D 73, 114504 (2006). https://doi.org/10.1103/PhysRevLett.110.172003. arXiv:hep-lat/0512020
[UKQCD 07] P.A. Boyle, J. Flynn, A. Jüttner, C. Sachrajda, J. Zanotti, Hadronic form factors in lattice QCD at small and vanishing momentum transfer. JHEP 0705, 016 (2007). https://doi.org/10.1088/1126-6708/2007/05/016. arXiv:hep-lat/0703005
[SPQcdR 04] D. Bećirević et al., The \(K \rightarrow \pi \) vector form factor at zero momentum transfer on the lattice. Nucl. Phys. B 705, 339–362 (2005). https://doi.org/10.1016/j.nuclphysb.2004.11.017. arXiv:hep-ph/0403217
C. Bernard, J. Bijnens, E. Gámiz, J. Relefors, Twisted finite-volume corrections to \(K_{l3}\) decays with partially-quenched and rooted-staggered quarks. JHEP 03, 120 (2017). https://doi.org/10.1007/JHEP03(2017)120. arXiv:1702.03416
G. Amoros, J. Bijnens, P. Talavera, QCD isospin breaking in meson masses, decay constants and quark mass ratios. Nucl. Phys. B 602, 87–108 (2001). https://doi.org/10.1016/S0550-3213(01)00121-3. arXiv:hep-ph/0101127
M. Lüscher, Properties and uses of the Wilson flow in lattice QCD. JHEP 08, 071 (2010). https://doi.org/10.1007/JHEP08(2010)071, https://doi.org/10.1007/JHEP03(2014)092. arXiv:1006.4518
[BMW 12A] S. Borsanyi, S. Dürr, Z. Fodor, C. Hoelbling, S.D. Katz et al., High-precision scale setting in lattice QCD. JHEP 1209, 010 (2012). https://doi.org/10.1007/JHEP09(2012)010. arXiv:1203.4469
D. Giusti, V. Lubicz, G. Martinelli, F. Sanfilippo, S. Simula, N. Tantalo et al., Leading isospin-breaking corrections to meson masses on the lattice. EPJ Web Conf. 175, 06002 (2018). https://doi.org/10.1051/epjconf/201817506002. arXiv:1710.06633
C.-Y. Seng, M. Gorchtein, H.H. Patel, M.J. Ramsey-Musolf, Reduced hadronic uncertainty in the determination of \(V_{ud}\). Phys. Rev. Lett. 121, 241804 (2018). https://doi.org/10.1103/PhysRevLett.121.241804. arXiv:1807.10197
[JLQCD 15C] B. Fahy, G. Cossu, S. Hashimoto, T. Kaneko, J. Noaki, M. Tomii, Decay constants and spectroscopy of mesons in lattice QCD using domain-wall fermions. PoS LATTICE2015, 074 (2016). arXiv:1512.08599
[HPQCD 09B] C.T.H. Davies, E. Follana, I. Kendall, G.P. Lepage, C. McNeile, Precise determination of the lattice spacing in full lattice QCD. Phys. Rev. D 81, 034506 (2010). https://doi.org/10.1103/PhysRevD.81.034506. arXiv:0910.1229
J. Gasser, H. Leutwyler, Chiral perturbation theory to one loop. Ann. Phys. 158, 142 (1984). https://doi.org/10.1016/0003-4916(84)90242-2
J. Bijnens, G. Ecker, Mesonic low-energy constants. Ann. Rev. Nucl. Part. Sci. 64, 149–174 (2014). https://doi.org/10.1146/annurev-nucl-102313-025528. arXiv:1405.6488
S.R. Sharpe, Applications of chiral perturbation theory to lattice QCD (Nara, Japan, 2005). arXiv:hep-lat/0607016
M. Golterman, Applications of chiral perturbation theory to lattice QCD. In Modern perspectives in lattice QCD: Quantum field theory and high performance computing. Proceedings, International School, 93rd Session, Les Houches, France, August 3–28, 2009 (2009), pp. 423–515. arXiv:0912.4042
C. Bernard, Effective field theories and lattice QCD. PoS CD15, 004 (2015). arXiv:1510.02180
M.E. Fisher, V. Privman, First-order transitions breaking O(n) symmetry: finite-size scaling. Phys. Rev. B 32, 447–464 (1985). https://doi.org/10.1103/PhysRevB.32.447
E. Brezin, J. Zinn-Justin, Finite size effects in phase transitions. Nucl. Phys. B 257, 867 (1985). https://doi.org/10.1016/0550-3213(85)90379-7
J. Gasser, H. Leutwyler, Light quarks at low temperatures. Phys. Lett. B 184, 83 (1987). https://doi.org/10.1016/0370-2693(87)90492-8
J. Gasser, H. Leutwyler, Thermodynamics of chiral symmetry. Phys. Lett. B 188, 477 (1987). https://doi.org/10.1016/0370-2693(87)91652-2
J. Gasser, H. Leutwyler, Spontaneously broken symmetries: effective Lagrangians at finite volume. Nucl. Phys. B 307, 763 (1988). https://doi.org/10.1016/0550-3213(88)90107-1
P. Hasenfratz, H. Leutwyler, Goldstone boson related finite size effects in field theory and critical phenomena with O(N) symmetry. Nucl. Phys. B 343, 241–284 (1990). https://doi.org/10.1016/0550-3213(90)90603-B
G. Colangelo, J. Gasser, H. Leutwyler, \(\pi \pi \) scattering. Nucl. Phys. B 603, 125–179 (2001). https://doi.org/10.1016/S0550-3213(01)00147-X. arXiv:hep-ph/0103088
G. Amoros, J. Bijnens, P. Talavera, Two point functions at two loops in three flavor chiral perturbation theory. Nucl. Phys. B 568, 319–363 (2000). https://doi.org/10.1016/S0550-3213(99)00674-4. arXiv:hep-ph/9907264
J.F. Donoghue, J. Gasser, H. Leutwyler, The decay of a light Higgs boson. Nucl. Phys. B 343, 341–368 (1990). https://doi.org/10.1016/0550-3213(90)90474-R
J. Bijnens, G. Colangelo, P. Talavera, The vector and scalar form factors of the pion to two loops. JHEP 05, 014 (1998). arXiv:hep-ph/9805389
[JLQCD/TWQCD 08] T. Kaneko et al., Pion vector and scalar form factors with dynamical overlap quarks. PoS LAT2008, 158 (2008). arXiv:0810.2590
A. Jüttner, Revisiting the pion’s scalar form factor in chiral perturbation theory. JHEP 1201, 007 (2012). https://doi.org/10.1007/JHEP01(2012)007. arXiv:1110.4859
S. Weinberg, Pion scattering lengths. Phys. Rev. Lett. 17, 616–621 (1966). https://doi.org/10.1103/PhysRevLett.17.616
J. Gasser, H. Leutwyler, Low-energy theorems as precision tests of QCD. Phys. Lett. 125B, 325–329 (1983). https://doi.org/10.1016/0370-2693(83)91294-7
J. Bijnens, G. Colangelo, G. Ecker, J. Gasser, M.E. Sainio, Elastic pi pi scattering to two loops. Phys. Lett. B 374, 210–216 (1996). https://doi.org/10.1016/0370-2693(96)00165-7. arXiv:hep-ph/9511397
J. Nebreda, J.R. Pelaez., Strange and non-strange quark mass dependence of elastic light resonances from SU(3) unitarized chiral perturbation theory to one loop. Phys. Rev. D 81, 054035 (2010). https://doi.org/10.1103/PhysRevD.81.054035. arXiv:1001.5237
L. Maiani, M. Testa, Final state interactions from Euclidean correlation functions. Phys. Lett. B 245, 585–590 (1990). https://doi.org/10.1016/0370-2693(90)90695-3
M. Lüscher, Volume dependence of the energy spectrum in massive quantum field theories. 1. Stable particle states. Commun. Math. Phys. 104, 177 (1986). https://doi.org/10.1007/BF01211589
M. Lüscher, Volume dependence of the energy spectrum in massive quantum field theories. 2. Scattering states. Commun. Math. Phys. 105, 153–188 (1986). https://doi.org/10.1007/BF01211097
M. Lüscher, Two particle states on a torus and their relation to the scattering matrix. Nucl. Phys. B 354, 531–578 (1991). https://doi.org/10.1016/0550-3213(91)90366-6
M. Lüscher, Signatures of unstable particles in finite volume. Nucl. Phys. B 364, 237–254 (1991). https://doi.org/10.1016/0550-3213(91)90584-K
S.M. Roy, Exact integral equation for pion pion scattering involving only physical region partial waves. Phys. Lett. 36B, 353–356 (1971). https://doi.org/10.1016/0370-2693(71)90724-6
B. Ananthanarayan, G. Colangelo, J. Gasser, H. Leutwyler, Roy equation analysis of pi pi scattering. Phys. Rept. 353, 207–279 (2001). https://doi.org/10.1016/S0370-1573(01)00009-6. arXiv:hep-ph/0005297
I. Caprini, G. Colangelo, H. Leutwyler, Regge analysis of the pi pi scattering amplitude. Eur. Phys. J. C 72, 1860 (2012). arXiv:1111.7160
[NPLQCD 07] S.R. Beane et al., Precise determination of the I=2 \(\pi \pi \) scattering length from mixed-action lattice QCD. Phys. Rev. D 77, 014505 (2008). https://doi.org/10.1103/PhysRevD.77.014505. arXiv:0706.3026
[ETM 09G] X. Feng, K. Jansen, D.B. Renner, The pi+ pi+ scattering length from maximally twisted mass lattice QCD. Phys. Lett. B 684, 268–274 (2010). https://doi.org/10.1016/j.physletb.2010.01.018. arXiv:0909.3255
Z. Fu, Lattice QCD study of the s-wave \(\pi \pi \) scattering lengths in the I=0 and 2 channels. Phys. Rev. D 87, 074501 (2013). https://doi.org/10.1103/PhysRevD.87.074501. arXiv:1303.0517
[ETM 15E] C. Helmes, C. Jost, B. Knippschild, C. Liu, J. Liu, L. Liu et al., Hadron–hadron interactions from N\(_{f}\) = 2 + 1 + 1 lattice QCD: isospin-2 \(\pi \)-\(\pi \) scattering length. JHEP 09, 109 (2015). https://doi.org/10.1007/JHEP09(2015)109. arXiv:1506.00408
[ETM 16C] L. Liu et al., Isospin-0 \(\pi \pi \) s-wave scattering length from twisted mass lattice QCD. Phys. Rev. D 96, 054516 (2017). https://doi.org/10.1103/PhysRevD.96.054516. arXiv:1612.02061
J.-W. Chen, D. O’Connell, R.S. Van de Water, A. Walker-Loud, Ginsparg-Wilson pions scattering on a staggered sea. Phys. Rev. D 73, 074510 (2006). https://doi.org/10.1103/PhysRevD.73.074510. arXiv:hep-lat/0510024
M.I. Buchoff, Isotropic and anisotropic lattice spacing corrections for I=2 pi-pi Scattering from Effective Field Theory. Phys. Rev. D 77, 114502 (2008). https://doi.org/10.1103/PhysRevD.73.074510. arXiv:0802.2931
S. Aoki, O. Bar, B. Biedermann, Pion scattering in Wilson chiral perturbation theory. Phys. Rev. D 78, 114501 (2008). https://doi.org/10.1103/PhysRevD.78.114501. arXiv:0806.4863
N.R. Acharya, F.-K. Guo, U.-G. Meissner, C.-Y. Seng, Connected and disconnected contractions in pion-pion scattering. Nucl. Phys. B 922, 480–498 (2017). https://doi.org/10.1016/j.nuclphysb.2017.07.012. arXiv:1704.06754
J. Bijnens, N. Danielsson, T.A. Lähde, Three-flavor partially quenched chiral perturbation theory at NNLO for meson masses and decay constants. Phys. Rev. D 73, 074509 (2006). https://doi.org/10.1103/PhysRevD.73.074509c. arXiv:hep-lat/0602003
J. Bijnens, I. Jemos, A new global fit of the \(L^r_i\) at next-to-next-to-leading order in chiral perturbation theory. Nucl. Phys. B 854, 631–665 (2012). https://doi.org/10.1016/j.nuclphysb.2011.09.013. arXiv:1103.5945
X. Du, Staggered chiral perturbation theory in the two-flavor case. Phys. Rev. D 82, 014016 (2010). https://doi.org/10.1103/PhysRevD.82.014016. arXiv:0911.2534
C. Bernard, M. Golterman, On the foundations of partially quenched chiral perturbation theory. Phys. Rev. D 88, 014004 (2013). https://doi.org/10.1103/PhysRevD.88.014004. arXiv:1304.1948
J. Bijnens, E. Bostrom, T.A. Lahde, Two-loop sunset integrals at finite volume. JHEP 01, 019 (2014). https://doi.org/10.1007/JHEP01(2014)019. arXiv:1311.3531
J. Bijnens, T. Rossler, Finite volume at two-loops in chiral perturbation theory. JHEP 01, 034 (2015). https://doi.org/10.1007/JHEP01(2015)034. arXiv:1411.6384
J. Bijnens, T. Rössler, Finite volume for three-flavour partially quenched chiral perturbation theory through NNLO in the Meson sector. JHEP 11, 097 (2015). https://doi.org/10.1007/JHEP11(2015)097. arXiv:1508.07238
O. Bär, G. Rupak, N. Shoresh, Simulations with different lattice Dirac operators for valence and sea quarks. Phys. Rev. D 67, 114505 (2003). https://doi.org/10.1103/PhysRevD.67.114505. arXiv:hep-lat/0210050
O. Bär, G. Rupak, N. Shoresh, Chiral perturbation theory at \(O(a^2)\) for lattice QCD. Phys. Rev. D 70, 034508 (2004). https://doi.org/10.1103/PhysRevD.70.034508. arXiv:hep-lat/0306021
O. Bär, C. Bernard, G. Rupak, N. Shoresh, Chiral perturbation theory for staggered sea quarks and Ginsparg-Wilson valence quarks. Phys. Rev. D 72, 054502 (2005). https://doi.org/10.1103/PhysRevD.72.054502. arXiv:hep-lat/0503009
J.-W. Chen, M. Golterman, D. O’Connell, A. Walker-Loud, Mixed action effective field theory: an addendum. Phys. Rev. D 79, 117502 (2009). https://doi.org/10.1103/PhysRevD.79.117502. arXiv:0905.2566
[SWME 10] T. Bae et al., \(B_K\) using HYP-smeared staggered fermions in \(N_f=2+1\) unquenched QCD. Phys. Rev. D 82, 114509 (2010). https://doi.org/10.1103/PhysRevD.82.114509. arXiv:1008.5179
J.A. Bailey, H.-J. Kim, W. Lee, S.R. Sharpe, Kaon mixing matrix elements from beyond-the-Standard-Model operators in staggered chiral perturbation theory. Phys. Rev. D 85, 074507 (2012). https://doi.org/10.1103/PhysRevD.85.074507. arXiv:1202.1570
[SWME 15] J.A. Bailey, H.-J. Kim, J. Kim, W. Lee, B. Yoon, Masses and decay constants of pions and kaons in mixed-action staggered chiral perturbation theory. Phys. Rev. D 96, 034522 (2017). https://doi.org/10.1103/PhysRevD.96.034522. arXiv:1504.02573
H. Leutwyler, A.V. Smilga, Spectrum of Dirac operator and role of winding number in QCD. Phys. Rev. D 46, 5607–5632 (1992). https://doi.org/10.1103/PhysRevD.46.5607
F.C. Hansen, Finite size effects in spontaneously broken SU(N)\(\times \)SU(N) theories. Nucl. Phys. B 345, 685–708 (1990). https://doi.org/10.1016/0550-3213(90)90405-3
F.C. Hansen, H. Leutwyler, Charge correlations and topological susceptibility in QCD. Nucl. Phys. B 350, 201–227 (1991). https://doi.org/10.1016/0550-3213(91)90259-Z
L. Giusti, P. Hernandez, M. Laine, P. Weisz, H. Wittig, Low-energy couplings of QCD from current correlators near the chiral limit. JHEP 0404, 013 (2004). https://doi.org/10.1088/1126-6708/2004/04/013. arXiv:hep-lat/0402002
P.H. Damgaard, M.C. Diamantini, P. Hernandez, K. Jansen, Finite-size scaling of meson propagators. Nucl. Phys. B 629, 445–478 (2002). https://doi.org/10.1016/S0550-3213(02)00145-1. arXiv:hep-lat/0112016
P.H. Damgaard, P. Hernandez, K. Jansen, M. Laine, L. Lellouch, Finite-size scaling of vector and axial current correlators. Nucl. Phys. B 656, 226–238 (2003). https://doi.org/10.1016/S0550-3213(03)00117-2. arXiv:hep-lat/0211020
S. Aoki, H. Fukaya, Chiral perturbation theory in a \(\theta \) vacuum. Phys. Rev. D 81, 034022 (2010). https://doi.org/10.1103/PhysRevD.81.034022. arXiv:0906.4852
R. Sommer, A new way to set the energy scale in lattice gauge theories and its applications to the static force and \(\alpha _s\) in SU(2) Yang-Mills theory. Nucl. Phys. B 411, 839–854 (1994). https://doi.org/10.1016/0550-3213(94)90473-1. arXiv:hep-lat/9310022
F. Bernardoni, P.H. Damgaard, H. Fukaya, P. Hernandez, Finite volume scaling of Pseudo Nambu-Goldstone Bosons in QCD. JHEP 10, 008 (2008). https://doi.org/10.1088/1126-6708/2008/10/008. arXiv:0808.1986
P. Hernandez, S. Necco, C. Pena, G. Vulvert, \(N_f=2\) chiral dynamics in the mixed chiral regime. PoS LAT2012, 204 (2012). arXiv:1211.1488
P.H. Damgaard, H. Fukaya, The chiral condensate in a finite volume. JHEP 01, 052 (2009). https://doi.org/10.1088/1126-6708/2009/01/052. arXiv:0812.2797
S. Aoki, H. Fukaya, Interpolation between the \(\epsilon \)- and p-regimes. Phys. Rev. D 84, 014501 (2011). https://doi.org/10.1103/PhysRevD.84.014501. arXiv:1105.1606
H. Fukaya, T. Suzuki, Extracting the electromagnetic pion form factor from QCD in a finite volume. Phys. Rev. D 90, 114508 (2014). https://doi.org/10.1103/PhysRevD.90.114508. arXiv:1409.0327
H. Leutwyler, Energy levels of light quarks confined to a box. Phys. Lett. B 189, 197 (1987). https://doi.org/10.1016/0370-2693(87)91296-2
P. Hasenfratz, The QCD rotator in the chiral limit. Nucl. Phys. B 828, 201–214 (2010). https://doi.org/10.1016/j.nuclphysb.2009.11.015. arXiv:0909.3419
F. Niedermayer, C. Weiermann, The rotator spectrum in the \(\delta \)-regime of the O(n) effective field theory in 3 and 4 dimensions. Nucl. Phys. B 842, 248–263 (2011). https://doi.org/10.1016/j.nuclphysb.2010.09.007. arXiv:1006.5855
M. Weingart, The QCD rotator with a light quark mass. arXiv:1006.5076
A. Hasenfratz, P. Hasenfratz, F. Niedermayer, D. Hierl, A. Schäfer, First results in QCD with 2+1 light flavors using the fixed-point action. PoS LAT2006, 178 (2006). arXiv:hep-lat/0610096
[QCDSF 10] W. Bietenholz et al., Pion in a box. Phys. Lett. B 687, 410–414 (2010). https://doi.org/10.1016/j.physletb.2010.03.063. arXiv:1002.1696
M.E. Matzelle, B.C. Tiburzi, Low-Energy QCD in the Delta Regime. Phys. Rev. D 93, 034506 (2016). https://doi.org/10.1103/PhysRevD.93.034506. arXiv:1512.05286
F. Niedermayer, P. Weisz, Matching effective chiral Lagrangians with dimensional and lattice regularizations. JHEP 04, 110 (2016). https://doi.org/10.1007/JHEP04(2016)110. arXiv:1601.00614
P. Di Vecchia, G. Veneziano, Chiral dynamics in the large N limit. Nucl. Phys. B 171, 253 (1980). https://doi.org/10.1016/0550-3213(80)90370-3
[TWQCD 09] Y.-Y. Mao, T.-W. Chiu, Topological susceptibility to the one-loop order in chiral perturbation theory. Phys. Rev. D 80, 034502 (2009). https://doi.org/10.1103/PhysRevD.80.034502. arXiv:0903.2146
V. Bernard, S. Descotes-Genon, G. Toucas, Topological susceptibility on the lattice and the three-flavour quark condensate. JHEP 1206, 051 (2012). https://doi.org/10.1007/JHEP06(2012)051. arXiv:1203.0508
V. Bernard, S. Descotes-Genon, G. Toucas, Determining the chiral condensate from the distribution of the winding number beyond topological susceptibility. JHEP 12, 080 (2012). https://doi.org/10.1007/JHEP12(2012)080. arXiv:1209.4367
[CERN 08] L. Giusti, M. Lüscher, Chiral symmetry breaking and the Banks-Casher relation in lattice QCD with Wilson quarks. JHEP 03, 013 (2009). https://doi.org/10.1088/1126-6708/2009/03/013. arXiv:0812.3638
T. Banks, A. Casher, Chiral symmetry breaking in confining theories. Nucl. Phys. B 169, 103 (1980). https://doi.org/10.1016/0550-3213(80)90255-2
G.P. Engel, L. Giusti, S. Lottini, R. Sommer, Chiral symmetry breaking in QCD with two light flavors. Phys. Rev. Lett. 114, 112001 (2015). https://doi.org/10.1103/PhysRevLett.114.112001. arXiv:1406.4987
S.R. Sharpe, Discretization errors in the spectrum of the Hermitian Wilson-Dirac operator. Phys. Rev. D 74, 014512 (2006). https://doi.org/10.1103/PhysRevD.74.014512. arXiv:hep-lat/0606002
S. Necco, A. Shindler, Corrections to the Banks-Casher relation with Wilson quarks. PoS CD12, 056 (2012). arXiv:1302.5595
E.V. Shuryak, J.J.M. Verbaarschot, Random matrix theory and spectral sum rules for the Dirac operator in QCD. Nucl. Phys. A 560, 306–320 (1993). https://doi.org/10.1016/0375-9474(93)90098-I. arXiv:hep-th/9212088
J.J.M. Verbaarschot, I. Zahed, Spectral density of the QCD Dirac operator near zero virtuality. Phys. Rev. Lett. 70, 3852–3855 (1993). https://doi.org/10.1103/PhysRevLett.70.3852. arXiv:hep-th/9303012
J.J.M. Verbaarschot, The spectrum of the QCD Dirac operator and chiral random matrix theory: the threefold way. Phys. Rev. Lett. 72, 2531–2533 (1994). https://doi.org/10.1103/PhysRevLett.72.2531. arXiv:hep-th/9401059
J.J.M. Verbaarschot, T. Wettig, Random matrix theory and chiral symmetry in QCD. Ann. Rev. Nucl. Part. Sci. 50, 343–410 (2000). https://doi.org/10.1146/annurev.nucl.50.1.343. arXiv:hep-ph/0003017
S.M. Nishigaki, P.H. Damgaard, T. Wettig, Smallest Dirac eigenvalue distribution from random matrix theory. Phys. Rev. D 58, 087704 (1998). https://doi.org/10.1103/PhysRevD.58.087704. arXiv:hep-th/9803007
P.H. Damgaard, S.M. Nishigaki, Distribution of the k-th smallest Dirac operator eigenvalue. Phys. Rev. D 63, 045012 (2001). https://doi.org/10.1103/PhysRevD.63.045012. arXiv:hep-th/0006111
F. Basile, G. Akemann, Equivalence of QCD in the \(\epsilon \)-regime and chiral random matrix theory with or without chemical potential. JHEP 12, 043 (2007). https://doi.org/10.1088/1126-6708/2007/12/043. arXiv:0710.0376
M. Kieburg, J.J.M. Verbaarschot, S. Zafeiropoulos, Random matrix models for the hermitian Wilson-Dirac operator of QCD-like theories. PoS LAT2012, 209 (2012). arXiv:1303.3242
G. Akemann, P.H. Damgaard, J.C. Osborn, K. Splittorff, A new chiral two-matrix theory for Dirac spectra with imaginary chemical potential. Nucl. Phys. B 766, 34–67 (2007). https://doi.org/10.1016/j.nuclphysb.2006.12.016. arXiv:hep-th/0609059
C. Lehner, S. Hashimoto, T. Wettig, The \(\epsilon \)-expansion at next-to-next-to-leading order with small imaginary chemical potential. JHEP 06, 028 (2010). https://doi.org/10.1007/JHEP06(2010)028. arXiv:1004.5584
C. Lehner, J. Bloch, S. Hashimoto, T. Wettig, Geometry dependence of RMT-based methods to extract the low-energy constants \(\Sigma \) and F. JHEP 1105, 115 (2011). https://doi.org/10.1007/JHEP05(2011)115. arXiv:1101.5576
[CERN-TOV 05] L. Del Debbio, L. Giusti, M. Lüscher, R. Petronzio, N. Tantalo, Stability of lattice QCD simulations and the thermodynamic limit. JHEP 02, 011 (2006). arXiv:hep-lat/0512021
[JLQCD/TWQCD 07B] H. Fukaya et al., Two-flavor lattice QCD in the \(\epsilon \)-regime and chiral random matrix theory. Phys. Rev. D 76, 054503 (2007). https://doi.org/10.1103/PhysRevD.76.054503. arXiv:0705.3322
[BGR 06] C.B. Lang, P. Majumdar, W. Ortner, The condensate for two dynamical chirally improved quarks in QCD. Phys. Lett. B 649, 225–229 (2007). https://doi.org/10.1016/j.physletb.2007.03.059. arXiv:hep-lat/0611010
T. DeGrand, Z. Liu, S. Schaefer, Quark condensate in two-flavor QCD. Phys. Rev. D 74, 094504 (2006). https://doi.org/10.1103/PhysRevD.74.094504. arXiv:hep-lat/0608019
P. Hasenfratz et al., 2+1 flavor QCD simulated in the \(\epsilon \)-regime in different topological sectors. JHEP 11, 100 (2009). https://doi.org/10.1088/1126-6708/2009/11/100. arXiv:0707.0071
T. DeGrand, S. Schaefer, Parameters of the lowest order chiral Lagrangian from fermion eigenvalues. Phys. Rev. D 76, 094509 (2007). https://doi.org/10.1103/PhysRevD.76.094509. arXiv:0708.1731
[JLQCD/TWQCD 08A] J. Noaki et al., Convergence of the chiral expansion in two-flavor lattice QCD. Phys. Rev. Lett. 101, 202004 (2008). https://doi.org/10.1103/PhysRevLett.101.202004. arXiv:0806.0894
J. Gasser, C. Haefeli, M.A. Ivanov, M. Schmid, Integrating out strange quarks in ChPT. Phys. Lett. B 652, 21–26 (2007). https://doi.org/10.1016/j.physletb.2007.06.058. arXiv:0706.0955
J. Gasser, C. Haefeli, M.A. Ivanov, M. Schmid, Integrating out strange quarks in ChPT: terms at order \(p^6\). Phys. Lett. B 675, 49–53 (2009). https://doi.org/10.1016/j.physletb.2009.03.056. arXiv:0903.0801
S. Dürr, Convergence issues in ChPT: a lattice perspective. PoS KAON13, 027 (2013). arXiv:1305.5758
G. Rupak, N. Shoresh, Chiral perturbation theory for the Wilson lattice action. Phys. Rev. D 66, 054503 (2002). https://doi.org/10.1103/PhysRevD.66.054503. arXiv:hep-lat/0201019
S. Aoki, Chiral perturbation theory with Wilson-type fermions including \(a^2\) effects: \(N_f = 2\) degenerate case. Phys. Rev. D 68, 054508 (2003). https://doi.org/10.1103/PhysRevD.68.054508. arXiv:hep-lat/0306027
C. Aubin, C. Bernard, Pion and kaon masses in staggered chiral perturbation theory. Phys. Rev. D 68, 034014 (2003). https://doi.org/10.1103/PhysRevD.68.034014. arXiv:hep-lat/0304014
C. Aubin, C. Bernard, Pseudoscalar decay constants in staggered chiral perturbation theory. Phys. Rev. D 68, 074011 (2003). https://doi.org/10.1103/PhysRevD.68.074011. arXiv:hep-lat/0306026
O. Bär, B. Horz, Charmless chiral perturbation theory for \(N_f=2+1+1\) twisted mass lattice QCD. Phys. Rev. D 90, 034508 (2014). https://doi.org/10.1103/PhysRevD.90.034508. arXiv:1402.6145
[ETM 13A] G. Herdoiza, K. Jansen, C. Michael, K. Ottnad, C. Urbach, Determination of low-energy constants of Wilson chiral perturbation theory. JHEP 1305, 038 (2013). https://doi.org/10.1007/JHEP05(2013)038. arXiv:1303.3516
[ETM 15A] A. Abdel-Rehim et al., Simulating QCD at the physical point with \(N_f=2\) Wilson twisted mass fermions at maximal twist. Phys. Rev. D 95 094515, (2015). https://doi.org/10.1103/PhysRevD.95.094515. arXiv:1507.05068
[HPQCD 15B] J. Koponen, F. Bursa, C.T.H. Davies, R.J. Dowdall, G.P. Lepage, The size of the pion from full lattice QCD with physical \(u\), \(d\), \(s\) and \(c\) Quarks. Phys. Rev. D 93 054503 (2016). https://doi.org/10.1103/PhysRevD.93.054503. arXiv:1511.07382
[JLQCD 09] H. Fukaya et al., Determination of the chiral condensate from 2+1-flavor lattice QCD. Phys. Rev. Lett. 104, 122002 (2010). https://doi.org/10.1103/PhysRevLett.104.122002. arXiv:0911.5555
[JLQCD/TWQCD 10A] H. Fukaya et al., Determination of the chiral condensate from QCD Dirac spectrum on the lattice. Phys. Rev. D 83, 074501 (2011). https://doi.org/10.1103/PhysRevD.83.074501. arXiv:1012.4052
[RBC/UKQCD 08A] P.A. Boyle et al., The pion’s electromagnetic form factor at small momentum transfer in full lattice QCD. JHEP 07, 112 (2008). https://doi.org/10.1088/1126-6708/2008/07/112. arXiv:0804.3971
[TWQCD 08] T.-W. Chiu, T.-H. Hsieh, P.-K. Tseng, Topological susceptibility in 2+1 flavors lattice QCD with domain-wall fermions. Phys. Lett. B 671, 135–138 (2009). https://doi.org/10.1016/j.physletb.2008.11.058. arXiv:0810.3406
[ETM 12] F. Burger, V. Lubicz, M. Muller-Preussker, S. Simula, C. Urbach, Quark mass and chiral condensate from the Wilson twisted mass lattice quark propagator. Phys. Rev. D 87, 034514 (2013). https://doi.org/10.1103/PhysRevD.87.034514, https://doi.org/10.1103/PhysRevD.87.079904. arXiv:1210.0838
F. Bernardoni, N. Garron, P. Hernandez, S. Necco, C. Pena, Light quark correlators in a mixed-action setup. PoS LAT2011, 109 (2011). arXiv:1110.0922
[TWQCD 11] T.-W. Chiu, T.-H. Hsieh, Y.-Y. Mao, Pseudoscalar meson in two flavors QCD with the optimal domain-wall fermion. Phys. Lett. B 717, 420–424 (2012). https://doi.org/10.1016/j.physletb.2012.09.067. arXiv:1109.3675
[TWQCD 11A] T.-W. Chiu, T.H. Hsieh, Y.Y. Mao, Topological susceptibility in two flavors lattice QCD with the optimal domain-wall fermion. Phys. Lett. B 702 131–134 (2011). arXiv:1105.4414
F. Bernardoni, P. Hernandez, N. Garron, S. Necco, C. Pena, Probing the chiral regime of \(N_{f}\)= 2 QCD with mixed actions. Phys. Rev. D 83, 054503 (2011). https://doi.org/10.1103/PhysRevD.83.054503. arXiv:1008.1870
A. Hasenfratz, R. Hoffmann, S. Schaefer, Low energy chiral constants from \(\epsilon \)-regime simulations with improved Wilson fermions. Phys. Rev. D 78, 054511 (2008). https://doi.org/10.1103/PhysRevD.78.054511. arXiv:0806.4586
[JLQCD/TWQCD 07] H. Fukaya et al., Lattice study of meson correlators in the \(\epsilon \)-regime of two-flavor QCD. Phys. Rev. D 77, 074503 (2008). https://doi.org/10.1103/PhysRevD.77.074503. arXiv:0711.4965
[JLQCD/TWQCD 07A] S. Aoki et al., Topological susceptibility in two-flavor lattice QCD with exact chiral symmetry. Phys. Lett. B 665, 294–297 (2008). https://doi.org/10.1016/j.physletb.2008.06.039. arXiv:0710.1130
Y. Aoki, S. Borsanyi, S. Dürr, Z. Fodor, S.D. Katz, S. Krieg et al., The QCD transition temperature: results with physical masses in the continuum limit II. JHEP 06, 088 (2009). https://doi.org/10.1088/1126-6708/2009/06/088. arXiv:0903.4155
[HotQCD 14] A. Bazavov et al., Equation of state in (2+1)-flavor QCD. Phys. Rev. D 90, 094503 (2014). https://doi.org/10.1103/PhysRevD.90.094503. arXiv:1407.6387
[QCDSF 13] R. Horsley, Y. Nakamura, A. Nobile, P. Rakow, G. Schierholz et al., Nucleon axial charge and pion decay constant from two-flavor lattice QCD. Phys. Lett. B 732, 41–48 (2014). https://doi.org/10.1016/j.physletb.2014.03.002. arXiv:1302.2233
G. Colangelo, S. Dürr, The pion mass in finite volume. Eur. Phys. J. C 33, 543–553 (2004). https://doi.org/10.1140/epjc/s2004-01593-y. arXiv:hep-lat/0311023
V. Gülpers, G. von Hippel, H. Wittig, The scalar pion form factor in two-flavor lattice QCD. Phys. Rev. D 89, 094503 (2014). https://doi.org/10.1103/PhysRevD.89.094503. arXiv:1309.2104
[JLQCD/TWQCD 09] S. Aoki et al., Pion form factors from two-flavor lattice QCD with exact chiral symmetry. Phys. Rev. D 80, 034508 (2009). https://doi.org/10.1103/PhysRevD.80.034508. arXiv:0905.2465
[CERN-TOV 06] L. Del Debbio, L. Giusti, M. Lüscher, R. Petronzio, N. Tantalo, QCD with light Wilson quarks on fine lattices (I): first experiences and physics results. JHEP 02, 056 (2007). arXiv:hep-lat/0610059
[JLQCD 15A] S. Aoki, G. Cossu, X. Feng, S. Hashimoto, T. Kaneko, J. Noaki et al., Light meson electromagnetic form factors from three-flavor lattice QCD with exact chiral symmetry. Phys. Rev. D 93, 034504 (2016). https://doi.org/10.1103/PhysRevD.93.034504. arXiv:1510.06470
[JLQCD 14] H. Fukaya, S. Aoki, S. Hashimoto, T. Kaneko, H. Matsufuru, J. Noaki, Computation of the electromagnetic pion form factor from lattice QCD in the \(\epsilon \) regime. Phys. Rev. D 90, 034506 (2014). https://doi.org/10.1103/PhysRevD.90.034506. arXiv:1405.4077
[PACS-CS 11A] O.H. Nguyen, K.-I. Ishikawa, A. Ukawa, N. Ukita, Electromagnetic form factor of pion from \(N_f=2+1\) dynamical flavor QCD. JHEP 04 122 (2011). https://doi.org/10.1007/JHEP04(2011)122. arXiv:1102.3652
[LHP 04] F.D.R. Bonnet, R.G. Edwards, G.T. Fleming, R. Lewis, D.G. Richards, Lattice computations of the pion form factor. Phys. Rev. D 72, 054506 (2005). https://doi.org/10.1103/PhysRevD.72.054506. arXiv:hep-lat/0411028
[ETM 17F] C. Alexandrou et al., Pion vector form factor from lattice QCD at the physical point. Phys. Rev. D 97, 014508 (2018). https://doi.org/10.1103/PhysRevD.97.014508. arXiv:1710.10401
[QCDSF/UKQCD 06A] D. Brömmel et al., The pion form factor from lattice QCD with two dynamical flavours. Eur. Phys. J. C 51, 335–345 (2007). https://doi.org/10.1140/epjc/s10052-007-0295-6. arXiv:hep-lat/0608021
S.R. Amendolia et al., A measurement of the space-like pion electromagnetic form factor. Nucl. Phys. B 277, 168 (1986). https://doi.org/10.1016/0550-3213(86)90437-2
M. Döring, B. Hu and M. Mai, Chiral Extrapolation of the Sigma resonance. arXiv:1610.10070
Z. Fu, X. Chen, \(I=0\) \(\pi \pi \) \(s\)-wave scattering length from lattice QCD. Phys. Rev. D 98, 014514 (2018). https://doi.org/10.1103/PhysRevD.98.014514. arXiv:1712.02219
Z. Fu, Lattice QCD calculation of \(\pi \pi \) scattering length. Commun. Theor. Phys. 57, 78–84 (2012). https://doi.org/10.1088/0253-6102/57/1/13. arXiv:1110.3918
[PACS-CS 13] K. Sasaki, N. Ishizuka, M. Oka, T. Yamazaki, Scattering lengths for two pseudoscalar meson systems. Phys. Rev. D 89, 054502 (2014). https://doi.org/10.1103/PhysRevD.89.054502. arXiv:1311.7226
[NPLQCD 11A] S.R. Beane, E. Chang, W. Detmold, H.W. Lin, T.C. Luu, K. Orginos et al., The I=2 pipi S-wave Scattering Phase Shift from Lattice QCD. Phys. Rev. D 85, 034505 (2012). https://doi.org/10.1103/PhysRevD.85.034505. arXiv:1107.5023
[NPLQCD 05] S.R. Beane, P.F. Bedaque, K. Orginos, M.J. Savage, I = 2 pi-pi scattering from fully-dynamical mixed-action lattice QCD. Phys. Rev. D 73, 054503 (2006). https://doi.org/10.1103/PhysRevD.73.054503. arXiv:hep-lat/0506013
T. Yagi, S. Hashimoto, O. Morimatsu, M. Ohtani, I=2 \(\pi \)-\(\pi \) scattering length with dynamical overlap fermion. arXiv:1108.2970
[CP-PACS 04] T. Yamazaki et al., I = 2 pi pi scattering phase shift with two flavors of O(a) improved dynamical quarks. Phys. Rev. D 70, 074513 (2004). https://doi.org/10.1103/PhysRevD.70.074513. arXiv:hep-lat/0402025
J. Bulava, B. Fahy, B. Horz, K.J. Juge, C. Morningstar, C.H. Wong, \(I=1\) and \(I=2\) \(\pi -\pi \) scattering phase shifts from \(N_{{\rm f}} = 2+1\) lattice QCD. Nucl. Phys. B 910, 842–867 (2016). https://doi.org/10.1016/j.nuclphysb.2016.07.024. arXiv:1604.05593
S. Dürr, Validity of ChPT - is \(M_\pi \)=135 MeV small enough?. PoS LATTICE2014, 006 (2015). arXiv:1412.6434
S. Dürr, \(M_\pi ^2\) versus \(m_q\): comparing CP-PACS and UKQCD data to chiral perturbation theory. Eur. Phys. J. C 29, 383–395 (2003). https://doi.org/10.1140/epjc/s2003-01245-x. arXiv:hep-lat/0208051
N.H. Fuchs, H. Sazdjian, J. Stern, How to probe the scale of \(\bar{q} q\) in chiral perturbation theory. Phys. Lett. B 269, 183–188 (1991). https://doi.org/10.1016/0370-2693(91)91472-8
J. Stern, H. Sazdjian, N.H. Fuchs, What \(\pi \)-\(\pi \) scattering tells us about chiral perturbation theory. Phys. Rev. D 47, 3814–3838 (1993). https://doi.org/10.1103/PhysRevD.47.3814. arXiv:hep-ph/9301244
S. Descotes-Genon, L. Girlanda, J. Stern, Paramagnetic effect of light quark loops on chiral symmetry breaking. JHEP 01, 041 (2000). arXiv:hep-ph/9910537
V. Bernard, S. Descotes-Genon, G. Toucas, Chiral dynamics with strange quarks in the light of recent lattice simulations. JHEP 1101, 107 (2011). https://doi.org/10.1007/JHEP01(2011)107. arXiv:1009.5066
[NPLQCD 06] S.R. Beane, P.F. Bedaque, K. Orginos, M.J. Savage, \(f_K/f_\pi \) in full QCD with domain wall valence quarks. Phys. Rev. D 75, 094501 (2007). https://doi.org/10.1103/PhysRevD.75.094501. arXiv:hep-lat/0606023
D. Boito, A. Francis, M. Golterman, R. Hudspith, R. Lewis, K. Maltman et al., Low-energy constants and condensates from ALEPH hadronic \(\tau \) decay data. Phys. Rev. D 92, 114501 (2015). https://doi.org/10.1103/PhysRevD.92.114501. arXiv:1503.03450
P.A. Boyle, L. Del Debbio, N. Garron, R.J. Hudspith, E. Kerrane, K. Maltman et al., Combined NNLO lattice-continuum determination of \(L\_{10}^r\). Phys. Rev. D 89, 094510 (2014). https://doi.org/10.1103/PhysRevD.89.094510. arXiv:1403.6729
[RBC/UKQCD 09] P.A. Boyle, L. Del Debbio, J. Wennekers, J.M. Zanotti, The S parameter in QCD from domain wall fermions. Phys. Rev. D 81, 014504 (2010). https://doi.org/10.1103/PhysRevD.81.014504. arXiv:0909.4931
[JLQCD 08A] E. Shintani et al., S-parameter and pseudo-Nambu–Goldstone boson mass from lattice QCD. Phys. Rev. Lett. 101, 242001 (2008). https://doi.org/10.1103/PhysRevLett.101.242001. arXiv:0806.4222
J. Bijnens, P. Talavera, Pion and kaon electromagnetic form-factors. JHEP 0203, 046 (2002). arXiv:hep-ph/0203049
M. Davier, L. Girlanda, A. Hocker, J. Stern, Finite energy chiral sum rules and tau spectral functions. Phys. Rev. D 58, 096014 (1998). https://doi.org/10.1103/PhysRevD.58.096014. arXiv:hep-ph/9802447
C. Jung, Status of dynamical ensemble generation. PoS LAT2009, 002 (2009). arXiv:1001.0941
G. Ecker, J. Gasser, A. Pich, E. de Rafael, the role of resonances in chiral perturbation theory. Nucl. Phys. B 321, 311–342 (1989). https://doi.org/10.1016/0550-3213(89)90346-5
G. Ecker, J. Gasser, H. Leutwyler, A. Pich, E. de Rafael, Chiral Lagrangians for massive spin 1 fields. Phys. Lett. B 223, 425–432 (1989). https://doi.org/10.1016/0370-2693(89)91627-4
[CP-PACS 07] S. Aoki et al., Lattice QCD Calculation of the rho Meson Decay Width. Phys. Rev. D 76, 094506 (2007). https://doi.org/10.1103/PhysRevD.76.094506. arXiv:0708.3705
X. Feng, K. Jansen, D.B. Renner, Resonance Parameters of the rho-Meson from Lattice QCD. Phys. Rev. D 83, 094505 (2011). https://doi.org/10.1103/PhysRevD.83.094505. arXiv:1011.5288
C.B. Lang, D. Mohler, S. Prelovsek, M. Vidmar, Coupled channel analysis of the rho meson decay in lattice QCD. Phys. Rev. D 84, 054503 (2011). https://doi.org/10.1103/PhysRevD.89.059903, https://doi.org/10.1103/PhysRevD.84.054503. arXiv:1105.5636
[CS 11] S. Aoki et al., \(\rho \) Meson decay in 2+1 flavor lattice QCD. Phys. Rev. D 84, 094505 (2011). https://doi.org/10.1103/PhysRevD.84.094505. arXiv:1106.5365
C. Pelissier, A. Alexandru, Resonance parameters of the rho-meson from asymmetrical lattices. Phys. Rev. D 87, 014503 (2013). https://doi.org/10.1103/PhysRevD.87.014503. arXiv:1211.0092
[HS 12A] J. J. Dudek, R.G. Edwards, C.E. Thomas, Energy dependence of the \(\rho \) resonance in \(\pi \pi \) elastic scattering from lattice QCD. Phys. Rev. D 87, 034505 (2013). https://doi.org/10.1103/PhysRevD.87.034505, https://doi.org/10.1103/PhysRevD.90.099902. arXiv:1212.0830
[BMW 14A] T. Metivet, Lattice study of \(\pi \pi \) scattering using \(N_f=2+1\) Wilson improved quarks with masses down to their physical values. PoS LATTICE2014, 079 (2015). https://doi.org/10.22323/1.214.0079. arXiv:1410.8447
X. Feng, S. Aoki, S. Hashimoto, T. Kaneko, Timelike pion form factor in lattice QCD. Phys. Rev. D 91, 054504 (2015). https://doi.org/10.1103/PhysRevD.91.054504. arXiv:1412.6319
D.J. Wilson, R.A. Briceno, J.J. Dudek, R.G. Edwards, C.E. Thomas, Coupled \(\pi \pi, K\bar{K}\) scattering in \(P\)-wave and the \(\rho \) resonance from lattice QCD. Phys. Rev. D 92, 094502 (2015). https://doi.org/10.1103/PhysRevD.92.094502. arXiv:1507.02599
[RQCD 15] G.S. Bali, S. Collins, A. Cox, G. Donald, M. Göckeler, C.B. Lang et al., \(\rho \) and \(K^*\) resonances on the lattice at nearly physical quark masses and \(N_f=2\). Phys. Rev. D 93, 054509 (2016). https://doi.org/10.1103/PhysRevD.93.054509. arXiv:1512.08678
D. Guo, A. Alexandru, R. Molina, M. Döring, Rho resonance parameters from lattice QCD. Phys. Rev. D 94, 034501 (2016). https://doi.org/10.1103/PhysRevD.94.034501. arXiv:1605.03993
Z. Fu, L. Wang, Studying the \(\rho \) resonance parameters with staggered fermions. Phys. Rev. D 94, 034505 (2016). https://doi.org/10.1103/PhysRevD.94.034505. arXiv:1608.07478
C. Alexandrou, L. Leskovec, S. Meinel, J. Negele, S. Paul, M. Petschlies et al., \(P\)-wave \(\pi \pi \) scattering and the \(\rho \) resonance from lattice QCD. Phys. Rev. D 96, 034525 (2017). https://doi.org/10.1103/PhysRevD.96.034525. arXiv:1704.05439
C. Andersen, J. Bulava, B. Hörz, C. Morningstar, The \(I=1\) pion-pion scattering amplitude and timelike pion form factor from \(N_{{\rm f}} = 2+1\) lattice QCD. Nucl. Phys. B 939, 145–173 (2019). https://doi.org/10.1016/j.nuclphysb.2018.12.018. arXiv:1808.05007
X.-Y. Guo, M.F.M. Lutz, On pion and kaon decay constants and chiral SU(3) extrapolations. Nucl. Phys. A 988, 36–47 (2019). https://doi.org/10.1016/j.nuclphysa.2019.04.001. arXiv:1810.07376
M.F.M. Lutz, R. Bavontaweepanya, C. Kobdaj, K. Schwarz, Finite volume effects in the chiral extrapolation of baryon masses. Phys. Rev. D 90, 054505 (2014). https://doi.org/10.1103/PhysRevD.90.054505. arXiv:1401.7805
M.F.M. Lutz, Y. Heo, X.-Y. Guo, On the convergence of the chiral expansion for the baryon ground-state masses. Nucl. Phys. A 977, 146–207 (2018). https://doi.org/10.1016/j.nuclphysa.2018.05.007. arXiv:1801.06417
G.C. Branco, L. Lavoura, J.P. Silva, CP violation. Int. Ser. Monogr. Phys. 103, 1–536 (1999)
M. Sozzi, Discrete symmetries and CP violation: From experiment to theory (Oxford University Press, Oxford, 2008), pp 1–550. https://doi.org/10.1093/acprof:oso/9780199296668.001.0001
G. Buchalla, A.J. Buras, M.E. Lautenbacher, Weak decays beyond leading logarithms. Rev. Mod. Phys. 68, 1125–1144 (1996). https://doi.org/10.1103/RevModPhys.68.1125. arXiv:hep-ph/9512380
A.J. Buras, Weak Hamiltonian, CP violation and rare decays. arXiv:hep-ph/9806471
L. Lellouch, Flavor physics and lattice quantum chromodynamics. In Modern perspectives in lattice QCD: Quantum field theory and high performance computing. Proceedings, International School, 93rd Session, Les Houches, France, August 3-28, 2009 (2011), pp. 629–698. arXiv:1104.5484
K. Anikeev et al., \(B\) physics at the Tevatron: Run II and beyond. arXiv:hep-ph/0201071
U. Nierste, Three lectures on meson mixing and CKM phenomenology, published in Dubna 2008, Heavy Quark Physics (HQP08), pp. 1–39. arXiv:0904.1869
A.J. Buras, D. Guadagnoli, Correlations among new CP violating effects in \(\Delta {F}=2\) observables. Phys. Rev. D 78, 033005 (2008). https://doi.org/10.1103/PhysRevD.78.033005. arXiv:0805.3887
A.J. Buras, D. Guadagnoli, G. Isidori, On \(\epsilon _K\) beyond lowest order in the operator product expansion. Phys. Lett. B 688, 309–313 (2010). https://doi.org/10.1016/j.physletb.2010.04.017. arXiv:1002.3612
T. Inami, C.S. Lim, Effects of superheavy quarks and leptons in low-energy weak processes \(K_L\rightarrow \mu \bar{\mu }\), \(K^+\rightarrow \pi ^+\nu \bar{\nu }\) and \(K^0\leftrightarrow \bar{K}^0\). Prog. Theor. Phys. 65, 297 (1981). https://doi.org/10.1143/PTP.65.297
J. Brod, M. Gorbahn, Next-to-next-to-leading-order charm-quark contribution to the CP violation parameter \(\epsilon _K\) and \(\Delta M_K\). Phys. Rev. Lett. 108, 121801 (2012). https://doi.org/10.1103/PhysRevLett.108.121801. arXiv:1108.2036
J. Brod, M. Gorbahn, \(\epsilon _K\) at next-to-next-to-leading order: The charm-top-quark contribution. Phys. Rev. D 82, 094026 (2010). https://doi.org/10.1103/PhysRevD.82.094026. arXiv:1007.0684
G. Martinelli, C. Pittori, C.T. Sachrajda, M. Testa, A. Vladikas, A general method for nonperturbative renormalization of lattice operators. Nucl. Phys. B 445, 81–108 (1995). https://doi.org/10.1016/0550-3213(95)00126-D. arXiv:hep-lat/9411010
[SWME 14] T. Bae et al., Improved determination of \(B_K\) with staggered quarks. Phys. Rev. D 89, 074504 (2014). https://doi.org/10.1103/PhysRevD.89.074504. arXiv:1402.0048
[ALPHA 07A] P. Dimopoulos et al., Non-perturbative renormalisation of \(\Delta F=2\) four-fermion operators in two-flavour QCD. JHEP 0805, 065 (2008). https://doi.org/10.1088/1126-6708/2008/05/065. arXiv:0712.2429
[ALPHA 18B] P. Dimopoulos et al., Non-Perturbative Renormalisation and Running of BSM Four-Quark Operators in \(N_f = 2\) QCD. Eur. Phys. J. C 78, 579 (2018). https://doi.org/10.1140/epjc/s10052-018-6002-y. arXiv:1801.09455
Z. Bai et al., Standard Model Prediction for Direct CP Violation in \(K \rightarrow \pi \pi \) Decay. Phys. Rev. Lett. 115, 212001 (2015). https://doi.org/10.1103/PhysRevLett.115.212001. arXiv:1505.07863
T. Blum et al., \(K \rightarrow \pi \pi \) \(\Delta I=3/2\) decay amplitude in the continuum limit. Phys. Rev. D 91, 074502 (2015). https://doi.org/10.1103/PhysRevD.91.074502. arXiv:1502.00263
Z. Bai, Long distance part of \(\epsilon _K\) from lattice QCD. PoS LATTICE2016, 309 (2017). https://doi.org/10.22323/1.256.0309. arXiv:1611.06601
[RBC/UKQCD 12F] N.H. Christ, T. Izubuchi, C. T. Sachrajda, A. Soni, J. Yu, Long distance contribution to the KL-KS mass difference. Phys. Rev. D 88, 014508 (2013). https://doi.org/10.1103/PhysRevD.88.014508. arXiv:1212.5931
Z. Bai, N.H. Christ, T. Izubuchi, C.T. Sachrajda, A. Soni, J. Yu, \(K_L-K_S\) Mass Difference from Lattice QCD. Phys. Rev. Lett. 113, 112003 (2014). https://doi.org/10.1103/PhysRevLett.113.112003. arXiv:1406.0916
N.H. Christ, X. Feng, G. Martinelli, C.T. Sachrajda, Effects of finite volume on the KL-KS mass difference. Phys. Rev. D 91, 114510 (2015). https://doi.org/10.1103/PhysRevD.91.114510. arXiv:1504.01170
Z. Bai, N.H. Christ, C.T. Sachrajda, The \(K_L\) - \(K_S\) mass difference. EPJ Web Conf. 175, 13017 (2018). https://doi.org/10.1051/epjconf/201817513017
N. Ishizuka, K. I. Ishikawa, A. Ukawa, T. Yoshié, Calculation of \(K \rightarrow \pi \pi \) decay amplitudes with improved Wilson fermion action in lattice QCD. Phys. Rev. D 92, 074503 (2105). https://doi.org/10.1103/PhysRevD.92.074503. arXiv:1505.05289
N. Ishizuka, K.I. Ishikawa, A. Ukawa, T. Yoshié, Calculation of \(K \rightarrow \pi \pi \) decay amplitudes with improved Wilson fermion action in non-zero momentum frame in lattice QCD. Phys. Rev. D 98, 114512 (2018). https://doi.org/10.1103/PhysRevD.98.114512. arXiv:1809.03893
N. Christ, X. Feng, Including electromagnetism in \(K\rightarrow \pi \pi \) decay calculations. EPJ Web Conf. 175, 13016 (2018). https://doi.org/10.1051/epjconf/201817513016. arXiv:1711.09339
A. Donini, P. Hernández, C. Pena, F. Romero-López, Nonleptonic kaon decays at large \(N_c\). Phys. Rev. D 94, 114511 (2016). https://doi.org/10.1103/PhysRevD.94.114511. arXiv:1607.03262
F. Romero-López, A. Donini, P. Hernández, C. Pena, Follow-up on non-leptonic kaon decays at large \(N_c\). In Proceedings, 36th International Symposium on Lattice Field Theory (Lattice 2018): East Lansing, MI, United States, July 22-28, 2018, vol. LATTICE2018 (2018), p. 278. https://doi.org/10.22323/1.334.0278. arXiv:1810.06285
[SWME 15B] J.A. Bailey, Y.-C. Jang, W. Lee, S. Park, Standard Model evaluation of \(\varepsilon _K\) using lattice QCD inputs for \(\hat{B}_K\) and \(V_{cb}\). Phys. Rev. D 92, 034510 (2015). https://doi.org/10.1103/PhysRevD.92.034510. arXiv:1503.05388
J.A. Bailey, S. Lee, W. Lee, J. Leem, S. Park, Updated evaluation of \(\epsilon _K\) in the standard model with lattice QCD inputs. Phys. Rev. D 98, 094505 (2018). https://doi.org/10.1103/PhysRevD.98.094505. arXiv:1808.09657
D. Bećirević et al., \(K^0 \bar{K}^0\) mixing with Wilson fermions without subtractions. Phys. Lett. B 487, 74–80 (2000). https://doi.org/10.1016/S0370-2693(00)00797-8. arXiv:hep-lat/0005013
[ALPHA 01] R. Frezzotti, P.A. Grassi, S. Sint, P. Weisz, Lattice QCD with a chirally twisted mass term. JHEP 08, 058 (2001). arXiv:hep-lat/0101001
[ALPHA 06] P. Dimopoulos et al., A precise determination of \(B_K\) in quenched QCD. Nucl. Phys. B 749, 69–108 (2006). https://doi.org/10.1016/j.nuclphysb.2006.04.033. arXiv:hep-ph/0601002
[ALPHA 07] P. Dimopoulos et al., Flavour symmetry restoration and kaon weak matrix elements in quenched twisted mass QCD. Nucl. Phys. B 776, 258–285 (2007). https://doi.org/10.1016/j.nuclphysb.2007.03.051. arXiv:hep-lat/0702017
R.S. Van de Water, S.R. Sharpe, \(B_K\) in staggered chiral perturbation theory. Phys. Rev. D 73, 014003 (2006). https://doi.org/10.1103/PhysRevD.73.014003. arXiv:hep-lat/0507012
P.H. Ginsparg, K.G. Wilson, A remnant of chiral symmetry on the lattice. Phys. Rev. D 25, 2649 (1982). https://doi.org/10.1103/PhysRevD.25.2649
V. Cirigliano, J.F. Donoghue, E. Golowich, Dimension eight operators in the weak OPE. JHEP 10, 048 (2000). https://doi.org/10.1088/1126-6708/2000/10/048. arXiv:hep-ph/0007196
A.J. Buras, M. Jamin, P.H. Weisz, Leading and next-to-leading QCD corrections to \(\epsilon \) parameter and \(B_0 - \bar{B}_0\) mixing in the presence of a heavy top quark. Nucl. Phys. B 347, 491–536 (1990). https://doi.org/10.1016/0550-3213(90)90373-L
[ETM 10A] M. Constantinou et al., BK-parameter from \(N_f = 2\) twisted mass lattice QCD. Phys. Rev. D 83, 014505 (2011). https://doi.org/10.1103/PhysRevD.83.014505. arXiv:1009.5606
[SWME 13A] T. Bae et al., Neutral kaon mixing from new physics: matrix elements in \(N_f=2+1\) lattice QCD. Phys. Rev. D 88, 071503 (2013). https://doi.org/10.1103/PhysRevD.88.071503. arXiv:1309.2040
[SWME 13] T. Bae et al., Update on \(B_K\) and \(\varepsilon _K\) with staggered quarks. PoS LATTICE2013, 476 (2013). arXiv:1310.7319
[SWME 11A] T. Bae et al., Kaon \(B\)-parameter from improved staggered fermions in \(N_f=2+1\) QCD. Phys. Rev. Lett. 109, 041601 (2012). https://doi.org/10.1103/PhysRevLett.109.041601. arXiv:1111.5698
[RBC/UKQCD 10B] Y. Aoki et al., Continuum limit of \(B_K\) from 2+1 flavor domain wall QCD. Phys. Rev. D 84 014503 (2011). https://doi.org/10.1103/PhysRevD.84.014503. arXiv:1012.4178
C. Aubin, J. Laiho, R.S. Van de Water, The neutral kaon mixing parameter \(B_K\) from unquenched mixed-action lattice QCD. Phys. Rev. D 81, 014507 (2010). https://doi.org/10.1103/PhysRevD.81.014507. arXiv:0905.3947
[ETM 10C] M. Constantinou et al., Non-perturbative renormalization of quark bilinear operators with \(N_f=2\) (tmQCD) Wilson fermions and the tree-level improved gauge action. JHEP 08, 068 (2010). https://doi.org/10.1007/JHEP08(2010)068. arXiv:1004.1115
F. Gabbiani, E. Gabrielli, A. Masiero, L. Silvestrini, A complete analysis of FCNC and CP constraints in general SUSY extensions of the standard model. Nucl. Phys. B 477, 321–352 (1996). https://doi.org/10.1016/0550-3213(96)00390-2. arXiv:hep-ph/9604387
[RBC/UKQCD 12E] P. A. Boyle, N. Garron, R. J. Hudspith, Neutral kaon mixing beyond the standard model with \(n_f = 2+1\) chiral fermions. Phys. Rev. D 86, 054028 (2012). https://doi.org/10.1103/PhysRevD.86.054028. arXiv:1206.5737
A.J. Buras, M. Misiak, J. Urban, Two loop QCD anomalous dimensions of flavor changing four quark operators within and beyond the standard model. Nucl. Phys. B 586, 397–426 (2000). https://doi.org/10.1016/S0550-3213(00)00437-5. arXiv:hep-ph/0005183
C.R. Allton, L. Conti, A. Donini, V. Gimenez, L. Giusti, G. Martinelli et al., B parameters for Delta S = 2 supersymmetric operators. Phys. Lett. B 453, 30–39 (1999). https://doi.org/10.1016/S0370-2693(99)00283-X. arXiv:hep-lat/9806016
A. Donini, V. Gimenez, L. Giusti, G. Martinelli, Renormalization group invariant matrix elements of Delta S = 2 and Delta I = 3/2 four fermion operators without quark masses. Phys. Lett. B 470, 233–242 (1999). https://doi.org/10.1016/S0370-2693(99)01300-3. arXiv:hep-lat/9910017
R. Babich, N. Garron, C. Hoelbling, J. Howard, L. Lellouch, C. Rebbi, K0 - anti-K0 mixing beyond the standard model and CP-violating electroweak penguins in quenched QCD with exact chiral symmetry. Phys. Rev. D 74, 073009 (2006). https://doi.org/10.1103/PhysRevD.74.073009. arXiv:hep-lat/0605016
A.J. Buras, J.-M. Gérard, Dual QCD Insight into BSM hadronic matrix elements for \(K^0-\bar{K}^0\) Mixing from Lattice QCD. Acta Phys. Polon. B 50, 121 (2019). https://doi.org/10.5506/APhysPolB.50.121. arXiv:1804.02401
[SWME 14C] J. Leem et al., Calculation of BSM Kaon B-parameters using Staggered Quarks. PoS LATTICE2014, 370 (2014). arXiv:1411.1501
[RBC/UKQCD 17A] P. Boyle et al., Neutral kaon mixing beyond the Standard Model with n\(_{f}\) = 2 + 1 chiral fermions. Part 2: non perturbative renormalisation of the \(\Delta F=2\) four-quark operators. JHEP 10, 054 (2017). https://doi.org/10.1007/JHEP10(2017)054. arXiv:1708.03552
P. Boyle, N. Garron, R. J. Hudspith, A. Juttner, J. Kettle, A. Khamseh et al., Beyond the Standard Model Kaon Mixing with Physical Masses. In Proceedings, 36th International Symposium on Lattice Field Theory (Lattice 2018): East Lansing, MI, United States, July 22-28, 2018, vol. LATTICE2018 (2019), p. 285. https://doi.org/10.22323/1.334.0285. arXiv:1812.04981
[ALPHA 13B] J. Heitger, G.M. von Hippel, S. Schaefer and F. Virotta, Charm quark mass and D-meson decay constants from two-flavour lattice QCD. PoS LATTICE2013, 475 (2014). arXiv:1312.7693
[FNAL/MILC 13] A. Bazavov et al., Charmed and strange pseudoscalar meson decay constants from HISQ simulations. PoS LATTICE2013, 405 (2014). arXiv:1312.0149
[FNAL/MILC 12B] A. Bazavov et al., Pseudoscalar meson physics with four dynamical quarks. PoS LAT2012, 159 (2012). arXiv:1210.8431
[PACS-CS 11] Y. Namekawa et al., Charm quark system at the physical point of 2+1 flavor lattice QCD. Phys.Rev. D 84, 074505 (2011). https://doi.org/10.1103/PhysRevD.84.074505. arXiv:1104.4600
[FNAL/MILC 05] C. Aubin, C. Bernard, C.E. DeTar, M. Di Pierro, E.D. Freeland et al., Charmed meson decay constants in three-flavor lattice QCD. Phys.Rev.Lett. 95, 122002 (2005). https://doi.org/10.1103/PhysRevLett.95.122002. arXiv:hep-lat/0506030
[TWQCD 14] W. Chen et al., Decay constants of pseudoscalar \(D\)-mesons in lattice QCD with Domain-Wall Fermion. Phys. Lett. B 736, 231–236 (2014). https://doi.org/10.1016/j.physletb.2014.07.025. arXiv:1404.3648
P. Boyle, A. Jüttner, M.K. Marinkovic, F. Sanfilippo, M. Spraggs, J.T. Tsang, An exploratory study of heavy domain wall fermions on the lattice. JHEP 04, 037 (2016). https://doi.org/10.1007/JHEP04(2016)037. arXiv:1602.04118
C. Bernard, J. Komijani, Chiral perturbation theory for all-staggered heavy-light Mesons. Phys. Rev. D 88, 094017 (2013). https://doi.org/10.1103/PhysRevD.88.094017. arXiv:1309.4533
CLEO collaboration, D. Besson et al., Improved measurements of \(D\) meson semileptonic decays to \(\pi \) and \(K\) mesons. Phys. Rev. D 80, 032005 (2009). https://doi.org/10.1103/PhysRevD.80.032005. arXiv:0906.2983
BESIII collaboration, M. Ablikim et al., Measurement of \(e^{+}e^{-}\rightarrow \pi ^{+}\pi ^{-}\psi (3686)\) from 4.008 to 4.600 GeV and observation of a charged structure in the \(\pi ^{\pm }\psi (3686)\) mass spectrum. Phys. Rev. D 96, 032004 (2017). https://doi.org/10.1103/PhysRevD.96.032004. arXiv:1703.08787
BESIII collaboration, M. Ablikim et al., Measurement of the branching fraction for the semi-leptonic decay \(D^{0(+)}\rightarrow \pi ^{-(0)}\mu ^+\nu _\mu \) and test of lepton universality. Phys. Rev. Lett. 121, 171803 (2018). https://doi.org/10.1103/PhysRevLett.121.171803. arXiv:1802.05492
P.F. Bedaque, Aharonov-Bohm effect and nucleon nucleon phase shifts on the lattice. Phys. Lett. B 593, 82–88 (2004). https://doi.org/10.1016/j.physletb.2004.04.045. arXiv:nucl-th/0402051
C. Sachrajda, G. Villadoro, Twisted boundary conditions in lattice simulations. Phys. Lett. B 609, 73–85 (2005). https://doi.org/10.1016/j.physletb.2005.01.033. arXiv:hep-lat/0411033
[ETM 11B] S. Di Vita, B. Haas, V. Lubicz, F. Mescia, S. Simula and C. Tarantino, Form factors of the \(D \rightarrow \pi \) and \(D \rightarrow K\) semileptonic decays with \(N_f = 2\) twisted mass lattice QCD. PoS LATTICE2010, 301 (2010). arXiv:1104.0869
[HPQCD 11C] J. Koponen et al., The D to K and D to \(\pi \) semileptonic decay form factors from lattice QCD. PoS LAT2011, 286 (2011). arXiv:1111.0225
[HPQCD 12B] J. Koponen, C. Davies, G. Donald, D to K and D to \(\pi \) semileptonic form factors from lattice QCD, Charm (2012). arXiv:1208.6242
[HPQCD 13C] J. Koponen, C. T. H. Davies, G. C. Donald, E. Follana, G. P. Lepage et al., The shape of the \(D \rightarrow K\) semileptonic form factor from full lattice QCD and \(V_{cs}\). arXiv:1305.1462
[ETM 18] V. Lubicz, L. Riggio, G. Salerno, S. Simula and C. Tarantino, Tensor form factor of \(D \rightarrow \pi (K) \ell \nu \) and \(D \rightarrow \pi (K) \ell \ell \) decays with \(N_f=2+1+1\) twisted-mass fermions. Phys. Rev. D 98, 014516 (2018). https://doi.org/10.1103/PhysRevD.98.014516. arXiv:1803.04807
D. Bećirević, B. Haas and F. Mescia, Semileptonic D-decays and lattice QCD. PoS LAT2007, 355 (2007). arXiv:0710.1741
D. Bećirević, A.B. Kaidalov, Comment on the heavy \(\rightarrow \) light form-factors. Phys. Lett. B 478, 417–423 (2000). https://doi.org/10.1016/S0370-2693(00)00290-2. arXiv:hep-ph/9904490
[FNAL/MILC 04] C. Aubin et al., Semileptonic decays of D mesons in three-flavor lattice QCD. Phys. Rev. Lett. 94, 011601 (2005). https://doi.org/10.1103/PhysRevLett.94.011601. arXiv:hep-ph/0408306
FOCUS collaboration, J. Link et al., Measurements of the \(q^{2}\) dependence of the \(D^0 \rightarrow K^{-} \mu ^{+} \nu \) and \(D^0 \rightarrow \pi ^{-} \mu ^{+} \nu \) form factors. Phys. Lett. B 607, 233–242 (2005). https://doi.org/10.1016/j.physletb.2004.12.036. arXiv:hep-ex/0410037
Belle collaboration, K. Abe et al., Measurement of \(D^0 \rightarrow \pi l \nu (K l \nu )\) and their form-factors. arXiv: hep-ex/0510003
[FNAL/MILC 12G] J. A. Bailey et al., Charm semileptonic decays and \(|V_{cs(d)}|\) from heavy clover quarks and 2+1 flavor asqtad staggered ensembles. PoS LAT2012, 272 (2012). arXiv:1211.4964
[JLQCD 17B] T. Kaneko, B. Colquhoun, H. Fukaya and S. Hashimoto, D meson semileptonic form factors in \(N_f\) = 3 QCD with Möbius domain-wall quarks. EPJ Web Conf. 175, 13007 (2018). https://doi.org/10.1051/epjconf/201817513007. arXiv:1711.11235
G. Colangelo, M. Procura, L. Rothen, R. Stucki, J Tarrus Castella, On the factorization of chiral logarithms in the pion form factors. JHEP 09, 081 (2012). https://doi.org/10.1007/JHEP09(2012)081. arXiv:1208.0498
J. Bijnens, I. Jemos, Hard Pion Chiral Perturbation Theory for \(B\rightarrow \pi \) and \(D\rightarrow \pi \) Formfactors. Nucl. Phys. B 840, 54–66 (2010). https://doi.org/10.1016/j.nuclphysb.2010.06.021, https://doi.org/10.1016/j.nuclphysb.2010.10.024. arXiv:1006.1197
[FNAL/MILC 15B] T. Primer, C. Bernard, C. DeTar, A. El-Khadra, E. Gámiz, J. Komijani et al., \(D\)-meson semileptonic form factors at zero momentum transfer in (2+1+1)-flavor lattice QCD. PoS LATTICE2015, 338 (2016). https://doi.org/10.1016/j.nuclphysb.2010.06.021, https://doi.org/10.1016/j.nuclphysb.2010.10.024. arXiv:1511.04000
[FNAL/MILC 17B] T. Primer et al., D meson semileptonic form factors with HISQ valence and sea quarks. PoS LATTICE2016, 305 (2017). https://doi.org/10.22323/1.256.0305
B. Chakraborty, C. Davies, J. Koponen, G.P. Lepage, \(D \rightarrow Kl{\nu }\) semileptonic decay using lattice QCD with HISQ at physical pion masses. EPJ Web Conf. 175, 13027 (2018). https://doi.org/10.1051/epjconf/201817513027. arXiv:1710.07334
S. Meinel, \(\Lambda _c \rightarrow \Lambda l^+ \nu _l\) form factors and decay rates from lattice QCD with physical quark masses. Phys. Rev. Lett. 118, 082001 (2017). https://doi.org/10.1103/PhysRevLett.118.082001. arXiv:1611.09696
BESIII collaboration, M. Ablikim et al., Measurement of the absolute branching fraction for \(\Lambda ^+_{c}\rightarrow \Lambda e^+\nu _e\). Phys. Rev. Lett. 115, 221805 (2015). https://doi.org/10.1103/PhysRevLett.115.221805. arXiv:1510.02610
BESIII collaboration, M. Ablikim et al., Measurement of the absolute branching fraction for \(\Lambda _c^+\rightarrow \Lambda \mu ^+\nu _{\mu }\). Phys. Lett. B 767, 42–47 (2017). https://doi.org/10.1016/j.physletb.2017.01.047. arXiv:1611.04382
T. Feldmann, M.W.Y. Yip, Form Factors for \(Lambda_b \rightarrow \Lambda \) Transitions in SCET. Phys. Rev. D 85, 014035 (2012). https://doi.org/10.1103/PhysRevD.85.014035, https://doi.org/10.1103/PhysRevD.86.079901. arXiv:1111.1844
V. Cirigliano, I. Rosell, \(\pi /K\rightarrow e \bar{\nu }_e\) branching ratios to \(O(e^2p^4)\) in Chiral Perturbation Theory. JHEP 10, 005 (2007). https://doi.org/10.1088/1126-6708/2007/10/005. arXiv:0707.4464
L. Riggio, G. Salerno, S. Simula, Extraction of \(|V_{cd}|\) and \(|V_{cs}|\) from experimental decay rates using lattice QCD \(D \rightarrow \pi (K) \ell \nu \) form factors. Eur. Phys. J. C 78, 501 (2018). https://doi.org/10.1140/epjc/s10052-018-5943-5. arXiv:1706.03657
LHCb, CMS collaboration, V. Khachatryan et al., Observation of the rare \(B^0_s\rightarrow \mu ^+\mu ^-\) decay from the combined analysis of CMS and LHCb data. Nature 522, 68–72 (2015). https://doi.org/10.1038/nature14474. arXiv:1411.4413
LHCb collaboration, R. Aaij et al., Measurement of the \(B^0_s\rightarrow \mu ^+\mu ^-\) branching fraction and effective lifetime and search for \(B^0\rightarrow \mu ^+\mu ^-\) decays. Phys. Rev. Lett. 118, 191801 (2017). https://doi.org/10.1103/PhysRevLett.118.191801. arXiv:1703.05747
Babar collaboration, J. Lees et al., Evidence of \(B\rightarrow \tau \nu \) decays with hadronic \(B\) tags. Phys. Rev. D 88, 031102 (2013). https://doi.org/10.1103/PhysRevD.88.031102. arXiv:1207.0698
Belle collaboration, B. Kronenbitter et al., Measurement of the branching fraction of \(B^{+} \rightarrow \tau ^{+} \nu _{\tau }\) decays with the semileptonic tagging method. Phys. Rev. D 92, 051102 (2015). https://doi.org/10.1103/PhysRevD.92.051102. arXiv:1503.05613
G. Buchalla, A.J. Buras, QCD corrections to rare K and B decays for arbitrary top quark mass. Nucl. Phys. B 400, 225–239 (1993). https://doi.org/10.1016/0550-3213(93)90405-E
C. Bobeth, M. Gorbahn, T. Hermann, M. Misiak, E. Stamou, M. Steinhauser, \(B_{s, d} \rightarrow l^+ l^-\) in the standard model with reduced theoretical uncertainty. Phys. Rev. Lett. 112, 101801 (2014). https://doi.org/10.1103/PhysRevLett.112.101801. arXiv:1311.0903
[ETM 13E] N. Carrasco, P. Dimopoulos, R. Frezzotti, V. Giménez, P. Lami et al., A \(N_f = 2 + 1 + 1\) ’twisted’ determination of the \(b\)-quark mass, \(f_{B}\) and \(f_{B_s}\). PoS LATTICE2013, 313 (2014). arXiv:1311.2837
[RBC/UKQCD 13A] O. Witzel, \(B\)-meson decay constants with domain-wall light quarks and nonperturbatively tuned relativistic \(b\)-quarks. PoS LATTICE2013, 377 (2014). arXiv:1311.0276
[ALPHA 13] F. Bernardoni, B. Blossier, J. Bulava, M. Della Morte, P. Fritzsch et al., B-physics with \(N_f=2\) Wilson fermions. PoS LATTICE2013, 381 (2014). arXiv:1309.1074
[ETM 13C] N. Carrasco et al., B-physics computations from Nf=2 tmQCD. PoS LATTICE2013, 382 (2014). arXiv:1310.1851
[ALPHA 12A] F. Bernardoni, B. Blossier, J. Bulava, M. Della Morte, P. Fritzsch et al., B-physics from HQET in two-flavour lattice QCD. PoS LAT2012, 273 (2012). arXiv:1210.7932
[ETM 12B] N. Carrasco, P. Dimopoulos, R. Frezzotti, V. Gimenez, G. Herdoiza et al., B-physics from the ratio method with Wilson twisted mass fermions. PoS LAT2012, 104 (2012). arXiv:1211.0568
[ALPHA 11] B. Blossier, J. Bulava, M. Della Morte, M. Donnellan, P. Fritzsch et al., \(M_b\) and \(f_B\) from non-perturbatively renormalized HQET with \(N_f=2\) light quarks. PoS LAT2011, 280 (2011). arXiv:1112.6175
[ETM 09D] B. Blossier et al., A proposal for B-physics on current lattices. JHEP 1004, 049 (2010). https://doi.org/10.1007/JHEP04(2010)049. arXiv:0909.3187
[HPQCD 05B] A. Gray et al., The upsilon spectrum and \(m_b\) from full lattice QCD. Phys.Rev. D 72, 094507 (2005). https://doi.org/10.1103/PhysRevD.72.094507. arXiv:hep-lat/0507013
[RBC/UKQCD 10C] C. Albertus et al., Neutral B-meson mixing from unquenched lattice QCD with domain-wall light quarks and static b-quarks. Phys.Rev. D 82, 014505 (2010). https://doi.org/10.1103/PhysRevD.82.014505. arXiv:1001.2023
K.G. Chetyrkin, M. Steinhauser, Short distance mass of a heavy quark at order \(\alpha _s^3\). Phys. Rev. Lett. 83, 4001–4004 (1999). https://doi.org/10.1103/PhysRevLett.83.4001. arXiv:hep-ph/9907509
N. Gray, D.J. Broadhurst, W. Grafe, K. Schilcher, Three loop relation of quark (modified) Ms and pole masses. Z. Phys. C 48, 673–680 (1990). https://doi.org/10.1007/BF01614703
D. Arndt, C.J.D. Lin, Heavy meson chiral perturbation theory in finite volume. Phys. Rev. D 70, 014503 (2004). https://doi.org/10.1103/PhysRevD.70.014503. arXiv:hep-lat/0403012
[HPQCD 12F] R.J. Dowdall, C. Davies, T. Hammant and R. Horgan, Precise heavy-light meson masses and hyperfine splittings from lattice QCD including charm quarks in the sea. Phys. Rev. D 86, 094510 (2012). https://doi.org/10.1103/PhysRevD.86.094510. arXiv:1207.5149
A. Lenz, U. Nierste, Theoretical update of \(B_s - \bar{B}_s\) mixing. JHEP 0706, 072 (2007). https://doi.org/10.1088/1126-6708/2007/06/072. arXiv:hep-ph/0612167
M. Beneke, G. Buchalla, I. Dunietz, Width difference in the \(B_s-\bar{B_s}\) system. Phys. Rev. D 54, 4419–4431 (1996). https://doi.org/10.1103/PhysRevD.54.4419, https://doi.org/10.1103/PhysRevD.83.119902. arXiv:hep-ph/9605259
[FNAL/MILC 11A] C. M. Bouchard, E. Freeland, C. Bernard, A. El-Khadra, E. Gamiz et al., Neutral \(B\) mixing from \(2+1\) flavor lattice-QCD: the Standard Model and beyond. PoS LAT2011, 274 (2011). arXiv:1112.5642
[HPQCD 06A] E. Dalgic, A. Gray, E. Gamiz, C. T. Davies, G. P. Lepage et al., \(B^0_{s} - \bar{B}^0_s\) mixing parameters from unquenched lattice QCD. Phys. Rev. D 76, 011501 (2007). https://doi.org/10.1103/PhysRevD.76.011501. arXiv:hep-lat/0610104
[ETM 12A] N. Carrasco et al., Neutral meson oscillations in the standard model and beyond from \(N_f=2\) twisted mass lattice QCD. PoS LAT2012, 105 (2012). arXiv:1211.0565
[FNAL/MILC 12] A. Bazavov, C. Bernard, C. Bouchard, C. DeTar, M. Di Pierro et al., Neutral B-meson mixing from three-flavor lattice QCD: determination of the SU(3)-breaking ratio \(\xi \). Phys. Rev. D 86, 034503 (2012). https://doi.org/10.1103/PhysRevD.86.034503. arXiv:1205.7013
[MILC 13B] C. Bernard, Neutral B mixing in staggered chiral perturbation theory. Phys. Rev. D 87, 114503 (2013). https://doi.org/10.1103/PhysRevD.87.114503. arXiv:1303.0435
M Della Morte, B. Jäger, T. Rae, H. Wittig, Improved interpolating fields for hadrons at non-zero momentum. Eur. Phys. J. A 48, 139 (2012). https://doi.org/10.1140/epja/i2012-12139-9. arXiv:1208.0189
[HPQCD 06] E. Dalgic et al., B meson semileptonic form-factors from unquenched lattice QCD. Phys. Rev. D 73, 074502 (2006). https://doi.org/10.1103/PhysRevD.73.074502, https://doi.org/10.1103/PhysRevD.75.119906. arXiv:hep-lat/0601021
[FNAL/MILC 08A] J. A. Bailey et al., The \(B \rightarrow \pi \ell \nu \) semileptonic form factor from three-flavor lattice QCD: a model-independent determination of \(|V_{ub}|\). Phys. Rev. D 79, 054507 (2009). https://doi.org/10.1103/PhysRevD.79.054507. arXiv:0811.3640
[FNAL/MILC 15] J. A. Bailey et al., \(|V_{ub}|\) from \(B\rightarrow \pi \ell \nu \) decays and (2+1)-flavor lattice QCD. Phys. Rev. D 92, 014024 (2015). https://doi.org/10.1103/PhysRevD.92.014024. arXiv:1503.07839
[RBC/UKQCD 15] J. M. Flynn, T. Izubuchi, T. Kawanai, C. Lehner, A. Soni, R. S. Van de Water et al., \(B \rightarrow \pi \ell \nu \) and \(B_s \rightarrow K \ell \nu \) form factors and \(|V_{ub}|\) from 2+1-flavor lattice QCD with domain-wall light quarks and relativistic heavy quarks. Phys. Rev. D 91, 074510 (2015). https://doi.org/10.1103/PhysRevD.91.074510. arXiv:1501.05373
[HPQCD 15A] B. Colquhoun, R. J. Dowdall, J. Koponen, C. T. H. Davies, G. P. Lepage, \(B \rightarrow \pi \ell \nu \) at zero recoil from lattice QCD with physical \(u/d\) quarks. Phys. Rev. D 93, 034502 (2016). https://doi.org/10.1103/PhysRevD.93.034502. arXiv:1510.07446
[HPQCD 12C] C. M. Bouchard, G. P. Lepage, C. J. Monahan, H. Na, J. Shigemitsu, Form factors for \(B\) and \(B_s\) semileptonic decays with NRQCD/HISQ quarks. PoS LAT2012, 118 (2012). arXiv:1210.6992
[HPQCD 13F] C. M. Bouchard, G. P. Lepage, J. C. Monahan, H. Na, J. Shigemitsu, \(B\) and \(B_s\) semileptonic decay form factors with NRQCD/HISQ quarks. PoS LATTICE2013, 387 (2014). arXiv:1310.3207
B. Colquhoun, S. Hashimoto, T. Kaneko, \(B \rightarrow \pi \ell \nu \) with Möbius Domain Wall Fermions. EPJ Web Conf. 175, 13004 (2018). https://doi.org/10.1051/epjconf/201817513004. arXiv:1710.07094
Z. Gelzer et al., Semileptonic \(B\)-meson decays to light pseudoscalar mesons on the HISQ ensembles. EPJ Web Conf. 175, 13024 (2018). https://doi.org/10.1051/epjconf/201817513024. arXiv:1710.09442
[HPQCD 14] C.M. Bouchard, G.P. Lepage, C. Monahan, H. Na, J. Shigemitsu, \(B_s \rightarrow K \ell \nu \) form factors from lattice QCD. Phys. Rev. D 90, 054506 (2014). https://doi.org/10.1103/PhysRevD.90.054506. arXiv:1406.2279
[ALPHA 14B] F. Bahr, F. Bernardoni, J. Bulava, A. Joseph, A. Ramos, H. Simma et al., Form factors for \({\rm B}_{{\rm s}} \rightarrow {{\rm K}}\ell \nu \) decays in Lattice QCD. In 8th International Workshop on the CKM Unitarity Triangle (CKM2014) Vienna, Austria, September 8-12, 2014 (2014). arXiv:1411.3916
C. J. Monahan, C. M. Bouchard, G. P. Lepage, H. Na, J. Shigemitsu, Form factor ratios for \(B_s \rightarrow K \, \ell \, \nu \) and \(B_s \rightarrow D_s \, \ell \, \nu \) semileptonic decays and \(|V_{ub}/V_{cb}|\). arXiv:1808.09285
[FNAL/MILC 17A] Y. Liu et al., \(B_s \rightarrow K \ell \nu \) Form Factors with 2+1 Flavors. EPJ Web Conf. 175, 13008 (2018). https://doi.org/10.1051/epjconf/201817513008. arXiv:1711.08085
M. Antonelli et al., Flavor physics in the quark sector. Phys. Rept. 494, 197–414 (2010). https://doi.org/10.1016/j.physrep.2010.05.003. arXiv:0907.5386
Z. Liu et al., Form factors for rare \(B\) decays: strategy, methodology, and numerical study. PoS LAT2009, 242 (2009). arXiv:0911.2370
[HPQCD 13E] C. Bouchard, G. P. Lepage, C. Monahan, H. Na, J. Shigemitsu, Rare decay \(B \rightarrow K \ell ^+ \ell ^-\) form factors from lattice QCD. Phys. Rev. D 88, 054509 (2013). https://doi.org/10.1103/PhysRevD.88.079901, https://doi.org/10.1103/PhysRevD.88.054509. arXiv:1306.2384
[FNAL/MILC 15D] J. A. Bailey et al., \(B\rightarrow Kl^+l^-\) decay form factors from three-flavor lattice QCD. Phys. Rev. D 93, 025026 (2016). https://doi.org/10.1103/PhysRevD.93.025026. arXiv:1509.06235
[FNAL/MILC 15E] J. A. Bailey et al., \(B\rightarrow \pi \ell \ell \) form factors for new-physics searches from lattice QCD. Phys. Rev. Lett. 115, 152002 (2015). https://doi.org/10.1103/PhysRevLett.115.152002. arXiv:1507.01618
[HPQCD 13D] C. Bouchard, G. P. Lepage, C. Monahan, H. Na, J. Shigemitsu, Standard Model predictions for \(B \rightarrow Kll\) with form factors from lattice QCD. Phys. Rev. Lett. 111, 162002 (2013). https://doi.org/10.1103/PhysRevLett.112.149902, https://doi.org/10.1103/PhysRevLett.111.162002. arXiv:1306.0434
[FNAL/MILC 15F] D. Du, A. X. El-Khadra, S. Gottlieb, A. S. Kronfeld, J. Laiho, E. Lunghi et al., Phenomenology of semileptonic B-meson decays with form factors from lattice QCD. Phys. Rev. D 93, 034005 (2016). https://doi.org/10.1103/PhysRevD.93.034005. arXiv:1510.02349
LHCb collaboration, R. Aaij et al., First measurement of the differential branching fraction and \(C\!P\) asymmetry of the \(B^\pm \rightarrow \pi ^\pm \mu ^+\mu ^-\) decay. JHEP 10, 034 (2015). https://doi.org/10.1007/JHEP10(2015)034. arXiv:1509.00414
C.B. Lang, D. Mohler, S. Prelovsek, R.M. Woloshyn, Predicting positive parity B\(_s\) mesons from lattice QCD. Phys. Lett. B 750, 17–21 (2015). https://doi.org/10.1016/j.physletb.2015.08.038. arXiv:1501.01646
M. Lage, U.-G. Meissner, A. Rusetsky, A Method to measure the antikaon-nucleon scattering length in lattice QCD. Phys. Lett. B 681, 439–443 (2009). https://doi.org/10.1016/j.physletb.2009.10.055. arXiv:0905.0069
V. Bernard, M. Lage, U.G. Meissner, A. Rusetsky, Scalar mesons in a finite volume. JHEP 01, 019 (2011). https://doi.org/10.1007/JHEP01(2011)019. arXiv:1010.6018
M. Doring, U.-G. Meissner, E. Oset, A. Rusetsky, Unitarized chiral perturbation theory in a finite volume: scalar meson sector. Eur. Phys. J. A 47, 139 (2011). https://doi.org/10.1140/epja/i2011-11139-7. arXiv:1107.3988
M.T. Hansen, S.R. Sharpe, Multiple-channel generalization of Lellouch-Luscher formula. Phys. Rev. D 86, 016007 (2012). https://doi.org/10.1103/PhysRevD.86.016007. arXiv:1204.0826
R.A. Briceno, Z. Davoudi, Moving multichannel systems in a finite volume with application to proton-proton fusion. Phys. Rev. D 88, 094507 (2013). https://doi.org/10.1103/PhysRevD.88.094507. arXiv:1204.1110
[HS 14] J.J. Dudek, R.G. Edwards, C.E. Thomas, D.J. Wilson, Resonances in coupled \(\pi K -\eta K\) scattering from quantum chromodynamics. Phys. Rev. Lett. 113, 182001 (2014). https://doi.org/10.1103/PhysRevLett.113.182001. arXiv:1406.4158
R.R. Horgan, Z. Liu, S. Meinel, M. Wingate, Lattice QCD calculation of form factors describing the rare decays \(B \rightarrow K^* \ell ^+ \ell ^-\) and \(B_s \rightarrow \phi \ell ^+ \ell ^-\). Phys. Rev. D 89, 094501 (2014). https://doi.org/10.1103/PhysRevD.89.094501. arXiv:1310.3722
R.R. Horgan, Z. Liu, S. Meinel, M. Wingate, Calculation of \(B^0 \rightarrow K^{*0} \mu ^+ \mu ^-\) and \(B_s^0 \rightarrow \phi \mu ^+ \mu ^-\) observables using form factors from lattice QCD. Phys. Rev. Lett. 112, 212003 (2014). https://doi.org/10.1103/PhysRevLett.112.212003. arXiv:1310.3887
[RBC/UKQCD 15B] J. Flynn, A. Jüttner, T. Kawanai, E. Lizarazo, O. Witzel, Hadronic form factors for rare semileptonic \(B\) decays. In Proceedings, 33rd International Symposium on Lattice Field Theory (Lattice 2015), vol. LATTICE2015 (2016), p. 345. arXiv:1511.06622
J. Flynn, T. Izubuchi, A. Jüttner, T. Kawanai, C. Lehner, E. Lizarazo et al., Form factors for semi-leptonic \(B\) decays. PoS LATTICE2016, 296 (2016). https://doi.org/10.22323/1.256.0296. arXiv:1612.05112
E. Lizarazo, O. Witzel, Non-perturbative determinations of \(B\)-meson decay constants and semi-leptonic form factors. PoS ICHEP2016, 558 (2016). https://doi.org/10.22323/1.282.0558. arXiv:1612.06113
A. Sirlin, Large \(m_W\), \(m_Z\) behavior of the \(O(\alpha )\) corrections to semileptonic processes mediated by \(W\). Nucl. Phys. B 196, 83 (1982). https://doi.org/10.1016/0550-3213(82)90303-0
M.E. Luke, Effects of subleading operators in the heavy quark effective theory. Phys. Lett. B 252, 447–455 (1990). https://doi.org/10.1016/0370-2693(90)90568-Q
[FNAL/MILC 04A] M. Okamoto et al., Semileptonic \(D \rightarrow \pi /K\) and \(B \rightarrow \pi /D\) decays in 2+1 flavor lattice QCD. Nucl. Phys. Proc. Suppl. 140, 461–463 (2005). https://doi.org/10.1016/j.nuclphysbps.2004.11.151. arXiv:hep-lat/0409116
[FNAL/MILC 13B] S.-W. Qiu , C. DeTar, A. X. El-Khadra, A. S. Kronfeld, J. Laiho et al., Semileptonic decays \(B\rightarrow D^{(*)}l\nu \) at nonzero recoil. PoS LATTICE2013, 385 (2014). arXiv:1312.0155
M. Atoui, V. Morenas, D. Becirevic, F. Sanfilippo, \(b_s \rightarrow d_s \ell \nu _\ell \) near zero recoil in and beyond the standard model. Eur. Phys. J. C 74, 2861 (2014). https://doi.org/10.1140/epjc/s10052-014-2861-z. arXiv:1310.5238
[FNAL/MILC 08] C. Bernard et al., The \(\bar{B} \rightarrow D^{*} \ell \bar{\nu }\) form factor at zero recoil from three-flavor lattice QCD: a model independent determination of \(|V_{cb}|\). Phys. Rev. D 79, 014506 (2009). https://doi.org/10.1103/PhysRevD.79.014506. arXiv:0808.2519
[FNAL/MILC 14] J. A. Bailey et al., Update of \(|V_{cb}|\) from the \(\bar{B}\rightarrow D^*\ell \bar{\nu }\) form factor at zero recoil with three-flavor lattice QCD. Phys. Rev. D 89, 114504 (2014). https://doi.org/10.1103/PhysRevD.89.114504. arXiv:1403.0635
[FNAL/MILC 15C] J. A. Bailey et al., \(B\rightarrow D\ell \nu \) form factors at nonzero recoil and |V\(_{cb}\)| from 2+1-flavor lattice QCD. Phys. Rev. D 92, 034506 (2015). https://doi.org/10.1103/PhysRevD.92.034506. arXiv:1503.07237
[HPQCD 15] H. Na, C. M. Bouchard, G. P. Lepage, C. Monahan, J. Shigemitsu, \(B\rightarrow D \ell \nu \) form factors at nonzero recoil and extraction of \(|V_{cb}|\). Phys. Rev. D 92, 054510 (2015). https://doi.org/10.1103/PhysRevD.92.054510. arXiv:1505.03925
C.J. Monahan, H. Na, C. M. Bouchard, G. P. Lepage, J. Shigemitsu, \(B_{(s)}\rightarrow D_{(s)}\) semileptonic decays with NRQCD-HISQ valence quarks. PoS LATTICE2016, 298 (2016). arXiv:1611.09667
[HPQCD 17] C. J. Monahan, H. Na, C. M. Bouchard, G. P. Lepage, J. Shigemitsu, \(B_s \rightarrow D_s \ell \nu \) Form Factors and the Fragmentation Fraction Ratio \(f_s/f_d\). Phys. Rev. D 95, 114506 (2017). https://doi.org/10.1103/PhysRevD.95.114506. arXiv:1703.09728
J. Harrison, C. Davies, M. Wingate, \(|V_{cb}|\) from the \(\bar{B}^0 \rightarrow D^{*+} \ell ^- \bar{\nu }\) zero-recoil form factor using \(2+1+1\) flavour HISQ and NRQCD. PoS LATTICE2016, 287 (2017). https://doi.org/10.22323/1.256.0287. arXiv:1612.06716
[HPQCD 17B] J. Harrison, C. Davies, M. Wingate, Lattice QCD calculation of the \({{B}_{(s)}\rightarrow D_{(s)}^{*}\ell {\nu }}\) form factors at zero recoil and implications for \({|V_{cb}|}\). Phys. Rev. D 97, 054502 (2018). https://doi.org/10.1103/PhysRevD.97.054502. arXiv:1711.11013
A. Datta, S. Kamali, S. Meinel, A. Rashed, Phenomenology of \( {\Lambda }_b\rightarrow {\Lambda }_c\tau {\overline{\nu }}_{\tau } \) using lattice QCD calculations. JHEP 08, 131 (2017). https://doi.org/10.1007/JHEP08(2017)131. arXiv:1702.02243
[ETM 10B] B. Blossier et al., Average up/down, strange and charm quark masses with \(N_f=2\) twisted mass lattice QCD. Phys. Rev. D 82, 114513 (2010). https://doi.org/10.1103/PhysRevD.82.114513. arXiv:1010.3659
D. Bigi, P. Gambino, Revisiting \(B\rightarrow D \ell \nu \). Phys. Rev. D 94, 094008 (2016). https://doi.org/10.1103/PhysRevD.94.094008. arXiv:1606.08030
[FNAL/MILC 12C] J. A. Bailey et al., \(B_s\rightarrow D_s/B\rightarrow D\) semileptonic form-factor ratios and their application to BR(\(B^0_s\rightarrow \mu ^+\mu ^-\)). Phys.Rev. D 85, 114502 (2012). https://doi.org/10.1103/PhysRevD.85.114502, https://doi.org/10.1103/PhysRevD.86.039904. arXiv:1202.6346
LHCb collaboration, R. Aaij et al., Determination of \(f_s/f_d\) for \(7~\rm {TeV}\) \(pp\) collisions and a measurement of the branching fraction of the decay \(B_d\rightarrow D^-K^+\). Phys. Rev. Lett. 107, 211801 (2011). https://doi.org/10.1103/PhysRevLett.107.211801. arXiv:1106.4435
L. Randall, M.B. Wise, Chiral perturbation theory for \(B\rightarrow D^*\) and \(B\rightarrow D\) semileptonic transition matrix elements at zero recoil. Phys. Lett. B 303, 135–139 (1993). https://doi.org/10.1016/0370-2693(93)90057-O. arXiv:hep-ph/9212315
M.J. Savage, Heavy meson observables at one loop in partially quenched chiral perturbation theory. Phys. Rev. D 65, 034014 (2002). https://doi.org/10.1103/PhysRevD.65.034014. arXiv:hep-ph/0109190
S. Hashimoto, A.S. Kronfeld, P.B. Mackenzie, S.M. Ryan, J.N. Simone, Lattice calculation of the zero recoil form-factor of \(\bar{B} \rightarrow D^* \ell \bar{\nu }\): toward a model independent determination of \(|V_{cb}|\). Phys. Rev. D 66, 014503 (2002). https://doi.org/10.1103/PhysRevD.66.014503. arXiv:hep-ph/0110253
A. Lytle, B. Colquhoun, C. Davies, J. Koponen, C. McNeile, Semileptonic \(B_c\) decays from full lattice QCD. PoS BEAUTY2016, 069 (2016). https://doi.org/10.22323/1.273.0069. arXiv:1605.05645
[HPQCD 16] B. Colquhoun, C. Davies, J. Koponen, A. Lytle, C. McNeile, \(B_c\) decays from highly improved staggered quarks and NRQCD. PoS LATTICE2016, 281 (2016). https://doi.org/10.22323/1.256.0281. arXiv:1611.01987
W. Detmold, C. Lehner, S. Meinel, \(\Lambda _b \rightarrow p \ell ^-\bar{\nu }_\ell \) and \(\Lambda _b \rightarrow \Lambda _c \ell ^- \bar{\nu }_\ell \) form factors from lattice QCD with relativistic heavy quarks. Phys. Rev. D 92, 034503 (2016). https://doi.org/10.1103/PhysRevD.92.034503. arXiv:1503.01421
W. Detmold, C.J.D. Lin, S. Meinel, M. Wingate, \(\Lambda _b \rightarrow \Lambda \ell ^+\ell ^-\) form factors and differential branching fraction from lattice QCD. Phys. Rev. D 87, 074502 (2013). https://doi.org/10.1103/PhysRevD.87.074502. arXiv:1212.4827
W. Detmold, C.J.D. Lin, S. Meinel, M. Wingate, \(\Lambda _b \rightarrow p l^-\bar{\nu }_\ell \) form factors from lattice QCD with static b quarks. Phys. Rev. D 88, 014512 (2013). https://doi.org/10.1103/PhysRevD.88.014512. arXiv:1306.0446
LHCb collaboration, R. Aaij et al., Determination of the quark coupling strength \(|V_{ub}|\) using baryonic decays. Nat. Phys. 11, 743–747 (2015). https://doi.org/10.1038/nphys3415. arXiv:1504.01568
W. Detmold, S. Meinel, \(\Lambda _b \rightarrow \Lambda \ell ^+ \ell ^-\) form factors, differential branching fraction, and angular observables from lattice QCD with relativistic \(b\) quarks. Phys. Rev. D 93, 074501 (2016). https://doi.org/10.1103/PhysRevD.93.074501. arXiv:1602.01399
S. Meinel, G. Rendon, Lattice QCD calculation of form factors for \(\Lambda _b \rightarrow \Lambda (1520) \ell ^+ \ell ^-\) decays. PoS LATTICE2016, 299 (2016). https://doi.org/10.22323/1.256.0299. arXiv:1608.08110
S. Meinel, \(\Lambda _c \rightarrow N\) form factors from lattice QCD and phenomenology of \(\Lambda _c \rightarrow n \ell ^+ \nu _\ell \) and \(\Lambda _c \rightarrow p \mu ^+ \mu ^-\) decays. Phys. Rev. d 97, 034511 (2018). https://doi.org/10.1103/PhysRevD.97.034511. arXiv:1712.05783
Belle collaboration, I. Adachi et al., Measurement of \(B^- \rightarrow \tau ^- \bar{\nu }_\tau \) with a hadronic tagging method using the full data sample of Belle. Phys. Rev. Lett. 110, 131801 (2013). https://doi.org/10.1103/PhysRevLett.110.131801. arXiv:1208.4678
Babar collaboration, B. Aubert et al., A search for \(B^+ \rightarrow \ell ^+ \nu _{\ell }\) recoiling against \(B^{-}\rightarrow D^{0} \ell ^{-}\bar{\nu } X\). Phys. Rev. D 81, 051101 (2010). https://doi.org/10.1103/PhysRevD.81.051101. arXiv:0912.2453
Babar collaboration, P. del Amo Sanchez et al., Study of \(B \rightarrow \pi \ell \nu \) and \(B \rightarrow \rho \ell \nu \) Decays and Determination of \(|V_{ub}|\). Phys.Rev. D 83, 032007 (2011). https://doi.org/10.1103/PhysRevD.83.032007. arXiv:1005.3288
Babar collaboration, J. Lees et al., Branching fraction and form-factor shape measurements of exclusive charmless semileptonic B decays, and determination of \(|V_{ub}|\). Phys.Rev. D 86, 092004 (2012). arXiv:1208.1253
Belle collaboration, H. Ha et al., Measurement of the decay \(B^0\rightarrow \pi ^-\ell ^+\nu \) and determination of \(|V_{ub}|\). Phys.Rev. D 83, 071101 (2011). https://doi.org/10.1103/PhysRevD.83.071101. arXiv:1012.0090
Belle collaboration, A. Sibidanov et al., Study of exclusive \(B \rightarrow X_u \ell \nu \) Decays and Extraction of \(\Vert V_{ub}\Vert \) using full reconstruction tagging at the Belle Experiment. Phys. Rev. D 88, 032005 (2013). https://doi.org/10.1103/PhysRevD.88.032005. arXiv:1306.2781
P. Urquijo, Physics prospects at the Belle II experiment. Nucl. Part. Phys. Proc. 263–264, 15–23 (2015). https://doi.org/10.1016/j.nuclphysbps.2015.04.004
Belle II collaboration, E. Kou et al., The Belle II Physics Book. arXiv:1808.10567
I. Caprini, L. Lellouch, M. Neubert, Dispersive bounds on the shape of anti-B –> D(*) lepton anti-neutrino form-factors. Nucl. Phys. B 530, 153–181 (1998). https://doi.org/10.1016/S0550-3213(98)00350-2. arXiv:hep-ph/9712417
Belle collaboration, A. Abdesselam et al., Measurement of CKM Matrix Element \(|V_{cb}|\) from \(\bar{B} \rightarrow D^{*+} \ell ^{-} \bar{\nu }_\ell \). arXiv:1809.03290
D. Bigi, P. Gambino, S. Schacht, A fresh look at the determination of \(|V_{cb}|\) from \(B\rightarrow D^{*} \ell \nu \). Phys. Lett. B 769, 441–445 (2017). https://doi.org/10.1016/j.physletb.2017.04.022. arXiv:1703.06124
F.U. Bernlochner, Z. Ligeti, M. Papucci, D.J. Robinson, Tensions and correlations in \(|V_{cb}|\) determinations. Phys. Rev. D 96, 091503 (2017). https://doi.org/10.1103/PhysRevD.96.091503. arXiv:1708.07134
B. Grinstein, A. Kobach, Model-Independent Extraction of \(|V_{cb}|\) from \(\bar{B}\rightarrow D^* \ell \overline{\nu }\). Phys. Lett. B 771, 359–364 (2017). https://doi.org/10.1016/j.physletb.2017.05.078. arXiv:1703.08170
C.G. Boyd, B. Grinstein, R.F. Lebed, Constraints on form-factors for exclusive semileptonic heavy to light meson decays. Phys. Rev. Lett. 74, 4603–4606 (1995). https://doi.org/10.1103/PhysRevLett.74.4603. arXiv:hep-ph/9412324
C.G. Boyd, B. Grinstein, R.F. Lebed, Precision corrections to dispersive bounds on form-factors. Phys. Rev. D 56, 6895–6911 (1997). https://doi.org/10.1103/PhysRevD.56.6895. arXiv:hep-ph/9705252
Belle collaboration, R. Glattauer et al., Measurement of the decay \(B\rightarrow D\ell \nu _\ell \) in fully reconstructed events and determination of the Cabibbo-Kobayashi-Maskawa matrix element \(|V_{cb}|\). Phys. Rev. D 93, 032006 (2016). https://doi.org/10.1103/PhysRevD.93.032006. arXiv:1510.03657
BaBar collaboration, B. Aubert et al., Measurement of \(|V(cb)|\) and the Form-Factor Slope in \(\overline{B}\rightarrow D \ell ^-\overline{\nu }_\ell \) decays in events tagged by a fully reconstructed \(B\) Meson. Phys. Rev. Lett. 104, 011802 (2010). https://doi.org/10.1103/PhysRevLett.104.011802. arXiv:0904.4063
P. Gambino, K.J. Healey, S. Turczyk, Taming the higher power corrections in semileptonic B decays. Phys. Lett. B 763, 60–65 (2016). https://doi.org/10.1016/j.physletb.2016.10.023. arXiv:1606.06174
BaBar collaboration, J. P. Lees et al., A test of heavy quark effective theory using a four-dimensional angular analysis of \(\overline{B} \rightarrow D^\ast \ell ^- \overline{\nu }_\ell \). arXiv:1903.10002
P. Gambino, M. Jung, S. Schacht, The \(V_{cb}\) puzzle: an update. Phys. Lett. B 795, 386–390 (2019). https://doi.org/10.1016/j.physletb.2019.06.039. arXiv:1905.08209
S. Dittmaier et al., Handbook of LHC Higgs Cross Sections: 2. Differential Distributions. arXiv:1201.3084
LHC Higgs Cross Section Working Group collaboration, S. Heinemeyer et al., Handbook of LHC Higgs Cross Sections: 3. Higgs Properties. arXiv:1307.1347
LBNE collaboration, C. Adams et al., Scientific opportunities with the long-baseline neutrino experiment. arXiv:1307.7335
S. Dawson, A. Gritsan, H. Logan, J. Qian, C. Tully et al., Higgs Working Group Report of the Snowmass 2013 Community Planning Study. arXiv:1310.8361
A. Accardi et al., A critical appraisal and evaluation of modern PDFs. Eur. Phys. J. C 76, 471 (2016). https://doi.org/10.1140/epjc/s10052-016-4285-4. arXiv:1603.08906
G. P. Lepage, P. B. Mackenzie and M. E. Peskin, Expected precision of Higgs Boson partial widths within the standard model. arXiv:1404.0319
D. Buttazzo, G. Degrassi, P.P. Giardino, G.F. Giudice, F. Sala, A. Salvio et al., Investigating the near-criticality of the Higgs boson. JHEP 12, 089 (2013). https://doi.org/10.1007/JHEP12(2013)089. arXiv:1307.3536
J. R. Espinosa, Vacuum stability and the Higgs Boson. PoS LATTICE2013, 010 (2014). arXiv:1311.1970
G. P. Salam, The strong coupling: a theoretical perspective. In From My Vast Repertoire ...: Guido Altarelli’s Legacy (A. Levy, S. Forte and G. Ridolfi, eds.) (2019), pp. 101–121. https://doi.org/10.1142/9789813238053_0007. arXiv:1712.05165
W. Bernreuther, W. Wetzel, Decoupling of heavy quarks in the minimal subtraction scheme. Nucl. Phys. B 197, 228 (1982). https://doi.org/10.1016/0550-3213(82)90288-7
K. Chetyrkin, J.H. Kuhn, C. Sturm, QCD decoupling at four loops. Nucl. Phys. B 744, 121–135 (2006). https://doi.org/10.1016/j.nuclphysb.2006.03.020. arXiv:hep-ph/0512060
Y. Schröder, M. Steinhauser, Four-loop decoupling relations for the strong coupling. JHEP 01, 051 (2006). https://doi.org/10.1088/1126-6708/2006/01/051. arXiv:hep-ph/0512058
B.A. Kniehl, A.V. Kotikov, A.I. Onishchenko, O.L. Veretin, Strong-coupling constant with flavor thresholds at five loops in the anti-MS scheme. Phys. Rev. Lett. 97, 042001 (2006). https://doi.org/10.1103/PhysRevLett.97.042001. arXiv: hep-ph/0607202
M. Czakon, The Four-loop QCD beta-function and anomalous dimensions. Nucl. Phys. B 710, 485–498 (2005). https://doi.org/10.1016/j.nuclphysb.2005.01.012. arXiv:hep-ph/0411261
T. Luthe, A. Maier, P. Marquard, Y. Schröder, Towards the five-loop Beta function for a general gauge group. JHEP 07, 127 (2016). https://doi.org/10.1007/JHEP07(2016)127. arXiv:1606.08662
F. Herzog, B. Ruijl, T. Ueda, J.A.M. Vermaseren, A. Vogt, The five-loop beta function of Yang-Mills theory with fermions. JHEP 02, 090 (2017). https://doi.org/10.1007/JHEP02(2017)090. arXiv:1701.01404
P.A. Baikov, K.G. Chetyrkin, J.H. Kuhn, Five-Loop Running of the QCD coupling constant. Phys. Rev. Lett. 118, 082002 (2017). https://doi.org/10.1103/PhysRevLett.118.082002. arXiv:1606.08659
A.G. Grozin, M. Hoeschele, J. Hoff, M. Steinhauser, Simultaneous decoupling of bottom and charm quarks. JHEP 09, 066 (2011). https://doi.org/10.1007/JHEP09(2011)066. arXiv:1107.5970
K.G. Chetyrkin, J.H. Kuhn, M. Steinhauser, RunDec: A Mathematica package for running and decoupling of the strong coupling and quark masses. Comput. Phys. Commun. 133, 43–65 (2000). https://doi.org/10.1016/S0010-4655(00)00155-7. arXiv: hep-ph/0004189
F. Herren, M. Steinhauser, Version 3 of RunDec and CRunDec. Comput. Phys. Commun. 224, 333–345 (2018). https://doi.org/10.1016/j.cpc.2017.11.014. arXiv:1703.03751
F. Karbstein, A. Peters, M. Wagner, \({\Lambda }_{\overline{\rm MS}}^{({n}_f=2)}\) from a momentum space analysis of the quark-antiquark static potential. JHEP 1409, 114 (2014). https://doi.org/10.1007/JHEP09(2014)114. arXiv:1407.7503
[FlowQCD 15] M. Asakawa, T. Iritani, M. Kitazawa, H. Suzuki, Determination of Reference Scales for Wilson Gauge Action from Yang–Mills Gradient Flow. arXiv:1503.06516
K.-I. Ishikawa, I. Kanamori, Y. Murakami, A. Nakamura, M. Okawa, R. Ueno, Non-perturbative determination of the \(\Lambda \)-parameter in the pure SU(3) gauge theory from the twisted gradient flow coupling. JHEP 12, 067 (2017). https://doi.org/10.1007/JHEP12(2017)067. arXiv:1702.06289
N. Husung, M. Koren, P. Krah, R. Sommer, SU(3) Yang Mills theory at small distances and fine lattices. EPJ Web Conf. 175, 14024 (2018). https://doi.org/10.1051/epjconf/201817514024. arXiv:1711.01860
F. Karbstein, M. Wagner, M. Weber, Determination of \(\Lambda _{\overline{\rm MS}}^{(n_f=2)}\) and analytic parameterization of the static quark-antiquark potentialDetermination of \(\Lambda _{\overline{\rm MS}}^{(n_f=2)}\) and analytic parametrization of the static quark-antiquark potential. Phys. Rev. D 98, 114506 (2018). https://doi.org/10.1103/PhysRevD.98.114506. arXiv:1804.10909
H. Takaura, T. Kaneko, Y. Kiyo, Y. Sumino, Determination of \(\alpha _s\) from static QCD potential with renormalon subtraction. Phys. Lett. B 789, 598–602 (2019). https://doi.org/10.1016/j.physletb.2018.12.060. arXiv:1808.01632
H. Takaura, T. Kaneko, Y. Kiyo, Y. Sumino, Determination of \(\alpha _s\) from static QCD potential: OPE with renormalon subtraction and Lattice QCD. JHEP 04, 155 (2019). https://doi.org/10.1007/JHEP04(2019)155. arXiv:1808.01643
R. J. Hudspith, R. Lewis, K. Maltman, E. Shintani, \(\alpha _s\) from the Lattice Hadronic Vacuum Polarisation. arXiv:1804.10286
M. Kitazawa, T. Iritani, M. Asakawa, T. Hatsuda, H. Suzuki, Equation of state for SU(3) gauge theory via the energy-momentum tensor under gradient flow. Phys. Rev. D 94, 114512 (2016). https://doi.org/10.1103/PhysRevD.94.114512. arXiv:1610.07810
K. Nakayama, H. Fukaya, S. Hashimoto, Lattice computation of the Dirac eigenvalue density in the perturbative regime of QCD. Phys. Rev. D 98, 014501 (2018). https://doi.org/10.1103/PhysRevD.98.014501. arXiv:1804.06695
C.W. Bernard et al., The static quark potential in three flavor QCD. Phys. Rev. D 62, 034503 (2000). https://doi.org/10.1103/PhysRevD.62.034503. arXiv:hep-lat/0002028
G. Martinelli, C.T. Sachrajda, On the difficulty of computing higher twist corrections. Nucl. Phys. B 478, 660–686 (1996). https://doi.org/10.1016/0550-3213(96)00415-4. arXiv:hep-ph/9605336
S. Bethke, A. H. Hoang, S. Kluth, J. Schieck, I. W. Stewart et al., Workshop on Precision Measurements of \(\alpha _s\). arXiv:1110.0016
D. Boito, M. Golterman, K. Maltman, J. Osborne, S. Peris, Strong coupling from the revised ALEPH data for hadronic \(\tau \) decays. Phys. Rev. D 91, 034003 (2015). https://doi.org/10.1103/PhysRevD.91.034003. arXiv:1410.3528
D. Boito, M. Golterman, K. Maltman, S. Peris, Strong coupling from hadronic \(\tau \) decays: A critical appraisal. Phys. Rev. D 95, 034024 (2017). https://doi.org/10.1103/PhysRevD.95.034024. arXiv:1611.03457
[ALPHA 12] P. Fritzsch, F. Knechtli, B. Leder, M. Marinkovic, S. Schaefer et al., The strange quark mass and the \(\Lambda \) parameter of two flavor QCD. Nucl. Phys. B 865, 397–429 (2012). https://doi.org/10.1016/j.nuclphysb.2012.07.026. arXiv:1205.5380
[HotQCD 11] A. Bazavov, T. Bhattacharya, M. Cheng, C. DeTar, H. Ding et al., The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 85, 054503 (2012). https://doi.org/10.1103/PhysRevD.85.054503. arXiv:1111.1710
S. Necco, R. Sommer, The \(N_f = 0\) heavy quark potential from short to intermediate distances. Nucl. Phys. B 622, 328–346 (2002). https://doi.org/10.1016/S0550-3213(01)00582-X. arXiv:hep-lat/0108008
M. Lüscher, P. Weisz, Quark confinement and the bosonic string. JHEP 0207, 049 (2002). https://doi.org/10.1088/1126-6708/2002/07/049. arXiv:hep-lat/0207003
S. Sint, A. Ramos, On O(\(a^2\)) effects in gradient flow observables. PoS LATTICE2014, 329 (2015). arXiv:1411.6706
Z. Fodor, K. Holland, J. Kuti, S. Mondal, D. Nogradi et al., The lattice gradient flow at tree-level and its improvement. JHEP 1409, 018 (2014). https://doi.org/10.1007/JHEP09(2014)018. arXiv:1406.0827
[MILC 15] A. Bazavov et al., Gradient flow and scale setting on MILC HISQ ensembles. Phys. Rev. D 93, 094510. https://doi.org/10.1103/PhysRevD.93.094510. arXiv:1503.02769
V.G. Bornyakov et al., Wilson flow and scale setting from lattice QCD. arXiv:1508.05916
R. Sommer, Scale setting in lattice QCD. PoS LATTICE2013, 015 (2014). https://doi.org/10.22323/1.187.0015. arXiv:1401.3270
[ALPHA 16] M. Dalla Brida, P. Fritzsch, T. Korzec, A. Ramos, S. Sint, R. Sommer, Determination of the QCD \(\Lambda \)-parameter and the accuracy of perturbation theory at high energies. Phys. Rev. Lett. 117, 182001 (2016). https://doi.org/10.1103/PhysRevLett.117.182001. arXiv:1604.06193
[ALPHA 18] M. Dalla Brida, P. Fritzsch, T. Korzec, A. Ramos, S. Sint, R. Sommer, A non-perturbative exploration of the high energy regime in \(N_{{\rm f}}=3\) QCD. Eur. Phys. J. C 78, 372 (2018). https://doi.org/10.1140/epjc/s10052-018-5838-5. arXiv:1803.10230
M. Lüscher, P. Weisz, U. Wolff, A numerical method to compute the running coupling in asymptotically free theories. Nucl. Phys. B 359, 221–243 (1991). https://doi.org/10.1016/0550-3213(91)90298-C
S. Sint, On the Schrödinger functional in QCD. Nucl. Phys. B 421, 135–158 (1994). https://doi.org/10.1016/0550-3213(94)90228-3. arXiv:hep-lat/9312079
A. Coste, A. Gonzalez-Arroyo, J. Jurkiewicz, C. Korthals Altes, Zero momentum contribution to Wilson loops in periodic boxes. Nucl. Phys. B 262, 67 (1985). https://doi.org/10.1016/0550-3213(85)90064-1
M. Lüscher, R. Sommer, P. Weisz, U. Wolff, A precise determination of the running coupling in the \(SU(3)\) Yang-Mills theory. Nucl. Phys. B 413, 481–502 (1994). https://doi.org/10.1016/0550-3213(94)90629-7. arXiv:hep-lat/9309005
S. Sint, R. Sommer, The running coupling from the QCD Schrödinger functional: a one loop analysis. Nucl. Phys. B 465, 71–98 (1996). https://doi.org/10.1016/0550-3213(96)00020-X. arXiv:hep-lat/9508012
[ALPHA 99] A. Bode, P. Weisz, U. Wolff, Two loop computation of the Schrödinger functional in lattice QCD. Nucl. Phys. B 576, 517–539 (2000). https://doi.org/10.1016/S0550-3213(00)00187-5, https://doi.org/10.1016/S0550-3213(00)00187-5. arXiv:hep-lat/9911018
[CP-PACS 04] S. Takeda, S. Aoki, M. Fukugita, K.-I. Ishikawa, N. Ishizuka et al., A scaling study of the step scaling function in \(SU(3)\) gauge theory with improved gauge actions. Phys. Rev. D 70, 074510 (2004). https://doi.org/10.1103/PhysRevD.70.074510. arXiv:hep-lat/0408010
M. Lüscher, A semiclassical formula for the topological susceptibility in a finite space-time volume. Nucl. Phys. B 205, 483 (1982). https://doi.org/10.1016/0550-3213(82)90371-6
P. Fritzsch, A. Ramos, F. Stollenwerk, Critical slowing down and the gradient flow coupling in the Schrödinger functional. PoS Lattice 2013, 461 (2014). arXiv:1311.7304
M Dalla Brida, P. Fritzsch, T. Korzec, A. Ramos, S. Sint, R. Sommer, Slow running of the Gradient Flow coupling from 200 MeV to 4 GeV in \(N_{{\rm f}}=3\) QCD. Phys. Rev. D 95, 014507 (2017). https://doi.org/10.1103/PhysRevD.95.014507. arXiv:1607.06423
M. Lüscher, Step scaling and the Yang-Mills gradient flow. JHEP 06, 105 (2014). https://doi.org/10.1007/JHEP06(2014)105. arXiv:1404.5930
R. Narayanan, H. Neuberger, Infinite N phase transitions in continuum Wilson loop operators. JHEP 03, 064 (2006). https://doi.org/10.1088/1126-6708/2006/03/064. arXiv:hep-th/0601210
Z. Fodor, K. Holland, J. Kuti, D. Nogradi, C.H. Wong, The Yang-Mills gradient flow in finite volume. JHEP 1211, 007 (2012). https://doi.org/10.1007/JHEP11(2012)007. arXiv:1208.1051
P. Fritzsch, A. Ramos, The gradient flow coupling in the Schrödinger functional. JHEP 1310, 008 (2013). https://doi.org/10.1007/JHEP10(2013)008. arXiv:1301.4388
A. Ramos, The gradient flow running coupling with twisted boundary conditions. JHEP 11, 101 (2014). https://doi.org/10.1007/JHEP11(2014)101. arXiv:1409.1445
M Dalla Brida, M. Lüscher, SMD-based numerical stochastic perturbation theory. Eur. Phys. J. C 77, 308 (2017). https://doi.org/10.1140/epjc/s10052-017-4839-0. arXiv:1703.04396
[ALPHA 10A] F. Tekin, R. Sommer, U. Wolff, The running coupling of QCD with four flavors. Nucl. Phys. B 840, 114–128 (2010). https://doi.org/10.1016/j.nuclphysb.2010.07.002. arXiv:1006.0672
P. Perez-Rubio, S. Sint, Non-perturbative running of the coupling from four flavour lattice QCD with staggered quarks. PoS LAT2010, 236 (2010). arXiv:1011.6580
[ALPHA 04] M. Della Morte et al., Computation of the strong coupling in QCD with two dynamical flavours. Nucl. Phys. B 713, 378–406 (2005). https://doi.org/10.1016/j.nuclphysb.2005.02.013. arXiv:hep-lat/0411025
[ALPHA 01A] A. Bode et al., First results on the running coupling in QCD with two massless flavors. Phys. Lett. B 515, 49–56 (2001). https://doi.org/10.1016/S0370-2693(01)00857-7. arXiv:hep-lat/0105003
[ALPHA 98] S. Capitani, M. Lüscher, R. Sommer, H. Wittig, Nonperturbative quark mass renormalization in quenched lattice QCD. Nucl. Phys. B 544, 669–698 (1999). https://doi.org/10.1016/S0550-3213(98)00857-8. arXiv:hep-lat/9810063
J. Bulava, S. Schaefer, Improvement of \(N_f=3\) lattice QCD with Wilson fermions and tree-level improved gauge action. Nucl. Phys. B 874, 188–197 (2013). https://doi.org/10.1016/j.nuclphysb.2013.05.019. arXiv:1304.7093
M. Lüscher, P. Weisz, On-shell improved lattice gauge theories. Commun. Math. Phys. 97, 59 (1985). https://doi.org/10.1007/BF01206178
[JLQCD/CP-PACS 04] N. Yamada et al., Non-perturbative O(a)-improvement of Wilson quark action in three-flavor QCD with plaquette gauge action. Phys.Rev. D 71, 054505 (2005). https://doi.org/10.1103/PhysRevD.71.054505. arXiv:hep-lat/0406028
A. Gonzalez-Arroyo, M. Okawa, The string tension from smeared Wilson loops at large N. Phys. Lett. B 718, 1524–1528 (2013). https://doi.org/10.1016/j.physletb.2012.12.027. arXiv:1206.0049
C. Michael, The running coupling from lattice gauge theory. Phys. Lett. B 283, 103–106 (1992). https://doi.org/10.1016/0370-2693(92)91435-C. arXiv:hep-lat/9205010
[UKQCD 92] S.P. Booth et al., The running coupling from SU(3) lattice gauge theory. Phys. Lett. B 294, 385–390 (1992). https://doi.org/10.1016/0370-2693(92)91538-K. arXiv:hep-lat/9209008
W. Fischler, Quark-antiquark potential in QCD. Nucl. Phys. B 129, 157–174 (1977). https://doi.org/10.1016/0550-3213(77)90026-8
A. Billoire, How heavy must be quarks in order to build coulombic \(q \bar{q}\) bound states. Phys. Lett. B 92, 343 (1980). https://doi.org/10.1016/0370-2693(80)90279-8
M. Peter, The static potential in QCD: a full two loop calculation. Nucl. Phys. B 501, 471–494 (1997). https://doi.org/10.1016/S0550-3213(97)00373-8. arXiv:hep-ph/9702245
Y. Schröder, The static potential in QCD to two loops. Phys. Lett. B 447, 321–326 (1999). https://doi.org/10.1016/S0370-2693(99)00010-6. arXiv:hep-ph/9812205
N. Brambilla, A. Pineda, J. Soto, A. Vairo, The infrared behavior of the static potential in perturbative QCD. Phys. Rev. D 60, 091502 (1999). https://doi.org/10.1103/PhysRevD.60.091502. arXiv:hep-ph/9903355
A.V. Smirnov, V.A. Smirnov, M. Steinhauser, Three-loop static potential. Phys. Rev. Lett. 104, 112002 (2010). https://doi.org/10.1103/PhysRevLett.104.112002. arXiv:0911.4742
C. Anzai, Y. Kiyo, Y. Sumino, Static QCD potential at three-loop order. Phys. Rev. Lett. 104, 112003 (2010). https://doi.org/10.1103/PhysRevLett.104.112003. arXiv:0911.4335
N. Brambilla, A. Vairo, X Garcia i Tormo, J. Soto, The QCD static energy at NNNLL. Phys. Rev. D 80, 034016 (2009). https://doi.org/10.1103/PhysRevD.80.034016. arXiv:0906.1390
S. Necco, R. Sommer, Testing perturbation theory on the \(N_f = 0\) static quark potential. Phys. Lett. B 523, 135–142 (2001). https://doi.org/10.1016/S0370-2693(01)01298-9. arXiv:hep-ph/0109093
A. Bazavov, N. Brambilla, X Garcia i Tormo, P. Petreczky, J. Soto et al., Determination of \(\alpha _s\) from the QCD static energy. Phys. Rev. D 86, 114031 (2012). https://doi.org/10.1103/PhysRevD.86.114031. arXiv:1205.6155
[ETM 11C] K. Jansen, F. Karbstein, A. Nagy, M. Wagner, \(\Lambda _{\overline{\rm MS}}\) from the static potential for QCD with \(N_f=2\) dynamical quark flavors. JHEP 1201, 025 (2012). https://doi.org/10.1007/JHEP01(2012)025. arXiv:1110.6859
N. Brambilla, X Garcia i Tormo, J. Soto, A. Vairo, Precision determination of \(r_0\,\Lambda _{\overline{MS}}\) from the QCD static energy. Phys. Rev. Lett. 105, 212001 (2010). https://doi.org/10.1103/PhysRevLett.105.212001. arXiv:1006.2066
G.S. Bali, K. Schilling, Running coupling and the \(\Lambda \)-parameter from \(SU(3)\) lattice simulations. Phys. Rev. D 47, 661–672 (1993). https://doi.org/10.1103/PhysRevD.47.661. arXiv:hep-lat/9208028
K.G. Chetyrkin, A.L. Kataev, F.V. Tkachov, Higher order corrections to sigma-t (e+ e- –> Hadrons) in quantum chromodynamics. Phys. Lett. 85B, 277–279 (1979). https://doi.org/10.1016/0370-2693(79)90596-3
L.R. Surguladze, M.A. Samuel, Total hadronic cross-section in e+ e- annihilation at the four loop level of perturbative QCD. Phys. Rev. Lett. 66, 560–563 (1991). https://doi.org/10.1103/PhysRevLett.66.560
S.G. Gorishnii, A.L. Kataev, S.A. Larin, The O(\(\alpha _s^3\)) corrections to \(\sigma _\text{ tot }(e^+ e^- \rightarrow \text{ hadrons })\) and \(\Gamma (\tau ^- \rightarrow \nu _\tau + \text{ hadrons })\) in QCD. Phys. Lett. B 259, 144–150 (1991). https://doi.org/10.1016/0370-2693(91)90149-K
P.A. Baikov, K.G. Chetyrkin, J.H. Kuhn, Order \(\alpha _s^4\) QCD Corrections to Z and tau Decays. Phys. Rev. Lett. 101, 012002 (2008). https://doi.org/10.1103/PhysRevLett.101.012002. arXiv:0801.1821
I. Balitsky, M. Beneke, V.M. Braun, Instanton contributions to the \(\tau \) decay widths. Phys. Lett. B 318, 371–381 (1993). https://doi.org/10.1016/0370-2693(93)90142-5. arXiv:hep-ph/9309217
R. J. Hudspith, R. Lewis, K. Maltman, E. Shintani, Determining the QCD coupling from lattice vacuum polarization. In Proceedings, 33rd International Symposium on Lattice Field Theory (Lattice 2015), vol. LATTICE2015 (2016), p. 268. arXiv:1510.04890
[JLQCD 10] E. Shintani, S. Aoki, H. Fukaya, S. Hashimoto, T. Kaneko et al., Strong coupling constant from vacuum polarization functions in three-flavor lattice QCD with dynamical overlap fermions. Phys. Rev. D 82, 074505 (2010). https://doi.org/10.1103/PhysRevD.82.074505. arXiv:1002.0371[Erratum–ibid. D 89 (2014) 099903]
[JLQCD/TWQCD 08C] E. Shintani et al., Lattice study of the vacuum polarization function and determination of the strong coupling constant Phys. Rev. D 79, 074510 (2009). https://doi.org/10.1103/PhysRevD.79.074510. arXiv:0807.0556
R. Hudspith, R. Lewis, K. Maltman, E. Shintani, \(\alpha _s\) from the Hadronic Vacuum Polarisation. EPJ Web Conf. 175, 10006 (2018). https://doi.org/10.1051/epjconf/201817510006
[HPQCD 05A] Q. Mason et al., Accurate determinations of \(\alpha _s\) from realistic lattice QCD. Phys. Rev. Lett. 95, 052002 (2005). https://doi.org/10.1103/PhysRevLett.95.052002. arXiv:hep-lat/0503005
[HPQCD 08A] C. T. H. Davies et al., Update: accurate determinations of \(\alpha _s\) from realistic lattice QCD. Phys. Rev. D 78, 114507 (2008). arXiv:0807.1687
G.P. Lepage, P.B. Mackenzie, On the viability of lattice perturbation theory. Phys. Rev. D 48, 2250–2264 (1993). https://doi.org/10.1103/PhysRevD.48.2250. arXiv:hep-lat/9209022
K. Hornbostel, G. Lepage, C. Morningstar, Scale setting for \(\alpha _s\) beyond leading order. Phys. Rev. D 67, 034023 (2003). https://doi.org/10.1103/PhysRevD.67.034023. arXiv:hep-ph/0208224
[QCDSF/UKQCD 05] M. Göckeler, R. Horsley, A. Irving, D. Pleiter, P. Rakow, G. Schierholz et al., A determination of the Lambda parameter from full lattice QCD. Phys. Rev. D 73, 014513 (2006). https://doi.org/10.1103/PhysRevD.73.014513. arXiv:hep-ph/0502212
[SESAM 99] A. Spitz et al., \(\alpha _s\) from upsilon spectroscopy with dynamical Wilson fermions. Phys. Rev. D 60, 074502 (1999). https://doi.org/10.1103/PhysRevD.60.074502. arXiv:hep-lat/9906009
M. Wingate, T.A. DeGrand, S. Collins, U.M. Heller, From spectroscopy to the strong coupling constant with heavy Wilson quarks. Phys. Rev. D 52, 307–319 (1995). https://doi.org/10.1103/PhysRevD.52.307. arXiv:hep-lat/9501034
C.T.H. Davies, K. Hornbostel, G. Lepage, A. Lidsey, J. Shigemitsu et al., A precise determination of \(\alpha _s\) from lattice QCD. Phys. Lett. B 345, 42–48 (1995). https://doi.org/10.1016/0370-2693(94)01598-7. arXiv:hep-ph/9408328
S. Aoki, M. Fukugita, S. Hashimoto, N. Ishizuka, H. Mino et al., Manifestation of sea quark effects in the strong coupling constant in lattice QCD. Phys. Rev. Lett. 74, 22–25 (1995). https://doi.org/10.1103/PhysRevLett.74.22. arXiv:hep-lat/9407015
A.X. El-Khadra, G. Hockney, A.S. Kronfeld, P.B. Mackenzie, A determination of the strong coupling constant from the charmonium spectrum. Phys. Rev. Lett. 69, 729–732 (1992). https://doi.org/10.1103/PhysRevLett.69.729
[QCDSF/UKQCD 04A] M. Göckeler, R. Horsley, A. Irving, D. Pleiter, P. Rakow, G. Schierholz et al., Determination of \(\Lambda \) in quenched and full QCD: an update. Nucl. Phys. Proc. Suppl. 140, 228–230 (2005). https://doi.org/10.1016/j.nuclphysbps.2004.11.295. arXiv:hep-lat/0409166
S. Booth, M. Göckeler, R. Horsley, A. Irving, B. Joo, S. Pickles et al., The strong coupling constant from lattice QCD with \(N_f=2\) dynamical quarks. Nucl. Phys. Proc. Suppl. 106, 308–310 (2002). https://doi.org/10.1016/S0920-5632(01)01697-8. arXiv:hep-lat/0111006
[QCDSF/UKQCD 01] S. Booth, M. Göckeler, R. Horsley, A. Irving, B. Joo, S. Pickles et al., Determination of \(\Lambda _{\overline{\rm MS}}\) from quenched and \(N_f=2\) dynamical QCD. Phys. Lett. B 519, 229–237 (2001). https://doi.org/10.1016/S0370-2693(01)01103-0. arXiv:hep-lat/0103023
[HPQCD 03A] C. T. H. Davies et al., High-precision lattice QCD confronts experiment. Phys. Rev. Lett. 92, 022001 (2004). https://doi.org/10.1103/PhysRevLett.92.022001. arXiv:hep-lat/0304004
Q. J. Mason, High-precision lattice QCD: Perturbations in a non-perturbative world. Ph.D. thesis, Cornell U., LNS (2004)
A. Bochkarev, P. de Forcrand, Determination of the renormalized heavy quark mass in lattice QCD. Nucl. Phys. B 477, 489–520 (1996). https://doi.org/10.1016/0550-3213(96)00396-3. arXiv:hep-lat/9505025
K. Chetyrkin, J.H. Kuhn, C. Sturm, Four-loop moments of the heavy quark vacuum polarization function in perturbative QCD. Eur. Phys. J. C 48, 107–110 (2006). https://doi.org/10.1140/epjc/s2006-02610-y. arXiv:hep-ph/0604234
R. Boughezal, M. Czakon, T. Schutzmeier, Charm and bottom quark masses from perturbative QCD. Phys. Rev. D 74, 074006 (2006). https://doi.org/10.1103/PhysRevD.74.074006. arXiv:hep-ph/0605023
A. Maier, P. Maierhofer, P. Marqaurd, The second physical moment of the heavy quark vector correlator at \(O(\alpha _s^3)\). Phys. Lett. B 669, 88–91 (2008). https://doi.org/10.1016/j.physletb.2008.09.041. arXiv:0806.3405
A. Maier, P. Maierhofer, P. Marquard, A. Smirnov, Low energy moments of heavy quark current correlators at four loops. Nucl. Phys. B 824, 1–18 (2010). https://doi.org/10.1016/j.nuclphysb.2009.08.011. arXiv:0907.2117
Y. Kiyo, A. Maier, P. Maierhofer, P. Marquard, Reconstruction of heavy quark current correlators at \(O(\alpha _s^3)\). Nucl. Phys. B 823, 269–287 (2009). https://doi.org/10.1016/j.nuclphysb.2009.08.010. arXiv:0907.2120
J.H. Kühn, M. Steinhauser, C. Sturm, Heavy quark masses from sum rules in four-loop approximation. Nucl. Phys. B 778, 192–215 (2007). https://doi.org/10.1016/j.nuclphysb.2007.04.036. arXiv:hep-ph/0702103
K. Chetyrkin, J. Kuhn, A. Maier, P. Maierhofer, P. Marquard et al., Charm and bottom quark masses: An update. Phys. Rev. D 80, 074010 (2009). https://doi.org/10.1103/PhysRevD.80.074010. arXiv:0907.2110
B. Dehnadi, A.H. Hoang, V. Mateu, Bottom and charm mass determinations with a convergence test. JHEP 08, 155 (2015). https://doi.org/10.1007/JHEP08(2015)155. arXiv:1504.07638
A. Cucchieri, Gribov copies in the minimal Landau gauge: The Influence on gluon and ghost propagators. Nucl. Phys. B 508, 353–370 (1997). https://doi.org/10.1016/S0550-3213(97)00629-9. arXiv:hep-lat/9705005
L. Giusti, M. Paciello, C. Parrinello, S. Petrarca, B. Taglienti, Problems on lattice gauge fixing. Int. J. Mod. Phys. A 16, 3487–3534 (2001). https://doi.org/10.1142/S0217751X01004281. arXiv:hep-lat/0104012
A. Maas, J.M. Pawlowski, D. Spielmann, A. Sternbeck, L. von Smekal, Strong-coupling study of the Gribov ambiguity in lattice Landau gauge. Eur. Phys. J. C 68, 183–195 (2010). https://doi.org/10.1140/epjc/s10052-010-1306-6. arXiv:0912.4203
B. Alles, D. Henty, H. Panagopoulos, C. Parrinello, C. Pittori et al., \(\alpha _s\) from the nonperturbatively renormalised lattice three gluon vertex. Nucl. Phys. B 502, 325–342 (1997). https://doi.org/10.1016/S0550-3213(97)00483-5. arXiv:hep-lat/9605033
P. Boucaud, J. Leroy, H. Moutarde, J. Micheli, O. Pene et al., Preliminary calculation of \(\alpha _s\) from Green functions with dynamical quarks. JHEP 0201, 046 (2002). arXiv: hep-ph/0107278
P. Boucaud, J. Leroy, A. Le Yaouanc, A. Lokhov, J. Micheli et al., Asymptotic behavior of the ghost propagator in SU(3) lattice gauge theory. Phys. Rev. D 72, 114503 (2005). https://doi.org/10.1103/PhysRevD.72.114503. arXiv:hep-lat/0506031
P. Boucaud, J. Leroy, A. Le Yaouanc, A. Lokhov, J. Micheli et al., Non-perturbative power corrections to ghost and gluon propagators. JHEP 0601, 037 (2006). https://doi.org/10.1088/1126-6708/2006/01/037. arXiv:hep-lat/0507005
A. Sternbeck, K. Maltman, L. von Smekal, A. Williams, E. Ilgenfritz et al., Running \(\alpha _s\) from Landau-gauge gluon and ghost correlations. PoS LAT2007, 256 (2007). arXiv:0710.2965
Ph Boucaud, F. De Soto, J. Leroy, A. Le Yaouanc, J. Micheli et al., Ghost-gluon running coupling, power corrections and the determination of \(\Lambda _{\overline{\rm MS}}\). Phys. Rev. D 79, 014508 (2009). https://doi.org/10.1103/PhysRevD.79.014508. arXiv:0811.2059
[ETM 13D] B. Blossier et al., High statistics determination of the strong coupling constant in Taylor scheme and its OPE Wilson coefficient from lattice QCD with a dynamical charm. Phys. Rev. D 89, 014507 (2014). https://doi.org/10.1103/PhysRevD.89.014507. arXiv:1310.3763
[ETM 12C] B. Blossier, P. Boucaud, M. Brinet, F. De Soto, X. Du et al., The strong running coupling at \(\tau \) and \(Z_0\) mass scales from lattice QCD. Phys. Rev. Lett. 108, 262002 (2012). https://doi.org/10.1103/PhysRevLett.108.262002. arXiv:1201.5770
[ETM 11D] B. Blossier, P. Boucaud, M. Brinet, F. De Soto, X. Du et al., Ghost-gluon coupling, power corrections and \(\Lambda _{\overline{\rm MS}}\) from lattice QCD with a dynamical charm. Phys. Rev. D 85, 034503 (2012). https://doi.org/10.1103/PhysRevD.85.034503. arXiv:1110.5829
A. Sternbeck, K. Maltman, M. Müller-Preussker, L. von Smekal, Determination of \(\Lambda _{\overline{\rm MS}}\) from the gluon and ghost propagators in Landau gauge. PoS LAT2012, 243 (2012). arXiv:1212.2039
A. Sternbeck, E.-M. Ilgenfritz, K. Maltman, M. Müller-Preussker, L. von Smekal et al., QCD Lambda parameter from Landau-gauge gluon and ghost correlations. PoS LAT2009, 210 (2009). arXiv:1003.1585
[ETM 10F] B. Blossier et al., Ghost-gluon coupling, power corrections and \(\Lambda _{\overline{\rm MS}}\) from twisted-mass lattice QCD at \(N_f=2\). Phys. Rev. D 82, 034510 (2010). https://doi.org/10.1103/PhysRevD.82.034510. arXiv:1005.5290
E.-M. Ilgenfritz, C. Menz, M. Müller-Preussker, A. Schiller, A. Sternbeck, \(SU(3)\) Landau gauge gluon and ghost propagators using the logarithmic lattice gluon field definition. Phys. Rev. D 83, 054506 (2011). https://doi.org/10.1103/PhysRevD.83.054506. arXiv:1010.5120
F. De Soto, J. Rodriguez-Quintero, Notes on the determination of the Landau gauge OPE for the asymmetric three gluon vertex. Phys. Rev. D 64, 114003 (2001). https://doi.org/10.1103/PhysRevD.64.114003. arXiv:hep-ph/0105063
P. Boucaud, A. Le Yaouanc, J. Leroy, J. Micheli, O. Pene et al., Testing Landau gauge OPE on the lattice with a \(\langle A^2 \rangle \) condensate. Phys. Rev. D 63, 114003 (2001). https://doi.org/10.1103/PhysRevD.63.114003. arXiv:hep-ph/0101302
P. Boucaud, A. Le Yaouanc, J. Leroy, J. Micheli, O. Pene et al., Consistent OPE description of gluon two point and three point Green function? Phys. Lett. B 493, 315–324 (2000). https://doi.org/10.1016/S0370-2693(00)01149-7. arXiv:hep-ph/0008043
P. Boucaud, G. Burgio, F. Di Renzo, J. Leroy, J. Micheli et al., Lattice calculation of \(1 / p^2\) corrections to \(\alpha _s\) and of \(\Lambda _{{\rm QCD}}\) in the MOM scheme. JHEP 0004, 006 (2000). arXiv:hep-ph/0003020
D. Bećirević, P. Boucaud, J. Leroy, J. Micheli, O. Pene et al., Asymptotic scaling of the gluon propagator on the lattice. Phys. Rev. D 61, 114508 (2000). arXiv:hep-ph/9910204
D. Bećirević, P. Boucaud, J. Leroy, J. Micheli, O. Pene et al., Asymptotic behavior of the gluon propagator from lattice QCD. Phys. Rev. d 60, 094509 (1999). arXiv:hep-ph/9903364
P. Boucaud, J. Leroy, J. Micheli, O. Pene, C. Roiesnel, Three loop beta function and nonperturbative \(\alpha _s\) in asymmetric momentum scheme. JHEP 9812, 004 (1998). https://doi.org/10.1088/1126-6708/1998/12/004. arXiv:hep-ph/9810437
P. Boucaud, J. Leroy, J. Micheli, O. Pene, C. Roiesnel, Lattice calculation of \(\alpha _s\) in momentum scheme. JHEP 9810, 017 (1998). arXiv:hep-ph/9810322
K.G. Chetyrkin, J.H. Kuhn, Quartic mass corrections to R(had). Nucl. Phys. B 432, 337–350 (1994). https://doi.org/10.1016/0550-3213(94)90605-X. arXiv:hep-ph/9406299
J.-L. Kneur, A. Neveu, Chiral condensate from renormalization group optimized perturbation. Phys. Rev. D 92, 074027 (2015). https://doi.org/10.1103/PhysRevD.92.074027. arXiv:1506.07506
Particle Data Group collaboration, J. Beringer et al., Review of particle physics. Phys. Rev. D 86, 010001 (2012) (2013 partial update for the 2014 edition)
S. Syritsyn, Review of Hadron structure calculations on a lattice. PoS LATTICE2013, 009 (2014). https://doi.org/10.22323/1.187.0009. arXiv:1403.4686
S. Capitani, M Della Morte, D. Djukanovic, G. von Hippel, J. Hua, B. Jäger et al., Nucleon electromagnetic form factors in two-flavor QCD. Phys. Rev. D 92, 054511 (2015). https://doi.org/10.1103/PhysRevD.92.054511. arXiv:1504.04628
R.S. Sufian, Y.-B. Yang, A. Alexandru, T. Draper, J. Liang, K.-F. Liu, Strange quark magnetic moment of the nucleon at the physical point. Phys. Rev. Lett. 118, 042001 (2017). https://doi.org/10.1103/PhysRevLett.118.042001. arXiv:1606.07075
R. Gupta, Y.-C. Jang, H.-W. Lin, B. Yoon, T. Bhattacharya, Axial vector form factors of the nucleon from lattice QCD. Phys. Rev. D 96, 114503 (2017). https://doi.org/10.1103/PhysRevD.96.114503. arXiv:1705.06834
J. Green, N. Hasan, S. Meinel, M. Engelhardt, S. Krieg, J. Laeuchli et al., Up, down, and strange nucleon axial form factors from lattice QCD. Phys. Rev. D 95, 114502 (2017). https://doi.org/10.1103/PhysRevD.95.114502. arXiv:1703.06703
[CSSM/QCDSF/UKQCD 17] A. J. Chambers et al., Electromagnetic form factors at large momenta from lattice QCD. Phys. Rev. D 96, 114509 (2017). https://doi.org/10.1103/PhysRevD.96.114509. arXiv:1702.01513
C. Alexandrou, M. Constantinou, K. Hadjiyiannakou, K. Jansen, C. Kallidonis, G. Koutsou et al., Nucleon electromagnetic form factors using lattice simulations at the physical point. Phys. Rev. D 96, 034503 (2017). https://doi.org/10.1103/PhysRevD.96.034503. arXiv:1706.00469
C. Alexandrou, M. Constantinou, K. Hadjiyiannakou, K. Jansen, C. Kallidonis, G. Koutsou et al., Strange nucleon electromagnetic form factors from lattice QCD. Phys. Rev. D 97, 094504 (2018). https://doi.org/10.1103/PhysRevD.97.094504. arXiv:1801.09581
[PACS 18] K.-I. Ishikawa, Y. Kuramashi, S. Sasaki, N. Tsukamoto, A. Ukawa, T. Yamazaki, Nucleon form factors on a large volume lattice near the physical point in 2+1 flavor QCD. Phys. Rev. D 98, 074510 (2018). https://doi.org/10.1103/PhysRevD.98.074510. arXiv:1807.03974
H.-W. Lin et al., Parton distributions and lattice QCD calculations: a community white paper. Prog. Part. Nucl. Phys. 100, 107–160 (2018). https://doi.org/10.1016/j.ppnp.2018.01.007. arXiv:1711.07916
M.J. Savage, Nuclear Physics from Lattice QCD. Prog. Part. Nucl. Phys. 67, 140–152 (2012). https://doi.org/10.1016/j.ppnp.2011.12.008. arXiv:1110.5943
[NPLQCD 17] E. Chang, Z. Davoudi, W. Detmold, A. S. Gambhir, K. Orginos, M. J. Savage et al., Scalar, axial, and tensor interactions of light nuclei from lattice QCD. Phys. Rev. Lett. 120, 152002 (2018). https://doi.org/10.1103/PhysRevLett.120.152002. arXiv:1712.03221
J. Carlson, S. Gandolfi, F. Pederiva, S.C. Pieper, R. Schiavilla, K.E. Schmidt et al., Quantum Monte Carlo methods for nuclear physics. Rev. Mod. Phys. 87, 1067 (2015). https://doi.org/10.1103/RevModPhys.87.1067. arXiv:1412.3081
M.L. Wagman, F. Winter, E. Chang, Z. Davoudi, W. Detmold, K. Orginos et al., Baryon-Baryon Interactions and spin-flavor symmetry from lattice quantum chromodynamics. Phys. Rev. D 96, 114510 (2017). https://doi.org/10.1103/PhysRevD.96.114510. arXiv:1706.06550
T. Iritani, Two-baryon systems from HAL QCD method and the mirage in the temporal correlation of the direct method. EPJ Web Conf. 175, 05008 (2018). https://doi.org/10.1051/epjconf/201817505008. arXiv:1710.06147
H.W. Hamber, E. Marinari, G. Parisi, C. Rebbi, Considerations on numerical analysis of QCD. Nucl. Phys. B 225, 475 (1983). https://doi.org/10.1016/0550-3213(83)90528-X
G.P. Lepage, The analysis of algorithms for lattice field theory. Boulder ASI 1989(97–120), 97–120 (1989)
[QCDSF 06] A.A. Khan, M. Göckeler, P. Hägler, T. Hemmert, R. Horsley et al., Axial coupling constant of the nucleon for two flavours of dynamical quarks in finite and infinite volume. Phys. Rev. D 74, 094508 (2006). https://doi.org/10.1103/PhysRevD.74.094508. arXiv:hep-lat/0603028
[Mainz 12] S. Capitani, M. Della Morte, G. von Hippel, B. Jager, A. Jüttner et al., The nucleon axial charge from lattice QCD with controlled errors. Phys. Rev. D 86, 074502 (2012). https://doi.org/10.1103/PhysRevD.86.074502. arXiv:1205.0180
[RQCD 14] G.S. Bali, S. Collins, B. Glässle, M. Göckeler, J. Najjar, R.H. Rödl et al., Nucleon isovector couplings from \(N_f=2\) lattice QCD. Phys. Rev. D 91, 054501 (2015). https://doi.org/10.1103/PhysRevD.91.054501. arXiv:1412.7336
[RQCD 16] G.S. Bali, S. Collins, D. Richtmann, A. Schäfer, W. Söldner, A. Sternbeck, Direct determinations of the nucleon and pion \(\sigma \) terms at nearly physical quark masses. Phys. Rev. D 93, 094504 (2016). https://doi.org/10.1103/PhysRevD.93.094504. arXiv:1603.00827
[PACS-CS 09] K.-I. Ishikawa et al., SU(2) and SU(3) chiral perturbation theory analyses on baryon masses in 2+1 flavor lattice QCD. Phys. Rev. D 80, 054502 (2009). https://doi.org/10.1103/PhysRevD.80.054502. arXiv:0905.0962
[ETM 15D] A. Abdel-Rehim et al., Nucleon and pion structure with lattice QCD simulations at physical value of the pion mass. Phys. Rev. D 92, 114513 (2015), https://doi.org/10.1103/PhysRevD.92.114513, https://doi.org/10.1103/PhysRevD.93.039904. arXiv:1507.04936
[ETM 16A] A. Abdel-Rehim, C. Alexandrou, M. Constantinou, K. Hadjiyiannakou, K. Jansen, C. Kallidonis et al., Direct evaluation of the Quark content of nucleons from lattice QCD at the physical point. Phys. Rev. Lett. 116, 252001 (2016). https://doi.org/10.1103/PhysRevLett.116.252001. arXiv:1601.01624
[ETM 17B] C. Alexandrou, M. Constantinou, K. Hadjiyiannakou, K. Jansen, C. Kallidonis, G. Koutsou et al., Nucleon axial form factors using \(N_f\) = 2 twisted mass fermions with a physical value of the pion mass. Phys. Rev. D 96, 054507 (2017). https://doi.org/10.1103/PhysRevD.96.054507. arXiv:1705.03399
[ETM 17C] C. Alexandrou, M. Constantinou, K. Hadjiyiannakou, K. Jansen, C. Kallidonis, G. Koutsou et al., Nucleon spin and momentum decomposition using lattice QCD simulations. Phys. Rev. Lett. 119, 142002 (2017). https://doi.org/10.1103/PhysRevLett.119.142002. arXiv:1706.02973
[ETM 17] C. Alexandrou et al., Nucleon scalar and tensor charges using lattice QCD simulations at the physical value of the pion mass. Phys. Rev. D 95, 114514 (2017). https://doi.org/10.1103/PhysRevD.96.099906, https://doi.org/10.1103/PhysRevD.95.114514. arXiv:1703.08788
[PNDME 13] T. Bhattacharya, S.D. Cohen, R. Gupta, A. Joseph, H.-W. Lin, B. Yoon, Nucleon charges and electromagnetic form factors from 2+1+1-flavor lattice QCD. Phys. Rev. D 89, 094502 (2014). https://doi.org/10.1103/PhysRevD.89.094502. arXiv:1306.5435
[PNDME 15A] T. Bhattacharya, V. Cirigliano, S. Cohen, R. Gupta, A. Joseph, H.-W. Lin et al., Iso-vector and Iso-scalar Tensor Charges of the Nucleon from Lattice QCD. Phys. Rev. D 92, 094511 (2015). https://doi.org/10.1103/PhysRevD.92.094511. arXiv:1506.06411
[PNDME 15] T. Bhattacharya, V. Cirigliano, R. Gupta, H.-W. Lin, B. Yoon, Neutron electric dipole moment and tensor charges from lattice QCD. Phys. Rev. Lett. 115, 212002 (2015). https://doi.org/10.1103/PhysRevLett.115.212002. arXiv:1506.04196
[PNDME 16] T. Bhattacharya, V. Cirigliano, S. Cohen, R. Gupta, H.-W. Lin, B. Yoon, Axial, scalar and tensor charges of the nucleon from 2+1+1-flavor lattice QCD. Phys. Rev. D 94, 054508 (2016). https://doi.org/10.1103/PhysRevD.94.054508. arXiv:1606.07049
[CalLat 17] E. Berkowitz et al., An accurate calculation of the nucleon axial charge with lattice QCD. arXiv:1704.01114
[RBC/UKQCD 08B] T. Yamazaki et al., Nucleon axial charge in 2+1 flavor dynamical lattice QCD with domain wall fermions. Phys.Rev.Lett. 100, 171602 (2008). https://doi.org/10.1103/PhysRevLett.100.171602. arXiv:0801.4016
[RBC/UKQCD 09B] T. Yamazaki, Y. Aoki, T. Blum, H.-W. Lin, S. Ohta, S. Sasaki et al., Nucleon form factors with 2+1 flavor dynamical domain-wall fermions. Phys. Rev. D 79, 114505 (2009). https://doi.org/10.1103/PhysRevD.79.114505. arXiv:0904.2039
[RBC/UKQCD 10D] Y. Aoki, T. Blum, H.-W. Lin, S. Ohta, S. Sasaki, R. Tweedie et al., Nucleon isovector structure functions in (2+1)-flavor QCD with domain wall fermions. Phys. Rev. D 82, 014501 (2010). https://doi.org/10.1103/PhysRevD.82.014501. arXiv:1003.3387
[\(\chi \)QCD 13A] M. Gong et al., Strangeness and charmness content of the nucleon from overlap fermions on 2+1-flavor domain-wall fermion configurations. Phys. Rev. D 88, 014503 (2013). https://doi.org/10.1103/PhysRevD.88.014503. arXiv:1304.1194
[\(\chi \)QCD 15] M. Gong, Y.-B. Yang, J. Liang, A. Alexandru, T. Draper, K.-F. Liu, Strange and charm quark spins from the anomalous Ward identity. Phys. Rev. D 95, 114509 (2017). https://doi.org/10.1103/PhysRevD.95.114509. arXiv:1511.03671
[JLQCD 08B] H. Ohki, H. Fukaya, S. Hashimoto, T. Kaneko, H. Matsufuru, J. Noaki et al., Nucleon sigma term and strange quark content from lattice QCD with exact chiral symmetry. Phys. Rev. D 78, 054502 (2008). https://doi.org/10.1103/PhysRevD.78.054502. arXiv:0806.4744
[JLQCD 12A] H. Ohki, K. Takeda, S. Aoki, S. Hashimoto, T. Kaneko, H. Matsufuru et al., Nucleon strange quark content from \(N_f=2+1\) lattice QCD with exact chiral symmetry. Phys. Rev. D 87, 034509 (2013). https://doi.org/10.1103/PhysRevD.87.034509. arXiv:1208.4185
[JLQCD 18] N. Yamanaka, S. Hashimoto, T. Kaneko, H. Ohki, Nucleon charges with dynamical overlap fermions. Phys. Rev. D 98, 054516 (2018). https://doi.org/10.1103/PhysRevD.98.054516. arXiv:1805.10507
R. Babich, J. Brannick, R.C. Brower, M.A. Clark, T.A. Manteuffel, S.F. McCormick et al., Adaptive multigrid algorithm for the lattice Wilson-Dirac operator. Phys. Rev. Lett. 105, 201602 (2010). https://doi.org/10.1103/PhysRevLett.105.201602. arXiv:1005.3043
M. Lüscher, Deflation acceleration of lattice QCD simulations. JHEP 12, 011 (2007). https://doi.org/10.1088/1126-6708/2007/12/011. arXiv:0710.5417
G.S. Bali, S. Collins, A. Schafer, Effective noise reduction techniques for disconnected loops in Lattice QCD. Comput. Phys. Commun. 181, 1570–1583 (2010). https://doi.org/10.1016/j.cpc.2010.05.008. arXiv:0910.3970
T. Blum, T. Izubuchi, E. Shintani, New class of variance-reduction techniques using lattice symmetries. Phys. Rev. D 88, 094503 (2013). https://doi.org/10.1103/PhysRevD.88.094503. arXiv:1208.4349
A. Stathopoulos, J. Laeuchli, K. Orginos, Hierarchical probing for estimating the trace of the matrix inverse on toroidal lattices. arXiv:1302.4018
A. S. Gambhir, A. Stathopoulos, K. Orginos, B. Yoon, R. Gupta, S. Syritsyn, Algorithms for Disconnected Diagrams in Lattice QCD. PoS LATTICE2016, 265 (2016). https://doi.org/10.22323/1.256.0265. arXiv:1611.01193
[LHPC 10] J.D. Bratt et al., Nucleon structure from mixed action calculations using 2+1 flavors of asqtad sea and domain wall valence fermions. Phys. Rev. D 82, 094502 (2010). https://doi.org/10.1103/PhysRevD.82.094502. arXiv:1001.3620
B. Yoon et al., Controlling Excited-State Contamination in Nucleon Matrix Elements. Phys. Rev. D 93, 114506 (2016). https://doi.org/10.1103/PhysRevD.93.114506. arXiv:1602.07737
T.A. DeGrand, S. Schaefer, Improving meson two point functions in lattice QCD. Comput. Phys. Commun. 159, 185–191 (2004). https://doi.org/10.1016/j.cpc.2004.02.006. arXiv:hep-lat/0401011
R. Gupta, A. Patel, C.F. Baillie, G. Guralnik, G.W. Kilcup, S.R. Sharpe, QCD with dynamical Wilson Fermions. Phys. Rev. D 40, 2072 (1989). https://doi.org/10.1103/PhysRevD.40.2072
C. Thron, S. Dong, K. Liu, H. Ying, Pade - Z(2) estimator of determinants. Phys. Rev. D 57, 1642–1653 (1998). https://doi.org/10.1103/PhysRevD.57.1642. arXiv:hep-lat/9707001
S. Bernardson, P. McCarty, C. Thron, Monte Carlo methods for estimating linear combinations of inverse matrix entries in lattice QCD. Comput. Phys. Commun. 78, 256–264 (1993). https://doi.org/10.1016/0010-4655(94)90004-3
J. Foley et al., Practical all-to-all propagators for lattice QCD. Comput. Phys. Commun. 172, 145–162 (2005). https://doi.org/10.1016/j.cpc.2005.06.008. arXiv:hep-lat/0505023
S. Güsken, U. Löw, K.H. Mütter, R. Sommer, A. Patel, K. Schilling, Nonsinglet axial vector couplings of the Baryon octet in lattice QCD. Phys. Lett. B 227, 266–269 (1989). https://doi.org/10.1016/S0370-2693(89)80034-6
C. Alexandrou, F. Jegerlehner, S. Gusken, K. Schilling, R. Sommer, B meson properties from lattice QCD. Phys. Lett. B 256, 60–67 (1991). https://doi.org/10.1016/0370-2693(91)90219-G
B.C. Tiburzi, Time dependence of nucleon correlation functions in chiral perturbation theory. Phys. Rev. D 80, 014002 (2009). https://doi.org/10.1103/PhysRevD.80.014002. arXiv:0901.0657
O. Bär, Multi-hadron-state contamination in nucleon observables from chiral perturbation theory. EPJ Web Conf. 175, 01007 (2018). https://doi.org/10.1051/epjconf/201817501007. arXiv:1708.00380
O. Bär, Nucleon-pion-state contribution in lattice calculations of the nucleon charges \(g_A, g_T\) and \(g_S\). Phys. Rev. D 94, 054505 (2016). https://doi.org/10.1103/PhysRevD.94.054505. arXiv:1606.09385
O. Bär, Nucleon-pion-state contribution in lattice calculations of moments of parton distribution functions. Phys. Rev. D 95, 034506 (2017). https://doi.org/10.1103/PhysRevD.95.034506. arXiv:1612.08336
M.T. Hansen, H.B. Meyer, On the effect of excited states in lattice calculations of the nucleon axial charge. Nucl. Phys. B 923, 558–587 (2017). https://doi.org/10.1016/j.nuclphysb.2017.08.017. arXiv:1610.03843
B. Yoon et al., Isovector charges of the nucleon from 2+1-flavor QCD with clover fermions. Phys. Rev. D 95, 074508 (2017). https://doi.org/10.1103/PhysRevD.95.074508. arXiv:1611.07452
L. Maiani, G. Martinelli, M.L. Paciello, B. Taglienti, Scalar densities and Baryon mass differences in lattice QCD with Wilson Fermions. Nucl. Phys. B 293, 420 (1987). https://doi.org/10.1016/0550-3213(87)90078-2
S.J. Dong, K.F. Liu, A.G. Williams, Lattice calculation of the strangeness magnetic moment of the nucleon. Phys. Rev. D 58, 074504 (1998). https://doi.org/10.1103/PhysRevD.58.074504. arXiv:hep-ph/9712483
S. Capitani, B. Knippschild, M. Della Morte, H. Wittig, Systematic errors in extracting nucleon properties from lattice QCD. PoS LATTICE2010, 147 (2010). https://doi.org/10.22323/1.105.0147. arXiv:1011.1358
J. Bulava, M. Donnellan, R. Sommer, On the computation of hadron-to-hadron transition matrix elements in lattice QCD. JHEP 01, 140 (2012). https://doi.org/10.1007/JHEP01(2012)140. arXiv:1108.3774
S. Güsken, K. Schilling, R. Sommer, K.H. Mütter, A. Patel, Mass Splittings in the Baryon Octet and the Nucleon \(\sigma \) Term in Lattice QCD. Phys. Lett. B 212, 216–220 (1988). https://doi.org/10.1016/0370-2693(88)90528-X
R. Sommer, Current matrix elements with quenched Wilson fermions. Nucl. Phys. Proc. Suppl. 17, 513–517 (1990). https://doi.org/10.1016/0920-5632(90)90304-D
C. Bouchard, C.C. Chang, T. Kurth, K. Orginos, A. Walker-Loud, On the Feynman-Hellmann Theorem in Quantum Field Theory and the Calculation of Matrix Elements. Phys. Rev. D 96, 014504 (2017). https://doi.org/10.1103/PhysRevD.96.014504. arXiv:1612.06963
[CSSM/QCDSF/UKQCD 14] A. J. Chambers et al., Feynman-Hellmann approach to the spin structure of hadrons. Phys. Rev. D 90, 014510 (2014). https://doi.org/10.1103/PhysRevD.90.014510. arXiv:1405.3019
A.J. Chambers et al., Disconnected contributions to the spin of the nucleon. Phys. Rev. D 92, 114517 (2015). https://doi.org/10.1103/PhysRevD.92.114517. arXiv:1508.06856
B.J. Owen, J. Dragos, W. Kamleh, D.B. Leinweber, M.S. Mahbub, B.J. Menadue et al., Variational Approach to the Calculation of gA. Phys. Lett. B 723, 217–223 (2013). https://doi.org/10.1016/j.physletb.2013.04.063. arXiv:1212.4668
G. Fox, R. Gupta, O. Martin, S. Otto, Monte Carlo estimates of the mass gap of the O(2) and O(3) Spin Models in (1+1)-dimensions. Nucl. Phys. B 205, 188–220 (1982). https://doi.org/10.1016/0550-3213(82)90384-4
C. Michael, Adjoint sources in lattice gauge theory. Nucl. Phys. B 259, 58–76 (1985). https://doi.org/10.1016/0550-3213(85)90297-4
M. Lüscher, U. Wolff, How to calculate the elastic scattering matrix in two-dimensional quantum field theories by numerical simulation. Nucl. Phys. B 339, 222–252 (1990). https://doi.org/10.1016/0550-3213(90)90540-T
B. Blossier, M Della Morte, G. von Hippel, T. Mendes, R. Sommer, On the generalized eigenvalue method for energies and matrix elements in lattice field theory. JHEP 04, 094 (2009). https://doi.org/10.1088/1126-6708/2009/04/094. arXiv:0902.1265
J. Dragos, R. Horsley, W. Kamleh, D.B. Leinweber, Y. Nakamura, P.E.L. Rakow et al., Nucleon matrix elements using the variational method in lattice QCD. Phys. Rev. D 94, 074505 (2016). https://doi.org/10.1103/PhysRevD.94.074505. arXiv:1606.03195
K. Jansen, C. Liu, M. Luscher, H. Simma, S. Sint, R. Sommer et al., Nonperturbative renormalization of lattice QCD at all scales. Phys. Lett. B 372, 275–282 (1996). https://doi.org/10.1016/0370-2693(96)00075-5. arXiv:hep-lat/9512009
M. Lüscher, S. Sint, R. Sommer, P. Weisz, Chiral symmetry and O(a) improvement in lattice QCD. Nucl. Phys. B 478, 365–400 (1996). https://doi.org/10.1016/0550-3213(96)00378-1. arXiv:hep-lat/9605038
[RQCD 16A] G. S. Bali, E. E. Scholz, J. Simeth, W. Söldner, Lattice simulations with \(N_f=2+1\) improved Wilson fermions at a fixed strange quark mass. Phys. Rev. D 94, 074501 (2016). https://doi.org/10.1103/PhysRevD.94.074501. arXiv:1606.09039
A. Gerardin, T. Harris, H.B. Meyer, Non-perturbative renormalization and O\((a)\)-improvement of the non-singlet vector current with \(N_{{\rm f}}=2+1\) Wilson fermions and tree-level Symanzik improved gauge action. Phys. Rev. D 99, 014519 (2019). https://doi.org/10.1103/PhysRevD.99.014519. arXiv:1811.08209
R. Frezzotti, G. C. Rossi, Chirally improving Wilson fermions. I: O(a) improvement. JHEP 08, 007 (2004). arXiv:hep-lat/0306014
R. Frezzotti, G.C. Rossi, Twisted mass lattice QCD with mass nondegenerate quarks. Nucl. Phys. Proc. Suppl. 128, 193–202 (2004). https://doi.org/10.1016/S0920-5632(03)02477-0. arXiv:hep-lat/0311008
S. Capitani, M. Göckeler, R. Horsley, H. Perlt, P.E.L. Rakow, G. Schierholz et al., Renormalization and off-shell improvement in lattice perturbation theory. Nucl. Phys. V 593, 183–228 (2001). https://doi.org/10.1016/S0550-3213(00)00590-3. arXiv:hep-lat/0007004
T. Bhattacharya, R. Gupta, W. Lee, S.R. Sharpe, J.M.S. Wu, Improved bilinears in lattice QCD with non-degenerate quarks. Phys. Rev. D 73, 034504 (2006). https://doi.org/10.1103/PhysRevD.73.034504. arXiv:hep-lat/0511014
M. Bochicchio, L. Maiani, G. Martinelli, G.C. Rossi, M. Testa, Chiral symmetry on the lattice with Wilson fermions. Nucl. Phys. B 262, 331 (1985). https://doi.org/10.1016/0550-3213(85)90290-1
S. Sint, P. Weisz, Further results on O(a) improved lattice QCD to one loop order of perturbation theory. Nucl. Phys. B 502, 251–268 (1997). https://doi.org/10.1016/S0550-3213(97)00372-6. arXiv:hep-lat/9704001
Y. Taniguchi, A. Ukawa, Perturbative calculation of improvement coefficients to O(g**2a) for bilinear quark operators in lattice QCD. Phys. Rev. D 58, 114503 (1998). https://doi.org/10.1103/PhysRevD.58.114503. arXiv:hep-lat/9806015
P. Korcyl, G.S. Bali, Non-perturbative determination of improvement coefficients using coordinate space correlators in \(N_f=2+1\) lattice QCD. Phys. Rev. D 95, 014505 (2017). https://doi.org/10.1103/PhysRevD.95.014505. arXiv:1607.07090
M. Constantinou, M. Hadjiantonis, H. Panagopoulos, G. Spanoudes, Singlet versus nonsinglet perturbative renormalization of fermion bilinears. Phys. Rev. D 94, 114513 (2016). https://doi.org/10.1103/PhysRevD.94.114513. arXiv:1610.06744
G. S. Bali, S. Collins, M. Göckeler, S. Piemonte, A. Sternbeck, Non-perturbative renormalization of flavor singlet quark bilinear operators in lattice QCD. PoS LATTICE2016, 187 (2016). https://doi.org/10.22323/1.256.0187. arXiv:1703.03745
S. Dinter, V. Drach, R. Frezzotti, G. Herdoiza, K. Jansen, G. Rossi, Sigma terms and strangeness content of the nucleon with \(N_f=2+1+1\) twisted mass fermions. JHEP 08, 037 (2012). https://doi.org/10.1007/JHEP08(2012)037. arXiv:1202.1480
E.E. Jenkins, A.V. Manohar, Baryon chiral perturbation theory using a heavy fermion Lagrangian. Phys. Lett. B 255, 558–562 (1991). https://doi.org/10.1016/0370-2693(91)90266-S
T.N. Truong, Chiral perturbation theory and final state theorem. Phys. Rev. Lett. 61, 2526 (1988). https://doi.org/10.1103/PhysRevLett.61.2526
A. Walker-Loud et al., Light hadron spectroscopy using domain wall valence quarks on an Asqtad sea. Phys. Rev. D 79, 054502 (2009). https://doi.org/10.1103/PhysRevD.79.054502. arXiv:0806.4549
A. Torok, S.R. Beane, W. Detmold, T.C. Luu, K. Orginos, A. Parreno et al., Meson-Baryon scattering lengths from mixed-action lattice QCD. Phys. Rev. D 81, 074506 (2010). https://doi.org/10.1103/PhysRevD.81.074506. arXiv:0907.1913
E.E. Jenkins, A.V. Manohar, J.W. Negele, A. Walker-Loud, A lattice test of 1/N(c) Baryon mass relations. Phys. Rev. D 81, 014502 (2010). https://doi.org/10.1103/PhysRevD.81.014502. arXiv:0907.0529
A. Walker-Loud, Evidence for non-analytic light quark mass dependence in the baryon spectrum. Phys. Rev. D 86, 074509 (2012). https://doi.org/10.1103/PhysRevD.86.074509. arXiv:1112.2658
V. Bernard, N. Kaiser, J. Kambor, U.G. Meissner, Chiral structure of the nucleon. Nucl. Phys. B 388, 315–345 (1992). https://doi.org/10.1016/0550-3213(92)90615-I
S.R. Beane, M.J. Savage, Baryon axial charge in a finite volume. Phys. Rev. D 70, 074029 (2004). https://doi.org/10.1103/PhysRevD.70.074029. arXiv:hep-ph/0404131
R.E. Kass, A.E. Raftery, Bayes factors. J. Am. Stat. Assoc. 90, 773–795 (1995). https://doi.org/10.1080/01621459.1995.10476572. https://amstat.tandfonline.com/doi/pdf/10.1080/01621459.1995.10476572
H. Akaike, A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723 (1974). https://doi.org/10.1109/TAC.1974.1100705
T. Bhattacharya, V. Cirigliano, S.D. Cohen, A. Filipuzzi, M. Gonzalez-Alonso et al., Probing novel scalar and tensor interactions from (ultra)cold neutrons to the LHC. Phys. Rev. D 85, 054512 (2012). https://doi.org/10.1103/PhysRevD.85.054512. arXiv:1110.6448
UCNA collaboration, M. Mendenhall et al., Precision measurement of the neutron \(\beta \)-decay asymmetry. Phys.Rev. C 87, 032501 (2013). https://doi.org/10.1103/PhysRevC.87.032501. arXiv:1210.7048
UCNA collaboration, M. A. P. Brown et al., New result for the neutron \(\beta \)-asymmetry parameter \(A_0\) from UCNA. Phys. Rev. C 97, 035505 (2018). https://doi.org/10.1103/PhysRevC.97.035505. arXiv:1712.00884
D. Mund, B. Maerkisch, M. Deissenroth, J. Krempel, M. Schumann, H. Abele et al., Determination of the Weak Axial Vector Coupling from a measurement of the beta-asymmetry parameter a in neutron beta decay. Phys. Rev. Lett. 110, 172502. https://doi.org/10.1103/PhysRevLett.110.172502. arXiv:1204.0013
M. Ademollo, R. Gatto, Nonrenormalization theorem for the strangeness violating vector currents. Phys. Rev. Lett. 13, 264–265 (1964). https://doi.org/10.1103/PhysRevLett.13.264
J.F. Donoghue, D. Wyler, Isospin breaking and the precise determination of \(V_{ud}\). Phys. Lett. B 241, 243 (1990). https://doi.org/10.1016/0370-2693(90)91287-L
R. Alarcon et al., Precise measurement of neutron decay parameters (2007)
W. Wilburn et al., Measurement of the neutrino-spin correlation parameter \(b\) in neutron decay using ultracold neutrons. Rev. Mex. Fis. Suppl. 55, 119 (2009)
Nab collaboration, D. Pocanic et al., Nab: Measurement principles, apparatus and uncertainties. Nucl. Instrum. Methods A 611, 211–215 (2009). https://doi.org/10.1016/j.nima.2009.07.065. arXiv:0810.0251
M. Gonzalez-Alonso and J. Martin Camalich, Isospin breaking in the nucleon mass and the sensitivity of \(\beta \) decays to new physics. Phys. Rev. Lett. 112, 042501 (2014). https://doi.org/10.1103/PhysRevLett.112.042501. arXiv:1309.4434
J. Dudek et al., Physics Opportunities with the 12 GeV Upgrade at Jefferson Lab. Eur. Phys. J. A 48, 187 (2012). https://doi.org/10.1140/epja/i2012-12187-1. arXiv:1208.1244
Z. Ye, N. Sato, K. Allada, T. Liu, J.-P. Chen, H. Gao et al., Unveiling the nucleon tensor charge at Jefferson Lab: A study of the SoLID case. Phys. Lett. B 767, 91–98 (2017). https://doi.org/10.1016/j.physletb.2017.01.046. arXiv:1609.02449
H.-W. Lin, W. Melnitchouk, A. Prokudin, N. Sato, H. Shows, First Monte Carlo global analysis of nucleon transversity with lattice QCD constraints. Phys. Rev. Lett. 120, 152502 (2018). https://doi.org/10.1103/PhysRevLett.120.152502. arXiv:1710.09858
M. Radici, A. Bacchetta, First extraction of transversity from a global analysis of electron-proton and proton-proton data. Phys. Rev. Lett. 120, 192001 (2018). https://doi.org/10.1103/PhysRevLett.120.192001. arXiv:1802.05212
[Mainz 18] K. Ottnad, T. Harris, H. Meyer, G. von Hippel, J. Wilhelm, H. Wittig, Nucleon charges and quark momentum fraction with \(N_f=2+1\) Wilson fermions. In Proceedings, 36th International Symposium on Lattice Field Theory (Lattice 2018): East Lansing, MI, United States, July 22–28, 2018, vol. LATTICE2018 (2018), p. 129. https://doi.org/10.22323/1.334.0129. arXiv:1809.10638
[LHPC 12A] J. R. Green, M. Engelhardt, S. Krieg, J. W. Negele, A. V. Pochinsky, S. N. Syritsyn, Nucleon structure from lattice QCD using a nearly physical pion mass. Phys. Lett. B 734, 290–295 (2014). https://doi.org/10.1016/j.physletb.2014.05.075. arXiv:1209.1687
[LHPC 05] R.G. Edwards et al., The nucleon axial charge in full lattice QCD. Phys. Rev. Lett. 96, 052001 (2006). https://doi.org/10.1103/PhysRevLett.96.052001. arXiv:hep-lat/0510062
[RBC 08] H.-W. Lin, T. Blum, S. Ohta, S. Sasaki, T. Yamazaki, Nucleon structure with two flavors of dynamical domain-wall fermions. Phys. Rev. D 78, 014505 (2008). https://doi.org/10.1103/PhysRevD.78.014505. arXiv:0802.0863
[LHP/RBC/UKQCD 18] S. Ohta, Nucleon isovector axial charge in \(2+1\)-flavor domain-wall QCD with physical mass. In 36th International Symposium on Lattice Field Theory (Lattice 2018) East Lansing, MI, United States, July 22-28, 2018, vol. LATTICE2018 (2018), p. 128. https://doi.org/10.22323/1.334.0128. arXiv:1810.09737
[LHPC 12] J.R. Green, J.W. Negele, A.V. Pochinsky, S.N. Syritsyn, M. Engelhardt, S. Krieg, Nucleon scalar and tensor charges from lattice QCD with light Wilson Quarks. Phys. Rev. D 86, 114509 (2012). https://doi.org/10.1103/PhysRevD.86.114509. arXiv:1206.4527
M. Radici, A. Courtoy, A. Bacchetta, M. Guagnelli, Improved extraction of valence transversity distributions from inclusive dihedron production. JHEP 05, 123 (2015). https://doi.org/10.1007/JHEP05(2015)123. arXiv:1503.03495
Z.-B. Kang, A. Prokudin, P. Sun, F. Yuan, Extraction of Quark transversity distribution and collins fragmentation functions with QCD evolution. Phys. Rev. D 93, 014009 (2016). https://doi.org/10.1103/PhysRevD.93.014009. arXiv:1505.05589
Z.-B. Kang, private communication, Jun. 2015. (2015)
G. R. Goldstein, J. O. Gonzalez Hernandez, S. Liuti, Flavor dependence of chiral odd generalized parton distributions and the tensor charge from the analysis of combined \(\pi ^0\) and \(\eta \) exclusive electroproduction data. arXiv:1401.0438
M. Pitschmann, C.-Y. Seng, C.D. Roberts, S.M. Schmidt, Nucleon tensor charges and electric dipole moments. Phys. Rev. D 91, 074004 (2015). https://doi.org/10.1103/PhysRevD.91.074004. arXiv:1411.2052
M.A. Shifman, A.I. Vainshtein, V.I. Zakharov, Remarks on Higgs Boson Interactions with Nucleons. Phys. Lett. 78B, 443–446 (1978). https://doi.org/10.1016/0370-2693(78)90481-1
K.G. Chetyrkin, B.A. Kniehl, M. Steinhauser, Decoupling relations to O (alpha-s**3) and their connection to low-energy theorems. Nucl. Phys. B 510, 61–87 (1998). https://doi.org/10.1016/S0550-3213(98)81004-3, https://doi.org/10.1016/S0550-3213(97)00649-4. arXiv: hep-ph/9708255
R.J. Hill, M.P. Solon, Standard Model anatomy of WIMP dark matter direct detection II: QCD analysis and hadronic matrix elements. Phys. Rev. D 91, 043505 (2015). https://doi.org/10.1103/PhysRevD.91.043505. arXiv:1409.8290
European Muon collaboration, J. Ashman et al., A Measurement of the spin asymmetry and determination of the structure function g(1) in deep inelastic Muon-Proton scattering. Phys. Lett. B 206, 364 (1988). https://doi.org/10.1016/0370-2693(88)91523-7
X.-D. Ji, Gauge-Invariant Decomposition of Nucleon Spin. Phys. Rev. Lett. 78, 610–613 (1997). https://doi.org/10.1103/PhysRevLett.78.610. arXiv:hep-ph/9603249
R.L. Jaffe, A. Manohar, The G(1) Problem: Fact and Fantasy on the Spin of the Proton. Nucl. Phys. B 337, 509–546 (1990). https://doi.org/10.1016/0550-3213(90)90506-9
M. Pospelov, A. Ritz, Electric dipole moments as probes of new physics. Ann. Phys. 318, 119–169 (2005). https://doi.org/10.1016/j.aop.2005.04.002. arXiv: hep-ph/0504231
C. Baker, D. Doyle, P. Geltenbort, K. Green, M. van der Grinten et al., An Improved experimental limit on the electric dipole moment of the neutron. Phys. Rev. Lett. 97, 131801 (2006). https://doi.org/10.1103/PhysRevLett.97.131801. arXiv:hep-ex/0602020
C.-Y. Seng, Reexamination of the standard model nucleon electric dipole moment. Phys. Rev. C 91, 025502 (2015). https://doi.org/10.1103/PhysRevC.91.025502. arXiv:1411.1476
M. Engelhardt, Strange quark contributions to nucleon mass and spin from lattice QCD. Phys. Rev. D 86, 114510 (2012). https://doi.org/10.1103/PhysRevD.86.114510. arXiv:1210.0025
J.M. Alarcon, J Martin Camalich, J.A. Oller, The chiral representation of the \(\pi N\) scattering amplitude and the pion-nucleon sigma term. Phys. Rev. D 85, 051503 (2012). https://doi.org/10.1103/PhysRevD.85.051503. arXiv:1110.3797
Y.-H. Chen, D.-L. Yao, H.Q. Zheng, Analyses of pion-nucleon elastic scattering amplitudes up to \(O(p^4)\) in extended-on-mass-shell subtraction scheme. Phys. Rev. D 87, 054019 (2013). https://doi.org/10.1103/PhysRevD.87.054019. arXiv:1212.1893
M. Hoferichter, J. Ruiz de Elvira, B. Kubis, U.-G. Meissner, High-precision determination of the pion-nucleon \(\sigma \) term from Roy-Steiner equations. Phys. Rev. Lett. 115, 092301 (2015). https://doi.org/10.1103/PhysRevLett.115.092301. arXiv:1506.04142
[MILC 09D] D. Toussaint, W. Freeman, The Strange quark condensate in the nucleon in 2+1 flavor QCD. Phys. Rev. Lett. 103, 122002 (2009). https://doi.org/10.1103/PhysRevLett.103.122002. arXiv:0905.2432
[JLQCD 10A] K. Takeda, S. Aoki, S. Hashimoto, T. Kaneko, J. Noaki, T. Onogi, Nucleon strange quark content from two-flavor lattice QCD with exact chiral symmetry. Phys. Rev. D 83, 114506 (2011). https://doi.org/10.1103/PhysRevD.83.114506. arXiv:1011.1964
C. McNeile, A. Bazavov, C.T.H. Davies, R.J. Dowdall, K. Hornbostel, G.P. Lepage et al., Direct determination of the strange and light quark condensates from full lattice QCD. Phys. Rev. D 87, 034503 (2013). https://doi.org/10.1103/PhysRevD.87.034503. arXiv:1211.6577
P.E. Shanahan, A.W. Thomas, R.D. Young, Sigma terms from an SU(3) chiral extrapolation. Phys. Rev. D 87, 074503 (2013). https://doi.org/10.1103/PhysRevD.87.074503. arXiv:1205.5365
[QCDSF/UKQCD 11] R. Horsley, Y. Nakamura, H. Perlt, D. Pleiter, P. E. L. Rakow, G. Schierholz et al., Hyperon sigma terms for 2+1 quark flavours. Phys. Rev. D 85, 034506 (2012). https://doi.org/10.1103/PhysRevD.85.034506. arXiv:1110.4971
J. Martin Camalich, L. S. Geng, M. J. Vicente Vacas, The lowest-lying baryon masses in covariant SU(3)-flavor chiral perturbation theory. Phys. Rev. D 82, 074504 (2010). https://doi.org/10.1103/PhysRevD.82.074504. arXiv:1003.1929
[ETM 17A] C. Alexandrou, C. Kallidonis, Low-lying baryon masses using \(N_f=2\) twisted mass clover-improved fermions directly at the physical pion mass. Phys. Rev. D 96, 034511 (2017). https://doi.org/10.1103/PhysRevD.96.034511. arXiv:1704.02647
C. Kallidonis, private communication, Nov. 2018.
[ETM 09H] C. Alexandrou, R. Baron, J. Carbonell, V. Drach, P. Guichon, K. Jansen et al., Low-lying baryon spectrum with two dynamical twisted mass fermions. Phys. Rev. D 80, 114503 (2009). https://doi.org/10.1103/PhysRevD.80.114503. arXiv:0910.2419
[BMW 08] S. Dürr et al., Ab-initio determination of light hadron masses. Science 322, 1224–1227 (2008). https://doi.org/10.1126/science.1163233. arXiv:0906.3599
A. Crivellin, M. Hoferichter, M. Procura, Accurate evaluation of hadronic uncertainties in spin-independent WIMP-nucleon scattering: Disentangling two- and three-flavor effects. Phys. Rev. D 89, 054021 (2014). https://doi.org/10.1103/PhysRevD.89.054021. arXiv:1312.4951
M. Procura, B.U. Musch, T. Wollenweber, T.R. Hemmert, W. Weise, Nucleon mass: From lattice QCD to the chiral limit. Phys. Rev. D 73, 114510 (2006). https://doi.org/10.1103/PhysRevD.73.114510. arXiv:hep-lat/0603001
R.D. Young, A.W. Thomas, Octet baryon masses and sigma terms from an SU(3) chiral extrapolation. Phys. Rev. D 81, 014503 (2010). https://doi.org/10.1103/PhysRevD.81.014503. arXiv:0901.3310
X.L. Ren, L.S. Geng, J Martin Camalich, J. Meng, H. Toki, Octet baryon masses in next-to-next-to-next-to-leading order covariant baryon chiral perturbation theory. JHEP 12, 073 (2012). https://doi.org/10.1007/JHEP12(2012)073. arXiv:1209.3641
L. Alvarez-Ruso, T. Ledwig, J Martin Camalich, M.J. Vicente-Vacas, Nucleon mass and pion-nucleon sigma term from a chiral analysis of lattice QCD data. Phys. Rev. D 88, 054507 (2013). https://doi.org/10.1103/PhysRevD.88.054507. arXiv:1304.0483
X.-L. Ren, L.-S. Geng, J. Meng, Scalar strangeness content of the nucleon and baryon sigma terms. Phys. Rev. D 91, 051502 (2015). https://doi.org/10.1103/PhysRevD.91.051502. arXiv:1404.4799
X.-L. Ren, L. Alvarez-Ruso, L.-S. Geng, T. Ledwig, J. Meng, M .J.Vicente Vacas, Consistency between SU(3) and SU(2) covariant baryon chiral perturbation theory for the nucleon mass. Phys. Lett. B 766, 325–333 (2017). https://doi.org/10.1016/j.physletb.2017.01.024. arXiv:1606.03820
X.-Z. Ling, X.-L. Ren, L.-S. Geng, Pion-nucleon sigma term revisited in covariant baryon chiral perturbation theory. Phys. Lett. B 783, 7–12 (2018). https://doi.org/10.1016/j.physletb.2018.05.063. arXiv:1710.07164
J. Ruiz de Elvira, M. Hoferichter, B. Kubis, U.-G. Meissner, Extracting the \(\sigma \)-term from low-energy pion-nucleon scattering. J. Phys. G 45, 024001 (2018). https://doi.org/10.1088/1361-6471/aa9422. arXiv:1706.01465
K.G. Wilson, Confinement of quarks. Phys. Rev. D 10, 2445–2459 (1974). https://doi.org/10.1103/PhysRevD.10.2445
Y. Iwasaki, Renormalization group analysis of lattice theories and improved lattice action: two-dimensional nonlinear O(N) sigma model. Nucl. Phys. B 258, 141–156 (1985). https://doi.org/10.1016/0550-3213(85)90606-6
T. Takaishi, Heavy quark potential and effective actions on blocked configurations. Phys. Rev. D 54, 1050–1053 (1996). https://doi.org/10.1103/PhysRevD.54.1050
P. de Forcrand et al., Renormalization group flow of SU(3) lattice gauge theory: numerical studies in a two coupling space. Nucl. Phys. B 577, 263–278 (2000). https://doi.org/10.1016/S0550-3213(00)00145-0. arXiv:hep-lat/9911033
M.G. Alford, W. Dimm, G.P. Lepage, G. Hockney, P.B. Mackenzie, Lattice QCD on small computers. Phys. Lett. B 361, 87–94 (1995). https://doi.org/10.1016/0370-2693(95)01131-9. arXiv:hep-lat/9507010
K. G. Wilson, Quarks and strings on a lattice. In New Phenomena in Subnuclear Physics, part A. Proceedings of the first half of the 1975 International School of Subnuclear Physics, Erice, Sicily, July 11–August 1, 1975, ed. by A. Zichichi (Plenum Press, New York, 1977), p. 69 (CLNS-321)
L.H. Karsten, J. Smit, Lattice fermions: species doubling, chiral invariance, and the triangle anomaly. Nucl. Phys. B 183, 103 (1981). https://doi.org/10.1016/0550-3213(81)90549-6
M. Lüscher, S. Sint, R. Sommer, P. Weisz, U. Wolff, Non-perturbative O(a) improvement of lattice QCD. Nucl. Phys. B 491, 323–343 (1997). https://doi.org/10.1016/S0550-3213(97)00080-1. arXiv:hep-lat/9609035
J.B. Kogut, L. Susskind, Hamiltonian formulation of Wilson’s lattice gauge theories. Phys. Rev. D 11, 395 (1975). https://doi.org/10.1103/PhysRevD.11.395
T. Banks, L. Susskind, J.B. Kogut, Strong coupling calculations of lattice gauge theories: (1+1)-dimensional exercises. Phys. Rev. D 13, 1043 (1976). https://doi.org/10.1103/PhysRevD.13.1043
L. Susskind, Lattice fermions. Phys. Rev. D 16, 3031–3039 (1977). https://doi.org/10.1103/PhysRevD.16.3031
N. Kawamoto, J. Smit, Effective Lagrangian and dynamical symmetry breaking in strongly coupled lattice QCD. Nucl. Phys. B 192, 100 (1981). https://doi.org/10.1016/0550-3213(81)90196-6
H.S. Sharatchandra, H.J. Thun, P. Weisz, Susskind fermions on a euclidean lattice. Nucl. Phys. B 192, 205 (1981). https://doi.org/10.1016/0550-3213(81)90200-5
E. Marinari, G. Parisi, C. Rebbi, Monte Carlo simulation of the massive Schwinger model. Nucl. Phys. B 190, 734 (1981). https://doi.org/10.1016/0550-3213(81)90048-1
C. Bernard, M. Golterman, Y. Shamir, Observations on staggered fermions at non-zero lattice spacing. Phys. Rev. D 73, 114511 (2006). https://doi.org/10.1103/PhysRevD.73.114511. arXiv:hep-lat/0604017
S. Prelovsek, Effects of staggered fermions and mixed actions on the scalar correlator. Phys. Rev. D 73, 014506 (2006). https://doi.org/10.1103/PhysRevD.73.014506. arXiv:hep-lat/0510080
C. Bernard, Staggered chiral perturbation theory and the fourth-root trick. Phys. Rev. D 73, 114503 (2006). https://doi.org/10.1103/PhysRevD.73.114503. arXiv:hep-lat/0603011
C. Bernard, C.E. DeTar, Z. Fu, S. Prelovsek, Scalar meson spectroscopy with lattice staggered fermions. Phys. Rev. D 76, 094504 (2007). https://doi.org/10.1103/PhysRevD.76.094504. arXiv:0707.2402
C. Aubin, J. Laiho, R.S. Van de Water, Discretization effects and the scalar meson correlator in mixed-action lattice simulations. Phys. Rev. D 77, 114501 (2008). https://doi.org/10.1103/PhysRevD.77.114501. arXiv:0803.0129
Y. Shamir, Locality of the fourth root of the staggered-fermion determinant: renormalization-group approach. Phys. Rev. D 71, 034509 (2005). https://doi.org/10.1103/PhysRevD.71.034509. arXiv:hep-lat/0412014
Y. Shamir, Renormalization-group analysis of the validity of staggered-fermion QCD with the fourth-root recipe. Phys. Rev. D 75, 054503 (2007). https://doi.org/10.1103/PhysRevD.75.054503. arXiv:hep-lat/0607007
W.-J. Lee, S.R. Sharpe, Partial flavor symmetry restoration for chiral staggered fermions. Phys. Rev. D 60, 114503 (1999). https://doi.org/10.1103/PhysRevD.60.114503. arXiv:hep-lat/9905023
S.R. Sharpe, R.S. Van de Water, Staggered chiral perturbation theory at next-to-leading order. Phys. Rev. D 71, 114505 (2005). https://doi.org/10.1103/PhysRevD.71.114505. arXiv:hep-lat/0409018
C. Bernard, M. Golterman, Y. Shamir, Effective field theories for QCD with rooted staggered fermions. Phys. Rev. D 77, 074505 (2008). https://doi.org/10.1103/PhysRevD.77.074505. arXiv:0712.2560
C. Aubin, C. Bernard, Staggered chiral perturbation theory for heavy-light mesons. Phys. Rev. D 73, 014515 (2006). https://doi.org/10.1103/PhysRevD.73.014515. arXiv:hep-lat/0510088
J. Komijani, C. Bernard, Staggered chiral perturbation theory for all-staggered heavy-light mesons. PoS LAT2012, 199 (2012). arXiv:1211.0785
J.A. Bailey, Staggered heavy baryon chiral perturbation theory. Phys. Rev. D 77, 054504 (2008). https://doi.org/10.1103/PhysRevD.77.054504. arXiv:0704.1490
S. Dürr, C. Hoelbling, Staggered versus overlap fermions: a study in the Schwinger model with \(N_f=0, 1, 2\). Phys. Rev. D 69, 034503 (2004). https://doi.org/10.1103/PhysRevD.69.034503. arXiv:hep-lat/0311002
S. Dürr, C. Hoelbling, Scaling tests with dynamical overlap and rooted staggered fermions. Phys. Rev. D 71, 054501 (2005). https://doi.org/10.1103/PhysRevD.71.054501. arXiv:hep-lat/0411022
S. Dürr, C. Hoelbling, Lattice fermions with complex mass. Phys. Rev. D 74, 014513 (2006). https://doi.org/10.1103/PhysRevD.74.014513. arXiv:hep-lat/0604005
[HPQCD 04] E. Follana, A. Hart, C.T.H. Davies, The index theorem and universality properties of the low-lying eigenvalues of improved staggered quarks. Phys. Rev. Lett. 93, 241601 (2004). https://doi.org/10.1103/PhysRevLett.93.241601. arXiv:hep-lat/0406010
S. Dürr, C. Hoelbling, U. Wenger, Staggered eigenvalue mimicry. Phys. Rev. D 70, 094502 (2004). https://doi.org/10.1103/PhysRevD.70.094502. arXiv:hep-lat/0406027
K.Y. Wong, R. Woloshyn, Systematics of staggered fermion spectral properties and topology. Phys. Rev. D 71, 094508 (2005). https://doi.org/10.1103/PhysRevD.71.094508. arXiv:hep-lat/0412001
[HPQCD/FNAL 11] G. C. Donald, C. T. Davies, E. Follana, A. S. Kronfeld, Staggered fermions, zero modes, and flavor-singlet mesons. Phys.Rev. D 84, 054504 (2011). https://doi.org/10.1103/PhysRevD.84.054504. arXiv:1106.2412
M. Creutz, Flavor extrapolations and staggered fermions. arXiv:hep-lat/0603020
M. Creutz, Diseases with rooted staggered quarks. PoS LAT2006, 208 (2006). arXiv:hep-lat/0608020
M. Creutz, The evil that is rooting. Phys. Lett. B 649, 230–234 (2007). https://doi.org/10.1016/j.physletb.2007.03.065. arXiv:hep-lat/0701018
M. Creutz, The author replies. (Chiral anomalies and rooted staggered fermions). Phys. Lett. B 649, 241–242 (2007). https://doi.org/10.1016/j.physletb.2007.04.017. arXiv:0704.2016
M. Creutz, Why rooting fails. PoS LAT2007, 007 (2007). arXiv:0708.1295
M. Creutz, Comment on “’t Hooft vertices, partial quenching, and rooted staggered QCD”. Phys. Rev. D 78, 078501 (2008). https://doi.org/10.1103/PhysRevD.78.078501. arXiv:0805.1350
M. Creutz, Comments on staggered fermions/Panel discussion. PoS CONFINEMENT8, 016 (2008). arXiv:0810.4526
C. Bernard, M. Golterman, Y. Shamir, S.R. Sharpe, Comment on ’chiral anomalies and rooted staggered fermions’. Phys. Lett. B 649, 235–240 (2007). https://doi.org/10.1016/j.physletb.2007.04.018. arXiv:hep-lat/0603027
C. Bernard, M. Golterman, Y. Shamir, S.R. Sharpe, ’t Hooft vertices, partial quenching, and rooted staggered QCD. Phys. Rev. D 77, 114504 (2008). https://doi.org/10.1103/PhysRevD.77.114504. arXiv:0711.0696
C. Bernard, M. Golterman, Y. Shamir, S.R. Sharpe, Reply to: Comment on ’t Hooft vertices, partial quenching, and rooted staggered QCD. Phys. Rev. D 78, 078502 (2008). https://doi.org/10.1103/PhysRevD.78.078502. arXiv:0808.2056
D.H. Adams, The rooting issue for a lattice fermion formulation similar to staggered fermions but without taste mixing. Phys. Rev. 77, 105024 (2008). https://doi.org/10.1103/PhysRevD.77.105024. arXiv:0802.3029
G ’t Hooft, Symmetry breaking through Bell-Jackiw anomalies. Phys. Rev. Lett. 37, 8–11 (1976). https://doi.org/10.1103/PhysRevLett.37.8
G. ’t Hooft, Computation of the quantum effects due to a four-dimensional pseudoparticle. Phys.Rev. D 14, 3432–3450 (1976). https://doi.org/10.1103/PhysRevD.18.2199, https://doi.org/10.1103/PhysRevD.14.3432
[MILC 99] K. Orginos, D. Toussaint, R.L. Sugar, Variants of fattening and flavor symmetry restoration. Phys. Rev. D 60, 054503 (1999). https://doi.org/10.1103/PhysRevD.60.054503. arXiv:hep-lat/9903032
[HPQCD 06B] E. Follana et al., Highly improved staggered quarks on the lattice, with applications to charm physics. Phys. Rev. D 75, 054502 (2007). https://doi.org/10.1103/PhysRevD.75.054502. arXiv:hep-lat/0610092
Y. Aoki, Z. Fodor, S. Katz, K. Szabo, The equation of state in lattice QCD: with physical quark masses towards the continuum limit. JHEP 0601, 089 (2006). https://doi.org/10.1088/1126-6708/2006/01/089. arXiv:hep-lat/0510084
A. Hasenfratz, F. Knechtli, Flavor symmetry and the static potential with hypercubic blocking. Phys. Rev. D 64, 034504 (2001). https://doi.org/10.1103/PhysRevD.64.034504. arXiv:hep-lat/0103029
S. Naik, On-shell improved lattice action for QCD with Susskind fermions and asymptotic freedom scale. Nucl. Phys. B 316, 238 (1989). https://doi.org/10.1016/0550-3213(89)90394-5
G.P. Lepage, Flavor-symmetry restoration and Symanzik improvement for staggered quarks. Phys. Rev. D 59, 074502 (1999). https://doi.org/10.1103/PhysRevD.59.074502. arXiv:hep-lat/9809157
P. Hasenfratz, Lattice QCD without tuning, mixing and current renormalization. Nucl. Phys. B 525401–409, (1998). https://doi.org/10.1016/S0550-3213(98)00399-X. arXiv:hep-lat/9802007
P. Hasenfratz, V. Laliena, F. Niedermayer, The index theorem in QCD with a finite cut-off. Phys. Lett. B 427, 125–131 (1998). https://doi.org/10.1016/S0370-2693(98)00315-3. arXiv:hep-lat/9801021
M. Lüscher, Exact chiral symmetry on the lattice and the Ginsparg-Wilson relation. Phys. Lett. B 428, 342–345 (1998). https://doi.org/10.1016/S0370-2693(98)00423-7. arXivhep-lat/9802011
H.B. Nielsen, M. Ninomiya, No go theorem for regularizing chiral fermions. Phys. Lett. B 105, 219 (1981). https://doi.org/10.1016/0370-2693(81)91026-1
H. Neuberger, Exactly massless quarks on the lattice. Phys. Lett. B 417, 141–144 (1998). https://doi.org/10.1016/S0370-2693(97)01368-3. arXiv:hep-lat/9707022
D.B. Kaplan, A method for simulating chiral fermions on the lattice. Phys. Lett. B 288, 342–347 (1992). https://doi.org/10.1016/0370-2693(92)91112-M. arXiv:hep-lat/9206013
Y. Shamir, Chiral fermions from lattice boundaries. Nucl. Phys. B 406, 90–106 (1993). https://doi.org/10.1016/0550-3213(93)90162-I. arXiv:hep-lat/9303005
V. Furman, Y. Shamir, Axial symmetries in lattice QCD with Kaplan fermions. Nucl. Phys. B 439, 54–78 (1995). https://doi.org/10.1016/0550-3213(95)00031-M. arXiv:hep-lat/9405004
T. Blum, A. Soni, QCD with domain wall quarks. Phys. Rev. D 56, 174–178 (1997). https://doi.org/10.1103/PhysRevD.56.174. arXiv:hep-lat/9611030
S. R. Sharpe, Future of chiral extrapolations with domain Wall Fermions. arXiv:0706.0218
A. Borici, Truncated overlap fermions. Nucl. Phys. Proc. Suppl. 83, 771–773 (2000). arXiv:hep-lat/9909057
A. Borici, Truncated overlap fermions: The Link between overlap and domain wall fermions. NATO Sci. Ser. C 553, 41–52 (2000). arXiv:hep-lat/9912040
W. Bietenholz, U. Wiese, Perfect lattice actions for quarks and gluons. Nucl. Phys. B 464, 319–352 (1996). https://doi.org/10.1016/0550-3213(95)00678-8. arXiv:hep-lat/9510026
P. Hasenfratz et al., The construction of generalized Dirac operators on the lattice. Int. J. Mod. Phys. C 12, 691–708 (2001). https://doi.org/10.1142/S0129183101001882. arXiv:hep-lat/0003013
P. Hasenfratz, S. Hauswirth, T. Jörg, F. Niedermayer, K. Holland, Testing the fixed-point QCD action and the construction of chiral currents. Nucl. Phys. B 643, 280–320 (2002). https://doi.org/10.1016/S0550-3213(02)00742-3. arXiv:hep-lat/0205010
C. Gattringer, A new approach to Ginsparg-Wilson fermions. Phys. Rev. D 63, 114501 (2001). https://doi.org/10.1103/PhysRevD.63.114501. arXiv:hep-lat/0003005
A. Hasenfratz, R. Hoffmann, S. Schaefer, Hypercubic smeared links for dynamical fermions. JHEP 05, 029 (2007). arXiv:hep-lat/0702028
C. Morningstar, M.J. Peardon, Analytic smearing of SU(3) link variables in lattice QCD. Phys. Rev. D 69, 054501 (2004). https://doi.org/10.1103/PhysRevD.69.054501. arXiv:hep-lat/0311018
[BMW 08A] S. Dürr et al., Scaling study of dynamical smeared-link clover fermions. Phys. Rev. D 79, 014501 (2009). https://doi.org/10.1103/PhysRevD.79.014501. arXiv:0802.2706
S. Capitani, S. Dürr, C. Hoelbling, Rationale for UV-filtered clover fermions. JHEP 11, 028 (2006). https://doi.org/10.1088/1126-6708/2006/11/028. arXiv:hep-lat/0607006
N. Isgur, M.B. Wise, Weak decays of heavy mesons in the static quark approximation. Phys. Lett. B 232, 113 (1989). https://doi.org/10.1016/0370-2693(89)90566-2
E. Eichten, B.R. Hill, An effective field theory for the calculation of matrix elements involving heavy quarks. Phys. Lett. B 234, 511 (1990). https://doi.org/10.1016/0370-2693(90)92049-O
N. Isgur, M.B. Wise, Weak transition form-factors between heavy mesons. Phys. Lett. B 237, 527 (1990). https://doi.org/10.1016/0370-2693(90)91219-2
W.E. Caswell, G.P. Lepage, Effective Lagrangians for bound state problems in QED, QCD and other field theories. Phys. Lett. B 167, 437 (1986). https://doi.org/10.1016/0370-2693(86)91297-9
G.T. Bodwin, E. Braaten, G.P. Lepage, Rigorous QCD analysis of inclusive annihilation and production of heavy quarkonium. Phys. Rev. D 51, 1125–1171 (1995). https://doi.org/10.1103/PhysRevD.55.5853, https://doi.org/10.1103/PhysRevD.51.1125. arXiv: hep-ph/9407339
[ALPHA 03] J. Heitger, R. Sommer, Nonperturbative heavy quark effective theory. JHEP 0402, 022 (2004). https://doi.org/10.1088/1126-6708/2004/02/022. arXiv:hep-lat/0310035
B. Thacker, G.P. Lepage, Heavy quark bound states in lattice QCD. Phys. Rev. D 43, 196–208 (1991). https://doi.org/10.1103/PhysRevD.43.196
G.P. Lepage, L. Magnea, C. Nakhleh, U. Magnea, K. Hornbostel, Improved nonrelativistic QCD for heavy quark physics. Phys. Rev. D 46, 4052–4067 (1992). https://doi.org/10.1103/PhysRevD.46.4052. arXiv:hep-lat/9205007
A.X. El-Khadra, A.S. Kronfeld, P.B. Mackenzie, Massive fermions in lattice gauge theory. Phys. Rev. D 55, 3933–3957 (1997). https://doi.org/10.1103/PhysRevD.55.3933. arXiv:hep-lat/9604004
N.H. Christ, M. Li, H.-W. Lin, Relativistic heavy quark effective action. Phys. Rev. D 76, 074505 (2007). https://doi.org/10.1103/PhysRevD.76.074505. arXiv:hep-lat/0608006
S. Aoki, Y. Kuramashi, S.-I. Tominaga, Relativistic heavy quarks on the lattice. Prog. Theor. Phys. 109, 383–413 (2003). https://doi.org/10.1143/PTP.109.383. arXiv:hep-lat/0107009
T. Ishikawa, Y. Aoki, J.M. Flynn, T. Izubuchi, O. Loktik, One-loop operator matching in the static heavy and domain-wall light quark system with O(a) improvement. JHEP 1105, 040 (2011). https://doi.org/10.1007/JHEP05(2011)040. arXiv:1101.1072
B. Blossier, Lattice renormalisation of O(a) improved heavy-light operators: an addendum. Phys. Rev. D 84, 097501 (2011). https://doi.org/10.1103/PhysRevD.84.097501. arXiv:1106.2132
[ALPHA 10B] B. Blossier, M. Della Morte, N. Garron, R. Sommer, HQET at order \(1/m\): I. Non-perturbative parameters in the quenched approximation. JHEP 1006, 002 (2010). https://doi.org/10.1007/JHEP06(2010)002. arXiv:1001.4783
R. Sommer, Non-perturbative QCD: renormalization, O(a)-improvement and matching to heavy quark effective theory (Nara, Japan, 2005). arXiv:hep-lat/0611020
M. Della Morte, Standard Model parameters and heavy quarks on the lattice. PoS LAT2007, 008 (2007). arXiv:0711.3160
[ALPHA 12D] B. Blossier et al., Parameters of heavy quark effective theory from \(N_f=2\) lattice QCD. JHEP 1209, 132 (2012). https://doi.org/10.1007/JHEP09(2012)132. arXiv:1203.6516
[ALPHA 10] B. Blossier et al., HQET at order 1/m: III. Decay constants in the quenched approximation. JHEP 1012, 039 (2010). https://doi.org/10.1007/JHEP12(2010)039. arXiv:1006.5816
[ALPHA 05A] M. Della Morte, A. Shindler, R. Sommer, On lattice actions for static quarks. JHEP 0508, 051 (2005). https://doi.org/10.1088/1126-6708/2005/08/051. arXiv:hep-lat/0506008
[HPQCD 10C] E. B. Gregory et al., Precise \(B\), \(B_s\) and \(B_c\) meson spectroscopy from full lattice QCD. Phys. Rev. D 83, 014506 (2011). https://doi.org/10.1103/PhysRevD.83.014506. arXiv:1010.3848
C.J. Morningstar, Radiative corrections to the kinetic couplings in nonrelativistic lattice QCD. Phys. Rev. D 50, 5902–5911 (1994). https://doi.org/10.1103/PhysRevD.50.5902. arXiv:hep-lat/9406002
T. Hammant, A. Hart, G. von Hippel, R. Horgan, C. Monahan, Radiative improvement of the lattice NRQCD action using the background field method and application to the hyperfine splitting of quarkonium states. Phys. Rev. Lett. 107, 112002 (2011). https://doi.org/10.1103/PhysRevLett.107.112002. arXiv:1105.5309
[HPQCD 11B] R. J. Dowdall et al., The upsilon spectrum and the determination of the lattice spacing from lattice QCD including charm quarks in the sea. Phys. Rev. D 85, 054509 (2012). https://doi.org/10.1103/PhysRevD.85.054509. arXiv:1110.6887
[HPQCD 12D] C. Monahan, J. Shigemitsu, R. Horgan, Matching lattice and continuum axial-vector and vector currents with NRQCD and HISQ quarks. Phys. Rev. D 87, 034017 (2013). arXiv:1211.6966
[HPQCD 10D] J. Koponen et al., Heavy-light current-current correlators. PoS LAT2010, 231 (2010). arXiv:1011.1208
J. Harada, S. Hashimoto, K.-I. Ishikawa, A. S. Kronfeld, T. Onogi et al., Application of heavy-quark effective theory to lattice QCD. 2. Radiative corrections to heavy-light currents. Phys. Rev. D 65, 094513 (2002). https://doi.org/10.1103/PhysRevD.71.019903, https://doi.org/10.1103/PhysRevD.65.094513. arXiv:hep-lat/0112044
B. Sheikholeslami, R. Wohlert, Improved continuum limit lattice action for QCD with Wilson fermions. Nucl. Phys. B 259, 572 (1985). https://doi.org/10.1016/0550-3213(85)90002-1
A.S. Kronfeld, Application of heavy quark effective theory to lattice QCD. 1. Power corrections. Phys. Rev. D 62, 014505 (2000). https://doi.org/10.1103/PhysRevD.62.014505. arXiv:hep-lat/0002008
J. Harada, S. Hashimoto, A.S. Kronfeld, T. Onogi, Application of heavy-quark effective theory to lattice QCD. 3. Radiative corrections to heavy-heavy currents. Phys. Rev. D 65, 094514 (2002). https://doi.org/10.1103/PhysRevD.65.094514. arXiv:hep-lat/0112045
A.X. El-Khadra, A.S. Kronfeld, P.B. Mackenzie, S.M. Ryan, J.N. Simone, The semileptonic decays \(B \rightarrow \pi \ell \nu \) and \(D\rightarrow \pi \ell \nu \) from lattice QCD. Phys. Rev. D 64, 014502 (2001). https://doi.org/10.1103/PhysRevD.64.014502. arXiv:hep-ph/0101023
[RBC/UKQCD 12A] Y. Aoki et al., Nonperturbative tuning of an improved relativistic heavy-quark action with application to bottom spectroscopy. Phys. Rev. D 86, 116003 (2012). https://doi.org/10.1103/PhysRevD.86.116003. arXiv:1206.2554
O. Witzel, Calculating B-meson decay constants using domain-wall light quarks and nonperturbatively tuned relativistic b-quarks. PoS LAT2012, 103 (2012). arXiv:1211.3180
[RBC/UKQCD 12B] T. Kawanai, R. S. Van de Water, O. Witzel, The \(B \rightarrow \pi \ell \nu \) form factor from unquenched lattice QCD with domain-wall light quarks and relativistic b-quarks. PoS LAT2012, 109 (2012). arXiv:1211.0956
C. Lehner, Automated lattice perturbation theory and relativistic heavy quarks in the Columbia formulation. PoS LAT2012, 126 (2012). arXiv:1211.4013
[CP-PACS/JLQCD 05] S. Aoki et al., Nonperturbative O(a) improvement of the Wilson quark action with the RG-improved gauge action using the Schrödinger functional method. Phys. Rev. D 73, 034501 (2006). https://doi.org/10.1103/PhysRevD.73.034501. arXiv:hep-lat/0508031
S. Aoki, Y. Kayaba, Y. Kuramashi, A perturbative determination of mass dependent O(a) improvement coefficients in a relativistic heavy quark action. Nucl. Phys. B 697, 271–301 (2004). https://doi.org/10.1016/j.nuclphysb.2004.07.017. arXiv:hep-lat/0309161
[CP-PACS/JLQCD/ALPHA 07] T. Kaneko et al., Non-perturbative improvement of the axial current with three dynamical flavors and the Iwasaki gauge action. JHEP 0704, 092 (2007). https://doi.org/10.1088/1126-6708/2007/04/092. arXiv:hep-lat/0703006
S. Aoki, Y. Kayaba, Y. Kuramashi, Perturbative determination of mass dependent O(a) improvement coefficients for the vector and axial vector currents with a relativistic heavy quark action. Nucl. Phys. B 689, 127–156 (2004). https://doi.org/10.1016/j.nuclphysb.2004.04.009. arXiv:hep-lat/0401030
D. Guazzini, R. Sommer, N. Tantalo, \(m_b\) and \(f_{B_s}\) from a combination of HQET and QCD. PoS LAT2006, 084 (2006). arXiv:hep-lat/0609065
[ETM 09E] B. Blossier et al., \(f_B\) and \(f_{B_s}\) with maximally twisted Wilson fermions. PoS LAT2009, 151 (2009). arXiv:0911.3757
M. Lüscher, P. Weisz, Perturbative analysis of the gradient flow in non-abelian gauge theories. JHEP 02, 051 (2011). https://doi.org/10.1007/JHEP02(2011)051. arXiv:1101.0963
[RBC 10] R. Arthur, P.A. Boyle, Step scaling with off-shell renormalisation. Phys. Rev. D 83, 114511 (2011). https://doi.org/10.1103/PhysRevD.83.114511. arXiv:1006.0422
C. Sturm, Y. Aoki, N.H. Christ, T. Izubuchi, C.T.C. Sachrajda, A. Soni, Renormalization of quark bilinear operators in a momentum-subtraction scheme with a nonexceptional subtraction point. Phys. Rev. D 80, 014501 (2009). https://doi.org/10.1103/PhysRevD.80.014501. arXiv:0901.2599
A. X. El-Khadra, E. Gamiz, A. S. Kronfeld, M. A. Nobes, Perturbative matching of heavy-light currents at one-loop. PoS LAT2007, 242 (2007). arXiv:0710.1437
S.R. Sharpe, R.L. Singleton Jr., Spontaneous flavor and parity breaking with Wilson fermions. Phys. Rev. D 58, 074501 (1998). https://doi.org/10.1103/PhysRevD.58.074501. arXiv:hep-lat/9804028
S.R. Sharpe, J.M.S. Wu, Twisted mass chiral perturbation theory at next-to-leading order. Phys. Rev. D 71, 074501 (2005). https://doi.org/10.1103/PhysRevD.71.074501. arXiv:hep-lat/0411021
S. Aoki, O. Bär, Twisted-mass QCD, O(a) improvement and Wilson chiral perturbation theory. Phys. Rev. D 70, 116011 (2004). https://doi.org/10.1103/PhysRevD.70.116011. arXiv:hep-lat/0409006
C.W. Bernard, M.F.L. Golterman, Partially quenched gauge theories and an application to staggered fermions. Phys. Rev. D 49, 486–494 (1994). https://doi.org/10.1103/PhysRevD.49.486. arXiv:hep-lat/9306005
M.F.L. Golterman, K.-C. Leung, Applications of partially quenched chiral perturbation theory. Phys. Rev. D 57, 5703–5710 (1998). https://doi.org/10.1103/PhysRevD.57.5703. arXiv:hep-lat/9711033
S.R. Sharpe, Enhanced chiral logarithms in partially quenched QCD. Phys. Rev. D 56, 7052–7058 (1997). https://doi.org/10.1103/PhysRevD.56.7052. arXiv:hep-lat/9707018
S.R. Sharpe, N. Shoresh, Physical results from unphysical simulations. Phys. Rev. D 62, 094503 (2000). https://doi.org/10.1103/PhysRevD.62.094503. arXiv:hep-lat/0006017
M. Golterman, T. Izubuchi, Y. Shamir, The role of the double pole in lattice QCD with mixed actions. Phys. Rev. D 71, 114508 (2005). https://doi.org/10.1103/PhysRevD.71.114508. arXiv:hep-lat/0504013
J.-W. Chen, D. O’Connell, A. Walker-Loud, Two meson systems with Ginsparg-Wilson valence quarks. Phys. Rev. D 75, 054501 (2007). https://doi.org/10.1103/PhysRevD.75.054501. arXiv:hep-lat/0611003
J.-W. Chen, D. O’Connell, A. Walker-Loud, Universality of mixed action extrapolation formulae. JHEP 04, 090 (2009). https://doi.org/10.1088/1126-6708/2009/04/090. arXiv:0706.0035
P. Ball, R. Zwicky, New results on \(B \rightarrow \pi, K, \eta \) decay form factors from light-cone sum rules. Phys. Rev. D 71, 014015 (2005). https://doi.org/10.1103/PhysRevD.71.014015. arXiv:hep-ph/0406232
D. Becirevic, A. L. Yaouanc, A. Oyanguren, P. Roudeau, F. Sanfilippo, Insight into \(D/B\rightarrow \pi \ell \nu _\ell \) decay using the pole models. arXiv:1407.1019
R.J. Hill, Heavy-to-light meson form-factors at large recoil. Phys. Rev. D 73, 014012 (2006). https://doi.org/10.1103/PhysRevD.73.014012. arXiv:hep-ph/0505129
G.P. Lepage, S.J. Brodsky, Exclusive processes in perturbative Quantum Chromodynamics. Phys. Rev. D 22, 2157 (1980). https://doi.org/10.1103/PhysRevD.22.2157
R. Akhoury, G.F. Sterman, Y. Yao, Exclusive semileptonic decays of \(B\) mesons into light mesons. Phys. Rev. D 50, 358–372 (1994). https://doi.org/10.1103/PhysRevD.50.358
L. Lellouch, Lattice constrained unitarity bounds for \(\bar{B}^0 \rightarrow \pi ^+ \ell \, \bar{\nu _l}\) decays. Nucl. Phys. B 479, 353–391 (1996). https://doi.org/10.1016/0550-3213(96)00443-9. arXiv:hep-ph/9509358
C. Bourrely, I. Caprini, L. Lellouch, Model-independent description of \(B \rightarrow \pi \ell \nu \) decays and a determination of \(|V_{ub}|\). Phys. Rev. D 79, 013008 (2009). https://doi.org/10.1103/PhysRevD.82.099902, https://doi.org/10.1103/PhysRevD.79.013008. arXiv:0807.2722
C. Bourrely, B. Machet, E. de Rafael, Semileptonic decays of pseudoscalar particles (M \(\rightarrow \) \(M^\prime \ell \nu _\ell \)) and short distance behavior of Quantum Chromodynamics. Nucl. Phys. B 189, 157 (1981). https://doi.org/10.1016/0550-3213(81)90086-9
C.G. Boyd, M.J. Savage, Analyticity, shapes of semileptonic form-factors, and \(\bar{B} \rightarrow \pi \ell \bar{\nu }\). Phys. Rev. D 56, 303–311 (1997). https://doi.org/10.1103/PhysRevD.56.303. arXiv:hep-ph/9702300
M.C. Arnesen, B. Grinstein, I.Z. Rothstein, I.W. Stewart, A precision model independent determination of \(|V_{ub}|\) from \(B \rightarrow \pi e \nu \). Phys. Rev. Lett. 95, 071802 (2005). https://doi.org/10.1103/PhysRevLett.95.071802. arXiv:hep-ph/0504209
T. Becher, R.J. Hill, Comment on form-factor shape and extraction of \(|V_{ub}|\) from \(B \rightarrow \pi l \nu \). Phys. Lett. B 633, 61–69 (2006). https://doi.org/10.1016/j.physletb.2005.11.063. arXiv:hep-ph/0509090
R.J. Hill, The Modern description of semileptonic meson form factors. eConf C060409, 027 (2006). arXiv:hep-ph/0606023
R.J. Hill, G. Paz, Model independent extraction of the proton charge radius from electron scattering. Phys. Rev. D 82, 113005 (2010). https://doi.org/10.1103/PhysRevD.82.113005. arXiv:1008.4619
R.J. Hill, G. Paz, Model independent analysis of proton structure for hydrogenic bound states. Phys. Rev. Lett. 107, 160402 (2011). https://doi.org/10.1103/PhysRevLett.107.160402. arXiv:1103.4617
Z. Epstein, G. Paz, J. Roy, Model independent extraction of the proton magnetic radius from electron scattering. Phys. Rev. D 90, 074027 (2014). https://doi.org/10.1103/PhysRevD.90.074027. arXiv:1407.5683
[CP-PACS 01] A. Ali Khan et al., Light hadron spectroscopy with two flavors of dynamical quarks on the lattice. Phys. Rev. D 65, 054505 (2002). https://doi.org/10.1103/PhysRevD.65.054505. arXiv:hep-lat/0105015
S. Dürr, G. Koutsou, The ratio \(m_c/m_s\) with Wilson fermions. Phys. Rev. Lett. 108, 122003 (2012). https://doi.org/10.1103/PhysRevLett.108.122003. arXiv:1108.1650
[ETM 07] B. Blossier et al., Light quark masses and pseudoscalar decay constants from \(N_f=2\) lattice QCD with twisted mass fermions. JHEP 04, 020 (2008). https://doi.org/10.1088/1126-6708/2008/04/020. arXiv:0709.4574
[ETM 09B] K. Jansen, A. Shindler, The \(\epsilon \)-regime of chiral perturbation theory with Wilson-type fermions. PoS LAT2009, 070 (2009). arXiv:0911.1931
[JLQCD 08] S. Aoki et al., \(B_K\) with two flavors of dynamical overlap fermions. Phys. Rev. D 77, 094503 (2008). https://doi.org/10.1103/PhysRevD.77.094503. arXiv:0801.4186
[JLQCD 02] S. Aoki et al., Light hadron spectroscopy with two flavors of \(O(a)\)- improved dynamical quarks. Phys. Rev. D 68, 054502 (2003). https://doi.org/10.1103/PhysRevD.68.054502. arXiv:hep-lat/0212039
[JLQCD 05] N. Tsutsui et al., Kaon semileptonic decay form factors in two-flavor QCD. PoS LAT2005, 357 (2006). arXiv:hep-lat/0510068
[QCDSF 07] D. Brömmel et al., Kaon semileptonic decay form factors from \(N_f = 2\) non-perturbatively \(O(a)\)-improved Wilson fermions. PoS LAT2007, 364 (2007). arXiv:0710.2100
[QCDSF/UKQCD 04] M. Göckeler et al., Determination of light and strange quark masses from full lattice QCD. Phys. Lett. B 639, 307–311 (2006). https://doi.org/10.1016/j.physletb.2006.06.036. arXiv:hep-ph/0409312
[QCDSF/UKQCD 06] M. Göckeler et al., Estimating the unquenched strange quark mass from the lattice axial Ward identity. Phys. Rev. D 73, 054508 (2006). https://doi.org/10.1103/PhysRevD.73.054508. arXiv:hep-lat/0601004
[RBC 04] Y. Aoki et al., Lattice QCD with two dynamical flavors of domain wall fermions. Phys. Rev. D 72, 114505 (2005). https://doi.org/10.1103/PhysRevD.72.114505. arXiv:hep-lat/0411006
[RBC 06] C. Dawson, T. Izubuchi, T. Kaneko, S. Sasaki, A. Soni, Vector form factor in \(K_{l3}\) semileptonic decay with two flavors of dynamical domain-wall quarks. Phys. Rev. D 74, 114502 (2006). https://doi.org/10.1103/PhysRevD.74.114502. arXiv:hep-ph/0607162
K. Osterwalder, E. Seiler, Gauge Field Theories on the Lattice. Annals Phys. 110, 440 (1978). https://doi.org/10.1016/0003-4916(78)90039-8
[SPQcdR 05] D. Bećirević et al., Non-perturbatively renormalised light quark masses from a lattice simulation with \(N_f= 2\). Nucl. Phys. B 734, 138–155 (2006). https://doi.org/10.1016/j.nuclphysb.2005.11.014. arXiv:hep-lat/0510014
[UKQCD 04] J.M. Flynn, F. Mescia, A.S.B. Tariq, Sea quark effects in \(B_K\) from \(N_f = 2\) clover-improved Wilson fermions. JHEP 11, 049 (2004). https://doi.org/10.1088/1126-6708/2004/11/049. arXiv:hep-lat/0406013
[HPQCD/UKQCD 06] E. Gamiz et al., Unquenched determination of the kaon parameter \(B_K\) from improved staggered fermions. Phys. Rev. D 73, 114502 (2006). https://doi.org/10.1103/PhysRevD.73.114502. arXiv:hep-lat/0603023
[JLQCD/TWQCD 08B] T.-W. Chiu et al., Topological susceptibility in (2+1)-flavor lattice QCD with overlap fermion. PoS LAT2008, 072 (2008). arXiv:0810.0085
[JLQCD/TWQCD 09A] J. Noaki et al., Chiral properties of light mesons with \(N_f=2+1\) overlap fermions. PoS LAT2009, 096 (2009). arXiv:0910.5532
[MILC 07] C. Bernard et al., Status of the MILC light pseudoscalar meson project. PoSLAT2007, 090 (2007). arXiv:0710.1118
[PACS-CS 08A] Y. Kuramashi, PACS-CS results for 2+1 flavor lattice QCD simulation on and off the physical point. PoS LAT2008, 018 (2008). arXiv:0811.2630
[QCDSF 11] G.S. Bali et al., The strange and light quark contributions to the nucleon mass from Lattice QCD. Phys. Rev. D 85, 054502 (2012). https://doi.org/10.1103/PhysRevD.85.054502. arXiv:1111.1600
[RBC/UKQCD 07A] D.J. Antonio et al., Neutral kaon mixing from 2+1 flavor domain wall QCD. Phys. Rev. Lett. 100, 032001 (2008). https://doi.org/10.1103/PhysRevLett.100.032001. arXiv:0702042
[RBC/UKQCD 11] C. Kelly, Continuum results for light hadronic quantities using domain wall fermions with the Iwasaki and DSDR gauge actions, PoS LAT2011, 285 (2011). arXiv:1201.0706
[SWME 11] J. Kim, C. Jung, H.-J. Kim, W. Lee, S.R. Sharpe, Finite volume effects in \(B_K\) with improved staggered fermions. Phys. Rev. D 83, 117501 (2011). https://doi.org/10.1103/PhysRevD.83.117501. arXiv:1101.2685
[ETM 17E] V. Lubicz, A. Melis, S. Simula, Masses and decay constants of \(D*_{(s)}\) and \(B*_{(s)}\) mesons with \(N_f = 2 + 1 + 1\) twisted mass fermions. Phys. Rev. D 96, 034524 (2017). https://doi.org/10.1103/PhysRevD.96.034524. arXiv:1707.04529
[FNAL/MILC 10] J.A. Bailey et al., \(B \rightarrow D^* \ell \nu \) at zero recoil: an update, PoS LAT2010, 311 (2010). arXiv:1011.2166
S. Meinel, Bottomonium spectrum at order \(v^6\) from domain-wall lattice QCD: Precise results for hyperfine splittings. Phys. Rev. D 82, 114502 (2010). https://doi.org/10.1103/PhysRevD.82.114502. arXiv:1007.3966
S.R. Beane, M.J. Savage, Nucleons in two flavor partially quenched chiral perturbation theory. Nucl. Phys. A 709, 319–344 (2002). https://doi.org/10.1016/S0375-9474(02)01086-2. arXiv:0203003
B.C. Tiburzi, Baryons with Ginsparg-Wilson quarks in a staggered sea. Phys. Rev. D 72, 094501 (2005). https://doi.org/10.1103/PhysRevD.72.094501. https://doi.org/10.1103/PhysRevD.79.039904. arXiv:hep-lat/0508019
A. Walker-Loud, Octet baryon masses in partially quenched chiral perturbation theory. Nucl. Phys. A 747, 476–507 (2005). https://doi.org/10.1016/j.nuclphysa.2004.10.007. arXiv:hep-lat/0405007
S. Steininger, U.-G. Meissner, N. Fettes, On wave function renormalization and related aspects in heavy fermion effective field theories. JHEP 09, 008 (1998). https://doi.org/10.1088/1126-6708/1998/09/008. arXiv:hep-ph/9808280
T. Becher, H. Leutwyler, Baryon chiral perturbation theory in manifestly Lorentz invariant form. Eur. Phys. J. C 9, 643–671 (1999). https://doi.org/10.1007/PL00021673. arXiv:hep-ph/9901384
[QCDSF/UKQCD 03] A. Ali Khan et al., The Nucleon mass in N(f) = 2 lattice QCD: Finite size effects from chiral perturbation theory. Nucl. Phys. B 689, 175–194 (2004). https://doi.org/10.1016/j.nuclphysb.2004.04.018. arXiv:hep-lat/0312030
J. Gasser, M.E. Sainio, A. Svarc, Nucleons with Chiral Loops. Nucl. Phys. B 307, 779–853 (1988). https://doi.org/10.1016/0550-3213(88)90108-3
R.D. Young, D.B. Leinweber, A.W. Thomas, S.V. Wright, Chiral analysis of quenched baryon masses. Phys. Rev. D 66, 094507 (2002). https://doi.org/10.1103/PhysRevD.66.094507. arXiv:hep-lat/0205017
W. Bietenholz et al., Flavour blindness and patterns of flavour symmetry breaking in lattice simulations of up, down and strange quarks. Phys. Rev. D 84, 054509 (2011). https://doi.org/10.1103/PhysRevD.84.054509. arXiv:1102.5300
J.A. Oller, M. Verbeni, J. Prades, Meson-baryon effective chiral lagrangians to O(q**3). JHEP 09, 079 (2006). https://doi.org/10.1088/1126-6708/2006/09/079. arXiv:hep-ph/0608204
M. Frink, U.-G. Meissner, On the chiral effective meson-baryon Lagrangian at third order, https://doi.org/10.1140/epja/i2006-10105-x. Eur. Phys. J.A29 (2006) 255–260, arXiv: hep-ph/0609256
J. Gegelia, G. Japaridze, Matching heavy particle approach to relativistic theory. Phys. Rev. D 60, 114038 (1999). https://doi.org/10.1103/PhysRevD.60.114038. arXiv:hep-ph/9908377
T. Fuchs, J. Gegelia, G. Japaridze, S. Scherer, Renormalization of relativistic baryon chiral perturbation theory and power counting. Phys. Rev. D 68, 056005 (2003). https://doi.org/10.1103/PhysRevD.68.056005. arXiv:hep-ph/0302117
M. Procura, T.R. Hemmert, W. Weise, Nucleon mass, sigma term and lattice QCD. Phys. Rev. D 69, 034505 (2004). https://doi.org/10.1103/PhysRevD.69.034505. arXiv:hep-lat/0309020
G. Colangelo, A. Fuhrer, C. Haefeli, The pion and proton mass in finite volume. Nucl. Phys. Proc. Suppl. 153, 41–48 (2006). https://doi.org/10.1016/j.nuclphysbps.2006.01.004. arXiv:hep-lat/0512002
S.R. Beane, Nucleon masses and magnetic moments in a finite volume. Phys. Rev. D D70, 034507 (2004). https://doi.org/10.1103/PhysRevD.70.034507. arXiv:hep-lat/0403015
Acknowledgements
We are very grateful to the external reviewers for providing detailed comments and suggestions on the draft of this review. These reviewers were Claude Bernard, Jérôme Charles, Paolo Gambino, Elvira Gámiz, Marc Knecht, Bira van Kolck, Laurent Lellouch, Zoltan Ligeti, Vittorio Lubicz, Kim Maltman, Aneesh Manohar, Emilie Passemar, Peter Petreczky, Nazario Tantalo, Tilo Wettig and Takeshi Yamazaki. The 2017 kick-off meeting for the present review was held at the University of Edinburgh and was supported by the Higgs Centre for Theoretical Physics. The 2018 mid-review meeting was held at Fermilab. We thank our hosts for their hospitality and financial support is gratefully acknowledged.
Members of FLAG were supported by funding agencies; in particular:
\(\bullet \) S.A. is supported in part by the Grant-in-Aid of the Japanese Ministry of Education, Sciences and Technology, Sports and Culture (MEXT) for Scientific Research (No. JP16H03978), by a priority issue (Elucidation of the fundamental laws and evolution of the universe) to be tackled by using Post “K” Computer, and by Joint Institute for Computational Fundamental Science (JICFuS).
\(\bullet \) Y.A. acknowledges support from JSPS KAKENHI grant No. 16K05320 and by the Post-K supercomputer project through JICFuS.
\(\bullet \) M.G. acknowledges support by the U.S. Department of Energy, Office of Science, Office of High Energy Physics under Contract No. DE-FG03-92ER40711.
\(\bullet \) R.G. acknowledges support by the U.S. Department of Energy, Office of Science, Office of High Energy Physics under Contract No. DE-AC52-06NA25396.
\(\bullet \) A.J. received funding from the STFC consolidated grant ST/P000711/1 and from the European Research Council under the European Union’s Seventh Framework Program (FP7/2007-2013)/ERC Grant agreement 279757.
\(\bullet \) D.L. would like to acknowledge support from Taiwanese MoST via grant number 105-2112-M-002-023-MY3.
\(\bullet \) A.P. is supported in part by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 757646, and by UK STFC grant ST/P000630/1.
\(\bullet \) The work of S.R.S. is supported in part by the US Department of Energy (grant DE-SC0011637).
\(\bullet \) S.D. likes to thank DFG for partial funding under SFB TRR-55.
\(\bullet \) H.F. acknowledges Japanese Grant-in-Aid for Scientific Research (JP18H01216 and JP18H04484).
\(\bullet \) G.H. and C.P. acknowledge support from the EU H2020-MSCA-ITN-2018-813942 (EuroPLEx), Spanish MICINN and MINECO grant FPA2015-68541-P (MINECO/FEDER), Spanish Agencia Estatal de Investigación through the grant ”IFT Centro de Excelencia Severo Ochoa SEV-2016-0597”, and the Ramón y Cajal Programme RYC-2012-0249.
\(\bullet \) S.H. is supported in part by JSPS KAKENHI Grant Number 18H03710.
\(\bullet \) S.A., Y.A., H.F., and S.H. are supported by the Post-K supercomputer project through the Joint Institute for Computational Fundamental Science (JICFuS).
\(\bullet \) S.C. acknowledges support through Deutsche Forschungsgemeinschaft Collaborative Research Centre/Transregio 55 (SFB/TRR 55) project and European Union Innovative Training Network Grant No. 813942 (EuroPLEx).
Author information
Authors and Affiliations
Corresponding author
Appendices
A Glossary
1.1 Lattice actions
In this appendix we give brief descriptions of the lattice actions used in the simulations and summarize their main features.
1.1.1 Gauge actions
The simplest and most widely used discretization of the Yang–Mills part of the QCD action is the Wilson plaquette action [962]:
where \(\beta \equiv 6/g_0^2\) (with \(g_0\) the bare gauge coupling) and the plaquette \(W_{\mu \nu }^{1\times 1}(x)\) is the product of link variables around an elementary square of the lattice, i.e.,
This expression reproduces the Euclidean Yang–Mills action in the continuum up to corrections of order \(a^2\). There is a general formalism, known as the “Symanzik improvement programme” [93, 94], which is designed to cancel the leading lattice artifacts, such that observables have an accelerated rate of convergence to the continuum limit. The improvement programme is implemented by adding higher-dimensional operators, whose coefficients must be tuned appropriately in order to cancel the leading lattice artifacts. The effectiveness of this procedure depends largely on the method with which the coefficients are determined. The most widely applied methods (in ascending order of effectiveness) include perturbation theory, tadpole-improved (partially resummed) perturbation theory, renormalization group methods, and the nonperturbative evaluation of improvement conditions.
In the case of Yang-Mills theory, the simplest version of an improved lattice action is obtained by adding rectangular \(1\times 2\) loops to the plaquette action, i.e.,
where the coefficients \(c_0, c_1\) satisfy the normalization condition \(c_0+8c_1=1\). The Symanzik-improved [726], Iwasaki [963], and DBW2 [964, 965] actions are all defined through Eq. (404) via particular choices for \(c_0, c_1\). Details are listed in Table 69 together with the abbreviations used in the summary tables. Another widely used variant is the tadpole Symanzik-improved [755, 966] action which is obtained by adding additional 6-link parallelogram loops \(W_{\mu \nu \sigma }^{1\times 1\times 1}(x)\) to the action in Eq. (404), i.e.,
where
allows for 1-loop improvement [726].
1.1.2 Light-quark actions
If one attempts to discretize the quark action, one is faced with the fermion doubling problem: the naive lattice transcription produces a 16-fold degeneracy of the fermion spectrum.
Wilson fermions
Wilson’s solution to the fermion doubling problem is based on adding a dimension-5 (irrelevant) operator to the lattice action. The Wilson-Dirac operator for the massless case reads [962, 967]
where \(\nabla _\mu ,\,\nabla _\mu ^*\) denote the covariant forward and backward lattice derivatives, respectively. The addition of the Wilson term \(a\nabla _\mu ^*\nabla _\mu \), results in fermion doublers acquiring a mass proportional to the inverse lattice spacing; close to the continuum limit these extra degrees of freedom are removed from the low-energy spectrum. However, the Wilson term also results in an explicit breaking of chiral symmetry even at zero bare quark mass. Consequently, it also generates divergences proportional to the UV cutoff (inverse lattice spacing), besides the usual logarithmic ones. Therefore the chiral limit of the regularized theory is not defined simply by the vanishing of the bare quark mass but must be appropriately tuned. As a consequence quark-mass renormalization requires a power subtraction on top of the standard multiplicative logarithmic renormalization. The breaking of chiral symmetry also implies that the nonrenormalization theorem has to be applied with care [888, 968], resulting in a normalization factor for the axial current which is a regular function of the bare coupling. On the other hand, vector symmetry is unaffected by the Wilson term and thus a lattice (point split) vector current is conserved and obeys the usual nonrenormalization theorem with a trivial (unity) normalization factor. Thus, compared to lattice fermion actions which preserve chiral symmetry, or a subgroup of it, the Wilson regularization typically results in more complicated renormalization patterns.
Furthermore, the leading-order lattice artifacts are of order a. With the help of the Symanzik improvement programme, the leading artifacts can be cancelled in the action by adding the so-called “Clover” or Sheikholeslami–Wohlert (SW) term [881]. The resulting expression in the massless case reads
where \(\sigma _{\mu \nu }=\frac{i}{2}[\gamma _\mu ,\gamma _\nu ]\), and \({\widehat{F}}_{\mu \nu }\) is a lattice transcription of the gluon field strength tensor \(F_{\mu \nu }\). The coefficient \(c_{\mathrm{sw}}\) can be determined perturbatively at tree-level (\(c_{\mathrm{sw}}= 1\); tree-level improvement or tlSW for short), via a mean field approach [755] (mean-field improvement or mfSW) or via a nonperturbative approach [969] (nonperturbatively improved or npSW). Hadron masses, computed using \(D_{\mathrm{sw}}\), with the coefficient \(c_{\mathrm{sw}}\) determined nonperturbatively, will approach the continuum limit with a rate proportional to \(a^2\); with tlSW for \(c_{\mathrm{sw}}\) the rate is proportional to \(g_0^2 a\).
Other observables require additional improvement coefficients [881]. A common example consists in the computation of the matrix element \(\langle \alpha \vert Q \vert \beta \rangle \) of a composite field Q of dimension-d with external states \(\vert \alpha \rangle \) and \(\vert \beta \rangle \). In the simplest cases, the above bare matrix element diverges logarithmically and a single renormalization parameter \(Z_Q\) is adequate to render it finite. It then approaches the continuum limit with a rate proportional to the lattice spacing a, even when the lattice action contains the Clover term. In order to reduce discretization errors to \({{\mathcal {O}}}(a^2)\), the lattice definition of the composite operator Q must be modified (or “improved”), by the addition of all dimension-\((d+1)\) operators with the same lattice symmetries as Q. Each of these terms is accompanied by a coefficient which must be tuned in a way analogous to that of \(c_{\mathrm{sw}}\). Once these coefficients are determined nonperturbatively, the renormalized matrix element of the improved operator, computed with a npSW action, converges to the continuum limit with a rate proportional to \(a^2\). A tlSW improvement of these coefficients and \(c_{\mathrm{sw}}\) will result in a rate proportional to \(g_0^2 a\).
It is important to stress that the improvement procedure does not affect the chiral properties of Wilson fermions; chiral symmetry remains broken.
Finally, we mention “twisted-mass QCD” as a method which was originally designed to address another problem of Wilson’s discretization: the Wilson-Dirac operator is not protected against the occurrence of unphysical zero modes, which manifest themselves as “exceptional” configurations. They occur with a certain frequency in numerical simulations with Wilson quarks and can lead to strong statistical fluctuations. The problem can be cured by introducing a so-called “chirally twisted” mass term. The most common formulation applies to a flavour doublet \({{\bar{\psi }}} = ( u \quad d)\) of mass-degenerate quarks, with the fermionic part of the QCD action in the continuum assuming the form [487]
Here, \(\mu _{\mathrm{q}}\) is the twisted-mass parameter, and \(\tau ^3\) is a Pauli matrix in flavour space. The standard action in the continuum can be recovered via a global chiral field rotation. The physical quark mass is obtained as a function of the two mass parameters m and \(\mu _{\mathrm{q}}\). The corresponding lattice regularization of twisted-mass QCD (tmWil) for \(N_{ f}=2\) flavours is defined through the fermion matrix
Although this formulation breaks physical parity and flavour symmetries, resulting in nondegenerate neutral and charged pions, is has a number of advantages over standard Wilson fermions. Firstly, the presence of the twisted-mass parameter \(\mu _{\mathrm{q}}\) protects the discretized theory against unphysical zero modes. A second attractive feature of twisted-mass lattice QCD is the fact that, once the bare mass parameter \(m_0\) is tuned to its “critical value” (corresponding to massless pions in the standard Wilson formulation), the leading lattice artifacts are of order \(a^2\) without the need to add the Sheikholeslami–Wohlert term in the action, or other improving coefficients [884]. A third important advantage is that, although the problem of explicit chiral symmetry breaking remains, quantities computed with twisted fermions with a suitable tuning of the mass parameter \(\mu _{\mathrm{q}}\), are subject to renormalization patterns which are simpler than the ones with standard Wilson fermions. Well known examples are the pseudoscalar decay constant and \(B_{\mathrm{K}}\).
Staggered fermions
An alternative procedure to deal with the doubling problem is based on Kogut-Susskind fermions [970, 971] and is now known under the name “staggered” fermion formulation [972,973,974]. Here the degeneracy is only lifted partially, from 16 down to 4. It has become customary to refer to these residual doublers as “tastes” in order to distinguish them from physical flavours. Taste changing interactions can occur via the exchange of gluons with one or more components of momentum near the cutoff \(\pi /a\). This leads to the breaking of the SU(4) vector symmetry among tastes, thereby generating order \(a^2\) lattice artifacts.
The residual doubling of staggered quarks (four tastes per flavour) is removed by taking a fractional power of the fermion determinant [975] – the “fourth-root procedure,” or, sometimes, the “fourth root trick.” This procedure would be unproblematic if the action had full SU(4) taste symmetry, which would give a Dirac operator that was block-diagonal in taste space. However, the breaking of taste symmetry at nonzero lattice spacing leads to a variety of problems. In fact, the fourth root of the determinant is not equivalent to the determinant of any local lattice Dirac operator [976]. This in turn leads to violations of unitarity on the lattice [977,978,979,980].
According to standard renormalization group lore, the taste violations, which are associated with lattice operators of dimension greater than four, might be expected to go away in the continuum limit, resulting in the restoration of locality and unitarity. However, there is a problem with applying the standard lore to this nonstandard situation: the usual renormalization group reasoning assumes that the lattice action is local. Nevertheless, Shamir [981, 982] shows that one may apply the renormalization group to a “nearby” local theory, and thereby gives a strong argument that that the desired local, unitary theory of QCD is reproduced by the rooted staggered lattice theory in the continuum limit.
A version of chiral perturbation that includes the lattice artifacts due to taste violations and rooting (“rooted staggered chiral perturbation theory”) can also be worked out [382, 983, 984] and shown to correctly describe the unitarity-violating lattice artifacts in the pion sector [978, 985]. This provides additional evidence that the desired continuum limit can be obtained. Further, it gives a practical method for removing the lattice artifacts from simulation results. Versions of rooted staggered chiral perturbation theory exist for heavy–light mesons with staggered light quarks but nonstaggered heavy quarks [986], heavy–light mesons with staggered light and heavy quarks [518, 987], staggered baryons [988], and mixed actions with a staggered sea [324, 326], as well as the pion-only version referenced above.
There is also considerable numerical evidence that the rooting procedure works as desired. This includes investigations in the Schwinger model [989,990,991], studies of the eigenvalues of the Dirac operator in QCD [992,993,994,995], and evidence for taste restoration in the pion spectrum as \(a\rightarrow 0\) [129, 166].
Issues with the rooting procedure have led Creutz [996,997,998,999,1000,1001,1002] to argue that the continuum limit of the rooted staggered theory cannot be QCD. These objections have however been answered in Refs. [126,127,128, 995, 1003,1004,1005,1006]. In particular, a claim that the continuum ’t Hooft vertex [1007, 1008] could not be properly reproduced by the rooted theory has been refuted [995, 1004].
Overall, despite the lack of rigorous proof of the correctness of the rooting procedure, we think the evidence is strong enough to consider staggered QCD simulations on a par with simulations using other actions. See the following reviews for further evidence and discussion: Refs. [125,126,127,128,129].
Improved staggered fermions
An improvement program can be used to suppress taste-changing interactions, leading to “improved staggered fermions,” with the so-called “Asqtad” [1009], “HISQ” [1010], “Stout-smeared” [1011], and “HYP” [1012] actions as the most common versions. All these actions smear the gauge links in order to reduce the coupling of high-momentum gluons to the quarks, with the main goal of decreasing taste-violating interactions. In the Asqtad case, this is accomplished by replacing the gluon links in the derivatives by averages over 1-, 3-, 5-, and 7-link paths. The other actions reduce taste changing even further by smearing more. In addition to the smearing, the Asqtad and HISQ actions include a three-hop term in the action (the “Naik term” [1013]) to remove order \(a^2\) errors in the dispersion relation, as well as a “Lepage term” [1014] to cancel other order \(a^2\) artifacts introduced by the smearing. In both the Asqtad and HISQ actions, the leading taste violations are of order \(\alpha _S^2 a^2\), and “generic” lattices artifacts (those associated with discretization errors other than taste violations) are of order \(\alpha _S a^2\). The overall coefficients of these errors are, however, significantly smaller with HISQ than with Asqtad. With the Stout-smeared and HYP actions, the errors are formally larger (order \(\alpha _S a^2\) for taste violations and order \(a^2\) for generic lattices artifacts). Nevertheless, the smearing seems to be very efficient, and the actual size of errors at accessible lattice spacings appears to be at least as small as with HISQ.
Although logically distinct from the light-quark improvement program for these actions, it is customary with the HISQ action to include an additional correction designed to reduce discretization errors for heavy quarks (in practice, usually charm quarks) [1010]. The Naik term is adjusted to remove leading \((am_c)^4\) and \(\alpha _S(am_c)^2\) errors, where \(m_c\) is the charm-quark mass and “leading” in this context means leading in powers of the heavy-quark velocity v (\(v/c\sim 1/3\) for \(D_s\)). With these improvements, the claim is that one can use the staggered action for charm quarks, although it must be emphasized that it is not obvious a priori how large a value of \(am_c\) may be tolerated for a given desired accuracy, and this must be studied in the simulations.
Ginsparg-Wilson fermions
Fermionic lattice actions, which do not suffer from the doubling problem whilst preserving chiral symmetry go under the name of “Ginsparg-Wilson fermions”. In the continuum the massless Dirac operator (D) anti-commutes with \(\gamma _5\). At nonzero lattice spacing a chiral symmetry can be realized if this condition is relaxed to [1015,1016,1017]
which is now known as the Ginsparg–Wilson relation [491]. The Nielsen–Ninomiya theorem [1018], which states that any lattice formulation for which D anticommutes with \(\gamma _5\) necessarily has doubler fermions, is circumvented since \(\{D,\gamma _5\}\ne 0\).
A lattice Dirac operator which satisfies Eq. (411) can be constructed in several ways. The so-called “overlap” or Neuberger-Dirac operator [1019] acts in four space-time dimensions and is, in its simplest form, defined by
\(D_{\mathrm{w}}\) is the massless Wilson-Dirac operator and \(|s|<1\) is a tunable parameter. The overlap operator \(D_{\mathrm{N}}\) removes all doublers from the spectrum, and can readily be shown to satisfy the Ginsparg-Wilson relation. The occurrence of the sign function \(\epsilon (A)\) in \(D_{\mathrm{N}}\) renders the application of \(D_{\mathrm{N}}\) in a computer program potentially very costly, since it must be implemented using, for instance, a polynomial approximation.
The most widely used approach to satisfying the Ginsparg-Wilson relation Eq. (411) in large-scale numerical simulations is provided by Domain Wall Fermions (DWF) [1020,1021,1022] and we therefore describe this in some more detail. Following early exploratory studies [1023]. this approach has been developed into a practical formulation of lattice QCD with good chiral and flavour symmetries leading to results which contribute significantly to this review. In this formulation, the fermion fields \(\psi (x,s)\) depend on a discrete fifth coordinate \(s=1,\ldots ,N\) as well as the physical 4-dimensional space-time coordinates \(x_\mu ,\,\mu =1\cdots 4\) (the gluon fields do not depend on s). The lattice on which the simulations are performed, is therefore a five-dimensional one of size \(L^3\times T\times N\), where \(L,\,T\) and N represent the number of points in the spatial, temporal and fifth dimensions respectively. The remarkable feature of DWF is that for each flavour there exists a physical light mode corresponding to the field q(x):
The left and right-handed modes of the physical field are located on opposite boundaries in the 5th dimensional space which, for \(N\rightarrow \infty \), allows for independent transformations of the left and right components of the quark fields, that is for chiral transformations. Unlike Wilson fermions, where for each flavour the quark-mass parameter in the action is fine-tuned requiring a subtraction of contributions of \({\mathcal {O}}(1/a)\) where a is the lattice spacing, with DWF no such subtraction is necessary for the physical modes, whereas the unphysical modes have masses of \({\mathcal {O}}(1/a)\) and decouple.
In actual simulations N is finite and there are small violations of chiral symmetry which must be accounted for. The theoretical framework for the study of the residual breaking of chiral symmetry has been a subject of intensive investigation (for a review and references to the original literature see, e.g., [1024]). The breaking requires one or more crossings of the fifth dimension to couple the left and right-handed modes; the more crossings that are required the smaller the effect. For many physical quantities the leading effects of chiral symmetry breaking due to finite N are parameterized by a residual mass, \(m_{\mathrm {res}}\). For example, the PCAC relation (for degenerate quarks of mass m) \(\partial _\mu A_\mu (x) = 2m P(x)\), where \(A_\mu \) and P represent the axial current and pseudoscalar density respectively, is satisfied with \(m=m^\mathrm {DWF}+m_\mathrm {res}\), where \(m^\mathrm {DWF}\) is the bare mass in the DWF action. The mixing of operators which transform under different representations of chiral symmetry is found to be negligibly small in current simulations. The important thing to note is that the chiral symmetry breaking effects are small and that there are techniques to mitigate their consequences.
The main price which has to be paid for the good chiral symmetry is that the simulations are performed in 5 dimensions, requiring approximately a factor of N in computing resources and resulting in practice in ensembles at fewer values of the lattice spacing and quark masses than is possible with other formulations. The current generation of DWF simulations is being performed at physical quark masses so that ensembles with good chiral and flavour symmetries are being generated and analysed [156]. For a discussion of the equivalence of DWF and overlap fermions see Refs. [1025, 1026].
A third example of an operator which satisfies the Ginsparg-Wilson relation is the so-called fixed-point action [1027,1028,1029]. This construction proceeds via a renormalization group approach. A related formalism are the so-called “chirally improved” fermions [1030].
Smearing
A simple modification which can help improve the action as well as the computational performance is the use of smeared gauge fields in the covariant derivatives of the fermionic action. Any smearing procedure is acceptable as long as it consists of only adding irrelevant (local) operators. Moreover, it can be combined with any discretization of the quark action. The “Asqtad” staggered quark action mentioned above [1009] is an example which makes use of so-called “Asqtad” smeared (or “fat”) links. Another example is the use of n-HYP smeared [1012, 1031], stout smeared [1032, 1033] or HEX (hypercubic stout) smeared [1034] gauge links in the tree-level clover improved discretization of the quark action, denoted by “n-HYP tlSW”, “stout tlSW” and “HEX tlSW” in the following.
In Table 70 we summarize the most widely used discretizations of the quark action and their main properties together with the abbreviations used in the summary tables. Note that in order to maintain the leading lattice artifacts of the actions as given in the table in nonspectral observables (like operator matrix elements) the corresponding nonspectral operators need to be improved as well.
1.1.3 Heavy-quark actions
Charm and bottom quarks are often simulated with different lattice-quark actions than up, down, and strange quarks because their masses are large relative to typical lattice spacings in current simulations; for example, \(a m_c \sim 0.4\) and \(am_b \sim 1.3\) at \(a=0.06\) fm. Therefore, for the actions described in the previous section, using a sufficiently small lattice spacing to control generic \((am_h)^n\) discretization errors at the physical b-quark mass is computationally demanding and has so far not been possible, with the first exception being the calculation of FNAL/MILC in [5] which uses the HISQ action and a lattice spacing of \(a \approx 0.03\) fm.
One alternative approach for lattice heavy quarks is direct application of effective theory. In this case the lattice heavy-quark action only correctly describes phenomena in a specific kinematic regime, such as Heavy-Quark Effective Theory (HQET) [1035,1036,1037] or Nonrelativistic QCD (NRQCD) [1038, 1039]. One can discretize the effective Lagrangian to obtain, for example, Lattice HQET [1040] or Lattice NRQCD [1041, 1042], and then simulate the effective theory numerically. The coefficients of the operators in the lattice-HQET and lattice-NRQCD actions are free parameters that must be determined by matching to the underlying theory (QCD) through the chosen order in \(1/m_h\) or \(v_h^2\), where \(m_h\) is the heavy-quark mass and \(v_h\) is the heavy-quark velocity in the the heavy–light meson rest frame.
Another approach is to interpret a relativistic quark action such as those described in the previous section in a manner suitable for heavy quarks. One can extend the standard Symanzik improvement program, which allows one to systematically remove lattice cutoff effects by adding higher-dimension operators to the action, by allowing the coefficients of the dimension 4 and higher operators to depend explicitly upon the heavy-quark mass. Different prescriptions for tuning the parameters correspond to different implementations: those in common use are often called the Fermilab action [1043], the relativistic heavy-quark action (RHQ) [1044], and the Tsukuba formulation [1045]. In the Fermilab approach, HQET is used to match the lattice theory to continuum QCD at the desired order in \(1/m_h\).
More generally, effective theory can be used to estimate the size of cutoff errors from the various lattice heavy-quark actions. The power counting for the sizes of operators with heavy quarks depends on the typical momenta of the heavy quarks in the system. Bound-state dynamics differ considerably between heavy–heavy and heavy–light systems. In heavy–light systems, the heavy quark provides an approximately static source for the attractive binding force, like the proton in a hydrogen atom. The typical heavy-quark momentum in the bound-state rest frame is \(|\vec {p}_h| \sim \Lambda _{\mathrm{QCD}}\), and heavy–light operators scale as powers of \((\Lambda _{\mathrm{QCD}}/m_h)^n\). This is often called “HQET power-counting”, although it applies to heavy–light operators in HQET, NRQCD, and even relativistic heavy-quark actions described below. Heavy–heavy systems are similar to positronium or the deuteron, with the typical heavy-quark momentum \(|\vec {p}_h| \sim \alpha _S m_h\). Therefore motion of the heavy quarks in the bound state rest frame cannot be neglected. Heavy–heavy operators have complicated power counting rules in terms of \(v_h^2\) [1042]; this is often called “NRQCD power counting.”
Alternatively, one can simulate bottom or charm quarks with the same action as up, down, and strange quarks provided that (1) the action is sufficiently improved, and (2) the lattice spacing is sufficiently fine. These qualitative criteria do not specify precisely how large a numerical value of \(am_h\) can be allowed while obtaining a given precision for physical quantities; this must be established empirically in numerical simulations. At present, both the HISQ and twisted-mass Wilson actions discussed previously are being used to simulate charm quarks. Simulations with HISQ quarks have employed heavier-quark masses than those with twisted-mass Wilson quarks because the action is more highly improved, but neither action has been used to simulate at the physical \(am_b\) until the recent calculation of FNAL/MILC in [5], where a lattice spacing of \(a \approx 0.03\) fm is available. All other calculations of heavy–light decay constants with these actions still rely on effective theories: the ETM collaboration interpolates between twisted-mass Wilson data generated near \(am_c\) and the static point [199], while the HPQCD collaboration, for the coarser lattice spacings, extrapolates HISQ data generated below \(am_b\) up to the physical point using an HQET-inspired series expansion in \((1/m_h)^n\) [72].
Heavy-quark effective theory
HQET was introduced by Eichten and Hill in Ref. [1036]. It provides the correct asymptotic description of QCD correlation functions in the static limit \(m_{h}/|\vec {p}_h| \!\rightarrow \! \infty \). Subleading effects are described by higher dimensional operators whose coupling constants are formally of \({{\mathcal {O}}}((1/m_{h})^n)\). The HQET expansion works well for heavy–light systems in which the heavy-quark momentum is small compared to the mass.
The HQET Lagrangian density at the leading (static) order in the rest frame of the heavy quark is given by
with
A bare quark mass \(m_{\mathrm{bare}}^{\mathrm{stat}}\) has to be added to the energy levels \(E^{\mathrm{stat}}\) computed with this Lagrangian to obtain the physical ones. For example, the mass of the B meson in the static approximation is given by
At tree-level \(m_{\mathrm{bare}}^{\mathrm{stat}}\) is simply the (static approximation of the) b-quark mass, but in the quantized lattice formulation it has to further compensate a divergence linear in the inverse lattice spacing. Weak composite fields are also rewritten in terms of the static fields, e.g.,
where the renormalization factor of the axial current in the static theory \(Z_{\mathrm{A}}^{\mathrm{stat}}\) is scale-dependent. Recent lattice-QCD calculations using static b quarks and dynamical light quarks [199, 562] perform the operator matching at 1-loop in mean-field improved lattice perturbation theory [1046, 1047]. Therefore the heavy-quark discretization, truncation, and matching errors in these results are of \({{\mathcal {O}}}(a^2 \Lambda _{\mathrm{QCD}}^2)\), \({{\mathcal {O}}} (\Lambda _{\mathrm{QCD}}/m_h)\), and \({{\mathcal {O}}}(\alpha _s^2, \alpha _s^2 a \Lambda _{\mathrm{QCD}})\).
In order to reduce heavy-quark truncation errors in B-meson masses and matrix elements to the few-percent level, state-of-the-art lattice-HQET computations now include corrections of \({{\mathcal {O}}}(1/m_h)\). Adding the \(1/m_{h}\) terms, the HQET Lagrangian reads
At this order, two other parameters appear in the Lagrangian, \(\omega _{\mathrm{kin}}\) and \(\omega _{\mathrm{spin}}\). The normalization is such that the tree-level values of the coefficients are \(\omega _{\mathrm{kin}}=\omega _{\mathrm{spin}}=1/(2m_{h})\). Similarly the operators are formally expanded in inverse powers of the heavy-quark mass. The time component of the axial current, relevant for the computation of mesonic decay constants is given by
and depends on two additional parameters \(c_{\mathrm{A}}^{(1)}\) and \(c_{\mathrm{A}}^{(2)}\).
A framework for nonperturbative HQET on the lattice has been introduced in Refs. [1040, 1048]. As pointed out in Refs. [1049, 1050], since \(\alpha _s(m_h)\) decreases logarithmically with \(m_h\), whereas corrections in the effective theory are power-like in \(\Lambda /m_h\), it is possible that the leading errors in a calculation will be due to the perturbative matching of the action and the currents at a given order \((\Lambda /m_h)^l\) rather than to the missing \({{\mathcal {O}}}((\Lambda /m_h)^{l+1})\) terms. Thus, in order to keep matching errors below the uncertainty due to truncating the HQET expansion, the matching is performed nonperturbatively beyond leading order in \(1/m_{h}\). The asymptotic convergence of HQET in the limit \(m_h \rightarrow \infty \) indeed holds only in that case.
The higher dimensional interaction terms in the effective Lagrangian are treated as space-time volume insertions into static correlation functions. For correlators of some multi-local fields \({{\mathcal {Q}}}\) and up to the \(1/m_h\) corrections to the operator, this means
where \(\langle {{\mathcal {Q}}} \rangle _{\mathrm{stat}}\) denotes the static expectation value with \({{\mathcal {L}}}^{\mathrm{stat}}(x) +{{\mathcal {L}}}^{\mathrm{light}}(x)\). Nonperturbative renormalization of these correlators guarantees the existence of a well-defined continuum limit to any order in \(1/m_h\). The parameters of the effective action and operators are then determined by matching a suitable number of observables calculated in HQET (to a given order in \(1/m_{h}\)) and in QCD in a small volume (typically with \(L\simeq 0.5\) fm), where the full relativistic dynamics of the b-quark can be simulated and the parameters can be computed with good accuracy. In Refs. [1048, 1051] the Schrödinger Functional (SF) setup has been adopted to define a set of quantities, given by the small volume equivalent of decay constants, pseudoscalar-vector splittings, effective masses and ratio of correlation functions for different kinematics, that can be used to implement the matching conditions. The kinematical conditions are usually modified by changing the periodicity in space of the fermions, i.e., by directly exploiting a finite-volume effect. The new scale L, which is introduced in this way, is chosen such that higher orders in \(1/m_hL\) and in \(\Lambda _{\mathrm{QCD}}/m_h\) are of about the same size. At the end of the matching step the parameters are known at lattice spacings which are of the order of 0.01 fm, significantly smaller than the resolutions used for large volume, phenomenological, applications. For this reason a set of SF-step scaling functions is introduced in the effective theory to evolve the parameters to larger lattice spacings. The whole procedure yields the nonperturbative parameters with an accuracy which allows to compute phenomenological quantities with a precision of a few percent (see Refs. [557, 1052] for the case of the \(B_{(s)}\) decay constants). Such an accuracy can not be achieved by performing the nonperturbative matching in large volume against experimental measurements, which in addition would reduce the predictivity of the theory. For the lattice-HQET action matched nonperturbatively through \({{\mathcal {O}}}(1/m_h)\), discretization and truncation errors are of \({{\mathcal {O}}}(a \Lambda ^2_{\mathrm{QCD}}/m_h, a^2 \Lambda ^2_{\mathrm{QCD}})\) and \({{\mathcal {O}}}((\Lambda _{\mathrm{QCD}}/m_h )^2)\).
The noise-to-signal ratio of static-light correlation functions grows exponentially in Euclidean time, \(\propto e^{\mu x_0}\) . The rate \(\mu \) is nonuniversal but diverges as 1/a as one approaches the continuum limit. By changing the discretization of the covariant derivative in the static action one may achieve an exponential reduction of the noise to signal ratio. Such a strategy led to the introduction of the \(S^{\mathrm{stat}}_{\mathrm{HYP1,2}}\) actions [1053], where the thin links in \(D_0\) are replaced by HYP-smeared links [1012]. These actions are now used in all lattice applications of HQET.
Nonrelativistic QCD
Nonrelativistic QCD (NRQCD) [1041, 1042] is an effective theory that can be matched to full QCD order by order in the heavy-quark velocity \(v_h^2\) (for heavy–heavy systems) or in \(\Lambda _{\mathrm{QCD}}/m_h\) (for heavy–light systems) and in powers of \(\alpha _s\). Relativistic corrections appear as higher-dimensional operators in the Hamiltonian.
As an effective field theory, NRQCD is only useful with an ultraviolet cutoff of order \(m_h\) or less. On the lattice this means that it can be used only for \(am_h>1\), which means that \({\mathcal {O}}(a^n)\) errors cannot be removed by taking \(a\rightarrow 0\) at fixed \(m_h\). Instead heavy-quark discretization errors are systematically removed by adding additional operators to the lattice Hamiltonian. Thus, while strictly speaking no continuum limit exists at fixed \(m_h\), continuum physics can be obtained at finite lattice spacing to arbitrarily high precision provided enough terms are included, and provided that the coefficients of these terms are calculated with sufficient accuracy. Residual discretization errors can be parameterized as corrections to the coefficients in the nonrelativistic expansion, as shown in Eq. (427). Typically they are of the form \((a|\vec {p}_h|)^n\) multiplied by a function of \(am_h\) that is smooth over the limited range of heavy-quark masses (with \(am_h > 1\)) used in simulations, and can therefore can be represented by a low-order polynomial in \(am_h\) by Taylor’s theorem (see Ref. [1054] for further discussion). Power-counting estimates of these effects can be compared to the observed lattice-spacing dependence in simulations. Provided that these effects are small, such comparisons can be used to estimate and correct the residual discretization effects.
An important feature of the NRQCD approach is that the same action can be applied to both heavy–heavy and heavy–light systems. This allows, for instance, the bare b-quark mass to be fixed via experimental input from \(\Upsilon \) so that simulations carried out in the B or \(B_s\) systems have no adjustable parameters left. Precision calculations of the \(B_s\)-meson mass (or of the mass splitting \(M_{B_s} - M_\Upsilon /2\)) can then be used to test the reliability of the method before turning to quantities one is trying to predict, such as decay constants \(f_B\) and \(f_{B_s}\), semileptonic form factors or neutral B mixing parameters.
Given the same lattice-NRQCD heavy-quark action, simulation results will not be as accurate for charm quarks as for bottom (\(1/m_b < 1/m_c\), and \(v_b < v_c\) in heavy–heavy systems). For charm, however, a more serious concern is the restriction that \(am_h\) must be greater than one. This limits lattice-NRQCD simulations at the physical \(am_c\) to relatively coarse lattice spacings for which light-quark and gluon discretization errors could be large. Thus recent lattice-NRQCD simulations have focused on bottom quarks because \(am_b > 1\) in the range of typical lattice spacings between \(\approx \) 0.06 and 0.15 fm.
In most simulations with NRQCD b-quarks during the past decade one has worked with an NRQCD action that includes tree-level relativistic corrections through \({{\mathcal {O}}}(v_h^4)\) and discretization corrections through \({{\mathcal {O}}}(a^2)\),
where the subscripts “t” and “\(t-a\)” denote that the heavy-quark, gauge, \(\mathbf {E}\), and \(\mathbf {B}\)-fields are on time slices t or \(t-a\), respectively. \(H_0\) is the nonrelativistic kinetic energy operator,
and \(\delta H\) includes relativistic and finite-lattice-spacing corrections,
\(m_h\) is the bare heavy-quark mass, \(\Delta ^{(2)}\) the lattice Laplacian, \({\varvec{\nabla }}\) the symmetric lattice derivative and \({\Delta ^{(4)}}\) the lattice discretization of the continuum \(\sum _i D^4_i\). \({\tilde{{\varvec{\nabla }}}}\) is the improved symmetric lattice derivative and the \(\tilde{\mathbf{E}}\) and \(\tilde{\mathbf{B}}\) fields have been improved beyond the usual clover leaf construction. The stability parameter n is discussed in Ref. [1042]. In most cases the \(c_i\)’s have been set equal to their tree-level values \(c_i = 1\). With this implementation of the NRQCD action, errors in heavy–light-meson masses and splittings are of \({{\mathcal {O}}}(\alpha _S \Lambda _{\mathrm{QCD}}/m_h )\), \({{\mathcal {O}}}(\alpha _S (\Lambda _{\mathrm{QCD}}/m_h)^2 )\), \({{\mathcal {O}}}((\Lambda _{\mathrm{QCD}}/m_h )^3)\), and \({{\mathcal {O}}}(\alpha _s a^2 \Lambda _{\mathrm{QCD}}^2)\), with coefficients that are functions of \(am_h\). 1-loop corrections to many of the coefficients in Eq. (427) have now been calculated, and are starting to be included in simulations [1055,1056,1057].
Most of the operator matchings involving heavy–light currents or four-fermion operators with NRQCD b-quarks and Asqtad or HISQ light quarks have been carried out at 1-loop order in lattice perturbation theory. In calculations published to date of electroweak matrix elements, heavy–light currents with massless light quarks have been matched through \({{\mathcal {O}}}(\alpha _s, \Lambda _\mathrm{QCD}/m_h, \alpha _s/(a m_h), \alpha _s \Lambda _{\mathrm{QCD}}/m_h)\), and four-fermion operators through \({{\mathcal {O}}}(\alpha _s, \Lambda _\mathrm{QCD}/m_h, \alpha _s/(a m_h))\). NRQCD/HISQ currents with massive HISQ quarks are also of interest, e.g., for the bottom-charm currents in \(B \rightarrow D^{(*)} l \nu \) semileptonic decays and the relevant matching calculations have been performed at 1-loop order in Ref. [1058]. Taking all the above into account, the most significant systematic error in electroweak matrix elements published to date with NRQCD b-quarks is the \({{\mathcal {O}}}(\alpha _s^2)\) perturbative matching uncertainty. Work is therefore underway to use current-current correlator methods combined with very high order continuum perturbation theory to do current matchings nonperturbatively [1059].
Relativistic heavy quarks
An approach for relativistic heavy-quark lattice formulations was first introduced by El-Khadra et al. [1043]. Here they showed that, for a general lattice action with massive quarks and non-Abelian gauge fields, discretization errors can be factorized into the form \(f(m_h a)(a|\vec {p}_h|)^n\), and that the function \(f(m_h a)\) is bounded to be of \({{\mathcal {O}}}(1)\) or less for all values of the quark mass \(m_h\). Therefore cutoff effects are of \({{\mathcal {O}}}(a \Lambda _{\mathrm{QCD}})^n\) and \({{\mathcal {O}}}((a|\vec {p}_h|)^n)\), even for  , and can be controlled using a Symanzik-like procedure. As in the standard Symanzik improvement program, cutoff effects are systematically removed by introducing higher-dimension operators to the lattice action and suitably tuning their coefficients. In the relativistic heavy-quark approach, however, the operator coefficients are allowed to depend explicitly on the quark mass. By including lattice operators through dimension n and adjusting their coefficients \(c_{n,i}(m_h a)\) correctly, one enforces that matrix elements in the lattice theory are equal to the analogous matrix elements in continuum QCD through \((a|\vec {p}_h|)^n\), such that residual heavy-quark discretization errors are of \({{\mathcal {O}}}(a|\vec {p}_h|)^{n+1}\).
, and can be controlled using a Symanzik-like procedure. As in the standard Symanzik improvement program, cutoff effects are systematically removed by introducing higher-dimension operators to the lattice action and suitably tuning their coefficients. In the relativistic heavy-quark approach, however, the operator coefficients are allowed to depend explicitly on the quark mass. By including lattice operators through dimension n and adjusting their coefficients \(c_{n,i}(m_h a)\) correctly, one enforces that matrix elements in the lattice theory are equal to the analogous matrix elements in continuum QCD through \((a|\vec {p}_h|)^n\), such that residual heavy-quark discretization errors are of \({{\mathcal {O}}}(a|\vec {p}_h|)^{n+1}\).
The relativistic heavy-quark approach can be used to compute the matrix elements of states containing heavy quarks for which the heavy-quark spatial momentum \(|\vec {p}_h|\) is small compared to the lattice spacing. Thus it is suitable to describe bottom and charm quarks in both heavy–light and heavy–heavy systems. Calculations of bottomonium and charmonium spectra serve as nontrivial tests of the method and its accuracy.
At fixed lattice spacing, relativistic heavy-quark formulations recover the massless limit when \((am_h) \ll 1\), recover the static limit when \((am_h) \gg 1\), and smoothy interpolate between the two; thus they can be used for any value of the quark mass, and, in particular, for both charm and bottom. Discretization errors for relativistic heavy-quark formulations are generically of the form \(\alpha _s^k f(am_h)(a |\vec {p}_h|)^n\), where k reflects the order of the perturbative matching for operators of \({{\mathcal {O}}}((a |\vec {p}_h|)^n)\). For each n, such errors are removed completely if the operator matching is nonperturbative. When \((am_h) \sim 1\), this gives rise to nontrivial lattice-spacing dependence in physical quantities, and it is prudent to compare estimates based on power-counting with a direct study of scaling behaviour using a range of lattice spacings. At fixed quark mass, relativistic heavy-quark actions possess a smooth continuum limit without power-divergences. Of course, as \(m_h \rightarrow \infty \) at fixed lattice spacing, the static limit is recovered and by then taking the continuum limit the corresponding power divergences are reproduced (see, e.g., Ref. [1060]).
The relativistic heavy-quark formulations in use all begin with the asymmetric (or anisotropic) Sheikholeslami–Wohlert (“clover”) action [1061]:
where \(D_\mu \) is the lattice covariant derivative and \(F_{\mu \nu }\) is the lattice field-strength tensor. Here we show the form of the action given in Ref. [1044]. The introduction of a space-time asymmetry, parameterized by \(\zeta \) in Eq. (428), is convenient for heavy-quark systems because the characteristic heavy-quark four-momenta do not respect space-time axis exchange (\(\vec {p}_h < m_h\) in the bound-state rest frame). Further, the Sheikoleslami–Wohlert action respects the continuum heavy-quark spin and flavour symmetries, so HQET can be used to interpret and estimate lattice discretization effects [1060, 1062, 1063]. We discuss three different prescriptions for tuning the parameters of the action in common use below. In particular, we focus on aspects of the action and operator improvement and matching relevant for evaluating the quality of the calculations discussed in the main text.
The meson energy-momentum dispersion relation plays an important role in relativistic heavy-quark formulations:
where \(M_1\) and \(M_2\) are known as the rest and kinetic masses, respectively. Because the lattice breaks Lorentz invariance, there are corrections proportional to powers of the momentum. Further, the lattice rest masses and kinetic masses are not equal (\(M_1 \ne M_2\)), and only become equal in the continuum limit.
The Fermilab interpretation [1043] is suitable for calculations of mass splittings and matrix elements of systems with heavy quarks. The Fermilab action is based on the hopping-parameter form of the Wilson action, in which \(\kappa _h\) parameterizes the heavy-quark mass. In practice, \(\kappa _h\) is tuned such that the the kinetic meson mass equals the experimentally-measured heavy-strange meson mass (\(m_{B_s}\) for bottom and \(m_{D_s}\) for charm). In principle, one could also tune the anisotropy parameter such that \(M_1 = M_2\). This is not necessary, however, to obtain mass splittings and matrix elements, which are not affected by \(M_1\) [1062]. Therefore in the Fermilab action the anisotropy parameter is set equal to unity. The clover coefficient in the Fermilab action is fixed to the value \(c_{\mathrm{SW}} = 1/u_0^3\) from mean-field improved lattice perturbation theory [755]. With this prescription, discretization effects are of \({{\mathcal {O}}}(\alpha _sa|\vec {p}_h|, (a|\vec {p}_h|)^2)\). Calculations of electroweak matrix elements also require improving the lattice current and four-fermion operators to the same order, and matching them to the continuum. Calculations with the Fermilab action remove tree-level \({{\mathcal {O}}}(a)\) errors in electroweak operators by rotating the heavy-quark field used in the matrix element and setting the rotation coefficient to its tadpole-improved tree-level value (see, e.g., Eqs. (7.8) and (7.10) of Ref. [1043]). Finally, electroweak operators are typically renormalized using a mostly nonperturbative approach in which the flavour-conserving light-light and heavy–heavy current renormalization factors \(Z_V^{ll}\) and \(Z_V^{hh}\) are computed nonperturbatively [1064]. The flavour-conserving factors account for most of the heavy–light current renormalization. The remaining correction is expected to be close to unity due to the cancellation of most of the radiative corrections including tadpole graphs [1060]; therefore it can be reliably computed at 1-loop in mean-field improved lattice perturbation theory with truncation errors at the percent to few-percent level.
The relativistic heavy-quark (RHQ) formulation developed by Li, Lin, and Christ builds upon the Fermilab approach, but tunes all the parameters of the action in Eq. (428) nonperturbatively [1044]. In practice, the three parameters \(\{m_0a, c_{\mathrm{SW}}, \zeta \}\) are fixed to reproduce the experimentally-measured \(B_s\) meson mass and hyperfine splitting (\(m_{B_s^*}-m_{B_s}\)), and to make the kinetic and rest masses of the lattice \(B_s\) meson equal [1065]. This is done by computing the heavy-strange meson mass, hyperfine splitting, and ratio \(M_1/M_2\) for several sets of bare parameters \(\{m_0a, c_\mathrm{SW}, \zeta \}\) and interpolating linearly to the physical \(B_s\) point. By fixing the \(B_s\)-meson hyperfine splitting, one loses a potential experimental prediction with respect to the Fermilab formulation. However, by requiring that \(M_1 = M_2\), one gains the ability to use the meson rest masses, which are generally more precise than the kinetic masses, in the RHQ approach. The nonperturbative parameter-tuning procedure eliminates \({{\mathcal {O}}}(a)\) errors from the RHQ action, such that discretization errors are of \({{\mathcal {O}}}((a|\vec {p}_h|)^2)\). Calculations of B-meson decay constants and semileptonic form factors with the RHQ action are in progress [1066, 1067], as is the corresponding 1-loop mean-field improved lattice perturbation theory [1068]. For these works, cutoff effects in the electroweak vector and axial-vector currents will be removed through \({{\mathcal {O}}}(\alpha _s a)\), such that the remaining discretization errors are of \({{\mathcal {O}}}(\alpha _s^2a|\vec {p}_h|, (a|\vec {p}_h|)^2)\). Matching the lattice operators to the continuum will be done following the mostly nonperturbative approach described above.
The Tsukuba heavy-quark action is also based on the Sheikholeslami–Wohlert action in Eq. (428), but allows for further anisotropies and hence has additional parameters: specifically the clover coefficients in the spatial \((c_B)\) and temporal \((c_E)\) directions differ, as do the anisotropy coefficients of the \(\vec {D}\) and \(\vec {D}^2\) operators [1045]. In practice, the contribution to the clover coefficient in the massless limit is computed nonperturbatively [1069], while the mass-dependent contributions, which differ for \(c_B\) and \(c_E\), are calculated at 1-loop in mean-field improved lattice perturbation theory [1070]. The hopping parameter is fixed nonperturbatively to reproduce the experimentally-measured spin-averaged 1S charmonium mass [514]. One of the anisotropy parameters (\(r_t\) in Ref. [514]) is also set to its 1-loop perturbative value, while the other (\(\nu \) in Ref. [514]) is fixed noperturbatively to obtain the continuum dispersion relation for the spin-averaged charmonium 1S states (such that \(M_1 = M_2\)). For the renormalization and improvement coefficients of weak current operators, the contributions in the chiral limit are obtained nonperturbatively [159, 1071], while the mass-dependent contributions are estimated using 1-loop lattice perturbation theory [1072]. With these choices, lattice cutoff effects from the action and operators are of \({{\mathcal {O}}}(\alpha _s^2 a|\vec {p}|, (a|\vec {p}_h|)^2)\).
Light-quark actions combined with HQET
The heavy-quark formulations discussed in the previous sections use effective field theory to avoid the occurence of discretization errors of the form \((am_h)^n\). In this section we describe methods that use improved actions that were originally designed for light-quark systems for B physics calculations. Such actions unavoidably contain discretization errors that grow as a power of the heavy-quark mass. In order to use them for heavy-quark physics, they must be improved to at least \({{\mathcal {O}}}(am_h)^2\). However, since \(am_b > 1\) at the smallest lattice spacings available in current simulations, these methods also require input from HQET to guide the simulation results to the physical b-quark mass.
The ETM collaboration has developed two methods, the “ratio method” [560] and the “interpolation method” [1073, 1074]. They use these methods together with simulations with twisted-mass Wilson fermions, which have discretization errors of \({\mathcal {O}}(am_h)^2\). In the interpolation method \(\Phi _{hs}\) and \(\Phi _{h\ell }\) (or \(\Phi _{hs}/\Phi _{h\ell }\)) are calculated for a range of heavy-quark masses in the charm region and above, while roughly keeping \(am_h \lesssim 0.5 \). The relativistic results are combined with a separate calculation of the decay constants in the static limit, and then interpolated to the physical b quark mass. In ETM’s implementation of this method, the heavy Wilson decay constants are matched to HQET using NLO in continuum perturbation theory. The static limit result is renormalized using 1-loop mean-field improved lattice perturbation theory, while for the relativistic data PCAC is used to calculate absolutely normalized matrix elements. Both, the relativistic and static limit data are then run to the common reference scale \(\mu _b = 4.5 \,\mathrm {GeV}\) at NLO in continuum perturbation theory. In the ratio method, one constructs physical quantities \(P(m_h)\) from the relativistic data that have a well-defined static limit (\(P(m_h) \rightarrow \) const. for \(m_h \rightarrow \infty \)) and evaluates them at the heavy-quark masses used in the simulations. Ratios of these quantities are then formed at a fixed ratio of heavy-quark masses, \(z = P(m_h) / P(m_h/\lambda )\) (where  ), which ensures that z is equal to unity in the static limit. Hence, a separate static limit calculation is not needed with this method. In ETM’s implementation of the ratio method for the B-meson decay constant, \(P(m_h)\) is constructed from the decay constants and the heavy-quark pole mass as \(P(m_h) = f_{h\ell }(m_h) \cdot (m^\mathrm{pole}_h)^{1/2}\). The corresponding z-ratio therefore also includes ratios of perturbative matching factors for the pole mass to \({\overline{\mathrm {MS}}}\) conversion. For the interpolation to the physical b-quark mass, ratios of perturbative matching factors converting the data from QCD to HQET are also included. The QCD-to-HQET matching factors improve the approach to the static limit by removing the leading logarithmic corrections. In ETM’s implementation of this method (ETM 11 and 12) both conversion factors are evaluated at NLO in continuum perturbation theory. The ratios are then simply fit to a polynomial in \(1/m_h\) and interpolated to the physical b-quark mass. The ratios constructed from \(f_{h\ell }\) (\(f_{hs}\)) are called z (\(z_s\)). In order to obtain the B meson decay constants, the ratios are combined with relativistic decay constant data evaluated at the smallest reference mass.
), which ensures that z is equal to unity in the static limit. Hence, a separate static limit calculation is not needed with this method. In ETM’s implementation of the ratio method for the B-meson decay constant, \(P(m_h)\) is constructed from the decay constants and the heavy-quark pole mass as \(P(m_h) = f_{h\ell }(m_h) \cdot (m^\mathrm{pole}_h)^{1/2}\). The corresponding z-ratio therefore also includes ratios of perturbative matching factors for the pole mass to \({\overline{\mathrm {MS}}}\) conversion. For the interpolation to the physical b-quark mass, ratios of perturbative matching factors converting the data from QCD to HQET are also included. The QCD-to-HQET matching factors improve the approach to the static limit by removing the leading logarithmic corrections. In ETM’s implementation of this method (ETM 11 and 12) both conversion factors are evaluated at NLO in continuum perturbation theory. The ratios are then simply fit to a polynomial in \(1/m_h\) and interpolated to the physical b-quark mass. The ratios constructed from \(f_{h\ell }\) (\(f_{hs}\)) are called z (\(z_s\)). In order to obtain the B meson decay constants, the ratios are combined with relativistic decay constant data evaluated at the smallest reference mass.
The HPQCD collaboration has introduced a method in Ref. [72] which we shall refer to as the “heavy HISQ” method. The first key ingredient is the use of the HISQ action for the heavy and light valence quarks, which has leading discretization errors of \({{\mathcal {O}}} \left( \alpha _s (v/c) (am_h)^2, (v/c)^2 (am_h)^4\right) \). With the same action for the heavy- and light-valence quarks it is possible to use PCAC to avoid renormalization uncertainties. Another key ingredient at the time of formulation was the availability of gauge ensembles over a large range of lattice spacings, in this case the library of \(N_f = 2\,+\,1\) asqtad ensembles made public by the MILC collaboration which include lattice spacings as small as \(a \approx 0.045\) fm. Since the HISQ action is so highly improved and with lattice spacings as small as 0.045 fm, HPQCD is able to use a large range of heavy-quark masses, from below the charm region to almost up to the physical b-quark mass with \(am_h \lesssim 0.85\). They then fit their data in a combined continuum and HQET fit (i.e., using a fit function that is motivated by HQET) to a polynomial in \(1/m_H\) (the heavy pseudoscalar-meson mass of a meson containing a heavy (h) quark).
This approach has been extended in recent work by the HPQCD and FNAL/MILC collaborations using the MILC-generated \(N_f=2\,+\,1\,+\,1\) HISQ ensembles with lattice spacings down to 0.03 fm [5]. These are being used by the HPQCD and the FNAL/MILC collaborations for their B-physics programmes and the corresponding analyses include heavy-quark masses at the physical b quark mass.
In Table 71 we list the discretizations of the quark action most widely used for heavy c and b quarks together with the abbreviations used in the summary tables. We also summarize the main properties of these actions and the leading lattice discretization errors for calculations of heavy–light meson matrix quantities with them. Note that in order to maintain the leading lattice artifacts of the actions as given in the table in nonspectral observables (like operator matrix elements) the corresponding nonspectral operators need to be improved as well.
1.2 Setting the scale
In simulations of lattice-QCD quantities such as hadron masses and decay constants are obtained in “lattice units” i.e., as dimensionless numbers. In order to convert them into physical units they must be expressed in terms of some experimentally known, dimensionful reference quantity Q. This procedure is called “setting the scale”. It amounts to computing the nonperturbative relation between the bare gauge coupling \(g_0\) (which is an input parameter in any lattice simulation) and the lattice spacing a expressed in physical units. To this end one chooses a value for \(g_0\) and computes the value of the reference quantity in a simulation: This yields the dimensionless combination, \((aQ)|_{g_0}\), at the chosen value of \(g_0\). The calibration of the lattice spacing is then achieved via
where \(Q|_{\mathrm{exp}}\) denotes the experimentally known value of the reference quantity. Common choices for Q are the mass of the nucleon, the \(\Omega \) baryon or the decay constants of the pion and the kaon. Vector mesons, such as the \(\rho \) or \(K^*\) meson, are unstable and therefore their masses are not very well suited for setting the scale, despite the fact that they have been used over many years for that purpose.
Another widely used quantity to set the scale is the hadronic radius \(r_0\), which can be determined from the force between static quarks via the relation [336]
If the force is derived from potential models describing heavy quarkonia, the above relation determines the value of \(r_0\) as \(r_0\approx 0.5\) fm. A variant of this procedure is obtained [688] by using the definition \(F(r_1)r_1^2=1.00\), which yields \(r_1\approx 0.32\) fm. It is important to realize that both \(r_0\) and \(r_1\) are not directly accessible in experiment, so that their values derived from phenomenological potentials are necessarily model-dependent. Inspite of the inherent ambiguity whenever hadronic radii are used to calibrate the lattice spacing, they are very useful quantities for performing scaling tests and continuum extrapolations of lattice data. Furthermore, they can be easily computed with good statistical accuracy in lattice simulations.
More recently, the so-called gradient flow scales \(t_0\) and \(w_0\) have become popular, because they can be computed with very high statistical accuracy in lattice simulations without introducing any systematics due to the analysis. The scales are based on the gradient flow procedure [271] which evolves the gauge fields in field space along a fictitious flow time t according to a local diffusion equation. The field at finite flow time can be shown to be renormalized [1075]. Expectation values of local gauge-invariant expressions of the field are physical quantities with a well-defined continuum limit and can hence be used to fix the scale. One example is provided by the gauge action density E(t). Its expectation value is used to define the reference scale \(t_0\) through the implicit equation [271]
Another example is the related observable
which is used to define the scale \(w_0\) via the condition [272]
Similarly to the hadronic radius, the values of \(t_0\) and \(w_0\) can not be determined from experiment, but only from within lattice QCD, yielding \(\sqrt{t_0}\approx 0.14\) fm and \(w_0 \approx 0.17\) fm (see, e.g., [699]). Nevertheless, they are very useful quantities for performing scaling tests and continuum extrapolations of lattice data.
1.3 Matching and running
The lattice formulation of QCD amounts to introducing a particular regularization scheme. Thus, in order to be useful for phenomenology, hadronic matrix elements computed in lattice simulations must be related to some continuum reference scheme, such as the \({\overline{\mathrm {MS}}}\)-scheme of dimensional regularization. The matching to the continuum scheme usually involves running to some reference scale using the renormalization group.
In principle, the matching factors which relate lattice matrix elements to the \({\overline{\mathrm {MS}}}\)-scheme, can be computed in perturbation theory formulated in terms of the bare coupling. It has been known for a long time, though, that the perturbative expansion is not under good control. Several techniques have been developed which allow for a nonperturbative matching between lattice regularization and continuum schemes, and are briefly introduced here.
Regularization-independent momentum subtraction
In the Regularization-independent Momentum Subtraction (“RI/MOM” or “RI”) scheme [468] a nonperturbative renormalization condition is formulated in terms of Green functions involving quark states in a fixed gauge (usually Landau gauge) at nonzero virtuality. In this way one relates operators in lattice regularization nonperturbatively to the RI scheme. In a second step one matches the operator in the RI scheme to its counterpart in the \({\overline{\mathrm {MS}}}\)-scheme. The advantage of this procedure is that the latter relation involves perturbation theory formulated in the continuum theory. The use of lattice perturbation theory can thus be avoided, and the continuum perturbation theory, which is technically more feasible for higher order calculations, could be applied if more precision is required. A technical complication is associated with the accessible momentum scales (i.e., virtualities), which must be large enough (typically several \(\mathrm {GeV}\)) in order for the perturbative relation to \({\overline{\mathrm {MS}}}\) to be reliable. The momentum scales in simulations must stay well below the cutoff scale (i.e., \(2\pi \) over the lattice spacing), since otherwise large lattice artifacts are incurred. Thus, the applicability of the RI scheme traditionally relies on the existence of a “window” of momentum scales, which satisfy
However, solutions for mitigating this limitation, which involve continuum limit, nonperturbative running to higher scales in the RI/MOM scheme, have recently been proposed and implemented [11, 12, 498, 1076].
Within the RI/MOM framework one has some freedom in the choice of the external momenta used in the Green functions. In the choice made in the original work, the virtuality of each external leg is nonzero, but that of the momentum transfer between different legs can vanish [468]. This leads to enhanced nonperturbative contributions that fall as powers of \(p^2\). An alternative choice that reduces these issues is the symmetric MOM scheme, in which virtualities in all channels are nonzero [1077]. This scheme is now widely used. To distinguish it from the original choice of virtualities, it is referred to as the RI/SMOM (or RI-SMOM) scheme, while the original choice is called the RI/MON (or RI-MOM) scheme.
Schrödinger functional
Another example of a nonperturbative matching procedure is provided by the Schrödinger functional (SF) scheme [172]. It is based on the formulation of QCD in a finite volume. If all quark masses are set to zero the box length remains the only scale in the theory, such that observables like the coupling constant run with the box size L. The great advantage is that the RG running of scale-dependent quantities can be computed nonperturbatively using recursive finite-size scaling techniques. It is thus possible to run nonperturbatively up to scales of, say, \(100\,\mathrm {GeV}\), where one is sure that the perturbative relation between the SF and \({\overline{\mathrm {MS}}}\)-schemes is controlled.
Perturbation theory
The third matching procedure is based on perturbation theory in which higher order are effectively resummed [755]. Although this procedure is easier to implement, it is hard to estimate the uncertainty associated with it.
Mostly nonperturbative renormalization
Some calculations of heavy–light and heavy–heavy matrix elements adopt a mostly nonperturbative matching approach. Let us consider a weak decay process mediated by a current with quark flavours h and q, where h is the initial heavy quark (either bottom or charm) and q can be a light (\(\ell = u,d\)), strange, or charm quark. The matrix elements of lattice current \(J_{hq}\) are matched to the corresponding continuum matrix elements with continuum current \({{{\mathcal {J}}}}_{hq}\) by calculating the renormalization factor \(Z_{J_{hq}}\). The mostly nonperturbative renormalization method takes advantage of rewriting the current renormalization factor as the following product:
The flavour-conserving renormalization factors \(Z_{V^4_{hh}}\) and \(Z_{V^4_{qq}}\) can be obtained nonperturbatively from standard heavy–light and light-light meson charge normalization conditions. \(Z_{V^4_{hh}}\) and \(Z_{V^4_{qq}}\) account for the bulk of the renormalization. The remaining correction \(\rho _{J_{hq}}\) is expected to be close to unity because most of the radiative corrections, including self-energy corrections and contributions from tadpole graphs, cancel in the ratio [1060, 1063]. The 1-loop coefficients of \(\rho _{J_{hq}}\) have been calculated for heavy–light and heavy–heavy currents for Fermilab heavy and both (improved) Wilson light [1060, 1063] and asqtad light [1078] quarks. In all cases the 1-loop coefficients are found to be very small, yielding sub-percent to few percent level corrections.
In Table 72 we list the abbreviations used in the compilation of results together with a short description.
1.4 Chiral extrapolation
As mentioned in the introduction, Symanzik’s framework can be combined with Chiral Perturbation Theory. The well-known terms occurring in the chiral effective Lagrangian are then supplemented by contributions proportional to powers of the lattice spacing a. The additional terms are constrained by the symmetries of the lattice action and therefore depend on the specific choice of the discretization. The resulting effective theory can be used to analyse the a-dependence of the various quantities of interest – provided the quark masses and the momenta considered are in the range where the truncated chiral perturbation series yields an adequate approximation. Understanding the dependence on the lattice spacing is of central importance for a controlled extrapolation to the continuum limit.
For staggered fermions, this program has first been carried out for a single staggered flavour (a single staggered field) [983] at \({\mathcal {O}}(a^2)\). In the following, this effective theory is denoted by S\(\chi \)PT. It was later generalized to an arbitrary number of flavours [382, 383], and to next-to-leading order [984]. The corresponding theory is commonly called Rooted Staggered chiral perturbation theory and is denoted by RS\(\chi \)PT.
For Wilson fermions, the effective theory has been developed in [380, 381, 1079] and is called W\(\chi \)PT, while the theory for Wilson twisted-mass fermions [124, 1080, 1081] is termed tmW\(\chi \)PT.
Another important approach is to consider theories in which the valence and sea quark masses are chosen to be different. These theories are called partially quenched. The acronym for the corresponding chiral effective theory is PQ\(\chi \)PT [1082,1083,1084,1085].
Finally, one can also consider theories where the fermion discretizations used for the sea and the valence quarks are different. The effective chiral theories for these “mixed action” theories are referred to as MA\(\chi \)PT [322,323,324,325, 1086,1087,1088].
Finite-Volume Regimes of QCD
Once QCD with \(N_{ f}\) nondegenerate flavours is regulated both in the UV and in the IR, there are \(3+N_{ f}\) scales in play: The scale \(\Lambda _\mathrm {QCD}\) that reflects “dimensional transmutation” (alternatively, one could use the pion decay constant or the nucleon mass, in the chiral limit), the inverse lattice spacing 1/a, the inverse box size 1/L, as well as \(N_{ f}\) meson masses (or functions of meson masses) that are sensitive to the \(N_{ f}\) quark masses, e.g., \(M_{\pi }^2\), \(2M_K^2-M_{\pi }^2\) and the spin-averaged masses of \({}^1S\) states of quarkonia.
Ultimately, we are interested in results with the two regulators removed, i.e., physical quantities for which the limits \(a \rightarrow 0\) and \(L \rightarrow \infty \) have been carried out. In both cases there is an effective field theory (EFT) which guides the extrapolation. For the \(a \rightarrow 0\) limit, this is a version of the Symanzik EFT which depends, in its details, on the lattice action that is used, as outlined in Sect. A.1. The finite-volume effects are dominated by the lightest particles, the pions. Therefore, a chiral EFT, also known as \(\chi \)PT, is appropriate to parameterize the finite-volume effects, i.e., the deviation of masses and other observables, such as matrix elements, in a finite-volume from their infinite volume, physical values. Most simulations of phenomenological interest are carried out in boxes of size \(L \gg 1/M_\pi \), that is in boxes whose diameter is large compared to the Compton wavelength that the pion would have, at the given quark mass, in infinite volume. In this situation the finite-volume corrections are small, and in many cases the ratio \(M_\mathrm {had}(L) / M_\mathrm {had}\) or f(L) /f, where f denotes some generic matrix element, can be calculated in \(\chi \)PT, such that the leading finite-volume effects can be taken out analytically. In the terminology of \(\chi \)PT this setting is referred to as the p-regime, as the typical contributing momenta \(p \sim M_\pi \gg 1/L\). A peculiar situation occurs if the condition \(L \gg 1/M_{\pi }\) is violated (while \(L\Lambda _\mathrm {QCD}\gg 1\) still holds), in other words if the quark mass is taken so light that the Compton wavelength that the pion would have (at the given \(m_q\)) in infinite volume, is as large or even larger than the actual box size. Then the pion zero-momentum mode dominates and needs to be treated separately. While this setup is unlikely to be useful for standard phenomenological computations, the low-energy constants of \(\chi \)PT can still be calculated, by matching to a re-ordered version of the chiral series, and following the details of the reordering such an extreme regime is called the \(\epsilon \)- or \(\delta \)-regime, respectively. Accordingly, further particulars of these regimes are discussed in Sect. 5.1 of this report.
1.5 Parameterizations of semileptonic form factors
In this section, we discuss the description of the \(q^2\)-dependence of form factors, using the vector form factor \(f_+\) of \(B\rightarrow \pi \ell \nu \) decays as a benchmark case. Since in this channel the parameterization of the \(q^2\)-dependence is crucial for the extraction of \(|V_{ub}|\) from the existing measurements (involving decays to light leptons), as explained above, it has been studied in great detail in the literature. Some comments about the generalization of the techniques involved will follow.
The vector form factor for \(B\rightarrow \pi \ell \nu \) All form factors are analytic functions of \(q^2\) outside physical poles and inelastic threshold branch points; in the case of \(B\rightarrow \pi \ell \nu \), the only pole expected below the \(B\pi \) production region, starting at \(q^2 = t_+ = (m_B+m_\pi )^2\), is the \(B^*\). A simple ansatz for the \(q^2\)-dependence of the \(B\rightarrow \pi \ell \nu \) semileptonic form factors that incorporates vector-meson dominance is the Bečirević-Kaidalov (BK) parameterization [530], which for the vector form factor reads:
Because the BK ansatz has few free parameters, it has been used extensively to parameterize the shape of experimental branching-fraction measurements and theoretical form-factor calculations. A variant of this parameterization proposed by Ball and Zwicky (BZ) adds extra pole factors to the expressions in Eq. (437) in order to mimic the effect of multiparticle states [1089]. A similar idea, extending the use of effective poles also to \(D\rightarrow \pi \ell \nu \) decays, is explored in Ref. [1090]. Finally, yet another variant (RH) has been proposed by Hill in Ref. [1091]. Although all of these parameterizations capture some known properties of form factors, they do not manifestly satisfy others. For example, perturbative QCD scaling constrains the behaviour of \(f_+\) in the deep Euclidean region [1092,1093,1094], and angular momentum conservation constrains the asymptotic behaviour near thresholds – e.g., \(\mathrm{Im}\,f_+(q^2) \sim (q^2-t_+)^{3/2}\) (see, e.g., Ref. [1095]). Most importantly, these parameterizations do not allow for an easy quantification of systematic uncertainties.
A more systematic approach that improves upon the use of simple models for the \(q^2\) behaviour exploits the positivity and analyticity properties of two-point functions of vector currents to obtain optimal parameterizations of form factors [651, 652, 1094, 1096,1097,1098,1099]. Any form factor f can be shown to admit a series expansion of the form
where the squared momentum transfer is replaced by the variable
This is a conformal transformation, depending on an arbitrary real parameter \(t_0<t_+\), that maps the \(q^2\) plane cut for \(q^2 \ge t_+\) onto the disk \(|z(q^2,t_0)|<1\) in the z complex plane. The function \(B(q^2)\) is called the Blaschke factor, and contains poles and cuts below \(t_+\) – for instance, in the case of \(B\rightarrow \pi \) decays,
Finally, the quantity \(\phi (q^2,t_0)\), called the outer function, is some otherwise arbitrary function that does not introduce further poles or branch cuts. The crucial property of this series expansion is that the sum of the squares of the coefficients
is a finite quantity. Therefore, by using this parameterization an absolute bound to the uncertainty induced by truncating the series can be obtained. The aim in choosing \(\phi \) is to obtain a bound that is useful in practice, while (ideally) preserving the correct behaviour of the form factor at high \(q^2\) and around thresholds.
The simplest form of the bound would correspond to \(\sum _{n=0}^\infty a_n^{2}=1\). Imposing this bound yields the following “standard” choice for the outer function
where \(t_-=(m_B-m_\pi )^2\), and \(\chi _{1^-}(0)\) is the derivative of the transverse component of the polarization function (i.e., the Fourier transform of the vector two-point function) \(\Pi _{\mu \nu }(q)\) at Euclidean momentum \(Q^2=-q^2=0\). It is computed perturbatively, using operator product expansion techniques, by relating the \(B\rightarrow \pi \ell \nu \) decay amplitude to \(\ell \nu \rightarrow B\pi \) inelastic scattering via crossing symmetry and reproducing the correct value of the inclusive \(\ell \nu \rightarrow X_b\) amplitude. We will refer to the series parameterization with the outer function in Eq. (442) as Boyd, Grinstein, and Lebed (BGL). The perturbative and OPE truncations imply that the bound is not strict, and one should take it as
where this holds for any choice of N. Since the values of |z| in the kinematical region of interest are well below 1 for judicious choices of \(t_0\), this provides a very stringent bound on systematic uncertainties related to truncation for \(N\ge 2\). On the other hand, the outer function in Eq. (442) is somewhat unwieldy and, more relevantly, spoils the correct large \(q^2\) behaviour and induces an unphysical singularity at the \(B\pi \) threshold.
A simpler choice of outer function has been proposed by Bourrely, Caprini and Lellouch (BCL) in Ref. [1095], which leads to a parameterization of the form
This satisfies all the basic properties of the form factor, at the price of changing the expression for the bound to
The constants \(B_{jk}\) can be computed and shown to be \(|B_{jk}|\lesssim {\mathcal {O}}(10^{-2})\) for judicious choices of \(t_0\); therefore, one again finds that truncating at \(N\ge 2\) provides sufficiently stringent bounds for the current level of experimental and theoretical precision. It is actually possible to optimize the properties of the expansion by taking
which for physical values of the masses results in the semileptonic domain being mapped onto the symmetric interval  (where this range differs slightly for the \(B^{\pm }\) and \(B^0\) decay channels), minimizing the maximum truncation error. If one also imposes that the asymptotic behaviour \(\mathrm{Im}\,f_+(q^2) \sim (q^2-t_+)^{3/2}\) near threshold is satisfied, then the highest-order coefficient is further constrained as
(where this range differs slightly for the \(B^{\pm }\) and \(B^0\) decay channels), minimizing the maximum truncation error. If one also imposes that the asymptotic behaviour \(\mathrm{Im}\,f_+(q^2) \sim (q^2-t_+)^{3/2}\) near threshold is satisfied, then the highest-order coefficient is further constrained as
Substituting the above constraint on \(a_N^{+}\) into Eq. (444) leads to the constrained BCL parameterization
which is the standard implementation of the BCL parameterization used in the literature.
Parameterizations of the BGL and BCL kind, to which we will refer collectively as “z-parameterizations”, have already been adopted by the BaBar and Belle collaborations to report their results, and also by the Heavy Flavour Averaging Group (HFAG, later renamed HFLAV). Some lattice collaborations, such as FNAL/MILC and ALPHA, have already started to report their results for form factors in this way. The emerging trend is to use the BCL parameterization as a standard way of presenting results for the \(q^2\)-dependence of semileptonic form factors. Our policy will be to quote results for z-parameterizations when the latter are provided in the paper (including the covariance matrix of the fits); when this is not the case, but the published form factors include the full correlation matrix for values at different \(q^2\), we will perform our own fit to the constrained BCL ansatz in Eq. (448); otherwise no fit will be quoted. We however stress the importance of providing, apart from parameterization coefficients, values for the form factors themselves (in the continuum limit and at physical quark masses) for a number of values of \(q^2\), so that the results can be independently parameterized by the readers if so wished.
The scalar form factor for \(B\rightarrow \pi \ell \nu \) The discussion of the scalar \(B\rightarrow \pi \) form factor is very similar. The main differences are the absence of a constraint analogue to Eq. (447) and the choice of the overall pole function. In our fits we adopt the simple expansion:
We do impose the exact kinematical constraint \(f_+ (0) = f_0 (0)\) by expressing the \(a_{N-1}^0\) coefficient in terms of all remaining \(a_n^+\) and \(a_n^0\) coefficients. This constraint introduces important correlations between the \(a_n^+\) and \(a_n^0\) coefficients; thus only lattice calculations that present the correlations between the vector and scalar form factors can be used in an average that takes into account the constraint at \(q^2 = 0\).
Finally we point out that we do not need to use the same number of parameters for the vector and scalar form factors. For instance, with \((N^+ = 3, N^0 = 3)\) we have \(a_{0,1,2}^+\) and \(a_{0,1}^0\), while with \((N^+ = 3, N^0 = 4)\) we have \(a_{0,1,2}^+\) and \(a_{0,1,2}^0\) as independent fit parameters. In our average we will choose the combination that optimizes uncertainties.
Extension to other form factors The discussion above largely extends to form factors for other semileptonic transitions (e.g., \(B_s\rightarrow K\) and \(B_{(s)} \rightarrow D^{(*)}_{(s)}\), and semileptonic D and K decays). Details are discussed in the relevant sections.
A general discussion of semileptonic meson decay in this context can be found, e.g., in Ref. [1100]. Extending what has been discussed above for \(B\rightarrow \pi \), the form factors for a generic \(H \rightarrow L\) transition will display a cut starting at the production threshold \(t_+\), and the optimal value of \(t_0\) required in z-parameterizations is \(t_0=t_+(1-\sqrt{1-t_-/t_+})\) (where \(t_\pm =(m_H\pm m_L)^2\)). For unitarity bounds to apply, the Blaschke factor has to include all sub-threshold poles with the quantum numbers of the hadronic current – i.e., vector (resp. scalar) resonances in \(B\pi \) scattering for the vector (resp. scalar) form factors of \(B\rightarrow \pi \), \(B_s\rightarrow K\), or \(\Lambda _b \rightarrow p\); and vector (resp. scalar) resonances in \(B_c\pi \) scattering for the vector (resp. scalar) form factors of \(B\rightarrow D\) or \(\Lambda _b \rightarrow \Lambda _c\).Footnote 90 Thus, as emphasized above, the control over systematic uncertainties brought in by using z-parameterizations strongly depends on implementation details. This has practical consequences, in particular, when the resonance spectrum in a given channel is not sufficiently well-known. Caveats may also apply for channels where resonances with a nonnegligible width appear. A further issue is whether \(t_+=(m_H+m_L)^2\) is the proper choice for the start of the cut in cases such as \(B_s\rightarrow K\ell \nu \) and \(B\rightarrow D\ell \nu \), where there are lighter two-particle states that project on the current (B,\(\pi \) and \(B_c\),\(\pi \) for the two processes, respectively).Footnote 91 In any such situation, it is not clear a priori that a given z-parameterization will satisfy strict bounds, as has been seen, e.g., in determinations of the proton charge radius from electron–proton scattering [1101,1102,1103].
The HPQCD collaboration pioneered a variation on the z-parameterization approach, which they refer to as a “modified z-expansion,” that is used to simultaneously extrapolate their lattice simulation data to the physical light-quark masses and the continuum limit, and to interpolate/extrapolate their lattice data in \(q^2\). This entails allowing the coefficients \(a_n\) to depend on the light-quark masses, squared lattice spacing, and, in some cases the charm-quark mass and pion or kaon energy. Because the modified z-expansion is not derived from an underlying effective field theory, there are several potential concerns with this approach that have yet to be studied. The most significant is that there is no theoretical derivation relating the coefficients of the modified z-expansion to those of the physical coefficients measured in experiment; it therefore introduces an unquantified model dependence in the form-factor shape. As a result, the applicability of unitarity bounds has to be examined carefully. Related to this, z-parameterization coefficients implicitly depend on quark masses, and particular care should be taken in the event that some state can move across the inelastic threshold as quark masses are changed (which would in turn also affect the form of the Blaschke factor). Also, the lattice-spacing dependence of form factors provided by Symanzik effective theory techniques may not extend trivially to z-parameterization coefficients. The modified z-expansion is now being utilized by collaborations other than HPQCD and for quantities other than \(D \rightarrow \pi \ell \nu \) and \(D \rightarrow K \ell \nu \), where it was originally employed. We advise treating results that utilize the modified z-expansion to obtain form-factor shapes and CKM matrix elements with caution, however, since the systematics of this approach warrant further study.
1.6 Summary of simulated lattice actions
In the following Tables 73, 74, 75, 76, 77 and 78 we summarize the gauge and quark actions used in the various calculations with \(N_f=2, 2\,+\,1\) and \(2\,+\,1\,+\,1\) quark flavours. The calculations with \(N_f=0\) quark flavours mentioned in Sect. 9 all used the Wilson gauge action and are not listed. Abbreviations are explained in Sects. A.1.1, A.1.2 and A.1.3, and summarized in Tables 69, 70 and 71.
B Notes
In the following Appendices we provide more detailed information on the simulations used to calculate the quantities discussed in Sects. 3–10. We present this information only for results that have appeared since FLAG 16. For earlier results the information is available in the corresponding Appendices B.1–7 of FLAG 16 [3]. The complete tables are available on the FLAG website http://flag.unibe.ch [4] (Tables 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101).
1.1 Notes to Sect. 3 on quark masses
1.2 Notes to Sect. 4 on \(|V_{ud}|\) and \(|V_{us}|\)
See Tables 102, 103, 104, 105, 106, 107, 108, 109 and 110.
1.3 Notes to Sect. 5 on low-energy constants
See Tables 111, 112, 113, 114, 115, 116, 117, 118 and 119.
1.4 Notes to Sect. 6 on kaon mixing
1.4.1 Kaon B-parameter \(B_K\)
See Tables 120, 121, 122 and 123.
1.4.2 Kaon BSM B-parameters
See Tables 124, 125, 126 and 127.
1.5 Notes to Sect. 7 on D-meson decay constants and form factors
See Tables 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141 and 142.
1.5.1 Form factors for semileptonic decays of charmed hadrons
See Tables 143, 144, 145, 146, 147 and 148.
1.6 Notes to Sect. 8 on B-meson decay constants, mixing parameters and form factors
1.6.1 \(B_{(s)}\)-meson decay constants
See Tables 149, 150, 151, 152 and 153.
1.6.2 \(B_{(s)}\)-meson mixing matrix elements
See Tables 154, 155, 156, 157 and 158.
1.6.3 Form factors entering determinations of \(|V_{ub}|\) (\(B \rightarrow \pi l\nu \), \(B_s \rightarrow K l\nu \), \(\Lambda _b \rightarrow pl\nu \))
No new calculations w.r.t. the previous FLAG report.
1.6.4 Form factors for rare decays of beauty hadrons
See Tables 159, 160, 161, 162 and 163.
1.6.5 Form factors entering determinations of \(|V_{cb}|\) (\(B_{(s)} \rightarrow D_{(s)}^{(*)} l\nu \), \(\Lambda _b \rightarrow \Lambda _c l\nu \)) and \(R(D_{(s)})\)
See Tables 164, 165, 166, 167, 168, 169 and 170.
1.7 Notes to Sect. 9 on the strong coupling \(\alpha _{\mathrm{s}}\)
1.7.1 Renormalization scale and perturbative behaviour
1.7.2 Continuum limit
1.8 Notes to Sect. 10 on nucleon matrix elements
See Tables 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208 and 209.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Aoki, S., Aoki, Y., Bečirević, D. et al. FLAG Review 2019. Eur. Phys. J. C 80, 113 (2020). https://doi.org/10.1140/epjc/s10052-019-7354-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-7354-7




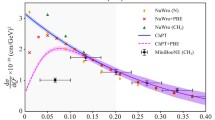
 the parameter values and ranges used to generate the data sets allow for a satisfactory control of the systematic uncertainties;
the parameter values and ranges used to generate the data sets allow for a satisfactory control of the systematic uncertainties; the parameter values and ranges used to generate the data sets allow for a reasonable attempt at estimating systematic uncertainties, which however could be improved;
the parameter values and ranges used to generate the data sets allow for a reasonable attempt at estimating systematic uncertainties, which however could be improved; the parameter values and ranges used to generate the data sets are unlikely to allow for a reasonable control of systematic uncertainties.
the parameter values and ranges used to generate the data sets are unlikely to allow for a reasonable control of systematic uncertainties.
 200 MeV
200 MeV  otherwise
otherwise at least three lattice spacings and at least two points below 0.1 fm and a range of lattice spacings satisfying
at least three lattice spacings and at least two points below 0.1 fm and a range of lattice spacings satisfying  at least two lattice spacings and at least one point below 0.1 fm and a range of lattice spacings satisfying
at least two lattice spacings and at least one point below 0.1 fm and a range of lattice spacings satisfying  otherwise
otherwise

 otherwise
otherwise and
and  ). However, as pion masses decrease, one must also account for the weakening of the pion couplings. In particular, 1-loop chiral perturbation theory [
). However, as pion masses decrease, one must also account for the weakening of the pion couplings. In particular, 1-loop chiral perturbation theory [

 otherwise
otherwise all leading isospin breaking effects are included in the lattice calculation
all leading isospin breaking effects are included in the lattice calculation isospin breaking effects are included using the electro-quenched approximation
isospin breaking effects are included using the electro-quenched approximation otherwise
otherwise nonperturbative
nonperturbative 1-loop perturbation theory or higher with a reasonable estimate of truncation errors
1-loop perturbation theory or higher with a reasonable estimate of truncation errors otherwise
otherwise corresponds to results included in the average or estimate (i.e., results that contribute to the black square below);
corresponds to results included in the average or estimate (i.e., results that contribute to the black square below); corresponds to results that are not included in the average but pass all quality criteria;
corresponds to results that are not included in the average but pass all quality criteria; corresponds to all other results;
corresponds to all other results; corresponds to FLAG averages or estimates; they are also highlighted by a gray vertical band.
corresponds to FLAG averages or estimates; they are also highlighted by a gray vertical band. corresponds to nonlattice results;
corresponds to nonlattice results; corresponds to Particle Data Group (PDG) results.
corresponds to Particle Data Group (PDG) results.

































 all points relevant in the analysis have
all points relevant in the analysis have  all points have
all points have  otherwise
otherwise verified over a range of a factor 4 change in
verified over a range of a factor 4 change in  agreement with perturbation theory over a range of a factor
agreement with perturbation theory over a range of a factor  otherwise
otherwise three lattice spacings with
three lattice spacings with  three lattice spacings with
three lattice spacings with  otherwise
otherwise 3 or more lattice spacings, at least 2 points below
3 or more lattice spacings, at least 2 points below  2 lattice spacings, at least 1 point below
2 lattice spacings, at least 1 point below  otherwise
otherwise



 in the continuum extrapolation.
in the continuum extrapolation.

 200 MeV
200 MeV  Otherwise
Otherwise Three or more source-sink separations
Three or more source-sink separations  Two or more source-sink separations,
Two or more source-sink separations,  Otherwise
Otherwise






 and a factor
and a factor  . An exception to the above is the situation where the correction terms are small anyway, i.e.,
. An exception to the above is the situation where the correction terms are small anyway, i.e.,  in the perturbative behaviour. This rating is, however, due to the overall estimated uncertainty, not to the rest of the data and analysis, which we use here.
in the perturbative behaviour. This rating is, however, due to the overall estimated uncertainty, not to the rest of the data and analysis, which we use here. for the continuum limit, in Boucaud 00A [
for the continuum limit, in Boucaud 00A [