1 Introduction

Ultra high intensity lasers have been developed significantly in these days, which are said to enable the experimental confirmations for the theoretically predicted quantum effects [1]. One of them is the Unruh effect [6–8]. It is a prediction that one, moving in the Minkowski space-time with linear constant acceleration, experiences the space-time as a thermal bath given by a canonical ensemble with the Unruh temperature, \(T_\mathrm{U} = \hbar \, a/(2\pi c \,k_B) \approx 4 \times 10^{-23}\,a{/}(\mathrm{{1}\,cm}{/}\mathrm{s}^2)\,[\mathrm{K}]\), where a is the acceleration.

In the above situation, we think that it is timely and meaningful to investigate the theoretical aspect of the phenomena of the Unruh effect. There are already considerations and attempts to detect the Unruh effect [1–5]. These exploit the Larmor radiation that an accelerating electron emits. Here the Larmor radiation they exploit is an additional Larmor radiation emitted by the Brownian motion rooted in the thermal bath given by the Unruh effect in the accelerating frame, in addition to the normal Larmor radiation. Such an additional Larmor radiation is called “Unruh radiation” in these papers.

One of the interesting points as regards the Unruh radiation is that although the Unruh effect itself is a phenomenon occurring only in the accelerating frame, the Brownian motion rooted in the thermal bath given by the Unruh effect in the accelerating frame is predicted in the inertial frame, and as a result the Unruh radiation is emitted in the inertial frame. If such a Brownian motion can be predicted, we assume for the thermal radiation in the inertial frame, which a particle heated by the Unruh effect in the accelerating frame emits, could also be predicted.

We hence propose the prediction mentioned above in this study. The point in our prediction is, although the Unruh effect occurs only in the accelerating frame, the Brownian motion rooted in the Unruh effect appears in the inertial frame, and the heat of the particle appears in the inertial frame. We call such a thermal radiation “Unruh thermal radiation”, and perform this study based on such Unruh thermal radiation.

Let us here turn to the recent detection of the Higgs particle [9, 10]. This leads us to the prediction that the realistic field’s vacuum energies are given by some Higgs potentials. Since the spontaneous symmetry breaking described by the Higgs potentials is restored by the thermal effect [11], the Unruh thermal radiation can also restore the spontaneous symmetry breaking. In this case, the vacuum energies with such a thermal correction affect the structure of the space-time by its role as the cosmological constant.

Hence, the purpose of this study is, based on our prediction for the Unruh thermal radiation mentioned in the fourth paragraph, to calculate the thermal field theory’s vacuum energy given by the Higgs type potential with the correction becoming the cause for the restoration of the spontaneous symmetry breaking. In this calculation we take into account that the background space-time varies due to the field theory’s corrected vacuum energy. Based on such an analysis, we investigate the phenomena.

We now will more specifically mention what we will do. We first consider a particle moving with a linear constant acceleration in the four-dimensional Minkowski space-time. Then, as mentioned earlier, if the prediction for the Brownian motion rooted in the Unruh effect is possible in the inertial frame, we propose a prediction in this paper for the thermal radiation, which we call the Unruh thermal radiation in the fourth paragraph, as well. As a result, in the inertial frame, the field in the neighborhood of the particle gets heated and the field’s vacuum energy gets a thermal correction. The field we consider in this study is a real scalar field described by the Klein–Gordon equation with a Higgs potential term, at finite temperature, where the temperature is brought about according to the imaginary time formalism. It is identified with the Unruh temperature. We then calculate the one-loop effective potential with the correction given by the Unruh thermal radiation, where the corrected one-loop effective potential describes the restoration of the spontaneous symmetry breaking. We perform this calculation taking into account that the background space-time is deformed due to the corrected one-loop effective potential’s role as the cosmological constant. Although the cosmological constant in our actual cosmology is not zero, taking the approximation that the space-time will be flat at zero temperature for simplicity in this study, we define the corrected one-loop effective potential to vanish at zero temperature. Based on such a corrected one-loop effective potential, we examine the amount of the energy corresponding to the change of the acceleration and the accelerating particle’s world-line for each acceleration.

We refer to a few basic papers on the spontaneous symmetry breaking and its restoration induced by the thermal effect and Unruh effect. In Ref. [11], the symmetry breaking and restoration in a flat space at finite temperature have been investigated. In Ref. [12], the restoration of the spontaneous symmetry breaking in a real scalar field in a Rindler space has been investigated. Further, the chiral condensation and the quark and diquark condensation in the Nambu–Jona-Lasinio model in the Rindler space have been investigated in Refs. [13] and [14], respectively. There are also papers concluding that the Unruh effect does not restore the spontaneous symmetry breaking in Rindler space [15, 16].

One may notice that the symmetry restorations in Refs. [12–14] are the ones in the accelerating frame. On the other hand, the symmetry restoration in this paper is the one in the inertial frame. Further, the phenomena in the situation that the spontaneous symmetry breaking is being restored with the deformed background space-times due to the corrected field’s vacuum energy by the Unruh thermal radiation have never been investigated so far, and we first investigate these in this paper. As for Refs. [15, 16], their conclusion does not apply to this study readily. Because their issue is how the restoration of the spontaneous symmetry breaking is in the accelerating frame. On the other hand, the issue we address in this paper is a phenomenology in the inertial frame provided that a particle becomes hot in the inertial frame by the Unruh temperature in the accelerating frame. Further, the thermal source in the restoration of the spontaneous symmetry in this paper is not the Unruh effect itself but the heat of the particle in the inertial frame rooted in the Unruh effect. As long as they can provide some mechanism that can cancel the Unruh effect in the accelerating frame, their conclusion does not apply to our study readily.

For the reason that the effective potentials in the realistic fields can be predicted to be some Higgs potential type, there is a certain probability that the phenomena similar to what we investigate in this paper are actually occurring in our world. This study would for this reason be important and intriguing.

We mention the organization of this paper. In Sect. 2, we give the background space-time and the model in the field theory in this study. In Sect. 3, introducing the finite temperature according to the imaginary formalism, we calculate the one-loop effective potential in the field theory at the finite temperature, and then we define it such that it can vanish at zero temperature. In Sect. 4, by regarding the one-loop effective potential obtained in Sect. 3 as the cosmological constant, we give the relation to fix the background space-time. In Sect. 5, we show the results in this study: the Hubble constant characterizing the variation of the de Sitter space and the variation of the shape of the one-loop effective potential against the temperature, and after that the amount of the energy corresponding to the change of the temperature at the each temperature and the accelerating particle’s world-line with the corrections. In Sect. 6, we make remarks on this study.

2 The model

We start with the following action:

$$\begin{aligned} S^M= & {} \int \mathrm{d}^4 x \sqrt{-g^M} \, \left( R^M + \frac{1}{2} \partial _\mu \phi \, \partial ^\mu \phi -\frac{1}{2} m^2 \phi ^2-\frac{\lambda }{4\,!}\phi ^4\right) \nonumber \\\equiv & {} \int \mathrm{d}^4 x \sqrt{-g^M} \, \left( R^M + \mathcal{L}^M \right) , \end{aligned}$$
(1)

where R and \(\phi \) are the scalar curvature and the real scalar field, respectively. \(m^2\) is some constant, negative in order to have a Higgs potential. In this paper, we attach “M” to the quantities given in the Minkowski space-time. On the other hand, we denote the quantities given in the Euclid space without “E”, except for the case that we need to distinguish it explicitly.

It will turn out later that the field’s effective potential plays the role of a positive cosmological constant. Hence we take the four-dimensional de Sitter space-time,Footnote 1

$$\begin{aligned} \mathrm{d}s_M^2 = \mathrm{d}t^2 - e^{2H^M t}\left( \mathrm{d}x^2 +\mathrm{d}y^2+\mathrm{d}z^2 \right) , \end{aligned}$$
(2)

as our background space-time, where the Hubble constant \(H^M\) is not fixed at this stage.

We now address the case of a particle moving with a linear constant acceleration a. Following the Unruh effect’s prediction, the particle experiences the space-time where the particle exists as a thermal bath with the Unruh temperature,

$$\begin{aligned} T_\mathrm{U} = \frac{a}{2\pi }, \end{aligned}$$
(3)

in the accelerating frame (we use the natural units.). Following our prediction for the Unruh thermal radiation mentioned in the fourth paragraph of Sect. 1, the particle is thought to have some temperature rooted in the Unruh temperature and to emit thermal radiation. The thermal radiation gradually decreases, getting away from the particle due to thermal dissipation in nature, and the radiation range is finite. However, in this paper, we take the radiation range from zero to infinity for simplicity in the analysis. We further regard the temperature distribution as uniform in the entire region.

3 One-loop effective potential at finite temperature

We calculate the one-loop effective potential of the real scalar field at finite temperature. To introduce the temperature, we perform a Wick rotation, \(t \rightarrow -i\,\tau \), and pose the requirement of periodicity with the period \(\beta = 1/T\) to the imaginary time direction. This T is identified in this study with the Unruh temperature \(T_\mathrm{U}\) given in Eq. (3) as mentioned in the last paragraph of Sect. 2. Then the background geometry (2) is transformed as

$$\begin{aligned} \mathrm{d}s_M^2 \rightarrow \mathrm{d}s^2 = -\mathrm{d}\tau ^2 -e^{2H\,\tau }\left( \mathrm{d}x^2 +\mathrm{d}y^2+\mathrm{d}z^2 \right) \end{aligned}$$
(4)

with \(H^M \rightarrow i H\), where we described the Hubble constant in the usual form using a scale factor and its time derivative, and the symbol “\(\rightarrow \)” means the manipulation of the Wick rotation. We use it in this sense in this paper. Correspondingly the probability amplitude with the action (1) is changed to the partition function by

$$\begin{aligned} Z= & {} \int \mathcal{D}\phi \, \exp \left( i \int \mathrm{d}^4x \sqrt{-g^M} \left( R^M + \mathcal{L}^M \right) \right) \end{aligned}$$
(5)
$$\begin{aligned}\rightarrow & {} \int \mathcal{D}\phi \, \exp \left( \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \, \left( R + \mathcal{L} \right) \right) \nonumber \\= & {} \exp \left( \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \, R \right) \nonumber \\&\cdot \int \mathcal{D}\phi \, \exp \left( \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \, \mathcal{L} \right) \nonumber \\\equiv & {} \exp \left( - \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \, \big (-R \big ) \right) \cdot Z_\phi . \end{aligned}$$
(6)

We denote the determinant of the metric and the Lagrangian density after the transformation as g and \(\mathcal{L}\), respectively.

We now consider the quantum fluctuation of \(\phi \) as \(\phi = \phi _0 + \delta \phi \), where \(\phi _0\) is the scalar field’s condensation independent of the space-time at the symmetry breaking phase, and \(\delta \phi \) is the quantum fluctuation. Then \(Z_\phi \) can be written as

$$\begin{aligned} Z_\phi= & {} \int \mathcal{D}\phi \, \exp \left( \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \, \mathcal{L} \right) \nonumber \\= & {} \exp \left( - \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \, \mathcal{L}_0 \right) \nonumber \\&\cdot \int \mathcal{D}(\delta \phi )\exp \left( - \frac{1}{2} \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \delta \phi \, G^{-1} \, \delta \phi \right) ,\nonumber \\ \end{aligned}$$
(7)

where

$$\begin{aligned} \mathcal{L}_0 = \frac{m^2}{2} \,\phi _0^2 + \frac{\lambda }{4!} \,\phi _0^4, \end{aligned}$$
(8)
$$\begin{aligned} G^{-1}= & {} e^{H \tau }\partial _z^2+\sqrt{g}\,(M^2 -3H\partial _\tau -\partial _\tau ^2). \end{aligned}$$
(9)

Here

$$\begin{aligned} M^2 \equiv m^2+\frac{\lambda }{2}\,\phi _0^2. \end{aligned}$$
(10)

Then integrating out the \(\delta \phi \), we obtain

$$\begin{aligned} Z_\phi= & {} \exp \left( - \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \,\mathcal{L}^\mathrm{E}_0 - \frac{1}{2} \, \log \,\mathrm{Det} \, G^{-1} \right) \nonumber \\\equiv & {} \exp (-\varGamma _E). \end{aligned}$$
(11)

Performing the Fourier transformation and evaluating the functional determinant, we obtain

$$\begin{aligned} \varGamma _E= & {} \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \,\, \mathcal{L}_0 \nonumber \\&+\,\frac{1}{2\beta \,(2\pi )^3} \sum _{n=-\infty }^{\infty } \int \mathrm{d}\tau \, \mathrm{d}^3x \, \mathrm{d}^3k \, \log \Big ( e^{Hu}k^2+\sqrt{g}\nonumber \\&\left( M^2-3iH\omega _n + \omega _n^2\right) \Big )\nonumber \\\equiv & {} \int \mathrm{d}^3x \cdot V, \end{aligned}$$
(12)

where \(\omega _n \equiv 2\pi n/\beta \) (n is integer). We make one comment. Now we have factored out \(\int \mathrm{d}^3x\). If factoring out the volume factor, the factor \(\int \mathrm{d}^4x \sqrt{g}\) should be factored out. However, our integrand function depends on u. Hence factoring out of all volume cannot be done at this moment. We, however, factor out the rest, \(\int \mathrm{d}\tau \sqrt{g}\), in view of Eq. (21).

We now evaluate the summation of n. To this aim, we rewrite the part concerned as

$$\begin{aligned}&\sum _{n=-\infty }^{\infty } \log \Big (e^{H \tau } k^2 + \sqrt{g}\, \left( M^2 - 3i H \omega _n + \omega _n^2 \right) \Big )\nonumber \\&\quad = \lim _{n \rightarrow \infty }3H \tau \, (2n+1) \,+ \sum _{n=-\infty }^{\infty } \log \Big ( e^{-2H \tau } k^2 + M^2 \nonumber \\&\qquad \qquad \qquad \qquad \qquad \quad \qquad -\, 3i H \omega _n + \omega _n^2 \Big ){.} \end{aligned}$$
(13)

Then once performing the derivative as \(\partial _\chi \log \left( \chi ^2 - 3i H \omega _n + \omega _n^2 \right) \), where \(\chi ^2 \equiv e^{-2H \tau } k^2 + M^2\), we perform the summation. After that, we integrate it. As a result, we obtain

$$\begin{aligned} V = V_{0}+V_{1}, \end{aligned}$$
(14)

where

$$\begin{aligned} V_{0}= & {} \int _0^\beta d \tau \, e^{3 H \tau } \, {\mathcal{L}_0},\end{aligned}$$
(15)
$$\begin{aligned} V_{1}= & {} \frac{1}{(2\pi )^2 \beta } \int \mathrm{d}\tau \, \mathrm{d}k \, \sqrt{g} \,\, k^2 \log \nonumber \\&\left[ -\sinh \left( \frac{\beta }{4} \left( \sqrt{9 H^2 + 4\left( e^{-2H \tau } k^2 + M^2 \right) }-3 H\right) \right) \right. \nonumber \\&\quad \left. \times \sinh \left( \frac{\beta }{4} \left( \sqrt{9 H^2 + 4\left( e^{-2H \tau } k^2 + M^2 \right) }+3 H \right) \right) \right] \nonumber \\&\quad + \frac{1}{2(2\pi )^3 \beta } \int \mathrm{d}\tau \, \mathrm{d}k^3 \lim _{n \rightarrow \infty }3H \tau \,(2n+1). \end{aligned}$$
(16)

Performing the rescaling \(k \rightarrow e^{H \tau }\, k\), we can write \(V_{1}\) as

$$\begin{aligned} V_{1}= & {} \frac{1}{(2\pi )^2 \beta } \int \mathrm{d}\tau \, \mathrm{d}k \, \sqrt{g} \,\, k^2 \, \log \nonumber \\&\left[ -\sinh \left( \frac{\beta }{4} \left( \sqrt{9 H^2+4 \left( k^2+M^2\right) }-3 H \right) \right) \right. \nonumber \\&\quad \left. \times \sinh \left( \frac{\beta }{4} \left( \sqrt{9 H^2 +4 \left( k^2+M^2\right) }+3 H \right) \right) \right] \nonumber \\&\quad + \frac{1}{2\beta \,(2\pi )^3} \int \mathrm{d}\tau \, \mathrm{d}k^3 \lim _{n \rightarrow \infty }3H \tau \,(2n+1). \end{aligned}$$
(17)

Pushing forward the calculation, we can write \(V_{1}\) as

$$\begin{aligned} V_{1}=V_{1,\,(T=0)}+V_{1,\,(T>0)}, \end{aligned}$$
(18)

where \(V_{1,\,(T=0)}\) and \(V_{1,\,(T>0)}\) are the contributions independent of the temperature and depending on the finite temperature as

$$\begin{aligned} V_{1,\,(T=0)}= & {} \frac{1}{4} \int _0^\beta \mathrm{d}\tau \,\sqrt{g}\, \int \frac{\mathrm{d}^3k}{(2\pi )^3}\,\sqrt{9 H^2 +4 \left( k^2+M^2\right) }{,}\nonumber \\ \end{aligned}$$
(19)
$$\begin{aligned} V_{1,\,(T>0)}= & {} \frac{1}{(2\pi )^2\beta } \int _0^\beta \mathrm{d}\tau \,\sqrt{g}\, \int \mathrm{d}k \, \,k^2\,\log \nonumber \\&\times \left[ \left( 1-e^{-\frac{\beta }{2} \left( \sqrt{9 H^2 +4 \left( k^2+M^2\right) }-3 H\right) }\right) \right. \nonumber \\&\times \left. \left( 1-e^{-\frac{\beta }{2} \left( \sqrt{9 H^2 +4 \left( k^2+M^2\right) }+3 H\right) }\right) \right] +\varOmega ,\nonumber \\ \end{aligned}$$
(20)

and

$$\begin{aligned} \varOmega= & {} \frac{1}{2\beta \,(2\pi )^3} \int \mathrm{d}\tau \, \mathrm{d}k^3 \left( \lim _{n\rightarrow \infty } 3 H \tau (2 n+1)\right. \nonumber \\&\left. +\, e^{3H \tau }(-2 \log (2)+ i \pi ) \right) . \end{aligned}$$
(21)

Now it can be seen that we can factor out by \(V \rightarrow \int \mathrm{d}\tau \, \sqrt{g} \cdot V\). By combining this with the factoring out of the space part performed in Eq. (12), we can now think of the factoring out of the whole volume factor as having been done.

Let us next turn to the squared mass in the effective potential, which is the coefficient of \(\phi _0^2{/2}\) and currently given as \(m^2\). It is assumed that it should be written as \(m_\mathrm{eff}^2 = m^2+ \, \delta m^2\) after evaluating the finite temperature contribution, where \(m_\mathrm{eff}^2\) is generally called the squared effective mass, and \(\delta m^2\) formally represents the finite temperature contribution to the coefficient of \(\phi _0^2{/2}\). (Our result at the one-loop order is given in Eq. (28).) Using this \(m_\mathrm{eff}^2\), \(M^2\) given in Eq. (10) is thought to be indeed given by \(M_\mathrm{eff}^2 \equiv m_\mathrm{eff}^2+\frac{\lambda }{2}\phi _0^2\). Correspondingly, the \(M^2\) in Eq. (20) are rewritten \(M_\mathrm{eff}^2\). We expand \(V_{1,\,(T>0)}\) around \(M_\mathrm{eff}^2=0\) to the linear order. Around the symmetry breaking restoration, \(m_\mathrm{eff}^2\) and \(\phi _0^2\) take small values, and \(M_\mathrm{eff}^2\) takes small values.

Finally, the one-loop effective potential we obtain with the factor out of the volume factor done above is

$$\begin{aligned} V = V_{0}+V_{1,\,(T=0)}+V_{1,\,(T>0)}, \end{aligned}$$
(22)

where now \(\displaystyle Z_\phi = \exp \left( -\int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \cdot V \right) \) and

$$\begin{aligned} V_{0} = {\mathcal{L}_0},\end{aligned}$$
(23)
$$\begin{aligned} V_{1,\,(T=0)}= & {} \frac{1}{4} \int \frac{\mathrm{d}^3k}{(2\pi )^3}\,\sqrt{9 H^2 +4 \left( k^2+M_\mathrm{eff}^2\right) },\end{aligned}$$
(24)
$$\begin{aligned} V_{1,\,(T>0)}= & {} \frac{1}{(2\pi )^2} \int \mathrm{d}k \, k^2 \Bigg \{ \frac{1}{\beta } \, \log \left[ \left( 1-e^{-\frac{\beta }{2} \left( \sqrt{9 H^2+4 k^2}-3 H\right) } \right) \right. \nonumber \\&\left. \left( 1-e^{-\frac{\beta }{2} \left( \sqrt{9 H^2+4 k^2}+3 H\right) } \right) \right] \nonumber \\&+ \frac{1}{\sqrt{9 H^2+4 k^2}} \left( \frac{1}{e^{\frac{\beta }{2} \left( \sqrt{9 H^2+4 k^2}+3 H\right) }-1}\right. \nonumber \\&\left. \left. +\frac{1}{e^{\frac{\beta }{2} \left( \sqrt{9 H^2+4 k^2}-3 H\right) }-1} \right) M_\mathrm{eff}^2 \right\} + \varOmega , \end{aligned}$$
(25)

and

$$\begin{aligned} \varOmega= & {} \frac{1}{2\beta \,(2\pi )^3} \, \int \mathrm{d}k^3 \left( \frac{1}{V_u} \int ^\beta _0\mathrm{d}\tau \,\lim _{n \rightarrow \infty } 3 H \tau (2n+1)\right. \nonumber \\&\left. -\,2 \log (2)+ i \pi \right) . \end{aligned}$$
(26)

Here, \(V_u\) is defined as \(\displaystyle V_u \equiv \int ^\beta _0 \mathrm{d}\tau \sqrt{g}=\left( -1+e^{H\,\beta }\right) /3H\). The above may agree with the case of flat space at \(H=0\).Footnote 2 It can be seen from order-counting that Eq. (24) diverges at the ultraviolet region. On the other hand, Eq. (25) does not diverge.

We now fix \(\delta m^2\) in \(m_\mathrm{eff}^2 = m^2+ \, \delta m^2\). It can be read out from the coefficient of \(\phi _0^2{/2}\). It specifically turns out that \(\delta m^2\) is given by the coefficient of \(M_\mathrm{eff}^2\) in \(V_{1,\,(T>0)}\) given in Eq. (25), and the result is

$$\begin{aligned} m_\mathrm{eff}^2= & {} m^2 + \frac{\lambda }{(2\pi )^2} \int \mathrm{d}k \,\frac{k^2}{\sqrt{9 H^2+4 k^2}} \nonumber \\&\left( \frac{1}{e^{\frac{\beta }{2} \left( \sqrt{9 H^2+4 k^2}+3 H\right) }-1} +\frac{1}{e^{\frac{\beta }{2} \left( \sqrt{9 H^2+4 k^2}-3 H\right) }-1} \right) .\nonumber \\ \end{aligned}$$
(28)

We now define the effective potential in our study. For this purpose, we think of the approximation that the space-time will be flat at \(T=0\). For this reason, we set our one-loop effective potential such that it can be zero when \(T=0\) at the symmetry breaking phase.Footnote 3 Writing such an effective potential as \( \Delta V(\beta )\), we set \(\Delta V(\beta )\) as

$$\begin{aligned} \Delta V(\beta ) \equiv V(\beta )-C = V_{0}(\phi )-V_{0}(\phi _0) + V_{1,(T>0)}, \end{aligned}$$
(29)

by subtracting a constant \(C \equiv V_{0}(\phi _0) +V_{1,(T=0)}+\varOmega \) from \(V(\beta )\). Correspondingly, \(Z_\phi \) is rewritten as follows:

$$\begin{aligned} Z_\phi= & {} \exp \left( -\int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \,\sqrt{g}\cdot V(\beta ) \right) \nonumber \\ {}\rightarrow & {} \exp \left( -\int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \,\sqrt{g}\cdot \Delta V(\beta ) \right) . \end{aligned}$$
(30)

We can see that \(\varOmega \) given in Eq. (26) is diverging. In this paper, we just ignore \(\varOmega \) in \(\Delta V(\beta )\).

We make a comment. We have performed the expansion of \(M_\mathrm{eff}^2\) to the linear order in the above. Generally the high temperature expansion is an expansion with regard to the ratio of \(M_\mathrm{eff}/T\). Our situation that \(M_\mathrm{eff}\) is smaller can be regarded as the situation that T is higher in the ratio of \(M_\mathrm{eff}/T\). Because of this, our expansion is equal to the high temperature expansion.

We now consider the contribution from the functional integral measure. The functional integral measure can be considered to be written as \(\mathcal{D}\phi =c\,\beta d\phi \), where c is some dimensionless number.Footnote 4 As a result, the contribution from the functional integral measure to the effective potential can be written in the following way:

$$\begin{aligned} Z_\phi= & {} \int \mathcal{D} \phi \exp \left( -\int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \,\sqrt{g}\cdot \mathcal{L}\right) \nonumber \\= & {} \int d\phi \, c \, \beta \exp \left( -\int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \,\sqrt{g}\cdot \mathcal{L} \right) \nonumber \\= & {} \exp \left( -\int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \,\sqrt{g}\right. \nonumber \\&\cdot \left. \left( V(\beta ) - \frac{1}{\mathrm{{Vol}}}(\log \beta + \log c)\right) \right) , \end{aligned}$$
(31)

where \(\displaystyle \mathrm{{Vol}} \equiv \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \,\sqrt{g}\). We can see that the contribution from the measure does not contribute due to the infinite contribution of \(\mathrm{{Vol}}\). Consequently, it turns out that we do not need to take into account the contribution from the functional integral measure.

The effective potential we consider is finally Eq. (29), and our \(Z_\phi \) can be written as

$$\begin{aligned} Z_\phi = \exp \left( -\int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \,\sqrt{g} \cdot \Delta V(\beta ) \right) . \end{aligned}$$
(32)

4 Fixing the background space-time

In this chapter, we obtain the equation to fix the background geometry by regarding the effective potential as the positive cosmological constant. Now our total partition function can be written as

$$\begin{aligned} Z= \exp \left( - \int _0^\beta \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \cdot \big ( -R + \Delta V(\beta ) \big ) \right) . \end{aligned}$$
(33)

We can generally describe the Wick rotation to the Einstein–Hilbert case as

$$\begin{aligned} iS^M= & {} \int \mathrm{d}^4x \, \sqrt{-g^M} \, \left( R^M-2\varLambda ^M \right) \end{aligned}$$
(34)
$$\begin{aligned}\rightarrow & {} \int \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \, \left( R - 2\varLambda \right) \nonumber \\= & {} - \int \mathrm{d}\tau \int \mathrm{d}^3x \, \sqrt{g} \, \left( -R + 2\varLambda \right) = -S{.} \end{aligned}$$
(35)

We can confirm that the Einstein equation in the Euclid de Sitter space (4) can be satisfied when \(\varLambda =-3H^2\).

Hence comparing Eqs. (33) and (34), we have the following equation:

$$\begin{aligned} 6H^2 = - \Delta V(\beta ) \big |_{\phi =\phi _0}, \end{aligned}$$
(36)

with \(\partial \left( \Delta V(\beta )\right) /\partial \phi =0\) to determine the condensation \(\phi _0\) at the spontaneous symmetry breaking phase. We actually have two unknown variables, H and \(\phi _0\), and we have two equations. Solving these simultaneously, we determine the Hubble constant H that characterizes the background space-time metric (4).

5 Space-time, and energy corresponding to the change of the acceleration and particle’s world-line

Solving Eq. (36) numerically, we obtain the results of the effective potential with the background space’s contribution and the Hubble constant H against the temperature. Based on these results, we perform an evaluation of the accelerating particle’s world-line and the amount of the energy corresponding to the change of the temperature at the each temperature. The temperature in the results is thought of as the Unruh temperature (3).

In our presentation, the red results represent the results obtained by solving for the two variables H and \(\phi _0\). On the other hand, the blue results represent the results obtained by solving only for \(\phi _0\) with fixing H to zero. Hence the blue points are the results in the flat space.

The parameters (\(m^2\), \(\lambda \)) are always taken to be (\(-1\), 1). At this time, it turns out that the critical temperature \(T_\mathrm{c}\) for the symmetry breaking restoration is given as \(T_\mathrm{c} \simeq 4.402482673\). Here, we determined \(T_\mathrm{c}\) from whether the values of the squared effective mass \(m_\mathrm{eff}^2\) (28) and the condensation \(\phi \) are numerically zero or not.

5.1 Effective potential and space-time

Let us first consider H against T. The points in Fig. 1 are the calculated results for the Hubble constant H, and the dotted line is a fitting result. The fitting function we have adopted is \(c_1\,T + c_2\,T^2\), where \(c_1\) and \(c_2\) are the fitting parameters. These are fixed as \((c_1,c_2)=(-0.0943597,0.173624)\) in our fitting.

Fig. 1
figure 1

The Hubble constant H defined in Eq. (2) against the temperature T. The dotted line is the fitting result

Full size image
Fig. 2
figure 2

The effective potential \(\Delta V\) defined at Eq. (29) against the condensation value \(\phi \) at various T. The red lines represent the results with the background space’s contribution (\(H\not =0\)), and the blue lines represent the results without the background space’s contribution (\(H=0\)). Although there is only an explanation for the red lines in the caption of the figure, as to the blue lines, the same kind of line is used for the results calculated at the same temperatures (Fig. 5). The right figure is just an enlarged view of the left figure, so that the results for \(T=1.0, 2.0\), and 3.0 can be well inspected

Full size image
Fig. 3
figure 3

The squared effective mass \(m_\mathrm{eff}^2\) in Eq. (28) and the condensation \(|\phi _0|\) against the temperature T

Full size image

We now have obtained the Hubble constant. We can see that, as T gets higher, H grows as in Fig. 1. Hence we can see that, as the temperature gets higher, the background space transforms to the de Sitter space gradually.

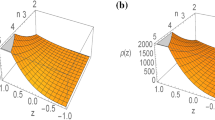
It turns out that the scalar curvature R is given by \(-12H^2\) on the background space given in Eq. (4). Substituting H, we can evaluate the background’s contribution in the effective potential. Thus, we can obtain Fig. 2 in which the effective potential with the background space’s contribution is plotted. We can see from Fig. 2 that the background space’s effect lowers the critical temperature. We show Fig. 3 (the numerical results of the squared effective mass \(m_\mathrm{eff}^2\) and the field’s condensation \(|\phi _0|\)) to support this.

Here it would be noteworthy that the Lagrangian density \(\mathcal{L}\) was expanded originally as \(\mathcal{L} \sim \sum _{n=0}^\infty \, \delta \phi ^{\,2n}\) before integrating out \(\delta \phi \), where \(\delta \phi \) means the fluctuation around the vacuum. As the temperature increases, since the concaves in the effective potential’s profile become locally shallower, the quantum fluctuation can grow higher. As a result, the higher order terms in the expansion become less able to be disregarded at higher temperatures. The profiles shown in Fig. 2 are the results obtained from the expansion to the one-loop order. For this reason, properly speaking, there might be some corrections in the shape at a greater distance away from the vacuum (expansion point) in the higher temperature results. We furthermore should notice that we have performed the expansion equivalent to the high temperature expansion as mentioned under Eq. (29). Hence one of the things we can say is that our analysis at the neighborhood of the vacuum in the higher temperature region that satisfies \(|M_\mathrm{eff}/T| \ll 1\) is precise.

Fig. 4
figure 4

The entropy density against the temperature T, obtained by calculating \(\partial F /\partial T\) numerically, where \(F=-R +\Delta V\) in Fig. 2

Full size image

5.2 Energy corresponding to the change of the acceleration and particle’s world-line

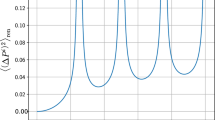
The effective potential we have calculated can be regarded as a free energy. We can hence read out the entropy density according to the general relation \(S = -\partial F / \partial T\) (S and F are the general entropy densities and free energies). We actually have evaluated it numerically at several temperatures. These results are shown in Fig. 4.

The entropy density in Fig. 4 can be interpreted as the amount of the energy corresponding to the unit temperature growth at each temperature. The temperature in this study is thought of as proportional to the acceleration through the Unruh effect (3).

We hence conclude that the amount of energy corresponding to the increase of acceleration at each acceleration is proportional to the entropy density in Fig. 4 at each temperature to which the acceleration corresponds. We further can see from Fig. 4 that the higher the acceleration gets, the more energy is required.

Fig. 5
figure 5

The world-lines of the uniformly accelerating particle at various T. The red lines represent the results with the background space’s contribution (\(H\not =0\)), and the blue lines represent the results without the background space’s contribution (\(H=0\)). Although there is only an explanation for the red lines in the caption of the figure, for the blue lines, the same kinds of line are used for the results calculated at the same temperatures as well as Fig. 2

Full size image

We next turn to the issue of the accelerating particle’s world-line. In our study, the space-time in the neighborhood of the accelerating particle is predicted to be the de Sitter space. Hence it is assumed that the accelerating particle’s world-line gets a correction compared with the case of a flat space.

To investigate, writing the position of the particle as \(r^\mu (u)\) (u is the proper time), we solve the geodesic equation in the de Sitter space-time (2) with a force added for the uniform acceleration of the particle, \(F^\mu = ma\,({r^1}'(u),{r^0}'(u),0,0)\). Concretely,

$$\begin{aligned} e^{2Hu}H \, ({r^1}')^2+{r^0}''= & {} F^0,\end{aligned}$$
(37)
$$\begin{aligned} 2H \, {r^0}' + {r^1}''= & {} F^1, \end{aligned}$$
(38)

where we have confined the motion of the particle to the (0, 1)-plane. H is assumed to have the temperature dependence obtained from the fitting in Sect. 5.1 and a is proportional to T through the Unruh effect (3). We solve the above numerically with the boundary condition:

$$\begin{aligned} \big (r^0(0),{r^0}'(0)\big ) = (0,1) \quad \mathrm{and} \quad \big (r^1(0), {r^1}'(0)\big ) =(0,0)\nonumber \\ \end{aligned}$$
(39)

at several T. As a result, we obtain the results shown in Fig. 5.

We can see that the Unruh thermal radiation has the effect of diminishing and enhancing the particle’s accelerations, respectively. (The particle’s acceleration can be read out from the gradients in Fig. 5.)

6 Remark

In this paper, corresponding to the prediction in Refs. [1–5] that an accelerating particle performs a Brownian motion in the inertial frame rooted in the Unruh effect in the accelerating frame, we have proposed that thermal radiation rooted in the Unruh effect is emitted from an accelerating particle in the inertial frame. We have named such a radiation “Unruh thermal radiation” in the fourth paragraph of Sect. 1.

We then have calculated the one-loop effective potential at finite temperature taking into account that the background space-time is deformed from the flat space-time to the de Sitter space-time due to the field theory’s corrected one-loop effective potential. In this paper, the temperature being expected to be proportional to the Unruh temperature, we have simply thought of the temperature as the Unruh temperature. The model we have considered has been a real scalar field described by the four-dimensional Klein–Gordon model with a Higgs potential term at finite temperature.

As for technicalities, we touch on a problem to be noticed particularly. It is the region where the Unruh thermal radiation can reach and the temperature distribution in that region. We have taken the radial direction in that region from zero to infinity and regarded the temperature distribution to be uniform in the entire region. However, in a realistic world, it should be finite and the temperature should gradually decline, at greater distance away from the particle (working as the thermal source). But if these were taken into account in the analysis, it is expected that the factoring out of the volume factor done in Eq. (12) becomes a problem. As a result, the analysis would become highly complicated. We are going to treat these issues more precisely in our future work.

As for our results, when a deformed background space-time is taken, it turns out that the critical temperature becomes smaller than the case that the background space-time is fixed to the static flat case. We further have revealed that the amount of the energy corresponding to an increase in acceleration at each acceleration increases as the acceleration gets higher and we have a correction in the world-line of the accelerating particle.

It would be intriguing to examine how our results turn out in the future as we develop the model to more realistic cases, and to confirm whether the tendencies obtained in our study are consistent or not compared with the experiments. Furthermore, the Unruh effect has a close relation with the Hawking temperature. The Hawking temperature at the moment is a result of semi-classical gravity, and it would be no surprise if it would get some correction in the full quantum gravity. In this sense, the future development of this study would also be intriguing.