Introduction

The seminal work of Seidel et al.1 demonstrated that DC conductivity is higher at domain walls (DWs) in BiFeO3 (BFO) than in the bulk, enabling signal transmission along the walls. This inspired a new paradigm for the design of DW-based nanoelectronic devices2,3,4,5,6,7,8,9,10,11,12, leading to the demonstration of DW-based diode and transistor operating in kHz range6,12. The push for higher frequencies13,14,15, used in modern computers, has led to a discovery of giant increase of the effective DW conductivity at GHz frequencies in recent microwave microscopy experiments15,16,17. The conductivity results from the excitation of soft DW-localized phonon modes, that are at the heart of switching, microwave dielectric loss, and dielectric constant enhancement in ferroelectrics15,18,19. They correspond to oscillations of the DW plane and can be excited by an AC electric field that favors one of the domains during its half period (Fig. 1a). Here we show that the frequency of these phonons can go from GHz all the way up to THz, going beyond the frequency range of modern surface acoustic wave-based cell phone transducers.

Fig. 1: Selection rules for activation of DW sliding modes under the electric field applied by the SMIM tip.
figure 1

a Excitation of a DW sliding mode is allowed when the field favors one of the domains; b, c when the field from the tip has the same projection on the polarizations of two domains, the excitation of the DW sliding mode is forbidden. c 71° domain wall corresponding to the P2 reversal in BFO. The wall is tilted to minimize the elastic energy due to strain mismatch between the two domains, thus breaking the mirror indicated with a dashed line. The pseudocubic coordinates x1, x2, x3 shown here are used throughout the paper and are referred to as the horizontal, out-of-plane and vertical directions.

Full size image

The results explain why the frequency range of the scanning microwave impedance microscopy (SMIM) anomaly is so wide and reveal DW-localized bands in the phonon spectra of ferroelectrics. We also address the peculiar selection rules for DW excitation. When the ferroelectric polarization component along the driving field is the same in the two domains across the wall, the DW vibration should not be excited (Fig. 1b), as seen at 180° walls on the ac face of YMnO315. However, this rule is violated in recent experiments on rhombohedral BFO, where polarization components along the field across the wall do not differ (Fig. 1c), while the DW mode is still excited and the effect is robust against extrinsic artefacts such as oxygen and bismuth vacancies, tip–sample interface, and Schottky barriers18. The results could inspire the exploration of DW-based nanosystems in THz frequency range, and lead to novel DW-based phononic nanodevices.

BFO is a rare room-temperature multiferroic with the largest spontaneous polarization among single-phase compounds known to date, and may be soon used in nano-devices20. Three types of ferroelectric DWs in the rhombohedral phase are distinguished by the number of polarization components being reversed21. The most puzzling data is on R71° DWs, at which the P2 component is reversed, and the polarization rotates by 71° across the wall, as seen in Fig. 1c. R71 DWs are often seen in BFO films grown on a [001] oriented substrate22,23, such as SrTiO3 and DyScO3. The sliding mode of this wall should not be excited by the field normal to the (100) surface, since neither domain is favored by the field, as seen in Fig. 1c. However, the AC impedance signal is still observed experimentally18, and exceeds DC conductivity by 5–6 orders of magnitude, thus significantly exceeding the possible contribution due to charged defects24,25. The important distinction between 180° DWs in YMnO3 and R71 DWs in BFO is their orientation with respect to the surface. YMnO3 DWs are mostly normal to the surface, while BFO R71 DWs are tilted away from the surface normal. In that case the combination of the surface and DW orientations breaks the symmetry, as seen in Fig. 1c. This symmetry breaking plays a key role in their response to electric fields, even when the simple selection rule, summarized in Fig. 1a, b, suggests no response.

Results

DW-localized phonons

We use the Ginzburg–Landau–Devonshire (GLD) model for DWs in BFO to capture the energetics of interacting ferroelectric polarization and strain (see Methods for details). The DW is tilted 45° away from the surface normal and bends near the surface to reduce the DW area, as shown in Fig. 2. Long-range strain textures emanate from the bent segments. P3 decrease in the blue area near the surface is driven by the compression ϵ33 and the tensile strain ϵ11 via electrostriction.

Fig. 2: Electric polarization and strain profiles at an R71 DW.
figure 2

Asymmetric polarization (a) and strain profiles (b, c) at the domain wall obtained by numerical energy minimization. Each polarization component in the bulk takes the value, marked in red on the color scale in a.

Full size image

The vibrational modes of the system with DWs are computed from the linearized equations of motion within a discretized Ginzburg–Landau model, and shown in Fig. 3a, b (see the Methods section for details). The DW breaks translational invariance and therefore the modes are not characterized by a well-defined quasimomentum. The traditional phonon band structure is then replaced by a spectral function, as seen in Fig. 3a, where the intensity at frequency ω and wavevector k indicates the content of plane waves with that wavevector in the eigenmodes at that frequency. For a translationally invariant system, sharp peaks would then appear in the spectral function \(A_j\left( {\omega ,\vec k} \right) = \mathop {\sum}\nolimits_\nu {\delta \left( {\omega \pm \omega _\nu } \right)\left| {\left\langle {\delta P_{j,\nu }\left( r \right)\left| {{\mathrm{exp}}\left( {i\vec k \cdot \vec r} \right)} \right.} \right\rangle } \right|^2}\) at frequencies ων of phonon modes ν, where δPj,ν(r) is the polarization profile due to the mode ν of unit amplitude. The long-ranged strain texture of the wall, shown in Fig. 2, is responsible for strong mixing between the DW sliding modes and acoustic phonons, whose frequency ranges overlap. This mixing is evident from the rays in the phonon polarization profile δP3, Fig. 3c (lower), repeating the shape of the strain texture, Fig. 2.

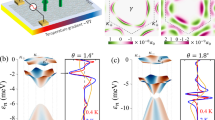
Fig. 3: DW-localized phonons and their SMIM signatures.
figure 3

a, b The phonon spectral function for polar modes in BFO with an R71 DW. The intense bands are the polar modes. The faint stripe at low energy, merging with the phonon band away from the zone center corresponds to the DW sliding modes. The labels in a, ①~⑤, are used to indicate the DW localized modes in e–i with correspondingly the same labels. The spectral weight extends to k ~ 2π/λ in the direction perpendicular to the wall, as seen in panel b. c The simulated SMIM loss signal across R71 DW I(r, ω). A peak at the DW and a signature from the long-range strain profile are seen at the sliding mode frequency. The notable asymmetry in the polarization profile, δP3(r) for the DW sliding mode that leads to the excitation of this mode by the vertical electric field is shown below; d the spectral function for both polar and acoustic phonons along the k|| direction (a cross-section of (a) and (b) through the Γ point). e–i Real-space polarization profile δP2(r) of the low frequency DW sliding e–g and breathing h, i modes (upper row), along with schematic illustrations of corresponding DW vibrations (below). The initial position of the DW is marked with white dashed lines.

Full size image

Figure 3a, b shows for every frequency ω the content of plane waves with \(P_2\sim e^{i\vec k \cdot \vec r}\) in modes of that frequency, while Fig. 3d shows the phonon dispersion along the wall. At low frequencies acoustic phonons are observed (their intensity is divided by 10 in Fig. 3d to make the DW branch visible). They correspond to strain modulations and mix with P2 modes due to electrostriction, \(f_q = - \frac{1}{2}\epsilon _{jk}q_{jklm}P_lP_m\). The V-shaped low frequency branch, marked with (1–3) in Fig. 3a, extends from around 10 GHz at Γ-point all the way to the bulk polar phonons, and corresponds to the DW sliding and wobbling modes, illustrated in Fig. 3e–g. The phonons in this branch disperse along the wall (along k||), but are localized in the perpendicular direction, and therefore their Fourier components extend to k⊥ ~ ±π/λ, where λ stands for the DW width. The intensity of the DW-localized branch is lower than that of the bulk phonons due to the low volume fraction occupied by DWs. The higher frequency modes are the bulk polar phonons.

Figure 3e–i shows δP2 profiles corresponding to some of the lowest frequency DW sliding modes (e–g) and breathing modes (h, i). The nodeless mode shown in the upper panel of Fig. 3e corresponds to the P2 increase at the wall during half-period of the oscillation, therefore adding the DW area to the positive domain. During another half-period the negative domain grows. Therefore this mode can be thought of as DW sliding, depicted schematically in the lower panels of Fig. 3e. A higher energy mode with a node in that branch, shown in the upper panel of Fig. 3f, corresponds to DW wobbling. The DW breathing modes, schematically shown in Fig. 3h, i, are found below the band of bulk polar modes, and are indicated with markers (4 and 5) in Fig. 3a.

SMIM signal simulations

Now we move to the origin of the SMIM signal. In the experiments, an AC electric field is applied between the tip and the back electrode, as shown in Fig. 1, and the current is measured. The phonons that have a non-zero energy in the oscillating field of the tip, \(- {\int} {dr\delta \vec P\left( {\vec r} \right) \cdot \vec E\left( {\vec r} \right)e^{i\omega t}}\), are excited and give rise to a displacement current component in phase with the field. The corresponding loss, \({\mathrm{Re}}{\int} {dr\vec j\left( r \right) \cdot \vec E\left( r \right)}\) is measured in addition to the Ohmic losses due to itinerant electrons. The amplitude xj of a phonon mode j with an eigenfrequency ωj is governed by the equation of motion

$$m_j\ddot x_j + \gamma _j\dot x_j + m_j\omega _j^2x_j = {\int} {dr\delta \vec P_j\left( {\vec r} \right) \cdot \vec E\left( {\vec r} \right)e^{i\omega t}} ,$$
(1)

where the mode is characterized by its effective mass mj, damping γj, and the spatial polarization profile δPj(r). The oscillating driving force on the right-hand side is due to the electric field \(\vec E\left( {\vec r} \right)e^{i\omega t}\) of the SMIM tip. The tip function E(r) mimics the electrostatic potential arising due to a voltage applied between the tip and the back electrode. It is a sum of the potential of a point charge, placed 20 nm above the surface, and an opposite image charge due to the back electrode. Damping of γ = 0.1 THz was used throughout the manuscript for illustration purposes, as we leave phonon–phonon interactions and phonon damping outside the scope of the present study. Looking for the solution in the form \(x_j = x_j^{\left( 0 \right)}e^{i\omega t}\), we obtain the loss power at the tip position \(\vec r\),

$$I\left( {\vec r,\omega } \right) = \omega ^2\gamma \mathop {\sum}\limits_j {\frac{{\left[ {{\int} {dr^{\prime}\;\vec E\left( {\overrightarrow {r^{\prime}} - \vec r} \right) \cdot \delta \vec P_j\left( {\overrightarrow {r^{\prime}} } \right)} } \right]^2}}{{m_j^2\left( {\omega _j^2 - \omega ^2} \right)^2\, +\, \omega ^2\gamma ^2}}} .$$
(2)

The frequency dependence is characterized by a Lorentzian. The integral in the numerator is negligible for phonons whose spatial oscillation period is much smaller than the length scale of the electric field inhomogeneity, roughly determined by the tip radius R, therefore the phonons with wavevectors \(k\lesssim R^{ - 1}\) are excited. Figure 3c shows the simulated signal for a BFO sample containing a R71 DW. An asymmetric peak at the DW and a weak signature due to the long-range strain features are visible. We note that Eq. (2) only describes the phonon contributions to SMIM signal, i.e., the contribution of bound charges. It does not capture contributions of itinerant carriers, mobile defects24, and artefacts seen in SMIM due to surface topography and Schottky barriers26.

Discussion

Figure 3c shows that SMIM conductivity is much higher at DW than in the bulk due to low-frequency DW sliding and wobbling modes. Their dispersion spans the whole GHz range and extends to the bulk polar phonon band, usually positioned at THz frequency. This explains why the GHz microwave conductivity at DWs in hexagonal manganites does not show a narrow peak in the frequency domain, but rather rises monotonically towards higher frequencies. The proximity of DW phonons to acoustic branches also leads to phonon scattering and affects thermal conductivity27. The low frequency of sliding modes is also behind the giant enhancement of the static dielectric permittivity19. In addition, soft DW phonons are responsible for mechanical softening phenomena, recently observed in several ferroelectrics28.

In materials with strong strain–polarization interactions, DWs are aligned into regular lattices by strain fields29,30, and spectral features similar to the ones in Fig. 3a, b are expected. Alternatively, when DWs are randomly oriented, the spectral weight of DW wobbling and breathing modes spreads along different directions, but the phonon density of states is expected to retain its shape, with the peak at GHz frequencies. The directionality of DWs and their populations in the sample can then be inferred from the orientation and intensity of low-energy branches, as discussed in Supplementary Note 2 and Supplementary Fig. 2.

The recent observation of nominally silent DW modes in BFO18 being activated is a surprising evidence that DW type and orientation control local AC conductivity. Possible DW orientations have been classified using symmetry and compatibility analyses31,32. In essence, the distances between ionic planes in the two domains must match along the wall. This is only possible for particular DW orientations, for which the strain components in the DW plane match at the wall (see Supplementary Eq. (3)). The energy penalty (see Supplementary Note 1 and Supplementary Fig. 1) for violating this condition scales linearly with the wall area, therefore fixing the DW orientation in the bulk. However, in thin films surface strain relaxation allows the DW to deviate from its optimal bulk orientation.

In an infinite bulk sample with a DW, a diagonal mirror plane Mdw(−1, 0, 1), shown by the dashed line in Fig. 1c, is a symmetry operation. This symmetry imposes the requirements: ϵ11 = ϵ33, ϵ12 = ϵ23. The surface of the thin film and the domain wall orientation together break this mirror symmetry mdw if they are not orthogonal. The stress at the tilted domain wall σjk = ∂f/∂ϵjk then acts on geometrically different regions from the left and right sides of the wall. The resulting asymmetric strain induces asymmetric polarization across the wall via electrostriction, Eq. (7). This phenomenon is observed in Fig. 4, where we simulated thin films with different surface orientations with respect to the crystallographic directions (different ways of cutting a film out of a slab). It is seen that the DW orients perpendicular to the [P1, 0, P3] direction, and a small bending near the surface is observed in Fig. 4a33,34,35,36. In very thin films, the wall deviates from the [101] orientation towards the surface normal. Figure 4b shows the polarization component normal to the surface. When the wall is tilted at 45°, the asymmetry of the polarization P3 is evident in Fig. 2a, especially near the surface where the polarization deviates the most from the bulk value. This asymmetry comes from the asymmetric strain, plotted in Fig. 2b, c. Even though the DW polarization profile is very narrow, the accompanying strain texture, emanating from the areas of DW bending near the surface33,34,35,36, extends surprisingly far37,38, as seen in Fig. 2b, c.

Fig. 4: Asymmetric ferroelectric polarization at an R71 DW.
figure 4

a Thin films with various surface orientations with respect to the crystallographic directions, indicated on the left. The DW normal is indicated by the arrow. b Normalized deviation of the vertical component of polarization \(\delta \left( {P_3} \right) = \frac{{P_3\left( r \right)\; - \;P_{3,bulk}}}{{P_{3,bulk}}}\) from its bulk value P3,bulk due to the stress at the DW.

Full size image

The polarization asymmetry eventually results in the asymmetry in the phonon polarization profile of the DW sliding mode, as seen in the lower panel of Fig. 3c. When the polarization component P3 interacts with the external electric field, normal to the surface, the electrostatic energy \(- {\int} {dr\vec E\left( {\vec r} \right) \cdot \vec P\left( {\vec r - \vec r_{DW}} \right)}\) results in a force on the wall due to \(\vec E \cdot \frac{{\partial \vec P\left( {\vec r \,- \,\vec r_{DW}} \right)}}{{\partial x_{1,DW}}} \,\ne\, 0\) and excitation of the DW vibration by the SMIM field.

In addition to SMIM, it may be possible to observe the DW-localized modes with inelastic neutron or X-ray scattering, although their intensity may be low due to low volume fraction occupied by DWs. Rapid quenching of a sample across the ferroelectric transition, leading to high DW densities39, or strain-induced generation and alignment of ferroelastic DWs40 should increase the intensity of these branches and enable their observation in inelastic neutron scattering experiments and other bulk spectroscopies.

In summary, the simulated phonon spectra reveal the DW-localized phonon branches starting from GHz and extending all the way to THz frequencies. This explains a wide frequency range of the conductivity anomaly observed in hexagonal manganites15 and other materials. The surprising activation of the nominally silent DW mode at R71° DWs in BFO is interpreted in terms of phonon polarization asymmetry due to the interplay of electrostriction and elastic compatibility at a tilted DW. The proposed way to simulate SMIM experiments may be used in emerging second-principles methodologies. Since the low-energy theory used here is rather general, similar phonon spectra must be expected for all ferroic materials, where the order parameter couples strongly to the lattice. We hope this work will motivate the experimental search for DW-localized phonon branches, guide the interpretation of SMIM studies and eventually inspire the development of high-speed DW-based phononic devices, extending surface acoustic wave-based technology to THz DW-based circuits.

Methods

Computational

In order to elucidate the essential physics that is responsible for the activation of the tilted R71 walls, we use a simplified GLD model41. To this end, we focus on the polar mode that connects the parent centrosymmetric phase with the ferroelectric one and consider its interactions with strains (through electrostriction), while neglecting octahedral rotations.

The free energy density, expanded near the centrosymmetric paraelectric parent structure is written as:

$$f = f_L + f_G + f_c + f_q + f_{fl},$$
(3)
$$f_L = \alpha _jP_j^2 + \frac{1}{2}\alpha _{jk}P_j^2P_k^2 + \alpha _{jkl}P_j^2P_k^2P_l^2,$$
(4)
$$f_G = \frac{1}{2}G_{jklm}\partial _kP_j\partial _mP_l,$$
(5)
$$f_c = \frac{1}{2}\epsilon _{jk}C_{jklm}\epsilon _{lm},$$
(6)
$$f_q = - \frac{1}{2}\epsilon _{jk}q_{jklm}P_lP_m,$$
(7)
$$f_{fl} = \frac{1}{2}f_{jklm}\left( {\epsilon _{jk}\partial _mP_l - P_l\partial _m\epsilon _{jk}} \right)$$
(8)

where Pj stands for the components of the ferroelectric polarization; the strain tensor ϵjk is related to symmetrized gradients of deformations uj as ϵjk = (∂kuj + ∂juk)/2, where the deformation vector \(\vec u\left( {\vec r} \right)\) relates points \(\vec r\) in the reference structure to \(\vec r + \vec u\left( {\vec r} \right)\) in the deformed structure; summation over repeated indices is implied. fL represents the distorted Mexican hat-shaped potential that determines the amplitude and anisotropy of the polarization. fG describes the energy penalty due to spatial variations of the polarization. fc describes elastic energy, while fq is the electrostriction term that refers to the interaction between polarization and strain. The flexoelectric coupling ff, that describes interactions of strain gradient with the polarization, was also included as in ref. 42, but does not change the qualitative results reported here. The parameters of the model were adopted from ref. 43. To obtain the equilibrium configuration, we minimize the free energy \({\int} {fd^3r}\) in Eq. (3) with respect to Pi, ui, by solving Euler–Lagrange equations with the Lagrangian density given by −f, namely δf/δPi(r) = 0, δf/δui(r) = 0 with δ being variational derivatives, using the finite element method as implemented in Fenics software44,45. The real space was discretized with element dimensions 0.4 nm. The simulated thin film was 60 nm thick and 180 nm wide, and a single DW was placed in the middle. Test calculations were performed for the 360 nm wide film to validate the long-range strain profile. Zero external stress boundary conditions were applied on the top surface while u3 = 0 was used at the bottom one. At the two ends in the x1 direction, both open and twisted boundary conditions were tested to ensure the absence of boundary effects within the domain wall area. Periodic boundary conditions were applied in the translational direction (x2) to mimic an infinite system.

Phonons are computed using a 20 × 1 × 20 square finite difference mesh with 0.4 nm elements and a single domain wall in the middle. The finite element size gives rise to a periodic lattice potential acting on the DW and gapping the sliding mode at 8 GHz46. It is analogous to a Pierls–Nabarro washboard potential in a realistic lattice. The resulting oscillation frequency is an order of magnitude higher than characteristic frequencies of DW vibrations due to electrostatic effects47.

The energy was minimized numerically and the equations of motion (Euler–Lagrange equations δL/δPi(r) = 0, δL/δui(r) = 0 for the Lagrangian density \(L = \frac{1}{2}\left( {M_{uu}\dot u^2 + M_{PP}\dot P^2} \right) - f\left( {P,u} \right)\)) were expanded to a linear order in small deviations \(\delta \vec u\left( {r,t} \right) = \delta \vec u\left( r \right)e^{ - i\omega t},\;\delta \vec P\left( {r,t} \right) = \delta \vec P\left( r \right)e^{ - i\omega t}\) around the equilibrium state. That leads to a standard generalized eigenvalue problem \(F_{jk}v_k^{\left( n \right)} = \omega ^{\left( n \right)}M_{jk}v_k^{\left( n \right)}\) for phonon polarization vectors νk containing all displacement and polarization variations \(\delta \vec u\left( r \right),\;\delta \vec P\left( r \right)\); force constants Fjk were computed as second derivatives of L and the mass of the polarization mode was chosen to fit the gap between acoustic and optical bands of the spectrum to DFT calculations48, MPP ≈ 3mO/V and Muu = (m Bi + m Fe + 3mO)/V, where V is the unit cell volume. Phonon polarization vectors were then projected on the plane waves to obtain the phonon spectral functions, shown in Fig. 3a, b, d.

In order to reproduce the realistic 45° tilt of the wall, necessary to simulate the SMIM signal, shown in Fig. 3c, we used a larger grid of 360 × 1 × 120 with 4 nm elements.