Dynamical Windings of Random Walks and Exclusion Models. Part I: Thermodynamic Limit in ℤ²

Abstract

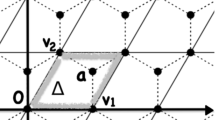
We consider a system consisting of a planar random walk on a square lattice, subjected to stochastic elementary local deformations. Both numerical and theoretical results are reported. Depending on the deformation transition rates, and specifically on a parameter η which breaks the symmetry between the left and right orientation, the winding distribution of the walk is modified, and the system can be in three different phases: folded, stretched and glassy. An explicit mapping is found, leading to consider the system as a coupling of two exclusion processes: particles of the first one move in a landscape defined by particles of the second one, and vice-versa. This can be viewed as an inhomogeneous exclusion process. For all closed or periodic initial sample paths, a convenient scaling permits to show a convergence in law (or almost surely on a modified probability space) to a continuous curve, the equation of which is given by a system of two non linear stochastic differential equations. The deterministic part of this system is explicitly analyzed via elliptic functions. In a similar way, by using a formal fluid limit approach, the dynamics of the system is shown to be equivalent to a system of two coupled Burgers equations.