Hydrodynamic limit of simple exclusion processes in symmetric random environments via duality and homogenization

Abstract

We consider continuous-time random walks on a random locally finite subset of $\mathbb {R}^d$ with random symmetric jump probability rates. The jump range can be unbounded. We assume some second-moment conditions and that the above randomness is left invariant by the action of the group $\mathbb {G}=\mathbb {R}^d$ or $\mathbb {G}=\mathbb {Z}^d$. We then add a site-exclusion interaction, thus making the particle system a simple exclusion process. We show that, for almost all environments, under diffusive space–time rescaling the system exhibits a hydrodynamic limit in path space. The hydrodynamic equation is non-random and governed by the effective homogenized matrix D of the single random walk, which can be degenerate. The above result covers a very large family of models including e.g. simple exclusion processes built from random conductance models on $\mathbb {Z}^d$ and on crystal lattices (possibly with long conductances), Mott variable range hopping, simple random walks on Delaunay triangulations, random walks on supercritical percolation clusters.

1 Introduction

The simple exclusion process is a fundamental interacting particle system obtained by adding a site-exclusion interaction to multiple random walks [26]. We assume here that particles lie on a random locally finite subset of ${\mathbb R} ^d$ (a simple point process) and allow the jump probability rates to be random as well, but symmetric (i.e. they do not depend on the orientation of the jump). We require that the law of the environment is stationary and ergodic w.r.t. the action of a group ${\mathbb G}$ of ${\mathbb R} ^d$-translations, ${\mathbb G}$ being the full group of translations or a subgroup isomorphic to ${\mathbb Z} ^d$. Under weak second moment assumptions on the jump rates and a percolation assumption assuring the existence of the process, we then prove for almost all environments that the simple exclusion process admits a hydrodynamic limit (HL) in path space with hydrodynamic equation $\partial _t \rho = \nabla \cdot ( D \nabla \rho )$, D being the non random effective homogenized matrix associated to a single random walk (D can also be degenerate). The above result (stated in Theorem 4.1 in Sect. 4) covers a very large class of simple exclusion processes in symmetric random environments, e.g. those obtained by adding a site-exclusion interaction to random walks on $\mathbb {Z}^d$ and on general crystal lattices with random (possibly arbitrarily long) conductances, to random walks performing a Mott variable range hopping, to simple random walks on Delaunay triangulations [18] or on supercritical percolation clusters (in Sect. 5 we discuss some examples). In Sect. 2 we provide a brief presentation of our class of models and our main result, without insisting on technicalities (faced in the subsequent sections). We discuss below how the present work relates with the existing literature, the strategy we have followed and the most original aspects of our contribution.

Given a realization of the environment the resulting simple exclusion process is non-gradient. The usual derivation of the HL for non-gradient interacting particle systems based on the method introduced by Varadhan and further developed by Quastel (cf. [26, 34, 39]) is very technical. It becomes even harder in the disordered case (cf. [14, 35]). On the other hand, for disordered simple exclusion processes with symmetric jump rates one can try to avoid the non-gradient machinery by exploiting some duality property between the particle system and the single random walk and some averaging property of the single random walk. This was first realized by Nagy in [33] for the simple exclusion process on ${\mathbb Z}$ with symmetric random jump rates. Nagy’s analysis had two main ingredients: a representation of the exclusion process in terms of compensated Poisson processes and the Markov semigroup of the random walk (see [33, Eq. (12), (13)] and a quenched CLT for the random walk uniformly in the starting point (see [33, Theorem 1]). Nagy’s representation (coming from duality) has been further generalized in [9, 10] and in [10] we showed that Nagy’s second ingredient can be replaced but a suitable homogenization result of the $L^2$-Markov semigroup of the random walk. The advantage comes from the fact that homogenization requires much weaker assumptions than quenched CLT’s (moreover, it is also more natural from a physical viewpoint: the light bulb turns on because of the motion of many electrons and not of a single one). One advantage of the approach based on Nagy’s representation and homogenization is that one can prove the HL without proving the uniqueness of the weak solution of the Cauchy problem associated to the hydrodynamic limit. On the other hand, one gets the HL at a fixed macroscopic time (in the form usually stated e.g. in [26]) but not in path space.

To gain the HL in path space, one has to prove the tightness of the empirical measure. This has been achieved in [22] by developing the method of corrected empirical measure (initially introduced in [24]). This method again relies on duality and on homogenization property of the resolvent of the random walk. Once proved the tightness one can proceed in two ways. If a uniqueness result for the Cauchy problem is available, one can try to push further the analysis of the corrected empirical measure and characterize all limit points of the empirical measures as in [22]. Otherwise, one can try to extend Nagy’s representation and use homogenization (or some averaging, in general) to get the HL for a fixed time, avoiding results of uniqueness. This has revealed useful e.g. for the subdiffusive system considered in [16], where a quenched CLT for varying and converging initial points was used instead of homogenization.

Of course, the above strategies have been developed in specific contexts and not in full generality. The applications to other models require some work, already in the choice of the right function spaces and topologies. In our proof we used the corrected empirical measure and homogenization to prove tightness. To proceed we have presented the two independent routes: by proving uniqueness for the Cauchy problem in weak form we characterize the limit points of the empirical measure continuing to work with the corrected one; alternatively we prove in “Appendix C” Nagy’s representation in our context and use homogenization to get the HL at a fixed time.

We comment now how our result differs from the previous contributions concerning the diffusive HL of simple exclusion processes in symmetric environments. The main novelty is the huge class of models for which the HL has been proved. In particular, (i) we go beyond the lattice (${\mathbb Z} ^d$ or toroidal) structure and deal with a very broad range of random environments including geometrically amorphous ones (think e.g. to a simple exclusion process on a Poisson point process), (ii) our assumptions on the jump rates are minimal and given by 2nd moment assumptions plus a percolation assumption for Harris’ percolation argument, (iii) we remove ellipticity conditions on the jump rates and treat also the case of degenerate effective homogenized matrix D, (iv) the jump range can be unbounded. Concerning Item (i) we point out that to gain such a generality we have used the theory of ${\mathbb G}$-stationary random measures, where ${\mathbb G} ={\mathbb R} ^d$, ${\mathbb Z} ^d$ (cf. [20, 21, 25]), in order to fix our general setting in Sect. 3. This also allows to describe the ergodic properties of the environment in terms of the Palm distribution. To achieve the HL in great generality we needed the same generality for the homogenization results. This part, which has also an independent interest, has been presented in the companion work [12], where our homogenization analysis is based on 2-scale convergence. Although [12] has been preliminary to the present work, here we have kept the presentation self-contained.

For completeness, we point out that Theorem 4.1 includes also as very special cases the HL in [10, 33, 36] (for the part concerning non-dynamical random environments in [36]). We recall that in [36] the authors prove the HL for the random conductance model on ${\mathbb Z} ^d$ with possibly time-dependent random conductances in a given interval [a, b], with $0<a<b<+\infty$. Finally, we point out that for reversible but not symmetric jump rates the homogenization results in [12] for a single random walk still hold, but the duality properties of the simple exclusion process fail. An explicit example is given by the simple exclusion process with site disorder treated in [14, 35]. In general, for reversible but not symmetric jump rates, the hydrodynamic limit is expected to be described by the non-linear equation $\partial _t \rho = \nabla \cdot (D(\rho ) \nabla \rho )$ with a density-dependent diffusion matrix $D(\rho )$. As rigorously proved in [35, Theorem 1] in the case of site-disorder, D(0) is expected to coincide with the effective homogenized matrix D associated to a single random walk.

Outline of the paper In Sect. 2 we give a non-technical presentation of setting and results. In Sect. 3 we present more precisely our setting and basic assumptions for the single random walk. In Sect. 4 we state our HL (see Theorem 4.1). In Sect. 5 we discuss some examples. In Sect. 6 we recall the homogenization results from [12] used in the proof of Theorem 4.1. In Sect. 7 we present the graphical construction of the simple exclusion process and analyze its Markov semigroup. In Sect. 8 we collect some results concerning duality. In Sect. 9 we recall some properties of the space $\mathcal M$ of Radon measures on ${\mathbb R} ^d$ and of the Skorohod space $D([0,T],\mathcal M)$ and show the uniqueness of the weak solution of the Cauchy problem. In Sect. 10 we study the family of typical environments, for which the HL will be proved. In Sect. 11 we prove Theorem 4.1. In “Appendix A” we present a model satisfying all our assumptions for which the effective homogenized matrix D is nonzero but degenerate. “Appendix B” concerns the proof of Proposition 7.4. In “Appendix C” we give an independent proof of the HL for fixed times by proving Nagy’s representation in our context and by using homogenization.

2 Overview

In this section we give a brief presentation of our context and results postponing a detailed discussion to Sects. 3 and 4. Not surprisingly, this story starts with a probability space $(\Omega , \mathcal F, \mathcal P)$. Here are the other characters: the group ${\mathbb G}$ acting on the probability space and acting by translations on ${\mathbb R} ^d$, a simple point process and a family of jump probability rates.

The group ${\mathbb G}$ can be ${\mathbb R} ^d$ or ${\mathbb Z} ^d$ (the former endowed with the Euclidean distance, the latter with the discrete topology). ${\mathbb G}$ is a measurable space endowed with the Borel $\sigma$-algebra and it acts on $(\Omega , \mathcal F, \mathcal P)$ by a family of maps $(\theta _g)_{g\in {\mathbb G} }$, with $\theta _g :\Omega \rightarrow \Omega$, such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \theta _0=\mathbbm {1},\\ \theta _g \circ \theta _{g'}= \theta _{g+g'} \text { for all } g,g'\in {\mathbb G} ,\\ \text {the map }{\mathbb G} \times \Omega \ni (g,\omega ) \mapsto \theta _g \omega \in \Omega \ \text {is measurable.} \end{array}\right. } \end{aligned}$$

(1)

The group ${\mathbb G}$ acts also on the space ${\mathbb R} ^d$ by translations. We denote its action by $(\tau _g)_{g\in {\mathbb G} }$, where $\tau _g:{\mathbb R} ^d\rightarrow {\mathbb R} ^d$ is given by

$$\begin{aligned} \tau _g x=x+ g_1v_1 + \cdots +g_d v_d\;, \qquad g=(g_1,\dots , g_d) \in {\mathbb G} , \end{aligned}$$

(2)

for a fixed basis $v_1, \dots , v_d$ of ${\mathbb R} ^d$. For many applications, $\tau _g x= x+g$. When dealing with processes on general lattices (as e.g. the triangular or hexagonal lattice on ${\mathbb R} ^2$), the general form (2) is more suited (see Sect. 5).

We assume to have a simple point process on ${\mathbb R} ^d$ defined on our probability space. In particular, to each $\omega \in \Omega$ we associate a locally finite subset ${\hat{\omega }} \subset {\mathbb R} ^d$ by a measurable map $\Omega \ni \omega \rightarrow {\hat{\omega }} \in \mathcal N$. Above, $\mathcal N$ is the measurable space of locally finite subsets of ${\mathbb R} ^d$ with $\sigma$-algebra generated by the sets $\{ |{\hat{\omega }} \cap A|=n\}$, where $A\subset {\mathbb R} ^d$ is Borel and $n \in {\mathbb N}$ (cf. [5]). As discussed in [5] one can introduce a metric d on $\mathcal N$ such that the above $\sigma$-algebra equals the Borel $\sigma$-algebra.

Finally, we fix a measurable function

$$\begin{aligned} c: \Omega \times {\mathbb R} ^d \times {\mathbb R} ^d \ni (\omega , x, y)\mapsto c_{x,y}(\omega ) \in [0,+\infty ) ,\end{aligned}$$

(3)

symmetric in x, y: $c_{x,y}(\omega )= c_{y,x}(\omega )$. As it will be clear below, only the value of $c_{x,y}(\omega )$ with $x\not =y$ in ${\hat{\omega }}$ will be relevant. Hence, without loss of generality, we take

$$\begin{aligned} c_{x,x}(\omega )\equiv 0 \text { and } c_{x,y}(\omega )\equiv 0 \text { if }\{x,y\}\not \subset {\hat{\omega }}. \end{aligned}$$

(4)

All the above objects are related by ${\mathbb G}$-invariance. As detailed in Sect. 3, we assume that $\mathcal P$ is stationary and ergodic for the action $(\theta _g)_{g\in {\mathbb G} }$. We recall that stationarity means that $\mathcal P\circ \theta _g^{-1}=\mathcal P$ for all $g\in {\mathbb G}$, while ergodicity means that $\mathcal P(A)=1$ for all translation invariant sets $A \in {\mathcal F}$, i.e. such that $\theta _g A= A$ for all $g\in {\mathbb G}$ (we can identity ${\mathbb G}$ with a subset of Euclidean translations by (2), thus motivating our terminology). We also assume that, for $\mathcal P$-a.a. $\omega \in \Omega$ and for all $g\in {\mathbb G}$, it holds

$$\begin{aligned}&\widehat{\theta _g\omega } =\tau _{-g} ( \hat{\omega }) , \end{aligned}$$

(5)

$$\begin{aligned}&c_{x,y} (\theta _g\omega )= c_{\tau _g x, \tau _g y} (\omega ) \qquad \forall x,y \in {\mathbb R} ^d . \end{aligned}$$

(6)

The minus sign in (5) could appear ugly, but indeed if one identifies ${\hat{\omega }}$ with the counting measure $\mu _\omega (A):= \sharp ( {\hat{\omega }} \cap A)$, one would restate (5) as $\mu _{\theta _g\omega } (A)= \mu _\omega ( \tau _g A)$ for all $A\subset {\mathbb R} ^d$ Borel.

Given the environment $\omega$, we will introduce by the standard graphical construction the simple exclusion process on $\hat{\omega }$ with probability rate $c_{x,y}(\omega )$ for a jump between x and y when the exclusion constraint is satisfied. As discussed in Sect. 7 this simple exclusion process is a Feller process whose Markov semigroup on $C(\{0,1\}^{{\hat{\omega }}})$ has infinitesimal generator $\mathcal L_\omega$ acting on local functions as

$$\begin{aligned} \mathcal L_{\omega } f(\eta ) = \sum _{x\in {\hat{\omega }}} \sum _{y\in {\hat{\omega }}}c_{x,y}(\omega ) \eta (x) \bigl ( 1- \eta (y)\bigr ) \left[ f( \eta ^{x,y})- f(\eta )\right] ,\;\; \eta \in \{0,1\}^{{\hat{\omega }}}. \end{aligned}$$

(7)

Above and in what follows, $\{0,1\}^{{\hat{\omega }}}$ is endowed with the product topology and $C(\{0,1\}^{{\hat{\omega }}})$ denotes the space of continuous functions on $\{0,1\}^{{\hat{\omega }}}$ endowed with the uniform topology. We recall that a function f on $\{0,1\}^{{\hat{\omega }}}$ is called local if $f(\eta )$ depends on $\eta$ only through $\eta (x)$ with x varying among a finite set. The configuration $\eta ^{x,y}$ is obtained from $\eta$ by exchanging the occupation variables at x and y, i.e.

$$\begin{aligned} \eta ^{x,y}(z)={\left\{ \begin{array}{ll} \eta (y) &{}\quad \text {if } z=x ,\\ \eta (x) &{}\quad \text {if } z=y ,\\ \eta (z) &{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(8)

The generator $\mathcal L_\omega$ given in (7) can be thought of as an exchange operator:

$$\begin{aligned} \mathcal L_\omega f (\eta ) = \sum _{\{x,y\}\subset {\hat{\omega }}} c_{x,y}(\omega ) \bigl [ f(\eta ^{x,y})-f(\eta ) \bigr ]. \end{aligned}$$

(9)

When the starting configuration is given by a single particle, the dynamics reduces to a random walk in random environment, denoted by $X_t^\omega$. In Sects. 3 and 4 we will fix basic assumptions assuring the existence of the above processes for all times for $\mathcal P$-a.a. $\omega$.

We can now present the content of our Theorem 4.1 (see Sect. 4), in which we show that, under suitable weak assumptions, for $\mathcal P$-a.a. environments $\omega$ the above simple exclusion process admits a hydrodynamic limit under diffusive rescaling. More precisely, for $\mathcal P$-a.a. $\omega$ the following holds. Fix an initial macroscopic profile given by a Borel function $\rho _0 :{\mathbb R} ^d \rightarrow [0,1]$. Suppose that for any $\varepsilon >0$ the simple exclusion process starts with an initial distribution $\mathfrak {m}_\varepsilon$ such that

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \mathfrak {m}_\varepsilon \left( \Big | \varepsilon ^d \sum _{x \in {\hat{\omega }}} \varphi (\varepsilon x) \eta (x) -\int _{{\mathbb R} ^d} \varphi (x) \rho _0(x) dx \Big |>\varepsilon \right) =0 \qquad \forall \varphi \in C_c({\mathbb R} ^d). \end{aligned}$$

Call ${\mathbb P} _{ \omega ,\mathfrak {m}_\varepsilon }^\varepsilon$ the law of the exclusion process on ${\hat{\omega }}$ with initial distribution $\mathfrak {m}_\varepsilon$ and generator $\varepsilon ^{-2} \mathcal L_ \omega$. Then for all $T>0$ one has

$$\begin{aligned}\lim _{\varepsilon \downarrow 0} {\mathbb P} ^\varepsilon _{ \omega ,\mathfrak {m}_\varepsilon } \left( \sup _{0\le t\le T} \Big | \varepsilon ^d \sum _{x \in {\hat{\omega }}} \varphi (\varepsilon x) \eta _t( x) - \int _{{\mathbb R} ^d} \varphi (x) \rho (x,t) dx\Big | >\delta \right) =0 \; \;\forall \varphi \in C_c({\mathbb R} ^d), \end{aligned}$$

where $\rho :{\mathbb R} ^d\times [0,\infty )\rightarrow {\mathbb R}$ is given by $\rho (x ,t ): =P_t \rho _0(x)$, $(P_t)_{t\ge 0}$ being the Markov semigroup on bounded measurable functions of the Brownian motion with diffusion matrix 2D.

Above D is the so called effective homogenized matrix. D is a $d\times d$ symmetric non-negative matrix, admitting a variational characterization in terms of the Palm distribution $\mathcal P_0$ associated to $\mathcal P$ (cf. Definition 3.3). D is related to the homogenization properties of the diffusively rescaled random walk $\varepsilon X^\omega _{ \varepsilon ^{-2} t}$ on $\varepsilon {\hat{\omega }}$ as discussed in [12]. Some of these properties are collected in Proposition 6.1.

3 Basic assumptions and homogenization

In this section we describe our setting and our basic assumptions for the single random walk $X_t^\omega$ (hence the site-exclusion interaction does not appear here). The context is the same of [12] with the simplification that the jump rates are symmetric, hence the counting measure on ${\hat{\omega }}$ is reversible for $X_t^\omega$.

We first fix some basic notation. We denote by $e_1, \dots , e_d$ the canonical basis of ${\mathbb R} ^d$, by $\ell (A)$ the Lebesgue measure of the Borel set $A\subset {\mathbb R} ^d$, by $a \cdot b$ the standard scalar product of $a,b\in {\mathbb R} ^d$. Given a topological space W, without further mention, W will be thought of as a measurable space endowed with the $\sigma$-algebra $\mathcal B(W)$ of its Borel subsets. $\mathcal N$ is the space of locally finite subset $\{x_i\}$ of ${\mathbb R} ^d$. $\mathcal N$ is endowed with a metric such that the Borel $\sigma$-algebra $\mathcal B(\mathcal N)$ is generated by the sets $\{ |{\hat{\omega }} \cap A|=n\}$, where $A\in \mathcal B( {\mathbb R} ^d)$ and $n \in {\mathbb N}$ (cf. [5]).

Recall that ${\mathbb G}$ acts on the probability space $(\Omega , \mathcal F, \mathcal P)$ by $(\theta _g)_{g\in {\mathbb G} }$ [see (1)] and that $\mathcal P$ is assumed to be stationary and ergodic for this action. Moreover, ${\mathbb G}$ acts on ${\mathbb R} ^d$ by $(\tau _g)_{g\in {\mathbb G} }$, where [cf. (2)]

$$\begin{aligned} \tau _g x= x+Vg , \qquad V:= [ v_1|v_2|\cdots |v_d]. \end{aligned}$$

(10)

Above, V is the matrix with columns given by the basis vectors $v_1,v_2, \dots , v_d$, fixed once and for all.

We set

$$\begin{aligned} \Delta := \{t_1 v_1 + \cdots + t_d v_d \,:\, (t_1,{\dots }, t_d) \in [0,1)^d\}. \end{aligned}$$

(11)

Given $x\in {\mathbb R} ^d$, the ${\mathbb G}$-orbit of x is defined as the set $\{\tau _g x\,:\, g\in {\mathbb G} \}$.

If ${\mathbb G} ={\mathbb R} ^d$, then the ${\mathbb G}$-orbit of the origin of ${\mathbb R} ^d$ equals ${\mathbb R} ^d$. In this case we introduce the function $g: {\mathbb R} ^d \rightarrow {\mathbb G}$ as follows:

$$\begin{aligned} {x= \tau _g 0=Vg\; \Longrightarrow \; g(x):=g}. \end{aligned}$$

(12)

Simply, for each $x\in {\mathbb R} ^d$, $g(x)=V^{-1}x$. When $V={\mathbb I}$ (as in many applications), we have $\tau _g x=x+g$ and therefore $g(x)=x$.

If ${\mathbb G} ={\mathbb Z} ^d$, $\Delta$ is a set of ${\mathbb G}$-orbit representatives for the action $(\tau _g)_{g\in {\mathbb G} }$. We introduce the functions $\beta : {\mathbb R} ^d \rightarrow \Delta$ and $g: {\mathbb R} ^d \rightarrow {\mathbb G}$ as follows:

$$\begin{aligned} x= \tau _g \bar{x} \text { and } \bar{x} \in \Delta \; \Longrightarrow \; \beta (x):=\bar{x} , \; g(x) := g. \end{aligned}$$

(13)

Hence, given $x\in {\mathbb R} ^d$, $\bar{x}$ denotes the unique element of $\Delta$ such that x and $\bar{x}$ are in the same ${\mathbb G}$-orbit, and g(x) denotes the unique element in ${\mathbb G}$ such that $x= \tau _{g(x)} \bar{x}$.

3.1 An example with ${\mathbb G} ={\mathbb Z} ^d$ and $V\not ={\mathbb I}$

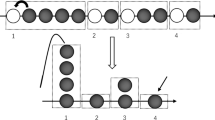
Although we will discuss several examples in Sect. 5, our mathematical objects for ${\mathbb G} ={\mathbb Z} ^d$ and $V\not ={\mathbb I}$ could appear very abstract at a first sight. To have in mind something concrete to which refer below, we present an example related to the random walk and the simple exclusion process on the infinite cluster of the supercritical site Bernoulli percolation on the hexagonal lattice (see Sect. 5 for a further discussion). Consider the hexagonal lattice graph $\mathcal L=(\mathcal V,\mathcal E)$ in ${\mathbb R} ^2$, partially drawn in Fig. 1. $\mathcal V$ and $\mathcal E$ denote respectively the vertex set and the edge set. The vectors $v_1$, $v_2$ in Fig. 1 form a fundamental basis for the hexagonal lattice.

Fig. 1

The parallelogram corresponds to the fundamental cell $\Delta$, the vectors $v_1,v_2$ are the columns of V, $\{0,a\}$ equals $\mathcal V\cap \Delta$

We take $\Omega :=\{0,1\}^\mathcal V$ endowed with the product topology and with the Bernoulli product probability measure $\mathcal P$ with supercritical parameter p. We set ${\mathbb G} :={\mathbb Z} ^2$. The action $(\theta _g )_{g\in {\mathbb Z} ^2}$ is given by $\theta _{(g_1,g_2)} \omega = ( \omega _{x-g_1 v_1 -g_2 v_2} ) _{x\in \mathcal V}$ if $\omega =(\omega _x) _{x\in \mathcal V}$ (note that $v_1,v_2$ are 2d vectors and not coordinates, while $(g_1,g_2)\in {\mathbb Z} ^2$). Trivially, $\mathcal P$ is stationary and ergodic for this action. The action of ${\mathbb Z} ^2$ on ${\mathbb R} ^2$ is given by the translations $\tau _{(g_1,g_2)}x:= x+g_1 v_1 +g_2 v_2$. Note that $V=[v_1|v_2]$.

The cell $\Delta$ in (11) is here the fundamental cell of the lattice $\mathcal L$ given by the parallelogram with ticked border in Fig. 1 (one has to remove the upper and right edges). Indeed, $\mathcal V=\cup _{g\in {\mathbb Z} ^d} \tau _g \{0,a\}$ and $\{0,a\}=\mathcal V\cap \Delta$. Then the map $\beta : {\mathbb R} ^2 \rightarrow \Delta$ in (13) is the map $\beta (x): =\bar{x}$ where $\bar{x}$ is the unique element of $\Delta$ such that $x =\bar{x} \text { mod } {\mathbb Z} v_1+{\mathbb Z} v_2$. Moreover, the map $g:{\mathbb R} ^2 \rightarrow {\mathbb Z} ^2$ in (13) assigns to x the only element $g=(g_1,g_2) \in {\mathbb Z} ^2$ such that $x\in \tau _g \Delta = \Delta + g_1 v_1 +g_2 v_2$.

We now describe the simple point process ${\hat{\omega }}$. As p is supercritical, for $\mathcal P$-a.a. $\omega$ the set $\{x\in \mathcal V\,:\, \omega _x=1\}$ has a unique infinite connected component $\mathcal C(\omega )$ inside the lattice $\mathcal L$. We set ${\hat{\omega }}:= \mathcal C(\omega )$. To extend this definition to all $\omega$, we set $\mathcal C(\omega ):=\emptyset$ if $\omega$ does not have a unique infinite connected component.

3.2 Palm distribution

We recall that we have a simple point process on ${\mathbb R} ^d$ defined on our probability space $(\Omega , \mathcal F,\mathcal P)$. This means that to each $\omega \in \Omega$ we associate a locally finite subset ${\hat{\omega }} \subset {\mathbb R} ^d$ by a measurable map $\Omega \ni \omega \rightarrow {\hat{\omega }} \in \mathcal N$. We now recall the definition of Palm distribution $\mathcal P_0$ associated to our simple point process by distinguishing between two main cases and a special subcase. For a more detailed discussion we refer to [12] and references therein. We remark that our treatment reduces to the one in [5] when ${\mathbb G} ={\mathbb R} ^d$, $\Omega =\mathcal N$, ${\hat{\omega }}=\omega$, $V={\mathbb I}$ (i.e. $\tau _g x=x+g)$ and $\theta _g \omega := \tau _{-g} \omega =\omega -g$. When ${\mathbb G} ={\mathbb R} ^d$ and in the special discrete case treated below, the Palm distribution $\mathcal P_0$ can be thought of as the probability measure $\mathcal P$ conditioned to the event $\{0\in {\hat{\omega }}\}$. For the special discrete case see (18) below, while for ${\mathbb G} ={\mathbb R} ^d$ some care is required as the above event has zero $\mathcal P$-probability (see [5, 40] for more details). We will write ${\mathbb E} [\cdot ]$ and ${\mathbb E} _0[\cdot ]$ for the expectation w.r.t. $\mathcal P$ and $\mathcal P_0$, respectively.¹

$\bullet$ Case ${\mathbb G} ={\mathbb R} ^d$. The intensity of the simple point process $\hat{\omega }$ is defined as

$$\begin{aligned} m:= {\mathbb E} \left[ \sharp \left( {\hat{\omega }} \cap [0,1)^d \right) \right] .\end{aligned}$$

(14)

We will assume that $m\in (0,+\infty )$. By the ${\mathbb G}$-stationarity of $\mathcal P$ we have $m \ell (B)={\mathbb E} \left[ \sharp \left( {\hat{\omega }} \cap B\right) \right]$ for any $B\in \mathcal B({\mathbb R} ^d)$. Then the Palm distribution $\mathcal P_0$ is the probability measure on $(\Omega ,\mathcal F)$ such that, for any $U\in \mathcal B({\mathbb R} ^d)$ with $0<\ell (U)<\infty$ ($\ell (U)$ is the Lebesgue measure of U),

$$\begin{aligned} \mathcal P_0(A):=\frac{1}{m \ell (U) }\int _\Omega d\mathcal P(\omega ) \sum _{x\in {\hat{\omega }} \cap U} \mathbbm {1}_A(\theta _{g(x)} \omega ) , \qquad \forall A\in \mathcal F.\end{aligned}$$

(15)

One can check that $\mathcal P_0$ has support inside the set $\Omega _0:=\{\omega \in \Omega \,:\, 0\in {\hat{\omega }}\}$.

$\bullet$ Case ${\mathbb G} ={\mathbb Z} ^d$. The intensity of the simple point process ${\hat{\omega }}$ is defined as

$$\begin{aligned} m:= {\mathbb E} \left[ \sharp \left( {\hat{\omega }} \cap \Delta \right) \right] / \ell (\Delta ) . \end{aligned}$$

(16)

By the ${\mathbb G}$-stationarity of $\mathcal P$, $m \ell (B)={\mathbb E} \left[ {\hat{\omega }}\left( B \right) \right]$ for any $B\in \mathcal B({\mathbb R} ^d)$ which is an overlap of translated cells $\tau _g \Delta$ with $g\in {\mathbb G}$. We will assume that $m\in (0,+\infty )$. Then the Palm distribution $\mathcal P_0$ is the probability measure on $\left( \Omega \times \Delta ,\mathcal F\otimes \mathcal B(\Delta )\right)$ such that

$$\begin{aligned} \mathcal P_0(A):=\frac{1}{m\, \ell (\Delta )}\int _\Omega d\mathcal P(\omega ) \sum _{x\in {\hat{\omega }} \cap \Delta } \mathbbm {1}_A( \omega ,x ) , \qquad \forall A\in \mathcal F\otimes \mathcal B(\Delta ) .\end{aligned}$$

(17)

$\mathcal P_0$ has support inside $\Omega _0:=\{(\omega , x)\in \Omega \times \Delta \,:\,x\in {\hat{\omega }}\}$.

Note that in the Example of Sect. 3.1, the set ${\hat{\omega }} \cap \Delta$ equals $\{0,a\}\cap \mathcal C(\omega )$, a being as in Fig. 1. Moreover, $\Omega _0= \{ (\omega , 0)\,:\, \omega \in \Omega , \;0 \in \mathcal C(\omega )\} \cup \{ (\omega , a)\,:\, \omega \in \Omega , \;a \in \mathcal C(\omega )\}$.

$\bullet$ Special discrete case: ${\mathbb G} ={\mathbb Z} ^d$, $V={\mathbb I}$ and ${\hat{\omega }} \subset {\mathbb Z} ^d$ $\forall \omega \in \Omega$ [see (10)]. This is a subcase of the previous one and in what follows we will call it simply special discrete case. Due to its relevance in discrete probability, we discuss it apart pointing out some simplifications. As $V={\mathbb I}$ we have $\Delta =[0,1)^d$. In particular (see the case ${\mathbb G} ={\mathbb Z} ^d$) $\mathcal P_0$ is concentrated on $\{ \omega \in \Omega :0\in {\hat{\omega }} \}\times \{0\}$. Hence we can think of $\mathcal P_0$ simply as a probability measure concentrated on the set $\Omega _0:=\{ \omega \in \Omega :0\in {\hat{\omega }}\}$. Formulas (16) and (17) then read

$$\begin{aligned} m:= \mathcal P(0\in {\hat{\omega }}) , \qquad \mathcal P_0(A):= \mathcal P\left( A\,|\, 0 \in {\hat{\omega }} \right) \qquad \forall A\in \mathcal F. \end{aligned}$$

(18)

In what follows, when treating the special discrete case, we will use the above identifications without explicit mention.

3.3 Basic assumptions

Recall that the jump probability rates are given by the measurable function $c_{x,y}(\omega )$ in (3), which is symmetric in x, y (i.e. $c_{x,y}(\omega )= c_{y,x}(\omega )$) and recall our convention (4). We also define

$$\begin{aligned} c_x(\omega ):= \sum _{y \in {\hat{\omega }} } c_{x,y} (\omega ) \qquad \forall x \in {\hat{\omega }}. \end{aligned}$$

(19)

We define the functions $\lambda _k:\Omega _0 \rightarrow [0,+\infty ]$ (for $k=0,2$) as follows:

$$\begin{aligned} \begin{aligned}&{\left\{ \begin{array}{ll} \lambda _k(\omega ):=\sum _{x\in {\hat{\omega }}} c_{0,x}(\omega )|x|^k &{} \quad {\text {Case }}{\mathbb G} ={\mathbb R} ^d \; {\text {and}}\\ \Omega _0=\{\omega \in \Omega \,:\, 0\in {\hat{\omega }}\} &{} \quad {\text {special discrete case}}, \end{array}\right. }\\&{\left\{ \begin{array}{ll} \lambda _k(\omega ,a):= \sum _{x\in {\hat{\omega }}} c_{a,x}(\omega )|x-a|^k \\ \Omega _0=\{(\omega , x)\in \Omega \times \Delta \,:\,x\in {\hat{\omega }} \} \end{array}\right. } \quad {\text {Case }}{\mathbb G} ={\mathbb Z} ^d. \end{aligned} \end{aligned}$$

(20)

For ${\mathbb G} ={\mathbb R} ^d$ and in the special discrete case, $\lambda _0(\omega )=c_0(\omega )$ for all $\omega \in \Omega _0$.

We collect below all our assumptions leading to homogenization of the massive Poisson equation of the diffusively rescaled random walk (some of them have already been mentioned in Sect. 2). We will not recall here the above homogenization results obtained in [12], as not necessary. On the other hand, we will collect some of their consequences in Proposition 6.1 in Sect. 6, since used in the proof of Theorem 4.1.

Assumptions for homogenization:

• (A1) $\mathcal P$ is stationary and ergodic w.r.t. the action $(\theta _g)_{g\in {\mathbb G} }$ of the group ${\mathbb G}$;

• (A2) the intensity m of the simple point process $\hat{\omega }$ is finite and positive [cf. (14), (16) and (18)];

• (A3) the $\omega$’s in $\Omega$ such that $\theta _g\omega \not = \theta _{g'} \omega$ for all $g\not =g'$ in ${\mathbb G}$ form a measurable set of $\mathcal P$-probability 1;

• (A4) the $\omega$’s in $\Omega$ such that, for all $g\in {\mathbb G}$ and $x,y \in {\mathbb R} ^d$,

  $$\begin{aligned}&\widehat{\theta _g\omega } =\tau _{-g}( {\hat{\omega }} ) , \end{aligned}$$

  (21)
  $$\begin{aligned}&c_{x,y} (\theta _g\omega )= c_{\tau _g x, \tau _g y} (\omega ) , \end{aligned}$$

  (22)

  form a measurable set of $\mathcal P$-probability 1;

• (A5) for $\mathcal P$-a.a. $\omega \in \Omega$, for all $x,y\in {\mathbb R} ^d$ it holds

  $$\begin{aligned} c_{x,y}(\omega ) = c_{y,x}(\omega )\,; \end{aligned}$$

  (23)

• (A6) for $\mathcal P$-a.a. $\omega \in \Omega$, given any $x,y \in {\hat{\omega }}$ there exists a path $x=x_0$, $x_1$,$\ldots , x_{n-1}, x_n =y$ such that $x_i \in {\hat{\omega }}$ and $c_{x_i, x_{i+1}}(\omega ) >0$ for all $i=0,1, \ldots , n-1$;

• (A7) $\lambda _0 , \lambda _2 \in L^1(\mathcal P_0)$;

• (A8) $L^2(\mathcal P_0)$ is separable.

The above assumptions implies that $\mathcal P$-a.s. the random walk $X_t^\omega$ on ${\hat{\omega }}$ introduced in Sect. 2 is well defined for all times $t\ge 0$ (recall that a set $A\subset \Omega$ is called translation invariant if $\theta _g A=A$ for all $g\in {\mathbb G}$):

Lemma 3.1

[12, Lemma 3.5] There exists a translation invariant measurable set $\mathcal A\subset \Omega$ with $\mathcal P(\mathcal A)=1$ such that, for all $\omega \in \mathcal A$, (i) $c_x(\omega )\in (0,+\infty )$ for all $x \in {\hat{\omega }}$ [cf. (19)], (ii) the continuous-time Markov chain on ${\hat{\omega }}$ starting at any $x_0\in {\hat{\omega }}$, with waiting time parameter $c_x(\omega )$ at $x\in {\hat{\omega }}$ and with probability $c_{x,y}(\omega )/c_x(\omega )$ for a jump from x to y, is non-explosive.

In Sect. 4 we will make an additional assumption [called Assumption (SEP)] assuring that the simple exclusion process introduced via the universal graphical construction is well defined for all times [see (7) for its generator on local functions]. Hence, by thinking the random walk $X_t^\omega$ as a simple exclusion process with only one particle, also Assumption (SEP) guarantees the well-definedness of $X_t^\omega$.

We now report some other comments on the above assumptions (A1),...,(A8) taken from [12, Section 2.4] (where more details are provided). By Zero-Infinity Dichotomy (see [5, Proposition 10.1.IV]) and Assumptions (A1) and (A2), for $\mathcal P$-a.a. $\omega$ the set ${\hat{\omega }}$ is infinite. (A3) is a rather superfluous assumption as one can add some randomness by enlarging $\Omega$ to assure (A3). The assumption of measurability in (A3) and (A4) is always satisfied for ${\mathbb G} ={\mathbb Z} ^d$ by (4) (as discussed in [12, Section 2.4], one can even weaken this requirement). Considering the random walk $X_t^\omega$, (A5) and (A6) correspond $\mathcal P$-a.s. to reversibility of the counting measure and to irreducibility. Finally, we point out that, by [3, Theorem 4.13], (A8) is fulfilled if $(\Omega _0,\mathcal F_0,\mathcal P_0)$ is a separable measure space where $\mathcal F_0:=\{A\cap \Omega _0\,:\, A\in \mathcal F\}$ (i.e. there is a countable family $\mathcal G\subset \mathcal F_0$ such that the $\sigma$-algebra $\mathcal F_0$ is generated by $\mathcal G$). For example, if $\Omega _0$ is a separable metric space and $\mathcal F_0= \mathcal B(\Omega _0)$ [which is valid if $\Omega$ is a separable metric space and $\mathcal F= \mathcal B(\Omega )$] then (cf. [3, p. 98]) $(\Omega _0,\mathcal F_0,\mathcal P_0)$ is a separable measure space and (A8) is valid.

We now explain why the Palm distribution $\mathcal P_0$ will play a crucial role in the hydrodynamic limit of the simple exclusion process. $\mathcal P_0$ is indeed the natural object to express the ergodic property of the environment when dealing with observables keeping track also of the local microscopic details of the environment. This is formalized by the following result which will be frequently used below (cf. [11, Appendix B], [12, Proposition 3.1] and recall that ${\mathbb E} _0$ denotes the expectation w.r.t. $\mathcal P_0$):

Proposition 3.2

Let $f: \Omega _0\rightarrow {\mathbb R}$ be a measurable function with $\Vert f\Vert _{L^1(\mathcal P_0)}<\infty$. Then there exists a translation invariant measurable subset $\mathcal A[f]\subset \Omega$ such that $\mathcal P(\mathcal A[f])=1$ and such that, for any $\omega \in \mathcal A[f]$ and any $\varphi \in C_c ({\mathbb R} ^d)$, it holds

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \int d \mu _\omega ^\varepsilon (x) \varphi (x ) f(\theta _{g( x/\varepsilon )} \omega )= \int dx\,m\varphi (x) \cdot {\mathbb E} _0[f] , \end{aligned}$$

(24)

where $\mu ^\varepsilon _\omega := \sum _{x\in {\hat{\omega }}} \varepsilon ^d \delta _{\varepsilon x}$.

We point out that the above proposition implies that $m=\lim _{\ell \uparrow \infty } \sharp ( {\hat{\omega }} \cap [-\ell ,\ell ]^d)/(2\ell )^d$ $\mathcal P$-a.s.

We can now also introduce the effective homogenized matrix D, defined in terms of the Palm distribution:

Definition 3.3

We define the effective homogenized matrix D as the unique $d\times d$ symmetric matrix such that:

$\bullet$ Case ${\mathbb G} ={\mathbb R} ^d$ and special discrete case

$$\begin{aligned} a \cdot Da =\inf _{ f\in L^\infty (\mathcal P_0) } \frac{1}{2}\int _{\Omega _0} d\mathcal P_0(\omega )\sum _{x\in {\hat{\omega }}} c_{0,x}(\omega ) \left( a\cdot x - \nabla f (\omega , x) \right) ^2 , \end{aligned}$$

(25)

for any $a\in {\mathbb R} ^d$, where $\nabla f (\omega , x) := f(\theta _{g(x)} \omega ) - f(\omega )$.

$\bullet$ Case ${\mathbb G} ={\mathbb Z} ^d$

$$\begin{aligned}&a \cdot Da \nonumber \\&\quad = \inf _{ f\in L^\infty (\mathcal P_0) } \frac{1}{2} \int _{\Omega \times \Delta }d\mathcal P_0(\omega ,x) \sum _{y \in {\hat{\omega }}} c_{x,y}(\omega ) \left( a\cdot (y-x) - \nabla f (\omega , x,y-x) \right) ^2 , \end{aligned}$$

(26)

for any $a\in {\mathbb R} ^d$, where $\nabla f (\omega , x,y-x) := f(\theta _{g(y)} \omega , \beta (y) ) - f(\omega ,x)$ [recall (13)].

We give some comments on the above definition of D. Firstly, it is well posed due to (A7). We also point out that the effective homogenized matrix D, which is defined by a variational formula, can be computed explicitly essentially only in dimension $d=1$ with positive conductances $c_{x,y}(\omega )$ only between nearest neighboring points x, y of ${\hat{\omega }}$ (see e.g. [2] and [4, Eq. (4.22)]). On the other hand, in the last years numerical approximation methods for D have been developed in quantitative stochastic homogenization theory (see e.g. [7]).

Under Assumption (A1),...,(A8) the random walk $X_t^\omega$ satisfies a weak form of central limit theorem where 2D equals the asymptotic diffusion matrix (cf. [12, Theorem 4.4]). Since the position of the random walk can be thought of as an antisymmetric additive functional of the environment viewed from the particle, D has the same structure of a Green–Kubo formula (cf. [4, 27, 29, 30, 38] and references therein).

Finally we introduce an additional assumption assuring a weak form of convergence for the $L^2$-Markov semigroup and the $L^2$-resolvent associated to the random walk $X_t^\omega$ as discussed in Sect. 6 [recall definition (11) of $\Delta$].

Additional assumption for semigroup and resolvent convergence:

• (A9) At least one of the following conditions is satisfied:

  • (i) for $\mathcal P$-a.a. $\omega$ $\exists C(\omega )>0$ such that

    $$\begin{aligned} \sharp ( {\hat{\omega }} \cap \tau _k \Delta ) \le C(\omega ) \text { for all } k\in {\mathbb Z} ^d ; \end{aligned}$$

    (27)

  • (ii) at cost to enlarge the probability space $\Omega$ one can define random variables $(N_k) _{k\in {\mathbb Z} ^d}$ with $\sharp ( {\hat{\omega }} \cap \tau _k \Delta ) \le N_k$ and such that, for some $C_0\ge 0$, it holds

    $$\begin{aligned}&\sup _{k \in {\mathbb Z} ^d} {\mathbb E} [N_k]<+\infty ,\qquad \sup _{k \in {\mathbb Z} ^d}{\mathbb E} \left[ N_k^2\right] <+\infty , \end{aligned}$$

    (28)
    $$\begin{aligned}&|\text {Cov}\,(N_k, N_{k'})| \le C_0 |k-k'| ^{-1} \qquad \forall k\not = k'\text { in }{\mathbb Z} ^d . \end{aligned}$$

    (29)

Remark 3.4

If one set $N_k:= \sharp ( {\hat{\omega }} \cap \tau _k \Delta )$ for $k\in {\mathbb Z} ^d$, then to check Condition (ii) in (A9) it is enough to check that ${\mathbb E} [N_0^2]<+\infty$ and (29) [due to (A1) and (A2)]. As discussed in [12, Remark 4.3], when ${\mathbb G} ={\mathbb R} ^d$, in (A9) one can replace the cells $\{\tau _k \Delta \}_{k \in {\mathbb Z} ^d}$ by the cells of any lattice partition of ${\mathbb R} ^d$.

4 Hydrodynamic limit

Given $\omega \in \Omega$ we consider the simple exclusion process on $\hat{\omega }$ with particle exchange probability rate $c_{x,y}(\omega )$. To have a well defined process for all times $t\ge 0$, $\mathcal P$-a.s., we will use in Sect. 7 Harris’ percolation argument [6]. To this aim, we define

$$\begin{aligned} \mathcal E_\omega :=\{ \,\{x,y\}\,:\, x,y \in {\hat{\omega }} , \; x\not =y\,\}. \end{aligned}$$

(30)

Then, given $\omega$, we associate to each unordered pair $\{x,y\}\in \mathcal E_\omega$ a Poisson process $( N_{x,y}(t))_{t\ge 0}$ with intensity $c_{x,y}(\omega )$, such that the $N_{x,y}(\cdot )$’s are independent processes when varying the pair $\{x,y\}$. The random object $( N_{x,y}(\cdot ) )_{\{x,y\}\in \mathcal E_\omega }$ takes value in the product space $D({\mathbb R} _+, {\mathbb N} )^{\mathcal E_\omega }$, $D({\mathbb R} _+, {\mathbb N} )$ being endowed with the standard Skorohod topology. In the rest, we will denote by $\mathcal K= ( \mathcal K_{x,y}(\cdot ) )_{\{x,y\}\in \mathcal E_\omega }$ a generic element of $D({\mathbb R} _+, {\mathbb N} )^{\mathcal E_\omega }$. Moreover, we denote by ${\mathbb P} _\omega$ the law on $D({\mathbb R} _+, {\mathbb N} )^{\mathcal E_\omega }$ of $( N_{x,y}(\cdot ) )_{\{x,y\}\in \mathcal E_\omega }$.

In this section we add the following assumption (we call it “SEP” for “simple exclusion process” as the assumption is introduced to assure the existence of the simple exclusion process):

Assumption (SEP). For $\mathcal P$-a.a. $\omega$ there exists $t_0=t_0(\omega )>0$ such that for ${\mathbb P} _\omega$-a.a. $\mathcal K$ the undirected graph $\mathcal G_{t_0}(\omega ,\mathcal K)$ with vertex set ${\hat{\omega }}$ and edges

$$\begin{aligned} \{ \{x,y\}\in \mathcal E_\omega \,:\, \mathcal K_{x,y}(t_0) \ge 1\}\end{aligned}$$

has only connected components with finite cardinality.

In Sect. 7 we discuss the universal graphical construction of the exclusion process on ${\hat{\omega }}$ under Assumption (SEP). For $\mathcal P$-a.a. $\omega$ the resulting process is a Feller process and the infinitesimal generator $\mathcal L_\omega$ acts on local functions as in (7) and (9) (see Proposition 7.4).

We denote by $\mathcal M$ the space of Radon measures on ${\mathbb R} ^d$ endowed with the vague topology and we denote by $D([0,T], \mathcal M)$ the Skorohod space of càdlàg paths from [0, T] to $\mathcal M$ endowed with the Skorohod metric (see Sect. 9 for details). For each $\varepsilon >0$ we consider the map

$$\begin{aligned} \{0,1\}^{{\hat{\omega }}}\ni \eta \mapsto \pi ^\varepsilon _\omega [\eta ]:=\varepsilon ^d \sum _{x\in {\hat{\omega }}} \eta (x) \delta _{\varepsilon x} \in \mathcal M.\end{aligned}$$

Above $\pi ^\varepsilon _\omega [\eta ]$ is the so called empirical measure associate to $\eta$. Given a path $\eta _\cdot = (\eta _s )_{0 \le s \le T}$ and given $t\in [0,T]$, we define $\pi ^\varepsilon _{\omega ,t} [ \eta _\cdot ]:= \pi ^\varepsilon _\omega [ \eta _t ]$.

In what follows, given $\varepsilon >0$ and a probability measure $\mathfrak {m}$ on $\{0,1\}^{ {\hat{\omega }}}$, we denote by ${\mathbb P} ^\varepsilon _{\omega , \mathfrak {m} }$ the law of the diffusively rescaled exclusion process on ${\hat{\omega }}$ with generator $\varepsilon ^{-2} \mathcal L_\omega$ and initial distribution $\mathfrak {m}$. Note that the time T is fixed and does not appear in the notation.

We denote by $(B_t)_{t\ge 0}$ the Brownian motion on ${\mathbb R} ^d$ with diffusion matrix given by 2D, D being the effective homogenized matrix (see Definition 3.3). As D is symmetric we can fix an orthonormal basis $\mathfrak {e}_1$,...,$\mathfrak {e}_d$ of eigenvectors of D, such that $\mathfrak {e}_1$,...,$\mathfrak {e}_{d_*}$ have positive eigenvalues, while the other basis vectors have zero eigenvalue. Then the Brownian motion $(B_t)_{t\ge 0}$ is not degenerate when projected on $\text {span}(\mathfrak {e}_1, \dots , \mathfrak {e}_{d_*})$, while no motion is present along $\text {span}(\mathfrak {e}_{d_*+1}, \dots , \mathfrak {e}_{d})$. Given a bounded function $f:{\mathbb R} ^d\rightarrow {\mathbb R}$ we set $P_t f(x):=E\left[ f(x+B_t)\right]$.

Theorem 4.1

Suppose that Assumptions (A1),...,(A9) and Assumption (SEP) are satisfied. Then there exists a translation invariant measurable set $\Omega _\mathrm{typ}\subset \Omega$ with $\mathcal P(\Omega _\mathrm{typ})=1$, such that for any $\omega \in \Omega _\mathrm{typ}$ the simple exclusion process is well defined for any initial distribution and exhibits the following hydrodynamic behavior.

Let $\rho _0: {\mathbb R} ^d \rightarrow [0,1]$ be a measurable function and let $\rho :{\mathbb R} ^d\times [0,\infty )\rightarrow [0,1]$ be the function $\rho (x,t):= P_t \rho _0 (x)$. Let $\{\mathfrak {m}_\varepsilon \}_{\varepsilon >0}$ be an $\varepsilon$-parametrized family of probability measures on $\{0,1\}^{\hat{\omega }}$ such that the random empirical measure $\pi _\omega ^\varepsilon [\eta ]$ in $\mathcal M$, with $\eta$ sampled according to $\mathfrak {m}_\varepsilon$, converges in probability to $\rho _0(x)dx$ inside $\mathcal M$. In other words, we suppose that, for all $\delta >0$ and $\varphi \in C_c({\mathbb R} ^d)$, it holds

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \mathfrak {m}_\varepsilon \left( \Big | \varepsilon ^d \sum _{x \in {\hat{\omega }}} \varphi (\varepsilon x) \eta (x) -\int _{{\mathbb R} ^d} \varphi (x) \rho _0(x) dx \Big |>\delta \right) =0. \end{aligned}$$

(31)

Then:

• (i) For all $T>0$, as $\varepsilon \downarrow 0$ the random path $( \pi ^\varepsilon _{\omega ,t} [ \eta _\cdot ])_{0\le t \le T}$ in $D ( [0,T], \mathcal M)$, with $\eta _\cdot =( \eta _t )_{0\le t \le T}$ sampled according to ${\mathbb P} ^\varepsilon _{\omega , \mathfrak {m}_\varepsilon }$, converges in probability to the deterministic path $(\rho (x,t) dx )_{0\le t \le T}$.

• (ii) For all $T>0$, $\varphi \in C_c({\mathbb R} ^d)$ and $\delta >0$, it holds

  $$\begin{aligned} \lim _{\varepsilon \downarrow 0} {\mathbb P} ^\varepsilon _{ \omega ,\mathfrak {m}_\varepsilon } \Big (\sup _{0\le t \le T}\Big | \varepsilon ^d \sum _{x \in {\hat{\omega }}} \varphi (\varepsilon x) \eta _t (x) - \int _{{\mathbb R} ^d} \varphi (x) \rho (x,t) dx\Big | >\delta \Big )=0. \end{aligned}$$

  (32)

The proof of the above theorem is given in Sect. 11 (Sect. 11.2 can be replaced by “Appendix C”, the two approaches are alternative). The function $\rho (x,t)= P_t \rho _0 (x)$ is the unique weak solution of the Cauchy system

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \rho = \nabla \cdot ( D \nabla \rho ) \quad {\text {for }} t>0 ,\\ \rho (0,\cdot ) = \rho _0 , \end{array}\right. } \end{aligned}$$

(33)

in the sense specified by Lemma 9.3 in Sect. 11.2.

Remark 4.2

Theorem 4.1 remains valid if Assumption (SEP) is replaced by any other assumption leading to Proposition 7.4 below. Indeed, the latter contains all the properties used in the proof provided in Sect. 11. See also Remark 6.2 for what concerns modifications to Assumption (A9).

Remark 4.3

The assumptions of Theorem 4.1 do not include that the effective homogenized matrix D is strictly positive definite. Checking this property can be a non-trivial task (see the discussion on the non-degeneracy of D in [12, Introduction and Section 5]). For an example of degenerate and nonzero D see “Appendix A”.

5 Some applications

There are plenty of examples to which Theorem 4.1 can be applied. We discuss here four main classes. The application of Theorem 4.1 to the simple exclusion process with random jump rates on the Delaunay triangulation is discussed in [18].

5.1 Nearest-neighbor random conductance model on ${\mathbb Z} ^d$, $d\ge 1$

We take ${\mathbb G} :={\mathbb Z} ^d$ acting on ${\mathbb R} ^d$ by standard translations, i.e. $\tau _g x=x+ g$. Let ${\mathbb E} ^d$ be the set of unoriented edges of ${\mathbb Z} ^d$ and endow $\Omega :=(0,+\infty )^{{\mathbb E} ^d}$ with the product topology. Given $\omega \in \Omega$, we write $\omega _{x,y}$ for the component of $\omega$ associated to the edge $\{x,y\}\in {\mathbb E} ^d$. The action $(\theta _x)_{x\in {\mathbb Z} ^d}$ is the standard one: $(\theta _x \omega ) _{a,b}:= \omega _{a+x,b+x}$. We set ${\hat{\omega }} := {\mathbb Z} ^d$, hence the exclusion process lives on ${\mathbb Z} ^d$. We define $c_{x,y}(\omega ):=\omega _{x,y}$ if $\{x,y\}\in {\mathbb E} ^d$ and $c_{x,y}(\omega ):=0$ otherwise. It is simple to check that Assumptions (A1),..., (A9) are satisfied whenever $\mathcal P$ is stationary and ergodic, $\mathcal P$ satisfies (A3) (which is a rather superfluous assumption, as already commented) and ${\mathbb E} [\omega _{x,y}]<+\infty$ for all $\{x,y\}\in {\mathbb E} ^d$. When $d=1$, D can be explicitly computed and one gets $D= 1/ {\mathbb E} [1/c_{0,1}(\omega )]\in [0,+\infty )$ (apply [2, Proposition 4.1 and Exercise 4.3] or use the characterization of D as a.s. limit (for $n\rightarrow +\infty$) of 2n times the effective conductivity under unit potential of the 1d resistor network with node set $[-n,n]\cap {\mathbb Z}$ and with nearest-neighbors conductances $c_{x,y}(\omega )$ [13]). For $d\ge 2$ the variational problem in (25) leading to D does not have an explicit solution.

Below, given $k>0$, we say that the random conductances $\omega _{x,y}$ are k-dependent if, given $A,B\subset {\mathbb Z} ^d$ with Euclidean distance between A and B larger than k, the random fields

$$\begin{aligned} \left( \omega _{x,y}\,:\,\{x,y\} \in {\mathbb E} ^d ,\; x,y\in A\right) \text { and }\left( \omega _{x,y}\,:\,\{x,y\} \in {\mathbb E} ^d ,\; x,y\in B\right) \end{aligned}$$

are independent (see [23, page 178] for a similar definition).

Proposition 5.1

Assumption (SEP) is satisfied if at least one of the following conditions is satisfied:

• (i) $\mathcal P$-a.s. there exists a constant $C(\omega )$ such that $\omega _{x,y}\le C(\omega )$ for all $\{x,y\}\in {\mathbb E} ^d$;

• (ii) under $\mathcal P$ the random conductances $\omega _{x,y}$ are independent;

• (iii) under $\mathcal P$ the random conductances $\omega _{x,y}$ are k-dependent with $k>0$.

We note that, by ergodicity, in Item (i) one could just restrict to a non-random upper bound C. Item (ii) is a special case of Item (iii).

Proof

We start with Item (i). As ${\mathbb P} _\omega ( \mathcal K_{x,y}(t_0)>0)= 1-e^{ - \omega _{x,y} t_0}$, it is enough to take $t_0$ small to have $1-e^{ - C (\omega ) t_0}< p_c$, $p_c>0$ being the critical probability for the Bernoulli bond percolation on ${\mathbb Z} ^d$.

Let us consider Items (ii) and (iii). We present an argument valid for all $d\ge 1$ (but for $d=1$ one can give easily a more direct proof). By ${\mathbb Z} ^d$-stationarity the distribution of $\omega _{x,y}$ depends only on the axis parallel to the edge $\{x,y\}$. To simplify the notation we suppose that the conductances are identically distributed with common distribution $\nu$ (otherwise one has just to deal with a finite family of distributions $\nu _1,\nu _2,\dots , \nu _d$ in the stochastic domination below). We observe that, for any $C_0>0$, the graph $\mathcal G_{t_0} (\omega ,\mathcal K)$ described in Assumption (SEP) is contained in the graph $\mathcal G'_{t_0}(\omega ,\mathcal K)$ with edges $\{x,y\}\in {\mathbb E} ^d$ such that

$$\begin{aligned} \omega _{x,y}> C_0 \qquad \text { or } \qquad {\left\{ \begin{array}{ll} \omega _{x,y} \le C_0,\\ \mathcal K_{x,y}(t_0)>0. \end{array}\right. } \end{aligned}$$

Given $e\in {\mathbb E} ^d$ we set $Y_e(\omega ,\mathcal K):=1$ if e is present in $\mathcal G'_{t_0}(\omega ,\mathcal K)$, otherwise we set $Y_e=0$. We define $\alpha (C_0):= \nu \left( (C_0 ,+\infty ) \right)$. Then, under ${\mathbb P} := \int d\mathcal P(\omega ) {\mathbb P} _\omega$, the random field $Y=(Y_e)_{e\in {\mathbb E} ^d}$ is stationary, satisfies ${\mathbb P} ( Y_e=1)\le \alpha (C_0) + (1-\alpha (C_0))( 1-e^{ - C _0 t_0})$ and is given by independent r.v.’s under (ii) and by k-dependent r.v.’s under (iii). Hence, fixed $p_*\in (0,p_c)$, we can first choose $C_0$ large and afterwards $t_0$ small to have ${\mathbb P} ( Y_e=1)\le p_*$. In particular, in case (ii) we conclude that ${\mathbb P}$-a.s. Y does not percolate. Similarly to [23, Theorem (7.65)] (invert the role between 0 and 1 there), by taking $p_*$ small enough we get that the random field Y is stochastically dominated by a subcritical Bernoulli bond percolation (i.e. of parameter smaller than $p_c$) and therefore ${\mathbb P}$-a.s. Y does not percolate. Hence, in both cases (ii) and (iii), by suitably choosing $C_0,t_0$, the graph $\mathcal G'_{t_0}(\omega ,\mathcal K)$ has only connected components with finite cardinality ${\mathbb P}$ a.s. (i.e. for $\mathcal P$-a.a. $\omega$ and for ${\mathbb P} _\omega$-a.a. $\mathcal K$). The same then must hold for $\mathcal G_{t_0}(\omega ,\mathcal K)\subset \mathcal G'_{t_0}(\omega ,\mathcal K)$. $\square$

5.2 Nearest-neighbor random conductance models on a generic crystal lattice

We consider a generic crystal lattice $\mathcal L=(\mathcal V,\mathcal E)$ in ${\mathbb R} ^d$, $d\ge 1$, as follows. We fix a basis $v_1,\ldots , v_d$ of ${\mathbb R} ^d$, write V for the matrix with columns $v_1,\ldots ,v_d$ and write $\Delta$ for the d-dimensional cell (11). Given $g\in {\mathbb G} :={\mathbb Z} ^d$, we denote by $\tau _g$ the translation (10), i.e. $\tau _g x = x+ V g$. We fix a finite set $\mathcal A\subset \Delta$. Then the vertex set $\mathcal V$ of the crystal lattice is given by $\sqcup _{g\in {\mathbb G} } ( \tau _g \mathcal A)$. The edge set $\mathcal E$ has to be a family of unoriented pairs of vertices $\{x,y\}$ with $x\not =y$ in $\mathcal V$, such that $\tau _g \mathcal E= \mathcal E$ for all $g\in {\mathbb G}$. In particular, the crystal lattice $\mathcal L=(\mathcal V,\mathcal E)$ is left invariant by the action $(\tau _g )_{g\in {\mathbb G} }$ on ${\mathbb R} ^d$. As an example consider the hexagonal lattice $\mathcal L=(\mathcal V,\mathcal E)$ in ${\mathbb R} ^2$ (cf. Sect. 3.1). Then $\mathcal A=\{0, a\}$ (see Fig. 1).

We take $\Omega := (0,+\infty )^{\mathcal E}$ endowed with the product topology and set $\omega _{x,y}:=\omega _{\{x,y\}}$. The action of $(\theta _g)_{g\in {\mathbb G} }$ on $\Omega$ is given by $\theta _g \omega : =(\omega _{x-Vg,y-Vg }\,:\, \{x,y\}\in \mathcal E)$ if $\omega =(\omega _{x,y}\,:\,\{x,y\}\in \mathcal E)$. For any $\omega \in \Omega$, we set ${\hat{\omega }} := \mathcal V$, hence our simple exclusion process lives on $\mathcal V$. The set $\Omega _0$ introduced after (17) equals $\Omega \times \mathcal A$ and, by (16), $m \ell (\Delta )= |\mathcal A|$. Hence [see (17)] $\mathcal P_0(d\omega ,dx)= \mathcal P(d\omega ) \otimes \mathrm{Av}_{u\in \mathcal A} \delta _u(dx)$, where $\mathrm{Av}$ denotes the arithmetic average and $\delta _u$ is the Dirac measure at u.

We set $c_{x,y}(\omega ):= \omega _{x,y}$ if $\{x,y\}\in \mathcal E$ and $c_{x,y}(\omega ):=0$ otherwise. If $\mathcal P$ satisfies (A1), (A2), (A3) and the crystal lattice is connected, then all assumptions (A1),...,(A9) are satisfied if $\sum _{y\in \mathcal V}\sum _{u \in \mathcal A} {\mathbb E} [ \omega _{u,y}]|y-u|^2<+\infty$. It the crystal lattice is locally finite (i.e. vertices have finite degree), then the above moment bound equal the bound ${\mathbb E} [\omega _{x,y}]<+\infty$ for $\{x,y\}\in \mathcal E$ (by ${\mathbb G}$-stationarity and local finiteness, we have just a finite family of bounds).

For locally finite crystal lattices, by reasoning as done for the lattice ${\mathbb Z} ^d$, we get that Assumption (SEP) is satisfied if the conductances $\omega _{x,y}$ are uniformly bounded or if the conductances $\omega _{x,y}$ are independent or k-dependent under $\mathcal P$.

5.3 Simple exclusion processes on marked simple point processes

We take ${\mathbb G} := {\mathbb R} ^d$ ($d\ge 1$) acting on ${\mathbb R} ^d$ by standard translations ($\tau _g x=x+ g$). $\Omega$ is given by the space of marked counting measures with marks in ${\mathbb R}$ [5], hence $(\Omega ,\mathcal F,\mathcal P)$ describes a marked simple point process [5]. By identifying $\omega$ with its support, we have $\omega =\{(x_i,E_i)\}$ where $E_i\in {\mathbb R}$ and the set $\{x_i\}$ is locally finite. The action $\theta _x$ on $\Omega$ is given by $\theta _x \omega :=\{ (x_i-x, E_i)\}$ if $\omega =\{(x_i, E_i)\}$. Our simple point process is obtained by setting ${\hat{\omega }} =\{x_i\}$ when $\omega =\{(x_i,E_i)\}$. We take

$$\begin{aligned} c_{x_i,x_j}(\omega ):= \exp \bigl \{ -|x_i-x_j| - u(E_{x_i},E_{x_j}) \bigr \}\,\qquad x_i\not =x_j , \end{aligned}$$

(34)

where $u:{\mathbb R} ^2 \rightarrow {\mathbb R}$ is a symmetric measurable function bounded from below. We point out that Mott random walk, used to model Mott variable range hopping in amorphous solids (see e.g. [15, 17] and references therein) is the random walk with jump rates $c_{x,y}(\omega )$ as above, with $u(a,b)=|E_a-E_b|+|E_a|+|E_b|$.

Suppose that $\mathcal P$ satisfies (A1),(A2) and (A3). Then $\mathcal P_0$ is simply the standard Palm distribution associated to the marked simple point process with law $\mathcal P$ [5]. Assumptions (A4), (A5), (A6) are automatically satisfied. As the above space $\Omega$ is Polish (see [5]) and $\Omega _0=\{\omega \,:\, 0 \in {\hat{\omega }}\}$ is a Borel subset of $\Omega$, $\Omega _0$ is separable and therefore (A8) is satisfied. As proven in [12, Section 5.4], (A7) is implied by the bound ${\mathbb E} \bigl [ |{\hat{\omega }} \cap [0,1]^d | ^{2} \bigr ]<+\infty$. Assumption (A9) is verified in numerous examples of marked simple point processes, including the Poisson point process (PPP) with intensity $m\in (0,+\infty )$. Assumption (SEP) is of percolation nature. We show its validity for PPP’s. Moreover, since one can consider as well other jump rates $c_{x,y}(\omega )$ for a random walk on a marked simple point process, we state our percolation result in a more general form.

Proposition 5.2

Suppose that under $\mathcal P$ the random set $\{x_i\}$ is a PPP with intensity $m\in (0,+\infty )$. Take jump rates $c_{x,y}(\omega )$ satisfying (22) in (A4) and (23) in (A5). Suppose that, for $\mathcal P$-a.a. $\omega$, $c_{x,y}(\omega ) \le g(|x-y|)$ for any $x,y \in {\hat{\omega }}$, where g(r) is a fixed bounded function such that the map $x \mapsto g(|x|)$ belongs to $L^1({\mathbb R} ^d, dx)$ [for example take $g(r)={C}e^{-r}$ for (34)]. Then Assumption (SEP) is satisfied.

Proof

Note that ${\mathbb P} _\omega ( \mathcal K_{x,y}(t) \ge 1)= 1- e^{-c_{x,y}(\omega )t} \le 1- \exp \{-g(|x-y|) t\}\le C_1 g(|x-y|) t$ for some fixed $C_1>0$ if we take $t\le 1$ (since g is bounded). We restrict to t small enough such that $C_1\Vert g\Vert _\infty t <1$ and $t\le 1$. Consider the random connection model [31] on a PPP with intensity m where an edge between $x\not =y$ is created with probability $C_1 g(|x-y|) t$. Due to the independence of the Poisson processes $N_{x,y}(\cdot )'s$ given $\omega$, one can couple the above random connection model with the field $(\omega , \mathcal K)$ with law ${\mathbb P} :=\int d \mathcal P(\omega ){\mathbb P} _\omega$ in a way that the graph in the random connection model contains the graph $\mathcal G_{t}(\omega ,\mathcal K)$. We choose $t=t_0$ small enough to have $m C_1 t_0 \int _{{\mathbb R} ^d} dx g(|x|) <1$. The above bound and the branching process argument in the proof of [31, Theorem 6.1] [cf. (6.3) there] imply that a.s. the random connection model has only connected components with finite cardinality. Hence the same must hold for $\mathcal G_{t_0}(\omega ,\mathcal K)$ $\square$

5.4 Simple exclusion processes on infinite clusters

For completeness we give an example associated to the random geometric structure introduced in Sect. 3.1. Recall that there $\mathcal L=(\mathcal V,\mathcal E)$ is the hexagonal lattice, $\Omega =\{0,1\}^{\mathcal V}$, $\mathcal P$ is a Bernoulli site percolation, ${\hat{\omega }} = \mathcal C(\omega )$ is the unique infinite percolation cluster inside $\mathcal L$ $\mathcal P$-a.s. We consider the simple exclusion process on $\mathcal C(\omega )$ with $c_{x,y}(\omega )=1$ if $x,y \in \mathcal C(\omega )$ and $\{x,y\}\in \mathcal E$. The it is trivial to check that Assumptions (A1),$\dots$,(A9) and (SEP) are all satisfied.

We now explain how Theorem 4.1 improves the hydrodynamic result given by [10, Theorem 2.2]. We take ${\mathbb G} :={\mathbb Z} ^d$ and $V:={\mathbb I}$ and define ${\mathbb E} ^d$ as in Example 5.1. We take $\Omega :=[0,+\infty )^{{\mathbb E} ^d}$ with the product topology. The action $(\theta _x)_{x\in {\mathbb Z} ^d}$ is the standard one as in Example 5.1. Let $\mathcal P$ be a probability measure on $\Omega$ stationary, ergodic and fulfilling (A3) for the above action. We assume that for $\mathcal P$-a.a. $\omega$ there exists a unique infinite connected component $\mathcal C(\omega )\subset {\mathbb Z} ^d$ in the graph given by the edges $\{x,y\}$ in ${\mathbb E} ^d$ with positive $\omega _{x,y}:=\omega _{\{x,y\}}$. We set ${\hat{\omega }}:=\mathcal C(\omega )$, $c_{x,y}(\omega ):=\omega _{x,y}$ if $\{x,y\}$ is an edge of $\mathcal C(\omega )$ and $c_{x,y}(\omega ):=0$ otherwise and assume that ${\mathbb E} [c_{0,e_i}]<+\infty$ for $i=1,2,\dots , d$. Then all Assumptions (A1),...,(A9) are satisfied. If at least one of the Items (i), (ii), (iii) in Proposition 5.1 is satisfied, then Assumption (SEP) is satisfied too (by the arguments in the proof of Proposition 5.1) and Theorem 4.1 applies, implying the hydrodynamic limit in path space. This result is stronger than [10, Theorem 2.2], since in [10] $c_{x,y}(\omega )$ has to be bounded uniformly in x, y and $\omega$, D has to be strictly positive definite and the hydrodynamic limit is for a fixed time.

6 Random walk semigroup and resolvent convergence by homogenizaton

In this section we recall the main results from [12] which will be used in the proof of Theorem 4.1. As in Proposition 3.2 we introduce the atomic measure

$$\begin{aligned} \mu _\omega ^\varepsilon := \sum _{ x\in {\hat{\omega }}} \varepsilon ^d \delta _{\varepsilon x}.\end{aligned}$$

(35)

We also introduce the set [recall (19)]

$$\begin{aligned} \begin{aligned} \Omega _1:=\{\omega \in \Omega \,:\, c_x(\omega ) <+\infty \; \forall x \in {\hat{\omega }} ,\;\; c_{x,y}(\omega )=c_{y,x}(\omega ) \;\forall x,y \in {\hat{\omega }}\}. \end{aligned} \end{aligned}$$

(36)

As explained in [12, Section 3.3], the set $\Omega _1$ is translation invariant and satisfies $\mathcal P(\Omega _1)=1$. Let us fix $\omega \in \Omega _1$. We call ${C_\mathrm{loc}}(\varepsilon {\hat{\omega }})$ the space of local functions $f : \varepsilon {\hat{\omega }} \rightarrow {\mathbb R}$ (here local means that f has finite support, i.e. f is zero outside a finite set).

We define

$$\begin{aligned} \mathcal D_\omega ^\varepsilon :=\left\{ f \in L^2(\mu _\omega ^\varepsilon )\,:\, \sum _{x\in {\hat{\omega }}} \sum _{y\in {\hat{\omega }}} c_{x,y}(\omega ) ( f(\varepsilon y) -f (\varepsilon x) )^2 <+\infty \right\} \end{aligned}$$

and introduce the bilinear form

$$\begin{aligned} \mathcal E_\omega ^\varepsilon (f,g) :=\frac{\varepsilon ^{d-2} }{2} \sum _{x\in {\hat{\omega }}} \sum _{y \in {\hat{\omega }} } c_{x,y}(\omega ) \bigl (f(\varepsilon y) - f (\varepsilon x ) \bigr )\bigl ( g(\varepsilon y) - g(\varepsilon x) \bigr ) \end{aligned}$$

with domain $\mathcal D_\omega ^\varepsilon$. Since $\omega \in \Omega _1$ it holds ${C_\mathrm{loc}} (\varepsilon {\hat{\omega }}) \subset \mathcal D_\omega ^\varepsilon$, as explained in [12, Section 3.3]. We call $\mathcal D_{\omega ,*}^\varepsilon$ the closure of ${C_\mathrm{loc}} (\varepsilon {\hat{\omega }})$ w.r.t. the norm $\Vert f\Vert _{L^2(\mu ^\varepsilon _\omega )} + \mathcal E_\omega ^\varepsilon (f,f)^{1/2}$. Then, as stated in [19, Example 1.2.5], the bilinear form $\mathcal E_\omega ^\varepsilon$ restricted to $\mathcal D_{\omega ,*}^\varepsilon$ is a regular Dirichlet form. In particular, there exists a unique nonpositive self-adjoint operator ${\mathbb L} ^\varepsilon _\omega$ in $L^2(\mu ^\varepsilon _\omega )$ such that $\mathcal D_{\omega ,*}^\varepsilon$ equals the domain of $\sqrt{-{{\mathbb L} }^\varepsilon _\omega }$ and $\mathcal E_\omega ^\varepsilon (f,f) = \Vert \sqrt{-{\mathbb L} ^\varepsilon _\omega } f\Vert ^2_{L^2(\mu ^\varepsilon _\omega )}$ for any $f\in \mathcal D_{\omega ,*}^\varepsilon$ (see [19, Theorem 1.3.1]). Due to [19, Lemma 1.3.2 and Exercise 4.4.1], ${\mathbb L} ^\varepsilon _\omega$ is the infinitesimal generator of the strongly continuous Markov semigroup $(P^\varepsilon _{\omega ,t} )_{t \ge 0}$ on $L^2(\mu ^\varepsilon _\omega )$ associated to the random walk $(\varepsilon X^\omega _{ \varepsilon ^{-2} t} )_{t\ge 0}$ on $\varepsilon {\hat{\omega }}$ defined in terms of holding times and jump probabilities (see Lemma 3.1). Hence, $P^\varepsilon _{\omega ,t} f(x) = E_x\bigl [ f(\varepsilon X^\omega _{ \varepsilon ^{-2} t}) \bigr ]$ for $f\in L^2(\mu ^\varepsilon _\omega )$ and $x\in \varepsilon {\hat{\omega }}$, $E_x$ denoting the expectation when the random walk starts at x. For completeness, although not used below, we report that (using that $\omega \in \Omega _1$) one can check that ${C_\mathrm{loc}} (\varepsilon {\hat{\omega }})\subset \mathcal D( {\mathbb L} ^\varepsilon _\omega )$ and that ${\mathbb L} ^\varepsilon _\omega f(\varepsilon x) = {\varepsilon ^{-2}}\sum _{y \in {\hat{\omega }}} c_{x,y}(\omega ) \left( f(\varepsilon y)-f(\varepsilon x) \right)$ for all $x \in {\hat{\omega }},\; \forall f\in {C_\mathrm{loc}}(\varepsilon {\hat{\omega }})$ (the series in the r.h.s. is well defined being absolutely convergent).

We recall that we write $( P_t )_{t \ge 0}$ for the Markov semigroup associated to the Brownian motion $(B_t)_{t\ge 0}$ on ${\mathbb R} ^d$ with diffusion matrix 2D given in Definition 3.3 (strictly speaking it would be natural here to refer to the semigroup on $L^2(mdx)$ but $P_t$ will be applied below to bounded functions, hence one can keep the same definition of $P_t$ as for Theorem 4.1). Given $\lambda >0$ we write $R^\varepsilon _{\omega ,\lambda }: L^2(\mu ^\varepsilon _\omega )\rightarrow L^2(\mu ^\varepsilon _\omega )$ for the resolvent associated to the random walk $\varepsilon X^\omega _{ \varepsilon ^{-2} t}$, i.e. $R^\varepsilon _{\omega ,\lambda }:= (\lambda -{\mathbb L} ^\varepsilon _\omega )^{-1} =\int _0^\infty e^{- \lambda s} P^\varepsilon _{\omega ,s} ds$. We write $R_\lambda : L^2(m dx) \rightarrow L^2(m dx)$ for the resolvent associated to the above Brownian motion $(B_t)_{t\ge 0}$.

Proposition 6.1

[12, Theorem 4.4] Let Assumptions (A1),...,(A9) be satisfied. Then there exists a translation invariant measurable set $\Omega _\sharp \subset \Omega$ with $\mathcal P( \Omega _\sharp )=1$ such that for any $\omega \in \Omega _\sharp$, any $f \in C_c({\mathbb R} ^d)$, $\lambda >0$, $t\ge 0$ it holds:

$$\begin{aligned}&\lim _{\varepsilon \downarrow 0} \int \bigl | P^\varepsilon _{\omega ,t} f(x) - P_t f (x) \bigr | d \mu ^\varepsilon _\omega (x)=0.\end{aligned}$$

(37)

$$\begin{aligned}&\lim _{\varepsilon \downarrow 0} \int \bigl | R^\varepsilon _{\omega ,\lambda } f(x) -R_\lambda f (x) \bigr | d \mu ^\varepsilon _\omega (x)=0. \end{aligned}$$

(38)

Remark 6.2

As stated in [12, Remark 4.5] Assumption (A9) is used in [12] only to prove for $\mathcal P$-a.a. $\omega$ that

$$\begin{aligned} \lim _{\ell \uparrow \infty } \varlimsup _{\varepsilon \downarrow 0} \int d \mu ^\varepsilon _\omega (x)\psi (|x|) \mathbbm {1}_{\{ |x| \ge \ell \}}=0 , \qquad \psi (r):=1/(1+ r^{d+1}) . \end{aligned}$$

(39)

Hence, in Theorem 4.1 one could replace (A9) by any other condition leading to the above property (39) $\mathcal P$-a.s.

For later use, we also point out that the $\omega$’s satisfying (39) form a translation invariant measurable set.

7 Graphical construction of the simple exclusion process

Let $t_0=t_0(\omega )$ be as in Assumption (SEP) in Sect. 4. Recall definition (30) of $\mathcal E_\omega$.

Definition 7.1

(Property $(P_r)$) Given $r\in {\mathbb N}$ we say that the pair $(\omega , \mathcal K)\in \Omega \times D({\mathbb R} _+,{\mathbb N} )^{\mathcal E_\omega }$ satisfies property $(P_r)$ if the undirected graph $\mathcal G^r_{t_0}(\omega ,\mathcal K)$ with vertex set ${\hat{\omega }}$ and edge set $\{ \{x,y\} \in \mathcal E_\omega \,:\, \mathcal K_{x,y}((r+1) t_0)> \mathcal K_{x,y} (r t_0) \}$ has only connected components with finite cardinality.

Recall definition (19) of $c_x(\omega )$.

Definition 7.2

(Set $\tilde{\Omega }$) The set $\tilde{\Omega }$ is given by the elements $\omega \in \Omega$ such that $c_x (\omega )<+\infty \;\forall x \in {\hat{\omega }}$ and such that the properties in Assumptions (A4) and (A5) are fulfilled [namely, (21), (22), (23) hold for all x, y, g].

As already pointed out in Sect. 6, the set $\Omega _1$ defined in (36) is a translation invariant set and $\mathcal P(\Omega _1)=1$. It is trivial to check that the same holds for $\tilde{\Omega }\subset \Omega _1$.

Definition 7.3

(Sets ${\mathbb K} _\omega$, $\Omega _*$) Fixed $\omega \in \Omega$, ${\mathbb K} _\omega$ is the set given by the elements $\mathcal K\in D({\mathbb R} _+,{\mathbb N} )^{\mathcal E_\omega }$ such that

• (i) $(\omega ,\mathcal K)$ satisfies property $(P_r)$ for all $r\in {\mathbb N}$;

• (ii) the jump time sets $\{ t>0\,: \mathcal K_{x,y}(t-)\not = \mathcal K_{x,y} (t) \}$ are disjoint as $\{x,y\}$ varies among $\mathcal E_\omega$;

• (iii) $\mathcal K_x(t):=\sum _{y: \{x,y\}\in \mathcal E_\omega } \mathcal K_{x,y}(t) <+\infty$ for all $x\in {\hat{\omega }}$ and $t\ge 0$.

We define $\Omega _*$ as the set of $\omega \in \tilde{\Omega }$ such that ${\mathbb P} _\omega ( {\mathbb K} _\omega )=1$.

Since $\mathcal P(\tilde{\Omega })=1$ and by the loss of memory of the Poisson point process, we have that $\mathcal P(\Omega _*)=1$. It is simple to check that $\Omega _*$ is translation invariant.

Also for later use, we now recall the graphical construction of the simple exclusion process. To this aim it is convenient to think the simple exclusion process as an exchange process.

Let us fix $\omega \in \Omega _*$ and $\mathcal K\in {\mathbb K} _\omega$. Given a particle configuration $\xi \in \{0,1\}^{{\hat{\omega }}}$ we now define a deterministic trajectory $(\eta ^\xi _t[\mathcal K])_{t \ge 0 }$ in $D({\mathbb R} _+,\{0,1\}^{{\hat{\omega }}} )$ and starting at $\xi$ by an iterative procedure. We set $\eta ^\xi _0[ \mathcal K]:=\xi$. Suppose that the deterministic trajectory has been defined up to time $r t_0$, $r\in {\mathbb N}$ (note that for $r=0$ this follows from our definition of $\eta ^\xi _0[ \mathcal K]$). As $\mathcal K\in {\mathbb K} _\omega$ all connected components of $\mathcal G^r_{t_0}(\omega ,\mathcal K)$ have finite cardinality. Let $\mathcal C$ be such a connected component and let

$$\begin{aligned}&\{s_1<s_2< \cdots<s_k\} \\&\quad =\bigl \{s \,: \mathcal K_{x,y}(s) = \mathcal K_{x,y}(s-)+1 , \;\{x,y\} \text { bond in } \mathcal C, \; r t_0 <s \le (r+1) t_0\bigr \}. \end{aligned}$$

As $\mathcal K\in {\mathbb K} _\omega$, the l.h.s. is indeed a finite set. The local evolution $\eta ^\xi _t[ \mathcal K](z)$ with $z \in \mathcal C$ and $r t_0 < t \le (r+1) t_0$ is described as follows. Start with $\eta ^\xi _{rt_0}[ \mathcal K]$ as configuration at time $r t_0$ in $\mathcal C$. At time $s_1$ exchange the values between $\eta (x)$ and $\eta (y)$ if $\mathcal K_{x,y}(s_1)= \mathcal K_{x,y}(s_1-)+1$ and $\{x,y\}$ is an edge in $\mathcal C$ (there is exactly one such edge as $\mathcal K\in {\mathbb K} _\omega$). Repeat the same operation orderly for times $s_2,s_3, \dots , s_k$. Then move to another connected component of $\mathcal G_{t_0}^r(\omega ,\mathcal K)$ and repeat the above construction and so on. As the connected components are disjoint, the resulting path does not depend on the order by which we choose the connected components in the above algorithm. This procedure defines $(\eta ^\xi _t[\mathcal K])_{ r t_0< t \le (r+1) t_0}$. Starting with $r=0$ and progressively increasing r by 1 we get the trajectory $(\eta ^\xi _t[\mathcal K])_{t\ge 0}$.

We recall that $C(\{0,1\}^{{\hat{\omega }}})$ is the space of continuous functions on $\{0,1\}^{{\hat{\omega }}}$ endowed with the uniform topology. Given $\omega \in \Omega _*$ we consider the probability space $( {\mathbb K} _\omega , {\mathbb P} _\omega )$, and write ${\mathbb E} _\omega$ for the associated expectation. We set

$$\begin{aligned} S(t) f (\xi ) := {\mathbb E} _\omega [ f( \eta ^\xi _t [\mathcal K])] , \qquad t\ge 0 ,\; f \in C(\{0,1\}^{{\hat{\omega }}}). \end{aligned}$$

Proposition 7.4

Take $\omega \in \Omega _*$ and fix $\xi \in \{0,1\}^{{\hat{\omega }}}$. Then the random trajectory $\bigl ( \eta ^\xi _t [\mathcal K]\bigr )_{t\ge 0}$ with $\mathcal K$ sampled in the probability space $( {\mathbb K} _\omega , {\mathbb P} _\omega )$ belongs to the Skorohod space $D( {\mathbb R} _+, \{0,1\}^{{\hat{\omega }}})$ and it starts at $\xi$. It describes a Feller process, called simple exclusion process. In particular, $( S(t) )_{t\ge 0}$ is a Markov semigroup on $C(\{0,1\}^{{\hat{\omega }}})$. Moreover, the domain of its infinitesimal generator $\mathcal L_\omega$ contains the family of local functions and for any local function f the function $\mathcal L_\omega f$ is given by the right hand sides of (7) and (9), which are absolutely convergent series in $C(\{0,1\}^{{\hat{\omega }}})$.

The above proposition can be derived by the standard arguments used for the graphical construction of the SEP usually presented under the assumption of finite range jumps (see e.g. [37, Section 2.1]). The only exception is given by the derivation of the identities (7) and (9) for local functions, due to possible unbounded jump range. We refer to “Appendix B” for the proof of (7) and (9).

8 Duality

In order to prove the tightness of the empirical measure by means of the corrected empirical one, we need to deal with non local functions on $\{0,1\}^{{\hat{\omega }}}$. In what follows we collect the extended results concerning $\mathcal L_\omega$ and Dynkin martingales, which will be used in Sect. 11.1. Recall (19).

In all this section we restrict to $\omega \in \Omega _*$ (cf. Definition 7.3).

Definition 8.1

Given a function $u : \varepsilon {\hat{\omega }} \rightarrow {\mathbb R}$ such that $\sum _{x\in {\hat{\omega }}} c_x (\omega ) |u(\varepsilon x) |<+\infty$, we define $\tilde{{\mathbb L} }^\varepsilon _\omega u(x) :=\varepsilon ^{-2} \sum _{y\in \hat{\omega }} c_{x,y} (\omega ) ( u(\varepsilon y) - u(\varepsilon x) )$.

By symmetry of the jump rates we have

$$\begin{aligned} \sum _{x\in {\hat{\omega }}} \sum _{y\in {\hat{\omega }}} c_{x,y} (\omega ) (| u(\varepsilon x)| + |u(\varepsilon y) |) =2 \sum _{x\in {\hat{\omega }}} c_x(\omega ) | u(\varepsilon x) |. \end{aligned}$$

(40)

Hence, if $\sum _{x\in {\hat{\omega }} } c_x (\omega ) |u(\varepsilon x) |<+\infty$, the series defining $\tilde{\mathbb L} ^\varepsilon _\omega u(x)$ is absolutely convergent for any $x\in {\hat{\omega }}$.

In what follows, to simplify the notation, we write $\pi ^\varepsilon _\omega (u)$, $\pi ^\varepsilon _{\omega ,t}(u)$ for the integral of u w.r.t. $\pi ^\varepsilon _\omega [\eta ]$, $\pi ^\varepsilon _{\omega ,t}[\eta ]$, respectively. Recall that ${\mathbb L} ^\varepsilon _\omega$ is the Markov generator in $L^2(\mu ^\varepsilon _\omega )$ of the random walk $(\varepsilon X_{\varepsilon ^{-2} t}^\omega )_{t\ge 0}$ (see Sect. 6). Recall that $\mathcal L_\omega$ is the Markov generator of the simple exclusion process in the function space $C(\{0,1\}^{{\hat{\omega }}})$ of continuous functions on $\{0,1\}^{\hat{\omega }}$ endowed with the uniform topology (see Proposition 7.4). We now state two lemmas which will be crucial when dealing with the corrected empirical measure. We postpone their proofs to the end of the section.

Lemma 8.2

(Duality) Suppose that $u : \varepsilon {\hat{\omega }} \rightarrow {\mathbb R}$ satisfies

$$\begin{aligned} \sum _{x\in {\hat{\omega }} } |u(\varepsilon x)|<+\infty \text { and } \sum _{x\in {\hat{\omega }} } c_x (\omega ) |u(\varepsilon x)| <+\infty . \end{aligned}$$

(41)

Then $\pi ^{\varepsilon } _{\omega }(u) =\varepsilon ^d\sum _{x\in {\hat{\omega }} } u(\varepsilon x) \eta (x)$ is an absolutely convergent series in $C(\{0,1\}^{{\hat{\omega }}})$. It belongs to the domain $\mathcal D(\mathcal L_\omega ) \subset C(\{0,1\}^{{\hat{\omega }}})$ of $\mathcal L_\omega$ and

$$\begin{aligned} \mathcal L_\omega \left( \pi ^\varepsilon _\omega (u)\right) = \varepsilon ^{d+2} \sum _{x\in {\hat{\omega }}} \eta (x) \tilde{\mathbb L} ^\varepsilon _\omega u (\varepsilon x) , \end{aligned}$$

(42)

the r.h.s. of (42) being an absolutely convergent series in $C(\{0,1\}^{{\hat{\omega }}})$. If, in addition to (41), it holds $u \in \mathcal D( {\mathbb L} ^\varepsilon _\omega )\subset L^2(\mu ^\varepsilon _\omega )$, then ${\mathbb L} ^\varepsilon _\omega u = \tilde{\mathbb L} ^\varepsilon _\omega u$ and in particular we have the duality relation

$$\begin{aligned} \mathcal L_\omega \left( \pi ^\varepsilon _\omega (u)\right) = \varepsilon ^{d+2} \sum _{x\in {\hat{\omega }}} \eta (x) {\mathbb L} ^\varepsilon _\omega u (\varepsilon x) . \end{aligned}$$

(43)

Let $u:\varepsilon {\hat{\omega }} \rightarrow {\mathbb R}$ be a function satisfying (41). As, by Lemma 8.2, $\pi ^{\varepsilon } _{\omega }(u) \in \mathcal D(\mathcal L_\omega )$, we can introduce on the Skorohod space $D\bigl ({\mathbb R} _+, \{0,1\}^{{\hat{\omega }}}\bigr )$ the Dynkin martingale $(\mathcal M^\varepsilon _{\omega ,t})_{t\ge 0}$ given by (see e.g. [26, Appendix 1] or [37, Section 3.2])

$$\begin{aligned} \mathcal M^\varepsilon _{\omega ,t} : = \pi ^{\varepsilon } _{\omega ,t}(u) - \pi ^{\varepsilon } _{\omega ,0}(u) -\varepsilon ^{-2} \int _0 ^t \mathcal L_\omega \left( \pi ^{\varepsilon } _{\omega }(u) \right) (\eta _s) ds . \end{aligned}$$

(44)

$(\mathcal M^\varepsilon _{\omega ,t})_{t\ge 0}$ is a square integrable martingale w.r.t. the filtered probability space $\left( D\bigl ({\mathbb R} _+, \{0,1\}^{{\hat{\omega }}}\bigr ), {\mathbb P} ^\varepsilon _{\omega ,\mathfrak {n}_\varepsilon }, (\mathcal F_t)_{t\ge 0}\right)$, $\mathfrak {n}_\varepsilon$ being an arbitrary initial distribution and $\mathcal F_t$ being the $\sigma$-field generated $\{\eta _s:0\le s\le t\}$. Square integrability follows from the property that $\Vert \mathcal M^\varepsilon _{\omega ,t} \Vert _\infty <+\infty$ as the same holds for all addenda in the r.h.s. of (44) (see Lemma 8.2).

Lemma 8.3

Let $u:\varepsilon {\hat{\omega }} \rightarrow {\mathbb R}$ be a function satisfying (41). Suppose in addition that $\sum _{x\in {\hat{\omega }}} c_x(\omega ) u(\varepsilon x )^2 <+\infty$. Then the sharp bracket process of $\mathcal M^\varepsilon _{\omega ,t}$ is given by $\langle \mathcal M^\varepsilon _{\omega }\rangle _t= \int _0 ^t B^\varepsilon _{\omega } (\eta _s)ds$, where

$$\begin{aligned} B^\varepsilon _{\omega }(\eta ) = \varepsilon ^{2d-2} \sum _{x\in {\hat{\omega }}} \sum _{y \in {\hat{\omega }}} c_{x,y}(\omega )\bigl [u(\varepsilon x)-u(\varepsilon y)\bigr ]^2 \eta (x) \bigl (1- \eta (y) \bigr ). \end{aligned}$$

(45)

Note that the bound $\sum _{x\in {\hat{\omega }}} c_x(\omega ) u(\varepsilon x )^2 <+\infty$ implies that the r.h.s. of (45) is an absolutely convergent series of functions in $C(\{0,1\}^{{\hat{\omega }}})$. For later use, we recall that $\langle \mathcal M^\varepsilon _{\omega }\rangle _t$ can be characterized as the unique predictable increasing process such that $(\mathcal M^\varepsilon _{\omega ,t})^2- \langle \mathcal M^\varepsilon _{\omega }\rangle _t$ is a martingale [28, Theorem 8.24].

Remark 8.4

In the proof of Theorem 4.1 (see Sect. 11.1) we will apply the above Lemmas 8.2 and 8.3 just to functions u of the form $R^\varepsilon _{\omega ,\lambda } \psi$ for suitable functions $\psi \in C_c ({\mathbb R} ^d)$, where $R^\varepsilon _{\omega ,\lambda } \psi$ is the resolvent introduced in Sect. 6.

Proof of Lemma 8.2

As $\sum _{x\in {\hat{\omega }} } |u(\varepsilon x) | <+\infty$, it is simple to check that the series defining $\pi ^{\varepsilon } _{\omega }(u)$ is indeed an absolutely convergent series of continuous functions w.r.t. the uniform norm. The same holds for the series corresponding to the r.h.s. of (42). Indeed, by (40), $\sum _{x\in {\hat{\omega }}} \Vert \eta (x) \tilde{\mathbb L} ^\varepsilon _\omega u (\varepsilon x) \Vert _\infty \le 2 \varepsilon ^{-2} \sum _{x\in {\hat{\omega }} } c_x(\omega ) |u(\varepsilon x) | <+\infty$.

When the function u is local, also the map $\eta \mapsto \pi ^\varepsilon _\omega (u)$ is local. By locality and Proposition 7.4, this map belongs to $\mathcal D(\mathcal L_\omega )$. In the case of local u, (42) follows from easy computations by (9). We now treat the general case. Given $n\in {\mathbb N}$, we define $u_n(\varepsilon x ):= u(\varepsilon x ){\mathbbm {1}}( |\varepsilon x | \le n)$. As observed above, $\pi ^{\varepsilon } _{\omega }(u_n)$ is a local function on $\{0,1\}^{{\hat{\omega }}}$ belonging to $\mathcal D(\mathcal L_\omega )$ and (42) holds with $u_n$ instead of u. We claim that

$$\begin{aligned}&\lim _{n \rightarrow \infty } \Vert \pi ^{\varepsilon } _{\omega }(u_n) - \pi ^{\varepsilon } _{\omega }(u) \Vert _\infty =0 , \end{aligned}$$

(46)

$$\begin{aligned}&\lim _{n \rightarrow \infty }\Vert \sum _{x\in {\hat{\omega }}} \eta (x) \tilde{\mathbb L} ^\varepsilon _\omega u_n (\varepsilon x) - \sum _{x\in {\hat{\omega }}} \eta (x) \tilde{\mathbb L} ^\varepsilon _\omega u (\varepsilon x) \Vert _\infty =0. \end{aligned}$$

(47)

As $\mathcal L_\omega$ is a closed operator being a Markov generator, (42) with $u_n$ instead of u, (46) and (47) imply that $\pi ^{\varepsilon } _{\omega }(u)\in \mathcal D(\mathcal L_\omega )$ and that (42) holds. To prove (46) and (47) it is enough to bound the uniform norms appearing there by, respectively, $\varepsilon ^d\sum _{x\in {\hat{\omega }}: |\varepsilon x|>n}| u(\varepsilon x) |$ and $2 \varepsilon ^{-2}\sum _{x\in {\hat{\omega }}: |\varepsilon x|>n} c_x(\omega ) |u(\varepsilon x) |$ and use (41). This concludes the proof of (42).

It remains to show that ${\mathbb L} ^\varepsilon _\omega u = \tilde{\mathbb L} ^\varepsilon _\omega u$ if $u \in \mathcal D( {\mathbb L} ^\varepsilon _\omega )\subset L^2(\mu ^\varepsilon _\omega )$ in addition to (41). Given a function $f\in C(\{0,1\}^{{\hat{\omega }}})$ we write $S(t) f (\eta ):={\mathbb E} _\eta [ f(\eta _t) ]$ for the Markov semigroup associated to the simple exclusion process (without any time rescaling). Then (42) can be read as

$$\begin{aligned} \lim _{t\downarrow 0}\sup _{\eta \in \{0,1\}^{{\hat{\omega }}} }\Big | \frac{\left( S(t) \pi ^{\varepsilon } _{\omega }(u)\right) (\eta )- \pi ^{\varepsilon } _{\omega }[\eta ](u)}{t}- \varepsilon ^{d+2} \sum _{x\in {\hat{\omega }}} \eta (x) \tilde{\mathbb L} ^\varepsilon _\omega u (\varepsilon x)\Big |=0. \end{aligned}$$

(48)

Given $x_0 \in {\hat{\omega }}$ we take $\eta$ corresponding to a single particle located at $x_0$. Then $\left( S(t) \pi ^{\varepsilon } _{\omega }(u)\right) (\eta )= \varepsilon ^d E_{x_0} [ u ( \varepsilon X^{\omega }_t) ]$ and (48) implies that $\frac{d}{dt} E_{x_0} [ u ( \varepsilon X^{\omega }_{\varepsilon ^{-2}t}) ]_{|t=0}= \tilde{\mathbb L} ^\varepsilon _\omega u (\varepsilon x_0)$. On the other hand, we know that $u \in \mathcal D({\mathbb L} ^\varepsilon _\omega )$. Hence

$$\begin{aligned} \lim _{t\downarrow 0}\sum _{x\in {\hat{\omega }}} \Big | \frac{ E_{x}\big [ u \big ( \varepsilon X^{\omega }_{\varepsilon ^{-2} t}\big )\big ] - u(x)}{t}- {\mathbb L} ^\varepsilon _\omega u (\varepsilon x)\Big |^2 =0, \end{aligned}$$

(49)

which implies that $\frac{d}{dt} E_{x_0} [ u ( \varepsilon X^{\omega }_{\varepsilon ^{-2}t}) ]_{|t=0}= {\mathbb L} ^\varepsilon _\omega u (\varepsilon x_0)$. Then it must be ${\mathbb L} ^\varepsilon _\omega u (\varepsilon x_0)=\tilde{\mathbb L} ^\varepsilon _\omega u (\varepsilon x_0)$. $\square$

Proof of Lemma 8.3

For u local both $\pi ^\varepsilon _\omega (u)$ and its square belong to $\mathcal D(\mathcal L_\omega )$ being local functions of $\eta$. Then the statement in the lemma can be checked by simple computations due to (9), Lemma 8.2 and [26, Lemma 5.1, Appendix 1] (equivalently, [37, Exercise 3.1 and Lemma 8.3]). For the computation of the sharp bracket process we just comment that, by using the symmetry of $c_{x,y}(\omega )$, one easily gets

$$\begin{aligned}&\mathcal L_\omega ( \pi ^\varepsilon _\omega (u)^2 )- 2 \pi ^\varepsilon _\omega (u) \mathcal L_\omega ( \pi ^\varepsilon _\omega (u) ) \\&\quad = \varepsilon ^{2d} \sum _{x\in {\hat{\omega }}} \sum _{y \in {\hat{\omega }}} c_{x,y}(\omega ) [ u(\varepsilon x)- u (\varepsilon y)]^2 \eta (x) (1- \eta (y)). \end{aligned}$$

We now move to the general case. For simplicity of notation we write $\mathcal M_t$, $B(\eta )$ instead of $\mathcal M^\varepsilon _{\omega ,t}$, $B^\varepsilon _\omega (\eta )$. Similarly, we define $\mathcal M_{n,t}$ and $B_n(\eta )$ as in (44) and (45) with u replaced by $u_n$, $u_n(\varepsilon x):= u(\varepsilon x) \mathbbm {1}(|\varepsilon x| \le n)$. Note that $\lim _{n \rightarrow +\infty }\sup _{t\in [0,T]} \Vert \mathcal M_t - \mathcal M_{n,t}\Vert _\infty =0$ for any $T>0$ [see (42), (46) and (47)]. Hence, by the characterization of the sharp bracket process recalled after Lemma 8.3 and by our results for the local case (applied to $u_n$), to get (45) it is enough to show that $\lim _{n\rightarrow \infty } \Vert B_n(\eta )-B(\eta ) \Vert _\infty =0$. To this aim it is enough to show that $\sum _{x\in {\hat{\omega }}} \sum _{y \in {\hat{\omega }}} c_{x,y}(\omega )\bigl [ u_n(\varepsilon x)- u_n (\varepsilon y)\bigr ]^2$ converges, as $n\rightarrow \infty$, to the analogous expression with u instead of $u_n$. This follows from the dominated convergence theorem, by dominating $\bigl [ u_n(\varepsilon x)- u_n (\varepsilon y)\bigr ]^2$ with $2 u(\varepsilon x)^2 + 2 u(\varepsilon y)^2$ and by using that $\sum _{x\in {\hat{\omega }}} \sum _{y \in {\hat{\omega }}} c_{x,y}(\omega )\bigl [ u(\varepsilon x)^2 + u(\varepsilon y)^2\bigr ]=2 \sum _{x\in {\hat{\omega }}} c_x(\omega ) u(\varepsilon x)^2<+\infty$. $\square$

9 Space $\mathcal M$ of Radon measures and Skorohod space $D([0,T], \mathcal M)$

Given a measure $\mu$ on ${\mathbb R} ^d$ and a real function G on ${\mathbb R} ^d$, we will denote by $\mu (G)$ the integral $\int d\mu (x) G(x)$. We denote by $\mathcal M$ the space of Radon measures on ${\mathbb R} ^d$, i.e. locally bounded Borel measures on ${\mathbb R} ^d$. $\mathcal M$ is endowed with the vague topology, for which $\mu _n \rightarrow \mu$ if and only if $\mu _n(f) \rightarrow \mu (f)$ for all $f\in C_c({\mathbb R} ^d)$. This topology can be defined through a metric, that we now recall also for later use (for more details, see e.g. [37, Appendix A.10]). To this aim we set $B_r:=\{x\in {\mathbb R} ^d: |x| \le r\}$. For each $\ell \in {\mathbb N}$ we choose a sequence of functions $(\varphi _{\ell , n})_{n \ge 0}$ such that²

• (i) $\varphi _{\ell , n} \in C^\infty _c ({\mathbb R} ^d)$ and $\varphi _{\ell , n}$ is supported on $B_{\ell +1}$;

• (ii) the family $(\varphi _{\ell , n})_{n \ge 0}$ contains a function with values in [0, 1], equal to 1 on $B_\ell$ and equal to 0 outside $B_{\ell +1}$;

• (iii) for each $\delta >0$ and $\varphi \in C^\infty _c({\mathbb R} ^d)$ with support in $B_\ell$ there exists $n\ge 0$ such that $\Vert \varphi _{\ell , n} - \varphi \Vert _\infty \le \delta$ and $\sup _{i,k=1}^d\Vert \partial ^2_{x_i, x_k} \varphi _{\ell , n} -\partial ^2_{x_i,x_k} \varphi \Vert _\infty \le \delta$.

For the existence of such a set of functions $\varphi _{\ell , n}$ we refer [37, Appendix A] and discuss only Item (iii) which is in part new. To deal with Item (iii) we use an extended version of the classical Weierstrass approximation theorem (see [32, Theorem 1.6.2]) implying that, for any compact set K, the family $\mathcal P$ of polynomial functions with rational coefficients is dense in $C^2({\mathbb R} ^d)$ w.r.t. to the semi-norm $\Vert f\Vert _K := \Vert f\Vert _{L^\infty (K)}+\sum _{i=1}^d \Vert \partial _{x_i} f\Vert _{L^\infty (K)}+ \sum _{i,j=1}^d \Vert \partial ^2_{x_i,x_j} f\Vert _{L^\infty (K)}$. For each $\ell$ fix a function $g_\ell$ as in Item (ii). Given $\varphi \in C^\infty _c({\mathbb R} ^d)$ as in Item (iii), by applying Leibniz rule to $\varphi -g_\ell f= g_\ell (\varphi -f)$, one easily gets that $\Vert \varphi - g_\ell f\Vert _{B_{\ell +1}}\le C(d) \Vert g_\ell \Vert _{B_{\ell +1}} \Vert \varphi - f\Vert _{B_{\ell +1}}$. Hence, to fulfill Item (iii), it is enough to include into $\{\varphi _{\ell ,n}\}$ the countable family of functions $\{ g_\ell f\, : \, f\in \mathcal P\}$.

Definition 9.1

By a relabeling, we write $( \varphi _j)_{j\in {\mathbb N} }$ for the family $( \varphi _{\ell , n})_{ \ell , n \in {\mathbb N} }$.

On $\mathcal M$ we define the metric $d_\mathcal M$ as $d_\mathcal M(\mu , \nu ):= \sum _{j=0}^\infty 2^{-j} \left( 1\wedge | \mu (\varphi _j) -\nu (\varphi _j) | \right)$. It can be proved that $(\mathcal M,d_\mathcal M)$ is a Polish space and that the topology induced by the metric $d_\mathcal M$ coincides with the vague topology (see e.g. [37, Appendix A.10], [5]).

We write $D([0,T],\mathcal M)$ for the Skorohod space of $\mathcal M$-valued càdlàg paths $(\mu _t)_{0\le t \le T}$. We recall (cf. [26, Section 4.1]) that $D([0,T],\mathcal M)$ is a Polish space endowed with the metric

$$\begin{aligned} d\left( \mu _\cdot , \nu _\cdot \right) := \inf _{\lambda \in \Lambda } \max \Big \{ \Vert \lambda \Vert , \sup _{0 \le t \le T} d_\mathcal M\bigl ( \mu _t,\nu _t \bigr ) \Big \} , \end{aligned}$$

(50)

where $\Lambda$ is the set of strictly increasing continuous functions $\lambda :[0,T]\rightarrow [0,T]$ with $\lambda (0)=0$, $\lambda (T)=T$, and $\Vert \lambda \Vert :=\sup _{s\not = t} \big |\ln [(\lambda (t)-\lambda (s))/(t-s)] \big |$. As a subset $A\subset \mathcal M$ is relatively compact if and only if $\sup \{\mu (K) \,:\, \mu \in A\}<+\infty$ for any compact set $K\subset {\mathbb R} ^d$ (cf. [37, Appendix A]), by the same arguments used in the proof of [26, prop 1.7, Chapter 4] one gets the following:

Lemma 9.2

Given an index set $\mathcal A$, a family of probability measures $\{ Q^\alpha \}_{\alpha \in \mathcal A}$ on $D([0,T],\mathcal M)$ is relatively compact (w.r.t. weak convergence) if and only if for any $j\in {\mathbb N}$ the family of probability measures $\{ Q^\alpha \circ \Phi _j ^{-1} \}_{\alpha \in \mathcal A}$ on $D([0,T],{\mathbb R} )$ is relatively compact, where

$$\begin{aligned} \Phi _j: D([0,T],\mathcal M)\ni (\mu _t )_{0\le t\le T} \mapsto (\mu _t(\varphi _j) )_{0\le t\le T}\in D([0,T],{\mathbb R} ). \end{aligned}$$

(51)

Recall that $B_r:=\{x\in {\mathbb R} ^d\,:\,|x|\le r\}$. The following fact can be obtained by suitably modifying and afterwards extend the proof of [37, Theorem A.28 in Appendix A]. W.r.t. the version in [37], we have removed the assumption of non-degenerate diffusion matrix and we have modified the mass bounds.

Lemma 9.3

Let $v_0: {\mathbb R} ^d\rightarrow {\mathbb R}$ be Borel and bounded. Let $\alpha : [0,T]\rightarrow \mathcal M$ be a map such that

• (i) $\alpha$ is continuous when $\mathcal M$ is endowed with the vague topology;

• (ii) $\alpha _0 (dx)=v_0(x) dx$;

• (iii) for all $\varphi \in C_c^\infty ({\mathbb R} ^d)$ and $t \in [0,T]$ it holds

  $$\begin{aligned} \int _{{\mathbb R} ^d} \varphi (x) \alpha _t( dx)= \int _{{\mathbb R} ^d} \varphi (x) \alpha _0(dx) +\int _0^t ds \int _{{\mathbb R} ^d} \nabla \cdot ( D \nabla \varphi )(x) \alpha _s(dx) \,; \end{aligned}$$

  (52)

• (iv) for some constants $C,r_0,\gamma >0$ it holds $\alpha _s( B_r) \le C r^\gamma$ for all $s\in [0,T]$ and all $r\ge r_0$.

Then $\alpha _t(dx)=P_t v_0(x) dx$ for all $t\in [0,T]$.

Proof

We distinguish two cases according to the non-degeneracy of D.

$\bullet$ Case D non-degenerate. The proof is the same of [37, Theorem A.28] apart of modifying [37, Eq. (A.40)]. To this aim, as in [37], let $f\in C_c^\infty ({\mathbb R} ^d)$ be a nonnegative, symmetric function with $\int _{{\mathbb R} ^d} f(x)dx=1$. Set $f^\epsilon (x):=\epsilon ^{-d} f(x/\epsilon )$ and $v^\epsilon (x,t):=\int _{{\mathbb R} ^d} f^\epsilon (x-y)\alpha _t(dy)$. Then [37, Eq. (A.40)] has to be replaced by the bound (for $0<\epsilon \le 1$)

$$\begin{aligned} |v^\epsilon (x,t) |\le \Vert f^\epsilon \Vert _\infty \alpha _t (x+ B_1) \le \Vert f^\epsilon \Vert _\infty \alpha _t( B_{r_0+1+|x|}) \le C \Vert f \Vert _\infty \epsilon ^{-d} (r_0+1+|x|)^\gamma , \end{aligned}$$

which holds uniformly in $t\in [0,T]$ due to Item (iv). The above bound is enough to apply [37, Theorem A.30] (which is a byproduct of [8, Theorems 1 and 7, Section 2.3]). Then one can proceed and conclude as in [37].

$\bullet$ Case D degenerate. Without loss, at cost of a linear change of coordinates, we can assume that D is diagonal with strictly positive eigenvalues on $e_1, e_2, \dots , e_{d_*}$, and zero eigenvalue on $e_{d_*+1}, \dots , e_d$ ($e_1,\dots , e_d$ being the canonical basis). By writing $p_t(\cdot ,\cdot )$ for the probability transition kernel of the Brownian motion on ${\mathbb R} ^{d_*}$ with non-degenerate diffusion matrix $2 \tilde{D}:=(2 D_{i,j})_{1\le i,j \le d_*}$, it holds

$$\begin{aligned} P_t v_0(x',x'') = \int _{{\mathbb R} ^{d_*}} p_t ( x', z') v_0( z', x'' ) dz'\,\qquad (x', x'')\in {\mathbb R} ^{d_*} \times {\mathbb R} ^{d-d_*}= {\mathbb R} ^d. \end{aligned}$$

(53)

Given $\psi \in C_c ^\infty ({\mathbb R} ^{d-d_*})$ with $\psi \ge 0$, we define $\tilde{\alpha }_t (dx')$ as the measure on ${\mathbb R} ^{d_*}$ given by $\tilde{\alpha }_t (B):= \int _{{\mathbb R} ^d} \mathbbm {1}_{B}(x') \psi (x'') \alpha _t(d x', d x'')$ for all Borel $B\subset {\mathbb R} ^{d_*}$. Above, and in what follows, $x'\in {\mathbb R} ^{d_*}$ and $x''\in {\mathbb R} ^{d-d_*}$. Then $\tilde{\alpha }_t\in \mathcal M({\mathbb R} ^{d_*})$, where $\mathcal M({\mathbb R} ^{d_*})$ is defined as $\mathcal M$ but with ${\mathbb R} ^{d_*}$ instead of ${\mathbb R} ^d$. Due to Item (i) the path $\tilde{\alpha }:[0,T]\rightarrow \mathcal M({\mathbb R} ^{d_*})$ is continuous. Due to Item (ii) we have $\tilde{\alpha }_0 ( dx') =\tilde{v}_0(x')d x'$ where $\tilde{v}_0(x'){:=}\int _{{\mathbb R} ^{d-d_*}} v_0 (x',x'') \psi (x'') dx''$ (trivially $\tilde{v}_0$ is bounded and Borel). Moreover, taking $\varphi (x',x''):=\tilde{\varphi }(x')\psi (x'')$ in Item (iii) with $\tilde{\varphi }\in C^\infty _c({\mathbb R} ^{d_*})$, we get that $\int _{{\mathbb R} ^{d_*}} \tilde{\varphi }(x') \tilde{\alpha }_t( dx')= \int _{{\mathbb R} ^{d_*}} \tilde{\varphi }(x') \tilde{\alpha }_0(dx') +\int _0^t ds \int _{{\mathbb R} ^{d_*}} \nabla \cdot (\tilde{D} \nabla \tilde{\varphi })(x') \tilde{\alpha }_s(dx')$. We set $\tilde{B}_r:=\{x'\in {\mathbb R} ^{d_*}\,:\, |x'|\le r\}$ and let $r_\psi$ be the minimal radius such that $\psi$ has support in the ball of ${\mathbb R} ^{d-d_*}$ centered at the origin with radius $r_\psi$. Then, due to Item (iv), it holds $\tilde{\alpha }_s ( \tilde{B}_r) = \int _{{\mathbb R} ^d} \mathbbm {1}_{\tilde{B}_r}(x') \psi (x'') \alpha _s(d x', d x'') \le C 2^\gamma r^\gamma$ if $r \ge \tilde{r}_0:= \max \{r_0,r_\psi \}$. Hence, we have checked that the path $\tilde{\alpha }$ satisfies the same conditions appearing in Lemma 9.3, restated for ${\mathbb R} ^{d_*}$ with D replaced by $\tilde{D}$. By the non-degenerate case we conclude that $\tilde{\alpha }_t (d x')=[ \int _{{\mathbb R} ^{d_*}} dz' p_t (x', z') \tilde{v}_0(z')] dx'$. Hence, for all $\tilde{\varphi }\in C_c({\mathbb R} ^d)$ and $\psi \in C_c ^\infty ({\mathbb R} ^{d-d_*})$ with $\psi \ge 0$, we have

$$\begin{aligned}&\int _{{\mathbb R} ^{d}} \tilde{\varphi }(x') \psi (x'') \alpha _t (dx',dx'') =\int _{{\mathbb R} ^{d_*}} dx' \tilde{\varphi }(x') \int _{{\mathbb R} ^{d_*}} dz' p_t (x', z') \tilde{v}_0(z')\nonumber \\&\quad =\int _{{\mathbb R} ^{d_*}} dx' \int _{{\mathbb R} ^{d-d_*}} d x'' \tilde{\varphi }(x') \psi (x'') \int _{{\mathbb R} ^{d_*}} dz'p_t (x', z') v_0(z',x'')\nonumber \\&\quad = \int _{{\mathbb R} ^{d_*}} dx' \int _{{\mathbb R} ^{d-d_*}} d x'' \tilde{\varphi }(x') \psi (x'') P_t v_0 (x',x''). \end{aligned}$$

(54)

By additivity and density we then get that $\alpha _t(dx) = P_t v_0(x) dx$. $\square$

10 Set $\Omega _\mathrm{typ}$ of typical environments

In this section we describe the set $\Omega _\mathrm{typ}$ of typical environments $\omega$ for which the properties stated in Theorem 4.1 will hold. We denote by $p^\varepsilon _{\omega ,t}(\cdot , \cdot )$ the transition probability kernel of $( \varepsilon X^\omega _{\varepsilon ^{-2} t})_{t\ge 0}$. Recall Definition 9.1.

Definition 10.1

(Set $\hat{\Omega }$) We define $\hat{\Omega }$ as the family of $\omega \in \Omega$ such that

$$\begin{aligned} \sum _{x\in {\hat{\omega }}} \sum _{y \in {\hat{\omega }}:\varepsilon y \in B_r} c_x(\omega ) \int _0^\infty e^{- t} p^\varepsilon _{\omega ,t}(\varepsilon x, \varepsilon y) dt<+\infty \end{aligned}$$

(55)

for all $\varepsilon , r\in (0,+\infty )$, where $B_r:=\{x\in {\mathbb R} ^d\,:\, |x|\le r\}$.

Definition 10.2

(Set $\Omega _\mathrm{typ}$) The set $\Omega _\mathrm{typ}$ is given by the environments $\omega \in \mathcal A[1]\cap \Omega _\sharp \cap \Omega _* \cap \hat{\Omega }$ satisfying (39) (see respectively Propositions 3.2 and 6.1, Definitions 7.3 and 10.1).

Remark 10.3

Due to Proposition 3.2, for any $\omega \in \Omega _\mathrm{typ}$ we have $\lim _{\varepsilon \downarrow 0} \mu ^\varepsilon _\omega (\varphi )= \int _{{\mathbb R} ^d} \varphi (x) m dx$ for all $\varphi \in C_c({\mathbb R} ^d)$.

Given $G\in {\{\varphi _j \}_{j\in {\mathbb N} }}$ and $\lambda >0$, we set $G^{(\lambda )} := \lambda G- \nabla \cdot D \nabla G$. Moreover, we denote by $G_{\omega , \lambda }^\varepsilon \in \mathcal D({\mathbb L} ^\varepsilon _\omega )$ the unique solution of $\lambda G_{\omega ,\lambda }^{\varepsilon }-{\mathbb L} ^\varepsilon _\omega G_{\omega ,\lambda }^{\varepsilon }= G^{(\lambda )}$ in ${\mathbb L} ^2(\mu _\omega ^\varepsilon )$. As $G_{\omega , \lambda }^\varepsilon = \int _0^\infty e^{- \lambda t} P^\varepsilon _{\omega ,t} G ^{(\lambda )} dt$ (for the notation see Sect. 6), we have the integral representation

$$\begin{aligned} G_{\omega , \lambda }^\varepsilon (\varepsilon x)= \sum _{y \in {\hat{\omega }}} \int _0^\infty e^{- \lambda t} p^\varepsilon _{\omega ,t}(\varepsilon x, \varepsilon y) G^{(\lambda )}(\varepsilon y)dt ,\qquad \forall x \in \hat{\omega }. \end{aligned}$$

(56)

Remark 10.4

If $\omega \in \Omega _\mathrm{typ}$, then for all $G\in {\{\varphi _j\}_{j\in {\mathbb N} }}$, $\varepsilon >0$ and $\lambda =1$ it holds

$$\begin{aligned} \sum _{x\in {\hat{\omega }}} c_x(\omega ) |G_{\omega , \lambda }^\varepsilon (\varepsilon x)|<+\infty \,\, \text { and }\,\,\sum _{x\in {\hat{\omega }}} c_x(\omega ) G_{\omega , \lambda }^\varepsilon (\varepsilon x)^2<+\infty . \end{aligned}$$

(57)

Indeed, by (56) we get that $\Vert G_{\omega , \lambda }^\varepsilon \Vert _\infty \le \Vert G^{(\lambda )}\Vert _\infty$. Hence, one has just to check the first bound in (57), which follows from (55) and (56) as $G^{(\lambda )}\in C^\infty _c({\mathbb R} ^d)$.

Proposition 10.5

$\Omega _\mathrm{typ}$ is measurable, translation invariant and $\mathcal P(\Omega _\mathrm{typ})=1$.

Proof

The sets $\mathcal A[1]$, $\Omega _\sharp$, $\Omega _*$ are translation invariant measurable sets of $\mathcal P$-probability one as stated in Propositions 3.2 and 6.1 and after Definition 7.3, respectively. The same holds for the set of $\omega$’s satisfying (39) as stated after Proposition 6.1.

To conclude it is enough to show that $\hat{\Omega }\cap \Omega _*$ is a translation invariant measurable set with $\mathcal P(\hat{\Omega }\cap \Omega _*)=1$. For what concerns measurability, it is enough to show that $\hat{\Omega }$ is measurable. Trivially, in Definition 10.1 one can restrict to $r\in {\mathbb Q} \cap (0,+\infty )$. It is also simple to check that one can restrict also to $\varepsilon \in {\mathbb Q} \cap (0,+\infty )$ by using that, given $0<\varepsilon _*<\varepsilon$ with $\varepsilon _*\in {\mathbb Q}$, it holds

$$\begin{aligned} \int _0^\infty e^{- t} p^\varepsilon _{\omega ,t}(\varepsilon x, \varepsilon y) dt&= \int _0^\infty e^{- t} p^1_{\omega ,\varepsilon ^{-2}t}( x, y) dt = \varepsilon ^2 \int _0^\infty e^{- \varepsilon ^2 s} p^1_{\omega ,s}( x, y) ds \nonumber \\&\le \varepsilon ^2 \int _0^\infty e^{- \varepsilon _* ^2 s} p^1_{\omega ,s}( x, y) ds\nonumber \\&= (\varepsilon /\varepsilon _* )^2 \int _0^\infty e^{- t} p^{\varepsilon _*}_{\omega ,t}(\varepsilon _* x, \varepsilon _* y) dt . \end{aligned}$$

(58)

Since in in Definition 10.1 one can restrict to $r,\varepsilon \in {\mathbb Q} \cap (0,+\infty )$ (hence to a countable set of parameters), we conclude that $\hat{\Omega }$ is measurable.

To prove that $\mathcal P(\hat{\Omega }\cap \Omega _*)=1$, it is enough to prove that, given $r,\varepsilon \in {\mathbb Q} \cap (0,+\infty )$, it holds $H(\omega )<+\infty$ for $\mathcal P$-almost all $\omega \in \Omega _*$ (recall that $\mathcal P(\Omega _*)=1$), where H denotes the l.h.s. of (55).

We treat the case ${\mathbb G} ={\mathbb R} ^d$ (the case ${\mathbb G} ={\mathbb Z} ^d$ can be reduced to the present one by the transformation described in [12, Section 6]). We also assume that $V={\mathbb I}$ in (10), w.l.o.g. at cost to apply an affine transformation. This implies that $\tau _g x= x+g$ and $g(x)=x$ [see (10) and (12)]. Given $\omega \in \Omega _*$ and given $x, y \in {\hat{\omega }}$ (see Definitions 7.2 and 7.3), we then have $p^\varepsilon _{\omega ,t}(\varepsilon x, \varepsilon y)=p^\varepsilon _{\omega ,t}(\varepsilon y, \varepsilon x) = p^\varepsilon _{\theta _y\omega ,t}(0, \varepsilon (x-y))$, $c_x(\omega )=c_{x-y}(\theta _y\omega )$ and $\widehat{\theta _y\omega }=\tau _{-y}{\hat{\omega }}={\hat{\omega }}-y$. We set $F(\xi ):=\sum _{z\in \hat{\xi }} c_z(\xi ) \int _0^\infty e^{- t}p^\varepsilon _{\xi ,t} (0, \varepsilon z) dt$ for $\xi \in \Omega _0=\{\xi \in \Omega \,:\, 0\in \hat{\xi }\}$. By the above observations, given $\omega \in \Omega _*$ we get

$$\begin{aligned} H(\omega ) = \sum _{y \in {\hat{\omega }}:\varepsilon y \in B_r} \sum _{z\in \widehat{\theta _y \omega }} c_z(\theta _y\omega ) \int _0^\infty e^{- t} p^\varepsilon _{\theta _y\omega ,t}(0, \varepsilon z) dt= \sum _{y \in {\hat{\omega }}:\varepsilon y \in B_r}F(\theta _y\omega ). \end{aligned}$$

(59)

Hence, to prove that $\mathcal P(\hat{\Omega }\cap \Omega _*)=1$, we just need to show that the last expression is finite $\mathcal P$-a.s. To this aim we apply Campbell’s identity (see [12, Appendix B]): for any nonnegative measurable function f on ${\mathbb R} ^d\times \Omega _0$ it holds

$$\begin{aligned} \int _{{\mathbb R} ^d}dx \int _{\Omega _0} d\mathcal P_0 ( \omega ) f(x, \omega ) =\frac{1}{m } \int _{\Omega }d\mathcal P(\omega ) \sum _{x\in {\hat{\omega }}} f(x , \theta _x \omega ) \end{aligned}$$

(60)

(we recall that $\mathcal P_0$ denotes the Palm distribution associated to $\mathcal P$). Taking $f(x,\omega ):= \mathbbm {1}_{B_r} (\varepsilon x) F(\omega )$ we get $\varepsilon ^{-d} \ell (B_r) {\mathbb E} _0[ F] = m^{-1} {\mathbb E} [ \sum _{x\in {\hat{\omega }}: \varepsilon x \in B_r} F (\theta _x \omega )]$, where ${\mathbb E} _0,{\mathbb E}$ denote the expectation w.r.t. $\mathcal P_0$, $\mathcal P$ respectively and $\ell (B_r)$ denotes the Lebesgue measure of the ball $B_r$. Hence, to conclude it is enough to show that ${\mathbb E} _0[F]<+\infty$. As it can be easily deduced from the proof of [12, Lemma 3.5], the Palm distribution $\mathcal P_0$ is a reversible and ergodic (w.r.t. time shifts) distribution for the environment viewed from the random walk, i.e. for the process $(\theta _{X_t^\omega }\omega ) _{t\ge 0}$. Indeed, in the proof of [12, Lemma 3.5] we considered the jump chain associated to the environment viewed from the random walk and proved that ${\mathbb E} [c_0]^{-1} c_0(\omega ) d \mathcal P_0(\omega )$ is reversible and ergodic for the jump chain. As accelerating time does not change the class of reversible and ergodic distributions, we get that $\mathcal P_0$ is a reversible and ergodic distribution also for the process $(\bar{\omega }_t)_{t\ge 0}$, $\bar{\omega }_t:=\theta _{ X^\omega _{\varepsilon ^{-2} t}} \omega$. On the other hand, by (A7), ${\mathbb E} _0 [ c_0]={\mathbb E} _0[\lambda _0]<+\infty$. Hence, by the $L^1$-Birkhoff ergodic theorem, we get $\lim _{t\rightarrow +\infty } \frac{1}{t} \int _0^t c_0( \bar{\omega }_s)ds= {\mathbb E} _0[ c_0]$ in $L^1({\mathbb P} _{\mathcal P_0})$, where ${\mathbb P} _{\mathcal P_0}$ is the law of the random path $(\bar{\omega }_t)_{t\ge 0}$ when the starting configuration $\omega$ is sampled with distribution $\mathcal P_0$. As the above limit implies the limit of expectations and $c_0(\theta _z\omega )=c_z(\omega )$, we have

$$\begin{aligned} \lim _{t\rightarrow +\infty } \frac{1}{t} \sum _{z\in {\hat{\omega }}}\int \mathcal P_0(d\omega ) \int _0^t p^\varepsilon _{\omega ,s} (0, \varepsilon z) c_z(\omega ) ds = {\mathbb E} _0 [ c_0]. \end{aligned}$$

(61)

Now note that, for some positive constant C, it holds

$$\begin{aligned} \begin{aligned} F(\omega ) \le C \sum _{n=0}^\infty \frac{e^{- n/2 }}{n+1} \sum _{z\in {\hat{\omega }}} \int _{n}^{n+1} p^\varepsilon _{\omega ,t} (0, \varepsilon z) c_z(\omega ) dt. \end{aligned} \end{aligned}$$

(62)

Hence, setting $a_n:= \frac{1}{n+1} \int \mathcal P_0(d \omega ) \sum _{z\in {\hat{\omega }}} \int _{0}^{n+1} p^\varepsilon _{\omega ,t} (0, \varepsilon z) c_z(\omega ) dt$, we get ${\mathbb E} _0[ F] \le C \sum _{n=0}^\infty e^{- n/2 } a_n$. By (61) we have $\lim _{n\rightarrow \infty } a_n = {\mathbb E} _0 [ c_0]<+\infty$, hence the series $\sum _{n=0}^\infty e^{- n/2 } a_n$ is finite, thus implying that ${\mathbb E} _0[ F] <+\infty$. This concludes the proof that $\mathcal P(\hat{\Omega }\cap \Omega _*)=1$

We now show that $\hat{\Omega }\cap \Omega _*$ is translation invariant (always restricting to ${\mathbb G} ={\mathbb R} ^d$ and $V={\mathbb I}$). Take $\varepsilon , r>0$, $g\in {\mathbb G}$ and $\omega \in \hat{\Omega }\cap \Omega _*$. Then we have

$$\begin{aligned} \begin{aligned} H(\theta _g \omega )&= \sum _{x\in \widehat{\theta _g \omega }} \sum _{y \in \widehat{\theta _g \omega }: \varepsilon y \in B_r } c_x(\theta _g \omega ) \int _0^\infty e^{- t} p^\varepsilon _{\theta _g\omega ,t}(\varepsilon x, \varepsilon y)dt \\&\le \sum _{a\in {\hat{\omega }}}\sum _{b \in {\hat{\omega }}: \varepsilon b \in B_{r+ \varepsilon |g|}} c_a(\omega ) \int _0^\infty e^{- t} p^\varepsilon _{\omega ,t}(\varepsilon a, \varepsilon b)dt <+\infty . \end{aligned} \end{aligned}$$

This proves that $\theta _g (\hat{\Omega }\cap \Omega _*)\subset \hat{\Omega }$ for all $g\in {\mathbb G}$. Using that $\Omega _*$ is translation invariant, it is then trivial to conclude that $\theta _g (\hat{\Omega }\cap \Omega _*)\subset \hat{\Omega }\cap \Omega _*$ for all $g \in {\mathbb G}$, which implies the translation invariance of $\hat{\Omega }\cap \Omega _*$. $\square$

11 Proof of Theorem 4.1

In Proposition 7.4 we discussed the existence of the simple exclusion process for $\omega \in \Omega _*\supset \Omega _\mathrm{typ}$. In Proposition 10.5 we showed that $\Omega _\mathrm{typ}$ is a translation invariant measurable set of $\mathcal P$-probability one. To get the hydrodynamic behavior we will proceed as follows. We fix $\omega \in \Omega _\mathrm{typ}$. We consider the random path $(\pi ^\varepsilon _{\omega ,t} [ \eta _\cdot ])_{0\le t\le T}$ with $\eta _\cdot$ sampled according to ${\mathbb P} ^\varepsilon _{ \omega ,\mathfrak {m}_\varepsilon }$. We call $Q^\varepsilon$ its law, which is a probability measure on $D([0,T], \mathcal M)$. Note that, to simplify the notation, $\omega$ is understood in $Q^\varepsilon$. We call ${Q^\star }$ the law of the deterministic path $\bigl ( \rho (x,t) dx \bigr )_{0\le t\le T}$ in $D([0,T], \mathcal M)$ where $\rho (x,t)= P_t \rho _0(x)$. To get Theorem 4.1 it is enough to prove that, for $\omega \in \Omega _\mathrm{typ}$, $Q^\varepsilon$ weakly converges to ${Q^\star }$. Indeed, this implies the convergence in probability of the random path $(\pi ^\varepsilon _{\omega ,t} [ \eta _\cdot ])_{0\le t\le T}$ towards $\bigl ( \rho (x,t) dx \bigr )_{0\le t\le T}$. As $\bigl ( \rho (x,t) dx \bigr )_{0\le t\le T}\in C([0,T], \mathcal M)$, the above convergence in probability implies (32) (cf. [1, page 124]).

By adapting the method of the corrected empirical process of [22] to the $L^2$-context and the unbounded domain ${\mathbb R} ^d$, we prove the tightness of $\{Q^\varepsilon \}$ in Sect. 11.1 (since $D([0,T], \mathcal M)$ is a Polish space, tightness is here equivalent to relative compactness, cf. [1, Theorems 5.1 and 5.2]). The homogenization result used in this part is given by (38).

After getting tightness, one can proceed in two ways. A first route is to show that all limit points of $\{Q^\varepsilon \}$ must equal $Q^\star$ since concentrated on continuous $\mathcal M$-valued paths solving in a weak sense the hydrodynamic equation with initial value $\rho _0(x) dx$ and satisfying suitable mass bounds on balls. Then one can invoke the uniqueness result for these weak solutions given by Lemma 9.3. This is the route followed in Sect. 11.2 in the same spirit of [22]. Again, the homogenization result used here is given by (38).

We now describe the second route. Due to tightness and by [1, Theorem 13.1], to prove that $Q^\varepsilon \Rightarrow {Q^\star }$ it is enough to show the finite dimensional distribution convergence and, by a union bound, the convergence for the distribution at a fixed time, i.e. that for any $t\ge 0$, $\delta >0$ and $\varphi \in C_c({\mathbb R} ^d)$ it holds

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} {\mathbb P} ^\varepsilon _{ \omega ,\mathfrak {m}_\varepsilon } \left( \Big | \varepsilon ^d \sum _{x \in {\hat{\omega }}} \varphi (\varepsilon x) \eta _t( x) - \int _{{\mathbb R} ^d} \varphi (x) \rho (x,t) dx\Big | >\delta \right) =0. \end{aligned}$$

(63)

This can be obtained by a completely autonomous analysis with two main ingredients: an extension to our context of Nagy’s representation of the simple exclusion process (based on duality with the random walk) and the homogenization limit (37). Note that here one does not need Lemma 9.3. We have discussed this second route in “Appendix C”.

11.1 Relative compactness of the empirical measure

To simplify the notation, we fix once and for all a sequence $\{\varepsilon _n\}$ of positive numbers with $\varepsilon _n \downarrow 0$. In what follows all limits $\varepsilon \downarrow 0$ have to be thought along the above sequence $\{\varepsilon _n\}$. By Lemma 9.2, to prove that the family $\{Q^\varepsilon \}$ is relatively compact as $\varepsilon \downarrow 0$ it is enough to prove that, given $G\in \{\varphi _j\}_{{j\in {\mathbb N} }}$ (cf. Definition 9.1), the $\varepsilon$-parameterized laws of the random paths $(\pi ^\varepsilon _{\omega ,t}(G))_{0\le t\le T}$ form a relatively compact family of probability measures on $D([0,T], {\mathbb R} )$ as $\varepsilon \downarrow 0$. Note that we have dropped from the notation the dependence on the path $\eta _\cdot$. By [26, Theorem 1.3, Chapter 4] and Aldous’ criterion given in [26, Proposition 1.6, Chapter 4], it is enough to prove that

• (i) for every $t\in [0,T]$ and every $\beta >0$, there exists $\ell >0$ such that $\varlimsup _{\varepsilon \downarrow 0} {\mathbb P} _{\omega ,\mathfrak {m}_\varepsilon } ^\varepsilon (| \pi ^\varepsilon _{\omega ,t}(G) |> \ell ) \le \beta$;

• (ii) calling $\mathfrak {I}_T$ the family of stopping times bounded by T w.r.t. to the filtration $(\mathcal F_t)_{t\ge 0}$, with $\mathcal F_t:=\sigma \{ \eta _s: 0 \le s \le t\}$, for any $\beta >0$ it holds

  $$\begin{aligned} \lim _{\gamma \downarrow 0} \varlimsup _{\varepsilon \downarrow 0}\sup _{ \begin{array}{c} \tau \in \mathfrak {I}_T\\ \theta \le \gamma \end{array}}{\mathbb P} ^\varepsilon _{\omega ,\mathfrak {m}_\varepsilon } \left( \left| \pi ^\varepsilon _{\omega ,\tau }(G)-\pi ^\varepsilon _{\omega ,(\tau +\theta )\wedge T }(G)\right| >\beta \right) =0. \end{aligned}$$

  (64)

Item (i) gives no problem. Indeed, $|\pi ^\varepsilon _{\omega ,t}(G) |\le \mu _\omega ^\varepsilon (|G|) \rightarrow \int dx m |G(x)| dx$ as $\omega \in \Omega _\mathrm{typ}$ (cf. Remark 10.3). Item (ii) is more delicate and can be treated by the corrected empirical measure. To this aim we fix $\lambda >0$ (let us take $\lambda =1$ as in Remark 10.4) and define $G^{(\lambda )}\in C^\infty _c({\mathbb R} ^d)$ as

$$\begin{aligned} G^{(\lambda )} := \lambda G- \nabla \cdot D \nabla G ,\end{aligned}$$

(65)

where D is the effective homogenized matrix (see Definition 3.3). As in Sect. 10, we define $G_{\omega ,\lambda }^{\varepsilon }$ as the unique element of $\mathcal D({\mathbb L} ^\varepsilon _\omega )\subset L^2(\mu ^\varepsilon _\omega )$ such that

$$\begin{aligned} \lambda G_{\omega ,\lambda }^{\varepsilon }-{\mathbb L} ^\varepsilon _\omega G_{\omega ,\lambda }^{\varepsilon }= G^{(\lambda )} \qquad \text { in }L^2(\mu ^\varepsilon _\omega ). \end{aligned}$$

(66)

By using the resolvent operators $R_\lambda$ and $R^\varepsilon _{\omega ,\lambda }$ defined in Sect. 6, we can restate the above definitions as

$$\begin{aligned} G=R_\lambda G^{(\lambda )} , \qquad G_{\omega ,\lambda }^{\varepsilon }= R_{\omega ,\lambda }^{\varepsilon }G^{(\lambda )}. \end{aligned}$$

(67)

We point out some standard bounds which we will be useful below. By taking the scalar product with $G_{\omega ,\lambda }^{\varepsilon }$ in the massive Poisson equation (66) and by applying Schwarz inequality, we get that

$$\begin{aligned}&\lambda \Vert G_{\omega ,\lambda }^{\varepsilon }\Vert _{L^2(\mu ^\varepsilon _\omega )} \le \Vert G^{(\lambda )} \Vert _{L^2(\mu ^\varepsilon _\omega )} , \end{aligned}$$

(68)

$$\begin{aligned}&\quad \big \langle G_{\omega ,\lambda }^{\varepsilon }, -{\mathbb L} ^\varepsilon _\omega G_{\omega ,\lambda }^{\varepsilon } \big \rangle _{L^2(\mu ^\varepsilon _\omega )} \le \big \langle G_{\omega ,\lambda }^{\varepsilon }, G^{(\lambda )} \big \rangle _{L^2(\mu ^\varepsilon _\omega )}\le \lambda ^{-1}\Vert G^{(\lambda )} \Vert ^2 _{L^2(\mu ^\varepsilon _\omega )} . \end{aligned}$$

(69)

We also note that

$$\begin{aligned} \big \langle G_{\omega ,\lambda }^{\varepsilon }, -{\mathbb L} ^\varepsilon _\omega G_{\omega ,\lambda }^{\varepsilon } \big \rangle _{L^2(\mu ^\varepsilon _\omega )} = \frac{\varepsilon ^{d-2} }{2} \sum _{x\in {\hat{\omega }}} \sum _{y \in {\hat{\omega }}} c_{x,y}(\omega )\bigl [ G_{\omega ,\lambda }^{\varepsilon } (\varepsilon x)- G_{\omega ,\lambda }^{\varepsilon } (\varepsilon y)\bigr ]^2. \end{aligned}$$

(70)

To justify (70) we proceed as follows. For any $f\in \mathcal D( {\mathbb L} ^\varepsilon _\omega )\subset \mathcal D( \sqrt{- {\mathbb L} ^\varepsilon _\omega })$ we have $\langle f, - {\mathbb L} ^\varepsilon _\omega f \rangle _{L^2(\mu ^\varepsilon _\omega )}= \Vert \sqrt{-{\mathbb L} ^\varepsilon _\omega } f\Vert ^2_{L^2(\mu ^\varepsilon _\omega )}= \mathcal E_\omega ^\varepsilon (f,f)$, the last identity being discussed in Sect. 6. By taking $f=G_{\omega ,\lambda }^{\varepsilon }$, we then get (70).

We now use our homogenization result for the resolvent convergence. Indeed, $\Omega _\mathrm{typ}\subset \Omega _\sharp$ and (67) and (38) imply that

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \varepsilon ^d \sum _{x\in {\hat{\omega }}} | G(\varepsilon x) - G_{\omega ,\lambda }^{\varepsilon } (\varepsilon x)| =0 . \end{aligned}$$

(71)

As $| \pi ^{\varepsilon } _{\omega ,t}(G) -\pi ^{\varepsilon } _{\omega ,t}(G_{\omega ,\lambda }^{\varepsilon }) |\le \varepsilon ^d \sum _{x\in {\hat{\omega }}} | G(\varepsilon x) - G_{\omega ,\lambda }^{\varepsilon } (\varepsilon x)|$, we get

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} {\mathbb P} ^\varepsilon _{\omega , \mathfrak {m}_\varepsilon } \left( \sup _{0\le t\le T} \bigl | \pi ^{\varepsilon } _{\omega ,t}(G) -\pi ^{\varepsilon } _{\omega ,t}\big (G_{\omega ,\lambda }^{\varepsilon }\big ) \bigr | >\delta \right) =0. \end{aligned}$$

(72)

By (72), to get Item (ii), it is enough to prove the same result with G replaced by $G_{\omega ,\lambda }^{\varepsilon }$, i.e. that for any $\beta >0$ it holds

$$\begin{aligned} \lim _{\gamma \downarrow 0} \varlimsup _{\varepsilon \downarrow 0}\sup _{ \begin{array}{c} \tau \in \mathfrak {I}_T\\ \theta \le \gamma \end{array}}{\mathbb P} ^\varepsilon _{\omega ,\mathfrak {m}_\varepsilon } \left( \left| \pi ^\varepsilon _{\omega ,\tau }\big (G_{\omega ,\lambda }^{\varepsilon }\big )-\pi ^\varepsilon _{\omega ,(\tau +\theta )\wedge T }\big (G_{\omega ,\lambda }^{\varepsilon }\big )\right| >\beta \right) =0. \end{aligned}$$

(73)

We have now to deal with the Dynkin martingale associated to $\pi ^{\varepsilon } _{\omega }(G_{\omega ,\lambda }^{\varepsilon })$. We will use below Lemmas 8.2 and 8.3. Let us check their hypotheses. Trivially, $G_{\omega ,\lambda }^{\varepsilon }\in \mathcal D({\mathbb L} ^\varepsilon _\omega )$ (by definition). We claim that

$$\begin{aligned}G_{\omega , \lambda }^\varepsilon \in L^1 (\mu ^\varepsilon _\omega ) ,\;\; \sum _{x\in {\hat{\omega }}} c_x(\omega ) |G_{\omega , \lambda }^\varepsilon (\varepsilon x)|<+\infty ,\;\; \sum _{x\in {\hat{\omega }}} c_x(\omega ) G_{\omega , \lambda }^\varepsilon (\varepsilon x)^2 <+\infty . \end{aligned}$$

The last two bounds follow from Remark 10.4. To derive the first one we observe that, by the integral representation (56) and the symmetry of $p^\varepsilon _{\omega ,t}(\cdot , \cdot )$, it holds $\Vert G_{\omega , \lambda }^\varepsilon \Vert _{L^1(\mu ^\varepsilon _\omega )} \le \Vert G^{(\lambda )}\Vert _{L^1(\mu ^\varepsilon _\omega )} /\lambda <+\infty$.

By applying Lemma 8.2, we get that $\pi ^{\varepsilon } _{\omega }(G_{\omega ,\lambda }^{\varepsilon })$ corresponds to an absolutely convergent series in $C(\{0,1\}^{{\hat{\omega }}})$ and, as function of $\eta$, belongs to the domain of $\mathcal L_\omega$. This observation allows us to introduce the Dynkin martingale

$$\begin{aligned} M^\varepsilon _{\omega ,t} : = \pi ^{\varepsilon } _{\omega ,t}\big (G_{\omega ,\lambda }^{\varepsilon }\big ) - \pi ^{\varepsilon } _{\omega ,0}\big (G_{\omega ,\lambda }^{\varepsilon }\big ) -\varepsilon ^{-2} \int _0 ^t \mathcal L_\omega \left( \pi ^{\varepsilon } _{\omega }\big (G_{\omega ,\lambda }^{\varepsilon } \big ) \right) (\eta _s) ds . \end{aligned}$$

(74)

By (43) and (66), we can rewrite $M^\varepsilon _{\omega ,t}$ as

$$\begin{aligned} M^\varepsilon _{\omega ,t}= \pi ^{\varepsilon } _{\omega ,t}\big (G_{\omega ,\lambda }^{\varepsilon }\big ) - \pi ^{\varepsilon } _{\omega ,0}\big (G_{\omega ,\lambda }^{\varepsilon }\big ) - \varepsilon ^{d} \sum _{x\in {\hat{\omega }}}\int _0^t \eta _s(x) \left( \lambda G_{\omega ,\lambda }^{\varepsilon } - G^{(\lambda )}\right) (\varepsilon x)ds . \end{aligned}$$

(75)

We can now prove (73). Due to (75) it is enough to prove that

$$\begin{aligned}&\lim _{\gamma \downarrow 0} \varlimsup _{\varepsilon \downarrow 0}\sup _{ \begin{array}{c} \tau \in \mathfrak {I}_T\\ \theta \le \gamma \end{array}}{\mathbb P} ^\varepsilon _{\omega ,\mathfrak {m}_\varepsilon } \left( \varepsilon ^{d} \theta \sum _{x\in {\hat{\omega }}} \left| \lambda G_{\omega ,\lambda }^{\varepsilon } - G^{(\lambda )}\right| (\varepsilon x) >\beta /2\right) =0 , \end{aligned}$$

(76)

$$\begin{aligned}&\quad \lim _{\gamma \downarrow 0} \varlimsup _{\varepsilon \downarrow 0}\sup _{ \begin{array}{c} \tau \in \mathfrak {I}_T\\ \theta \le \gamma \end{array}}{\mathbb P} ^\varepsilon _{\omega ,\mathfrak {m}_\varepsilon } \Big ( \Big |M^\varepsilon _{\omega ,(\tau +\theta )\wedge T}- M^\varepsilon _{\omega ,\tau } \Big | >\beta /2\Big )=0. \end{aligned}$$

(77)

$\bullet$ Proof of (76). The inequality inside (76) is indeed deterministic. As $\theta \le \gamma \downarrow 0$, to prove (76) it is enough to prove that

$$\begin{aligned} \varlimsup _{\varepsilon \downarrow 0} \varepsilon ^{d} \sum _{x\in {\hat{\omega }}} \left| \lambda G_{\omega ,\lambda }^{\varepsilon } - G^{(\lambda )}\right| (\varepsilon x)<+\infty . \end{aligned}$$

(78)

We have already observed that $\Vert G_{\omega , \lambda }^\varepsilon \Vert _{L^1(\mu ^\varepsilon _\omega )} \le \Vert G^{(\lambda )}\Vert _{L^1(\mu ^\varepsilon _\omega )} /\lambda$. Then, to get (78) it is enough to apply Remark 10.3.

$\bullet$ Proof of (77). We write ${\mathbb E} ^\varepsilon _{\omega ,\mathfrak {m}_\varepsilon }$ for the expectation w.r.t. ${\mathbb P} ^\varepsilon _{\omega ,\mathfrak {m}_\varepsilon }$. We bound the probability in (77) by $(2/\beta )^{2} {\mathbb E} ^\varepsilon _{\omega ,\mathfrak {m}_\varepsilon } \left[ (M^\varepsilon _{\omega ,(\tau +\theta )\wedge T} - M^\varepsilon _{\omega ,\tau })^2 \right]$. Using that $\tau$ is a stopping time and the form of the sharp bracket process in Lemma 8.3, we get [cf. (69) and (70)]

$$\begin{aligned} {\mathbb E} ^\varepsilon _{\omega ,\mathfrak {m}_\varepsilon } \left[ \big (M^\varepsilon _{\omega ,(\tau +\theta )\wedge T} - M^\varepsilon _{\omega ,\tau }\big )^2 \right]&\le \theta \varepsilon ^{2d-2} \sum _{x\in {\hat{\omega }}} \sum _{y \in {\hat{\omega }}} c_{x,y}(\omega )\bigl [ G_{\omega ,\lambda }^{\varepsilon } (\varepsilon x)- G_{\omega ,\lambda }^{\varepsilon } (\varepsilon y)\bigr ]^2\nonumber \\&= 2 \theta \varepsilon ^d \big \langle G_{\omega ,\lambda }^{\varepsilon } , -{\mathbb L} ^\varepsilon _\omega G_{\omega ,\lambda }^{\varepsilon } \big \rangle _{L^2(\mu ^\varepsilon _\omega )}\nonumber \\&\le 2\theta \varepsilon ^d \lambda ^{-1} \Vert G^{(\lambda )}\Vert ^2_{L^2(\mu ^\varepsilon _\omega )} . \end{aligned}$$

(79)

As $\omega \in \Omega _\mathrm{typ}$ (see Remark 10.3), as $\varepsilon {\downarrow } 0$ we have $\Vert G^{(\lambda )}\Vert ^2_{L^2(\mu ^\varepsilon _\omega )}\rightarrow C_0:= \int dx \,m G^{(\lambda )}(x) ^2$. In conclusion we have proved that the probability in (77) is bounded from above by $(2/\beta )^{2} 2 \theta \varepsilon ^d \lambda ^{-1} ( C_0+o(1))$ as $\varepsilon \downarrow 0$. This implies (77).

11.2 Characterization of the limit points

Recall that $\omega \in \Omega _\mathrm{typ}$ is fixed. Let Q be any limit point $\{Q^\varepsilon \}$ as $\varepsilon \downarrow 0$. We claim that Q is concentrated on paths $\alpha \in D([0,T],\mathcal M)$ satisfying the conditions of Lemma 9.3 with $v_0=\rho _0$. Then, by applying Lemma 9.3, we can conclude that $Q=\delta _{(\rho (x,t) dx)_{0 \le t \le T}}$, thus completing the proof of Theorem 4.1.

Let us prove our claim. Item (ii) in Lemma 9.3 follows from condition (31). We move to Item (iv). We recall that, for any integer $\ell \ge 0$, there is some [0, 1]-valued function $\varphi _{j_0}\in \{\varphi _j\}_{{j\in {\mathbb N} }}$ equal to 1 on $B_\ell$ and equal to zero outside $B_{\ell +1}$. Then, by Remark 10.3, we have for all $t\in [0,T]$ and for a suitable constant C(d) depending only on the dimension d that

$$\begin{aligned} \pi _{\omega ,t}^\varepsilon (\varphi _{j_0}) \le \mu ^\varepsilon _\omega (\varphi _{j_0}) {\mathop {\rightarrow }\limits ^{\varepsilon \downarrow 0}} m\int \varphi _{j_0}(x) dx \le C(d) m \ell ^d . \end{aligned}$$

(80)

Setting $H:=\{ \alpha \,:\, \sup _{0\le t\le T} \alpha _t (\varphi _{j_0}) \le 2 C(d) m \ell ^d \}$, we get $\lim _{\varepsilon \downarrow 0} {\mathbb P} ^\varepsilon _{ \omega ,\mathfrak {m}_\varepsilon }( \pi _{\omega ,\cdot }^\varepsilon \in H )=1$. As H is closed in $D([0,T],\mathcal M)$, we conclude that $Q(H)=1$. By varying $\ell$ in ${\mathbb N}$, this implies Item (iv) in Lemma 9.3 with $\gamma =d$.

We move to Item (iii). By Doob’s inequality and reasoning as in (79) we get

$$\begin{aligned} {\mathbb P} ^\varepsilon _{\omega , \mathfrak {m}_\varepsilon }\left( \sup _{t\in [0,T]} |M^\varepsilon _{\omega ,t} | \ge \delta \right) \le \delta ^{-2} {\mathbb E} ^\varepsilon _{\omega , \mathfrak {m}_\varepsilon }\big ( \big (M^\varepsilon _{\omega ,T} \big )^2\big ) \le 2 \delta ^{-2} T \varepsilon ^d \lambda ^{-1} \Vert G^{(\lambda )}\Vert ^2_{L^2(\mu ^\varepsilon _\omega )} {\mathop {\rightarrow }\limits ^{\varepsilon \downarrow 0}} 0 .\end{aligned}$$

(81)

By (65) and (71) (the latter is due to (38) in Proposition 6.1), we have

$$\begin{aligned} \sup _{0\le t\le T} \Big |\int _0^t \pi ^\varepsilon _{\omega ,s} \left( \lambda G_{\omega ,\lambda }^{\varepsilon } - G^{(\lambda )}- \nabla \cdot D \nabla G \right) ds \Big | \le T \varepsilon ^{d} \sum _{x\in {\hat{\omega }}} | \lambda G_{\omega ,\lambda }^{\varepsilon } - \lambda G | (\varepsilon x) {\mathop {\rightarrow }\limits ^{\varepsilon \downarrow 0}} 0. \end{aligned}$$

(82)

At this point, by combining (72), (75), (81) and (82) we get that

$$\begin{aligned} {\mathbb P} ^\varepsilon _{ \omega ,\mathfrak {m}_\varepsilon } \left( \sup _{0\le t\le T} | \pi ^{\varepsilon } _{\omega ,t}(G) - \pi ^{\varepsilon } _{\omega ,0}(G) -\int _0^t \pi ^{\varepsilon } _{\omega ,s}( \nabla \cdot D \nabla G ) ds |\le \delta \right) =1. \end{aligned}$$

(83)

As a consequence, given $G\in \{\varphi _j\}_{{j\in {\mathbb N} }}$, Q-a.s. it holds $\alpha _t(G)-\alpha _0(G)-\int _0^t \alpha _s ( \nabla \cdot D \nabla G ) ds =0$ for all $0\le t\le T$ (adapt the proof of [37, Lemma 8.7] to show that $\{ \alpha : \sup _{0\le t\le T} | \alpha _t(G) - \alpha _0(G) -\int _0^t \alpha _s ( \nabla \cdot D \nabla G ) ds |\le \delta \}$ is closed in $D([0,T],\mathcal M)$). By the construction of $\{\varphi _j\}_{{j\in {\mathbb N} }}$ in Sect. 9, given a generic $\varphi \in C_c^\infty ({\mathbb R} ^d)$ with support in some $B_\ell$, we know that for each $\delta >0$ there exists $G\in \{\varphi _j\}_{{j\in {\mathbb N} }}$ with support in $B_{\ell +1}$ such that $\Vert G - \varphi \Vert _\infty \le \delta$ and $\sup _{1\le i,k\le d}\Vert \partial ^2_{x_i, x_k} G -\partial ^2_{x_i,x_k} \varphi \Vert _\infty \le \delta$. Hence both $\sup _{0 \le t \le T}\bigl | \alpha _t (G) -\alpha _t(\varphi ) \bigr |$ and $\sup _{0 \le t \le T}\bigl | \alpha _t ( \nabla \cdot D \nabla G ) -\alpha _t( \nabla \cdot D \nabla \varphi ) \bigr |$ can be bounded by $C\delta \sup _{0\le t \le T} \alpha _t(B_{\ell +1})$, where $C=C(D)$. Due to Item (iv) (already proved) and by density, we conclude that Q-a.s. it holds $\alpha _t(\varphi )-\alpha _0(\varphi )-\int _0^t \alpha _s ( \nabla \cdot D \nabla \varphi ) ds =0$ for all $0\le t\le T$ and all $\varphi \in C^\infty _c({\mathbb R} ^d)$. Hence Item (iii) in Lemma 9.3 is verified.

We now check Item (i) in Lemma 9.3. By Remark 10.3, given $G\in \{\varphi _j\}_{{j\in {\mathbb N} }}$ we get

$$\begin{aligned} \sup _{\begin{array}{c} 0\le s\le t\le T\\ |t-s| < \beta \end{array}} \Big | \int _s^t \pi ^{\varepsilon } _{\omega ,u}( \nabla \cdot D \nabla G ) du \Big |\le \beta \varepsilon ^{d} \sum _{x\in {\hat{\omega }}} |\nabla \cdot D \nabla G (\varepsilon x) | {\mathop {\rightarrow }\limits ^{\varepsilon \downarrow 0}} C(G)\beta . \end{aligned}$$

(84)

We set $\tilde{H}:=\{ \alpha \,:\, |\alpha _t(G)-\alpha _s(G)|\le 2 C(G) \beta \text { for all } 0\le s\le t\le T \text { with }|t-s|< \beta \}$. By combining (83) and (84) we get $\lim _{\varepsilon \downarrow 0}{\mathbb P} ^\varepsilon _{ \omega ,\mathfrak {m}_\varepsilon }( \pi _{\omega ,\cdot }^\varepsilon \in \tilde{H})=1$. As $\tilde{H}$ is closed in $D([0,T],\mathcal M)$, we conclude that $Q(\tilde{H})=1$. By varying G among $\{\varphi _j\}_{{j\in {\mathbb N} }}$ and by taking $\beta \downarrow 0$ along a sequence, we get that $Q(C([0,T],\mathcal M) )=1$.

Appendices

Appendix A. An example of degenerate nonzero effective homogenized matrix D

In this appendix we present a model satisfying Assumptions (A1),...(A9) and (SEP) for which the effective homogenized matrix D is nonzero but degenerate.

All product spaces appearing below are endowed with the product topology. We take $\Omega := (0,2)^{{\mathbb Z} ^2} \times (0,2)^{{\mathbb Z} }$. We denote a generic element of $\Omega$ as $\omega =\left( (u_x)_{x\in {\mathbb Z} ^2}, (a_s)_{s\in {\mathbb Z} }\right)$. The probability measure $\mathcal P$ on $\Omega$ is such that, under $\mathcal P$, all coordinates are independent random variables, all $u_x$’s are uniformly distributed on (1, 2) and all $a_s$’s are identically distributed with ${\mathbb E} [a_s^{-1}]=+\infty$. We take $\hat{\omega }:={\mathbb Z} ^2$ and ${\mathbb G} ={\mathbb Z} ^2$. The action of ${\mathbb G}$ on $\Omega$ is the following:

$$\begin{aligned} \theta _g \omega := \left( (u_{x-g})_{x\in {\mathbb Z} ^2}, (a_{s-g_2})_{s\in {\mathbb Z} }\right) \text { if } g=(g_1,g_2)\in {\mathbb Z} ^2 ,\;\; \omega =\left( (u_x)_{x\in {\mathbb Z} ^2}, (a_s)_{s\in {\mathbb Z} }\right) . \end{aligned}$$

${\mathbb G}$ acts on ${\mathbb Z}$ by standard translations: $\tau _g x:= x+g$, $g\in {\mathbb G}$. The random conductance field is defined as

$$\begin{aligned} c_{x,y}(\omega ):= {\left\{ \begin{array}{ll} u_z &{} \text { if } \{x,y\}= \{z, z+e_1\} , \;\;\; z \in {\mathbb Z} ^2 ,\\ a_{z_2} &{} \text { if } \{x,y\}= \{z, z+e_2\} ,\;\;\; z=(z_1,z_2) \in {\mathbb Z} ^2 ,\\ 0 &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$

The geometric idea behind the definition of $\omega$ and the action $(\theta _g)_{g\in {\mathbb Z} ^2}$ is that we attach to each point $x=(x_1,x_2)$ the two numbers $u_x$ and $a_{x_2}$ and we think of $u_x$ as the conductance of the edge $\{x,x+e_1\}$ and of $a_{x_2}$ as the conductance of the edge $\{x,x+e_2\}$.

We claim that all Assumptions (A1),...,(A9) and (SEP) are satisfied. Indeed, trivially $\mathcal P$ is stationary. To check the ergodicity of $\mathcal P$ we introduce the bijection $\Phi : \Omega \rightarrow \Gamma ^{{\mathbb Z} }$ where $\Gamma =(0,2)^{{\mathbb Z} \cup \{*\}}$ as

$$\begin{aligned} \Phi (\omega ) = (\gamma _s) _{s \in {\mathbb Z} }\,\qquad \qquad (\gamma _s)_{t}:= {\left\{ \begin{array}{ll} u_{(t,s)} &{} \text { if } t\in {\mathbb Z} ,\\ a_s &{} \text { if } t=* , \end{array}\right. } \end{aligned}$$

whenever $\omega =\left( (u_x)_{x\in {\mathbb Z} ^2}, (a_s)_{s\in {\mathbb Z} }\right)$. Simply, we organize the elements of $\omega$ in rows having in mind the above geometric idea of $\omega$. We write $\mathcal Q$ for the probability measure on $\Gamma ^{{\mathbb Z} }$ such that $\mathcal Q(\mathcal B):= \mathcal P(\Phi ^{-1}(\mathcal B))$ for all Borel sets $\mathcal B\subset \Gamma ^{{\mathbb Z} }$. Then under $\mathcal Q$ the coordinates $\gamma _s$ are i.i.d. random variables. As a consequence $\mathcal Q$ is ergodic w.r.t. standard shifts of $\Gamma ^{{\mathbb Z} }$. Take now a translation invariant measurable set $\mathcal A\subset \Omega$. Then $\theta _{te_2} \mathcal A=\mathcal A$ for all $t\in {\mathbb Z}$ and therefore $\Phi (\mathcal A)$ is left invariant by the standard shifts of $\Gamma ^{{\mathbb Z} }$. Due to the ergodicity of $\mathcal Q$ we obtain that $\mathcal P(\mathcal A)=\mathcal Q(\Phi (\mathcal A))\in \{0,1\}$. This concludes the proof that $\mathcal P$ is ergodic. All other Assumptions (A2),...,(A9) are trivially satisfied. To check (SEP) it is enough to argue as in the proof of Proposition 5.1 in case (i).

Let us now prove that $D_{1,1}>0$ and $D_{i,j}=0$ for $(i,j)\not = (1,1)$.

As in the derivation of [2, Prop. 4.1] one can lower bound the scalar product $a\cdot Da$ by $C \sum _{x=e_1,e_2} (a\cdot x)^2 / {\mathbb E} [ 1/c_{0,x}(\omega )]$ with $C>0$. Taking $a=e_1$ and using that $c_{0,e_1}(\omega )=u_0 \ge 1$ $\mathcal P$-a.s., we get that $D_{1,1}>0$.

We now show that if $D_{2,2}=0$ then $D_{1,2}=D_{2,1}=0$. Recall that in general D is a symmetric and positive semidefinite matrix. Having nonnegative eigenvalues, the determinant of D is nonnegative, i.e. $D_{1,1} D_{2,2}-D_{1,2}D_{2,1}\ge 0$. Since $D_{2,2}=0$ and $D_{1,2}=D_{2,1}$, we then get that $-D_{1,2}^2\ge 0$, thus implying that $D_{1,2}=D_{2,1}=0$.

It remains to prove that $D_{2,2}=0$. Note that, by (18) and since ${\hat{\omega }}={\mathbb Z} ^2$, it holds $\mathcal P=\mathcal P_0$ and $\Omega =\Omega _0$. Then (25) implies that

$$\begin{aligned} D_{2,2}=\inf _{ f\in L^\infty (\mathcal P) } \frac{1}{2}\int _{\Omega } d\mathcal P(\omega )\sum _{x={\pm }e_1, {\pm }e_2} c_{0,x}(\omega ) \left( x_2- \nabla f (\omega , x) \right) ^2 , \end{aligned}$$

(85)

where $\nabla f (\omega , x) := f(\theta _{x} \omega ) - f(\omega )$. Let $\mathcal W$ be the family of bounded measurable functions on $\Omega$ depending only on the coordinates $(a_s)_{s\in {\mathbb Z} }$. Then $\nabla f (\omega , {\pm }e_1) = f(\theta _{e_ 1}\omega ) - f(\omega )=0$. Using also that $c_{x,y}(\omega ) \le 2$, due to (85) we get

$$\begin{aligned} D_{2,2}&\le 2 \inf _{ f\in \mathcal W} \frac{1}{2}\int _{\Omega } d\mathcal P(\omega )\sum _{x= {\pm }e_2} \left( {\pm }1 - \nabla f (\omega , x) \right) ^2\nonumber \\&=2 \inf _{ f\in L^\infty ( (0,2)^{\mathbb Z} ) } \frac{1}{2}\int _{(0,2)^{\mathbb Z} } d\bar{\mathcal P} ( \bar{a} )\sum _{x= {\pm }1} \left( x - \bar{\nabla } f (\bar{a} , x) \right) ^2 , \end{aligned}$$

(86)

where $\bar{a} \in (0,2)^{{\mathbb Z} }$, $\bar{\mathcal P}$ is the probability measure on $(0,2)^{\mathbb Z}$ making the coordinates into i.i.d. random variables with the same distribution of $a_0$ under $\mathcal P$, $\bar{\theta } _x$ is the standard shift operator on $(0,2)^{{\mathbb Z} }$ and $\bar{\nabla } f (\bar{a} , x) = f(\bar{\theta } _x \bar{a}) - f (\bar{a})$. Then the last expression in (86) is twice the effective homogenized coefficient for the nearest-neighbor random conductance model on ${\mathbb Z}$ with i.i.d. conductances given by $(\bar{a}_s)_{s\in {\mathbb Z} }$. Since $\bar{a}_0^{-1}$ has infinite expectation under $\bar{\mathcal P}$, we get that this coefficient is zero (see the discussion in Sect. 5.1 for $d=1$).

Appendix B. Proof of (7) and (9) for local functions f

Recall the notation of Sect. 7. We take $\omega \in \Omega _*$ and $\xi \in \{0,1\}^{\hat{\omega }}$. Below $\mathcal K$ will always vary in ${\mathbb K} _\omega$, without further mention. Given $t\in (0,t_0]$ we denote by $\mathcal G_{t}(\omega ,\mathcal K)$ the undirected graph with vertex set ${\hat{\omega }}$ and edge set $\{ \{x,y\}\in \mathcal E_\omega \,:\, \mathcal K_{x,y}(t) >0\}$. We recall that $\mathcal E_\omega =\{\{x,y\}\,:\, x,y \in {\hat{\omega }},\, x\not =y \}$. As $\mathcal G_{t}(\omega ,\mathcal K)$ is a subgraph of $\mathcal G_{t_0}(\omega ,\mathcal K)$, the graph $\mathcal G_{t}(\omega ,\mathcal K)$ has only connected components of finite cardinality. Moreover, as $t\le t_0$, one can check that $\eta _t^\xi [\mathcal K]$ can be obtained by the graphical construction detailed in Sect. 7 but working with the graph $\mathcal G_{t}(\omega ,\mathcal K)$ instead of $\mathcal G_{t_0}(\omega ,\mathcal K)$.

Let $f : \{0,1\}^{{\hat{\omega }}} \rightarrow {\mathbb R}$ be a local function. Let $A\subset {\hat{\omega }}$ be a finite set such that $f(\eta )$ is defined in terms only of $\eta (x)$ with $x\in A$. We set $\mathcal E_{A}:=\{\{x,y\} \in \mathcal E_\omega \,:\, \{x,y\} \cap A \not = \emptyset \}$ (as $\omega$ is fixed, in the notation we do not stress the dependence of $\mathcal E_A$ from $\omega$). As $\omega \in \Omega _*\subset \Omega _1$ [see (36) and Definition 7.3], we have

$$\begin{aligned} c_A(\omega ) := \sum _{\{x,y\} \in \mathcal E_{A}} c_{x,y}(\omega )\le \sum _{x\in A} \sum _{y \in {\hat{\omega }}} c_{x,y}(\omega ) = \sum _{x\in A}c_x(\omega ) <+\infty . \end{aligned}$$

(87)

Due to the above bound, it is simple to check that the r.h.s.’s of (7) and (9) are absolutely convergent series in $C(\{0,1\}^{\hat{\omega }})$ defining the same function, that we denote by $\hat{\mathcal L}_\omega f$. Hence we just need to prove that $\mathcal L_\omega f= \hat{\mathcal L}_\omega f$.

We note that $\mathcal K_A(t):= \sum _{\{x,y\} \in \mathcal E_A} \mathcal K_{x,y}(t)$ is a Poisson random variable (cf. also Item (iii) in Definition 7.3) with finite parameter $c_A(\omega )$. In particular, it holds

$$\begin{aligned} {\mathbb P} _\omega ( \mathcal K_A(t) \ge 2) = 1- e^{-c_A(\omega ) t} (1+ c_A(\omega ) t) \le C(\omega ) t^2. \end{aligned}$$

(88)

When $\mathcal K_A(t)=1$, we define the pair $\{x_0,y_0\}$ as the only edge in $\mathcal E_A$ such that $\mathcal K_{x_0,y_0}(t)=1$. To have a univocally defined labelling, we fix a total order $\prec$ of $\hat{\omega }$. If the pair has only one point in A, then we call this point $x_0$ and the other one $y_0$. Otherwise, we call $x_0$ the minimal point inside the pair w.r.t. the order $\prec$.

Claim B.1

Let F be the event that (i) $\mathcal K_A(t)=1$ and (ii) $\{x_0, y_0\}$ is not a connected component of $\mathcal G_t (\omega , \mathcal K)$. Then ${\mathbb P} _\omega (F) =o(t)$.

Proof of Claim B.1

We first show that $F\subset G$, where

$$\begin{aligned} G=\bigl \{ \mathcal K_A(t)=1 , \; x_0\in A ,\; y_0\not \in A ,\; \exists z \in \hat{\omega } \setminus (A \cup \{y_0\}) \text { with } \mathcal K_{y_0,z}(t)\ge 1\bigr \}. \end{aligned}$$

To prove the above inclusion suppose first that $\mathcal K_A(t)=1$ and $x_0,y_0\in A$. Then $\{x_0,y_0\}$ must be a connected component in $\mathcal G_t (\omega ,\mathcal K)$ otherwise we would contradict $\mathcal K_A(t)=1$. Hence, the event F implies that $x_0\in A$ and $y_0 \not \in A$. By F, $\{x_0,y_0\}$ is not a connected component of $\mathcal G_t (\omega ,\mathcal K)$, and therefore there exists a point $z\in \hat{\omega }\setminus \{x_0,y_0\}$ such that $\mathcal K_{x_0,z}(t) \ge 1$ or $\mathcal K_{y_0,z}(t)\ge 1$. The first case cannot indeed occur as $\mathcal K_A(t)=1$. By the same reason, in the second case it must be $z\not \in A$. Hence, we conclude that there exists $z\in \hat{\omega } \setminus (A\cup \{y_0\})$ such that $\mathcal K_{y_0,z}(t)\ge 1$. This concludes the proof that $F\subset G$.

We have

$$\begin{aligned} {\mathbb P} _\omega (G)&\le \sum _{x\in A} \sum _{y \in \hat{\omega } \setminus A} {\mathbb P} _\omega \left( \mathcal K_{x,y}(t)=1 , \sum _{z\in \hat{\omega } \setminus (A\cup \{y\})} \mathcal K_{y,z}(t) \ge 1\right) \nonumber \\&\le t \sum _{x\in A} \sum _{y \in \hat{\omega } } c_{x,y}(\omega ) e^{- c_{x,y}(\omega ) t} \big (1- e^{-c_y(\omega ) t}\big ). \end{aligned}$$

(89)

By (87) and the dominated convergence theorem applied to the last expression in (89), we get $\lim _{t\downarrow 0} {\mathbb P} _\omega (G)/t=0$. As $F\subset G$, the same holds for F. $\square$

Now let H be the event that (i) $\mathcal K_A(t)=1$ and (ii) $\{x_0, y_0\}$ is a connected component of $\mathcal G_t (\omega , \mathcal K)$. Moreover, given $\{x,y\}\in \mathcal E_A$, we set $H_{x,y}:= H \cap \bigl \{\{x_0,y_0\}=\{x,y\}\,\bigr \}$. Due to (88) and Claim B.1 we get

$$\begin{aligned} {\mathbb P} _\omega ( \{\mathcal K_A(t)=0\} \cup H ) = 1-o(t) . \end{aligned}$$

(90)

Hence we have $S(t) f (\xi ) -f(\xi ) =\sum _{ \{x,y\}\in \mathcal E_A}[ f(\xi ^{x,y}) -f (\xi ) ]{\mathbb P} _\omega ( H_{x,y}) + \Vert f\Vert _\infty o(t)$. As ${\mathbb P} _\omega (F)=o(t)$, we can rewrite the r.h.s. as

$$\begin{aligned} \begin{aligned}&\sum _{\{ x,y\}\in \mathcal E_A} [ f(\xi ^{x,y}) -f (\xi ) ]{\mathbb P} _\omega ( \{ \mathcal K_A(t)=1\}\cap \{ \{x_0, y_0\} =\{x,y\}\}) + \Vert f\Vert _\infty o(t)\\&=t \sum _{\{ x,y\}\in \mathcal E_A} [ f(\xi ^{x,y}) -f (\xi ) ] c_{x,y} (\omega ) e^{- c_A(\omega ) t}+ \Vert f\Vert _\infty o(t). \end{aligned} \end{aligned}$$

As $\lim _{t\downarrow 0} o(t)/t = 0$ uniformly in $\xi$, by the dominated convergence theorem we can conclude that $\hat{\mathcal L}_\omega f = \mathcal L_\omega f$.

Appendix C. Convergence at a fixed time

In this appendix we prove (63) for any $\omega \in \Omega _\mathrm{typ}$, $t>0$, $\delta >0$ and $\varphi \in C_c({\mathbb R} ^d)$ [the case $t=0$ follows from (31)]. To this aim recall the semigroups $P_t$ and $P^\varepsilon _{\omega ,t}$ discussed before Proposition 6.1 in Sect. 6. Recall also the sets $\Omega _\sharp$, $\tilde{\Omega }$, $\Omega _*$ and $\Omega _\mathrm{typ}$ (cf. respectively Proposition 6.1, Definitions 7.2, 7.3 and 10.2). One main tool to get (63) will be the following fact, that we will prove at the end:

Lemma C.1

Fix $\omega \in \Omega _\mathrm{typ}$, $\delta >0$, $t>0$, $\varphi \in C_c({\mathbb R} ^d)$ and let $\mathfrak {n}_\varepsilon$ be an $\varepsilon$-parametrized family of probability measures on $\{0,1\}^{\hat{\omega }}$. Then it holds

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} {\mathbb P} ^\varepsilon _{\omega , \mathfrak {n}_\varepsilon } \Big (\Big | \varepsilon ^d \sum _{x\in \hat{\omega }} \varphi (\varepsilon x) \eta _t (x )- \varepsilon ^d \sum _{x\in \hat{\omega }} \eta _0(x) P_{\omega , t}^\varepsilon \varphi (\varepsilon x) \Big | >\delta \Big )=0. \end{aligned}$$

(91)

Remark C.2

The second sum in (91) can be an infinite series. It is anyway absolutely convergent as it can be bounded by $\sum _{x\in \hat{\omega }} P_{\omega , t}^\varepsilon {|\varphi |} (\varepsilon x)= \sum _{x\in \hat{\omega }} |\varphi (\varepsilon x)|$ (by using the symmetry of the rates for $\omega \in \Omega _\mathrm{typ} \subset \Omega _* \subset \tilde{\Omega }$).

Let us first prove (63). As $\int \varphi (x) \rho (x,t) dx= \int \rho _0(x) P_t \varphi (x) dx$, we can bound

$$\begin{aligned}&\Big | \varepsilon ^d \sum _{x \in \hat{\omega }} \varphi (\varepsilon x) \eta _t(x) - \int _{{\mathbb R} ^d} \varphi (x) \rho (x,t) dx \Big |\nonumber \\&\le \Big | \varepsilon ^d \sum _{x\in \hat{\omega }} \varphi (\varepsilon x) \eta _t(x) - \varepsilon ^d \sum _{x\in \hat{\omega }} \eta _0(x) P_{\omega , t}^\varepsilon \varphi (\varepsilon x) \Big |\nonumber \\&\quad + \Big | \varepsilon ^d \sum _{x\in \hat{\omega }} \eta _0(x) P_{\omega , t}^\varepsilon \varphi (\varepsilon x)-\varepsilon ^d \sum _{x\in \hat{\omega }} \eta _0(x) P_t \varphi (\varepsilon x) \Big |\nonumber \\&\quad + \Big | \varepsilon ^d \sum _{x\in \hat{\omega }} \eta _0(x) P_t \varphi (\varepsilon x) - \int _{{\mathbb R} ^d} \rho _0(x) P_t \varphi (x) dx\Big |=:I_1+I_2+I_3. \end{aligned}$$

(92)

Trivially we can bound $I_2 \le \varepsilon ^d \sum _{x\in \hat{\omega }} | P_{\omega , t}^\varepsilon \varphi (\varepsilon x)-P_t \varphi (\varepsilon x) |$. The r.h.s. goes to zero as $\varepsilon \downarrow 0$ as $\Omega _\mathrm{typ}\subset \Omega _\sharp$ [cf. (37)]. By combining this limit with Lemma C.1, to prove (63) we only need to show that $\lim _{\varepsilon \downarrow 0} \mathfrak {m}_\varepsilon (I_3>\delta ) =0$. The continuous function $P_t\varphi$ decays fast to infinity. In particular, for some $C>0$ we have $| P_t\varphi |(z) \le C \psi (|z|)$ for all $z\in {\mathbb R} ^d$, where $\psi (r):=1/(1+ r^{d+1})$. Due to (39) and since $\omega \in \Omega _\mathrm{typ}$, we can fix $\ell$ such that $\int _{{\mathbb R} ^d} \psi (|z|) \mathbbm {1}_{\{ |z| \ge \ell \}}dz < \delta /(5C)$ and $\varlimsup _{\varepsilon \downarrow 0} \int _{{\mathbb R} ^d} d \mu ^\varepsilon _\omega (z)\psi (|z|) \mathbbm {1}_{\{ |z| \ge \ell \}}\le \delta /(5C)$. This implies for $\varepsilon$ small that

$$\begin{aligned} \varepsilon ^d \sum _{x\in {\hat{\omega }} } | P_t \varphi | (\varepsilon x)\mathbbm {1}_{\{ |\varepsilon x | \ge \ell \}}\le \delta /5 , \qquad \int _{{\mathbb R} ^d} |P_t\varphi |(z) \mathbbm {1}_{\{ |z| \ge \ell \}} dz \le \delta /5. \end{aligned}$$

(93)

Then we fix a function $\tilde{\varphi }\in C_c ({\mathbb R} ^d)$ such that $|\tilde{\varphi }| \le | P_t\varphi |$ and $\tilde{\varphi }(x)= P_t\varphi (x)$ if $|x| \le \ell$. Hence, due to (93), to prove that $\lim _{\varepsilon \downarrow 0} \mathfrak {m}_\varepsilon (I_3>\delta ) =0$ it is enough to show that

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \mathfrak {m}_\varepsilon \left( \Big | \varepsilon ^d \sum _{x\in {\hat{\omega }}} \eta _0(x) \tilde{\varphi }(\varepsilon x) - \int _{{\mathbb R} ^d} \rho _0(x)\tilde{\varphi }(x) dx\Big | >\delta /5 \right) =0. \end{aligned}$$

(94)

The above limit follows from our assumption on $\mathfrak {m}_\varepsilon$ [cf. (31) in Theorem 4.1]. This concludes the derivation of (63) assuming Lemma C.1.

We now give the proof of Lemma C.1:

Proof of Lemma C.1

It is convenient here to work with the non speeded-up exclusion process with formal generator $\mathcal L_\omega$ [cf. (7) and (9)]. We write ${\mathbb P} _{\omega , \mathfrak {n}_\varepsilon }$ for its law on the path space $D({\mathbb R} _+, \{0,1\}^{{\hat{\omega }}})$, when starting with distribution $\mathfrak {n}_\varepsilon$. Then we can restate (91) as

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} {\mathbb P} _{\omega , \mathfrak {n}_\varepsilon } \left( \Big | \varepsilon ^d \sum _{x\in {\hat{\omega }}} \varphi (\varepsilon x) \eta _{\varepsilon ^{-2} t} (x )- \varepsilon ^d \sum _{x\in {\hat{\omega }}} \eta _0(x) P_{\omega , t}^\varepsilon \varphi (\varepsilon x) \Big | >\delta \right) =0. \end{aligned}$$

(95)

We divide the proof of (95) in some main steps.

$\bullet$ Step 1: Reduction to distributions $\bar{\mathfrak {n}}_\varepsilon$ concentrating on configurations having a finite number of particles. We think of the exclusion process as built according to the graphical construction described in Sect. 7, after sampling $\eta _0$ with distribution $\mathfrak {n}_\varepsilon$. As $\omega \in \Omega _\mathrm{typ}\subset \Omega _*$ we have ${\mathbb P} _\omega ({\mathbb K} _\omega )=1$. Given $x\in {\hat{\omega }}$, $r \in {\mathbb N}$ and $\mathcal K\in {\mathbb K} _\omega$, we denote by $\mathcal C_r(x)$ the connected component of x in the graph $\mathcal G_{t_0} ^r (\omega , \mathcal K)$. Fix $s\in (r t_0, (r+1) t_0]$. Due to the graphical construction, if we know $\mathcal K$, then to determine $\eta ^\xi _s[\mathcal K](x)$ we only need to know $\eta _{r t_0}^\xi [ \mathcal K](z)$ with $z \in \mathcal C_r(x)$ (and this holds for any $\xi \in \{0,1\}^{{\hat{\omega }}}$). By iterating the above argument we conclude that, knowing $\mathcal K$, the value of $\eta ^\xi _s[\mathcal K](x)$ is determined by $\xi (z)$ as z varies in the finite set

$$\begin{aligned} Q_r(x):=\cup _{z_r \in \mathcal C_r (x) } \cup _{z_{r-1} \in \mathcal C_{r-1}(z_r) } \cdots \cup _{ z_1\in \mathcal C_1(z_2)} \mathcal C_0(z_1).\end{aligned}$$

The above set $Q_r(x)$ is finite as $\mathcal K\in {\mathbb K} _\omega$. As $\varphi$ has compact support, we can take $\ell >0$ such that $\varphi$ has support in the ball $B_\ell$ of radius $\ell$ centered at the origin. Then, by the above considerations, given $t>0$ for $\ell _*=\ell _*(\omega , \varepsilon ,t)$ large enough we have ${\mathbb P} _\omega ( A^c_{\omega ,\varepsilon ,t}) \le \varepsilon$, where

$$\begin{aligned} A_{\omega ,\varepsilon ,t}:=\bigl \{\mathcal K\in {\mathbb K} _\omega \,:\, \cup _{\begin{array}{c} x \in {\hat{\omega }}: \\ \varepsilon |x| \le \ell \end{array}} Q_{r(\varepsilon ^{-2}t)}(x) \subset B_{\ell _*} \bigr \} \end{aligned}$$

and $r(\varepsilon ^{-2}t)$ is the unique integer $r\ge 0$ such that $\varepsilon ^{-2}t\in (r t_0, (r+1) t_0]$. Note that, when the event $A_{\omega ,\varepsilon ,t}$ takes place, the value $\varepsilon ^d \sum _{x\in {\hat{\omega }}} \varphi (\varepsilon x) \eta ^\xi _ { \varepsilon ^{-2} t}[\mathcal K](x)$ depends on $\xi$ only through $\xi (z)$ with $z \in {\hat{\omega }} \cap B_{\ell _*}$.

As $\omega \in \Omega _\mathrm{typ}$ [see (39)] and since $P_t \varphi$ decays fast to infinity, we have $\varlimsup _{L \uparrow \infty }\,\varlimsup _{ \varepsilon \downarrow 0} \int d \mu ^\varepsilon _\omega (z) |P _t \varphi |(z)\mathbbm {1} _{\{| z | > L\}}=0$. In particular, we can fix $L_*=L_*(\varphi , \omega )$, such that $\varlimsup _{ \varepsilon \downarrow 0} \int d \mu ^\varepsilon _\omega (z) |P _t \varphi |(z)\mathbbm {1} _{\{| z | > L_*\}}\le \delta /4$. On the other hand, as $\omega \in \Omega _\mathrm{typ}\subset \Omega _\sharp$ [cf. (37) in Proposition 6.1] for $\varepsilon$ small enough we have $\int d \mu ^\varepsilon _\omega (z) |P_{\omega , t}^\varepsilon \varphi (z)-P_t \varphi (z) |\le \delta /4$. Due to the above observations, for $\varepsilon$ small it holds $\varepsilon ^d \sum _{x\in {\hat{\omega }}: |x | \ge L_* /\varepsilon } \xi (x)| P_{\omega , t}^\varepsilon \varphi | (\varepsilon x) \le \delta /2$ for all $\xi \in \{0,1\}^{{\hat{\omega }}}$.

Call $\overline{\mathfrak {n}}_\varepsilon$ the law of the following random configuration in $\{0,1\}^{{\hat{\omega }}}$: sample $\xi$ with law $\mathfrak {n}_\varepsilon$, then set the particle number of $\xi$ equal to zero at any site $x \in {\hat{\omega }}$ with $|x| > \ell _*\vee (L_*/\varepsilon )$. By the above considerations, to get (95) it is enough to prove the same limit with $\mathfrak {n}_\varepsilon$ replaced by $\overline{\mathfrak {n}}_\varepsilon$ and with $\delta$ replaced by $\delta /2$. The fact that the constant $\ell _*\vee (L_*/\varepsilon )$ depends on $\varepsilon , \omega , \varphi ,t$ does not interfere with the arguments presented below (moreover, $\omega$, $\varphi$, t can be thought as fixed).

$\bullet$ Step 2: special pathwise representation of $\eta ^\xi _t[\mathcal K](x)$. We fix $\xi \in \{0,1\}^{{\hat{\omega }}}$ with a finite number of particles. On the probability space $({\mathbb K} _\omega , {\mathbb P} _\omega )$ (cf. Definition 7.3) we introduce the martingales $(M^\xi _y(t))_{t\ge 0}$, with y varying among $\hat{\omega }$, by setting $M^\xi _y(0):=0$ and

$$\begin{aligned} dM^\xi _{y} (t) :=\sum _{z \in \hat{\omega }} \bigl (\eta ^\xi _{t-}[\mathcal K](z)- \eta _{t-}^\xi [\mathcal K](y)\bigr ) dA_{y,z}(t) , \;\;A_{y,z}(t):= \mathcal K_{y,z}(t) - c_{y,z}(\omega ) t. \end{aligned}$$

(96)

The key observation now, going back to [33] and proved below, is that the symmetry of the jump rates implies the following pathwise representation for all $x \in {\hat{\omega }}$ and $\mathcal K\in {\mathbb K} _\omega$:

$$\begin{aligned} \eta ^\xi _t[\mathcal K](x)= \sum _{y\in {\hat{\omega }}} p_\omega (t,x,y )\xi (y) + \sum _{y \in {\hat{\omega }}} \int _0^t p_\omega (t-s,x,y) dM^\xi _{y} (s). \end{aligned}$$

(97)

Above $p_\omega (t,x,y)$ is the probability to be at y for the random walk $X^\omega _\cdot$ starting at x (before we used the notation $p^1_{\omega ,t}(x,y)$, which would not be very readable in the rest). We first show that the r.h.s. of (97) is well posed and afterwards we check (97) itself.

$\odot$ Step 2.a: the r.h.s. of (97) is well posed. As $\omega \in \Omega _\mathrm{typ}$ it holds $c_y(\omega ):= \sum _{z\in \hat{\omega }}c_{y,z}(\omega ) <+\infty$ for all $y \in {\hat{\omega }}$. As $\mathcal K\in {\mathbb K} _\omega$, by Definition 7.3 we also have $\mathcal K_y(t)<+\infty$ for all $y\in {\hat{\omega }}$ and $t\ge 0$.

As $\xi$ has a finite number of particles, the first sum in the r.h.s. of (97) is trivially finite. We now show that the second sum in the r.h.s. is absolutely convergent, thus implying that the r.h.s. of (97) is well posed. To this aim call $D= D(\mathcal K, \xi )$ the set of points $y\in {\hat{\omega }}$ such that $\eta ^\xi _s[\mathcal K](y)=1$ for some $s\in [0,t]$. By the graphical construction and since $\xi$ has a finite number of particles, D is a finite set. We also note that, if $| \eta ^\xi _{s_-}[\mathcal K](z) - \eta _{s-}[\mathcal K](y)|$ is nonzero, then y or z must belong to D. Hence we can bound

$$\begin{aligned}&\sum _{y \in {\hat{\omega }}} \sum _{z \in {\hat{\omega }}}\int _0^t p_\omega (t-s ,x,y) \big |\eta _{s-}^\xi [\mathcal K](z)- \eta _{s-}^\xi [\mathcal K](y)\big |c_{y,z}(\omega ) ds\nonumber \\ {}&\le t \sum _{y\in D}\sum _{z\in {\hat{\omega }}} c_{y,z}(\omega )+t \sum _{y \in {\hat{\omega }}}\sum _{z\in D} c_{y,z}(\omega ) = 2t \sum _{y\in D}c_y(\omega )<+\infty \end{aligned}$$

(98)

and (using also that $\mathcal K_{y,z}(s)=\mathcal K_{z,y}(s)$)

$$\begin{aligned}&\sum _{y \in {\hat{\omega }}} \sum _{z\in {\hat{\omega }}} \int _0^t p_\omega (t-s,x,y) \big |\eta _{s-}^\xi [\mathcal K](z)- \eta _{s-}^\xi [\mathcal K](y)\big | d\mathcal K_{y,z}(s)\nonumber \\&\le \sum _{y \in {\hat{\omega }}} \sum _{z\in {\hat{\omega }}} \int _0^t \mathbbm {1} (y \in D \text { or } z\in D) d\mathcal K_{y,z}(s) \le 2 \sum _{v\in D} \mathcal K_v(t) <+\infty . \end{aligned}$$

(99)

As a byproduct of (98) and (99) the second series in the r.h.s. of (97) is absolutely convergent.

$\odot$ Step 2.b: proof of (97). We now verify (97) (the proof is different from the one in [33], which does not adapt well to our setting). To this aim we fix $\mathcal K\in {\mathbb K} _\omega$. Recall the finite set D introduced in Step 2.a. Let $t_1<t_2< \cdots <t_n$ be the jump times of the Poisson processes $\mathcal K_v(\cdot )$ up to time t, as v varies among D. Let $a_i,b_i\in {\hat{\omega }}$ be such that $\mathcal K_{a_i,b_i}(t_i)= \mathcal K_{a_i,b_i}(t_i-)+1$ (the pair $\{a_i,b_i\}$ is univocally determined, the way we label its elements will be irrelevant). We set $t_0:=0$, $t_{n+1}:=t$. As (see Step 2.a) the series in the r.h.s. of (97) are absolutely convergent, we have

$$\begin{aligned}&\sum _{y \in {\hat{\omega }}} \int _0^t p_\omega (t-s,x,y) dM^\xi _{y} (s)=A_1-A_2 , \nonumber \\&A_1:=\sum _{i=0}^n \sum _{y \in {\hat{\omega }}} \sum _{z\in \hat{\omega }} \bigl ( \eta ^\xi _{t_i}[\mathcal K](z)- \eta ^\xi _{t_i}[\mathcal K](y) \bigr ) \int _{(t_i,t_{i+1}]} p_\omega (t-s,x,y)d\mathcal K_{y,z}(s) ,\nonumber \\&A_2:= \sum _{i=0}^n \sum _{y \in {\hat{\omega }}} \sum _{z\in \hat{\omega }} c_{y,z}(\omega ) \bigl ( \eta ^\xi _{t_i}[\mathcal K](z)- \eta ^\xi _{t_i}[\mathcal K](y) \bigr ) \int _{t_i}^{t_{i+1}} p_\omega (t-s,x,y) ds . \end{aligned}$$

(100)

Consider the expression $\bigl ( \eta ^\xi _{t_i}[\mathcal K](z)- \eta ^\xi _{t_i}[\mathcal K](y) \bigr ) d\mathcal K_{y,z}(s)$. If it is nonzero, then $\{y,z\}$ intersects D and s is a jump time of $\mathcal K_{y,z}(\cdot )=\mathcal K_{z,y}(\cdot )$. In particular, it must be $s\in \{t_1,t_2,\dots , t_n\}$ and $\{y,z\}=\{a_i,b_i\}$ if $s=t_i$. The above considerations imply that $A_1=\sum _{i=0}^{n-1} C_i$, where

$$\begin{aligned} C_i := \bigl ( \eta ^\xi _{t_i}[\mathcal K](b_{i+1})- \eta ^\xi _{t_i}[\mathcal K](a_{i+1}) \bigr ) \bigl [ p_\omega (t-t_{i+1} ,x,a_{i+1})- p_\omega (t-t_{i+1} ,x,b_{i+1})\bigr ]. \end{aligned}$$

We write $E_x$ for the expectation w.r.t. the random walk $(X^\omega _t)_{t\ge 0}$ on ${\hat{\omega }}$ starting at x. Fixed $i\in \{1,\dots , n\}$, we consider the function $f_i: {\hat{\omega }}\rightarrow {\mathbb R}$ given by $f_i(a):= \eta ^\xi _{t_i}[\mathcal K](a)$. Note that $f_i$ has finite support. Since ${\tilde{{\mathbb L} }_\omega ^1} f_i (y)= \sum _{z\in \hat{\omega }} c_{y,z}(\omega ) \bigl ( \eta ^\xi _{t_i}[\mathcal K](z)- \eta ^\xi _{t_i}[\mathcal K](y) \bigr )$ (cf. Definition 8.1), we have

$$\begin{aligned} \begin{aligned} A_2&=\sum _{i=0}^n \sum _{y\in {\hat{\omega }}} {\tilde{{\mathbb L} }^1_\omega } f_i (y) \int _{t_i}^{t_{i+1}} p_\omega (t-s,x,y) ds\\&= \sum _{i=0}^n \sum _{y\in {\hat{\omega }}} \int _{t- t_{i+1}} ^{t-t_i} p_\omega (s,x,y) {\tilde{{\mathbb L} }^1_\omega } f_i (y) ds = \sum _{i=0}^n \int _{t- t_{i+1}}^{t-t_i} \frac{d}{ds} E_{x} [\eta ^\xi _{t_i}[\mathcal K](X^\omega _s)]ds\\&= \sum _{i=0}^n \left( E_{x} \big [\eta ^\xi _{t_i}[\mathcal K]\big ( X^\omega _{t-t_{i} }\big )\big ]-E_{x} \big [\eta _{t_i}^\xi [\mathcal K]\big ( X^\omega _{t-t_{i+1} }\big )\big ] \right) . \end{aligned} \end{aligned}$$

Note that the third identity can be derived from Proposition 7.4 (recall that $\Omega _\mathrm{typ}\subset \Omega _*$) as the random walk can be thought of as a simple exclusion process with just one particle (having (9) on local functions of $\eta$, it is enough to compute $\mathcal L_\omega F$ with $F(\eta ):= \sum _{a\in \Delta _i} f(a) \eta (a)$, $\Delta _i$ being the finite support of $f_i$, and evaluate $\mathcal L_\omega F$ on configurations with just one particle). Since, for $1\le i \le n$ and $u\in {\hat{\omega }}$, it holds

$$\begin{aligned} \begin{aligned} \eta ^\xi _{ t_i }[\mathcal K](u) = \eta ^\xi _{t_{i-1}}[\mathcal K](u)&+ ( \delta _{u,a_i}-\delta _{u,b_i}) \big [\eta ^\xi _{t_{i-1}}[\mathcal K](b_i) - \eta ^\xi _{t_{i-1}}[\mathcal K](a_i) \big ] , \end{aligned} \end{aligned}$$

we have $E_{x} [\eta ^\xi _{t_i}[\mathcal K](X^\omega _{t-t_{i} })]= E_{x} [\eta ^\xi _{t_{i-1}}[\mathcal K](X^\omega _{t-t_{i} })]+C_{i-1}$. Hence we can write

$$\begin{aligned} \begin{aligned}A_2&= E_{x} \big [\eta ^\xi _0[\mathcal K]\big (X^\omega _{t}\big )\big ]+\sum _{i=1}^n \big (E_{x} \big [\eta ^\xi _{t_{i-1}}[\mathcal K] \big (X^\omega _{t-t_{i} }\big )\big ]+C_{i-1}\big ) -\sum _{i=0}^n E_{x} \big [\eta ^\xi _{t_i}[\mathcal K] \big (X^\omega _{t-t_{i+1} }\big )\big ] \\&= E_{x} \big [\xi \big (X^\omega _{t} \big )\big ]-E_{x}^\omega \big [\eta ^\xi _{t_n}[\mathcal K] \big (X^\omega _{0} \big )\big ]+A_1= \sum _{y\in {\hat{\omega }}} p_\omega (t,x,y )\xi (y)-\eta ^\xi _{t}[\mathcal K](x)+A_1. \end{aligned} \end{aligned}$$

The above identity and (100) imply (97).

$\bullet$ Step 3: Conclusion. Recall that, due to Step 1, to prove (95) it is enough to prove the same limit with $\mathfrak {n}_\varepsilon$ replaced by $\overline{\mathfrak {n}}_\varepsilon$ and with $\delta$ replaced by $\delta /2$. We denote by ${\mathbb E} _\omega$ the expectation w.r.t. ${\mathbb P} _{\omega }$. By the symmetry $p_\omega (t,x,y)= p_\omega (t,y,x)$, we have

$$\begin{aligned} \varepsilon ^d \sum _{x\in {\hat{\omega }}} \varphi (\varepsilon x) \sum _{y\in {\hat{\omega }}} p_\omega (t,x,y )\xi (y)=\varepsilon ^d \sum _{x\in {\hat{\omega }}} \xi (x) P_{\omega , t}^\varepsilon \varphi (\varepsilon x) , \qquad \forall \xi \in \{0,1\}^{{\hat{\omega }}}. \end{aligned}$$

Hence, due to (97), in order to conclude the proof of (95) it is enough to show that

$$\begin{aligned} \lim _{\varepsilon \downarrow 0} \int d \bar{\mathfrak {n}}_\varepsilon (\xi ) {\mathbb E} _{\omega } \left[ \left( \varepsilon ^d \sum _{x\in {\hat{\omega }}} \varphi (\varepsilon x) \sum _{y \in {\hat{\omega }}} \int _0^{ \varepsilon ^{-2} t } p_\omega (\varepsilon ^{-2} t-s,x,y) dM^\xi _{y} (s) \right) ^2\right] =0. \end{aligned}$$

(101)

Due to (96), we can rewrite the expression inside the $(\cdot )$-brackets as

$$\begin{aligned} \begin{aligned}&\mathcal R_\varepsilon ^\xi [\mathcal K]: = \frac{\varepsilon ^d}{2} \sum _{x\in {\hat{\omega }}} \sum _{y \in {\hat{\omega }}} \sum _{z \in {\hat{\omega }}} \varphi (\varepsilon x) \cdot \\&\;\;\;\; \int _0^{\varepsilon ^{-2} t} \big [ \eta _{s-}^\xi (z) - \eta _{s-}^\xi (y)\big ] \bigl ( p_\omega (\varepsilon ^{-2} t-s,x,y) - p_\omega (\varepsilon ^{-2} t-s, x,z)\bigr ) d A_{y,z} (s) \\&\quad = \frac{\varepsilon ^d}{2} \sum _{y \in {\hat{\omega }}} \sum _{z \in {\hat{\omega }}} \int _0^{\varepsilon ^{-2} t} \big [ \eta _{s-}^\xi (z) - \eta _{s-}^\xi (y)\big ] \left( P^1_{\omega , \frac{t}{\varepsilon ^2}-s } \varphi (\varepsilon y)- P^1_{\omega ,\frac{t}{ \varepsilon ^{2} }-s} \varphi (\varepsilon z)\right) d A_{y,z} (s) \end{aligned} \end{aligned}$$

where $\eta _\cdot ^\xi =\eta _\cdot ^\xi [\mathcal K]$. As the $A_{y,z}(\cdot )$’s are orthogonal martingales by varying $\{y,z\}$ (while $A_{y,z}(\cdot )=A_{z,y}(\cdot )$), similarly to [33] we get (using the symmetry of $p_\omega (s, \cdot , \cdot )$)

$$\begin{aligned} \begin{aligned}&\int d \bar{\mathfrak {n}}_\varepsilon (\xi ) {\mathbb E} _{\omega } \big [(\mathcal R_\varepsilon ^\xi )^2\big ]\le \frac{\varepsilon ^{2d}}{{2}}\sum _{y \in {\hat{\omega }} } \sum _{z \in {\hat{\omega }}}\int _0^{\varepsilon ^{-2} t} c_{y,z}(\omega ) \bigl ( P^1_{\omega , s} \varphi (\varepsilon y)- P^1_{\omega , s} \varphi (\varepsilon z)\bigr )^2ds\\&\quad ={\varepsilon ^d} \int _0^{ t} \langle P^\varepsilon _{\omega , s} \varphi , - {\mathbb L} _\omega ^\varepsilon P^\varepsilon _{\omega , s} \varphi \rangle _{L^2 (\mu _\omega ^\varepsilon )}= -\frac{\varepsilon ^d}{{2}} \int _0^{ t} \frac{d}{ds} \Vert P^\varepsilon _{\omega , s} \varphi \Vert ^2_{L^2(\mu _\omega ^\varepsilon )}ds\\&\quad = \frac{\varepsilon ^d}{{2}} \Vert P^\varepsilon _{\omega , 0} \varphi \Vert ^2_{L^2(\mu _\omega ^\varepsilon )}-\frac{ \varepsilon ^d}{{2}} \Vert P^\varepsilon _{\omega , t} \varphi \Vert ^2_{L^2(\mu _\omega ^\varepsilon )} \le \frac{ \varepsilon ^d}{{2}} \Vert \varphi \Vert ^2_{L^2(\mu _\omega ^\varepsilon )}{\mathop {\longrightarrow }\limits ^{\varepsilon \rightarrow 0}}0. \end{aligned} \end{aligned}$$

This concludes the proof of (101). $\square$