Abstract
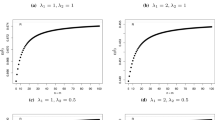
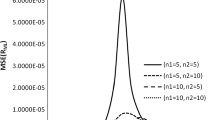
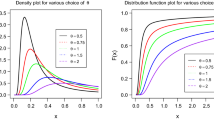
The problem of estimating R = P(X < Y) originated in the context of reliability where Y represents the strength subjected to a stress X. In this paper we consider the problem of estimating R when X and Y have independent normal distributions with equal coefficient of variation. The maximum likelihood estimation of R when the coefficient of variation is known and when it is unknown is studied. The asymptotic variance of the estimators are obtained and asymptotic confidence intervals are provided. An example is presented to illustrate the procedure. Finally some simulation studies are carried out to study the coverage probability and the lengths of the confidence interval. In particular, lengths of the confidence intervals are compared with and without the assumption of common coefficient of variation. It is observed that the assumption of common coefficient of variation results in considerably tighter intervals.
Similar content being viewed by others
REFERENCES
Awad, A. N. and Gharraf, M. K. (1986). Estimation of P(Y < X) in the Burr case: a comparative study, Comm. Statist. Simulation Comput., 15(2), 389–403.
Bamber, D. (1975). The area above the ordinal dominance graph and the area below the receiver operating characteristic graphs, J. Math. Psych., 12, 387–415.
Birnbaum, Z. W. (1956). On a use of Mann-Whitney statistics, Proc. Third Berkeley Symp. in Math. Statist. Probab., Vol. I, 13–17, Univ. of California Press, Berkeley.
Casella, G. and Berger, R. L. (1990). Statistical Inference, Brooks/Cole, Pacific Grove.
Church, J. D. and Harris, B. (1970). The estimation of reliability from stress-strength relationship, Technometrics, 12, 49–54.
Constantine, K., Tse, S. and Karson, M. (1986). Estimation of P(Y < X) in the gamma case, Comm. Statist. Simulation Comput., 15(2), 365–388.
Downton, F. (1973). The estimation of P(Y < X) in the normal case, Technometrics, 15, 551–558.
Gerig, T. M. and Sen, A. R. (1980). MLE in two normal samples but unknown population coefficients of variations, J. Amer. Statist. Assoc., 75, 704–708.
Govindarajulu, Z. (1967). Two sided confidence limits for P(X < Y) based on normal samples of X and Y, Sankhya Ser. B, 29, 35–40.
Gupta, R. C. and Ma, S. (1996). Testing the equality of coefficients of variation in k normal populations, Comm. Statist. Theory Methods, 25(1), 115–132.
Halperin, M., Gilbert, P. R. and Lachin, J. M. (1987). Distribution free confidence intervals for P(X 1 < X 2), Biometrics, 43, 71–80.
Kendall, M. G. and Stuart, A. (1967). The Advanced Theory of Statistics, Vol. 2, Hafner Publishing, New York.
Lohrding, R. K. (1969a). A test of equality of two normal means assuming homogeneous coefficients of variation, Ann. Math. Statist., 40(4), 1374–1385.
Lohrding, R. K. (1969b). Likelihood ratio tests of equal mean when the variances are heterogeneous, Ph.D. Dissertation, Kansas State University, Manhattan, Kansas.
Mazumdar, M. (1970). Some estimates of reliability using interference theory, Naval Res. Logist. Quart., 17, 159–165.
McCool, J. I. (1991). Inference on P(Y < X) in the Weibull case, Comm. Statist. Simulation Comput., 20(1), 129–148.
Nelson, W. (1990). Accelerated Testing, Wiley, New York.
Owen, D. B., Craswell, K. J. and Hanson, D. L. (1964). Nonparametric upper confidence bounds for P(Y < X) and confidence limits for P(Y < X) when X and Y are normal, J. Amer. Statist. Assoc., 59, 906–924.
Rao, C. R. (1965). Linear Statistical Inference and Its Applications, Wiley, New York.
Reiser, B. and Faraggi, D. (1994). Confidence bounds for Pr(a'x > b'y), Statistics, 25, 107–111.
Reiser, B. and Guttman, I. (1986). Statistical inference for P(Y < X): normal case, Technometrics, 28, 253–257.
Reiser, B. and Guttman, I. (1987). A comparison of three point estimators for P(Y < X) in the normal case, Comput. Statist. Data Anal., 5, 59–66.
Simonoff, J. S., Hochberg, Y. and Reiser, B. (1986). Alternative estimation procedures for Pr(X < Y) in categorized data, Biometrics, 42, 895–907.
Sinha, B. K., Rao, B. R. and Clement, B. (1978). Behrens-Fisher problem under the assumption of homogeneous coefficients of variation. Comm. Statist. Theory Methods. 7, 637–656.
Wolfe, D. A. and Hogg, R. V. (1971). On constructing statistics and reporting data, Amer. Statist., 25, 27–30.
Author information
Authors and Affiliations
About this article
Cite this article
Gupta, R.C., Ramakrishnan, S. & Zhou, X. Point and Interval Estimation of P(X < Y): The Normal Case with Common Coefficient of Variation. Annals of the Institute of Statistical Mathematics 51, 571–584 (1999). https://doi.org/10.1023/A:1003910408020
Issue Date:
DOI: https://doi.org/10.1023/A:1003910408020