Fact Checking in Knowledge Graphs with Ontological Subgraph Patterns

Abstract

Given a knowledge graph and a fact (a triple statement), fact checking is to decide whether the fact belongs to the missing part of the graph. Facts in real-world knowledge bases are typically interpreted by both topological and semantic context that is not fully exploited by existing methods. This paper introduces a novel fact checking method that explicitly exploits discriminant subgraph structures. Our method discovers discriminant subgraphs associated with a set of training facts, characterized by a class of graph fact checking rules. These rules incorporate expressive subgraph patterns to jointly describe both topological and ontological constraints. (1) We extend graph fact checking rules (${\mathsf{GFCs}}$) to a class of ontological graph fact checking rules (${\mathsf{OGFCs}}$). ${\mathsf{OGFCs}}$ generalize ${\mathsf{GFCs}}$ by incorporating both topological constraints and ontological closeness to best distinguish between true and false fact statements. We provide quality measures to characterize useful patterns that are both discriminant and diversified. (2) Despite the increased expressiveness, we show that it is feasible to discover ${\mathsf{OGFCs}}$ in large graphs with ontologies, by developing a supervised pattern discovery algorithm. To find useful ${\mathsf{OGFCs}}$ as early as possible, it generates subgraph patterns relevant to training facts and dynamically selects patterns from a pattern stream with a small update cost per pattern. We verify that ${\mathsf{OGFCs}}$ can be used as rules and provide useful features for other statistical learning-based fact checking models. Using real-world knowledge bases, we experimentally verify the efficiency and the effectiveness of ${\mathsf{OGFC}}$-based techniques for fact checking.

1 Introduction

Knowledge graphs have been utilized to support emerging applications, for example, Web search [8], recommendation [33], and decision making [17]. Real-life knowledge bases often contain two components: (1) a knowledge graph G that consists of a set of facts, where each fact is a triple statement 〈$v_x$, $\texttt {{ r}}, v_{y}$〉, that contains a subject entity $v_x$, an object entity $v_y$, and a predicate r that encodes the relationship between $v_x$ and $v_y$; and (2) an external ontology O [7, 35, 46] to support organizing meta-data such as types and labels. An ontology is typically a graph that contains a set of concepts and their relationships in terms of semantic closeness, such as ${\mathsf{subclassOf}}$, ${\mathsf{isSameAs}}$, ${\mathsf{Synonym}}$ [2, 46, 48]. Among the cornerstones of knowledge base management is the task of fact checking. Given a knowledge graph G and a fact t, it is to decide whether t belongs to the missing part of G. The verified facts can be used to (1) directly refine incomplete knowledge bases [3, 8, 23, 32], (2) provide cleaned evidence for error detection in dirty knowledge bases [4, 16, 27, 44], (3) improve the quality of knowledge search [31, 34], and (4) integrate multiple knowledge bases [8, 10].

Facts in knowledge graphs are often associated with nontrivial regularities that are jointly described by imposing both topological constraints and ontological closeness. Such regularities can be captured by subgraphs associated with the facts. How to exploit these associated subgraphs and ontologies to effectively support fact checking in knowledge graphs? Consider the following example.

Example 1.

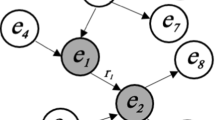
The graph $G_1$ in Fig. 1 illustrates a fraction of DBpedia [23] that depicts the facts about philosophers (e.g., “Plato”). The knowledge base is associated with an ontology $O_1$, which depicts semantic relationships among the concepts (e.g., “philosopher”) that are referred by the entity type in $G_1$. A user is interested in finding “whether a logician (‘Cicero’) or a theologian (‘St. Augustine’) as $v_x$ is influenced by a philosopher (‘Plato’) as $v_y$”.

It is observed that graph patterns help explain the existence of certain entities and relationships in knowledge bases [26]. Consider a rule represented by a graph pattern $P_1$ associated with philosophers, which states that “if a philosopher $v_x$gave one or more speeches that cited a book of $v_y$with the same topic, then $v_x$is likely to be influenced by $v_y$”. One may want to apply this rule to verify whether Cicero is influenced by Plato. Nevertheless, such rule cannot be directly applied, as Cicero is not directly labeled by “philosopher”. On the other hand, as “logician” (resp. “masterpiece”) is a type semantically close to the concept “philosopher” (resp. “speech”) in the philosopher ontology $O_1$, “Cicero” and “Plato” should be considered as matches of $P_1$, and the triple 〈Cicero, $\texttt {influencedBy}$, Plato〉 should be true in $G_1$. Similarly, another fact 〈St. Augustine, $\texttt {influencedBy}$, Plato〉 should be identified as true facts, given that (a) “theologian” and “writtenWork” are semantically close to “philosopher” and “book” in $O_1$, respectively, and (b) there is a subgraph of $G_1$ that contains “St. Augustine” and “Plato,” and matches $P_1$.

Consider another example, a business knowledge base $G_2$ from a fraction of a real-world offshore activity network [19] in Fig. 1. To find whether an active broker (close to active intermediary) $\texttt {A}$ is likely to serve a company $\texttt {C}$ in transition, a pattern $P_2$ that explains such an action may identify $G_2$ by stating that “${\texttt {\textit{A}}}$ is likely an intermediary of ${\texttt {\textit{C}}}$ if it served for a dissolved (closed) company ${\texttt {\textit{D}}}$, which has the same shareholder ${\texttt {\textit{O}}}$ and one or more service providers with ${\texttt {\textit{C}}}$”.

Subgraph patterns with “weaker” constraints may not explain facts well. Consider a graph pattern $P_1'$ obtained by removing the edge $\texttt {cited}$ (speech, book) from $P_1$. Although “Cicero” and “Plato” match $P_1'$, a false fact 〈Cicero, $\texttt {influencedBy}$, John Stuart Mill〉 also matches $P_1'$ because “John Stuart Mill” also has a book belonging to the “Ancient Philosophy” (not shown). Thus, $P_1'$ alone does not distinguish between true and false facts for $\texttt {influencedBy}$ (philosopher, philosopher) well. However, as “Cicero” does not have a speech citing a book of “John Stuart Mill,” the fact is identified as false by $P_1$, since it does not satisfy the constraints.

Fig. 1

Facts and their associated subgraphs. Subgraphs suggest the existence of facts by jointly describing topology and semantic constraints. These subgraphs can be identified by approximate graph pattern matching via associated ontologies

These graph patterns can be easily interpreted as rules, and the matches of the graph patterns readily provide instance-level evidence to “explain” the facts. These matches also indicate more accurate predictive models for various facts. We ask the following questions: How to jointly characterize and discover useful patterns with subgraphs and ontologies? and How to use these patterns to support fact checking in large knowledge graphs?

Contribution. We propose models and algorithms that explicitly incorporate discriminant subgraphs and ontologies to support fact checking in knowledge graphs.

(1) We extend graph fact checking rules (${\mathsf{GFCs}}$) [26] to a class of ontological graph fact checking rules (${\mathsf{OGFCs}}$) (Sect. 2). ${\mathsf{OGFCs}}$ incorporate discriminant graph patterns as the antecedent and generalized triple patterns as the consequent and build a unified model to check multiple types of facts by graph pattern matching with ontology closeness. We adopt computationally efficient pattern models and closeness functions to ensure tractable fact checking via ${\mathsf{OGFCs}}$.

We develop statistical measures (e.g., support, confidence, significance, and diversity) to characterize useful ${\mathsf{OGFCs}}$ (Sect. 3). Based on these measures, we formulate the top-k ${\mathsf{OGFC}}$ discovery problem to mine useful ${\mathsf{OGFCs}}$ for fact checking.

(2) We develop a feasible supervised discovery algorithm to compute ${\mathsf{OGFCs}}$ over a set of training facts (Sect. 4). In contrast to conventional pattern mining, the algorithm solves a submodular optimization problem with provable optimality guarantees, by a single scan of a stream of patterns, and incurs a small cost for each pattern.

(3) To evaluate the applications of ${\mathsf{OGFCs}}$, we apply ${\mathsf{OGFCs}}$ to enhance rule-based and learning-based models to the fact checking task, by developing two such classifiers. The first model directly uses ${\mathsf{OGFCs}}$ as rules. The second model extracts instance-level features from the matches of patterns induced by ${\mathsf{OGFCs}}$ to learn a classifier (Sect. 4.2).

(4) Using real-world knowledge bases, we experimentally verify the efficiency of ${\mathsf{OGFC}}$-based techniques (Sect. 5). We found that the discovery of ${\mathsf{OGFCs}}$ is feasible over large graphs. ${\mathsf{OGFC}}$-based fact checking also achieves high accuracy and outperforms its counterparts using Horn clause rules and path-based learning. We also show that the models are highly interpretable by providing case studies.

Our work nontrivially extends graph fact checking rules (${\mathsf{GFC}}$) [26] with the following new contributions that are not addressed by ${\mathsf{GFC}}$ techniques: (1) new rule models that incorporate semantic closeness in ontology beyond label equality, (2) improved rule discovery algorithms that incorporate ontological subgraph matching and ontological pattern growth strategy, (3) a unified model for multiple types of facts with semantic closeness, which is unlike ${\mathsf{GFCs}}$ that need to build a separate model for each single triple pattern, and (4) experimental studies that verify the effectiveness of adding ontologies to the ${\mathsf{GFC}}$ models.

Related work. We categorize the related work as follows.

Fact checking. Fact checking has been studied for unstructured data [13, 36] and structured (relational) data [18, 45], mostly relying on text analysis and crowd sourcing. Automatic fact checking in knowledge graphs is not addressed in these work. Beyond relational data, the following methods have been studied to predict triples in graphs.

(1) Rule-based models extract association rules to predict facts. ${\mathsf{AMIE}}$ (or its improved version ${\mathsf{AMIE+}}$) discovers rules with conjunctive Horn clauses [14, 15] for knowledge base enhancement. Beyond Horn rules, GPARs [11] discover association rules in the form of $Q \Rightarrow p$, with a subgraph pattern Q and a single edge p. It recommends users via co-occurred frequent subgraphs.

(2) Supervised link prediction has been applied to train predictive models with latent features extracted from entities [8, 22]. Recent works make use of path features [5, 6, 16, 37, 42]. The paths involving targeted entities are sampled from 1-hop neighbors [6] or via random walks [16], or constrained to be shortest paths [5]. Discriminant paths with the same ontology are grouped to generate training examples in [37].

Rule-based models are easy to interpret but usually cover only a subset of useful patterns [31]. It is also expensive to discover useful rules (e.g., via subgraph isomorphism) [11]. On the other hand, latent feature models are more difficult to be interpreted [31] compared with rule models [15]. Our work aims to balance the interpretability and model construction cost. (a) In contrast to ${\mathsf{AMIE}}$  [15], we use more expressive rules enhanced with graph patterns to express both constant and topological context of facts. Unlike [11], we use approximate pattern matching for ${\mathsf{OGFCs}}$ instead of subgraph isomorphism, since the latter may produce redundant examples and is computationally hard in general. (b) ${\mathsf{OGFCs}}$ can induce useful and discriminant features from patterns and subgraphs, beyond path features [6, 16, 42]. (c) ${\mathsf{OGFCs}}$ can be used as a stand-alone rule-based method. They also provide context-dependent features to support supervised link prediction to learn highly interpretable models. These are not addressed in [11, 15].

Ontological graph pattern matching. Ontology-based pattern matching has been proposed to replace the label equality with grouping semantically related labels [24, 46]. Wu et al. [46] revises subgraph isomorphism with a quantitative metric which measures the similarity between the query and its matches in the graph. We adopt ontology-based matching introduced in [46] and the closeness function between concepts (labels) to find ${\mathsf{OGFCs}}$ with semantically related labels.

Graph pattern mining. Frequent pattern mining defined by subgraph isomorphism has been studied for a single graph. GRAMI [9] discovers frequent subgraph patterns without edge labels. Parallel algorithms are also developed for association rules with subgraph patterns [11]. In contrast, (1) we adopt approximate graph pattern matching for feasible fact checking, rather than subgraph isomorphism as in [9, 11]. (2) We develop a more feasible stream mining algorithm with optimality guarantees on rule quality, which incurs a small cost to process each pattern. (3) Supervised graph pattern mining over observed ground truth is not discussed in [9, 11]. In contrast, we develop supervised pattern discovery algorithms that compute discriminant patterns that best distinguish between the observed true and false facts. None of these works discuss supervised graph pattern discovery and their applications for fact checking.

Graph dependency. Data dependencies have been extended to capture inconsistencies in graph data. Functional dependencies for graphs (${\mathsf{GFDs}}$) [12] enforce topological and value constraints by incorporating graph patterns with variables and subgraph isomorphism. Ontology functional dependencies (OFD) on relational data have been proposed to capture synonyms and is-a relationships defined in an ontology [2]. These hard constraints are useful for detecting and cleaning data inconsistencies for follow-up fact checking tasks [31]. On the other hand, they are often violated by incomplete knowledge graphs [31] and thus can be overkill for discovering useful substructures when applied to fact checking. We focus on “soft rules” to infer new facts toward data completion rather than identifying errors with hard constraints [34]. While hard rules are designed to enforce value constraints on node attribute values to capture data inconsistencies, ${\mathsf{OGFCs}}$ can be viewed as a class of association rules that incorporates approximate graph pattern matching with ontology closeness functions to identify missing facts. The semantics and applications of ${\mathsf{OGFCs}}$ are quite different from their counterparts in these data dependencies.

2 Fact Checking with Graph Patterns

We review the notions of knowledge graphs and fact checking. We then introduce a class of rules that incorporate graph patterns and ontologies for fact checking.

2.1 Graphs, Ontologies, and Patterns

Knowledge graphs. A knowledge graph [8] is a directed graph $G=(V, E, L)$, which consists of a finite set of nodes V, a set of edges $E\subseteq V\times V$. Each node $v\in V$ (resp. edge $e\in E$) carries a label L(v) (resp. L(e)) that encodes the content of v (resp. e) such as types, names, or property values.

Ontologies. An ontology is a directed graph O = $(V_o, E_o)$, where $V_o$ is a set of concept labels and $E_o\subseteq V_o\times V_o$ is a set of semantic relations among the concept nodes. In practice, an edge $(l,l')\in E_o$ may encode three types of relations [21], including: (a) equivalence states l and $l'$ are semantically equivalent, thereby representing “refersTo” or “knownAs”; (b) hyponyms states that l is a kind of $l'$, such as “isA” or “subclassOf” that enforces a preorder over $V_o$; and (c) descriptive states that l is described by another $l'$ in terms of, for example, “association,” “partOf” or “similarTo”. In practice, an ontology may encode taxonomies, thesauri, or RDF schemas.

Label closeness function Given an ontology O and a concept label l, a label closeness function ${\mathsf{osim}} (\cdot )$ computes a set of labels close to l, i.e., ${\mathsf{osim}} (l, O)=\{l'|{\mathsf{dist}} (l, l')\le 1 - \beta \}$, where (1) ${\mathsf{dist}} (\cdot ):$ $V_o\times V_o\rightarrow [0,1]$ computes a relevant score between l and $l'$, and (2) $\beta$ (resp. $(1 - \beta )$) is a similarity (resp. distance) bound. One may set ${\mathsf{dist}} (l, l')$ as the normalized sum of the edge weights along a shortest (undirected) path between l to $l'$ in O [21, 46]. For equivalence, hyponym, descriptive edges modeled in O, tunable weights $w_1$, $w_2,$ and $w_3$ can be assigned respectively, to differentiate equivalence, inheritance, and association properties [21].

Example 2.

Consider the knowledge graph $G_1$ in Fig. 1. A fact 〈$v_x$, $\texttt {{ r}}$, $v_y$ 〉 = 〈Cicero, $\texttt {influencedBy}$, Plato〉 is encoded by an edge in G with label “${\mathsf{influencedBy}}$ ” between the subject node $v_x$ and the object node $v_y$. The label of $v_x$ encodes its name “Cicero” and carries a type x = “philosopher”; similarly for $v_y$ with name “Plato” and type y = “philosopher”. By setting $w_{1} = 0.0$, $w_{2}=0.1$, and $w_{3}=0.4$, the corresponding ontology $O_1$ of $G_1$ (Fig. 1) suggests that (1) ${\mathsf{dist}} (\textit{theologian}, \textit{philosopher})=0.4$, ${\mathsf{dist}} (\textit{theologian}, \textit{logician})=0.4$, and ${\mathsf{dist}} (\textit{philosopher}, \textit{logician})=0.1$, and thus these concepts are close to each other if the threshold $\beta =0.6$; (2) ${\mathsf{dist}} (\textit{speech}, \textit{book})=0.3$, ${\mathsf{dist}} (\textit{speech}$, $\textit{writternWork}) = 0.2$, and ${\mathsf{dist}} (\textit{book}, \textit{writternWork})=0.1$, and thus these concepts are close to each other if the threshold $\beta =0.7$.

Fact checking in knowledge graphs. Given a knowledge graph G = (V, E, L) and a new fact t = 〈$v_x$, $\texttt {{ r}}$, $v_y$〉 , where $v_x$ and $v_y$ are in G, and $t\notin E$, the task of fact checking is to compute a model M to decide whether the relation r exists between $v_x$ and $v_y$ [31]. This task can be represented by a binary query in the form of 〈$v_x$, $\texttt {{ r}?}$, $v_y$〉 , where the model M outputs “true” or “false” for the query.

We study how subgraphs and ontologies can be jointly explored to support effective fact checking for knowledge graphs. To characterize useful subgraphs and concept labels, we introduce a class of ontology-based subgraph patterns, which extends its counterpart in graph fact checking rules (${\mathsf{GFCs}}$) [26] with ontology closeness.

Subgraph patterns. A subgraph pattern $P(x, y)=(V_P, E_P, L_P)$ is a directed graph that contains a set of pattern nodes $V_P$ and pattern edges $E_P$, respectively. Each pattern node $u_p\in V_P$ (resp. edge $e_p\in E_P$) has a label $L_P(u_p)$ (resp. $L_P(e_p)$). Moreover, it contains two designated anchored nodes $u_x$ and $u_y$ in $V_P$ of types x and y, respectively. Specifically, when it contains a single pattern edge with label r between $u_x$ and $u_y$, P is called a triple pattern, denoted as r(x, y).

We next extend the approximate pattern matching [26] with ontologies.

Ontological pattern matching. Given a graph G, a pattern P(x, y), and a function ${\mathsf{osim}} (\cdot )$, for a pattern node $v_P$ of P(x, y), a node v in G is a candidate of $v_P$ if $L(v)\in {\mathsf{osim}} (L_P(v_P), O)$. A candidate of a pattern edge $e_P$ = $(v_P, v_P')$ in G is an edge e = $(v,v')$ such that (a) v (resp. $v'$) is a candidate of $v_P$ (resp. $v_P'$), and (b) $L(e)\in {\mathsf{osim}} (L_P(e_P), O)$.

Match relation. Given P(x, y), G, O and function ${\mathsf{osim}} (\cdot )$, a pair of nodes $(v_x, v_y)$ match P(x, y), or P covers the pair $(v_x, v_y)$, if (1) there exists a matching relation $R\subseteq V_P\times V$ such that for each pair $(u, v)\in R$, (a) v is a candidate of u (verified by the ontology closeness function ${\mathsf{osim}} (\cdot )$), (b) for every edge $e_P=(u, u')\in E_P$, there exists a candidate $e'$ = $(v, v')\in E$ and $(u',v')\in R$; (c) for every edge $e_P'=(u', u)\in E_P$, there exists a candidate $e''$ = $(v', v)\in E$ and $(u',v')\in R$; and (2) $(u_x, v_x)\in R$ and $(u_y, v_y)\in R$, i.e., $v_x$ (resp. $v_y$) is a match of $u_x$ (resp. $u_y$), respectively.

Example 3.

Consider $G_1$ and its associated ontology $O_1$ in Fig. 1. Given the label “philosopher,” a set of close labels ${\mathsf{osim}} (\textit{philosopher}, O_1)$ may include $\{$ philosopher, logician, theologian$\}$. Similarly, ${\mathsf{osim}} (\textit{speech}, O_1)$ may include $\{$speech, writtenWork, masterpiece$\}$, and ${\mathsf{osim}} (\textit{book}, O_1)$ may contain $\{\textit{writtenWork}, \textit{book}\}$.

Remarks. As observed in [26, 28, 39, 40], subgraph patterns defined by, for example, subgraph isomorphism may be an overkill in capturing meaningful patterns and is computationally expensive (NP-hard). Moreover, it generates (exponentially) many isomorphic subgraphs and thus introduces redundant features for model learning [26]. In contrast, it is in ${\mathcal O}(|V_P|(|V_P|+|V|)(|E_P|+|E|))$ time to find whether a fact is covered by an approximate pattern [26]. The tractability carries over to the validation of ${\mathsf{OGFCs}}$ (Sect. 4). To ensure feasible fact checking in large knowledge graphs and ontologies, we shall consider ontological pattern matching to balance the expressiveness and computational cost of our rule model.

2.2 Ontological Graph Fact Checking Rules

We now introduce our rule model that incorporates graph patterns and ontologies.

Rule model. An ontological graph fact checking rule (denoted as ${\mathsf{OGFC}}$) is in the form of $\varphi : P(x,y)$ $\rightarrow r(x, y)$, where (1) P(x, y) and r(x, y) are two graph patterns carrying the same pair of anchored nodes $(u_x, u_y)$, and (2) r(x, y) is a triple pattern and is not in P(x, y).

Semantics. Given a knowledge graph G, an ontology O, and a closeness function ${\mathsf{osim}} (\cdot )$, an ${\mathsf{OGFC}}$ $\varphi : P(x,y) \rightarrow r(x, y)$ states that “a fact 〈$v_x$, $\texttt {{ r}}$, $v_y$〉 holds between $v_x$ and $v_y$ in G, if $(v_x, v_y)$ is covered by P in terms of O and ${\mathsf{osim}} (\cdot )$.”

Example 4.

Consider the patterns and graphs in Fig. 1. To verify the influence between two philosophers, an ${\mathsf{OGFC}}$ is $\varphi _1:P_1(x,y)\rightarrow$ $\texttt {influencedBy}$(x, y). Pattern $P_1$ has two anchored nodes x and y, both with type philosopher, and covers the pair $(\texttt {Cicero}$, $\texttt {Plato})$ in $G_1$. To verify the service between a pair of matched entities $(\texttt {A}, \texttt {C})$, another ${\mathsf{OGFC}}$ is $\varphi _2 : P_2(x,y) \rightarrow$ $\texttt {intermediaryOf}$(x, y). Note that with subgraph isomorphism, $P_1$ induces two subgraphs of $G_1$ that only differ by entities with label speech and masterpiece. It is impractical for users to inspect such highly overlapped subgraphs with subgraph isomorphism.

Remarks. We compare ${\mathsf{OGFCs}}$ with two models below. (1) Horn rules are adopted by ${\mathsf{AMIE+}}$  [14], in the form of $\bigwedge B_i\rightarrow r(x,y)$, where each $B_i$ is an atom (fact) carrying variables. It mines only closed (each variable appears at least twice) and connected (atoms transitively share variables/entities to all others) rules. We allow general approximate graph patterns in ${\mathsf{OGFCs}}$ to mitigate missing data and capture richer context features for supervised models (Sect. 4). (2) The association rules with graph patterns [11] have similar syntax with ${\mathsf{OGFCs}}$ but adopt strict subgraph isomorphism for social recommendation. In contrast, we define ${\mathsf{OGFCs}}$ with semantics and quality measures (Sect. 3) specified for observed true and false facts to support fact checking. (3) The ${\mathsf{GFC}}$ model [26] is a special case of ${\mathsf{OGFCs}}$ in which ${\mathsf{osim}} (\cdot )$ enforces label equality ($\beta =1$).

3 Supervised ${\mathsf{OGFC}}$ Discovery

To characterize useful ${\mathsf{OGFCs}}$, we introduce a set of metrics that jointly measure pattern significance and rule models, which extend their counterparts from established rule models [15] and discriminant patterns [47], and are specialized for a set of training facts. We then formalize the supervised ${\mathsf{OGFC}}$ discovery problem.

Statistical measures. Our measures are defined over a knowledge graph G, an ontology O (with function ${\mathsf{osim}} (\cdot )$), and a set of training facts $\varGamma$. The training facts $\varGamma$ consists of a set of true facts $\varGamma ^+$ in G, and a set of false facts $\varGamma ^-$ that are known not in G, respectively. Extending the silver standard in knowledge base completion [34], (1) $\varGamma ^+$ can be usually sampled from manually cleaned knowledge bases [29]; and (2) $\varGamma ^-$ are populated following the partial closed-world assumption (see “Confidence”).

We use the following notations. Given an ${\mathsf{OGFC}}$ $\varphi : P(x,y) \rightarrow r(x, y)$, a graph G, facts $\varGamma ^+$ and $\varGamma ^-$, (1) $P(\varGamma ^+)$ (resp. $P(\varGamma ^-)$) refers to the set of training facts in $\varGamma ^+$ (resp. $\varGamma ^-$) that are covered by P(x, y) in $\varGamma ^+$ (resp. $\varGamma ^-$) in terms of O and ${\mathsf {osim}} (\cdot )$. $P(\varGamma )$ is defined as $P(\varGamma ^+) \cup P(\varGamma ^-)$, i.e., all the facts in $\varGamma$ covered by P. (2) $r(\varGamma ^+)$, $r(\varGamma ^-)$, and $r(\varGamma )$ are defined similarly.

Support and confidence. The support of an ${\mathsf{OGFC}}$ $\varphi : P(x,y) \rightarrow r(x, y)$, denoted by ${\mathsf{supp}} (\varphi , G, \varGamma )$ (or simply ${\mathsf{supp}} (\varphi )$), is defined as

$$\begin{aligned} {\mathsf{supp}} (\varphi )=\frac{|P(\varGamma ^+)\cap r(\varGamma ^+)|}{|r(\varGamma ^+)|} \end{aligned}$$

Intuitively, the support is the fraction of the true facts that are instances of r(x, y), and those also satisfy the constraints of the subgraph pattern P(x, y) over the ontology O and the closeness function ${\mathsf{osim}} (\cdot )$. It extends the head coverage, a practical version for rule support [15] to address triple patterns r(x, y) that has not many matches due to the incompleteness of knowledge bases.

Given two patterns $P_1(x, y)$ and $P_2(x,y)$, we say $P_2(x, y)$ refines $P_1(x, y)$ (denoted by $P_1(x, y) \preceq P_2(x, y)$, if $P_1$ is a subgraph of $P_2$ and they pertain to the same pair of anchored nodes $(u_x, u_y)$. We show that the support of ${\mathsf{OGFCs}}$ preserves anti-monotonicity in terms of pattern refinement.

Lemma 1.

For graph G, given any two ${\mathsf{OGFCs}}$ $\varphi _1 : P_1(x, y)\rightarrow r(x,y)$ and $\varphi _2 : P_2(x, y)\rightarrow r(x,y)$, if $P_1(x, y) \preceq P_2(x, y)$, ${\mathsf{supp}} (\varphi _2)\le {\mathsf{supp}} (\varphi _1)$.

Proof sketch.

It suffices to show that any pair $(v_{x_2}, v_{y_2})$ covered by $P_2$ in G is also covered by $P_1(x,y)$. Assume there exists a pair $(v_{x_2}, v_{y_2})$ covered by $P_2$ but not by $P_1$, and assume w.l.o.g. $v_{x_2}$ does not match the anchored node $u_x$ in $P_1$. Then, there exists either (a) an edge $(u_x, u)$ (or $(u, u_x)$) in $P_1$ such that no edge $(v_{x_2}, v)$ (or $(v, v_{x_2})$) is a match, or (b) a node u as an ancestor or a descendant of $u_x$ in $P_1$, such that no ancestor or descendant of $v_{x_2}$ in G is a match. As $P_2$ refines $P_1$, both (a) and (b) lead to that $v_{x_2}$ is not covered by $P_2$, which contradicts the definition of approximate patterns. $\square$

Extending partial closed-world assumption. Following rule discovery in incomplete knowledge base [15], we extend partial closed-world assumption ($\mathsf{PCA}$) to characterize the confidence of ${\mathsf{OGFCs}}$. Given a triple pattern r(x, y) and a true instance 〈$v_x$, $\texttt {{ r}}$, $v_y$〉 $\in r(\varGamma ^+)$, an ontology-based $\mathsf{PCA}$ assumes that a missing instance 〈$v_x$, $\texttt {{ r}}$, $v_y'$〉 of r(x, y) is a false fact if $L(v_y')\not \in {\mathsf{osim}} (L(v_y), O)$. In other words, for a given entity $v_x$, it assumes that $r(\varGamma ^+)$ contains all the true facts about $v_x$ that pertain to specific r. Given the ontology and the function ${\mathsf{osim}} (\cdot )$ that tolerates concept label dissimilarity, it will identify a fact as false only when it claims a fact that connects $v_x$ and $v_y'$ via r, and $v_y'$ is not ontologically close to any known entity that is connected to $v_x$ via r. This necessarily extends the conventional $\mathsf{PCA}$ (where ${\mathsf{osim}} (\cdot )$ simply enforces label equality, i.e., $\beta =1$) to reduce the impact of facts that may not be counted as “false” due to the true facts that are ontologically close to them.

We define a normalizer set $P(\varGamma ^+)_N$, which contains all the pairs $(v_x, v_y)$ from $P(\varGamma ^+)$ that have at least a false counterpart under the ontology-based $\mathsf{PCA}$. The confidence of $\varphi$ in G, denoted as ${\mathsf{conf}} (\varphi , G, \varGamma )$ (or simply ${\mathsf{conf}} (\varphi )$), is defined as

$$\begin{aligned} {\mathsf{conf}} (\varphi ) = \frac{|P(\varGamma ^+)\cap r(\varGamma ^+)|}{|P(\varGamma ^+)_N|} \end{aligned}$$

The confidence measures the probability that an ${\mathsf{OGFC}}$ holds over the entity pairs that satisfy P(x, y), normalized by the facts that are assumed to be false under $\mathsf{PCA}$. We follow the ontology-based $\mathsf{PCA}$ to construct false facts in our experimental study.

Significance. We next quantify how significant an ${\mathsf{OGFC}}$ is in “distinguishing” between the true and false facts, by extending the G-test score [47]. This test verifies the null hypothesis of whether the number of true facts “covered” by P(x, y) fits to the distribution in the false facts. If not, P(x, y) is considered to be significant. Specifically, the score (denoted as ${\mathsf{sig}} (\varphi ,p,n)$, or simply ${\mathsf{sig}} (\varphi )$) is defined as

$$\begin{aligned} {\mathsf{sig}} (\varphi ) = 2|\varGamma ^+|\left( p\ln \frac{p}{n} + (1-p)\ln \frac{1-p}{1-n}\right) \end{aligned}$$

where p (resp. n) is the frequency of the facts covered by pattern P of $\varphi$ in $\varGamma ^+$ (resp. $\varGamma ^-$), i.e., $p=\frac{|P(\varGamma ^+)|}{|\varGamma ^+|}$ (resp. $n=\frac{|P(\varGamma ^-)|}{|\varGamma ^-|}$). As ${\mathsf{sig}} (\varphi )$ is not anti-monotonic, a common practice is to use a “rounded up” score to find significant patterns [47]. We adopt an upper bound of ${\mathsf{sig}} (\varphi )$, denoted as $\hat{{\mathsf{sig}}}(\varphi , p, n)$ (or $\hat{\mathsf{sig}} (\varphi )$ for simplicity), which is defined as $\tanh (\max \{{\mathsf{sig}} (\varphi , p, \delta ), {\mathsf{sig}} (\varphi , \delta , n)\})$, where $\delta$ > 0 is a small constant (to prevent the case that $\hat{{\mathsf{sig}}}(\varphi )=\infty$), and $\hat{{\mathsf{sig}}}$ is normalized to [0, 1] by the hyperbolic function $\tanh (\cdot )$. We show the following results.

Lemma 2.

Given graph G, for any two ${\mathsf{OGFCs}}$ $\varphi _1 : P_1(x, y) \rightarrow r(x, y)$ and $\varphi _2 : P_2(x, y) \rightarrow r(x, y)$, $\hat{{\mathsf{sig}}}(\varphi _2) \le \hat{{\mathsf{sig}}}(\varphi _1)$ if $\varphi _1 \preceq \varphi _2$.

Proof.

As $\hat{{\mathsf{sig}}}(\varphi )=\tanh (\max \{{\mathsf{sig}} (\varphi , p, \delta ), {\mathsf{sig}} (\varphi , \delta , n)\})$, it suffices to show that both ${\mathsf{sig}} (\varphi , p, \delta )$ and ${\mathsf{sig}} (\varphi , \delta , n)$ are anti-monotonic in terms of rule refinement.

(1) As ${\mathsf{sig}} (\varphi , p, \delta )=2|\varGamma ^+|(p\ln \frac{p}{\delta } + (1-p)\ln \frac{1-p}{1-\delta })$, the derivative w.r.t. p is

$$\begin{aligned} {\mathsf{sig}} '_p(\varphi , p, \delta )=2|\varGamma ^+|\left( \ln \frac{p}{1-p} - \ln \frac{\delta }{1-\delta }\right) \end{aligned}$$

Also, as ${\mathsf{sig}} (\varphi , \delta , n)=2|\varGamma ^+|(\delta \ln \frac{\delta }{n} + (1-\delta )\ln \frac{1 - \delta }{1 - n})$, the derivative w.r.t. n is

$$\begin{aligned} {\mathsf{sig}} '_n(\varphi , \delta , n)=2|\varGamma ^+|\left( \frac{1 - \delta }{1 - n} - \frac{\delta }{n}\right) =2|\varGamma ^+|\left( \frac{n - \delta }{n(1 - n)}\right) \end{aligned}$$

When $\delta \le \min \{p, n\}$, both ${\mathsf{sig}} '_p(\varphi , p, \delta ) \ge 0$ and ${\mathsf{sig}} '_n(\varphi , \delta , n) \ge 0$. Hence, both ${\mathsf{sig}} (\varphi , p, \delta )$ and ${\mathsf{sig}} (\varphi , \delta , n)$ are monotonic w.r.t. p and n, respectively.

(2) Given Lemma 1, we have $p_2 \le p_1$ and $n_2 \le n_1$ if $\varphi _1 \preceq \varphi _2$. Then, ${\mathsf{sig}} (\varphi _2, p_2, \delta ) \le {\mathsf{sig}} (\varphi _1, p_1, \delta )$ and ${\mathsf{sig}} (\varphi _2, \delta , n_2) \le {\mathsf{sig}} (\varphi _1, \delta , n_1)$, thus

$$\begin{aligned} \max \{{\mathsf{sig}} (\varphi _2, p_2, \delta ), {\mathsf{sig}} (\varphi _2, \delta , n_2)\} \le \max \{{\mathsf{sig}} (\varphi _1, p_1, \delta ), {\mathsf{sig}} (\varphi _1, \delta , n_1)\} \end{aligned}$$

and therefore $\hat{{\mathsf{sig}}}(\varphi _2) \preceq \hat{{\mathsf{sig}}}(\varphi _1)$. This completes the proof of Lemma 2. $\square$

Redundancy-aware selection. In practice, one wants to find ${\mathsf{OGFCs}}$ with both high significance and low redundancy. Indeed, a set of ${\mathsf{OGFCs}}$ can be less useful if they “cover” the same set of true facts in $\varGamma ^+$. We introduce a bi-criteria function that favors significant ${\mathsf{OGFCs}}$ that cover more diversified true facts. Given a set of ${\mathsf{OGFCs}}$ $\mathcal{S}$, when the set of true facts $\varGamma ^+$ is known, the coverage score of $\mathcal{S}$, denoted as ${\mathsf{cov}} (\mathcal{S})$, is defined as

$$\begin{aligned} {\mathsf{cov}} (\mathcal{S}) = {\mathsf{sig}} (\mathcal{S}) + {\mathsf{div}} (\mathcal{S}) \end{aligned}$$

The first term, defined as ${\mathsf{sig}} (\mathcal{S})=\sqrt{\sum _{\varphi \in \mathcal{S}}\hat{\mathsf{sig}} (\varphi )}$, aggregates the total significance of ${\mathsf{OGFCs}}$ in $\mathcal{S}$. The second term is defined as

$$\begin{aligned} {\mathsf{div}} (\mathcal{S})=\left( \sum _{t\in \varGamma ^+}\sqrt{\sum _{\varphi \in \varPhi _t(\mathcal{S})} {\mathsf{supp}} (\varphi )} \right) \big / |\varGamma ^+| \end{aligned}$$

where $\varPhi _t(\mathcal{S})$ refers to the ${\mathsf{OGFCs}}$ in $\mathcal{S}$ that cover a true fact $t \in \varGamma ^+$. ${\mathsf{div}} (\mathcal{S})$ quantifies the diversity of $\mathcal{S}$ and follows a reward function [25]. Intuitively, it rewards the diversity in that there is more benefit in selecting an ${\mathsf{OGFC}}$ that covers new facts, which are not covered by other ${\mathsf{OGFCs}}$ in $\mathcal{S}$ yet. Both terms are normalized to $(0, \sqrt{|\mathcal{S}|}]$.

The coverage score favors ${\mathsf{OGFCs}}$ that cover more distinct true facts with more discriminant patterns. We next show that ${\mathsf{cov}} (\cdot )$ is well defined in terms of diminishing returns. That is, adding a new ${\mathsf{OGFC}}$ $\varphi$ to a set $\mathcal{S}$ improves its significance and coverage at least as much as adding it to any superset of $\mathcal{S}$ (diminishing gain to $\mathcal{S}$). This also verifies that ${\mathsf{cov}} (\cdot )$ employs submodularity [30], a property widely used to justify goodness measures for set mining. Define the marginal gain ${\mathsf{mg}} (\varphi , \mathcal {S})$ of an ${\mathsf{OGFC}}$ $\varphi$ to a set $\mathcal{S}$ ($\varphi \notin \mathcal {S}$) as ${\mathsf{cov}} (\mathcal{S}\cup \{\varphi \})$-${\mathsf{cov}} (\mathcal{S})$. We have the following result.

Lemma 3.

The function ${\mathsf{cov}} (\cdot )$ is a monotone submodular function for ${\mathsf{OGFCs}}$ that is for any two sets $\mathcal{S}_1$ and $\mathcal{S}_2$, (1) if $\mathcal{S}_1\subseteq \mathcal {S}_2$, then ${\mathsf{cov}} (\mathcal {S}_1)\le {\mathsf{cov}} (\mathcal {S}_2)$, and (2) if $\mathcal{S}_1\subseteq \mathcal {S}_2$ and for any ${\mathsf{OGFC}}$ $\varphi \notin \mathcal{S}_2$, ${\mathsf{mg}} (\varphi , \mathcal {S}_2)\le {\mathsf{mg}} (\varphi , \mathcal {S}_1)$.

Proof.

We show that both parts pertaining to ${\mathsf{cov}} (\mathcal{S})$, i.e., ${\mathsf{sig}} (\mathcal{S})$ and ${\mathsf{div}} (\mathcal{S})$, are monotone submodular functions w.r.t. $\mathcal{S}$, and therefore ${\mathsf{cov}} (\mathcal{S})$ is a monotone submodular function w.r.t. $\mathcal{S}$.

(1) We show that both ${\mathsf{sig}} (\mathcal{S})$ and ${\mathsf{div}} (\mathcal{S})$ are monotone functions w.r.t. $\mathcal{S}$. Each term ${\mathsf{sig}} (\varphi )$ is positive, and the sum ${\sum _{\varphi \in {\mathcal{S}_1}}{\mathsf{sig}} (\varphi )}\le {\sum _{\varphi \in {\mathcal{S}_2}}{\mathsf{sig}} (\varphi )}$, since every $\varphi$ in $\mathcal{S}_1$ is also in $\mathcal{S}_2$ for any two sets $\mathcal{S}_1 \subseteq \mathcal{S}_2$ of ${\mathsf{OGFCs}}$. Hence, ${\mathsf{sig}} (\mathcal{S})$ is a monotone function w.r.t. the set $\mathcal{S}$.

We denote the term $\sqrt{\sum _{\varphi \in \varPhi _t(\mathcal{S})}{\mathsf{supp}} (\varphi )}$ in ${\mathsf{div}} (\mathcal{S})$ as $T_t{(\mathcal{S})}$. For each term $T_t(\mathcal{S})$ in ${\mathsf{div}} (\mathcal{S})$, similarly, ${\mathsf{supp}} (\varphi )$ is positive, and we have ${\sum _{\varphi \in \varPhi _t(\mathcal{S}_1)}{\mathsf{supp}} (\varphi )}$ $\le {\sum _{\varphi \in \varPhi _t(\mathcal{S}_2)}{\mathsf{supp}} (\varphi )}$, since every $\varphi$ in $\varPhi _t(\mathcal{S}_1)$ that covers t is also in $\varPhi _t(\mathcal{S}_2)$ for any two sets $\mathcal{S}_1 \subseteq \mathcal{S}_2$ of ${\mathsf{OGFCs}}$. Hence, each term $T_t(\mathcal{S})$ in ${\mathsf{div}} (\mathcal{S})$ is a monotone function w.r.t. $\mathcal{S}$, and thus ${\mathsf{div}} (\mathcal{S})$ is a monotone function w.r.t. $\mathcal{S}$.

(2) Next, we show that both ${\mathsf{sig}} (\mathcal{S})$ and ${\mathsf{div}} (\mathcal{S})$ are submodular functions w.r.t. $\mathcal{S}$. For any ${\mathsf{OGFC}}$ $\varphi ' \not \in \mathcal{S}$, the marginal gain for ${\mathsf{sig}} (\mathcal{S})$ is: ${\mathsf{sig}} (\mathcal{S}\cup \{\varphi '\}) - {\mathsf{sig}} (\mathcal{S})$ = $(\sum _{\varphi \in \mathcal{S}\cup \{\varphi '\}} {\mathsf{sig}} (\varphi ))^{\frac{1}{2}} - {\mathsf{sig}} (\mathcal{S})$ = $({\mathsf{sig}} ^2(\mathcal{S}) + {\mathsf{sig}} (\varphi '))^{\frac{1}{2}} - {\mathsf{sig}} (\mathcal{S})$ = ${\mathsf{sig}} (\varphi ') \big / (({\mathsf{sig}} ^2(\mathcal{S}) + {\mathsf{sig}} (\varphi '))^{\frac{1}{2}} + {\mathsf{sig}} (\mathcal{S}))$ , which is an anti-monotonic function w.r.t. ${\mathsf{sig}} (\mathcal{S})$. As ${\mathsf{sig}} (\mathcal{S})$ is monotonic w.r.t. $\mathcal{S}$, for any two sets $\mathcal{S}_1 \subseteq \mathcal{S}_2$ and $\varphi ' \not \in \mathcal{S}_2$, ${\mathsf{sig}} (\mathcal{S}_2 \cup \{\varphi '\}) - {\mathsf{sig}} (\mathcal{S}_2) \le {\mathsf{sig}} (\mathcal{S}_1 \cup \{\varphi '\}) - {\mathsf{sig}} (\mathcal{S}_1)$. Hence, ${\mathsf{sig}} (\mathcal{S})$ is submodular w.r.t. $\mathcal{S}$.

Similarly, for any ${\mathsf{OGFC}}$ $\varphi ' \not \in \mathcal{S}$, the marginal gain of ${\mathsf{div}} (\cdot )$ for each term $T_t(\mathcal{S})$ is: $T_t(\mathcal{S}\cup \{\varphi '\}) - T_t(\mathcal{S}) = (\sum _{\varphi \in \varPhi _t(\mathcal{S}\cup \{\varphi '\})}{\mathsf{supp}} (\varphi ))^{\frac{1}{2}} - T_t(\mathcal{S})$. If $\varphi '$ does not cover t, then $T_t(\mathcal{S}\cup \{\varphi '\}) - T_t(\mathcal{S}) = 0$. Otherwise, if $\varphi '$ covers t, following the similar process for ${\mathsf{sig}} (\mathcal{S})$, we have $T_t(\mathcal{S}\cup \{\varphi '\}) - T_t(\mathcal{S}) = {\mathsf{supp}} (\varphi ') \big / (T^2_t(\mathcal{S}) + {\mathsf{supp}} (\varphi '))^{\frac{1}{2}} + T_t(\mathcal{S}))$, which is an anti-monotonic function w.r.t. $T_t(\mathcal{S})$. As $T_t(\mathcal{S})$ is monotonic w.r.t. $\mathcal{S}$, for any two sets $\mathcal{S}_1 \subseteq \mathcal{S}_2$ and $\varphi ' \not \in \mathcal{S}_2$, $T_t(\mathcal{S}_1) \le T_t(\mathcal{S}_2)$. Hence, $T_t(\mathcal{S}_2 \cup \{\varphi '\}) - T_t(\mathcal{S}_2) \le T_t(\mathcal{S}_1 \cup \{\varphi '\}) - T_t(\mathcal{S}_1)$, no matter whether $\varphi '$ covers t. Thus, each term $T_t(\mathcal{S})$ in ${\mathsf{div}} (\mathcal{S})$ is a submodular function w.r.t. $\mathcal{S}$ and ${\mathsf{div}} (\mathcal{S})$ is hence a submodular function w.r.t. $\mathcal{S}$.

In summary, both ${\mathsf{sig}} (\mathcal{S})$ and ${\mathsf{div}} (\mathcal{S})$ are monotone submodular functions w.r.t. $\mathcal{S}$, and ${\mathsf{cov}} (\mathcal{S})$ is a monotone submodular function w.r.t. $\mathcal{S}$. Lemma 3 thus follows. $\square$

We now formulate the top-k ${\mathsf{OGFC}}$ discovery problem over observed facts.

Top-k supervised ${\mathsf{OGFC}}$ discovery. Given a graph G, a corresponding ontology O with an ontology closeness function ${\mathsf{osim}} (\cdot )$, a support threshold $\sigma$, a confidence threshold $\theta$, training facts $\varGamma$ as instances of a triple pattern r(x, y), and integer k, the problem is to identify a set $\mathcal{S}$ of top-k ${\mathsf{OGFCs}}$ that pertain to r(x, y), such that (a) for each ${\mathsf{OGFC}}$ $\varphi \in \mathcal {S}$, ${\mathsf{supp}} (\varphi )\ge \sigma$, ${\mathsf{conf}} (\varphi )\ge \theta$, and (b) ${\mathsf{cov}} (\mathcal {S})$ is maximized.

4 Discovery Algorithm

4.1 Top-k ${\mathsf{OGFC}}$ Discovery

Unsurprisingly, the supervised discovery problem for ${\mathsf{OGFCs}}$ is intractable. A naive “enumeration-and-verify” algorithm that generates and verifies all k-subsets of ${\mathsf{OGFC}}$ candidates is clearly impractical for large G, O, and $\varGamma$. We introduce efficient algorithms with near-optimality guarantees. Before we introduce these algorithms, we first introduce a common building-block procedure that computes the pairs covered by a subgraph pattern (“pattern matching” procedure).

Procedure $\mathsf{PMatch}$. We start with procedure $\mathsf{PMatch}$, an ontology-aware graph pattern matching procedure. Given knowledge graph G, ontology O, and closeness function ${\mathsf{osim}} (\cdot )$, for a subgraph pattern P(x, y), it computes the node pairs $(v_x, v_y)$ that can be covered by P(x, y). In a nutshell, the algorithm extends the approximate matching procedure that computes a graph dual-simulation relation [28], while the candidates are dynamically determined by ${\mathsf{osim}} (\cdot )$ and O. More specifically, $\mathsf{PMatch}$ first finds the candidate matches $v \in V$ of each node $u \in V_P$, such that v has a type that is close to u determined by ${\mathsf{osim}} (\cdot )$ and O. It then iteratively refines the match set that violates topological constraints of P by the definition of the matching relation R, until the match set cannot be further refined.

Complexity. Note that it takes a once-for-all preprocessing to identify all similar labels in the ontology O, in time ${\mathcal O}(|V_P|(|V_O|+|E_O|)$, following a traversal of O. Given that O is typically small (and thus its diameter is a small constant), the computation of ${\mathsf{osim}} (\cdot )$ for given labels is in O(1). It then takes $\mathcal {O}((|V_P|+|V|)(|E_P|+|E|))$ time to compute the matching relation for each pattern.

We next introduce ${\mathsf{OGFC}}$ discovery algorithms.

“Batch + Greedy”. We start with an algorithm (denoted as $\mathsf{OGFC\_batch}$) that takes a batch pattern discovery and a greedy selection as follows. (1) Apply graph pattern mining (e.g., Apriori [20]) to generate and verify all the graph patterns $\mathcal{P}$. The verification is specialized by an operator $\mathsf{Verify}$, which invokes the pattern matching algorithm $\mathsf{PMatch}$ to compute the support and confidence for each pattern. (2) Invoke a greedy algorithm to do k ${\mathsf{OGFC}}$ passes of $\mathcal{P}$. In each iteration i, it selects the pattern $P_i$, such that the corresponding ${\mathsf{OGFC}}$ $\varphi _i:P_i(x,y)\rightarrow r(x,y)$ maximizes the marginal gain ${\mathsf{cov}} (\mathcal {S}_{i-1}\cup \{\varphi _i\})$ - ${\mathsf{cov}} (\mathcal {S}_{i-1})$ , and then it updates $\mathcal {S}_i$ as $\mathcal {S}_{i-1}\cup \{\varphi _i\}$.

$\mathsf{OGFC\_batch}$ guarantees a $(1-\frac{1}{e})$ approximation, following Lemma 3 and the seminal result in [30]. Nevertheless, it requires the verification of all patterns before the construction of ${\mathsf{OGFCs}}$. The selection further requires k passes of all the verified patterns. This can be expensive for large G and $\varGamma$.

We can do better: In contrast to “batch processing” the pattern discovery and sequentially applying the verification, we organize newly generated patterns in a stream and interleave pattern generation and verification to assemble new patterns to top-k ${\mathsf{OGFCs}}$ with small update costs. This requires a single scan of all patterns with early termination, without waiting for all patterns to be verified. Capitalizing on stream-based optimization [1, 40], we develop a near-optimal algorithm to discover ${\mathsf{OGFCs}}$. Our main results are shown below.

Theorem 1.

Given a constant $\epsilon$ > 0, there exists a stream algorithm that computes top-k ${\mathsf{OGFCs}}$ with the following guarantees:

• (1) It achieves an approximation ratio $(\frac{1}{2}-\epsilon )$;

• (2) It performs a single pass of all processed patterns $\mathcal{P}$, with update cost in $O( (b + |\varGamma _b|)^2 + \frac{\log k}{\epsilon })$, where b is the largest edge number of the patterns, and $\varGamma _b$ is the b hop neighbors of the entities in $\varGamma$.

Fig. 2

Algorithm $\mathsf{OGFC\_stream}$  

As a proof of Theorem 1, we next introduce such a stream discovery algorithm.

“Stream + Sieve”. Our supervised discovery algorithm, denoted as $\mathsf{OGFC\_stream}$ (illustrated in Fig. 2), interleaves pattern generation and ${\mathsf{OGFC}}$ selection as follows.

(1) Ontology-aware pattern stream generation. The algorithm $\mathsf{OGFC\_stream}$ invokes a procedure $\mathsf{PGen}$ to produce a pattern stream $\mathcal{P}$ (line 2 and 8). Unlike $\mathsf{OGFC\_batch}$ that verifies patterns against entire graph G, it partitions facts $\varGamma$ to blocks and iteratively spawns and verifies patterns by visiting local neighbors of the facts in each block. This progressively finds patterns that better “purify” the labels of only those facts they cover and thus reduces unnecessary enumeration and verification. Instead of using exact matching triples [26], ${\mathsf{OGFC}}$ leverages the ontology O and the closeness function ${\mathsf{osim}} (\cdot )$ to group ontologically similar triples for partitioning.

(2) Selection on-the-fly. $\mathsf{OGFC\_stream}$ invokes a procedure $\mathsf{PSel}$ (line 7) to select patterns and construct ${\mathsf{OGFCs}}$ on the fly. To achieve the optimality guarantee, it applies the stream-sieving strategy in stream data summarization [1]. In a nutshell, it estimates the optimal value of a monotonic submodular function $F(\cdot )$ with multiple “sieve values,” initialized by the maximum coverage score of single patterns (Sect. 3), i.e., ${\mathsf{maxpcov}}$=$\max _{P\in \mathcal{P}}({\mathsf{cov}} (P))$ (lines 4-5), and eagerly constructs ${\mathsf{OGFCs}}$ with high marginal benefits that refines sieve values progressively.

The above two procedures interact with each other: Each pattern verified by $\mathsf{PGen}$ is sent to $\mathsf{PSel}$ for selection. The algorithm terminates when no new pattern can be verified by $\mathsf{PGen}$ or the set $\mathcal{S}$ can no longer be improved by $\mathsf {PSel}$ (as will be discussed). We next introduce the details of procedures $\mathsf {PGen}$ and $\mathsf {PSel}$.

Procedure $\mathsf {PGen}$. Procedure $\mathsf {PGen}$ improves its “batch” counterpart in $\mathsf {OGFC\_batch}$ by locally generating patterns that cover particular sets of facts, following a manner of decision tree construction. It maintains the following structures in each iteration i: (1) a pattern set $\mathcal{P}_i$, which contains graph patterns of size (number of pattern edges) i, and is initialized as a size-0 pattern that contains anchored nodes $u_x$ and $u_y$ only; (2) a partition set ${\varGamma _i}(P)$, which records the sets of facts $P(\varGamma ^+)$ and $P(\varGamma ^+)$, is initialized as $\{\varGamma ^+, \varGamma ^-\}$, for each pattern $P\in$ $\mathcal{P}_i$. At iteration i, it performs the following.

(1) For each block $B\in {\varGamma _{i-1}}$, $\mathsf {PGen}$ generates a set of graph patterns $\mathcal{P}_i$ with size i. A size-i pattern P is constructed by adding a triple pattern $e(u, u')$ to its size-($i-1$) counterpart $P'$ in $\mathcal{P}_{i-1}$. Moreover, it only inserts $e(u, u')$ with instances from the neighbors of the matches of $P'$ based on closeness function ${\mathsf{osim}}$.

(2) For each pattern $P\in \mathcal{P}_i$, $\mathsf {PGen}$ computes its support, confidence, and significance (G-test) by invoking procedure $\mathsf {Verify}$ as in the algorithm $\mathsf {OGFC\_batch}$ and prunes $\mathcal{P}_i$ by removing unsatisfied patterns. It refines $P'(\varGamma ^+)$ and $P'(\varGamma ^-)$ to $P(\varGamma ^+)$ and $P(\varGamma ^-)$ accordingly. Note that $P(\varGamma ^+)\subseteq P'(\varGamma ^+)$, and $P(\varGamma ^-)\subseteq P'(\varGamma ^-)$. Once a promising pattern P is verified,  $\mathsf {PGen}$ returns P to procedure $\mathsf {PSel}$ for the construction of top-k ${\mathsf{OGFCs}}$ $\mathcal{S}$.

Fig. 3

Procedure $\mathsf {PSel}$: Sieve values induce sieve sets to cache promising subgraph patterns. Subgraph patterns are verified and top patterns are selected in iterative discovery and selection

Procedure $\mathsf {PSel}$. To compute the set of ${\mathsf{OGFCs}}$ $\mathcal{S}$ that maximizes ${\mathsf{cov}} (\mathcal{S})$ for a given r(x, y), it suffices for procedure $\mathsf {PSel}$ to compute top-k graph patterns that maximize ${\mathsf{cov}} (\mathcal{S})$ accordingly. It solves a submodular optimization problem over the pattern stream that specializes the sieve-streaming technique [1] to ${\mathsf{OGFCs}}$.

Sieve streaming. [1, 26] Given a monotone submodular function $F(\cdot )$, a constant $\epsilon$>0, and element set $\mathcal{D}$, sieve streaming finds top-k elements $\mathcal{S}$ that maximizes $F(\mathcal{S})$ as follows. It first finds the largest value of singleton sets $m=\max _{e\in \mathcal{D}}F(\{e\})$ and then uses a set of sieve values $(1+\epsilon )^j$ (j is an integer) to discretize the range $[m, k*m]$. As the optimal value, denoted as $F(\mathcal {S}^*)$, is in $[m, k*m]$, there exists a value $(1+\epsilon )^j$ that “best” approximates $F(\mathcal {S}^*)$. For each sieve value v, a set of top patterns $\mathcal {S}_v$ is maintained, by adding patterns with a marginal gain at least $(\frac{v}{2}-F(\mathcal {S}_v))/(k-|\mathcal {S}_v|)$. It is shown that selecting the sieve of best k elements produces a set $\mathcal{S}$ with $F(\mathcal {S})\ge (\frac{1}{2} - \epsilon )F(\mathcal {S}^*)$ [1].

A direct application of the above sieve streaming for ${\mathsf{OGFCs}}$ seems infeasible: One needs to find the maximum ${\mathsf{cov}} (\varphi )$ (or ${\mathsf{cov}} (P)$ for fixed r(x, y)), which requires to verify the entire pattern set. Capitalizing on data locality of graph pattern matching, Lemma 3, and Lemma 1, we show that this is doable for ${\mathsf{OGFCs}}$ with a small cost.

Lemma 4.

It is in $O(|\varGamma _1|)$ time to compute the maximum ${\mathsf{cov}} (P)$.

This can be verified by observing that ${\mathsf{cov}} (\cdot )$ also preserves anti-monotonicity in terms of pattern refinement, because ${\mathsf{sig}} (\mathcal{S})$ is an aggregation of ${\mathsf{sig}} (\varphi )$ and ${\mathsf{div}} (\mathcal{S})$ is an aggregation of support, both of which hold the anti-monotonicity for single patterns. For any two patterns P(x, y) and $P^\prime (x, y)$, if $P\preceq P^\prime$, ${\mathsf{cov}} (\mathcal{S}\cup \{P^\prime \}) \le {\mathsf{cov}} (\mathcal{S}\cup \{P\})$. Thus, the value $\max _{P\in \mathcal{P}}{\mathsf{cov}} (P)$ must be from a single-edge pattern. That is, procedure $\mathsf {PSel}$ only needs to cache at most $|\varGamma _1|$ size-1 patterns from $\mathsf {PGen}$ to find the global maximum ${\mathsf{cov}} (P)$ (lines 4-5 of $\mathsf {OGFC\_stream}$).

The rest of $\mathsf {PSel}$ follows the sieve-streaming strategy, as illustrated in Fig. 3. The ${\mathsf{OGFCs}}$ are constructed with the top-k graph patterns (line 8).

Optimization. To further prune unpromising patterns, procedure $\mathsf {PGen}$ estimates an upper bound $\hat{\mathsf{mg}} (P, \mathcal{S}_{v_j})$ (line 5 of $\mathsf {PSel}$) without verifying a new size-b pattern P. If $\hat{\mathsf{mg}} (P,\mathcal{S}_{v_j}) < (\frac{v_j}{2} - \hat{\mathsf{cov}} (\mathcal{S}_{v_j})) \big / (k-|\mathcal{S}_{v_j}|)$, P is skipped without further verification.

To this end, $\mathsf {PGen}$ first traces to an ${\mathsf{OGFC}}$ $\varphi ' : P'(x,y)\rightarrow r(x,y)$, where $P'$ is a verified sub-pattern of P, and P is obtained by adding a triple pattern $r'$ to $P'$. It estimates an upper bound of the support of the ${\mathsf{OGFC}}$ $\varphi :P(x,y)\rightarrow r(x,y)$ as $\hat{\mathsf{supp}} (\varphi )={\mathsf{supp}} (\varphi ')$-$\frac{l}{|r(\varGamma ^+)|}$, where l is the number of the facts in $r(\varGamma ^+)$ that have no match of $r'$ in their i hop neighbors (thus cannot be covered by P). Similarly, one can estimate an upper bound for p and n in ${\mathsf{sig}} (\cdot )$ and thus get an upper bound $\hat{\mathsf{sig}} _b(\varphi )$ for $\hat{\mathsf{sig}} (\varphi )$. For each t in $\varGamma ^+$, denote term $\sqrt{\sum _{\varphi \in \varPhi _t(\mathcal{S})}{\mathsf{supp}} (\varphi )}$ in ${\mathsf{div}} (\mathcal{S})$ as $T_t(\mathcal{S})$; it then computes $\hat{\mathsf{mg}} (P, \mathcal{S})$ as

$$\begin{aligned} \hat{\mathsf{mg}} (P, \mathcal{S}) = \frac{\hat{\mathsf{sig}} _b(\varphi )}{2{{\mathsf{sig}} (\mathcal{S})}}+\left( \sum _{t \in P(\varGamma ^+)}\tfrac{\hat{\mathsf{supp}} (\varphi )}{2{T_t(\mathcal{S})}}\right) \big /{|\varGamma ^+|} \end{aligned}$$

To see that $\hat{{\mathsf{mg}}}(P, \mathcal{S})$ is an upper bound for ${\mathsf{mg}} (P, \mathcal{S})$, one may note that the marginal gains for the significance part $\hat{\mathsf{sig}} (\mathcal{S})$ and the diversity part ${\mathsf{div}} (\mathcal{S})$ are both defined in terms of square roots. Given any two positive numbers $a_1$ and $a_2$, an upper bound of $\sqrt{a_1 + a_2} - \sqrt{a_1}$ is $\frac{a_2}{2\sqrt{a_1}}$. We apply this inequality to each square root term. Take significance for example, ${\mathsf{sig}} (\mathcal{S}\cup \{P\})- {\mathsf{sig}} (\mathcal{S}) \le \sqrt{{\mathsf{sig}} ^2(\mathcal{S})+\hat{\mathsf{sig}} _b(P)}-\sqrt{{\mathsf{sig}} ^2(\mathcal{S})}$. When substituting $a_1$ and $a_2$ in the inequality by ${\mathsf{sig}} ^2(\mathcal{S})$ and $\hat{\mathsf{sig}} _b(P)$, respectively, we can have the upper bound $\frac{\hat{\mathsf{sig}} _b(\varphi )}{2{\mathsf{sig}} (\mathcal{S})}$. For the other terms in ${\mathsf{div}} (\mathcal{S})$, we can apply the inequality similarly to obtain the upper bound for each square root term.

Performance analysis. Denote the total patterns verified by $\mathsf {OGFC\_stream}$ as $\mathcal{P}$, it takes $O(|\mathcal{P}|(b+|\varGamma _b|)^2)$ time to compute the pattern matches and verify the patterns. Each time a pattern is verified, it takes $O(\frac{\log k}{\epsilon })$ time to update the set $\mathcal {S}_v$. Thus, the update time for each pattern is in $O((b+|\varGamma |_b)^2 + \frac{\log k}{\epsilon })$.

The approximation ratio follows the analysis of optimizing stream summarization [1], by viewing patterns as data items that carry a benefit, and the general pattern coverage as the utility function to be optimized. Specifically, (1) there exists a sieve value $v_j=(1+\epsilon )^j \in [{\mathsf{maxpcov}}, k*{\mathsf{maxpcov}} ]$ that is closest to $F(\mathcal {S}^*)$, say, $(1 - 2\epsilon )F(\mathcal {S}^*) \le v_j \le F(\mathcal {S}^*)$; and (2) the set $\mathcal {S}_{v_j}$ is a $(\frac{1}{2}-\epsilon )$ answer for an estimation of $F(\mathcal {S}^*)$ with sieve value $v_j$. Indeed, if ${\mathsf{mg}} (P, \mathcal {S}_{v_j})$ satisfies the test in $\mathsf {PSel}$ (line 5), then ${\mathsf{cov}} (\mathcal {S}_{v_j})$ is at least $\frac{v_j|\mathcal {S}|}{2k}=\frac{v_j}{2}$ (when $|\mathcal {S}|=k$). Following [1], there exists at least a value $v_j \in \mathcal{S}_V$ that best estimates the optimal ${\mathsf{cov}} (\cdot )$ and thus achieves approximation ratio $(\frac{1}{2}-\epsilon )$. Thus, selecting ${\mathsf{OGFCs}}$ with patterns from the sieve sets having the largest coverage guarantees approximation ratio $(\frac{1}{2}-\epsilon )$.

The above analysis completes the proof of Theorem 1.

4.2 ${\mathsf{OGFC}}$-based Fact Checking

The ${\mathsf{OGFCs}}$ can be applied to enhance fact checking as rule models or via supervised link prediction. We introduce two ${\mathsf{OGFC}}$-based models.

Generating training facts. Given a knowledge graph G = (V, E, L) and a triple pattern r(x, y), we generate training facts $\varGamma$ as follows. (1) For each fixed r(x, y), a set of true facts $\varGamma ^+$ is sampled from the matches of r(x, y) in the knowledge graph G. For each true fact 〈$v_x$, $\texttt {{ r}}$, $v_y$〉 $\in \varGamma ^+$, we further introduce “noise” by replacing their labels to semantically close counterparts asserted by ontology labels from O and ${\mathsf{osim}} (\cdot )$. This generates a set of true facts that approximately match r(x, y). (2) Given $\varGamma ^+$, a set of false facts $\varGamma ^-$ is sampled under the ontology-based PCA (Sect. 3). A missing fact t= $v_x$, $\texttt {{ r}}$, $v_y'$ is considered as a false fact only when (a) there exists a true fact 〈$v_x$, $\texttt {{ r}}$, $v_y$〉 in $\varGamma ^+$, and (b) $L(v_y) \not \in {\mathsf{osim}} (L(v_y'), O)$. We follow the silver standard [34] to only generate false facts that are not seen in the existed facts in G, thus $\varGamma ^+\cap \varGamma ^-$ = $\emptyset$.

Using ${\mathsf{OGFCs}}$ as rules. Given facts $\varGamma$, a rule-based model, denoted as ${\mathsf{OFact}} _R$, invokes algorithm $\mathsf {OGFC\_stream}$ to discover top-k ${\mathsf{OGFCs}}$ $\mathcal{S}$ as fact checking rules. Given a new fact t= $v_x$, $\texttt {{ r}}$, $v_y$ , it follows a “hit and miss” convention [15] and checks whether there exists an ${\mathsf{OGFC}}$ $\varphi$ in $\mathcal {S}$ that covers t (i.e., both the consequent and antecedent of $\varphi$ cover t), in terms of ontology O and function ${\mathsf{osim}} (\cdot )$. If so, ${\mathsf{OFact}} _R$ accepts t, otherwise, it rejects t.

Using ${\mathsf{OGFCs}}$ in supervised link prediction. Useful instance-level features can be extracted from the patterns and their matches induced by ${\mathsf{OGFCs}}$ to train classifiers. We develop a second model (denoted as $\mathsf {OFact}$) that adopts the following specifications. For each example t= 〈$v_x$, $\texttt {{ r}}$, $v_y$〉 $\ \in \varGamma$, $\mathsf {OFact}$ constructs a feature vector of size k, where each entry encodes the presence of the ith ${\mathsf{OGFC}}$ $\varphi _i$ in the top-k ${\mathsf{OGFCs}}$ $\mathcal{S}$. The class label of the example t is true (resp. false) if $t \in \varGamma ^+$ (resp. $\varGamma ^-$).

By default, $\mathsf {OFact}$ adopts logistic regression, which is experimentally verified to achieve slightly better performance than others (e.g., Naive Bayes and SVM). We find that $\mathsf {OFact}$ outperforms ${\mathsf{OFact}} _R$ over real-world graphs (See Sect. 5).

5 Experimental Study

Using real-world knowledge bases, we empirically evaluate the efficiency of ${\mathsf{OGFC}}$ discovery and the effectiveness of ${\mathsf{OGFC}}$-based fact checking.

Knowledge Graphs. We used five real-world knowledge graphs, including (1) $\mathsf {YAGO}$  [41] (version 2.5), a knowledge base that contains 2.1M entities with 2273 distinct labels, 4.0M edges with 33 distinct labels, and 15.5K triple patterns; (2) ${\mathsf{DBpedia}}$  [23] (version 3.8), a knowledge base that contains 2.2M entities with 73 distinct labels, 7.4M edges with 584 distinct labels, and 8.2K triple patterns; (3) ${\mathsf{Wikidata}}$  [43] (RDF dumps 20160801), a knowledge base that contains 10.8M entities with 18383 labels, 41.4M edges of 693 relationships, and 209K triple patterns; (4) ${\mathsf{MAG}}$  [38], a fraction of an academic graph with 0.6M entities (e.g., papers, authors, venues, affiliations) of 8565 labels and 1.71M edges of six relationships (cite, coauthorship); and (5) ${\mathsf{Offshore}}$  [19], a social network of offshore entities and financial activities, which contains 1M entities (e.g., company, country, person, etc.) with 357 labels, 3.3M relationships (e.g., establish, close, etc.) with 274 labels, and 633 triple patterns. We use ${\mathsf{Offshore}}$ mostly for case studies.

Ontologies. We have extracted ontologies for each knowledge graphs, either from their knowledge base sources like ${\mathsf{YAGO}}$¹, $\mathsf {DBpedia}$², and $\mathsf {Wikidata}$³. For datasets that do not have external ontologies such as $\mathsf {MAG}$ and $\mathsf {Offshore}$, we extend graph summarization [40] to construct ontologies. Specifically, we start with a set of manually selected seed concept labels (e.g., conferences, institutions and authors from $\mathsf {MAG}$) and extend these ontologies by grouping their frequently co-occurred labels in the node content (e.g., venues, universities, collaborators). We manually cleaned these ontologies to ensure their applicability.

Methods. We implemented the following methods in JAVA: (1) $\mathsf {OGFC\_stream}$, compared with (a) its “Batch + Greedy” counterpart $\mathsf {OGFC\_batch}$ (Sect. 4), (b) ${\mathsf{AMIE+}}$ [14] that discovers ${\mathsf{AMIE}}$ rules, (c) $\mathsf {PRA}$  [22], the path ranking algorithm that trains classifiers with path features from random walks, and (d) $\mathsf {KGMiner}$  [37], a variant of PRA that makes use of features from discriminant paths; (2) fact checking models ${\mathsf{OFact}} _R$ and $\mathsf {OFact}$, compared with learning models (and also denoted) by ${\mathsf{AMIE+}}$, $\mathsf {PRA}$, and $\mathsf {KGMiner}$, respectively. For practical comparison, we set a pattern size (the number of pattern edges) bound $b=4$ for ${\mathsf{OGFC}}$ discovery.

Ontology closeness. We apply weighted path lengths in ${\mathsf{osim}} (\cdot )$, in which each edge on a path has a weight according to one of the three types of relations (Sect. 2.1) (1) Given ontology O and two labels l and $l'$, the closeness of l and $l'$ is defined as ${1 - {\mathsf{dist}} (l, l')}$, where ${\mathsf{dist}} (l, l')$ is the sum of weights on the shortest path between l and $l'$ in the ontology O, normalized in range [0, 1]. (2) Given a threshold $\beta$, ${\mathsf{osim}} (l, O)$ is defined as all the concept labels from O with closeness no less than $\beta$. By default, we set $\beta$ = 1, i.e., the subgraph patterns enforce label equality by ensuring ${\mathsf{dist}} (l,l')$ = 0, which is same as ${\mathsf{GFCs}}$. As will be shown, varying $\beta$ provides trade-off between discovery cost and model accuracy.

Model configuration. For a fair comparison, we made effort to calibrate the models and training/testing sets with consistent settings. (1) For the supervised link prediction methods ($\mathsf {OFact}$, $\mathsf {PRA}$, and $\mathsf {KGMiner}$), we sample $80\%$ of the facts in a knowledge graph as the training facts $\varGamma$, and $20\%$ edges as testing set $\mathcal{T}$. For example, we use in total 107 triple patterns over $\mathsf {DBpedia}$, and each triple pattern has 5K-50K instances. In $\varGamma$ (resp. $\mathcal{T}$), $20\%$ are true examples $\varGamma ^+$ (resp. $\mathcal{T}^+$), and $80\%$ are false examples $\varGamma ^-$ (resp. $\mathcal{T}^-$). We generate $\varGamma ^-$ and $\mathcal{T}^-$ under ontology-based $\mathsf {PCA}$ (Sect. 3) for all the models. For all methods, we use logistic regression to train the classifiers (which is the default settings of $\mathsf {PRA}$ and $\mathsf {KGMiner}$). (2) For rule-based ${\mathsf{OFact}} _R$ and ${\mathsf{AMIE+}}$, we discover rules that cover the same set of $\varGamma ^+$. We set the size of ${\mathsf{AMIE+}}$ rule body to be 3, comparable to the number of pattern edges in our work. (3) We evaluate the impact of ontology closeness constraints to the efficiency and the effectiveness of ${\mathsf{OGFC}}$-based models, by varying the closeness threshold $\beta$.

Overview of results. We find the following. (1) It is feasible to discover ${\mathsf{OGFCs}}$ in large graphs (Exp-1). For example, it takes 211 seconds for $\mathsf {OGFC\_stream}$ to discover ${\mathsf{OGFCs}}$ over $\mathsf {YAGO}$ with 4 million edges and 3000 training facts. On average, it outperforms ${\mathsf{AMIE+}}$ by 3.4 times. (2) ${\mathsf{OGFCs}}$ can improve the accuracy of fact checking models (Exp-2). For example, it achieves additional $30\%$, $20\%,$ and $5\%$ gain of precision over $\mathsf {DBpedia}$, and $20\%$, $15\%,$ and $16\%$ gain of $F_1$ score over $\mathsf {Wikidata}$ when compared with ${\mathsf{AMIE+}}$, $\mathsf {PRA}$, and $\mathsf {KGMiner}$, respectively. (3) The ontological closeness ${\mathsf{osim}}$ and threshold $\beta$ enable trade-offs between discovering cost and effectiveness. With smaller threshold $\beta$, while $\mathsf {OGFC\_stream}$ takes more time to discover ${\mathsf{OGFCs}}$, these rules can cover more training instances and verify more missing facts that are not covered by their counterparts induced by larger $\beta$. (4) Our case study shows that $\mathsf {OFact}$ yields interpretable models (Exp-3).

We next report the details of our findings.

Exp-1: Efficiency. We report the efficiency of $\mathsf {OGFC\_stream}$, compared with $\mathsf {PRA}$, ${\mathsf{AMIE+}}$, and $\mathsf {OGFC\_batch}$, and study the efficiency with ontology closeness by varying $\beta$. ${\mathsf{KGMiner}}$ is omitted, since it has unstable learning time and is not comparable.

${{{{Varying |E|}}}}$. For $\mathsf {DBpedia}$, fixing $|\varGamma ^+|=15K$, support threshold $\sigma =0.1$, confidence threshold $\theta$= 0.005, $k=200$, we sampled five graphs from $\mathsf {DBpedia}$, with size (number of edges) varied from 0.6M to 1.8M; for $\mathsf {Wikidata}$, fixing $|\varGamma ^+|=6K$, $\sigma =0.001$, $\theta =5\times 10^{-5}$, $k=50$, we sampled five graphs, with size varied from 0.4M to 2.0M edges. Figure 4a, b shows that all methods take longer time over larger |E|, as expected. (1) Figure 4a shows that $\mathsf {OGFC\_stream}$ is on average 3.2 (resp. 4.1) times faster than ${\mathsf{AMIE}}$ + (resp. $\mathsf {OGFC\_batch}$) over $\mathsf {DBpedia}$ due to its approximate matching scheme and top-k selection strategy. (2) Although ${\mathsf{AMIE+}}$ is faster than $\mathsf {OGFC\_stream}$ over smaller graphs, we find that it returns few rules due to low support. Enlarging rule size (e.g., to 5) ${\mathsf{AMIE+}}$ does not run to completion. (3) The cost of $\mathsf {PRA}$ is less sensitive due to that it samples a (predefined) fixed number of paths, but it does not perform well in $\mathsf {Wikidata}$ (Fig. 4b). (4) $\mathsf {OGFC\_stream}$ outperforms the other three in $\mathsf {Wikidata}$ except $|E|=0.4M$ (Fig. 4b), which is because $\mathsf {OGFC\_stream}$ has an overhead to compute ${\mathsf{maxpcov}}$ and allocate sieves but too few rules can be discovered in small data.

Varying ${|\varGamma ^{+}|}$. For $\mathsf {DBpedia}$, fixing $|E|=1.8M$, $\sigma =0.1$, $\theta =0.005$, $k=200$, we varied $|\varGamma ^+|$ from 3K to 15K; for $\mathsf {Wikidata}$, fixing $|E|=2M$, $\sigma =0.001$, $\theta =5\times 10^{-5}$, $k=50$, we varied $\varGamma ^+$ from 1200 to 6000. As shown in Fig. 4c, d, while all the methods take longer time for larger $|\varGamma ^+|$, $\mathsf {OGFC\_stream}$ scales best with $|\varGamma ^+|$ due to its stream selection strategy. In $\mathsf {DBpedia}$, $\mathsf {OGFC\_stream}$ achieves comparable efficiency with $\mathsf {PRA}$ and outperforms $\mathsf {OGFC\_batch}$ and ${\mathsf{AMIE+}}$ by 3.54 and 5.1 times on average, respectively. In $\mathsf {Wikidata}$, ${\mathsf{OGFC\_stream}}$ outperforms others except $|\varGamma ^+|=1200$, which is still because an overhead for small data with too few rules.

Fig. 4

Efficiency of $\mathsf {OGFC\_stream}$

Varying σ. Fixing $|E|=1.8M$, $|\varGamma ^+|=15K$, $\theta =0.005$, $k=200$, we varied $\sigma$ from 0.05 to 0.25 in $\mathsf {DBpedia}$. As shown in Fig. 4e, $\mathsf {OGFC\_batch}$ takes longer time over smaller $\sigma$, due to more patterns and ${\mathsf{OGFC}}$ candidates need to be verified. On the other hand, $\mathsf {OGFC\_stream}$ is much less sensitive due to that it terminates early without verifying all patterns.

Varying k. Fixing $|E|=1.8M$, $\sigma =0.1$, $\theta =0.005$, we varied k from 200 to 1000 in $\mathsf {DBpedia}$. Figure 4f shows that $\mathsf {OGFC\_stream}$ is more sensitive to k due to it takes longer time to find k best patterns for each sieve value. Although $\mathsf {OGFC\_batch}$ is less sensitive, the major bottleneck is its verification cost. In addition, we found that with larger $\epsilon$, less number of patterns are needed; thus, $\mathsf {OGFC\_stream}$ takes less time.

Varying ${\beta }$. We next evaluate the impact of $\beta$ to the cost of ${\mathsf{OGFCs}}$ discovery. We fix $|E|=1.2M$, $\sigma ={0.01}$, $\theta =0.005$, $b=4$, and $k=200$ for $\mathsf {YAGO}$, and $|E|=1.5M$, $\sigma =0.1$, $\theta ={0.005}$, $b=4$, and $k=200$ for $\mathsf {DBpedia}$, we varied $\beta$ from 1 to 0.5. On the one hand, Fig. 4g, h shows that it takes longer time to discover ${\mathsf{OGFCs}}$ for smaller $\beta$ for both $\mathsf {OGFC\_stream}$ and $\mathsf {OGFC\_batch}$. This is because the pattern verification cost increases due to more candidates introduced by ${\mathsf{osim}} (\cdot )$. On the other hand, $\mathsf {OGFC\_stream}$ improves $\mathsf {OGFC\_batch}$ better over smaller $\beta$ due to its early termination. For example, it is 2.1, 4.4 and 8.14 times faster than $\mathsf {OGFC\_batch}$ over $\mathsf {DBpedia}$ when $\beta$ is 1 (using label equality), 0.75 and 0.5, respectively. Compared with ${\mathsf{GFCs}}$ ($\beta =1$), $\mathsf {OGFC\_stream}$ is on average five times slower when $\beta =0.75$ and is on average 15 times slower when $\beta =0.50$ over $\mathsf {DBpedia}$. Actually, enabling ontologies will enlarge training set $\varGamma ^+$, which takes longer time as verified in Fig. 4c, d. However, a benefit of ${\mathsf{OGFCs}}$ is to build a unified model for multiple triple patterns r(x, y), rather than building a separate model for each r(x, y) as in ${\mathsf{GFCs}}$. In practice, users can select applicable $\beta$ (closer to 1) to avoid including many similar labels.

Exp-2: Accuracy. We report the accuracy of all the models in Table 1.

Rule-based models. We apply the same support threshold $\sigma =0.1$ for ${\mathsf{AMIE+}}$ and ${\mathsf{OFact}} _R$. We set $\theta =0.005$ for ${\mathsf{OFact}} _R$ and set $k=200$. We sample 20 triple patterns and report the average accuracy. As shown in Table 1, ${\mathsf{OFact}} _R$ constantly improves ${\mathsf{AMIE+}}$ with up to $21\%$ gain in prediction rate, and with comparable performance for other cases. We found that ${\mathsf{AMIE+}}$ reports rules with high support but not necessarily meaningful, while ${\mathsf{OGFCs}}$ capture more meaningful context (see Exp-3). Both models have relatively high recall but low precision; due to that, they have a better chance to cover missing facts but may introduce errors when hitting false facts.

Supervised models. We next compare $\mathsf {OFact}$ with supervised link prediction models. $\mathsf {OFact}$ achieves the highest prediction rates and $F_1$ scores. It outperforms $\mathsf {PRA}$ with $12\%$ gain on precision and $23\%$ gain on recall on average and outperforms $\mathsf {KGMiner}$ with $16\%$ gain on precision and $19\%$ recall. Indeed, $\mathsf {OFact}$ extracts useful features from ${\mathsf{OGFCs}}$ with both high significance and diversity, beyond path features.

Table 1 Effectiveness: average accuracy

We next evaluate the impact of factors to the model accuracy and study the impact of ontology closeness by varying $\beta$ in Fig. 5.

Varying ${\sigma }$ and ${\theta }$. For $\mathsf {Wikidata}$, fixing $|E|=2.0M$, $|\varGamma ^+|=135K$, and $k=200$, we varied $\sigma$ from 0.05 to 0.25 and compare patterns with confidence 0.02 and 0.04, respectively, as shown in Fig. 5a. For $\mathsf {YAGO}$, fixing $|E|=1.5M$, $|\varGamma ^+|=250K$, and $k=200$, we varied $\sigma$ from 0.05 to 0.25 and compare patterns with confidence 0.001 and 0.002, respectively, as shown in Fig. 5b. Both figures show that $\mathsf {OFact}$ and ${\mathsf{OFact}} _R$ have lower prediction rates when support threshold (resp. confidence) is higher (resp. lower). That is because fewer patterns can be discovered with higher $\sigma$, leading to more “misses” in facts, while higher confidence leads to stronger association of patterns and more accurate predictions. In general, $\mathsf {OFact}$ achieves higher prediction rate than ${\mathsf{OFact}} _R$.

Varying ${|\varGamma ^{+}|}$. For $\mathsf {Wikidata}$, fixing $|E|=2.0M$, $|\varGamma ^{+}|=135K$, $\sigma =0.001$, $\theta =5\times 10^{-5}$, $k=200$, we vary $|\varGamma ^+|$ from 75K to 135K as shown in Fig. 5c; for $\mathsf {YAGO}$, fixing $|E|=1.5M$, $\sigma =0.01$, $\theta =0.005$, $k=200$, we vary $|\varGamma ^+|$ from 50K to 250K as shown in Fig. 5d. Both figures show that $\mathsf {OFact}$ and ${\mathsf{OFact}} _R$ have higher prediction rate when providing more examples. Their precisions (not shown) follow a similar trend.

Varying k. For $\mathsf {Wikidata}$, fixing $|E|=2.0M$, $\varGamma ^+=135K$, $\sigma =0.001$, $\theta =5\times 10^{-5}$, we varied k from 50 to 250. Figure 5e shows the prediction rate first increases and then decreases. For rule-based model, more rules increase the accuracy by covering more true facts, while increasing the risk of hitting false facts. For supervised link prediction, the model will be under-fitting with few features for small k and will be over-fitting with too many features due to large k. We observe that $k=200$ is a best setting for high prediction rate. This also explains the need for top-k discovery instead of a full enumeration of graph patterns.

Varying b. For $\mathsf {Wikidata}$, fixing $|E|=2.0M$, $\sigma =0.001$, $\theta =5 \times 10^{-5}$, and $k=200$, for $\mathsf {YAGO}$, fixing $|E|=1.5M$, $\sigma =0.01$, $\theta =0.005$, and $k=200$, for both data, we select 200 size 2 patterns and 200 size 3 patterns to train the models. Figure 5f verifies an interesting observation: Smaller patterns contribute more to recall and larger patterns contribute more to precision, because smaller patterns are more likely to “hit” new facts, while larger patterns have stricter constraints for correct prediction of true fact.

Varying ${\beta }$. Using the same setting as in Fig. 4g, h, we report the impact of $\beta$ to the accuracy of ${\mathsf{OGFC}}$-based models. Figure 5g and h shows that with smaller $\beta$, $\mathsf {OFact}$ and ${\mathsf{OFact}} _R$ achieve higher recall but retain reasonable precision. Indeed, smaller $\beta$ allows rules to be learned from more training examples and cover more missing facts. As $\beta$ is varied from 1 to 0.75 (resp. 0.5), for $\mathsf {YAGO}$, the recall of $\mathsf {OFact}$ increases from $45\%$ to $56\%$ (resp. $70\%$) with at most $5\%$ (resp. $9\%$) loss in precision; for $\mathsf {DBpedia}$, the recall of $\mathsf {OFact}$ increases from $31\%$ to $42\%$ (resp. $55\%$) with at most $1\%$ (resp. $4\%$) loss in precision. Note that for $\beta =1$, the results are the same as using ${\mathsf{GFCs}}$ without ontologies, which have much lower recalls than $\mathsf {OFact}$. This justifies the benefit of introducing ontological matching.

Fig. 5

Impact factors to accuracy

Exp-3: Case study. We perform case studies to evaluate the applications of ${\mathsf{OGFCs}}$.

Test cases. A test case consists of a triple pattern r(x, y) and a set of test facts that are ontologically close to r(x, y). According to the type information on nodes and edges, the triple patterns are categorized in:

(a) Functional cases refer to functional predicates (a “one-to-one” mapping) of relationship r between node $v_x$ and node $v_y$. For a relationship “capitalOf,” two locations can only map to each other through it, for example, “London” is the capital of “UK”.

(b) Pseudo-functional predicates can be “one-to-many,” but have high functionality (a.k.a. “usually functional”). For example, relationships like “graduatedFrom” are not necessary functional, but are functional for many “persons”.

(c) Inverse Pseudo-functional are those facts with inversed pseudo-functional predicates (“many-to-one”), like “almaMaterOf”.

(d) Non-Functional facts allow “many-to-many” mapping, such as “workFor” between “person” and “organization”.

Table 2 Case study: $F_1$ scores over 30 test cases

Accuracy. We show 30 r(x, y) cases from each category and report their overall $F_1$ scores in Table. 2. Non-functional cases are those allow “many-to-many” relations, in which case $\mathsf {PCA}$ may not hold [14]. We found that $\mathsf {OFact}$ performs well for all test cases, especially for those non-functional ones. Indeed, the relaxation of label equality by the ontology closeness in both pattern matching and the ontology-based $\mathsf {PCA}$ helps improve the fact checking models in recall without losing much precision (Fig. 5h, g), and the graph patterns of ${\mathsf{OGFCs}}$ mitigate the non-functional bases with enriched context.

Interpretability. We further illustrate three top ${\mathsf{OGFCs}}$ in Fig. 6, which contribute to highly important features in $\mathsf {OFact}$ with high confidence and significance over a real-world financial network $\mathsf {Offshore}$ and two knowledge graphs $\mathsf {DBpedia}$ and $\mathsf {Wikidata}$.

Fig. 6

Real-world ${\mathsf{OGFCs}}$ discovered by $\mathsf {OFact}$

(1) ${\mathsf{OGFC}}$ $\varphi _3$ : $P_3(x, y)\rightarrow$ $\texttt {hasSameNameAndRegDate}$(company, company) ($\mathsf {Offshore}$) states that two (anonymous) companies are likely to have the same name and registration date if they share shareholder and beneficiary, and one is registered and within jurisdiction in Panama, and the other is active in Panama. This ${\mathsf{OGFC}}$ has support 0.12 and confidence 0.0086 and is quite significant. For the same r(x, y), ${\mathsf{AMIE+}}$ discovers a top rule as $\texttt {registerIn}$(x, Jurisdiction_in_Panama) $\wedge$ $\texttt {registerIn}$(y, Jurisdiction_in_Panama) and implies x and y has the same name and registration date. This rule has a low prediction rate.

(2) ${\mathsf{OGFC}}$ $\varphi _4$ : $P_4(x, y) \rightarrow$ $\texttt {relevant}$(TVShow, film) ($\mathsf {DBpedia}$) states that a TV show and a film have relevant content if they have the common language, authors, and producers. This ${\mathsf{OGFC}}$ has support 0.15 and a high confidence and significant score. Within bound 3, ${\mathsf{AMIE+}}$ reports a top rule as $\texttt {Starring}$$(x, z)\wedge$ $\texttt {Starring}$$(y, z)\rightarrow$ $\texttt {relevant}$(x, y) , which has low accuracy. This rule also identifies relevant relationships between BBC programs (e.g., “BBC News at Six”) and other programs that are relevant to “TVShow” and “Films” respectively, enabled by ontological matching. These facts cannot be captured by ${\mathsf{GFCs}}$ or ${\mathsf{AMIE}}$.

(3) ${\mathsf{OGFC}}$ $\varphi _5$ : $P_5(x, y) \rightarrow$ $\texttt {influences}$(writer, philosopher) ($\mathsf {Wikidata}$) states that a writer $v_x$ influences a philosopher $v_y$, if $v_x$ influences a philosopher p and a scholar s, who both influences a philosopher $v_y$. This rule identifies true facts such as 〈Bertrand Russel, $\texttt {influences}$, Ludwig Wittgenstein〉, the influence between a logician and a philosopher, enabled by ontological matching following $O_2$.

6 Conclusion

We have introduced ${\mathsf{OGFCs}}$, a class of rules that incorporate graph patterns to predict facts in knowledge graphs. We developed an ontology-aware rule discovery algorithm to find useful ${\mathsf{OGFCs}}$ for observed true and false facts, which selects the top discriminant graph patterns generated in a stream. We have shown that ${\mathsf{OGFCs}}$ can be readily applied as rule models or provide useful instance-level features in supervised link prediction. The benefit of enabling ontologies is to build a unified model for multiple triple patterns. Our experimental study has verified the effectiveness and efficiency of ${\mathsf{OGFC}}$-based techniques. We have evaluated ${\mathsf{OGFCs}}$ with real-world graphs and pattern models. One future topic is to extend ${\mathsf{OGFC}}$ techniques for entity resolution, social recommendation, anomaly detection, and data imputation. A second direction is to extend ${\mathsf{OGFC}}$ model to cope with multi-label knowledge graphs or property graphs. A third future work is to develop scalable ${\mathsf{OGFCs}}$-based models and methods with parallel graph mining and distributed rule learning.