1 Introduction

Coal and gas outburst is an extremely complex gas dynamic phenomenon encountered in the production of underground coal mine and characterized by sudden eruption of a large amount of gas and coal from the coal tunnel or stope within a very short period of time (Lama and Saghafi 2002; Skoczyla 2012). China is one of the countries in the world which facing the most serious outburst risks, since almost half of the world’s coal and gas outburst accidents happened in China (Wang et al. 2015a, b). With the increase of mining depth and intensity, the complexity of geological structure, gas content and pressure increase, the risk of coal and gas outburst disaster is also growing (Chen 2011; Fan et al. 2017). However, research progress on coal and gas outburst is limited in recent years.

Experts from different countries have worked on the outburst mechanism and prediction model (Beamish and Crosdale 1998; Cao et al. 2003; Alexeev et al. 2004; Xu et al. 2006; Aguado and Nicieza 2007; Wold et al. 2008; Li et al. 2016; Fan et al. 2016). Currently, almost none of a single theory can fully explain all phenomena of occurring coal and gas outburst. The quantitative analysis is also difficult to accomplish. Because of the dangers of coal and gas outburst, the field test of the outburst is difficult to complete. Thus with the aid of physical simulation, observing simulation phenomenon of coal and gas outburst is very important in the laboratory (Xue et al. 2011). Physical simulation of coal and gas outburst has been rapid developed in recent years. Yuan, Yin, and Liu, et al. have carried out large-scale coal and gas outburst experiments, but research on the similarity theory of coal and gas outburst is still remain rare (Yin et al. 2013, 2015; Liu et al. 2015; Yuan 2016). Zhang deduced the similarity criteria of physical and mechanical parameters by dimensional analysis in the perspective of mechanics, resulting in the similarity criteria which cover geometrical, load and material properties, but the relationship between stress and gas pressure is unknown (Zhang et al. 2016). Hu indicated the similarity criteria of three-dimensional solid–fluid coupling from solid–fluid coupling (Hu et al. 2007). Wang derived gas pressure ratio is \(p_{p} :p_{m} = 1\), mechanical ratio \(C_{E} = C_{{\sigma^{2} }}\) on the basis of solid–fluid coupling model and energy model. However, the mechanics ratio contradicts with \(C_{E} = C_{\sigma }\) that derived by \(E = \sigma /\varepsilon\) (Wang et al. 2015a, b). Wang discussed the defor-mation of similar material and gas flow similar under the condition of triaxial compression (Wang et al. 2017). In general, there is no intact similar theory to guide physical experiment of coal and gas outburst.

The similar material research has mainly two stages. No additive phase and pulverized coal directly compressed as samples in the absence of any additives (Skochinski 1953; Neliekl and Topolnicki 1994; Skoczylas et al. 2014). For example, Skoczylas formed 48 mm diameter, length of 110 mm briquettes using fine coal, and prepared coal briquettes of various porosity from 13.5% to 33%, and the coal briquettes have the similar mechanical and gaseous properties with normal and altered coal in 2014 (Skochinski 1953, 2012). Deng formed briquettes of IV, V type strength using fine coal in cold pressure method (Deng et al. 1989). However, the cold briquettes prepared solely relying on pressure condition without any additives such as water, diesel, oil, sand, lime, gypsum and other materials have low strength (Meng et al. 1996; Jiang and Guo 1999). In the researches of the additive phase, Ou formed coal samples with different physical and mechanical properties by controlling the mixture of pulverized coal and tar (Ou 2012). Zhang investigated the influence of various materials on similar material properties (Zhang et al. 2016). Wang resoundingly simulated gas seepage test in the similar materials using pulverized coal, cement, sand, activated carbon, which has a great boost to the development of similar material (Wang et al. 2017). The problems of similar material are that the intensity of physical and mechanical properties, the adsorption, desorption characteristics of similar material are lower than raw coal.

The similarity criteria and similar materials research have great help on the development of outburst physical simulation. This article will put forward similarity criteria which can describe the whole process of coal and gas outburst by using mechanics model, solid–fluid coupling model and energy model, and choose similar numbers by considering the current experiment conditions and the simulation requirement. Based on above analysis, we present a more reasonable ratio of simulation material, and analyze the influence of various factors on the similar material. Research results can help the theoretical and experimental development of outburst.

2 Similarity criteria

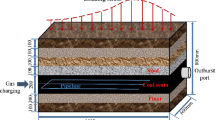
Coal and gas outburst is a complex mechanics process, and there is no accurate physical equation to describe the whole process of outburst. The non-dimensional was used to analyze mechanical model. The equation analysis method was applied to analyze fluid–solid coupling model in inoculation stage of outburst, and the proposed energy model was used to deduce similar criteria. The similarity criteria are unity and contradiction, because it is difficult to perfectly simulate outburst in the laboratory. Therefore, we choose the key factors to conduct outburst experiment (Fig. 1). The prototype parameters is the subscript p, model parameters is the subscript m in the paper.

Fig. 1
figure 1

The derivation process of the similar criteria

Full size image

2.1 Similarity criteria of mechanics model

The problems of outburst are solved usually by classic elastic–plastic mechanics. The basic equations include balance differential equation, geometric equation, constitutive equations, boundary conditions and initial conditions etc., thus the dimensional analysis method is adopted to analyze the involved physical quantities.

The outburst criterion is expressed as follows in the form of implicit function:

$$f(l,E,v,c,\varphi ,\psi ,\varepsilon ,R,p,\sigma ,W) = 0$$
(1)

where \(l\) is the length, \(E\) is the elastic modulus, \(v\) is poisson’s ratio, \(c\) is cohesion, \(\varphi\) is the internal friction angle, \(\psi\) is the dilation angle, \(\varepsilon\) is strain, \(R\) is the uniaxial compressive strength,\(p\) is the gas press, \(\sigma\) is the press, \(W\) is the load.

The function contains 11 ratios in similar conditions, \(C_{l}\), \(C_{E}\), \(C_{\nu }\), \(C_{c}\), \(C_{\varphi }\), \(C_{\psi }\), \(C_{\varepsilon }\), \(C_{R}\), \(C_{\sigma }\), \(C_{P}\), \(C_{W}\). The independent dimension is length and force. The corresponding non-dimensional function relations are as follow:

$$f(1,1,v,c/E,\varphi ,\psi ,\varepsilon ,R/E,p/E,\sigma /E,W/l) = 0$$
(2)

Based on the type of above parameters, we get 9 π numbers, \(\nu\), \(c/E\), \(\varphi\), \(\psi\), \(\varepsilon\), \(R/E\), \(P/E\), \(\sigma /E\), \(W/l\). There are 5 ratios, they are \(C_{E}\), \(C_{\nu }\), \(C_{\phi }\), \(C_{\psi }\), \(C_{\varepsilon }\), and \(C_{\nu }\) = \(C_{\phi }\) = \(C_{\psi }\) = \(C_{\varepsilon }\) = 1. The other parameters such as \(C_{c}\), \(C_{R}\), \(C_{\sigma }\), \(C_{W}\) rely on \(C_{l}\) and \(C_{E}\).

2.2 Similarity criteria of solid–liquid coupling model

Similarity criterion is derived based on solid–fluid coupling model proposed by Zhao (Hu et al. 2007).

Coal balance equation:

$$\sigma_{ij,i} + X_{j} = \rho \frac{{\partial^{2} \mu_{i} }}{{\partial t^{2} }}$$
(3)
$$\sigma_{ij,i} = G\nabla^{2} u{ + }(\lambda { + }G)\frac{{\partial {\text{e}}}}{{\partial {\text{x}}}}$$
(4)

Gas seepage equation:

$$K_{x} \frac{{\partial^{2} p}}{{\partial^{2} x}} + K_{y} \frac{{\partial^{2} p}}{{\partial^{2} y}} + K_{y} \frac{{\partial^{2} p}}{{\partial^{2} y}} = S\frac{\partial p}{\partial t} + \frac{\partial e}{\partial t} + w$$
(5)
$${\text{Effective}}\;{\text{stress}}\;{\text{equation:}}\;\overline{{\sigma_{ij} }} = \sigma_{ij} { - }\alpha p$$
(6)

where \(\sigma_{ij}\) is the total stress tensor; \(X_{j}\) is the volume force; \(\rho\) is the density; \(\mu_{i}\) is the matrix displacemen; G is the shear modulus; \(\lambda\) is the lame constant; e is the volume strain; \(K_{x}\), \(K_{\text{y}}\), \(K_{\text{z}}\) are permeability coefficient of three coordinate direction respectively; \(\overline{{\sigma_{ij} }}\) is the effective stress; \(\alpha\) is the Biolt coefficient; \(\gamma\) is the bulk density.

Similarly transforms:

$$\begin{aligned} & C_{G} G_{m} \frac{{C_{u} }}{{C_{l}^{2} }}\nabla^{2} u_{m} + C_{\lambda } \lambda_{m} \frac{{C_{e} }}{{C_{l} }}\frac{{\partial e_{m} }}{{\partial x_{m} }} + C_{G} G_{m} \frac{{C_{e} }}{{C_{l} }}\frac{{\partial e_{m} }}{{\partial x_{m} }} \\ & \quad + \,C_{\gamma } X_{m} = C_{\rho } \rho_{m} \frac{{C_{u} }}{{C_{t}^{2} }}\frac{{\partial^{2} u_{m} }}{{\partial t_{m}^{2} }} \\ \end{aligned}$$
(7)

According to the similarity theory, the similar physical phenomena will be expressed by the same differential equation. We gain 5 non-dimensional similar criteria to ensure that the prototype is similar to model, it is necessary to satisfy these five similar criterias.

$$\begin{aligned} \pi_{ 1} & {\text{ = C}}_{G} \frac{{C_{u} }}{{C_{l} }},\quad \pi_{2} = C_{\lambda } \frac{{C_{e} }}{{C_{l} }},\quad \pi_{ 3} { = }C_{G} \frac{{C_{e} }}{{C_{l} }} \\ \pi_{4} & = C_{\gamma } ,\quad \pi_{5} = C_{\rho } \frac{{C_{u} }}{{C_{l}^{2} }} \\ \end{aligned}$$
(8)
$$\begin{aligned} \pi_{2} & = \pi_{3} \to C_{G} = C_{\lambda } ; \\ \pi_{1} & = \pi_{3} ,C_{u} = C_{e} C_{l} \to C_{e} = 1,C_{u} = C_{l} ; \\ \pi_{3} & = \pi_{4} ,C_{G} C_{e} = C_{\gamma } C_{l} \to C_{G} = C_{E} ,C_{e} = 1, \\ C_{E} & = C_{\gamma } C_{l} \;C_{\gamma } = 1 \to C_{E} = C_{l} ; \\ C_{\sigma } & = C_{E} C_{e} \to C_{\sigma } = C_{\gamma } C_{l} ,\;{\text{when}}\;C_{\gamma } = 1,C_{\sigma } = C_{l} ; \\ \pi_{1} & = \pi_{5} ,\pi_{4} = \pi_{5} \to C_{t} = \sqrt {C_{e} C_{l} } ,C_{t} = \sqrt {C_{l} } ; \\ \end{aligned}$$

Gas seepage equation similarly transforms:

$$\begin{aligned} & \frac{{C_{K} C_{p} }}{{C_{x}^{2} }}K_{m} \frac{{\partial^{2} p_{m} }}{{\partial x_{m}^{2} }} + \frac{{C_{K} C_{p} }}{{C_{y}^{2} }}K_{m} \frac{{\partial^{2} p_{m} }}{{\partial y_{m}^{2} }} \\ & + \,\frac{{C_{K} C_{p} }}{{C_{z}^{2} }}K_{m} \frac{{\partial^{2} p_{m} }}{{\partial z_{m}^{2} }} = C_{s} S_{m} \frac{{C_{p} }}{{C_{t} }}\frac{{\partial p_{m} }}{{\partial t_{m} }} + \frac{{C_{e} }}{{C_{t} }}\frac{{\partial e_{m} }}{{\partial t_{m} }} + C_{w} w_{m} \\ \end{aligned}$$
(9)
$$\begin{aligned} \pi_{ 6} & = \frac{{C_{K} C_{p} }}{{C_{x}^{2} }},\pi_{ 7} { = }\frac{{C_{K} C_{p} }}{{C_{y}^{2} }},\pi_{ 8} { = }\frac{{C_{K} C_{p} }}{{C_{z}^{2} }} \\ \pi_{9} & {\text{ = C}}_{\text{s}} \frac{{C_{p} }}{{C_{l} }},\pi_{10} { = }\frac{{C_{e} }}{{C_{t} }} \\ \end{aligned}$$
(10)
$$\begin{aligned} \pi_{5} & = \pi_{6} = \pi_{7} = \pi_{9} \to \\ C_{p} & = C_{\gamma } C_{l} ,C_{t} = \sqrt {C_{l} } ,C_{x} = C_{y} = C_{z} = C_{l}, C_{K} = \frac{{\sqrt {C_{l} } }}{{C_{\gamma } }},C_{K} = \sqrt {C_{l} } ; \\ \pi_{5} & = \pi_{6} = \pi_{7} = \pi_{8} \to C_{s} = \frac{1}{{C_{\gamma } \sqrt {C_{l} } }}\;C_{s} = \frac{1}{{\sqrt {C_{l} } }}; \\ \end{aligned}$$

when \(C_{\alpha } = 1,\quad C_{p} = C_{\gamma } \,C_{l} ,\quad C_{\gamma } = 1 \to C_{p} = C_{l}\).

According to the above analysis, we get similarity criteria based on the solid–fluid coupling theory.

$$\begin{aligned} C_{u} & = C_{l} ,\quad C_{E} = C_{\gamma } C_{l} ,\quad C_{\sigma } = C_{\gamma } C_{l} ,\quad C_{p} = C_{\gamma } C_{l} \\ C_{t} & = \sqrt {C_{l} } ,\quad C_{K} = \frac{{\sqrt {C_{l} } }}{{C_{\gamma } }}\quad C_{s} = \frac{1}{{\sqrt {C_{l} } }} \\ \end{aligned}$$
(11)

In the process of similar material preparation, similar material density can be consistent with the prototype. When \(C_{\gamma }\) = 1, we have \(C_{\sigma } = C_{l}\), \(C_{E} = C_{l}\), \(C_{p} = C_{l}\). Participants generally determine the geometric ratio according to the test conditions firstly, in the outburst simulation experiment. Geometric ratio usually takes 10–20. For example, when \(C_{l}\) = 20, then \(C_{\sigma } { = }C_{E} { = }C_{p}\). In the experiment, the stress and elastic modulus can be implemented, while gas pressure was turned to 1/20 of the model is not reasonable. For example, prototype gas pressure is 1 MPa, then the test gas pressure is 1/20 MPa. According to the absorption theory, coal and gas outburst is not possible to occur because low adsorption capacity causes low gas pressure. Similarly, when applied the same values of stress and gas pressure as the prototype in experiment, the geometric ratio \(C_{l}\) = 1, this is not possible in the laboratory.

2.3 Similarity criteria of engery model

Outburst is the process of energy accumulation, transfer and release. Energy model constructs the relation between energy consumption and the potential, summaries the whole process of coal and gas outburst, therefore the energy equation is an effective way to derive similar criteria (Zhang et al. 2016). This paper derives similarity criteria on the basis of the energy equation which was put forward by Hu et al. (2015).

$$\begin{aligned} & \frac{{\pi (1 - 2\mu )\sigma_{0}^{2} R_{p}^{3} }}{E} + \int_{{\frac{L}{2Rp}}}^{1} {\left[ {\left( {\frac{{R_{pl} }}{{R_{p} }}} \right)^{3} - 1 + \frac{{k^{2} \left( {1 + \mu } \right)}}{{2\left( {1 - 2\mu } \right)\sigma_{0}^{2} }}\left( {1 - \frac{{R_{p}^{3} }}{{R_{pl}^{3} }}} \right)} \right]d\cos \varphi } \\ &+\, \eta np_{0} \ln \left( {\frac{{p_{0} }}{{p_{a} }}} \right)V_{s} = \xi \frac{2c\cos \varphi }{{10\left( {1 - \sin \varphi } \right)}}V_{s} + \frac{1}{2}V_{s} \rho v_{0}^{2} \\ \end{aligned}$$
(12)
$$R_{p} = R_{0} \left[ {\frac{{3\left( {\sigma_{0} + c\cot \varphi } \right)\left( {1 - \sin \varphi } \right)}}{{\left( {3 + \sin \varphi } \right)c\cot \varphi }}} \right]^{{\frac{1 - \sin \varphi }{4\sin \varphi }}}$$
(13)
$$R_{pl} = L\cos \varphi + \sqrt {R_{p}^{2} - L^{2} \sin^{2} \varphi }$$
(14)
$$k = - \sigma_{0} + \cot \varphi \left[ {\left( {\frac{{R_{p} }}{{R_{0} }}} \right)^{{\frac{4\sin \varphi }{1 - \sin \varphi }}} - 1} \right]$$
(15)
$$V_{s} = 2\uppi\int_{0}^{\arccos (L/2Rp)} {\sin \varphi \int_{{R_{p} }}^{{L\cos \varphi + \sqrt {R_{P}^{2} - L^{2} \sin^{2} \varphi } }} {r^{2} \text{d}r\text{d}\varphi } }$$
(16)

where \(\sigma_{0}\) is the in situ stress, n is the porosity,\(v_{0}\) is the pulverized coal pouring velocity, \(p_{a}\) is the atmospheric pressure, \(\eta\) and \(\xi\) are ratio, \(R_{p}\) is the radius of energy release area, \(R_{0}\) is the radius of roadway, \(V_{s}\) is the volume of energy release area.

Equations are dimensionless processing

$$\pi \left( {1 - 2\mu } \right)a^{3} \int_{{\frac{L}{{2aR_{0} }}}}^{1} {\left\{ {\left( {\frac{L\cos \varphi }{{aR_{0} }} + \sqrt {1 - \frac{L}{{aR_{0} }}\sin^{2} \varphi } } \right)^{3} - 1 + \frac{1 + \mu }{{2\left( {1 - 2\mu } \right)}}]\left[ { - 1 + \frac{c}{{\sigma_{0} }}\cos \varphi \left( {a^{{\frac{4\sin \varphi }{1 - \sin \varphi }}} - 1} \right)} \right]^{2} \times \left( {1 - \frac{1}{{\frac{L}{{aR_{0} }}\cos \varphi + \sqrt {1 - \frac{L}{{aR_{0} }}\sin^{2} \varphi } }}} \right)^{3} } \right\}d\cos \varphi + } \frac{{\eta np_{0} E}}{{\sigma_{0}^{2} }}\ln \left( {\frac{{p_{o} }}{{p_{a} }}} \right)b = \frac{b\cos \varphi }{{5\left( {1 - \sin \varphi } \right)}}\frac{cE\xi }{{\sigma_{0}^{2} }} + \frac{b}{2}\frac{{\rho V^{2} E}}{{\sigma_{0}^{2} }}$$
(17)
$$a = \left[ {\frac{{3\left( {\sigma_{0} + c\cot \varphi } \right)\left( {1 - \sin \varphi } \right)}}{{\left( {3 + \sin \varphi } \right)c\cos \varphi }}} \right]^{{\frac{1 - \sin \varphi }{4\sin \varphi }}}$$
(18)
$$b = 2\pi \int_{0}^{{\arccos \frac{L}{{2aR_{0} }}}} {\sin \varphi \int_{a}^{{\frac{L}{{R_{0} }}\cos \varphi + \sqrt {a^{2} - \frac{{L^{2} }}{{R_{0}^{2} }}\sin \varphi } }} {y^{2} dyd\varphi } }$$
(19)

According to the similarity theory, non-dimensional coefficient of equation is similar numeral \(\pi_{1}^{\prime } {-}\pi_{8}^{\prime }\).

$$\begin{aligned} & \pi^{\prime}_{1} { = }\frac{{\eta {\text{n}}p_{0} E}}{{\sigma_{0}^{2} }},\quad \pi^{\prime}_{2} = \frac{\xi cE}{{\sigma_{0}^{2} }},\quad \pi^{\prime}_{3} = \frac{{\rho v^{2} E}}{{\sigma_{0}^{2} }},\quad \pi^{\prime}_{4} = \frac{c}{{\sigma_{0} }},\quad \pi^{\prime}_{5} = \frac{{p_{0} }}{{p_{a} }},\quad \pi^{\prime}_{6} = \frac{L}{{R_{0} }},\quad \pi^{\prime}_{ 7} { = }\varphi ,\quad \pi^{\prime}_{ 8} { = }\mu \\ & \pi^{\prime}_{5} \to C_{p} = p_{p} /p_{m} = 1; \\ & \pi^{\prime}_{1} \to C_{E} = C_{{\sigma^{2} }} ; \\ & \pi^{\prime}_{4} \to C_{\text{c}} { = }C_{\sigma } ; \\ & \pi^{\prime}_{7} ,\pi^{\prime}_{8} , \to C_{\mu } = C_{\varphi } = 1; \\ \end{aligned}$$

Through discuss above, the similarity criteria based on energy model is derived.

$$\begin{aligned} &C_{p} = 1,\quad C_{\gamma } = 1,\quad C_{\text{n}} { = }1,\quad C_{\eta } { = }1, \hfill \\ &C_{\varphi } = 1,\quad C_{\text{c}} = C_{\sigma } ,\quad C_{E} = C_{{\sigma^{2} }} ,\quad C_{\mu } = 1 \hfill \\ \end{aligned}$$
(20)

We found the result that \(C_{E} = C_{{\sigma^{2} }}\), but it conflicts with \(C_{\sigma } = C_{E}\) deduced by \(E = \sigma /\varepsilon\). As a whole, one of the similarity criteria derived from the three kinds of mode is insufficient certainly. Because of outburst is a complex process affected by many factors, we can only choose the main factors to ensure the approximate similarity. Based on the mechanical model, we realized that mechanics parameter such as the uniaxial compressive strength, elastic modulus and poisson’s ratio should be similar, to guarantee the mechanical similarity of outburst. Based on the solid–fluid model, the similarity relations between mechanical parameters and geometric dimensions were concluded. These similar relations can guarantee the deformation and failure similarity of outburst. Based on the energy model, we obtained the similar relations between geometry and gas pressure, which can ensure the similarity of energy accumulation, transferring and releasing. Based on the above 3 methods, we achieve the similarity criteria of coal and gas outburst.

$$\begin{aligned} C_{u} & = C_{l} ,\quad C_{E} = C_{l} ,\quad C_{\sigma } = C_{l} ,\quad C_{p} = 1, \\ C_{\gamma } & { = }1,\quad C_{t} = \sqrt {C_{l} } ,\quad C_{K} = \frac{{\sqrt {C_{l} } }}{{C_{\gamma } }},\quad C_{s} = \frac{1}{{\sqrt {C_{l} } }} \\ \end{aligned}$$
(21)

3 Similar materials

In the similar simulation, the characteristics of similar material determine the accuracy of the similar model. Similar material components generally includes aggregate, cementations and accessories. The density of aggregate should be similar to raw coal, to simplify the similarity criteria of outburst. At the same time,we choose coal as the aggregate of similar materials because of its good adsorption performance. Mechanical strength of sample that suppressed by coal dust is too low to meet the standard of large scale simulation test. So the cementations were added to adjust similar material compressive parameters. The other materials includes water, sand and activated carbon. In order to make cement play a corresponding cementation role, we should add proper amount of water. Study shows that, when moisture is less than 8%, the mechanical strength of similar material is very low. When the moisture is more than 13%, similar material is too wet, and will affect molding and strength. To make similar material porosity is closer to the actual coal seams, selecting 40–20 mesh sand to adjust porosity of materials. Furthermore in order to make the similar material approach the adsorption and desorption characteristics of coal seam, we add proper amount of activated carbon to adjust similar material adsorption(Table 1; Figs. 2, 3).

Table 1 Coal-like material and composition
Full size table
Fig. 2
figure 2

Site location of Songzao Block, Chongqing, China

Full size image
Fig. 3
figure 3

Compositions of coal-like materials

Full size image

Many factors including cement, sand, water, activated carbon, have effect on the properties of similar material. We determine preliminarily proportion of each material in similar material proportion, and take uniform experiment design method (Tables 2, 3).

Table 2 Uniform design table of 5 factors and 12 levels
Full size table
Table 3 Coal-like material experimental design (mass ratio  %)
Full size table

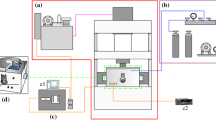
In order to test the physical and mechanical properties of similar materials, we made a number of cylindrical specimens. The size is \(\phi 50\,\text{mm} \times 100\,\text{mm}\). The preparation process is as follows.

Break the raw coal from Yuyang M8 coal seam by crusher, using the standard screen, the pulverized coal with particle size of 80–40 mesh and 40–20 mesh is selected.

Select 40–20 mesh sand,and Φ2.6 mm × 5.6 mm particle size activated carbon. Weigh pulverized coal, cement and auxiliary materials, water.

Dissolve cement in water, and stir in aggregate. Take similar material into the mold, and form a specimen by cold pressing molding under pressure 25 MPa. Holding 30 min, then take out, finally maintain coal specimen (Fig. 4).

Fig. 4
figure 4

50 mm × 100 mm similar material samples

Full size image

4 Result and discussion

4.1 Density

In Fig. 5a, the curve shows that the relationship between cement and similar material density. The fitting curve is \(\rho { = 0} . 0 0 3 5 7x_{ 1} { + 1} . 3 4 8 2 2\). With the increase of cement percentage, similar material density increases, they are the approximate linear correlation. This shows that the density of cement is greater than other raw materials’. Similar material density can meet the original density by adjusting the ratio of cementations. In Fig. 5b, the density relationship between the sand and similar material is “S” curve. The influence of sand on the similar material density is smaller than other materials. Figure 5c shows the density relationship between material ‘cement +Sand’ and similar material. The fitting equation is \(\rho { = 0} . 0 0 3 4 3x_{2} { + 1} . 3 4 1\). Compared with Fig. 5a the impact of cement on the density similar materials is further proved. The density of M8 coal is 1.34–1.39 g/cm3. The density of similar material is in good agreement with the density of raw coal, therefore \(C_{\rho } = 1\) can be achieved.

Fig. 5
figure 5

Density relationship between cement, sand and coal-like material

Full size image

4.2 Porosity

The porosity of coal refers to the volume of the coal pores in the total volume of coal. The relationship among the porosity of coal, true density, and apparent density is as follow:

$$k = \frac{1}{{\rho_{p} }} - \frac{1}{{\rho_{t} }}$$
(22)

where \(\rho_{t}\) is the true density,\(\rho_{t}\) is the apparent density.

True density and apparent density are available in experiment. The wider the difference between true density and apparent, the greater the porosity. After drying,we could calculate the apparent density by weighing quality using electronic weighing scales, measuring the diameter and height of specimen.The true density is measured by 5E automatic industrial analyzer according to the coal industrial analysis method GB/T212-2008.

As shown in Table 4, the density and porosity of similar materials are consistent with those of raw coal, realizeing \(C_{\text{n}} = 1\).

Table 4 Porosity of sample
Full size table

4.3 Uniaxial compressive strength

We measured mechanical parameters by TAW-200 microcomputer control electro-hydraulic servo rock triaxial testing machine. Two specimens in each group were choosed to determine uniaxial compressive strength(UCS). The average of strength was taken. Tested stress–strain curve of similar materials is shown in Fig. 6.

Fig. 6
figure 6

Typical stress–strain curve of similar materials

Full size image

Components of similar material have important influence on uniaxial compressive strength (UCS). Figure 7a shows that cement content impacts on UCS. The relationship between cement and UCS is \(R = 0.1194x_{3} - 0.2145\)\(0 \le x_{3} \le 15.45\%\). The proportion of cementation in similar material increases linearly with the strength of similar material specimen. Figure 7b shows the ‘cement + sand’ content impacts on UCS. The relationship is \(R = 0. 1 1 0 9x_{ 4} - 0. 1 3 8 4\) \(( 5. 5\le x_{ 4} \le 1 7 {\text{\% )}}\). Compared Fig. 7a with b, the proportion of sand has very little influence on UCS of similar materials, while the cement material has a crucial effect on UCS. Figure 7c shows the ‘water/cement’ content how to impact on UCS. The relationship is \(R{ = }0.4604{ + }2.4077x_{5}^{ - 1.19}\) \((0.5769 \le x_{5} \le 1.55)\). The water content has significant influence on UCS. When the ‘water/cement’ is \(0.5769 \le x_{5} \le 1.55\), UCS will reduce with the increase of the ratio of ‘water/cement’ in a negative exponent form. Water content and drying time should be controlled to meet the strength requirements of similar material. For example, when \(C_{l} = 20\), UCS of coal is about 10–20 MPa, and UCS of similar material is 0.5–1 MPa by theoretical calculation. UCS of similar material specimen are 0.543–1.803 MPa, which can meet the similar criteria.

Fig. 7
figure 7

Effect of cement, sand and water content on uniaxial compressive strength

Full size image

4.4 Adsorption and desorption

  1. (1)

    Adsorption

Because of the explosive risk of gas, the non-explosive gases such as CO2 and N2 are often used as experimental gas for the similar simulation tests. Research shows that the amount of CO2 adsorbed in the same coal sample is more than that of CH4. When the adsorption pressure is high, the ratio approximately 2 times. Considering the similar simulation test‘s geometry size is big, a large amount of gas used in the experiments. To avoid danger, the simulation experiment uses CO2 as experiment gas. Therefore, it is necessary to study the similarity between adsorption performance of CO2 on similar material and that of CH4 on raw coal. The industrial composition analysis and porosity measurement of similar materials were carried out. The adsorption isotherms of CH4 and CO2 were measured by HCA high pressure capacity adsorption.

Figures 8 and 9 are CO2 isothermal adsorption curve of sample No. 5, No. 6. The Langmuir equation is \(Q = abp/(1 + bp)\),which can be transformed as the form of \(p/Q = P/a + 1/ab\). We can get the relationship \(p /Q\)–\(p\) and adsorption constant a, b.

Fig. 8
figure 8

CO2 adsorption isotherm curve of No. 5

Full size image
Fig. 9
figure 9

CO2 adsorption isotherm curve of No. 6

Full size image

In Figs. 10 and 11 we found the relationship curve of adsorption constant are \(p/Q = 0.707p + 0.02084\), a = 33.92, b = 1.414 and \(p/Q = 0.893p + 0.02078\), a = 42.97, b = 1.12. The similar material absorbed CO2 curve shows a good linear relationship, and can be described by the Langmuir equation. Similarly, we get the CH4 isothermal adsorption curve of No.5 specimen, No.6 specimen, and M8 coal specimen (Table 5).

Fig. 10
figure 10

\(p /Q\)–\(p\) and adsorption constant of number 5

Full size image
Fig. 11
figure 11

\(p /Q\)–\(p\) and adsorption constant of number 6

Full size image
Table 5 Gas adsorption constant, industrial analysis of No. 5, 6 and M8
Full size table

The Figs. 12 and 13 show adsorption of similar material is similar to coal. Added un-adsorption materials such as cement, sand, water will lead to similar material’s adsorption ability reduce, compared with the raw coal. However, the adsorption capacity of similar materials can be compensated by using CO2 with stronger adsorption capacity as experimental gas. This makes the adsorption properties of CO2 adsorbed in similar materials have good similarity with CH4 adsorbed in raw coal.

Fig. 12
figure 12

The adsorption curves of M8 and No. 5

Full size image
Fig. 13
figure 13

The adsorption curves of M8 and No. 6

Full size image
  1. (2)

    Desorption

Initial velocity of methane diffusion represents the velocity of gas desorption. The initial velocity of methane diffusion of M8 coal and No.5–No.7 specimens are determined by WFC-2 gas radiation initial velocity tester.

The result is shown in Table 6.

Table 6 Initial velocity of CH4 and CO2 diffusion of M8, No. 5–7 coal similar materials specimens
Full size table

Table 6 and Fig. 14 show initial velocity of CH4 diffusion of the M8 coal seam is 22–43 mL/s. Initial velocity of CO2 diffusion of No.5–7 coal similar materials specimens is 35–39 mL/s. With the increasing of cement proportion, initial velocity of diffusion decreases. When cement proportion is 2%–13%, similar material initial velocity of CO2 diffusion is about 25 mL/s–47 mL/s. Therefore, desorption property of similar material can meet the test requirements.

Fig. 14
figure 14

Initial velocity of CH4 and CO2 diffusion of similar materials specimens

Full size image

4.5 Reasonable matching of coal and gas outburst simulation material

When UCS is 1 MPa. reasonable proportion matching can be calculated as follows:

The cement is 6.58%, and ‘water/cement’ is 1.23. Thus water is 8.093%. Therefore, reasonable proportion of similar materials is shown in Table 7 when the UCS is 1 MPa. When crushed coal is used as the main composition, it can controls the density, gas adsorption and desorption of similar material. So we choose crused coal as the main material of similar material, sand and activated carbon as compensation. This method can ensure density, porosity, gas adsorption and desorption performance meet corresponding that of coal seam when the cement proportion is fixed and UCS and other mechanical properties are constant. Ultimately, reasonable proportion of similar materials can be achieved.

Table 7 Reasonable matching of similar material when the UCS is 1 MPa
Full size table

5 Conclusion

  1. (1)

    Coal and gas outburst is a complex process affected by many factors. We can only seize the main factors of coal and gas outburst to ensure the approximate similarity. Based on the mechanics model, mechanics parameter such as the UCS, elastic modulus, poisson’s ratio is similar, which can guarantee the mechanics similarity of coal and gas outburst. We get the similar relation between mechanical parameters and geometric dimensions, and the similar relationship between the permeability and geometry size on the basis of a solid–fluid coupling model, which can guarantee the similarity of the deformation and failure during coal and gas outburst.

  2. (2)

    According to the energy model,we obtained the similar relations between geometry and gas pressure, which ensure the similarity of energy accumulation, transfering and releasing. From the analysis of 3 methods, we get the similarity criteria of coal and gas outburst.

    $$C_{u} = C_{l} ,\quad C_{E} = C_{l} ,\quad C_{\sigma } = C_{l} ,\quad C_{p} = 1,\quad C_{\gamma } { = }1,\quad C_{t} = \sqrt {C_{l} } \;C_{K} = \frac{{\sqrt {C_{l} } }}{{C_{\gamma } }},\quad C_{s} = \frac{1}{{\sqrt {C_{l} } }}$$
  3. (3)

    Further more, a reasonable maching of similar materials was put forward, that is of pulverized coal as aggregate, cement as the cementing agent, sand, activated carbon material, and water. When compared with raw coal, the similar material has the same density and porosity, and has the similar characteristics of high compressive strength, adsorption and desorption. These properties provide a support to carry out the experiment of coal and gas outburst in the future.