Introduction

Grey relational analysis (GRA) is part of grey system theory [5] which is suitable for solving a variety of multiple attribute decision-making (MADM) problems with uncertain information. GRA solves MADM problems by aggregating incommensurate attributes for each alternative into a single composite value, while the weight of each attribute is subject to the decision maker’s judgment. When such information is unavailable, equal weights seem to be a norm. However, this is often the source of controversies for the final ranking results. Therefore, how to properly select the attribute weights is a main source of difficulty in the application of this technique. Fortunately, the development of modern operational research has provided us two excellent tools called data envelopment analysis (DEA) and analytic hierarchy process (AHP), which can be used to derive attribute weights in GRA.

DEA is an objective data-oriented approach to assess the relative performance of a group of decision-making units (DMUs) with multiple inputs and outputs [4]. In the field of GRA, DEA models without explicit inputs are applied, i.e., the models in which only pure outputs or index data are taken into account (see [10, 23, 25]). The other combined GRA and DEA methodologies can be found in the literature, such as using GRA for the selection of inputs and outputs in DEA [3, 22], using GRA for ranking efficient DMUs in DEA with crisp data [7], and using GRA for ranking DMUs in DEA with grey data, i.e., the unknown numbers which have clear upper and lower limits [16].

In these models, each DMU or alternative can freely choose its own favorable system of weights to maximize its performance. However, this freedom of choosing weights is equivalent to keeping the preferences of a decision maker out of the decision process. In fact, an alternative may be indicated as the best one by assigning zero values to the weights of some attributes and neglecting the importance of these attributes in a decision-making process.

Fig. 1
figure 1

An integrated approach to GRA, DEA, and AHP

Full size image

Alternatively, AHP is a subjective data-oriented procedure which can reflect the relative importance of a set of attributes and alternatives based on the formal expression of the decision maker’s preferences. AHP usually involves three basic functions: structuring complexities, measuring on a ratio scale, and synthesizing [20]. The application of AHP with GRA can be seen in [2, 9, 24].

However, AHP has been a target of criticism because of the arbitrary nature of the ranking process (see [1], [21, p35] and [6]). In fact, the AHP weights are based on the experts’ personal experiences and the subjective judgments. If the selection of experts is different, the weights obtained will be different (see [13, 14]).

To overcome the problematic issue of confronting the contradiction between the objective weights in DEA and subjective weights in AHP, this research proposes an integrated DEA and AHP approach in deriving the attribute weights in the field of GRA. This can be implemented by incorporating weight bounds using AHP in DEA-based GRA models. It is worth pointing out that the models proposed in this article are not brand-new models in the DEA-AHP literature. Conceptually, they are parallel to the ratio-based DEA models using AHP, as discussed in [17]. Nevertheless, it is the first time that these models are applied to the field of GRA. In addition, as far as we know, nothing in the existing literature discusses the simultaneous application of DEA and AHP methodologies in the field of GRA.

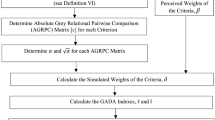
Methodology

This research has been organized to proceed along the following stages (Fig. 1):

  1. 1.

    Computing grey relational coefficients using GRA procedure to obtain the required (output) data for DEA-based GRA models.

  2. 2.

    Computing the grey relational grade of each alternative using a DEA-based GRA model which is applied in a minimax DEA-based GRA model.

  3. 3.

    Obtaining an optimal set of weights for each alternative using the minimax DEA-based GRA model without weight bounds (minimum grey relational loss \(\theta _{\min })\).

  4. 4.

    Computing the priority weights of attributes for all alternatives using AHP, which impose weight bounds into the minimax DEA-based GRA model.

  5. 5.

    Obtaining an optimal set of weights for each alternative using the minimax DEA-based GRA model by imposing weight bounds on attribute weights, using AHP (maximum grey relational loss \(\theta _{\max })\).

  6. 6.

    Measuring the performance of each alternative in terms of the relative closeness to the priority weights of attributes. For this purpose, we develop a parameter distance model. Increasing a parameter in a defined range of grey relational loss, we explore the tradeoff relationship between the grey relational grade and the priority weights of attributes for each alternative. This may result in various ranking positions for each alternative in comparison with the other alternatives.

Multi-attribute grey relational analysis

In the grey relational analysis method, alternative \(A_i (i=1,2,\ldots ,m)\) is characterized by a vector \(Y_i =(y_{i1}, y_{i2},\ldots ,y_{{in}})\) of values of attribute \(C_j (j=1,2,\ldots ,n)\). The term \(Y_i \) can be translated into the comparability sequence \(R_i =\left( {r_{i1} ,r_{i2},\ldots ,r_{{in}} } \right) \) using the following equations:

$$\begin{aligned} r_{ij}= & {} \frac{y_{ij} -y_{j(\min )} }{y_{j(\max )} -y_{j{(\min )}}} \quad \forall \; i,j \; \hbox {for desirable attributes}, \end{aligned}$$
(1)
$$\begin{aligned} r_{ij}= & {} \frac{y_{j(\max )} -y_{ij} }{y_{j(\max )} -y_{j {(\min )}}} \quad \forall \; i,j \; \hbox {for undesirable attributes},\nonumber \\ \end{aligned}$$
(2)

where \(y_{j(\max )} =\max \{y_{1j},y_{2j},\ldots ,y_{mj} \}\) and \(y_{j(\min )} =\min \{y_{1j}, y_{2j},\ldots ,y_{mj}\}\). Now, let \(A_0\) be a virtual ideal alternative which is characterized by a reference sequence \(U_0 =\left( {[u_{01},u_{02},\ldots ,u_{0n}} \right) \) of the maximum values of attribute \(C_j \) as follows:

$$\begin{aligned} u_{0j} =\max \{r_{1j}, r_{2j},\ldots ,r_{mj}\} \quad \forall \; j. \end{aligned}$$
(3)

To measure the degree of similarity between \(r_{ij} \) and \(u_{0j} \) for each attribute, the grey relational coefficient, \(\xi _{ij} \), can be calculated as follows:

$$\begin{aligned} \xi _{ij} =\frac{\min _i \min _j \left| {u_{0j} -r_{ij} } \right| +\rho \max _i \max _j \left| {u_{0j} -r_{ij} } \right| }{\left| {u_{0j} -r_{ij} } \right| +\rho \max _i \max _j \left| {u_{0j} -r_{ij} } \right| }, \end{aligned}$$
(4)

where \(\rho \in [0,1]\) is the distinguishing coefficient, generally \(\rho =0.5\). It should be noted that the final results of GRA for MADM problems are very robust to changes in the values of \(\rho \). Therefore, selecting the different values of \(\rho \) would only slightly change the rank order of attributes.

To find an aggregated measure of similarity between alternative \(A_i \), characterized by the comparability sequence \(R_i \), and the ideal alternative \(A_0 \), characterized by the reference sequence \(U_0 \), over all the attributes, the grey relational grade, \(\Gamma _i \), can be computed as follows:

$$\begin{aligned} \Gamma _i =\sum _{j=1}^n {w_j \xi _{ij} }, \end{aligned}$$
(5)

where \(w_j \) is the weight of attribute \(C_j \) and \(\sum \nolimits _{j=1}^n {w_j } =1\). In practice, expert judgments are often used to obtain the weights of attributes. When such information is unavailable, equal weights seem to be a norm. Nonetheless, the use of equal weights does not place an alternative in the best ranking position in comparison with the other alternatives. In the next section, we show how DEA can be used to obtain the optimal weights of attributes for each alternative in GRA.

DEA-based GRA models

Since all the grey relational coefficients are benefit (output) data, a DEA-based GRA model can be formulated similar to a classical DEA model without explicit inputs [15]:

$$\begin{aligned}&\Gamma _k =\max \sum _{j=1}^n {w_j \xi _{kj} } \end{aligned}$$
(6)
$$\begin{aligned}&\hbox {s}.\hbox {t}.\sum _{j=1}^n {w_j \xi _{ij} } \le 1 \quad \forall \, i, \end{aligned}$$
(7)
$$\begin{aligned}&w_j >0 \quad \forall \, j, \end{aligned}$$
(8)

where \(\Gamma _k \) is the grey relational grade for alternative under assessment \(A_k \)(known as a decision-making unit in the DEA terminology). k is the index for the alternative under assessment, where k ranges over 1, 2,..., m. \(w_j \) is the weight of attribute \(C_j (j=1,2,\ldots ,n)\). The first set of constraints (7) assures that if the computed weights are applied to a group of m alternatives, \((i=1,2,\ldots ,m)\), they do not attain a grade of larger than 1. The process of solving the model is repeated to obtain the optimal grey relational grade and the optimal weights required to attain such a grade for each alternative. The objective function (6) in this model maximizes the ratio of the grey relational grade of alternative \(A_k \) to the maximum grey relational grade across all alternatives for the same set of weights \(( {{\max \Gamma _k }/{\mathop {\mathrm{max}}\limits _{i=1,\ldots ,m} \Gamma _i }} )\). Hence, an optimal set of weights in the DEA-based GRA model represents \(A_k \) in the best light in comparison with all the other alternatives. It should be noted that the grey relational coefficients are normalized data. Consequently, the weights attached to them are also normalized. In addition, adding the constraint \(\sum \nolimits _{j=1}^n {w_j } =1\) to the DEA-based GRA model is not recommended here. In fact, the sum-to-one constraint is a non-homogeneous constraint (i.e., its right-hand side is a non-zero free constant) which can lead to underestimation of the grey relational grades of alternatives or infeasibility in the DEA-based GRA model (see [18]).

Minimax DEA-based GRA model using AHP

We develop our formulation based on a simplified version of the generalized distance model (see [8]). Let \(\Gamma _k^*(k=1,2,\ldots ,m)\) be the best attainable grey relational grade for the alternative under assessment, calculated from the DEA-based GRA model . We want the grey relational grade, \(\Gamma _k (w)\), calculated from the vector of weights \(w=(w_1,\ldots ,w_n )\) to be closest to \(\Gamma _k^*\). Our definition of “closest” is that the largest distance is at its minimum. Hence, we choose the form of the minimax model: \(\min _w \max _k \{\Gamma _k^*-\Gamma _k (w)\}\) to minimize a single deviation which is equivalent to the following linear model:

$$\begin{aligned}&\mathrm{Min} \, \theta \end{aligned}$$
(9)
$$\begin{aligned}&\hbox {s}.\hbox {t}.\Gamma _k^*-\sum _{j=1}^n {w_j \xi _{kj} } \le \theta , \end{aligned}$$
(10)
$$\begin{aligned}&\sum _{j=1}^n {w_j \xi _{ij} } \le \Gamma _i^*\quad \forall \; i, \end{aligned}$$
(11)
$$\begin{aligned}&\theta \le 1, \end{aligned}$$
(12)
$$\begin{aligned}&\theta ,w_j \ge 0, \quad \forall \; j. \end{aligned}$$
(13)

The combination of Eqs. (9)–(13) forms a minimax DEA-based GRA model that identifies the minimum grey relational loss \(\theta _{\min } \) needed to arrive at an optimal set of weights. The first constraint ensures that each alternative loses no more than \(\theta \) of its best attainable relational grade, \(\Gamma _k^*\). The second set of constraints satisfies that the relational grades of all alternatives are less than or equal to their upper bound of \(\Gamma _k^*\). It should be noted that for each alternative, the minimum grey relational loss \(\theta =0\). Therefore, the optimal set of weights obtained from the minimax DEA-based GRA model is exactly similar to that obtained from the DEA-based GRA model.

On the other hand, the priority weights of attributes are defined out of the internal mechanism of DEA by AHP. To more clearly demonstrate how AHP is integrated into the newly proposed minimax DEA-based GRA model, this research presents an analytical process in which alternatives’ weights are bounded by the AHP method. The AHP procedure for imposing weight bounds may be broken down into the following steps:

Step 1: A decision maker makes a pairwise comparison matrix of different attributes, denoted by B with the entries of \(b_{hq} (h=q=1,2,\ldots ,n)\). The comparative importance of attributes is provided by the decision maker using a rating scale. [20] recommends using a 1–9 scale.

Step 2: The AHP method obtains the priority weights of attributes by computing the eigenvector of matrix B(Eq. 14), \(e=(e_1, e_2,\ldots ,e_j )^{T}\), which is related to the largest eigenvalue, \(\lambda _{\max }\):

$$\begin{aligned} Be=\lambda _{\max } e. \end{aligned}$$
(14)

To determine whether or not the inconsistency in a comparison matrix is reasonable, the random consistency ratio, C.R., can be computed by the following equation:

$$\begin{aligned} \mathrm{C.R.}=\frac{\lambda _{\max } -N}{({N}-1)\mathrm{R.I.}}, \end{aligned}$$
(15)

where R.I. is the average random consistency index and N is the size of a comparison matrix.

To estimate the maximum relational loss \(\theta _{\max } \) necessary to achieve the priority weights of attributes for each alternative, the following set of constraints is added to the minimax DEA-based GRA model:

$$\begin{aligned} w_j =\alpha e_j \quad \forall \; j. \end{aligned}$$
(16)

The set of constraint (16) changes the priority weights of attributes to weights for the new system by means of a scaling factor \(\alpha \). The scaling factor \(\alpha \) is added to avoid the possibility of contradicting constraints leading to infeasibility or underestimating the grey relational grade of alternatives (see [18]).

A parametric distance model

In this stage, we develop a parametric distance model that can be solved repeatedly to generate the various sets of weights for the discrete values of the parameter \(\theta \), such that \(0\le \theta \le \theta _{\max } \). Let \(w(\theta )\) be a vector of attribute weights for a given value of parameter \(\theta \). Let \(w^{*}(\theta _{\max } )\) be the vector of priority weights of attributes obtained from the minimax DEA-based GRA model after adding the set of constraints (16). Our objective is to minimize the total deviations between \(w(\theta )\) and \(w^{*}(\theta _{\max } )\) with the shortest Euclidian distance measure subject to constraints (10)–(13):

$$\begin{aligned} \hbox {Min} \, Z_k (\theta )=\left( {\sum _{j=1}^n {\left( {w_j -w_j^*(\theta _{\max } )} \right) ^{2}} } \right) ^{1/2} \end{aligned}$$
(17)

s.t. constraints (10)–(13).

Because the range of deviations computed by the objective function is different for each alternative, it is necessary to normalize it using relative deviations rather than absolute ones (see [19]). Hence, the normalized deviations can be computed by

$$\begin{aligned} \Delta _k (\theta )=\frac{Z_k^*(0)-Z_k^*(\theta )}{Z_k^*(0)} \end{aligned}$$
(18)

where \(Z_k^*(\theta )\) is the optimal value of the objective function for \(0\le \theta \le \theta _{\max } \). We define \(\Delta _k (\theta )\) as a measure of closeness which represents the relative closeness of each alternative to the weights obtained from the minimax DEA-based GRA model in the range [0, 1] after imposing weight bounds (16) to it. Increasing the parameter \((\theta )\), we shift the optimal set of weights obtained from the minimax DEA-based GRA model to its corresponding weights bounded by AHP. In this way, we explore the tradeoff relationship between the grey relational grade and the priority weights of attributes for each alternative. This may lead to different ranking positions for each alternative in comparison with the other alternatives. It should be noted that in a special case, where the parameter \(\theta =\theta _{\max } =0\), we assume \(\Delta _k (\theta )= 1\).

A numerical example: dispatching rule selection

In this section, we present the application of the proposed approach for production scheduling problems using nine alternatives dispatching rules and five performance attributes. The processed data have been adopted from [12]. Table 1 shows the results of grey relational generating for dispatching rule selection problem based on Eq. (2). The notations in Table 1 are as follows: MD minimum deviation, SPT shortest processing time, SLK slack, DD due date, GCMD generalized cumulative minimum deviation, COST, VALUE, COV cost over time, and LPT longest processing time. A full description of both dispatching rules and performance attributes can be found in [11].

Table 1 Results of grey relational generating for the dispatching rule selection problem
Full size table
Table 2 Pairwise comparison matrix of five attributes
Full size table
Table 3 Results of grey relational coefficient for dispatching rule selection problem
Full size table

Table 2 shows the results of a pairwise comparison matrix in the AHP model as constructed by the author in the Expert Choice software. The priority weight for each attribute would be the average of the elements in the corresponding row of the normalized matrix of pairwise comparison, as shown in the last column of Table 2. One can argue that the priority weights of attributes must be judged by production scheduling experts. However, since the aim of this section is just to show the application of the proposed approach on numerical data, we see no problem to use our judgment alone.

Using Eq. (4), all grey relational coefficients are computed to provide the required (output) data for the DEA-based GRA model, as shown in Table 3.

Solving the minimax DEA-based GRA model for the dispatching rule under assessment, we obtain an optimal set of weights with minimum grey relational loss \((\theta _{\min })\). It should be noted that the value of the grey relational grade of all dispatching rules calculated from the minimax DEA-based GRA model is identical to that calculated from the DEA-based GRA model. Therefore, the minimum grey relational loss for the dispatching rule under assessment is \(\theta _{\min } =0\) (Table 4). This implies that the measure of relative closeness to the AHP weights for the dispatching rule under assessment is \(\Delta _k (\theta _{\min } )=0\). On the other hand, solving the minimax DEA-based GRA model for the dispatching rule under assessment after adding the set of constraints (16), we adjust the priority weights of attributes (outputs) obtained from AHP in such a way that they become compatible with the weights’ structure in the minimax DEA-based GRA model. This results in the maximum grey relational loss, \(\theta _{\max } \), for the dispatching rule under assessment (Table 4). In addition, this implies that the measure of relative closeness to the AHP weights for the dispatching rule under assessment is \(\Delta _k (\theta _{\max } )= 1\).

Table 4 Minimum and maximum grey relational losses for each dispatching rule
Full size table
Table 5 Optimal weights of minimax DEA-based GRA model for all dispatching rules bounded by AHP
Full size table
Table 6 Ranking position of each dispatching rule based on the minimum distance to priority weights of attributes
Full size table

Table 5 presents the optimal weights of attributes as well as its scaling factor for all dispatching rules. It should be noted that the priority weights of AHP (Table 2) used for incorporating weight bounds on the attribute weights are obtained as \(e_j =\frac{w_j }{\alpha }\).

Going one step further to the solution process of the parametric distance model, we proceed to the estimation of total deviations from the AHP weights for each dispatching rule, while the parameter \(\theta \) is \(0\le \theta \le \theta _{\max } \). Table 6 represents the ranking position of each dispatching rule based on the minimum deviation from the priority weights of attributes for \(\theta =0\). It should be noted that in a special case, where the parameter \(\theta =\theta _{\max } =0\), we assume \(\Delta _k (\theta )=1.\) Table 6 shows that SLK is the best alternative in terms of the grey relational grade and its relative closeness to the priority weights of attributes.

Nevertheless, increasing the value of \(\theta \) from 0 to \(\theta _{\max }\) has two main effects on the performance of the other dispatching rules: improving the priority of attributes (i.e., getting closer to AHP weights) and reducing the value of the grey relational grade. This, of course, is a phenomenon, one expects to observe frequently.

The graph of \(\Delta (\theta )\) versus \(\theta \), as shown in Fig. 2, is used to describe the tradeoff relationship between the grey relational grade and the priority of attributes for each dispatching rule as parameter \(\theta \) varies from 0 to \(\theta _{\max }\). This may result in different ranking positions for each dispatching rule in comparison with the other dispatching rules. Note that at \(\theta =0\), the dispatching rules can be ranked based on \(Z_k^*(0)\) from the closest to the furthest from the priority weights of attributes. For instance, at \(\theta =0\), COV, MD, and SPT with grey relational grades of one are ranked in the second, third, and fourth places, respectively, while GCMD, VALUE, and LPT with grey relational grades of less than one are ranked in the ninth, eighth, and sixth places, respectively (Tables 4, 6). However, with a small grey relational loss at \(\theta =0.01\), COV, MD, and SPT take the third, eighth, and seventh places, while GCMD, VALUE, and LPT take the fourth, second, and fifth places in the rankings, respectively. Using this example, as a guideline, it is relatively easy to rank the dispatching rules in terms of distance to the priority weights of attributes. At \(\theta =0.02\), COV moves up into the second place again, while VALUE drops into the third place. It is clear that both measures, \(Z_k^*(0)\) and \(\Delta _k (\theta )\), are necessary to explain the ranking position of each alternative (Appendix A).

Fig. 2
figure 2

Relative closeness to the priority weights of attributes [\(\Delta \) (\(\theta )\)], versus grey relational loss (\(\theta )\) for each dispatching rule

Full size image

Conclusion

We develop an integrated approach based on DEA and AHP methodologies for deriving the attribute weights in GRA. We define two sets of attribute weights in a minimax DEA-based GRA framework. The first set represents the weights of attributes with minimum grey relational loss. The second set represents the corresponding priority weights of attributes, using AHP, with maximum grey relational loss. We assess the performance of each alternative (or DMU) in comparison with the other alternatives based on the relative closeness of the first set of weights to the second set of weights. Improving the measure of relative closeness in a defined range of grey relational loss, we explore the various ranking positions for the alternative under assessment in comparison with the other alternatives. To demonstrate the effectiveness of the proposed approach, an illustrative example of a production scheduling problem using nine alternatives dispatching rules and five attributes is carried out.