1 Introduction

In the field of ocean engineering, there is a strong requirement for prediction of extreme values of design parameters which affects the operability and structural integrity. Prediction of severe nonlinear loads and large-amplitude motions is, therefore, of great importance to the safety of offshore marine systems. Computational schemes for predicting responses in small-amplitude linear incident waves are presently well established and most of the codes routinely used by marine and offshore industries for these evaluations are based on a 3D singularity distribution method using the frequency-domain free-surface Green function. As regards evaluation of nonlinear responses in large-amplitude waves, there can be several approaches for solution of this nonlinear problem: (1) a second-order frequency-domain solution based on perturbation theory (Faltinsen 1990; Chakrabarti 1990), (2) a mixed Eulerian–Lagrangian (MEL) approach which was originally developed by Longuet-Higgins and Cokelet (1976) for 2D nonlinear wave studies and subsequently followed up for wave–structure interactions (e.g. Beck 1994; Ferrant 1996) and (3) application of Reynolds-averaged Navier–Stokes equation (RANSE)-based CFD solvers (Mousaviraad et al. 2010; Bunnik et al. 2010). The latter two methods can in principle be applied to study extreme wave–structure interaction involving steep nonlinear waves. However, requirement of high computational effort by these approaches prohibits their routine usage by the offshore industries particularly during the preliminary design phase. RANSE solvers at present appear more suitable for studying specific problems of interest such as rolling response close to roll resonant period, sloshing and violent motion of fluid in confined spaces where fluid viscosity plays an important role as opposed to the global forces and motions. For ships and large offshore structures in the near future the main workhorse method likely to remain will be based on potential flow formulations. The ITTC Specialist Committee on CFD in Marine Hydrodynamics remarks that RANSE-based CFD methods are not efficient methods for obtaining response amplitude operators (RAOs) for a range of wave headings, frequencies, and wave steepness (ITTC 2014). At the same time, as the offshore sector is moving towards ultra deep water and new application areas for offshore structures continue to appear, the industry is witnessing emergence of various novel hybrid offshore configurations like SPAR platforms with heave damping plates, floating offshore wind turbines with large and high above water parts exposed to dynamic wind loads, etc.Thus there is a strong practical demand for an generalized computing tool applicable to a wide variety of marine structures for routine use to predict extreme design parameters, and also having the provision to incorporate effects of forces arising from variety of other sources without suffering by high computational cost.

In this paper, we present development of a practical computational tool for large-amplitude nonlinear steep waves interacting with practical 3D offshore and ship structures. The method follows a numerical wave tank (NWT) approach where the interaction hydrodynamics of wave radiation and diffraction effects are determined based on an MEL type of scheme. At this time, it will be useful to provide a brief review of full nonlinear MEL studies applied to wave–structure interactions. Faltinsen (1977) studied the full nonlinear wave–structure interaction problem of interior sloshing in a tank based on an MEL approach in two dimensions (2D). In a 3D NWT, (Xü and Yue 1992; Zhang et al. 1996) used MEL approach to simulate extreme and overturning waves but without any structure in the wave field. Beck (1994) developed a time-domain solution for floating bodies using a desingularised method. A study on the motion of a floating truncated vertical cylinder using a 3D MEL in a regular wave was carried out by Ferrant (1996). In this study, only vertical motions were allowed and the other degrees of freedom (DOF) were inhibited. Cointe et al. (1990) applied a domain decomposition scheme for 2D floating body simulations. Domain decomposition method within the MEL scheme for the 3D floating body problem has also been applied by Wu and Taylor (1996) and Kashiwagi (2000) among others. More recently, Bai and Eatock Taylor (2009) applied the domain decomposition method to investigate fully nonlinear wave interaction of fixed and freely floating flared structures. Qiu and Peng (2013) used a panel-free method for the body-exact problem in the time domain. One of the important numerical problems of an MEL-type time-domain solution scheme for the full nonlinear floating body problem is associated with the coupling between hydrodynamic forces and rigid body motions which tend to cause numerical instability inhibiting long-duration time-domain simulation. Many improved numerical schemes have been devised to handle this coupling, e.g. the acceleration potential method of Tanizawa (1995, (1996), the implicit coupled scheme of Dombre et al. (2015).

In addition to the limited works mentioned above, there are a large number of other studies on application of MEL scheme for the floating body simulations addressing different numerical aspects which can be found in Tanizawa (2000). Most of these works have attempted to solve the full nonlinear wave structure interaction in an NWT. However, despite drastic improvement in computational power, many challenges are still faced in studying full nonlinear interactions of floating bodies by an MEL type of approach, particularly if long-duration simulations are desired for realistic practical and complex configurations. On the other hand, driven by the need of the industry to study the effect of steep waves on structures, a variety of so-called blended methods and methods that are based on a variety of levels of simplifying approximation have also been developed over the years. An overview of such methods can be found in the recent review article of Hiradis et al. (2014).

The basic objective of the present work is to come up with a solution scheme in time domain within the framework of an NWT in which large-amplitude and steep incident waves can be made to interact with offshore structures, and the influence of the important nonlinearities of these waves on the loads and responses can be captured with only modest computational effort. In addition, the scheme should in principle be capable of considering a wide variety of emerging novel type of structures, multi-body interactions, etc. Practical offshore structures are also exposed to forces from many other sources besides waves, e.g. wind, current, mooring lines and risers, Morison forces, DP thrusters forces, etc. In this regard, versatility of time-domain solvers is well known over frequency-domain solvers. In many of the existing time-domain solvers used by the offshore industry, the wave structure interaction part is determined in the frequency domain by codes such as WAMIT and the computed hydrodynamic radiation and diffraction forces are then transformed to time domain using impulse-response function (IRF) following the formulation of Cummins (1962). The influence of external forces can be incorporated by adding these forces and moments on the right-hand side of the equations of motions. Indeed, use of IRF-based formulation is very popular in time-domain simulation of ships and floating bodies and it has been used for a variety of applications. The frequency-dependent added mass and damping needed for evaluating the memory-integral term in these formulations are usually found from a linear frequency-domain hydrodynamic solution. For simulations involving speed-dependent ship motions, these are usually determined from strip-theory formulations with suitable modifications to take into account the forward speed-dependent corrections (De Kat and Paulling 1989; Fonseca and Guedes-Soares 1998; Ayaz et al. 2006), while 3D linear hydrodynamic solvers are used for simulations involving stationary floating offshore configurations (Chitrapu et al. 1993; Kim et al. 2013). Similarly the diffraction forces are also usually determined from linear frequency-domain solutions and transformed into time domain. These IRF-based formulations can also take into account the incident Froude–Krylov (F–K) forces evaluated on the exact wetted hull of the object under the incident wave profile (De Kat and Paulling 1989; Chitrapu and Ertekin 1995).

The present approach differs from these IRF-based time-domain formulations in which the hydrodynamic interaction part of radiation and diffraction is determined in the time domain directly as the solution progresses in time. Although termed numerical wave tank, the present scheme differs from the usual nonlinear NWT approach where waves are created in a tank by physical movement of a wave-maker. Here the structure is made to appear in an existing incident wave field in a 3D circular domain. The solution methodology for time evolution of forces and motions are, however, similar to the full nonlinear MEL scheme. At this time it may be instructive to bring out the advantage and drawback of the present scheme in comparison to the IRF-based formulations. In the present method, the incident waves can be defined by any desired wave theory including a fully nonlinear steady numerical wave model, and thus it is possible to capture the exact F–K nonlinear forces. This is also possible in the IRF-based formulation although in almost all past works the incident waves are either described by linear waves or by Stokes 2nd order wave (e.g. Grochowalski et al. 1998). An advantage of using the nonlinear numerical wave is that it does not require any approximation to capture the wave kinematics for the part between the exact and the mean free surface. The other important feature of the present scheme is that the body boundary condition for the diffraction potential can be specified using this nonlinear incident potential even though the surface over which it is applied is the mean body surface. Although theoretically inconsistent, since nonlinear wave kinematics is larger in magnitude compared to the linear wave kinematics, this is expected to yield a better approximation of the nonlinear wave diffraction effect than fully linear wave diffraction.

The present method also provide possibilities of capturing further nonlinearities associated with wave diffraction by applying the body impermeability condition through a mapping of the exact wetted surface to the mean body surface following the idea similar (but not exactly same) to the ‘body-exact’ version of the 3D ship motion LAMP code (Lin et al. 1994). This idea is explained later in the paper. Among the other beneficial features, multi-body interactions are straightforward in the present method including capturing the free-surface elevations in the gap between the objects. As the solution provides the free-surface elevations over the entire domain at every time step, it is also straightforward to determine the air-gap or under-deck clearance based on the nonlinear incident wave. Preliminary results demonstrating both these features have been presented below. It is also straightforward to consider Morison members and include the Morison forces based on the exact wetted surface of the members as in Chitrapu et al. (1993) but here these forces can be determined using the full nonlinear incident wave kinematics. Overall the solution method can provide rich information on the body responses and the free-surface elevations over the entire domain, with the potential to successively improve upon the scheme for capturing nonlinearities associated with wave diffraction. The major limitation of the method is that it is not applicable for the forward speed problem.

Numerical computations are carried out for a wall-sided barge, the flared S175 hull and a twin pontoon six-column semisubmersible. Since a fully consistent linear solution emerges when incident waves are taken as linear waves and all forces are determined on the mean wetted surface, the linearized computations are first validated against the usual 3D frequency-domain Green function-based results as well as with experimental results and other Rankine panel time-domain results. For these linear computations, extremely stable and long-duration simulation results could be obtained. As the method is developed for stationary floating bodies undergoing oscillations about the mean positions, it cannot be applied if the body is allowed to freely drift. The problem of a freely drifting body is essentially equivalent to the forward speed ship motion problem where the mean drift speed can be considered as the forward speed. Thus, if motion simulations of a body is desired which is not moored or otherwise unrestrained from horizontal motions, then restrictions in horizontal motions need to be artificially imposed. This is presently done by evaluating the nonlinear F–K forces on the horizontally restraint location of the hull. This, however, is not a serious drawback as in reality all stationary structures have some sort of horizontal restraint from mooring lines, risers, DP systems or tethers in case of TLPs. Very long-duration stable results have been achieved from the adopted approximate nonlinear method capturing some of the important nonlinear features. Finally, detailed comparative studies between the linear and the approximate nonlinear solutions are presented to bring out the influence of steep large-amplitude wave effects on loads and responses.

2 The hydrodynamic problem and its numerical solution

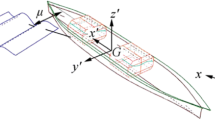
The boundary value problem (BVP) is formulated based on potential flow theory assuming fluid to be inviscid, incompressible, and homogeneous and the flow is irrotational. Fluid motions can thus be prescribed in terms of velocity potential \(\phi \) whose gradient is the fluid velocity vector \(\overrightarrow{v} =\nabla \phi \). Consider a surface piercing body \(B\) in a fluid domain \(\Omega \) bounded on top by the free surface \(\partial \Omega _{F}\), internally by instantaneous wetted body surface \(\partial \Omega _{B}\), on the bottom by a rigid bottom surface \(\partial \Omega _{D}\), and externally by a hypothetical vertical control surface \(\partial \Omega _{C}\). Figure 1 shows the fluid domain and the various boundaries. The right-handed Cartesian coordinate system Oxyz has its origin ‘O’ on the undisturbed free surface with O\(z\) directing vertically upwards.

Fig. 1
figure 1

Computational domain and coordinate system

Full size image

The BVP for \(\phi \) is specified by the following equations:

$$\begin{aligned}&\nabla ^2\phi (x,y,z;t)=0 \quad \hbox {on}\quad \Omega \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial \phi }{\partial n}=\overrightarrow{V}_H \cdot \overrightarrow{n} \quad \hbox {on} \quad \partial \Omega _B (t) \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial \phi }{\partial n}=0\quad \hbox {on}\quad \partial \Omega _D \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial \eta }{\partial t}+\frac{\partial \phi }{\partial x}\frac{\partial \eta }{\partial x}+\frac{\partial \phi }{\partial y}\frac{\partial \eta }{\partial y}-\frac{\partial \phi }{\partial z}=0 \quad \hbox {on}\quad \partial \Omega _F (t) \end{aligned}$$
(4a)
$$\begin{aligned}&\frac{\partial \phi }{\partial t}+\frac{1}{2}(\nabla \phi \cdot \nabla \phi )+g\eta =0 \quad \hbox {on} \quad \partial \Omega _F(t) \end{aligned}$$
(4b)

In addition, on the exterior control surface \(\partial \Omega _{C}\) a suitable radiation condition needs to be applied. In the above, \(\eta \) is the free surface elevation, ‘\(g\)’ is gravitational constant, ‘\(t\)’ is time, ‘\(h\)’ is water depth, \(\overrightarrow{V}_{H}\) represents the velocity vector at any point on the body surface, and \(\overrightarrow{n}\) is the exterior normal to the surface.

In a typical NWT approach, the numerical solution scheme is formed by first writing the following well-known boundary integral equation derived from application of Green’s second identity to \(\phi \) and the basic source \(G=1/4\pi r\) using Eq. (1),

$$\begin{aligned}&\sigma (P)\phi (P)-\int \int \limits _{\partial \Omega } \left( \phi (Q)\frac{\partial G(P,Q)}{\partial n_Q }\right. \nonumber \\&\left. \qquad \qquad \qquad \qquad \qquad \quad -G(P,Q)\frac{\partial \phi (Q)}{\partial n_Q }\right) \,\hbox {d}(\partial \Omega )\!=\!0 \end{aligned}$$
(5)

Here, \(\partial \Omega \) is the total boundary surface encompassing the domain \(\Omega \), \(P\) and \(Q\) are field and source points, respectively, \(r=\vert \vec {x}(P)-\vec {x}(Q)\vert \) and \(\sigma (P)\) is the solid angle on \(\partial \Omega \) at \(P\). The flat bottom surface \(\partial \Omega _{D }\) from \(\partial \Omega \) in Eq. (5) can be removed by modifying \(G\), i.e. by taking image of \(Q\) about this surface. As regards the exterior boundary, there are several schemes available to remove \(\partial \Omega _C \) from \(\partial \Omega \) in (5) through implementation of a suitable exterior condition. In the present work, this surface is removed from \(\partial \Omega \) using a numerical beach as will be discussed later. These modifications allow the integration in (5) to be applied only over the free surface and the wetted body surface. Discretization of \(\partial \Omega \) into surface panels and suitable assumption on variation of the boundary variables \(\phi \) and \(\partial \phi /\partial n\) over the panels can transform (5) into a set of linear equations of the form:

$$\begin{aligned}{}[A]\left\{ {\begin{array}{l} \phi \\ \partial \phi /\partial n \\ \end{array}} \right\} =[B]\left\{ {\begin{array}{l} \partial \phi /\partial n \\ \phi \\ \end{array}} \right\} \end{aligned}$$
(6)

Here, \([A]\) and \([B]\) are functions of the simple source and its normal derivative integrated over the panels and thus purely dependent on geometry of \(\partial \Omega \). Equation (6), therefore, allows determination of \(\phi \) on the body surface and \(\partial \phi /\partial n\) on the free surface if \(\partial \phi /\partial n\) on the body surface and \(\phi \) on the free surface are known.

The MEL scheme for NWT simulation briefly proceeds as follows. If at any instant the normal velocity \(\partial \phi /\partial n\) on body surface and potential \(\phi \) on the free surface are known, then from (6) the unknown data of \(\phi \) on the body surface and \(\partial \phi /\partial n\) on the free surfaces can be determined. From the evaluated \(\phi \) on the body surface, using suitable difference schemes in time and space, pressures and thus forces on the body can be found from Bernoulli’s equation. Time integration of the body equations of motion will then give \(\partial \phi /\partial n\) on the body surface through the body condition Eq. (2) for the next instant. Similarly, through integration of the nonlinear free-surface constraints (4a, 4b) \(\phi \) on the free surface can be found. Note that in these time integrations, not only the boundary data are evolving; the geometry of the surfaces also advances to their new positions. The process is now repeated as the solution progresses in time. This in brief completes an overly simplified description of the nonlinear MEL solution for the full nonlinear wave–structure interactions. In reality, however, there are numerous details that require proper resolution if a successful solution is to be achieved. These are associated with evaluation of the pressure on the body surface which requires evaluation of the time derivative of \(\phi \), handling numerical instability that is associated with the evolving free surface, proper treatment of the exterior boundary condition to ensure no reflection from this surface, etc. Apart from satisfactory treatment of all these details, another serious concern of the full nonlinear solution scheme is the very large computing time that this method demands. This arises from the need to solve the linear Eq. (6) at every time step, perhaps multiple times depending on the time-integration rules used. This is because as the geometry is evolving both matrices \([A]\) and \([B]\) change at every time step. It should also be noted that usually \([A]\) and \([B]\) are full matrices and thus special solution schemes that apply to tri-diagonal matrices cannot be used here. On the other hand, if the surface over which (5) is applied remains invariant with time, then (6) can be cast in the form:

$$\begin{aligned} \left\{ {\begin{array}{l} \phi \\ \partial \phi /\partial n \\ \end{array}} \right\} =[A]^{-1}[B]\left\{ {\begin{array}{l} \partial \phi /\partial n \\ \phi \\ \end{array}} \right\} \end{aligned}$$
(7)

The matrix \([C]=[A]^{-1}[B]\) in this case needs to be determined only once reducing Eq. (7) to only a simple matrix multiplication at every time step. The purpose of the present development is to use this simplification through suitable approximations but based on practical considerations. For 3D large volume structures particularly with relatively small water-plane areas, usually the radiated waves are much smaller compared to incident waves. Similarly the diffracted waves are also usually smaller compared to incident waves for realistic 3D structures. Note that full reflection takes place when waves are normally incident on a vertical wall. For 3D structures, it can thus be conjectured that overall the diffracted wave field will be of smaller amplitude compared to the incident waves. Therefore a linearization approximation for the radiation and diffracted wave fields may be justified within practical limits of applicability.

With the above approximation, we now proceed as follows. First, the incident wave potential \(\phi _I \) is taken out from the total potential \(\phi \) and the difference is defined as the \(\phi _P\):

$$\begin{aligned} \phi _P =\phi -\phi _I \end{aligned}$$
(8)

\(\phi _P\) is further decomposed into radiation potential (\(\phi _R\)) and diffraction potential (\(\phi _D\)):

$$\begin{aligned} \phi _P =\phi _R +\phi _D \end{aligned}$$
(9)

The boundary value problem for \(\phi \) defined by [Eqs. (1)–(4b)] applies for both \(\phi _R\) and \(\phi _D\) with the simplification that the free surface and body boundary conditions are now linearized and thus applied on the mean time invariant surfaces:

$$\begin{aligned}&\frac{\partial \eta _R }{\partial t}-\frac{\partial \phi _R }{\partial z}=0;\quad \frac{\partial \phi _R }{\partial t}+g\eta _R =0 \quad \hbox {on}\quad z=0\nonumber \\&\frac{\partial \phi _R }{\partial n}=\vec {V}_H \cdot \vec {n}\quad \hbox {on}\quad \partial \Omega _B (0)\end{aligned}$$
(10)
$$\begin{aligned}&\frac{\partial \eta _D }{\partial t}-\frac{\partial \phi _D }{\partial z}=0;\quad \frac{\partial \phi _D }{\partial t}+g\eta _D =0 \quad \hbox {on}\quad z=0\nonumber \\&\frac{\partial \phi _D }{\partial n}=-\frac{\partial \phi _I }{\partial n} \quad \hbox {on}\quad \partial \Omega _B (0) \end{aligned}$$
(11)

Here, \(\eta _R \) and \(\eta _D \) are the total radiated and diffracted wave elevations associated with the corresponding potentials \(\phi _R\) and \(\phi _D \).

The integral relation (5) can now be applied separately to \(\phi _R \) and \(\phi _D \). To discard \(\partial \Omega _C\) from \(\partial \Omega \) in (5) following Cointe et al. (1990) and Tanizawa (1996) we introduce a damping layer to an annular zone extending from \(R=R_0 \) to \(R=R_1 =R_0 +\beta R\) adjacent to the exterior surface \(\partial \Omega _C \) located at \(R=R_1 \) (here \(R=\sqrt{x^2+y^2} \) is the radial distance). Over this zone, the free-surface conditions are written as:

$$\begin{aligned} \frac{\partial \phi }{\partial t}= & {} -g\eta -\nu (R_e )\phi \nonumber \\ \frac{\partial \eta }{\partial t}= & {} \frac{\partial \phi }{\partial z}-\nu (R_e )\eta \end{aligned}$$
(12)

where \(\nu (R_e )\) is a damping coefficient defined by:

$$\begin{aligned} \nu (R_e )=\alpha \omega \left( {\frac{R-R_0 }{\lambda }}\right) ^2 \end{aligned}$$
(13)

In Eq. (13) \(\omega \) and \(\lambda \) are wave frequency and wave length, respectively. Parameter \(\alpha \) controls the strength of the damping and \(\beta \) the extent of the damping zone. These values govern the effectiveness of the damping zone. The purpose of this damping zone is to ensure that by the time the outgoing waves from the body wave reach the outer surface, both \(\eta \) and \(\phi \) reduce to zero. It may be remarked here that a proper implementation of the exterior condition is crucial in successful development of a fully nonlinear MEL-type NWT simulations, and research in this direction is still continuing as can be seen from the recent survey of various schemes available for treatment of this exterior surface by Kim et al. (2014). In 2D NWT, wave amplitudes do not decay with distance, but in 3D NWT the outgoing wave amplitudes attenuate with the radial distance and the absorbing or damping zone works well if properly tuned. In the present case since we are applying this numerical beach for absorbing linearized radiated and diffracted waves, the beach works very well with the values of \(\alpha =1\) and \(\beta \) ranging from 0.5 to 1 depending on wave frequency, as the results below will demonstrate.

For the solution to progress in time, along with integration of the free-surface constraints (10) and (11), the equations of body motion also need to be integrated. The body motions can be written in the Newtonian framework as:

$$\begin{aligned}{}[M]\{\ddot{\vec {\xi }}\}=\{\overrightarrow{f}\} \end{aligned}$$
(14)

where \(\{\vec {\xi }\}\) is the body displacement and \(\{\vec {f}\}\) is the generalized forces imposed on the body. \(\{\vec {f}\}\) is composed of hydrodynamic forces \(\{\vec {f}_H \}\), hydrostatic forces \(\{\vec {f}_S \}\) and any other external forces like wind, current, mooring line load, etc. to which the structure may be exposed. Computation of hydrodynamic forces at every time step requires determination of the time derivative of the corresponding potentials, i.e. \(\partial \phi _R /\partial t\) and \(\partial \phi _D /\partial t\) terms. Evaluation of the time derivative of the potential particularly in the context of fully nonlinear floating body simulation is not trivial. If a straightforward backward difference scheme is used for its evaluation, then the solution develops numerical instability. The literature on floating body simulations by MEL method indicates that special techniques have to be devised to determine this pressure term to ensure numerical stability of the simulation algorithm (Sen 1993; Tanizawa 2000). Noting that integral relation (5) also applies for \(\partial \phi /\partial t\) if this term on the body surface can be directly determined from such an integral equation without resorting to numerical differentiation, then the numerical instability problem can be avoided. Such a procedure will require specification of the appropriate boundary conditions for the \(\partial \phi /\partial t\) problem, in particular the body surface boundary condition. This means that \(\partial ^2\phi /\partial t\,\partial n\) on the wetted hull need to be stated. Such a condition was explicitly derived by Tanizawa (1995, (2000) by defining acceleration potential. This method for computing the time derivative of potential is termed acceleration potential method which has been subsequently used by several workers in nonlinear NWT simulation studies (e.g. Koo and Kim 2004).

In the present case, we devise a scheme similar to this acceleration potential method but due to the linearization of the corresponding potentials (\(\phi _R ,\phi _D\)), the implementation is somewhat different and simpler than the original acceleration potential method of Tanizawa (1995). We remark that for the purely diffraction problem, computing \(\partial \phi _D /\partial t\) by application of a backward numerical differentiation does not pose any difficulty and no instabilities are encountered. It is also straightforward to solve \(\partial \phi _D /\partial t\) through an integral relation as the body condition for this problem is known \(\partial /\partial n\,(\partial \phi _D /\partial t)=-\partial /\partial n\,(\partial \phi _I /\partial t)\). Same remarks also apply for evaluation of \(\partial \phi _R /\partial t\) for the forced oscillation or a purely radiation problem with specified body motions. Difficulties related to numerical instability arises in evaluating the \(\partial \phi _R /\partial t\) term for the floating body motion simulations where the equations of motion need to be integrated to establish the body boundary condition.

The procedure devised in our work is as follows. For a point fixed on the body, following Kang and Gong (1990), the normal derivative of the time derivative of potential is written as:

$$\begin{aligned} \frac{\partial }{\partial n}\frac{d\phi }{dt}=\vec {n}\cdot \left( {\dot{\vec {v}}_G +\ddot{\vec {\theta }}\times \vec {r}_P -\dot{\vec {\theta }}\times \vec {v}_G }\right) \end{aligned}$$
(15)

where \(v_G \) and \(\dot{\vec {\theta }}\) are the translation and angular velocities of the rigid body at the centre of gravity (CG) of the body, \(\vec {r}_P \) is the position vector of the considered point on the body surface from the CG, and the symbol \(d/dt\) represents differentiation following a fixed point. We can write:

$$\begin{aligned} \vec {n}\cdot \left( {\dot{\vec {v}}+\ddot{\vec {\theta }}\times \vec {r}-\dot{\vec {\theta }}\times \vec {v}}\right) =\sum \limits _{i=1}^6 {a_i } n_i \end{aligned}$$
(16)

where \(\vec {n}=(n_1 ,n_2 ,n_3 )\), \(\vec {r}\times \vec {n}=(n_4 ,n_5 ,n_6 )\) and

$$\begin{aligned} a_i= & {} \left( {\dot{\vec {v}}_G -\dot{\vec {\theta }}\times \vec {v}_G }\right) _i,\quad i=1,2,3 \nonumber \\= & {} (\ddot{\vec {\theta }})_{i-3}, \quad i=4,5,6 \end{aligned}$$
(17)

where the subscript on the right-hand side of the vector quantities in parenthesis represents the three components of the vectors, respectively. The time derivative of the total potential \(\partial \phi /\partial t\) is now decomposed as:

$$\begin{aligned} \frac{d\phi }{dt}=\sum \limits _{i=1}^6 {a_i \frac{d\phi _i }{dt}+\frac{d\phi _7 }{dt}} \end{aligned}$$
(18)

The boundary conditions applicable to these component potentials are: for \(i=1,\ldots ,6\)

$$\begin{aligned}&\frac{\partial }{\partial n}\left( {\frac{d\phi _i }{dt}}\right) =n_i \quad \hbox {on}\quad \partial \Omega _B (t)\nonumber \\&\frac{d\phi _i }{dt}=0 \quad \hbox {on}\quad \partial \Omega _F (t) \end{aligned}$$
(19)

and

$$\begin{aligned}&\frac{\partial }{\partial n}\left( {\frac{d\phi _7 }{dt}}\right) =0 \quad \hbox {on}\quad \partial \Omega _B (t)\nonumber \\&\frac{d\phi _7 }{dt}=\vec {V}_F \cdot \nabla \phi -\frac{1}{2}( {\nabla \phi })^2-gz\quad \hbox {on}\quad \partial \Omega _F (t) \end{aligned}$$
(20)

where \(\vec {V}_F\) is velocity of material points on the free surface.

Considering Eqs. (8) and (9), and the linearization of \(\phi _R\) and \(\phi _D \), we can write:

$$\begin{aligned} \phi= & {} \phi _P +\phi _I=\sum \limits _{i=1}^6 {a_i } \phi _i +\phi _7 \nonumber \\= & {} \sum \limits _{i=1}^6 {a_i } \phi _i +\left\{ (\phi _R^*+\phi _D)+\phi _I \right\} \nonumber \\= & {} \sum \limits _{i=1}^6 {a_i } \phi _i +\left\{ \phi _7^*+\phi _I \right\} \end{aligned}$$
(21)

In the above, \(\phi _R =\sum _{i=1}^6 {a_i } \phi _i +\phi _R^*\) which means the total radiation potential has been split into two parts with \(\phi _R^*\) representing one part of it. This part combined with the diffraction potential \(\phi _D \) is written as \(\phi _7^*\). This means \(\phi _7^*=\phi _R^*+\phi _D \). Since both \(\phi _R \) and \(\phi _D \) satisfy the linear free-surface conditions as per the approximations used here, the boundary condition for the time derivative of the \(\phi _7^*\) is obtained as:

$$\begin{aligned}&\frac{\partial }{\partial n}\left( {\frac{d\phi _7^*}{dt}}\right) =-\frac{\partial }{\partial n}\left( {\frac{d\phi _I }{dt}}\right) \quad \hbox {on}\quad \partial \Omega _B (0)\nonumber \\&\frac{d\phi _7^*}{dt}=-g(\eta _D +\eta _R ) \quad \hbox {on}\quad \partial \Omega _F (0)\quad \hbox {i.e. on}\quad z=0 \end{aligned}$$
(22)

Because of linearization, in Eq. (22) as well as in Eq. (19) \(d/dt\equiv \partial /\partial t,\) and thus (19) also applies on the mean time invariant position of body and free surface.

It is instructive here to provide an explanation for the need to split the radiation potential and combine a part of it with the diffraction potential. This arose purely from the requirement of deriving the body boundary condition for radiation potential time derivative, i.e. the \(\partial /\partial n\,(\partial \phi _R /\partial t)\) term for fixed collocation points on the body surface, which is necessary for solving \(\partial \phi _R /\partial t\) directly through a discretized integral relation similar to (5) to determine linear dynamic pressure term. Note that our interest is actually the determination of the total pressure \(\partial (\phi _R +\phi _D )/\partial t\). As no expression for \(\partial /\partial n\,(\partial \phi _R /\partial t)\) for fixed points on the body surface could be arrived at, \(\phi _R \) was split into two parts, one part is the sum of the terms \(\phi _i ,i=1,6\) and the other part is \(\phi _R^*\). The expressions for the time derivatives of \(\phi _i \) as well as \(\phi _R^*\) combined with \(\phi _D \) (which is written here as \(\phi _7^*=\phi _R^*+\phi _D )\) are now derived. This process thus enables determination of components of total linear pressure from radiation and diffraction directly from the solution of an integral relation without resorting to any numerical differentiation. The free-surface boundary conditions for the time derivatives of \(\phi _i \) in (19) indicate that these potentials can be called the infinite-frequency components of the radiation potentials for unit accelerations in different modes.

The hydrodynamic force \(\vec {f}_H \) is obtained from integration of pressure over the body surface. Considering the assumptions on the components of \(\phi \) made above, this force expression is obtained as:

$$\begin{aligned} \vec {f}_H= & {} -\rho \int \limits _{\partial \Omega _B (t)} {\left[ {\frac{\partial \phi }{\partial t}+\frac{1}{2}(\nabla \phi )^2} \right] \,\left\{ {\frac{\vec {n}}{\vec {r}\times \vec {n}}} \right\} \,\hbox {d}\partial \Omega } \nonumber \\= & {} -\rho \int \limits _{\partial \Omega _B (0)} {\frac{\partial }{\partial t}\left[ {\sum \limits _{i=1}^6 {a_i \phi _i +\phi _7^*} } \right] \,\left\{ {\frac{\vec {n}}{\vec {r}\times \vec {n}}} \right\} \,\hbox {d}\partial \Omega }\nonumber \\&-\rho \int \limits _{\partial \Omega _B (t)} {\left[ {\frac{\partial \phi _I }{\partial t}+\frac{1}{2}(\nabla \phi _I )^2} \right] \,\left\{ {\frac{\vec {n}}{\vec {r}\times \vec {n}}} \right\} \,\hbox {d}\partial \Omega } \nonumber \\= & {} \vec {f}_{RD} +\vec {f}_I \end{aligned}$$
(23)

The first term of 2nd line in Eq. (23) denoted as \(\vec {f}_{RD} \) is the force due to combined diffraction and radiation potentials, evaluated on the mean body surface, and the second term denoted as \(\vec {f}_I \) is the Froude–Krylov (F–K) force. \(\vec {f}_{RD}\) can be written as:

$$\begin{aligned} \vec {f}_{RD}= & {} -\rho \int \limits _{\partial \Omega _B (0)} \frac{\partial }{\partial t}\sum \limits _{i=1}^6 {a_i \phi _i } \left\{ {\frac{\vec {n}}{\vec {r}\times \vec {n}}} \right\} \,\hbox {d}\partial \Omega \nonumber \\&-\rho \int \limits _{\partial \Omega _B (0)} {\frac{\partial \phi _7^*}{\partial t}\left\{ {\frac{\vec {n}}{\vec {r}\times \vec {n}}} \right\} \,\hbox {d}\partial \Omega } \end{aligned}$$
(24)

Using Eq. (17), the first term on R.H.S. of Eq. (24) denoted as \(\vec {f}_R^*\) in component form is:

$$\begin{aligned} f_{Ri}^*=-\rho \int \limits _{\partial \Omega _B (0)} {\sum \limits _{j=1}^6 {a_j m_i \frac{\partial \phi _j }{\partial t}\,\hbox {d}\partial \Omega } } \end{aligned}$$
(25)

In Eq. (25) \(m_i \) is the generalized normal which is equal to \(n_i \) for \(i=1, 2, 3\) and equal to \((\vec {r}\times \vec {n})_{i-3} \) for \(i=4, 5, 6\). Defining

$$\begin{aligned} \alpha _{ij} =\rho \int \limits _{\partial \Omega _B (0)} {\sum \limits _{j=1}^6 {m_i \frac{\partial \phi _j }{\partial t}\,\hbox {d}\partial \Omega } } \end{aligned}$$
(26)

Using (17), we can now write:

$$\begin{aligned} f_{Ri}^*= & {} -\sum \limits _{j=1}^6 {\ddot{\xi }_j } \alpha _{ij} +\sum \limits _{j=1}^3 {(\dot{\vec {\theta }}\times \vec {v}_G )_j \alpha _{ij} }; \quad i=1,2,3 \nonumber \\= & {} -\sum \limits _{j=1}^6 {\ddot{\xi }_j } \alpha _{ij};\quad i=4,5,6 \end{aligned}$$
(27)

In writing (27), we have used \(\dot{\xi }_i =(\vec {v}_G )_i ,\,i=1,2,3\) and \(=(\dot{\vec {\theta }})_{i-3} ,i=4,5,6\). For convenience, force in Eq. (27) can be expressed in vector form as \(\vec {f}_R^1 +\vec {f}_R^2 \) with the first term representing the force given by the \(\ddot{\vec {\xi }}_j \alpha _{ij} \) term and note that \(\vec {f}_R^2 \) contributes only to the linear forces but not to the moments. By bringing \(\vec {f}_R^1 \) to the L.H.S. of the equations of motion, (14) can be expressed as:

$$\begin{aligned} \left[ {[M]+[\alpha ]} \right] \{\ddot{\vec {\xi }}\}=\{\vec {f}^*\} \end{aligned}$$
(28)

where \([\alpha ]\{\ddot{\xi }\}=-\{\vec {f}_R^1 \};\,\{\vec {f}^*\}=\{\vec {f}\}-\{\vec {f}_R^1 \}\). Note that \(\{\vec {f}\}\) composes of the total hydrodynamic force \(\{\vec {f}_H \}\), hydrostatic force \(\{\vec {f}_S \}\), and any other external forces such as mooring restoring forces that may be present. In Eq. (28) part of the radiation forces that are frequency independent and depending only on the body geometry can be expressed in the form \(-[\alpha ]\{\ddot{\bar{\xi }}\}\) has been moved to the R.H.S and combined with the rigid mass–inertia terms. The applicable free-surface condition in determination of the terms in \([\alpha ]\) suggests these to be analogous to frequency-independent added masses.

The force represented by the 2nd term of R.H.S. of (24) composes of forces from the pressure term given by \(\partial \phi _7^*/\partial t\,=\partial \phi _R^*/\partial t+\partial \phi _D /\partial t\), that is, this force is the combined effect of diffraction and part of radiation. As regards the F–K force \(\vec {f}_I \) Eq. (23) expresses it as integration over the wetted body surface. This raises the following questions. The first one is that the force/moment needs to be described with respect to a body-fixed coordinate system. However, the forces due to the radiation and diffraction are being computed on the mean position of the hull which is defined in inertial system. Transforming the evaluated forces from body-fixed to inertial system and vice-versa are, however, easily achieved through transformation matrix \([R]\) (and its inverse given by its transpose). As the radiation and diffraction forces, \(\vec {f}_{RD}\) in (23) are based on linearization assumption, these forces remain same in both the coordinate systems under this approximation. Thus, the equations of motion (14) can be written in the moving body coordinate system, and the evaluated \(\vec {f}_{RD} \) can be directly added to the incident forces (see e.g. Sen 2002). The second question is on the exact wetted surface. This surface should be formed by the instantaneous location of the hull under the combined wave profile of incident, radiation and diffraction (indeed, in full nonlinear solutions, such decomposition itself is not possible). Here, the forces are evaluated under the incident wave profile, which is consistent with the linearization approximation of the radiation and diffraction effects as linear free-surface conditions on the surface \(z = 0\) are applied to these potentials.

The solution proceeds as follows. The \(\alpha _{ij} \) terms are constant and independent of time requiring only one-time evaluation. These are thus pre-computed before the time simulations starts. For the time-simulation procedure, for any instance first we solve the \(\phi _R \) and \(\phi _D \) problems using (5) from which \(\eta _D \) and \(\eta _R \) are found from time integration of Eqs. (10) and (11) following an MEL procedure. For the same time instant, we also solve the time derivative problem, and find the force due to pressure term \(\partial \phi _7^*/\partial t\), that is the 2nd term of \(\vec {f}_{RD} \) in (24). After evaluating and adding \(\vec {f}_I \) (as well as \(\vec {f}_R^2 )\), the motion Eq. (14) are integrated and the solution advances in time. A flowchart of the time-stepping procedure is shown in Fig. 2. If it is desired to find the diffraction and radiation forces, these can be computed independently by applying appropriate numerical difference schemes to the evaluated \(\phi _D ,\phi _R \) on the body surface and integrating the resulting pressures. Note that forces thus evaluated are not used in the time advancement of the solution and, therefore, do not influence numerical stability of the simulation algorithm.

Fig. 2
figure 2

A brief flowchart of the time-integration procedure; the superscripts in \(\eta _{R}\), \(\eta _{D}\) and \(\bar{\xi }\) terms represent the iteration level in the time integration

Full size image

As regards the hydrostatic forces, along with the incident wave pressure the hydrostatic pressure term is also integrated over the instantaneous wetted hull under the incident profile. The body weight force is also to be considered in this case. If a consistently linear solution is desired, then the incident wave forces are determined on the mean wetted surface using only the linear pressure term and hydrostatic restoring forces are expressed by the well-known hydrostatic restoring coefficient terms. The body weight in this case is not taken into account as this is nullified by the buoyancy force for a body in equilibrium.

3 Results and discussion

Computations are performed for three geometries, a rectangular barge, a six-column twin pontoon semisubmersible, and the S175 hull. Relevant data on geometric particulars and the computational domain are shown in Table 1, and Fig. 3 displays the panelization of the body and free surface (for the semisubmersible case, only a part of the free surface is displayed). At the outset, to verify the developed MEL-based time-domain simulation scheme, we carry out the fully linearized calculation and compare the results with available computational and experimental results. The present calculations are able to generate extremely long-duration time-histories of motions over all frequencies. Figure 4 shows sample results for motion time-histories of the semisubmersible and the S175 hull. As can be seen, the algorithm remains stable and motion amplitudes are steady for the entire duration of the simulation run time. Comparisons are made with the Green function-based frequency-domain solution, available experimental data of Pinkster (1980) and the Rankine panel-based method SWAN-2 (Sclavounos 1996). For the present results, motion amplitudes are found from long-duration motion histories similar to Fig. 4. Comparison of the motion RAOs for wave heading \(\beta =13^{\circ }\) for all three structures are displayed in Figs. 5, 6, and 7. The code used for the frequency-domain Green function calculations is SOFORCE (Singh and Dhavalikar 2004), a code developed at Indian Register of Shipping which has been fully tested and benchmarked against other industry standard codes like WAMIT.

Fig. 3
figure 3

Body panels and free-surface panels a rectangular barge, b six-column semisubmersible and c S175 hull

Full size image
Table 1 Particulars of the three hull surface and relevant details of the NWT domain
Full size table

The translational motions surge (\(\xi _{1}\)), sway (\(\xi _{2}\)), and heave (\(\xi _{3}\)) are non-dimensionalized by wave amplitude (\(\xi _{a})\) and the angular motions roll (\(\xi _{4}\)), pitch (\(\xi _{5}\)), and yaw (\(\xi _{6}\)) are non-dimensionalized by wave number and wave amplitude (\(k\xi _{a}\) where \(k\) given by \(2\pi /\lambda \) is wave number, \(\lambda \) is wave length). RAOs are plotted against non-dimensionalized frequency \(\omega \sqrt{\nabla ^{1/3}/\hbox {g}} \). As can be seen, the comparisons for all three geometries in general show good agreement, particularly at higher frequency range. Semisubmersible results show that the captured natural period in heave by two numerical methods is different from the experimental results. For S175 hull, roll predicted by the present method as well as by frequency-domain code at the resonant frequency is conspicuously higher than SWAN-2 results because the former two computations are performed without incorporating any viscous roll damping unlike in SWAN-2 computations. Some differences, however, do exist particularly with the SWAN-2 code at the low-frequency range, but the agreement with the frequency-domain Green function-based method which is presently taken as standard method in offshore industry for linear wave–structure interactions is good over the entire frequency range. Considering that the three results are from three different methods and the uncertainties that exist in motions and loads for complex offshore configuration (see e.g. Hiradis et al. 2014), the overall agreement between the results can be termed good. Computations have also been made for beam waves and head waves (90\(^{\circ }\) and 180\(^{\circ }\) heading, respectively) and similar (and better) agreement is found in all cases, comparable to the bow-quartering case (the bow-quartering wave-heading results are presented here since at this heading all six modes of motions are present; in beam and head waves some of the motions are zero or negligible due to geometric symmetry).

Fig. 4
figure 4

Time-histories of the motion responses from the fully linearized algorithm. a Semisubmersible motions for wave period \((T) = 14\) s, wave height \((H_w)= 12\) m, wave heading \((\beta ) = 135^{\circ }\). b S175 hull motions for \(T = 12\) s, \(H_w= 10\) m, \(\beta 135^{\circ }\)

Full size image
Fig. 5
figure 5

Six degree of freedom (DOF) motion RAOs of barge at \(\beta = 135^{\circ }\)

Full size image
Fig. 6
figure 6

Motion RAOs of semisubmersible for wave heading \((\beta ) =135^{\circ }\)

Full size image
Fig. 7
figure 7

Motion RAOs of S175 hull for wave heading \((\beta ) =135^{\circ }\)

Full size image

The present linear computations are also directly compared with the SWAN-2 generated motion time-histories. Figure 8 shows a sample comparison for the S175 hull in head wave conditions. The height of this wave is taken very small, \(H_w =2\) m \((H_w /\lambda \approx 1/75)\) to ensure SWAN-2 to produce linear results. As can be seen, results compare well for both heave and pitch. Similar comparisons have been made for many different frequencies and wave headings, and agreements are found to be good in all cases. These results, therefore, confirm that for linear wave–structure interactions the present method is able to generate results comparable in accuracy with results from available codes for realistic practical geometries.

Fig. 8
figure 8

Heave and pitch time series results of the S175 hull for \(T = 10\) s, \(H_w= 2\) m, \(\beta =180^{\circ }\)

Full size image

We now proceed to the approximate nonlinear computations. The incident waves in these computations are taken as the fully nonlinear steady waves defined by the Fourier approximation-based numerical method given by Rienecker and Fenton (1981). This numerical method generates steady periodic nonlinear waves for steepness up to near breaking range and is similar to the stream function-based nonlinear water waves. For these calculations, however, we find that if the body is free in six DOF and fully unrestrained and, therefore, free to drift, the solution breaks down. The drifted location of the body over which the exact F–K forces are evaluated gets progressively shifted from the mean location over which the linearized diffraction effects are being computed. The problem of a freely drifting body is essentially same as the forward speed problem where the forward speed can be considered as the mean drift velocity. Since the present formulation is for a floating body with mean zero speed, the solution becomes invalid if the body is allowed to drift freely. For a forward speed problem, solution schemes based on Rankine panel method need to be formulated using a ship-fixed moving coordinate system. This is a different problem in which the specification of the boundary value problem itself gets modified through inclusion of forward speed-dependent terms, in particular in the free-surface conditions and the pressure term.

Almost all available 3D numerical methods for steep wave interaction with floating structures consider either three DOF motions of heave, pitch, roll or full six DOF with mooring lines restraining the body from freely drifting (see Ma and Yan 2009 and references therein). In a recent work by Watai et al. (2015), where a similar Rankine panel approach was applied for the fully linear problem of two side-by-side floating bodies, the horizontal motions of one body was fully restrained, and on the other body sway, yaw, and roll were fully restricted and surge was restrained through a spring. For the present approximate nonlinear calculations, it is clear that the method cannot be applied if the body is allowed to freely drift since the displaced location of the body needs to remain as an oscillation or perturbation about the mean location. In other words, the body’s horizontal motions need to be restrained. In practical application, all stationary floating objects have some restraining mechanism against free drifting, either through mooring lines or DP systems or tethers as in the case of a TLP (see e.g. Ma and Yan 2009; Chitrapu and Ertekin 1995). All these restraining mechanisms produce horizontal spring forces and moment on the body.

Allowing the body 3 DOF of heave, roll, and pitch is essentially equivalent to taking infinitely large spring stiffness in the horizontal plane restricting the horizontal motions of surge, sway, and yaw completely. On the other hand, a soft spring with low stiffness will allow all 6 modes of motions. For the present scheme, numerical experiments have shown that the influence of horizontal spring stiffness on the vertical plane motions is negligible. Thus, if the interest is in simulating heave, pitch, and roll motions only, then it is possible to generate meaningful results by restricting the horizontal motions completely. Since one of our objective is to generate long-duration motion time-histories for stationary (zero-Froude number) floating bodies using the approximate nonlinear method and be able to capture at least part of the important nonlinear features associated with large-amplitude waves, initially we perform computations by constraining the body’s horizontal motions completely. Implementation of this constraint in the algorithm is achieved by evaluating the nonlinear F–K forces and moments (in all six modes) over the exact wetted surface and under the incident wave profile formed by the body displaced in heave, pitch, and roll but restricted from sway, surge, and yaw. Restricting the horizontal motions in the evaluation of forces may be taken as another approximation in our blended nonlinear approach, physically equivalent to attaching a horizontal spring of infinite stiffness to the body. Note that in a consistent linear scheme, all forces are evaluated at the mean location of the body. For the above approximate nonlinear scheme, Figs. 9 and 10 displays the heave, roll, and pitch motions of the S175 hull and the barge in a wave of period \((T_{P})\) 12 s, height \((H_{w})\) 10 m, and heading (\(\beta \)) 135\(^{\circ }\). These and numerous other results for different geometries have shown that the algorithm remains extremely stable and is able to generate very long-duration motion histories displaying steady periodic characteristics.

Fig. 9
figure 9

Heave, roll, and pitch motions of the S175 hull for wave parameters: \(T=12\) s, \(H_{w}=10\) m, \(\beta =135^{\circ }\)

Full size image
Fig. 10
figure 10

Heave, roll, and pitch motions of the barge for wave parameters: same as in Fig. 9

Full size image

Having achieved long-duration results using the above modified form of the approximate nonlinear calculations, comparisons are now made to investigate the nature and extent of nonlinearities in the response histories. In presenting these results, forces and moments are non-dimensionalized by the \(\rho g\nabla \) and \(\rho g\nabla L\) where \(\rho \) is the density of sea water, \(\nabla \) is the mean under water volume and \(L\) is the body length. For clarity only a part of time history is displayed, although simulation is performed for over a very long duration, mostly exceeding 100 periods. In all plots, numerical results computed based on linear formulation (incident F–K force and hydrostatics restoring forces determined on mean location) are termed as ‘linear’ and the results computed based on approximated nonlinear formulation (incident F–K and hydrostatic forces are determined on the horizontally restrained location) are termed as ‘approx. nonlinear’.

Figure 11 shows the heave and roll motion of the barge in beam waves for wave of period 12 s \((\lambda /L\approx 1.49)\), and height 10 m. Heave and pitch motions in head sea condition for the same wave are shown in Fig. 12. It is seen that for this wave in beam sea, nonlinear predictions of roll is slightly higher than the corresponding linear results, but the pitch results are less influenced by incident wave nonlinearity. However, in a longer wave of period \(T= 18\) s. \((\lambda /L\approx 3.3)\) in head sea condition shown in Fig. 13, nonlinearities have some influence both on the amplitude and on the frequency components for pitch motions.

Fig. 11
figure 11

Heave and roll motions of the barge for wave parameters: \(T = 12\) s, \(H_w= 10\) m, \(\beta =90^{\circ }\)

Full size image
Fig. 12
figure 12

Heave and pitch motions of the barge for wave parameters: \(T = 12\) s, \(H_w= 10\) m, \(\beta =180^{\circ }\)

Full size image
Fig. 13
figure 13

Heave and pitch motions of the barge for wave parameters: \(T = 18\) s, \(H_w=10\) m, \(\beta =180^{\circ }\)

Full size image

Figure 14 displays the F–K forces on S175 hull for a wave of \(T=12\) s. (\(\lambda /L\approx 1.25\)), \(H_w =10\) m, \(\beta =135^{\circ }\). This hull, unlike the barge has a significant flare and thus incident forces as well as the hydrostatic restoring forces are expected to have pronounced nonlinear characteristics. As expected, results display considerable nonlinearities particularly in sway, roll, and yaw forces and moments. The non-dimensional hydrostatic forces and moments are shown in Fig. 15 which verifies similar nonlinear features. The motions for this case shown in Fig. 16 also reflect similar nonlinearities.

Fig. 14
figure 14

Incident forces and moments on S175 hull for wave parameters: (\(T = 12\) s, \(H_w= 10\) m, \(\beta =135^{\circ }\))

Full size image
Fig. 15
figure 15

Hydrostatic restoring forces/moments for the S175 hull for wave parameter: same as in Fig. 14

Full size image
Fig. 16
figure 16

Heave, roll, and pitch motions of the S175 hull for wave parameter: same as in Fig. 14

Full size image

Figure 17 shows the comparison of motions of the freely floating unmoored semisubmersible. Linear and approximate nonlinear results show negligible differences in the computed vertical motions. Numerical simulations have also been performed over a wide range of frequencies and wave heights, and in general it is found that the influence of nonlinearities as expected is largest for the S175 hull, followed by the barge and least significant for the semisubmersible configurations signifying that incident wave nonlinearities are mostly associated with the above water hull geometry: the larger and more flared this part is, the larger is the nonlinear influence.

Fig. 17
figure 17

Heave, roll and pitch motions of the semisubmersible for wave parameter: \(T = 14\) s, \(H_w= 12\) m, \(\beta =135^{\circ }\)

Full size image

We now show motions of the semisubmersible with mooring lines. A spread mooring with six lines is introduced and mooring lines are modelled as linear springs. The stiffness of each line is taken as 50 kN/m which is a realistic value for this size of a semisubmersible. The mooring forces are then expressed as \(\{\vec {f}_M \}=[c_M ]\{\xi \}\) and the equivalent linear restoring coefficients \([c_M ]\) are determined by adding the contribution from each line after proper resolution, as outlined in Faltinsen (1990). For this case, the F–K forces are determined on the exact displaced wetted surface without any restriction on its horizontal position. Figure 18 shows all the six modes of motion. There is an initial transient in surge and sway motions and these periods correspond well with theoretically estimated natural periods in these modes. Investigations have shown that these transients can be absorbed within a few periods (typically 2–5 periods) if a small damping of the order of 5 % of critical damping is introduced in the horizontal mode motions. The important observation from this result is that long-duration simulation with exact F–K forces on the displaced position of the hull is achievable if there is a physical restriction imposed on the horizontal plane motions through mooring lines. This particular case have shown insignificant difference between the motions except in yaw, but in a much longer wave of period 20 s. shown in Fig. 19, all the three horizontal plane motions show a mean offset of the body after the initial transients have decayed.

Fig. 18
figure 18

Six DOF motions of the semisubmersible with mooring lines for wave (\(T=14\) s, \(H_w= 12\) m, \(\beta =135^{\circ }\)); (here approx. nonlinear implies F–K force and hydrostatic restoring forces computed on exact wetted surface at displaced location)

Full size image
Fig. 19
figure 19

Six DOF motions of the semisubmersible with mooring lines for wave (\(T=20\) s, \(H_w= 16\) m, \(\beta =135^{\circ }\)) (approx. nonlinear implies same as described in Fig. 18)

Full size image

As mentioned previously, the present method can be applied straightforward for the multi-body case. In this case, the body surface will consist of panels over body-1 followed by body-2, etc. After determining the pressures over each body panel, all that is needed is to integrate the pressures over the respective body surfaces to determine the forces and moments over each body, taking care of the fact that the moments need to be defined with respect to the individual body coordinate systems. The equations of motions for each body can then be integrated independently. The details of the free-surface elevations surrounding the bodies can also be captured as the solution progresses. Figure 20 shows a preliminary result for a shuttle tanker lying in parallel to an FPSO with a 20m gap in between and the total perturbed wave elevation (i.e. the free-surface elevation excluding the incident wave) for an incident wave which is a linear wave of height 2 m and period 9sec at 180\(^{\circ }\) heading. The length, breadth, and draft of the FPSO and the shuttle tanker are (325, 58, 30 m) and (264, 46, 23 m), respectively. It can be seen that the method could capture the increased wave elevation within the gap region.

Fig. 20
figure 20

FPSO and shuttle tanker lying parallel with 20 m gap (top), and the free-surface elevation for the total perturbed wave field in a incident wave of \(T= 9\) s, \(H_w= 2\) m, and \(\beta =180^{\circ }\) (bottom)

Full size image

Figure 21 shows preliminary results on air-gap studies for a semisubmersible exposed to a nonlinear incident beam wave of height 14 m and period 10 s. The plot shows the total free-surface elevation as well as the total perturbed wave at a given instant. The bottom plot reveals that the perturbed wave height below the deck is relatively large compared to the rest of the region and thus important in predicting the under-deck clearance. Figure 22 shows the time-histories of deck height (\(z_D\)), free-surface elevation (\(\eta \)) and the air-gap (\(z_D -\eta \)) for a point located at the centre of the deck, that is at the horizontal location \((x,y)=(0,0)\). Results are shown for computations performed with both linear as well as steady nonlinear incident wave with height 14 m, period 10 s. and heading 90\(^{\circ }\). Careful observation reveals that the minimum air-gap obtained for nonlinear incident wave is lower by about 0.5 m as compared to the values obtained with linear wave case. Figure 23 shows a similar comparison for a twin pontoon four-column semisubmersible. The semisubmersible in this case has pontoon sizes of \(90~\times 15~\times ~6.5\) m spaced at 60 m, and the columns are of diameter 9 m longitudinally spaced at 69 m. The deck of the semisubmersible is taken at 10 m above mean water line. The results are for incident wave of height 10 m, period 10 s in heading of 135\(^{\circ }\). and the point is located at \((x,y)=(-44.17,-26.17)\) which is the centre of the free-surface panel adjacent to the inside of the aft-starboard side column. As can be seen, here also the minimum air-gap clearance for the computation with nonlinear incident wave predicts about 0.5 m lower as compared to the computation with linear incident wave. These preliminary results, therefore, reveal the importance of nonlinearities in the incident wave in predicting minimum air-gap clearance. The importance of nonlinearities in incident wave height for practical air-gap predictions has also been discussed in Sweetman (2004) where the incident waves used were Stokes 2nd order wave. As discussed by the author, there are several levels of approximate methods for practical air-gap predictions, and incident wave nonlinearity is an important contributor to the minimum air-gap. The present method can yield minimum air-gap considering full nonlinear incident waves in the time domain which turned out to be lower than when prediction are made with linear waves. Following the methods proposed in Sweetman (2004), the results from regular nonlinear incident computations can be statistically analysed to derive important design information in irregular waves. Detailed studies on multi-body simulations as well as under-deck clearance including validation will be reported in subsequent work. Here, these preliminary results are presented to demonstrate the capability and versatility of the method in yielding results of practical importance.

Fig. 21
figure 21

Semisubmersible exposed to a nonlinear incident wave of \(T=10\) s, \(H_w= 14\) m, \(\beta =90^{\circ }\); top plot shows the 3D view of total free-surface elevation and the bottom plot shows the 2D contour plot of perturbed wave elevation

Full size image
Fig. 22
figure 22

Time history of deck height, free-surface elevation (incident \(+\) perturbed) and the air-gap for a point at the centre of the deck located at \((x, y)=(0,0)\) for an incident beam wave (90\(^{\circ }\)) with height 14 m, period 10 s. a Linear Airy’s wave and b full nonlinear numerical wave

Full size image
Fig. 23
figure 23

Comparison of air-gap clearance between computations performed with linear wave and nonlinear wave at horizontal location \((x, y) = (-44.17,-26.70)\); the incident wave is of height 10 m and period 10 s, heading of 135\(^{\circ }\)

Full size image

It is also mentioned earlier that the present method allows for a possibility of modelling partial nonlinear effects associated with the diffracted wave field by a suitable mapping of the wetted hull at every time step. The idea here is as follows. Referring to Fig. 24, the top diagram (a) shows the body at its mean location along with a schematic panelization. It is this geometry that is being used in the integral Eq. (5). The bottom diagram (b) shows the body in its instantaneous location under the nonlinear incident wave profile. The time invariant body panels in (a) can be mapped through a suitable mapping procedure to the panels in the wetted surface (b), i.e. collocation point \(P_i (0)\) is mapped to the point \(P_i (t)\). The applicable body boundary condition for the diffraction potential expressed in terms of the incident wave normal velocity \(\,\partial \phi _I /\partial n\) [see Eq. (11)] is now evaluated for the point \(P_i (t)\) based on the nonlinear incident wave potential and applied at the point \(P_i (0)\) for the discretized solution. The procedure is theoretically inconsistent, but it is expected to capture some of the nonlinearities associated with the diffraction potential. In other words, this may give a closer approximation to the nonlinear diffraction than using a fully linear diffraction. This procedure of mapping the underwater hull follows from a similar idea used in the highest version of the LAMP code, the LAMP-4 body-exact version in the 3D ship motion calculations (Lin et al. 1994) which has also been implemented by Singh and Sen (2007a, (2007b) with reasonably good results.

Fig. 24
figure 24

Illustration for mapping in applying the body boundary condition for diffraction potential

Full size image

It should be noted that in the LAMP code, the mapping of the exact hull to the computational domain is somewhat different than what is proposed here because of the difference in the basic solution method. Whether such a procedure will produce results closer to the full nonlinear solution can only be confirmed after implementing such scheme and carrying out a detailed investigation in comparison to available nonlinear results. A form of this implementation for the case of wave diffraction for a bottom-mounted vertical cylinder have shown that this procedure yields a time history of diffraction forces with larger positive peak and lower negative peak as wave amplitude increases (Sen and Srinivasan 2007). The important point is that the method allows for possibilities of such extensions which may be able to provide improved estimates of large-amplitude wave effects on the structures.

4 Concluding remarks

A time-domain simulation method is developed for studying the interaction of large-amplitude nonlinear incident waves with 3D floating structures. The method is formulated based on a 3D MEL type of approach for solving the interaction hydrodynamics of radiation and diffraction effects with simplifying approximation of linearization of these potentials. The introduced approximations allow meaningful practical results to be obtained for realistic offshore and ship geometries with reasonable and moderate computing resources making the method suitable for routine industry usage. The method is also versatile and in principle can accommodate influence of external forces arising from other sources to which the emerging complex offshore structures may be exposed. There are also possibilities to account for certain nonlinearities associated with the radiation and diffraction through modification of the appropriate boundary conditions, e.g. using a modified form of the body boundary conditions for the diffraction potential [the 2nd Eq. of (11)] through a mapping of \(\partial \Omega _B (t)\) to \(\partial \Omega _B (0)\), as briefly discussed here. The versatility of this method also makes it suitable for studying multi-body interactions, under-deck clearance study using full nonlinear incident wave, etc. Presently some preliminary results are demonstrated to show the capabilities of the developed tool, detail applications will be addressed in subsequent works.

The present study comprises of the following elements in the development process of a robust and generalized tool for time-domain simulation of wave–structure interactions:

  • Computational results based on linear formulation are verified with results from other frequency domain and time-domain solvers. Comparison of computed results by the present scheme shows good agreement with other solvers.

  • Nonlinear interaction problem is pursued by taking into account the nonlinearities arising from the incident wave F–K forces and nonlinear hydrostatic restoring forces.

  • Long-duration simulation in a steep nonlinear incident wave is presented. Steady periodic long-duration simulation results are achieved for both linear and nonlinear formulation by devising techniques for computation of the linear dynamic pressure terms, introduction of an artificial dissipative beach. The method is not suitable for a freely drifting body. Thus if the body has no restraint in the horizontal plane, then such restraints need to be imposed artificially to restrict its motion in the horizontal plane.

From the extensive computations carried out for three realistic geometries, the following observations could be made:

  • In the nonlinear method, comparison of linear and nonlinear computations shows that for wall-sided structures like a rectangular barge with large upper hull part, some differences exist in the computed F–K forces while the differences in the restoring forces are less significant but the vertical motion response shows considerable variations from linear formulation results.

  • For S175 containership hull, significant variations in the F–K forces, restoring forces, and motions between linear and nonlinear computations can be observed. This is clearly due to the flare of the hull resulting in the so-called geometric nonlinearity. For such flared hulls, large-amplitude motions cause a considerable change in the wetted surface of the hull.

  • For six-column twin pontoon semisubmersible, minor variations between linear and nonlinear results are observed for all wave headings, including F–K forces, unlike in the case of a rectangular barge which also is wall sided. This is perhaps due to the fact that the semisubmersible has low volume part above water plane, that is, the variation in the exact wetted surface and the mean surface volume is relatively much small for this geometry.