1 Introduction

The numerical simulation of metal-cutting processes is complicated mainly by two factors. First one is the material constitutive model. It must adequately represent deformation behavior during high strain rate loading as well as low strain rate loading under a range of temperatures, and account for hardening and softening processes. Material models are usually calibrated based on experimental data from material testing covering the relevant range of loading conditions of the intended application. The magnitudes of strain and strain rate involved in metal cutting are several orders of magnitude higher than those generated from conventional material tension and compression testing. A highly desirable feature is therefore a material model that can be extrapolated outside the calibration range. This is not trivial since materials exhibit different strain hardening and softening characteristics at different strains, strain rates, and temperatures. The advantage of using a physically based plasticity model is an expected larger domain of validity compared with phenomenological models, because physically based models are related to the underlying physics of the deformation coupled to the microstructural evolution. The second challenge is concerned with the modeling and numerical realization of large configuration changes. Numerical simulations of machining process involves large strains and angular distortions, multiple contacts and self-contact, generation of new boundaries, and fracture with multiple cracks and defragmentation. All of them are difficult to handle using standard finite-element methods.

The purpose of this paper is to apply the particle finite-element method (PFEM) [1–3] to solve the problems associated with the large changes in configuration and use a physically based plasticity model [4, 5] to extrapolate the material behavior outside the calibration range.

The rest of the paper is organized as follows. Section 2 is devoted to the description of PFEM and the modifications introduced here concerning insertion and removal of particles. In Sect. 3, the basic equations for conservation of linear momentum, mass conservation, and heat transfer for a continuum using a generalized Lagrangian framework is presented. Section 4 deals with the variational formulation of the continuous problem presented in Sect. 3. Then the mixed finite-element discretization using simplicial element with equal order approximation for the displacement, the pressure, and the temperature is presented, and the relevant matrices and vectors of the discretized problem are given in Sect. 5. Section 6 presents the \(J_2 \) plasticity model at finite deformation and a description of the physical-based plasticity model. Details of the implicit solution of the Lagrangian FEM equations in time using an updated Lagrangian approach and a Newton–Raphson-type iterative scheme are presented in Sect. 7. Section 8 focuses on a set of representative numerical simulations of metal-cutting processes using PFEM and a physical-based constitutive model. Finally, in Sect. 9, some concluding remarks are presented.

2 The particle finite-element method

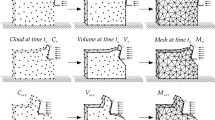
The particle finite-element method (PFEM) is a FEM-based particle method [1], initially proposed for the solution of the continuous fluid mechanics equations. The main objectives were, on the one hand, to develop a method to eliminate the convective terms in the governing equations. On the other hand, the introduction of a technology, based on the alpha shape method used in other areas, able to deal with free boundary surfaces is a secondary objective. The interpretation of the method has evolved from a meshless method, in which the nodes are supposed to be particles that move according to simple rules of motion, to a sort of updated Lagrangian approach in which the advantages of the standard FEM formulation for the solution of the incremental problem are used.

Although PFEM was initially applied to problems in the field of fluid mechanics, it is being currently applied to a wide range of simulation problems [6–9]: filling, erosion, mixing processes, thermoviscous processes and thermal diffusion problems, among others. First applications of PFEM to solid mechanics are found in [10–15] to problems involving large strains and rotations, multibody contacts and creation of new surfaces (riveting, powder filling, and machining).

Applications to the response of rockfill dams on overtopping conditions, via a non-Newtonian fluid, can be found in [16].

2.1 The particle finite-element method on fluid mechanics

In the PFEM approach, the continuum material is modeled using an updated formulation, and the finite-element method is used to solve the variational incremental problem. Hence, a mesh, discretizing the domain, is generated in order to solve the governing equations. In this context, discretization nodes can be regarded as material points whose motion is followed during the time stepping solution. The PFEM, typically, consists of the following steps

  1. 1.

    Fill the domain with a set of points referred to as ‘particles’. The accuracy of the numerical solution is clearly dependent on the considered number of particles.

  2. 2.

    Generate a finite-element mesh using the particles as nodes. This is achieved using a Delaunay triangulation [17, 18].

  3. 3.

    Identify the external boundaries to impose the boundary conditions and to compute the domain integrals. In this step, the Alpha Shape method [19, 20] is used for the boundary recognition.

  4. 4.

    Solve the nonlinear Lagrangian form of the governing equations finding displacement, velocity and pressure at every node of the mesh.

  5. 5.

    Update the particle positions using the computed values of displacement, velocity and pressure.

  6. 6.

    Go back to step 2 and repeat for the next time step.

The continuous reconnection introduced in step 2 is the key strategy to circumvent the typical mesh distortion generated when a description is used with problems involving large strains.

In this solution scheme, not only is the numerical solution of the equations critical from the computational point of view, but also are the generation of a new mesh and the identification of the boundaries.

2.1.1 Identification of the boundaries

In a Lagrangian framework, the external boundary and the reference volume are defined by the position of the material particles. Every time the mesh is regenerated, the particles belonging to the boundary may change, and the new boundary nodes (and therefore the particles) have to be identified. The Delaunay triangulation generates the convex hull of the set of particles. Moreover, the convex hull may not be conformal with the external boundaries. A possibility to overcome this problem is to correct the generated mesh using the so-called \(\alpha \)-shape method to remove the unnecessary triangles from the mesh using a criterion based on the mesh distortion. The \(\alpha \)-shape method can also be used for the identification of the fluid particles which separate from the rest of the domain.

2.2 The particle finite-element method solid mechanics

The PFEM is a set of numerical strategies combined for the solution of large deformation problems. The standard algorithm of the PFEM for the solution of solid mechanics problems contains the following steps.

  1. 1.

    Definition of the domain(s) \(\Omega _n \) in the last converged configuration, \(t={ }^nt\), keeping existing spatial discretization \(\bar{{\Omega }}_n \).

  2. 2.

    Transference of variables by a smoothing process—from Gauss points to nodes.

  3. 3.

    Discretization of the given domain(s) in a set of particles of infinitesimal size—elimination of existing connectivities \(\bar{{\Omega }}_n \) .

  4. 4.

    Reconstruction of the mesh through a triangulation of the domain’s convex-hull and the definition of the boundary applying the \(\alpha \)-shape method [19, 20], defining a new spatial discretization \(\bar{{\Omega }}_n \).

  5. 5.

    A contact method to recognize the multibody interaction.

  6. 6.

    Transference of information, interpolating nodal variables into the Gauss points.

  7. 7.

    Solution of the system of equations for \({ }^{n+1}t={}^nt+\Delta t\) .

  8. 8.

    Go back to step 1 and repeat the solution process for the next time step.

2.3 The particle finite-element method in the numerical simulation of metal-cutting processes

The standard PFEM presents some weaknesses when applied in orthogonal cutting simulation. For example, the external surface generated using \({\varvec{\alpha }}\)-shape may affect the mass conservation, the chip shape, the absence of equilibrium on the boundary due to the introduction of artificial perturbations, and generation of unphysical welding of the workpiece material and the chip.

To deal with this problem, in this work, the use of a constrained Delaunay algorithm is proposed. Furthermore, addition and removal of particles are the principal tools, which are employed for sidestepping the difficulties, associated with deformation-induced element distortion, and for resolving the different scales of the solution.

In the numerical simulation of metal-cutting process, despite the continuous Delaunay triangulation, elements arise with unacceptable aspect ratios; for this reason, the mesh is also subjected to a Laplacian smoothing algorithm to smooth a mesh. For each node in a mesh, a new position is chosen based on the position of neighbors, and the node is moved there. In the case that a mesh is topologically a rectangular grid, then this operation produces the Laplacian of the mesh. These procedures are applied locally and not in every time step. Specific size metrics control node insertion and removal, while the Laplacian smoothing algorithm drives the repositioning of nodes.

In summary, the enhancement of the PFEM takes place in three main areas: the dynamic process for the discretization of the domain into particles, varying the number of them depending on the deformation of the body; transference of the internal variables, from a nodal smoothing through a variable projection; and the boundary recognition, eliminating the geometric criterion of the \(\alpha \)-shape method.

2.3.1 Data transfer of internal variables

The transference of internal variables or element information between evolving meshes within the field of PFEM is critical in the numerical simulation of process like machining as is shown in [14, 15]. In this work, the authors show that the nodal scheme presented in [10] generates unphysical spring back of the machined surface and sub-estimation of the cutting and feed forces.

Due to the insertion, removal, and relocation of particles through Laplacian smoothing, the transference of gauss point variables is set directly through a mesh projection instead of traditional nodal smoothing [13]. The projection is carried out by a direct search of the position of the integration point of the new connectivity, over the former mesh. The use of this transference scheme give an improved computational efficiency. The use of the projector operator to transfer internal variables guarantees the preservation of the stress free state for the portions of the domains that do not yield. In this zone, there is no insertion, removal or relocation of particles, most of the finite elements of the stress free region remain the same before and after the Delaunay triangulation, getting as a result no diffusion of the internal variables in the stress free zone. More details about the data transfer of internal variables in the numerical simulations are found in [13–15].

3 Governing equations for a Lagrangian Continuum

Consider a domain containing a deformable material which evolves in time due to the external and internal forces and prescribed displacements and thermal conditions from an initial configuration at time \(t=0\) to a current configuration at time \(t=t_{n}\). The volume V and its boundaries \(\Gamma \) at the initial and current configurations are denoted as \(({ }^0V,{ }^0\Gamma )\) and \(({ }^nV,{ }^n\Gamma )\), respectively. The aim is to find a spatial domain that the material occupies, and at same time obtain velocities, strain rates, stresses and temperature in the updated configuration at time \({ }^{n+1}t={ }^nt+\Delta t\). In the following, a left super index denotes the configuration where the variable is computed.

3.1 Momentum equations

The equation of conservation of linear momentum for a deformable continuum are written in a Lagrangian description as

$$\begin{aligned} \rho \frac{Dv_i }{Dt}-\frac{\partial ^{n+1}\sigma _{ij} }{\partial ^{n+1}x_j }-{ }^{n+1}b_i =0,\quad i,j=1,\ldots ,n_\mathrm{s} \,{in }^{n+1}V\nonumber \\ \end{aligned}$$
(1)

In Eq. (1), \({}^{n+1}V\) is the analysis domain in the updated configuration at time \({}^{n+1}t\) with boundary \({}^{n+1}\Gamma \), \(v_i\) and \(b_i \) are the velocity and the body force components along the Cartesian axis, \(\rho \) is the density, \(n_\mathrm{s} \) is the number of space dimensions, \(^{n+1}x_j \) is the position of the material point at time \({ }^{n+1}t\) and \(^{n+1}\sigma _{ij} \) are the Cauchy stresses in \({ }^{n+1}V\) and \(\frac{Dv_i }{Dt}\) is the material derivative of the velocity field.

The Cauchy stresses are split in the deviatoric \(s_{ij} \) and pressure p components as

$$\begin{aligned} \sigma _{ij} =s_{ij} +p\delta _{ij} \end{aligned}$$
(2)

where \(\delta _{ij} \) is the Kronecker delta. The pressure is assumed to be positive for a tension state.

3.2 Thermal balance

The thermal balance equation in the current configuration is written in a Lagrangian framework as

$$\begin{aligned}&\rho c\frac{DT}{Dt}-\frac{\partial }{\partial { }^{n+1}x_i }\left( k\frac{\partial T}{\partial { }^{n+1}x_i }\right) \quad +{ }^{n+1}Q=0,\nonumber \\&\quad i,j=1,\ldots ,n_\mathrm{s} \,in\, {}^{n+1}V \end{aligned}$$
(3)

where T is the temperature, c is the thermal capacity, k is the thermal conductivity and Q is the heat source.

3.3 Mass balance

The mass conservation equation can be written for solids domain as

$$\begin{aligned} -\frac{1}{\kappa }\frac{Dp}{Dt}+\varepsilon _V =0 \end{aligned}$$
(4)

where \(\kappa \) is bulk elastic moduli of the solid material, \(\frac{Dp}{Dt}\) is the material derivative of the pressure field, and \(\varepsilon _V \) is the volumetric strain rate defined as the trace of the rate of deformation tensor defined as

$$\begin{aligned} d_{ij} =\frac{1}{2}\left( {\frac{\partial v_i }{\partial x_j }+\frac{\partial v_j }{\partial x_i }} \right) \end{aligned}$$
(5)

For a general time interval \(\left[ {{ }^nt,{ }^{n+1}t} \right] \), Eq. (4) is discretized as

$$\begin{aligned} -\frac{1}{\kappa }({ }^{n+1}p-{ }^np)+\varepsilon _V \Delta t=0 \end{aligned}$$
(6)

Equations (1), (3) and (4) are completed by the standard boundary conditions.

3.4 Boundary conditions

3.4.1 Mechanical problem

The boundary conditions at the Dirichlet \(\Gamma _v \) and Neumann \(\Gamma _t \) boundaries with \(\Gamma =\Gamma _v \cup \Gamma _t \) are

$$\begin{aligned}&v_i -v_i^P =0 \quad \hbox { on }\Gamma _v \end{aligned}$$
(7)
$$\begin{aligned}&\sigma _{ij} n_j -t_i^P =0 \quad \hbox { on }\Gamma _t ,i=1,\ldots n_\mathrm{s} \end{aligned}$$
(8)

where \(v_i^P \) and \(t_i^P \) are the prescribed velocities and the prescribed tractions, respectively.

3.4.2 Thermal problem

$$\begin{aligned}&{ }^{n+1}T-{ }^{n+1}T{ }^P=0 \quad \hbox { on }{ }^{n+1}\Gamma _T \end{aligned}$$
(9)
$$\begin{aligned}&k\frac{\partial T}{\partial n}+{ }^{n+1}q_n^p = 0 \quad \; \hbox { on }{ }^{n+1}\Gamma _q \end{aligned}$$
(10)

where \(T^{p}\) and \(q_n^p \) are the prescribed temperature and the prescribed normal heat flux at the boundaries \(\Gamma _T \) and \(\Gamma _q \), respectively, and n is a vector in the direction normal to the boundary.

4 Variational formulation

4.1 Momentum equations

Multiplying Eq. (1) by arbitrary test function \(w_i \) with dimensions of velocity and integrating over the updated domain \({ }^{n+1}V\) gives the weighted residual form of the momentum equations as [21, 22]

$$\begin{aligned} \int \limits _{{}^{n+1}V} {\left( {-\frac{\partial ^{n+1}\sigma _{ij} }{\partial ^{n+1}x_j }-{ }^{n+1}b_i } \right) } w_i =0 \end{aligned}$$
(11)

In Eq. (11), the inertial term \(\rho \frac{Dv_i }{Dt}\) is neglected because in the problems of interest in this work, this term is much smaller than the other terms appearing in Eq. (11).

Integrating by parts the terms involving \(\sigma _{ij} \) and using the tractions boundary conditions (8) yields the weak form of the momentum equation as

$$\begin{aligned}&\int \limits _{{ }^{n+1}V} {\delta \varepsilon _{ij} ^{n+1}\sigma _{ij} } \mathrm{d}V-\int \limits _{{ }^{n+1}V} {w_i { }^{n+1}b_i } \mathrm{d}V \nonumber \\&\quad -\int \limits _{{ }^{n+1}\Gamma _t } {{ }^{n+1}w_i { }^{n+1}t_i^p } \mathrm{d}V=0 \end{aligned}$$
(12)

where \(\delta \varepsilon _{ij} =\frac{1}{2}\left( {\frac{\partial w_i }{\partial { }^{n+1}x_j }+\frac{\partial w_j }{\partial { }^{n+1}x_i }} \right) \) is a virtual strain rate field. Equation (12) is the standard form of the principle of virtual power [21, 22].

Using (2), Eq. (12) gives the following expression

$$\begin{aligned}&\int \limits _{{ }^{n+1}V} {\delta \varepsilon _{ij} ^{n+1}s_{ij} } \mathrm{d}V+\int \limits _{^{n+1}V} {\delta \varepsilon _{ij} ^{n+1}p\delta _{ij} } \mathrm{d}V-\int \limits _{^{n+1}V} {w_i { }^{n+1}b_i } \mathrm{d}V \nonumber \\&\quad -\int \limits _{^{n+1}\Gamma _t } {w_i { }^{n+1}t_i^p } \mathrm{d}V=0 \end{aligned}$$
(13)

Introducing, \(\mathbf{w}\), \(\mathbf{s}\) and \(\delta \mathbf{e}\), the vectors of test function, deviatoric stresses and virtual strain rates respectively; \(\mathbf{b}\) and \(\mathbf{t}^{p}\) the body forces and tractions vectors, respectively, and \(\mathbf{m}\) an auxiliary vector in Eq. (13), yields

$$\begin{aligned}&\int \limits _{{n+1}_V} {\delta \varvec{{\upvarepsilon }}^{Tn+1}\mathbf{s}} \mathrm{d}V+\int \limits _{{n+1}_V} {\delta \varvec{{\upvarepsilon }}^{T}\mathbf{m}^{n+1}p} \mathrm{d}V \nonumber \\&\quad -\int \limits _{{n+1}V} {\mathbf{w}^{T}{ }^{n+1}{} \mathbf{b}} \mathrm{d}V-\int \limits _{{n+1}\Gamma _t} {{ }^T\mathbf{w}{ }^{n+1}{} \mathbf{t}^{p}} \mathrm{d}V=0 \end{aligned}$$
(14)

where the matrices introduced in Eq. (14) are defined in reference [23, 24].

4.2 Mass conservation equation

To obtain the mass conservation, Eq. (6) is multiplied by an arbitrary test function q, defined over the analysis domain. Integrating over \({ }^{n+1}V\) yields

$$\begin{aligned} \int \limits _{{ }^{n+1}V} {-\frac{q}{\kappa }({ }^{n+1}p-{ }^np)} \mathrm{d}V+\int \limits _{{ }^{n+1}V} {q\varepsilon _V \Delta t} \mathrm{d}V=0 \end{aligned}$$
(15)

4.2.1 Stabilized mass conservation equation: the polynomial pressure projection (PPP)

Mixed formulations have to satisfy additional mathematical conditions, which guarantee its stability. This condition is known as BB-condition, named after its inventors Babuska and Brezzi. In this approach, a stabilized formulation based on the so-called polynomial pressure projection (PPP) is presented and applied to Stokes equation in [25, 26] is used. The method is obtained by modification of the mixed variational equations using a local \(L_2 \) polynomial pressure projection. Unlike other stabilization methods, the PPP does not require the specification of a mesh-dependent stabilization parameter or the calculation of higher-order derivatives. In addition, PPP can be implemented at the elementary level and reduces to a simple modification of the mass conservation equation as follows:

(16)

where \(\alpha \) is a stabilization parameter, \(\mu \) the material shear modulus and is the best approximation of the pressure in the space of polynomial of order 0.

The best approximation of the pressure field in the space of polynomial of order 0 is given by

(17)

4.3 Thermal balance equation

Application of the standard weighted residual methods to the thermal balance Eqs. (3), (9) and (10) leads, after standard operations, to [22]

$$\begin{aligned}&\int \limits _{{ }^{n+1}V} {\hat{{w}}\rho c\frac{DT}{Dt}} \mathrm{d}V+\int \limits _{{ }^{n+1}V} {\frac{\partial \hat{{w}}}{\partial { }^{n+1}x_i }\left( k\frac{\partial T}{\partial { }^{n+1}x_i }\right) \mathrm{d}V} \nonumber \\&\quad +\int \limits _{{ }^{n+1}V} {\hat{{w}}{ }^{n+1}Q\mathrm{d}V+} \int \limits _{{ }^{n+1}V} {\hat{{w}}{ }^{n+1}q_n^p d\Gamma } =0 \end{aligned}$$
(18)

where \(\hat{{w}}\) are the space-weighting functions for the temperature.

5 Finite-element discretization

The analysis domain is discretized into finite elements with n nodes in the standard manner leading to a mesh with a total number of \(N_\mathrm{e} \) elements and N nodes. In the present work, a simple three-noded linear triangle (\(n = 3\)) with local linear shape functions \(N_i^\mathrm{e} \) defined for each node n of the elemente is used. The displacement, the velocity, the pressure, and the temperature are interpolated over the mesh in terms of their nodal values in the same manner using the global linear shape function \(N_j \) spanning over the nodes sharing node j. In matrix format and 2D problems, we have

$$\begin{aligned} \mathbf{u}=\mathbf{N}_u \bar{\mathbf{u}}, \,\, \mathbf{v}=\mathbf{N}_v \bar{\mathbf{v}},\,\, \hbox { p}=\mathbf{N}_p \bar{\mathbf{p}}, \,\, \hbox { T}=\mathbf{N}_T \bar{\mathbf{T}} \end{aligned}$$
(19)

where

$$\begin{aligned}&\bar{\mathbf{u}}=\left\{ {{\begin{array}{l} {\bar{\mathbf{u}}^{1}} \\ {\bar{\mathbf{u}}^{2}} \\ \vdots \\ {\bar{\mathbf{u}}^{N}} \\ \end{array} }} \right\} \hbox { with }\bar{\mathbf{u}}^{i}=\left\{ {{\begin{array}{l} {u_1^i } \\ {u_2^i } \\ \end{array} }} \right\} ,\, \bar{\mathbf{v}}=\left\{ {{\begin{array}{l} \bar{\mathbf{v}}^{1} \\ \bar{\mathbf{v}}^{2} \\ \vdots \\ \bar{\mathbf{v}}^{N} \\ \end{array} }} \right\} \hbox { with } \nonumber \\&\bar{\mathbf{v}}^{i}=\left\{ {{\begin{array}{l} {v_1^i } \\ {v_2^i } \\ \end{array}}} \right\} ,\, \bar{\mathbf{p}}=\left\{ {{\begin{array}{l} {\bar{{p}}^{1}} \\ {\bar{{p}}^{2}} \\ \vdots \\ {\bar{{p}}^{N}} \\ \end{array}}} \right\} ,\, \bar{\mathbf{T}}=\left\{ {{\begin{array}{l} \bar{{T}}^{1} \\ \bar{{T}}^{2} \\ \vdots \\ \bar{{T}}^{N} \\ \end{array}}} \right\} \nonumber \\&\quad \mathbf{N}_u =\mathbf{N}_v =\left[ \begin{array}{llll} \mathbf{N}_1 &{} \mathbf{N}_2&{} \cdots &{} \mathbf{N}_N \\ \end{array} \right] \nonumber \\&\quad \mathbf{N}_p =\mathbf{N}_T =\left[ \begin{array}{llll} N_{1} &{} N_{2} &{} \cdots &{} N_{N} \\ \end{array} \right] \end{aligned}$$
(20)

with \(\mathbf{N}_j =N_j \mathbf{I}_2 \) where \(\mathbf{I}_2 \) is the \(2\times 2\) identity matrix.

Substituting Eq. (19) into Eqs. (13),(16) and (18) while choosing a Galerkin formulation with leads to the following system of algebraic equations

$$\begin{aligned}&\mathbf{F}_\mathrm{res,mech} = \mathbf{F}_{\mathbf{u},\mathrm{int}} (\bar{\mathbf{u}},\bar{\mathbf{p}}) -\mathbf{F}_{\mathbf{u},\mathrm{ext}} =0 \nonumber \\&\mathbf{F}_\mathrm{res,mass} =\mathbf{F}_{p,\mathrm{press}} (\bar{\mathbf{p}})-\mathbf{F}_{p,\mathrm{vol}} (\bar{\mathbf{u}}) \nonumber \\&\quad +\,\mathbf{F}_{p,\mathrm{stab}} (\bar{\mathbf{p}})-\mathbf{F}_{p,press,n} ({ }^n\bar{\mathbf{p}})=0 \nonumber \\&\mathbf{F}_\mathrm{res,therm} =\mathbf{F}_{\theta ,\mathrm{dyn}} ({\dot{\bar{\mathbf{T}}}})-\mathbf{F}_{\theta ,\mathrm{int}} (\bar{\mathbf{T}}) \nonumber \\&\quad +\,\mathbf{F}_{\theta ,\mathrm{ext}} (\bar{\mathbf{T}})=0 \end{aligned}$$
(21)

where

$$\begin{aligned}&\mathbf{F}_{\mathbf{u},\mathrm{int}} (\bar{\mathbf{u}},\bar{\mathbf{p}})=\int \limits _{{ }^{n+1}V} {\mathbf{B}_u^T { }^{n+1}\sigma } \mathrm{d}V \end{aligned}$$
(22)
$$\begin{aligned}&\mathbf{F}_{\mathbf{u},\mathrm{ext}} =\int \limits _{{ }^{n+1}V} {\mathbf{N}^{T}{ }^{n+1}{} \mathbf{b}} \mathrm{d}V-\int \limits _{{ }^{n+1}\Gamma _t } {\mathbf{N}^{T}{ }^{n+1}{} \mathbf{t}^{p}} d\Gamma \end{aligned}$$
(23)
$$\begin{aligned}&\mathbf{F}_{p,\mathrm{press}} (\bar{\mathbf{p}})=\int \limits _{{ }^{n+1}V} {\frac{1}{\kappa }{} \mathbf{N}^{T}{} \mathbf{N}\bar{\mathbf{p}}\mathrm{d}V} \end{aligned}$$
(24)

The term \(\mathbf{F}_{p,press,n} ({ }^n\bar{\mathbf{p}})\) is exactly the same term as in Eq. (24), but the nodal pressure is evaluated at time \({ }^nt\)

$$\begin{aligned} \mathbf{F}_{p,\mathrm{vol}} (\bar{\mathbf{u}})=\mathbf{Q}^{Tn+1}\bar{\mathbf{u}} \end{aligned}$$
(25)

where the element form of the \(\mathbf{Q}\) matrix is given by

$$\begin{aligned}&\mathbf{Q}^{(e)}=\int \limits _{{ }^{n+1}V^{(e)}} {\mathbf{B}_{ui}^{(e)T} \mathbf{m}N_j^{(e)} \mathrm{d}V} \end{aligned}$$
(26)
$$\begin{aligned}&\quad \mathbf{F}_{p,\mathrm{stab}} (\bar{\mathbf{p}})= \mathop {\mathbf{A}}\limits _{e=1}^{N_e} \int \limits _{{ }^{n+1}V^{(e)}} {\frac{\alpha }{\mu }} \left( \mathbf{N}^{(e)}{} \mathbf{N}^{T(e)} -{\tilde{\mathbf{N}}}^{(e)}{\tilde{\mathbf{N}}}^{T(e)}\right) \mathbf{p}^{(e)}\mathrm{d}V \nonumber \\\end{aligned}$$
(27)
$$\begin{aligned}&\quad \mathbf{F}_{T,\mathrm{dyn}} ({\dot{\bar{\mathbf{T}}}})=\int \limits _{{ }^{n+1}V} {\rho c\mathbf{NN}^{T}{\dot{\bar{\mathbf{T}}}}\mathrm{d}V} \end{aligned}$$
(28)
$$\begin{aligned}&\quad \mathbf{F}_{\theta ,\mathrm{int}} (\bar{\mathbf{T}})=\int \limits _{{ }^{n+1}V} {k\mathbf{B}_\theta ^T \mathbf{B}_\theta } \bar{\mathbf{T}}\mathrm{d}V-\int \limits _{{ }^{n+1}V} {\mathbf{N}^{T}} Q\mathrm{d}V \end{aligned}$$
(29)
$$\begin{aligned}&\quad \mathbf{F}_{\theta ,\mathrm{ext}} (\bar{\mathbf{T}})=\int \limits _{{ }^{n+1}\Gamma _q } {\mathbf{N}^{T}q_n^p } d\Gamma \end{aligned}$$
(30)

In Eq. (21), \({\dot{\bar{\mathbf{T}}}}\) denotes the material time derivative of the nodal temperature.

In finite-element computations, the above force vectors are obtained as the assemblies of element vectors. Given a nodal point, each component of the global force associated with a particular global node is obtained as the sum of the corresponding contributions from the element force vectors of all elements that share the node. In this work, the element force vectors are evaluated using Gaussian quadrature.

Note that Eq. (21) involves the geometry at the updated configuration \(({ }^{n+1}V)\). This geometry is unknown; hence the solution of Eq. (21) has to be found iteratively. The iterative solution scheme proposed in this work is presented in the next section.

6 The constitutive model

6.1 Thermoelastoplasticity model at finite strains

In metal-forming processes like machining, elastic strain are in the order of \(10^{-4}\), whereas plastic strains can be of the order of \(10^{-1}\) to 10 [27]. In case elastic strains are neglected, the model is not able to predict residual stresses and the springback of the machined surface. For this reason, the constitutive model is developed for small elastic and large plastic deformation, instead of a more complex model that use large elastic large plastic deformation (See. [13–15]). An example of modeling of machining processes using a fluid mechanics approach is presented in [28]. A valuable implication of the small elastic strains is that the rate of deformation tensor \(d_{ij} =\frac{1}{2}\left( {\frac{\partial v_i }{\partial x_j }+\frac{\partial v_j }{\partial x_i }} \right) \) inherits the additive structure of classical small strain elastoplasticity:

$$\begin{aligned} \mathbf{d}=\mathbf{d}^{e}+\mathbf{d}^{p} \end{aligned}$$
(31)

where \(\mathbf{d}^{e}\) and \(\mathbf{d}^{p}\) are the elastic and plastic parts of the rate of deformation tensor, respectively.

6.1.1 Elastic response

Let a material with a hypo-elastic constitutive equation like

$$\begin{aligned} L_v (\tau )=\mathbf{c}:(\mathbf{d}-\mathbf{d}^{p}) \end{aligned}$$
(32)

where \(L_v (\cdot )\) denotes the Lie objective stress rate, and \(\tau \) denotes the Kirchhoff stress tensor. It can be assume that the special elasticity \(\mathbf{c}\) tensor is given by

$$\begin{aligned} \mathbf{c}=2\mu \left( \mathbf{I}-\frac{1}{3}{} \mathbf{1}\otimes \mathbf{1}\right) +\kappa \mathbf{1}\otimes \mathbf{1} \end{aligned}$$
(33)

where \(\mathbf{I}\) and \(\mathbf{1}\), with components \(I_{abcd} =(\delta _{ac} \delta _{bd} +\delta _{ad} \delta _{cd} )/2\) and \(1_{ab} =\delta _{ab} \), are the fourth- and second-order symmetric unit tensors, respectively. The parameters \(\mu \) and \(\kappa \) represent the shear and the bulk elastic modulus, respectively.

6.1.2 Yield condition

The yield condition used in this work is the von Misses–Huber yield criterion. This criterion is formulated in terms of the second invariant of the Kirchhoff stress tensor \(J_2 =\frac{1}{2}\hbox {dev}\tau :\hbox {dev}\tau \). Hence, the von Mises yield criterion (henceforth simply called the Mises criterion) can be stated as

$$\begin{aligned} f(\tau )= & {} \sqrt{2J_2 }-\sqrt{\frac{2}{3}}\sigma _y =\left\| {\hbox {dev}\tau } \right\| -\sqrt{\frac{2}{3}}\sigma _y (\bar{{\varepsilon }}^{p},\rho _i ,c_\mathrm{v} )=0\nonumber \\ \end{aligned}$$
(34)

where \(\sigma _y \) denotes the flow stress, \(\bar{{\varepsilon }}^{p}\) is the hardening parameter or plastic strain, \(\rho _i \) denotes the immobile dislocations density, and \(c_\mathrm{v} \) is the vacancy fraction. The set of nonlinear-coupled differential equations describing the evolution of \(\rho _i \) and \(c_\mathrm{v} \) are presented in Sect. 6.2.

6.1.3 Flow rule

As is customary in the framework of incremental plasticity, the concept of flow rule is applied to obtain the plastic rate of deformation tensor \(\mathbf{d}^{p}\) in terms of the plastic flow direction tensor \(\mathbf{n}=\frac{\hbox {dev}\tau }{\left\| {\hbox {dev}\tau } \right\| }\) associated to the yield surface:

$$\begin{aligned} \mathbf{d}^{p}=\dot{\lambda }{} \mathbf{n}=\dot{\lambda }\frac{\hbox {dev}\tau }{\left\| {\hbox {dev}\tau } \right\| } \end{aligned}$$
(35)

and the evolution equation for the accumulated effective plastic strain \(\bar{{\varepsilon }}^{p}\) is governed by

$$\begin{aligned} \dot{\bar{{\varepsilon }}}^{p}=\sqrt{\frac{2}{3}}\dot{\lambda } \end{aligned}$$
(36)

where \(\dot{\lambda }\) is the consistency parameter or plastic multiplier subject to the standard Kuhn–Tucker loading/unloading conditions

$$\begin{aligned} \dot{\lambda }\ge 0, \hbox { f}(\tau )\le 0 \,\, , \,\, \dot{\lambda }\hbox {f}(\tau )=0 \end{aligned}$$
(37)

Along with the consistency condition [29] complete the formulation of the model.

$$\begin{aligned} \dot{\lambda }\dot{\hbox {f}}(\tau )=0. \end{aligned}$$
(38)

6.2 Physical-based models

Physical-based models are models where the physical mechanisms are underlying the deformation in contrast to empirical models, which are of a more curve-fitting nature. However, due to the need for averaging and also limited knowledge about some of the relations making up the model, physical-based models need also be calibrated. Two different types of physical-based models exist. One option is to explicitly include variables from physics as internal state variables. The other possibility is to determine the format of the constitutive equation based on knowledge about the physical mechanisms causing the deformation. The latter is a so-called “model-based-phenomenology” Some advantages of physical-based models is the possibility to link effects from other scales, e.g. via parameters for grain size or models for microstructural evolution that extends the model validity to a larger domain. This may extrapolate the validity of the model outside their range of calibration. This requires that the physical mechanisms implemented in the models still dominate the deformation in the extended range.

The dislocation density model considers dislocation glide and climb processes contributions to the plastic straining. The yield limit in this approach is separated into two components according to [4, 5, 30–32]

$$\begin{aligned} \sigma _y =\sigma _G +\sigma ^{*} \end{aligned}$$
(39)

\(\sigma _G \) and \(\sigma ^{*}\) are the long-range athermal component and the short-range contributions to the flow stress, respectively. The first component \(\sigma _G \), is the stress needed to overcome the long-range interactions lattice distortions due to the dislocation substructure. The second component, \(\sigma ^{*}\), is the stress needed for the dislocation to pass through the lattice and to pass short-range obstacles. Thermal vibrations will then also assist the dislocation when passing an obstacle. The long-range stress component is commonly written as;

$$\begin{aligned} \sigma _G =m\alpha \mu b\sqrt{\rho _i } \end{aligned}$$
(40)

where m is the Taylor orientation factor, \(\alpha \) is a proportionality factor, \(\mu \) is the temperature dependent shear modulus, b is the magnitude of Burgers vector and \(\rho _i \) is the immobile dislocation density. The short-range stress components may be written as,

(41)

where \(\Delta F\) denote the required free energy needed to overcome the lattice resistance or obstacles without assistance from external stress, denote the athermal flow strength required to move the dislocation past barriers without assistance of thermal energy, \(\dot{\bar{{\varepsilon }}}_{ref} \) denote the reference strain rate. The exponent p and q characterize the barrier profiles and usually have values between \(0\le p\le 1\) and \(0\le q\le 2\) respectively.

6.2.1 Structure evolution

The evolution of the structure is considered to consist of a hardening and a recovery process. The used model assumes that the mobile dislocation density is stress and strain independent and much smaller than the immobile ones. Hence the evolution equation is written;

$$\begin{aligned} \dot{\rho }_i =\dot{\rho }_i^{(+)} -\dot{\rho }_{i(\hbox {glide})}^{(-)} -\dot{\rho }_{i(\hbox {climb})}^{(-)} \end{aligned}$$
(42)

where index i denotes the immobile dislocations. The increase in immobile dislocation density is assumed to be related to the plastic strain rate and may therefore be written according to

$$\begin{aligned} \dot{\rho }_i^{(+)} =\frac{m}{b}\frac{1}{\Lambda }\dot{\bar{{\varepsilon }}}^{p} \end{aligned}$$
(43)

where m is the Taylor orientation factor, b is the Burgers vector and \(\Lambda \)denote the mean free path. Mobile dislocations in this model are assumed to move an average distance (mean free path), \(\Lambda \), according to the relation

$$\begin{aligned} \frac{1}{\Lambda }=\frac{1}{s}+\frac{1}{g_\mathrm{s} } \end{aligned}$$
(44)

\(g_\mathrm{s} \) and s denote the size of the grains and the subcell, respectively.

The effect of grain size on flow stress, the Petch–Hall effect, is accounted for this way and contributes to the hardening. The size of subcells is related to the immobile DD by the parameter \(K_\mathrm{c} \)

$$\begin{aligned} s=K_\mathrm{c} \frac{1}{\sqrt{\rho _i }} \end{aligned}$$
(45)

The recovery may occur by dislocation glide and/or climb. The former is described by

$$\begin{aligned} \dot{\rho }_{i(\hbox {glide})}^{(-)} =\Omega \rho _i \dot{\bar{{\varepsilon }}}^{p} \end{aligned}$$
(46)

where \(\Omega \) is a recovery function which depends on the temperature and strain rate. Recovery by climb is describe by

$$\begin{aligned} \dot{\rho }_{i(\hbox {climb})}^{(-)} =2c_\gamma \frac{D_\mathrm{v} }{c_\mathrm{v}^\mathrm{eq} }\frac{\mu b^{3}}{kT}(\rho _i^2 -\rho _\mathrm{eq}^2 )c_\mathrm{v} \end{aligned}$$
(47)

where \(c_\mathrm{v} \) is the vacancy fraction, \(c_\mathrm{v}^\mathrm{eq} \) is the thermal equilibrium vacancy concentration, \(D_\mathrm{v} \) is the diffusivity and \(c_\gamma \) is a calibration parameter.

6.2.2 Vacancy generation and migration

Recovery of dislocations and diffusion of solute atoms are associated with the control generation and motion of vacancies. They affect recovery by climb, as described above. Climb is a nonconservative motion, where a dislocation moves out of the glide plane onto another glide plane. Motion of jogged screw dislocations creates vacancies by nonconservative motion of jogs [4], while annihilation of vacancies may take place at grain boundaries and at dislocations. The mono-vacancy evolution equation presented in [4, 5] is used in this study:

$$\begin{aligned} \dot{c}_\mathrm{v}= & {} \left[ {\chi \frac{\Omega _0 }{Q_\mathrm{vf} }\sigma _y +\zeta \frac{c_j }{4b^{2}}\frac{\Omega _0 }{b}} \right] \dot{\bar{{\varepsilon }}}_p -D_\mathrm{vm} \left( {\frac{1}{K_\mathrm{c}^2 }\rho _i +\frac{1}{g^{2}}} \right) \nonumber \\&\times (c_\mathrm{v} -c_\mathrm{v}^\mathrm{eq} )+\dot{c}_\mathrm{v}^\mathrm{eq} \end{aligned}$$
(48)

where \(\sigma _y\) is the flow stress, \(\chi \) is the fraction of mechanical work used for vacancy generation, \(Q_\mathrm{vf} \) is the activation energy for vacancy formation, \(\zeta \) is the net neutralization effect of vacancy emitting and vacancy-absorbing jogs, \(c_j\) is the concentration of thermal jogs, \(\Omega _0\cdot \) is the atomic volume, and \(D_\mathrm{vm} \) refers to vacancy migration.

6.3 Stress update algorithm

6.3.1 Thermoelastoplasticity model at finite strains

An implicit integration of the constitutive model presented in Sect. 6.1 is summarized in Box 1.

6.3.2 Physical-based models

figure a

Given the increment in effective plastic strain and the effective plastic strain rate obtained in the radial-return stress update algorithm (Box 1), the only unknowns of Eq. (42) and (48) are immobile dislocation density and the vacancy concentration. An implicit time discretization of the set of two coupled differential Eqs. (42) and (48) can be obtained as [4, 5]:

$$\begin{aligned}&\Delta \rho _i -\left( {\frac{m}{b}\frac{1}{\Lambda }-\Omega \rho _i } \right) \dot{\bar{{\varepsilon }}}^{p}\Delta t+2c_\gamma \frac{D_\mathrm{v}}{c_\mathrm{v}^\mathrm{eq} }\frac{\mu b^{3}}{kT} \nonumber \\&\quad \times (\rho _i^2 -\rho _\mathrm{eq}^2)c_\mathrm{v} \Delta t=0 \nonumber \\&\Delta c_\mathrm{v} -\left[ {\chi \frac{\Omega _0 }{Q_\mathrm{vf} }\sigma _y +\zeta \frac{c_j }{4b^{2}}\frac{\Omega _0 }{b}} \right] \dot{\bar{{\varepsilon }}}_p \Delta t+D_\mathrm{vm}\nonumber \\&\quad \times \left( {\frac{1}{K_\mathrm{c}^2 }\rho _i +\frac{1}{g^{2}}} \right) (c_\mathrm{v} -c_\mathrm{v}^\mathrm{eq} )\Delta t-\dot{c}_\mathrm{v}^\mathrm{eq} \Delta t=0 \end{aligned}$$
(49)

where \(\Delta \rho _i ={ }^{n+1}\rho _i -{ }^n\rho _i \), \(\Delta c_\mathrm{v} ={ }^{n+1}c_\mathrm{v} -{ }^nc_\mathrm{v} \) and \(\Delta t\) is the time step increment.

This set can be written in a vector form as

$$\begin{aligned} \mathbf{H}=\mathbf{0} \end{aligned}$$
(50)

The linearization of the system gives

$$\begin{aligned} \mathbf{H}_{(i)} +\frac{\partial \mathbf{H}_{(i)} }{\partial \mathbf{q}}\delta \mathbf{q}=0 \end{aligned}$$
(51)

where the subscript i is an iteration counter and \(\mathbf{q}\) is a vector containing the internal state variables

$$\begin{aligned} \mathbf{q}^{T}=(\rho _i ,c_\mathrm{v} ) \end{aligned}$$
(52)

The iterative changes in the internal state variables can now be computed as

$$\begin{aligned} \delta \mathbf{q}_{(i)} =-\left[ {\frac{\partial \mathbf{H}_{(i)} }{\partial \mathbf{q}}} \right] ^{-1}{} \mathbf{H}_{(i)} \end{aligned}$$
(53)

This set is solved by an implicit Newton–Raphson method. When the iterative changes \(\delta \mathbf{q}\) are small enough, the iterations are terminated, and the internal state variables are updated as

$$\begin{aligned}&{ }^{n+1}{} \mathbf{q}={ }^n\mathbf{q}+\Delta \mathbf{q} \end{aligned}$$
(54)
$$\begin{aligned}&\Delta \mathbf{q}=\sum _{i=1}^\mathrm{niter} {\delta \mathbf{q}_{(i)} } \end{aligned}$$
(55)

where niter is the number of iterations necessary to reach the desired tolerance of the Newton–Raphson method. More details about the matrix \(\frac{\partial \mathbf{H}_{(i)} }{\partial \mathbf{q}}\) are given in the Appendix and in [4].

7 Transient solution of the discretized equations

Equation (21) are solved in time with an uncoupled (mechanical–thermal) implicit Newton–Raphson-type iterative scheme. The basic steps within a time increment \(\left[ {n \cdot n+1} \right] \) are

  • Initialize variables

    $$\begin{aligned}&\left( { }^{n+1}{} \mathbf{x}^{1},{ }^{n+1}\bar{\mathbf{u}}^{1},{ }^{n+1}\tau ^{1},{ }^{n+1}\bar{\mathbf{p}}^{1},{ }^{n+1}\bar{\mathbf{T}}^{1},{ }^{n+1}\bar{{\varepsilon }}^{p} ,{ }^{n+1}\rho _i ,{ }^{n+1}c_\mathrm{v}\right) \\&\quad \leftarrow \left( { }^n\mathbf{x},{ }^n\bar{\mathbf{u}},{ }^n\tau ,{ }^n\bar{\mathbf{p}}^{1},{ }^n\bar{\mathbf{T}},{ }^n\bar{{\varepsilon }}_{p} ,{ }^n\rho _i ,{ }^nc_\mathrm{v} \right) \end{aligned}$$

  • In the following, \((\cdot )^{i}\) denotes a value computed at the ith iteration.

  • Iteration loop: \(i=1,\ldots ,N_{iter}\). For each iteration

Mechanical problem

Step 1 Compute the nodal displacement increments and the nodal pressure, from Eq. (21):

$$\begin{aligned} \mathbf{K}\left[ {{\begin{array}{l} {\Delta \mathbf{u}} \\ {\Delta \bar{\mathbf{p}}} \\ \end{array} }} \right] =-\left[ {{\begin{array}{l} {{ }^{n+1}{} \mathbf{F}_\mathrm{res,mech}^i } \\ {{ }^{n+1}{} \mathbf{F}_\mathrm{res,mass}^i } \\ \end{array} }} \right] \end{aligned}$$
(56)

The iteration matrix \(\mathbf{K}\) is given by

$$\begin{aligned} \mathbf{K}=\left[ {{\begin{array}{ll} \mathbf{K}_{uu} &{} \mathbf{K}_{up} \\ \mathbf{K}_{pu} &{} \mathbf{K}_{pp} \\ \end{array} }} \right] \end{aligned}$$
(57)

where \(\mathbf{K}_{uu}\), \(\mathbf{K}_{up} \),\(\mathbf{K}_{pu} \) and \(\mathbf{K}_{pp} \) are given by the following expressions

$$\begin{aligned}&{} \mathbf{K}_{uu,ij} = \int \limits _{{ }^{n+1}V} {\mathbf{B}_i^{eT} \left( \mathbf{C}_T^\mathrm{dev} -2p\mathbf{I}\right) \mathbf{B}_j^\mathrm{e} \mathrm{d}V} +\int \limits _{{ }^{n+1}V} {\mathbf{G}_i^T \sigma \mathbf{G}_j \mathrm{d}V} \nonumber \\&{} \mathbf{K}_{up,ij} = \int \limits _{{ }^{n+1}V} {\mathbf{B}_i^{eT} \mathbf{m}N_j^\mathrm{e} \mathrm{d}V} \nonumber \\&{} \mathbf{K}_{pu} = \mathbf{K}_{up}\nonumber \\&{} \mathbf{K}_{pp} \int \limits _{{ }^{n+1}V} {\frac{1}{\kappa }{} \mathbf{N}^{eT}\mathbf{N}^{e}\mathrm{d}V}+\int \limits _{{ }^{n+1}V} {\frac{\alpha }{\mu }} \left( \mathbf{N}^{e}{} \mathbf{N}^{eT}-{\tilde{\mathbf{N}}}^{e}{\tilde{\mathbf{N}}}^{eT}\right) \mathrm{d}V\nonumber \\ \end{aligned}$$
(58)

where \(\mathbf{C}_T^\mathrm{dev} \) is the deviatoric part of the consistent algorithmic matrix emanating from the linearization of Eq. (21) (a) with respect to the nodal displacements [21].

Step 2 Update the nodal displacements and nodal pressure:

$$\begin{aligned} { }^{n+1}\bar{\mathbf{u}}^{i+1}= & {} { }^{n+1}\bar{\mathbf{u}}^{i}+\Delta \mathbf{u} \nonumber \\ { }^{n+1}\bar{\mathbf{p}}^{i+1}= & {} { }^{n+1}\bar{\mathbf{p}}^{i}+\Delta \bar{\mathbf{p}} \end{aligned}$$
(59)

Step 3 Update the nodal coordinates and the incremental deformation gradient:

$$\begin{aligned} { }^{n+1}{} \mathbf{x}^{i+1}= & {} { }^{n+1}{} \mathbf{x}^{i}+\Delta \mathbf{u} \nonumber \\ { }^{n+1}F_{ij}^{i+1}= & {} \frac{\partial { }^{n+1}x_i^{i+1} }{\partial { }^nx_j } \end{aligned}$$
(60)

Step 4 Compute the deviatoric Cauchy stresses from Box 1.

Step 5 Compute the stresses:

$$\begin{aligned} { }^{n+1}\sigma _{ij} =\hbox {dev(}{ }^{n+1}\tau )+\bar{{p}}\delta _{ij} \end{aligned}$$
(61)

Step 6 Check convergence

Verify the following conditions:

$$\begin{aligned}&\left\| {{ }^{n+1}\bar{\mathbf{u}}^{i+1}-{ }^{n+1}\bar{\mathbf{u}}^{i}} \right\| \le e_u \left\| {{ }^n\bar{\mathbf{u}}} \right\| \nonumber \\&\left\| {{ }^{n+1}\bar{\mathbf{p}}^{i+1}-{ }^{n+1}\bar{\mathbf{p}}^{i}} \right\| \le e_p \left\| {{ }^n\bar{\mathbf{p}}} \right\| \end{aligned}$$
(62)

where \(e_u \) and \(e_p \) are the prescribed error norms. In the examples presented in this paper, the error norms are set to \(e_u =e_p =10^{-3}\) . If conditions (62) are satisfied, the solution of the thermal problem in the updated configuration\({ }^{n+1}{} \mathbf{x}\) is accepted. Otherwise, make the iteration counter \(i\leftarrow i+1\) and repeat Steps 1–6.

Thermal problem

  • Iteration loop: \(i=1,\ldots ,N_{iter} \) . For each iteration:

Step 7 Compute the nodal temperatures

$$\begin{aligned} \left[ {\int \limits _{{ }^{n+1}V} {\frac{\rho c}{\Delta t}{} \mathbf{NN}^{T}\mathrm{d}V} +\int \limits _{{ }^{n+1}V} {k\mathbf{B}_\theta ^T \mathbf{B}_\theta } } \right] \Delta \bar{\mathbf{T}}=-{ }^{n+1}{} \mathbf{F}_\mathrm{res,therm}^i\nonumber \\ \end{aligned}$$
(63)

Step 8 Update the nodal temperatures

$$\begin{aligned} { }^{n+1}\bar{\mathbf{T}}^{i+1}={ }^{n+1}\bar{\mathbf{T}}^{i}+\Delta \bar{\mathbf{T}} \end{aligned}$$
(64)

Step 9 Check convergence

$$\begin{aligned} \left\| {{ }^{n+1}\bar{\mathbf{T}}^{i+1}-{ }^{n+1}\bar{\mathbf{T}}^{i}} \right\| \le e_T \left\| {{ }^n\bar{\mathbf{T}}} \right\| \end{aligned}$$
(65)

where \(e_T \) is the error norm in the balance of energy. In the examples presented in this work, the error norm is set to \(e_T =10^{-5}\). If condition (65) is satisfied, the solution of the physical-based plasticity model Eq. (49) is accepted. Otherwise, make the iteration counter \(i\leftarrow i+1\) and repeat Steps 7–9.

Physical-based models

  • Iteration loop: \(i=1,\ldots ,N_{iter} \) . For each iteration:

Step 10 Compute the gauss point increment of dislocation density \(\rho _i\) and vacancy concentration \(c_\mathrm{v} \) given the value of temperature and strain rate obtained in in the solution of the thermal and mechanical problems, respectively.

$$\begin{aligned} \delta \mathbf{q}_{(i)} =-\left[ {\frac{\partial \mathbf{H}_{(i)} }{\partial \mathbf{q}}} \right] ^{-1}{} \mathbf{H}_{(i)} \end{aligned}$$
(66)

Step 11 Update the gauss point value of the \(\rho _i\) and vacancy concentration \(c_\mathrm{v}\)

$$\begin{aligned} { }^{n+1}{} \mathbf{q}={ }^n\mathbf{q}+\Delta \mathbf{q} \end{aligned}$$
(67)

Step 12 Check convergence of the physical-based constitutive model.

$$\begin{aligned} \left\| {\delta \rho _i(i)} \right\|\le & {} e_p \left\| {{ }^n\rho _i} \right\| \nonumber \\ \left\| {\delta c_\mathrm{v}(i)} \right\|\le & {} e_p \left\| {{ }^nc_\mathrm{v} } \right\| \end{aligned}$$
(68)

where \(e_p \) is the error norm in the physical-based constitutive model. In the examples presented in this work, a value of \(e_p =10^{-8}\) is used. If conditions (68) are satisfied then make \(n\leftarrow n+1\) and proceed to the next time step. Otherwise, make the iteration counter \(i\leftarrow i+1\) and repeat Steps 10–12.

Fig. 1
figure 1

2D plane strain PFEM model of orthogonal cutting: a initial set of particles, b initiation of the chip

Full size image

8 Examples, result and discussion

The ability of PFEM to adaptively insert and remove particles and improve mesh quality is crucial in the problems presented from here on. Then, it is possible to maintain a reasonable shape of elements and also capture gradients of strain, strain rate, and temperature. The PFEM strategy does not require a criterion for modelling of the chip separation from the workpiece.

The friction condition is an important factor that influences chip formation. Friction on the tool–chip interface is a nonconstant function dependent of normal and shear stress distributions. Normal stresses are largest in the sticking contact region near the tool tip. The stress in the sliding zone along the contact interface from the tool tip to the point where the chip separates from the tool rake face is controlled by frictional shear stress. A variety of complex friction models exists; however, the lack of input data to these models is a limiting factor. The model for tool–chip interface employed in this study is the Coulomb friction model. The friction coefficient \(\mu = 0.5\) was selected following the value used in [30, 33, 34].

The heat generated in metal cutting has a significant effect on the chip formation. The heat generation mechanisms are the plastic work done in the primary and secondary shear zones and the sliding friction in the tool–chip contact interface. Generated heat does not have sufficient time to diffuse away and temperature rise in the work material is mainly due to localized adiabatic conditions. A standard practice in the numerical simulations of mechanical cutting is to assume the fraction of plastic work transformed into heat equal to 0.9, see [30, 32, 34].

An orthogonal cutting operation was employed to mimic 2D plain strain conditions. The depth of cut, used for all the test cases, was equal to 3 mm. The dimension of the workpiece was 8 \(\times \) 1.6 mm. A horizontal velocity corresponding to the cutting speed was applied to the particles at the right side of the tool as is given in Table 1. The particles along the bottom and the left sides of the workpiece were fixed. Material properties for the workpiece material are shown in Appendix 2. Material properties of the tool were assumed as thermoelastic.

Table 1 Cutting data in simulations
Full size table
Fig. 2
figure 2

Intermediate stages of the chip formation: a time \(3.14\times 10-4 \hbox { s}\), b time \(6.28\times 10-4 \hbox { s}\)

Full size image
Table 2 Measured and simulated cutting forces
Full size table

The workpiece was discretized with 105 particles, see Fig. 1a. The tool geometry was discretized by 2298 tree-node thermomechanical elements. Due to adaptive insertion and removal of particles, the average number of particles increased up to 4800. The effect of insertion of particles near the tool tip is illustrated in Figs. 1b and 2a, b for the test case no. 2. The insertion of particles was controlled by the equidistribution of plastic power.

Fig. 3
figure 3

Effective plastic strain rate

Full size image
Fig. 4
figure 4

Temperature distribution

Full size image

8.1 Cutting and feed forces

The loading histories of simulated forces for test no 2, see Fig. 6b, were evaluated at the chip tool interface. Average values of the computed forces in the steady state region are compared with the experimental results in Table 2. The error used for the evaluation of the computed results is computed as

$$\begin{aligned} \mathrm{Error} = \frac{\mathrm{Computed}-\mathrm{Measured}}{\mathrm{Measured}} \times 100~\% \end{aligned}$$
(69)
figure b

The Table 2 shows that the cutting force was overestimated in all tests by about 15 %. Meanwhile, the feed force was underestimated by about 5 %. The results presented in the table above were compared with the results in Svoboda et al [30], showing that PFEM is able to predict results to those obtained using (FEM). The errors in Table 2 must be related to the context where they will be used, namely the cutting tool manufacturing industry. Literature overview [4] show that in the industrial production of nominally identical cutting tool as well as variations in material properties of nominally the same material can cause variations around the 10 % in forces. Estimated errors below 10 % indicate a good model fit for the purpose.

Fig. 5
figure 5

Dislocation density distribution

Full size image
Fig. 6
figure 6

Excess of vacancy concentration distribution

Full size image
Fig. 7
figure 7

A comparison of the predicted chip shape. a PFEM, b FEM

Full size image

8.2 Material response

All figures presented in this section correspond to the steady state conditions. The results shown are for the cutting velocity of \(180\,\hbox {m\, min}^{-1}\) and feed of 0.15 mm. Figure 3 illustrates distribution of plastic strain rates in the primary and the secondary shear zones. Figure 3 presents a maximum plastic strain rate value of 80,000 \(\hbox {s}^{-1}\) .

Temperature fields are presented in Fig. 4. Maximum temperature was generated in the contact between the chip and rake face of the tool.

The dislocation density (DD) and vacancy concentration are shown in Figs. 5 and 6, respectively. In the area close to the outer surface of the formed chip with lower-temperature level, the increased dislocation density controls the hardening, Fig. 5. Initial value of DD \(10^{6}\hbox { mm}^{-2}\) was increased up to \(10^{9} \hbox { mm}^{-3}\). In the domains of the highest temperature concentrated close to the tool rake face, Fig. 6, the significant generation of vacancies coupled with the dislocation recovery is present, see Fig. 5.

8.3 A comparison between FEM and PFEM

In order to validate PFEM as an effective strategy to deal with machining problems, we present a small comparison with MSC.Marc based on the FEM. The comparison is performed with test no. 2 presented in Sect. 8 of this work. It is important to mention that there are some differences and similarities between the formulations used in MSC.Marc and our in-house PFEM code. They use distinct formulation, finite elements, convergence criteria, and contact laws. Main differences between the numerical models are listed below:

Table 3 SANMAC 316L—material parameters
Full size table
Table 4 Known or assumed parameters
Full size table

  • MSC.Marc uses a quadrilateral finite element with reduced integration, whereas PFEM uses a linear displacement linear pressure-stabilized finite element.

  • MSC.Marc uses Coulomb friction law, while PFEM uses a regularized Coulomb friction law.

  • MSC.Marc uses a convergence criterion of relative displacement and forces of 0.01, whereas PFEM uses a convergence criterion of relative displacement of 0.001.

  • MSC.Marc is a FEM-based code implemented in noninterpreting languages, while PFEM is implemented in a vectorized Matlab-based code.

  • MSC.Marc uses adaptive mesh refinement schemes, whereas PFEM uses insertion, removal, and relocation of particles for avoiding the difficulties, associated with deformation-induced element distortion, and for resolving the different scales of the solution.

Figure 7 compares the predicted chip shapes using PFEM and PFEM showing a reasonable agreement. In our previous work [30], the FEM predicted chip shape was compared with experimental results showing similar shapes in the experimental and the numerical approach.

For the reasons mentioned above, the numerical model setup with PFEM is considered to be accurate enough to compete with current commercial softwares based in the FEM method (Abaqus, AdvantEdge, Deform, MSC.Marc) [13, 15]. Concerning with the computational cost, a MATLAB code with the PFEM implementation was used for this comparison. The calculation time in a serial execution was similar to the commercial ones. We guess that, with an implementation in a more optimized programming language, the PFEM would be clearly faster.

9 Conclusions

A Lagrangian formulation for analysis of metal-cutting processes involving thermally coupled interactions between deformable continua is presented. The governing equations for the generalized continuum are discretized using elements with equal linear interpolation for the displacement and the temperature. The merits of the formulation in terms of its general applicability have been demonstrated in the solutions of four representative numerical simulations of orthogonal cutting using the PFEM.

In this work, a dislocation density model has been used together with PFEM to virtually reproduce orthogonal cutting of AISI 316L steel. Numerical results obtained using PFEM have been compared with both experimental results and numerical results. Also, results of the numerical model developed within this work are in agreement with experimental results and can predict forces close to the required precision.

A comparison with FEM results show that the PFEM model gives similar results and is accurate enough to compete with the commercial software in the market.