1 Introduction

High-voltage direct-current transmission based on voltage source converter (VSC-HVDC) systems are a new type of DC transmission technology with fully controllable power electronic devices, which is one key technology in the research and development of the smart grid [1]. The characteristics of the converter structure and the control strategy of the VSC-HVDC system result in high peak value and fast rising speed of the DC side fault current. A large fault current can easily damage converter components and protective devices [2, 3], yet is difficult to eliminate immediately. Therefore, current-limiting technology is introduced to suppress the DC side fault current, and slow down the capacitor voltage drops. Meanwhile, this technology can effectively protect equipment [4], relax the requirements on the DC breaker in terms of the speed and capacity, and reduce the difficulty of designing the protection scheme.

As current-limiting technology is critical to the VSC-HVDC system, much related research has been performed and results achieved. Reference [5] analyzed the influence of the location of resistance-type superconductive fault current limiters (SFCLs) on the DC side fault. They pointed out that installing the resistance-type SFCL on the DC side could successfully limit the DC fault current in the case of a DC line fault. Reference [6] studied the current-limiting effect of the resistance-type SFCL in the single-pole ground fault and inter-pole fault at the DC side, and the simulation results revealed that the resistance-type SFCL has a significant effect on the DC side fault. Reference [7] examined application cases of the resistance-type SFCL in a three-terminal VSC-HVDC system, and proved the limiting effect of this STCL on various types of DC side fault current. Reference [8] analyzed the performance of the resistance-type SFCL in a multi-terminal VSC-HVDC system connected with an offshore wind farm, and their transient analysis for different perturbations proved that the resistance-type SFCL can reduce the fault current for both DC and AC faults. Reference [9] analyzed the coordination of fault current limitation in an electric power grid with multiple SFCLs to further limit fault current rise. Reference [10] proposed a new resistance-type SFCL that can reduce the fault current to 50% of the original value within 2 ms. To limit the fault current, the resistance of the fault circuit is increased by installing a resistance-type SFCL in the VSC-HVDC system.

Some literatures have also proposed limiting the fault current by increasing the circuit inductance [11]. Reference [12] designed an inductive SFCL and the simulation results revealed that this SFCL has a significant effect on the DC side fault. Reference [13] analyzed the impact of different inductance values in the VSC-HVDC system on the DC side fault current. Reference [14] offered an optimal design scheme of installing the current-limiting inductor in a multi-terminal VSC-HVDC system, and proved that this scheme can effectively deaccelerate the rise in fault current. Reference [15] designed a protective inductor for the VSC-HVDC system of an offshore wind farm to limit the current. The coordination relationships among converter, DC circuit breaker and DC SFCL were studied and some technical indicators were proposed to evaluate the performance of the SFCL in [16].

Though inductors at the DC side can serve as current limiters, large reactance will reduce the dynamic response speed and can easily cause parallel resonance. In normal operation, the equivalent inductance of saturated iron-core fault current limiters (SI-FCL) is so small that it has no effect on the VSC-HVDC system. When a DC side fault occurs, the equivalent inductance increases rapidly to limit the fault current. Thus, this approach is superior to installing inductors.

Some researches have also investigated the current-limiting effect of the SI-FCL in the VSC-HVDC system. Reference [11] proved the current-limiting effect of the SI-FCL in the VSC-HVDC system. Reference [17] analyzed the transient process of the DC side fault in the VSC-HVDC system with the SI-FCL, and gave the relationship between the peak value of the fault current and the SI-FCL parameters. Reference [18] analyzed the leakage magnetic flux of the SI-SFCL and proposed the equivalent magnetic circuit model considering the effect of leakage magnetic flux. Reference [19] introduced the application of the active SI-SFCL in the VSC-HVDC system.

The analysis method in these papers solves the DC side circuit differential equation with the equivalent inductance of the SI-FCL in the DC side fault condition. However, owing to the nonlinearity of the equivalent inductance, the calculation involved is enormous and error prone. Other researches mainly focused on the application of the SI-FCL to the AC system, which is not applicable to the VSC-HVDC system [20,21,22].

To analyze the current-limiting effect of the SI-FCL in the VSC-HVDC system, this paper analyzes the energy exchange between the SI-FCL and the DC capacitor after the DC side fault occurs. The relationship between the DC side fault current and the parameters of the SI-FCL is studied, and a rapid and effective analytical method of the current-limiting performance of the SI-FCL is proposed in this paper.

2 Analysis of energy variation process of SI-FCL with changing magnetic flux density

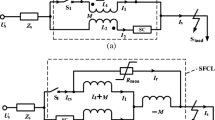
The basic structure of the SI-FCL is shown in Fig. 1, which includes one iron-core, one coil connected with the DC side of the VSC-HVDC system, and one excitation coil with a DC-biased source circuit. To reduce the run-time loss, the excitation coil can be made of superconductive materials.

Fig. 1
figure 1

Structure of SI-FCL for VSC-HVDC system

Full size image

In Fig. 1, coil 1 is the excitation coil and coil 2 is the coil connected with the DC side of the VSC-HVDC system; N1 is the turn number of coil 1 and N2 is the turn number of coil 2; i1 is the current of coil 1 generally excited by a constant current source; thus, i1 is considered as constant; i2 is the current of the DC side of the VSC-HVDC system.

The topology of the VSC-HVDC system with SI-FCLs is shown in Fig. 2. To limit the DC side fault current, SI-FCLs are installed in the converter station export. The locations are also shown in Fig. 2.

Fig. 2
figure 2

Topology of VSC-HVDC system with SI-FCLs

Full size image

As shown in Fig. 3, the magnetic flux density–magnetic field intensity B–H curve of the iron core used in the SI-SFCL is divided into the saturated region and the unsaturated region signified by points K1 and K2. When the VSC-HVDC system works normally, the magnetic flux density of the iron core is in the positive saturated region, the permeability of the iron core is small, and the equivalent inductance of the SI-FCL is extremely small; thus, its influence on the VSC-HVDC system is slight. When a DC side short-circuit fault occurs, the greatly increased fault current forces the magnetic flux density of the core into the non-saturated region. Subsequently, the equivalent inductance of the SI-FCL rises rapidly with the increase in permeability, and the fault current is limited by the SI-FCL.

Fig. 3
figure 3

B–H curve of iron core

Full size image

From the perspective of electromagnetic energy conservation, the electric energy is absorbed and converted into magnetic field energy by the SI-FCL after a DC side fault. Thereafter, the magnetic field energy draws the magnetic flux density from the positive saturated region into the unsaturated region. During this process, the magnetic permeability of the iron core increases, and so does the equivalent inductance of the SI-FCL. The energy conversion of the SI-FCL is analyzed at the stage when the magnetic flux density moves from the positive saturated region into the unsaturated region.

2.1 Theoretical analysis of energy change of SI-FCL with varying magnetic flux density

For simplicity, it is assumed that the cross-section areas of the iron core denoted by S are identical. The magnetic flux density is B. The relationship between the magnetic flux density B and the current of the DC side of the VSC-HVDC system i2 can be expressed by the following equation according to the relevant knowledge of magnetic circuit analysis [23]:

$$i_{2} = \frac{{N_{1} i_{1} - Hl}}{{N_{2} }}$$
(1)

where l is the overall length of the core; H is the magnetic field intensity. From the energy calculation formula, we can see that the energy variation of the SI-FCL in the period of t1–t2 is:

$$\Delta W_{L} = \int_{{t_{1} }}^{{t_{2} }} {u_{2} i_{2} } {\text{d}}t = Sl\int_{{B_{1} }}^{{B_{2} }} {\frac{B}{\mu }{\text{d}}B} - SN_{1} i_{1} B_{2} + SN_{1} i_{1} B_{1}$$
(2)

where B1 is the magnetic flux density at time t1; B2 is the magnetic flux density at time t2; S is the cross-section of the iron core.

According to the B–H curve in Fig. 3, the energy variation of the SI-FCL after the fault is:

$$\begin{aligned} \Delta W_{L} & = Sl\int_{{B_{m} }}^{{B_{k} }} {\frac{B}{\mu }{\text{d}}B - SN_{1} i_{1} B_{k} + SN_{1} i_{1} B_{m} } \\ & \quad + Sl\int_{{B_{k} }}^{{B_{t} }} {\frac{B}{\mu }{\text{d}}B - SN_{1} i_{1} B_{t} + SN_{1} i_{1} B_{k} } \\ \end{aligned}$$
(3)

where Bm is the magnetic flux density before the fault and in the saturated region; Bt is the magnetic flux density at a time point after the fault and in the non-saturated region; Bk is the magnetic flux density of point K1.

Because the variation of the magnetic flux density in the saturated region is negligible, Bm≈Bk. Hence, (3) can be simplified as follow:

$$\Delta W_{L} = Sl\int_{{B_{k} }}^{{B_{t} }} {\frac{B}{\mu }{\text{d}}B} - SN_{1} i_{1} B_{t} + SN_{1} i_{1} B_{k}$$
(4)

According to the B–H curve of the iron core in Fig. 3, we obtain the permeability–magnetic flux density μ1–B curve shown in Fig. 4 that depicts the μ–B relationship of the core. It can be seen from the Fig. 4, that the μ–B curve is linear in the unsaturated region.

Fig. 4
figure 4

μ–B curve of iron core

Full size image

Therefore, the first-order polynomial can be used to fit the relationship between the permeability μ and the magnetic flux density B with high accuracy. The fitting equation is:

$$\mu = \left\{ {\begin{array}{ll} {mB + n} \hfill & {0 \le B \le B_{k} } \hfill \\ { - mB + n} \hfill & { - B_{k} \le B < 0} \hfill \\ \end{array} } \right.$$
(5)

where the values of m and n depend on the material of the iron core.

The μ2–B curve in Fig. 4 is obtained from (5). Compared with the μ1–B curve, it can be seen that (5) can well fit the non-saturated region of the μ–B curve, but is not consistent with the saturated region.

According to (3) and (5), when the magnetic flux density B changes from the positive saturation region to the unsaturated region, the relationship between the energy variation ΔWL and the magnetic flux density Bt is:

$$\Delta W_{L} = \left\{ {\begin{array}{*{20}l} \begin{aligned} &\frac{Slm}{{k^{2} }}\ln \left( {\frac{{\mu_{{B_{k} }} }}{{k\mu_{{B_{t} }} + m}}} \right) - S\frac{l}{k}\left( {B_{k} - B_{t} } \right) \hfill \\ & \,\,\,\, +\,SN_{1} i_{1} \left( {B_{k} - B_{t} } \right)\qquad 0 \le B_{t} \le B_{k} \hfill \\ \end{aligned} \\ \begin{aligned} &\frac{Slm}{{k^{2} }}\ln \left( {\frac{{\mu_{{B_{k} }} }}{{ - k\mu_{{B_{t} }} + m}}} \right) - S\frac{l}{k}\left( {B_{k} + B_{t} } \right) \hfill \\& \,\,\,\, +\, SN_{1} i_{1} \left( {B_{k} - B_{t} } \right)\qquad - B_{k} \le B_{t} < 0 \hfill \\ \end{aligned} \\ \end{array} } \right.$$
(6)

where μBk is the permeability when the magnetic flux density is Bk.

When the magnetic flux density is in the unsaturated region, the relationship between the energy variation and the magnetic flux density can be reflected by (6). Thus, the variation of magnetic field energy can be calculated by (6) only when the magnetic flux density varies from the knee point to the unsaturated region.

2.2 Simulation and verification of SI-FCL energy change with varying magnetic flux density

To verify the correctness of (6), a simulation model of the SI-FCL is established in PSpice. A single-phase transformer model with saturated characteristics was built to simulate the SI-FCL, and the parameters of the model are listed in Table 1.

Table 1 Parameters of SI-FCL simulation model
Full size table

The excitation coil is connected to a ramp-type current source that generates current to drive the magnetic flux density of the SI-FCL from the positive saturated region across the unsaturated region into the negative saturated region. Current i2, voltage u2, and the magnetic flux density are recorded constantly in the simulation. According to (2), the energy variation of the SI-FCL from the simulation start time to a certain time can be calculated, and then the relationship between the energy variation and magnetic flux density can be obtained, which is shown as the ΔWL1–B curve in Fig. 5 with cross marks.

Fig. 5
figure 5

Relationship between energy variation and magnetic flux density

Full size image

Based on (6), the relationship between the energy variation and the magnetic flux density is calculated and shown as the ΔWL2–B curve in Fig. 5 with circle marks.

In Fig. 5, the two curves coincide well when the magnetic flux density varies from the positive saturated region near the point K1 to the unsaturated region. Equation (6) proves to be accurate in calculating the energy variation of the SI-FCL with the magnetic flux density ranging from the positive saturated region to the unsaturated region.

3 Current-limiting performance analysis of SI-FCL in VSC-HVDC system

The structure of the two-level VSC-HVDC system is shown in Fig. 2. The DC side faults in the system can be categorized as two-pole short-circuit fault, single-pole short-circuit fault and disconnection fault, among which the two-pole short-circuit fault is the most harmful. Therefore, this paper analyzes the energy exchange process of the DC side in the case of a two-pole short-circuit fault. On this basis, the current-limiting performance of the SI-FCL is studied.

When a DC side fault occurs, the insulated-gate bipolar transistors of the inverter will be blocked under self-protection. At this time, the capacitor voltage Udc is greater than the peak value of the inter-phase voltage of the AC side. Additionally, the AC side system cannot supply power to the DC side system through the free-wheel diodes. The DC side system can be regarded as a circuit structure in which the capacitor discharges to the short-circuit point. After the capacitor voltage drops below the peak value of the inter-phase voltage of the AC side, the free-wheel diodes will turn on, and will most likely be damaged by the fault current [3]. Therefore, the SI-FCL that provides ample time for the breaker to clear the fault should limit the fault current and delay the voltage drop time of the capacitor before the free-wheel diodes turns on.

In the most serious scenario, in which the resistance of the SI-FCL ignored, and a short-circuit fault occurs at the junction of the DC rail and the power cable, the DC side system is equivalent to the simplified circuit as shown in Fig. 6 until the free-wheel diodes turn on.

Fig. 6
figure 6

Equivalent circuit of DC side system after a two-pole short-circuit fault

Full size image

For the circuit shown in Fig. 6, the capacitor voltage at initial time t1 is denoted as Udc1, a time point after the fault is denoted as t2, and the voltage at time t2 is denoted as Udc2. The energy variation of the capacitor in the period t1–t2 is:

$$\Delta W_{c} = \frac{1}{2}CU_{\text{dc1}}^{2} - \frac{1}{2}CU_{\text{dc2}}^{2}$$
(7)

As observed from the equivalent circuit in Fig. 6, the electric field energy variation of the capacitor is equal to the magnetic field energy variation of the SI-FCL, ΔWc = ΔWL. According to the relationship between ΔWL and the magnetic flux density B shown in Fig. 5, it can be seen that the magnetic flux density B will gradually alter from the positive saturated region to the negative saturated region as the energy variation increases.

As can be seen from the B–H curve shown in Fig. 3, the magnetic field intensity H is reduced rapidly when the magnetic flux density B changes from the positive saturated region to the unsaturated region. Meanwhile, the current i2 increases rapidly, which can be seen from (1). When the magnetic flux density B is in the unsaturated region, the magnetic field intensity H converts slowly, and the current i2 is basically stable at a fixed value. When the magnetic flux density B enters the negative saturated region, the magnetic field intensity H will decrease rapidly again, the current i2 will dramatically increase, and the SI-FCL will no longer limit the fault current of the DC side. Therefore, to achieve the desired current-limiting effect, the energy released by the capacitor should remain below what can drive the magnetic flux density B from the positive saturated region across the unsaturated region into the negative saturated region.

Combining (6) and (7), when the magnetic flux density B varies from the positive saturated region into the unsaturated region, the relationship between the energy variation of the SI-FCL and the energy variation of the capacitor is:

$$\frac{1}{2}CU_{\text{dc1}}^{2} - \frac{1}{2}CU_{\text{dc2}}^{2} =\left\{ \begin{aligned} &\frac{Slm}{{k^{2} }}\ln \left( {\frac{{\mu_{{B_{k} }} }}{{k\mu_{{B_{t} }} + m}}} \right) - S\frac{l}{k}\left( {B_{k} - B_{t} } \right) \\& \;\;\; + SN_{1} i_{1} \left( {B_{k} - B_{t} } \right)\quad 0 \le B_{t} \le B_{k} \\ &\frac{Slm}{{k^{2} }}\ln \left( {\frac{{\mu_{{B_{k} }} }}{{ - k\mu_{{B_{t} }} + m}}} \right) - S\frac{l}{k}\left( {B_{k} + B_{t} } \right) \\&\;\;\;+ SN_{1} i_{1} \left( {B_{k} - B_{t} } \right)\quad - B_{k} \le B_{t} < 0 \end{aligned} \right.$$
(8)

It is noted that in (8) the magnetic flux density Bt is in the unsaturated region. Once the magnetic flux density moves from the non-saturated region to the negative saturated region, the μ–B curve is no longer consistent with (5), and (8) fails to reflect the relationship between the energy variation of the SI-FCL and that of the capacitor.

The capacitor voltage that turns on the free-wheel diodes is Udc,min. In the extreme case that the capacitor voltage drops to Udc,min, the energy absorbed by the SI-FCL is not sufficient to draw the magnetic flux density B into the negative saturated region, signified by point K2.

According to (2), for B not to reach the negative saturated region, the condition is:

$$2SN_{1} i_{1} B_{k} \ge \frac{1}{2}CU_{\text{dc1}}^{2} - \frac{1}{2}CU_{\text{dc,min}}^{2}$$
(9)

Let \(\Delta W_{L,\hbox{max} } = 2SN_{1} i_{1} B_{k}\), then ΔWL,max denotes the maximum energy absorbed by the SI-FCL when the magnetic flux density B stays out of the negative saturated region. Let \(\Delta W_{c,\hbox{max} } = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}CU_{{{\text{dc}}1}}^{2} - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}CU_{\text{dc,min}}^{2}\), then ΔWc,max represents the energy variation of the capacitor when the voltage drops to Udc,min, and (9) can be expressed as:

$$\Delta W_{{L,{ \hbox{max} }}} \ge \Delta W_{{c,{ \hbox{max} }}}$$
(10)

Equation (10) is a criterion used to determine whether the SI-FCL has current-limiting ability all the time before the capacitor voltage drops to Udc,min.

When the capacitance and voltage level of the VSC-HVDC system are given, if the criterion is met, the SI-FCL will have current-limiting ability all the time before the capacitor voltage drops to Udc,min and the fault current i2 will not surge. Otherwise, the SI-FCL will not always have current-limiting ability and thus cannot achieve the desired performance.

The SI-FCL is designed to limit the fault current to an acceptable level. In addition, the SI-FCL applied in the VSC-HVDC system is also used to extend the time before the voltage drops to Udc,min. Therefore, in addition to analyzing whether the SI-FCL has current-limiting ability in the process when the capacitor voltage drops from the initial state Udc1 to Udc,min, the maximum fault current (i2,max) and the duration of this process (T) also needs to be obtained.

When the magnetic flux density B is in the unsaturated region, the current i2 can be calculated by (11) derived from (1) and (5).

$$i_{2} = \left\{ {\begin{array}{*{20}l} {\frac{{N_{1} i_{1} - \frac{Bl}{kB + m}}}{{N_{2} }} \qquad \;\; 0 \le B \le B_{k} } \\ {\frac{{N_{1} i_{1} - \frac{Bl}{ - kB + m}}}{{N_{2} }} \qquad -B_{k} \le B < 0} \\ \end{array} } \right.$$
(11)

Depending on whether (10) is met before the capacitor voltage drops to Udc,min, the calculation of i2,max can be divided into two cases:

Case 1: the SI-FCL has current-limiting ability constantly during this voltage drop process. In this case, (8) is used to calculate the magnetic flux density Bmin when the capacitor voltage is Udc,min. With Bmin substituted into (11), the maximum fault current i2,max,I is known.

Case 2: the SI-FCL does not always have current-limiting ability during this process. In this case, the magnetic flux density of the SI-FCL will enter the negative saturated region, after which the fault current will surge before the capacitor voltage drops to Udc,min. By substituting the magnetic flux density at point K2 into (11), the maximum fault current i2,max,II can be obtained.

In normal operation, the iron core of the SI-FCL works in the saturated state so that the equivalent inductance is small. To ensure that the core is saturated, N1i1 must be very large. When a DC side fault occurs, the magnetic flux density enters the unsaturated region. As shown in Fig. 3, when the core is in the unsaturated state, the magnetic field intensity is small and changes little. Meanwhile, the variation range of the current i2 is small, and it can be assumed that i2 is approximately constant.

According to the capacitor discharge formula, it is known that:

$$i_{2} = - C\frac{{{\text{d}}U_{\text{dc}} }}{{{\text{d}}t}}$$
(12)

Setting T is the time for the capacitor voltage to fall to Udc,min. Depending on whether the condition (10) can be satisfied during the process before the capacitor voltage drops to Udc,min, the calculation of T is divided into two cases:

Case 1: the SI-FCL has current-limiting ability all the time during this process. In this case, the maximum fault current is i2,max,I. If the fault current is set to i2,max,I, the shortest time Tmin,I for capacitor voltage to fall from Udc1 to Udc,min is:

$$T_{\text{min,I}} = \frac{{C\left( {U_{\text{dc1}} - U_{\text{dc,min}} } \right)}}{{i_{{2,{\text{max,I}}}} }}$$
(13)

Case 2: the SI-FCL does not always have current-limiting ability during this process. In this case, by substituting the magnetic flux density at point into (8), the voltage Udc,s when the fault current begins to surge can be obtained as:

$$U_{\text{dcs}} = \sqrt {U_{\text{dc1}}^{2} - {{4SN_{1} i_{1} B_{k} } \mathord{\left/ {\vphantom {{4SN_{1} i_{1} B_{k} } C}} \right. \kern-0pt} C}}$$
(14)

As the variation range of the current i2 is narrow, it is assumed that the current i2 is i2,max,II. In addition, the shortest time for capacitor voltage to fall from Udc1 to Udc,s is:

$$T_{\text{min,s}} = \frac{{C\left( {U_{\text{dc1}} - U_{\text{dc,s}} } \right)}}{{i_{{2,{\text{max,II}}}} }}$$
(15)

Assuming that the fault current remains i2,max,II, the shortest time for capacitor voltage to fall from Udc1 to Udc,min is:

$$T_{{\hbox{min} ,{\text{s}}}}^{\prime } = \frac{{C\left( {U_{\text{dc1}} - U_{\text{dc,min}} } \right)}}{{i_{{2,{\text{max,II}}}} }}$$
(16)

The time for capacitor voltage to fall from Udc1 to Udc,min is Tmin,II, and Tmin,II is greater than Tmin,s. After the capacitor voltage drops to Udc,s, the DC side fault current surges, and Tmin,II must be less than \(T_{\text{min,s}}^{\prime }\). Thus, Tmin,II satisfies the condition as follow:

$$T_{\text{min,s}} < T_{\text{min,II}} < T_{\text{min,s}}^{\prime }$$
(17)

Through the analysis of the SI-FCL in the VSC-HVDC system, the criterion is found for determining whether the SI-FCL has current-limiting ability all the time before the capacitor voltage drops to Udc,min. By further analyzing the process in which the capacitor voltage drops from the initial state Udc1 to Udc,min, the current level to which the fault current is limited, and the time for the capacitor voltage to drop from Udc1 to Udc,min are obtained.

4 Case study and simulation verification

To verify the correctness of the theoretical analysis above, a two-level VSC-HVDC system model of ± 35 kV (Udc = 70 kV) is built in PSpice. The model structure is shown in Fig. 2, and the parameters of the model are listed in Table 2.

Table 2 Parameters of the two-level VSC-HVDC system model
Full size table

The transmission capacity is 20 MW, and the rated current i2rated is calculated as 0.3 kA. For the two-level VSC-HVDC system, the free-wheel diodes turn on once the capacitor voltage drops to the peak value of the inter-phase voltage at the AC side, so Udc,min is calculated as 49.497 kV.

The capacitor voltage and fault current are shown in Figs. 7 and 8, when a two-pole short-circuit fault occurs 5 km away from the rectifier at 0.1 s. It can be seen that the capacitor voltage drops rapidly to zero without the SI-FCL while the fault current rises rapidly and reaches 17.69 kA, approximately 60 times higher than the rated current.

Fig. 7
figure 7

Capacitor voltage of the VSC-HVDC system without an SI-FCL

Full size image
Fig. 8
figure 8

DC side fault current of VSC-HVDC system without an SI-FCL

Full size image

To verify the correctness of the theoretical analysis of the SI-FCL, the SI-FCLs A and B are separately connected in the VSC-HVDC system. The parameters of SI-FCL A are listed in Table 3.

Table 3 Parameters of SI-FCL A
Full size table

The current-limiting performance of SI-FCL A and B can be analyzed by the theory presented in Section 3.

Assuming that the two-pole short-circuit fault occurs at the junction of the DC rail and the power cable, the energy variation of the capacitor ΔWc,max is 2.45×106 J, and the energy variation of the SI-FCL A ΔWL,max is 2.48×106 J. It can be seen from (10) that the SI-FCL has current-limiting ability before the capacitor voltage drops to Udc,min. The SI-FCL A meets the condition of case 1. Therefore, the magnetic flux density Bmin is about 2.238 T, the maximum fault current i2,max,I is 1.017 kA, and Tmin,I is about 40.2 ms. The above theoretical calculations were made for the most serious fault conditions (resistance of the DC side is 0). When a DC side fault occurs at other locations, the line resistance is greater than 0, so the current-limiting effect of the SI-FCL can be better.

When a two-pole short-circuit fault occurs at 5 km away from the rectifier at 0.1 s, the capacitor voltage and fault current of the VSC-HVDC system with SI-FCL A are shown in Figs. 9 and 10. It can be seen that the time T for capacitor voltage to fall from Udc1 to Udc,min is extended to 40.8 ms by the SI-FCL A. In addition, the maximum fault current is about 1.04 kA. The results obtained by the simulation and theoretical analysis of SI-FCL A are basically the same.

Fig. 9
figure 9

Capacitor voltage of VSC-HVDC system with SI-FCL A

Full size image
Fig. 10
figure 10

DC side fault current of VSC-HVDC system with SI-FCL A

Full size image

The parameters of SI-FCL B are listed in Table 4.

Table 4 Parameters of SI-FCL B
Full size table

Assuming that the two-pole short-circuit fault occurs at the junction of the DC rail and the power cable in the VSC-HVDC system with SI-FCL B. The energy variation of the capacitor ΔWc,max is 2.45×106 J, and the energy variation of the SI-FCL B is 1.49×106 J. It can be seen from (10) that the SI-FCL will lose current-limiting ability before the capacitor voltage drops to Udc,min. The SI-FCL B meets the condition of case 2, and the current surge occurs before the capacitor voltage drops to Udc,min. The magnetic flux density Bk substituted into (11) and (14), the maximum fault current before the current surges is about 1.389 kA, and the voltage Udc,s is 57.271 kV. The shortest time Tmin,s for the capacitor voltage to fall from Udc1 to Udc,s is 18.3 ms. Assuming that the fault current remains 1.389 kA, the shortest time \(T_{\text{min,s}}^{\prime }\) for capacitor voltage to fall from Udc1 to Udc,min is 29.5 ms. Therefore, the time for the capacitor voltage to drop to Udc,min is longer than 18.3 ms and less than 29.5 ms.

When a two-pole short-circuit fault occurs 5 km away from the rectifier at 0.1 s, the capacitor voltage and fault current of the VSC-HVDC system with SI-FCL B are shown in Figs. 11 and 12. It can be seen that the time T for capacitor voltage to fall from Udc1 to Udc,min is 23.8 ms, and the maximum fault current is approximately 1.409 kA before the current surges. When the fault current surges, the capacitor voltage is 57.653 kV, and the time T′ for capacitor voltage to fall from Udc1 to Udc,s is 18.7 ms. The results obtained by the simulation and theoretical analysis of SI-FCL B are basically the same.

Fig. 11
figure 11

Capacitor voltage of VSC-HVDC system with SI-FCL B

Full size image
Fig. 12
figure 12

DC side fault current of VSC-HVDC system with SI-FCL B

Full size image

The simulation of the VSC-HVDC system with different SI-FCLs shows that the method analyzing the performance of the SI-FCL based on the electromagnetic energy conversion mechanism is correct. The method gives the criterion for determining whether the SI-FCL has current-limiting ability constantly before the capacitor voltage drops to Udc,min. In addition, the maximum fault current and the time for capacitor voltage to fall from Udc1 to Udc,min can also be calculated accurately by this method.

5 Conclusion

This paper has examined the performance of the SI-FCL in a VSC-HVDC system. From the perspective of electromagnetic energy conversion, the relationship between the electromagnetic energy and the magnetic flux density of the SI-FCL has been analyzed. Based on the study of the electromagnetic energy conversion process after the DC side fault, the relationship between the fault current and the magnetic flux density of the SI-FCL and that between the time for the capacitor voltage dropping to Udc,min and the DC side fault current have been given.

The method identifying the current-limiting characteristic of the SI-FCL in the VSC-HVDC system is based on the analysis of the energy conversion of the DC side fault. On this basis, the time for capacitor voltage to drop to Udc,min and the maximum fault current in the case of a constantly current-limiting-capable SI-FCL can be obtained if the parameters of the SI-FCL and the VSC-HVDC system are given. This method avoids the complex differential calculation of solving the DC side fault transient process in the time domain, and its accuracy has been demonstrated through a case study and simulation.