1 Introduction

The higher penetration level of renewable energy resources requires improved flexibility measures in the power networks. The relative low cost and abundance of natural gas fuel resources as a result of recent developments in the extraction techniques (hydrofracturing and horizontal drilling), the increase in the environmental concerns in electricity generation, and the higher efficiency of gas-fired electricity generation technology increased the dependence of electricity infrastructure system on the natural gas network [1]. Expected low natural gas prices in the 2016–2040 is projected to adding 175 GW generation capacity of natural gas-fired generation technology annually, which accounts for 36% of the total annual capacity increase [2]. Such increasing trends in natural gas-fired generation resources led to investigating the interdependence among the bulk electricity and natural gas energy systems [3,4,5].

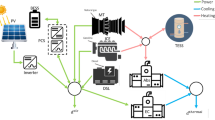
The installed capacity of the combined heat and power (CHP) in the U.S. is 70 GW which accounts for almost 7% of total generation capacity [6]. The CHP generation technology that is leveraged by the customers in the distribution networks, improves the energy efficiency and further highlights the interdependence among natural gas and electricity distribution networks. Microgrids equipped with CHP technology, provide the expected reliability and service quality by effectively coordinating the operation among electricity and natural gas distribution networks. The physical layer of the electricity network in microgrids – that operate in grid-connected or island mode – is composed of demand entities (consumers), distributed generation units, and distribution cables. The natural gas distribution network is composed of the source points, gas-fired distributed generation units, heaters, and natural gas pipelines.

In [4], several factors including physical characteristics, the operational procedures, types of the electricity generation plants, and availability of electricity and natural gas supply were addressed as potential factors that affect the operation of the interconnected natural gas and electricity networks. The scheduling of interdependent energy networks by determining the optimal coupling matrix and controlling the flow of electricity, natural gas, and district heat flow is addressed in [7]. It is shown in [8] that the integrated operation of electricity and natural gas networks will lead to savings in energy costs.

There are several perceptions of resilience. In [9], resilience is defined as the capability of a system to withstand major disruptions with acceptable degradation in performance and capability to recover within acceptable time and cost. In [10], resilience is defined as the ability to prepare and adapt to the evolving conditions, withstand the disruptions, and recover rapidly from them. This paper adopted the first definition of resilience; therefore, the vulnerable components in islanded microgrids are determined to avoid the disruption in service as a result of deliberate disruptions.

Resilience in electricity network was addressed by several publications [11,12,13,14,15]. In [11], a simulation-based approach is proposed to address the margin and sensitivity of the electricity distribution network with respect to the resources for repair and recovery. The proposed model could be used for distribution system operators to assess the ability of the system to accommodate large disturbances by adjusting system repair resources. A two-step stochastic programming framework is proposed in [12] to mitigate the socioeconomic cost of microgrids that are exposed to the stochastic natural disasters. The proposed approach showed the potential of microgrids for improving the resilience of the electricity network. In [13], static power system vulnerability is addressed using a bi-level optimization problem with transmission line switching. The objective is to determine the most destructive interdiction plan with the highest loss of load in the power network. An improved interdiction model that identifies maximal electric grid attacks in short-term (seconds to minutes) and medium term (minutes to days) is addressed in [14]. The proposed model identifies the potential cascading failures that may lead to large blackouts. In [15], a tri-level defender-attacker-defender model is proposed and solved using the column and constraint generation methodology for improving the grid survivability under contingencies. The resilience of natural gas network is addressed in [16] by procuring a response strategy to energy shortage and evaluating its quantified effectiveness in various scenarios.

While earlier research investigated the resilience of electricity networks against deliberate disruptions, the interaction among electricity and natural gas networks to provide effective resilience measures should be further investigated [17]. This paper addresses the reinforcement strategies in islanded microgrids with electricity and natural gas distribution networks, that are exposed to deliberate disruptions considering the uncertainties in electricity and heat demand. The presented framework identifies the critical components that should be reinforced to ensure the energy supply continuity in the microgrid’s distribution network while capturing the uncertainties imposed by volatility of electricity and heat demands.

2 Problem formulation

The problem is formulated as a bi-level optimization problem that yields the vulnerable components in the microgrid with electricity and natural gas distribution network. The preventive reinforcement strategies in the interdependent electricity and natural gas networks are procured by identifying the vulnerable components and the potential consequences of disruptions in an islanded microgrid. The objective of the upper-level problem is to maximize the expected operation cost of the microgrid by disrupting the vulnerable elements in the electricity and natural gas networks considering limited resources for such disruptions. The objective of the lower-level problem is to minimize the expected operation cost of the islanded microgrid once it is exposed to the deliberate disruptions. As shown in Fig. 1, by incorporating the duality theory, the bi-level optimization problem is formulated as a single level mixed integer programming (MIP) problem. The objective function of the MIP problem is the same as the objective function of the upper-level problem as given in (1).

Fig. 1
figure 1

Solution framework for the proposed bi-level optimization problem

Full size image
$$ {\text{max }} OP_{pri} = \mathop \sum \limits_{t} \left\{ {\rho_{t} \left[ {\mathop \sum \limits_{i} F_{c,i} \left( {P_{i,t}^{e} } \right) + VOLL^{e} \cdot \mathop \sum \limits_{j} \left( {P_{j,t}^{e,D} - P_{j,t}^{e,d} } \right) + \mathop \sum \limits_{k} F_{c,k} \left( {P_{k,t}^{h} } \right) + VOLL^{h} \cdot \mathop \sum \limits_{j} \left( {P_{j,t}^{h,D} - P_{j,t}^{h,d} } \right)} \right]} \right\} $$
(1)

where \( i \) is the index for the gas-fired distributed generation unit; \( l \) is the index for the electricity distribution line; \( p \) is the index for the natural gas pipeline; \( t \) is the index for scenario. The production cost function for gas-fired distributed generation unit \( i \) and heater \( k \) are presented by \( F_{c,i} \) and \( F_{c,k} \). The indices for electricity and heat energy are presented by \( e \) and \( h \). In addition, the value of lost load for electricity and heat demands are shown by \( VOLL^{e} \) and \( VOLL^{h} \) respectively. The probability of scenario \( t \) is shown as \( \rho_{t} \). The generation dispatch of gas-fired distributed generation is shown as \( P_{i,t}^{e} \), the electricity and heat demand at node \( j \) in scenario \( t \) are shown as \( P_{j,t}^{e,D} \) and \( P_{j,t}^{h,D} \) respectively. The served electricity and heat demand at node \( j \) in scenario \( t \) are shown as \( P_{j,t}^{e,d} \) and \( P_{j,t}^{h,d} \) respectively. The generated heat by heater \( k \) at node \( j \) in scenario \( t \) is shown as \( P_{k,t}^{h} \). The resources for disruption are limited by (2) where \( M \) is the total available resources for disruption. The required resources to reinforce gas-fired distributed generation units, distribution lines and natural gas pipelines are shown by \( M_{i} \), \( M_{l} \), and \( M_{p} \) respectively.

$$ \mathop \sum \limits_{i}^{NG} M_{i} (1 - UX_{i} ) + \mathop \sum \limits_{l}^{NL} M_{l} \left( {1 - UY_{l} } \right) + \mathop \sum \limits_{p}^{NP} M_{p} \left( {1 - UZ_{p} } \right) \le M $$
(2)

The decisions on disrupting gas-fired distributed generation units, distribution lines, and natural gas pipelines are represented by the binary variables \( UX_{i} \), \( UY_{l} \), and \( UZ_{p} \) respectively. Here, 0 indicates that the component is disrupted and consequently unavailable, and 1 indicates that the component is not disrupted and is available. The total number of gas-fired distributed generation units, electricity distribution lines, and natural gas pipelines are shown by \( NG \), \( NL \), and \( NP \) respectively. The objective of the lower-level problem is given in (3), where the expected operation cost \( OP_{pri} \) of the microgrid exposed to disruption is minimized. As formulated in (3), the objective of the lower-level problem is to minimize the expected operation cost of the microgrid.

$$ {\text{min}}\quad OP_{pri} = \mathop \sum \limits_{t} \left\{ {\rho_{t} \left[ {\mathop \sum \limits_{i} F_{c,i} \left( {P_{i,t}^{e} } \right) + VOLL^{e}\mathop \sum \limits_{j} \left( {P_{j,t}^{e,D} - P_{j,t}^{e,d} } \right) + \mathop \sum \limits_{k} F_{c,k} \left( {P_{k,t}^{h} } \right) + VOLL^{h} \mathop \sum \limits_{j} \left( {P_{j,t}^{h,D} - P_{j,t}^{h,d} } \right)} \right]} \right\} $$
(3)

The expected operation cost is determined by the probability associated with each scenario, the generation cost of gas-fired distributed generation units and heaters in addition to the penalty associated with the electricity and heat demand curtailments in each scenario. Here, the constraints associated with the lower-level problem are given in (4)–(26) where the dual variables of the equality and inequality constraints are shown by \( \mu \), \( \lambda \), \( \gamma \) and \( \tau \). The real and reactive power injection at node \( j \), are presented by \( P_{j,t}^{inj} \) and \( Q_{j,t}^{inj} \), as shown in (4) and (5) respectively.

$$ \mathop \sum \limits_{{i \in GG_{j} }} P_{i,t}^{e} - P_{j,t}^{e,d} = P_{j,t}^{inj} \quad\quad \left( {\lambda_{1}^{j,t} } \right) $$
(4)
$$ \mathop \sum \limits_{{i \in GG_{j} }} Q_{i,t}^{e} - Q_{j,t}^{e,d} = Q_{j,t}^{inj} \quad\quad \left( {\lambda_{2}^{j,t} } \right) $$
(5)

where \( P_{i,t}^{e} \) and \( Q_{i,t}^{e} \) are the decision variables associated with the real and reactive dispatch of gas-fired distributed generation unit \( i \) that is connected to node \( j \) in scenario \( t \) respectively. Furthermore, generation unit \( i \) belongs to the group of generators that is connected to the node \( j \) as shown by \( GG_{j} \). The served real and reactive electricity demand at node \( j \) in scenario \( t \) are shown by \( P_{j,t}^{e,d} \) and \( Q_{j,t}^{e,d} \) respectively. The real and reactive generation dispatch of gas-fired distributed generation units are limited by (6) and (7).

$$ P_{i}^{ \hbox{min} } UX_{i} \le P_{i,t}^{e} \le P_{i}^{ \hbox{max} } UX_{i} \quad\quad (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{1}^{i,t} ,\bar{\mu }_{1}^{i,t} ) $$
(6)
$$ Q_{i}^{ \hbox{min} } UX_{i} \le Q_{i,t}^{e} \le Q_{i}^{ \hbox{max} } UX_{i} \quad\quad \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{2}^{i,t} ,\bar{\mu }_{2}^{i,t} } \right) $$
(7)

The real and reactive generation capacity of the gas-fired distributed generation unit \( i \) are shown as \( P_{i}^{ \hbox{max}} \) and \( Q_{i}^{ \hbox{max} } \) respectively. Similarly, \( P_{i}^{ \hbox{min} } \) and \( Q_{i}^{ \hbox{min} } \) are the minimum real and reactive generation capacity of gas-fired distributed generation unit \( i \), respectively. It is assumed that the demand is curtailable and the real and reactive electricity demand curtailment at node \( j \) is no more than to the real and reactive electricity demand as presented by (8) and (9) respectively.

$$ 0 \le P_{j,t}^{e,D} - P_{j,t}^{e,d} \le P_{j,t}^{e,D} \quad\quad \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{3}^{j,t} ,\bar{\mu }_{3}^{j,t} } \right) $$
(8)
$$ 0 \le Q_{j,t}^{e,D} - Q_{j,t}^{e,d} \le Q_{j,t}^{e,D}\quad \quad \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{4}^{j,t} ,\bar{\mu }_{4}^{j,t} } \right) $$
(9)

The real and reactive electricity demand in scenario \( t \) at node \( j \) is represented by \( P_{j,t}^{e,D} \) and \( Q_{j,t}^{e,D} \), respectively. The admittance of the distribution line is calculated in (10), considering the binary variables associated with the disruptions in the distribution line.

$$ y_{j,o} = g_{j,o} + {\text{j}}b_{j,o} = \frac{{r_{j,o} UY_{j,o} }}{{r_{j,o}^{2} + x_{j,o}^{2} }} - {\text{j}}\frac{{x_{j,o} UY_{j,o} }}{{r_{j,o}^{2} + x_{j,o}^{2} }} $$
(10)

where \( y_{j,o} \), \( g_{j,o} \), \( b_{j,o} \), \( r_{j,o} \), \( x_{j,o} \) are admittance, conductance, susceptance, resistance, and reactance of distribution line that connects node \( j \) to node \( o \). The linearized AC power flow for real/reactive power injection is shown in (11) and (12) as suggested in [18].

$$ \begin{aligned} P_{j,t}^{inj} & = \left( {2V_{j,t} - 1} \right)G_{j,j} \\ &\quad + \mathop \sum \limits_{{o\left( {o \ne j} \right)}}^{NB} \left[ {G_{j,o} \left( {V_{j,t} + V_{o,t} - 1} \right) + B_{j,o} \left( {\theta_{j,t} - \theta_{o,t} } \right)} \right]\quad\quad \left( {\lambda_{3}^{j,t} } \right) \\ \end{aligned} $$
(11)
$$ \begin{aligned} Q_{j,t}^{inj} & = - \left( {2V_{j,t} - 1} \right)B_{j,j} \\ & \quad+ \mathop \sum \limits_{{o\left( {o \ne j} \right)}}^{NB} \left[ { - B_{j,o} \left( {V_{j,t} + V_{o,t} - 1} \right) + G_{j,o} \left( {\theta_{j,t} - \theta_{o,t} } \right)} \right]\quad\quad \left( {\lambda_{4}^{j,t} } \right) \\ \end{aligned} $$
(12)

where \( V_{j,t} \) and \( V_{o,t} \) are the voltage magnitudes on nodes \( j \) and \( o \); \( \theta_{j,t} \) and \( \theta_{o,t} \) are the voltage angles on nodes \( j \) and \( o \); \( NB \) is the total number of nodes; \( G_{j,o} \) and \( B_{j,o} \) are the elements of conductance and susceptance matrices. The real, reactive and apparent power transmitted through the distribution line is given in (13), (14) and (15) respectively.

$$ PL_{j,o}^{t} = - G_{j,o} \left( {V_{j,t} - V_{o,t} } \right) + B_{j,o} \left( {\theta_{j,t} - \theta_{o,t} } \right)\quad\quad \left( {\lambda_{5,t}^{j,o} } \right) $$
(13)
$$ QL_{j,o}^{t} = B_{j,o} \left( {V_{j,t} - V_{o,t} } \right) + G_{j,o} \left( {\theta_{j,t} - \theta_{o,t} } \right) \quad\quad \left( {\lambda_{6,t}^{j,o} } \right) $$
(14)
$$ SL_{j,o}^{t} = PL_{j,o}^{t} + \xi_{j,o} QL_{j,o}^{t} \quad\quad \left( {\lambda_{7,t}^{j,o} } \right) $$
(15)

In (13)–(15), the real, reactive, and apparent power transferred on the line between nodes \( j \) and \( o \) for scenario \( t \) are shown by \( PL_{j,o}^{t} \), \( QL_{j,o}^{t} \), \( SL_{j,o}^{t} \), respectively. In (15), the auxiliary parameter ξ is determined by the demand power factor as discussed in [18]. The apparent power that flows in the distribution line (\( SL_{j,o}^{t} \)) is limited by the capacity of the distribution line (\( SL_{j,o}^{ \hbox{max} } \)) as expressed in (16).

$$ - SL_{j,o}^{ \hbox{max} } \le SL_{j,o}^{t} \le SL_{j,o}^{ \hbox{max} }\quad \quad \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{5,t}^{j,o} ,\bar{\mu }_{5,t}^{j,o} } \right) $$
(16)

The limitations on the voltage phase angle and magnitude in distribution network are given in (17) and (18), where \( V^{ \hbox{max} } \), \( V^{ \hbox{min} } \), \( \theta^{ \hbox{max} } \), \( \theta^{ \hbox{min} } \) are the maximum and minimum voltage magnitudes and maximum and minimum voltage phase angles respectively. The nodal natural gas flow balance at node \( j \) is shown by (19).

$$ \theta^{ \hbox{min} } \le \theta_{j,t} \le \theta^{ \hbox{max} } \quad\quad \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{6}^{j,t} ,\bar{\mu }_{6}^{j,t} } \right) $$
(17)
$$ V^{ \hbox{min} } \le V_{j,t} \le V^{ \hbox{max} } \quad\quad \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{7}^{j,t} ,\bar{\mu }_{7}^{j,t} } \right) $$
(18)
$$ \begin{aligned} & \mathop \sum \limits_{{s \in GS_{j} }} A_{j} v_{s,t} - \mathop \sum \limits_{{p \in P_{F,j} }} f_{j,o}^{p,t} + \mathop \sum \limits_{{p \in P_{T,j} }} f_{j,o}^{p,t} \\ &\quad = \mathop \sum \limits_{{k \in HH_{j} }} \frac{{P_{k,t}^{h} }}{{C_{gh}^{k} }} + \mathop \sum \limits_{{i \in GG_{j} }} \frac{{P_{i,t}^{e} }}{{C_{ge}^{i} }} \quad\quad \left( {\gamma_{1}^{j,t} } \right) \\ \end{aligned} $$
(19)

The injected and withdrawn volumes of natural gas at node \( j \) are equal. The natural gas is used to produce heat and electricity at CHP units with respective conversion factors. Here \( s \) is the index for natural gas resource, \( GS_{j} \) is the group of all natural gas resources that are connected to the node \( j \), \( A_{j} \) is the node-natural gas resource connectivity matrix, and \( v_{s,t} \) is the volume of natural gas supply \( s \) in scenario t. The natural gas flow in pipeline \( p \) that connects the nodes \( j \) and \( o \) in scenario \( t \), is \( f_{j,o}^{p,t} \) and the set of pipelines starting from node \( j \) and ending to node \( j \) are shown by \( P_{F,j} \) and \( P_{T,j} \) respectively. The set of heaters at node \( j \) is presented by \( HH_{j} \). Here \( C_{gh}^{k} \) is the natural gas-to-heat conversion coefficient for heater \( k \) and \( C_{ge}^{i} \) is the natural gas-to-electricity conversion coefficient for gas-fired distributed generation \( i \). The availability of natural gas pipelines is determined by the disruption decisions given in (20), where the maximum natural gas flow on pipeline \( p \) that links node \( j \) and o. is given by \( f_{j,o}^{{p,{ \hbox{max} }}} \).

$$ - \,f_{j,o}^{{p,{ \hbox{max} }}} UZ_{p} \le f_{j,o}^{p,t} \le f_{j,o}^{{p,{ \hbox{max} }}} UZ_{p} \quad \quad\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{1,t}^{j,o} ,\bar{\tau }_{1,t}^{j,o} } \right) $$
(20)

The impact of nodal natural gas pressure on the natural gas flow among interconnected nodes \( j \) and \( o \) is given in (21), where \( \pi_{j} \) is the natural gas pressure at node \( j \), \( \pi_{j}^{\prime } \) is the initial natural gas pressure on node \( j \), \( C_{p} \) is a constant which is determined by the physical characteristics of natural gas pipeline \( p \), and \( K \) is a large number.

$$ \begin{aligned} & f_{j,o}^{p,t} - K\left( {1 - UZ_{p} } \right) \le \frac{{C_{p} \left( {\pi_{j}^{'} \pi_{j,t} - \pi_{o}^{'} \pi_{o,t} } \right)}}{{\sqrt {\left( {\pi_{j}^{'} } \right)^{2} - \left( {\pi_{o}^{'} } \right)^{2} } }} \\ & \le\, f_{j,o}^{p,t} + K\left( {1 - UZ_{p} } \right) \quad\quad \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{2,t}^{j,o} ,\bar{\tau }_{2,t}^{j,o} } \right) \\ \end{aligned} $$
(21)

The natural gas pressure at node \( j \) is limited by (22) where \( \pi^{ \hbox{max} } \) and \( \pi^{ \hbox{min} } \) are the maximum and minimum pressure in the natural gas distribution network. The served heat demand at node \( j \) (\( P_{j}^{h,d} \)) is lower than the total heat demand (\( P_{j}^{h,D} \)), as given by (23).

$$ \pi^{ \hbox{min} } \le \pi_{j,t} \le \pi^{ \hbox{max} } \quad\quad \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{3}^{j,t} ,\bar{\tau }_{3}^{j,t} } \right) $$
(22)
$$ P_{j,t}^{h,d} \le P_{j,t}^{h,D} \quad\quad \left( {\tau_{4}^{j,t} } \right) $$
(23)

The capacity of natural gas supply is further limited by (24), where \( v_{s}^{ \hbox{max} } \) and \( v_{s}^{ \hbox{min} } \) are the maximum and minimum volume of natural gas resource \( s \). If all electricity of a node is curtailed, the heat demand will be also curtailed as shown in (25). The heat demand is served either by the CHP unit as the bi-product of electricity generation or by burning natural gas in heater as shown in (26). Here, \( C_{gh}^{i} \) is the natural gas-to-heat conversion coefficient for gas-fired distributed generation unit \( i \).

$$ v_{s}^{ \hbox{min} } \le v_{s,t} \le v_{s}^{ \hbox{max} } \quad\quad \left( {\underline{\tau}_{5}^{s,t} },\bar{\tau }_{5}^{s,t} \right) $$
(24)
$$ P_{j,t}^{h,d} \le KP_{j,t}^{e,d} \quad\quad \left( {\tau_{6}^{j,t} } \right) $$
(25)
$$ 0 \le P_{j,t}^{h,d} \sum\limits_{{i \in GG_{i} }} {\frac{{(C_{gh}^{i} )P_{i,t}^{e} }}{{C_{gh}^{i} }}} + \sum\limits_{{k \in HH_{j} }} {P_{k,t}^{h} } \quad\quad \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{7}^{j,t} ,\bar{\tau }_{7}^{j,t} } \right) $$
(26)

The dual formulation of the lower-level problem is given in (27)–(43), where the objective of the dual form of the lower-level problem (\( OP_{dual} \)) is given in (27) and the constraints of the dual problem are represented in (28)–(43).

$$ \begin{aligned} & {\text{max}}~\quad OP_{{dual}} = \mathop \sum \limits_{t} \left\{ {\mathop \sum \limits_{i} (P_{i}^{{{\text{min}}}} UX_{i} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu } _{1}^{{i,t}} - P_{i}^{{{\text{max}}}} UX_{i} \bar{\mu }_{1}^{{i,t}} } \right. \\ & + ~Q_{i}^{{{\text{min}}}} UX_{i} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu } _{2}^{{i,t}} - Q_{i}^{{{\text{max}}}} UX_{i} \bar{\mu }_{2}^{{i,t}} ) + \mathop \sum \limits_{j} ( - P_{j}^{{e,D}} \bar{\mu }_{3}^{{j,t}} - Q_{j}^{{e,D}} \bar{\mu }_{4}^{{j,t}} \\ & - G_{{j,j}} \lambda _{3}^{{j,t}} + B_{{j,j}} \lambda _{4}^{{j,t}} - P_{j}^{{h,D}} \tau _{4}^{{j,t}} ~ + V^{{{\text{min}}}} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu } _{7}^{{j,t}} - V^{{{\text{max}}}} \bar{\mu }_{7}^{j} + \theta ^{{{\text{min}}}} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu } _{6}^{{j,t}} \\ & - \theta ^{{{\text{max}}}} \bar{\mu }_{6}^{{j,t}} + \pi ^{{{\text{min}}}} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau } _{3}^{{j,t}} - \pi ^{{{\text{max}}}} \bar{\tau }_{3}^{{j,t}} ) \\ & + \mathop \sum \limits_{j} \mathop \sum \limits_{{o\left( {j \ne o} \right)}} \left( { - f_{{j,o}}^{{p,{\text{max}}}} UZ_{p} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau } _{1}^{{j,o,t}} + \bar{\tau }_{1}^{{j,o,t}} } \right) - K\left( {1 - UZ_{p} } \right)\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau } _{2}^{{j,o,t}} + \bar{\tau }_{2}^{{j,o,t}} } \right) - SL_{{j,o}}^{{{\text{max}}}} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu } _{5}^{{j,o,t}} + \bar{\mu }_{5}^{{j,o,t}} } \right)} \right) \\ & \left. { + \mathop \sum \limits_{s} v_{s}^{{{\text{min}}}} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau } _{5}^{{s,t}} - v_{s}^{{{\text{max}}}} \bar{\tau }_{5}^{{s,t}} } \right\} \\ \end{aligned} $$
(27)
$$ \mathop \sum \limits_{{i \in GG_{i} }} \lambda_{1}^{j,t} + \frac{{\left( {C_{gh}^{i} \bar{\tau }_{7}^{j,t} - \gamma_{1}^{j,t} } \right)}}{{C_{ge}^{i} }} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{1}^{i,t} - \bar{\mu }_{1}^{i,t} = \rho_{t} \partial F_{c,i} {P_{i,t}^{e} } /\partial P_{i,t}^{e} \quad\quad\left( {P_{i,t}^{e} } \right) $$
(28)
$$ \mathop \sum \limits_{{i \in GG_{i} }} (\lambda_{2}^{j,t} ) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{1}^{i,t} - \bar{\mu }_{1}^{i,t} = 0\quad\quad \left( {Q_{i,t}^{e} } \right) $$
(29)
$$ - \lambda_{1}^{j,t} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{3}^{j,t} + \bar{\mu }_{3}^{j,t} + K\tau_{6}^{j,t} = - \rho^{t} VOLL^{e} \quad\quad \left( {P_{j,t}^{e,d} } \right) $$
(30)
$$ - \lambda_{2}^{j,t} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{4}^{j,t} + \bar{\mu }_{4}^{j,t} = 0\quad\quad \left( {Q_{j,t}^{e,d} } \right) $$
(31)
$$ \lambda_{1}^{j,t} + \lambda_{3}^{j,t} = 0\quad \quad\left( {P_{j,t}^{inj} } \right) $$
(32)
$$ \lambda_{2}^{j,t} + \lambda_{4}^{j,t} = 0\quad\quad \left( {Q_{j,t}^{inj} } \right) $$
(33)
$$ \begin{aligned} & - 2 G_{j,j} \lambda_{3}^{j,t} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{7}^{j,t} - \bar{\mu }_{7}^{j,t} + 2 B_{j,j} \lambda_{4}^{j,t} \\ & - \mathop \sum \limits_{{o\left( {o \ne j} \right)}}^{NB} \begin{array}{*{20}c} {\left[ {G_{j,o} \left( {\lambda_{3}^{j,t} + \lambda_{3}^{o,t} } \right) - B_{j,o} \left( {\lambda_{4}^{j,t} + \lambda_{4}^{o,t} } \right) } \right]} \\ { } \\ \end{array} \\ & + G_{j,o} \left( {\lambda_{5}^{j,o,t} - \lambda_{5}^{o,j,t} } \right) - B_{j,o} \left( {\lambda_{6}^{j,o,t} + \lambda_{6}^{o,j,t} } \right) = 0\quad\quad \left( {V_{j,t} } \right) \\ \end{aligned} $$
(34)
$$ \begin{aligned} & \mathop \sum \limits_{{o\left( {o \ne j} \right)}}^{NB} \left[ {B_{j,o} \left( { - \lambda_{3}^{j,t} + \lambda_{3}^{o,t} } \right) - G_{j,o} \left( {\lambda_{4}^{j,t} - \lambda_{4}^{o,t} } \right) } \right] \\ & - B_{j,o} \left( {\lambda_{5}^{j,o,t} - \lambda_{5}^{o,j,t} } \right) - G_{j,o} \left( {\lambda_{6}^{j,o,t} - \lambda_{6}^{o,j,t} } \right) \\ & + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{6}^{j,t} - \bar{\mu }_{6}^{j,t} = 0 \quad\quad \left( {\theta_{j,t} } \right) \\ \end{aligned} $$
(35)
$$ \lambda_{5}^{j,o,t} - \lambda_{7}^{j,o,t} = 0 \quad\quad \left( {PL_{j,o,t} } \right) $$
(36)
$$ \lambda_{6}^{j,o,t} - \xi_{j,o} \lambda_{7}^{j,o,t} = 0\quad\quad \left( {QL_{j,o,t} } \right) $$
(37)
$$ \lambda_{7}^{j,o,t} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{5}^{j,o,t} - \bar{\mu }_{5}^{j,o,t} = 0 \quad\quad \left( {SL_{j,o,t} } \right) $$
(38)
$$ c_{p} \pi_{j}^{'} \left( {\frac{{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{2}^{j,o,t} - \bar{\tau }_{2}^{j,o,t} } }}{{\sqrt {\left( {\pi_{j}^{'} } \right)^{2} - \left( {\pi_{o}^{'} } \right)^{2} } }} - \frac{{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{2}^{o,j,t} - \bar{\tau }_{2}^{o,j,t} }}}{{\sqrt {\left( {\pi_{o}^{'} } \right)^{2} - \left( {\pi_{j}^{'} } \right)^{2} } }}} \right) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{3}^{j,t} - \bar{\tau }_{3}^{j,t} = 0\quad\quad \left( {\pi_{j,t} } \right) $$
(39)
$$ \mathop \sum \limits_{{s \in GS_{j} }} A_{j} \gamma_{1}^{j,t} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{5}^{s,t} + \bar{\tau }_{5}^{s,t} = 0 \quad\quad \left( {v_{s,t} } \right) $$
(40)
$$ \begin{aligned} - \mathop \sum \limits_{{p \in P_{f,j} }} \gamma_{1}^{j,t} + \mathop \sum \limits_{{p \in P_{t,j} }} \gamma_{1}^{j,t} \hfill \\ + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{1}^{j,o,t} - \bar{\tau }_{1}^{j,o,t} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{2}^{j,o,t} + \bar{\tau }_{2}^{j,o,t} = 0 \quad\quad \left( {f_{j,o,t}^{p} } \right) \hfill \\ \end{aligned} $$
(41)
$$ - \tau_{4}^{j,t} - \tau_{6}^{j,t} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tau }_{7}^{j,t} - \bar{\tau }_{7}^{j,t} = - \rho_{t} \cdot VOLL^{h} \quad\quad \left( {P_{j,t}^{h,d} } \right) $$
(42)
$$ \mathop \sum \limits_{{k \in HH_{j} }} (\frac{{ - \gamma_{1}^{j,t} }}{{C_{gh}^{k} }} + \bar{\tau }_{7}^{j,t} ) = \rho_{t} \partial F_{c,i} \left( {P_{k,t}^{h} } \right)/\partial P_{k,t}^{h} \quad\quad \left( {P_{k,t}^{h} } \right) $$
(43)

As the decisions on binary variables were made in the upper-level problem, these variables are fixed in the lower-level problem and it is possible to formulate the dual form of the lower-level problem [19]. In other words, the lower-level problem is reflected as a set of constraints that ensures the feasibility of the decisions made in the upper-level problem. The dual formulation of the lower-level problem is used to transform the lower-level optimization problem into a set of constraints. In addition to the primal and dual constraints of the lower-level problem, the strong duality condition that is shown in (44), is formulated as a constraint. This constraint shows that the objective of the primal form of the lower-level problem is equal to the objective of its dual form. Therefore, the lower-level problem is formulated as a set of constraints represented by (4)–(26), (28)–(43) and (44). The constraints (4)–(26) are corresponding to the primal form of the lower-level problem, while (28)–(43) are associated with the dual form. In (43), \( C_{gh}^{k} \) is a constant representing the conversion factor of natural gas to heat for heater k. The left-hand side of this constraint is linear. The right-hand side is the derivative of cost function with respect to the heat energy for heater \( k \) which is the marginal cost for the heater. Assuming a quadratic cost function, the marginal cost function is also a linear function. Therefore, the right-hand side of this equation is linear. The marginal cost function can be approximated by piece-wise linear representation. Here, the lower-level problem is represented by a set of primal and dual constraints which form the feasible region for the upper-level problem. Using the primal and dual constraints, the bi-level optimization problem is transformed into a single level optimization problem.

$$ OP_{primal} = OP_{dual} $$
(44)

In the presented formulation, all nonlinear terms are transformed into linear form. In this section, the nonlinear constraints are listed and the linearization approach is presented. These nonlinear terms are formed as a result of binary to continuous variable multiplication in the dual formulation and the AC power flow constraints. In (27) there are three types of binary-to-continuous terms, which are associated with the generator, distribution line, and pipelines, respectively. The binary decision variables associated with the electricity distribution lines are incorporated in the admittance matrix as illustrated in (10). The constraints (11)–(14) contain 10 binary-to-continuous terms and (34) and (35) have 8 distinguished binary-to-continuous terms. As mentioned in the previous part, (20) and (21) are the linearized form of the nonlinear formulation (45). Once the binary variable (\( UZ_{p} \)) in (45) is set to one, the first equality constraint will be presented as two inequality constraints as shown in (21) where both inequality constraints are binding. Once the binary variable (\( UZ_{p} \)) is set to zero, the inequality constraints given in (21) are relaxed, i.e. the natural gas flow in the disrupted pipeline that connects two nodes is not dependent on the difference between the nodal pressures at the nodes. Also, the natural gas flow is set to zero as shown in (20). Other binary-to-continuous nonlinear terms are linearized using the same technique.

$$ f_{j,o,t}^{p} = \left\{ {\begin{array}{*{20}l} { \frac{{C_{p} \left( {\pi_{j}^{'} \pi_{j,t} - \pi_{o}^{'} \pi_{o,t} } \right)}}{{\sqrt {\left| {\left( {\pi_{j}^{'} } \right)^{2} - \left( {\pi_{o}^{'} } \right)^{2} } \right|} }}} & {UZ_{p} = 1} \\ 0 & {UZ_{p} = 0} \\ \end{array} } \right. $$
(45)

The preventive reinforcement strategy is procured through several steps in which the resilience of microgrid at each step is measured based on the reinforcement strategy for generation and distribution components. Figure 2 shows the process to improve the resilience of the microgrid using successive reinforcements. The solution of the bi-level optimization problem at each step procures the vulnerable components that should be reinforced in the next step. The iterative process for reinforcing the energy conversion and distribution components continues until the operator’s anticipated level of resilience is achieved. In order to quantify the resilience measure, the resilience index (r) is formulated as (46). Here, \( \gamma \) and \( \gamma_{0} \) are the expected operation costs of the microgrid in normal and contingency conditions respectively and \( M \) is the total available resources for disruptions. The resilience index shows the vulnerability of microgrid to deliberate disruptions at each step. The lower the resilience index is, the more vulnerable the microgrid is to deliberate disruptions. Therefore, the resilience index increases as the microgrid components are reinforced against disruptions.

Fig. 2
figure 2

Preventive reinforcement procedure

Full size image
$$ r = e^{\frac{{\gamma_{0} - \gamma }}{M}}$$
(46)

3 Case study

In the case study, an islanded microgrid with 13 nodes, 13 electricity distribution lines, 13 electricity demands, 7 heat demands, 7 natural gas pipelines, and 5 CHP units is considered. The conversion efficiency of natural gas to electricity and natural gas to heat for each CHP is 34% and 50% respectively. The data related to the natural gas pipelines and the electricity distribution lines, as well as the characteristics of CHP units, are presented in Tables 1 and 2 respectively. As the equipment used for heat transfer (such as pumps or fans) use electricity, disruption in electricity supply at nodes that result in total electricity demand curtailment will also cause total curtailment of heat demand. The electricity and heat demands and their respective values of lost load (VOLL) are listed in Table 3. The assigned VOLL determines the prominence of demands to be served. Here, the constant of natural gas, \( c_{p} \), is dependent on length, friction, diameter, temperature, and gas composition [20]. The total available natural gas is equal to 50 standard cubic meter (SCM) in this case study. The phase angles, voltage magnitude, and natural gas pressure at nodes are restricted between − π to π, 0.95–1.05 per unit, 54 to 57 bar, respectively. The resistance and inductive reactance of the distribution network cables are \( r = 0.0918\;\Omega /1000\;{\text{m}} \) and \( x = 0.1213\;\;\Omega /1000\;{\text{m}} \) respectively. CPLEX 12.6 is used as the solver for this case study.

Table 1 Electricity and natural gas networks’ characteristics
Full size table
Table 2 CHP unit characteristics
Full size table
Table 3 Electricity and heat demand
Full size table

The disruption costs for generators, natural gas pipelines, and electricity distribution lines are $4500, $3500 and $1500 respectively. The required resources to disrupt gas-fired distributed generation unit, distribution line and natural gas pipeline are 10 times higher than the reinforcement cost. The available budget for disruption in islanded microgrid is $10000. The following cases were considered to evaluate the effectiveness of proposed preventive reinforcement strategy on enhancing the energy supply resiliency:

Case 1 :

Sequential reinforcement of electricity and natural gas networks (deterministic solution).

Case 2 :

Sequential reinforcement of electricity and natural gas networks (stochastic solution).

3.1 Case 1

The reinforcement strategy is continued until no generation, distribution and natural gas pipeline can be disrupted considering the available resources for the attacker. Table 4 shows a selected number of steps in the sequence of reinforcements in the microgrid’s electricity and natural gas network. As shown in this table, as more reinforcements were made through the steps, the operation cost of the microgrid decreases as a result of less electricity and heat demand curtailment and reduction in the number of vulnerable components in the electricity and natural gas networks. For example, at step 4 of reinforcement, the operation cost is decreased from $25514 to $22655 as a result of less electricity and heat demand curtailment. The electric load curtailment at step 4 is 882 kW which is decreased from 1617 kW in step 3. The developed reinforcement strategy at this step led to improvement in the resilience index. The resilience index is increased from 0.2861 at step 3 to 0.3301 at step 4. The increase in the resilience index requires more investment in reinforcing the electricity and natural gas network components. As shown in Table 4, the reinforcement cost is increased from $29000 at step 3 to $38000 at this step. The increase in the reinforcement cost is because of reinforcing L5, L6, L10 in electricity distribution network and P7 in the natural gas distribution network. As shown in Table 4, the reinforcement cost increases with the increase in the number of reinforced components.

Table 4 Outcome of sequential preventive reinforcement
Full size table

3.2 Case 2

In this case, the uncertainties in demand were captured in microgrids by generating 3000 scenarios using Monte Carlo simulation. The error in the forecasted demand is determined by employing truncated normal distribution with a mean value equals to the forecasted demand and a standard deviation equals to 10% percentage of the forecasted demand. As such problem has a large computation burden while there are several similar scenarios in which can be reduced to much smaller number of scenarios. Fast backward, fast backward/forward and fast backward/backward are among selected scenario reduction techniques. Here, backward/forward method is utilized to procure twelve district scenarios. The probability of the scenario discussed in Case 1 is 24% and eleven other scenarios have the probability of 2%, 1.5%, 1.5%, 4%, 3%, 3%, 10%, 7.5%, 7.5%, 18% and 18%.

In step 0, the impact of disruption on electricity and natural gas networks is evaluated with no preventive reinforcement in these networks. In normal condition and before any disruptions, the expected operation cost of the microgrid is $530. The vulnerable components, in this step, considering the budget attack as $10000, are distribution lines L7 as well as the pipeline P1 and gas-fired unit G3. The deliberate disruption in this step will lead to electricity and heat demand curtailments in all nodes. The expected operation cost increases from $530 in normal condition to $82,098 in this step. Figure 3 shows the topology of the network with the presumed outages. As shown in this figure, the electricity demands in all nodes are curtailed as there is no gas supply for G1, G2, G4, G5 and G3 is disrupted. The heat demands in nodes 2, 4-6, 8, 9, 11, and 13 are curtailed as disruption of P1 prevent natural gas delivery to these nodes. The resilience index, in this step, is 0.0003.

Fig. 3
figure 3

Disruption in step 0 of Case 2

Full size image

In the first step of reinforcement, distribution lines L7 as well as the pipeline P1 and gas-fired unit G3 are reinforced. Therefore, the disruption cost for the reinforced line is $3000, the disruption cost for pipeline P1 is $7000, and the disruption cost for gas-fired unit G3 is $9000. In the first step, the distribution lines L2, L6, and L7 as well as pipeline P3 are disrupted. Figure 4 shows the topology of the network with the presumed outages.

Fig. 4
figure 4

Disruption in step 1 of Case 2

Full size image

As the natural gas pipeline P3 supplies nodes 6, 8, 9, and 11 in the natural gas network of the microgrid, disruption of this pipeline will lead to electric and heat load curtailment at these nodes. The heat load on nodes 4, 6, 8, 9, and 11 are curtailed, as electricity curtailment in node 4 led to heat curtailment on this node. In this step, the electricity network of the microgrid is divided into three electrically islanded networks consisting of nodes {1, 2, 12, 13}, nodes {3, 4} and nodes {5, 6, 7, 8, 9, 10, 11}. The operation cost, in this step, is $63263 and the resilience index is 0.0019.

Table 5 shows the steps in the sequence of reinforcements in the microgrid’s electricity and natural gas network considering the uncertainties in microgrid’s demand. Because of the uncertainty in demand, the expected operation cost at initial step of reinforcement is increased compared to the deterministic solution. The expected operation cost of the microgrid at step 0 is $82098 which is 4.8% more than that in Case 1. In addition, the expected operation of the microgrid with resiliency index equal to one is 8.81% higher than the operation cost in Case 1.

Table 5 Outcome of sequential preventive reinforcement with uncertainties in demand
Full size table

Similar to Case 1, as more reinforcements were made through the steps, the expected operation cost of the microgrid decreases because of less electricity and heat demand curtailment and reduction in the number of vulnerable components in the electricity and natural gas networks. The expected operation cost microgrid at step 4 is significantly decreased (i.e. 25.58%) compared to that in step 3 and the resiliency index is increased from 0.0056 at step 3 to 0.0250 at step 4.

4 Conclusion

This paper presents an approach for strategic reinforcement and optimal operation of microgrids with electricity and natural gas networks that are exposed to deliberate disruptions considering the uncertainties in electricity and heat demand. The output of the presented approach determines the highest expected operation cost of the microgrid as a result of the deliberate disruption. A reinforcement strategy is proposed based on the determined vulnerable components in the interdependent electricity and natural gas networks. As a result of the proposed reinforcement strategy, the cost of disruption for the reinforced components is increased and therefore, the disrupted components are less vulnerable to outages in next iterations. Consequently, the penalty associated with the curtailed demand is decreased through the iterations as shown in a case study. The proposed resilience measure shows the resilience of the microgrid as it is exposed to deliberate disruptions. It is shown that as more components are reinforced in the microgrid’s interdependent energy networks, the reinforcement cost is increased and the expected operation cost is decreased.