1 Introduction

Smart grids have played an important role in the security of grid operations and the stability of energy supply [1]. A smart grid is an integration of the power network and information network. Compared to traditional electrical grids, smart grids are environmentally-friendly and more intelligent in the information communication. Energy generators in traditional electrical grids, which primarily consume fossil fuel as their energy source, produce about 41% of the whole world greenhouse gases and have a huge negative effect on the environment [2]. With the appearance of problems with fossil energy depletion and the greenhouse effect, energy generation in smart grids through renewable energy resources, such as wind power, solar power, and geothermal power, has become an attractive alternative and contributes to solving the problem [3,4,5]. Furthermore, in traditional electrical grids, information is delivered in a single direction. Only grids can manage and control energy to satisfy the demand of consumers. Grids and consumers can both participate in the energy management in smart grids via the information network [6], which contributes to promoting the utilization of renewable energy resources and reducing the emission of greenhouse gases.

In order to improve the functions of smart grids on the demand side, the concept of demand-side management (DSM) is proposed to reduce the energy cost of consumers, shift energy consumption from peak hours to reduce peak-to-average ratio (PAR) and balance power supply and demand [7,8,9]. DSM programs can be conducted effectively primarily due to their dynamic pricing schemes such as time-of-use (ToU) pricing [10], real-time pricing (RTP) [11] and critical-peak pricing. Most of consumers who want to reduce their costs are willing to shift their energy consumption from peak demand hours to off-peak hours because of the high price in peak hours. In fact, consumers in demand-side primarily refer to the users who consume energy to satisfy their requirements as residential users, commercial users and industrial users. However, residential DSM has attracted more attention due to residential users being responsible for about 40% of global energy consumption [12]. Moreover, DSM has become more significant for smart grids especially when renewable energy generation is introduced into the smart house. Photovoltaic (PV) generation, which has been widely applied as a type of renewable energy generation, can be installed in the common household for providing energy [13, 14]. Since PV only works during daylight, PV generation usually requires a storage system to store the produced energy and then this storage provides energy for loads during peak hours to reduce the user’s cost [15]. However, it brings more challenges for DSM to schedule energy consumption when storage is introduced into the DSM, such as the optimization of storage capacity [16, 17]. Storage capacity, which is related to various aspects (user’s loads, price policy and characteristics of renewable energy sources), is an important factor for the cost of residential users. Users must pay more for storage depreciation cost when the PV is supplied with a large capacity storage system. However, storage with small capacity cannot satisfy user’s demand during peak hours, which causes the rise of energy costs. Therefore, optimization of storage capacity is a non-negligible problem for PV-storage systems in DSM programs.

Recently, many researchers have proposed various DSM programs to manage the energy consumption of residential users. The problem of optimizing storage capacity in DSM programs has also been studied in some literatures with implementing different methods. The authors [18] propose a mixed-integer linear programming framework for DSM to optimize the capacity of PV and an energy storage system when considering the variability of loads during weekday-weekend and different seasons. Guo et al. [19] provided an online control algorithm, which incorporated renewable energy generation, home appliances and battery storage, to achieve a clear trade-off between users’ cost and energy storage capacity. Moreover, the authors [20] focused on the Monte Carlo and particle swarm optimization to schedule capacity of wind turbines and batteries in smart households while considering the statistical characters of the load, renewable energy generation and energy price. Specifically, different from aforementioned methods, a game-theoretic method, which has been extensively employed as a solution to solve the problems of optimization for DSM [21,22,23], is also studied in DSM with storage in literature [24,25,26,27,28]. The authors [24] adopted a dynamic non-cooperative repeated game to determine optimal energy trading amounts for the next day considering the existence of community energy storage devices. Literature [25] designed an auction-based mechanism to determine the internal prices of renewable energy sources with a non-cooperative Stackelberg game in the scenario where each residential unit has an energy storage and they can share storage with the controller. The authors [27] proposed a Stackelberg game among the utility provider and users to minimize their cost when considering energy storage devices selling back energy. Adika et al. [28] formulated a non-cooperative game to reduce users’ energy bills via coordinating the charging and discharging of batteries with a high penetration of household batteries.

However, few literatures consider the optimization of the storage capacity in DSM programs with game-theoretic methods. In this paper, based on the ToU pricing mechanism and battery storage, we primarily focus on combining the optimization of battery capacity and energy consumption with the non-cooperative game-theoretic method under the scenario in which each user has a PV-battery system and other household appliances. Compared to previous research on DSM programs with game theory, residential users in the scenario not only consider energy consumption behavior but also battery capacity in order to reduce energy cost. In brief, the main contributions of this paper can be summarized as follows: 1) An energy consumption management program is proposed for multiple residential users using a game-theoretic method to obtain the scheduled energy consumption and optimal capacity for reducing users’ costs in three approaches, including shifting loads from on-peak hours to off-peak hours, selling energy back to the grid by PV generation and providing energy for users during peak demand hours with using batteries; 2) The existence of the Nash equilibrium and optimal battery capacity for the proposed on-cooperative game approach are both proved mathematically; 3) Simulations are conducted to confirm the effectiveness and efficiency of the approach and the results show that not only the cost of the residential user can be reduced but the PAR of the grid is also reduced.

The rest of this paper is organized as follows. The system model is introduced in Sect. 2. In Sect. 3, we formulate the non-cooperative game approach and prove the existence of the Nash Equilibrium and optimal battery capacity. The simulation is presented to verify the theoretical analysis in Sect. 4. Finally, Sect. 5 concludes this paper.

2 System model

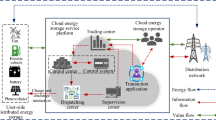
As shown in Fig. 1, a scenario is considered with multiple residential users and a single utility company (energy source) as part of the wholesale electricity market. Assume that each user owns a smart meter with the function of energy consumption scheduling. All smart meters are connected to the power line and information network. Users receive price policy and send desired demand to the company via the information network. Users in the scenario have shiftable and unshiftable loads and a PV-storage system, all of which are controlled by the DSM except for the unshiftable loads, which primarily refer to household appliances such as lights and refrigerators, whose operation time is stable and unscheduled. Shiftable loads can be scheduled and are prone to delay, such as washing machines and EVs. PV offers energy for users’ loads and charges the battery in the daylight. Users can sell surplus energy back to the company after PV has satisfied the loads and battery.

Fig. 1
figure 1

A scenario contains N residential users with smart meters, a PV-storage system, information network, and power line

Full size image

2.1 Energy consumption model

Suppose there are N residential users in the scenario with a set of \({\mathcal{N}} = \left\{ {1,2, \ldots ,N} \right\}\). A day is divided into H time slots, which is denoted by \({\mathcal{H}} = \left\{ {1,2, \ldots ,H} \right\}\). For residential user \(n \in {\mathcal{N}}\), let l h n denote the total energy consumption of unshiftable and shiftable loads in time slot \(h \in {\mathcal{H}}\), and the daily energy consumption of loads for user n is denoted by:

$$\varvec{l}_{n} = \left[ {l_{n}^{1} , \ldots ,l_{n}^{h} , \ldots ,l_{n}^{H} } \right]$$
(1)

Due to the existence of a PV-battery system, the PV-battery and utility company can offer the energy for household loads during working time. Let x h n denote the energy demand sent to the utility company by user n in time slot \(h \in {\mathcal{H}}\), and the daily energy demand is formulated as:

$$\varvec{x}_{n} = \left[ {x_{n}^{1} , \ldots ,x_{n}^{h} , \ldots ,x_{n}^{H} } \right]$$
(2)

The total energy demand across all users in time slot h can be calculated as:

$$X_{h} = \sum\limits_{n = 1}^{N} {x_{n}^{h} }$$
(3)

To calculate the PAR in the total energy demand, the daily and average energy demand are calculated as follows [29]:

$$X_{peak} = \mathop {\hbox{max} }\limits_{{h \in {\mathcal{H}}}} X_{h}$$
(4)

and

$$X_{avg} = \frac{1}{H}\sum\limits_{{h \in {\mathcal{H}}}} {X_{h} }$$
(5)

Therefore, the PAR in total energy demand is expressed as:

$${\text{PAR}} = \frac{{X_{peak} }}{{X_{avg} }} = H\frac{{\mathop {\hbox{max} }\limits_{{h \in {\mathcal{H}}}} X_{h} }}{{\sum\limits_{{h \in {\mathcal{H}}}} {X_{h} } }}$$
(6)

2.2 Energy cost model

Energy cost function refers to a type of pricing mechanism formulated by utility companies. An effective cost function can be employed to encourage residential users to positively take part in their energy consumption scheduling programs. To fairly charge the cost of energy consumption by users, we make the following assumptions:

  1. 1)

    A utility company has a responsibility for satisfying the demand of all users at any time, hence the energy cost in any time slot \(h \in {\mathcal{H}}\) is a function of the total energy demand Xh by N users.

  2. 2)

    The energy cost in a certain time slot is always increasing and smooth or at least a piecewise smooth function with respect to the energy demand Xh.

  3. 3)

    The cost in peak demand hours is higher than that in off-peak demand hours. That is, the cost of the user is not only related to the energy amount they consume but also the time slot when they consume.

Based on the above assumptions, a quadratic cost function is utilized in most of the literature due to the nature of the increasing and strictly convex function [9, 30], and the function is:

$$C_{h} \left( {X_{h} } \right) = a_{h} X_{h}^{2} + b_{h} X_{h}$$
(7)

where ah > 0, bh ≥ 0 are fixed parameters with high values in peak demand hours; Ch(Xh) is the total cost of N users for energy demand Xh in time slot h. Therefore, the cost of user n can be calculated as:

$$C_{n,h} = \left( {a_{h} X_{h} + b_{h} } \right)x_{n}^{h} = p_{h} \left( {X_{h} } \right)x_{n}^{h}$$
(8)

where ph(Xh) represents the energy price in time slot h. According to the price model ph(Xh), the model can guarantee the growth of the energy price with the increase of Xh, which will effectively convince the consumers to shift their peak-time consumption to off-peak hours. Furthermore, the energy price can affect users ’consumption behavior via regulating ah and bh in different time slots. Following the adopted energy price model, the total cost for residential user n in a whole day can be calculated as follows:

$$C_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} } \right) = \sum\limits_{h = 1}^{H} {\left[ {p_{h} \left( {X_{h} } \right)x_{n}^{h} } \right]}$$
(9)

where \(\varvec{x}_{ - n} = \left[ {\varvec{x}_{1} , \cdots ,\varvec{x}_{n - 1} ,\varvec{x}_{n + 1} , \cdots ,\varvec{x}_{N} } \right]\) denotes the energy demand across all users except user n. According to (9), residential users can reduce their energy cost by using the following approaches: 1) making the best use of the PV-battery system to reduce the energy purchased from the utility company; 2) shifting loads from peak hours to off-peak hours to avoid the higher energy price.

2.3 PV generation

Generally, in the hybrid system containing PV-battery generation, the schedule of energy from the utility company, the PV and battery storage is a complex process for a household energy management system [31]. Considering that the cost of energy from a PV system is cheaper than that from the utility company, the priorities of energy obtained from the PV in this paper are defined as follows: at any working time in the daylight, the energy output can be employed to provide energy for household loads and then the batteries; when energy is still surplus after satisfying the loads and batteries, it can be sold back to the utility company allowing for making a profit from trading. For user n, assume that the energy output of PV generation is en,h ≥ 0 in time slot h. PV provides energy e l n, h  ≥ 0 for household loads and energy e b n, h  ≥ 0 for charging the batteries respectively. Hence, surplus energy is en,h − e l n, h  − e b n, h  ≥ 0, in which en,h − e l n, h  − e b n, h  = 0 which represents that the user has no surplus energy to sell. Accordingly, the profit that user n is making from trading in a whole day is equal to:

$$G_{n} = \sum\limits_{h = 1}^{H} {\lambda_{s} } \left( {e_{n,h} - e_{n,h}^{l} - e_{n,h}^{b} } \right)$$
(10)

where λs > 0 is the energy selling price in cents/kWh. At present, the profit making from trading is usually conducted via energy price subsidies by the government in China. Currently, the subsidy standard λs is 6.3 cents/kWh for distributed PV generation [32].

The cost of generation should be considered in the users’ daily cost. In this paper, the cost of PV generation is calculated by dividing the total cost of PV, including those for investment, operation, and maintenance, which is expressed as the cost of PV generation per unit electricity [18]. Hence, the daily cost of PV generation can be expressed as follows:

$$C_{n}^{PV} = \sum\limits_{h = 1}^{H} {\lambda_{n}^{PV} } e_{n,h}$$
(11)

where λ PV n is the cost of generation per unit energy in cents/kWh. It depends on many factors, such as type and size of the PV, solar resources in the area and maintenance costs.

2.4 Energy storage system

The storage system is an indispensable appliance for PV generation and is also a significant object of energy consumption scheduling in DSM. In this scenario, the chief task of the battery is to store the surplus energy after PV generation, satisfying household loads. And then, the battery provides energy for loads in peak demand hours to reduce energy cost. Presently, a variety of batteries with different materials and technologies are available on the market, such as Sodium/Sulfur batteries, Zinc/Bromine batteries and lithium-ion batteries [33]. These batteries can only be charged and discharged for a finite number of times. Thereby, the depreciation cost cannot be ignored, which varies with materials, technologies and capacities. It is usually defined as a quadratic function of charging/discharging power or a linear function of capacity [20, 34]. In this paper, the depreciation cost is assumed to be a linear function of battery capacity. Suppose battery capacity of the residential user n is yn kWh, which can be scheduled within a certain range:

$$y_{n} \in \left[ {y_{n}^{l} ,y_{n}^{u} } \right]$$
(12)

where y l n is the minimum capacity and y u n is the maximum capacity. Let C bat n denote the daily depreciation cost of the battery which can be expressed as follows:

$$C_{n}^{bat} \left( {y_{n} } \right) = \lambda_{n}^{bat} y_{n}$$
(13)

where λ bat n is the depreciation cost per unit of battery capacity in cents/kWh and is correlated with the type of battery. The depreciation cost (13) is a linear increasing function with respect to battery capacity yn. Users have to pay more depreciation cost with the increasing of battery capacity. However, users will pay a higher energy cost to the utility company if capacity is too small to store sufficient energy from PV generation. Therefore, the optimal battery capacity contributes to reducing user’s daily cost.

Meanwhile, a number of different battery parameters must be considered, such as charging and discharging efficiency. Due to the conversion loss of the battery in the process of charging/discharging, let 0 < ηch < 1 and 0 < ηdis < 1 represent battery charging/discharging efficiency respectively. Suppose the energy state of the battery for user n in a whole day is expressed as:

$$\varvec{s}_{n} = \left[ {s_{n}^{1} , \cdots ,s_{n}^{h} , \cdots ,s_{n}^{H} } \right]$$
(14)

Since there is a limitation of battery capacity, we can determine the following inequality constraints:

$$0 \le s_{n}^{h} \le y_{n}$$
(15)

Let binary variables k h ch and k h dis represent the operation patterns of the battery in time slot h. k h ch =1 and k h dis =1 refer to the charging and discharging pattern respectively. A battery cannot charge and discharge at the same time, therefore:

$$k_{ch}^{h}\,+\,k_{dis}^{h} \le 1$$
(16)

The energy state of the battery in any time slot h can be calculated as follows:

$$s_{n}^{h + 1} = s_{n}^{h} + \eta_{ch} e_{n,h}^{b} - 1/\eta_{dis} \cdot b_{n,h}^{l}$$
(17)

In (17), e b n, h is the energy charged to the battery by PV generation and b l n, h is the energy discharged from the battery for satisfying user’s loads. The maximal charging and discharging energy should be lower than a certain value, thus e b n, h and b l n, h is satisfied by:

$$e_{n,h}^{b} \le k_{ch}^{h} B_{ch}$$
(18)

and

$$b_{n,h}^{l} \le k_{dis}^{h} B_{dis}$$
(19)

where Bch is the maximal energy charged to the battery and Bdis is the maximal energy discharged from the battery.

For user n, the total household loads consume energy l h n in time slot h, where PV generation provides e l n, h , the battery provides b l n, h and the utility company provides x h n . On the basis of the energy balance principle, x h n , e l n, h , b l n, h , you can satisfy the following equation:

$$l_{n}^{h} = x_{n}^{h} + e_{n,h}^{l} + b_{n,h}^{l}$$
(20)

According to (20), one can see that the energy consumption scheduling of users can be translated into scheduling the purchasing strategy from the utility company and usage strategy of the PV-battery system. When the energy users consumption in time slot h is lower than the energy provided by the PV generation or battery, there is no need for the user to buy energy from the company. When energy consumption is more than the provided energy, the user only needs to buy the remaining energy after PV generation and the battery satisfy the loads.

3 Game formulation and analysis

3.1 Daily cost minimization

Household energy consumption scheduling becomes complicated since the existence of a PV-battery system. Users have to pay for the cost of energy purchased from the utility company, the cost of PV generation and the depreciation cost of the battery. In addition, users can make a profit via selling energy back to the company. Hence, the total cost of user n in a whole day can be calculated as:

$$F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right) = C_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} } \right) + C_{n}^{bat} \left( {y_{n} } \right) + C_{n}^{PV} - G_{n}$$
(21)

According to (9)–(13), user n’s daily cost can be written as:

$$\begin{aligned} F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right){ = }\sum\limits_{h = 1}^{H} {\left[ {p_{h} \left( {X_{h} } \right)x_{n}^{h} } \right]} + \lambda_{n}^{bat} y_{n} + \lambda_{s} \sum\limits_{h = 1}^{H} {e_{n,h}^{b} } \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; +\, \lambda_{s} \sum\limits_{h = 1}^{H} {e_{n,h}^{l} } +\, \left( {\lambda_{n}^{PV} - \lambda_{s} } \right)\sum\limits_{h = 1}^{H} {e_{n,h} } \hfill \\ \end{aligned}$$
(22)

In this scenario, if PV generation supplies a large capacity battery that cannot be fully charged, a part of the storage space is wasted, which will increase user’s daily cost. Therefore, battery capacity in the range of [y l n , y u n ] can be fully charged by PV generation in its working time. PV provides energy e b n, h for the battery in time slot h and the battery will obtain ηche b n, h considering the charging efficiency. That is:

$$\lambda_{s} \sum\limits_{h = 1}^{H} {e_{n,h}^{b} } = \lambda_{s} y_{n} /\eta_{ch}$$
(23)

Additionally,

$$\sum\limits_{h = 1}^{H} {e_{n,h}^{l} } = \sum\limits_{h = 1}^{H} {l_{n}^{h} } - \sum\limits_{h = 1}^{H} {x_{n}^{h} } - \sum\limits_{h = 1}^{H} {b_{n,h}^{l} }$$
(24)

where ∑  H h=1 b l n, h  = ηdisyn.

Therefore, (22) is equal to:

$$F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right){ = }\sum\limits_{h = 1}^{H} {\left( {p_{h} \left( {X_{h} } \right) - \lambda_{s} } \right)x_{n}^{h} } + \lambda_{n}^{bat + } y_{n} + \varphi$$
(25)

where

$$\lambda_{n}^{bat + } = \lambda_{n}^{bat} + \lambda_{s} /\eta_{ch} - \eta_{dis} \lambda_{s}$$
(26)

and

$$\varphi = \lambda_{s} \sum\limits_{h = 1}^{H} {l_{n}^{h} } + \left( {\lambda_{n}^{PV} - \lambda_{s} } \right)\sum\limits_{h = 1}^{H} {e_{n,h} }$$
(27)

Our target is to find an optimal battery capacity and the best strategy of energy consumption for all users so that the daily cost of each user will be minimized:

$$\mathop {\hbox{min} }\limits_{{x_{n}^{h} \in \varvec{x}_{n} ,\forall n \in {\mathcal{N}}}} \;F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)$$
(28)

where constraints are (15)–(20). The best energy demand strategy and optimal battery capacity can be found by searching the optimal solution of problem (28) in the feasible region.

3.2 Non-cooperative game formulation

Game-theoretic methods can be employed to optimize energy consumption of users because they can capture the features of interactions among users. Games can be divided into cooperative games and non-cooperative games according to the presence or absence of agreements among the players. Generally, players in the cooperative game aim to minimize/maximize the total group cost/profit of all players and then search the overall optimal solution for each player by solving the optimization problem; while in the non-cooperative game, players only aim to minimize/maximize their own cost/profit and then search the Nash equilibrium. In this paper, considering the selfishness of human beings and that each user is only concerned about his/her cost, we formulate the model via a non-cooperative game.

Consequently, the non-cooperative game among users can be formulated as follow.

  1. 1)

    Players: users in the set \({\mathcal{N}}\);

  2. 2)

    Strategies: each user \(n \in {\mathcal{N}}\) selects its strategy by scheduling household loads to maximize its payoff;

  3. 3)

    Payoffs: \(P_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\) for user n is defined as follows:

    $$P_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right) = - F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)$$
    (29)

Based on the payoff function of residential users, they are willing to schedule their shiftable loads to minimize their cost until the Nash equilibrium of the game is reached. Let \(\left( {\varvec{x}_{1}^{*} , \cdots ,\varvec{x}_{n}^{*} , \cdots ,\varvec{x}_{N}^{*} } \right)\) denote the Nash equilibrium and optimal battery capacity is y * n , then:

$$P_{n} \left( {\varvec{x}_{n}^{*} ,\varvec{x}_{ - n}^{*} ,y_{n}^{*} } \right) \ge P_{n} \left( {\tilde{\varvec{x}}_{n}^{*} ,\tilde{\varvec{x}}_{ - n}^{*} ,y_{n} } \right)$$
(30)

and

$$P_{n} \left( {\tilde{\varvec{x}}_{n}^{*} ,\tilde{\varvec{x}}_{ - n}^{*} ,y_{n} } \right) \ge P_{n} \left( {\varvec{x}_{n} ,\tilde{\varvec{x}}_{ - n}^{*} ,y_{n} } \right)$$
(31)

where \(\left( {\tilde{\varvec{x}}_{n}^{*} ,\tilde{\varvec{x}}_{ - n}^{*} } \right)\) denotes the Nash equilibrium corresponding to battery capacity yn. Once the Nash equilibrium of the non-cooperative game among all users is reached, the payoff of user n will be damaged by deviating from x * n , ∀n ∊ N. The existence and uniqueness of the Nash equilibrium are proved mathematically in the following propositions 1 and 2. The proof of propositions 1 and 2 is performed on the basis of fixed battery capacity yn. When battery capacity is determined, the PV-battery system can be taken as a type of household load, whose energy consumption is negative. Energy demand of users can be obtained via scheduling household loads, including shiftable loads and PV-battery systems.

Proposition 1

For user \(n \in {\mathcal{N}}\), daily cost function \(F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\) is continuously differentiable in \(\varvec{x}_{n}\). For each fixed vector \(\varvec{x}_{n}\) and yn, \(F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\) is convex in \(\varvec{x}_{n}\).

Proof

Due to the continuous characteristics of the daily cost function \(F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\), it is continuously differentiable in \(\varvec{x}_{n}\). After calculation, the Hessian of \(F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\) is a positive semi-definite, therefore, \(F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\) is convex in \(\varvec{x}_{n}\) [35].

Proposition 1 shows that the daily cost \(F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\) is continuously differentiable and convex in \(\varvec{x}_{n}\) because the energy cost \(C_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} } \right)\) has a continuous quadratic form with respect to \(\varvec{x}_{n}\). Proposition 1 is the precondition of proving proposition 2.

Proposition 2

For \(\forall n \in {\mathcal{N}},h \in {\mathcal{H}}\), the Nash equilibrium of the non-cooperative game exists and is also unique.

Proof

Since the function \(F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\) is convex in \(\varvec{x}_{n}\), According to the [36, Th. 6], the Nash equilibrium of the non-cooperative game exists and is also unique.

Proposition 3

The unique Nash equilibrium \(\left( {\varvec{x}_{n}^{*} ,\varvec{x}_{ - n}^{*} } \right)\) in the game is Pareto optimality.

Proof

A strategy state is Pareto optimality when no one can increase their payoff by modifying the users’ strategies without damaging other users’ payoff [24]. According to proposition 2, the non-cooperative game has the Nash equilibrium among users and each user has improved its strategy for the highest payoff based on other users’ strategies. That is, no one can increase its payoff without the permission of changing other users’ strategies [37]. Therefore, we can conclude that equilibrium \(\left( {\varvec{x}_{n}^{*} ,\varvec{x}_{ - n}^{*} } \right)\) in the game is the Pareto optimality.

Proposition 2 demonstrates that there is a unique Nash equilibrium of the non-cooperative game for a fixed capacity but the Nash equilibrium will be different along with the change of battery capacity. Based on proposition 3, it shows that the strategy of energy consumption among residential users will reach a Pareto optimality and no user can increase its payoff without damaging other users’ payoffs.

Proposition 4

For battery capacity yn ∊ [y l n , y u n ] and the energy consumption vector \(\varvec{l}_{n}\) of user n, there is a unique battery capacity yn that can make the daily cost function \(F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\) be the minimum.

Proof

See “Appendix A”.

Proposition 4 shows there exits an optimal battery capacity in the range of [y l n , y u n ]. The meaning of y * n can be understood as that there is a specific value of cost \(F_{n} \left( {\varvec{x}_{n} ,\varvec{x}_{ - n} ,y_{n} } \right)\) with a certain battery capacity and only y * n can make the cost minimum. From the above propositions 1–3, one can see that the non-cooperative game we proposed based on the payoff function (29) which can encourage residential users to make a best strategy of energy consumption and optimal battery capacity for reducing their cost.

3.3 Distributed algorithm

A distributed algorithm is proposed to optimize battery capacity and schedule energy consumption of the users. It is implemented based on the ToU pricing policy which can encourage users to participate in energy consumption scheduling. This algorithm shows the interactions among residential users as it is employed in each user’s smart meter, where users select their own strategy according to other users’ strategies. The algorithm progresses by assuming a static battery capacity when the user solves his/her optimization problem (28). Since function (28) is strictly convex, it can be solved by convex programming techniques such as the interior point method (IPM) and will always have a unique solution for the fixed parameters of function [29]. Each of the Nash equilibriums will be reached according to different battery capacities. Comparing the daily costs corresponding to these capacities and the Nash equilibriums, the algorithm will select the minimal cost and obtain the best response strategy and optimal battery capacity. More details about the distributed algorithm for the non-cooperative game are shown in Algorithm 1.

figure a

4 Simulation results

An analytical case study in this section is presented to verify the performance and effectiveness of the proposed game approach for residential users optimizing their battery capacity and scheduling their energy consumption.

In this paper, ToU is adopted and a whole day is divided into H = 24 hours which are classified into different segments with different pricing parameters. According to energy consumption behavior of residential users, a whole day can be divided into three segments: off-peak hours, mid-peak hours and on-peak hours. The interval from 0:00 to 7:00 belongs to off-peak hours due to having the least energy consumption of loads. The intervals from 7:00 to 17:00 and from 22:00 to 24:00 belong to mid-peak hours. Residential users begin to use household loads intensively during the interval from 17:00 to 22:00 and this period belongs to on-peak hours. Each segment has a specific value of ah and bh with maximal value in peak demand hours and minimal value in off-peak demand hours.

In the simulation, assume that there are N = 5 residential users. Each user has between 10 to 15 nonshiftable loads that cannot participate in the energy consumption management, including refrigerator, light, heater and so on. Figure 2 shows the energy consumption distribution of non-shiftable loads in each hour across 5 users. Moreover, we assume that each user has three shiftable loads, including dishwasher (daily consumption: 1.39–1.5 kWh), washing machine (daily consumption: 1.49–1.53 kWh) and electric vehicle (daily consumption: 4 kWh). For the shiftable load dishwasher, we assume that it works 2 hours, 1 hour between 7:00 and 9:00 and 1 hour between 18:00 and 22:00. For the washing machine, it works 1 hour between 19:00 and 22:00. For the electric vehicle, we assume that it can be charged from 22:00 to 24:00 and from 0:00 to 7:00 the day after. As for PV generation, it is obvious that users can benefit more if there are more daylight hours or higher energy output of the PV. Furthermore, energy output and daylight hours have greater influence on the battery capacity optimization when users supply their storage system. However, no matter what the energy output and daylight hours will be, the effectiveness of the proposed method in this paper will not be influenced. Therefore, without loss of generality, we suppose that each smart house in the scenario installs a 2 kW rooftop PV generation system. Energy output in a certain day, which is shown in Fig. 3, is assumed based on the predicted data in [38]. Additionally, user’s battery capacity is assumed in the range of [1.0, 5.0] kWh and the battery can be charged during PV working time from 6:00 to 17:00. The time slots of the discharging battery can be any time except charging time, yet user’s cost is dependent on the discharging time, which will be the least when the battery discharges in the peak demand hours. Hence the time slot of the discharging battery is from 17:00 to 22:00. The maximum energy charged/discharged to/from the battery in an hour are both 1.5 kWh; charging and discharging efficiency of the battery are both 92% [9]; daily depreciation cost of the battery is assumed to be 7.2 cents/kWh [20]. More details about parameters in the simulation can be found in Tables 1 and 2.

Fig. 2
figure 2

Energy consumption of non-shiftable loads across 5 users

Full size image
Fig. 3
figure 3

Energy output of PV generation in a certain day

Full size image
Table 1 Parameters of pricing model
Full size table
Table 2 Parameters of the PV-battery system
Full size table

Figure 4 shows the total energy consumption by 5 residential users in a whole day: Fig. 4a is initial energy consumption without scheduling and Fig. 4b is optimal energy consumption with game approach. In the initial situation, the dishwasher works at 7:00 and 19:00, the washing machine works at 20:00, and the electric vehicle charges from 22:00 to 24:00 and the next day from 0:00 to 2:00. In Fig. 4a, one can see that the maximal consumption achieves 11.65 kWh between 20:00 and 21:00, while the least consumption is only about 0.5 kWh between 2:00 and 6:00. In Fig. 4b, the shiftable loads of 5 users have been shifted across different hours of the day, for example, the charging time slots of the EV have been shifted to the interval from 0:00 to 7:00 in which the energy price is lower than for other time slots.

Fig. 4
figure 4

Energy consumption of residential users

Full size image

Figure 5 shows that the proposed game approach contributes to reducing the PAR in each user’s daily energy demand sent to the utility company and the PAR in the total energy demand. The individual PAR in the figure is calculated as follows:

$${\text{PAR}}_{n} = H\frac{{\mathop {\hbox{max} }\limits_{h \in H} x_{n}^{h} }}{{\sum\limits_{h \in H} {x_{n}^{h} } }}$$
(32)
Fig. 5
figure 5

PAR in each user’s daily energy demand and the PAR in the total daily energy demand by all users

Full size image

In order to demonstrate the advantage of the proposed game approach, we take into account the situation that users take part in the DSM but there is no game behavior among the users. That is, each user optimizes its strategy without considering the influence of other users and will not modify its strategy according to other users’ strategies. We can see that the PAR in the total energy demand which is sent to the utility company is 4.18 in the initial situation. When all users participate in the DSM without game, PAR reduces to 2.66. Furthermore, it declines to 2.13 when the non-cooperative game approach is employed. Additionally, the individual PAR is distributed around the PAR in the total energy demand and it is also reduced when DSM is employed, for example, PAR in user 4’s energy demand is reduced from 4.11 to 2.74, and then to 2.00.

There are 5 residential users in the simulation and each user has an optimal battery capacity and strategy of energy consumption after the Nash equilibrium among 5 users is reached. To facilitate the analysis, we take user 1 as the example which is shown in Figs. 6 and 7. Figure 6 shows the energy distribution of PV generation. Figure 6a is the initial distribution of the PV with battery capacity 1.5 kWh, in which PV generation only provides energy for the user’s loads from 6:00 to 9:00 and begins to charge the battery at 9:00 until the battery is fully charged at 12:00. After satisfying loads and battery charging, approximately one-third of the produced energy (1.98 kWh) is sold back to the utility company. While users all take part in the non-cooperative game in Fig. 6b, one can see that almost all of the produced energy is used to satisfy loads and battery needs. The battery is charged from 9:00 to 16:00, which consumes energy of 3.59 kWh. Figure 7 shows the energy consumption of user 1 in a whole day. Energy consumption of loads in the daylight from 9:00 to 16:00 is all covered by PV generation. In peak demand hours between 17:00 and 22:00, the battery is employed to provide energy for loads to reduce the energy consumption during such period because of the high energy price. Since the existence of energy consumption scheduling, there is a more evenly distributed energy demand across different hours of the day.

Fig. 6
figure 6

Energy distribution of PV generation

Full size image
Fig. 7
figure 7

Energy consumption of residential user 1 with game optimization

Full size image

Daily energy costs of users corresponding to different battery capacities are shown in Fig. 8. Selecting different battery capacities will lead to the differences of daily cost for each user. Each user’s cost decreases first and then increases with the increase of battery capacity from 1 kWh to 5 kWh, which represents a minimal value corresponding to the optimal capacity. The optimal battery capacities are 3.3 kWh for user 1, 3.8 kWh for user 2, 4.3 kWh for user 3, 3.5 kWh for user 4, and 3.9 kWh for user 5. Due to the limitation in space, the optimal battery capacities in the situation of DSM without game are not shown in the figure. The optimal battery capacities are 3.3, 3.8, 4.2, 3.4, and 3.8 kWh respectively. Figure 9 shows the cost of each residential user for three situations “without DSM,” “DSM without game” and “DSM with game.” In the situation without DSM, one can see that the daily costs of the 5 users are $1.96, $1.83, $1.78, $1.86, and $1.89 respectively. When DSM is employed without game, the daily costs are $1.82, $1.68, $1.61, $1.72, and $1.73 respectively. However, when users all participate in the energy consumption scheduling with game approach, their daily costs have reduced to $1.73, $1.58, $1.51, $1.63 and $1.63.

Fig. 8
figure 8

Energy cost corresponding to battery capacity

Full size image
Fig. 9
figure 9

Energy cost of residential users

Full size image

5 Conclusion

In this paper, we have presented a non-cooperative game approach among residential users for optimizing battery capacity and scheduling their energy consumption in the scenario where the users are selfish and compete to reduce their own cost. The bidirectional energy trading is also considered by allowing users to buy and sell energy from/to the utility company with PV generation. The proposed method can help users choose an optimal battery capacity which is optimized according to energy price, household loads and depreciation cost of the battery. Simulation results shows that: when users all have optimal battery capacity and scheduled energy consumption, their costs reduces approximately 11%–15% compared to the initial situation without scheduling and the PAR in the total energy demand and the PAR in each user’s energy demand are both reduced about 50%. It demonstrates that the proposed game approach can not only reduce the costs of the residential user but also contributes to reducing the PAR of the grid.