1 Introduction

With the technology of renewable generation becoming mature, the penetration of distributed generations (DGs) connected to the distribution network is growing rapidly. Generally, renewable DGs connect to the grid through power electronic converters, which reduces the total inertia and deteriorate system damping property. With the penetration level of DG increasing, such converter-dominant power distribution infrastructure will suffer from the lacking of inertial and damping. Meanwhile, the power system is prone to become unstable if the penetration of converter type DGs reaches a certain threshold [1, 2].

On the other hand, the high controllability and fast response of power electronic devices provide unique opportunity to provide virtual inertia and damping through the power converters. The basic idea is known as virtual synchronous generator (VSG) which can behave as synchronous generator (SG) with inertia and damping, so as to enhance the system stability. VSG is playing an increasingly important role in power systems due to its controllability and flexibility, especially in microgrids and active distribution power networks [3, 4].

The original concept of VSG is proposed in the Europe VSYNC project [5, 6], after that, many other kinds of VSG are presented to improve the performance, including the synchronous-VSC and the synchronverter [7,8,9,10,11]. In view of the operational advantages, the voltage-controlled VSG is attracting more and more attentions, including VSG modelling [5, 8], control strategy design [10,11,12,13] and stability analysis [14, 15].

The VSG control strategy has been one of the major research directions in recent years. In [10], a VSG with the functionality of constant PQ control and V/f control is proposed, which can meet various operation requirements. The constant power control strategy with droop mechanism is designed to allocate the active and reactive power between multiple VSGs [11]. A comprehensive control framework with frequency, angle and virtual torque control loops is developed to further imitate the behavior of a SG [12].

It is worth mentioning that the aforementioned methods are developed under balanced and normal grid voltage conditions. However, the distribution grid voltage is influenced by many factors, such as overloads, startup of motors and asymmetric faults, which all may result in asymmetric or symmetric voltage sags [16]. Moreover, current unbalance, power oscillation or even overcurrent may be emerged when traditional VSG control strategies are adopted under voltage sags, which may cause VSG protection or outage.

In the field of traditional inverter control, voltage sags have been shown to be one of the greatest challenges for inverters control in order to keep them operating normally. In [17], a current reference calculation method is introduced to provide voltage support. Reference [18] aims at reducing active power oscillation to exploit the maximum capability of distributed generation. In [19, 20], the selection of a proper current reference is proposed to override grid faults and meet different power quality requirements. Other interesting methods have also been reported to address this issue, which manage to either balance three phase currents, or reduce the active or reactive power oscillations under unbalanced grid voltage [21, 22].

Nevertheless, the proposed inverter control methods under voltage sags are mainly for the current-controlled inverter that can be equivalent to a current source. The VSG, however, is emulated as a voltage-source, which is inherently distinct from the traditional inverter. The traditional inverter unbalanced control strategies cannot be mechanically applied to the VSG control under unbalanced voltage. Therefore, another significant concern related to VSG control is the ability to operate well under the conditions of voltage sags, which is important but about which few researches have been conducted.

Some inspirations are drawn from the traditional inverter control strategies under voltage sags. To provide balanced current or constant active power output under unbalanced grid voltage, the improved VSG control strategy is proposed in [23, 24], respectively. They are helpful and enlightening for designing VSG unbalanced control though they are simple without considering additional important targets.

Motivated by the aforementioned issues, a flexible unbalanced control strategy for VSG is comprehensively studied in this paper. The proposed flexible control strategy is cascaded with novel current reference generator (CRG) and power reference generator (PRG) together with the basic VSG controller and a double sequence frame current regulator, which can flexibly meet different operation requirements under varying voltage conditions. The control strategy is advantageous in twofold: ① current reference generator is an essential module to achieve different unbalanced control objectives, which manages to either balance three phase currents, or provide constant active or reactive power; ② power reference generator with peak current limitation is another important module, which can make full utilization of the maximum current to provide power supports and avoid overcurrent tripping or device damage.

The rest of the paper is organized as follows. The basic problem formulation including VSG control topology and essential properties are introduced in Section 2. The cascaded control framework and design process are presented in Section 3. Experimental results in Section 4 corroborate the claimed features of the proposed controller. Conclusions are drawn in Section 5.

2 Basic problem formulation

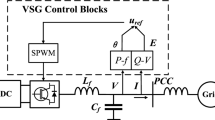
In general, a VSG consists of primary circuit and control strategy. The schematic diagram of VSG is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of VSG

Full size image

The primary circuit includes a three-phase full bridge converter and LC filter, which is almost the same as a conventional inverter. The control strategy is the core of VSG that can make it mimic the operation mechanism as a SG. The basic VSG algorithm is described by [23, 24]:

$$\left\{ \begin{aligned} J\frac{{{\text{d}}\Delta \omega }}{{{\text{d}}t}} = \frac{{P^{*} }}{\omega } - \frac{{P_{e} }}{\omega } - D\Delta \omega \hfill \\ \frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \omega \hfill \\ \frac{1}{{K_{q} }}\int {(Q^{*} - Q_{e} ) + D_{q} (v_{rms}^{*} - v_{rms} )} = E \hfill \\ \end{aligned} \right.$$
(1)

where P * and Q * are the reference of active power and reactive power; P e and Q e are the electromagnetic active power and reactive power, which can be calculated through v = [v a v b v c]T and i = [i a i b i c]T; e = [e a e b e c]T is the output voltage of the IGBTs; E is the magnitude; D p , D q , J are the damping coefficient, voltage droop coefficient and system inertia, respectively; K q is the integral coefficient; ω and θ are the virtual angle speed and virtual angular. The voltage reference e * can be composed as \(E\angle \theta\)

When VSG is operated under unbalanced voltage sags, the output current and power are strongly affected by the PCC voltage. Similar to common grid-connected inverters, the negative sequence components of VSG also appear when the voltage is asymmetrical, which may distort the current and power waveforms. The VSG output power can be obtained as follows [23]:

$$\left\{ \begin{aligned} p = p_{0} + p_{c2} \cos (2\omega t) + p_{s2} \sin (2\omega t) \hfill \\ q = q_{0} + q_{c2} \cos (2\omega t) + q_{s2} \sin (2\omega t) \hfill \\ \end{aligned} \right.$$
(2)

where p 0 and q 0 are the average value of active and reactive power; p c2, p s2, q c2, q s2 are the double frequency oscillations of the power.

From (2), it can be seen that the double frequency oscillations are produced under unbalanced voltage sags, where the negative sequence voltage and current are not equal to zero. The active and reactive power can be calculated by:

$$\left[ \begin{aligned} p_{0} \hfill \\ q_{0} \hfill \\ p_{s2} \hfill \\ p_{c2} \hfill \\ q_{c2} \hfill \\ q_{s2} \hfill \\ \end{aligned} \right] = \frac{3}{2}\left[ {\begin{array}{*{20}c} \begin{aligned} v_{d}^{ + } \hfill \\ v_{q}^{ + } \hfill \\ \end{aligned} & \begin{aligned} v_{q}^{ + } \hfill \\ - v_{d}^{ + } \hfill \\ \end{aligned} & \begin{aligned} v_{d}^{ - } \hfill \\ v_{q}^{ - } \hfill \\ \end{aligned} & \begin{aligned} v_{q}^{ - } \hfill \\ - v_{d}^{ - } \hfill \\ \end{aligned} \\ \begin{aligned} v_{q}^{ - } \hfill \\ v_{d}^{ - } \hfill \\ \end{aligned} & \begin{aligned} - v_{d}^{ - } \hfill \\ v_{q}^{ - } \hfill \\ \end{aligned} & \begin{aligned} - v_{q}^{ + } \hfill \\ v_{d}^{ + } \hfill \\ \end{aligned} & \begin{aligned} v_{d}^{ + } \hfill \\ v_{q}^{ + } \hfill \\ \end{aligned} \\ {v_{q}^{ - } } & { - v_{d}^{ - } } & {v_{q}^{ + } } & { - v_{d}^{ + } } \\ { - v_{d}^{ - } } & { - v_{q}^{ - } } & {v_{d}^{ + } } & {v_{q}^{ + } } \\ \end{array} } \right]\;\left[ \begin{aligned} i_{d}^{ + } \hfill \\ i_{q}^{ + } \hfill \\ i_{d}^{ - } \hfill \\ i_{q}^{ - } \hfill \\ \end{aligned} \right]$$
(3)

From (3), it can be concluded that there are only four control freedoms (i + d , i + q , i − d , i − q ) for controlling six variables (p 0, q 0, p s2, p c2, q s2, q c2). As a result, it is difficult to achieve multiple objectives at the same time. For instance, it is very difficult to provide constant active power (p s2 and p c2 are eliminated) and obtain balanced current simultaneously.

3 Proposed flexible control strategy

3.1 Cascaded control framework

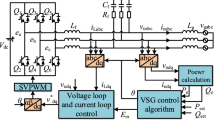
To achieve different control objectives as well as remain the properties of VSG, the proposed flexible control strategy is designed as a cascaded control framework, which mainly includes four modules: basic VSG algorithm, a novel CRG, an innovative PRG, and a typical current regulator. The cascaded control framework is designed as shown in Fig. 2.

Fig. 2
figure 2

Cascaded control framework

Full size image

From Fig. 2, it can be seen that the CRG and PRG are the kernel and novel modules of the proposed control framework. Thereinto, the CRG is used to generate current reference, which can achieve the targets of current balancing, constant active or reactive power output under unbalanced voltage. The PRG is mainly in charge of producing power reference to make full use of the maximum allowance current to provide power supports and avoid overcurrent for VSG under unbalanced voltage sags. Furthermore, the basic VSG algorithm and the typical current regulator including the positive and negative sequence control loops have been described in detail in [23, 24]. Thus the CRG and PRG will be elaborated hereinafter.

3.2 Current reference generator

As previously analysis, when VSG operates under unbalanced voltage sags, the primary objective is to either balance the grid injected currents, or deliver constant active or reactive power. CRG is a key component of the proposed control strategy since it can obtain the current reference for different objectives. That is to say, the control strategy can flexibly achieve these objectives by injecting different amounts of positive and negative sequence current reference produced by the current reference generator.

3.2.1 Balanced current mode

To some extent, unbalanced or distorted current cannot be accepted from the point view of power utilities. To obtain symmetrical grid-connected currents, only positive sequence components are required, where the negative sequence current reference is forced at zero. However, the positive sequence current cannot be calculated by (3) directly due to the influence of traditional VSG control. Therefore, the voltage reference produced by the traditional VSG controller and the circuit equation should be utilized to calculate the positive sequence current reference, which is inherently difference from traditional inverter control. From the VSG topology in Fig. 1, it can be deduced that:

$$\left[ \begin{aligned} e_{d} \hfill \\ e_{q} \hfill \\ \end{aligned} \right]{ = }\left[ \begin{aligned} v_{d}^{ + } \hfill \\ v_{q}^{ + } \hfill \\ \end{aligned} \right] + \left[ {\begin{array}{*{20}c} {Lp + R} & { - \omega L} \\ {\omega L} & {Lp + R} \\ \end{array} } \right]\left[ \begin{aligned} i_{d}^{ + } \hfill \\ i_{q}^{ + } \hfill \\ \end{aligned} \right]$$
(4)

where p = d/dt, which represents the differential operator; L is the total inductance from the VSG to the grid. And the other variables have been explained in Fig. 1. Owing to VSG controller, the stable value can approach to the predefined reference value. Therefore, (4) can be transformed into frequency domain as:

$$\begin{aligned} \left[ \begin{aligned} I_{d}^{ + } (s) \hfill \\ I_{q}^{ + } (s) \hfill \\ \end{aligned} \right]{ = }\left[ {\begin{array}{*{20}c} {Ls + R} & { - \omega L} \\ {\omega L} & {Ls + R} \\ \end{array} } \right]^{ - 1} \left( {\left[ \begin{aligned} E_{d}^{{}} (s) \hfill \\ E_{q}^{{}} (s) \hfill \\ \end{aligned} \right] - \left[ \begin{aligned} V_{d}^{ + } (s) \hfill \\ V_{q}^{ + } (s) \hfill \\ \end{aligned} \right]} \right) \hfill \\ { = }\frac{1}{{(Ls + R)^{2} + (\omega L)^{2} }}\left[ {\begin{array}{*{20}c} {(Ls + R)\Delta V_{d}^{ + } (s) + \omega L\Delta V_{q}^{ + } (s)} \\ {(Ls + R)\Delta V_{q}^{ + } (s) - \omega L\Delta V_{d}^{ + } (s)} \\ \end{array} } \right] \hfill \\ \end{aligned}$$
(5)

where \(\Delta V_{d}^{ + } \left( s \right) = E_{d} \left( s \right) - V_{d}^{ + } \left( s \right)\); \(\Delta V_{q}^{ + } \left( s \right) = E_{q} \left( s \right) - V_{q}^{ + } \left( s \right)\); s is the complex frequency.

Based on the Laplace final-value theorem, the positive sequence current reference can be deduced from (5), which is shown as follows:

$$\left[ \begin{aligned} i_{d}^{{{ + }*}} \hfill \\ i_{q}^{{{ + }*}} \hfill \\ \end{aligned} \right]{ = }\frac{1}{{R^{2} + (\omega L)^{2} }}\left[ {\begin{array}{*{20}c} {R\Delta v_{d}^{ + } + \omega L\Delta v_{q}^{ + } } \\ {R\Delta v_{q}^{ + } - \omega L\Delta v_{d}^{ + } } \\ \end{array} } \right]$$
(6)

where \(\Delta v_{d}^{ + } = e_{d} - v_{d}^{ + }\); \(\Delta v_{q}^{ + } = e_{q} - v_{q}^{ + }\).

It is worth noting that the final output power, especially the average value of power, does not rely on the exact circuit parameters (R or L), because the output power of the integral control loop in VSG control can be adjusted automatically. The proof process is shown in Appendix A.

Furthermore, the output power oscillations are depressed because the negative sequence current is eliminated. Therefore, if high quality of grid-connected current is desired, the balanced current mode (BCM) will be the best choice.

3.2.2 Constant active power mode

As mentioned before, one way to provide constant active power is to make p c2 and p s2 equal to zero. That is:

$$\left[ {\begin{array}{*{20}c} {v_{q}^{ - } } & { - v_{d}^{ - } } \\ {v_{d}^{ - } } & {v_{q}^{ - } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d}^{ + } } \\ {i_{q}^{ + } } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} { - v_{q}^{ + } } & {v_{d}^{ + } } \\ {v_{d}^{ + } } & {v_{q}^{ + } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d}^{ - } } \\ {i_{q}^{ - } } \\ \end{array} } \right] = 0$$
(7)

From (7), it can be seen that the reference of positive and negative sequence current should be included in the control system in order to eliminate active power fluctuation. The negative sequence current reference can be easily obtained from (7).

$$\left[ {\begin{array}{*{20}c} {i_{d}^{ - *} } \\ {i_{q}^{ - *} } \\ \end{array} } \right]{ = }\frac{ - 1}{{(v_{d}^{ + } )^{2} + (v_{q}^{ + } )^{2} }}\left[ {\begin{array}{*{20}c} { - v_{q}^{ + } v_{q}^{ - } + v_{d}^{ + } v_{d}^{ - } } & {v_{q}^{ + } v_{d}^{ - } + v_{d}^{ + } v_{q}^{ - } } \\ {v_{d}^{ + } v_{q}^{ - } + v_{q}^{ + } v_{d}^{ - } } & { - v_{d}^{ + } v_{d}^{ - } + v_{q}^{ + } v_{q}^{ - } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d}^{ + *} } \\ {i_{q}^{ + *} } \\ \end{array} } \right]$$
(8)

Equation (8) indicates that the negative sequence current reference can be conveniently derived with positive sequence current reference. Under this control condition, the active power fluctuation is deeply reduced, but the quadrature magnitudes of oscillating reactive power is also large due to the negative sequence currents are not removed. Thereby, the constant active power mode (CAPM) is mainly suitable in the situation that constant active power flow is desired.

3.2.3 Constant reactive power mode

For some large capacity power generation equipment, the capability to provide stable reactive power supports is strongly required. Similar to the active power oscillation control, taking q c2 = q s2 = 0 is the basic idea to ensure constant reactive power output. That is:

$$\left[ {\begin{array}{*{20}c} {v_{q}^{ - } } & { - v_{d}^{ - } } \\ {v_{d}^{ - } } & {v_{q}^{ - } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d}^{ + } } \\ {i_{q}^{ + } } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} { - v_{q}^{ + } } & {v_{d}^{ + } } \\ {v_{d}^{ + } } & {v_{q}^{ + } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d}^{ - } } \\ {i_{q}^{ - } } \\ \end{array} } \right] = 0$$
(9)

Dealing with (9), the injected negative sequence current reference used to reduce the reactive power oscillation is generated by:

$$\left[ {\begin{array}{*{20}c} {i_{d}^{ - *} } \\ {i_{q}^{ - *} } \\ \end{array} } \right]{ = }\frac{1}{{(v_{d}^{ + } )^{2} + (v_{q}^{ + } )^{2} }}\left[ {\begin{array}{*{20}c} { - v_{q}^{ + } v_{q}^{ - } + v_{d}^{ + } v_{d}^{ - } } & {v_{q}^{ + } v_{d}^{ - } + v_{d}^{ + } v_{q}^{ - } } \\ {v_{d}^{ + } v_{q}^{ - } + v_{q}^{ + } v_{d}^{ - } } & { - v_{d}^{ + } v_{d}^{ - } + v_{q}^{ + } v_{q}^{ - } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d}^{ + *} } \\ {i_{q}^{ + *} } \\ \end{array} } \right]$$
(10)

From (8) and (10), it is interesting to notice that those two results are opposite, which provide much more convenience to unify the algorithm. Therefore, (6), (8) and (10) can be combined as:

$$\left[ {\begin{array}{*{20}c} \begin{aligned} i_{d}^{ + *} \hfill \\ i_{q}^{ + *} \hfill \\ i_{d}^{ - *} \hfill \\ \end{aligned} \\ {i_{q}^{ - *} } \\ \end{array} } \right]{ = }\frac{1}{{(v_{d}^{ + } )^{2} + (v_{q}^{ + } )^{2} }}\left[ {\begin{array}{*{20}c} \begin{aligned} \;(v_{d}^{ + } )^{2} + (v_{q}^{ + } )^{2} \hfill \\ \;\;\;\;\;\;\;\;\;\;0 \hfill \\ N( - v_{q}^{ + } v_{q}^{ - } + v_{d}^{ + } v_{d}^{ - } ) \hfill \\ \end{aligned} & \begin{aligned} \;\;\;\;\;\;\;\;0 \hfill \\ (v_{d}^{ + } )^{2} + (v_{q}^{ + } )^{2} \hfill \\ N(v_{q}^{ + } v_{d}^{ - } + v_{d}^{ + } v_{q}^{ - } ) \hfill \\ \end{aligned} \\ {N(v_{d}^{ + } v_{q}^{ - } + v_{q}^{ + } v_{d}^{ - } )} & {N( - v_{d}^{ + } v_{d}^{ - } + v_{q}^{ + } v_{q}^{ - } )} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d}^{ + *} } \\ {i_{q}^{ + *} } \\ \end{array} } \right]$$
(11)

where N is the unifying factor, which is an integer in the range of [−1, 1]. In fact, N can be used to select the required control targets. When N = 0, (11) can be combined with (6), which the injected grid current is balanced. Similarly, when N = ±1, (11) converts to (10) and (8) to remove active power and reactive power oscillation. Therefore, it is flexible to customize the control objectives for different demands.

3.3 Power reference generator

If the active power or reactive power reference is constant, current may exceed the maximum allowable value during voltage sags. To avoid the risk of overcurrent, the active and reactive power reference should be obtained through a power calculator instead of a predefined value. For different control objects, there are corresponding power references.

3.3.1 Peak current calculation

As a basic part of the PRG, the peak current calculation is applied to quantitatively analyse the relationship between the power and allowable output current under voltage sags. In order to elaborate the calculation process, take the ‘CAPM’ as an example. When the control objective is CAPM, use (3) and make p c2 and p s2 equal to zero again. The output current in dq axis can be determined as:

$$\left[ \begin{aligned} i_{d}^{ + } \hfill \\ i_{q}^{ + } \hfill \\ i_{d}^{ - } \hfill \\ i_{q}^{ - } \hfill \\ \end{aligned} \right] = \frac{{2p_{0} }}{{3\left( {D_{1} - D_{2} } \right)}}\left[ \begin{array}{c} v_{d}^{ + } \hfill \\ v_{q}^{ + } \hfill \\ - v_{d}^{ - } \hfill \\ - v_{q}^{ - } \hfill \\ \end{array} \right] + \frac{{2q_{0} }}{{3\left( {D_{1} + D_{2} } \right)}}\left[ \begin{array}{c} v_{q}^{ + } \hfill \\ - v_{d}^{ + } \hfill \\ v_{q}^{ - } \hfill \\ - v_{d}^{ - } \hfill \\ \end{array} \right]$$
(12)

where \(D_{1} = \left( {v_{d}^{ + } } \right)^{2} + \left( {v_{q}^{ + } } \right)^{2}\), \(D_{2} = \left( {v_{d}^{ - } } \right)^{2} + \left( {v_{q}^{ - } } \right)^{2}\).

Then, applying the inverse Park transformation to (12), the instantaneous values of VSG output currents can be expressed as:

$$\left[ \begin{aligned} i_{\text{a}}^{ + } \hfill \\ i_{\text{b}}^{ + } \hfill \\ i_{\text{c}}^{ + } \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} {K_{1} \cos \theta^{ + } + K_{2} \sin \theta^{ + } } & {K_{2} \cos \theta^{ + } - K_{1} \sin \theta^{ + } } \\ {K_{1} \cos \left( {\theta^{ + } - \frac{2}{3}\uppi} \right) + K_{2} \sin \left( {\theta^{ + } - \frac{2}{3}\uppi} \right)} & {K_{2} \cos \left( {\theta^{ + } - \frac{2}{3}\uppi} \right) - K_{1} \sin \left( {\theta^{ + } - \frac{2}{3}\uppi} \right)} \\ {K_{1} \cos \left( {\theta^{ + } + \frac{2}{3}\uppi} \right) + K_{2} \sin \left( {\theta^{ + } + \frac{2}{3}\uppi} \right)} & {K_{2} \cos \left( {\theta^{ + } + \frac{2}{3}\uppi} \right) - K_{1} \sin \left( {\theta^{ + } + \frac{2}{3}\uppi} \right)} \\ \end{array} } \right]\left[ \begin{aligned} v_{d}^{ + } \hfill \\ v_{q}^{ + } \hfill \\ \end{aligned} \right]$$
(13)
$$\left[ \begin{aligned} i_{\text{a}}^{ - } \hfill \\ i_{\text{b}}^{ - } \hfill \\ i_{\text{c}}^{ - } \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} {K_{2} \sin \theta^{ - } - K_{1} \cos \theta^{ - } } & {K_{1} \sin \theta^{ - } + K_{2} \cos \theta^{ - } } \\ {K_{2} \sin \left( {\theta^{ - } - \frac{2}{3}\uppi} \right) - K_{1} \cos \left( {\theta^{ - } - \frac{2}{3}\uppi} \right)} & {K_{1} \sin \left( {\theta^{ - } - \frac{2}{3}\uppi} \right) + K_{2} \cos \left( {\theta^{ - } - \frac{2}{3}\uppi} \right)} \\ {K_{2} \sin \left( {\theta^{ - } + \frac{2}{3}\uppi} \right) - K_{1} \cos \left( {\theta^{ - } + \frac{2}{3}\uppi} \right)} & {K_{1} \sin \left( {\theta^{ - } + \frac{2}{3}\uppi} \right) + K_{2} \cos \left( {\theta^{ - } + \frac{2}{3}\uppi} \right)} \\ \end{array} } \right]\left[ \begin{aligned} v_{d}^{ - } \hfill \\ v_{q}^{ - } \hfill \\ \end{aligned} \right]$$
(14)

where \(K_{1} = \frac{{2p_{0} }}{{3(D_{1} - D_{2} )}}\); \(K_{2} = \frac{{2q_{0} }}{{3(D_{1} + D_{2} )}}\); θ + = ωt + φ +, θ - = −ωt + φ −, which are the positive and negative sequence reference angles; φ + and φ − are arbitrary angle. Furthermore, the instantaneous values of the phase currents can be obtained from (13) and (14). Take phase A for instance, the peak value of output current can be expressed as:

$$\begin{aligned} i_{\text{a}} & = \left( {K_{1} v_{d}^{ + } + K_{2} v_{q}^{ + } } \right)\cos \theta^{ + } + \left( {K_{2} v_{d}^{ + } - K_{1} v_{q}^{ + } } \right)\sin \theta^{ + } + \\ & \quad \left( {K_{2} v_{q}^{ - } - K_{1} v_{d}^{ - } } \right)\cos \theta^{ - } + \left( {K_{1} v_{q}^{ - } + K_{2} v_{d}^{ - } } \right)\sin \theta^{ - } \\ \end{aligned}$$
(15)

Let \(A_{1} = K_{1} v_{d}^{ + } + K_{2} v_{q}^{ + }\), \(A_{2} = K_{2} v_{d}^{ + } - K_{1} v_{q}^{ + }\), A 3 = K 2 v − q  − K 1 v − d , A 4 = K 1 v − q  + K 2 v − d . Then the current peak value of phase A can be extracted from (15) by using trigonometric formula, that is:

$$i_{{{\text{a}}m}} = \sqrt {A_{1}^{2} + A_{2}^{2} + A_{3}^{2} + A_{4}^{2} + 2\sqrt {A_{1}^{2} + A_{2}^{2} } \sqrt {A_{3}^{2} + A_{4}^{2} } \cos (\Delta \varphi - \varphi^{\prime})}$$
(16)

where Δφ = θ + + θ - = φ + + φ −, \(\varphi^{\prime} = \arctan \;\frac{{A_{2} }}{{A_{1} }} + \arctan \;\frac{{A_{4} }}{{A_{3} }}\).

In the same way, the current peak value of phase B and phase C can be express as

$$i_{{{\text{b}}m}} = \sqrt {A_{1}^{2} + A_{2}^{2} + A_{3}^{2} + A_{4}^{2} + 2\sqrt {A_{1}^{2} + A_{2}^{2} } \sqrt {A_{3}^{2} + A_{4}^{2} } \cos \left( {\Delta \varphi - \varphi^{\prime} - \frac{2}{3}\uppi} \right)}$$
(17)
$$i_{{{\text{c}}m}} = \sqrt {A_{1}^{2} + A_{2}^{2} + A_{3}^{2} + A_{4}^{2} + 2\sqrt {A_{1}^{2} + A_{2}^{2} } \sqrt {A_{3}^{2} + A_{4}^{2} } \cos \left( {\Delta \varphi - \varphi^{\prime} + \frac{2}{3}\uppi} \right)}$$
(18)

From (16)–(18), it can be seen clearly that the possible maximum current will appear in phase A, B and C when Δφ = φ ′, \(\Delta \varphi = \varphi^{\prime} + \frac{2}{3}\uppi\), \(\Delta \varphi = \varphi^{\prime} - \frac{2}{3}\uppi\), respectively. The maximum current value can be expressed as:

$$I_{m} = \sqrt {A_{1}^{2} + A_{2}^{2} } { + }\sqrt {A_{3}^{2} + A_{4}^{2} }$$
(19)

Then substituting A 1, A 2, A 3 and A 4 to (19), the maximum current of VSG in CAPM can also be expressed as:

$$I_{m} = \sqrt {\left( {\frac{{2p_{0} }}{{3\left( {D_{1} - D_{2} } \right)}}} \right)^{2} { + }\left( {\frac{{2q_{0} }}{{3\left( {D_{1} + D_{2} } \right)}}} \right)^{2} } \left( {\sqrt {D_{1} } + \sqrt {D_{2} } } \right)$$
(20)

From (20), it can be seen that I m is strongly related with p 0 and q 0. As a consequence, p 0 and q 0 deeply depend upon the power reference. Therefore, one effective way to reasonably reduce I m is changing the value of power reference automatically.

3.3.2 Power reference calculation

Take CAPM for instance again. If the permissible peak current of VSG is I max, which means that I m should be less than I max. Generally, I max is set below the overcurrent protection threshold to avoid the risk of overcurrent shutdown of VSG. Then, combining with (20), the active and reactive power reference must be limited by means of the following condition to avoid VSG overcurrent.

$$\sqrt {\left( {\frac{{P^{*} }}{{D_{1} - D_{2} }}} \right)^{2} { + }\left( {\frac{{Q^{*} }}{{D_{1} + D_{2} }}} \right)^{2} } \le \frac{{1.5I_{\hbox{max} } }}{{\sqrt {D_{1} } + \sqrt {D_{2} } }}$$
(21)

When asymmetric voltage sags happen, the VSG output current can be limited to the maximum allowed value if (21) is satisfied. However, (21) only gives the condition for current limitation, which cannot certainly generate the active and reactive power reference due to two unknown parameters (P * and Q *) in only one function. It is worth noting that during voltage sags, one of the important functionality of VSG is to provide power support for the power grid. And in general, the reactive power demand is a little larger than the active power. Thus, it is reasonable to design the reactive power reference to be no less than the active power reference during voltage sags. That is:

$$P^{*} = kQ^{*} \;\;\;\;\;\;\;\;\;\;0 \le k \le 1$$
(22)

Then, the power reference of CAPM can be determined by solving (21) and (22).

$$\left\{ \begin{aligned} Q_{1}^{*} = \frac{{1.5\left( {D_{1} + D_{2} } \right)\left( {\sqrt {D_{1} } - \sqrt {D_{2} } } \right)I_{\hbox{max} } }}{{\sqrt {k^{2} \left( {D_{1} + D_{2} } \right)^{2} + \left( {D_{1} - D_{2} } \right)^{2} } }} \hfill \\ P_{1}^{*} = kQ_{1}^{*} \hfill \\ \end{aligned} \right.$$
(23)

From (23), it can be seen that there are two potential problems. One is that little current margin has been left, which may lead to overcurrent due to a small disturbance or inaccuracy. The other is that the calculation turns out too complicated for practical application. Therefore, (23) should be simplified in a reasonable way.

Firstly, it can be proved that when 0≤k≤1, \(\frac{{1.5(D_{1} + D_{2} )}}{{\sqrt {k^{2} (D_{1} + D_{2} )^{2} + (D_{1} - D_{2} )^{2} } }} > 1\). Consequently, (23) can be facilitated into a more effective form:

$$\left\{ \begin{aligned} Q_{{}}^{ *} { = }\left( {V^{ + } - V^{ - } } \right)I_{\hbox{max} } \hfill \\ P_{{}}^{ *} = kQ_{{}}^{ *} \hfill \\ \end{aligned} \right.$$
(24)

where V + and V − are the amplitude of positive and negative sequence grid voltage.

They can be obtained by \(V^{ + } = \sqrt {(v_{d}^{ + } )^{2} + (v_{q}^{ + } )^{2} }\) and \(V^{ - } = \sqrt {(v_{d}^{ - } )^{2} + (v_{q}^{ - } )^{2} }\).

3.3.3 Unified form of PRG

As mentioned above, the process of peak current calculation and power reference calculation in CAPM are illustrated in detail. The PRG of constant reactive power mode (CRPM) and BCM can be obtained in the same way as previously analysis. To facilitate the description, the PRG of CRPM and BCM are simply described as follows.

1) PRG of CRPM

PRG of CRPMWhen the control objective is to provide constant reactive power, the output currents in dq axis can be determined as:

$$\left[ \begin{aligned} i_{d}^{ + } \hfill \\ i_{q}^{ + } \hfill \\ i_{d}^{ - } \hfill \\ i_{q}^{ - } \hfill \\ \end{aligned} \right] = \frac{{2p_{0} }}{{3\left( {D_{1} + D_{2} } \right)}}\left[ \begin{aligned} v_{d}^{ + } \hfill \\ v_{q}^{ + } \hfill \\ - v_{d}^{ - } \hfill \\ - v_{q}^{ - } \hfill \\ \end{aligned} \right] + \frac{{2q_{0} }}{{3\left( {D_{1} - D_{2} } \right)}}\left[ \begin{aligned} v_{q}^{ + } \hfill \\ - v_{d}^{ + } \hfill \\ v_{q}^{ - } \hfill \\ - v_{d}^{ - } \hfill \\ \end{aligned} \right]$$
(25)

Then the reference power of CRPM is given by:

$$\left\{ \begin{aligned} Q_{2}^{*} = \frac{{1.5\left( {D_{1} + D_{2} } \right)\left( {\sqrt {D_{1} } - \sqrt {D_{2} } } \right)I_{\hbox{max} } }}{{\sqrt {\left( {D_{1} + D_{2} } \right)^{2} + k^{2} \left( {D_{1} - D_{2} } \right)^{2} } }} \hfill \\ P_{2}^{*} = kQ_{2}^{*} \hfill \\ \end{aligned} \right.$$
(26)

Furthermore, (26) can be simplified as

$$\left\{ \begin{aligned} Q_{2}^{ *} { = }\left( {V^{ + } - V^{ - } } \right)I_{\hbox{max} } \hfill \\ P_{2}^{ *} = kQ_{2}^{ *} \hfill \\ \end{aligned} \right.$$
(27)

which is exactly similar to (24).

2) PRG of BCM

PRG of BCMWhen the target is to produce balanced currents, the output currents in dq axis can be expressed as:

$$\left[ \begin{aligned} i_{d}^{ + } \hfill \\ i_{q}^{ + } \hfill \\ \end{aligned} \right]{ = }\frac{{2P^{*} }}{{3D_{1} }}\left[ \begin{aligned} e_{d}^{ + } \hfill \\ e_{q}^{ + } \hfill \\ \end{aligned} \right] + \frac{{2Q^{*} }}{{3D_{1} }}\left[ \begin{aligned} e_{q}^{ + } \hfill \\ - e_{d}^{ + } \hfill \\ \end{aligned} \right]$$
(28)

It can be seen that negative sequence current does not appear in (28), which has been eliminated to ensure balanced current under voltage sags. The power reference in this scenario is given by:

$$\left\{ \begin{aligned} Q_{3}^{ *} { = }\frac{{1.5\sqrt {D_{1} } I_{\hbox{max} } }}{{\sqrt {1 + k^{2} } }} \hfill \\ P_{3}^{ *} = kQ_{3}^{ *} \hfill \\ \end{aligned} \right.$$
(29)

For simplicity, the constant \(\frac{1.5}{{\sqrt {1 + k^{2} } }}\) can be ignored when 0≤k≤1. Thus a simplified form can be derived as:

$$\left\{ \begin{aligned} Q_{3}^{ *} { = }V^{ + } I_{\hbox{max} } \hfill \\ P_{3}^{ *} = kQ_{3}^{ *} \hfill \\ \end{aligned} \right.$$
(30)

Comparing (24), (25) and (30), it is obvious that these three equations admits the following unified expression.

$$\left\{ \begin{aligned} Q^{*} { = }\left( {V^{ + } - N^{2} V^{ - } } \right)I_{\hbox{max} } \hfill \\ P^{*} = kQ^{*} \hfill \\ \end{aligned} \right.$$
(31)

where 0 ≤ k ≤ 1; N is the unifying factor, which has the same meanings as in (13). It should be noticed that in order to exploit the maximum capability of the inverter, k should be set to 1 to produce more active power while achieving the goal of limiting the peak current as well as providing active power support.

Moreover, to enhance the flexibility of PRG, the preset power reference should also be contained in the PRG. Therefore, (31) can be expanded as:

$$\left\{ \begin{aligned} Q^{*} { = }\left\{ \begin{aligned} \left( {V^{ + } - N^{2} V^{ - } } \right)I_{\hbox{max} } \;\;\;\;\;\;\;{\text{when}}\;\;{\text{Enb = 1}} \hfill \\ Q_{set} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{when}}\;\;{\text{Enb = 0}}\; \hfill \\ \end{aligned} \right. \hfill \\ P^{*} = \left\{ \begin{aligned} kQ^{*} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{when}}\;\;{\text{Enb = 1}} \hfill \\ P_{set} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{when}}\;\;{\text{Enb = 0}} \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned} \right.$$
(32)

where ‘Enb’ represents the enable signal of PRG. When ‘Enb’ equals to 1, the PRG is used to calculate the power reference without exceeding I max. Otherwise, the power reference can be manually preset as expected values when VSG operates under balanced grid voltages.

Based on the aforementioned analysis, the proposed control framework endows the VSG with the ability of meeting various demands of balancing the grid current or providing constant power without overcurrent. The proposed flexible control strategy for VSG LVRT control is shown in Fig. 3, which contains critical control modules and important equations mentioned before.

Fig. 3
figure 3

Block diagram of proposed flexible control strategy

Full size image

In general, it is difficult to determine the best control parameter that coordinates with existing PI controllers. During unbalanced grid voltage sags, it is even more complicated to examine system stability with given parameters. The main reason is that not only positive sequence model, but also negative sequence model and the VSG model should be jointly considered for the unbalanced grid. The asymmetric and comprehensive modelling, parameter design and stability analysis of VSG LVRT control under unbalanced voltage sags would be a subject of future research. One feasible way for parameters design is to adopt the proper parameters that work well under the balanced grid [25,26,27], and regulate them combining with practical experience.

4 Experimental verification

4.1 Experimental platform

Based on the schematic diagram in Fig. 1, a downscale experimental platform has been built to verify the proposed flexible control strategy for VSG LVRT. Thereinto, the semikron three-phase full-bridge converter, LC filter and some other components are utilized to construct the VSG primary circuit. The proposed flexible control strategy is implemented on a digital signal processor (DSP), which can acquire voltage and current data and deploy control commands to the power converter.

Additionally, the DC power source is emulated by a lithium-ion batteries energy storage system (BESS). The grid unbalanced voltage sag is emulated by changing the tap positions of three single-phase voltage regulators connected to the grid. The oscilloscope and host PC are adopted to constitute a monitor and display system, which can acquire and deal with the operation data. The system parameters are listed in Table 1. The experimental platform is shown in Fig. 4.

Table 1 Main parameters of experimental platform
Full size table
Fig. 4
figure 4

Experimental platform

Full size image

4.2 Experimental results

Firstly, the characteristics of the emulated voltage sag are presented in Fig. 5. The voltage sag is used to mimic the real behavior of the most common and typical single-phase short circuit fault, which is time varying and has two transient segments. From Fig. 5, it can be seen that the sag duration is about 0.3 s (from 0.05 s to 0.35 s). The RMS voltage droops from 30 V RMS to about 20 V, which indicates the deep of the voltage sag is approximately 70%.

Fig. 5
figure 5

Voltage sag characterization

Full size image

Then, the comparison results under different control modes taken on the test platform will be presented in the following paragraph, which can be expected as verification for the proposed control strategy.

Case A: traditional VSG control mode

Experimental results of the traditional VSG control under unbalanced voltage sag are shown below, which can be used to compare with the results of other modes.

As can be seen in the Fig. 6, the current waveform is highly unbalanced and distorted during voltage sag. Obviously, the current exceeds I max, which may leads to overcurrent or even tripping. Meanwhile, the double frequency fluctuations of active and reactive power occur during the sag. There is a large deviation between the real value and the set value of the power.

Fig. 6
figure 6

Phase current and power waveform under traditional VSG control mode

Full size image

Consequently, VSG cannot work well during voltage sag under traditional control mode. Therefore, the displayed results below mainly focus on the proposed control strategy. The results are elaborated in two parts for the purpose of comprehensiveness: the mode with constant power set value (Enb=0 in (31)) and the mode with power calculation value (Enb=1 in (31)).

Case B: balanced current mode

As previously stated, the object of BCM is to balance the current under voltage sag. The experimental results are shown in Fig. 7.

Fig. 7
figure 7

Phase current and power waveform under BCM

Full size image

Note that, in Fig. 7, the current becomes more balanced and the magnitudes of power oscillations are remarkably reduced compared with those in Fig. 6, owing to the BCM which eliminates the negative sequence currents. Furthermore, comparing Fig.7a and b, it is clear that the currents exceed the constraint when using constant power set value during voltage sag. On contrary, the current is reduced within the constraint when using the power calculation value instead of a constant value. And the reactive power is also produced due to the P * and Q * are set as the same (where k = 1 in (32)) in the calculation procedure.

Case C: constant active power mode

With the target of decreasing the VSG active power oscillations under unbalanced voltage sag, the result is shown in Fig. 8.

Fig. 8
figure 8

Phase current and power waveform under CAPM

Full size image

Similarly, the results in Fig. 8 demonstrate that the output active power can be maintained almost at a constant when utilizing the proposed CAPM. However, the current shown in Fig. 8a is overcurrent. On contrary, as shown in Fig. 8b, the current is decreased and the active and reactive power is also provided. It indicates that the calculating power reference value is much more reliable than that of the predefined constant value.

Case D: constant reactive power mode

In this experiment, the advantage of eliminating reactive power oscillations is illustrated in Fig. 9.

Fig. 9
figure 9

Phase current and power waveform under CRPM

Full size image

From Fig. 9, it can be seen that the provided reactive power remains almost constant with smaller fluctuation when the proposed CRPM is applied. Of course, comparing with the method of using predefined power value, the currents are within the threshold value when using the calculating power reference.

In summary, it can be seen that the experimental results meets the demonstration of theoretical analysis. The target of balancing current, maintaining constant power delivery and making full use of the maximum allowing current can be flexibly achieved by utilizing the presented flexible control strategy.

5 Conclusion

VSG is advantageous in many ways in power converter based distributed generations. To enhance the operating characteristics of VSG under different operation demands and unbalanced grid voltage sag, a flexible control strategy for VSG LVRT is presented. A current CRG and a PRG are developed and integrated in the proposed cascaded control framework. Several control objectives are automatically fulfilled with typical demands: to balance the injected currents, to deliver constant active power or reactive power, and to make full use of the allowable current without overcurrent while providing power supports. Theoretical analysis and experimental results verify the validness and effectiveness of the proposed control strategy. Additionally, the control strategy can also be extended to implement more control targets to enhance the capability of VSG low voltage ride through.