1 Introduction

High levels of traffic in metropolis areas have become a critical social problem of the twenty-first century. Congestion pricing, as part of traffic demand management (TDM) strategies, is a significant economic tool which has been implemented in several cities around the world [1]. It mitigates the congestion level by encouraging the commuters enough to alter their behavior, such as their departure time, route or mode of transport [2, 3]. Congestion pricing schemes can be categorized into two groups: the first-best and the second-best strategies. In the first-best strategy, the well-known Pigouvian formula [4] is used to calculate the negative externalities which should be paid by the drivers. It is applied by charging tolls over all links of the network, so that the user equilibrium flow pattern shifts toward a socially preferred pattern. However, this is not a practical strategy, because of the political and social resistance against all roads tolled. On the other hand, the second-best policy is more acceptable to the public since it settles charges on a limited subset of the links. First applied in Singapore in 1975, cordon pricing is the most appropriate second-best policy for network authorities due to its practicality, effectiveness and social acceptance. Cordon pricing follows three main objectives in general: alleviating congestion, enhancing the environmental indices and generating revenue [5]. In the conventional form of cordon pricing, the commuters are charged on entry into a specific zone, enclosed by a hypothetical cordon line. Mostly implemented on the central business districts, this second-best strategy can reduce the intensity of congestion within the cordoned area by deflecting the routes from entry or changing the mode of transport. May et al. [6], Shepherd et al. [7, 8], Santos et al. [9], May et al. [10], Zhang and Yang [11] and Gholami et al. [12] are among those who investigated the impact of the entry-based cordon pricing on the performance of transportation systems. Although a single layer cordon has a positive effect on reducing the congestion inside, it may cause unwilling congestion outside the cordoned area. In order to tackle this deficiency, some researchers suggested that using multilayer cordons can improve the geographical coverage of cordon pricing [10, 12, 13]. May et al. [10], Zou et al. [14] and Gholami et al. [12] argued against cordon pricing by showing that there may exist more effective toll points in the whole network than on the cordon line, providing that the total number of tolled links is not changed. Based on their experiments, relaxing the constraint of keeping the cordon line closed can increase the social benefits of community. However, implementation of such a strategy encounters practical issues since it does not form a coherent geographical district and is mentally hard to be perceived and accepted by the users. May et al. [6] pointed out that cordon pricing can affect only the trips with the origins outside and the destinations inside the cordoned area. They implemented a bidirectional charging plan which can enhance the overall performance of the pricing.

Area pricing is known as an appropriate surrogate for cordon pricing, as it can influence the incoming, outgoing and inner traffic flows within a specific area. Maruyama and Sumalee [15] compared cordon and area pricing strategies in terms of social welfare, demonstrating that the latter is superior to the former. Fujishima [16] investigated these two toll designs and concluded that the cordon pricing is better if long-distance commuting is prevalent, while area pricing is dominant where central urban area is relatively large. Zhang et al. [17] compared them and found out that area pricing is superior to cordon pricing. They showed numerically that the larger area or the higher tolls do not necessarily result that either of them performs better.

Despite the acceptable performance, the typical cordon and area pricing plans have an inherently serious drawback: They do not take into account the real externalities imposed by drivers to the system. In these toll designs, every vehicle riding inside the predefined area is charged with the same toll level, regardless of the distance it travels, the time it spends moving, the speed it has and the real congestion it causes. Besides technical weakness, this drawback limits the applicability of these policies in an equity and social acceptance perspective. Hence, researchers investigated time-dependent, speed-dependent and distance-dependent pricing strategies in a broader framework of cordon-based pricing. May and Milne [5] studied the time-dependent cordon tolling and showed the superiority of this policy against the conventional entry-based cordon pricing. Liu et al. [18] proposed a mathematical programming model with equilibrium constraint for the speed-based toll design of a cordon. They considered the speed criterion as a penalty term in the objective function and used genetic algorithm to solve the problem. However, time-dependent and speed-dependent cordon-based tolls are believed to encourage commuters for aggressive driving behavior in the pursuance of less charges. This results in safety issues, limiting their application such as the rejection of them in London [19]. Distance-based cordon pricing is the most favorite policy as it does not provoke unsafe driving and is more justice centered. In this policy, drivers are charged relative to the distance they travel within the cordoned area: The longer the route is, the higher the toll should be. It is worthwhile noting that the well-known electronic road pricing system in Singapore will be transformed into a distance-based pricing system from 2020 as the next generation of congestion pricing [20]. May and Milne [5], Mitchell et al. [21] and Namdeo and Mitchell [22] studied the linear distance-based toll design where the charges are linearly proportional to the distance travelled. Using linear tolls, the generalized travel cost becomes link-wise additive, meaning that the travel cost of a path would be equal to the sum of the travel cost of the links comprising the path. Distance-based pricing is often, in practice, nonlinear [23]; however, using nonlinear tolls converts the problem into a nonadditive space, so that finding a user equilibrium solution requires formulating a complementarity problem (instead of an optimization problem) which is very hard to solve. Meng et al. [24] made the problem additive by replacing each possible path in the cordon with a dummy link. However, applying the technique of dummy links for a large-scale network imposes intense computational burden from the exhausting enumeration of all available paths within the cordoned area. Lawphongpanich and Yin [23] used piecewise linear toll functions for two-part tariff as an approximation of nonlinear tolls. They formulated the problem as a convex optimization model and used coordinate search algorithm to solve it. Sun et al. [25] considered multiple intervals for the piecewise linear function and proposed a bi-level programming problem, in which the lower-level problem is a path-based tolled user equilibrium problem solved by the gradient projection method, and the upper level one is a multi-objective optimization problem solved by a genetic algorithm. Liu et al. [26] proposed a robust min–max optimization model for nonlinear distance-based tolls inside a cordoned zone to consider the stochastic day-to-day dynamics. They assumed that the tolls follow a piecewise linear function and applied the metaheuristic algorithm of artificial bee colony to solve the problem. After all, either linear or nonlinear, the distance-based pricing has two main disadvantages:

  1. (1)

    It encourages the drivers to reduce their toll by using shorter routes, even if they are highly congested. This logical response is in contrary to the objective of congestion pricing. To cope with the problem, Liu et al. [27] proposed a model for a joint nonlinear distance and time-based toll design, in which the latter compensate for the deficiency of the former. Despite the novelty, the time-based tolling evokes safety issues in the real world instances.

  2. (2)

    It may destroy the desired function of cordoned area by creating congestion inside the cordon around its boundary. This phenomenon is logically expected because of the low charges assigned to low mileage travels within the cordon.

Most of the researches on TDM strategies are based upon static traffic assignment. But, in order to devise an efficient strategy, it is of necessity to recognize the time variation of traffic flows using a dynamic traffic assignment model. Lo and Szeto [28] compared the static and dynamic traffic distribution trends in evaluating traffic management schemes. They came to conclusion that the static theory is not suitable, especially when facing with congested networks wherein junction blockage is common. Johnson et al. [29] compared static with dynamic paradigms in solving the network design problem and indicated the difference between their results. They claimed that the variation of flow in the peak hour should not be neglected as is done in the static models. Jonson [30] examined the effects of using dynamic versus static traffic assignment on the outcomes of the network design problem.

Subsequently, various researchers carried out studies on the congestion pricing in dynamic paradigms with taking account of time-varying traffic flows. Bearing in mind the complexity and computational difficulties of using a dynamic model, the literature is mainly focused on the first-best rather than the second-best strategies [31,32,33]. Interested readers are referred to Cheng et al. [34] for further information on the subject. There are a few researches dedicated to the second-best tolling design based on a dynamic traffic assignment model. De Palma et al. [35] analyzed road pricing schemes using the dynamic network equilibrium simulator METROPOLIS. They presented an iterative algorithm to solve the problem for the area and cordon pricing plans. Lin et al. [36] proposed a bi-level programming model which applies the cellular transmission model (CTM) for the dynamic tolled user equilibrium problem. They used a dual variable approximation method to solve the model for second-best scenarios. Chung et al. [37] developed a robust bi-level cellular particle swarm optimization model, where the lower-level problem is a dynamic loading model, and the upper level one is a dynamic system optimum problem which aims at adjusting tolls on predefined locations. Furthermore, there are some studies about dynamic congestion pricing where the traffic flows are based on the macroscopic fundamental diagrams instead of traffic equilibrium laws [38,39,40,41].

The main contributions of this paper include: (1) presenting a hybrid entry- and distance-based cordon charging plan which can enhance the performance of the system compared with the distinct entry-based and distance-based policies; (2) developing a dynamic tolled traffic assignment algorithm capable of dealing with our congestion pricing designs; (3) showing by example that the dynamic approach is more realistic for modeling the cordon pricing problem than the static approach. The paper is organized as follows. In the next section, the hybrid pricing scheme is introduced and its main properties are noted. Section 3 describes the dynamic tolled network loading model and algorithm. The proposed method for determining the optimum toll levels is presented in Sect. 4. Section 5 provides the numerical results for the test network, and the final section gives the concluding remarks.

2 Hybrid pricing scheme

As mentioned above, entry-based cordon pricing is not completely equitable in a sense that it does not consider the real externalities imposed by vehicles to the whole network. In this strategy, every vehicle is charged with the same toll while passing certain points at the cordon boundary, regardless of what the route of the travel is. On the other side, applying the distance-based pricing inside a cordoned area may cause unwanted congestion within the cordon around the boundary. These drawbacks limit the applicability and performance of this policy. In this paper, a hybrid entry- and distance-based strategy is proposed to circumvent these issues. In the hybrid layout, the toll consists of two parts: (1) a certain amount of charge for entering the cordon, and (2) a fee proportional to the distance travelled within the cordoned area. The first part prevents unnecessary trips into the cordoned area, while the second part provides more equity to the users traveling inside. This is further to note that the vehicle traveling outside the cordon line is free of charge.

Figure 1 illustrates schematic patterns of entry-based, distance-based and hybrid toll designs for a specific entry into the cordoned area. As can be seen, the joint design has inherited the properties of its parent designs; it consists of a positive y-intercept showing the entry toll and a positive slop representing the toll per unit distance travelled. In other words, the line of the hybrid toll (dashed line in Fig. 1) can be considered as a generalized toll design, as it can be converted to the entry-based and distance-based designs with setting to zero the line's slope and intercept, respectively.

Fig. 1
figure 1

Schematic designs of entry-based, distance-based and joint cordon tolls

Full size image

In a mathematical perspective, the objective of congestion pricing is to minimize the total travel time of travelers in an optimization model, subjected to the constraint that the route choice behavior of drivers is affected by tolling. According to the following theorem, we can easily see that the hybrid regime dominates the others.

Theorem 1

The objective function value of the optimum solution to the hybrid pricing model (\(Z_{\text{h}}\)) is a lower bound of those to the corresponding entry-based (\(Z_{\text{e}}\)) and distance-based (\(Z_{\text{d}}\)) ones.

Proof

It is obvious that the hybrid pricing model is a relaxation of each entry-based and distance-based pricing models. So, the solution spaces of the latter two problems are subsets of that of the hybrid model. Considering each space contains a finite number of solutions, we should have \(Z_{\text{h}} \le Z_{\text{e}}\) and \(Z_{\text{h}} \le Z_{\text{d}}\).□

Theorem 1 shows that using the proposed joint design may improve the system performance compared with the distinct designs of entry- and distance-based strategies. This result is further explained below using a simple example.

Consider a network with six nodes and eight links, as depicted in Fig. 2. Assume there are two origin–destination (OD) pairs A and B starting from origin 1 and ending at destinations 4 and 6, respectively. As can be seen, there are three paths connecting OD pair A (e.g., path 1–5–3–4) and two paths connecting OD pair B (e.g., path 1–5–6). The figure shows an imaginary cordon line which surrounds a cordon zone including a triangle formed between nodes 2, 3 and 4, so links (2, 4), (3, 2) and (3, 4) are the tolled links within the cordon area. For vehicles entering the cordoned zone, there are two stations located near the ends of links (1, 2) and (5, 3), which present the entry links to the cordoned area. Three different cordon toll designs are considered as follows:

Fig. 2
figure 2

Small network and cordoned area

Full size image

Entry-based tolling: vehicles are charged on entry into the cordoned area. The entry links (1, 2) and (5, 3) activate this toll.

Distance-based tolling: vehicles driving within the cordoned area are charged with tolls proportional to their distance travelled. The cordoned links (2, 4), (3, 2) and (3, 4) count these tolls.

Joint tolling: vehicles entering the cordon area are charged with both the entry- and distance-based tolls.

As can be noticed, the entry-based layout can affect OD pair B by deflecting flows from path 1–5–3–6 crossing the cordon line to path 1–5–6 which is external to the cordon. However, it cannot directly alter flow distribution of OD pair A, since all the paths between the OD pair are charged equally at the cordon stations. As a result, this plan is not fully efficient in diverting the traffic flow from the cordoned area. The distance-based scheme can obviously change the flow pattern among the routes of OD pair A, following their different traveling lengths inside the cordoned zone. On the other hand, it is unable to affect flow distribution between the paths of OD pair B, because none of them traverse the tolled links inside the zone. Hence, this toll design cannot optimally prohibit vehicles from entering the cordoned area. On the contrary, the hybrid regime yields the optimal state by diverting the flows of both OD pairs from passing over the cordon line.

3 Dynamic tolled network loading

Javani et al. [42] proposed a path-based capacity-restrained dynamic traffic assignment model, whose specific feature is allowing for an evaluation of many TDM strategies within the strategic transportation planning framework. An important extension of this model would be the inclusion of the tolls applied to the cordoned area, so that the resulting model suits for analyzing the cordon pricing strategies included in the paper. Such an extended model is discussed below.

3.1 Mathematical model

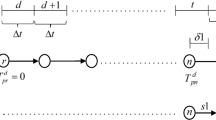
Consider \(G = (N,A)\) as the graph representing a transportation network with node set \(N\) and link set A. Each link \(a \in A\) corresponds to a pair \((n,\,m)\) of the nodes in N, where n is the tail and m is the head node of the link. Assume G is strongly connected, and let \(A_{p} \subseteq A\) be the set of links and \(N_{p} \subseteq N\) be the set of nodes on each path p in G. Assume \(A^{\prime} \subseteq A\) is the set of entry links to and \(A^{\prime\prime} \subseteq A\) is the set of tolled links within the cordoned area. Also, denote by \(r(p)\) the origin node of path \(p\), and let \(A_{pn} \subseteq A_{p}\) be the set of links which connect \(r(p)\) to each node \(n \in N_{p}\). Considering that the demand rate is known for each OD pair \(i\) and departure interval \(d\), the equilibrium dynamic tolled traffic assignment problem for the given parameters \(\delta\) and \(\gamma\) can be stated as the following model. (The definitions of other needed variables and the parameters are given in Table 1.)

Table 1 Variables and parameters used in problem P
Full size table
$$\begin{aligned} & P(\delta ,\gamma ): \\ & \hbox{min} \, Z_{\delta ,\gamma } (x(h)) = \sum\limits_{a \in A} {\sum\limits_{t \in D} {\int_{0}^{{x_{a}^{t} }} {f_{a}^{t} (\omega )} } } {\text{d}}\omega + \sum\limits_{{a \in A^{\prime}}} {\sum\limits_{{t \in D^{\prime}}} {x_{a}^{t} \frac{\delta }{\phi }} } + \sum\limits_{{a \in A^{\prime\prime}}} {\sum\limits_{{t \in D^{\prime}}} {x_{a}^{t} \cdot l_{a} \frac{\gamma }{\phi }} } , \\ \end{aligned}$$
(1)
$$\begin{aligned} {\text{s}} . {\text{t}} .\hfill \\ \sum\limits_{{p \in P_{i} }} {h_{p}^{d} } = q_{i}^{d} \quad \forall i \in I, \, d \in D, \hfill \\ \end{aligned}$$
(2)
$$h_{p}^{d} \ge 0\quad \forall \, p \in P_{i} ,\,\,i \in I, \, d \in D,$$
(3)
$$x_{a}^{t} = \sum\limits_{i \in I} {\sum\limits_{{p \in P_{i} :\,a \in A_{p} }} {\sum\limits_{d \in D} {h_{p}^{d} \,\alpha_{pa}^{dt} } } } \quad \forall a \in A, \, t \in D,$$
(4)
$$T_{pn}^{d} = \left\{ {\begin{array}{*{20}c} {\sum\limits_{{a \in A_{pn} }} {\sum\limits_{t \in D} {f_{a}^{t} (x_{a}^{t} )\,\alpha_{pa}^{dt} } } } & {{\text{if}}\,n \in N_{p} - r(p)} \\ 0 & {{\text{if}}\,n = r(p)} \\ \end{array} } \right.\quad \forall p \in P_{i} ,\,\,i \in I, \, n \in N_{p} , \, d \in D,$$
(5)
$$\alpha_{pa}^{dt} \in \{ 0,\,1\} \quad \forall p \in P_{i} ,\,\,i \in I, \, a \in A_{p} , { }d \in D, \, t \in D,$$
(6)
$$\sum\limits_{t \in D} {\alpha_{pa}^{dt} } = 1\quad \forall p \in P_{i} ,\,\,i \in I, \, a \in A_{p} , { }d \in D,$$
(7)
$$(T_{pn}^{d} + (d - t - 1)\,\Delta t)\,\alpha_{pk}^{dt} \le 0\quad \forall \,p \in P_{i} ,\,\,i \in I, \, k = (n,\,m) \in A_{p} , \, d \in D, \, t \in D,$$
(8)
$$(T_{pn}^{d} + (d - t)\,\Delta t)\,\alpha_{pk}^{dt} \ge 0\quad \forall \,p \in P_{i} ,\,\,i \in I, \, k = (n,\,m) \in A_{p} , \, d \in D, \, t \in D.$$
(9)

Equation (1) represents the objective function of the tolled dynamic traffic assignment model, which includes three terms as follows. The left-hand term is the Beckmann’s objective function [43] in the dynamic paradigm; the middle term shows the total revenue from entry tolls; and the right-hand term represents the total distance-based tolls collected. Equations (2) and (3) force the flow conservation and nonnegativity constraints to be satisfied. Equation (4) expresses the relationship between the dynamic link and path flows, established by using the path-link incidence variables \(\alpha_{pa}^{dt}\). According to Eq. (5), for every \(n \in N_{p}\), \(T_{pn}^{d}\) equals the sum of (1) the total travel time of the links belonging to \(A_{pn}\) in the time intervals that the path reaches their tail nodes, (2) the toll paid to enter the cordoned area through the links in \(A_{pn}\) (if applicable) and (3) the toll charged for driving within the cordoned zone on the links in \(A_{pn}\) (if applicable). Equation (6) requires the incidence variables \(\alpha_{pa}^{dt}\) to be integers taking 0 or 1, and Eq. (7) implies that the flow on path \(p\) which departs in time interval \(d\) reaches each link on the path in only one time interval included in \(D\). Finally, (8) and (9) result

$$(t - d)\,\Delta \,t \le T_{pn}^{d} \le (t + 1 - d)\,\Delta \,t\quad \text{for} \;k = (n,\,m) \in A_{p} \,\,\text{such} \,{\text {that}}\,\,\alpha_{pk}^{dt} = 1,$$
(10)

implying the consistency between \(T_{pn}^{d}\) and the time interval that path \(p\) reaches the tail note of link \(k\).

Equations (1–9) represent a dynamic tolled user equilibrium traffic assignment model which is appropriate for analyses of the cordon pricing strategies mentioned above. Based on the work of Bliemer et al. [44], the proposed model is categorized as the class of the capacity-restrained dynamic traffic assignment models in which link physical capacities may be exceeded, and queues and spillbacks are not considered explicitly.

3.2 Solution method

The path-based dynamic traffic assignment algorithm proposed by Javani et al. [42] is used to solve the optimization problem P given the parameters \(\delta\) and \(\gamma\). The idea is to divide the model into subproblems SP1 and SP2 corresponding to Eqs. (1–5) and (6–10), respectively. It is to note that by setting the path-link variable \(\alpha_{pa}^{dt}\) to 0 or 1, Eqs. (1–5) become similar to the conventional static traffic assignment problem, so that they can be solved with ordinary traffic assignment algorithms. Besides, Eqs. (6–10) provide the temporally continuous path flows with considering \(\alpha_{pa}^{dt}\) as variable.

The solution algorithm initiates with an arbitrary set of variables \(\alpha_{pa}^{dt}\), in such a way that Eqs. (6–10) are satisfied. It follows an iterative procedure: solving problem SP1 with the current values of \(\alpha_{pa}^{dt}\) to obtain the equilibrium path flows and solving the SP2 with the last calculated path and link flows to adjust the incidence variables. This loop is repeatedly executed until a convergence criterion is met. Brief descriptions of how the subproblems are solved are given in the following subsections.

3.2.1 Solving subproblem SP1

The algorithm decomposes the subproblem SP1 in terms of OD pairs and departure intervals and separately solves each in a successive linearization framework. Considering the variables \(\alpha_{pa}^{dt}\) as fixed binary values, the subproblem gets similar to the conventional static traffic assignment model. Therefore, it is appropriate to apply an existing traffic assignment algorithm with some augmentation required for dealing with the special structure of tensor \([\alpha_{pa}^{dt} ]\). As was performed in [42], we adopt the static algorithm developed by Javani and Babazadeh [45] to solve the subproblem. At each iteration of this algorithm, a column generation technique is utilized for generating active paths per OD pair and departure time interval, taking into account the generalized path travel times defined as

$$\varGamma_{p}^{d} = \sum\limits_{{a \in A_{p} }} {\sum\limits_{t \in D} {f_{a}^{t} (x_{a}^{t} )\,\alpha_{pa}^{dt} } } + \sum\limits_{{a \in A_{p} \cap A^{\prime}}} {\,\sum\limits_{{t \in D^{\prime}}} {\frac{\delta }{\phi }\alpha_{pa}^{dt} } } + \sum\limits_{{a \in A_{p} \cap A^{\prime\prime}}} {\,\sum\limits_{{t \in D^{\prime}}} {l_{a} \frac{\gamma }{\phi }\alpha_{pa}^{dt} \quad \forall \, p \in P_{i} ,i \in I,d \in D} } ,$$
(11)

in which the first term is the ordinary travel time on path \(p\) and the last two terms serve as the time values of the tolls charged on the path for entering into and riding within the cordoned area, respectively. Next, the subproblem SP1 is decomposed into OD pairs and departure time intervals, and each one is solved separately while holding the variables \(\alpha_{pa}^{dt}\) fixed. The path flows \(h_{p}^{d}\) are updated once the subproblem of each OD pair and departure interval is solved. The algorithm iterates in this manner until a solution as close to the optimal solution of SP1 is attained.

3.2.2 Solving subproblem SP2

The subproblem SP2 is solved for the path-link variables \(\alpha_{pa}^{dt}\), assuming that the link flows \(x_{a}^{t}\) are fixed at their current values. Because the information of active paths is stored in the random access memory (RAM), a simple path tracing scheme can be used to update the variables \(\alpha_{pa}^{dt}\) based on the current values of path travel times \(T_{pn}^{d}\). The following explains this in further detail.

Consider \(P_{i}^{d + } \subseteq P_{i}\) as the set of active paths pertaining to OD pair \(i\) and departure interval \(d\) in the current iteration, and we are tracing path \(p \in P_{i}^{d + }\) and have now reached node \(n \in N_{p}\). At this point, the travel time \(T_{pn}^{d}\) has been computed by the process using Eq. (5), and we are moving forward on link \(k = (n,m) \in A_{p}\). To update \(\alpha_{pk}^{dt}\) for each time interval \(t \in D\), the time interval \(\hat{t} \in D\) that the flow on path \(p\) reaches node \(n\) is first computed as below:

$$\hat{t} = \left[ {\frac{{T_{pn}^{d} }}{\Delta t}} \right] + d,$$
(12)

where \([\upsilon ]\) gives the integer part of number \(\upsilon\). Afterward, the values of \(\alpha_{pk}^{dt}\) are computed according to conditions (5–9) as

$$\alpha_{pk}^{dt} = \left\{ {\begin{array}{*{20}c} 1, & {t = \hat{t}} \\ 0, & {t \ne \hat{t}} \\ \end{array} } \right.\quad \forall t \in D. $$
(13)

The tracing process continues in the topological order until the destination node of path \(p\) is reached. Moreover, a solution to the subproblem SP2 is obtained by repeating the process for all the active paths in the network.

Javani et al. [42] suggested applying an averaging technique along with the tracing scheme to speed up the convergence of the variables \(\alpha_{ps}^{dt}\) to their optimal values. This is performed by substituting \(T_{pn}^{d}\) in Eq. (5) with a weighted average of its current value and the value it had at the previous iteration. More details are available in [42].

4 Optimal cordon tolls

The congestion pricing problem can be considered as an optimization programming model with the objective of minimizing the total travel time of all travelers in the network, subjected to the constraint that the route choice behavior of the drivers is governed by the known system parameters and the unknown tolls which are to be optimized. Since only the on-entry- and distance-based cordon tolls are considered in this paper, the optimization model can be therefore written as

$$\hbox{min} \,\,S(x,\delta ,\gamma ) = \sum\limits_{a \in A} {\sum\limits_{t \in D} {x_{a}^{t} \cdot f_{a}^{t} (x_{a}^{t} )} } ,$$
(14)
$$\begin{aligned} & {\text{s}} . {\text{t}} .\\ & x\,\,\text{solves} \,\,{P} (\delta ,\gamma ), \\ \end{aligned}$$
(15)
$$0 \le \delta \le \delta_{\hbox{max} } ,$$
(16)
$$0 \le \gamma \le \gamma_{\hbox{max} } ,$$
(17)

where S is the total travel time experienced by travelers and \(\delta\) and \(\gamma\) are the entry toll and the rate of distance toll (i.e., toll per unit distance), respectively, which are bounded from above by \(\delta_{\hbox{max} }\) and \(\gamma_{\hbox{max} }\) in that order.

The above model is known as a nonlinear bi-level programming program. It is well known that such programs are inherently non-convex and therefore cannot be solved using the standard optimization methods. We instead suggest an enumeration algorithm which performs a grid search of the whole problem space. This can serve as a reliable method to find the global optimum with tunable precision, while having a drawback that imposes a large amount of computational burden for high-precision solutions. We set up a very fine grid points to obtain a precise solution, because we mainly aim to analyze the productivity of the hybrid pricing, not to provide an efficient solution algorithm. The enumeration algorithm iterates through the grid points to determine the optimum toll level, as depicted in Fig. 3.

Fig. 3
figure 3

Flowchart of the applied enumeration algorithm

Full size image

5 Numerical results

The cordon pricing strategies discussed above, i.e., the entry-based, distance-based and joint tolling schemes, are evaluated through the solution of the pricing model (14–17) for the well-known Sioux Falls network. This network has 24 nodes, 76 arcs, 552 OD pairs and 3606 hundreds of vehicle trips per dayFootnote 1 [46]. Besides, to fulfill the purpose of the paper, a cordon line is defined around the central part of the network. Figure 4 illustrates this network along with the determined cordoned area. As can be seen, there are 10 exit or entry stations on the cordon line, surrounding 6 links within the cordoned area.

Fig. 4
figure 4

Sioux Falls network and cordoned area

Full size image

Table 2 shows the settings of the pricing problem for the Sioux Falls network. To generate the dynamic demand matrices, the daily OD matrix given in [46] is multiplied by 0.1 to convert from vehicles per day to vehicles per hour (in total 3606 hundreds of vehicle trips per hour). Then, the peak hour matrix is distributed among four successive 15-min departure intervals with shares of 20%, 30%, 30% and 20%, respectively. Two additional time intervals with the same length are also included to let all peak hour trips to reach their destinations. In other words, for each test case, the dynamic loading algorithm is applied for an analysis period including six 15-min time intervals of which the first four are the peak hour departure intervals. Moreover, both the entry-based and distance-based tolls are assumed to be applied only during the peak hour (i.e., no toll is charged in the last two time intervals). The following dynamic travel time function is applied in the model:

$$f_{a}^{t} (x_{a}^{t} ) = A_{a} + B_{a} \left( {{{x_{a}^{t} } \mathord{\left/ {\vphantom {{x_{a}^{t} } {\Delta t}}} \right. \kern-0pt} {\Delta t}}} \right)^{4} \quad \forall a \in A,\,\,t \in D,$$
(18)

where \(A_{a}\) and \(B_{a}\) are the same parameters as used in [46]. These parameters as well as the length of the links assumed are provided in Table 3.

Table 2 Parameters of cordon pricing problem for Sioux Falls
Full size table
Table 3 Links parameters for Sioux Falls (\(A_{a}\) in hours; \(B_{a}\) in h/[100 vehicles/h]4)
Full size table

The following relative gap (RG) is used to measure the convergence of a solution to the dynamic user equilibrium condition:

$${\text{RG}} = \frac{{\sum\nolimits_{d \in D} {\sum\nolimits_{i \in I} {\sum\nolimits_{{p \in p_{i}^{d + } }} {h_{p}^{d} T_{p}^{d} } } } - \sum\nolimits_{d \in D} {\sum\nolimits_{i \in I} {\sum\nolimits_{{p \in p_{i}^{d + } }} {h_{p}^{d} u_{i}^{d} } } } }}{{\sum\nolimits_{d \in D} {\sum\nolimits_{i \in I} {\sum\nolimits_{{p \in p_{i}^{d + } }} {h_{p}^{d} T_{p}^{d} } } } }},$$
(19)

where \(u_{i}^{d}\) is the minimum generalized path travel time for OD pair i and departure time d and \(\varGamma_{p}^{d}\) is the generalized travel time on path \(p\) as given in Eq. (11).

In the following subsections, first, the performance of the proposed joint cordon pricing scheme is analyzed and compared to its entry-based and distance-based counterparts. Second, the efficiency of the three toll designs in reducing the level of congestion in cordoned area is investigated. Finally, it is demonstrated that using the proposed dynamic tolled traffic assignment model is more suited and reliable for assessing the pricing plans than its static counterpart. In all experiments, the dynamic assignment algorithm is terminated after an RG of 10−6 or less is achieved. The total enumeration algorithm was coded in MATLAB 7.1 [48] and linked to the available C++ code of the assignment algorithm. All results reported below were produced on a laptop with an Intel 2.50 GHz CPU and 8 GB RAM.

5.1 Entry-based, distance-based or hybrid regime?

Apart from the validity of the congestion pricing, there is a serious debate about which of the cordon and distance-based pricing schemes or combinations of them would be the best treatment for the congestion problems within the urban areas. Having their own efficiencies and deficiencies, the distance-based pricing has won more favor in the previous researches mostly under the static loading conditions (see, e.g., [5, 21, 22]). To compare these policies in the more realistic case of dynamic loading, the proposed model is solved considering wide ranges of entry- and distance-based tolls for the cordoned test network.

The enumeration algorithm was performed by varying \(\delta\) from 0 to 3 and \(\gamma\) from 0 to 1 with increments of 0.01, resulting in 30,401 regularly distributed grid points within the problem space. This is a grid search on the feasible hybrid toll point, covering also the points of entry-based tolls (\(\gamma = 0\)) and distance-based tolls (\(\delta = 0\)) as bounded solutions.

Figure 5 shows a 3-D surface of surveyed solutions, generated by applying a two-dimensional low-pass filter [49], where the vertical axis represents the total travel time of the travelers during the full analysis period (as the objective performance measure of tolling) and horizontal axes show the entry toll and the distance toll rate each. As can be seen, the surface has an extremely non-convex shape and, although not explicitly shown, reaches the minimum height at point \(\delta = 0.17\) and \(\gamma = 0.08\). To explore where this point lies in the problem space, a biharmonic interpolation technique was applied to construct a clear 3-D plot of the points in a neighborhood of the optimum solution. The intended surface and the corresponding contour plot are plotted together in Fig. 6. Figure 7 illustrates the variation of total travel time with distance-based toll increases from \(\delta = 0\) to \(\delta = 3\), while the entry toll is kept fixed at the optimum level of \(\gamma = 0.08\). As it is shown in this figure, the objective function has many local optima around the global optimum point \(\delta = 0.17\).

Fig. 5
figure 5

Variation of total travel time with toll levels for Sioux Falls

Full size image
Fig. 6
figure 6

Surface plot (above) and counter plot (down) in a neighborhood of optimum toll levels for Sioux Falls

Full size image
Fig. 7
figure 7

Variation of total travel time with distance-based toll at entry toll \(\delta = 0.17\) for Sioux Falls

Full size image

Figure 8 depicts the same analysis as above but for the total monetary revenue from the peak hour charges, i.e., the sum of two last terms of Eq. (1) multiplied by \(\phi\). As expected, higher levels of tolls result in higher revenues. Also, the figure illustrates that the amount of revenue is more sensitive to changes in entry toll as compared to changes in the rate of distance toll.

Fig. 8
figure 8

Variation of total revenue with toll levels for Sioux Falls

Full size image

Table 4 shows the comparison of the total travel times and total revenues from the considered cordon pricing schemes at their optimal solutions. As can be seen, the hybrid regime has the best performance in reducing the total travel time, indicated by a significantly higher reduction percentage than the others. The entry-based system performs considerably worse, while the distance-based tolling demonstrates a very weak performance. Moreover, the hybrid regime generates the highest level of revenue, distance-based tolling the lowest level of revenue, and entry-based tolling an intermediate level. High levels of outcome can create opportunities for remarkable investments in public transport infrastructures, while some social resistance and dissatisfaction may arise limiting the total revenue from tolls. Table 5 represents the same results as the previous table but with the collected revenue limited to 1300 $. Measuring the percent reduction in total travel time, it is demonstrated that the distance-based scheme is clearly outperformed by the entry-based scheme, which is in turn clearly outperformed by the hybrid layout. It is worth mentioning that the reported reductions in the total travel times are somehow conservative, since the cordon pricing may cause the drivers changing their modes or departure times following their attempts to avoid paying tolls.

Table 4 Optimal designs of cordon pricing schemes for Sioux Falls
Full size table
Table 5 Optimal designs of cordon pricing schemes with revenue restriction of 2 × 103 $ for Sioux Falls
Full size table

5.2 Congestion reduction in cordoned area

One of the main goals of cordon pricing is to mitigate the level of congestion within a cordoned area. The volume-to-capacity ratio is a criterion commonly used for measuring the congestion level of a single link or the whole network. Table 6 displays the average of this ratio in the peak hour (i.e., the first four 15-min intervals) across the links within the cordoned area for the no-toll state as well as the alternative toll designs. As shown in this table, distance-based and hybrid schemes can partly alleviate the congestion level in the cordoned area, but the entry-based regime shows a weak performance. Moreover, in contrast to the results of Table 4 about the reduction in total travel time, the distance-based tolling system clearly outbeats the entry-based system in mitigating the congestion level inside the cordoned area.

Table 6 Volume-to-capacity ratios within cordon area for different toll designs for Sioux Falls
Full size table

5.3 Change in input flow to cordoned area

As mentioned above, the distance-based pricing may cause unwilling congestion inside the cordon near its boundary. To verify the claim, the total input volume to the cordoned area in all time intervals is analyzed as a measure of cordon boundary congestion. Table 7 shows the comparison of this measure for the alternative pricing designs as well as for the no-toll state. As demonstrated, the distance-based pricing shows a poor performance in preventing vehicles from entering the cordon, while the entry-based and hybrid regimes provide much better results. It is interesting to note that the total OD demand with the origins outside the cordoned zone and destination inside equals 7980 vehicles per hours. No matter what strategy is used, these trips cannot be eliminated from entering the zone when OD demands are treated as fixed values. However, noting the result for the no-toll scenario in Table 7, there are a number of 3342 (\(= 11322 - 7980\)) vehicles passing inside the cordon zoned, but whose origins and destinations are outside the cordon's boundary. Parts of this traffic are diverted from entry into the priced zone, affected by different pricing policy. Table 8 shows the performance of the considered tolling plans about rerouting the vehicles out of the cordoned area. As expected, the results are in accordance with those in Table 7.

Table 7 Input flow to cordoned area for different toll designs for Sioux Falls
Full size table
Table 8 Diverted flow from cordoned area for different toll designs for Sioux Falls
Full size table

5.4 Static versus dynamic approach

As explained above, dynamic traffic assignment models are generally more appropriate than static models to assessing the TDM plans, considering their ability in reproducing traffic flow more realistically. Aside from the computational efficiency of static models, the important question arises is how reliable these models are, and if they may cause detrimental results.

To eliminate the above ambiguity, the hybrid toll design from static modeling approach is compared against that obtained above by the dynamic approach. To obtain the former, the pricing problem (14–17) should be solved with considering that set D includes only a single time interval of 60-min duration. In this special case, \({P} (\delta ,\gamma )\) becomes a static tolled traffic loading model (notice that the variable \(\alpha_{pa}^{dt}\) and the corresponding constraints (1–5) are removed from the problem in this case). Applying the total enumeration technique, the optimum solution to the static model of the pricing problem is given by \(\delta = 0.15\) and \(\gamma = 0.03\), which are obviously lower than those established by the dynamic formulation. This toll design can be evaluated by the dynamic tolled assignment model to distinguish whether or not it would be really effective. Table 9 shows the comparison of the performance of the optimal hybrid tolls from the static and dynamic approaches evaluated under both the static and dynamic loading conditions. According to Table 9, the following conclusions can be remarked:

Table 9 Optimal hybrid toll designs from static and dynamic modeling approaches for Sioux Falls
Full size table
  1. (1)

    For all different toll levels, including the no-toll state, the static traffic assignment model underestimates the total travel time of the travelers by around 9%–10% compared with its dynamic counterpart. In other words, the static model cannot reflect the network congestion precisely. This is in accordance with the results provided in [42].

  2. (2)

    The optimum toll design obtained by the static approach cannot perform adequately well under dynamic loading conditions. As can be seen in the table, it attains a realistic total travel time of 8247 h, which is well above the minimum of 8283 h provided by the dynamic approach. Therefore, the static formulation of the problem may not be reliable as a standard modeling approach.

  3. (3)

    Evaluating a toll design with the static loading model may yield detrimental results. It is demonstrated that the total travel time of the optimum toll design (i.e., \(\delta = 0.17\) and \(\gamma = 0.08\)) under static loading conditions equals 7484, which is ridiculously more than the same value in the no-toll state (i.e., 7477 h). In other words, using the static traffic assignment model may cause some really beneficial pricing alternatives to be rejected.

  4. (4)

    Static modeling slightly overestimated the total amount of collected tolls when comparing to its dynamic counterpart.

6 Conclusions

In this paper, a new hybrid pricing layout was presented which is a combination of the entry-based and distance-based schemes. The new policy offers a flexible framework which allows the authorities to adjust the tolls charged for various purposes and conditions. Furthermore, a dynamic tolled traffic assignment model was developed to evaluate different pricing schemes under realistic time-varying flow conditions. The cordon pricing problem was formulated as bi-level programming model with the objective of minimizing the total travel time of the travelers, and an enumeration algorithm was devised which makes a grid search to explore for an optimal solution within the problem space. A cordoned version of the well-known Sioux Falls network was used for the evaluation of the proposed joint design against its entry-based and distance-based counterparts. The following are the results of the numerical example:

  1. (1)

    The hybrid regime is superior in reducing the total travel time of the travelers in the whole analysis period and generates the highest amount of collected tolls within the peak hour as well. Also, it performs the best in terms of mitigating the congestion within the cordoned area of the network during the peak hour.

  2. (2)

    Comparing the distinct entry-based and distance-based tolling systems showed that the former outperforms the latter in total travel time saving and revenue collection, but fails to perform better when focusing on the congestion level within the cordoned area.

  3. (3)

    The distance-based tolling system is strongly outperformed by the entry-based and hybrid schemes in diverting drivers from entry into the cordoned area.

  4. (4)

    A comparison between the results from static and dynamic modeling approaches revealed some surprising points. First, the static network loading model significantly underestimates the total travel time of the travelers and slightly overestimates the total collected tolls, compared with its dynamic counterpart. Second, the static approach provides a solution that is away from the optimality under dynamic loading conditions and therefore may not be considered as a reliable approach. Third, the static assignment cannot produce a realistic evaluation of the pricing policies, so that some beneficial alternatives may be rejected.

The above results vouch for the applicability and advantages of the proposed method for the cordon tolling problem at planning levels. Although the results are limited to the scale of our test network, they strongly encourage further investigations on the effects of such policies on real life networks. However, designing a heuristic or metaheuristic approach capable of dealing with large-scale problems may be required. In addition, using more sophisticated dynamic traffic assignment model which can consider the queue formation phenomena may be helpful in future researches.