Skip to main content
SpringerLink
Log in

Pressure and shear stress analysis in a normal triangular tube bundle based on experimental flow velocity field

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

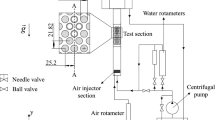
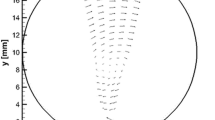
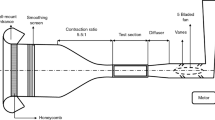
This paper presents the experimental vector velocity field obtained through the spatial filter velocimetry technique in a normal triangular tube bundle test section with tubes of 20 mm O.D. and transverse pitch of 25.2 mm. The experiments were conducted for water flows and Reynolds numbers ranging from 447 to 1842. The pressure field was estimated based on the velocity results by solving the Poisson equation. The shear stress around the tubes was analyzed calculating the viscous and Reynolds stresses. The results for turbulence strength and flow vorticity were calculated and discussed. All the analyses were performed using a second-order finite difference scheme to estimate the partial derivatives. The results indicate that the spatial filter velocimetry technique provides accurate velocity data and is suitable to be applied to complex geometries. In addition, the obtained velocity fields show that the SFV technique is capable of capturing asymmetric flow distributions, which switch from time to time, indicating a suitable spatial and temporal resolution for the experimental conditions evaluated in the present study.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Abbreviations

\(\bar{P}\) :

Average pressure (Pa)

x :

Relative to x axis (m)

y :

Relative to y axis (m)

z :

Relative to z axis (m)

V :

Actual velocity (m/s)

\(\bar{V}\) :

Average velocity (m/s)

v :

Velocity fluctuation (m/s)

u rms :

Turbulence strength (m/s)

I :

Image intensity (–)

F :

Filter (–)

t :

Time (s)

f :

Frequency (Hz)

L :

Spacing between each strip of the spatial filter (μm)

Q :

Volumetric flow rate (l/min)

d :

Tube diameter

j :

Superficial velocity (m/s)

Re:

Reynolds number based on superficial velocity and tube diameter (= j.d/ν) (–)

\(\rho\) :

Density (kg/m3)

\(\tau\) :

Shear stress (Pa)

\(\mu\) :

Dynamic viscosity (Pa.s)

\(\nu\) :

Kinetic viscosity (m2/s)

\(\omega\) :

Vorticity (1/s)

ε :

Relative error (–)

i :

Index notation

j :

Index notation

l:

Relative to liquid phase

D:

Dominant frequency

sf:

Spatial filter applied

References

  1. Kanizawa FT, Ribatski G (2016) Two-phase flow patterns across triangular tube bundles for air–water upward flow. Int J Multiph Flow 80:43–56. https://doi.org/10.1016/j.ijmultiphaseflow.2015.11.004

    Article  Google Scholar 

  2. Kanizawa FT, Ribatski G (2016) Void fraction predictive method based on the minimum kinetic energy. J Braz Soc Mech Sci Eng 38(1):209–225. https://doi.org/10.1007/s40430-015-0446-x

    Article  Google Scholar 

  3. Paul SS, Tachie MF, Ormiston SJ (2007) Experimental study of turbulent cross-flow in a staggered tube bundle using particle image velocimetry. Int J Heat Fluid Flow 28(3):441–453. https://doi.org/10.1016/j.ijheatfluidflow.2006.06.001

    Article  Google Scholar 

  4. Hosokawa S, Tomiyama A (2012) Spatial filter velocimetry based on time-series particle images. Exp Fluids 52(6):1361–1372. https://doi.org/10.1007/s00348-011-1259-z

    Article  Google Scholar 

  5. Iwaki C, Cheong KH, Monji H, Matsui G (2005) Vertical, bubbly, cross-flow characteristics over tube bundles. Exp Fluids 39(6):1024. https://doi.org/10.1007/s00348-005-0036-2

    Article  Google Scholar 

  6. Iwaki C, Cheong KH, Monji H, Matsui G (2004) PIV measurement of the vertical cross-flow structure over tube bundles. Exp Fluids 37(3):350–363. https://doi.org/10.1007/s00348-004-0823-1

    Article  Google Scholar 

  7. Hosokawa S, Mikihara I, Tomiyama A (2013) Development of a submersible small fiber LDV probe and its application to flows in a 4 × 4 rod bundle. Nucl Eng Des 263:342–349. https://doi.org/10.1016/j.nucengdes.2013.06.009

    Article  Google Scholar 

  8. Hayashi K, Hosokawa S, Tomiyama A (2014) Void distribution and bubble motion in bubbly flows in a 4 × 4 rod bundle. Part II: Numerical simulation. J Nucl Sci Technol 51(5):580–589. https://doi.org/10.1080/00223131.2014.882802

    Article  Google Scholar 

  9. Hosokawa S, Hayashi K, Tomiyama A (2014) Void distribution and bubble motion in bubbly flows in a 4 × 4 rod bundle. Part I: Experiments. J Nucl Sci Technol 51(2):220–230. https://doi.org/10.1080/00223131.2013.862189

    Article  Google Scholar 

  10. Ozturk NA, Ozalp C, Canpolat C, Sahin B (2016) PIV measurements of flow through normal triangular cylinder arrays in the passage of a model plate-tube heat exchanger. Int J Heat Fluid Flow 61:531–544. https://doi.org/10.1016/j.ijheatfluidflow.2016.06.013

    Article  Google Scholar 

  11. Delgado M, Lee S, Hassan YA, Anand NK (2018) Flow visualization study at the interface of alternating pitch tube bundles in a model helical coil steam generator using particle image velocimetry. Int J Heat Mass Transf 122:614–628. https://doi.org/10.1016/j.ijheatmasstransfer.2018.02.014

    Article  Google Scholar 

  12. Delgado M, Hassan YA, Anand NK (2019) Experimental flow visualization study using particle image velocimetry in a helical coil steam generator with changing lateral pitch geometry. Int J Heat Mass Transf 133:756–768. https://doi.org/10.1016/j.ijheatmasstransfer.2018.12.152

    Article  Google Scholar 

  13. Lee S, Delgado M, Lee SJ, Hassan YA (2018) Experimental investigation of the isothermal flow field across slant 5-tube bundles in helically coiled steam generator geometry using PIV. Nucl Eng Des 338:261–268. https://doi.org/10.1016/j.nucengdes.2018.08.012

    Article  Google Scholar 

  14. Fujisawa N, Tanahashi S, Srinivas K (2005) Evaluation of pressure field and fluid forces on a circular cylinder with and without rotational oscillation using velocity data from PIV measurement. Meas Sci Technol 16(4):989. https://doi.org/10.1088/0957-0233/16/4/011

    Article  Google Scholar 

  15. Hosokawa S, Moriyama S, Tomiyama A, Takada N (2003) PIV measurement of pressure distributions about single bubbles. J Nucl Sci Technol 40(10):754–762. https://doi.org/10.1080/18811248.2003.9715416

    Article  Google Scholar 

  16. Charonko JJ, King CV, Smith BL, Vlachos PP (2010) Assessment of pressure field calculations from particle image velocimetry measurements. Meas Sci Technol 21(10):105401. https://doi.org/10.1088/0957-0233/21/10/105401

    Article  Google Scholar 

  17. De Kat R, Van Oudheusden BW (2012) Instantaneous planar pressure determination from PIV in turbulent flow. Exp Fluids 52(5):1089–1106. https://doi.org/10.1007/s00348-011-1237-5

    Article  Google Scholar 

  18. Chisholm D (1984) Two-phase vertical upflow through tube banks with bypass lanes. Int J Heat Fluid Flow 5(1):51–53. https://doi.org/10.1016/0142-727X(84)90016-X

    Article  Google Scholar 

  19. Kanizawa FT, Ribatski G (2017) Void fraction and pressure drop during external upward two-phase crossflow in tube bundles–part I: Experimental investigation. Int J Heat Fluid Flow 65:200–209. https://doi.org/10.1016/j.ijheatfluidflow.2016.04.012

    Article  Google Scholar 

  20. Kanizawa FT, Ribatski G (2017) Void fraction and pressure drop during external upward two-phase cross flow in tube bundles–part II: Predictive methods. Int J Heat Fluid Flow 65:210–219. https://doi.org/10.1016/j.ijheatfluidflow.2016.08.003

    Article  Google Scholar 

  21. De Paula AV, Endres LAM, Möller SV (2012) Bistable features of the turbulent flow in tube banks of triangular arrangement. Nucl Eng Des 249:379–387. https://doi.org/10.1016/j.nucengdes.2012.04.024

    Article  Google Scholar 

  22. De Paula AV, Möller SV (2018) On the chaotic nature of bistable flows. Exp Therm Fluid Sci 94:172–191. https://doi.org/10.1016/j.expthermflusci.2018.01.006

    Article  Google Scholar 

  23. Keogh DB, Meskell C (2015) Bi-stable flow in parallel triangular tube arrays with a pitch-to-diameter ratio of 1.375. Nucl Eng Des 285:98–108. https://doi.org/10.1016/j.nucengdes.2015.01.009

    Article  Google Scholar 

  24. Kim HJ, Durbin PA (1988) Investigation of the flow between a pair of circular cylinders in the flopping regime. J Fluid Mech 196:431–448. https://doi.org/10.1017/S0022112088002769

    Article  Google Scholar 

  25. Tennekes H, Lumley JL (1972) A first course in turbulence. MIT Press, New York

    MATH  Google Scholar 

  26. Pope SB (2000) Turbulent flows. Cambridge University Press, Cambridge

    Book  Google Scholar 

  27. Mathieu J, Scott J (2000) An introduction to turbulent flow. Cambridge University Press, Cambridge

    Book  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge FAPESP (State of São Paulo research foundation agency, Brazil) for the doctorate scholarship (Contract Number 2016/20200-2) of the first author, Douglas Martins Rocha, and for the internship at Kobe University (Contract Number 2015/00854-5) of the second author, Fabio Toshio Kanizawa. The authors also appreciate the supports by FAPERJ, Grant Number FAPERJ E-26/203.261/2017 (234197) and CNPq, Grant Number 305673/2017-3. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001.

Author information

Authors and Affiliations

  1. Heat Transfer Research Group, Department of Mechanical Engineering, São Carlos School of Engineering, University of São Paulo, São Carlos, SP, Brazil

    Douglas Martins Rocha & Gherhardt Ribatski

  2. Department of Mechanical Engineering, School of Engineering, Universidade Federal Fluminense, Niterói, RJ, Brazil

    Fabio Toshio Kanizawa

  3. Graduate School of Engineering, Kobe University, 1-1 Rokkodai, Nada, Kobe, 657-8501, Japan

    Kosuke Hayashi & Akio Tomiyama

  4. Faculty of Societal Safety Science, Kansai University, 7-1 Hakubai, Takatsuki, Osaka, 569-1098, Japan

    Shigeo Hosokawa

Authors
  1. Douglas Martins Rocha
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fabio Toshio Kanizawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kosuke Hayashi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shigeo Hosokawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Akio Tomiyama
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Gherhardt Ribatski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Douglas Martins Rocha.

Additional information

Technical Editor: William Wolf, Ph.D.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rocha, D.M., Kanizawa, F.T., Hayashi, K. et al. Pressure and shear stress analysis in a normal triangular tube bundle based on experimental flow velocity field. J Braz. Soc. Mech. Sci. Eng. 42, 201 (2020). https://doi.org/10.1007/s40430-020-02293-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-020-02293-7

Keywords

Search

Navigation