1 Introduction

Solving systems of equations is well-studied problem. There are many methods for the numerical solution. Among other things, linear systems of equations are obtained as a result of the approximation of differential or integral equations used for modelling boundary problems (Brebbia et al. 1984). Transformation from the differential (integral) equations into system of algebraic equations is not yet the solution of the problem. To obtain unique solution of linear system of equations, the matrix determinant should be different from zero, and the matrix should be well conditioned. It is possible, that linear system of equations obtained as the result of approximation of differential (integral) equations may not meet conditions determining its unique solution.

In recent years, boundary problems are modelled by integral equations using interval numbers [for example (Piasecka Belkhayat and Korczak 2014; Zalewski et al. 2009)]. Such modelling of problems is more reliable, because it gives opportunity to include measurement errors in modelling the shape of boundary and boundary conditions. However, problem of interval modelling the shape of boundary is still open. Many authors [for example (Dessombz et al. 2001; Muhanna et al. 2005; Piasecka Belkhayat and Korczak 2014; Zalewski et al. 2009)] defined only boundary conditions and input parameters as intervals. In process of modelling boundary problems, intervals appears as measurement errors in data definition. Numerical solution of such problems is reduced to solving interval systems of equations. Solving these systems is more complicated than solving the ones with precise elements. It requires application of interval arithmetic (Hayes 2003; Krämer 2013; Moore et al. 2009).

Methods of solving systems of equations were examined in case of rounding errors (for example, generated by hardware decoding of floating-points operations) (Krämer et al. 2006; Rump 2014). The authors applied interval arithmetic to solve such systems. Rounding errors are described by very narrow intervals. They are significantly smaller then measurement errors and may be ignored in modelling of boundary problems. In this case, direct application of methods described in Krämer et al. (2006) and Rump (2014) gives wide width of solution intervals. It is useless in practical point of view.

In this paper, we apply three selected numerical methods for solving interval linear systems of equations, i.e. the Gauss elimination method (Neumaier 1990), the LU decomposition method (Goldsztejn and Chambert 2007) and the Jacobi iterative method (Markov 1999). We also apply directed interval arithmetic (Markov 1995) to minimize width of interval solutions. Because of lack of implementation of directed interval arithmetic in well-known libraries, such as C-XSC or Intlab, we implement own C++ class based on double-precision floating-point type.

In this paper, the basic concepts of interval numbers are presented. Selected numerical methods for solving interval linear systems of equations are described. The aim of this study is to test the effectiveness of mentioned methods for solving interval systems of equations obtained during solving boundary value problems. To solve such problems, classical boundary element method (BEM) (Brebbia et al. 1984) or its modification based on parametric integral systems of equations (PIES) (Zieniuk 2013) can be used. Analysis of the results is performed in terms of their accuracy, depending on the size and conditioning of the matrix of the system of equations.

2 Basic concepts of interval numbers

Interval numbers were determined by the interval, whose left endpoint had to be smaller than the right one. These numbers are called proper numbers, classical intervals or just intervals and they are presented as follows (Kearfott et al. 2005; Moore et al. 2009):

$$\begin{aligned} \mathbf x =[ \underline{x},\overline{x} ]=\lbrace x | \underline{x} \le x \le \overline{x} \rbrace \end{aligned}$$
(1)

To operate on these numbers special interval arithmetic was created and it is generally defined by the formula (where \(\circ \in \lbrace +,-,\cdot ,/\rbrace \)) (Hayes 2003):

$$\begin{aligned} \mathbf x \circ \mathbf y =[ \underline{x},\overline{x} ] \circ [ \underline{y},\overline{y} ]=[\mathrm{min}(\underline{x} \circ \underline{y}, \underline{x} \circ \overline{y}, \overline{x} \circ \underline{y}, \overline{x} \circ \overline{y}), \mathrm{max}(\underline{x} \circ \underline{y}, \underline{x} \circ \overline{y}, \overline{x} \circ \underline{y}, \overline{x} \circ \overline{y})]\nonumber \\ \end{aligned}$$
(2)

Our objective is to estimate the range of a function. Formula (2) provides the exact description of the range of each arithmetic operation over given intervals. During the development of various methods using interval numbers (Dawood 2011; Hansen and Walster 2004; Neumaier 1990), it turns out that it is impossible to obtain opposite and inverse element of such numbers. Thus problem occurs in solving simple interval equation as well as in interval systems of equations. For this purpose, an extension of classical intervals by improper numbers has been proposed (Markov 1995). These are numbers which the upper endpoint is smaller than the lower one. Such an extension was called directed or extended intervals (Popova 2001). In addition, two operators were added to get inverse and opposite element of the given number. They allow to obtain additional arithmetic operators of subtraction and division:

$$\begin{aligned} \mathbf x \ominus \mathbf y&= [ \underline{x}-\underline{y},\overline{x}-\overline{y} ]\end{aligned}$$
(3)
$$\begin{aligned} \mathbf x \oslash \mathbf y&= {\left\{ \begin{array}{ll} \left[ \underline{x}/\underline{y},\overline{x}/\overline{y} \right] &{}\text {for } \mathbf{{x}} > 0, \mathbf{{y}} > 0 \\ \left[ \overline{x}/\overline{y},\underline{x}/\underline{y}\right] &{}\text {for } \mathbf{{x}} < 0, \mathbf{{y}} < 0 \\ \left[ \overline{x}/\underline{y},\underline{x}/\overline{y} \right] &{}\text {for } \mathbf{{x}} > 0, \mathbf{{y}} < 0 \\ \left[ \underline{x}/\overline{y},\overline{x}/\underline{y} \right] &{}\text {for } \mathbf{{x}} < 0, \mathbf{{y}} > 0 \\ \left[ \overline{x}/\underline{y},\underline{x}/\underline{y} \right] &{}\text {for } \mathbf{{x}} \in 0, \mathbf{{y}} < 0 \\ \left[ \underline{x}/\overline{y},\overline{x}/\overline{y} \right] &{}\text {for } \mathbf{{x}} \in 0, \mathbf{{y}} > 0 \\ \end{array}\right. } \end{aligned}$$
(4)

3 Methods of solving interval systems of equations

General matrix form of interval system of equations can be written as follows (Neumaier 1990; Shary 2012):

$$\begin{aligned} \mathbf A \mathbf x = \mathbf b \end{aligned}$$
(5)

where A is a matrix of interval coefficients, x is a vector of interval solutions, and b is a vector of intervals. There are many methods of solving such system of equations. However, we should apply directed intervals, due to the way of modelling described in Chapter 4. Therefore in this paper, we use the LU method presented in Goldsztejn and Chambert (2007), the Jacobi method discussed by Markov (1999) and the Gauss elimination method (Neumaier 1990) as one of the most commonly used methods. Selected methods, tested and fully analysed, were presented below.

3.1 Gauss elimination method

The best-known and widely used method in the real numbers domain is the Gauss elimination method. A major step in solving interval system of equations using this method (Neumaier 1990) is to transform the matrix coefficients from the formula (5) to the following form:

$$\begin{aligned} \left[ \begin{array}{cccc}\mathbf{{a}}_{11}&{}\quad \mathbf{{a}}_{12}&{}\quad \ldots &{}\quad \mathbf{{a}}_{1n}\\ 0&{}\quad \mathbf{{a}}_{22}&{}\quad \ldots &{}\quad \mathbf{{a}}_{2n}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad 0&{}\quad \ldots &{}\quad \mathbf{{a}}_{nn}\end{array}\right] \left[ \begin{array}{c} \mathbf{{x}}_1 \\ \mathbf{{x}}_2\\ \vdots \\ \mathbf{{x}}_n \end{array}\right] =\left[ \begin{array}{c} \mathbf{{b}}_1 \\ \mathbf{{b}}_2\\ \vdots \\ \mathbf{{b}}_n \end{array}\right] \end{aligned}$$
(6)

To achieve the matrix A and the vector b, the following formulas are used:

$$\begin{aligned} \mathbf{{a}}^{(i+1)}_{jk}=\mathbf{{a}}^{(i)}_{jk} \ominus \mathbf{{a}}^{(i)}_{ik}\cdot \mathbf{{a}}^{(i)}_{ji} \oslash \mathbf{{a}}^{(i)}_{ii}, \quad \mathbf{{b}}^{(i+1)}_{k}=\mathbf{{b}}^{(i)}_{k} \ominus \mathbf{{b}}^{(i)}_{i}\cdot \mathbf{{a}}^{(i)}_{ki} \oslash \mathbf{{a}}^{(i)}_{ii} \end{aligned}$$
(7)

where \(i=1,2,\ldots ,n\) and \(j,k=i+1,i+2,\ldots ,n\).

With an upper triangular matrix (6) it is easy to determine the value of the solution vector. Starting from the last row, elements of the matrix A are equal to the value in corresponding row of the vector b. The only difference between the presented method and the method with the real numbers is to use the interval arithmetic.

3.2 The LU decomposition method

An extension of the Gauss elimination method is the LU decomposition method. In this method, the matrix A of the system of equation (5) can be written as the product of two triangular matrices: lower L and upper U (Goldsztejn and Chambert 2007):

$$\begin{aligned} \mathbf A =\mathbf L \cdot \mathbf U , \quad \text {where}:\quad \mathbf L = \left[ \begin{array}{cccc}1&{}\quad 0&{}\quad \ldots &{}\quad 0\\ \mathbf{{l}}_{21}&{}\quad 1&{}\quad \ldots &{}\quad 0\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \mathbf{{l}}_{n1}&{}\quad \mathbf{{l}}_{n2}&{}\quad \ldots &{}\quad 1\end{array}\right] \quad \mathbf U = \left[ \begin{array}{cccc}\mathbf{{u}}_{11}&{}\quad \mathbf{{u}}_{12}&{}\quad \ldots &{}\quad \mathbf{{u}}_{1n}\\ 0&{}\quad \mathbf{{u}}_{22}&{}\quad \ldots &{}\quad \mathbf{{u}}_{2n}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad 0&{}\quad \ldots &{}\quad \mathbf{{u}}_{nn}\end{array}\right] \end{aligned}$$
(8)

The solution of interval system of equations is reduced to solving two interval systems of equations with the triangular matrices:

$$\begin{aligned} \mathbf L \cdot \mathbf U \cdot \mathbf x = \mathbf b \Rightarrow \mathbf U \cdot \mathbf x = \mathbf z \quad \mathbf L \cdot \mathbf z = \mathbf b \end{aligned}$$
(9)

The elements of the matrix L and U are calculated alternately. First, the values in the row of the U matrix are calculated, then the column of the L matrix. The corresponding elements of the matrix for all \(i \in \lbrace 1,2,\ldots ,n \rbrace \) can be calculated:

$$\begin{aligned} \mathbf{{u}}_{ij}&= \mathbf{{a}}_{ij} \ominus \sum _{k=1}^{i-1}\mathbf{{l}}_{jk}\cdot \mathbf{{u}}_{kj} \quad \text {for} \, j \in \lbrace i,i+1,\ldots ,n \rbrace \end{aligned}$$
(10)
$$\begin{aligned} \mathbf{{l}}_{ji}&= 1 \oslash \mathbf{{u}}_{ii} \left( \mathbf{{a}}_{ji} \ominus \sum _{k=1}^{i-1}\mathbf{{l}}_{jk}\cdot \mathbf{{u}}_{ki}\right) \quad \text {for} \, j \in \lbrace i+1,i+2,\ldots ,n \rbrace \end{aligned}$$
(11)

Analysing the Eq. (11), it can be seen that the method will not work if the value of any element on the diagonal of the matrix U will be equal to zero (Goldsztejn and Chambert 2007).

3.3 The Jacobi method

Another method of solving linear systems of equations is the iterative Jacobi method (Markov 1999). In this method, the interval system of Eq. (5) is solved by the following formula:

$$\begin{aligned} \mathbf x _{i+1}=\mathbf T ^{-1} \cdot \left( \mathbf b \ominus (\mathbf A \ominus \mathbf T ) \cdot \mathbf x _{i} \right) \end{aligned}$$
(12)

where \(\mathbf x _{i}\) is the next approximation of the solution vector, A is the matrix of interval coefficients, b is a vector of intervals, T and \(\mathbf T ^{-1}\) are matrices defined as follows:

$$\begin{aligned} \mathbf T&= \mathbf T (\mathbf A )= (\mathbf{{t}}_{ij}) \quad \text {where} \quad \mathbf{{t}}_{ii}=\mathbf{{a}}_{ii}, ~\mathbf{{t}}_{ij}=0 \quad \text {for} \quad i \ne j\end{aligned}$$
(13)
$$\begin{aligned} \mathbf T ^{-1}&= \mathbf T ^{-1}(\mathbf A )= (\mathbf{{t}}^{*}_{ij}) \quad \text {where} \quad \mathbf{{t}}^{*}_{ij}=1 \oslash \mathbf{{a}}_{ii},~\mathbf{{t}}^{*}_{ij}=0 \quad \text {for}\, i \ne j \end{aligned}$$
(14)

Substituting (13) and (14) into (12) we can find solution of the system (5):

$$\begin{aligned} \mathbf{{x}}_{i}=\left( \mathbf{{b}}_{i} \ominus \sum _{j=1,j \ne i}^{n}\mathbf{{a}}_{ij} \cdot \mathbf{{x}}_{j} \right) \oslash \mathbf{{a}}_{ii} \end{aligned}$$
(15)

Calculation are performed until the difference between calculated value and the value from previous iteration is small enough.

4 Analysis of solutions of interval linear system of equations obtained during numerical solving of boundary value problems

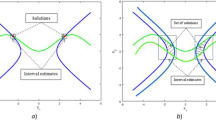
To solve boundary value problems, we can apply boundary element method (Brebbia et al. 1984) based on boundary integral equations (BIE) and similarly parametric integral equations system (Zieniuk 2013; Zieniuk et al. 2012, 2014; Kużelewski and Zieniuk 2014) which is a modification of classical BIE. Numerical solution of the problems using mentioned methods is reduced to solve linear system of equations. The system is defined on boundary of solving problem. However, first of all we should define the problem. It means that the shape of boundary should be presented as an interval. Such intervals include measurement errors \(\varepsilon \) which are associated with defining the boundary (Fig. 1). They are not included in classical modelling (use of real numbers). In practice, to define this problem the boundary should be presented as some band with a width \(\varepsilon \), which includes measurement error. It is assumed that the precise boundary is located within the band (bold line in the Fig. 1 labelled as b). The bounds of interval band are the inner edge a and the outer edge c.

Fig. 1
figure 1

Schematic modelling of interval boundary

Full size image

Solution of a boundary problem with a shape of boundary defined as interval is reduced to solving interval system of equations. In this paper, modelling of the problem described by Navier–Lamé equations was considered. The aim of the research is to examine the effectiveness of methods of solving interval system of equations. Such system can be obtained by MEB (or PIES). Process of modelling of boundary problem is carried out two times, separately for the inner and outer edges. As result of this strategy, two linear systems of equations are obtained (16). The first of these relates to the inner edge (a on the Fig. 1) and the second to the outer edge (c on the Fig. 1) of band.

$$\begin{aligned}&\left[ \begin{array}{cccc}\underline{a}_{11}&{}\quad \underline{a}_{12}&{}\quad \ldots &{}\quad \underline{a}_{1n}\\ \underline{a}_{21}&{}\quad \underline{a}_{22}&{}\quad \ldots &{}\quad \underline{a}_{2n}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \underline{a}_{n1}&{}\quad \underline{a}_{n2}&{}\quad \ldots &{}\quad \underline{a}_{nn}\end{array}\right] \cdot \left[ \begin{array}{c}\underline{x}_{1}\\ \underline{x}_{2}\\ \vdots \\ \underline{x}_{n} \end{array}\right] \!=\! \left[ \begin{array}{c}\underline{b}_{1}\\ \underline{b}_{2}\\ \vdots \\ \underline{b}_{n} \end{array}\right] \quad \left[ \begin{array}{cccc}\overline{a}_{11}&{}\quad \overline{a}_{12}&{}\quad \ldots &{}\quad \overline{a}_{1n}\\ \overline{a}_{21}&{}\quad \overline{a}_{22}&{}\quad \ldots &{}\quad \overline{a}_{2n}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \overline{a}_{n1}&{}\quad \overline{a}_{n2}&{}\quad \ldots &{}\quad \overline{a}_{nn}\end{array}\right] \cdot \left[ \begin{array}{c}\overline{x}_{1}\\ \overline{x}_{2}\\ \vdots \\ \overline{x}_{n} \end{array}\right] = \left[ \begin{array}{c}\overline{b}_{1}\\ \overline{b}_{2}\\ \vdots \\ \overline{b}_{n} \end{array}\right] \nonumber \\ \end{aligned}$$
(16)

Interval system of equations is obtained combining elements matrices and vectors in (16). We decided to examine the efficiency of methods described in Sect. 3. To solve such a system, the classical and directed interval arithmetic were used. Finally, obtained solutions were compared.

4.1 Differences between traditional and directed intervals arithmetic

The main objective of traditional interval computations is to find enclosure [all possible values of x from Eq. (5)]. Directed interval arithmetic is focused on minimizing of solution error and it gives narrower intervals than classic one. Solution of the system of two equations using classical interval arithmetic (Hansen and Walster 2004) gives significantly wider intervals than using directed intervals (Markov 1999). Therefore, it was decided to check the case of linear system of 12 equations. For this purpose, the boundary value problem defined in the triangular area was considered. The system of equations generated during the numerical solution of the problem has been solved by the LU decomposition method. The results of application classical interval arithmetic and directed one are presented in Table 1.

Table 1 Solution of the system of equations using classical and directed interval arithmetic
Full size table

It turns out that for system of 12 equations interval width of results for classical intervals is much greater than for directed ones, as well as in case of 2 equations. It is also noted that the middle value of classical interval solution is more shifted from the real number (b in Fig. 1) than directed one. It is connected with the fact that traditional intervals gives all possible solutions, which is usually useless in practice. Additionally, it is more accurate to use directed intervals because modelling problem in a way presented in Sect. 4 may produce improper intervals. Therefore, we decided to focus only on application of directed interval arithmetic.

4.2 Tests for systems with a small number of equations

To test the effectiveness of three selected methods of solving systems of equations described in Sect. 3, the problem defined in the triangular area with the generated system of 24 equations was examined. First to solve the system, the Jacobi iterative method was applied. Unfortunately, the method does not always converge to the correct result. It also happened in this case. Because it often happens that the Jacobi method fails, we decided to examine properties of generated system. For this purpose, the condition number has been calculated. It turned out that this is quite high value, much different from the 1. Therefore, to improve the condition of the matrix, we decided to make the following preconditioning of the system (5) (Neumaier 1990):

$$\begin{aligned} \text {mid}(\mathbf A )^{-1}\cdot \mathbf A \cdot \mathbf x = \text {mid}(\mathbf A )^{-1}\cdot \mathbf b \end{aligned}$$
(17)

where mid\(([\underline{x},\overline{x}])=(\underline{x}+\overline{x})/2\) is the middle value of interval. Therefore, the equation is multiplied by the inverse matrix of middle values.

After the implementation of such transformation, the system has been solved by the Jacobi method. Because it is the iterative method which results does not always converge to the correct solution, it was decided to test the LU decomposition method and the Gauss elimination method. In case of solving the preconditioned system of equations, the results obtained by these methods are very close to the ones from the Jacobi method. However, the direct application (without preconditioning) of the LU decomposition or the Gauss elimination method slightly decreases the solution interval. This phenomenon is observed only at systems with a small number of equations. To verify the correctness and accuracy of the results obtained by different methods, relative error of the solutions is presented in (Fig. 2).

Fig. 2
figure 2

Relative error of each value of obtained solution for selected methods (asterisk indicates solution after the preconditioning)

Full size image

In this case, relative error is specified by absolute value of interval solution to precise one with application of degenerate intervals (Markov 1995). The exact value became a value of a precise solution (b in the Fig. 1), therefore, the formula of relative error was described in the following form:

$$\begin{aligned} \delta = \Delta \mathbf x \oslash \mathbf x _{0} = ([\underline{x},\overline{x}]-[x_0,x_0]) \oslash [x_0,x_0] \end{aligned}$$
(18)

where: x interval solution of system equations, \(\mathbf x _{0}\) precise solution. Figure 2 shows, that after the preconditioning, the relative error of all considered methods is very similar. However, direct application of the LU decomposition or the Gauss elimination method to the generated system reduces slightly the error value. The correctness of these solutions was checked additionally by multiplying them by a matrix of coefficients A and then the comparison with a right-hand vector b. The results confirmed the correctness of the methods for solving the system of equations. The difference between the values turned out to be small.

4.3 Tests for linear systems with a large number of equations

In the case of system of 24 equations, the differences between the methods are quite hardly visible. Therefore, it was decided to examine boundary value problem which required solution of the system of 96 equations. It turned out that in case of such system, conditioning of the matrix is deteriorating. Application of the Gauss elimination method gave slightly worse results than the LU decomposition method. In the Jacobi method, the convergence problem occurred. Therefore, the further analysis focuses on the LU decomposition method. Figure 3 shows relative error of selected solutions calculated by (18).

Fig. 3
figure 3

Relative error of selected interval solution using the LU and the LU* methods (asterisk indicates solution after the preconditioning)

Full size image

Solutions were obtained by the LU method and preconditioned LU method (17). It turned out that preconditioning influences the improvement of results. Significant difference between selected maximum values of the relative errors is seen in Fig. 3. In addition, in case of the LU* method, improvements of the middle value of error can be noted. This is closer to the expected zero than in the case of the LU method. Another disadvantage of direct application of the LU method is that interval solution not always contains the precise solution. This problem does not appear in preconditioned LU method. Therefore, despite slightly worse value in the case of systems of 24 equations, we should apply preconditioned methods.

4.4 Influence of measurement error size \(\varepsilon \) into the solution

Until now, systems of equations have been created by taking relatively small measurement error (the value \(\varepsilon \) in Fig. 1). The value of \(\varepsilon =0.001\), and maximum length of the boundary of triangular area was 1. Therefore, it was decided to examine the change of solutions when the value of \(\varepsilon \) is changed. Figure 4 shows the relationship between the lower and upper endpoint of the interval solution, and the precise solution for different values of measurement error \(\varepsilon \).

Fig. 4
figure 4

Values of the interval and real number solutions vectors depending on measurement error \(\varepsilon \)

Full size image

It can be seen, that for each element of the solution vector, the precise solution (grey bar) is always between the ends of the interval (black and white bars). In addition, it can be seen that the change of the width of selected errors affects the intervals width of the obtained solutions. Respectively for the value \(\varepsilon =0.1\), a quite large differences of the interval solution were observed. Sometimes the values were change from negative to positive. In case of the \(\varepsilon = 0.01\) bars are closer, but still difference between some values can be clearly seen. Only in the case of \(\varepsilon =0.001\) difference is almost invisible.

5 Conclusions

This paper presents the effectiveness of the methods used to solve interval systems of equations generated during the numerical solution of boundary value problems. Comparison of three selected methods of solving such systems was performed using directed interval arithmetic. The Gauss elimination and the LU decomposition methods work well with systems of 24 equations. However, in case of 96 equations it may happen that the interval does not contain a precise solution. The reason for this behaviour of methods is ill-conditioned matrix obtained from PIES. Therefore, it seems reasonable to use preconditioned methods. After transformation, the effectiveness of both methods improved, whereas the middle of the interval relative error was closer to zero. In case of solving ill-conditioned linear systems of 96 equations, the LU method allows to get a little bit narrower intervals than the Gauss elimination method. In case of the Jacobi method, the main problem turns out to be the convergence of the method. Preconditioning increases the likelihood of convergence significantly, but does not guarantee that each problem can be solved. As a result, it was found, that the best method for solving interval systems of equations is preconditioned LU decomposition method. The main objective of this study was try to get a correct solution from practical point of view. The intervals are generated by measurement errors which appear during the modelling of boundary value problem. The intervals appeared in the process of data definition. This paper is a necessary step to our further work on uncertainty in solving boundary value problems. For further work, the application of fuzzy sets (Reiser et al. 2013) can be considered. In this case, interval solutions should be analysed as suitable alpha-cuts.