Quadrature iterative method for numerical solution of two-dimensional linear fuzzy Fredholm integral equations

Abstract

In this paper, first, we propose an iterative method based on quadrature formula for solving two-dimensional linear fuzzy Fredholm integral equations (2DLFFIE). Then, we prove the error estimation of the method. In addition, we show the numerical stability analysis of the method with respect to the choice of the first iteration. Finally, supporting examples are also provided.

Introduction

The study of fuzzy differential and integral equations begins with the research of Kaleva [13] and Seikkala [21]. As we know, showing the existence and uniqueness solution of these equations is very important. So, to this end, many authors applied the Banach’s fixed point theorem and the method of successive approximations. Recently, many researchers proposed numerical methods for solving fuzzy Fredholm integral equations (FFIEs). To see more details about solving FFIE, one can refer to [2, 4–6, 8–12, 15, 16, 18, 19, 22, 23].

Solving linear and nonlinear FFIEs based on iterative method is done by many authors but for the first time, solving 2DLFFIEs was studied by authors of [18] that the authors proved the existence and uniqueness solution of these equations by using Banach’s fixed point theorem. In addition, in [19], authors presented a numerical method for solving two-dimensional nonlinear FFIEs by using an iterative method. Recently, authors of [7, 14, 17, 20] proposed some numerical approaches to solve 2DLFFIEs.

Here, we propose a numerical method for solving (3.1). In addition, we present the estimation error and the numerical stability analysis. The rest of the paper is organized as follows: In “Preliminaries”, we review some properties for fuzzy-number-valued functions, such as continuity, boundedness, fuzzy Henstock and fuzzy Riemann integrability and fuzzy quadrature rules . In “2D linear fuzzy Fredholm integral equations”, we propose a new approach based on quadrature rule and iterative method to solve 2DLFFIEs. In “Convergence analysis”, we investigate convergence analysis of the proposed method. Considering the numerical stability analysis of the proposed method is done in “Numerical stability analysis”. Finally, some numerical examples are presented in “Numerical examples”.

Preliminaries

At first, we present some basic definitions and necessary results about fuzzy set theory.

Definition 2.1

[1] A fuzzy number is a function $u:\mathbb {R}\rightarrow [0,1]$ with the following properties:

• 1. u is normal, i.e. $\exists x_{0}\in \mathbb {R}$; $u(x_{0})=1$.

• 2. $u(\eta x+(1-\eta )y)\ge \min \{u(x),u(y)\}\forall x,y\in \mathbb {R},\forall \eta \in [0,1]$ (u is called a convex fuzzy subset).

• 3. u is upper semicontinuous on $\mathbb {R}$, i.e., $\forall x_{0}\in \mathbb {R}$ and $\forall \epsilon >0$, $\exists$ neighborhood $V(x_{0}):u(x)\le u(x_{0})+\epsilon , \forall x\in V(x_{0})$.

• 4. The set $\overline{supp(u)}$ is compact in $\mathbb {R}$ (where $supp(u):=\{x\in \mathbb {R}; u(x)>0\}$).

The set of all fuzzy numbers is denoted by $\mathbb {R}_{F}$.

Definition 2.2

[1] For $0<r\le 1$ and $u\in \mathbb {R}_{F}$ define $[u]^{r}:=\{x\in \mathbb {R}: u(x)\ge r\}$ and

$$\begin{aligned}{}[u]^{0}:=\overline{\{x\in \mathbb {R}: u(x)>0\}}. \end{aligned}$$

It is well known that for each $r\in [0,1]$, $[u]^{r}$ is a closed and bounded interval of $\mathbb {R}$. For $\tilde{u}$, $\tilde{v}\in \mathbb {R}_{F}$ and $\lambda \in \mathbb {R}$, we define uniquely the sum $\tilde{u}\oplus \tilde{v}$ and the product $\lambda \odot \tilde{u}$ by

$$\begin{aligned} \,[\tilde{u}\oplus \tilde{v}]^{r}=[\tilde{u}]^{r}+[\tilde{v}]^{r},[\lambda \odot \tilde{u}]^{r}=\lambda [\tilde{u}]^{r},\forall r\in [0,1], \end{aligned}$$

where $[\tilde{u}]^{r}+[\tilde{v}]^{r}$ means the usual addition of two intervals (as subsets of $\mathbb {R}$). Also, $\lambda [\tilde{u}]^{r}$ means the usual product between a scalar and a subset of $\mathbb {R}$. Notice $1\odot \tilde{u}=\tilde{u}$ and it holds $\tilde{u}\oplus \tilde{v}=\tilde{v}\oplus \tilde{u}$, $\lambda \odot \tilde{u}=\tilde{u}\odot \lambda$. If $0\le r_{1}\le r_{2}\le 1$ then $[\tilde{u}]^{r_{2}}\subseteq [\tilde{u}]^{r_{1}}$. Actually $[\tilde{u}]^{r}=[\tilde{u}_{-}^{(r)},\tilde{u}_{+}^{(r)}]$, where $\tilde{u}_{-}^{(r)}\le \tilde{u}_{+}^{(r)}$, $\tilde{u}_{-}^{(r)}$, $\tilde{u}_{+}^{(r)}\in \mathbb {R}$, $\forall r\in [0,1]$. For $\lambda >0$ one has $\lambda \tilde{u}_{\pm }^{(r)}=(\lambda \odot \tilde{u})_{\pm }^{(r)}$, respectively.

Definition 2.3

[1] Define $D:\mathbb {R}_{F}\times \mathbb {R}_{F}\rightarrow \mathbb {R}_{+}$ by

$$\begin{aligned} D(\tilde{u},\tilde{v}):= \sup _{r\in [0,1]}\max \bigg \{\left| \tilde{u}_{-}^{(r)}-\tilde{v}_{-}^{(r)}\right| , \left| \tilde{u}_{+}^{(r)}-\tilde{v}_{+}^{(r)}\right| \bigg \}\\= & {} \sup _{r\in [0,1]} \text{ Hausdorff } \text{ distance } ([\tilde{u}]^{r},[\tilde{v}]^{r}),\\ \end{aligned}$$

where $[\tilde{v}]^{r}=[\tilde{v}_{-}^{(r)},\tilde{v}_{+}^{(r)}]$; $\tilde{u}$, $\tilde{v}\in \mathbb {R}_{F}$. Clearly, D is a metric on $\mathbb {R}_{F}$. Also $(\mathbb {R}_{F},D)$ is a complete metric space, with the following properties [1]:

$$\begin{aligned} D(\tilde{u}\oplus \tilde{w},\tilde{v}\oplus \tilde{w})& \,=\, D(\tilde{u},\tilde{v}), \forall \tilde{u},\tilde{v},\tilde{w}\in \mathbb {R}_{F},\\ D(k'\odot \tilde{u},k'\odot \tilde{v}) &\,=\, \left| k'\right| D(\tilde{u},\tilde{v}),\forall \tilde{u},\tilde{v}\in \mathbb {R}_{F},\forall k'\in \mathbb {R},\\ D(\tilde{u}\oplus \tilde{v},\tilde{w}\oplus \tilde{e})&\le D(\tilde{u},\tilde{w})+D(\tilde{v},\tilde{e}),\forall \tilde{u},\tilde{v},\tilde{w},\tilde{e}\in \mathbb {R}_{F}.\\ \end{aligned}$$

Definition 2.4

[1] Let $f,g:\mathbb {R}\rightarrow \mathbb {R}_{F}$ be fuzzy number valued functions. The distance between f, g is defined by

$$\begin{aligned} D^{*}(f,g):=\sup _{x\in \mathbb {R}} D(f(x),g(x)). \end{aligned}$$

Lemma 2.5

[1]

• 1. If we denote $\tilde{0}:=\chi _{\{0\}}$ , then $\tilde{0}\in \mathbb {R}_{F}$ is the neutral element with respect to $\oplus$ , i.e., $\tilde{u}\oplus \tilde{0}=\tilde{0}\oplus \tilde{u}=\tilde{u}$, $\forall \tilde{u}\in \mathbb {R}_{F}$.

• 2. With respect to $\tilde{0}$ , none of $\tilde{u}\in \mathbb {R}_{F}$, $\tilde{u}\ne \tilde{0}$ has opposite in $\mathbb {R}_{F}$.

• 3. Let $\alpha$, $\beta \in \mathbb {R}: \alpha .\beta \ge 0$ , and any $\tilde{u}\in \mathbb {R}_{F}$ , we have $(\alpha +\beta )\odot \tilde{u}=\alpha \odot \tilde{u}\oplus \beta \odot \tilde{u}$ . For general $\alpha$, $\beta \in \mathbb {R}$ , the above property is false.

• 4. For any $\gamma \in \mathbb {R}$ and any $\tilde{u}$, $\tilde{v}\in \mathbb {R}_{F}$ , we have $\gamma \odot (\tilde{u}\oplus \tilde{v})=\gamma \odot \tilde{u}\oplus \gamma \odot \tilde{v}$.

• 5. For any $\gamma$, $\eta \in \mathbb {R}$ and any $\tilde{u}\in \mathbb {R}_{F}$ , we have $\gamma \odot (\eta \odot \tilde{u})=(\gamma \odot \eta )\odot \tilde{u}$.

If we denote $\left\| \tilde{u}\right\| _{F}:=D(\tilde{u},\tilde{0})$, $\forall \tilde{u}\in \mathbb {R}_{F}$ , then $\left\| .\right\| _{F}$ has the properties of a usual norm on $\mathbb {R}_{F}$ , i.e.,

$$\begin{aligned} \left\| \tilde{u}\right\| _{F}&\,=\, 0\text{ iff } \tilde{u}=\tilde{0},\left\| \lambda \odot \tilde{u}\right\| _{F}=\left| \lambda \right| .\left\| \tilde{u}\right\| _{F},\\ \left\| \tilde{u}\oplus \tilde{v}\right\| _{F}&\le \left\| \tilde{u}\right\| _{F}+\left\| \tilde{v}\right\| _{F},\left\| \tilde{u}\right\| _{F}-\left\| \tilde{v}\right\| _{F}\le D(\tilde{u},\tilde{v}). \end{aligned}$$

Notice that $(\mathbb {R}_{F},\oplus ,\odot )$ is not a linear space over $\mathbb {R}$ , and consequently $(\mathbb {R}_{F},\left\| .\right\| _{F})$ is not a normed space. Here $\sum ^{*}$ denotes the fuzzy summation.

Definition 2.6

[13] A fuzzy valued function $f:[a,b]\rightarrow \mathbb {R}_{F}$ is said to be continuous at $x_{0}\in [a,b]$, if for each $\epsilon >0$ there exists $\delta >0$ such that $D(f(x),f(x_{0}))<\epsilon$, whenever $x\in [a,b]$ and $\left| x-x_{0}\right| <\delta$. We say that f is fuzzy continuous on [a, b] if f is continuous at each $x_{0}\in [a,b]$, and denotes the space of all such functions by $C_{F}[a,b]$.

Definition 2.7

[3] Let $f:[a,b]\rightarrow \mathbb {R}_{F}$ be a bounded mapping. Then the function $\omega _{[a,b]}(f,.):\mathbb {R}_{+}\cup \{0\}\rightarrow \mathbb {R}_{+}$

$$\begin{aligned} \omega _{[a,b]}(f,\delta )=\sup \{D(f(x),f(y));x,y\in [a,b],\left| x-y\right| \le \delta \}, \end{aligned}$$

is called the modulus of oscillation of f on [a, b].

If $f\in C_{F}[a,b]$ (i.e. $f:[a,b]\rightarrow \mathbb {R}_{F}$ is continuous on [a, b]), then $\omega _{[a,b]}(f,\delta )$ is called uniform modulus of continuity of f.

The following properties will be very useful in what follows.

Theorem 2.8

[3] The following statements, concerning the modulus of oscillation, are true:

• 1. $D(f(x),f(y))\le \omega _{[a,b]}(f,\left| x-y\right| ),$ $\forall x,y\in [a,b]$,

• 2. $\omega _{[a,b]}(f,\delta )$ is a nondecreasing mapping in $\delta$,

• 3. $\omega _{[a,b]}(f,0)=0$,

• 4. $\omega _{[a,b]}(f,\delta _{1}+\delta _{2})\le \omega _{[a,b]}(f,\delta _{1})+\omega _{[a,b]}(f,\delta _{2})$, $\forall \delta _{1}$, $\delta _{2}\ge 0$,

• 5. $\omega _{[a,b]}(f,n\delta )\le n\omega _{[a,b]}(f,\delta )$, $\forall \delta \ge 0$, $n\in \mathbb {N},$

• 6. $\omega _{[a,b]}(f,\eta \delta )\le (\eta +1)\omega _{[a,b]}(f,\delta )$, $\forall \delta$, $\eta \ge 0$.

Definition 2.9

[1] Let $f:[a,b]\rightarrow \mathbb {R}_{F}$. We say that f is fuzzy-Riemann integrable to $I\in \mathbb {R}_{F}$ if for any $\epsilon >0$, there exists $\delta >0$ such that for any division $P=\{[u,v];\xi \}$ of [a, b] with the norms $\Delta (p) <\delta$, we have

$$\begin{aligned} D\left( \sum _{p}^{~~~~~*}(v-u)\odot f(\xi ),I\right) < \, \epsilon , \end{aligned}$$

where $\sum ^{~~*}$ denotes the fuzzy summation. We choose to write

$$\begin{aligned} I:=(FR)\int _{a}^{b}f(x)\mathrm{d}x. \end{aligned}$$

We also call an f as above (FR)-integrable.

Lemma 2.10

[1] If $f,g:[a,b]\subseteq \mathbb {R}\rightarrow \mathbb {R}_{F}$ are fuzzy continuous functions, then the function $F:[a,b]\rightarrow \mathbb {R}_{+}$ defined by $F(x):=D(f(x),g(x))$ is continuous on [a, b], and

$$\begin{aligned} D\left( (FR)\int _{a}^{b}f(x)\mathrm{d}x,(FR)\int _{a}^{b}g(x)\mathrm{d}x\right) \le \int _{a}^{b}D(f(x),g(x))\mathrm{d}x. \end{aligned}$$

Theorem 2.11

[3] Let $f:[a,b]\rightarrow \mathbb {R}_{F}$ be a Henstock integrable, bounded mapping. Then, for any division $a=x_{0}<x_{1}<\cdots <x_{n}=b$ and any points $\xi _{i}\in [x_{i-1},x_{i}]$ we have

$$\begin{aligned} D\left( (FH)\int _{a}^{b}f(t)dt,\sum _{i=1}^{n}(x_{i}-x_{i-1})\odot f(\xi _{i})\right) \le \sum _{i=1}^{n}(x_{i}-x_{i-1})\omega _{[x_{i-1},x_{i}]}(f,x_{i}-x_{i-1}). \end{aligned}$$

By the above theorem, the following result holds:

Corollary 2.12

[3] Let $f:[a,b]\rightarrow \mathbb {R}_{F}$ be a Henstock integrable, bounded mapping. Then

$$\begin{aligned}&D\left( (FH)\displaystyle \int _{a}^{b}f(t)dt,\frac{b-a}{6}\odot \left( f(a)\oplus 4\odot f\left( \frac{a+b}{2}\right) \oplus f(b)\right) \right) \\&\quad \quad \le 3(b-a)\omega _{[a,b]}\left( f,\frac{b-a}{6}\right) . \end{aligned}$$

Definition 2.13

[18] Suppose that $f:[a,b]\times [c,d]\rightarrow \mathbb {R}_{f}$ is a bounded mapping. The function $\omega _{[a,b]\times [c,d]}(f,.):\mathbb {R}_{+}\cup \{0\}\rightarrow \mathbb {R}_{+}$ defined by

$$\begin{aligned} \omega _{[a,b]\times [c,d]}(f,\delta )&=\sup \{D(f(x,y),f(s,t)); x,s\in [a,b]; y,t\in [c,d]; \\&\quad \;\sqrt{(x-s)^{2}+(y-t)^{2}}\le \delta \}, \end{aligned}$$

is called modules of oscillation of f on $[a,b]\times [c,d]$. In addition, if $f\in C_{F}([a,b]\times [c,d])$, then $\omega _{[a,b]\times [c,d]}(f,\delta )$ is called uniform modules of continuity of f.

Theorem 2.14

[18] The following properties hold:

• 1. $D(f(x,y),f(s,t))\le \omega _{[a,b]\times [c,d]}(f,\sqrt{(x-s)^{2}+(y-t)^{2}}), \forall x,s\in [a,b], y,t\in [c,d];$

• 2. $\omega _{[a,b]\times [c,d]}(f,\delta )$ is a nondecreasing mapping in $\delta$;

• 3. $\omega _{[a,b]\times [c,d]}(f,0)=0$;

• 4. $\omega _{[a,b]\times [c,d]}(f,\delta _{1}+\delta _{2})\le \omega _{[a,b]\times [c,d]}(f,\delta _{1})+\omega _{[a,b]\times [c,d]}(f,\delta _{2})$, $\forall \delta _{1},\delta _{2}\ge 0$;

• 5. $\omega _{[a,b]\times [c,d]}(f,n\delta )\le n\omega _{[a,b]\times [c,d]}(f,\delta )$, $\forall \delta \ge 0$, $n\in \mathbb {N}$;

• 6. $\omega _{[a,b]\times [c,d]}(f,\lambda \delta )\le (\lambda +1)\omega _{[a,b]\times [c,d]}(f,\delta )$, $\forall \lambda ,\delta \ge 0$.

Corollary 2.15

[18] We have

$$\begin{aligned} \underline{(FR)\int _{c}^{d}\int _{a}^{b}f(s,t;r)dsdt}&=\int _{c}^{d}\int _{a}^{b}\underline{f}(s,t,r)dsdt,\\ \overline{(FR)\int _{c}^{d}\int _{a}^{b}f(s,t;r)dsdt}&=\int _{c}^{d}\int _{a}^{b}\overline{f}(s,t,r)dsdt.\\ \end{aligned}$$

Theorem 2.16

[18] If f and g are Henstock integrable mapping on $[a,b]\times [c,d]$ and if D(f(s, t), g(s, t)) is Lebesgue integrable, then

$$\begin{aligned}&D\left( (FH)\int _{c}^{d}\int _{a}^{b}f(s,t)dsdt,(FH)\int _{c}^{d}\int _{a}^{b}g(s,t)dsdt\right) \nonumber \\& \quad \le (L)\int _{c}^{d}\int _{a}^{b}D(f(s,t),g(s,t))dsdt. \end{aligned}$$

(2.1)

Definition 2.17

[18] A function $f:[a,b]\times [c,d]\rightarrow \mathbb {R}_{F}$ is said to be L-Lipschitz, if

$$\begin{aligned} D(f(x,y),f(s,t))\le L\sqrt{(x-s)^{2}+(y-t)^{2}}, \end{aligned}$$

(2.2)

$\forall x,s\in [a,b]$, $y,t\in [c,d]$.

Theorem 2.18

[18] Let $f:[a,b]\times [c,d]\rightarrow \mathbb {R}_{F}$ be Henstock integrable, bounded mappings. Then, for any divisions $a=x_{0}<x_{1}<\cdots <x_{n}=b$ and $c=y_{0}<y_{1}<\cdots <y_{n}=d$ and any points $\xi _{i}\in [x_{i-1},x_{i}]$ and $\eta _{j}\in [y_{j-1},y_{j}]$, one has

$$\begin{aligned}&D\left( (FH)\int _{c}^{d}(FH)\int _{a}^{b}f(s,t)dsdt,\sum _{j=1}^{n}\sum _{i=1}^{n}(x_{i}-x_{i-1})(y_{j}-y_{j-1})\odot f(\xi _{i},\eta _{j})\right) \\&\quad \le \sum _{i=1}^{n}(x_{i}-x_{i-1})(y_{j}-y_{j-1}) \omega _{[x_{i-1},x_{i}]\times [y_{j-1},y_{j}]}\left( f,\sqrt{(x_{i}-x_{i-1})^{2}+(y_{j}-y_{j-1})^{2}}\right) .\nonumber \end{aligned}$$

Corollary 2.19

[18] Let $f:[a,b]\times [c,d]\rightarrow \mathbb {R}_{F}$ be a two-dimensional Henstock integrable, bounded mapping. Then

$$\begin{aligned} \begin{array}{ll} &D\bigg ((FH)\displaystyle\int _{c}^{d}(FH)\displaystyle\int _{a}^{b}f(s,t)dsdt,\frac{(b-a)(d-c)}{36}\odot \bigg (f(a,c)\oplus f(a,d)\bigg .\bigg .\\ & \quad\oplus 4\odot f\left( a,\frac{c+d}{2}\right) \oplus 4 \odot f\left( \frac{a+b}{2},c\right) \oplus 16\odot f\left( \frac{a+b}{2},\frac{a+c}{2}\right) \\ & \quad \bigg .\bigg .\oplus 4\odot f\left( \frac{a+b}{2},d\right) \oplus 4\odot f\left( b,\frac{c+d}{2}\right) \oplus f(b,c)\oplus f(b,d)\bigg )\bigg )\\ & \quad\le (b-a)(d-c)\omega _{[a,b]\times [c,d]}\left( f,\frac{(b-a)(d-c)}{36}\right) . \end{array} \end{aligned}$$

(2.3)

2D linear fuzzy Fredholm integral equations

Consider 2DLFFIE as follows

$$\begin{aligned} F(s,t)=f(s,t)\oplus \lambda \odot (FR)\int _{c}^{d}(FR)\int _{a}^{b}k(s,t,x,y)\odot F(x,y)\mathrm{d}x\mathrm{d}y, \end{aligned}$$

(3.1)

where $\lambda >0$, k(s, t, x, y) is an arbitrary positive function on $[a,b]\times [c,d]\times [a,b]\times [c,d]$ and $f:[a,b]\times [c,d]\rightarrow \mathbb {R}_{F}$. We assume that k is continuous and, therefore, it is uniformly continuous with respect to (s, t). So, there exists $M>0$ such that $M=\max \limits _{s,x\in [a,b],t,y\in [c,d]}\left| k(s,t,x,y)\right|$. Here, we present a quadrature iterative method for solving this equation.

Theorem 3.1

[18] Let the function k(s, t, x, y) be continuous and positive for $s,x\in [a,b]$, and $t,y\in [c,d]$, and let $f:[a,b]\times [c,d]\rightarrow \mathbb {R}_{F}$ be continuous on $[a,b]\times [c,d]$. Also, suppose f(x,t) that is not zero. If $B=\lambda M(b-a)(d-c)<1$ then the fuzzy integral equation (3.1) has a unique solution $F^{*}\in X$ where

$$\begin{aligned} X=\{f:[a,b]\times [c,d]\rightarrow \mathbb {R}_{F}; f \text{ is } \text{continous}\}, \end{aligned}$$

is the space of two-dimensional fuzzy continuous functions with the metric

$$\begin{aligned} D^{*}(f,g)=\sup \limits _{s\in [a,b], t\in [c,d]}D(f(s,t),g(s,t)), \end{aligned}$$

and it can be obtained by the following successive approximations method

$$\begin{aligned} F_{0} (s,t) & = f(s,t), \\ F_{m} (s,t) & = f(s,t) \oplus \lambda \odot (FR)\int_{c}^{d} {(FR)} \int_{a}^{b} k (s,t,x,y) \\ & \quad \odot F_{{m - 1}} (x,y){\text{d}}x{\text{d}}y,\quad \forall m \ge 1. \\ \end{aligned}$$

(3.2)

Moreover, the sequence of successive approximations, $(F_{m})_{m\ge 1}$ converges to the solution $F^{*}$. Furthermore, the following error bound holds

$$\begin{aligned} D^{*}(F^{*},F_{m})\le \frac{B^{m+1}}{1-B}M_{1},\forall m\ge 1, \end{aligned}$$

(3.3)

where $M_{1}=\sup _{s\in [a,b],t\in [c,d]}\left\| F(s,t)\right\| _{F}$.

Now, we propose a numerical method to solve (3.1). In this way, we assume 2DLFFIE (3.1) and uniform partitions of the interval $[a,b]\times [c,d]$

$$\begin{aligned} \Delta _{x}: a=s_{0}<s_{1}<\cdots<s_{2n-1}<s_{2n}=b, \end{aligned}$$

(3.4)

with $s_{i}=a+ih$, where $h=\frac{b-a}{2n}$, $i=0,\cdots ,2n$ and

$$\begin{aligned} \Delta _{y}: c=t_{0}<t_{1}<\cdots<t_{2n-1}<t_{2n}=d, \end{aligned}$$

(3.5)

with $t_{j}=c+jh'$, where $h'=\frac{d-c}{2n}$, $j=0,\cdots ,2n$. So, the following iterative procedure gives the approximate solution of (3.1) in point (s, t) as follows

$$\begin{aligned} \begin{array}{ll} u_{0}(s,t)&{}=f(s,t) \\ u_{m}(s,t)&{}=f(s,t)\oplus \frac{\lambda hh'}{9}\odot \sum _{j=1}^{n}\sum _{i=1}^{n}\Big (k(s,t,s_{2i-2},t_{2j-2})\odot u_{m-1}(s_{2i-2},t_{2j-2})\Big . \\ \Big .&{}\quad \oplus k(s,t,s_{2i-2},t_{2j})\odot u_{m-1}(s_{2i-2},t_{2j}) \oplus k(s,t,s_{2i},t_{2j-2})\odot u_{m-1}(s_{2i},t_{2j-2}) \\ &{}\quad \oplus k(s,t,s_{2i},t_{2j})\odot u_{m-1}(s_{2i},t_{2j})\oplus 4\Big (k(s,t,s_{2i-2},t_{2j-1})\odot u_{m-1}(s_{2i-2},t_{2j-1}) \\ &{}\quad \oplus k(s,t,s_{2i-1},t_{2j-2})\\ &{}\quad \odot u_{m-1}(s_{2i-1},t_{2j-2})\oplus k(s,t, s_{2i},t_{2j-1})\odot u_{m-1}(s_{2i},t_{2j-1}) \\ &{}\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot u_{m-1}(s_{2i-1},t_{2j})\Big )\oplus 16k(s,t,s_{2i-1},t_{2j-1})\\ &{}\quad \odot u_{m-1}(s_{2i-1},t_{2j-1})\Big ). \end{array} \end{aligned}$$

(3.6)

Convergence analysis

In this section, we obtain an error estimate between the exact solution and the approximate solution of 2DLFFIE (3.1).

Theorem 4.1

Under the hypotheses of Theorem 3.1 and $\lambda >0$ , the iterative procedure (3.6) converges to the unique solution of (3.1), $F^{*}$ , and its error estimate is as follows

$$\begin{aligned} D^{*} (F^{*} ,u_{m} ) & \le \frac{{B^{{m + 1}} }}{{1 - B}}M_{1} \\ & \quad + \frac{{10B}}{{9(1 - B)}}(\omega _{{[a,b] \times [c,d]}} (f,hh^{\prime}) + \frac{B}{{M(1 - B)}}\left\| f \right\|\omega _{{st}} (k,hh^{\prime}) \\ & \quad + \frac{1}{{M(1 - B)}}\left\| f \right\|\omega _{{xy}} (k,hh^{\prime})). \\ \end{aligned}$$

(4.1)

where

$$\begin{aligned} \omega _{st}(k,\delta )&=\sup \{\left| k(s_{1},t_{1},x,y)-k(s_{2},t_{2},x,y)\right| : \sqrt{(s_{2}-s_{1})^{2}+(t_{2}-t_{1})^{2}}\le \delta \}, \nonumber \\&\forall \delta \ge 0,\forall s_{1},s_{2}\in [a,b], t_{1},t_{2}\in [c,d] \end{aligned}$$

(4.2)

$$\begin{aligned} \omega _{xy}(k,\delta )&=\sup \{\left| k(s,t,x_{1},y_{1})-k(s,t,x_{2},y_{2})\right| : \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\le \delta \}, \nonumber \\&\forall \delta \ge 0, x_{1},x_{2}\in [a,b], y_{1},y_{2}\in [c,d] \end{aligned}$$

(4.3)

Proof

Considering iterative procedure (3.6), for all $(s,t)\in [a,b]\times [c,d]$, we have

$$\begin{aligned}&D(F_{1}(s,t),u_{1}(s,t))= D\bigg (f(s,t)\oplus \lambda \odot (FR)\int _{c}^{d}(FR)\int _{a}^{b}k(s,t,x,y)\\&\quad \odot F_{0}(x,y)\mathrm{d}x\mathrm{d}y,f(s,t)\oplus \frac{\lambda hh'}{9}\odot \sum _{j=1}^{n}\sum _{i=1}^{n}\bigg ((k(s,t,s_{2i-2},t_{2j-2})\odot u_{0}(s_{2i-2},t_{2j-2})\big .\\ \big .&\quad \oplus k(s,t,s_{2i-2},t_{2j})\odot u_{0}(s_{2i-2},t_{2j}) \oplus k(s,t,s_{2i},t_{2j-2})\odot u_{0}(s_{2i},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j})\odot u_{0}(s_{2i},t_{2j}))\\ {}&\quad \oplus 4(k(s,t,s_{2i-2},t_{2j-1})\odot u_{0}(s_{2i-2},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j-2})\odot u_{0}(s_{2i-1},t_{2j-2})\\&\quad \oplus k(s,t, s_{2i},t_{2j-1})\odot u_{0}(s_{2i},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot u_{0}(s_{2i-1},t_{2j}))\\&\quad \oplus 16 k(s,t,s_{2i-1},t_{2j-1})\odot u_{0}(s_{2i-1},t_{2j-1})\bigg )\bigg )\\&=D\bigg (\lambda \odot \sum _{j=1}^{n}\sum _{i=1}^{n}(FR)\int _{t_{2j-2}}^{t_{2j}}(FR)\int _{s_{2i-2}}^{s_{2i}}k(s,t,x,y)\odot f(x,y)\mathrm{d}x\mathrm{d}y, \end{aligned}$$

$$\begin{aligned}&\quad \frac{\lambda hh'}{9}\odot \sum _{j=1}^{n}\sum _{i=1}^{n}\bigg (k(s,t,s_{2i-2},t_{2j-2})\odot f(s_{2i-2},t_{2j-2})\big .\\ \big .&\quad \oplus k(s,t,s_{2i-2},t_{2j})\odot f(s_{2i-2},t_{2j}) \oplus k(s,t,s_{2i},t_{2j-2})\odot f(s_{2i},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j})\odot f(s_{2i},t_{2j})\\&\quad \oplus 4(k(s,t,s_{2i-2},t_{2j-1})\odot f(s_{2i-2},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j-2})\odot f(s_{2i-1},t_{2j-2})\\&\quad \oplus k(s,t, s_{2i},t_{2j-1})\odot f(s_{2i},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot f(s_{2i-1},t_{2j}))\\&\quad \oplus 16 k(s,t,s_{2i-1},t_{2j-1})\odot f(s_{2i-1},t_{2j-1})\bigg )\bigg )\\&\le \lambda \sum _{j=1}^{n}\sum _{i=1}^{n}D\bigg (\int _{t_{2j-2}}^{t_{2j}}\int _{s_{2i-2}}^{s_{2i}}k(s,t,x,y)\odot f(x,y)\mathrm{d}x\mathrm{d}y,\\&\quad \frac{hh'}{9}\odot \bigg (k(s,t,s_{2i-2},t_{2j-2})\odot f(s_{2i-2},t_{2j-2})\big .\\ \big .&\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot f(s_{2i-2},t_{2j}) \oplus k(s,t,s_{2i},t_{2j-2})\odot f(s_{2i},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j})\odot f(s_{2i},t_{2j})\\&\quad \oplus 4(k(s,t,s_{2i-2},t_{2j-1})\odot f(s_{2i-2},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j-2})\odot f(s_{2i-1},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j-1})\odot f(s_{2i},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot f(s_{2i-1},t_{2j}))\\&\quad \oplus 16 k(s,t,s_{2i-1},t_{2j-1})\odot f(s_{2i-1},t_{2j-1})\bigg )\bigg ). \end{aligned}$$

Using Corollary 2.19, we have

$$\begin{aligned} D(F_{1} (s,t),u_{1} (s,t)) & \le \lambda \sum\limits_{{j = 1}}^{n} {\sum\limits_{{i = 1}}^{n} {(s_{{2i}} - s_{{2i - 2}} )} } (t_{{2j}} - t_{{2j - 2}} ) \\ & \quad { \times }\omega _{{[s_{{2i - 2}} ,s_{{2i}} ] \times [t_{{2j - 2}} ,t_{{2j}} ]}} \left( {kf,\frac{{hh^{\prime}}}{9}} \right), \\ & \le \frac{{10}}{9}\lambda \sum\limits_{{j = 1}}^{n} {\sum\limits_{{i = 1}}^{n} {(s_{{2i}} - s_{{2i - 2}} )} } (t_{{2j}} - t_{{2j - 2}} ) \\ & \quad{ \times }\omega _{{[s_{{2i - 2}} ,s_{{2i}} ] \times [t_{{2j - 2}} ,t_{{2j}} ]}} \left( {kf,hh^{\prime}} \right). \\ \end{aligned}$$

Since $(\alpha ,\gamma ),(\beta ,\eta )\in [s_{2i-2},s_{2i}]\times [t_{2j-2},t_{2j}]$ with $\sqrt{(\alpha -\beta )^{2}+(\gamma -\eta )^{2}}\le hh'$, we have

$$\begin{aligned} D\bigg (f(\alpha ,\gamma )&\odot k(s,t,\alpha ,\gamma ),f(\beta ,\eta )\odot k(s,t,\beta ,\eta )\bigg ) \\&\le D\bigg (f(\alpha ,\gamma )\odot k(s,t,\alpha ,\gamma ),f(\beta ,\eta )\odot k(s,t,\alpha ,\gamma )\bigg )\\&\quad +D\bigg (f(\beta ,\eta )\odot k(s,t,\alpha ,\gamma ),f(\beta ,\eta )\odot k(s,t,\beta ,\eta )\bigg )\\&\le \left| k(s,t,\alpha ,\gamma )\right| D\bigg (f(\alpha ,\gamma ),f(\beta ,\eta )\bigg )\\&\quad +\left| k(s,t,\alpha ,\gamma )-k(s,t,\beta ,\eta )\right| D\bigg (f(\beta ,\eta ),\tilde{0}\bigg )\\&\le M\omega _{[s_{2i-2},s_{2i}]\times [t_{2j-2},t_{2j}]}(f,hh')+\omega _{xy}(k,hh')\left\| f\right\| . \end{aligned}$$

Taking supremum from above inequality, we conclude that,

$$\begin{aligned} \omega _{[s_{2i-2},s_{2i}]\times [t_{2j-2},t_{2j}]}(kf,hh')\le M\omega _{[s_{2i-2},s_{2i}]\times [t_{2j-2},t_{2j}]}(f,hh')+\omega _{xy}(k,hh')\left\| f\right\| . \end{aligned}$$

(4.4)

Therefore,

$$\begin{aligned} D^{*}(F_{1},u_{1})&\le \frac{10B}{9}\omega _{[a,b]\times [c,d]}(f,hh')+\frac{10B}{9M}\omega _{xy}(k,hh')\left\| f\right\| .\\ \end{aligned}$$

Now, for $m=2$, it follows that

$$\begin{aligned} D(F_{2}(s,t),u_{2}(s,t))&=D(f(s,t),f(s,t))\\&\quad +D\bigg (\lambda \odot (FR)\int _{c}^{d}(FR)\int _{a}^{b}k(s,t,x,y)\odot F_{1}(x,y)\mathrm{d}x\mathrm{d}y,\\&\quad \frac{\lambda hh'}{9}\sum _{j=1}^{n}\sum _{i=1}^{n}\bigg ((k(s,t,s_{2i-2},t_{2j-2})\odot u_{1}(s_{2i-2},t_{2j-2})\big .\\ \big .&\quad \oplus k(s,t,s_{2i-2},t_{2j})\\&\quad \odot u_{1}(s_{2i-2},t_{2j}) \oplus k(s,t,s_{2i},t_{2j-2})\odot u_{1}(s_{2i},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j})\odot u_{1}(s_{2i},t_{2j}))\\&\quad \oplus 4(k(s,t,s_{2i-2},t_{2j-1})\odot u_{1}(s_{2i-2},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j-2})\odot u_{1}(s_{2i-1},t_{2j-2})\\&\quad \oplus k(s,t, s_{2i},t_{2j-1})\odot u_{1}(s_{2i},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot u_{1}(s_{2i-1},t_{2j}))\\&\quad \oplus 16 k(s,t,s_{2i-1},t_{2j-1})\odot u_{1}(s_{2i-1},t_{2j-1})\bigg )\bigg )\\&\le \lambda \sum _{j=1}^{n}\sum _{i=1}^{n}\bigg (D\bigg (\int _{t_{2j-2}}^{t_{2j}}\int _{s_{2i-2}}^{s_{2i}}k(s,t,x,y)\odot F_{1}(x,y)\mathrm{d}x\mathrm{d}y,\\&\quad \frac{hh'}{9}\odot \bigg ((k(s,t,s_{2i-2},t_{2j-2})\odot F_{1}(s_{2i-2},t_{2j-2})\big . \end{aligned}$$

$$\begin{aligned} \big .&\quad \oplus k(s,t,s_{2i-2},t_{2j})\odot F_{1}(s_{2i-2},t_{2j}) \oplus k(s,t,s_{2i},t_{2j-2})\odot F_{1}(s_{2i},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j})\odot F_{1}(s_{2i},t_{2j}))\\&\quad \oplus 4(k(s,t,s_{2i-2},t_{2j-1})\odot F_{1}(s_{2i-2},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j-2})\odot F_{1}(s_{2i-1},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j-1})\odot F_{1}(s_{2i},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot F_{1}(s_{2i-1},t_{2j}))\\&\quad \oplus 16 k(s,t,s_{2i-1},t_{2j-1})\odot F_{1}(s_{2i-1},t_{2j-1})\bigg )\bigg )\\&\quad +D\bigg (\frac{hh'}{9}((k(s,t,s_{2i-2},t_{2j-2})\odot F_{1}(s_{2i-2},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i-2},t_{2j})\odot F_{1}(s_{2i-2},t_{2j})\\&\quad \oplus k(s,t,s_{2i},t_{2j-2})\odot F_{1}(s_{2i},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j})\odot F_{1}(s_{2i},t_{2j}))\\&\quad \oplus 4(k(s,t,s_{2i-2},t_{2j-1})\odot F_{1}(s_{2i-2},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j-2})\odot F_{1}(s_{2i-1},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j-1})\odot F_{1}(s_{2i},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot F_{1}(s_{2i-1},t_{2j}))\\&\quad \oplus 16 k(s,t,s_{2i-1},t_{2j-1})\odot F_{1}(s_{2i-1},t_{2j-1})),\\&\frac{hh'}{9}((k(s,t,s_{2i-2},t_{2j-2})\odot u_{1}(s_{2i-2},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i-2},t_{2j})\odot u_{1}(s_{2i-2},t_{2j})\\&\quad \oplus k(s,t,s_{2i},t_{2j-2})\odot u_{1}(s_{2i},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j})\odot u_{1}(s_{2i},t_{2j}))\\&\quad \oplus 4(k(s,t,s_{2i-2},t_{2j-1})\odot u_{1}(s_{2i-2},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j-2})\odot u_{1}(s_{2i-1},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j-1})\odot u_{1}(s_{2i},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot u_{1}(s_{2i-1},t_{2j}))\\&\quad \oplus 16 k(s,t,s_{2i-1},t_{2j-1})\odot u_{1}(s_{2i-1},t_{2j-1})\bigg )\\&\le \frac{10B}{9}\omega _{[a,b]\times [c,d]}(F_{1},hh') +\frac{10B}{9M}\omega _{xy}(k,hh')\left\| F_{1}\right\| \\&\quad +\frac{\lambda hh'}{9}\sum _{j=1}^{n}\sum _{i=1}^{n}\bigg (\left| k(s,t,s_{2i-2},t_{2j-2})\right| D\left( F_{1}(s_{2i-2},t_{2j-2}),u_{1}(s_{2i-2},t_{2j-2})\right) \\&\quad +\left| k(s,t,s_{2i-2},t_{2j})\right| D\left( F_{1}(s_{2i-2},t_{2j}),u_{1}(s_{2i-2},t_{2j})\right) \\&\quad +\left| k(s,t,s_{2i},t_{2j-2})\right| D\left( F_{1}(s_{2i},t_{2j-2}),u_{1}(s_{2i},t_{2j-2})\right) \\&\quad +\left| k(s,t,s_{2i},t_{2j})\right| D\left( F_{1}(s_{2i},t_{2j}),u_{1}(s_{2i},t_{2j})\right) \end{aligned}$$

$$\begin{aligned}&\quad +4\left| k(s,t,s_{2i-2},t_{2j-1})\right| D\left( F_{1}(s_{2i-2},t_{2j-1}),u_{1}(s_{2i-2},t_{2j-1})\right) \\&\quad +4\left| k(s,t,s_{2i-1},t_{2j-2})\right| D\left( F_{1}(s_{2i-1},t_{2j-2}),u_{1}(s_{2i-1},t_{2j-2})\right) \\&\quad +4\left| k(s,t,s_{2i},t_{2j-1})\right| D\left( F_{1}(s_{2i},t_{2j-1}),u_{1}(s_{2i},t_{2j-1})\right) \\&\quad +4\left| k(s,t,s_{2i-1},t_{2j})\right| D\left( F_{1}(s_{2i-1},t_{2j}),u_{1}(s_{2i-1},t_{2j})\right) \\&\quad +16\left| k(s,t,s_{2i-1},t_{2j-1})\right| D\left( F_{1}(s_{2i-1},t_{2j-1}),u_{1}(s_{2i-1},t_{2j-1})\right) \bigg ) \end{aligned}$$

So, we have the following result:

$$\begin{aligned} D^{*} (F_{2} ,u_{2} ) & \le \frac{{10B}}{9}\omega _{{[a,b] \times [c,d]}} (F_{1} ,hh^{\prime}) + \frac{{10B}}{{9M}}\omega _{{xy}} (k,hh^{\prime})\left\| {F_{1} } \right\| \\ & \quad + \lambda M(b - a)(d - c)D^{*} (F_{1} ,u_{1} ) \\ \end{aligned}$$

By induction, for $m\ge 3$, we obtain

$$\begin{aligned} D^{*}(F_{m},u_{m})&\le \frac{10B}{9}\omega _{[a,b]\times [c,d]}(F_{m-1},hh')+\frac{10B}{9M}\omega _{xy}(k,hh')\left\| F_{m-1}\right\| \\&\quad +BD^{*}(F_{m-1},u_{m-1}),\\ D^{*}(F_{m-1},u_{m-1})&\le \frac{10B}{9}\omega _{[a,b]\times [c,d]}(F_{m-2},hh')+\frac{10B}{9M}\omega _{xy}(k,hh')\left\| F_{m-2}\right\| \\&\quad +BD^{*}(F_{m-2},u_{m-2}),\\ D^{*}(F_{m-2},u_{m-2})&\le \frac{10B}{9}\omega _{[a,b]\times [c,d]}(F_{m-3},hh')+\frac{10B}{9M}\omega _{xy}(k,hh')\left\| F_{m-3}\right\| \\&\quad +BD^{*}(F_{m-3},u_{m-3}),\\&\vdots\qquad \vdots \qquad \vdots \\ D^{*}(F_{1},u_{1})&\le \frac{10B}{9}\omega _{[a,b]\times [c,d]}(F_{0},hh')+\frac{10B}{9M}\omega _{xy}(k,hh')\left\| F_{0}\right\| \\&\quad +BD^{*}(F_{0},u_{0}). \end{aligned}$$

Then

$$\begin{aligned} \begin{array}{ll} D^{*}(F_{m},u_{m})&{}\le \frac{10B}{9}(\omega _{[a,b]\times [c,d]}(F_{m-1},hh')+B\omega _{[a,b]\times [c,d]}(F_{m-2},hh')\\ &{}\quad +B^{2}\omega _{[a,b]\times [c,d]}(F_{m-3},hh')+\cdots +B^{m-1}\omega _{[a,b]\times [c,d]}(f,hh'))\\ &{}\quad +\frac{10B}{9M}\omega _{xy}(k,hh')(\left\| F_{m-1}\right\| +B\left\| F_{m-2}\right\| +\cdots +B^{m-1}\left\| F_{0}\right\| ). \end{array} \end{aligned}$$

(4.5)

On the other hand, we have:

$$\begin{aligned} D(F_{m} (s_{1} ,t_{1} ),F_{m} (s_{2} ,t_{2} )) &= D(f(s_{1} ,t_{1} ) \oplus \lambda \odot (FR) \\ & \quad \times \int_{c}^{d} {(FR)} \int_{a}^{b} k (s_{1} ,t_{1} ,x,y) \odot F_{{m - 1}} (x,y){\text{d}}x{\text{d}}y, \\ & \quad \times f(s_{2} ,t_{2} ) \oplus \lambda \odot (FR)\int_{c}^{d} {(FR)} \int_{a}^{b} k (s_{2} ,t_{2} ,x,y) \odot F_{{m - 1}} (x,y){\text{d}}x{\text{d}}y) \\ & \le D(f(s_{1} ,t_{1} ),f(s_{2} ,t_{2} )) + \lambda \int_{c}^{d} {\int_{a}^{b} {\left| {k(s_{1} ,t_{1} ,x,y) - k(s_{2} ,t_{2} ,x,y)} \right|} } \\ & \quad \times D(F_{{m - 1}} (x,y),\tilde{0}){\text{d}}x{\text{d}}y, \\ \end{aligned}$$

therefore, we see that

$$\begin{aligned} \omega _{[a,b]\times [c,d]}(F_{m},hh')\le \omega _{[a,b]\times [c,d]}(f,hh')+\frac{B}{M}\omega _{st}(k,hh')\left\| F_{m-1}\right\| , \end{aligned}$$

(4.6)

for any $(s_{1},t_{1}), (s_{2},t_{2})\in [a,b]\times [c,d]$ with $\sqrt{(s_{1}-s_{2})^{2}+(t_{1}-t_{2})^{2}}\le hh'$.

By using above inequality and (4.5), we obtain

$$\begin{aligned} D^{*}(F_{m},u_{m})&\le \frac{10B}{9}\omega _{[a,b]\times [c,d]}(f,hh')(1+B+B^{2}+\cdots +B^{m-1})\\&\quad +\frac{10B^{2}}{9M}\omega _{st}(k,hh')(\left\| F_{m-2}\right\| +B\left\| F_{m-3}\right\| +B^{2}\left\| F_{m-4}\right\| \\&\quad +\cdots +B^{m-2}\left\| F_{0}\right\| )\\&\quad +\frac{10B}{9M}\omega _{xy}(k,hh')(\left\| F_{m-1}\right\| +B\left\| F_{m-2}\right\| +B^{2}\left\| F_{m-3}\right\| \\&\quad +\cdots +B^{m-1}\left\| F_{0}\right\| ). \end{aligned}$$

Now, by using (3.2), we conclude that

$$\begin{aligned} D(F_{m}(s,t),F_{m-1}(s,t))&=D(f(s,t)\oplus \lambda \odot \\&\quad (FR)\int _{c}^{d}(FR)\int _{a}^{b}k(s,t,x,y)\odot F_{m-1}(x,y)\mathrm{d}x\mathrm{d}y,\\&\quad f(s,t)\oplus \lambda \odot (FR)\int _{c}^{d}(FR)\int _{a}^{b}k(s,t,x,y)\odot \\&\quad F_{m-2}(x,y)\mathrm{d}x\mathrm{d}y)\\&\le\, \lambda \int _{c}^{d}\int _{a}^{b}\left| k(s,t,x,y)\right| D(F_{m-1}(x,y),F_{m-2}(x,y))\mathrm{d}x\mathrm{d}y\\&\le \,\lambda M(d-c)(b-a)D^{*}(F_{m-1},F_{m-2})\\&\le \,B^{m-1}D^{*}(F_{1},F_{0}). \end{aligned}$$

Consequently,

$$\begin{aligned} D(F_{m}(s,t),F_{0}(s,t))&\le D(F_{m}(s,t),F_{m-1}(s,t))+\cdots +D(F_{1}(s,t),F_{0}(s,t)). \end{aligned}$$

Taking supremum for $s,t\in [a,b]\times [c,d]$ from the above inequality, we have

$$\begin{aligned} D^{*}(F_{m},F_{0})&\le (B^{m-1}+B^{m-2}+\cdots +B+1)D^{*}(F_{1},F_{0})\\&\le \frac{1}{1-B}D^{*}(F_{1},F_{0}). \end{aligned}$$

It is obvious that

$$\begin{aligned} D(F_{1}(s,t),F_{0}(s,t))&=D(f(s,t)\oplus \lambda (FR)\int _{c}^{t}(FR)\int _{a}^{b}k(s,t,x,y)\odot \\&\quad F_{0}(x,y)\mathrm{d}x\mathrm{d}y,f(s,t))\\&\le \lambda \int _{c}^{d}\int _{a}^{b}\left| k(s,t,x,y)\right| D(f(x,y),\tilde{0})\mathrm{d}x\mathrm{d}y\\&\le \lambda (d-c)(b-a)M\left\| f\right\| =B\left\| f\right\| , \end{aligned}$$

and

$$\begin{aligned} D(F_{m}(s,t),\tilde{0})&\le D(F_{m}(s,t),F_{0}(s,t))+D(F_{0}(s,t),\tilde{0})\\&\le \frac{1}{1-B}D^{*}(F_{1},F_{0})+\left\| f\right\| \\&\le \frac{1}{1-B}\left\| f\right\| . \end{aligned}$$

Therefore, we see that

$$\begin{aligned} D^{*} (F_{m} ,u_{m} ) & \le \frac{{10B}}{{9(1 - B)}}(\omega _{{[a,b] \times [c,d]}} (f,hh^{\prime}) \\ & \quad + \frac{B}{{M(1 - B)}}\left\| f \right\|\omega _{{st}} (k,hh^{\prime}) \\ & \quad + \frac{1}{{M(1 - B)}}\left\| f \right\|\omega _{{xy}} (k,hh^{\prime})). \\ \end{aligned}$$

$\square$

Numerical stability analysis

To show the numerical stability analysis of the proposed method in previous section, we consider another starting approximation $g(s,t)=Y_{0}(s,t)$ such that $\exists \epsilon >0$ for which $D(F_{0}(s,t),Y_{0}(s,t))<\epsilon ,\forall s,t\in [a,b]\times [c,d]$. The obtained sequence of successive approximations is

$$\begin{aligned} Y_{m}(s,t)=g(s,t)\oplus \lambda \odot (FR)\int _{c}^{d}(FR)\int _{a}^{b}k(s,t,x,y)\odot Y_{m-1}(x,y)\mathrm{d}x\mathrm{d}y, \end{aligned}$$

and using the same iterative method, the terms of produced sequence are

$$\begin{aligned} v_{0}(s,t)&=Y_{0}(s,t)=g(s,t),\\ v_{m}(s,t)&=g(s,t)\oplus \frac{\lambda hh'}{9}\odot \sum _{j=1}^{n}\sum _{i=1}^{n}\bigg (k(s,t,s_{2i-2}, t_{2j-2})\odot v_{m-1}(s_{2i-2},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i-2},t_{2j}) \odot v_{m-1}(s_{2i-2},t_{2j}) \oplus k(s,t,s_{2i},t_{2j-2}) \odot v_{m-1}(s_{2i},t_{2j-2})\\&\quad \oplus k(s,t,s_{2i},t_{2j}) \odot v_{m-1}(s_{2i},t_{2j}) \oplus 4\bigg (k(s,t,s_{2i-2},t_{2j-1})\odot \\&\quad v_{m-1}(s_{2i-2},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j-2})\odot v_{m-1}(s_{2i-1},t_{2j-2}) \oplus k(s,t,s_{2i},t_{2j-1})\odot \\&\quad v_{m-1}(s_{2i},t_{2j-1})\\&\quad \oplus k(s,t,s_{2i-1},t_{2j})\odot \\&\quad v_{m-1}(s_{2i-1},t_{2j})\bigg )\oplus 16 k(s,t,s_{2i-1},t_{2j-1})\odot \\&\quad v_{m-1}(s_{2i-1},t_{2j-1})\bigg ). \end{aligned}$$

Definition 5.1

The proposed algorithm based on iterative method applied to solve 2DLFFIE (3.1) is said to be numerically stable with respect to the choice of the first iteration if there exist four independent constants $k_{1},k_{2},k_{3},k_{4}>0$ such that

$$\begin{aligned} D^{*}(u_{m},v_{m})&\le k_{1}\epsilon +k_{2}\bigg (\omega _{[a,b]\times [c,d]}(f,hh') \nonumber \\&+\omega _{[a,b]\times [c,d]}(g,hh')\bigg )+k_{3}\omega _{st}(k,hh')+k_{4}\omega _{xy}(k,hh'), \end{aligned}$$

(5.1)

where $h=\frac{b-a}{2n}$, $h'=\frac{d-c}{2n}$,

$$\begin{aligned} k_{1}&=\frac{1}{1-B},k_{2}=\frac{10B}{9(1-B)},k_{3}=\frac{10B^{2}}{9M(1-B)^{2}} \\&\quad (\left\| f\right\| +\left\| g\right\| ),k_{4}=\frac{10B}{9M(1-B)^{2}}(\left\| f\right\| +\left\| g\right\| ). \end{aligned}$$

Theorem 5.2

Under the assumptions of Theorem 4.1 , the presented method (3.6) is numerically stable with respect to the choice of the first iteration.

Proof

At first, we obtain that

$$\begin{aligned} D(u_{m}(s,t),v_{m}(s,t))&\le D(u_{m}(s,t),F_{m}(s,t))+D(F_{m}(s,t),Y_{m}(s,t))\\&\quad +D(Y_{m}(s,t),v_{m}(s,t))\\&\le \frac{10B}{9(1-B)}\bigg (\omega _{[a,b]\times [c,d]}(f,hh')\\&\quad +\frac{B}{M(1-B)}\left\| f\right\| \omega _{st}(k,hh')+\frac{1}{M(1-B)}\left\| f\right\| \omega _{xy}(k,hh')\bigg )\\&\quad +D(F_{m}(s,t),Y_{m}(s,t))\\&\quad + \frac{10B}{9(1-B)}\bigg (\omega _{[a,b]\times [c,d]}(g,hh')\\&\quad +\frac{B}{M(1-B)}\left\| g\right\| \omega _{st}(k,hh')+\frac{1}{M(1-B)}\left\| g\right\| \omega _{xy}(k,hh')\bigg ). \end{aligned}$$

However,

$$\begin{aligned} D(F_{m}(s,t),Y_{m}(s,t))&=D\bigg (f(s,t)\oplus \lambda \odot (FR)\int _{c}^{d} (FR)\int _{a}^{b}k(s,t,x,y)\odot \\&\quad F_{m-1}(x,y)\mathrm{d}x\mathrm{d}y,\\&\quad g(s,t)\oplus \lambda \odot (FR)\int _{c}^{d} (FR)\int _{a}^{b}k(s,t,x,y)\odot \\&\quad Y_{m-1}(x,y)\mathrm{d}x\mathrm{d}y\bigg )\\&\le D(f(s,t),g(s,t))\\&\quad +\lambda D\bigg ((FR)\int _{c}^{d}(FR)\int _{a}^{b}k(s,t,x,y)\odot F_{m-1}(x,y)\mathrm{d}x\mathrm{d}y,\\&\quad (FR)\int _{c}^{d}(FR)\int _{a}^{b}k(s,t,x,y)\odot Y_{m-1}(x,y)\mathrm{d}x\mathrm{d}y\bigg )\\&\le \epsilon +\lambda (FR)\int _{c}^{d}(FR)\int _{a}^{b}\left| k(s,t,x,y)\right| \\&\quad D(F_{m-1}(x,y),Y_{m-1}(x,y))\mathrm{d}x\mathrm{d}y. \end{aligned}$$

We conclude that

$$\begin{aligned} D^{*}(F_{m},Y_{m})\le \epsilon +\lambda \int _{c}^{d}\int _{a}^{b}MD^{*}(F_{m-1},Y_{m-1})\mathrm{d}x\mathrm{d}y=\epsilon +BD^{*}(F_{m-1},Y_{m-1}), \end{aligned}$$

and thus

$$\begin{aligned} D^{*}(F_{m},Y_{m})&\le \epsilon +BD^{*}(F_{m-1},Y_{m-1})\\ D^{*}(F_{m-1},Y_{m-1})&\le \epsilon +BD^{*}(F_{m-2},Y_{m-2})\\ D^{*}(F_{m-2},Y_{m-2})&\le \epsilon +BD^{*}(F_{m-3},Y_{m-3})\\ \vdots&\quad \quad \vdots \\ D^{*}(F_{1},Y_{1})&\le \epsilon +BD^{*}(F_{0},Y_{0}). \end{aligned}$$

So,

$$\begin{aligned} D^{*}(F_{m},Y_{m})&\le \epsilon +B\bigg (\epsilon +BD^{*}(F_{m-2},Y_{m-2})\bigg )\\&\le \epsilon +B\epsilon +B^{2}\bigg (\epsilon +BD^{*}(F_{m-3},Y_{m-3})\bigg )\\&\le \epsilon +B\epsilon +B^{2}\epsilon +B^{3}\bigg (\epsilon +BD^{*}(F_{m-4},Y_{m-4})\bigg )\\&\quad \quad \quad \vdots \\&\le \epsilon +B\epsilon +B^{2}\epsilon +B^{3}\epsilon +\cdots +B^{m}D^{*}(F_{0},Y_{0})\\&\le \epsilon \bigg (1+B+B^{2}+B^{3}+\cdots +B^{m}\bigg )\le \frac{\epsilon }{1-B}. \end{aligned}$$

Therefore,

$$\begin{aligned} D^{*}(u_{m},v_{m})&\le \frac{10B}{9(1-B)}\bigg (\omega _{[a,b]\times [c,d]}(f,hh')\\&\quad +\frac{B}{M(1-B)}\left\| f\right\| \omega _{st}(k,hh')+\frac{1}{M(1-B)}\left\| f\right\| \omega _{xy}(k,hh')\bigg )\\&\quad +\frac{\epsilon }{1-B}\\&\quad + \frac{10B}{9(1-B)}\bigg (\omega _{[a,b]\times [c,d]}(g,hh')\\&\quad +\frac{B}{M(1-B)}\left\| g\right\| \omega _{st}(k,hh')+\frac{1}{M(1-B)}\left\| g\right\| \omega _{xy}(k,hh')\bigg ), \end{aligned}$$

where

$$\begin{aligned} k_{1}&=\frac{1}{1-B},k_{2}=\frac{10B}{9(1-B)},\\ k_{3}&=\frac{10 B^{2}}{9M(1-B)^{2}}(\left\| f\right\| +\left\| g\right\| ),k_{4}=\frac{10B}{9M(1-B)^{2}}(\left\| f\right\| +\left\| g\right\| ). \end{aligned}$$

$\square$

Numerical examples

In this section, we apply the proposed method in “2D linear fuzzy Fredholm integral equations” for solving two examples. In addition, we compare the absolute errors of the obtained results with the results of the method [18].

Example 6.1

[14] Consider the linear integral equation

$$\begin{aligned} F(s,t)=f(s,t)\oplus (FR)\int _{0}^{1}(FR)\int _{0}^{1}k(s,t,x,y)\odot F(x,y)\mathrm{d}x\mathrm{d}y, \end{aligned}$$

(6.1)

with

$$\begin{aligned} k(s,t,x,y)&=s^{2}tx,\\ \underline{f}(s,t,r)&=(r^{2}+r)s \sin \left( \frac{t}{2}\right) ,\\ \overline{f}(s,t,r)&=(4-r^{3}-r)s \sin \left( \frac{t}{2}\right) . \end{aligned}$$

The exact solution of this example is

$$\begin{aligned} \underline{F}^{*}(s,t,r)&=(r^{2}+r)\left( s \sin \left( \frac{t}{2}\right) -\frac{16}{21}\left( \cos \left( \frac{1}{2}\right) -1\right) s^{2}t\right) ,\\ \overline{F}^{*}(s,t,r)&=(4-r^{3}-r)\left( s \sin \left( \frac{t}{2}\right) -\frac{16}{21}\left( \cos \left( \frac{1}{2}\right) -1\right) s^{2}t\right) . \end{aligned}$$

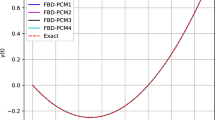
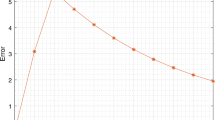
By using the proposed method and the method [18] for $h=h'=\frac{1}{10}, \frac{1}{20}$, $m=5,7$ and $r\in \{0.00,0.25,0.50,0.75,1.00\}$ in $(s_{0},t_{0})=(0.5,0.5)$, we present the absolute errors in Tables 1, 2, 3, and 4

Example 6.2

[14] Consider the following fuzzy Fredholm integral equation (6.1) with

$$\begin{aligned} \underline{f}(s,t,r)&=r\left( st+\frac{1}{676}(s^{2}+t^{2}-2)\right) ,\\ \overline{f}(s,t,r)&=(2-r)\left( st+\frac{1}{676}(s^{2}+t^{2}-2)\right) , \end{aligned}$$

and kernel

$$\begin{aligned} k(s,t,x,y)=\frac{1}{169}(s^{2}+t^{2}-2)(x^{2}+y^{2}-2), 0\le s,t,x,y\le 1. \end{aligned}$$

The exact solution is

$$\begin{aligned} \underline{F}^{*}(s,t,r)&=rst,\\ \overline{F}^{*}(s,t,r)&=(2-r)st. \end{aligned}$$

To compare the absolute errors for the proposed method and the method [18], see Tables 5, and 6

Table 1 The absolute errors on the level sets with $h=h'=\frac{1}{10}$, $m=5$ for Example 6.1 by using the method [18] in $(s_{0},t_{0})=(0.5,0.5)$

Table 2 The absolute errors on the level sets with $h=h'=\frac{1}{20}$, $m=7$ for Example 6.1 by using the method [18] in $(s_{0},t_{0})=(0.5,0.5)$

Table 3 The absolute errors on the level sets with $h=h'=\frac{1}{10}$, $m=5$ for Example 6.1 by using the proposed method in $(s_{0},t_{0})=(0.5,0.5)$

Table 4 The absolute errors on the level sets with $h=h'=\frac{1}{20}$, $m=7$ for Example 6.1 by using the proposed method in $(s_{0},t_{0})=(0.5,0.5)$

Table 5 The absolute errors on the level sets with $h=h'=\frac{1}{10}$, $m=5$ for Example 6.2 by using the method [18] in $(s_{0},t_{0})=(0.5,0.5)$, respectively

Table 6 The absolute errors on the level sets with $h=h'=\frac{1}{10}$, $m=5$ for Example 6.2 by using the proposed method in $(s_{0},t_{0})=(0.5,0.5)$, respectively

Conclusions

To approximate the solution of 2DLFFIEs, we developed a quadrature iterative method. We prove the convergence analysis (Theorem 4.1) and the numerical stability analysis (Theorem 5.2) of the proposed method with respect to the choice of the first iteration. Obtained results show that the proposed method can be a suitable method for solving 2DLFFIEs.