Introduction

Recently, the high-field THz pulses have been generated from large-scale accelerators using ultrashort electron bunches. For example, peak field of 44 MV/cm has been obtained via coherent transition radiation in the Linac Coherent Light Source [1]. In the laser-based schemes, THz pulses with field strength >8 MV/cm at 1 kHz repetition rate have been generated via two-color laser filamentation [2]. Single-cycle THz pulse with field strength up to 36 MV/cm can be generated by optical rectification of a mid infrared laser in a large-size nonlinear organic crystals assembly [3]. Electromagnetic radiations have been generated by the interaction of ultrashort lasers with gas-jet plasmas [4, 5] and water vapor [6]. In addition to these, other methods that have produced high-field THz pulses (but only with components <20 THz) include difference frequency mixing process of two near-infrared lasers in second-order nonlinear crystals [7], and optical rectification (with component limited to <1.5 THz) in lithium niobate (LiNbO3) crystals with tilted laser front [8]. Besides, high-field THz radiations can be generated from relativistic laser irradiated plasmas via various mechanisms [9,10,11,12].

Several experiments employ plasma as a nonlinear medium for the generation of THz radiation by using sub picosecond laser pulses and energetic electron beams [13], since the plasma has the advantage of handling very high field with a remarkable property of being not damaged and having strong nonlinearity [14]. Malik et al. [15] have analytically investigated the THz generation by tunnel ionization of a gas jet with superposed femtosecond laser pulses shone onto it after passing through an axicon. In this mechanism, the temporal evolution of plasma density and hence, oscillatory current density via oscillating dipoles gives rise to the emission of THz radiation. Electron positron plasma has been suggested for high-efficient THz generation by using laser pulse [16]. All the methods suggest that the intense THz radiation can be achieved when very high-intensity lasers are employed in the plasma. However, under that situation, the electron motion will become relativistic and hence, their mass will be varied. This situation is considered in the present article along with the use of coshyperbolic-Gaussian lasers.

Coshyperbolic-Gaussian lasers

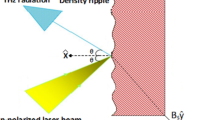
We consider linearly polarized cosh-Gaussian electromagnetic beams propagating along the z-axis. Their electric fields are along the y-axis, given by

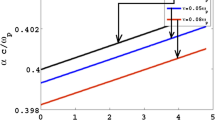
$$ \vec{E}_{j} = E_{0} \cosh \left( {\tfrac{ys}{b}} \right)\exp \left( { - \left( {\tfrac{ys}{b}} \right)^{p} } \right)\exp \left( {i\left( {k_{j} z - \omega_{j} t} \right)} \right)\hat{y}, $$

together with j = 1, 2 and p as the index of the lasers. Here E 0 is the amplitude of the fields; b is the beam width of the lasers. Figure 1 shows the profile of the incident laser beam when p ≥ 2 and for different values of the skewness parameter s.

Fig. 1
figure 1

Electric field distribution of the incident laser profile

Full size image

Relativistic ponderomotive force

We use the cold fluid equations for electrons with their number density n 0 and velocity υ under the impact of lasers fields. Hence, the electrons oscillatory velocity is obtained as

$$ \vec{\upsilon }_{j} = \frac{{e\vec{E}_{j} }}{{mi\omega_{j} }}. $$
(1)

Here we neglect the effect of collisions in the plasma because collision effect is not significant for high-intensity laser beam. The density n obeys the continuity equation \( \frac{\partial n}{\partial t} + \vec{\nabla } \cdot \left( {n\vec{\upsilon }} \right) = 0 \). In view of the high-intensity lasers, we consider relativistic motion of the electrons. The relativistic ponderomotive force in the presence of an intense electromagnetic beam can be represented [17, 18] as

$$ \vec{F}_{p} = - mc^{2} \vec{\nabla }\left( {\gamma - 1} \right)\;{\text{together with}}\;\gamma = \left( {1 - \frac{{\left| {\upsilon_{1} + \upsilon_{2} } \right|}}{{c^{2} }}^{2} } \right)^{{ - \tfrac{1}{2}}} . $$
(2)

Here m is the rest mass of the electron, c is the velocity of the light, and υ 1 and υ 2 are the oscillatory drift velocities of the electrons. The use of Eq. (1) in Eq. (2) yields the ponderomotive force as

$$ \vec{F}_{p} = - mc^{2} \vec{\nabla }\left( {1 - \frac{2A}{{c^{2} \omega_{1} \omega_{2} }}\cos \left( {kz - \omega t} \right)} \right)^{{ - \tfrac{1}{2}}} , $$
(3)

where \( A = \frac{{e^{2} E_{0}^{2} }}{{m^{2} }}\cosh^{2} \left( {\frac{ys}{b}} \right)e^{{ - 2\left( {\tfrac{ys}{b}} \right)^{p} }} ,\,k = k_{1} - k_{2} \) and ω = ω 1−ω 2.

We obtain the following expression for the ponderomotive force:

$$ \vec{F}_{p}^{\text{NL}} = \frac{{imc^{2} A}}{{\omega_{1} \omega_{2} }}\left( {1 - \frac{{2Ac^{2} }}{{\omega_{1} \omega_{2} }}\cos (kz - \omega t)} \right)^{{ - \tfrac{3}{2}}} \left[ {\left( {2p\left( {\frac{ys}{b}} \right)^{p - 1} \frac{s}{b} - \tanh \left( {\frac{ys}{b}} \right)\frac{s}{b}} \right)\cos \left( {kz - \omega t} \right)\hat{y} + k\sin \left( {kz - \omega t} \right)\hat{z}} \right]. $$
(4)

This nonlinear force causes perturbations in the density of the plasma. These perturbations generate space charge potential that leads to the linear density perturbations. The nonlinear density perturbations are obtained as

$$ n_{1}^{\text{NL}} = \frac{{n_{0} \vec{\nabla } \cdot \vec{F}_{p}^{\text{NL}} }}{{m\omega^{2} }}. $$
(5)

Finally, the nonlinear velocity of the electrons is obtained from equation of motion as

$$ \vec{V}^{\text{NL}} = - \left( {\frac{{\omega^{2} \left( {\omega^{2} - \omega_{p}^{2} } \right) + \omega_{p}^{2} \omega^{2} }}{{mi\omega^{3} \left( {\omega^{2} - \omega_{p}^{2} } \right)}}} \right)\vec{F}_{p} . $$
(6)

Here, ω p is the plasma frequency given by \( \omega_{p} = \sqrt {\frac{{4\pi n_{0} e^{2} }}{m}} \).

The nonlinear current density can be obtained from \( {\vec{J}}^{\text{NL}} = - \frac{1}{2}ne{\vec{V}}^{\text{NL}} \), where n = n 0 + n 2. Here n 2 is the ripple density in the plasma given as \( n_{2} = n_{\alpha } e^{i\alpha z} \) together with α as the wave number of the ripples produced in the plasma and n α as the amplitude of the density ripples. These density ripples are generally used to achieve the resonance condition. These ripples in density may be produced using various techniques, which involve transmissive ring grating and a patterned mask where the control of ripple parameters might be possible by changing the groove structure, groove period, and duty cycle in such a grating and by adjusting the period and size of the mask [19,20,21,22,23]. Finally, the nonlinear current density is obtained as

$$ \vec{J}_{y}^{\text{NL}} = - \frac{1}{2}n_{\alpha } e^{i\alpha z} e\left[ { - \frac{{\omega^{2} \left( {\omega^{2} - \omega_{p}^{2} } \right) + \omega_{p}^{2} \omega^{2} }}{{mi\omega^{3} \left( {\omega^{2} - \omega_{p}^{2} } \right)}}\vec{F}_{py} } \right]. $$
(7)

Calculation of electric field of terahertz radiation

The wave equation that governs the emitted THz radiation is given by

$$ - \nabla^{2} \vec{E}_{\text{THz}} + \vec{\nabla }(\vec{\nabla } \cdot \vec{E}_{\text{THz}} ) = \frac{4\pi i\omega }{{c^{2} }}\vec{J}^{\text{NL}} + \frac{{\omega^{2} }}{{c^{2} }}\varepsilon \vec{E}_{\text{THz}} . $$
(8)

Here \( \vec{E}_{\text{THz}} \) is the electric field associated with the THz radiation and ε is dielectric constant of the plasma amounting to \( 1 - \frac{{\omega_{p}^{2} }}{{\omega^{2} }} \). From Eq. (8), we get the amplitude of the THz radiation as

$$ \begin{aligned} E_{{{{THz}}y}} =\left[\begin{array}{l} - \frac{4\pi i\omega mz}{{c^{2} 2k^{{\prime }} }}\frac{{en_{\alpha } e^{i\alpha z} }}{2}\left( {\frac{{Ac^{2} }}{{\omega_{1} \omega_{2}}}} \right) ^{{-\frac{1}{2}}} \frac{1}{2\sqrt 2 }\left[ {\cos \left( {kz - \omega t} \right)} \right]^{{ - \frac{3}{2}}} -\frac{4\pi i\omega z}{{c^{2} 2k^{{\prime }} }}\frac{em{n_{\alpha } e^{i\alpha z} }}{2} \\ \left( {\frac{{Ac^{2} }}{{\omega_{1} \omega_{2} }}} \right) ^{{-\frac{1}{2}}} {\frac{3}{4}}\left( {\frac{{Ac^{2} }}{{\omega_{1} \omega_{2} }}} \right)^{ - 1} \frac{1}{2\sqrt 2 }\left[ {\cos \left( {kz - \omega t} \right)} \right]^{{ - \frac{5}{2}}} \end{array} \right] \times \left[ {CD\cos \left( {kz - \omega t} \right)} \right] \end{aligned} $$
(9)

Here C and D are frequency-dependent terms defined as \( C = 2p\left( {\frac{ys}{b}} \right)^{p - 1} \frac{s}{b} - \frac{s}{b}\tanh \left( {\frac{ys}{b}} \right) \) and \( D = \frac{i\omega }{{m\left( {\omega^{2} - \omega_{p}^{2} } \right)}} \) and k′ = k + α.

In order to find the amplitude of the THz radiation, we analyze the expression (9). This relation can be bifurcated into two different expressions as shown in Eq. (10), indicating that it is superposition of two different waves. This is the consequence of the different components of the ponderomotive force. Finally, we achieve the following expression for E THz:

$$ E_{\text{THz}} = J\cos \left( {kz - \omega t} \right) + R\cos^{2} \left( {kz - \omega t} \right). $$
(10)

Here J and R are the amplitudes of the different wave components that are generated due to the relativistic ponderomotive force nonlinearity in the plasma. The symbols J, R and G are defined as

$$ J = - {\text{GCD}},\quad R = - \frac{\text{GADC}}{{3\omega_{1} \omega_{2} c^{2} }}\;{\text{and}}\;G = - \frac{{\pi i\omega zn_{\alpha } em}}{{2\sqrt 2 c^{2} k^{{\prime }} }}\left( {\frac{{Ac^{2} }}{{\omega_{1} \omega_{2} }}} \right)^{{ - \tfrac{1}{2}}} . $$

For the high-intensity laser, where a part of its energy is used in heating of the electrons in the plasma, the resonance condition is expected to be modified as \( \omega = \sqrt {\omega_{p}^{2} + k^{2} \upsilon_{\text{th}}^{2} } \), where υ th is the thermal velocity of the electrons. However, the second term would play a significant role only when \( k \) is very large, i.e. for the short wavelength laser pulses. So it is clear that the resonance condition is departed from ω = ω p when one considers the heating in the plasma and under this situation reduced THz field would be realized (clear from Fig. 3, later).

Results and discussion

This section deals with the results obtained from Eq. (10) for the electric field of THz radiation. The following set of parameters has been used in the numerical analysis: \( E_{0} = 2.7 \times 10^{12} V/m,b = 0.01 \times 10^{ - 2} m,s = 0.6,\omega = 1.15\omega_{p} ,\omega_{1} = 1.65 \times 10^{15} {\text{rad/s}} \) and ω p  = 2.0×1013 rad/s. This is seen that out of two components of fields, given by Eq. (10), only one component (second term) dominates and is solely responsible for the THz amplitude.

Figure 1 shows the electric field distribution of the incident lasers. This is clear that a dip occurs in the peak of the fields when p > 2. As the skewness parameter s is increased this dip takes a prominent form in the incident laser profile. Figure 2 shows the output profile (normalized amplitude) of the THz radiation with the normalized distance, when n α  = 0.3n 0. The maximum amplitude occurs at particular values of y/b. Peak positions are symmetric in nature because of skewness parameter s. Maximum amplitudes correspond to the higher SG index lasers. A comparison of Figs. 1 and 2 shows that in general two peaks of the emitted THz radiation are obtained for the lasers having one peak. However, when there is a dip in the peak value of the lasers field, small peaks start generating in the produced radiations. Also the higher peak is further enhanced for the larger dip in the incident laser profile. This is true for the lasers having higher skewness in their profiles (s > 0.6).

Fig. 2
figure 2

The profile of electric field of emitted THz radiation

Full size image

The dependence of THz field on the ripple amplitude n α and beating frequency ω is shown in Fig. 3. It is evident that the amplitude E THz is high when n α carries higher values, but it decreases sharply when the resonance condition ω ~ ω p is departed. Ripples in plasma density play a positive role to enhance the THz amplitude because large numbers of electrons participate for the generation of nonlinear current so amplitude of THz field increases accordingly.

Fig. 3
figure 3

Variation of THz radiation normalized field with beating frequency ω and density ripple amplitude n α , for the same parameters as in Fig. 2

Full size image

In order to find the effect of beam width of the lasers on the THz radiation, we have plotted the intensity (normalized by \( \left| {E_{0} } \right|^{2} \), i.e. the intensity of lasers) with b and p in Fig. 4. Here, we clearly observe that the lasers with lower beam width produce intense radiation and the same is the case with higher index lasers (p). These results are in agreement with the observations made by other researchers [24,25,26].

Fig. 4
figure 4

Variation of normalized intensity of the generated THz radiation with beam width of the lasers

Full size image

Comparative study

Kumar et al. [27] have studied the Gaussian lasers beam beating for THz generation. Our results are comparable to their observations when we consider the relativistic case and use coshyperbolic-Gaussian lasers. Flat top or super-Gaussian like lasers destabilize as these propagate in the medium leading to two separate peaks in THz profile, whereas Gaussian-like beam retains its shape as it propagates through the medium. Therefore, the THz field in Fig. 2 shows small intensity peak at the center. In nonrelativistic cases the SG index plays important role to enhance the amplitude of the THz [26], but in case of relativistic ponderomotive force the density ripples are found to enhance the amplitude significantly, whereas SG index does not play that much significant role. Main difference between the results obtained in relativistic and nonrelativistic cases is that multiple components appear in Eq. [10] as obtained by Bituk and Fedorov [28] also.

Conclusions

When we consider the relativistic effect in plasma due to the higher intensity lasers, the emitted THz radiation is not found to be focused at a single place, rather it is focused at least at two places. These amplitudes carry different magnitudes. We can create multiple focal THz radiation by creating a dip in the electric field peak of the beating lasers. Other effects of the beam width and density ripples are found to be the similar as in nonrelativistic case.