Motivation

The management of stochastic inventories is a critical issue for the success of modern business, particularly in retail industry. While profit maximization/cost minimization served as a milestone objective for so long, in economics, the default assumption is that the decision makers are usually risk-averse, meaning that the individuals have a positive and diminishing marginal utility of money. Risk-averse behavior of the decision makers affects their future choices and decisions, a matter which has been acknowledged by a good deal of the literature. It intensely influences ordering, pricing and other marketing decisions in business environments. Risk attitudes are modeled by the utility functions. The “utility” is an economic term referring to the total satisfaction attained from consuming a good or a service. Therefore, the satisfaction of a surplus made by some trade/business is not necessarily well assessed by the expected value; rather, the utility is the rational valuation of the surplus from the decision makers’ perspective. For instance, if some individuals are to choose between a cash money of $500 or a probable payoff of (−$1000 or $5000) both of equal chances, many will choose the sure amount of $500 while the expected value of the second option is $2000. This shows the failure of expected value theory and demonstrates the need for a theory that explains such a behavior. Note that even when the probability of the maximum reward is high, say 0.95, some will prefer the cash of $500 (those who are highly loss-averse). Utility theory has successfully explained the natural/cognitive behavior of individuals who are making decisions. In the classical problem, the newsvendor must decide how much to order under the assumption of risk-neutral behavior. However, few percent of individuals in the globe may be found risk-neutral. Indeed, most of us tend to be more loss-averse than risk-averse (Wei et al. 2014; Meng et al. 2017; Dalalah et al. 2016).

For this reason, this paper deals with the newsvendor problem with the utilities taken care of. However, the selection of the utility function is not a straightforward task. In fact, it has been emphasized by a significant deal of the literature that the utilities should be bounded; otherwise, a classical Petersburg paradox cannot be explained neither by the expected value nor by unbounded utilities (Pfiffelmann 2011). Consequently, the category of exponential functions (shown in “The utility and certainty equivalents” section) serves as a good utility choice that has asymptotic lower and upper bounds.

Utilities have a significant impact on the newsvendor choices. Recently, the topic of risk attitudes has attracted a remarkable attention by researchers from supply chain and revenue management fields (Dalalah and Khaled 2016). However, few studies have addressed the utility in the newsvendor problem; to the best of our knowledge, none considered bounded utilities. Moreover, the normal distribution has not been taken into consideration for utility maximization of bounded exponential functions. Consequently, this paper addresses the problem of maximizing the expected exponential utilities for a normal demand. The impact of loss aversion is analyzed to help the newsvendor find the best stocking quantity according to his/her risk behavior. In addition, the factors that affect the resulting risk premiums such as the parameters of loss aversion, the costs and demand standard deviations are analyzed.

This paper is organized as follows: A literature review is presented in “Literature review” section followed by the utility and certainty equivalents in “The utility and certainty equivalents” section. The expected utility of normally distributed rewards is presented in The expected utility of the normal distribution section, followed by the newsvendor problem under risk aversion in “Utility of loss-averse newsvendor of normal demand” section. Later, the effect of risk aversion on the optimal order quantity is given in “The effect of loss aversion on the optimal stocking quantity” section. Risk premiums are discussed in “Risk premiums: a sensitivity analysis” section. Finally, the conclusions are presented in “Conclusions” section.

Literature review

The classical newsvendor (NV) model is a prevalent framework in operations management. The simplest and most elementary version of the newsvendor problem is to optimize the costs/profits by finding stocking quantity a newsvendor should order when the future demand is stochastic. The problem deals with the maximization of the expected profits which are measured by the surplus of money end of the day. The classical NV model has served as a main structure for several real applications that can be found in different aspects of business. In fact, the newsvendor problem can be found in inventory management, supply chain management, manufacturing sectors, scheduling, option pricing models, sports, fashion, telecom and many other areas (Chen et al. 2004; Liu et al. 2006; Dalalah et al. 2015; Khorasani and Almasifard 2018; Mahsa and Ata 2018). The classical version of the newsvendor problem has been extensively studied in the literature under the consideration of different conditions such as multiple products and different pricing methods. Due to its closed-form solution, the classical problem represents an elegant structure of stochastic inventory models.

Good surveys of the newsvendor problem can be found in the handbook of Tsan-Ming (2012) which demonstrates the use and implications of the newsvendor models in realistic applications. For example, at the firm level, one important extension is the interface between marketing and operations that influences the decision making. In some newsvendor problems, the demand is stimulated by sale prices; in others, the demand is driven by the inventory or by some marketing instruments. Newsvendor pricing techniques can be found in Petruzzi and Dada (1999). Pricing under stochastic demand that is characterized by an increasing generalized failure rate has been addressed by Yao et al. (2006). In Lariviere and Porteus (2001) as an example, the coordination with wholesale price contracts was addressed for the classical newsvendor model. Recently, Hardik and Ashaba (2018) proposed a joint pricing model for an inventory of deteriorating items with stochastic demand and promotional efforts. In the same context, Panda et al. (2019) presented a credit policy approach in a two-warehouse inventory model for deteriorating items with price- and stock-dependent demand under partial backlogging.

In the past, some papers considered the inventory as a marketing performance measure such as Gerchak and Wang (1994). In their study, they considered endogenous demand and exogenous prices. In the same context, Balakrishnan et al. (2004) investigated the deterministic complement for the newsvendor problem. The same problem has been extended by Balakrishnan et al. (2008) to general inventory-dependent demand. In Dana and Petruzzi (2001), optimizing both the stocking quantity and the price for demand-stimulating products was considered to jointly solve for both variables, i.e., price and quantity. It has been shown that when the demand is affected by retailer’s sales efforts, a win–win situation for both the customer and the retailer may be achieved, Taylor (2002). Similar analysis has been conducted by Krishnan et al. (2004) to address the impact of retailers on altering the demands.

Mirbahador et al. (2013) developed a model for solving two-echelon inventory system of perishable items in a supply chain via a case study scenario. A similar study was presented by Naser Ghasemi (2015) to develop economic production quantity (EPQ) models for non-instantaneous deteriorating items. Two-warehouse system of non-instantaneous deterioration products with promotional effort and inflation over a finite time horizon is presented by Palanivel et al. (2018). Demand’s means that are increasing as a function of the advertising expenditures have been considered in an early work of Gerchak and Parlar (1987) where mixed optimization has been used to solve the decision variables. The model of Gerchak and Parlar (1987) has been extended by Khouja and Robbins (2003) to address three different cases, namely the demand of constant variance, the demand of constant coefficient of variation and an increasing coefficient of variation. In Wang et al. (2010a, b and Wang and Zhou 2011), an advertisement-sensitive demand has been considered for revenue sharing contract for the entire supply chain coordination.

Maximization of the expected utility was considered by Dana and Petruzzi (2001). In their model, the demand is stimulated by the inventory and prices. They found that higher inventories held may attract the customers. Different newsvendor objective functions were studied in Tie and Qiying (2013) such as maximizing the expected utility and maximizing the probability of achieving some level of profit. Under the consideration of concave and differentiable utility function, Eeckhoudt et al. (1995) showed that the optimal order quantity will be smaller for risk-averse persons as compared to risk-neutral ones. The first order optimality conditions for risk-averse expectations of utility were demonstrated by Keren and Pliskin (2006), particularly for uniform demand. Risk aversion and pricing along with emergency ordering have been studied by Agrawal and Seshadri (2000). The utilities used are strictly increasing and twice differentiable as a function of the potential rewards. In addition to above, Federgruen and Chen (2000) and Choi et al. (2008) addressed the trade-offs of the mean variance where the later explored different attitudes toward risk. The conditional value at risk (CVaR)—one of the special risk metrics—has been also considered in the newsvendor problem. For instance, Gotoh and Takano (2007) proposed an optimality model to minimize the CVaR and to find the optimal order quantities. We can also find different pricing and ordering strategies that have been introduced by Chen et al. (2009). Their results were compared to risk-neutral newsvendors.

The management of the newsvendor problem from the behavioral aspects has been studied in the literature, specifically, from the social and cognitive theories point of view as in Gino and Pisano (2008) and Bendoly et al. (2010), where the later studied the behavioral economics and judgment in decision making. Dynamic pricing of finite inventories and heterogeneous population was a successful approach of Su (2008). He showed that the compositions of customers’ population may affect the optimal results. Puspita et al. (2018) studied the optimal replenishment and credit policy in a supply chain inventory model under two levels of trade credit with time- and credit-sensitive demand and default risk. Their major objective was to determine the retailer’s optimal credit period and cycle time such that the total profit per unit time is maximized.

Loss aversion, as another perspective of decision making, is intuitively appealing and well supported in marketing, finance and organizational behavior. Indeed, most of the references listed in this article demonstrate that the decision-making behavior of managers is consistent with loss aversion. Moreover, it has been verified by literature studies that loss aversion has a substantial impact on the newsvendor decisions. Loss-averse models have been slightly explored under the utility theory. Wang and Webster (2009) and Hui et al. (2016) are among the first to study such a problem.

The newsvendor problem of seasonal demand has been addressed by Aviv and Pazgal (2008) with the presence of forward-looking customers. Their work falls under the concept of strategic customers who to a certain extent can cooperate with the seller. Further analysis of strategic customers has been presented by Xuanming and Zhang (2008). They showed that the optimal stocking quantities can be lower than those found in the case of the classical newsvendor problem due to strategic customers. Strategic customers of risk aversion were considered in Tie and Qiying (2013) where different utility functions have been employed to find the optimal stocking quantity when the customers are exposed to the seller prices but not the quantities.

To study the newsvendor’s risk attitude, many researchers have adopted the utility approach such as (Meng et al. 2017; Hui et al. 2016; Wang and Webster 2009; Guo and Chen 2000; Eeckhoudt et al. 1995). For instance, Meng et al. (2017) employed anchoring as an approach for competitive newsvendors. Loss-averse newsvendor’s problem has been solved using a robust optimization in Hui et al. (2016) which has been formerly considered in Wang and Webster (2009). Eeckhoudt et al. (1995) studied the newsvendor problem with risk-averse decision makers. Other researchers have used the possibility theory instead of the conventional probability theory as in Guo and Chen (2000). Alkhaledi et al. (2018) used a scaled utility function to highlight the impact of losses as compared to gains in the newsvendor problem.

While the utility theory has been considered in several studies in the literature, yet, to the best of our knowledge, no existing study has considered risk premiums of the newsvendor problem that maximizes the expected utility of normal demand distribution. In contrast, this paper presents a model to maximize the utility under normal demands, where an elegant formulation is established for the solution of the optimal stocking quantity. The effect of different loss-averse attitudes on the optimal stocking quantity is analyzed under the assumption of normal demand and exponential utilities. Moreover, the resulting risk premiums versus the value of risk aversion, cost components and demand standard deviations are analyzed.

The utility and certainty equivalents

The theory of utility is a methodological framework for the assessment of alternatives/options/choices that are made by individuals, firms or any businesses process. The utility refers to the satisfaction that a choice offers to the decision maker. Therefore, the utility theory assumes that any decision is made based on the principle of utility maximization. The best choice is the one that provides the highest satisfaction (utility) to the decision maker. It is usually described by a function that maps the monetary values to their utility values, where u(x) is the utility of a quantity x. For example, consider a discrete gamble L that is denoted by its payoffs and probabilities, i.e., L(x1, p1; …; xn, pn). The expected utility of this gamble is given by \( E\left[ {u\left( x \right)} \right] = \mathop \sum \nolimits_{1}^{n} u(x_{i} )p_{i} . \)

Risk aversion is described by a strictly increasing concave function for positive net wealth. Loss aversion, on the other hand, is described by a strictly decreasing but convex function for negative net wealth. Loss aversion is a debatable matter that is still under research investigation. The general conditions of loss aversion can be found in many references in our references list. Note that the exponential function can satisfy some of these conditions to a certain extent. Due to the evidence that the utilities must be bounded (the reader is referred to Petersburgh paradox), the exponential utility function has become one interesting formulation that supports bounded utilities. A classical form of the exponential function as a utility of the net wealth is given by:

$$ u\left( x \right) = \left\{ {\begin{array}{*{20}l} {1 - {\text{e}}^{ - \nu x} ,} \hfill & {x \ge 0} \hfill \\ {{\text{e}}^{\lambda x} - 1,} \hfill & {x < 0} \hfill \\ \end{array} } \right. $$
(1)

where \( \nu ,\lambda > 0 \). The coefficient of the absolute risk aversion is defined as:

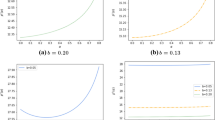
$$ A\left( x \right) = \frac{{u^{{\prime \prime }} \left( x \right)}}{{u^{{\prime }} \left( x \right)}} $$
(2)

While the exponential function captures all risk-averse characteristics, loss-averse characteristics are moderately captured by the same exponential category. Two main coefficients are considered in our study, namely the coefficient of risk aversion (ν) and the coefficient of loss aversion (λ). Higher values of ν mean higher risk aversion, and similarly, higher values of λ mean higher loss aversion to a certain extent. When ν = λ, loss aversion will have the same impact as that of risk aversion (i.e., the newsvendor fears the loss as much as he regrets the possible gains). However, when ν > λ, the decision maker tends to be more risk-averse; contrariwise, he/she will be more loss-averse if ν < λ (i.e., more anxiety from loss). Figure 1 shows the bounded utility.

Fig. 1
figure 1

Risk and loss aversion of bounded utilities

Full size image

The certainty equivalents (CE) are estimated by the utility functions. CE is the sure payoff that an agent/investor would have to receive to be indifferent between that sure payoff and (probabilistic payoffs). Clearly, the individuals will guess their CE’s according to their risk attitudes. Those who are risk-averse tend to underestimate the expected value, while those who are risk seekers tend to overestimate the probabilistic payoffs.

To rationally explain some decision-making behaviors, the utilities should be bounded. The evidence of bounded utilities can be demonstrated easily via the simple gamble of Petersburg paradox. Petersburg paradox is thoroughly explained in Pfiffelmann (2011). In short, consider a gamble in which the player will win $2n when a coin lands heads up, where n refers to the nth throw at which the coin lands heads up for the first time. The gamble is terminated at the first landing of heads. Clearly, the expected value of such a gamble is ∞ which brings a violation to the expected value theory, where

$$ {\text{EV}} = \frac{1}{2} \times 2 + \left( {\frac{1}{2}} \right)^{2} \times 2^{2} + \cdots + \left( {\frac{1}{2}} \right)^{n} \times 2^{n} + \cdots = \infty $$
(3)

Although the expected value is unimaginable, real experiments revealed that an individual only pays an amount of almost $3 for such a gamble (Pfiffelmann 2011). To explain this, we can show easily that the expected utility has a limit for this gamble when the exponential utility function is employed.

The certainty equivalents can be found using the inverse of the expected utility function (Fig. 2). The reason for this is owed to the assumption that both the expected utility value and CE will have the same utility from the perspective of the evaluator. Therefore, the certainty equivalent of a risky asset is given by:

Fig. 2
figure 2

Risk attitudes illustrated, where CE denotes certainty equivalent, RP risk premium, EV expected value, and \( u^{ - 1} \left( \cdot \right) \) the inverse transform of the utility function u

Full size image
$$ {\text{CE}} = u^{ - 1} \left( {E\left[ {u\left( x \right)} \right]} \right) $$
(4)

The expected utility of the normal distribution

For a continuous potential reward X of the probability density function f(x), the expected utility is expressed by the form:

$$ E\left[ {u\left( x \right)} \right] = \mathop \int \nolimits_{ - \infty }^{\infty } u\left( x \right)f\left( x \right){\text{d}}x $$
(5)

Let X ~ N(µ,σ), where \( f\left( x \right) = \frac{{{\text{e}}^{{ - \frac{{\left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}}} }}{{\sqrt {2\pi \sigma^{2} } }} \) and \( F\left( x \right) \) is the corresponding cumulative function. By considering the above utility in (1), the expected utility can be found by the following:

$$ E\left[ {u\left( x \right)} \right] = \frac{1}{{\sqrt {2\pi \sigma^{2} } }}\mathop \int \nolimits_{ - \infty }^{\infty } \left( {1 - {\text{e}}^{ - \nu x} } \right){\text{e}}^{{\frac{{ - \left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}}} {\text{d}}x $$
(6)

which is simply expressed as:

$$ E\left[ {u\left( x \right)} \right] = \frac{1}{{\sqrt {2\pi \sigma^{2} } }}\mathop \int \nolimits_{ - \infty }^{\infty } {\text{e}}^{{\frac{{ - \left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}}} {\text{d}}x - \frac{1}{{\sqrt {2\pi \sigma^{2} } }}\mathop \int \nolimits_{ - \infty }^{\infty } {\text{e}}^{{ - \left( {\nu x + \frac{{\left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} {\text{d}}x $$

Write the power part in the integration as:

$$ \nu x + \frac{{\left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }} = \frac{{\left( {x - \mu + \nu \sigma^{2} } \right)^{2} }}{{2\sigma^{2} }} + \nu \left( {\mu - \nu \frac{{\sigma^{2} }}{2}} \right), $$
(7)

The expected utility can be expressed as:

$$ E\left[ {u\left( x \right)} \right] = 1 - {\text{e}}^{{ - \nu \left( {\mu - \nu \frac{{\sigma^{2} }}{2}} \right)}} \mathop \int \nolimits_{ - \infty }^{\infty } \frac{{{\text{e}}^{{ - \frac{{\left( {x - \mu + \nu \sigma^{2} } \right)^{2} }}{{2\sigma^{2} }}}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x $$
(8)

However, \( \mathop \int \nolimits_{ - \infty }^{\infty } \frac{{{\text{e}}^{{ - \frac{{\left( {x - \mu '} \right)^{2} }}{{2\sigma^{2} }}}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x = 1 \), where \( \mu^{{\prime }} = \mu - \nu \sigma^{2} \), and accordingly, the expected utility reduces to the expression:

$$ E\left[ {u\left( x \right)} \right] = 1 - {\text{e}}^{{ - \nu \left( {\mu - \nu \frac{{\sigma^{2} }}{2}} \right)}} $$
(9)

The above expected utility applies only when the payoffs are normally distributed. The utility can be increased by maximizing the quantity \( \mu - \nu \frac{{\sigma^{2} }}{2} \). Equation (9) states that an agent who is facing continuous and normally distributed probable payoffs should seek those of lower variances and higher averages. This result conforms to the findings in risk management where less risk is observed in the probable payoffs of narrow ranges and higher values. The above interesting formula has been repeatedly reported in the literature.

Utility of loss-averse newsvendor of normal demand

In this section, a loss-averse newsvendor model is considered along with a normally distributed demand. In particular, we consider a single risk-averse retailer who must determine how many units to order of some product. The demand is i.i.d. (i.e., independent and identically distributed) which is denoted by a random variable X, where X ~ N(µ,σ). The demand data represent a sequence of random variables that have the same probability distribution of mutual independence.

The retailer’s utility function is given by (1), where \( u^{{\prime }} \left( x \right) > 0 \) and \( u^{{\prime \prime }} \left( x \right) < 0 \). The retailer faces a cost of c per unit of the product which can be sold to customers at a full price of p. Leftover units will be salvaged at a price of s, where s < c < p. Since the demand is random, the retailer must determine the optimal stocking quantity to maximize his expected utility instead of maximizing the expected profits. No strategic planning between the retailer and customers may take place in this setting. For a specific order quantity, if the realized demand is low, the leftover quantities will be sold at the salvage value; hence, the cost of overage is given by \( c_{\text{o}} = c - s \). On the other hand, when the stocked quantities are low, lost opportunities may arise; hence, the cost of underage is given by \( c_{\text{u}} = p - c \). While the classical newsvendor problem results in an elegant structure, with utility maximization, the solution of the problem gets more intricate where more efforts are required to find the optimal stocking quantity.

Let the stocking quantity be \( Q \). When the demand x is less than \( Q \) in a cost newsvendor model, the retailer’s drop in wealth will be given by: \( c_{\text{o}} \left( {Q - x} \right) \) and therefore the expected utility is given by \( \mathop \int \nolimits_{ - \infty }^{Q} u\left( { - c_{\text{o}} \left( {Q - x} \right)} \right)f\left( x \right){\text{d}}x \). Similarly, when the demand is greater than the order quantity \( Q \), the expected drop in wealth is \( c_{\text{u}} \left( {x - Q} \right) \) and the expected utility is given by \( \mathop \int \nolimits_{Q}^{\infty } u\left( { - c_{\text{u}} \left( {x - Q} \right)} \right)f\left( x \right){\text{d}}x \). By summing the two terms, we get:

$$ E\left[ {u\left( Q \right)} \right] = \mathop \int \nolimits_{ - \infty }^{Q} u\left( { - c_{\text{o}} \left( {Q - x} \right)} \right)f\left( x \right){\text{d}}x + \mathop \int \nolimits_{Q}^{\infty } u\left( { - c_{\text{u}} \left( {x - Q} \right)} \right)f\left( x \right){\text{d}}x $$
(10)

Since a cost model is considered, here, the second part of the utility function is used (i.e., x < 0). Substitute both the utility and the demand distribution in (10) to get the following expression:

$$ E\left[ {u\left( Q \right)} \right] = \mathop \int \nolimits_{ - \infty }^{Q} \left( {{\text{e}}^{{ - c_{\text{o}} \lambda \left( {Q - x} \right)}} - 1} \right)\frac{{{\text{e}}^{{\frac{{ - \left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x + \mathop \int \nolimits_{Q}^{\infty } \left( {{\text{e}}^{{ - c_{\text{u}} \left( {x - Q} \right)}} - 1} \right)\frac{{{\text{e}}^{{\frac{{ - \left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x $$
(11)

Let \( K = - c_{\text{o}} \lambda \) and \( L = c_{\text{u}} \lambda \), hence, the above expands to the following:

$$ E\left[ {u\left( Q \right)} \right] = \mathop \int \nolimits_{ - \infty }^{Q} {\text{e}}^{KQ} \frac{{{\text{e}}^{{ - \left( {Kx + \frac{{\left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x - \mathop \int \nolimits_{ - \infty }^{Q} \frac{{{\text{e}}^{{\frac{{ - \left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x + \mathop \int \nolimits_{Q}^{\infty } e^{LQ} \frac{{{\text{e}}^{{ - \left( {Lx + \frac{{\left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x - \mathop \int \nolimits_{Q}^{\infty } \frac{{e^{{\frac{{ - \left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x. $$

Note that the second and fourth integration parts sum to 1, and hence, we get:

$$ E\left[ {u\left( Q \right)} \right] = \mathop \int \nolimits_{ - \infty }^{Q} \frac{{e^{KQ} }}{{\sqrt {2\pi \sigma^{2} } }}e^{{ - \left( {Kx + \frac{{\left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} {\text{d}}x + \mathop \int \nolimits_{Q}^{\infty } \frac{{{\text{e}}^{LQ} }}{{\sqrt {2\pi \sigma^{2} } }}e^{{ - \left( {Lx + \frac{{\left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} {\text{d}}x - 1 $$
(12)

Using the simplified expression in (7), we get the following:

$$ E\left[ {u\left( Q \right)} \right] = \mathop \int \nolimits_{ - \infty }^{Q} {\text{e}}^{KQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu + K\sigma^{2} } \right)^{2} }}{{2\sigma^{2} }} + K\left( {\mu - K\frac{{\sigma^{2} }}{2}} \right)} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x + \mathop \int \nolimits_{Q}^{\infty } {\text{e}}^{LQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu + L\sigma^{2} } \right)^{2} }}{{2\sigma^{2} }} + L\left( {\mu - L\frac{{\sigma^{2} }}{2}} \right)} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x - 1 $$

For simplicity, let \( \mu_{a} = \mu - K\sigma^{2} \), \( \mu_{b} = \mu - L\sigma^{2} \), \( O = \mu - K\frac{{\sigma^{2} }}{2} \) and \( U = \mu - L\frac{{\sigma^{2} }}{2} \) to get the following:

$$ E\left[ {u\left( Q \right)} \right] = \mathop \int \nolimits_{ - \infty }^{Q} {\text{e}}^{KQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }} + KO} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x + \mathop \int \nolimits_{Q}^{\infty } {\text{e}}^{LQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{b} } \right)^{2} }}{{2\sigma^{2} }} + LU} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x - 1 $$
(13)

By taking the constants out of the integration, the above is simplified to:

$$ E\left[ {u\left( Q \right)} \right] = \underbrace {{{\text{e}}^{ - KO} \mathop \int \nolimits_{ - \infty }^{Q} {\text{e}}^{KQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x }}_{A\left( Q \right)} + \underbrace {{{\text{e}}^{ - LU} \mathop \int \nolimits_{Q}^{\infty } {\text{e}}^{LQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{b} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x - 1}}_{B\left( Q \right)} $$
(14)

A visual inspection of the above expression shows that it has a unique maximum as a function of \( Q \). The optimal order quantity can be found by \( \frac{\text{d}}{{{\text{d}}Q}}E\left[ {u\left( Q \right)} \right] = 0 \), where \( \frac{\text{d}}{{{\text{d}}Q}}E\left[ {u\left( Q \right)} \right] = \frac{{{\text{d}}A\left( Q \right)}}{{{\text{d}}Q}} + \frac{{{\text{d}}B\left( Q \right)}}{{{\text{d}}Q}} \). Using Leibniz law for the first part, we get:

$$ \frac{{{\text{d}}A\left( Q \right)}}{{{\text{d}}Q}} = {\text{e}}^{ - KO} \left( {{\text{e}}^{KQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {Q - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }} \times 1 + \mathop \int \nolimits_{ - \infty }^{Q} K{\text{e}}^{KQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x} \right) $$

The above is also equivalent to:

$$ \frac{{{\text{d}}A\left( Q \right)}}{{{\text{d}}Q}} = {\text{e}}^{KQ} \frac{{{\text{e}}^{{ - \left( {KO + \left( {\frac{{\left( {Q - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }}} \right)} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }} + {\text{e}}^{ - KO} \mathop \int \nolimits_{ - \infty }^{Q} K{\text{e}}^{KQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x $$
(15)

Recall that \( \mu_{a} = \mu - K\sigma^{2} \) and \( O = \mu - K\frac{{\sigma^{2} }}{2} \), and using a similar operation in (7), the power in the first expression will be:

$$ KO + \left( {\frac{{\left( {Q - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }}} \right) = K\left( {\mu - K\frac{{\sigma^{2} }}{2}} \right) + \frac{{\left( {Q - \mu + K\sigma^{2} } \right)^{2} }}{{2\sigma^{2} }} = KQ + \frac{{\left( {Q - \mu } \right)^{2} }}{{2\sigma^{2} }}. $$

Accordingly, the expression (13) reduces to the following form:

$$ \frac{{{\text{d}}A\left( Q \right)}}{{{\text{d}}Q}} = \frac{{{\text{e}}^{KQ} }}{{\sqrt {2\pi \sigma^{2} } }}e^{{ - \left( {KQ + \frac{{\left( {Q - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} + {\text{e}}^{ - KO} \mathop \int \nolimits_{ - \infty }^{Q} K{\text{e}}^{KQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x $$

which also equals to:

$$ \frac{{{\text{d}}A\left( Q \right)}}{{{\text{d}}Q}} = \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {Q - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }} + K{\text{e}}^{ - KO} {\text{e}}^{KQ} \mathop \int \nolimits_{ - \infty }^{Q} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x $$
(16)

As for the integration part above, it represents another normal distribution of a mean \( \mu_{a} \) and a standard deviation of σ. Let \( _{a} \) be a cumulative density function of this normal distribution where

$$ \Psi _{a} \left( x \right) = \mathop \int \nolimits_{ - \infty }^{x} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{a} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x. $$
(17)

Therefore, we have:

$$ \frac{{{\text{d}}A\left( Q \right)}}{{{\text{d}}Q}} = \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {Q - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }} + K{\text{e}}^{{K\left( {Q - O} \right)}}\Psi _{a} \left( Q \right) $$
(18)

For part B of the expression in (14), a similar procedure can be followed, where

$$ \frac{{{\text{d}}B\left( Q \right)}}{{{\text{d}}Q}} = - {\text{e}}^{ - LU} \times {\text{e}}^{LQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {Q - \mu_{b} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }} \times 1 + {\text{e}}^{ - LU} \mathop \int \nolimits_{Q}^{\infty } L{\text{e}}^{LQ} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{b} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x $$

which by similar analysis of the first part will result in:

$$ \frac{{{\text{d}}B\left( Q \right)}}{{{\text{d}}Q}} = - \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {Q - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }} + L{\text{e}}^{{L\left( {Q - U} \right)}} \mathop \int \nolimits_{Q}^{\infty } \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{b} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x $$
(19)

It should be noted that the integration part above represents a normal distribution with a mean of \( \mu_{b} \) and a standard deviation of σ. Therefore, a new normal distribution given by the cumulative density function \( \Psi _{b} \left( x \right) \) is expressed as:

$$ \Psi _{b} \left( x \right) = \mathop \int \nolimits_{ - \infty }^{x} \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {x - \mu_{b} } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }}{\text{d}}x $$
(20)

where

$$ \frac{{{\text{d}}B\left( Q \right)}}{{{\text{d}}Q}} = - \frac{{{\text{e}}^{{ - \left( {\frac{{\left( {Q - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)}} }}{{\sqrt {2\pi \sigma^{2} } }} + L{\text{e}}^{{L\left( {Q - U} \right)}} \times \left( {1 -\Psi _{b} \left( Q \right)} \right) $$
(21)

Finally, summing the derivatives of parts A and B and equating by “0” result in the following optimality formula:

$$ \frac{{{\text{d}}E\left[ {u\left( Q \right)} \right]}}{{{\text{d}}Q}} = K{\text{e}}^{{K\left( {Q - O} \right)}}\Psi _{a} \left( Q \right) + L{\text{e}}^{{L\left( {Q - U} \right)}} \times \left( {1 -\Psi _{b} \left( Q \right)} \right) = 0 $$

By solving the above, we get an elegant formulation as follows:

$$ \frac{{\Psi _{a} \left( Q \right)}}{{1 -\Psi _{b} \left( Q \right)}} = - \frac{{L{\text{e}}^{{L\left( {Q - U} \right)}} }}{{K{\text{e}}^{{K\left( {Q - O} \right)}} }} $$
(22)

where \( \mu_{a} = \mu - K\sigma^{2} \), \( \mu_{b} = \mu - L\sigma^{2} \), \( O = \mu - K\frac{{\sigma^{2} }}{2} \), \( U = \mu - L\frac{{\sigma^{2} }}{2} \), and both \( \Psi _{a} \) and \( \Psi _{b} \) have the same standard deviation of σ. An alternative formulation of the above is given by:

$$ \frac{{\Psi _{a} \left( Q \right)}}{{1 -\Psi _{b} \left( Q \right)}} = \frac{{c_{\text{u}} }}{{c_{\text{o}} }}{\text{e}}^{{\left( {L - K} \right)\left[ {Q - \mu + \left( {L + K} \right)\frac{{\sigma^{2} }}{2}} \right]}} $$
(23)

The above expression is an implicit function of \( Q \). Closed-form solution of \( Q \) is not attainable, and hence, a simple algorithm can be implemented, which can be done by a simple incremental search in Excel. More importantly, the two resulting cumulative distributions \( \Psi _{a} \) and \( \Psi _{b} \) have the same standard deviation of σ; however, with shifted means around µ, recall that \( K \) and \( L \) have opposite signs. Figure 3 depicts the two distributions, where \( \Psi _{a} \left( Q \right) = \int\nolimits_{Q} {\psi_{a} } \left( x \right){\text{d}}x \) refers to the cumulative distribution of the expected utility in the case of overstocking and \( \Psi _{b} \left( Q \right) = \int\nolimits_{Q} {\psi_{b} } \left( x \right){\text{d}}x \) refers to the cumulative distribution of utilities upon understocking. The distance between the two distributions is \( \lambda \sigma^{2} \left( {c_{\text{o}} + c_{\text{u}} } \right) \).

Fig. 3
figure 3

The three distributions: the demand (middle), overage (right) and underage (left), all having the same standard deviation (σ)

Full size image

More importantly, the two distributions approach the exact demand distribution when λ approaches “0” (i.e., risk neutrality); indeed, a value of “0” reduces the model to the classical newsvendor problem, where

$$ \mathop {\lim }\limits_{\lambda \to 0} - \frac{{c_{\text{u}} }}{{c_{\text{o}} }}{\text{e}}^{{Q\left( {L + K} \right)}} {\text{e}}^{{\mu \left( {K - L} \right) + \left( {L + K} \right)\left( {L - K} \right)\frac{{\sigma^{2} }}{2}}} = \frac{{c_{\text{u}} }}{{c_{\text{o}} }} $$
$$ \frac{{\Psi _{a} \left( Q \right)}}{{1 -\Psi _{b} \left( Q \right)}} = \frac{{c_{\text{u}} }}{{c_{\text{o}} }}. $$
(24)

We also have \( \mathop {\lim }\limits_{\lambda \to 0}\Psi _{a} \left( Q \right) = F\left( Q \right) \) and \( \lim_{\lambda \to 0}\Psi \left( Q \right) = F\left( Q \right) \) for the same reason above. In this case, we know that \( \Psi _{a} \left( Q \right) =\Psi _{b} \left( Q \right) = F\left( Q \right) \), and hence, the solution reduces to the following where \( \lambda = 0 \):

$$ F\left( Q \right) = \frac{{c_{\text{u}} }}{{c_{\text{o}} + c_{\text{u}} }} $$
(25)

The above analysis shows that when an exponential utility function is used, the optimal order quantity of the classical newsvendor will serve as an upper limit of utility-optimal quantity when \( c_{\text{u}} > c_{\text{o}} \) and as a lower limit when \( c_{\text{o}} > c_{\text{u}} \). This is if the optimal order quantity of the classical newsvendor is denoted by either \( Q_{{(c_{\text{o}} > c_{\text{u}} )}} \) or \( Q_{{(c_{\text{u}} > c_{\text{o}} )}} \) and that of our model is \( Q_{\text{u}} \), then for any positive values of \( c_{\text{o}} \), \( c_{\text{u}} \), \( \mu \), λ and σ we have \( Q_{{(c_{\text{o}} > c_{\text{u}} )}} < Q_{\text{u}} < Q_{{(c_{\text{u}} > c_{\text{o}} )}} \).

The effect of loss aversion on the optimal stocking quantity

In this section, we will explore the relationship between the risk aversion parameter λ and the optimal order quantity \( Q \) which can be easily estimated for any selected costs values, demand means and standard deviations. Evidently, the loss aversion (λ) yields higher quantity than \( Q_{{(c_{\text{o}} > c_{\text{u}} ) }} \) and smaller quantity than \( Q_{{(c_{\text{u}} > c_{\text{o}} )}} \) with an asymptotic approach to the mean (µ) as λ increases. The effect of the loss aversion parameter (λ) on the optimal order quantity is shown in the numerical example presented in Fig. 4. The bottom curve shows the optimal quantities as a function of (λ) where \( c_{\text{o}} = 25 \), \( c_{\text{u}} = 5 \), µ = 100, σ = 25, while the curve on the top shows the utility-optimal quantities when \( c_{\text{o}} = 5 \), \( c_{\text{u}} = 25 \), µ = 100, σ = 25.

Fig. 4
figure 4

Utility-optimal order quantity versus the loss aversion parameter λ. For this numerical example, µ = 100, σ = 25 and \( c_{\text{o}} = 25 \), \( c_{\text{u}} = 5 \) for the bottom curve and \( c_{\text{o}} = 5 \), \( c_{\text{u}} = 25 \) for the top curve

Full size image

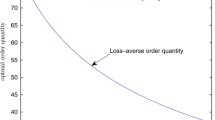
The closer to risk neutrality, the closer the optimal order quantity to that of the classical newsvendor problem. This behavior is explained in the limit given in (24). Figure 4 and 5 show that the optimal order quantity of the utility model approaches the optimal order quantity of the classical newsvendor problem (100 units for the case of equal underage and overage costs). Higher risk attitudes entail smaller optimal quantity if \( c_{\text{u}} > c_{\text{o}} \). Contrariwise, it will result in higher optimal quantity if \( c_{\text{o}} > c_{\text{u}} \), all owed to high overage/underage costs.

Fig. 5
figure 5

The objective function of the expected utility for different newsvendor settings, where λ = 0.04, µ = 100, σ = 25

Full size image

The optimal order quantity will be less than the mean value (µ) when the overage cost is higher than the underage cost. Contrarily, the utility-optimal quantity will be higher than (µ) when the underage cost is higher than the overage cost. By increasing the loss aversion, the newsvendor tends to order as much as the mean value of (µ). Clearly, low loss aversion means that the newsvendor tends to be risk-neutral; thereby, the NV behaves like the classical newsvendor problem. The classical newsvendor problem yields an optimal quantity of 183 for the first case and 217 for the second case. Of note, these two quantities serve as the minimum and the maximum bounds of the utility-optimal quantity for the same values that are given in Fig. 4.

For any loss aversion value (λ), the utility-optimal quantity is always less than the classical optimal quantity when the underage cost is high. Contrarily, also, it is always higher than the classical optimal quantity when the overage cost is high. Clearly, low loss aversion means getting closer to risk neutrality, i.e., the classical newsvendor.

For further sensitivity analysis, the overage and underage costs (\( c_{\text{o}} \) and \( c_{\text{u}} \)) were tested for different values using Eq. (5). Figure 5 shows that as the overage cost \( c_{\text{o}} \) increases, the peak of the objective function gets lower; thereby, lower optimal quantities are computed. Of note, the utility objective function is bounded by its highest profile when \( c_{\text{o}} \) = \( c_{\text{u}} \); therefore, the highest utility is achieved when both cost components are same. On the other hand, when the underage cost (\( c_{\text{u}} \)) increases, it will result in higher utility-optimal quantities. However, the magnitude of the decrease/increase in the optimal quantities gets smaller as the difference in the cost components gets higher (Fig. 6).

Fig. 6
figure 6

Utility-optimal order quantity versus the demand standard deviation, where \( c_{\text{o}} = 25 \), \( c_{\text{u}} = 5 \), µ = 100, λ = 0.04

Full size image

Figure 7 depicts the behavior of the optimal order quantity of the exponential utility as a function of the standard deviation. The results conform to the findings of Eq. (9), where high σ values result in low utility-optimal quantity. It is noteworthy mentioning that smaller standard deviation will make the two distributions \( \psi_{a} \left( Q \right) \) and \( \psi_{b} \left( Q \right) \) approach each other; therefore, the optimal value will approach the mean value (µ) as σ decreases.

Fig. 7
figure 7

The resulting risk premiums and certainty equivalents versus the loss aversion parameter λ, where \( c_{\text{o}} = 25 \), \( c_{\text{u}} = 5 \), µ = 100, σ = 25

Full size image

Risk premiums: a sensitivity analysis

Risk premiums are defined in economics as the additional return an investor expects from holding a risky asset (i.e., probable payoffs) rather than holding a risk-free one (i.e., sure payoffs). It also refers to the extra amount of money an investor would take to hold the risky investment. Essentially, this is the difference between the total expected return from the investment and the proper estimated risk-free return. Risk premiums are measured by:

$$ {\text{RP}}_{i} = {\text{EV}}_{i} - {\text{CE}}_{i} $$
(26)

where \( {\text{RP}}_{i} \) is the risk premium, \( {\text{EV}}_{i} \) is the expected value, and \( {\text{CE}}_{i} \) is the certainty equivalent of a risky asset i.

The utility newsvendor model has been considered from the cost point of view which justifies the negative values of risk premiums while, in fact, the magnitude of risk premiums is the issue that matters. An increase in the magnitude refers to higher amount of money that is requested by the newsvendor to hold this business. Higher risk premiums also make the sales unattractable to the customers. Hence, risk-averse investors tend to raise their prices. To explore the effect of loss aversion parameter (λ) on the risk premiums, first we consider a utility model of the given parameters: \( c_{\text{o}} = 25 \), \( c_{\text{u}} = 5 \), µ = 100, σ = 25. The results are demonstrated in Table 1 which shows the resulting optimal order quantities, the optimal utility value, the certainty equivalents and finally the risk premiums. Equation (4) is used for the certainty equivalents and Eq. (26) for the risk premiums. Different values of λ were tested to study the effect of loss aversion on the risk premiums. The expected costs were found according to the calculated optimal quantity using the same parameters above for the classical newsvendor of normal demand, i.e., no utility is taken into consideration. Risk premiums are simply the difference between the expected value and the certainty equivalent.

Table 1 Risk premiums versus the loss aversion parameter (λ) where \( c_{\text{o}} = 25 \), \( c_{\text{u}} = 5 \), µ = 100, σ = 25
Full size table

The absolute values of the risk premiums increase by increasing the loss aversion. This behavior is not preferred to customers as higher loss aversion increases the premiums; thereby, higher expectations and returns are anticipated by the newsvendor. High risk premiums will not encourage an individual to hold the risky asset compared to risk-free one. The behavior of certainty equivalent versus the parameter λ is shown in Fig. 7. Indeed, the magnitude of the certainty equivalents increases by increasing the loss aversion parameter. This also increases the gap between the expectations and the certainties which results in an increase in the magnitudes of risk premiums, i.e., an indication of lower willingness to carry the risky asset.

Another example is presented to test the effect of underage cost, where \( c_{\text{o}} = 5 \), µ = 100, σ = 25, λ = 0.04. Different underage cost values were tested, and the resulting certainty equivalents and risk premiums are shown in Table 2. The magnitude of risk premiums increases as the underage cost increases. This pattern is depicted in Fig. 8. Clearly, for both the certainty equivalents, the expected values will get higher when the underage costs increase. That said, by increasing the underage cost, the newsvendor willingness to hold this inventory problem will decrease.

Table 2 The results of the classical newsvendor and the utility newsvendor models, where \( c_{\text{o}} = 5 \), µ = 100, σ = 25, λ = 0.04
Full size table
Fig. 8
figure 8

Risk premiums and the certainty equivalents of the utility newsvendor versus the underage cost, where \( c_{\text{o}} = 5 \), µ = 100, σ = 25, λ = 0.04

Full size image

As for the overage cost, similar patterns of the certainty equivalents and the risk premiums can be observed. For instance, when \( c_{\text{u}} = 5 \), µ = 100, σ = 25 and λ = 0.04, the magnitude of RP will increase as shown in Fig. 9. In short, the risk premiums will increase when the gap between the overage and the underage costs gets wider.

Fig. 9
figure 9

Risk premiums versus overage cost, where \( c_{\text{u}} = 5 \), µ = 100, σ = 25, λ = 0.04

Full size image

As for the effect of the demand standard deviation (σ), our results conform to the findings of Eq. (9), where lower standard deviations are more preferred. The results of different σ values are shown in Table 3, Figs. 9 and 10. Clearly, the gap between the expected costs and the certainty equivalents increases by increasing σ. Therefore, higher uncertainty yields higher risk premiums, a matter which may not be preferred by the investors and the customers. Figure 10 shows the risk premiums versus the standard deviation. Less willingness to hold the risky asset will result in the increase in σ. The parameters used for this instance are: \( c_{\text{o}} = c_{\text{u}} = 5 \), µ = 100 and λ = 0.04.

Table 3 The risk premiums (last column) for different demand standard deviations, where \( c_{\text{o}} = c_{\text{u}} = 5 \), µ = 100 and λ = 0.04
Full size table
Fig. 10
figure 10

Certainty equivalents, expected cost and risk premiums versus σ where \( c_{\text{o}} = c_{\text{u}} = 5 \), µ = 100 and λ = 0.04

Full size image

To summarize, risk premiums will increase as loss aversion increases. In other words, loss-averse investors request additional fund to be inspired to hold the newsvendor problem. Moreover, increasing the gap between the overage and underage costs will increase the risk premium. Similarly, higher uncertainties in the payoffs will also result in higher risk premiums indicating more unwillingness to hold the risky newsvendor problem.

Conclusions

In this paper, loss aversion in the newsvendor problem is addressed under the assumption of bounded utility. Two of models have been considered, namely the normal and the exponential functions. To the best of our knowledge, no existing study has dealt with this combination of bounded exponential utilities along with a normal demand distribution.

The expected utility of normally distributed payoffs was derived first to help later in the derivation of the utility-optimal formula. An elegant formulation was found, and the optimal quantities were calculated by simple numerical search owed to the implicit expression of the optimal quantity \( Q \). The analysis showed that the classical newsvendor optimal quantity represents a lower/upper bound on the utility-optimal quantities when \( (c_{\text{o}} > c_{\text{u}} )/(c_{\text{u}} > c_{\text{o}} ) \). As loss aversion vanishes by decreasing the parameter λ, the utility model approaches that of the classical newsvendor model.

For the case of normal demand, two other normal distributions of shifted means but similar standard deviations resulted in the last optimality form. The gap between the two distributions is affected by the magnitude of loss aversion, where low loss aversion entails closer distributions. The two distributions will coincide when loss aversion disappears. Conversely, higher demand standard deviation will place the two distributions further apart, which also entails more risk and therefore lower utility-optimal quantities.

As for the risk premiums (RP), the magnitude of RP increases as loss aversion, overage and underage costs increase. Higher demand standard deviations will also increase the magnitude of RP. Higher risk premiums mean that the newsvendor willingness to hold the risky asset decreases as compared to risk-neutral case.

The formulas in (22) and (23) represent a new pair of equations that contribute to the literature related to the newsvendor problem under loss aversion. The presented formulas are advantageous for finding the optimal order quantities of short-shelf life products when loss is an important factor in the decision-making process.

This study addressed the utility newsvendor of a single period and fixed prices. Future extensions can be directed toward multiperiod models and pricing schemes. Other directions may involve discount models and strategic suppliers of long-term commitments. Time series demand patterns and other utility functions are also possible for future extensions.